ỦY BAN NHÂN DÂN QUẬN LIÊN CHIỂU
TRƯỜNG THCS NGUYỄN LƯƠNG BẰNG BÀI 22
TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC ĐẠI SỐ Giáo viên : Hà Duy Ninh Thành phố : Đà Nẵng Sách
: Kết nối tri thức với cuộc sống CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI GIẢNG HÔM NAY! x  y
Xét phân thức đại số : 3 3 x  y
Liệu phân thức nào đơn giản nhưng bằng phân thức trên không ?
1 . TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC
 Nhận biết tính chất cơ bản của phân thức đại số.
Nếu nhân cả tử và mẫu của phân thức với 2x ta được phân thức mới nào ?
Giải thích vì sao phân thức mới nhận được bằng phân thức đã cho.
• Khi nhân cả tử và mẫu của phân thức với 2x ta được :
2x(x  y)
2x(x  y)
Phân thức mới nhận được bằng phân thức đã cho vì cả tử và
mẫu của phân thức đều nhân cùng với một số.
1 . TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC
 Nhận biết tính chất cơ bản của phân thức đại số.
Tử và mẫu của phân thức có nhân tử chung là Viết phân thức
nhận được sau khi chia cả tử và mẫu của phân thức này cho nhân tử chung đó.
So sánh phân thức mới nhận được với phân thức đã cho.
 Chia cả tử và mẫu của phân thức này cho nhân tử chung , ta có x 1 2 x  x 1
Vậy phân thức mới được rút gọn và mất đi nhân tử chung
1 . TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC
 Nhận biết tính chất cơ bản của phân thức đại số.
 Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức
khác đa thức 0 thì được một phân thức bằng phân thức đã cho :
( M là một đa thức khác đa thức 0)
 Nếu tử và mẫu của một phân thức có nhân tử chung thì khi chia
cả tử và mẫu cho nhân tử chung đó ta được một phân thức bằng phân thức đã cho :
( N là một nhân tử chung)
1 . TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC
 Nhận biết tính chất cơ bản của phân thức đại số.
 Áp dụng tính chất cơ bản của phân thức, ta có : 2x  2 2(x 1) 2   2 x  1
(x  1)(x 1) x  1
1 . TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC
 Nhận biết tính chất cơ bản của phân thức đại số. 2y
 Khẳng định trên là đúng. Vì nhân cả tử và mẫu của
với đa thức , ta được : 3(x  y) 2 2 .
y 15xy(x  y)
30xy (x  y)  2
3(x  y).15xy(x  y)
45xy(x  y)
1 . TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC
 Nhận biết tính chất cơ bản của phân thức đại số.
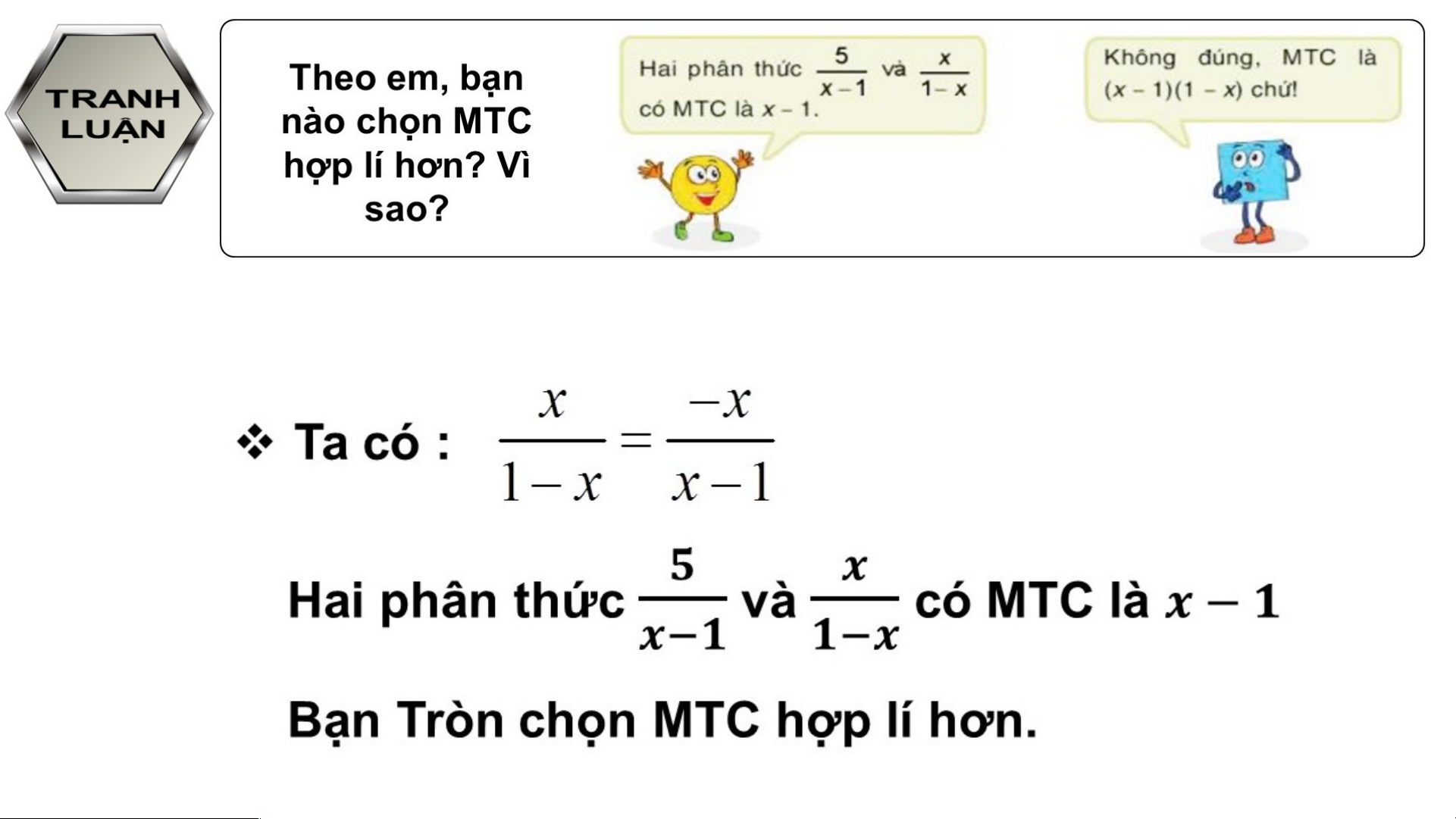
 Nhân cả tử và mẫu của phân thức với , ta được : .( x  1)  x 
(x  1).( 1) 1 x Chú ý :
• Ta có quy tắc đổi dấu : Nếu đổi dấu cả tử và mẫu của một phân
thức thì được một phân thức bằng phân thức đã cho 2 . VẬN DỤNG .
a) Rút gọn phân thức .
 Cách rút gọn một phân thức
• Rút gọn một phân thức là biến đổi phân thức đó thành một
phân thức mới bằng nó nhưng đơn giản hơn. 2 . VẬN DỤNG .
a) Rút gọn phân thức .
Phân tích tử và mẫu của phân thức thành nhân tử và tìm các
nhân tử chung của chúng. 2 2x  2x 2x(x 1)  Ta có :  2 x  1
(x 1)(x  1) Nhân tử chung là 2 . VẬN DỤNG .
a) Rút gọn phân thức .
Chia cả tử và mẫu của phân thức cho các nhân tử chung , ta
nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn. 2 2x  2x 2x(x 1) 2x  Ta có :   2 x  1
(x 1)(x  1) x 1 Chú ý :
 Muốn rút gọn một phân thức đại số ta làm như sau :
- Phân tích tử và mẫu thành nhân tử để tìm nhân tử chung
- Chia cả tử và mẫu cho nhân tử chung đó. 2 . VẬN DỤNG .
a) Rút gọn phân thức . 2 x  xy
x(x  y) x
 Ta có : P    2 3 3(xy  y ) 2
3y (x  y) 2 3y 2 . VẬN DỤNG .
a) Rút gọn phân thức . x  y x  y 1  Ta có :   3 3 2 2 x 2 2  y
(x  y)(x  xy  y )
x  xy  y 2 . VẬN DỤNG .
a) Rút gọn phân thức .
 Bạn tròn làm thế là sai.
Vì bạn bỏ hai số hạng giống nhau của cả tử và mẫu là 2x chứ
không phải chia cho nhân tử chung của cả tử và mẫu. Bài tập
HƯỚNG DẪN VỀ NHÀ 1
Ghi nhớ kiến thức trong bài 2 Hoàn thành bài tập SBT 3 Chuẩn bị bài sau BÀI HỌC KẾT THÚC
CẢM ƠN CÁC EM ĐÃ LẮNG NGHE!
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38
• Slide 39
• Slide 40