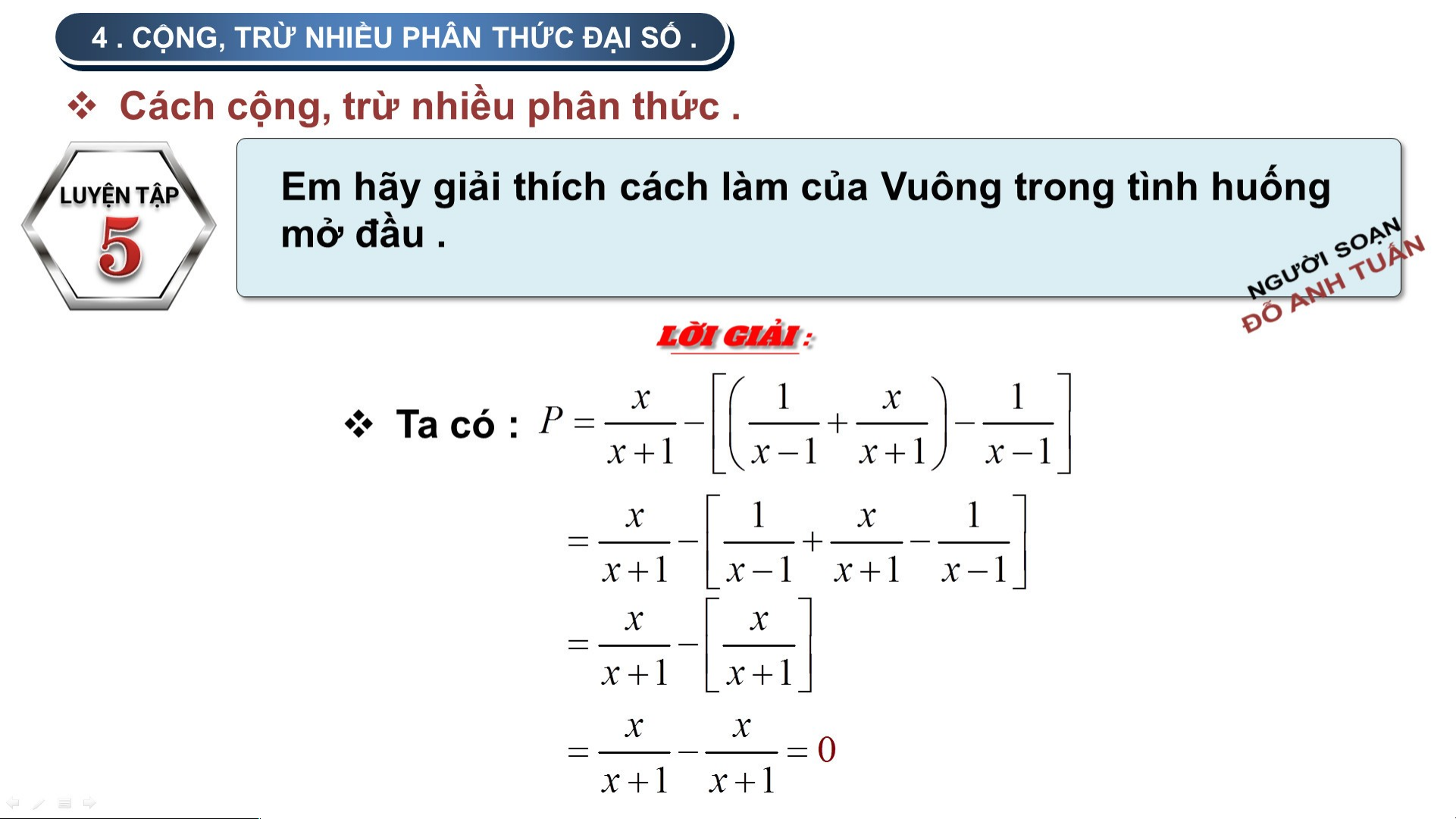
Làm thế nào mà bạn
Vuông thấy ngay được kết quả thế nhỉ?
1 . CỘNG HAI PHÂN THỨC CÙNG MẪU .
 Quy tắc cộng hai phân thức cùng mẫu .
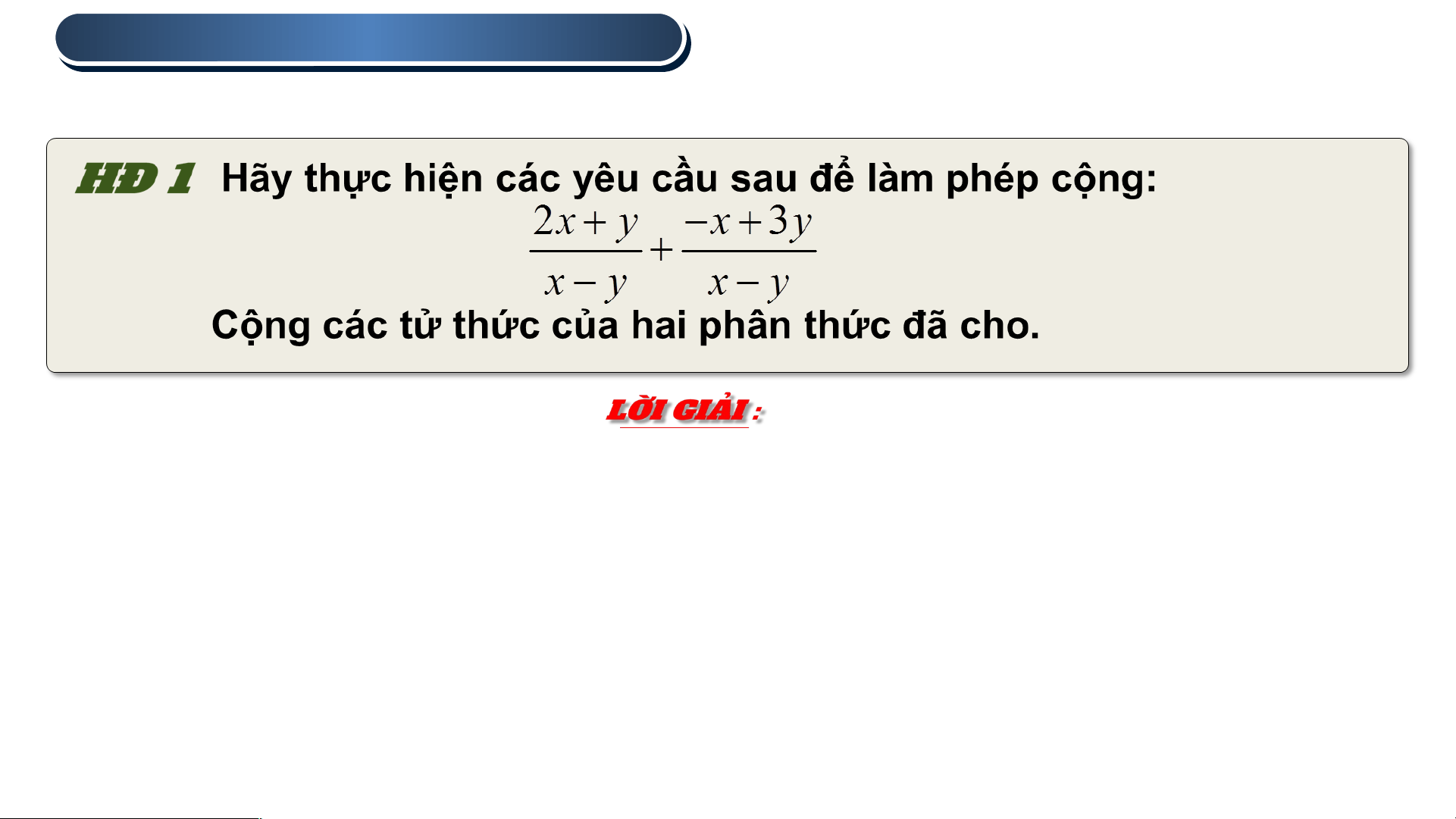
 Cộng các tử thức của hai phân thức, ta có:
2x  y  x  3y x  4y
1 . CỘNG HAI PHÂN THỨC CÙNG MẪU .
 Quy tắc cộng hai phân thức cùng mẫu .
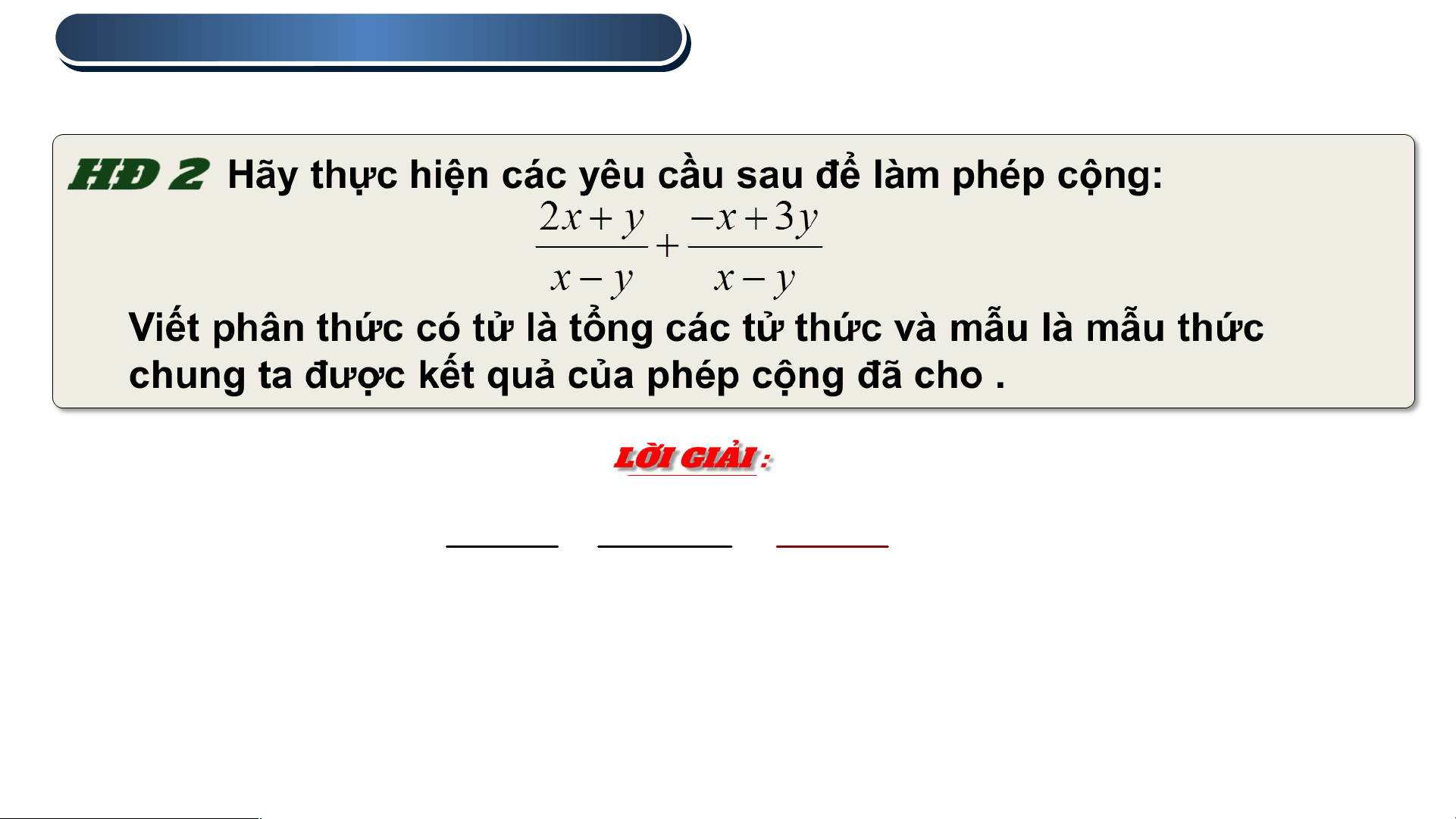
2x  y  x  3y x  4y   x  y x  y x  y
1 . CỘNG HAI PHÂN THỨC CÙNG MẪU .
 Quy tắc cộng hai phân thức cùng mẫu . Chú ý :
• Kết quả của phép cộng hai phân thức được gọi là tổng của hai
phân thức đó . Ta thường viết tổng dưới dạng rút gọn.
1 . CỘNG HAI PHÂN THỨC CÙNG MẪU .
 Quy tắc cộng hai phân thức cùng mẫu . 2 2 2  Ta có : 5x 5  10x 5x  5  10x 5(x  2x 1)    x  1 x  1 x  1 x  1 2 5(x  1)  5  (x  1) x  1
1 . CỘNG HAI PHÂN THỨC CÙNG MẪU .
 Quy tắc cộng hai phân thức cùng mẫu .
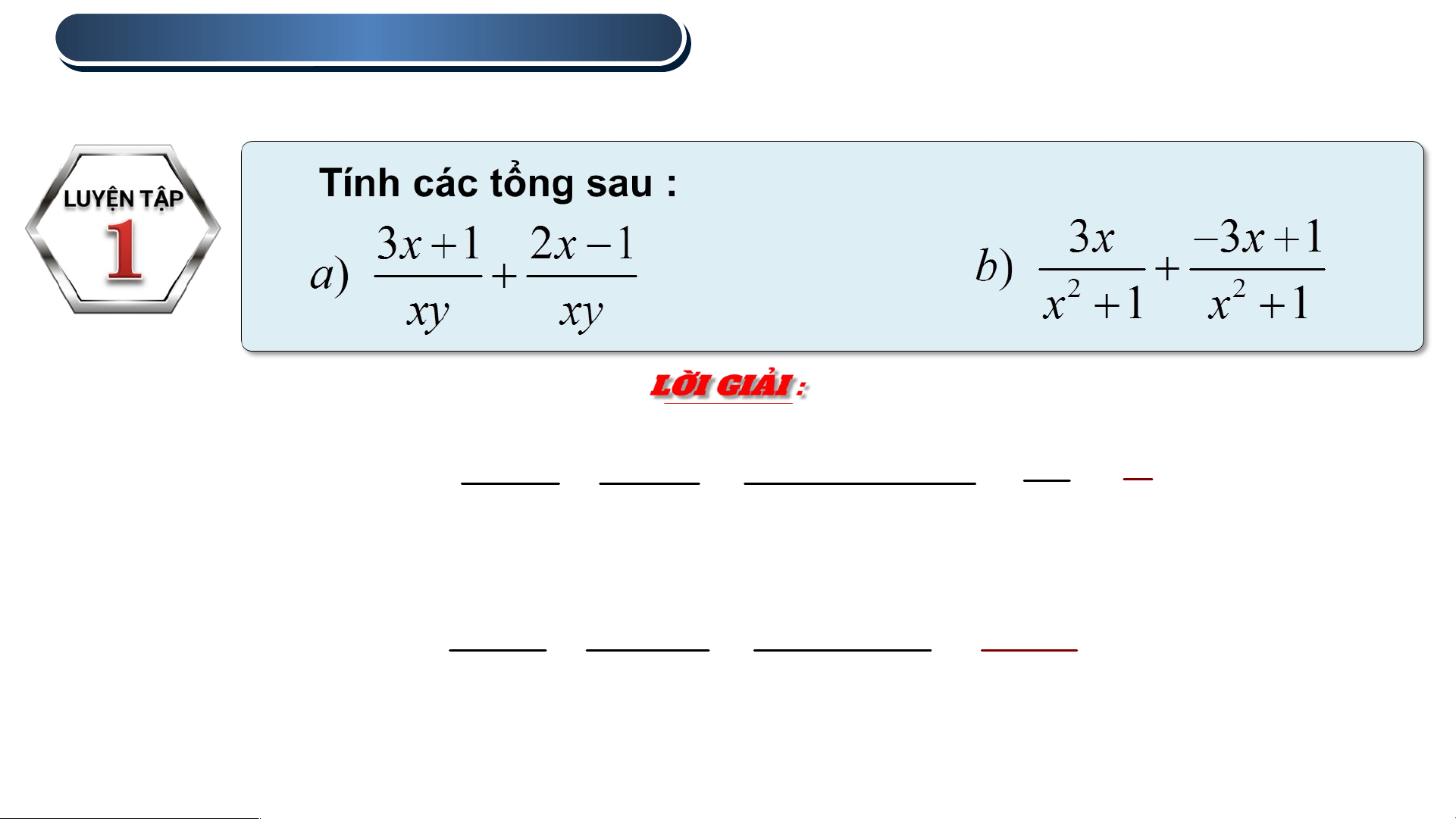
a) Ta có : 3x 1 2x  1
3x 1 2x  1 5x 5     xy xy xy xy y b) Ta có : 3x  3x 1 3x  3x 1 1    2 2 2 x 1 x 1 x 1 2 x 1
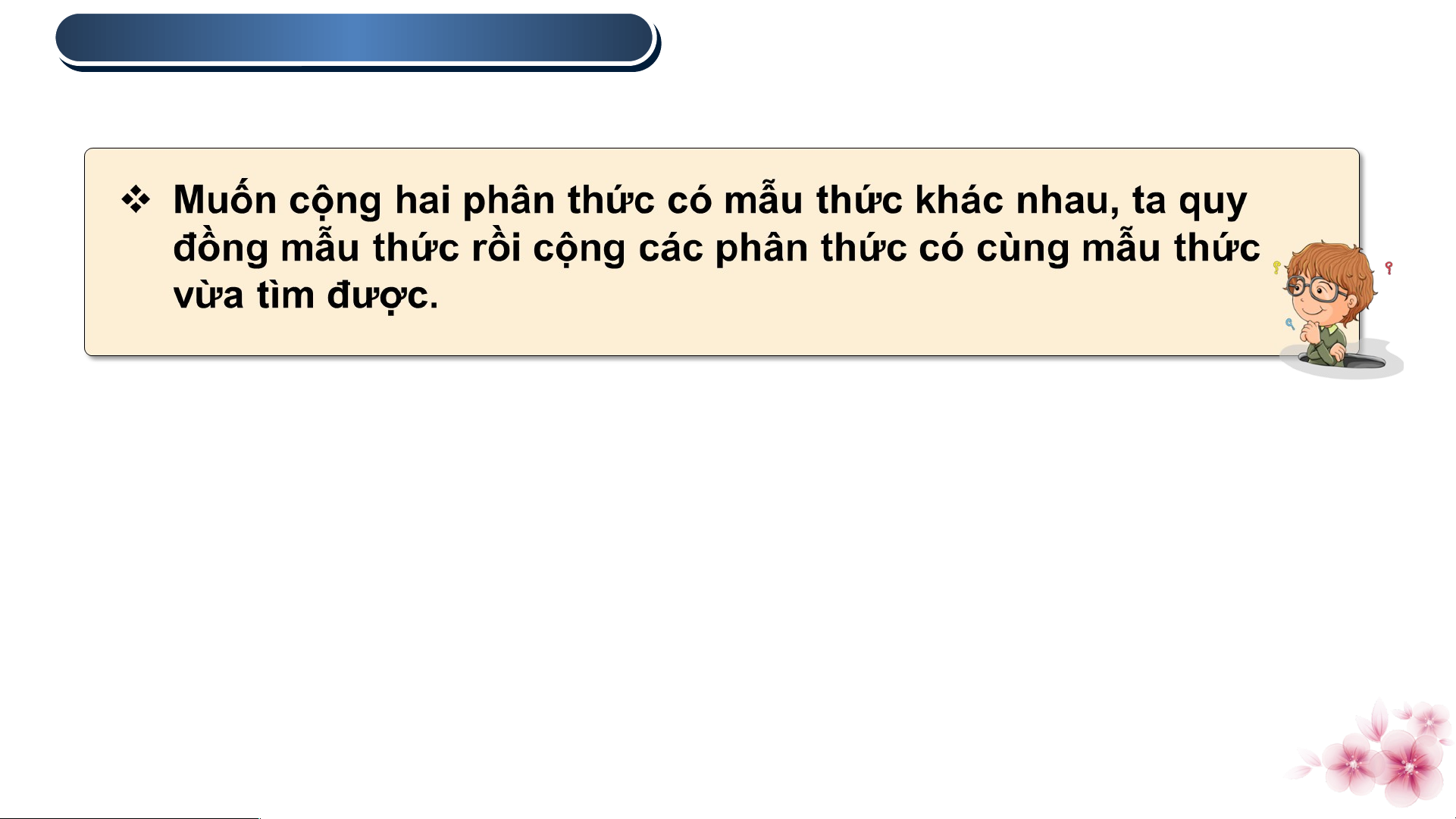
2 . CỘNG HAI PHÂN TH TH ỨC KHÁC MẪU
 Quy tắc cộng hai phân thức khác mẫu.  MTC :
Nhân tử phụ của x là y
Nhân tử phụ của y là x
Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng 1 y  1  x  ;  x xy y xy
2 . CỘNG HAI PHÂN TH TH ỨC KHÁC MẪU
 Quy tắc cộng hai phân thức khác mẫu. y  x y  x  Ta có :   xy xy xy 1  1 y  x Vậy :   x y xy
2 . CỘNG HAI PHÂN TH TH ỨC KHÁC MẪU
 Quy tắc cộng hai phân thức khác mẫu.
2 . CỘNG HAI PHÂN TH TH ỨC KHÁC MẪU
 Quy tắc cộng hai phân thức khác mẫu.
 Quy đồng mẫu hai phân thức đã cho : 5 5(1 x) 3 3x  ;  x x(1 x) 1 x x(1 x) Do đó : 5(1 x)  3x 5  2x   x(1 x) x(1 x)
2 . CỘNG HAI PHÂN TH TH ỨC KHÁC MẪU
 Quy tắc cộng hai phân thức khác mẫu.
 Quy đồng mẫu hai phân thức đã cho : 5 5.5y 25y   2 2
2x (6x  y)
2x (6x  y).5y 2
10x y(6x  y) 3 3.2x 6x  
5xy(6x  y)
5xy(6x  y).2x 2
10x y(6x  y) 5 3 25y  6x Do đó :   2 2
2x (6x  y) 5xy(6x  y) 10x y(6x  y)
3 . TRỪ HAI PHÂN THỨC .
 Quy tắc trừ hai phân thức. x  1 2x  3
x  1 (2x  3)  Ta có :   x 1 x 1 x 1
x  1 2x  3  x  y  3   x 1 x 1
 Để có cả bộ Giáo án Pp Toán 8 – KNTT , xin liên hệ :
Đỗ Anh Tuấn - Zalo : 0918.790.615
Thầy (cô) có thể tham khảo trước nội dung các bài giảng tại đây :
https://sites.google.com/view/giaoandientu-doanhtuan/to%C3%A1n-
8/k%E1%BA%BFt-n%E1%BB%91i-tri-th%E1%BB%A9c?authuser= (copy
đường link và dán vào trình duyệt )
• Tất cả bài giảng đều do một người soạn ( Đỗ Anh Tuấn) nên chất lượng đồng đều
từ bài đầu đến bài cuối.
• Bài giảng được thực hiện công phu và đầy đủ các bài tập và luyện tập .
• Đặt biệt là phân môn Hình học : các hình vẽ được vẽ chuẩn xác và rõ nét hơn cả
SGK ( Đây là điểm khác biệt lớn của bộ Giáo án này )
Tất cả bài tập Hình học đều có hình minh hoạ đầy đủ , giúp việc dạy học dễ dàng .
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35