ỦY BAN NHÂN DÂN QUẬN LIÊN CHIỂU
TRƯỜNG THCS NGUYỄN LƯƠNG BẰNG
Bài 27 KHÁI NIỆM HÀM SỐ VÀ ĐỒ THỊ HÀM SỐ (2 tiết) Giáo viên : Hà Duy Ninh Thành phố : Đà Nẵng Sách
: Kết nối tri thức với cuộc sống ĐẶT VẤN ĐỀ
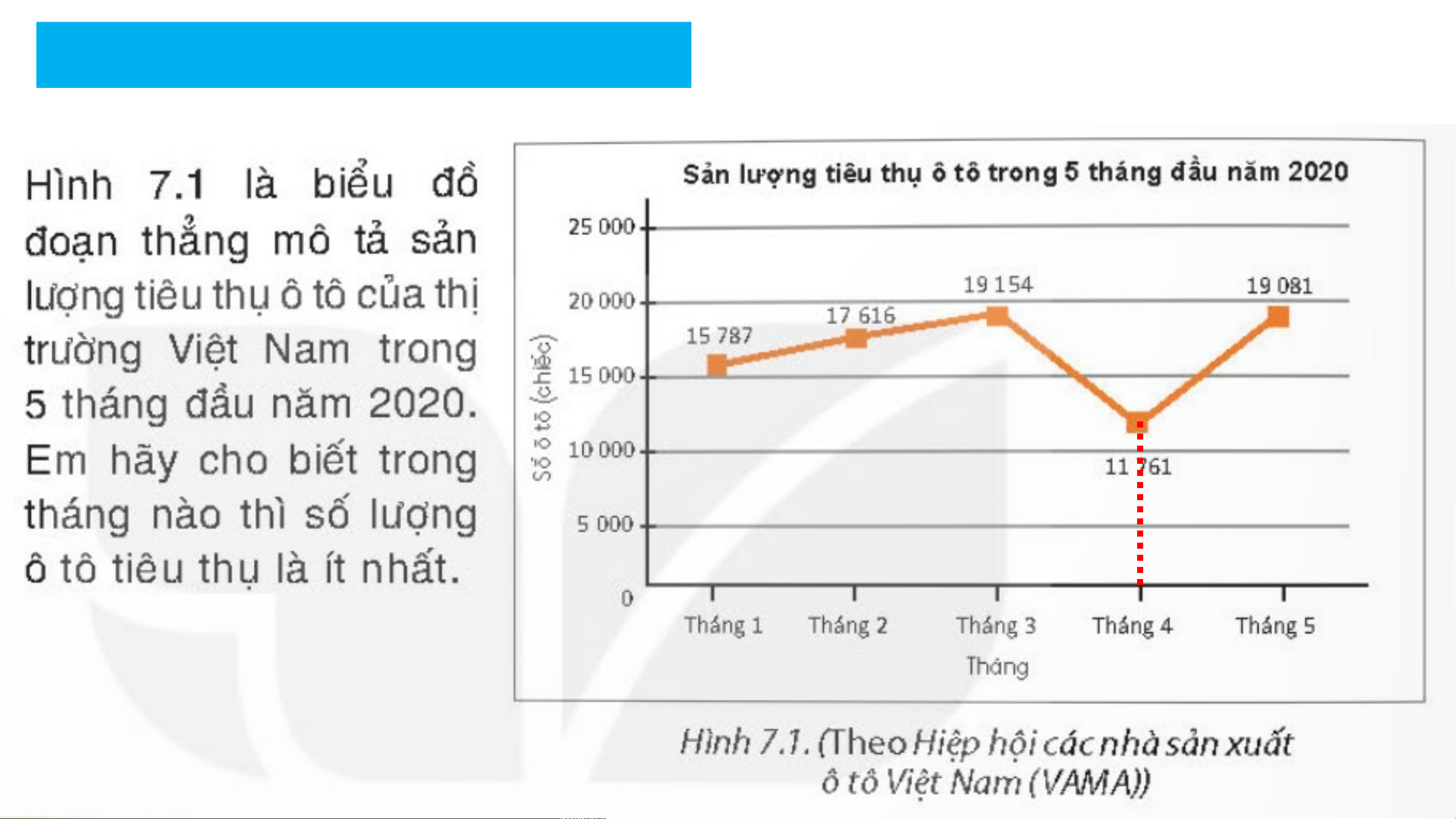
Xác định điểm thấp nhất rồi vẽ đường
vuông góc xuống trục ngang: Tháng 4
Biểu đồ đoạn thẳng là một hàm số.
Chúng ta hiểu kĩ hơn trong bài này a) t 1 2 3 4 S 60 120 180 240
b) Với mỗi giá trị của t , ta xác đinh được một giá trị tương ứng của S
a) Nhiệt độ của Hà Nội vào thời điểm 12 giờ trưa ngày hôm đó là 120C
b) Trong bảng với mỗi giá trị t ta xác định được 1 giá trị tương ứng T
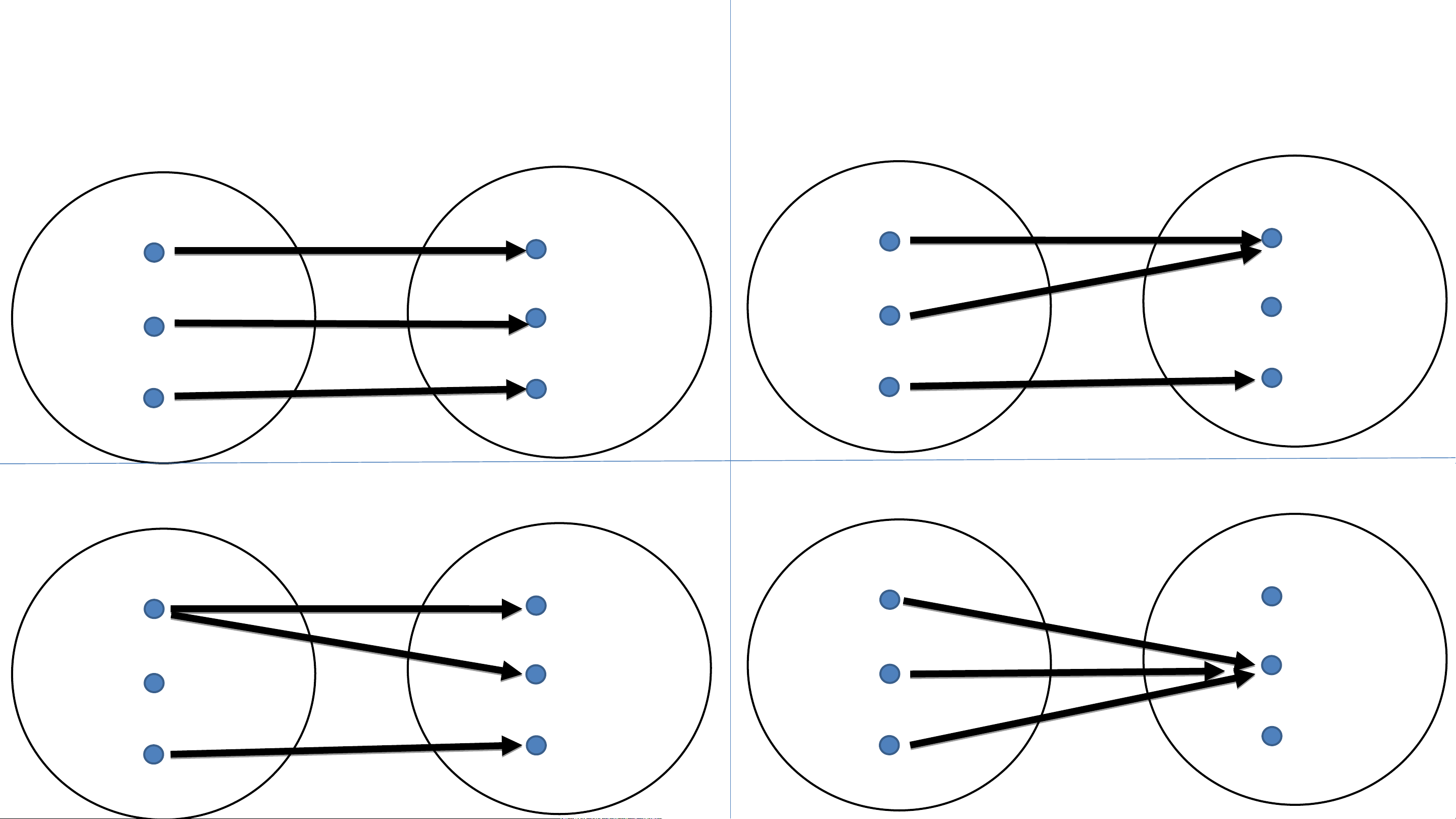
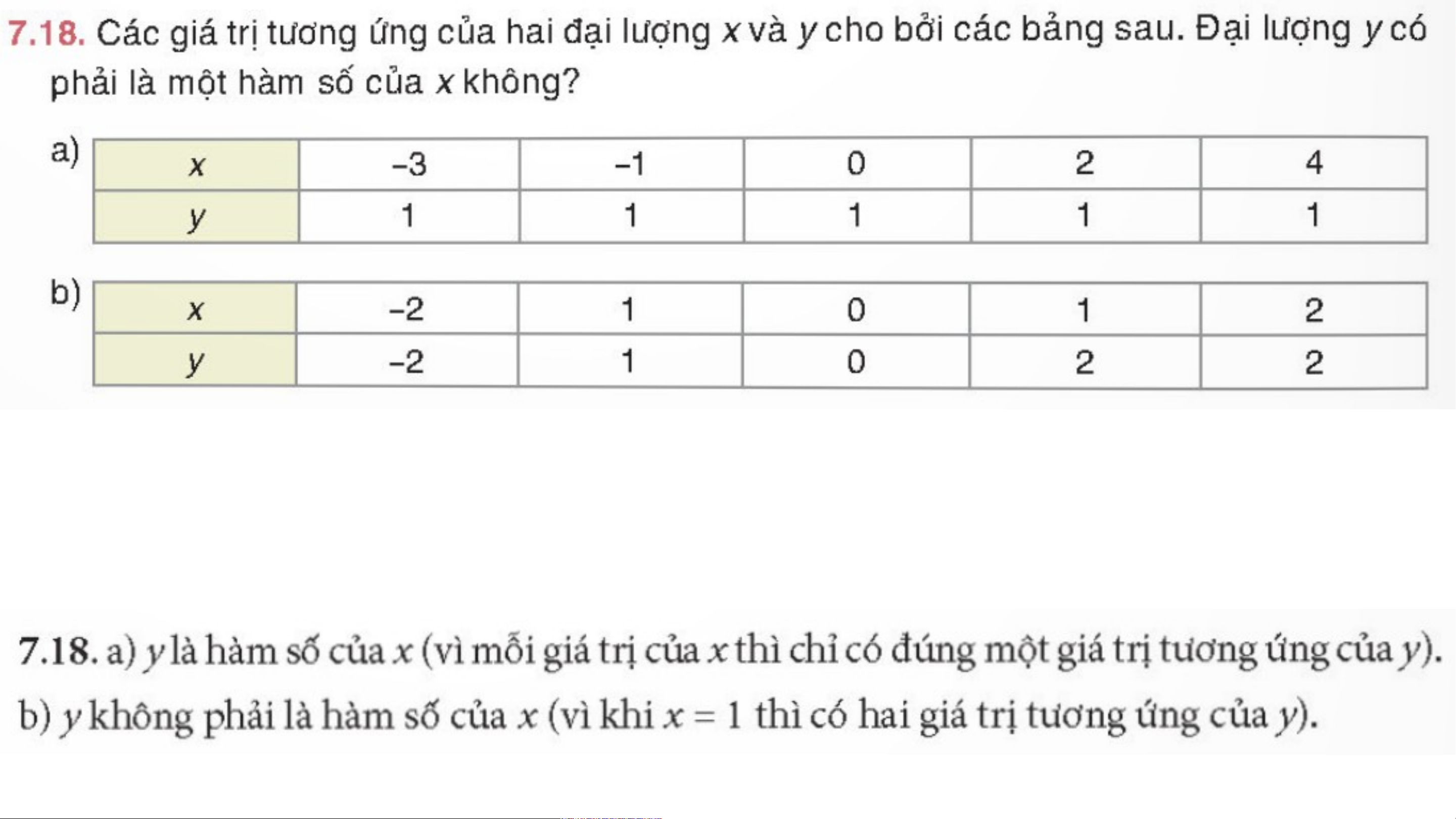
Giải thích về hàm số cho bằng Bảng y là hàm số của x y là hàm số của x X y X y 1 4 1 4 5 2 5 2 6 3 6 3 X
Y không là hàm số của x y X y là hàm số của x y 1 4 1 4 2 5 2 5 6 3 6 3
Công thức tính thời gian di chuyển t (giờ) của một ô tô chuyển động trên quãng
đường dài 150km với vận tốc không đổi v(km/h) là:
Thời gian t là hàm số của vận tốc v, khi v = 60 thì t = 2,5 giờ
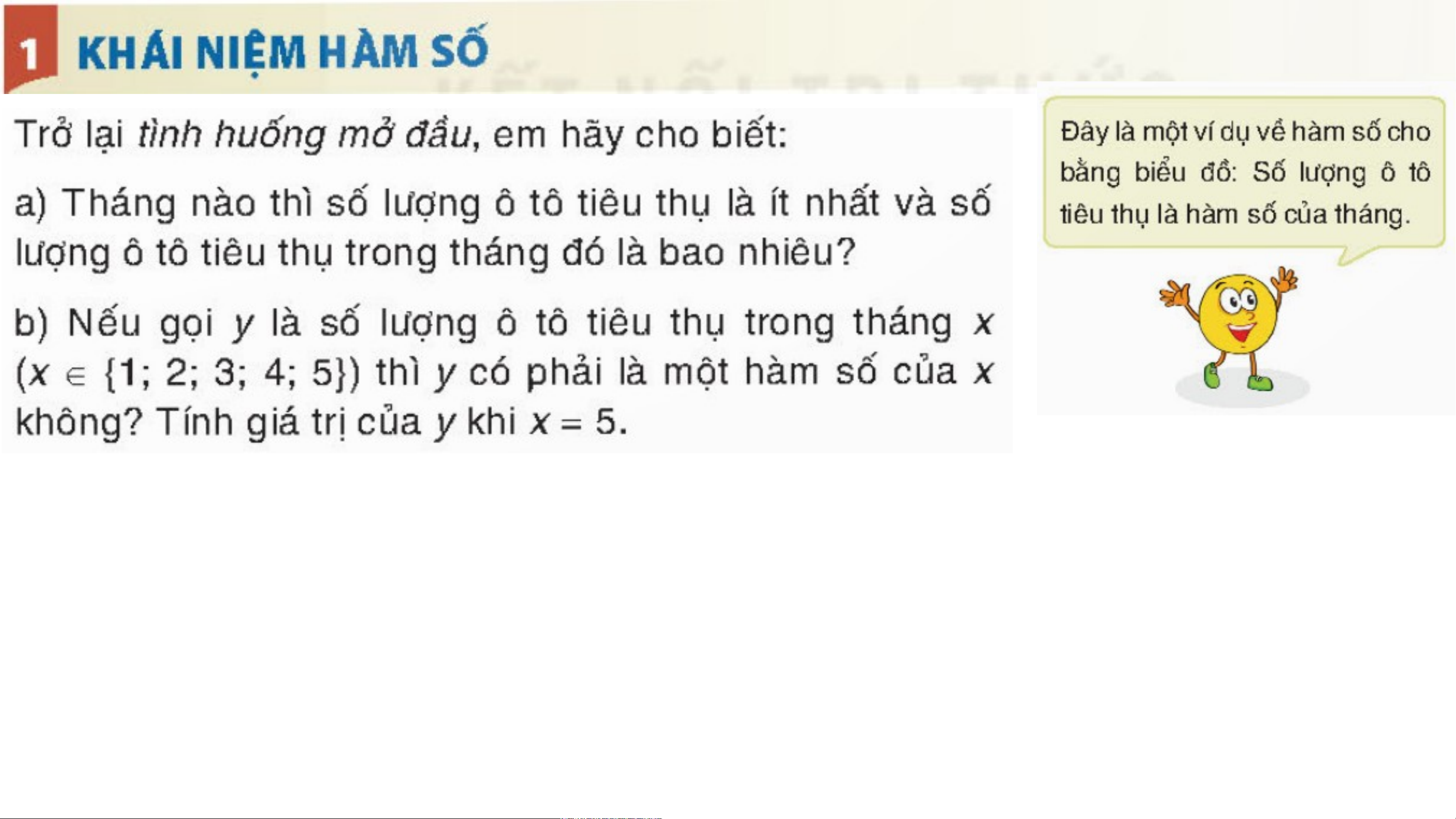
a) Số lượng ô tô tiêu thụ ít nhất vào tháng 4 số lượng là 11761
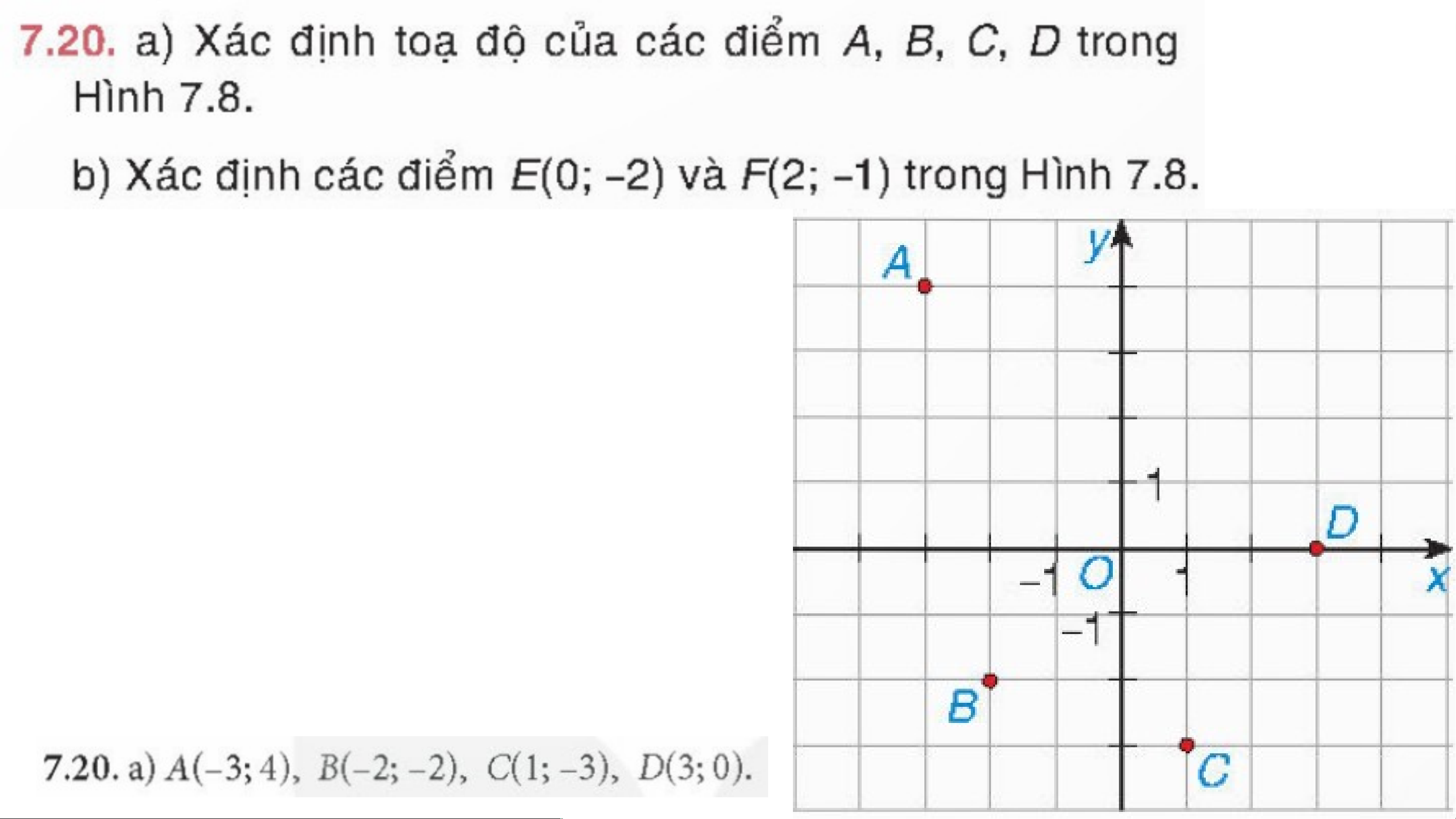
b) y là hàm số của x, với x = 5 thì y =19081 a) • M(-2;4) • N(1;-2) • P(2;0) • Q(0;-3)
b) Kí hiệu các điểm R, S trên hình
↓ Người ta quy ước đánh
số từ 1 đến 4 cho các góc phần tư bằng số La Mã
Góc phần tư thứ nhất, ký
hiệu là góc I, là góc phần
tư bao gồm các điểm có
tung độ và hoành độ đều dương. Tương tự theo hướng ngược chiều kim
đồng hồ để đặt tên cho
các góc phần tư tiếp theo
Góc phần tư thứ nhất, ký hiệu I, là góc phần tư bao gồm các điểm có tung độ và hoành độ đều dương.
Góc phần tư thứ hai, ký hiệu II , là góc phần tư bao gồm các điểm có hoành độ âm, tung độ dương
Góc phần tư thứ ba, ký hiệu III , là góc phần tư bao gồm các điểm có hoành độ âm, tung độ âm
Góc phần tư thứ tư, ký hiệu IV , là góc phần tư bao gồm các điểm có hoành độ dương, tung độ âm KẾT Ế NỐI CUỘ I C SỐNG “BÀ B N À C Ờ V C U Ờ V A U ” A
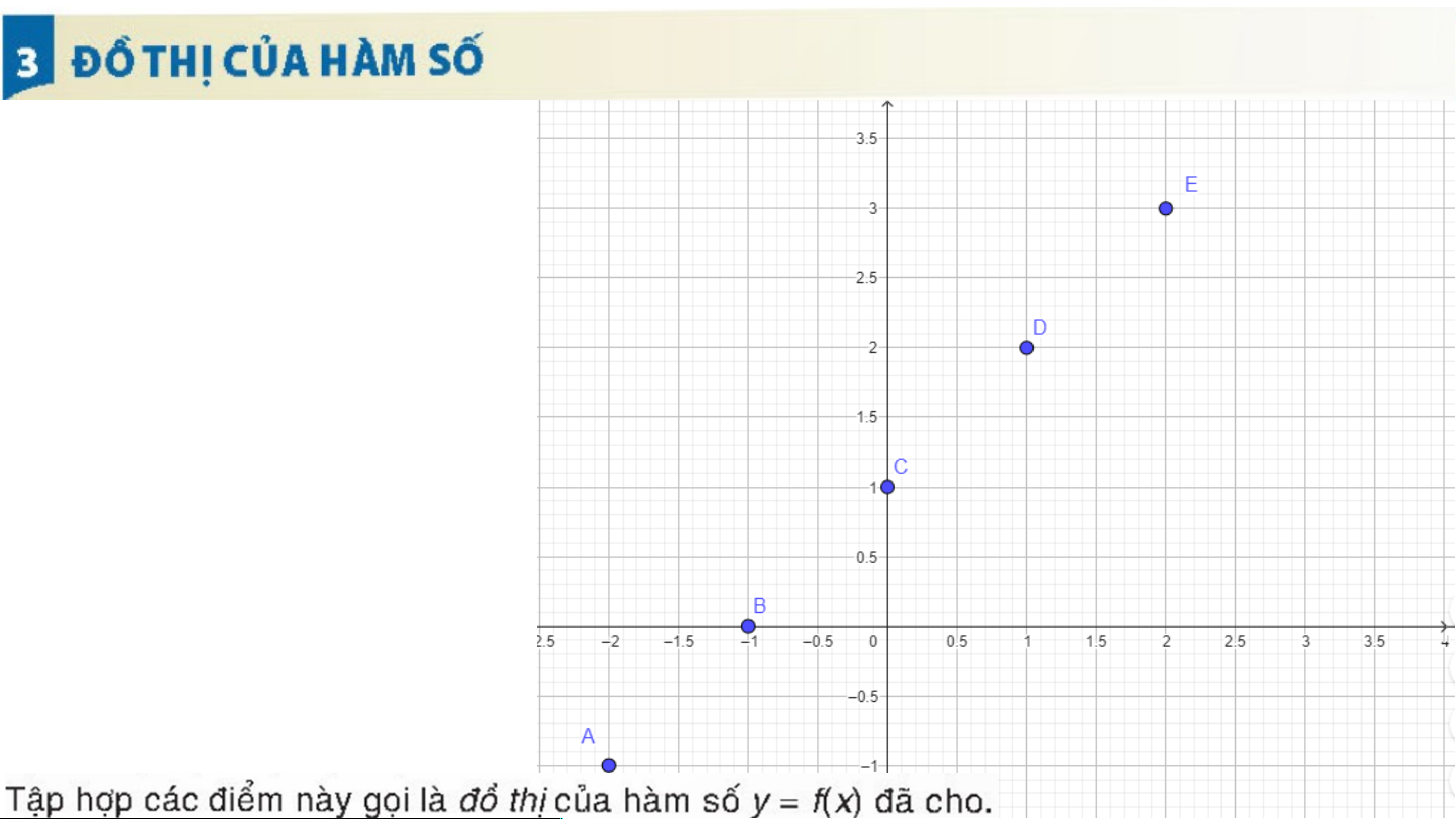
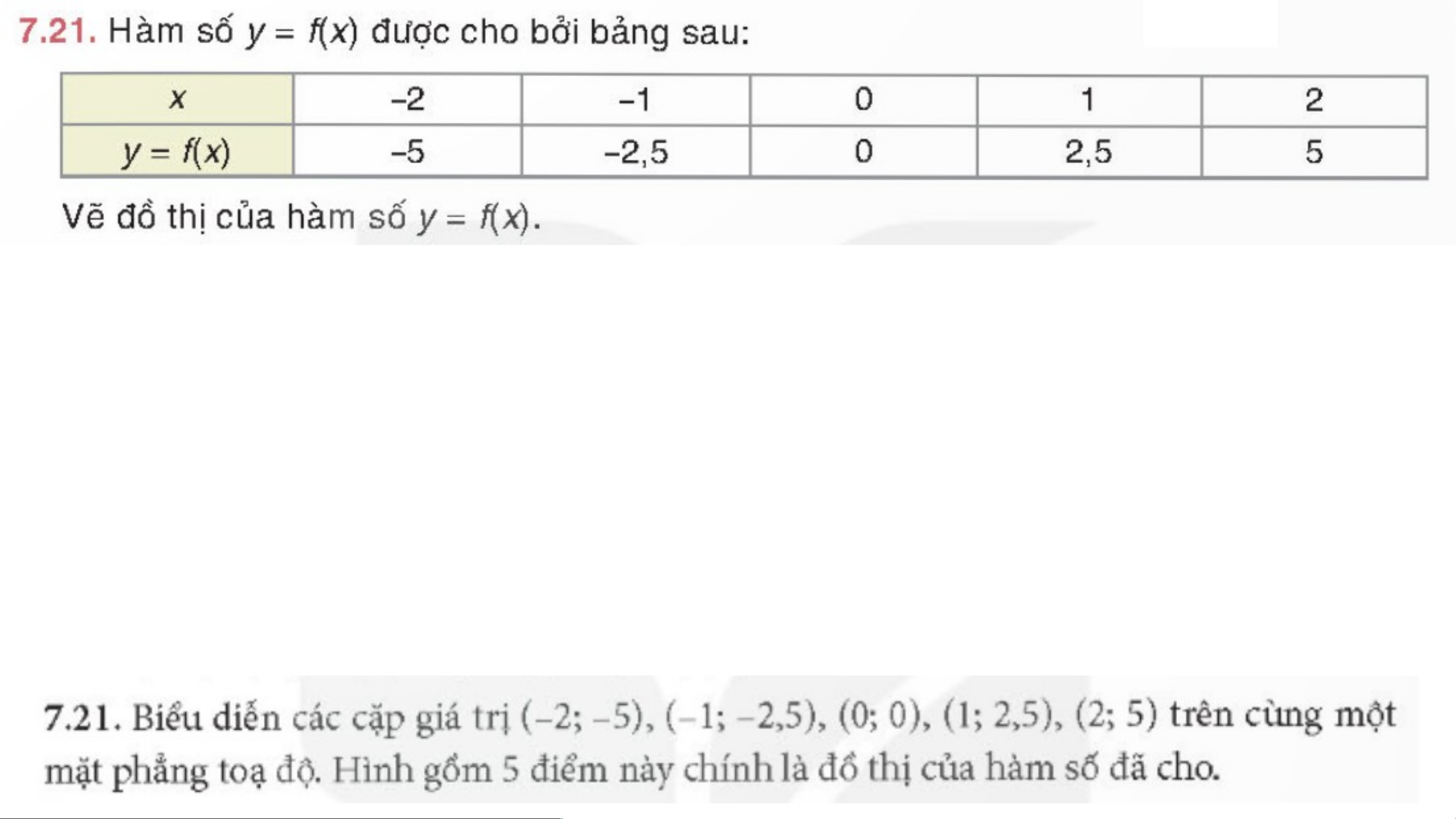
a) Tập hợp các cặp giá trị tương ứng của x và y là:
{(-2;-1);(-1;0);(0;1);(1;2);(2;3)} y
b) Đặt tên tọa độ và biểu
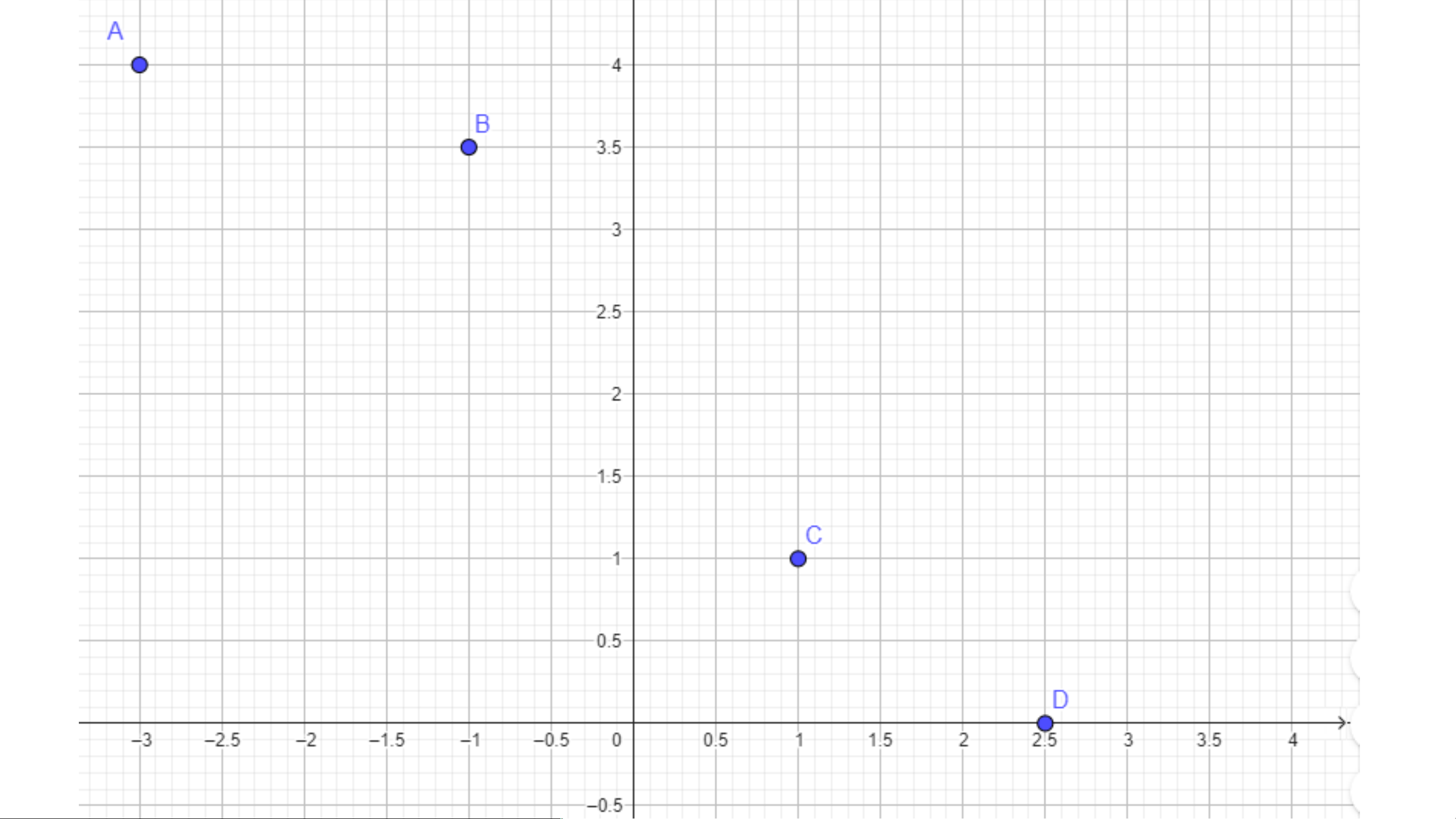
điễn các điểm trên trục tọa độ Oxy: A(-2;-1) B(-1;0) C(0;1) D(2;3) x Đặt tên tọa độ: • A(-3;4) • B(-1;3,5) • C(1;1) • D(2,5;0) y x
HƯỚNG DẪN VỀ NHÀ 1
Ghi nhớ kiến thức trong bài 2
Hoàn thành bài tập SGK, SBT 3 Chuẩn bị bài mới
Document Outline

• Slide 1
• Slide 2
• ĐẶT VẤN ĐỀ
• Slide 4
• Slide 5
• Slide 6
• Giải thích về hàm số cho bằng Bảng
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
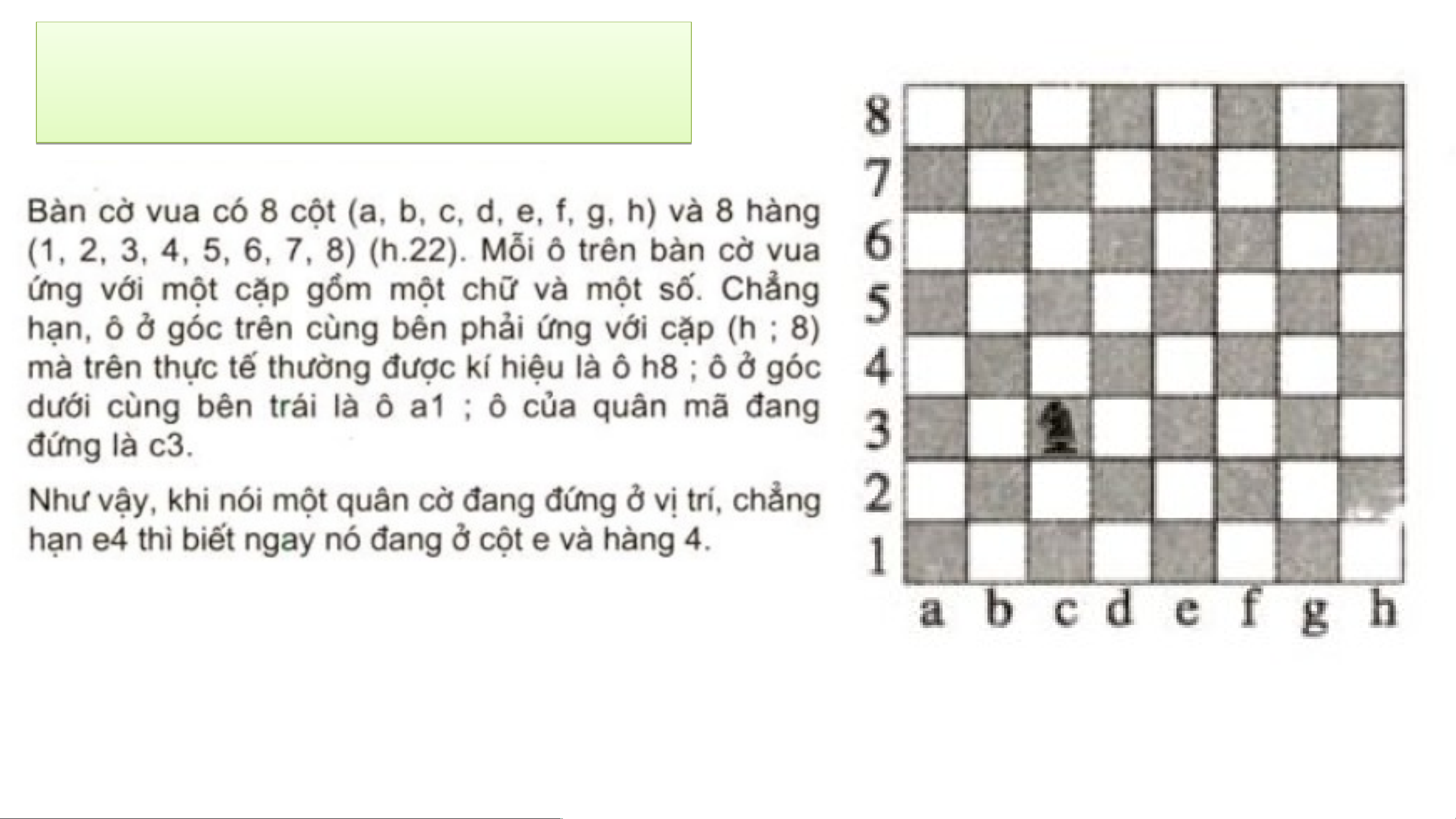
• KẾT NỐI CUỘC SỐNG “BÀN CỜ VUA”
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38