













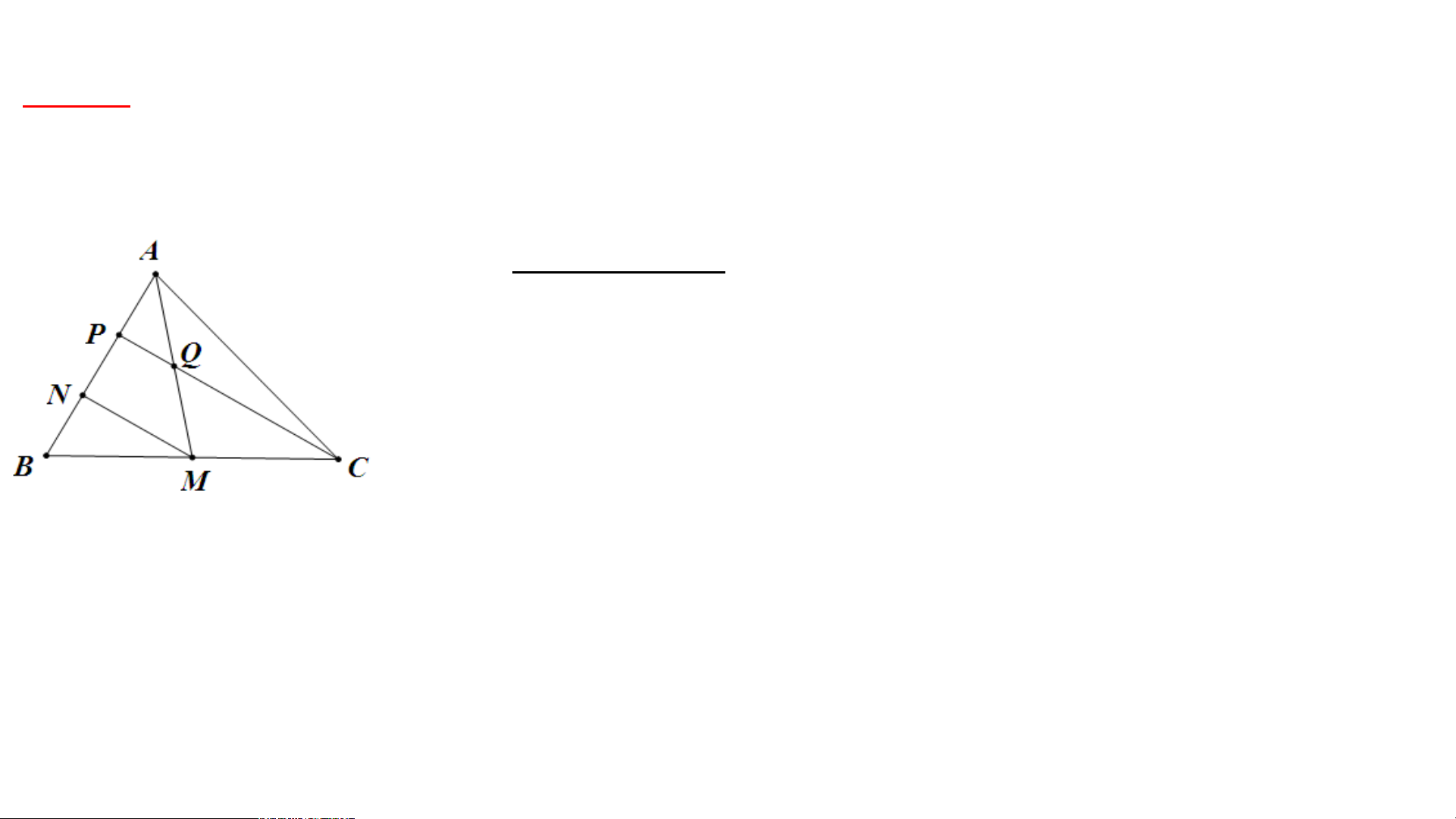







Preview text:
CHÀO MỪNG CÁC THẦY GIÁO, CÔ GIÁO
CÙNG CÁC EM HỌC SINH VỀ DỰ GIỜ TIẾT HỌC Năm học: 2023-2024 TRÒ CHƠI TRỐN TÌM
CÙNG BẠCH TUYẾT VÀ CÁC CHÚ LÙN LUẬT CHƠI:
+ Có tất cả 5 câu hỏi, gọi học sinh lần lượt trả lời các câu hỏi.
+ Mỗi câu hỏi có 10 giây để suy nghĩ và ai nhanh hơn được trả lời.
+ Nếu học sinh trả lời đúng thì một chú lùn sẽ xuất hiện và bạn đó
được nhận 01 phần quà bí ẩn trong hộp.
+ Nếu học sinh trả lời sai thì các con vật sẽ xuất hiện nhường lại quyền trả lời cho bạn khác. START
Câu 1. Đoạn thẳng nối trung Hết Giờ 12
điểm hai cạnh của một tam giác 9 3 6
gọi là đường gì trong tam giác: A. Đường trung trực B. Đường trung bình C. Đường trung tuyến D. Đường phân giác ĐÚNG RỒI START Hết Giờ
Câu 2. Điền từ thích hợp vào … : 12 9 3
“Đường trung bình của tam giác 6
thì … với cạnh thứ ba và …”
A. Vuông góc – bằng nửa C. Giao nhau – bằng nửa cạnh đó cạnh đó B. Song song – bằng nửa D. Song song – gấp đôi cạnh đó cạnh đó ĐÚNG RỒI START
Câu 3. Một tam giác có số đường Hết Giờ 12 trung bình là: 9 3 6 A. B. C. D. ĐÚNG RỒI START Hết Giờ
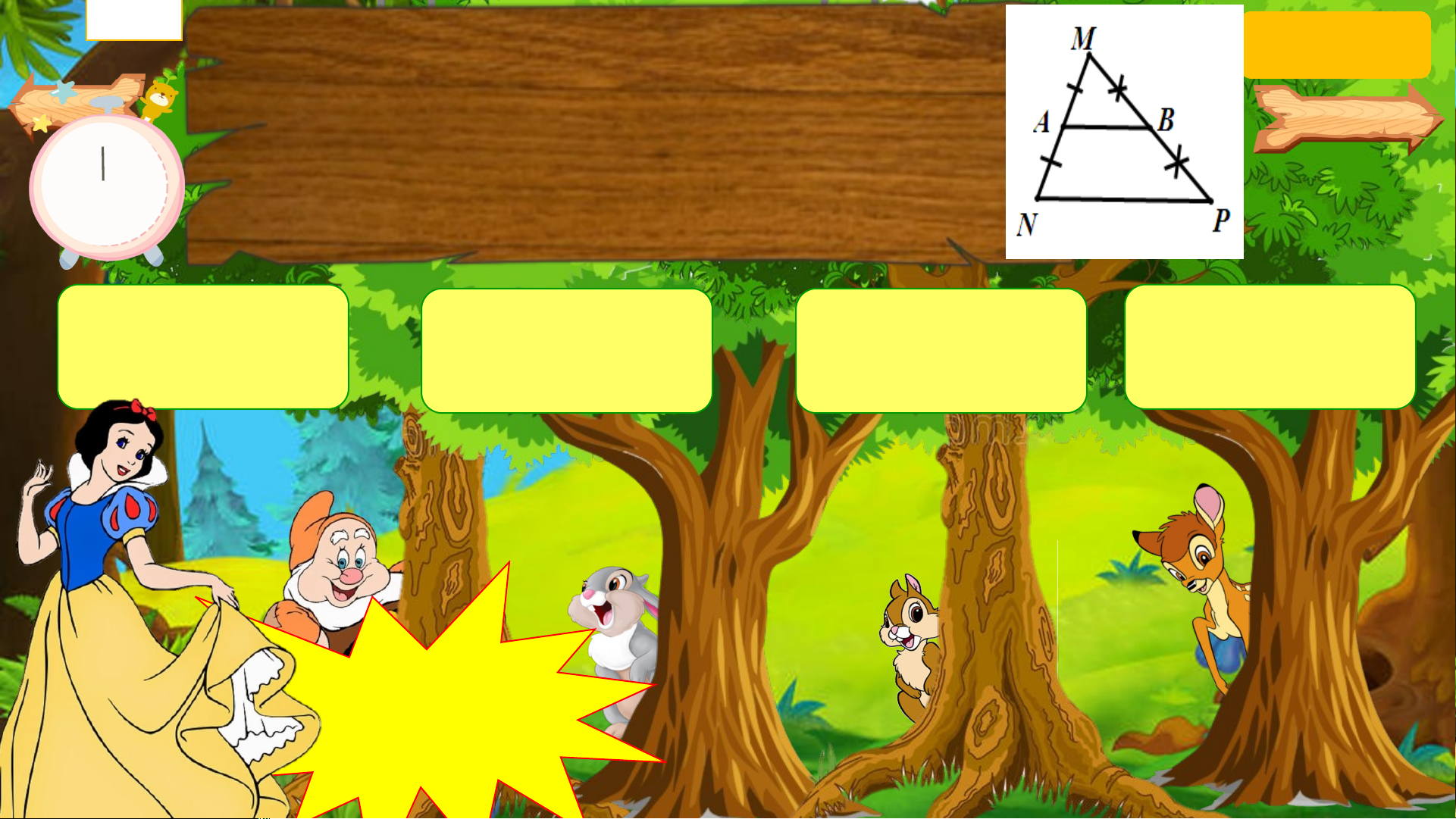
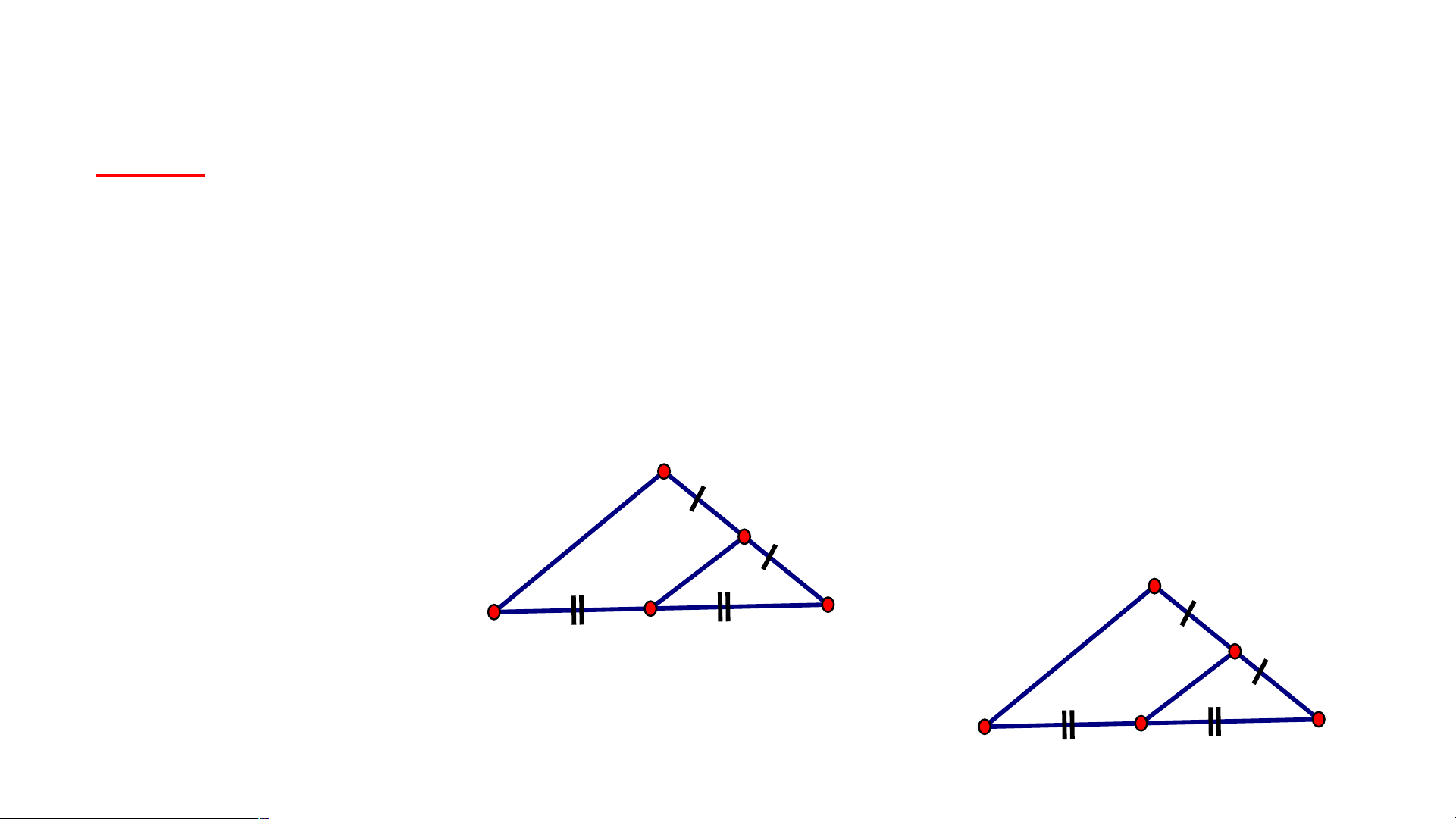
Câu 4. Cho có là đường
trung bình của tam giác (như hình 12 9 3
vẽ). cm . Độ dài đoạn 6 là: A. B. C. D. ĐÚNG RỒI START Hết Giờ Câu 5. Cho hình vẽ. 12 Độ dài đoạn là: 9 3 6 A. cm B. cm C. cm D. cm ĐÚNG RỒI
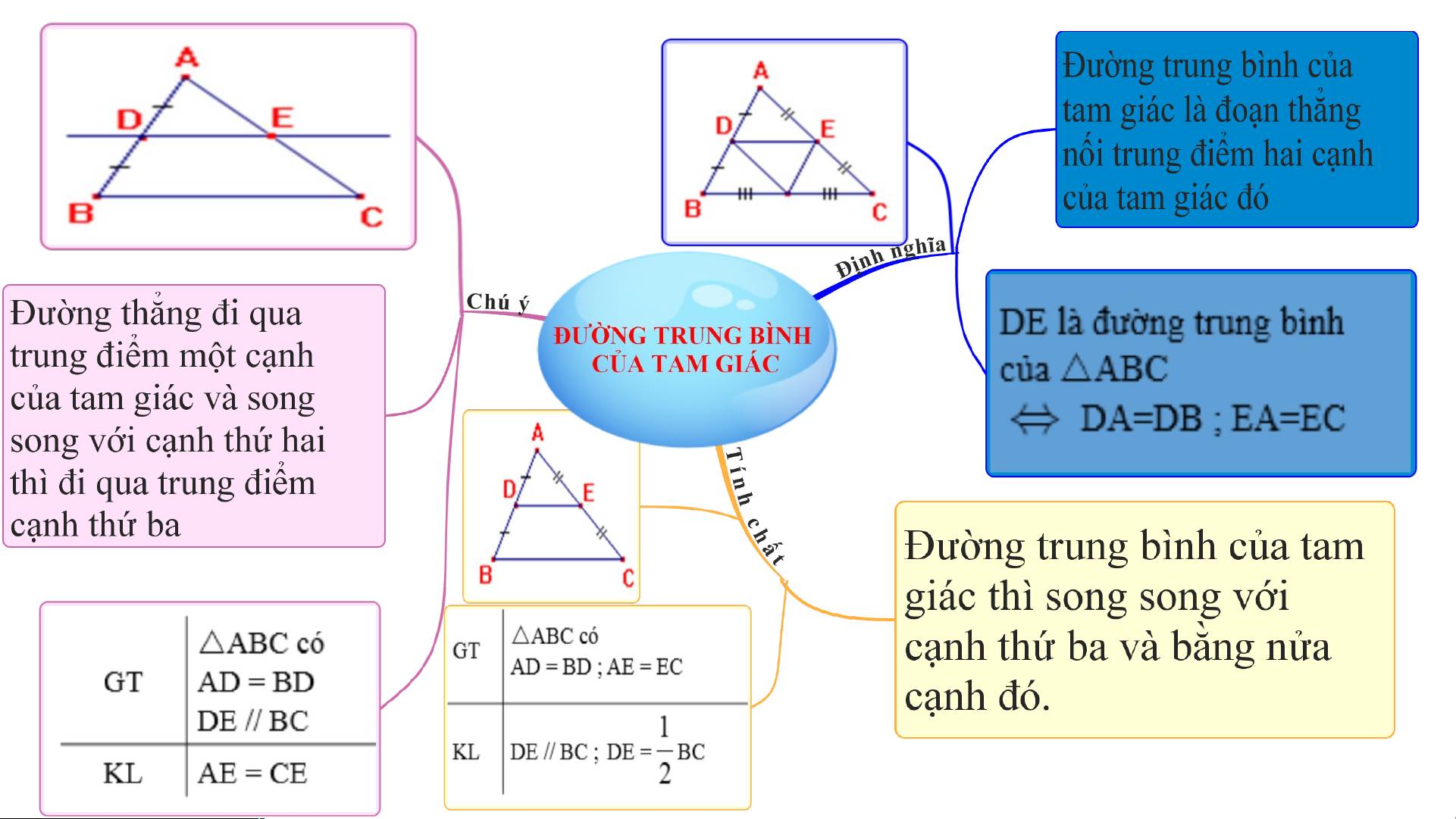
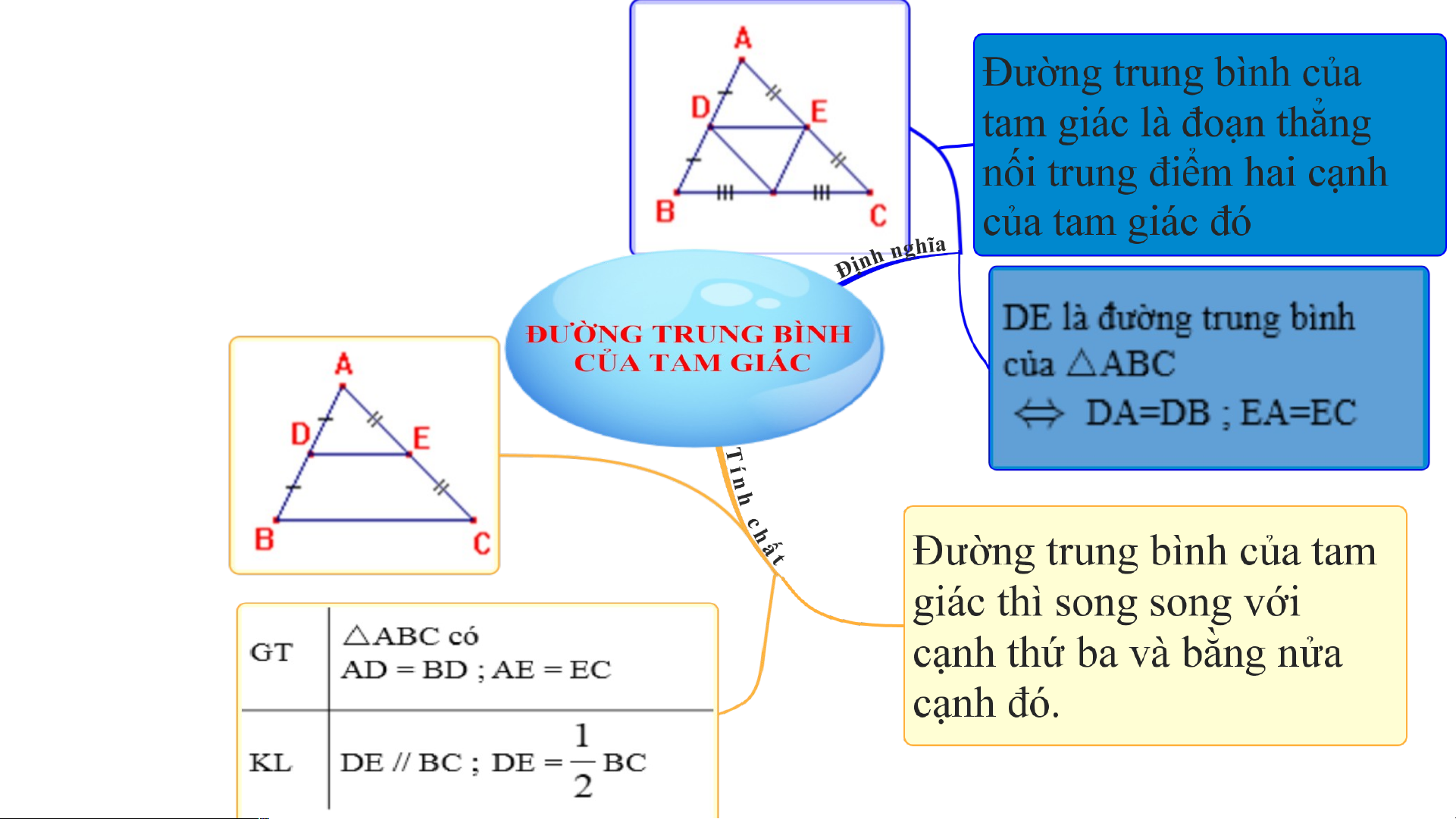
ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
PHIẾU HỌC TẬP SỐ 1 -
Nêu định nghĩa và tính chất của đường trung bình của tam giác ? -
Nếu một đường thẳng đi qua trung điểm một cạnh
của tam giác, song song với cạnh thứ hai thì có tính chất gì đặc biệt?
(Nêu rõ nội dung, vẽ hình và tóm tắt dưới dạng kí hiệu)
CÁC DẠNG BÀI TẬP CỦA CHỦ ĐỀ
DẠNG 1: Tính độ dài đoạn thẳng.
DẠNG 2: Chứng minh các hệ thức về cạnh.
DẠNG 3: Chứng minh tứ giác đặc biệt: hình bình hành,
hình thoi, hình vuông, hình chữ nhật…
DẠNG 4: Chứng minh hai đường thẳng song song, ba điểm thẳng hàng.
DẠNG 5: Các bài toán thực tế. TIÊU CHÍ ĐÁNH GIÁ
- Đi đúng đường về tổ và giải thích đúng cách tính
của mỗi hình được 10 điểm
- Tính đúng mỗi hình 1,0 điểm
- Giải thích đúng mỗi hình 1,0 điểm
- Nếu đi nhầm đường trừ 0,25 điểm/ lần
- Điểm tính cho tất cả các thành viên trong nhóm. MẬT THƯ
Bài 1:Tính x , y trong các hình sau để tìm đúng đường
cho Ong con về tổ bạn nhé! B START x HÌNH 1 D 1,5m 2m E 8m C A HÌNH 4 HÌNH 2 HÌNH 3
TÊN HỌC SINH:…………………… 1,5 ĐIỂM:……….. 4,5 7,5 7,5 6 4 8 6 7,5 5
TÊN HỌC SINH:…………………… 1,5 ĐIỂM:……….. 4,5 7,5 7,5 6 4 8 6 7,5 5
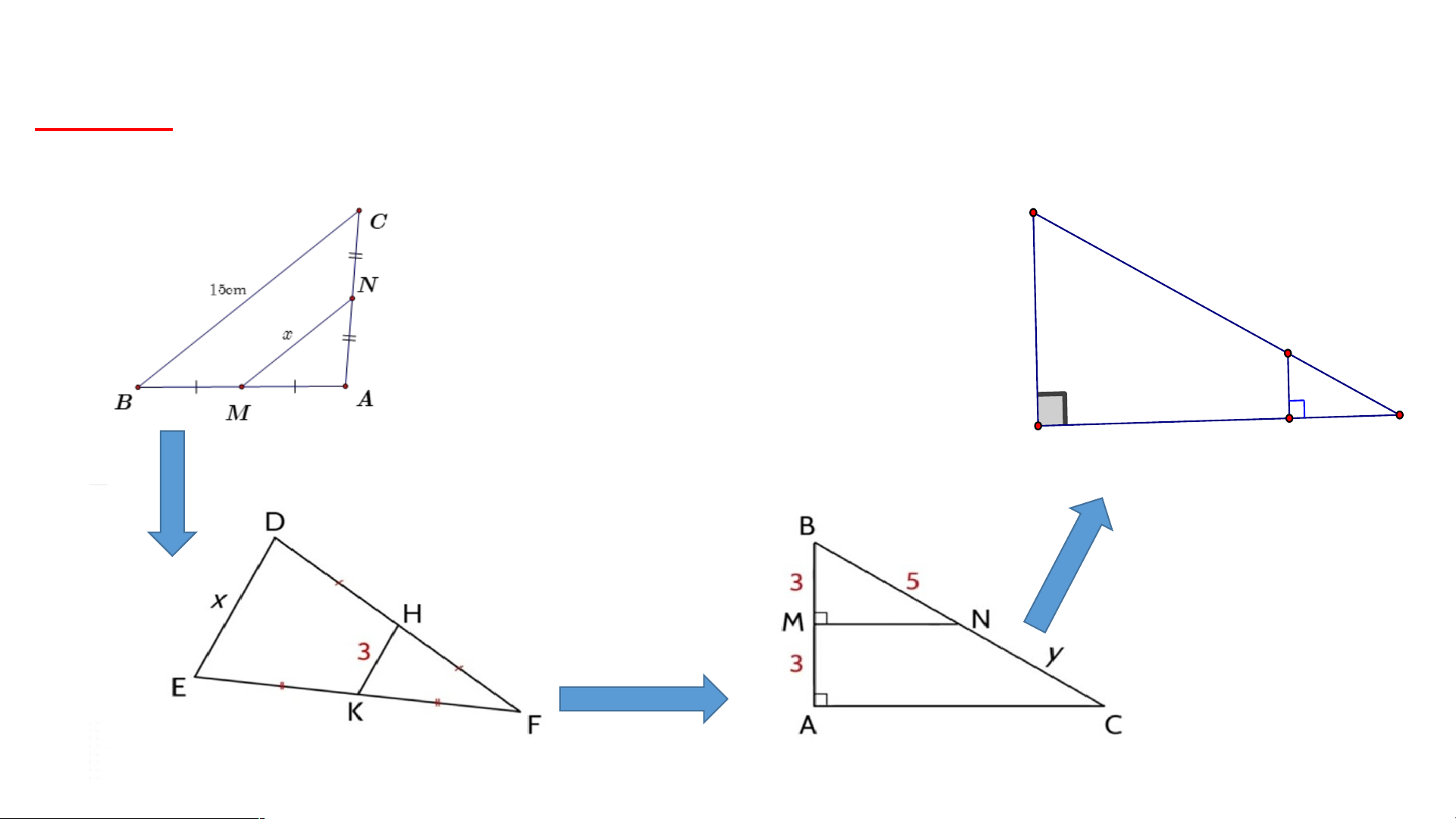
Ta có M,N lần lượt là trung điểm của AB,AC HÌNH 1
Nên MN là đường trung bình của tam giác ABC 1 1 ⇒ 𝑀𝑁 = 𝐵𝐶 .15 2 ⇒ 𝑥= 2 =7,5 𝑐𝑚
Ta có H,K lần lượt là trung điểm của DF,EF
Nên HK là đường trung bình của tam giác DEF 1 1
⇒ 𝐻𝐾 = 𝐷𝐸 . 𝑥 2
⇒ 3= 2 ⇒ 𝑥=2.3=6 𝑐𝑚 𝑀𝑁 Ta có ⊥ 𝐴𝐵
𝐴𝐶 ⊥ 𝐴𝐵 }⇒ 𝑀 𝑁 /¿ 𝐴𝐶
Mà MA = MB = 3 nên NC = NB = y = 5 𝐴𝐵 ⊥ 𝐴𝐸 Ta
𝐶𝐷 ⊥ 𝐴𝐸 }⇒ 𝐴 𝐵/¿ 𝐶𝐷 có x
Theo hệ quả định lí Thales có𝐶𝐷 𝐸𝐶
𝐴𝐵= 𝐸𝐴 ⇒ 𝐴𝐵 . 𝐸𝐶=𝐶𝐷 . 𝐸𝐴
𝐶𝐷 . 𝐸𝐴 1,5.10 HÌNH 4 ⇒ 𝐴𝐵= 𝐸𝐶 = =7,5 𝑚=𝑥 2 TIÊU CHÍ ĐÁNH GIÁ
- Đi đúng đường về tổ và giải thích đúng cách tính
của mỗi hình được 10 điểm
- Tính đúng mỗi hình 1,0 điểm
- Giải thích đúng mỗi hình 1,0 điểm
- Nếu đi nhầm đường trừ 0,25 điểm/ lần
- Điểm tính cho tất cả các thành viên trong nhóm.
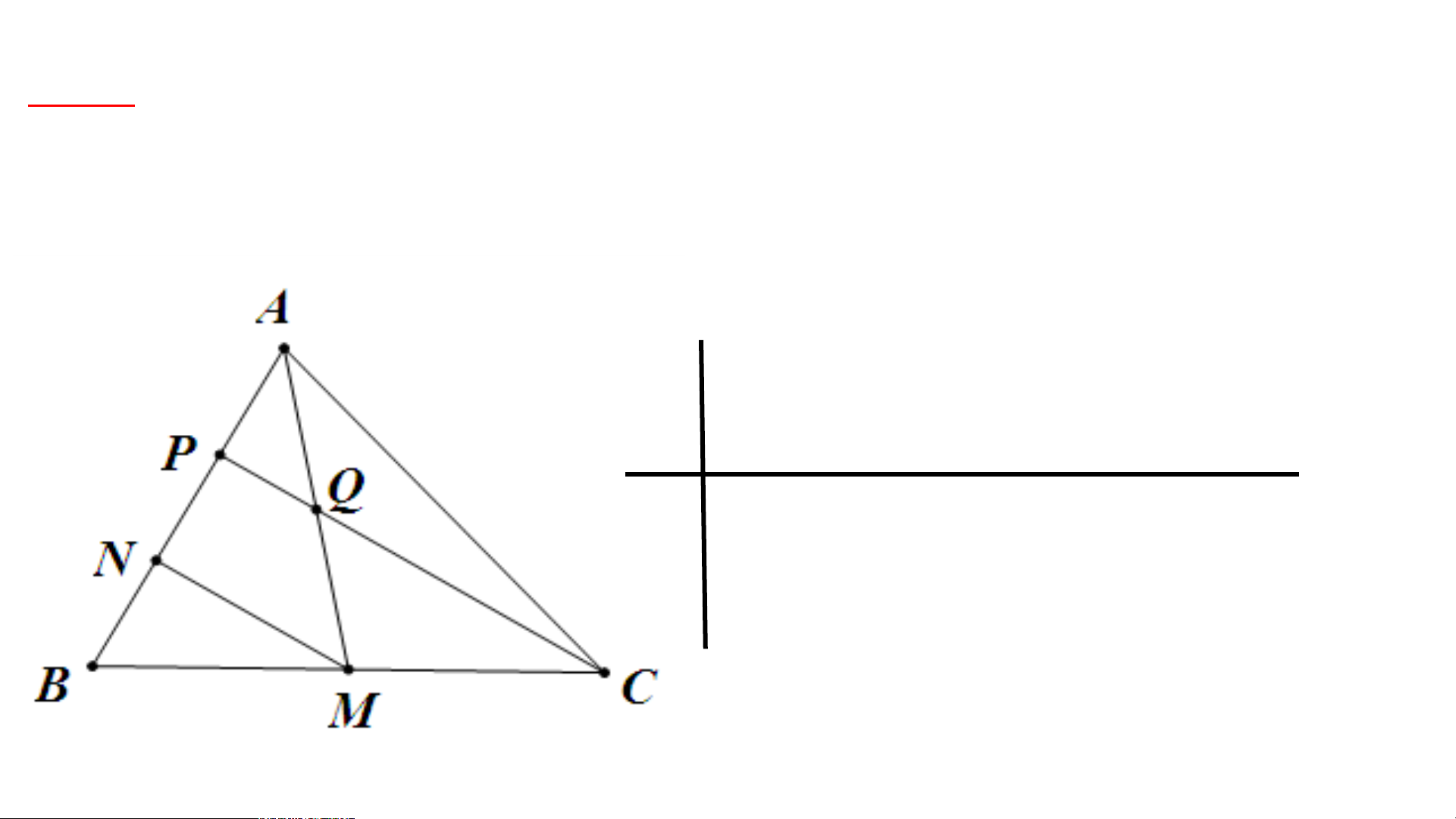
Bài 2: Cho có là đường trung tuyến, các điểm , phân biệt thuộc
cạnh sao cho . Gọi là giao điểm của và . Chứng minh: a) MN//CP b) c)
, là đường trung tuyến, GT KL a) MN//CP , b) c)
Bài 2. Cho có là đường trung tuyến, các điểm , phân biệt thuộc
cạnh sao cho . Gọi là giao điểm của và . Chứng minh: a) MN//CP b) c) Chứng minh a) Nối với có (gt);
( do là đường trung tuyến)
là đường trung bình của tam giác b) có (gt); (cmt)
Bài 2: Cho có là đường trung tuyến, các điểm , phân biệt thuộc
cạnh sao cho . Gọi là giao điểm của và . Chứng minh: a) MN//CP b) c) Chứng minh c) có (gt); (cmt)
là đường trung bình của tam giác Có (cmt) ; (cmt) hay
Bài 3:Bài toán thực tế
Giữa hai điểm B và C bị ngăn cách bởi hồ nước (như hình dưới).
Hãy xác định độ dài BC mà không cần phải bơi qua hồ.
Biết rằng đoạn thẳng KI dài 250 m và K là trung điểm
của AB, I là trung điểm của AC.
Bài 4: Cho tứ giác có lần lượt là trung điểm của các cạnh
. Chứng minh tứ giác là hình bình hành. Chứng minh: Nối B với D có (gt); (gt)
là đường trung bình của và có (gt); (gt)
là đường trung bình của và Tứ giác có: (cùng ) là hình bình hành. Học và ghi nhớ định
HƯỚNG DẪN VỀ NHÀ nghĩa, tính chất, chú ý
1 đường trung bình của tam giác. DẶN DÒ 2 Thực hiện các bài tập về nhà NHIỆM VỤ VỀ NHÀ
Bài 1. Cho , điểm thuộc cạnh sao cho .
Gọi là trung điểm của , là giao điểm của và . Chứng minh rằng .
Bài 2. Cho nhọn có là trực tâm. Gọi
lần lượt là trung điểm của đoạn thẳng .
Chứng minh tứ giác là hình chữ nhật. BÀI TẬP ÁP DỤNG
Bài 1 Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi
xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài
mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em
hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu
(xem hình vẽ minh họa) ? D P D E Q C P E Q C
Bài 2:Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã
làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như
hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người
thợ đã làm thanh ngang đó dài bao nhiêu cm ? A M N C B
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31




