CHÀO MỪNG CÁC EM
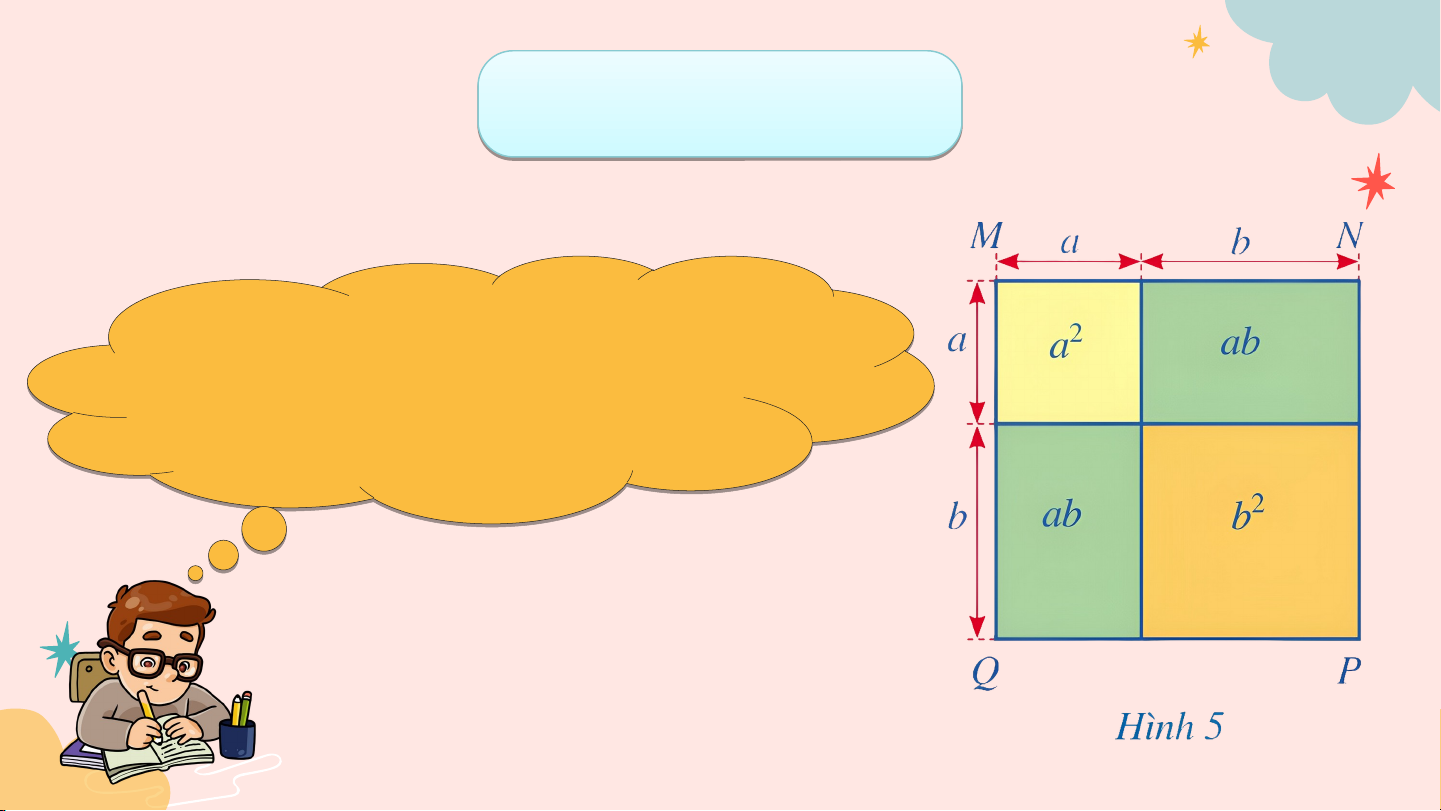
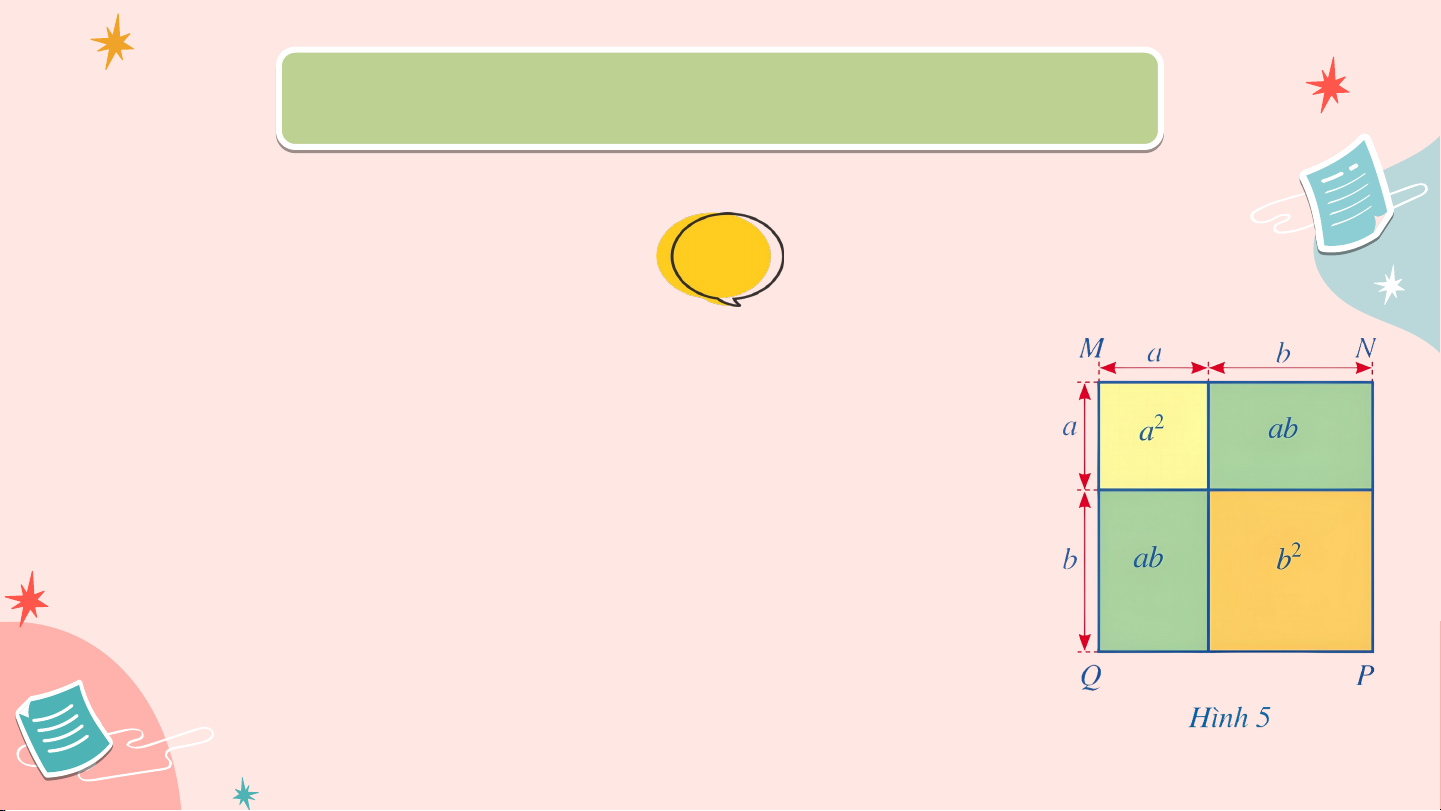
ĐẾN VỚI BÀI GIẢNG HÔM NAY KHỞI ĐỘNG Di D ện títc í h của h hì của nh hì v nh uông uô MN M P N Q Q (H ( ì H nh ì 5) 5) c ó ó thể t t hể ítnh nh theo t nhữ heo ng nhữ c ng ách nào? ách BÀI 3:
HẰNG ĐẲNG THỨC ĐÁNG NHỚ NỘI DUNG BÀI HỌC I. Hằng đẳng thức II. II
Hằng đẳng thức đáng nhớ I. HẰNG ĐẲNG THỨC
Thảo luận nhóm đôi, hoàn thành HĐ1.
HĐ 1. Xét hai biểu thức: và
Tìm giá trị của mỗi biểu thức và rồi so sánh hai giá trị đó
trong mỗi trường hợp sau: a) Tại b) Tại ;
Thảo luận nhóm đôi, hoàn thành HĐ1. HĐ 1. Giải
a) Thay vào biểu thức và , ta được: +) ; +) Vậy tại thì .
Thảo luận nhóm đôi, hoàn thành HĐ1. HĐ 1. Giải
b) Thay vào biểu thức và , ta được: +) ; +) . Vậy tại thì . NHẬN XÉT
Trong mỗi trường hợp trên, giá trị của biểu thức luôn bằng giá trị của biểu thức KẾT LUẬN
Nếu hai biểu thức P và Q nhận giá trị như nhau với mọi giá trị của biến
thì ta nói P = Q là một đồng nhất thức hay một hằng đẳng thức Ví dụ 1 ụ Chứng minh rằng: Giải Ta có: Vậy Luy u ệ y n t n ập ậ p 1 Chứng minh rằng: Giải Ta có: (đpcm) II.
HẰNG ĐẲNG THỨC ĐÁNG NHỚ 1. 1 Bìn B h p h hư h ơn ơ g n g củ c a m a ột ộ t tổ t n ổ g, m g ột ộ hiệ h u
Thảo luận nhóm bốn, hoàn thành HĐ2. HĐ 2.
a) Giải bài toán nêu trong phần mở đầu b) So sánh và c) So sánh và 1. 1 Bìn B h p h hư h ơn ơ g n g củ c a m a ột ộ t tổ t n ổ g, m g ột ộ hiệ h u HĐ 2. Giải Cách 1: Cách 2: 1. 1 Bìn B h p h hư h ơn ơ g n g củ c a m a ột ộ t tổ t n ổ g, m g ột ộ hiệ h u HĐ 2. Giải b) c) (𝑎+𝑏)2
𝑎2+2𝑎𝑏+𝑏2 (𝑎− 𝑏)2
𝑎2−2𝑎𝑏+𝑏2
Với hai biểu thức , tùy ý, ta có: ; Ví dụ í d 2 Tính: a) ; b) ; c) Giải a) b) c) V í d ụ ụ 1B
4 ác Ngọc dự định gấp một khối lập phương có cạnh là 5
cm. Sau khi xem xét lại, bác Ngọc quyết định tăng độ dài cạnh của
khối lập phương thêm (cm). Viết đa thức biểu thị phần thể tích
tăng thêm của khối lập phương mới so với khối lập phương dự định gấp ban đầu theo Giải
Vậy đa thức biểu thị phần thể tích tăng thêm của khối lập
phương mới do với khối lập phương dự định gấp ban đầu là: () LUYỆN TẬP TƯỚI HOA TRONG CHẬU TRÒ CHƠI Câu hỏi 1: Khai triển ta được A. A C. B. D. Bà B i à tập tậ 3: 3: SGK K – – tr. tr 23
Viết mỗi biểu thức sau dưới dạng tích: Giải a) ; Giả b) ; e) c) ; d) ; e) ; f) Bà B i à tập tậ 3: 3: SGK K – – tr. tr 23
Viết mỗi biểu thức sau dưới dạng tích: Giải a) ; Giả b) ; g) c) ; d) ; e) ; f) VẬN DỤNG Bà B i à tập t 4: 4 SGK SG – – tr t . r 23 2
Tính giá trị của mỗi biểu thức: a) tại b) tại Giả i i a) Ta có: . Tại ta có: . Vậy tại . Bà B i à tập t 4: 4 SGK SG – – tr t . r 23 2
Tính giá trị của mỗi biểu thức: a) tại b) tại Giả i i b) Ta có:
Thay vào biểu thức B, ta được: . . Vậy tại . CẢM ƠN CÁC EM
ĐÃ LẮNG NGHE BÀI GIẢNG
Document Outline

• Slide 1
• Slide 2
• BÀI 3: HẰNG ĐẲNG THỨC ĐÁNG NHỚ
• II.
• I.
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• II.
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• LUYỆN TẬP
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• VẬN DỤNG
• Slide 26
• Slide 27
• Slide 28