










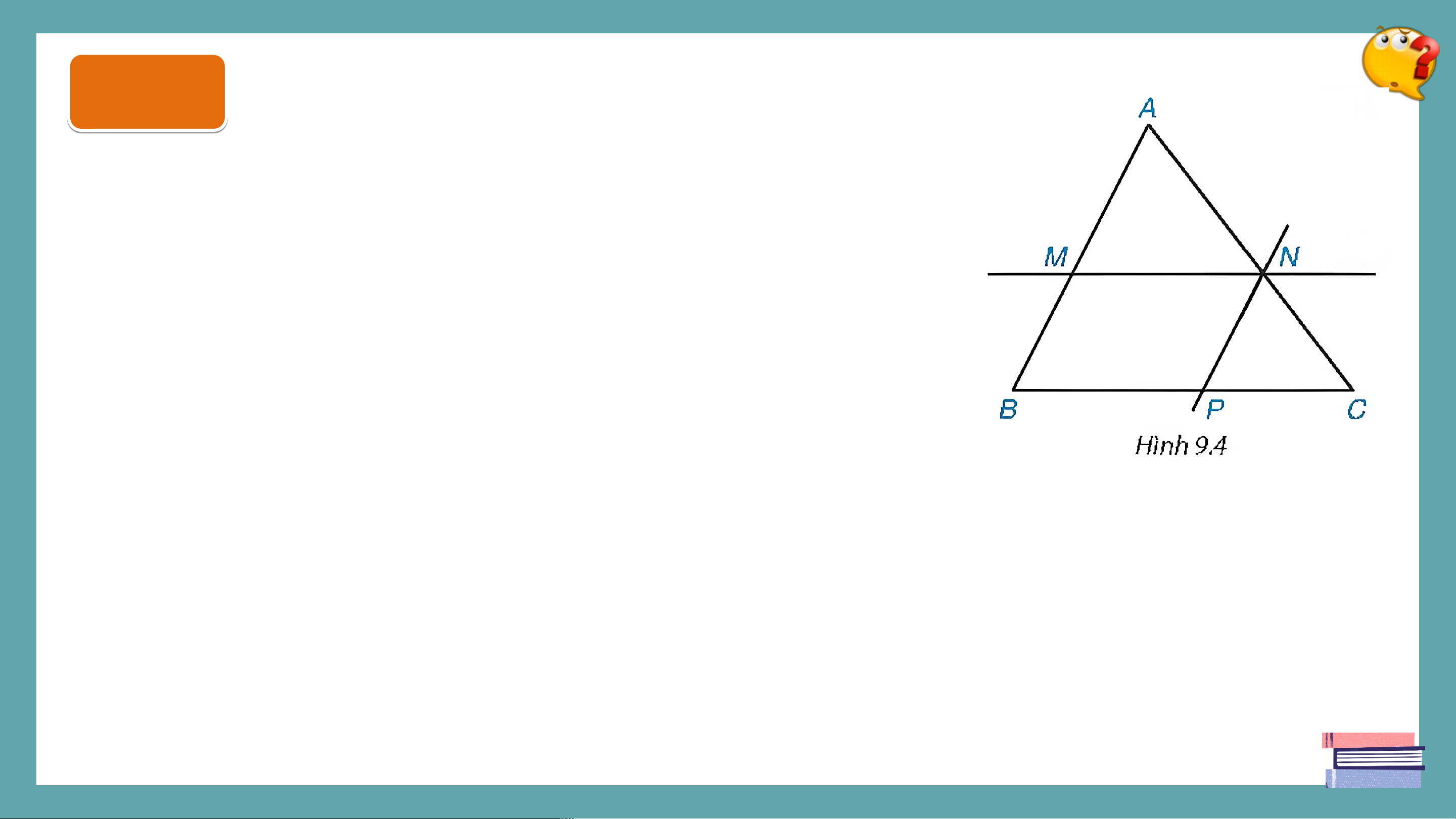












Preview text:
NHIỆT LIỆT CHÀO MỪNG
CÁC EM ĐẾN VỚI BÀI HỌC MỚI! KHỞI ĐỘNG
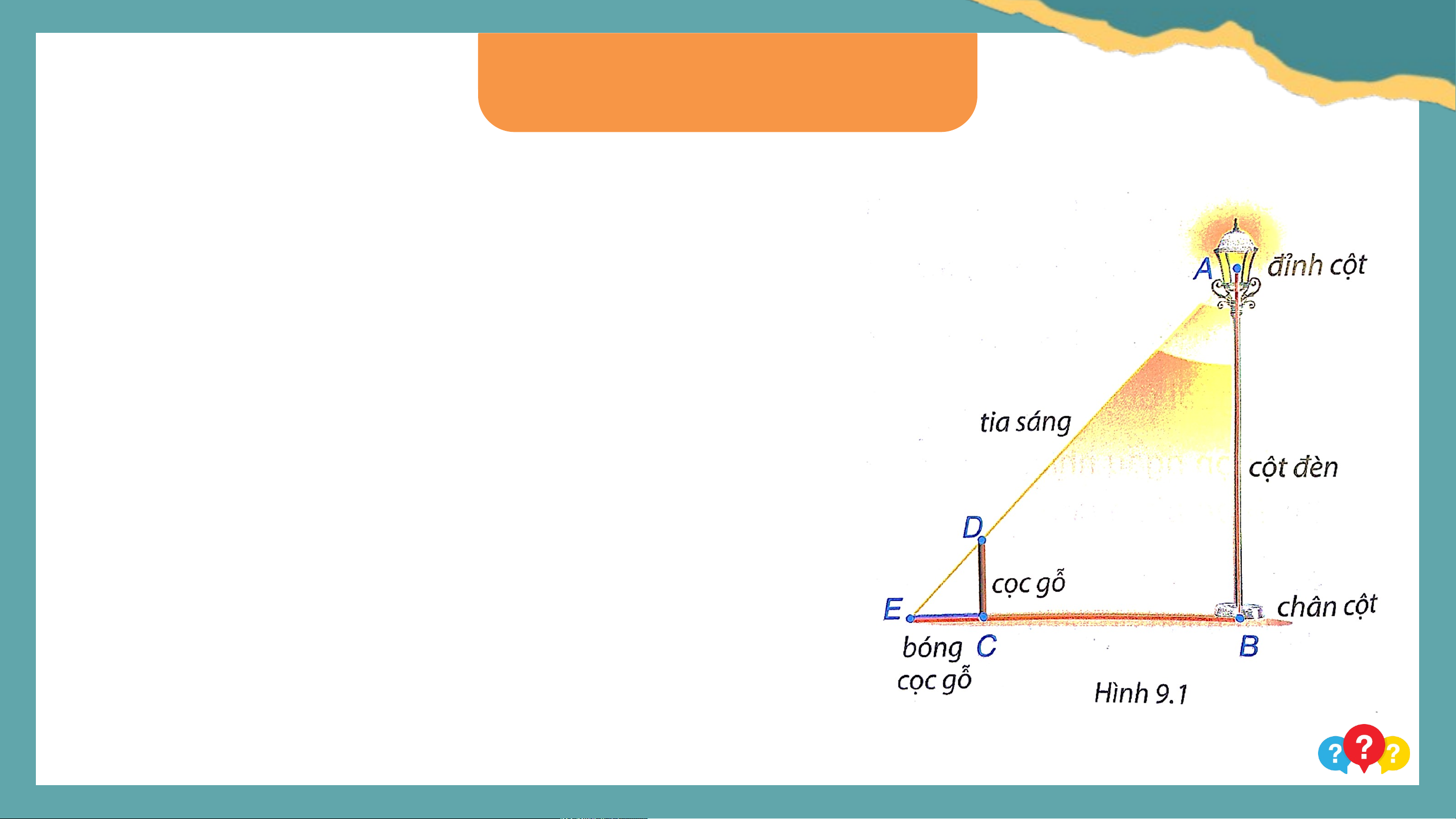
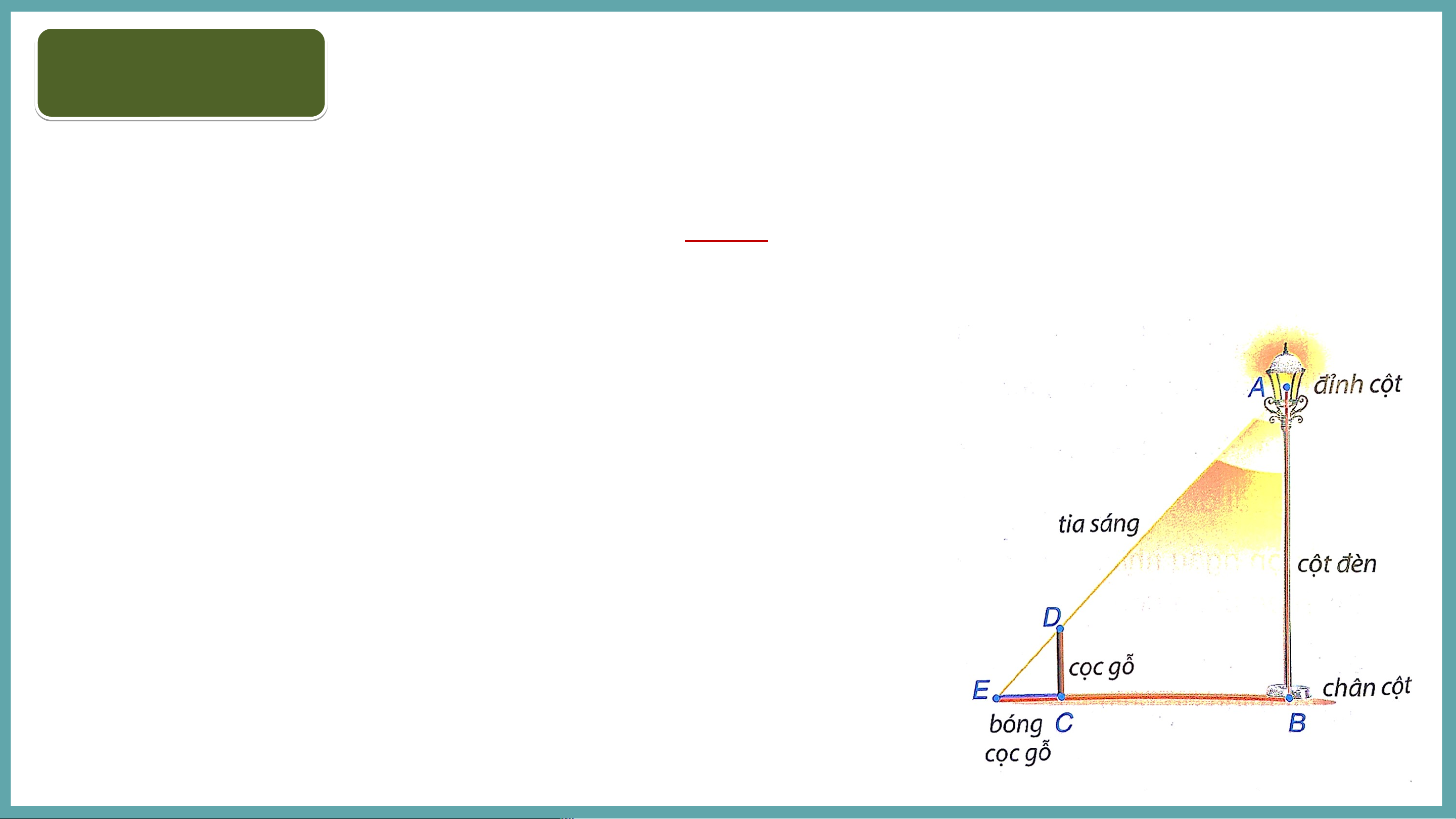
Có một chiếc bóng điện được mắc trên đỉnh
(điểm ) của cột đèn thẳng đứng. Để tính
chiều cao của cột đèn, bác Dương cắm một
chiếc cọc gỗ (đoạn ) thẳng đứng trên mặt đất
rồi đo chiều dài bóng của cọc gỗ do ánh đèn
điện tạo ra và đo khoảng cách từ điểm đến
chân cột đèn (điểm ). Theo em, bác Dương
đã tính như thế nào để ra được chiều cao cột đèn?
CHƯƠNG IX. TAM GIÁC ĐỒNG DẠNG BÀI 33. HAI TAM GIÁC ĐỒNG DẠNG 01 ĐỊNH NGHĨA NỘI DUNG BÀI HỌC 02 ĐỊNH LÍ ĐỊ Đ NH N H NGHĨA N I H Đ H 1
Đ Trong hình 9.2, và
là hai tam giác có các cạnh tương ứng
song song và các góc tương ứng bằng nhau, tức là và
Nhìn hình vẽ, hãy cho biết giá trị các tỉ số
sau 𝐴𝐵 𝐵𝐶 𝐴𝐶 ; ; .
𝐷𝐸 𝐸 𝐹 𝐷𝐹 Giải
Qua sát hình ảnh ta thấy: KHÁI NIỆM
Tam giác gọi là đồng dạng với tam giác nếu:
Tam giác đồng dạng với tam giác được kí hiệu (viết theo thứ tự cặp đỉnh tương ứng).
Tỉ số được gọi là tỉ số đồng dạng của với . Nhận xét:
Nếu với tỉ số đồng dạng thì với tỉ số đồng dạng . Do vậy khi thì ta nói
hai tam giác và đồng dạng với nhau.
Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng .
Đặc biệt, mọi tam giác đồng dạng với chính nó.
Nếu với tỉ số đồng dạng và với tỉ số đồng dạng thì với tỉ số đồng dạng . Ví
V dụ 1 Cho và là hai tam giác đều có
Chứng minh rằng và tìm tỉ số đồng dạng. Giải Ta có và .
Do vậy hai tam giác và có:
Vậy với tỉ số đồng dạng 3 . 4 Luyện yệ tập 1
Trong các tam giác được vẽ trên ô lưới vuông, có một cặp tam giác đồng dạng. Hãy chỉ
ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng. Giải:
Ta thấy với tỉ số đồng dạng .
Hoặc: với tỉ số đồng dạng . THỬ T HỬ HÁCH NHỎ HÁC Cho . Chứng minh rằng:
a) Nếu tam giác cân tại thì tam giác cân tại đỉnh
b) Nếu tam giác đều thì tam giác đều; c) Nếu thì Giải a) Vì và Nếu cân tại cân tại Giải b) đều.
c) Giả sử với hệ số đồng dạng . Suy ra: ĐỊ Đ NH N H LÍ II HĐ H 2 Đ
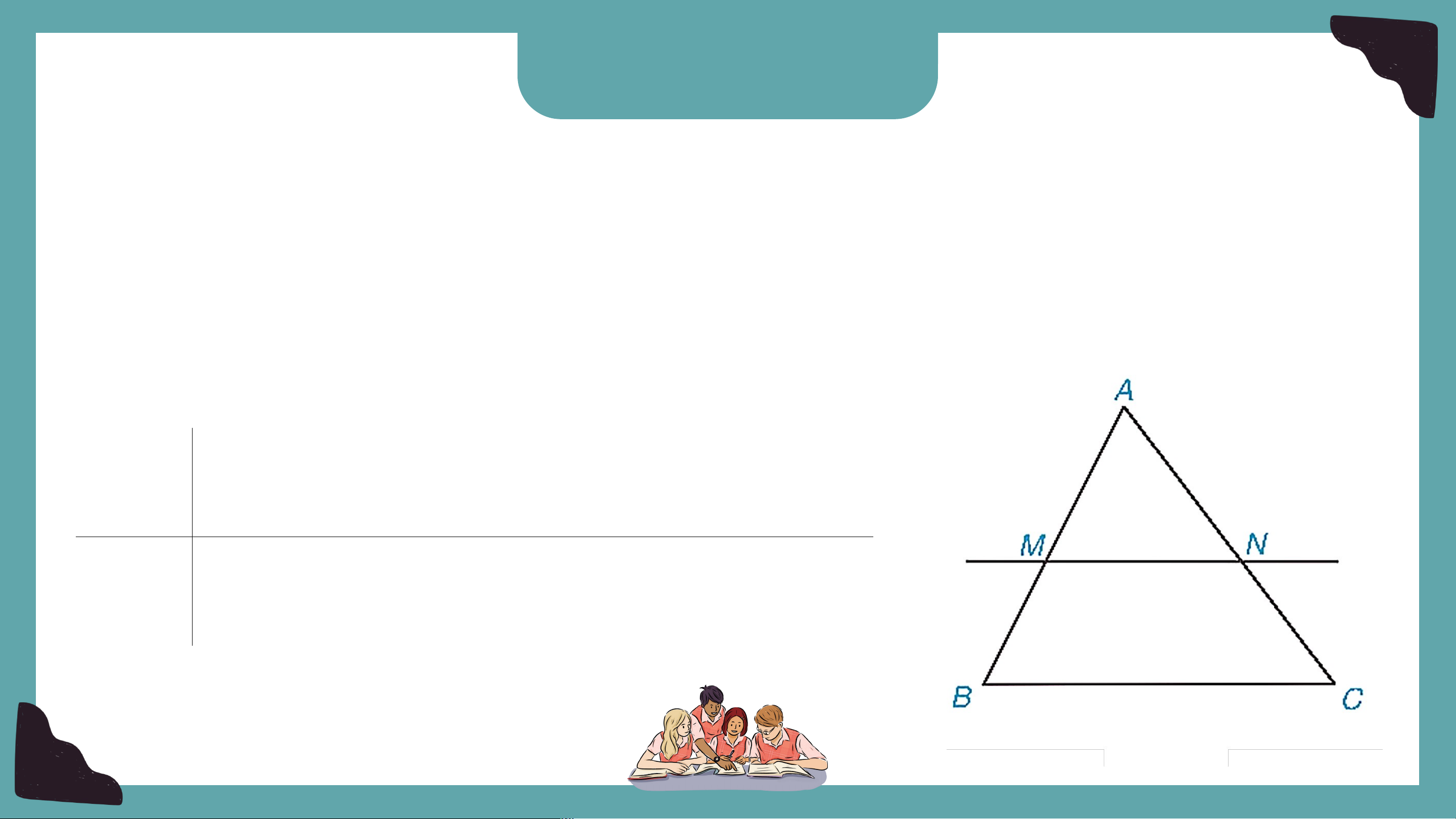
Cho tam giác và các điểm lần lượt nằm trên các
cạnh sao cho song song với như Hình 9.4.
- Hãy viết các cặp góc bằng nhau của hai tam giác
và giải thích vì sao chúng bằng nhau.
- Kẻ đường thẳng đi qua song song với và cắt tại . Hãy chứng tỏ và suy ra
- Tam giác và tam giác có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng. Giải Vì (giả thiết) Xét và có: chung, tức là: (1) ; (đồng vị) (2) Ta có ; (giả thiết) là hình bình hành . Từ (1)(2)(3) suy ra . ĐỊNH LÍ
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với
cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho. GT () KL Chú ý:
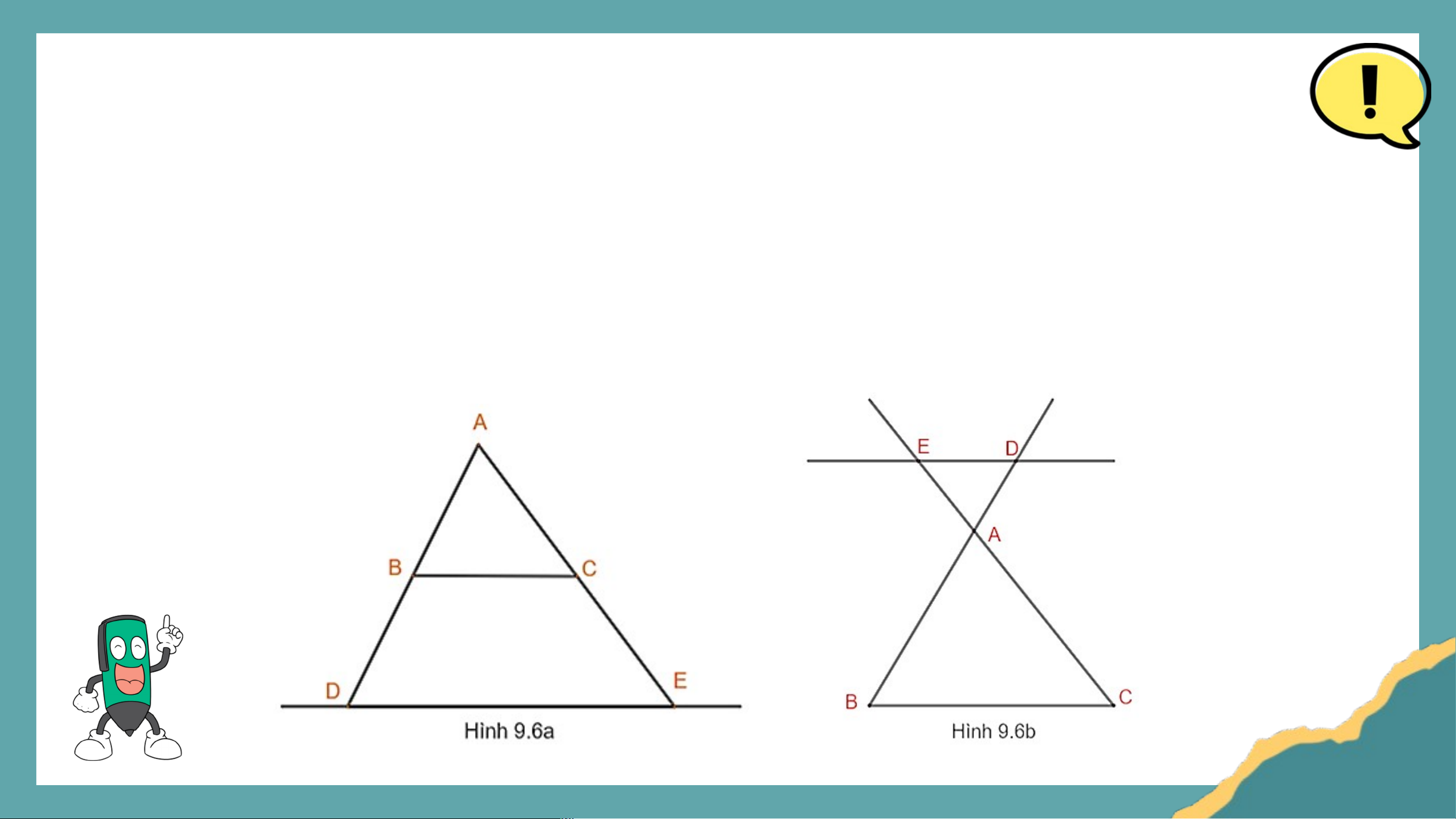
Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo
dài của hai cạnh tam giác. Chẳng hạn, trong Hình 9.6 có . Khi đó, . Ví dụ dụ 2
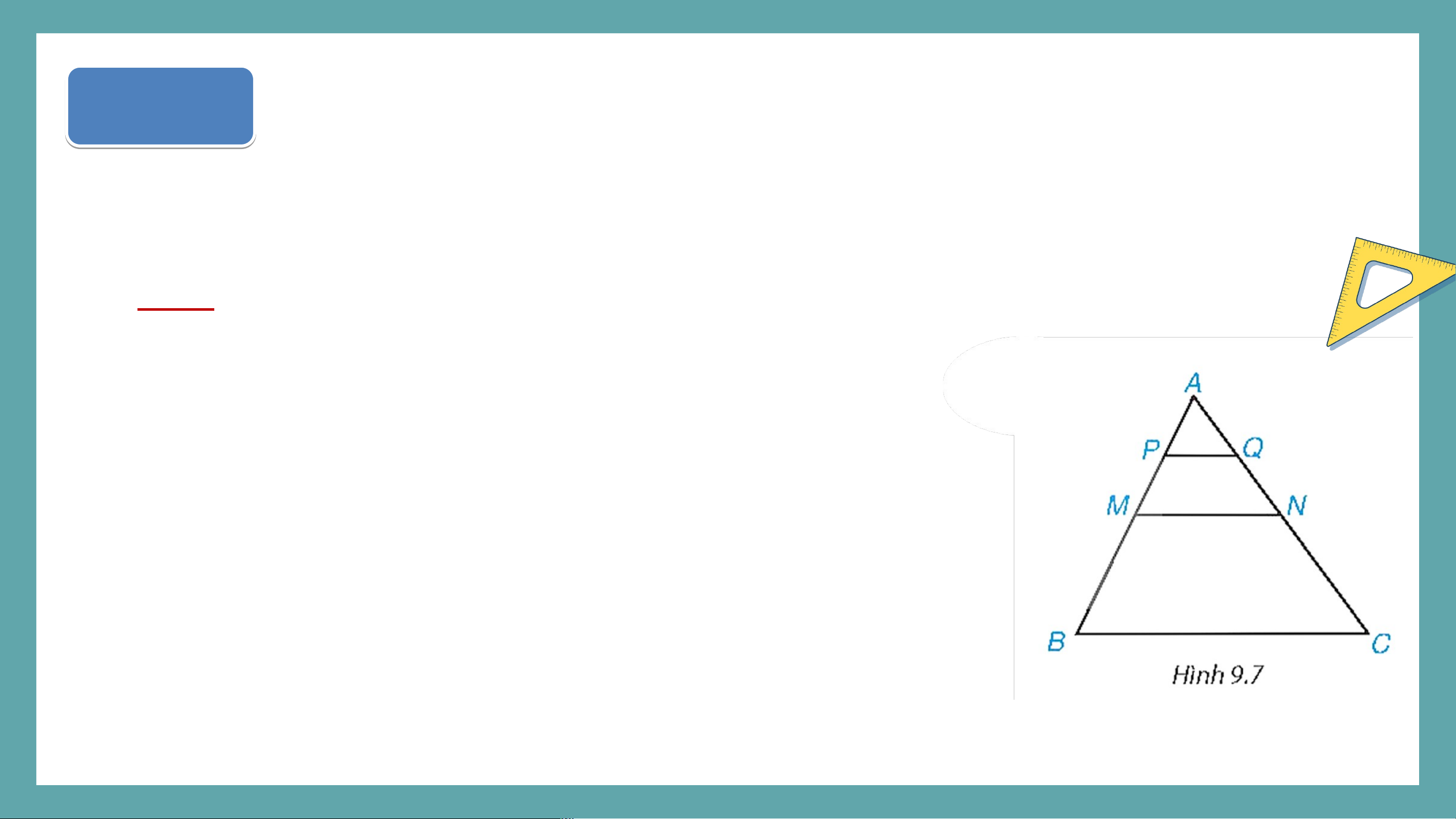
Cho Hình 9.7, trong đó lần lượt là trung điểm của
lần lượt là trung điểm của . Hãy liệt kê tất cả các cặp tam giác (phân biệt) đồng dạng. Giải
Tam giác có lần lượt là trung điểm của nên là đường trung bình của tam giác . Suy ra . (1)
Do đó (theo định lí trên).
Tương tự, là đường trung bình của tam giác nên . (2) Ví dụ dụ 2
Cho Hình 9.7, trong đó lần lượt là trung điểm của
lần lượt là trung điểm của . Hãy liệt kê tất cả các cặp tam giác (phân biệt) đồng dạng. Giải
Do đó (theo định lí trên). Từ (1) và (2), suy ra .
Do đó (theo định lí trên).
Vậy có tất cả ba cặp tam giác đồng dạng là: Luy L ệ uy n ệ n tậ t p 2 ậ
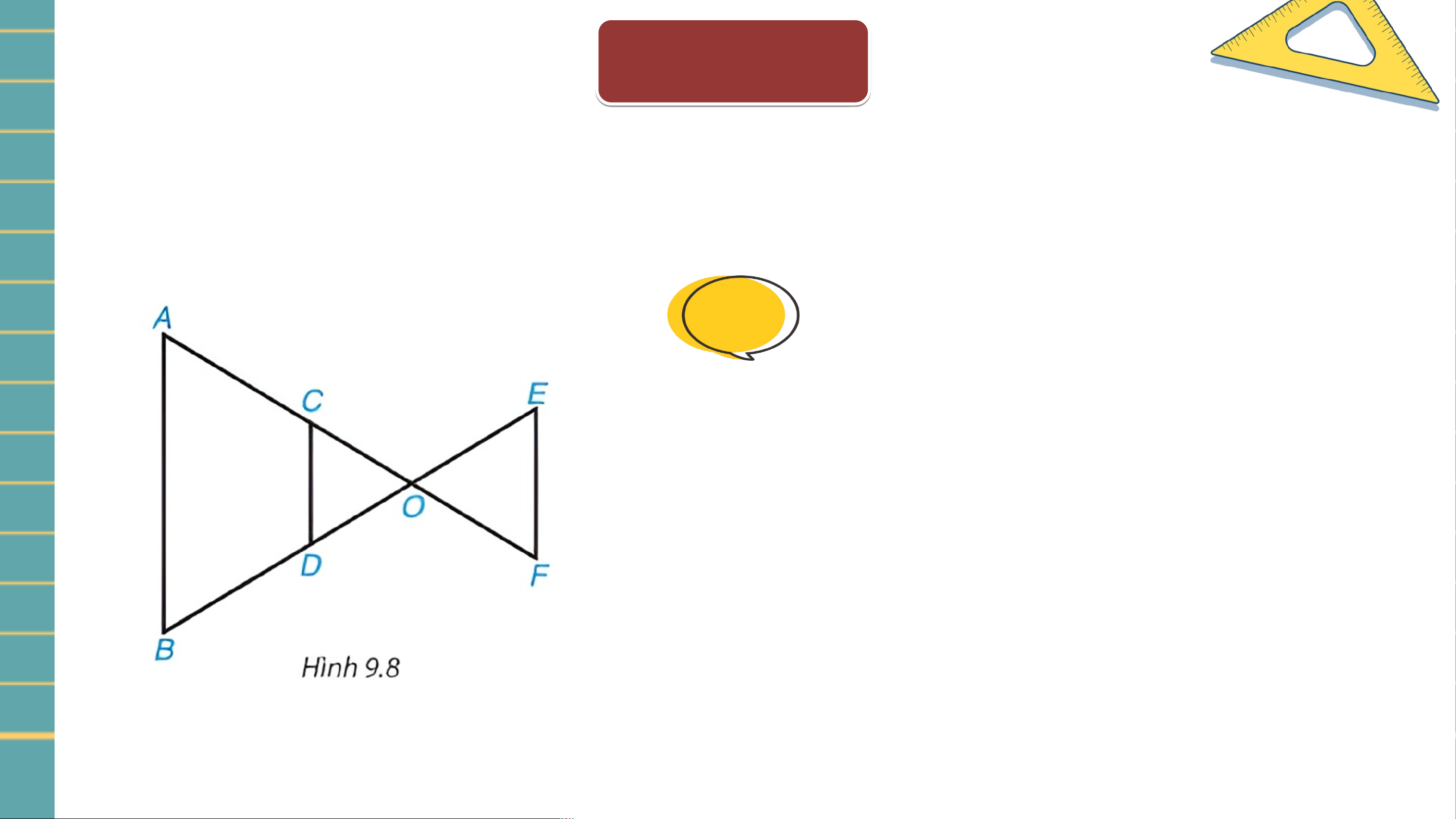
Trong hình 9.8, các đường thẳng song song với nhau. Hãy liệt kê ba cặp tam
giác (phân biệt) đồng dạng. Giải • Vì và nên • Vì và nên • Vì và nên VẬN Ậ D N Ụ D N Ụ G N
Trở lại tình huống mở đầu, hãy giải thích bác Dương đã tính được
chiều cao cột đèn như thế nào, biết cọc gỗ cao và Giải: Vì (cùng vuông góc với ) Theo định lí trên thì
Như vậy, chỉ cần đo chiều dài bóng cọc gỗ (đọan ),
khoảng cách thì với chiều cao đã biết, bác Dương tính được chiều cao . Theo công thức trên, m. LUYỆN LU TẬ YỆN P TẬ
CÂU HỎI TRẮC NGHIỆM
Câu 1. Hãy chọn câu sai
A. Hai tam giác bằng nhau thì đồng dạng
B. Hai tam giác đều luôn đồng dạng với nhau
C. Hai tam giác đồng dạng là hai tam giác có tất cả các cặp
góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ
D. Hai tam giác vuông luôn đồng dạng với nhau
Câu 2. Nếu tam giác ABC có MN//BC (với M ∈ AB,N ∈ AC) thì A. ΔAMN đồng dạng với C. ΔAMN đồng dạng với ΔACB ΔABC B. ΔABC đồng dạng với D. ΔABC đồng dạng với ∆MNA ΔANM Câu C âu 3. 3 Hã H y c ã họ y c n c họ â n c u â đún ú g n . A. A. Hai H t am gi am ác bằ b ng n nhau C. .Hai H t am gi g ác b ác ằn ằ g g nhau thì hì đồng dạng thì h không đồng dạng đồng B. B H ai ai tam t gi ác đồng ác d đồng ạn ạ g g D. .Hai H t am giác gi vuông l vuông uô u n n thì t bằng n bằng ha h u đồn ồ g g dạng vớ dạng i nhau
Câu 4. Cho tam giác ABC và hai điểm M,N lần lượt thuộc các cạnh
BC,AC sao cho MN//AB. Chọn kết luận đúng. A. ΔAMN đồng dạng với C. ΔNMC đồng dạng với ΔABC ΔABC B. ΔABC đồng dạng với D. ΔCAB đồng dạng với ∆MNC ΔCMN Câu 5 C . âu 5 Cho đồng Cho đ dạng ồng với ; dạng cm . S cm ố đo . S là ? ố đo A. C. B. D. Bài 9.1 (SGK – tr82)
Cho ΔABC ∽ ΔMNP, khẳng định nào sau đây không đúng? Giải a) ΔMNP ∽ ΔABC Từ giả thiết, ta có b) ΔBCA ∽ ΔNPM
Các cặp đỉnh tương ứng là: c) ΔCAB ∽ ΔPNM
tương ứng với ; tương ứng với ; tương ứng với . d) ΔACB ∽ ΔMNP
Bài 9.2 (SGK – tr82) Khẳng định nào sau đây là đúng?
a) Hai tam giác bằng nhau thì đồng dạng với nhau
b) Hai tam giác bất kì đồng dạng với nhau
c) Hai tam giác đều bất kì đồng dạng với nhau
d) Hai tam giác vuông bất kì đồng dạng với nhau
e) Hai tam giác đồng dạng thì bằng nhau VẬN VẬ DỤ N N DỤ G N
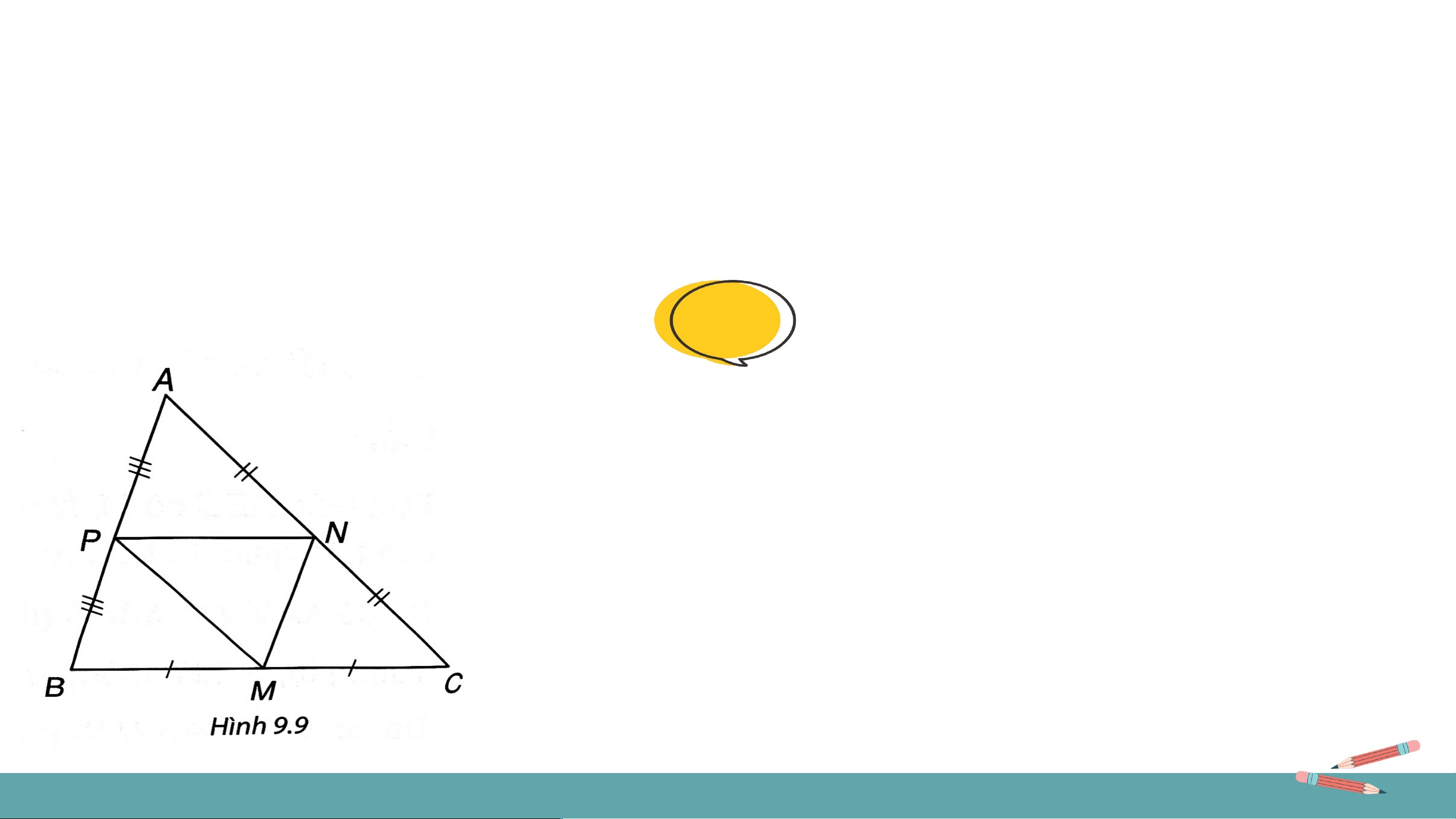
Bài 9.3 (SGK – tr82) Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt
là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà
chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng. Giải Xét và có: (so le trong) và chung (g.c.g) Tương tự ta có:
Bài 9.3 (SGK – tr82) Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt
là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà
chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng. Giải là đường trung bình
Vậy đôi một bằng nhau và cùng đồng dạng với
Cả 5 tam giác đôi một đồng dạng với nhau.
Bài 9.4 (SGK – tr82) Cho tam giác cân tại đỉnh và tam giác cân tại đỉnh . Biết rằng ,
. Chứng minh và tìm tỉ số đồng dạng. Giải: cân tại nên Tương tự cân tại Vì nên từ (1)(2) suy ra
Lấy lần lượt là trung điểm của thì ta có (đồng vị) Giải: Xét và có : (giả thiết); (cmt); (cmt) (g.c.g) Mà (vì )
Do đó với tỉ số đồng dạng
HƯỚNG DẪN VỀ NHÀ Chuẩn bị trước Ôn tập kiến thức Hoàn thành Bài 34. Ba trường đã học bài tập trong SBT
hợp đồng dạng của hai tam giác CẢM ƠN CÁC EM
ĐÃ THEO DÕI BÀI GIẢNG!
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37




