








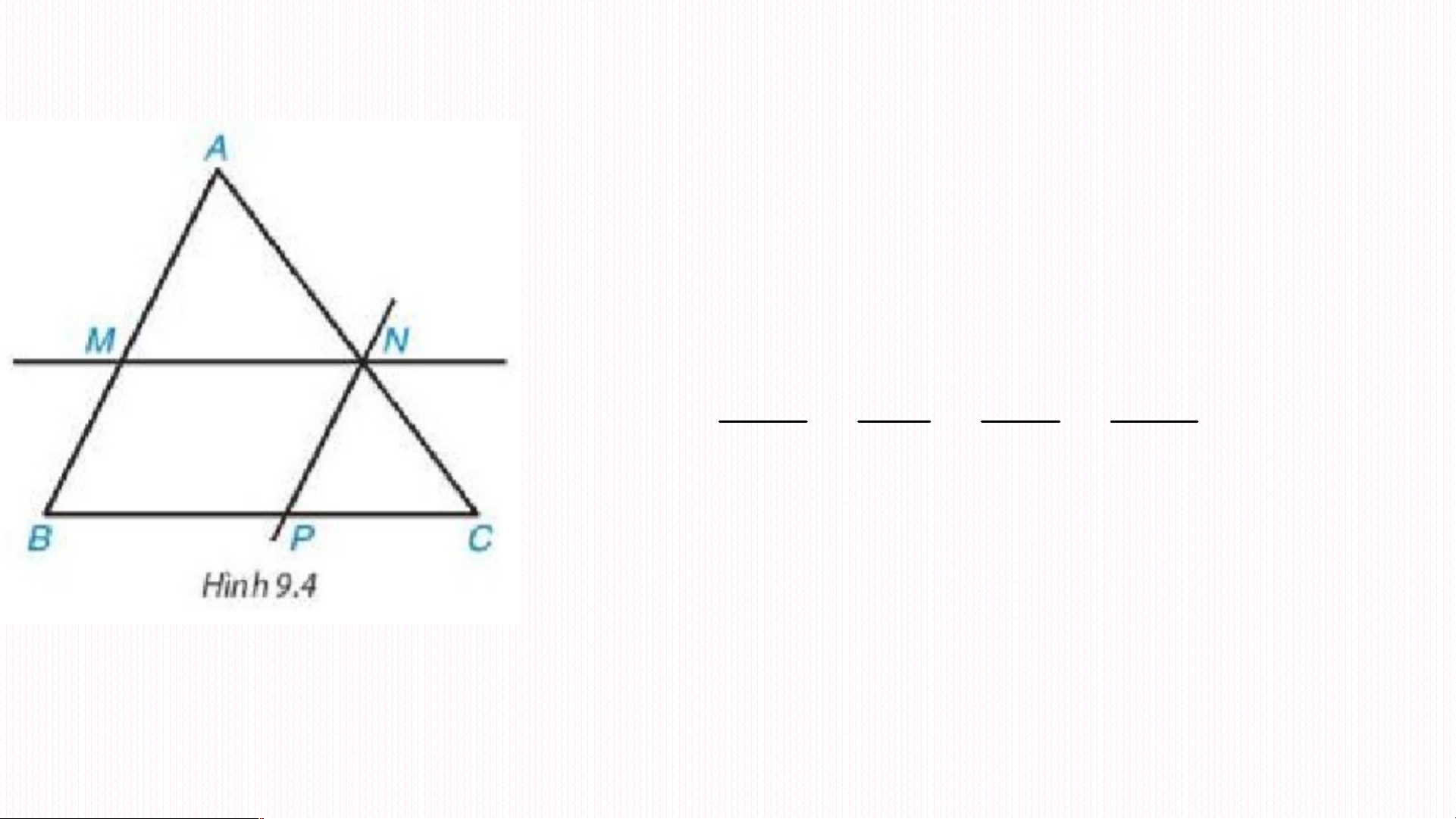
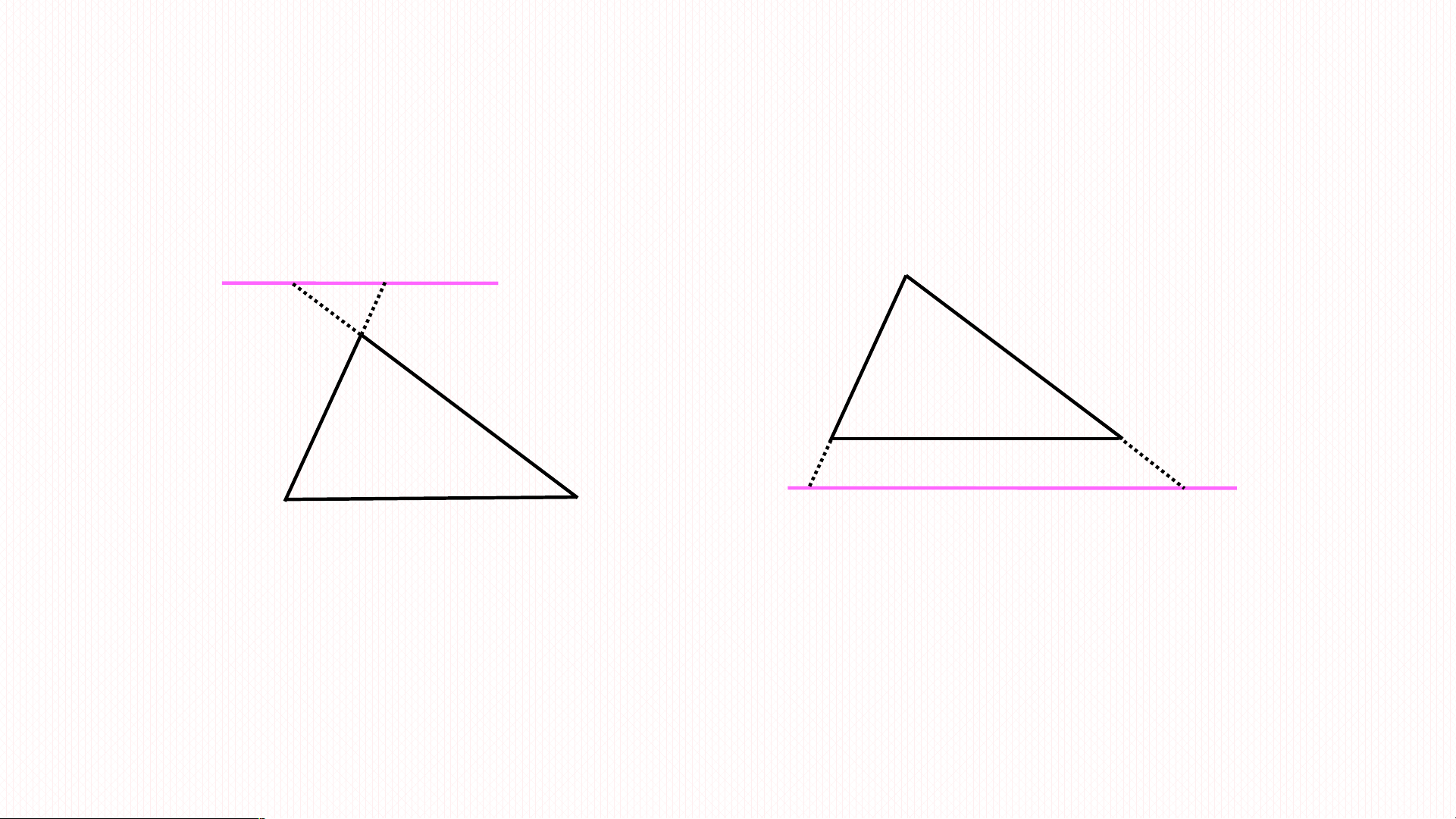



Preview text:
ỦY BAN NHÂN DÂN QUẬN LIÊN CHIỂU
TRƯỜNG THCS NGUYỄN LƯƠNG BẰNG
MỞ ĐẦU VỀ XÁC SUẤT CỦA BIẾN CỐ
BÀI 33: HAI TAM GIÁC ĐỒNG DẠNG Giáo viên : Hà Duy Ninh Thành phố : Đà Nẵng Sách
: Kết nối tri thức với cuộc sống
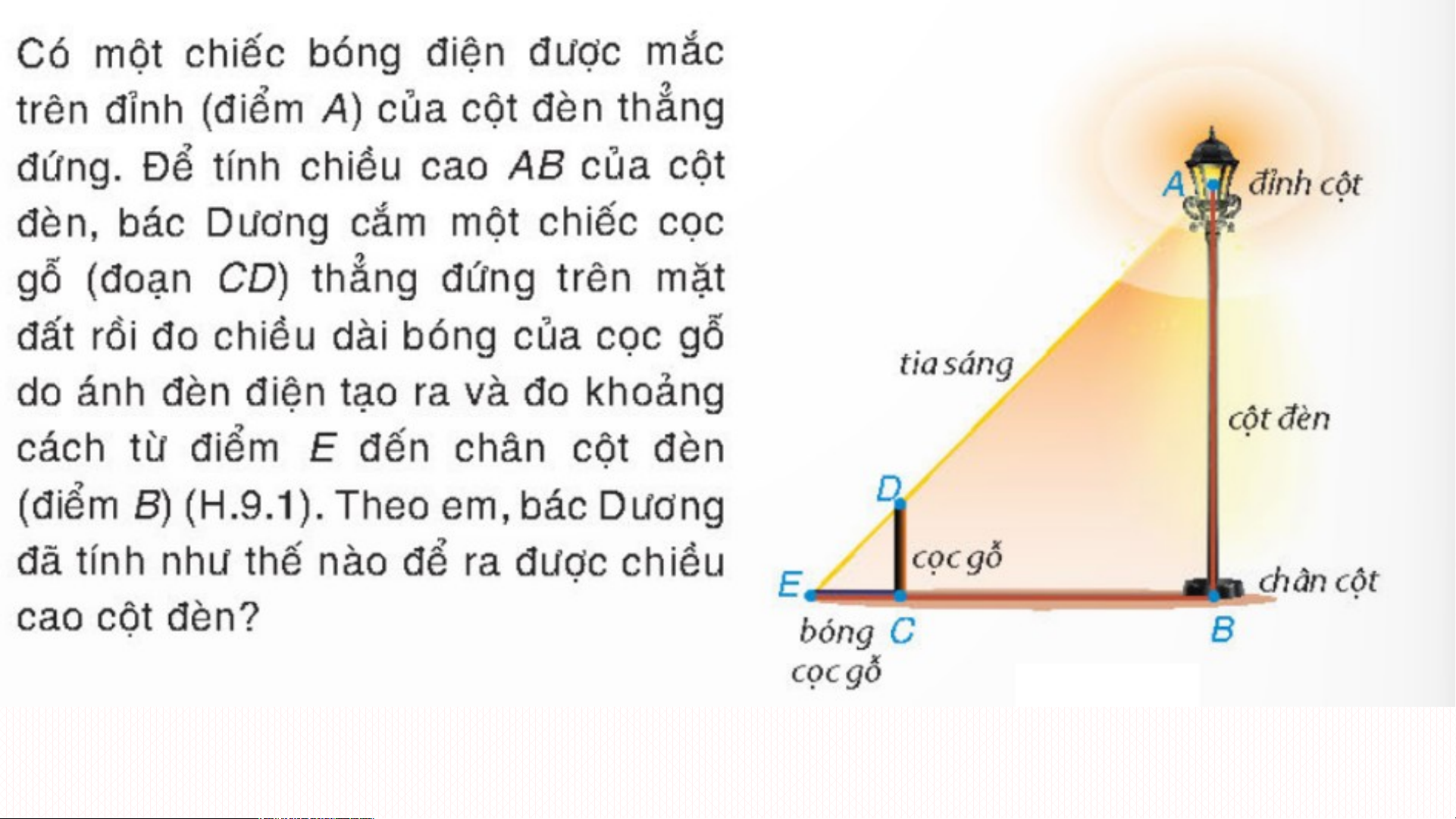
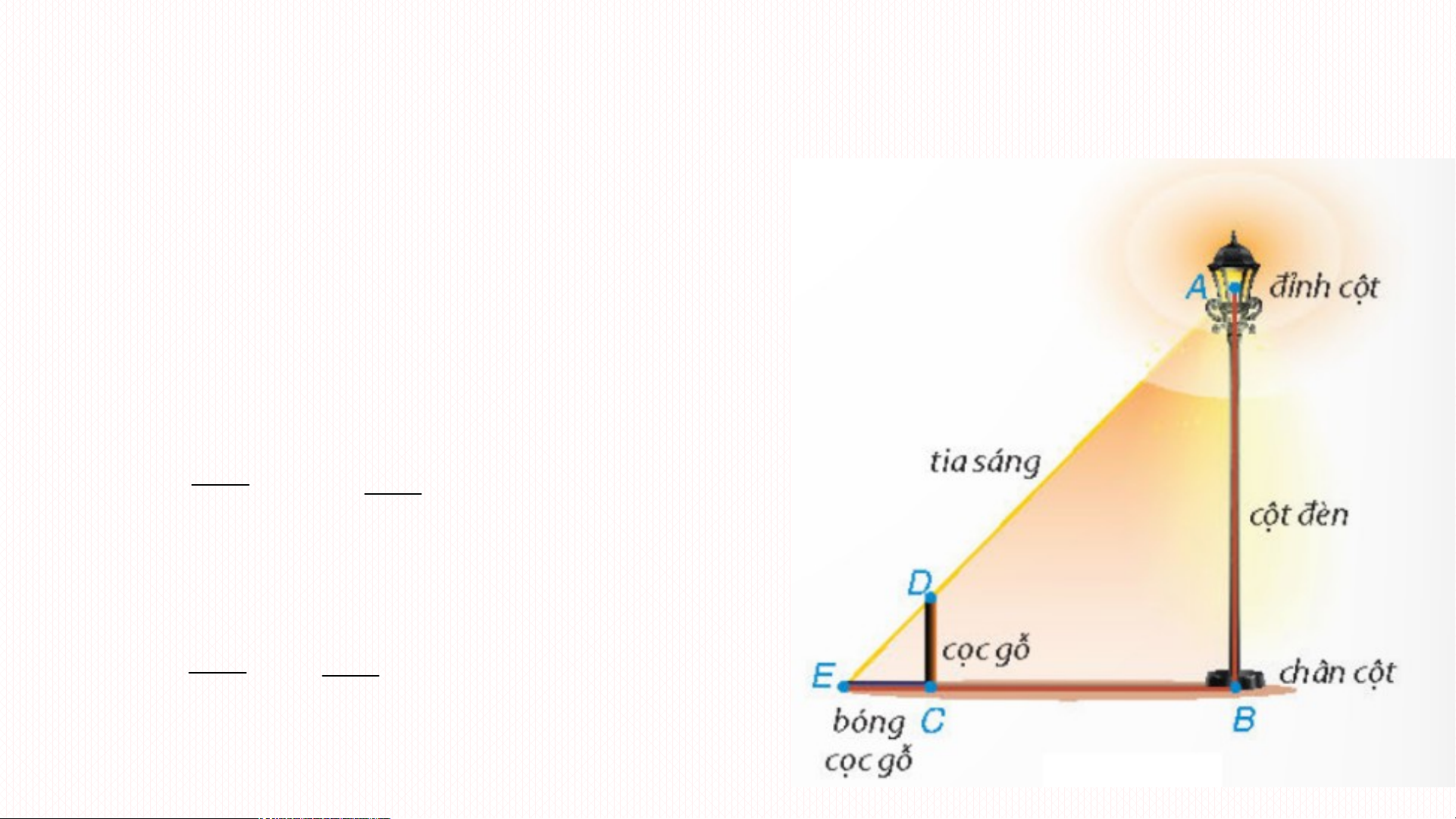
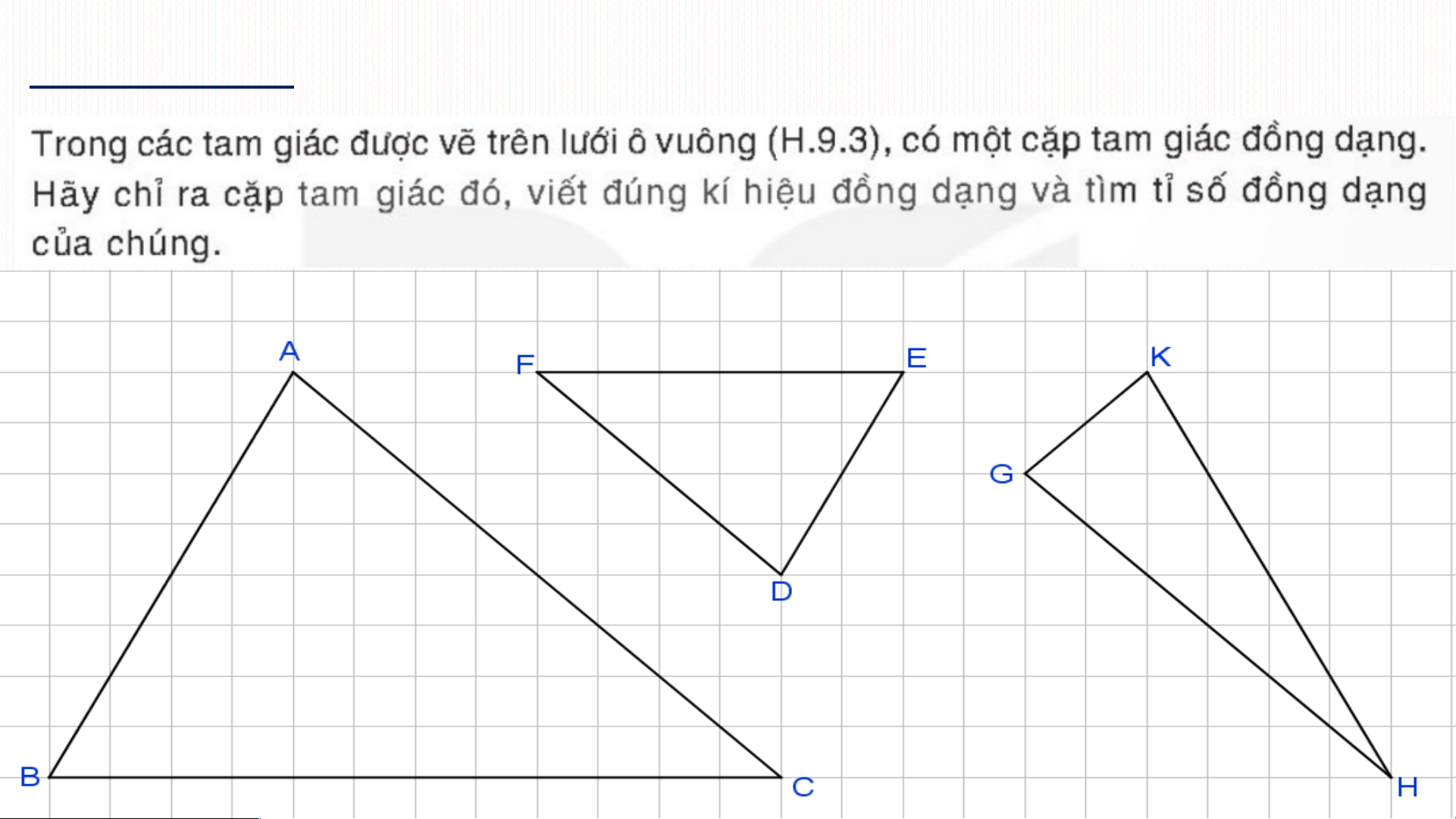
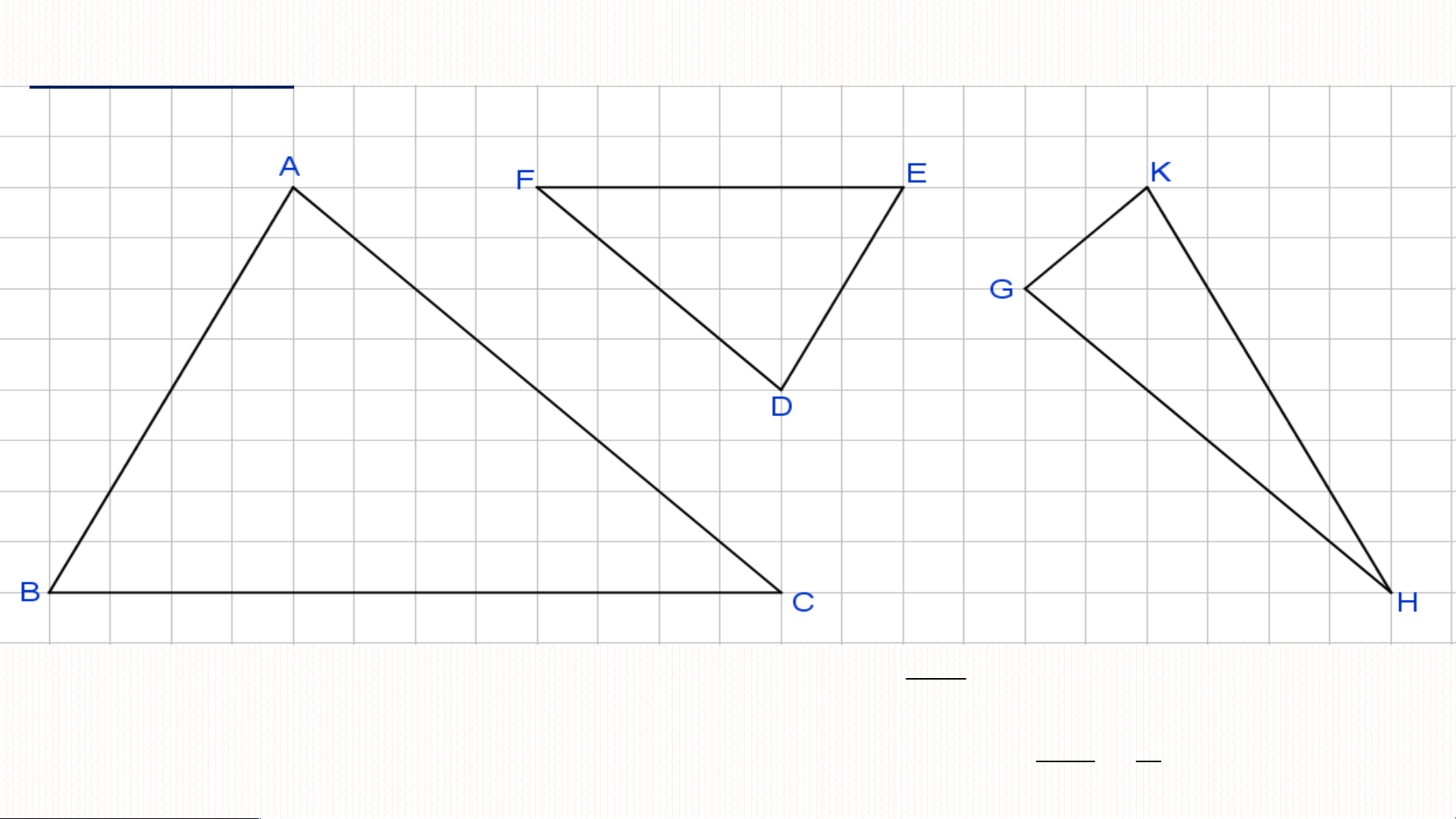
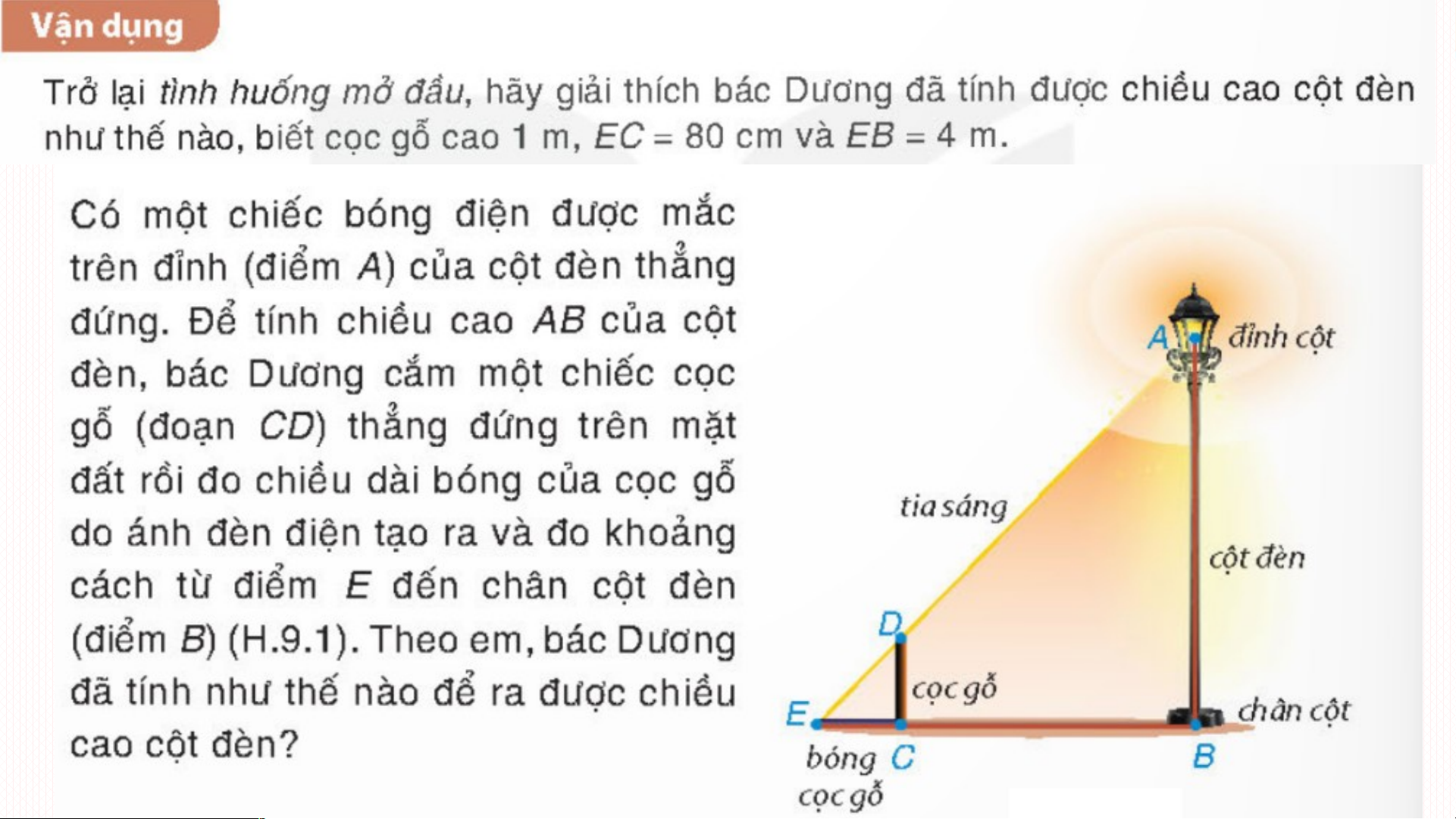
BÀI 33: HAI TAM GIÁC ĐỒNG DẠNG BÀI TOÁN MỞ ĐẦU
Như vậy để tính chiều cao cột đèn ta sNh ử ậ đ n ụ x ngé t v đ ị ịn trí h l h í ai Th cạ al n èsh D là C ch v ưà a AB đủ ?cần
tìm tỉ lệ giữa các cạnh của tam giác D DC EC //AB và AEB.
Dựa vào định lí Thalès nhận xét về
Khi đó hai tam giác DEC và AEB ED EC ha đ i ư tỉ ợc lệ gọi là và gì? EA EB
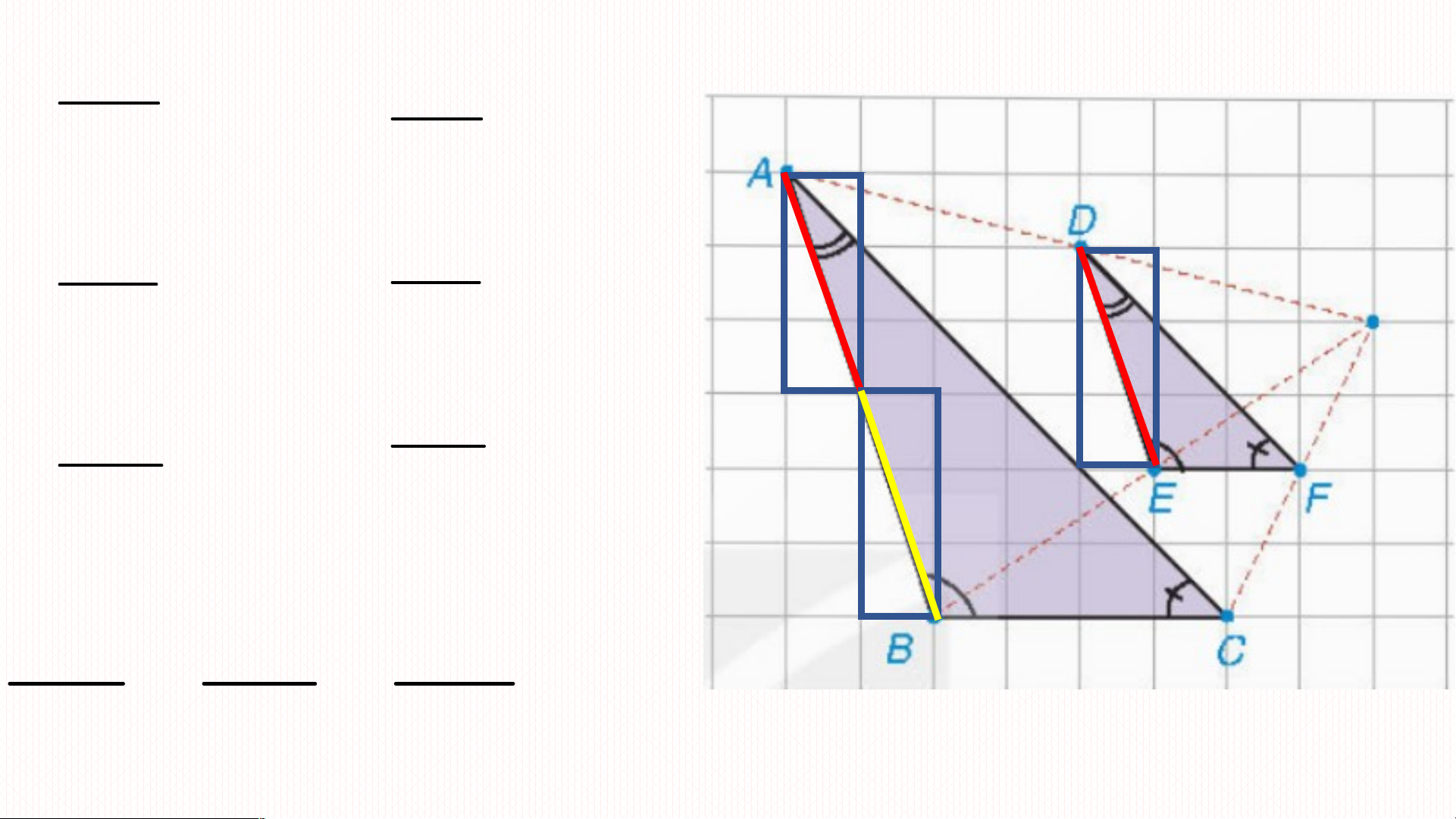
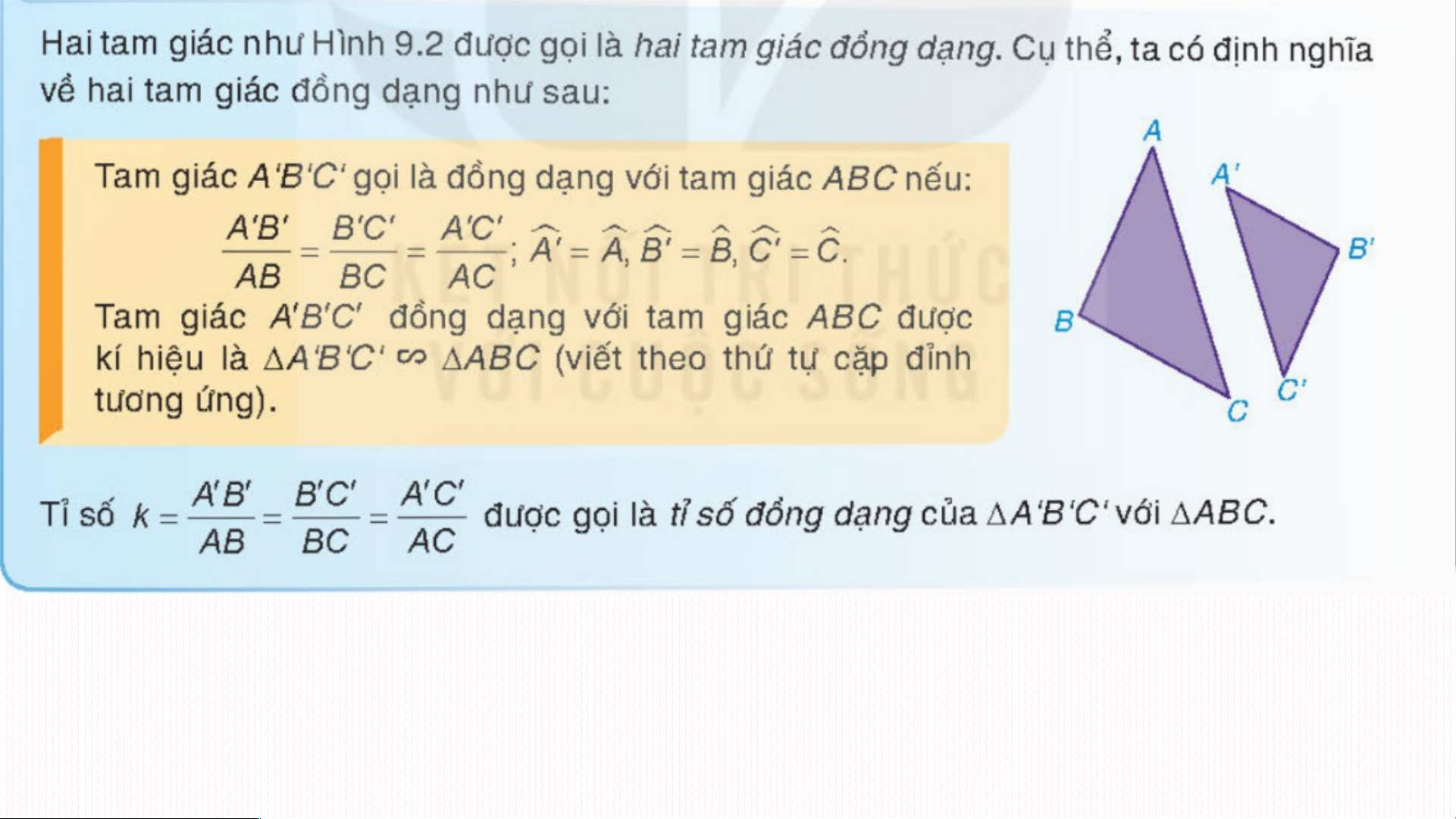
Vì DC//AB nên theo định lí Thalès ED EC = EA EB AB ? AB DE 2 DE BC BC ? 2 EF EF CA CA ? 2 FD FD AB BC CA 2 DE EF FD ∽∽∽∽ Ví dụ 1:
Cho ABC và A’B’C’ là hai tam giác đều có AB = 4cm; A’B’ = 3cm. Chứng minh rằng A’B’C’ ∽
ABC và tìm tỉ số đồng dạng. Giải:
Ta có BC = CA = AB = 4cm; B’C’ = C’A’ = A’B’ = 3cm. 0 0 A B C 6 0 ;A ' B ' C ' 60 A'B' B'C' C'A' 3 Do vậy A’B’C’ và ABC có = = = AB BC CA 4 và A A ';B B ';C C ' 3 Vậy A’B’C’ ∽
ABC và tỉ số đồng dạng là . 4 Luyện tập 1: Luyện tập 1: BC ABC
DEF với tỉ số đồng dạng bằng ∽ = 2 EF ( Hoặc DEF ∽
ABC với tỉ số đồng dạng bằng EF 1 ) BC 2 Thử thách nhỏ: a) N B C P suy ra MNP cân tại M. b) 0 0 0 M A 6 0 ; N B 6 0 ;P C 6 0 suy ra MNP đều. c) Giả sử ABC ∽
MNP với tỉ số đồng dạng bằng k >0. Suy ra AB AC BC MN= ;MP= ; NP= k k k
Mà AB AC BC nên MN MP NP HĐ 2: +) M B ; N C
(các cặp góc so le trong); A chung
+) tứ giác BMNP là hình bình hành nên MN = BP. Suy ra MN BP AN AM BC BC AC AB Do đó AMN ∽ ABC. 2. ĐỊNH LÝ
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song
với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho. A ABC
GT MN // BC (M AB; N AC) M N a KL AMN ∽ ABC B C Chú ý
Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài hai
cạnh của tam giác và song song với cạnh còn lại. A E D A B C B C D E ABC ∽ ADE ABC ∽ ADE
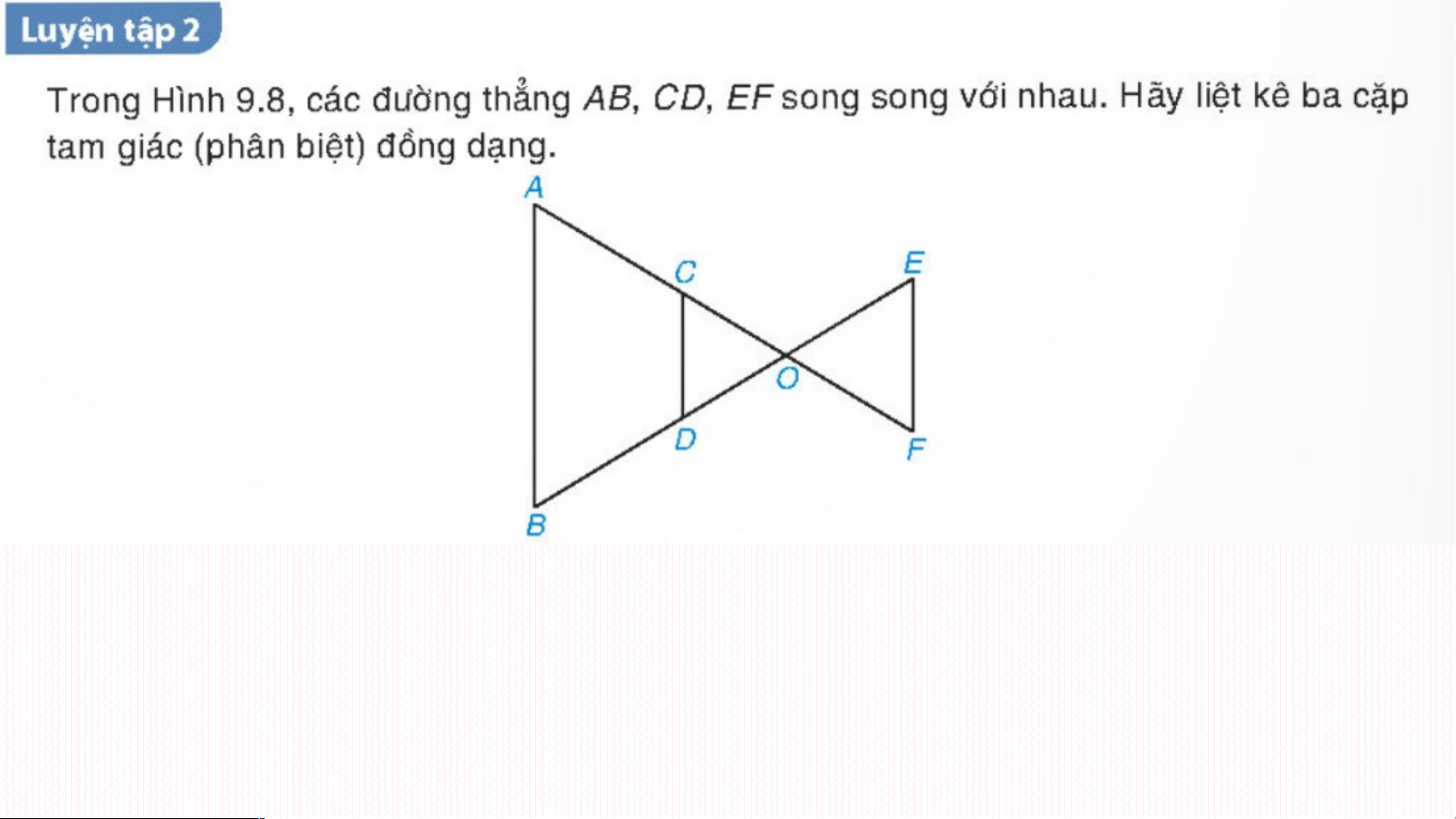
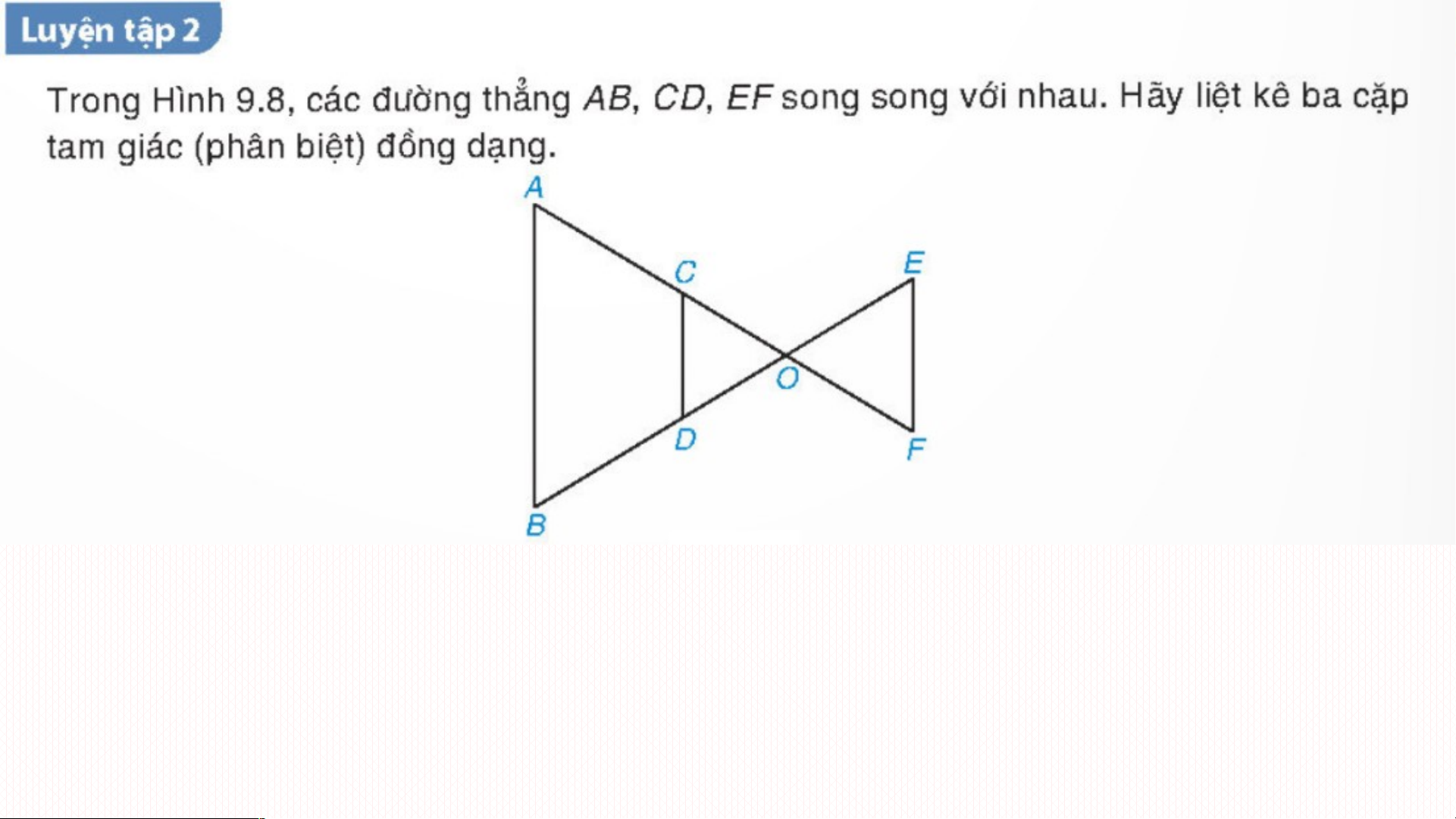
- Vì C OA, D OB và CD//AB nên OCD ∽ OAB
- Vì E OB, F OA (kéo dài) và EF//AB nên OEF ∽ OBA
- Vì F OC, E OD (kéo dài) và EF//CD nên OFE ∽ OCD Vận dụng:
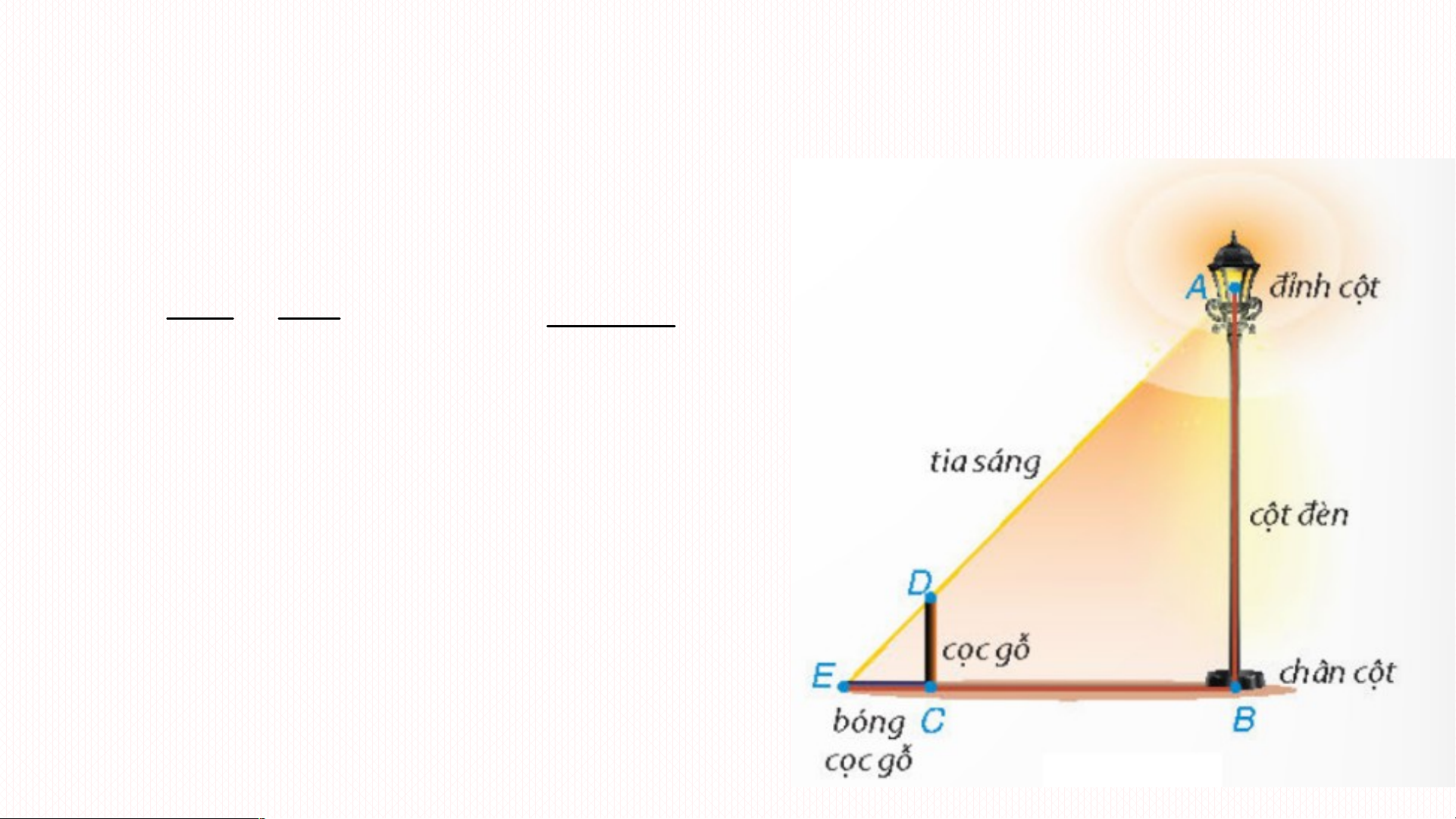
Vì CD // AB (cùng vuông góc với BC) Theo định lý thì DEC ∽ DEB DC EC EB.DC Suy ra hay AB AB EB EC
Như vậy chỉ cần đo chiều dài bóng
cọc gỗ (đoạn EC), khoảng cách EB
thì với chiều cao CD đã biết, bác
Dương tính được chiều cao AB của cột điện.
Theo công thức trên thì AB = 5m. Bài tập 9.1: Cho ABC ∽
MNP Các khẳng định sau đúng hay sai? 1. MNP ∽ ABC ĐÚNG 2. BCA ∽ NPM ĐÚNG 3. CAB ∽ PMN ĐÚNG 4. ACB = MNP SAI Bài t p ậ 9.2: Kh n ẳ g đ n
ị h nào sau đây là đúng ?
a) Hai tam giác bằng nhau thì đ n ồ g d n ạ g v i n ớ hau ĐÚNG KHÔNG ĐÚNG
b) Hai tam giác bất kì đ n ồ g d n ạ g v i ớ nhau c) Hai tam giác đ u ề b t ấ kì đ n ồ g d n ạ g v i n ớ hau ĐÚNG
d) Hai tam giác vuông bất kì đ n ồ g d n ạ g v i n ớ hau KHÔNG ĐÚNG e) Hai tam giác đ n
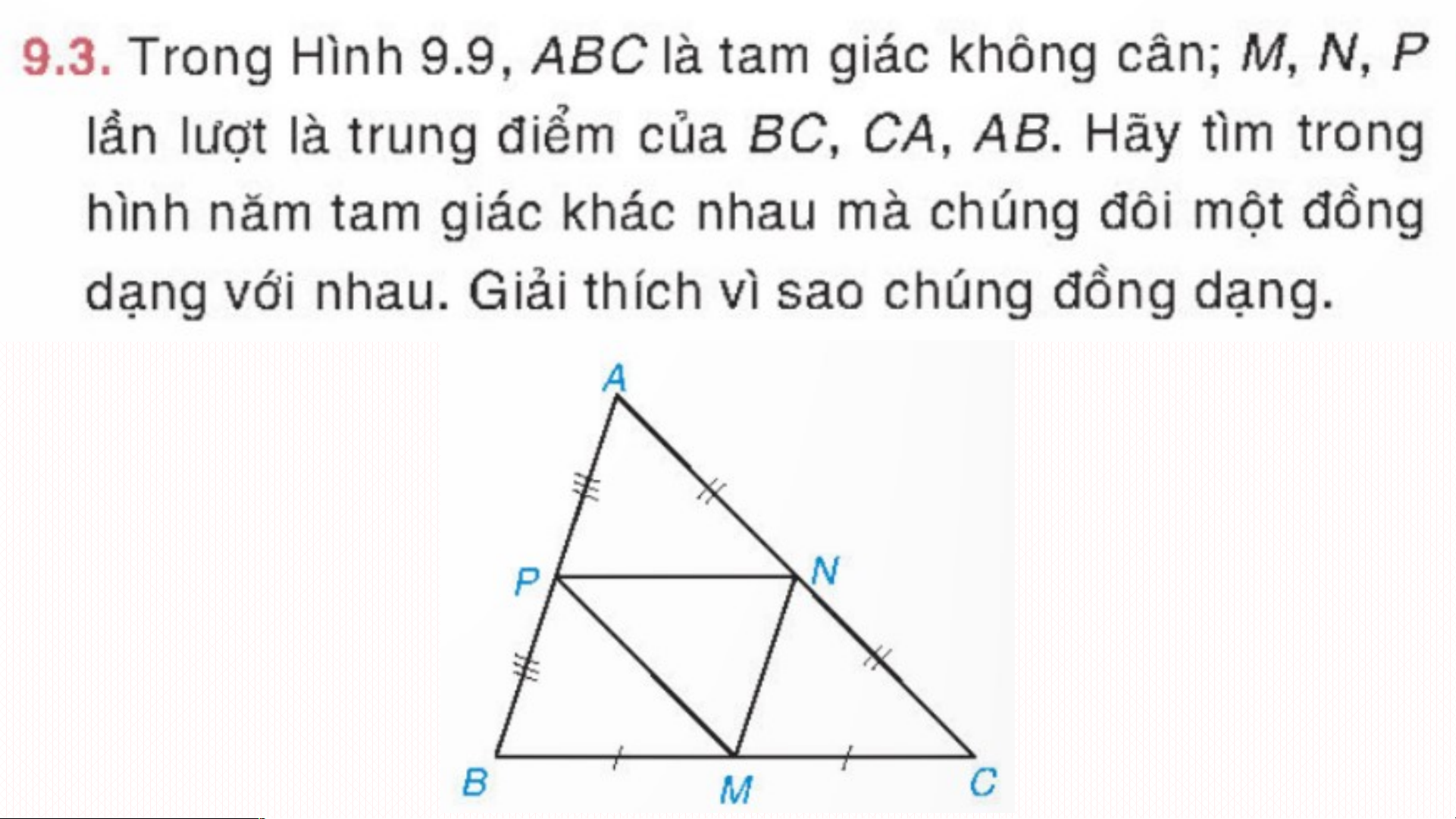
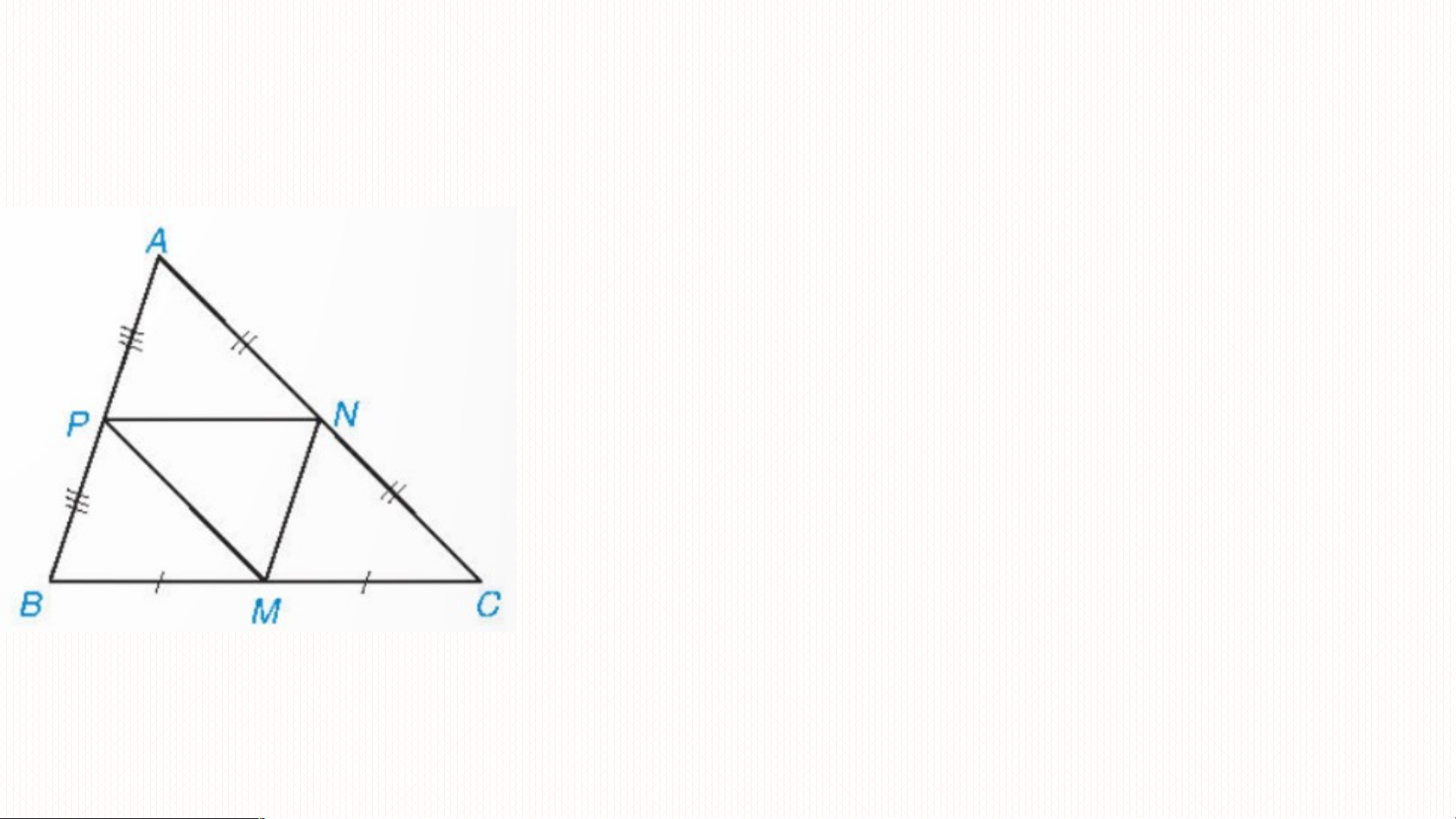
ồ g dạng thì bằng nhau KHÔNG ĐÚNG Xét APN và MNP có Bài t p ậ 9.3: APN M NP;ANP M P N ( các góc so le trong) PN là cạnh chung Nên APN = MNP Tương tự: PBM = MNP ; NMC = MNP
Do vậy bốn tam giác APN; PBM; NMC;
MNP cùng đồng dạng với nhau.
Ta lại có PN //BC ( đường trung bình) nên APN ∽ ABC
Vậy 5 tam giác APN; PBM; NMC; MNP và ABC đôi một đồng dạng.
HƯỚNG DẪN VỀ NHÀ 1
Ghi nhớ kiến thức trong bài 2
Hoàn thành bài tập SGK, SBT 3 Chuẩn bị bài mới
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32




