





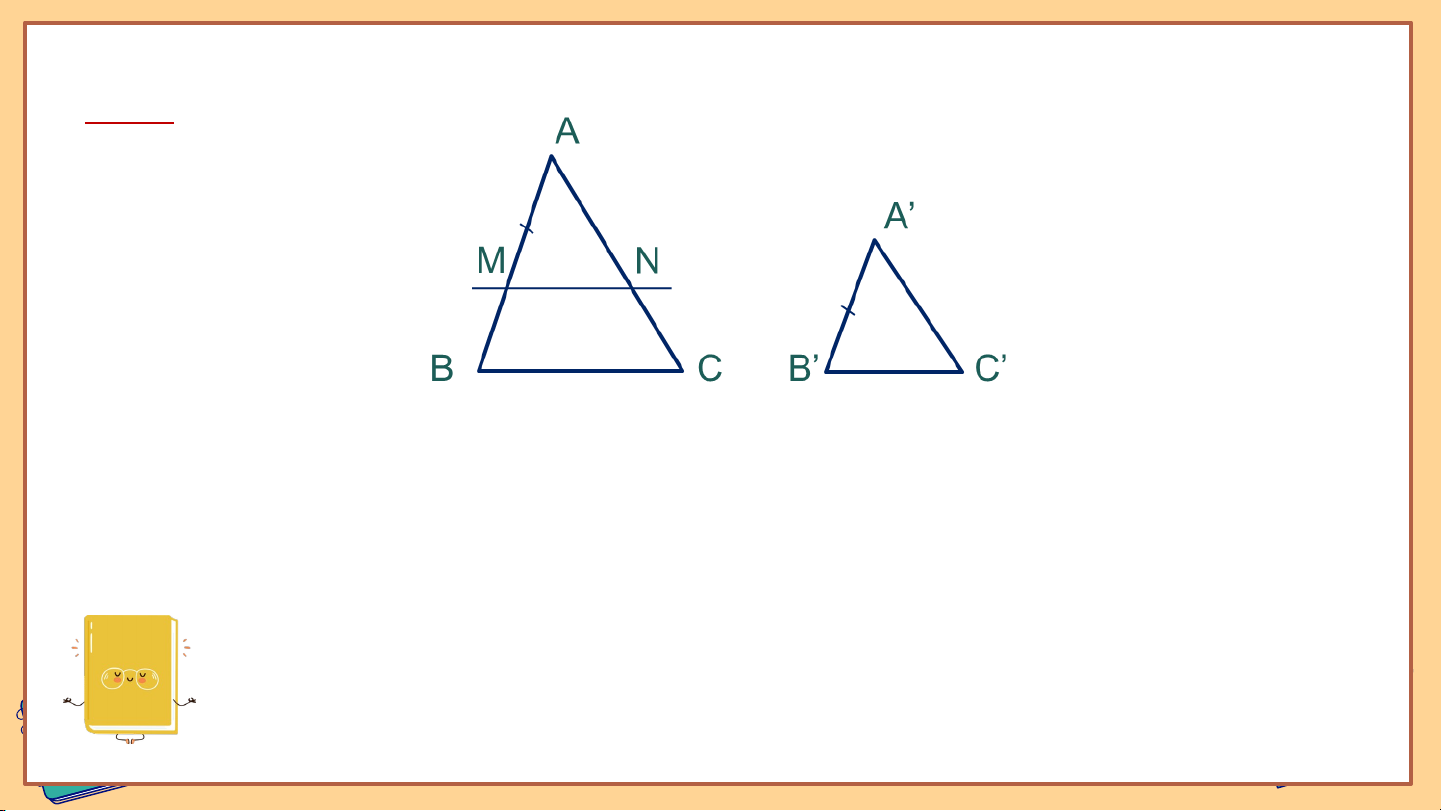
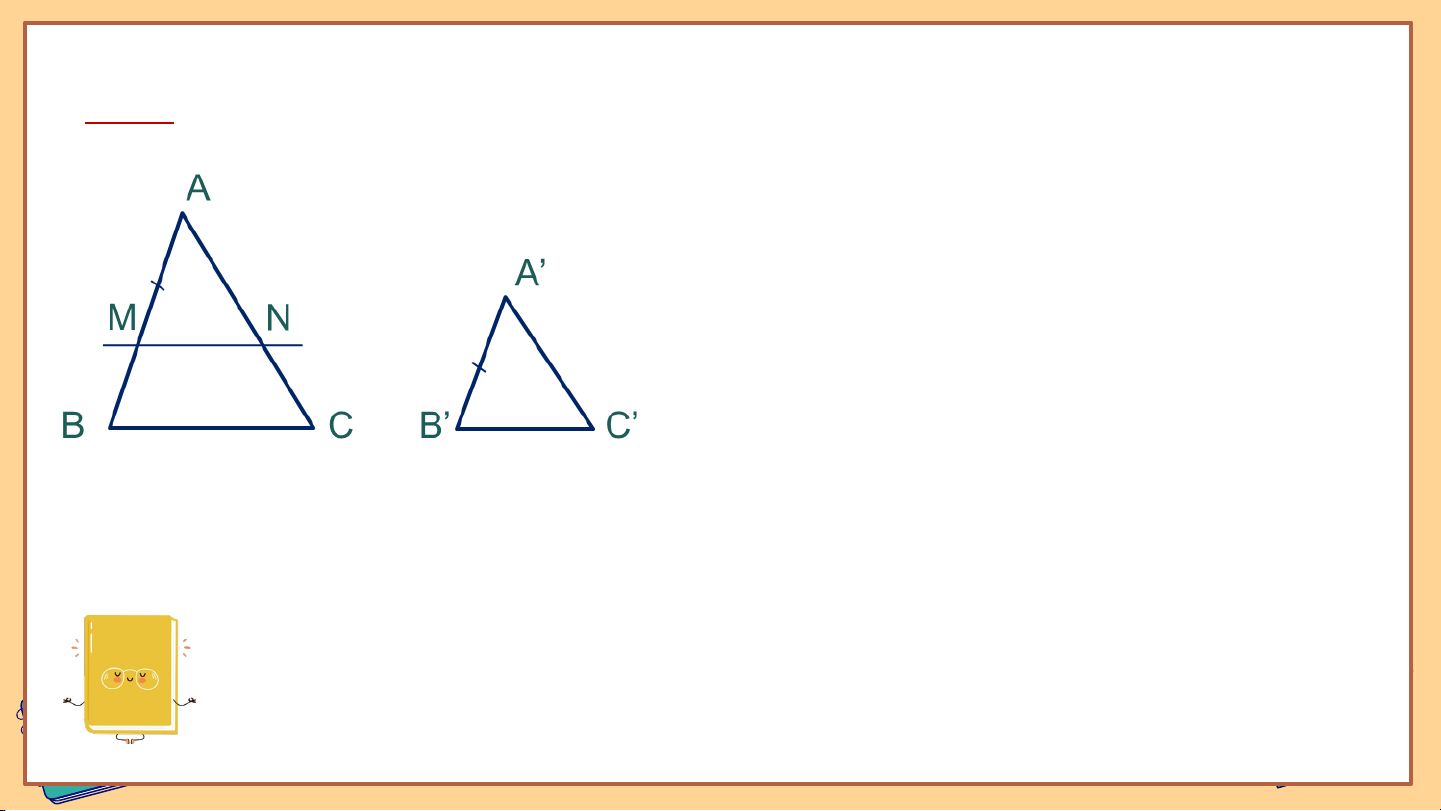
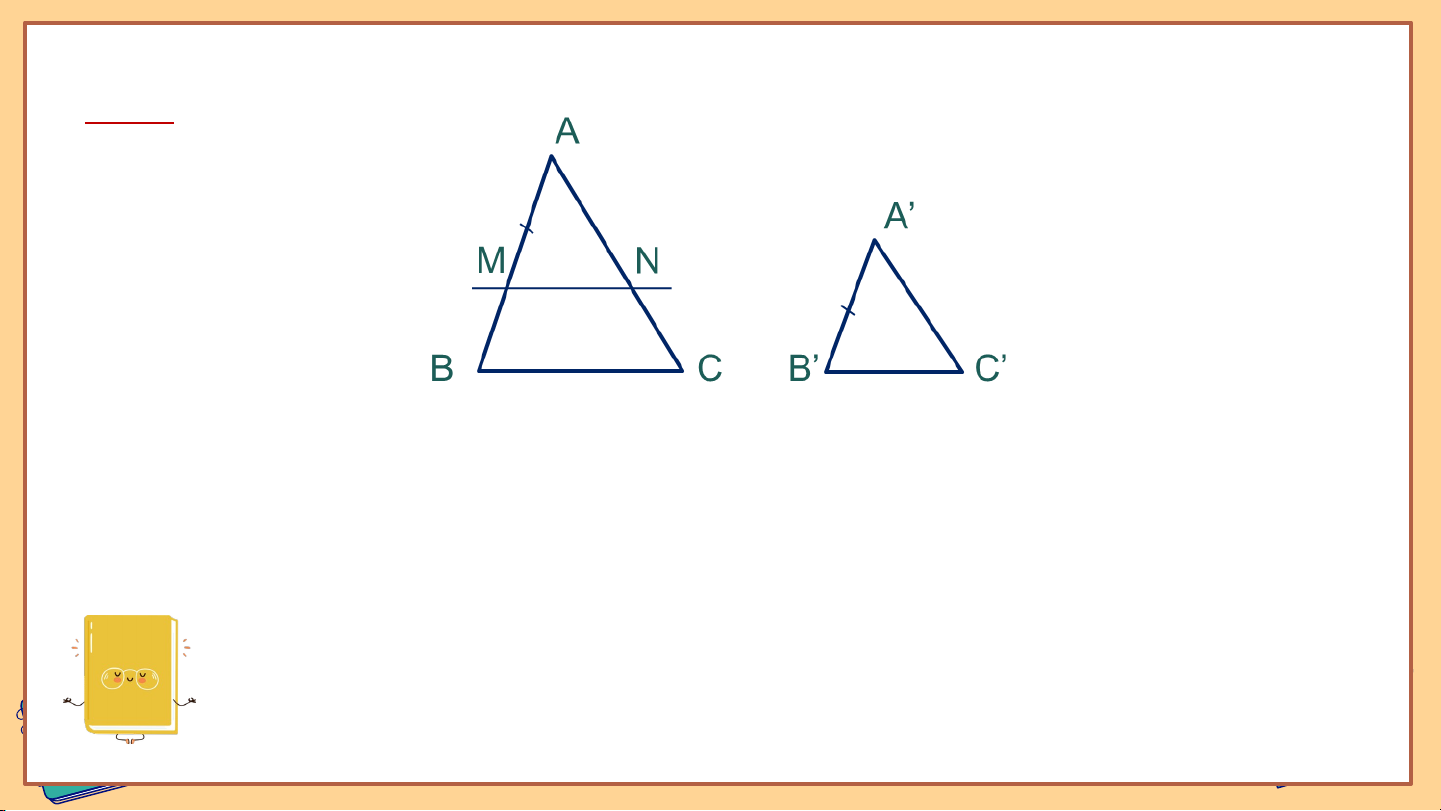





Preview text:
BÀI 34. BA TRƯỜNG HỢP
ĐỒNG DẠNG CỦA HAI TAM GIÁC CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC NGÀY HÔM NAY! KHỞI ĐỘNG
Trong bóng đá, độ khó của mỗi pha ghi bàn còn được tính bởi góc
sút vào cầu môn là rộng hay hẹp. Nếu biết độ rộng của khung thành
là 7,32 m, trái bóng cách hai cọt gôn lần lượt là 10,98 m và 14,64 m
thì em có cách nào để đo
được góc sút ở vị trí này bởi
các dụng cụ học tập không? CHƯƠNG IX.
TAM GIÁC ĐỒNG DẠNG
BÀI 34. BA TRƯỜNG HỢP
ĐỒNG DẠNG CỦA HAI TAM GIÁC NỘI DUNG BÀI HỌC
01 Trường hợp đồng dạng thứ nhất của tam giác
02 Trường hợp đồng dạng thứ hai của tam giác
03 Trường hợp đồng dạng thứ ba của tam giác 1. Trư rường hợ ng hợ p đ p đồng ồng dạn d g ạng thứ thứ nhất c hất ủ của t a am tam giá i c ác
Trường hợp đồng dạng cạnh – cạnh – cạnh
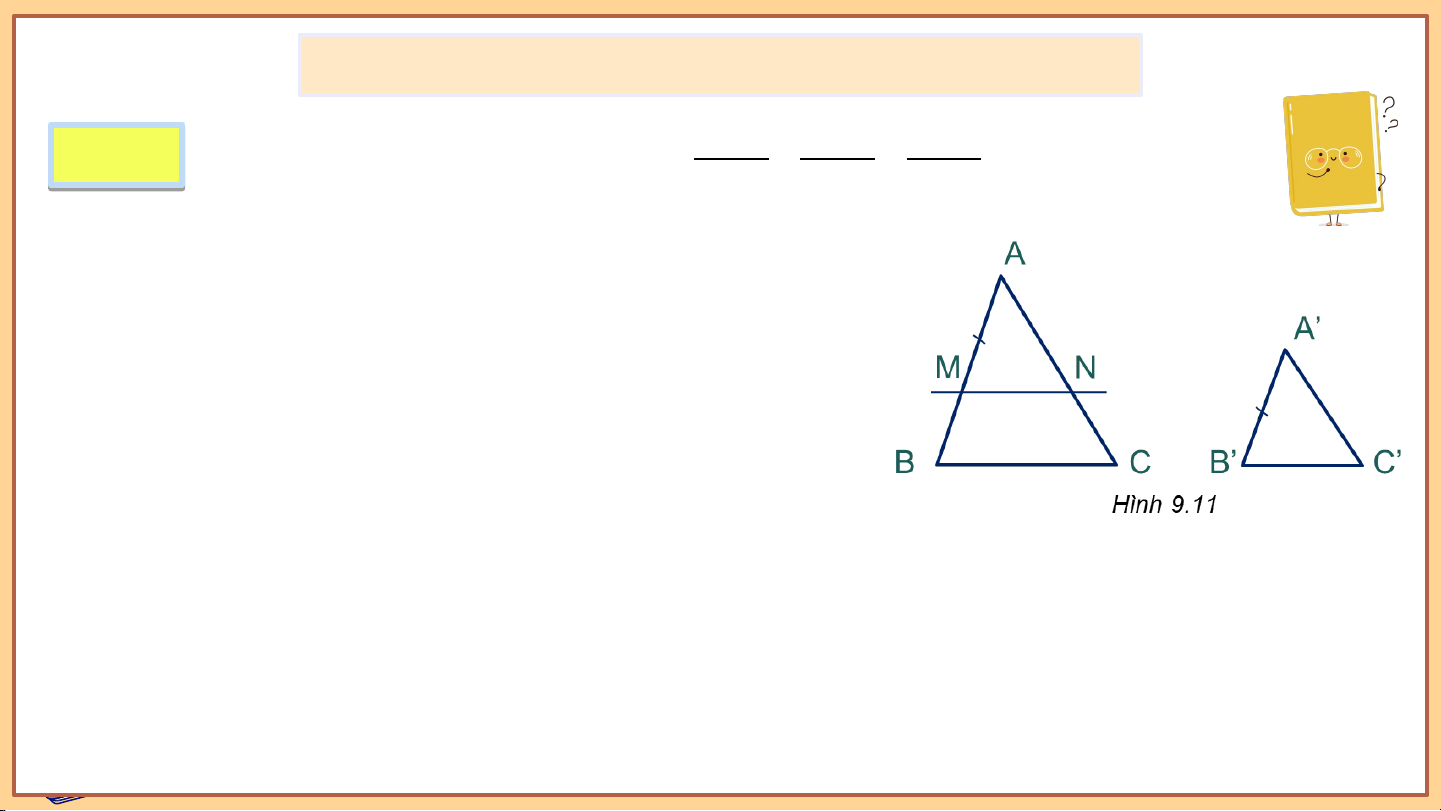
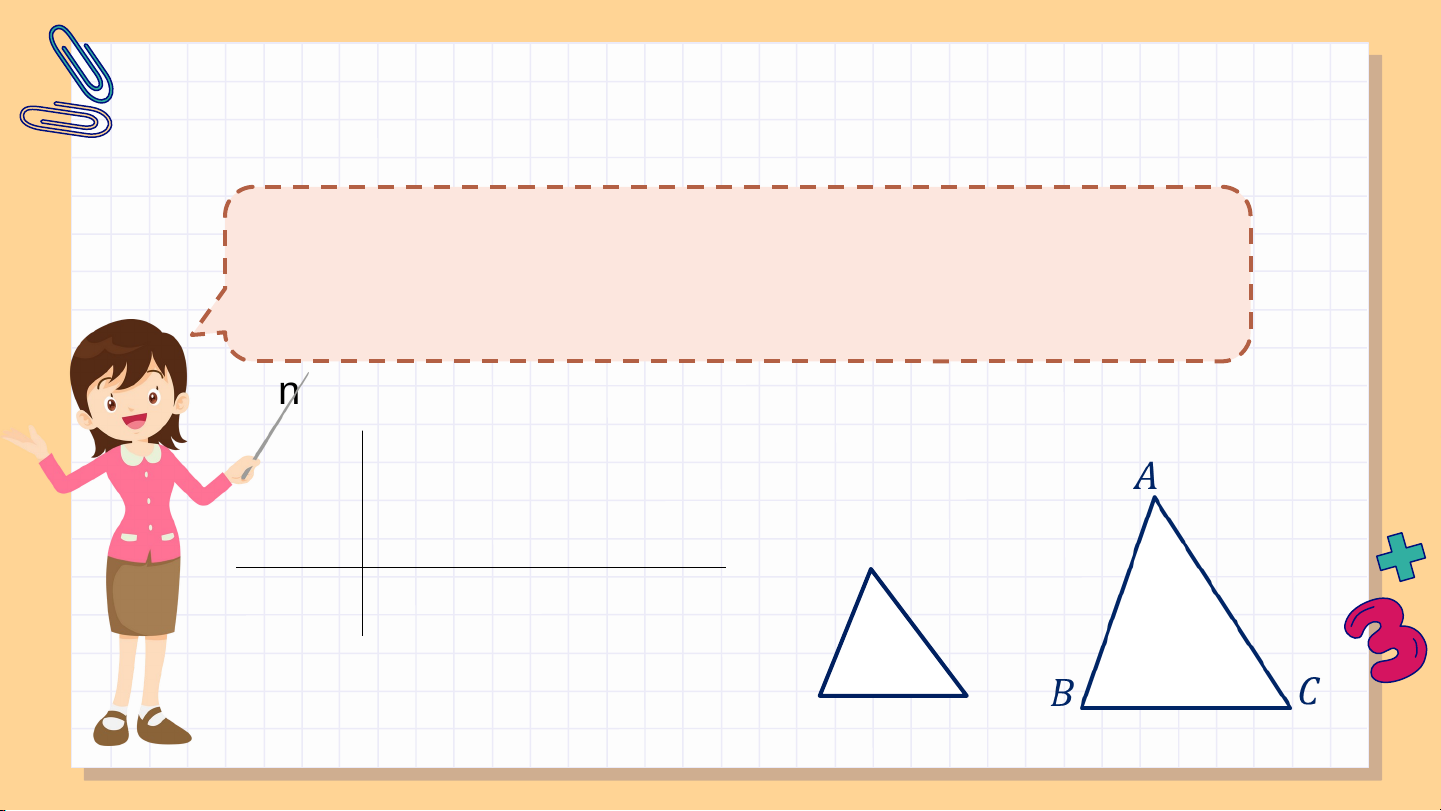
𝐴′ 𝐵′ 𝐴′𝐶′ 𝐵′𝐶′ HĐ 1 H Cho hai tam giác và có = = 𝐴𝐵 𝐴𝐶 𝐵𝐶
a) Nếu thì hai tam giác có đồng dạng với nhau không? Vì sao?
b) Nếu như hình 9.11. Trên đoạn thẳng lấy điểm sao
cho Kẻ đường thẳng qua song song với và cắt tại . - Hãy giải thích vì sao -
Hãy chứng tỏ rằng để suy ra (c.c.c) -
Hai tam giác và có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
c) Nếu thì tam giác có đồng dạng với tam giác không? Vì sao? Giải: a) Nếu thì và (c.c.c) Do đó Giải: b) vì . Vì (do ) nên Giải:
c) Nếu , bằng cách đổi vai trò và cho nhau thì theo phần b) . ĐỊNH LÍ
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của
tam giác kia thì hai tam giác đó đồng dạng với nhau. , GT 𝐴′ KL 𝐵′ 𝐶 ′
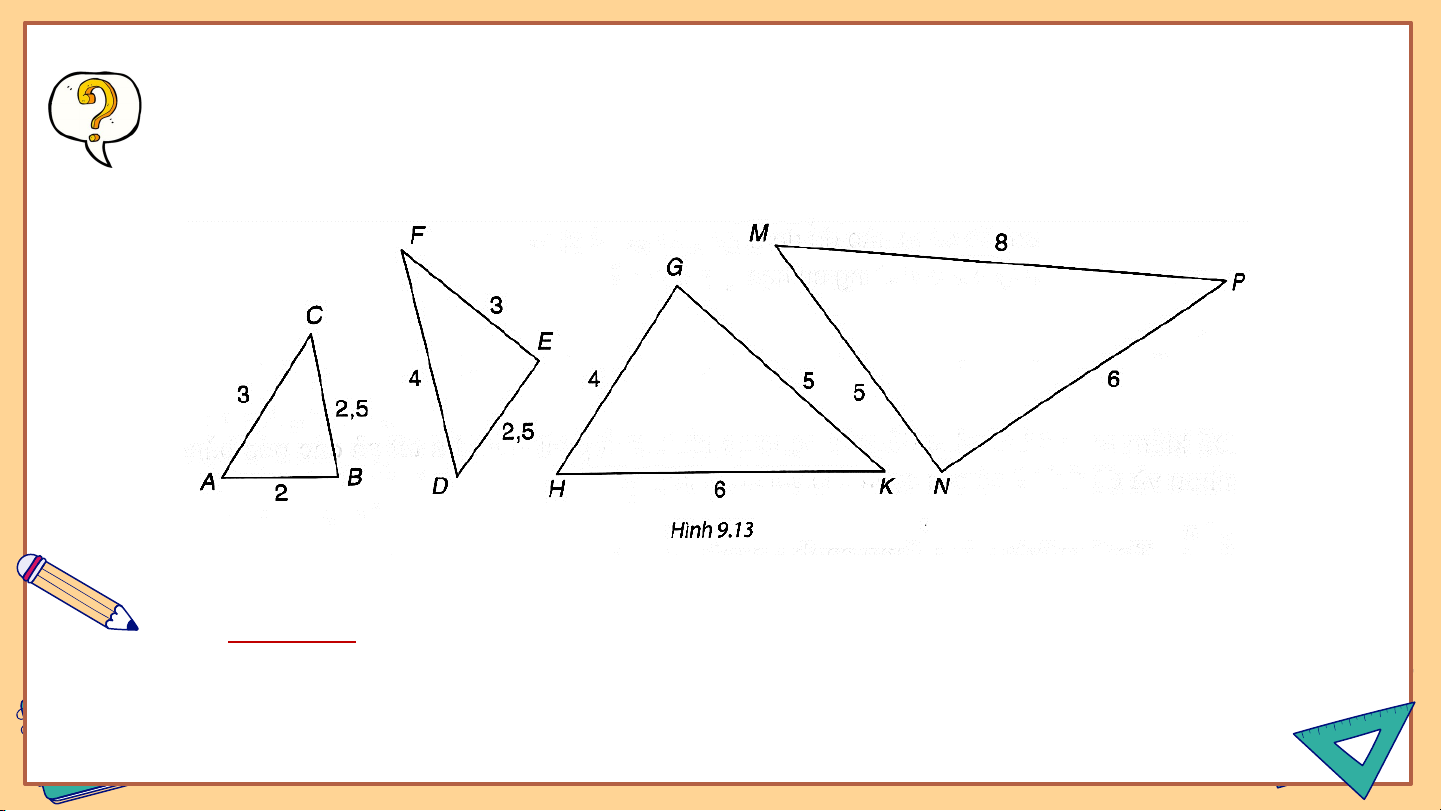
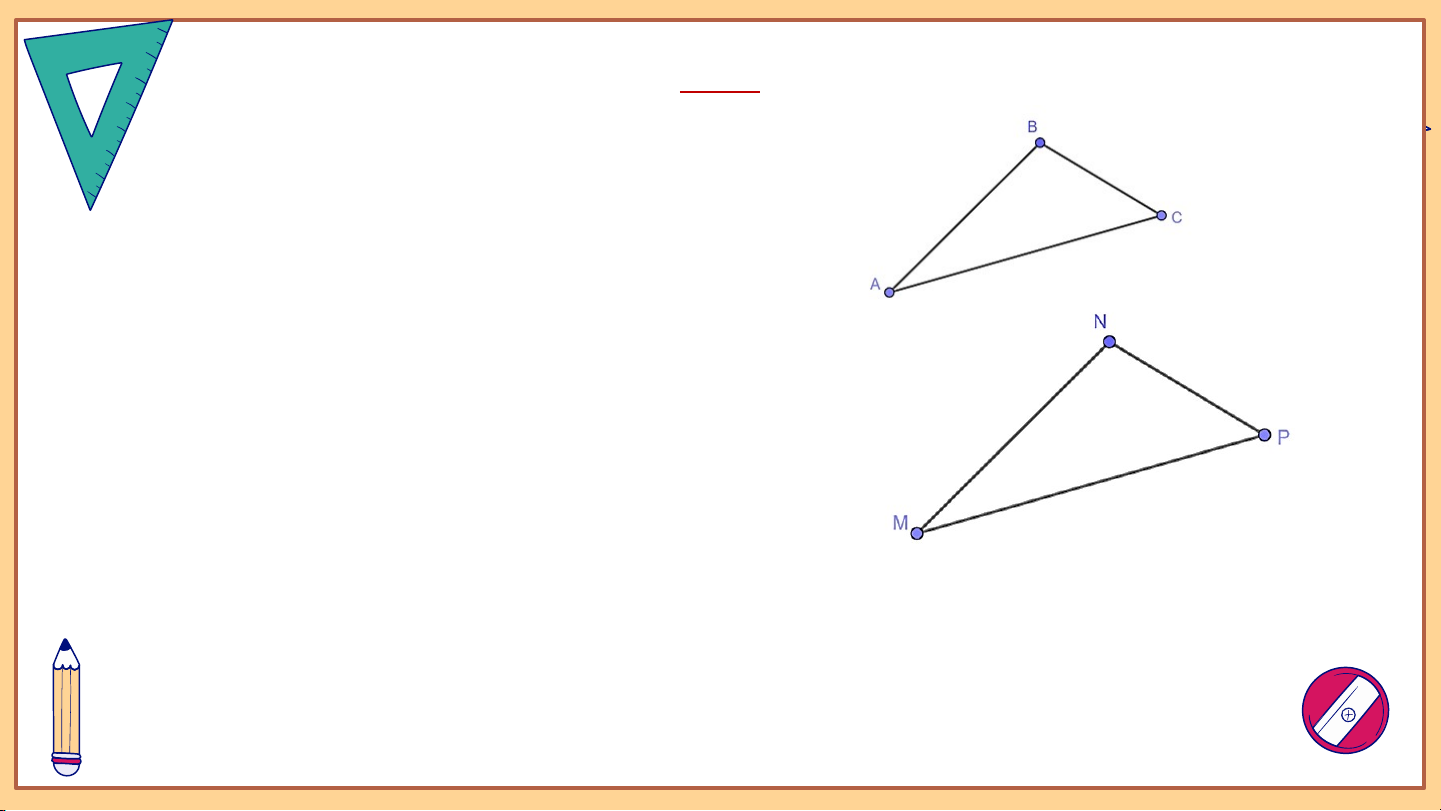
Những cặp tam giác nào dưới đây (hình 9.13) là đồng dạng? (các kích
thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
Trả lời: (c.c.c). Vì: (c.c.c). Vì: Ví dụ 1:
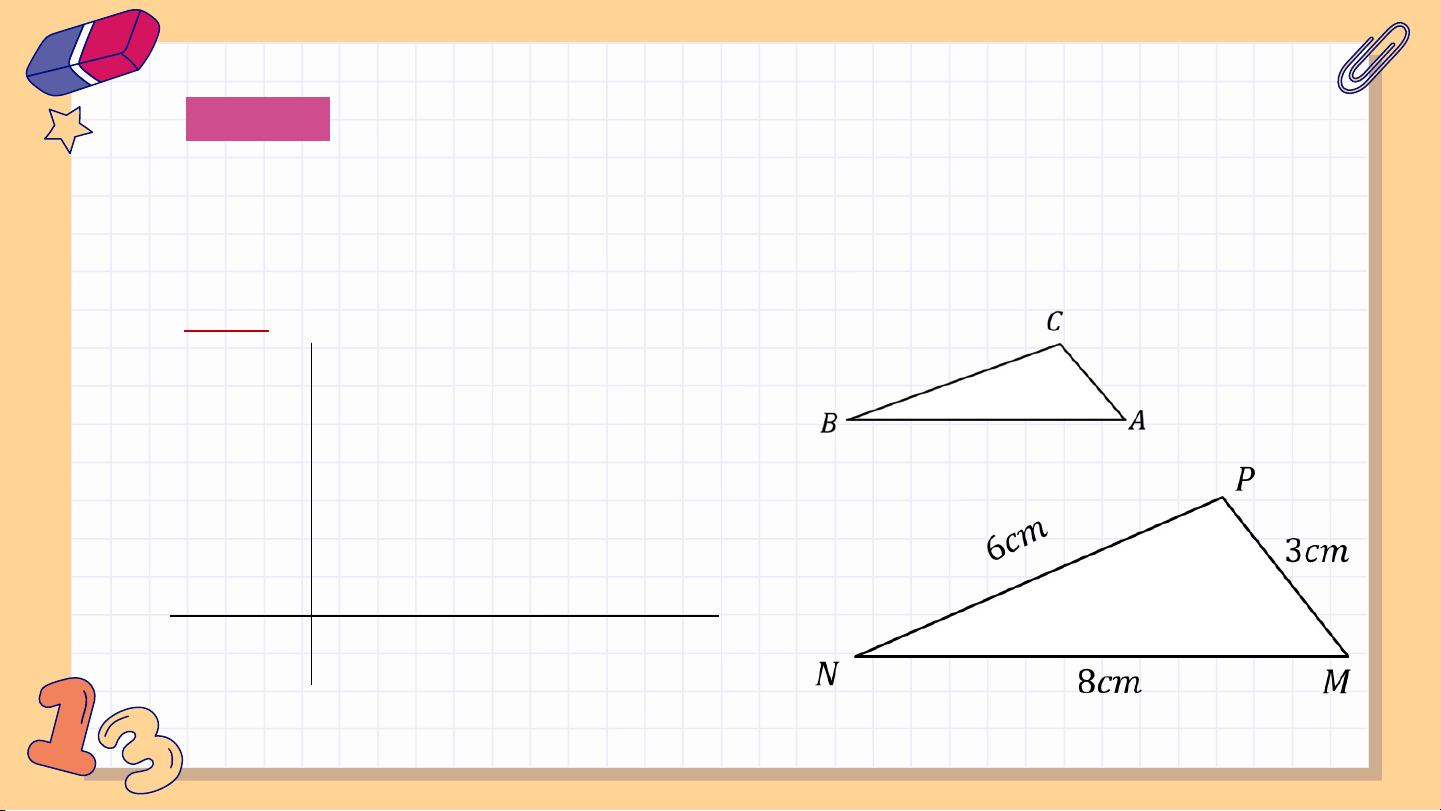
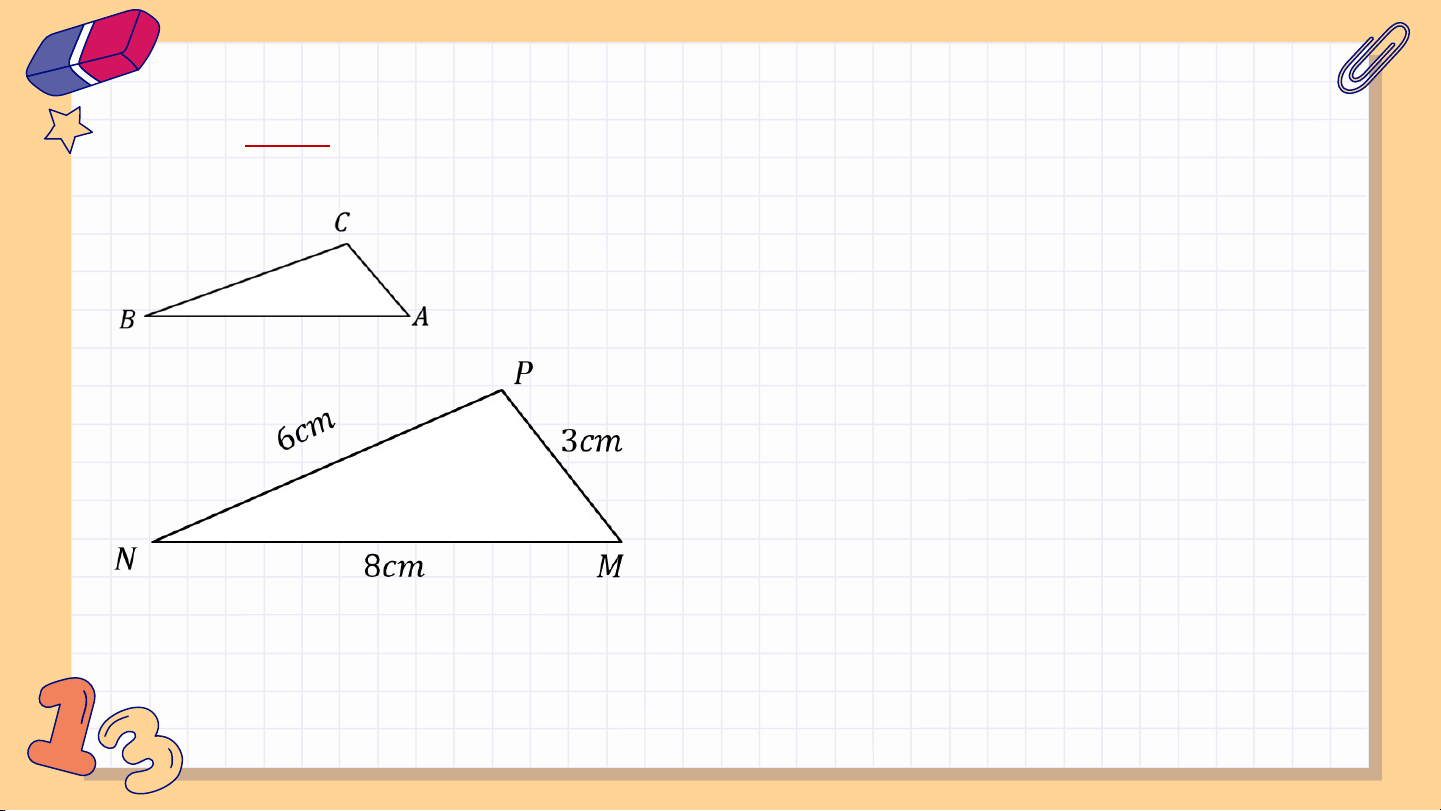
Cho các tam giác và có , . Chứng minh rằng Giải: , GT KL Giải: Từ giả thiết ta có và Vậy và có: Do đó . Luyện tập 1
Cho tam giác có chu vi bằng và tam giác có chu vi bằng . Biết rằng . Chứng minh Giải: : cm : cm Xét và có: Vậ V n d n ụn ụ g
Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh
tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và
hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được. Giải: • Vẽ với các số đo: (cm)
• Gọi điểm đặt trái bóng là ,
Chân hai cột gôn là và . Thì ta có hình minh họa: Ta có: (c.c.c) GIÚP ONG VỀ TỔ
Câu 1. Cho hai tam giác và có , khi đó ta có: A
∆ 𝑅𝑆𝐾 ∽ ∆ 𝑃𝑄𝑀 HẾT B
∆ 𝑅𝑆𝐾 ∽ ∆ 𝑄𝑃𝑀 GIỜ C
∆ 𝑅𝑆𝐾 ∽ ∆ 𝑀𝑃𝑄 D
∆ 𝑅𝑆𝐾 ∽ ∆ 𝑄𝑀𝑃
Câu 2. Cho đồng dạng với . Biết cm ;
cm ; cm cm. Chọn câu đúng A
𝑁𝑃=12𝑐𝑚; 𝐴𝐶=2,5𝑐𝑚 HẾT B
𝑁𝑃=2,5𝑐𝑚; 𝐴𝐶=12𝑐𝑚 GIỜ C
𝑁𝑃=5 𝑐𝑚; 𝐴𝐶=10𝑐𝑚 D
𝑁𝑃=10 𝑐𝑚; 𝐴𝐶=5𝑐𝑚
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- NỘI DUNG BÀI HỌC
- 1. Trường hợp đồng dạng thứ nhất của tam giác
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21




