Nam và Việt muốn đo chiều cao của cột cờ
ở sân trường mà hai bạn không trèo lên
được. Vào buổi chiều, Nam đo thấy bóng
cột cờ dài 6m và bóng của Việt dài 70cm.
Nam hỏi Việt cao bao nhiêu, Việt trả lời là
cao 1,4m. Nam liền reo lên: “Tớ biết cột cờ
cao bao nhiêu rồi đấy”
Vậy làm thế nào mà Nam
biết được chiều cao của cột cờ?
1 . ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG B B' A C A' C'
1 . ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG
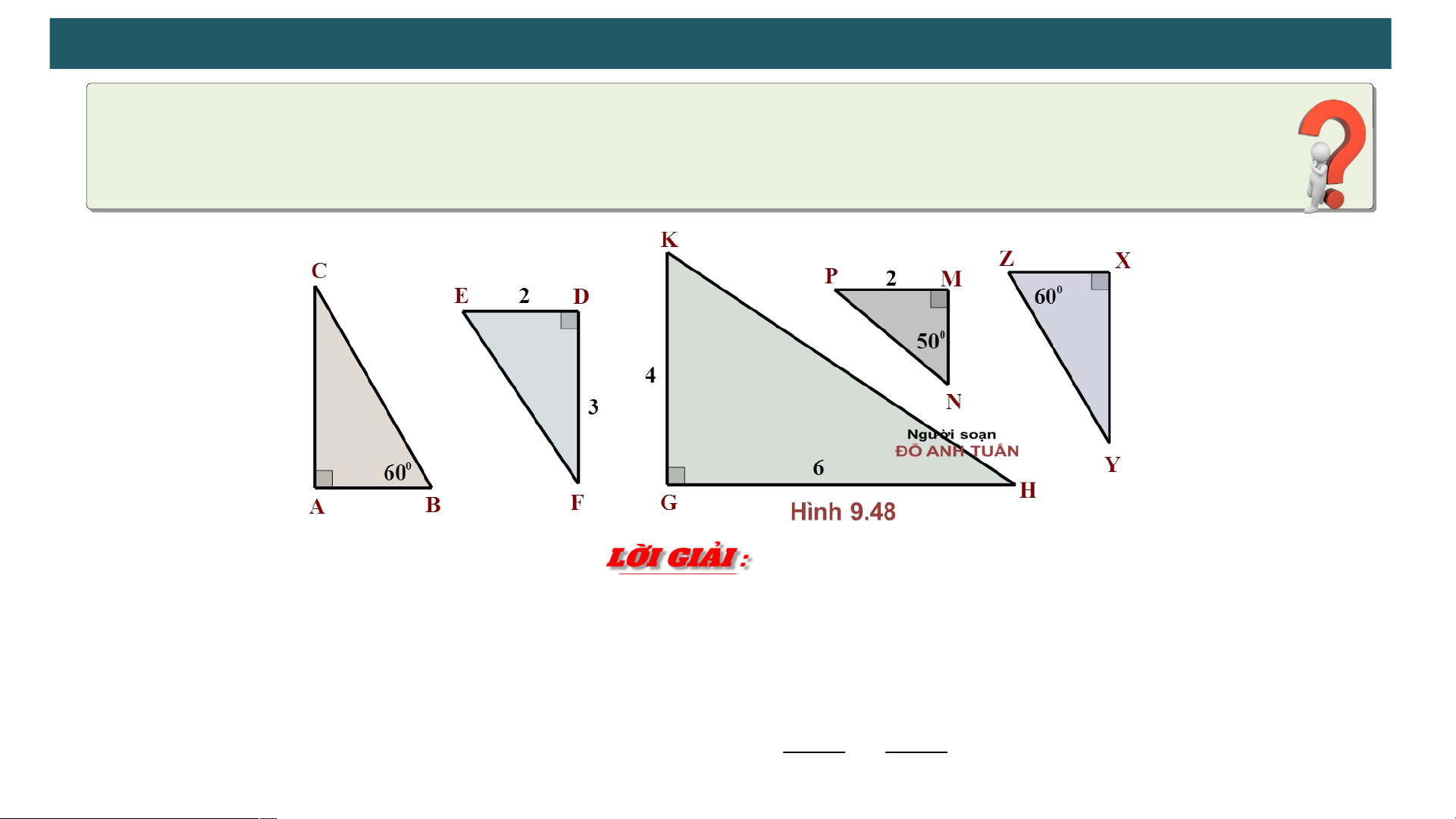
 Câu hỏi : Hãy chỉ ra hai cặp tam giác vuông đồng dạng có trong hình 9.48
 Các cặp tam giác vuông đồng dạng:     A  BC  X
 YZ ( A X ; B Z  )  ED DF   EDF  KGB ; EDF KGH       KG GF   
1 . ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG
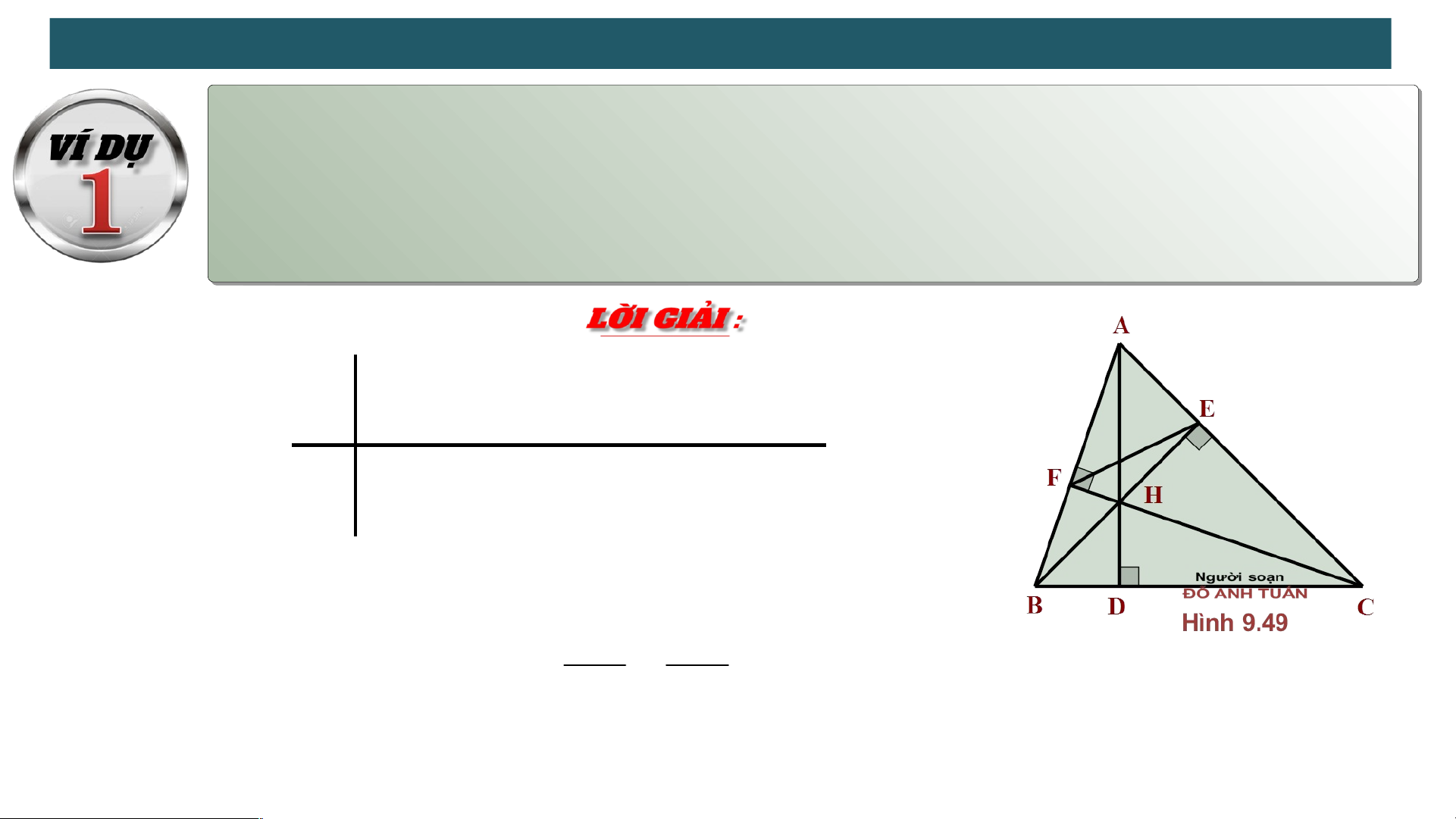
Cho tam giác ABC có đường cao AD, BE, CF cắt nhau tại điểm H. Chứng minh rằng : a. b. AEFABC
ABC, đường cao AD, BE, CF GT đồng quy tại H KL a) H . A HD H .
B HE HC.HF b) A  EF  A  BC
a) Hai tam giác vuông AHF và CHD có : Do đó AHFCHD . Suy ra : HA HF  HC HD Hay H .
A HD HC.HF (1)
Tương tự ta có nên 2 tam giác vuông AHE và BHD đồng dạng với nhau
1 . ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG
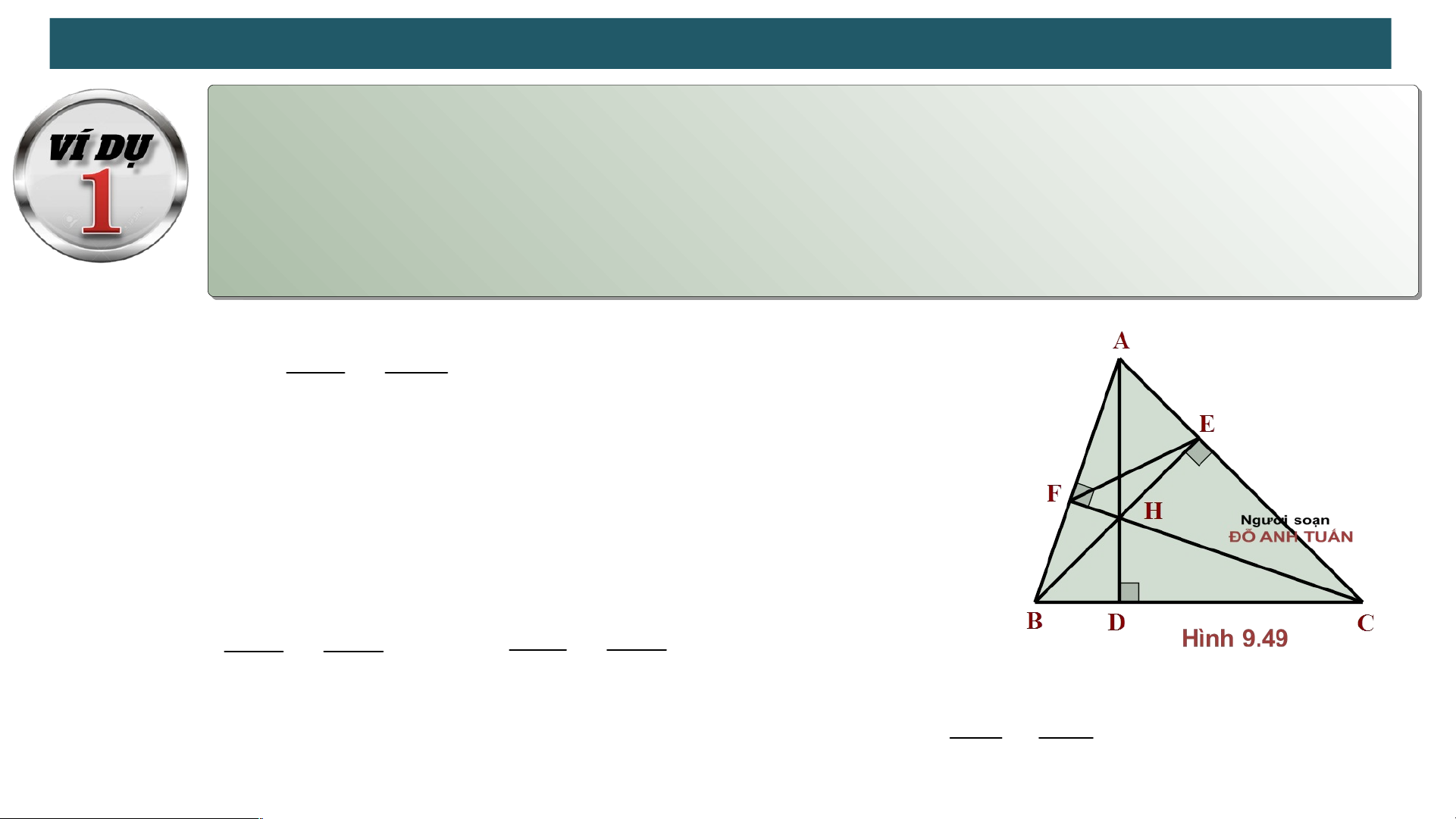
Cho tam giác ABC có đường cao AD, BE, CF cắt nhau tại
điểm H. Chứng minh rằng : a. b. AEFABC HA HF Suy ra :  Hay H . A HD H . B HE (2) HB HD
Từ (1) và (2) suy ra : H . A HD H .
B HE HC.HF
b) Hai tam giác vuông ABE và ACF có góc A chung nên ABEACF. Suy ra : AE AB AE AF  Hay  AF AC AB AC
Hai tam giác vuông AEF và ABC có góc A chung và AE AF  AB AC nên AEFABC (c.g.c)
1 . ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG
a) Hai tam giác vuông ABC và A'B'C' có nên
chúng đồng dạng với nhau . A' B ' A'C '
b) Vì ABCA’B’C’ nên :  AB AC 0, 7 1, 4 6 Hay  Suy ra : AC 1  , 4. 1  2(m) 6 AC 0,7
 Ta có: CX = 2,4 – 1,6 = 0,8(m) MN = 1 + 19 = 20 (cm)
Xét 2 tam giác vuông MXC và MYA có: góc M
chung và nên chúng đồng dạng MX XC 1 0,8   Hay  Hình 9.51 MY YA 20 YA Suy ra : YA 2  0.0,8 16  (cm)
Suy ra : AB BY YA 1  , 6 16 17  , 6(cm)
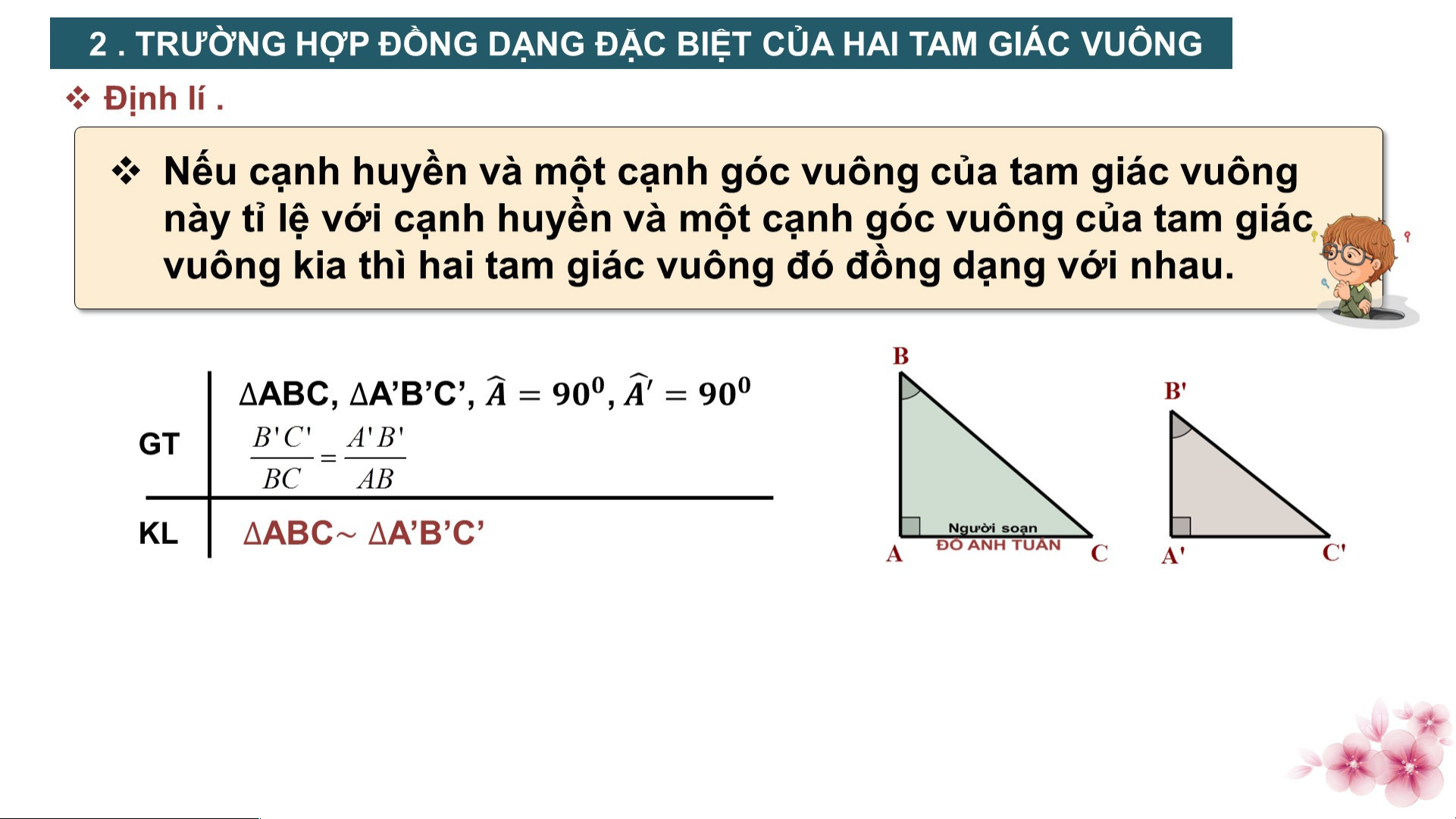
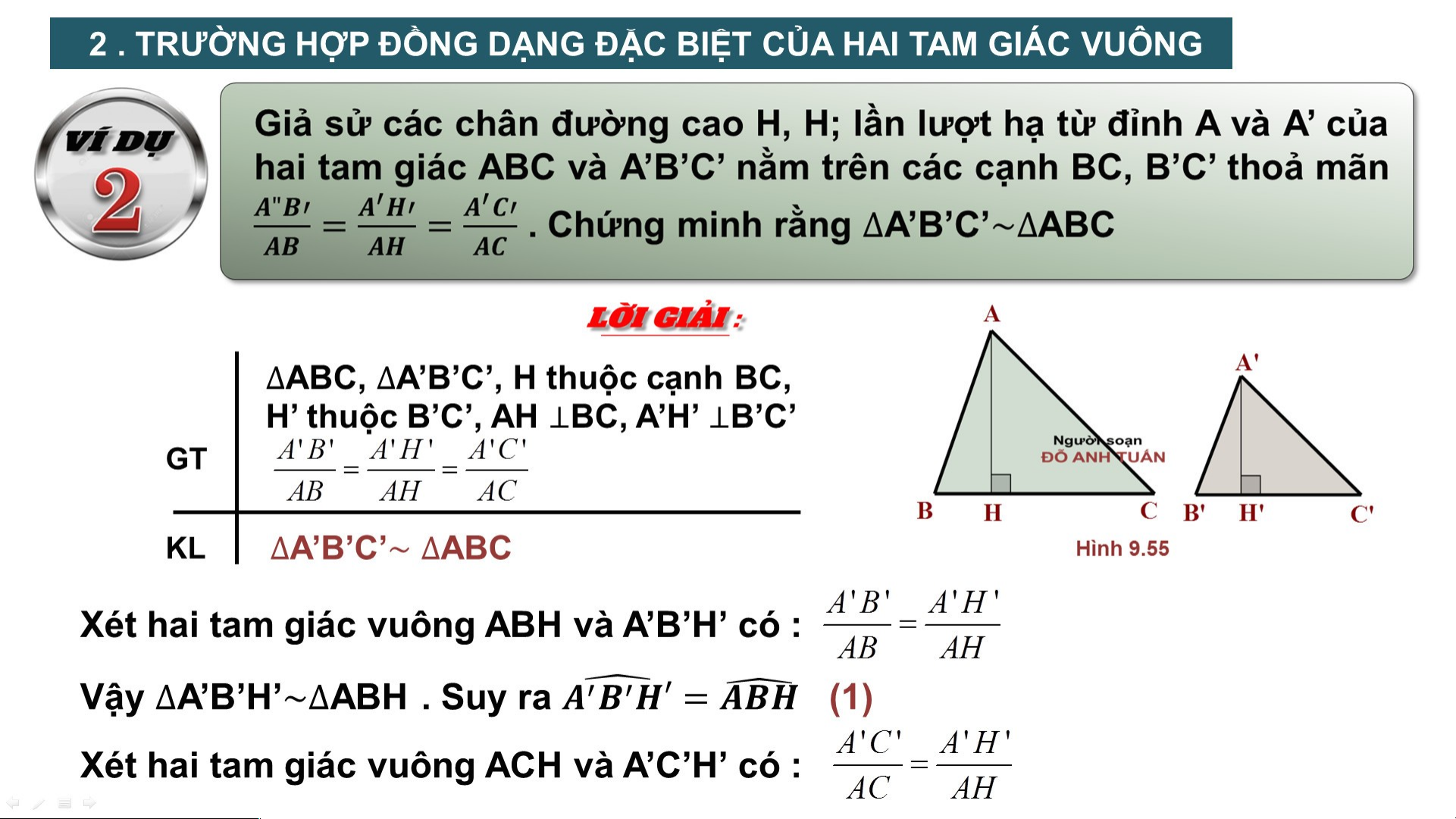
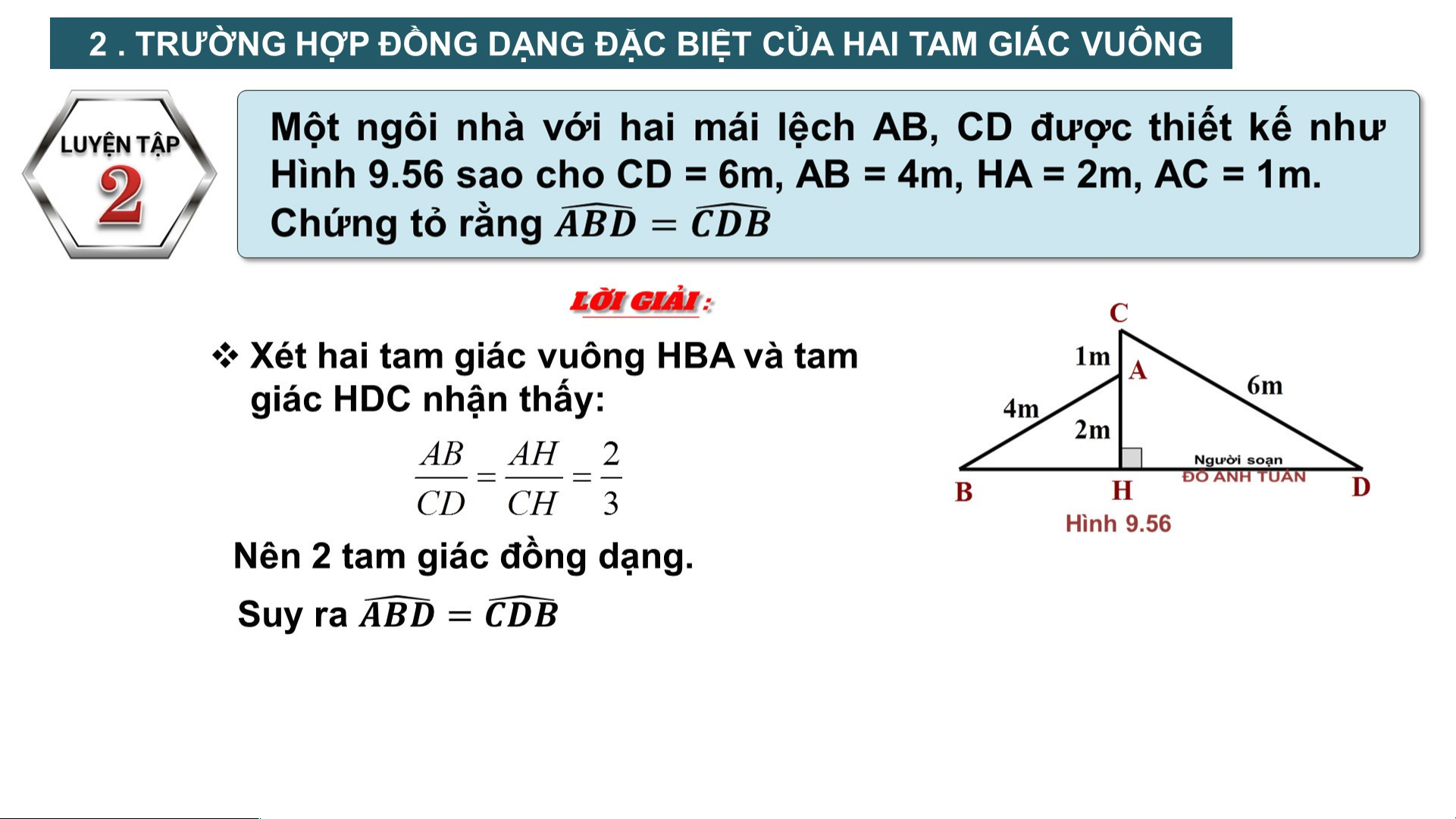
2 . TRƯỜNG HỢP ĐỒNG DẠNG ĐẶC BIỆT CỦA HAI TAM GIÁC VUÔNG
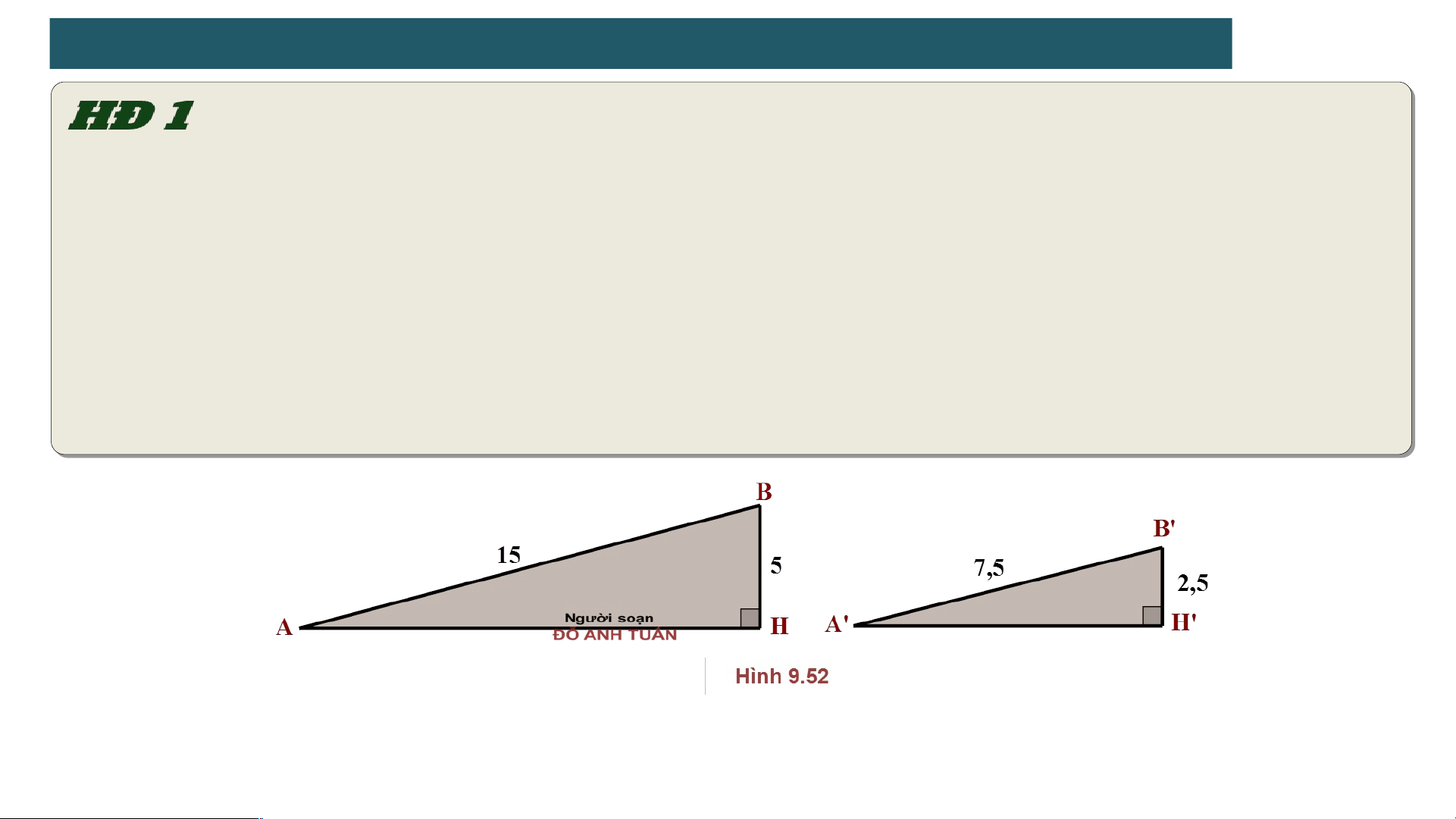
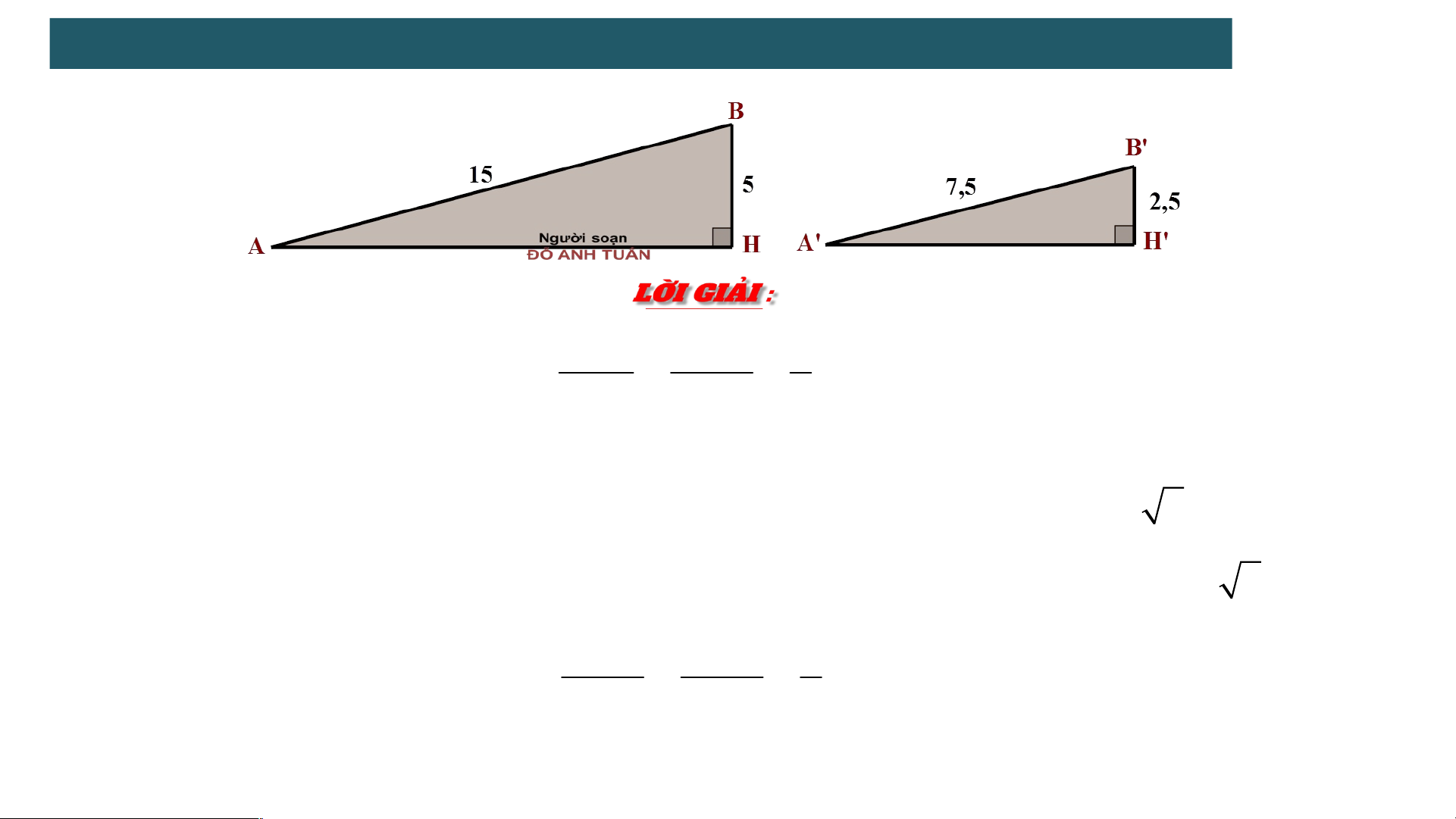
Các tam giác vuông AHB và A'H'B' mô tả hai con dốc có chiều dài lần lượt là
AB = 15m, A′B′ = 7,5m và độ cao lần lượt là BH = 5m, B′H′ = 2,5m.
Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B' -
Nhận xét về 2 đại lượng : và -
Dùng định lí Pythagore để tính AH và A’H’ -
So sánh các đại lượng và -
Hai tam giác vuông A’H’B’ và AHB có đồng dạng không? Từ đó rút ra kết luận gì về
độ dốc của 2 con dốc ?
2 . TRƯỜNG HỢP ĐỒNG DẠNG ĐẶC BIỆT CỦA HAI TAM GIÁC VUÔNG A' B ' B ' H ' 1 Ta có :   AB BH 2
Áp dụng định lí Pythagore ta có : 2 2 2 2 2
AH AB  BH 1  5  5 2  00  AH 1  0 2 2 2 2 2 2
A' H ' A' B '  B ' H ' 7,  5  2, 5 50   A ' H ' 5  2 A' H ' B ' H ' 1    AH BH 2
Do đó 2 tam giác vuông A’H’B’ và AHB đồng dạng.
 Để có cả bộ Giáo án Pp Toán 8 – KNTT , xin liên hệ :
Đỗ Anh Tuấn - Zalo : 0918.790.615
Thầy (cô) có thể tham khảo trước nội dung các bài giảng tại đây :
https://sites.google.com/view/giaoandientu-doanhtuan/to%C3%A1n-
8/k%E1%BA%BFt-n%E1%BB%91i-tri-th%E1%BB%A9c?authuser= (copy
đường link và dán vào trình duyệt )
• Tất cả bài giảng đều do một người soạn ( Đỗ Anh Tuấn) nên chất lượng đồng đều
từ bài đầu đến bài cuối.
• Bài giảng được thực hiện công phu và đầy đủ các bài tập và luyện tập .
• Đặt biệt là phân môn Hình học : các hình vẽ được vẽ chuẩn xác và rõ nét hơn cả
SGK ( Đây là điểm khác biệt lớn của bộ Giáo án này )
Tất cả bài tập Hình học đều có hình minh hoạ đầy đủ , giúp việc dạy học dễ dàng .
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27