Kim tự tháp Kheops ở Ai Cập được
xây dựng vào khoảng 2500 năm trước
Công nguyên là một trong những công
trình cổ nhất và duy nhất còn tồn tại
trong số bảy kì quan thế giới cổ đại. Kim
tự tháp này có dạng hình chóp tứ giác
đều cao 147m, cạnh đáy dài 230m (Hình 10.17) Hình 10.17
Hỏi kim tự tháp Kheops có
thể tích bằng bao nhiêu?
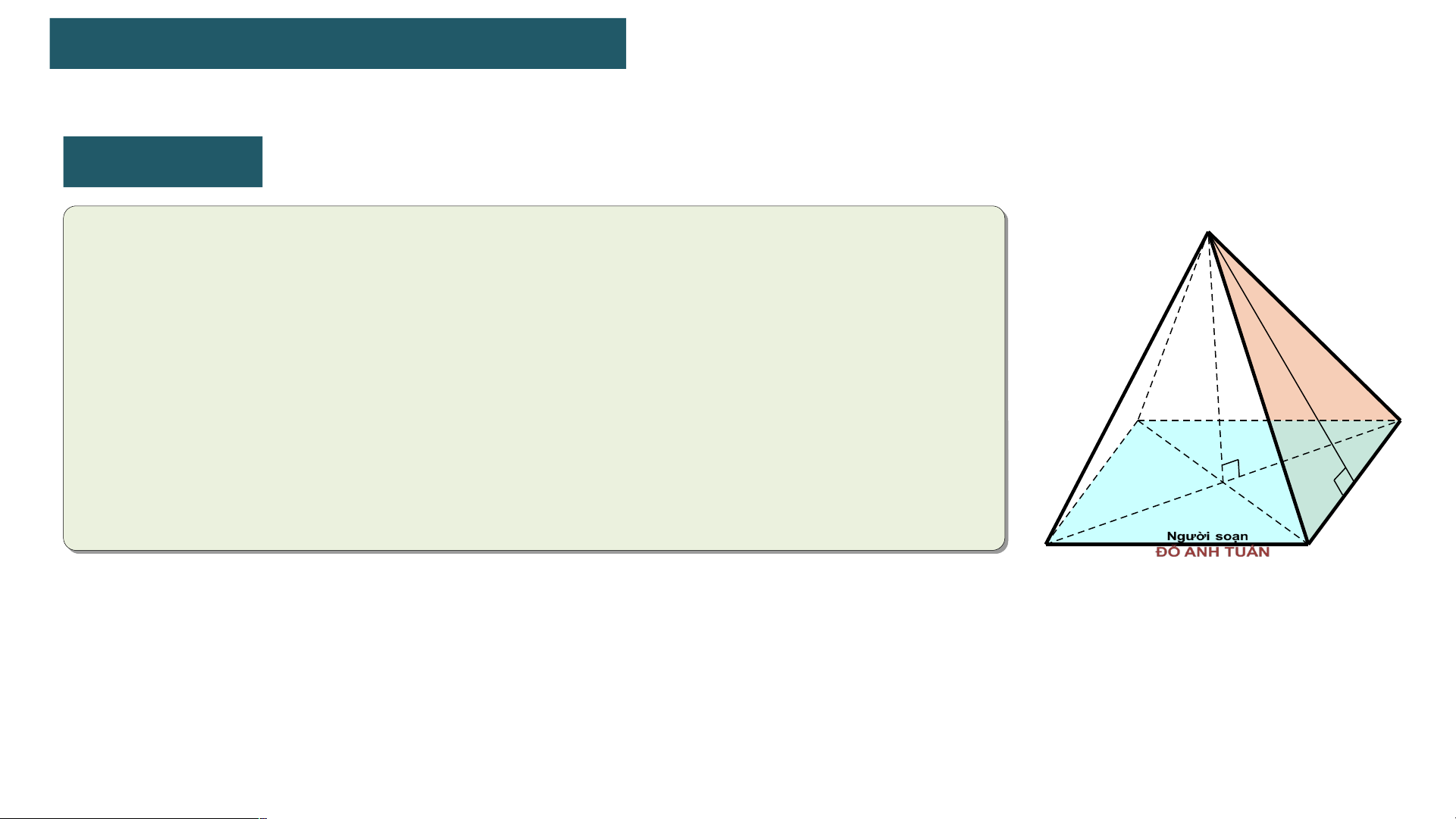
1 . HÌNH CHÓP TỨ GIÁC ĐỀU
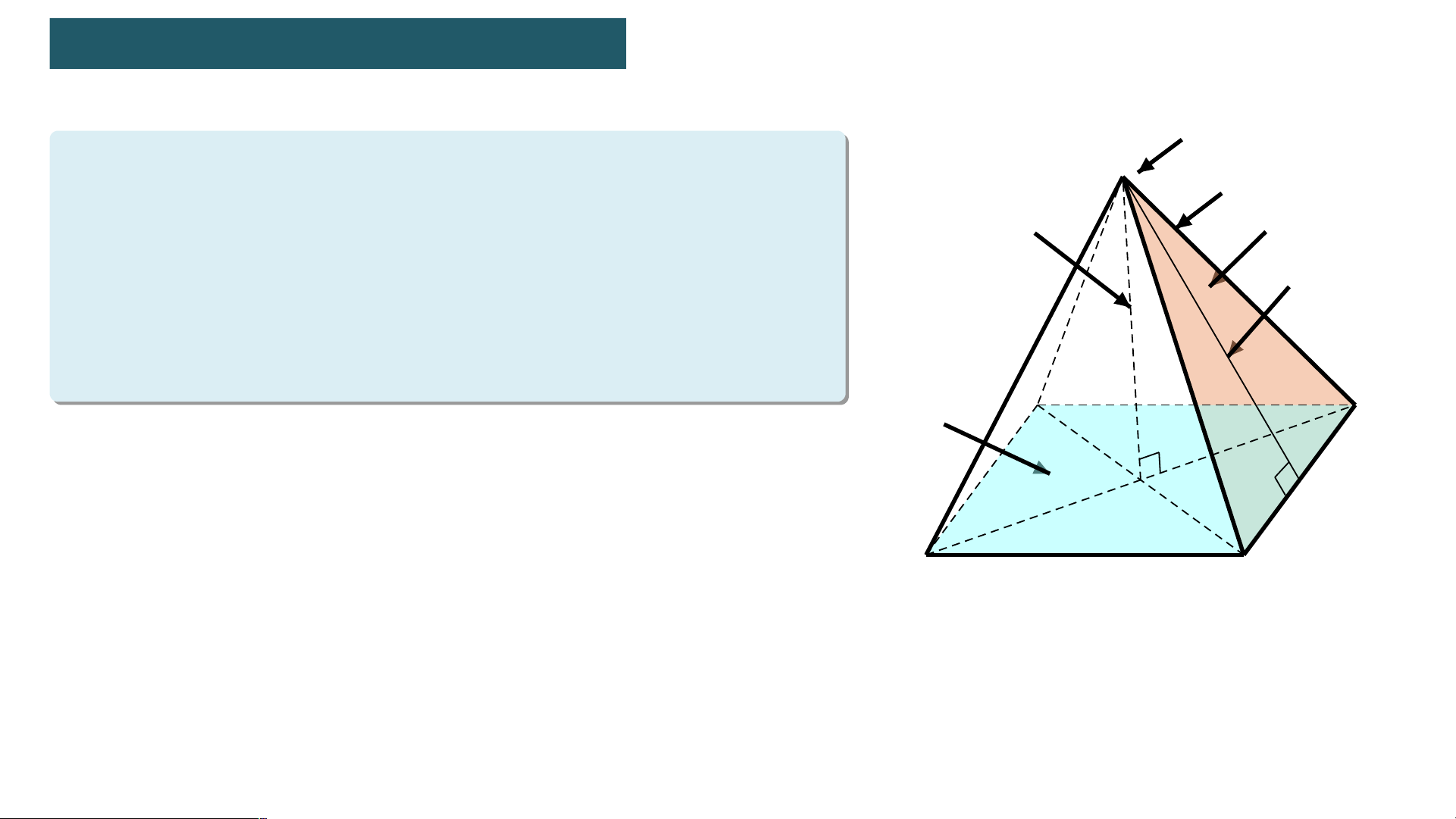
 Hình chóp tứ giác đều. Đỉnh
• Hình chóp S.ABCD trong Hình 10.18 có S Cạnh bên
đáy ABCD là hình vuông, các mặt bên Đường cao Mặt bên
là những tam giác cân bằng nhau, có Trung đoạn
chung đỉnh. Ta gọi S.ABCD là hình chóp tứ giác đều . A Mặt đáy D H O B C Hình 10.18
1 . HÌNH CHÓP TỨ GIÁC ĐỀU
 Hình chóp tứ giác đều.
Quan sát hình 10.18 để kể tên đỉnh, các cạnh bên Đỉnh S Cạnh bên - Đỉnh: S Đường cao Mặt bên Trung đoạn
- Cạnh bên: SD, SC, SA, SB A Mặt đáy D H O B C Hình 10.18
1 . HÌNH CHÓP TỨ GIÁC ĐỀU
 Hình chóp tứ giác đều.
Quan sát hình 10.18. Gọi tên đường cao, trung đoạn của hình chóp. Đỉnh S Cạnh bên Đường - Đường cao: SO cao Mặt bên Trung đoạn - Trung đoạn: SH A Mặt đáy D H O B C Hình 10.18
1 . HÌNH CHÓP TỨ GIÁC ĐỀU
 Hình chóp tứ giác đều.
Quan sát hình 10.18. Gọi tên các mặt bên và mặt đáy của hình chóp. Đỉnh S Cạnh bên Đường
- Mặt bên: SCD, SAB, SBC, SAD cao Mặt bên Trung đoạn - Mặt đáy: ABCD A Mặt đáy D H O B C Hình 10.18
1 . HÌNH CHÓP TỨ GIÁC ĐỀU
 Hình chóp tứ giác đều. Nhận xét : S
Hình chóp tứ giác đều có :
• Mặt đáy là hình vuông, các mặt bên là các tam
giác cân bằng nhau có chung đỉnh.
• Chân đường cao kẻ từ đỉnh tới mặt đáy là A D
điểm cách đều các đỉnh của mặt đáy (giao điểm hai đường chéo) H O B C
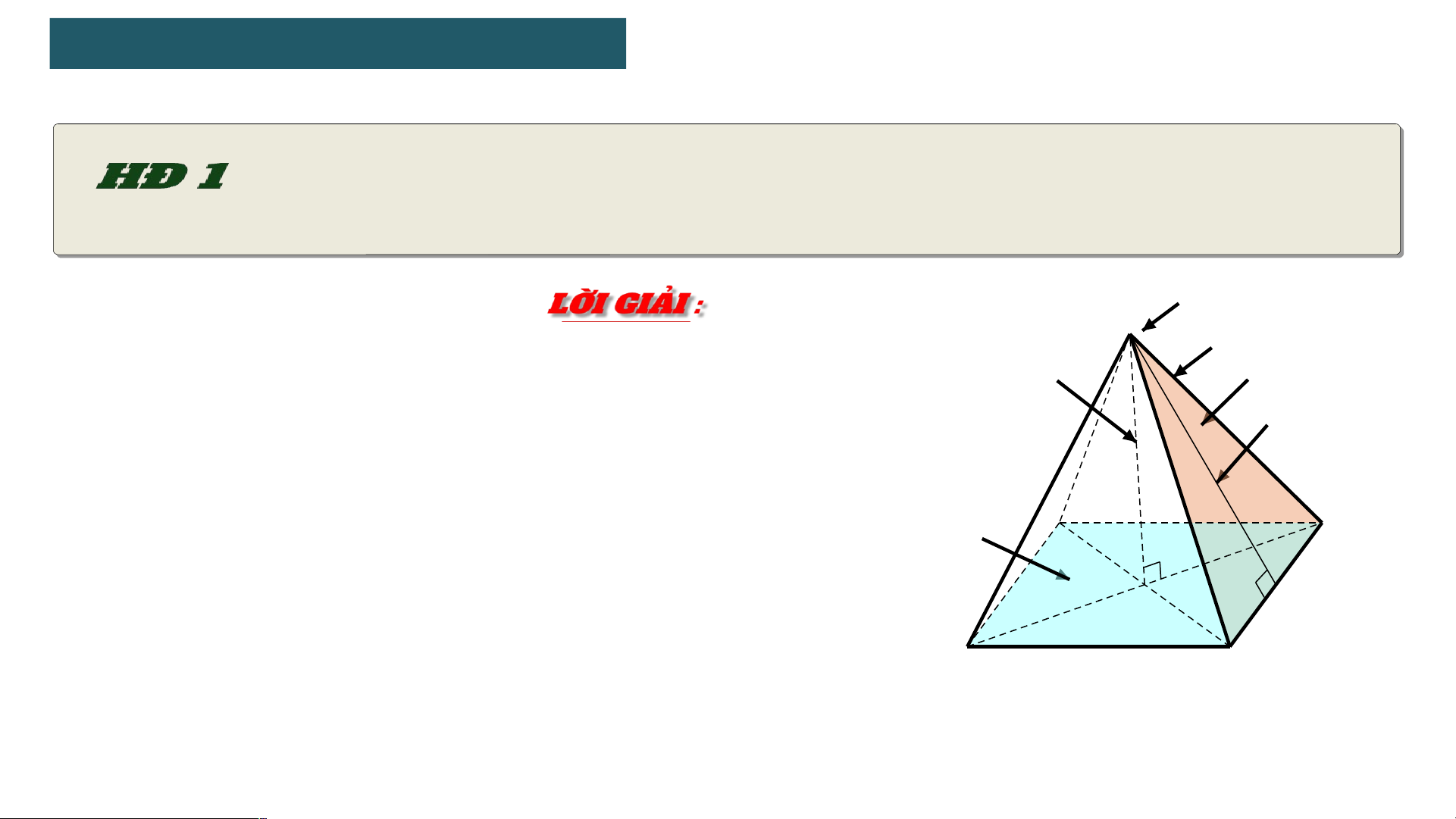
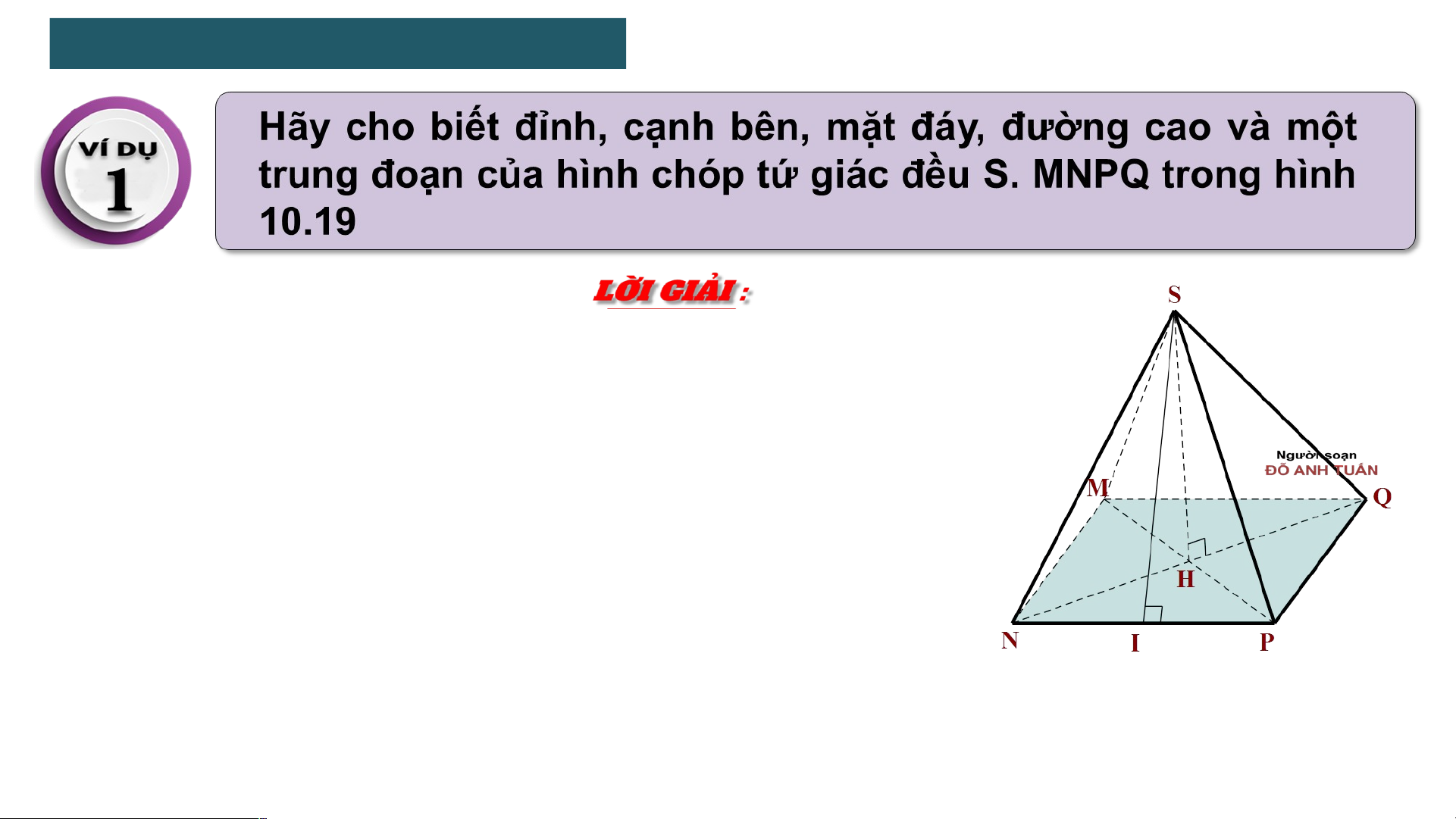
1 . HÌNH CHÓP TỨ GIÁC ĐỀU  Đỉnh : S
• Các cạnh bên : SM, SN, SP, SQ
• Các mặt bên là các tam giác cân bằng nhau SMN, SNP, SPO, SOM
• Mặt đáy là hình vuông MNPQ • Đường cao SH
• Trung đoạn SI
1 . HÌNH CHÓP TỨ GIÁC ĐỀU Thực hành
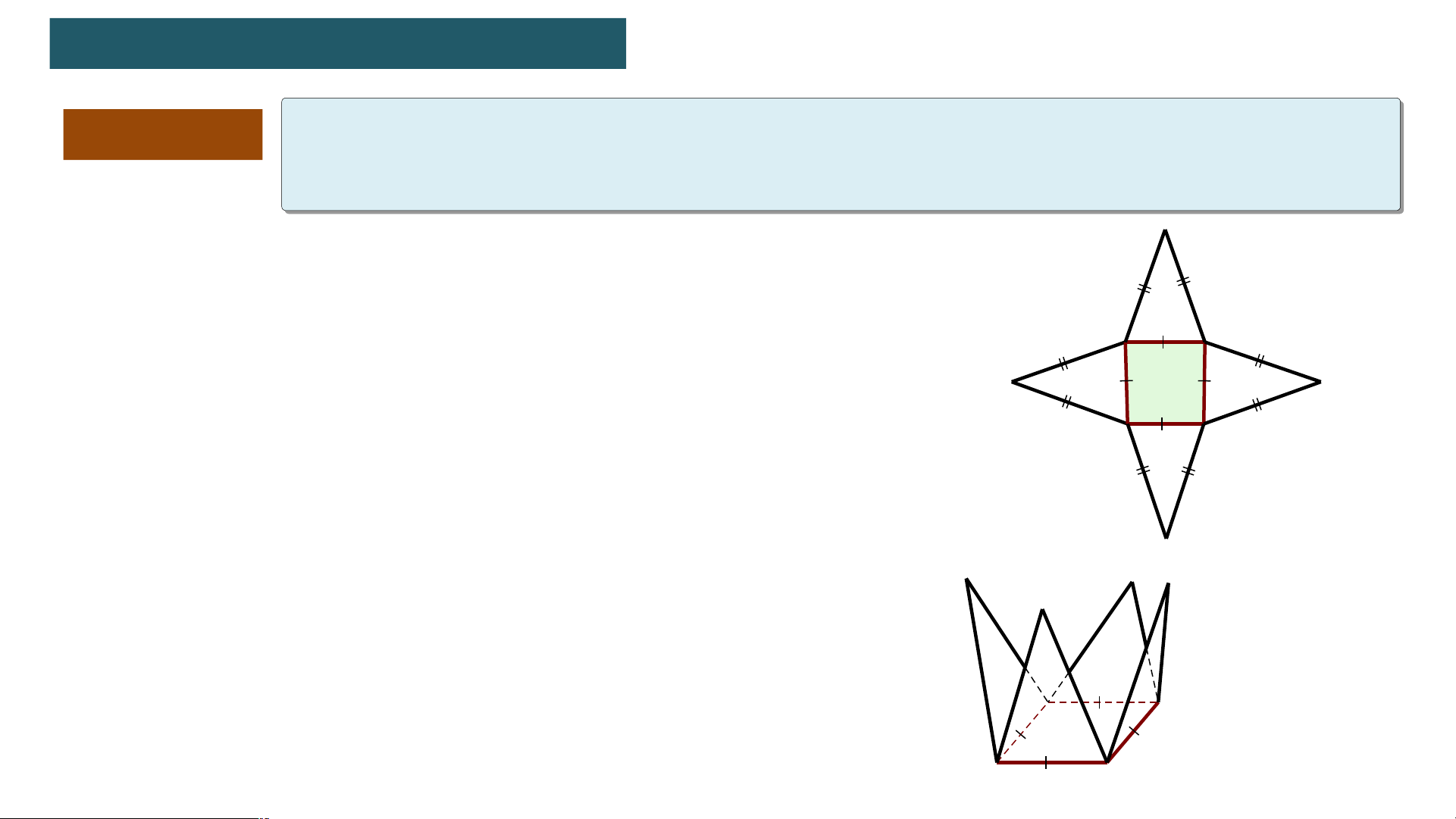
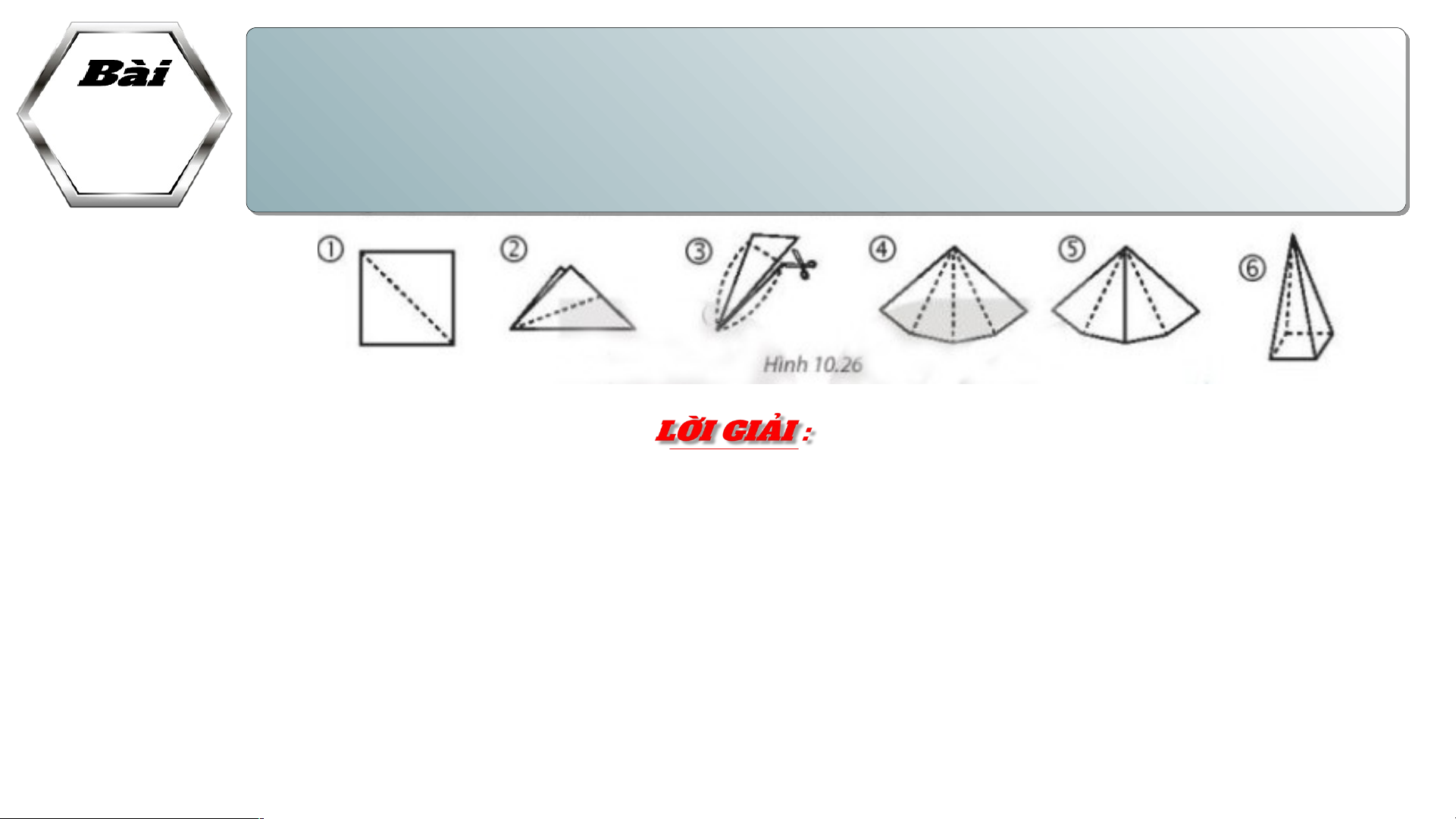
Cắt và gấp miếng bìa thành hình chóp tam tứ giác đều theo hướng dẫn sau :
Bước 1 : Vẽ hình khai triển theo mẫu và cắt theo viền ( Hình 10.20)
Bước 2 : Gấp theo các đường màu cam, ta được
hình chóp tam giác đều (Hình 10.21) Hình 10.20 Hình 10.21
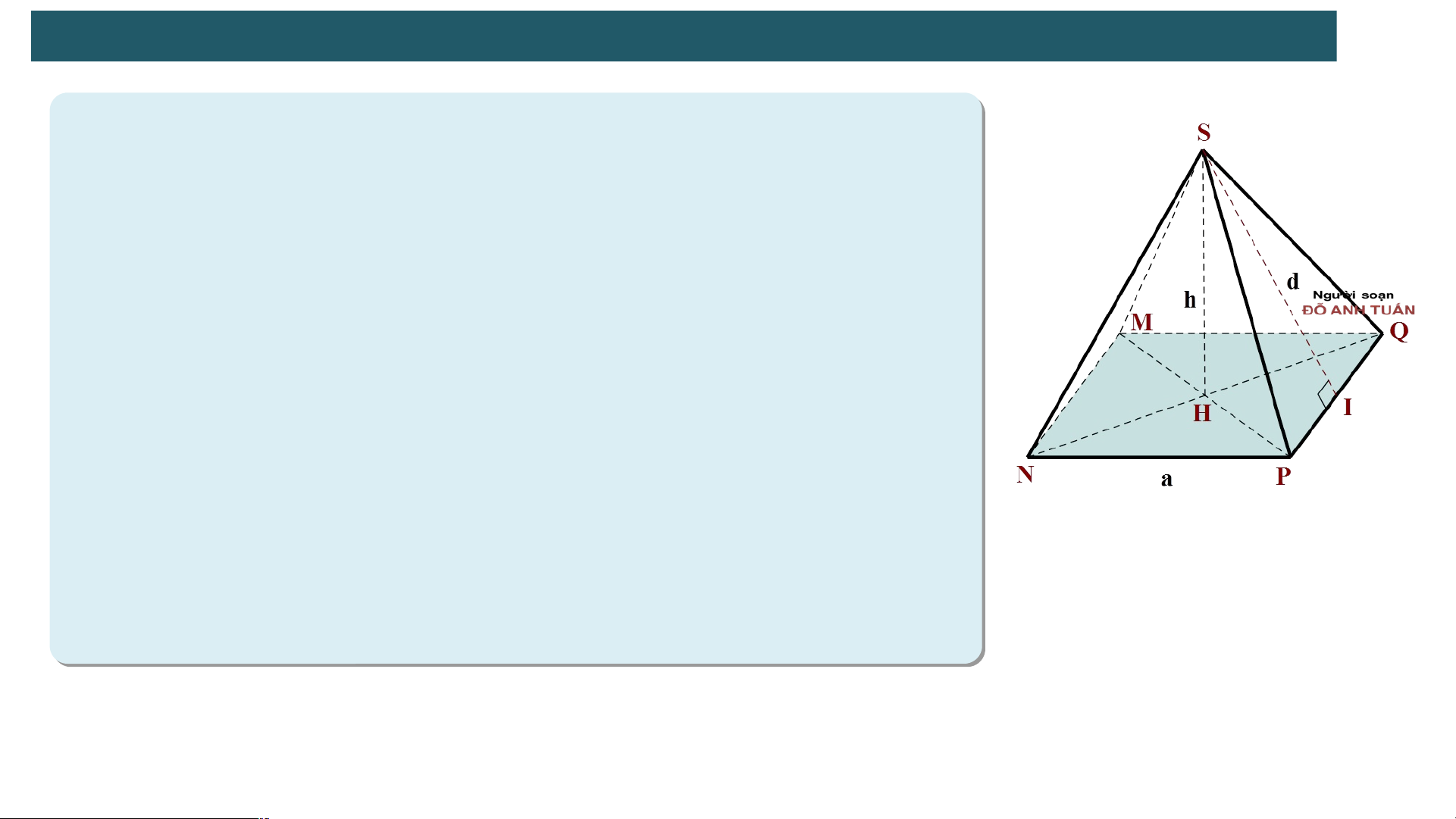
2 . DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH CỦA HÌNH CHÓP TỨ GIÁC ĐỀU
• Diện tích xung quanh của hình chóp tứ giác
đều bằng tích của nửa chu vi đáy với trung đoạn :
Trong đó p là nửa chu vi đáy d là trung đoạn
• Thể tích của hình chóp tứ giác đều bằng 1/3
tích của diện tích đáy với chiều cao của nó :
Trong đó S là diện tích đáy
h là chiều cao hình chóp.
2 . DIỆN TÍCH XUNG QUANH VÀ THỂ TÍCH CỦA HÌNH CHÓP TỨ GIÁC ĐỀU
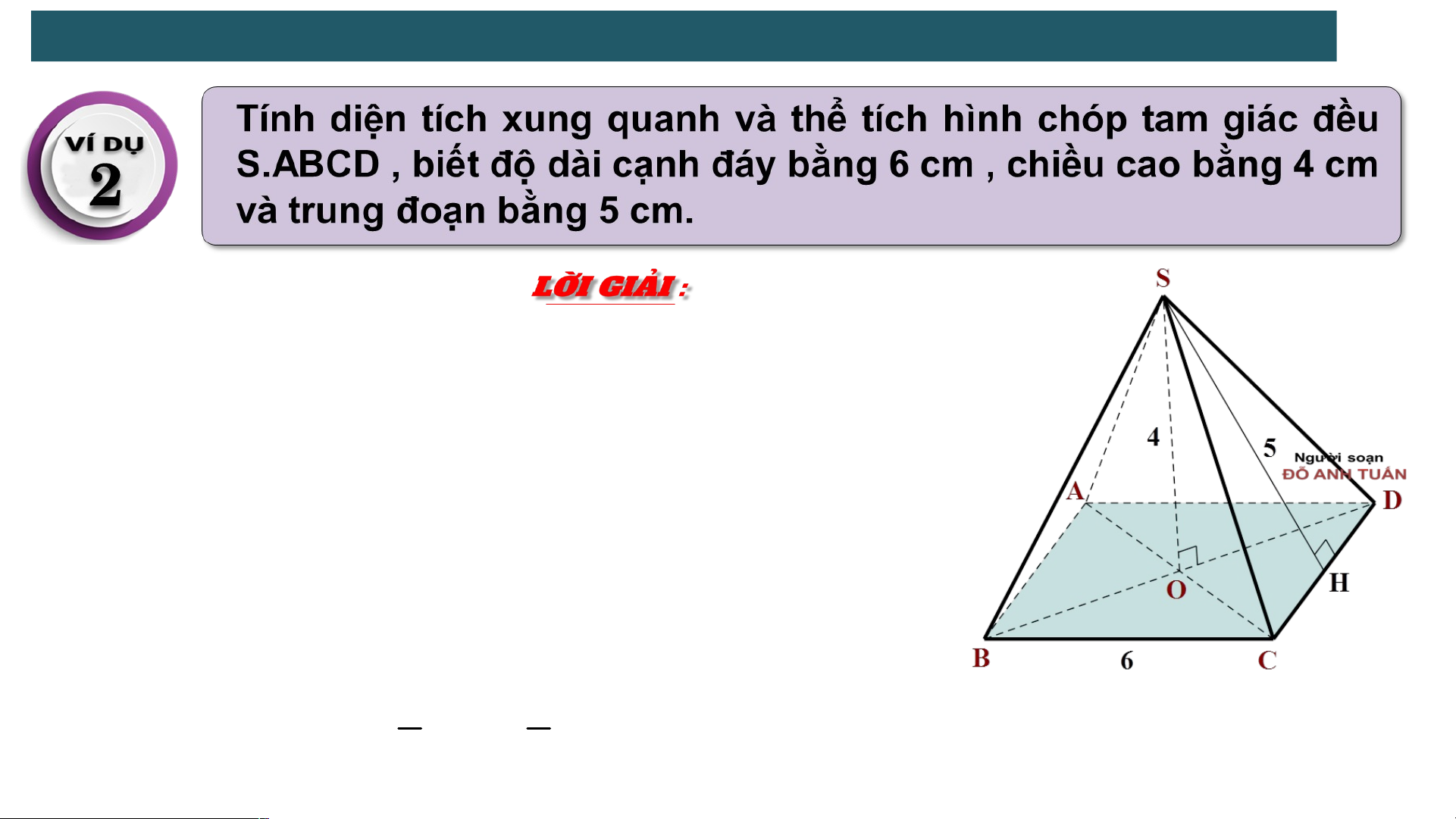
 Nửa chu vi đáy ABCD là : (4 . 6) : 2 = 12 (cm)
Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là : 2 S  . p d 12.  5 6  0 (cm ) xq
Diện tích đáy ABCD là : S = 62 = 36 (cm2)
Thể tích của hình chóp tứ giác đều S.ABCD là : 1 1 3
V  S.h  .36.4 4  ( 8 cm ) 3 3
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
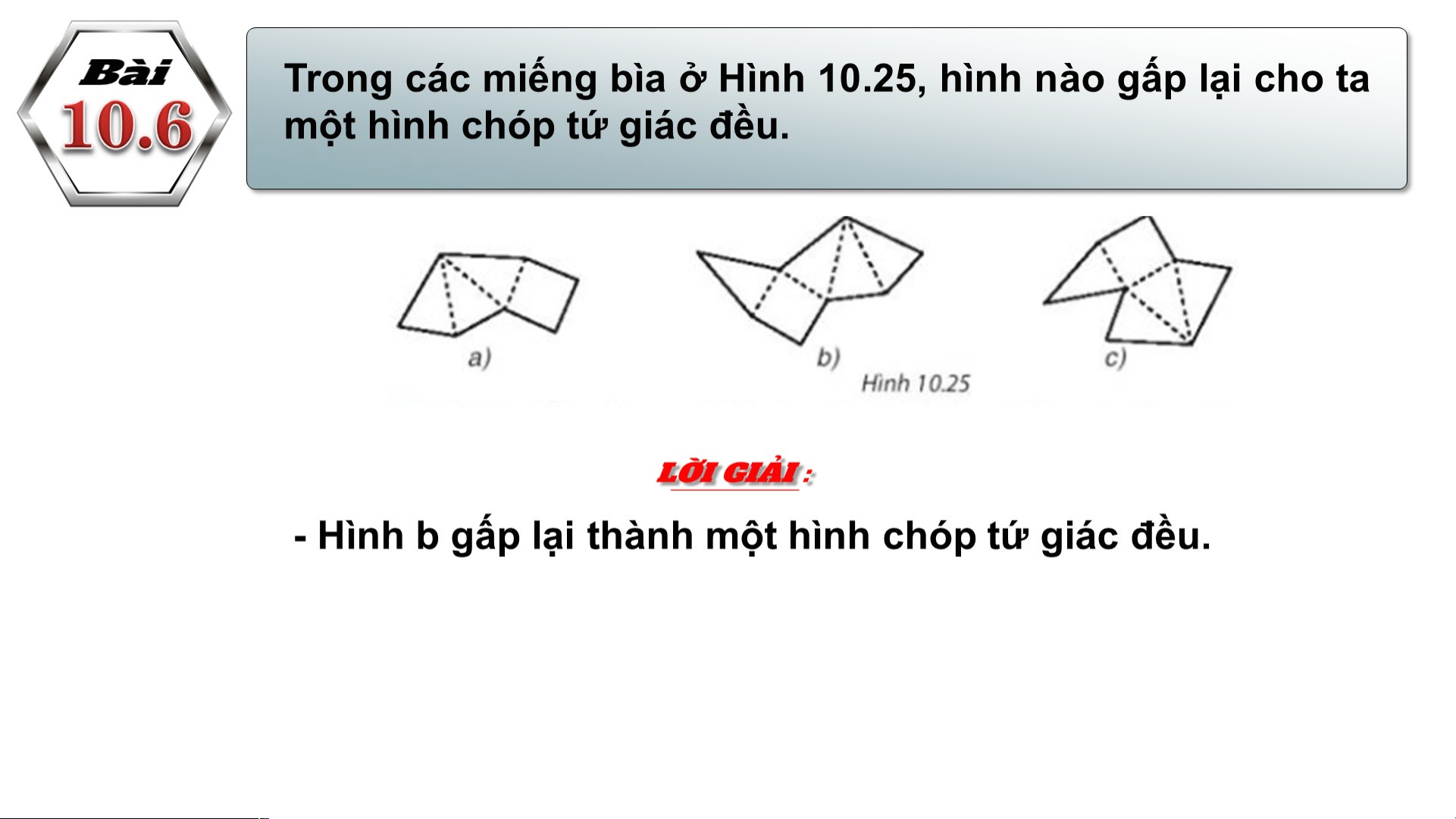
Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao
tác như hình 10.26 để có thể ghép được các mặt bên của
10.7 hình chóp tứ giác đều.
- Thực hiện theo yêu cầu của đề bài
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và không có tên người soạn )
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23