Giáo án điện tử Toán 8 Bài 4 Cánh diều: Tính chất đường phân giác của tam giác
Bài giảng PowerPoint Toán 8 Bài 4 Cánh diều: Tính chất đường phân giác của tam giác hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 8. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 8
Môn: Toán 8
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
CHÀO MỪNG CÁC EM
ĐÃ ĐẾN VỚI BUỔI HỌC! PHẠM THỊ LOAN
GV : TRƯỜNG THCS TRẦN PHÚ KHỞI Đ I ỘNG
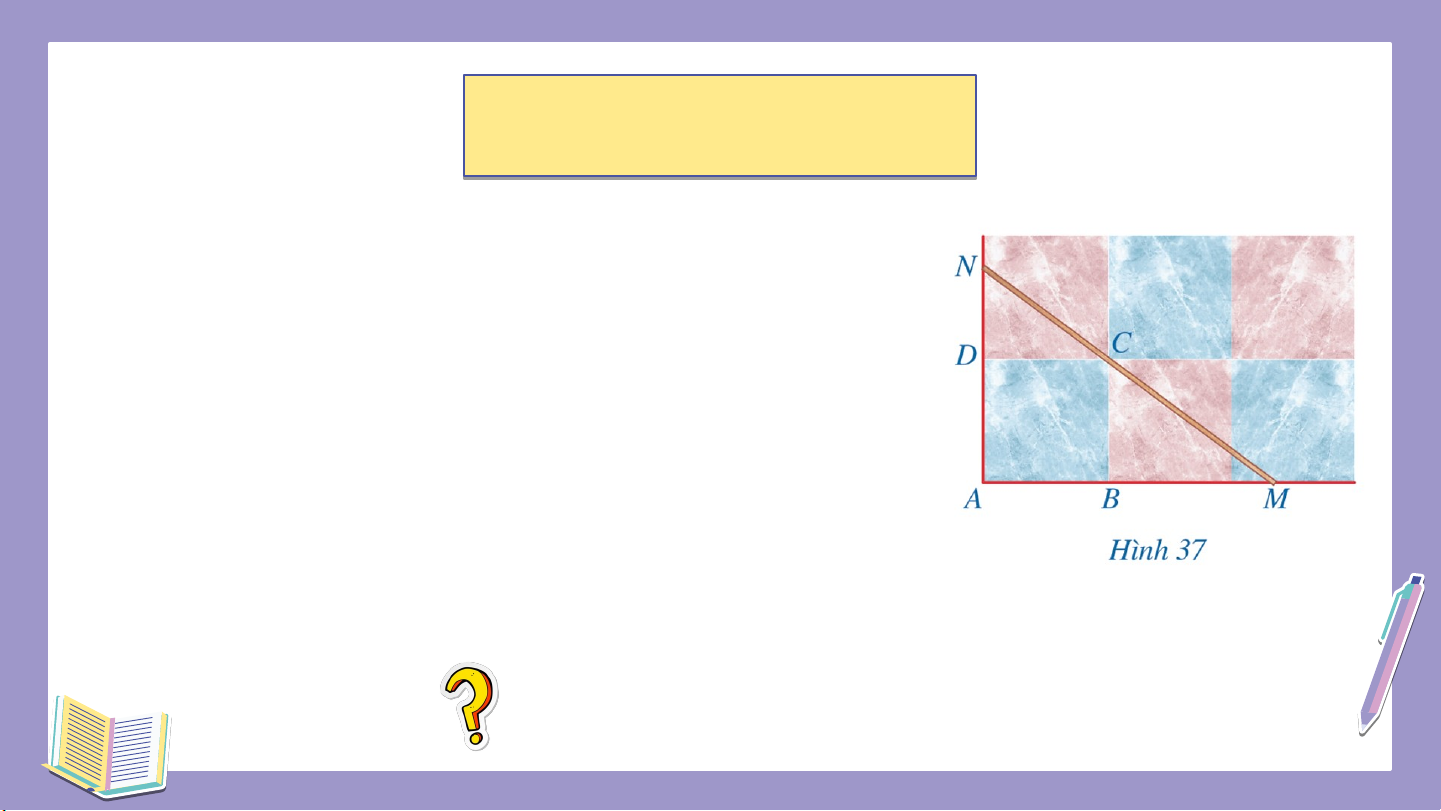
Hình 37 minh họa một phần sân nhà bạn Duy được
lát bởi các viên gạch hình vuông khít nhau, trong
đó các điểm là bốn đỉnh của một viên gạch. Bạn
Duy đặt một thước gỗ trên mặt sân sao cho thước
gỗ luôn đi qua điểm và cắt tia tại , cắt tia tại . Bạn
Duy nhận thấy ta luôn có tỉ lệ thức .
Tại sao ta luôn có tỉ lệ thức
BÀI 4. TÍNH CHẤT ĐƯỜNG
PHÂN GIÁC CỦA TAM GIÁC
HOẠT ĐỘNG NHÓM: Thảo luận cặp đôi hoàn
thành cột 1 và cột 2 trong bảng sau K (Know) W (Want) L (Learn) (Điều em biết) (Điều em muốn biết) (Điều em học được)
Hãy viết những điều Viết những điều em
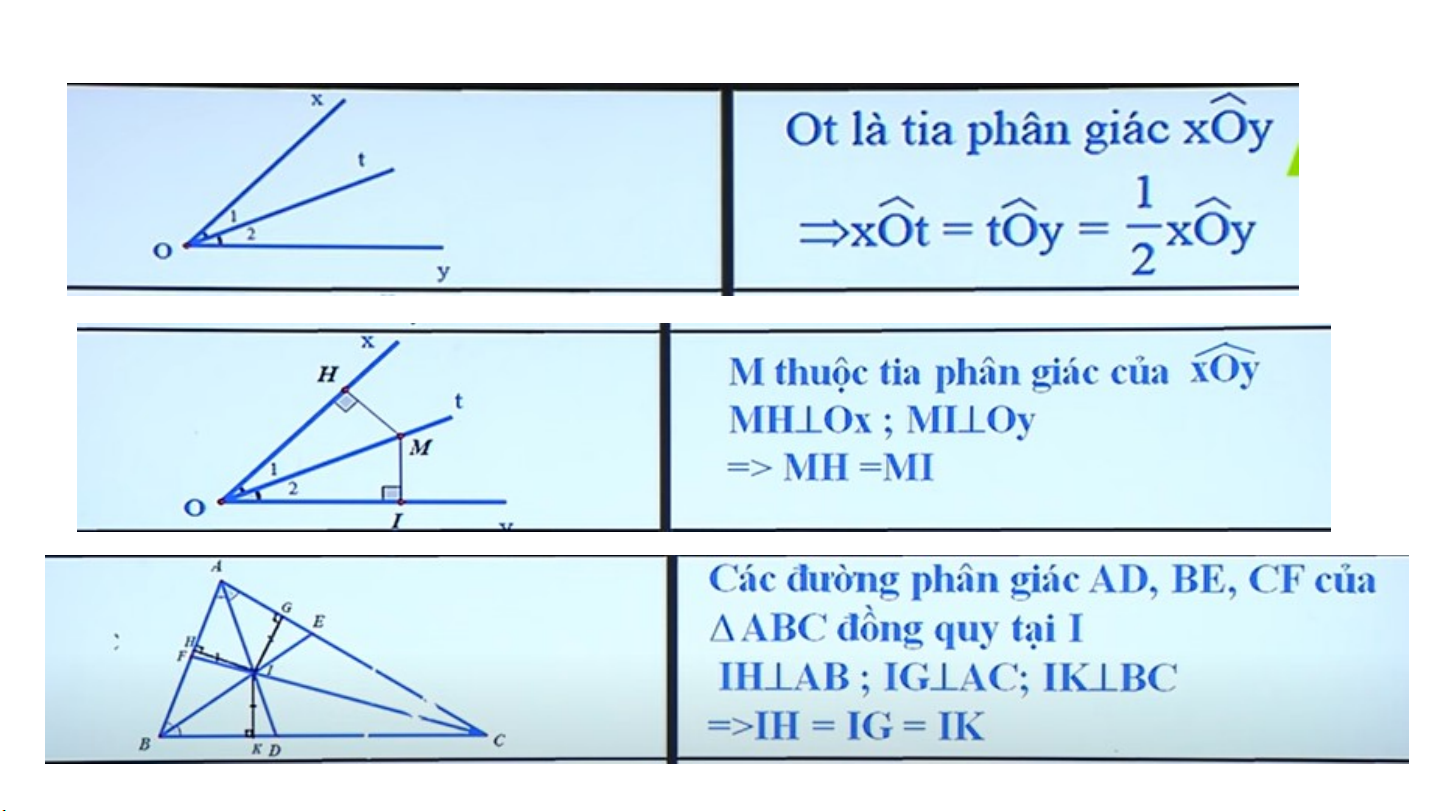
em đã biết về đường muốn biết trong bài học phân giác này HĐ 1 H
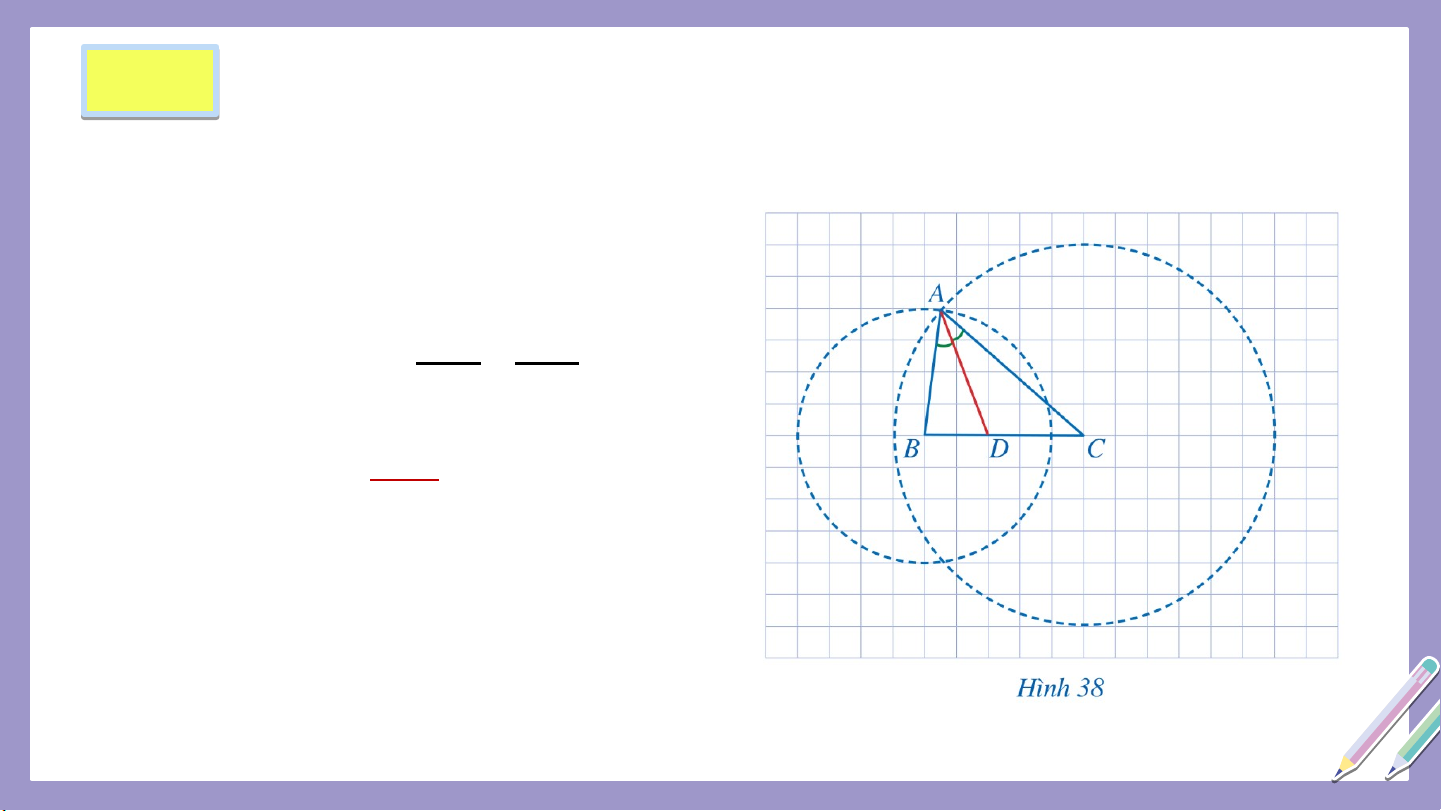
Trong Hình 38, tam giác có là đường phân giác của góc . Giả sử mỗi ô
vuông của lưới ô vuông có độ dài cạnh bằng 1 cm.
Tính độ dài các đoạn thẳng .
Tính độ dài các đoạn thẳng . 𝐷𝐵 𝐴𝐵 . So sánh các tỉ số
𝐷𝐶 = 𝐴𝐶 Giải Nhận xét Nh
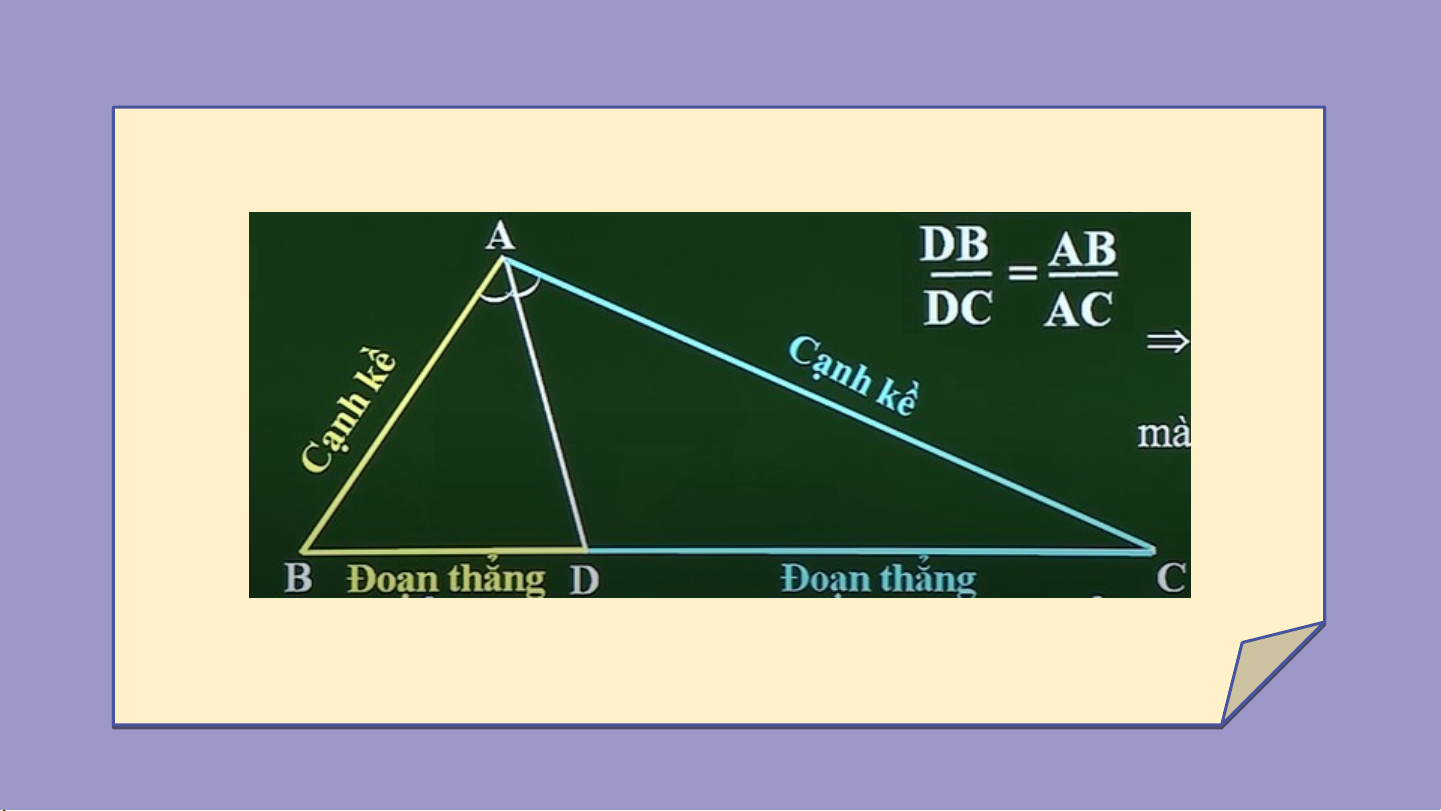
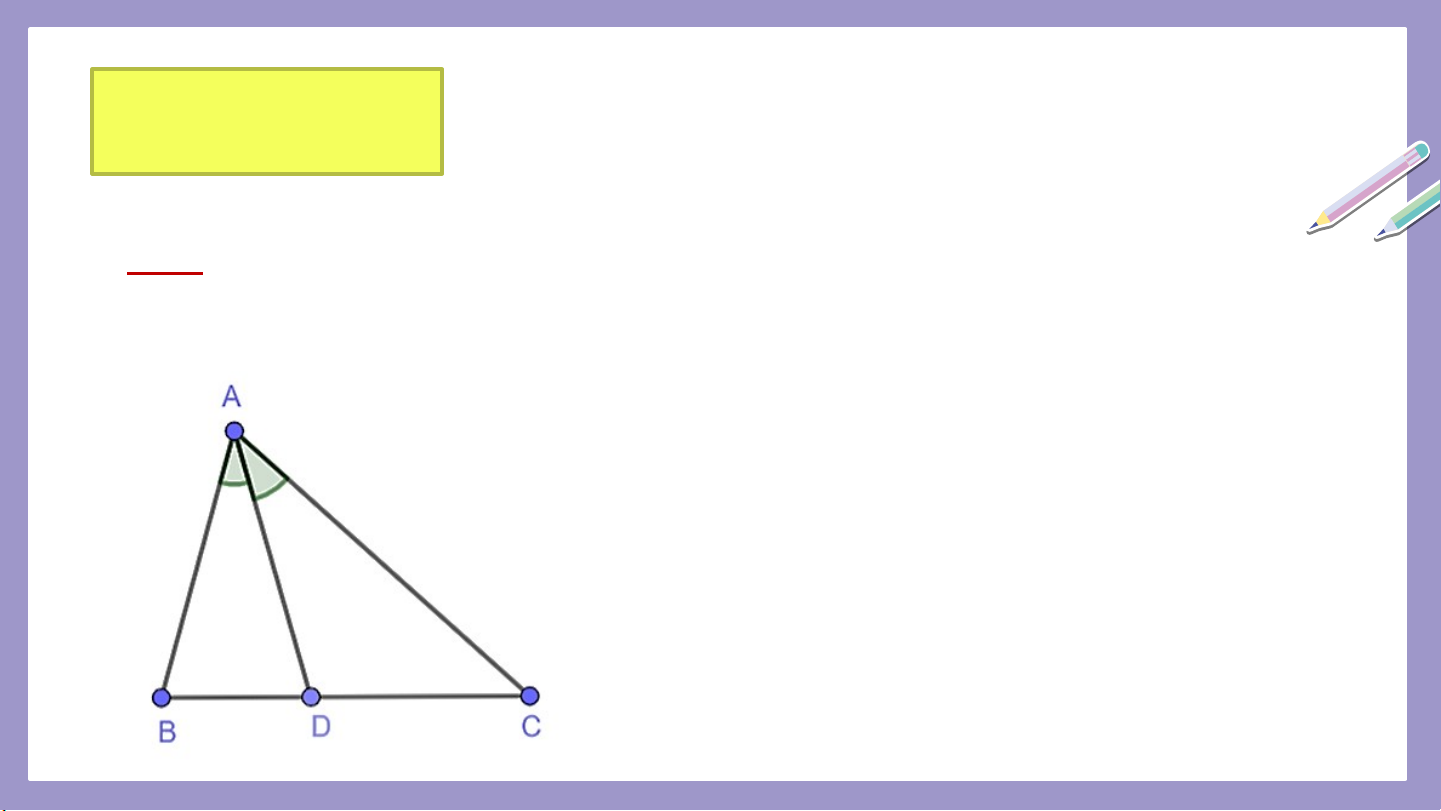
Trong , đường phân giác chia cạnh đối diện
thành hai đoạn thẳng tỉ lệ với hai cạnh kề .
Trong tam giác, đường phân giác của một góc chia
cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
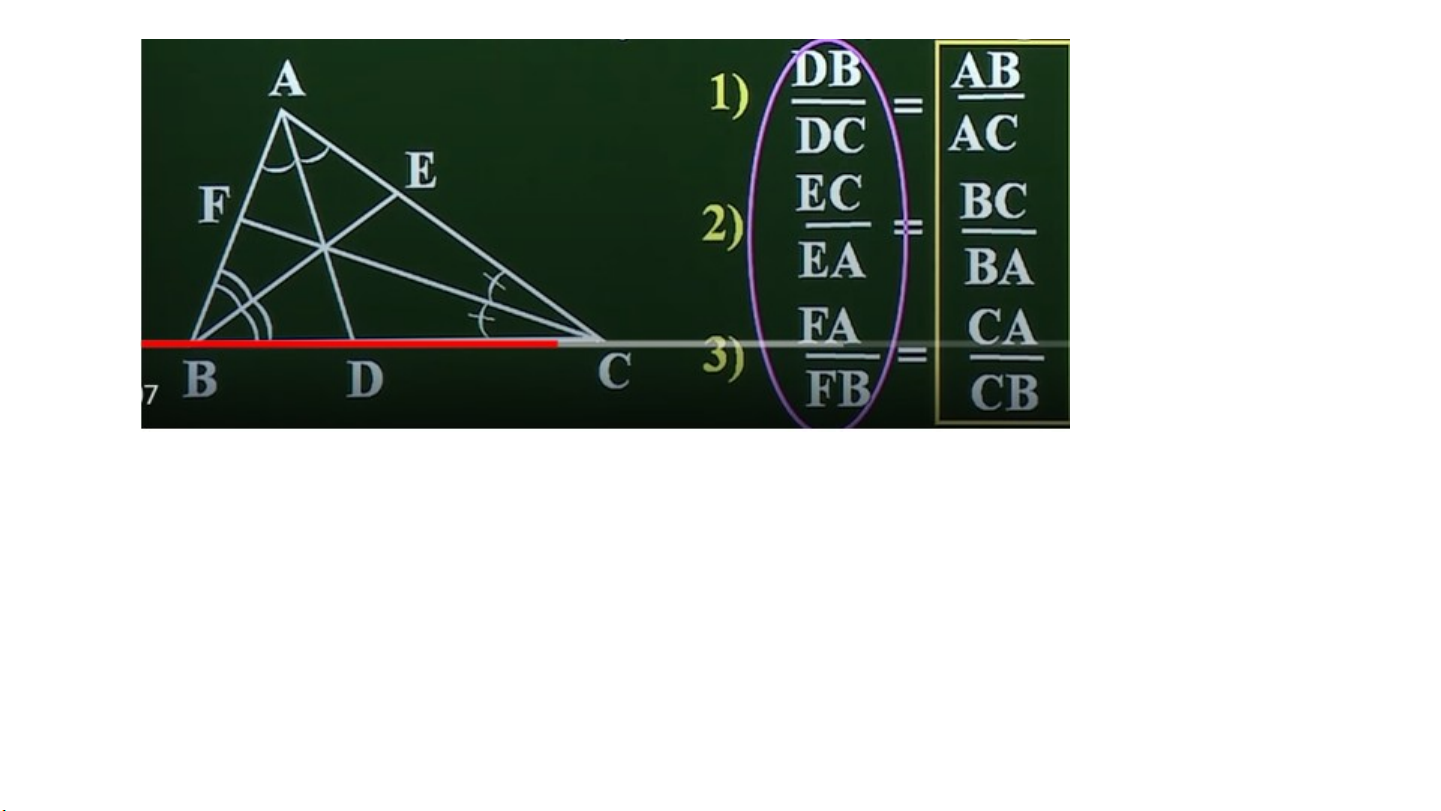
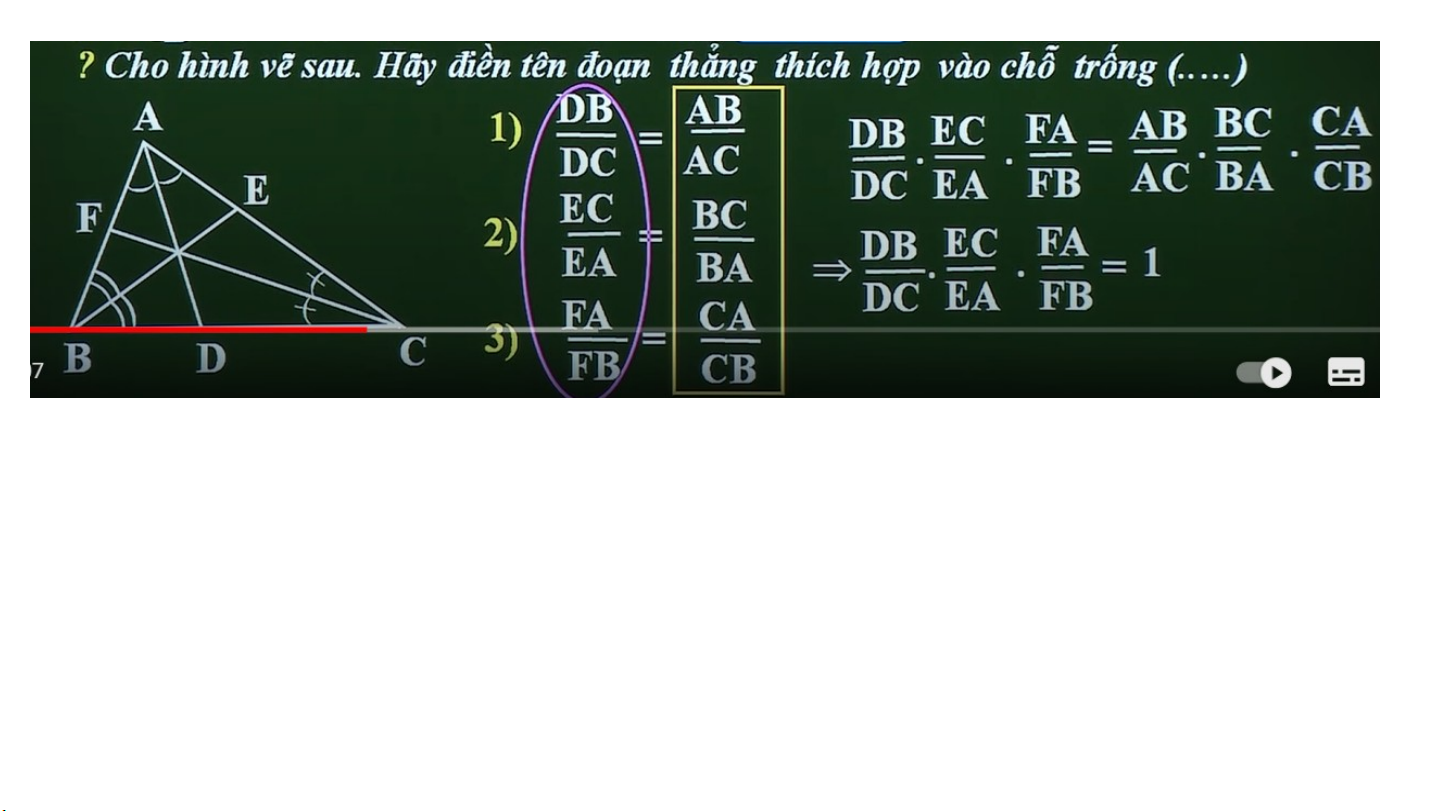
Cho hình vẽ sau , hãy điền tên đoạn thẳng thích hợp vào … 1) 2) 3)
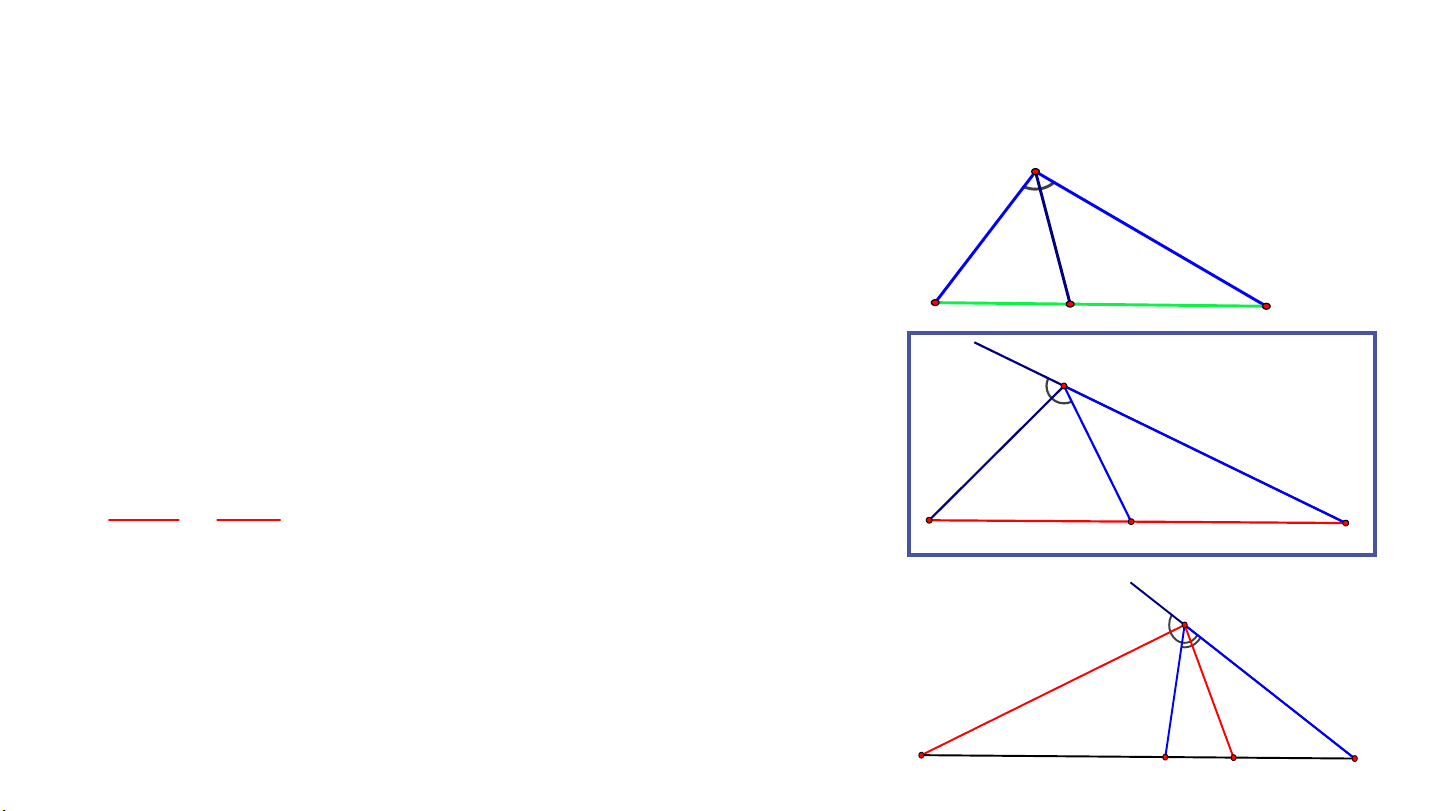
Định lí vẫn đúng đối với tia phân giác
của góc ngoài của tam giác. x 2 A 1 x D’ B C A y Trong hình trên ta có: B C (AB = AC)
TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC A 1. Định lí Hình 1
là tia phân giác của B C ⇒ D A Chú ý
* AD’ là phân giác ngoài của ABC D B ' B A ⇒ = (AB ≠ AC) D' B C C D' AC
* , có là phân giác góc trong, là phân giác góc ngoài A đỉnh : Hình 2 ⇒ D' B D C
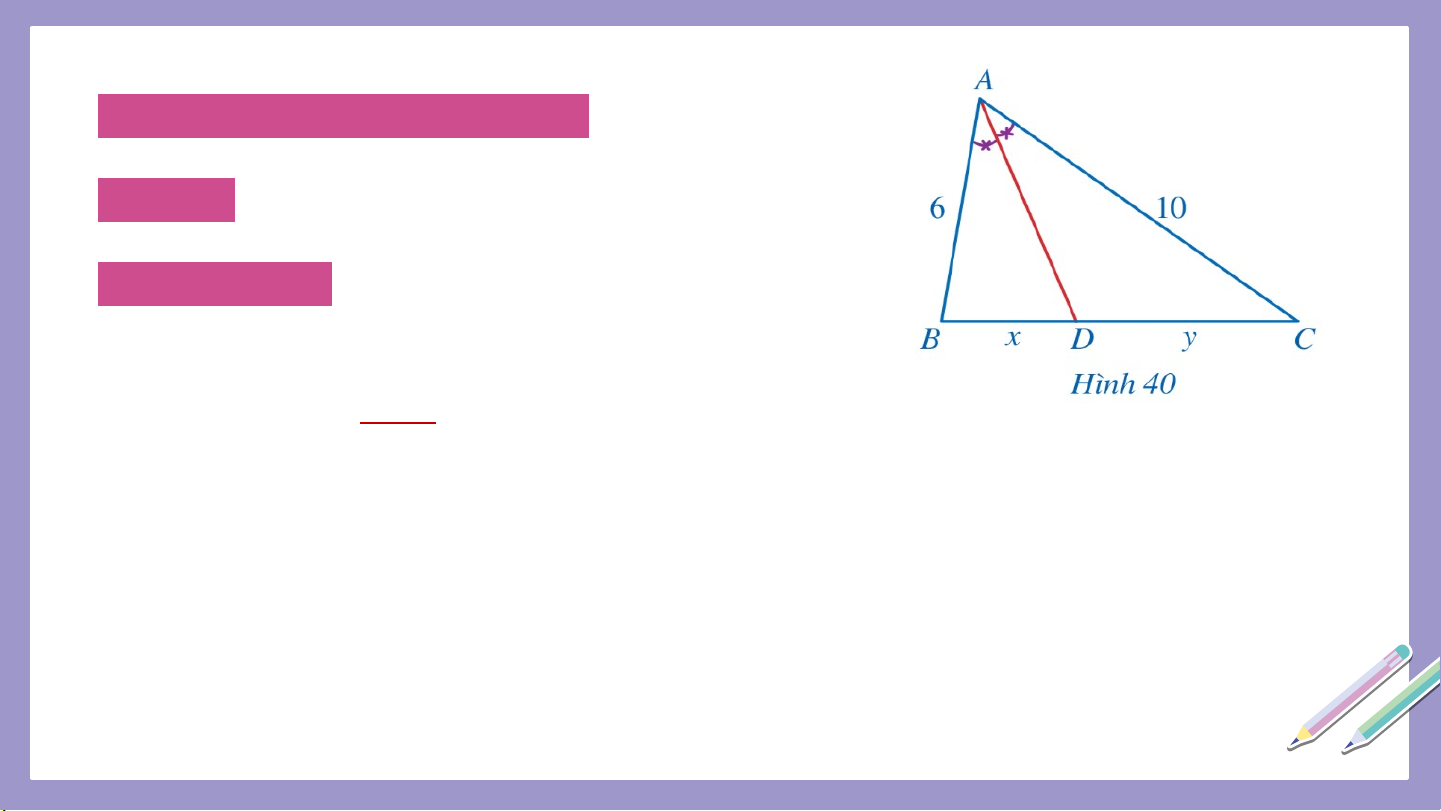
Ví dụ 1: Quan sát Hình 40. a) Tính b) Tính , biết Giải
a) Xét tam giác có là đường phân giác của góc nên (tính chất đường phân giác) Suy ra
Ví dụ 1: Quan sát Hình 40. a) Tính b) Tính , biết Giải b) Ta có suy ra
Theo tính chất của dãy tỉ số bằng nhau ta có: Suy ra
Ví dụ 2: Cho tam giác có là một đường phân giác và là
giao điểm ba đường phân giác của tam giác đó (Hình 41). Tính và Giải
Xét tam giác có là đường phân giác của góc nên Suy ra , do đó
Theo tính chất của dãy tỉ số bằng nhau ta có: .
Xét tam giác có là đường phân giác của góc nên . Suy ra Luyện tập 1
Giải bài toán nêu trong phần mở đầu. Giải
• Vì là hình vuông nên là tia phân giác của
là đường phân giác trong .
• Áp dụng tính chất đường phân giác trong tam giác ta có:
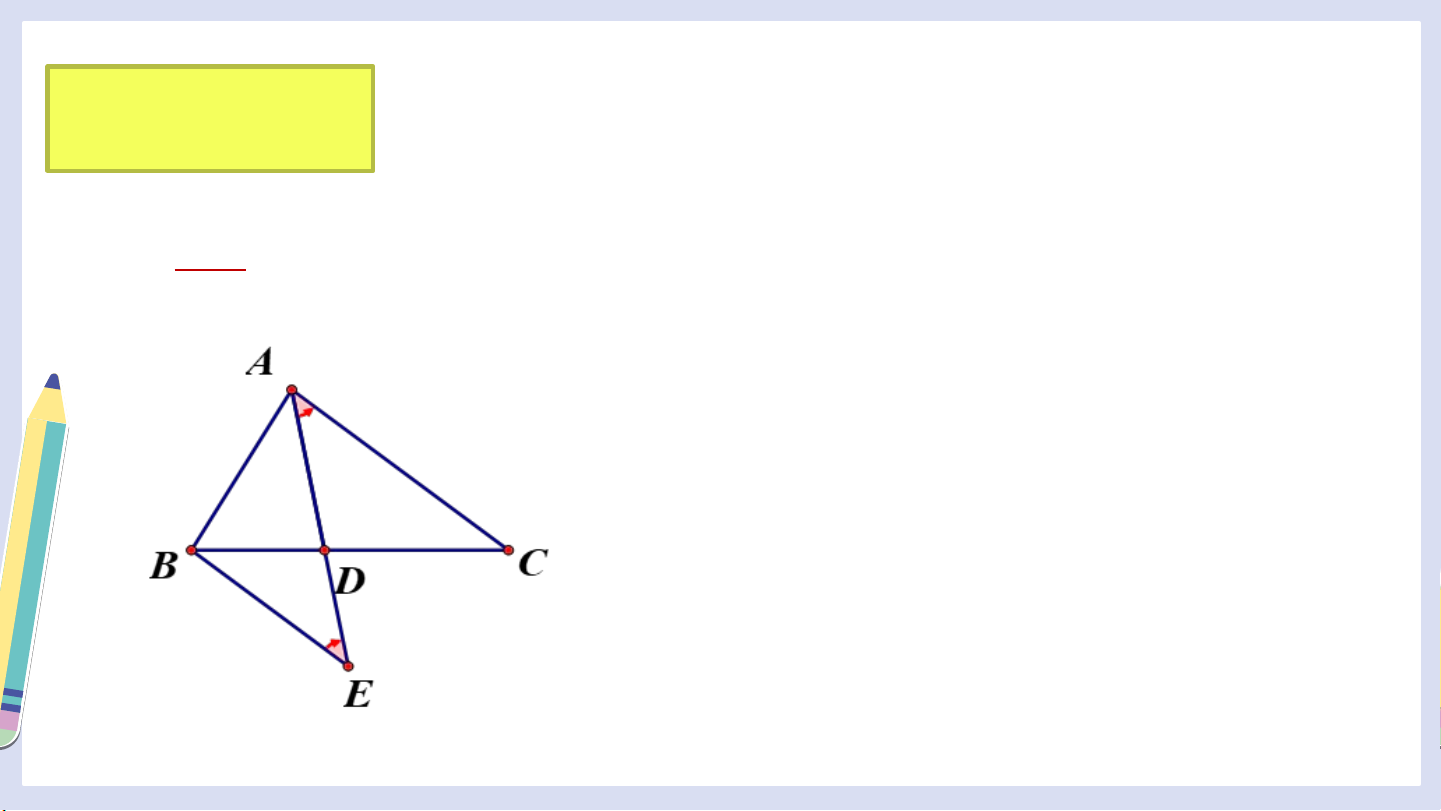
Cho tam giác có là đường phân giác. Chứng Luyện tập 2 minh . Giải
Xét có là đường phân giác Mà
Ví dụ 3: Cho tam giác có là đường trung tuyến. Gọi lần lượt là đường phân giác của các tam
giác và . Giả sử cắt tại . Chứng minh và là trung điểm của . Giải
Xét tam giác có là đường phân giác của góc nên
Xét tam giác có là đường phân giác của góc nên Mà nên Suy ra
Vì thế (định lí Thalès đảo trong tam giác ).
Áp dụng hệ quả của định lí Thalès trong hai tam giác và , ta có: và . Suy ra
Mà nên . Do đó là trung điểm của .
Cho tam giác , điểm thuộc cạnh sao cho .
Luyện tập 4 Chứng minh là tia phân giác của góc . Giải Lấy thuộc sao cho
Theo hệ quả định lí Thalès, có: Mà nên Khi đó cân tại Mà nên
Vậy là phân giác của góc . HƯỚNG D ẪN VỀ NHÀ
Ôn tập kiến thức đã học.
Hoàn thành bài tập trong 1,2,3 SÁCH GIÁO KHOA. CẢM ƠN CÁC EM ĐÃ THEO DÕI BÀI HỌC!
Document Outline
- Slide 1
- KHỞI ĐỘNG
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Nhận xét
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- HƯỚNG DẪN VỀ NHÀ
- Slide 25