Trường THCS …..
Chào mừng quý thầy cô đến dự giờ thăm lớp! LỚP: 8 GV: …………………….
THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU GIÁO HỌC VIÊN SINH  SGK  SGK  Kế hoạch bài dạy  Thước thẳng  Thước thẳng
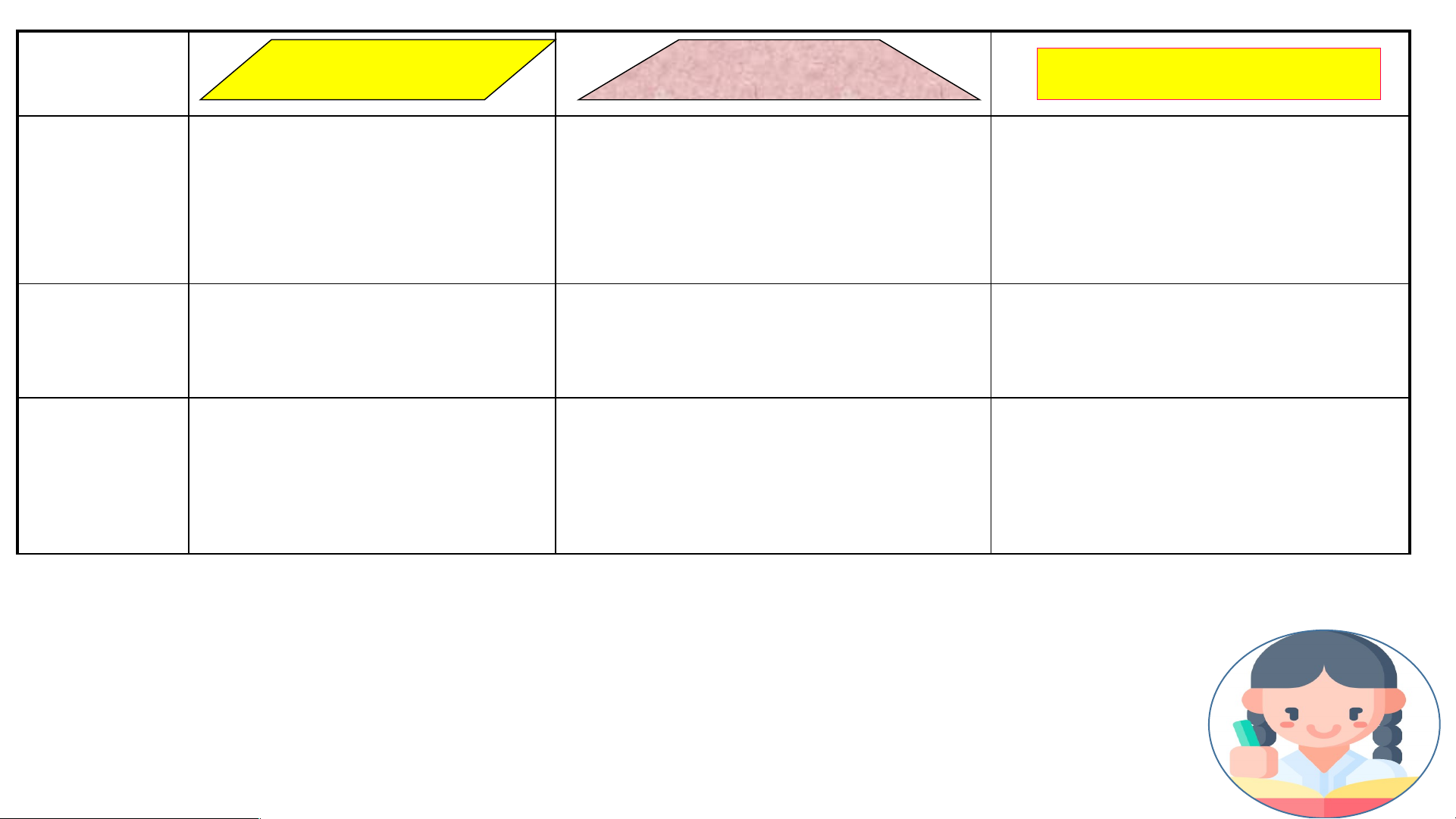
 Bảng phụ (máy chiếu) CHÚ THÍCH HĐ: HĐ: HĐ: CÁ NHÂN CẶP ĐÔI NHÓM 01 KHỞI ĐỘNG Hình bình hành Hình thang cân Hình chữ nhật Cạnh Các cạnh Hai cạnh bên ..... b.ằng nhau đố so i n ... g ..... son..g... .. và... .. b ... ằn ..... g n.. h.au
Các cạnh đối song song và bằng nhau Góc Các góc ..... H ... ai ..... gó .. c ... k .. ề ..... m ... ột .. đ... á .. y đối b .. ằn..g..... n ... ha .. u ................ bằng nhau.
Bốn góc bằng nhau và bằng 900 Đường Hai đường chéo Hai đường chéo
Hai đường chéo bằng nhau và chéo ...... cắ ..... t ..... nh .... a ..... u t ..... ại ...... tr ..... un..... g điểm ........ bằ .. n ... g .. n... h .. a ... u ....
cắt nhau tại trung điểm của mỗi của mỗi đường đường
Hãy nêu các tính chất của hình bình hành và hình thang
cân, hình chữ nhật bằng cách điền vào bảng trên?
BÀI 5. HÌNH CHỮ NHẬT (Tiết 2) LỚP ： 8 GV: …………………… HÌNH CHỮ NHẬT (tiết 2)
III DẤU HIỆU NHẬN BIẾT 02 HÌNH THÀNH KIẾN THỨC
III. DẤU HIỆU NHẬN BIẾT
Hoạt động 3 trang 110 SGK
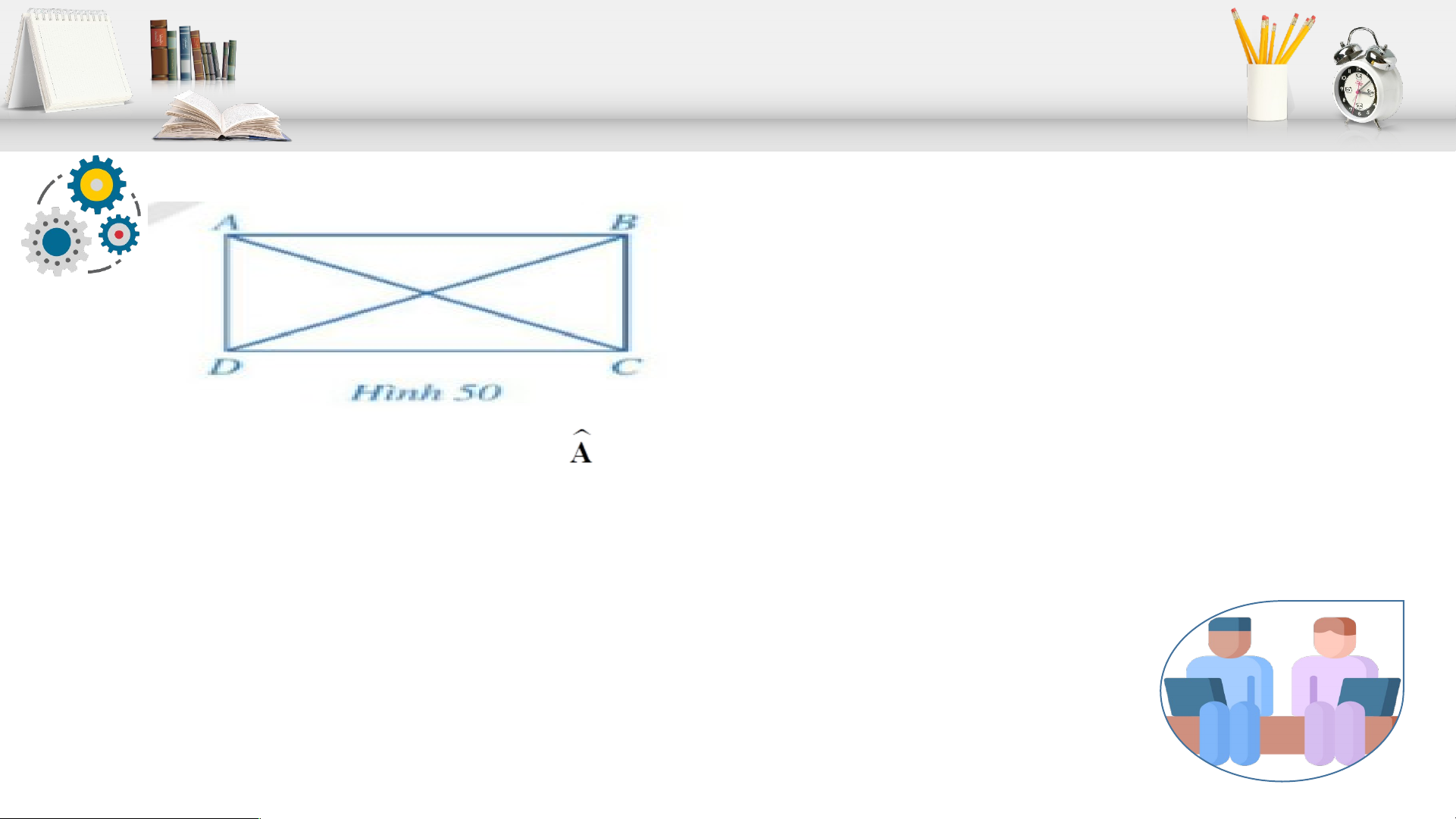
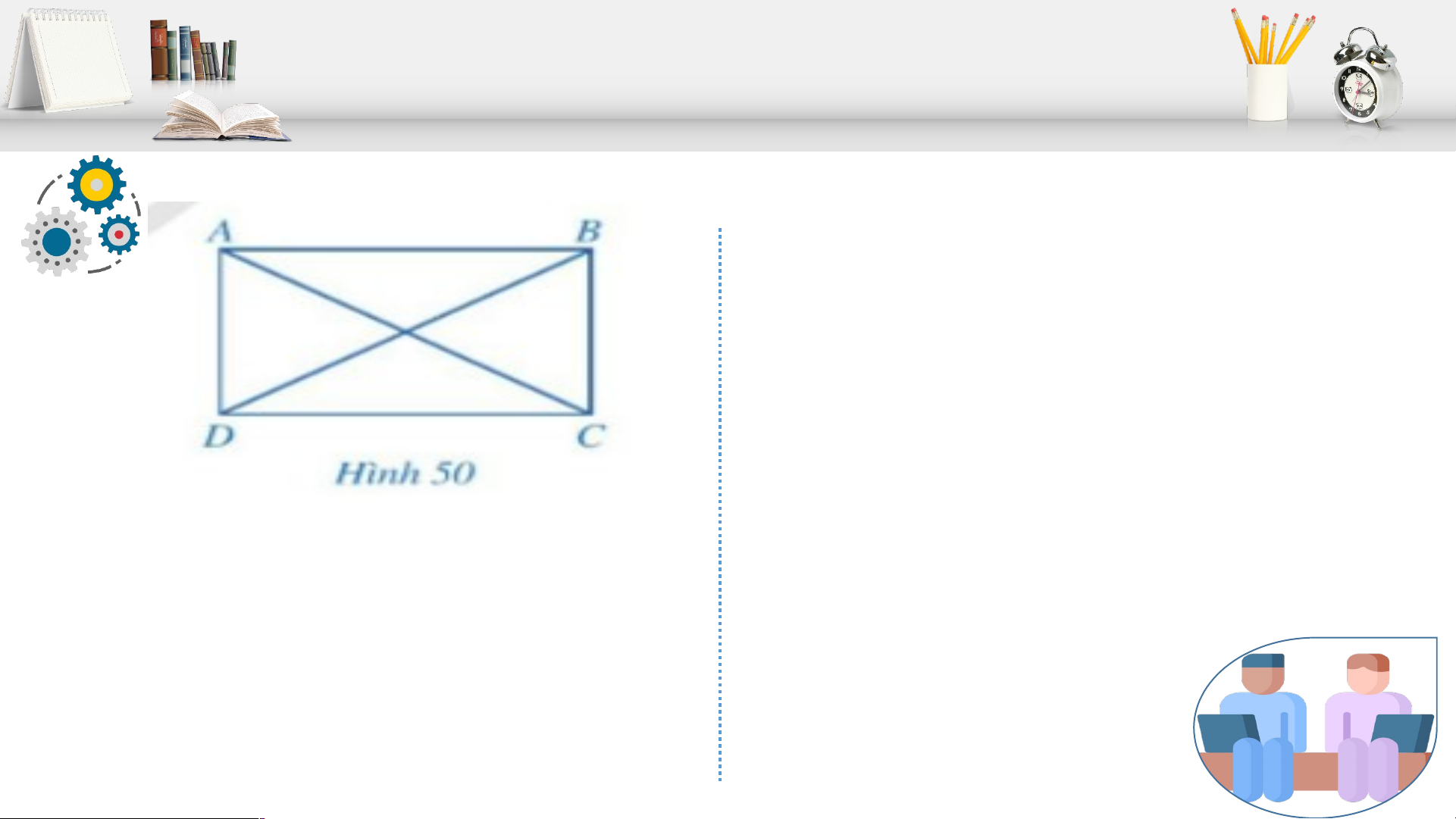
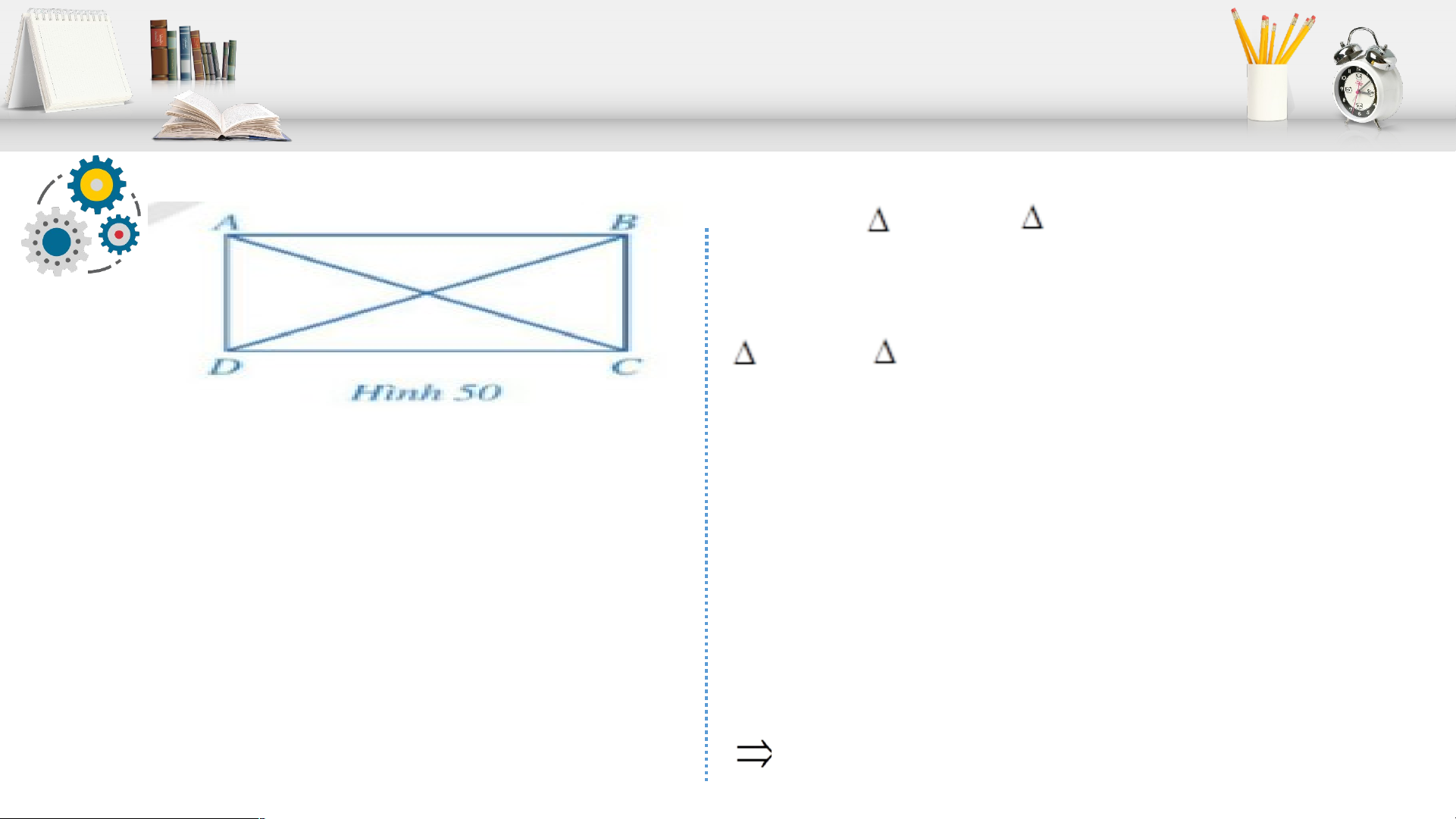
a) Cho hình bình hành ABCD có = 900. ABCD có phải là hình chữ nhật hay không?
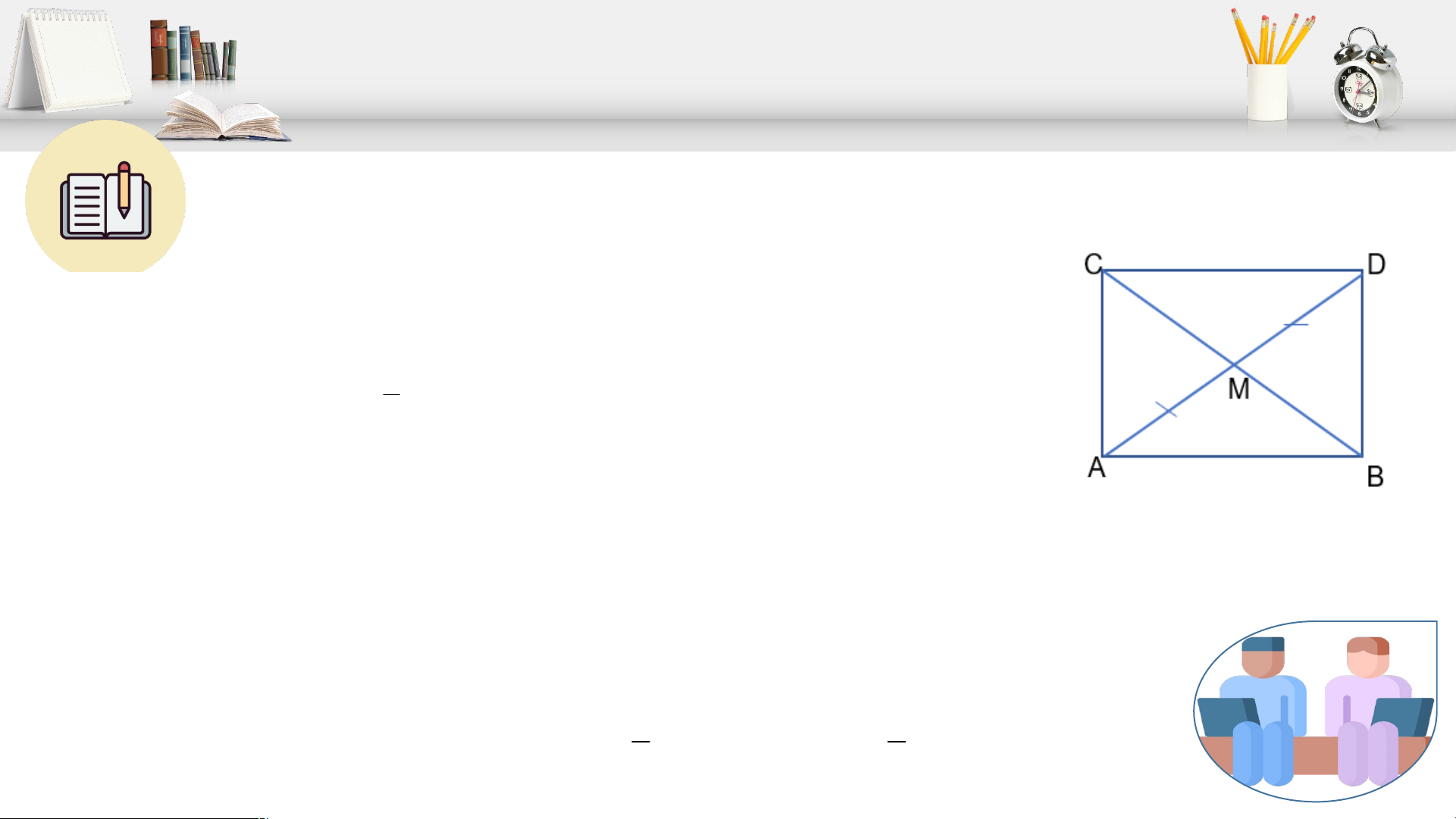
b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau?
+) Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh góc ABC và góc DCB.
+) ABCD có phải là hình chữ nhật hay không?
III. DẤU HIỆU NHẬN BIẾT
Hoạt động 3 trang 110 SGK Giải     0 A C 90
(2 góc đối của hình bình hành ABCD) (1) Mà      0
A B +C+ D = 360 (Tổng các góc của 1 tứ giác)   0      (  )
0  ( 0  0)  0 B D = 360 A C = 360 90 90 180     0 B D = 90 (2)    
a) Cho hình bình hành ABCD có  A = 900. Từ (1) và (2)     0 A B C D = 90
ABCD có phải là hình chữ nhật hay 
ABCD là hình chữ nhật. không?
III. DẤU HIỆU NHẬN BIẾT
Hoạt động 3 trang 110 SGKb) Xét ABC và DCB có:
AB = DC (2 cạnh đối của hbh ABCD) BC chung; AC = BD (gt) ABC = DCB (c - c - c).  
 ABC DCB (2 góc tương ứng ) (1)
b) Cho hình bình hành ABCD có hai
Trong hình bình hành ABCD có các cặp
đường chéo AC và BD bằng nhau?
góc đối bằng nhau nên   ABC ADC
+) Hai tam giác ABC và DCB có bằng và (2)   DCB DAB
nhau hay không? Từ đó, hãy so sánh góc Từ (1) và (2)    
 ABC ADCDCB DAB ABC và góc DCB.
Mặt khác trong một tứ giác tổng các góc sẽ bằng 3600
+) ABCD có phải là hình chữ nhật hay         0 ABC ADC DCB DAB = 90 không?
ABCD là hình chữ nhật.
III. DẤU HIỆU NHẬN BIẾT Ghi nhớ:
+) Hình bình hành có một góc vuông là hình chữ nhât.
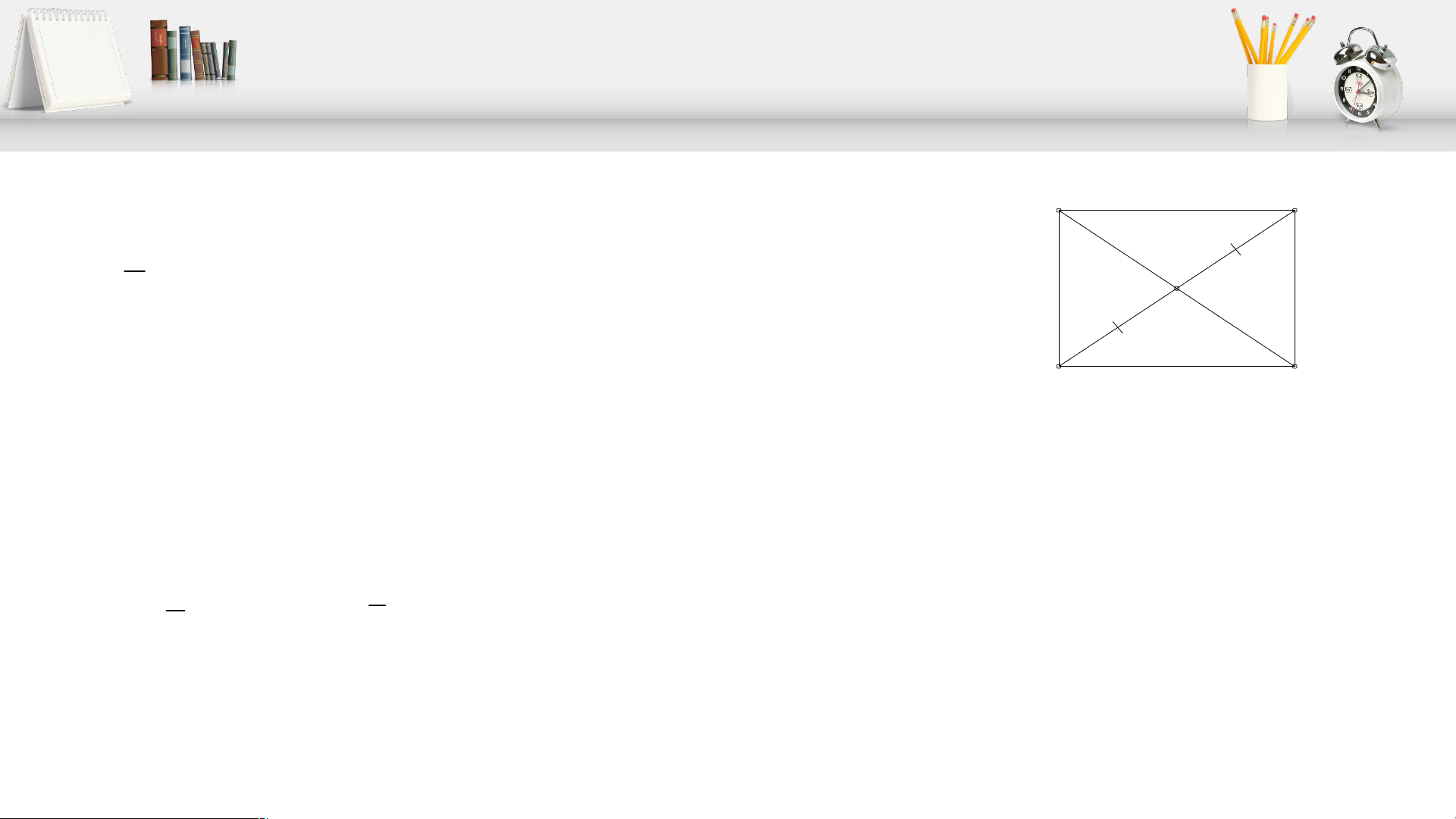
+) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhât.
III. DẤU HIỆU NHẬN BIẾT
Ví dụ 3 trang 111 SGK B A M D C 1
Cho tam giác ABC có đường trung tuyến AM A th M = ỏa BCmãn 2
. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh:
a) Tứ giác ABDC là hình chữ nhật;
b) Tam giác ABC vuông tại A.
III. DẤU HIỆU NHẬN BIẾT
Ví dụ 3 trang 111 SGK
Cho tam giác ABC có đường trung tuyến AM B A thỏa mãn 1 AM = BC
2 Trên tia đối của tia MA lấy điểm D sao cho M D C MD = MA. Chứng minh: a ) T ứ g i ác A B D C l à h ì n h c h ữ n h ật; Giải a) b )V ì T tứ am giác ác ABDC BC v c u ó h ôn a g i đ tạiư ờn
A. g chéo AD, BC cắt nhau tại
trung điểm M của mỗi đường nên ABDC là hình bình hành. Do 1 1 AM = B C A M v = à A
D (Vì D là trung điểm của AD) nên BC 2= AD 2
Hình bình hành ABDC có hai đường chéo AD, BC bằng
nhau nên ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật nên . Suy ra tam giác ABC vuông tại A.
Nhận xét: Nếu một tam giác có đường trung tuyến
ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông. 03 LUYỆN TẬP Bài 1 trang 111 SGK
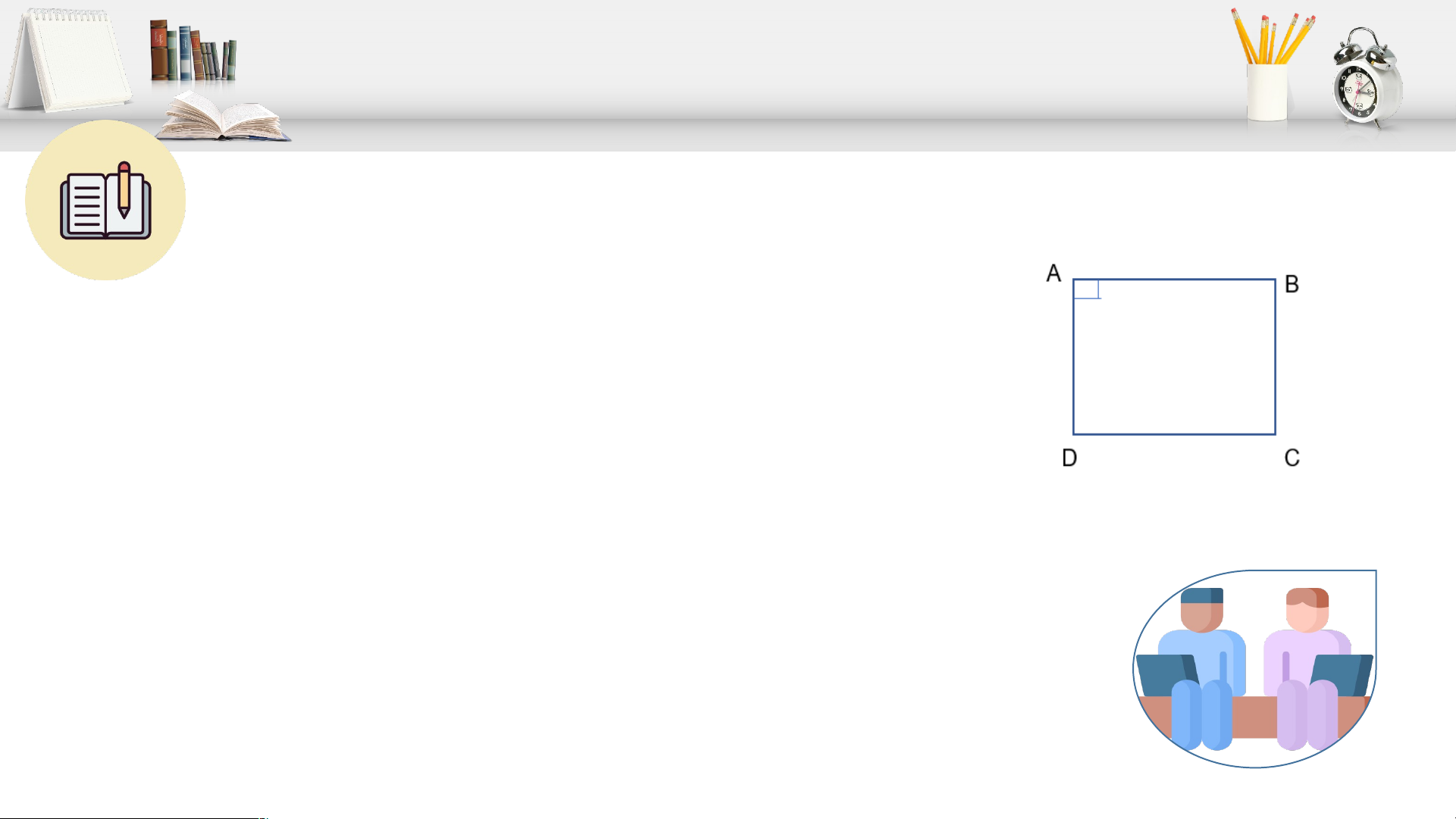
Cho hình thang cân ABCD có AB // CD, . C   0 A 90 hứng
minh ABCD là hình chữ nhật. Giải:
ABCD là hình thang cân và AB//CD nên:
2 góc kề đáy AB là     0 A B 90   0     (  ) 
0  ( 0  0)  0 C D = 360 - A B 360 90 90 180
2 góc kề đáy CD là         0 C D C D 90
Tứ giác ABCD có 4 góc vuông nên là hình chữ nhật. Bài 2 trang 111 SGK
Cho tam giác ABC vuông tại A có M là trung điểm cúa cạnh BC. Trên tia
đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh tứ giác ABDC
là hình chữ nhật và AM = 1 BC 2 Giải
Trên tia đối của tia MA lấy điểm D sao cho MD = MA
 M là trung điểm của AD. Tứ giác ABCD có 2 đường chéo là AD và BC
cắt nhau tại trung điểm của mỗi đường nên là hình bình hành. Lại có góc A
vuông nên là hình chữ nhật (đpcm)
 2 đường chéo AD = BC. Mà AM = 1 AD nên AM = 1 BC (đpcm ) 2 2 LƯU Ý:
Hình thang cân có một góc 1
vuông là hình chữ nhật. 2 Dấu hiệu
Trong tam giác vuông, đường nhận biết
2 trung tuyến ứng với cạnh
huyền bằng nửa cạnh huyền 04 VẬN DỤNG
EM TẬP LÀM THỦ MÔN LUẬT CHƠI
- Học sinh xung phong làm thủ môn bắt bóng.
- Để bắt được trái bóng em phải trả lời đúng 1 câu hỏi trắc nghiệm, nếu trả lời sai
bóng sẽ bay vào lưới và em là người thua cuộc.
- Những thủ môn xuất sắc không để thủng lưới sẽ nhận được 1 phần thưởng của cô.
Câu 1: Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M
vẽ ME song song với AB và MF song song với AC. Hãy xác định điều
kiện của ΔABC để tứ giác AEMF là hình chữ nhật. : A. ΔABC vuông tại A
B. ΔABC vuông tại B D. ΔABC đều
C. ΔABC vuông tại C
Câu 2: Hãy chọn câu trả lời đúng. Hình bình hành ABCD là hình chữ nhật khi: A. AB = BC B. BC = CD C. AC = BD D. AC⊥ BD
Câu 3: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền
BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB,
AC. Tứ giác ADME là hình gì? A. Hình thang B. Hình bình hành C. Hình chữ nhật D. Hình vuông
Câu 4: Độ dài đường trung tuyến ứng với cạnh huyền của tam giác
vuông có các cạnh góc vuông bằng 5cm, 12cm là: A. 13 cm B. 10 cm D. 6,5 cm C. 6 cm Bài 4 trang 111 SGK
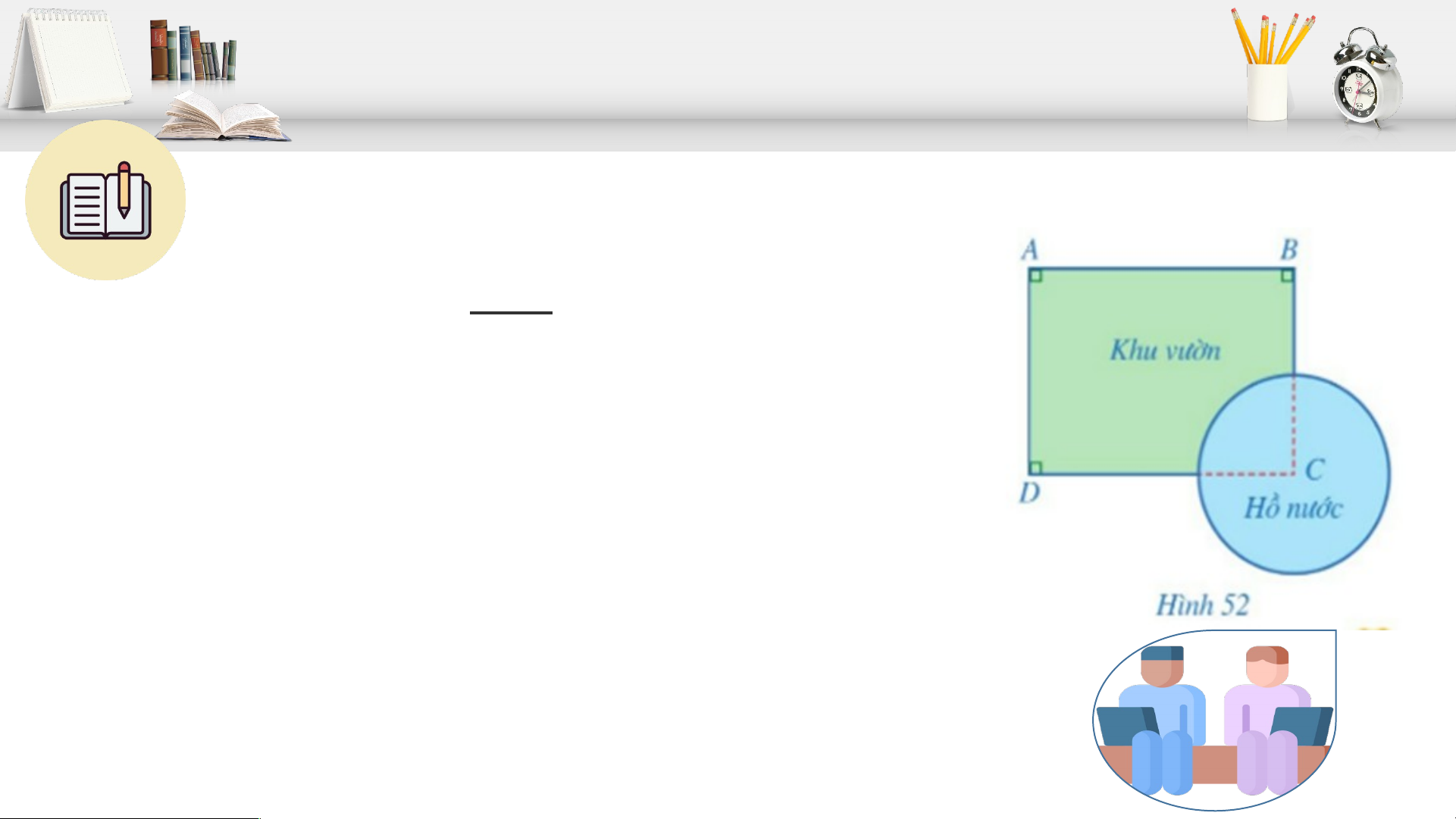
Một khu vườn có dạng tứ giác ABCD với
các góc A, B, D là góc vuông,
AB = 400 m, AD = 300 m. Người ta đã làm
một cái hồ nước có dạng hình tròn, khi đó
vị trí C không còn nằm trong khu vườn nữa
(Hình 52). Tính khoảng cách từ vị trí C đến mỗi vị trí A, B, D. Bài 4 trang 111 SGK Giải:
Tứ giác ABCD có 3 góc A, B, D là góc vuông nên góc
C còn lại cũng là góc vuông. Vậy ABCD là hình chữ nhật. Suy ra:
CB = AD = 300m. Khoảng cách từ C đến B là 300m.
CD = AB = 400m. Khoảng cách từ C đến D là 400m.
Xét tam giác vuông ADC có:
AC2 = AD2 + DC2 = 3002 + 4002 = 25000  AC =500.
Vậy khoảng cách từ C đến A là 500m. CÓ THỂ EM CHƯA BIẾT Tỉ l ệ khung hình 4 16 3 9
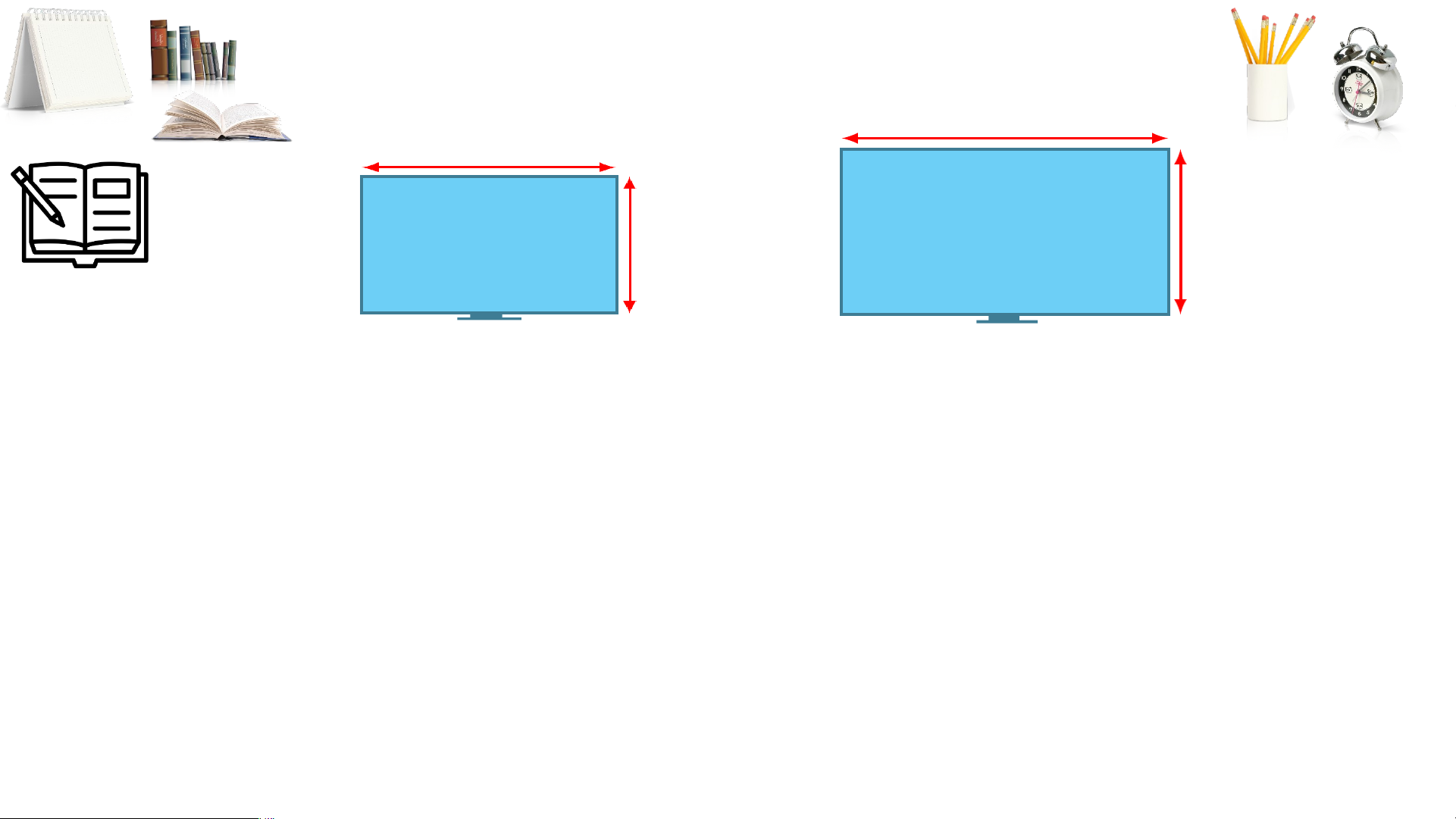
Tỉ lệ khung hình 4 : 3
Tỉ lệ khung hình 16 : 9 Hình 54
+) Tỉ lệ khung hình (còn gọi là tỉ lệ hình ảnh) thể hiện tỉ lệ của chiều
rộng và chiều cao (theo cùng đơn vị đo) của một khung hình có dạng hình chữ nhật.
+) Chẳng hạn, ta có thể hiểu khung hình ti vi có tỉ lệ 16:
9 là khung hình ti vi có dạng hình chữ nhật với chiều
rộng là 16 đơn vị và chiều cao là 9 đơn vị.
+) Ngày nay, các thiết bị như màn hình máy tính, màn
hình ti vi, ... thường sử dụng hai tỉ lệ khung hình là 4: 3 và 16: 9 (Hình 54). CÓ THỂ EM CHƯA BIẾT Tỉ l ệ khung hình 4 16 3 9
Tỉ lệ khung hình 4 : 3
Tỉ lệ khung hình 16 : 9 Hình 54
+) Tỉ lệ khung hình 4: 3 được sử dụng phổ biến trên các màn hình máy tính, phù
hợp làm việc văn phòng hoặc dùng cho truyển hình tiêu chuẩn, máy quay phim.
+) Tỉ lệ khung hình 16: 9 là tỉ lệ chuẩn quốc tế hiện nay phổ biến nhất trên các
thiết bị công nghệ như màn hình điện thoại, ti vi, màn hình LED, ... Đặc điểm nổi
bật của khung hình tỉ lệ 16: 9 là cho phép hình ảnh/video được hiển thị sắc nét, trọn vẹn màn hình
HƯỚNG DẪN VỀ NHÀ Học và ghi nhớ: Định 1 nghĩa, tính chất, dấu
hiệu nhận biết hình chữ nhật. DẶN DÒ 2 BT VN: 1,2,3,4 SBT. Chuẩn bị bài mới: 3
Bài 6. Hình thoi THANK YOU!
Chúc các con học tốt!
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33