












Preview text:
CHÀO MỪNG CÁC EM
ĐÃ ĐẾN VỚI BUỔI HỌC! KHỞI ĐỘNG
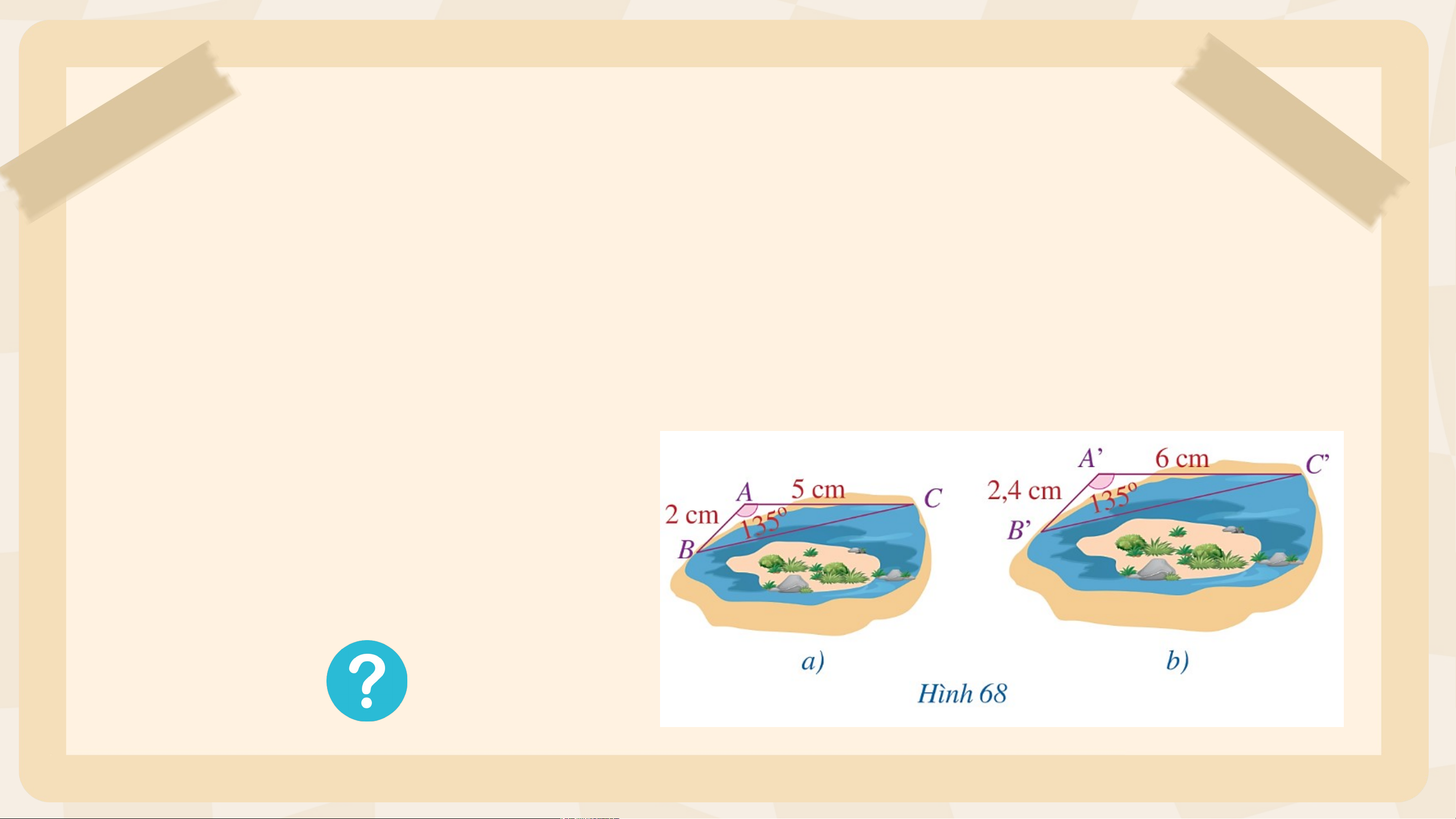
Bạn Hoàng và bạn Thu cùng vẽ bản đồ một ốc đảo và ba vị trí với tỉ lệ bản đồ
khác nhau. Bạn Hoàng dùng ba điểm A,B,C lần lượt biểu thị các vị trí thứ nhất,
thứ hai, thứ ba (H.68a). Bạn Thu dùng ba điểm A’,B’,C’ lần lượt biểu thị ba vị trí đó (H.68b)
Hai tam giác A’B’C’ và ABC có đồng dạng hay không ?
CHƯƠNG VIII. TAM GIÁC ĐỒNG DẠNG. HÌNH ĐỒNG DẠNG
BÀI 7. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI CỦA TAM GIÁC NỘI DUNG BÀI HỌC I
Trường hợp đồng dạng thứ hai: Cạnh – góc – cạnh
Áp dụng trường hợp đồng dạng thứ hai II
của tam giác vào tam giác vuông
I. Trường hợp đồng dạng thứ
hai: Cạnh – góc – cạnh
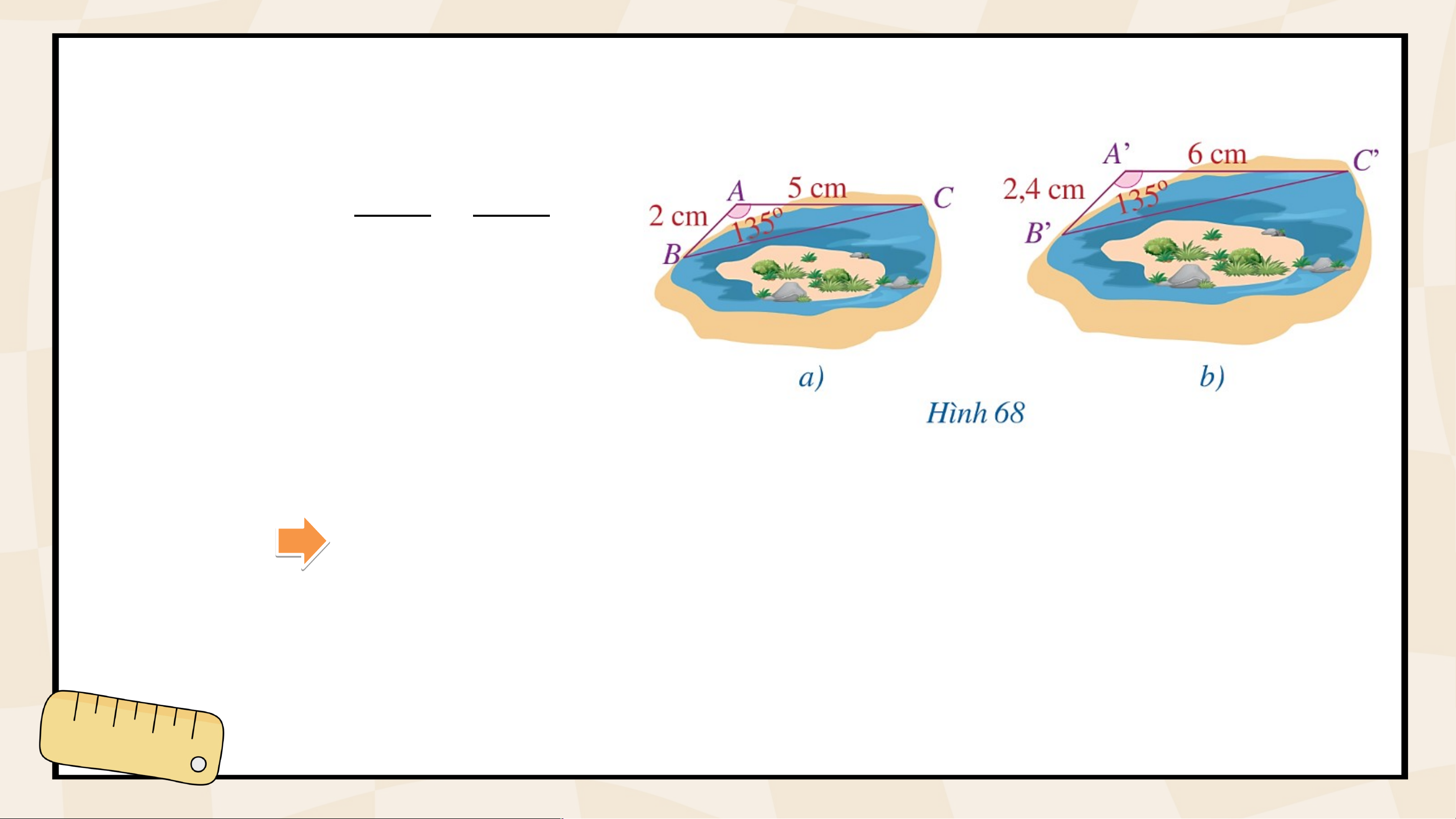
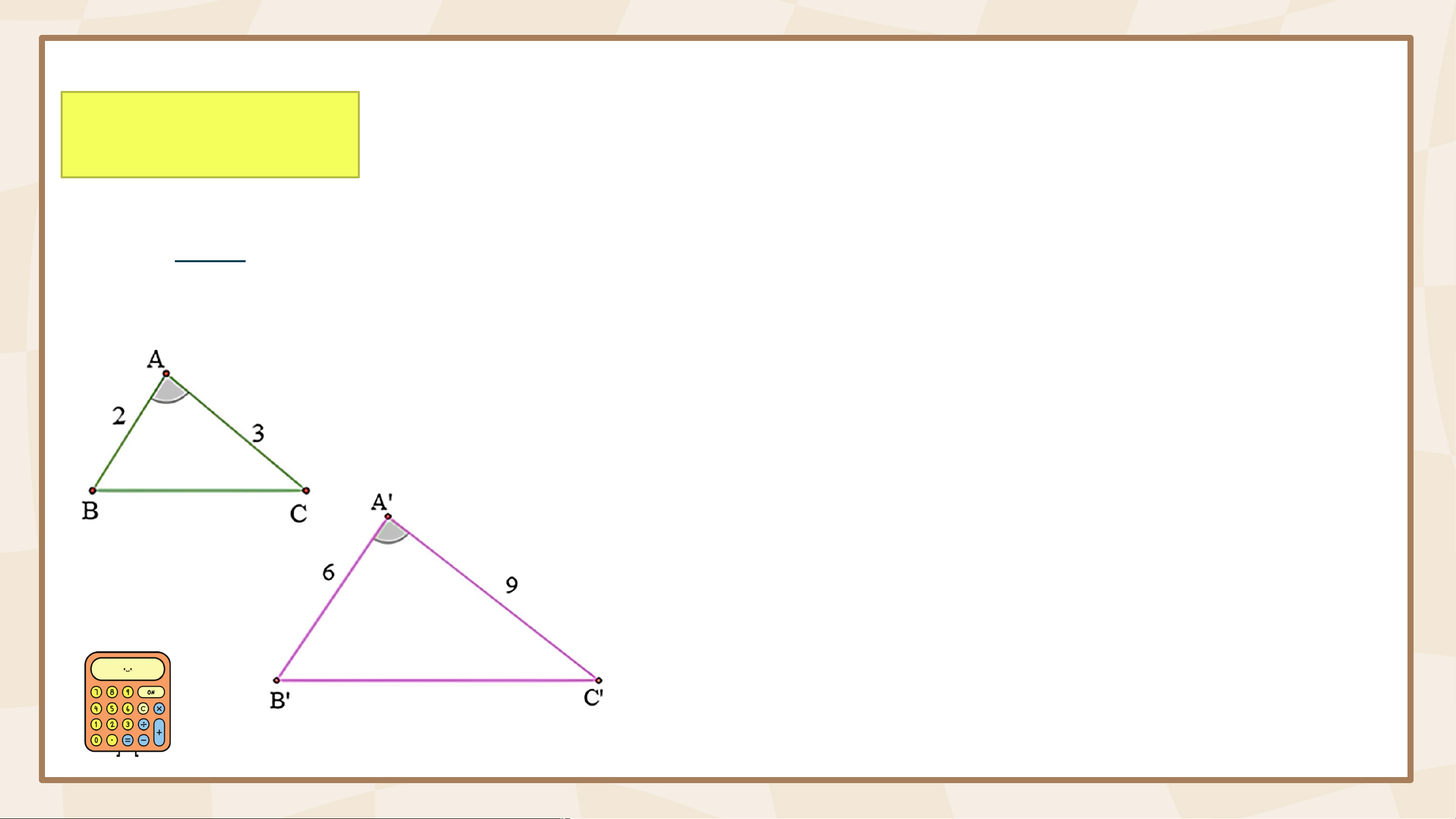
HĐ1: Quan sát Hình 68 và so sánh: 𝐴′ 𝐵′ 𝐴′ 𝐶′ v à
a) Các tỉ số 𝐴𝐵 𝐴𝐶 b) Các góc và Ta có: Định lí
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia
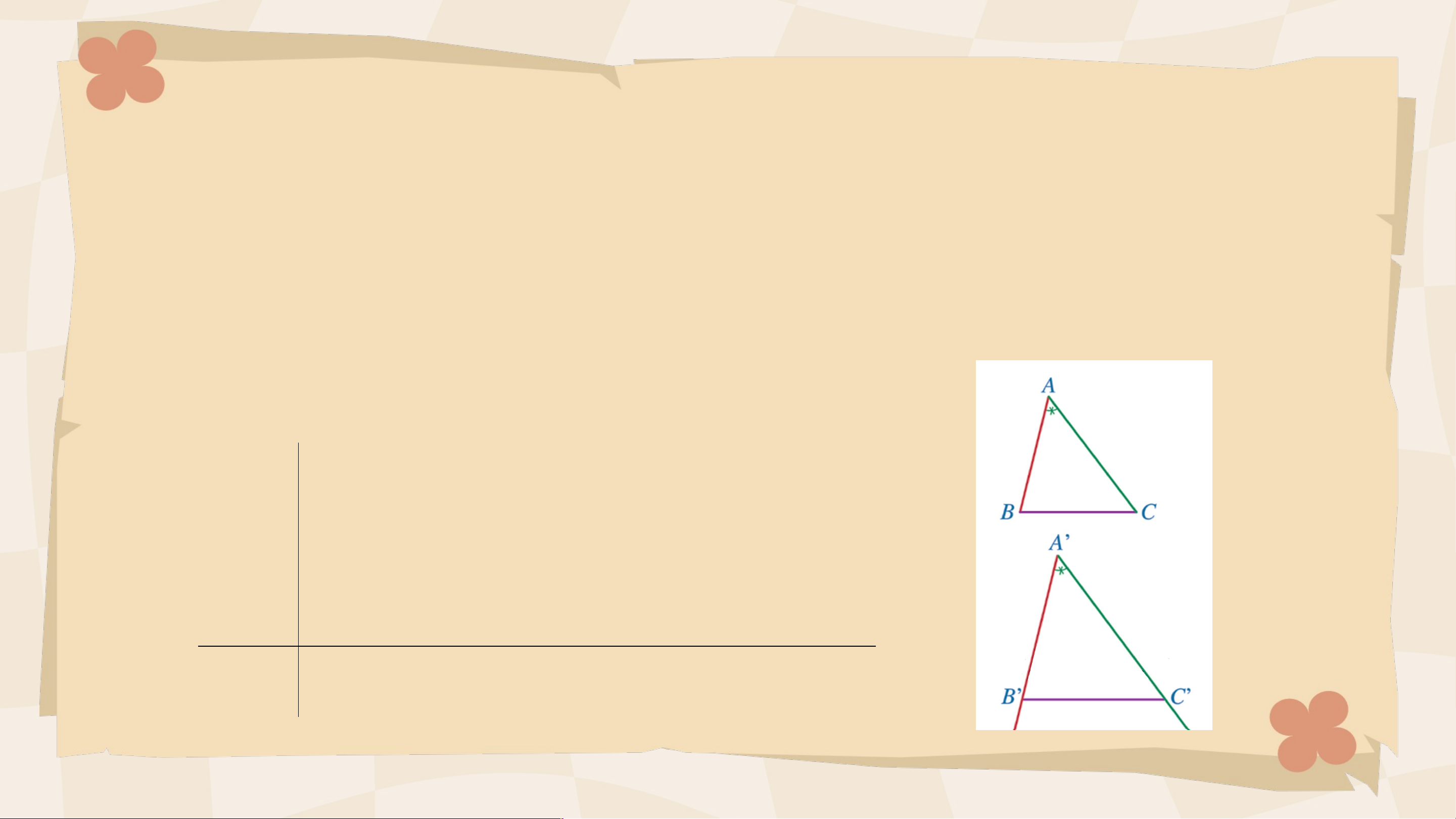
và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng. GT KL Chứng minh: • Trường hợp 1: Khi đó: Suy ra (c.g.c). Vậy • Trường hợp 2:
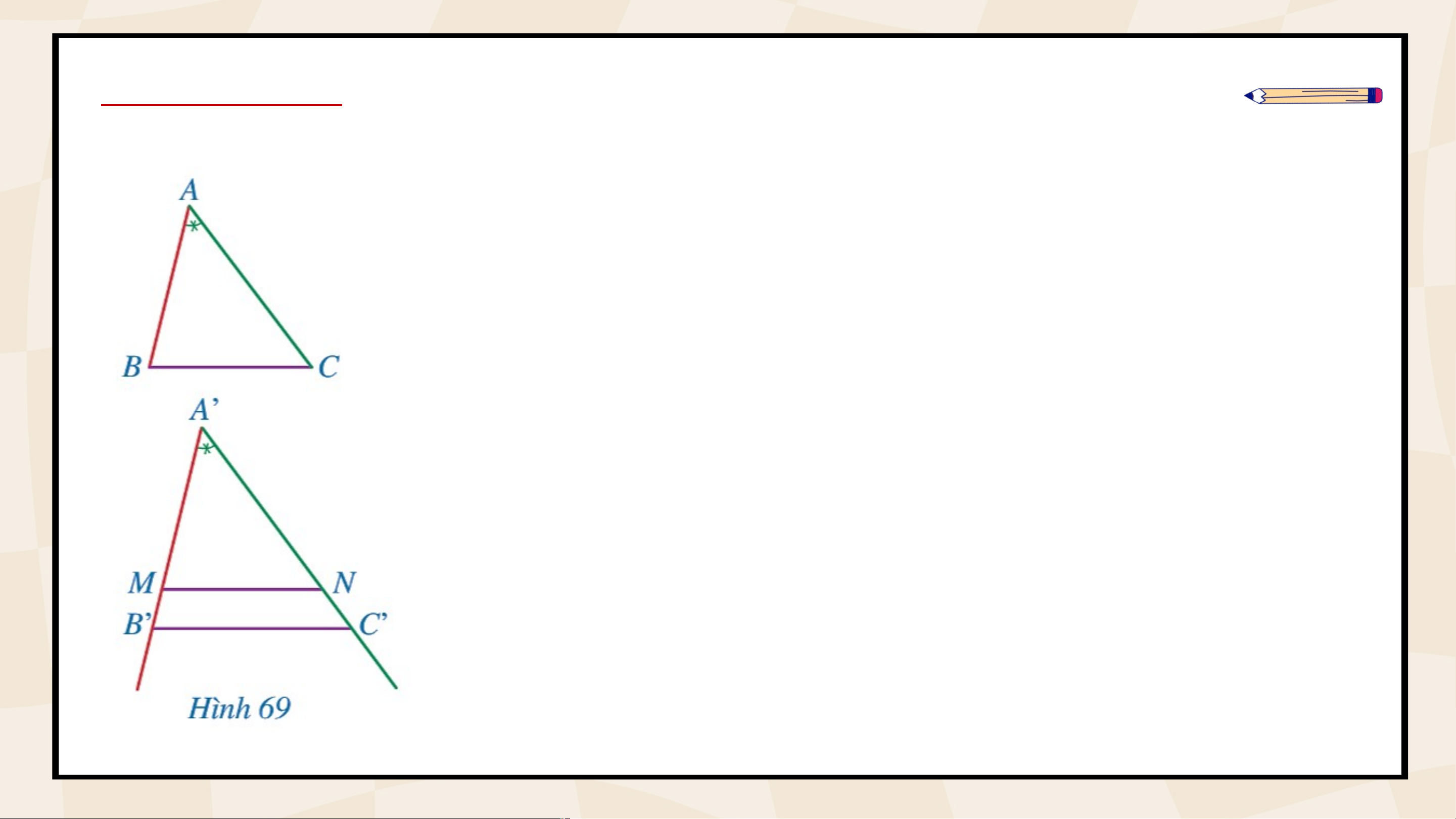
Trên tia lấy điểm thoả mãn .
Trên tia lấy điểm thoả mãn (Hình 69). Xét hai tam giác và có suy ra (c.g.c). Chứng minh: Vậy Vì và nên
Suy ra (định lí Thalès đảo).
Từ đó theo định lí trang 72 ta có Từ và ta suy ra
Ví dụ 1: Quan sát Hình 70 và chỉ ra hai cặp tam giác đồng dạng: Giải
Xét hai tam giác và , ta có: Suy ra Lại có . Vậy
Xét hai tam giác và , ta có: Suy ra Lại có . Vậy Luyện tập 1
Cho hai tam giác và thoả mãn và . Chứng minh . Giải Ta có:
Xét hai tam giác và , ta có:
(các cặp góc tương ứng) LUYỆN TẬP GẤU CON HAM ĂN
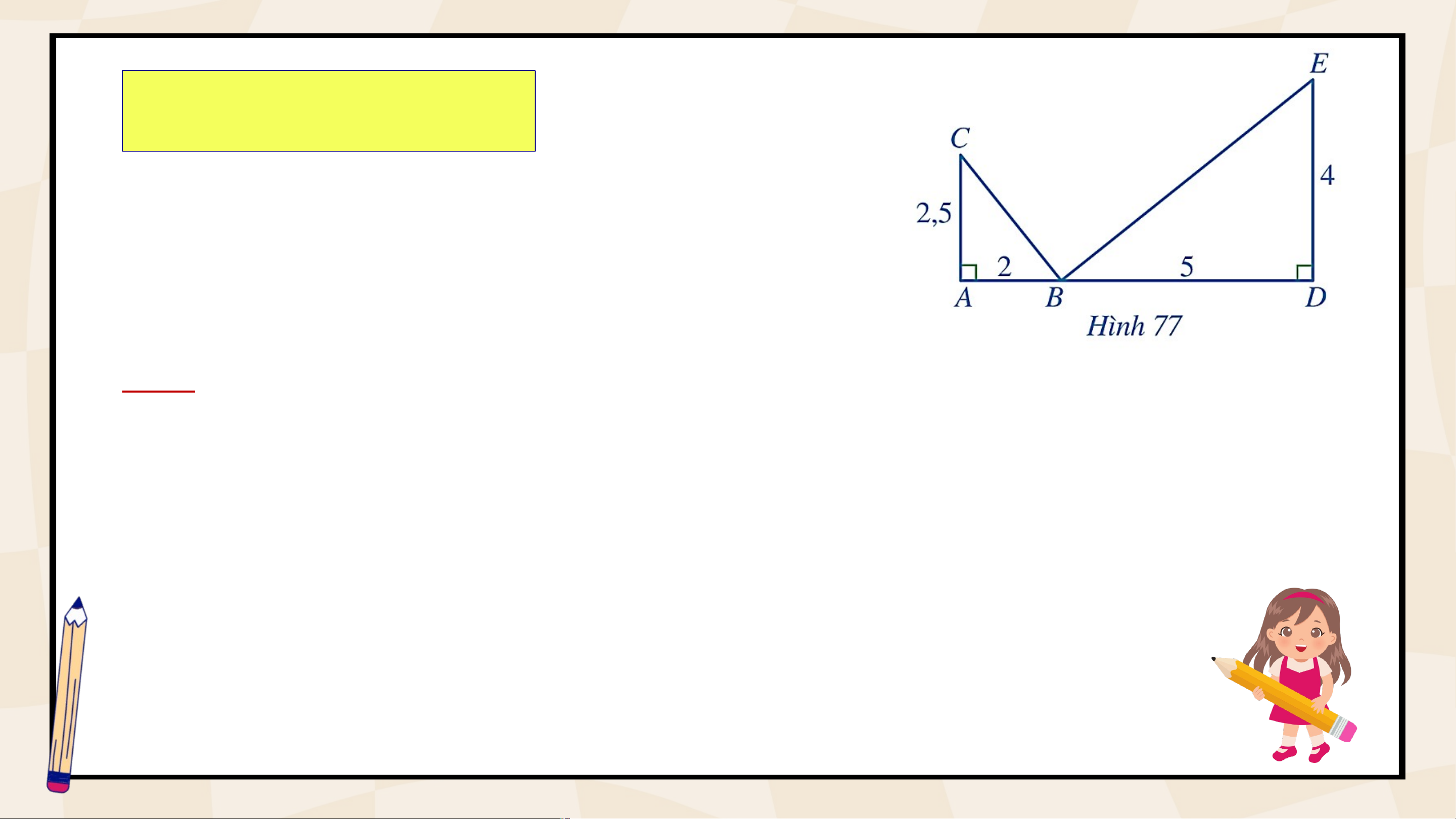
Câu 1. Hãy chọn câu đúng. Nếu và có ; A. đồng dạng với C. đồng dạng với B. đồng dạng với D. đồng dạng với Bài 4 (SGK – tr.82) Cho Hình 77, chứng minh: a) b) . Giải b) vuông tại có: mà (cmt). Suy ra mà . Do đó: Hay VẬN DỤNG Bài 5 (SGK – tr.82) Cho .
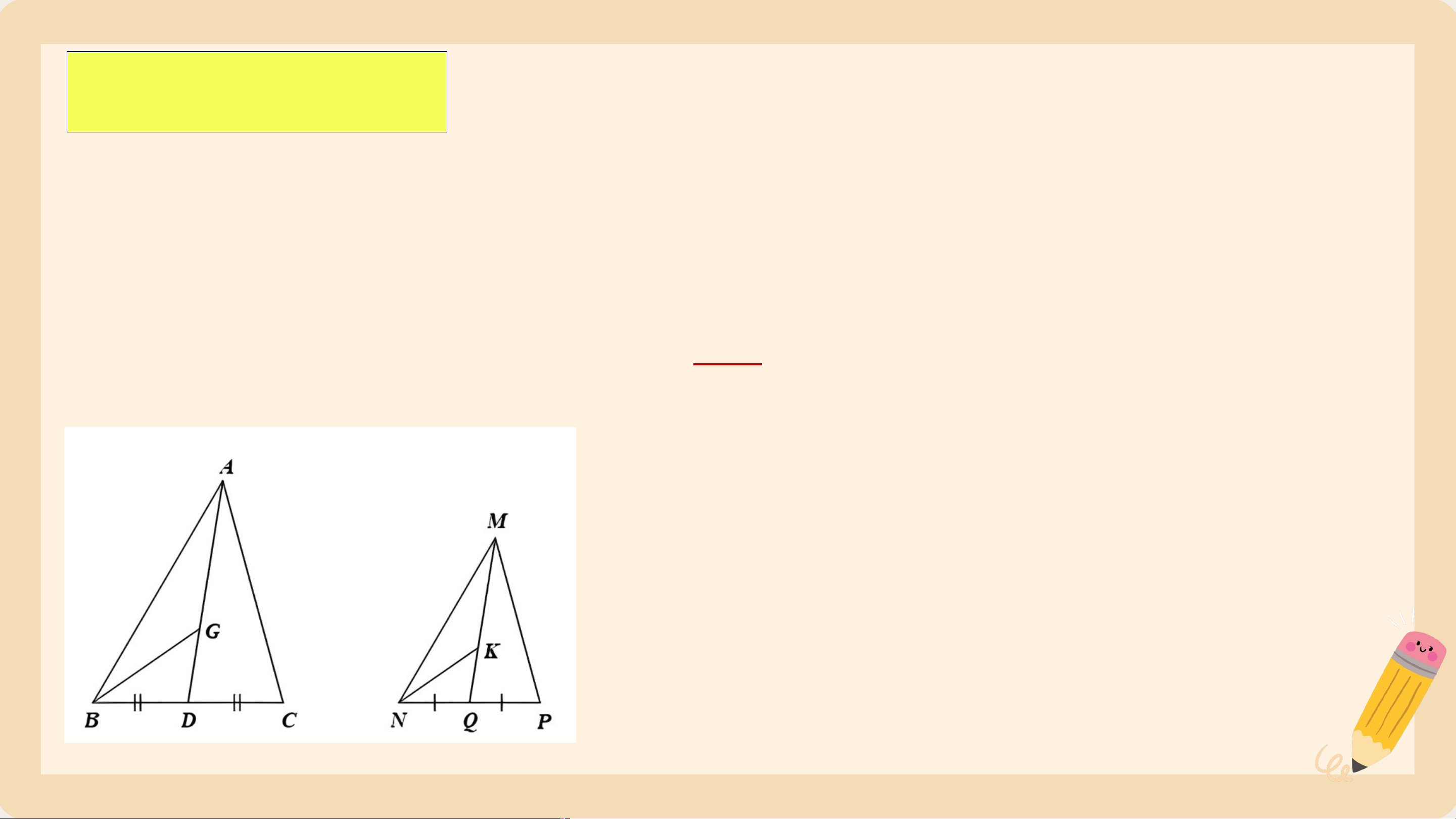
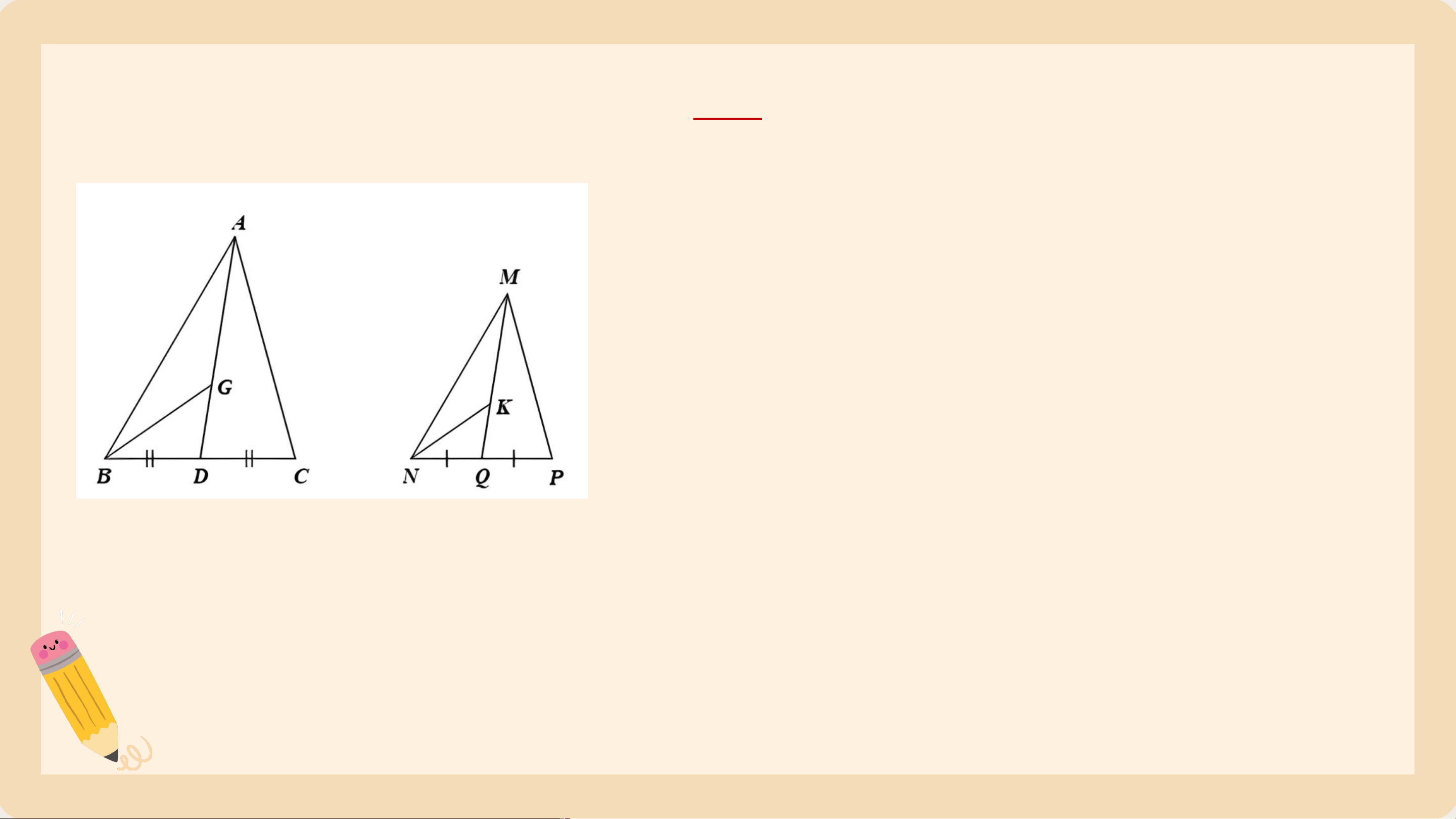
a) Gọi và lần lượt là trung điểm của và . Chứng minh .
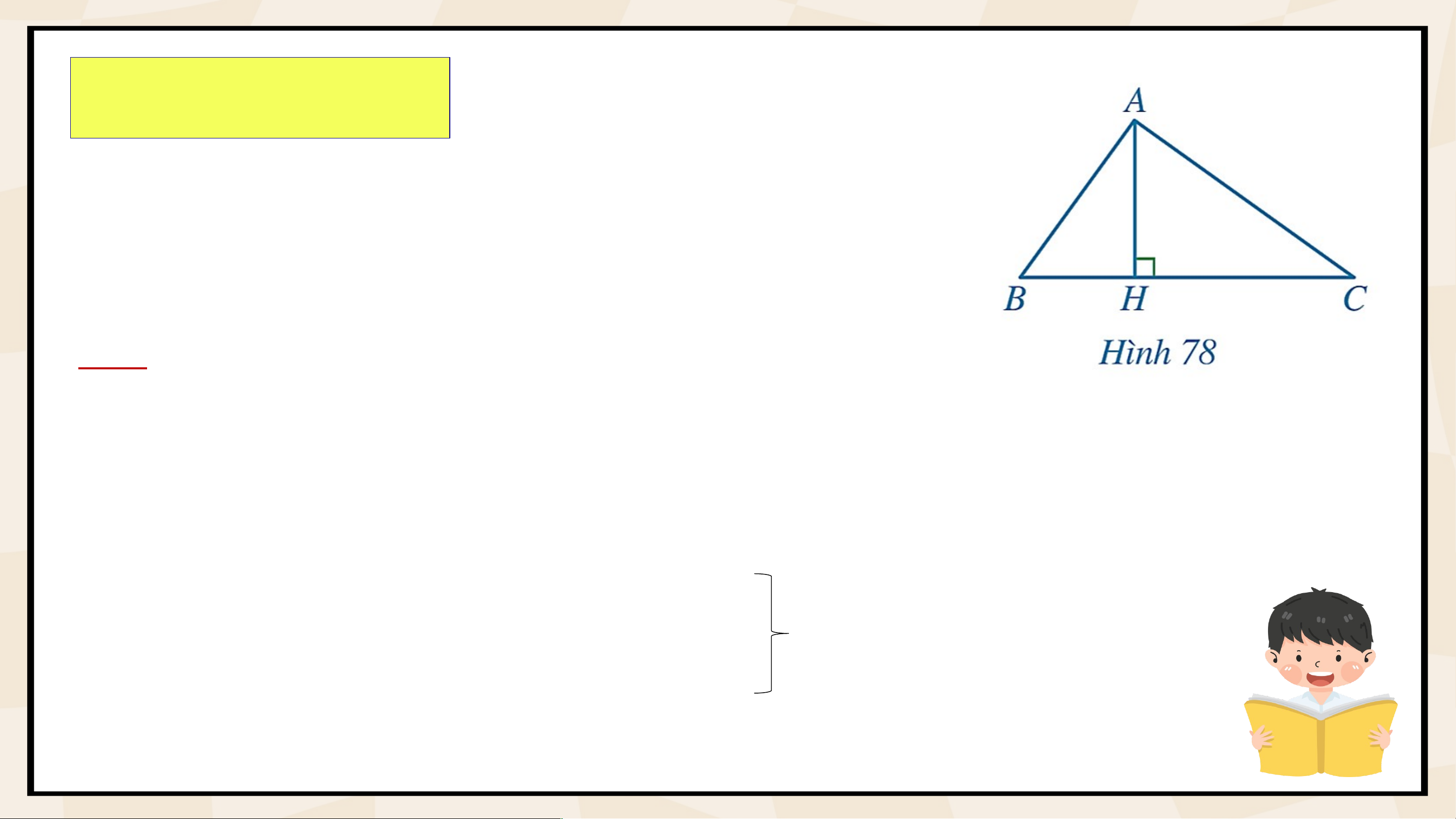
b) Gọi và lần lượt là trọng tâm của hai tam giác và . Chứng minh Giải a) Ta có: và mà (D là trung điểm ) ( là trung điểm ) Do đó: và (c.g.c) Giải b) Ta có: (cmt) và ; Mà ( là trọng tâm ); ( là trọng tâm ) Do đó: và (c.g.c) Bài 6 (SGK – tr.82) Cho Hình 78, biết Chứng minh: a) ∆ b) Tam giác vuông tại . Giải a) Ta có: ; Mà Do đó: (c.g.c) b) Do vuông tại có: ⇒ ^ 𝐻𝐴𝐵+^
𝐻𝐴𝐶=90𝑜 Vậy hay vuông tại . Bài 7 (SGK – tr.82)
Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo
góc, làm thế nào đo được khoảng cách giữa hai vị trí trên thực tế, biết
rằng có vị trí thoả mãn
Bạn Vy làm như sau: Vẽ tam giác có
Bạn Vy lấy thước đo khoảng cách giữa hai điểm và nhận được kết
quả . Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí trên thực tế
khoảng . Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy. Giải Đổi Ta có: Suy ra: Do đó: (c.g.c) Do đó: hay .
HƯỚNG DẪN VỀ NHÀ Hoàn thành Ôn tập kiến Chuẩn bị bài bài tập trong thức đã học sau Bài 8 SBT CẢM ƠN CÁC EM ĐÃ THAM GIA BUỔI HỌC!
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23




