














Preview text:
BÀI TẬP CUỐI CHƯƠNG III
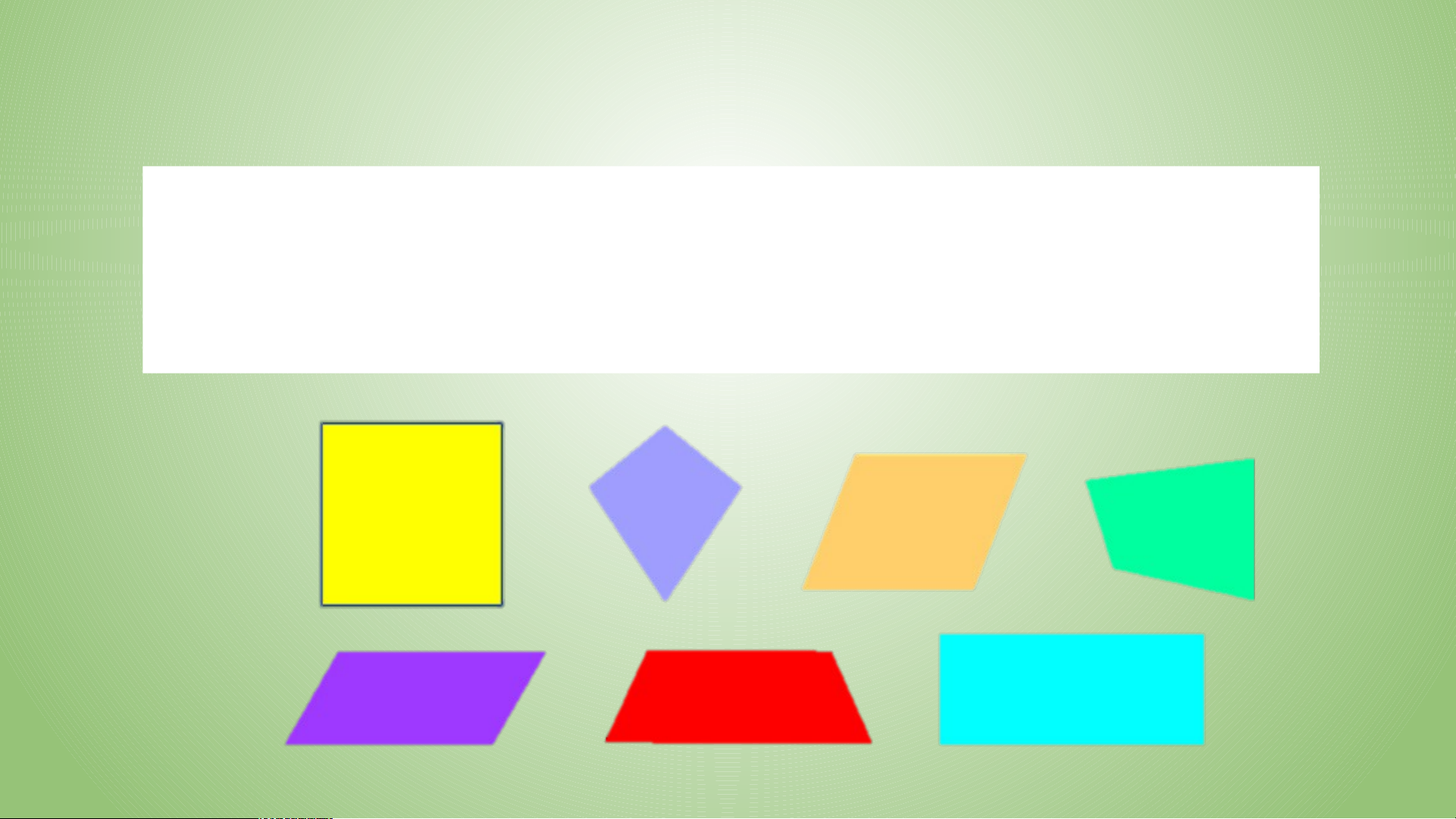
Toán 8 - Kết nối tri thức Hoạt động 1: TRÒ CHƠI HÁI CAM ?
Câu 1. Khẳng định nào sau đây là đúng?
A. Tứ giác có hai cạnh đối song song là hình bình hành.
B. Tứ giác có hai cạnh đối bằng nhau là hình bình hành.
C. Tứ giác có hai góc đối bằng nhau là hình bình hành.
D. Tứ giác có các cạnh đối song song là hình bình hành.
Câu 2: Tứ giác dưới đây là hình thoi theo dấu hiệu nào?
A. Tứ giác có 4 cạnh bằng nhau
C. Tứ giác có hai đường chéo vuông góc
B. Hình bình hành có hai đường
D. Tứ giác có hai đường chéo giao chéo bằng nhau
nhau tại trung điểm mỗi đường
Câu 3: Khẳng định nào sau đây là sai?
A. Hình chữ nhật có hai đường chéo bằng nhau.
B. Hình chữ nhật có hai đường chéo cắt nhau tại trung điểm mỗi đường.
C. Hình chữ nhật có hai cạnh kề bằng nhau.
D. Trong hình chữ nhật, giao của hai đường chéo là tâm của hình chữ nhật đó.
BÀI TẬP CUỐI CHƯƠNG III
Đại diện các nhóm lên trình bày sơ đồ đã chuẩn bị trước đó. HOẠT Đ N Ộ G 2
Dấu hiệu nhận biết hình chữ nhật.
Dấu hiệu nhận biết hình thoi.
Dấu hiệu nhận biết hình vuông.
Dấu hiệu nhận biết hình bình hành. NHIỆM VỤ NHÓM 1
Nhóm đôi: Thảo luận nhóm trả lời câu hỏi:
Hình chữ nhật, tính chất.
Dấu hiệu nhận biết hình chữ nhật. NHIỆM VỤ NHÓM 2
Nhóm đôi: Thảo luận nhóm trả lời câu hỏi:
Hình thoi, tính chất.
Dấu hiệu nhận biết hình thoi. NHIỆM VỤ NHÓM 3
Nhóm đôi: Thảo luận nhóm trả lời câu hỏi:
Hình vuông, tính chất.
Dấu hiệu nhận biết hình vuông NHIỆM VỤ NHÓM 4
Nhóm đôi: Thảo luận nhóm trả lời câu hỏi:
Hình bình hành, tính chất.
Dấu hiệu nhận biết hình bình hành.
Hoạt động 3: Luyện tập
BÀI TẬP TRẮC NGHIỆM
3.39. Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.
C. Nếu tứ giác có hai góc tù thì góc còn lại phải nhọn.
D. Không có tứ giác nào có ba góc tù.
BÀI TẬP TRẮC NGHIỆM
3.40. Trong các khẳng định sau, khẳng định nào
đúng? Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau là hình bình hành.
b) Tứ giác có hai cặp cạnh bằng nhau là hình bình hành.
c) Tứ giác có ba góc vuông là hình chữ nhật.
d) Tứ giác có ba cạnh bằng nhau là hình thoi.
BÀI TẬP TRẮC NGHIỆM
3.41. Trong các khẳng định sau, khẳng định nào đúng?
Khẳng định nào sai?
a) Tứ giác có hai đường chéo bằng nhau và hai cạnh đối
nào cũng bằng nhau là hình chữ nhật.
b) Tứ giác có hai cạnh đối nào cũng bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh song song và hai đường chéo
bằng nhau là hình thang cân.
d) Tứ giác có hai cạnh song song và hai cạnh còn lại
bằng nhau là hình bình hành.
BÀI TẬP TỰ LUẬN
3.42. Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và ột
cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân THẢO LUẬN NHÓM
Gọi O là giao điểm của AC và BD. Xét ∆ACD và ∆BDC có: Xét ∆ABC và ∆BAD có: AD = BC (giả thiết) AD = BC (giả thiết) AC = BD (giả thiết) AC = BD (giả thiết) Cạnh CD chung Cạnh AB chung
Do đó ∆ADC = ∆BCD (c.c.c)
Do đó ∆ABC = ∆BAD (c.c.c)
Suy ra DAC=CBD (hai góc tương
Suy ra ADB =ACB (hai góc tương ứng).
ứng).Suy ra OAB=OCD mà hai góc này ở vị trí so le trong. Do đó AB // CD.
Tứ giác ABCD có AB // CD nên ABCD là hình thang.
Hình thang ABCD có hai đường chéo AC = BD.
Do đó tứ giác ABCD là hình thang cân.
Vậy nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân.
BÀI TẬP TỰ LUẬN
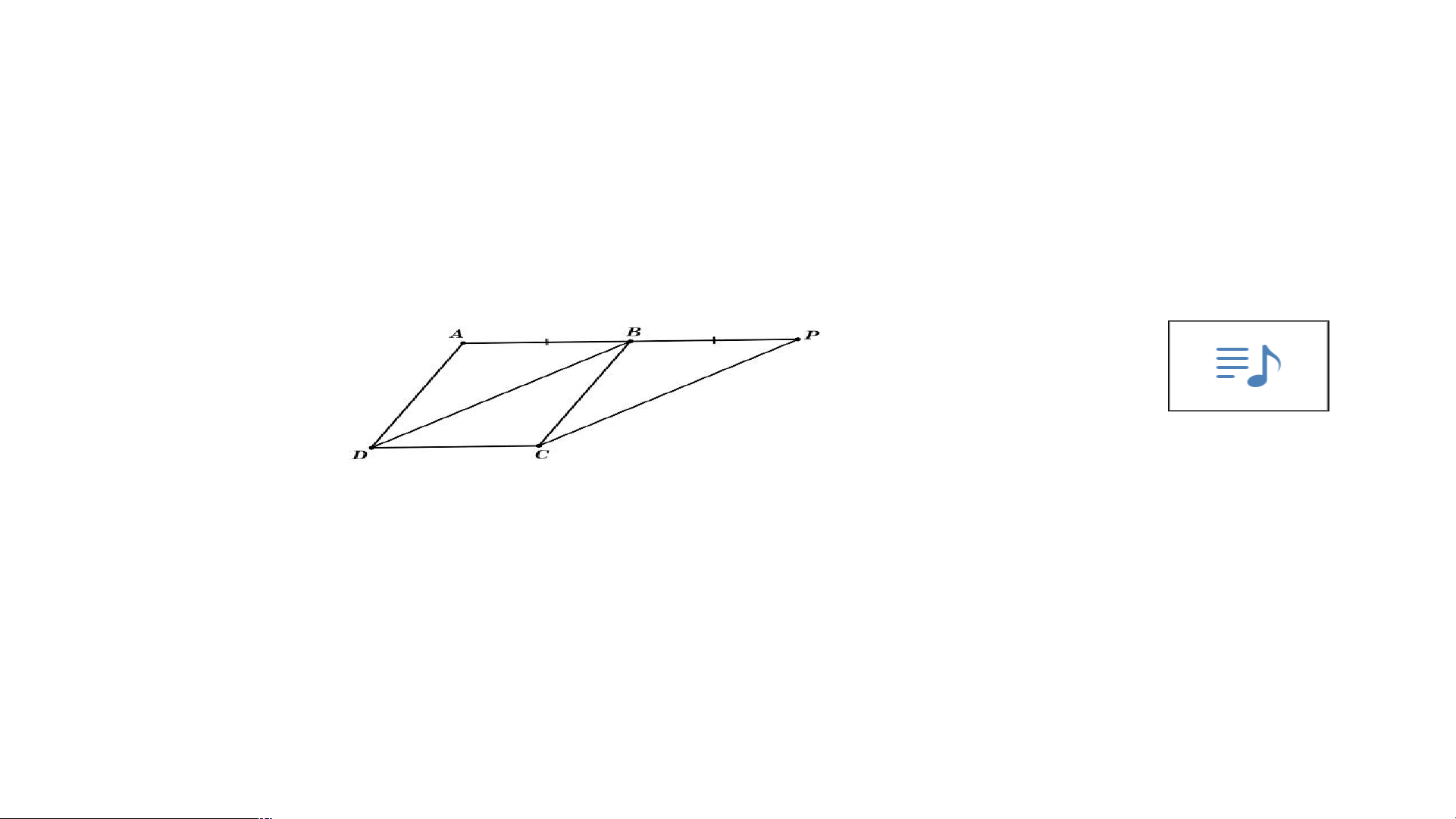
3.43. Cho hình bình hành ABCD. Lấy điểm P trên tia AB sao cho AP = 2 AB.
a) Tứ giác BPCD có phải là hình bình hành không? Tại sao?
b) Khi tam giác ABD vuông cân tại A, hãy tính số đo các góc của tứ giác BPCD. THẢO LUẬN NHÓM
a) Xét tứ giác BPCD ta có: BP // CD, BP = CD (cùng bằng AB) suy ra BPCD là hình bình hành
b) ABD vuông cân tại A suy ra AB = AD, do đó ABCD là hình vuông
Khi đó BD là phân giác ABC⇒ DBC=45o ⇒ DBP= 45o +90o= 135o PCD = DBP =135o
BD//PC ⇒ BPC = ABD = 45o (hai góc đồng vị) BDC=BPC= 45o
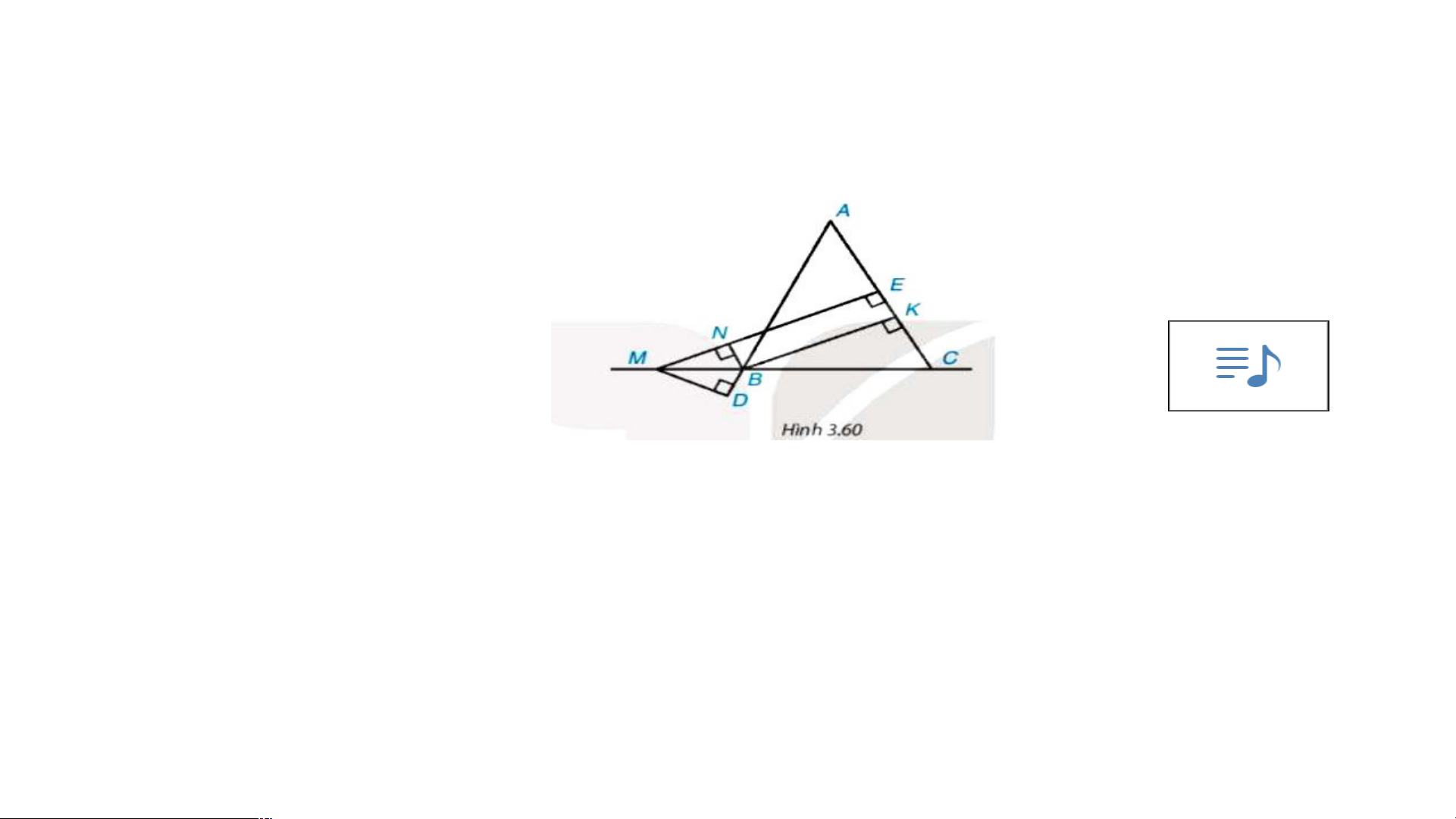
3.45. Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở
giữa M và C. Gọi E và K lần lượt là chân đường vuông góc hạ từ M và từ B
xuống AC, còn N là chân đường vuông góc hạ từ B xuống ME (H.3.60) THẢO LUẬN NHÓM
a) Xét tứ giác BKEN có: BKE=KEN=ENB=90o
Suy ra tứ giác BKEN là hình chữ nhật
b) D là chân đường vuông góc hạ từ M đến AB
Ta có BN // AC (do BKNE là hình chữ nhật) suy ra MBN=BCA(hai góc đồng vị) MBD=ABC (đối đỉnh)
Mà ABC=BCA(tam giác ABC cân tại A) suy ra MBN=MBD
Xét tam giác vuông MBD và MBN ta có: AB chung ABC=BCA
Suy ra ΔMBD = ΔMBN (cạnh huyền – góc nhọn) Suy ra MD = MN
Lại có: BK = NE = ME – MN suy ra BK = NE = ME − MD
HƯỚNG DẪN VỀ NHÀ 01 02 03 Ôn tập kiến thức Hoàn thành bài tập Chuẩn bị bài sau 3.44 đã học chương III
HẸN GẶP LẠI CÁC EM TRONG TIẾT HỌC SAU!
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- NHIỆM VỤ NHÓM 1
- NHIỆM VỤ NHÓM 2
- NHIỆM VỤ NHÓM 3
- NHIỆM VỤ NHÓM 4
- BÀI TẬP TRẮC NGHIỆM
- BÀI TẬP TRẮC NGHIỆM
- BÀI TẬP TRẮC NGHIỆM
- THẢO LUẬN NHÓM
- THẢO LUẬN NHÓM
- THẢO LUẬN NHÓM
- HƯỚNG DẪN VỀ NHÀ
- Slide 20




