

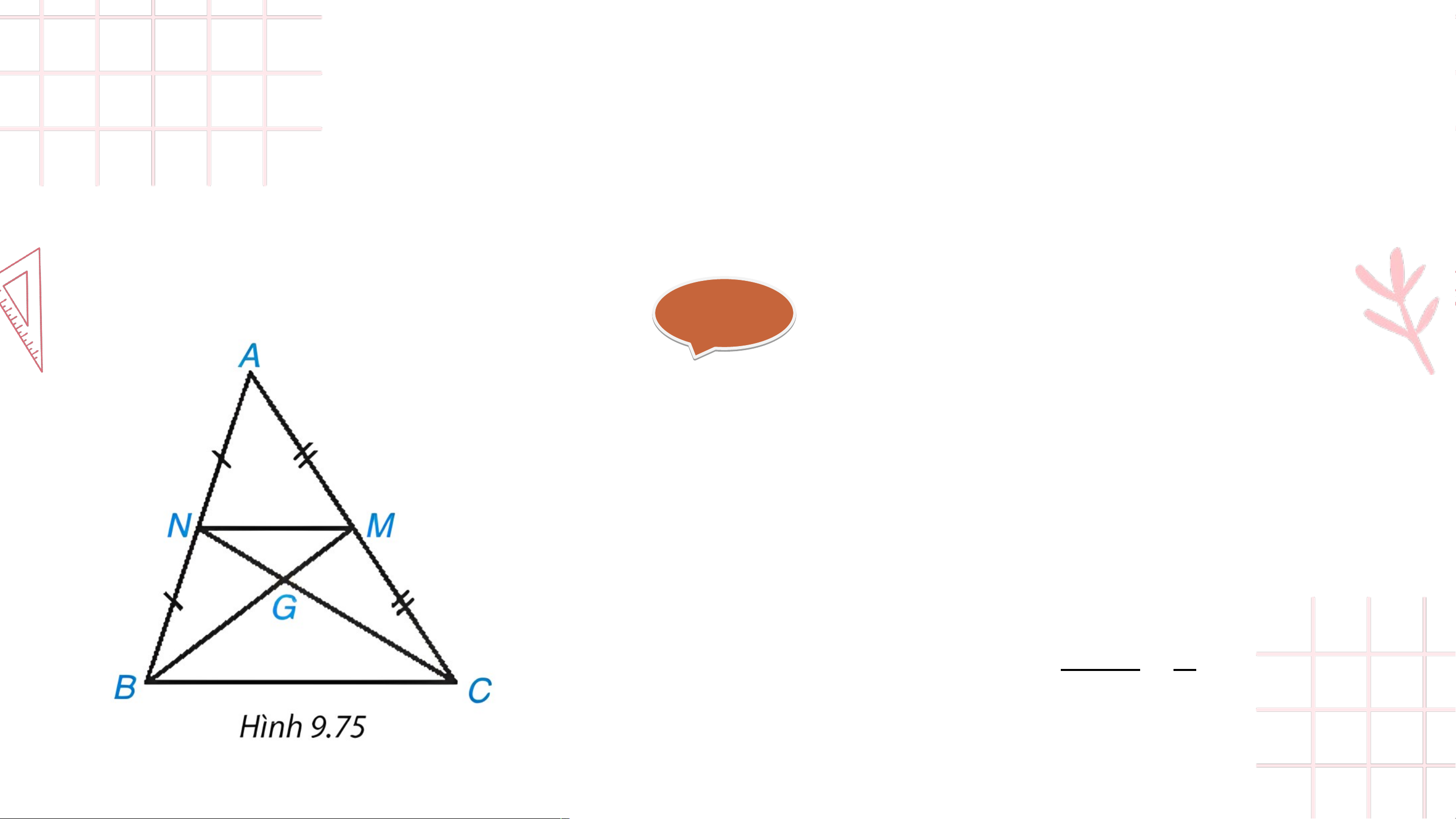

Preview text:
ÔN TẬP KIẾN THỨC ĐÃ HỌC TRONG CHƯƠNG IX HOẠT ĐỘNG NHÓM Nh N óm 1 Nhóm 2 m Hai ta t m m giác c Ba
B trường hợp đồng dạng g của đồng dạng hai tam t giác Nh N óm 3 Nhóm 4 Định n h lí íPytha h g a o g r o e e Các trường hợp đồng ng dạng của và à Ứng Ứn d ụn ụ g n hai tam t giác vuôn uô g Nhóm 1 Nhóm 2 Nhóm 3 Nhóm 4
BÀI TẬP TRẮC NGHIỆM
9.37. Cho ABC là tam giác không cân. Biết ΔA′B′C′ ∽
ΔABC. Khẳng định nào sau đây là đúng? A. ΔA′C′B′ ∽ ΔACB C. ΔB′A′C′ ∽ ΔBCA B. ΔB′C′A′ ∽ ΔBAC D. ΔA′C′B′ ∽ ΔABC
BÀI TẬP TRẮC NGHIỆM 3.98. Cho ΔA B ′ C ′ ′
∽ ΔABC với tỉ số đồng dạng bằng 2.
Khẳng định nào sau đây là đúng: 𝐴𝐵 𝐴𝐵 𝐴′ 𝐵′ 𝐴′ 𝐵′ 𝐴. =2 𝐵. =2 𝐶 . 𝐷. 𝐴′ 𝐵′ 𝐴′𝐶′ 𝐴𝐵 =2 𝐴𝐶 =2
BÀI TẬP TRẮC NGHIỆM
9.39 Trong các bộ ba số đo dưới đây, đâu là số đo ba cạnh của một tam giác vuông? A. 3 m; 5 m; 6 m C. 1 cm; 0,5 cm; 1,25 cm B. 6 m; 8 m; 10 m D. 9 m; 16 m; 25 m
BÀI TẬP TRẮC NGHIỆM
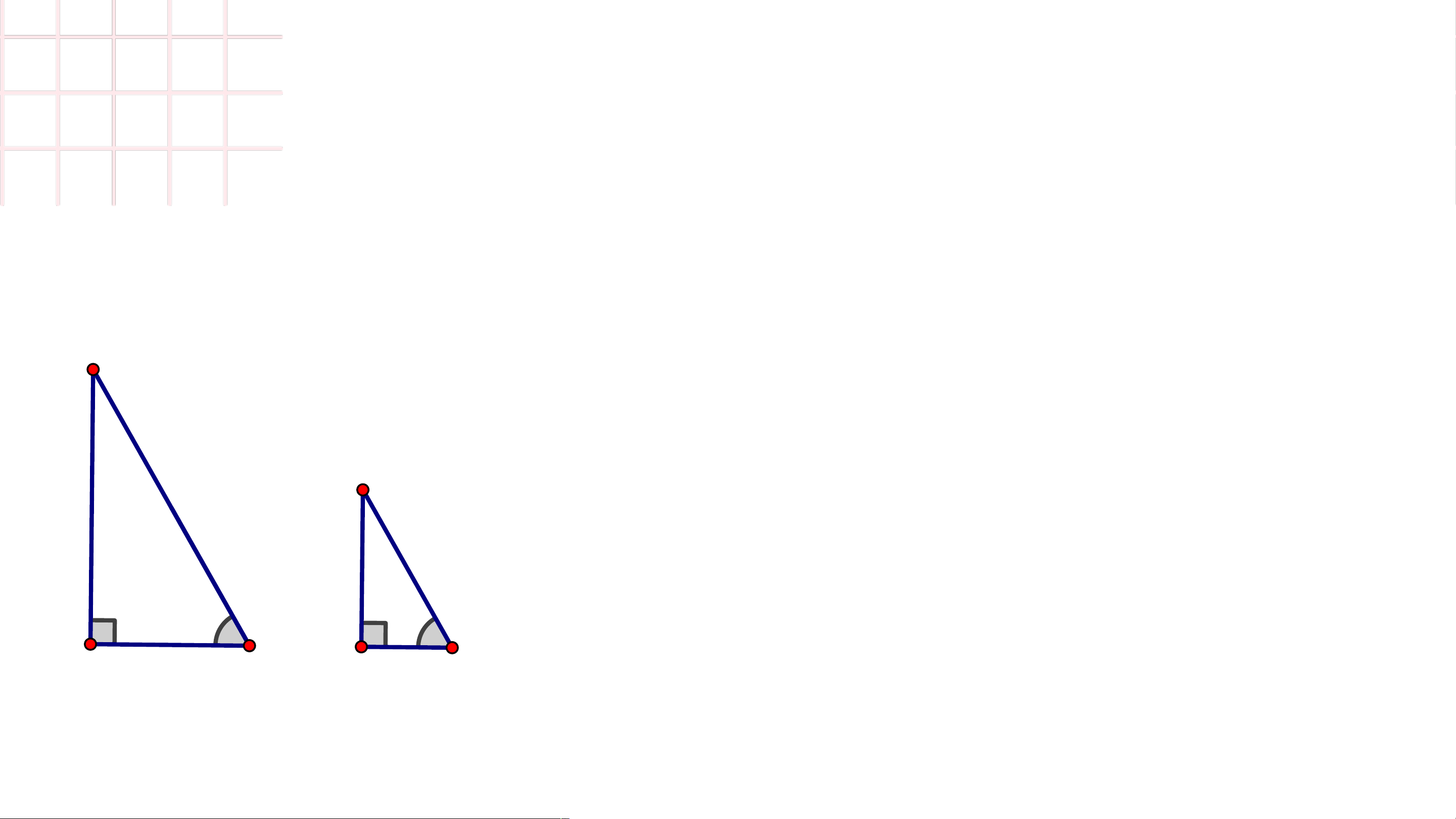
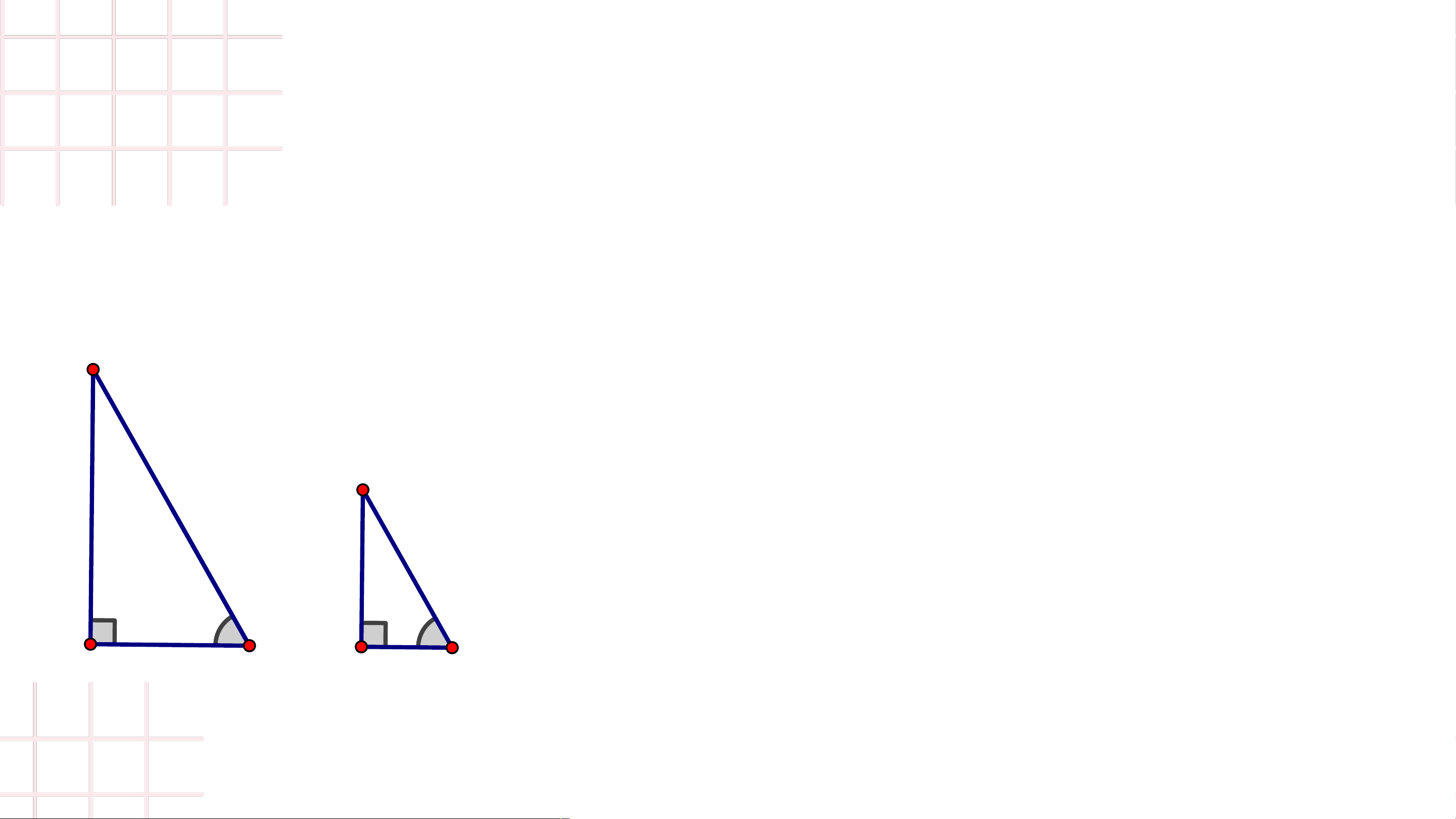
9.40 Cho tam giác ABC vuông tại A (ABAC) và tam giác DEF vuông tại D
(DEDF). Điều nào dưới đây không suy ra ΔABC ∽ ΔDEF A. B. C. D. LUYỆN TẬP
B à i 9
.4 1 ( S GK – t ra n g 1 1
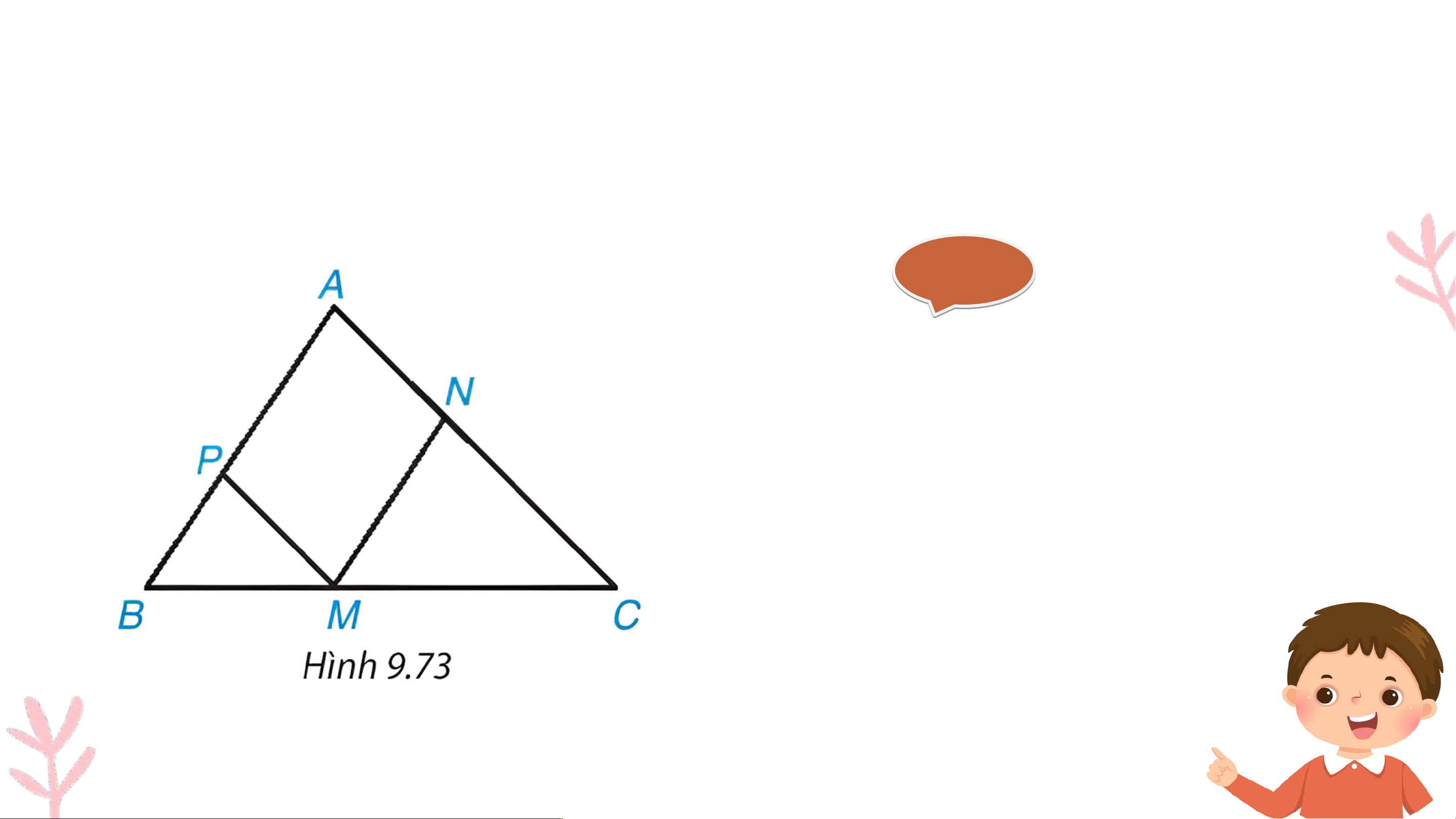
0 ) Cho hình 9.73, biết rằng MN // AB, MP // AC.
Hãy liệt kê ba cặp hai tam giác (khác nhau) đồng dạng có trong hình Gi G ải ả ∆BMP ∽ ∆BCA ; ∆MCN ∽ ∆BCA; ∆BMP ∽ ∆MCN.
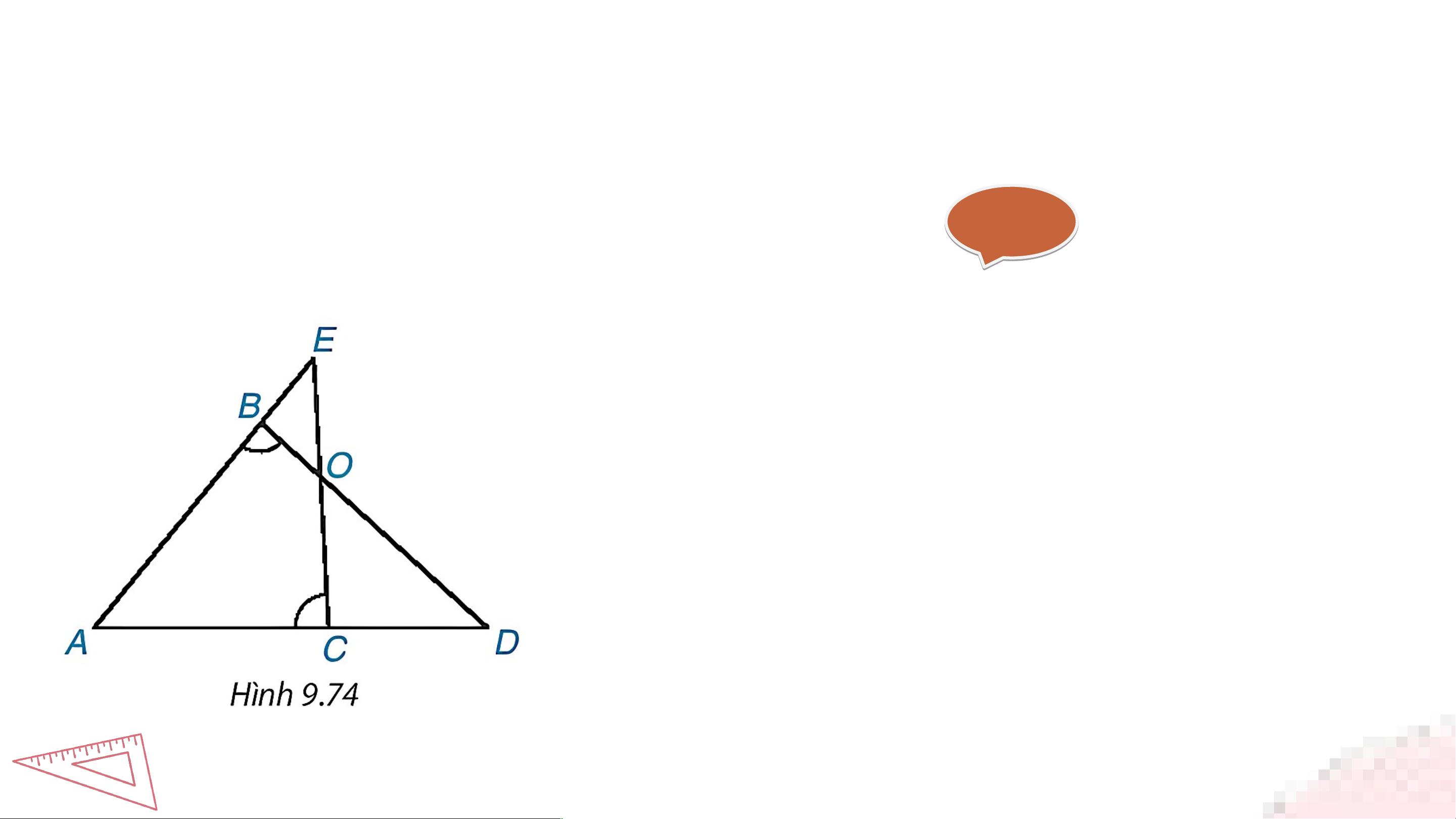
Bài 9.42 (SGK – trang 110) Cho hình 9.74, biết rằng Chứng minh rằng và . Giả i i Xét và có: (gt) ; chung Do đó (g.g) Suy ra Xét và có: (đối đỉnh); Do đó (g.g)
Bài 9.47 (SGK – trang 111) Để tính được chiều cao gần đúng của kim tự tháp Ai
Cập, người ta nắm 1 cây cọc cao 1m vuông góc với mặt đất và đo được bóng cây cọc
trên mặt đất là 1,5m. Khi đó chiều dài bóng của kim tự tháp trên mặt đất là 208,2 m.
Hỏi kim tự tháp cao bao nhiêu mét? B
Chiều cao của kim tự tháp và bóng của nó tạo thành ABC vuông tại A B'
Khi đó: chiều dài cái bóng là đoạn AC = 208,2m ? 1m
Chiều cao của cây cọc và bóng của nó tạo thành A’B’C’ C A A'
C' vuông tại A’ 208,2m 1,5m
Khi đó: Chiều cao cây cọc là đoạn A’B’ = 1m
Chiều dài cái bóng cây cọc là đoạn A’C’ = 1,5m
Bài 9.47 (SGK – trang 111) Để tính được chiều cao gần đúng của kim tự tháp Ai
Cập, người ta nắm 1 cây cọc cao 1m vuông góc với mặt đất và đo được bóng cây cọc
trên mặt đất là 1,5m. Khi đó chiều dài bóng của kim tự tháp trên mặt đất là 208,2 m.
Hỏi kim tự tháp cao bao nhiêu mét? B
Vì cùng 1 thời điểm trong ngày, tia sáng tạo với mặt đất các góc bằng nhau () B'
Xét ABC và A’B’C’ có: ?
Suy ra ABC A’B’C’ (g – g) 1m Do đó C A A' C' 208,2m 1,5m Hay AB = 138,8
Vậy chiều cao của kim tự tháp là 138,8 mét
Bài 9.43 (SGK – trang 110) Hai đường trung tuyến của tam giác cắt nhau
tại điểm (H.9.75). Chứng minh rằng tam giác đồng dạng với tam giác và tìm tỉ số đồng dạng. Giải ả và có: (so le trong) (g.g) 𝑀𝑁 1
với tỉ số đồng dạng bằng 𝐵𝐶 =2
HƯỚNG DẪN VỀ NHÀ Chuẩn bị trước Ghi nhớ Hoàn thành các bài mới kiến thức trong bài bài tập trong SBT Hình chóp tam giác đều VẬN DỤNG
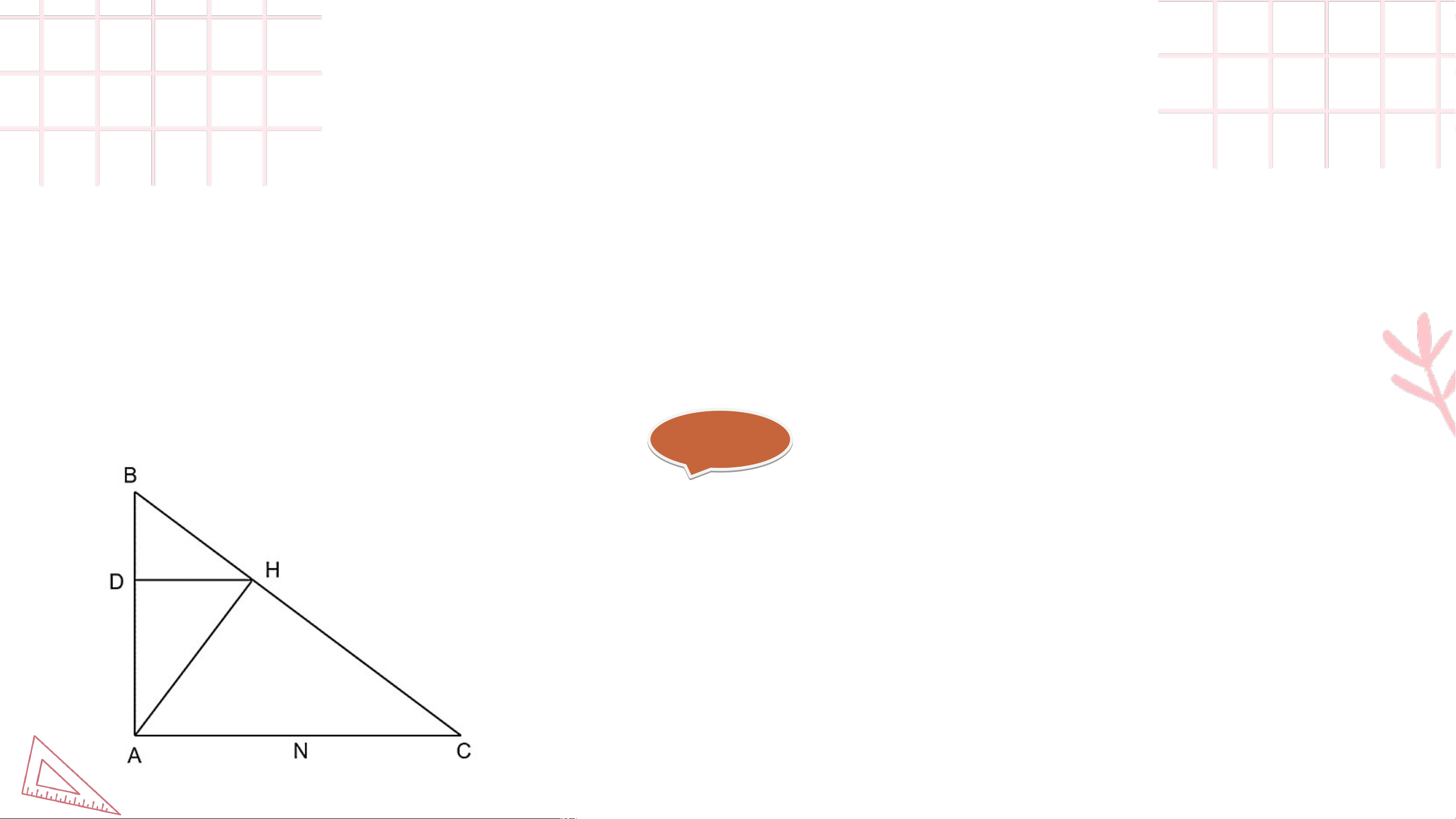
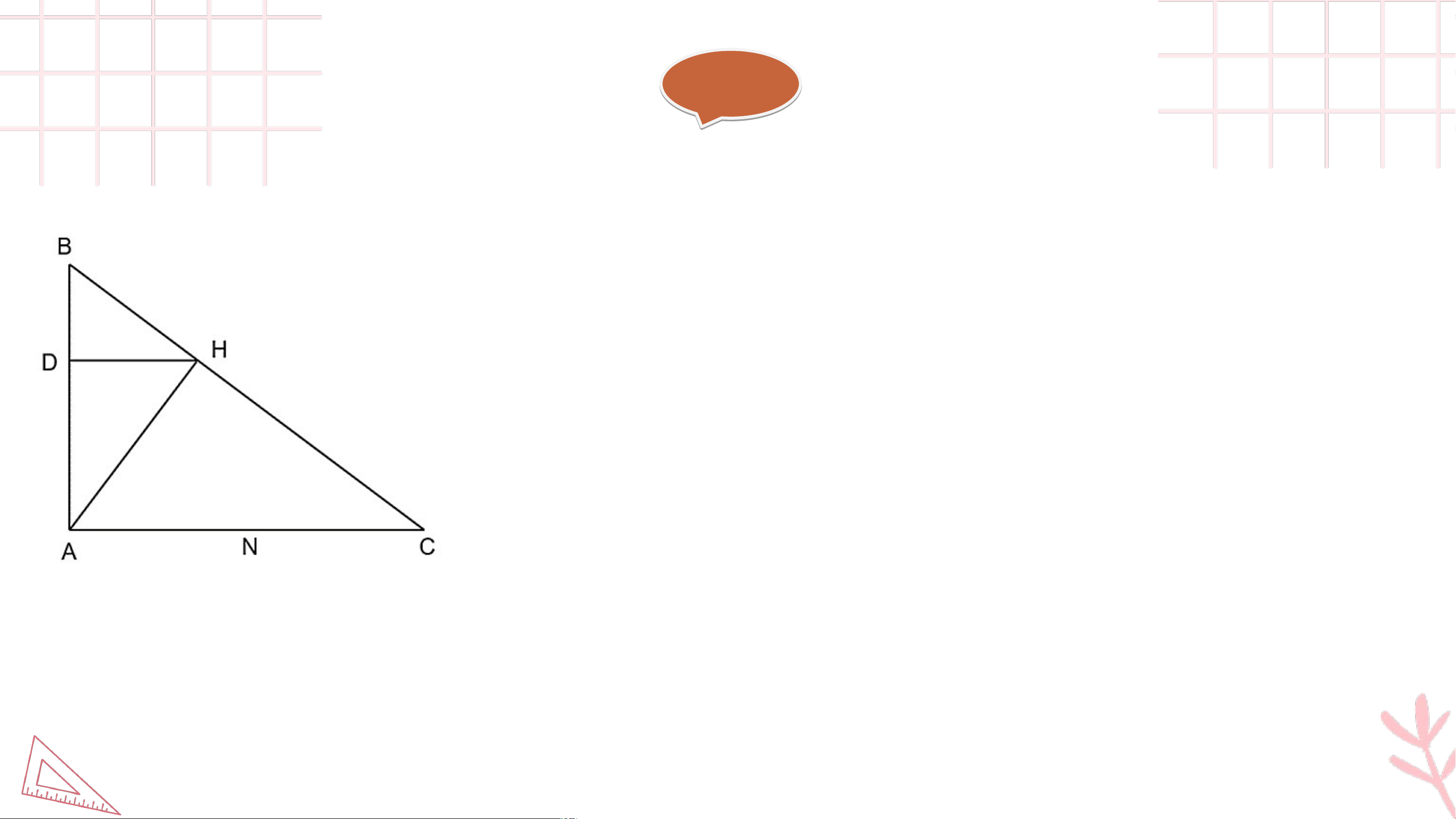
Bài 9.44 (SGK – trang 111) Cho tam giác vuông tại có . Gọi lần lượt là các đường
cao kẻ từ đỉnh của tam giác và đỉnh của tam giác . a) Chứng minh rằng
b) Tính độ dài các đoạn thẳng . Giải ả
a) (vuông tại ) và (vuông tại ) có: (cặp góc nhọn) Giả i i ả b) (cm) (cm) (cm) (cm) (cm)
Bài 9.45 (SGK – trang 111)
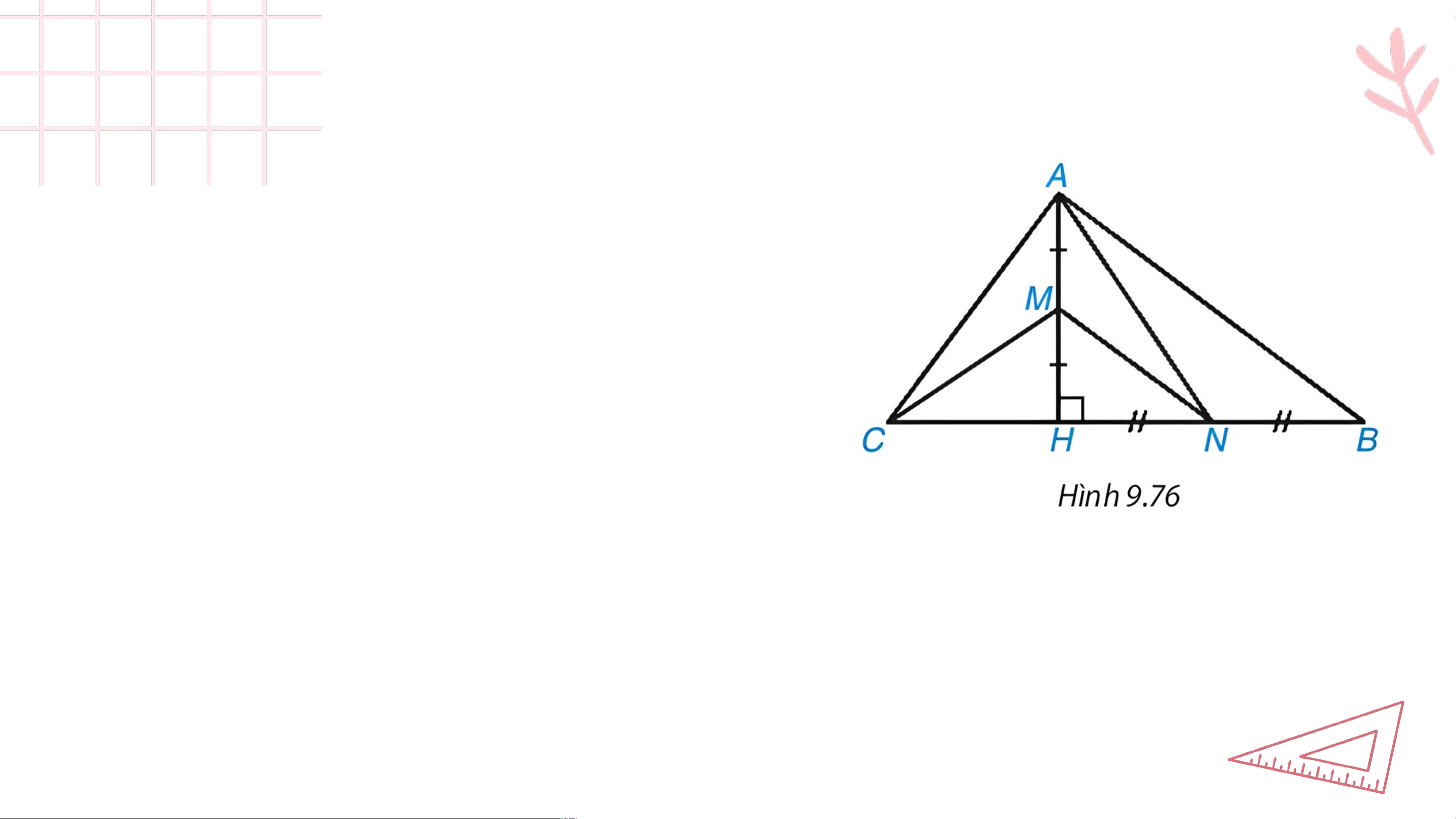
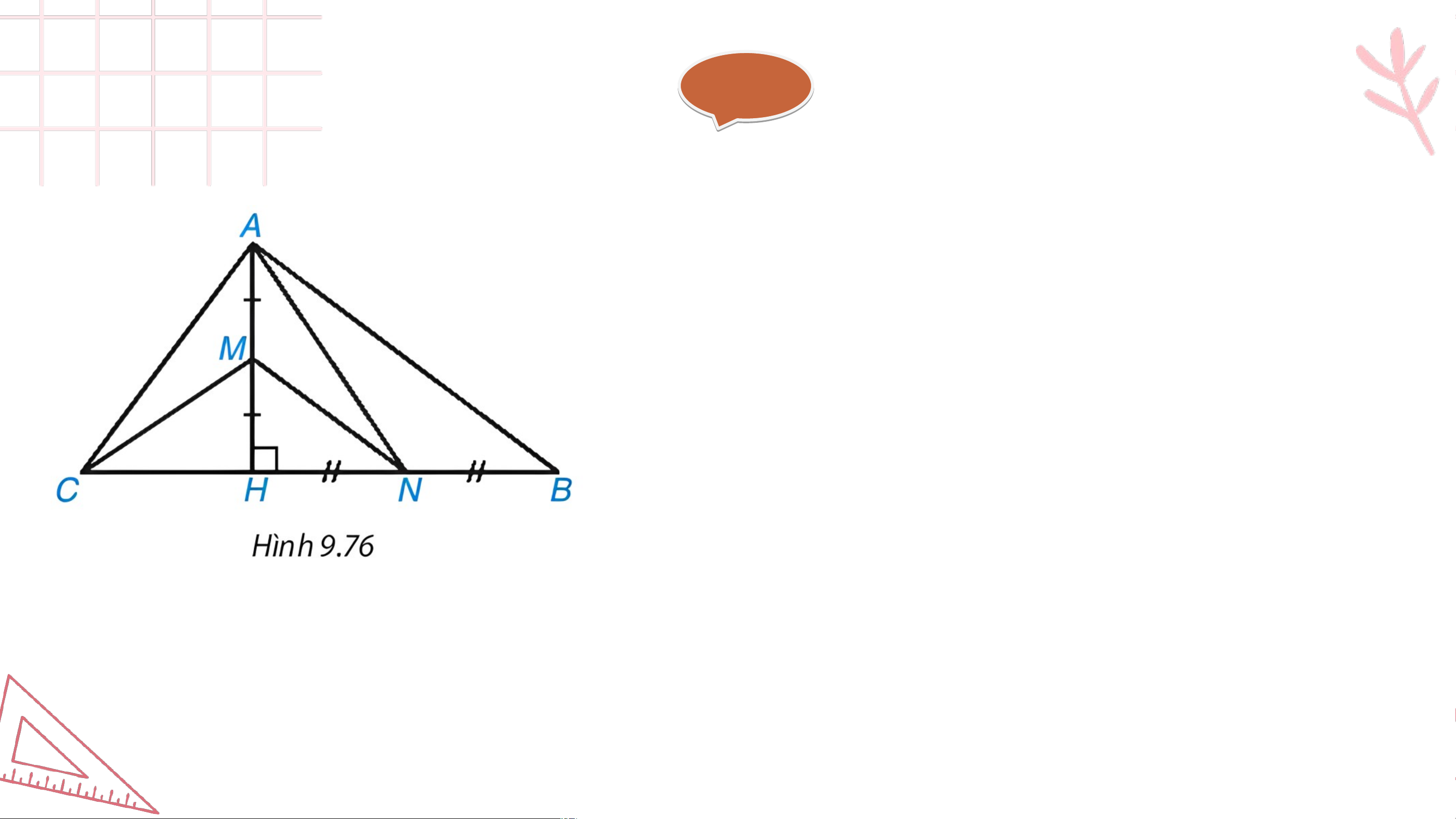
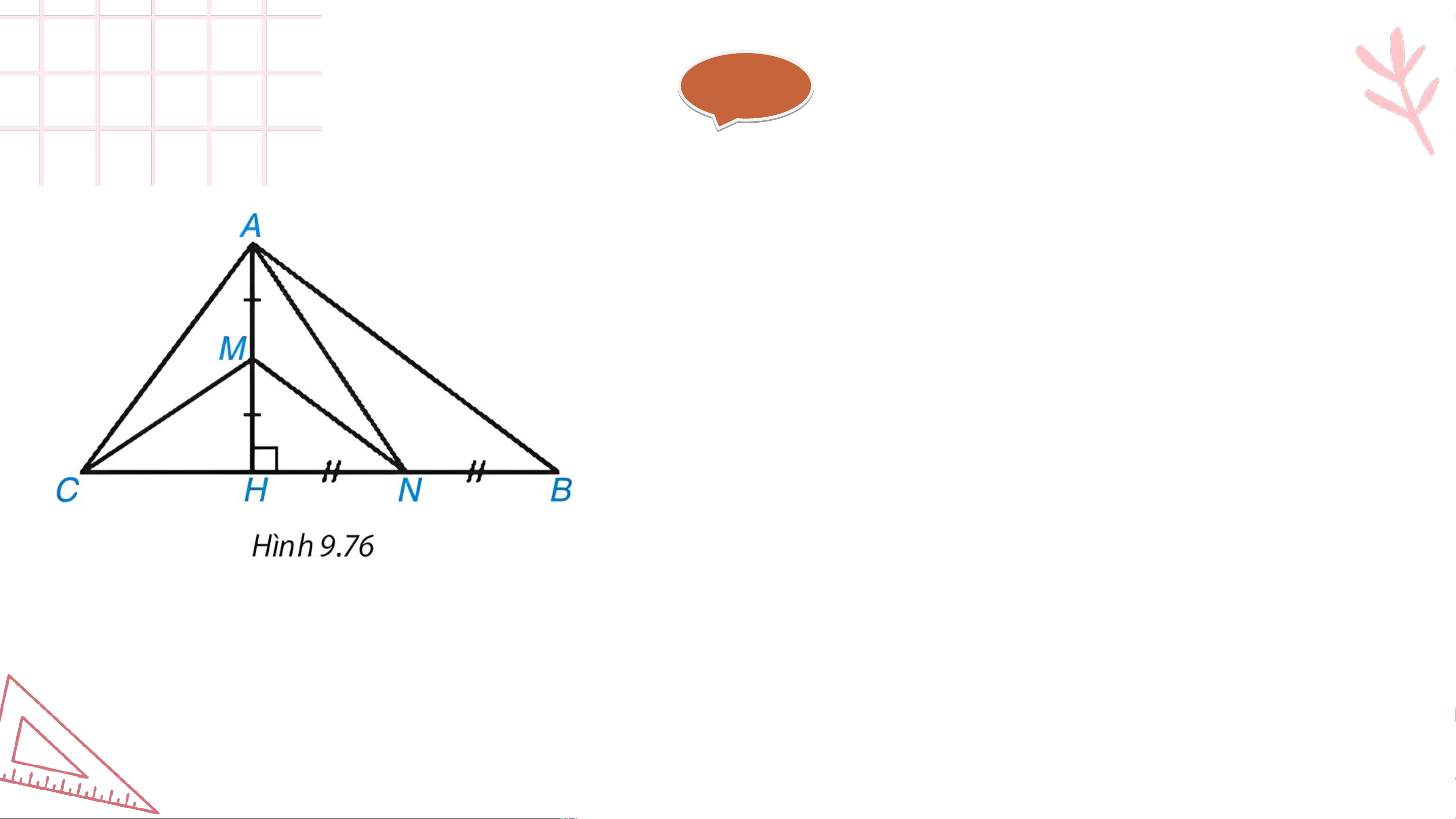
Cho tam giác có đường cao . Biết . Lấy lần
lượt là trung điểm của .
a) Chứng minh rằng là tam giác vuông tại b) Chứng minh rằng và
c) Tính diện tích tam giác Giải ả a) Ta có: (cm) (cm) (cm)
Do đó nên vuông tại (định lí Pythagore đảo). Giải ả b) và nên có: (gt) ; (cmt), mà . Vậy là trực tâm của c) Ta có:
Bài 9.46 (SGK – trang 111)
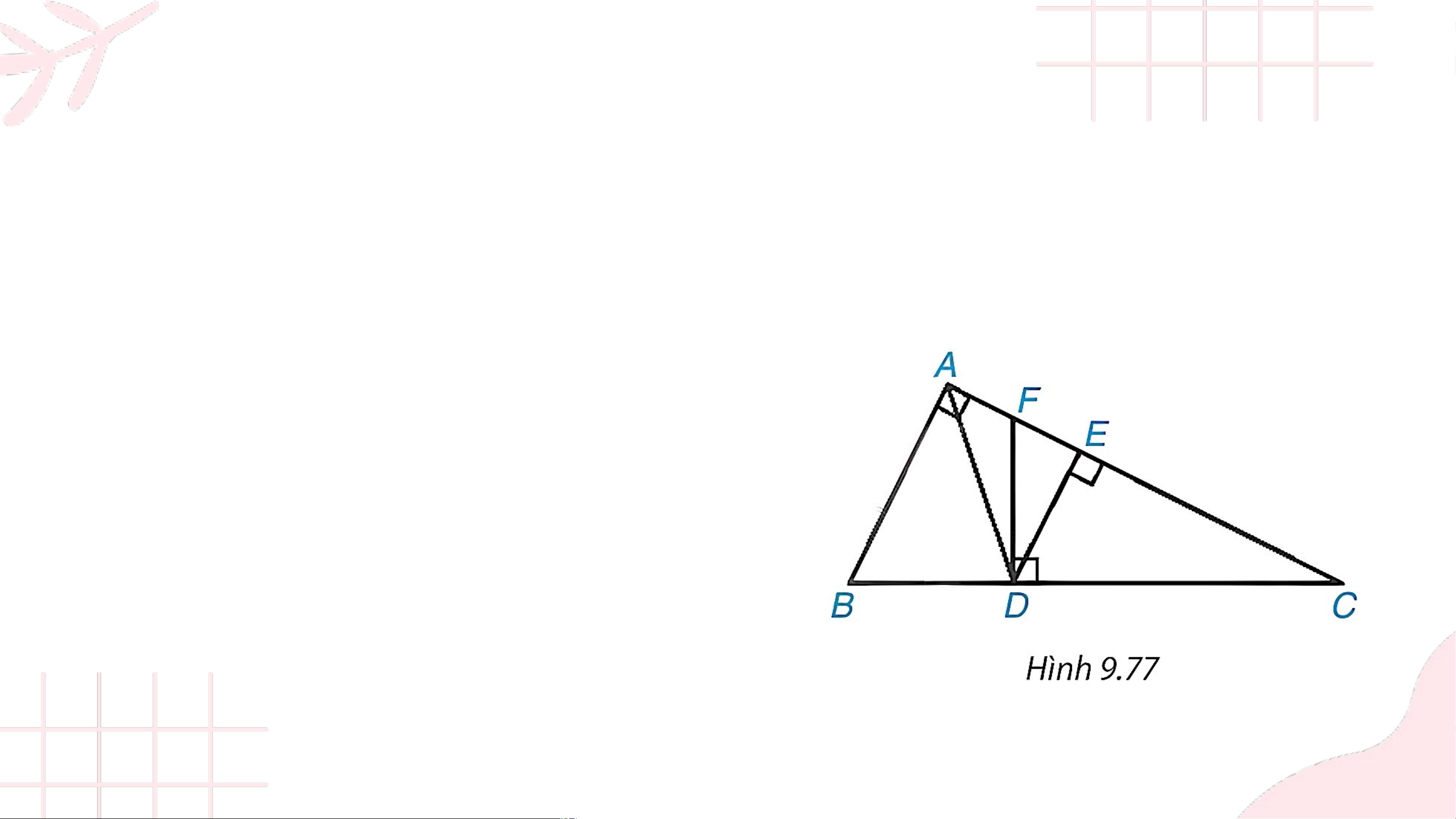
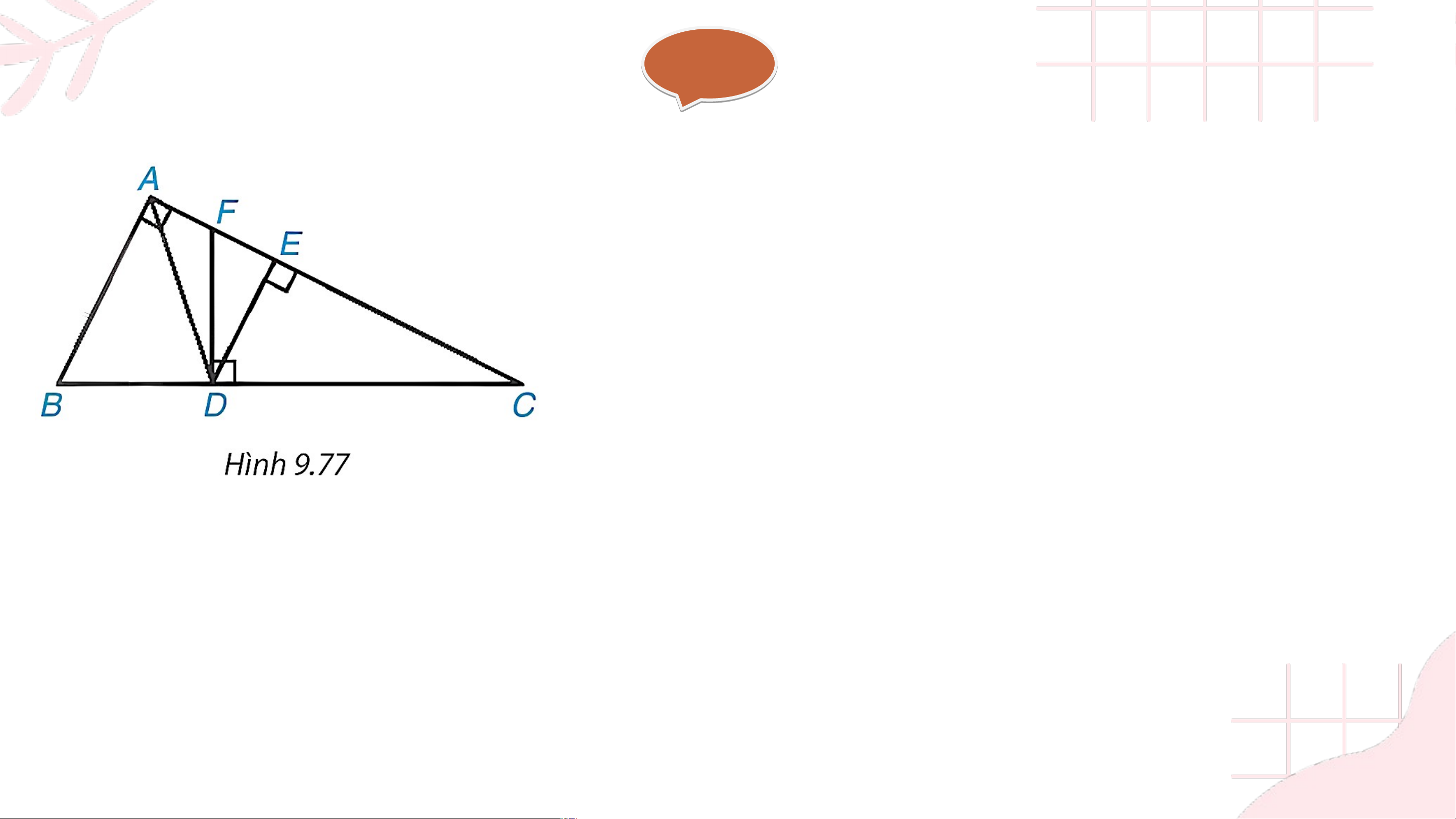
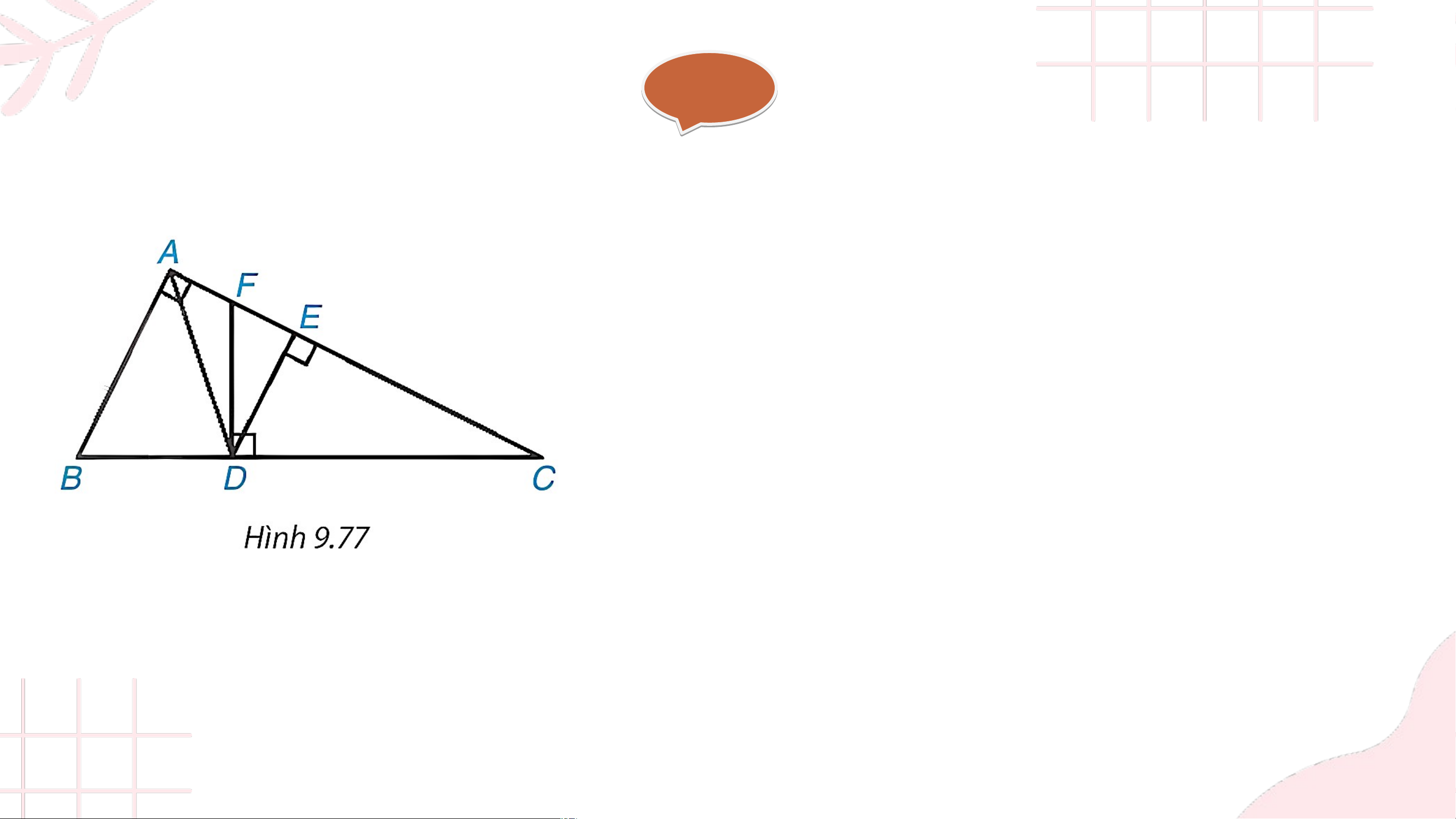
Cho tam giác vuông tại và các điểm như Hình 9.77 sao cho là phân giác của góc
và lần lượt vuông góc với và . Chứng minh rằng: a) , từ đó suy ra b) c) Giải
a) Kẻ đường thẳng qua vuông góc với , cắt tại Vì nên và Do vậy (1) (1)
Theo định lí Thalès, ta có: Giải
b) (vuông tại ) và (vuông tại ) có: chung (1 cặp góc nhọn) c) Từ câu b Do đó
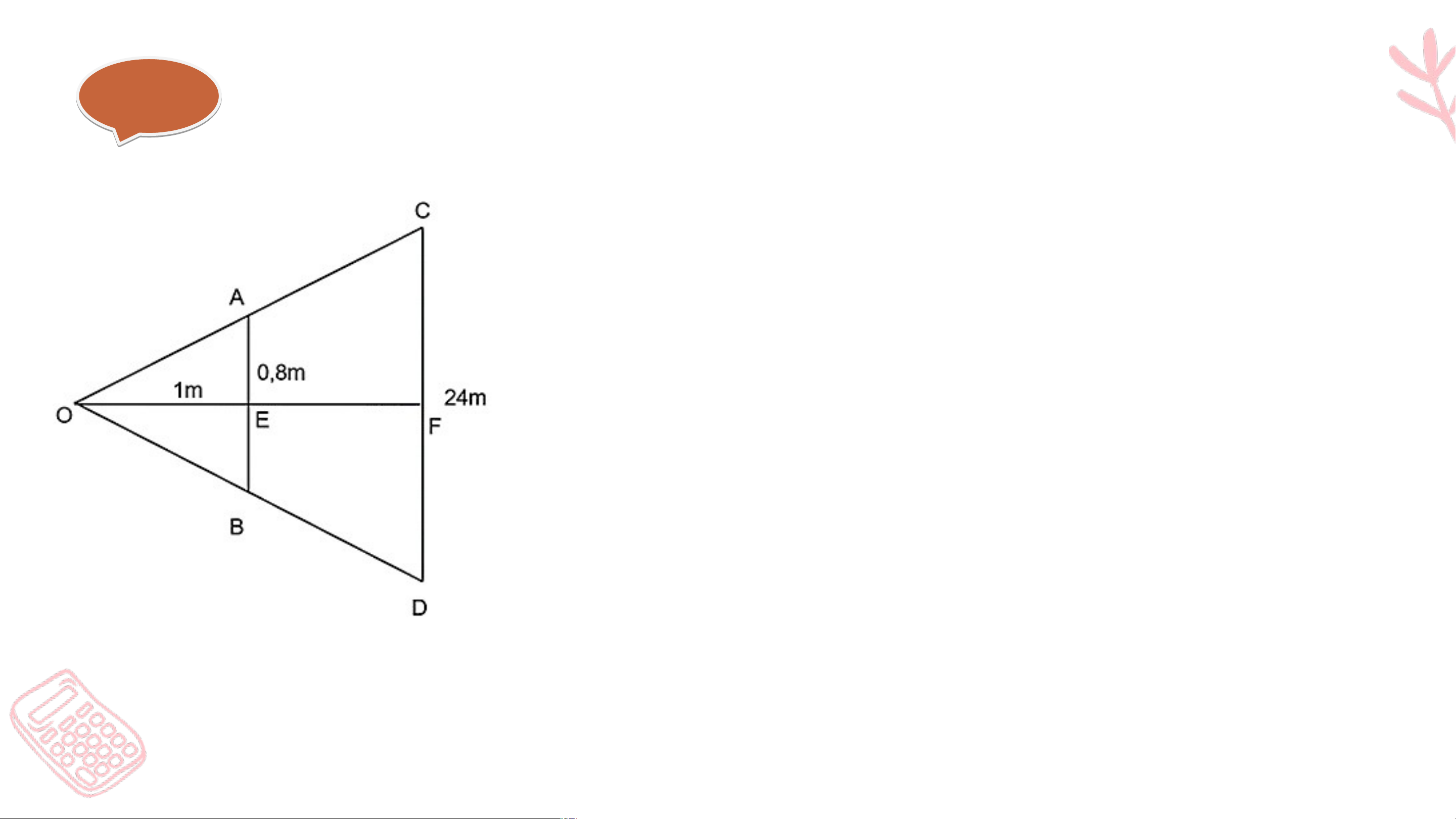
Bài 9.48 (SGK – trang 111)
Từ căn hộ chung cư nhà mình, bạn Lan đứng cách cửa sổ 1m nhìn sang tòa
nhà đối diện thì vừa nhìn thấy đúng tất cả 6 tầng của tòa nhà đó. Biết rằng
cửa sổ nhà Lan cao 80cm và mỗi tầng của tòa nhà đối diện 4m. Hỏi khoảng
cách từ căn hộ nhà Lan đến tòa nhà đối diện là bao nhiêu? Giả i i ả Có m ; m ; (m) Xét và có : m
Vậy khoảng cách từ căn hộ nhà Lan đến tòa nhà đối diện là 29m.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- BÀI TẬP TRẮC NGHIỆM
- BÀI TẬP TRẮC NGHIỆM
- BÀI TẬP TRẮC NGHIỆM
- BÀI TẬP TRẮC NGHIỆM
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28




