Giáo án điện tử Toán 8 Kết nối tri thức: Luyện tập chung (trang 121)

KIẾN THỨC CƠ BẢN VỀ HÌNH CHÓP TỨ GIÁC ĐỀU
Hình chóp tứ giác đều là
01 hình có đáy là hình vuông và
các mặt bên là các tam giác cân bằng nhau
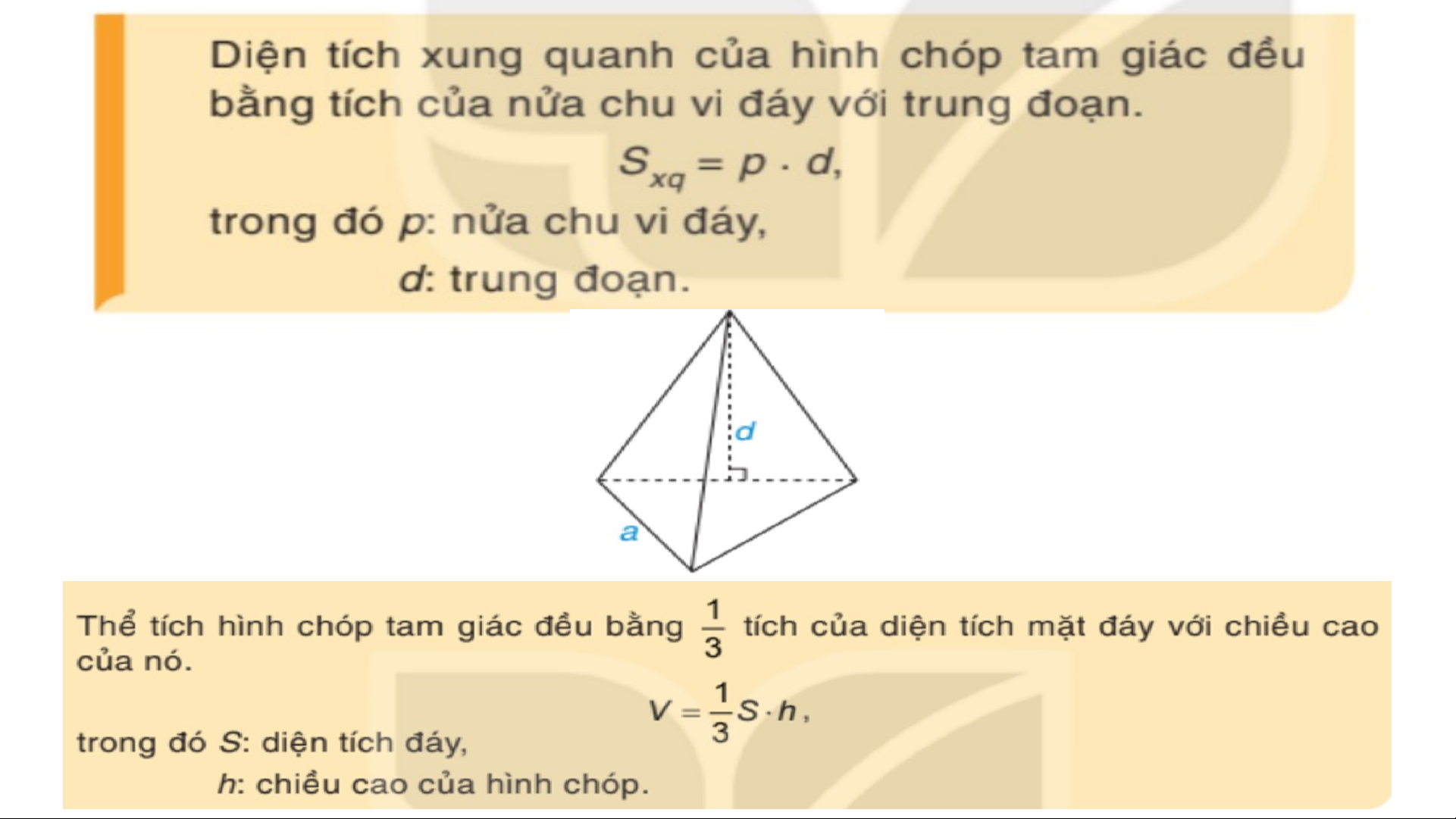
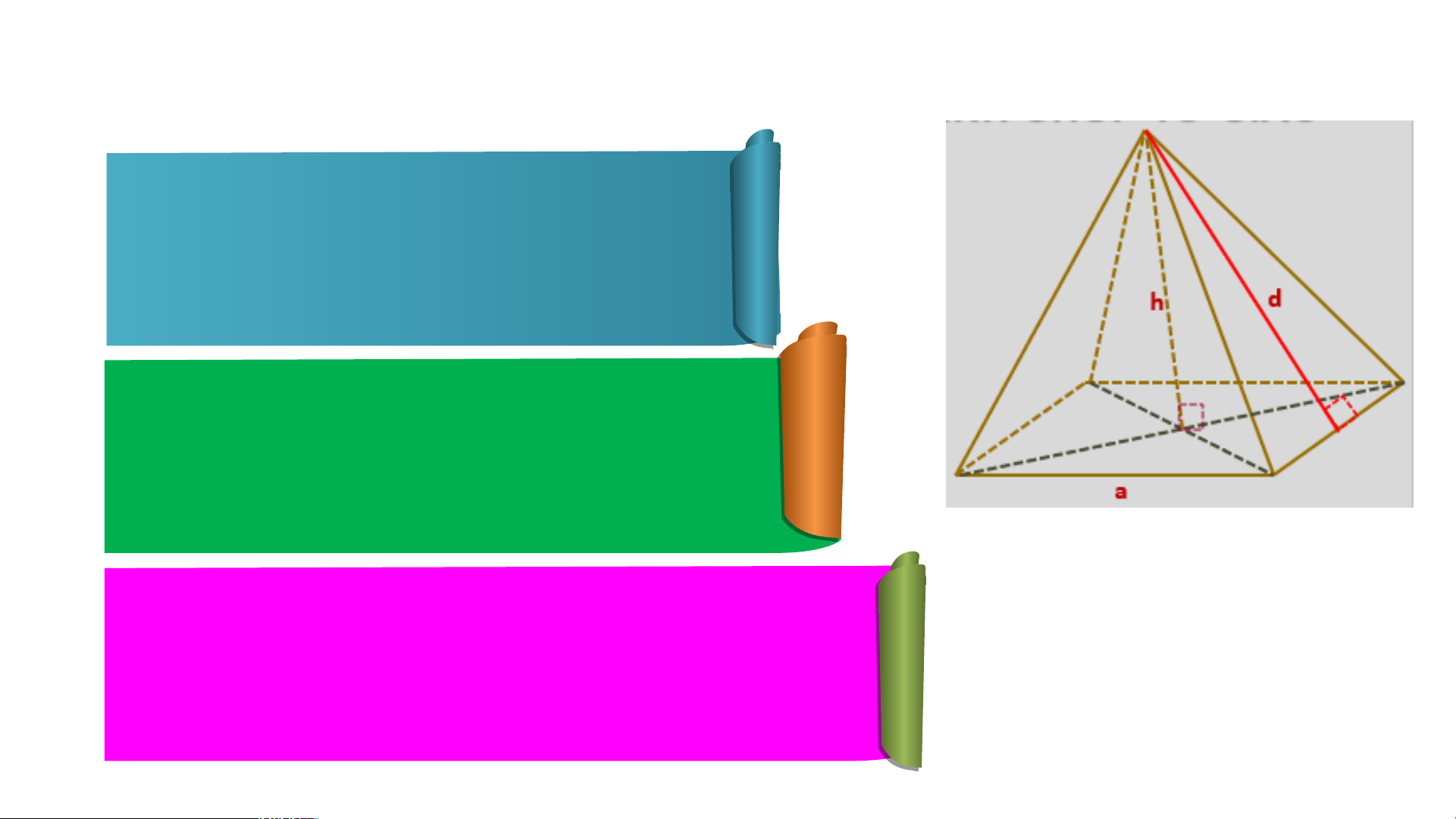
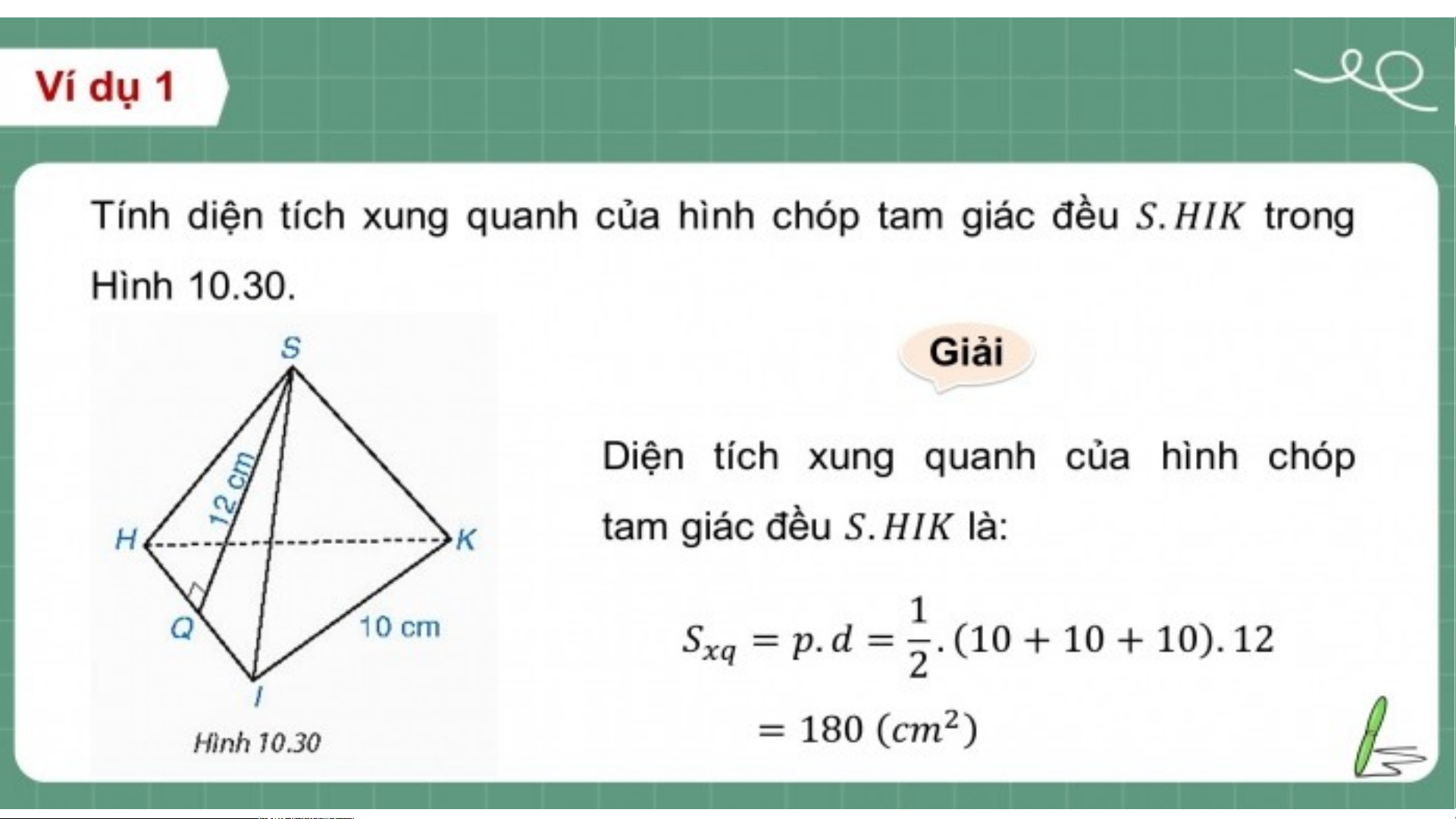
Công thức tính diện tích xung quanh : = p.d
02 Công thức tính diện tích toàn phần: S = S + S tp xq đ
Công thức tính thể tích của hình chóp
03 tứ giác đều V = S.d D C TIẾT 59.
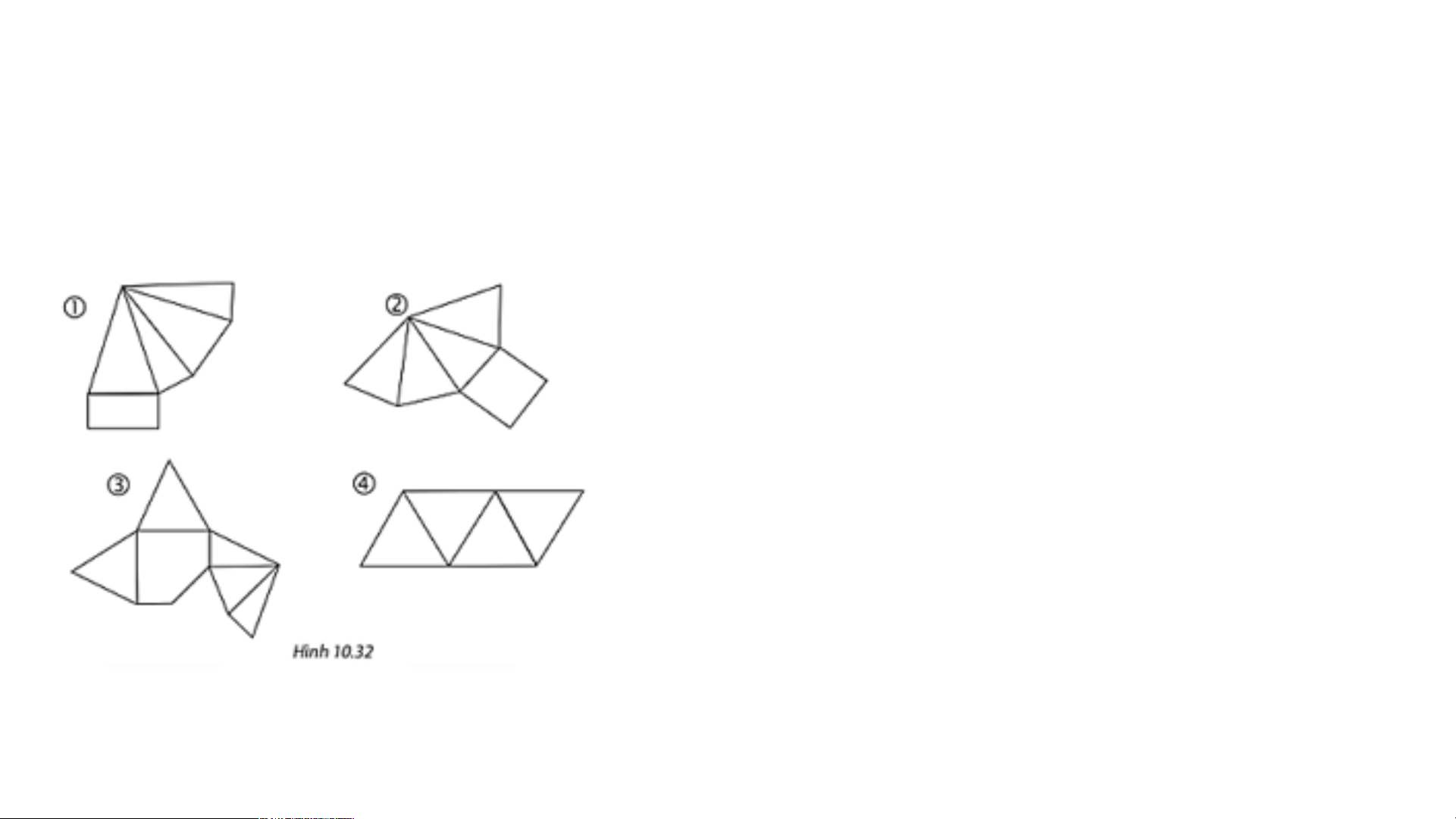
Bài 10.12 trang 122: Trong các miếng bìa ở Hình 10.32, miếng bìa
nào khi gấp và dán lại thì được một hình chóp tam giác đều, miếng
nào thì được một hình chóp tứ giác đều.
Miếng bìa 4 gấp và dán lại được hình chóp tam giác đều.
Miếng bìa 2 gấp và dán lại được hình chóp tứ giác đều.
Miếng bìa 1 và miếng bìa 3 không
không có đáy là hình vuông hay hình
tam giác nên không thỏa mãn.
Bài 10.11 trang 121: Tính thể tích của hình chóp tam giác đều
S.ABC, biết diện tích đáy của nó bằng 15,6 cm2, chiều cao bằng 10 cm.
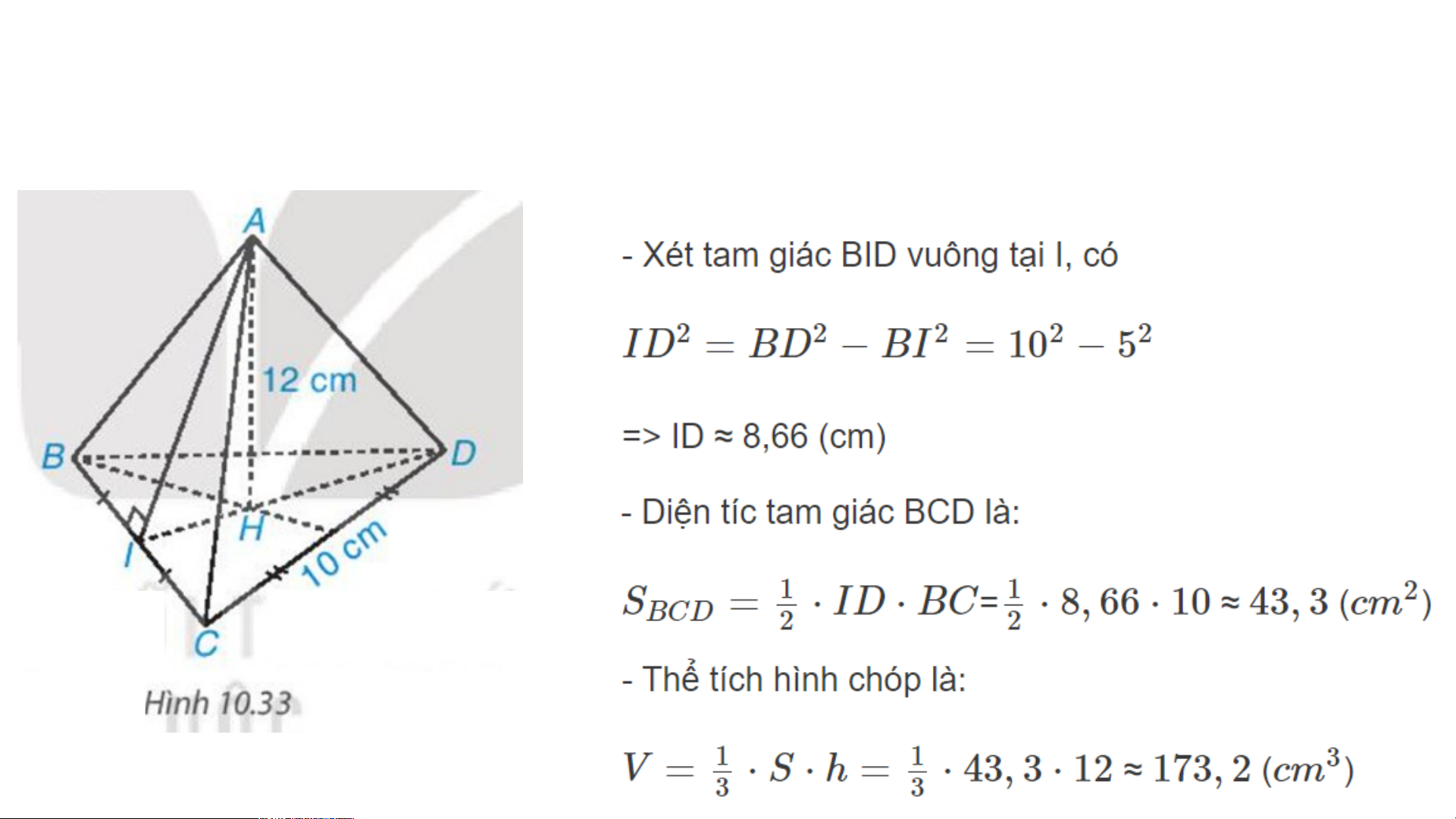
Bài 10.13 trang 122: Tính thể tích hình chóp tam giác đều A.BCD có độ dài
cạnh đáy bằng 10 cm, chiều cao bằng 12 cm (H.10.33), biết ≈ 8,66 GIẢI:
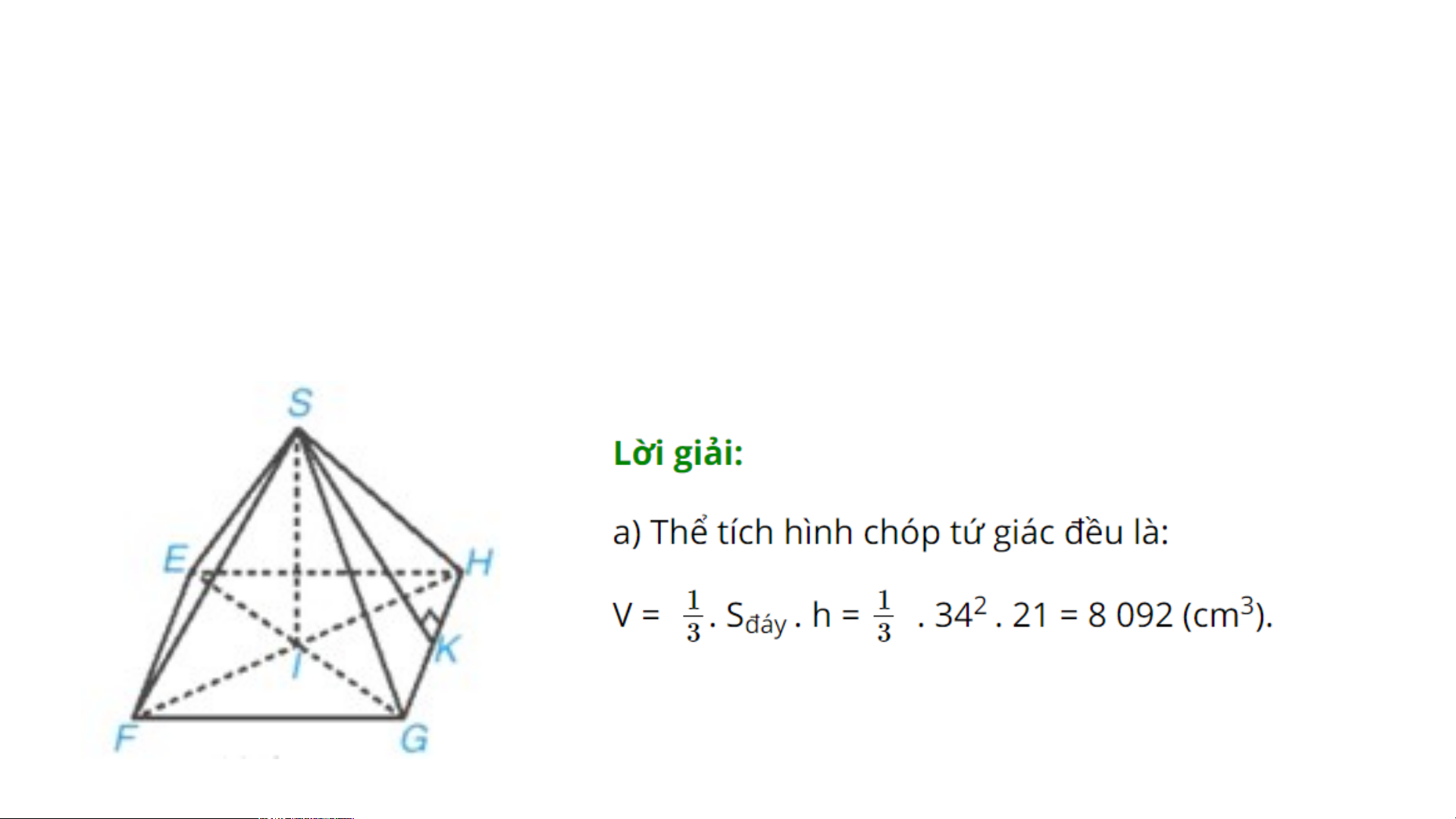
Bài 10.14 trang 122. Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng
Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m
a) Tính thể tích hình chóp
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết
rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.
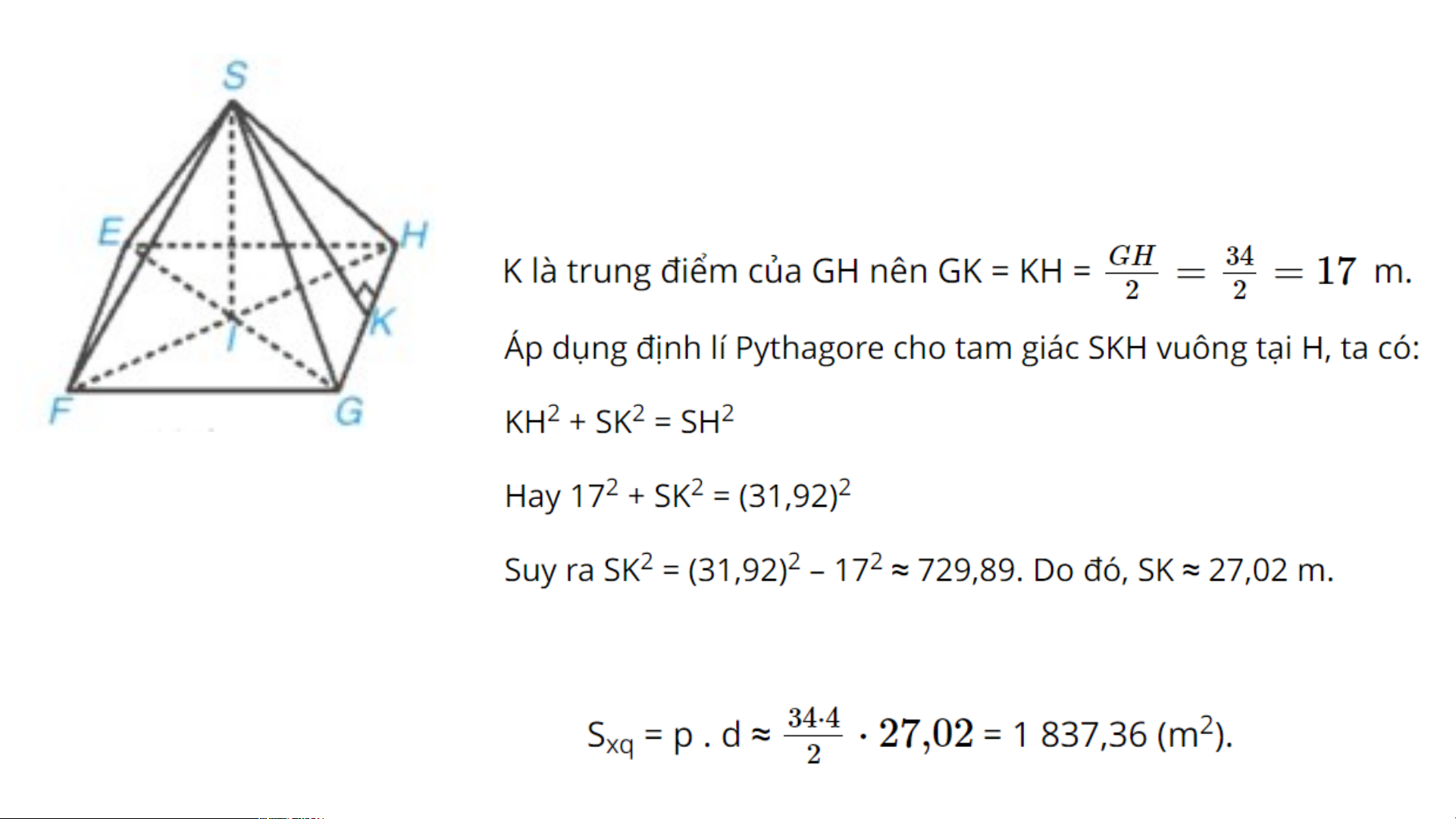
b) Ta có SI = 21 m, EF = FG = GH = HE =
34 m, SE = SF = SG = SH = 31,92 m.
SK là một trung đoạn của hình chóp.
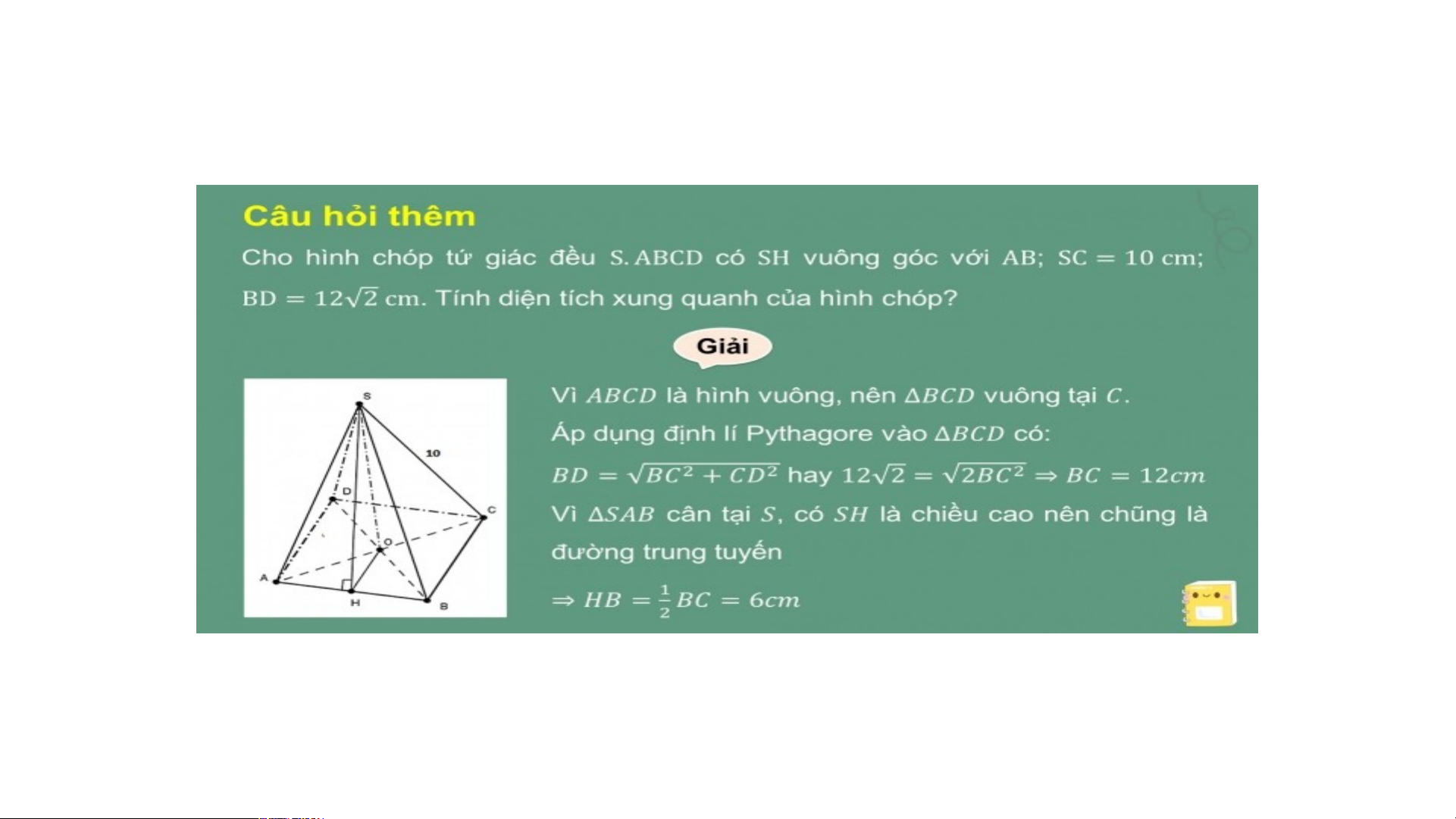
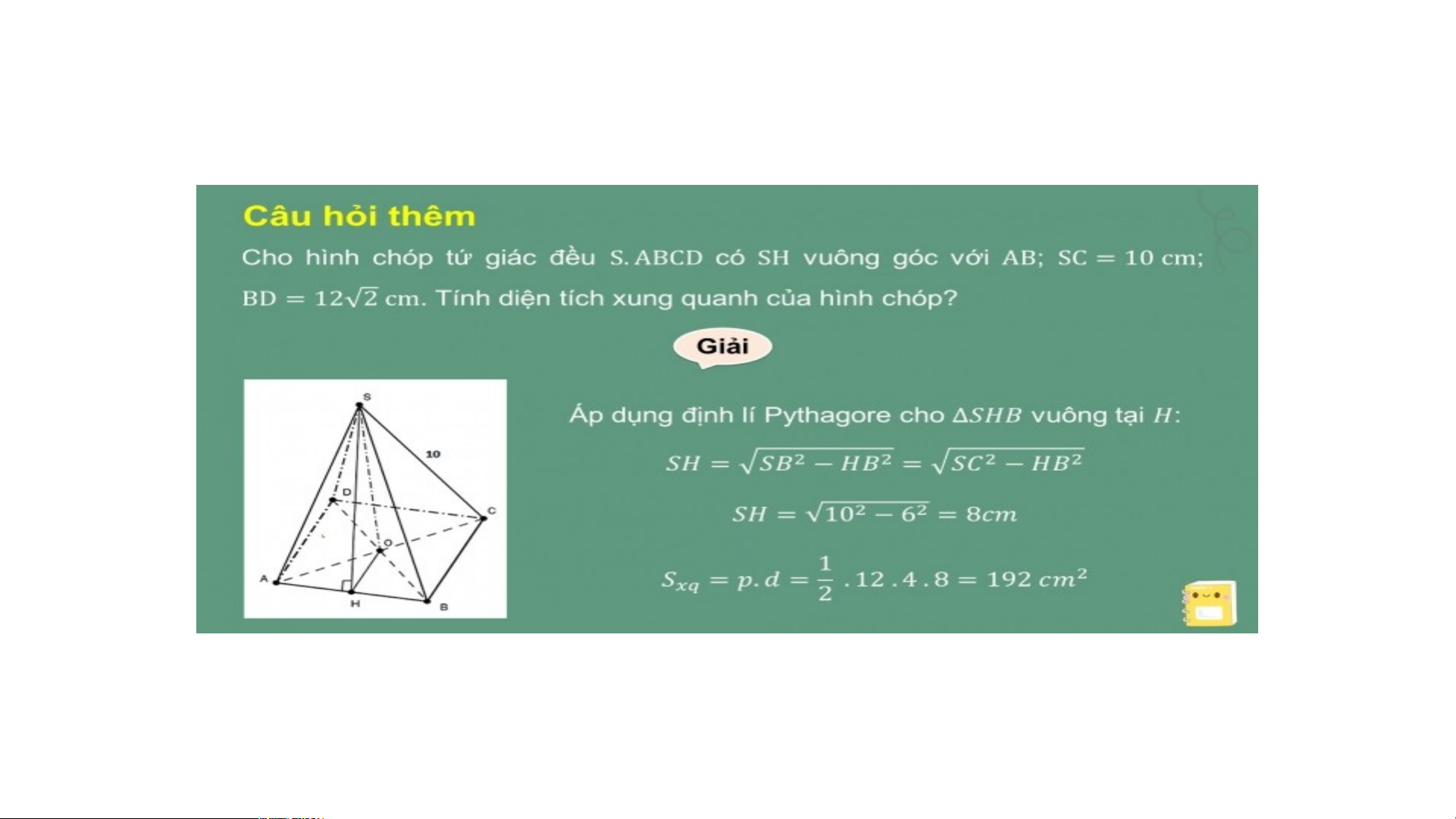
Diện tích xung quanh của hình chóp tứ giác đều là: BÀI TẬP THÊM
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18