








Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC NGÀY HÔM NAY!
GV: NGUYỄN THỊ PHƯƠNG KHÁNH
THCS&THPT NÀ PHẶC Chứng g minh hình bình hàn à h Chứn ứ g minh cá c c đ oạn thẳn ẳ g, cá c c g ó g c bằn ằ g nhau VÒNG QUAY MAY MẮN T 1 2 iếp 3 4 5 QUAY
Câu 1. Khẳng định nào sau đây là đúng?
A. Tứ giác có hai cạnh đối song song là hình bình hành.
B. Tứ giác có hai cạnh đối bằng nhau là hình bình hành.
C. Tứ giác có hai góc đối bằng nhau là hình bình hành.
D. Tứ giác có các cạnh đối song song là hình bình hành. D QUAY A Y VỀ V
Câu 2. Khẳng định nào sau đây là sai ?
A. Tứ giác có hai cặp cạnh đối song song là hình bình hành. B.
B Hình thang có hai góc kề một đáy bằng nhau là hình bình hành.
C. Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
D. Tứ giác có hai cặp góc đối bằng nhau là hình bình hành. QUAY A Y VỀ V
Câu 3. Khẳng định nào sau đây là sai ?
A. Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
B. Hình thang có hai cạnh bên song song là hình bình hành.
C. Hình thang có hai đường chéo bằng nhau là hình bình hành.
D. Tứ giác có hai đường chéo cắt nhau tại trung điểm
của mỗi đường là hình bình hành. QUAY A Y VỀ V
Câu 4. Chọn câu sai. ABCD là hình bình hành. Khi đó: A. AB = CD B. AD = BC C. D. D AC = BD QUAY A Y VỀ V
Câu 5. Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu: D QUAY A Y VỀ V TIẾT 8 + 9. LUYỆN TẬP CHUNG Bài Bài tập t 3. ập 19 3. 19 trang tr ang 63 s 63 gk g
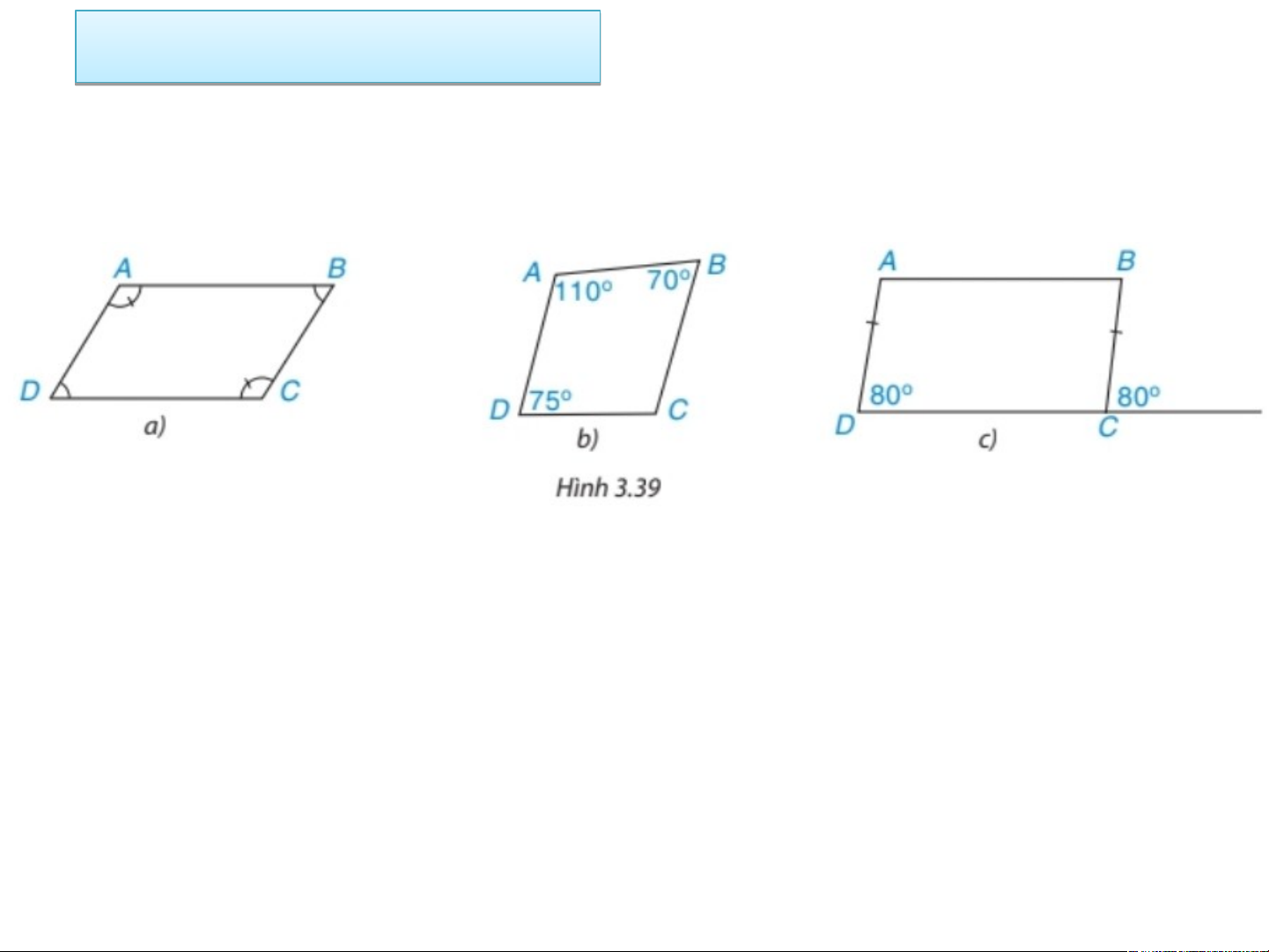
Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao? Bài giải
a) là hình bình hành vì có các cặp góc đối bằng nhau
b) Không là hình bình hành vì có cặp góc đối không bằng nhau
c) là hình bình hành vì có AD = BC, AD // BC Bài Bài tập t 3. ập 20 3. 20 trang tr ang 63 s 63 gk g
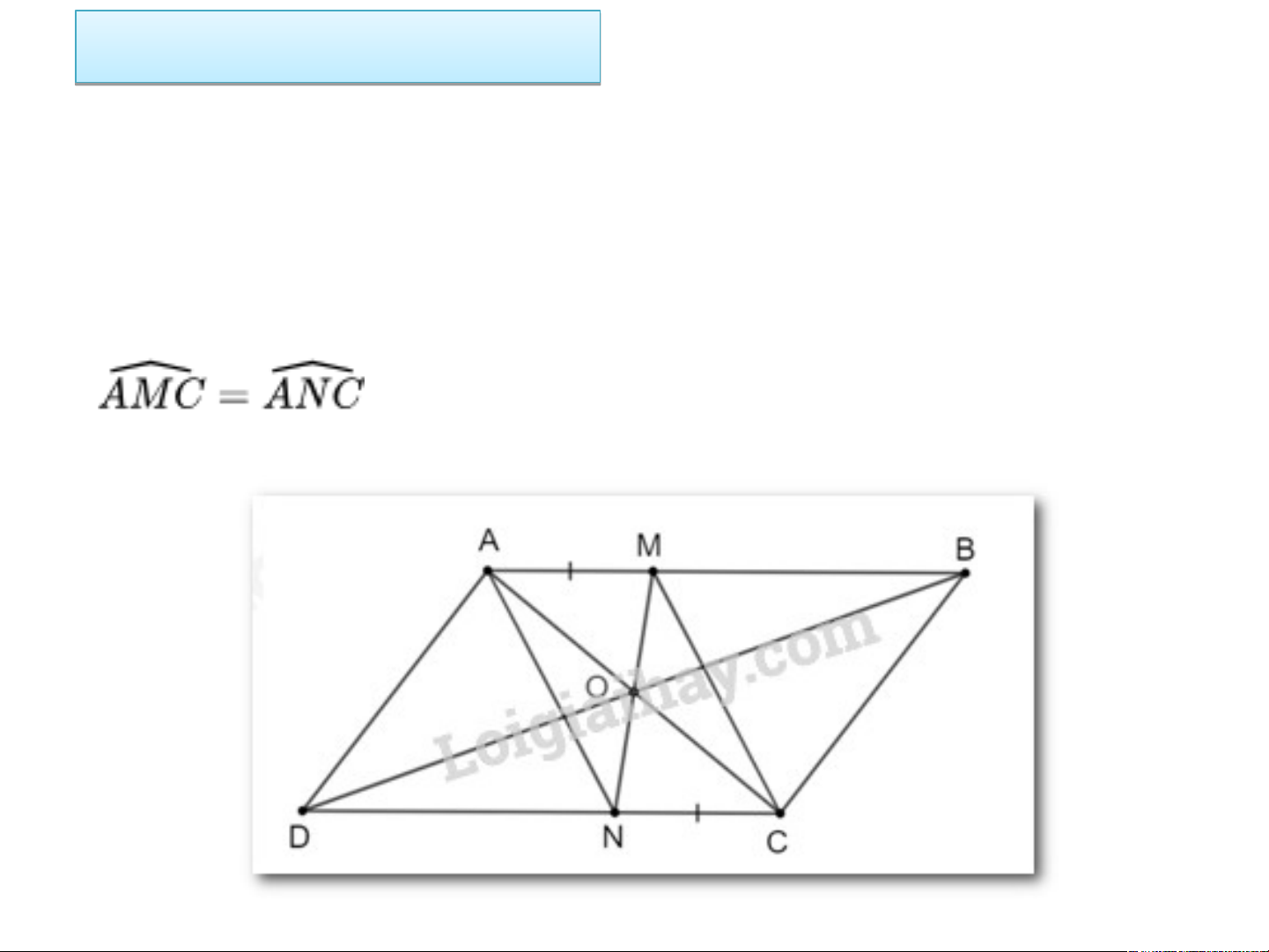
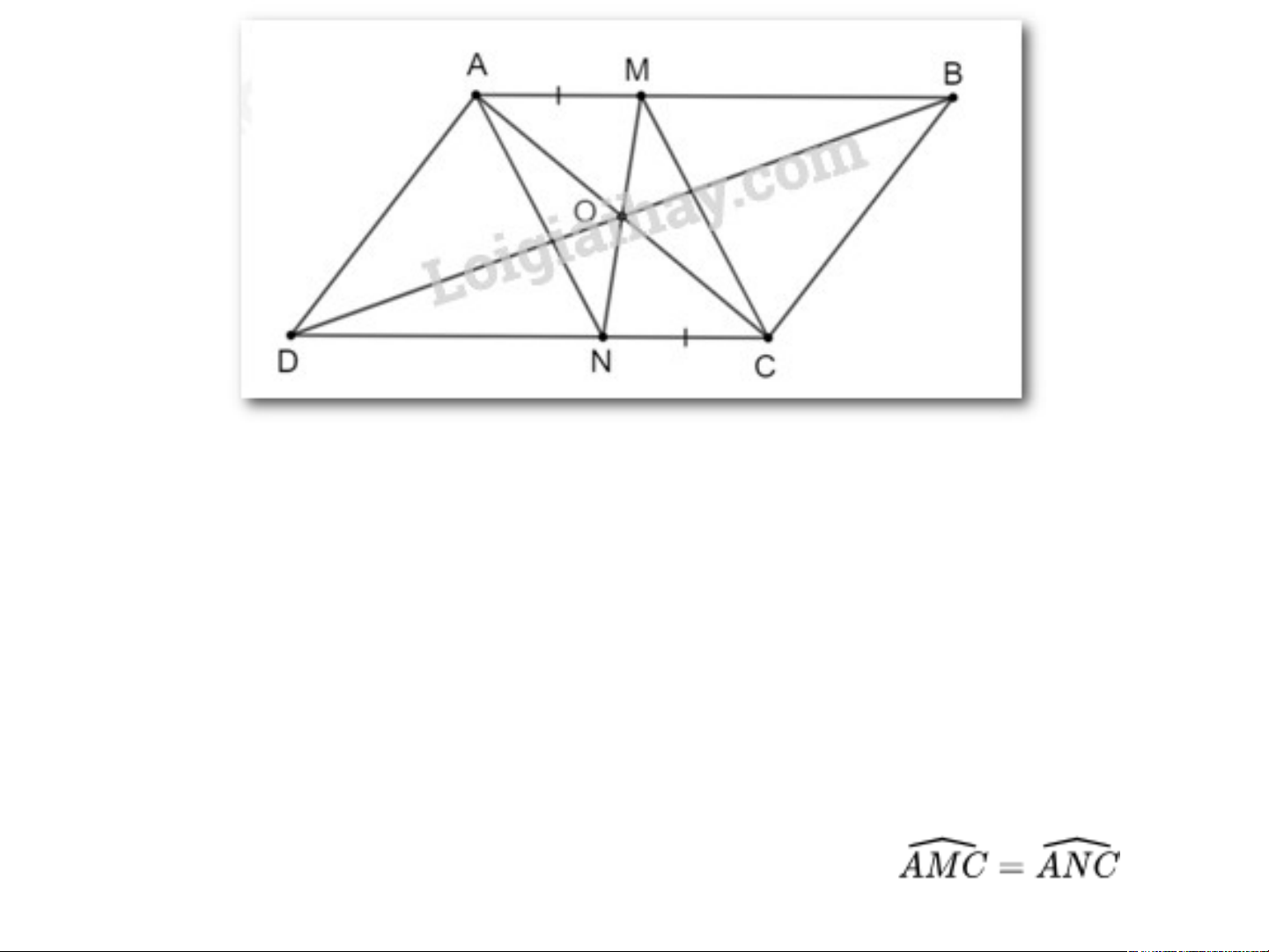
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh
AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng: a) AN = CM b) Chứng minh
a) Vì ABCD là hình bình hành nên AB // CD.
Tứ giác AMCN có AM // CN (vì AB // CD); AM = CN (giả thiết).
Suy ra, tứ giác AMCN là hình bình hành. Do đó AN = CM
b) Vì tứ giác AMCN là hình bình hành suy ra Bài Bài tập t 3. ập 21 3. 21 trang tr ang 63 s 63 gk g
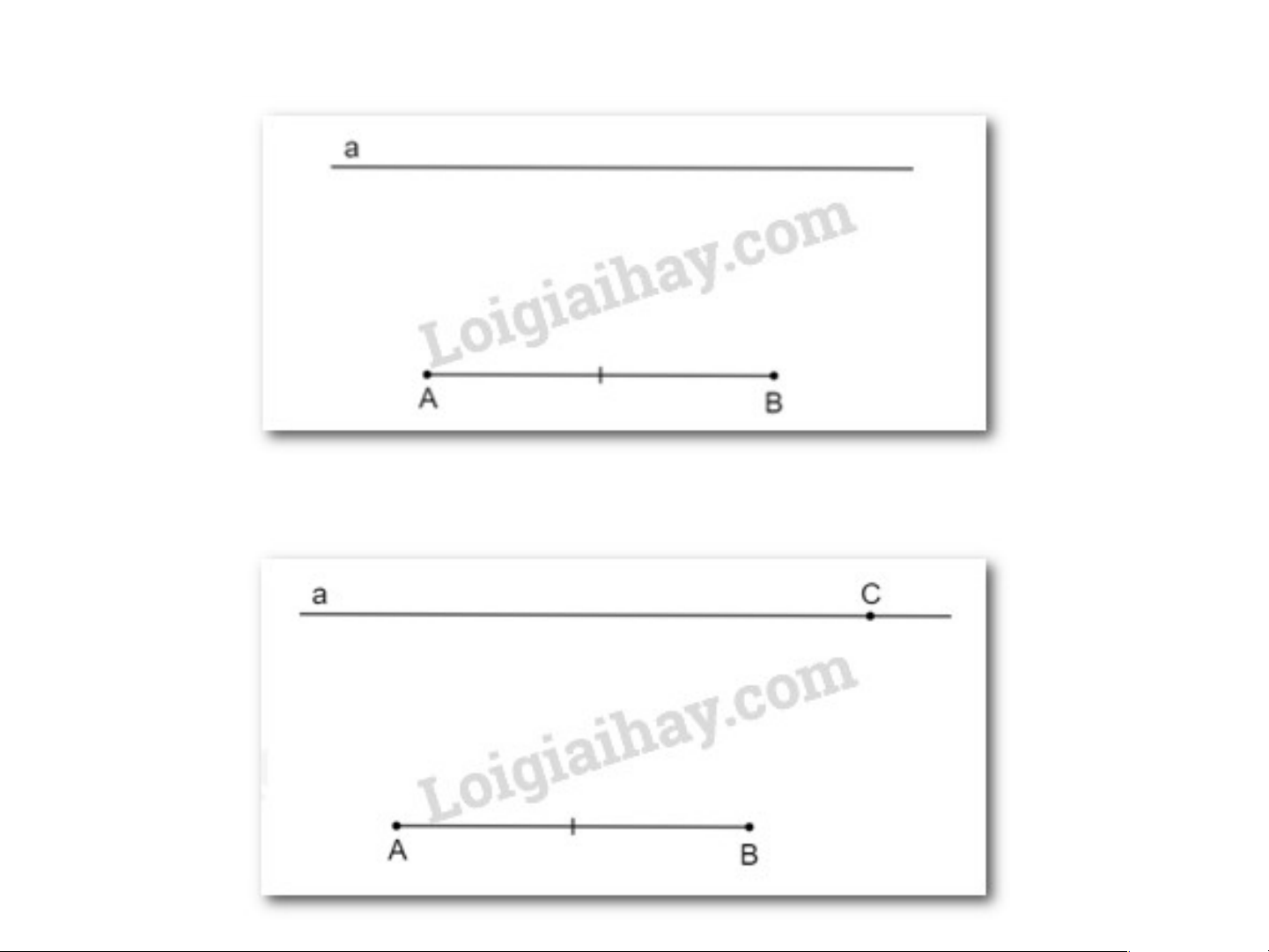
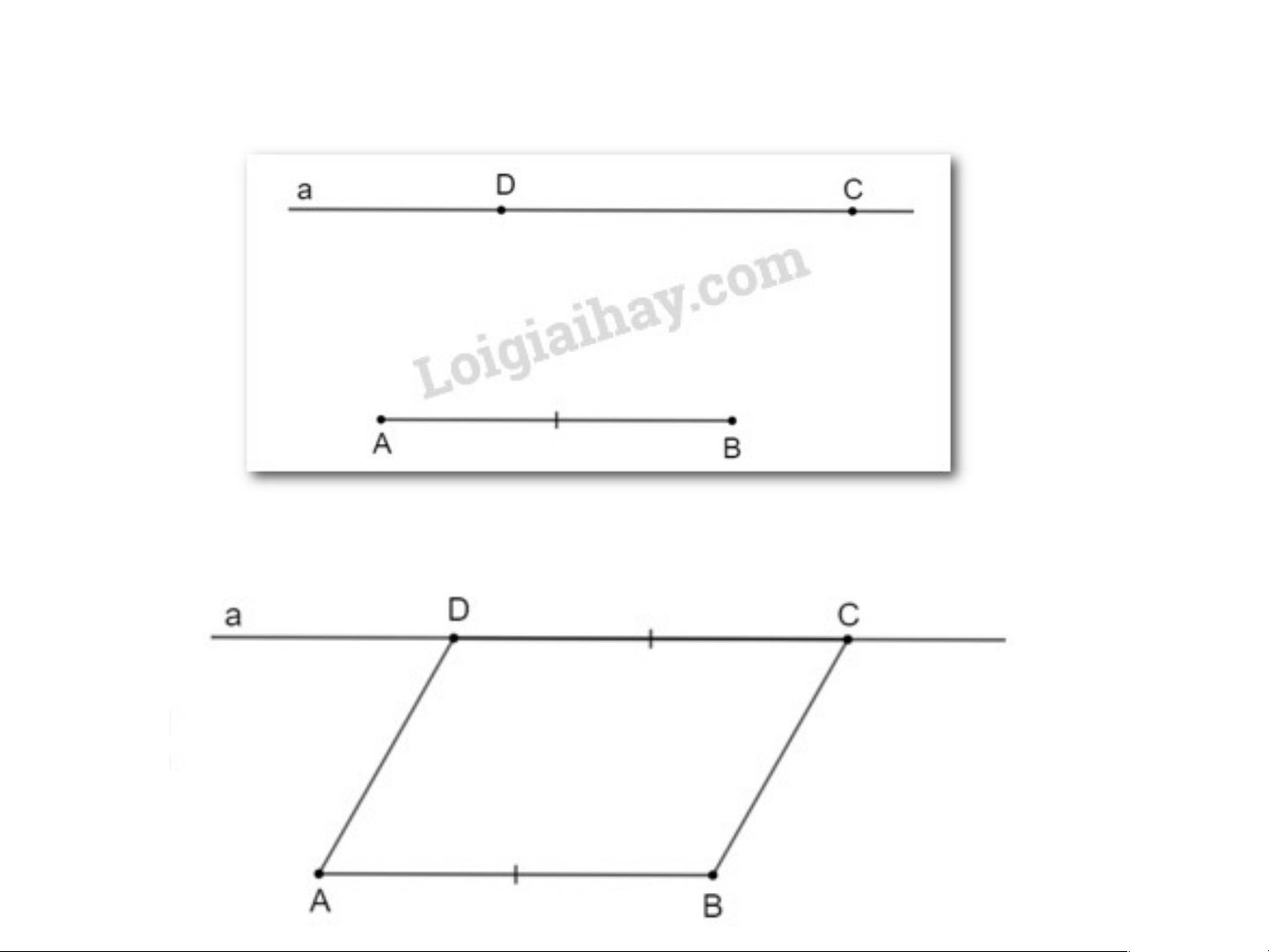
Vẽ tứ giác ABCD theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB Bước 2. Lấy điểm C ∈ a
Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.
Hãy giải thích tại sao tứ giác ABCD là hình bình hành.
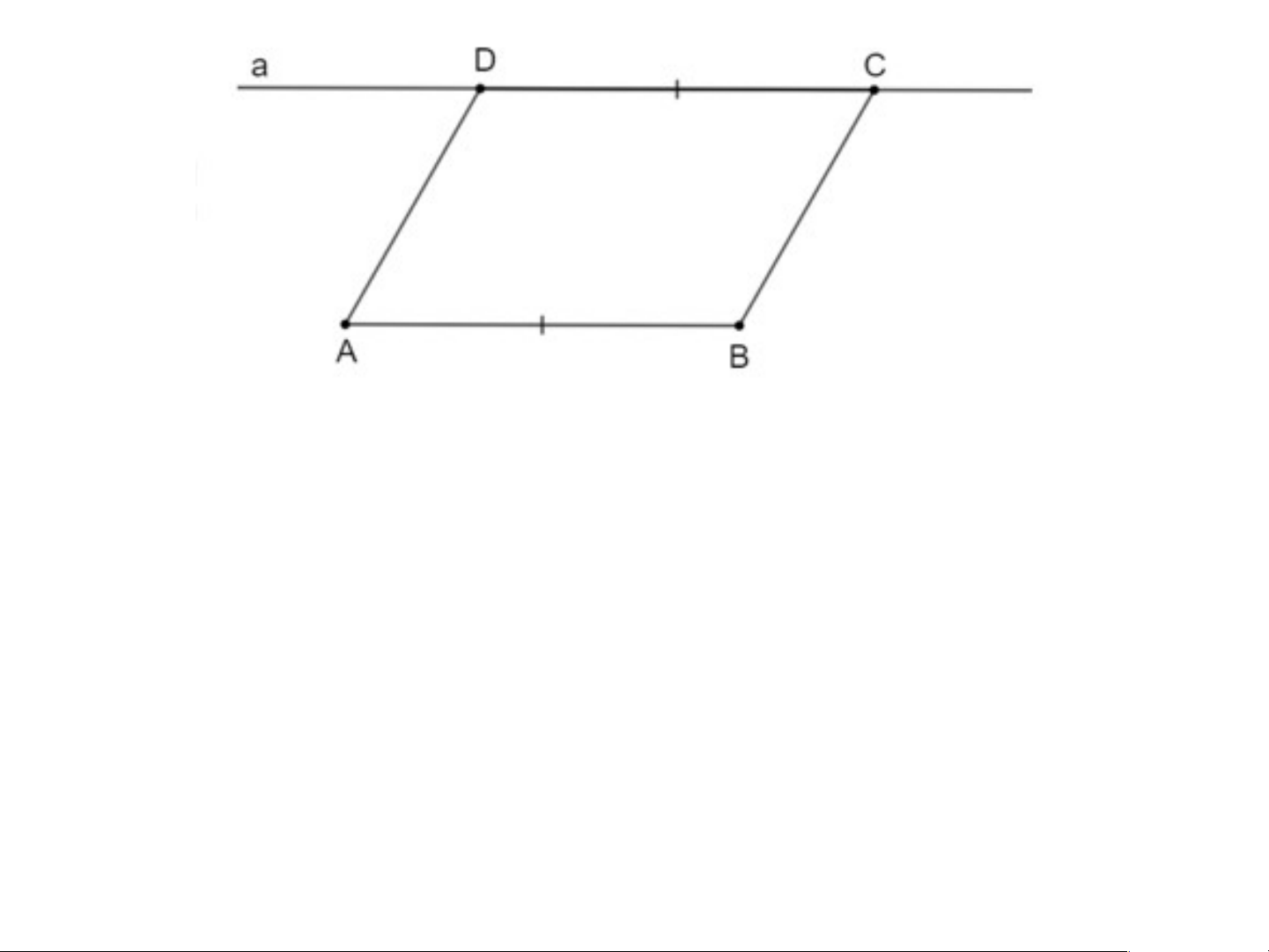
Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB Bước 2. Lấy điểm C ∈ a
Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.
Nối AD, BC ta có tứ giác ABCD là hình bình hành
Tứ giác ABCD là hình bình hành do:
• AB // CD (vì AB // a; C, D ∈ a); • AB = CD (giả thiết). Bài Bài tập t 3. ập 22 3. 22 trang tr ang 63 s 63 gk g
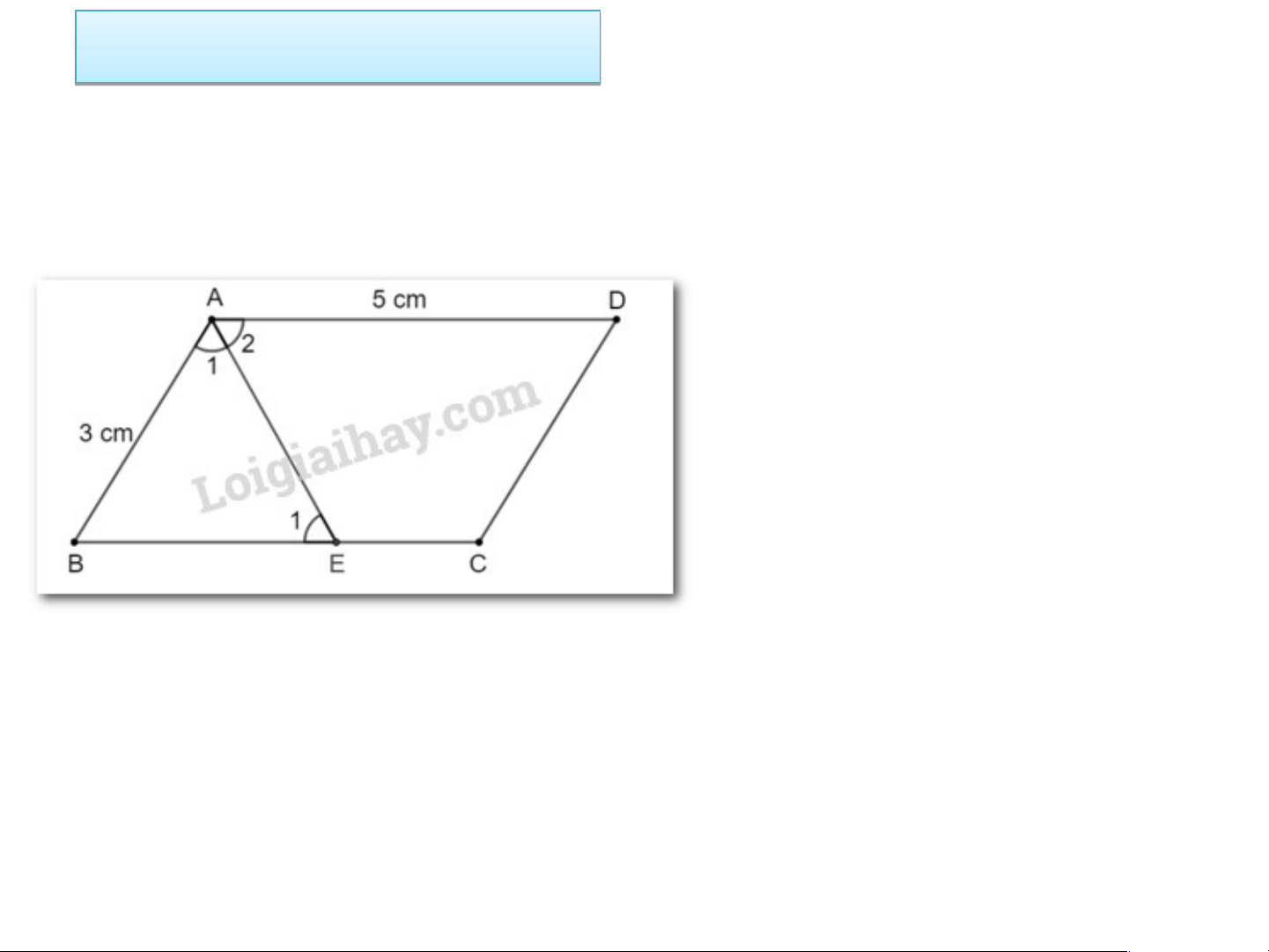
Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
b) Tính khoảng cách từ giao điểm đó đến điểm C.
a) Vì AD > AB (5 cm > 3 cm)
nên tia phân giác của góc A cắt cạnh BC.
b) Gọi E là giao điểm của tia phân giác góc A với cạnh BC. Ta có: = (so le trong) = (AE là phân giác ) = cân tại B BE = AB = 3cm EC = 2cm Bài Bài tập t 3. ập 23 3. 23 trang tr ang 63 s 63 gk g
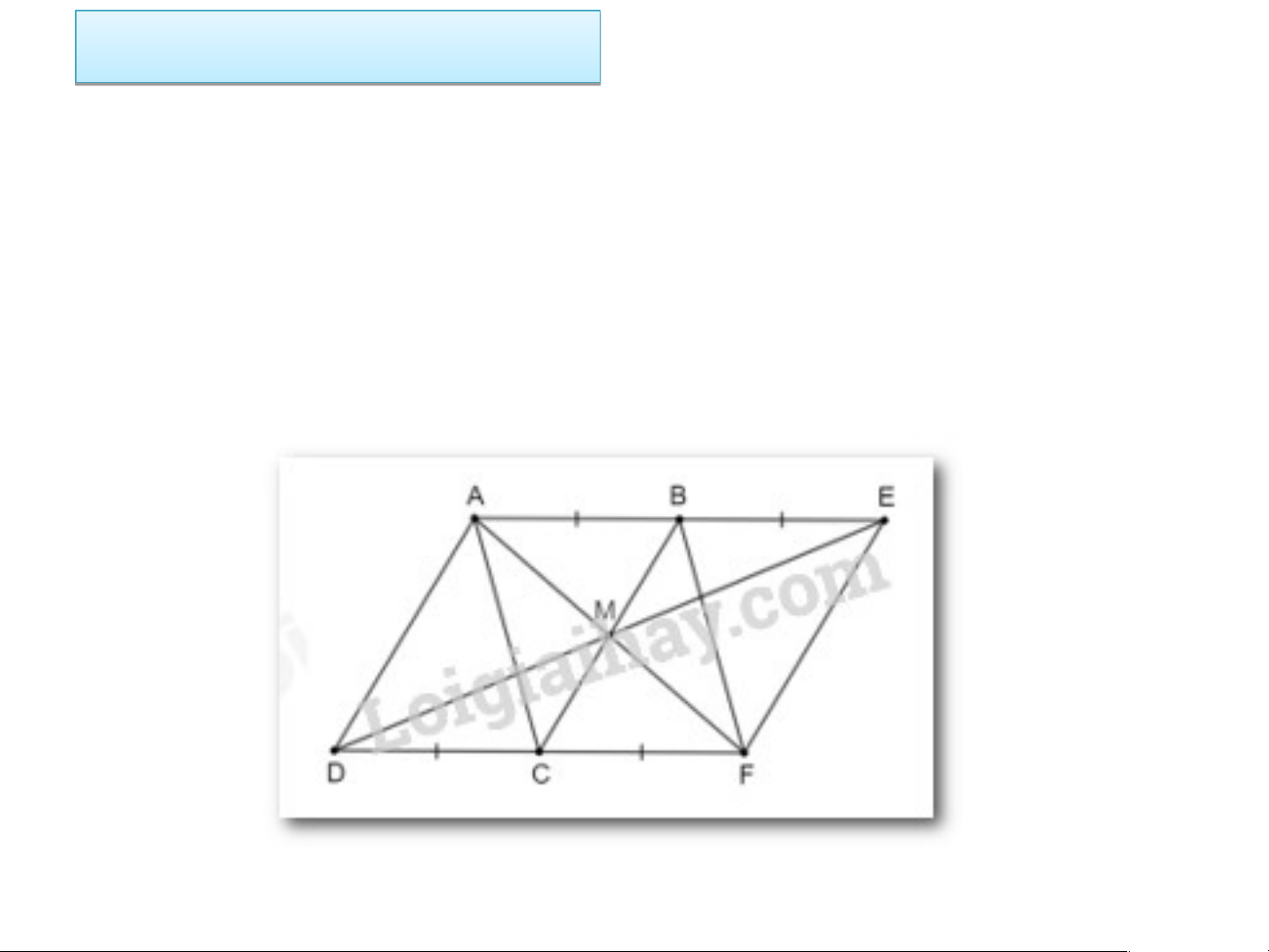
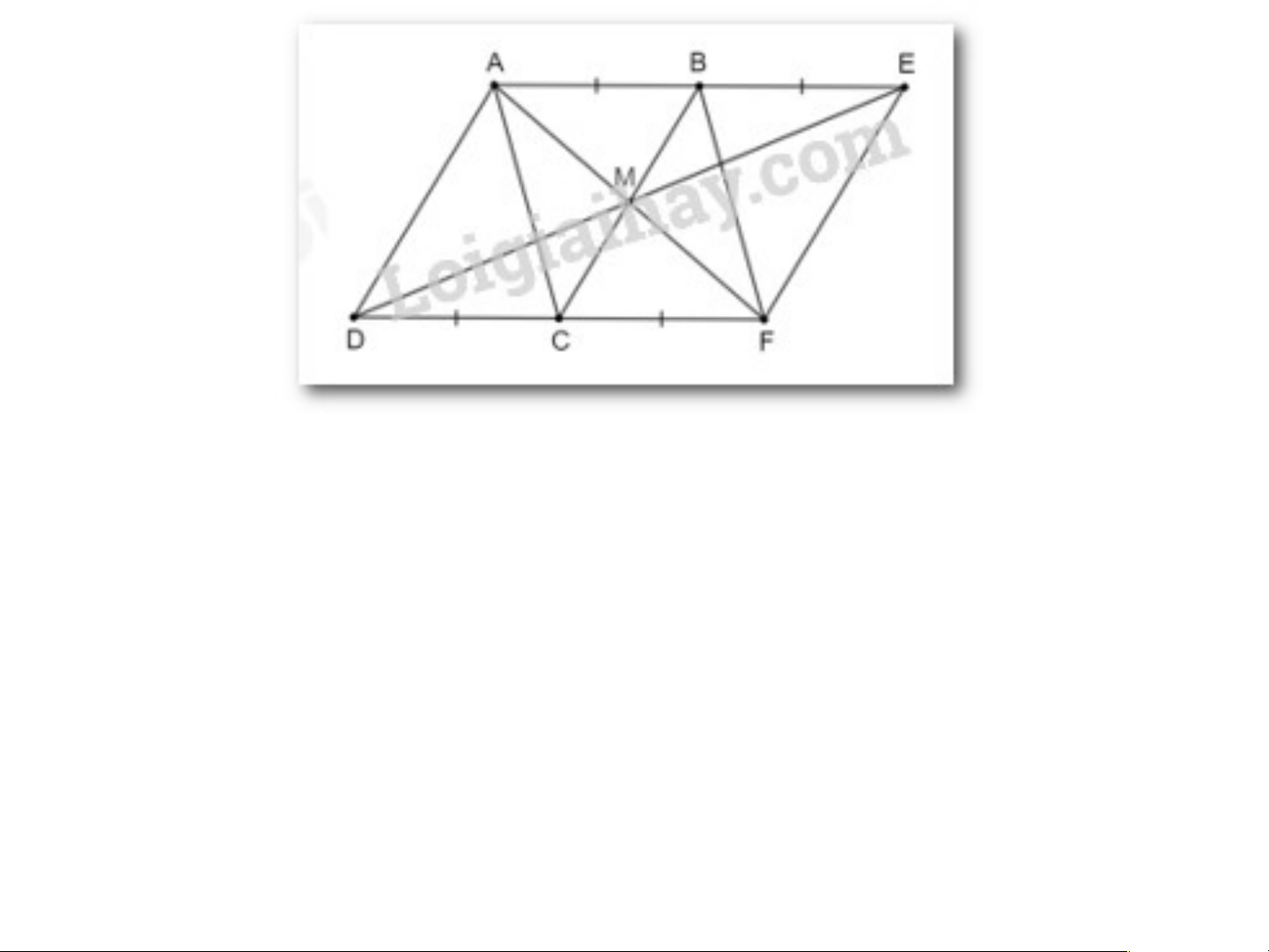
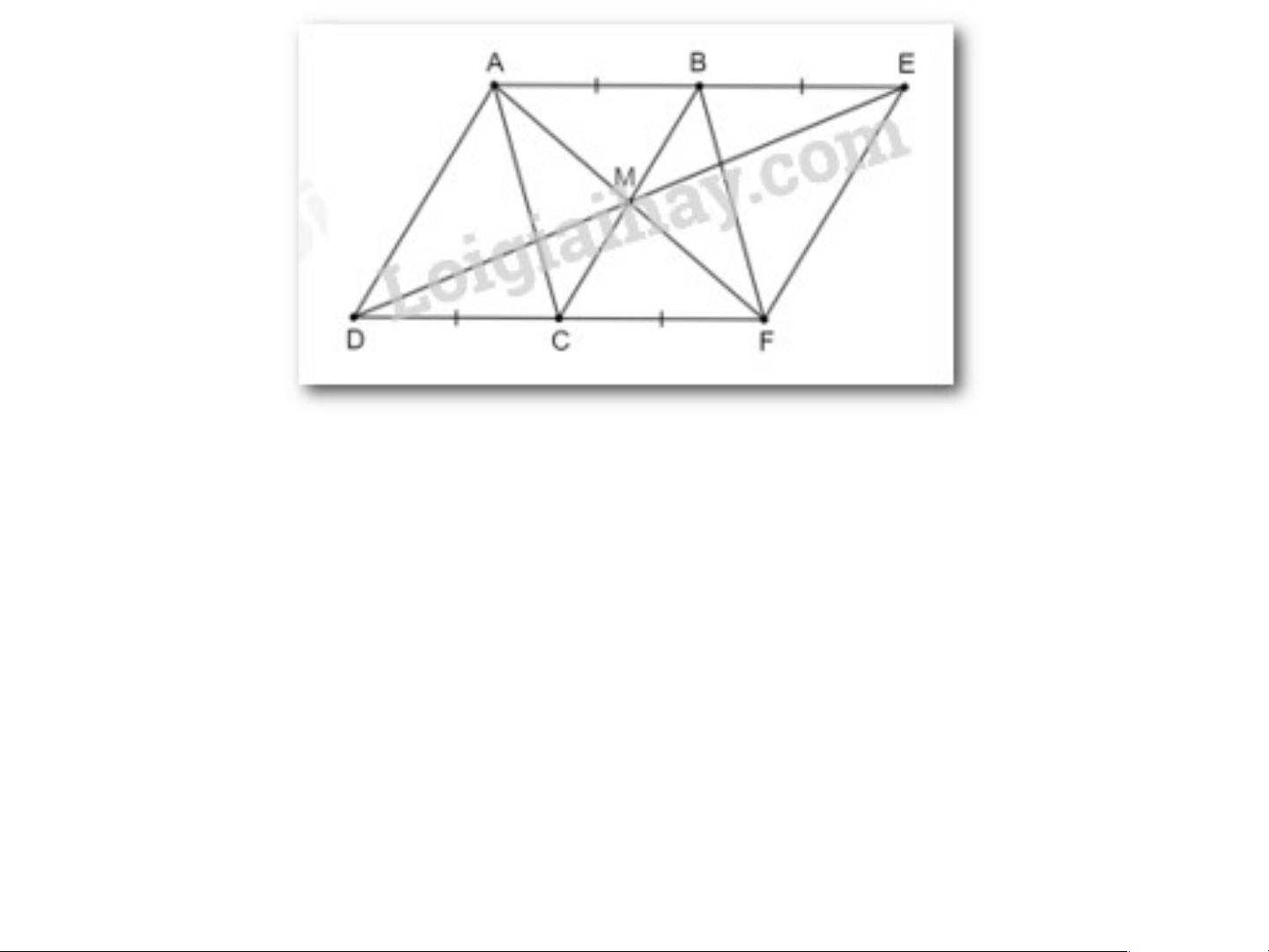
Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của
AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau
a) Vì ABCD là hình bình hành nên AB = CD; AB // CD.
Mà hai điểm B, C lần lượt là trung điểm AE, DF.
Suy ra AE = DF; AB = BE = CD = CF.
Tứ giác AEFD có AE // DF (vì AB // CD); AE = DF (c/m trên).
Do đó tứ giác AEFD là hình bình hành.
Tứ giác ABFC có AB // CF (vì AB // CD); AB = CF (c/m trên).
Do đó tứ giác ABFC là hình bình hành.
b) Vì hình bình hành AEFD có hai đường chéo AF và DE nên chúng
cắt nhau tại trung điểm của mỗi đường, ta gọi giao điểm đó là M.
Hình bình hành ABFC có hai đường chéo AF và BC.
Mà M là trung điểm của AF.
Suy ra M cũng là trung điểm của BC.
Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau. Bà B i t i ậ t p 3 . 3 2 . 4 4 tr a tr ng n 6 g 3 6 s gk
Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.
b) Hỏi tìm được bao nhiêu điểm như vậy? Lời giải
a) Gọi ba điểm không thẳng hàng đó là A, B, C. Khi đó ta cần tìm
điểm D để bốn điểm A, B, C, D là 4 đỉnh của hình bình hành. Gọi (H)
là hình bình hành cần tìm.
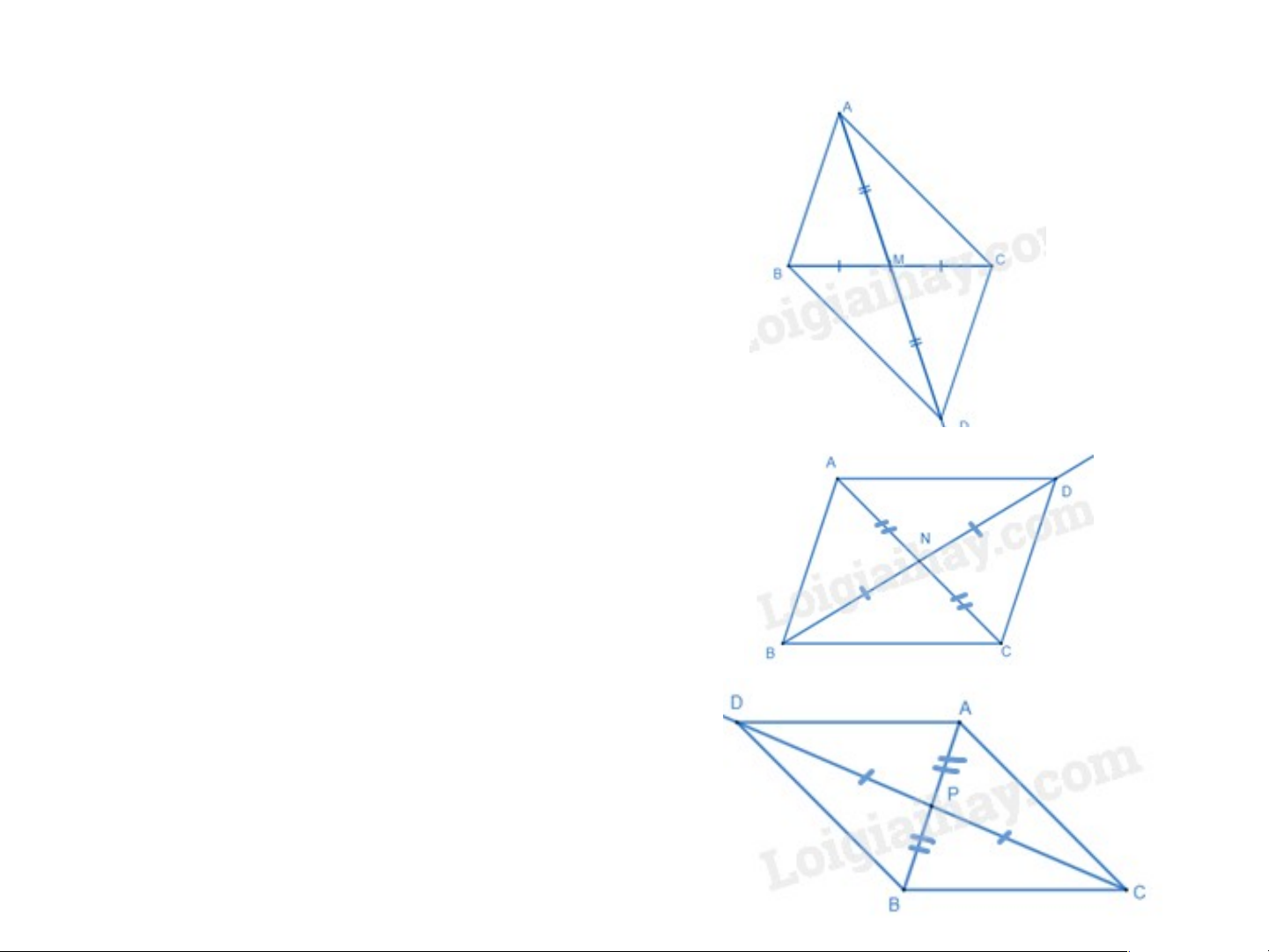
+ TH1. Nếu A là đỉnh đối của D trong
(H), khi đó trung điểm của AD trùng với trung điểm của BC.
Gọi M là trung điểm của BC. Ta có M
cũng là trung điểm của AD. Trên tia đối
của tia MA lấy điểm D sao cho AM =
MD, ta được hình bình hành ABDC là (H).
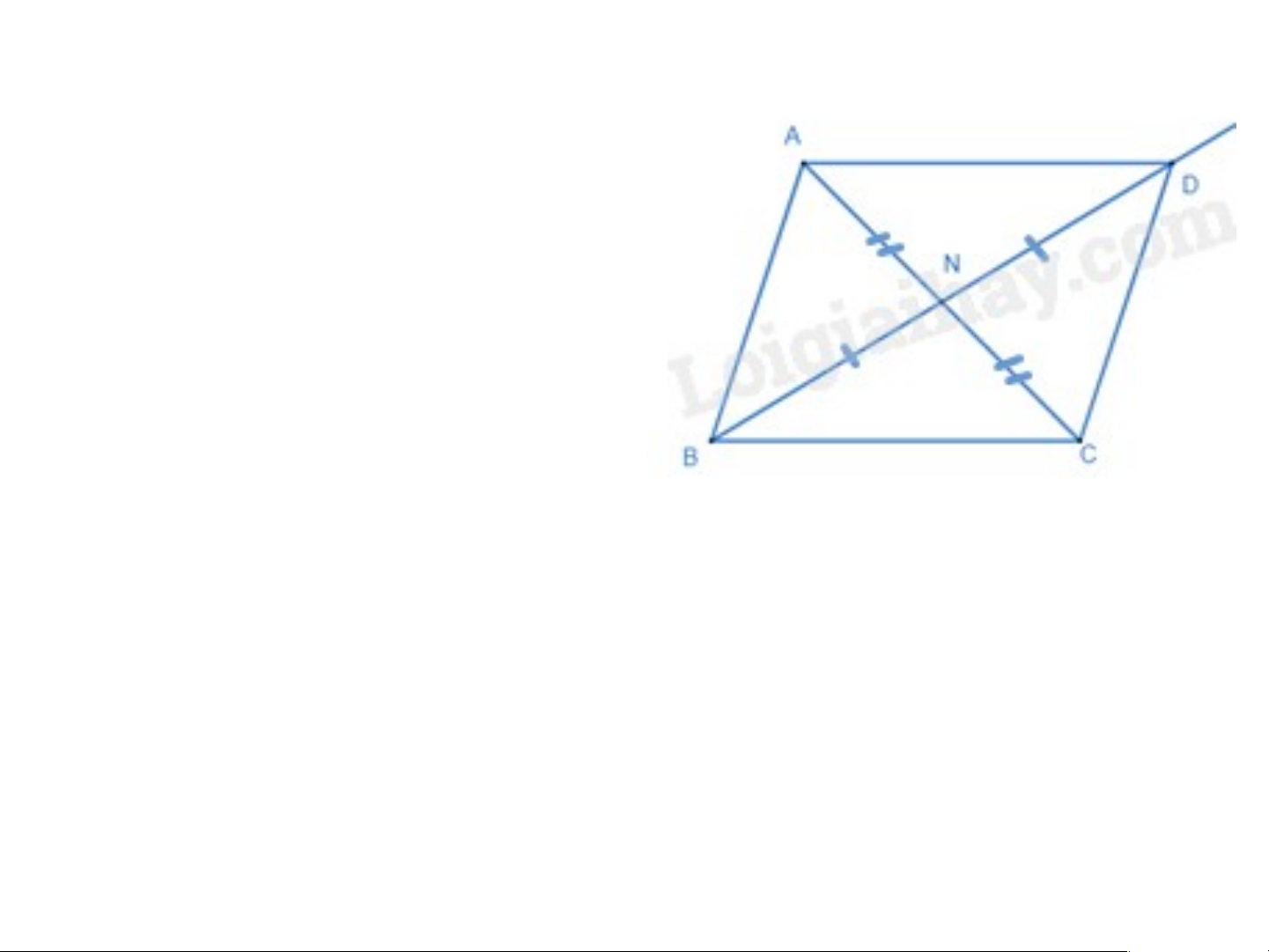
+ TH2. Nếu B là đỉnh đối của D
trong (H), khi đó trung điểm của
BD trùng với trung điểm của AC.
Gọi N là trung điểm của AC. Ta có
N cũng là trung điểm của BD. Trên
tia đối của tia NB lấy điểm D sao
cho BN = ND, ta được hình bình hành ABCD là (H).
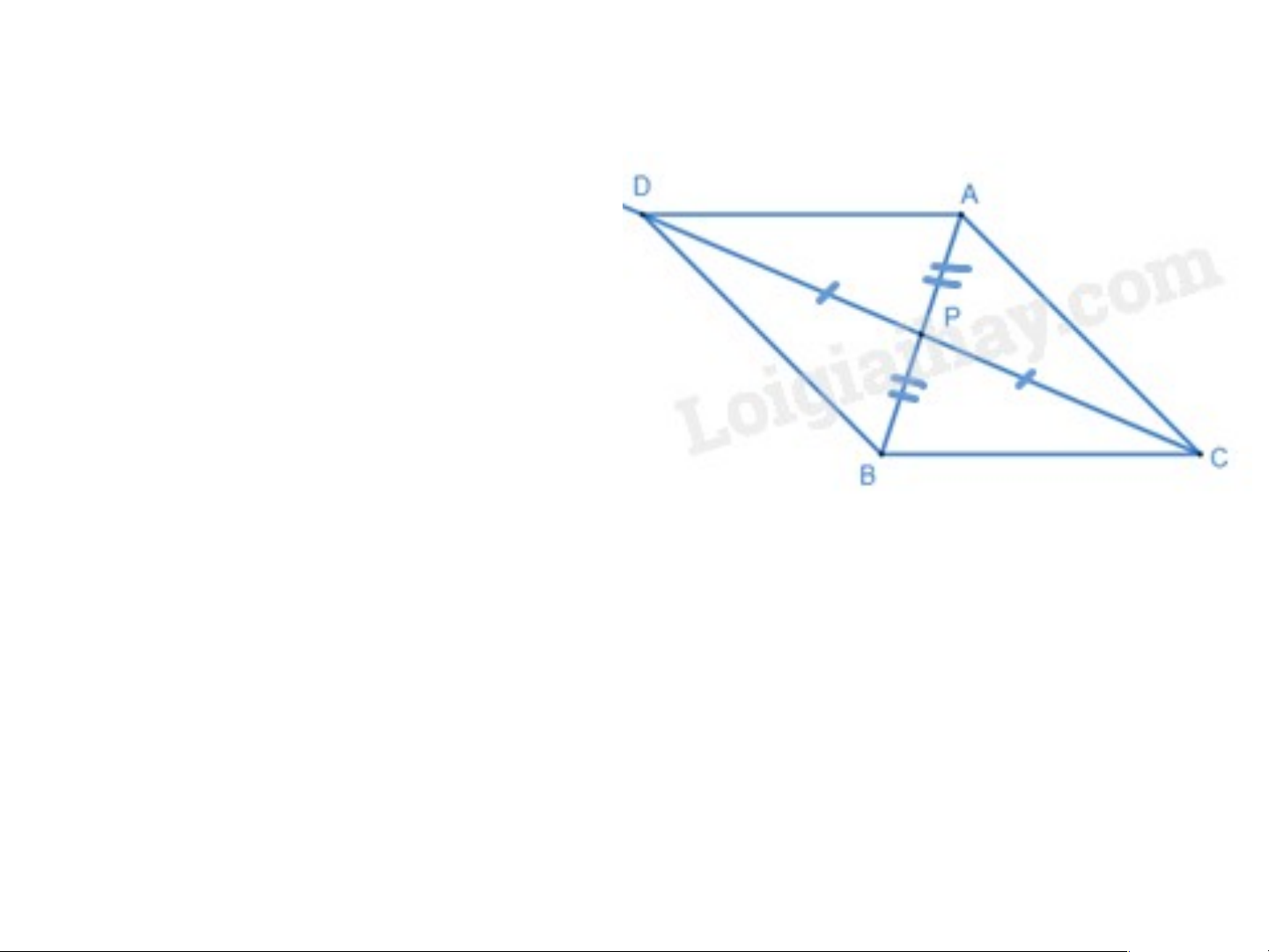
+ TH3. Nếu C là đỉnh đối của D
trong (H), khi đó trung điểm
của CD trùng với trung điểm của AB.
Gọi P là trung điểm của AB. Ta
có P cũng là trung điểm của
CD. Trên tia đối của tia PC lấy điểm D sao cho CP = PD, ta
được hình bình hành ACBD là (H).
b) Theo phần a, ta thấy có 3 điểm D thỏa mãn yêu cầu bài toán.
Khi D là đỉnh đối của A thì ta có hình bình hành ABDC.
Khi D là đỉnh đối của B thì ta có hình bình hành ABCD.
Khi D là đỉnh đối của A thì ta có hình bình hành ACBD.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26




