Giáo án Giải tích 12 cơ bản – Phạm Việt Hương

Giới thiệu đến quý thầy, cô giáo và các em Giáo án Giải tích 12 cơ bản – Phạm Việt Hương. Mời mọi người đón xem.

103 52 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 12

Môn: Toán 12

Thông tin:

133 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 1
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
12A3
Chương I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT
VÀ VẼ ĐỒ THỊ HÀM SỐ
Tiết dạy: 01 Bài 1: SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức:
Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm
này với đạo hàm.
Nắm được qui tắc xét tính đơn điệu của hàm số.
Kĩ năng:
Biết vận dụng qui tắc xét tính đơn điệu của một hàm số và dấu đạo hàm của nó.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đạo hàm ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tính đạo hàm của các hàm số: a)
2
2
x
y 
, b)
1
y
x
. Xét dấu đạo hàm của các hàm số đó?
Đ. a)
yx' 
b)
.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Nhắc lại các kiến thức liên quan tới tính đơn điệu của hàm số
Dựa vào KTBC, cho HS
nhận xét dựa vào đồ thị của các
hàm số.
H1. Hãy chỉ ra các khoảng
đồng biến, nghịch biến của các
hàm số đã cho?
H2. Nhắc lại định nghĩa tính
đơn điệu của hàm số?
-8 -6 -4 -2 2 4 6 8
-5
5
x
y
Đ1.
2
2
x
y 
đồng biến trên (–∞;
0), nghịch biến trên (0; +∞)
1
y
x
nghịch biến trên (–∞; 0),
(0; +∞)
I. Tính đơn điệu của hàm số
1. Nhắc lại định nghĩa
Giả sử hàm số y = f(x) xác
định trên K.
y = f(x) đồng biến trên K
x
1
, x
2
K: x
1
< x
2
f(x
1
) < f(x
2
)
12
12
( ) ( )
0
f x f x
xx
,
x
1
,x
2
K (x
1
x
2
)
y = f(x) nghịch biến trên K
x
1
, x
2
K: x
1
< x
2
f(x
1
) > f(x
2
)
12
12
( ) ( )
0
f x f x
xx
,
x
1
,x
2
K (x
1
x
2
)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 2
H3. Nhắc lại phương pháp xét
tính đơn điệu của hàm số đã
biết?
H4. Nhận xét mối liên hệ giữa
đồ thị của hàm số và tính đơn
điệu của hàm số?
GV hướng dẫn HS nêu nhận
xét về đồ thị của hàm số.
Đ4.
y > 0 HS đồng biến
y < 0 HS nghịch biến
Nhận xét:
Đồ thị của hàm số đồng biến
trên K là một đường đi lên từ
trái sang phải.
Đồ thị của hàm số nghịch
biến trên K là một đường đi
xuống từ trái sang phải.
Hoạt động 2: Tìm hiểu mối liên hệ giữa tính đơn điệu của hàm số và dấu của đạo hàm
Dựa vào nhận xét trên, GV
nêu định lí và giải thích.
2. Tính đơn điệu và dấu của
đạo hàm:
Định lí: Cho hàm số y = f(x)
có đạo hàm trên K.
Nếu f '(x) > 0,
xK
thì y = f(x) đồng biến trên K.
Nếu f '(x) < 0,
xK
thì y = f(x) nghịch biến trên K.
Chú ý: Nếu f
(x) = 0,
xK
thì f(x) không đổi trên K.
Hoạt động 3: Áp dụng xét tính đơn điệu của hàm số
Hướng dẫn HS thực hiện.
H1. Tính y và xét dấu y ?
HS thực hiện theo sự hướng
dẫn của GV.
Đ1.
a) y = 2 > 0, x
x


y'
y


b) y = 2x – 2
x


y'


1
0
y
VD1: Tìm các khoảng đơn
điệu của hàm số:
a)
21yx
b)
2
2y x x
Hoạt động 4: Củng cố
Nhấn mạnh:
– Mối liên quan giữa đạo hàm
và tính đơn điệu của hàm số.
x
O
y
x
O
y
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 3
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Sự đồng biến, nghịch biến của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
12A3
Tiết dạy: 02 Bài 1: SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm
này với đạo hàm.
Nắm được qui tắc xét tính đơn điệu của hàm số.
Kĩ năng:
Biết vận dụng qui tắc xét tính đơn điệu của một hàm số và dấu đạo hàm của nó.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đạo hàm ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm các khoảng đơn điệu của hàm số
4
21yx
?
Đ. Hàm số đồng biến trong khoảng (0; +∞), nghịch biến trong khoảng (–∞; 0).
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu thêm về mối liên hệ giữa đạo hàm và tính đơn điệu của hàm số
GV nêu định lí mở rộng và
giải thích thông qua VD.
x
y’
y


0
0+ +
0


I. Tính đơn điệu của hàm số
2. Tính đơn điệu và dấu của
đạo hàm
Chú ý:
Giả sử y = f(x) có đạo hàm
trên K. Nếu f
(x)
0 (f
(x)
0),
x
K và f
(x) = 0 chỉ tại một
số hữu hạn điểm thì hàm số
đồng biến (nghịch biến) trên K.
VD2: Tìm các khoảng đơn
điệu của hàm số y = x
3
.
Hoạt động 2: Tìm hiểu qui tắc xét tính đơn điệu của hàm số
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 4
GV hướng dẫn rút ra qui tắc
xét tính đơn điệu của hàm số.
II. Qui tắc xét tính đơn điệu
của hàm số
1. Qui tắc
1) Tìm tập xác định.
2) Tính f
(x). Tìm các điểm x
i
(i
= 1, 2, …, n) mà tại đó đạo
hàm bằng 0 hoặc không xác
định.
3) Săpx xếp các điểm x
i
theo
thứ tự tăng dần và lập bảng
biến thiên.
4) Nêu kết luận về các khoảng
đồng biến, nghịch biến của
hàm số.
Hoạt động 3: Áp dụng xét tính đơn điệu của hàm số
Chia nhóm thực hiện và gọi
HS lên bảng.
GV hướng dẫn xét hàm số:
trên
0
2
;


.
H1. Tính f(x) ?
Các nhóm thực hiện yêu cầu.
a) đồng biến (–; –1), (2; +)
nghịch biến (–1; 2)
b) đồng biến (–; –1), (–1; +)
Đ1. f(x) = 1 – cosx 0
(f(x) = 0 x = 0)
f(x) đồng biến trên
0
2
;


với
0
2
x

ta có:
f x x x( ) sin
> f(0) = 0
2. Áp dụng
VD3: Tìm các khoảng đơn
điệu của các hàm số sau:
a)
32
11
22
32
y x x x
b)
1
1
x
y
x
VD4: Chứng minh:
sinxx
trên khoảng
0;
2



.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Mối liên quan giữa đạo hàm
và tính đơn điệu của hàm số.
– Qui tắc xét tính đơn điệu của
hàm số.
– Ứng dụng việc xét tính đơn
điệu để chứng minh bất đẳng
thức.
4. BÀI TẬP VỀ NHÀ:
Bài 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 5
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
12A3
Tiết dạy: 03 Bài 2: CỰC TRỊ CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức:
Mô tả được các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
Mô tả được các điều kiện đủ để hàm số có điểm cực trị.
Kĩ năng:
Sử dụng thành thạo các điều kiện đủ để tìm cực trị.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Xét tính đơn điệu của hàm số:
2
( 3)
3

x
yx
?
Đ. ĐB:
4
; ,(3; )
3

 


, NB:
4
;3
3



.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm cực trị của hàm số
Dựa vào KTBC, GV giới
thiệu khái niệm CĐ, CT của
hàm số.
Nhấn mạnh: khái niệm cực trị
mang tính chất "địa phương".
H1. Xét tính đơn điệu của hàm
số trên các khoảng bên trái,
bên phải điểm CĐ?
Đ1.
Bên trái: hàm số ĐB f
(x)
0
Bên phái: h.số NB f
(x)
0.
I. KHÁI NIỆM CỰC ĐẠI,
CỰC TIỂU
Định nghĩa:
Cho hàm số y = f(x) xác định
và liên tục trên khoảng (a; b)
và điểm x
0
(a; b).
a) f(x) đạt CĐ tại x
0
h > 0,
f(x) < f(x
0
),
x
S(x
0
, h)\ {x
0
}.
b) f(x) đạt CT tại x
0
h > 0,
f(x) > f(x
0
),
x
S(x
0
, h)\ {x
0
}.
Chú ý:
a) Điểm cực trị của hàm số;
Giá trị cực trị của hàm số;
Điểm cực trị của đồ thị hàm số.
b) Nếu y = f(x) có đạo hàm
trên (a; b) và đạt cực trị tại x
0
(a; b) thì f
(x
0
) = 0.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 6
Hoạt động 2: Tìm hiểu điều kiện đủ để hàm số có cực trị
GV phác hoạ đồ thị của các
hàm số:
a)
21 yx
b)
2
( 3)
3

x
yx
Từ đó cho HS nhận xét mối
liên hệ giữa dấu của đạo hàm
và sự tồn tại cực trị của hàm
số.
GV hướng dẫn thông qua
việc xét hàm số
yx
.
a) không có cực trị.
b) có CĐ, CT.
II. ĐIỀU KIỆN ĐỦ ĐỂ HÀM
SỐ CÓ CỰC TRỊ
Định lí 1: Giả sử hàm số y =
f(x) liên tục trên khoảng K =
00
( ; )x h x h
và có đạo hàm
trên K hoặc K \ {x
0
} (h > 0).
a) f
(x) > 0 trên
00
( ; )x h x
,
f
(x) < 0 trên
00
( ; )x x h
thì x
0
là một điểm CĐ của f(x).
b) f
(x) < 0 trên
00
( ; )x h x
,
f
(x) > 0 trên
00
( ; )x x h
thì x
0
là một điểm CT của f(x).
Nhận xét: Hàm số có thể đạt
cực trị tại những điểm mà tại
đó đạo hàm không xác định.
Hoạt động 3: Áp dụng tìm điểm cực trị của hàm số
GV hướng dẫn các bước thực
hiện.
H1.
– Tìm tập xác định.
– Tìm y
.
– Tìm điểm mà y = 0 hoặc
không tồn tại.
– Lập bảng biến thiên.
– Dựa vào bảng biến thiên để
kết luận.
Đ1.
a) D = R
y = –2x; y = 0 x = 0
Điểm CĐ: (0; 1)
b) D = R
y =
2
3 2 1xx
;
y = 0
1
1
3

x
x
Điểm CĐ:
1 86
;
3 27



,
Điểm CT:
(1;2)
c) D = R \ {–1}
2
2
' 0, 1
( 1)
yx
x
Hàm số không có cực trị.
VD1: Tìm các điểm cực trị của
hàm sô:
a)
2
( ) 1 y f x x
b)
32
( ) 3 y f x x x x
c)
31
()
1

x
y f x
x
Hoạt động 4: Củng cố
Nhấn mạnh:
– Khái niệm cực trị của hàm
số.
– Điều kiện cần và điều kiện
đủ để hàm số có cực trị.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 7
4. BÀI TẬP VỀ NHÀ:
Làm bài tập 1, 3 SGK.
Đọc tiếp bài "Cực trị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
12A3
Tiết dạy: 04 Bài 2: CỰC TRỊ CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Mô tả được các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
Mô tả được các điều kiện đủ để hàm số có điểm cực trị.
Kĩ năng:
Sử dụng thành thạo các điều kiện đủ để tìm cực trị.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu và cực trị của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Tìm điểm cực trị của hàm số:
3
31 y x x
?
Đ. Điểm CĐ: (–1; 3); Điểm CT: (1; –1).
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu Qui tắc tìm cực trị của hàm số
Dựa vào KTBC, GV cho HS
nhận xét, nêu lên qui tắc tìm
cực trị của hàm số.
HS nêu qui tắc.
III. QUI TẮC TÌM CỰC TRỊ
Qui tắc 1:
1) Tìm tập xác định.
2) Tính f
(x). Tìm các điểm tại
đó f
(x) = 0 hoặc f
(x) không
xác định.
3) Lập bảng biến thiên.
4) Từ bảng biến thiên suy ra
các điểm cực trị.
Hoạt động 2: Áp dụng qui tắc 1 tìm cực trị của hàm số
Cho các nhóm thực hiện.
Các nhóm thảo luận và trình
bày.
a) CĐ: (–1; 3); CT: (1; –1).
b) CĐ: (0; 2);
VD1: Tìm các điểm cực trị của
hàm số:
a)
2
( 3)y x x
b)
42
32 y x x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 8
CT:
31
;
24




,
31
;
24



c) Không có cực trị
d) CĐ: (–2; –3); CT: (0; 1)
c)
1
1
x
y
x
d)
2
1
1

xx
y
x
Hoạt động 3: Tìm hiểu qui tắc 2 để tìm cực trị của hàm số
GV nêu định lí 2 và giải
thích.
H1. Dựa vào định lí 2, hãy nêu
qui tắc 2 để tìm cực trị của hàm
số?
Đ1. HS phát biểu.
Định lí 2:
Giả sử y = f(x) có đạo hàm cấp
2 trong
00
( ; )x h x h
(h > 0).
a) Nếu f
(x
0
) = 0, f

(x
0
) > 0
thì x
0
là điểm cực tiểu.
b) Nếu f
(x
0
) = 0, f

(x
0
) < 0
thì x
0
là điểm cực đại.
Qui tắc 2:
1) Tìm tập xác định.
2) Tính f
(x). Giải phương trình
f
(x) = 0 và kí hiệu x
i
là nghiệm
3) Tìm f

(x) và tính f

(x
i
).
4) Dựa vào dấu của f

(x
i
) suy
ra tính chất cực trị của x
i
.
Hoạt động 4: Áp dụng qui tắc 2 để tìm cực trị của hàm số
Cho các nhóm thực hiện.
Các nhóm thảo luận và trình
bày.
a) CĐ: (0; 6)
CT: (–2; 2), (2; 2)
b) CĐ:
4
xk
CT:
3
4
xk
VD2: Tìm cực trị của hàm số:
a)
4
2
26
4
x
yx
b)
sin2yx
Hoạt động 5: Củng cố
Nhấn mạnh:
– Các qui tắc để tìm cực trị của
hàm số.
– Nhận xét qui tắc nên dùng
ứng với từng loại hàm số.
Câu hỏi: Đối với các hàm số
sau hãy chọn phương án đúng:
1) Chỉ có CĐ.
2) Chỉ có CT.
3) Không có cực trị.
4) Có CĐ và CT.
a)
32
53 y x x x
b)
32
53 y x x x
c)
2
4
2

xx
y
x
a) Có CĐ và CT
b) Không có CĐ và CT
c) Có CĐ và CT
d) Không có CĐ và CT
Đối với các hàm đa thức bậc
cao, hàm lượng giác, … nên
dùng qui tắc 2.
Đối với các hàm không có
đạo hàm không thể sử dụng qui
tắc 2.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 9
d)
4
2
x
y
x
4. BÀI TẬP VỀ NHÀ:
Làm bài tập 2, 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 05 Bài 2: BÀI TẬP CỰC TRỊ CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức:
Mô tả được các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
Mô tả được các điều kiện đủ để hàm số có điểm cực trị.
Kĩ năng:
Sử dụng thành thạo các điều kiện đủ để tìm cực trị.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu và cực trị của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Sử dụng qui tắc 1 để tìm cực trị của hàm số
Cho các nhóm thực hiện.
H1. Nêu các bước tìm điểm
cực trị của hàm số theo qui tắc
1?
Các nhóm thảo luận và trình
bày.
Đ1.
a) CĐ: (–3; 71); CT: (2; –54)
b) CT: (0; –3)
c) CĐ: (–1; –2); CT: (1; 2)
d) CT:
13
;
22



1. Tìm các điểm cực trị của
hàm số:
a)
32
2 3 36 10 y x x x
b)
42
23 y x x
c)
d)
2
1 y x x
Hoạt động 2: Sử dụng qui tắc 2 để tìm cực trị của hàm số
Cho các nhóm thực hiện.
H1. Nêu các bước tìm điểm
cực trị của hàm số theo qui tắc
2?
Các nhóm thảo luận và trình
bày.
Đ1.
a) CĐ: (0; 1); CT: (1; 0)
b) CĐ:
6
xk
2. Tìm các điểm cực trị của
hàm số:
a)
42
21 y x x
b)
sin2y x x
c)
sin cosy x x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 10
CT:
6
xl
c) CĐ:
2
4
xk
CT:
(2 1)
4
xl
d) CĐ: x = –1; CT: x = 1
d)
53
21 y x x x
Hoạt động 3: Vận dụng cực trị của hàm số để giải toán
H1. Nêu điều kiện để hàm số
luôn có một CĐ và một CT?
Hướng dẫn HS phân tích yêu
cầu bài toán.
H2. Nếu x = 2 là điểm CĐ thì
y(2) phải thoả mãn điều kiện
gì?
H3. Kiểm tra với các giá trị m
vừa tìm được?
Đ1. Phương trình y
= 0 có 2
nghiệm phân biệt.
2
' 3 2 2 y x mx
= 0 luôn
có 2 nghiệm phân biệt.
 = m
2
+ 6 > 0, m
Đ2.
y(2) = 0
1
3


m
m
Đ3.
m = –1: không thoả mãn
m = –3: thoả mãn
3. Chứng minh rằng với mọi m,
hàm số
32
21 y x mx x
luôn có một điểm CĐ và một
điểm CT.
4. Xác định giá trị của m để
hàm số
2
1
x mx
y
xm
đạt CĐ
tại x = 2.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Điều kiện cần, điều kiện đủ
để hàm số có cực trị.
– Các qui tắc tìm cực trị của
hàm số.
4. BÀI TẬP VỀ NHÀ:
Làm các bài tập còn lại trong SGK và bài tập thêm.
Đọc trước bài "Giá trị lớn nhất và giá trị nhỏ nhất của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 11
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 06 Bài 3: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT
CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức:
Biết các khái niệm GTLN, GTNN của hàm số trên một tập hợp số.
Nắm được qui tắc tìm GTLN, GTNN của hàm số.
Kĩ năng:
Biết cách tìm GTLN, GTNN của hàm số trên một đoạn, một khoảng.
Phân biệt việc tìm GTLN, GTNN với tìm cực trị của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu và cực trị của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Cho hàm số
32
1y x x x
. Hãy tìm cực trị của hàm số. So sánh giá trị cực trị với
21yy( ), ( )
?
Đ.
1 32
3 27
CÑ
yy



,
10
CT
yy()
;
29y()
,
10y()
.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm GTLN, GTNN của hàm số
Từ KTBC, GV dẫn dắt đến
khái niệm GTLN, GTNN của
hàm số.
GV cho HS nhắc lại định
nghĩa GTLN, GTNN của hàm
số.
GV hướng dẫn HS thực hiện.
H1. Lập bảng biến thiên của
hàm số ?
Các nhóm thảo luận và trình
bày.
Đ1.
x
y’
y
0 1
0
-3



– +
0
31f x f
( ; )
min ( ) ( )

f(x) không có GTLN trên
I. ĐỊNH NGHĨA
Cho hàm số y = f(x) xác định
trên D.
a)
00
D
f x M
f x M x D
x D f x M
max ( )
( ) ,
: ( )
b)
00
D
f x m
f x m x D
x D f x m
min ( )
( ) ,
: ( )
VD1: Tìm GTLN, GTNN của
hàm số sau trên khoảng (0; +∞)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 12
(0;+∞)
Hoạt động 2: Tìm hiểu cách tìm GTLN, GTNN của hàm số trên một khoảng
GV hướng dãn cách tìm
GTLN, GTNN của hàm số liên
tục trên một khoảng.
H1. Lập bảng biến thiên của
hàm số ?
Đ1.
x
y’
y
-1
0
–
+
–6




16
R
yymin ( )
không có GTLN.
II. CÁCH TÍNH GTLN,
GTNN CỦA HÀM SỐ LIÊN
TỤC TRÊN MỘT KHOẢNG
Dựa vào bảng biến thiên để
xác định GTLN, GTNN của
hàm số liên tục trên một
khoảng.
VD2: Tính GTLN, GTNN của
hàm số
2
25y x x
.
Hoạt động 3: Vận dụng cách tìm GTLN, GTNN của hàm số để giải toán
GV hướng dẫn cách giải
quyết bài toán.
H1. Tính thể tích khối hộp ?
H2. Nêu yêu cầu bài toán ?
H3. Lập bảng biến thiên ?
Đ1.
2
20
2
a
V x x a x x( ) ( )



Đ2. Tìm x
0
0
2
a
;



sao cho
V(x
0
) có GTLN.
Đ3.
3
0
2
2
27
a
a
max V x
;
()



VD3: Cho một tấm nhôm hình
vuông cạnh a. Người ta cắt ở
bốn góc bốn hình vuông bằng
nhau, rồi gập tấm nhôm lại
thành một cái hộp không nắp.
Tính cạnh của các hình vuông
bị cắt sao cho thể tích của khối
hộp là lớn nhất.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách tìm GTLN, GTNN của
hàm số liên tục trên một
khoảng.
4. BÀI TẬP VỀ NHÀ:
Làm bài tập 4, 5 SGK.
Đọc tiếp bài "GTLN, GTNN của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 13
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 07 Bài 3: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT
CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Biết các khái niệm GTLN, GTNN của hàm số trên một tập hợp số.
Nắm được qui tắc tìm GTLN, GTNN của hàm số.
Kĩ năng:
Biết cách tìm GTLN, GTNN của hàm số trên một đoạn, một khoảng.
Phân biệt việc tìm GTLN, GTNN với tìm cực trị của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về cực trị và GTLN, GTNN của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm GTLN, GTNN của hàm số
2
32y x x
?
Đ.
31
24
R
max y y




; không có GTNN.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách tìm GTLN, GTNN của hàm số liên tục trên một đoạn
Từ KTBC, GV đặt vấn đề đối
với hàm số liên tục trên một
đoạn.
GV giới thiệu định lí.
GV cho HS xét một số VD.
Từ đó dẫn dắt đến qui tắc tìm
GTLN, GTNN.
VD: Tìm GTLN, GTNN của
hàm số
2
yx
trên đoạn được
chỉ ra:
a) [1; 3] b) [–1; 2]
-1 1 2 3
-8
-6
-4
-2
2
4
6
8
x
y
a)
13
11yy
;
min ( )
13
39max y y
;
()
b)
12
00yy
;
min ( )

12
24max y y
;
()

II. CÁCH TÍNH GTLN,
GTNN CỦA HÀM SỐ TRÊN
MỘT ĐOẠN
1. Định lí
Mọi hàm số liên tục trên một
đoạn đều có GTLN và GTNN
trên đoạn đó.
2. Qui tắc tìm GTLN, GTNN
của hàm số liên tục trên đoạn
[a; b]
Tìm các điểm x
1
, x
2
, …, x
n
trên khoảng (a; b), tại đó f
(x)
bằng 0 hoặc không xác định.
Tính f(a), f(x
1
), …, f(x
n
), f(b).
Tìm số lớn nhất M và số nhỏ
nhất m trong các số trên.
[a b]
[a b]
M max f x m f x
;
;
( ), min ( )
Hoạt động 2: Vận dụng cách tìm GTLN, GTNN của hàm số để giải toán
Cho các nhóm thực hiện.
Các nhóm thảo luận và trình
VD1: Tìm GTLN, GTNN của
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 14
Chú ý các trường hợp khác
nhau.
bày.
2
3 2 1y x x'
1
0
3
1
x
y
x
'


1 59
3 27
y




;
11y()
a) y(–1) = 1; y(2) = 4
12
1 1 1y y y
;
min ( ) ( )
12
24max y y
;
()

b) y(–1) = 1; y(0) = 2
10
11yy
;
min ( )
10
1 59
3 27
max y y
;



c) y(0) = 2; y(2) = 4
02
11yy
;
min ( )
02
24max y y
;

d) y(2) = 4; y(3) = 17
23
24yy
;
min ( )
23
3 17max y y
;

hàm số
32
2y x x x
trên
đoạn:
a) [–1; 2] b) [–1; 0]
c) [0; 2] d) [2; 3]
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách tìm GTLN, GTNN của
hàm số liên tục trên một đoạn.
– So sánh với cách tìm GTLN,
GTNN của hàm số liên tục trên
một khoảng.
4. BÀI TẬP VỀ NHÀ:
Làm bài tập 1, 2, 3 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 15
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 08 Bài 3: BÀI TẬP GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT
CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức: Củng cố:
Các khái niệm GTLN, GTNN của hàm số trên một tập hợp số.
Các qui tắc tìm GTLN, GTNN của hàm số.
Kĩ năng:
Tìm được GTLN, GTNN của hàm số trên một đoạn, một khoảng.
Phân biệt việc tìm GTLN, GTNN với tìm cực trị của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về cực trị và GTLN, GTNN của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tìm GTLN, GTNN của hàm số liên tục trên một đoạn
H1. Nêu các bước thực hiện ?
Đ1.
a)
44
44
05
05
41 40
8 40
yy
yy
[ ; ]
;
[ ; ]
;
min ; max
min ; max

b)
03
03
25
25
1
56
4
6 552
yy
yy
[ ; ]
;
[ ; ]
;
min ; max
min ; max

c)
24
24
11
11
2
0
3
13
yy
yy
[ ; ]
;
[ ; ]
;
min ; max
min ; max


d)
11 11
13yy
[ ; ] [ ; ]
min ; max


1. Tính GTLN, GTNN của
hàm số:
a)
32
3 9 35y x x x
trên các đoạn [–4; 4], [0; 5].
b)
42
32y x x
trên các đoạn [0; 3], [2; 5]
c)
2
1
x
y
x
trên các đoạn [2; 4], [–3; –2].
d)
54yx
trên [–1; 1].
Hoạt động 2: Luyện tập tìm GTLN, GTNN của hàm số liên tục trên một khoảng
H1. Nêu các bước thực hiện ?
Đ1.
a)
4
R
ymax
; không có GTNN
b)
1
R
ymax
; không có GTNN
c)
; không có GTLN
d)
0
4y
( ; )
min

;không có GTLN
2. Tìm GTLN, GTNN của các
hàm số sau:
a)
2
4
1
y
x
b)
34
43y x x
c)
yx
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 16
d)
4
0y x x
x
()
Hoạt động 3: Vận dụng GTLN, GTNN để giải toán
Hướng dẫn HS cách phân
tích bài toán.
H1. Xác định hàm số ? Tìm
GTLN, GTNN của hàm số ?
Đ1.
3) S = x (8 – x), (0 < x < 8)
Để S lớn nhất thì x = 4.
maxS = 16
4) P =
48
x
x
0 4 3x
Để P nhỏ nhất thì x =
43
minP =
16 3
3. Trong số các hình chữ nhật
có cùng chu vi 16 cm, hãy tìm
hình chữ nhật có diện tích lớn
nhất.
4. Trong số các hình chữ nhật
cùng có diện tích 48 cm
2
, hãy
tìm hình chữ nhật có chu vi
nhỏ nhất.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Các cách tìm GTLN, GTNN
của hàm số.
– So sánh với cách tìm GTLN,
GTNN của hàm số liên tục trên
một khoảng.
– Cách vận dụng GTLN,
GTNN để giải toán.
4. BÀI TẬP VỀ NHÀ:
Đọc trước bài "Đường tiệm cận".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 09 Bài 4: ĐƯỜNG TIỆM CẬN
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
Kĩ năng:
Tìm được đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
Củng cố cách tìm giới hạn, giới hạn một bên của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 17
Học sinh: SGK, vở ghi. Ôn tập cách tính giới hạn của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Cho hàm số
2
1
x
y
x
. Tính các giới hạn:
xx
yylim , lim
 
?
Đ.
1
x
ylim


,
1
x
ylim


.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm đường tiệm cận ngang của đồ thị hàm số
Dẫn dắt từ VD để hình thành
khái niệm đường tiệm cận
ngang.
VD: Cho hàm số
2
1
x
y
x
(C). Nhận xét khoảng cách từ
điểm M(x; y) (C) đến đường
thẳng : y = –1 khi x ∞.
H1. Tính khoảng cách từ M
đến đường thẳng ?
H2. Nhận xét khoảng cách đó
khi x +∞ ?
GV giới thiệu khái niệm
đường tiệm cận ngang.
Đ1. d(M, ) =
1y
Đ2. dần tới 0 khi x +∞.
I. ĐƯỜNG TIỆM CẬN
NGANG
1. Định nghĩa
Cho hàm số y = f(x) xác định
trên một khoảng vô hạn.
Đường thẳng y = y
0
là tiệm
cận ngang của đồ thị hàm số y
= f(x) nếu ít nhất một trong các
điều kiện sau được thoả mãn:
0
x
f x ylim ( )

,
0
x
f x ylim ( )

Chú ý: Nếu
0
xx
f x f x ylim ( ) lim ( )
 

thì ta viết chung
0
x
f x ylim ( )

Hoạt động 2: Tìm hiểu cách tìm tiệm cận ngang của đồ thị hàm số
Cho HS nhận xét cách tìm
TCN .
H1. Tìm tiệm cận ngang ?
Các nhóm thảo luận và trình
bày.
Đ1.
a) TCN: y = 2
b) TCN: y = 0
c) TCN: y = 1
d) TCN: y = 0
2. Cách tìm tiệm cận ngang
Nếu tính được
0
x
f x ylim ( )

hoặc
0
x
f x ylim ( )

thì đường
thẳng y = y
0
là TCN của đồ thị
hàm số y = f(x).
VD1: Tìm tiệm cận ngang cuẩ
đồ thị hàm số:
a)
21
1
x
y
x
b)
2
1
1
x
y
x
c)
2
2
32
1
xx
y
xx


d)
1
7
y
x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 18
H2. Tìm tiệm cận ngang ?
Đ2.
a) TCN: y = 0
b) TCN: y =
1
2
c) TCN: y = 1
d) TCN: y = 1
VD2: Tìm tiệm cận ngang cuẩ
đồ thị hàm số:
a)
2
1
3
x
y
xx
b)
3
21
x
y
x
c)
2
2
32
35
xx
y
xx


d)
7
x
y
x
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách tìm tiệm cận ngang của
đồ thị hàm số.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Đường tiệm cận".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 10 Bài 4: ĐƯỜNG TIỆM CẬN (tt)
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
Kĩ năng:
Tìm được đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
Củng cố cách tìm giới hạn, giới hạn một bên của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập cách tính giới hạn của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Cho hàm số
23
1
x
y
x
(C). Tìm tiệm cận ngang của (C) ? Tính
1x
ylim
,
1x
ylim
?
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 19
Đ.
1x
ylim
,
1x
ylim
.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm đường tiệm cận đứng của đồ thị hàm số
Dẫn dắt từ VD để hình thành
khái niệm tiệm cận đứng.
VD: Cho hàm số
2
1
x
y
x
có
đồ thị (C). Nhận xét về khoảng
cách từ điểm M(x; y) (C)
đến đường thẳng : x = 0 khi x
1
+
?
H1. Tính khoảng cách từ M
đến ?
H2. Nhận xét khoảng cách đó
khi x 1
+
?
GV giới thiệu khái niệm tiệm
cận đứng.
Đ1. d(M, ) =
1x
.
Đ2. dần tới 0.
II. ĐƯỜNG TIỆM CẬN
ĐỨNG
1. Định nghĩa
Đường thẳng x = x
0
đgl tiệm
cận đứng của đồ thị hàm số y
= f(x) nếu ít nhất một trong các
điều kiện sau được thoả mãn:
0
xx
fxlim ( )

0
xx
fxlim ( )

0
xx
fxlim ( )

0
xx
fxlim ( )

Hoạt động 2: Tìm hiểu cách tìm tiệm cận đứng của đồ thị hàm số
GV cho HS nhận xét cách
tìm TCĐ.
H1. Tìm tiệm cận đứng ?
Các nhóm thảo luận và trình
bày.
Đ1.
a) TCĐ: x = 3
b) TCĐ: x = 1
c) TCĐ: x = 0; x = 3
d) TCĐ: x = –7
2. Cách tìm tiệm cận đứng
của đồ thị hàm số
Nếu tìm được
0
xx
fxlim ( )

hoặc
0
xx
fxlim ( )

,
hoặc
0
xx
fxlim ( )

,
hoặc
0
xx
fxlim ( )

thì đường thẳng x = x
0
là TCĐ
của đồ thị hàm số y = f(x).
VD1: Tìm tiệm cận đứng của
đồ thị hàm số:
a)
21
3
x
y
x
b)
2
1
1
xx
y
x

c)
2
1
3
x
y
xx
d)
1
7
y
x
VD2: Tìm TCĐ và TCN của
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 20
H2. Tìm tiệm cận đứng và tiệm
cận ngang ?
Đ2.
a) TCĐ: x = 1; x = 2
TCN: y = 0
b) TCĐ: x = 1; x = –2
TCN: y = 0
c) TCĐ: x =
1
2
TCN: y =
1
2
d) TCĐ: không có
TCN: y = 1
đồ thị hàm số:
a)
2
1
32
x
y
xx

b)
2
3
2
x
y
xx

c)
3
21
x
y
x
d)
2
2
3
2
xx
y
xx


Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách tìm tiệm cận đứng và
tiệm cận ngang của đồ thị hàm
số.
– Nhắc lại cách tính giới hạn
của hàm số.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 11 Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ
CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức:
Biết sơ đồ tổng quát để khảo sát hàm số.
Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức
ax b
y
a x b''
.
Kĩ năng:
Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
Biết cách tìm giao điểm của hai đồ thị.
Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 21
2. Kiểm tra bài cũ: (3')
H. Nhắc lại định lí về tính đơn điệu, cực trị của hàm số?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu sơ đồ khảo sát hàm số
GV cho HS nhắc lại cách
thực hiện từng bước trong sơ
đồ.
H1. Nêu một số cách tìm tập
xác định của hàm số?
H2. Nhắc lại định lí về tính
đơn điệu và cực trị của hàm
số?
H3. Nhắc lại cách tìm tiệm cận
của đồ thị hàm số ?
H4. Nêu cách tìm giao điểm
của đồ thị với các trục toạ độ ?
Đ1.
– Mẫu # 0.
– Biểu thức trong căn bậc hai
không âm.
Đ2. HS nhắc lại.
Đ3. HS nhắc lại.
Đ4.
– Tìm giao điểm với trục tung:
Cho x = 0, tìm y.
– Tìm giao điểm với trục
hoành:
Giải pt: y = 0, tìm x.
I. SƠ ĐỒ KHẢO SÁT HÀM
SỐ
1. Tập xác định
2. Sự biến thiên
– Tính y
.
– Tìm các điểm tại đó y
= 0
hoặc y
không xác định.
– Tìm các giới hạn đặc biệt và
tiệm cận (nếu có).
– Lập bảng biến thiên.
– Ghi kết quả về khoảng đơn
điệu và cực trị của hàm số.
3. Đồ thị
– Tìm toạ độ giao điểm của đồ
thị với các trục toạ độ.
– Xác định tính đối xứng của
đồ thị (nếu có).
– Xác định tính tuần hoàn (nếu
có) của hàm số.
– Dựa vào bảng biến thiên và
các yếu tố xác định ở trên để
vẽ.
Hoạt động 2: Áp dụng khảo sát và vẽ đồ thị hàm số bậc nhất
Cho HS nhắc lại các điều đã
biết về hàm số
y ax b
, sau
đó cho thực hiện khảo sát theo
sơ đồ.
Các nhóm thảo luận, thực
hiện và trình bày.
+ D = R
+ y = a
+ a > 0: hs đồng biến
+ a < 0: hs nghịch biến
+ a = 0: hs không đổi
VD1: Khảo sát sự biến thiên và
vẽ đồ thị hàm số
y ax b
Hoạt động 3: Áp dụng khảo sát và vẽ đồ thị hàm số bậc hai
Cho HS nhắc lại các điều đã
biết về hàm số
2
y ax bx c
, sau đó cho thực hiện khảo sát
theo sơ đồ.
Các nhóm thảo luận, thực
hiện và trình bày.
+ D = R
+ y = 2ax + b
a > 0
x
y’
y
0
2
b
a




4a
+
–
a < 0
VD2: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
2
y ax bx c
(a 0)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 22
x
y’
y
0
2
b
a


4a


–
+
Hoạt động 4: Củng cố
Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các tính chất hàm số đã học.
Câu hỏi: Khảo sát sự biến
thiên và vẽ đồ thị hàm số:
a)
2
43y x x
b)
2
23y x x+
4. BÀI TẬP VỀ NHÀ:
Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 12 Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ
CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Biết sơ đồ tổng quát để khảo sát hàm số.
Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức
ax b
y
a x b''
.
Kĩ năng:
Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
Biết cách tìm giao điểm của hai đồ thị.
Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại sơ đồ khảo sát hàm số?
Đ.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 23
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khảo sát hàm số bậc ba
Cho HS thực hiện lần lượt
các bước theo sơ đồ.
Các nhóm thực hiện và trình
bày.
+ D = R
+ y =
2
36xx
y = 0
2
0
x
x

+
x
ylim


;
x
ylim


+ BBT
+ x = 0 y = –4
y = 0
2
1
x
x

+ Đồ thị
II. KHẢO SÁT MỘT SỐ
HÁM ĐA THỨC VÀ HÀM
PHÂN THỨC
1. Hàm số
32
y ax bx cx d
(a 0)
VD1: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
32
34y x x
Cho HS thực hiện lần lượt
các bước theo sơ đồ.
Các nhóm thực hiện và trình
bày.
+ D = R
+ y =
2
3 1 1x()
< 0, x
+
x
ylim


;
x
ylim


+ BBT
+ x = 0 y = 2
y = 0 x = 1
+ Đồ thị
VD2: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
32
3 4 2y x x x
Hoạt động 2: Tìm hiểu các dạng đồ thị của hàm số bậc ba
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 24
Hoạt động 3: Củng cố
Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các dạng đồ thị của hàm số
bậc ba.
Câu hỏi: Các hàm số sau thuộc
dạng nào?
a)
3
y x x
b)
3
y x x
c)
3
y x x
d)
3
y x x
Các nhóm thảo luận và trả lời
a) a > 0, > 0 b) a > 0, < 0
c) a < 0, < 0 d) a < 0, > 0
4. BÀI TẬP VỀ NHÀ:
Bài 1 SGK.
Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 25
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 13 Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ
CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Biết sơ đồ tổng quát để khảo sát hàm số.
Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức
ax b
y
a x b''
.
Kĩ năng:
Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
Biết cách tìm giao điểm của hai đồ thị.
Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại sơ đồ khảo sát hàm số?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khảo sát hàm số bậc ba
Cho HS thực hiện lần lượt
các bước theo sơ đồ.
Các nhóm thực hiện và trình
bày.
+ D = R
+ y =
2
41xx()
y = 0
1
1
0
x
x
x

+
x
ylim


;
x
ylim


+ BBT
+ Đồ thị
x = 0 y = –3
y = 0
3
3
x
x

Hàm số đã cho là hàm số
II. KHẢO SÁT MỘT SỐ
HÁM ĐA THỨC VÀ HÀM
PHÂN THỨC
2. Hàm số
42
y ax bx c
(a 0)
VD1: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
42
23y x x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 26
chẵn Đồ thị nhận trục tung
làm trục đối xứng.
Cho HS thực hiện lần lượt
các bước theo sơ đồ.
Các nhóm thực hiện và trình
bày.
+ D = R
+ y =
2
21xx()
y = 0 x = 0
+
x
ylim


;
x
ylim


+ BBT
+ Đồ thị
x = 0 y =
3
2
y = 0 x = 1
Đồ thị nhận trục tung làm trục
đối xứng.
VD2: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
4
2
3
22
x
yx
Hoạt động 2: Tìm hiểu các dạng đồ thị của hàm số trùng phương
Hoạt động 3: Củng cố
Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các dạng đồ thị của hàm số
bậc bốn trùng phương.
Câu hỏi: Các hàm số sau thuộc
dạng nào?
a)
42
y x x
b)
42
y x x
c)
42
y x x
d)
42
y x x
Các nhóm thảo luận và trả lời
4. BÀI TẬP VỀ NHÀ:
Bài 2 SGK.
Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 27
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 14 Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ
CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Biết sơ đồ tổng quát để khảo sát hàm số.
Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức
ax b
y
a x b''
.
Kĩ năng:
Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
Biết cách tìm giao điểm của hai đồ thị.
Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại sơ đồ khảo sát hàm số?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khảo sát hàm số nhất biến
Cho HS thực hiện lần lượt
các bước theo sơ đồ.
Các nhóm thực hiện và trình
bày.
+ D = R \ {–1}
+ y =
2
3
1x()
< 0, x –1
+ TCĐ: x = –1
TCN: y = –1
+ BBT
x
y’
y




–
–
–1
–1
–1
+ Đồ thị
x = 0 y = 2
y = 0 x = 2
Giao điểm của hai tiệm cận
là tâm đối xứng của đồ thị.
II. KHẢO SÁT MỘT SỐ
HÁM ĐA THỨC VÀ HÀM
PHÂN THỨC
3. Hàm số
ax b
y
cx d
(c 0, ad – bc 0)
VD1: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
2
1
x
y
x

Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 28
Cho HS thực hiện lần lượt
các bước theo sơ đồ.
Các nhóm thực hiện và trình
bày.
+ D = R \
1
2



+ y =
2
5
21x()
> 0, x
1
2
+ TCĐ: x =
1
2
TCN: y =
1
2
+ BBT
x
y’
y
1
2
1
2




1
2
+
+
+ Đồ thị
x = 0 y = –2
y = 0 x = 2
Đồ thị nhận giao điểm của 2
tiệm cận làm tâm đối xứng.
VD2: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
2
21
x
y
x
Hoạt động 2: Tìm hiểu các dạng đồ thị của hàm số nhất biến
Hoạt động 3: Củng cố
Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các dạng đồ thị của hàm số
nhất biến.
Câu hỏi: Các hàm số sau thuộc
dạng nào? Tìm các tiệm cận
của chúng:
Các nhóm thảo luận và trả lời
0
ad – bc > 0
x
y
0
ad – bc < 0
x
y
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 29
a)
21
1
x
y
x
b)
21
1
x
y
x
4. BÀI TẬP VỀ NHÀ:
Bài 3 SGK.
Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 15 Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ
CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Biết sơ đồ tổng quát để khảo sát hàm số.
Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức
ax b
y
a x b''
.
Kĩ năng:
Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
Biết cách tìm giao điểm của hai đồ thị.
Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm toạ độ giao điểm của đồ thị hai hàm số:
22
2 3 2y x x y x x,
?
Đ.
57
10
24
; , ;




.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách xét sự tương giao của các đồ thị
Từ KTBC, GV cho HS nêu
cách tìm giao điểm của hai đồ
thị.
(1) đgl phương trình hoành
độ giao điểm của hai đồ thị.
Các nhóm thảo luận và trình
bày.
III. SỰ TƯƠNG GIAO CỦA
CÁC ĐỒ THỊ
Cho hai hàm số:
y = f(x) (C
1
) và y = g(x) (C
2
).
Để tìm hoành độ giao điểm của
(C
1
) và (C
2
), ta giải phương
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 30
trình: f(x) = g(x) (1)
Giả sử (1) có các nghiệm là x
0
,
x
1
, … Khi đó, các giao điểm là
0 0 0 1 1 1
M x f x M x f x; ( ) , ; ( )
,
…
Nhận xét: Số nghiệm của (1)
bằng số giao điểm của (C
1
),
(C
2
).
Hoạt động 2: Áp dụng xét sự tương giao của hai đồ thị
Cho HS thực hiện.
H1. Lập pt hoành độ giao
điểm?
Hướng dẫn HS giải pt bậc ba.
Chú ý điều kiện mẫu khác 0.
H2. Lập pt hoành độ giao điểm
của đồ thị và trục hoành?
H3. Nêu điều kiện để đồ thị cắt
trục hoành tại 3 điểm phân biệt
Các nhóm thực hiện và trình
bày.
Đ1.
a)
3 2 3 2
3 5 2 2 3x x x x
32
3 5 8 0xx
x = –1
b)
2
24
24
1
x
xx
x
32
30
1
xx
x

0
3
x
x
c)
2
31
1
x
x
x
2
2 1 0x()
1
2
x
Đ2.
22
1 3 0x x mx m( )( )
Đ3. Pt có 3 nghiệm phân biệt
22
30x mx m
có 2
nghiệm phân biệt, khác 1
2
0
1 3 0mm
22
1
m
m

VD1: Tìm toạ độ giao điểm
của đồ thị hai hàm số:
a)
32
35y x x
(C
1
)
32
223y x x
(C
2
)
b)
24
1
x
y
x
2
24y x x
c)
2
1
x
y
x
31yx
VD2: Tìm m để đồ thị hàm số
22
13y x x mx m( )( )
cắt trục hoành tại 3 điểm phân
biệt.
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách xét sư tương giao giữa
hai đồ thị.
– Số giao điểm của hai đồ thị
bằng số nghiệm của phương
trình hoành độ giao điểm.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 31
4. BÀI TẬP VỀ NHÀ:
Bài 5, 6, 7, 8, 9 SGK.
Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 16 Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ
CỦA HÀM SỐ (tt)
I. MỤC TIÊU:
Kiến thức:
Biết sơ đồ tổng quát để khảo sát hàm số.
Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức
ax b
y
a x b''
.
Kĩ năng:
Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
Biết cách tìm giao điểm của hai đồ thị.
Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm toạ độ giao điểm của đồ thị hai hàm số:
32
7 2 5y x x x y x,
?
Đ.
1 7 5 5 2 5 5 5 2 5( ; ), ; , ;
.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách biện luận số nghiệm của phương trình bằng đồ thị
H1. Nhắc lại cách giải phương
trình bằng đồ thị đã biết ?
GV giơ
i thiệu phương pháp.
Đ1. Vẽ các đồ thị trên cùng
một hệ trục. Dựa vào đồ thị để
kết luận.
IV. BIỆN LUẬN SỐ
NGHIỆM CỦA PHƯƠNG
TRÌNH BẰNG ĐỒ THỊ
Xét ph.trình: F(x, m)=0 (1)
– Biến đổi (1) về dạng:
f(x) = g(m) (2)
– Khi đó (2) có thể xem là pt
hoành độ giao điểm của 2 đồ
thị: (C): y = f(x)
(d): y = g(m)
(trong đó y = f(x) thường là
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 32
hàm số đã được khảo sát và vẽ
đồ thị, (d) là đường thẳng cùng
phương với trục hoành).
– Dựa vào đồ thị (C), từ số
giao điểm của (C) và (d) ta suy
ra số nghiệm của (2), cũng là
số nghiệm của (1).
Hoạt động 2: Áp dụng biện luận số nghiệm của phương trình bằng đồ thị
H1. Khảo sát và vẽ đồ thị hàm
số ?
GV hướng dẫn HS biện luận
số giao điểm của (C) và (d).
Đ1. HS thực hiện nhanh.
2
2
m
m

: (1) có 1 nghiệm
2
2
m
m

: (1) có 2 nghiệm
–2 < m < 2: (1) có 3 nghiệm
VD1: Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
32
32y x x
(C)
Dựa vào đồ thị, biện luận theo
m số nghiệm của phương trình:
32
32x x m
(1)
Hoạt động 3: Ôn tập bài toán tiếp tuyến
H1. Nhắc lại ý nghĩa hình học
của đạo hàm ?
GV hướng dẫn HS cách giải
bài toán 2. (Bài toán 3 dành
cho HS khá giỏi).
H2. Nêu dạng phương trình
đường thẳng đi qua (x
0
; y
0
) và
có hệ số góc k ?
H2. Tìm toạ độ giao điểm của
(C) và trục hoành ?
Đ1. Hệ số góc của tiếp tuyến
k = f(x
0
).
Đ2.
00
y y k x x()
Đ3.
3
2 3 0xx
1
2
x
x

+ Pttt của (C) tại (–1; 0):
y = 0
+ Pttt của (C) tại (2; 0):
y = –9(x – 2)
V. TIẾP TUYẾN
Bài toán 1: Viết phương trình
tiếp tuyến của (C): y = f(x) tại
điểm
0 0 0
M x f x; ( )
(C).
0 0 0
y y f x x x'( ).( )
(y
0
= f(x
0
))
Bài toán 2: Viết phương trình
tiếp tuyến của (C): y = f(x),
biết tiếp tuyến có hệ số góc k.
Gọi (x
0
; y
0
) là toạ độ của
tiếp điểm.
f
(x
0
) = k (*)
Giải pt (*), tìm được x
0
.
Từ đó viết pttt.
Bài toán 3: Viết phương trình
tiếp tuyến của (C): y = f(x),
biết tiếp tuyến đi qua điểm
A(x
1
; y
1
).
VD2: Viết phương trình tiếp
tuyến của đồ thị (C) của hàm
số sau tại các giao điểm của
(C) với trục hoành:
3
23y x x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 33
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ:
Bài 5, 6, 7, 8, 9 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 17 Bài 5: BÀI TẬP KHẢO SÁT SỰ BIẾN THIÊN
VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức: Củng cố:
Sơ đồ khảo sát hàm số.
Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức
ax b
y
a x b''
.
Kĩ năng:
Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
Biết cách tìm giao điểm của hai đồ thị.
Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
Biết viết phương trình tiếp tuyến của đồ thị hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba
H1. Nhắc lại các bước khảo sát
và vẽ đồ thị hàm số bậc ba?
Các nhóm thực hiện và trình
bày.
Đ1.
a)
x
y’
y
–1
1
0
0
4
0
– +
–




1. Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
a)
3
23y x x
b)
32
9y x x x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 34
b)
x
y’
y
+




x
y
O 1
–1
4
2
2
–2
x
y
1–1
O
11
–9
Hoạt động 2: Luyện tập khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn trùng phương
H1. Nhắc lại các bước khảo sát
và vẽ đồ thị hàm số bậc bốn
trùng phương?
Các nhóm thực hiện và trình
bày.
Đ1.
a)
x
y’
y
+



–1 0
1
0 00 +
––
1
1
2

b)
x
y’
y
0
0
3
+ –




2. Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
a)
42
22y x x
b)
24
23y x x
-3 -2 -1 1 2 3
-1
1
2
3
4
5
6
7
8
9
x
y
-2 -1 1 2
-1
1
2
3
x
y
Hoạt động 3: Luyện tập khảo sát sự biến thiên và vẽ đồ thị hàm số nhất biến
H1. Nhắc lại các bước khảo sát
và vẽ đồ thị hàm số nhất biến?
Các nhóm thực hiện và trình
bày.
Đ1.
a)
x
y’
y
2
+ +




–1
–1
b)
3. Khảo sát sự biến thiên và
vẽ đồ thị hàm số:
a)
12
24
x
y
x
b)
2
21
x
y
x

-4 -3 -2 -1 1 2 3 4 5 6 7
-4
-3
-2
-1
1
2
3
4
x
y
O
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 35
x
y’
y
+ +




1
2
1
2
1
2
-3 -2 -1 1 2 3 4 5
-3
-2
-1
1
2
3
x
y
O
Hoạt động 4: Luyện tập xét sự tương giao giữa các đồ thị
H1. Nêu đk để đồ thị hàm số
cắt trục hoành tại 3 điểm phân
biệt ?
H2. Nêu đk để đồ thị các hàm
số cắt nhau tại 2 điểm phân
biệt ?
Đ1. Pt hoành độ giao điểm có 3
nghiệm phân biệt:
32
3 1 2 1 0mx mx m x()
2
1 2 1 0x mx mx( )( )
2
1
2 1 0 2
x
mx mx ()

(2) có 2 nghiệm pb, khác –1
0
0
2 2 0
m
m
'
1
0
m
m

Đ2. Pt hoành độ giao điểm có 2
nghiệm phân biệt:
2
23
2
1
x x m
xm
x


2
1
xm
x
2
1
2
xm
m
1. Tìm m để đồ thị hàm số sau
cắt trục hoành tại ba điểm phân
biệt:
32
3 1 2 1y mx mx m x()
2. Tìm m để đồ thị các hàm số
sau cắt nhau tại hai điểm phân
biệt:
2
23
2
1
x x m
y y x m
x
;

Hoạt động 5: Luyện tập biện luận số nghiệm của phương trình bằng đồ thị
H1. Khảo sát và vẽ đồ thị hàm
số ?
H2. Biến đổi phương trình?
H3. Biện luận số giao điểm của
(C) và (d)?
Đ1. Các nhóm khảo sát và vẽ
nhanh đồ thị hàm số.
-3 -2 -1 1 2 3
-2
2
x
y
m+1
O
Đ2.
3
30x x m
3
3 1 1x x m
Đ3.
2
2
m
m

: pt có 1 nghiệm
2
2
m
m

: pt có 2 nghiệm
–2 < m < 2: pt có 3 nghiệm
3. Khảo sát và vẽ đồ thị (C)
của hàm số:
3
31y x x
.
Dựa vào đồ thị (C), biện luận
số nghiệm của phương trình
sau theo m:
3
30x x m
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 36
Hoạt động 6: Luyện tập viết phương trình tiếp tuyến của đồ thị hàm số
H1. Để viết pttt, cần tìm các
giá trị nào ?
Đ1. x
0
, y(x
0
).
42
00
1 1 7
1
4 2 4
xx
0
1x 
Tại
7
1
4
;



, pttt là:
7
21
4
yx()
1
2
4
yx
Tại
7
1
4
;



, pttt là:
7
21
4
yx()
1
2
4
yx
4. Viết phương trình tiếp tuyến
của (C):
42
11
1
42
y x x
tại điểm có tung độ bằng
7
4
.
Hoạt động 7: Củng cố
Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ:
Bài tập ôn chương
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 37
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 18 + 19 BÀI TẬP ÔN CHƯƠNG I
I. MỤC TIÊU:
Kiến thức: Củng cố:
Tính đơn điệu của hàm số.
Cực trị của hàm số, GTLN, GTNN của hàm số.
Đường tiệm cận.
Khảo sát hàm số.
Kĩ năng:
Xác định thành thạo các khoảng đơn điệu của hàm số.
Tính được cực đại, cực tiểu của hàm số (nếu có).
Xác định được các đường tiệm cận của đồ thị hàm số (nếu có).
Lập bảng biến thiên và vẽ đồ thị hàm số một cách thành thạo.
Tính được GTLN, GTNN của hàm số.
Giải được một số bài toán liên quan đến khảo sát hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập khảo sát hàm số
H1. Nêu đk để hàm số đồng
biến trên D ?
H2. Nêu đk để hàm số có 1 CĐ
và 1 CT ?
H3. Phân tích yêu cầu bài
toán?
* Gv: Khi nào thì hàm số đồng
biến nghịch biến.
Cho học sinh thảo luận nhóm
và gọi học sinh lên trả lời câu
Đ1. f
(x)
0, x D
2
3 2 2 1 0x mx m()
,x
2
2 1 0mm'
m = 1
Đ2. f
(x) = 0 có 2 nghiệm phân
biệt.
2
2 1 0mm'
m 1
Đ3. Giải bất phương trình:
f

(x) > 6x
6x – 6m > 6x m < 0
* Hs: Thảo luận theo nhóm và
lên bảng làm bài tập theo yêu
cầu của giáo viên.
B ài 1. Cho hàm số:
32
3 3 2 1 1f x x mx m x( ) ( )
a) Xác định m để hàm số đồng
biến trên tập xác định.
b) Với giá trị nào của m, hàm
số có một CĐ và một CT.
c) Xác định m để f

(x) > 6x.
Bài 2: Tìm các khoảng đơn
điệu của các hàm số:
* y = -x
3
+ 2x
2
– x - 7
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 38
hỏi và bảng làm
* Gv: Sửa bài và cho điểm.
* Gv: Để tìm tiệm cận ngang,
tiệm cận đứng ta phải làm thế
nào?
Cho học sinh thảo luận nhóm
và gọi học sinh lên trả lời câu
hỏi và bảng làm bài tập.
2
1
' 3 4 1 0
1
3
x
y x x
x
Hàm số đồng biến trong
khoảng (
1
3
; 1), nghịch biến
trong các khoảng
1
;;
3




1; 
.
* Hàm số
x5
y
1x
làm tương
tự.
* Hs: Thảo luận theo nhóm và
lên bảng làm bài tập theo yêu
cầu của giáo viên.
23
lim lim 2
2
xx
x
y
x
 

nên y =-2 là tiệm cận ngang.
22
23
lim lim
2
xx
x
y
x



Nên x = 2 là tiệm cận đứng
Bài 3: Tìm tiệm cận của hàm
của hàm số:
2x 3
y
2x
Hoạt động 2: Luyện tập giải các bài toán liên quan đến khảo sát hàm số
Cho HS làm nhanh câu a).
H1. Nêu đk để đường thẳng
luôn cắt (C) tại 2 điểm phân
biệt ?
H2. Nhận xét tính chất của
hoành độ các giao điểm M, N ?
H3. Tính MN ?
Đ1. Pt hoành độ giao điểm
luôn có 2 nghiệm phân biệt.
3
2
1
x
xm
x

2
2 1 3 0
1
x m x m
x
()

2
3 16
20
m' ( )

Đ2. là các nghiệm của pt:
2
2 1 3 0x m x m()
1
2
3
2
MN
MN
m
xx
m
xx.
Đ3.
2 2 2
M N M N
MN x x y y( ) ( )
=
2
5
3 16
4
m()



2. a) Khảo sát và vẽ đồ thị (C)
của hàm số
3
1
x
y
x
b) Chứng minh rằng với mọi
m, đường thẳng
2y x m
luôn cắt (C) tại hai điểm phân
biệt M, N. Xác định m sao cho
độ dài MN là nhỏ nhất.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 39
H4. Tính f
(x), f
(sinx) ?
H5. Giải pt f
(x) = 0? Suy ra
nghiệm của pt: f
(sinx) = 0 ?
H6. Tính f

(x) và giải pt
0fx''( )
?
5
16 20
4
.
minMN =
25
khi m = 3
Đ4. f
(x) =
2
4xx
2
4f inx x inx'(s ) sin s
Đ5.
2
0 4 0f x x x'( )
1 17
2
x
[–1; 1]
Pt: f
(sinx) = 0 vô nghiệm.
Đ6.
1
2 1 0
2
f x x x''( )
Pttt tại
1 47
2 12
;



:
17 1 47
4 2 12
yx



3. Cho hàm số
32
11
46
32
f x x x x()
a) Giải pt:
0f inx'(s )
.
b) Viết pttt của đồ thị hàm số
tại điểm có hoành độ là nghiệm
của phương trình
0fx''( )
.
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ:
Chuẩn bị kiểm tra 1 tiết chương I.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 40
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 20 Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG 1
I. MỤC TIÊU:
Kiến thức:
Ôn tập toàn bộ kiến thức trong chương I.
Kĩ năng:
Khảo sát sự biến thiên và vẽ đồ thị hàm số.
Giải các bài toán về tính đơn điệu, cực trị, GTLN, GTNN, tiệm cận.
Giải các bài toán liên quan đến khảo sát hàm số: sự tương giao, biện luận số nghiệm của
phương trình bằng đồ thị, viết phương trình tiếp tuyến với đồ thị.
Thái độ:
Rèn luyện tính cẩn thận, chính xác.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: Ôn tập toàn bộ kiến thức chương 1.
III. MA TRẬN ĐỀ:
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Tính đơn điệu
3
0,5
1,5
Cực trị, GTLN – GTNN
3
0,5
1,5
Tiệm cận
2
0,5
1,0
Khảo sát hàm số
1
3,0
3,0
Các bài toán liên quan
1
3,0
3,0
Tổng
4,0
3,0
3,0
10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm)
Câu 1: Hàm số
32
34y x x
đồng biến trên khoảng:
A. (0; 2) B. (

; 0) và (2;

) C. (

; 2) D. (0; +∞)
Câu 2: Hàm số
42
23y x x
đồng biến trên khoảng:
A. (–∞; 0) B. (–∞; –1) C. (1; +∞) D. (0; +∞)
Câu 3: Hàm số
1
2
x
y
x
nghịch biến trên khoảng:
A. (–∞; +∞) B. (–∞; 2) C. (2; +∞) D. (–2; +∞)
Câu 4: Hàm số
32
34y x x
đạt cực tiểu tại điểm:
A. x = 0 B. x = 2 C. x = 4 D. không có
Câu 5: Hàm số
42
23y x x
đạt cực đại tại điểm:
A. x = –1 B. x = 1 C. x = 0 D. x = 3
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 41
Câu 6: Hàm số
1
2
x
y
x
có mấy điểm cực trị:
A. 0 B. 1 C. 2 D. 3
Câu 7: Đồ thị hàm số
2
1
3
x
y
xx
có bao nhiêu tiệm cận:
A. 0 B. 1 C. 2 D. 3
Câu 8: Đồ thị hàm số
2
3
2
x
y
xx

có bao nhiêu tiệm cận đứng:
A. 0 B. 1 C. 2 D. 3
B. Phần tự luận: (6 điểm) Cho hàm số :
32
33y x x
.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
b) Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trình:
32
3x x m
.
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
B
A
D
B
C
A
D
C
B. Phần tự luận: Mỗi câu 3 điểm
a)
32
33y x x
D = R
2
36y x x' 
y = 0 x = 0, x = –2
xx
yylim ; lim
 
 
x
y’
y
-2 0
00
1
-3




++ –
x = 0 y = –3;
x = 1 y = 1; x = –3 y = –3
b)
32
3x x m
32
3 3 3x x m
(*)
0
4
m
m
: (*) có 1 nghiệm
0
4
m
m
: (*) có 2 nghiệm 0 < m < 4: (*) có 3 nghiệm
VI. KẾT QUẢ KIỂM TRA:
Lớp
Sĩ số
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
12S1
53
12S2
54
12S3
54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
-4 -3 -2 -1 1 2 3 4
-4
-3
-2
-1
1
2
3
4
x
y
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 42
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Chương II: HÀM SỐ LUỸ THỪA – HÀM SỐ MŨ –
HÀM SỐ LOGARIT
Tiết dạy: 21 Bài 1: LUỸ THỪA
I. MỤC TIÊU:
Kiến thức:
Biết các khái niệm và tính chất của luỹ thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ không
nguyên và luỹ thừa với số mũ thực.
Biết khái niệm và tính chất của căn bậc n.
Kĩ năng:
Biết dùng các tính chất của luỹ thừa để rút gọn biểu thức, so sánh những biểu thức có chứa luỹ thừa.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại một số qui tắc luỹ thừa với số mũ nguyên dương?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu luỹ thừa với số mũ nguyên
H1. Nhắc lại định nghĩa và tính
chất của luỹ thừa với số mũ
nguyên dương ?
H2. Biến đổi các số hạng theo cơ
số thích hợp ?
H3. Phân tích các biểu thức thành
nhân tử ?
Đ1.
m
m n m n m n
n
n
m mn n n n
n
n
n
a
a .a a ; a
a
a a ; (ab) a .b
aa
b
b






Đ2.
10
3 10 9
1
.27 3 .3 3
3





4 2 4 4
(0,2) .25 5 .5 1

9
1 7 9
1
128 . 2 .2 4
2





A = 8.
Đ3.
I. KHÁI NIỆM LUỸ THỪA
1. Luỹ thừa với số mũ nguyên
Cho n là một số nguyên dương.
Với a tuỳ ý:
n
n thöøa soá
a a.a....a
Với a
0:
0n
n
1
a 1; a
a

(a: cơ số, n: số mũ)
Chú ý:
0n
0 , 0
không có nghĩa.
Luỹ thừa với số mũ nguyên có
các tính chất tương tự như luỹ
thừa với số mũ nguyên dương.
VD1: Tính giá trị của biểu thức
10
3
9
4 2 1
1
A .27
3
1
(0,2) .25 128 .
2








VD2: Rút gọn biểu thức:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 43
2
2 1 1
a 2 2 2
a 2(a 1)
(1 a ) a

3
22
a1
1 a a(a 1)

B =
2
3
2 1 1 2
a 2 2 2 a
B.
(1 a ) a 1 a






(a 0, a 1)
Hoạt động 2: Biện luận số nghiệm của phương trình
n
xb
H1. Dựa vào đồ thị, biện luận số
nghiệm của các phương trình:
34
x b, x b
?
GV hướng dẫn HS biện luận. Từ
đó nêu nhận xét.
2. Phương trình
n
xb
(*)
a) n lẻ:
(*) luôn có nghiệm duy nhất.
b) n chẵn:
+ b < 0: (*) vô nghiệm.
+ b = 0: (*) có 1 nghiệm x = 0
+ b > 0: (*) có 2 nghiệm đối
nhau.
Hoạt động 3: Tìm hiểu khái niệm và tính chất căn bậc n
Dựa vào việc giải phương trình
n
xb
, GV giới thiệu khái niệm
căn bậc n.
H1. Tìm các căn bậc hai của 4?
Lưu ý HS phân biệt kí hiệu 2 giá
trị căn bậc n của một số dương.
GV hướng dẫn HS nhận xét một
số tính chất của căn bậc n.
H2. Thực hiện phép tính ?
Đ1. 2 và –2.
Đ2.
A =
5
32 2
B =
3
3
33
3. Căn bậc n
a) Khái niệm
Cho b
R, n
N
*
(n
2). Số a
đgl căn bậc n của b nếu
n
ab
.
Nhận xét:
n lẻ, b tuỳ ý: có duy nhất một
căn bậc n của b, kí hiệu
n
b
n chẵn:
+ b < 0: không có căn bậc n của
b.
+ b = 0: căn bậc n của 0 là 0.
+ b > 0: có hai căn trái dấu, kí
hiệu giá trị dương là
n
b
, còn giá
trị âm là
n
b
.
b) Tính chất của căn bậc n
n n n
a. b ab
;
n
n
n
aa
b
b
m
n
nm
aa
;
n
k nk
aa
n
n
a khi n leû
a
a khi n chaün
VD3: Rút gọn biểu thức:
A =
5
5
48.
; B =
3
33
Hoạt động 4: Củng cố
Nhấn mạnh:
– Định nghĩa và tính chất của luỹ
thừa với số mũ nguyên.
– Định nghĩa và tính chất của căn
bậc n.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 44
4. BÀI TẬP VỀ NHÀ:
Bài 1 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 22 Bài 1: LUỸ THỪA (tt)
I. MỤC TIÊU:
Kiến thức:
Biết các khái niệm và tính chất của luỹ thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ
không nguyên và luỹ thừa với số mũ thực.
Biết khái niệm và tính chất của căn bậc n.
Kĩ năng:
Biết dùng các tính chất của luỹ thừa để rút gọn biểu thức, so sánh những biểu thức có chứa
luỹ thừa.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số tính chất của căn bậc n?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu luỹ thừa với số mũ hữu tỉ
GV nêu định nghĩa.
H1. Viết dưới dạng căn thức?
H2. Phân tích tử thức thành
nhân tử ?
Đ1.
A =
3
11
82
B =
3
3
11
4
8
4

Đ2.
4. Luỹ thừa với số mũ hữu tỉ
Cho a
R, a > 0 và
m
r
n
,
trong đó m
Z, n
N, n
2.
m
n
rm
n
a a a
Đặc biệt:
1
n
n
aa
VD1: Tính giá trị các biểu thức
A =
1
3
1
8



; B =
3
2
4
VD2: Rút gọn biểu thức:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 45
5 5 1 1
4 4 4 4
x y xy xy x y



C = xy.
C =
55
44
4
4
x y xy
xy
(x, y > 0)
Hoạt động 2: Tìm hiểu khái niệm luỹ thừa với số mũ vô tỉ
GV cho HS nhận xét kết quả
bảng tính
3
n
r
. Từ đó GV nêu
định nghĩa.
HS tính và nêu nhận xét.
5. Luỹ thừa với số mũ vô tỉ
Cho a
R, a > 0,
là số vô tỉ.
Ta gọi giới hạn của dãy số
n
r
a
là luỹ thừa của a với số
mũ
, kí hiệu
a
.
n
r
aalim
với
n
rlim
Chú ý:
11
(
R)
Hoạt động 3: Tìm hiểu tính chất của luỹ thừa với số mũ thực
H1. Nhắc lại các tính chất của
luỹ thừa với số mũ nguyên
dương ?
H2. Nêu tính chất tương tự cho
luỹ thừa với số mũ thực ?
H3. Biến đổi tử và mẫu về luỹ
thừa với cơ số a ?
H4. Ta cần so sánh các số nào?
Đ1. HS nhắc lại.
Đ2. Các nhóm lần lượt nêu tính
chất.
Đ3.
7 1 2 7 3
a a a.

22
2 2 2
aa

D =
5
a
31
3 1 2
aa
5 3 4 5
a a a.

E = a
Đ4. Vì cùng cơ số nên chỉ cần
so sánh các số mũ.
2 3 12 18 3 2
2
A < B
II. TÍNH CHẤT CỦA LUỸ
THỪA VỚI SỐ MŨ THỰC
Cho a, b
R, a, b > 0;
,
R. Ta có:
a a a.
;
a
a
a

aa

;
ab a b( ) .
aa
b
b



a > 1:
aa


a < 1:
aa


VD3. Rút gọn biểu thức:
D =
7 1 2 7
22
22
aa
a
.

(a > 0)
E =
31
31
5 3 4 5
a
aa.

VD4: So sánh các số:
A =
23
5
và B =
32
5
Hoạt động 4: Củng cố
Nhấn mạnh:
– Định nghĩa và tính chất của
luỹ thừa với số mũ hữu tỉ, số
mũ thực.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 46
4. BÀI TẬP VỀ NHÀ:
Bài 2, 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 23 Bài 2: HÀM SỐ LUỸ THỪA
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm và tính chất của hàm số luỹ thừa.
Biết công thức tính đạo hàm của hàm số luỹ thừa.
Biết dạng đồ thị của hàm số luỹ thừa.
Kĩ năng:
Biết khảo sát hàm số luỹ thừa.
Tính được đạo hàm của hàm số luỹ thừa.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Cho VD một số hàm số luỹ thừa đã học?
Đ.
2
1
y x y y x
x
;;
, …
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm hàm số luỹ thừa
H1. Cho VD một số hàm luỹ
thừa và vẽ đồ thị của chúng ?
H2. Nhận xét tập xác định của
các hàm số đó ?
GV nêu chú ý.
Đ1. Các nhóm thảo luận và
trình bày.
1
21
2
y x y x y x y x; ; ;
-3 -2 -1 1 2 3
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
x
y
y = x
y = x
2
y = x
-1
y = x
1/2
I. KHÁI NIỆM
Hàm số
yx
với
R đgl
hàm số luỹ thừa.
Chú ý: Tập xác định của hàm
số
yx
tuỳ thuộc vào giá trị
của
:
nguyên dương: D = R
0
nguyeân aâm
: D = R \ {0}
không nguyên: D = (0;+∞)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 47
H3. Dựa vào yếu tố nào để xác
định tập xác định của hàm số
luỹ thừa ? Từ đó chỉ ra điều
kiện xác định của hàm số ?
Đ3. Dựa vào số mũ .
a) 1 – x > 0 D = (–∞; 1)
b)
2
20x
D =
22( ; )
c)
2
10x 
D = R \ {–1; 1}
d)
2
20xx
D = (–∞; –1) (2; +∞)
VD1: Tìm tập xác định của các
hàm số:
a)
1
3
1yx()

b)
3
2
5
2yx()
c)
22
1yx()

d)
22
2y x x()
Hoạt động 2: Tìm hiểu công thức tính đạo hàm của hàm số luỹ thừa
H1. Nhắc lại công thức tính
đạo hàm của hàm số
n
yx
với n nguyên dương ?
H2. Thực hiện phép tính ?
Đ1.
1nn
x nx()
Đ2.
a)
4
3
4
y
x
b)
5
3
2
3
yx

c)
31
3yx
d)
1
yx
II. ĐẠO HÀM CỦA HÀM
SỐ LUỸ THỪA
1
xx

(x > 0)
1
u u u.

VD2: Tính đạo hàm:
a)
3
4
yx
b)
2
3
yx
c)
3
yx
d)
yx
Hoạt động 3: Vận dụng tính đạo hàm của hàm số luỹ thừa
H1. Thực hiện phép tính?
Đ2.
a)
3
2
2 4 1
3 2 1
x
y
xx
()

b)
2 2 1
62
31
x
y
x
'
()
c)
31
35yx' ( )
d)
1
2
3
31
2
yx' ( )

VD2: Tính đạo hàm:
a)
2
2
3
21y x x
b)
2
2
31yx

c)
3
5yx()
d)
2
31yx()

Hoạt động 4: Củng cố
Nhấn mạnh:
– Tập xác định của hàm số luỹ
thừa phụ thuộc vào số mũ .
– Công thức tính đạo hàm của
hàm số luỹ thừa.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đóc tiếp bài "Hàm số luỹ thừa".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 48
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 24 Bài 2: HÀM SỐ LUỸ THỪA (tt)
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm và tính chất của hàm số luỹ thừa.
Biết công thức tính đạo hàm của hàm số luỹ thừa.
Biết dạng đồ thị của hàm số luỹ thừa.
Kĩ năng:
Biết khảo sát hàm số luỹ thừa.
Tính được đạo hàm của hàm số luỹ thừa.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu tập xác định và công thức tính đạo hàm của hàm số luỹ thừa?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khảo sát hàm số luỹ thừa
GV hướng dẫn HS khảo sát
và vẽ đồ thị hàm số
yx
theo từng bước của sơ đồ khảo
sát.
Các nhóm thảo luận và trả
lời.
III. KHẢO SÁT HÀM SỐ
LUỸ THỪA
yx
Tập khảo sát
Sự biến thiên
Giới hạn đặc biệt
Tiệm cận
Bảng biến thiên
Đồ thị
yx
( > 0)
(0; +∞)
1
0yx

, x > 0
0
0
x
x
xxlim ; lim



Không có
yx
( < 0)
(0; +∞)
1
0yx

, x > 0
0
0
x
x
xxlim ; lim



TCN: trục Ox
TCĐ: trục Oy
Chú ý: Khi khảo sát hàm số
luỹ thừa với số mũ cụ thể, ta
phải xét hàm số đó trên toàn
bộ tập xác định của nó.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 49
Hoạt động 2: Áp dụng khảo sát và vẽ đồ thị của hàm số luỹ thừa
H1. Thực hiện các bước khảo
sát và vẽ đồ thị ?
H2. Thực hiện các bước khảo
sát và vẽ đồ thị ?
Đ1. Các nhóm thảo luận và
trình bày.
D = (0; +∞)
7
4
3
4
yx'

< 0, x D
TCĐ: x = 0; TCN: y = 0
BBT:
Đồ thị
Đ2. Các nhóm thảo luận và
trình bày.
D = R \ {0}
< 0, x D
TCĐ: x = 0; TCN: y = 0
BBT:
x
y’
y
0
0
0
–
–




Đồ thị
Hàm số
3
yx
là hàm số lẻ
nên đồ thị nhận gốc toạ độ làm
tâm đối xứng.
VD1: Khảo sát sự biến thiên và
vẽ đồ thị hàm số
3
4
yx
.
VD2: Khảo sát sự biến thiên và
vẽ đồ thị hàm số
3
yx
O
y
x
3
yx
Hoạt động 3: Củng cố
Nhấn mạnh:
– Tính chất và đồ thị của hàm
số luỹ thừa.
Bảng tóm tắt
> 0
< 0
Đạo hàm
1
yx'
1
yx'
Chiều biến thiên
Luôn đồng biến
Luôn nghịch biến
Tiệm cận
Không có
TCN: trục Ox
TCĐ: trục Oy
Đồ thị
Luôn đi qua điểm (1; 1)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 50
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc trước bài "Logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 25 Bài 3: LOGARIT
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm và tính chất của logarit.
Biết các qui tắc tính logarit và công thức đổi cơ số.
Biết các khái niệm logarit thập phân, logarit tự nhiên.
Kĩ năng:
Biết vận dụng định nghĩa để tính một số biểu thức chứa logarit đơn giản.
Biết vận dụng các tính chất của logarit vào các bài toán biến đổi, tính toán các biểu thức
chứa logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Giải các phương trình:
2 8 3 81 2 3
x x x
;;
?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm logarit
Dẫn dắt từ KTBC, GV nêu
định nghĩa logarit.
H1. Nhận xét giá trị biểu thức
a
?
H2. Thực hiện phép tính và
giải thích ?
Đ1.
a
> 0, b > 0
Đ2.
a)
2
8log
= 3 vì
3
28
I. KHÁI NIỆM LOGARIT
1. Định nghĩa
Cho a, b > 0, a
1.
a
b a blog
Chú ý: không có logarit của số
âm và số 0.
VD1: Tính:
a)
2
8log
b)
1
3
9log
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 51
b)
1
3
9log
= –2 vì
2
1
9
3



c)
1
2
4log
= –2 vì
2
1
4
2



d)
3
1
27
log
= –3 vì
3
1
3
27
c)
1
2
4log
d)
3
1
27
log
Hoạt động 2: Tìm hiểu tính chất của logarit
GV hướng dẫn HD nhận xét
các tính chất.
H1. Thực hiện phép tính ?
a
0
= 1
10
a
log
a
1
= a
1
a
alog
Đ1.
a)
3
25
3
log
=
3
2
5
2
35
log
b)
1
2
8log
=
3
1
2
1
3
2
log




c)
2
1
7
4
log
=
2
2
1
2
7
1
2
7
log



d)
5
1
3
1
25
log



=
5
2
1
2
3
1
5
3
log



2. Tính chất
Cho a, b > 0, a
1.
1 0 1
a
aa
b
a
a
a b a
log
log ; log
; log ( )


VD2: Tính:
a)
3
25
3
log
b)
1
2
8log
c)
2
1
7
4
log
d)
5
1
3
1
25
log



Hoạt động 3: Tìm hiểu qui tắc tính logarit
H1. Cho
35
12
22bb,
. Tính
2 1 2 2 2 1 2
b b b blog log ;log
.
So sánh kết quả ?
GV nêu định lí.
H2. Thực hiện phép tính ?
Đ1.
2 1 2 2
2 1 2
3 5 8
8
bb
bb
log log
log
2 1 2 2 2 1 2
b b b blog log ; log
Đ2.
a) =
6
36 2log
b)
1 1 1
2 2 2
1 1 1
2
3 3 3
log log log
c) =
1
3
27 3log 
d) =
5
125 3log
II. QUI TẮC TÍNH
LOGARIT
1. Logarit của 1 tích
Cho a, b
1
, b
2
> 0, a
1.
1 2 1 2a a a
b b b blog ( ) log log
Chú ý: Định lí trên có thể mở
rộng cho tích của n số dương:
11a n a a n
b b b blog ( ... ) log ... log
VD3: Tính:
a)
66
94log log
b)
1 1 1
2 2 2
13
22
38
log log log
c)
1 1 1
3 3 3
9
53
5
log log log
d)
55
5
75
3
log log
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 52
Hoạt động 4: Củng cố
Nhấn mạnh:
– Định nghĩa logarit.
– Qui tắc tính logarit.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 26 Bài 3: LOGARIT (tt)
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm và tính chất của logarit.
Biết các qui tắc tính logarit và công thức đổi cơ số.
Biết các khái niệm logarit thập phân, logarit tự nhiên.
Kĩ năng:
Biết vận dụng định nghĩa để tính một số biểu thức chứa logarit đơn giản.
Biết vận dụng các tính chất của logarit vào các bài toán biến đổi, tính toán các biểu thức
chứa logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa logarit và tính:
21
4
1
log ; log 2
8
?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu các qui tắc tính logarit
Tương tự như logarit của 1
tích, GV cho HS nhận xét.
II.QUI TẮC TÍNH LOGARIT
2. Logarit của 1 thương
Cho a, b
1
, b
2
> 0, a
1.
a a a
b
bb
b
1
12
2
log log log
Đặc biệt:
aa
b
b
1
log log
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 53
H1. Thực hiện phép tính ?
GV hướng dẫn HS chứng
minh.
H2. Thực hiện phép tính ?
Đ1.
a) =
2
log 8 3
b) =
3
1
log 2
9

c) =
1
5
log 25 2
d)
7
1
log 1
7

Đặt
a
b b alog
Đ2.
a) =
2
7
2
2
log 2
7
b) =
1
2
5
1
log 5
2

VD1: Tính:
a)
22
log 120 log 15
b)
33
log 16 log 144
c)
11
55
log 16 log 400
d)
77
log 30 log 210
3. Logarit của 1 luỹ thừa
Cho a, b > 0; a
1;
tuỳ ý:
aa
bblog log
Đặc biệt:
n
aa
bb
n
1
log log
VD2: Tính:
a)
1
7
2
log 4
b)
55
1
log 3 log 15
5
Hoạt động 2: Tìm hiểu công thức đổi cơ số
H1. Cho a = 4, b = 64, c = 2.
Tính
a c c
bablog ,log ,log
. Từ đó
rút ra nhận xét?
GV hướng dẫn HS chứng
minh.
H2. Thực hiện phép tính ?
Đ1.
c a c
a b blog .log log
a
b
cc
ba
log
log log
=
ac
balog .log
Đ2.
a)
82
1
log 9 log 9
3
b)
4 2 2
1
log 15 log 15 log 15
2

c)
1
3
13
27
log 2 log 2
III. ĐỔI CƠ SỐ
Cho a, b, c > 0; a, c
1.
c
a
c
b
b
a
log
log
log
Đặc biệt:
a
b
b
a
1
log
log
(b
1)
a
a
bb
1
log log
(
0)
VD3: Tính:
a)
3 8 6
log 6.log 9.log 2
b)
4
log 15
2
c)
1
27
log 2
3
Hoạt động 3: Tìm hiểu khái niệm logarit thập phân, logarit tự nhiên
GV giới thiệu khái niệm
logarit thập phân và logarit tự
nhiên.
GV hướng dẫn HS sử dụng
MTBT để tính.
HS theo dõi và thực hành
trên MTBT.
2
log3
log 3 1,5850
log2

IV. LOGARIT THẬP PHÂN,
LOGARIT TỰ NHIÊN
1. Logarit thập phân
b b b
10
lg log log
2. Logarit tự nhiên
e
bbln log
Chú ý: Muốn tính
a
blog
với a
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 54
3
ln0,8
log 0,8 0,2031
ln3
10 và a
e, bằng MTBT, ta có thể
sử dụng công thức đổi cơ số.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Qui tắc tính logarit.
– Công thức đổi cơ số.
4. BÀI TẬP VỀ NHÀ:
Bài 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 27 Bài 3: BÀI TẬP LOGARIT
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm và tính chất của logarit.
Các qui tắc tính logarit và công thức đổi cơ số.
Các khái niệm logarit thập phân, logarit tự nhiên.
Kĩ năng:
Biết vận dụng định nghĩa để tính một số biểu thức chứa logarit đơn giản.
Biết vận dụng các tính chất của logarit vào các bài toán biến đổi, tính toán các biểu thức
chứa logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: ()
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập các qui tắc tính logarit
H1. Nêu qui tắc cần sử dụng ?
Đ1.
A = –1
B =
4
3
C = 9 + 16 = 25
D = 16.25 = 400
1. Thực hiện các phép tính:
A =
21
4
42log .log
B =
5 27
1
9
25
log .log
C =
3
2
2
3
49
log
log
D =
3 81
2 2 4 5
9
log log
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 55
H2. Nêu qui tắc cần sử dụng ?
H3. Nêu cách so sánh ?
Đ2.
A =
4 3 2
5 6 7
B =
22
68
C = lg1 = 0
D =
Đ3.
a)
73
4 1 5log log
b)
0 3 5
2 0 3
,
log log
c)
52
30 3 10log log
2. Thực hiện các phép tính:
A =
3 9 9
5 36 4 7
81 27 3
log log log

B =
57
68
25 49
log log
C =
00
1 89lg(tan ) ... lg(tan )
D =
8 4 2
16log log (log )


3. So sánh các cặp số:
a)
37
54log , log
b)
0 3 5
23
,
log , log
c)
25
10 30log , log
Hoạt động 2: Luyện tập vận dụng công thức đổi cơ số
GV hướng dẫn HS cách tính.
H1. Phân tích 1350 thành tích
các luỹ thừa của 3, 5, 30 ?
H2. Tính
3
5log
theo c ?
H3. Tính
14
2log
?
Đ1. 1350 =
2
3 5 30..
30
1350log
= 2a + b + 1
Đ2.
3 3 3
15
5 15 1
3
log log log
=
1
1
c
Đ3.
14
2log
=
14 14
14
17
7
log log
= 1 – a
4. Tính giá trị của biểu thức
logarit theo các biểu thức đã
cho:
a) Cho
30 30
35ablog , log
.
Tính
30
1350log
theo a, b.
b) Cho
15
3c log
.
Tính
25
15log
theo c.
c) Cho
14 14
75ablog , log
.
Tính
35
28log
theo a, b.
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách vận dụng các qui tắc,
công thức đổi cơ số để tính các
biểu thức logarit.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc trước bài "Hàm số mũ. Hàm số logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 56
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 28 Bài 4: HÀM SỐ MŨ – HÀM SỐ LOGARIT
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm và tính chất của hàm số mũ, hàm số logarit.
Biết công thức tính đạo hàm của hàm số mũ, hàm số logarit.
Biết dạng đồ thị của hàm số mũ, hàm số logarit.
Kĩ năng:
Biết vận dụng tính chất của các hàm số mũ, hàm số logarit vào việc so sánh hai số, hai biểu thức
chứa mũ và logarit.
Biết vẽ đồ thị các hàm số mũ, hàm số logarit.
Tính được đạo hàm của hàm số mũ, hàm số logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các qui tắc tính luỹ thừa với số mũ thực ?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm hàm số mũ
GV nêu bài toán "lãi kép".
Hướng dẫn HS cách tính. Từ đó
giới thiệu khái niệm hàm số mũ.
H1. Tính số tiền lãi và tiền lĩnh
sau năm thứ nhất, thứ hai, …?
H2. Cho HS xét?
H3. Nêu sự khác nhau giữa hàm
số luỹ thừa và hàm số mũ?
Đ1. Các nhóm tính và điền vào
bảng.
1
2
3
Lãi
0,7
0,0749
Lĩnh
1,7
1,1449
P(1+r)
P(1+r)
2
Đ2.
Hàm số mũ: a), b), d)
Đ3. Các nhóm thảo luận và trình
bày.
Bài toán lãi kép:
Vốn: P = 1 triệu
Lãi suất: r = 7% / năm
Qui cách lãi kép: tiền lãi sau 1
năm được nhập vào vốn.
Tính: số tiền lĩnh được sau n năm
?
I. HÀM SỐ MŨ
1. Định nghĩa
Cho a > 0, a
1. Hàm số
x
ya
đgl hàm số mũ cơ số a.
VD1: Trong các hàm số sau, hàm
số nào là hàm số mũ:
a)
x
y 3
b)
x
y
3
5
c)
yx
4
d)
x
y 4
Chú ý:
Cơ số
Số mũ
HS mũ
K.đổi
B.thiên
HS LT
B.thiên
K.đổi
Hoạt động 2: Tìm hiểu công thức tính đạo hàm của hàm số mũ
GV nêu các công thức.
2. Đạo hàm của hàm số mũ
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 57
H1. Thực hiện phép tính ?
Đ1.
a)
x
y
1
2 .ln2
b)
x
y
24
2.5 .ln5
c)
xx
yx
2
(2 1).8 .ln8

d)
x
ye
21
2.
t
t
e
t
0
1
lim 1
xx
ee
;
uu
e e u.
xx
a a aln
uu
a a a uln .
VD2: Tính đạo hàm:
a)
x
y
1
2
b)
x
y
24
5
c)
xx
y
2
8
d)
x
ye
21
Hoạt động 3: Khảo sát hàm số mũ
GV hướng dẫn HS khảo sát 2
hàm số:
x
x
yy
1
2,
2

. Từ đó
tổng kết sơ đồ khảo sát hàm số
mũ.
HS theo dõi và thực hiện
3. Khảo sát hàm số mũ
x
ya
(a > 0, a 1)
Tập xác định
Đạo hàm
Giới hạn:
Tiệm cận
Bảng biến thiên
Đồ thị
x
ya
(a > 1)
D = R
x
y a a.ln
> 0, x
xx
xx
aalim 0, lim
 

TCN: trục Ox
x
ya
(0 < a < 1)
D = R
x
y a a.ln
< 0, x
xx
xx
aalim , lim 0
 
TCN: trục Ox
Hoạt động 4: Củng cố
Nhấn mạnh:
– Công thức tính đạo hàm của
hàm số mũ.
– Các dạng đồ thị của hàm số mũ.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Hàm số mũ. Hàm số logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 58
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 29 Bài 4: HÀM SỐ MŨ – HÀM SỐ LOGARIT (tt)
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm và tính chất của hàm số mũ, hàm số logarit.
Biết công thức tính đạo hàm của hàm số mũ, hàm số logarit.
Biết dạng đồ thị của hàm số mũ, hàm số logarit.
Kĩ năng:
Biết vận dụng tính chất của các hàm số mũ, hàm số logarit vào việc so sánh hai số, hai biểu thức
chứa mũ và logarit.
Biết vẽ đồ thị các hàm số mũ, hàm số logarit.
Tính được đạo hàm của hàm số mũ, hàm số logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Tính đạo hàm của các hàm số:
,
inx
y
s
3
?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm hàm số logarit
GV nêu định nghĩa hàm số
logarit.
H1. Cho VD hàm số logarit ?
H2. Nêu điều kiện xác định ?
Đ1. Các nhóm cho VD.
Đ2.
a) 2x + 1 > 0 D =
b)
xx
2
3 2 0
D = (–∞; 1) (2; +∞)
c)
D = (–1; 1)
d)
xx
2
10
D = R
II. HÀM SỐ LOGARIT
1. Định nghĩa
Cho a > 0, a
1. Hàm số
đgl hàm số logarit cơ
số a.
VD1:
y x y x
31
4
log , log
y x y x y x
5
log , ln , lg
VD2: Tìm tập xác định của các
hàm số:
a)
yx
2
log (2 1)
b)
y x x
2
3
log ( 3 2)
c)
x
y
x
1
ln
1

d)
y x x
2
lg( 1)
Hoạt động 2: Tìm hiểu công thức tính đạo hàm của hàm số logarit
GV nêu công thức.
2. Đạo hàm của hàm số logarit
a
x
xa
1
log
ln
(x > 0)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 59
H1. Thực hiện phép tính ?
Đ1.
a)
y
x
2
(2 1)ln2
b)
x
y
xx
2
23
( 3 2)ln3

c)
y
x
2
2
1

d)
x
y
xx
2
21
( 1)ln10

a
u
u
ua
log
ln
Đặc biệt:
x
x
1
ln
u
u
u
ln
VD3: Tính đạo hàm:
a)
yx
2
log (2 1)
b)
y x x
2
3
log ( 3 2)
c)
x
y
x
1
ln
1

d)
y x x
2
lg( 1)
Hoạt động 3: Khảo sát hàm số logarit
GV hướng dẫn HS khảo sát 2
hàm số:
y x y x
21
2
log , log
.
Từ đó tổng hợp sơ đồ khảo sát.
3. Khảo sát hàm số logarit
(a > 0, a 1)
Tập xác định
Sự biến thiên
Giới hạn
Tiệm cận
Bảng biến thiên
Đồ thị
(a > 1)
D = (0; +∞)
> 0, x > 0
a
x
x
0
lim log
a
x
xlim log


TCĐ: trục Oy
(0 < a < 1)
D = (0; +∞)
< 0, x > 0
a
x
x
0
lim log
a
x
xlim log


TCĐ: trục Oy
Hoạt động 4: Củng cố
Nhấn mạnh:
– Công thức tính đạo hàm của
hàm số logarit.
– Các dạng đồ thị của hàm số
logarit.
4. BÀI TẬP VỀ NHÀ:
Bài 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 60
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 30 + 31 Bài 4: BÀI TẬP HÀM SỐ MŨ – HÀM SỐ LOGARIT
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm và tính chất của hàm số mũ, hàm số logarit.
Công thức tính đạo hàm của hàm số mũ, hàm số logarit.
Các dạng đồ thị của hàm số mũ, hàm số logarit.
Kĩ năng:
Biết vận dụng tính chất của các hàm số mũ, hàm số logarit vào việc so sánh hai số, hai biểu
thức chứa mũ và logarit.
Biết vẽ đồ thị các hàm số mũ, hàm số logarit.
Tính được đạo hàm của hàm số mũ, hàm số logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hàm số mũ và hàm số logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tính đạo hàm của hàm số mũ, hàm số logarit
H1. Thực hiện phép tính ?
Đ1.
a)
x
y e x cos x2 ( 1) 6 2
b)
x
y x inx cosx10 2 (s ln2. )
c)
x
x
y
1 ( 1)ln3
3

d)
y x cosx
x
1
64
e)
x
y
xx
2
21
( 1)ln10

f)
x
y
x
2
1 ln
ln3
1. Tính đạo hàm của các hàm
số sau:
a)
x
y xe x2 3sin2
b)
x
y x x
2
5 2 cos
c)
x
x
y
1
3
d)
y x x x
2
3 ln 4sin
e)
y x x
2
log( 1)
f)
x
y
x
3
log
Hoạt động 2: Luyện tập khảo sát hàm số mũ, hàm số logarit
H1. Nêu điều kiện xác định ?
Đ1.
a) 5 – 2x > 0 D =
5
;
2




b)
xx
2
20
D = (–∞; 0) (2; +∞)
c)
xx
2
4 3 0
D = (–∞; 1) (3; +∞)
2. Tìm tập xác định của hàm
số:
a)
yx
2
log (5 2 )
b)
y x x
2
3
log ( 2 )
c)
y x x
2
1
5
log ( 4 3)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 61
H2. Vẽ đồ thị trên cùng hệ trục
va nhận xét?
Từ đó nêu thành nhận xét
tổng quát:
+ Đồ thị các hàm số
x
ya
,
x
ya
đối xứng nhau qua trục
tung.
+ Đồ thị các hàm số
,
a
yx
1
log
đối xứng nhau qua
trục hoành.
+ Đồ thị các hàm số
x
ya
,
đối xứng nhau qua
dường thẳng y = x.
d)
x
x
32
0
1
D =
2
;1
3



Đ2. Các nhóm thảo luận và
trình bày.
-4 -3 -2 -1 1 2 3 4
-4
-3
-2
-1
1
2
3
4
x
y
y = 4
x
x
y
1
4



yx
4
log
yx
1
4
log
+ Đồ thị các hàm số
x
y 4
,
x
y
1
4



đối xứng nhau qua
trục tung.
+ Đồ thị các hàm số
,
yx
1
4
log
đối xứng nhau qua
trục hoành.
+ Đồ thị các hàm số
x
y 4
,
đối xứng nhau qua
dường thẳng y = x.
d)
x
y
x
0,4
32
log
1
3. Vẽ đồ thị các hàm số sau
(trên cùng một hệ trục):
x
y 4
,
x
y
1
4



,
yx
1
4
log
Nhận xét mối quan hệ giữa đồ
thị của các hàm số trên.
Hoạt động 3: Củng cố
Nhấn mạnh:
– Các công thức tính đạo hàm.
– Dạng đồ thị của hàm số mũ
và logarit.
Cho HS hệ thống các công
thức tính đạo hàm của hàm số
mũ, luỹ thừa và logarit (điền
vào bảng).
Bảng đạo hàm của các hàm số luỹ thừa, mũ, logarit
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc trước bài " Phương trình mũ và phương trình logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 62
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 32 Bài 5: PHƯƠNG TRÌNH MŨ – PHƯƠNG TRÌNH LOGARIT
I. MỤC TIÊU:
Kiến thức:
Biết được cách giải một số dạng phương trình mũ và phương trình logarit.
Kĩ năng:
Giải được một số phương trình mũ và phương trình logarit đơn giản bằng các phương pháp
đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hàm số mũ và hàm số logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ:
H. Nêu một số tính chất của hàm số mũ?
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm phương trình mũ
GV nêu bài toán, hướng dẫn
HS giải. Từ đó nêu khái niệm
phương trình mũ.
H1. Tìm công thức nghiệm ?
Hướng dẫn HS nhận xét số
giao điểm của 2 đồ thị.
H2. Giải phương trình ?
n
n
PP(1 0,084)
n
PP2
n
(1,084) 2
n =
1,084
log 2 8,59
n = 9.
Đ1.
x
ab
Đ2.
a) 2x – 1 = 0
x
1
2
b) –3x + 1 = 2
x
1
3

I. PHƯƠNG TRÌNH MŨ
Bài toán: Một người gửi tiết
kiệm với lãi suất r = 8,4%/năm
và lãi hàng năm được nhập vào
vốn (lãi kép). Hỏi sau bao
nhiêu năm người đó thu được
gấp đôi số tiền ban đầu?
1. Phương trình mũ cơ bản
x
ab
(a > 0, a
1)
b > 0:
x
ab
b
0: ph.trình vô nghiệm.
Minh hoạ bằng đồ thị: Số
nghiệm của phương trình bằng
số giao điểm của 2 đồ thị của 2
hàm số
x
ya
và y = b.
VD1: Giải các phương trình:
a)
x21
41
b)
c)
xx
2
31
1
2
2

d)
xx
2
3
1
5
25
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 63
c)
xx
2
3 1 1
x
x
1
2
d)
xx
2
32
x
x
1
2
Hoạt động 2: Tìm hiểu cách giải một số phương trình mũ đơn giản
H1. So sánh x, y nếu
xy
aa
?
H2. Đưa về cùng cơ số ?
H3. Nêu điều kiện của t ?
H4. Đặt ẩn phụ thích hợp ?
H5. Lấy logarit hai vế theo cơ
số nào ?
Đ1. x = y
Đ2.
a)
xx5 7 1
33
22
x = 1
b)
xx2(3 1) 8 2
33

x = 0
c)
xx
2
( 2) 4 3
22
x
x
1
2
d)
x
6 36
x = 2
Đ3. t > 0 vì a
x
> 0, x
Đ4.
a)
x
t 3
b)
x
t 2
c)
x
t 4
Đ5.
a) chọn cơ số 3
b) chọn cơ số 2.
2. Cách giải một số phương
trình mũ đơn giản
a) Đưa về cùng cơ số
f x g x)
a a f x g x
( ) (
( ) ( )
VD3: Giải các phương trình:
a)
x
x
1
57
2
(1,5)
3



b)
xx3 1 8 2
93

c)
x
x
2
2
43
1
2
2



d)
xx1
3 .2 72
b) Đặt ẩn phụ
f x f x
a b c
2 ( ) ( )
0
fx
t a t
at bt c
()
2
,0
0

VD4: Giải các phương trinh:
a)
xx
9 4.3 45 0
b)
xx1
4 2 8 0
c)
xx
16 17.4 16 0
c) Logarit hoá
f x g x
ab
( ) ( )
Lấy logarit hai vế với cơ số bất
kì.
VD5: Giải các phương trình:
a)
xx
2
3 .2 1
b)
x x x x
2 2 2 2
1 2 1
2 2 3 3
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách giải các dạng phương
trình mũ.
– Chú ý điều kiện t = a
x
> 0.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Hàm số mũ. Hàm số logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 64
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 33 Bài 5: PHƯƠNG TRÌNH MŨ – PHƯƠNG TRÌNH LOGARIT (tt)
I. MỤC TIÊU:
Kiến thức:
Biết được cách giải một số dạng phương trình mũ và phương trình logarit.
Kĩ năng:
Giải được một số phương trình mũ và phương trình logarit đơn giản bằng các phương pháp
đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hàm số mũ và hàm số logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số tính chất của hàm số logarit?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm phương trình logarit
Gv nêu định nghĩa phương
trình logarit.
H1. Cho VD phương trình
logarit?
Hướng dẫn HS nhận xét số
giao điểm của 2 đồ thị.
H2. Giải phương trình?
Đ1.
x
1
2
log 4
xx
2
44
log 2log 1 0
Đ2.
a)
x
4
3
b) x = –1; x = 2
b) x = –1; x = 9
II. PHƯƠNG TRÌNH
LOGARIT
Phương trình logarit là
phương trình có chứa ẩn số
trong biểu thức dưới dấu
logarit.
1. Ph.trình logarit cơ bản
b
a
x b x alog
Minh hoạ bằng đồ thị:
Đường thẳng y = b luôn cắt đồ
thị hàm số
tại một
điểm với
b
R.
Phương trình
(a >
0, a
1) luôn có duy nhất một
nghiệm
b
xa
.
VD1: Giải các phương trình:
a)
x
3
1
log
4
b)
xx
2
log ( 1) 1
c)
xx
2
3
log ( 8 ) 2
Hoạt động 2: Tìm hiểu cách giải một số phương trình logarit đơn giản
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 65
Lưu ý điều kiện của biểu thức
dưới dấu logarit.
H1. Đưa về cơ số thích hợp ?
H2. Đưa về cùng cơ số và đặt
ẩn phụ thích hợp ?
GV hướng dẫn HS tìm cách
giải.
H3. Giải phương trình?
Đ1.
a) Đưa về cơ số 3: x = 81
b) Đưa về cơ số 2: x = 32
c) Đưa về cơ số 2: x =
12
2
d) Đưa về cơ số 3: x = 27
Đ2.
a) Đặt
tx
2
log
x
x
1
2
4
b) Đặt
txlg
, t 5, t –1
x
x
100
1000
c) Đặt
tx
5
log
x = 5
Dựa vào định nghĩa.
Đ3.
a)
xx2
5 2 2

x
x
0
2
b)
xx2
3 8 3

x = 2
c)
x
26 3 25
x = 0
2. Cách giải một số phương
trình logarit đơn giản
a) Đưa về cùng cơ số
aa
f x g x
f x g x
f x hoaëc g x
log ( ) log ( )
( ) ( )
( ) 0 ( ( ) 0)

VD2: Giải các phương trình:
a)
xx
39
log log 6
b)
x x x
2 4 8
log log log 11
c)
x x x
4 1 8
16
log log log 7
d)
x x x
31
3
3
log log log 6
b) Đặt ẩn phụ
aa
A f x B f x C
2
log ( ) log ( ) 0
a
t f x
At Bt C
2
log ( )
0
VD3: Giải các phương trình:
a)
xx
2
12
2
log log 2
b)
xx
12
1
5 lg 1 lg


c)
x
x
5
1
log log 2
5

c) Mũ hoá
a
f x g xlog ( ) ( )
gx
f x a
()
()
VD4: Giải các phương trình:
a)
x
x
2
log (5 2 ) 2
b)
x
x
3
log (3 8) 2
c)
x
5
log (26 3 ) 2
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách giải các dạng phương
trình logarit.
– Chú ý điều kiện của các phép
biến đổi logarit.
4. BÀI TẬP VỀ NHÀ:
Bài 3, 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 66
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 34 Bài 5: BÀI TẬP PHƯƠNG TRÌNH MŨ –
PHƯƠNG TRÌNH LOGARIT
I. MỤC TIÊU:
Kiến thức: Củng cố:
Cách giải một số dạng phương trình mũ và phương trình logarit.
Kĩ năng:
Giải được một số phương trình mũ và phương trình logarit đơn giản bằng các phương pháp
đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số.
Nhận dạng được phương trình.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về phương trình mũ và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập phương pháp đưa về cùng cơ số
H1. Nêu cách giải ?
Chú ý điều kiện của các phép
biến đổi logarit.
Đ1. Đưa về cùng cơ số.
a)
x
3
2
b) x = –2
c) x = 0; x = 3
d) x = 9
e) vô nghiệm
f) x = 7
g) x = 6
h) x = 5
1. Giải các phương trình sau:
a)
x32
(0,3) 1
b)
x
1
25
5



c)
xx
2
32
24

d)
xx7 1 2
(0,5) .(0,5) 2

e)
xx
33
log (5 3) log (7 5)
f)
xxlg( 1) lg(2 11) lg2
g)
xx
22
log ( 5) log ( 2) 3
h)
x x x
2
lg( 6 7) lg( 3)
Hoạt động 2: Luyện tập phương pháp đặt ẩn phụ
H1. Nêu cách giải ?
Chú ý điều kiện của ẩn phụ.
Đ1. Đặt ẩn phụ.
a) Đặt
x
t 8
x = 1
b) Đặt
x
t
2
3



x = 0
c) Đặt
tx
2
log
x
x
1
2
d) Đặt
txlg
x
x
10
1000
2. Giải các phương trình sau:
a)
xx
64 8 56 0
b)
x x x
3.4 2.6 9
c)
x
x
2
24
1
log 2log 0
d)
xx
13
1
5 lg 3 lg


Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 67
Hoạt động 3: Luyện tập phương pháp logarit hoá – mũ hoá
H1. Nêu cách giải ?
Chú ý điều kiện của các phép
biến đổi.
Đ1. Logarit hoá hoặc mũ hoá.
a) Lấy logarit cơ số 3 hai vế
x = 0;
x
3
log 5
b) Lấy logarit cơ số 2 hai vế
x = 2;
x
2
2
1 log 5
2log 5

c) Lấy logarit cơ số 2 hai vế
x
32
3
log (log 3)
1 log 2
d) Lấy logarit cơ số 2 hai vế
x = 1;
x
2
2
2(log 3 1)
log 3

e)
xx1
6 7 7


x = 0
f)
xx1 2 1
4.3 1 3


x
x
0
1
g)
xx21
3.2 1 2

x
x
0
1

h)
xx3
9 2 2

x
x
0
3
3. Giải các phương trình sau:
a)
2
5 .3 1
xx
b)
21
1
5 .2 50
x
x
x
c)
32
23
xx
d)
3
2
3 .2 6
x
x
x
e)
7
log (6 7 ) 1
x
x
f)
1
3
log (4.3 1) 2 1
x
x
g)
2
log (3.2 1) 2 1 0
x
x
h)
5
log (3 )
2
log (9 2 ) 5
x
x

Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách giải các dạng phương
trình.
– Điều kiện của các phép biến
đổi phương trình.
Giởi thiệu thêm phương pháp
hàm số cho HS khá, giỏi.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc trước bài "Bất phương trình mũ – Bất phương trình logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 68
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 35 + 36 Bài 6: BẤT PHƯƠNG TRÌNH MŨ –
BẤT PHƯƠNG TRÌNH LOGARIT
I. MỤC TIÊU:
Kiến thức:
Biết được cách giải một số dạng bất phương trình mũ và bất phương trình logarit.
Kĩ năng:
Giải được một số bất phương trình mũ và bất phương trình logarit đơn giản bằng các
phương pháp đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về phương trình mũ và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số cách giải phương trình mũ và logarit?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách giải bất phương trình mũ
GV nêu dạng bất phương
trình mũ và hướng dẫn HS biện
luận.
H1. Khi nào bất phương trình
có nghiệm, vô nghiệm?
H2. Nêu cách giải?
H3. Nêu cách biến đổi?
Các nhóm thảo luận và trình
bày.
Đ2. Đưa về cơ số 3.
xx
2
2
33
xx
2
2
–1 < x < 2
Đ3. Chia 2 vế cho
x
10
.
Đặt
x
t
2
5



, t > 0
I. BẤT PH.TRÌNH MŨ
1. Bất ph.trình mũ cơ bản
x
ab
với a > 0, a
1.
xxx
hoaëc a b a b a b( , , )
Minh hoạ bằng đồ thị:
x
ab
Tập nghiệm
a > 1
0 < a < 1
b
0
R
R
b > 0
a
blog ;
a
b;log
2. Bất ph.trình mũ đơn giản
VD1: Giải bất phương trình:
VD2: Giải bất phương trình:
x x x2
4 2.5 10
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 69
S =
2
5
log 2;




Hoạt động 2: Tìm hiểu cách giải bất phương trình logarit
GV nêu dạng bất phương
trình mũ và hướng dẫn HS biện
luận.
H1. Khi nào bất phương trình
có nghiệm, vô nghiệm?
H2. Biến đổi bất phương trình?
Chú ý điều kiện của các phép
biến đổi.
H3. Nêu cách giải?
Đ2.
x x x
xx
2
2
5 10 6 8
6 8 0
–2 < x < 1
Đ3. Đặt
tx
2
log
tt
2
6 8 0
4 x 16
II. BPT LOGARIT
1. BPT logarit cơ bản
a
xblog
với a > 0, a 1
aaa
hoaëc x b x b x blog ,log ,log
Minh hoạ bằng đồ thị:
a
xblog
Tập nghiệm
a > 1
0 < a < 1
Nghiệm
b
xa
b
xa0 
2. Bất ph.trình mũ đơn giản
VD1: Giải bất phương trình:
x+ x x
2
11
22
log (5 10) log ( 6 8)
VD2:
xx
2
22
log 6log 8 0
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách giải bất phương trình
mũ và logarit.
– Cách vận dụng tính đơn điệu
của hàm số mũ và logarit.
– Chú ý điều kiện của các phép
biến đổi.
Câu hỏi: Lập bảng biện luận
đối với các bất phương trình
tương tự:
xxx
a b a b a b,,
aaa
x b x b x blog ,log ,log
x
ab
Tập nghiệm
a > 1
0 < a < 1
b
0
b > 0
a
b;log
a
blog ;
a
xblog
Tập nghiệm
a > 1
0 < a < 1
Nghiệm
b
xa0 
b
xa
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Chuẩn bị máy tính bỏ túi.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 70
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 37 + 38
Bài 6: BÀI TẬP BẤT PHƯƠNG TRÌNH MŨ & LOGARIT
I. MỤC TIÊU:
Kiến thức:
- Nắm vững phương pháp giải bpt mũ,bpt logarit và vận dụng để giải đượcác bpt mũ ,bpt logarit
Kĩ năng:
- Sử dụng thành thạo tính đơn điệu hàm số mũ ,logaritvà nhận biết điều kiện bài toán
Thái độ:
- Vận dụng được tính logic, biết đưa bài toán lạ về quen, học tập nghiêm túc, hoạt động tich cực
II. CHUẨN BỊ:
Giáo viên: Phiếu học tập, câu hỏi trắc nghiệm
Học sinh : Bài tập giải ở nhà, nắm vững phương pháp giải
III. PHƯƠNG PHÁP : gợi mỡ ,vấn đáp-Hoạt động nhóm
IV. HOẠT ĐỘNG DẠY HỌC:
1. Ổn dịnh tỏ chức:
2. Kiểm tra bài cũ: 3’ Giải bpt sau:a./ Log
2
(x+4) < 3 b/ 5
2x-1
> 125
3. Bài mới
HĐ1: Giải bpt mũ
Hoạt động giáo viên
Hoạt động học sinh
Ghi bảng
HĐTP1-Yêu cầu học sinh nêu
phương pháp giải bpt a
x
> b
a
x
< b
- GVsử dụng bảng phụ ghi tập
nghiêm bpt
GV phát phiếu học tập1 và 2
- Giao nhiệm vụ các nhóm giải
-Gọi đại diện nhóm trình bày
trên bảng,các nhóm còn lại nhận
xét
GV nhận xét và hoàn thiện bài
giải
HĐTP2:GV nêu bài tập
Hướng dẫn học sinh nêu cách
giải
-Gọi HS giải trên bảng
-Gọi HS nhận xét bài giải
- GV hoàn thiện bài giải
- Trả lời
_ HS nhận xét
-Giải theo nhóm
-Đại diện nhóm trình
bày lời giải trên bảng
-Nhận xét
-Nêu các cách giải
-HSgiải trên bảng
-nhận xét
Bài 1: Giải bpt sau:
1/
93
3
2
xx
(1)
2/
2833
12
xx
(2)
Giải:
(1)
023
2
xx
21 x
(2)
283.
3
1
3.9
xx
133 x
x
Bài tập2 :giải bpt
4
x
+3.6
x
– 4.9
x
< 0(3)
Giải:
(3)
04
3
2
3
3
2
2
xx
Đặt t =
0,
3
2
t
x
bpt trở thành t
2
+3t – 4 <
0
Do t > 0 ta đươc 0< t<1
0. x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 71
HĐ2: Giải bpt logarit
-Gọi HS nêu cách giải bpt
Log
a
x >b ,Log
a
x <b và ghi tập
nghiệm trên bảng
GV : phát phiếu học tập 3
Gọi đại diện nhóm trả lời
Gọi HS nhận xét
GV hoàn thiện bài giải
- Gọi học sinh đưa các cơ số trong
phương trình a) về dạng phân số
và tìm mối liên hệ giữa các phân
số đó.
- Yêu cầu học sinh vận dụng giải
bất phương trình trên.
- Cho hs nêu phương pháp giải bpt
lôgarit:
log ( ) log ( ) (*)
(1 0)
aa
f x g x
a

- Hướng dẫn cho hoc sinh vận
dụng phương pháp trên để giải
bpt.
-Giáo viên nhận xét và hoàn thiện
lời giải của hoc sinh.
-Nêu cách giải
Nhóm giải trên phiếu
học tập
Đại diện nhóm trình bày
trên bảng
Nhóm còn lại nhận xét
- Trả lời theo yêu cầu
của giáo viên.
25
0,4 ; 2,5
52

Nếu đặt
2
5
t
thì
51
2 t
- Thảo luận và lên bảng
trình bày.
- Trả lời theo yêu cầu
của gv.
Đk:
( ) 0
( ) 0
fx
gx
+ Nếu
1a
thì
(*)
( ) ( )f x g x
+ Nếu
01a
thì
(*)
( ) ( )f x g x
- Thảo luận và lên bảng
trình bày.
Bài 3: giải bất phương trình sau:
a) a)
1
(0,4) (2,5) 1,5
xx

2
2 5 5 3
.
5 2 2 2
22
2 3. 5 0
55
2
1
5
25
52
25
52
1
xx
xx
x
x
x
x










b)
2
13
3
log ( 6 5) 2log (2 ) 0x x x
(*)
Đk:
2
6 5 0
1
20
xx
x
x


22
33
22
log (2 ) log ( 6 5)
(2 ) 6 5
1
21
2
x x x
x x x
xx
Tập nghiệm
1
;1
2
T


HĐ3 củng cố : 5’
Bài 1: tập nghiệm bất phương trình :
2
2x 3x
35
53



A/
1 1 1
;1 / ;1 / ;1 / ;1
2 2 2
CD

B
Bài 2: Tập nghiệm bất phương trình:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 72
2
1
2
log 5x+7 0
/ 3; / 2;3 / ;2 / ;3
x
A B C D

  
Dặn dò : Về nhà làm bài tập 8/90 SGK
Phụ lục : Phiếu học tập 3
0,2 5 0,2
log log 5 log 3xx
4. BÀI TẬP VỀ NHÀ:
- Bài 2 a,b,d
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 39 + 40 + 41 Bài dạy: ÔN TẬP CHƯƠNG II
I. MỤC TIÊU:
Kiến thức: Củng cố:
Luỹ thừa với số mũ thực.
Khảo sát hàm số luỹ thừa.
Logarit và các qui tắc tính logarit.
Khảo sát hàm số mũ, hàm số logarit.
Phương trình, bất phương trình mũ và logarit.
Kĩ năng:
Khảo sát các hàm số luỹ thừa, hàm số mũ, hàm số logarit.
Tính logarit và biến đổi các biểu thức chứa logarit.
Giải các phương trình, bất phương trình mũ và logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức chương II
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Khảo sát các tính chất của hàm số luỹ thừa, hàm số mũ và hàm số logarit
H1. Phân loại hàm số và nêu
điều kiện xác định của hàm số
?
Đ1.
a)
x
3 3 0
D = R \ {1}
b)
x
x
1
0
23
1. Tìm tập xác định của hàm số
a)
x
y
1
33
b)
x
y
x
1
log
23
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 73
D =
3
( ;1) ;
2

 


c)
xx
2
12 0
D =
( ; 3) (4; ) 
d)
xx
25 5 0
D = [0; +∞)
c)
y x x
2
log 12
d)
xx
y 25 5
Hoạt động 2: Củng cố phép tính logarit
H1. Nêu qui tắc cần sử dụng ?
H2. Tính
5
log 7
?
H3. Phân tích
3
5
49
log
8
?
Đ1.
a)
a
xlog
= 8
b)
a
xlog
= 11
Đ2.
a
5 25
log 7 2log 7 2
Đ3. M =
55
3 log 49 log 8
=
5
2
3
3 2log 7
log 5



=
a
b
9
12
2. Cho
aa
bclog 3, log 2
.
Tính
a
xlog
với:
a) x =
a b c
32
b) x =
ab
c
4
3
3
3. Cho
ab
25 2
log 7 , log 5
.
Tính M =
3
5
49
log
8
theo a, b.
Hoạt động 3: Giải phương trình, bất phương trình mũ, logarit
H1. Nếu cách giải ?
Chú ý: x > 1
x
7
log 0
.
- Gọi học sinh nhắc lại phương
pháp giải phương trình mũ.
- Yêu cầu học sinh vận dụng
làm bài tập trên.
- Gọi học sinh nhắc lại phương
pháp giải phương trình lôgarit.
- Tìm điều kiện để các lôgarit
Đ1.
a) Đưa về cơ số 3 và 5.
x 3
35
53
x = –3
b) Chia 2 vế cho
x
16
.
Đặt
x
t
3
4



, t > 0.
x = 1
c)
x
7
log ( 1) 0
x = 8
d)
x
3
log 3
x = 27
- Trả lời theo yêu cầu của giáo
viên.
(*)
x
ab
Nếu
0b
thì pt (*) VN
Nếu
0b
thì pt (*) có nghiệm
duy nhất
log
a
xb
- Thảo luận và lên bảng trình
bày
4. Giải các phương trình sau:
a)
x x x x4 3 4 3
3 3.5 5 3
b)
x x x
4.9 12 3.16 0
c)
x x x
7 7 7
log ( 1)log log
d)
x x x
31
3
3
log log log 6
5. Giải các phương trình mũ và
lôgarit sau:
a)
22
2 3.2 1 0
xx
2
4.2 3.2 1 0
2 1 0
1
2
4
2
xx
x
x
x
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 74
có nghĩa?
- Hướng dẫn hs sử dụng các
công thức
+
log log
a
a
bb
+
log log log .
a a a
b c b c
+
log
a
b
ab
để biến đổi
phương trình đã cho
- Yêu cầu học sinh vận dụng
làm bài tập trên.
- Gọi hoc sinh nhắc lại công
thức lôgarit thập phân và
lôgarit tự nhiên.
- Cho học sinh quan sát
phương trình c) để tìm phương
pháp giải.
- Giáo viên nhận xét, hoàn
chỉnh lời giải.
H2. Nêu cách giải ?
- Trả lời theo yêu cầu của giáo
viên.
log
b
a
x b x a
Đk:
10
0
a
x

- Thảo luận và lên bảng trình
bày.
- Nhắc lại theo yêu cầu của
giáo viên.
10
log lg
log ln
e
xx
xx
- Thảo luận để tìm phương
pháp giải.
Đ2.
a) Đưa về cùng cơ số
2
5
.
Đặt
x
t
2
5



, t > 0.
tt
2
2 3 5 0
t
5
2
b)
21
8
11
log ( 2) log 3 5
63
xx
(*)
Đk:
20
2
3 5 0
x
x
x



2
2
2
2
2
(*) log ( 2) 2
log (3 5)
log [( 2)(3 5)]=2
3 11 10 4
3 11 6 0
3
3
2
2
3
x
x
xx
xx
xx
x
x
x

c)
lg lg lg
4.4 6 18.9 0
x x x
(3)
(3)
2lg lg
lg 2
lg
22
4. 18 0
33
2 9 2
3 4 3
2
20
3
1
lg 2
100
xx
x
x
xx




6. Giải các bất phương trình
sau:
a)
xx1
(0,4) (2,5) 1,5

b)
xx
2
0,2 0,2
log 5log 6
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 75
x < –1.
b) Đặt
tx
0,2
log
.
tt
2
5 6 0
2 < t < 3
0,008 < x < 0,04.
- Trả lời theo yêu cầu của giáo
viên.
log
b
a
x b x a
Đk:
10
0
a
x

- Thảo luận và lên bảng trình
bày.
- Nhắc lại theo yêu cầu của
giáo viên.
10
log lg
log ln
e
xx
xx
- Thảo luận để tìm phương
pháp giải.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Các tính chất của hàm số luỹ
thừa, hàm số mũ, hàm số
logarit.
– Cách giải các dạng phương
trình, bất phương trình mũ và
logarit.
4. BÀI TẬP VỀ NHÀ:
Chuẩn bị kiểm tra 1 tiết chương II.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 76
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 42 Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG II
I. MỤC TIÊU:
Kiến thức:
Ôn tập toàn bộ kiến thức trong chương II.
Kĩ năng:
Các qui tắc luỹ thừa và logarit.
Khảo sát các tính chất của hàm số luỹ thừa, hàm số mũ và hàm số logảit.
Giải phương trình, bất phương trình mũ và logarit.
Thái độ:
Rèn luyện tính cẩn thận, chính xác.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: Ôn tập toàn bộ kiến thức chương 2.
III. MA TRẬN ĐỀ:
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Luỹ thừa
1
0,5
0,5
Logarit
2
0,5
1,0
Hàm số luỹ thừa – Mũ –
Logarit
2
0,5
3
0,5
2,5
Phương trình – Bất
phương mũ , logarit
1
2,0
2
2,0
6,0
Tổng
2,5
1,5
2,0
4,0
10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (2 điểm) Chọn phương án đúng nhất:
Câu 1: Giá trị của biểu thức
A
2 6 4
2 6 4
( 3) .( 15) .8
9 .( 5) .( 6)


bằng:
A) 16 B) 256 C) 64 D)
256
9
Câu 2: Giá trị của biểu thức
A
3
2
log 2
log 3
49
bằng:
A) 8 B) 12 C) 16 D) 25
Câu 3: Cho
blg3
. Tính
lg900
theo b :
A) 2(b + 1) B) b + 2 C) b + 30 D) b + 100
Câu 4: Tập xác định của hàm số
y x x
1
2
2
( 3 4)
là:
A) (–∞; –4) (1; +∞) B) (–4; 1) C) (–∞; –4) D) (1; +∞)
Câu 5: Tập xác định của hàm số
x
y
x
3
1
log
1
là:
A) (–∞; –1) B) (1; +∞) C) (–1; 1) D) (–∞; –1) (1; +∞)
Câu 6: Cho hàm số
f x x x
3
2
( ) 1
. Tính
f (0)
?
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 77
A) 3 B) 1 C)
1
3
D)
2
3
Câu 7: Cho hàm số
xx
f x e
2
2
()
. Tính
f (0)
?
A) 0 B) 1 C) 2 D) e
Câu 8: Cho hàm số
f x x( ) ln(sin )
. Tính
f
4



?
A) 0 B) 1 C)
3
D)
2
B. Phần tự luận: (8 điểm) Giải các phương trình, bất phương trình sau:
a)
x x x
2.14 3.49 4 0
b)
xx1
2
log (5 25 ) 2

c)
xx
2
1
2
log ( 5 6) 3
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
B
D
A
B
D
C
C
B
B. Phần tự luận: Mỗi câu 2 điểm
a)
x x x
2.14 3.49 4 0
xx2
77
3. 2 1 0
22
x
tt
tt
2
7
,0
2
3 2 1 0




x
tt
t loaïi
t
7
,0
2
1 ( )
1
3





x
71
23



x
7
2
1
log
3
b)
xx1
2
log (5 25 ) 2

xx2
5 5.5 4 0
x
tt
tt
2
5 , 0
5 4 0

x
tt
t
t
5 , 0
1
4

x
x
51
54
x
x
5
0
log 4
c)
xx
2
1
2
log ( 5 6) 3
xx
23
5 6 2
xx
2
5 14 0
x
x
2
7

VI. KẾT QUẢ KIỂM TRA:
Lớp
Sĩ số
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
12S1
53
12S2
54
12S3
54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 78
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Chương III: NGUYÊN HÀM – TÍCH PHÂN VÀ ỨNG DỤNG
Tiết dạy: 43 Bài 1: NGUYÊN HÀM
I. MỤC TIÊU:
Kiến thức:
Hiểu khái niệm nguyên hàm của một hàm số.
Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
Các phương pháp tính nguyên hàm.
Kĩ năng:
Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính
nguyên hàm từng phần.
Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn
giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại các công thức tính đạo hàm của các hàm số luỹ thừa, mũ, logarit?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm nguyên hàm
GV dẫn dắt từ VD sau để
giới thiệu khái niệm nguyên
hàm của hàm số.
VD: Tìm hàm số F(x) sao cho:
F
(x) = f(x)
nếu: a) f(x) = 3x
2
với x
R
b) f(x) =
x
2
1
cos
vôùi x ;
22





H1. Tìm nguyên hàm ?
H2. Nêu nhận xét về các
nguyên hàm của một hàm số ?
Các nhóm thảo luận và trình
bày.
a) F(x) =
x
3
;
x
3
+ 3;
x
3
– 2; ...
b) F(x) = tanx; tanx – 5; …
Đ1.
a) F(x) =
x
2
;
x
2
+ 2;
x
2
– 5,..
b) F(x) = lnx; lnx + 1; lnx – 3, ..
Đ2. Các nguyên hàm của một
hàm số sai khác một tham số
cộng.
I. NGUYÊN HÀM VÀ TÍNH
CHẤT
1. Nguyên hàm
Cho hàm số f(x) xác định tren
K
R. Hàm số F(x) đgl
nguyên hàm của f(x) trên K
nếu, với
x
K ta có:
F x f x( ) ( )
VD1: Tìm một nguyên hàm
của các hàm số sau:
a) f(x) = 2x trên R
b) f(x) =
x
1
trên (0; +
)
Định lí 1:
Nếu F(x) là 1 nguyên hàm của
f(x) trên K thì với mỗi hằng số
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 79
GV cho HS nhận xét và phát
biểu.
GV giới thiệu kí hiệu họ
nguyên hàm của một hàm số.
H3. Tìm 1 nguyên hàm ?
G x f x)( ) (
F x G x( ) ( ) 0

F(x) – G(x) = C
Đ3.
a)
xdx=x C
2
2
b)
ds s C
s
1
ln
c)
tdt t Ccos sin
C, G(x) = F(x) + C cũng là 1
nguyên hàm của f(x) trên K.
Định lí 2:
Nếu F(x) là 1 nguyên hàm của
f(x) trên K thì mọi nguyên hàm
của f(x) trên K đều có dạng
F(x) + C, với C là một hằng số.
Nhận xét:
Nếu F(x) là 1 nguyên hàm của
f(x) trên K thì F(x) + C, C
R
là họ tất cả các nguyên hàm
của f(x) trên K. Kí hiệu:
f x dx F x C( ) ( )
VD2: Tìm họ nguyên hàm:
a) f(x) = 2x b) f(s) =
s
1
c) f(t) = cost
Hoạt động 2: Tìm hiểu tính chất của nguyên hàm
GV hướng dẫn HS nhận xét
và chứng minh các tính chất.
GV nêu một số VD minh hoạ
các tính chất.
H1. Tìm nguyên hàm ?
x dx= x+C(cos ) cos
x x x
e dx=3 e dx=3e C3

x dx=-3cosx+2lnx+C
x
2
3sin



Đ1.
a)
x
f x dx= inx C
2
( ) 2s
2

b)
x
f x dx=x e C
3
( ) 5
c)
f x dx= x cosx C
3
1
()
6

d)
f x dx= x x C
3
21
( ) sin2
32

2. Tính chất của nguyên hàm
f x dx=f(x)+C()
kf x dx=k f x dx( ) ( )

(k
0)
f x g x dx= f x dx
g x dx
( ) ( ) ( )
()



VD3: Tìm nguyên hàm:
a)
f x x cosx( ) 2
b)
x
f x x e
2
( ) 3 5
c)
f x x inx
2
1
( ) s
2

d)
f x x cos x( ) 2
Hoạt động 3: Củng cố
Nhấn mạnh:
– Mối liên hệ giữa đạo hàm và
nguyên hàm.
– Các tính chất của nguyên
hàm.
4. BÀI TẬP VỀ NHÀ:
Bài 1 SGK.
Đọc tiếp bài "Nguyên hàm".
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 80
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 44 Bài 1: NGUYÊN HÀM (tt)
I. MỤC TIÊU:
Kiến thức:
Hiểu khái niệm nguyên hàm của một hàm số.
Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
Các phương pháp tính nguyên hàm.
Kĩ năng:
Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính
nguyên hàm từng phần.
Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn
giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa và tính chất của nguyên hàm?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu sự tồn tại nguyên hàm
GV nêu định lí.
H1. Xét tính liên tục của hàm số
trên tập xác định của nó?
Đ1.
a)
f x x
2
3
()
liên tục trên khoảng
(0; +∞) .
x dx= x C
25
33
3
5
b)
fx
x
2
1
()
sin
liên tục trên từng
khoảng
kk( ;( 1) )

.
dx= x C
x
2
1
cot
sin

3. Sự tồn tại nguyên hàm
Định lí 3:
Mọi hàm số liên tục trên K đều có
nguyên hàm trên K.
VD1: Chứng tỏ các hàm số sau có
nguyên hàm:
a)
f x x
2
3
()
b)
fx
x
2
1
()
sin
c)
x
fx( ) 2
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 81
c)
x
fx( ) 2
liên tục trên R.
x
x
dx= C
2
2
ln2
Hoạt động 2: Tìm hiểu bảng nguyên hàm
GV cho HS tính và điền vào
bảng.
GV nêu chú ý.
Các nhóm thảo luận và trình
bày.
dx=C0
x dx= x C
1
1
( 1)
1

dx= x C
x
1
ln
xx
e dx=e C
4. Bảng nguyên hàm của một s ố
hàm số
x
x
a
a dx= C a a
a
( 0, 1)
ln
xdx x Ccos sin
xdx x Csin cos
dx x C
x
2
1
tan
cos

dx x C
x
2
1
cot
sin
Chú ý: Tìm nguyên hàm của 1
hàm số được hiểu là tìm nguyên
hàm trên từng khoảng xác định
của nó.
Hoạt động 3: Áp dụng bảng nguyên hàm
Cho HS tính.
H1. Nêu cách tìm ?
Các nhóm tính và trình bày.
A =
x x C
3
3
2
3
3

B =
x
xC
1
3
3sin
ln3

C =
x x Ctan cot
D =
xC
x
1
ln 
Đ1. Tìm họ nguyên hàm F(x) của
hàm số, sau đó sử dụng giả thiết
để tìm tham số C.
a)
x
F x x x C
4
2
( ) 2 5
4
F(1) = 3 C =
1
4
b) F(x) = 3x – 5sinx + C
F() = 2 C = 2 – 3.
c)
x
F x x C
2
5
( ) 3ln
2
F(e) = 1 C =
e
2
25
2
d)
x
F x x C
2
( ) ln
2
F(1) =
3
2
C = 1
VD2: Tính:
A =
x dx
x
2
3
2
1
2




B =
x
x dx
1
(3cos 3 )
C =
dx
xx
22
1
sin .cos
D =
x
dx
x
2
1
VD3: Tìm một nguyên hàm của
hàm số, biết:
a)
f x x x F
3
( ) 4 5; (1) 3
b)
f x x F( ) 3 5cos ; ( ) 2
c)
x
f x F e
x
2
35
( ) ; ( ) 1

d)
x
f x F
x
2
13
( ) ; (1)
2

Hoạt động 4:
Nhấn mạnh:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 82
– Bảng nguyên hàm.
4. BÀI TẬP VỀ NHÀ:
Bài 2 SGK.
Đọc tiếp bài "Nguyên hàm".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 45 Bài dạy: ÔN TẬP HỌC KÌ I
I. MỤC TIÊU:
Kiến thức: Củng cố:
Các tính chất của hàm số.
Khảo sát sự biến thiên và vẽ dồ thị hàm số.
Phép tính luỹ thừa, logarit.
Tính chất của các hàm số luỹ thừa, mũ, logarit.
Các dạng phương trình, bất phương trình mũ, logarit.
Kĩ năng:
Khảo sát thành thạo các tính chất của hàm số.
Vận dụng được các tính chất của hàm số để giải toán.
Thành thạo trong việc khảo sát sự biến thiên và vẽ đồ thị hàm số.
Thành thạo thực hiện các phép tính về luỹ thừa và logarit.
Giải thành thạo phương trình, bất phương trình mũ, logarit đơn giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức trong học kì 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình ôn tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Ôn tập khảo sát hàm số bậc ba
H1. Nêu các bước khảo sát
hàm số? Nêu một số đặc điểm
của hàm số bậc ba?
Đ1.
-2 -1 1 2 3
-2
-1
1
2
3
x
y
-m
1. Cho hàm số
32
44 y x x x
a) Khảo sát sự biến thiên và vẽ
đồ thị (C) của hàm số.
b) Biện luận theo m, số nghiệm
của phương trình:
32
4 4 0 x x x m
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 83
H2. Nêu cách biện luận số
nghiệm của phương trình bằng
đồ thị ?
Đ2.
32
27
0

m
m
: 1 nghiệm
32
27
0

m
m
: 2 nghiệm
32
0
27
m
: 3 nghiệm
Hoạt động 2: Ôn tập khảo sát hàm số bậc bốn trùng phương
H1. Nêu một số đặc điểm của
hàm số bậc bốn trùng phương?
H2. Nêu cách viết phương
trình tiếp tuyến của (C)?
Đ1.
-2 -1 1 2 3
-2
-1
1
2
3
x
y
Đ2. Pttt:
88yx
2. Cho hàm số
42
23 y x x
a) Khảo sát sự biến thiên và vẽ
đồ thị (C) của hàm số.
b) Viết phương trình tiếp tuyến
d của (C), biết d song song với
đường thẳng y = 8x.
Hoạt động 3: Ôn tập khảo sát hàm số nhất biến
H1. Nêu một số đặc điểm của
hàm số nhất biến?
H2. Nêu cách biện luận số giao
điểm của 2 đồ thị?
H3. Nêu cách tìm các điểm
thuộc đồ thị có toạ độ nguyên ?
Đ1.
-3 -2 -1 1 2 3 4 5 6 7
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
x
y
A
Đ2.
Phương trình đường thẳng d:
28 y kx k
Phương trình hoành độ giao
điểm của d và (C):
2
8 4 20 0
2
kx x k
x
41 k
: 0 giao điểm
4
1


k
k
: 1 giao điểm
4
1


k
k
: 2 giao điểm
Đ3.
4
2
y
x
Z x – 2 là
ước số của 4.
x = 3; 1; 4; 0; 6; –2
3. Cho hàm số
4
2
y
x
.
a) Khảo sát sự biến thiên và vẽ
đồ thị (C) của hàm số.
b) Một đường thẳng d đi qua
điểm A(–2; 8) và có hệ số góc
k. Biện luận theo k số giao
điểm của d và (C).
c) Tìm các điểm M(x; y) (C)
có toạ độ nguyên.
Hoạt động 4: Củng cố
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 84
Nhấn mạnh:
– Các bước khảo sát và vẽ đồ
thị hàm số.
– Đặc điểm và dạng đồ thị của
các loại hàm số trong chương
trình.
– Cách giải một số bài toán
liên quan đến khảo sát hàm số.
4. BÀI TẬP VỀ NHÀ:
Bài tập ôn Học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 46 Bài dạy: ÔN TẬP HỌC KÌ I (tt)
I. MỤC TIÊU:
Kiến thức: Củng cố:
Các tính chất của hàm số.
Khảo sát sự biến thiên và vẽ dồ thị hàm số.
Phép tính luỹ thừa, logarit.
Tính chất của các hàm số luỹ thừa, mũ, logarit.
Các dạng phương trình, bất phương trình mũ, logarit.
Kĩ năng:
Khảo sát thành thạo các tính chất của hàm số.
Vận dụng được các tính chất của hàm số để giải toán.
Thành thạo trong việc khảo sát sự biến thiên và vẽ đồ thị hàm số.
Thành thạo thực hiện các phép tính về luỹ thừa và logarit.
Giải thành thạo phương trình, bất phương trình mũ, logarit đơn giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức trong học kì 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình ôn tập)
H.
Đ.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 85
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Ôn tập giải phương trình mũ
H1. Nêu cách giải?
Cho các nhóm thảo luận và
trình bày.
Đ1.
Đưa về cùng cơ số.
a)
9 21
4 91



x
b)
53
35



x
Đặt ẩn phụ
c)
2
55
20
22
xx
d)
2
33
3. 1 0
22
xx
e)
2
33
4. 5. 9 0
22
x
x
f)
32
55
20
22
xx
Phân tích thành nhân tử.
g)
( 2)( 2 2 ) 0
x
xx
1. Giải các phương trình sau:
a)
1 2 1 2
9 9 9 4 4 4
x x x x x x
b)
1 3 4 2
7.3 5 3 5
x x x x
c)
21
25 10 2

x x x
d)
4 2.6 3.9
x x x
e)
2
4.3 9.2 5.6
x
xx
f)
31
125 50 2

x x x
g)
2
(3 2 ) 2(1 2 ) 0
xx
xx
Hoạt động 2: Ôn tập giải phương trình logarit
H1. Nêu cách giải?
Chú ý điều kiện của các phép
biến đổi.
Đ1.
Đưa về cùng cơ số
a)
2
22
log ( 3) log (3 5) xx
b)
22
log( 1) logxx
c)
22
1
log ( 2) log
2
xx
d)
3
3
log 2 9x
Đặt ẩn phụ
e) Đặt
2
log ( 1)tx
f) Đặt
2
logtx
2. Giải các phương trình sau:
a)
2
22
log ( 3) log (6 10) 1 0 xx
b)
5
1
2log( 1) log log
2
x x x
c)
4
log ( 2).log 2 1
x
x
d)
22
33
log ( 2) log 4 4 9 x x x
e)
( 1) 2
log 16 log ( 1)

x
x
f)
22
2
log 4 .log 12
x
xx
Hoạt động 3: Ôn tập giải bất phương trình mũ, logarit
H1. Nêu cách giải?
Chú ý sử dụng tính đồng
biến, nghịch biến của hàm số
mũ, hàm số logarit.
Đ1.
Đưa về cùng cơ số
a)
2
7
5



x
d)
2 (2 3) 0
4 2.2 0


xx
xx
e)
2
3 2 14
14 0

x x x
x
Đặt ẩn phụ
3. Giải các bất phương trình
sau:
a)
2 1 2
2 5 2 5
x x x x
+ <
b)
11
3.4 35.6 2.9 0

x x x
c)
1
9 4.3 27 0
xx
d)
2
1
log (4 2 )

xx
x
e)
2
22
log 3 2 log 14 x x x
f)
2 3 17
3.2 2.3 6


y
x
y
x
g)
22
6
log log 3


xy
xy
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 86
b)
2
33
18 35. 12 0
22
xx
c)
2
3 12.3 27 0
xx
Đưa về hệ phương trình đại
số
f)
17
3 2 6


uv
uv
g)
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách giải các dạng phương
trinh, bất phương trình mũ,
logarit.
– Điều kiện của các phép biến
đổi.
4. BÀI TẬP VỀ NHÀ:
Chuẩn bị kiểm tra Học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 47 KIỂM TRA HỌC KÌ 1
I. MỤC TIÊU:
Kiến thức:
Ôn tập toàn bộ kiến thức trong học kì 1.
Kĩ năng:
Khảo sát thành thạo các tính chất của hàm số.
Vận dụng được các tính chất của hàm số để giải toán.
Thành thạo trong việc khảo sát sự biến thiên và vẽ đồ thị hàm số.
Thành thạo thực hiện các phép tính về luỹ thừa và logarit.
Giải thành thạo phương trình, bất phương trình mũ, logarit đơn giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác.
THI THEO ĐỀ CHUNG CỦA SỞ GIÁO DỤC HÀ GIANG
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 87
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 48 Bài 1: NGUYÊN HÀM (tt)
I. MỤC TIÊU:
Kiến thức:
Hiểu khái niệm nguyên hàm của một hàm số.
Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
Các phương pháp tính nguyên hàm.
Kĩ năng:
Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính
nguyên hàm từng phần.
Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn
giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số công thức tính nguyên hàm?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu phương pháp đổi biến số
GV cho HS xét VD, từ đó
giới thiệu định lí.
VD:
a) Cho
10
( 1)
x dx
.
Đặt u = x –1.
Hãy viết
10
( 1)x dx
theo u, du.
b) Cho
ln
x
dx
x
. Đặt t = lnx.
Hãy viết
ln x
x
theo t, dt.
GV hướng dẫn HS chứng
minh định lí.
Các nhóm thảo luận và trình
bày.
a) u = x – 1 du = dx
10
( 1)x dx
=
10
u du
b) t = lnx dt =
dx
x
ln x
x
= tdt
( ( )) ( ( )). ( )
F u x f u x u x
II. PHƯƠNG PHÁP TÍNH
NGUYÊN HÀM
1. Phương pháp đổi biến số
Định lí:
Nếu
( ) ( )
f u du F u C
và
hàm số u = u(x) có đạo hàm
liên tục thì:
( ( ( )). ( ) ( ( ))

f u u x u x dx F u x C
Hệ quả: Với u = ax + b (a
0)
ta có:
1
( ) ( )
f ax b dx F ax b C
a
Chú ý: Nêu tính nguyên hàm
theo biến mới u thì sau khi tính
nguyên hàm phải trở lại biến x
ban đầu bằng cách thay u bởi
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 88
u(x).
Hoạt động 2: Áp dụng phương pháp đổi biến số
Hướng dẫn HS cách đổi biến.
H1. Nêu cách đổi biến ?
Các nhóm thảo luận và trình
bày.
a) t = 3x – 1
A =
1
cos(3 1)
3
xC
b) t = x + 1
B =
3
1 1 1
( 1) 4( 1) 3





C
xx
c) t = 3 – 2x
C =
4
1
8(3 2 )
C
x
d) t = cosx
D =
ln cosxC
Đ1.
e)
2
1tx
E =
2
1
2
x
e
C
f)
tx
F =
2
x
eC
g)
tantx
G =
tan x
e
h)
lntx
H =
4
ln
4
x
C
VD1: Tính
A =
sin(3 1)
x dx
B =
5
( 1)
x
dx
x
C =
5
(3 2 )
dx
x
D =
tan
xdx
VD2: Tính:
E =
2
1
.
x
x e dx
F =
x
e
dx
x
G =
tan
2
cos
x
e
dx
x
H =
Hoạt động 3:
Nhấn mạnh:
– Cách sử dụng phương pháp
đổi biến để tìm nguyên hàm.
Câu hỏi: Lập bảng nguyên
hàm của hàm số hợp?
u x dx u x C'( ) ( )
ux
u x u x dx= C
1
()
( ) . ( )
1
( –1)
ux
dx u x C
ux
. ( )
ln ( )
()

u x u x
e u x dx e C
( ) ( )
. ( )

ux
ux
a
a u x dx C
a
()
()
. ( )
ln

(a > 0, a 1)
u x u x dx u x Ccos ( ). ( ) sin ( )

u x u x dx u x Csin ( ). ( ) cos ( )
ux
dx u x C
ux
2
()
tan ( )
cos ( )

ux
dx u x C
ux
2
()
cot ( )
sin ( )
4. BÀI TẬP VỀ NHÀ:
Bài 3 SGK.
Bài tập ôn Học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 89
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 49 Bài 1: NGUYÊN HÀM (tt)
I. MỤC TIÊU:
Kiến thức:
Hiểu khái niệm nguyên hàm của một hàm số.
Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
Các phương pháp tính nguyên hàm.
Kĩ năng:
Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính
nguyên hàm từng phần.
Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn
giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số công thức tính nguyên hàm?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu phương pháp tính nguyên hàm từng phần
Dẫn dắt từ VD, GV giới thiệu
phương pháp tính nguyên hàm
từng phần.
VD: Tính
xx( cos )
;
x x dx( cos )
;
xdxcos
.
Từ đó tính
x xdxsin
.
GV nêu định lí và hướng dẫn
HS chứng minh.
xx( cos )
= cosx – xsinx
x x dx( cos )
= xcosx + C
1
xdxcos
= sinx + C
2
x xdxsin
=–xcosx+sinx +C
uv u v uv()

uv uv u v()

2. Phương pháp tính nguyên
hàm từng phần
Định lí: Nếu hai hàm số u =
u(x) và v = v(x) có đạo hàm
liên tục trên K thì:
udv uv vdu

Hoạt động 2: Áp dụng phương pháp tính nguyên hàm từng phần
GV hướng dẫn HS cách phân
tích.
HS theo dõi và thực hành.
a) Đặt
x
ux
dv e dx
A =
xx
xe e C
VD1: Tính:
A =
x
xe dx
B =
x xdxcos
C =
xdxln
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 90
H1. Nêu cách phân tích ?
b) Đặt
ux
dv xdxcos
B =
x x x Csin cos
c) Đặt
ux
dv dx
ln
C =
x x x Cln 
d) Đặt
ux
dv xdxsin
D =
x x x Ccos sin
Đ1.
e) Đặt
ux
dv xdx
2
5
sin

E=
x cosx x inx C
2
( 3) 2 s
f) Đặt
u x x
dv xdx
2
23
cos
F=
x x x x C
2
( 1) sin 2 cos
g) Đặt
ux
dv dx
2
ln
G=
x x x x x C
2
ln 2 ln 2
h) Đặt
tx
2
H=
t
te dt
1
2
=
tt
te e C
1
()
2

=
xx
x e e C
22
2
1
2

D =
x xdxsin
VD2: Tính:
E =
x xdx
2
( 5)sin
F =
x x xdx
2
( 2 3)cos
G =
x dx
2
ln( 1)
H =
x
x e dx
2
3
Hoạt động 3: Củng cố
Nhấn mạnh:
– Phương pháp tính nguyên
hàm từng phần.
Câu hỏi: Nêu cách phân tích
một số dạng thường gặp?
P x xdx( )sin
P x xdx( )cos
x
P x e dx()
P x xdx( )ln
u
P(x)
P(x)
P(x)
lnx
dv
sinxdx
cosxdx
x
e dx
P(x)dx
4. BÀI TẬP VỀ NHÀ:
Bài 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 91
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 50 Bài 1: BÀI TẬP NGUYÊN HÀM
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm nguyên hàm của một hàm số.
Các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
Các phương pháp tính nguyên hàm.
Kĩ năng:
Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính
nguyên hàm từng phần.
Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn
giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Củng cố khái niệm nguyên hàm
H1. Nhắc lại định nghĩa
nguyên hàm của một hàm số?
H2. Nhắc lại bảng nguyên
hàm?
Đ1. F(x) = f(x)
a) Cả 2 đều là nguyên hàm của
nhau.
b)
2
sin x
là 1 nguyên hàm của
sin2x
c)
4
1



x
e
x
là 1 nguyên hàm
của
2
2
1



x
e
x
Đ2.
a)
5 7 2
3 6 3
3 6 3
4 7 2
x x x C
b)
2 ln2 1
(ln2 1)

x
x
C
e
c)
11
cos8 cos2
34



x x C
d)
11
ln
3 1 2
x
C
x
1. Trong các cặp hàm số sau,
hàm số nào là 1 nguyên hàm
của hàm số còn lại:
a)

xx
e và e
b)
2
sin2 sinx và x
c)
2
24
11

xx
e và e
xx
2. Tìm nguyên hàm của các
hàm số sau:
a)
3
1
()

xx
fx
x
b)
21
()
x
x
fx
e
c)
( ) sin5 .cos3f x x x
d)
1
()
(1 )(1 2 )

fx
xx
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 92
Hướng dẫn cách phân tích
phân thức.
1 1 1 2
(1 )(1 2 ) 3 1 1 2




x x x x
Hoạt động 2: Luyện tập phương pháp đổi biến số
H1. Nêu công thức đổi biến ?
Đ1.
a) t = 1 – x A =
10
(1 )
10

x
C
b) t = 1 + x
2
B =
5
2
2
1
(1 )
5
xC
c) t = cosx C =
4
1
cos
4
xC
d) t = e
x
+ 1 D =
1
1

x
C
e
3. Sử dụng phương pháp đổi
biến, hãy tính:
a)
9
(1 )
x dx
b)
3
2
2
(1 )
x x dx
c)
3
cos sin
x xdx
d)
1
2

xx
dx
ee
Hoạt động 3: Luyện tập phương pháp nguyên hàm từng phần
H1. Nêu cách phân tích?
Đ1.
a)
ln(1 )
ux
dv xdx
A =
22
11
( 1)ln(1 )
2 4 2
x
x x x C
b)
2
21
x
u x x
dv e dx
B =
2
( 1)
x
e x C
c)
sin(2 1)

ux
dv x dx
C =
1
cos(2 1) sin(2 1)
24
x
x x C
d)
1
cos

ux
dv xdx
D =
(1 )sin cos x x x C
4. Sử dụng phương pháp
nguyên hàm từng phần, hãy
tính:
a)
ln(1 )
x x dx
b)
2
( 2 1)
x
x x e dx
c)
sin(2 1)
x x dx
d)
(1 )cos
x xdx
Hoạt động 4: Củng cố
Nhấn mạnh:
– Bảng các nguyên hàm.
– Các sử dụng các phương
pháp tính nguyên hàm.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc trước bài "Tích phân".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 93
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 51 Bài 2: TÍCH PHÂN
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm diện tích hình thang cong.
Biết định nghĩa tích phân của hàm số liên tục.
Biết các tính chất và các phương pháp tính tích phân.
Kĩ năng:
Tìm được tích phân của một số hàm số đơn giản bằng định nghĩa hoặc phương pháp tích
phân từng phần.
Sử dụng được phương pháp đổi biến số để tính tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập công thức đạo hàm và nguyên hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa và tính chất của nguyên hàm?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm diện tích hình thang cong
Cho HS nhắc lại tính diện
tích hình thang vuông. Từ đó
dẫn dắt đến nhu cầu tính diện
tích "hình thang cong".
GV dẫn dắt cách tìm diện
tích hình thang cong thông qua
VD: Tính diện tích hình thang
cong giới hạn bởi đường cong
y = f(x) = x
2
, trục hoành và các
đường thẳng x = 0; x = 1.
Với x [0; 1], gọi S(x) là
diện tích phần hình thang cong
I. KHÁI NIỆM TÍCH PHÂN
1. Diện tích hình thang cong
Cho hàm số y = f(x) liên tục,
không đổi dấu trên đoạn [a; b]
Hình phẳng giới hạn bởi đồ thị
của hàm số y = f(x), trục Ox và
hai đường thẳng x = a, x = b
đgl hình thang cong.
Cho hình thang cong giới
hạn bởi các đường thẳng x = a,
x = b (a < b), trục hoành và
đường cong y = f(x) liên tục,
không âm trên [a; b]. Giả sử
F(x) là một nguyên hàm của
f(x) thì diện tích của hình thang
cong cần tìm là: F(b) – F(a)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 94
nằm giữa 2 đt vuông góc với
trục Ox tại 0 và x.
C.minh: S(x) là một nguyên
hàm của f(x) trên [0;1].
Hoạt động 2: Tìm hiểu định nghĩa tích phân
GV nêu định nghĩa tích phân
và giải thích.
Minh hoạ bằng VD.
2. Định nghĩa tích phân
Cho f(x) là hàm số liên tục trên
[a; b]. Giả sử F(x) là một
nguyên hàm của f(x) trên [a; b]
Hiệu số F(b) – F(a) đgl tích
phân từ a đến b của f(x).
( ) ( ) ( ) ( )
b
b
a
a
f x dx F x F b F a
b
a
: dấu tích phân
a: cận dưới, b: cận trên
Qui ước:
( ) 0
a
a
f x dx
;
( ) ( )

ba
ab
f x dx f x dx
Hoạt động 3: Áp dụng định nghĩa tính tích phân
H1. Tìm nguyên hàm của hàm
số?
GV nêu nhận xét.
Đ1.
a)
2
2
2 2 2
1
1
2 2 1 3
xdx x
b)
1
1
1
ln ln ln1 1
e
e
dt t e
t
VD1: Tính tích phân:
a)
2
1
2
xdx
b)
1
1
e
dt
t
Nhận xét:
a) Tích phân của một hàm số
không phụ thuộc vào kí hiệu
biến số.
( ) ( ) ( )
b b b
a a a
f x dx f t dt f u du
b) Ý nghĩa hình học: Nếu f(x)
liên tục và không âm trên [a;
b] thì
()
b
a
f x dx
là diện tích của
hình thang cong giới hạn bởi
đồ thị hàm số f(x), trục Ox và
hai đường thẳng x = a, x = b:
()
b
a
S f x dx
Hoạt động 4: Củng cố
Nhấn mạnh:
– Định nghĩa tích phân.
– Ý nghĩa hình học của tích
phân.
4. BÀI TẬP VỀ NHÀ:
Bài 1 SGK.
Đọc tiếp bài "Tích phân".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 95
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 52 Bài 2: TÍCH PHÂN (tt)
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm diện tích hình thang cong.
Biết định nghĩa tích phân của hàm số liên tục.
Biết các tính chất và các phương pháp tính tích phân.
Kĩ năng:
Tìm được tích phân của một số hàm số đơn giản bằng định nghĩa hoặc phương pháp tích
phân từng phần.
Sử dụng được phương pháp đổi biến số để tính tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập công thức nguyên hàm, định nghĩa tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa tích phân?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo
viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu các tính chất của tích phân
H1. Chứng minh các
tính chất?
Đ1. Các nhóm thảo luận và trình bày.
b
b
a
a
kf x dx kF x( ) ( )
b
b
a
a
f x g x dx F x G x[ ( ) ( )] ( ( ) ( ))
cb
cb
ac
ac
f x dx f x dx F x F x( ) ( ) ( ) ( )

II. TÍNH CHẤT CỦA TÍCH
PHÂN
1.
bb
aa
kf x dx k f x dx( ) ( )

2.
b
a
bb
aa
f x g x dx
f x dx g x dx
[ ( ) ( )]
( ) ( )


3.
b c b
a a c
f x dx f x dx f x dx( ) ( ) ( )
(a < c < b)
Hoạt động 2: Áp dụng các tính chất của tích phân
H1. Gọi HS tính.
Đ1. các nhóm thực hiện và trình bày.
A =
x
x
4
3
3
2
1
2
3



= 35
VD1: Tính các tích phân:
a)
x x dx
4
2
1
( 3 )
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 96
H2. Xét dấu hàm số
dưới dấu GTTĐ?
B =
x
xx
3
4
2
1
33
4



C =
x
x
2
1
11
ln ln2
2



D =
e
xx
x
x
23
1
1
ln
23



Đ2.
A=
xdx xdx
01
10
24

B =
xdx xdx
2
0
2 sin sin






C =
x x dx x x dx
12
22
01
( ) ( )

D =
x dx x dx x dx
1 1 3
2 2 2
3 1 1
( 1) (1 ) ( 1)

b)
x x dx
3
3
1
( 2 1)
c)
x
dx
x
2
2
1
1
d)
e
x x dx
x
x
2
2
1
11



VD2: Tính các tích phân:
a)
x x dx
1
1
3
b)
xdx
2
0
1 cos2
c)
x x dx
2
2
0
d)
x dx
3
2
3
1
Hoạt động 3: Tìm hiểu cách tính tích phân bằng phương pháp đổi biến số thứ nhất
GV dẫn dắt đến phương
pháp.
Xét VD: Cho I =
x dx
1
2
0
(2 1)
.
a) Tính I bằng cách khai triển
x
2
(2 1)
.
b) Đặt t = 2x + 1.
Tính J =
t
t
g t dt
(1)
(0)
()
.
GV nêu định lí.
GV hướng dẫn HS thực hiện.
HS thực hiện theo sự hướng
dẫn của GV.
a) I =
x x dx
1
2
0
13
(4 4 1)
3
b) J =
t dt
3
2
1
1 13
33
I = J
Đặt
x t ttan ,
22

.
xt
t
2
1
()
cos
.
I =
dt
tt
4
22
0
1
.
1 tan cos
=
4
III. PHƯƠNG PHÁP TÍNH
TÍCH PHÂN
1. Phương pháp đổi biến số
Định lí 1: Cho hàm số f(x) liên
tục trên [a; b]. Giả sử hàm số x
=
(t) có đạo hàm liên tục trên
đoạn [
;
] sao cho
(
) = a,
(
) = b và a
(t)
b với
t
[
;
]. Khi đó:
b
a
f x dx f t t dt( ) ( ) ( )


VD1: Tính I =
dx
x
1
2
0
1
1
Hoạt động 4: Tìm hiểu cách tính tích phân bằng phương pháp đổi biến số thứ hai
GV giới thiệu định lí 2
Định lí 2: Cho hàm số f(x) liên
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 97
GV hướng dẫn cách đổi biến.
Đặt u = sinx.
I =
u du
1
2
0
1
3
tục trên [a; b]. Nếu hàm số u =
u(x) có đạo hàm liên tục trên
[a; b] và
u(x)
với mọi x
[a; b] sao cho f(x) =
g[u(x)]u
(x), g(u) liên tục trên
[
;
] thì:
ub
b
a u a
f x dx g u du
()
()
( ) ( )

VD2: Tính
I =
x xdx
2
2
0
sin .cos
Hoạt động 5: Áp dụng tính tích phân bằng phương pháp đổi biến số
H1. Sử dụng cách đổi biến
nào?
Đ1.
a) Đặt t = 1 – x
A =
t t dt
1
19
0
1
(1 )
420

b) Đặt t = e
x
+ 1
B =
dt
t
3
2
3
ln
2
c) Đặt x = sint
C =
t
dt
t
6
0
cos
cos
=
6
d) Đặt
xt3tan
D =
dt
dx
tt
3
22
0
3
3
cos (tan 1)
=
3
9
VD3: Tính các tích phân sau:
a)
x x dx
1
19
0
(1 )
b)
x
x
e
dx
e
ln2
0
1
c)
dx
x
1
2
2
0
1
1
d)
dx
x
3
2
0
1
3
Hoạt động 6: Củng cố
Nhấn mạnh:
– Cách sử dụng các dạng của
phương pháp đổi biến số để
tính tích phân.
4. BÀI TẬP VỀ NHÀ:
Bài 3 SGK.
Đọc tiếp bài "Tích phân".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 98
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 53 Bài 2: TÍCH PHÂN (tt)
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm diện tích hình thang cong.
Biết định nghĩa tích phân của hàm số liên tục.
Biết các tính chất và các phương pháp tính tích phân.
Kĩ năng:
Tìm được tích phân của một số hàm số đơn giản bằng định nghĩa hoặc phương pháp tích
phân từng phần.
Sử dụng được phương pháp đổi biến số để tính tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập công thức nguyên hàm, định nghĩa tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các cách đổi biến số để tính tích phân?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách tính tích phân bằng phương pháp tích phân từng phần
GV dẫn dắt từ VD để giới
thiệu phương pháp tích phân
từng phần.
VD: Tính
x
x e dx( 1)
bằng
phương pháp tính nguyên hàm
từng phần.
Từ đó tính
x
x e dx
1
0
( 1)
.
GV nêu định lí
HS tính I =
x
x e dx( 1)
Đặt
x
ux
dv e dx
1

I = (x + 1)e
x
–
x
e dx
= xe
x
+ C
xx
x e dx xe e
1
1
0
0
( 1)
III. PHƯƠNG PHÁP TÍNH
TÍCH PHÂN
2. Phương pháp tích phân
từng phần
Định lí : Nếu u = u(x) và v =
v(x) là hai hàm số có đạo hàm
liên tục trên [a; b] thì:
bb
b
a
aa
udv uv vdu

Hoạt động 2: Áp dụng tính tích phân bằng phương pháp tích phân từng phần
H1. Nêu cách phân tích?
Đ1.
a) Đặt
ux
dv xdxsin
A =
x x xdx
2
2
0
0
( cos ) cos

=1
b) Đặt
ux
dv xdxcos
VD1: Tính các tích phân:
a)
x xdx
2
0
sin
b)
x xdx
2
0
cos
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 99
B =
x x xdx
2
2
0
0
( sin ) sin 1
2
c) Đặt
x
ux
dv e dx
C =
xx
xe e dx
ln2
ln2
0
0
2ln2 1
d) Đặt
ux
dv xdx
ln
D =
e
e
xe
x xdx
22
1
1
11
ln
2 2 4

c)
x
xe dx
ln2
0
d)
e
x xdx
1
ln
Hoạt động 3: Áp dụng tính tích phân một số dạng khác
GV hướng dẫn cách tính.
a) Phân tích phan thức
xx
xx
2
1 1 1
32
56



b) Đặt
tx
2
1
c) Biến đổi tích thành tổng
x x x x
1
sin2 .cos (sin3 sin )
2

d) Đặt
x
te 1
VD2: Tính các tích phân:
a)
dx
xx
1
2
0
56
b)
x x dx
22
2
0
1
c)
x xdx
4
0
sin2 .cos
d)
x
x
e
dx
e
1
0
1
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách sử dụng phương pháp
tích phân từng phần để tính
tích phân.
– Một số dạng sử dụng phương
pháp tích phân từng phần.
4. BÀI TẬP VỀ NHÀ:
Bài 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 100
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 54 + 55 Bài 2: BÀI TẬP TÍCH PHÂN
I. MỤC TIÊU:
Kiến thức: Củng cố:
Định nghĩa và tính chất của tích phân.
Các phương pháp tính tích phân.
Kĩ năng:
Sử dụng định nghĩa để tính tích phân.
Sử dụng các phương pháp tính tích phân để tính các tích phân đơn giản.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình tluyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tính tích phân bằng định nghĩa
H1. Nêu cách biến đổi hàm số
để từ đó sử dụng định nghĩa
tích phân?
Đ1. Các nhóm thực hiện và
trình bày.
a)
x x x x
1 1 1
( 1) 1


A = ln2
b) Khai triển đa thức
B =
34
3
c) C = 0
d) Biến đổi tích thành tổng
D = 0
1. Tính các tích phân:
a)
dx
xx
2
1
2
1
( 1)
b)
x x dx
2
2
0
( 1)
c)
x dx
2
0
sin
4



d)
x xdx
2
2
sin3 .cos5
Hoạt động 2: Luyện tập tính tích phân bằng phương pháp đổi biến số
H1. Nêu cách đổi biến?
Đ1.
a) Đặt t = 1 + x
A =
5
3
b) Đặt x = sint
B =
4
2. Tính các tích phân:
a)
x
dx
x
3
2
3
0
2
(1 )
b)
x dx
1
2
0
1
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 101
c) Đặt t = 1 + xe
x
C = ln(1 + e)
d) Đặt x = asint
D =
6
c)
x
x
ex
dx
xe
1
0
(1 )
1
d)
a
dx
ax
2
22
0
1
Hoạt động 3: Luyện tập tính tích phân bằng phương pháp tích phân từng phần
H1. Nêu cách phân tích?
Đ1.
a) Đặt
ux
dv xdx
1
sin

A = 2
b) Đặt
ux
dv x dx
2
ln
B =
e
3
1
(2 1)
9
c) Đặt
ux
dv dx
ln( 1)

C = 2ln2 – 1
d) Đặt
x
u x x
dv e dx
2
21
D = –1
3. Tính các tích phân:
a)
x xdx
2
0
( 1)sin
b)
e
x xdx
2
1
ln
c)
x dx
1
0
ln(1 )
x
x x e dx
1
2
0
( 2 1)

Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách sử dụng các phương
pháp tính tích phân.
4. BÀI TẬP VỀ NHÀ:
Bài tập còn lại.
Đọc trước bài "Ứng dụng của tích phân trong hình học".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 102
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 56 Bài 3: ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
I. MỤC TIÊU:
Kiến thức:
Biết các công thức tính diện tích, thể tích nhờ tích phân.
Kĩ năng:
Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
Củng cố phép tính tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu ý nghĩa hình học của tích phân?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách tính diện tích hình phẳng giới hạn bởi 1 đường cong và trục Ox
H1. Nhắc lại ý nghĩa hình
học của tích phân?
H2. Nếu f(x)
0 trên [a; b],
thì ta có thể tính diện tích
hình phẳng đó như thế nào?
Đ1. Diện tích hình phẳng giới
hạn bởi đồ thị hàm số f(x) liên
tục, không âm trên [a; b], trục
hoành và 2 đường thẳng x = a, x
= b:
b
a
S f x dx()
Đ2. Tính diện tích hình đối xứng
qua trục hoành.
I. TÍNH DIỆN TÍCH HÌNH
PHẲNG
1. Hình phẳng giới hạn bởi 1
đường cong và trục hoành
Diện tích hình phẳng giới hạn
bởi đồ thị hàm số f(x) liên tục,
trục hoành và 2 đường thẳng x
= a, x = b:
b
a
S f x dx()
Chú ý: Nếu trên [a; b] hàm số
f(x) giữ nguyên một dấu thì:
bb
aa
f x dx f x dx( ) ( )

Hoạt động 2: Áp dụng tính diện tích hình phẳng
H1. Thiết lập công thức tính?
Đ1.
S x dx
3
2
0
= 9 (đvdt)
VD1: Tính diện tích hình
phẳng giới hạn bởi các đường:
y = x
2
, x = 0, x = 3, trục Ox.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 103
H2. Thiết lập công thức tính?
H3. Thiết lập công thức tính?
-4 -3 -2 -1 1 2 3 4
-1
1
2
3
4
5
6
7
8
9
x
y
O
Đ2.
S x dx
0
2
( sin )

= 1 (đvdt)
-4π/5 -3π/5 -2π/5 -π/5 π/5 2π/5 3π/5 4π/5
-1
1
x
y
O
Đ3.
S x dx x dx x dx
2 0 2
3 3 3
1 1 0
()

=
17
4
-2 -1 1 2 3
-1
1
2
3
4
5
6
7
8
9
x
y
O
VD2: Tính diện tích hình
phẳng giới hạn bởi các đường:
y = sinx, x =
2
, x = 0, y = 0.
VD3: Tính diện tích hình
phẳng giới hạn bởi các đường:
y = x
3
, y = 0, x = –1, x = 2.
Hoạt động 3: Tìm hiểu cách tính diện tích hình phẳng giới hạn bởi 2 đường cong
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 104
GV minh hoạ bằng hình
vẽ và cho HS nhận xét tìm
công thức tính diện tích.
GV nêu chú ý
S = S
1
– S
2
2. Hình phẳng giới hạn bởi hai đường
cong
Cho hai hàm số y = f
1
(x) và y = f
2
(x)
liên tục trên [a; b]. Diện tích của hình
phẳng giới hạn bởi đồ thị của hai hàm
số và các đường thẳng x = a, x = b
được tính bởi công thức:
b
a
S f x f x dx
12
( ) ( )
Chú ý: Nếu trên đoạn [
;
] biểu thức
f
1
(x) – f
2
(x) không đổi dấu thì:
f x f x dx f x f x dx
1 2 1 2
( ) ( ) ( ) ( )





Hoạt động 2: Áp dụng tính diện tích hình phẳng
GV hướng dẫn các bước
xác định hình phẳng và
thiết lập công thức tính
diện tích.
H1. Nêu các bước thực
hiện?
H2. Nêu các bước thực
hiện?
Tìm hoành độ giao điểm
của 2 đường: x = –2, x = 1
S x x dx
1
32
2
(4 3 )
27
4
Đ1. Các nhóm thảo luận và
trình bày.
Hoành độ giao điểm:
x
4
S x x dx
0
cos sin

=
x x dx
4
0
cos sin
+
+
x x dx
4
cos sin
=
22
Đ2.
Hoành độ giao điểm:
x = –2, x = 0, x = 1
S x x x dx
1
32
2
2
VD1: Tính diện tích hình phẳng giới
hạn bởi các đường:
y x x
32
3
, y = 4.
-2 -1 1
1
2
3
4
x
y
VD2: Tính diện tích hình phẳng giới
hạn bởi các đường: y = cosx, y = sinx, x
= 0, x = .
π/2 π
-1
1
x
y
VD3: Tính diện tích hình phẳng giới
hạn bởi các đường:
y x x
3

,
y x x
2

.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 105
=
x x x dx
0
32
2
2

+
+
x x x dx
1
32
0
2
=
37
12
-2 -1 1
-6
-5
-4
-3
-2
-1
1
x
y
Hoạt động 3: Củng cố
Nhấn mạnh:
– Cách xác định hình
phẳng.
– Cách thiết lập công thức
tính diện tích.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3 SGK.
Đọc tiếp bài "Ứng dụng của tích phân trong hình học".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 57 Bài 3: ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC (tt)
I. MỤC TIÊU:
Kiến thức:
Biết các công thức tính diện tích, thể tích nhờ tích phân.
Kĩ năng:
Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
Củng cố phép tính tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu công thức tính diện tích hình phẳng giới hạn bởi hai đường cong?
Đ.
b
a
S f x f x dx
12
( ) ( )
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 106
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách tính thể tích vật thể
GV dùng hình vẽ để minh
hoạ và giải thích.
II. TÍNH THỂ TÍCH
1. Thể tích của vật thể
Cắt một vật thể T bởi hai mặt
phẳng (P) và (Q) vuông góc với
trục Ox lần lượt tại x = a, x = b (a
< b). Một mặt phẳng tuỳ ý vuông
góc với Ox tại điểm x (a
x
b)
cắt T theo thiết diện có diện tích là
S(x). Giả sử S(x) liên tục trên [a;
b]. Khi đó thể tích V của phần vật
thể T giới hạn bởi hai mặt phẳng
(P), (Q) được tính theo công thức:
b
a
V S x dx()
Hoạt động 2: Áp dụng tính thể tích khối lăng trụ
H1. Nhắc lại công thức tính
thể tích khối lăng trụ?
GV hướng dẫn HS cách xây
dựng công thức.
H2. Tính diện tích thiết diện?
Đ1. V = Bh
Chọn trục Ox // đường
cao, còn 2 đáy nằm trong 2
mặt phẳng vuông góc với
Ox tại x = 0, x = h
Đ2. S(x) = B (0 x h)
V =
h
h
Bdx Bx Bh
0
0

2. Thể tích khối lăng trụ
Tính thể tích khối lăng trụ có diện
tích đáy bằng B và chiều cao h.
V = B.h
Hoạt động 3: Áp dụng tính thể tích khối chóp
H1. Nhắc lại công thức tính
thể tích khối chóp?
GV hướng dẫn HS cách xây
dựng công thức.
H2. Tính diện tích thiết diện?
Đ1. V =
Bh
1
3
Chọn trục Ox vuông góc
với mp đáy tại I sao cho gốc
O S và có hướng
OI
. OI
= h.
Đ2.
x
S x B
h
2
2
()
h
x Bh
V B dx
h
2
2
0
3

3. Thể tích khối chóp
Thể tích khối chóp có chiều cao h
và diện tích đáy B.
V =
Bh
1
3
Hoạt động 4: Áp dụng tính thể tích khối chóp cụt
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 107
GV hướng dẫn HS cách xây
dựng công thức.
H1. Tính diện tích thiết diện?
Chọn trục Ox trùng với
đường cao, O S. Hai mặt
phẳng đáy cắt Ox tại I và I.
Đặt OI = b, OI = a (a < b)
Đ1.
x
S x B
b
2
2
()
b
a
x b a a ab b
V B dx B
bb
2 2 2
22
.
3

=
h B BB B
1
3


a
B B h b a
b
2
2
;




4. Thể tích khối chóp cụt
Thể tích khối chóp cụt có chiều cao
h và diện tích hai đáy là B, B
.
V =
h B BB B
1
3


Hoạt động 5: Củng cố
Nhấn mạnh:
– Cách xây dựng các công
thức tính thể tích các khối
lăng trụ, chóp, chóp cụt.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc tiếp bài "Ứng dụng của tích phân trong hình học".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 108
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 58 Bài 3: ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC (tt)
I. MỤC TIÊU:
Kiến thức:
Biết các công thức tính diện tích, thể tích nhờ tích phân.
Kĩ năng:
Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
Củng cố phép tính tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về diện tích, thể tích.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu công thức tính thể tích vật thể?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách tính thể tích khối tròn xoay
H1. Nhắc lại khái niệm khối
tròn xoay?
GV hướng dẫn HS xây
dựng công thức tính thể tích
khối tròn xoay.
H2. Tính diện tích thiết
diện?
Đ1. HS nhắc lại.
Đ2.
S x f x
2
( ) ( )
b
a
V f x dx
2
()
III. THỂ TÍCH KHỐI TRÒN
XOAY
1. Thể tích khối tròn xoay tạo bởi
một hình thang cong giới hạn bởi đồ
thị hàm số y = f(x), trục Ox, hai
đường thẳng x = a, x = b (a < b)
quay quanh trục Ox được tính bởi
công thức:
b
a
V f x dx
2
()
Hoạt động 2: Áp dụng tính thể tích khối nón tròn xoay
GV hướng dẫn HS xây
dựng công thức.
H1. Xác định phương trình
đường thẳng OA?
Chọn hệ trục sao cho trục
hoành trùng với trục hình
nón, O S.
Đ1.
R
f x x
h
()
2. Thể tích khối nón tròn xoay có
chiều cao h và bán kính đáy R là:
V R h
2
1
3
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 109
h
R
V x dx R h
h
2
2
0
1
3





O
x
y
I
A
x
h
M
R
Hoạt động 3: Áp dụng tính thể tích hình cầu
GV hướng dẫn HS xây
dựng công thức.
H1. Xác định phương trình
cung nửa đường tròn?
Đ1.
f x R x
22
()
R
R
V R x dx
22
()

=
R
3
4
3
3. Thể tích hình cầu bán kính R là:
VR
3
4
3
Hoạt động 4: Áp dụng tính thể tích khối tròn xoay
H1. Lập công thức tính?
Đ1.
V xdx
2
2
0
sin
2

VD1: Cho hình phẳng giới hạn bởi
đường cong y = sinx, trục Ox, x = 0,
x = . Tính thể tích khối tròn xoay
thu được khi quay hình này xung
quanh trục Ox.
Hoạt động 5: Củng cố
Nhấn mạnh:
– Cách xây dựng các công
thức tính thể tích các khối
tròn xoay.
4. BÀI TẬP VỀ NHÀ:
Bài 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 110
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 59 Bài 3: BÀI TẬP ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
I. MỤC TIÊU:
Kiến thức:
Củng cố các công thức tính diện tích, thể tích nhờ tích phân.
Kĩ năng:
Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
Củng cố phép tính tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về diện tích, thể tích.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tính diện tích hình phẳng
H1. Nêu các bước tính diện
tích hình phẳng?
H2. Nêu các bước thực
hiện?
Đ1.
a) HĐGĐ: x = –1, x = 2
S x x dx
2
2
1
9
2
2
b) HĐGĐ:
x x e
e
1
,
e
e
S x dx
1
ln 1
=
e
e
x dx x dx
1
1
1
(1 ln ) (1 ln )

=
e
e
1
2
c) HĐGĐ: x = 3, x = 6
S x x x dx
6
22
3
( 6) (6 )
= 9
Đ2.
PTTT:
yx43
HĐGĐ: x = 0, x = 2
1. Tính diện tích hình phẳng giới
hạn bởi các đường:
a)
y x y x
2
,2
b)
y x yln , 1
c)
y x y x x
22
( 6) , 6
2. Tính diện tích hình phẳng giới
hạn bởi đường cong (C):
yx
2
1
,
tiếp tuyến với (C) tại điểm M(2; 5)
và trục Oy.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 111
S x x dx
2
2
0
8
1 4 3
3
Hoạt động 2: Luyện tập tính thể tích vật thể tròn xoay
H1. Nêu các bước thực
hiện?
H2. Viết phương trình OM,
toạ độ điểm P?
Đ1.
a) HĐGĐ: x = –1, x = 1
V x dx
1
22
1
16
(1 )
15

b)
V xdx
2
2
0
cos
2

c)
V xdx
4
2
0
tan 1
4




Đ2. (OM): y = tan.x
P(Rcos; 0)
R
V x dx
cos
22
0
tan .

=
R
3
3
(cos cos )
3

3. Tính thể tích khối tròn xoay do
hình phẳng giới hạn bởi các đường
sau quay quanh trục Ox:
a)
y x y
2
1 , 0
b)
y x y x xcos , 0, 0,
c)
y x y x xtan , 0, 0,
4
4. Cho tam giác vuông OPM có
cạnh OP nằm trên trục Ox. Đặt OM
= R,
POM
R0 , 0
3



Tính thể tích khối tròn xoay thu
được khi quay tam giác đó quanh
trục Ox.
Hoạt động 3: Củng cố
Nhấn mạnh:
– Các bước giải bài toán
tính diện tích và thể tích.
4. BÀI TẬP VỀ NHÀ:
Bài tập ôn chương III.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 112
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 60 + 61 Bài dạy: ÔN TẬP CHƯƠNG III
I. MỤC TIÊU:
Kiến thức: Củng cố:
Định nghĩa nguyên hàm. Bảng nguyên hàm. Phương pháp tính nguyên hàm.
Định nghĩa tích phân. Tính chất và phương pháp tính tích phân.
Ứng dụng của tích phân để tính diện tích, thể tích.
Kĩ năng:
Thành thạo trong việc tính nguyên hàm, tích phân.
Thành thạo trong việc tính diện tích, thể tích bằng công cụ tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học trong chương III.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Ôn tập tính nguyên hàm của hàm số
H1. Nêu cách tìm nguyên
hàm của hàm số?
H2. Nêu cách tính?
Đ1.
a) Khai triển đa thức
4 3 2
3 11
( ) 3
23
F x x x x x C
b) Biến đổi thành tổng
11
( ) cos4 cos8
8 32
F x x x C
c) Phân tích thành tổng
11
( ) ln
21

x
F x C
x
d) Khai triển đa thức
3
2
3
( ) 3
32
x
xx
e
F x e e x C
Đ2.
a) PP nguyên hàm từng phần
( 2)cos sin A x x x C
b) Khai triển
5 3 1
2 2 2
24
2
53
B x x x C
c) Sử dụng hằng đẳng thức
2
1
2
xx
C e e x C
1. Tìm nguyên hàm của các
hàm số:
a)
( ) ( 1)(1 2 )(1 3 ) f x x x x
b)
2
( ) sin4 .cos 2f x x x
c)
2
1
()
1
fx
x
d)
3
( ) ( 1)
x
f x e
2. Tính:
a)
(2 )sin
x xdx
b)
2
( 1)
x
dx
x
c)
3
1
1
x
x
e
dx
e
d)
2
1
(sin cos )
dx
xx
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 113
d)
sin cos 2cos
4



x x x
1
tan
24



D x C
Hoạt động 2: Ôn tập tính tích phân
H1. Nêu cách tính?
H2. Nêu cách tính?
Đ1.
a) Đổi biến:
1tx
2
2
1
8
2 ( 1)
3
A t dt
b) Tách phân thức
64
11
36
1
1839
14
B x x dx
c) Tích phân từng phần 2 lần
6
2
(13 1)
27
Ce
d)
1 sin2 sin cos x x x
=
2 sin
4



x
22D
Đ2.
a) Biến đổi thành tổng.
A
8

b) Bỏ dấu GTTĐ:
B
1
ln2
c) Phân tích thành tổng:
C
1
ln3
2

d) Khai triển:
D
3
5
32


3. Tính:
a)
3
0
1
x
dx
x
b)
64
3
1
1
x
dx
x
c)
2
23
0
x
x e dx
d)
0
1 sin2
xdx
4. Tính:
a)
2
2
0
cos2 sin
x xdx
b)
1
1
22
xx
dx
c)
2
2
0
1
23
dx
xx
d)
2
0
( sin )
x x dx
Hoạt động 3: Ôn tập tính diện tích, thể tích
H1. Nêu các bước thực hiện?
Đ1.
HĐGĐ: x = 0, x = 1
S x x dx
1
2
0
2 1 (1 ) 1
2
V x x dx
1
22
0
4 (1 ) (1 )


=
4
3
5. Xét hình phẳng giới hạn bởi
y x y x
2
2 1 , 2(1 )
a) Tính diện tích hình phẳng.
b) Tính thể tích khối tròn xoay
tạo thành khi quay hình phẳng
quanh trục Ox.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Các phương pháp tính
nguyên hàm, tích phân.
– Các bước giải bài toán tính
diện tích và thể tích.
4. BÀI TẬP VỀ NHÀ:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 114
Chuẩn bị kiểm tra 1 tiết.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 62 Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG III
I. MỤC TIÊU:
Kiến thức: Củng cố:
Định nghĩa nguyên hàm. Bảng nguyên hàm. Phương pháp tính nguyên hàm.
Định nghĩa tích phân. Tính chất và phương pháp tính tích phân.
Ứng dụng của tích phân để tính diện tích, thể tích.
Kĩ năng:
Thành thạo trong việc tính nguyên hàm, tích phân.
Thành thạo trong việc tính diện tích, thể tích bằng công cụ tích phân.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học trong chương III.
III. MA TRẬN ĐỀ:
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Nguyên hàm
4
0,5
2,0
Tích phân
4
0,5
2
2,0
6,0
Ứng dụng
1
2,0
2,0
Tổng
4,0
4,0
2,0
10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm) Chọn phương án đúng nhất:
Câu 1: Tính A =
3
xdx
.
A)
4
3
4
3
A x C
B)
4
3
3
4
A x C
C)
3
4
3
4
A x C
D)
2
3
3
2
A x C
Câu 2: Tính A =
sin5
xdx
.
A)
cos5
5
x
AC
B)
5cos5 A x C
C)
cos5
5

x
AC
D)
cos5 A x C
Câu 3: Tính A =
5
2
x
dx
.
A)
5
5ln2.2
x
AC
B)
5
5.2
x
AC
C)
5
5
.2
ln2

x
AC
D)
5
2
5ln2

x
AC
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 115
Câu 4: Tính A =
5
x
e dx
.
A)
5
5
x
A e C
B)
5
1
5

x
A e C
C)
1
5

x
A e C
D)
5
x
A e C
Câu 5: Tính
8
3
1
A xdx
.
A)
20A
B)
4
3
4 2 1
4
A
C)
45
4
A
D)
4
4
4 2 1
3
A
Câu 6: Tính
0
sin5
A xdx
.
A)
0A
B)
1
5
A
C)
1
5
A
D)
2
5
A
Câu 7: Tính
1
5
0
2
x
A dx
.
A)
31
5ln2
A
B)
155A
C)
155ln2A
D)
155
ln2
A
Câu 8: Tính
ln2
5
0
x
A e dx
.
A)
155A
B)
1
5
A
C)
5A
D)
31
5
A
B. Phần tự luận: (6 điểm)
Bài 1: (4 điểm) Tính các tích phân sau:
2
0
(2 )sin

I x xdx
,
ln2
2
0
1
x
x
e
J dx
e
Bài 2: (2 điểm) Tính hình phẳng giới hạn bởi các đường sau:
32
1 y x x
và
3
42 y x x
.
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
B
A
D
B
C
D
A
D
B. Phần tự luận: Mỗi câu 2 điểm
Bài 1:a)
2
0
(2 )sin

I x xdx
. Đặt
2
sin cos



u x du dx
dv xdx v x
I =
2
2
0
0
(2 )cos cos
x x xdx
=
22
0
0
(2 )cos sin

x x x
= 1
b)
ln2
2
0
1
x
x
e
J dx
e
. Đặt t =
1
x
e
dt =
x
e dx
.
02
ln2 3
xt
xt
J =
3
3
2
2
12
ln 1 ln
3
t
dt t t
t
Bài 2: Phương trình hoành độ giao điểm của hai đường:
32
1 y x x
và
3
42 y x x
.
3 2 3
1 4 2 x x x x
1
3
x
x
Diện tích: S =
3
3 2 3
1
1 4 2
x x x x dx
=
3
2
1
4
( 4 3)
3
x x dx
VI. KẾT QUẢ KIỂM TRA:
Lớp
Sĩ số
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 116
SL
%
SL
%
SL
%
SL
%
SL
%
12S1
53
12S2
54
12S3
54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Chương IV: SỐ PHỨC
Tiết dạy: 63 Bài 1: SỐ PHỨC
I. MỤC TIÊU:
Kiến thức:
Hiểu các khái niệm số phức, phần thực, phần ảo của một số phức, môđun của số phức, số
phức liên hợp.
Hiểu ý nghĩa hình học của khái niệm môđun và số phức liên hợp.
Kĩ năng:
Tính được môđun của số phức.
Tìm được số phức liên hợp của một số phức.
Biểu diễn được một số phức trên mặt phẳng toạ độ.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về toạ độ trên mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Giải các phương trình:
xx
22
1 0; 1 0
?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm số i
GV giới thiệu khái niệm số i
1. Số i
Nghiệm của phương trình
x
2
10
là số i.
i
2
1
Hoạt động 2: Tìm hiểu định nghĩa số phức
GV nêu định nghĩa số phức.
H1. Cho VD số phức? Chỉ ra
Đ1. Các nhóm thực hiện.
2. Định nghĩa số phức
Mỗi biểu thức dạng
a bi
,
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 117
phần thực và phần ảo?
i25
,
i23
,
i13
,
i13
i0
,
i50
trong đó a, b
R,
i
2
1
đgl
một số phức.
a: phần thực, b: phần ảo.
Tập số phức: C.
Chú ý: Phần thực và phần ảo
của một số phức đều là những
số thực.
Hoạt động 3: Tìm hiểu khái niệm hai số phức bằng nhau
GV nêu định nghĩa hai số
phức bằng nhau.
GV nêu chú ý.
H1. Khi nào hai số phức bằng
nhau?
H2. Khi nào z là số thực, là số
ảo?
H3. Khi nào z là số thực, là số
ảo?
Đ1. Các nhóm thực hiện.
a)
xx
yy
2 1 2
3 2 4
x
y
1
3
b)
1 2 5
3 1 3

x
y
15
2
13
3
x
y
c)
3 9 12
3 5 7

x
y
7
2

x
y
d)
2 3 2 1
(3 1) 3 7
xy
yx
2
0
x
y
Đ2.
a)
3 5 0b
5
3
b
b)
2 1 0a
1
2
a
Đ3.
c) là số ảo
d) là số thực
3. Số phức bằng nhau
Hai số phức là bằng nhau nếu
phần thực và phần ảo của
chúng tương ứng bằng nhau.
ac
a bi c di
bd
Chú ý:
Mỗi số thực a được coi là
một số phức với phần ảo bằng
0: a = a + 0i
Như vậy, a
R
a
C
Số phức 0 + bi đgl số thuần
ảo và viết đơn giản là bi:
bi = 0 + bi
Đặc biệt, i = 0 + 1i.
Số i : đơn vị ảo
VD1: Tìm các số thực x, y để z
= z':
a)
(2 1) (3 2)
( 2) ( 4)
z x y i
z x y i
b)
(1 2 ) 3
5 (1 3 )
z x i
z y i
c)
( 3 9) 3
12 (5 7)
z x i
z y i
d)
(2 3) (3 1)
(2 1) (3 7)
z x y i
z y x i
VD2: Cho số phức
(2 1) (3 5) z a b i
Tìm a, b để:
a) z là số thực
b) z là số ảo
VD3: Trong các số phức sau,
số nào là số thực, số nào là số
ảo:
a)
00
sin30 cos30 i
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 118
b)
00
sin30 cos30 i
c)
00
cos90 sin90 i
d)
00
sin90 cos90 i
Hoạt động 4: Củng cố
Nhấn mạnh:
– Ý nghĩa của số i.
– Định nghĩa số phức, phần
thực, phần ảo.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 64 Bài 1: SỐ PHỨC (tt)
I. MỤC TIÊU:
Kiến thức:
Hiểu các khái niệm số phức, phần thực, phần ảo của một số phức, môđun của số phức, số
phức liên hợp.
Hiểu ý nghĩa hình học của khái niệm môđun và số phức liên hợp.
Kĩ năng:
Tính được môđun của số phức.
Tìm được số phức liên hợp của một số phức.
Biểu diễn được một số phức trên mặt phẳng toạ độ.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức và mặt phẳng toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa số phức? Cho VD?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu biểu diễn hình học của số phức
GV giới thiệu cách biểu
diễn hình học của số phức.
H1. Nhận xét về sự tương
Đ1. Tương ứng 1–1.
4. Biểu diễn hình học số phức
Điểm M(a; b) trong một hệ toạ
độ vuông góc của mặt phẳng
đgl điểm biểu diễn số phức
z a bi
.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 119
ứng giữa cặp số (a; b) với toạ
độ của điểm trên mặt phẳng?
H2. Biểu diễn các số phức
trên mp toạ độ?
H3. Nhận xét về các số thực,
số thuần ảo?
Đ2. Các nhóm thực hiện.
Đ3. Các điểm biểu diễn số thực
nằm trên Ox, các điểm biểu diễn
số ảo nằm trên trục Oy.
VD1: Biểu diễn các số phức
sau trên mặt phẳng toạ độ:
a)
32zi
b)
23zi
c)
32 zi
d)
3zi
e)
4z
Hoạt động 2: Tìm hiểu khái niệm môđun của số phức
GV giới thiệu khái niệm
môđun của số phức.
H1. Gọi HS tính.
H2. Phân tích YCBT?
Đ1. Các nhóm thực hiện.
a), b), c)
13z
d)
3z
e)
4z
Đ2.
22
0ab
0
0
a
b
0z
5. Môđun của số phức
Độ dài của
OM
đgl môđun
của số phức z và kí hiệu
z
.
22
z a bi a b
VD2: Tính môđun của các số
phức sau:
a)
32zi
b)
23zi
c)
32 zi
d)
3zi
e)
4z
VD3: Tìm số phức có môđun
bằng 0.
Hoạt động 3: Tìm hiểu khái niệm số phức liên hợp
GV giới thiệu khái niệm số
phức liên hợp.
H1. Nhận xét mối liên hệ
giữa 2 số phức liên hợp?
H2. Tìm số phức liên hợp?
Đ1. Các nhóm thảo luận và trình
bày.
Đ2. Các nhóm thực hiện.
a)
32zi
b)
23zi
c)
32 zi
d)
3zi
6. Số phức liên hợp
Cho số phức
z a bi
. Ta gọi
a bi
là số phức liên hợp của
z và kí hiệu là
z a bi
.
Chú ý:
Trên mặt phẳng toạ độ, các
điểm biểu diễn z và
z
đối xứng
nhau qua trục Ox.
zz
zz
VD4: Tìm số phức liên hợp
của các số phức sau:
a)
32zi
b)
23zi
c)
32 zi
d)
3zi
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 120
e)
4z
e)
4z
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách biểu diễn số phức trên
mặt phẳng toạ độ.
– Môđun của số phức, số
phức liên hợp.
4. BÀI TẬP VỀ NHÀ:
Bài 3, 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 65 Bài 1: BÀI TẬP SỐ PHỨC
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm số phức, phần thực, phần ảo của một số phức, môđun của số phức, số phức liên
hợp.
Ý nghĩa hình học của khái niệm môđun và số phức liên hợp.
Kĩ năng:
Tính được môđun của số phức.
Tìm được số phức liên hợp của một số phức.
Biểu diễn được một số phức trên mặt phẳng toạ độ.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập xác định phần thực, phần ảo của số phức, số phức bằng nhau
H1. Xác định phần thực và
phần ảo của số phức?
Đ1. HS thực hiện.
a)
1,
ab
b)
2, 1 ab
c)
2 2, 0ab
1. Tìm phần thực và phần ảo
của số phức:
a)
1
zi
b)
2zi
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 121
H2. Khi nào 2 số phức bằng
nhau?
d)
0, 7 ab
Đ2.
a)
3 2 1
2 1 ( 5)
xx
yy
3
2
4
3
x
y
b)
2 2 3
2 2 1
x y x y
y x y x
0
1
x
y
c)
22z
d)
7zi
2. Tìm các số thực x, y để
zz
, biết:
a)
(3 2) (2 1)
( 1) ( 5)
z x y i
z x y i
b)
(2 ) (2 )
( 2 3) ( 2 1)
z x y y x i
z x y y x i
Hoạt động 2: Luyện tập biểu diễn số phức trên mặt phẳng toạ độ
H1. Nêu cách biểu diễn số
phức trên mặt phẳng toạ độ?
x
y
–2
O
a)
x
y
3
O
b)
Đ1.
– Phần thực: hoành độ
– Phần ảo: tung độ
x
y
2O
c)
–1
x
y
3
O
d)
1
3. Trên mặt phẳng toạ độ, tìm
tập hợp điểm biểu diễn số phức
z thoả điều kiện:
a) Phần thực của z bằng –2
b) Phần ảo của z bằng 3
c) Phần thực của z thuộc (–1;2)
d) Phần ảo của z thuộc [1; 3]
Hoạt động 3: Luyện tập tính môđun và tìm số phức liên hợp
H1. Nêu công thức tính
môđun của số phức?
H2. Xác định điểm M?
H3. Nêu định nghĩa số phức
liên hợp?
Đ1.
22
z a b
a)
7z
b)
11z
c)
5z
d)
3z
Đ2.
a) Đường tròn (O; 1)
b) Hình tròn (O; 1)
c) Hình vành khăn
d) Điểm A(0; 1)
Đ3.
a)
12zi
b)
23 zi
c)
5z
d)
7zi
4. Tính môđun của các số
phức:
a)
23 zi
b)
23zi
c)
5z
d)
3zi
5. Trên mặt phẳng toạ độ, tìm
tập hợp điểm biểu diễn các số
phức z thoả điều kiện:
a)
1z
b)
1z
c)
12z
d)
1z
và phần ảo bằng 1.
6. Tìm số phức liên hợp của số
phức:
a)
12zi
b)
23 zi
c)
5z
d)
7zi
Hoạt động 4: Củng cố
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 122
Nhấn mạnh:
– Cách biểu diễn số phức trên
mặt phẳng toạ độ.
– Môđun của số phức, số
phức liên hợp.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc trước bài "Cộng, trừ và nhân số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 66 Bài 2: CỘNG, TRỪ VÀ NHÂN SỐ PHỨC
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm phép cộng, phép trừ, phép nhân số phức.
Kĩ năng:
Vận dụng thành thạo các phép toán cộng, trừ và nhân số phức.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa số phức, môđun, số phức liên hợp?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu phép cộng, phép trừ số phức
GV nêu cách tính.
H1. Nêu qui tắc thực hiện
phép tính?
Đ1. Cộng (trừ) hai phần thực,
hai phần ảo.
a) A =
8 10 i
b) B =
32 i
c) C =
89 i
d) D =
33i
1. Phép cộng và phép trừ
Phép cộng và phép trừ hai số phức
được thực hiện theo qui tắc cộng, trừ
đa thức.
( ) ( ) ( ) ( ) a bi c di a c b d i
( ) ( ) ( ) ( ) a bi c di a c b d i
VD1: Thực hiện phép tính:
a)
(3 2 ) (5 8 ) ii
b)
(7 5 ) (4 3 ) ii
c)
(5 2 ) (3 7 ) ii
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 123
d)
(1 6 ) (4 3 ) ii
Hoạt động 2: Tìm hiểu phép nhân hai số phức
GV nêu cách tính.
H1. Nhắc lại các tính chất
của phép cộng và phép
nhân các số thực?
H2. Gọi HS tính?
Đ1. giao hoán, kết hợp, phân
phối.
Đ2. Các nhóm thực hiện.
a)
Ai14 23
b)
Bi24 10
c)
Ci22 7
d)
D 13
2. Phép nhân
Phép nhân hai số phức được thực
hiện theo qui tắc nhân đa thức rồi
thay
i
2
1
trong kết quả nhận được.
a bi c di ac bd ad bc i( )( ) ( ) ( )
Chú ý: Phép cộng và phép nhân các
số phức có tất cả các tính chất của
phép cộng và phép nhân các số thực.
VD2: Thực hiện phép tính:
a)
ii(5 2 )(4 3 )
b)
ii(2 3 )(6 4 )
c)
ii(2 3 )(5 4 )
d)
ii(3 2 )(3 2 )
Hoạt động 3: Áp dụng phép cộng và phép nhân các số phức
H1. Nêu các tính?
Đ1. Thực hiện phép tính, sau
đó tìm số phức liên hợp.
a)
zi7
b)
zi37
c)
zi3
d)
zi37
e)
zi22 7
f)
zi2 23
g)
zi2 23
h)
zi22 7
VD3: Tìm số phức liên hợp của các
số phức sau:
a)
z i i(2 3 ) (5 4 )
b)
z i i(2 3 ) (5 4 )
c)
z i i(2 3 ) (5 4 )
d)
z i i(2 3 ) (5 4 )
e)
z i i(2 3 )(5 4 )
f)
z i i(2 3 )(5 4 )
g)
z i i(2 3 )(5 4 )
h)
z i i(2 3 )(5 4 )
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách thực hiện phép
cộng, phép nhân các số
phức.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4, 5 SGK.
Chứng minh:
z z z z
z z z z
z z z z
1 2 1 2
1 2 1 2
1 2 1 2
..
Đọc tiếp bài "Cộng, trừ và nhân số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 124
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 67 Bài 2: BÀI TẬP CỘNG, TRỪ VÀ NHÂN SỐ PHỨC
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm phép cộng, phép trừ, phép nhân số phức.
Kĩ năng:
Vận dụng thành thạo các phép toán cộng, trừ và nhân số phức.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập phép cộng, phép trừ số phức
H1. Nhắc lại cách thực hiện
phép cộng, trừ các số phức?
H2. Gọi HS tính.
Đ1.
a)
i5
b)
i3 10
c)
i1 10
d)
i3
Đ2.
a)
u v i u v i3 2 , 3 2
b)
u v i u v i1 4 , 1 8
c)
u v i u v i2 , 12
d)
u v i u v i19 2 , 11 2
1. Thực hiện các phép tính sau:
a)
ii(3 5 ) (2 4 )
b)
ii( 2 3 ) ( 1 7 )
c)
ii(4 3 )–(5–7 )
d)
ii(2 3 ) (5 4 )
2. Tính u + v, u – v với:
a)
u v i3, 2
b)
u i v i1 2 , 6
c)
u i v i5 , 7
d)
u v i15, 4 2
Hoạt động 2: Luyện tập phép nhân hai số phức
H1. Nhắc lại cách thực hiện
phép nhân các số phức?
H2. Nêu cách tính?
Đ1.
a)
i13
b)
i10 4
c)
i20 15
d)
i20 8
Đ2.
i i i i
32
.
i i i
4 2 2
.1
i i i i
54
.
Nếu
n q r r4 , 0 4
3. Thực hiện các phép tính sau:
a)
ii(3 2 )(2 3 )
b)
ii( 1 )(3 7 )
c)
i5(4 3 )
d)
ii( 2 5 ).4
4. Tính
i i i
3 4 5
,,
. Nêu cách
tính
n
i
với n là một số tự nhiên
tuỳ ý.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 125
H3. Nêu cách tính?
thì
nr
ii
Đ3. Sử dụng hằng đẳng thức.
a)
i5 12
b)
i46 9
c)
i2
d)
i25
5. Thực hiện phép tính:
a)
i
2
(2 3 )
b)
i
3
(2 3 )
c)
i
2
(1 )
d)
ii
3
(1 ) 3
Hoạt động 3: Áp dụng phép cộng và phép nhân các số phức
H1. Thực hiện phép tính?
Đ1.
a)
i1
b)
i7 6 2
c) 13
d)
i17
6. Xác định phần thực, phần ảo
của các số sau:
a)
i i i(2 4 ) (3 2 )
b)
i
2
23
c)
ii(2 3 )(2 3 )
d)
i i i(2 )(3 )
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách thực hiện phép cộng,
phép nhân các số phức.
4. BÀI TẬP VỀ NHÀ:
Đọc trước bài "Phép chia số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 126
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 68 Bài 3: PHÉP CHIA SỐ PHỨC
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm số phức nghịch đảo, phép chia hai số phức.
Kĩ năng:
Biết tìm được nghịch đảo của một số phức.
Biết thực hiện được phép chia hai số phức.
Biết thực hiện các phép tính trong một biểu thức chứa các số phức.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại khái niệm số phức liên hợp, phép cộng, nhân các số phức?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu tổng và tích của hai số phức liên hợp
GV cho HS thực hiện
một số VD, rồi cho HS
nhận xét kết quả.
VD: Cho z.
Tính
z z z z,.
?
a)
zi23
b)
zi53
c)
zi53
d)
zi23
GV cho HS nêu nhận xét.
Các nhóm thực hiện và trình
bày.
z
z
zz
zz.
2+3i
2–3i
4
13
5–3i
5+3i
10
34
–5–3i
–5+3i
–10
34
–2+3i
–2–3i
–4
13
HS phát biểu.
1. Tổng và tích của hai số phức
liên hợp
Tổng của một số phức với số
phức liên hợp của nó bằng hai lần
phần thực của số phức đó:
z z a2
Tích của một số phức với số
phức liên hợp của nó bằng bình
phương môđun của số phức đó.
z z a b z
2
22
.
Nhận xét: Tổng và tích của hai số
phức liên hợp là một số thực
Hoạt động 2: Tìm hiểu phép chia hai số phức
H1. Phát biểu phép chia 2
số thực?
GV cho HS phát biểu
định nghĩa phép chia 2 số
phức.
Đ1.
a
c a bc
b
(b 0)
HS phát biểu.
2. Phép chia hai số phức
Chia số phức c + di cho số phức a
+ bi khác 0 là tìm số phức z sao
cho:
c + di = (a + bi)z
Số phức z đgl thương trong phép
chia c + di cho a + bi.
Kí hiệu:
c di
z
a bi
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 127
GV hướng dẫn cách thực
hiện.
Giả sử
i
z
i
42
1
i z i(1 ) 4 2
i i z i i(1 )(1 ) (1 )(4 2 )
zi2 6 2
zi3
VD1: Thực hiện phép chia
i42
cho
i1
.
Tổng quát:
Để tìm thương
c di
z
a bi
ta thực
hiện các bước sau:
– Đưa về dạng:
a bi z c di()
– Nhân cả 2 vế với số phức liên
hợp của a + bi, ta được:
a b z ac bd ad bc i
22
( ) ( ) ( )
– Nhân cả 2 vế với
ab
22
1
:
z ac bd ad bc i
ab
22
1
( ) ( )
Chú ý: Trong thực hành, để tính
thương
c di
a bi
, ta nhân cả tử và
mẫu với số phức liên hợp của
a bi
.
Hoạt động 3: Áp dụng thực hiện phép chia số phức
H1. Gọi HS tính.
Đ1.
a)
i i i
i
i i i
3 2 (3 2 )(2 3 ) 12 5
2 3 (2 3 )(2 3 ) 13 13
b)
i i i
i
i i i
1 (1 )(2 3 ) 1 5
2 3 (2 3 )(2 3 ) 13 13
c)
i i i
i
i i i
6 3 (6 3 )( 5 ) 15 30
5 5 ( 5 ) 25 25
VD2: Thực hiện các phép chia
sau:
a)
i
i
32
23
b)
i
i
1
23
c)
i
i
63
5
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách thực hiện phép chia
các số phức.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 128
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 69 Bài 3: BÀI TẬP PHÉP CHIA SỐ PHỨC
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm số phức nghịch đảo, phép chia hai số phức.
Kĩ năng:
Biết tìm được nghịch đảo của một số phức.
Biết thực hiện được phép chia hai số phức.
Biết thực hiện các phép tính trong một biểu thức chứa các số phức.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tìm số phức nghịch đảo
H1. Nêu cách tìm?
Đ1. Tìm
z
1
.
a)
i
zi
1 1 1 2
1 2 5 5
b)
i
z
i
1 1 2 3
11 11
23
c)
i
zi
11
d)
i
z
i
1 1 5 3
28 28
53
1. Tìm số phức nghịch đảo của
các số phức sau:
a)
zi12
b)
zi23
c)
zi
d)
zi53
Hoạt động 2: Luyện tập phép chia hai số phức
H1. Nêu cách tính?
Đ1. Nhân cả tử và mẫu với số
phức liên hợp của mẫu.
a)
i
i
2
32
=
i
47
13 13
b)
i
i
i
1 2 2 6 2 2 3
77
23

c)
i
i
i
5 15 10
2 3 13 13

2. Thực hiện các phép chia sau:
a)
i
i
2
32
b)
i
i
12
23
c)
i
i
5
23
d)
i
i
52
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 129
H2. Gọi HS tính.
d)
i
i
i
52
25
Đ2.
a)
i
i
1 2 3
2 3 13 13

b)
i
i
1 1 3
22
13
22

c)
i
i
i
32
23
d)
i
i
i
3 4 16 13
4 17 17

3. Thực hiện các phép tính sau:
a)
i
1
23
b)
i
1
13
22
c)
i
i
32
d)
i
i
34
4
Hoạt động 3: Vận dụng phép chia số phức
H1. Nêu cách tìm?
Đ1.
a)
i
zi
i
2
12

b)
zi
i
1 1 3
1 3 10 10
c)
zi
i
4 8 4
2 5 5
d)
z i z i( 2 )( 2 ) 0
zi
zi
2
2

4. Tìm số phức z thoả mãn:
a)
iz i20
b)
i z z(2 3 ) 1
c)
iz(2 ) 4 0
d)
z
2
40
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách thực hiện phép chia
các số phức.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 130
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 70 Bài 4: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
I. MỤC TIÊU:
Kiến thức:
Biết cách giải phương trình bậc hai với hệ số thực.
Căn bậc hai của một số thực âm.
Kĩ năng:
Biết tìm nghiệm phức của phương trình bậc hai với hệ số thực.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Giải phương trình:
z i z i( 2 )( 2 ) 0
?
Đ.
z i z i2 ; 2
.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu căn bậc hai của số thực âm
H1. Nhắc lại thế nào là căn
bậc hai của số thực dương a ?
GV giới thiệu khái niệm căn
bậc 2 của số thực âm.
H2. Tìm và điền vào bảng?
Đ1.
b là căn bậc 2 của a nếu
ba
2
.
Đ2. Các nhóm thực hiện yêu cầu
a
–2
–3
–4
căn
bậc 2
i 2
i 3
i2
1. Căn bậc hai của số thực
âm
Căn bậc hai của –1 là i và –i.
Căn bậc hai của số thực a <
0 là
ia
.
VD1: Tìm các căn bậc hai của
các số sau: –2, –3, –4.
Hoạt động 2: Tìm hiểu phương trình bậc hai với hệ số thực
H1. Nhắc lại cách giải
phương trình bậc hai?
GV nêu nhận xét.
Đ1. Xét
=
b ac
2
4
.
= 0: PT có 1 nghiệm thực
b
x
a2

> 0: PT có 2 nghiệm thực
phân biệt
b
x
a
1,2
2

< 0: PT không có nghiệm
thực.
2. Phương trình bậc hai với
hệ số thực
Xét phương trình bậc hai:
ax bx c
2
0
(với a, b, c
R, a
0)
Tính
=
b ac
2
4
.
Trong trường hợp
< 0, nếu
xét trong tập số phức, ta vẫn có
2 căn bậc hai thuần ảo của
là
i
. Khi đó, phương
trình có 2 nghiệm phức được
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 131
H2. Nêu các bước giải
phương trình bậc hai?
GV hướng dẫn HS nêu nhận
xét.
Đ2. HS thực hiện lần lượt các
bước.
= –3
i
x
1,2
13
2

Các nhóm thảo luận và trình
bày.
xác định bởi công thức:
bi
x
a
1,2
2

VD2: Giải phương trình sau
trên tập số phức:
xx
2
10
Nhận xét: Trên tập số phức:
Mọi PT bậc hai đều có 2
nghiệm (có thể trùng nhau).
Tổng quát, mọi PT bậc n (n
1):
nn
n
a x a x a
1
01
... 0
với a
0
, a
1
, …, a
n
C, a
0
0
đều có n nghiệm phức (có thể
trùng nhau).
Hoạt động 3: Áp dụng giải phương trình bậc hai
H1. Gọi HS giải.
Đ1.
a)
xi
1,2
3
b)
xi
1,2
12
c)
i
x
1,2
3 11
10
d)
x
x
1
3

VD3: Giải các phương trình
sau trên tập số phức:
a)
x
2
30
b)
xx
2
2 3 0
c)
xx
2
5 3 1 0
d)
xx
2
2 3 0
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách tính căn bậc hai của số
thực âm.
– Cách giải phương trình bậc
hai với hệ số thực.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 132
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 71 Bài 4: BÀI TẬP PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
I. MỤC TIÊU:
Kiến thức: Củng cố:
Cách giải phương trình bậc hai với hệ số thực.
Căn bậc hai của một số thực âm.
Kĩ năng:
Biết tìm nghiệm phức của phương trình bậc hai với hệ số thực.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tìm căn bậc hai của số thực âm
H1. Nêu công thức tìm căn
bậc hai phức của số thực âm?
Đ1.
a
các căn bậc hai phức
–7
ii7; 7
–8
ii2 2; 2 2
–12
ii2 3; 2 3
–20
ii2 5; 2 5
–121
ii11; 11
1. Tìm các căn bậc hai phức
của các số sau:
–7; –8; –12; –20; –121
Hoạt động 2: Luyện tập giải phương trình bậc hai với hệ số thực
H1. Nêu cách giải?
H2. Nêu cách giải?
Đ1.
a)
z
1,2
15
2
b)
zi
1,2
12
c)
zi
1,2
23
d)
i
z
1,2
1 23
4

Đ2.
a)
i
z
1,2
12
3
b)
i
z
1,2
3 47
14

2. Giải các phương trình sau
trên tập số phức:
a)
zz
2
10
b)
zz
2
2 5 0
c)
zx
2
4 7 0
d)
xx
2
2 3 0
3. Giải các phương trình sau
trên tập số phức:
a)
zz
2
3 2 1 0
b)
zz
2
7 3 2 0
c)
zz
2
5 7 11 0
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Giải tích 12 chuẩn
GV: Phạm Việt Phương 133
c)
i
z
1,2
7 171
10
d)
zi4
d)
z
2
16 0
Hoạt động 3: Vận dụng giải phương trình bậc hai
H1. Nêu cách giải?
H2. Viết công thức nghiệm và
tính
zz
12
,
zz
12
?
H3. Nêu cách tìm?
Đ1.
a)
z z i
1,2 3,4
2; 3
b)
z i z i
1,2 3,4
2; 5
c)
z z i
1 2,3
2; 1 3
d)
i
zz
1 2,3
33
1;
2

Đ2.
Xét < 0.
bi
z
a
1,2
2


b
zz
a
12
,
c
zz
a
12
Đ3.
x z x z( )( ) 0
x z z x z z
2
( ) 0
(*)
mà
z z a zz a b
22
2,
nên
(*)
x ax a b
2 2 2
20
4. Giải các phương trình sau
trên tập số phức:
a)
zz
42
60
b)
zz
42
7 10 0
c)
z
3
80
d)
z z z
32
4 6 3 0
5. Cho a, b, c
R, a
0, z
1
, z
2
là các nghiệm của phương trình
az bz c
2
0
. Hãy tính
zz
12
và
zz
12
?
6. Cho số phức
z a bi
. Tìm
một phương trình bậc hai với
hệ số thực nhận z và
z
làm
nghiệm.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách tính căn bậc hai của số
thực âm.
– Cách giải phương trình bậc
hai với hệ số thực.
– Cách vận dụng việc giải
phương trình bậc hai với hệ
số thực.
4. BÀI TẬP VỀ NHÀ:
Bài tập ôn chương IV.
Chuẩn bị kiểm tra 1 tiết chương IV.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
| 1/133
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 12A3
Chương I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT
VÀ VẼ ĐỒ THỊ HÀM SỐ Tiết dạy: 01
Bài 1: SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ I. MỤC TIÊU: Kiến thức:
 Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm này với đạo hàm.
 Nắm được qui tắc xét tính đơn điệu của hàm số. Kĩ năng:
 Biết vận dụng qui tắc xét tính đơn điệu của một hàm số và dấu đạo hàm của nó. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đạo hàm ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
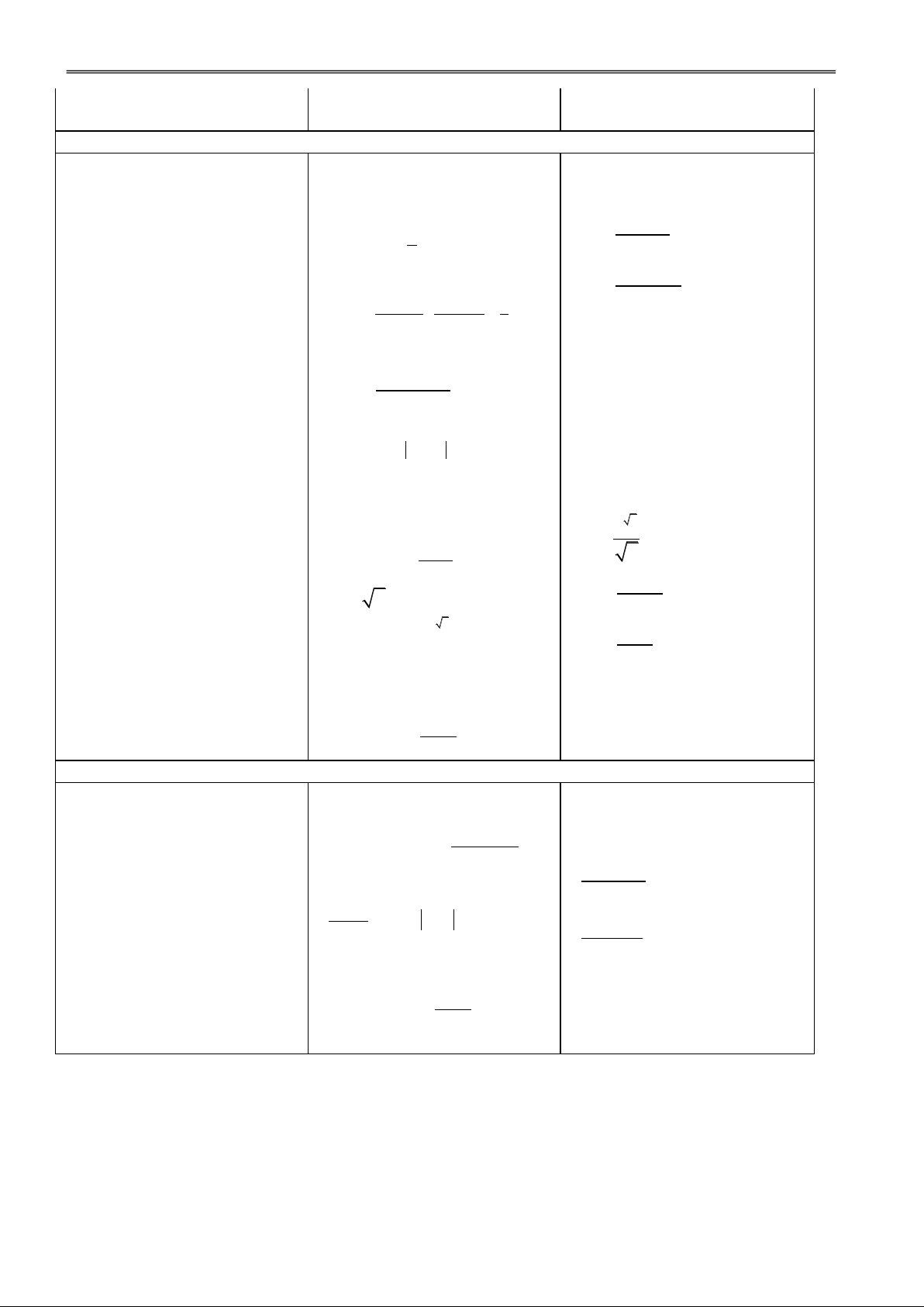
2. Kiểm tra bài cũ: (5') 2 x 1
H. Tính đạo hàm của các hàm số: a) y   , b) y
. Xét dấu đạo hàm của các hàm số đó? 2 x 1
Đ. a) y '  x b) y '   . 2 x 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Nhắc lại các kiến thức liên quan tới tính đơn điệu của hàm số y
I. Tính đơn điệu của hàm số
1. Nhắc lại định nghĩa  5 Dựa vào KTBC, cho HS
Giả sử hàm số y = f(x) xác
nhận xét dựa vào đồ thị của các x định trên K. hàm số. -8 -6 -4 -2 2 4 6 8
y = f(x) đồng biến trên K  -5
x1, x2 K: x1 < x2 f(x1) < f(x2) f x Đ1.
 ( ) f (x ) 
H1. Hãy chỉ ra các khoảng 1 2 0 , x x
đồng biến, nghịch biến của các 2 x 1 2 y    hàm số
đồng biến trên (–∞;
x1,x2 K (x1 x2) đã cho? 2
0), nghịch biến trên (0; +∞)
y = f(x) nghịch biến trên K 1  y
x1, x2 K: x1 < x2
x nghịch biến trên (–∞; 0), f(x1) > f(x2) (0; +∞) f x
H2. Nhắc lại định nghĩa tính  ( ) f (x ) 1 2  0 , đơn điệu của hàm số? x x 1 2 x K (x 1,x2 1 x2) GV: Phạm Việt Phương 1
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
H3. Nhắc lại phương pháp xét
tính đơn điệu của hàm số đã biết? Đ4.
y > 0  HS đồng biến
H4. Nhận xét mối liên hệ giữa y < 0  HS nghịch biến
đồ thị của hàm số và tính đơn y điệu của hàm số? Nhận xét:
 GV hướng dẫn HS nêu nhận
Đồ thị của hàm số đồng biến
xét về đồ thị của hàm số. x
trên K là một đường đi lên từ O trái sang phải. y
Đồ thị của hàm số nghịch x
biến trên K là một đường đi O
xuống từ trái sang phải.
Hoạt động 2: Tìm hiểu mối liên hệ giữa tính đơn điệu của hàm số và dấu của đạo hàm
 Dựa vào nhận xét trên, GV
2. Tính đơn điệu và dấu của
nêu định lí và giải thích. đạo hàm:
Định lí: Cho hàm số y = f(x) có đạo hàm trên K.
Nếu f '(x) > 0, x   K
thì y = f(x) đồng biến trên K.
Nếu f '(x) < 0, x   K
thì y = f(x) nghịch biến trên K.
Chú ý: Nếu f (x) = 0, x   K
thì f(x) không đổi trên K.
Hoạt động 3: Áp dụng xét tính đơn điệu của hàm số
 Hướng dẫn HS thực hiện.
 HS thực hiện theo sự hướng VD1: Tìm các khoảng đơn dẫn của GV. điệu của hàm số:
H1. Tính y và xét dấu y ? Đ1.
a) y  2x 1 a) y = 2 > 0, x b) 2
y x  2x x   y' y   b) y = 2x – 2 x  1  y' 0 y  
Hoạt động 4: Củng cố Nhấn mạnh:
– Mối liên quan giữa đạo hàm
và tính đơn điệu của hàm số. GV: Phạm Việt Phương 2
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Sự đồng biến, nghịch biến của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 12A3 Tiết dạy: 02
Bài 1: SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm này với đạo hàm.
 Nắm được qui tắc xét tính đơn điệu của hàm số. Kĩ năng:
 Biết vận dụng qui tắc xét tính đơn điệu của một hàm số và dấu đạo hàm của nó. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đạo hàm ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm các khoảng đơn điệu của hàm số 4 y  2x 1?
Đ. Hàm số đồng biến trong khoảng (0; +∞), nghịch biến trong khoảng (–∞; 0). 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu thêm về mối liên hệ giữa đạo hàm và tính đơn điệu của hàm số
I. Tính đơn điệu của hàm số
 GV nêu định lí mở rộng và
2. Tính đơn điệu và dấu của giải thích thông qua VD. đạo hàm Chú ý: x  0 
Giả sử y = f(x) có đạo hàm y’ + 0 +
trên K. Nếu f (x) 0 (f(x) 0), 
x K và f(x) = 0 chỉ tại một y 0
số hữu hạn điểm thì hàm số 
đồng biến (nghịch biến) trên K.
VD2: Tìm các khoảng đơn
điệu của hàm số y = x3.
Hoạt động 2: Tìm hiểu qui tắc xét tính đơn điệu của hàm số GV: Phạm Việt Phương 3
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
II. Qui tắc xét tính đơn điệu
 GV hướng dẫn rút ra qui tắc của hàm số
xét tính đơn điệu của hàm số. 1. Qui tắc
1) Tìm tập xác định.
2) Tính f(x). Tìm các điểm xi (i
= 1, 2, …, n) mà tại đó đạo
hàm bằng 0 hoặc không xác định.
3) Săpx xếp các điểm xi theo
thứ tự tăng dần và lập bảng biến thiên.
4) Nêu kết luận về các khoảng
đồng biến, nghịch biến của hàm số.
Hoạt động 3: Áp dụng xét tính đơn điệu của hàm số 2. Áp dụng
 Chia nhóm thực hiện và gọi  Các nhóm thực hiện yêu cầu. HS lên bảng.
a) đồng biến (–; –1), (2; +)
VD3: Tìm các khoảng đơn nghịch biến (–1; 2)
điệu của các hàm số sau:
b) đồng biến (–; –1), (–1; +) 1 1
y x x x  a) 3 2 2 2 3 2  x 1
GV hướng dẫn xét hàm số: b) y x  1   trên 0;   .  2  H1. Tính f(x) ? Đ1. VD4: Chứng minh:
f(x) = 1 – cosx  0 x  sin x (f(x) = 0  x = 0)      trên khoảng  0; 
f(x) đồng biến trên 0;     2  .  2   với 0 x    ta có: 2
f (x)  x sin x > f(0) = 0
Hoạt động 4: Củng cố Nhấn mạnh:
– Mối liên quan giữa đạo hàm
và tính đơn điệu của hàm số.
– Qui tắc xét tính đơn điệu của hàm số.
– Ứng dụng việc xét tính đơn
điệu để chứng minh bất đẳng thức.
4. BÀI TẬP VỀ NHÀ:  Bài 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 4
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 12A3 Tiết dạy: 03
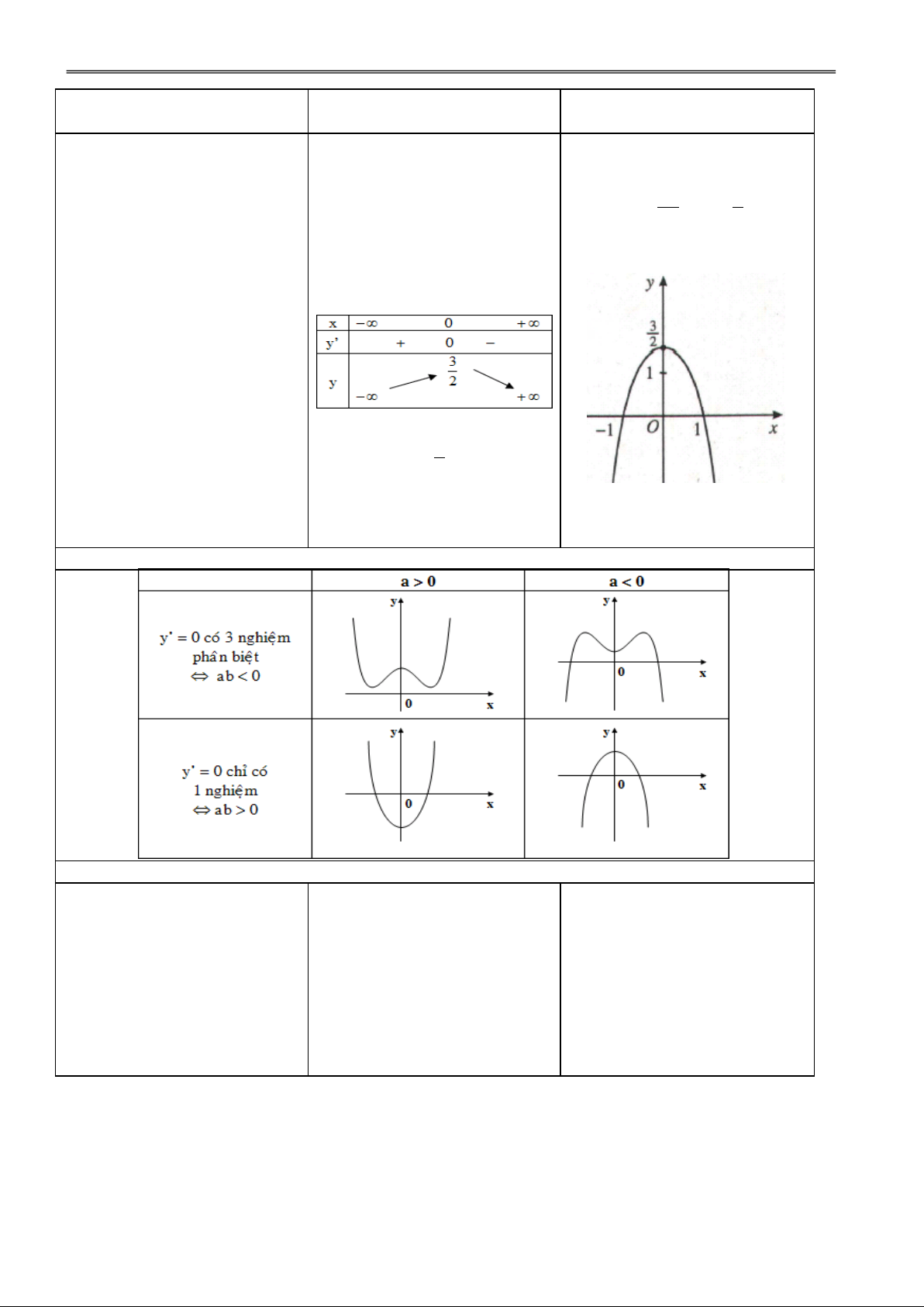
Bài 2: CỰC TRỊ CỦA HÀM SỐ I. MỤC TIÊU: Kiến thức:
 Mô tả được các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
 Mô tả được các điều kiện đủ để hàm số có điểm cực trị. Kĩ năng:
 Sử dụng thành thạo các điều kiện đủ để tìm cực trị. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3') x
H. Xét tính đơn điệu của hàm số: 2 y  (x  3) ? 3    4  Đ. ĐB: 4   ;  ,(3; )  , NB:  ;3.  3   3  3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
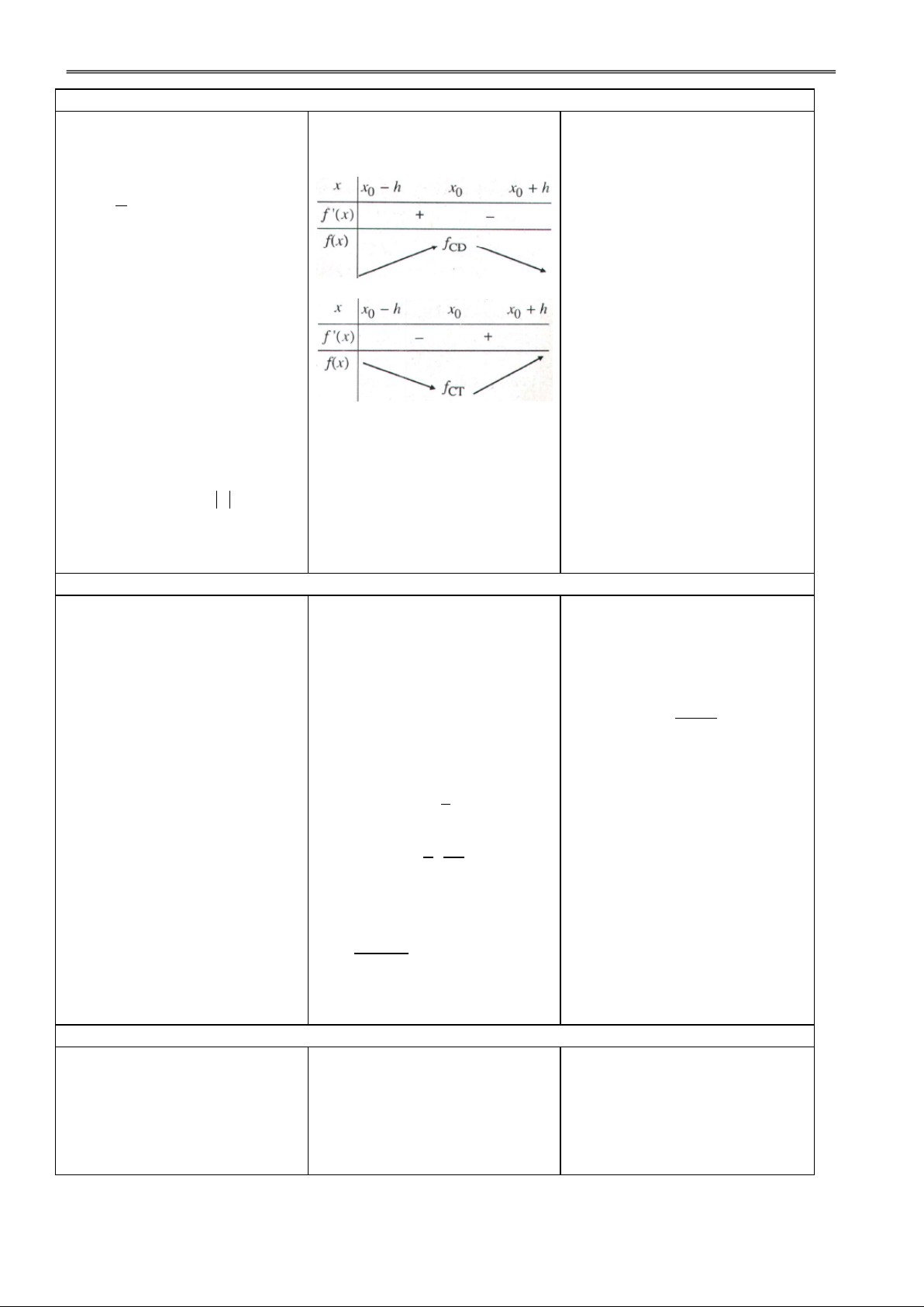
Hoạt động 1: Tìm hiểu khái niệm cực trị của hàm số
 Dựa vào KTBC, GV giới
I. KHÁI NIỆM CỰC ĐẠI,
thiệu khái niệm CĐ, CT của CỰC TIỂU hàm số. Định nghĩa:
Cho hàm số y = f(x) xác định
Nhấn mạnh: khái niệm cực trị
và liên tục trên khoảng (a; b)
mang tính chất "địa phương".
và điểm x0 (a; b).
a) f(x) đạt CĐ tại x0 h > 0,
f(x) < f(x0), x S(x0, h)\ {x0}.
b) f(x) đạt CT tại x0 h > 0,
f(x) > f(x0), x S(x0, h)\ {x0}. Chú ý:
H1. Xét tính đơn điệu của hàm Đ1.
a) Điểm cực trị của hàm số;
số trên các khoảng bên trái, Bên trái: hàm số ĐB  f(x) 0 Giá trị cực trị của hàm số; bên phải điểm CĐ?
Bên phái: h.số NB  f(x) 0. Điểm cực trị của đồ thị hàm số.
b) Nếu y = f(x) có đạo hàm
trên (a; b) và đạt cực trị tại x0
(a; b) thì f(x0) = 0. GV: Phạm Việt Phương 5
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Hoạt động 2: Tìm hiểu điều kiện đủ để hàm số có cực trị
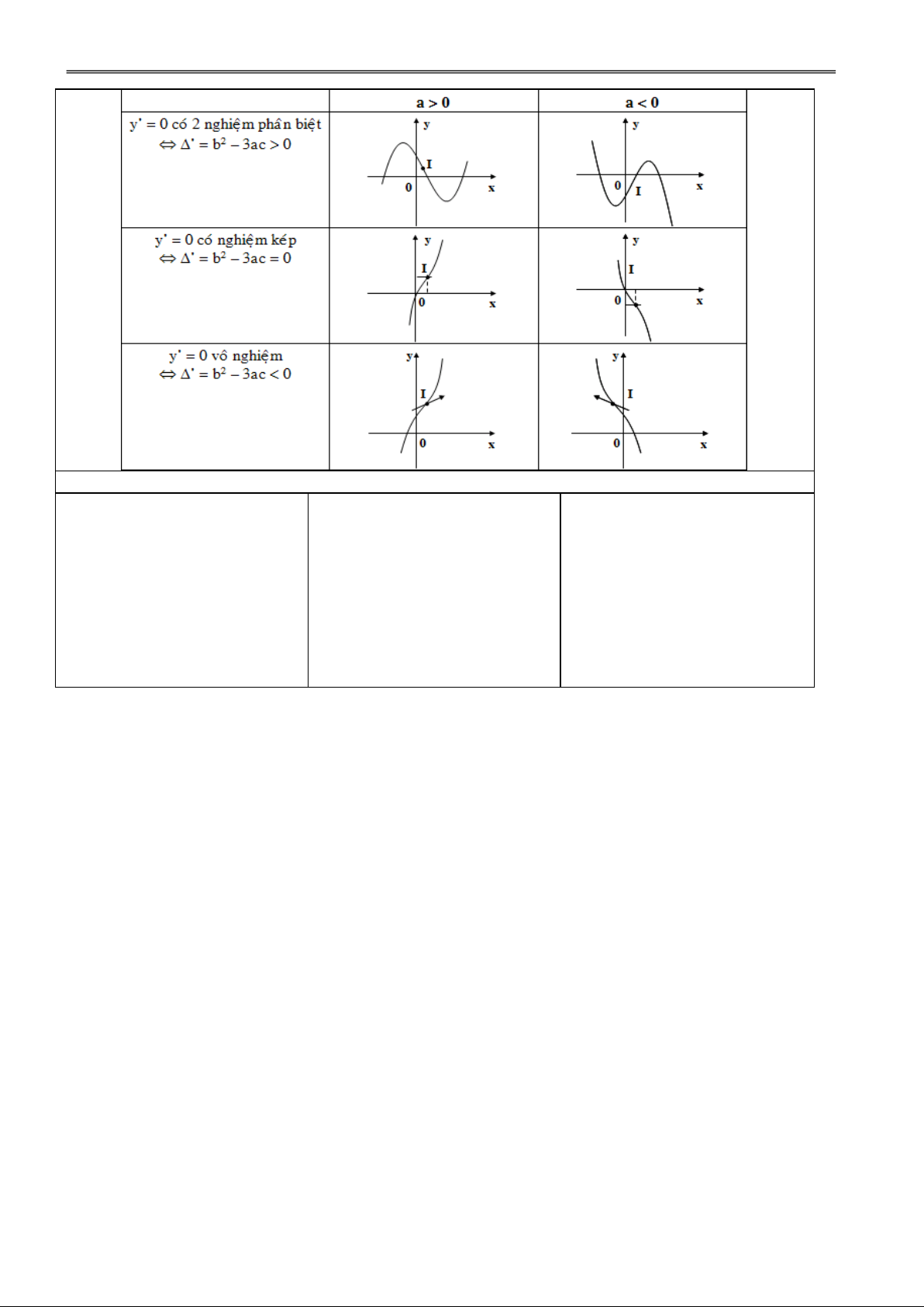
 GV phác hoạ đồ thị của các 
II. ĐIỀU KIỆN ĐỦ ĐỂ HÀM hàm số: a) không có cực trị. SỐ CÓ CỰC TRỊ a) y  2  x 1 b) có CĐ, CT.
Định lí 1: Giả sử hàm số y =
f(x) liên tục trên khoảng K = x b) 2 y  (x  3) (x  ;
h x h) và có đạo hàm 3 0 0
Từ đó cho HS nhận xét mối
trên K hoặc K \ {x0} (h > 0).
liên hệ giữa dấu của đạo hàm
a) f(x) > 0 trên (x  ; h x ) , 0 0
và sự tồn tại cực trị của hàm
f(x) < 0 trên (x ; x h) thì x0 số. 0 0
là một điểm CĐ của f(x).
b) f(x) < 0 trên (x  ; h x ) , 0 0
f(x) > 0 trên (x ; x h) thì x 0 0 0
là một điểm CT của f(x).
 GV hướng dẫn thông qua
việc xét hàm số y x .
Nhận xét: Hàm số có thể đạt
cực trị tại những điểm mà tại
đó đạo hàm không xác định.
Hoạt động 3: Áp dụng tìm điểm cực trị của hàm số
 GV hướng dẫn các bước thực
VD1: Tìm các điểm cực trị của hiện. Đ1. hàm sô: H1. a) D = R a) 2
y f (x)  x 1 – Tìm tập xác định.
y = –2x; y = 0  x = 0 b) 3 2
y f (x)  x x x  3 – Tìm y. Điểm CĐ: (0; 1) x  – 3 1
Tìm điểm mà y = 0 hoặc b) D = R
c) y f (x)  không tồn tại. x  y = 2
3x  2x 1 ; 1
– Lập bảng biến thiên.  x  1
– Dựa vào bảng biến thiên để y = 0   kết luận. 1 x    3   Điểm CĐ: 1 86   ;   3 27  , Điểm CT: (1;2) c) D = R \ {–1} 2 y '   0,x  1  2 (x 1)
 Hàm số không có cực trị.
Hoạt động 4: Củng cố Nhấn mạnh:
– Khái niệm cực trị của hàm số.
– Điều kiện cần và điều kiện
đủ để hàm số có cực trị. GV: Phạm Việt Phương 6
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Làm bài tập 1, 3 SGK.
 Đọc tiếp bài "Cực trị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 12A3 Tiết dạy: 04
Bài 2: CỰC TRỊ CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Mô tả được các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
 Mô tả được các điều kiện đủ để hàm số có điểm cực trị. Kĩ năng:
 Sử dụng thành thạo các điều kiện đủ để tìm cực trị. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu và cực trị của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Tìm điểm cực trị của hàm số: 3
y x  3x 1?
Đ. Điểm CĐ: (–1; 3); Điểm CT: (1; –1). 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu Qui tắc tìm cực trị của hàm số
 Dựa vào KTBC, GV cho HS  HS nêu qui tắc.
III. QUI TẮC TÌM CỰC TRỊ
nhận xét, nêu lên qui tắc tìm Qui tắc 1: cực trị của hàm số.
1) Tìm tập xác định.
2) Tính f(x). Tìm các điểm tại
đó f(x) = 0 hoặc f(x) không xác định.
3) Lập bảng biến thiên.
4) Từ bảng biến thiên suy ra các điểm cực trị.
Hoạt động 2: Áp dụng qui tắc 1 tìm cực trị của hàm số
 Cho các nhóm thực hiện.
 Các nhóm thảo luận và trình VD1: Tìm các điểm cực trị của bày. hàm số:
a) CĐ: (–1; 3); CT: (1; –1). a) 2
y x(x  3) b) CĐ: (0; 2); b) 4 2
y x  3x  2 GV: Phạm Việt Phương 7
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn x  3 1   3 1  1 CT:   y  ;   ,  ;   c)  x  2 4   2 4  1 c) Không có cực trị 2 x x 1 d) y
d) CĐ: (–2; –3); CT: (0; 1) x 1
Hoạt động 3: Tìm hiểu qui tắc 2 để tìm cực trị của hàm số
 GV nêu định lí 2 và giải Định lí 2: thích.
Giả sử y = f(x) có đạo hàm cấp 2 trong (x  ;
h x h) (h > 0). 0 0
a) Nếu f(x0) = 0, f(x0) > 0
thì x0 là điểm cực tiểu.
b) Nếu f(x0) = 0, f(x0) < 0
thì x0 là điểm cực đại.
H1. Dựa vào định lí 2, hãy nêu Đ1. HS phát biểu.
qui tắc 2 để tìm cực trị của hàm Qui tắc 2: số?
1) Tìm tập xác định.
2) Tính f(x). Giải phương trình
f(x) = 0 và kí hiệu xi là nghiệm
3) Tìm f(x) và tính f(xi).
4) Dựa vào dấu của f(xi) suy
ra tính chất cực trị của xi.
Hoạt động 4: Áp dụng qui tắc 2 để tìm cực trị của hàm số
 Cho các nhóm thực hiện.
 Các nhóm thảo luận và trình VD2: Tìm cực trị của hàm số: bày. 4 x a) CĐ: (0; 6) 2 y   x  a) 2 6 4 CT: (–2; 2), (2; 2) y   b) sin 2x b) CĐ: x    k 4 3 CT: x    k 4
Hoạt động 5: Củng cố Nhấn mạnh:
– Các qui tắc để tìm cực trị của hàm số.
– Nhận xét qui tắc nên dùng
 Đối với các hàm đa thức bậc
ứng với từng loại hàm số.
cao, hàm lượng giác, … nên dùng qui tắc 2.
Câu hỏi: Đối với các hàm số
 Đối với các hàm không có
sau hãy chọn phương án đúng:
đạo hàm không thể sử dụng qui 1) Chỉ có CĐ. tắc 2. 2) Chỉ có CT.
3) Không có cực trị. 4) Có CĐ và CT. a) 3 2
y x x  5x  3 a) Có CĐ và CT b) Không có CĐ và CT b) 3 2
y  x x  5x  3 c) Có CĐ và CT 2 x x  4 d) Không có CĐ và CT c) y x  2 GV: Phạm Việt Phương 8
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn x  4 d) y x  2
4. BÀI TẬP VỀ NHÀ:
 Làm bài tập 2, 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 05
Bài 2: BÀI TẬP CỰC TRỊ CỦA HÀM SỐ I. MỤC TIÊU: Kiến thức:
 Mô tả được các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số.
 Mô tả được các điều kiện đủ để hàm số có điểm cực trị. Kĩ năng:
 Sử dụng thành thạo các điều kiện đủ để tìm cực trị. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu và cực trị của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Sử dụng qui tắc 1 để tìm cực trị của hàm số
 Cho các nhóm thực hiện.
 Các nhóm thảo luận và trình 1. Tìm các điểm cực trị của bày. hàm số:
H1. Nêu các bước tìm điểm Đ1. a) 3 2
y  2x  3x  36x 10
cực trị của hàm số theo qui tắc a) CĐ: (–3; 71); CT: (2; –54) b) 4 2
y x  2x  3 1? b) CT: (0; –3)
c) CĐ: (–1; –2); CT: (1; 2) 1 c) y x   x 1 3  d) CT:  ;   d) 2 y x x 1 2 2 
Hoạt động 2: Sử dụng qui tắc 2 để tìm cực trị của hàm số
 Cho các nhóm thực hiện.
 Các nhóm thảo luận và trình 2. Tìm các điểm cực trị của bày. hàm số:
H1. Nêu các bước tìm điểm Đ1. a) 4 2
y x  2x 1
cực trị của hàm số theo qui tắc a) CĐ: (0; 1); CT: (1; 0)
b) y  sin 2x x 2?  b) CĐ: x   
c) y  sin x  cos x k 6 GV: Phạm Việt Phương 9
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn  d) 5 3
y x x  2x 1 CT: x     l 6  c) CĐ: x   2  k 4  CT: x   (2l 1) 4 d) CĐ: x = –1; CT: x = 1
Hoạt động 3: Vận dụng cực trị của hàm số để giải toán
H1. Nêu điều kiện để hàm số Đ1. Phương trình y = 0 có 2 3. Chứng minh rằng với mọi m,
luôn có một CĐ và một CT? nghiệm phân biệt. hàm số 3 2
y x mx  2x 1  2
y '  3x  2mx  2 = 0 luôn luôn có một điểm CĐ và một có 2 nghiệm phân biệt. điểm CT.
  = m2 + 6 > 0, m
Hướng dẫn HS phân tích yêu
4. Xác định giá trị của m để cầu bài toán. 2 x mx 1
H2. Nếu x = 2 là điểm CĐ thì Đ2. hàm số y  đạt CĐ x
y(2) phải thoả mãn điều kiện mm  1  gì? tại x = 2. y(2) = 0   m   3
H3. Kiểm tra với các giá trị m vừa tìm được? Đ3. m = –1: không thoả mãn m = –3: thoả mãn
Hoạt động 4: Củng cố Nhấn mạnh:
– Điều kiện cần, điều kiện đủ
để hàm số có cực trị.
– Các qui tắc tìm cực trị của hàm số.
4. BÀI TẬP VỀ NHÀ:
 Làm các bài tập còn lại trong SGK và bài tập thêm.
 Đọc trước bài "Giá trị lớn nhất và giá trị nhỏ nhất của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 10
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 06
Bài 3: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ I. MỤC TIÊU: Kiến thức:
 Biết các khái niệm GTLN, GTNN của hàm số trên một tập hợp số.
 Nắm được qui tắc tìm GTLN, GTNN của hàm số. Kĩ năng:
 Biết cách tìm GTLN, GTNN của hàm số trên một đoạn, một khoảng.
 Phân biệt việc tìm GTLN, GTNN với tìm cực trị của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu và cực trị của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
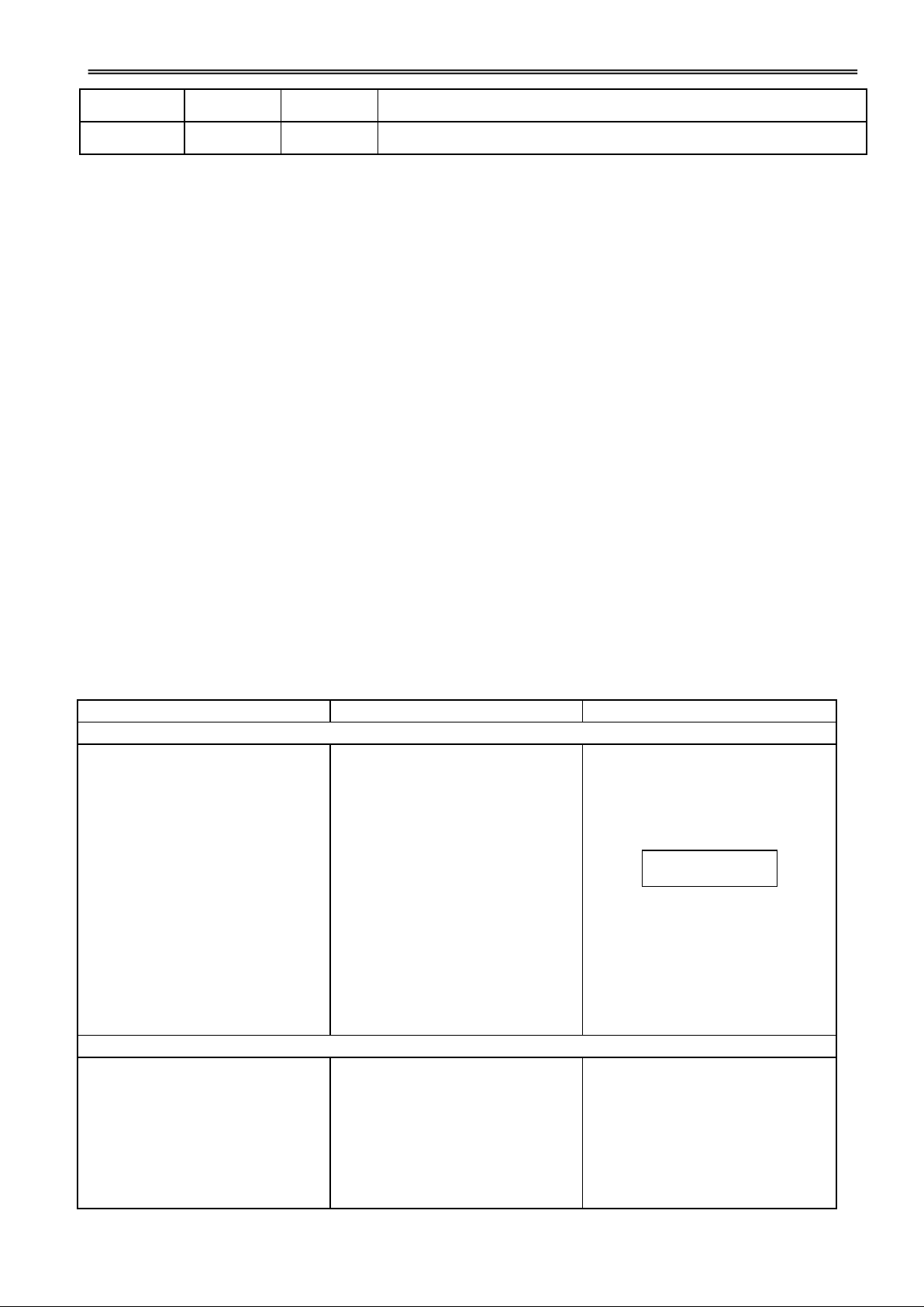
2. Kiểm tra bài cũ: (5') H. Cho hàm số 3 2
y x x x 1. Hãy tìm cực trị của hàm số. So sánh giá trị cực trị với y( 2  ), y 1 ( )?  1  32 Đ. CÑ yy    ,
 1  0 ; y( )   , y( )  .  CT y y( ) 2 9 1 0 3  27 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm GTLN, GTNN của hàm số
 Từ KTBC, GV dẫn dắt đến I. ĐỊNH NGHĨA khái niệm GTLN, GTNN của
Cho hàm số y = f(x) xác định hàm số. trên D.
 GV cho HS nhắc lại định  Các nhóm thảo luận và trình
max f (x)  M
nghĩa GTLN, GTNN của hàm bày. D a)
f (x)  M, x   D số.   x
  D : f (x )  M  0 0
min f (x)  m D b)
f (x)  m, x   D   x
  D : f (x )  m  0 0
 GV hướng dẫn HS thực hiện.
H1. Lập bảng biến thiên của Đ1.
VD1: Tìm GTLN, GTNN của hàm số ? x 0 1 
hàm số sau trên khoảng (0; +∞) y’ – 0 +   y -3
 min f (x)  3   f 1 ( ) (0;) f(x) không có GTLN trên GV: Phạm Việt Phương 11
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn (0;+∞)
Hoạt động 2: Tìm hiểu cách tìm GTLN, GTNN của hàm số trên một khoảng
 GV hướng dãn cách tìm II. CÁCH TÍNH GTLN,
GTLN, GTNN của hàm số liên
GTNN CỦA HÀM SỐ LIÊN tục trên một khoảng.
TỤC TRÊN MỘT KHOẢNG
Dựa vào bảng biến thiên để
xác định GTLN, GTNN của
hàm số liên tục trên một khoảng.
H1. Lập bảng biến thiên của Đ1.
VD2: Tính GTLN, GTNN của hàm số ? x  -1  hàm số 2
y x  2x 5 . y’ – 0 +   y –6
 min y y( 1  )  6  R không có GTLN.
Hoạt động 3: Vận dụng cách tìm GTLN, GTNN của hàm số để giải toán
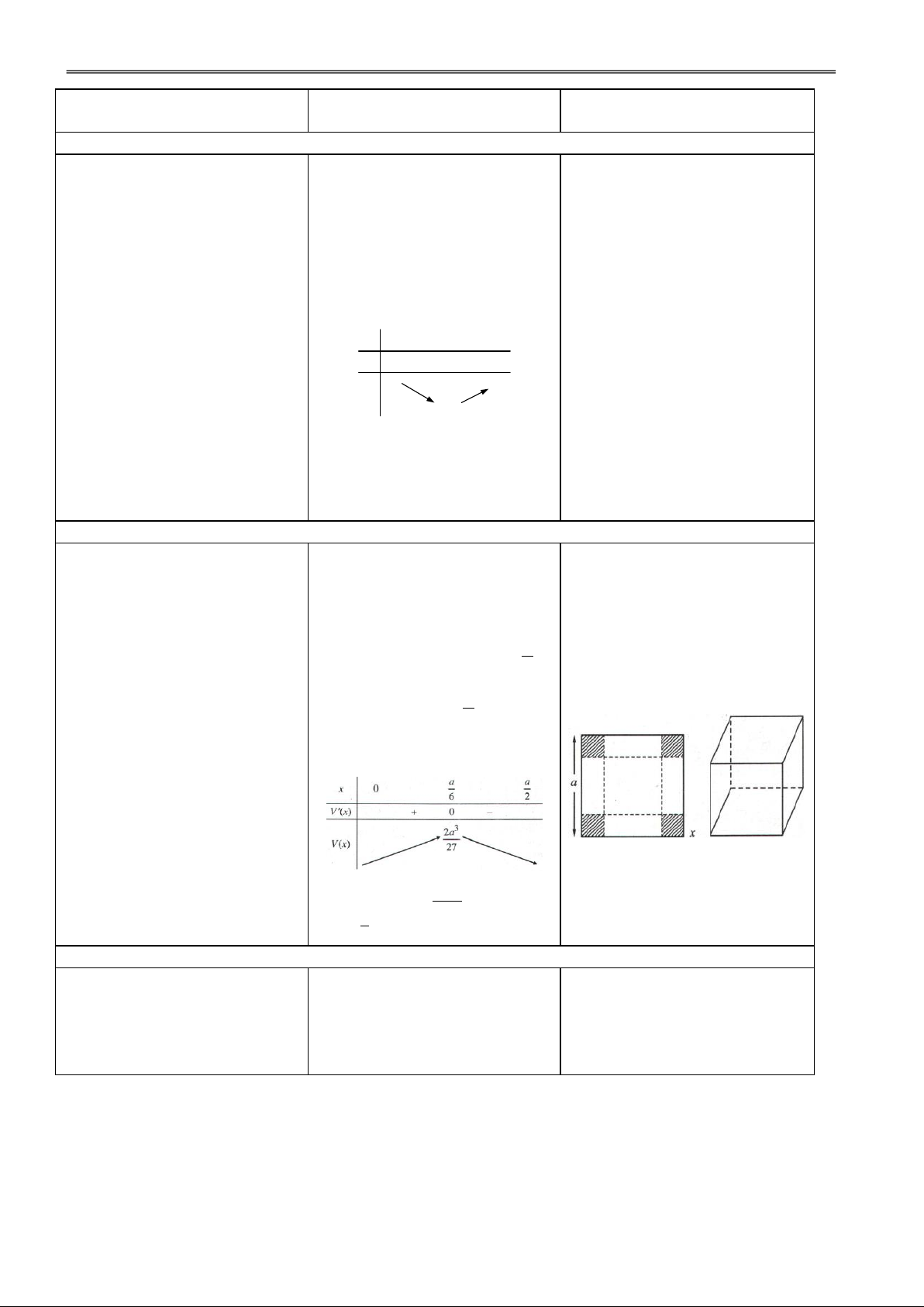
 GV hướng dẫn cách giải
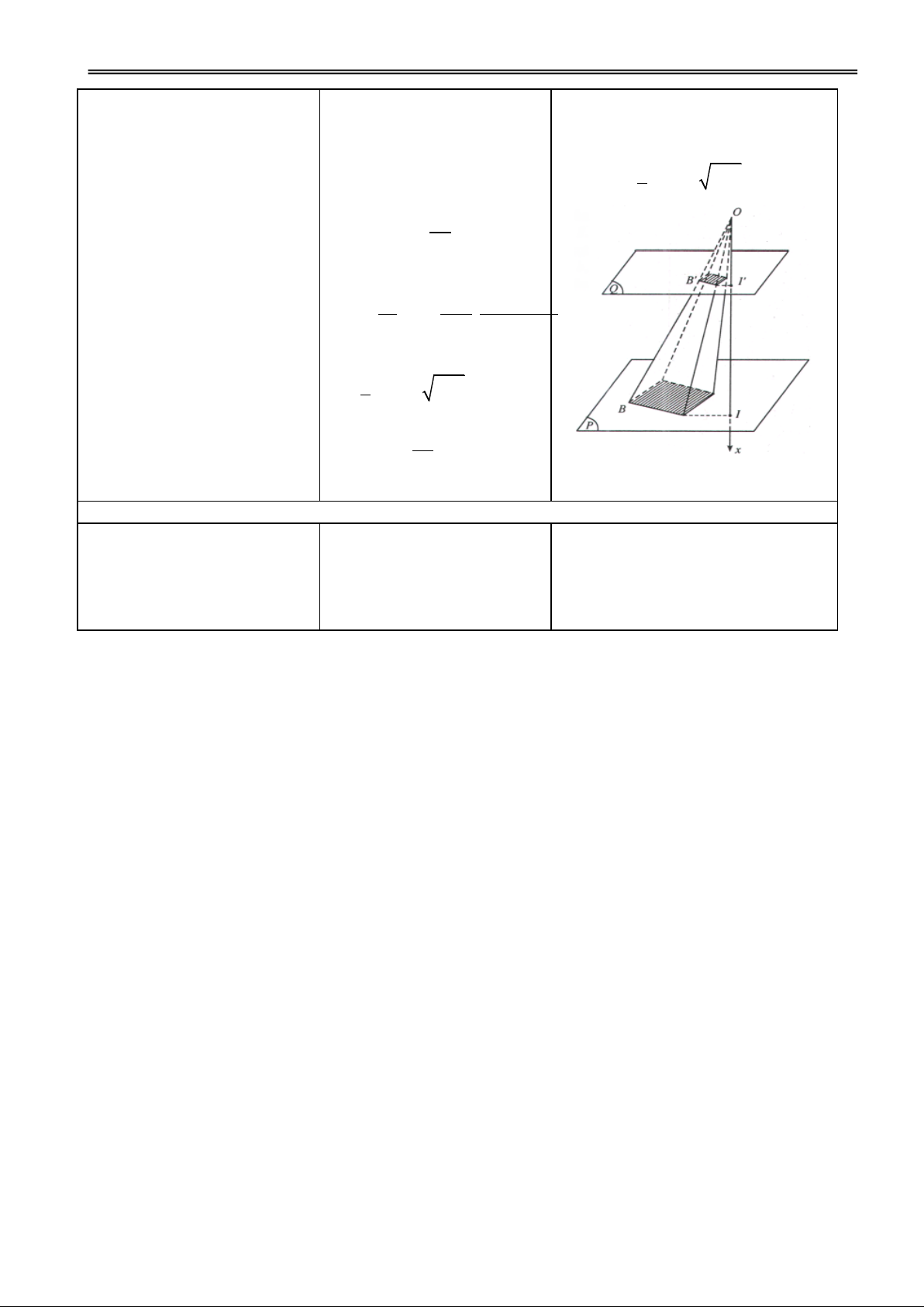
VD3: Cho một tấm nhôm hình quyết bài toán.
vuông cạnh a. Người ta cắt ở
bốn góc bốn hình vuông bằng
H1. Tính thể tích khối hộp ? Đ1.
nhau, rồi gập tấm nhôm lại  a
thành một cái hộp không nắp. 2
V(x)  x(a x)   x  2 0  
Tính cạnh của các hình vuông 2 
H2. Nêu yêu cầu bài toán ?
bị cắt sao cho thể tích của khối  a Đ2. Tìm x  ; hộp là lớn nhất. 0  0   2  sao cho V(x0) có GTLN.
H3. Lập bảng biến thiên ? Đ3. 3 a  2 max V (x)   a  27 0;   2 
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách tìm GTLN, GTNN của
hàm số liên tục trên một khoảng.
4. BÀI TẬP VỀ NHÀ:  Làm bài tập 4, 5 SGK.
 Đọc tiếp bài "GTLN, GTNN của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 12
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 07
Bài 3: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Biết các khái niệm GTLN, GTNN của hàm số trên một tập hợp số.
 Nắm được qui tắc tìm GTLN, GTNN của hàm số. Kĩ năng:
 Biết cách tìm GTLN, GTNN của hàm số trên một đoạn, một khoảng.
 Phân biệt việc tìm GTLN, GTNN với tìm cực trị của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về cực trị và GTLN, GTNN của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm GTLN, GTNN của hàm số 2
y  x  3x  2 ?  3  1
Đ. max y y    ; không có GTNN. R  2  4 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách tìm GTLN, GTNN của hàm số liên tục trên một đoạn
 Từ KTBC, GV đặt vấn đề đối II. CÁCH TÍNH GTLN,
với hàm số liên tục trên một
GTNN CỦA HÀM SỐ TRÊN đoạn. MỘT ĐOẠN y
GV giới thiệu định lí. 1. Định lí 8
Mọi hàm số liên tục trên một 6 4
đoạn đều có GTLN và GTNN 2 trên đoạn đó. x
 GV cho HS xét một số VD. -1 1 2 3 -2
Từ đó dẫn dắt đến qui tắc tìm
2. Qui tắc tìm GTLN, GTNN -4 GTLN, GTNN.
của hàm số liên tục trên đoạn -6
VD: Tìm GTLN, GTNN của -8 [a; b]  hàm số 2 y x
Tìm các điểm x1, x2, …, xn trên đoạn được a)
min y y( )   1 1 1; 
trên khoảng (a; b), tại đó f(x) chỉ ra: 3
bằng 0 hoặc không xác định. a) [1; 3] b) [–1; 2]
max y y( )   3 9 1;  3
Tính f(a), f(x1), …, f(xn), f(b). b)
min y y( ) 
Tìm số lớn nhất M và số nhỏ  0 0 1  ;2
nhất m trong các số trên.
max y y( ) 
M max f (x), m  min f (x)  2 4 1  ;2 [a b ; ] [a b ; ]
Hoạt động 2: Vận dụng cách tìm GTLN, GTNN của hàm số để giải toán
 Cho các nhóm thực hiện.
 Các nhóm thảo luận và trình VD1: Tìm GTLN, GTNN của GV: Phạm Việt Phương 13
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn bày. hàm số 3 2
y x x x  2 trên đoạn: 2
y'  3x  2x 1 a) [–1; 2] b) [–1; 0]  c) [0; 2] d) [2; 3] 1 x y'      0 3  x 1  1  59 y   ; y( )   1 1 3  27 
a) y(–1) = 1; y(2) = 4
Chú ý các trường hợp khác  min y y( 1  )  y 1 ( ) 1 nhau.  1  ;2
max y y( )   2 4 1  ;2 b) y(–1) = 1; y(0) = 2
min y y( )   1 1 1  0 ;   1  59
max y y      1  0 ;   3  27 c) y(0) = 2; y(2) = 4
min y y( )   1 1 0;2
max y y 2   4 0 2 ;  d) y(2) = 4; y(3) = 17
min y y( )   2 4 2;  3
max y y 3   17 2;  3
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách tìm GTLN, GTNN của
hàm số liên tục trên một đoạn.
– So sánh với cách tìm GTLN,
GTNN của hàm số liên tục trên một khoảng.
4. BÀI TẬP VỀ NHÀ:
 Làm bài tập 1, 2, 3 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 14
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 08
Bài 3: BÀI TẬP GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ I. MỤC TIÊU:
Kiến thức: Củng cố:
 Các khái niệm GTLN, GTNN của hàm số trên một tập hợp số.
 Các qui tắc tìm GTLN, GTNN của hàm số. Kĩ năng:
 Tìm được GTLN, GTNN của hàm số trên một đoạn, một khoảng.
 Phân biệt việc tìm GTLN, GTNN với tìm cực trị của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về cực trị và GTLN, GTNN của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tìm GTLN, GTNN của hàm số liên tục trên một đoạn
H1. Nêu các bước thực hiện ? Đ1.
1. Tính GTLN, GTNN của
min y   ; max y  hàm số:  41 40 4  ;4 [ 4  ;4] a) min y  ; max y  a) 3 2
y x 3x 9x  35  8 40 0;  5 [0 5 ; ]
trên các đoạn [–4; 4], [0; 5]. 1
min y   ; max y  b) 4 2
y x 3x  2 56 b) 0;  3 4 [0 3 ; ]
trên các đoạn [0; 3], [2; 5] min y  ; max y   6 552 2  x 2;  5 [2 5 ; ] c) y  1 x 2 min y  0; max y
trên các đoạn [2; 4], [–3; –2]. c) 2;4 [2;4] 3 min y  ; max y
d) y  5  4x trên [–1; 1].  ;  1 3 11 [ 11  ; ] d) min y  1; max y  3 [ 1  1 ; ] [ 1  1 ; ]
Hoạt động 2: Luyện tập tìm GTLN, GTNN của hàm số liên tục trên một khoảng
H1. Nêu các bước thực hiện ? Đ1.
2. Tìm GTLN, GTNN của các
a) max y  4 ; không có GTNN hàm số sau: R 4
b) max y  1 ; không có GTNN a) y R 2 1 x
c) min y  0 ; không có GTLN
y x x R b) 3 4 4 3
d) min y  4 ;không có GTLN c) y x (0;) GV: Phạm Việt Phương 15
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 4 d) y x  (x  0) x
Hoạt động 3: Vận dụng GTLN, GTNN để giải toán
 Hướng dẫn HS cách phân
3. Trong số các hình chữ nhật tích bài toán.
có cùng chu vi 16 cm, hãy tìm
H1. Xác định hàm số ? Tìm Đ1.
hình chữ nhật có diện tích lớn GTLN, GTNN của hàm số ?
3) S = x (8 – x), (0 < x < 8) nhất.
 Để S lớn nhất thì x = 4.  maxS = 16 48 
4. Trong số các hình chữ nhật 0  x  4 3  4) P = x x
cùng có diện tích 48 cm2, hãy
tìm hình chữ nhật có chu vi
 Để P nhỏ nhất thì x = 4 3 nhỏ nhất.  minP = 16 3
Hoạt động 4: Củng cố Nhấn mạnh:
– Các cách tìm GTLN, GTNN của hàm số.
– So sánh với cách tìm GTLN,
GTNN của hàm số liên tục trên một khoảng. – Cách vận dụng GTLN, GTNN để giải toán.
4. BÀI TẬP VỀ NHÀ:
 Đọc trước bài "Đường tiệm cận".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 09
Bài 4: ĐƯỜNG TIỆM CẬN I. MỤC TIÊU: Kiến thức:
 Biết khái niệm đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số. Kĩ năng:
 Tìm được đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
 Củng cố cách tìm giới hạn, giới hạn một bên của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ. GV: Phạm Việt Phương 16
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Học sinh: SGK, vở ghi. Ôn tập cách tính giới hạn của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')  x H. Cho hàm số 2 y
. Tính các giới hạn: lim y, lim y x ? 1 x x Đ. lim y  1  , lim y  1  . x x 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm đường tiệm cận ngang của đồ thị hàm số
 Dẫn dắt từ VD để hình thành
I. ĐƯỜNG TIỆM CẬN
khái niệm đường tiệm cận NGANG ngang. 1. Định nghĩa x
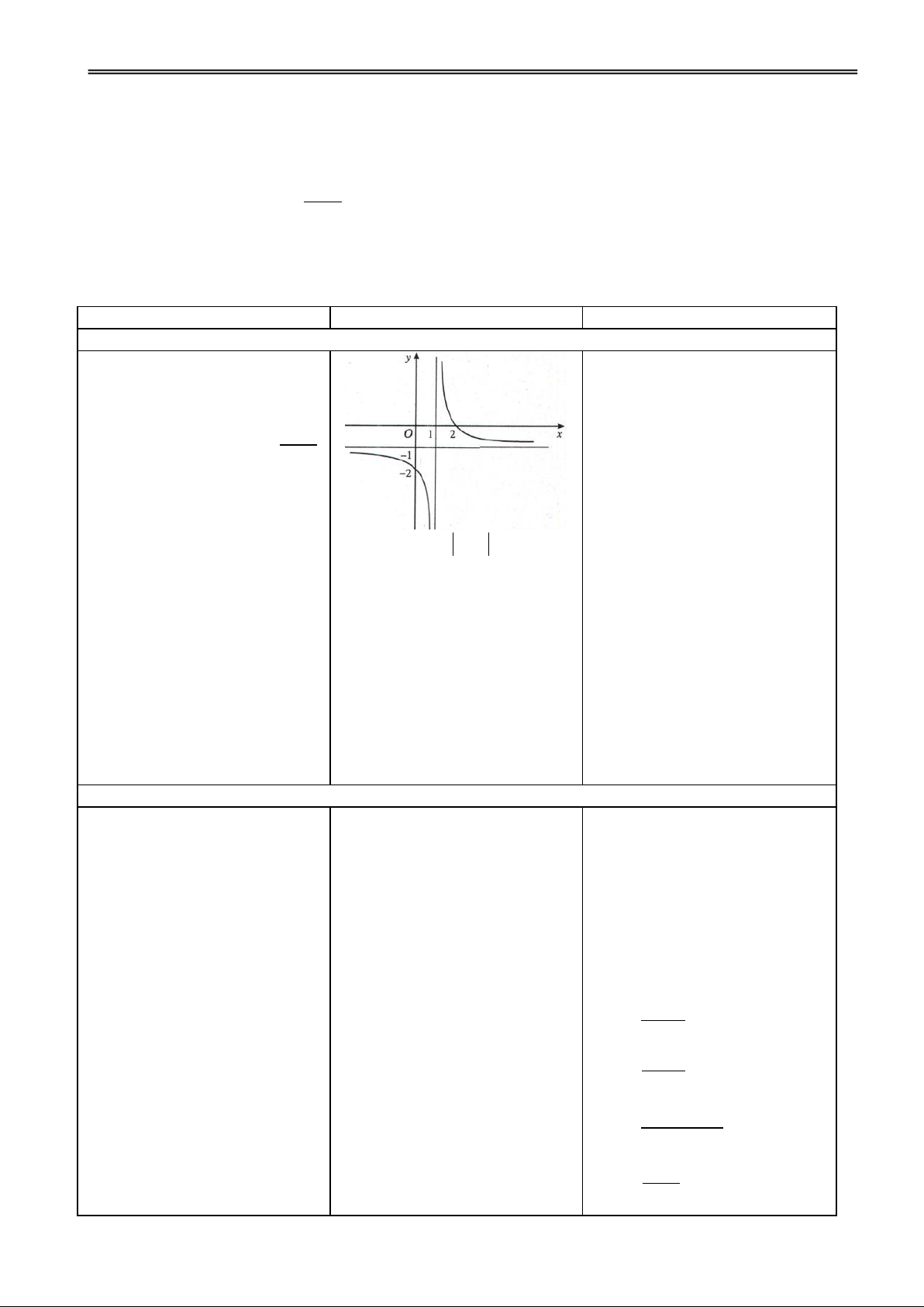
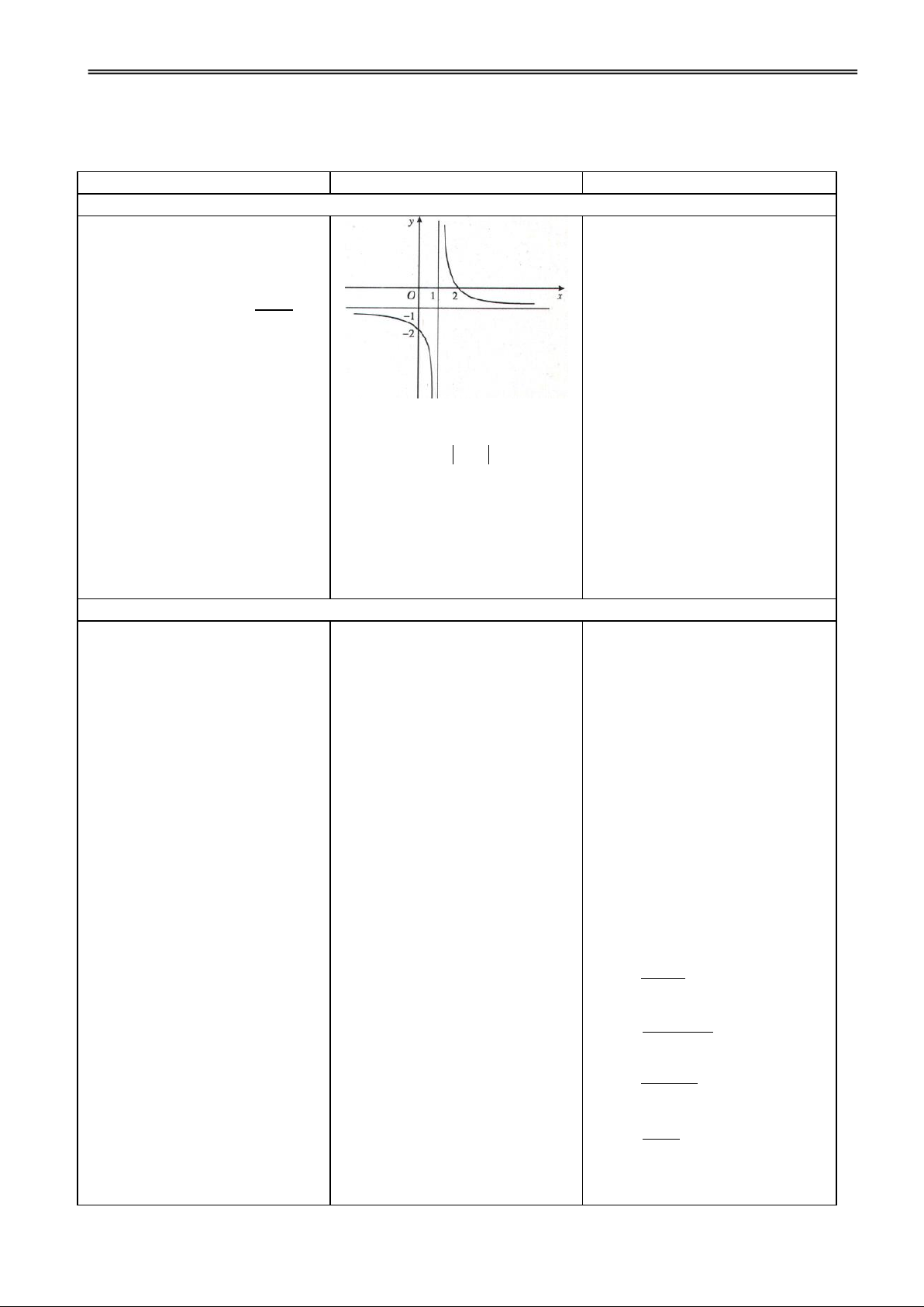
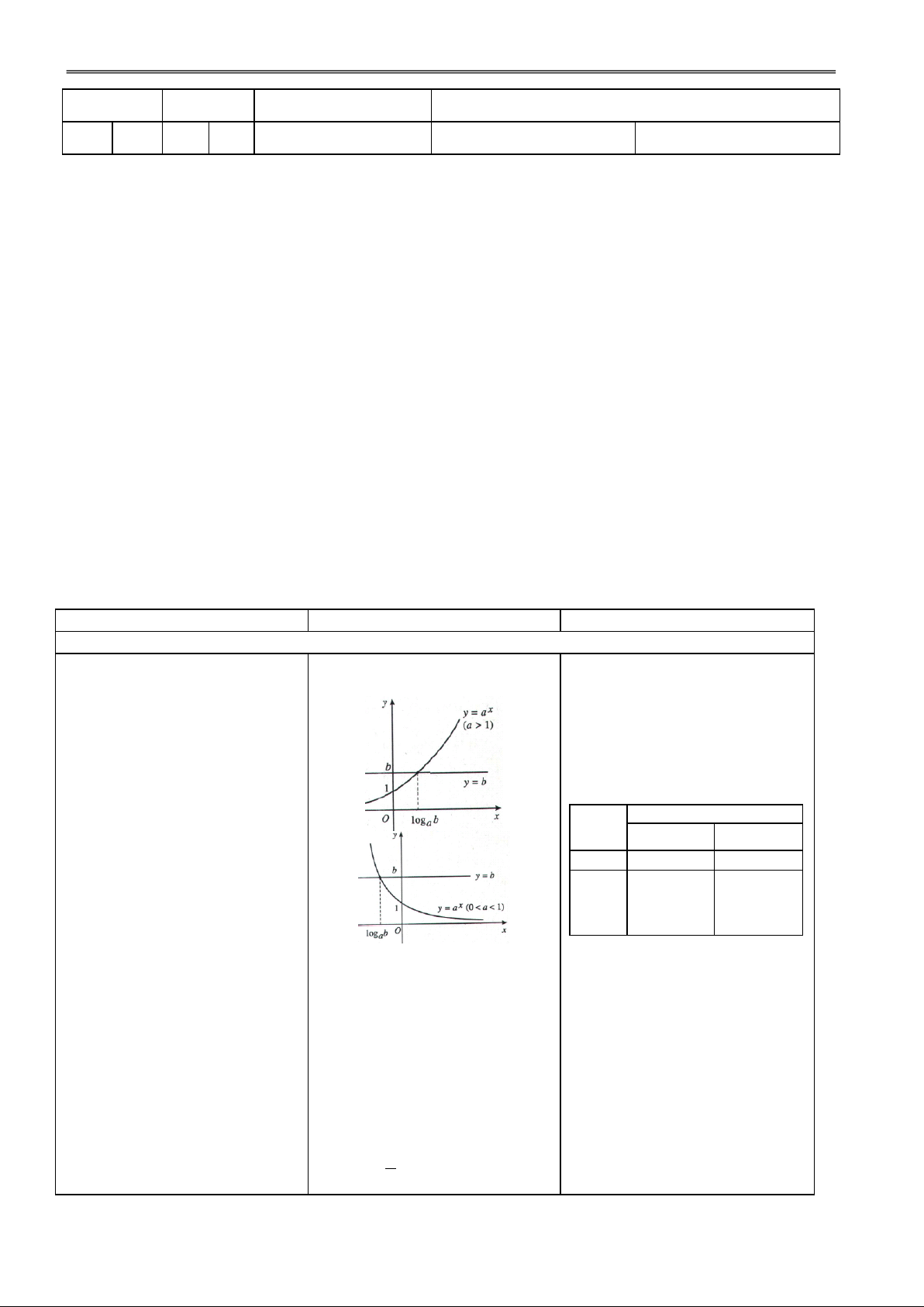
Cho hàm số y = f(x) xác định VD: Cho hàm số 2 y x
trên một khoảng vô hạn. 1
(C). Nhận xét khoảng cách từ
Đường thẳng y = y0 là tiệm cận ngang điểm M
của đồ thị hàm số y
(x; y)  (C) đến đường
= f(x) nếu ít nhất một trong các
thẳng : y = –1 khi x  ∞.
điều kiện sau được thoả mãn:
H1. Tính khoảng cách từ M Đ1. d(M, ) = y 1
lim f (x)  y đến đường thẳng  , ? 0 x
lim f (x)  y
H2. Nhận xét khoảng cách đó Đ2. 0
dần tới 0 khi x  +∞. x khi x  +∞ ? Chú ý: Nếu
 GV giới thiệu khái niệm
lim f (x)  lim f (x)  y 0 đường tiệm cận ngang. x x  thì ta viết chung
lim f (x)  y 0 x
Hoạt động 2: Tìm hiểu cách tìm tiệm cận ngang của đồ thị hàm số
 Cho HS nhận xét cách tìm  Các nhóm thảo luận và trình 2. Cách tìm tiệm cận ngang TCN . bày.
Nếu tính được lim f (x)  y 0 x
hoặc lim f (x)  y thì đường 0 x thẳng y = y
0 là TCN của đồ thị hàm số y = f(x).
H1. Tìm tiệm cận ngang ? Đ1.
VD1: Tìm tiệm cận ngang cuẩ a) TCN: y = 2 đồ thị hàm số: b) TCN: y = 0 x c) TCN: y = 1 2 1 a) y  d) TCN: y = 0 x  1 x 1 y  b) 2 x 1 2 x  3x  2 c) y  2 x x 1 1 d) y x  7 GV: Phạm Việt Phương 17
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
H2. Tìm tiệm cận ngang ? Đ2.
VD2: Tìm tiệm cận ngang cuẩ a) TCN: y = 0 đồ thị hàm số: 1 x 1 b) TCN: y = a) y  2 2 x  3x c) TCN: y = 1 x  3 d) TCN: y = 1 b) y x  2 1 2 x  3x  2 c) y  2 x  3x  5 x d) y x  7
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách tìm tiệm cận ngang của đồ thị hàm số.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Đường tiệm cận".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 10
Bài 4: ĐƯỜNG TIỆM CẬN (tt) I. MỤC TIÊU: Kiến thức:
 Biết khái niệm đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số. Kĩ năng:
 Tìm được đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
 Củng cố cách tìm giới hạn, giới hạn một bên của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập cách tính giới hạn của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5') x H. Cho hàm số 2 3 y  lim y lim y
x  (C). Tìm tiệm cận ngang của (C) ? Tính , ? 1 x   1  x 1  GV: Phạm Việt Phương 18
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Đ. lim y   , lim y   . x   1  x 1  3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
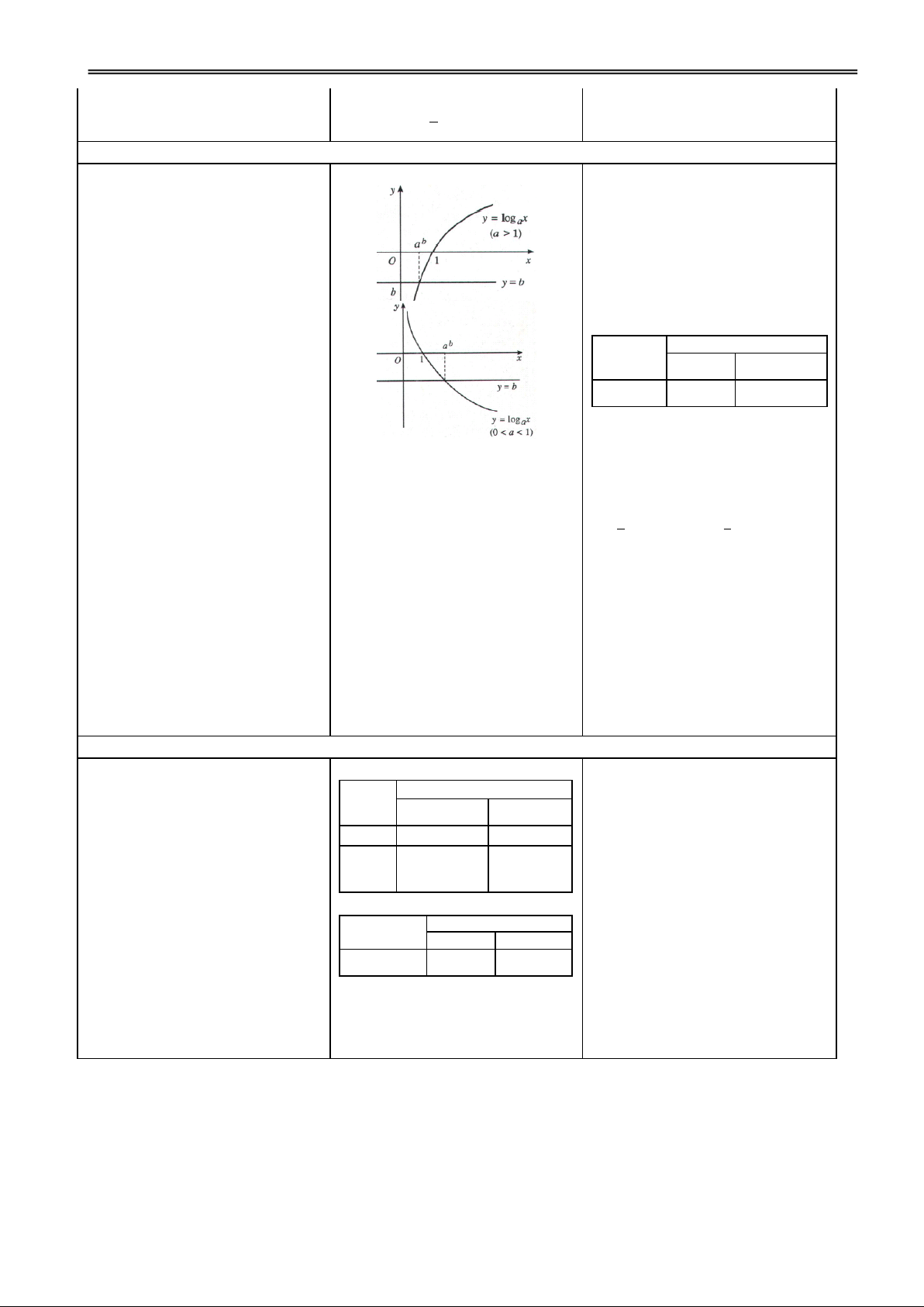
Hoạt động 1: Tìm hiểu khái niệm đường tiệm cận đứng của đồ thị hàm số
 Dẫn dắt từ VD để hình thành
II. ĐƯỜNG TIỆM CẬN
khái niệm tiệm cận đứng. ĐỨNG 1. Định nghĩax
Đường thẳng x = x0 đgl tiệm VD: Cho hàm số 2 y x có 
cận đứng của đồ thị hàm số y 1
đồ thị (C). Nhận xét về khoảng
= f(x) nếu ít nhất một trong các
điều kiện sau được thoả mãn: cách từ điểm M(x; y)  (C) đến đường thẳng 
lim f (x)   : x = 0 khi x x x   0 1+ ?
lim f (x)   x x 
H1. Tính khoảng cách từ M Đ1. 0 d(M, ) = x 1 . đến 
lim f (x)   ? x x 
H2. Nhận xét khoảng cách đó Đ2. 0 dần tới 0.
lim f (x)   khi x  1+ ? x x 
 GV giới thiệu khái niệm tiệm 0 cận đứng.
Hoạt động 2: Tìm hiểu cách tìm tiệm cận đứng của đồ thị hàm số
 GV cho HS nhận xét cách  Các nhóm thảo luận và trình 2. Cách tìm tiệm cận đứng tìm TCĐ. bày.
của đồ thị hàm số
Nếu tìm được lim f (x)   xx0
hoặc lim f (x)   , x x  0
hoặc lim f (x)   , x x  0
hoặc lim f (x)   x x  0
thì đường thẳng x = x0 là TCĐ
của đồ thị hàm số y = f(x).
VD1: Tìm tiệm cận đứng của đồ thị hàm số:
H1. Tìm tiệm cận đứng ? Đ1. 2x 1 a) TCĐ: x = 3 a) y x b) TCĐ: x = 1  3 c) TCĐ: x = 0; x = 3 2 x x 1 b) y  d) TCĐ: x = –7 x  1 x 1 c) y  2 x  3x 1 d) y x  7
VD2: Tìm TCĐ và TCN của GV: Phạm Việt Phương 19
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
H2. Tìm tiệm cận đứng và tiệm Đ2. đồ thị hàm số: cận ngang ? a) TCĐ: x = 1; x = 2 x 1 y TCN: y = 0 a)  2 b) TCĐ: x = 1; x = – x x  2 3 2 x  TCN: y = 0 3 b) y  2 x x  2 c) TCĐ: x = 1 2 x  3 c) y  1 2x 1 TCN: y = 2 2 x x  3 d) TCĐ: không có d) y  2 x x  2 TCN: y = 1
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách tìm tiệm cận đứng và
tiệm cận ngang của đồ thị hàm số.
– Nhắc lại cách tính giới hạn của hàm số.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 11
Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ I. MỤC TIÊU: Kiến thức:
 Biết sơ đồ tổng quát để khảo sát hàm số.
 Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức ax b
y a'xb'. Kĩ năng:
 Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
 Biết cách tìm giao điểm của hai đồ thị.
 Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp. GV: Phạm Việt Phương 20
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
2. Kiểm tra bài cũ: (3')
H. Nhắc lại định lí về tính đơn điệu, cực trị của hàm số? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu sơ đồ khảo sát hàm số
 GV cho HS nhắc lại cách
I. SƠ ĐỒ KHẢO SÁT HÀM
thực hiện từng bước trong sơ SỐ đồ. 1. Tập xác định
H1. Nêu một số cách tìm tập Đ1. 2. Sự biến thiên xác định của hàm số? – Mẫu # 0. – Tính y.
– Biểu thức trong căn bậc hai – Tìm các điểm tại đó y = 0 không âm.
hoặc y không xác định.
H2. Nhắc lại định lí về tính Đ2. HS nhắc lại.
– Tìm các giới hạn đặc biệt và
đơn điệu và cực trị của hàm
tiệm cận (nếu có). số?
– Lập bảng biến thiên.
– Ghi kết quả về khoảng đơn
H3. Nhắc lại cách tìm tiệm cận Đ3. HS nhắc lại.
điệu và cực trị của hàm số. của đồ thị hàm số ? 3. Đồ thị
– Tìm toạ độ giao điểm của đồ
H4. Nêu cách tìm giao điểm Đ4.
thị với các trục toạ độ.
của đồ thị với các trục toạ độ ? – Tìm giao điểm với trục tung:
– Xác định tính đối xứng của  Cho x = 0, tìm y.
đồ thị (nếu có).
– Tìm giao điểm với trục – Xác định tính tuần hoàn (nếu hoành: có) của hàm số.
 Giải pt: y = 0, tìm x.
– Dựa vào bảng biến thiên và
các yếu tố xác định ở trên để vẽ.
Hoạt động 2: Áp dụng khảo sát và vẽ đồ thị hàm số bậc nhất
 Cho HS nhắc lại các điều đã  Các nhóm thảo luận, thực VD1: Khảo sát sự biến thiên và
biết về hàm số y ax b , sau hiện và trình bày.
vẽ đồ thị hàm số y ax b
đó cho thực hiện khảo sát theo + D = R sơ đồ. + y = a + a > 0: hs đồng biến
+ a < 0: hs nghịch biến + a = 0: hs không đổi
Hoạt động 3: Áp dụng khảo sát và vẽ đồ thị hàm số bậc hai
 Cho HS nhắc lại các điều đã  Các nhóm thảo luận, thực VD2: Khảo sát sự biến thiên và biết về hàm số 2
y ax bx c hiện và trình bày. vẽ đồ thị hàm số:
, sau đó cho thực hiện khảo sát + D = R 2
y ax bx c (a  0) theo sơ đồ. + y = 2ax + b a > 0 b   x  2a y’ – 0 +   y   4a a < 0 GV: Phạm Việt Phương 21
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn b   x  2a y’ + 0 –  y  4a  
Hoạt động 4: Củng cố Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các tính chất hàm số đã học.
Câu hỏi: Khảo sát sự biến
thiên và vẽ đồ thị hàm số: a) 2
y x  4x  3 b) 2
y  x  2x 3 +
4. BÀI TẬP VỀ NHÀ:
 Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 12
Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Biết sơ đồ tổng quát để khảo sát hàm số.
 Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức ax b
y a'x .  b' Kĩ năng:
 Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
 Biết cách tìm giao điểm của hai đồ thị.
 Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại sơ đồ khảo sát hàm số? Đ. GV: Phạm Việt Phương 22
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khảo sát hàm số bậc ba
 Cho HS thực hiện lần lượt  Các nhóm thực hiện và trình II. KHẢO SÁT MỘT SỐ
các bước theo sơ đồ. bày.
HÁM ĐA THỨC VÀ HÀM + D = R PHÂN THỨC 1. Hàm số + y = 2 3x  6x x      2  3 2 y ax bx cx d (a  0) y = 0   x  0
VD1: Khảo sát sự biến thiên và
+ lim y   ; lim y   x x vẽ đồ thị hàm số: + BBT 3 2
y x  3x  4 + x = 0  y = –4 x  2  y = 0   x 1 + Đồ thị
 Cho HS thực hiện lần lượt  Các nhóm thực hiện và trình VD2: Khảo sát sự biến thiên và các bước theo sơ đồ. bày. vẽ đồ thị hàm số: + D = R 3 2
y  x  3x  4x  2 + y = 2 3
 (x 1) 1 < 0, x
+ lim y   ; lim y   x x + BBT + x = 0  y = 2 y = 0  x = 1 + Đồ thị
Hoạt động 2: Tìm hiểu các dạng đồ thị của hàm số bậc ba GV: Phạm Việt Phương 23
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Hoạt động 3: Củng cố Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các dạng đồ thị của hàm số bậc ba.
Câu hỏi: Các hàm số sau thuộc  Các nhóm thảo luận và trả lời dạng nào?
a) a > 0,  > 0 b) a > 0,  < 0 a) 3
y x x b) 3
y x x c) a < 0,  < 0 d) a < 0,  > 0 c) 3
y  x x d) 3
y  x x
4. BÀI TẬP VỀ NHÀ:  Bài 1 SGK.
 Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 24
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 13
Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Biết sơ đồ tổng quát để khảo sát hàm số.
 Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức ax b
y a'x .  b' Kĩ năng:
 Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
 Biết cách tìm giao điểm của hai đồ thị.
 Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại sơ đồ khảo sát hàm số? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khảo sát hàm số bậc ba
 Cho HS thực hiện lần lượt  Các nhóm thực hiện và trình II. KHẢO SÁT MỘT SỐ
các bước theo sơ đồ. bày.
HÁM ĐA THỨC VÀ HÀM + D = R PHÂN THỨC 2. Hàm số + y = 2 4x(x 1) x   4 2
y ax bx c (a  0) 1
y = 0   x  1  x  0
VD1: Khảo sát sự biến thiên và vẽ đồ thị hàm số:
+ lim y   ; lim y   x x 4 2
y x  2x 3 + BBT + Đồ thị x = 0  y = –3 x   3 y = 0   x  3
Hàm số đã cho là hàm số GV: Phạm Việt Phương 25
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
chẵn  Đồ thị nhận trục tung làm trục đối xứng.
 Cho HS thực hiện lần lượt  Các nhóm thực hiện và trình VD2: Khảo sát sự biến thiên và các bước theo sơ đồ. bày. vẽ đồ thị hàm số: + D = R 4 x 2 3 y    x  + y = 2 2  x(x 1) 2 2 y = 0  x = 0
+ lim y   ; lim y   x x + BBT + Đồ thị 3 x = 0  y = 2 y = 0  x =  1
Đồ thị nhận trục tung làm trục đối xứng.
Hoạt động 2: Tìm hiểu các dạng đồ thị của hàm số trùng phương
Hoạt động 3: Củng cố Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các dạng đồ thị của hàm số bậc bốn trùng phương.
Câu hỏi: Các hàm số sau thuộc  Các nhóm thảo luận và trả lời dạng nào? a) 4 2
y x x b) 4 2
y x x c) 4 2
y  x x d) 4 2
y  x x
4. BÀI TẬP VỀ NHÀ:  Bài 2 SGK.
 Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 26
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 14
Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Biết sơ đồ tổng quát để khảo sát hàm số.
 Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức ax b
y a'x .  b' Kĩ năng:
 Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
 Biết cách tìm giao điểm của hai đồ thị.
 Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại sơ đồ khảo sát hàm số? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
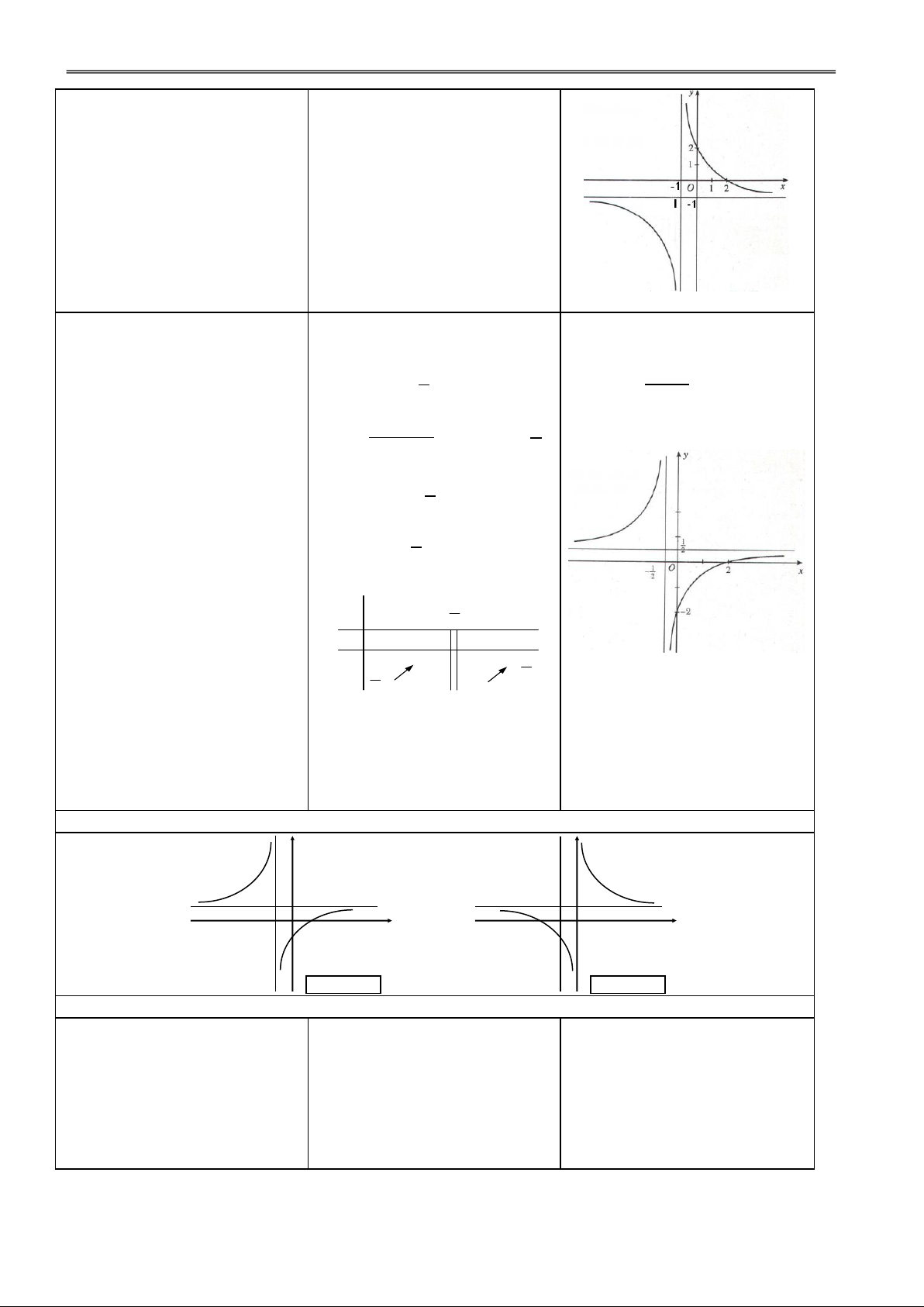
Hoạt động 1: Tìm hiểu khảo sát hàm số nhất biến
 Cho HS thực hiện lần lượt  Các nhóm thực hiện và trình II. KHẢO SÁT MỘT SỐ
các bước theo sơ đồ. bày.
HÁM ĐA THỨC VÀ HÀM + D = R \ {–1} PHÂN THỨC 3 ax b + y =  < 0, x  –1
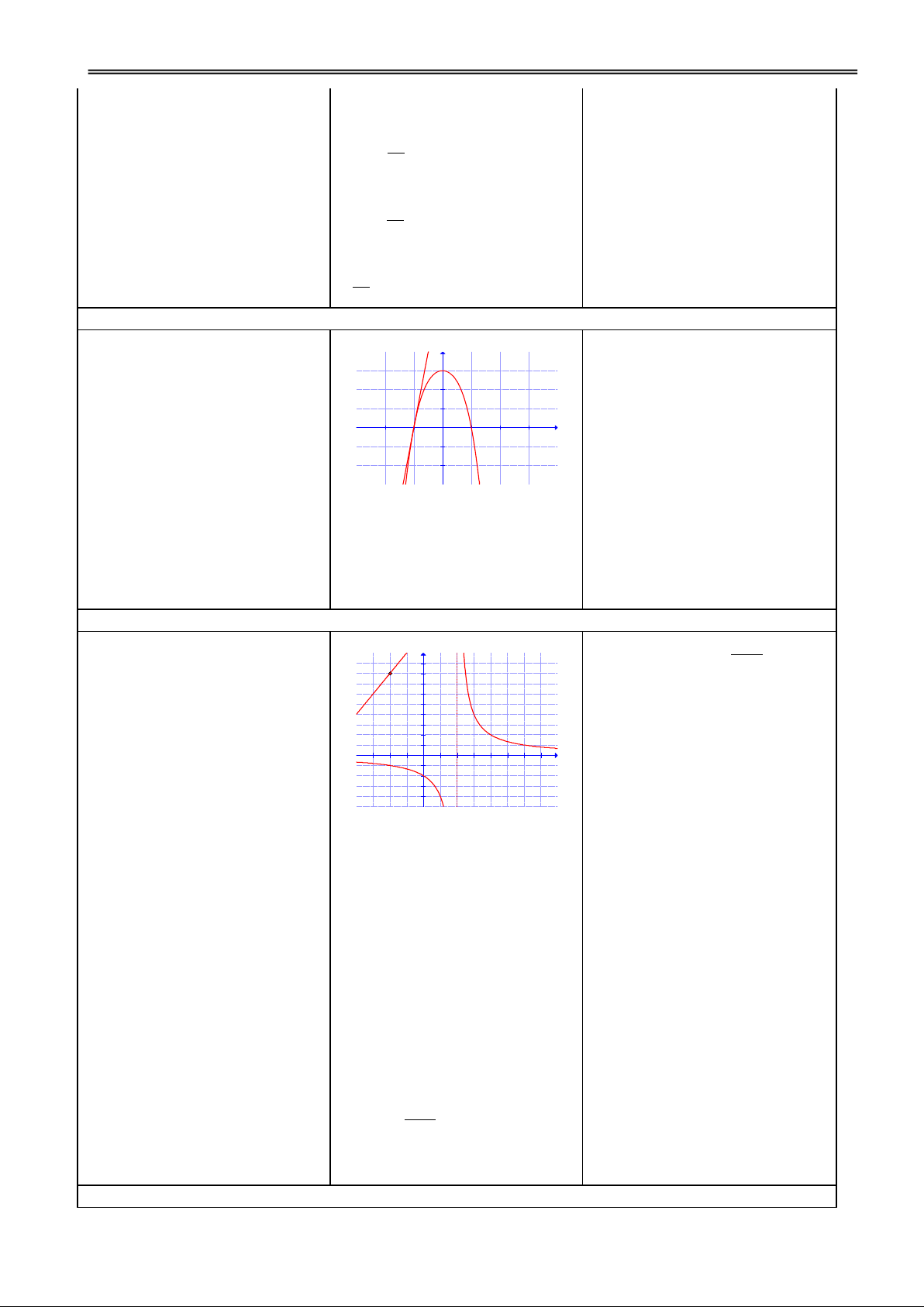
3. Hàm số y 2 (x 1) cx d + TCĐ: x = –1 (c  0, ad – bc  0) TCN: y = –1 + BBT
VD1: Khảo sát sự biến thiên và vẽ đồ thị hàm số: x  –1  x  2 y’ – – y  –  x  1 1 y  –1 + Đồ thị x = 0  y = 2 y = 0  x = 2
Giao điểm của hai tiệm cận
là tâm đối xứng của đồ thị. GV: Phạm Việt Phương 27
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
 Cho HS thực hiện lần lượt  Các nhóm thực hiện và trình VD2: Khảo sát sự biến thiên và các bước theo sơ đồ. bày. vẽ đồ thị hàm số:  1  x  2 + D = R \   y   2 2x 1 5 1 + y = > 0, x   2 (2x 1) 2 + TCĐ: x = 1  2 1 TCN: y = 2 + BBT 1 x    2 y’ + +  1 y 1 2  2 + Đồ thị x = 0  y = –2 y = 0  x = 2
Đồ thị nhận giao điểm của 2
tiệm cận làm tâm đối xứng.
Hoạt động 2: Tìm hiểu các dạng đồ thị của hàm số nhất biến y y 0 x 0 x ad – bc > 0 ad – bc < 0
Hoạt động 3: Củng cố Nhấn mạnh:
– Sơ đồ khảo sát hàm số.
– Các dạng đồ thị của hàm số nhất biến.
Câu hỏi: Các hàm số sau thuộc  Các nhóm thảo luận và trả lời
dạng nào? Tìm các tiệm cận của chúng: GV: Phạm Việt Phương 28
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 2x 1 2x 1 a) y y x b) 1 x 1
4. BÀI TẬP VỀ NHÀ:  Bài 3 SGK.
 Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 15
Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Biết sơ đồ tổng quát để khảo sát hàm số.
 Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức ax b
y a'x .  b' Kĩ năng:
 Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
 Biết cách tìm giao điểm của hai đồ thị.
 Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm toạ độ giao điểm của đồ thị hai hàm số: 2 2
y x  2x 3, y  x x  2 ?   Đ.  ;  5 7 1 0 ,  ;    2 4  . 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách xét sự tương giao của các đồ thị
 Từ KTBC, GV cho HS nêu  Các nhóm thảo luận và trình III. SỰ TƯƠNG GIAO CỦA
cách tìm giao điểm của hai đồ bày. CÁC ĐỒ THỊ thị. Cho hai hàm số:
y = f(x) (C1) và y = g(x) (C2).
 (1) đgl phương trình hoành
Để tìm hoành độ giao điểm của
độ giao điểm của hai đồ thị.
(C1) và (C2), ta giải phương GV: Phạm Việt Phương 29
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn trình: f(x) = g(x) (1)
Giả sử (1) có các nghiệm là x0,
x1, … Khi đó, các giao điểm là
M x ; f (x ) , M x ; f (x ) , 0  0 0  1  1 1  …
Nhận xét: Số nghiệm của (1)
bằng số giao điểm của (C1), (C2).
Hoạt động 2: Áp dụng xét sự tương giao của hai đồ thị  Cho HS thực hiện.
 Các nhóm thực hiện và trình VD1: Tìm toạ độ giao điểm bày.
của đồ thị hai hàm số:
H1. Lập pt hoành độ giao Đ1. a) 3 2
y x 3x  5 (C1) điểm? a) 3 2 3 2
x 3x 5  2
x  2x 3 3 2 y  2
x  2x 3 (C2)   x x
Hướng dẫn HS giải pt bậc ba. 3 2 3 5 8  0  x = –1 2x  4 y  2x  4 b)
 x x x   b) 2 2 4 1
Chú ý điều kiện mẫu khác 0. x 1
y  x x   2 2 4 3 2 x  3x  0 x  0     x  1 x  3 2 x y  2 x c)   x x 1 c) 3 1 x 1 y  3  x 1  ( x  )  2 2 1 0  1 x  2
VD2: Tìm m để đồ thị hàm số 2 2
H2. Lập pt hoành độ giao điểm Đ2.
y  (x  )(x mx m  ) 1 3
của đồ thị và trục hoành?
cắt trục hoành tại 3 điểm phân 2 2
(x  )(x mx m  )  1 3 0 biệt.
H3. Nêu điều kiện để đồ thị cắt
trục hoành tại 3 điểm phân biệt Đ3. Pt có 3 nghiệm phân biệt  2 2
x mx m 3  0 có 2
nghiệm phân biệt, khác 1    0  2 1
  m m  3  0   2   m  2  m  1 
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách xét sư tương giao giữa hai đồ thị.
– Số giao điểm của hai đồ thị
bằng số nghiệm của phương
trình hoành độ giao điểm. GV: Phạm Việt Phương 30
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Bài 5, 6, 7, 8, 9 SGK.
 Đọc tiếp bài "Khảo sát sự biến thiên và vẽ đồ thị của hàm số".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 16
Bài 5: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ (tt) I. MỤC TIÊU: Kiến thức:
 Biết sơ đồ tổng quát để khảo sát hàm số.
 Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức ax b
y a'x .  b' Kĩ năng:
 Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
 Biết cách tìm giao điểm của hai đồ thị.
 Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Tìm toạ độ giao điểm của đồ thị hai hàm số: 3 2
y x x  7x, y  2  x  5 ? ( 1
 ;7), 5;5  2 5, 5;5  2 5 Đ. . 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách biện luận số nghiệm của phương trình bằng đồ thị
H1. Nhắc lại cách giải phương Đ1. Vẽ các đồ thị trên cùng IV. BIỆN LUẬN SỐ
trình bằng đồ thị đã biết ?
một hệ trục. Dựa vào đồ thị để NGHIỆM CỦA PHƯƠNG kết luận.
TRÌNH BẰNG ĐỒ THỊ
 GV giới thiệu phương pháp.
Xét ph.trình: F(x, m)=0 (1)
– Biến đổi (1) về dạng: f(x) = g(m) (2)
– Khi đó (2) có thể xem là pt
hoành độ giao điểm của 2 đồ thị: (C): y = f(x) (d): y = g(m)
(trong đó y = f(x) thường là GV: Phạm Việt Phương 31
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
hàm số đã được khảo sát và vẽ
đồ thị, (d) là đường thẳng cùng
phương với trục hoành).
– Dựa vào đồ thị (C), từ số
giao điểm của (C) và (d) ta suy
ra số nghiệm của (2), cũng là số nghiệm của (1).
Hoạt động 2: Áp dụng biện luận số nghiệm của phương trình bằng đồ thị
H1. Khảo sát và vẽ đồ thị hàm Đ1. HS thực hiện nhanh.
VD1: Khảo sát sự biến thiên và số ? vẽ đồ thị hàm số: 3 2
y x  3x  2 (C)
Dựa vào đồ thị, biện luận theo 
m số nghiệm của phương trình:
GV hướng dẫn HS biện luận 
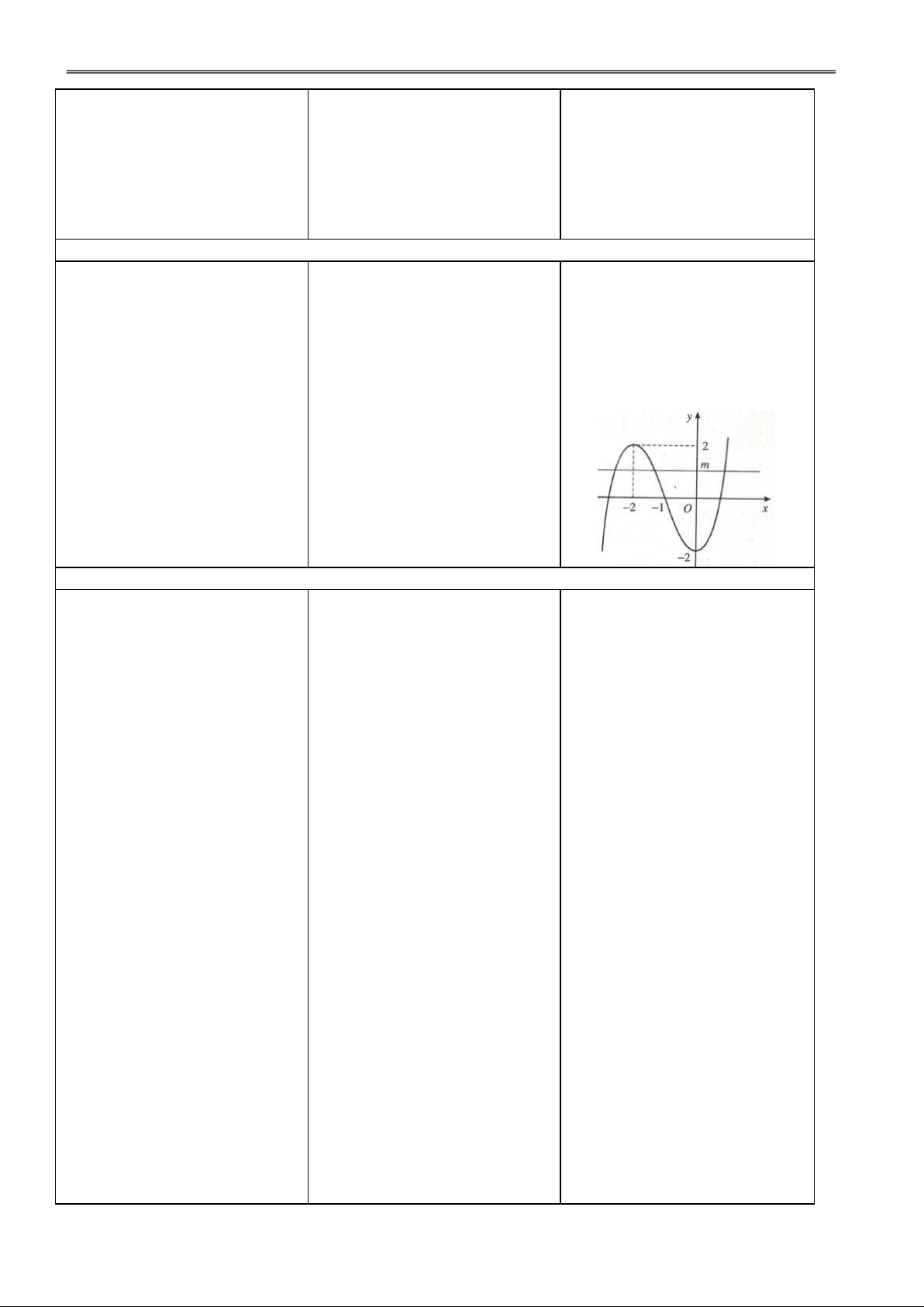
số giao điểm của (C) và (d). m  3 2
x x   m (1) 2  3 2 : (1) có 1 nghiệm  m  2 m  2   : (1) có 2 nghiệm m  2
–2 < m < 2: (1) có 3 nghiệm
Hoạt động 3: Ôn tập bài toán tiếp tuyến
H1. Nhắc lại ý nghĩa hình học Đ1. Hệ số góc của tiếp tuyến V. TIẾP TUYẾN của đạo hàm ? k = f(x0).
Bài toán 1: Viết phương trình
tiếp tuyến của (C): y = f(x) tại
điểm M x ; f (x )  (C). 0  0 0 
 GV hướng dẫn HS cách giải
bài toán 2. (Bài toán 3 dành
y y f '(x ).(x x ) 0 0 0 cho HS khá giỏi). (y0 = f(x0))
Bài toán 2: Viết phương trình
H2. Nêu dạng phương trình Đ2. y y k(x x )
tiếp tuyến của (C): y = f(x), đường thẳng đi qua 0 0 (x0; y0) và
biết tiếp tuyến có hệ số góc k. có hệ số góc k ?  Gọi (x
0; y0) là toạ độ của tiếp điểm. f(x0) = k (*)
Giải pt (*), tìm được x 0. Từ đó viết pttt.
Bài toán 3: Viết phương trình tiếp tuyến của (C): y = f(x), biết tiếp tuyến đi qua điểm A(x1; y1). x  
H2. Tìm toạ độ giao điểm của Đ3. 1 3
2  3x x  0  
VD2: Viết phương trình tiếp (C) và trục hoành ? x  2
tuyến của đồ thị (C) của hàm
+ Pttt của (C) tại (–1; 0):
số sau tại các giao điểm của y = 0 (C) với trục hoành:
+ Pttt của (C) tại (2; 0): 3
y  2  3x x y = –9(x – 2) GV: Phạm Việt Phương 32
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ:  Bài 5, 6, 7, 8, 9 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 17
Bài 5: BÀI TẬP KHẢO SÁT SỰ BIẾN THIÊN
VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ I. MỤC TIÊU:
Kiến thức: Củng cố:
 Sơ đồ khảo sát hàm số.
 Biết các dạng đồ thị của các hàm số bậc ba, bậc bốn trùng phương, hàm phân thức ax b
y a'x .  b' Kĩ năng:
 Biết cách khảo sát và vẽ đồ thị của các hàm số trong chương trình.
 Biết cách tìm giao điểm của hai đồ thị.
 Biết cách dùng đồ thị của hàm số để biện luận số nghiệm của một phương trình.
 Biết viết phương trình tiếp tuyến của đồ thị hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập khảo sát sự biến thiên và vẽ đồ thị hàm số bậc ba
 Các nhóm thực hiện và trình 1. Khảo sát sự biến thiên và bày.
vẽ đồ thị hàm số:
H1. Nhắc lại các bước khảo sát Đ1. a) 3
y  2  3x x
và vẽ đồ thị hàm số bậc ba? a)
y x x x x  – b) 3 2 9 1 1  y’ – 0 + 0 –  4 y 0  GV: Phạm Việt Phương 33
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn y 4 b) 2 x   y’ + –2 –1 O 1 2 x  y  y 11 –1 O 1 x –9
Hoạt động 2: Luyện tập khảo sát sự biến thiên và vẽ đồ thị hàm số bậc bốn trùng phương
 Các nhóm thực hiện và trình 2. Khảo sát sự biến thiên và bày.
vẽ đồ thị hàm số: a) 4 2
y x  2x  2
H1. Nhắc lại các bước khảo sát Đ1.
và vẽ đồ thị hàm số bậc bốn a) b) 2 4 y  2
x x  3 trùng phương? y x  –1 0 9 1  8 7 y’ – 0 + 0 – 0 + 6 5  2  4 y 3 2 1 1 1 x -3 -2 -1 1 2 3 -1 b) x  0  y y’ 3 + 0 – 2 3 1 y x   -2 -1 1 2 -1
Hoạt động 3: Luyện tập khảo sát sự biến thiên và vẽ đồ thị hàm số nhất biến
 Các nhóm thực hiện và trình 3. Khảo sát sự biến thiên và bày.
vẽ đồ thị hàm số: 1 2xx  2
H1. Nhắc lại các bước khảo sát Đ1. y y  a) 2x  b) 4 2x  1
và vẽ đồ thị hàm số nhất biến? a) y 4 x  2  3 2 y’ + + 1  – x 1 O -4 -3 -2 -1 1 2 3 4 5 6 7 y -1 -2 –1  -3 -4 b) GV: Phạm Việt Phương 34
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn y 1 x    3 2 2 y’ + + 1 x O 1  -3 -2 -1 1 2 3 4 5 y  2 -1 1 -2   2 -3
Hoạt động 4: Luyện tập xét sự tương giao giữa các đồ thị
H1. Nêu đk để đồ thị hàm số Đ1. Pt hoành độ giao điểm có 3 1. Tìm m để đồ thị hàm số sau
cắt trục hoành tại 3 điểm phân nghiệm phân biệt:
cắt trục hoành tại ba điểm phân biệt ? 3 2 mx  biệt: 3mx  1
(  2m)x 1 0 3 2
y mx  3mx  1 (  2m)x 1  2
(x 1)(mx  2mx 1)  0 x  1    2
mx  2mx 1  0 (2)
 (2) có 2 nghiệm pb, khác –1 m  0   '  0  2   2m  0 m  1    m  0
2. Tìm m để đồ thị các hàm số
H2. Nêu đk để đồ thị các hàm Đ2. Pt hoành độ giao điểm có 2 sau cắt nhau tại hai điểm phân
số cắt nhau tại 2 điểm phân nghiệm phân biệt: biệt: biệt ? 2
2x  3x m x m 2 2 x
x x m  2 3 1 y
; y  2x m x x 1 2m  x  2m     1 x  1 m   2
Hoạt động 5: Luyện tập biện luận số nghiệm của phương trình bằng đồ thị
H1. Khảo sát và vẽ đồ thị hàm Đ1. Các nhóm khảo sát và vẽ 3. Khảo sát và vẽ đồ thị (C) số ? nhanh đồ thị hàm số. của hàm số: 3
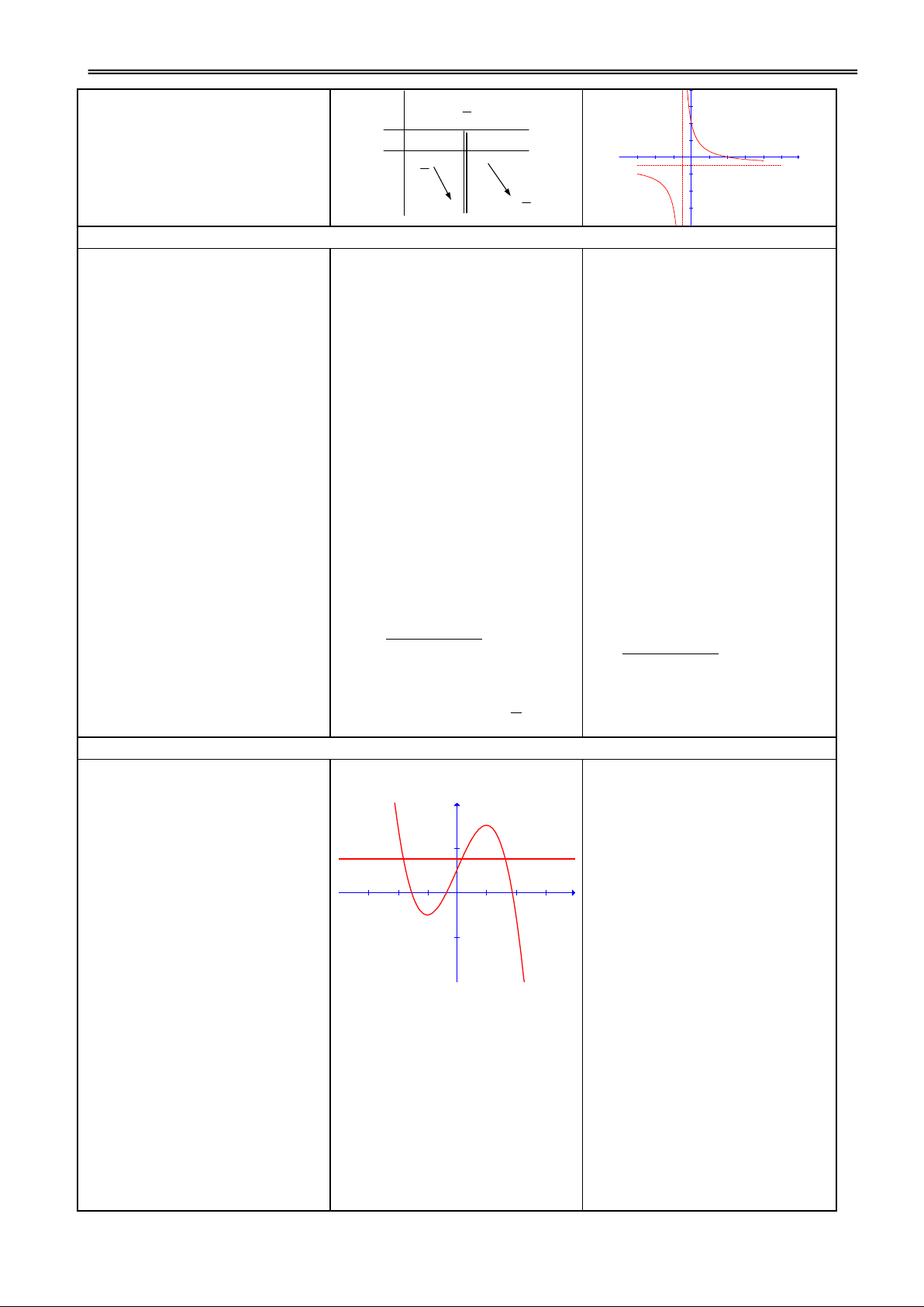
y  x  3x 1. y
Dựa vào đồ thị (C), biện luận
số nghiệm của phương trình 2 m+1 sau theo m: x 3
x x m  -3 -2 -1 O 1 2 3 3 0 -2
H2. Biến đổi phương trình? Đ2. 3
x 3x m  0  3
x  3x 1 m 1
H3. Biện luận số giao điểm của Đ3. (C) và (d)? m  2   : pt có 1 nghiệm m  2 m  2   : pt có 2 nghiệm m  2
–2 < m < 2: pt có 3 nghiệm GV: Phạm Việt Phương 35
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Hoạt động 6: Luyện tập viết phương trình tiếp tuyến của đồ thị hàm số
H1. Để viết pttt, cần tìm các Đ1. x0, y(x0).
4. Viết phương trình tiếp tuyến giá trị nào ? 1 1 7 1 1 4 2 x x 1 của (C): 4 2
y x x 1 0 0 4 2 4 4 2  x  1 0
tại điểm có tung độ bằng 7 .   4  Tại 7 1;  , pttt là:  4  7 1 y
 2(x 1)  y  2x  4 4    Tại 7  1;  , pttt là:  4  7 y   2  (x 1) 4  1 y  2  x  4
Hoạt động 7: Củng cố Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ: Bài tập ôn chương
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 36
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy
Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 18 + 19
BÀI TẬP ÔN CHƯƠNG I I. MỤC TIÊU:
Kiến thức: Củng cố:
 Tính đơn điệu của hàm số.
 Cực trị của hàm số, GTLN, GTNN của hàm số.  Đường tiệm cận.  Khảo sát hàm số. Kĩ năng:
 Xác định thành thạo các khoảng đơn điệu của hàm số.
 Tính được cực đại, cực tiểu của hàm số (nếu có).
 Xác định được các đường tiệm cận của đồ thị hàm số (nếu có).
 Lập bảng biến thiên và vẽ đồ thị hàm số một cách thành thạo.
 Tính được GTLN, GTNN của hàm số.
 Giải được một số bài toán liên quan đến khảo sát hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về khảo sát hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập khảo sát hàm số
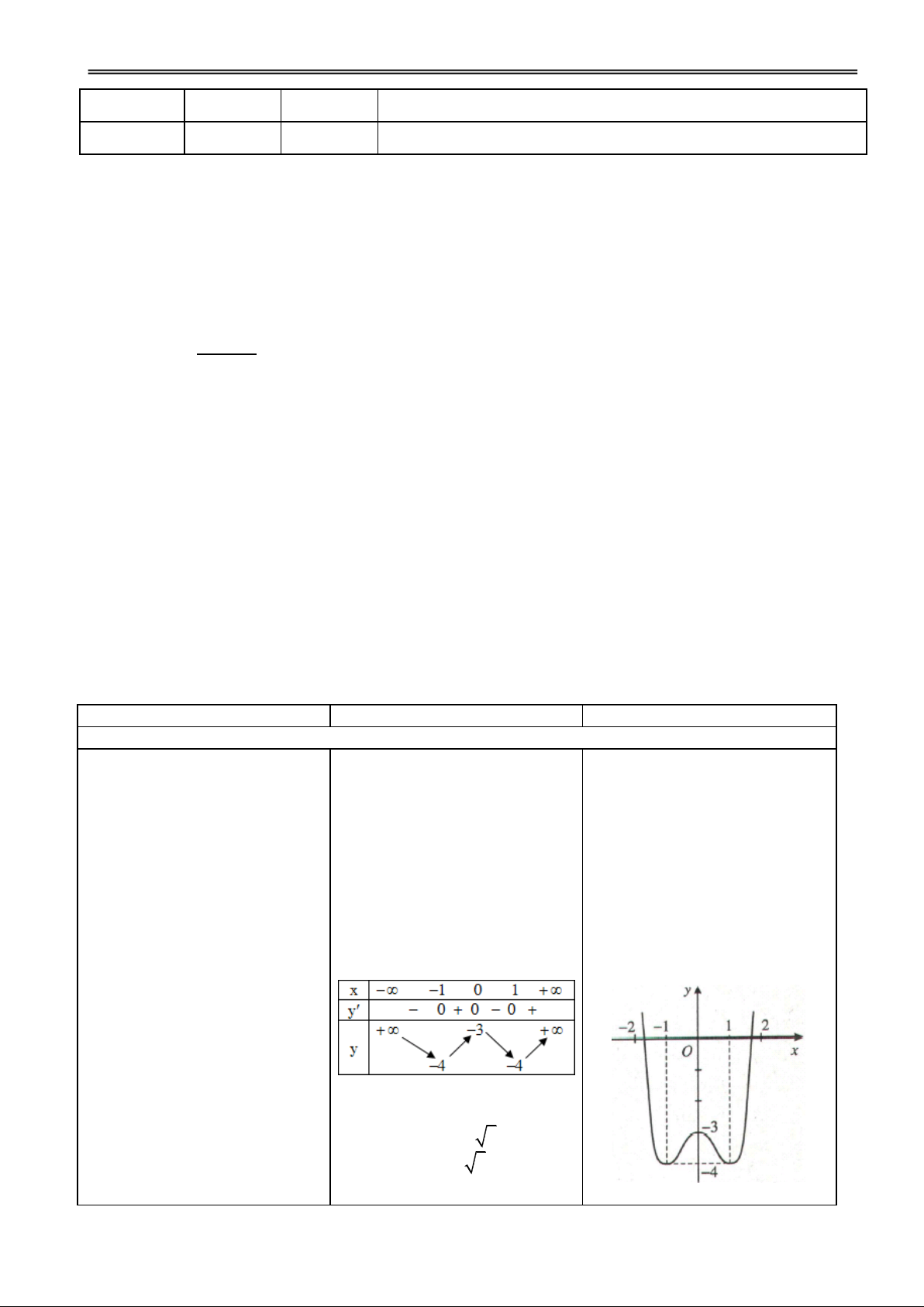
B ài 1. Cho hàm số:
H1. Nêu đk để hàm số đồng Đ1. f(x) 0, x  D 3 2
f (x)  x 3mx 3(2m 1)x 1 biến trên D ?  2
3(x  2mx  2m 1)  0 ,x a) Xác định m để hàm số đồng
biến trên tập xác định.  2
'  m  2m 1 0
b) Với giá trị nào của m, hàm  m = 1
số có một CĐ và một CT.
c) Xác định m để f(x) > 6x.
H2. Nêu đk để hàm số có 1 CĐ Đ2. f(x) = 0 có 2 nghiệm phân và 1 CT ? biệt.  2
'  m  2m 1 0  m  1
H3. Phân tích yêu cầu bài Đ3. toán?
Giải bất phương trình:
f(x) > 6x
6x – 6m > 6x  m < 0
* Gv: Khi nào thì hàm số đồng biến nghịch biến.
* Hs: Thảo luận theo nhóm và Bài 2
: Tìm các khoảng đơn
Cho học sinh thảo luận nhóm lên bảng làm bài tập theo yêu điệu của các hàm số:
và gọi học sinh lên trả lời câu cầu của giáo viên. * y = -x3 + 2x2 – x - 7 GV: Phạm Việt Phương 37
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn hỏi và bảng làm x 1 2  y '  3
x  4x 1  0 
* Gv: Sửa bài và cho điểm. 1 x   3
Hàm số đồng biến trong khoảng 1 ( ; 1), nghịch biến 3  1   trong các khoảng ; ;    3   1;  .  * Hàm số x 5 y  làm tương 1 x tự.
Bài 3: Tìm tiệm cận của hàm
* Gv: Để tìm tiệm cận ngang, 
tiệm cận đứng ta phải làm thế của hàm số: 2x 3 
* Hs: Thảo luận theo nhóm và y 2  x nào?
lên bảng làm bài tập theo yêu
Cho học sinh thảo luận nhóm cầu của giáo viên.
và gọi học sinh lên trả lời câu 2x  3
hỏi và bảng làm bài tập. lim y  lim  2  x
x x  2
nên y =-2 là tiệm cận ngang. 2x  3 lim y  lim     x2 x2 2  x
Nên x = 2 là tiệm cận đứng
Hoạt động 2: Luyện tập giải các bài toán liên quan đến khảo sát hàm số
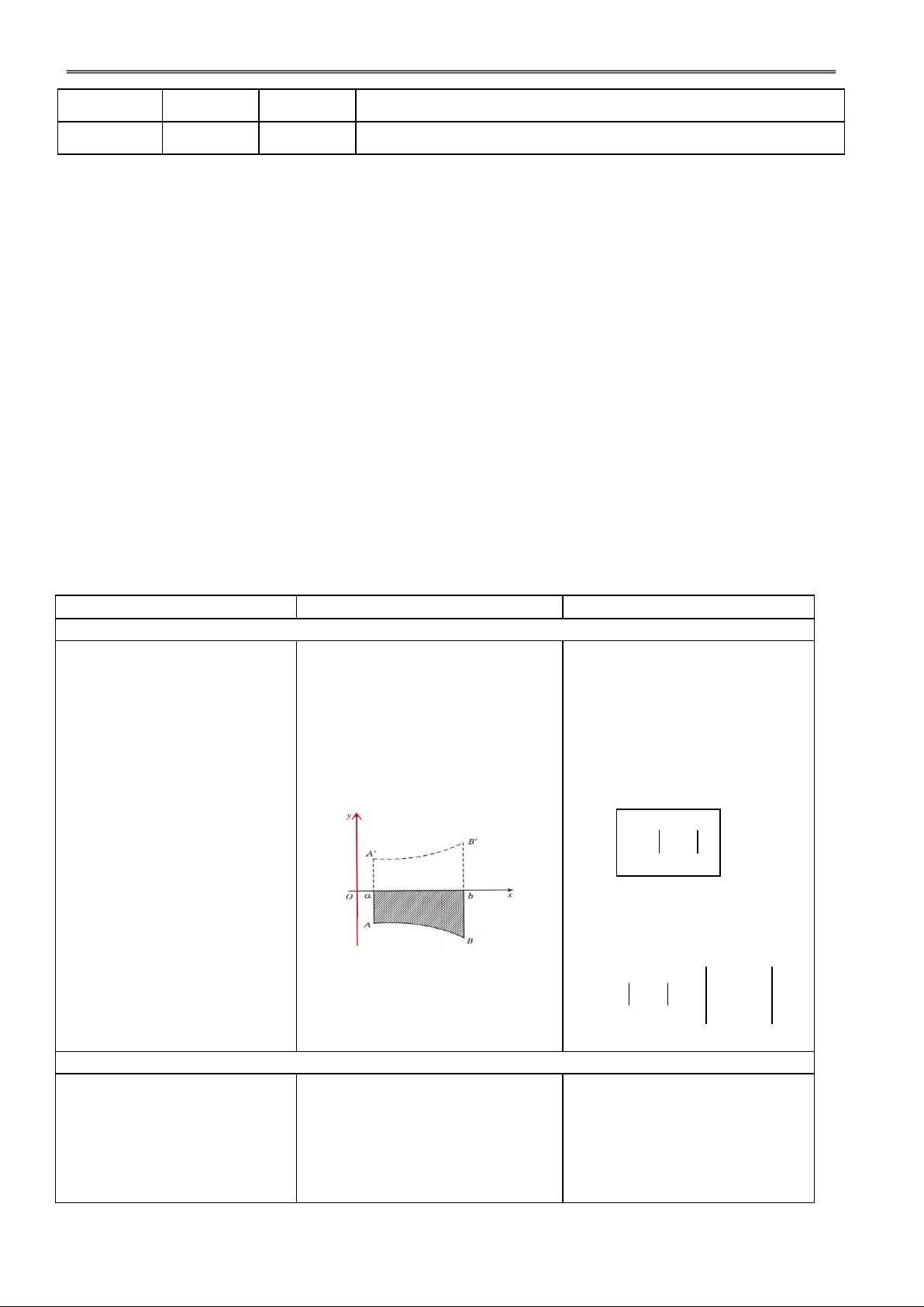
 Cho HS làm nhanh câu a).
2. a) Khảo sát và vẽ đồ thị (C)
H1. Nêu đk để đường thẳng Đ1. Pt hoành độ giao điểm x
luôn cắt (C) tại 2 điểm phân luôn có 2 nghiệm phân biệt. của hàm số 3 y x 1 biệt ?
x  3  x m
b) Chứng minh rằng với mọi 2 x 1
m, đường thẳng y  2x m  2
x  (m  )x m
luôn cắt (C) tại hai điểm phân  2 1  3  0  x
biệt M, N. Xác định m sao cho  1 
độ dài MN là nhỏ nhất.  2
'  (m  3) 16    2   0
H2. Nhận xét tính chất của Đ2. là các nghiệm của pt:
hoành độ các giao điểm M, N ? 2
2x  (m 1)x m  3  0  m 1
xM xN     2  m  3 xM.xN   2 H3. Tính MN ? Đ3. 2 2 2
MN  (xM xN) (yM yN) 5 =  2 (m 3) 16    4 GV: Phạm Việt Phương 38
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 5 .  16  20 4  minMN = 2 5 khi m = 3
Đ4. f(x) = 2
x x  4
H4. Tính f(x), f(sinx) ? 3. Cho hàm số 2
f '(sinx)  sin x sinx  4 1 1
f (x)  x x x  3 2 4 6 3 2
H5. Giải pt f(x) = 0? Suy ra Đ5. 2
f '(x)  0  x x  4  0 a) Giải pt: f '(sinx)  0 .
nghiệm của pt: f(sinx) = 0 ? 1 17
b) Viết pttt của đồ thị hàm số  x    [–1; 1] 2
tại điểm có hoành độ là nghiệm 
của phương trình f ' (x)  0 .
Pt: f(sinx) = 0 vô nghiệm. Đ6.
H6. Tính f(x) và giải pt f ' (x)  0 ? 1
f ' (x)  2x 1  0  x  2    Pttt tại 1 47  ;   2 12  : 17  1  47 y    x    4  2  12
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ:
 Chuẩn bị kiểm tra 1 tiết chương I.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 39
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 20
Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG 1 I. MỤC TIÊU: Kiến thức:
 Ôn tập toàn bộ kiến thức trong chương I. Kĩ năng:
 Khảo sát sự biến thiên và vẽ đồ thị hàm số.
 Giải các bài toán về tính đơn điệu, cực trị, GTLN, GTNN, tiệm cận.
 Giải các bài toán liên quan đến khảo sát hàm số: sự tương giao, biện luận số nghiệm của
phương trình bằng đồ thị, viết phương trình tiếp tuyến với đồ thị. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: Ôn tập toàn bộ kiến thức chương 1. III. MA TRẬN ĐỀ: Nhận biết Chủ đề Thông hiểu Vận dụng Tổng TNKQ TL TNKQ TL TNKQ TL Tính đơn điệu 3 1,5 0,5 Cực trị, GTLN – GTNN 3 1,5 0,5 Tiệm cận 2 1,0 0,5 Khảo sát hàm số 1 3,0 3,0 Các bài toán liên quan 1 3,0 3,0 Tổng 4,0 3,0 3,0 10,0
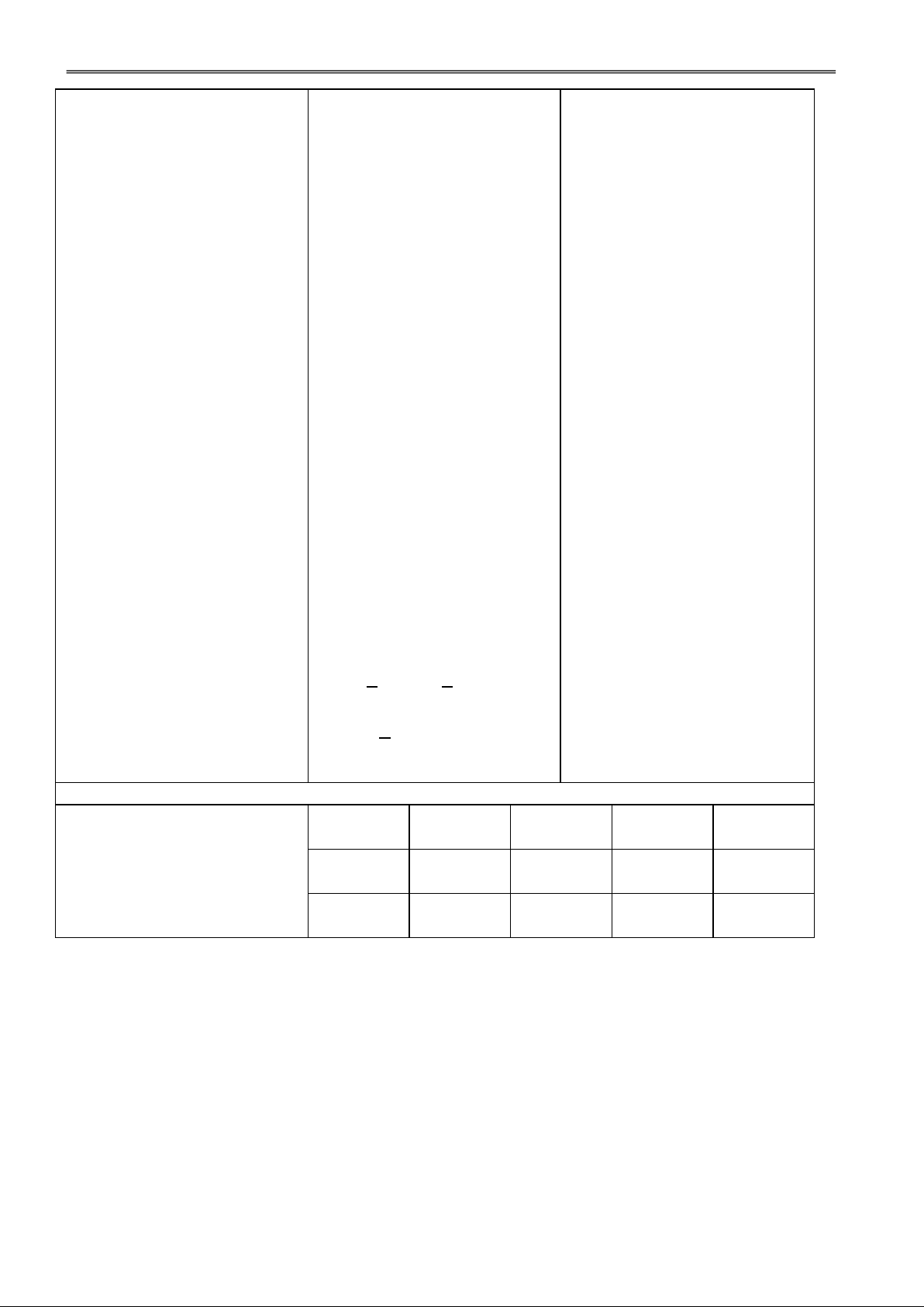
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm) Câu 1: Hàm số 3 2
y x 3x  4 đồng biến trên khoảng: A. (0; 2)
B. (  ; 0) và (2;  ) C. (  ; 2) D. (0; +∞) Câu 2: Hàm số 4 2
y  x  2x  3 đồng biến trên khoảng: A. (–∞; 0) B. (–∞; –1) C. (1; +∞) D. (0; +∞)  x Câu 3: Hàm số 1
y x nghịch biến trên khoảng: 2 A. (–∞; +∞) B. (–∞; 2) C. (2; +∞) D. (–2; +∞) Câu 4: Hàm số 3 2
y x 3x  4 đạt cực tiểu tại điểm: A. x = 0 B. x = 2 C. x = 4 D. không có Câu 5: Hàm số 4 2
y  x  2x  3 đạt cực đại tại điểm: A. x = –1 B. x = 1 C. x = 0 D. x = 3 GV: Phạm Việt Phương 40
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn x Câu 6: Hàm số 1 y
có mấy điểm cực trị: 2  x A. 0 B. 1 C. 2 D. 3 x Câu 1
7: Đồ thị hàm số y  có bao nhiêu tiệm cận: 2 x  3x A. 0 B. 1 C. 2 D. 3 x Câu 3
8: Đồ thị hàm số y
có bao nhiêu tiệm cận đứng: 2 x x  2 A. 0 B. 1 C. 2 D. 3
B. Phần tự luận: (6 điểm) Cho hàm số : 3 2
y x  3x 3.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số .
b) Dựa vào đồ thị (C), biện luận theo m số nghiệm của phương trình: 3 2
x 3x m .
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 B A D B C A D C
B. Phần tự luận: Mỗi câu 3 điểm a) 3 2
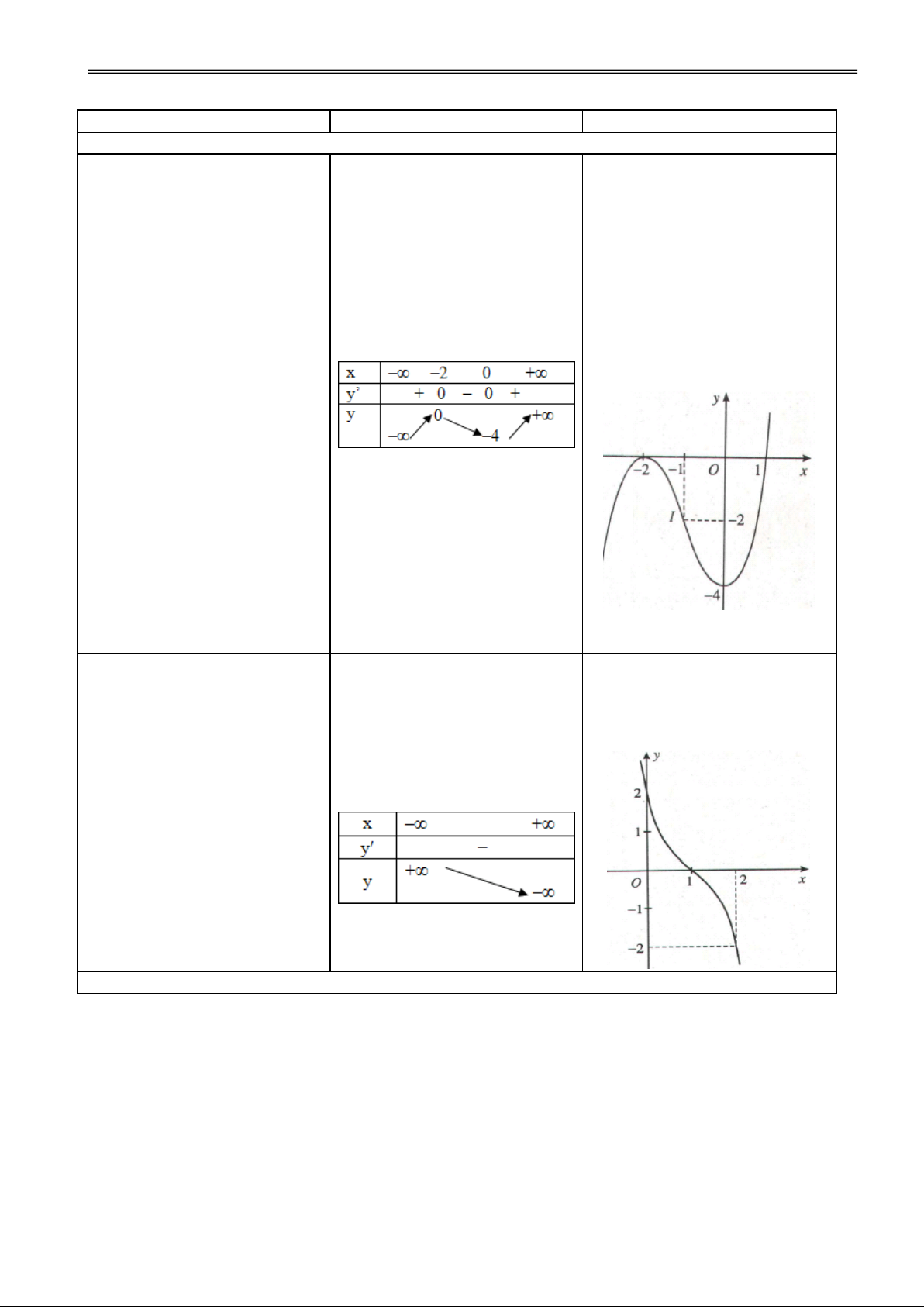
y x  3x 3  D = R  2
y'  3x  6x  y = 0  x = 0, x = –2  lim y   ;  lim y   y x x 4  3 x  -2 0  2 y’ + 0 – 0 + 1 1  x y -4 -3 -2 -1 1 2 3 4  -1 -3 -2  x = 0  y = –3; -3
x = 1  y = 1; x = –3  y = –3 -4 b) 3 2
x 3x m  3 2
x 3x 3  m 3 (*) m  0 m  0   : (*) có 1 nghiệm 
: (*) có 2 nghiệm  0 < m < 4: (*) có 3 nghiệm m  4 m  4
VI. KẾT QUẢ KIỂM TRA: Lớp 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Sĩ số SL % SL % SL % SL % SL % 12S1 53 12S2 54 12S3 54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 41
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1
Chương II: HÀM SỐ LUỸ THỪA – HÀM SỐ MŨ – HÀM SỐ LOGARIT Tiết dạy: 21 Bài 1: LUỸ THỪA I. MỤC TIÊU: Kiến thức:
 Biết các khái niệm và tính chất của luỹ thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ không
nguyên và luỹ thừa với số mũ thực.
 Biết khái niệm và tính chất của căn bậc n. Kĩ năng:
 Biết dùng các tính chất của luỹ thừa để rút gọn biểu thức, so sánh những biểu thức có chứa luỹ thừa. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại một số qui tắc luỹ thừa với số mũ nguyên dương? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu luỹ thừa với số mũ nguyên
H1. Nhắc lại định nghĩa và tính Đ1.
I. KHÁI NIỆM LUỸ THỪA
chất của luỹ thừa với số mũ m
1. Luỹ thừa với số mũ nguyên  a nguyên dương ? m n m n mn a .a  a ;  a
Cho n là một số nguyên dương. n a n  Với a tuỳ ý: n a  a.a. . a  m a  mn n n n  a ; (ab)  a .b n thöøa soá n n  a  a  1     0 n
Với a 0: a  1; a  n  b  b n a
(a: cơ số, n: số mũ) Chú ý:  0 n
0 , 0 không có nghĩa.
Luỹ thừa với số mũ nguyên có
các tính chất tương tự như luỹ
thừa với số mũ nguyên dương.
H2. Biến đổi các số hạng theo cơ Đ2. số thích hợp ? 10
VD1: Tính giá trị của biểu thức  1   3  10 9   .27  3 .3  3 10  1   3   3  A    .27   3  4  2  4 4 (0,2) .25 5 .5  1 9  4  2  1   1  9  (0,2) .25 128 .  1   1  7  9 128 .  2     2 .2  4  2   A = 8.
H3. Phân tích các biểu thức thành Đ3.
VD2: Rút gọn biểu thức: nhân tử ? GV: Phạm Việt Phương 42
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn a 2 2 2 3  2     a 2(a 1) a 2 2 2 a B    . 2 1  1 (1 a ) a 2 1  1  2 (1 a ) a  1 a 3 a 1 (a  0, a  1)  2  2 1 a a(a 1)  B = 2
Hoạt động 2: Biện luận số nghiệm của phương trình n x  b
H1. Dựa vào đồ thị, biện luận số 
nghiệm của các phương trình: 2. Phương trình n x b (*) a) n lẻ: 3 4 x  b, x  b ?
(*) luôn có nghiệm duy nhất. b) n chẵn:
 GV hướng dẫn HS biện luận. Từ
+ b < 0: (*) vô nghiệm. đó nêu nhận xét.
+ b = 0: (*) có 1 nghiệm x = 0
+ b > 0: (*) có 2 nghiệm đối nhau.
Hoạt động 3: Tìm hiểu khái niệm và tính chất căn bậc n 3. Căn bậc n
 Dựa vào việc giải phương trình a) Khái niệm n
x  b, GV giới thiệu khái niệm
Cho b R, n N* (n 2). Số a căn bậc n.
đgl căn bậc n của b nếu n a  b . Nhận xét:
H1. Tìm các căn bậc hai của 4?  Đ1.
n lẻ, b tuỳ ý: có duy nhất một 2 và –2.
căn bậc n của b, kí hiệu n b n chẵn:
+ b < 0: không có căn bậc n của b.
+ b = 0: căn bậc n của 0 là 0.
+ b > 0: có hai căn trái dấu, kí
Lưu ý HS phân biệt kí hiệu 2 giá
hiệu giá trị dương là n b , còn giá
trị căn bậc n của một số dương. trị âm là n  b .
b) Tính chất của căn bậc n
GV hướng dẫn HS nhận xét một n
số tính chất của căn bậc n. a a n n n a. b  ab ; n  n b b n am n m n k nk  a ; a  a n n a  khi n leû a    a khi n chaün
H2. Thực hiện phép tính ? Đ2. 5 A = 3  2  2 
VD3: Rút gọn biểu thức:  5 5 3 A = 4. 8  ; B = 3 3 3 3 3 B =  3
Hoạt động 4: Củng cố Nhấn mạnh:
– Định nghĩa và tính chất của luỹ
thừa với số mũ nguyên.
– Định nghĩa và tính chất của căn bậc n. GV: Phạm Việt Phương 43
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Bài 1 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 22
Bài 1: LUỸ THỪA (tt) I. MỤC TIÊU: Kiến thức:
 Biết các khái niệm và tính chất của luỹ thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ
không nguyên và luỹ thừa với số mũ thực.
 Biết khái niệm và tính chất của căn bậc n. Kĩ năng:
 Biết dùng các tính chất của luỹ thừa để rút gọn biểu thức, so sánh những biểu thức có chứa luỹ thừa. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số tính chất của căn bậc n? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu luỹ thừa với số mũ hữu tỉ  GV nêu định nghĩa.
4. Luỹ thừa với số mũ hữu tỉ m r
Cho a R, a > 0 và n ,
trong đó m Z, n N, n 2. m r n n m
a a a 1 n n a a Đặc biệt:
H1. Viết dưới dạng căn thức? Đ1.
VD1: Tính giá trị các biểu thức 1 1 A = 3  1 8 2  3 1 3  A =   2 4  1 1  8  ; B = B = 3 4   3 8 4
H2. Phân tích tử thức thành Đ2.
VD2: Rút gọn biểu thức: nhân tử ? GV: Phạm Việt Phương 44
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 5 5  1 1  5 5   4 4 4 4
x y xy xyx y  4 4 x y xy C = (x, y > 0)  C = xy. 4 4 x y
Hoạt động 2: Tìm hiểu khái niệm luỹ thừa với số mũ vô tỉ
 GV cho HS nhận xét kết quả  HS tính và nêu nhận xét.
5. Luỹ thừa với số mũ vô tỉ bảng tính r
Cho a R, a > 0, là số vô tỉ.
3 n . Từ đó GV nêu
Ta gọi giới hạn của dãy số định nghĩa.  rn a
là luỹ thừa của a với số
mũ , kí hiệu a. r n
a  lim a với   lim nr Chú ý:
1  1 ( R)
Hoạt động 3: Tìm hiểu tính chất của luỹ thừa với số mũ thực
H1. Nhắc lại các tính chất của Đ1. HS nhắc lại.
II. TÍNH CHẤT CỦA LUỸ
luỹ thừa với số mũ nguyên
THỪA VỚI SỐ MŨ THỰC dương ?
Cho a, b R, a, b > 0; , R. Ta có:
H2. Nêu tính chất tương tự cho Đ2. Các nhóm lần lượt nêu tính a
luỹ thừa với số mũ thực ?     chất. a a .  a ; a a   a  a    
; (ab)  a b .   a a    b b  
a > 1: a a       
a < 1: a a    
H3. Biến đổi tử và mẫu về luỹ Đ3. thừa với cơ số a ?
VD3. Rút gọn biểu thức: 7 1  2 7 3 a a .  a 7 1  2 7 a a .   D = (a > 0)   2 2 2 2 2 a a    22 a  2 2  D = 5 a    a   3 1 3 1 3 1   3 1 2 aa E = 5 3  4 5 a a . 5 3  4 5 a a .  a  E = a
H4. Ta cần so sánh các số nào?
VD4: So sánh các số: Đ4.
Vì cùng cơ số nên chỉ cần so sánh các số mũ. A = 2 3 5 và B = 3 2 5 2 3  12  18  3 2 2  A < B
Hoạt động 4: Củng cố Nhấn mạnh:
– Định nghĩa và tính chất của
luỹ thừa với số mũ hữu tỉ, số mũ thực. GV: Phạm Việt Phương 45
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Bài 2, 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 23
Bài 2: HÀM SỐ LUỸ THỪA I. MỤC TIÊU: Kiến thức:
 Biết khái niệm và tính chất của hàm số luỹ thừa.
 Biết công thức tính đạo hàm của hàm số luỹ thừa.
 Biết dạng đồ thị của hàm số luỹ thừa. Kĩ năng:
 Biết khảo sát hàm số luỹ thừa.
 Tính được đạo hàm của hàm số luỹ thừa. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Cho VD một số hàm số luỹ thừa đã học? Đ. 2 1
y x ; y  ; y x , … x 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm hàm số luỹ thừa
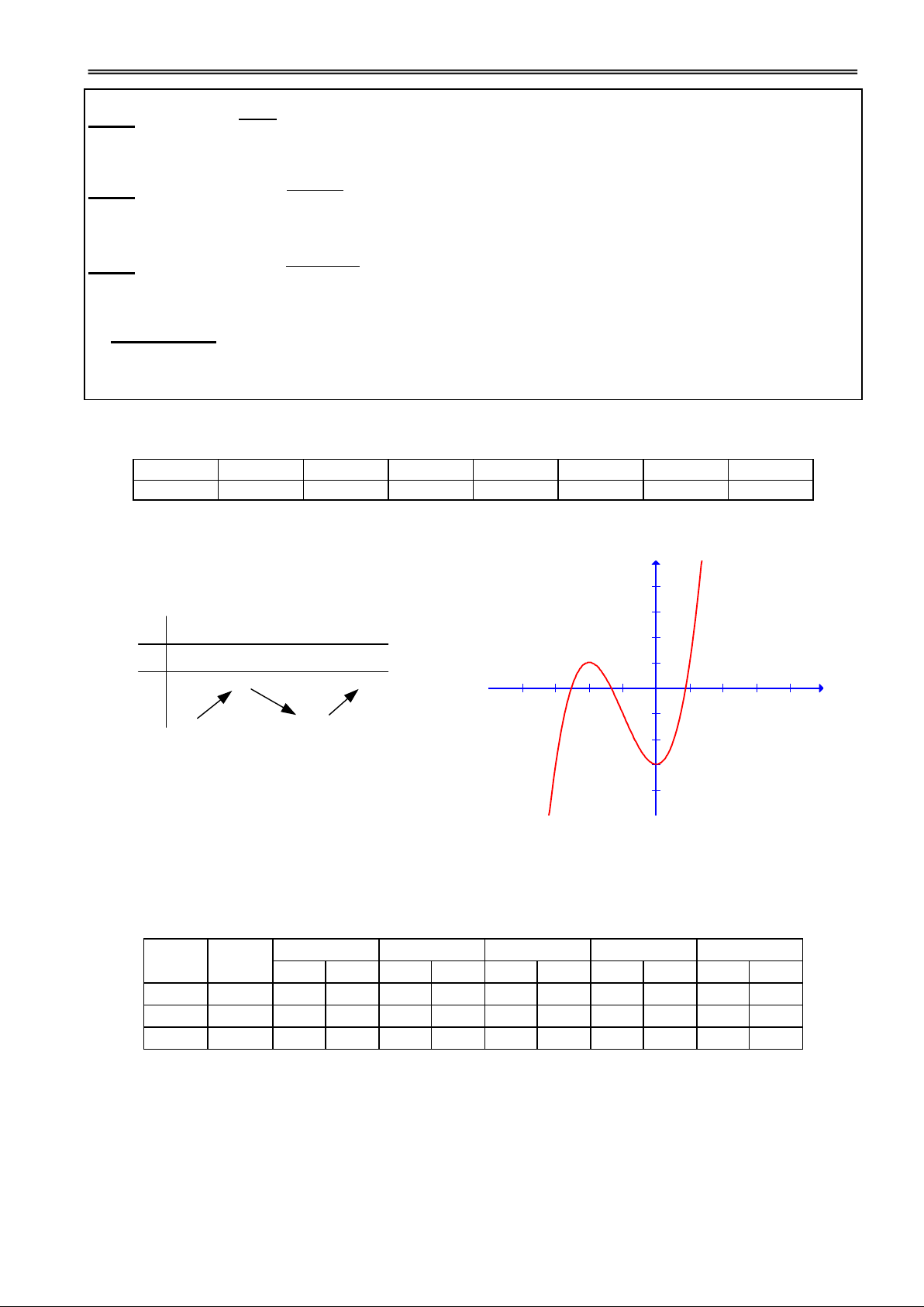
H1. Cho VD một số hàm luỹ Đ1. Các nhóm thảo luận và I. KHÁI NIỆM
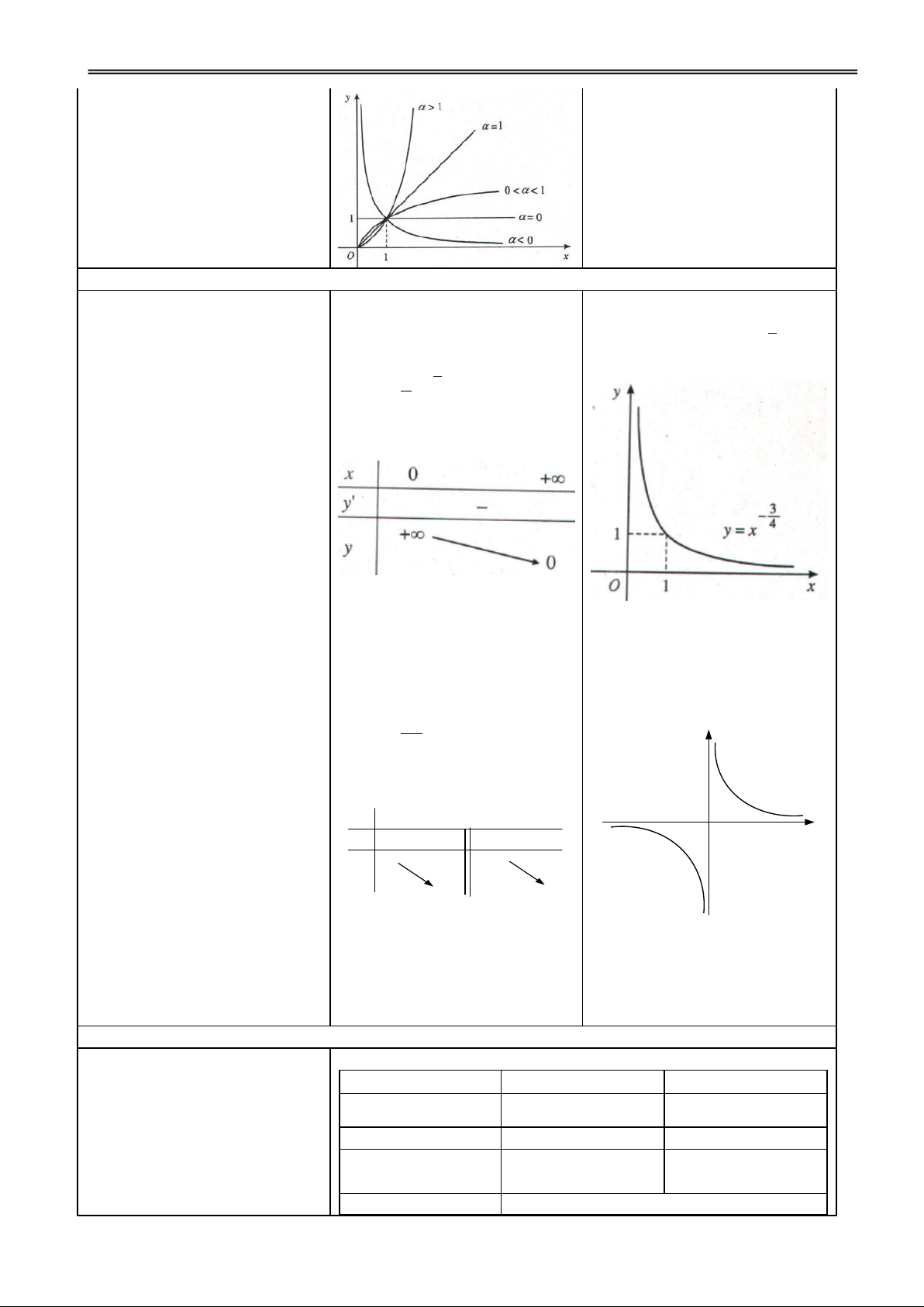
thừa và vẽ đồ thị của chúng ? trình bày. Hàm số y x 
với R đgl 1
hàm số luỹ thừa. 2 1  2
y x; y x ; y x ; y x
H2. Nhận xét tập xác định của Chú ý: các hàm số đó ?
Tập xác định của hàm y 7 6 y = x2 số y x 
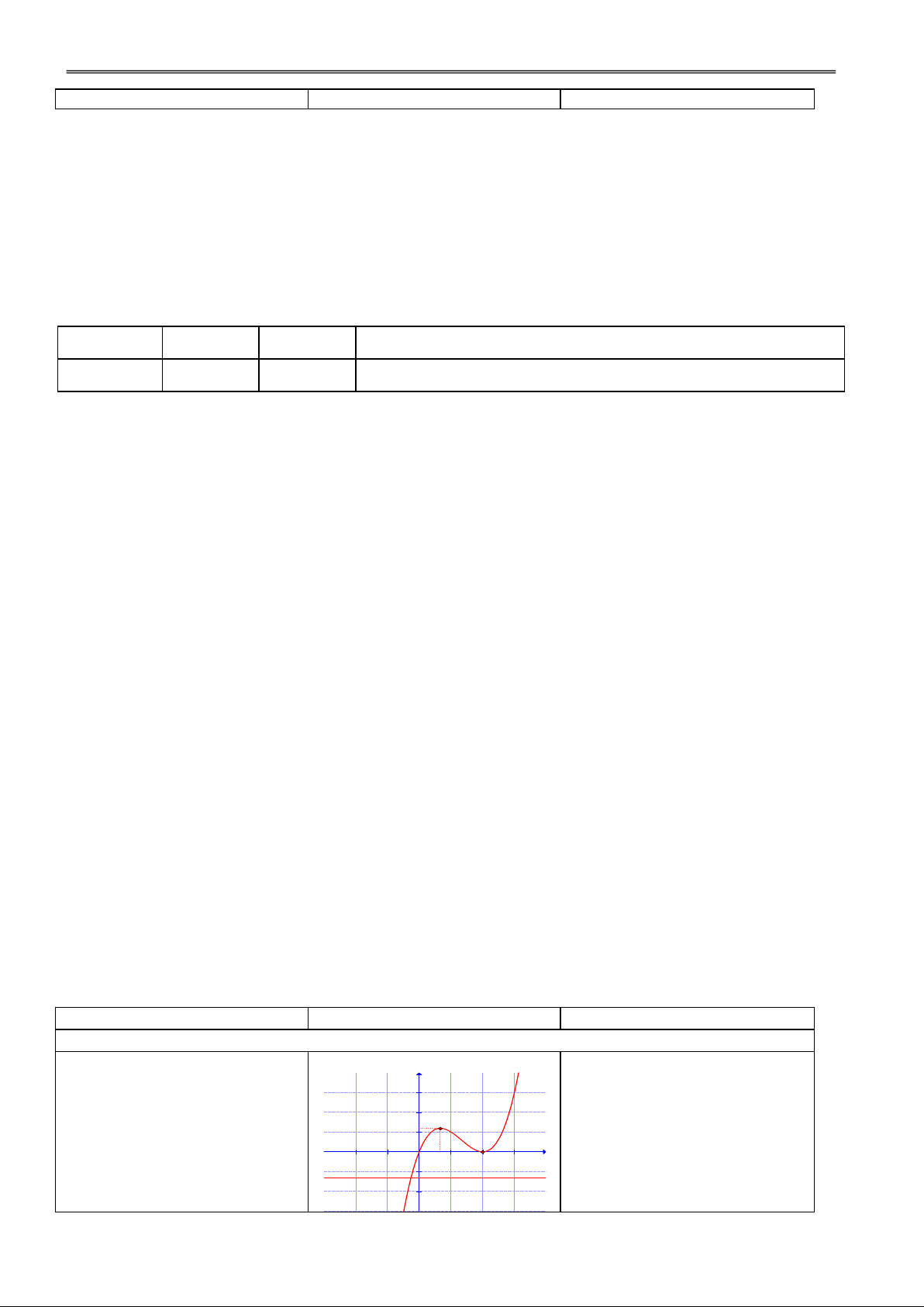
tuỳ thuộc vào giá trị 5  y = x-1 GV nêu chú ý. 4 của : 3 y = x 2  y = x1/2
nguyên dương: D = R 1 x -3 -2 -1 1 2 3   nguyeân aâm -1  : D = R \ {0} -2    -3 0 -4 -5 
không nguyên: D = (0;+∞) -6 -7 GV: Phạm Việt Phương 46
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
H3. Dựa vào yếu tố nào để xác Đ3. Dựa vào số mũ .
VD1: Tìm tập xác định của các
định tập xác định của hàm số a) 1 – x > 0  D = (–∞; 1) hàm số:
luỹ thừa ? Từ đó chỉ ra điều  x  1 
kiện xác định của hàm số ? b) 2 2 0 a) 3 y  1 (  x)  D = ( 2; 2) 3 2 c) 2 x 1 0 b) 5
y  (2  x )  D = R \ {–1; 1} c) 2 2 y (x 1)   d) 2
x x  2  0
y  (x x  )
 D = (–∞; –1)  (2; +∞) d) 2 2 2
Hoạt động 2: Tìm hiểu công thức tính đạo hàm của hàm số luỹ thừa
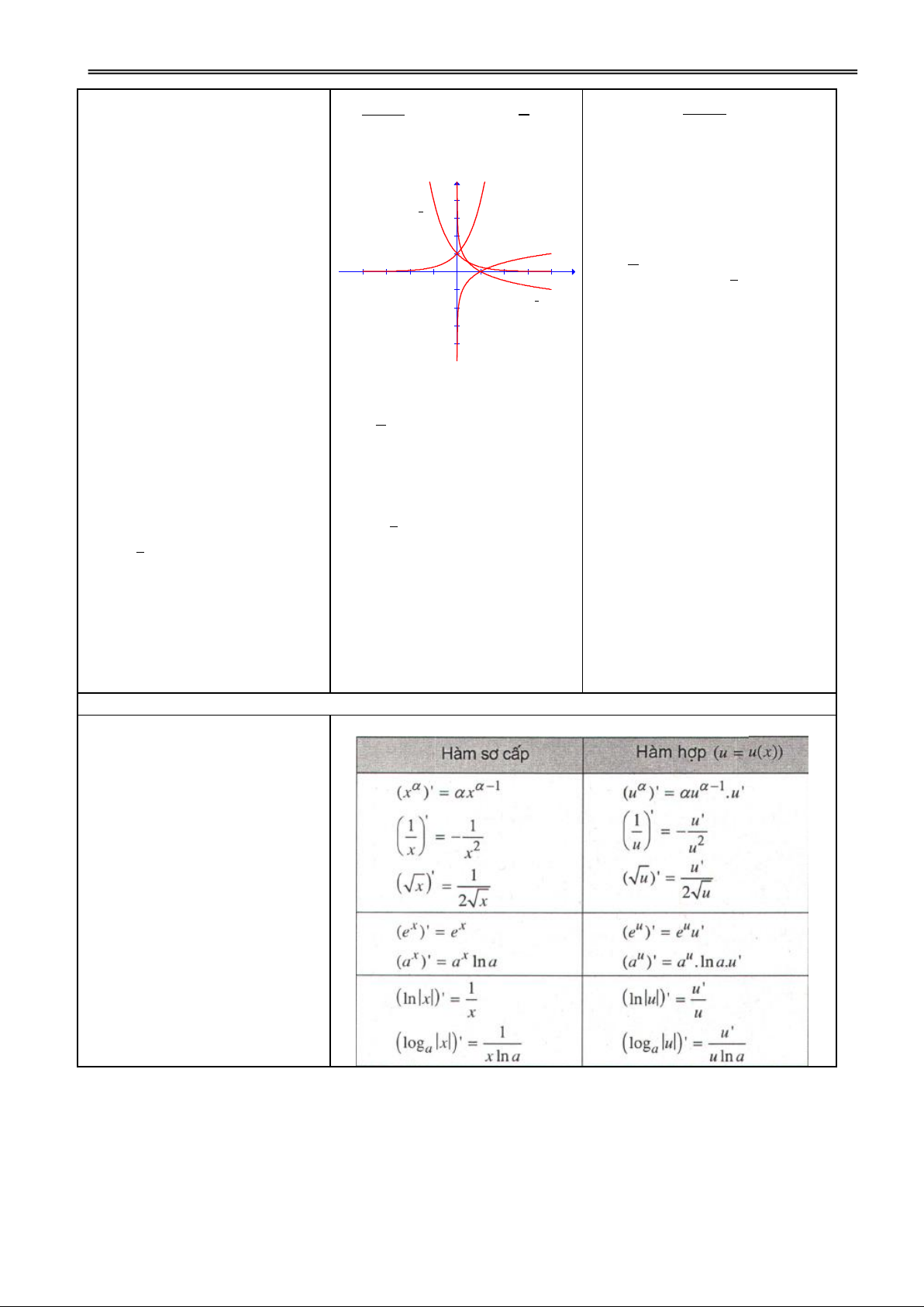
H1. Nhắc lại công thức tính Đ1.
II. ĐẠO HÀM CỦA HÀM đạo hàm của hàm số n y x n nSỐ LUỸ THỪA 1 (x )  nx với n nguyên dương ?      1 x
  x  (x > 0)     1 u  u u . 
H2. Thực hiện phép tính ? Đ2.
VD2: Tính đạo hàm: 5 3 2  3 2  a) y  b)  3 y   x a) 4 y x b) 3 y x 4 4 x 3 c) 3 y x d) y x  c) 3 1 y 3x    d) 1 y x    
Hoạt động 3: Vận dụng tính đạo hàm của hàm số luỹ thừa
H1. Thực hiện phép tính? Đ2.
VD2: Tính đạo hàm: 2(4x 1) a) y 
y  2x x  2 2 3 3 a) 1 2 3 2x x 1  6  x 2 y   2 3x   2 b) 1 b) y '  2 2 1 3 ( x 1)  c) 3 y  5 (  x) c) 3 1 y' 3 5 ( x)       d) 2 y  3 ( x 1) 1 3  d) 2 y'  3 ( x 1) 2
Hoạt động 4: Củng cố Nhấn mạnh:
– Tập xác định của hàm số luỹ
thừa phụ thuộc vào số mũ .
– Công thức tính đạo hàm của hàm số luỹ thừa.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đóc tiếp bài "Hàm số luỹ thừa".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 47
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 24
Bài 2: HÀM SỐ LUỸ THỪA (tt) I. MỤC TIÊU: Kiến thức:
 Biết khái niệm và tính chất của hàm số luỹ thừa.
 Biết công thức tính đạo hàm của hàm số luỹ thừa.
 Biết dạng đồ thị của hàm số luỹ thừa. Kĩ năng:
 Biết khảo sát hàm số luỹ thừa.
 Tính được đạo hàm của hàm số luỹ thừa. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu tập xác định và công thức tính đạo hàm của hàm số luỹ thừa? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khảo sát hàm số luỹ thừa
 GV hướng dẫn HS khảo sát  Các nhóm thảo luận và trả III. KHẢO SÁT HÀM SỐ
và vẽ đồ thị hàm số lời. y x 
LUỸ THỪA y x 
theo từng bước của sơ đồ khảo sát. y x  ( > 0) y x  ( < 0)  Tập khảo sát  (0; +∞)  (0; +∞)   y x       y x      Sự biến thiên 1 0 , x > 0 1 0 , x > 0      Giới hạn đặc biệt
 lim x  0; lim x    lim x  ;  lim x  0 x    0 x x0 x  Tiệm cận  Không có  TCN: trục Ox  Bảng biến thiên  TCĐ: trục Oy   Đồ thị
Chú ý: Khi khảo sát hàm số
luỹ thừa với số mũ cụ thể, ta
phải xét hàm số đó trên toàn
bộ tập xác định của nó. GV: Phạm Việt Phương 48
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Hoạt động 2: Áp dụng khảo sát và vẽ đồ thị của hàm số luỹ thừa
H1. Thực hiện các bước khảo Đ1. Các nhóm thảo luận và VD1: Khảo sát sự biến thiên và sát và vẽ đồ thị ? trình bày. 3   D = (0; +∞) vẽ đồ thị hàm số 4 y x . 7 3   4
y '   x < 0, x  D 4  TCĐ: x = 0; TCN: y = 0  BBT:  Đồ thị
H2. Thực hiện các bước khảo Đ2. Các nhóm thảo luận và sát và vẽ đồ thị ?
VD2: Khảo sát sự biến thiên và trình bày.  vẽ đồ thị hàm số 3 y x  D = R \ {0}  3 y '   < 0, x  D 4 x y  TCĐ: x = 0; TCN: y = 0 3 y x   BBT: x  0  y’ – – O x 0  y  0  Đồ thị Hàm số 3 y x  là hàm số lẻ
nên đồ thị nhận gốc toạ độ làm tâm đối xứng.
Hoạt động 3: Củng cố Nhấn mạnh: Bảng tóm tắt
– Tính chất và đồ thị của hàm  > 0  < 0 số luỹ thừa. Đạo hàm  1 y' x    1 y'  x Chiều biến thiên Luôn đồng biến Luôn nghịch biến Tiệm cận Không có TCN: trục Ox TCĐ: trục Oy Đồ thị Luôn đi qua điểm (1; 1) GV: Phạm Việt Phương 49
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc trước bài "Logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 25 Bài 3: LOGARIT I. MỤC TIÊU: Kiến thức:
 Biết khái niệm và tính chất của logarit.
 Biết các qui tắc tính logarit và công thức đổi cơ số.
 Biết các khái niệm logarit thập phân, logarit tự nhiên. Kĩ năng:
 Biết vận dụng định nghĩa để tính một số biểu thức chứa logarit đơn giản.
 Biết vận dụng các tính chất của logarit vào các bài toán biến đổi, tính toán các biểu thức chứa logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3') x x x
H. Giải các phương trình: 2  8; 3  81; 2  3 ? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm logarit
 Dẫn dắt từ KTBC, GV nêu
I. KHÁI NIỆM LOGARIT định nghĩa logarit. 1. Định nghĩa
Cho a, b > 0, a 1.
H1. Nhận xét giá trị biểu thức log 
a b    a b a ?
Đ1. a > 0,   b > 0
Chú ý: không có logarit của số âm và số 0.
H2. Thực hiện phép tính và giải thích ? VD1: Tính: Đ2. a) log 8 b) log 9 2 1 a) log 8 = 3 vì 3 2  8 2 3 GV: Phạm Việt Phương 50
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 2   1  log 1 log b) log 9 = –2 vì    9 c) 4 d) 1 3 1  3  27 2 3 2   1  c) log 4 = –2 vì    4 1  2  2 1  d) log = –3 vì 3 1 3  3 27 27
Hoạt động 2: Tìm hiểu tính chất của logarit
 GV hướng dẫn HD nhận xét  2. Tính chất các tính chất. a0 = 1  log 1  0 a
Cho a, b > 0, a 1. log  log 1 0; log a 1 a a a1 = a  1 a a log b a ab; log (a )   a
H1. Thực hiện phép tính ? VD2: Tính: Đ1. 2 log 5 a) 3 3 b) log 8 2 1 2 log 5  log 5 2 3 3  a) 3 3 =  5 2 1 3   log 1  1 log 5  1  3 b) log 8 = log    3  7 1 1  c) 2 4 d)   2   25  2 2 2 1 log  1 2 log   2 1 7 2  c) 2 7 4 =     7  1 log 2  1 2  5   log   5 1 3 5  1  3 d)       25  =  3
Hoạt động 3: Tìm hiểu qui tắc tính logarit Đ1. II. QUI TẮC TÍNH H1. Cho 3 5
b  2 ,b  2 . Tính 1 2
log b  log b    LOGARIT
log b  log b ;log b b 3 5 8 . 2 1 2 2 2 1 2 2 2 1 2 log b b  8
1. Logarit của 1 tích So sánh kết quả ? 2 1 2 Cho a, b
 log b  log b ; log b b
1, b2 > 0, a 1. 2 1 2 2 2 1 2
loga(b b )  loga b  loga b  1 2 1 2 GV nêu định lí.
Chú ý: Định lí trên có thể mở
rộng cho tích của n số dương:
log (b . b. )  log b . . log b a 1 n a 1 a n
H2. Thực hiện phép tính ? Đ2. VD3: Tính: a) = log 36  2 log 9  log 4 6 a) 6 6 1 1 1 1 3 b) 2 log  log  log log  log  log 1 1 1 b) 2 2 3 3 3 1 1 1 3 8 2 2 2 2 2 2 c) = log 27  3  1 9 c) log 5  log  log 3 3 1 1 1 5 3 3 3 d) = log 125  3 5 5 d) log 75  log 5 5 3 GV: Phạm Việt Phương 51
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Hoạt động 4: Củng cố Nhấn mạnh: – Định nghĩa logarit. – Qui tắc tính logarit.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 26 Bài 3: LOGARIT (tt) I. MỤC TIÊU: Kiến thức:
 Biết khái niệm và tính chất của logarit.
 Biết các qui tắc tính logarit và công thức đổi cơ số.
 Biết các khái niệm logarit thập phân, logarit tự nhiên. Kĩ năng:
 Biết vận dụng định nghĩa để tính một số biểu thức chứa logarit đơn giản.
 Biết vận dụng các tính chất của logarit vào các bài toán biến đổi, tính toán các biểu thức chứa logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3') 1
H. Nêu định nghĩa logarit và tính: log2 ; log1 2 8 ? 4 Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu các qui tắc tính logarit
 Tương tự như logarit của 1
II.QUI TẮC TÍNH LOGARIT tích, GV cho HS nhận xét.
2. Logarit của 1 thương
Cho a, b1, b2 > 0, a 1. b1 log
 log b  log b a a 1 a b 2 2 1
Đặc biệt: loga  loga b b GV: Phạm Việt Phương 52
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn VD1: Tính: a) log2120  log215
H1. Thực hiện phép tính ? Đ1. b) log 16  log 144 3 3 a) = log2 8  3 c) log 16  log 400 1 1 1 b) = lo 3 g  2  5 5 9 d) log 30  log 210 log 25  2  7 7 c) = 1
3. Logarit của 1 luỹ thừa 5
Cho a, b > 0; a 1; tuỳ ý: 1 d) log  7  1 
log b  log b 7 a aĐặc biệt:
GV hướng dẫn HS chứng  minh. Đặt log    n 1
a b b a
loga b  loga b n VD2: Tính:
H2. Thực hiện phép tính ? Đ2. 1 7 log 4 2 a) 2 2 a) = 7 log 1 2 2  7 b) log5 3  log515 5 1  1 b) = 2 lo 5 g 5   2
Hoạt động 2: Tìm hiểu công thức đổi cơ số
H1. Cho a = 4, b = 64, c = 2. Đ1. III. ĐỔI CƠ SỐ
Tính loga b,logc a,logc b . Từ đó
logc a.loga b logc b
Cho a, b, c > 0; a, c 1. rút ra nhận xét? logc b log b a logc a
 GV hướng dẫn HS chứng  b   b a alog log log  c c Đặc biệt: minh. log b.log a 1 = a c
loga b  log a (b 1) b 1 log  b
log b ( 0) a a
H2. Thực hiện phép tính ? Đ2. VD3: Tính: 1 log 6.log 9.log 2 a) log 9  log 9 a) 3 8 6 8 2 3 log 2 1 log 15 1 2 27 3 b) log b) 4 c) 4 15  log215  log2 15 2 1  c) 3 log 1 2  lo 3 g 2 27
Hoạt động 3: Tìm hiểu khái niệm logarit thập phân, logarit tự nhiên
 GV giới thiệu khái niệm
IV. LOGARIT THẬP PHÂN,
logarit thập phân và logarit tự LOGARIT TỰ NHIÊN nhiên.
1. Logarit thập phân
lgb  logb  log b 10
 GV hướng dẫn HS sử dụng  HS theo dõi và thực hành 2. Logarit tự nhiên MTBT để tính. trên MTBT. lnb  loge b log3 log 3  1,5850
Chú ý: Muốn tính log với a 2 log2 a b GV: Phạm Việt Phương 53
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn ln0,8 10 và a  lo
e, bằng MTBT, ta có thể 3 g 0,8   0  ,2031 ln3
sử dụng công thức đổi cơ số.
Hoạt động 4: Củng cố Nhấn mạnh: – Qui tắc tính logarit.
– Công thức đổi cơ số.
4. BÀI TẬP VỀ NHÀ:  Bài 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 27
Bài 3: BÀI TẬP LOGARIT I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm và tính chất của logarit.
 Các qui tắc tính logarit và công thức đổi cơ số.
 Các khái niệm logarit thập phân, logarit tự nhiên. Kĩ năng:
 Biết vận dụng định nghĩa để tính một số biểu thức chứa logarit đơn giản.
 Biết vận dụng các tính chất của logarit vào các bài toán biến đổi, tính toán các biểu thức chứa logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: () H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập các qui tắc tính logarit
H1. Nêu qui tắc cần sử dụng ? Đ1.
1. Thực hiện các phép tính: A = –1 A = log 4.log 2 2 1 4 4 B =  3 1 log .log C = 9 + 16 = 25 B = 9 5 27 25 D = 16.25 = 400 log log 2 3 C = 2 3 4  9 2 log 24 log 5 D = 3 81 9 GV: Phạm Việt Phương 54
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
2. Thực hiện các phép tính:
H2. Nêu qui tắc cần sử dụng ? Đ2. log 5 log 36 4 log 7 A = 3 9 9 81  27  3 A = 4 3 2 5  6  7 log 6 log 8 B = 5 7 25  49 B = 2 2 6  8 C = 0 0
lg(tan1 ) . . lg(tan89 ) C = lg1 = 0 log log (log ) D = log 1  0 D = 16   8 8 4 2
3. So sánh các cặp số:
H3. Nêu cách so sánh ? Đ3. a) log 5, log 4 3 7 a) log 4  1  log 5 7 3 b) log 2, log 3 0 3 , 5 b) log 2  0  log 3 0 3 , 5 c) log 10, log 30 2 5 c) log 30  3  log 10 5 2
Hoạt động 2: Luyện tập vận dụng công thức đổi cơ số
 GV hướng dẫn HS cách tính.
4. Tính giá trị của biểu thức
H1. Phân tích 1350 thành tích Đ1.
logarit theo các biểu thức đã 1350 = 2 3 5 . 3 . 0
các luỹ thừa của 3, 5, 30 ?  cho: log 1350 = 2a + b + 1 30 a) Cho a  log 3, b  log 5 . 30 30
H2. Tính log 5 theo c ? 3 Đ2. log Tính 1350 theo a, b. 30 15 b) Cho c  log 3 . log 5  log  log 151 15 3 3 3 3 Tính log 15 theo c. 25 1 = 1
c) Cho a  log 7, b  log 5 . c 14 14 log H3. Tính log 2 ? Đ3. Tính 28 theo a, b. 14 35 log 14 2 = log 1 log 7 14 14 14 7 = 1 – a
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách vận dụng các qui tắc,
công thức đổi cơ số để tính các biểu thức logarit.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc trước bài "Hàm số mũ. Hàm số logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 55
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 28
Bài 4: HÀM SỐ MŨ – HÀM SỐ LOGARIT I. MỤC TIÊU: Kiến thức:
 Biết khái niệm và tính chất của hàm số mũ, hàm số logarit.
 Biết công thức tính đạo hàm của hàm số mũ, hàm số logarit.
 Biết dạng đồ thị của hàm số mũ, hàm số logarit. Kĩ năng:
 Biết vận dụng tính chất của các hàm số mũ, hàm số logarit vào việc so sánh hai số, hai biểu thức chứa mũ và logarit.
 Biết vẽ đồ thị các hàm số mũ, hàm số logarit.
 Tính được đạo hàm của hàm số mũ, hàm số logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các qui tắc tính luỹ thừa với số mũ thực ? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm hàm số mũ
 GV nêu bài toán "lãi kép". Bài toán lãi kép:
Hướng dẫn HS cách tính. Từ đó Vốn: P = 1 triệu
giới thiệu khái niệm hàm số mũ. Lãi suất: r = 7% / năm
H1. Tính số tiền lãi và tiền lĩnh
Qui cách lãi kép: tiền lãi sau 1
sau năm thứ nhất, thứ hai, …?
Đ1. Các nhóm tính và điền vào năm được nhập vào vốn. bảng.
Tính: số tiền lĩnh được sau n năm ? 1 2 3 Lãi 0,7 0,0749 I. HÀM SỐ MŨ Lĩnh 1,7 1,1449 P(1+r) P(1+r)2 1. Định nghĩa
Cho a > 0, a 1. Hà m số x y a
đgl hàm số mũ cơ số a. H2. Cho HS xét?
VD1: Trong các hàm số sau, hàm Đ2. số nào là hàm số mũ:  Hàm số mũ: a), b), d) x   x y 3 y 3  5 a) b)  x c) y x 4 d) y 4 
H3. Nêu sự khác nhau giữa hàm
số luỹ thừa và hàm số mũ?
Đ3. Các nhóm thảo luận và trình Chú ý: bày. Cơ số Số mũ HS mũ K.đổi B.thiên HS LT B.thiên K.đổi
Hoạt động 2: Tìm hiểu công thức tính đạo hàm của hàm số mũ
 GV nêu các công thức.
2. Đạo hàm của hàm số mũ GV: Phạm Việt Phương 56
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn t e 1  lim 1 0  t t   x e  xue u e ; e u .    x a  x a lna u a  u a lna u . 
H1. Thực hiện phép tính ? Đ1. x a) y 1   2 .ln2
VD2: Tính đạo hàm: xx y 1 2   x y 2 4 5   b) y 2 4   2.5 .ln5 a) b) x x x x x c) y  x 2 (2 1).8 .ln8 c) y 2 8   d) y e2 1   x d) y e2 1 2.   
Hoạt động 3: Khảo sát hàm số mũ
 GV hướng dẫn HS khảo sát 2  HS theo dõi và thực hiện
3. Khảo sát hàm số mũ x hàm số: x y y 1 2 ,  . Từ đó
y a (a > 0, a 1) x 2
tổng kết sơ đồ khảo sát hàm số mũ. x x
y a (a > 1)
y a (0 < a < 1)  Tập xác định  D = R  D = R x x
y  a .lna
y  a .lna Đạo hàm > 0, x < 0, x  x x x x Giới hạn:
 lim a  0, lim a    lim a   ,  lim a  0 x x x x  Tiệm cận  TCN: trục Ox  TCN: trục Ox  Bảng biến thiên  Đồ thị
Hoạt động 4: Củng cố Nhấn mạnh:
– Công thức tính đạo hàm của hàm số mũ.
– Các dạng đồ thị của hàm số mũ.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Hàm số mũ. Hàm số logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 57
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 29
Bài 4: HÀM SỐ MŨ – HÀM SỐ LOGARIT (tt) I. MỤC TIÊU: Kiến thức:
 Biết khái niệm và tính chất của hàm số mũ, hàm số logarit.
 Biết công thức tính đạo hàm của hàm số mũ, hàm số logarit.
 Biết dạng đồ thị của hàm số mũ, hàm số logarit. Kĩ năng:
 Biết vận dụng tính chất của các hàm số mũ, hàm số logarit vào việc so sánh hai số, hai biểu thức chứa mũ và logarit.
 Biết vẽ đồ thị các hàm số mũ, hàm số logarit.
 Tính được đạo hàm của hàm số mũ, hàm số logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về luỹ thừa và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')  inx
H. Tính đạo hàm của các hàm số: x x
y e 2 2 , y s  3 ? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm hàm số logarit
 GV nêu định nghĩa hàm số II. HÀM SỐ LOGARIT logarit. 1. Định nghĩa
Cho a > 0, a 1. Hàm số
y  loga x đgl hàm số logarit cơ số a.
H1. Cho VD hàm số logarit ?
Đ1. Các nhóm cho VD.  log ,  log VD1: y x y x 3 1 4
y  log x, y  ln x, y  lg x 5
H2. Nêu điều kiện xác định ? Đ2.  1 
a) 2x + 1 > 0  D =   ;
VD2: Tìm tập xác định của các 2    hàm số: 2  log (2 1)
b) x  3x  2  0 a) y x 2
 D = (–∞; 1)  (2; +∞) 2
b) y  log (x  3x  2) x 1 3 c)  0 x 1 x  D = (–1; 1) 1 c) y  ln x 1 2
d) x x  1  0  D = R 2
d) y  lg(x x  1)
Hoạt động 2: Tìm hiểu công thức tính đạo hàm của hàm số logarit  GV nêu công thức.
2. Đạo hàm của hàm số logarit  1 log   a x
x lna (x > 0) GV: Phạm Việt Phương 58
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn u  loga u  ulna Đặc biệt: x 1 ln  ln 
H1. Thực hiện phép tính ? Đ1.     x   u u u 2  a) y  (2x 1)ln2
VD3: Tính đạo hàm: 2x  3 a) y  log (2x 2 1) b) y 
(x2  3x  2)ln3 2
b) y  log (x  3x 3  2) 2 c) y   x y 1  ln x2 1 c) x 1 2x 1 2  lg(  1) d) y  d) y x x
(x2  x 1)ln10
Hoạt động 3: Khảo sát hàm số logarit
 GV hướng dẫn HS khảo sát 2
3. Khảo sát hàm số logarit
hàm số: y  log x, y  log x y  log x 2 1 . a (a > 0, a  1) 2
Từ đó tổng hợp sơ đồ khảo sát.
y  loga x (a > 1)
y  loga x (0 < a < 1)   D = (0; +∞)  D = (0; +∞) Tập xác định 1 1        Sự biến thiên y
x lna > 0, x > 0 y
x lna < 0, x > 0  Giới hạn  lim log  
 lim log x    a xa x 0  x 0   Tiệm cận lim loga x   lim loga x    x x Bảng biến thiên  TCĐ: trục Oy  TCĐ: trục Oy  Đồ thị  
Hoạt động 4: Củng cố Nhấn mạnh:
– Công thức tính đạo hàm của hàm số logarit.
– Các dạng đồ thị của hàm số logarit.
4. BÀI TẬP VỀ NHÀ:  Bài 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 59
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 30 + 31
Bài 4: BÀI TẬP HÀM SỐ MŨ – HÀM SỐ LOGARIT I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm và tính chất của hàm số mũ, hàm số logarit.
 Công thức tính đạo hàm của hàm số mũ, hàm số logarit.
 Các dạng đồ thị của hàm số mũ, hàm số logarit. Kĩ năng:
 Biết vận dụng tính chất của các hàm số mũ, hàm số logarit vào việc so sánh hai số, hai biểu
thức chứa mũ và logarit.
 Biết vẽ đồ thị các hàm số mũ, hàm số logarit.
 Tính được đạo hàm của hàm số mũ, hàm số logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hàm số mũ và hàm số logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính đạo hàm của hàm số mũ, hàm số logarit
H1. Thực hiện phép tính ? Đ1.
1. Tính đạo hàm của các hàm x a) y  e
2 (x 1)  6cos2x số sau: x x
a) y  2xe  3sin 2x
b) y  10x  2 (sinx  ln 2 c . osx) 2 xx
b) y  5x  2 cos x c) y 1 ( 1)ln3   x 3 x  c) y 1  1 x 3
d) y  6x   c 4 osx x 2
d) y  3x  ln x  4sin x 2x 1 2 e) y 
e) y  log(x x  1)
(x2  x 1)ln10 log x 1 ln x f) y 3  f) y  x x2 ln3
Hoạt động 2: Luyện tập khảo sát hàm số mũ, hàm số logarit
H1. Nêu điều kiện xác định ? Đ1.
2. Tìm tập xác định của hàm  5  số:  ;   a) 5 – 2x > 0  D =  2 
a) y  log (5  2x 2 ) 2  2  0 2  log (  2 ) b) x x b) y x x 3
 D = (–∞; 0)  (2; +∞) 2
c) y  log (x  4x 1  3) 2
c) x  4x  3  0 5
 D = (–∞; 1)  (3; +∞) GV: Phạm Việt Phương 60
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 3x  2  2  3x  2  0   ;1 d) y  log d)  D =  1 x  3  0,4 1 x
H2. Vẽ đồ thị trên cùng hệ trục Đ2. Các nhóm thảo luận và va nhận xét? trình bày.
3. Vẽ đồ thị các hàm số sau y
(trên cùng một hệ trục): x 4  1  y = 4x y    x  4  y  4  log 3 , y x 4 2 x y  log x   1 4 y 1   log x  4  , y x   1 -4 -3 -2 -1 1 2 3 4 4 -1 y  log x 1 4 -2
Nhận xét mối quan hệ giữa đồ -3
thị của các hàm số trên. -4
 Từ đó nêu thành nhận xét + Đồ thị các hàm số x y  4 , tổng quát: x   + Đồ thị các hàm số x
y a , y 1
  4 đối xứng nhau qua   x y a 
đối xứng nhau qua trục trục tung. tung.
+ Đồ thị các hàm số y  log x 4 ,
+ Đồ thị các hàm số y  loga x , y  log x 1 đối xứng nhau qua y  log x 1 đối xứng nhau qua 4 a trục hoành. trục hoành. + Đồ thị các hàm số x y  4 , + Đồ thị các hàm số x
y a , y  log x 4 đối xứng nhau qua
y  loga x đối xứng nhau qua dường thẳng y = x. dường thẳng y = x.
Hoạt động 3: Củng cố Nhấn mạnh:
Bảng đạo hàm của các hàm số luỹ thừa, mũ, logarit
– Các công thức tính đạo hàm.
– Dạng đồ thị của hàm số mũ và logarit.
 Cho HS hệ thống các công
thức tính đạo hàm của hàm số
mũ, luỹ thừa và logarit (điền vào bảng).
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc trước bài " Phương trình mũ và phương trình logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 61
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 32
Bài 5: PHƯƠNG TRÌNH MŨ – PHƯƠNG TRÌNH LOGARIT I. MỤC TIÊU: Kiến thức:
 Biết được cách giải một số dạng phương trình mũ và phương trình logarit. Kĩ năng:
 Giải được một số phương trình mũ và phương trình logarit đơn giản bằng các phương pháp
đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hàm số mũ và hàm số logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ:
H. Nêu một số tính chất của hàm số mũ?
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm phương trình mũ
 GV nêu bài toán, hướng dẫn  n I. PHƯƠNG TRÌNH MŨ  
HS giải. Từ đó nêu khái niệm n P P(1 0,084)
Bài toán: Một người gửi tiết n phương trình mũ. n
P  2P  (1,084)  2
kiệm với lãi suất r = 8,4%/năm  n = lo
và lãi hàng năm được nhập vào 1 g ,084 2  8,59 
vốn (lãi kép). Hỏi sau bao n = 9.
nhiêu năm người đó thu được
gấp đôi số tiền ban đầu? x a b x  log b
H1. Tìm công thức nghiệm ? Đ1. a
1. Phương trình mũ cơ bản x
a b (a > 0, a 1) x
b > 0: a b x  log b a
b 0: ph.trình vô nghiệm.
 Hướng dẫn HS nhận xét số
giao điểm của 2 đồ thị.
Minh hoạ bằng đồ thị: Số
nghiệm của phương trình bằng
số giao điểm của 2 đồ thị của 2 hàm số x
y a và y = b.
VD1: Giải các phương trình:
H2. Giải phương trình ? Đ2. 2x 1  3  x 1  a) 4 1 b) 3  9 a) 2x – 1 = 0  x 1  2 x2 3x 1  1 c) 2  2 d) b) –3x + 1 = 2  x 1    1 3 x2 3x 5  25 GV: Phạm Việt Phương 62
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn x 1
c) x2  3x  1  1    x  2 x 1
d) x2  3x  2    x  2
Hoạt động 2: Tìm hiểu cách giải một số phương trình mũ đơn giản Đ1.
2. Cách giải một số phương
H1. So sánh x, y nếu x y a a ? x = y trình mũ đơn giản
a) Đưa về cùng cơ số f (x) g(x) aa
f (x)  g(x)
H2. Đưa về cùng cơ số ? Đ2.
VD3: Giải các phương trình: 5x7 x 1   3   3  x 1       a) 2  2  x = 1     5x7 2 a) (1,5)     3  b) 2(3x 1  ) 8x 2 3 3    x = 0 3x 1  8x2 b) 9  3 2 x 1 c) (x 2) 4 3  x 2  2  2  x 2 x  2  1  c) 43x    2  2  d) x 6  36  x = 2  d) x x 1 3 .2  72 b) Đặt ẩn phụ 2 f (x) f (x) abc  0
H3. Nêu điều kiện của t ?
Đ3. t > 0 vì ax > 0, x  f (x
t a ),t  0   2
at bt c  0 Đ4.
VD4: Giải các phương trinh:
H4. Đặt ẩn phụ thích hợp ? x x x a) t  3 a) 9  4.3  45  0 x x x 1 4 2   8  0 b) t  2 b) x x x 16 17.4 16  0 c) t  4 c) c) Logarit hoá f (x) g(x) ab
Lấy logarit hai vế với cơ số bất kì. Đ5.
VD5: Giải các phương trình:
H5. Lấy logarit hai vế theo cơ a) chọn cơ số 3 x x2 3 .2 1 số nào ? a) b) chọn cơ số 2. x2  x2  x2 x2 1 2 1  2  2  3  3 b)
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách giải các dạng phương trình mũ.
– Chú ý điều kiện t = ax > 0.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Hàm số mũ. Hàm số logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 63
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 33
Bài 5: PHƯƠNG TRÌNH MŨ – PHƯƠNG TRÌNH LOGARIT (tt) I. MỤC TIÊU: Kiến thức:
 Biết được cách giải một số dạng phương trình mũ và phương trình logarit. Kĩ năng:
 Giải được một số phương trình mũ và phương trình logarit đơn giản bằng các phương pháp
đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hàm số mũ và hàm số logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số tính chất của hàm số logarit? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm phương trình logarit
 Gv nêu định nghĩa phương II. PHƯƠNG TRÌNH trình logarit. LOGARIT
Phương trình logarit là
H1. Cho VD phương trình Đ1. log x
phương trình có chứa ẩn số 1  4 logarit? 2
trong biểu thức dưới dấu 2
log x  2log x 1 0 logarit. 4 4
1. Ph.trình logarit cơ bản b
loga x b x a
Minh hoạ bằng đồ thị:
Hướng dẫn HS nhận xét số
Đường thẳng y = b luôn cắt đồ
giao điểm của 2 đồ thị.
thị hàm số y  log x tại một a
điểm với b R.
Phương trình loga x b (a >
0, a 1) luôn có duy nhất một nghiệm b x a .
H2. Giải phương trình? Đ2.
VD1: Giải các phương trình: a) x 4  3 b) x = –1; x = 2 1 log  b) x = –1; x = 9 a) x 3 4
b) log x(x 1  2 ) 1 2 c) log (x  8x 3 )  2
Hoạt động 2: Tìm hiểu cách giải một số phương trình logarit đơn giản GV: Phạm Việt Phương 64
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
2. Cách giải một số phương
trình logarit đơn giản
 Lưu ý điều kiện của biểu thức
a) Đưa về cùng cơ số dưới dấu logarit.
loga f (x)  loga g(x)
f (x)  g(x)  
f (x)  0 (hoaëc g(x)  0)
VD2: Giải các phương trình:
H1. Đưa về cơ số thích hợp ? Đ1.
a) log x  log x  6
a) Đưa về cơ số 3: x = 81 3 9
b) Đưa về cơ số 2: x = 32
b) log x  log x  log x 2 4 8  11
c) Đưa về cơ số 2: x = 12 2 c) log x  log x  log x 4 1 8  7
d) Đưa về cơ số 3: x = 27 16 d) log x  log x  log x 3  6 3 1 3 b) Đặt ẩn phụ A 2
log f (x)  Blog f (x) C  0 a a
t  log f (x)  a
At2  Bt C  0
VD3: Giải các phương trình:
H2. Đưa về cùng cơ số và đặt Đ2. 2 ẩn phụ thích hợp ? log  log  2  1 a) x x 1 2
a) Đặt t  log x x   2 2  2  1 2 x  4 b)  1
b) Đặt t  lg x
5  lg x 1 lg x , t  5, t  –1 1 x 100 c) log x  log  2   5 x 5 x 1000
c) Đặt t  log x 5  x = 5 c) Mũ hoá
GV hướng dẫn HS tìm cách  Dựa vào định nghĩa. log ( )  ( ) giải. a f x g x g xf x a ( ) ( ) 
H3. Giải phương trình? Đ3.
VD4: Giải các phương trình: x 2 xx  0 a) 5 2 2      xx  2
a) log (5  2 )  2  x 2 x 2 x x b) 3 8 3     x = 2
b) log (3  8)  2  x 3 x c) 26  3  25  x = 0 x c) lo 5 g (26  3 )  2
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách giải các dạng phương trình logarit.
– Chú ý điều kiện của các phép biến đổi logarit.
4. BÀI TẬP VỀ NHÀ:  Bài 3, 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 65
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 34
Bài 5: BÀI TẬP PHƯƠNG TRÌNH MŨ –
PHƯƠNG TRÌNH LOGARIT I. MỤC TIÊU:
Kiến thức: Củng cố:
 Cách giải một số dạng phương trình mũ và phương trình logarit. Kĩ năng:
 Giải được một số phương trình mũ và phương trình logarit đơn giản bằng các phương pháp
đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số.
 Nhận dạng được phương trình. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về phương trình mũ và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập phương pháp đưa về cùng cơ số
H1. Nêu cách giải ?
Đ1. Đưa về cùng cơ số.
1. Giải các phương trình sau: 3x2 a) (0,3) 1 a) x 3  2 x  1  b) x = –2    25 b)  5  c) x = 0; x = 3
Chú ý điều kiện của các phép d) x = 9 x2 3  x2 biến đổi logarit. 2  4 c) e) vô nghiệm x7 1 2  x f) x = 7 d) (0,5) .(0,5)  2 g) x = 6
e) log (5x  3)  log (7x 3 3  5) h) x = 5
f) lg(x 1)  lg(2x 11)  lg 2
g) log (x  5)  log (x 2 2  2)  3 2
h) lg(x  6x  7)  lg(x  3)
Hoạt động 2: Luyện tập phương pháp đặt ẩn phụ
H1. Nêu cách giải ?
Đ1. Đặt ẩn phụ.
2. Giải các phương trình sau: a) Đặt x t  8 x x  x = 1 a) 64  8  56  0 x x x x  3.4  2.6  9
Chú ý điều kiện của ẩn phụ.   b) b) Đặt t 2   3    x = 0 2 1 c) log x 2  2 log4  0 x  1 x
c) Đặt t  log x 2   x  2 1 3 d)   1 x  10
5 lg x 3 lg x
d) Đặt t  lg x   x  1000 GV: Phạm Việt Phương 66
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
Hoạt động 3: Luyện tập phương pháp logarit hoá – mũ hoá
H1. Nêu cách giải ?
Đ1. Logarit hoá hoặc mũ hoá.
3. Giải các phương trình sau:
a) Lấy logarit cơ số 3 hai vế 2 a) 5 .3 x x 1
 x = 0; x   log3 5 2 x 1 
 Chú ý điều kiện của các phép x
b) Lấy logarit cơ số 2 hai vế x 1  b) 5 .2 50 biến đổi. 1 x x  log 5 c) 3 2 2  3  x = 2; x 2   2log 3x 2 5 d) x x2 3 .2  6
c) Lấy logarit cơ số 2 hai vế x e) log (6  7 ) 1 x log (log 3) 7  x 3 2  x 1
log (4.3  1)  2x 1 1 log f) 3 3 2 x
d) Lấy logarit cơ số 2 hai vế g) lo 2
g (3.2 1)  2x 1  0 2(log 3 1) x log (3 ) log (9  2 )  5 x  x = 1; x 2   h) 5 log 2 2 3 x 1x e) 6  7  7  x = 0 x 1  2x 1  x  0 f) 4.3 1  3   x  1 x 2x 1 x  0 g) 3.2 1 2      x  1 x 3 xx  0 h) 9 2 2      x  3
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách giải các dạng phương trình.
– Điều kiện của các phép biến đổi phương trình.
 Giởi thiệu thêm phương pháp
hàm số cho HS khá, giỏi.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc trước bài "Bất phương trình mũ – Bất phương trình logarit".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 67
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 35 + 36
Bài 6: BẤT PHƯƠNG TRÌNH MŨ –
BẤT PHƯƠNG TRÌNH LOGARIT I. MỤC TIÊU: Kiến thức:
 Biết được cách giải một số dạng bất phương trình mũ và bất phương trình logarit. Kĩ năng:
 Giải được một số bất phương trình mũ và bất phương trình logarit đơn giản bằng các
phương pháp đưa về cùng cơ số, logarit hoá, mũ hoá, đặt ẩn phụ, tính chất của hàm số. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về phương trình mũ và logarit.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số cách giải phương trình mũ và logarit? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách giải bất phương trình mũ
 GV nêu dạng bất phương  Các nhóm thảo luận và trình I. BẤT PH.TRÌNH MŨ
trình mũ và hướng dẫn HS biện bày.
1. Bất ph.trình mũ cơ bản luận. x
a b với a > 0, a 1. x x x
H1. Khi nào bất phương trình
(hoaëc a b,a b,a b) có nghiệm, vô nghiệm?
Minh hoạ bằng đồ thị: x Tập nghiệm a b a > 1 0 < a < 1 b 0 R R b > 0 log  ;  loga ba b;
2. Bất ph.trình mũ đơn giản
Đ2. Đưa về cơ số 3.
VD1: Giải bất phương trình: H2. Nêu cách giải? x2 x x2x 2 2 3  9 3
 3  x x  2  –1 < x < 2
VD2: Giải bất phương trình:
H3. Nêu cách biến đổi? Đ3. Chia 2 vế cho x 10 . x 2x x 4  2.5  10 x   Đặt t 2   5   , t > 0 GV: Phạm Việt Phương 68
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn  S =  log2 2;    5 
Hoạt động 2: Tìm hiểu cách giải bất phương trình logarit II. BPT LOGARIT
 GV nêu dạng bất phương
1. BPT logarit cơ bản
trình mũ và hướng dẫn HS biện
loga x b với a > 0, a  1 luận.
hoaëc loga x b,loga x b,loga x b
H1. Khi nào bất phương trình có nghiệm, vô nghiệm?
Minh hoạ bằng đồ thị: lo Tập nghiệm a g x b a > 1 0 < a < 1 Nghiệm b x a b 0  x a
2. Bất ph.trình mũ đơn giản
VD1: Giải bất phương trình:
H2. Biến đổi bất phương trình? Đ2.
log (5x+10)  log (x2  6x 8) 5
 x 10  x2  6x 8 1 1  2 2
x2  6x  8  0
 Chú ý điều kiện của các phép biến đổi.  –2 < x < 1 2
VD2: log x  6 log x 2 2  8  0 H3. Nêu cách giải?
Đ3. Đặt t  log x 2 2 t t 6  8  0  4  x  16
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách giải bất phương trình x a b Tập nghiệm mũ và logarit. a > 1 0 < a < 1
– Cách vận dụng tính đơn điệu b 0
của hàm số mũ và logarit. loga b; – ;  log
Chú ý điều kiện của các phép b > 0 a b biến đổi.
Câu hỏi: Lập bảng biện luận log  Tập nghiệm
đối với các bất phương trình a x b a > 1 0 < a < 1 tương tự: Nghiệm b 0  x a b x a x x x
a b,a b,a b
loga x b,loga x b,loga x b
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Chuẩn bị máy tính bỏ túi.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 69
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 37 + 38
Bài 6: BÀI TẬP BẤT PHƯƠNG TRÌNH MŨ & LOGARIT I. MỤC TIÊU: Kiến thức:
- Nắm vững phương pháp giải bpt mũ,bpt logarit và vận dụng để giải đượcác bpt mũ ,bpt logarit Kĩ năng:
- Sử dụng thành thạo tính đơn điệu hàm số mũ ,logaritvà nhận biết điều kiện bài toán Thái độ:
- Vận dụng được tính logic, biết đưa bài toán lạ về quen, học tập nghiêm túc, hoạt động tich cực II. CHUẨN BỊ:
Giáo viên: Phiếu học tập, câu hỏi trắc nghiệm
Học sinh : Bài tập giải ở nhà, nắm vững phương pháp giải
III. PHƯƠNG PHÁP : gợi mỡ ,vấn đáp-Hoạt động nhóm
IV. HOẠT ĐỘNG DẠY HỌC:
1. Ổn dịnh tỏ chức:
2. Kiểm tra bài cũ: 3’ Giải bpt sau:a./ Log 2 (x+4) < 3 b/ 52x-1 > 125 3. Bài mới HĐ1: Giải bpt mũ
Hoạt động giáo viên
Hoạt động học sinh Ghi bảng
HĐTP1-Yêu cầu học sinh nêu - Trả lời
phương pháp giải bpt ax > b Bài 1: Giải bpt sau: a x < b _ HS nhận xét 2  x  1/ 3 3x  9 (1)
- GVsử dụng bảng phụ ghi tập x2 x 1    nghiêm bpt 2/3 3 28 (2) Giải:
GV phát phiếu học tập1 và 2 -Giải theo nhóm 2
 x x  
- Giao nhiệm vụ các nhóm giải (1) 3 2 0  
-Gọi đại diện nhóm trình bày -Đại diện nhóm trình 1 x  2
trên bảng,các nhóm còn lại nhận bày lời giải trên bảng x 1 (2)  3 . 9  3 . x  28 xét -Nhận xét 3
GV nhận xét và hoàn thiện bài
 3x  3  x  1 giải Bài tập2 :giải bpt 4x +3.6x – 4.9x < 0(3) Giải: 2  x x 2   2  HĐTP2:GV nêu bài tập (3)     3   4  0  3   3 
Hướng dẫn học sinh nêu cách -Nêu các cách giải  x 2  giải
Đặt t =   ,t  0 bpt trở thành t2 +3t – 4 < -HSgiải trên bảng  3  -Gọi HS giải trên bảng -nhận xét 0
-Gọi HS nhận xét bài giải
Do t > 0 ta đươc 0< t<1  . x  0
- GV hoàn thiện bài giải GV: Phạm Việt Phương 70
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn HĐ2: Giải bpt logarit
-Gọi HS nêu cách giải bpt -Nêu cách giải Loga x >b ,Loga x nghiệm trên bảng
GV : phát phiếu học tập 3
Gọi đại diện nhóm trả lời Nhóm giải trên phiếu Gọi HS nhận xét học tập GV hoàn thiện bài giải
Đại diện nhóm trình bày trên bảng Nhóm còn lại nhận xét
Bài 3: giải bất phương trình sau:
- Gọi học sinh đưa các cơ số trong - Trả lời theo yêu cầu a) a) x x 1 (0, 4) (2,5)   1,5
phương trình a) về dạng phân số của giáo viên. x x
và tìm mối liên hệ giữa các phân     2 5 2 5 5 3   .  số đó.       0, 4 ; 2,5 5 2  5  2  2  2 2 x x 2 5 1 Nếu đặt  2   2  t  thì   2  3.  5  0     5 2 t  5   5 
- Yêu cầu học sinh vận dụng giải x  bất phương trình trên.  2    1   
- Thảo luận và lên bảng  5 x   2  5    trình bày.    x    5  2 2 5    
- Cho hs nêu phương pháp giải bpt - Trả lời theo yêu cầu  5  2 lôgarit: của gv.  x  1 
log f (x)  log g(x) (*)  f (x)  0 a a Đk:  b) (1  a  0) g(x)  0 2
log (x  6x  5)  2log (2  x)  0 (*) 1 3 + Nếu a  1 thì 3 (*)  f ( ) x g( ) x Đk: + Nếu 2 0  a  1 thì
x  6x  5  0   
- Hướng dẫn cho hoc sinh vận x 1 (*)  f ( ) x g( ) x 2  x  0
dụng phương pháp trên để giải bpt.
- Thảo luận và lên bảng trình bày. 2 2
log (2  x)  log (x  6x  5) 3 3 2 2
 (2  x)  x  6x  5 1
 2x  1  x
-Giáo viên nhận xét và hoàn thiện 2 lời giải của hoc sinh. 1  Tập nghiệm T  ;1   2  HĐ3 củng cố : 5’ 2 2x 3x  
Bài 1: tập nghiệm bất phương trình : 3 5     5  3 1  1   1  A/ ;1 B / ;1 C / ;1 D /         ;1 2  2   2 
Bài 2: Tập nghiệm bất phương trình: GV: Phạm Việt Phương 71
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn log  2 x  5x+7  0 1  2 A / 3;  B / 2;3 C /  ;  2 D /  ;  3
Dặn dò : Về nhà làm bài tập 8/90 SGK
Phụ lục : Phiếu học tập 3 log x  log x  5  log 3 0,2 5   0,2
4. BÀI TẬP VỀ NHÀ: - Bài 2 a,b,d Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1
Tiết dạy: 39 + 40 + 41
Bài dạy: ÔN TẬP CHƯƠNG II I. MỤC TIÊU:
Kiến thức: Củng cố:
 Luỹ thừa với số mũ thực.
 Khảo sát hàm số luỹ thừa.
 Logarit và các qui tắc tính logarit.
 Khảo sát hàm số mũ, hàm số logarit.
 Phương trình, bất phương trình mũ và logarit. Kĩ năng:
 Khảo sát các hàm số luỹ thừa, hàm số mũ, hàm số logarit.
 Tính logarit và biến đổi các biểu thức chứa logarit.
 Giải các phương trình, bất phương trình mũ và logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức chương II
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Khảo sát các tính chất của hàm số luỹ thừa, hàm số mũ và hàm số logarit
H1. Phân loại hàm số và nêu Đ1.
1. Tìm tập xác định của hàm số
điều kiện xác định của hàm số x
a) 3  3  0  D = R \ {1} y 1  ? a) x 1 x 3  3 b)  0 2x 3 x 1
b) y  log 2x 3 GV: Phạm Việt Phương 72
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn  3  2   log  12 D = ( ;  1) ; c) y x x 2    x x y  25  5 2 d)
c) x x 12  0  D = ( ;  3  )(4; )  x x
d) 25  5  0  D = [0; +∞)
Hoạt động 2: Củng cố phép tính logarit
H1. Nêu qui tắc cần sử dụng ? Đ1.
2. Cho loga b  3, loga c  2  . a) loga x = 8 Tính log a x với: log b) a x = 11 3 2 a) x = a b c a4 3 b b) x = c3 3. Cho log
7  a, log 5  b 25 2 . H2. Tính log log 7  2log 7  2 5 7 ? Đ2. a 5 25 49 49 Đ3. Tính M = log M = 3lo 3 5 g 49  log5 8 5 H3. Phân tích log 8 theo a, b. 3 5 8 ?  3  = 3 2 log5 7   log 5    2 9 = 12a b
Hoạt động 3: Giải phương trình, bất phương trình mũ, logarit
H1. Nếu cách giải ? Đ1.
4. Giải các phương trình sau:
a) Đưa về cơ số 3 và 5. x4 x3 x4 x3 a) 3  3.5  5  3 x 3  3   5  x x x 4.9 12 3.16  0 b)       5   3   x = –3
c) log (x 1) log x  log x 7 7 7 b) Chia 2 vế cho x 16 . d) log x  log x  log x 3  6 3 1 x   3 Đặt t 3     4  , t > 0.  x = 1 
Chú ý: x > 1  log x 7  0 . c) log (x 7 1)  0  x = 8 d) log x 3  3  x = 27
- Gọi học sinh nhắc lại phương
5. Giải các phương trình mũ và
pháp giải phương trình mũ.
- Trả lời theo yêu cầu của giáo viên. lôgarit sau: xx    x  a) 2 2 2 3.2 1 0 a b (*)
Nếu b  0 thì pt (*) VN 2
 4.2 x  3.2x 1  0
Nếu b  0 thì pt (*) có nghiệm
duy nhất x  log b x 2  1   0 a
- Yêu cầu học sinh vận dụng 
- Thảo luận và lên bảng trình  làm bài tập trên. x 1  bày  2   4    x 2
- Gọi học sinh nhắc lại phương
pháp giải phương trình lôgarit.
- Tìm điều kiện để các lôgarit GV: Phạm Việt Phương 73
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn có nghĩa? b)
- Hướng dẫn hs sử dụng các - Trả lời theo yêu cầu của giáo 1 1 công thức viên. log (x  2)   log 3x  5 2 1 6 3 8   log b
x b x a + log  ab log b (*) a a  1   a  0 Đk: Đk:
+ log b  log c  log . b c     a a ax  0 x 2 0   x  2 + a  log a b để biến đổi 3  x  5  0 b phương trình đã cho
- Yêu cầu học sinh vận dụng
(*)  log (x  2)  2 2 làm bài tập trên.  log (3x  5)
- Thảo luận và lên bảng trình 2 bày.
 log [(x  2)(3x  5)]=2 2
- Gọi hoc sinh nhắc lại công 2    
thức lôgarit thập phân và 3x 11x 10 4 lôgarit tự nhiên. 2
 3x 11x  6  0 x  3
- Cho học sinh quan sát
phương trình c) để tìm phương  2  x  3    pháp giải. x 2  3 c) lg x lg x lg 4.4 6 18.9 x    0
- Giáo viên nhận xét, hoàn chỉnh lời giải. (3)
- Nhắc lại theo yêu cầu của (3) giáo viên. 2 lg x lg x log x  lg x  2   2  10  4.  18  0     log x  ln x  3   3  e lg x 2  
- Thảo luận để tìm phương  2  9  2     pháp giải.      3  4  3    lgx  2    2   0    3  1  lg x  2   x 100
H2. Nêu cách giải ? Đ2.
6. Giải các bất phương trình 2 a) Đưa về cùng cơ số sau: 5 . x x 1  a) (0,4)  (2,5) 1,5 x   2 Đặt t 2   b) log x 5log x 0,2 0,2  6  5    , t > 0. 2 t 2  t 3 5  0  t 5  2 GV: Phạm Việt Phương 74
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn  x < –1. b) Đặt t  log x 0,2 . 2 t t
5  6  0  2 < t < 3  0,008 < x < 0,04.
- Trả lời theo yêu cầu của giáo viên. log b
x b x a a 1   a  0 Đk:  x  0
- Thảo luận và lên bảng trình bày.
- Nhắc lại theo yêu cầu của giáo viên. log x  lg x 10 log x  ln x e
- Thảo luận để tìm phương pháp giải.
Hoạt động 4: Củng cố Nhấn mạnh:
– Các tính chất của hàm số luỹ
thừa, hàm số mũ, hàm số logarit.
– Cách giải các dạng phương
trình, bất phương trình mũ và logarit.
4. BÀI TẬP VỀ NHÀ:
 Chuẩn bị kiểm tra 1 tiết chương II.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 75
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 42
Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG II I. MỤC TIÊU: Kiến thức:
 Ôn tập toàn bộ kiến thức trong chương II. Kĩ năng:
 Các qui tắc luỹ thừa và logarit.
 Khảo sát các tính chất của hàm số luỹ thừa, hàm số mũ và hàm số logảit.
 Giải phương trình, bất phương trình mũ và logarit. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: Ôn tập toàn bộ kiến thức chương 2. III. MA TRẬN ĐỀ: Nhận biết Chủ đề Thông hiểu Vận dụng Tổng TNKQ TL TNKQ TL TNKQ TL Luỹ thừa 1 0,5 0,5 Logarit 2 1,0 0,5
Hàm số luỹ thừa – Mũ – 2 3 2,5 Logarit 0,5 0,5 Phương trình – Bất 1 2 phương mũ , logarit 6,0 2,0 2,0 Tổng 2,5 1,5 2,0 4,0 10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (2 điểm) Chọn phương án đúng nhất: 2 6 4 ( 3  ) .( 1  5) .8
Câu 1: Giá trị của biểu thức A  2 6 4 bằng: 9 .( 5  ) .( 6)  256 A) 16 B) 256 C) 64 D) 9 log 3 log 2
Câu 2: Giá trị của biểu thức A 2 3  4  9 bằng: A) 8 B) 12 C) 16 D) 25
Câu 3: Cho lg3  b . Tính lg900 theo b : A) 2(b + 1) B) b + 2 C) b + 30 D) b + 100 1 Câu 2
4: Tập xác định của hàm số y  x x 2 ( 3  4) là:
A) (–∞; –4)  (1; +∞) B) (–4; 1) C) (–∞; –4) D) (1; +∞) x 1
Câu 5: Tập xác định của hàm số y  3 log x1 là: A) (–∞; –1) B) (1; +∞) C) (–1; 1)
D) (–∞; –1)  (1; +∞)
Câu 6: Cho hàm số f x 3  x2 ( )
x 1 . Tính f (0) ? GV: Phạm Việt Phương 76
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 1 2 A) 3 B) 1 C) 3 D) 3 Câu 7: Cho hàm số x x f x e 2 2 ( )   . Tính f (  0) ? A) 0 B) 1 C) 2 D) e   
Câu 8: Cho hàm số f (x)  ln(sin x) . Tính f  4  ?   A) 0 B) 1 C) 3 D) 2
B. Phần tự luận: (8 điểm) Giải các phương trình, bất phương trình sau: x x x x 1  x 2 a) 2.14  3.49  4  0 b) log2(5  25 )  2 c) log (x  5x 1  6)  3  2
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 B D A B D C C B
B. Phần tự luận: Mỗi câu 2 điểm 2x x x   7  x x x  7   7 
t    ,t  0
a) 2.14  3.49  4  0  3.   2  1  0  2   2     2    t2 3  2t 1  0 x    t 7    ,t  0   2  x  7  1 1  t  1  l(oaïi)      x  log7   2  3 3  2 t 1   3 x 1  x x 2x x
t  5 , t  0 b) log2(5
 25 )  2  5  5.5  4  0   t2  t 5  4  0  x
t  5 , t  0  x 5 1 x  0  t 1      x 5  4 x  log  5 4 t  4 2 2 3 2 x  2  c) log (x  5x 1  6)  3
  x  5x  6  2  x 5x 14  0   x  7 2
VI. KẾT QUẢ KIỂM TRA: Lớp 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Sĩ số SL % SL % SL % SL % SL % 12S1 53 12S2 54 12S3 54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 77
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1
Chương III: NGUYÊN HÀM – TÍCH PHÂN VÀ ỨNG DỤNG Tiết dạy: 43 Bài 1: NGUYÊN HÀM I. MỤC TIÊU: Kiến thức:
 Hiểu khái niệm nguyên hàm của một hàm số.
 Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
 Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
 Các phương pháp tính nguyên hàm. Kĩ năng:
 Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần.
 Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại các công thức tính đạo hàm của các hàm số luỹ thừa, mũ, logarit? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm nguyên hàm
 GV dẫn dắt từ VD sau để  Các nhóm thảo luận và trình I. NGUYÊN HÀM VÀ TÍNH
giới thiệu khái niệm nguyên bày. CHẤT hàm của hàm số. 1. Nguyên hàm
VD: Tìm hàm số F(x) sao cho:
Cho hàm số f(x) xác định tren
a) F(x) = x3 ; x3 + 3; x3 – 2; ... F(x) = f(x)
b) F(x) = tanx; tanx – 5; …
K R. Hàm số F(x) đgl
nếu: a) f(x) = 3x2 với x R
nguyên hàm của f(x) trên K 1
nếu, với x K ta có: b) f(x) = 2 cos x
F (x)  f (x)     vôùi x  ; 2 2   
H1. Tìm nguyên hàm ?
VD1: Tìm một nguyên hàm Đ1. của các hàm số sau:
a) F(x) = x2 ; x2 + 2; x2 – 5,.. a) f(x) = 2x trên R
b) F(x) = lnx; lnx + 1; lnx – 3, .. 1 b) f(x) =
trên (0; +) x
H2. Nêu nhận xét về các
nguyên hàm của một hàm số ?
Đ2. Các nguyên hàm của một Định lí 1:
hàm số sai khác một tham số Nếu F(x) là 1 nguyên hàm của cộng.
f(x) trên K thì với mỗi hằng số GV: Phạm Việt Phương 78
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
G(x)  f (x)
C, G(x) = F(x) + C cũng là 1
nguyên hàm của f(x) trên K.
GV cho HS nhận xét và phát biểu. Định lí 2:
Nếu F(x) là 1 nguyên hàm của
F(x)G(x )  0
f(x) trên K thì mọi nguyên hàm F(x) – G(x) = C
của f(x) trên K đều có dạng
F(x) + C, với C là một hằng số.
 GV giới thiệu kí hiệu họ Nhận xét:
nguyên hàm của một hàm số.
Nếu F(x) là 1 nguyên hàm của
f(x) trên K thì F(x) + C, C R
là họ tất cả các nguyên hàm
của f(x) trên K. Kí hiệu: f (x d
) x F(x)  C
H3. Tìm 1 nguyên hàm ? Đ3.
VD2: Tìm họ nguyên hàm: 2 a) 2xdx=x C  1 a) f(x) = 2x b) f(s) = 1 s b)
ds  ln s Cs c) f(t) = cost
c) costdt  sin t C
Hoạt động 2: Tìm hiểu tính chất của nguyên hàm
 GV hướng dẫn HS nhận xét
2. Tính chất của nguyên hàm
và chứng minh các tính chất.  f (x d ) x=f(x)+C
 GV nêu một số VD minh hoạ  các tính chất.  ( ) ( )  
kf x dx=k f x dx (k 0)
(cos x)dx=cos x+C  
f (x) g(x) dx= f (x d)xx x xe
3 dx=3 e dx=3e C   g(x d ) x  2 
3sin x dx=-3cosx+2lnx+Cx
H1. Tìm nguyên hàm ? Đ1.
VD3: Tìm nguyên hàm: x2
a) f (x)  x  2cosx a) f (x d ) x=  2sinx C  2 2 x
b) f (x)  3x e 5 3 x b) f (x d ) x=x e 5  C  1 2 c) f (x)  x  sinx 1 2 3 c) f (x d
) x= x cosx C  6
d) f (x)  x cos2x 2 3 1 d) f (x d ) x=
x  sin2x C  3 2
Hoạt động 3: Củng cố Nhấn mạnh:
– Mối liên hệ giữa đạo hàm và nguyên hàm.
– Các tính chất của nguyên hàm.
4. BÀI TẬP VỀ NHÀ:  Bài 1 SGK.
 Đọc tiếp bài "Nguyên hàm". GV: Phạm Việt Phương 79
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 44
Bài 1: NGUYÊN HÀM (tt) I. MỤC TIÊU: Kiến thức:
 Hiểu khái niệm nguyên hàm của một hàm số.
 Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
 Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
 Các phương pháp tính nguyên hàm. Kĩ năng:
 Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần.
 Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa và tính chất của nguyên hàm? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu sự tồn tại nguyên hàm  GV nêu định lí.
3. Sự tồn tại nguyên hàm Định lí 3:
Mọi hàm số liên tục trên K đều có nguyên hàm trên K.
H1. Xét tính liên tục của hàm số Đ1.
VD1: Chứng tỏ các hàm số sau có
trên tập xác định của nó? 2 nguyên hàm: a) f x x3 ( )  liên tục trên khoảng 2 2 5 a) f x x3 ( )  3 (0; +∞) .
x3dx= x3  C  1 5 b) f (x)  2 1 sin x b) f (x)  2 liên tục trên từng x sin x c) f (x)  2
khoảng (k ;(k  1) ) . 1
dx= cot x C  2 sin x GV: Phạm Việt Phương 80
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn x
c) f (x)  2 liên tục trên R. x x 2 2 dx=C  ln2
Hoạt động 2: Tìm hiểu bảng nguyên hàm
 GV cho HS tính và điền vào  Các nhóm thảo luận và trình 4. Bảng nguyên hàm của một s ố bảng. bày. hàm số x x a dx= 0 Ca dx=
C (a  0,a  1)  lna dx=x+C
cos xdx  sin x C   1  1 
sin xdx  cos x Cx dx= xC (  1  )   1
1 dx  tanx C
1dx=ln x C  2 cos x x 1 x x e dx=e C
dx  cot x C  2 sin x  GV nêu chú ý.
Chú ý: Tìm nguyên hàm của 1
hàm số được hiểu là tìm nguyên
hàm trên từng khoảng xác định của nó.
Hoạt động 3: Áp dụng bảng nguyên hàm  Cho HS tính.
 Các nhóm tính và trình bày. VD2: Tính: 2 3 3  2 1  2 A =
x  3 x C  3 A = x dx   3 2   x x 1  3 x 1 B = 3sin x   C  B = (3cos x  3 dx )  ln3
C = tan x  cot x C 1 C = dx  1 2 sin x 2 .cos x D = ln x   C x x 1 dx D =  H1. Nêu cách tìm ? x2
Đ1. Tìm họ nguyên hàm F(x) của
hàm số, sau đó sử dụng giả thiết VD3: Tìm một nguyên hàm của để tìm tham số C. hàm số, biết: 3 x4
a) f (x)  x  4x  5; F(1)  3 2 a) F(x) 
 2x  5x C
( )  3  5cos ; ( )  2 4 b) f x x F 1  x2 3 5 F(1) = 3  C =  c) f (x)  ; F e ( ) 1 4 x
b) F(x) = 3x – 5sinx + C x2 1 3
F() = 2  C = 2 – 3. d) f (x)  ; F(1)  x 2 x2 5
c) F(x)  3ln x   C 2  e2 2 5 F(e) = 1  C = 2 x2 d) F(x)   ln x C 2 3 F(1) = 2  C = 1 Hoạt động 4: Nhấn mạnh: GV: Phạm Việt Phương 81
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn – Bảng nguyên hàm.
4. BÀI TẬP VỀ NHÀ:  Bài 2 SGK.
 Đọc tiếp bài "Nguyên hàm".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 45
Bài dạy: ÔN TẬP HỌC KÌ I I. MỤC TIÊU:
Kiến thức: Củng cố:
 Các tính chất của hàm số.
 Khảo sát sự biến thiên và vẽ dồ thị hàm số.
 Phép tính luỹ thừa, logarit.
 Tính chất của các hàm số luỹ thừa, mũ, logarit.
 Các dạng phương trình, bất phương trình mũ, logarit. Kĩ năng:
 Khảo sát thành thạo các tính chất của hàm số.
 Vận dụng được các tính chất của hàm số để giải toán.
 Thành thạo trong việc khảo sát sự biến thiên và vẽ đồ thị hàm số.
 Thành thạo thực hiện các phép tính về luỹ thừa và logarit.
 Giải thành thạo phương trình, bất phương trình mũ, logarit đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức trong học kì 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình ôn tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Ôn tập khảo sát hàm số bậc ba
H1. Nêu các bước khảo sát Đ1. 1. Cho hàm số 3 2
y x  4x  4x
hàm số? Nêu một số đặc điểm y
a) Khảo sát sự biến thiên và vẽ 3 của hàm số bậc ba?
đồ thị (C) của hàm số. 2
b) Biện luận theo m, số nghiệm 1 x của phương trình: -2 -1 1 2 3 -1 3 2
x  4x  4x m  0 -m -2 GV: Phạm Việt Phương 82
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
H2. Nêu cách biện luận số Đ2.
nghiệm của phương trình bằng  32 m   đồ thị ?  27  : 1 nghiệm m  0  32 m    27  : 2 nghiệm m  0 32   m  0 : 3 nghiệm 27
Hoạt động 2: Ôn tập khảo sát hàm số bậc bốn trùng phương
H1. Nêu một số đặc điểm của Đ1. 2. Cho hàm số 4 2
y  x  2x  3
hàm số bậc bốn trùng phương? y
a) Khảo sát sự biến thiên và vẽ 3
đồ thị (C) của hàm số. 2 1
b) Viết phương trình tiếp tuyến x
d của (C), biết d song song với -2 -1 1 2 3 -1 đường thẳng y = 8x. -2
Đ2. Pttt: y  8x 8
H2. Nêu cách viết phương
trình tiếp tuyến của (C)?
Hoạt động 3: Ôn tập khảo sát hàm số nhất biến
H1. Nêu một số đặc điểm của Đ1. y  hàm số nhất biến? 3. Cho hàm số 4 . y 9 x  A 2 8 7
a) Khảo sát sự biến thiên và vẽ 6 5
đồ thị (C) của hàm số. 4 3
b) Một đường thẳng d đi qua 2 1 x
điểm A(–2; 8) và có hệ số góc -3 -2 -1 1 2 3 4 5 6 7 -1
k. Biện luận theo k số giao -2 -3 điểm của d và (C). -4
c) Tìm các điểm M(x; y)  (C)
H2. Nêu cách biện luận số giao Đ2. có toạ độ nguyên. điểm của 2 đồ thị?
Phương trình đường thẳng d:
y kx  2k  8
Phương trình hoành độ giao điểm của d và (C):
kx x k    2 8 4 20 0 x  2 4   k  1  : 0 giao điểm k  4   : 1 giao điểm k  1  k  4   : 2 giao điểm k  1 
H3. Nêu cách tìm các điểm Đ3. 4 y   Z  x – 2 là
thuộc đồ thị có toạ độ nguyên ? x  2 ước số của 4.  x = 3; 1; 4; 0; 6; –2
Hoạt động 4: Củng cố GV: Phạm Việt Phương 83
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Nhấn mạnh:
– Các bước khảo sát và vẽ đồ thị hàm số.
– Đặc điểm và dạng đồ thị của
các loại hàm số trong chương trình.
– Cách giải một số bài toán
liên quan đến khảo sát hàm số.
4. BÀI TẬP VỀ NHÀ:
 Bài tập ôn Học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 46
Bài dạy: ÔN TẬP HỌC KÌ I (tt) I. MỤC TIÊU:
Kiến thức: Củng cố:
 Các tính chất của hàm số.
 Khảo sát sự biến thiên và vẽ dồ thị hàm số.
 Phép tính luỹ thừa, logarit.
 Tính chất của các hàm số luỹ thừa, mũ, logarit.
 Các dạng phương trình, bất phương trình mũ, logarit. Kĩ năng:
 Khảo sát thành thạo các tính chất của hàm số.
 Vận dụng được các tính chất của hàm số để giải toán.
 Thành thạo trong việc khảo sát sự biến thiên và vẽ đồ thị hàm số.
 Thành thạo thực hiện các phép tính về luỹ thừa và logarit.
 Giải thành thạo phương trình, bất phương trình mũ, logarit đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức trong học kì 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình ôn tập) H. Đ. GV: Phạm Việt Phương 84
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Ôn tập giải phương trình mũ
 Cho các nhóm thảo luận và 1. Giải các phương trình sau: trình bày. a) x x 1  x2 x x 1  x2 9  9  9  4  4  4 H1. Nêu cách giải? Đ1. b) x 1  x3 x4 x2 7.3 5  3 5
 Đưa về cùng cơ số. c) x x 2x 1 25 10 2    x x xx   9  21 d) 4 2.6 3.9 a)     x 4  91 e) x x 2 4.3  9.2  5.6  x x x x 5  3 f) 3 1 125 50 2    b)     x x 3  5 g) 2
x  (3  2 )x  2(1 2 )  0  Đặt ẩn phụ 2  x x 5   5  c)
      2  0  2   2  2  x x 3   3  d)
3.     1  0  2   2  x x 2  3   3  e)
4.   5.   9  0  2   2  3x 2  x 5   5  f)
      2  0  2   2 
 Phân tích thành nhân tử. g) (  2)(  2  2x x x )  0
Hoạt động 2: Ôn tập giải phương trình logarit H1. Nêu cách giải? Đ1.
2. Giải các phương trình sau:  Đưa về cùng cơ số a) 2
log (x  3)  log (6x 10) 1  0 2 2 a) 2
log (x  3)  log (3x  5) 1  2 2 b) 5 2 log(x 1) 
log x  log x
Chú ý điều kiện của các phép b) 2 2
log(x 1)  log x 2 biến đổi.
c) log (x  2).log 2  1 1 4 x
c) log (x  2)  log x 2 2 2 d) 2 2 log (x  2)  log
x  4x  4  9 3 3  x  d) 3 log x  2  9 e) log 16 log ( 1) ( x 1  ) 2 3  Đặt ẩn phụ f) 2 2 log 4x .log x  12 x 2
e) Đặt t  log (x 1) 2
f) Đặt t  log x 2
Hoạt động 3: Ôn tập giải bất phương trình mũ, logarit H1. Nêu cách giải? Đ1.
3. Giải các bất phương trình  Đưa về cùng cơ số sau: xxx x  x + <  2  a) 2 1 2 2 5 2 5 a)    7 xx x   b) 1 1 3.4 35.6  2.9  0  5
Chú ý sử dụng tính đồng x x     c) 1 9 4.3 27 0 x x
biến, nghịch biến của hàm số 2 (2  3)  0 x x d)  d) 1 log (4  2 )  x 2 mũ, hàm số logarit. x x 4  2.2  0 e) log  2
x  3x  2  log x 14 2  2   2
x  3x  2  x 14 e) 
2x  3y 17 x 14  0 f)  3
 .2x  2.3y  6  Đặt ẩn phụ x y  6 g) 
log x  log y  3  2 2 GV: Phạm Việt Phương 85
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 2  x x 3   3 
b) 18   35.  12  0  2   2  c) 2
3 x 12.3x  27  0
 Đưa về hệ phương trình đại số u v 17 f)  3
u  2v  6 x y  6 g)  xy  8
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách giải các dạng phương
trinh, bất phương trình mũ, logarit.
– Điều kiện của các phép biến đổi.
4. BÀI TẬP VỀ NHÀ:
 Chuẩn bị kiểm tra Học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 47 KIỂM TRA HỌC KÌ 1 I. MỤC TIÊU: Kiến thức:
 Ôn tập toàn bộ kiến thức trong học kì 1. Kĩ năng:
 Khảo sát thành thạo các tính chất của hàm số.
 Vận dụng được các tính chất của hàm số để giải toán.
 Thành thạo trong việc khảo sát sự biến thiên và vẽ đồ thị hàm số.
 Thành thạo thực hiện các phép tính về luỹ thừa và logarit.
 Giải thành thạo phương trình, bất phương trình mũ, logarit đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác.
THI THEO ĐỀ CHUNG CỦA SỞ GIÁO DỤC HÀ GIANG GV: Phạm Việt Phương 86
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 48
Bài 1: NGUYÊN HÀM (tt) I. MỤC TIÊU: Kiến thức:
 Hiểu khái niệm nguyên hàm của một hàm số.
 Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
 Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
 Các phương pháp tính nguyên hàm. Kĩ năng:
 Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần.
 Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số công thức tính nguyên hàm? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu phương pháp đổi biến số
 GV cho HS xét VD, từ đó  Các nhóm thảo luận và trình II. PHƯƠNG PHÁP TÍNH
giới thiệu định lí. bày. NGUYÊN HÀM VD: a) u = x – 1  du = dx
1. Phương pháp đổi biến số Định lí: a) Cho 10 ( 1)  x dx .  10
(x 1) dx = 10 u du Đặt Nếu ( )  ( )   f u du F u C và u = x –1. dx b) t = lnx  dt = Hãy viết 10
(x 1) dx theo u, du. x
hàm số u = u(x) có đạo hàm liên tục thì: ln  ln x
b) Cho  x dx . Đặt t = lnx. = tdt  x x ( ( ( )). ( )  ( ( )) 
f u u x u x dx F u x C Hãy viết ln x theo t, dt. x
Hệ quả: Với u = ax + b (a 0)  
GV hướng dẫn HS chứng  F(u(x))  f (u( ) x ).  u ( ) x ta có: minh định lí. 1 (  )  (  )   f ax b dx F ax b C a
Chú ý: Nêu tính nguyên hàm
theo biến mới u thì sau khi tính
nguyên hàm phải trở lại biến x
ban đầu bằng cách thay u bởi GV: Phạm Việt Phương 87
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn u(x).
Hoạt động 2: Áp dụng phương pháp đổi biến số
 Hướng dẫn HS cách đổi biến.  Các nhóm thảo luận và trình VD1: Tính bày. A = sin(3 1)  x dx a) t = 3x – 1 1  B =  x dx x   5  A = cos(3 1) C (x 1) 3 b) t = x + 1 C =  dx 1  1 1  5 (3  2x)  B =   C 3  
(x 1)  4(x 1) 3  D = tan  xdx c) t = 3 – 2x  1 C =  C 4 8(3  2x) d) t = cosx
D = ln cos x C VD2: Tính:
H1. Nêu cách đổi biến ? 2 Đ1. 1 E = .   x x e dx e) 2 t x 1 x e 2 x 1  F =  dx e  E =  C x 2 tan x e f) t x G =  dx 2 cos x  F = 2 x eC 3 ln g) t  tan x H =  x dx x  G = tanx e h) t  ln x 4 ln x  H =  C 4 Hoạt động 3: Nhấn mạnh: u'(x d
) x u(x)  C  cosu(x) u
. (x)dx  sinu(x)  C
– Cách sử dụng phương pháp  1 
đổi biến để tìm nguyên hàm. sinu(x) u
. (x)dx  cosu(x)  C   ( ) u(x) u x u . (x d ) x=C
Câu hỏi: Lập bảng nguyên  1 u(x)
hàm của hàm số hợp? (  –1)
dx  tanu(x)  C  2 cos u(x) u
. (x) dx  ln u(x) Cu(x)
u(x) dx  cotu(x)C  2 u(x) u(x e
ux dx e ) . ( )  C  sin u(x) u(x) u(x) a a u . (x d ) x   C  lna (a > 0, a  1)
4. BÀI TẬP VỀ NHÀ:  Bài 3 SGK.
 Bài tập ôn Học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 88
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 49
Bài 1: NGUYÊN HÀM (tt) I. MỤC TIÊU: Kiến thức:
 Hiểu khái niệm nguyên hàm của một hàm số.
 Biết các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
 Phân biệt rõ một nguyên hàm với họ nguyên hàm của một hàm số.
 Các phương pháp tính nguyên hàm. Kĩ năng:
 Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần.
 Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số công thức tính nguyên hàm? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu phương pháp tính nguyên hàm từng phần
 Dẫn dắt từ VD, GV giới thiệu
2. Phương pháp tính nguyên
phương pháp tính nguyên hàm  hàm từng phần từng phần. (x cos x)
Định lí: Nếu hai hàm số u =
= cosx – xsinx
u(x) và v = v(x) có đạo hàm
VD: Tính (x cos x);
(x cos x)dx  = xcosx + C1
liên tục trên K thì:
(x cos x)dx  ; cos xdx  . cos xdx
udv uv vdu = sinx + C   2
Từ đó tính x sin xdx  .  x sin xdx
=–xcosx+sinx +C 
GV nêu định lí và hướng dẫn HS chứng minh.  u
( v)  uv uv  uv  u
( v)  uv
Hoạt động 2: Áp dụng phương pháp tính nguyên hàm từng phần
 GV hướng dẫn HS cách phân  HS theo dõi và thực hành. VD1: Tính: tích. u x x A = xe dx  a) Đặt  xdv e dx B = x cos xdxx x
A = xe e C C = ln xdx  GV: Phạm Việt Phương 89
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
b) Đặt u x D = x sin xdx  
dv  cos xdx
B = x sin x  cos x C   ln c) Đặt u x  dv dx
 C = x ln x x C   d) Đặt u x
dv  sin xdx
D = x cos x  sin x C
H1. Nêu cách phân tích ? Đ1.  2 VD2: Tính:
e) Đặt u x  5  2
dv  sin xdx
E = (x  5)sin xdx   2 2 E= (  x 3 c
) osx  2xsinx C F = (x  2x 3)cos xdx   2 2
f) Đặt u x  2x  3  G = ln(x 1 d ) x
dv  cos xdx x2 3 H = x e dx   2
F= (x 1) sin x  2x cos x C  2
g) Đặt u  ln x  dv dx  2
G= x ln x  2x ln x  2x C h) Đặt t x2  1 1  t t t H= te dt t
( e e ) C 2  = 2 1  x2 x x e e 2 2  = C 2
Hoạt động 3: Củng cố Nhấn mạnh: ( )sin ( )cos ( ) ( )ln – P x xdxP x xdxx P x e dxP x xdx  Phương pháp tính nguyên hàm từng phần.  u P(x) P(x) P(x) lnx
Câu hỏi: Nêu cách phân tích
một số dạng thường gặp? dv sinxdx cosxdx x e dx P(x)dx
4. BÀI TẬP VỀ NHÀ:  Bài 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 90
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 50
Bài 1: BÀI TẬP NGUYÊN HÀM I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm nguyên hàm của một hàm số.
 Các tính chất cơ bản của nguyên hàm. Bảng nguyên hàm của một số hàm số.
 Các phương pháp tính nguyên hàm. Kĩ năng:
 Tìm được nguyên hàm của một số hàm số đơn giản dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần.
 Sử dụng được các phương pháp tính nguyên hàm để tìm nguyên hàm của các hàm số đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Bảng công thức đạo hàm và nguyên hàm.
Học sinh: SGK, vở ghi. Ôn tập các công thức đạo hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Củng cố khái niệm nguyên hàm H1. Nhắc
lại định nghĩa Đ1. F(x) = f(x)
1. Trong các cặp hàm số sau,
nguyên hàm của một hàm số?
a) Cả 2 đều là nguyên hàm của hàm số nào là 1 nguyên hàm nhau. của hàm số còn lại: x x b) 2
sin x là 1 nguyên hàm của a)   e và e sin2x b) 2
sin 2x và sin x  4  x 2 c) 1  e   x    là 1 nguyên hàm 2 4 x x
c) 1  e và 1  e x   x  2  2  của 1  x e x
H2. Nhắc lại bảng nguyên Đ2.
2. Tìm nguyên hàm của các hàm? 5 7 2 3 6 3 hàm số sau: a) 3 6 3 x x x C  1 4 7 2 a) ( )  x x f x x 3 2  ln 2 1 x b)  C x e (ln 2 1) 2x 1 b) f (x)  1  1  x e
c)   cos8x  cos 2x   C f x  3  4  c) ( ) sin 5 . x cos 3x  1 1 1 x f x  d) ln  C d) ( )  x  3 1 2x (1 )(1 2x) GV: Phạm Việt Phương 91
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
 Hướng dẫn cách phân tích  1 1  1 2     phân thức. 
(1 x)(1 2x)
3 1 x 1 2x
Hoạt động 2: Luyện tập phương pháp đổi biến số
H1. Nêu công thức đổi biến ? Đ1.
3. Sử dụng phương pháp đổi 10 (1 x) biến, hãy tính: a) t = 1 – x  A =   C 10 a) 9 (1 )  x dx b) t = 1 + x2  3 2 5 b) 2  1 (1 )  x x dx B = 2 2
(1 x )  C 5 c) 3 cos sin  x xdx 1 c) t = cosx  C = 4
 cos x C 4 d) 1  dx xe x e  2 d) t = ex + 1  D = 1   C 1 x e
Hoạt động 3: Luyện tập phương pháp nguyên hàm từng phần
H1. Nêu cách phân tích? Đ1.
4. Sử dụng phương pháp
u  ln(1 x)
nguyên hàm từng phần, hãy a)  dv xdx tính: 1 1 x a) ln(1 )  x x dx A = 2 2
(x 1) ln(1 x)  x   C 2 4 2 b) 2 (  2 1)  x x x e dx 2
u x  2x 1 b)  c) sin(2 1)  x x dx dv x e dx d) (1 )cos  x xdx B = x 2
e (x 1)  C u x c) 
dv  sin(2x 1)dx x 1
C =  cos(2x 1)  sin(2x 1)  C 2 4 u 1 x d) 
dv  cos xdx
D = (1 x)sin x  cos x C
Hoạt động 4: Củng cố Nhấn mạnh: – Bảng các nguyên hàm.
– Các sử dụng các phương pháp tính nguyên hàm.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc trước bài "Tích phân".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 92
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 51 Bài 2: TÍCH PHÂN I. MỤC TIÊU: Kiến thức:
 Biết khái niệm diện tích hình thang cong.
 Biết định nghĩa tích phân của hàm số liên tục.
 Biết các tính chất và các phương pháp tính tích phân. Kĩ năng:
 Tìm được tích phân của một số hàm số đơn giản bằng định nghĩa hoặc phương pháp tích phân từng phần.
 Sử dụng được phương pháp đổi biến số để tính tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập công thức đạo hàm và nguyên hàm.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa và tính chất của nguyên hàm? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm diện tích hình thang cong
 Cho HS nhắc lại tính diện
I. KHÁI NIỆM TÍCH PHÂN
tích hình thang vuông. Từ đó
1. Diện tích hình thang cong
dẫn dắt đến nhu cầu tính diện
Cho hàm số y = f(x) liên tục, tích "hình thang cong".
không đổi dấu trên đoạn [a; b]
Hình phẳng giới hạn bởi đồ thị
của hàm số y = f(x), trục Ox và
hai đường thẳng x = a, x = b
đgl hình thang cong.
 GV dẫn dắt cách tìm diện
Cho hình thang cong giới
tích hình thang cong thông qua
hạn bởi các đường thẳng x = a,
VD: Tính diện tích hình thang
x = b (a < b), trục hoành và
cong giới hạn bởi đường cong
đường cong y = f(x) liên tục,
y = f(x) = x2, trục hoành và các
không âm trên [a; b]. Giả sử
đường thẳng x = 0; x = 1.
F(x) là một nguyên hàm của
f(x) thì diện tích của hình thang
cong cần tìm là: F(b) – F(a)
 Với x  [0; 1], gọi S(x) là
diện tích phần hình thang cong GV: Phạm Việt Phương 93
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
nằm giữa 2 đt vuông góc với trục Ox tại 0 và x.
C.minh: S(x) là một nguyên hàm của f(x) trên [0;1].
Hoạt động 2: Tìm hiểu định nghĩa tích phân
 GV nêu định nghĩa tích phân
2. Định nghĩa tích phân và giải thích.
Cho f(x) là hàm số liên tục trên
[a; b]. Giả sử F(x) là một
nguyên hàm của f(x) trên [a; b]
Hiệu số F(b) – F(a) đgl tích
phân từ a đến b của f(x). b b
f (x)dx F(x)  F( )
b F(a)  a a b
: dấu tích phân a
a: cận dưới, b: cận trên Qui ước: Minh hoạ bằng VD. a b a
f (x)dx  0 
; f (x)dx   f (x)   dx a a b
Hoạt động 3: Áp dụng định nghĩa tính tích phân
H1. Tìm nguyên hàm của hàm Đ1.
VD1: Tính tích phân: số? 2 2 e 2 1 a) 2 2 2 2   2 1  3  xdx x a) 2  xdx b)  dt 1 t 1 1 1 e 1 e b) dt  ln t e   1 ln ln1 1  t Nhận xét:  1 GV nêu nhận xét.
a) Tích phân của một hàm số
không phụ thuộc vào kí hiệu biến số. b b b
f (x)dx
f (t)dt f (u)    du a a a
b) Ý nghĩa hình học: Nếu f(x)
liên tục và không âm trên [a; b b] thì f (x) 
dx là diện tích của a
hình thang cong giới hạn bởi
đồ thị hàm số f(x), trục Ox và
hai đường thẳng x = a, x = b: b S f (x)  dx a
Hoạt động 4: Củng cố Nhấn mạnh:
– Định nghĩa tích phân.
– Ý nghĩa hình học của tích phân.
4. BÀI TẬP VỀ NHÀ:  Bài 1 SGK.
 Đọc tiếp bài "Tích phân".
IV. RÚT KINH NGHIỆM, BỔ SUNG: GV: Phạm Việt Phương 94
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 52
Bài 2: TÍCH PHÂN (tt) I. MỤC TIÊU: Kiến thức:
 Biết khái niệm diện tích hình thang cong.
 Biết định nghĩa tích phân của hàm số liên tục.
 Biết các tính chất và các phương pháp tính tích phân. Kĩ năng:
 Tìm được tích phân của một số hàm số đơn giản bằng định nghĩa hoặc phương pháp tích phân từng phần.
 Sử dụng được phương pháp đổi biến số để tính tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập công thức nguyên hàm, định nghĩa tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa tích phân? Đ. 3. Giảng bài mới:
Hoạt động của Giáo
Hoạt động của Học sinh viên Nội dung
Hoạt động 1: Tìm hiểu các tính chất của tích phân
H1. Chứng minh các Đ1. Các nhóm thảo luận và trình bày.
II. TÍNH CHẤT CỦA TÍCH tính chất? b b PHÂN kf (x d ) x  
kF(x) a b b a
1. kf (x d
) x k f (x d ) x   b b a a
[ f (x)  g(x) d
] x  (F(x)  G(x))  a 2. a b c b
[ f (x)  g(x) d ] x c bf (x d
) x f (x d
) x F(x)  
a F(x) c a a c b b f (x d
) x g(x d ) x   a a b c b 3. f (x d
) x f (x d
) x f (x d ) x    a a c
(a < c < b)
Hoạt động 2: Áp dụng các tính chất của tích phân H1. Gọi HS tính.
Đ1. các nhóm thực hiện và trình bày.
VD1: Tính các tích phân: 4  4 3 3  2 x a) (x  3 x d ) x  A =   2x2   3  = 35 1 1 GV: Phạm Việt Phương 95
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 3  3 4  x 2 3 b)
(x  2x 1 d ) x  B =   x x  3 3  4  1 1 2 2 x 1  1  1 ln dx   ln2  c)  2 C = xx    1 x 1 2 e e  1 1 2   x2 1 x3  d) x    x dx   x 2  D =   ln x    1 x   2 x 3  1 Đ2.
H2. Xét dấu hàm số
VD2: Tính các tích phân: dưới dấu GTTĐ? 0 1 2 1  4 A= xdx xdx   a)
x 3xdx  1  0 1   2  2 B = 2  sin xdx  sin xdx      b) 1 cos2xdx   0   0 1 2 2 2 2 C = (x x d
) x  (x x d ) x   2 c) x x dx  0 1 0 D = 3 1  1 3 2 d) x 1dx  (x2 1 d
) x  (1 x2 d
) x  (x2 1 d ) x    3  3  1  1
Hoạt động 3: Tìm hiểu cách tính tích phân bằng phương pháp đổi biến số thứ nhất
 GV dẫn dắt đến phương  HS thực hiện theo sự hướng III. PHƯƠNG PHÁP TÍNH pháp. dẫn của GV. TÍCH PHÂN 1 1 13
1. Phương pháp đổi biến số Xét VD: Cho I = (2x 2 1) dx  2
. a) I = (4x  4x 1 d ) x   Định lí 1: 3
Cho hàm số f(x) liên 0 0
tục trên [a; b]. Giả sử hàm số x
a) Tính I bằng cách khai triển 3 1
= (t) có đạo hàm liên tục trên 2 13 x 2 (2 1) b) J = t dt   . 3 3
đoạn [; ] sao cho () = a, 1 b) Đặt t = 2x + 1. 
() = b và a (t) b với t t(1) I = J
[; ]. Khi đó: Tính J = g t ( d ) t  . bf (x d ) x f    t() t(0)  t( d ) t a  GV nêu định lí. 1 1  VD1: Tính I = dx
GV hướng dẫn HS thực hiện.   1 x2 0
 Đặt x  tant,  t  2 2 . 1  xt ( )  2 . cos t  4 1 dt  I = .  2 = 1 tan t 2 4 0 cos t
Hoạt động 4: Tìm hiểu cách tính tích phân bằng phương pháp đổi biến số thứ hai
 GV giới thiệu định lí 2
Định lí 2: Cho hàm số f(x) liên GV: Phạm Việt Phương 96
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
tục trên [a; b]. Nếu hàm số u =
u(x) có đạo hàm liên tục trên
[a; b] và u(x) với mọi x
[a; b] sao cho f(x) =
g[u(x)]u(x), g(u) liên tục trên
[; ] thì: b u(b) f (x d ) x g u ( d ) u   a u(a) 
GV hướng dẫn cách đổi biến.  Đặt u = sinx. VD2: Tính 1 2 1   I = u du   3 2 0 2
I = sin x.cos xdx  0
Hoạt động 5: Áp dụng tính tích phân bằng phương pháp đổi biến số
H1. Sử dụng cách đổi biến Đ1.
VD3: Tính các tích phân sau: nào? a) Đặt t = 1 – x 1 19 1
a) x(1 x) dx  19 1 A = (1 t t ) dt   0 420 0 ln2 x e b) Đặt t = ex + 1 b) dxx 3 0 e 1 dt 3 B =  ln  1 t 2 2 2 1 c) Đặt x = sint c) dx  2  0 1 x 6 cost  3 1 C = dt  cost = 6 d) dx  2 0 0 x  3
d) Đặt x  3 tant  3 3 dt D = dx  2 3 cos t 2 0 (tan t 1) 3 = 9
Hoạt động 6: Củng cố Nhấn mạnh:
– Cách sử dụng các dạng của
phương pháp đổi biến số để tính tích phân.
4. BÀI TẬP VỀ NHÀ:  Bài 3 SGK.
 Đọc tiếp bài "Tích phân".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 97
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 53
Bài 2: TÍCH PHÂN (tt) I. MỤC TIÊU: Kiến thức:
 Biết khái niệm diện tích hình thang cong.
 Biết định nghĩa tích phân của hàm số liên tục.
 Biết các tính chất và các phương pháp tính tích phân. Kĩ năng:
 Tìm được tích phân của một số hàm số đơn giản bằng định nghĩa hoặc phương pháp tích phân từng phần.
 Sử dụng được phương pháp đổi biến số để tính tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập công thức nguyên hàm, định nghĩa tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các cách đổi biến số để tính tích phân? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách tính tích phân bằng phương pháp tích phân từng phần
 GV dẫn dắt từ VD để giới 
III. PHƯƠNG PHÁP TÍNH HS tính I = x (x 1 e ) dx
thiệu phương pháp tích phân TÍCH PHÂN từng phần. u x 1
2. Phương pháp tích phân Đặt  x VD: Tính x (x 1 e ) dxtừng phần bằng dv e dx
Định lí : Nếu u = u(x) và v =
phương pháp tính nguyên hàm  x I = (x + 1)ex – e dx
v(x) là hai hàm số có đạo hàm từng phần. = xex + C
liên tục trên [a; b] thì: 1 1 b b Từ đó tính x (x 1 e ) dx  1 b .  x x (x 1 e ) dx xe
udv uv vdu 0  e a 0 0 a a  GV nêu định lí
Hoạt động 2: Áp dụng tính tích phân bằng phương pháp tích phân từng phần
H1. Nêu cách phân tích? Đ1.
VD1: Tính các tích phân: u x  a) Đặt 
dv  sin xdx 2 sin a) x xdx    0 2 
A = (x cos x 2 )  cos xdx 0  =1 2 0 b) x cos xdx  u x 0 b) Đặt 
dv  cos xdx GV: Phạm Việt Phương 98
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn  ln2  x 2 c) xe dx  2 ( sin ) sin    1 B = x x xdx 0  2 0 0 eu x d) x ln xdx  c) Đặt  xdv e dx 1 ln2 ln2 x x C = xe 0  e dx  2ln2 1  0 u  ln x d) Đặt  dv xdx e 2 e x 1 e2 1 D = ln x xdx   2 1 2 4 1
Hoạt động 3: Áp dụng tính tích phân một số dạng khác
 GV hướng dẫn cách tính. 
VD2: Tính các tích phân: a) Phân tích phan thức 1 dx 1 1 1 a)    2 0 x  5x  6
x2  5x  6 x 3 x  2 2 2
b) Đặt t x2 1 2 b) x x d 1 x  0
c) Biến đổi tích thành tổng  4 x x 1
sin2 .cos  (sin3x  sin x) sin 2 .cos 2 c) x xdx  0 d) Đặt x t e 1 1 x e d) dxx 0 1 e
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách sử dụng phương pháp
tích phân từng phần để tính tích phân.
– Một số dạng sử dụng phương
pháp tích phân từng phần.
4. BÀI TẬP VỀ NHÀ:  Bài 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 99
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 54 + 55
Bài 2: BÀI TẬP TÍCH PHÂN I. MỤC TIÊU:
Kiến thức: Củng cố:
 Định nghĩa và tính chất của tích phân.
 Các phương pháp tính tích phân. Kĩ năng:
 Sử dụng định nghĩa để tính tích phân.
 Sử dụng các phương pháp tính tích phân để tính các tích phân đơn giản. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình tluyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính tích phân bằng định nghĩa
H1. Nêu cách biến đổi hàm số Đ1. Các nhóm thực hiện và 1. Tính các tích phân:
để từ đó sử dụng định nghĩa trình bày. 2 1 tích phân? 1 1 1 a) dx    x(x 1) a) x(x 1) x x 1 1 2 A = ln2 2 b) Khai triển đa thức 2
b) x(x  1) dx  34 0 B = 3  c) C = 0 2   
d) Biến đổi tích thành tổng sin    c) x dx  4  0  D = 0  2 d) sin3x.cos5xdx    2
Hoạt động 2: Luyện tập tính tích phân bằng phương pháp đổi biến số
H1. Nêu cách đổi biến? Đ1.
2. Tính các tích phân: a) Đặt t = 1 + x 3 x2 5 a) dx  A = 3 3 0  x 2 (1 ) b) Đặt x = sint 1  2 b) 1 x dx  B = 4 0 GV: Phạm Việt Phương 100
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn c) Đặt t = 1 + xex 1 x e (1 x) C = ln(1 + e) c) dxx 0 1 xe d) Đặt x = asint a  2 1 D = d) dx  6 a2  x2 0
Hoạt động 3: Luyện tập tính tích phân bằng phương pháp tích phân từng phần
H1. Nêu cách phân tích? Đ1.
3. Tính các tích phân: u x  a) Đặt 1 
dv  sin xdx 2
a) (x  1)sin xdx  A = 2 0 u  ln x e b) Đặt  2
dv x2dx b) x ln xdx  1 1 B = ( e3 2 1) 1 9 c) ln(1 x d ) x
u  ln(x 1) 0 c) Đặt  dv dx 1 2 x (x 2x 1 e )    dx  C = 2ln2 – 1 0
u x2 2x 1 d) Đặt  x
dv e dx D = –1
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách sử dụng các phương pháp tính tích phân.
4. BÀI TẬP VỀ NHÀ:  Bài tập còn lại.
 Đọc trước bài "Ứng dụng của tích phân trong hình học".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 101
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 56
Bài 3: ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC I. MỤC TIÊU: Kiến thức:
 Biết các công thức tính diện tích, thể tích nhờ tích phân. Kĩ năng:
 Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
 Củng cố phép tính tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu ý nghĩa hình học của tích phân? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách tính diện tích hình phẳng giới hạn bởi 1 đường cong và trục Ox
H1. Nhắc lại ý nghĩa hình Đ1. Diện tích hình phẳng giới I. TÍNH DIỆN TÍCH HÌNH học của tích phân?
hạn bởi đồ thị hàm số f(x) liên PHẲNG
tục, không âm trên [a; b], trục 1. Hình phẳng giới hạn bởi 1
hoành và 2 đường thẳng x = a, x đường cong và trục hoành = b:
Diện tích hình phẳng giới hạn b
bởi đồ thị hàm số f(x) liên tục,
S f (x dx ) 
trục hoành và 2 đường thẳng x a = a, x = b: b
S f (x)dx a
Chú ý: Nếu trên [a; b] hàm số
f(x) giữ nguyên một dấu thì:
H2. Nếu f(x) 0 trên [a; b], Đ2. Tính diện tích hình đối xứng b b
thì ta có thể tính diện tích qua trục hoành.
f (x)dx f (x d ) x  
hình phẳng đó như thế nào? a a
Hoạt động 2: Áp dụng tính diện tích hình phẳng
H1. Thiết lập công thức tính? Đ1.
VD1: Tính diện tích hình 3
phẳng giới hạn bởi các đường: 2 S x dx  = 9 (đvdt)
y = x2, x = 0, x = 3, trục Ox. 0 GV: Phạm Việt Phương 102
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn y 9 8 7 6 5 4 3 2
H2. Thiết lập công thức tính? 1
VD2: Tính diện tích hình x -4 -3 -2 -1 O 1 2 3 4 -1
phẳng giới hạn bởi các đường: Đ2.  0
y = sinx, x =  2 , x = 0, y = 0. S  (sin x d ) x  = 1 (đvdt)   2 y 1 x -4π/5 -3π/5 -2π/5 -π/5 O π/5 2π/5 3π/5 4π/5 -1
VD3: Tính diện tích hình
H3. Thiết lập công thức tính?
phẳng giới hạn bởi các đường:
y = x3, y = 0, x = –1, x = 2. Đ3. 2 0 2 S
x3 dx  (x3 d
) x x3dx    1  1  0 17 = 4 y 9 8 7 6 5 4 3 2 1 x -2 -1 O 1 2 3 -1
Hoạt động 3: Tìm hiểu cách tính diện tích hình phẳng giới hạn bởi 2 đường cong GV: Phạm Việt Phương 103
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
 GV minh hoạ bằng hình
2. Hình phẳng giới hạn bởi hai đường
vẽ và cho HS nhận xét tìm cong
công thức tính diện tích.
Cho hai hàm số y = f1(x) và y = f2(x)
liên tục trên [a; b]. Diện tích của hình
phẳng giới hạn bởi đồ thị của hai hàm
số và các đường thẳng x = a, x = b
được tính bởi công thức: b
S f (x)  f (x)dx S = S 1 2 1 – S2 a
Chú ý: Nếu trên đoạn [; ] biểu thức
f1(x) – f2(x) không đổi dấu thì:  GV nêu chú ý  
f (x)  f (x)dx   f (x)  f (x) dx  1 2   1 2   
Hoạt động 2: Áp dụng tính diện tích hình phẳng
 GV hướng dẫn các bước  Tìm hoành độ giao điểm VD1: Tính diện tích hình phẳng giới
xác định hình phẳng và của 2 đường: x = –2, x = 1 hạn bởi các đường: y x3  x2 3 , y = 4.
thiết lập công thức tính 1 y diện tích. 3 2
S  (4  x  3x d ) x  4 3 2  2 27  1 4 x -2 -1 1
VD2: Tính diện tích hình phẳng giới
H1. Nêu các bước thực Đ1. Các nhóm thảo luận và hạn bởi các đường: y = cosx, y = sinx, x hiện? trình bày. = 0, x = . 
Hoành độ giao điểm: x y 4  1
S  cos x  sin x dx  0 x  π/2 π 4 =
cos x  sin x dx  + -1 0  +
cos x sin x dx   4 = 2 2
VD3: Tính diện tích hình phẳng giới
H2. Nêu các bước thực Đ2. hạn bởi các đường: y x3   x hiện? , Hoành độ giao điểm: y x x2   x = –2, x = 0, x = 1 . 1 S
x3  x2  2x dx  2  GV: Phạm Việt Phương 104
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 0 y 3 2 =
x x  2x dx  + 1 x 2  -2 -1 1 1 -1 3 2 +
x x  2x dx  -2 0 -3 37 -4 = -5 12 -6
Hoạt động 3: Củng cố Nhấn mạnh: – Cách xác định hình phẳng.
– Cách thiết lập công thức tính diện tích.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3 SGK.
 Đọc tiếp bài "Ứng dụng của tích phân trong hình học".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 57
Bài 3: ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC (tt) I. MỤC TIÊU: Kiến thức:
 Biết các công thức tính diện tích, thể tích nhờ tích phân. Kĩ năng:
 Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
 Củng cố phép tính tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tích phân.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu công thức tính diện tích hình phẳng giới hạn bởi hai đường cong? b
Đ. S f (x)  f (x)dx  1 2 a GV: Phạm Việt Phương 105
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách tính thể tích vật thể
 GV dùng hình vẽ để minh II. TÍNH THỂ TÍCH hoạ và giải thích.
1. Thể tích của vật thể
Cắt một vật thể T bởi hai mặt
phẳng (P) và (Q) vuông góc với
trục Ox lần lượt tại x = a, x = b (a
< b). Một mặt phẳng tuỳ ý vuông
góc với Ox tại điểm x (a x b)
cắt T theo thiết diện có diện tích là
S(x). Giả sử S(x) liên tục trên [a;
b]. Khi đó thể tích V của phần vật
thể T giới hạn bởi hai mặt phẳng
(P), (Q) được tính theo công thức: b
V S(x d ) x a
Hoạt động 2: Áp dụng tính thể tích khối lăng trụ
H1. Nhắc lại công thức tính Đ1. V = Bh
2. Thể tích khối lăng trụ
thể tích khối lăng trụ?
Tính thể tích khối lăng trụ có diện
 GV hướng dẫn HS cách xây
tích đáy bằng B và chiều cao h. dựng công thức.
 Chọn trục Ox // đường V = B.h
cao, còn 2 đáy nằm trong 2
mặt phẳng vuông góc với
H2. Tính diện tích thiết diện? Ox tại x = 0, x = h
Đ2. S(x) = B (0  x  h) hh V = Bdx Bx  0  Bh 0
Hoạt động 3: Áp dụng tính thể tích khối chóp
H1. Nhắc lại công thức tính 1
3. Thể tích khối chóp thể tích khối chóp? Đ1. V = Bh 3
Thể tích khối chóp có chiều cao h
và diện tích đáy B.
GV hướng dẫn HS cách xây  Chọn trục Ox vuông góc 1 dựng công thức. V = Bh
với mp đáy tại I sao cho gốc 3
O  S và có hướng OI . OI = h.
H2. Tính diện tích thiết diện? 2 x
Đ2. S(x)  B h2 h x2 BhV B dx   h2 3 0
Hoạt động 4: Áp dụng tính thể tích khối chóp cụt GV: Phạm Việt Phương 106
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
 GV hướng dẫn HS cách xây  Chọn trục Ox trùng với 4. Thể tích khối chóp cụt dựng công thức.
đường cao, O  S. Hai mặt Thể tích khối chóp cụt có chiều cao
phẳng đáy cắt Ox tại I và I. h và diện tích hai đáy là B, B.
Đặt OI = b, OI = a (a < b)
1 hBBB B V = 3
H1. Tính diện tích thiết diện? x2
Đ1. S(x)  B b2  b x2
b a a2  ab b2
V B dx B .  2 2 3 a b b
1 hBBB B = 3 a2   B  B
; h b a  b2   
Hoạt động 5: Củng cố Nhấn mạnh:
– Cách xây dựng các công
thức tính thể tích các khối
lăng trụ, chóp, chóp cụt.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc tiếp bài "Ứng dụng của tích phân trong hình học".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 107
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 58
Bài 3: ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC (tt) I. MỤC TIÊU: Kiến thức:
 Biết các công thức tính diện tích, thể tích nhờ tích phân. Kĩ năng:
 Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
 Củng cố phép tính tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về diện tích, thể tích.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu công thức tính thể tích vật thể? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách tính thể tích khối tròn xoay
H1. Nhắc lại khái niệm khối Đ1. HS nhắc lại.
III. THỂ TÍCH KHỐI TRÒN tròn xoay? XOAY
1. Thể tích khối tròn xoay tạo bởi  GV hướng dẫn HS xây
một hình thang cong giới hạn bởi đồ
dựng công thức tính thể tích
thị hàm số y = f(x), trục Ox, hai khối tròn xoay.
đường thẳng x = a, x = b (a < b)
quay quanh trục Ox được tính bởi công thức:
H2. Tính diện tích thiết Đ2. 2 b
S(x)   f (x) 2 diện?
V   f (x dx )  b  2 a
V   f (x dx )  a
Hoạt động 2: Áp dụng tính thể tích khối nón tròn xoay
 GV hướng dẫn HS xây  Chọn hệ trục sao cho trục
2. Thể tích khối nón tròn xoay có dựng công thức.
hoành trùng với trục hình
chiều cao h và bán kính đáy R là: nón, O  S. 1 2   V R h 3 R
H1. Xác định phương trình Đ1. f (x)  x h đường thẳng OA? GV: Phạm Việt Phương 108
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn h 2 y   R  1 2 A
V    x dx   R h R  h  3 M 0 I O x h x
Hoạt động 3: Áp dụng tính thể tích hình cầu  GV hướng dẫn HS xây
3. Thể tích hình cầu bán kính R là: dựng công thức. 4   V R3 3
H1. Xác định phương trình Đ1. 2 2
f (x)  R x cung nửa đường tròn? R  2 2 V   (R x d ) x  R 4 =  R3 3
Hoạt động 4: Áp dụng tính thể tích khối tròn xoay
H1. Lập công thức tính?  2
VD1: Cho hình phẳng giới hạn bởi 2 
Đ1. V   sin xdx  
đường cong y = sinx, trục Ox, x = 0, 2 0
x = . Tính thể tích khối tròn xoay
thu được khi quay hình này xung quanh trục Ox.
Hoạt động 5: Củng cố Nhấn mạnh:
– Cách xây dựng các công
thức tính thể tích các khối tròn xoay.
4. BÀI TẬP VỀ NHÀ:  Bài 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 109
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 59
Bài 3: BÀI TẬP ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC I. MỤC TIÊU: Kiến thức:
 Củng cố các công thức tính diện tích, thể tích nhờ tích phân. Kĩ năng:
 Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.
 Củng cố phép tính tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về diện tích, thể tích.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính diện tích hình phẳng
H1. Nêu các bước tính diện Đ1.
1. Tính diện tích hình phẳng giới tích hình phẳng? a) HĐGĐ: x = –1, x = 2 hạn bởi các đường: 2 2 2 9
a) y x , y x  2 S
x x  2dx   2  ln , 1 1  b) y x y 1 2 2  , 
c) y  (x  6) , y  6x x b) HĐGĐ: x x e e e
S  ln x 1dx  1 e 1 e = (1 ln x d
) x  (1 ln x d ) x   1 1 e 1 =  e  2 e c) HĐGĐ: x = 3, x = 6 6 S  (x 2
 6)  (6x x 2 ) dx  3 = 9
2. Tính diện tích hình phẳng giới
H2. Nêu các bước thực Đ2. hiện?
hạn bởi đường cong (C):y x2 1,
PTTT: y  4x  3
tiếp tuyến với (C) tại điểm M(2; 5) HĐGĐ: x = 0, x = 2 và trục Oy. GV: Phạm Việt Phương 110
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 2
S x2   x dx 8 1 4 3   3 0
Hoạt động 2: Luyện tập tính thể tích vật thể tròn xoay
H1. Nêu các bước thực Đ1.
3. Tính thể tích khối tròn xoay do hiện? a) HĐGĐ: x = –1, x = 1
hình phẳng giới hạn bởi các đường 1 sau quay quanh trục Ox: 2 2 16
V   (1 x ) dx    15 2
a) y  1 x , y  0 1 
b) y  cos x, y  0, x  0, x    2 2 
b) V   cos xdx    2
c) y  tan x, y  0, x  0, x  0 4 c)  4 V 2  tan xdx   1       4    0
4. Cho tam giác vuông OPM có
H2. Viết phương trình OM,
cạnh OP nằm trên trục Ox. Đặt OM toạ độ điểm P?
Đ2. (OM): y = tan.x    P(Rcos; 0)
= R, POM    0    , R  0 3    Rcos  2 2 V   tan .x dx
Tính thể tích khối tròn xoay thu 0
được khi quay tam giác đó quanh  R3 trục Ox. 3 = (cos  cos ) 3
Hoạt động 3: Củng cố Nhấn mạnh:
– Các bước giải bài toán
tính diện tích và thể tích.
4. BÀI TẬP VỀ NHÀ:
 Bài tập ôn chương III.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 111
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 60 + 61
Bài dạy: ÔN TẬP CHƯƠNG III I. MỤC TIÊU:
Kiến thức: Củng cố:
 Định nghĩa nguyên hàm. Bảng nguyên hàm. Phương pháp tính nguyên hàm.
 Định nghĩa tích phân. Tính chất và phương pháp tính tích phân.
 Ứng dụng của tích phân để tính diện tích, thể tích. Kĩ năng:
 Thành thạo trong việc tính nguyên hàm, tích phân.
 Thành thạo trong việc tính diện tích, thể tích bằng công cụ tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học trong chương III.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Ôn tập tính nguyên hàm của hàm số
H1. Nêu cách tìm nguyên Đ1.
1. Tìm nguyên hàm của các hàm của hàm số? a) Khai triển đa thức hàm số: 3 11
a) f (x)  (x 1)(1  2x)(1  3x) 4 3 2 F (x)  x
x  3x x C 2 3 b) 2 f ( ) x  sin 4 . x cos 2x
b) Biến đổi thành tổng 1 f x  1 1 c) ( ) 2 F x   x x  1  x ( ) cos 4 cos8 C 8 32 d) x 3 f ( ) x  (e 1) c) Phân tích thành tổng 1 1 x F(x)  ln  C 2 1 x d) Khai triển đa thức 3x e 3 2 F (x)   x e  3 x
e x C 3 2 Đ2. H2. Nêu cách tính? 2. Tính:
a) PP nguyên hàm từng phần a) (2  )sin  x xdx
A  (x  2) cos x  sin x C 2 b) Khai triển  ( 1) b)  x dx 5 3 1 2 4 x 2 2 2 B x
x  2x C 3x e  5 3 1 c)  dx
c) Sử dụng hằng đẳng thức x e 1 1 1 2  x x C e
e x C d)  dx 2 x  2 (sin cos x) GV: Phạm Việt Phương 112
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn   
d) sin x  cos x  2 cos x    4  1    D  tan  x    C 2  4 
Hoạt động 2: Ôn tập tính tích phân H1. Nêu cách tính? Đ1. 3. Tính:
a) Đổi biến: t  1 x 3 a)  x dx 2 8 1  x 2
A  2 (t 1)dt   0 3 64 1 1  b) Tách phân thức b)  x dx 3 x 1 64 2 B   1 1  1839 3 6 xx dx   c) 2 3  x x e dx 14 1 0
c) Tích phân từng phần 2 lần   2 d) 1 sin 2  xdx 6 C  (13e 1) 0 27
d) 1 sin 2x  sin x  cos x    = 2 sin  x    D  2 2  4  H2. Nêu cách tính? Đ2. 4. Tính:     2
a) Biến đổi thành tổng. A 8 a) 2 cos 2 sin  x xdx 0 b) Bỏ dấu GTTĐ: B 1  1 ln2 b) 2  2  x x dx c) Phân tích thành tổng: 1  2 1 c)  dx C 1   ln3 2 2 x  2x  3 0 3   5  d) Khai triển: D   d) 2 ( sin )  x x dx 3 2 0
Hoạt động 3: Ôn tập tính diện tích, thể tích
H1. Nêu các bước thực hiện? Đ1.
5. Xét hình phẳng giới hạn bởi HĐGĐ: x = 0, x = 1 y   x2 2 1
, y  2(1 x) 1 S 2
1 x2 (1 x)dx       1 
a) Tính diện tích hình phẳng. 2 0
b) Tính thể tích khối tròn xoay 1
tạo thành khi quay hình phẳng V 4 
 (1 x2) (1 x 2) d       x quanh trục Ox. 0 4 =  3
Hoạt động 4: Củng cố Nhấn mạnh: – Các phương pháp tính nguyên hàm, tích phân.
– Các bước giải bài toán tính diện tích và thể tích.
4. BÀI TẬP VỀ NHÀ: GV: Phạm Việt Phương 113
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
 Chuẩn bị kiểm tra 1 tiết.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 62
Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG III I. MỤC TIÊU:
Kiến thức: Củng cố:
 Định nghĩa nguyên hàm. Bảng nguyên hàm. Phương pháp tính nguyên hàm.
 Định nghĩa tích phân. Tính chất và phương pháp tính tích phân.
 Ứng dụng của tích phân để tính diện tích, thể tích. Kĩ năng:
 Thành thạo trong việc tính nguyên hàm, tích phân.
 Thành thạo trong việc tính diện tích, thể tích bằng công cụ tích phân. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học trong chương III. III. MA TRẬN ĐỀ: Nhận biết Chủ đề Thông hiểu Vận dụng Tổng TNKQ TL TNKQ TL TNKQ TL Nguyên hàm 4 2,0 0,5 Tích phân 4 2 6,0 0,5 2,0 Ứng dụng 1 2,0 2,0 Tổng 4,0 4,0 2,0 10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm) Chọn phương án đúng nhất: Câu 1: Tính A = 3  xdx. 4 4 4 3 3 3 2 3  A) 3 A x C B) 3 A x C C) 4 A x C D) 3 A   xC 3 4 4 2 Câu 2: Tính A = sin5  xdx . cos 5x cos 5x A) A    C B) A  5
 cos5x C C) A   C
D) A   cos5x C 5 5 Câu 3: Tính A = 5 2  xdx . 5 5 2 x A) 5  5ln 2.2 x AC B) 5  5.2 x AC C) 5  .2 x AC D) A   C ln 2 5ln 2 GV: Phạm Việt Phương 114
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Câu 4: Tính A = 5  x e dx . 1 1 A) 5  5 x A eC B) 5  x A eC C)  x A e C D)  5 x A e C 5 5 8 Câu 5: Tính 3 A   xdx . 1 3 45 4 A) A  20 B) A   4 4 2   1 C) A  D) A   4 4 2   1 4 4 3 
Câu 6: Tính A  sin5  xdx . 0 1 1 2 A) A  0 B) A  C) A   D) A  5 5 5 1 Câu 7: Tính 5  2  x A dx . 0 31 155 A) A  B) A  155 C) A  155ln 2 D) A  5ln 2 ln 2 ln 2 Câu 8: Tính 5   x A e dx . 0 1 31 A) A  155 B) A  C) A  5 D) A  5 5
B. Phần tự luận: (6 điểm)  2 ln 2 2 x Bài 1: e
(4 điểm) Tính các tích phân sau:
I  (2  x)sin  xdx , J   dx x e 1 0 0
Bài 2: (2 điểm) Tính hình phẳng giới hạn bởi các đường sau: 3 2
y x x 1 và 3
y x  4x  2 .
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 B A D B C D A D
B. Phần tự luận: Mỗi câu 2 điểm  2 u  2  xdu  dx
Bài 1:a) I  (2  x)sin  xdx . Đặt   
dv  sin xdx
v  cos x 0   2   I = 2
(2  x)cos x  cos  xdx = 2 2 (
 2  x)cos x  sin x = 1 0 0 0 0 ln 2 2 x e
x  0  t  2 b) J  
dx . Đặt t = x
e  1  dt = x e dx .  x e 1
x  ln 2  t  3 0 3 1 3 2 J =    ln  1 ln  t dt t t 2 t 3 2
Bài 2: Phương trình hoành độ giao điểm của hai đường: 3 2
y x x 1 và 3
y x  4x  2 . x 1 3 2 3
x x  1  x  4x  2   x  3 3 3 4 Diện tích: S = 3 2 3  1  4  2  x x x x dx = 2 (  4  3)   x x dx 3 1 1
VI. KẾT QUẢ KIỂM TRA: Lớp Sĩ số 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 GV: Phạm Việt Phương 115
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn SL % SL % SL % SL % SL % 12S1 53 12S2 54 12S3 54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1
Chương IV: SỐ PHỨC Tiết dạy: 63 Bài 1: SỐ PHỨC I. MỤC TIÊU: Kiến thức:
 Hiểu các khái niệm số phức, phần thực, phần ảo của một số phức, môđun của số phức, số phức liên hợp.
 Hiểu ý nghĩa hình học của khái niệm môđun và số phức liên hợp. Kĩ năng:
 Tính được môđun của số phức.
 Tìm được số phức liên hợp của một số phức.
 Biểu diễn được một số phức trên mặt phẳng toạ độ. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về toạ độ trên mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3') 2 2
H. Giải các phương trình: x 1  0; x 1  0 ? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm số i
 GV giới thiệu khái niệm số i
1. Số i
Nghiệm của phương trình
x2 1 0 là số i. i2  1 
Hoạt động 2: Tìm hiểu định nghĩa số phức
 GV nêu định nghĩa số phức.
2. Định nghĩa số phức
H1. Cho VD số phức? Chỉ ra Đ1. Các nhóm thực hiện.
Mỗi biểu thức dạng a bi , GV: Phạm Việt Phương 116
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
phần thực và phần ảo? 2  i 5 ,  2  i 3 , 1 i
3 , 1 i 3 trong đó a, b R, i2  1  đgl
0 i , 5 i 0
một số phức.
a: phần thực, b: phần ảo. Tập số phức: C.
Chú ý: Phần thực và phần ảo
của một số phức đều là những số thực.
Hoạt động 3: Tìm hiểu khái niệm hai số phức bằng nhau
 GV nêu định nghĩa hai số
3. Số phức bằng nhau phức bằng nhau.
Hai số phức là bằng nhau nếu
phần thực và phần ảo của
chúng tương ứng bằng nhau. a c
a bi c di   b d Chú ý: GV nêu chú ý.
Mỗi số thực a được coi là
một số phức với phần ảo bằng 0: a = a + 0i
Như vậy, a R a C
Số phức 0 + bi đgl số thuần ảo
và viết đơn giản là bi: bi = 0 + bi
Đặc biệt, i = 0 + 1i.
Số i : đơn vị ảo
H1. Khi nào hai số phức bằng Đ1. Các nhóm thực hiện.
VD1: Tìm các số thực x, y để z nhau?
2x 1  x  2 x  1 = z': a)   
z x   y  3
y  2  y  4 y  3 (2 1) (3 2)i a)  z
  x   y   ( 2) ( 4)i 1  5 x   1   2x  5 
z  (1 2x)  i 3 2 b)    b)  z  3 1 3y  1  3
  5  (1 3y)i y    3
z  (3x  9)  3  i  3  x  9 12 x  7  c)  z
 12  (5y  7)i c)    3   5y  7 y  2
z  (2x  3)  (3y 1)  i
x   y  x  d)  2 3 2 1 2 d)    z
  (2y 1)  (3x  7)i
(3y 1)  3x  7  y  0 VD2: Cho số phức
H2. Khi nào z là số thực, là số Đ2. z a   b  ảo? (2 1) (3 5)i 5
a) 3b  5  0  b   Tìm a, b để: 3 a) z là số thực 1
b) 2a 1  0  a  b) z là số ảo 2
H3. Khi nào z là số thực, là số Đ3.
VD3: Trong các số phức sau, ảo?
số nào là số thực, số nào là số c) là số ảo ảo: d) là số thực a) 0 0 sin 30  i cos 30 GV: Phạm Việt Phương 117
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn b) 0 0 sin 30  i cos 30 c) 0 0 cos 90  i sin 90 d) 0 0 sin 90  i cos 90
Hoạt động 4: Củng cố Nhấn mạnh:
– Ý nghĩa của số i.
– Định nghĩa số phức, phần thực, phần ảo.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 64
Bài 1: SỐ PHỨC (tt) I. MỤC TIÊU: Kiến thức:
 Hiểu các khái niệm số phức, phần thực, phần ảo của một số phức, môđun của số phức, số phức liên hợp.
 Hiểu ý nghĩa hình học của khái niệm môđun và số phức liên hợp. Kĩ năng:
 Tính được môđun của số phức.
 Tìm được số phức liên hợp của một số phức.
 Biểu diễn được một số phức trên mặt phẳng toạ độ. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức và mặt phẳng toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa số phức? Cho VD? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu biểu diễn hình học của số phức
 GV giới thiệu cách biểu
4. Biểu diễn hình học số phức
diễn hình học của số phức.
Điểm M(a; b) trong một hệ toạ
độ vuông góc của mặt phẳng
đgl điểm biểu diễn số phức
H1. Nhận xét về sự tương
z a bi .
Đ1. Tương ứng 1–1. GV: Phạm Việt Phương 118
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
ứng giữa cặp số (a; b) với toạ
độ của điểm trên mặt phẳng?
Đ2. Các nhóm thực hiện.
VD1: Biểu diễn các số phức
H2. Biểu diễn các số phức
sau trên mặt phẳng toạ độ: trên mp toạ độ?
a) z  3  2i
b) z  2  3i c) z  3   2i d) z  3i e) z  4 Đ3.
H3. Nhận xét về các số thực,
Các điểm biểu diễn số thực số thuần ảo?
nằm trên Ox, các điểm biểu diễn
số ảo nằm trên trục Oy.
Hoạt động 2: Tìm hiểu khái niệm môđun của số phức
 GV giới thiệu khái niệm
5. Môđun của số phức môđun của số phức.
Độ dài của OM đgl môđun
của số phức z và kí hiệu z . 2 2
z a bi a b H1. Gọi HS tính.
Đ1. Các nhóm thực hiện.
VD2: Tính môđun của các số z  phức sau: a), b), c) 13 z   d) z  3 a) 3 2i z   e) z  4 b) 2 3i z    c) 3 2i d) z  3i e) z  4 H2. Phân tích YCBT? a
VD3: Tìm số phức có môđun Đ2. 0 2 2
a b  0   bằng 0. b  0  z  0
Hoạt động 3: Tìm hiểu khái niệm số phức liên hợp
 GV giới thiệu khái niệm số
6. Số phức liên hợp phức liên hợp.
Cho số phức z a bi . Ta gọi
a bi là số phức liên hợp của
z và kí hiệu là z a bi . Chú ý:
Trên mặt phẳng toạ độ, các
H1. Nhận xét mối liên hệ Đ1.
điểm biểu diễn z và z đối xứng
giữa 2 số phức liên hợp?
Các nhóm thảo luận và trình bày. nhau qua trục Ox. z z z z
H2. Tìm số phức liên hợp?
Đ2. Các nhóm thực hiện.
VD4: Tìm số phức liên hợp của
a) z  3  2i các số phức sau: z  
b) z  2  3i a) 3 2i z   c) z  3   2i b) 2 3i z    d) z  3i c) 3 2i d) z  3i GV: Phạm Việt Phương 119
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn e) z  4 e) z  4
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách biểu diễn số phức trên mặt phẳng toạ độ.
– Môđun của số phức, số phức liên hợp.
4. BÀI TẬP VỀ NHÀ:  Bài 3, 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 65
Bài 1: BÀI TẬP SỐ PHỨC I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm số phức, phần thực, phần ảo của một số phức, môđun của số phức, số phức liên hợp.
 Ý nghĩa hình học của khái niệm môđun và số phức liên hợp. Kĩ năng:
 Tính được môđun của số phức.
 Tìm được số phức liên hợp của một số phức.
 Biểu diễn được một số phức trên mặt phẳng toạ độ. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập xác định phần thực, phần ảo của số phức, số phức bằng nhau
H1. Xác định phần thực và Đ1. HS thực hiện.
1. Tìm phần thực và phần ảo
phần ảo của số phức?
a) a  1, b    của số phức: z  
b) a  2, b  1  a) 1  i
b) z  2  i a b  c) 2 2, 0 GV: Phạm Việt Phương 120
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
d) a  0, b  7 c) z  2 2 d) z  7i
H2. Khi nào 2 số phức bằng Đ2. nhau?  3
2. Tìm các số thực x, y để x  3
x  2  x 1  z   a)   2  z , biết:
2y 1  (y  5) 4 
z  (3x  2)  (2y 1)i y   a)  3 z
  (x 1)  (y  5)i
2x y x  2y  3 x  0 b)   
z  (2x y)  (2y x)  i
2y x y  2x 1 y 1 b)  z
  x y   y x  ( 2 3) ( 2 1)i
Hoạt động 2: Luyện tập biểu diễn số phức trên mặt phẳng toạ độ
H1. Nêu cách biểu diễn số Đ1.
3. Trên mặt phẳng toạ độ, tìm
phức trên mặt phẳng toạ độ?
– Phần thực: hoành độ
tập hợp điểm biểu diễn số phức y – Phần ảo: tung độ
z thoả điều kiện: 3 y a) Phần thực của y z bằng –2 y 3
b) Phần ảo của z bằng 3
c) Phần thực của z thuộc (–1;2) –2 O x O x 1 d) Phần ảo của – z thuộc [1; 3] 1 O 2 x O x a) b) c) d)
Hoạt động 3: Luyện tập tính môđun và tìm số phức liên hợp
H1. Nêu công thức tính Đ1. 2 2
z a b
4. Tính môđun của các số môđun của số phức? phức: a) z  7 a) z  2   i 3 b) z  11
b) z  2  3i c) z  5 c) z  5  d) z  3 d) z i 3
H2. Xác định điểm M? Đ2.
5. Trên mặt phẳng toạ độ, tìm
tập hợp điểm biểu diễn các số a) Đường tròn (O; 1) phức b) Hình tròn (O; 1)
z thoả điều kiện: z  c) Hình vành khăn a) 1 d) Điểm A(0; 1) z  b) 1 c) 1  z  2
d) z  1 và phần ảo bằng 1.
H3. Nêu định nghĩa số phức Đ3.
6. Tìm số phức liên hợp của số liên hợp? a) phức: z  1 i 2 z  
b) z   2  i 3 a) 1 i 2 c) z  5
b) z   2  i 3 d) z  7i c) z  5 d) z  7i
Hoạt động 4: Củng cố GV: Phạm Việt Phương 121
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Nhấn mạnh:
– Cách biểu diễn số phức trên mặt phẳng toạ độ.
– Môđun của số phức, số phức liên hợp.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc trước bài "Cộng, trừ và nhân số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 66
Bài 2: CỘNG, TRỪ VÀ NHÂN SỐ PHỨC I. MỤC TIÊU: Kiến thức:
 Biết khái niệm phép cộng, phép trừ, phép nhân số phức. Kĩ năng:
 Vận dụng thành thạo các phép toán cộng, trừ và nhân số phức. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa số phức, môđun, số phức liên hợp? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu phép cộng, phép trừ số phức  GV nêu cách tính.
1. Phép cộng và phép trừ
Phép cộng và phép trừ hai số phức
được thực hiện theo qui tắc cộng, trừ đa thức.
(a bi)  (c di)  (a c)  (b d )i
H1. Nêu qui tắc thực hiện Đ1. Cộng (trừ) hai phần thực, (a bi)  (c di)  (a c)  (b d )i phép tính? hai phần ảo. a) A = 8  10i
VD1: Thực hiện phép tính: b) B = 3  2i
a) (3  2i)  (5  8i) c) C = 8  9i
b) (7  5i)  (4  3i) d) D = 3   3i
c) (5  2i)  (3  7i) GV: Phạm Việt Phương 122
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
d) (1 6i)  (4  3i)
Hoạt động 2: Tìm hiểu phép nhân hai số phức  GV nêu cách tính. 2. Phép nhân
Phép nhân hai số phức được thực
hiện theo qui tắc nhân đa thức rồi thay i2  1
trong kết quả nhận được.
(a bi) c (  di)  a
( c bd)  a
( d bc i)
H1. Nhắc lại các tính chất Đ1. giao hoán, kết hợp, phân Chú ý:
của phép cộng và phép phối.
Phép cộng và phép nhân các
số phức có tất cả các tính chất của nhân các số thực?
phép cộng và phép nhân các số thực. H2. Gọi HS tính?
Đ2. Các nhóm thực hiện.
VD2: Thực hiện phép tính:
a) A  14  2 i 3 a) (5  i 2 )(4  i 3 )
b) B  24 1 i 0 (2 3 )(6  4 )
c) C  22  i 7 b) i i d) D  13 c) (2  i 3 )(5 i 4 ) d) (3  i 2 )(3 i 2 )
Hoạt động 3: Áp dụng phép cộng và phép nhân các số phức H1. Nêu các tính?
Đ1. Thực hiện phép tính, sau VD3: Tìm số phức liên hợp của các
đó tìm số phức liên hợp. số phức sau:
a) z  7  i
a) z  (2  i 3 ) (5 i 4 ) b) z  3   i 7
b) z  (2  i 3 )(5 i 4 ) c) z  3  i
c) z  (2  i 3 ) (5 i 4 ) d) z  3   i 7
d) z  (2  i 3 ) (5 i 4 )
e) z  22  i 7
e) z  (2  i 3 )(5 i 4 ) f) z  2   2 i 3  (2  3 )(5 4 ) g) z  2   2 i 3 f) z i i
h) z  22  i 7
g) z  (2  i 3 )(5 i 4 )
h) z  (2  i 3 )(5 i 4 )
Hoạt động 4: Củng cố Nhấn mạnh: – Cách thực hiện phép cộng, phép nhân các số phức.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3, 4, 5 SGK.  Chứng minh:
z z z z 1 2 1 2
z z z z 1 2 1 2 z z .  z .z 1 2 1 2
 Đọc tiếp bài "Cộng, trừ và nhân số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 123
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 67
Bài 2: BÀI TẬP CỘNG, TRỪ VÀ NHÂN SỐ PHỨC I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm phép cộng, phép trừ, phép nhân số phức. Kĩ năng:
 Vận dụng thành thạo các phép toán cộng, trừ và nhân số phức. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập phép cộng, phép trừ số phức
H1. Nhắc lại cách thực hiện Đ1.
1. Thực hiện các phép tính sau:
phép cộng, trừ các số phức? a) 5  i a) (3  i 5 )  (2  i 4 ) b) 3  1 i 0 b) ( 2   i 3 )  ( 1   i 7 ) c) 1  1 i 0 c) (4  i 3 ) –(5 – i 7 ) d) 3   i d) (2  i 3 ) (5 i 4 ) H2. Gọi HS tính. Đ2.
2. Tính u + v, u – v với:  3,  2 a) u v i
a) u v  3  i
2 , u v  3  i 2 1 2 ,  6
b) u v  1 i
4 , u v  1 i 8 b) u i v i  5 ,  7 
c) u v   i 2 ,
u v  1 i 2 c) u i v i 15,  4  2
d) u v  19  i
2 , u v  11 i 2 d) u v i
Hoạt động 2: Luyện tập phép nhân hai số phức
H1. Nhắc lại cách thực hiện Đ1.
3. Thực hiện các phép tính sau: phép nhân các số phức? a) i 13  a) (3  i 2 )(2  i 3 ) b) 1  0  i 4 b) ( 1
  i)(3  i 7 ) c) 20 1 i 5 c) 5(4  i 3 ) d) 20  i 8 d) ( 2   i 5 ). i 4 3 4 5 H2. Nêu cách tính? Đ2.
4. Tính i , i , i . Nêu cách
i3  i2 i.  i  tính n i
với n là một số tự nhiên 4 2 2 tuỳ ý. i i i. 1
i5  i4 i.  i
Nếu n  4q r, 0  r  4 GV: Phạm Việt Phương 124
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn thì n r i i
Đ3. Sử dụng hằng đẳng thức. H3. Nêu cách tính? a) 5  1 i 2
5. Thực hiện phép tính: b) 4  6  i 9 a)  i 2 (2 3 ) c) i 2  b)  i 3 (2 3 ) d) 2   i 5 c)  i 2 (1 ) 3
d) (1 i)  i 3
Hoạt động 3: Áp dụng phép cộng và phép nhân các số phức
H1. Thực hiện phép tính? Đ1.
6. Xác định phần thực, phần ảo a) 1  i của các số sau:
a) i  (2  i 4 ) (3 i 2 ) b) 7   6 i 2 c) 13  2 2  i 3  b) d) 1 i 7 c) (2  i 3 )(2  i 3 )
d) i(2  i)(3  i)
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách thực hiện phép cộng, phép nhân các số phức.
4. BÀI TẬP VỀ NHÀ:
 Đọc trước bài "Phép chia số phức".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 125
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 68
Bài 3: PHÉP CHIA SỐ PHỨC I. MỤC TIÊU: Kiến thức:
 Biết khái niệm số phức nghịch đảo, phép chia hai số phức. Kĩ năng:
 Biết tìm được nghịch đảo của một số phức.
 Biết thực hiện được phép chia hai số phức.
 Biết thực hiện các phép tính trong một biểu thức chứa các số phức. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại khái niệm số phức liên hợp, phép cộng, nhân các số phức? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu tổng và tích của hai số phức liên hợp
 GV cho HS thực hiện  Các nhóm thực hiện và trình 1. Tổng và tích của hai số phức
một số VD, rồi cho HS bày. liên hợp nhận xét kết quả.
Tổng của một số phức với số VD: Cho z.
phức liên hợp của nó bằng hai lần
Tính z z , z.z ? z z z z z.z
phần thực của số phức đó: a) z  2  i 3 2+3i 2–3i 4 13
z z a 2 b) z  5  i 3 5–3i 5+3i 10 34
Tích của một số phức với số c) z  5   i 3 –5–3i –5+3i –10 34
phức liên hợp của nó bằng bình d) z  2   i 3 –2+3i –2–3i –4 13
phương môđun của số phức đó. z z a b z 2 2 2 .   
 GV cho HS nêu nhận xét.  HS phát biểu.
Nhận xét: Tổng và tích của hai số
phức liên hợp là một số thực
Hoạt động 2: Tìm hiểu phép chia hai số phức
H1. Phát biểu phép chia 2 a
2. Phép chia hai số phức số thực?
c a bc Đ1. b (b  0)
Chia số phức c + di cho số phức a
+ bi khác 0 là tìm số phức z sao  GV cho HS phát biểu  cho: HS phát biểu.
định nghĩa phép chia 2 số c + di = (a + bi)z phức.
Số phức z đgl thương trong phép
chia c + di cho a + bi. c di Kí hiệu: z a bi GV: Phạm Việt Phương 126
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
VD1: Thực hiện phép chia 4  i 2 cho 1 i .
 GV hướng dẫn cách thực 4  i 2  Tổng quát: hiện.  z  Giả sử 1  i c di zĐể tìm thương ta thực
(1 i)z  4  i 2 a bi
 (1i)(1 i)z  (1i)(4  i 2 )
hiện các bước sau: – Đưa về dạng: 2z  6  i
2  z  3i
(a bi)z c di
– Nhân cả 2 vế với số phức liên
hợp của a + bi, ta được: a2  b2 (
)z  (ac bd) (ad bc i) 1
– Nhân cả 2 vế với : a2  b2 z 1 
(acbd) a
( d bc i) a2  b2
Chú ý: Trong thực hành, để tính c di thương
, ta nhân cả tử và a bi
mẫu với số phức liên hợp của a bi .
Hoạt động 3: Áp dụng thực hiện phép chia số phức H1. Gọi HS tính. Đ1.
VD2: Thực hiện các phép chia a) sau: 3 i 2 (3 i 2 )(2  i 3 ) 12 5 3 i 2    i 2 a)  i 3 (2  i 3 )(2  i 3 ) 13 13 2  i 3 1 i b) b) 2  i 3 1 i (1 i)(2  i 3 ) 1  5    i 6  i 3 2  i 3 (2  i 3 )(2  i 3 ) 13 13 c) i 5 c) 6  i 3 (6  i 3 )( i 5 ) 15 30    i i 5 i 5 (  i 5 ) 25 25
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách thực hiện phép chia các số phức.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3, 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 127
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 69
Bài 3: BÀI TẬP PHÉP CHIA SỐ PHỨC I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm số phức nghịch đảo, phép chia hai số phức. Kĩ năng:
 Biết tìm được nghịch đảo của một số phức.
 Biết thực hiện được phép chia hai số phức.
 Biết thực hiện các phép tính trong một biểu thức chứa các số phức. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tìm số phức nghịch đảo H1. Nêu cách tìm? 1
1. Tìm số phức nghịch đảo của Đ1. Tìm z . các số phức sau: 1 2 1 1 1 2 a) z i a)    i z 1 i 2 5 5 b) z  2  i 3 c) z i 1 1 2 3 b)    i  5 3 z d) z i 2  i 3 11 11 1 1 c)   i z i 1 1 5 3 d)    i z 5  i 3 28 28
Hoạt động 2: Luyện tập phép chia hai số phức H1. Nêu cách tính?
Đ1. Nhân cả tử và mẫu với số 2. Thực hiện các phép chia sau:
phức liên hợp của mẫu. 2  i 2  i 4 7 a) 3 i2 a)  3 i 2 = i 13 13 1 i 2
1 i 2 2  6 2 2  3 b) 2  i b)   i 3 2  i 3 7 7 i 5 i 5 1  5 10 c) 2 i3 c)   i 2  i 3 13 13 5 i 2 d) i GV: Phạm Việt Phương 128
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 5 i 2  2   i 5 d) i
3. Thực hiện các phép tính sau: H2. Gọi HS tính. Đ2. 1 a) 1 2 3 2  i 3 a)   i 2  i 3 13 13 1 b) 1 1 3 1 3 b)   i i 1 3 2 2 2 2  i 2 2 3 i 2 c) 3 i 2 i c)  2   i 3 i 3 i 4 d) 3 i 4 16 13 4 i d)   i 4 i 17 17
Hoạt động 3: Vận dụng phép chia số phức H1. Nêu cách tìm? Đ1.
4. Tìm số phức z thoả mãn: 2   i
a) iz  2  i  0 a) z  1 i 2 i b) (2  i 3 )z z 1 1  1 3
c) (2  i)z  4  0 b) z     i 1  i 3 10 10 d) z2  4  0 4 8 4 c) z    i 2  i 5 5 d) (z i 2 )(z i 2 )  0
 z   i 2  z i 2
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách thực hiện phép chia các số phức.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3, 4 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 129
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 70
Bài 4: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC I. MỤC TIÊU: Kiến thức:
 Biết cách giải phương trình bậc hai với hệ số thực.
 Căn bậc hai của một số thực âm. Kĩ năng:
 Biết tìm nghiệm phức của phương trình bậc hai với hệ số thực. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Giải phương trình: (z i 2 )(z i 2 )  0?
Đ. z i 2 ; z   i 2 . 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu căn bậc hai của số thực âm
H1. Nhắc lại thế nào là căn Đ1.
1. Căn bậc hai của số thực
bậc hai của số thực dương a ? 2 âm
b là căn bậc 2 của a nếu b a . 
Căn bậc hai của –1 là i và –i.
 GV giới thiệu khái niệm căn 
Căn bậc hai của số thực a <
bậc 2 của số thực âm. 0 là i a .
H2. Tìm và điền vào bảng?
VD1: Tìm các căn bậc hai của
Đ2. Các nhóm thực hiện yêu cầu các số sau: – 2, –3, –4. a –2 –3 –4 căn bậc 2 i  2  i 3 i 2 
Hoạt động 2: Tìm hiểu phương trình bậc hai với hệ số thực H1.
Nhắc lại cách giải Đ1. 2
2. Phương trình bậc hai với
Xét  = b  4ac . phương trình bậc hai?  hệ số thực
= 0: PT có 1 nghiệm thực
Xét phương trình bậc hai: b x   2
ax bx c  0 2a
(với a, b, c R, a 0)
> 0: PT có 2 nghiệm thực 2 b
Tính = b  4ac . x   phân biệt 1,2  2a  
Trong trường hợp < 0, nếu
< 0: PT không có nghiệm
xét trong tập số phức, ta vẫn có thực. GV nêu nhận xét.
2 căn bậc hai thuần ảo của
là i . Khi đó, phương
trình có 2 nghiệm phức được GV: Phạm Việt Phương 130
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn
xác định bởi công thức: b i x1,2  2a
Đ2. HS thực hiện lần lượt các
H2. Nêu các bước giải bước.
VD2: Giải phương trình sau phương trình bậc hai? trên tập số phức: 1   i 3 2  = –3  x1,2  2
x x 1 0
Nhận xét: Trên tập số phức:
 Các nhóm thảo luận và trình
GV hướng dẫn HS nêu nhận
Mọi PT bậc hai đều có 2 xét. bày.
nghiệm (có thể trùng nhau).
Tổng quát, mọi PT bậc n (n n n 1  1): a x a x 0 1  . . n a  0
với a0, a1, …, an C, a0 0
đều có n nghiệm phức (có thể trùng nhau).
Hoạt động 3: Áp dụng giải phương trình bậc hai H1. Gọi HS giải. Đ1.
VD3: Giải các phương trình sau trên tập số phức: a) xi 1,2 3 a) x2  3  0 b) x    i 1,2 1 2 2
b) x  2x  3  0 3 i 11 2 c) x
c) 5x  3x 1  0 1,2  10 2
d) x  2x  3  0 x  1 d)  x  3
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách tính căn bậc hai của số thực âm.
– Cách giải phương trình bậc hai với hệ số thực.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3, 4, 5 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 131
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 71
Bài 4: BÀI TẬP PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC I. MỤC TIÊU:
Kiến thức: Củng cố:
 Cách giải phương trình bậc hai với hệ số thực.
 Căn bậc hai của một số thực âm. Kĩ năng:
 Biết tìm nghiệm phức của phương trình bậc hai với hệ số thực. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về số phức.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tìm căn bậc hai của số thực âm
H1. Nêu công thức tìm căn Đ1.
1. Tìm các căn bậc hai phức
bậc hai phức của số thực âm? a
các căn bậc hai phức của các số sau: – – 7 i  7; i 7 7; –8; –12; –20; –121 –8 i 2 2; i 2 2 –12 i 2 3; i 2 3 –20 i 2 5; i 2 5 –121 1  i 1 ; 1 i 1
Hoạt động 2: Luyện tập giải phương trình bậc hai với hệ số thực H1. Nêu cách giải? Đ1.
2. Giải các phương trình sau 1 5 trên tập số phức: a) z1,2  2 2
a) z z 1  0    2 b) z i 1,2 1 2
b) z  2z  5  0 2  4  7  0 c) z   i c) z x 1,2 2 3 2
d) 2x x  3  0 1   i z 23  d) 1,2 4 H2. Nêu cách giải? Đ2.
3. Giải các phương trình sau 1 i 2 trên tập số phức: a) z1,2  3 2 a)  z 3  2z 1 0 3   i 47 2 b) z 7  z 3  2  0 b) z1,2  14 2 c) z 5  z 7 11 0 GV: Phạm Việt Phương 132
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Giải tích 12 chuẩn 7  i 171 d) z2 16  0 c) z1,2  10 d) z   i 4
Hoạt động 3: Vận dụng giải phương trình bậc hai H1. Nêu cách giải? Đ1.
4. Giải các phương trình sau trên tập số phức: a) z
  2; z i  3 1,2 3,4 4 2
a) z z  6  0 b) zi  2; z i 1,2 3,4  5 4 2 b) z z 7 10  0 c) z  2; z  1   i 1 2,3 3 c) z3  8  0 3   i 3 3 2
d) z  4z  6z  3  0 d) z  1  ; z 1 2,3  2
5. Cho a, b, c R, a 0, z
H2. Viết công thức nghiệm và Đ2. 1, z2
là các nghiệm của phương trình tính z z Xét  < 0. 1 2 , z z 1 2 ?
az2  bz c  0. Hãy tính b i z  1,2  z z 2a 1 2 và z z 1 2 ? b c
z z   z z 1 2 a , 1 2  a H3. Nêu cách tìm? Đ3.   . Tìm
6. Cho số phức z a bi
một phương trình bậc hai với
(x z)(x z )  0
hệ số thực nhận z và z làm  2
x  (z z )x zz  0 (*) nghiệm.
mà z z a zz a2  b2 2 , nên 2 2 2 (*)  x a
2 x a b  0
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách tính căn bậc hai của số thực âm.
– Cách giải phương trình bậc hai với hệ số thực.
– Cách vận dụng việc giải
phương trình bậc hai với hệ số thực.
4. BÀI TẬP VỀ NHÀ:
 Bài tập ôn chương IV.
 Chuẩn bị kiểm tra 1 tiết chương IV.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 133