Giáo án Hình học 12 cơ bản cô Phạm Việt Hương

Giới thiệu đến quý thầy, cô giáo và các em Giáo án Hình học 12 cơ bản cô Phạm Việt Hương. Mời mọi người đón xem.

93 47 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 12

Môn: Toán 12

Thông tin:

88 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 1
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
12A3
Chương I: KHỐI ĐA DIỆN
Tiết dạy: 01 Bài 1: KHÁI NIỆM VỀ KHỐI ĐA DIỆN
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm khối lăng trụ, khối chóp, khối chóp cụt, khối đa diện.
Biết khái niệm hai hình đa diện bằng nhau.
Kĩ năng:
Vẽ thành thạo các khối đa diện đơn giản.
Biết cách phân chia và lắp ghép các khối đa diện đơn giản.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hình học không gian ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Cho hình hộp ABCD.ABCD. Hãy xác định các mặt, các đỉnh, các cạnh của hình hộp?
Đ. 6 mặt, 8 đỉnh, 12 cạnh.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Nhắc lại định nghĩa hình
lăng trụ, hình chóp, hình chóp
cụt?
H2. Nêu một số hình ảnh thực
tế về hình lăng trụ, hình chóp,
hình chóp cụt?
Đ1. Các nhóm thảo luận và
phát biểu.
Đ2.
– HLT: hộp bánh, …
– HC: kim tự tháp, …
– HCC: quả cân, …
I. KHỐI LĂNG TRỤ VÀ
KHỐI CHÓP
Khối lăng trụ (khối chóp,
khối chóp cụt) là phần không
gian được giới hạn bởi một
hình lăng trụ (hình chóp, hình
chóp cụt) kể cả hình lăng trụ
(hình chóp, hình chóp cụt) ấy.
Tên gọi và các thành phần:
đỉnh, cạnh, mặt bên, … được
đặt tương ứng với hình tương
ứng.
Điểm trong – Điểm ngoài
GV cho HS quan sát một số
Các nhóm thảo luận và trình
II. KHÁI NIỆM VỀ HÌNH
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 2
hình cụ thể và hướng dẫn rút ra
nhận xét.
GV cho HS nêu định nghĩa
hình đa diện.
GV giới thiệu một số hình và
cho HS nhận xét hình nào là
hình đa diện, không là hình đa
diện.
GV hướng dẫn HS nhận xét.
H1. Nêu một số vật thể thực tế
là những khối đa diện?
bày.
HS quan sát và trả lời.
– Hình đa diện:
– Không là hình đa diện:
Đ1. Viên kim cương, …
ĐA DIỆN VÀ KHỐI ĐA
DIỆN
1. Khái niệm về hình đa diện
Hình đa diện là hình được tạo
bởi một số hữu hạn các đa giác
thoả mãn hai tính chất:
a) Hai đa giác phân biệt chỉ có
thể: hoặc không có điểm
chung, hoặc chỉ có một đỉnh
chung, hoặc chỉ có một cạnh
chung.
b) Mỗi cạnh của đa giác nào
cũng là cạnh chung của đúng
hai đa giác.
2. Khái niệm về khối đa diện
Khối đa diện là phần không
gian được giới hạn bởi một
hình đa diện, kể cả hình đa
diện đó.
Tên gọi và các thành phần:
đỉnh, cạnh, mặt bên, … được
đặt tương ứng với hình đa diện
tương ứng.
Điểm trong – Điểm ngoài
Miền trong – Miền ngoài
Mỗi hình đa diện chia các
điểm còn lại của không gian
thành hai miền không giao
nhau là miền trong và miền
ngoài của hình đa diện, trong
đó chỉ có miền ngoài là chứa
hoàn toàn một đường thẳng
nào đấy.
Hoạt động 3: Củng cố
Nhấn mạnh:
– Khái niệm hình đa diện, khối
đa diện.
Câu hỏi: Cho VD về khối đa
diện, không là khối đa diện?
4. BÀI TẬP VỀ NHÀ:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 3
Bài 1, 2 SGK.
Đọc tiếp bài "Khái niệm về khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 02 Bài 1: KHÁI NIỆM VỀ KHỐI ĐA DIỆN (tt)
I. MỤC TIÊU:
Kiến thức:
Biết khái niệm khối lăng trụ, khối chóp, khối chóp cụt, khối đa diện.
Biết khái niệm hai hình đa diện bằng nhau.
Kĩ năng:
Vẽ thành thạo các khối đa diện đơn giản.
Vận dụng thành thạo một số phép biến hình.
Biết cách phân chia và lắp ghép các khối đa diện đơn giản.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về phép biến hình ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu khái niệm hình đa diện?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Nhắc lại định nghĩa phép
biến hình và phép dời hình
trong mặt phẳng?
H2. Nhắc lại định nghĩa các
phép tịnh tiến, phép đối xứng
tâm, đối xứng trục trong mặt
phẳng?
Đ1. HS nhắc lại.
Đ2. HS nhắc lại.
III. HAI ĐA DIỆN BẰNG
NHAU
1. Phép dời hình trong không
gian
Trong không gian, quy tắc
đặt tương ứng mỗi điểm M với
điểm M
xác định duy nhất đgl
một phép biến hình trong
không gian.
Phép biến hình trong không
gian đgl phép dời hình nếu nó
bảo toàn khoảng cách giữa hai
điểm tuỳ ý.
a) Phép tịnh tiến theo vectơ
v
v
T M M MM v: ' '
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 4
b) Phép đối xứng qua mặt
phẳng (P)
P
D M M
()
:'
– Nếu M
(P) thì M
M,
– Nếu M
(P) thì MM
nhận
(P) làm mp trung trực.
c) Phép đối xứng tâm O
O
D M M:'
– Nếu M
O thì M
O,
– Nếu M
O thì MM
nhận O
làm trung điểm.
d) Phép đối xứng qua đường
thẳng
D M M:'
– Nếu M
thì M
M,
– Nếu M
thì MM
nhận
làm đường trung trực.
Nhận xét:
Thực hiện liên tiếp các phép
dời hình sẽ được một phép dời
hình.
Nếu phép dời hình biến (H)
thành (H
) thì nó biến đỉnh,
mặt, cạnh của (H) thành đỉnh,
mặt, cạnh tương ứng của (H
).
Hoạt động 2: Áp dụng tìm ảnh của một hình qua một phép dời hình
Hướng dẫn HS thực hiện.
Các nhóm thảo luận và trình
bày.
VD1: Cho hình lập phương
ABCD.ABCD có tâm O.
Tìm ảnh của tứ giác ABCD
qua:
a) Phép tịnh tiến theo
v AA'
.
b) Phép đối xứng qua mặt
phẳng (BBDD).
c) Phép đối xứng tâm O.
d) Phép đối xứng qua đường
thẳng AC.
Hoạt động 3: Tìm hiểu khái niệm hai hình bằng nhau
H1. Tìm phép dời hình biến
hình này thành hình kia?
Đ1. Xét phép đối xứng tâm O.
2. Hai hình bằng nhau
Hai hình đgl bằng nhau nếu
có một phép dời hình biến hình
này thành hình kia.
Hai đa diện đgl bằng nhau
nếu có một phép dời hình biến
đa diện này thành đa diện kia.
VD2: Cho hình hộp
ABCD.ABCD. Chứng minh
hai lăng trụ ABD.ABD và
BCD.BCD bằng nhau.
Hoạt động 4: Tìm hiểu sự phân chia và lắp ghép các khối đa diện
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 5
Cho HS quan sát 3 hình (H),
(H
1
), (H
2
) và hướng dẫn HS
nhận xét.
Các nhóm thảo luận và trình
bày.
– (H
1
), (H
2
) không có chung
điểm trong nào.
– (H
1
), (H
2
) ghép lại thành (H).
IV. PHÂN CHIA VÀ LẮP
GHÉP CÁC KHỐI ĐA DIỆN
Nếu khối đa diện (H) là hợp
của hai khối đa diện (H
1
) và
(H
2
) sao cho (H
1
) và (H
2
)
không có chung điểm trong
nào thì ta nói có thể chia được
khối đa diện (H) thành hai khối
đa diện (H
1
) và (H
2
), hay có
thể lắp ghép hai khối đa diện
(H
1
) và (H
2
) với nhau để được
khối đa diện (H).
GV hướng dẫn HS chia các
khối đa diện.
Các nhóm thảo luận và trình
bày.
VD1: Cho khối lập phương
ABCD.ABCD.
a) Chia khối lập phương thành
2 khối lăng trụ.
b) Chia khối lăng trụ
ABD.ABD thành 3 khối
tứ diện.
Nhận xét: Một khối đa diện
bất kì luôn có thể phân chia
được thành những khối tứ diện.
Cho các nhóm thực hiện.
Các nhóm thảo luận và trình
bày.
Chia lăng trụ thành 5 tứ diện
AA’BD, B’A’BC’, CBC’D,
D’C’DA’ và DA’BC’.
VD2: Chia một khối lập
phương thành 5 khối tứ diện.
D'
C'
C
B
A'
B'
A
D
H1. Nêu cách chia?
Đ1.
+ Chia khối lập phương thành
2 khối lăng trụ ABD.ABD và
VD3: Chia một khối lập
phương thành 6 khối tứ diện
bằng nhau.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 6
H2. Nêu cách chứng minh các
khối tứ diện bằng nhau?
BCD.BCD.
+ Chia lăng trụ ABD.A’B’D’
thành 3 tứ diện BA’B’D’,
AA’BD’ và ADBD’.
+ Chứng minh 3 khối tứ diện
bằng nhau:
A BD
D BA B D AA BD
( ' ')
: ' ' ' ' '
ABD
D AA BD ADBD
( ')
: ' ' '
+ Làm tương tự đối với lăng
trụ BCD.B’C’D’.
Chia được hình lập phương
thành 6 tứ diện bằng nhau.
D'
C'
C
B
A'
B'
A
D
Hoạt động 6: Củng cố
Nhấn mạnh:
– Cách phân chia và lắp ghép
các khối đa diện.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Khái niệm về khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 03 Bài 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU
I. MỤC TIÊU:
Kiến thức:
Nắm được định nghĩa khối đa diện lồi.
Hiểu được thế nào là khối đa diện đều.
Nhận biết được các loại khối đa diện đều.
Kĩ năng:
Biết phân biệt khối đa diện lồi và không lồi.
Biết được một số khối đa diện đều và chứng minh được một khối đa diện là đa diện đều.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu khái niệm khối đa diện?
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 7
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV cho HS quan sát một số
khối đa diện, hướng dẫn HS
nhận xét, từ đó giới thiệu khái
niệm khối đa diện lồi.
H1. Cho VD về khối đa diện
lồi, không lồi?
Khối đa diện lồi
Khối đa diện không lồi
Đ1. Khối lăng trụ, khối chóp,
…
I. KHỐI ĐA DIỆN LỒI
Khối đa diện (H) đgl khối đa
diện lồi nếu đoạn thẳng nối hai
điểm bất kì của (H). Khi đó đa
diện xác định (H) đgl đa diện
lồi.
Nhận xét: Một khối đa diện là
khối đa diện lồi khi và chỉ khi
miền trong của nó luôn nằm về
một phía đối với mỗi mặt
phẳng chứa một mặt của nó.
Cho HS quan sát khối tứ diện
đều, khối lập phương. Từ đó
giới thiệu khái niệm khối đa
diện đều.
GV giới thiệu 5 loại khối đa
diện đều.
H1. Đếm số đỉnh, số cạnh, số
mặt của các khối đa diện đều?
Đ1. Các nhóm đếm và điền vào
bảng.
II. KHỐI ĐA DIỆN ĐỀU
Khối đa diện đều là khối đa
diện lồi có các tính chất sau:
a) Mỗi mặt của nó là một đa
giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh
chung của đúng q mặt.
Khối đa diện đều như vậy đgl
khối đa diện đều loại (p; q).
Định lí: Chỉ có 5 loại khối đa
diện. Đó là các loại [3; 3], [4;
3], [3; 4], [5; 3], [3; 5].
Bảng tóm tắt của 5 loại khối
đa diện đều
H1. Nêu các bước chứng
minh?
Đ1.
– Chứng minh các mặt đều là
những đa giác đều.
– Xác định loại khối đa diện
VD1: Chứng minh rằng:
a) Trung điểm các cạnh của
một tứ diện đều là các đỉnh của
một hình bát diện đều.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 8
đều.
b) Tâm các mặt của một hình
lập phương là các đỉnh của một
hình bát diện đều.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Nhận dạng khối đa diện đều.
– Cách chứng minh khối đa
diện đều.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4, 5 SGK.
Đọc tiếp bài "Khái niệm về khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 04 Bài 2: BÀI TẬP KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU
I. MỤC TIÊU:
Kiến thức:
Khắc sâu lại định nghĩa và các tính chất của khối đa diện lồi, khối đa diện đều.
Nhận biết được các loại khối đa diện lồi, khối đa diện đều.
Kĩ năng:
Biết chứng minh khối đa diện đều và giải các bài tập về khối đa diện lồi và khối đa diện đều.
Rèn luyện kỹ năng vẽ hình không gian.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện lồi, khối đa diện đều.
III. HOẠT ĐỘNG DẠY HỌC:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 9
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Tính độ dài cạnh của (H)?
H2. Tính diện tích toàn phần
của (H) và (H) ?
H3. Nhận xét các tứ giác
ABFD và ACFE?
H4. Chứng minh IB = IC = ID
= IE ?
Đ1.
b =
2
2a
Đ2.
S = 6a
2
S =
3
8
3
8
2
2
a
a
23
S
S '
Đ3. Các tứ giác đó là nhứng
hình thoi.
AF BD, AF CE
Đ4. Vì AI (BCDE) và AB =
AC = AD = AE.
BCDE là hình vuông.
1. Cho hình lập phương (H)
cạnh bằng a. Gọi (H) là hình
bát diện đều có các đỉnh là tâm
các mặt của (H). Tính tỉ số diện
tích toàn phần của (H) và (H).
2. Cho hình tứ diện đều
ABCDEF. Chứng minh rằng:
a) Các đoạn thẳng AF, BD, CE
đôi một vuông góc với nhau và
cắt nhau tại trung điểm mỗi
đường.
b) ABFD, AEFC và BCDE là
những hình vuông.
H1. Ta cần chứng minh điều gì
?
Đ1. G
1
G
2
= G
2
G
3
=
G
3
G
4
=
G
4
G
1
= G
4
G
2
= G
1
G
3
=
3
a
3. Chứng minh rằng tâm các
mặt của hình tứ diện đều là các
đỉnh của một hình tứ diện đều.
Nhấn mạnh:
– Nhận dạng khối đa diện đều.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 10
– Cách chứng minh khối đa
diện đều.
4. BÀI TẬP VỀ NHÀ:
Đọc trước bài "Khái niệm về thể tích của khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 05 Bài 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm thể tích của khối đa diện.
Nắm được các công thức tính thể tích của một số khối đa diện cụ thể.
Kĩ năng:
Tính được thể tích của khối lăng trụ, khối chóp.
Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Thế nào là khối đa diện lồi, khối đa diện đều? Nêu một số công thức tính thể tích đã biết?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu khái niệm thể tích khối đa diện
GV nêu một số cách tính thể
tích vật thể và nhu cầu cần tìm
ra cách tính thể tích những
khối đa diện phức tạp.
GV giới thiệu khái niệm thể
tích khối đa diện.
HS tham gia thảo luận.
Nêu một công thức tính thể
tích đã biết.
I. KHÁI NIỆM VỀ THỂ
TÍCH KHỐI ĐA DIỆN
Thể tích của khối đa diện (H)
là một số dương duy nhất V
(H)
thoả mãn các tính chất sau:
a) Nếu (H) là khối lập phương
có cạnh bằng 1 thì V
(H)
= 1.
b) Nếu hai khối đa diện (H
1
),
(H
2
) bằng nhau thì V
(H1)
=V(
H2
).
c) Nếu khối đa diện (H) được
phan chia thành hai khối đa
diện (H
1
), (H
2
) thì
V
(H)
= V
(H1)
+ V
(H2)
.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 11
V
(H)
cũng đgl thể tích của
hình đa diện giới hạn khối đa
diện (H).
Khối lập phương có cạnh
bằng 1 đgl khối lập phương
đơn vị.
GV hướng dẫn HS tìm cách
tính thể tích của khối hộp chữ
nhât.
VD1: Tính thể tích của khối
hộp chữ nhật có 3 kích thước là
những số nguyên dương.
H1. Có thể chia (H
1
) thành bao
nhiêu khối (H
0
) ?
H2. Có thể chia (H
2
) thành bao
nhiêu khối (H
1
) ?
H3. Có thể chia (H) thành bao
nhiêu khối (H
2
) ?
GV nêu định lí.
Đ1. 5 V
(H1)
= 5V
(H0)
= 5
Đ2. 4 V
(H2)
= 4V
(H1)
= 4.5
= 20
Đ3. 3 V
(H)
= 3V
(H2)
= 3.20
= 60
Định lí: Thể tích của một khối
hộp chữ nhật bằng tích ba kích
thước của nó.
V = abc
Cho HS thực hiện.
Các nhóm tính và điền vào
bảng.
VD2: Gọi a, b, c, V lần lượt là
ba kích thước và thể tích của
khối hộp chữ nhật. Tính và
điền vào ô trống:
a
b
c
V
1
2
3
4
3
24
1
2
2
3
1
1
3
1
Nhấn mạnh:
– Khái niệm thể tích khối đa
diện.
– Công thức tính thể tích khối
hộp chữ nhật.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 12
4. BÀI TẬP VỀ NHÀ:
Đọc tiếp bài "Khái niệm về thể tích của khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 06 Bài 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm thể tích của khối đa diện.
Nắm được các công thức tính thể tích của một số khối đa diện cụ thể.
Kĩ năng:
Tính được thể tích của khối lăng trụ, khối chóp.
Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hình lăng trụ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Thế nào là thể tích khối đa diện?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu công thức tính thể tích khối lăng trụ
H1. Khối hộp chữ nhật có phải
là khối lăng trụ không?
GV giới thiệu công thức tính
thể tích khối lăng trụ.
Đ1. Là khối lăng trụ đứng.
II. THỂ TÍCH KHỐI LĂNG
TRỤ
Định lí: Thể tích khối lăng trụ
bằng diện tích đáy B nhân với
chiều cao h.
V = Bh
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 13
Cho HS thực hiện.
Các nhóm tính và điền kết
quả vào bảng.
VD1: Gọi S, h, V lần lượt là
thể diện tích đáy, chiều cao và
thể tích khối lăng trụ. Tính và
điền vào ô trống:
S
h
V
8
7
8
4
8
4
3
2
12
H1. Nhắc lại khái niệm lăng
trụ đứng, lăng trụ đều?
H2. Xác định góc giữa AC và
đáy?
H3. Tính chiều cao của lăng
trụ?
H4. Xác định góc giữa BC và
mp(AACC) ?
H5. Tính AC, CC ?
Đ1. HS nhắc lại.
Đ2.
0
60AC A''
Đ3. h = CC = AC.tan60
0
=
6a
V = S
ABCD
.CC =
3
6a
Đ4.
0
30BCA
Đ5. AC = AB.cot30
0
= 3b
CC =
22
22AC AC b' 
V =
3
6b
.
BT1: Cho lăng trụ đều
ABCD.ABCD cạnh đáy
bằng a. Góc giữa đường chéo
AC và đáy bằng 60
0
. Tính thể
tích của hình lăng trụ.
BT2: Hình lăng trụ đứng
ABC.ABC có đáy ABC là
một tam giác vuông tại A, AC
= b,
0
60C
. Đường chéo BC
của mặt bên BBCC tạo với
mp(AACC) một góc 30
0
.
Tính thể tích của lăng trụ.
A
B
C
A’
B’
C’
0
30
0
60
Nhấn mạnh:
– Công thức thể tích khối lăng
trụ.
– Tính chất của hình lăng trụ
đứng, lăng trụ đều.
4. BÀI TẬP VỀ NHÀ:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 14
Đọc tiếp bài "Khái niệm về thể tích của khối đa diện".
Bài tập thêm.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 07 Bài 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm thể tích của khối đa diện.
Nắm được các công thức tính thể tích của một số khối đa diện cụ thể.
Kĩ năng:
Tính được thể tích của khối lăng trụ, khối chóp.
Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hình chóp.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Nhắc lại định nghĩa và tính chất của hình chóp đều?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu công thức tính thể tích khối chóp
GV giới thiệu công thức tính
thể tích khối chóp.
H1. Nhắc lại khái niệm đường
cao của hình chóp?
Đ1. Đoạn vuông góc hạ từ đỉnh
đến đáy của hình chóp.
S
A
B
C
D
H
III. THỂ TÍCH KHỐI
CHÓP
Định lí: Thể tích khối chóp
bằng
1
3
diện tích đáy B nhân
với chiều cao h.
V =
1
3
Bh
Hoạt động 2: Áp dụng tính thể tích khối chóp
Cho HS thực hiện.
Các nhóm tính và điền kết
quả vào bảng.
VD1: Gọi S, h, V lần lượt là
thể diện tích đáy, chiều cao và
thể tích khối chóp. Tính và
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 15
điền vào ô trống:
S
h
V
8
7
8
4
8
4
3
2
12
H1. Tính chiều cao của hình
chóp ?
H2. Tính thể tích khối chóp
C.ABC theo V ?
H3. Nhận xét thể tích của hai
khối chóp C.ABFE và
C.ABBA ?
H4. So sánh diện tích của hai
tam giác CFE và CBA ?
H5. Tính thể tích khối (H) ?
Đ1.
a) h = SO =
22
SA AO
=
2
2
3
a
b
b)
2
2 2 2 2
3
6
3
a
h OM
a
h SA OA b
.tan tan


2
4
b
a
.tan
tan
2
4
b
h
.tan
tan
Đ2.
V
C.A
B
C
=
1
3
V
V
ABB
A
=
2
3
V
Đ3.
V
C.ABFE
=
1
2
V
C.ABB
A
=
1
3
V
Đ4. S
C
FE
= 4S
C
B
A
V
C.E
F
C
=
4
3
V
Đ5. V
(H)
=
2
3
V
1
2
H
C E F C
V
V
()
. ' ' '
BT1: Cho hình chóp tam giác
đều S.ABC. Tính thể tích khối
chóp nếu biết:
a) AB = a và SA = b.
b) SA = b và góc giữa mặt bên
và đáy bằng .
S
A
B
C
O
M
BT2: Cho hình lăng trụ tam
giác ABC.ABC. Gọi E, F lần
lượt là trung điểm của AA,
BB. Đường thẳng CE cắt CA
tại E. Đường thẳng CF cắt
CB tại F. Gọi V là thể tích
khối lăng trụ ABC.ABC.
a) Tính thể tích khối chóp
C.ABFE theo V.
b) Gọi khối đa diện (H) là phần
còn lại của khối lăng trụ
ABC.ABC sau khi cắt bỏ đi
khối chóp C.ABFE. Tính tỉ số
thể tích của (H) và của khối
chóp C.CEF.
Nhấn mạnh:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 16
– Công thức thể tích khối chóp.
– Tính chất của hình chóp đều.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 08 Bài 3: BÀI TẬP KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm thể tích của khối đa diện.
Các công thức tính thể tích của một số khối đa diện cụ thể.
Kĩ năng:
Tính được thể tích của khối lăng trụ, khối chóp.
Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tính thể tích khối lăng trụ
H1. Xác định góc giữa AA và
đáy ?
H2. Tính chiều cao AO ?
H3. Chứng minh BC (AAO)
Đ1. A cách đều A, B, C
AO (ABC)
0
60A AO'
Đ2. AO =
3
3
a
AO = a
V = S
ABC
.AO =
3
3
4
a
Đ3. BC AO, BC AO
BC (AAO) BC AA
1. Cho lăng trụ tam giác ABC.
ABC có đáy ABC là một tam
giác đều cạnh a và điểm A
cách đều các điểm A, B, C.
Cạnh bên AA tạo với mặt
phẳng đáy một góc 60
0
.
a) Tính thể tích khối lăng trụ.
b) Chứng minh BCCB là một
hình chữ nhật.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 17
BC BB
BCCB là hình chữ nhật.
A’
B’C’
A
BC
O
H
H1. Xác định đường cao của tứ
diện ?
H2. Viết công thức tính thể
tích khối tứ diện CDFE ?
H3. Tính CE, CF, FE, DF ?
Đ1. DF (CFE)
Đ2. V =
1
3
CFE
S DF.
Đ3.
CE =
2
22
AD a
CF =
6
3
a
; FE =
6
6
a
DF =
3
3
a
V =
3
36
a
2. Cho tam giác ABC vuông
cân ở A và AB = a. Trên
đường thẳng qua C và vuông
góc với mp(ABC) lấy điểm D
sao cho CD = a. Mặt phẳng qua
C vuông góc với BD cắt BD tại
F và cắt AD tại E. Tính thể tích
khối tứ diện CDFE theo a.
A
B
C
D
F
E
Hướng dẫn HS xác định đỉnh
và đáy hình chóp để tính thể
tích.
H1. Tính diện tích các tam giác
SBC và SBC ?
H2. Tính tỉ số chiều cao của
hai khối chóp ?
H3. Tính thể tích của hai khối
chóp ?
Đỉnh A, đáy SBC,
Đỉnh A, đáy SBC.
Đ1. S
SBC
=
1
2
SB SC BSC. .sin
S
SB
C
=
1
2
SB SC B SC'. '.sin ' '
Đ2.
h SA
h SA
''
Đ3.
V
SABC
=
1
3
SBC
Sh.
V
SB'C
=
1
3
SB C
Sh
''
.'
3. Cho hình chóp S.ABC. Trên
các đoạn thẳng SA, SB, SC lần
lượt lấy 3 điểm A, B, C khác
S. Chứng minh:
S A B C
S ABC
V
SA SB SC
V SA SB SC
. ' ' '
.
' ' '
..
A
A’
C
B
B’
C’
H
H’
S
h
h'
Nhấn mạnh:
– Cách vận dụng các công thức
tính thể tích các khối đa diện.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 18
4. BÀI TẬP VỀ NHÀ:
Bài tập ôn chương 1 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 09 + 10 Bài dạy: ÔN TẬP CHƯƠNG 1
I. MỤC TIÊU:
Kiến thức: Củng cố:
Nắm được khái niệm hình đa diện, khối đa diện.
Hai khối đa diện bằng nhau.
Phân chia và lắp ghép khối đa diện.
Đa điện đều và các loại đa diện đều.
Thể tích các khối đa diện.
Kĩ năng:
Nhận biết được các đa diện và khối đa diện.
Biết cách phân chia và lắp ghép các khối đa diện để giải các bài toán thể tích.
Vận dụng các công thức tính thể tích khối đa diện vào việc giải toán.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức chương 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tính thể tích khối đa diện
H1. Xác định góc giữa mặt bên
và đáy?
H2. Tính chu vi và diện tích
của ABC ?
H3. Tính chiều cao của hình
Đ1.
0
60SEH SJH SFH
HE = HJ = HF
H là tâm đường tròn nội tiếp
ABC.
Đ2. p = 9a, S =
2
66a
HE = r =
26
3
Sa
p
1. Cho hình chóp tam giác
S.ABC có AB = 5a, BC = 6a,
CA = 7a. Các mặt bên SAB,
SBC, SCA tạo với đáy một góc
60
0
. Tính thể tích khối chóp đó.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 19
chóp ?
Đ3.
h = SH =
0
60 2 2HE a.tan
V =
3
83a
.
A
B
C
S
H
F
E
J
0
60
H1. Xác định tỉ số thể tích của
hai khối chóp ?
H2. Tính SD, SA ?
H3. Tính thể tích khối chóp
S.ABC ?
Đ1.
S DBC
S ABC
V
SD
V SA
.
.
Đ2. SA =
3
4
a
, SD =
53
12
a
5
8
SD
SA
Đ3. V
S.ABC
=
3
3
12
a
V
S.DBC
=
3
53
96
a
.
2. Cho hình chóp tam giác đều
S.ABC có cạnh AB = a. Các
cạnh bên SA, SB, SC tạo với
đáy một góc 60
0
. Gọi D là giao
điểm của SA với mặt phẳng
qua BC và vuông góc với SA.
a) Tính tỉ số thể tích của hai
khối chóp S.DBC và S.ABC.
c) Tính thể tích của khối chóp
S.DBC.
A
B
C
S
E
H
D
0
60
Hướng dẫn HS tính thể tích
khối chóp tam giác bằng nhiều
cách khác nhau.
H1. Xác định đường cao và
đáy của khối chóp bằng các
cách khác nhau?
H2. Xác định công thức tính
thể tích khối chóp theo 2 cách
?
H3. Tính diện tích ABC ?
Đ1.
– Đáy OBC, đường cao AO.
– Đáy ABC, đường cao OH.
Đ2.
V
1
3
OBC
S OA.
1
3
ABC
S OH.
Đ3. S
ABC
=
1
2
AE BC.
=
2 2 2 2 2 2
1
2
a b b c c a
OH =
3
ABC
V
S
3. Cho hình chóp tam giác
O.ABC có ba cạnh OA, OB,
OC đôi một vuông góc với
nhau và OA = a, OB = b, OC =
c. Tính độ dài đường cao OH
của hình chóp.
O
B
C
A
H
E
a
b
c
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 20
=
2 2 2 2 2 2
abc
a b b c c a
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách vận dụng các công thức
tính thể tích các khối đa diện.
– Cách vận dụng thể tích để
giải toán.
4. BÀI TẬP VỀ NHÀ:
Chuẩn bị kiểm tra 1 tiết chương 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 11 Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG 1
I. MỤC TIÊU:
Kiến thức:
Ôn tập toàn bộ kiến thức trong chương I.
Kĩ năng:
Nhận biết được các hình đa diện và khối đa diện.
Tính được thể tích của các khối đa diện đơn giản.
Vận dụng các công thức tính thể tích khối đa diện vào việc giải toán.
Thái độ:
Rèn luyện tính cẩn thận, chính xác.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: Ôn tập toàn bộ kiến thức chương 1.
III. MA TRẬN ĐỀ:
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Khái niệm khối đa
diện
1
0,5
0,5
Khối đa diện lồi và
khối đa diện đều
1
0,5
0,5
Thể tích khối đa diện
2
0,5
4
0,5
1
3,0
1
3,0
9,0
Tổng
2,0
2,0
3,0
3,0
10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 21
Câu 1: Các mặt của khối tứ diện đều là:
A. Hình tam giác đều B. Hình vuông C. Hình ngũ giác đều D. Hình thoi.
Câu 2: Trong một hình đa diện, mỗi đỉnh là đỉnh chung của ít nhất:
A. 2 mặt B. 3 mặt C. 4 mặt D. 5 mặt
Câu 3: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 5a là:
A. 125a
3
B.
3
125
3
a
C.
3
125
4
a
D.
3
125 3
4
a
Câu 4: Thể tích của khối lăng trụ bằng
3
83a
, chiều cao bằng 2a. Diện tích đáy của khối lăng trụ đó bằng:
A.
43a
B.
2
43a
C.
3
43a
D.
43
Câu 5: Thể tích của khối chóp tam giác S.ABC với đáy ABC là tam giác đều cạnh bằng
3a
, SA vuông góc với
đáy và SA =
3a
là:
A.
3
9a
B.
3
27a
C.
3
9
4
a
D.
3
93
4
a
Câu 6: Cho khối lập phương ABCD.ABCD cạnh bằng a. Thể tích của khối tứ diện AABD bằng
A.
3
4
a
B.
3
2
a
C.
3
3
a
D.
3
6
a
Câu 7: Cho khối lập phương ABCD.ABCD. Tỉ số thể tích của khối AABC và khối AABD bằng:
A. 1 B. 2 C.
1
2
D.
1
6
Câu 8: Cho khối lập phương ABCD.ABCD. Tỉ số thể tích của khối AABC và khối lập phương
ABCD.ABCD bằng:
A. 1 B. 2 C.
1
2
D.
1
6
II. Phần tự luận: (6 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và SA
vuông góc với đáy.
a) Tính thể tích khối chóp S.ABC.
b) Tính khoảng cách từ A đến mặt phẳng (SBC).
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
A
B
D
B
C
D
A
D
B. Phần tự luận: Mỗi câu 3 điểm
a) Hình vẽ (0,5 điểm)
V =
1
.
3
ABC
S SA
(0,5 điểm)
S
ABC
=
2
2
a
(1,0 điểm)
V =
3
6
a
(1,0 điểm)
b) Vẽ AH (SBC)
V =
1
.
3
SBC
S AH
=
3
6
a
(1,0 điểm)
S
SBC
=
2
2
2
a
(1,0 điểm)
S
A
B
C
D
H
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 22
AH =
32
2
SBC
V
a
S
(1,0 điểm)
VI. KẾT QUẢ KIỂM TRA:
Lớp
Sĩ số
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
12S1
53
12S2
54
12S3
54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Chương II: MẶT NÓN, MẶT TRỤ, MẶT CẦU
Tiết dạy: 12 Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm chung về mặt tròn xoay.
Hiểu được khái niệm mặt nón tròn xoay, phân biệt được các khái niệm: mặt nón tròn xoay,
hình nón tròn xoay, khối nón tròn xoay. Biết công thức tính diện tích xung quanh hình nón
tròn xoay, thể tích khối nón tròn xoay.
Nắm được khái niệm mặt trụ tròn xoay, phân biệt được các khái niệm: mặt trụ tròn xoay,
hình trụ tròn xoay, khối trụ tròn xoay. Biết công thức tính diện tích xung quanh hình trụ tròn
xoay, thể tích khối trụ tròn xoay.
Kĩ năng:
Vẽ thành thạo các mặt trụ và mặt nón.
Tính được diện tích và thể tích của hình trụ, hình nón.
Phân chia mặt trụ và mặt nón bằng mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hình học không gian.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại những điều đã biết về hình nón, hình trụ?
Đ.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 23
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Nêu tên một số đồ vật mà
mặt ngoài có hình dạng là các
mặt tròn xoay?
GV dùng hình vẽ minh hoạ
cho sự tạo thành mặt tròn xoay
Đ1. Các nhóm thảo luận và
trình bày.
Lọ hoa, chiếc nón, cái ly, …
I. SỰ TẠO THÀNH MẶT
TRÒN XOAY
Trong KG, cho mp (P) chứa
đường thẳng
và một đường
(C). Khi quay (P) quanh
một
góc 360
0
thì mỗi điểm M trên
(C) vạch ra một đường tròn có
tâm O thuộc
và nằm trên mp
vuông góc với
. Khi đó (C) sẽ
tạo nên một hình đgl mặt tròn
xoay.
(C) đgl đường sinh của mặt
tròn xoay đó.
đgl trục của
mặt tròn xoay.
GV dùng hình vẽ minh hoạ
và hướng dẫn cho HS nhận biết
được cách tạo thành mặt nón
tròn xoay.
H1. Mô tả đường sinh, trục,
đỉnh của cái nón?
Đ1. Các nhóm thảo luận và
trình bày.
1. Mặt nón tròn xoay
Trong mp (P) có hai đường
thẳng d và
cắt nhau tại điểm
O và tạo thành góc nhọn
. Khi
quay (P) xung quanh
thì d
sinh ra một mặt tròn xoay đgl
mặt nón tròn xoay đỉnh O.
gọi là trục, d gọi là đường
sinh, góc 2
gọi là góc ở đỉnh
của mặt nón đó.
GV dùng hình vẽ minh hoạ
và hướng dẫn cho HS nhận biết
được cách tạo thành mặt trụ
tròn xoay.
H1. Mô tả đường sinh, trục,
đỉnh của hộp sữa (lon)?
Đ1. Các nhóm thảo luận và
trình bày.
2. Mặt trụ tròn xoay
Trong mp (P) cho hai đường
thẳng
và l song song nhau,
cách nhau một khoảng bằng r.
Khi quay (P) xung quanh
thì
l sinh ra một mặt tròn xoay đgl
mặt trụ tròn xoay.
gọi là
trục, l gọi là đường sinh, r là
bán kính của mặt trụ đó.
Nhấn mạnh:
– Sự tạo thành của mặt tròn
xoay.
– Các khái niệm đường sinh,
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 24
trục của mặt tròn xoay.
Cau hỏi: Nêu tên một số đồ
vật có hình dạng là mặt nón,
mặt trụ.
4. BÀI TẬP VỀ NHÀ:
Bài 1 SGK.
Làm một số mô hình biểu diễn mặt trụ tròn xoay, mặt nón tròn xoay.
Đọc tiếp bài "Khái niệm mặt tròn xoay".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 13 Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm chung về mặt tròn xoay.
Hiểu được khái niệm mặt nón tròn xoay, phân biệt được các khái niệm: mặt nón tròn xoay, hình nón
tròn xoay, khối nón tròn xoay. Biết công thức tính diện tích xung quanh hình nón tròn xoay, thể tích
khối nón tròn xoay.
Nắm được khái niệm mặt trụ tròn xoay, phân biệt được các khái niệm: mặt trụ tròn xoay, hình trụ
tròn xoay, khối trụ tròn xoay. Biết công thức tính diện tích xung quanh hình trụ tròn xoay, thể tích
khối trụ tròn xoay.
Kĩ năng:
Vẽ thành thạo các mặt trụ và mặt nón.
Tính được diện tích và thể tích của hình trụ, hình nón.
Phân chia mặt trụ và mặt nón bằng mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa mặt nón tròn xoay?
Đ.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 25
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV dùng hình vẽ để minh hoạ
và hướng dẫn HS cách tạo ra hình
nón tròn xoay.
H1. Xác định khoảng cách từ đỉnh
đến đáy?
GV giới thiệu khái niệm khối
nón.
H2. Phân biệt hình nón và khối
nón?
Đ1. h = OI.
Đ2. Các nhóm thảo luận và trả lời.
I. NẶT NÓN TRÒN XOAY
1. Mặt nón tròn xoay
2. Hình nón tròn xoay
Cho
OIM vuông tại I. Khi quay
nó xung quanh cạnh góc vuông OI
thì đường gấp khúc OMI tạo
thành một hình đgl hình nón tròn
xoay.
– Hình tròn (I, IM): mặt đáy
– O: đỉnh
– OI: đường cao
– OM: đường sinh
– Phần mặt tròn xoay sinh ra bởi
OM: mặt xung quanh.
3. Khối nón tròn xoay
Phần không gian được giới hạn
bởi một hình nón tròn xoay kể cả
hình nón đó đgl khối nón tròn
xoay.
– Điểm ngoài: điểm không thuộc
khối nón.
– Điểm trong: điểm thuộc khối
nón nhưng không thuộc hình nón.
– Đỉnh, mặt đáy, đường sinh
GV giới thiệu khái niệm hình
chóp nội tiếp hình nón, diện tích
xung quanh hình nón.
H1. Tính diện tích hình quạt?
4. Diện tích xung quanh của
hình nón
a) Một hình chóp đgl nội tiếp hình
nón nếu đáy của hình chóp là đa
giác nội tiếp đường tròn đáy của
hình nón và đỉnh của hình chóp là
đỉnh của hình nón.
Diện tích xung quanh của hình
nón là giới hạn của diện tích xung
quanh của hình chóp đều nội tiếp
hình nón đó khi số cạnh đáy tăng
lên vô hạn.
b) Diện tích xung quanh của hình
nón bằng nửa tích độ dài đường
tròn đáy với độ dài đường sinh :
xq
S rl
Diện tích toàn phần của hình nón
bằng tổng diện tích xung quanh
và diện tích đáy.
Chú ý: Nếu cắt mặt xung quanh
của hình nón theo một đường sinh
rồi trải ra trên một mp thì ta được
một hình quạt có bán kính bằng
độ dài đường sinh và một cung
tròn có độ dài bằng chu vi đường
tròn đáy của hình nón. Khi đó:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 26
Đ1.
quaït
S rl
xq quaït
S S rl

Hoạt động 3: Tìm hiểu công thức tính thể tích của khối nón
GV giới thiệu khái niệm và
công thức tính thể tích khối nón.
H1. Nhắc lại công thức tính thể
tích khối chóp?
Đ1.
V Bh
1
3
5. Thể tích khối nón
Thể tích khối nón là giới hạn của
thể tích khối chóp đều nội tiếp
khối nón đó khi số cạnh đáy tăng
lên vô hạn.
V r h
2
1
3
Hoạt động 4: Củng cố
Nhấn mạnh:
– Các khái niệm hình nón, khối
nón.
– Công thức tính diện tích xung
quanh, thể tích của khối nón.
4. BÀI TẬP VỀ NHÀ:
Bài 2, 3, 4, 6, 9 SGK.
Đọc tiếp bài "Khái niệm mặt tròn xoay".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 14 Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm chung về mặt tròn xoay.
Hiểu được khái niệm mặt nón tròn xoay, phân biệt được các khái niệm: mặt nón tròn xoay, hình nón
tròn xoay, khối nón tròn xoay. Biết công thức tính diện tích xung quanh hình nón tròn xoay, thể tích
khối nón tròn xoay.
Nắm được khái niệm mặt trụ tròn xoay, phân biệt được các khái niệm: mặt trụ tròn xoay, hình trụ
tròn xoay, khối trụ tròn xoay. Biết công thức tính diện tích xung quanh hình trụ tròn xoay, thể tích
khối trụ tròn xoay.
Kĩ năng:
Vẽ thành thạo các mặt trụ và mặt nón.
Tính được diện tích và thể tích của hình trụ, hình nón.
Phân chia mặt trụ và mặt nón bằng mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 27
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa mặt trụ tròn xoay?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV dùng hình vẽ để minh
hoạ và hướng dẫn HS cách tạo
ra hình trụ tròn xoay.
H1. Xác định khoảng cách
giữa hai đáy?
GV giới thiệu khái niệm khối
trụ.
H2. Phân biệt hình trụ và khối
trụ?
H3. Cho VD các vật thể có
dạng hình trụ, khối trụ?
Đ1. h = AB
Đ3. Hộp sữa, một số chi tiết
máy.
III. MẶT TRỤ TRÒN
XOAY
1. Mặt trụ tròn xoay
2. Hình trụ tròn xoay
Xét hình chữ nhật ABCD. Khi
quay hình đó xung quanh
đường thẳng chứa 1 cạnh,
chẳng hạn AB, thì đường gấp
khúc ADCB tạo thành 1 hình
đgl hình trụ tròn xoay.
– Hai đáy.
– Đường sinh.
– Mặt xung quanh.
– Chiều cao.
3. Khối trụ tròn xoay
Phần không gian được giới
hạn bởi một hình trụ kể cả hình
trụ đó đgl khối trụ tròn xoay.
– Điểm ngoài.
– Điểm trong.
– Mặt đáy, đường sinh, chiều
cao
GV giới thiệu khái niệm hình
lăng trụ nội tiếp hình trụ, diện
tích xung quanh hình trụ.
4. Diện tích xung quanh của
hình trụ
a) Một hình lăng trụ đgl nội
tiếp một hình trụ nếu hai đáy
của hình lăng trụ nội tiếp hai
đường tròn đáy của hình trụ.
Diện tích xung quanh của hình
trụ là giới hạn của diện tích
xung quanh của hình lăng trụ
đều nội tiếp hình trụ khi số
cạnh đáy tăng lên vô hạn.
b) Diện tích xung quanh của
hình trụ bằng tích độ dài
đường tròn đáy và độ dài
đường sinh.
xq
S rl2
Diện tích toàn phần của hình
trụ bằng tổng diện tích xung
quanh và diện tích của hai đáy.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 28
H1. Tính diện tích hình chữ
nhật?
Đ1.
hcn
S rl2
Chú ý: Nếu cắt mặt xung
quanh của hình trụ theo một
đường sinh, rồi trải ra trên một
mp thì sẽ được một hình chữ
nhật có một cạnh bằng đường
sinh l và một cạnh bằng chu vi
đường tròn đáy.
xq hcn
S S rl2

Hoạt động 3: Tìm hiểu công thức tính thể tích của khối trụ
GV giới thiệu khái niệm và
công thức tính thể tích khối trụ.
H1. Nhắc lại công thức tính thể
tích khối lăng trụ?
Đ1. V = Bh
5. Thể tích khối trụ
Thể tích khối trụ là giới hạn
của thể tích khối lăng trụ đều
nội tiếp khối trụ đó khi số cạnh
đáy tăng lên vô hạn.
V r h
2
Hoạt động 4: Củng cố
Nhấn mạnh:
– Các khái niệm hình trụ, khối
trụ.
– Công thức tính diện tích
xung quanh, thể tích của khối
trụ.
4. BÀI TẬP VỀ NHÀ:
Bài 5, 7, 8, 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 29
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 15 Bài 1: BÀI TẬP KHÁI NIỆM VỀ MẶT TRÒN XOAY
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm hình nón, khối nón, hình trụ, khối trụ.
Công thức tính diện tích xung quanh hình nón tròn xoay, thể tích khối nón tròn xoay.
Công thức tính diện tích xung quanh hình trụ tròn xoay, thể tích khối trụ tròn xoay.
Kĩ năng:
Vẽ thành thạo các mặt trụ và mặt nón.
Tính được diện tích và thể tích của hình trụ, hình nón.
Phân chia mặt trụ và mặt nón bằng mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập..
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Xác định đường sinh của
hình nón?
H2. Tính S
xq
?
H3. Tính chiều cao khối chóp?
Đ1. l = OM = 2a
Đ2. S
xq
= rl = 2a
2
Đ3. h = OI =
a 3
.
V =
a
3
3
3
1. Cho tam giác OIM vuông tại
I, góc
IOM
0
30
, IM = a. Khi
quay OIM quanh cạnh góc
vuông OI thì đường gấp khúc
OMI tạo thành một hình nón
tròn xoay.
a) Tính diện tích xung quanh
của hình nón đó.
b) Tính thể tích khối nón tròn
xoay tạo thành.
H4. Xác định khoảng cách từ
tâm của đáy đến thiết diện?
Đ4. OH SI (I là trung điểm
của AB)
2. Cho hình nón tròn xoay có
đường cao h = 20cm, bán kính
đáy r = 25 cm.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 30
OH OS OI
2 2 2
1 1 1

OI = 15 (cm)
SAB
S SO OI
1
.
2
= 25 (cm
2
)
a) Tính diện tích xung quanh
của hình nón.
b) Tính thể tích khối nón tạo
thành.
c) Một thiết diện đi qua đỉnh
của hình nón có khoảng cách
từ tâm của đáy đến mp chứa
thiết diện là 12 cm. Tính diện
tích thiết diện đó.
S
A
B
O
H
I
h
l
H5. Tính bán kính đáy, chiều
cao, đường sinh của hình nón?
H6. Tính S
xq
, S
đáy
, V của khối
nón?
H7. Xác định góc giữa
mp(SBC) và đáy hình nón?
Đ5.
a
r
2
2
,
a
h
2
2
, l = a
Đ6.
xq
a
S
2
2
2
ñaùy
a
S
2
2
;
a
V
3
2
12
Đ7.
SHO
0
60
SBC
a
S
2
2
3
3. Cắt hình nón đỉnh S bởi mp
đi qua trục ta đwọc một tam
giác vuông cân có cạnh huyền
bằng
a 2
.
a) Tính diện tích xung quanh,
diện tích đáy và thể tích của
khối nón tương ứng.
b) Cho dây cung BC của đường
tròn đáy hình nón sao cho
mp(SBC) tạo với mp chứa đáy
hình nón một góc 60
0
. Tính
diện tích tam giác SBC.
S
A
O
l
B
H
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách vẽ hình nón.
– Cách xác định các yếu tố:
đường cao, đường sinh, bán
kính đáy của hình nón.
– Các tính chất HHKG.
4. BÀI TẬP VỀ NHÀ:
Bài tập còn lại.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 31
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 16 Bài 2: MẶT CẦU
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm chung về mặt cầu.
Giao của mặt cầu và mặt phẳng.
Giao của mặt cầu và đường thẳng.
Công thức diện tích khối cầu và diện tích mặt cầu.
Kĩ năng:
Vẽ thành thạo các mặt cầu.
Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
Biết tính diện tích mặt cầu và thể tích khối cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại khái niệm hình tròn xoay? Cách tạo thành hình nón, hình trụ?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Chỉ ra một số đồ vật có
dạng mặt cầu?
H2. Nhận xét về khái niệm mặt
cầu trong KG và đường tròn
trong mp?
Đ1. Các nhóm thảo luận và
trình bày.
Quả bóng, quả địa cầu, ..
Đ2. Các nhóm thảo luận và
trình bày.
I. MẶT CẦU VÀ CÁC KHÁI
NIỆM LIÊN QUAN ĐẾN
MẶT CẦU
1. Mặt cầu
Tập hợp những điểm M trong
KG cách điểm O cố định một
khoảng không đổi bằng r (r >
0) đgl mặt cầu tâm O bán kính
r. Kí hiệu S(O; r).
S O r M OM r( ; ) 
– Dây cung
– Đường kính
Một mặt cầu được xác định
nếu biết tâm và bán kính của
nó.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 32
Hoạt động 2: Tìm hiểu khái niệm khối cầu
H1. Nhắc lại cách xét VTTĐ
giữa 1 điểm với 1 đường tròn?
Từ đó nêu cách xét VTTĐ giữa
1 điểm và 1 mặt cầu?
GV nêu khái niệm khối cầu.
Đ1. So sánh độ dài OA với bán
kính r.
2. Điểm nằm trong và nằm
ngoài mặt cầu. Khối cầu
Cho S(O; r) và điểm A bất kì.
– OA = r
A nằm trên (S)
– OA < r
A nằm trong (S)
– OA > r
A nằm ngoài (S)
Tập hợp các điểm thuộc S(O;
r) cùng với các điểm nằm trong
mặt cầu đó đgl khối cầu hoặc
hình cầu tâm O bán kính r.
Hoạt động 3: Tìm hiểu cách biểu diễn mặt cầu
GV dùng hình vẽ minh hoạ
giới thiệu khái niệm kinh
tuyến, vĩ tuyến.
H1. Nhắc lại khái niệm kinh
tuyến, vĩ tuyến trong địa lí?
GV cho HS tự vẽ hình biểu
diễn của mặt cầu, nhận xét và
rút ra cách biểu diễn mặt cầu.
H2. Tam giác AOB có đặc
điểm gì?
H3. Điểm O thuộc mp cố định
nào?
Đ1. Các nhóm thảo luận và
trình bày.
HS thực hành.
Đ2. Tam giác cân tại O.
Đ3. Mp trung trực của AB.
3. Đường kinh tuyến và vĩ
tuyến của mặt cầu
– Mặt cầu là mặt tròn xoay
được tạo bởi một nửa đường
tròn quay quanh trục chứa nửa
đường kính của đường tròn đó
– Giao tuyến của mặt cầu với
các nửa mp có bờ là trục của
mặt cầu đgl kinh tuyến của
mặt càu.
– Giao tuyến (nếu có) của mặt
cầu với các mp vuông góc với
trục đgl vĩ tuyến của mặt cầu.
– Hai giao điểm của mặt cầu
với trục đgl hai cực.
4. Biểu diễn mặt cầu
Nhận xét: Hình biểu diễn của
mặt cầu qua phép chiếu vuông
góc là một hình tròn.
– Vẽ một đường tròn có tâm và
bán kính là tâm và bán kính
của mặt cầu.
– Vẽ thêm một vài kinh tuyến,
vĩ tuyến của mặt cầu đó.
VD1: Tìm tập hợp tâm các mặt
cẩu luôn đi qua hai điểm cố
định A, B cho trước.
A
B
O
H
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 33
Nhấn mạnh:
– Khái niệm mặt cầu.
– Cách biểu diễn mặt cầu.
4. BÀI TẬP VỀ NHÀ:
Bài 1 SGK.
Đọc tiếp bài "Mặt cầu".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 17 Bài 2: MẶT CẦU (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm chung về mặt cầu.
Giao của mặt cầu và mặt phẳng.
Giao của mặt cầu và đường thẳng.
Công thức diện tích khối cầu và diện tích mặt cầu.
Kĩ năng:
Vẽ thành thạo các mặt cầu.
Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
Biết tính diện tích mặt cầu và thể tích khối cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa mặt cầu và VTTĐ giữa 1 điểm và mặt cầu?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Giữa h và r có bao nhiêu
trường hợp xảy ra?
GV minh hoạ bằng hình vẽ
và hướng dẫn HS nhận xét.
Đ1. 3 trường hợp.
h > r; h = r; h < r
Các nhóm quan sát và trình
bày.
II. GIAO CỦA MẶT CẦU
VÀ MẶT PHẲNG
Cho mặt cầu S(O; r) và mp (P).
Đặt h = d(O, (P)).
h > r
(P) và (S) không có
điểm chung.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 34
H2. Nêu điều kiện để (P) tiếp
xúc với (S)?
GV giới thiệu khái niệm
đường tròn lớn, mặt phẳng
kính.
Đ2. (P) OH tại H.
h = r
(P) tiếp xúc với (S).
h < r
(P) cắt (S) theo
đường tròn tâm H, bán kính
r r h
22

.
Chú ý:
Điều kiện cần và đủ để (P)
tiếp xúc với S(O; r) tại H là (P)
vuông góc với OH tại H.
Nếu h = 0 thì (P) cắt (S) theo
đường tròn tâm O bán kính r.
Đường tròn này đgl đường
tròn lớn và (P) đgl mặt phẳng
kính của mặt cầu (S).
Hoạt động 2: Áp dụng VTTĐ của mặt phẳng và mặt cầu
H1. Tính bán kính của đường
tròn giao tuyến?
H2. Tính
PQ
rr,

?
H3. Xét VTTĐ của (P) và (S)?
Đ1.
rr
rr
2
2
3
22



Đ2.
P
r r a
22

,
Q
r r b
22

vì a < b nên
PQ
rr

Đ3. Các nhóm thực hiện.
d
3
4
5
5
r
5
4
4
8
VT
TĐ
cắt
tiếp
xúc
k
cắt
VD1: Hãy xác định đường tròn
giao tuyến của mặt cầu S(O; r)
và mp (P) biết khoảng cách từ
O đến (P) bằng
r
2
.
VD2: Cho mặt cầu S(O; r), hai
mặt phẳng (P), (Q) có khoảng
cách đến O lần lượt bằng a và b
với 0 < a < b < r. Hãy so sánh
các bán kính của các đường
tròn giao tuyến.
VD3: Gọi d là khoảng cách từ
tâm O của mặt cầu S(O; r) đến
mặt phẳng (P). Điền vào chỗ
trồng.
Hoạt động 3: Củng cố
Nhấn mạnh:
– Vị trí tương đối của mp và
mặt cầu.
– Cách xác định tâm và tính
bán kính của đường tròn giao
tuyến.
4. BÀI TẬP VỀ NHÀ:
Bài 3, 4 SGK.
Đọc tiếp bài "Mặt cầu".
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 35
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 18 Bài 2: MẶT CẦU (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm chung về mặt cầu.
Giao của mặt cầu và mặt phẳng.
Giao của mặt cầu và đường thẳng.
Công thức diện tích khối cầu và diện tích mặt cầu.
Kĩ năng:
Vẽ thành thạo các mặt cầu.
Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
Biết tính diện tích mặt cầu và thể tích khối cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các VTTĐ giữa mặt phẳng và mặt cầu?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV hướng dẫn HS nhận xét
từng trường hợp.
H1. Nêu điều kiện để tiếp xúc
với (S) tại H?
Đ1. vuông góc OH tại H.
III. GIAO CỦA MẶT CẦU
VỚI ĐƯỜNG THẲNG. TIẾP
TUYẾN CỦA MẶT CẦU
Cho mặt cầu S(O; r) và đường
thẳng
. Gọi d = d(O,
).
d > r
và (S) không có điểm
chung.
d = r
tiếp xúc với (S).
d < r
cắt (S) tại hai điểm
M, N phân biệt.
Chú ý:
Điều kiện cần và đủ để đường
thẳng
tiếp xúc với mặt cầu S(O;
r) tại điểm H là
vuông góc với
bán kính OH tại H.
đgl tiếp
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 36
H2. Nhắc lại tính chất tiếp tuyến
của đường tròn trong mặt phẳng?
Từ đó GV hướng dẫn HS nêu
nhận xét đối với tiếp tuyến của
mặt cầu trong KG.
Đ2.
– Tại mỗi điểm trên đường tròn có
1 tiếp tuyến.
– Qua 1 điểm nằm ngoài đường
tròn có 2 tiếp tuyến. Các đoạn tiếp
tuyến là bằng nhau.
tuyến, H đgl tiếp điểm.
Nếu d = 0 thì
đi qua tâm O và
cắt (S) tại hai điểm A, B. AB là
đường kính của (S).
Nhận xét:
a) Qua một điểm A nằm trên mặt
cầu S(O; r) có vô số tiếp tuyến
của (S). Tất cả các tiếp tuyến này
đều nằm trên mặt phẳng tiếp xúc
với (S) tại A.
b) Qua một điểm A nằm ngoài
mặt cầu S(O; r) có vô số tiếp
tuyến với (S). Các tiếp tuyến này
tạo thành một mặt nón đỉnh A.
Khi đó độ dài các đoạn thẳng k ẻ
từ A đến các tiếp điểm đều bằng
nhau.
Hoạt động 2: Tìm hiểu khái niệm mặt cầu nội tiếp, ngoại tiếp hình đa diện
GV giới thiệu khái niệm mặt
cầu nội tiếp, ngoại tiếp hình đa
diện (minh hoạ bằng hình vẽ).
S
A
B
C
D
Mặt cầu đgl nội tiếp hình đa
diện nếu mặt cầu đó tiếp xúc với
tất cả các mặt của hình đa diện.
Mặt cầu đgl ngoại tiếp hình đa
diện nếu tất cả các đỉnh của hình
đa diện đều nằm trên mặt cầu.
Hoạt động 3: Áp dụng VTTĐ của đường thẳng và mặt cầu
H1. Chứng tỏ điểm O cách đều
các dỉnh của hình lập phương?
Tính OA?
H2. Chứng tỏ điểm O cách dều
các cạnh của hình lập phương?
Tính khoảng cách từ O đến các
cạnh của hình lập phương?
H3. Chứng tỏ điểm O cách dều
các mặt của hình lập phương?
Tính khoảng cách từ O đến các
mặt của hình lập phương?
Đ1.
OA =
a 3
2
Đ2. d =
a 2
2
Đ3. d =
a
2
VD1: Cho hình lập phương
ABCD.ABCD có cạnh bằng a.
Hãy xác định tâm và bán kính của
mặt cầu:
a) Đi qua 8 đỉnh của hình lập
phương.
b) Tiếp xúc với 12 cạnh của hình
lập phương.
c) Tiếp xúc với 6 mặt của hình lập
phương.
A
B C
D
A’
B’
C’
D’
O
Hoạt động 4: Củng cố
Nhấn mạnh:
– Cách xét VTTĐ của đường
thẳng và mặt cầu.
– Khái niệm mặt cầu nội tiếp,
ngoại tiếp hình đa diện.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 37
4. BÀI TẬP VỀ NHÀ:
Bài 5, 6, 7, 8, 9 SGK.
Đọc tiếp bài "Mặt cầu".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 19 Bài 2: MẶT CẦU (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm chung về mặt cầu.
Giao của mặt cầu và mặt phẳng.
Giao của mặt cầu và đường thẳng.
Công thức diện tích khối cầu và diện tích mặt cầu.
Kĩ năng:
Vẽ thành thạo các mặt cầu.
Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
Biết tính diện tích mặt cầu và thể tích khối cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các VTTĐ giữa đường thẳng và mặt cầu?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Nhắc lại công thức tính
diện tích mặt cầu và thể tích
khối cầu đã biết?
Đ1.
Sr
2
4
;
Vr
3
4
3
IV. CÔNG THỨC TÍNH
DIỆN TÍCH MẶT CẦU VÀ
THỂ TÍCH KHỐI CẦU
Cho mặt cầu S(O; r).
Diện tích mặt cầu:
Sr
2
4
Thể tích khối cầu:
Vr
3
4
3
Chú ý:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 38
H2. Tính diện tích đường tròn
lớn ?
Đ2.
ñt
Sr
2
Diện tích mặt cầu bằng 4 lần
diện tích hình tròn lớn của mặt
cầu đó.
Thể tích khối cầu bằng thể
tích khối chóp có diện tích đáy
bằng diện tích mặt cầu và có
chiều cao bằng bán kính của
khối cầu đó.
Hoạt động 2: Áp dụng tính diện tích mặt cầu và thể tích khối cầu
GV cho các nhóm tính.
Các nhóm tính và điền vào
bảng.
r
1
2
3
4
S
đt
4
9
16
S
mc
4
16
36
64
V
4
3
32
3
36
256
3
VD1: Cho mặt cầu S có bán
kính r. Tính diện tích đường
tròn lớn, diện tích mặt cầu và
thể tích khối cầu.
H1. Tính cạnh của hình lập
phương theo r?
Đ1.
Cạnh hình lập phương nội
tiếp mặt cầu:
a =
r 2
V
1
=
r
3
22
Cạnh hình lập phương ngoại
tiếp mặt cầu:
b = 2r
Vr
3
2
8
VD2: Cho mặt cầu bán kính r.
Tính thể tích của hình lập
phương:
a) Nội tiếp mặt cầu.
b) Ngoại tiếp mặt cầu.
O
r
a
a 2
O
I J
KL
H
H1. Chứng minh OA = OB =
OC = OS ?
H2. Tính SC ?
Đ1.
SAC vuông tại A
OA = OC = OS
SBC vuông tại B
OB = OC = OS
Đ2.
AC AB BC a
2 2 2 2
3
SC SA AC a
2 2 2 2
4
SC = 2a
R = a.
VD3: Cho hình chóp S.ABC
có đáy ABC là tam giác vuông
tại B và SA (ABC). Gọi O là
trung điểm của SC.
a) Chứng minh A, B, C, S cùng
nằm trên một mặt cầu.
b) Cho SA = BC = a và AB =
a 2
. Tính bán kính mặt cầu
trên.
S
A
B
C
O
a
a
a 2
Hoạt động 4: Củng cố
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 39
Nhấn mạnh:
– Cách xác định tâm và bán
kính mặt cầu.
– Công thức tính diện tích mặt
cầu và thể tích khối cầu.
4. BÀI TẬP VỀ NHÀ:
Bài 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 20+21 Bài 2: BÀI TẬP MẶT CẦU
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm chung về mặt cầu.
Giao của mặt cầu và mặt phẳng.
Giao của mặt cầu và đường thẳng.
Công thức diện tích khối cầu và diện tích mặt cầu.
Kĩ năng:
Vẽ thành thạo các mặt cầu. Xác định tâm và bán kính của mặt cầu.
Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
Biết tính diện tích mặt cầu và thể tích khối cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV hướng dẫn HS cách xác
định tâm mặt cầu ngoại tiếp
hình chóp đều.
H1. Nhận xét tính chất của tam
giác SAC?
H2. Nhận xét tứ giác OIAH?
Đ1. SAC vuông tại S
OS = OA = OC
OS = OA = OC = OB = OD
1. Cho hình chóp tứ giác đều
S.ABCD có tất cả các cạnh đều
bằng a. Xác định tâm và bán
kính mặt cầu ngoại tiếp hình
chóp.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 40
H3. Tính bán kính mặt cầu ?
H4. Nhận xét tính chất tâm O
của mặt cấu ngoại tiếp hình
chóp?
H5. Xác định bán kính mặt
cầu?
O là tâm của mặt cầu ngoại
tiếp hình chóp S.ABCD.
Đ3. R = OA =
a 2
2
Đ3. OA = OB = OC = OS
O và O thuộc mp trung
trực của SC.
Đ5. R = OA =
OI AI
22
=
a b c
2 2 2
2

S
A B
C
D
O
2. Cho hình chóp S.ABC có
SA = a, SB = b, SC = c và ba
cạnh SA, SB, SC đôi một
vuông góc. Xác định tâm và
bán kính của mặt cầu ngoại
tiếp hình chóp.
S
A
B
C
H
O
I
Hoạt động 2: Chứng minh tính chất liên quan đến mặt cầu
H1. Nhắc lại tính chất tương tự
đối với đường tròn trong mp?
H2. Tính phương tích của điểm
M đối với đường tròn lớn qua
A, B?
H3. Nhận xét các tiếp tuyến vẽ
từ A và B?
Đ1. Trong mp(MA, MC) ta có:
MA.MB = MC.MD
Đ2. MA.MB =
dr
22
Đ3. AI = AM, BI = BM
ABI = ABM
AMB AIB
3. Từ một điểm M nằm ngoài
mặt cầu S(O; r) kẻ hai đường
thẳng cắt mặt cầu lần lượt tại
A, B và C, D.
a) Chứng minh:
MA.MB = MC.MD
b) Đặt MO = d. Tính MA.MB
theo r và d.
M
A
B
C
D
O
4. Cho mặt cầu S(O; r) tiếp xúc
với mp (P) tại I. Gọi M là một
điểm nằm trên mặt cầu nhưng
không phải là điểm đối xứng
với I qua O. Từ M kẻ hai tiếp
tuyến của mặt cầu cắt (P) tại A
và B. CMR:
AMB AIB
.
O
M
A
B
I
P
Hoạt động 3: Tập hợp điểm liên quan đến mặt cầu
H1. Nêu bài toán tương tự
trong mặt phẳng?
Đ1. Tập hợp các điểm M trong
mp nhìn đoạn AB cố định dưới
một góc vuông là đường tròn
đường kính AB.
5. Tìm tập hợp các điểm M
trong KG luôn nhìn đoạn thẳng
AB cố định dưới một góc
vuông.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 41
H2. Nhận xét tính chất tâm O
của một mặt cầu?
Đ2. Lấy A, B, C (C).
O là tâm mặt cầu OA = OB
= OC
O nằm trên trục của đường
tròn (C).
6. Tìm tập hợp tâm các mặt cầu
luôn chứa một đường tròn (C)
cố định.
Nhấn mạnh:
– Các tính chất của mặt cầu.
– Cách xác định tâm và bán
kính của mặt cầu.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Bài tập ôn học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 22 Bài dạy: ÔN TẬP HỌC KÌ I
I. MỤC TIÊU:
Kiến thức:
Ôn tập toàn bộ kiến thức học kì 1.
Kĩ năng:
Thành thạo giải bài toán tính thể tích khối đa diện và vận dụng thể thích khối đa diện để giải
toán hình học.
Thành thạo giải bài toán tính thể tích khối tròn xoay.
Thành thạo xác định tâm và bán kính mặt cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với khối đa điện, khối tròn xoay.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học trong học kì 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Xác định tính chất tứ giác
Đ1.
1. Cho hình chóp S.ABCD có
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 42
BCNM?
H2. Xác định đường cao của
hình chóp SBCNM?
H3. Tính diện tích đáy và
chiều cao của hình chóp?
(BCM) // AD MN // AD
BC AB
BC BM
BC SA

BCNM là hình thang vuông
với đường cao BM
Đ2. Do (SBM) (BCNM) nên
trong (SBM) vẽ SH BM
SH (BCNM) SH là
đường cao.
Đ3.
SA AB a
0
tan60 3
MN SM
AD SA
a
MN
4
3
a
BM
2
3
BCNM
a
S
2
10
33
SB = 2a
AB AM
SB MS
1
2

BM là phân giác của
SBH
SH SB a
0
.sin30
đáy ABCD là hình chữ nhật
với AB = a, AD = 2a, cạnh SA
vuông góc với đáy, cạnh SB
tạo với mặt phẳng đáy một góc
60
0
. Trên cạnh SA lấy điểm M
sao cho AM =
a 3
3
. Mặt
phẳng (BCM) cắt cạnh SD tại
N. Tính thể tích khối chóp
S.BCNM.
S
A
B C
D
M
N
H
2a
a
H1. Xác định góc giữa hai mp
(ABC) và (ABC)?
H2. Tính tan ?
H3. Nêu cách tính thể tích khối
chóp A.BCCB?
Đ1. E là trung điểm của BC.
AE BC
A E BC
ABC A BC AEA,

Đ2.
AH=
A A AH
22
=
ba
22
1
93
3
tan =
A H b a
HE a
22
23
Đ3.
A BCC B ABCA B C A ABC
V V V

=
ABC
A H S
2
.
3
=
a b a
2 2 2
3
6
2. Cho hình lăng trụ
ABC.ABC có AABC là hình
chóp tam giác đều, cạnh đáy
AB = a, cạnh bên AA = b. Gọi
là góc giữa hai mặt phẳng
(ABC) và (ABC). Tính tan
và thể tích khối chóp
A.BBCC.
A’
B
C
A
H
E
B’
C’
H1. Xác định tính chất thiết
diện AMKN?
Gọi V
1
= V
ABCDMKN
V
2
= V
AMKNA
B
C
D
Đ1. AK MN AMKN là
hình thoi.
3. Cho hình lập phương
ABCD.ABCD có cạnh bằng
a và điểm K thuộc cạnh CC
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 43
H2. Tính thể tích V
1
?
H3. Tính thể tích khối lập
phương?
Đ2. V
1
= 2V
ABCKM
=
BCKM
AB S
1
2. .
3
=
a a a a
a
3
22
3 3 3 2 3




Đ3. V = a
3
V
2
= V – V
1
=
a
3
2
3
sao cho CK =
a
2
3
. Mặt phẳng
(P) qua A, K và song song với
BD, chia khối lập phương
thành hai khối đa diện. Tính
thể tích của hai khối đa diện
đó.
A’
B
C
A
B’
C’
D
D’
O’
O
I
K
M
N
Nhấn mạnh:
– Công thức tính thể tích khối
chóp, khối lăng tụ.
– Một số cách tính thể tích
khối đa diện.
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Tính độ dài đường sinh,
bán kính đáy và chiều cao của
hình nón?
H2. Nhắc lại công thức tính
S
xq
, S
tp
, V của khối nón?
Đ1.
l = a
r = OA =
a 2
2
= h
Đ2.
S
xq
= rl =
a
2
2
2
S
tp
= S
xq
+ S
đáy
=
a
2
21
2
V =
rh
2
1
3
=
a
3
1
2
12
1. Thiết diện qua trục của một
hình nón là một tam giác
vuông cân có cạnh góc vuông
bằng a.
a) Tính diện tích xung quanh
và diện tích toàn phần của hình
nón.
b) Tính thể tích khối nón tương
ứng.
S
A BO
a a
r
H1. Xác định góc giữa AB và
trục của hình trụ?
H2. Xác định thiết diện ?
H3. Nhắc lại công thức tính
S
xq
, S
tp
, V của khối trụ?
Đ1. AA // OO
BAA
0
30
A B AA R
0
.tan30


Đ2. Thiết diện là hình chữ nhật
AABB.
S
AA
BB
= AA.BA =
R
2
3
Đ3.
S
xq
= 2rh =
R
2
23
V = r
2
h =
R
3
3
2. Một hình trụ có bán kính đáy
R và đường cao
R 3
. A và B
là 2 điểm trên 2 dường tròn đáy
sao cho góc hợp bởi AB và
trục của hình trụ là 30
0
.
a) Tính diện tích thiết diện qua
AB và song song với trục của
hình trụ.
b) Tính S
xq
, S
tp
, V của khối trụ.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 44
A
B
A’
O
O’
0
30
H
B’
Hoạt động 3: Củng cố giải toán liên quan đến khối cầu
H1. Xác định góc giữa cạnh
bên và đáy?
H2. Nêu tính chất của tâm mặt
cầu ngoại tiếp?
H3. Tính bán kính mặt cầu?
Đ1.
SAH
0
60
SAC là tam giác đều.
Đ2. OA = OB = OC = OD= OS
O SH và O là tâm của
đường tròn ngoại tiếp SAC
O là trọng tâm của SAC
Đ3.
R = SO =
SH
2
3
=
AC 3
3
=
a 6
3
3. Cho một hình chóp tứ giác
đều có cạnh đáy là a, cạnh bên
hợp với đáy một góc 60
0
.
a) Xác định tâm và bán kính
mặt cầu ngoại tiếp hình chóp.
b) Tính diện tích mặt cầu và
thể tích khối cầu tương ứng.
S
O
A
B
a
C
D
H
0
60
Hoạt động 4: Củng cố
Nhấn mạnh:
– Công thức tính thể tích khối
nón, khối trụ, khối cầu.
– Cách xác định tâm và bán
kính của mặt cầu.
4. BÀI TẬP VỀ NHÀ:
Chuẩn bị kiểm tra học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy:23
KỂM TRA HỌC KÌ 1
THI THEO ĐỀ CHUNG CỦA SỞ
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 45
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy:24
ÔN TẬP CHƯƠNG II
I. Mục tiêu:
+ Về kiến thức:
- Hệ thống các kiến thức cơ bản về mặt tròn xoay và các yếu tố cơ bản về mặt tròn xoay như
trục, đường sinh,...
- Phân biệt được các khái niệm về mặt và khối nón, trụ, cầu và các yếu tố liên quan.
- Nắm vững các công thức tính diện tích xung quanh và thể tích của khối nón, khối trụ, công
thức tính diện tích mặt cầu và thể tích khối cầu.
+ Về kỹ năng:
- Vận dụng được các công thức vào việc tính diện tích xung quanh và thể tích của các khối :
nón, trụ, cầu.
- Rèn luyện kĩ năng vẽ hình cho học sinh.
+ Về tư duy và thái độ:
- Rèn luyện tính tích cực, sáng tạo, cẩn thận.
II. Chuẩn bị của giáo viên và học sinh:
+ Giáo viên:Giáo án, bảng phụ, phiếu học tập.
+ Học sinh: Dụng cụ học tập, SGK,...
III. Phương pháp: Gợi mở, giải quyết vấn đề.
IV. Tiến trình bài học:
Tiết 1:
1. Ổn định tổ chức:
2. Kiểm tra bài cũ:
CH1: Ghi các công thức tính diện tích và thể tích các mặt và khối:nón, trụ, cầu.
Mặt nón-Khối nón
Mặt trụ-Khối trụ
Mặt cầu-Khối cầu
Diện tích
S
xq
=
S
xq
=
S=
Thể tích
V=
V=
V=
GV chính xác hóa kiến thức, đánh giá và ghi điểm.
3. Bài mới:
* Hoạt động 1: Giải bài toán đúng sai.
Hoạt động của giáo viên
Hoạt động của học sinh
Ghi bảng
Đọc đề BT1 SGK
CH1: Qua 3 điểm A,B,C có bao
nhiêu mặt phẳng.
CH2: Xét vị trí tương đối giữa
mp (ABC) và mặt cầu và trả lời
câu a.
CH3: Theo đề mp(ABC) có qua
tâm O của mặt cầu không.
CH4: Dựa vào giả thiết nào để
+ Xem đề SGK /T50
+ Trả lời: Có duy nhất
mp(ABC)
+ Mp(ABC) cắt mặt cầu theo
giao tuyến là đường tròn qua
A,B,C. Suy ra kết quả a đúng.
+ Chưa biết (Có 2 khả năng)
+ Dựa vào CH3 suy ra: b-
Không đúng
c-Không đúng.
+Dựa vào giả thiết:
ABC
=90
0
và kết quả câu a
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 46
khẳng định AB là đường kính
của đường tròn hay không.
*Hoạt động 2: Kết hợp BT2 và BT5 SGK/T50
Hoạt động của giáo viên
Hoạt động của học sinh
Ghi bảng
Nêu đề: Cho tứ diện đều
ABCD cạnh a. Gọi H là hình
chiếu của A trên mp(BCD). N
là trung điểm CD
a- Chứng minh HB=HC=HD.
Tính độ dài đoạn AH.
b- Tính S
xq
và V của khối nón
tạo thành khi quay miền tam
giác AHN quanh cạnh AH.
c- Tính S
xq
và V của khối trụ
có đường tròn đáy ngoại tiếp
tam giác BCD và chiều cao
AH.
Hoạt động 2.1:
CH1: Có nhận xét gì về các
tam giác AHB, AHC, AHD.
Nêu cách tính AH.
Hoạt động 2.2:
CH: Để tính S
xq
của mặt nón và
V của khối nón, cần xác định
các yếu tố nào?
+Gọi một hs lên bảng thực
hiện.
+Cho các hs còn lại nhận xét
bài giải, gv đánh giá và ghi
điểm
Hoạt động 2.3:
CH: Để tính S
xq
của mặt trụ và
V của khối trụ, cần xác định
các yếu tố nào?
+Gọi một hs lên bảng thực
hiện.
+Cho các hs còn lại nhận xét
bài giải, gv đánh giá và ghi
điểm
- Vẽ hình (GV hướng dẫn nếu
cần)
TL: Chúng là 3 tam giác vuông
bằng nhau.
Suy ra HB=HC=HD
AH=
22
BHAB
+Cần xác định độ dài đường
sinh l = AN, bán kính đường
tròn đáy r = HN và đường cao
h=AH.
+Cần xác định độ dài đường
sinh l = AB, bán kính đường
tròn đáy r = BH và đường cao
h=l
a) AH
(BCD)
=> Các tam giác AHB, AHC,
AHD vuông tại H
Lại có: AH cạnh chung
AB=AC=AD(ABCD là
tứ diện đều)
=> 3 tam giác AHB, AHC,
AHD bằng nhau
Suy ra HB=HC=HD
*AH=
22
BHAB
=
3
2
2
a
a
=
3
6a
b) Khối nón tạo thành có:
3
6
6
3
2
3
a
AHh
a
HNr
a
ANl
S
xq
=
rl=
.
6
3a
.
2
3a
=
4
2
a
V=
hB.
3
1
=
3
6
.
12
.
3
1
2
aa
=
108
6
3
a
c) Khối trụ tạo thành có:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 47
3
6
3
3
a
AHhl
a
HBr
S
xq
=2
rl
=2
.
3
3a
3
6a
=
3
22
2
a
V=B.h=
3
6
.
3
.
2
aa
=
9
6.
3
a
*Hoạt động 3: BT 6/50 SGK
Hoạt động của giáo viên
Hoạt động của học sinh
Ghi bảng
+ Nêu đề.
Hoạt động 3.1: Xác định tâm
và bán kính của mặt cầu ngoại
tiếp hình chóp.
CH 1: Trình bày pp xác định
tâm mặt cầu ngoại tiếp hình
chóp.
+ Nhận xét câu trả lời của hs
và nhắc lại các bước:
1. Xác định trục Δ của đường
tròn ngoại tiếp đa giác đáy.
2. Xác định mặt phẳng trung
trực (
) (hoặc đường trung
trực d) của cạnh bên bất kì.
3. Xác định giao điểm của Δ
với (
) (hoặc của Δ với d) .
Đó chính là tâm mặt cầu cần
tìm.
CH 2: Đường tròn ngoại tiếp
hình vuông ABCD có trục là
đường thẳng nào?
CH 3: Có nhận xét gì về hai
tam giác SAO và SMO
’
. Nêu
cách tính bán kính R của mặt
cầu.
+ HS vẽ hình
+ Lắng nghe và trả lời.
+ Suy nghĩ trả lời câu hỏi.
+ Đó là hai tam giác vuông có
chung góc nhọn nên chúng
đồng dạng
=>
SM
SO
SO
SA
'
a. Gọi O’, R lần lượt là tâm
và bán kính của mặt cầu
Vì O’A=O’B=O’C=O’D
=> O’ thuộc SO (1)
Trong (SAO), gọi M là trung
điểm của SA và d là đường
trung trực của đoạn SA
Vì O’S = O’A
=> O’ thuộc d (2)
Từ (1) và (2) =>O’=SO
d
+ R = O
’
S.
Hai tam giác vuông SAO và
SMO
’
đồng dạng nên:
SO
SMSA
SO
.
'
Trong đó
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 48
Hoạt động 3.2: Tính diện tích
mặt cầu và thể tích khối cầu.
CH : Nêu lại công thức tính
diện tích mặt cầu và thể tích
khối cầu.
+ S = 4πR
2
+ V =
3
3
4
R
SA=
2
3
22
a
OASO
=> SO
'
=
4
3a
=R
b) Mặt cầu có bán kính R=
4
3a
nên:
+ S=4π
2
)
4
3
(
a
=
4
9
2
a
+ V=
3
)
4
3
(
3
4 a
=
16
9
3
a
4. Củng cố:
*Hoạt động 4: Giải bài tập trắc nghiệm theo nhóm(củng cố toàn bài)
Câu 1) Cho hình lập phương ABCD.A
’
B
’
C
’
D
’
có cạnh bằng a.
1.1 Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông
ABCD và A
’
B
’
C
’
D
’
. Diện tích S là:
A) πa
2
B)
2
2
a
C)
3
2
a
D)
2
2
2
a
1.2 Gọi S
’
là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng AC
’
khi
quay xung quanh trục AA
’
. Diện tích S
’
là:
A) πa
2
B)
3
2
a
C)
2
2
a
D)
6
2
a
Câu 2) Số mặt cầu chứa một đường tròn cho trước là:
A) 1 B) 2 C) vô số D) 0
Cho các nhóm nêu đáp án và đại diện trình bày phương pháp giải theo chỉ định câu hỏi của GV.
GV nhận xét, đánh giá và ghi điểm cho nhóm.
5. Dặn dò:
- Về nhà làm các bài tập ôn chương còn lại
- Chuẩn bị cho bài kiểm tra 1 tiết vào tiết tiếp theo.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 49
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Chương III: PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN
Tiết dạy: 25 Bài 1: HỆ TOẠ ĐỘ TRONG KHÔNG GIAN
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm toạ độ của điểm và vectơ trong không gian.
Biểu thức toạ độ của các phép toán vectơ.
Phương trình mặt cầu.
Kĩ năng:
Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
Viết được phương trình mặt cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại định nghĩa toạ độ của điểm và vectơ trong mặt phẳng?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV sử dụng hình vẽ để giới
thiệu hệ trục toạ độ trong
không gian.
H1. Đọc tên các mặt phẳng toạ
độ?
H2. Nhận xét các vectơ
i
,
j
,
k
?
Đ1. (Oxy), (Oyz), (Ozx).
Đ2. Đôi một vuông góc với
nhau.
I. TOẠ ĐỘ CỦA ĐIỂM VÀ
CỦA VECTƠ
1. Hệ toạ độ
Hệ toạ độ Đề–các vuông góc
trong không gian là hệ gồm 3
trục x
Ox, y
Oy, z
Oz vuông
góc với nhau từng đôi một, với
các vectơ đơn vị
i
,
j
,
k
.
i j k
2 2 2
1
i j j k k i. . . 0
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 50
GV hướng dẫn HS phân tích
OM
theo các vectơ
i
,
j
,
k
.
Cho HS biểu diễn trên hình
vẽ.
Các nhóm thực hiện.
2. Toạ độ của một điểm
M(x; y; z)
OM xi yj zk
VD1: Xác định các điểm
M(0;0;0), A(0; 1; 2), B(1; 0;
2), C(1; 2; 0) trong không gian
Oxyz.
Hoạt động 3: Tìm hiểu khái niệm toạ độ của vectơ
H1. Nhắc lại định lí phân tích
vectơ theo 3 vectơ không đồng
phẳng trong không gian?
GV giới thiệu định nghĩa và
cho HS nhận xét mối quan hệ
giữa toạ độ điểm M và
OM
.
H2. Xác định toạ độ các đỉnh
của hình hộp?
H3. Xác định toạ độ của các
vectơ?
Đ1.
a a a a a a i a j a k
1 2 3 1 2 3
( ; ; )
Toạ độ của
OM
cũng là toạ
độ điểm M.
O
A
B
C
D
D’
C’
B’
A’
x
y
z
M
a
b
c
Đ2.
B(a; 0; 0), D(0; b; 0), A(0; 0;c)
C(a; b; 0), C(a; b; c), D(0;b;c)
Đ3.
AB a( ;0;0)
,
AC a b( ; ;0)
AC a b c( ; ; )
,
a
AM b c; ; )
2



3. Toạ độ của vectơ
a a a a a a i a j a k
1 2 3 1 2 3
( ; ; )
Nhận xét:
M x y z OM x y z( ; ; ) ( ; ; )
Toạ độ của các vectơ đơn vị:
i j k(1;0;0), (0;1;0), (0;0;1)
0 (0;0;0)
VD2: Trong KG Oxyz, cho
hình hộp chữ nhật
ABCD.ABCD có đỉnh A
trùng với O, các vectơ
AB AD,
AA
theo thứ tự cùng hướng
với
i j k,,
và AB = a, AD = b,
AA = c. Tính toạ độ các vectơ
AB AC AC AM, , ,
, với M là
trung điểm của cạnh CD.
Hoạt động 4: Củng cố
Nhấn mạnh:
– Khái niệm toạ độ của điểm,
của vectơ trong KG.
– Liên hệ với toạ độ của điểm,
của vectơ trong MP.
4. BÀI TẬP VỀ NHÀ:
Đọc tiếp bài "Hệ toạ độ trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 51
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 26 Bài 1: HỆ TOẠ ĐỘ TRONG KHÔNG GIAN (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm toạ độ của điểm và vectơ trong không gian.
Biểu thức toạ độ của các phép toán vectơ.
Phương trình mặt cầu.
Kĩ năng:
Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
Viết được phương trình mặt cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa toạ độ của điểm và vectơ trong không gian?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV cho HS nhắc lại các tính
chất tương tự trong mp và
hướng dẫn HS chứng minh.
H1. Phát biểu các hệ quả?
Các nhóm thảo luận và trình
bày.
a a i a j a k
b b i b j b k
1 2 3
1 2 3
Đ1.
Hai vectơ bằng nhau các
toạ độ tương ứng bằng nhau
Hai vectơ cùng phương
các toạ độ của vectơ này bằng
k lần toạ độ tương ứng của
vectơ kia
II. BIỂU THỨC TOẠ ĐỘ
CỦA CÁC PHÉP TOÁN
VECTƠ
Định lí: Trong KG Oxyz, cho:
a a a a b b b b
1 2 3 1 2 3
( ; ; ), ( ; ; )
.
a b a b a b a b
1 1 2 2 3 3
( ; ; )
a b a b a b a b
1 1 2 2 3 3
( ; ; )
ka k a a a ka ka ka
1 2 3 1 2 3
( ; ; ) ( ; ; )
(k
R)
Hệ quả:
ab
a b a b
ab
11
22
33
Với
b 0
:
a b cuøng phöông
a kb
k R a kb
a kb
11
22
33
,
:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 52
Toạ độ vectơ bằng toạ độ
điểm ngọn trừ toạ độ điểm gốc
Toạ độ trung điểm đoạn
thẳng bằng trung bình cộng toạ
độ hai điểm mút.
Cho
A A A B B B
A x y z B x y z( ; ; ), ( ; ; )
B A B A B A
AB x x y y z z( ; ; )
M là trung điểm của đoạn AB:
A B A B A B
x x y y z z
M ;;
2 2 2



Hoạt động 2: Tìm hiểu biểu thức toạ độ của tích vô hướng
GV cho HS nhắc lại các tính
chất tương tự trong mp và
hướng dẫn HS chứng minh.
Các nhóm thảo luận và trình
bày.
III. TÍCH VÔ HƯỚNG
1. Biểu thức toạ độ của tích
vô hướng
Định lí: Trong KG Oxyz, cho:
a a a a b b b b
1 2 3 1 2 3
( ; ; ), ( ; ; )
.
a b a b a b a b
1 1 2 2 3 3
.
2. Ứng dụng
a a a a
222
1 2 3
B A B A B A
AB x x y y z z
2 2 2
( ) ( ) ( )
a b a b a b
ab
a a a b b b
1 1 2 2 3 3
2 2 2 2 2 2
1 2 3 1 2 3
cos( , )
.

a b a b a b a b
1 1 2 2 3 3
0
Hoạt động 3: Áp dụng biểu thức toạ độ các phép toán vectơ
H1. Xác định toạ độ các vectơ?
Đ1.
AB ( 2;1;2)
,
AC ( 1;3; 3)
,
BC (1;2; 5)
,
AM
31
;2;
22



AC AB3 ( 7;6;3)
AB AC2 (0; 5;8)
AB AC.0
VD1: Trong KG Oxyz, cho
A(1;1;1), B(–1;2;3), C(0;4;–2).
a) Tìm toạ độ các vectơ
AB
,
AC
,
BC
,
AM
(M là trung
điểm của BC).
b) Tìm toạ độ của vectơ:
AC AB3
,
AB AC2
c) Tính các tích vô hướng:
AB AC.
,
AB AC.2
Hoạt động 4: Củng cố
Nhấn mạnh:
– Các biểu thức toạ độ các
phép toán vectơ trong KG.
– Liên hệ với toạ độ của điểm,
của vectơ trong MP.
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4 SGK.
Đọc tiếp bài "Hệ toạ độ trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 53
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 27 Bài 1: HỆ TOẠ ĐỘ TRONG KHÔNG GIAN (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được khái niệm toạ độ của điểm và vectơ trong không gian.
Biểu thức toạ độ của các phép toán vectơ.
Phương trình mặt cầu.
Kĩ năng:
Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
Viết được phương trình mặt cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các biểu thức toạ độ các phép toán vectơ trong không gian?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Nhắc lại phương trình
đường tròn trong MP?
H2. Tính khoảng cách IM?
H3. Gọi HS tính?
Đ1.
x a y b r
2 2 2
( ) ( )
Đ2.
IM x a y b z c
2 2 2
( ) ( ) ( )
Đ3.
x y z
2 2 2
( 1) ( 2) ( 3) 25
IV. PHƯƠNG TRÌNH MẶT
CẦU
Định lí: Trong KG Oxyz, mặt
cầu (S) tâm I(a; b; c), bán kính
r có phương trình:
x a y b z c r
2 2 2 2
( ) ( ) ( )
VD1: Viết phương trình mặt
cầu có tâm I(1; –2; 3) và bán
kính r = 5.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 54
GV hướng dẫn HS nhận xét
điều kiện để phương trình là
phương trình mặt cầu.
GV hướng dẫn HS cách xác
định.
H1. Biến đổi về dạng tổng bình
phương?
H2. Xác định a, b, c, r?
Đ1.
x y z
2 2 2 2
( 2) ( 1) ( 3) 3
Đ2. a = –2, b = 1, c = –3, r = 3
Nhận xét: Phương trình:
x y z ax by cz d
2 2 2
2 2 2 0
với
a b c d
2 2 2
0
là
phương trình mặt cầu có tâm
I(–a; –b; –c) và bán kính
r a b c d
2 2 2
.
VD2: Xác định tâm và bán
kính của mặt cầu có phương
trình:
x y z x y z
2 2 2
4 2 6 5 0
Hoạt động 3: Áp dụng phương trình mặt cầu
H1. Gọi HS xác định?
H2. Xác định tâm và bán kính?
Đ1. Các nhóm thực hiện và
trình bày.
a)
Ir(2;1; 3), 8
b)
Ir( 1;2;3), 3
c)
Ir(4; 2;1), 5
d)
Ir( 2;1;2), 2
Đ2.
b)
r IA 29
c)
Ir
7 29
;3;1 ,
22



VD3: Xác định tâm và bán
kính của mặt cầu có phương
trình:
x y z
2 2 2
( 2) ( 1) ( 3) 64
x y z
2 2 2
( 1) ( 2) ( 3) 9
x y z x y z
2 2 2
8 4 2 4 0
x y z x y z
2 2 2
4 2 4 5 0
VD4: Viết phương trình mặt
cầu (S):
a) (S) có tâm I(1; –3; 5), r =
3
b) (S) có tâm I(2; 4; –1) và đi
qua điểm A(5; 2; 3)
c) (S) có đường kính AB với
A(2; 4; –1), B(5; 2; 3)
Hoạt động 4: Củng cố
Nhấn mạnh:
– Các dạng phương trình mặt
cầu.
– Cách xác định mặt cầu.
4. BÀI TẬP VỀ NHÀ:
Bài 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 55
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 28 Bài 1: BÀI TẬP HỆ TOẠ ĐỘ TRONG KHÔNG GIAN
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm toạ độ của điểm và vectơ trong không gian.
Biểu thức toạ độ của các phép toán vectơ.
Phương trình mặt cầu.
Kĩ năng:
Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
Viết được phương trình mặt cầu.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
H1. Nêu cách tính?
H1. Nhắc lại tính chất trọng
tâm tam giác?
H3. Nêu hệ thức vectơ xác
định các đỉnh còn lại của hình
Đ1.
d
1 55
11; ;
33


e ( 0; 27;3)
f
5 11
; ; 6
22


g
33 17
4; ;
22



Đ2.
GA GB GC 0
A B C
G
A B C
G
A B C
G
x x x
x
y y y
y
z z z
z
2
33
0
3
4
33






Đ3.
C(2;0;2)
,
A (3;5; 6)
,
1. Cho ba vectơ
a (2; 5;3)
,
b (0;2; 1)
,
c (1;7;2)
. Tính
toạ độ của các vectơ:
d a b c
1
43
3
e a b c42
f a b c
1
2
2
g a b c
1
3
2
2. Cho ba điểm
A(1; 1;1)
,
B(0;1;2)
,
C(1;0;1)
. Tìm toạ độ
trọng tâm G của ABC.
3. Cho h.hộp ABCD.ABCD
biết
A(1;0;1)
,
B(2;1;2)
,
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 56
hộp?
H4. Nêu công thức tính?
H5. Nêu công thức tính?
B (4;6; 5)
,
D (3;4; 6)
Đ4.
a)
ab.
= 6
b)
ab.
= –21
Đ5.
a)
ab
5
cos ,
26.14
b)
ab
0
, 90
.
D(1; 1;1)
,
C (4;5; 5)
. Tính toạ
độ các đỉnh còn lại của hình
hộp.
4. Tính
ab.
với:
a)
a (3;0; 6)
,
b (2; 4;0)
b)
ab(1; 5;2), (4;3; 5)
5. Tính góc giữa hai vectơ
ab,
a)
ab(4;3;1), ( 1;2;3)
b)
ab(2;5;4), (6;0; 3)
Hoạt động 2: Luyện tập phương trình mặt cầu
H1. Nêu cách xác định ?
H2. Nêu cách xác định mặt
cầu?
Đ1.
a)
I(4;1;0)
, R = 4
b)
I( 2; 4;1)
, R = 5
c)
I(4; 2; 1)
, R = 5
d)
I
45
1; ;
32




, R =
19
6
Đ2.
a) Tâm I(3; –2; 2), bk R = 3
x y z
2 2 2
( 3) ( 1) ( 5) 9
b) Bán kính R = CA =
5
x y z
2 2 2
( 3) ( 3) ( 1) 5
6. Tìm tâm và bán kính của các
mặt cầu có phương trình:
a)
x y z x y
2 2 2
8 2 1 0
b)
x y z x y z
2 2 2
4 8 2 4 0
c)
x y z x y z
2 2 2
8 4 2 4 0
d)
x y z
x y z
2 2 2
3 3 3
6 8 15 3 0
7. Lập phương trình mặt cầu:
a) Có đường kính AB với A(4;
–3; 7), B(2; 1; 3).
b) Đi qua điểm A(5; –2; 1) và
có tâm C(3; –3; 1).
Hoạt động 3: Củng cố
Nhấn mạnh:
– Các biểu thức toạ độ của các
phép toán vectơ.
– Cách lập phương trình mặt
cầu, cách xác định tâm và bán
kính mặt cầu.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Đọc trước bài "Phương trình mặt phẳng"
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 57
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 29 Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG
I. MỤC TIÊU:
Kiến thức:
Nắm được vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
Nắm được sự xác định mặt phẳng. Phương trình tổng quát của mặt phẳng.
Điều kiện để hai mặt phẳng song song, vuông góc.
Kĩ năng:
Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
Xác định được hai mặt phẳng song song, vuông góc.
Tính được khoảng cách từ một điểm đến mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số tính chất cơ bản của phép toán về vectơ?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
GV giới thiệu định nghĩa
VTPT của mặt phẳng.
H1. Một mp có bao nhiêu
VTPT?
n
P
Đ1. Vô số VTPT, chúng cùng
phương với nhau.
I. VECTƠ PHÁP TUYẾN
CỦA MẶT PHẲNG
Định nghĩa: Cho mp (P). Nếu
vectơ
n
0
và có giá vuông
góc với (P) thì
n
đgl vectơ
pháp tuyến của (P).
Chú ý: Nếu
n
là VTPT của (P)
thì
kn
(k
0) cũng là VTPT
của (P).
H1. Tính toạ độ các vectơ
AB
,
AC
,
BC
?
H2. Tính
,


AB AC
,
,


AB BC
?
H3. Xác định một VTPT của
các mặt phẳng (Oxy), (Oyz)?
Đ1.
(2;1; 2)AB
,
( 12;6;0)AC
,
( 14;5;2)BC
Đ2.
,,
(12;24;24)
AB AC AB BC
Đ3.
()
Oxy
nk
,
()
Oyz
ni
VD1: Tìm một VTPT của mặt
phẳng:
a) Qua A(2; –1; 3), B(4; 0; 1),
C(–10; 5; 3).
b) Qua A(2; 0; 0), B(0; 2; 0),
C(0; 0; 2).
c) Mặt phẳng (Oxy).
d) Mặt phẳng (Oyz).
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 58
Hoạt động 3: Tìm hiểu phương trình tổng quát của mặt phẳng
GV hướng dẫn HS giải bài toán
1.
H1. Nêu điều kiện để M (P)?
GV hướng dẫn nhanh bài toán 2.
GV nêu định nghĩa phương trình
tổng quát của mặt phẳng và
hướng dẫn HS nêu nhận xét.
H2. Chỉ ra một VTPT của (P)?
Đ1. M (P)
0
M M n
Đ2.
( ; ; )n A B C
II. PHƯƠNG TRÌNH TỔNG
QUÁT CỦA MẶT PHẲNG
Bài toán 1: Trong KG Oxyz, cho
mp (P) đi qua
0 0 0 0
( ; ; )M x y z
và
nhận
( ; ; )n A B C
làm VTPT.
Điều kiện cần và đủ để M(x; y; z)
(P) là:
0 0 0
( ) ( ) ( ) 0 A x x B y y C z z
Bài toán 2: Trong KG Oxyz, tập
hợp các điểm M(x; y; z) thoả PT:
0 Ax By Cz D
(A, B, C
không đồng thời bằng 0) là một
mặt phẳng nhận vectơ
( ; ; )n A B C
làm VTPT.
1. Định nghĩa: Phương trình
0 Ax By Cz D
, trong đó
2 2 2
0 A B C
, đgl phương
trình tổng quát của mặt phẳng.
Nhận xét:
a) (P):
0 Ax By Cz D
(P) có 1 VTPT là
( ; ; )n A B C
.
b) PT của (P) qua
0 0 0 0
( ; ; )M x y z
và có VTPT
( ; ; )n A B C
là:
0 0 0
( ) ( ) ( ) 0 A x x B y y C z z
Hoạt động 4: Tìm hiểu các trường hợp riêng của phương trình tổng quát của mặt phẳng
GV hướng dẫn HS xét các
trường hợp riêng.
H1. Khi (P) đi qua O, tìm D?
H2. Phát biểu nhận xét khi một
trong các hệ số A, B, C bằng 0?
Đ1. D = 0
Đ2. Hệ số của biến nào bằng 0 thì
(P) song song hoặc chứa trục ứng
với biến đó.
2. Các trường hợp riêng
a) D = 0
(P) đi qua O.
b) A = 0
()
()
P Ox
P Ox
c) A = B = 0
( ) ( )
( ) ( )
P Oxy
P Oxy
H3. Tìm giao điểm của (P) với
các trục toạ độ?
Đ3. (P) cắt các trục Ox, Oy, Oz
lần lượt tại A(a; 0; 0), B(0; b; 0),
C(0; 0; c).
Nhận xét: Nếu các hệ số A, B, C,
D đều khác 0 thì có thể đưa
phương trình của (P) về dạng:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 59
1
x y z
a b c
(2)
(2) đgl phương trình của mặt
phẳng theo đoạn chắn.
H1. Gọi HS tìm?
H2. Xác định một VTPT của mặt
phẳng?
Đ1.
a)
(4; 2; 6) n
b)
(2;3;0)n
Đ2.
a)
, ( 1;4; 5)


n AB AC
(P):
4 5 2 0 x y z
b) (P):
1
1 2 3
x y z
6 3 2 6 0 x y z
VD1: Xác định một VTPT của
các mặt phẳng:
a)
4 2 6 7 0 x y z
b)
2 3 5 0 xy
VD2: Lập phương trình của mặt
phẳng đi qua các điểm:
a) A(1; 1; 1), B(4; 3; 2), C(5; 2; 1)
b) A(1; 0; 0), B(0; 2; 0), C(0; 0; 3)
Nhấn mạnh:
– Phương trình tổng quát của mặt
phẳng.
– Các trường hợp riêng
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2, 3, 4, 5 SGK.
Đọc tiếp bài "Phương trình mặt phẳng".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 60
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 30 Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
Nắm được sự xác định mặt phẳng. Phương trình tổng quát của mặt phẳng.
Điều kiện để hai mặt phẳng song song, vuông góc.
Kĩ năng:
Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
Xác định được hai mặt phẳng song song, vuông góc.
Tính được khoảng cách từ một điểm đến mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về phương trình mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Tìm các VTPT của hai mặt phẳng:
12
( ): 2 3 1 0, ( ):2 4 6 1 0 P x y z P x y z
?
Đ.
12
(1; 2;3), (2; 4;6) nn
.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai mặt phẳng song song
H1. Xét quan hệ giữa hai
VTPT khi hai mặt phẳng song
song?
H2. Xét quan hệ giữa hai mặt
phẳng khi hai VTPT của chúng
cùng phương?
H3. Nêu điều kiện để
(P
1
)//(P
2
), (P
1
) cắt (P
2
)?
Đ1. Hai VTPT cùng phương.
Đ2. Hai mặt phẳng song song
hoặc trùng nhau.
Đ3. (P
1
)//(P
2
)
1 1 1 2 2 2
12
( ; ; ) ( ; ; )
A B C k A B C
D kD
III. ĐIỀU KIỆN ĐỂ HAI MP
SONG SONG, VUÔNG GÓC
1. Điều kiện để hai mặt phẳng
song song
Trong KG cho 2 mp (P
1
), (P
2
):
1 1 1 1 1
( ): 0 P A x B y C z D
2 2 2 2 2
( ): 0 P A x B y C z D
12
( ) ( )PP
1 1 1 2 2 2
12
( ; ; ) ( ; ; )
A B C k A B C
D kD
12
( ) ( )PP
1 1 1 2 2 2
12
( ; ; ) ( ; ; )
A B C k A B C
D kD
(P
1
) cắt (P
2
)
1 1 1 2 2 2
( ; ; ) ( ; ; )A B C k A B C
VD1: Cho hai mp (P
1
) và (P
2
):
(P
1
):
40 x my z m
(P
2
):
2 ( 2) 4 0 x y m z
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 61
H4. Xác định VTPT của (P)?
1 1 1 1
2 2 2 2
A B C D
A B C D
m = 2
(P
1
) cắt (P
2
) m 2
Đ4. Vì (P) // (Q) nên (P) có
VTPT
(2; 3;1)n
.
(P):
2( 1) 3( 2) 1( 3) 0 x y z
2 3 11 0 x y z
Tìm m để (P
1
) và (P
2
):
a) song song
b) trùng nhau
c) cắt nhau.
VD2: Viết PT mp (P) đi qua
điểm M(1; –2; 3) và song song
với mp (Q):
2 3 5 0 x y z
.
H1. Xét quan hệ giữa hai
VTPT khi hai mp vuông góc?
H2. Xác định điều kiện hai mp
vuông góc?
H2. Xác định cặp VTCP của
(P)?
H3. Xác định VTPT của (P)?
Đ1.
1 2 1 2
( ) ( ) P P n n
Đ2.
1 2 1 2 1 2 1 2
( ) ( ) 0 P P A A B B C C
1
2
m
Đ2. (P) có cặp VTCP là:
( 1; 2;5) AB
và
(2; 1;3)
Q
n
Đ3.
, ( 1;13;5)


PQ
n AB n
(P):
13 5 5 0 x y z
2. Điều kiện để hai mặt phẳng
vuông góc
1 2 1 2 1 2 1 2
( ) ( ) 0 P P A A B B C C
VD3: Xác định m để hai mp
sau vuông góc với nhau:
(P):
2 7 2 0 x y mz
(Q):
3 2 15 0 x y z
VD4: Viết phương trình mp
(P) đi qua hai điểm A(3; 1; –1),
B(2; –1; 4) và vuông góc với
mp (Q):
2 3 1 0 x y z
.
Nhấn mạnh:
– Điều kiện để hai mp song song,
vuông góc.
– Cách lập phương trình mặt
phẳng song song hoặc vuông góc
với mp đã cho.
Cách viết khác của điều kiện để
hai mp song song, trùng nhau.
1 1 1 1
12
2 2 2 2
( ) ( )
A B C D
PP
A B C D
1 1 1 1
12
2 2 2 2
( ) ( )
A B C D
PP
A B C D
4. BÀI TẬP VỀ NHÀ:
Bài 5, 6, 7, 8 SGK.
Đọc tiếp bài "Phương trình mặt phẳng".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 62
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 31 Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
Nắm được sự xác định mặt phẳng. Phương trình tổng quát của mặt phẳng.
Điều kiện để hai mặt phẳng song song, vuông góc.
Kĩ năng:
Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
Xác định được hai mặt phẳng song song, vuông góc.
Tính được khoảng cách từ một điểm đến mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về phương trình mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu điều kiện để hai mặt phẳng song song, trùng nhau, cắt nhau?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu cách tính khoảng cách từ một điểm đến một mặt phẳng
GV hướng dẫn HS chứng
minh định lí.
H1. Xác định toạ độ vectơ
10
MM
?
H2. Nhận xét hai vectơ
10
MM
và
n
?
H3. Tính
10
.M M n
bằng hai
cách?
Đ1.
1 0 0 1 0 1 0 1
( ; ; ) M M x x y y z z
Đ2. Hai vectơ cùng phương.
Đ3.
1 0 1 0
..M M n M M n
=
0 1 0 1 0 1
( ) ( ) ( ) A x x B y y C z z
IV. KHOẢNG CÁCH TỪ
MỘT ĐIỂM ĐẾN MỘT
MẶT PHẲNG
Định lí: Trong KG Oxyz, cho
(P):
0 Ax By Cz D
và
điểm
0 0 0 0
( ; ; )M x y z
.
0 0 0
0
2 2 2
,( )

Ax By Cz D
d M P
A B C
Hoạt động 2: Áp dụng khoảng cách từ một điểm đến một mặt phẳng
H1. Gọi HS tính?
Đ1.
a)
4
( ,( ))
3
d M P
b)
11
( ,( ))
3
d M P
c)
( ,( )) 27d M P
VD1: Tính khoảng cách từ
điểm M đến mp(P):
a) M(1; –2; 13)
(P):
2 2 3 0 x y z
b) M(2; –3; 5)
(P):
2 2 6 0 x y z
c) M(1; –4; –2)
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 63
H2. Nhắc lại cách tính khoảng
cách giữa hai mp song song?
H3. Xác định bán kính mặt cầu
(S)?
H4. Xác định VTPT của (P)?
d)
( ,( )) 2d M P
Đ2. Bằng khoảng cách từ 1
điểm trên mp này đến mp kia.
a) Lấy M(0; 0; –1) (Q).
(( ),( )) ( ,( )) 3d P Q d M P
b) Lấy M(0; 1; 0) (P)
4
(( ),( )) ( ,( ))
9
d P Q d M Q
Đ3. R =
( ,( ))d I P
a)
2 2 2
162
( 3) ( 5) ( 2)
7
x y z
b)
2
2 2 2
23
( 1) ( 4) ( 7)
11



x y z
Đ4.
n IM
a)
(P):
4( 1) 2( 3) 2 0 x y z
b)
( ):6( 7) 2( 1) 3( 5) 0 P x y z
(P):
5 14 0 x y z
d) M(3; 1; –2)
(P) (Oxy)
VD2: Tính khoảng cách giữa
hai mp song song (P) và (Q):
a) (P):
2 2 11 0 x y z
(Q):
2 2 2 0 x y z
b) (P):
4 8 1 0 x y z
(Q):
4 8 5 0 x y z
VD3: Viết pt mặt cầu (S) có
tâm I và tiếp xúc với mp (P):
a)
(3; 5; 2)
( ):2 3 1 0

I
P x y z
b)
(1;4;7)
( ):6 6 7 42 0
I
P x y z
VD4: Viết pt mặt phẳng (P)
tiếp xúc với mặt cầu (S) tại M:
a)
2 2 2
( ):( 3) ( 1) ( 2) 24
( 1;3;0)
S x y z
M
b)
2 2 2
( ):( 1) ( 3) ( 2) 49
(7; 1;5)
S x y z
M
Nhấn mạnh:
– Công thức tính khoảng cách từ 1
điểm đến 1 mặt phẳng.
– Ứng dụng công thức tính
khaongr cách từ 1 điểm đến 1 mp.
4. BÀI TẬP VỀ NHÀ:
Bài 9, 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 64
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 32 - 33
Bài 2: BÀI TẬP PHƯƠNG TRÌNH MẶT PHẲNG
I. MỤC TIÊU:
Kiến thức: Củng cố:
Khái niệm vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
Phương trình tổng quát của mặt phẳng.
Điều kiện để hai mặt phẳng song song, vuông góc.
Kĩ năng:
Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
Xác định được hai mặt phẳng song song, vuông góc.
Tính được khoảng cách từ một điểm đến mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về phương trình mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập lập phương trình mặt phẳng
H1. Nêu công thức? Cần xác
định thêm các yếu tố nào?
H2. Cần xác định các yếu tố
nào?
Đ1.
0 0 0
( ) ( ) ( ) 0 A x x B y y C z z
a) (P):
2 3 5 16 0 x y z
b)
, (2; 6;6) n u v
(P):
3 3 9 0 x y z
c) (P):
1
3 2 1
x y z
d)
, ( 2; 1; 1)


n AC AD
(P):
2 14 0 x y z
Đ2.
a) (P) qua trung điểm I(3; 2; 5)
và có VTPT
(2; 2; 4) AB
(P):
2 9 0 x y z
b)
, (10;9;5)



n AB CD
(P):
10 9 5 74 0 x y z
c)
(2; 1;3)
PQ
nn
(P):
2 3 11 0 x y z
1. Viết ptmp (P):
a) Đi qua M(1; –2; 4) và nhận
(2;3;5)n
làm VTPT.
b) Đi qua A(0; –1; 2) và song
song với giá của mỗi vectơ
(3;2;1), ( 3;0;1) uv
.
c) Đi qua A(–3; 0; 0), B(0; –2;
0), C(0; 0; –1).
d) Đi qua A(5; 1; 3), C(5; 0; 4).
D(4; 0; 6).
2. Viết ptmp (P):
a) Là mp trung trực của đoạn
AB với A(2; 3; 7), B(4; 1; 3).
b) Qua AB và song song với
CD với A(5; 1; 3), B(1; 6; 2),
C(5; 0; 4), D(4; 0; 6).
c) Qua M(2; –1; 2) và song
song với (Q):
2 3 4 0 x y z
d) Qua A(1; 0; 1), B(5; 2; 3) và
vuông góc với (Q):
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 65
d)
, (1;0; 2)


PQ
n AB n
(P):
2 1 0 xz
2 7 0 x y z
.
H1. Nêu đk để hai mp song
song, cắt nhau, trùng nhau?
Đ1.
a) (P)//(Q)
2 3 5
8 6 2

m
n
4
4

m
n
b) (P)//(Q)
3 5 3
2 3 1

m
n
9
2
10
3


m
n
3. Xác định các giá trị của m, n
để mỗi cặp mp sau: song song,
cắt nhau, trùng nhau:
a) (P):
2 3 5 0 x my z
(Q):
8 6 2 0 nx y z
b) (P):
3 5 3 0 x y mz
(Q):
2 3 1 0 x ny z
H1. Nêu công thức tính ?
Hướng dẫn HS cách sử dụng pp
toạ độ để giải toán.
H2. Xác định toạ độ các đỉnh của
hlp?
H3. Viết pt hai mp (ABD) và
(BCD)?
Đ1.
a)
( ,( )) 5d A P
b)
( ,( )) 2d A P
x
y
z
A
B C
D
A’
B’ C’
D’
Đ2. A(0;0;0), B(1;0;0), C(1;1;0),
D(0;1;0), A(0;0;1), B(1;0;1),
C(1;1;1), D(0;1;1)
Đ3.
(ABD):
0 x y z
(BCD):
10 x y z
(ABD) // (BCD)
1
(( ),( ))
3
d AB D BC D
4. Tính khoảng cách từ A(2; 4; –
3) đế các mp sau:
a) (P):
2 2 9 0 x y z
b) (P):
0x
5. Cho hlp ABCD.ABCD có
cạnh bằng 1.
a) CMR hai mp (ABD) và
(BCD) song song với nhau.
b) Tính khoảng cách giữa hai mp
trên.
Nhấn mạnh:
– Cách viết phương trình mặt
phẳng.
– Cách sử dụng công thức tính
khoảng cách từ một điểm đến một
mặt phẳng.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
Chuẩn bị kiểm tra 1 tiết.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 66
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 34 Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN
I. MỤC TIÊU:
Kiến thức:
Nắm được phương trình tham số của đường thẳng.
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
Vị trí tương đối giữa đường thẳng và mặt phẳng.
Kĩ năng:
Viết được phương trình tham số của đường thẳng.
Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng và mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại thế nào là VTCP của đường thẳng, VTPT của mặt phẳng?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu phương trình tham số của đường thẳng
H1. Nêu điều kiện để M ?
GV nêu định nghĩa.
a
M
0
M
Đ1.
M 
0
,M M a
cùng phương
0
M M ta
I. PT THAM SỐ CỦA
ĐƯỜNG THẲNG
Định lí: Trong KG Oxyz, cho
đường thẳng
đi qua điểm
M
0
(x
0
; y
0
; z
0
) và nhận vectơ
1 2 3
( ; ; )a a a a
làm VTCP. Điều
kiện cần và đủ để điểm
M(x;y;z) nằm trên
là có một
số thực t sao cho:
01
02
03



x x ta
y y ta
z z ta
Định nghĩa: Phương trình
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 67
H2. Nhắc lại pt tham số của đt
trong mặt phẳng?
GV nêu chú ý.
Đ2.
01
02


x x ta
y y ta
tham số của đường thẳng
đi
qua điểm M
0
(x
0
; y
0
; z
0
) và có
VTCP
1 2 3
( ; ; )a a a a
là phương
trình có dạng:
01
02
03



x x ta
y y ta
z z ta
trong đó t là tham số.
Chú ý: Nếu a
1
, a
2
, a
3
đều khác
0 thì có thể viết phương trình
của
dưới dạng chính tắc:
0 0 0
1 2 3

x x y y z z
a a a
H1. Gọi HS thực hiện.
H2. Xác định một VTCP và
một điểm của đường thẳng?
H3. Xác định một VTCP của
?
GV hướng dẫn cách xác định
toạ độ một điểm M .
Đ1. Các nhóm thực hiện và
trình bày.
Đ2.
( 1; 1;5) AB
, A(2;3;–1)
PTTS của AB:
2
3
15


xt
yt
zt
Đ3.
Vì (P) nên
an
= (2;–3;6)
PTTS của :
22
43
36


xt
yt
zt
Cho t = t
0
, thay vào PT của .
Với t = 0 M(–1; 3; 5)
VD1: Viết PTTS của đường
thẳng đi qua điểm M
0
và có
VTCP
a
, với:
a)
(1;2; 3), ( 1;3;5) Ma
b)
(0; 2;5), (0;1;4)Ma
c)
(1;3; 1), (1;2; 1) Ma
d)
(3; 1; 3), (1; 2;0) Ma
VD2: Cho các điểm A(2;3;–1),
B(1; 2; 4), C(2; 1; 0), D(0;1;2).
Viết PTTS của các đường
thẳng AB, AC, AD, BC.
VD3: Viết PTTS của đi qua
điểm A và vuông góc với mặt
phẳng (P):
a)
( 2;4;3), ( ):2 3 6 19 0 A P x y z
b)
(3;2;1), ( ): 2 5 4 0 A P x y
c) A(1; –1; 0), (P)(Oxy)
d) A(2; –3; 6), (P)(Oyz)
VD4: Cho đường thẳng có
PTTS. Hãy xác định một điểm
M và một VTCP của .
:
12
33
54


xt
yt
zt
Nhấn mạnh:
– Các dạng PTTS và PTCT của
đường thẳng
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 68
4. BÀI TẬP VỀ NHÀ:
Bài 1, 2 SGK.
Đọc tiếp bài "Phương trình đường thẳng trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 35 Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được phương trình tham số của đường thẳng.
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
Vị trí tương đối giữa đường thẳng và mặt phẳng.
Kĩ năng:
Viết được phương trình tham số của đường thẳng.
Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu cách viết PTTS của đường thẳng?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai đường thẳng song song
H1. Nhắc lại các VTTĐ của 2
đường thẳng trong KG?
H2. Nêu điều kiện để hai
M
d
d’
a
a
Đ1. song song, cắt nhau, trùng
nhau, chéo nhau.
Đ2. d và d không có điểm
II. ĐIỀU KIỆN ĐỂ HAI
ĐƯỜNG THẲNG SONG
SONG, CẮT NHAU, CHÉO
NHAU
1. Điều kiện để hai đường
thẳng song song
Gọi
1 2 3 1 2 3
( ; ; ), ( ; ; )
a a a a a a a a
lần lượt là VTCP của d và d
.
Lấy M(x
0
; y
0
; z
0
)
d.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 69
đường thẳng song song?
chung và hai VTCP cùng
phương.
d // d

a ka
Md
d
d

a ka
Md
H1. Xác định các VTCP của d
và d?
H2. Lấy 1 điểm M d, chứng
tỏ M d?
H3. Xác định VTCP của ?
H4. Xác định VTCP của d?
Đ1.
(1;2; 1)a
,
(2;4; 2)
a
,
aa
cùng phương.
Đ2. M(1; 0; 3) d
M d.
Đ3.
Vì // d nên cũng nhận
VTCP của d làm VTCP.
Đ4.
a)
( 3;4; 2) a
b)
(4; 2;3)a
c)
(4;2;3)a
d)
(2;3;4)a
VD1: Chứng minh hai đường
thẳng sau song song song:
a)
22
1
: 2 ; : 2 4
3
52





xt
xt
d y t d y t
zt
zt
b)
12
12
: 2 ; : 2
32
32



xt
xt
d y t d y t
zt
zt
c)
1 2 3
:
9 6 3
7 6 5
:
6 4 2


x y z
d
x y z
d
d)
21
:
4 6 8
72
:
6 9 12





x y z
d
x y z
d
VD2: Viết phương trình đường
thẳng đi qua điểm A và song
song với đường thẳng d cho
trước:
a) A(2; –5; 3), d:
23
34
52



xt
yt
zt
b) A(1; –3; 2), d:
34
22
31



xt
yt
zt
c) A(4; –2; 2),
d:
2 5 2
4 2 3

x y z
d) A(5; 2; –3),
d:
3 1 2
2 3 4

x y z
Nhấn mạnh:
– Điều kiện để hai đường thẳng
song song, trùng nhau.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 70
– Cách xác định một điểm nằm
trên đường thẳng.
4. BÀI TẬP VỀ NHÀ:
Bài 3 SGK.
Đọc tiếp bài "Phương trình đường thẳng trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 36 Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được phương trình tham số của đường thẳng.
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
Vị trí tương đối giữa đường thẳng và mặt phẳng.
Kĩ năng:
Viết được phương trình tham số của đường thẳng.
Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu điều kiện để hai đường thẳng song song, trùng nhau?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai đường thẳng cắt nhau
H1. Hai đường thẳng cắt nhau
có mấy điểm chung?
Đ1. 1 điểm chung duy nhất.
II. ĐIỀU KIỆN ĐỂ HAI ĐT
SONG SONG, CẮT NHAU,
CHÉO NHAU
2. Điều kiện để hai đường
thẳng cắt nhau
Cho 2 đường thẳng
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 71
d:
01
02
03



x x ta
y y ta
z z ta
, d
:
''
01
''
02
''
03



x x t a
y y t a
z z t a
d và d
cắt nhau
hệ pt ẩn t,
t
sau có đúng 1 nghiệm:
''
0 1 0 1
''
0 2 0 2
''
0 3 0 3
x ta x t a
y ta y t a
z ta z t a
(*)
Chú ý: Giả sử hệ (*) có
nghiệm, để tìm toạ độ giao
điểm M
0
của d và d
ta có thể
thay t
0
vào PTTS của d hoặc
thay t
0
vào PTTS của d
.
H1. Gọi HS thực hiện.
H2. Nêu điều kiện để hai
đường thẳng cắt nhau?
Đ1. Các nhóm thực hiện và
trình bày.
Đ2. Hệ phương trình có
nghiệm duy nhất.
VD1: Tìm giao điểm của hai
đường thẳng sau:
a)
22
1
: 2 3 , : 2
3
13





xt
xt
d y t d y t
zt
zt
b)
1
: 2 2
1
1 2 1
:
3 1 1




xt
d y t
zt
x y z
d
c)
1
3
: 1 2 , : 2
3
4




xt
xt
d y t d y t
zt
zt
d)
5
32
: 2 3 , : 1 4
64
20




xt
xt
d y t d y t
zt
zt
VD2: Tìm m để hai đường
thẳng d và d cắt nhau. Khi đó
tìm toạ độ giao điểm của chúng
a)
1
1
: , : 2 2
12
3




xt
x mt
d y t d y t
zt
zt
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 72
b)
2
1
: 3 2 , : 1
23





xt
xt
d y t d y t
z m t
zt
Hoạt động 3: Củng cố
Nhấn mạnh:
– Điều kiện để hai đường thẳng
cắt nhau.
– Cách tìm giao điểm của hai
đường thẳng cắt nhau.
4. BÀI TẬP VỀ NHÀ:
Bài 3, 4 SGK.
Đọc tiếp bài "Phương trình đường thẳng trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 37 Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt)
I. MỤC TIÊU:
Kiến thức:
Nắm được phương trình tham số của đường thẳng.
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
Vị trí tương đối giữa đường thẳng và mặt phẳng.
Kĩ năng:
Viết được phương trình tham số của đường thẳng.
Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu điều kiện để hai đường thẳng song song, trùng nhau, cắt nhau?
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai đường thẳng cắt nhau
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 73
H1. Nêu điều kiện để hai
đường thẳng chéo nhau?
d
d’
a
a
Đ1. Không cùng phương và
không cắt nhau.
II. ĐIỀU KIỆN ĐỂ HAI ĐT
SONG SONG, CẮT NHAU,
CHÉO NHAU
3. Điều kiện để hai đường
thẳng chéo nhau
Cho 2 đường thẳng
d:
x x ta
y y ta
z z ta
01
02
03



, d
:
x x t a
y y t a
z z t a
''
01
''
02
''
03



d và d
chéo nhau
hai VTCP
không cùng phương và hệ pt ẩn
t, t
sau vô nghiệm:
x ta x t a
y ta y t a
z ta z t a
''
0 1 0 1
''
0 2 0 2
''
0 3 0 3
(*)
d
d
aa
H1. Gọi HS thực hiện.
GV hướng dẫn cách viết
phương trình đường vuông góc
chung của hai đường thẳng
chéo nhau.
Đ1. Các nhóm thực hiện và
trình bày.
Lấy M d, N d
Từ điều kiện
MN d
MN d
, ta tìm
được M, N.
Khi đó đường vuông góc
chung là đường thẳng MN.
VD1: Chứng tỏ các cặp đường
thẳng sau chéo nhau:
a)
xt
xt
d y t d y t
zt
zt
13
12
: 1 3 , : 2 2
5
12




b)
xt
xt
d y t d y t
zt
zt
2
12
: 3 , : 1
23
32



c)
x y z
d
x y z
d
21
:
3 2 2
11
:
1 2 4




d)
x y z
d
x y z
d
7 3 9
:
1 2 1
3 1 1
:
7 2 3


VD2: Chứng tỏ các đường
thẳng sau chéo nhau? Viết
phương trình đường vuông góc
chung của 2 đường thẳng đó:
a)
xt
xt
d y t d y t
zt
zt
23
32
: 1 4 , : 4
24
12




Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 74
b)
xt
xt
d y t d y t
zt
zt
23
12
: 3 , : 1 2
23
44



Hoạt động 3: Tìm hiểu VTTĐ giữa đường thẳng và mặt phẳng
H1. Nêu các trường hợp về
VTTĐ giữa đường thẳng và
mặt phẳng?
H2. Nêu mối quan hệ giữa số
giao điểm và VTTĐ của đt,
mp?
Đ1.
d // (P), d cắt (P), d (P)
Đ2.
d // (P) 0 giao điểm
d cắt (P) 1 giao điểm
d (P) vô số giao điểm
*) VTTĐ GIỮA ĐƯỜNG
THẲNG VÀ MẶT PHẲNG
Cho (P):
Ax By Cz D 0
,
d:
x x ta
y y ta
z z ta
01
02
03



.
Xét phương trình:
A x ta B y ta
C z ta D
0 1 0 2
03
( ( )
( ) 0
(1)
Nếu (1) vô nghiệm thì d // (P)
Nếu (1) có đúng 1 nghiệm t
0
thì d cắt (P) tại điểm M
0
.
Nếu (1) có vô số nghiệm thì d
thuộc (P).
Hoạt động 4: Áp dụng xét VTTĐ của đường thẳng và mặt phẳng
H1. Lập phương trình và giải?
H2. Nêu cách xét?
Đ1. Các nhóm thực hiện và
trình bày.
a)
tt(2 ) (3 ) 1 3 0
4 = 0 PT vô nghiệm
d // (P)
b)
ttt(1 2 ) (1 ) (1 ) 3 0
0 = 0 PT vô số nghiệm
d (P)
c)
t t t(1 5 ) (1 4 ) (1 3 ) 3 0
4t = 0 PT có nghiệm t = 0
d cắt (P) tại A(1; 1; 1)
Đ2.
C1: Dựa vào mối quan hệ giữa
VTCP của d và VTPT của (P).
C2: Dựa vào số nghiệm của hệ
phương trình
d
P()
.
VD1: Tìm số giao điểm của
mặt phẳng (P):
x y z 30
và đường thẳng d:
a) d:
xt
yt
z
2
3
1


b) d:
xt
yt
zt
12
1
1



c) d:
xt
yt
zt
15
14
13



VD2: Xét VTTĐ của đường
thẳng d và mặt phẳng (P):
a)
d x t y t z t
P x y z
: 2 ; 1 ; 3
( ): 10 0
b)
d x t y t z t
P x y z
: 3 2; 1 4 ; 4 5
( ): 4 3 6 5 0
c)
x y z
d
P x y z
12 9 1
:
4 3 1
( ):3 5 2 0

Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 75
H3. Nêu điều kiện ứng với
từng trường hợp?
Đ3.
d cắt (P)
an
d // (P)
an
MP
0
()
(M
0
d)
d (P)
an
MP
0
()
(M
0
d)
d (P)
an,
cùng phương
VD3: Cho đường thẳng d và
mặt phẳng (P). Tìm m, n để:
i) d cắt (P) ii) d // (P)
iii) d (P) iv) d (P)
a)
x y z
d
mm
P x y z
1 2 3
:
2 1 2
( ): 3 2 5 0

b)
d x t y t z t
P m x y z n
: 3 4 ; 1 4 ; 3
( ):( 1) 2 4 9 0
Nhấn mạnh:
– Các trường hợp về VTTĐ của
đường thẳng và mặt phẳng.
– Cách tìm giao điểm của đường
thẳng và mặt phẳng.
4. BÀI TẬP VỀ NHÀ:
Bài 5, 6, 7, 8, 9, 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy:38
Bài 3: BÀI TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN
I. MỤC TIÊU:
Kiến thức: Củng cố:
Phương trình tham số của đường thẳng.
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
Vị trí tương đối giữa đường thẳng và mặt phẳng.
Kĩ năng:
Viết được phương trình tham số của đường thẳng.
Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 76
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập viết phương trình tham số của đường thẳng
H1. Nêu điều kiện xác định
PTTS của đường thẳng?
H2. Nêu cách xác định hình
chiếu d của d trên (P)?
Đ1. Biết được 1 điểm và 1
VTCP.
a) d:
xt
yt
zt
52
43
1



b) d:
xt
yt
zt
2
1
3


c) d:
xt
yt
zt
22
3
34

d) d:
xt
yt
zt
13
22
3



Đ2.
Xác định (Q) d, (Q) (P).
– M
0
d M
0
(Q)
–
Q P d
n n a,


Xác định d = (P) (Q)
d là h.chiếu của d trên (P).
– Lấy M (P)(Q) M d
–
d P Q
a n n
'
,


a) d:
xt
yt
z
2
32
0

b) d:
x
yt
zt
0
32
13

1. Viết PTTS của đường thẳng
d trong mỗi trường hợp sau:
a) d đi qua M(5; 4; 1) và có
VTCP
a (2; 3;1)
.
b) d đi qua điểm A(2; –1; 3) và
vuông góc (P):
x y z 50
c) d đi qua B(2; 0; –3) và song
song với :
xt
yt
zt
12
33
4

d) d đi qua P(1; 2; 3),Q(4; 4; 4)
2. Viết PTTS của đường thẳng
d là hình chiếu vuông góc của
đường thẳng d:
xt
yt
zt
2
32
13


lần
lượt trên các mặt phẳng (P):
a) (P) (Oxy) b) (P) (Oyz)
Hoạt động 2: Luyện tập xét VTTĐ của hai đường thẳng
H1. Nêu cách xét VTTĐ của
hai đường thẳng?
Đ1.
C1: Xét quan hệ hai VTCP
C2: Xét số nghiệm của hệ PT
a) d và d cắt nhau tại M(3; 7;
18)
b) d // d
c) d và d chéo nhau
3. Xét VTTĐ của các cặp đt:
a) d:
xt
yt
zt
32
23
64

, d:
xt
yt
zt
5
14
20


b) d:
xt
yt
zt
1
2
3



, d:
xt
yt
zt
12
12
22


Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 77
c) d:
xt
yt
zt
1
22
3


, d:
xt
yt
z
1
32
1


H1. Nêu cách tìm?
Đ1.
Giải hệ pt:
d
P()
, từ số nghiệm
suy ra số giao điểm của d và
(P).
a) d cắt (P) tại (0; 0; –2)
b) d // (P)
c) d (P)
4. Tìm số giao điểm của đường
thẳng d với mặt phẳng (P):
a) d:
xt
yt
zt
12 4
93
1



,
(P):
x y z3 5 2 0
b) d:
xt
yt
zt
1
2
12



,
(P):
x y z3 1 0
c) d:
xt
yt
zt
1
12
23



(P):
x y z 40
Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ:
Bài tập thêm.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 78
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 39
Bài 3: BÀI TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt)
I. MỤC TIÊU:
Kiến thức: Củng cố:
Phương trình tham số của đường thẳng.
Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
Vị trí tương đối giữa đường thẳng và mặt phẳng.
Kĩ năng:
Viết được phương trình tham số của đường thẳng.
Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập tìm điểm đối xứng của 1 điểm qua 1 đường thẳng
H1. Xác định 1 VTCP của ?
H2. Nêu cách xác định điểm
H?
H3. Nêu cách xác định điểm
A?
H4. Xác định khoảng cách từ
A đến ?
Đ1.
a (1;2;1)
Đ2.
H
AH a
H t t t
AH a
(2 ;1 2 ; )
.0

t
1
2

H
31
;0;
22



Đ3.
H là trung điểm của AA
A
A
A
x
AA AH y
z
'
'
'
2
20
1

Đ4.
d(A, ) = AH
1. Cho điểm A(1; 0; 0) và
đường thẳng :
xt
yt
zt
2
12


a) Tìm toạ độ điểm H là hình
chiếu của A trên .
b) Tìm toạ độ điểm A đối
xứng với A qua .
c) Tính khoảng cách từ A đến
.
Hoạt động 2: Luyện tập tìm điểm đối xứng của 1 điểm qua 1 mặt phẳng
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 79
H1. Nêu cách xác định điểm
H?
H2. Nêu cách xác định điểm
M?
H3. Nhắc lại công thức tính
khoảng cách từ 1 điểm đến mặt
phẳng?
Đ1.
– Xác định đi qua M và
vuông góc với (P).
:
x t y t z t1 ; 4 ; 2
– H là giao điểm của và (P)
H(–1; 2; 0)
Đ2.
H là trung điểm của MM
MM MH2
M(–3;0;–2)
Đ3.
d(M, (P)) =
Ax By Cz D
A B C
0 0 0
2 2 2

2. Cho điểm M(1; 4; 2) và mặt
phẳng (P):
x y z 10
.
a) Tìm toạ độ điểm H là hình
chiếu vuông góc của điểm M
trên mặt phẳng (P).
b) Tìm toạ độ điểm M đối
xứng với M qua (P).
c) Tính khoảng cách từ M đến
(P).
GV hướng dẫn cách chọn hệ
trục toạ độ.
H1. Xác định toạ độ của hình
lập phương?
H2. Lập phương trình các mặt
phẳng (ABD), (BDC)?
H3. Tính khoảng cách từ A đến
các mặt phẳng (ABD),
(BDC)?
Chọn hệ toạ độ Oxyz sao cho:
O A,
i AB j AD k AA,,
Đ1. A(0; 0; 1), B(1; 0; 0),
D(0; 1; 0), B(1; 0; 1),
D(0; 1; 1), C(1; 1; 0)
Đ2.
(ABD):
x y z 10
(BDC):
x y z 20
Đ3.
d(A, (ABD)) =
1
3
d(A, (BDC)) =
2
3
3. Cho hình lập phương
ABCD.ABCD có cạnh bằng
1. Tính khoảng cách từ đỉnh A
đến các mặt phẳng (ABD) và
(BDC).
Nhấn mạnh:
– Cách vận dụng phương trình
đường thẳng, mặt phẳng để giải
toán.
– Cách giải toán HHKG bẳng
phương pháp toạ độ.
4. BÀI TẬP VỀ NHÀ:
Bài tập ôn HK 2.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 80
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 40 -41
ÔN TẬP CHƯƠNG III
I. MỤC TIÊU:
- Về kiến thức:
+ Học sinh nắm vững hệ tọa độ trong không gian, tọa độ của véc tơ , của điểm, phép toán
về véc tơ.
+ Viết được phương trình mặt cầu, phương trình đường thẳng và vị trí tương đối của chúng.
+ Tính được các khoảng cách: giữa hai điểm, từ một điểm đến mặt phẳng.
- Về kiến thức:
+ Rèn luyện kỹ năng làm toán trên véc tơ.
+ Luyện viết phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng.
+ Phối hợp các kiến thức cơ bản, các kỹ năng cơ bản để giải các bài toán mang tính tổng
hợp bằng phương pháp tọa độ.
- Về tư duy và thái độ:
+ Rèn luyện tính chính xác, tư duy lôgíc.
+ Rèn khả năng quan sát sự liên hệ giữa song song và vuông góc.
II/ CHUẨN BỊ:
- Giáo viên: Giáo án, phiếu học tập, bảng phụ.
- Học sinh: giải bài tập ôn chương, các kiến thức cơ bản trong chương.
III/ PHƯƠNG PHÁP: Hỏi đáp , hoạt động nhóm.
IV/ TIẾN TRÌNH BÀI HỌC:
1/ Ổn định tổ chức:
2/ Kiểm tra bài cũ:
3/ Bài mới:
tiết 40
Hoạt động 1:
Hoạt động của học sinh
Hoạt động của giáo viên
Nội dung ghi bảng
-Treo bảng phụ 1
-Gọi 2 học sinh lên bảng
giải bài tập 1a; 1b
-Nhẩm, nhận xét , đánh giá
-Hỏi để học sinh phát hiện
ra cách 2:
ADACAB ,,
không
đồng phẳng
-Hỏi: Khoảng cách từ A
đến(BCD) được tính như
thế nào?
-Phát phiếu HT1
-Làm bài tập1
-Hai học sinh được lên bảng.
-Lớp theo dõi; nhận xét, nêu
ý kiến khác.
-Trả lời câu hỏi và áp dụng
vào bài tập 1c.
-Nhận phiếu HT1 và trả lời
BT1:
a/P/trình mp(BCD):
x-2y-2z+2 = 0 (1)
Tọa độ điểm A không thỏa
mãn phương trình mp(1) nên
A không thuộc mặt phẳng
(BCD)
b/
Cos(AB,CD)=
2
2
.
.
CDAB
CDAB
Vậy (AB,CD)= 45
0
c/ d(A, (BCD)) = 1
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 81
Hoạt động 2:
Hoạt động của học sinh
Hoạt động của giáo viên
Nội dung ghi bảng
BT4:
- Hướng dẫn gợi ý học sinh
làm .
Câu hỏi: Tìm véctơ chỉ
phương của đường thẳng
AB? ∆?
BT 6:
a/Gợi ý, hướng dẫn để học
sinh tự tìm ra cách giải
bài 6a
b/ Hỏi
d)(
quan hệ
giữa
n
và
d
u
?
BT2: Nêu phương trình mặt
cầu?
-Tìm tâm và bán kính r của
(S) ở bài tập 2a
-Gợi mở để h/s phát hiện ra
hướng giải bài 2c
- Hai học sinh lên bảng
giải bài tập 4a; 4b
- Theo dõi, nhận xét
- Từ hướng dẫn của giáo
viên rút ra cách tìm giao
điểm của đường và mặt.
Suy nghĩ, trả lời, suy ra
hướng giải quyết bài tập
6b.
Trả lời câu hỏi của giáo
viên, trình bày bài giải lên
bảng.
Suy ra hướng giải bài 2c
BT4:
a/
AB
= (2;-1;3); phương
trình đường thẳng AB:
3t 3- z
t- y
2t 1 x
b/(∆) có vécctơ chỉ phương
)5;4;2(
u
và đi qua M nên
p/trình tham số của (
):
)(
5t - 5- z
4t- 3 y
2t 2 x
Rt
BT6: a/Toạ độ giao điểm của
đường thẳng d và mp
)(
là
nghiệm của hệ phương trình:
02-z-5y3x
t 1 z
3t 9 y
4t 12 x
ĐS: M(0; 0; -2)
b/ Ta có vtpt của mp
)(
là:
)1;3;4(
d
un
.P/t mp
)(
:
4(x- 0)+ 3(y- 0)+ (z+ 2)= 0
4x + 3y + z +2 = 0.
BT2:a/ Tâm I(1, 1, 1)
Bán kính
62r
.
b/(S):(x-1)
2
+(y-1)
2
+(z-1)
2
=62
c/ Mp
)(
tiếp xúcvới mặt
cầu(S) tại A, Suy ra
)(
có
vtpt là
)6;1;5( IA
. vậy
phương trình của mp
)(
là:
5(x-6) + 1(y-2) – 6(z+5)=0
Hay 5x + y – 6z – 62 = 0.
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 82
tiết 41
Hoạt động 3:
Bài toán vận dụng kiến thức tổng hợp
BT7: Gọi 2 h/sinh lên bảng
giải bài tập 7a, 7b.
-Theo dõi, nhận xét, đánh
giá
Vẽ hình, gợi mở để h/sinh
phát hiện ra đ/thẳng
A
d
M
BT9 Vẽ hình, hướng dẫn
học sinh nhận ra hình chiếu
H của M trên mp
)(
và cách
xác định H
M
H
Hai h/sinh lên bảng giải.
Lớp theo dõi, nhận xét.
Quan sát, theo dõi đễ phát
hiện
u
Theo dõi, suy nghĩ nhìn ra
H và cách tìm H
BT7:
a/ Pt mp
)(
có dạng:
6(x+1) – 2(y-2) – 3(z+3) = 0
Hay 6x -2y - 3z +1 = 0
b/ ĐS M(1; -1; 3).
c/ Đường thẳng
thoả mãn
các yêu cầu của đề bài chính
là đường thẳng đi qua A và
M. Ta có
)6;3;2( MA
.
Vậy p/trình đường thẳng
:
)(
6t3 z
3t- 1- y
2t 1 x
Rt
BT9 Gọi d là đường thẳng
qua M và vuông góc với
mp
)(
, pt đt (d) là:
)(
2t2 z
t- 1- y
2t 1 x
Rt
d cắt
)(
tại H. Toạ độ của H
là nghiệm của hệ:
)(
0112zy2x
2t2 z
t- 1- y
2t 1 x
Rt
Suy ra H(-3; 1; -2).
Hoạt động 4:
Hướng dẫn những bài tập 10, 11,12.
BT 11:
-Treo bảng phụ 2
Oxz
M
d
M'
d'
- Nhìn bảng phụ
- Theo dõi, suy nghĩ và
tìm ra cách giải
bài tập 11.
Nhìn hình ,suy nghĩ và
tìm ra cách giải.
BT 11
)0;1;0(uxy)O(
j
cắt d
g/điểm M(t; -4+t; 3-t)
cắt d
’
g/điểm
N(1-2t’;-3+t’;4-5t’)
Suy ra
jkMN
p/trình
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 83
- Hướng dẫn, gợi ý học sinh
phát hiện ra hướng giải bài
tập 11
BT12
-Vẽ hình
-Gợi mở, hướng dẫn học
sinh tìm ra cách giải bt này.
Phát phiếu HT2
-Nhận phiếu và trả lời
BT12
- Tìm hình chiếu H của A trên
-A
’
là điểm đối xứng của A qua
Khi H là trung điểm AA
/
.
Từ đó suy toạ độ A
/
.
4/ Củng cố toàn bài:
- Các yếu tố cần thiết để lập phương trình: đường thẳng, mặt phẳng, mặt cầu.
- Cách xác định điểm đối xứng của M qua mp
)(
, qua đường thẳng
5/ Bài tập về nhà : Hoàn thành bài tập 8; 11; 12.
V/ PHỤ LỤC
Phiếu HT 1:
Cho
)6;0;3( a
;
)0;4;2( b
. Chọn mệnh đề sai:
A.
)6;12;3(3 ba
B.
)0;0;6(. ba
C. Cos(
5
1
), ba
D.
6. ba
Phiếu HT 2:
1/ Phương trình mặt cầu đường kính AB với A(4, -3, 7); B(2, 1, 3) là:
A. (x+3)
2
+ (y-1)
2
+ (z+5)
2
= 9 B. (x+3)
2
+ (y-1)
2
+ (z+5)
2
= 35
C. (x- 3)
2
+ (y+1)
2
+ (z-5)
2
= 9 D. (x- 3)
2
+ (y+1)
2
+ (z-5)
2
= 35.
2/ Phương trình mặt phẳng qua A(1, 2, 3) và song song với mặt phẳng (P): x + 2y – 3z = 0 là:
A. x + 2y – 3z – 4 = 0 B. x + 2y – 3z + 7 = 0
C. x + 2y – 3z + 4 = 0 D. x + 2y – 3z – 7 = 0
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 84
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 42 Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG III
I. MỤC TIÊU:
Kiến thức: Củng cố:
Biểu thức toạ độ của các phép toán vectơ trong KG.
Phương trình mặt cầu.
Khái niệm vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
Phương trình tổng quát của mặt phẳng.
Điều kiện để hai mặt phẳng song song, vuông góc.
Kĩ năng:
Thành thạo các phép tính về biểu thức toạ độ của các phép toán vectơ trong KG.
Biết lập phương trình mặt cầu.
Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
Xác định được hai mặt phẳng song song, vuông góc.
Tính được khoảng cách từ một điểm đến mặt phẳng.
Thái độ:
Rèn luyện tính cẩn thận, chính xác.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về toạ độ vectơ, phương trình mặt cầu, mặt phẳng.
III. MA TRẬN ĐỀ:
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Tổng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Toạ độ của điểm và
vectơ
2
0,5
1
0,5
1
2,0
3,5
Phương trình mặt cầu
1
0,5
1
0,5
1
2,0
3,0
Phương trình mặt
phẳng
2
0,5
1
0,5
1
2,0
3,5
Tổng
2,5
1,5
4,0
2,0
10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm)
Câu 1: Cho 2 điểm A(1; 2; –3) và B(6; 5; –1). Nếu OABC là hình bình hành thì toạ độ điểm C là:
A) (5; 3; 2) B) (–5;–3;–2) C) (3;5;–2) D) (–3;–5;–2)
Câu 2: Cho các vectơ
(1;2;3); ( 2;4;1); ( 1;3;4) a b c
. Vectơ
2 3 5v a b c
có toạ độ là:
A) (7; 3; 23) B) (23; 7; 3) C) (3; 7; 23) D) (7; 23; 3)
Câu 3: Cho 3 điểm A(2; 1; 4), B(–2; 2; –6), C(6; 0; –1). Tích
AB AC.
bằng:
A) –67 B) 65 C) 67 D) 33
Câu 4: Cho mặt cầu (S):
x y z x y z
2 2 2
8 4 2 4 0
. Bán kính R của mặt cầu (S) là:
A) R = 2 B) R =
88
C) R = 5 D) R =
17
Câu 5: Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là:
A)
x y z
2 2 2
( 3) ( 1) 9
B)
x y z
2 2 2
( 3) ( 1) 9
C)
x y z
2 2 2
( 3) ( 1) 9
D)
x y z
2 2 2
( 3) ( 1) 3
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 85
Câu 6: Cho 3 điểm A(1; –2; 1), B(–1; 3; 3), C(2; –4; 2). Một VTPT
n
của mặt phẳng (ABC) là:
A)
n ( 1;9;4)
B)
n (9;4; 1)
C)
n (9;4;1)
D)
n (4;9; 1)
Câu 7: Cho hai mặt phẳng song song (P):
nx y z7 6 4 0
và (Q):
x my z3 2 7 0
. Khi đó
giá trị của m và n là:
A)
mn
7
;9
3

B)
mn
3
;9
7

C)
mn
7
;1
3

D)
nm
7
;9
3

Câu 8: Khoảng cách giữa hai mặt phẳng (P):
x y z2 3 5 0
và (Q):
x y z2 3 1 0
bằng:
A)
6
14
B)
4
14
C) 4 D) 6
II. Phần tự luận: (6 điểm) Trong không gian Oxyz, cho tứ diện ABCD với A(1; 6; 2), B(5; 1; 3),
C(4; 0; 6), D(5; 0; 4).
a) Xác định toạ độ trọng tâm G của tam giác ABC. So sánh các vectơ
DA DB DC
và
DG
.
b) Viết phương trình mặt phẳng (ABC).
c) Viết phương trình mặt cầu (S) có tâm D và tiếp xúc với mặt phẳng (ABC).
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
A
C
D
C
C
B
A
B
B. Phần tự luận: Mỗi câu 2 điểm
a)
G
10 7 11
;;
3 3 3



(1 điểm)
DA DB DC DG3
(1 điểm)
b)
AB AC(4; 5;1), (3; 6;4)
(0,5 điểm)
n AB AC, ( 14; 13; 9)


(0,5 điểm)
mp(ABC):
x y z14 13 9 110 0
(1 điểm)
c) d(D,(ABC)) =
4
446
(1 điểm)
(S):
x y z
2 2 2
8
( 5) ( 4)
223
(1 điểm)
VI. KẾT QUẢ KIỂM TRA:
Lớp
Sĩ số
0 – 3,4
3,5 – 4,9
5,0 – 6,4
6,5 – 7,9
8,0 – 10
SL
%
SL
%
SL
%
SL
%
SL
%
12S1
53
12S2
53
12S3
54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 86
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 43 - 44 ÔN CUỐI NĂM
I. MỤC TIÊU:
Kiến thức: Củng cố:
Hệ toạ độ trong không gian.
Phương trình mặt cầu.
Phương trình mặt phẳng.
Phương trình đường thẳng.
Khoảng cách.
Kĩ năng:
Thực hiện các phép toán trên toạ độ của vectơ.
Lập phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng.
Dùng phương pháp toạ độ tính được các loại khoảng cách cơ bản trong không gian.
Giải các bài toán hình học không gian bằng phương pháp toạ độ.
Thái độ:
Liên hệ được với nhiều vấn đề trong thực tế với bài học.
Phát huy tính độc lập, sáng tạo trong học tập.
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về toạ độ trong không gian.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh
Nội dung
Hoạt động 1: Luyện tập vận dụng phương trình mặt phẳng
H1. Nêu cách chứng minh 4
điểm tạo thành tứ diện?
H2. Nêu cách tính góc giữa hai
đường thẳng?
H3. Nêu cách tính độ dài
đường cao của hình chóp
A.BCD?
H4. Nêu điều kiện để (P) cắt
(S) theo một đường tròn?
H5. Nêu cách xác định tâm J
Đ1. Chứng minh 4 điểm không
đồng phẳng.
– Viết ptmp (BCD)
(BC):
x y z2 2 2 0
– Chứng tỏ A (BCD).
Đ2.
AB CD
AB CD
AB CD
.2
cos ,
.2

(AB, CD) = 45
0
.
Đ3. h = d(A, (BCD)) = 1
Đ4. d(I, (P)) < R
1. Cho 4 điểm A(1; 0; 0), B(0;
1; 0), C(0; 0; 1), D(–2; 1; –1).
a) Chứng minh A, B, C, D là 4
đỉnh của 1 tứ diện.
b) Tìm góc giữa hai đường
thẳng AB và CD.
c) Tính độ dài đường cao của
hình chóp A.BCD.
2. Cho mặt cấu (S):
x y z
2 2 2
( 3) ( 2) ( 1) 100
và mặt phẳng (P):
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 87
của đường tròn (C)?
H6. Tính bán kính R của (C)?
Đ5. J là hình chiếu của I trên
(P) J(–1; 2; 3)
Đ6. R =
Rd
22
= 8
x y z2 2 9 0
Mặt phẳng (P) cắt (S) theo một
đường tròn (C). Hãy xác định
toạ độ tâm và bán kính của (C).
H1. Nêu công thức ptmp?
H2. Nêu cách tìm giao điểm
của d và (P)?
H3. Nêu cách xác định ?
H4. Nêu cách xác định đường
thẳng ?
Đ1.
A x x B y y C z z
0 0 0
( ) ( ) ( ) 0
(P):
x y z6 2 3 1 0
Đ2. Giải hệ pt
d
P()
M(1; –1; 3)
Đ3. chính là đường thẳng
AM :
xt
yt
zt
12
13
36


Đ4.
– (Oxz) có VTCP
j (0;1;0)
– Gọi M(t; –4+t; 3–t),
M((1–2t; –3+t; 4–5t)
lần lượt là giao điểm của với
d và d.
MM kj
tt
t t k
tt
1 2 0
1
1 5 0
t
t
3
7
2
7
M
3 25 18
;;
7 7 7



:
x y t z
3 25 18
;;
7 7 7
3. Cho điểm A(–1; 2; –3),
vectơ
a (6; 2; 3)
và đường
thẳng d:
xt
yt
zt
13
12
35


.
a) Viết ptmp (P) chứa điểm A
và vuông góc với giá của
a
.
b) Tìm giao điểm của d và (P).
c) Viết ptđt đi qua A, vuông
góc với giá của
a
và cắt d.
4. Viết ptđt vuông góc với
mp(Oxz) và cắt hai đường
thẳng:
d:
xt
yt
zt
4
3

, d:
xt
yt
zt
12
3
45


Nhấn mạnh:
– Cách vận dụng phương trình
đường thẳng, mặt phẳng để giải
toán.
4. BÀI TẬP VỀ NHÀ:
Chuẩn bị kiểm tra HK 2.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Trường THPT Nà Chì năm học 2011 - 2012 Giáo án Hình học12 chuẩn
GV: Phạm Việt Phương 88
Ngày dạy
Tiết dạy
Lớp dạy
Tên HS vắng mặt
12A1
Tiết dạy: 45 Bài dạy: KIỂM TRA HỌC KÌ 2
I. MỤC TIÊU:
Kiến thức:
Ôn tập toàn bộ kiến thức trong học kì 2.
Kĩ năng:
Thực hiện các phép toán trên toạ độ của vectơ.
Lập phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng.
Dùng phương pháp toạ độ tính được các loại khoảng cách cơ bản trong không gian.
Giải các bài toán hình học không gian bằng phương pháp toạ độ.
Thái độ:
Rèn luyện tính cẩn thận, chính xác.
II. CHUẨN BỊ:
THI THEO ĐỀ CHUNG CỦA SỞ
| 1/88
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 12A3
Chương I: KHỐI ĐA DIỆN Tiết dạy: 01
Bài 1: KHÁI NIỆM VỀ KHỐI ĐA DIỆN I. MỤC TIÊU: Kiến thức:
 Biết khái niệm khối lăng trụ, khối chóp, khối chóp cụt, khối đa diện.
 Biết khái niệm hai hình đa diện bằng nhau. Kĩ năng:
 Vẽ thành thạo các khối đa diện đơn giản.
 Biết cách phân chia và lắp ghép các khối đa diện đơn giản. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hình học không gian ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
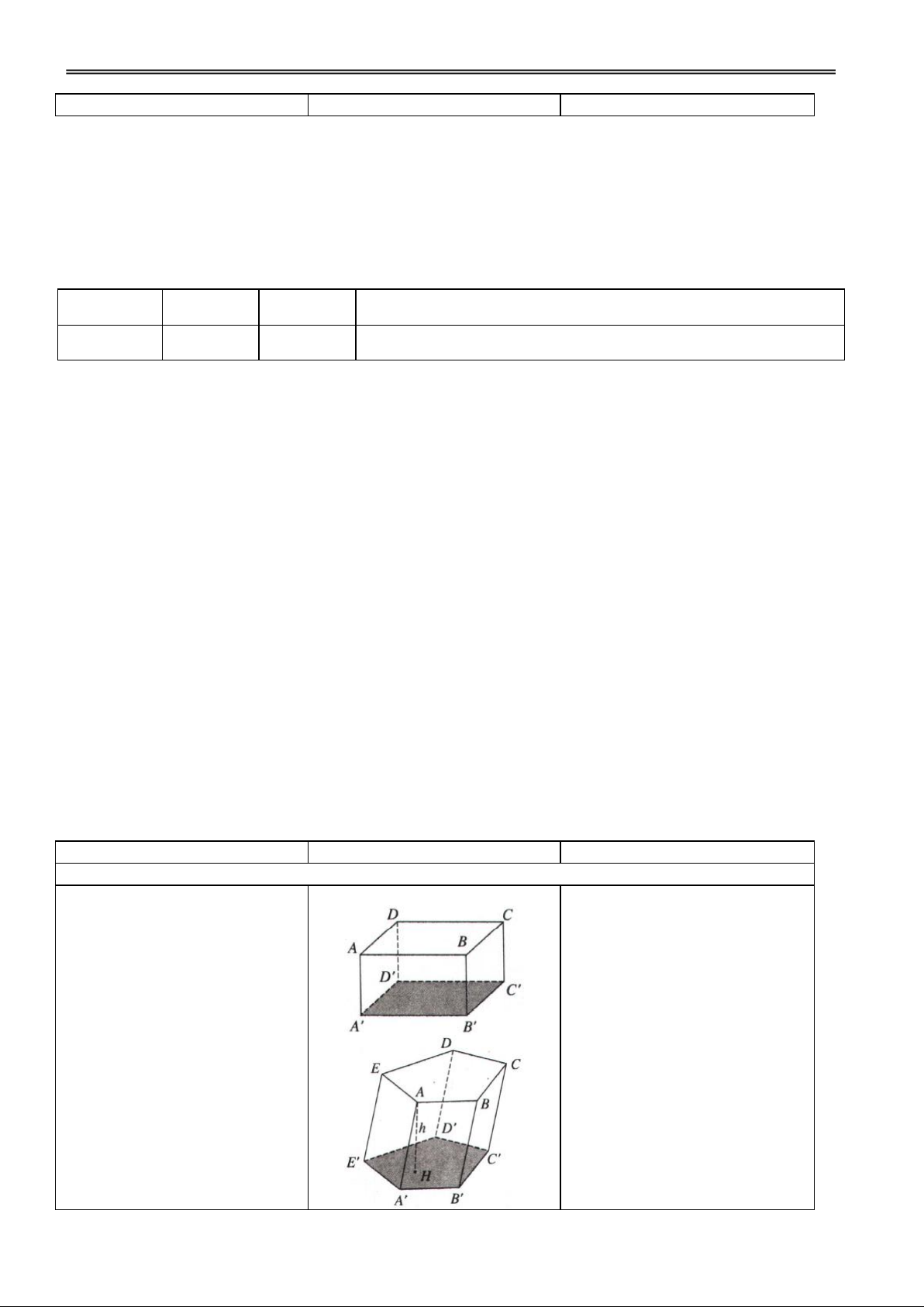
H. Cho hình hộp ABCD.ABCD. Hãy xác định các mặt, các đỉnh, các cạnh của hình hộp?
Đ. 6 mặt, 8 đỉnh, 12 cạnh. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
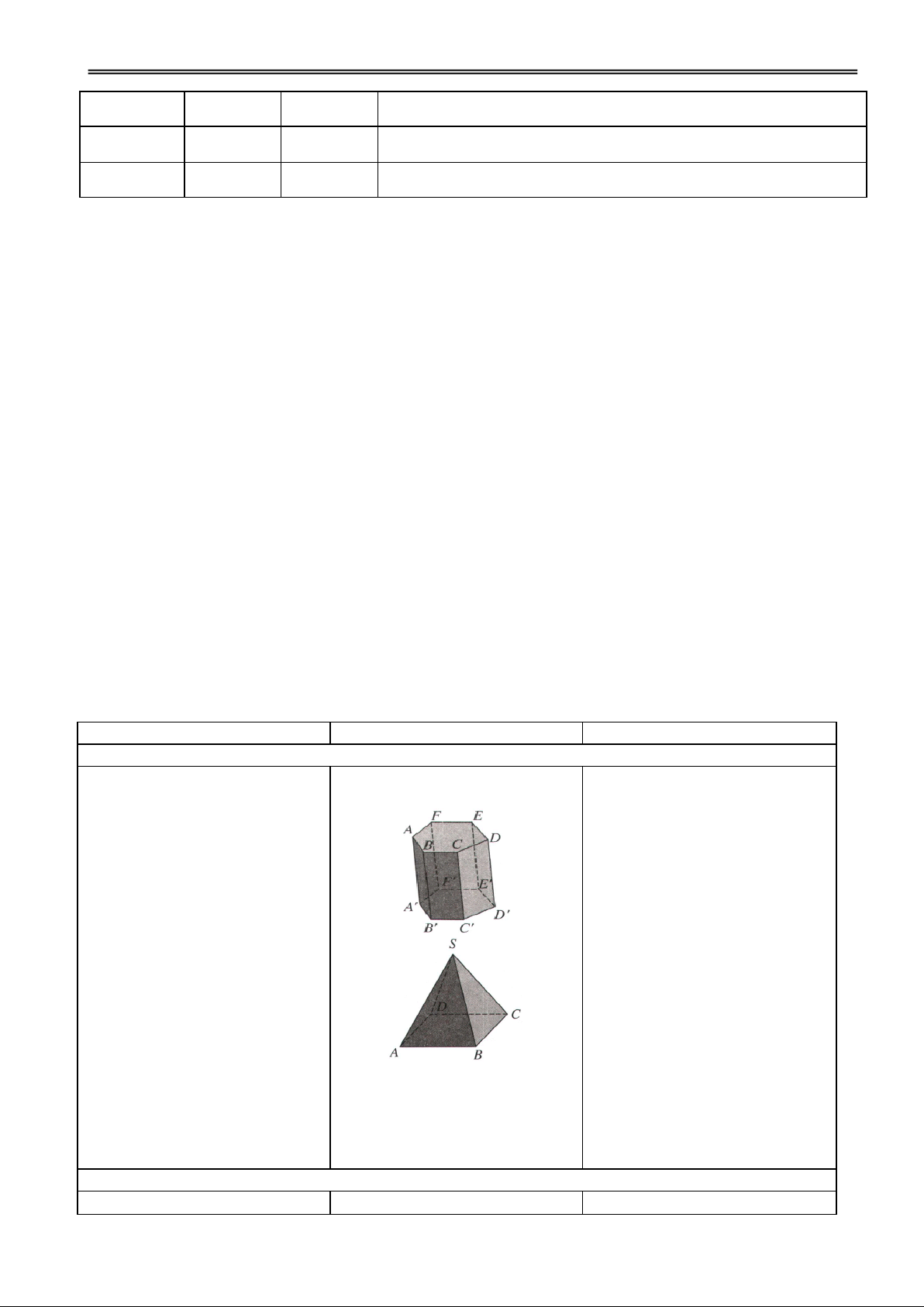
Hoạt động 1: Tìm hiểu khái niệm khối lăng trụ và khối chóp
H1. Nhắc lại định nghĩa hình Đ1. Các nhóm thảo luận và I. KHỐI LĂNG TRỤ VÀ
lăng trụ, hình chóp, hình chóp phát biểu. KHỐI CHÓP cụt?
Khối lăng trụ (khối chóp,
khối chóp cụt) là phần không
gian được giới hạn bởi một
hình lăng trụ (hình chóp, hình
chóp cụt) kể cả hình lăng trụ
(hình chóp, hình chóp cụt) ấy.
Tên gọi và các thành phần:
đỉnh, cạnh, mặt bên, … được
đặt tương ứng với hình tương ứng.
H2. Nêu một số hình ảnh thực Đ2.
Điểm trong – Điểm ngoài
tế về hình lăng trụ, hình chóp, – HLT: hộp bánh, … hình chóp cụt? – HC: kim tự tháp, … – HCC: quả cân, …
Hoạt động 2: Tìm hiểu khái niệm hình đa diện và khối đa diện
 GV cho HS quan sát một số  Các nhóm thảo luận và trình II. KHÁI NIỆM VỀ HÌNH GV: Phạm Việt Phương 1
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
hình cụ thể và hướng dẫn rút ra bày.
ĐA DIỆN VÀ KHỐI ĐA nhận xét. DIỆN
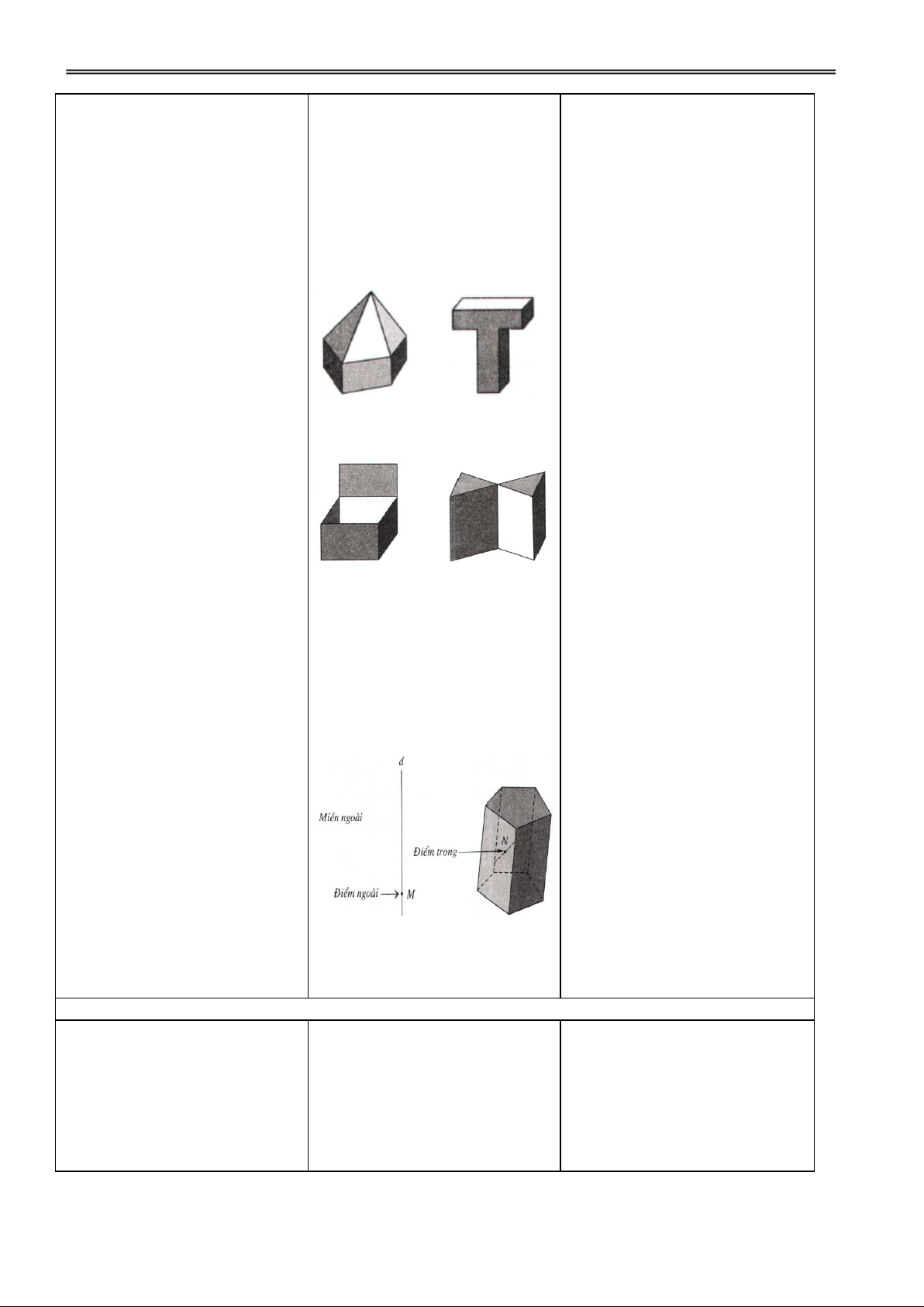
1. Khái niệm về hình đa diện
 GV cho HS nêu định nghĩa
Hình đa diện là hình được tạo hình đa diện.
bởi một số hữu hạn các đa giác
thoả mãn hai tính chất:
a) Hai đa giác phân biệt chỉ có
 GV giới thiệu một số hình và  HS quan sát và trả lời.
thể: hoặc không có điểm
cho HS nhận xét hình nào là – Hình đa diện:
chung, hoặc chỉ có một đỉnh
hình đa diện, không là hình đa
chung, hoặc chỉ có một cạnh diện. chung.
b) Mỗi cạnh của đa giác nào
cũng là cạnh chung của đúng hai đa giác.
– Không là hình đa diện:
2. Khái niệm về khối đa diện
Khối đa diện là phần không
gian được giới hạn bởi một
hình đa diện, kể cả hình đa diện đó.
Tên gọi và các thành phần:
đỉnh, cạnh, mặt bên, … được
đặt tương ứng với hình đa diện tương ứng.
Điểm trong – Điểm ngoài
Miền trong – Miền ngoài
 GV hướng dẫn HS nhận xét.
Mỗi hình đa diện chia các
điểm còn lại của không gian
thành hai miền không giao
nhau là miền trong và miền
ngoài của hình đa diện, trong
đó chỉ có miền ngoài là chứa
hoàn toàn một đường thẳng nào đấy.
H1. Nêu một số vật thể thực tế Đ1. Viên kim cương, …
là những khối đa diện?
Hoạt động 3: Củng cố Nhấn mạnh:
– Khái niệm hình đa diện, khối đa diện.
Câu hỏi: Cho VD về khối đa
diện, không là khối đa diện?
4. BÀI TẬP VỀ NHÀ: GV: Phạm Việt Phương 2
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn  Bài 1, 2 SGK.
 Đọc tiếp bài "Khái niệm về khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 02
Bài 1: KHÁI NIỆM VỀ KHỐI ĐA DIỆN (tt) I. MỤC TIÊU: Kiến thức:
 Biết khái niệm khối lăng trụ, khối chóp, khối chóp cụt, khối đa diện.
 Biết khái niệm hai hình đa diện bằng nhau. Kĩ năng:
 Vẽ thành thạo các khối đa diện đơn giản.
 Vận dụng thành thạo một số phép biến hình.
 Biết cách phân chia và lắp ghép các khối đa diện đơn giản. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về phép biến hình ở lớp 11.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu khái niệm hình đa diện? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu một số phép dời hình trong không gian
H1. Nhắc lại định nghĩa phép Đ1. HS nhắc lại.
III. HAI ĐA DIỆN BẰNG
biến hình và phép dời hình NHAU trong mặt phẳng?
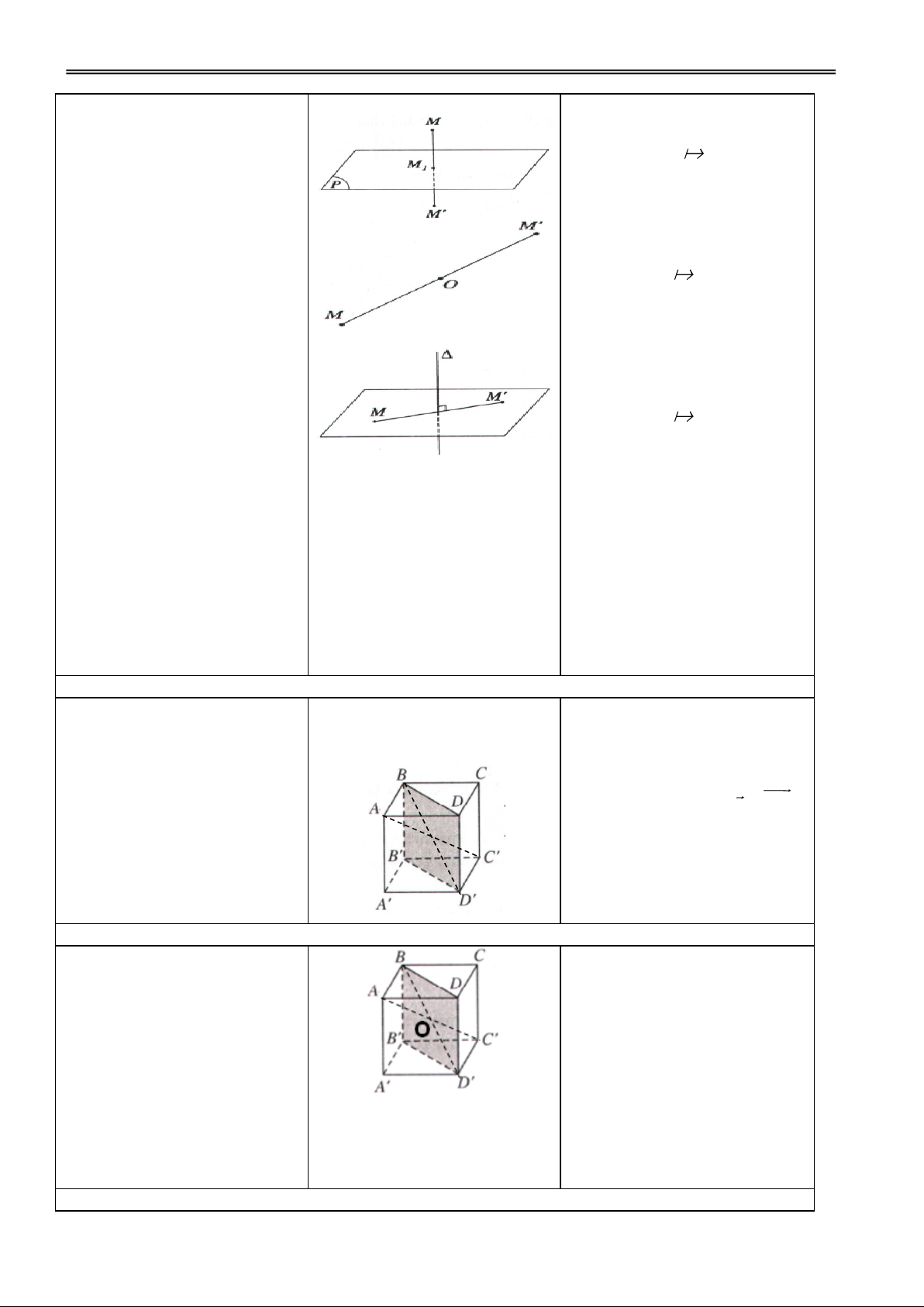
1. Phép dời hình trong không gian
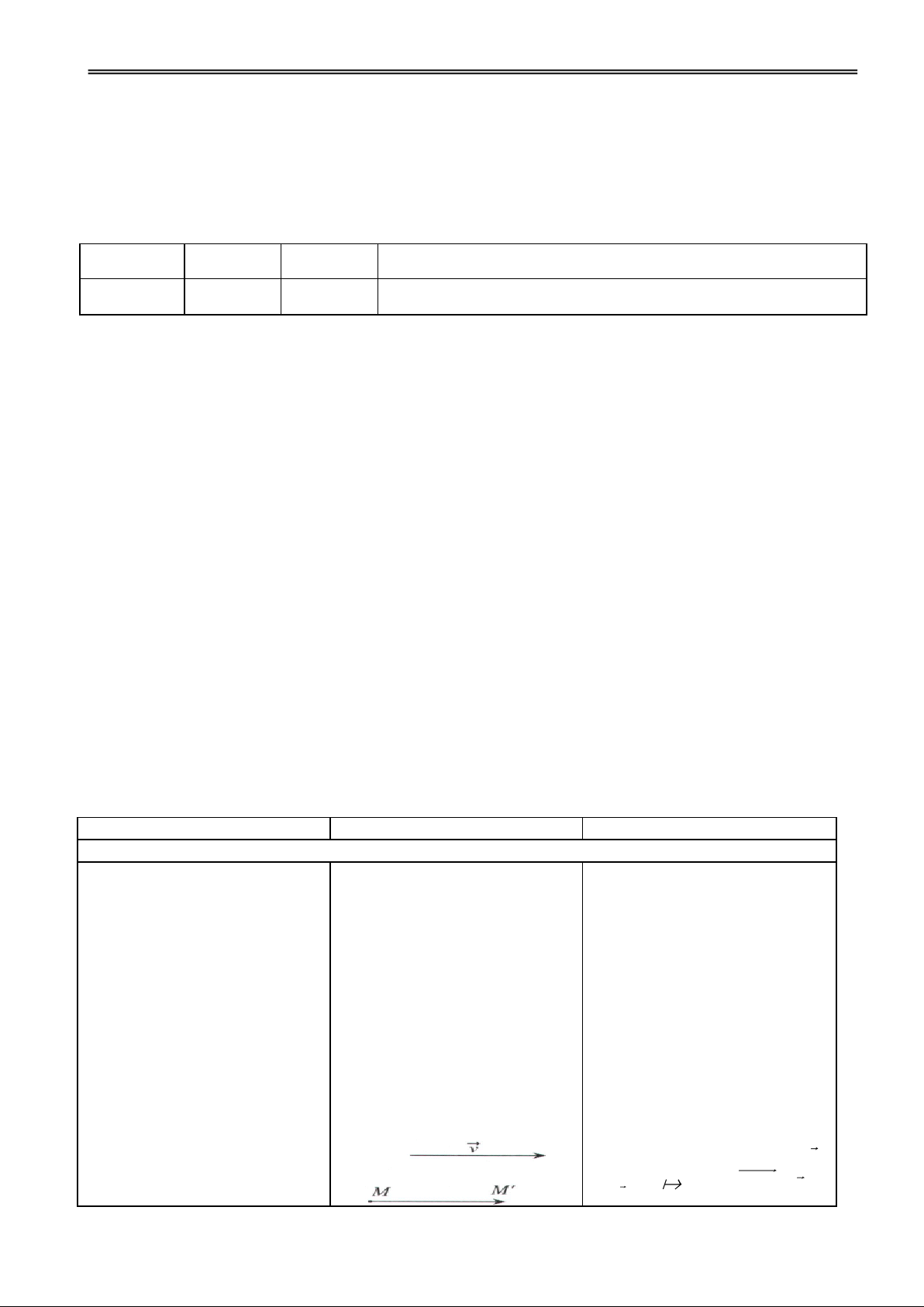
Trong không gian, quy tắc
đặt tương ứng mỗi điểm M với
điểm M xác định duy nhất đgl
một phép biến hình trong không gian.
Phép biến hình trong không
gian đgl phép dời hình nếu nó
bảo toàn khoảng cách giữa hai
H2. Nhắc lại định nghĩa các Đ2. HS nhắc lại. điểm tuỳ ý.
phép tịnh tiến, phép đối xứng
a) Phép tịnh tiến theo vectơ v
tâm, đối xứng trục trong mặt : '  '  phẳng? v T M M MM v GV: Phạm Việt Phương 3
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
b) Phép đối xứng qua mặt phẳng (P) D P M M ( ) : '
– Nếu M (P) thì M M,
– Nếu M (P) thì MM nhận
(P) làm mp trung trực.
c) Phép đối xứng tâm O O D : M M '
– Nếu M O thì M O,
– Nếu M O thì MM nhận O làm trung điểm.
d) Phép đối xứng qua đường thẳng D : M M ' 
– Nếu M thì M M,
– Nếu M thì MM nhận làm đường trung trực. Nhận xét:
Thực hiện liên tiếp các phép
dời hình sẽ được một phép dời hình.
Nếu phép dời hình biến (H)
thành (H) thì nó biến đỉnh,
mặt, cạnh của (H) thành đỉnh,
mặt, cạnh tương ứng của (H).
Hoạt động 2: Áp dụng tìm ảnh của một hình qua một phép dời hình
 Hướng dẫn HS thực hiện.
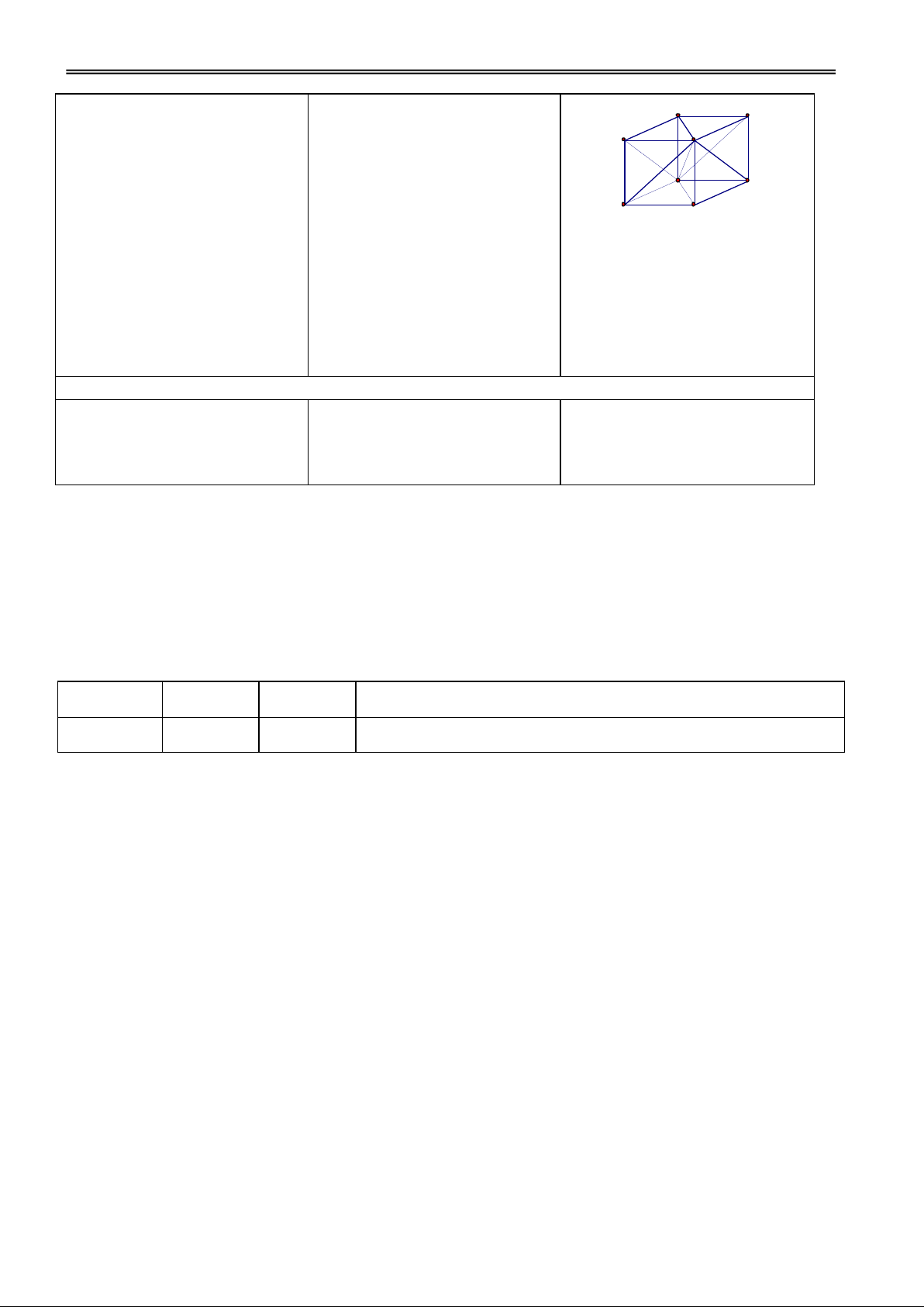
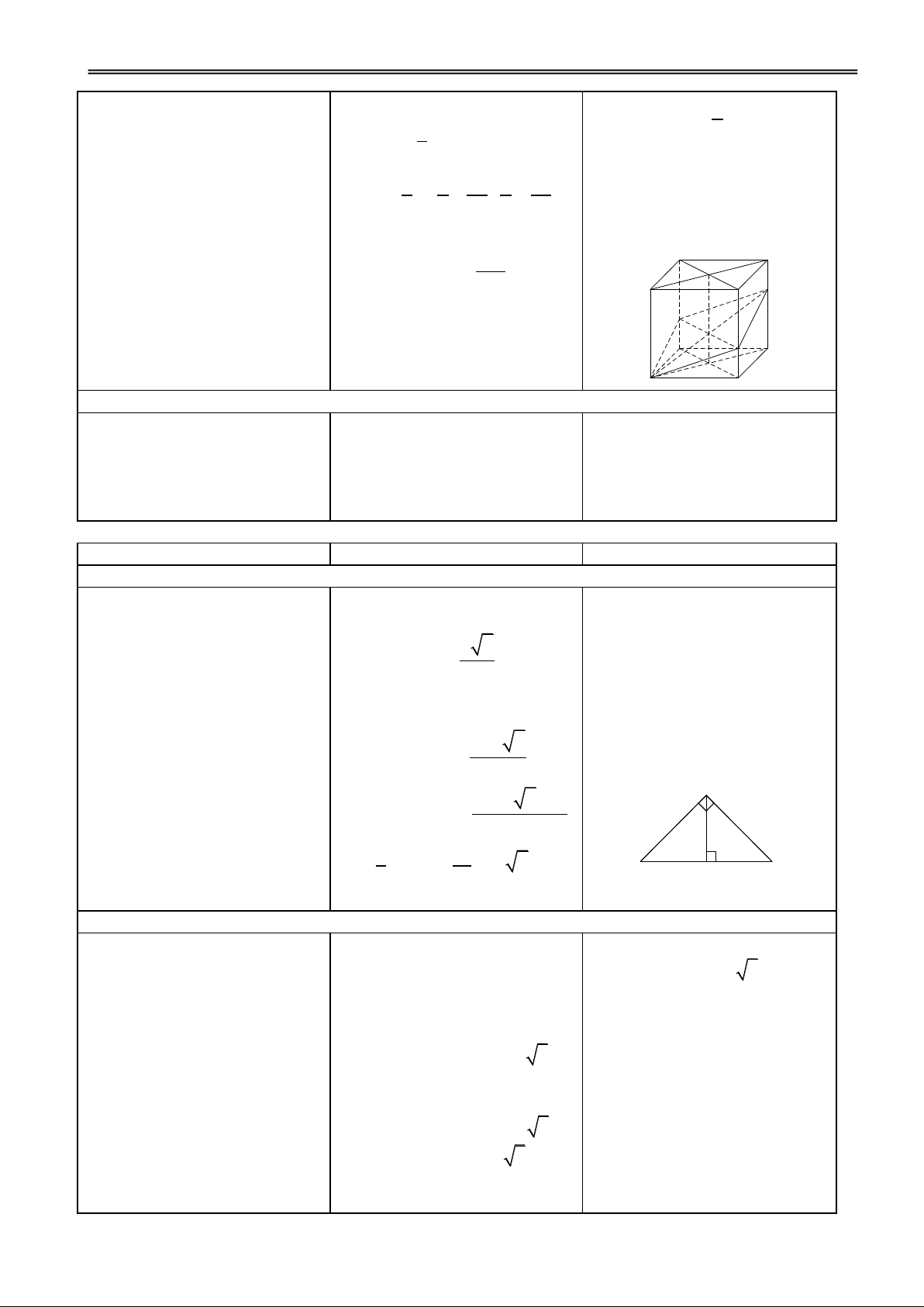
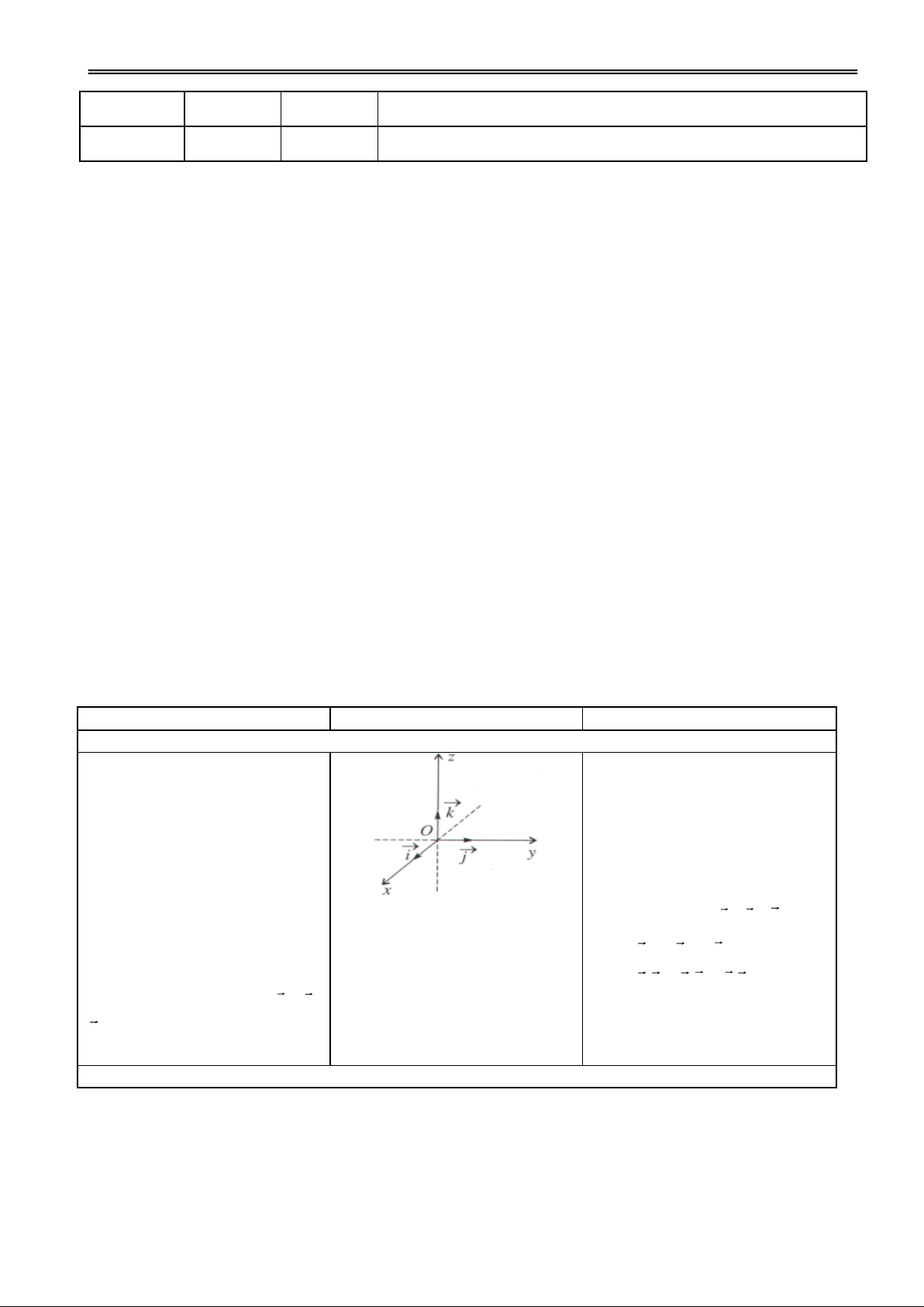
 Các nhóm thảo luận và trình VD1: Cho hình lập phương bày.
ABCD.ABCD có tâm O.
Tìm ảnh của tứ giác ABCD qua:
a) Phép tịnh tiến theo v AA' .
b) Phép đối xứng qua mặt phẳng (BBDD).
c) Phép đối xứng tâm O.
d) Phép đối xứng qua đường thẳng AC.
Hoạt động 3: Tìm hiểu khái niệm hai hình bằng nhau
2. Hai hình bằng nhau
Hai hình đgl bằng nhau nếu
có một phép dời hình biến hình này thành hình kia.
Hai đa diện đgl bằng nhau
nếu có một phép dời hình biến
đa diện này thành đa diện kia.
H1. Tìm phép dời hình biến Đ1. Xét phép đối xứng tâm O. VD2: Cho hình hộp hình này thành hình kia?
ABCD.ABCD. Chứng minh
hai lăng trụ ABD.ABD và BCD.BCD bằng nhau.
Hoạt động 4: Tìm hiểu sự phân chia và lắp ghép các khối đa diện GV: Phạm Việt Phương 4
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
 Cho HS quan sát 3 hình (H),  Các nhóm thảo luận và trình IV. PHÂN CHIA VÀ LẮP
(H1), (H2) và hướng dẫn HS bày.
GHÉP CÁC KHỐI ĐA DIỆN nhận xét.
– (H1), (H2) không có chung Nếu khối đa diện (H) là hợp điểm trong nào.
của hai khối đa diện (H1) và
– (H1), (H2) ghép lại thành (H). (H2) sao cho (H1) và (H2)
không có chung điểm trong
nào thì ta nói có thể chia được
khối đa diện (H) thành hai khối
đa diện (H1) và (H2), hay có
thể lắp ghép hai khối đa diện
(H1) và (H2) với nhau để được khối đa diện (H).
Hoạt động 5: Phân chia và lắp ghép các khối đa diện
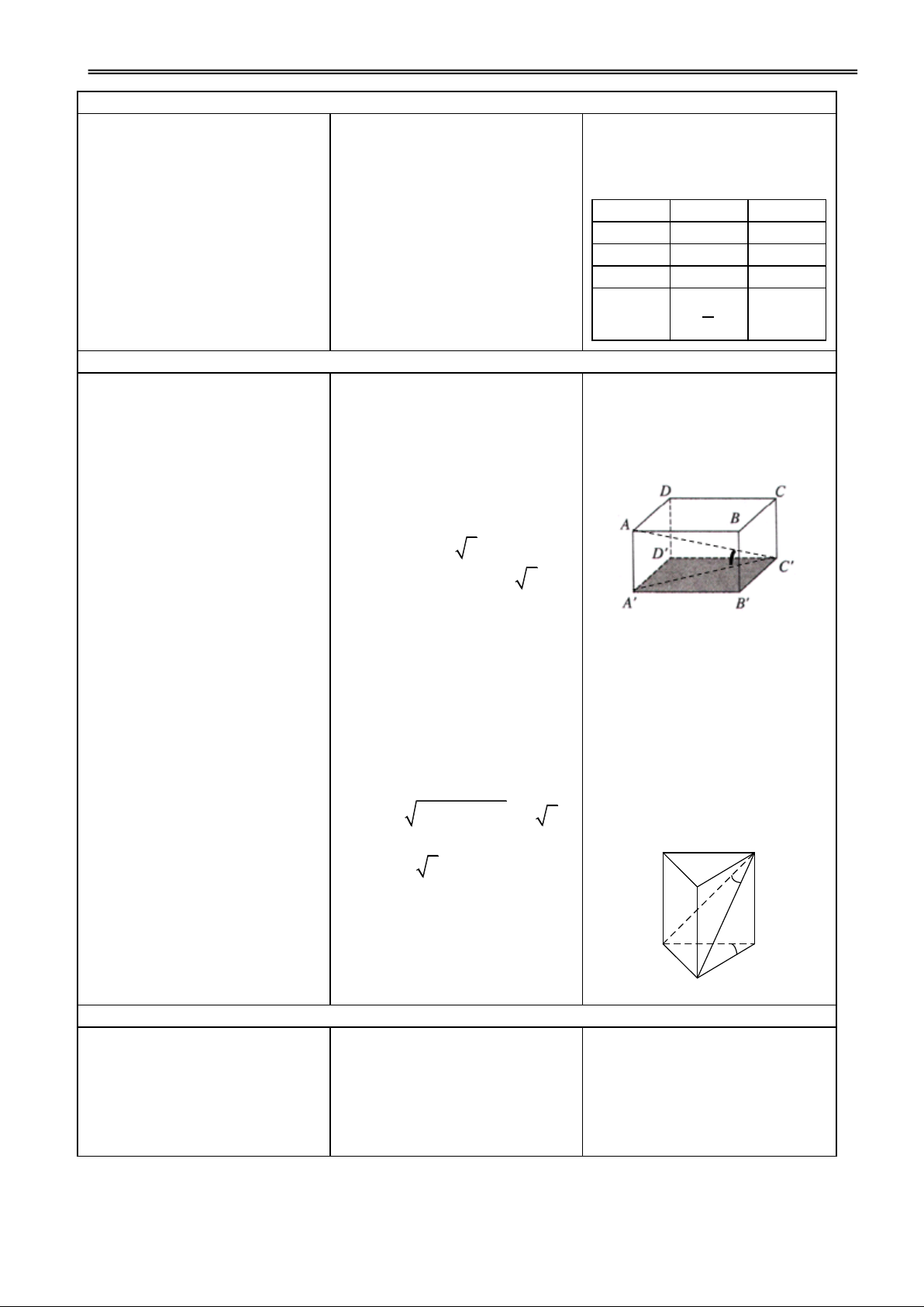
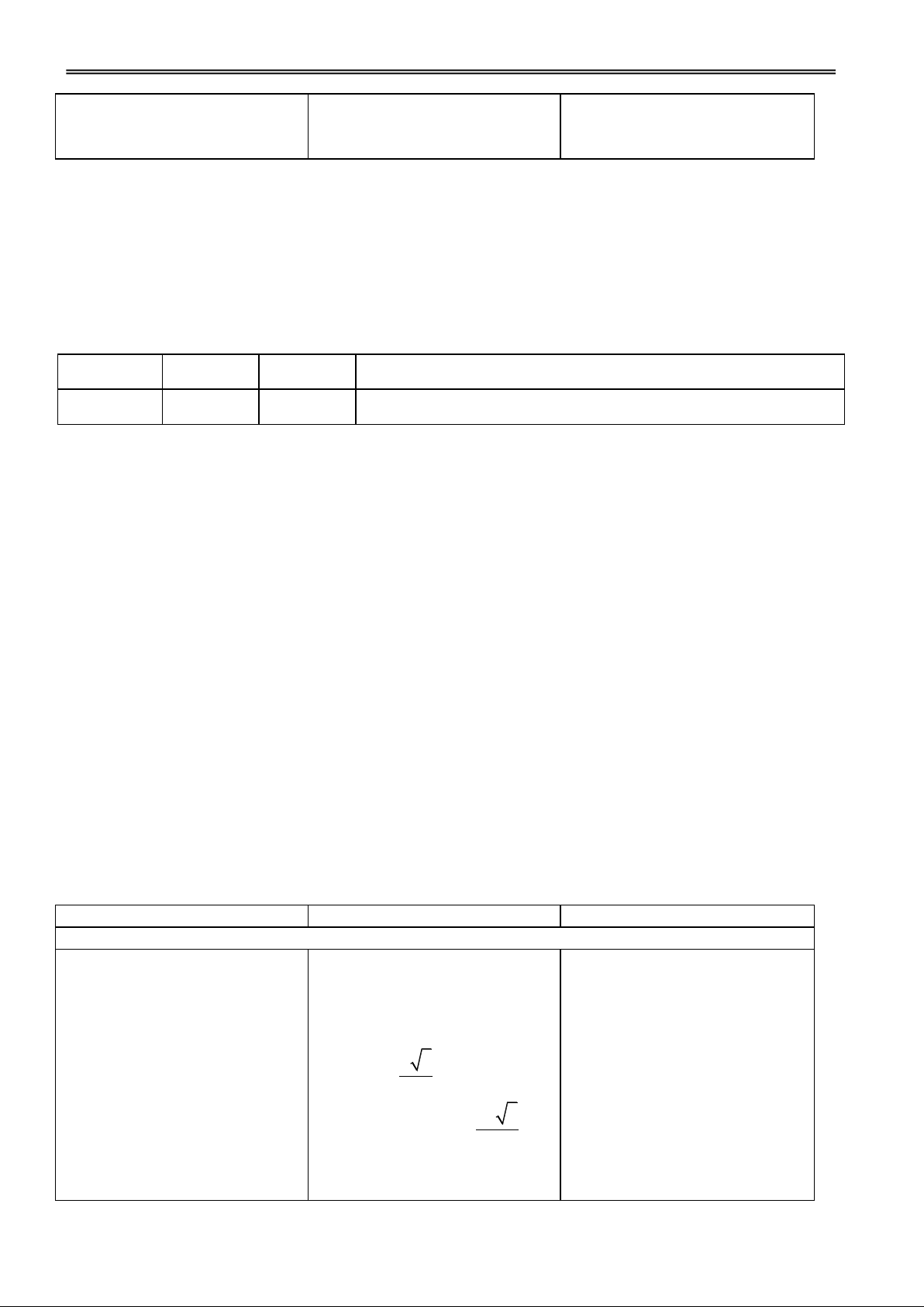
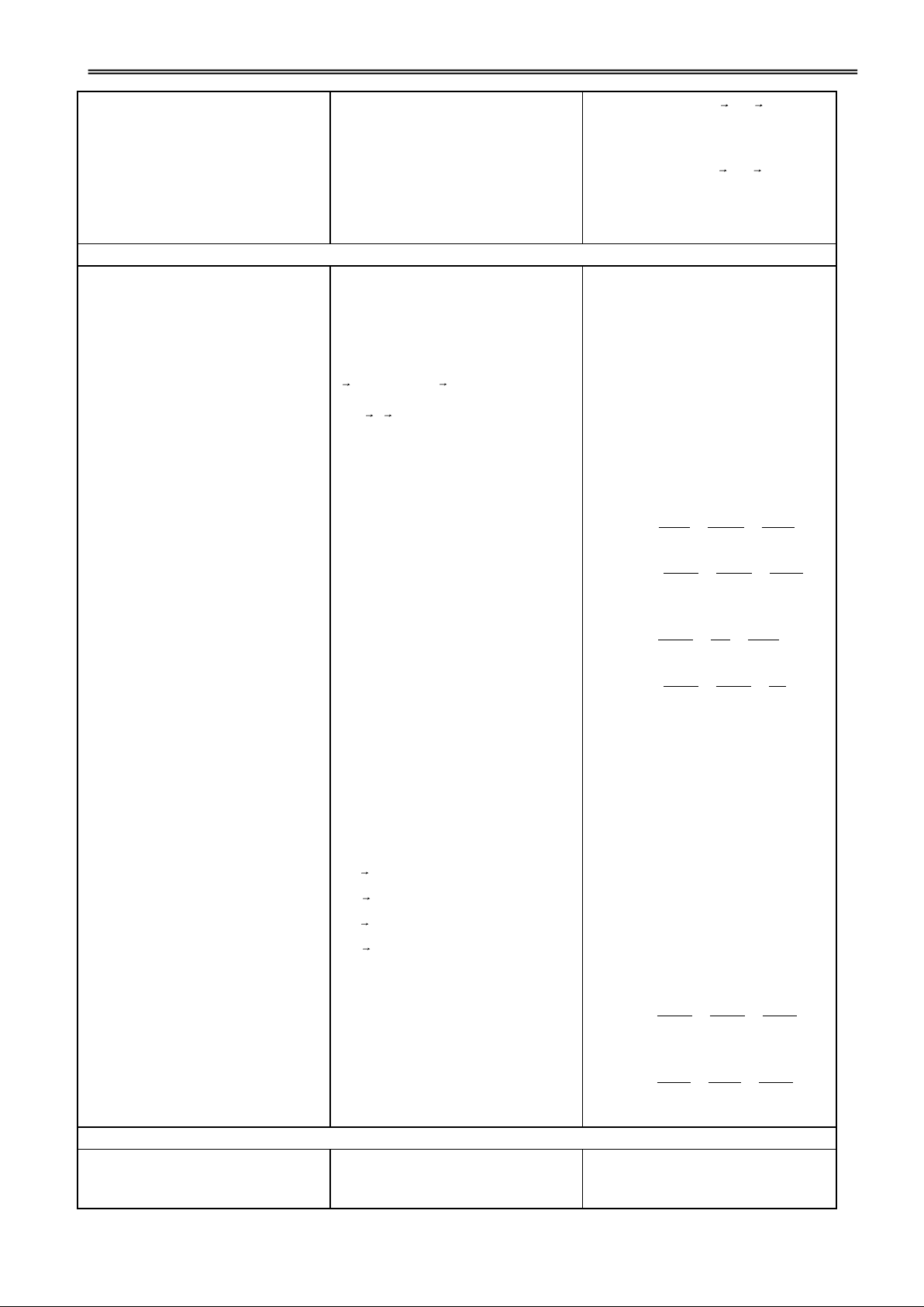
 GV hướng dẫn HS chia các  Các nhóm thảo luận và trình VD1: Cho khối lập phương khối đa diện. bày. ABCD.ABCD.
a) Chia khối lập phương thành 2 khối lăng trụ. b) Chia khối lăng trụ
ABD.ABD thành 3 khối tứ diện.
Nhận xét: Một khối đa diện
bất kì luôn có thể phân chia
được thành những khối tứ diện.
 Cho các nhóm thực hiện.
 Các nhóm thảo luận và trình VD2: Chia một khối lập bày.
phương thành 5 khối tứ diện.
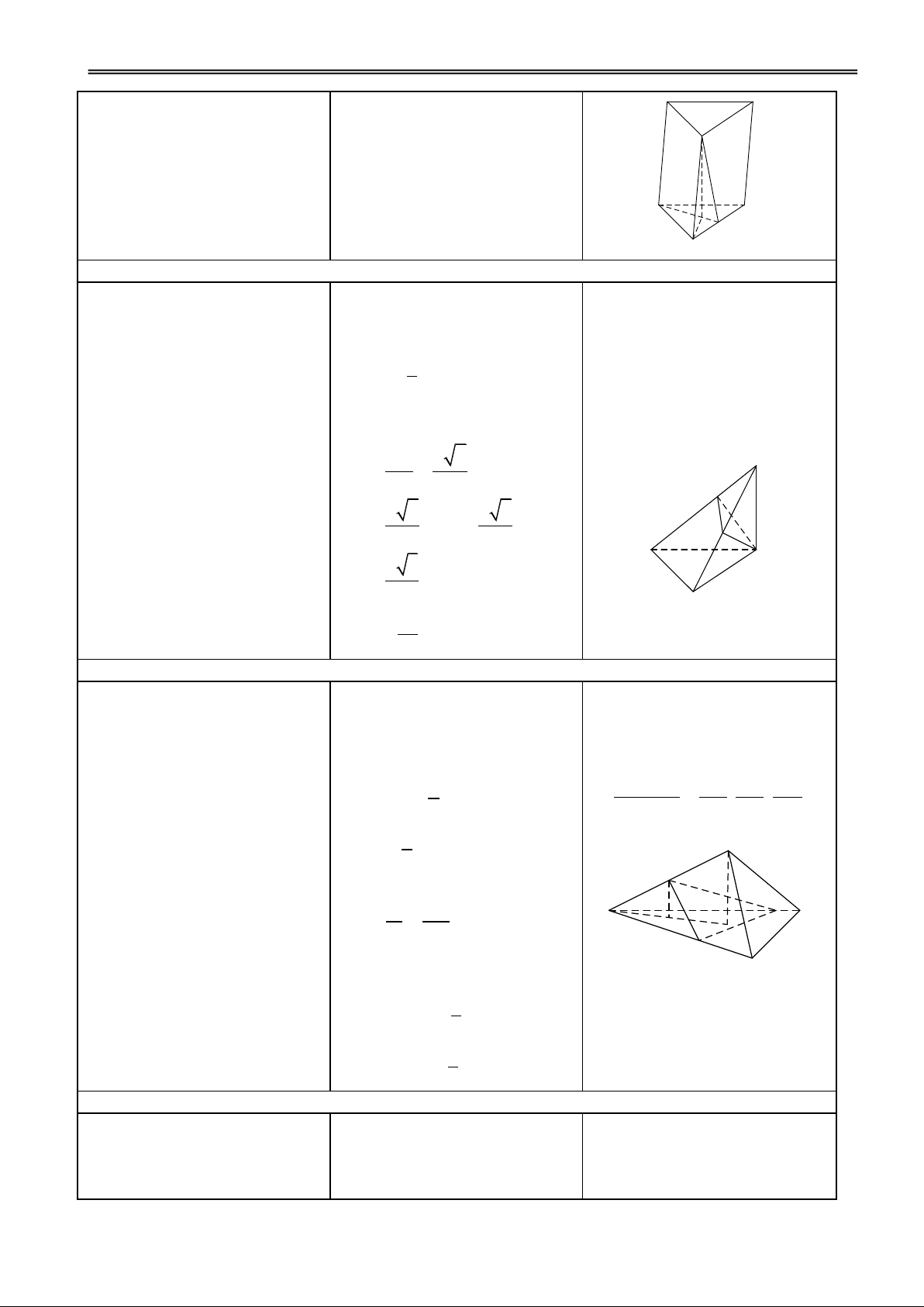
Chia lăng trụ thành 5 tứ diện D C
AA’BD, B’A’BC’, CBC’D, D’C’DA’ và DA’BC’. A B C' D' A' B' H1. Nêu cách chia? Đ1.
VD3: Chia một khối lập
+ Chia khối lập phương thành
phương thành 6 khối tứ diện
2 khối lăng trụ ABD.ABD và bằng nhau. GV: Phạm Việt Phương 5
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn BCD.BCD. D C
+ Chia lăng trụ ABD.A’B’D’
thành 3 tứ diện BA’B’D’, A B AA’BD’ và ADBD’. C'
H2. Nêu cách chứng minh các + Chứng minh 3 khối tứ diện D'
khối tứ diện bằng nhau? bằng nhau: A' B' D A BD BA B D AA BD ( ' ') : ' ' ' ' '
D ABD AA BD ADBD ( ') : ' ' '
+ Làm tương tự đối với lăng trụ BCD.B’C’D’.
 Chia được hình lập phương
thành 6 tứ diện bằng nhau.
Hoạt động 6: Củng cố Nhấn mạnh:
– Cách phân chia và lắp ghép các khối đa diện.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Khái niệm về khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy
Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 03
Bài 2: KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU I. MỤC TIÊU: Kiến thức:
 Nắm được định nghĩa khối đa diện lồi.
 Hiểu được thế nào là khối đa diện đều.
 Nhận biết được các loại khối đa diện đều. Kĩ năng:
 Biết phân biệt khối đa diện lồi và không lồi.
 Biết được một số khối đa diện đều và chứng minh được một khối đa diện là đa diện đều. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu khái niệm khối đa diện? GV: Phạm Việt Phương 6
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm khối đa diện lồi
 GV cho HS quan sát một số
I. KHỐI ĐA DIỆN LỒI
khối đa diện, hướng dẫn HS
Khối đa diện (H) đgl khối đa
nhận xét, từ đó giới thiệu khái
diện lồi nếu đoạn thẳng nối hai
niệm khối đa diện lồi.
điểm bất kì của (H). Khi đó đa
diện xác định (H) đgl đa diện lồi. Khối đa diện lồi
Nhận xét: Một khối đa diện là
khối đa diện lồi khi và chỉ khi
miền trong của nó luôn nằm về
một phía đối với mỗi mặt
phẳng chứa một mặt của nó. Kh
ối đa diện không lồi
H1. Cho VD về khối đa diện lồi, không lồi? Đ1.
Khối lăng trụ, khối chóp, …
Hoạt động 2: Tìm hiểu khái niệm khối đa diện đều
 Cho HS quan sát khối tứ diện
II. KHỐI ĐA DIỆN ĐỀU
đều, khối lập phương. Từ đó
Khối đa diện đều là khối đa
giới thiệu khái niệm khối đa
diện lồi có các tính chất sau: diện đều.
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh
chung của đúng q mặt.
Khối đa diện đều như vậy đgl
khối đa diện đều loại (p; q).
 GV giới thiệu 5 loại khối đa
Định lí: Chỉ có 5 loại khối đa diện đều.
diện. Đó là các loại [3; 3], [4;
3], [3; 4], [5; 3], [3; 5].
Bảng tóm tắt của 5 loại khối
H1. Đếm số đỉnh, số cạnh, số Đ1. Các nhóm đếm và điền vào đa diện đều
mặt của các khối đa diện đều? bảng.
Hoạt động 3: Áp dụng chứng minh khối đa diện đều
H1. Nêu các bước chứng Đ1.
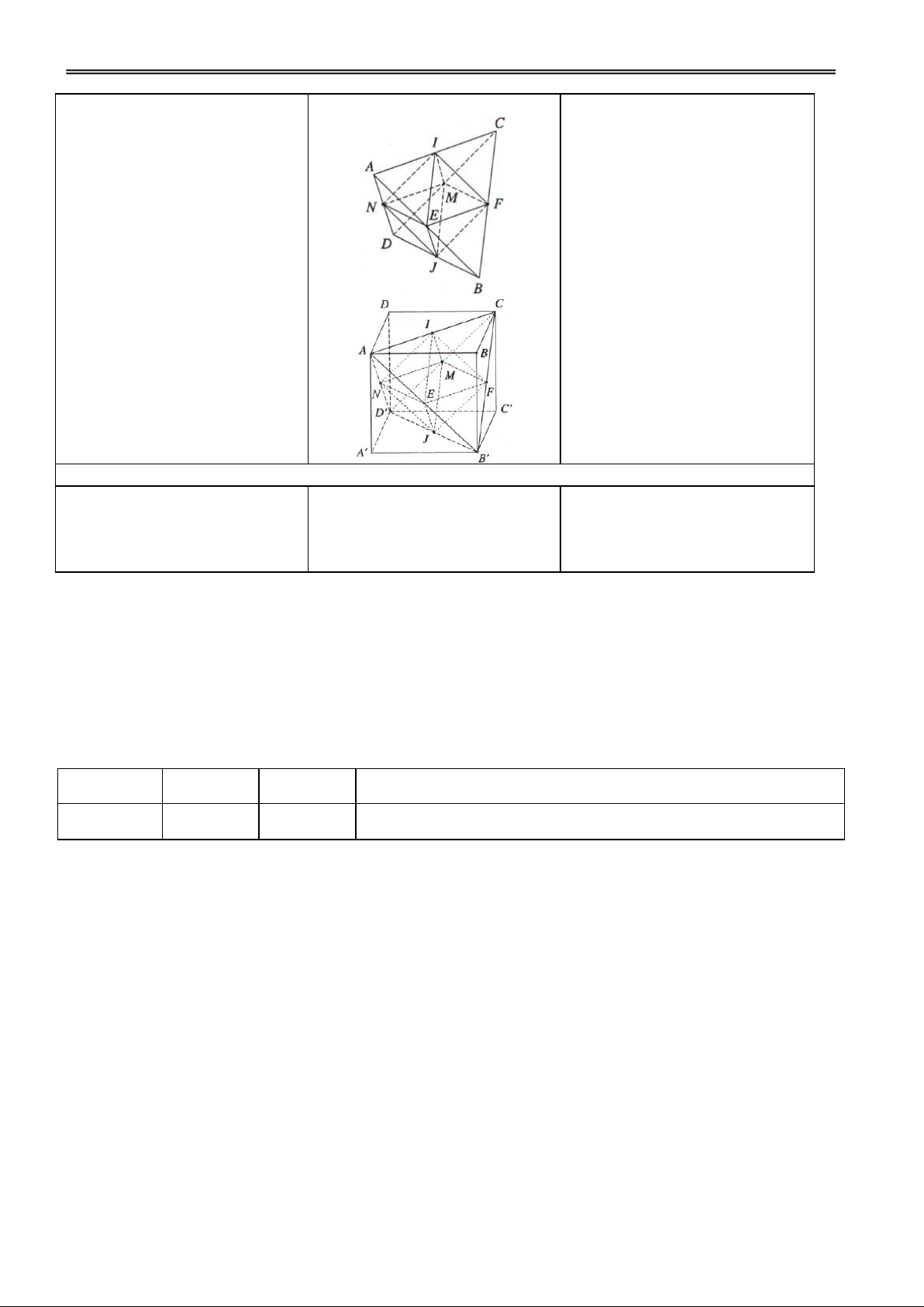
VD1: Chứng minh rằng: minh?
– Chứng minh các mặt đều là a) Trung điểm các cạnh của những đa giác đều.
một tứ diện đều là các đỉnh của
– Xác định loại khối đa diện một hình bát diện đều. GV: Phạm Việt Phương 7
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn đều.
b) Tâm các mặt của một hình
lập phương là các đỉnh của một hình bát diện đều.
Hoạt động 4: Củng cố Nhấn mạnh:
– Nhận dạng khối đa diện đều.
– Cách chứng minh khối đa diện đều.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3, 4, 5 SGK.
 Đọc tiếp bài "Khái niệm về khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 04
Bài 2: BÀI TẬP KHỐI ĐA DIỆN LỒI VÀ KHỐI ĐA DIỆN ĐỀU I. MỤC TIÊU: Kiến thức:
 Khắc sâu lại định nghĩa và các tính chất của khối đa diện lồi, khối đa diện đều.
 Nhận biết được các loại khối đa diện lồi, khối đa diện đều. Kĩ năng:
 Biết chứng minh khối đa diện đều và giải các bài tập về khối đa diện lồi và khối đa diện đều.
 Rèn luyện kỹ năng vẽ hình không gian. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện lồi, khối đa diện đều.
III. HOẠT ĐỘNG DẠY HỌC: GV: Phạm Việt Phương 8
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập vận dụng tính chất của khối đa diện đều
H1. Tính độ dài cạnh của (H)? Đ1.
1. Cho hình lập phương (H) a 2 cạnh
bằng a. Gọi (H) là hình b =
bát diện đều có các đỉnh là tâm 2
H2. Tính diện tích toàn phần Đ2.
các mặt của (H). Tính tỉ số diện của (H) và (H) ?
tích toàn phần của (H) và (H). S = 6a2 2 a 3 S = 8 2  a 3 8  S  2 3 S '
H3. Nhận xét các tứ giác Đ3.
2. Cho hình tứ diện đều
Các tứ giác đó là nhứng ABFD và ACFE? ABCDEF. Chứng minh rằng: hình thoi.
a) Các đoạn thẳng AF, BD, CE  AF  BD, AF  CE
đôi một vuông góc với nhau và
cắt nhau tại trung điểm mỗi
H4. Chứng minh IB = IC = ID đường.
Đ4. Vì AI  (BCDE) và AB = = IE ? b) ABFD, AEFC và BCDE là AC = AD = AE. những hình vuông.  BCDE là hình vuông.
Hoạt động 2: Luyện tập chứng minh khối đa diện đều
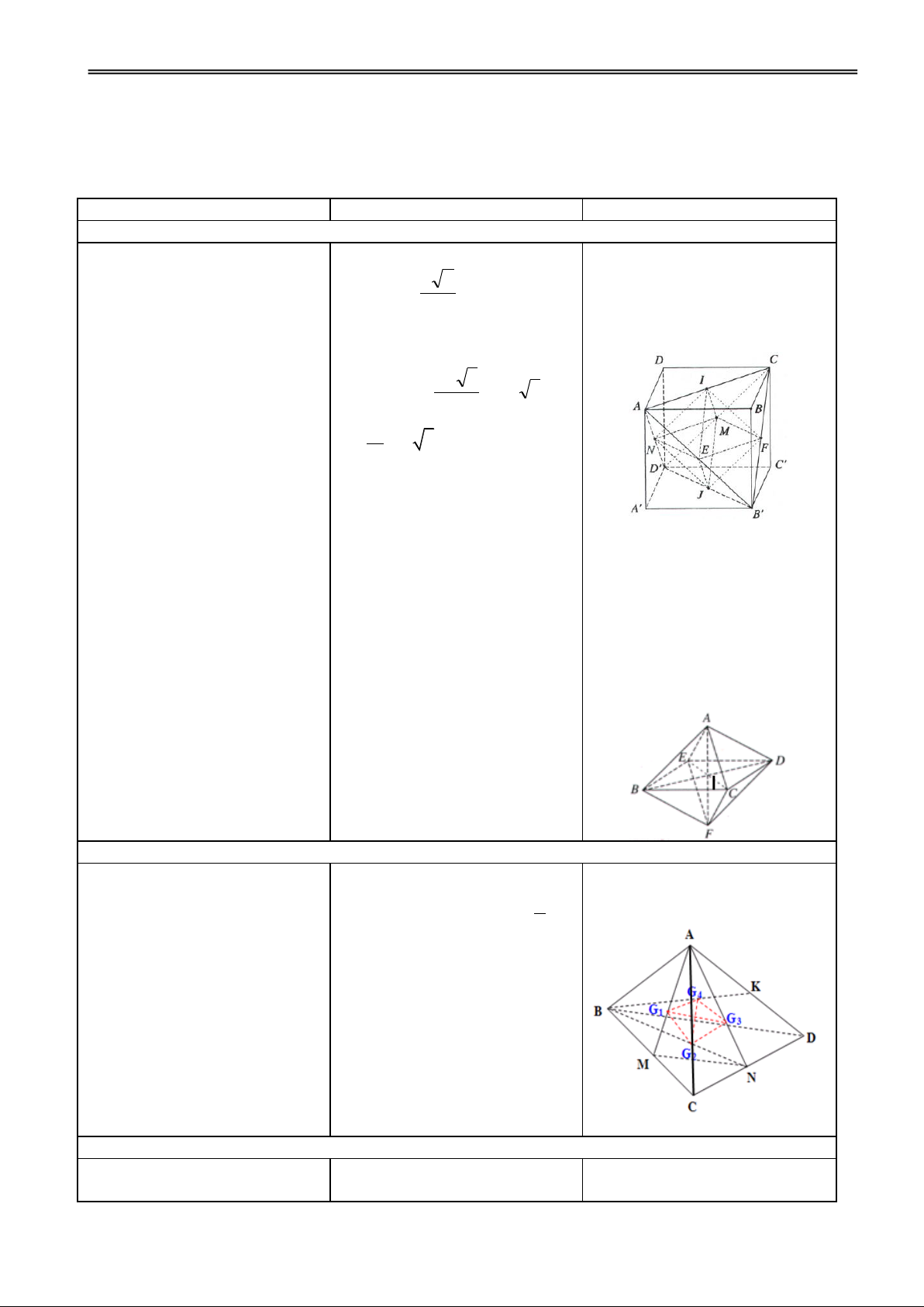
H1. Ta cần chứng minh điều gì Đ1. G
3. Chứng minh rằng tâm các 1G2 = G2G3 = G3G4 = ?
mặt của hình tứ diện đều là các G a 4G1 = G4G2 = G1G3 =
đỉnh của một hình tứ diện đều. 3
Hoạt động 3: Củng cố Nhấn mạnh:
– Nhận dạng khối đa diện đều. GV: Phạm Việt Phương 9
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
– Cách chứng minh khối đa diện đều.
4. BÀI TẬP VỀ NHÀ:
 Đọc trước bài "Khái niệm về thể tích của khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 05
Bài 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm thể tích của khối đa diện.
 Nắm được các công thức tính thể tích của một số khối đa diện cụ thể. Kĩ năng:
 Tính được thể tích của khối lăng trụ, khối chóp.
 Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Thế nào là khối đa diện lồi, khối đa diện đều? Nêu một số công thức tính thể tích đã biết? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm thể tích khối đa diện
 GV nêu một số cách tính thể  HS tham gia thảo luận.
I. KHÁI NIỆM VỀ THỂ
tích vật thể và nhu cầu cần tìm Nêu một công thức tính thể
TÍCH KHỐI ĐA DIỆN
ra cách tính thể tích những tích đã biết.
Thể tích của khối đa diện (H)
khối đa diện phức tạp.
là một số dương duy nhất V(H)
thoả mãn các tính chất sau:
 GV giới thiệu khái niệm thể
a) Nếu (H) là khối lập phương tích khối đa diện.
có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1),
(H2) bằng nhau thì V(H1)=V(H2).
c) Nếu khối đa diện (H) được
phan chia thành hai khối đa diện (H1), (H2) thì V(H) = V(H1) + V(H2). GV: Phạm Việt Phương 10
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
V(H) cũng đgl thể tích của
hình đa diện giới hạn khối đa diện (H).
Khối lập phương có cạnh
bằng 1 đgl khối lập phương đơn vị.
Hoạt động 2: Tìm hiểu cách thiết lập công thức tính thể tích khối hộp chữ nhật
 GV hướng dẫn HS tìm cách
VD1: Tính thể tích của khối
tính thể tích của khối hộp chữ
hộp chữ nhật có 3 kích thước là nhât. những số nguyên dương.
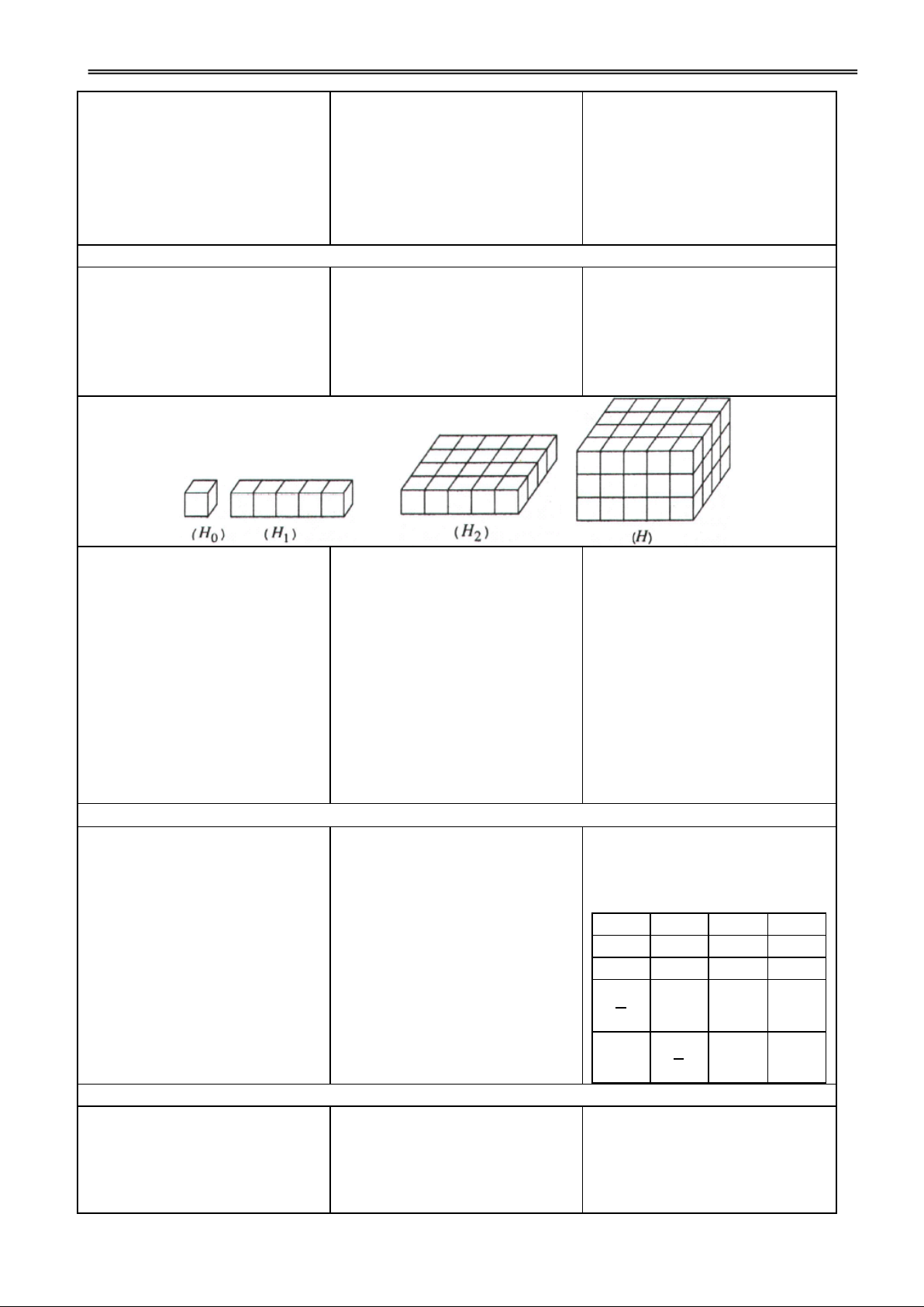
H1. Có thể chia (H1) thành bao Đ1. 5  V(H1) = 5V(H0) = 5 nhiêu khối (H0) ?
H2. Có thể chia (H2) thành bao Đ2. 4  V(H2) = 4V(H1) = 4.5 nhiêu khối (H1) ? = 20
H3. Có thể chia (H) thành bao Đ3. 3  V (H) = 3V(H2) = 3.20 nhiêu khối (H2) ? = 60
Định lí: Thể tích của một khối
hộp chữ nhật bằng tích ba kích  GV nêu định lí. thước của nó. V = abc
Hoạt động 3: Áp dụng tính thể tích của khối hộp chữ nhật  Cho HS thực hiện.
 Các nhóm tính và điền vào VD2: Gọi a, b, c, V lần lượt là bảng.
ba kích thước và thể tích của
khối hộp chữ nhật. Tính và điền vào ô trống: a b c V 1 2 3 4 3 24 1 2 3 2 1 1 1 3
Hoạt động 4: Củng cố Nhấn mạnh:
– Khái niệm thể tích khối đa diện.
– Công thức tính thể tích khối hộp chữ nhật. GV: Phạm Việt Phương 11
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
4. BÀI TẬP VỀ NHÀ:
 Đọc tiếp bài "Khái niệm về thể tích của khối đa diện".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 06
Bài 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm thể tích của khối đa diện.
 Nắm được các công thức tính thể tích của một số khối đa diện cụ thể. Kĩ năng:
 Tính được thể tích của khối lăng trụ, khối chóp.
 Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hình lăng trụ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Thế nào là thể tích khối đa diện? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu công thức tính thể tích khối lăng trụ
H1. Khối hộp chữ nhật có phải Đ1. Là khối lăng trụ đứng.
II. THỂ TÍCH KHỐI LĂNG
là khối lăng trụ không? TRỤ
Định lí: Thể tích khối lăng trụ
 GV giới thiệu công thức tính
bằng diện tích đáy B nhân với
thể tích khối lăng trụ. chiều cao h. V = Bh GV: Phạm Việt Phương 12
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Hoạt động 2: Áp dụng tính thể tích khối lăng trụ  Cho HS thực hiện.
 Các nhóm tính và điền kết VD1: Gọi S, h, V lần lượt là quả vào bảng.
thể diện tích đáy, chiều cao và
thể tích khối lăng trụ. Tính và điền vào ô trống: S h V 8 7 8 4 8 4 3 12 2
Hoạt động 3: Vận dụng tính thể tích của khối lăng trụ
H1. Nhắc lại khái niệm lăng Đ1. HS nhắc lại. BT1: Cho lăng trụ đều
trụ đứng, lăng trụ đều? ABCD.ABCD cạnh đáy
bằng a. Góc giữa đường chéo
H2. Xác định góc giữa AC và Đ2. 0 AC' A'  60
AC và đáy bằng 600. Tính thể đáy?
tích của hình lăng trụ.
H3. Tính chiều cao của lăng Đ3. h = CC = AC.tan600 trụ? a = 6  V = S a ABCD.CC = 3 6
BT2: Hình lăng trụ đứng
H4. Xác định góc giữa BC và Đ4.
ABC.ABC có đáy ABC là 0 BCA  30 mp(AACC) ?
một tam giác vuông tại A, AC = b, 0
C  60 . Đường chéo BC
H5. Tính AC, CC ?
Đ5. AC = AB.cot300 = 3b
của mặt bên BBCC tạo với
mp(AACC) một góc 300. CC = 2 2
AC '  AC  2 2b Tính thể tích của lăng trụ. A’ C’  V = 3 b 6 . 0 B’ 30 A 0 C 60 B
Hoạt động 4: Củng cố Nhấn mạnh:
– Công thức thể tích khối lăng trụ.
– Tính chất của hình lăng trụ đứng, lăng trụ đều.
4. BÀI TẬP VỀ NHÀ: GV: Phạm Việt Phương 13
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
 Đọc tiếp bài "Khái niệm về thể tích của khối đa diện".  Bài tập thêm.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 07
Bài 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm thể tích của khối đa diện.
 Nắm được các công thức tính thể tích của một số khối đa diện cụ thể. Kĩ năng:
 Tính được thể tích của khối lăng trụ, khối chóp.
 Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về hình chóp.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (5')
H. Nhắc lại định nghĩa và tính chất của hình chóp đều? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu công thức tính thể tích khối chóp
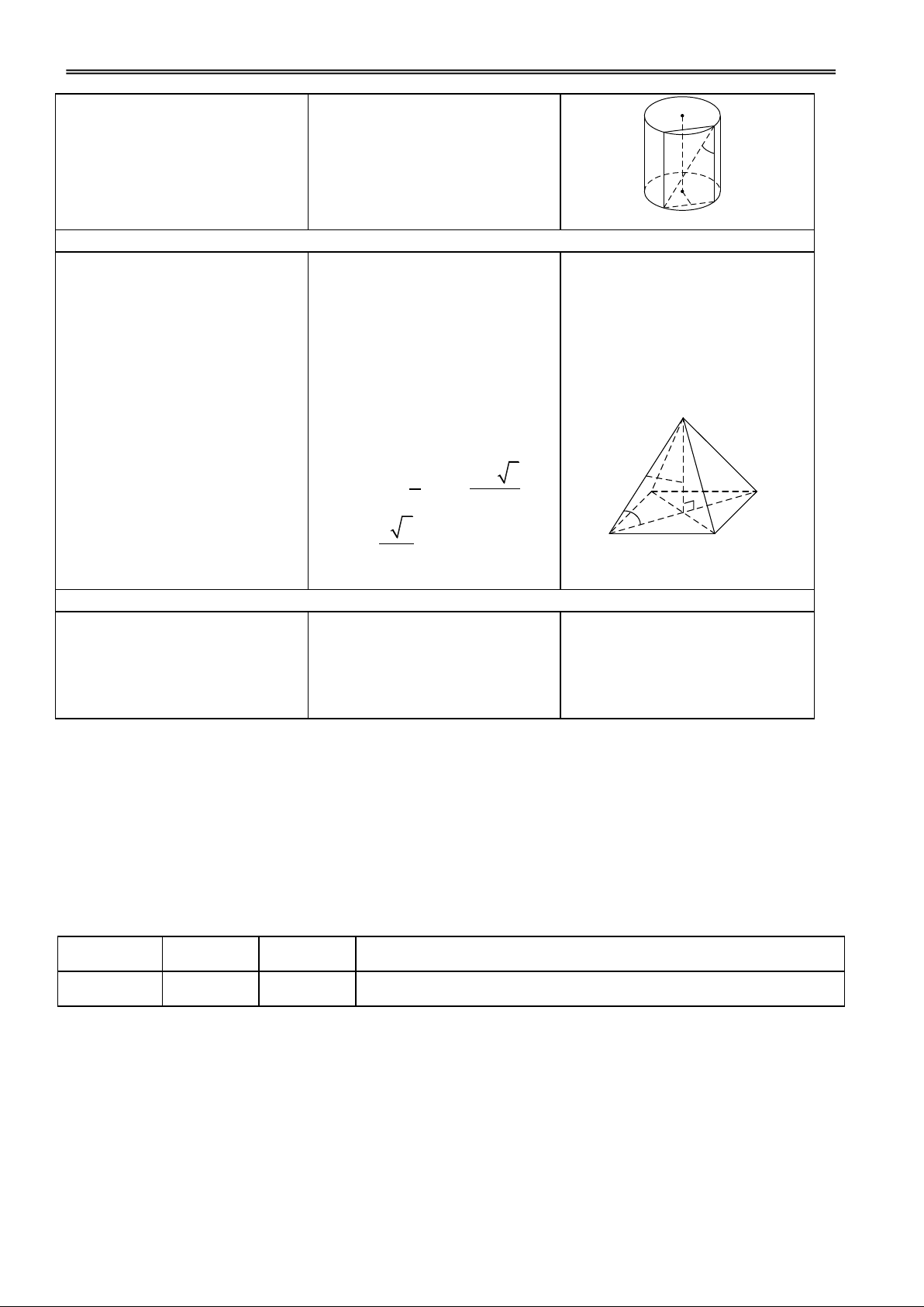
 GV giới thiệu công thức tính III. THỂ TÍCH KHỐI thể tích khối chóp. CHÓP
Định lí: Thể tích khối chóp
H1. Nhắc lại khái niệm đường Đ1. Đoạn vuông góc hạ từ đỉnh cao của hình chóp? bằng 1
đến đáy của hình chóp.
diện tích đáy B nhân 3 S với chiều cao h. 1 V = Bh 3 D A H B C
Hoạt động 2: Áp dụng tính thể tích khối chóp  Cho HS thực hiện.
 Các nhóm tính và điền kết VD1: Gọi S, h, V lần lượt là quả vào bảng.
thể diện tích đáy, chiều cao và
thể tích khối chóp. Tính và GV: Phạm Việt Phương 14
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn điền vào ô trống: S h V 8 7 8 4 8 4 3 12 2
Hoạt động 3: Vận dụng tính thể tích của khối chóp
H1. Tính chiều cao của hình Đ1.
BT1: Cho hình chóp tam giác chóp ?
đều S.ABC. Tính thể tích khối a) h = SO = 2 2 SA AO chóp nếu biết: 2 a a) AB = a và SA = b. 2 b  =
b) SA = b và góc giữa mặt bên 3 và đáy bằ b) ng . S  a 3
h OM.tan  tan  6  2  a 2 2 2 2
h SA OA b   C 3 A b  O M  a .tan  B 2 4  tan  bh .tan  2 4  tan 
BT2: Cho hình lăng trụ tam
H2. Tính thể tích khối chóp Đ2.
giác ABC.ABC. Gọi E, F lần C.ABC theo V ? 1 V
lượt là trung điểm của AA, VC.ABC = 3
BB. Đường thẳng CE cắt CA 2
tại E. Đường thẳng CF cắt  V V ABBA = 3
CB tại F. Gọi V là thể tích
H3. Nhận xét thể tích của hai Đ3.
khối lăng trụ ABC.ABC. khối chóp C.ABFE và 1 1
a) Tính thể tích khối chóp V V C.ABFE = VC.ABBA = C.ABBA ? 2 3 C.ABFE theo V.
b) Gọi khối đa diện (H) là phần
còn lại của khối lăng trụ
H4. So sánh diện tích của hai Đ4. S
ABC.ABC sau khi cắt bỏ đi CFE = 4SCBA
tam giác CFE và CBA ?
khối chóp C.ABFE. Tính tỉ số 4  V V C.EFC =
thể tích của (H) và của khối 3 chóp C.CEF.
H5. Tính thể tích khối (H) ? Đ5. 2 V V (H) = 3 V  (H) 1  V 2
C.E'F'C'
Hoạt động 4: Củng cố Nhấn mạnh: GV: Phạm Việt Phương 15
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
– Công thức thể tích khối chóp.
– Tính chất của hình chóp đều.
4. BÀI TẬP VỀ NHÀ:
 Bài 1, 2, 3, 4, 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 08
Bài 3: BÀI TẬP KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm thể tích của khối đa diện.
 Các công thức tính thể tích của một số khối đa diện cụ thể. Kĩ năng:
 Tính được thể tích của khối lăng trụ, khối chóp.
 Tính được tỉ số thể tích các khối đa diện được tách ra từ một khối đa diện. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập kiến thức đã học về khối đa diện.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính thể tích khối lăng trụ
H1. Xác định góc giữa AA và Đ1. A cách đều A, B, C
1. Cho lăng trụ tam giác ABC. đáy ?  AO  (ABC)
ABC có đáy ABC là một tam 
giác đều cạnh a và điểm A 0 A' AO  60
cách đều các điểm A, B, C.
H2. Tính chiều cao AO ? a
Cạnh bên AA tạo với mặt 3 Đ2. AO =  AO = a phẳng đáy một góc 600. 3
a) Tính thể tích khối lăng trụ. 3 a 3
b) Chứng minh BCCB là một  V = SABC.AO = 4 hình chữ nhật.
H3. Chứng minh BC  (AAO) Đ3. BC  AO, BC  AO
 BC  (AAO)  BC  AA GV: Phạm Việt Phương 16
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn  BC  BB C’ B’
 BCCB là hình chữ nhật. A’ C B O H A
Hoạt động 2: Luyện tập tính thể tích khối chóp
H1. Xác định đường cao của tứ Đ1. DF  (CFE)
2. Cho tam giác ABC vuông diện ? cân ở A và AB = a. Trên
đường thẳng qua C và vuông
H2. Viết công thức tính thể
góc với mp(ABC) lấy điểm D 1
tích khối tứ diện CDFE ? Đ2. V = S CFE D . F
sao cho CD = a. Mặt phẳng qua 3
C vuông góc với BD cắt BD tại
H3. Tính CE, CF, FE, DF ? Đ3.
F và cắt AD tại E. Tính thể tích
khối tứ diện CDFE theo a. AD a 2 CE =  D 2 2 F a 6 a 6 CF = ; FE = E 3 6 a B 3 C DF = 3 A 3 a  V = 36
Hoạt động 3: Luyện tập tính tỉ số thể tích của khối đa diện
 Hướng dẫn HS xác định đỉnh  Đỉnh A, đáy SBC,
3. Cho hình chóp S.ABC. Trên
và đáy hình chóp để tính thể Đỉnh A, đáy SBC.
các đoạn thẳng SA, SB, SC lần tích.
lượt lấy 3 điểm A, B, C khác S. Chứng minh:
H1. Tính diện tích các tam giác 1 S
V .A'B'C SA' SB' SC ' ' SBC và SB  . . C ? Đ1. S SB S . C.sin BSC SBC = 2 S V .ABC SA SB SC 1 S SB' S
. C '.sin B'SC ' A SBC = 2 A’ h
H2. Tính tỉ số chiều cao của Đ2. hai khối chóp ? h' C’ h' SA' C  S h SA H’ H B’
H3. Tính thể tích của hai khối Đ3. B chóp ? 1 V S h . SABC = SBC 3 1 V S h SB'C = SB'C'. ' 3
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách vận dụng các công thức
tính thể tích các khối đa diện. GV: Phạm Việt Phương 17
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
4. BÀI TẬP VỀ NHÀ:
 Bài tập ôn chương 1 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 09 + 10
Bài dạy: ÔN TẬP CHƯƠNG 1 I. MỤC TIÊU:
Kiến thức: Củng cố:
 Nắm được khái niệm hình đa diện, khối đa diện.
 Hai khối đa diện bằng nhau.
 Phân chia và lắp ghép khối đa diện.
 Đa điện đều và các loại đa diện đều.
 Thể tích các khối đa diện. Kĩ năng:
 Nhận biết được các đa diện và khối đa diện.
 Biết cách phân chia và lắp ghép các khối đa diện để giải các bài toán thể tích.
 Vận dụng các công thức tính thể tích khối đa diện vào việc giải toán. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa diện.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập toàn bộ kiến thức chương 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính thể tích khối đa diện
H1. Xác định góc giữa mặt bên Đ1. 0
SEH SJH SFH  60 1. Cho hình chóp tam giác và đáy?  S.ABC có AB = 5a, BC = 6a, HE = HJ = HF  CA = 7a. Các mặt bên SAB,
H là tâm đường tròn nội tiếp 
SBC, SCA tạo với đáy một góc ABC.
600. Tính thể tích khối chóp đó.
H2. Tính chu vi và diện tích của  2 ABC ?
Đ2. p = 9a, S = 6 6a S 2 6a  HE = r =  p 3
H3. Tính chiều cao của hình GV: Phạm Việt Phương 18
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn chóp ? Đ3. S h = SH = 0
HE.tan60  2 2a  V = 3 8 3a . J A C 0 60 H E F B
Hoạt động 2: Luyện tập tính tỉ số thể tích khối đa diện
H1. Xác định tỉ số thể tích của Đ1.
2. Cho hình chóp tam giác đều hai khối chóp ? S.ABC có cạnh AB = a. Các S V .DBC SDV SA
cạnh bên SA, SB, SC tạo với S.ABC
đáy một góc 600. Gọi D là giao H2. Tính SD, SA ? a a
điểm của SA với mặt phẳng Đ2. 3 5 3 SA = , SD =
qua BC và vuông góc với SA. 4 12 SD
a) Tính tỉ số thể tích của hai 5   khối chóp S.DBC và S.ABC. SA 8
c) Tính thể tích của khối chóp S.DBC.
H3. Tính thể tích khối chóp 3 a Đ3. 3 S V S.ABC ? S.ABC = 12 D  5 3 V a S.DBC = 3 . 96 0 60 A C H E B
Hoạt động 3: Vận dụng thể tích của khối đa diện để giải toán
 Hướng dẫn HS tính thể tích
3. Cho hình chóp tam giác
khối chóp tam giác bằng nhiều O.ABC có ba cạnh OA, OB, cách khác nhau.
OC đôi một vuông góc với
H1. Xác định đường cao và Đ1. nhau và OA = a, OB = b, OC =
đáy của khối chóp bằng các – Đáy OBC, đường cao AO.
c. Tính độ dài đường cao OH cách khác nhau?
– Đáy ABC, đường cao OH. của hình chóp. A
H2. Xác định công thức tính Đ2.
thể tích khối chóp theo 2 cách 1 a  S O . A H ? V OBC 3 c O C 1  S b ABC O . H E 3 B
H3. Tính diện tích ABC ? Đ3. 1 S AE B . C ABC = 2 1 = 2 2 2 2 2 2
a b b c c a 2 V  3 OH = SABC GV: Phạm Việt Phương 19
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn abc = 2 2 2 2 2 2
a b b c c a
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách vận dụng các công thức
tính thể tích các khối đa diện.
– Cách vận dụng thể tích để giải toán.
4. BÀI TẬP VỀ NHÀ:
 Chuẩn bị kiểm tra 1 tiết chương 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 11
Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG 1 I. MỤC TIÊU: Kiến thức:
 Ôn tập toàn bộ kiến thức trong chương I. Kĩ năng:
 Nhận biết được các hình đa diện và khối đa diện.
 Tính được thể tích của các khối đa diện đơn giản.
 Vận dụng các công thức tính thể tích khối đa diện vào việc giải toán. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: Ôn tập toàn bộ kiến thức chương 1. III. MA TRẬN ĐỀ: Nhận biết Chủ đề Thông hiểu Vận dụng Tổng TNKQ TL TNKQ TL TNKQ TL Khái niệm khối đa 1 0,5 diện 0,5 Khối đa diện lồi và 1 0,5 khối đa diện đều 0,5
Thể tích khối đa diện 2 4 1 1 9,0 0,5 0,5 3,0 3,0 Tổng 2,0 2,0 3,0 3,0 10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm) GV: Phạm Việt Phương 20
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Câu 1: Các mặt của khối tứ diện đều là: A. Hình tam giác đều B. Hình vuông
C. Hình ngũ giác đều D. Hình thoi.
Câu 2: Trong một hình đa diện, mỗi đỉnh là đỉnh chung của ít nhất: A. 2 mặt B. 3 mặt C. 4 mặt D. 5 mặt
Câu 3: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 5a là: 125 125 125 3 A. 125a3 B. 3 a C. 3 a D. 3 a 3 4 4
Câu 4: Thể tích của khối lăng trụ bằng 3
8 3a , chiều cao bằng 2a. Diện tích đáy của khối lăng trụ đó bằng: 2 3 A. 4 3a B. 4 3a C. 4 3a D. 4 3
Câu 5: Thể tích của khối chóp tam giác S.ABC với đáy ABC là tam giác đều cạnh bằng 3a , SA vuông góc với
đáy và SA = 3a là: 3 9a 3 9 3a A. 3 9a B. 3 27a C. D. 4 4
Câu 6: Cho khối lập phương ABCD.ABCD cạnh bằng a. Thể tích của khối tứ diện AABD bằng 3 a 3 a 3 a 3 a A. B. C. D. 4 2 3 6
Câu 7: Cho khối lập phương ABCD.ABCD. Tỉ số thể tích của khối AABC và khối AABD bằng: 1 1 A. 1 B. 2 C. D. 2 6
Câu 8: Cho khối lập phương ABCD.ABCD. Tỉ số thể tích của khối AABC và khối lập phương ABCD.ABCD bằng: 1 1 A. 1 B. 2 C. D. 2 6
II. Phần tự luận: (6 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a và SA vuông góc với đáy.
a) Tính thể tích khối chóp S.ABC.
b) Tính khoảng cách từ A đến mặt phẳng (SBC).
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 A B D B C D A D
B. Phần tự luận: Mỗi câu 3 điểm a)  Hình vẽ (0,5 điểm) S 1  V = S .  SA (0,5 điểm) ABC 3 2 a H  SABC = (1,0 điểm) 2 A D 3 a  V = (1,0 điểm) B C 6 b)  Vẽ AH  (SBC) 1 3 a  V = S .  AH SBC = (1,0 điểm) 3 6 2  SSBC = 2 a (1,0 điểm) 2 GV: Phạm Việt Phương 21
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn 3V 2  AH =  a (1,0 điểm) S 2 SBC
VI. KẾT QUẢ KIỂM TRA: Lớp 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Sĩ số SL % SL % SL % SL % SL % 12S1 53 12S2 54 12S3 54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1
Chương II: MẶT NÓN, MẶT TRỤ, MẶT CẦU Tiết dạy: 12
Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm chung về mặt tròn xoay.
 Hiểu được khái niệm mặt nón tròn xoay, phân biệt được các khái niệm: mặt nón tròn xoay,
hình nón tròn xoay, khối nón tròn xoay. Biết công thức tính diện tích xung quanh hình nón
tròn xoay, thể tích khối nón tròn xoay.
 Nắm được khái niệm mặt trụ tròn xoay, phân biệt được các khái niệm: mặt trụ tròn xoay,
hình trụ tròn xoay, khối trụ tròn xoay. Biết công thức tính diện tích xung quanh hình trụ tròn
xoay, thể tích khối trụ tròn xoay. Kĩ năng:
 Vẽ thành thạo các mặt trụ và mặt nón.
 Tính được diện tích và thể tích của hình trụ, hình nón.
 Phân chia mặt trụ và mặt nón bằng mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hình học không gian.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại những điều đã biết về hình nón, hình trụ? Đ. GV: Phạm Việt Phương 22
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
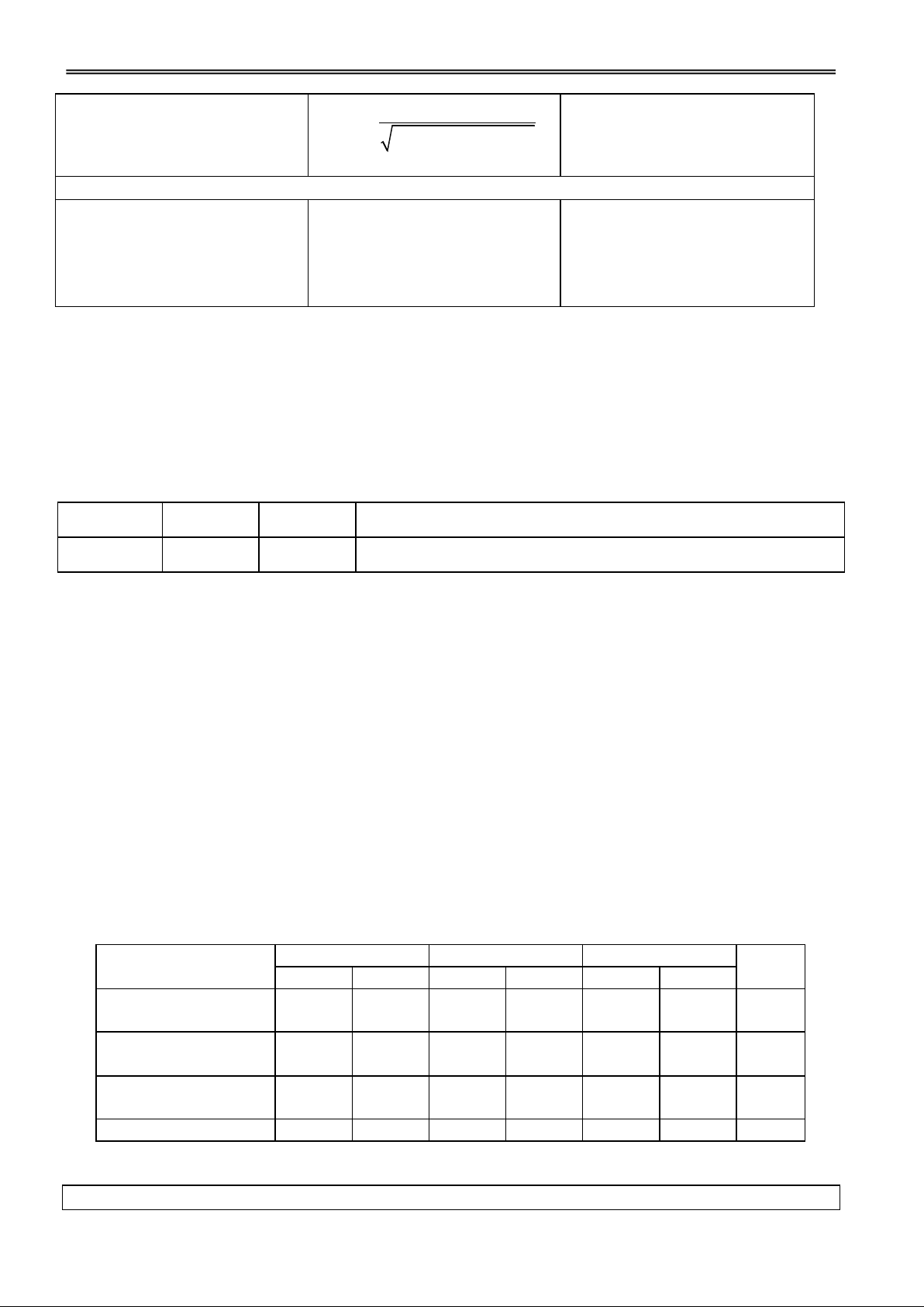
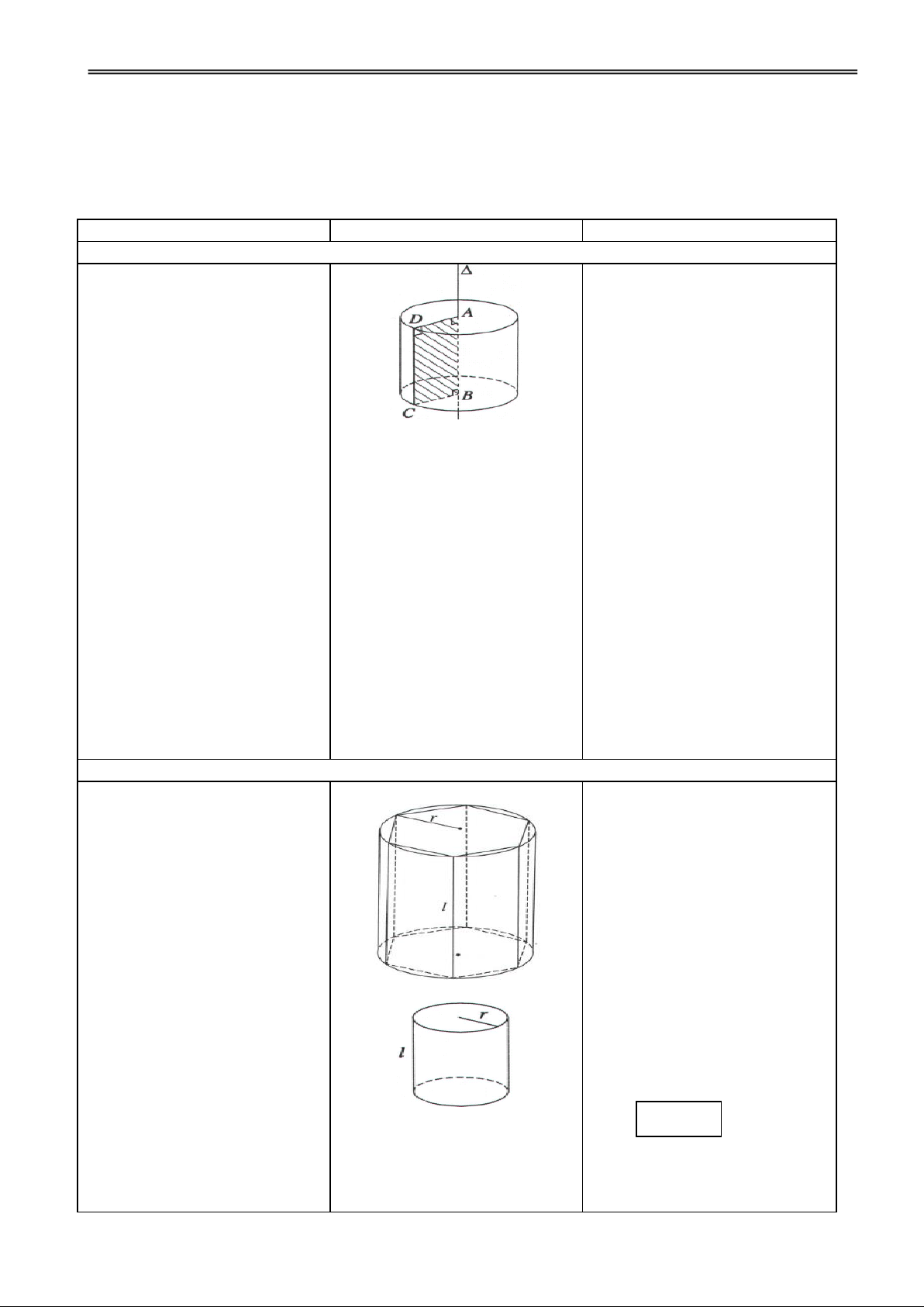
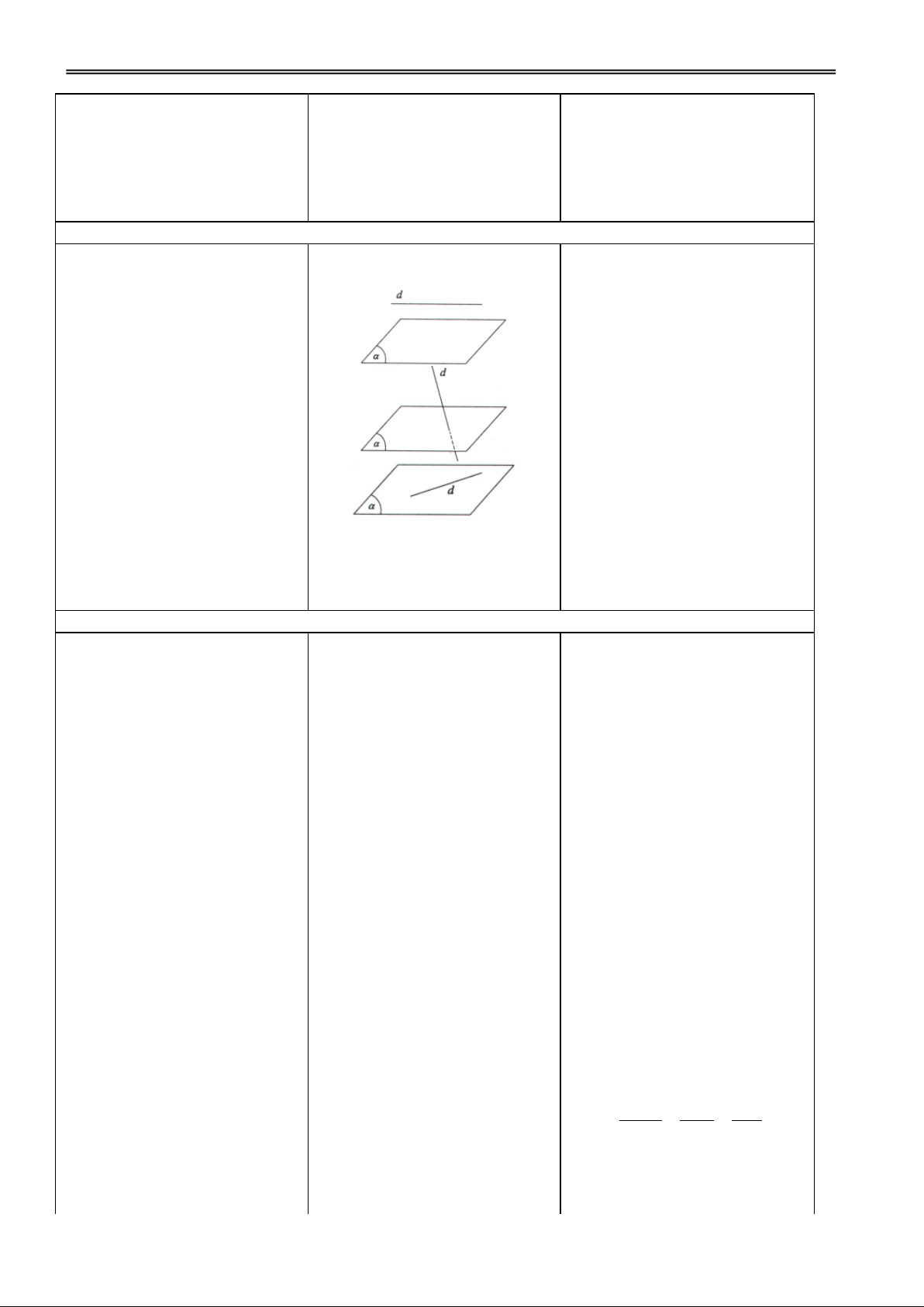
Hoạt động 1: Tìm hiểu khái niệm mặt tròn xoay
H1. Nêu tên một số đồ vật mà Đ1. Các nhóm thảo luận và I. SỰ TẠO THÀNH MẶT
mặt ngoài có hình dạng là các trình bày. TRÒN XOAY mặt tròn xoay?
Lọ hoa, chiếc nón, cái ly, …
Trong KG, cho mp (P) chứa
đường thẳng và một đường
 GV dùng hình vẽ minh hoạ
(C). Khi quay (P) quanh một
cho sự tạo thành mặt tròn xoay
góc 3600 thì mỗi điểm M trên
(C) vạch ra một đường tròn có
tâm O thuộc và nằm trên mp
vuông góc với . Khi đó (C) sẽ
tạo nên một hình đgl mặt tròn xoay.
(C) đgl đường sinh của mặt
tròn xoay đó. đgl trục của mặt tròn xoay.
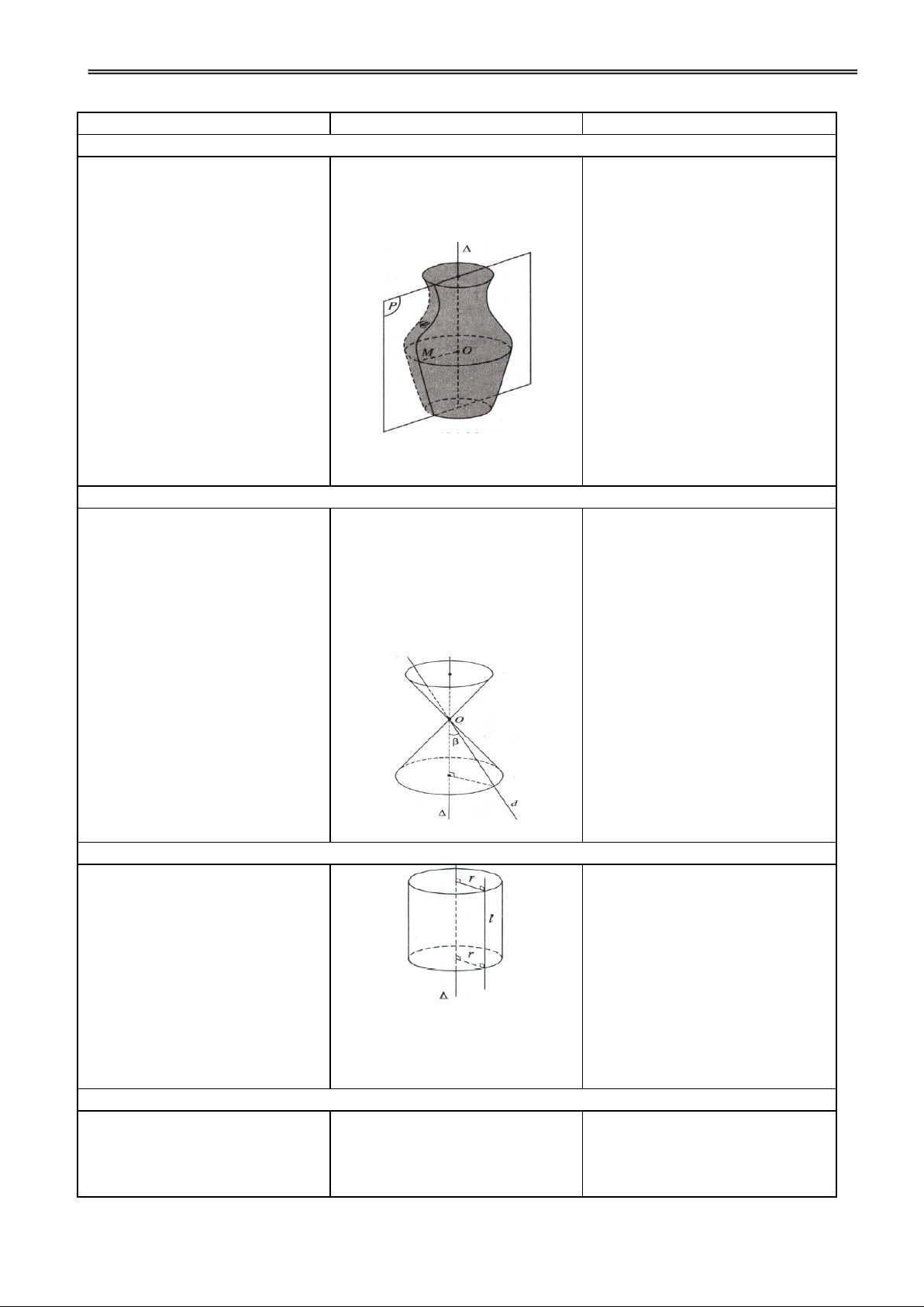
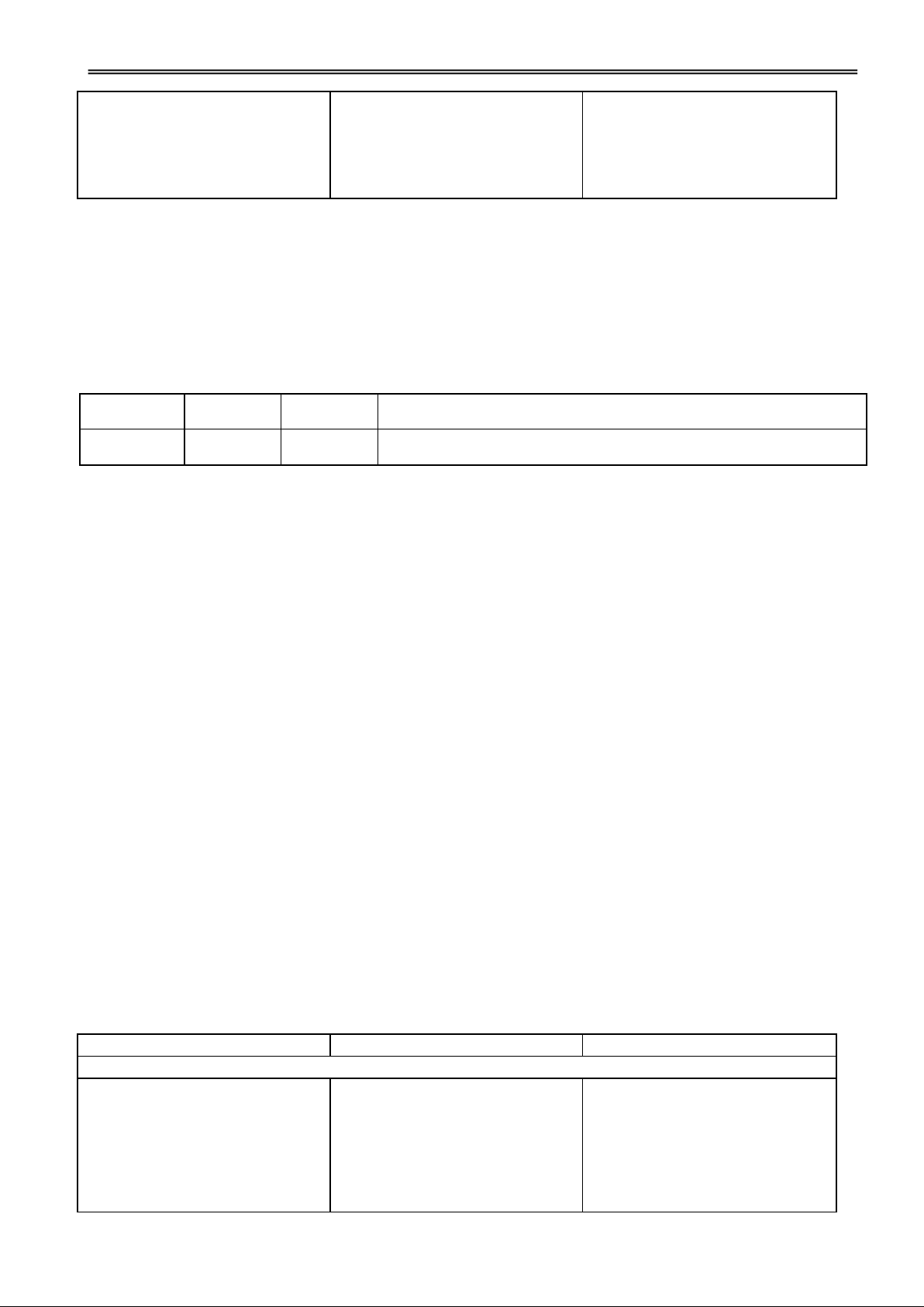
Hoạt động 2: Tìm hiểu sự tạo thành mặt nón tròn xoay
 GV dùng hình vẽ minh hoạ
1. Mặt nón tròn xoay
và hướng dẫn cho HS nhận biết
Trong mp (P) có hai đường
được cách tạo thành mặt nón
thẳng d và cắt nhau tại điểm tròn xoay.
O và tạo thành góc nhọn . Khi
quay (P) xung quanh thì d
H1. Mô tả đường sinh, trục, Đ1. Các nhóm thảo luận và sinh ra một mặt tròn xoay đgl đỉnh của cái nón? trình bày.
mặt nón tròn xoay đỉnh O.
gọi là trục, d gọi là đường
sinh, góc 2 gọi là góc ở đỉnh của mặt nón đó.
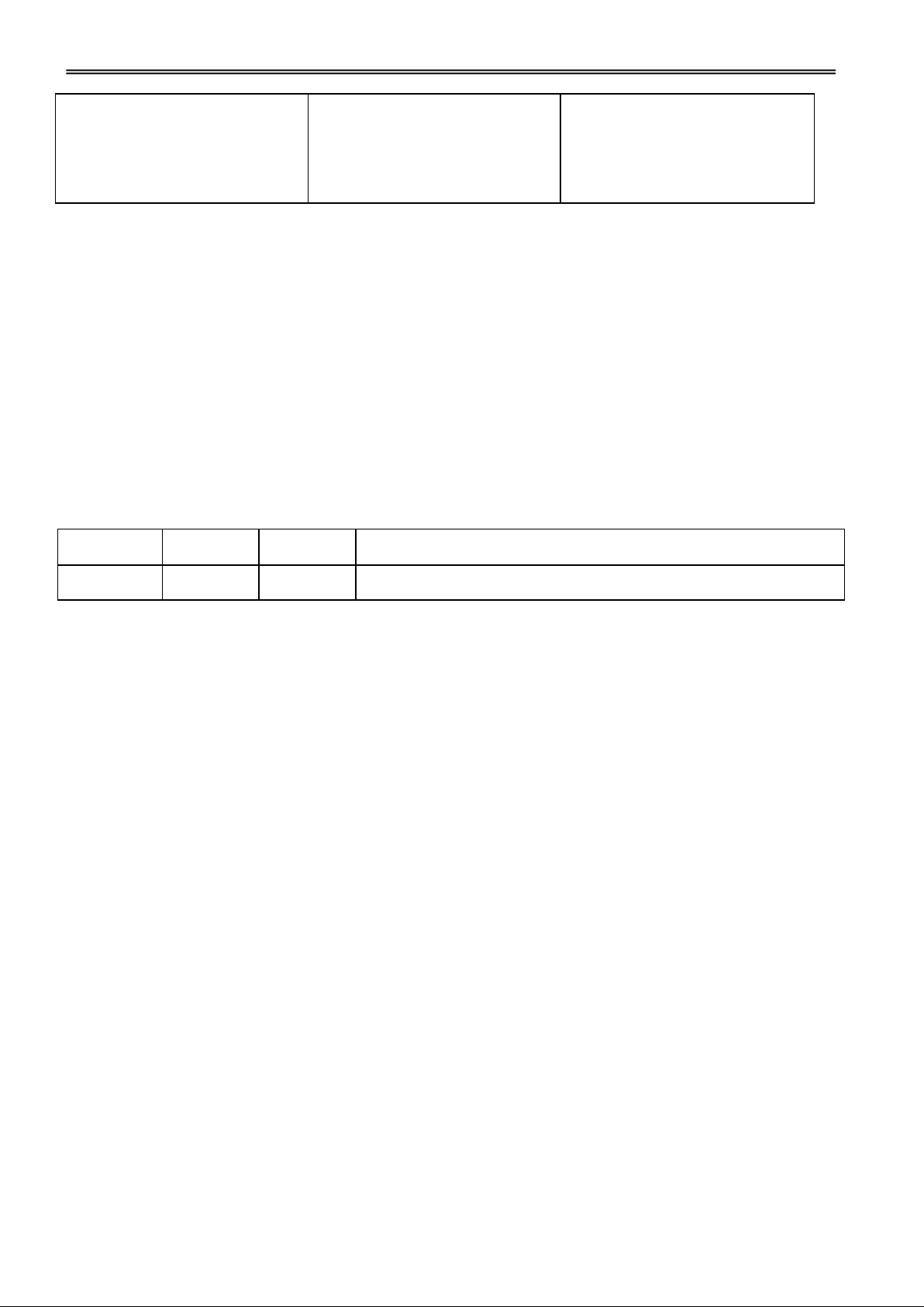
Hoạt động 3: Tìm hiểu sự tạo thành mặt trụ tròn xoay
 GV dùng hình vẽ minh hoạ
2. Mặt trụ tròn xoay
và hướng dẫn cho HS nhận biết
Trong mp (P) cho hai đường
được cách tạo thành mặt trụ
thẳng và l song song nhau, tròn xoay.
cách nhau một khoảng bằng r.
Khi quay (P) xung quanh thì
l sinh ra một mặt tròn xoay đgl
mặt trụ tròn xoay. gọi là
H1. Mô tả đường sinh, trục, Đ1. Các nhóm thảo luận và trục, l gọi là đường sinh, r là
đỉnh của hộp sữa (lon)? trình bày.
bán kính của mặt trụ đó.
Hoạt động 4: Củng cố Nhấn mạnh:
– Sự tạo thành của mặt tròn xoay.
– Các khái niệm đường sinh, GV: Phạm Việt Phương 23
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
trục của mặt tròn xoay.
Cau hỏi: Nêu tên một số đồ
vật có hình dạng là mặt nón, mặt trụ.
4. BÀI TẬP VỀ NHÀ:  Bài 1 SGK.
 Làm một số mô hình biểu diễn mặt trụ tròn xoay, mặt nón tròn xoay.
 Đọc tiếp bài "Khái niệm mặt tròn xoay".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 13
Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm chung về mặt tròn xoay.
 Hiểu được khái niệm mặt nón tròn xoay, phân biệt được các khái niệm: mặt nón tròn xoay, hình nón
tròn xoay, khối nón tròn xoay. Biết công thức tính diện tích xung quanh hình nón tròn xoay, thể tích khối nón tròn xoay.
 Nắm được khái niệm mặt trụ tròn xoay, phân biệt được các khái niệm: mặt trụ tròn xoay, hình trụ
tròn xoay, khối trụ tròn xoay. Biết công thức tính diện tích xung quanh hình trụ tròn xoay, thể tích khối trụ tròn xoay. Kĩ năng:
 Vẽ thành thạo các mặt trụ và mặt nón.
 Tính được diện tích và thể tích của hình trụ, hình nón.
 Phân chia mặt trụ và mặt nón bằng mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa mặt nón tròn xoay? Đ. GV: Phạm Việt Phương 24
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm hình nón, khối nón tròn xoay
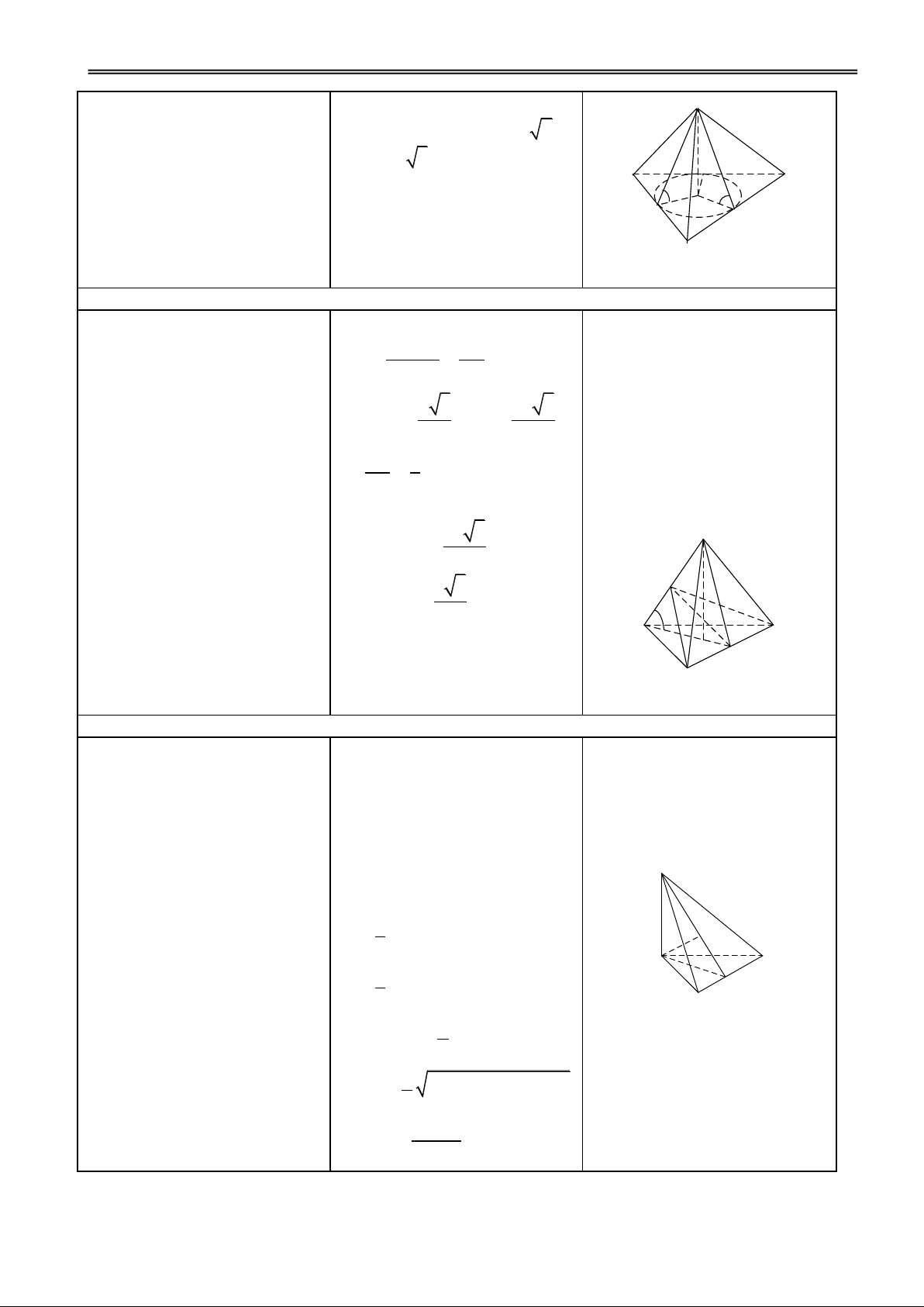
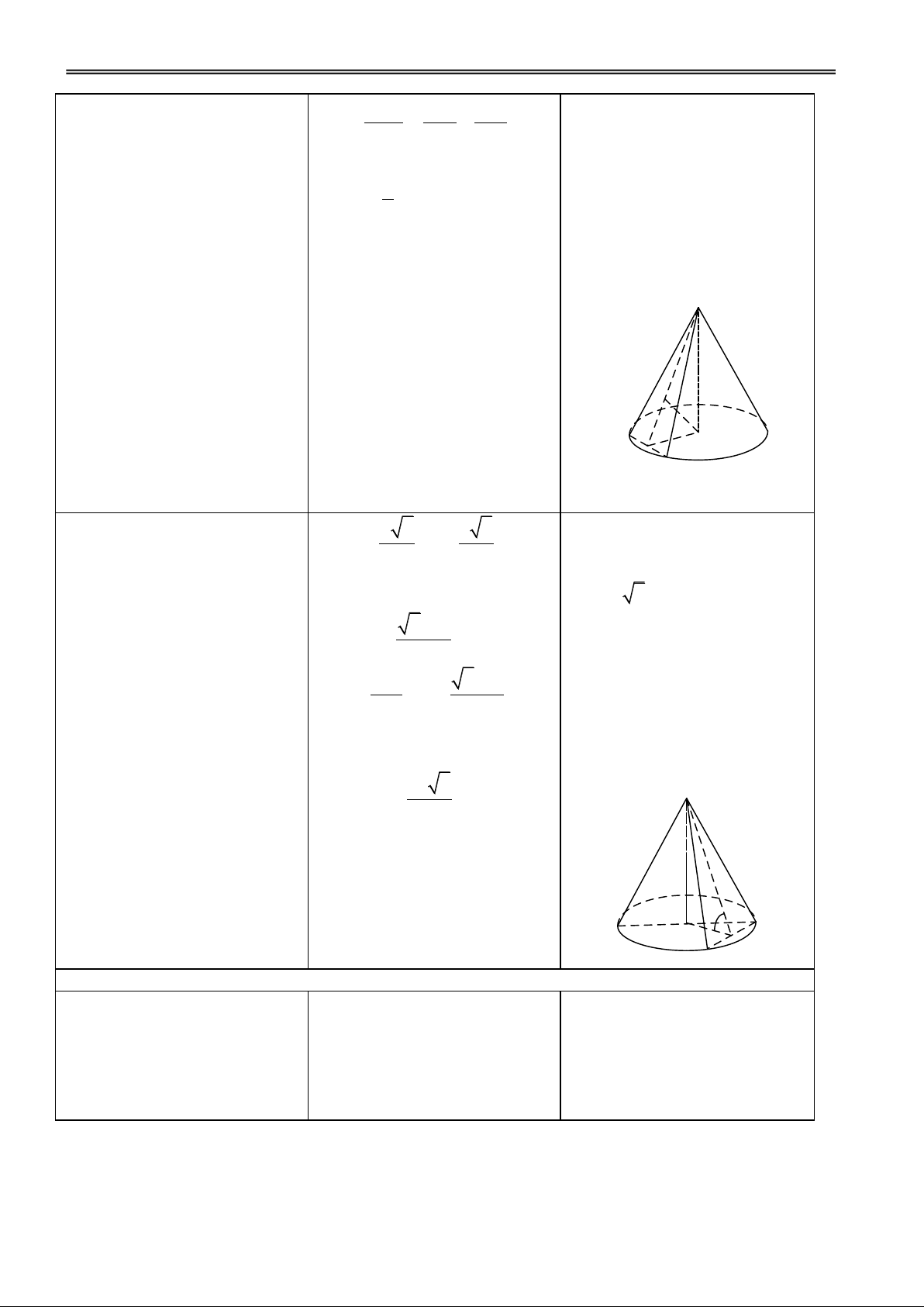
 GV dùng hình vẽ để minh hoạ
I. NẶT NÓN TRÒN XOAY
và hướng dẫn HS cách tạo ra hình
1. Mặt nón tròn xoay nón tròn xoay.
2. Hình nón tròn xoay
Cho OIM vuông tại I. Kh i q u ay
nó xung quanh cạnh góc vuông OI
thì đường gấp khúc OMI tạo
thành một hình đgl hình nón tròn
H1. Xác định khoảng cách từ đỉnh Đ1. h = OI. xoay. đến đáy?
– Hình tròn (I, IM): mặt đáy – O: đỉnh – OI: đường cao – OM: đường sinh
– Phần mặt tròn xoay sinh ra bởi OM: mặt xung quanh.
 GV giới thiệu khái niệm khối
3. Khối nón tròn xoay nón.
Phần không gian được giới hạn
bởi một hình nón tròn xoay kể cả
H2. Phân biệt hình nón và khối Đ2. Các nhóm thảo luận và trả lời. hình nón đó đgl khối nón tròn nón? xoay.
– Điểm ngoài: điểm không thuộc khối nón.
– Điểm trong: điểm thuộc khối
nón nhưng không thuộc hình nón.
– Đỉnh, mặt đáy, đường sinh
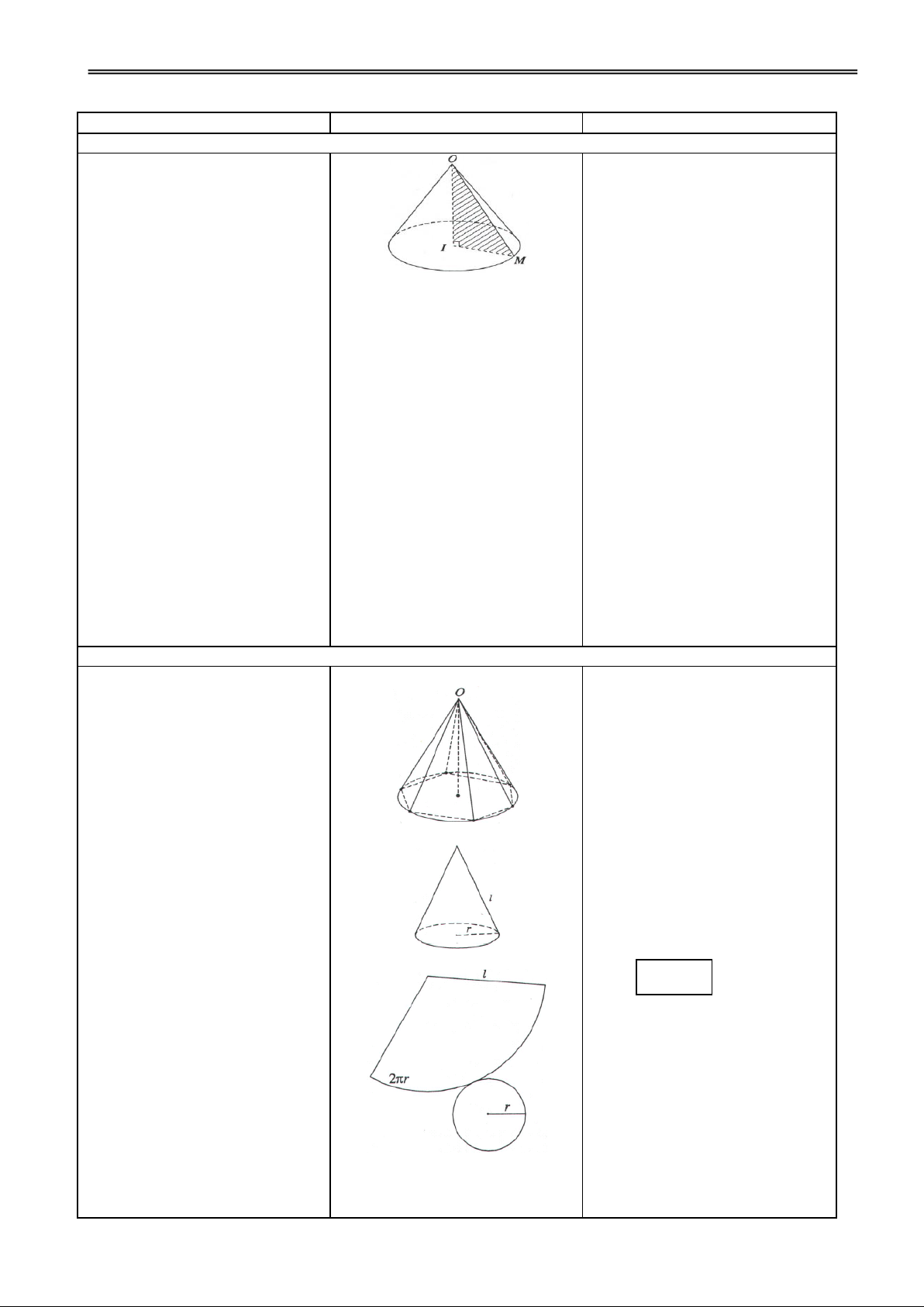
Hoạt động 2: Tìm hiểu công thức tính diện tích xung quanh của hình nón
 GV giới thiệu khái niệm hình
4. Diện tích xung quanh của
chóp nội tiếp hình nón, diện tích hình nón xung quanh hình nón.
a) Một hình chóp đgl nội tiếp hình
nón nếu đáy của hình chóp là đa
giác nội tiếp đường tròn đáy của
hình nón và đỉnh của hình chóp là
đỉnh của hình nón.
Diện tích xung quanh của hình
nón là giới hạn của diện tích xung
quanh của hình chóp đều nội tiếp
hình nón đó khi số cạnh đáy tăng lên vô hạn.
b) Diện tích xung quanh của hìn h
nón bằng nửa tích độ dài đường
tròn đáy với độ dài đường sinh : Sxq  rl
Diện tích toàn phần của hình nón
bằng tổng diện tích xung quanh
và diện tích đáy. Chú ý:
Nếu cắt mặt xung quanh
của hình nón theo một đường sinh
rồi trải ra trên một mp thì ta được
một hình quạt có bán kính bằng
độ dài đường sinh và một cung
tròn có độ dài bằng chu vi đường
H1. Tính diện tích hình quạt?
tròn đáy của hình nón. Khi đó: GV: Phạm Việt Phương 25
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn Đ1. q
S uaït  rl Sxq q
S uaït rl
Hoạt động 3: Tìm hiểu công thức tính thể tích của khối nón
 GV giới thiệu khái niệm và
5. Thể tích khối nón
công thức tính thể tích khối nón.
Thể tích khối nón là giới hạn của 1
thể tích khối chóp đều nội tiếp
H1. Nhắc lại công thức tính thể Đ1. V Bh
khối nón đó khi số cạnh đáy tăng tích khối chóp? 3 lên vô hạn. 1 2 V  r h 3
Hoạt động 4: Củng cố Nhấn mạnh:
– Các khái niệm hình nón, khối nón.
– Công thức tính diện tích xung
quanh, thể tích của khối nón.
4. BÀI TẬP VỀ NHÀ:  Bài 2, 3, 4, 6, 9 SGK.
 Đọc tiếp bài "Khái niệm mặt tròn xoay".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 14
Bài 1: KHÁI NIỆM VỀ MẶT TRÒN XOAY (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm chung về mặt tròn xoay.
 Hiểu được khái niệm mặt nón tròn xoay, phân biệt được các khái niệm: mặt nón tròn xoay, hình nón
tròn xoay, khối nón tròn xoay. Biết công thức tính diện tích xung quanh hình nón tròn xoay, thể tích khối nón tròn xoay.
 Nắm được khái niệm mặt trụ tròn xoay, phân biệt được các khái niệm: mặt trụ tròn xoay, hình trụ
tròn xoay, khối trụ tròn xoay. Biết công thức tính diện tích xung quanh hình trụ tròn xoay, thể tích khối trụ tròn xoay. Kĩ năng:
 Vẽ thành thạo các mặt trụ và mặt nón.
 Tính được diện tích và thể tích của hình trụ, hình nón.
 Phân chia mặt trụ và mặt nón bằng mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay. GV: Phạm Việt Phương 26
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa mặt trụ tròn xoay? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
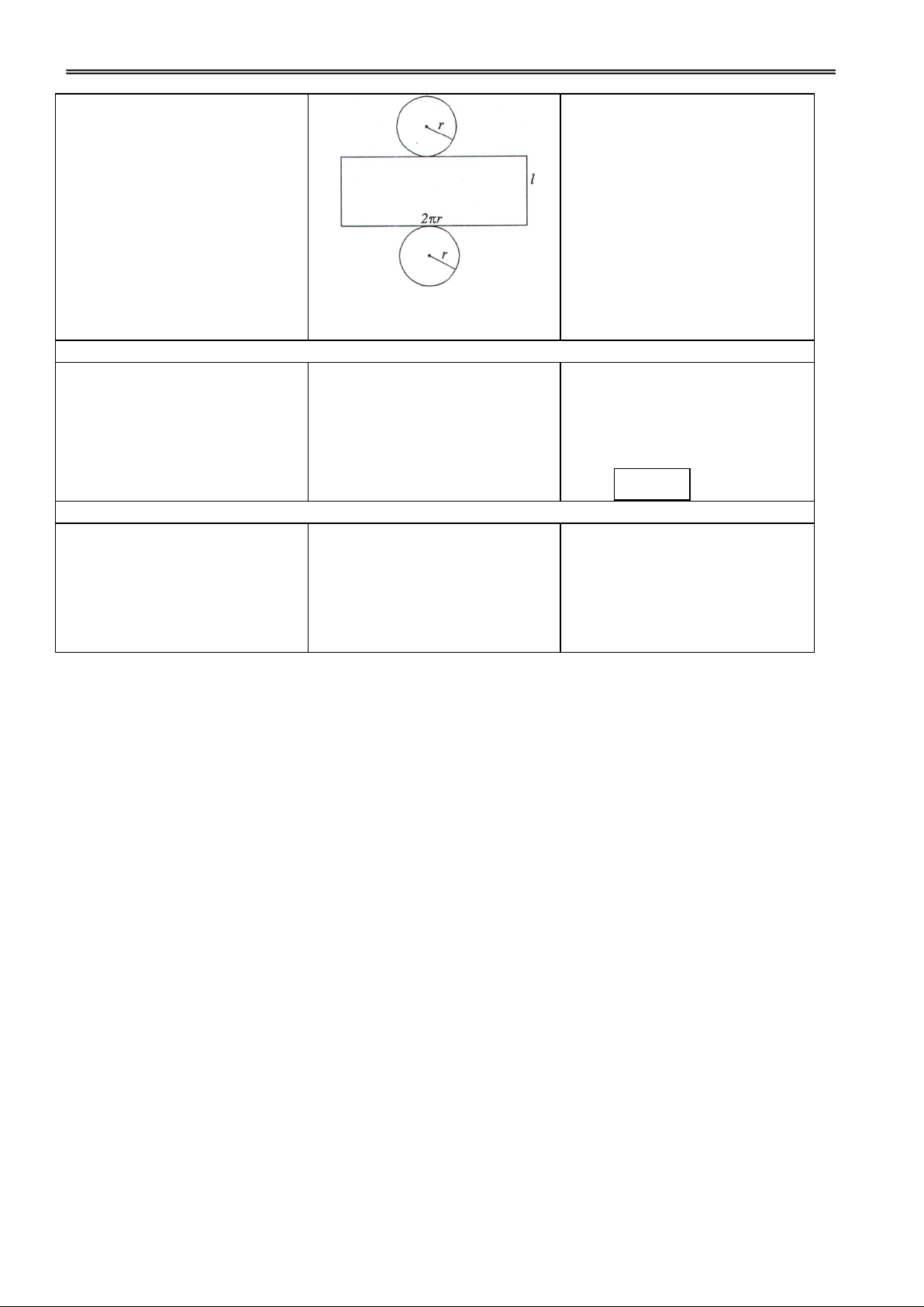
Hoạt động 1: Tìm hiểu khái niệm hình trụ, khối trụ tròn xoay
 GV dùng hình vẽ để minh III. MẶT TRỤ TRÒN
hoạ và hướng dẫn HS cách tạo XOAY ra hình trụ tròn xoay.
1. Mặt trụ tròn xoay
2. Hình trụ tròn xoay
Xét hình chữ nhật ABCD. Khi
quay hình đó xung quanh
đường thẳng chứa 1 cạnh,
chẳng hạn AB, thì đường gấp Đ1. h = AB
khúc ADCB tạo thành 1 hình
H1. Xác định khoảng cách
đgl hình trụ tròn xoay. giữa hai đáy? – Hai đáy. – Đường sinh. – Mặt xung quanh. – Chiều cao.
 GV giới thiệu khái niệm khối trụ.
3. Khối trụ tròn xoay
Phần không gian được giới
H2. Phân biệt hình trụ và khối
hạn bởi một hình trụ kể cả hình trụ?
trụ đó đgl khối trụ tròn xoay.
Đ3. Hộp sữa, một số chi tiết – Điểm ngoài.
H3. Cho VD các vật thể có máy. – Điểm trong.
dạng hình trụ, khối trụ?
– Mặt đáy, đường sinh, chiều cao
Hoạt động 2: Tìm hiểu công thức tính diện tích xung quanh của hình trụ
4. Diện tích xung quanh của
 GV giới thiệu khái niệm hình hình trụ
lăng trụ nội tiếp hình trụ, diện
a) Một hình lăng trụ đgl nội tích xung quanh hình trụ.
tiếp một hình trụ nếu hai đáy
của hình lăng trụ nội tiếp hai
đường tròn đáy của hình trụ.
Diện tích xung quanh của hình
trụ là giới hạn của diện tích
xung quanh của hình lăng trụ
đều nội tiếp hình trụ khi số
cạnh đáy tăng lên vô hạn.
b) Diện tích xung quanh của
hình trụ bằng tích độ dài
đường tròn đáy và độ dài đường sinh. Sxq  2rl
Diện tích toàn phần của hình
trụ bằng tổng diện tích xung
quanh và diện tích của hai đáy. GV: Phạm Việt Phương 27
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
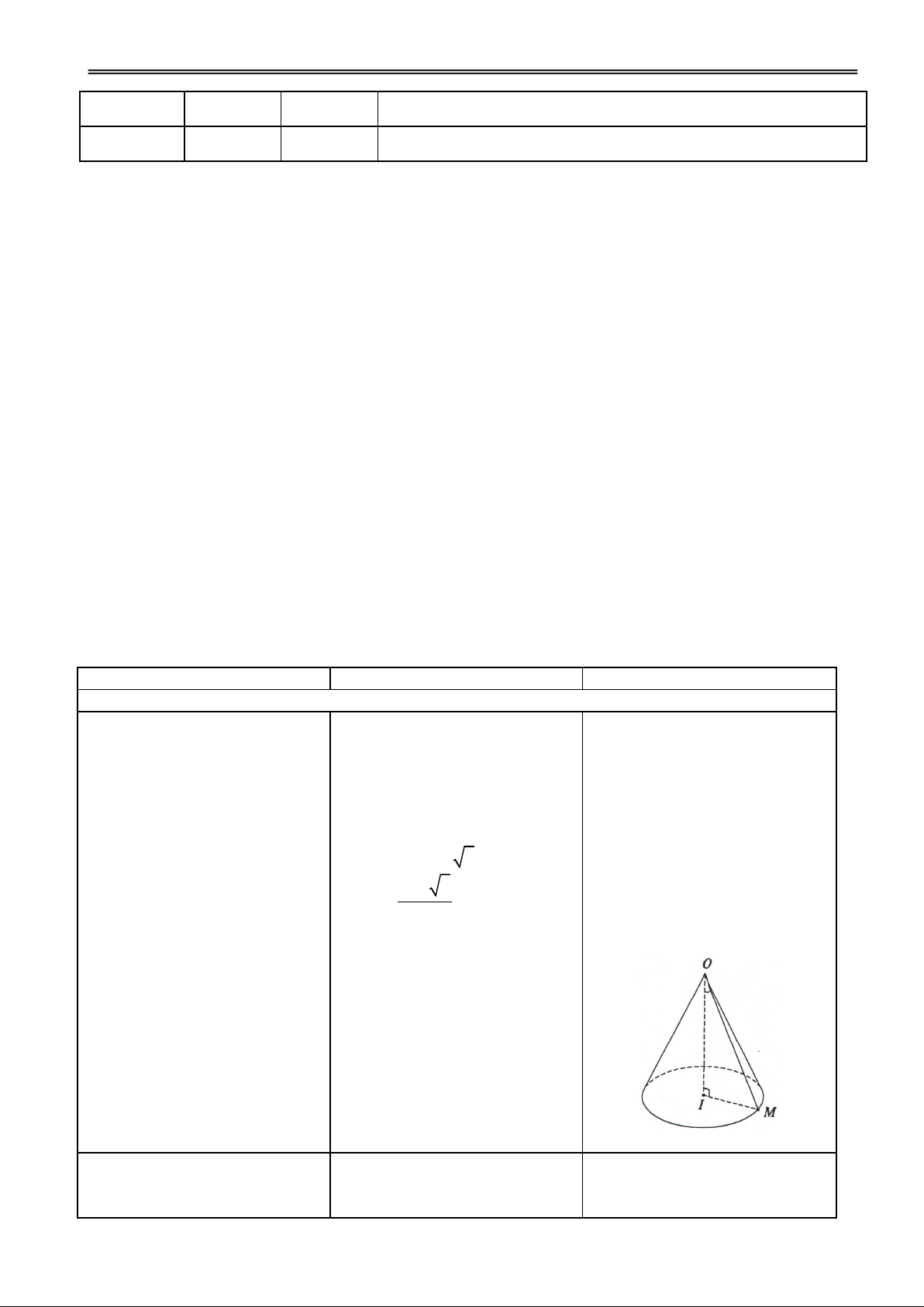
Chú ý: Nếu cắt mặt xung
quanh của hình trụ theo một
đường sinh, rồi trải ra trên một
mp thì sẽ được một hình chữ
nhật có một cạnh bằng đường
H1. Tính diện tích hình chữ
sinh l và một cạnh bằng chu vi nhật? đường tròn đáy. Sxq h S cn  2rl Đ1. h
S cn  2rl
Hoạt động 3: Tìm hiểu công thức tính thể tích của khối trụ
 GV giới thiệu khái niệm và
5. Thể tích khối trụ
công thức tính thể tích khối trụ.
Thể tích khối trụ là giới hạn
của thể tích khối lăng trụ đều
H1. Nhắc lại công thức tính thể Đ1. V = Bh
nội tiếp khối trụ đó khi số cạnh tích khối lăng trụ?
đáy tăng lên vô hạn. 2 V  r h
Hoạt động 4: Củng cố Nhấn mạnh:
– Các khái niệm hình trụ, khối trụ.
– Công thức tính diện tích
xung quanh, thể tích của khối trụ.
4. BÀI TẬP VỀ NHÀ:  Bài 5, 7, 8, 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 28
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 15
Bài 1: BÀI TẬP KHÁI NIỆM VỀ MẶT TRÒN XOAY I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm hình nón, khối nón, hình trụ, khối trụ.
 Công thức tính diện tích xung quanh hình nón tròn xoay, thể tích khối nón tròn xoay.
 Công thức tính diện tích xung quanh hình trụ tròn xoay, thể tích khối trụ tròn xoay. Kĩ năng:
 Vẽ thành thạo các mặt trụ và mặt nón.
 Tính được diện tích và thể tích của hình trụ, hình nón.
 Phân chia mặt trụ và mặt nón bằng mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối tròn xoay.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập..
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính diện tích xung quanh và thể tích khối nón
1. Cho tam giác OIM vuông tại
H1. Xác định đường sinh của Đ1. l = OM = 2a I, góc IOM 0  30 , IM = a. Khi hình nón? quay OIM quanh cạnh góc
vuông OI thì đường gấp khúc H2. Tính Sxq?
Đ2. Sxq = rl = 2a2
OMI tạo thành một hình nón tròn xoay.
H3. Tính chiều cao khối chóp?
Đ3. h = OI = a 3 .
a) Tính diện tích xung quanh a3 3 của hình nón đó.  V =
b) Tính thể tích khối nón tròn 3 xoay tạo thành.
H4. Xác định khoảng cách từ Đ4. OH  SI (I là trung điểm 2. Cho hình nón tròn xoay có
tâm của đáy đến thiết diện? của AB)
đường cao h = 20cm, bán kính đáy r = 25 cm. GV: Phạm Việt Phương 29
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn 1 1 1
a) Tính diện tích xung quanh   của hình nón.
OH2 OS2 OI2
b) Tính thể tích khối nón tạo  OI = 15 (cm) thành. S 1
c) Một thiết diện đi qua đỉnh SAB SO O . I 2 = 25 (cm2)
của hình nón có khoảng cách
từ tâm của đáy đến mp chứa
thiết diện là 12 cm. Tính diện tích thiết diện đó. S l H h A I O B a a
3. Cắt hình nón đỉnh S bởi mp
H5. Tính bán kính đáy, chiều Đ5. r 2  h 2  2 , 2 , l = a
đi qua trục ta đwọc một tam
cao, đường sinh của hình nón?
giác vuông cân có cạnh huyền bằng a 2 . 2
a) Tính diện tích xung quanh, H6. Tính S 2a xq, Sđáy, V của khối Đ6. S
diện tích đáy và thể tích của nón? xq 2 khối nón tương ứng. a2 a3 2
b) Cho dây cung BC của đường ñ S aùy V  2 ; 12
tròn đáy hình nón sao cho
mp(SBC) tạo với mp chứa đáy
hình nón một góc 600. Tính H7.
Xác định góc giữa Đ7. SHO 0  60 diện tích tam giác SBC. mp(SBC) và đáy hình nón? a2 2  S SBC  S 3 l A B O H
Hoạt động 4: Củng cố Nhấn mạnh: – Cách vẽ hình nón.
– Cách xác định các yếu tố:
đường cao, đường sinh, bán kính đáy của hình nón. – Các tính chất HHKG.
4. BÀI TẬP VỀ NHÀ:  Bài tập còn lại.
IV. RÚT KINH NGHIỆM, BỔ SUNG: GV: Phạm Việt Phương 30
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 16 Bài 2: MẶT CẦU I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm chung về mặt cầu.
 Giao của mặt cầu và mặt phẳng.
 Giao của mặt cầu và đường thẳng.
 Công thức diện tích khối cầu và diện tích mặt cầu. Kĩ năng:
 Vẽ thành thạo các mặt cầu.
 Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
 Biết tính diện tích mặt cầu và thể tích khối cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt tròn xoay.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại khái niệm hình tròn xoay? Cách tạo thành hình nón, hình trụ? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
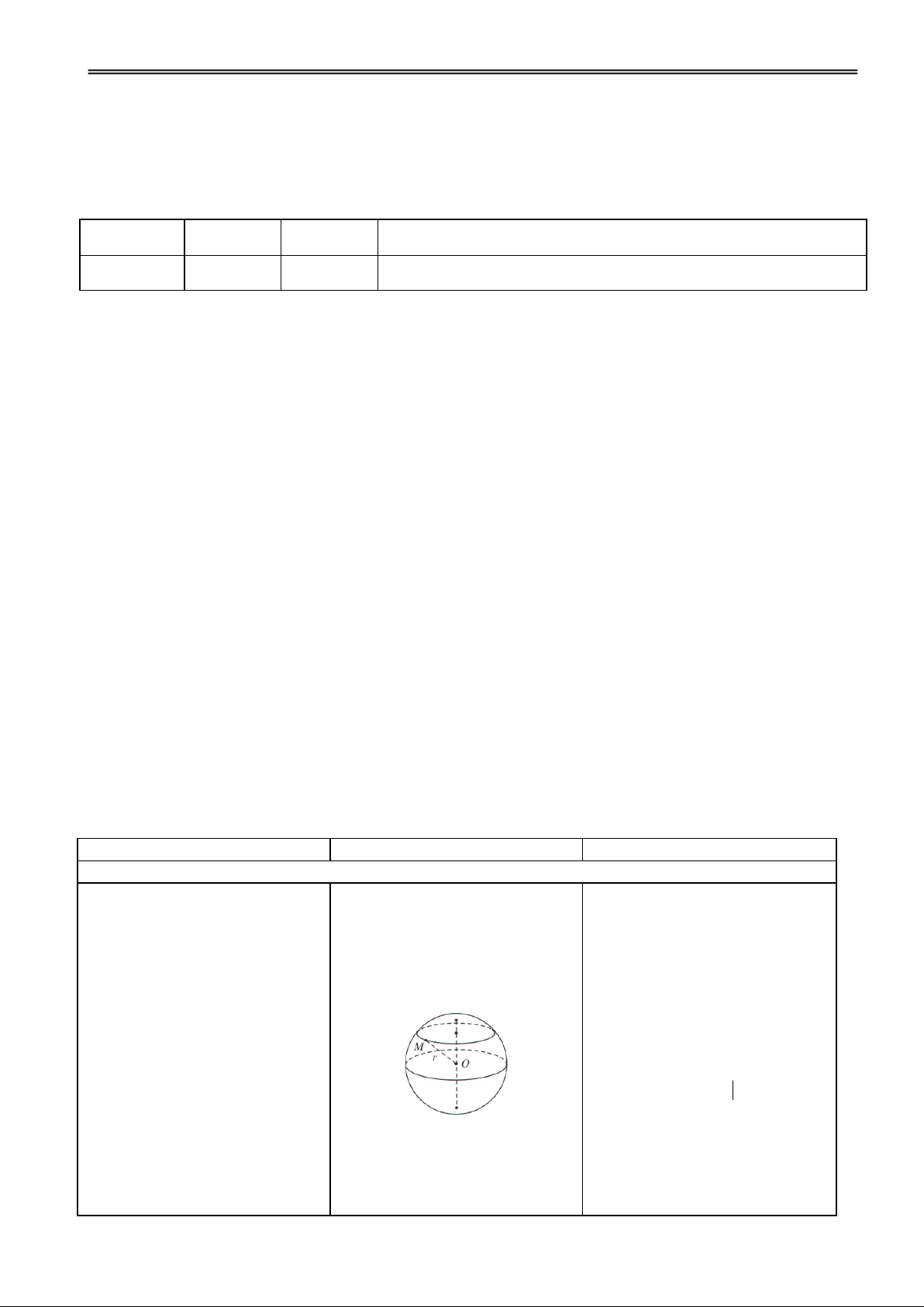
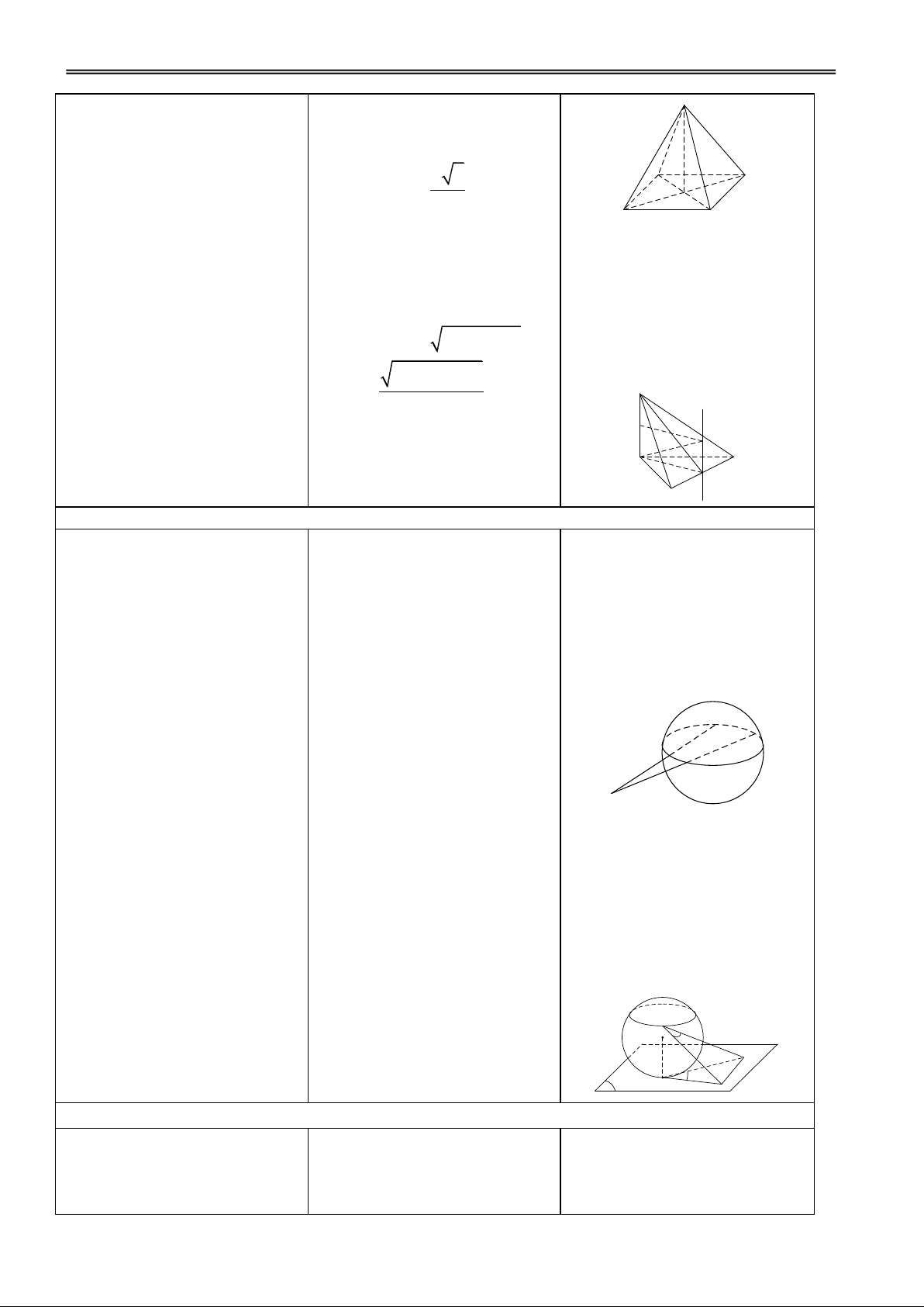
Hoạt động 1: Tìm hiểu khái niệm mặt cầu
H1. Chỉ ra một số đồ vật có Đ1. Các nhóm thảo luận và I. MẶT CẦU VÀ CÁC KHÁI dạng mặt cầu? trình bày.
NIỆM LIÊN QUAN ĐẾN
Quả bóng, quả địa cầu, .. MẶT CẦU 1. Mặt cầu
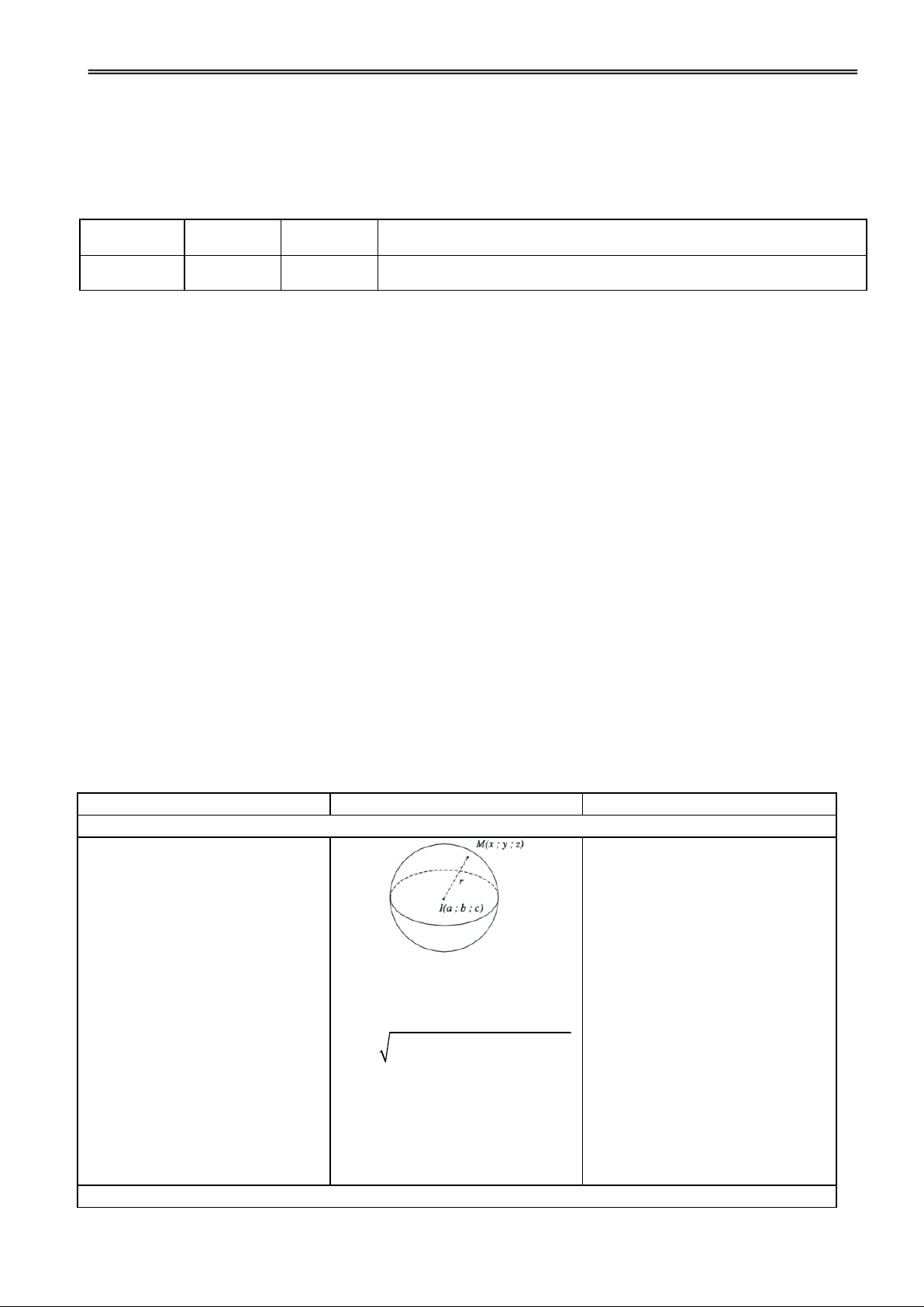
H2. Nhận xét về khái niệm mặt Đ2. Các nhóm thảo luận và Tập hợp những điểm M trong
cầu trong KG và đường tròn trình bày.
KG cách điểm O cố định một trong mp?
khoảng không đổi bằng r (r >
0) đgl mặt cầu tâm O bán kính r. Kí hiệu S(O; r). S O
( ;r)  M OM   r – Dây cung – Đường kính
Một mặt cầu được xác định
nếu biết tâm và bán kính của nó. GV: Phạm Việt Phương 31
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Hoạt động 2: Tìm hiểu khái niệm khối cầu
H1. Nhắc lại cách xét VTTĐ Đ1. So sánh độ dài OA với bán 2. Điểm nằm trong và nằm
giữa 1 điểm với 1 đường tròn? kính r.
ngoài mặt cầu. Khối cầu
Từ đó nêu cách xét VTTĐ giữa
Cho S(O; r) và điểm A bất kì. 1 điểm và 1 mặt cầu?
– OA = r A nằm trên (S)
– OA < r A nằm trong (S)
– OA > r A nằm ngoài (S)
 GV nêu khái niệm khối cầu.
Tập hợp các điểm thuộc S(O;
r) cùng với các điểm nằm trong
mặt cầu đó đgl khối cầu hoặc
hình cầu tâm O bán kính r.
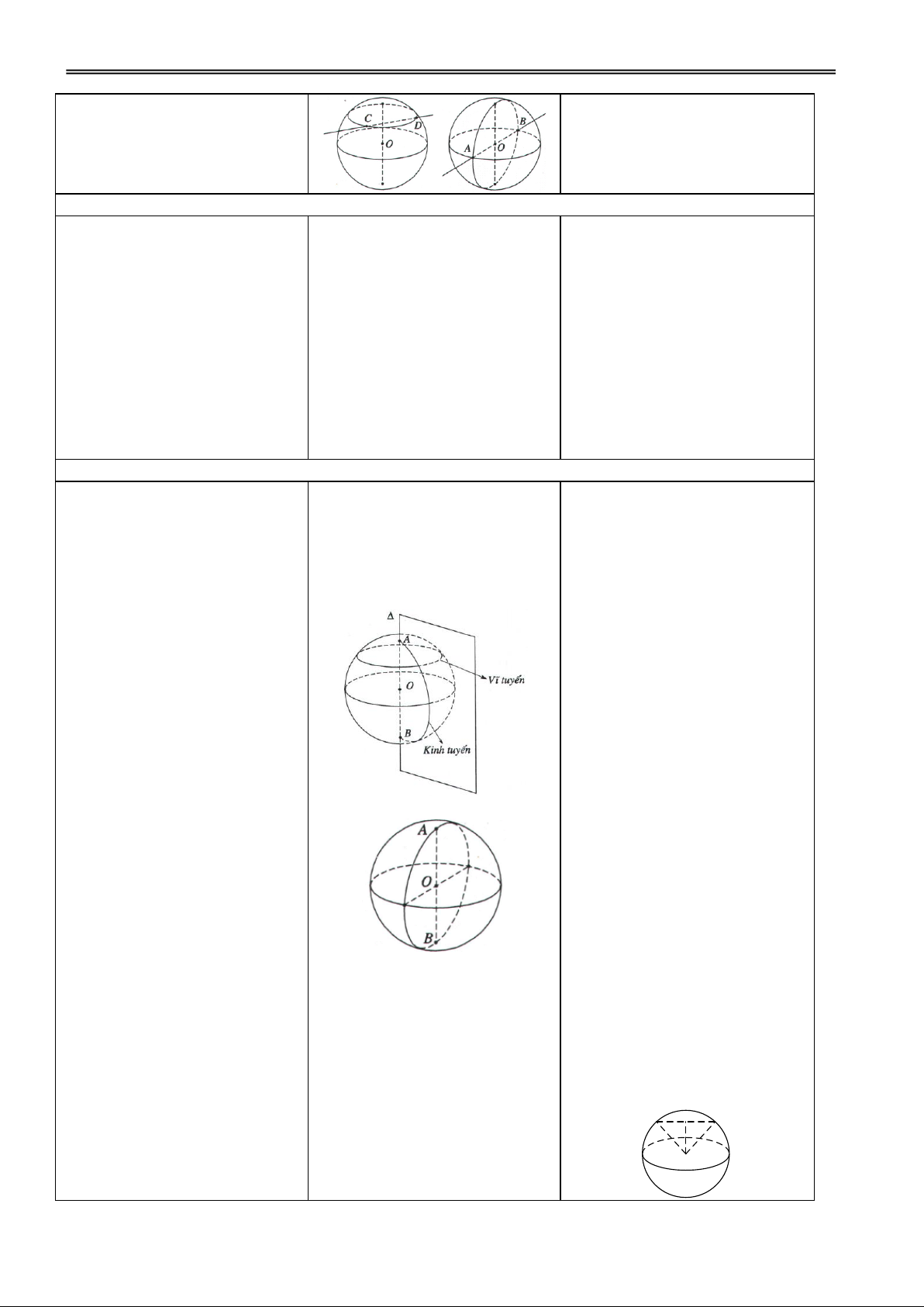
Hoạt động 3: Tìm hiểu cách biểu diễn mặt cầu
 GV dùng hình vẽ minh hoạ
3. Đường kinh tuyến và vĩ
giới thiệu khái niệm kinh
tuyến của mặt cầu tuyến, vĩ tuyến.
– Mặt cầu là mặt tròn xoay
được tạo bởi một nửa đường
H1. Nhắc lại khái niệm kinh Đ1. Các nhóm thảo luận và tròn quay quanh trục chứa nửa
tuyến, vĩ tuyến trong địa lí? trình bày.
đường kính của đường tròn đó
– Giao tuyến của mặt cầu với
các nửa mp có bờ là trục của
mặt cầu đgl kinh tuyến của mặt càu.
– Giao tuyến (nếu có) của mặt
cầu với các mp vuông góc với
trục đgl vĩ tuyến của mặt cầu.
– Hai giao điểm của mặt cầu
với trục đgl hai cực.  
GV cho HS tự vẽ hình biểu HS thực hành.
4. Biểu diễn mặt cầu
diễn của mặt cầu, nhận xét và
Nhận xét: Hình biểu diễn của
rút ra cách biểu diễn mặt cầu.
mặt cầu qua phép chiếu vuông
góc là một hình tròn.
– Vẽ một đường tròn có tâm v à
bán kính là tâm và bán kính của mặt cầu.
– Vẽ thêm một vài kinh tuyến,
vĩ tuyến của mặt cầu đó.
H2. Tam giác AOB có đặc Đ2. Tam giác cân tại O.
VD1: Tìm tập hợp tâm các mặt điểm gì?
cẩu luôn đi qua hai điểm cố định A, B cho trước.
H3. Điểm O thuộc mp cố định Đ3. Mp trung trực của AB. nào? A H B O GV: Phạm Việt Phương 32
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Hoạt động 4: Củng cố Nhấn mạnh: – Khái niệm mặt cầu.
– Cách biểu diễn mặt cầu.
4. BÀI TẬP VỀ NHÀ:  Bài 1 SGK.
 Đọc tiếp bài "Mặt cầu".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
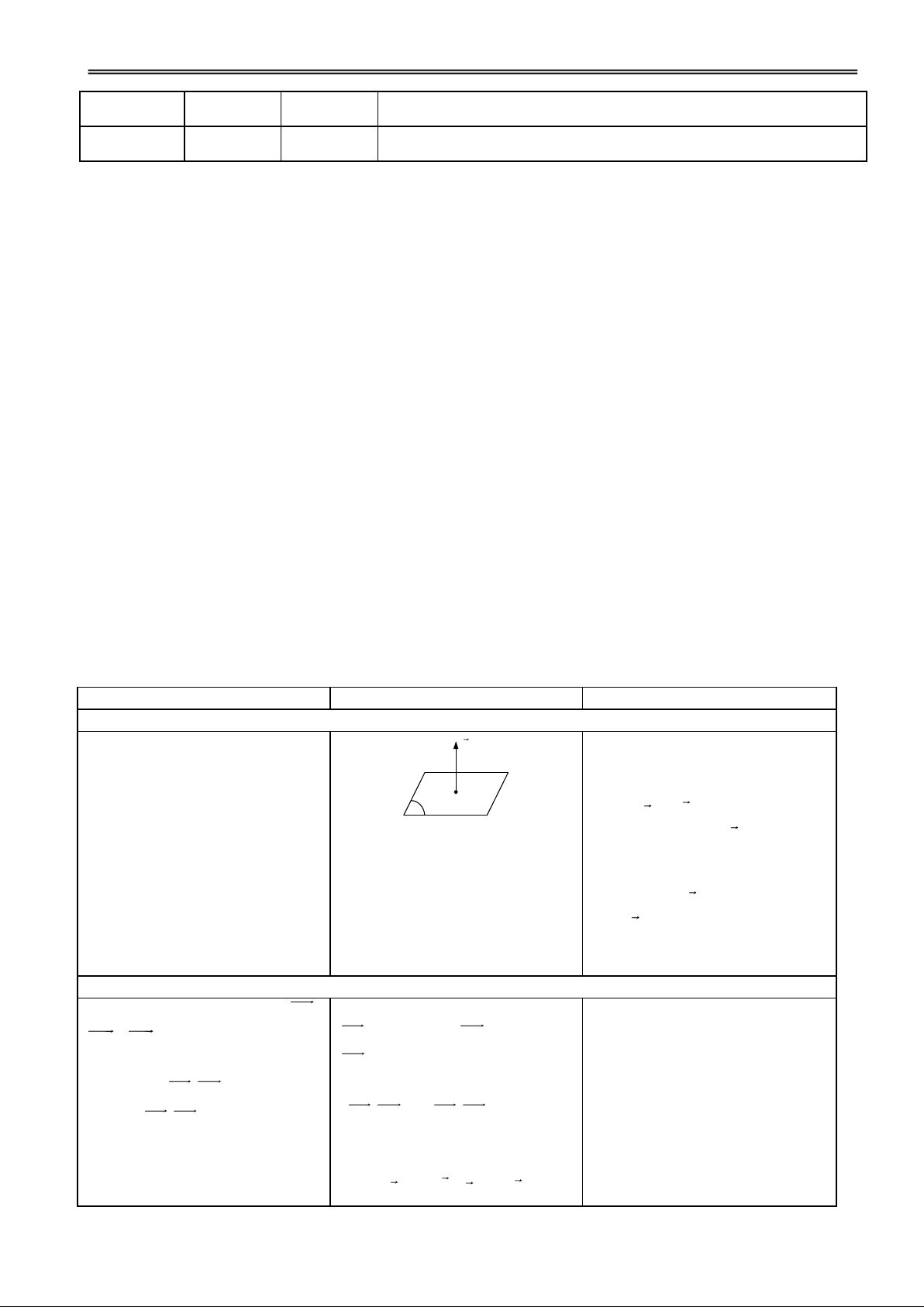
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 17
Bài 2: MẶT CẦU (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm chung về mặt cầu.
 Giao của mặt cầu và mặt phẳng.
 Giao của mặt cầu và đường thẳng.
 Công thức diện tích khối cầu và diện tích mặt cầu. Kĩ năng:
 Vẽ thành thạo các mặt cầu.
 Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
 Biết tính diện tích mặt cầu và thể tích khối cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa mặt cầu và VTTĐ giữa 1 điểm và mặt cầu? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
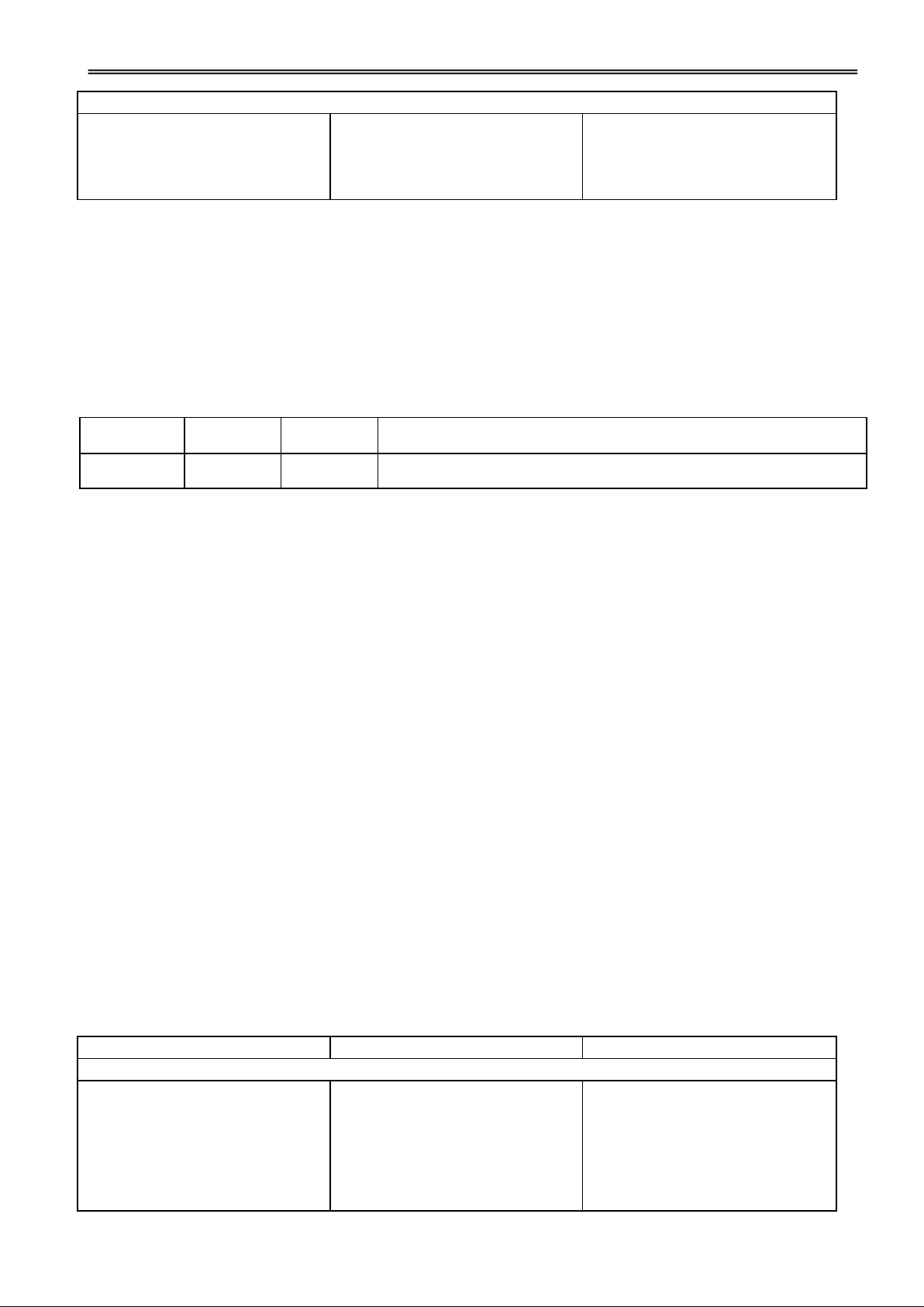
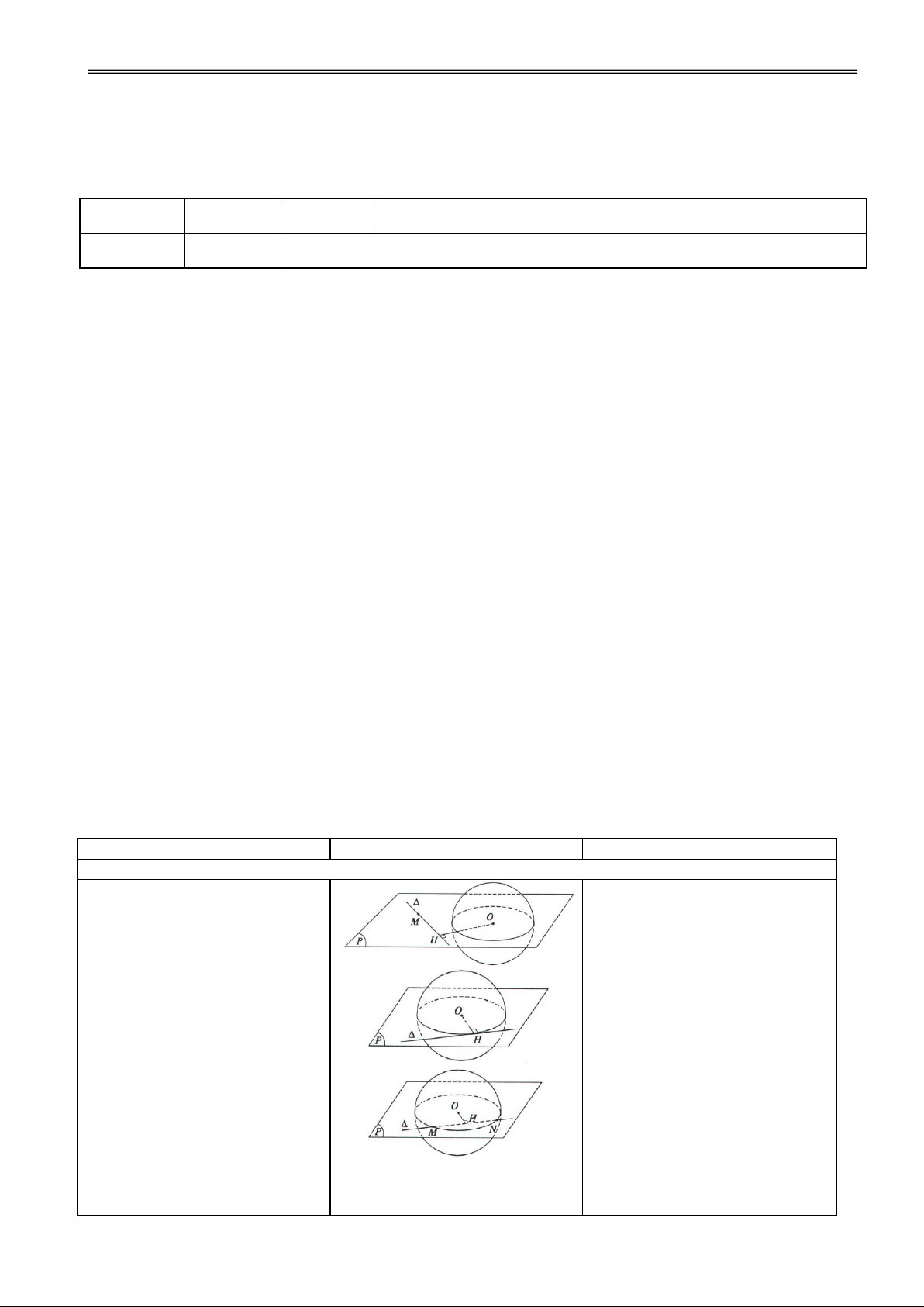
Hoạt động 1: Tìm hiểu vị trí tương đối của mặt cầu và mặt phẳng
H1. Giữa h và r có bao nhiêu Đ1. 3 trường hợp.
II. GIAO CỦA MẶT CẦU trường hợp xảy ra? h > r; h = r; h < r VÀ MẶT PHẲNG
Cho mặt cầu S(O; r) và mp (P).
 GV minh hoạ bằng hình vẽ  Các nhóm quan sát và trình Đặt h = d(O, (P)).
và hướng dẫn HS nhận xét. bày.
h > r (P) và (S) không có điểm chung. GV: Phạm Việt Phương 33
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
h = r (P) tiếp xúc với (S).
h < r (P) cắt (S) theo
đường tròn tâm H, bán kính r r2 h2    . Chú ý:
Điều kiện cần và đủ để (P)
tiếp xúc với S(O; r) tại H là (P)
vuông góc với OH tại H.
Nếu h = 0 thì (P) cắt (S) theo
H2. Nêu điều kiện để (P) tiếp
đường tròn tâm O bán kính r. xúc với (S)?
Đường tròn này đgl đường Đ2. tròn lớn (P)  OH tại H.
và (P) đgl mặt phẳng
 GV giới thiệu khái niệm
kính của mặt cầu (S).
đường tròn lớn, mặt phẳng kính.
Hoạt động 2: Áp dụng VTTĐ của mặt phẳng và mặt cầu
H1. Tính bán kính của đường Đ1.
VD1: Hãy xác định đường tròn tròn giao tuyến?
giao tuyến của mặt cầu S(O; r)  r 2 2  r 3
r  r    
và mp (P) biết khoảng cách từ  2  2 r O đến (P) bằng 2 .
VD2: Cho mặt cầu S(O; r), hai H2. Tính   Đ2. P r , Q r ?
mặt phẳng (P), (Q) có khoảng 2 2  2 2 
cách đến O lần lượt bằng a và b P
r r a , Q
r r b với 0 < a < b < r. Hãy so sánh
vì a < b nên r  r
các bán kính của các đường P Q tròn giao tuyến.
H3. Xét VTTĐ của (P) và (S)?
Đ3. Các nhóm thực hiện.
VD3: Gọi d là khoảng cách từ
tâm O của mặt cầu S(O; r) đến d 3 4 5 5
mặt phẳng (P). Điền vào chỗ r 5 4 4 8 trồng. VT cắt tiếp k cắt TĐ xúc
Hoạt động 3: Củng cố Nhấn mạnh:
– Vị trí tương đối của mp và mặt cầu.
– Cách xác định tâm và tính
bán kính của đường tròn giao tuyến.
4. BÀI TẬP VỀ NHÀ:  Bài 3, 4 SGK.
 Đọc tiếp bài "Mặt cầu". GV: Phạm Việt Phương 34
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 18
Bài 2: MẶT CẦU (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm chung về mặt cầu.
 Giao của mặt cầu và mặt phẳng.
 Giao của mặt cầu và đường thẳng.
 Công thức diện tích khối cầu và diện tích mặt cầu. Kĩ năng:
 Vẽ thành thạo các mặt cầu.
 Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
 Biết tính diện tích mặt cầu và thể tích khối cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các VTTĐ giữa mặt phẳng và mặt cầu? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu vị trí tương đối của mặt cầu và đường thẳng
 GV hướng dẫn HS nhận xét
III. GIAO CỦA MẶT CẦU từng trường hợp.
VỚI ĐƯỜNG THẲNG. TIẾP
TUYẾN CỦA MẶT CẦU
Cho mặt cầu S(O; r) và đường
thẳng . Gọi d = d(O, ).
d > r và (S) không có điểm chung.
d = r tiếp xúc với (S).
d < r cắt (S) tại hai điểm M, N phân biệt. Chú ý:
Điều kiện cần và đủ để đường
H1. Nêu điều kiện để  tiếp xúc
thẳng tiếp xúc với mặt cầu S(O; với (S) tại H?
Đ1.  vuông góc OH tại H.
r) tại điểm H là vuông góc với
bán kính OH tại H. đgl tiếp GV: Phạm Việt Phương 35
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
tuyến, H đgl tiếp điểm.
Nếu d = 0 thì đi qua tâm O và
cắt (S) tại hai điểm A, B. AB là
đường kính của (S). Nhận xét:
a) Qua một điểm A nằm trên mặt
H2. Nhắc lại tính chất tiếp tuyến
cầu S(O; r) có vô số tiếp tuyến
của đường tròn trong mặt phẳng?
của (S). Tất cả các tiếp tuyến này
 Từ đó GV hướng dẫn HS nêu
đều nằm trên mặt phẳng tiếp xúc
nhận xét đối với tiếp tuyến của Đ2. với (S) tại A. mặt cầu trong KG.
– Tại mỗi điểm trên đường tròn có b) Qua một điểm A nằm ngoài 1 tiếp tuyến.
mặt cầu S(O; r) có vô số tiếp
– Qua 1 điểm nằm ngoài đường tuyến với (S). Các tiếp tuyến này
tròn có 2 tiếp tuyến. Các đoạn tiếp tạo thành một mặt nón đỉnh A. tuyến là bằng nhau.
Khi đó độ dài các đoạn thẳng k ẻ
từ A đến các tiếp điểm đều bằng nhau.
Hoạt động 2: Tìm hiểu khái niệm mặt cầu nội tiếp, ngoại tiếp hình đa diện
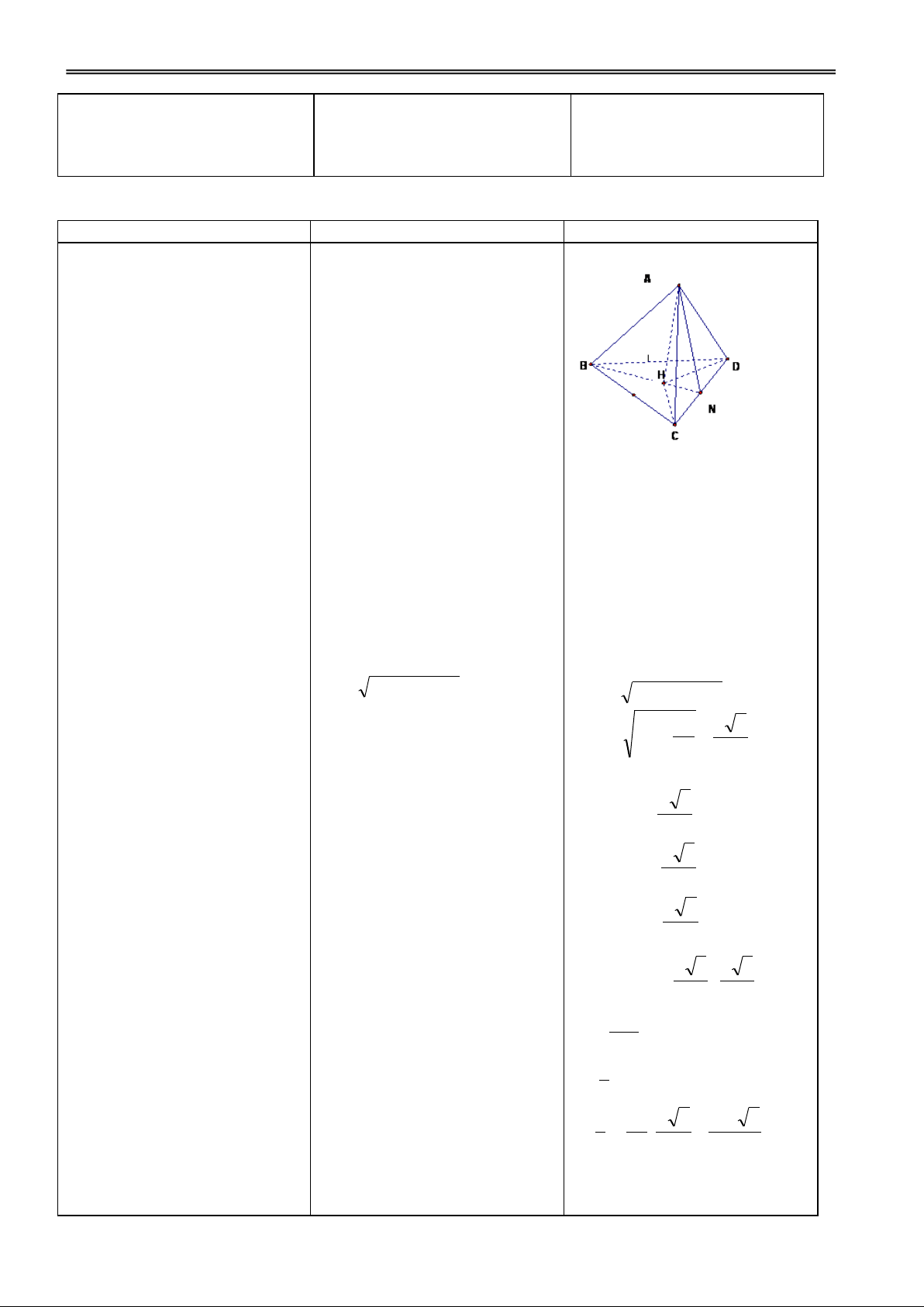
 GV giới thiệu khái niệm mặt S
Mặt cầu đgl nội tiếp hình đa
cầu nội tiếp, ngoại tiếp hình đa
diện nếu mặt cầu đó tiếp xúc với
diện (minh hoạ bằng hình vẽ).
tất cả các mặt của hình đa diện. D
Mặt cầu đgl ngoại tiếp hình đa C
diện nếu tất cả các đỉnh của hình
đa diện đều nằm trên mặt cầu. A B
Hoạt động 3: Áp dụng VTTĐ của đường thẳng và mặt cầu
H1. Chứng tỏ điểm O cách đều Đ1.
VD1: Cho hình lập phương
các dỉnh của hình lập phương? a 3
ABCD.ABCD có cạnh bằng a. Tính OA? OA =
Hãy xác định tâm và bán kính của 2 mặt cầu:
a) Đi qua 8 đỉnh của hình lập
H2. Chứng tỏ điểm O cách dều a 2 phương.
các cạnh của hình lập phương? Đ2. d = 2
b) Tiếp xúc với 12 cạnh của hình
Tính khoảng cách từ O đến các lập phương.
cạnh của hình lập phương?
c) Tiếp xúc với 6 mặt của hình lập phương. B C
H3. Chứng tỏ điểm O cách dều a D A
các mặt của hình lập phương? Đ3. d = 2
Tính khoảng cách từ O đến các O
mặt của hình lập phương? B’ C’ A’ D’
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách xét VTTĐ của đường thẳng và mặt cầu.
– Khái niệm mặt cầu nội tiếp,
ngoại tiếp hình đa diện. GV: Phạm Việt Phương 36
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Bài 5, 6, 7, 8, 9 SGK.
 Đọc tiếp bài "Mặt cầu".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Ngày dạy
Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 19
Bài 2: MẶT CẦU (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm chung về mặt cầu.
 Giao của mặt cầu và mặt phẳng.
 Giao của mặt cầu và đường thẳng.
 Công thức diện tích khối cầu và diện tích mặt cầu. Kĩ năng:
 Vẽ thành thạo các mặt cầu.
 Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
 Biết tính diện tích mặt cầu và thể tích khối cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các VTTĐ giữa đường thẳng và mặt cầu? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
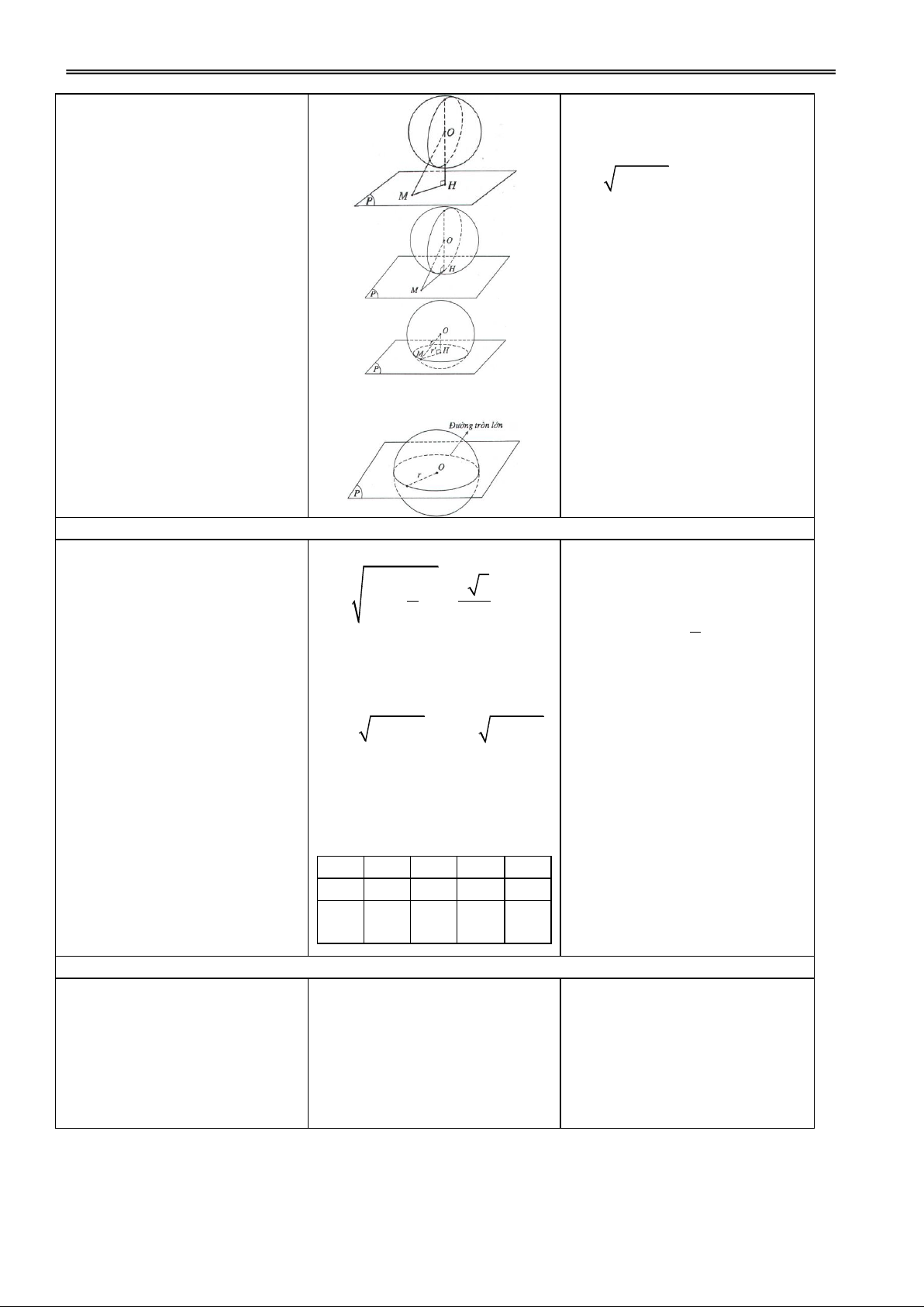
Hoạt động 1: Tìm hiểu công thức tính diện tích mặt cầu và thể tích khối cầu
H1. Nhắc lại công thức tính Đ1. IV. CÔNG THỨC TÍNH
diện tích mặt cầu và thể tích 4
DIỆN TÍCH MẶT CẦU VÀ khối cầu đã biế    t? S r2 4 ; V r3 3
THỂ TÍCH KHỐI CẦU
Cho mặt cầu S(O; r).
Diện tích mặt cầu: S r2 4
Thể tích khối cầu: 4
V  r3 3 Chú ý: GV: Phạm Việt Phương 37
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
H2. Tính diện tích đường tròn Đ2.  
Diện tích mặt cầu bằng 4 lần lớn ? ñt S r2 
diện tích hình tròn lớn của mặt cầu đó.
Thể tích khối cầu bằng thể
tích khối chóp có diện tích đáy
bằng diện tích mặt cầu và có
chiều cao bằng bán kính của khối cầu đó.
Hoạt động 2: Áp dụng tính diện tích mặt cầu và thể tích khối cầu  GV cho các nhóm tính.
 Các nhóm tính và điền vào VD1: Cho mặt cầu S có bán bảng.
kính r. Tính diện tích đường
tròn lớn, diện tích mặt cầu và r 1 2 3 4 thể tích khối cầu. Sđt  4 9 16 S mc 4 16 36 64 32 256 4  36  V  3 3 3
H1. Tính cạnh của hình lập Đ1.
VD2: Cho mặt cầu bán kính r. phương theo r?
 Cạnh hình lập phương nội Tính thể tích của hình lập tiếp mặt cầu: phương: a) Nội tiếp mặt cầu. a = r 2
b) Ngoại tiếp mặt cầu.  V1 = r3 2 2 a 2 r a O H
 Cạnh hình lập phương ngoại I J tiếp mặt cầu: b = 2r O  V r3 2 8 L K
H1. Chứng minh OA = OB = Đ1.
VD3: Cho hình chóp S.ABC OC = OS ? SAC vuông tại A
có đáy ABC là tam giác vuông  OA = OC = OS
tại B và SA  (ABC). Gọi O là SBC vuông tại B trung điểm của SC.  OB = OC = OS
a) Chứng minh A, B, C, S cùng
nằm trên một mặt cầu. H2. Tính SC ? Đ2. b) Cho SA = BC = a và AB = 2 2 2 2
AC AB BC a
3 a 2 . Tính bán kính mặt cầu 2 2 2 2 trên.
SC SA AC a 4  S SC = 2a  O R = a. a A C a a 2 B
Hoạt động 4: Củng cố GV: Phạm Việt Phương 38
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn Nhấn mạnh:
– Cách xác định tâm và bán kính mặt cầu.
– Công thức tính diện tích mặt
cầu và thể tích khối cầu.
4. BÀI TẬP VỀ NHÀ:  Bài 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 20+21
Bài 2: BÀI TẬP MẶT CẦU I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm chung về mặt cầu.
 Giao của mặt cầu và mặt phẳng.
 Giao của mặt cầu và đường thẳng.
 Công thức diện tích khối cầu và diện tích mặt cầu. Kĩ năng:
 Vẽ thành thạo các mặt cầu. Xác định tâm và bán kính của mặt cầu.
 Biết xác định giao của mặt cầu với mặt phẳng và đường thẳng.
 Biết tính diện tích mặt cầu và thể tích khối cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với mặt cầu.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về mặt cầu.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Xác định tâm và bán kính mặt cầu
 GV hướng dẫn HS cách xác
1. Cho hình chóp tứ giác đều
định tâm mặt cầu ngoại tiếp
S.ABCD có tất cả các cạnh đều hình chóp đều.
bằng a. Xác định tâm và bán
H1. Nhận xét tính chất của tam Đ1. SAC vuông tại S
kính mặt cầu ngoại tiếp hình giác SAC?  OS = OA = OC chóp.
H2. Nhận xét tứ giác OIAH?  OS = OA = OC = OB = OD GV: Phạm Việt Phương 39
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
 O là tâm của mặt cầu ngoại S tiếp hình chóp S.ABCD.
H3. Tính bán kính mặt cầu ? a 2 D C Đ3. R = OA = 2 O A B Đ3.
H4. Nhận xét tính chất tâm O OA = OB = OC = OS
của mặt cấu ngoại tiếp hình  O   và O thuộc mp trung 2. Cho hình chóp S.ABC có SA = a, SB = b, SC = c và ba chóp? trực của SC. cạnh SA, SB, SC đôi một
vuông góc. Xác định tâm và
H5. Xác định bán kính mặt Đ5. 2 2
R = OA = OI AI
bán kính của mặt cầu ngoại cầu? 2 2 2 tiếp hình chóp.
a b c = 2 C  H O S B I A
Hoạt động 2: Chứng minh tính chất liên quan đến mặt cầu
H1. Nhắc lại tính chất tương tự Đ1. Trong mp(MA, MC) ta có:
3. Từ một điểm M nằm ngoài
đối với đường tròn trong mp? MA.MB = MC.MD
mặt cầu S(O; r) kẻ hai đường
thẳng cắt mặt cầu lần lượt tại
H2. Tính phương tích của điểm Đ2. 2 2 A, B và C, D.
MA.MB = d r
M đối với đường tròn lớn qua a) Chứng minh: A, B? MA.MB = MC.MD b) Đặt MO = d. Tính MA.MB theo r và d. B D A O C M
4. Cho mặt cầu S(O; r) tiếp xúc
H3. Nhận xét các tiếp tuyến vẽ Đ3. AI = AM, BI = BM
với mp (P) tại I. Gọi M là một từ A và B?  ABI = ABM
điểm nằm trên mặt cầu nhưng
AMB AIB
không phải là điểm đối xứng
với I qua O. Từ M kẻ hai tiếp
tuyến của mặt cầu cắt (P) tại A
và B. CMR: AMB AIB . M O A I P B
Hoạt động 3: Tập hợp điểm liên quan đến mặt cầu
H1. Nêu bài toán tương tự Đ1. Tập hợp các điểm M trong 5. Tìm tập hợp các điểm M trong mặt phẳng?
mp nhìn đoạn AB cố định dưới trong KG luôn nhìn đoạn thẳng
một góc vuông là đường tròn AB cố định dưới một góc đường kính AB. vuông. GV: Phạm Việt Phương 40
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
H2. Nhận xét tính chất tâm O Đ2. Lấy A, B, C  (C).
6. Tìm tập hợp tâm các mặt cầu của một mặt cầu?
O là tâm mặt cầu  OA = OB luôn chứa một đường tròn (C) = OC cố định.
 O nằm trên trục của đường tròn (C).
Hoạt động 4: Củng cố Nhấn mạnh:
– Các tính chất của mặt cầu.
– Cách xác định tâm và bán kính của mặt cầu.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Bài tập ôn học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 22
Bài dạy: ÔN TẬP HỌC KÌ I I. MỤC TIÊU: Kiến thức:
 Ôn tập toàn bộ kiến thức học kì 1. Kĩ năng:
 Thành thạo giải bài toán tính thể tích khối đa diện và vận dụng thể thích khối đa diện để giải toán hình học.
 Thành thạo giải bài toán tính thể tích khối tròn xoay.
 Thành thạo xác định tâm và bán kính mặt cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với khối đa điện, khối tròn xoay.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học trong học kì 1.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Củng cố tính thể tích khối đa diện
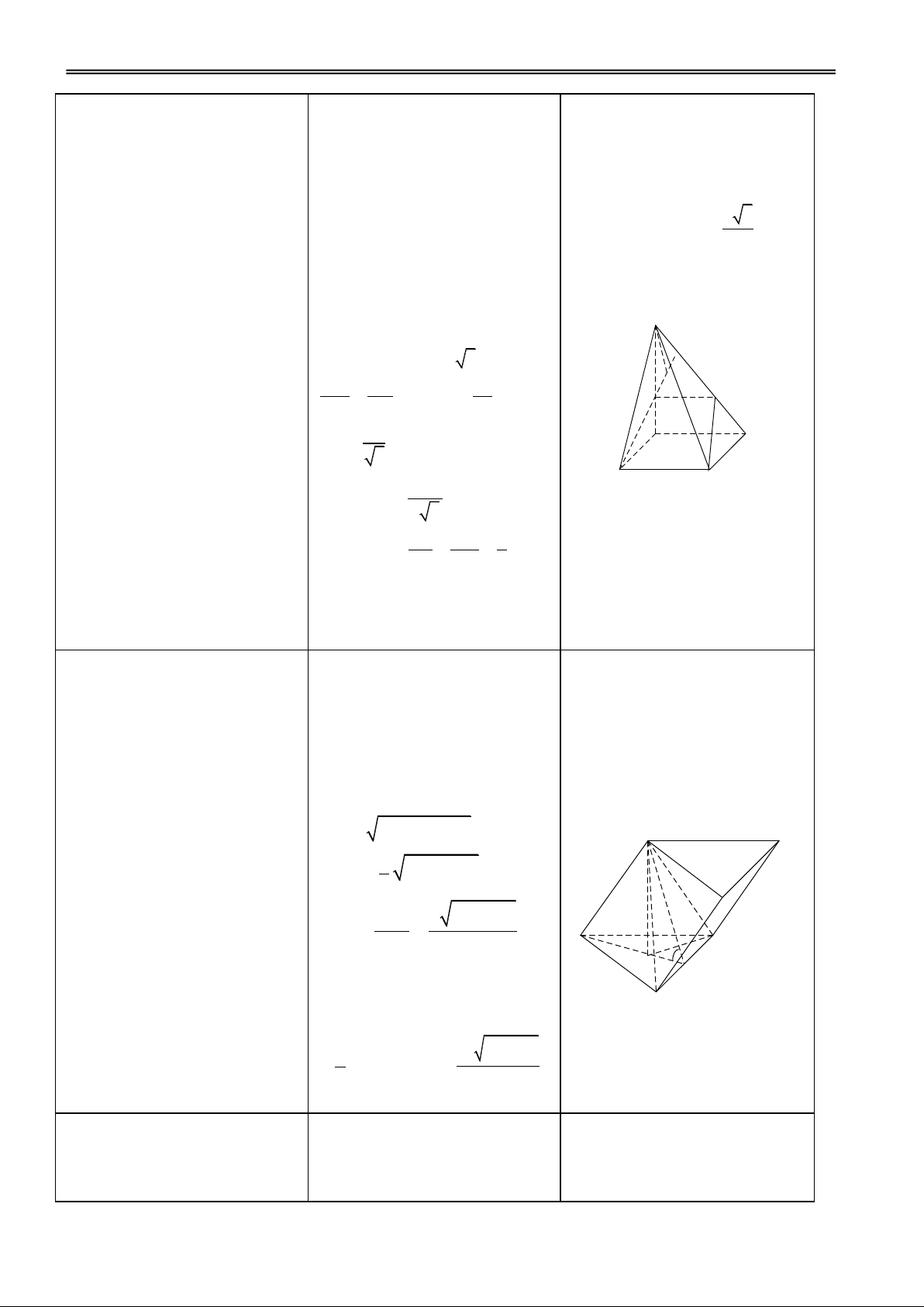
H1. Xác định tính chất tứ giác Đ1.
1. Cho hình chóp S.ABCD có GV: Phạm Việt Phương 41
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn BCNM? (BCM) // AD  MN // AD
đáy ABCD là hình chữ nhật BC AB
với AB = a, AD = 2a, cạnh SA   BC BMBC SA
vuông góc với đáy, cạnh SB 
tạo với mặt phẳng đáy một góc BCNM là hình thang vuông với đường cao BM
600. Trên cạnh SA lấy điểm M a 3
H2. Xác định đường cao của sao cho AM = . Mặt Đ2. 3 hình chóp SBCNM? Do (SBM)  (BCNM) nên trong (SBM) vẽ SH  BM
phẳng (BCM) cắt cạnh SD tại 
N. Tính thể tích khối chóp SH  (BCNM)  SH là đường cao. S.BCNM. Đ3. S
H3. Tính diện tích đáy và chiều cao của hình chóp? 0
SA ABtan60  a 3 MN SM a H   MN 4  AD SA 3 N M a BM 2  D A 3 a 2 B 2a C  10a SBCNM  3 3 AB AM 1 SB = 2a    SB MS 2
 BM là phân giác của SBH  0
SH SB.sin30  a
H1. Xác định góc giữa hai mp Đ1. E là trung điểm của BC. 2. Cho hình lăng trụ (ABC) và (ABC)? AE BC
ABC.ABC có AABC là hình  
chóp tam giác đều, cạnh đáy
AE BC
AB = a, cạnh bên AA = b. Gọi
  ABC, ABC  AEA
 là góc giữa hai mặt phẳng
(ABC) và (ABC). Tính tan H2. Tính tan ? Đ2. và thể tích khối chóp 2 2 A.BBCC. AH=
AA AH A’ C’ 1 2 2 = b 9  a 3 3 B’ 2 2 AH 2 b 3  a tan =  HE a A C H E
H3. Nêu cách tính thể tích khối Đ3. chóp A.BCCB? VVV B ABCCBABCAB C   AABC 2
a2 b2  a2 3 = AH S . ABC 3  = 6
H1. Xác định tính chất thiết Đ1. AK  MN  AMKN là 3. Cho hình lập phương diện AMKN? hình thoi.
ABCD.ABCD có cạnh bằng  Gọi V1 = VABCDMKN
a và điểm K thuộc cạnh CC V2 = VAMKNABCD GV: Phạm Việt Phương 42
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
H2. Tính thể tích V1? Đ2. V1 = 2VABCKM 2 1 sao cho CK = a . Mặt phẳng 3 = 2. AB. B S CKM 3
(P) qua A, K và song song với 3  
BD, chia khối lập phương 2 a 2a a a = a   
thành hai khối đa diện. Tính 3  3 3  2 3
thể tích của hai khối đa diện
H3. Tính thể tích khối lập Đ3. V = a3 đó. phương? a3 2 D’ C’  V O’ 2 = V – V1 = 3 A’ B’ K N I D M C O A B
Hoạt động 4: Củng cố Nhấn mạnh:
– Công thức tính thể tích khối chóp, khối lăng tụ.
– Một số cách tính thể tích khối đa diện.
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Củng cố giải toán liên quan đến khối nón
H1. Tính độ dài đường sinh, Đ1.
1. Thiết diện qua trục của một
bán kính đáy và chiều cao của l = a
hình nón là một tam giác hình nón? a 2
vuông cân có cạnh góc vuông r = OA = 2 = h bằng a.
a) Tính diện tích xung quanh
H2. Nhắc lại công thức tính
và diện tích toàn phần của hình Đ2.
Sxq, Stp, V của khối nón? nón.  a2 2
b) Tính thể tích khối nón tương Sxq = rl = 2 ứng.  a2  2   1 S Stp = Sxq + Sđáy = 2 a a 1 2 1 r V =  r h  2 3 = a3 12 A O B
Hoạt động 2: Củng cố giải toán liên quan đến khối trụ
H1. Xác định góc giữa AB và 
2. Một hình trụ có bán kính đáy trục của hình trụ?
Đ1. AA // OO  BAA 0  30 0
R và đường cao R 3 . A và B
AB AA.tan30  R
là 2 điểm trên 2 dường tròn đáy
H2. Xác định thiết diện ?
Đ2. Thiết diện là hình chữ nhật sao cho góc hợp bởi AB và AABB.
trục của hình trụ là 300.
SAABB = AA.BA = R2 3
a) Tính diện tích thiết diện qua
AB và song song với trục của
H3. Nhắc lại công thức tính Đ3. hình trụ.
Sxq, Stp, V của khối trụ? 
b) Tính Sxq, Stp, V của khối trụ. Sxq = 2rh = R2 2 3 V = r2h =  R3 3 GV: Phạm Việt Phương 43
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn O A B’ 0 30 O’ H A’ B
Hoạt động 3: Củng cố giải toán liên quan đến khối cầu
H1. Xác định góc giữa cạnh Đ1. SAH 0  60
3. Cho một hình chóp tứ giác bên và đáy? 
đều có cạnh đáy là a, cạnh bên SAC là tam giác đều.
hợp với đáy một góc 600.
H2. Nêu tính chất của tâm mặt Đ2.
a) Xác định tâm và bán kính OA = OB = OC = OD= OS cầu ngoại tiếp? 
mặt cầu ngoại tiếp hình chóp.
O  SH và O là tâm của
b) Tính diện tích mặt cầu và
đường tròn ngoại tiếp SAC
thể tích khối cầu tương ứng. 
O là trọng tâm của SAC S
H3. Tính bán kính mặt cầu? Đ3. 2 AC 3 R = SO = SH O 3 = 3 D C 0 60 a 6 H = a 3 A B
Hoạt động 4: Củng cố Nhấn mạnh:
– Công thức tính thể tích khối
nón, khối trụ, khối cầu.
– Cách xác định tâm và bán kính của mặt cầu.
4. BÀI TẬP VỀ NHÀ:
 Chuẩn bị kiểm tra học kì 1.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy:23 KỂM TRA HỌC KÌ 1
THI THEO ĐỀ CHUNG CỦA SỞ GV: Phạm Việt Phương 44
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy:24 ÔN TẬP CHƯƠNG II I. Mục tiêu: + Về kiến thức:
- Hệ thống các kiến thức cơ bản về mặt tròn xoay và các yếu tố cơ bản về mặt tròn xoay như trục, đường sinh,...
- Phân biệt được các khái niệm về mặt và khối nón, trụ, cầu và các yếu tố liên quan.
- Nắm vững các công thức tính diện tích xung quanh và thể tích của khối nón, khối trụ, công
thức tính diện tích mặt cầu và thể tích khối cầu. + Về kỹ năng:
- Vận dụng được các công thức vào việc tính diện tích xung quanh và thể tích của các khối : nón, trụ, cầu.
- Rèn luyện kĩ năng vẽ hình cho học sinh.
+ Về tư duy và thái độ:
- Rèn luyện tính tích cực, sáng tạo, cẩn thận.
II. Chuẩn bị của giáo viên và học sinh:
+ Giáo viên:Giáo án, bảng phụ, phiếu học tập.
+ Học sinh: Dụng cụ học tập, SGK,...
III. Phương pháp: Gợi mở, giải quyết vấn đề.
IV. Tiến trình bài học: Tiết 1:
1. Ổn định tổ chức:
2. Kiểm tra bài cũ:
CH1: Ghi các công thức tính diện tích và thể tích các mặt và khối:nón, trụ, cầu. Mặt nón-Khối nón Mặt trụ-Khối trụ Mặt cầu-Khối cầu Diện tích Sxq= Sxq= S= Thể tích V= V= V=
GV chính xác hóa kiến thức, đánh giá và ghi điểm. 3. Bài mới:
* Hoạt động 1: Giải bài toán đúng sai.
Hoạt động của giáo viên
Hoạt động của học sinh Ghi bảng Đọc đề BT1 SGK + Xem đề SGK /T50
CH1: Qua 3 điểm A,B,C có bao + Trả lời: Có duy nhất nhiêu mặt phẳng. mp(ABC)
CH2: Xét vị trí tương đối giữa + Mp(ABC) cắt mặt cầu theo
mp (ABC) và mặt cầu và trả lời giao tuyến là đường tròn qua câu a.
A,B,C. Suy ra kết quả a đúng.
+ Chưa biết (Có 2 khả năng)
CH3: Theo đề mp(ABC) có qua + Dựa vào CH3 suy ra: b-
tâm O của mặt cầu không. Không đúng c-Không đúng. 
CH4: Dựa vào giả thiết nào để +Dựa vào giả thiết: ABC =900 và kết quả câu a GV: Phạm Việt Phương 45
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
khẳng định AB là đường kính
của đường tròn hay không.
*Hoạt động 2: Kết hợp BT2 và BT5 SGK/T50
Hoạt động của giáo viên
Hoạt động của học sinh Ghi bảng
Nêu đề: Cho tứ diện đều - Vẽ hình (GV hướng dẫn nếu
ABCD cạnh a. Gọi H là hình cần)
chiếu của A trên mp(BCD). N là trung điểm CD a- Chứng minh HB=HC=HD. Tính độ dài đoạn AH.
b- Tính Sxq và V của khối nón
tạo thành khi quay miền tam giác AHN quanh cạnh AH.
c- Tính Sxq và V của khối trụ
có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao a) AH  (BCD) AH.
=> Các tam giác AHB, AHC, Hoạt động 2.1: AHD vuông tại H
CH1: Có nhận xét gì về các Lại có: AH cạnh chung tam giác AHB, AHC, AHD. AB=AC=AD(ABCD là Nêu cách tính AH. tứ diện đều)
TL: Chúng là 3 tam giác vuông => 3 tam giác AHB, AHC, bằng nhau. AHD bằng nhau Suy ra HB=HC=HD Suy ra HB=HC=HD AH= 2 2 AB BH 2 *AH= 2 AB BH 2 a a 6 = 2 a  = 3 3
b) Khối nón tạo thành có: a 3 l AN Hoạt động 2.2:  2 CH: Để tính S  xq của mặt nón và a 3
V của khối nón, cần xác định r HN  6 các yếu tố nào?  
+Gọi một hs lên bảng thực a 6
+Cần xác định độ dài đường h AH  hiện.
sinh l = AN, bán kính đường  3
+Cho các hs còn lại nhận xét tròn đáy r = HN và đường cao a 3 a 3
bài giải, gv đánh giá và ghi S . h=AH. xq=  rl=  . điểm 6 2 Hoạt động 2.3: 2 a  =
CH: Để tính Sxq của mặt trụ và 4
V của khối trụ, cần xác định 1 các yếu tố nào? V= B h . 3
+Gọi một hs lên bảng thực 3 hiện. 1 2 a a 6 a  6
+Cần xác định độ dài đường = . . =
+Cho các hs còn lại nhận xét 3 12 3 108
sinh l = AB, bán kính đường
bài giải, gv đánh giá và ghi
c) Khối trụ tạo thành có:
tròn đáy r = BH và đường cao điểm h=l GV: Phạm Việt Phương 46
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn a 3 r HB    3  a 6
l h AH   3 Sxq=2 rl a 3 a 6 2 2 a  2 =2 . = 3 3 3 2 a a 6 . 3 a 6 V=B.h= . . = 3 3 9
*Hoạt động 3: BT 6/50 SGK
Hoạt động của giáo viên
Hoạt động của học sinh Ghi bảng + Nêu đề. + HS vẽ hình
Hoạt động 3.1: Xác định tâm
và bán kính của mặt cầu ngoại tiếp hình chóp.
CH 1: Trình bày pp xác định + Lắng nghe và trả lời.
tâm mặt cầu ngoại tiếp hình chóp.
a. Gọi O’, R lần lượt là tâm
+ Nhận xét câu trả lời của hs
và bán kính của mặt cầu
và nhắc lại các bước: Vì O’A=O’B=O’C=O’D
1. Xác định trục Δ của đường => O’ thuộc SO (1)
tròn ngoại tiếp đa giác đáy.
Trong (SAO), gọi M là trung
2. Xác định mặt phẳng trung
điểm của SA và d là đường
trực ( ) (hoặc đường trung trung trực của đoạn SA
trực d) của cạnh bên bất kì. Vì O’S = O’A
3. Xác định giao điểm của Δ => O’ thuộc d (2)
với ( ) (hoặc của Δ với d) .
Từ (1) và (2) =>O’=SO  d
Đó chính là tâm mặt cầu cần tìm.
CH 2: Đường tròn ngoại tiếp
hình vuông ABCD có trục là đường thẳng nào?
+ Suy nghĩ trả lời câu hỏi.
CH 3: Có nhận xét gì về hai
tam giác SAO và SMO’. Nêu + R = O’S.
cách tính bán kính R của mặt + Đó là hai tam giác vuông có Hai tam giác vuông SAO và cầu.
chung góc nhọn nên chúng SMO’ đồng dạng nên: đồng dạng ' SA SM . SO SA SO SO =>  SO' SM Trong đó GV: Phạm Việt Phương 47
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Hoạt động 3.2: Tính diện tích a 2 2 3
mặt cầu và thể tích khối cầu.
SA= SO OA
CH : Nêu lại công thức tính 2
diện tích mặt cầu và thể tích 3a => SO'= =R khối cầu. 4 + S = 4πR2 4 3a + V = 3
b) Mặt cầu có bán kính R= R  3 4 nên: + S=4π 3a 9 2 a  2 ( ) = 4 4 4 3a 9 3 a  + V= 3  ( ) = 3 4 16 4. Củng cố:
*Hoạt động 4: Giải bài tập trắc nghiệm theo nhóm(củng cố toàn bài)
Câu 1) Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a.
1.1 Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông
ABCD và A’B’C’D’. Diện tích S là: 2 A) πa a  2 2 B) 2 a  2 C) 2 a  3 D) 2
1.2 Gọi S’ là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng AC’ khi
quay xung quanh trục AA’. Diện tích S’ là: A) πa2 B) 2 a  3 C) 2 a  2 D) 2 a  6
Câu 2) Số mặt cầu chứa một đường tròn cho trước là: A) 1 B) 2 C) vô số D) 0
Cho các nhóm nêu đáp án và đại diện trình bày phương pháp giải theo chỉ định câu hỏi của GV.
GV nhận xét, đánh giá và ghi điểm cho nhóm. 5. Dặn dò:
- Về nhà làm các bài tập ôn chương còn lại
- Chuẩn bị cho bài kiểm tra 1 tiết vào tiết tiếp theo. GV: Phạm Việt Phương 48
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1
Chương III: PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN Tiết dạy: 25
Bài 1: HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm toạ độ của điểm và vectơ trong không gian.
 Biểu thức toạ độ của các phép toán vectơ.
 Phương trình mặt cầu. Kĩ năng:
 Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
 Viết được phương trình mặt cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại định nghĩa toạ độ của điểm và vectơ trong mặt phẳng? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm hệ toạ độ trong không gian
 GV sử dụng hình vẽ để giới
I. TOẠ ĐỘ CỦA ĐIỂM VÀ
thiệu hệ trục toạ độ trong CỦA VECTƠ không gian. 1. Hệ toạ độ
Hệ toạ độ Đề–các vuông góc
trong không gian là hệ gồm 3
trục xOx, yOy, zOz vuông
góc với nhau từng đôi một, với
các vectơ đơn vị i Đ1. , j , k .
H1. Đọc tên các mặt phẳng toạ (Oxy), (Oyz), (Ozx). 2 2 2 độ?
i j k 1 .  .  .  0 Đ2. i j j k k i
Đôi một vuông góc với
H2. Nhận xét các vectơ i , j , nhau. k ?
Hoạt động 2: Tìm hiểu khái niệm toạ độ của một điểm GV: Phạm Việt Phương 49
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
 GV hướng dẫn HS phân tích
2. Toạ độ của một điểm
OM theo các vectơ i , j , k .
M(x; y; z) OM xi yj zk
VD1: Xác định các điểm M(0;0;0), A(0; 1; 2), B(1; 0;
 Cho HS biểu diễn trên hình  Các nhóm thực hiện.
2), C(1; 2; 0) trong không gian vẽ. Oxyz.
Hoạt động 3: Tìm hiểu khái niệm toạ độ của vectơ
H1. Nhắc lại định lí phân tích Đ1.
3. Toạ độ của vectơ
vectơ theo 3 vectơ không đồng a  (a ;a ;a )  a a i a j a k a  (a ;a ;a )  a a i a j a k phẳng trong không gian? 1 2 3 1 2 3 1 2 3 1 2 3
GV giới thiệu định nghĩa và Nhận xét:
cho HS nhận xét mối quan hệ  Toạ độ của OM cũng là toạ độ điểm M.
M(x; y;z)  OM  (x; y;z)
giữa toạ độ điểm M và OM . z 
Toạ độ của các vectơ đơn vị: A’ D’
i  (1;0;0), j  (0;1;0),k  (0;0;1) M c B’ C’
0  (0;0;0) A D O b y a B
VD2: Trong KG Oxyz, cho C x hình hộp chữ nhật
H2. Xác định toạ độ các đỉnh Đ2. của hình hộp?
ABCD.ABCD có đỉnh A
B(a; 0; 0), D(0; b; 0), A(0; 0;c)
trùng với O, các vectơ AB, AD
C(a; b; 0), C(a; b; c), D(0;b;c)
AA theo thứ tự cùng hướng
H3. Xác định toạ độ của các Đ3. vectơ?
với i , j,k và AB = a, AD = b, AB  (a;0;0)  ( ; ;0) , AC a b
AA = c. Tính toạ độ các vectơ  a  
AC  (a;b;c)
AB, AC, AC , AM , với M là
, AM   ;b;c) 2  
 trung điểm của cạnh CD.
Hoạt động 4: Củng cố Nhấn mạnh:
– Khái niệm toạ độ của điểm, của vectơ trong KG.
– Liên hệ với toạ độ của điểm, của vectơ trong MP.
4. BÀI TẬP VỀ NHÀ:
 Đọc tiếp bài "Hệ toạ độ trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 50
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 26
Bài 1: HỆ TOẠ ĐỘ TRONG KHÔNG GIAN (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm toạ độ của điểm và vectơ trong không gian.
 Biểu thức toạ độ của các phép toán vectơ.
 Phương trình mặt cầu. Kĩ năng:
 Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
 Viết được phương trình mặt cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu định nghĩa toạ độ của điểm và vectơ trong không gian? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu biểu thức toạ độ của các phép toán vectơ trong không gian
 GV cho HS nhắc lại các tính  Các nhóm thảo luận và trình II. BIỂU THỨC TOẠ ĐỘ
chất tương tự trong mp và bày. CỦA CÁC PHÉP TOÁN
hướng dẫn HS chứng minh. VECTƠ
a a i a j a k
Định lí: Trong KG Oxyz, cho: 1 2 3
b b i b j b k
a  (a ;a ;a ), b  (b ;b ;b ) 1 2 3 1 2 3 1 2 3 .
a b a
(  b ;a b ;a b ) 1 1 2 2 3 3
a b  (a b ;a b ;a b 1 1 2 2 3 3)
ka k(a ;a ;a )  (ka ;ka ;ka ) 1 2 3 1 2 3 (k R) Hệ quả: Đ1.a b 1 1
H1. Phát biểu các hệ quả?  
a b  a b 2 2
Hai vectơ bằng nhau  các
toạ độ tương ứng bằng nhau  a b  3 3    Với b 0 :
Hai vectơ cùng phương 
a,b cuøng phöông
các toạ độ của vectơ này bằng a kb
k lần toạ độ tương ứng của 1 1 vectơ kia
 k R : a kb 2 2  a kb  3 3 GV: Phạm Việt Phương 51
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Cho A(x ;y ;z ),B(x ;y ;z ) A A A B B B
Toạ độ vectơ bằng toạ độ
điểm ngọn trừ toạ độ điểm gốc
AB  (x x ; y y ;z z ) B A B A B A
M là trung điểm của đoạn AB:
 Toạ độ trung điểm đoạn
x x y y z z
thẳng bằng trung bình cộng toạ A B A B A B M  ; ; 2 2 2    độ hai điểm mút.
Hoạt động 2: Tìm hiểu biểu thức toạ độ của tích vô hướng
 GV cho HS nhắc lại các tính  Các nhóm thảo luận và trình III. TÍCH VÔ HƯỚNG
chất tương tự trong mp và bày.
1. Biểu thức toạ độ của tích
hướng dẫn HS chứng minh. vô hướng
Định lí: Trong KG Oxyz, cho:
a  (a ;a ;a ), b  (b ;b ;b 1 2 3 1 2 3) . a b
.  a b a b a b 1 1 2 2 3 3 2. Ứng dụng  2 2 2
a a a a 1 2 3  2 2 2
AB  (xB xA) (yB yA) ( Bz zA)
a b a b a b  1 1 2 2 3 3
cos(a,b) 
a2 a2 a2. b2 b2 b2 1 2 3 1 2 3
a b a b a b a b 1 1 2 2 3 3  0
Hoạt động 3: Áp dụng biểu thức toạ độ các phép toán vectơ
H1. Xác định toạ độ các vectơ? Đ1.
VD1: Trong KG Oxyz, cho AB  ( 2  ;1;2),
A(1;1;1), B(–1;2;3), C(0;4;–2). AC  ( 1  ;3; 3  )
a) Tìm toạ độ các vectơ AB , , BC AC  (1;2; 5  )
, BC , AM (M là trung , điểm của BC).   AM 3 1 
b) Tìm toạ độ của vectơ:   ;2; 2 2   
AC  3AB , AB  2AC
AC  3AB  ( 7  ;6;3)
c) Tính các tích vô hướng: AB.2AC
AB  2AC  (0; 5  ;8) AB.AC , AB.AC  0
Hoạt động 4: Củng cố Nhấn mạnh:
– Các biểu thức toạ độ các phép toán vectơ trong KG.
– Liên hệ với toạ độ của điểm, của vectơ trong MP.
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3, 4 SGK.
 Đọc tiếp bài "Hệ toạ độ trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG: GV: Phạm Việt Phương 52
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 27
Bài 1: HỆ TOẠ ĐỘ TRONG KHÔNG GIAN (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được khái niệm toạ độ của điểm và vectơ trong không gian.
 Biểu thức toạ độ của các phép toán vectơ.
 Phương trình mặt cầu. Kĩ năng:
 Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
 Viết được phương trình mặt cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu các biểu thức toạ độ các phép toán vectơ trong không gian? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu phương trình mặt cầu
IV. PHƯƠNG TRÌNH MẶT CẦU
Định lí: Trong KG Oxyz, mặt
cầu (S) tâm I(a; b; c), bán kính r có phương trình:
H1. Nhắc lại phương trình 2 2 2 2 2 2 2
(x a)  (y b)  (z c)  r đường tròn trong MP?
Đ1. (x a)  (y b)  r
H2. Tính khoảng cách IM? Đ2.
IM x a 2  y b 2  z c 2 ( ) ( ) ( )
VD1: Viết phương trình mặt H3. Gọi HS tính? Đ3.
cầu có tâm I(1; –2; 3) và bán x 2   y 2   z 2 ( 1) ( 2) ( 3)  25 kính r = 5.
Hoạt động 2: Tìm hiểu dạng khác của phương trình mặt cầu GV: Phạm Việt Phương 53
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
 GV hướng dẫn HS nhận xét
Nhận xét: Phương trình:
điều kiện để phương trình là
x2  y2  z2  a 2 x b 2 y c
2 zd  0 phương trình mặt cầu. 2 2 2 với
a b c d  0 là
phương trình mặt cầu có tâm
I(–a; –b; –c) và bán kính r a2 b2 c2     d .
VD2: Xác định tâm và bán
GV hướng dẫn HS cách xác
kính của mặt cầu có phương định. trình:
H1. Biến đổi về dạng tổng bình Đ1. 2 2 2 phương? x 2   y 2   z 2 2 ( 2) ( 1) (  3)  3
x y z  4x 2y  6z  5  0
H2. Xác định a, b, c, r?
Đ2. a = –2, b = 1, c = –3, r = 3
Hoạt động 3: Áp dụng phương trình mặt cầu
H1. Gọi HS xác định?
Đ1. Các nhóm thực hiện và VD3: Xác định tâm và bán trình bày.
kính của mặt cầu có phương a) I(2;1; 3  ), r  8 trình: b) I( 1  ;2;3), r  3 x 2   y 2   z 2 ( 2) ( 1) (  3)  64 c) I(4; 2  ;1), r  5 2 2 2
(x 1)  (y  2)  (z 3)  9 d) I( 2  ;1;2), r  2
x2  y2  z2 8x  4y  2z  4  0 2 2 2
x y z  4x  2y  4z  5  0
H2. Xác định tâm và bán kính?
VD4: Viết phương trình mặt Đ2. cầu (S):
b) r IA  29
a) (S) có tâm I(1; –3; 5), r = 3  7  29
b) (S) có tâm I(2; 4; –1) và đi
c) I  ;3;1, r   2  2 qua điểm A(5; 2; 3)
c) (S) có đường kính AB với A(2; 4; –1), B(5; 2; 3)
Hoạt động 4: Củng cố Nhấn mạnh:
– Các dạng phương trình mặt cầu.
– Cách xác định mặt cầu.
4. BÀI TẬP VỀ NHÀ:  Bài 5, 6 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 54
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 28
Bài 1: BÀI TẬP HỆ TOẠ ĐỘ TRONG KHÔNG GIAN I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm toạ độ của điểm và vectơ trong không gian.
 Biểu thức toạ độ của các phép toán vectơ.
 Phương trình mặt cầu. Kĩ năng:
 Thực hành thành thạo các phép toán về vectơ, tính khoảng cách giữa hai điểm.
 Viết được phương trình mặt cầu. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và toạ độ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập biểu thức toạ độ của các phép toán vectơ H1. Nêu cách tính? Đ1.
1. Cho ba vectơ a  (2; 5  ;3),   d 1 55  11; ; b  (0;2; 1
 ) , c  (1;7;2) . Tính 3 3   
toạ độ của các vectơ: e  (0; 2  7;3) d a 1 4  b c 3   f 5 11  3   ; ; 6    2 2 
e a b 4  c 2   1 g 33 17   4; ;
f  a  2b c 2 2    2 g 1
a b c 3 2
H1. Nhắc lại tính chất trọng Đ2. GA GB GC  0
2. Cho ba điểm A(1; 1  ;1) , tâm tam giác? 
xA xB C x
B(0;1;2), C(1;0;1) . Tìm toạ độ x 2 G   3 3  trọng tâm G của ABC. 
yA yB C y   G y   0  3 
z z z 4 A B C G z    3 3
H3. Nêu hệ thức vectơ xác Đ3.
định các đỉnh còn lại của hình
3. Cho h.hộp ABCD.ABCD
C(2;0;2), A(3;5; 6  ), biết A(1;0;1) , B(2;1;2) , GV: Phạm Việt Phương 55
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn hộp? B(4;6; 5  ) , D(3;4; 6  ) D(1; 1  ;1), C(4;5; 5  ) . Tính toạ
độ các đỉnh còn lại của hình hộp. Đ4.
H4. Nêu công thức tính? 4. Tính a b . với: a) a b . = 6 a) a  (3; 0; 6  ) , b  (2; 4  ;0) b) a b . = –21 b) a  (1; 5  ;2), b  (4;3; 5  )
H5. Nêu công thức tính? Đ5.
5. Tính góc giữa hai vectơ a, b 5
a) a  (4;3;1), b  ( 1  ;2;3)
a) cosa, b   26.14
b) a  (2;5;4), b  (6;0; 3  ) 0
b) a,b   90 .
Hoạt động 2: Luyện tập phương trình mặt cầu
H1. Nêu cách xác định ? Đ1.
6. Tìm tâm và bán kính của các a) I(4;1; 0) , R = 4
mặt cầu có phương trình: b) I( 2  ; 4  ;1), R = 5 2 2 2
a) x y z  8x  2y 1  0 c) I(4; 2  ; 1  ), R = 5 2 2 2
b) x y z  4x y 8 2z 4  0   19 d) I 4 5 1; ;  2 2 2
c) x y z  8x  4y  2z  4  0  3 2  , R = 6 d) 2 2 2
3x  3y  3z  6
x  8y 15z  3  0
H2. Nêu cách xác định mặt Đ2.
7. Lập phương trình mặt cầu: cầu?
a) Tâm I(3; –2; 2), bk R = 3
a) Có đường kính AB với A(4; x 2   y 2   z 2 ( 3) ( 1)
(  5)  9 –3; 7), B(2; 1; 3).
b) Đi qua điểm A(5; –2; 1) và b) Bán kính R = CA = 5 có tâm C(3; –3; 1). x 2   y 2   z 2 ( 3) ( 3) ( 1)  5
Hoạt động 3: Củng cố Nhấn mạnh:
– Các biểu thức toạ độ của các phép toán vectơ.
– Cách lập phương trình mặt
cầu, cách xác định tâm và bán kính mặt cầu.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Đọc trước bài "Phương trình mặt phẳng"
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 56
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 29
Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG I. MỤC TIÊU: Kiến thức:
 Nắm được vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
 Nắm được sự xác định mặt phẳng. Phương trình tổng quát của mặt phẳng.
 Điều kiện để hai mặt phẳng song song, vuông góc. Kĩ năng:
 Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
 Xác định được hai mặt phẳng song song, vuông góc.
 Tính được khoảng cách từ một điểm đến mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về vectơ và mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu một số tính chất cơ bản của phép toán về vectơ? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu khái niệm vectơ pháp tuyến của mặt phẳng
 GV giới thiệu định nghĩa n
I. VECTƠ PHÁP TUYẾN VTPT của mặt phẳng. CỦA MẶT PHẲNG
Định nghĩa: Cho mp (P). Nếu P
vectơ n 0 và có giá vuông
góc với (P) thì n đgl vectơ
pháp tuyến của (P).
H1. Một mp có bao nhiêu Đ1. Vô số VTPT, chúng cùng Chú ý: Nếu n là VTPT của (P) VTPT? phương với nhau.
thì kn (k 0) cũng là VTPT của (P).
Hoạt động 2: Áp dụng tìm VTPT của mặt phẳng
H1. Tính toạ độ các vectơ AB , Đ1.
VD1: Tìm một VTPT của mặt AC AB  (2;1; 2  ) , AC  ( 1  2;6;0) , phẳng: , BC ?
a) Qua A(2; –1; 3), B(4; 0; 1), BC  ( 1  4;5;2) C(–10; 5; 3).
H2. Tính  A , B AC   , Đ2.
b) Qua A(2; 0; 0), B(0; 2; 0), AB AC    AB BC  A , B BC   ? ,  ,  C(0; 0; 2). c) Mặt phẳng (Oxy).  (12;24;24) d) Mặt phẳng (Oyz).
H3. Xác định một VTPT của Đ3.
các mặt phẳng (Oxy), (Oyz)? nk , ni (Oxy ) (Oyz) GV: Phạm Việt Phương 57
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Hoạt động 3: Tìm hiểu phương trình tổng quát của mặt phẳng
 GV hướng dẫn HS giải bài toán
II. PHƯƠNG TRÌNH TỔNG 1.
QUÁT CỦA MẶT PHẲNG
Bài toán 1: Trong KG Oxyz, cho
H1. Nêu điều kiện để M  (P)?
Đ1. M  (P)  M M n
mp (P) đi qua M (x ; y ; z ) và 0 0 0 0 0 nhận n  ( ;
A B;C) làm VTPT.
Điều kiện cần và đủ để M(x; y; z) (P) là: (
A x x )  B( y y )  C(z z )  0 0 0 0
Bài toán 2: Trong KG Oxyz, tập
GV hướng dẫn nhanh bài toán 2.
hợp các điểm M(x; y; z) thoả PT:
Ax By Cz D  0 (A, B, C
không đồng thời bằng 0) là một mặt phẳng nhận vectơ
 GV nêu định nghĩa phương trình n  ( ;
A B;C) làm VTPT.
tổng quát của mặt phẳng và
hướng dẫn HS nêu nhận xét.
1. Định nghĩa: Phương trình
Ax By Cz D  0 , trong đó 2 2 2
A B C  0 , đgl phương
trình tổng quát của mặt phẳng. Nhận xét:
H2. Chỉ ra một VTPT của (P)? Đ2. n  ( ; A B;C)
a) (P): Ax By Cz D  0
(P) có 1 VTPT là n  ( ; A B;C) . b) PT của (P) qua
M (x ; y ; z ) 0 0 0 0 và có VTPT n  ( ;
A B;C) là: (
A x x )  B( y y )  C(z z )  0 0 0 0
Hoạt động 4: Tìm hiểu các trường hợp riêng của phương trình tổng quát của mặt phẳng
 GV hướng dẫn HS xét các
2. Các trường hợp riêng trường hợp riêng.
a) D = 0 (P) đi qua O.
H1. Khi (P) đi qua O, tìm D? Đ1. D = 0 (P)  Ox
H2. Phát biểu nhận xét khi một Đ2. Hệ số của biến nào bằng 0 thì b) A = 0
trong các hệ số A, B, C bằng 0? (P) Ox
(P) song song hoặc chứa trục ứng với biến đó. (P) (Oxy)
c) A = B = 0  (P)  (Oxy)
H3. Tìm giao điểm của (P) với Đ3. (P) cắt các trục Ox, Oy, Oz Nhận xét: Nếu các hệ số A, B, C, các trục toạ độ?
lần lượt tại A(a; 0; 0), B(0; b; 0), D đều khác 0 thì có thể đưa C(0; 0; c).
phương trình của (P) về dạng: GV: Phạm Việt Phương 58
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn x y z   1 (2) a b c
(2) đgl phương trình của mặt
phẳng theo đoạn chắn.
Hoạt động 5: Áp dụng phương trình mặt phẳng H1. Gọi HS tìm? Đ1.
VD1: Xác định một VTPT của a) n  (4; 2  ; 6  ) các mặt phẳng: b) n  (2;3;0)
a) 4x  2 y  6z  7  0
b) 2x  3y  5  0
H2. Xác định một VTPT của mặt Đ2.
VD2: Lập phương trình của mặt phẳng? phẳng đi qua các điểm:
a) n  A , B AC  ( 1  ;4; 5  ) 
a) A(1; 1; 1), B(4; 3; 2), C(5; 2; 1)
(P): x  4 y  5z  2  0
b) A(1; 0; 0), B(0; 2; 0), C(0; 0; 3) x y z b) (P):   1 1 2 3
 6x  3y  2z  6  0
Hoạt động 6: Củng cố Nhấn mạnh:
– Phương trình tổng quát của mặt phẳng.
– Các trường hợp riêng
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2, 3, 4, 5 SGK.
 Đọc tiếp bài "Phương trình mặt phẳng".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 59
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 30
Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
 Nắm được sự xác định mặt phẳng. Phương trình tổng quát của mặt phẳng.
 Điều kiện để hai mặt phẳng song song, vuông góc. Kĩ năng:
 Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
 Xác định được hai mặt phẳng song song, vuông góc.
 Tính được khoảng cách từ một điểm đến mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về phương trình mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Tìm các VTPT của hai mặt phẳng: (P ) : x  2y  3z 1  0, (P ) : 2x  4y  6z 1  0 ? 1 2 Đ. n  (1; 2  ;3), n  (2; 4  ;6) . 1 2 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai mặt phẳng song song
H1. Xét quan hệ giữa hai Đ1. Hai VTPT cùng phương.
III. ĐIỀU KIỆN ĐỂ HAI MP
VTPT khi hai mặt phẳng song SONG SONG, VUÔNG GÓC song?
1. Điều kiện để hai mặt phẳng song song
H2. Xét quan hệ giữa hai mặt Đ2. Hai mặt phẳng song song Trong KG cho 2 mp (P1), (P2):
phẳng khi hai VTPT của chúng hoặc trùng nhau.
(P ) : A x B y C z D  0 1 1 1 1 1 cùng phương?
(P ) : A x B y C z D  0 2 2 2 2 2
(P) (P ) 1 2
(A ;B ;C )  k(A ;B ;C ) 1 1 1 2 2 2   D   kD 1 2
(P)  (P ) 1 2
(A ;B ;C )  k(A ;B ;C ) 1 1 1 2 2 2   D kD  1 2  (P1) cắt (P2)
(A ;B ;C )  k(A ;B ;C ) 1 1 1 2 2 2 H3. Nêu điều kiện
để Đ3. (P1)//(P2)
VD1: Cho hai mp (P1) và (P2):
(P1)//(P2), (P1) cắt (P2)?  A B C
 ( ; ; ) k(A ;B ;C )
(P1): x my  4z m  0 1 1 1 2 2 2  D   kD (P
x y m z   1 2 2): 2 ( 2) 4 0 GV: Phạm Việt Phương 60
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn A B C D Tìm m để (P 1 1 1 1     m = 2 1) và (P2): A B C D a) song song 2 2 2 2 b) trùng nhau (P
1) cắt (P2)m  2
H4. Xác định VTPT của (P)? Đ4. c) cắt nhau. Vì (P) // (Q) nên (P) có VTPT
VD2: Viết PT mp (P) đi qua n  (2; 3  ;1) .
điểm M(1; –2; 3) và song song
 (P): 2(x 1) 3(y  2) 1(z 3)  0 với mp (Q): 2x 3y z 5  0 .
 2x  3y z 11  0
Hoạt động 2: Tìm hiểu điều kiện để hai mặt phẳng vuông góc
H1. Xét quan hệ giữa hai Đ1. (P )  (P )  n n
2. Điều kiện để hai mặt phẳng 1 2 1 2 VTPT khi hai mp vuông góc? vuông góc
(P )  (P )  A A B B C C  0 1 2 1 2 1 2 1 2
H2. Xác định điều kiện hai mp Đ2.
VD3: Xác định m để hai mp vuông góc?
(P )  (P )  A A B B C C  0 1 2 1 2 1 2 1 2 sau vuông góc với nhau:  1
x y mz   (P): 2 7 2 0 m   2
(Q): 3x y  2z 15  0
H2. Xác định cặp VTCP của Đ2. (P) có cặp VTCP là:
VD4: Viết phương trình mp (P)? AB  ( 1  ; 2  ;5) và n  (2; 1
 ;3) (P) đi qua hai điểm A(3; 1; –1), Q
B(2; –1; 4) và vuông góc với
H3. Xác định VTPT của (P)?
mp (Q): 2x y  3z 1  0 .
Đ3. n   AB,n   ( 1  ;13;5) PQ  
(P): x 13y  5z  5  0
Hoạt động 3: Củng cố Nhấn mạnh:
– Điều kiện để hai mp song song, vuông góc.
– Cách lập phương trình mặt
phẳng song song hoặc vuông góc với mp đã cho.
Cách viết khác của điều kiện để
hai mp song song, trùng nhau. A B C D 1 1 1 1 (P ) (P )     1 2 A B C D 2 2 2 2 A B C D 1 1 1 1
(P )  (P )     1 2 A B C D 2 2 2 2
4. BÀI TẬP VỀ NHÀ:  Bài 5, 6, 7, 8 SGK.
 Đọc tiếp bài "Phương trình mặt phẳng".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... GV: Phạm Việt Phương 61
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 31
Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
 Nắm được sự xác định mặt phẳng. Phương trình tổng quát của mặt phẳng.
 Điều kiện để hai mặt phẳng song song, vuông góc. Kĩ năng:
 Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
 Xác định được hai mặt phẳng song song, vuông góc.
 Tính được khoảng cách từ một điểm đến mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về phương trình mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu điều kiện để hai mặt phẳng song song, trùng nhau, cắt nhau? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu cách tính khoảng cách từ một điểm đến một mặt phẳng
 GV hướng dẫn HS chứng
IV. KHOẢNG CÁCH TỪ minh định lí.
MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG
Định lí: Trong KG Oxyz, cho (P):
Ax By Cz D  0 và
H1. Xác định toạ độ vectơ Đ1.
điểm M (x ; y ; z ) . 0 0 0 0 M M ?
M M x x y y z  1 0 ( ; ; z )
Ax By Cz  1 0 0 1 0 1 0 1  D d M ,(P)  0  0 0 0
H2. Nhận xét hai vectơ M M Đ2. Hai vectơ cùng phương. 2 2 2 1 0
A B C và n ?
H3. Tính M M .n bằng hai Đ3. M M .n M M . n = 1 0 1 0 1 0 cách? (
A x x )  B( y y )  C(z z ) 0 1 0 1 0 1
Hoạt động 2: Áp dụng khoảng cách từ một điểm đến một mặt phẳng H1. Gọi HS tính? Đ1.
VD1: Tính khoảng cách từ 4 điểm M đến mp(P):
a) d (M ,(P))  3 a) M(1; –2; 13) 11
(P): 2x  2 y z  3  0 d M P  b) ( , ( )) 3 b) M(2; –3; 5)
c) d (M ,(P))  27
(P): 2x y  2z  6  0 c) M(1; –4; –2) GV: Phạm Việt Phương 62
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
d) d (M ,(P))  2
(P): x y  5z 14  0 d) M(3; 1; –2) (P)  (Oxy)
H2. Nhắc lại cách tính khoảng
VD2: Tính khoảng cách giữa
cách giữa hai mp song song?
Đ2. Bằng khoảng cách từ 1 hai mp song song (P) và (Q):
điểm trên mp này đến mp kia. a)
(P): x  2 y  2z 11  0
a) Lấy M(0; 0; –1)  (Q).
(Q): x  2 y  2z  2  0
d ((P), (Q))  d (M , (P))  3 b) (P): 4x y  8z 1 0 b) Lấy M(0; 1; 0)  (P)
(Q): 4x y  8z  5  0 4
d ((P),(Q))  d (M ,(Q))  9
H3. Xác định bán kính mặt cầu
VD3: Viết pt mặt cầu (S) có (S)?
tâm I và tiếp xúc với mp (P): Đ3.
R = d (I ,(P)) I(3; 5  ; 2  ) a) a) 
(P) : 2x y  3z 1  0 162 2 2 2
(x  3)  ( y  5)  (z  2)  I(1;4;7) 7 b)   P
x y z   b) ( ) : 6 6 7 42 0 2  23 2 2 2
(x 1)  ( y  4)  (z  7)     11 
H4. Xác định VTPT của (P)?
VD4: Viết pt mặt phẳng (P)
tiếp xúc với mặt cầu (S) tại M: Đ4. n IM a) a) 2 2 2 (P): S x   y   z   4(
x 1)  2(y  3)  2z  0 ( ) : ( 3) ( 1) ( 2) 24 b) M ( 1  ;3;0)
(P) : 6(x  7)  2( y  1)  3(z  5)  0 b) 2 2 2
(S) : (x 1)  ( y  3)  (z  2)  49 M (7; 1  ;5)
Hoạt động 3: Củng cố Nhấn mạnh:
– Công thức tính khoảng cách từ 1
điểm đến 1 mặt phẳng.
– Ứng dụng công thức tính
khaongr cách từ 1 điểm đến 1 mp.
4. BÀI TẬP VỀ NHÀ:  Bài 9, 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 63
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 32 - 33
Bài 2: BÀI TẬP PHƯƠNG TRÌNH MẶT PHẲNG I. MỤC TIÊU:
Kiến thức: Củng cố:
 Khái niệm vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
 Phương trình tổng quát của mặt phẳng.
 Điều kiện để hai mặt phẳng song song, vuông góc. Kĩ năng:
 Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
 Xác định được hai mặt phẳng song song, vuông góc.
 Tính được khoảng cách từ một điểm đến mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về phương trình mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập lập phương trình mặt phẳng
H1. Nêu công thức? Cần xác Đ1. 1. Viết ptmp (P):
định thêm các yếu tố nào? (
A x x )  B( y y )  C(z z )  0 a) Đi qua M(1; –2; 4) và nhận 0 0 0
a) (P): 2x  3y  5z 16  0
n  (2;3;5) làm VTPT.
b) n  u,v  (2; 6  ;6)
b) Đi qua A(0; –1; 2) và song
song với giá của mỗi vectơ
(P): x  3y  3z  9  0
u  (3; 2;1), v  ( 3  ;0;1) . x y z c) (P):   1
c) Đi qua A(–3; 0; 0), B(0; –2; 3  2  1  0), C(0; 0; –1).
d) n  AC, AD  ( 2  ; 1  ; 1  )
d) Đi qua A(5; 1; 3), C(5; 0; 4).
(P): 2x y z 14  0 D(4; 0; 6).
H2. Cần xác định các yếu tố Đ2. 2. Viết ptmp (P): nào?
a) (P) qua trung điểm I(3; 2; 5) a) Là mp trung trực của đoạn
và có VTPT AB  (2; 2  ; 4  )
AB với A(2; 3; 7), B(4; 1; 3).  b) Qua AB và song song với
(P): x y  2z  9  0
CD với A(5; 1; 3), B(1; 6; 2),
b) n  A ,
B CD  (10;9;5) C(5; 0; 4), D(4; 0; 6).
 (P): 10x  9y  5z  74  0 c) Qua M(2; –1; 2) và song
c) n n  (2; 1  ;3)
song với (Q): 2x y  3z  4  0 P Q
d) Qua A(1; 0; 1), B(5; 2; 3) và
(P): 2x y  3z 11  0 vuông góc với (Q): GV: Phạm Việt Phương 64
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn d)
x y z  
n   AB, n   (1;0; 2)  2 7 0 . PQ  
(P): x  2z 1  0
Hoạt động 2: Luyện tập xét VTTĐ giữa hai mặt phẳng
H1. Nêu đk để hai mp song Đ1.
3. Xác định các giá trị của m, n
song, cắt nhau, trùng nhau? 2 m 3 5 
để mỗi cặp mp sau: song song, a) (P)//(Q)     n 8  6  2 cắt nhau, trùng nhau: m  4
a) (P): 2x my  3z  5  0   n  4 
(Q): nx  8y  6z  2  0
x y mz   3 5  m 3  b) (P): 3 5 3 0 b) (P)//(Q)     2 n 3  1
(Q): 2x ny  3z 1  0  9 m     2  10 n    3
Hoạt động 3: Luyện tập tính khoảng cách từ một điểm đến một mặt phẳng
H1. Nêu công thức tính ? Đ1.
4. Tính khoảng cách từ A(2; 4; – a) d ( , A (P))  5 3) đế các mp sau: b) d ( , A (P))  2
a) (P): 2x y  2z  9  0 b) (P): x  0 z A’
5. Cho hlp ABCD.ABCD có  D’
Hướng dẫn HS cách sử dụng pp cạnh bằng 1.
toạ độ để giải toán. B’ C’ a) CMR hai mp (ABD) và D A y
(BCD) song song với nhau.
b) Tính khoảng cách giữa hai mp B C trên. x
H2. Xác định toạ độ các đỉnh của Đ2. A(0;0;0), B(1;0;0), C(1;1;0), hlp? D(0;1;0), A(0;0;1), B(1;0;1), C(1;1;1), D(0;1;1)
H3. Viết pt hai mp (ABD) và Đ3. (BCD)?
(ABD): x y z  0
(BCD): x y z 1  0  (ABD) // (BCD)  1 d((A B
D ),(BCD))  3
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách viết phương trình mặt phẳng.
– Cách sử dụng công thức tính
khoảng cách từ một điểm đến một mặt phẳng.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
 Chuẩn bị kiểm tra 1 tiết.
IV. RÚT KINH NGHIỆM, BỔ SUNG: GV: Phạm Việt Phương 65
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 34
Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN I. MỤC TIÊU: Kiến thức:
 Nắm được phương trình tham số của đường thẳng.
 Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
 Vị trí tương đối giữa đường thẳng và mặt phẳng. Kĩ năng:
 Viết được phương trình tham số của đường thẳng.
 Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
 Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng và mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nhắc lại thế nào là VTCP của đường thẳng, VTPT của mặt phẳng? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu phương trình tham số của đường thẳng a I. PT THAM SỐ CỦA M ĐƯỜNG THẲNG
Định lí: Trong KG Oxyz, cho M0
đường thẳng đi qua điểm
M0(x0; y0; z0) và nhận vectơ
H1. Nêu điều kiện để M   ? Đ1. a làm VTCP. Điều
(a ;a ;a ) 1 2 3
kiện cần và đủ để điểm
M  M M , a cùng phương 0
M(x;y;z) nằm trên là có một M M ta 0 số thực t sao cho:
x x ta 0 1 
y y ta 0 2  z z   ta 0 3  GV nêu định nghĩa.
Định nghĩa: Phương trình GV: Phạm Việt Phương 66
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
tham số của đường thẳng đi
qua điểm M0(x0; y0; z0) và có
H2. Nhắc lại pt tham số của đt Đ2.
VTCP a  (a ;a ;a ) là phương 1 2 3 trong mặt phẳng?
x x ta trình có dạng: 0 1  y y   ta
x x ta 0 2 0 1 
y y ta 0 2  z z   ta 0 3
trong đó t là tham số.  GV nêu chú ý.
Chú ý: Nếu a1, a2, a3 đều khác
0 thì có thể viết phương trình
của dưới dạng chính tắc: x x y y z z 0 0 0   a a a 1 2 3
Hoạt động 2: Áp dụng viết phương trình tham số của đường thẳng
H1. Gọi HS thực hiện.
Đ1. Các nhóm thực hiện và VD1: Viết PTTS của đường trình bày.
thẳng  đi qua điểm M0 và có VTCP a , với: a) M (1;2; 3  ),a  ( 1  ;3;5) b) M (0; 2  ;5),a  (0;1;4) c) M (1;3; 1  ),a  (1;2; 1  ) M   a   d) (3; 1; 3), (1; 2;0)
H2. Xác định một VTCP và Đ2.
VD2: Cho các điểm A(2;3;–1),
một điểm của đường thẳng?
B(1; 2; 4), C(2; 1; 0), D(0;1;2). AB  ( 1  ; 1  ;5) , A(2;3;–1) Viết PTTS  của các đường x  2  t thẳng AB, AC, AD, BC.  
PTTS của AB:  y  3  t   z    1 5t
H3. Xác định một VTCP của Đ3.
VD3: Viết PTTS của  đi qua ?
Vì   (P) nên a n = (2;–3;6) điểm A và vuông góc với mặt  x  2   2t phẳng (P):   a) ( A 2
 ;4;3), (P): 2x  3y  6z 19  0
PTTS của :  y  4  3t A P x y    b) (3;2;1), ( ) : 2 5 4 0 z  3  6t c) A(1; –1; 0), (P)(Oxy) d) A(2; –3; 6), (P)(Oyz) 
GV hướng dẫn cách xác định 
VD4: Cho đường thẳng  có
toạ độ một điểm M 
Cho t = t0, thay vào PT của . . Với t = 0 
PTTS. Hãy xác định một điểm M(–1; 3; 5)  
M   và một VTCP của .  x  1   2t
: y  3  3t
z  5  4t
Hoạt động 3: Củng cố Nhấn mạnh:
– Các dạng PTTS và PTCT của đường thẳng GV: Phạm Việt Phương 67
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
4. BÀI TẬP VỀ NHÀ:  Bài 1, 2 SGK.
 Đọc tiếp bài "Phương trình đường thẳng trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 35
Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được phương trình tham số của đường thẳng.
 Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
 Vị trí tương đối giữa đường thẳng và mặt phẳng. Kĩ năng:
 Viết được phương trình tham số của đường thẳng.
 Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
 Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu cách viết PTTS của đường thẳng? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai đường thẳng song song d’
II. ĐIỀU KIỆN ĐỂ HAI a d ĐƯỜNG THẲNG SONG
SONG, CẮT NHAU, CHÉO a NHAU
1. Điều kiện để hai đường M thẳng song song
Gọi a  (a ;a ;a ), a  (a ;a ;a )
H1. Nhắc lại các VTTĐ của 2 Đ1. song song, cắt nhau, trùng 1 2 3 1 2 3 đường thẳng trong KG?
lần lượt là VTCP của d và d. nhau, chéo nhau. Lấy M(x
0; y0; z0) d.
H2. Nêu điều kiện để hai Đ2. d và d không có điểm GV: Phạm Việt Phương 68
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn đường thẳng song song? chung và hai VTCP cùng
a ka phương.
d // d M d
a ka
d d M d
Hoạt động 2: Áp dụng xét điều kiện để hai đường thẳng song song
VD1: Chứng minh hai đường thẳng sau song song song:
x  2  2t x   1 t  
a) d y t
d  y   t
H1. Xác định các VTCP của d Đ1. : 2 ; : 2 4   z   và d 3 t
z   t ? 5 2 a  (1; 2; 1
 ) , a  (2;4; 2)   x  1   2t x  
a, a cùng phương. 1 2t  
b) d : y  2  t ; d : y  2  t z  3 2  t
z    t
H2. Lấy 1 điểm M  d, chứng Đ2. M(1; 0; 3)  d 3 2 tỏ M  d?  M  d. c) x 1 y  2 z  3 d :   9 6 3 x  7 y  6 z  5 d :   6 4 2 d) x  2 y z  1 d   : 4 6  8  x  7 y  2 dz :   6  9 12
VD2: Viết phương trình đường
thẳng  đi qua điểm A và song
H3. Xác định VTCP của ? Đ3.
song với đường thẳng d cho
Vì  // d nên  cũng nhận trước: VTCP của d làm VTCP.
x  2  3t  y  
H4. Xác định VTCP của d? Đ4. a) A(2; –5; 3), d: 3 4t
a) a  (3; 4;2)
z  5  2t b) a  (4; 2  ;3)
x  3  4t  c) a  (4;2;3)
b) A(1; –3; 2), d:  y  2  2t d) a  (2;3;4)  z  3t 1 c) A(4; –2; 2), x  2 y  5 z  2 d:   4 2 3 d) A(5; 2; –3), x  3 y 1 z  2 d:   2 3 4
Hoạt động 3: Củng cố Nhấn mạnh:
– Điều kiện để hai đường thẳng song song, trùng nhau. GV: Phạm Việt Phương 69
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
– Cách xác định một điểm nằm trên đường thẳng.
4. BÀI TẬP VỀ NHÀ:  Bài 3 SGK.
 Đọc tiếp bài "Phương trình đường thẳng trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 36
Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được phương trình tham số của đường thẳng.
 Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
 Vị trí tương đối giữa đường thẳng và mặt phẳng. Kĩ năng:
 Viết được phương trình tham số của đường thẳng.
 Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
 Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu điều kiện để hai đường thẳng song song, trùng nhau? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai đường thẳng cắt nhau
II. ĐIỀU KIỆN ĐỂ HAI ĐT SONG SONG, CẮT NHAU, CHÉO NHAU
H1. Hai đường thẳng cắt nhau Đ1. 1 điểm chung duy nhất.
2. Điều kiện để hai đường có mấy điểm chung? thẳng cắt nhau
Cho 2 đường thẳng GV: Phạm Việt Phương 70
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn ' '
x x t
x x ta a 0 1 0 1   
d: y y ta , d: ' '
y y ta 0 2  0 2  z z   ta ' '
z z t 0 3  a 0 3
d và d cắt nhau hệ pt ẩn t,
t sau có đúng 1 nghiệm: ' '
x ta x ta 0 1 0 1  ' '
y ta y ta (*) 0 2 0 2  ' '
z ta z t  a 0 3 0 3
Chú ý: Giả sử hệ (*) có
nghiệm, để tìm toạ độ giao
điểm M0 của d và d ta có thể
thay t0 vào PTTS của d hoặc thay t
0 vào PTTS của d.
Hoạt động 2: Áp dụng xét điều kiện để hai đường thẳng cắt nhau
H1. Gọi HS thực hiện.
Đ1. Các nhóm thực hiện và VD1: Tìm giao điểm của hai trình bày. đường thẳng sau:
x  2  2t x 1 t   
d y   t d  y    t a) : 2 3 , : 2   z  3  t
z 1 3t x 1 td y   : 2 2t  b) z 1 t x 1 y  2 z 1 d   : 3 1 1
x   t 1 x  3t   
c) d :  y 1 2t ,d :  y  2t   z  3  t
z  4  t
x  5 t x  3   2t   
d) d : y  2
  3t ,d : y  1   4t  
z  6  4t
z  20  t
H2. Nêu điều kiện để hai Đ2.
Hệ phương trình có VD2: Tìm m để hai đường đường thẳng cắt nhau? nghiệm duy nhất.
thẳng d và d cắt nhau. Khi đó
tìm toạ độ giao điểm của chúng
x 1 t x 1 mt   
a) d :  y t
, d :  y  2  2t   z  1   2t
z  3 t GV: Phạm Việt Phương 71
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
x  2  t x 1 t   
b) d : y  3  2t ,d : y 1 t  
z m t
z  2  3t
Hoạt động 3: Củng cố Nhấn mạnh:
– Điều kiện để hai đường thẳng cắt nhau.
– Cách tìm giao điểm của hai đường thẳng cắt nhau.
4. BÀI TẬP VỀ NHÀ:  Bài 3, 4 SGK.
 Đọc tiếp bài "Phương trình đường thẳng trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 37
Bài 3: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt) I. MỤC TIÊU: Kiến thức:
 Nắm được phương trình tham số của đường thẳng.
 Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
 Vị trí tương đối giữa đường thẳng và mặt phẳng. Kĩ năng:
 Viết được phương trình tham số của đường thẳng.
 Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
 Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (3')
H. Nêu điều kiện để hai đường thẳng song song, trùng nhau, cắt nhau? Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Tìm hiểu điều kiện để hai đường thẳng cắt nhau GV: Phạm Việt Phương 72
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn d
II. ĐIỀU KIỆN ĐỂ HAI ĐT SONG SONG, CẮT NHAU, a CHÉO NHAU
3. Điều kiện để hai đường thẳng chéo nhau a
Cho 2 đường thẳng d’
x x ta
x x'  ta'
H1. Nêu điều kiện để hai Đ1. Không cùng phương và 0 1  0 1  ' '     đường thẳng chéo nhau?
y y ta y y t a không cắt nhau. d: 0 2 , d: 0 2
z z ta  ' '  0 3
z z ta  0 3
d và d chéo nhau hai VTCP
không cùng phương và hệ pt ẩn
t, t sau vô nghiệm:
x ta x'  ta' 0 1 0 1  ' '
y ta y ta 0 2 0 2 (*)
z ta z'  ta'  0 3 0 3
d d a a
Hoạt động 2: Áp dụng xét điều kiện để hai đường thẳng chéo nhau
H1. Gọi HS thực hiện.
Đ1. Các nhóm thực hiện và VD1: Chứng tỏ các cặp đường trình bày. thẳng sau chéo nhau: a) x 1 t 2 x 1 t 3    d : y  1   t
3 ,d : y  2   t 2 
z  5 t  z  1   t 2  x 1 t 2 x t 2   
b) d : y  3  t
,d : y 1 t z  2   t 3  z  3  t 2 
x  2 y 1 z d :   c) 3 2  2 x y 1 z d 1  :   1 2 4
x  7 y  3 z d  9 :   d) 1 2 1 
x  3 y 1 z d 1  :   7  2 3
 GV hướng dẫn cách viết  Lấy M  d, N  d
VD2: Chứng tỏ các đường
phương trình đường vuông góc MN d
thẳng sau chéo nhau? Viết
chung của hai đường thẳng Từ điều kiện  , ta tìm MN d
phương trình đường vuông góc chéo nhau.
chung của 2 đường thẳng đó: được M, N.
Khi đó đường vuông góc a)
chung là đường thẳng MN.  x  3  t 2 x  2  t 3   
d : y 1 t
4 ,d : y  4  t z  2   t 4  z 1 t 2  GV: Phạm Việt Phương 73
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn b) x 1 t 2 x  2   t 3    d : y  3
  t,d : y 1 t 2 
z  2  t3  z  4   t 4 
Hoạt động 3: Tìm hiểu VTTĐ giữa đường thẳng và mặt phẳng
H1. Nêu các trường hợp về Đ1.
*) VTTĐ GIỮA ĐƯỜNG
VTTĐ giữa đường thẳng và
d // (P), d cắt (P), d  (P) THẲNG VÀ MẶT PHẲNG mặt phẳng?
Cho (P): Ax By Cz D  0 ,
x x ta 0 1 
d: y y ta 0 2 .
z z ta  0 3 Xét phương trình:
A(x ta B(y ta 0 1 0 2 )  (1)
C(z ta )  D  0 0 3
Nếu (1) vô nghiệm thì d // (P)
Nếu (1) có đúng 1 nghiệm t0
thì d cắt (P) tại điểm M0.
H2. Nêu mối quan hệ giữa số Đ2.
Nếu (1) có vô số nghiệm thì d
giao điểm và VTTĐ của đt, d // (P)  0 giao điểm thuộc (P). mp?
d cắt (P)  1 giao điểm
d  (P)  vô số giao điểm
Hoạt động 4: Áp dụng xét VTTĐ của đường thẳng và mặt phẳng
H1. Lập phương trình và giải?
Đ1. Các nhóm thực hiện và VD1: Tìm số giao điểm của trình bày.
mặt phẳng (P): x y z  3  0
a) (2  t)  (3  t)  1  3  0 và đường thẳng d:  4 = 0  PT vô nghiệm x  2  t   d // (P)
a) d: y  3  t z 1
b) (1  2t)  (1  t)  (1  t)  3  0 x  1 2t  
0 = 0  PT vô số nghiệm y  1 t b) d: 
z 1 t d  (P) x  1 t 5  c)
c) d: y  1 4t (1 t
5 )  (1 4t)  (1 t 3 )  3  0  z  1 t 3
 4t = 0 PT có nghiệm t = 0
 d cắt (P) tại A(1; 1; 1)
VD2: Xét VTTĐ của đường H2. Nêu cách xét? Đ2.
thẳng d và mặt phẳng (P):
C1: Dựa vào mối quan hệ giữa
d : x t
2 ;y 1 t;z  3  t a) 
VTCP của d và VTPT của (P). (
P) : x y z 10  0
C2: Dựa vào số nghiệm của hệ
d : x t
3  2;y 1 4t;z  4t  5 d phương trình b)   . (
P): 4x  3y  6z  5  0 (  P) 
x 12 y  9 z 1 d :   c)  4 3 1 (
 P):3x  5y z  2  0 GV: Phạm Việt Phương 74
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn Đ3.
VD3: Cho đường thẳng d và
H3. Nêu điều kiện ứng với d cắt (P)  a n
mặt phẳng (P). Tìm m, n để: từng trường hợp? a n i) d cắt (P) ii) d // (P)
d // (P)  M P (M0  d)  iii) d  (P) iv) d  (P) 0 ( )  a x 1 y  2 z  3  nd :  
d  (P)  M P (M0  d) a)  m 2m 1 2  0 ( ) (
 P): x  3y  2z  5  0
d  (P)  a,n cùng phương b)
d : x  3  t
4 ;y 1 4t;z  3   t ( 
P) : (m 1)x  2y  4z n  9  0
Hoạt động 5: Củng cố Nhấn mạnh:
– Các trường hợp về VTTĐ của
đường thẳng và mặt phẳng.
– Cách tìm giao điểm của đường thẳng và mặt phẳng.
4. BÀI TẬP VỀ NHÀ:
 Bài 5, 6, 7, 8, 9, 10 SGK.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy:38
Bài 3: BÀI TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN I. MỤC TIÊU:
Kiến thức: Củng cố:
 Phương trình tham số của đường thẳng.
 Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
 Vị trí tương đối giữa đường thẳng và mặt phẳng. Kĩ năng:
 Viết được phương trình tham số của đường thẳng.
 Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
 Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng. GV: Phạm Việt Phương 75
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập viết phương trình tham số của đường thẳng
H1. Nêu điều kiện xác định Đ1. Biết được 1 điểm và 1 1. Viết PTTS của đường thẳng PTTS của đường thẳng? VTCP.
d trong mỗi trường hợp sau:
x  5  2t
a) d đi qua M(5; 4; 1) và có 
a) d: y  4  t 3 VTCP a  (2; 3  ;1) .
z 1 t
b) d đi qua điểm A(2; –1; 3) và x  2  t
vuông góc (P): x y z  5  0 
b) d: y  1  t
c) d đi qua B(2; 0; –3) và song
z  3  tx  1 2t
x  2  2t
song với : y  3   t 3  y t 3 z  4t c) d: z  3   4t
d) d đi qua P(1; 2; 3),Q(4; 4; 4) x  1 t 3 
d) d: y  2  2t  z  3  t Đ2.
Xác định (Q)  d, (Q)  (P).
H2. Nêu cách xác định hình –
2. Viết PTTS của đường thẳng M0  d  M0  (Q)
chiếu d của d trên (P)?
d là hình chiếu vuông góc của – Q n   P n , d a  x  2  t  
Xác định d = (P)  (Q)
đường thẳng d: y  3  2t lần
 d là h.chiếu của d trên (P).
z 1 t3
– Lấy M  (P)(Q)  M  d lượt trên các mặt phẳng (P): – d a   P n Q n ' ,  a) (P)  (Oxy) b) (P) (Oyz) x  2  t
a) d: y  3  2t z  0 x  0 
b) d: y  3  2t
z 1 t3
Hoạt động 2: Luyện tập xét VTTĐ của hai đường thẳng
H1. Nêu cách xét VTTĐ của Đ1.
3. Xét VTTĐ của các cặp đt: hai đường thẳng?
C1: Xét quan hệ hai VTCP
x  3  2t
x  5 t
C2: Xét số nghiệm của hệ PT  
y  2  t 3 y  1   4t a) d và d a) d: , d: cắt nhau tại M(3; 7;
z  6  4t
z  20  t 18) b) d // d x  1 t
x 1 2t c) d và d   chéo nhau
b) d: y  2  t , d:y  1   2t
z  3 t
z  2  2t GV: Phạm Việt Phương 76
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn x  1 t
x 1 t  
c) d: y  2  2t , d:y  3  2t z t3  z 1
Hoạt động 3: Luyện tập xét VTTĐ của đường thẳng và mặt phẳng H1. Nêu cách tìm? Đ1.
4. Tìm số giao điểm của đường
thẳng d với mặt phẳng (P): Giải hệ pt: d(  , từ số nghiệm  P)
x  12  4t
suy ra số giao điểm của d và a)
d: y  9  t 3 ,
z 1 t (P).
a) d cắt (P) tại (0; 0; –2)
(P): 3x  5y z  2  0 b) d // (P) x  1 t  c) d  (P) b)
d: y  2  t ,
z 1 2t
(P): x  3y z  1  0 x  1 t  c)
d: y  1 2t
z  2  t3
(P): x y z  4  0
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách giải các dạng toán.
4. BÀI TẬP VỀ NHÀ:  Bài tập thêm.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 77
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 39
Bài 3: BÀI TẬP PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN (tt) I. MỤC TIÊU:
Kiến thức: Củng cố:
 Phương trình tham số của đường thẳng.
 Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau.
 Vị trí tương đối giữa đường thẳng và mặt phẳng. Kĩ năng:
 Viết được phương trình tham số của đường thẳng.
 Biết cách xác định toạ độ một điểm thuộc đường thẳng và toạ độ một vectơ chỉ phương khi
biết phương trình tham số của đường thẳng.
 Biết cách xét vị trí tương đối giữa đường thẳng và mặt phẳng. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về đường thẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tìm điểm đối xứng của 1 điểm qua 1 đường thẳng
H1. Xác định 1 VTCP của ? Đ1.
1. Cho điểm A(1; 0; 0) và a (1;2;1)   x  2  t
đường thẳng : y  1 2t
H2. Nêu cách xác định điểm Đ2. z t H? H 
H(2  t;1 2t;t)
a) Tìm toạ độ điểm H là hình   AH aAH a.  0 chiếu của A trên .    
b) Tìm toạ độ điểm A đối    t 1    H 3 1  ;0;  xứng với A qua . 2  2 2 
c) Tính khoảng cách từ A đến
H3. Nêu cách xác định điểm Đ3. . A?
H là trung điểm của AA xA'  2  
AA  2AH  yA'  0 z  1   A'
H4. Xác định khoảng cách từ Đ4. A đến ? d(A, ) = AH
Hoạt động 2: Luyện tập tìm điểm đối xứng của 1 điểm qua 1 mặt phẳng GV: Phạm Việt Phương 78
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
H1. Nêu cách xác định điểm Đ1.
2. Cho điểm M(1; 4; 2) và mặt H?
– Xác định  đi qua M và phẳng (P): x y z 1  0 . vuông góc với (P).
a) Tìm toạ độ điểm H là hình
:x 1 t;y  4  t;z  2  t
chiếu vuông góc của điểm M – trên mặt phẳng (P).
H là giao điểm của  và (P)
b) Tìm toạ độ điểm M  H(–1; 2; 0) đối
H2. Nêu cách xác định điểm Đ2. xứng với M qua (P). M?
c) Tính khoảng cách từ M đến
H là trung điểm của MM (P).
MM  2MH M(–3;0;–2)
H3. Nhắc lại công thức tính
khoảng cách từ 1 điểm đến mặt Đ3. phẳng?
Ax By Cz D 0 0 0 d(M, (P)) =
A2  B2  C2
Hoạt động 3: Luyện tập giải toán HHKG bằng phương pháp toạ độ
 GV hướng dẫn cách chọn hệ  Chọn hệ toạ độ Oxyz sao cho: 3. Cho hình lập phương trục toạ độ.
ABCD.ABCD có cạnh bằng
O  A, i AB, j AD,k AA
1. Tính khoảng cách từ đỉnh A
H1. Xác định toạ độ của hình
đến các mặt phẳng (ABD) và lập Đ1. phương? A(0; 0; 1), B(1; 0; 0), (BDC). D(0; 1; 0), B(1; 0; 1), D(0; 1; 1), C(1; 1; 0)
H2. Lập phương trình các mặt Đ2.
phẳng (ABD), (BDC)?
(ABD): x y z  1  0
(BDC): x y z  2  0
H3. Tính khoảng cách từ A đến Đ3. các mặt phẳng (ABD), 1 (BDC)? d(A, (ABD)) = 3 2 d(A, (BDC)) = 3
Hoạt động 4: Củng cố Nhấn mạnh:
– Cách vận dụng phương trình
đường thẳng, mặt phẳng để giải toán.
– Cách giải toán HHKG bẳng phương pháp toạ độ.
4. BÀI TẬP VỀ NHÀ:  Bài tập ôn HK 2.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 79
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 40 -41 ÔN TẬP CHƯƠNG III I. MỤC TIÊU: - Về kiến thức:
+ Học sinh nắm vững hệ tọa độ trong không gian, tọa độ của véc tơ , của điểm, phép toán về véc tơ.
+ Viết được phương trình mặt cầu, phương trình đường thẳng và vị trí tương đối của chúng.
+ Tính được các khoảng cách: giữa hai điểm, từ một điểm đến mặt phẳng. - Về kiến thức:
+ Rèn luyện kỹ năng làm toán trên véc tơ.
+ Luyện viết phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng.
+ Phối hợp các kiến thức cơ bản, các kỹ năng cơ bản để giải các bài toán mang tính tổng
hợp bằng phương pháp tọa độ.
- Về tư duy và thái độ:
+ Rèn luyện tính chính xác, tư duy lôgíc.
+ Rèn khả năng quan sát sự liên hệ giữa song song và vuông góc. II/ CHUẨN BỊ:
- Giáo viên: Giáo án, phiếu học tập, bảng phụ.
- Học sinh: giải bài tập ôn chương, các kiến thức cơ bản trong chương.
III/ PHƯƠNG PHÁP: Hỏi đáp , hoạt động nhóm.
IV/ TIẾN TRÌNH BÀI HỌC: 1/ Ổn định tổ chức: 2/ Kiểm tra bài cũ: 3/ Bài mới: tiết 40 Hoạt động 1:
Hoạt động của học sinh
Hoạt động của giáo viên Nội dung ghi bảng -Treo bảng phụ 1 -Làm bài tập1 BT1:
-Gọi 2 học sinh lên bảng
-Hai học sinh được lên bảng. a/P/trình mp(BCD): giải bài tập 1a; 1b
-Lớp theo dõi; nhận xét, nêu x-2y-2z+2 = 0 (1)
-Nhẩm, nhận xét , đánh giá ý kiến khác.
Tọa độ điểm A không thỏa
-Hỏi để học sinh phát hiện
mãn phương trình mp(1) nên ra cách 2:
A không thuộc mặt phẳng
AB, AC, AD không (BCD) đồng phẳng
-Trả lời câu hỏi và áp dụng b/ vào bài tập 1c. -Hỏi: Khoảng cách từ A . AB CD 2
đến(BCD) được tính như Cos(AB,CD)=  . AB CD 2 thế nào? Vậy (AB,CD)= 450
-Nhận phiếu HT1 và trả lời c/ d(A, (BCD)) = 1 -Phát phiếu HT1 GV: Phạm Việt Phương 80
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn Hoạt động 2:
Hoạt động của học sinh
Hoạt động của giáo viên Nội dung ghi bảng BT4: BT4:
- Hướng dẫn gợi ý học sinh - Hai học sinh lên bảng
a/ AB = (2;-1;3); phương làm . giải bài tập 4a; 4b trình đường thẳng AB: x   1 2t  
Câu hỏi: Tìm véctơ chỉ y - t - Theo dõi, nhận xét 
phương của đường thẳng   z -  3 3t AB? ∆?
b/(∆) có vécctơ chỉ phương  u  ( ; 2  ; 4  ) 5 và đi qua M nên 
p/trình tham số của (  ): x  2  2t  y  - 3 4t (t R)  z - 5t - 5 
BT6: a/Toạ độ giao điểm của
đường thẳng d và mp() là
- Từ hướng dẫn của giáo
nghiệm của hệ phương trình: viên rút ra cách tìm giao   x  12 4t BT 6:
điểm của đường và mặt.    y 9  3t
a/Gợi ý, hướng dẫn để học   z 
sinh tự tìm ra cách giải 1 t   bài 6a 3x  5y - z - 2   0 ĐS: M(0; 0; -2)
b/ Ta có vtpt của mp( ) là:   n u  ( ) 1 ; 3 ; 4  .P/t mp( ) : d 4(x- 0)+ 3(y- 0)+ (z+ 2)= 0
b/ Hỏi ( )  d quan hệ  4x + 3y + z +2 = 0. giữa   n
Suy nghĩ, trả lời, suy ra  và u ? BT2:a/ Tâm I(1, 1, 1) d
hướng giải quyết bài tập Bán kính r  62 . 6b. b/(S):(x-1)2+(y-1)2+(z-1)2=62
BT2: Nêu phương trình mặt
c/ Mp ( ) tiếp xúcvới mặt cầu? cầu(S) tại A, Suy ra có ( )
-Tìm tâm và bán kính r của vtpt là IA   . vậy (S) ở bài tập 2a ; 1 ; 5 ( 6)
Trả lời câu hỏi của giáo phương trình của mp là:
-Gợi mở để h/s phát hiện ra ( ) hướng giải bài 2c
viên, trình bày bài giải lên 5(x-6) + 1(y-2) – 6(z+5)=0 bảng. Hay 5x + y – 6z – 62 = 0.
Suy ra hướng giải bài 2c GV: Phạm Việt Phương 81
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn tiết 41 Hoạt động 3:
Bài toán vận dụng kiến thức tổng hợp
BT7: Gọi 2 h/sinh lên bảng
Hai h/sinh lên bảng giải. BT7: giải bài tập 7a, 7b. Lớp theo dõi, nhận xét. a/ Pt mp ( ) có dạng:
-Theo dõi, nhận xét, đánh
6(x+1) – 2(y-2) – 3(z+3) = 0 giá Hay 6x -2y - 3z +1 = 0
Vẽ hình, gợi mở để h/sinh b/ ĐS M(1; -1; 3).
phát hiện ra đ/thẳng 
c/ Đường thẳng  thoả mãn
các yêu cầu của đề bài chính
Quan sát, theo dõi đễ phát 
là đường thẳng đi qua A và hiện u M. Ta có MA  ( ; 2  ; 3 6) . d
Vậy p/trình đường thẳng  : x  1  2t   y - - 1 3t (t R)  z  3  6t  A M
BT9 Gọi d là đường thẳng qua M và vuông góc với Theo dõi, suy nghĩ nhìn ra , pt đt (d) là: mp ( ) H và cách tìm H x  1  2t
BT9 Vẽ hình, hướng dẫn  y  - - 1 t (t R)
học sinh nhận ra hình chiếu  H của M trên mp z  2  2t ( ) và cách  xác định H d cắt
( ) tại H. Toạ độ của H M là nghiệm của hệ: x  1  2t  y  - - 1 t  (t R) z  2  2t  H 2x
  y  2z 11  0 Suy ra H(-3; 1; -2). Hoạt động 4:
Hướng dẫn những bài tập 10, 11,12. BT 11: - Nhìn bảng phụ BT 11   -Treo bảng phụ 2 - Theo dõi, suy nghĩ và   (O xy)  u   ( ) 0 ; 1 ; 0  j tìm ra cách giải
 cắt d g/điểm M(t; -4+t; 3-t) bài tập 11.  cắt d’ g/điểm M N(1-2t’;-3+t’;4-5t’)  d
Suy ra MN k j  p/trình  M' d' Oxz Nhìn hình ,suy nghĩ và tìm ra cách giải. GV: Phạm Việt Phương 82
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
- Hướng dẫn, gợi ý học sinh
phát hiện ra hướng giải bài tập 11 BT12 BT12 -Vẽ hình
- Tìm hình chiếu H của A trên 
-Gợi mở, hướng dẫn học
-A’ là điểm đối xứng của A qua 
sinh tìm ra cách giải bt này. Khi H là trung điểm AA/. Phát phiếu HT2
-Nhận phiếu và trả lời Từ đó suy toạ độ A/.
4/ Củng cố toàn bài :
- Các yếu tố cần thiết để lập phương trình: đường thẳng, mặt phẳng, mặt cầu.
- Cách xác định điểm đối xứng của M qua mp ( ) , qua đường thẳng 
5/ Bài tập về nhà : Hoàn thành bài tập 8; 11; 12. V/ PHỤ LỤC Phiếu HT 1:   Cho a  ; 3 ( ; 0  ) 6 ; b  ( ; 2  ; 4 ) 0 . Chọn mệnh đề sai:    
A. a  3b  ( ; 12 ; 3  ) 6 B. . a b  ; 6 ( 0 ) 0 ;   1   C. Cos( a,b)  D. . a b  6 5 Phiếu HT 2:
1/ Phương trình mặt cầu đường kính AB với A(4, -3, 7); B(2, 1, 3) là:
A. (x+3)2 + (y-1)2 + (z+5)2 = 9
B. (x+3)2 + (y-1)2 + (z+5)2 = 35
C. (x- 3)2 + (y+1)2 + (z-5)2 = 9
D. (x- 3)2 + (y+1)2 + (z-5)2 = 35.
2/ Phương trình mặt phẳng qua A(1, 2, 3) và song song với mặt phẳng (P): x + 2y – 3z = 0 là: A. x + 2y – 3z – 4 = 0 B. x + 2y – 3z + 7 = 0
C. x + 2y – 3z + 4 = 0 D. x + 2y – 3z – 7 = 0 GV: Phạm Việt Phương 83
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 42
Bài dạy: KIỂM TRA 1 TIẾT CHƯƠNG III I. MỤC TIÊU:
Kiến thức: Củng cố:
 Biểu thức toạ độ của các phép toán vectơ trong KG.
 Phương trình mặt cầu.
 Khái niệm vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.
 Phương trình tổng quát của mặt phẳng.
 Điều kiện để hai mặt phẳng song song, vuông góc. Kĩ năng:
 Thành thạo các phép tính về biểu thức toạ độ của các phép toán vectơ trong KG.
 Biết lập phương trình mặt cầu.
 Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.
 Xác định được hai mặt phẳng song song, vuông góc.
 Tính được khoảng cách từ một điểm đến mặt phẳng. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. II. CHUẨN BỊ:
Giáo viên: Giáo án. Đề kiểm tra.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về toạ độ vectơ, phương trình mặt cầu, mặt phẳng. III. MA TRẬN ĐỀ: Nhận biết Chủ đề Thông hiểu Vận dụng Tổng TNKQ TL TNKQ TL TNKQ TL
Toạ độ của điểm và 2 1 1 3,5 vectơ 0,5 0,5 2,0 Phương trình mặt cầu 1 1 1 3,0 0,5 0,5 2,0 Phương trình mặt 2 1 1 3,5 phẳng 0,5 0,5 2,0 Tổng 2,5 1,5 4,0 2,0 10,0
IV. NỘI DUNG ĐỀ KIỂM TRA:
A. Phần trắc nghiệm: (4 điểm)
Câu 1: Cho 2 điểm A(1; 2; –3) và B(6; 5; –1). Nếu OABC là hình bình hành thì toạ độ điểm C là: A) (5; 3; 2) B) (–5;–3;–2) C) (3;5;–2) D) (–3;–5;–2)
Câu 2: Cho các vectơ a  (1;2;3); b  ( 2  ;4;1); c  ( 1
 ;3;4) . Vectơ v  2a 3b  5c có toạ độ là: A) (7; 3; 23) B) (23; 7; 3) C) (3; 7; 23) D) (7; 23; 3)
Câu 3: Cho 3 điểm A(2; 1; 4), B(–2; 2; –6), C(6; 0; –1). Tích AB.AC bằng: A) –67 B) 65 C) 67 D) 33
Câu 4: Cho mặt cầu (S): x2  y2  z2  8x  4y  2z  4  0 . Bán kính R của mặt cầu (S) là: A) R = 2 B) R = 88 C) R = 5 D) R = 17
Câu 5: Cho 2 điểm A(2; 4; 1), B(–2; 2; –3). Phương trình mặt cầu đường kính AB là: 2 2 2 2 2 2
A) x  (y  3)  (z 1)  9
B) x  (y  3)  (z 1)  9 2 2 2 2 2 2
C) x  (y  3)  (z 1)  9
D) x  (y  3)  (z 1)  3 GV: Phạm Việt Phương 84
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Câu 6: Cho 3 điểm A(1; –2; 1), B(–1; 3; 3), C(2; –4; 2). Một VTPT n của mặt phẳng (ABC) là: A) n  ( 1  ;9;4) B) n  (9; 4; 1  ) C) n  (9; 4;1) D) n  (4;9; 1  )
Câu 7: Cho hai mặt phẳng song song (P): nx  7y  6z  4  0 và (Q): 3x my  2z  7  0 . Khi đó
giá trị của m và n là: 7 3 7 7
A) m  ; n  9  ;  9  ;  1  ;  9 3 B) m n 7 C) m n 3 D) n m 3
Câu 8: Khoảng cách giữa hai mặt phẳng (P): 2x y z
3  5  0 và (Q): 2x y z 3 1  0 bằng: 6 4 A) B) C) 4 D) 6 14 14
II. Phần tự luận: (6 điểm) Trong không gian Oxyz, cho tứ diện ABCD với A(1; 6; 2), B(5; 1; 3), C(4; 0; 6), D(5; 0; 4).
a) Xác định toạ độ trọng tâm G của tam giác ABC. So sánh các vectơ DA DB DC và DG .
b) Viết phương trình mặt phẳng (ABC).
c) Viết phương trình mặt cầu (S) có tâm D và tiếp xúc với mặt phẳng (ABC).
V. ĐÁP ÁN VÀ BIỂU ĐIỂM:
A. Phần trắc nghiệm: Mỗi câu đúng 0,5 điểm Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 A C D C C B A B
B. Phần tự luận: Mỗi câu 2 điểm   a) G 10 7 11  ; ; 3 3 3    (1 điểm)
DA DB DC D 3 G (1 điểm) b) AB  (4; 5  ;1), AC  (3; 6  ;4) (0,5 điểm)
n  AB, AC  ( 1  4; 1  3; 9  ) (0,5 điểm)
mp(ABC): 14x 13y  9z 110  0 (1 điểm) 4 c) d(D,(ABC)) = (1 điểm) 446 2 2 2 8
(S): (x  5)  y  (z  4)  223 (1 điểm)
VI. KẾT QUẢ KIỂM TRA: Lớp 0 – 3,4 3,5 – 4,9 5,0 – 6,4 6,5 – 7,9 8,0 – 10 Sĩ số SL % SL % SL % SL % SL % 12S1 53 12S2 53 12S3 54
VII. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 85
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 43 - 44 ÔN CUỐI NĂM I. MỤC TIÊU:
Kiến thức: Củng cố:
 Hệ toạ độ trong không gian.
 Phương trình mặt cầu.
 Phương trình mặt phẳng.
 Phương trình đường thẳng.  Khoảng cách. Kĩ năng:
 Thực hiện các phép toán trên toạ độ của vectơ.
 Lập phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng.
 Dùng phương pháp toạ độ tính được các loại khoảng cách cơ bản trong không gian.
 Giải các bài toán hình học không gian bằng phương pháp toạ độ. Thái độ:
 Liên hệ được với nhiều vấn đề trong thực tế với bài học.
 Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về toạ độ trong không gian.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập) H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập vận dụng phương trình mặt phẳng
H1. Nêu cách chứng minh 4 Đ1. Chứng minh 4 điểm không 1. Cho 4 điểm A(1; 0; 0), B(0;
điểm tạo thành tứ diện? đồng phẳng.
1; 0), C(0; 0; 1), D(–2; 1; –1). – Viết ptmp (BCD)
a) Chứng minh A, B, C, D là 4
(BC): x  2y  2z  2  0 đỉnh của 1 tứ diện. – Chứng tỏ A  (BCD).
b) Tìm góc giữa hai đường thẳng AB và CD.
H2. Nêu cách tính góc giữa hai Đ2.
c) Tính độ dài đường cao của đường thẳng? hình chóp A.BCD. . 2 cos ,  AB CD AB CD   AB C . D 2  (AB, CD) = 450.
H3. Nêu cách tính độ dài
đường cao của hình chóp Đ3. h = d(A, (BCD)) = 1 A.BCD?
H4. Nêu điều kiện để (P) cắt
2. Cho mặt cấu (S):
(S) theo một đường tròn? Đ4. d(I, (P)) < R x 2   y 2   z 2 ( 3) ( 2) ( 1) 100 và mặt phẳng (P):
H5. Nêu cách xác định tâm J GV: Phạm Việt Phương 86
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn của đường tròn (C)?
Đ5. J là hình chiếu của I trên
2x  2y z  9  0 (P)  J(–1; 2; 3)
Mặt phẳng (P) cắt (S) theo một
H6. Tính bán kính R của (C)? Đ6. 2 2
đường tròn (C). Hãy xác định
R = R d = 8
toạ độ tâm và bán kính của (C).
Hoạt động 2: Luyện tập vận dụng phương trình đường thẳng
H1. Nêu công thức ptmp? Đ1.
3. Cho điểm A(–1; 2; –3),
A(x x )  B(y y )  C(z z
vectơ a  (6;2;3) 0 0 0 )  0 và đường
 (P): 6x  2y  3z 1  0 x  1 t 3   thẳng d: y  1   2t .
H2. Nêu cách tìm giao điểm Đ2. Giải hệ pt d
z  3 t5 của d và (P)? (  P)
a) Viết ptmp (P) chứa điểm A  M(1; –1; 3)
và vuông góc với giá của a .
b) Tìm giao điểm của d và (P).
H3. Nêu cách xác định ?
Đ3.  chính là đường thẳng c) Viết ptđt  đi qua A, vuông x  1 2t
góc với giá của a và cắt d. AM  : y  1   t 3
z  3 6t
H4. Nêu cách xác định đường Đ4. thẳng 
4. Viết ptđt  vuông góc với ?
–   (Oxz)   có VTCP mp(Oxz) và cắt hai đường j  (0;1;0) thẳng:
– Gọi M(t; –4+t; 3–t), x tx 1 t 2 
M((1–2t; –3+t; 4–5t)  
y  4  ty  3   t
lần lượt là giao điểm của  d: , d: với
z  3  t  z  4  t 5  d và d. 1 
 2t  t  0 
MM  kj  1
  t  t k 1    t 5   t  0 t 3      7   M 3 25 18  ; ;  t 2    7 7 7   7   3 25 18
: x  ; y    t;z   7 7 7
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách vận dụng phương trình
đường thẳng, mặt phẳng để giải toán.
4. BÀI TẬP VỀ NHÀ:
 Chuẩn bị kiểm tra HK 2.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... GV: Phạm Việt Phương 87
Trường THPT Nà Chì năm học 2011 - 2012
Giáo án Hình học12 chuẩn
Ngày dạy Tiết dạy Lớp dạy Tên HS vắng mặt 12A1 Tiết dạy: 45
Bài dạy: KIỂM TRA HỌC KÌ 2 I. MỤC TIÊU: Kiến thức:
 Ôn tập toàn bộ kiến thức trong học kì 2. Kĩ năng:
 Thực hiện các phép toán trên toạ độ của vectơ.
 Lập phương trình mặt cầu, phương trình mặt phẳng, phương trình đường thẳng.
 Dùng phương pháp toạ độ tính được các loại khoảng cách cơ bản trong không gian.
 Giải các bài toán hình học không gian bằng phương pháp toạ độ. Thái độ:
 Rèn luyện tính cẩn thận, chính xác. II. CHUẨN BỊ:
THI THEO ĐỀ CHUNG CỦA SỞ GV: Phạm Việt Phương 88