Giao thoa Ánh sáng - Slide Chương 1 môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Chương 1 GIAO THOA ÁNH SÁNG
1.1. Quang lộ. Định lý Malus. Hàm sóng của ánh sáng và cường độ sáng
1.2. Giao thoa ánh sáng cho bởi 2 nguồn kết hợp
(khe Young): hình dạng, vị trí vân (thừa nhận kết
quả); giao thoa của ánh sáng trắng
1.4. Vân giao thoa cùng độ dày trên bản mỏng: bản hình nêm, vân Newton
1.5. Ứng dụng giao thoa: giao thoa kế Michelson.
1. Quang lộ. Định lý Malus. Hàm sóng của ánh sáng và cường độ sáng a. Quang lộ
Địnhnghĩa:QuanglộgiữahaiđiểmA,B(trong n
môitrườngđồngtính,cóchiếtsuấtn,cáchnhau A d B
mộtđoạnbằngd)làđoạnđườngánhsáng
truyềnđượctrongchânkhôngtrongkhoảngthời
gianbằngkhoảngthờigianmàánhsángđi hết
đoạnđườngABtrongmôitrường. d L = ct =c =nd v 1 n n2 d d
Quanglộcủa ánhsángtruyềnqua nmôitrường n A 1 3 2
cóchiếtsuấtkhácnhauđược xácđịnh: d3 n B L =å ndii i 1 = ds
Nếuánhsángtruyềnquamôitrườngkhông
đồngnhấtcóchiếtsuấtthayđổiliêntục. A n B L= nds B ò A
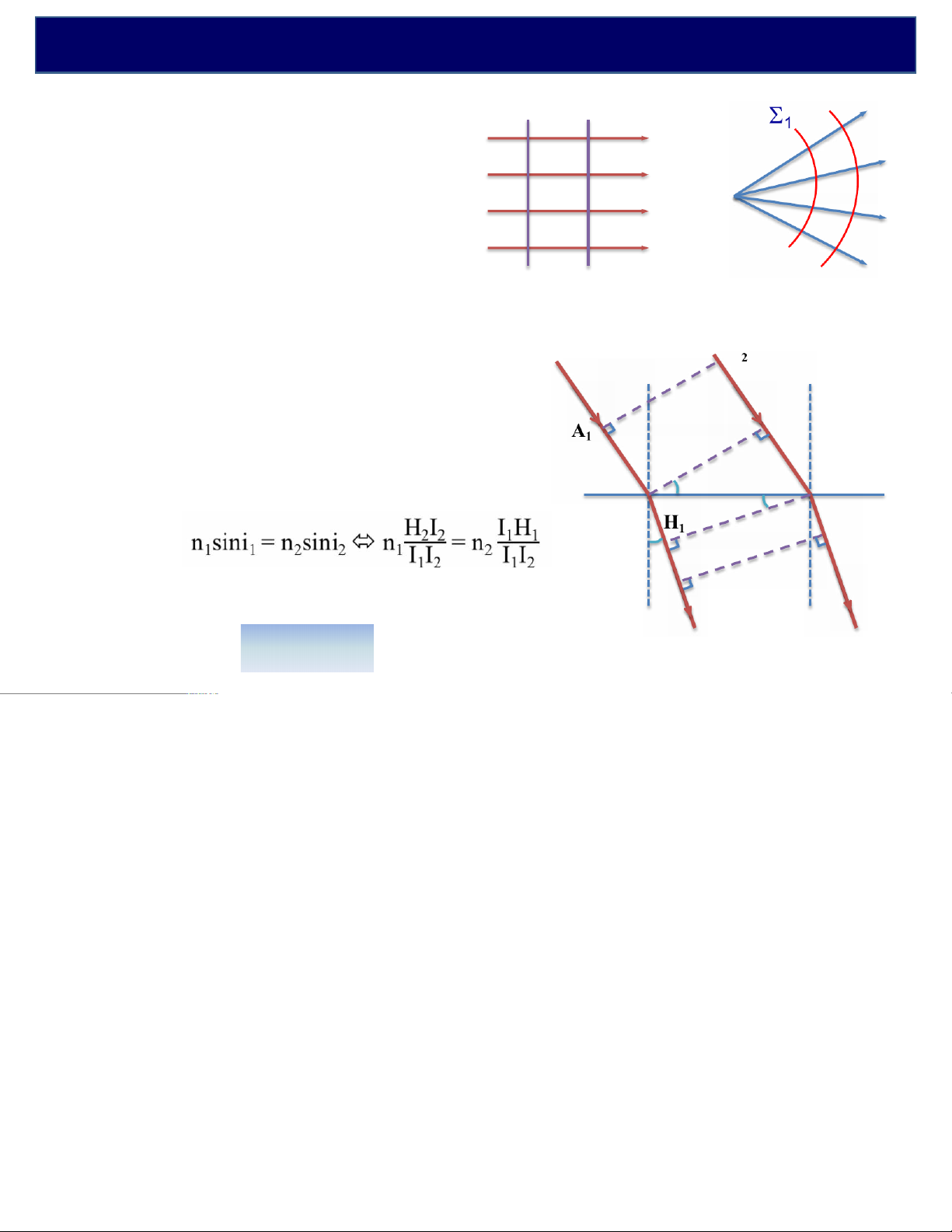
1. Quang lộ. Định lý Malus. Hàm sóng của ánh sáng và cường độ sáng b. Định lý Malus S2 S1S2 Mặt trực giao:
Mặt vuông góc với các tia sáng của một chùm sáng.
Định lý Malus: Quang lộ của các tia sáng giữa hai mặt trực giao của một chùm sáng thì bằng nhau. Chứng minh: A L1 = n1A I 1 + (n 1 2I1H + 1 n2H1B1) L2 = (n1A2H2+ n1H2I ) 2 + n I 2 2B2 H2 Ta có: i1 A1I1= A2H2 CD i1 I2 H1B1= I B 2 2 i I 2 1 Mặt khác: B2 i2 Ta được: nH I n H I B1 = 1 2 2 2 1 1 ® L =L1 2
1. Quang lộ. Định lý Malus. Hàm sóng của ánh sáng và cường độ sáng
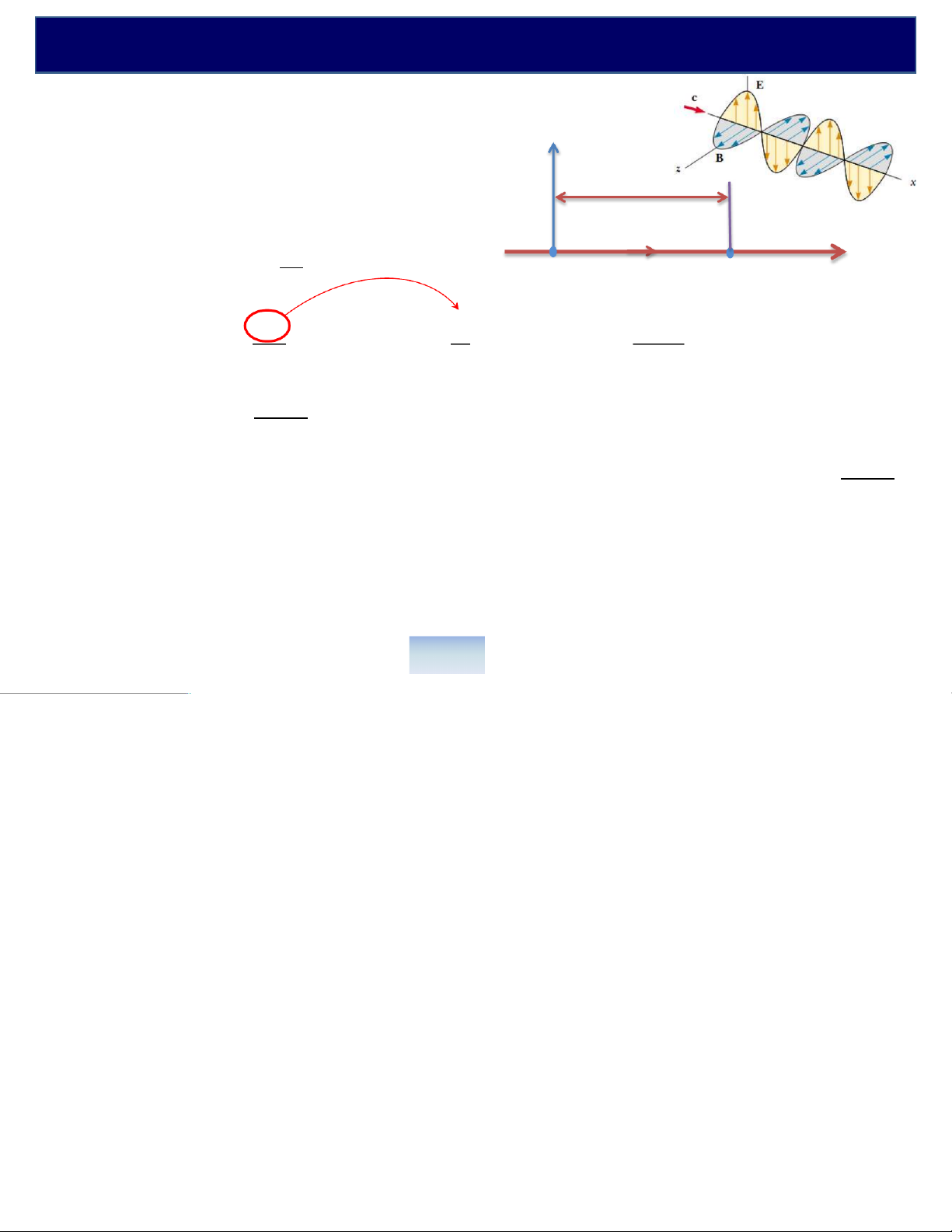
c. Hàm sóng ánh sáng
Phương trình dao động sóng sáng tại O: !" E xa 0cos = t (w) d
Dao động sóng sáng tại M có dạng: ! v cosæö d xa tw O My =- ç÷ èø v ndL L
với L = nd là quang lộ æ ö æö æ 2 ö p xa - co -s t ww a cosco t s = = =- ç ÷ ç÷w a ç t ÷ của tia sáng trên è c ø èø ccT è ø đoạn OM cosæö 2p L ®=- xa çt÷wl là hàm sóng ánh sáng èø o cosæö 2p L
Nếu truyền theo chiều ngược lại, hàm sóng ánh sáng có dạng: x = a + ç÷ twl èø o d. Cường độ sáng
Cường độ sáng tại một điểm có trị số bằng năng lượng truyền qua một đơn vị
diện tích đặt vuông góc với phương truyền ánh sáng trong một đơn vị thời gian.
Như vậy, cường độ sáng tại một điểm tỉ lệ với bình phương biên độ dao động sáng tại điểm đó 2 I = a
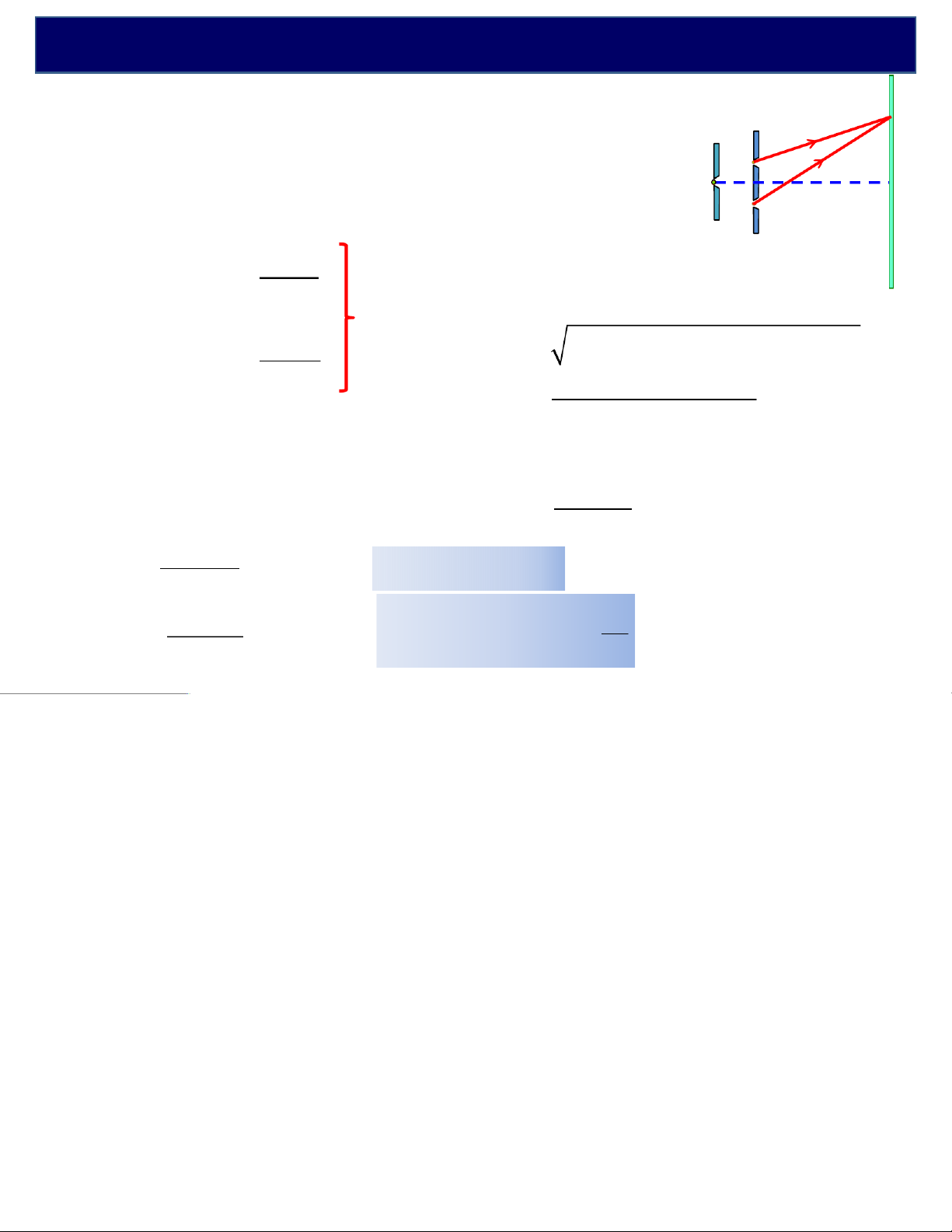
2. Giao thoa ánh sáng cho bởi 2 nguồn kết hợp (khe Young) vThí nghiệm P1P2 P3
KL: Sự giao nhau của hai sóng ánh sáng tạo nên trong không
gian những vùng tối và những vùng sáng xen kẽ nhau gọi là
hiện tượng giao thoa ánh sáng.
2. Giao thoa ánh sáng cho bởi 2 nguồn kết hợp (khe Young)
a. Điều kiện cực đại và cực tiểu giao thoa P
Giả sử dao động sáng tại S1và S2do nguồn S gửi tới có dạng: x S1 1 a 1cos t w = và S x 2 a 2cos t w = O S2
Gọi L1và L2là quang lộ của tia sáng gửi từ S1, S2tới P: æö 2p L1 xa cots wl =- ç÷
Dao động sáng tổng hợp tại P: 1P1 èø o xx x 1P2Pa cos t = + = (w + ) j æö 2p L a a a a a 2 Trong đó: 22 = + + 2cos( j- ) j xa cos t wl =- ç÷ 1 2 12 1 2 2P2 èø a s a insin j j o 1 12+ 2 tgaa jj= j coscos 1 12+ 2 2 22 I Cường độ sáng t a ại P: a a aa = = + + 2cos( j ) 1 2 12 1j - 2 LL -
Iphụ thuộc vào hiệu pha ban đầu: 2 1 1 jj-= 2 2p l
àphụ thuộc hiệu quang lộ o LL- k = ØNếu: 2 1 2 2 pp ® L -L = kλ 21 ο k= 0, ± 1,± → P sáng 2.... lo LL- k λ 2 1 = + ο ØNếu: 2pp (2 1) ® L - L =(2k +1) 2 k 21 = 0, ± 1,± → P t 2.... ối lo
2. Giao thoa ánh sáng cho bởi 2 nguồn kết hợp (khe Young)
b. Hình dạng và vị trí vân giao thoa
Điều kiện vân sáng: L -L = kλ 21 ο k
với = 0, ± 1,± 2....
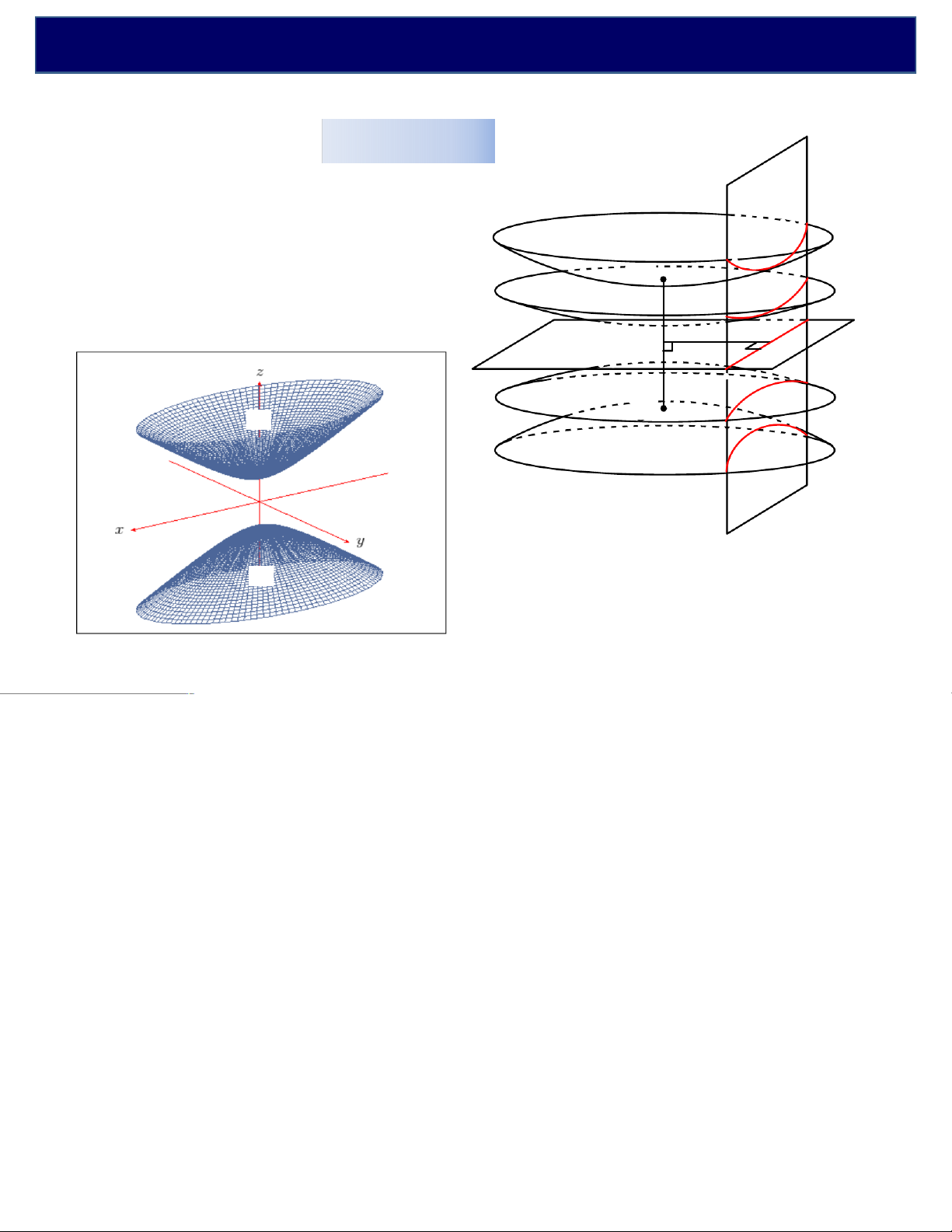
Quĩ tích tất cả các điểm trong
không gian có hiệu khoảng cách å2 k= 2
tới hai điểm cố định không đổi là S1 å 2 k= 1
mặt hypecboloit tròn xoay. 1 k= 0 å0 å k= -1 -1 S2 S1 1 å-2 k= -2
Quĩ tích các điểm sáng nhất và tối
nhất là mặt hypecboloit tròn xoay S2
xen kẽ trong không gian, riêng
mặt k = 0 là mặt phẳng trung trực của S1S2.
2. Giao thoa ánh sáng cho bởi 2 nguồn kết hợp (khe Young)
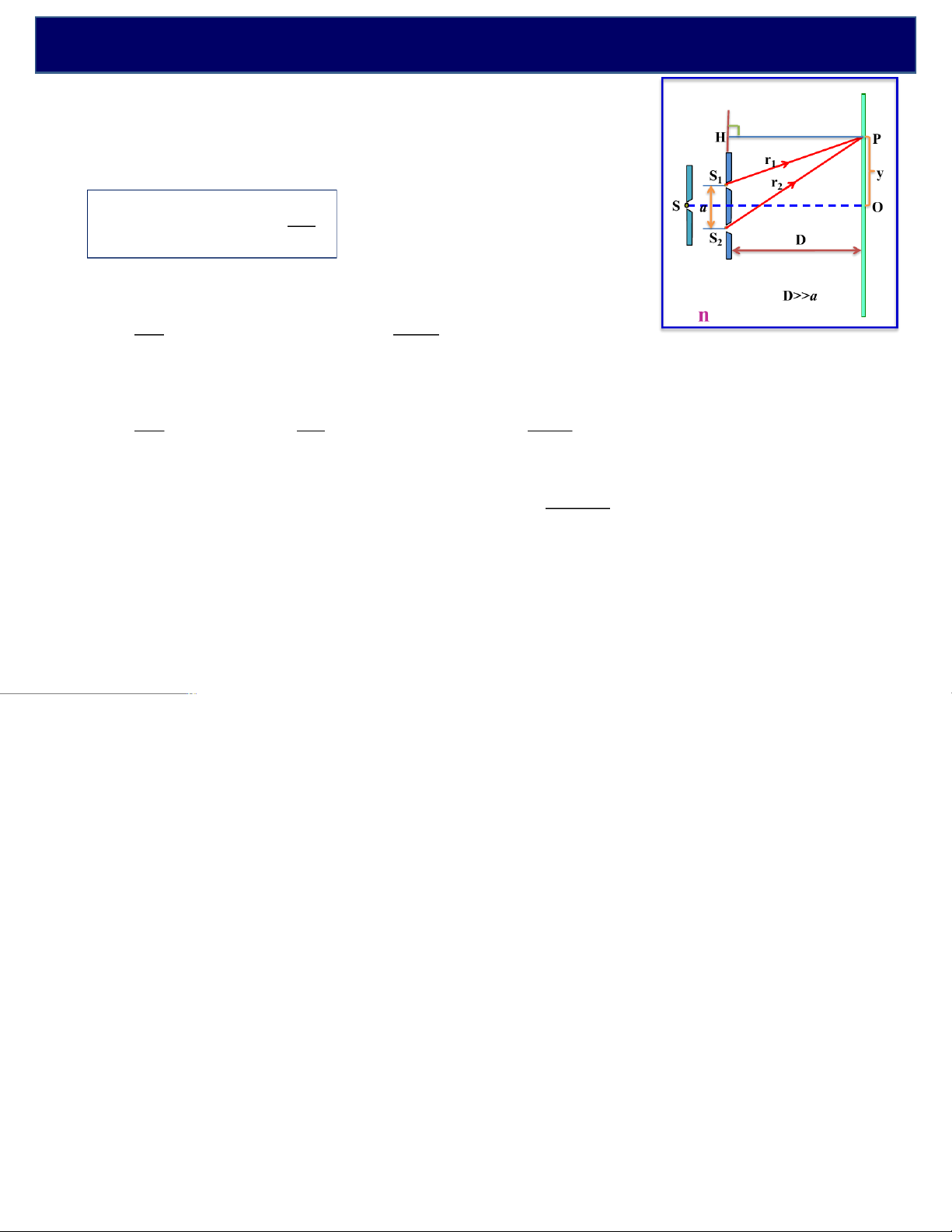
c. Vị trí vân sáng và khoảng vân Hiệu quang lộ: L L L nrnrn rr -=- 2 1 2 1 () 21 ( )na ®D L = n - r = r y 21 D
•Vị trí vân sáng: na λD DL = = yk l ®o y =k na với k so = ± 0;1 ± ;2... D s
•Vị trí vân tối: na l λD DL = yk = ( +2 1) o ® o
y = (2k + 1)2na với k= ± 0;1 ± ;2... t D 2 t loD •Khoảng vân:
i = y (k) - y (k - 1) = na s s
d. Giao thoa của ánh sáng trắng Tự đọc
3.Hiệntượnggiaothoa do phảnxạ- ThínghiệmLoyld
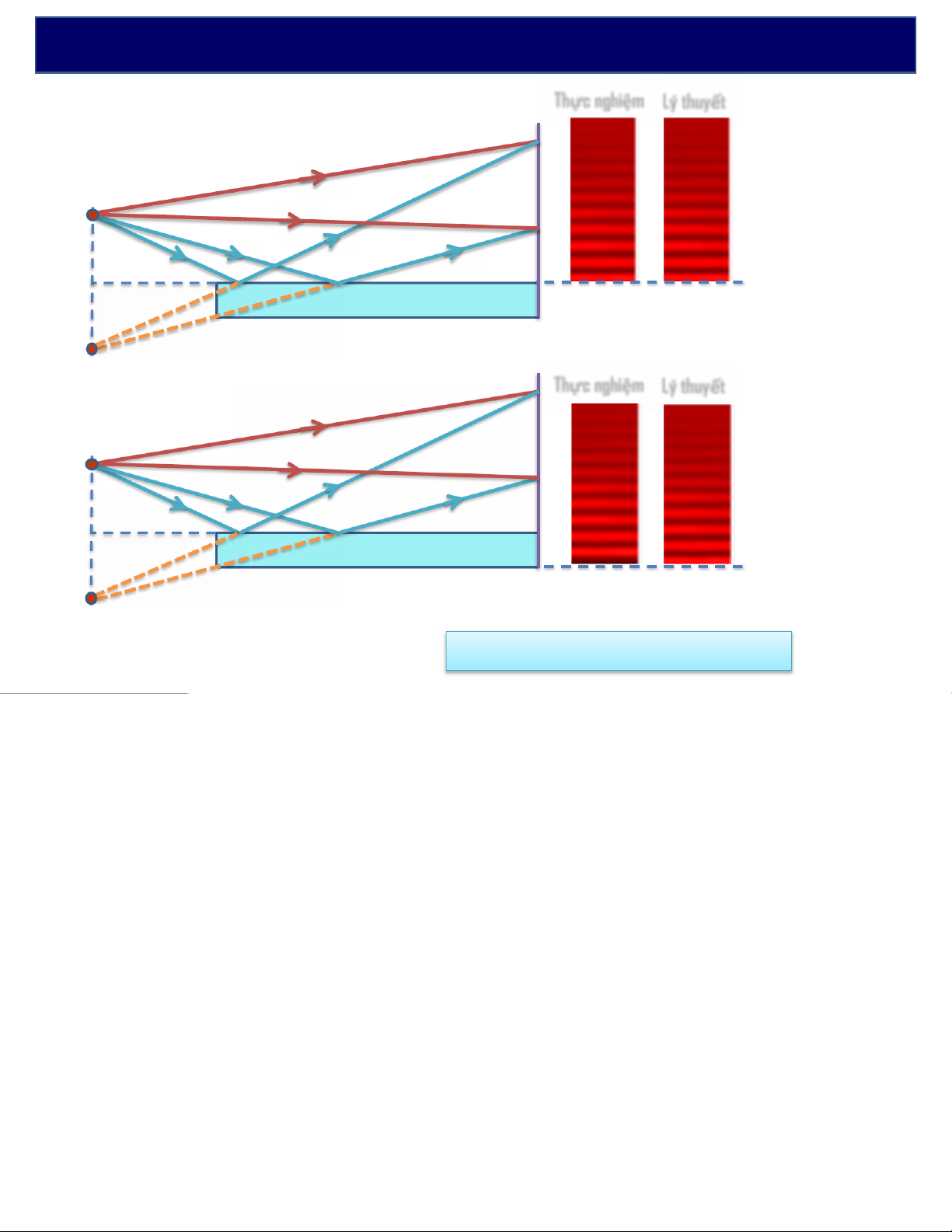
TH1: Chiết suất môi trường: n> n’
Thực nghiệmLý thuyết KL: n > n’ thì kết quả thực n
nghiệm và lý S thuyết hoàn P toàn phù hợp I n’ O S’
TH2: Chiết suất môi trường: n< n’ Thực nghiệmLý thuyết n KL: n < n’ thì kết quả thực S
nghiệm và lý P thuyết hoàn toàn ngược I O n’ nhau
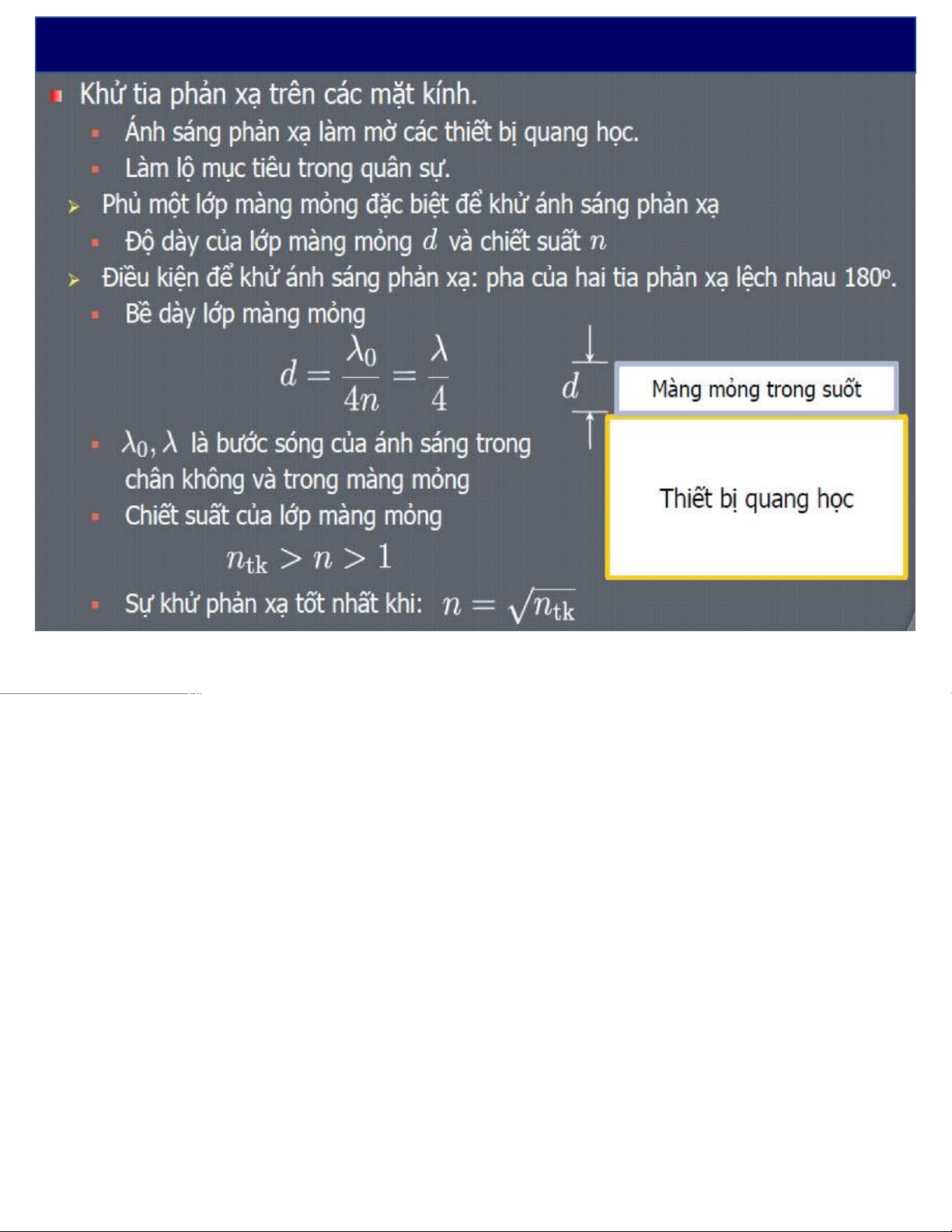
è Khitiasángphảnxạtừmôitrườngkémchiếtquangvào môitrường S’
chiếtquangthìquanglộcủatiasángdài thêm lo/2.
L = [SIP] = n(SI+IP) + lo/2
4. Vân giao thoa cùng độ dày trên bản mỏng: bản hình nêm, vân Newton
a. Bản mỏng có bề dày thay đổi - Vân cùng độ dày ØXét: - Nguồn điểm O
- Bản mỏng bề dày thay đổi,
-d:bề dày bản mỏng
ØCác tia chiếu đến bản mỏng tại điểm M: O -i1:góc tới -i - Tia phản xạ OM (1) 2:góc khúc xạ - Tia khúc xạ OBCM (2)
là các tia kết hợp gặp nhau tại M àgiao thoa à
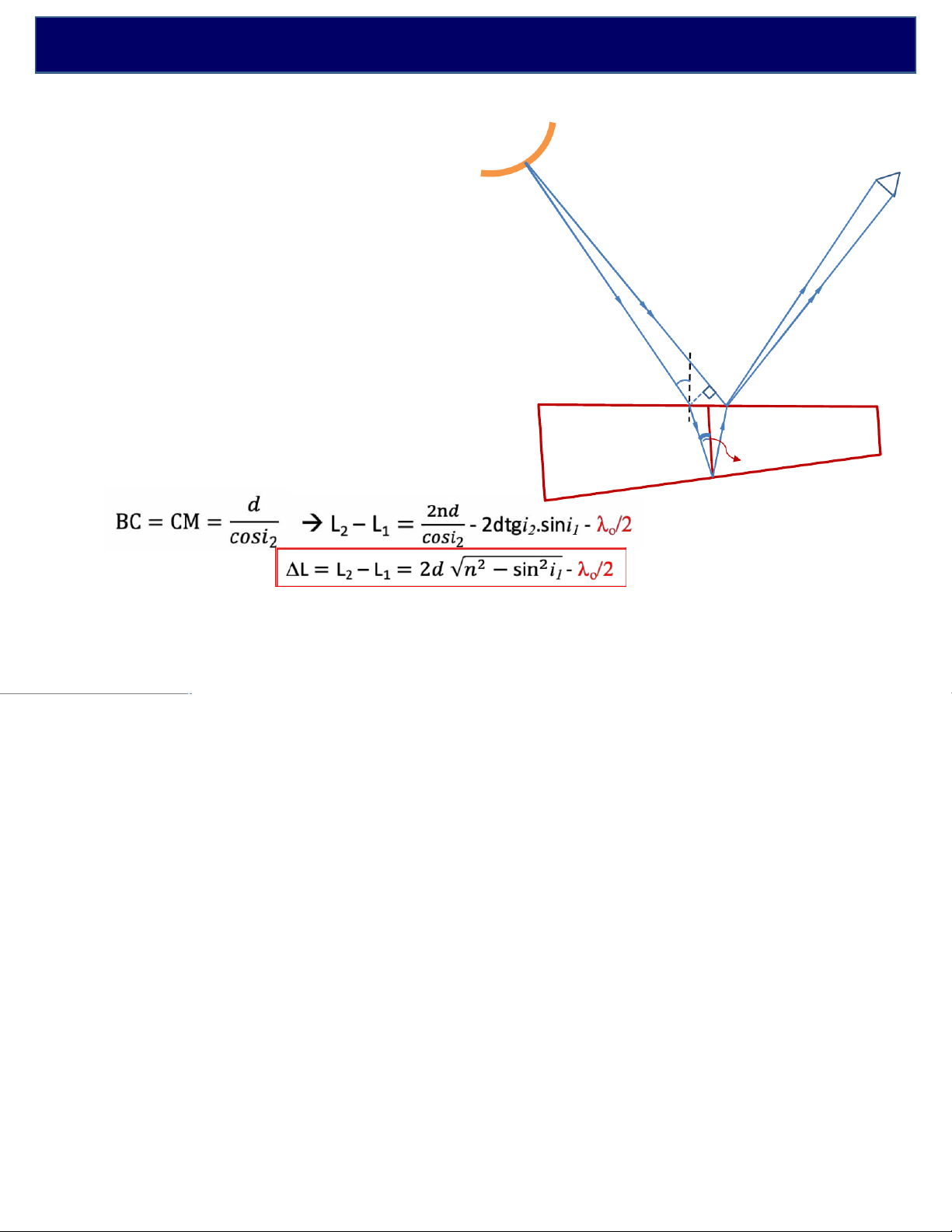
vân giao thoa xuất hiện trên mặt trên của bản mỏng ØHiệu quang lộ i1
L2– L1= OB + n(BC + CM) – (OM + lo/2) R M Gần đúng: OM – OB »RM B
L2– L1= n(BC + CM) – RM – lo/2 i2 d
RM = BMsini1= 2dtgi2.sini1n C
-i1coi như không đổi d àDL phụ thuộc . -
Mỗi vân sáng/tối ứng với một giá trị xác định của dàvân cùng độ dày.
4. Vân giao thoa cùng độ dày trên bản mỏng: bản hình nêm, vân Newton
Hình ảnh giao thoa bản mỏng Váng dầu Bong bóng xà phòng Đĩa CD
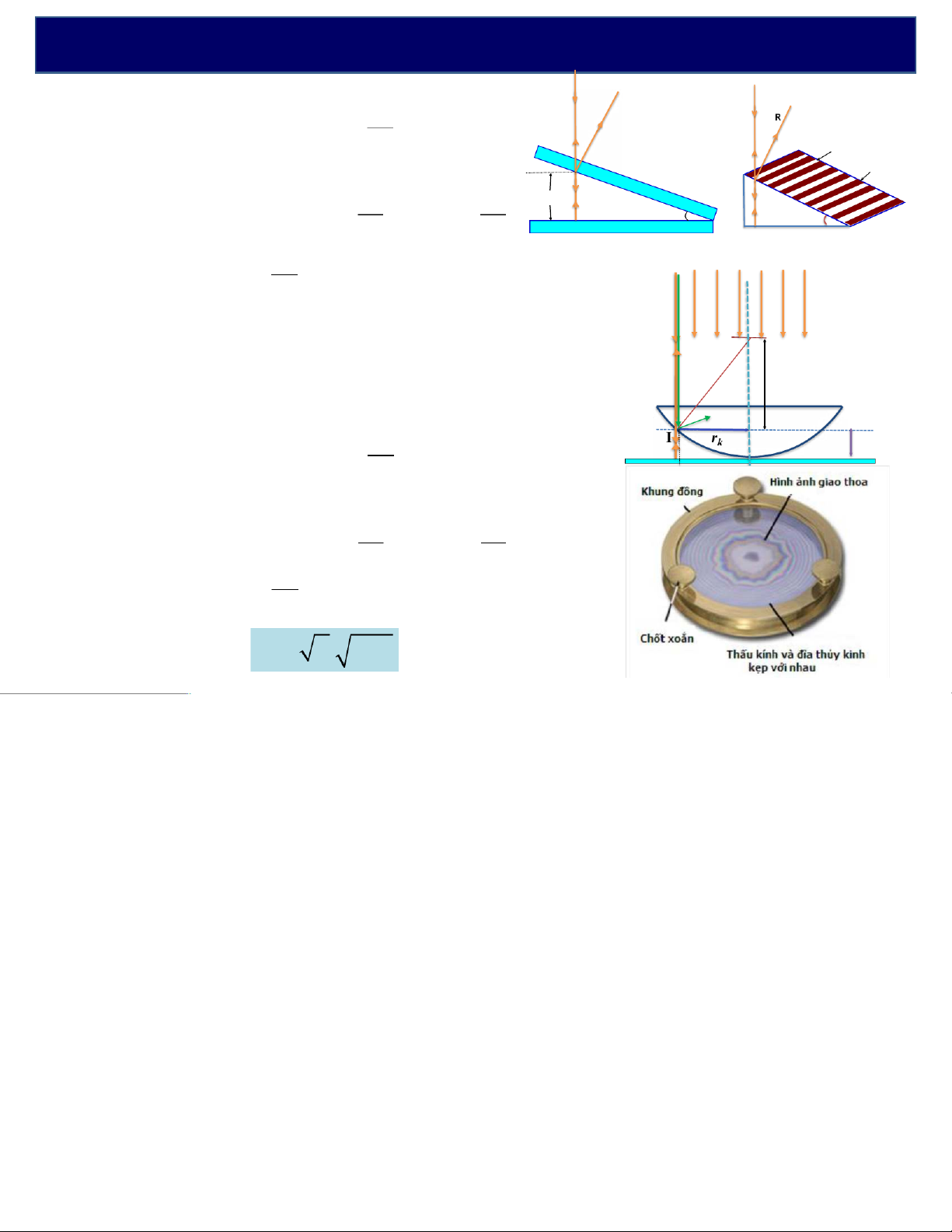
4. Vân giao thoa cùng độ dày trên bản mỏng: bản hình nêm, vân Newton S vNêm không khí S l R Hiệu quang lộ: o 2 LL -=1 2 d + 2 vân sáng G1
chỉphụthuộcvàobềdàydcủalớpkhôngkhí. i vân tối G1 I I ll d Điểm Itối kh i: oo ¢ C 2 LL-= 12d + = (21 k + ) K a a C K 22 G G 2 2 C l Vịtrívân d tối: = k o k = với 0,1, 2,3... 2 -
Cạnh nêm CC’ ứng với d = 0 (k=0) là một vân tối. O -
Các vân tối là các đoạn thẳng định xứ ở mặt dưới R
tấm kính G1và song song với cạnh nêm CC’. R-dk vVântrònNewton l dk Hiệu quang lộ: o 2 LL -=1 2 d + 2
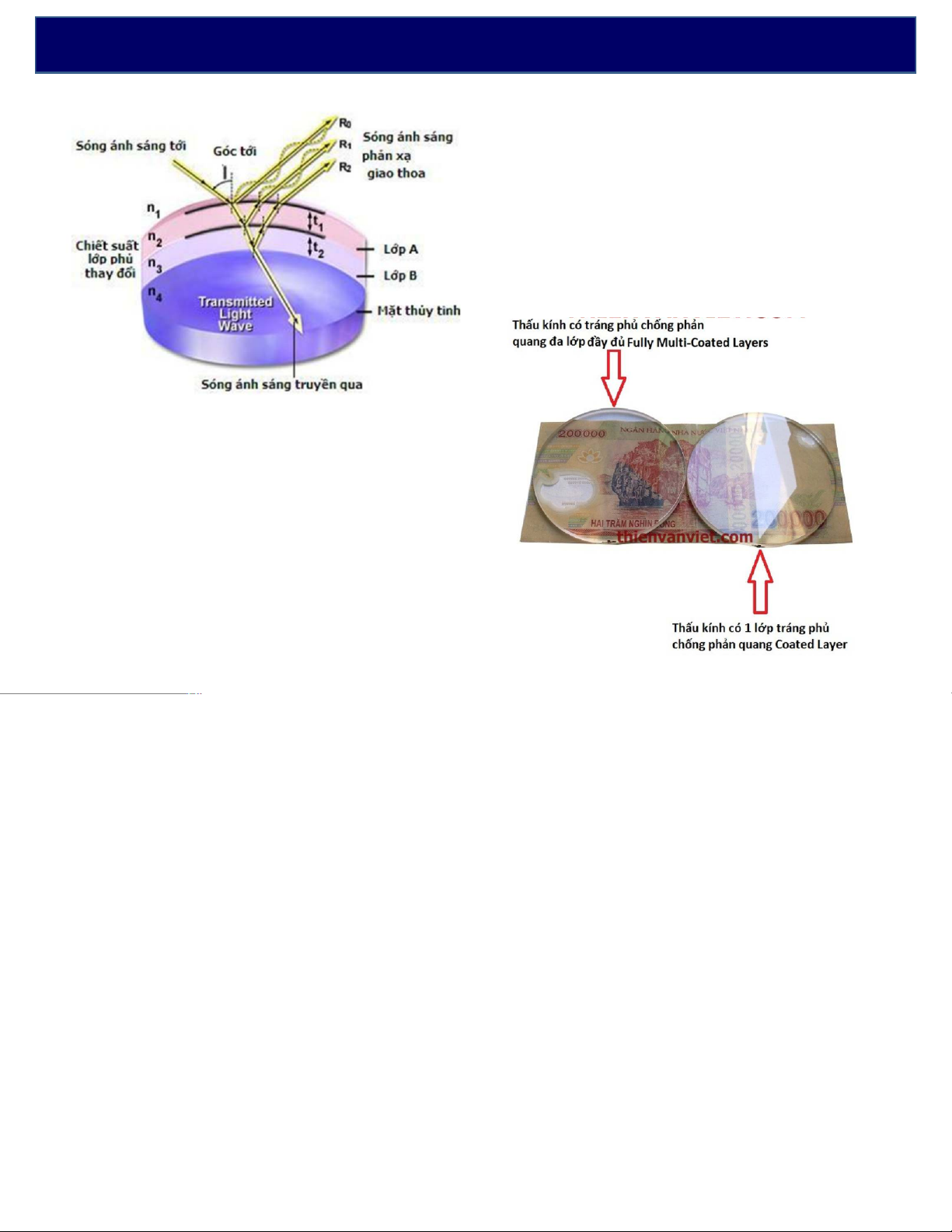
chỉphụthuộcvàobềdàydcủalớpkhôngkhí. ll Điểm Itối khi: oo 2 LL-= 12d + = (21 k + ) 22 l Vịtrívân d tối: = k o k = với 0,1, 2,3... 2 Bánkínhvântối: r k.R l ko= 4.Ứngdụnggiaothoa 4.Ứngdụnggiaothoa 4.Ứngdụnggiaothoa 4.Ứngdụnggiaothoa 4.Ứngdụnggiaothoa 4.Ứngdụnggiaothoa
1 CƠ SỞ CỦA QUANG HÌNH HỌC
1.1 Định luật về sự truyền thẳng của ánh sáng
Trong môi trường trong suốt đồng tính và đẳng hướng, ánh sáng truyền theo đường thẳng.
1.2 Định luật về tác dụng độc lập của các tia sáng
Tác dụng của các chùm sáng khác nhau thì độc lập với nhau, nghĩa là tác dụng của một
chùm sáng này không phụ thuộc vào sự có mặt hay không của các chùm sáng khác.
1.3 Định luật của Descartes thứ nhất
Tia phản xạ nằm trong mặt phẳng tới (mặt Pháp tuyến Tia tới Tia p/xạ
phẳng chứa tia tới và pháp tuyến) và góc tới bằng góc phản xạ. i= i ' ii’
1.4 Định luật của Descartes thứ hai MT n1
Tia khúc xạ nằm trong mặt phẳng tới và tỉ
số giữa sin góc tới và sin góc khúc xạ là MT n2
một số không đổi và bằng chiết suất tỉ đối giữa hai môi trường. r Tia k/xạ sin in= 21 sin r
Hiện tượng phản xạ toàn phần Điều kiện: n > n 1 2 i > i gh r i igh