














Preview text:
DẠI HỌC QUỐC GIA THÀNH PHỐ HỒ CHÍ MINH
TRƯÍNG DẠI HỌC BÁCH KHOA
Nguyễn Dình Huy (Chủ biên)
Nguyễn Quốc Lân, Lê Xuân Dại TOÁN CAO CẤP
GIẢI TÍCH HÀM MộT BIẾN
NHÀ XUẤT BẢN ĐẠI HỌC QUỐC GIA TP HỒ CHÍ MINH 2015 51 89/176-05 Mã số: 8I092M5 GD-05 Lďi nói dầu
Cuốn sách dành cho các bạn sinh viȇn trmờng Dại học Bách Khoa TpHCM.
Trong biȇn soạn khȏng thễ tránh khỏi sai sót và nhầm lấn mong bạn dọc cho ý kiến. Mọi góp ý
gải về dịa chỉ: ytkadai@hcmut.edu.vn Ngày 13 tháng 01 năm 2014 Nhóm tác giả Mṇc lṇc
LỜi nói đầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . i
Mực lực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ii
ChG6ng 1. GIÎI HẠN CỦA DÃY SỐ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.1. Khái ni»m dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2. GiỚi hạn của dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3. GiỚi hạn của dãy đ6n đi»u. Định lj Weierstrass . . . . . . . . . . . . . . . . . . . . . . . 8
1.4. Các phG6ng pháp tìm giỚi hạn của dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.5. Bài tªp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
LỜi giải bài tªp chG6ng 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
ChG6ng 2. GIÎI HẠN VÀ TÍNH LIÊN TỤC CỦA HÀM MộT BIẾN . . . . . . . . 18
2.1. GiỚi hạn của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.2. GiỚi hạn vô cùng bé của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
2.3. GiỚi hạn vô cùng lỚn của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.4. Hàm số liên tực . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.5. Bài tªp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
ChG6ng 3. ĐẠO HÀM VÀ VI PHÂN CỦA HÀM MộT BIẾN . . . . . . . . . . . . . . . 32
3.1. Khái ni»m đạo hàm của hàm một biến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.2. Đạo hàm cấp cao. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
3.3. Vi phân của hàm một biến . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
3.4. Tìm giỚi hạn dạng vô định theo qui tắc L’ Hopital. . . . . . . . . . . . . . . . . . . . 41
3.5. Khai triển Taylor - Maclaurin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
3.6. Khảo sát và vẽ đồ thị hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
3.7. Bài tªp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
ChG6ng 4. PHÉP TÍNH TÍCH PHÂN CỦA HÀM MộT BIẾN . . . . . . . . . . . . . . . 54
4.1. Nguyên hàm và tích phân bất định . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 MỤC LỤC 1
4.2. PhG6ng pháp tính tích phân bất định. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.3. Tích phân của nhfing hàm hfiu tỉ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
4.4. Tích phân của hàm vô tỉ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .61
4.5. Tích phân của hàm lGỢng giác. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
4.6. Tích phân xác định. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
4.7. PhG6ng pháp tính tích phân xác định. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
4.8. Tích phân suy rộng loại 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
4.9. Tích phân suy rộng loại 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
4.10. Ứng dựng của tích phân. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
4.11. Bài tªp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
ChG6ng 5. PHƯƠNG TRÌNH VI PHÂN THÔNG THƯÍNG. . . . . . . . . . . . . . . . . . . . .94
5.1. PhG6ng trình vi phân cấp một. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
5.2. Bài tªp phG6ng trình vi phân cấp một. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
5.3. PhG6ng trình vi phân cấp hai vỚi h» số hằng. . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
5.4. Bài tªp phG6ng trình vi phân cấp hai. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
5.5. H» phG6ng trình vi phân. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
5.6. Bài tªp h» phG6ng trình vi phân. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .121
CÁC ĐỀ THI TRẮC NGHI M GIỮA KỲ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
6.1. Đề thi gifia kj giải tích 1- Ca 1 năm 2012-2013. . . . . . . . . . . . . . . . . . . . . . . . 124
CÁC ĐỀ THI TỰ LU N CUỐI KỲ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
7.1. Đề thi cuối kj giải tích 1- Ca 1 năm học 2013-2014. . . . . . . . . . . . . . . . . . . . 130
7.2. Đề thi cuối kj giải tích 1- Ca 2 năm học 2013-2014. . . . . . . . . . . . . . . . . . . . 130
CHƯƠNG TRÌNH MATLAB. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .142
Tài li»u tham khảo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144 Chương1
GIÎI HẠN CỦA DÃY SỐ
1.1. Khái ni»m dãy số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2. GiỚi hạn của dãy số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.3. GiỚi hạn của dãy đ6n đi»u. Định lj Weierstrass. . . . . . . . . . . . . . . . . . . . . . . . 8
1.4. Các phG6ng pháp tìm giỚi hạn của dãy số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8
1.5. Bài tªp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
LỜi giải bài tªp chG6ng 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15
1.1 Khái ni»m dãy số
Di»n tích hình tròn đGỢc xấp xỉ bỞi di»n tích của nhfing đa giác đều
Tính gần dúng di¾n tích của hình tròn có bán kính R
Hình 1.1: Di¾n tích hình tròn dmợc xấp xỉ bởi di¾n tích của nhãng da giác dều
A = lim An = πR2. n→∞
1.1 Khái ni»m dãy số 3
1.1.1 Dịnh nghĩa dãy số
Định nghĩa 1.1. Ánh xạ f : N —→ R tà t¾p hợp số tự nhiȇn lȇn t¾p hợp số thực R dmợc gọi là dãy số.
Dãy số dmợc kí hi¾u là (xn). xn dmợc gọi là phần tả tỗng quát thá n của dãy số.
Ví dị 1.1.1. 1 1 1
Cho dãy (xn) với xn = thì x , . . . n
1 = 1, x2 = 2, . . . , xn = n
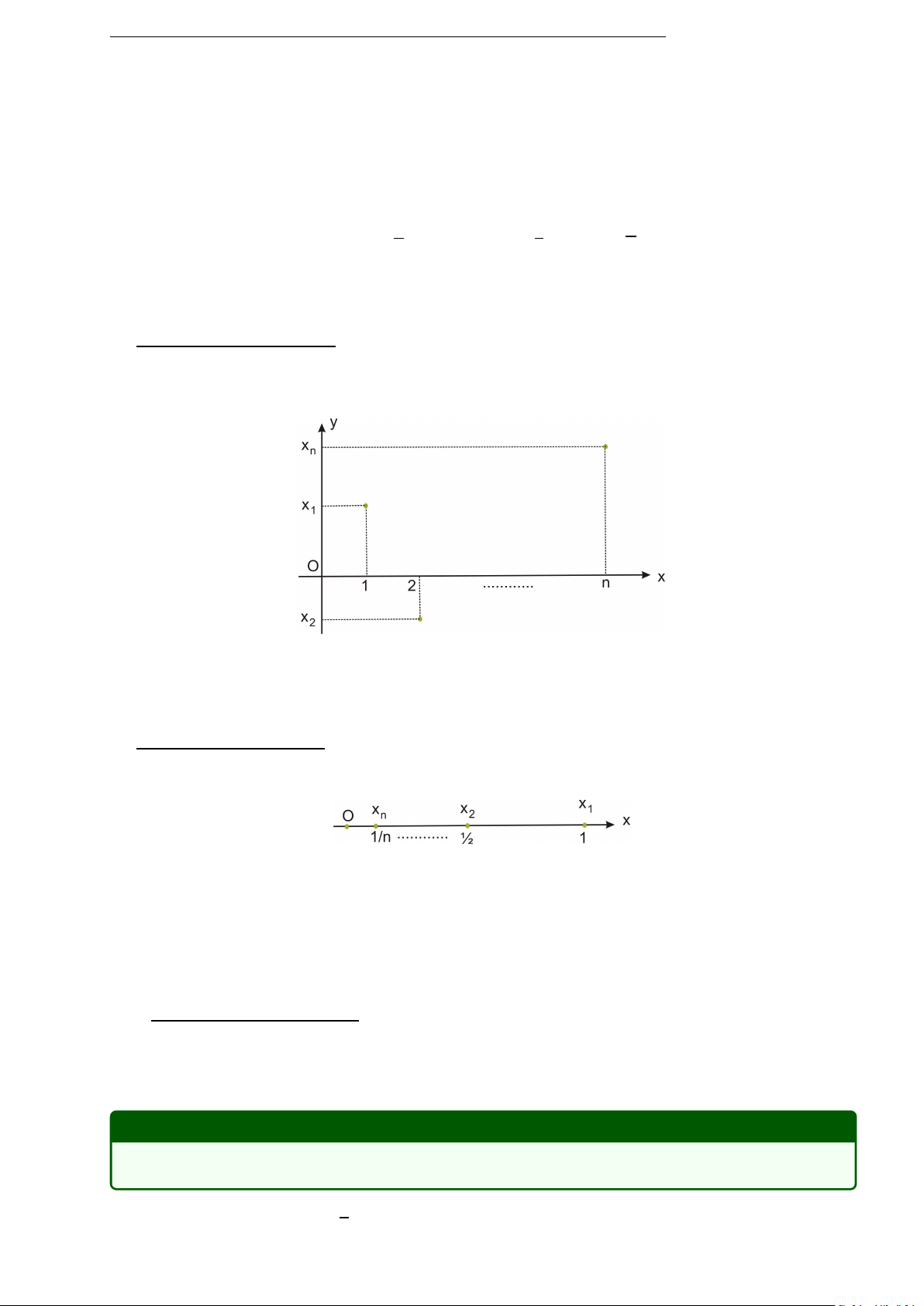
1.1.2 Sfi biểu diễn hình học của dãy số PhG6ng pháp thf í nhất.
Dãy số (xn) dmợc biễu diến bằng dồ thị của nó tà nhãng diễm (n, xn).
Hình 1.2: Biễu diến dãy số trȇn m°t phẫng PhG6ng pháp thf í hai.
Dãy số (xn) dmợc biễu diến bởi nhãng diễm của trục Ox
Hình 1.3: Biễu diến dãy số trȇn trục số thực
1.1.1 Tính chất của dãy số
1. Tính tăng và tính giảm.
Định nghĩa 1.2. Dãy số (xn) dmợc gọi là dãy tăng (dãy giảm) nếu nhm với mọi n ∈ N luȏn có bất
dẫng thác xn < xn+1(xn > xn+1).
Định lj 1.1: Bất đẳng thfíc Bernoulli.
Nếu số h > —1 và h /= 0 thì luȏn có bất dẫng thác (1 + h)n > 1 + nh với mọi số tự nhiȇn n ≥ 2. 1 n
Ví dị 1.1.2. Dãy xn = 1 + n ,(n ∈ N) là dãy tăng. 4
GIďI HẠN CỦA DÃY SỐ 1 n
Chfíng minh. Vì x
> 0 nȇn ta chỉ cần cháng minh xn+1 n = 1 + > 1. Ta có x n n xn+1 1 (1 + )n+1 (n+2 n+2 n+1 n+1)n+1 n + 1 n+1 ! = = = n+1 n + 1 . n2 + 2n = n+1 . = xn (1 + 1 n n n2 n )n ( n+1 )n n+1 n + 2n + 1 n = 1 — 1 n+1 n + 1 . > 1 1 n + 1 . = n .n + 1 = 1 (n + 1) — 2 n n + 1 n n + 1 n
Nhm v¾y xn < xn+1□ 1 n+1
Ví dị 1.1.3. Dãy số xn = 1 + , (n n ∈ N) là dãy giảm. x
Chfíng minh. Vì x = (1 + 1 )n+1 > 0 nȇn ta chỉ cần cháng minh n > 1. Ta có n n xn+1 xn (1 + 1 )n+1 n+1 n+2 = ( n+1 )n+1 n = n = ! n . n
n2 + 2n + 1 n+2 n = . x = n+1 (1 + 1 n+2 n+2 n+2 n + 1 n2 + 2n n + 1 n+1 )n+2 ( ) n+1 n+1 1 n+2 n 1 n n + 1 n = 1 + . > 1 + . = . n(n + 2) = 1. n + 1 n n + 1 n n + 1
Nhm v¾y xn > xn+1□ 2. Tính bị ch°n.
Định nghĩa 1.3. Dãy số (xn) ⊂ R dmợc gọi là bị ch°n trȇn (dmới), nếu nhm tồn tại số IM ∈ R (m ∈ R),
sao cho với mọi ∀n ∈ N luȏn có xn ≤ M(xn ≥ m).
Số M (m) dmợc gọi là c¾n trȇn (c¾n dmới) của dãy (xn).
Định nghĩa 1.4. Dãy số (xn) ⊂ R dmợc gọi là bị ch°n, nếu nó bị ch°n trȇn và ch°n dmới có nghĩa là
nếu nhm tồn tại số IM, m ∈ R sao cho với mọi ∀n ∈ N luȏn có m ≤ xn ≤ M.
Định nghĩa 1.5. Dãy số (xn) ⊂ R dmợc gọi là khȏng bị ch°n trȇn (dmới), nếu nhm với mọi số
∀M ∈ R (m ∈ R), tồn tại số hạng của dãy số xn0 sao cho xn0 > M (xn0 < m). 1 n+1
Ví dị 1.1.4. Dãy số x 1 + n = (n n
∈ N) bị ch°n dmới bởi số m = 0, và bị ch°n trȇn bởi số
M = (1 + 1)2 = 4. Chfíng minh.
Vì dãy này là dãy giảm nȇn với mọi ∀n ∈ N luȏn có xn ≤ x1 = 4.
Với mọi ∀n ∈ N ta có xn > 0□
Ví dị 1.1.5. Dãy số xn = (1 + 1 n)n, (n ∈ N) bị ch°n dmới bởi số m = 0 và bị ch°n trȇn bởi số M = 4. 1 n 1 n+1
Chfíng minh. Với mọi ∀n ∈ N luȏn có x 1 + < 1 +
n > 0, và xn = n n ≤ 4□
1.2 Giói hạn của dãy số 5
Hình 1.4: Ý nghĩa hình học của giới hạn của dãy số
1.2 Giďi hạn của dãy số
1.2.1 Nhfing khái ni»m c6 bản
Định nghĩa 1.6. Số a ∈ R dmợc gọi là giỚi hạn của dãy (xn) ⊂ R, nếu nhm với mọi ∀ε > 0 tồn tại
số N = N(ε) sao cho với mọi ∀n > N luȏn có bất dẫng thác |xn — a| < ε.
Chú j. Nếu số a ∈R là giới hạn của dãy (xn) ⊂ R thì ta viết là lim xn = a. n→∞
Định nghĩa 1.7. Dãy số (xn) ⊂ R có giới hạn hãu hạn a ∈ R dmợc gọi là dãy hội tự đến a. Khi dó
ta viết là xn → a.
Định nghĩa 1.8. Dãy số (xn) ⊂ R dmợc gọi là phân kj nếu nhm mọi số ∀a ∈ R khȏng là giới hạn
của dãy số này, có nghĩa là a khȏng tồn tại ho°c bằng ∞.
1.2.2 Tính chất của giďi hạn hfiu hạn của dãy số Định lj 1.2
Mọi dãy hội tụ (xn) ⊂ R dều bị ch°n.
Chú j. Diều ngmợc lại khȏng dúng. Ví dụ dãy an = (—1)n bị ch°n nhmng phȃn kỳ. Định lj 1.3
Nếu dãy số (xn) ⊂ R có giới hạn hãu hạn a thì giới hạn dó là duy nhất. Định lj 1.4
Nếu dãy số (xn) ⊂ R và (yn) ⊂ R có giới hạn hãu hạn tmơng áng là a và b thì: 1. lim |x n→∞ n| = |a|. 2. lim (x n→∞
n ± yn) = a ± b
3. lim (xn.yn) = a.b. n→∞ x
4. Nếu bỗ sung thȇm diều ki¾n b /= 0 thì ta có lim n a = . n→∞ yn b
1.2.3 Nhfing giďi hạn c6 bản 6
GIďI HẠN CỦA DÃY SỐ
Nhfing giỚi hạn c6 bản 1. lim qn = 0, p | ln n
q| < 1. n→∞ 6. lim = 0, nα
∀p, ∀α > 0. n→∞ 1 2. lim = 0, α > 0. 7. √n n→∞ nα lim
np = 1, ∀p. n→∞ 1 √n 3. lim = 0, α > 0.
8. lim a = 1, a > 0. n→∞ lnα n n→∞ n 1 4. lim = 0. 9. lim 1 + 1 = e. n→∞ en n→∞ n np n 5. lim ∀p. 10. lim 1 + a a
n→∞ en = 0, = e , n→∞ n ∀a.
Chú j. Với p, α > 0, a > 1, khi n → ∞ thì
lnp n << nα << an << n! << nn 1.2.4 Dịnh lj kẹp Định lj 1.5 Nếu
( xn≤ yn ≤ zn, ∀n>n0
lim xn = lim zn = a n→∞ n→∞ thì lim yn = a. n→∞
Hình 1.5: Hình ảnh minh họa dịnh lý kẹp 7n
Ví dị 1.2.1. Tìm giới hạn lim . n→∞ nn Giải. Ta có 7n 7 0 < nn < n
, ∀n > 8. 8 7 n mà lim
= 0 nȇn lim 7n = 0. n→∞ 8 n→∞ nn
1.2.5 Giďi hạn vô cùng của dãy số
Định nghĩa 1.9. Số +∞(—∞; ∞) dmợc gọi giới hạn của dãy số (xn) ⊂ R, nếu nhm với mọi ∀M > 0 tồn
tại số N = N(M) > 0 sao cho với mọi ∀n > N luȏn có bất dẫng thác xn > M(xn < —M; |xn| > M). Chú j. 1 1 = 0; ∞ 0 = ∞
1.2 Giói hạn của dãy số 7
Ví dị 1.2.2. Dãy số xn = qn(n ∈ N) với q > 1 có giới hạn lim qn = +∞. n→∞
Chfíng minh. Vì 0 < 1 q< 1 nȇn theo giới hạn cơ bản, ta có 1 lim n = lim 1n = 0. n→∞ q n→∞ q
Lấy 1 số M > 0 bất kỳ và d°t ε = 1 > 0, khi dó theo dịnh nghĩa giới hạn thì dối với số ε > 0 này M
tồn tại số N = N(ε) > 0 sao cho với mọi ∀n > N luȏn có bất dẫng thác | 1 — 0| = 1 < ε = 1 , có qn qn M
nghĩa là qn > M( ∀n > N). Nhm v¾y lim qn = +∞□ n→∞
Ví dị 1.2.3. Dãy số xn = qn(n ∈ N) với q < —1 có giới hạn lim qn = ∞. n→∞
Chfíng minh. Vì 0 < |1 q| < 1 nȇn theo giới hạn cơ bản, ta có l 1 1 n im n →∞ | = lim 1 | n = lim n = 0. q n→∞ |q| n→∞ |q |
Lấy 1 số M > 0 bất kỳ và d°t ε = 1 > 0, khi dó theo dịnh nghĩa giới hạn thì dối với số ε > 0 này M
tồn tại số N = N(ε) > 0 sao cho với mọi ∀n > N luȏn có bất dẫng thác || 1 | — 0| = 1 < ε = 1 , có qn |q|n M
nghĩa là |xn| = |qn| = |q|n > M(∀n > N). Nhm v¾y lim qn = ∞□ n→∞
Chú j. Số +∞ và —∞ trong trmờng hợp này khȏng là giới hạn của dãy xn = qn(n ∈ N) với
q < —1. Vì với mọi số chắn n thì xn = qn > 0, còn với mọi số lẻ n thì xn = qn < 0. 1.2.6 Dãy con
Định nghĩa 1.10. Cho dãy số (xn) ⊂ R và n1 < n2 < . . . < nk < . . . một dãy số tự nhiȇn tăng bất
kỳ, khi dó dãy số xn1 , xn2, . . . , xn , . . . k
dmợc gọi là dãy con của dãy (xn). Dãy con dmợc kí hi¾u là (xn ). k
Định nghĩa 1.11. Số c ∈ R dmợc gọi là giỚi hạn riêng của dãy (xn), nếu nhm tồn tại dãy con (xn )
k của dãy (xn), hội tụ dến số c.
Ví dị 1.2.4. Cho dãy (xn) với xn = (—1)n. Với n = 2k thì dãy {1, 1, . . . , 1, . . .} dmợc gọi là 1 dãy con
của dãy (xn) và giới hạn riȇng của nó x2k → 1, k → ∞. Với n = 2k + 1 thì dãy {—1, —1, . . . , —1, . . .}
cũng là 1 dãy con của dãy (xn) và giới hạn riȇng của nó x2k+1 → —1, k → ∞.
1.2.7 Mối quan h» gifia giďi hạn riêng và giďi hạn của dãy số hội tṇ
Nếu nhm dãy (xn) hội tụ dến số a, thì với mọi dãy con (xn ) k
của dãy (xn), giới hạn của nó là a. lim xn = a ⇒ = lim xn = a n→∞ k k→∞ Định lj 1.6
Nếu dãy (xn) hội tụ thì tất cả giới hạn riȇng của dãy (xn) dều bằng nhau và bằng giới hạn của dãy số (xn).
Chú j. Dễ cháng minh dãy (xn) phȃn kỳ ta làm nhm sau:
Cách 1. Chỉ ra 2 dãy con hội tụ về 2 giới hạn riȇng khác nhau.
Cách 2. Chỉ ra 1 dãy con phȃn kỳ. 8
GIďI HẠN CỦA DÃY SỐ
Ví dị 1.2.5. Nói chung dối với một số dãy số thì có thễ tồn tại nhãng giới hạn riȇng khác nhau.
Dối với dãy (xn) = (—1)n (n ∈ N), dãy con của nó (x2k) = (—1)2k = 1 và (x2k—1) = (—1)2k—1 = —1
có giới hạn riȇng lần lmợt là 1 và -1. Chúng khȏng bằng nhau.
Ví dị 1.2.6. Khȏng phải với dãy số nào cũng có giới hạn riȇng.
Dãy số 1, 2, . . . , n, . . . khȏng có giới hạn riȇng.
1.3 Giďi hạn của dãy d6n di»u. Dịnh lj Weierstrass Định lj 1.7
Nếu dãy số dơn di¾u tăng (giảm) (xn) ⊂ R bị ch°n trȇn (dmới)
x1 ≤ x2 ≤ . . . ≤ xn ≤ . . . ≤ y
(x1 ≥ x2 ≥ . . . ≥ xn ≥ . . . ≥ z),
thì nó có giới hạn hãu hạn. Còn nếu nhm dãy số dơn di¾u tăng (giảm) (xn) ⊂ R khȏng bị ch°n
trȇn (dmới) thì giới hạn của nó là +∞(—∞).
Ví dị 1.3.1. Cháng minh rằng dãy số (xn) = (1 + 1 n)n(n ∈ N) có giới hạn hãu hạn. Giới hạn này dmợc kí hi¾u là e.
Chfíng minh. Nhm ta dã biết dãy (xn) trȇn là dãy tăng và bị ch°n trȇn. Vì v¾y theo dịnh lý
Weierstrass tồn tại giới hạn hãu hạn 1 n lim 1 + = e. n→∞ n
Chú j. Số e là số siȇu vi¾t (khȏng phải là số dại số). Nó khȏng là nghi¾m của da thác với h¾ số
nguyȇn có b¾c n ≥ 1.
Số e ≈ 2, 718281828459045, số này còn dmợc gọi là số Neper hay số Ole.
1.4 Các phG6ng pháp tìm giďi hạn của dãy số
1.4.1 Dùng biến dổi dại số dể tìm giďi hạn của dãy số n3
Ví dị 1.4.1. Tìm giới hạn I = lim n2 .
n→∞ n + 1 — n2 + 1 Giải. 1
I = lim n2(n2 + 1) — n3(n + 1) = lim n2 — n3 = lim n — 1 = = —1. n→∞ (n + 1)(n2 + 1)
n→∞ (n + 1)(n2 + 1)
n→∞ (1 + 1 )(1 + 1 ) n n2
Ví dị 1.4.2. Tìm giới hạn I = lim (n + 1)4 — (n — 1)4 .
n→∞ (n2 + 1)2 — (n2 — 1)2 Giải. 2n(n2 + 1)
I = lim (n + 1 — n + 1)(n + 1 + n — 1)((n + 1)2 + (n — 1)2) = lim n→∞
(n2 + 1 — n2 + 1)(n2 + 1 + n2 — 1) n→∞ n2 = ∞.
1.4 Các phương pháp tìm giói hạn của dãy số 9 1
Ví dị 1.4.3. Tìm giới hạn I = lim √ .
n→∞ n( n2 — 1 — n) Giải. √ q n2 — 1 + n 1 — 1 + 1 n2 I = lim = lim
n→∞ n(n2 — 1 — n2) n→∞ 1 = = —2. √n2 + 1—n
Ví dị 1.4.4. Tìm giới hạn I = lim √ . n→∞ n + 1 — √n Giải. √ q q √
(n2 + 1 — n2)( n + 1 + n) 1 + 1 + 1 √ = lim n q I = lim n2
(n + 1 — n)( n2 + 1 + n) n 1 = 0. n→∞ n→∞ 1 + √ n2 + 1 n2 + 1 — n
Ví dị 1.4.5. Tìm giới hạn I = lim √ √ . n→∞ n3 + 1 — n n Giải. √ √ q √
(n2 + 1 — n2)( n3 + 1 + n n) n + + n n3 1 I = lim √ = lim q 3 3 2 = ∞.
n→∞ (n + 1 — n )( n + 1 + n) n→∞ 1 + 1 n + 2 √4 √
n3 + n — n 1
Ví dị 1.4.6. Tìm giới hạn I = lim √ .
n→∞ n + 2 + n + 1 Giải. q q 1 4 1 + — 1 n n3 n I = lim q = 0. n→∞ 1 + 2 1 1 n + + n n2
1.4.2 Dùng dịnh lj kẹp tìm giďi hạn của dãy số
Ví dị 1.4.7. Tìm giới hạn
1 + 22 + . . . + nn lim n→∞ nn . Giải. D°t
1 + 22 + . . . + nn an = nn . Khi dó ta có nn
n1 + n2 + . . . + nn nn+1 — n nn — 1 n n
1 = nn ≤ an ≤ = = . < . nn (n — 1)nn nn n — 1 n — 1 n Vì → 1 nȇn a n — 1
n → 1 khi n → ∞. 1
Ví dị 1.4.8. Tìm giới hạn I = lim n→∞ √n! Giải.
Bằng phmơng pháp qui nạp toán học ta có thễ cháng minh dmợc n! > n2
4 , ∀n ∈ N. 1 2 2
Do dó 0 < √ < n. M°t khác lim n = 0 nȇn I = 0. n! n→∞ 10
GIďI HẠN CỦA DÃY SỐ
Ví dị 1.4.9. Tìm giới hạn I = lim √nn n→∞ Giải.
Theo cȏng thác nhị thác Newton ta có √ √ n(n √ √ n = (1 + ( — 1)
n n — 1))n = 1 + n( n n — 1) + +
( n n — 1)2 + . . . + ( n n — 1)n. 2 r √ √ 2
Với mọi ∀n > 1 ta có n > n(n—1)( n n — 1)2. Do dó với mọi ∀n > 1, 0 < n n — 1 < . 2 r n — 1 2 √ M°t khác lim = 0 nȇn
n n — 1 = 0 hay I = 1. lim n→∞ n — 1 n→∞
Ví dị 1.4.10. √
Tìm giới hạn I = lim n a, a > 1. n→∞ Giải.
Theo cȏng thác nhị thác Newton ta có √ √ n(n √ √ a = (1 + ( — 1)
n a — 1))n = 1 + n( n a — 1) + +
( n a — 1)2 + . . . + ( n a — 1)n. 2 √ √ a
Với a > 1 ta có a > n( n a — 1). Do dó 0 < n a — 1 < . n a √ M°t khác lim
= 0 nȇn lim n a — 1 = 0 hay I = 1. n→∞ n n→∞
Ví dị 1.4.11. Tìm giới hạn I = lim qn, |q| < 1. n→∞
Nếu q = 0 thì I = 0.1 1
Nếu q /= 0 thì ta có > 1, do dó
= 1 + h, h > 0. Theo bất dẫng thác Bernoulli (1.1) ở trang |q| |q| 3, ta có 1 1
= (1 + h)n > 1 + nh > nh ⇒ 0 < |q|n < . |q|n nh 1 M°t khác lim = 0 nȇn I = 0. n→∞ nh
Ví dị 1.4.12. Tìm giới hạn I = lim n , a > 1. n→∞ an
Theo cȏng thác nhị thác Newton ta có an = (1 + (a — 1))n = 1 + n(a — 1) n(n +
— 1)(a — 1)2 + ... + (a — 1)n. 2 n 2
Với a > 1 ta có an > n(n—1)(a — 1)2. Do dó 0 < < . M°t khác 2 2 an
(n — 1)(a — 1)2 lim = 0 nȇn I = 0.
n→∞ (n — 1)(a — 1)2 ( 1)n
Ví dị 1.4.13. I = lim — n→+∞ nα , α > 0 Giải.
Với α > 0 ta có —1 n ≤ (—1) ≤ 1 nα nα nα 1 M°t khác lim —1 = lim = 0 nȇn I = 0. n→∞ nα n→∞ nα
1.4 Các phương pháp tìm giói hạn của dãy số 11
1.4.3 Sfi dṇng giďi hạn c6 bản 1 + 7n+2
Ví dị 1.4.14. Tìm giới hạn của dãy an = 3 — 7n 1 + 72 1
Chia tả số và mấu số cho 7n ta dmợc lim a = lim 7n = —49 vì lim = 0. n 3 n→∞ n→∞ 7n 1 n→∞ 7n
Ví dị 1.4.15. Tìm giới hạn lim 2n+2 + 3n+3 n→∞ 2n + 3n
Chia tả số và mấu số cho 3n ta có 4.2n 3n + 33 an = 2n 3n + 1
Do dó lim a = lim 4.2n
3n + 33 = 27 vì lim 2n = 0. n n n→∞ n 2 →∞ 3n n + 1 →∞ 3n
5.2n — 3.5n+1
Ví dị 1.4.16. Tìm giới hạn lim
n→∞ 100.2n + 2.5n
Chia tả số và mấu số cho 5n ta có 5.2n 5n — 3.5
an = 100.2n 5n + 2 n 5.2 — 3.5 15 2n
Do dó lim a = lim 5n = — vì lim = 0. n n→∞
n→∞ 100.2n 5n + 2 2 n→∞ 5n
Ví dị 1.4.17. Tìm giới hạn lim (—1)n.6n — 5n+1
n→∞ 5n — (—1)n.6n+1
Chia tả số và mấu số cho (—6)n ta có 1 — 5.5n a (—6)n n = 5n (—6)n — 6 5.5n 1
Do dó lim a = lim — (—6)n = n —1 n→∞ n 5n 6 →∞ (—6)n — 6 5n vì lim n = 0. n→∞ (—6)
Ví dị 1.4.18. Tìm giới hạn lim 2n + 3—n
n→∞ 2—n — 3n
Chia tả số và mấu số cho 3n ta có 2n + 1 a = 3n 9n n 1 6n 1
Do dó lim a = lim 2n + 1 3n
9n = 0 vì lim 2n = lim 1 = lim 1 = 0. n 1 n→∞ n→∞ 6 n n 1 n→∞ 3n →∞ 9n n→∞ 6n (—1)n + 1
Ví dị 1.4.19. Tìm giới hạn lim n n→∞ n2 1 — (—1)n
Chia tả số và mấu số cho (—1)n ta có 1 + (—1)n an = n (—1)n 1 n2
Do dó lim an = lim 1 + (—1)n n = —1 vì n→∞ n→∞ (—1)n n2 1 (—1)n n lim (—1) = lim n→∞ n n→∞ n2 = 0. 12
GIďI HẠN CỦA DÃY SỐ
1.4.4 Dùng dịnh lj Weierstrass về sfi tồn tại giďi hạn của dãy d6n di»u 1 1 1
Ví dị 1.4.20. Cháng minh rằng dãy an = 5+ 1 + 52 + 1 + ... + 5n + 1 hội tụ. Giải.
Dãy an là dãy dơn di¾u tăng. Th¾t v¾y, vì 1
an+1 = an + 5n+1 + 1
nȇn an+1 > an.
Dãy an bị ch°n trȇn. Th¾t v¾y 1 1 1 1 1 1 1 — 1 1 1 1 an = + + . . . + < + = 5 5n+1 = . 5 + 1 52 + 1 5n + 1 5 52 + . . . + 5n 1 — 1 1 — < 4 5n 4 5
Nhm v¾y, dãy an dã cho dơn di¾u tăng và bị ch°n trȇn nȇn nó hội tụ. 1 1 1
Ví dị 1.4.21. Cháng minh rằng dãy an = 3+ 1 + 32 + 2 + ... + 3n + n hội tụ. Giải.
Dãy an là dãy dơn di¾u tăng. Th¾t v¾y, vì 1
an+1 = an + 3n+1 + n + 1
nȇn an+1 > an.
Dãy an bị ch°n trȇn. Th¾t v¾y 1 1 1 1 1 1 1 — 1 1 1 1 an = + + . . . + < + + . . . + = 3 3n+1 1 . 3 + 1 32 + 2 3n + n 3 32 3n 1 — 1 = — < 2 3n 2 3
Nhm v¾y, dãy an dã cho dơn di¾u tăng và bị ch°n trȇn nȇn nó hội tụ. 2n
Ví dị 1.4.22. Cháng minh rằng dãy an =
hội tụ và tìm giới hạn của nó. n!
Giải. Dãy an là dãy dơn di¾u giảm. Th¾t v¾y, vì 2n+1 an+1 = (n+1)! 2 =
< 1, ∀n > 1. 2n an n + 1 n!
nȇn an+1 < an.
Dãy an bị ch°n dmới bởi 0 vì an > 0. Nhm v¾y, dãy an dã cho dơn di¾u giảm và bị ch°n dmới nȇn nó hội tụ. 2
Giả sả lim an = a. = a n→∞ Ta có an+1 n
n + 1 . Lấy giới hạn 2 vế của dẫng thác này khi n → ∞ ta dmợc lim an+1 = lim 2 . lim an. n→∞
n→∞ n + 1 n→∞ 2n
Do dó a = 0.a ⇒ a = 0. V¾y lim = 0. n→∞ n! √ √
Ví dị 1.4.23. Cho dãy a1 = 2, an+1 = 2an. Cháng minh rằng dãy (an) hội tụ và tìm giới hạn của nó.
1.4 Các phương pháp tìm giói hạn của dãy số 13 Giải.
Dãy an là dãy dơn di¾u tăng vì a1 < a2 < a3 < . . . .
Ta sẽ cháng minh dãy an bị ch°n trȇn bởi 2. √ √ √
Th¾t v¾y, a1 = 2, a2 = 2a1 < 2.2 = 2.
Giả sả dã cháng minh dmợc rằng an ≤ 2. Ta sẽ cháng minh an+1 ≤ 2. √ √
Th¾t v¾y, an+1 = 2an ≤ 2.2 = 2. V¾y theo nguyȇn lý qui nạp ta có an ≤ 2, ∀n ∈ N
Nhm v¾y, dãy an dã cho dơn di¾u tăng và bị ch°n trȇn nȇn nó hội tụ. Giả sả lim √ a 2 = 2a
n = a. Ta có an+1 = 2an ⇒ an+1 n
n. Lấy giới hạn 2 vế của dẫng thác này khi n → ∞ →∞ ta dmợc lim 2 a = 2. lim an. n→∞ n+1 n→∞ ⇒ √ Do dó a2 = 2.a
a = 0 a = 2. Vì an > 2 nȇn a = 2. V¾y lim an = 2. W n→∞ r √ √ √ q √
Ví dị 1.4.24. Cho dãy x1 = a, x2 = a + a, . . . , xn = a + a + . . . + a, a > 0. Cháng ` ˛ ¸ x n dấ u căn
minh rằng dãy (xn) hội tụ và tìm giới hạn của nó.
Giải. Dãy an là dãy dơn di¾u tăng vì x1 < x2 < x3 < . . . . Ta sẽ cháng minh dãy xn bị ch°n trȇn √ bởi a + 1. √ √ √ √ √ √ √ √
Th¾t v¾y, x1 = a < a + 1, x2 =
a + a < √a + a + 1 < a + 2 a + 1 = a + 1.
Giả sả dã cháng minh dmợc rằng xn ≤ √a + 1. Ta sẽ cháng minh xn+1 ≤ √a + 1. √ √ √ √ √
Th¾t v¾y, xn+1 = a + xn <
a + a + 1 <
a + 2 a + 1 = a + 1. V¾y theo nguyȇn lý qui √ √
nạp ta có xn ≤ a + 1, ∀n ∈ N
Nhm v¾y, dãy xn dã cho dơn di¾u tăng và bị ch°n trȇn nȇn nó hội tụ. Giả sả lim √a + x 2 = a + x n ⇒ xn+1 n.
n→∞ xn = x. Ta có xn+1 =
Lấy giới hạn 2 vế của dẫng thác này khi n → ∞ ta dmợc lim 2 x = a + lim xn. n→∞ n+1 n→∞ √ √ √ 1 — 1 + 4a W 1 + 1 + 4a
Do dó x2 = a + x ⇒ x = x =
. Vì x > 0 nȇn x = 1 + 1 + 4a. V¾y √ 2 2 n 2 lim x 1 + 4a n = 1 + . n→∞ 2
1.4.5 Sfi dṇng giďi hạn của số e
Sả dụng giới hạn của số e tính giới hạn dạng 1∞ 1 n lim 1 + = e n→∞ n 1 un
Nếu lim un = ∞ thì lim 1 + = e n→∞ n→∞ un n
Ví dị 1.4.25. 1 Tìm giới hạn lim 1 + , k ∈ N n→∞ n + k 14
GIďI HẠN CỦA DÃY SỐ Giải. 1 n 1 (n+k). n lim 1 + = lim n+k 1 + = e1 = e. n→∞ n + k n→∞ n + k n n
Ví dị 1.4.26. Tìm giới hạn lim . n→∞ n + 1 Giải. 1 n 1 —(n+1). n lim 1 = lim −(n+1) 1 = e—1. — — n→∞ n + 1 n→∞ n + 1 1 n
Ví dị 1.4.27. Tìm giới hạn lim 1 + . n→∞ 2n Giải. n 1 n 2n lim 1 1 + 2n. = lim 1 + 1 = e2 . n→∞ 2n n→∞ 2n 2n + 1 2n
Ví dị 1.4.28. Tìm giới hạn lim n→∞ 2n . 1 2n lim
2n + 1 2n = lim 1 + n→∞ 2n n→∞ 2n = e.
1.4.6 Chfíng minh dãy số phân kj
Dễ cháng minh dãy (xn) phȃn kỳ ta làm nhm sau:
Cách 1. Chỉ ra 2 dãy con hội tụ về 2 giới hạn riȇng khác nhau.
Cách 2. Chỉ ra 1 dãy con phȃn kỳ. 2n + 3
Ví dị 1.4.29. Cháng minh rằng dãy a = ( 1)n phȃn kỳ. n — 3n + 1
Giải. Xét 2 dãy con với chỉ số chắn và lẻ ta có 2.2k + 3 2 a k = (—1)2k → 2, 3.2k + 1 3 2
a k+1 = (—1)2k+1 2.(2k + 1) + 3 → —2 3.(2k + 1) + 1 3
khi k → ∞. V¾y tồn tại 2 dãy con có giới hạn khác nhau nȇn dãy dã cho phȃn kỳ.
1.4.7 Tóm tắt các khái ni»m c6 bản của chG6ng 1
GiỚi hạn của dãy số
1. Nhãng giới hạn cơ bản 2. Dịnh lý kẹp 3. Dịnh lý Weierstrass
4. Giới hạn của số e
5. Dùng mối quan h¾ giãa giới hạn riȇng và giới hạn của dãy số cháng minh dãy số phȃn kỳ






