TRƯỜNG ĐẠI HỌC DUY TÂN ---------- 0 O 0 ----------- GIÁO TRÌNH THÍ NGHIỆM VẬT LÝ ĐẠI CƯƠNG A1
DÙNG CHO SINH VIÊN HỆ ĐẠI HỌC & CAO ĐẲNG
(Tài liệu lưu hành nội bộ) Đà Nẵng, năm 2021
Phần 1. LÝ THUYẾT SAI SỐ Bài mở đầu CÁCH XÁC ĐỊNH SAI SỐ
CỦA PHÉP ĐO CÁC ĐẠI LƯỢNG VẬT LÝ
Vật lý học là một môn khoa học thực nghiệm, những định lý, định luật, thuyết…. được
xây dựng từ thực nghiệm. Vì vậy, thí nghiệm thực hành Vật lý là một phần quan trọng
không thể thiếu của môn học Vật lý trong chương trình học tập của sinh viên, học sinh ở
các trường đại học, cao đẳng và trung học phổ thông. Mục đích của nó là giúp sinh viên, học sinh:
1. Hiểu biết sâu sắc hơn những hiện tượng, định luật, định lý trong phần lý thuyết vật lý.
2. Nắm bắt được một số phương pháp đo và dụng cụ đo các đại lượng vật lý cơ bản,
đồng thời biết cách đánh giá độ chính xác các kết quả của phép đo.
3. Rèn luyện tác phong thực nghiệm khoa học, góp phần xây dựng phương pháp
nghiên cứu khoa học cần thiết cho kỹ sư, cử nhân tương lai.
Để học tập tốt phần thí nghiệm - thực hành Vật lý, trước tiên người tiến hành thí
nghiệm phải hiểu rõ được phép đo các đại lượng Vật lý và cách tính sai số các phép đo này.
I. THẾ NÀO LÀ PHÉP ĐO CÁC ĐẠI LƯỢNG VẬT LÝ
Mỗi tính chất vật lý của các đối tượng vật chất được đặc trưng bởi một đại lượng
vật lý như: độ dài, khối lượng, thời gian, vận tốc, gia tốc, nhiệt độ, ...
Để xác định định tính và định lượng các tính chất vật lý người ta phải tiến hành
phép đo các đại lượng vật lý. Phép đo các đại lượng vật lý là phép so sánh nó với một đại
lượng cùng loại được quy ước chọn làm đơn vị đo. Công cụ giúp chúng ta thực hiện việc
so sánh trên được gọi là dụng cụ đo.
+ Nếu so sánh trực tiếp đại lượng cần đo với dụng cụ đo thì ta gọi đó là phép đo trực tiếp.
+ Những đại lượng không so sánh với dụng cụ đo mà được xác định thông qua các
đại lượng đo trực tiếp bằng các công thức toán học thì ta gọi đó là phép đo gián tiếp.
Kết quả phép đo một đại lượng vật lý được biểu diễn bởi một giá trị bằng số kèm
theo đơn vị đo tương ứng. Thí dụ: độ dài của một cạnh cửa là L = 3,5m, khối lượng của
một vật là m = 3kg, vận tốc của một chiếc ôtô là v = 60m/s,...
Muốn thực hiện các phép đo người ta phải xây dựng lý thuyết của các phương pháp
đo và sử dụng các dụng cụ đo như thước milimét, cân kỹ thuật, đồng hồ bấm giây, nhiệt
kế, ampekế, vôn kế, ...
Hiện nay chúng ta dùng các đơn vị đo được quy định trong bảng đo lường hợp
pháp của nước Việt Nam dựa trên cơ sở của hệ đơn vị quốc tế SI (Système International Unit) bao gồm:
+ Đơn vị cơ bản: như độ dài: mét (m), khối lượng: kilôgam (kg), thời gian: giây (s),
cường độ dòng điện: ampe (A), cường độ sáng: candela (cd), lượng chất: mole (mol)…
+ Đơn vị dẫn xuất: như đơn vị đo vận tốc: mét trên giây (m/s), đơn vị đo cường độ
điện trường: Vôn trên mét V/m,...
II. SAI SỐ CỦA CÁC ĐẠI LƯỢNG ĐO
1. Nguyên nhân gây sai số
Độ nhạy và độ chính xác của dụng cụ đo bị giới hạn bởi giác quan của người làm
thí nghiệm thiếu nhạy cảm, điều kiện của các lần đo không thật ổn định, lý thuyết của
phương pháp đo có tính chất gần đúng, ... Do đó, không thể đo chính xác tuyệt đối giá trị
thực của đại lượng vật lý cần đo, nói cách khác là kết quả của phép đo có sai số. Như vậy
khi tiến hành phép đo, không những ta phải xác định giá trị của đại lượng cần đo, mà phải
các định cả sai số của kết quả đo.
* Vấn đề sai số: có nhiều loại sai số gây ra bởi nhiều nguyên nhân khác nhau,
trong đó người tiến hành thí nghiệm cần chú ý các loại sai số quan trọng sau: sai số ngẫu
nhiên và sai số hệ thống.
Sai số ngẫu nhiên là loại sai số khiến cho kết quả đo khi thì lớn hơn, khi thì nhỏ
hơn giá trị thực của đại lượng cần đo. Ví dụ: khi đo thời gian rơi tự do của một vật ta
không thể bấm đồng hồ đúng thời điểm vật bắt đầu rơi cũng như không thể bấm đúng thời
điểm vật bắt đầu chạm đất, mà thường bấm nhanh hơn hay chậm hơn các thời điểm thật
của nó. Sự không cẩn thận khi đo cũng là một trong những nguyên nhân gây ra sai số
ngẫu nhiên. Rõ ràng ta không thể khử được sai số ngẫu nhiên nhưng ta có thể giảm nhỏ
giá trị của nó bằng cách thực hiện đo cẩn thận nhiều lần trong cùng điều kiện và xác định
giá trị trung bình của nó dựa trên cơ sở của phép tính xác suất thống kê.
Sai số dụng cụ là sai số do bản thân dụng cụ, thiết bị gây ra. Thiết bị càng hoàn
thiện thì sai số dụng cụ càng nhỏ, nhưng thực tế không thể khử hết sai số dụng cụ
Sai số hệ thống là sai số làm cho kết quả đo hoặc bao giờ cũng lớn hơn hoặc bao
giờ cũng nhỏ hơn giá trị thực của đại lượng cần đo. Ví dụ: một đồng hồ chạy nhanh mỗi
phút 0,1s thì trong phép đo thời gian ta luôn luôn được khoảng thời gian lớn hơn thời gian
thực mà hiện tượng vật lý xảy ra. Sai số hệ thống thường do người làm thực nghiệm thiếu
cẩn thận, do dụng cụ đo chưa được hiệu chỉnh đúng, vì thế sai số hệ thống là loại sai số
có thể khử được, vấn đề này người làm thực nghiệm tự chú ý khắc phục.
Tóm lại khi làm thí nghiệm chúng ta cần biết cách xác định hai loại sai số là sai số
ngẫu nhiên của phép đo và sai số của dụng cụ đo. Mặt khác trong quá trình thí nghiệm thì
người tiến hành phải hết sức cẩn thận trong việc sử dụng dụng cụ đo và trong xử lý kết quả đo.
2. Cách xác định sai số của phép đo các đại lượng đo trực tiếp
Phép đo các đại lương đo trực tiếp là phép đo mà kết quả của nó được đọc ngay
trên thang của dụng cụ đo.
Giả sử đại lượng cần đo F có giá trị chính xác là A.
Nếu đo trực tiếp đại lượng này n lần trong cùng điều kiện, ta sẽ nhận được các giá
trị A1, A2, A3,...,An khác với giá trị A. Nhưng theo lý thuyết của phép tính xác suất thống
kê, các giá trị A1, A2, A3,...,An được phân bố đều đặn về cả hai phái lân cận giá trị chính xác A.
Khi đó nếu số lần đo n là lớn, giá trị trung bình của chúng là:    ... n A1 A2 A3 A 1 A  n   i A n n i1
Đây là giá trị gần đúng với giá trị A và được gọi là giá trị trung bình của đại lượng cần đo F.
Giá trị tuyệt đối của các hiệu số giữa những giá trị đo được A1, A2, A3,...,An và giá
trị trung bình A được gọi là sai số tuyệt đối của mỗi lần đo. A  A  A 1 1 A  A  A 2 2 ....................... A   A  A n n
Giá trị trung bình của các sai số tuyệt đối trong mỗi lần đo được gọi là sai số tuyệt
đối trung bình của đại lượng F trong các lần đo, đó cũng là sai số ngẫu nhiên (trung bình) của phép đo. A  A  ..  .  1 n A  1 2 n A    n  i i A n 1
Sai số tuyệt đối của phép đo (A) được xác định bằng tổng của sai số tuyệt đối
trung bình của các lần đo A
 và sai số dụng cụ (A)dc: A   A   A  DC
Nó cho biết giá trị trung bình của khoảng giá trị chính xác A của đại lượng cần đo
F. Như vậy giá trị chính xác của đại lượng A được viết là: A  A  A SAI SỐ TỈ ĐỐI
Độ chính xác của kết quả phép đo đại lượng F được đánh giá bằng sai số tỉ đối của
đại lượng cần đo F. Đó là tỷ số giữa sai số tuyệt đối A với giá trị trung bình A Đại lượng A  A  .100% A
Sai số tỉ đối trung bình biểu diễn theo tỷ lệ phần trăm (%). Giá trị của nó càng nhỏ
thì phép đo càng chính xác.
Thí dụ: Dùng thước Panme có độ chính xác (tức độ chia nhỏ nhất) là 0,01mm để đo 5 lần
đường kính D của một ống trụ kim loại, ta được giá trị ghi trong bảng đo dưới đây: Lần đo D (mm ) D (mm) i 1 21,52 0,014 2 21,48 0,026 3 21,51 0,004 4 21,53 0,024 5 21,49 0,016 Giá trị Trung bình 21,506 0,017
Giá trị trung bình của đường kính D là:
21,52  21,48  21,51 21,53  21,49 D   21,506mm 5
Sai số tuyệt đối của từng lần đo được tính là: D
  D D với i 1, 2, 3,.. n i i
(kết quả có trên bảng trên)
Thước Panme có độ chính xác là 0,01mm, tức là sai số dụng cụ trong trường
hợp này bằng 0,01mm nên sai số tuyệt đối của phép đo được tính bằng:
D  D  D  0,017  0,01 0,027mm dc
Sau khi làm tròn ta được D = 0,03 mm
Kết quả là: D = (21,51  0,30) mm
 Các quy tắc làm tròn số
a. Sai số tuyệt đối của phép đo không bao giờ chính xác hơn sai số của dụng cụ đo, trong
ví dụ trên thước cặp chỉ đo được chính xác tới 0,01mm, nên kết quả sai số chỉ cần giữ
lại số đầu tiên sau dấu phẩy: D = 1,64mm thì hai con số 6 và 4 là không chính xác,
do đó phải làm tròn thành 0,2mm.
b. Các sai số tuyệt đối và tương đối được quy tròn sao cho chúng chỉ viết tối đa với 2
chữ số có nghĩa. Còn giá trị trung bình của đại lượng cần đo phải quy tròn đến chữ
số có nghĩa cùng bậc với sai số tuyệt đối của nó. Tất cả các chữ số đều là số có nghĩa
kể cả số 0, trừ những số 0 đầu tiên nằm ở phía bên trái của các chữ số ( ví dụ 0,32 có
2 chữ số có nghĩa, số 0,0320 có 4 chữ số có nghĩa, số 03023 có 4 chữ số có nghĩa).
Việc giữ lại một hay hai chữ số có nghĩa tùy thuộc vào độ chính xác của dụng cụ đo,
trong trường hợp dụng cụ có độ chính xác cao chúng ta giữ lại hai chữ số có nghĩa,
trong trường hợp độ chính xác của dụng cụ thấp hơn ta giữ lại một chữ số có nghĩa
sao cho phù hợp với quy tắc a.
c. Việc làm tròn số tuân theo quy tắc thông thường, nghĩa là các số từ 5 đến 9 quy thành
10, còn các số từ 0 đến 4 quy thành 0; ví dụ 2,05 viết thành 2,1; 3,42 viết thành 3,4.
 Cách xác định sai số dụng cụ a.
Thông thường, sai số dụng cụ lấy bằng giá trị của độ chính xác (tức bằng một độ
chia nhỏ nhất) của dụng cụ đo, trừ trừơng hợp một độ chia nhỏ nhất của dụng cụ có kích
thước quá lớn so với khả năng phân giải của mắt người làm thí nghiệm thì có thể lấy phân nửa độ chia. b.
Đối với các đồng hồ điện (ampekế, vônkế, ...) thì sai số dụng cụ (A)dc được tính
theo công thức: (A)dc = .Am
Trong đó Am là giá trị cực đại trên thang đo của đồng hồ điện.  là cấp chính xác
của đồng hồ đo điện (ghi trên mặt thang đo) và nó biểu thị sai số tương đối (tính ra phần
trăm) của giá trị cực đại Am của đồng hồ đo điện.
Ví dụ: Một miliampekế có cấp chính xác là  = 1 và thang đo sử dụng có giá trị
cực đại Im = 100 mA, thì sai số dụng cụ của bất kỳ giá trị nào mà nó đo được trên thang
đo này cũng có giá trị bằng: (I)dc = 1%.100 = 1mA
Nếu thang đo có 100 vạch chia thì độ chia nhỏ nhất trên thang đo của miliampekế
có giá trị bằng 1mA. Khi đó không được phép lấy sai số dụng cụ bằng 1/ 2 độ chia nhỏ
nhất trên thang đo của miliampekế.
Thí dụ 2: Một miliampekế có cấp chính xác  = 1,5 và thang đo sử dụng giá trị
cực đại Im = 100 mA, thì sai số dụng cụ của bất kỳ giá trị nào mà nó đo được trên thang
đo này cũng có giá trị bằng: (I)dc = 1,5%.100 = 1,5mA
Nếu thang đo có 100 vạch chia thì độ chia nhỏ nhất trên thang đo của miliampe
kế có giá trị bằng 1mA. Khi đó không được phép lấy sai số dụng cụ bằng một độ chia nhỏ
nhất trên thang đo của miliampe kế (bằng 1mA) mà phải lấy sai số dụng cụ bằng 1,5mA. c.
Sai số dụng cụ của các thiết bị đo hiện số được xác định bằng tổng của sai số tính
được theo cấp chính xác và tùy thuộc thang đo như đối với đồng hồ đo điện (mục b) cộng
với một đơn vị của chữ số cuối cùng hiện lên màn hình. Ví dụ một đồng hồ vôn kế hiện
số có cấp chính xác là 1 ( = 1%), ta dùng thang đo có giá trị cực đại Umax = 10 V; giá
trị hiệu điện thế đang đo hiện trên màn hình là 5,7 V (một đơn vị của chữ số cuối cùng,
số 7 tương ứng với 0,1 V); sai số dụng cụ
(U)dc = 1%.10V + 0,1V = 0,2V.
3. Cách xác định sai số đối với phép đo các đại lượng đo gián tiếp
a) Phép đo gián tiếp: là phép đo mà kết qủa đo được xác định gián tiếp thông qua các đại
lượng đo trực tiếp được biểu diễn bằng quan hệ qua những công thức hay quan hệ hàm
giữa các đại lượng cần đo với các đại lượng đo trực tiếp.
Thí dụ: Khối lượng riêng được xác định gián tiếp qua công thức m   trong đó khối V
lượng m được đo trực tiếp bằng cân kỹ thuật, thể tích V được đo bằng thước kẹp,...
b) Cách tính sai số của phép đo gián tiếp
Giả sử đại lượng cần đo F liên hệ với các đại lượng đo trực tiếp x, y, z theo hàm số F = f ( x, y, z )
Để xác định sai số tuyệt đối của đại lượng F ta làm như sau: + Lấy vi phân hàm F F F  F dF  d . x  d . y  .dz x  y z 
+ Dựa vào phương pháp toán học ta thay các dấu vi phân bằng dấu gia số. F = F  F  F . x   .y   . z x y z 
+ Vì không biết rõ chiều thay đổi (tăng hay giảm) của các sai số x, y, z ta phải
chọn giá trị lớn nhất của sai số F bằng cách lấy tổng trị tuyệt đối của các vi phân riêng
phần trong biểu thức trên:    F F F F  . x   . y   . z  x  y  z 
Sai số tương đối cũng có thể xác định theo phép tính vi phân như sau:
 Tính loga nêpe của hàm số: lnF = ln f(x, y, z) dF
 Tính vi phân toàn phần của lnF: d(lnF) = F dF
 Rút gọn biểu thức vi phân toàn phần
bằng cách gộp những vi phân riêng phần F
chứa cùng vi phân của biến số dx, hoặc dy, hoặc dz.
 Lấy tổng trị tuyệt đối của vi phân riêng phần. Thay dấu vi phân “d” bằng dấu sai
số “”, đồng thời thay x, y, z bằng các giá trị trung bình của chúng.
Thí dụ: Đo lực ma sát của ổ trục quay theo công thức f h  1 h ms = mg. 2 h  1 h2
Theo quy tắc nêu trên, trước hết ta tính
Lnfms = ln m + ln g + ln (h1 - h2) - ln (h1 + h2)
Sau đó, tính vi phân toàn phần của ln fms df dm dg d (h  h ) d (h  h ) ms 1 2 1 2     f m g h  h h  h ms 1 2 1 2
Rút gọn biểu thức của vi phân toàn phần ta tìm được: df dm dg ( 2 h .dh  h .dh ) ms 2 1 1 2    2 2 f m g  ms h h 1 2
Lấy tổng giá trị tuyệt đối của các vi phân riêng phần bằng cách thay dấu (-) trước
dh2 thành dấu (+). Thay dấu vi phân “d” bằng dấu sai số “” và thay các đại lượng đo trực
tiếp bằng các giá trị trung bình của chúng: m  g  2(h . h   h . h  ) 2 1 1 2  f    ms 2 2 m g h  h 1 2
Chú ý: Ta có thể tính sai số của phép đo gián tiếp tuân theo hai quy tắc như sau:
a) Nếu công thức của đại lượng cần đo F là một tổng hoặc một hiệu của đại lượng đo trực
tiếp x và y, thì tính sai số tuyệt đối trung bình trước: F = x  y F   x   y
Sau đó mới tính giá trị trung bình F và suy ra sai số tỉ đối.
b) Ngược lại, nếu công thức của đại lượng cần đo F là một tích số hay một thương số của
đại lượng đo trực tiếp x và y, thì phải tính sai số tương đối trước: F = x . y hoặc F = x y Và x y  F   x   y   x y
Sau khi xác định được sai số tỉ đối , ta mới tính giá trị trung bình F và suy ra sai số tuyệt đối.
c) Vì các sai số được quy tròn và giữ lại hai số có nghĩa, trong công thức tính sai số
tương đối, nếu có một số hạng lớn gấp 10 lần một số hạng khác, ta có thể bỏ qua số hạng
này, với điều kiện tổng của tất cả các số hạng bỏ đi vẫn nhỏ hơn nhiều so với số hạng lớn giữ lại.
d) Nếu trong công thức tính đại lượng cần đo F có chứa những số cho trước (không
ghi sai số kèm theo) hoặc chứa những hằng số thì sai số của chúng được xác định kèm theo quy tắc sau:
Sai số tuyệt đối của đại lượng cho trước lấy bằng một đơn vị của những chữ số cuối cùng của nó.
Thí dụ: Cho D = 12,0 mm thì lấy D = 0,1 mm
Đối với những hằng số như (, g, e,...) thì lấy giá trị của hằng số đến chữ số mà sai
số tương đối của hằng số đó nhỏ hơn hoắc bằng 1/10 giá trị của ít nhất một sai số tương
đối của hằng số đó trong công thức tính.
Ví dụ: Thể tích của khối trụ được tính theo công thức 1 2
V   D .h, biết đường 4
kính đáy trụ D = ( 30,2  0,1) mm và chiều cao của trụ h = (50,1  0,1) mm. Vì V  2D h  2. 1 , 0 1 , 0            , 0 0086 V  D h  3 , 0 2 50 1 , 
Nên phải lấy  = 3,141 để  , 0 001   ,
0 0003  0,0086/10 = 0,00086  1 , 3 41 Khi đó 3 V  1 , 3 41.30 3 , 5 . 0 1 ,  4752 3 , 95  4752mm Và V  ..V  4752 . 0089 , 0  29 , 42  40 mm3
Kết quả: V = 4750  40 mm3
Hay viết thành: V = (475  4) .10 mm 3;  = 0,009 = 0,9%
Phương pháp đồ thị biểu diễn kết quả đo
Ngoài phương pháp biểu diễn kết quả đo trên, phương pháp biểu diễn kết quả đo
bằng đồ thị được ứng dụng nhiều trong thí nghiệm vật lý. Phương pháp này cho phép:
1/ Thể hiện một cách trực quan sự phụ thuộc hàm số của một đại lượng vật lý này vào
một đại lượng vật lý khác. Thí dụ: nghiên cứu sự phụ thuộc của điện trở dây dẫn vào nhiệt
độ t, ta được các số liệu trong bảng dưới đây:
t ( 0C) 0,0  0,1 1,0  0,1 2,0  0,1 3,0  0,1 4,0  0,1 5,0  0,1
R () 20  2 60  3 80  2 100  3 120  2 140  2
Căn cứ vào bảng số liệu trên, vẽ đồ thị biểu diễn hàm số R = f (t) như sau:
a/ Vẽ một hệ trục tọa độ vuông góc trên giấy kẻ ô milimét. Chọn tỷ lệ thích hợp trên các
trục để đồ thị được cân đối, rõ ràng, chính xác.
Trên trục tung ghi các giá trị của R, trên trục
hoành ghi các giá trị của t.
b/ Với mỗi cặp giá trị tương ứng của R và t,
vẽ một điểm đánh dấu bằng một chữ thập
có kích thước ngang bằng giá trị sai số của R.
c/ Vẽ đường biểu diễn thành một đường
liên tục (thẳng hoặc cong) sao cho giao điểm của các chữ thập phân bố đều về cả hai phía
của nó. Đường biểu diễn như vậy là đường trung bình của các điểm đo được.
2/ Nội suy các giá trị của hàm số ứng với các giá trị của đối số không có trong bảng số liệu nêu trên:
Sau khi vẽ đồ thị R = f (t) theo các số liệu đã đo được, ta có thể tìm được giá trị của
điện trở R1 tương ứng với nhiệt độ t1 đã cho bằng cách đặt giá trị của t1 lên trục hoành,
rồi kẻ một đường song song với trục tung đi qua điểm t1 và cắt đồ thị tại một điểm M nào đó.
Tung độ của điểm M cho biết giá trị của điện trở R1 . Muốn xác định sai số R của
điện trở ta lấy giá trị  t rồi kẻ hai đường bao đi qua hai điểm -R và +R cắt đồ thị ở
hai điểm. Từ hai điểm này, kẻ hai đường song song với trục hoành, giao điểm của hai
đường đo với trục tung xác định giá trị  R.
Phần 2: CÁC BÀI THÍ NGHIỆM Bài thí nghiệm số 1
XÁC ĐỊNH THỂ TÍCH CÁC VẬT RẮN ĐỒNG CHẤT CÓ DẠNG ĐỐI
XỨNG VÀ CÂN KHỐI LƯỢNG CỦA VẬT TRÊN CÂN KỸ THUẬT I. CÁC DỤNG CỤ ĐO
a) Thước kẹp: Thước kẹp là dụng cụ đo độ dài.
- Độ chính xác: Chính là sai số của dụng cụ đo có giá trị là 0,02mm hoặc 0,05mm. Hình ảnh thước kẹp: Ngàm trên Ngàm dưới - Cấu tạo: T
Cấu tạo thước kẹp gồm một thước chính T (thước cố
định) được chia đều thành từng milimét và một Du xích 0 5 10
(thước trượt) được chế tạo sao cho N độ chia của nó có độ n
dài đúng bằng N-1 độ chia của thước chính. Gọi a là giá trị 0 m
của mỗi độ chia trên thước chính, b là giá trị của mỗi độ T’
chia trên Du xích, ta có điều kiện: a
N.b  (N  1).a  (a b)  N Đặt a   N
Đại lượng  được gọi là độ chính xác của Du xích, nó cho biết độ sai lệch giữa giá
trị mỗi độ chia của thước chính và mỗi độ chia của Du xích.
Độ chia trên thước T là a = 1mm nên nếu số vạch trên Du xích là N = 50 thì  = 0,02
mm; Nếu N = 20 thì  = 0,05 mm.
Cách đo và đọc số liệu:
- Đưa vật cần đo vào giữa hai ngàm của thước kẹp. Nếu đo đường kính
trong thì dùng ngàm trên, nếu đo đường kính ngoài thì dùng ngàm dưới.
- Dùng ta đẩy núm nhỏ phía trên thước chính sao cho hai ngàm của thước
sít chặt vào vật, vặn núm nhỏ chặt lại để cố định thước.
- Căn cứ vào vị trí của các vạch trên thước chính và du xích để đọc số liệu.
Gọi d là giá trị cần đo, ta có công thức đọc như sau: d  n  . m
Trong đó: n là số vạch chia trên thước chính nằm giữa hai vạch số 0 trên thước
chính và du xích. Hay là số vạch trên thước chính nằm bên trái vạch số 0 của thước phụ.
m là vạch thứ m trên thước phụ, trùng nhất với vạch bất kỳ trên thước chính.
 là sai số hay cấp chính xác của thước. 21
Ví dụ: Ta dùng thước có   0,02mm . Theo hình vẽ trên, ta đọc phép đo như sau:
d  13 21.0,02  13,42mm
b) Thước Panme: Là dụng cụ đo độ dài từ 0 – 25mm. - Độ chính xác: 0,01mm  Cấu tạo: 2 1 4 3 5 6
Gồm một cán thước hình chữ U mang trục vít vi cấp 1 và đầu tựa cố định 2.
Một thước kép có các độ chia nằm sole nhau, cách nhau 0,05mm nằm phía trên và
phía dưới của đường thẳng chuẩn nằm ngang trên thân trụ 3.
Một cần gạt nhỏ 4 dùng hãm trục vít 1. Một thước tròn có 50 độ chia bằng nhau
nằm ở sát mép trái của trụ rỗng 5, bao quanh thân trụ 3.
Khi vặn đầu 6 của trục vít 1, thước tròn sẽ quanh và tịnh tiến theo bước ren h =
0,05mm của trục vít 1. Như vậy, khi thước tròn quay đúng một vòng ứng với N = 50 độ
chia thì đồng thời nó tịnh tiến một đoạn h = 0,5mm dọc theo thước kép. Mỗi độ chia trên
thước tròn ứng với giá trị: h 0,5     0,01mm N 50
Giá trị này được gọi là sai số của dụng cụ đo hay cấp chính xác của dụng cụ đo.
 Cách đo và đọc số liệu
Để đo chiều dài vật nhỏ nào đó, chúng ta làm theo các bước sau:
+ Vặn đầu 6 của trục vít 1 ngược chiều kim đồng hồ sao cho nghe tiếng tạch tạch văng
lên thì dừng lại, kiểm tra xem vạch số 0 trên mép thước tròn đã trùng với đường chuẩn
nằm ngang và mép thước tròn trùng với vạch số 0 trên trước cố định 3 chưa, Nếu chưa
trùng thì yêu cầu giáo viên hướng dẫn hiệu chỉnh thước cho đúng như trên.
+ Vặn đầu 6 của trục vít 1 cùng chiều kim đồng hồ cho đến khi bỏ vừa vật cần đo vào
giữa hai khe 1 và 2 một cách dễ dàng. Sau đó vặn đầu 6 của trục vít 1 ngược chiều kim
đồng hồ (KHÔNG ĐƯỢC CẦM TRÊN TRỤ RỖNG 5 ĐỂ QUAY) sao cho nghe tiếng
kêu tạch tạch thì ta phải gạt nhỏ 4 dùng hãm trục vít 1 lại để tiến hành đọc số liệu:
Có hai trường hợp xảy ra khi đo:
+ Nếu mép thước tròn nằm sát bên phải vạch chia thứ N của thước milimet ở
phía trên đường chuẩn ngang, đồng thời đường chuẩn ngang sát vạch thứ n của thước tròn thì: d  N  0, 01.n (m ) m
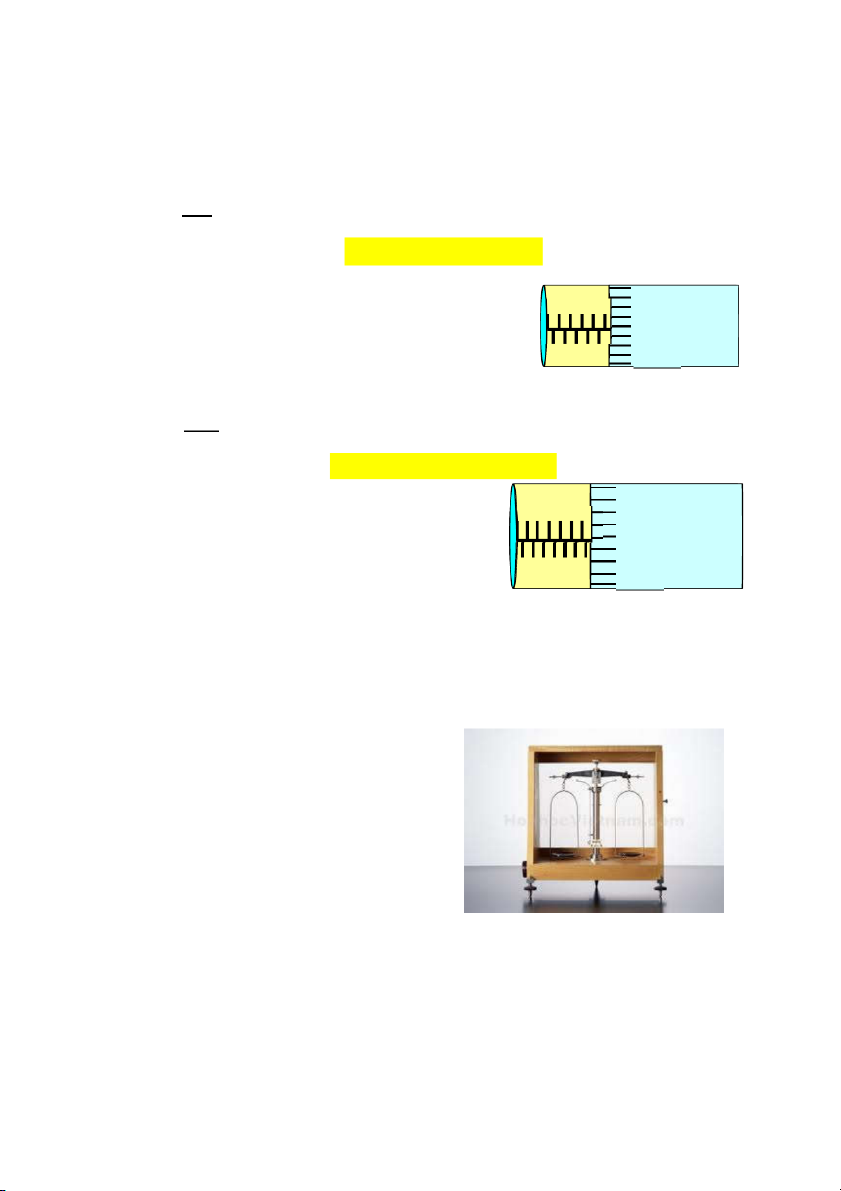
Ví dụ: Giả sử hệ thống các vạch trên thước được 1 50 0 1 2 3 4 5
biểu diễn như hình vẽ. 49 48 Ta đọc như sau: 47 46
d  5  48.0,01  5,48mm 45
+ Nếu mép thước tròn nằm sát bên phải vạch chia thứ N của thước milimet ở
phía dưới đường chuẩn ngang, đồng thời đường chuẩn ngang sát vạch thứ n của thước tròn thì: d  N  0,5  0,01.n (m ) m
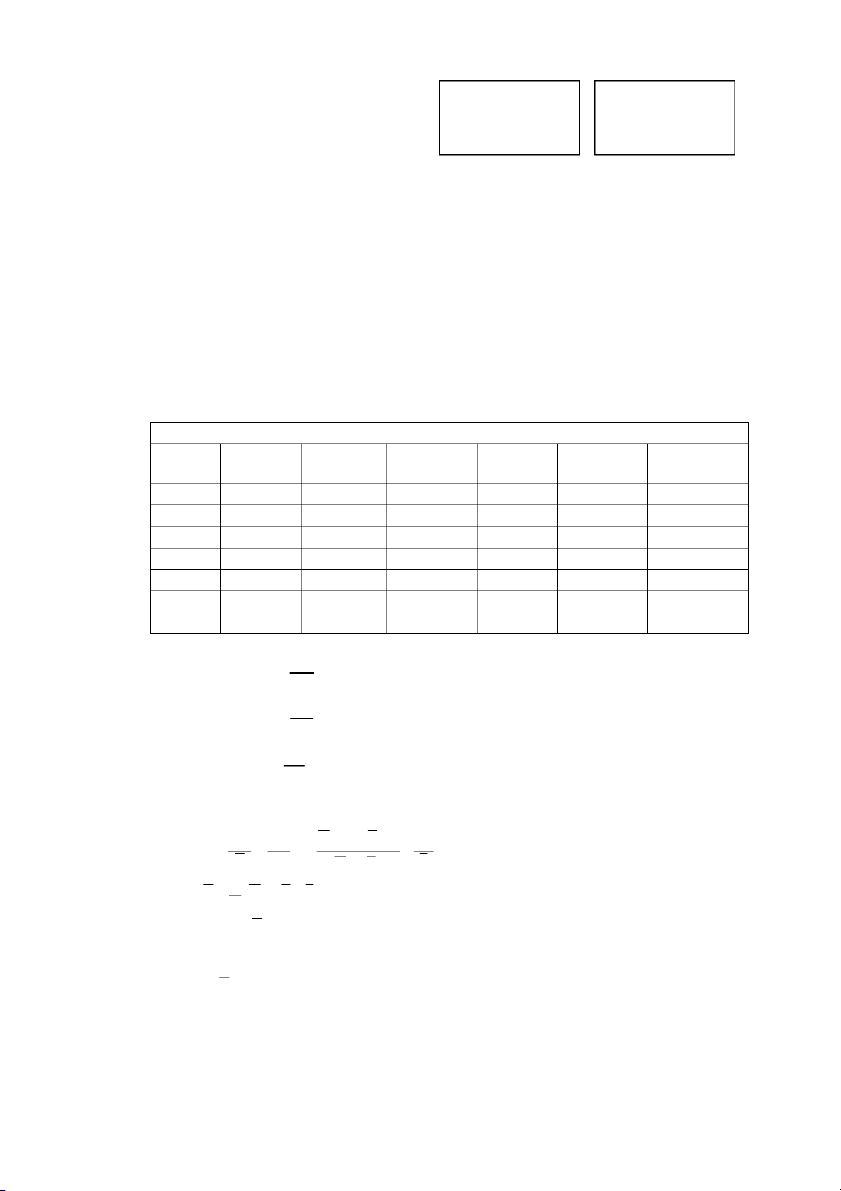
Ví dụ: Giả sử hệ thống các vạch trên thước được 1
biểu diễn như hình vẽ. 50 0 1 2 3 4 5 6 49 Ta đọc như sau: 48 47 d 6 0  ,5 4  7.0,01 6,97 mm 46 45 44 43 42 Chú ý:
- Các giá trị n, N là số vạch chia nên là các số nguyên.
- Không được cầm trụ rỗng 5 quay khi sít vật để đo.
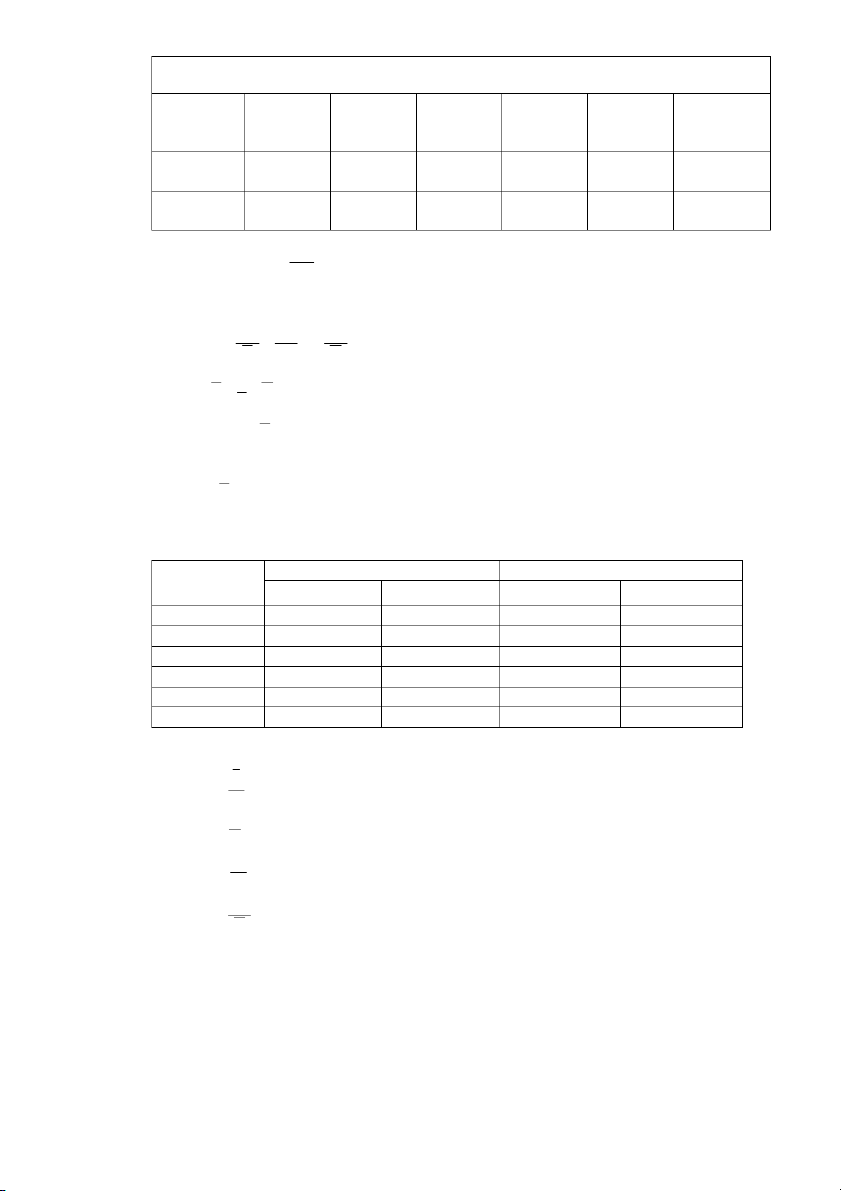
c) Cân kỹ thuật là dụng cụ đo khối lượng
của các vật trong giới hạn 0 - 200g với độ chính xác 0,02g.  Cấu tạo
Cân kỹ thuật có cấu tạo gồm phần
chính là một đòn cân làm bằng hợp kim nhẹ,
trên đòn cân có khắc các độ chia từ 0 đến 50.
Ở chính giữa thân của đòn cân có gắn một
con dao O hình lăng trụ tam giác bằng thép Cân kỹ thuật
cứng, cạnh của con dao quay xuống phía
dưới và đặt tựa trên mặt phẳng ngang (bằng đá mã nảo) trên đỉnh của trụ cân. Ơ hai đầu
của đòn cân cũng có hai con dao O1 và O2 tương tự như con dao O. Các cạnh của hai con
dao O1 và O2 quay lên trên và được đặt song song với cạnh của con dao O, đồng thời
chúng nằm cách đều cạnh của con dao O nên các cánh tay đòn OO1 bằng OO2 = L. Trên
hai con dao O1 và O2 có treo hai chiếc móc mang hai đĩa cân giống nhau. Nhờ một kim
dài K gắn vào đòn cân (ở ngay phía dưới con dao O) và một thước nhỏ T trên thân chân
trụ, ta có thể xác định chỉ đúng số 0 của thước nhỏ T. Có thể điều chỉnh vị trí cân bằng
của cân nhờ hai vít nhỏ Đ ở mỗi đầu của đòn cân. Toàn bộ cân đặt trên đế cân đựng trong
tủ kính, dưới đế cân có hai vít xoay V dùng điều chỉnh cho trụ cân thẳng đứng.
Ở mặt trước của trụ cân có một núm xoay N dùng nâng hoặc hạ đòn cân lên xuống theo
phương thẳng đứng. Khi nâng đòn cân lên, cạnh của con dao O không tựa trên mặt phẳng
ngang của trụ cân: “cân ở vị trí nghỉ ”. Khi hạ đòn cân xuống cạnh của con dao O tỳ lên
mặt phẳng ngang và đòn cân có thể dao động nhẹ quanh cạnh của con dao O: “ cân ở vị
trí làm việc “. Đồng thời còn có một hộp gỗ đựng các quả cân từ 10 đến 100g. Có thể dịch
chuyển một quả cân nhỏ C đặt ngay trên đòn cân - gọi là con mã, để thêm (hay bớt) những
khối lượng nhở hơn hoặc bằng 1g vào các đĩa cân.
Muốn cân một vật có khối lượng m ứng với trọng lượng p = mg, ta đặt lên đĩa cân bên
trái. Sau đó đặt các quả cân theo thứ tự từ lớn đến nhỏ lên đĩa cân bên phải cho tới khi
vặn ném xoay N để đòn cân nằm ở vị trí “làm việc”, thì đầu dưới của kim K dao động nhẹ
về hai phía của số 0 trên thước T ở chân trụ cân. Khi đó tổng khối lượng m của các quả
cân đặt trên đĩa cân bên phải ứng với trọng lượng p’ = m’.g. Ap dụng quy tắt momen lực
đối với cạnh của con dao O ở vị trí cân bằng của đòn cân, ta có đẳng thức: . p L  p '.L 1 2
Vì L1 = L2 nên p = p’ và suy ra m = m’
Như vậy khi cân ở vị trí ”làm việc” cân bằng: khối lượng của vật ở hai đĩa bên trái và
phải của cân đúng bằng nhau. II. TRÌNH TỰ THÍ NGHIỆM
1. Xác định thể tích của ống trụ rỗng kim loại bằng thước kẹp a) Mục đích thí nghiệm
- Làm quen với các dụng cụ đo độ dài như thước kẹp để đo chiều dài của vật.
- Đo gián tiếp thể tích của các vật có dạng đối xứng.
- Biết tính sai số và viết kết quả của phép đo trực tiếp, gián tiếp. b) Dụng cụ thí nghiệm
- Thước kẹp 0 – 15mm, độ chính xác là 0,02mm; 0,05mm.
- Hai mẫu vật cần đo là hai vòng đồng rỗng, hình trụ. c) Tiến hành
- Thể tích hình trụ rỗng được tính theo công thức  2 2 V  .(D d ).h 4
Trong đó: D là đường kính ngoài ống trụ
d là đường kính trong ống trụ
h là chiều cao ống trụ
- Hiệu chỉnh thước kẹp: Đẩy hai ngàm thước sít vào nhau sao cho hai vạch số 0 trên hai
thước trùng sát nhau thì được. Nếu chưa trùng thì yêu cầu giáo viên hướng dẫn hiệu chỉnh.
- Lần lượt đo đường kính trong d, đường kính ngoài D, chiều cao h của vòng đồng rỗng.
Đo 5 lần rồi ghi vào bảng số liệu 1.
- Tiến hành xử lý sai số theo mẫu và viết kết quả.
2. Xác định thể tích viên bi thép bằng thước panme a) Mục đích thí nghiệm
- Làm quen với các dụng cụ đo độ dài như thước panme để đo chiều dài của vật.
- Đo gián tiếp thể tích của các vật có dạng đối xứng.
- Biết tính sai số và viết kết quả của phép đo trực tiếp, gián tiếp. b) Dụng cụ thí nghiệm
- Thước kẹp 0 – 25mm, độ chính xác là 0,01mm.
- Hai mẫu vật cần đo là viên bi thép. c) Tiến hành
- Thể tích viên bi thép được tính theo công thức 1 3
V  . D Trong đó: D là đường kính viên bi 6
- Hiệu chỉnh thước panme.
- Lần lượt đo đường kính D của viên bi. Đo 5 lần rồi ghi vào bảng số liệu 2.
- Tiến hành xử lý sai số theo mẫu và viết kết quả.
3. Xác định khối lượng vật bằng cân kỹ thuật a) Mục đích thí nghiệm
- Làm quen với dụng cụ đo độ dài là cân kỹ thuật để đo khối lượng của vật.
- Đo trực tiếp khối lượng của một số mẫu vật.
- Biết tính sai số và viết kết quả của phép đo trực tiếp, gián tiếp. b) Dụng cụ thí nghiệm
- Cân kỹ thuật, có độ chính xác 0,02g
- Hai mẫu vật cần đo là viên bi thép, vòng đồng rỗng.
- Hộp đựng quả cân, có khối lượng từ 10mg đến 500g.
c) Tiến trình thí nghiệm - Hiệu chỉnh cân.
- Đối với cân kỹ thuật có đòn cân (cánh tay đòn) bằng nhau, trọng lượng P của khối
lượng vật bằng trọng lượng P0 của các quả cân. Nên khối lượng của vật cần cân bằng khối
lượng của các quả cân. m = m0
- Tiến hành cân không tải nhằm xác định độ nhạy và độ chính xác của cân: (cân 5 lần)
+ Chưa đặt vật hoặc các quả cân lên đĩa cân. Gạt con mã về vị trí số 0 trên đòn cân.
+ Vặn núm xoay N ngược chiều kim đồng hồ để cân hoạt động trong trạng
thái không tải. Nếu kim chỉ thị K không chỉ đúng vạch số 0 hoặc không dao động
đều xung quanh vạch số 0 trên thước T thì hạ cân xuống ở trạng thái tĩnh (bằng
cách xoay núm N cùng chiều kim đồng hồ) và tiến hành điều chỉnh các núm ở
hai bên đòn cân đến khi cân thăng bằng.
+ Khi cân đang ở trạng thái ”nghỉ”. Đặt quả cân 10mg lên đĩa cân bên trái,
sau đó đưa cân lên ở trạng thái hoạt động. Đọc số độ chia n trên thước T ứng với
số vạch mà kim K lệch khỏi vạch số 0 trên thước T.
+ Tính độ nhạy S của cân theo công thức: n S  (do chia / mg) 10
+ Đại lượng nghịch đảo của độ nhạy S gọi là độ chính xác của cân : 1   (mg / do chia) S
- Cân 5 lần khối lượng mẫu vật rồi ghi vào bảng số liệu 3.
+ Khi cân đang ở trạng thái nghỉ. Đặt mẫu vật cần cân vào 1 đĩa cân, lựa
chọn các quả cân từ bé đến lớn đặt vào đĩa cân còn lại. Vặn núm xoay N ngược
chiều kim đồng hồ để nâng cân lên ở trạng thái hoạt động. Nếu kim chỉ thị K
dao động đều quanh vạch số 0 hoặc chỉ đúng vạch số 0 trên thước T thì hạ cân
xuống. Khối lượng tổng cộng các quả cân chính là khối lượng của mẫu vật cần cân.
- Tiến hành xử lý sai số theo mẫu và viết kết quả.
4. Xác định khối lượng riêng  của thanh trụ kim loại
Sau khi đo được thể tích V và khối lượng, của thanh trụ kim loại, ta có thể xác định
khối lượng riêng  của nó theo công thức và tính sai số phép đo. m   V III. Câu hỏi kiểm tra
1. Trình bày cấu tạo của thước kẹp, nguyên tắc của Du xích thẳng và độ chính xác của
nó. Nói rõ cách đo độ dài của một vật bằng thước kẹp.
2. Trình bày nguyên tắc cấu tạo của thước panme và độ chính xác của nó. Nói rõ cách đo
đường kính của một vật bằng thước panme. 3. V 
Dựa vào công thức (1), tìm công thức tính sai số tương đối
đối với thể tích V của V thanh trụ kim loại.
4. Trình bày nguyên tắc cấu tạo của cân kỹ thuật và độ chính xác của nó. Nói rõ cách cân
khối lượng của một vật trên cân kỹ thuật.
5. Viết công thức xác định khối lượng riêng  của thanh trụ kim loại. Tìm biểu thức tính sai số tương đối 
 của thanh trụ kim loại. 
Trường Đại học Duy Tân Xác nhận của Giáo viên
Họ và tên: ……………………
Lớp:…………………Tổ:……
BÀI BÁO CÁO THÍ NGHIỆM SỐ 1
XÁC ĐỊNH THỂ TÍCH CÁC VẬT RẮN CÓ DẠNG ĐỐI XỨNG
VÀ CÂN MẪU VẬT TRÊN CÂN KỸ THUẬT I. MỤC ĐÍCH THÍ NGHIỆM
..................................................................................................................................
.................................................................................................................................. II. KẾT QUẢ THÍ NGHIỆM
1. Xác định thể tích của chiếc vòng đồng (khối trụ rỗng)
Bảng 1 Độ chính xác của thước kẹp: ………..(mm) D d d h h Lần đo D (.10-3m) (.10-3m) (.10-3m) (.10-3m ) (.10-3m) (.10-3m) 1 2 3 4 5 Trung bình
a. Tính sai số tuyệt đối của phép đo 3 D D
D ........... ..................... .....................10        (m) dc 3 d d
d .............................. ....................10        m dc 3 h h h         m dc
.................................. .....................10
b. Tính sai số và kết quả phép đo thể tích vòng đồng V  D.D  d .d h    2.  ................. 2 2 V  D d h  2 2
V  (D d ).h ................... 4  V
  .V ..........................
c. Kết quả của phép đo
V  V  V  .................... ........... ..........
2. Xác định thể tích của khối cầu (viên bi thép)
Bảng 2 Độ chính xác của thước panme:…………….(mm) Trung Lần đo 1 2 3 4 5 bình 3 D(.10 m) 3 D  (.10 m)
a. Tính sai số tuyệt đối của phép đo 3 D D
D ........... ..................... .....................10         (m) dc
b. Tính sai số và kết quả phép đo thể tích viên bi V   D       3.  ................. V  D 1 3
 V  .D  ................... 6
 V  .V  ..........................
c. Kết quả của phép đo
V  V  V  .................... ........... ..........
3. Cân khối lượng mẫu vật trên cân kỹ thuật Bảng 3. Cân không tải Cân có tải Lần đo n n 3 m (.10 kg) 3 m (.10  kg) 0 0 1 2 3 4 5 Trung bình
a) Xác định độ nhạy và độ chính xác của cân n  S   ................... 10 1  
........................... S
b) Tính sai số và độ nhạy của phép cân khối lượng 3 m m m
................... ................(10        kg) 0 0 m   
.100% ....................................(%) m Meeting ID: 954 3721 2857 Passcode: 3y605t Bài thí nghiệm số 2
XÁC ĐỊNH MÔMEN QUÁN TÍNH CỦA TRỤ ĐẶC CÓ TRỤC QUAY
ĐỐI XỨNG VÀ LỰC MA SÁT CỦA Ổ TRỤC QUAY Dụng cụ:
1. Bộ thiết bị vật lý MC - 965 (bánh xe có trục quay, giá đỡ có ổ trục quay, quả
nặng, dây treo, hộp chân đế)
2. Thước kẹp 0 - 150mm, chính xác 0,02mm
3. Máy đo thời gian đa năng hiện số MC - 963A
4. Đầu cảm biến thu phát quang điện hồng ngoại
5. Hộp điều khiển khởi động máy I. CƠ SỞ LÝ THUYẾT 
Gia tốc góc  của một vật rắn quay quanh một trục cố định  tỷ lệ thuận với
momen lực M tác dụng lên vật rắn và tỷ lệ nghịch với momen quán tính I của vật
rắn đó đối với trục quay : M  I. 
Đó là phương trình cơ bản của chuyển động quay của vật rắn. Momem quán tính
I đặc trưng cho quán tính của vật rắn trong chuyển động quay và được đo bằng đơn vị kg.m2.
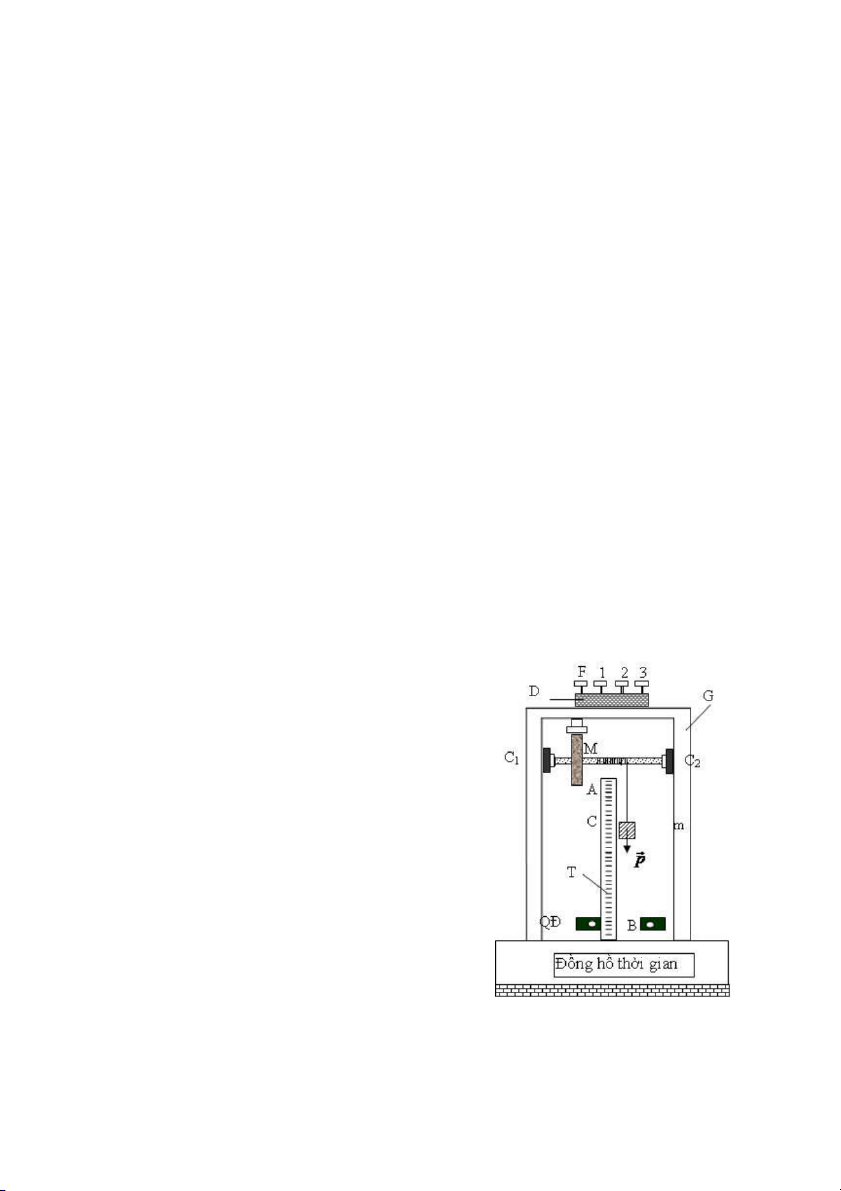
Có thể xác định momen quán tính của
một bánh xe và lực ma sát của ổ trục quay của
nó nhờ bộ thiết bị vật lý MC - 965 (hình 1).
Một bánh xe khối lượng M có trục quay gối
trong hai ổ trục C1 C2 gắn cố định vào giá đỡ
G dựng thẳng đứng trên hộp chân đế H. Một
sợi dây mảnh và không giãn được cuốn xít
nhau thành một lớp trên trục quay: một đầu
buộc vào trục, đầu kia treo quả nặng khối
lượng m. Vị trí của quả nặng m được xác định
trên thước milimét T. Nhờ bộ điều khiển Đ (có
4 núm bấm F -1- 2- 3) nối với máy đo thời
gian hiện số MC - 963 và đầu cảm biến quang
điện QĐ, ta có thể dể dàng khởi động máy và
tự động đo khoảng thời gian chuyển động của
hệ vật gồm quả nặng m và bánh xe M.
Lúc đầu, bánh xe M đứng yên và quả
nặng m ở vị trí A có độ cao h1 so với vị trí thấp nhất của nó tại B, vậy thế năng dự
trữ của vật là mgh1. Sau đó thả cho hệ vật chuyển động dưới tác dụng của trọng lực  
p  m.g của quả nặng. Khi đó quả nặng m tịnh tiến từ A đến B, đồng thời bánh xe
M quay quanh trục nằm ngang của ns. Thế năng dự trữ mgh1 của hệ vật chuyển một 2 2
phần thành động năng tịnh tiến mv của qủa nặng và động năng quay  I của 2 2
bánh xe (kể cả trục quay của nó), phần còn lại dùng để thắng công cản của lực ma
sát Ac = fms.h1 trong hai ổ trục quay C1C2.
Áp dụng định luật biến đổi và bảo toàn cơ năng cho quá trình chuyển động này
của hệ vật nói trên từ A đến B, ta có 2 2 mg.h mv I 1 = + + fms.h1 (2) 2 2
Khi quả nặng m đến vị trí thấp nhất, theo quán tính, trụ đặc tiếp tục quay và
quấn dây làm cho quả nặng lên đên độ cao h2. Theo định lý thế năng, ta có: f .(h  h )  mg(h  h ) ms 1 2 1 2 h  h (3) 1 2  f  ms mg h h 1 2
Vì quả nặng m chuyển động thẳng nhanh dần đều trên đoạn đường AB = h1 trong
khoảng thời gian t, nên vận tốc của nó tại vị trí thấp nhất B có giá trị bằng: 2h1 v  (4) t
Vận tốc này đồng thời cũng là vật tốc dài của một điểm trên trục quay của bánh
xe M tại thời điểm t (kể từ khi bánh xe bắt đầu quay). Nó liên hệ với vận tốc góc 
và bán kính r của trục quay bởi hệ thức v   . Từ đó suy ra: r  = h . 2 1 (5) t.r
thay các đại lượng trên vào (2), ta tìm được: 2 md h 2 2 I  (gt 1) 4 h (h h ) 1 1 2
Trong thí nghiệm này, ta sẽ xác định được lực ma sát fms trong ổ trục quay và
momen quán tính I của bánh xe ( kể cả trục quay của nó) theo các công thức (3) và
(6) bằng cách đo bán kính r của trục quay, đo thời gian chuyển động t của hệ vật,
đo các độ cao h1 và h2 của quả nặng và biết trước khối lượng của quả nặng.