













































Preview text:
lOMoARcPSD| 36207943 1 Giới thiệu môn học
Môn toán cao cấp cung cấp những kiến thức nền tảng và bổ trợ cho các môn như kinh tế vi mô,
kinh tế vĩ mô, lý thuyết xác suất, thống kê ứng dụng, kinh tế lượng, dự báo kinh tế, v.v.
Mặc dù tất cả các trường uy tín trên thế giới đều có học phần tương tự toán cao cấp cho sinh
viên năm nhất, nhiều sinh viên và giảng viên đại học ở Việt Nam chưa hiểu "vì sao cần học những
kiến thức cơ sở" này? Liên hệ một chút, khi muốn học chơi cờ, chơi đàn hay một môn gì mới, ban
đầu chúng ta cần hiểu rõ về "cách chơi", "luật chơi", có đúng vậy không? Các môn khoa học nói
chung và toán nói riêng cũng hơi giống như vậy! Nếu ta muốn sử dụng được các phương pháp toán
học định lượng để nghiên cứu các hiện tượng hay quy luật trong thực tiễn, ta cần biết các kiến thức
cơ sở của toán. Những cơ sở cơ bản nhất nằm trong đại số tuyến tính và giải tích. Đó là nội dung
chính của học phần này.
Chú ý rằng, hiểu rõ "luật chơi" chỉ là điều kiện cần, chưa bảo đảm để bạn sẽ trở thành kiện tướng
cờ thực sự hay là một nghệ sỹ với những bản nhạc tuyệt vời. Muốn đạt tới đó, cần có đủ đam mê và quá trình rèn luyện.
Hướng tới giáo dục 4.0, trong tài liệu này bên cạnh khối kiến thức căn bản về đại số và giải tích,
chúng tôi bổ sung một số yếu tố mới, với mục tiêu: 1.
Đưa môn học đến gần hơn với các môn cơ sở ngành và môn chuyên ngành. Đặc biệtchú ý
tới các ứng dụng trực tiếp của kiến thức đại số tuyến tính, giải tích trong kinh tế, kinh doanh và quản lý. 2.
Xây dựng hệ thống bài học gắn với các môn học khác và gắn với thực tiễn. Hình thứchọc tập
đa dạng để tạo điều kiện cho việc triển khai lớp học linh hoạt, phù hợp với nhiều đối tượng chuyên ngành khác nhau. 3.
Tạo thói quen và rèn luyện kỹ năng tìm kiếm, phân tích, tổng hợp, làm việc nhóm,thuyết
trình ... thông qua các bài tập mở, bài tập nhóm, bài tập trình bày. 4.
Giới thiệu cách sử dụng phần mềm, khuyến khích sinh viên thử nghiệm lập trình để xử lý
những bài tập tính toán phức tạp, tiếp cận xử lý các bài toán trong thực tiễn. Chương1
Ma trận và hệ phương trình tuyến tính
Sau khi học xong chương này, người học có những kĩ năng và kiến thức sau:
1. Hiểu về ma trận, hệ phương trình tuyến tính và ứng dụng của chúng trong kinh tế vàtrong đời sống thực tế.
2. Tính toán được với các phép toán thông dụng trên ma trận và sử dụng được các phépbiến đổi sơ cấp của ma trận.
3. Phân tích được các mô hình tuyến tính trong kinh tế: mô hình cân bằng cung cầu, môhình cân
bằng kinh tế vĩ mô, mô hình Input-Output của Leontief.
4. Sử dụng được máy tính cầm tay và các phần mềm hỗ trợ để tính toán trên ma trận,hệ phương trình. 1.1
Ma trận và các phép toán
Trong thực tế, chúng ta thường gặp nhiều bài toán cần xử lý nhiều dữ liệu cùng tính chất. Để
thuận tiện cho việc quan sát và làm việc trên các dữ liệu như vậy, người ta có thể sắp xếp chúng
thành các hàng, cột (các "ma trận hàng, cột" hay "vectơ") hoặc các bảng gồm có nhiều cột, nhiều
hàng (các "ma trận"). Trên các cột hay các bảng như vậy, người ta có thể xây dựng các phép toán để
xử lý dữ liệu theo từng mục đích cụ thể. Ví dụ bảng tổng số lượng bán ra của một cửa hàng trà sữa
với hai loại trà tương ứng với 3 cỡ ly to, vừa và nhỏ sau mỗi ngày là một bảng 2 x3 như sau: Ly nhỏ (200ml) Ly vừa (400ml) Ly lớn (600ml) lOMoARcPSD| 36207943 2
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH Trà sữa Matcha 112 358 289 Hồng trà 140 321 254 1.1.1 Khái niệm ma trận
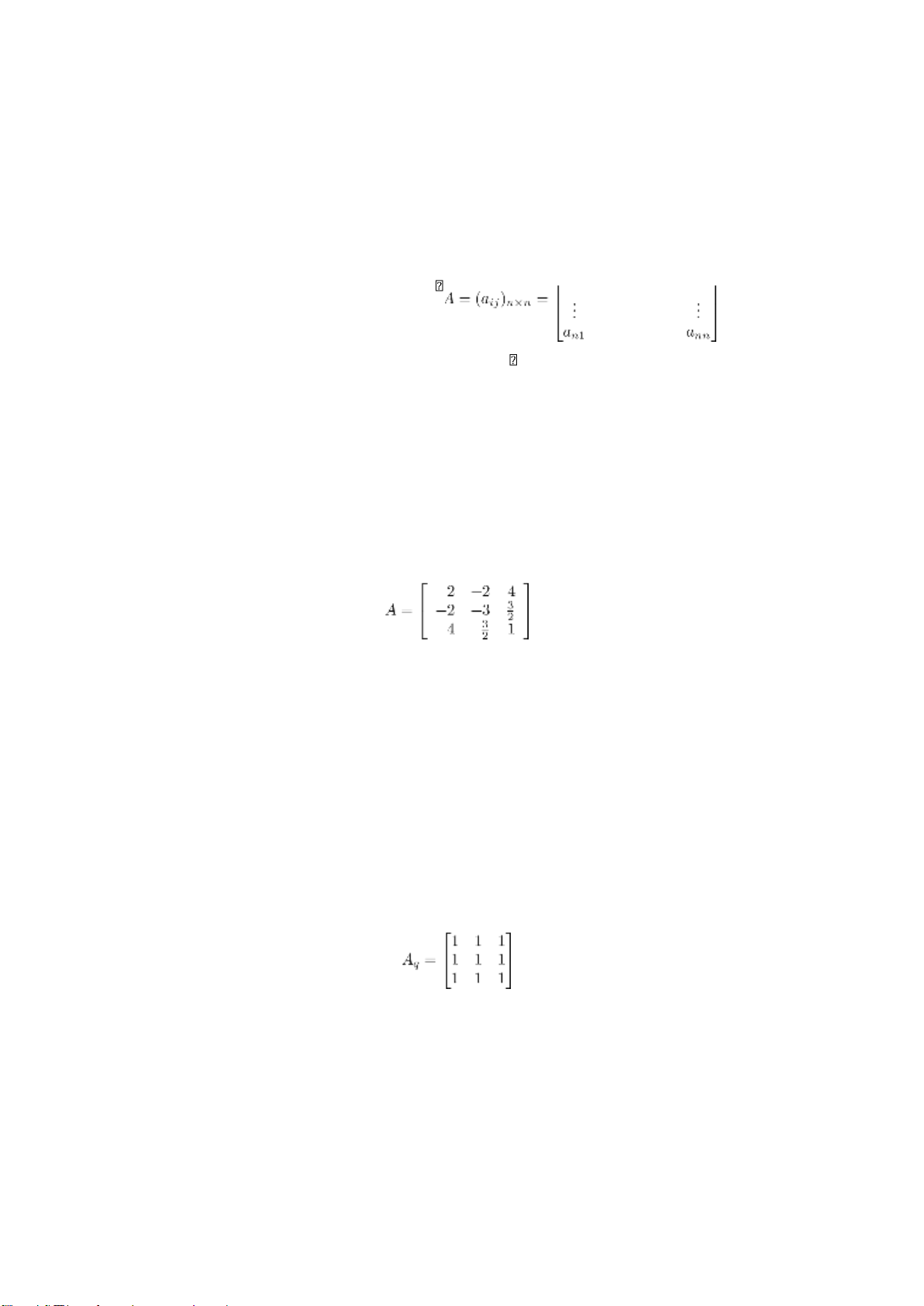
Ma trận là một bảng số hình chữ nhật gồm m dòng và n cột. Ma trận ký hiệu bằng các chữ cái A,
B, C.... và biểu diễn dưới dạng sau: a11 a12 a13 ... a1n
A = a21 a22 a23 . . a2n ...am1 am2 am3 . . amn hoặc dưới dạng a11 a12 a13 ... a1n A = a21 a22 a23 ... a2n
. . . . . . . . . . . . . . am1 am2 am3 ...
amn Ma trận ở trên có cấp m × n. 3 lOMoARcPSD| 36207943 3
1.1.2 Một số dạng ma trận
1. Ma trận vuông là ma trận mà số dòng bằng với số cột. Một ma trận vuông cấp n × n còn được
gọi tắt là ma trận vuông cấp n. Trong một ma trận vuông A = (aij)n×n, các phần tử a11,. .,ann
được gọi là các phần tử thuộc đường chéo chính của ma trận.
2. Ma trận chéo là ma trận vuông mà các phần tử không nằm trên đường chéo chính đềubằng 0.
3. Ma trận tam giác trên (dưới) là ma trận vuông mà các phần từ nằm dưới (trên) đườngchéo chính đều bằng 0.
4. Ma trận đơn vị là ma trận chéo mà các phần tử trên đường chéo chính đều bằng 1.
5. Ma trận cột (dòng) là ma trận chỉ có một cột (dòng).
6. Ma trận không (kí hiệu bởi O) là ma trận mà tất cả các phần tử đều bằng 0. 1.1.3
Các phép toán trên ma trận
1. Phép cộng (trừ) hai ma trận A và B được thực hiện bằng cách cộng (trừ) các phần tử ở các vị
trí tương ứng. Như vậy hai phép toán này chỉ thực hiện được khi hai ma trận A và B có cùng cấp.
2. Phép nhân một ma trận với một số thực λ được thực hiện bằng cách nhân λ tới tất cả các
phần tử của ma trận đó.
3. Phép nhân ma trận A cho ma trận B được thực hiện bằng cách lấy từng dòng của A (từ trên
xuống dưới) nhân vô hướng với từng cột của ma trận B (từ trái sang phải). Phép nhân AB chỉ
thực hiện được khi số cột của A bằng với số dòng của B. 4. Phép chuyển vị của A được thực
hiện bằng cách chuyển dòng của A thành cột. Ma trận chuyển vị của A được kí hiệu là At 1.2
Ma trận bậc thang dòng và các phép biến đổi sơ cấp
Một ma trận được gọi là ma trận bậc thang dòng nếu
• Dòng có tất cả các phần tử bằng 0 luôn nằm dưới các dòng khác không.
• Với hai dòng khác 0 bất kì, phần từ khác 0 đầu tiên tính từ trái sang phải của dòng trên luôn ở
bên trái so với của các dòng dưới.
Các phép biến đổi sơ cấp (viết tắt là bđsc):
1. Đổi chỗ hai dòng cho nhau: di ↔ dj.
2. Nhân một dòng với một số khác 0 di 7→ αdi,α 6= 0.
3. Thêm (bớt) vào một dòng, một tích vô của một số với một dòng khác di 7→ di + αdj. Ví dụ. 1.3 Hạng của ma trận.
Hạng của một ma trận A là số dòng khác 0 của ma trận bậc thang tương ứng với nó, và được kí hiệu là rank(A). Ví dụ. Cho ma trận lOMoARcPSD| 36207943 4
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH . 1.4. ĐỊNH THỨC
Bằng các phép biến đổi sơ cấp, ta đưa ma trận A về dạng bậc thang theo dòng như sau: 1 2 4 1 2 4 1 2 4
A = 0 21 −−−−−−−d37→d3−d→1 0
21 −−−−−−−d3→7d3−d→2 0 2 1 . 1 4 5 0 2 1 0 0 0
Như vậy, rank(A) = 2. 1.4 Định thức
Định thức của một ma trận A, kí hiệu là det(A), hoặc là |A|, được định nghĩa bằng phương pháp
quy nạp (công thức Laplace) như sau:
• Nếu A = (a)1×1 thì detA = |A| = a. • Nếu . • Nếu . • Nếu
A khai triển theo dòng thứ
detA = ai1Ai1 + ai2Ai2 + ··· + ainAin,
trong đó Aij là tích của (−1)i+j nhân với định thức của ma trận vuông cấp n−1 nhận được từ A
bằng cách xoá đi dòng i, cột j. Aij được gọi là phần bù đại số của aij.
Lưu ý. Ngoài khai triển theo dòng, định thức còn có thể được khai triển theo cột bằng công thức tương tự. 1.4.1
Tính định thức bằng các phép biến đổi sơ cấp
Định thức của ma trận bậc thang .
là det(A) = 2.5.7 = 70. Như vậy, định thức của ma trận tam giác trên (vuông) bằng với tích các phần
tử trên đường chéo (chính). Mà ta đã biết các phép biến đổi sơ cấp có thể đưa ma trận về dạng
bậc thang (trong trường hợp của ma trận vuông thì một ma trận bậc thang theo dòng là một ma
trận tam giác trên), nên ta có thể sử dụng các phép biến đổi sơ cấp để đưa ma trận về dạng bậc
thang và từ đó tính định thức. Tuy nhiên, các phép biến đổi sơ cấp sẽ làm thay đổi giá trị định thức như sau:
1. Phép bđsc thứ nhất di ↔ dj làm cho định thức đổi dấu.
2. Phép bđsc thứ hai di 7→ αdi làm cho định thức mới bằng α lần định thức cũ.
3. Phép bđsc thứ ba di 7→ di − αdj không làm thay đổi giá trị định thức. lOMoARcPSD| 36207943 5
Ví dụ 1.4.1. Tính định thức của ma trận sau .
Ta thực hiện các phép bđsc như sau để đưa A về dạng bậc thang: .
Định thức của ma trận bậc thang sau cùng bằng với 3. Tuy nhiên, trong quá trình bđsc ta đã sử
dụng phép bđsc d1 ↔ d2 (làm thay đổi dấu của định thức) và
(làm định thức thay đổi
lần). Nên detA = (−1) × 2 × 3 = −6. ———————————————— ——————————— —— 1.5 Ma trận khả nghịch
Ma trận vuông A cấp n × n được gọi là khả nghịch nếu tồn tại một ma trận vuông B cùng cấp
sao cho AB = BA = In, trong đó In là ma trận đơn vị cấp n. Khi đó B được gọi là ma trận nghịch đảo
của A, và được kí hiệu bởi A−1.
Định lý 1.5.1. Ma trận vuông A cấp n khả nghịch khi và chỉ khi một trong hai điều kiện tương đương sau được thoả mãn:
• rank(A) = n, • detA 6= 0.
Thuật toán tìm nghịch đảo bằng các phép biến đổi sơ cấp:
1. Để tìm nghịch đảo (nếu có) của ma trận vuông A cấp n, ta lập ma trận mở rộng [A|In].
2. Biến đổi sơ cấp trên các dòng của [A|In] để đưa nó về dạng [In|B]. Nếu không thể biến đổi
được như thế, nghĩa là trong quá trình biến đổi sơ cấp, ma trận bên trái xuất hiện một dòng
bằng không thì A không khả nghịch. Ngược lại, nếu thực hiện được thì A khả nghịch và nghịch
đảo của A là ma trận B.
Thuật toán tìm nghịch đảo của ma trận vuông A bằng định thức:
1. Tính detA. Nếu detA = 0 thì kết luận là A không khả nghịch. Nếu detA 6= 0 thì kết luận là A
khả nghịch và chuyển sang bước tiếp theo để tìm nghịch đảo của A. 2. Tìm ma trận phụ hợp của
PA, là ma trận cùng cấp với A và được định nghĩa bởi (PA)ij = Aij, trong đó Aij là phần bù đại số của aij.
3. Ma trận nghịch đảo của A lúc này được xác định bởi . 1.6
Hệ phương trình tuyến tính - Định lý Kronecker- Capelli
Xét một hệ phương trình tuyến tính như sau:
a1x + b1y + c1z + d1t = e1
a2x + b2y + c2z + d2t = e2 a3x +
b3y + c3z + d3t = e3
a4x + b4y
+ c4z + d4t = e4 lOMoARcPSD| 36207943 6
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Hệ phương trình trên tương đương ở dạng ma trận như sau:
Do các kí hiệu ẩn x,y,z,t không đóng vai trò quan trọng, nên ta có thể viết lại hệ phương trình trên
theo dạng ma trận mở rộng như sau: a1 b1 c1 d1e1 a2 b2 c2 d2e2
a3 b3 c3 d3e3
a4 b4 c4 d4e4
Tương tự như vậy với hệ phương trình tuyến tính bất kì, ta có thể biểu diễn dưới dạng ma trận mở
rộng. Câu hỏi được đặt ra là liệu chúng ta có thể sử dụng các tính chất của ma trận để xét nghiệm
của hệ phương trình tuyến tính tương ứng được hay không. Định lý Kronecker-Capelli sẽ cho chúng
ta đáp án cho câu hỏi này.
Định lý Kronecker-Capelli. Cho hệ phương trình Ax = b, trong đó A là một ma trận (thực) cấp m × n
và b là một ma trận cột có m dòng, còn x là ma trận ẩn cấp n × 1. Lúc đó ta có: lOMoARcPSD| 36207943
1.7. MÔ HÌNH TUYẾN TÍNH TRONG KINH TẾ 7
1. Hệ phương trình vô nghiệm nếu rank(A) < rank(A|b). 2. Hệ có nghiệm duy nhất nếu rank(A)
= rank(A|b) = n, ở đây n là số cột của ma trận A, đồng thời cũng là số ẩn xuất hiện trong hệ phương trình trên.
3. Hệ có vô số nghiệm phụ thuộc n − rank(A) tham số nếu rank(A) = rank(A|b) < n. 1.6.1
Hệ Cramer và phương pháp giải
Hệ phương trình Ax = b, trong đó A là một ma trận vuông khả nghịch được gọi là một hệ Cramer.
Định lý Cramer khẳng định rằng lúc này hệ có nghiệm duy nhất, xác định bởi ,
trong đó D = detA 6= 0 và Di là định thức của ma trận nhận được từ A bằng cách thay cột thứ i bởi b.
1.6.2 Hệ phương trình tuyến tính thuần nhất và đặc trưng của nghiệm của hệ này
Hệ phương trình tuyến tính Ax = b, trong đó b là ma trận 0, được gọi là hệ phương trình tuyến
tính thuần nhất. Hệ phương trình tuyến tính thuần nhất luôn có ít nhất một nghiệm là x = 0. Theo
định lý Kronecker-Cappelli, hệ này có nghiệm duy nhất x = 0 khi và chỉ khi rank(A) = n, trong đó n
là số cột của A (cũng chính là số ẩn của hệ phương trình trên). Cũng theo định lý Kronecker-Capelli,
nếu rank(A) = r < n thì hệ có vô số nghiệm phụ thuộc vào n − r tham số. Giả sử n − r tham số trên
là a1,. .,an−r. Lúc đó với mỗi i bằng cách gắn cho ai giá trị 1 và các aj,j 6= i giá trị 0, ta được n − r
nghiệm x1,...,xn−r. Lúc đó ta dễ dàng thấy tập nghiệm của hệ phương trình thuần nhất trên là tập
{α1x1 + ··· + αn−rxn−r : α1,...,αn−r ∈ R}.
Hệ nghiệm x1,...,xn−r như trên được gọi là một hệ nghiệm cơ bản của hệ phương trình tuyến tính thuần nhất đã cho.
Giả sử ta có một hệ phương trình tổng quát Ax = b và ta biết một nghiệm riêng x0 của hệ này. Lúc
đó, tất cả các nghiệm của hệ này sẽ là x0 + xtn, trong đó xtn là nghiệm của hệ thuần nhât Ax = 0. 1.7
Một số mô hình tuyến tính trong kinh tế
Mô hình hóa các vấn đề trong kinh tế về mô hình toán là việc làm thường xuyên của các nhà
kinh tế. Sau khi chuyển đổi một vấn đề phát biểu dưới quan điểm kinh tế về một bài toán, các nhà
kinh tế/nhà toán học sẽ dựa trên các công cụ của toán học để giải quyết vấn đề, rút ra kết luận,
phân tích đánh giá và trả kết quả về dưới dạng các phát biểu của kinh tế. Dựa trên các kết quả đó,
người làm kinh tế sẽ tìm được câu trả lời cho vấn đề của mình. Sau đây, chúng ta tìm hiểu một số
mô hình rất điển hình trong kinh tế. 1.7.1
Mô hình cân bằng thị trường (mô hình cung cầu)
Nói một cách nôm na, cân bằng thị trường đối với một loại hàng hóa là trạng thái mà tại đó giá
của hàng hoá được chấp nhận từ cả người bán và người mua.
Ví dụ 1.7.1. Tại một quầy thịt, giá 1kg thịt rút sườn vào buổi sáng là 95.000 đồng. Quầy thịt vẫn có
người mua như các ngày trong tháng. Như vậy, mức giá 95.000 đồng/kg là giá cân bằng đối với
mặt hàng này. Tuy nhiên, vào thời điểm gần tết, nhu cầu về thịt tăng mạnh, lượng thịt cung cấp dù
tăng nhưng vẫn không đáp ứng được nhu cầu mua dẫn đến giá thịt tăng cao. Khi giá tăng cao,
người dân lại có xu hướng giảm lượng mua. Từ đó, giá sẽ giảm xuống dần đến mức cân bằng. lOMoARcPSD| 36207943 8
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Từ ví dụ trên, ta thấy rằng giá được thị trường chấp nhận chính là giá thỏa mãn nhu cầu người
mua và khả năng cung cấp của người bán. Sau đây, ta xem khả năng cung cấp và nhu cầu mua là
hai hàm theo biến giá và kí kiệu chúng lần lượt bởi Qs và Qd. Ta thấy rằng:
• Khi giá tăng, người bán sẽ muốn bán nhiều, nên hàm Qs(p) là một hàm tăng theo giá p.
• Khi giá tăng, người mua sẽ giảm hoạt động mua, nên hàm cầu Qd(p) là một hàm giảm theo giá p.
• Khi giao dịch mua bán được thực hiện tức là người mua chấp nhận giá của người bán thì giá
đó được gọi là giá tại điểm cân bằng. Như vậy giá tại điểm cân bằng là mức giá p làm cho
hàm cung và hàm cầu bằng nhau: Qs(p) = Qd(p).
Trong trường hợp các hàm cung, cầu là các hàm tuyến tính thì ta có Qs(p) = −a0 + a1p và Qd(p) = b0
− b1p với a0,a1,b0,b1 dương. Và lúc này mô hình cân bằng có dạng:
Ví dụ 1.7.2. Cho hàm cung và hàm cầu theo giá của một loại hàng hóa là Qs = −5+p và Qd = 55 − 3p.
• Giá cân bằng thị trường là nghiệm của phương trình:
Qs = Qd ⇔ −5 + p = 55 − 3p ⇔ p = 15.
Vậy giá cân bằng là p = 15 (đơn vị tiền tệ).
• Khi thị trường đạt cân bằng về giá thì lượng cung bằng lượng cầu và bằng với
Qs = Qd = Qs(15) = Qd(15) = −5 + 15 = 10 đơn vị hàng hóa.
Trong thị trường, có rất nhiều loại hàng hóa khác nhau, giá của loại hàng hóa này sẽ ảnh hưởng
đến lượng cung và lượng cầu của loại hàng hóa kia. Ví dụ như khi thịt heo tăng giá mạnh, người
dân có xu hướng giảm mua thịt heo mà thay vào đó người ta sẽ mua các sản phẩm thay thế như
cá biển, cá đồng,v.v. Việc chuyển hướng mua này cho thấy sự thay đổi về nhu cầu và ảnh hưởng
đến khả năng cung ứng. Từ đó, ảnh hưởng đến giá thành của thịt và của cả các loại hải sản. Trong
trường hợp này, ta xét mô hình cân bằng thị trường tổng quát: Trong đó,
• biến giá pi là giá hàng hóa thứ i;
• hàm cung Qsi là lượng cung của hàng hóa thứ i;
• hàm cầu Qdi là hàm cầu đối với hàng hóa thứ i, i = 1,2,. .,n.
Chuyển vế và đặt cij = aij − bij, ta được hệ phương trình tuyến tính:
c11p1 + c12p2 + c13p3 + ··· + c1npn = −c10
c21p1 + c22p2 + c23p3 + ··· + c2npn = −c20 ···
cn1p1 + cn2p2 + cn3p3 + ··· + cnnpn = −cn0
Giải hệ này ta tìm được giá cân bằng cho n loại hàng hóa đã cho.
Ví dụ: Xét một thị trường gồm 3 loại hàng hóa. Hàm cung và hàm cầu thỏa mãn các điều kiện sau:
Qs1 = −2 + 4p1 − p2 − p3,
Qs2 = −1 + p1 + 4p2 − p3, Qs3 = −2 − p1 + p2 + 4p3, Qd1 = 10
− 2p1 + p2 + p3,
Qd2 = 1 + p1 − 2p2 + p3,
Qd3 = 3 + p1 + 2p2 − 2p3. lOMoARcPSD| 36207943
1.7. MÔ HÌNH TUYẾN TÍNH TRONG KINH TẾ 9
Hệ phương trình xác định điểm cân bằng là .
Vậy, giá cân bằng mỗi loại là p1 = 3,p2 = 1,p3 = 2. Ta cũng gọi bộ (3,1,2) là điểm cân bằng của thị
trường. Ta tính được lượng hàng cân bằng của từng loại như sau:
Qs1 = Qd1 = 7,
Qs2 = Qd2 = 4,
Qs3 = Qd3 = 4. 1.7.2
Mô hình cân bằng kinh tế vĩ mô
Trong một nền kinh tế đóng, nghĩa là không có quan hệ kinh tế đối ngoại, ta có mô hình cân bằng như sau:
Y = C + I + G.
• Với Y (Income) là tổng thu nhập quốc dân, C (Consumption) là tổng tiêu dùng của dân cư, I
(Invesment), G (Government)là mức chi tiêu chính phủ.
• Hàm tiêu dùng phụ thuộc vào thu nhập, được biểu thị dưới dạng tuyến tính: C = aY +b.
• Khoảng đầu tư không ngắn hạn của chính phủ có thể được cố định, tức I = I0.
• Khoản tài khóa (mức tiêu dùng chính phủ) cũng được cố định G = G0.
• Thuế được tính từ thu nhập theo dạng hàm: T = d + tY .
Từ đây, ta được mô hình cân bằng kinh tế vĩ mô:
Giải hệ ta tìm được mức thu nhập quốc dân Y , mức tiêu dùng C và mức thuế cân bằng T. Câu hỏi
Các hệ số a,b,d,t thuộc miền nào trên trục số và vì sao? Ví dụ. Giả sử trong một quốc gia trong năm
nay, mức đầu tư cố định của chính phủ là I0 = 2500 (triệu USD), mức chi tiêu cố định của chính phủ
là G0 = 500 (triệu USD); còn tổng thu nhập quốc dân Y , tổng mức tiêu dùng dân cư C và tổng thuế
T thỏa mãn các điều kiện sau:
C = 800 + 0.3(Y − T),
T = 500 + 0.1T.
Theo mô hình cân bằng kinh tế vĩ mô ta có Y = C + I0 + G0. Thay các giá trị đã cho của I0,G0 vào hệ
phương trình cân bằng ta được:
Biến đổi và giải hệ ta được: , lOMoARcPSD| 36207943 10
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
Vậy tổng thu nhập, chi tiêu và thuế ở mức cân bằng lần lượt là: Y = 5000, C = 2000, T = 1000. 1.7.3 Mô hình IS-LM
Trong mô hình cân bằng kinh tế vĩ mô, ta giả thiết là tổng đầu tư không đổi I = I0 tức lãi suất
bằng 0. Tuy nhiên, theo một quy luật tự nhiên thì lãi suất không thể bằng 0, khi lãi suất càng cao
thì đầu tư càng giảm. Điều này cho thấy rằng hàm đầu tư là một hàm biến động ngược so với lãi
suất. Ta giả sử hàm đầu tư có dạng:
I = b1 − a1r,
(a1,b1 > 0).
Từ đây ta được phương trình cân bằng hàng hóa .
Hay a1r = b+b1+G0 −(1−a)Y . Phương trình này được gọi là Phương trình (IS), biểu thị quan hệ giữa
lãi suất và thu nhập khi thị trường hàng hóa cân bằng (tổng cung bằng tổng cầu).
Trong thị trường tiền tệ, nhu cầu tiền mặt đồng biến với tổng thu nhập Y và nghịch biến với lãi suất
r. Giả sử hàm cầu có dạng tuyến tính:
L = b2Y − a2r,
(a2 > 0,b2 > 0)
Giả sử lượng cung tiền mặt là M0. Trong điều kiện thị trường cân bằng tiền tệ ta có:
M0 = L ⇔ M0 = b2Y − a2r ⇔ a2r = b2Y − M0 (LM).
Phương trình này cho thấy khi thu nhập tăng thì lãi suất cũng tăng.
Như vậy, ta được hệ phương trình IS-LM được xếp thứ tự trong hệ như sau:
(LM). Ví dụ 1.7.3. Giả sử tại một
quốc gia trong năm nay mức chi tiêu cố định của chính phủ là G0 = 500( triệu USD); lượng cung tiền
mặt là M0 = 1000 (triệu USD) còn tổng thu nhập quốc dân Y , tổng mức đầu tư chính phủ I, tổng
mức tiêu dùng dân cư C, lượng cầu tiền mặt và mức lãi suất r thỏa mãn các điều kiện:
I = 2500 − 50r,
C = 500 + 0.4Y,
L = 0.6Y − 200r. Theo mô hình IS-LM, ta có
Y = C + I + G0 ⇔ Y = (500 + 0.4Y ) + (2500 − 50r) + 500 ⇔ 50r = 350 − 0.6Y. Vậy
phương trình (IS) là: 50r = 350 − 0.6Y.
Lượng cung cầu tiền tệ cân bằng tức là:
L = M0 ⇔ 0.6Y − 200r = 1000 ⇔ 200r = 0.6Y − 1000. Vậy
phương trình (LM): 200r = 0.6Y − 1000.
Mức thu nhập Y là lãi suất r ở trạng thái cân bằng thị trường là nghiệm của hệ hương trình:
Vậy thu nhập cân bằng và lãi suất cân bằng là Y = 5000 và r = 10. lOMoARcPSD| 36207943
1.7. MÔ HÌNH TUYẾN TÍNH TRONG KINH TẾ 11 1.7.4
Mô hình Input-Output của Leontief
Trong mô hình này, khái niệm ngành được xét theo nghĩa thuần túy sản xuất. Các giả thuyết của mô hình:
• Mỗi ngành kinh tế chỉ sản xuất một loại hàng hóa.
• Mỗi ngành đều sử dụng một tỉ lệ cố định các sản phẩm của ngành khác làm đầu vào cho sản suất đầu ra của mình.
• Khi đầu vào thay đổi k lần thì đầu ra cũng thay đổi k lần.
Giả sử một nền kinh tế gồm n ngành sản xuất, ngành 1,2,3,. .,n.
• Gọi xi là giá trị tổng cầu1 về sản phẩm của ngành i,i = 1,2,. .,n.
• Nhu cầu các hộ tiêu dùng và các nhà xuất khẩu gọi là giá trị cầu cuối cùng, đặt là bi,i = 1,2,. .,n.
• Ngành j cần mua sản phẩm ngành i để làm nguyên liệu đầu vào sản xuất, ta kí hiệu là xij.
Khi đó, tổng cầu ngành i được xác định bởi cầu ngành i của các ngành j và cầu cuối bi hay
xi = xi1 + xi2 + xi3 + · + xik + bi.
Công thức tỉ lệ chi phí đầu vào của ngành j đối với sản phẩm .
Công thức này được giả định là không thay đổi trong suốt quá trình sản xuất. Ý nghĩa aij: Để ngành
j sản xuất ra 1 đơn vị giá trị sản phẩm thì cần mua aij đơn vị giá trị nguyên liệu đầu vào-sản phẩm, của ngành i.
Giả sử a12 = 0.2, có nghĩa là để sản xuất ra 1 đồng giá trị ngành 2 cần mua 0.2 đồng nguyên liệu
đầu vào sản phẩm của ngành 1, làm nguyên liệu cho quá trình sản xuất. Nếu đặt a11 a12 ··· A = (aik) = a31 a a nn3n 32 ··· ... ... ... an2 ··· ... an1 a
a1n a21 a22 ··· a2n
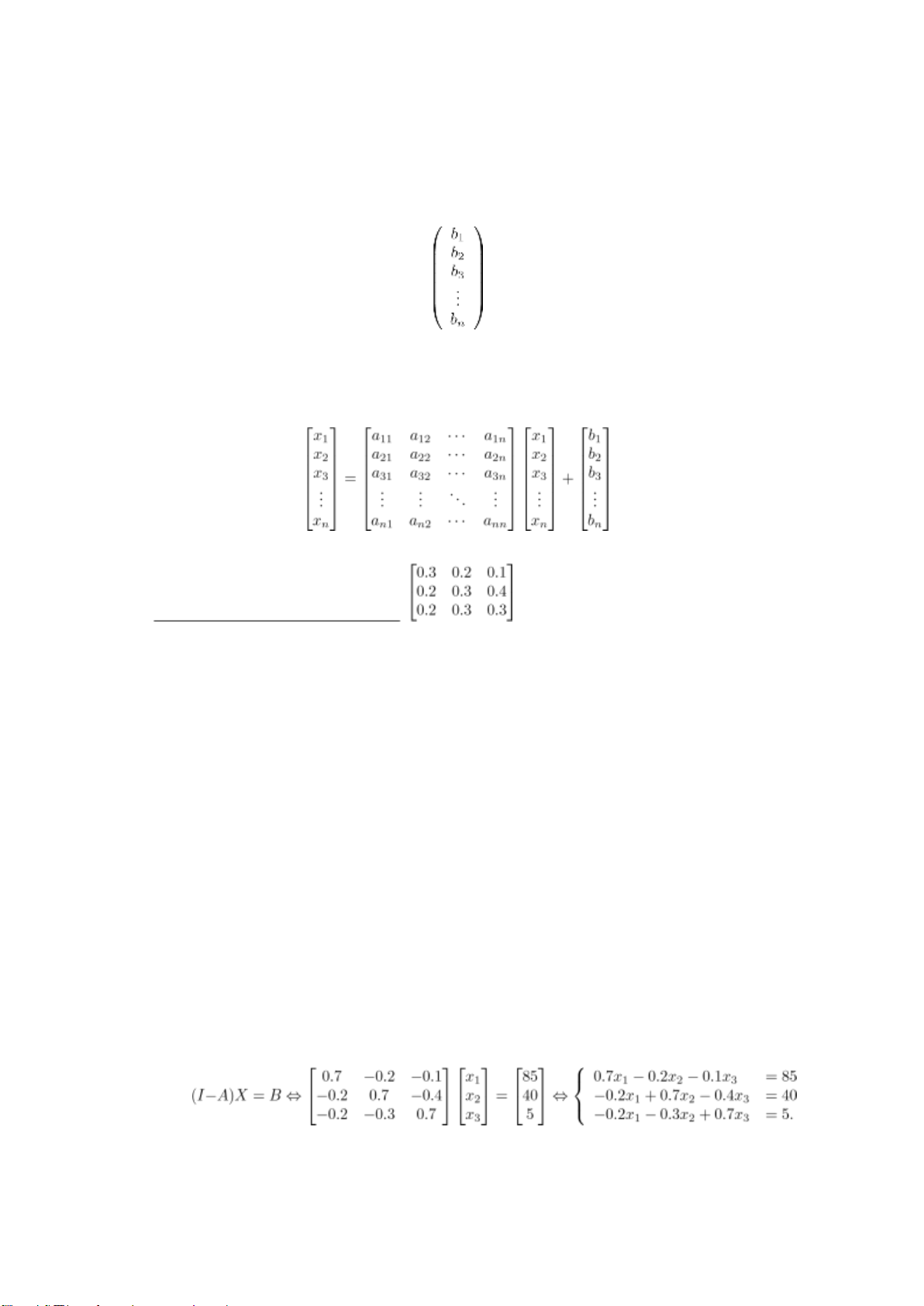
Ở đây, hàng biểu diễn cho dữ liệu đầu vào và cột biểu diễn cho dữ liệu đầu ra. Ma trận tổng cầu: x1 x2 X = x3 ...
1 Tham khảo thêm tại https://vi.wikipedia.org/wiki/Nguyên_lý_cung_-_cầu lOMoARcPSD| 36207943 12
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH xn
Vectơ cầu cuối (nhu cầu của người dân và nhu cầu xuất khẩu):
Từ phương trình (1) ta thay xij = aijxk, ta được
xi = ai1x1 + ai2
i = 1,2,3,. .,n.
Hay biểu diễn phương trình dưới dạng ma trận là X = AX + b. Tức là:
Ví dụ: Giả sử một quốc gia có 3 ngành kinh tế với ma trận hệ số đầu vào là
a) Giải thích ý nghĩa hệ số 0.4 ở dòng 2, cột 3 của ma trận đầu vào.
b) Tìm hệ số tỉ phần gia tăng a0j của từng ngành (j = 1,2,3). Giải thích ý nghĩa của hệ số a03.
c) Tìm đầu ra cho mỗi ngành biết rằng cầu cuối của mỗi ngành lần lượt là 85, 40, 5.
d) Tìm cầu cuối của mỗi ngành biết đầu ra của mỗi ngành lần lượt là 40, 40, 30. Bài Giải.
a) Hệ số a23 ở dòng 2 cột 3 có nghĩa là để sản xuất 1 USD giá trị hàng hóa của ngành 3
cần chi ra 0.4 USD mua hàng háo của ngành 2.
b) Hệ số tỉ phần gia tăng a0j của từng ngành (j = 1,2,3)
X a01 = 1 − (0.3 + 0.2 + 0.2) = 0.3
X a02 = 1 − (0.2 + 0.3 + 0.3) = 0.2
X a03 = 1 − (0.1 + 0.4 + 0.3) = 0.2
Ý nghĩa của a02 = 0.2: tỉ phần gia tăng trong tổng giá trị hàng hóa của ngành 2 là 20%. Nói
cách khác, trong sản xuất của mình, ngành 2 đã tạo ra 20% giá trị gia tăng sau khi trừ mọi chi phí.
c) Theo giả thiết ta có cầu cuối B = (b1,b2,b3)t = (85,40,5)t. Do đó, đầu ra X =
(x1,x2,x3)t là nghiệm của hệ phương trình
Với I là ma trận đơn vị cấp 3. Giải hệ ta được đầu ra mỗi ngành lần lượt là
x1 = 200,x2 = 200,x3 = 150. lOMoARcPSD| 36207943
1.7. MÔ HÌNH TUYẾN TÍNH TRONG KINH TẾ 13
d) Vì đầu ra X = (x1,x2,x3)t là (40,40,30) nên cầu cuối B = (b1,b2,b3)t xác định bởi hệ thức. .
Vậy cầu cuối của mỗi ngành lần lượt là 17,8,1. lOMoARcPSD| 36207943 14
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
1.8. TÍNH TOÁN VỚI PHẦN MỀM
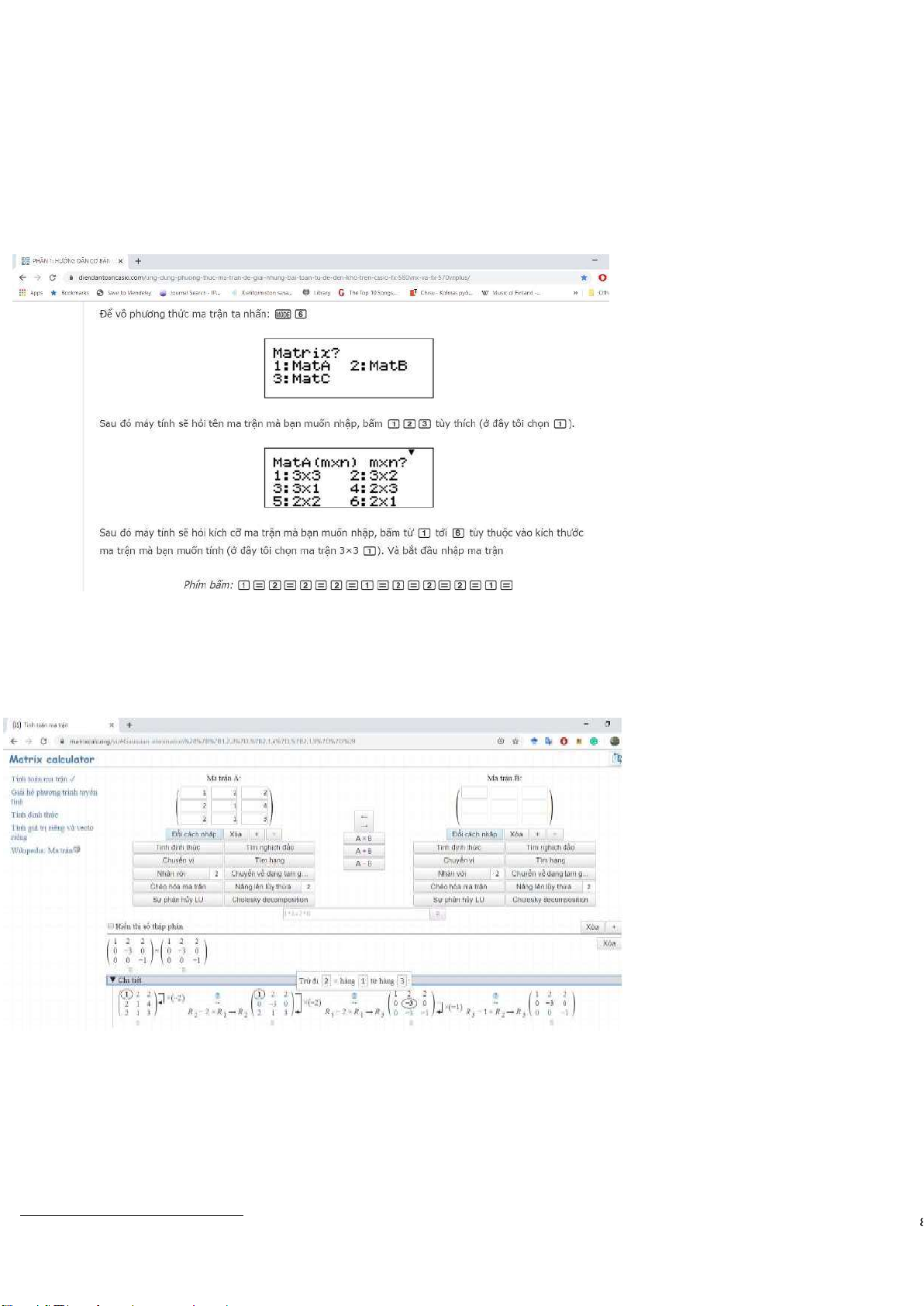
1.8 Hướng dẫn sử dụng máy tính cầm tay và các phần mềm tính toán trên ma trận
Máy tính cầm tay có thể hỗ trợ tốt cho nhiều tính toán với ma trận và hệ phương trình kích cỡ nhỏ2
Hình 1.1: Cách nhập và tính toán với ma trận trên máy cầm tay Casio.
Ngoài ra, ta cũng có thể sử dụng trang web Matrix calculator3 để thực hiện một số phép toán cơ bản
trên ma trận, ví dụ như dưới đây.
Hình 1.2: Biến đổi ma trận về dạng tam giác.
Thực hiện phép toán nghịch đảo và phép nhân hai ma trận, ta viết biểu thức tính vào ô trống ngay
giữa hai ma trận như hình bên dưới:
2 https://diendantoancasio.com/ung-dung-phuong-thuc-ma-tran-\de-giai-nhung-bai-toan-tu-de-den-kho-tren-casio-fx-5 3https://matrixcalc.org/vi/ lOMoARcPSD| 36207943 15
Hình 1.3: Phép toán nghịch đảo và phép nhân. 1.9
Một số bài tập và thực hành cuối chương 1
1. (Bài tập làm việc nhóm). Nhóm hãy tìm hiểu thêm về các ứng dụng của ma trận và hệ phương
trình tuyến tính trong thực tiễn. Từ đó nhóm chuẩn bị bài trình bày trước lớp (powerpoint
hoặc tương đương), tối thiểu gồm hai ứng dụng cụ thể.
2. (Bài tập rèn luyện tiếng Anh học thuật). Tìm hiểu và trình bày theo ý bạn các nội dung được
đề cập trong video sau: The beauty I see in algebra.
3. (Bài tập thực hành). Sử dụng máy tính cầm tay3, phần mềm Excel4 (hoặc tương tự), website
doza6 hoặc matrix calculator5 để tính toán với một số ma trận bạn tự chọn. So sánh kết quả,
ưu và nhược điểm (nếu có) của các công cụ nói trên. Đọc thêm về thuật toán giải hệ phương
trình tuyến tính trên máy tính, liên hệ với kiến thức vừa học trong chương này.
4. Giả sử trên thị trường hiện có 3 công ty chuỗi cửa hàng đồ ăn nhanh A, B, C đangcạnh tranh
nhau. Trong đó công ty A chiếm 20% thị phần, B chiếm 60% và C chiếm 20%. Khảo sát về mức
độ trung thành của khách hàng trong năm tới ta thu được số liệu sau:
A sẽ giữ được 85% khách hàng nhưng 5% nói sẽ chuyển sang B và 10% sẽ chuyển sangC.
B sẽ giữ được 55% khách hàng nhưng 15% nói sẽ chuyển sang A và 30% sẽ chuyển sang C.
C sẽ giữ được 85% khách hàng nhưng 10% nói sẽ chuyển sang A và 5% sẽ chuyển sangB.
Năm tới thị phần của công ty A, B, C sẽ lần lượt là bao nhiêu?
5. Hàm cung của một mặt hàng là QS = 5P − 25 (P có đơn vị là đô la, Q có đơn vị là sản phẩm).
Xác định giá thấp nhất được bán của loại sản phẩm trên? Giải thích vì sao?
6. Xét một thị trường gồm hai loại hàng hóa. Hàm cung, hàm cầu và giá của chúng thỏa mãn các điều kiện sau:
Qd1 = 150 − 2p1 + p2;
Qs1 = −45 + 2p1 Qd2
= 75 + 2p1 − 2p2; Qs2 = −30 + 3p2.
Lượng cung cầu cân bằng của từng loại hàng hóa là bao nhiêu? Nhận xét về mối liên hệ giữa
hai loại hàng hóa trên (chúng thay thế lẫn nhau giống như xe bus với xe taxi hay được thường
tiêu thụ cùng nhau giống như máy tính và máy in)?
1.9. MỘT SỐ BÀI TẬP VÀ THỰC HÀNH CUỐI CHƯƠNG 1
3 https://diendantoancasio.com/ung-dung-phuong-thuc-ma-tran-de-giai-nhung-bai-toan-tu-de-den-kho-tren-casio-fx-58
4 https://www.youtube.com/watch?v=3jn8fas_MAc&t=98s 6doza.pro 5 https://matrixcalc.org/vi/ lOMoARcPSD| 36207943 16
CHƯƠNG 1. MA TRẬN VÀ HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
7. Ta có mô hình kinh tế vĩ mô với đơn vị là (tỷ đô la) như sau: Chi dùng của chính phủlà G =
180; phần đầu tư chung là I = 540 và tiêu dùng của quốc gia là C = 0.8Y + 120 (trong đó Y là thu nhập quốc gia).
Tại vị trí cân bằng kinh tế, thu nhập quốc gia Y là bao nhiêu?
8. Nếu hàm cung và cầu của thị trường gồm một loại hàng hóa cho bởi phương trình sau
P = aQS + b;
P = cQD + d.
Trong đó P (price) là giá hàng hóa và Q (quantity) là số lượng cung hoặc cầu. Ta cần điều kiện
gì cho a, b, c, d để phương trình có ý nghĩa về mặt kinh tế và tồn tại điểm cân bằng?
9. Giả sử nền kinh tế có hai ngành nông nghiệp và năng lượng. Mỗi 1 đô la giá trị nông nghiệp
cần 0.4 từ chính nó và 0.2 từ năng lượng; phía năng lượng cần 0.2 từ nông nghiệp và 0.1 từ
chính nó. Nhu cầu bên ngoài là 12 tỷ đô là từ nông nghiệp và 9 tỷ đô la từ năng lượng. Tìm: a. Ma trận Input - Output?
b. Tỷ phần gia tăng của ngành nông nghiệp và ngành năng lượng?
c. Tại vị trí cân bằng, nên sản xuất bao nhiêu tỷ đô la nông nghiệp và bao nhiêu tỷđô la năng lượng? lOMoAR cPSD| 36207943 17 lOMoARcPSD| 36207943 18 Chương2
Không gian Rn và sơ lược về không gian vectơ
Sau khi học xong chương này, người học có những kỹ năng và kiến thức sau:
1. Hiểu về ý nghĩa của vectơ trong đời sống cũng như trong kinh tế.
2. Thực hiện được các tính toán trên vectơ.
3. Xét được tính độc lập tuyến tính, phụ thuộc tuyến tính của một hệ vectơ.
4. Xét được một hệ vectơ có phải là cơ sở của không gian đã chỉ ra hay không và tính được toạ
độ của vectơ theo một cơ sở bất kì.
5. Sử dụng được máy tính cầm tay cũng như các ứng dụng trên máy vi tính để tính toán với các vectơ.
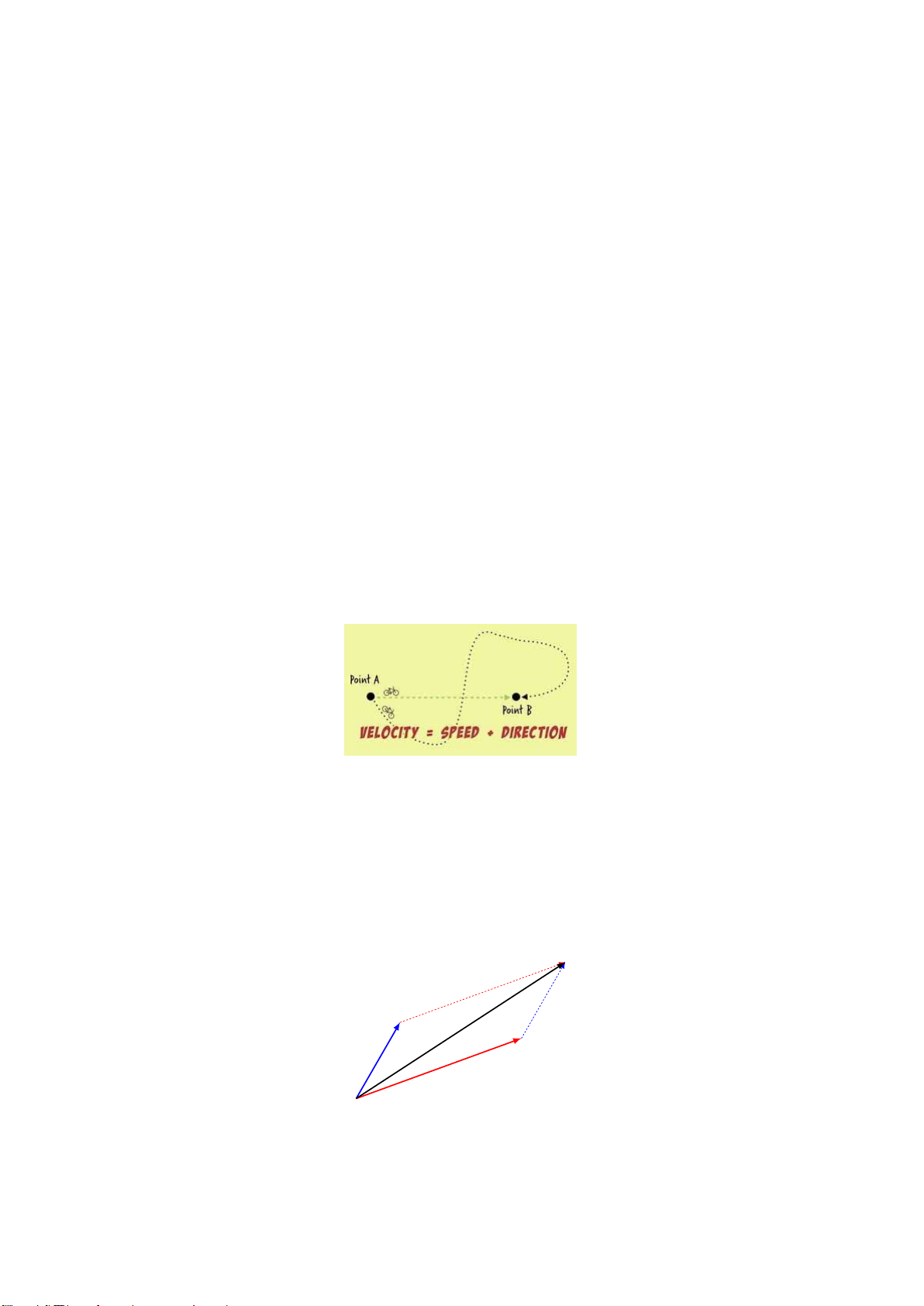
Một vectơ là một đại lượng có độ dài (magnitude) và hướng (direction). Ví dụ như vận tốc là một
vectơ trong khi đó tốc độ là một đại lượng vô hướng.
Hai vectơ là bằng nhau nếu chúng có cùng độ dài và cùng hướng (không cần phải xuất phát từ cùng một điểm). 2.0.1 Các phép toán trên vectơ
Phép cộng. Để cộng hai vectơ u và v, ta vẽ một vectơ có cùng hướng và độ dài với vectơ v nhưng
xuất phát tử đỉnh của vectơ u. Lúc đó, u+v là vectơ xuất phát tử gốc của vectơ u và kết thúc ở đỉnh
của vectơ v mới được vẽ lại. Trong hệ trục toạ độ Descartes, tổng của hai vectơ u = (a1,...,an) và v
= (b1,...,bn) là vectơ u+v có toạ độ là u+v = (a1 +b1,. .,an +bn). ~ v ~ + ~ ~ u v u ~ v 17
CHƯƠNG 2. KHÔNG GIAN VECTƠ RN
Phép trừ. Vì v −u = v +(−u), nên hiệu v −u bằng với tổng của vectơ v và vectơ −u, trong đó vectơ
−u là vectơ có cùng phương và độ dài với vectơ u nhưng ngược hướng. lOMoARcPSD| 36207943 ~ u ~ v ~ − ~ v u ~ ~ u v
Phép nhân vô hướng. Lấy α là một số thực bất kì, lúc đó vectơ αu là vectơ có cùng phương với
vectơ u, nhưng có độ dài bằng |α| lần độ dài của u, đồng thời αu có cùng (ngược) hướng với u nếu
α > 0 (α < 0). 2 ~ u ~ u
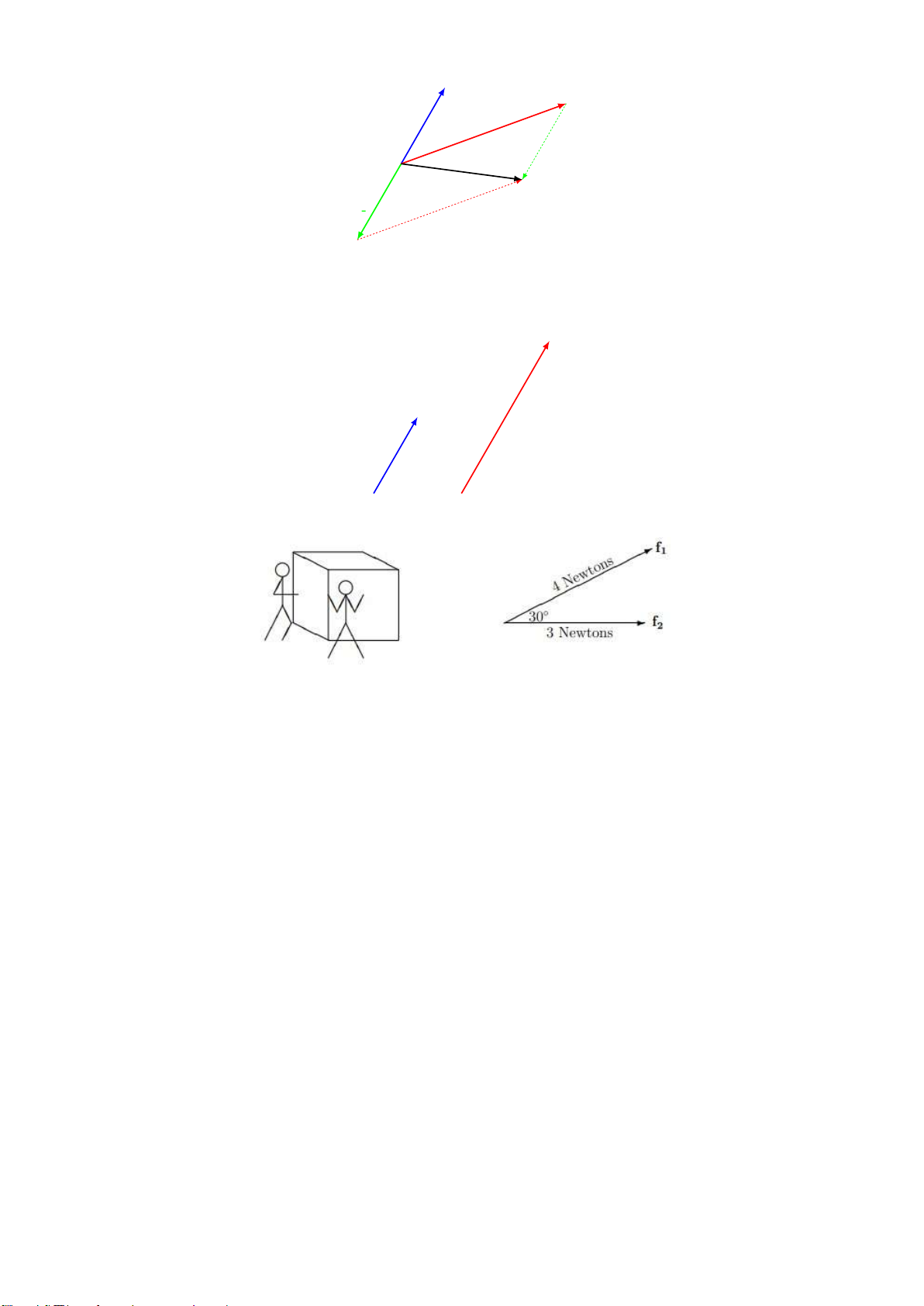
Bài tập. Hai sinh viên cùng đẩy một vật nặng với lực và góc độ như sau:
Hỏi hướng di chuyển và độ dài dịch chuyển của vật thể như thế nào? 2.1
Tổ hợp tuyến tính - biểu diễn tuyến tính
Trong không gian vectơ Rn, cho một hệ m + 1 vectơ
v1,v2,. .,vm, và v.
Lúc đó biểu diễn a1v1 + a2v2 + ··· + amvm, trong đó a1,a2,. .,am là các số thực, được gọi là một tổ hợp
tuyến tính của hệ v1,v2,. .,vm. Nếu tồn tại một tổ hợp tuyến tính của hệ v1,. .,vm mà bằng với vectơ v
thì ta nói v biểu diễn tuyến tính qua hệ v1,. .,vm. Một tổ hợp tuyến tính được gọi là tầm thường nếu
các hệ số a1,. .,am đều bằng 0. Sử dụng định lý Kronecker-Capelli đã học ở Chương I, ta dễ dàng chứng minh định lý sau:
Định lý 2.1.1. • v biểu diễn tuyến tính được qua v1,v2,. .,vm khi và chỉ khi rank(A) = rank(A|v), trong
đó A là ma trận tạo thành từ các cột v1,. .,vm.
• v biểu diễn tuyến tính duy nhất được qua v1,v2,. .,vm khi và chỉ khi rank(A) = rank(A|v) = m. 2.2. HẠNG CỦA HỆ VECTƠ 19 2.2 Hạng của hệ vectơ
Trong Rn, ta nói hệ m vectơ v1,v2,. .,vm có hạng là r, kí hiệu là rank(v1,v2,. .,vm) = r, nếu tồn tại r
vectơ trong hệ sao cho r vectơ độc lập tuyến tính và tất cả các vectơ còn lại trong hệ đều biểu diễn
tuyến tính được qua hệ r vectơ này. Định lý. lOMoARcPSD| 36207943 20
rank(v1,v2,. .,vm) = rank(A),
trong đó A là ma trận tạo thành từ các cột v1,. .,vm. 2.3
Độc lập và phụ thuộc tuyến tính
Một hệ m vectơ v1,...,vm trong Rn được gọi là độc lập tuyến tính nếu vectơ O chỉ có duy nhất một
cách biểu diễn tuyến tính qua hệ bởi tổ hợp tuyến tính tầm thường. Ngược lại thì ta nói hệ phụ thuộc tuyến tính.
Định lý. Hệ vectơ v1,...,vm độc lập tuyến tính khi và chỉ khi rank(A) = m, trong đó A = [v1 v2 . . vm] là
ma trận tạo thành từ các vectơ v1,. .,vm viết theo cột. 2.4
Cơ sở, số chiều và toạ độ
Một hệ vectơ (sắp thứ tự) v1,...,vm trong Rn được gọi là một cơ sở của Rn nếu như hệ này độc lập
tuyến tính và mọi vectơ trong Rn đều biểu diễn tuyến tính được qua hệ trên. Ví dụ. Hệ (v1 = (1,0),v2
= (0,1)) là một cơ sở của R2, vì mọi vectơ u trong R2 đều có dạng u = (a,b) với a,b ∈ R. Nên u = av1
+ bv2. Vì vậy hệ (v1,v2) là một cơ sở của R2. Định lý. Trong Rn, hệ v1,...,vm là một cơ sở của Rn khi và
chỉ khi m = n (tức là số vectơ trong hệ bằng với "số chiều" của không gian đã cho và v1,v2,. .,vm là
một hệ độc lập tuyến tính.
Như vậy, một hệ n vectơ v1,. .,vn trong không gian Rn là một cơ sở khi và chỉ khi det(A) 6= 0, trong
đó A = [v1 v2 ...vm] là ma trận tạo thành từ các vectơ trong hệ.
Số chiều. Số vectơ của mỗi cơ sở trong không gian vectơ được gọi là số chiều của không gian vectơ
đó. Ví dụ như số chiều của Rn là n, và ta kí hiệu là dim(Rn) = n.
Toạ độ. Trong Rn, cho cơ sở (B) = (b1,b2,...,bn). Khi đó, mỗi vectơ trong Rn đều biểu diễn tuyến tính
được một cách duy nhất qua (B), tức là cho một vectơ b bất kì, ta luôn tìm được một bộ n số thực
x1,x2,. .,xn sao cho
x = x1b1 + x2b2 + ··· + xnbn.
Bộ n số thực (x1,...,xn) được gọi toạ độ của vectơ x theo cơ sở (B). Ta kí hiệu là
[x](B) = (x1,x2,...,xn). 2.5
Thực hành với phần mềm
Việc tìm hạng, xét tính độc lập hay phụ thuộc tuyến tính của các véc tơ có thể thông qua phép
biến đổi sơ cấp, hoặc/và sử dụng các công cụ online để hỗ trợ kiểm tra 6, xem hình 2.5. 2.6
Một số bài tập và thực hành cuối chương 2
1. (Bài tập nhóm). Nhóm hãy tìm hiểu thêm về các ứng dụng của không gian véc tơ trong thực
tiễn, chuẩn bị bài trình bày trước lớp (powerpoint hoặc tương đương), tối thiểu gồm hai ứng
dụng cụ thể. Có thể tham khảo sách Fuad Aleskerov et al. “Linear Algebra for Economists”7:
phần 2.3 trang 27, 2.4 trang 29, 6.5 trang 101.
2. (Bài tập rèn luyện tiếng Anh học thuật). Tìm hiểu và trình bày theo ý bạn các nội dung được
đề cập trong video Why is linear algebra useful?.
CHƯƠNG 2. KHÔNG GIAN VECTƠ RN 6 https://matrixcalc.org/vi/
7 http://93.174.95.29/_ads/432193591563C6CD1C0060CD4371CA0C lOMoARcPSD| 36207943
Hình 2.1: Tìm hạng của một hệ véc tơ bằng cách chuyển ma trận tương ứng với hệ véc tơ về dạng bậc thang.
3. (Bài tập thực hành). Sử dụng máy tính cầm tay, Excel, hoặc các công cụ online doza8, matrix
calculator9 để tính toán với một số hệ véc tơ (bao gồm hệ chứa tham số) do bạn tự chọn.
4. Cho một công ty gồm 5 nhân viên, hệ số lương của các nhân viên lần lượt là (2.67;3.33; 6.2;
3.66; 4.98). Biết mức lương cơ bản theo quy định hiện hành là 1 490 000 đồng/tháng, mức
phụ cấp cố định của công ty là 25% và phụ cấp ăn trưa là 700 000 đồng/tháng. Sử dụng phép
toán trên véc tơ tính lương tháng của 5 nhân viên nói trên? Chương3
Sơ lược về toán tử tuyến tính và dạng toàn phương
Sau khi học xong chương này, người học đạt được những kiến thức và kỹ năng sau:
• Hiểu được tầm quan trọng của giá trị riêng, vectơ riêng trong khoa học và trong thực tiễn.
• Tính được giá trị riêng, vectơ riêng, xét được tính chéo hoá cũng như chéo hoá được ma trận vuông cấp nhỏ.
• Hiểu về dạng toàn phương: đưa được dạng toàn phương về dạng chính tắc, xét dấu được dạng toàn phương.
• Sử dụng được các phần mềm để hỗ trợ tính toán phức tạp.
Theo một cuộc điều tra lao động nam tại Mỹ năm 1996, tỷ lệ có việc làm là x0 = 0.95 và tỷ lệ thất
nghiệp y0 = 0.05. Sau mỗi tuần, ở nhóm có việc, xác suất bị mất việc là 0.002. Ở nhóm thất nghiệp,
xác suất có việc ở tuần sau đó là 0.136. Sau 100 tuần, tỷ lệ có việc và thất nghiệp sẽ là: . (3.1)
Ma trận chuyển trạng thái ở trên là một ví dụ về toán tử tuyến tính. Việc tính toán giá trị (x100,y100)
có thể khá lâu nếu ta không có máy tính hỗ trợ. Trong chương này chúng ta sẽ bàn về toán tử tuyến 8 doza.pro 9 https://matrixcalc.org/vi/ lOMoARcPSD| 36207943 22
tính và một số các khái niệm liên quan. Làm việc với chúng sẽ trở nên bớt phức tạp và thú vị hơn nhiều. 3.1
Giá trị riêng và vectơ riêng của ma trận
Phép chuyển hình trong hình 3.1 là một toán tử tuyến tính. Bằng cách chọn cơ sở phù hợp, toán
tử tuyến tính trên tương đương với một ma trận. Vectơ màu xanh có một đặc điểm là nó không
thay đổi về phương sau toán tử tuyến tính bên trên. Và nó được gọi là một vectơ riêng của toán tử
tuyến tính đó, hay ma trận của toán tử tuyến tính đó. Như vậy, nói một cách nôm na, một vectơ v
là một vectơ riêng của một ma trận vuông A nếu Av có cùng phương với v, nghĩa là Av = λv với λ là
một số thực. Số thực λ như thế được gọi là một giá trị riêng của A ứng với vectơ riêng v. Nếu cho
trước một giá trị riêng λ, thì một vectơ v 6= 0 thoả mãn Av = λv cũng được gọi là một vectơ riêng
của A ứng với giá trị riêng λ.
Định nghĩa. Cho một ma trận vuông A, một số thực λ được gọi là một giá trị riêng của A nếu tồn tại
một vectơ v 6= 0 sao cho Av = λv.
Vectơ v như trên được gọi là một vectơ riêng của A ứng với giá trị riêng λ. 21 lOMoARcPSD| 36207943
Hình 3.1: "Ánh xạ" chuyển từ hình bên trái sang hình bên phải ở bên trên là một toán tử tuyến tính
từ không gian 2 chiều sang không gian 2 chiều.
3.1.1 Cách tìm giá trị riêng và vectơ riêng Cho một ma trận vuông A, λ
là một giá trị riêng của A khi và chỉ khi
∃v 6= 0 : Av = λv ⇐⇒
∃v 6= 0 : (A − λI)v = 0 ⇐⇒
det(A − λv) = 0
Vậy tập các giá trị riêng của ma trận A là tập tất cả nghiệm của đa thức (theo λ) PA(λ) := det(A − λI).
Cho một ma trận vuông A cùng với một giá trị riêng λ, thì v 6= 0 là một vectơ riêng của A ứng
với λ khi và chỉ khi v là nghiệm của
(A − λI)v = 0. Như vậy, việc tìm giá trị riêng của ma trận
được quy về việc giải phương trình PA(λ) = 0 và việc tìm vectơ riêng ứng với giá trị riêng λ được
quy về việc giải hệ phương trình tuyến tính (A − λI)v = 0. 3.1.2 Chéo hoá ma trận Xét ma trận . Thì A có GTR: λ1 = 3, VTR: GTR: λ1 = 4, VTR: .
3.2. SƠ LƯỢC VỀ DẠNG TOÀN PHƯƠNG 23 lOMoARcPSD| 36207943 24
CHƯƠNG 3. TOÁN TỬ TUYẾN TÍNH VÀ DẠNG TOÀN PHƯƠNG Suy ra Đặt Thì ta có Hay .
Quá trình như trên được gọi là quá trình chéo hoá ma trận A.
Cho một ma trận A vuông bất kì, ta nói A chéo hoá được nếu tồn tại một ma trận khả nghịch
cùng cấp P, sao cho P−1AP là ma trận chéo. Lúc đó ma trận P được gọi là ma trận làm chéo hoá A,
còn ma trận chéo D = P−1AP được gọi là dạng chéo của A.
Giả sử P−1AP = D là một ma trận chéo. Thì ta dễ dàng suy ra
det(A − λI) = det(P−1(A − λI)P) = det(D − λI).
Nên nếu A chéo hoá được thì tập giá trị riêng của A chính là tập hợp các phần tử trên đường chéo
của D. Hơn nữa, cột thứ i của P chính là một vectơ riêng của P tương ứng với giá trị riêng (D)ii. Vì
vậy ta có thuật toán chéo hoá ma trận như sau.
Thuật toán chéo hoá ma trận vuông A.
1. Lập đa thức đặc trưng PA(λ) = det(A − λI).
2. Giải phương trình PA(λ) = 0 để tìm các giá trị riêng (thực) λ1,. .,λk. 3. Với mỗi giá trị riêng λ,
giải hệ phương trình (theo v) (A − λI)v = 0. Đếm số tham số xuất hiện trong mỗi hệ nghiệm
(cững chính là số chiều của không gian vectơ riêng tương ứng với mỗi λ).
4. Nếu tổng số tham số xuất hiện ở bước 3 ít hơn số bậc của ma trận A thì ta khẳng định A không
chéo hoá được. Trong trường hợp tổng số tham số bằng với số bậc thì ma trận chéo hoá
được. Lúc đó ma trận làm chéo hoá A là ma trận tạo thành từ các vectơ cơ bản ở bước 3, và
ma trận dạng chéo của A tương ứng là ma trận các vectơ riêng tương ứng. 3.2
Sơ lược về dạng toàn phương
Một dạng toàn phương n biến thực định nghĩa bởi:
q = a11x21 + ··· + annx2n + 2 X aijxixj, 1≤i≤n
trong đó aij ∈ R, còn x1,. .,xn là n biến số (thực).
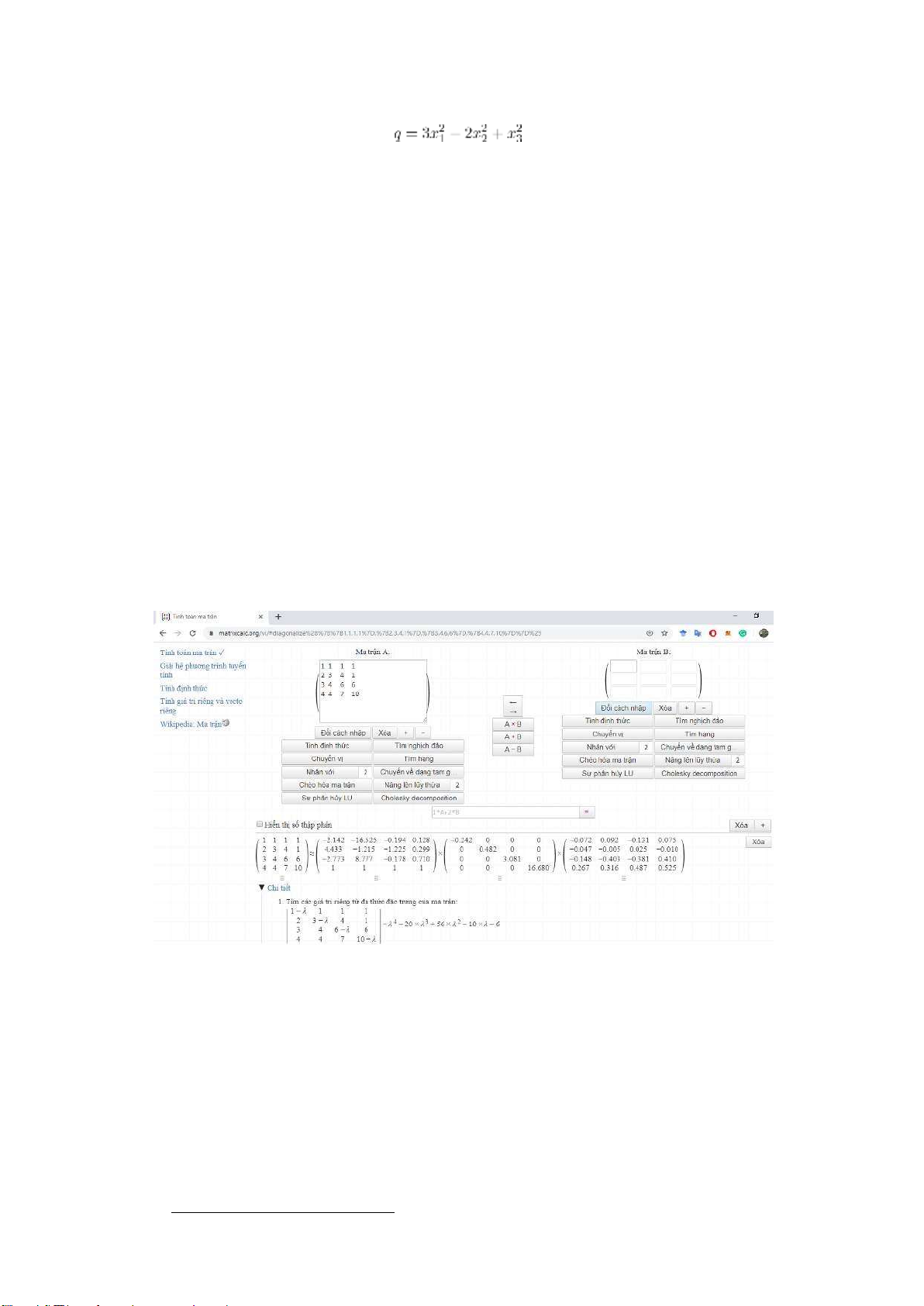
Ví dụ 3.2.1. Đa thức sau đây là một dạng toàn phương 3 biến:
q = 2x2 − 3y2 − 4xy + 8xz lOMoARcPSD| 36207943 3.2.1
Biểu diễn ma trận của dạng toàn phương Cho dạng toàn phương
q = a11x21 + ··· + annx2n + 2 X aijxixj. 1≤i≤n Ma trận a11 a12 ··· ... ... an2 ··· ,
a1n a21 a22 ··· a2n
trong đó aji = aij, được gọi là ma trận của dạng toàn phương q bên trên.
Xét ma trận dòng x = (x1 x2 . . xn). Thì ta có q = xAxt.
Ví dụ 3.2.2. Ma trận của dạng toàn phương q = 2x2 − 3y2 + z2 − 4xy + 8xz + 3yz là
Ta dễ dàng thấy nếu A là ma trận của một dạng toàn phương thì A = At, hay nói cách khác, A là một ma trận đối xứng. 3.2.2
Hạng của dạng toàn phương
Hạng của dạng toàn phương q, kí hiệu bởi rank(q), được định nghĩa là hạng của ma trận biểu diễn của nó.
Ví dụ 3.2.3. Cho dạng toàn phương
q = x2 + y2 + z2 + 2xy + 2xz + 2yz. Thì ta có
rank(q) = 1 vì ma trận biểu diễn của q , có hạng là 1. 3.2.3 Dạng chính tắc
Dạng toàn phương q được gọi là dạng chính tắc nếu ma trận biểu diễn của q có dạng chéo. Lúc
đó, các hệ số aii nằm trên đường chéo được gọi là các hệ số chính tắc của q.
Định lý (Luật quán tính Sylvester) Mỗi dạng toàn phương q luôn có thể đổi biến để đưa về dạng
chính tắc. Nhìn chung thì dạng chính tắc của q là không duy nhất mà phụ thuộc vào cách đổi biến.
Trong mỗi dạng chính tắc của q, số các hệ số chính tắc khác 0, số các hệ số dương và số các hệ số
âm không phụ thuộc cách đổi biến. Ta gọi số các hệ số dương (âm) của A là chỉ số dương (âm) quán tính của q.
Ví dụ 3.2.4. Nếu dạng toàn phương 3 biến q có dạng chính tắc là lOMoARcPSD| 36207943 26
CHƯƠNG 3. TOÁN TỬ TUYẾN TÍNH VÀ DẠNG TOÀN PHƯƠNG ,
thì chỉ số quán tính dương của q là 2, trong khi đó chỉ số âm quán tính của q là 1 và hạng của q là 3.
3.3. TÍNH TOÁN VỚI PHẦN MỀM 25 3.2.4
Dấu của dạng toàn phương
Cho một dạng toàn phương q. Khi đó,
1. q được gọi là không âm nếu mọi hệ số chính tắc của q đều dương.
2. q được gọi là xác định dương nếu q không âm và số các hệ số chính tắc đúng bằng số biến của q.
3. q được gọi là không dương nếu mọi hệ số chính tắc của q đều âm.
4. q được gọi là xác định âm nếu q không dương và số các hệ số chính tắc đúng bằng số biến của q.
5. Nếu hệ số chính tắc của q có cả âm và dương thì ta nói q đổi dấu. 3.3 Thực hành phần mềm
Việc tìm hoặc kiểm tra kết quả về giá trị riêng, véc tơ riêng và chéo hóa ma trận, kể cả những
ma trận có tham số sẽ đơn giản hơn thông qua phần mềm online. Các bước tính toán được giải
thích chi tiết, xem thêm hình 3.2.
Hình 3.2: Tính nghiệm của phương trình đặc trưng và chéo hóa ma trận 4 × 4. 3.4
Một số bài tập và thực hành cuối chương 3
1. (Bài tập nhóm). Nhóm hãy tìm hiểu thêm về các ứng dụng của giá trị riêng và vector riêng
trong thực tế, chuẩn bị bài trình bày trước lớp (powerpoint hoặc tương đương). Có thể tham
khảo sách Fuad Aleskerov et al. “Linear Algebra for Economists”10 phần 9.1 trang 149 hoặc website thetalog.com11.
10 http://93.174.95.29/_ads/432193591563C6CD1C0060CD4371CA0C
11 https://thetalog.com/thetaflow/pca2d-visualizer/?fbclid=IwAR0k5vk7h2ZUFybrLYeGz9v9NVz-\
jLTGjnK0mWvnBomrGl7qInmrJjDuubo lOMoARcPSD| 36207943
2. (Bài tập rèn luyện tiếng Anh học thuật). Tìm hiểu và trình bày tóm tắt các nội dung được nêu
trong trang wikipedia về giá trị riêng và véc tơ riêng12.
3. (Bài tập thực hành). Sử dụng phần mềm online doza13 hoặc matrix calculator14 để tìm giá trị
riêng và véc tơ riêng của một ma trận (ánh xạ tuyến tính) do bạn tự chọn.
4. Dùng giá trị riêng, véc tơ riêng và chéo hóa ma trận để xử lý tình huống nêu ra ở đầuchương
này: tính tỷ lệ có việc làm và tỷ lệ thất nghiệp sau 100 tuần với số liệu của Mỹ: .
12 https://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors 13 doza.pro 14 https://matrixcalc.org/vi/ lOMoARcPSD| 36207943 28
CHƯƠNG 3. TOÁN TỬ TUYẾN TÍNH VÀ DẠNG TOÀN PHƯƠNG Chương4 Quy hoạch tuyến tính
Sau khi học xong chương này, người học đạt được những kiến thức và kỹ năng sau:
1. Hiểu được bài toán quy hoạch tuyến tính.
2. Hiểu được ý nghĩa của bài toán quy hoạch tuyến tính trong kinh tế cũng như trongđời sống.
3. Hiểu được định nghĩa của các phương án và ý tưởng của phương pháp đơn hình.
4. Sử dụng được các phần mềm trên máy vi tính để xử lý bài toán quy hoạch tuyến tính. 4.1 Bài toán vận tải
Một bài toán vận tải (transportation problem) là một bài toán tìm phương án vận chuyển giữa
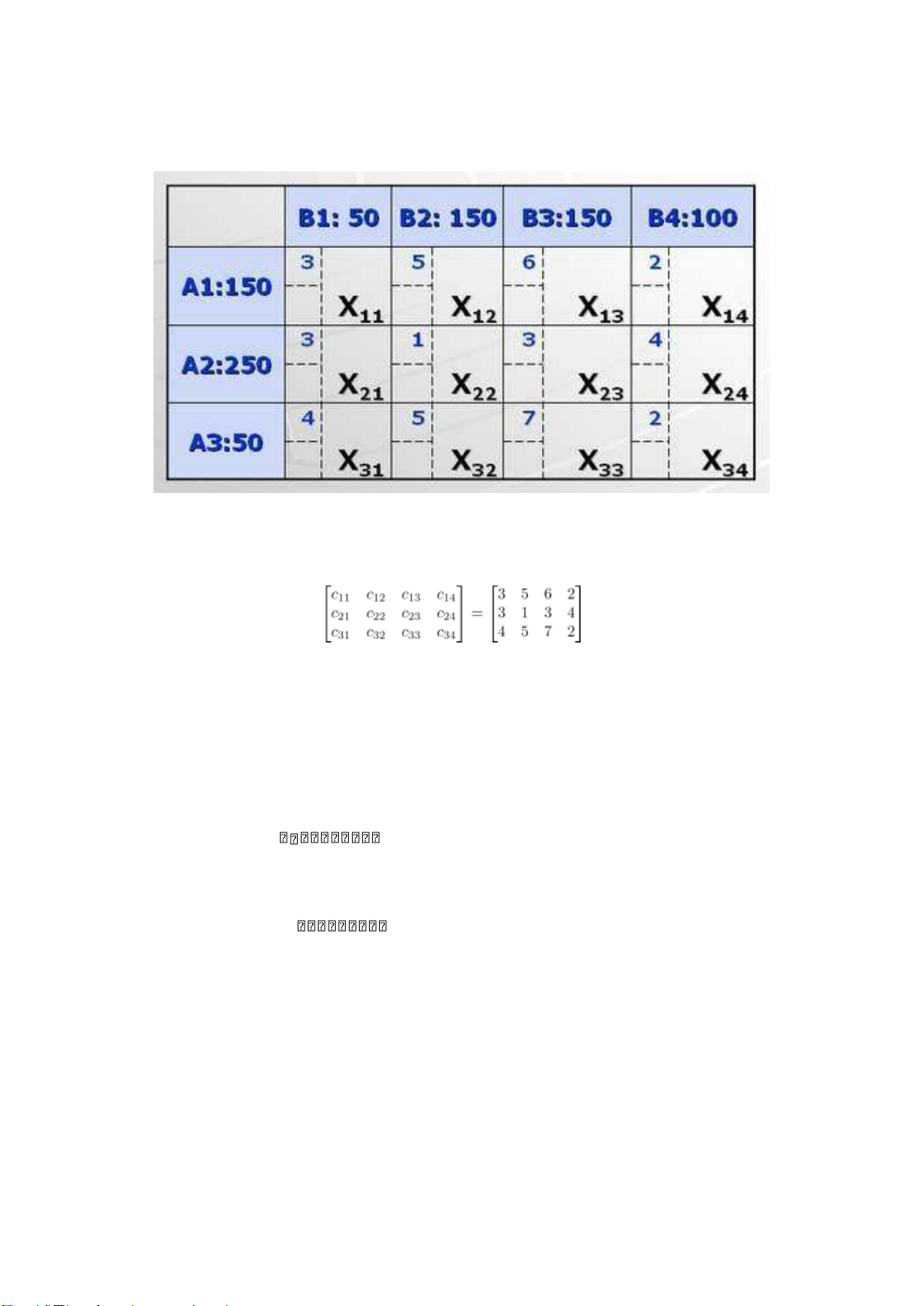
các "kho hàng" và "cửa hàng" sao cho có lợi nhất. Ví dụ, ta có 3 kho hàng Ai và 4 cửa hàng Bi như sau: Trong đó,
1. Kho hàng Ai có ai tấn hàng.
2. Cửa hàng Bi cần bi tấn hàng.
3. Chi phí vận chuyển từ Ai sang Bj là cij (nghìn USD) trên mỗi tấn hàng.
Câu hỏi được đặt ra là tìm phương án vận chuyển tiết kiệm nhất?
Đặt xij là số tấn hàng chuyển từ Ai tới Bj.Ta sẽ gọi ma trận
(xij) là một phương án vận chuyển. Như vậy, bài toán vận
tải là bài toán tìm phương án vận chuyển xij sao cho chi
phí vận chuyển là ít nhất
Mỗi phương án vận chuyển xij sẽ tốn của chúng ta chi phí là: G = Xcijxij. ij 27 lOMoAR cPSD| 36207943
CHƯƠNG 4. QUY HOẠCH TUYẾN TÍNH
Để đơn giản, ta xét một trường hợp cụ thể như sau:
Nghĩa là kho hàng A1 có a1 = 150 tấn hàng, kho hàng A2 có a2 = 250 tấn hàng, kho hàng
A3 có a3 = 50 tấn hàng; và cửa hàng B1 cần 50 tấn hàng, cửa hàng B2 cần 150 tấn hàng, cửa hàng B3
cần 150 tấn hàng, cửa hàng B4 cần 100 tấn hàng. Ngoài ra, chi phí để vận chuyển mỗi tẫn hàng từ
kho Ai đến kho Bj là .
Do kho hàng Ai chỉ có ai tấn hàng và cửa hàng Bj chỉ cần bj tấn hàng. Nên ta có các ràng
buộc (lý tưởng) như sau:
x11 + x12 + x13 + x14 = 150
x21 + x22 + x23 + x24 = 250
x31 + x32 + x33 + x34 = 50 x (I) 11 + x21 + x31 = 50
x12 + x22 + x32 = 150
x13 + x23 + x33 = 150
x14 + x24 + x34 = 100
Như vậy, bài toán trở thành tìm phương án (xij) thoả mãn các ràng buộc (I) phía trên sao cho hàm chi phí
G = 3x11 + 5x12 + 6x13 + 2x14 + 3x21 + x22 + 3x23 + 4x24 + 4x31 + 5x32 + 7x33 + 2x34
đạt giá trị thấp nhất.
Vì cả hàm mục tiêu G và các ràng buộc đều là các hàm tuyến tính nên bài toán vận tải là một bài
toán quy hoạch tuyến tính. Như vậy một bài toán quy hoạch tuyến tính là một bài toán tìm giá trị
lớn nhất hay nhỏ nhất của một hàm mục tiêu với một hệ các ràng buộc (là các phương trình hoặc
bất phương trình), trong đó cả hàm mục tiêu lẫn các ràng buộc phải là các hàm tuyến tính. lOMoARcPSD| 36207943 30 4.2
Phương án và phương án tối ưu
Giả sử ta có một bài toán quy hoạch tuyến tính như sau: tìm xij sao cho hàm mục tiêu G = 3x11
4.3. PHƯƠNG PHÁP ĐƠN HÌNH 29
đạt giá trị nhỏ nhất, với các ràng buộc: = 150 = 250 = 50 = 50
+ 5x12 + 6x13 + 2x14 + 3x21 + x22 + 3x23 + 4x24 + 4x31 + 5x32 + 7x33 + 2x34 x12 + x22 + x32 = 150
x1314 + x2324 + x3334 ij =
150Rn x + x + x = 100
Khi đó, một phương án (PA) là một ma trận (x ) trong
sao cho nó thoả mãn tất cả các ràng buộc.
Ví dụ 4.2.1. Một trường hợp tối ưu. Ma trận .
là một phương án. Một phương án được gọi là phương án tối ưu (PATƯ) nếu nó làm cho hàm mục
tiêu đạt được cực trị (trong trường hợp này là cực tiểu). 4.3
Giới thiệu ý tưởng của phương pháp đơn hình
Để giải một bài toán quy hoạch tuyến tính, ta có thể sử dụng phương pháp đơn hình. Phương
pháp đơn hình là phương pháp mà ta xuất phát từ một phương án (cực biên), sau đó ta sẽ dựa vào
các hàm mục tiêu và các hàm ràng buộc để tìm một phương án tốt hơn, nghĩa là phương án mới
này làm cho hàm mục tiêu đạt gần giá trị tối ưu hơn. Trong trường hợp của bài toán vận tải bên
trên, phương án mới sẽ làm cho chi phí nhỏ hơn. Sau đó, ta kiểm tra xem phương án mới này đã
là phương án tối ưu chưa. Nếu nó là phương án tối ưu thì ta dừng lại. Ngược lại, nếu phương án
mới chưa tối ưu thì ta sẽ tìm phương án mới tốt hơn và lặp lại các bước bên trên. Thuật toán đơn
hình đã được chứng minh là sẽ dừng sau một số hữu hạn bước. 4.4 Thực hành phần mềm
Tính toán với phần mềm Chúng ta có thể sử dụng nhiều phần mềm để giải bài toán quy hoạch
tuyến tính. Sau đây là một số thao tác đơn giản với Excel. Sử dụng Add-in Solver, lOMoARcPSD| 36207943
Hình 4.1: Thực hiện nhập liệu, đưa các điều kiện vào bảng và xây dựng hàm mục tiêu nhập hàm
mục tiêu và các điều kiện kèm theo, sau đó yêu cầu "solve": Kết quả thu được 4.5
Một số bài tập và thực hành cuối chương 4
1. (Bài tập nhóm). Nhóm hãy tìm hiểu thêm về các ứng dụng của quy hoạch tuyến tính trong
thực tế, chuẩn bị một bài trình bày trước lớp (powerpoint hoặc tương đương).
2. (Bài tập rèn luyện tiếng Anh học thuật). Nghe hiểu và thực hành theo nội dung được trình
bày trong video về Excel 15.
CHƯƠNG 4. QUY HOẠCH TUYẾN TÍNH
Hình 4.2: Nhập hàm mục tiêu và các điều kiện vào bảng hỏi Solver.
15 https://www.youtube.com/watch?v=dsNQrW7ZiFw lOMoARcPSD| 36207943 32
Hình 4.3: Kết quả trả về tự điền vào các ô trống khối lượng của "X" và kết quả của hàm mục tiêu.
4.5. MỘT SỐ BÀI TẬP VÀ THỰC HÀNH CUỐI CHƯƠNG 4 31
3. (Bài tập thực hành). Sử dụng Excel hoặc phần mềm tương đương để giải bài toán vận tải
trong phần 4.1 hoặc một bài quy hoạch tuyến tính do bạn tự chọn. lOMoARcPSD| 36207943 Chương5 Hàm một biến số
Sau khi học chương này, người học sẽ có các kỹ năng và kiến thức sau:
1. Hiểu được một số ứng dụng của hàm số và các hàm thông dụng trong mô
hìnhkinh tế đơn giản: hàm doanh thu, lợi nhuận, chi phí, hàm lợi ích, etc.
2. Sử dụng được đạo hàm để tính xấp xỉ giá trị cận biên của các hàm kinh tế, hệ
sốco giãn của các hàm cung và cầu, etc.
3. Xử lý được các bài toán tối ưu trong kinh tế.
4. Sử dụng được phần mềm máy tính hỗ trợ các bài toán phức tạp.
5.1 Hàm số một biến
Định nghĩa 5.1 Một hàm số thực (real-valued function) của biến x với tập xác định
(domain) D là một quy tắc mà mỗi một giá trị của x ∈ D xác định duy nhất một giá trị
của hàm số. Giá trị của hàm số f tại x thường được ký hiệu là y = f(x).
Ví dụ 5.1 Giá của sản phẩm P là hàm của lượng cầu Q, biểu diễn là P = 300 − 2Q.
Hệ số 2 ở đây có đơn vị là $/sản phẩm.
Khi Q = 50 (sản phẩm) thì giá của chúng là P = 200$.
Ví dụ 5.2 (Lương và tiền thưởng). Giả sử một nhân viên bán hàng nhận được mức
lương theo hợp đồng kèm theo mức thưởng. Trong hợp đồng quy định rằng lương
hàng tháng gồm có ba phần. Phần lương cơ bản là 7 triệu đồng, phần hoa hồng là
10% doanh số bán hàng, phần thưởng thêm của tháng là 5 triệu nếu nhân viên bán
hàng có thể đạt doanh thu trên 200 triệu trong tháng đó.
Gọi s là doanh thu bán hàng của nhân viên và p là tiền lương hàng tháng của nhân
viên đó, ta có hàm số p theo s là: 7 + 0.1s, s < 200 p = ( 12 + 0.1s, s ≥ 200 33
Ta thấy hàm số này là hàm đồng biến và gián đoạn tại điểm s = 200. Vẽ đồ thị biểu diễn hàm trên?
Giả sử nhân viên A đạt doanh số bán hàng trong tháng là 190 triệu, lương của A là 7 + 10% × 190 = 26 triệu; lOMoARcPSD| 36207943 34
CHƯƠNG 5. HÀM MỘT BIẾN SỐ
Nhân viên B đã đạt doanh số 190 triệu vào ngày 25 của tháng và rất muốn đạt mức
200 triệu để có thêm thưởng. B thông báo với các khách hàng tiềm năng của mình là
nếu khách ký hợp đồng với giá trị tối thiểu là 10 triệu trước ngày cuối cùng của tháng
thì B sẽ tặng khách quà tặng có giá trị tương đương 8% giá trị hợp đồng của khách.
Một số khách hàng thích chương trình này và B đã có thêm doanh số vượt 10 triệu.
Hỏi thu nhập của B khi đó ít nhất sẽ là bao nhiêu? So sánh với thu nhập của A thì thế nào?
Ví dụ 5.3 Tổng sản phẩm quốc nội (Gross National Product) sau t năm được cho bởi
mô hình dự báo sau:
GNP = 80e0.04t.
Sau bao nhiêu năm thì tổng sản phẩm quốc nội có giá trị là 100 tỷ $?
Ta cần giải phương trình sau: 100 = 80e0.04t ⇒ 0.04t = ln(1.25). Ta thu được t xấp xỉ 5.58 năm.
5.2 Giới hạn của hàm số (limit of a function)
Định nghĩa 5.2 (Giới hạn trái). Hàm số f(x) có giới hạn trái bằng L tại điểm a nếu với
mọi ǫ > 0, nhỏ tùy ý, thì tồn tại một số δ > 0 sao cho khi a − δ < x < a ta có |f(x) − L| < ǫ, ký hiệu
Ví dụ 5.4 Xét hàm số .
Ta có limx→0− f(x) = −1.
Định nghĩa 5.3 (Giới hạn phải). Hàm số f(x) có giới hạn phải bằng L tại điểm a nếu với
mọi ǫ > 0, nhỏ tùy ý, thì tồn tại một số δ > 0 sao cho khi a < x < a + δ ta có |f(x) − L| < ǫ, ký hiệu
Ví dụ 5.5 Xét hàm số .
Ta có limx→0+ f(x) = 1.
Định nghĩa 5.4 Hàm số f(x) gọi là có giới hạn tại điểm a nếu nó có giới hạn trái và giới
hạn phải bằng nhau, tức là
lim f(x) = lim f(x) = lim f(x). x→a x→a− x→a+ lOMoARcPSD| 36207943 35 5.3. ĐẠO HÀM Ví dụ 5.6 . 5.3 Đạo hàm
Định nghĩa 5.5 . Cho hàm số f : D → R. Hàm f được gọi là có đạo hàm tại điểm x0 nếu
tồn tại giới hạn hữu hạn (tương tự, .
Giá trị giới hạn đó gọi là đạo hàm của hàm f tại x0, ký hiệu là f′(x0).
5.3.1 Đạo hàm của một số hàm sơ cấp
• C′ = 0; (xα)′ = αxα−1 (α 6= 0)
• (ex)′ = ex; log(x)′ = x1
5.3.2 Quy tắc tính đạo hàm
• Đạo hàm của hàm tổng, hiệu (u ± v)′ = u′ ± v′
• Đạo hàm của hàm tích (uv)′ = u′v + uv′ • Đạo hàm hàm thương
• Đạo hàm hàm hợp: cho hàmy′(u),u′(x) thì y = f(u) và u = g(x) nếu tồn tại đạo
hàm (f(g(x))′ = g′(x)f′(g(x)) lOMoARcPSD| 36207943 36
CHƯƠNG 5. HÀM MỘT BIẾN SỐ
• sốĐạo hàm hàm ẩn cho ở dạng tham số: chox = x(t),y = y(t)(t ∈ D,x′(t) 6=
0,∀ty∈(xD) )xác định bởi phương trình tham. Khi đó: . 5.4
Các ứng dụng của đạo hàm trong kinh tế
Ký hiệu của một số biến và hàm thường gặp trong kinh tế: • Giá (price): p hoặc P; • Lao động (Labor): L; • Vốn (Capital): K;
• Hàm lợi ích (Utility): U;
• Chi phí (Total Cost): TC;
• Doanh thu (Total Revenue): TR;
• Lợi nhuận (Profit) π = TR − TC. 5.4.1
Giá trị cận biên (marginal value)
Trong kinh tế học, lượng thay đổi của hàm y = y(x) tại x0 khi x tăng lên một đơn vị gọi
là giá trị cận biên (marginal value). Ta ký hiệu là My(x0). Coi sự thay đổi của x là khá
nhỏ, ta có xấp xỉ sau đây: .
Trong thực hành, đôi khi ta viết dấu bằng thay cho dấu xấp xỉ.
Ví dụ 5.7 Hàm của giá theo số lượng cầu là P = 100−2Q. Tính doanh thu cận biên, nếu
hiện tại lượng cầu Q = 15 sản phẩm?
Giải: Hàm doanh thu là R = PQ = (100 − 2Q)Q. Với Q = 15 ta có:
MR ≈ (R)′ = 100 − 4Q = 100 − 4 · 15 = 40. lOMoARcPSD| 36207943 37
5.4.2 Quy luật lợi ích cận biên giảm dần
Các hàm biểu diễn lợi ích (thu nhập, doanh thu, lợi nhuận ...) đều tuân theo quy luật
lợi ích cận biên giảm dần.
Ví dụ 5.8 Bạn rất thích ăn kẹo sô cô la. Hàm "lợi ích" của bạn sẽ tăng khi bạn được ăn
kẹo. Ăn chiếc đầu, bạn thấy rất tuyệt! Thêm một chiếc, vẫn rất ngon (lợi ích cận biên
còn cao)! Thêm chiếc nữa, cảm giác ngon miệng có giảm đi chút ít. Nếu thêm chiếc
nữa, rồi chiếc nữa, thì lợi ích cận biên sẽ ra sao?
Lợi ích cận biên sẽ luôn giảm dần. Dưới góc nhìn của hàm số, hàm biểu diễn lợi ích là
các hàm có đạo hàm cấp 1 giảm dần, tức là đạo hàm cấp 2 âm.
5.4. CÁC ỨNG DỤNG CỦA ĐẠO HÀM TRONG KINH TẾ
5.4.3 Hệ số co giãn - elasticity
Giả sử rằng một loại xe hơi tuần trước có giá 500 triệu và một loại điện thoại di động
có giá 5 triệu. Tuần này chiếc xe hơi giảm 10 triệu, còn điện thoại giảm 1 triệu. a.
Thực chất xe hơi hay điện thoại đã có biến động về giá lớn hơn, xét tương
đối với giátrị của sản phẩm? b.
Phản ứng của người tiêu dùng sẽ như thế nào? Làm sao để so sánh sự thay
đổi tươngđối về lượng cầu với sự thay đổi tương đối của giá sản phẩm?
Trong thực tiễn, ta sử dụng khái niệm hệ số co giãn để xem xét sự thay đổi tương
đối của biến y(x)(ví dụ cung hoặc cầu) so với biến x (ví dụ như giá cả).
Định nghĩa 5.6 Hệ số co giãn của y(x) theo biến x: .
Hệ số co giãn tương ứng với một điểm x0: Khi x tăng từ mức x = x0 lên 1% (hay một
khoảng đủ nhỏ), ta có: .
Ví dụ 5.9 Giả sử giá rượu bia tăng lên 5% làm lượng cầu giảm đi 3%. Vậy hệ số co giãn
của cầu theo giá là bao nhiêu?
Hệ số co giãn của cầu theo giá là: -3% / (5%) = -0.6.
Ví dụ 5.10 (Hệ số co giãn tại một điểm). Hàm cầu của một loại hàng hóa là .
Tính hệ số co giãn của cầu theo giá tại P = 5$. Ước lượng tỷ lệ thay đổi về cầu khi giá tăng 2%.
Giải. Tại P = 5 ta có Q = 80. Hệ số co giãn của cầu theo giá tại P = 5 là: lOMoARcPSD| 36207943 38
CHƯƠNG 5. HÀM MỘT BIẾN SỐ
Q′(P)P/Q = −4000 × 5−3 × 5/80 = −2.
Khi giá từ 5$ tăng khoảng 2% thì cầu sẽ giảm khoảng 4%.
Chú ý 5.1 Nếu
• |ǫ| > 1 thì ta nói co giãn mạnh;
• |ǫ| < 1 là co giãn yếu;
• |ǫ| = 1 thì ta có co giãn đơn vị hay đẳng co.
Trong trường hợp bài toán trên là co giãn mạnh vì | − 2| = 2 > 1.
5.5 Bài toán tối ưu của hàm một biến số (optimization of one-variable function)
Định nghĩa 5.7 Hàm f(x) được gọi là có cực đại toàn cục tại x∗ nếu
f(x∗) ≥ f(x), ∀x.
f(x) được gọi là có cực đại địa phương tại x0 nếu tồn tại ǫ > 0 rất nhỏ.
f(x0) ≥ f(x),
∀x0 − ǫ ≤ x ≤ x0 + ǫ.
Định nghĩa 5.8 Hàm f(x) được gọi là có cực tiểu toàn cục tại x∗ nếu
f(x∗) ≤ f(x), ∀x.
f(x) được gọi là có cực tiểu địa phương tại x0 nếu tồn tại ǫ > 0 rất nhỏ,
f(x0) ≤ f(x),
∀x0 − ǫ ≤ x ≤ x0 + ǫ.
Chú ý 5.2 Cho hàm số f(x). Để tìm cực trị ta thực hiện như sau:
Bước 1: Tìm các điểm tới hạn x0, tức là f′(x0) = 0 hoặc điểm x0 mà tại đó không tồn
tại đạo hàm. Bước 2: Xét bảng biến thiên:
• Nếu qua x0 hàm f′ đổi dấu từ âm sang dương thì hàm số f có cực tiểu
• Nếu qua x0 hàm f′ đổi dấu từ dương sang âm thì hàm số f có cực đại
• Nếu tại x0 hàm f′ không đổi dấu thì hàm f không có cực trị tại x0.
Để thay thế bước 2 ta có thể xét dấu của đạo hàm cấp 2:
• Nếu f′(x0) = 0 và f′′(x0) < 0 thì hàm số f(x) có cực đại tại x0,
• Nếu f′(x0) = 0 và f′′(x0) > 0 thì hàm số f(x) có cực tiểu tại x0. lOMoARcPSD| 36207943 39
Nếu cần tìm giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [a,b] thì ta so sánh hàm
số tại điểm cực trị với các giá trị của hàm số tại các điểm a,b.
Ví dụ 5.11 Xét quan hệ giữa nhà xuất bản và tác giả sách. Giả sử hàm giá theo cầu là
p = 100 − x, hàm doanh thu của nhà xuất bản là R = px = (100 − x)x. Hàm chi phí là C
= 25x. Giả sử tất cả sách in ra được bán hết và nhà xuất bản sẽ trả cho tác giả 10%
phí bản quyền. Khi đó thu nhập của tác giả sách là:
y(x) = 0.1px = 0.1(100x − x2).
Còn lợi nhuận của nhà xuất bản là:
π(x) = R(x) − C(x) − y(x) = 65x − 0.9x2. a.
Tác giả muốn đặt ra một cái giá và lượng sách cần in để sao cho thu nhập
anh ta đạtcực đại. Giá đó là bao nhiêu và cần in bao nhiêu bản? b.
Phía nhà xuất bản cũng muốn có lợi nhuận tối đa, vậy giá họ muốn đưa ra là
baonhiêu và cần in khoảng bao nhiêu cuốn sách?
5.6. THỰC HÀNH LẬP TRÌNH
Giải. Ta có y′(xA) = 0 ⇒ xA = 50. Do đó giá sách tác giả mong muốn sẽ là:
pA = 100 − xA = 50$.
Đối với nhà xuất bản thì họ cũng muốn đạt lợi nhuận tối đa, do đó ta có lượng sách
mà nhà xuất bản muốn in sẽ xấp xỉ bằng:
π′(xB) = 65 − 1.8xB = 0 ⇒ xB ≈ 36.
Giá tương ứng xấp xỉ pB = 64$.
So sánh hai kết quả ta thấy rằng nhà xuất bản muốn đưa ra giá bán sách cao hơn và
in ít bản hơn tác giả sách mong muốn.
5.6 Thực hành lập trình
Trong chương trước ta đã biết dùng Excel để giải bài toán quy hoạch tuyến tính. Với
bài toán phi tuyến mức độ đơn giản, Excel hỗ trợ xử lý tương đối hiệu quả: ví dụ chạy trên Excel
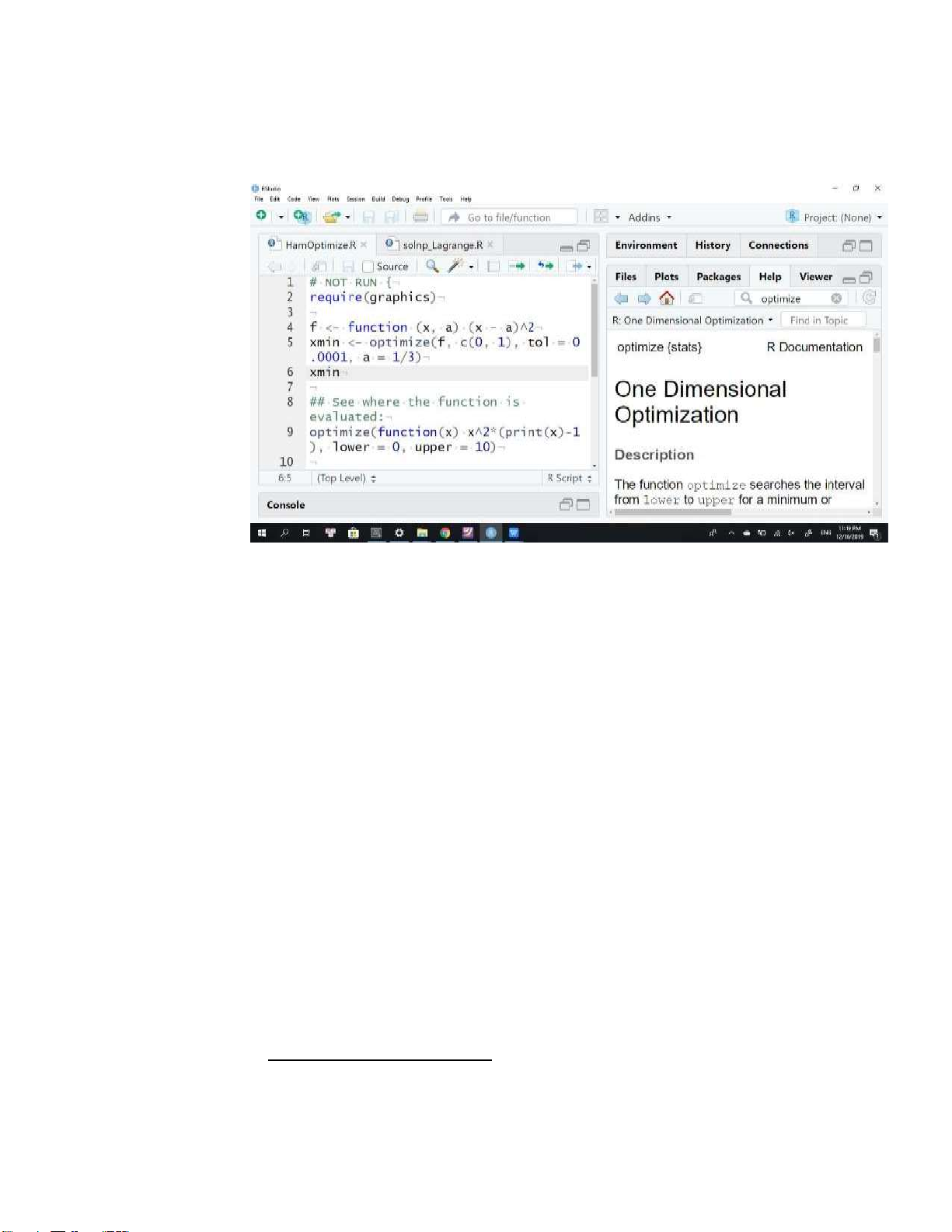
Trong phần này ta sẽ thử dùng ngôn ngữ R để giải quyết bài toán tối ưu ở trên.
1. Cài đặt R trước rồi tới Rstudio, file cài có ở trên web: bấm vào đây
2. Sau đó khởi động Rstudio để bắt đầu lập trình trên R: bấm vào đây. lOMoARcPSD| 36207943 40
CHƯƠNG 5. HÀM MỘT BIẾN SỐ
Hình 5.1: Tối ưu một biến với hàm optimize() trên R.
5.7 Một số bài tập và thực hành cuối chương 5
1. (Tiếng Anh học thuật và thực hành lập trình). Đọc hiểu phần hướng dẫn thực hành và chạy thử hàm optimize():
https://www.rdocumentation.org/packages/stats/versions/3.6.1/topics/opti mize.
2. (Bài tập nhóm). Lập trình giải bài một số bài tập cuối chương Differentiation
trong sách "Mathematics for economics and business", Ian Jacques 16. Mỗi
nhóm làm một hoặc hai bài tương ứng với các nội dung ứng dụng khác nhau,
giải thích phần lập trình qua một bài trình bày ngắn để nói về kết quả nhóm làm được.
3. Hàm tổng doanh thu làTÌm hàm lợi nhuận biên và tính giá trị lợi nhuận biên
tạiTR = 50Q−3Q2 và hàm tổng chi phí làQ = 3. Nêu ý nghĩa củaTC = 20+2Q. kết quả.
16 http://93.174.95.29/_ads/96A8076441FD5FA8966D6B303EFE4497 lOMoAR cPSD| 36207943 41
4. Hàm cầu của một loại hàng hóa làcầu Q theo giá P, khi giá
P = 95 − Q2 −
4Q. Tính hệ số co giãn của
P = 50($)? Nêu ý nghĩa của kết quả tìm được và nhận
xét sự co giãn ở đây là co giãn mạnh hay yếu, hay đẳng co?
5. Hàm doanh thu cận biên là MR = 36 − 2Q và hàm chi phí cận biên là MC =
3($). Biết chi phí cố định là 20($), tìm lợi nhuận tối ưu? lOMoARcPSD| 36207943 Chương6
Hàm nhiều biến (function of multi-variables)
Sau khi học xong chương này, người học có thể:
• Hiểu được một số ứng dụng của hàm nhiều biến trong thực tế, ví dụ hàm thuầnnhất
và bài toán quy mô sản xuất.
• Sử dụng được đạo hàm riêng để phân tích giá trị biên, tính xấp xỉ hệ số co giãncủa các hàm kinh tế.
• Giải được bài toán tối ưu không điều kiện và tối ưu có điều kiện trong kinh tế, vídụ
bài toán liên quan tới tối ưu hóa lợi nhuận, bài toán lượng cầu Marshall, lượng cầu Hick.
• Dùng được phần mềm hỗ trợ giải bài toán phức tạp.
6.1 Hàm nhiều biến
Định nghĩa 6.1 Hàm f của hai biến số x,y trên tập xác định D là một quy tắc mỗi giá trị của
x,y ∈ D thu được một giá trị z = f(x,y). Các biến x,y là biến độc lập và z là biến phụ thuộc.
Ví dụ 6.1 R. Frisch and T. Haavelmo đã đưa ra mô hình tiêu thụ sữa của các hộ gia đình như sau:
trong đó z là mức tiêu thụ sữa, p là giá sữa, m là mức thu nhập của hộ gia đình.
Ví dụ 6.2 Hàm hai biến thường xuất hiện nhiều trong kinh tế, chẳng hạn như hàm Cobb-
Douglas về năng xuất dựa trên vốn sở hữu và lao động. Mô hình tổng quát như sau:
F(K,L) = AKαLβ. 41 lOMoARcPSD| 36207943 43
Mở rộng định nghĩa của hàm hai biến ta có hàm của n biến số x1,x2,. .,xn, ký hiệu y =
f(x1,x2,...,xn).
Định nghĩa 6.2 Hàm thực f là hàm thuần nhất bậc s nếu: f(tX) = tsf(X).
Hàm Cobb-Douglas nêu trên là hàm thuần nhất. Thông thường trong bài toán quy mô sản
xuất ta xét một hàm thuần nhất như trên và xét t > 1. Giả sử hàm sản xuất là thuần nhất bậc s. Ta có
• s > 1: hiệu quả sản xuất tăng theo quy mô,
• s = 1: hiệu quả sản xuất không đổi theo quy mô,
• s < 1: hiệu quả sản xuất giảm theo quy mô.
6.2 Đạo hàm của hàm hai biến số
Xét hàm số z = f(x,y). Ta muốn biết z thay đổi thế nào nếu ta thay đổi các giá trị của x, y.
Nếu ta cố định biến y, tức là coi y như là hằng số thì khi đó ta có đạo hàm của hàm z theo
biến x. Nếu cố định biến x thì ta có đạo hàm của z theo biến y.
Các đạo hàm của z theo các biến x,y như vậy được gọi là các đạo hàm riêng, ký hiệu là ∂x∂z
và ∂y∂z hoặc zx′ ,zy′ .
Về mặt toán học ta có định nghĩa của các đạo hàm riêng như sau.
Định nghĩa 6.3 Cho hàm z = f(x,y) đạo hàm riêng của f theo các biến được xác định như sau
Đạo hàm riêng cấp 2 của hàm z = f(x,y) theo các biến x,y, ký hiệu hoặc (
) được định nghĩa như sau: .
Ma trận đạo hàm cấp 2 gọi là ma trận Hessian, luôn đối xứng. Dạng ma trận tổng quát: f11′′ ′′ f12 ′′ f22 ... lOMoARcPSD| 36207943 44
CHƯƠNG 6. HÀM NHIỀU BIẾN (FUNCTION OF MULTI-VARIABLES) f ′′ ′′ fn2 ...n H = 21 f′′1
6.3. HÀM BIÊN VÀ HỆ SỐ CO GIÃN
Ví dụ 6.3 Tìm các đạo hàm riêng cấp 1 và cấp 2 của hàm số a. z =
f(x,y) = x3y + x2y2 + x + y2; b. .
6.3 Hàm biên và hệ số co giãn
Ví dụ 6.4 Hàm sản lượng nông nghiệp y = f(K,L,T), trong đó K là vốn, L là lao động và T
là vùng sản xuất. Khi đó
xấp xỉ sản lượng biên theo vốn, nó cho ta biết tốc độ thay đổi
của sản lượng theo sự thay đổi của vốn K. Ví dụ nếu
thì khi tăng lượng vốn lên h
đơn vị thì sản suất tăng thêm 5h đơn vị. Xét hàm sản xuất f có dạng mô hình Cobb-Douglas
y = f(K,L,T) = 2K2L3T4.
a. Tính hàm sản xuất biên và hệ số co giãn theo biến vốn, lao động và vùng sảnxuất,
biết K = K0,L = L0,T = T0.
b. Ma trận Hessian các đạo hàm cấp 2 của hàm f là ma trận cấp mấy? Ma trận này có
đối xứng không? (Gợi ý:
Ví dụ 6.5 Nhu cầu tiền mặt M ở nước Mỹ trong giai đoạn 1929-1952 được ước lượng cho
bởi hàm sau: M = 0.14Y +76.03(r−2)−0.84, (r > 2). Trong đó Y là thu nhập quốc gia, r là
lãi suất (%). Hãy tìm biểu diễn của hàm biên, hệ số co giãn tại điểm (Y0,r0) cho trước và
tính ma trận Hessian. (Gợi ý: Ma trân Hessian là ma trận vuông cấp 2).
6.4 Cực trị hàm nhiều biến
Cho hàm z = f(x,y), ta muốn tìm giá trị lớn nhất và nhỏ nhất của z. Ta giả sử rằng hàm f
đạt cực đại tại điểm (x0,y0). Nếu ta cố định giá trị y tại y0 thì hàm số g(x) = f(x,y0) sẽ có
cực đại tại x0, tương tự hàm h(y) = f(x0,y) đạt cực đại tại điểm y0. lOMoARcPSD| 36207943 45
6.4.1 Cực trị tự do
Định lý 6.1 (Điều kiện cần và đủ để hàm số đạt cực trị). Cho hàm hai biến z = f(x,y) để
hàm số có cực trị tại điểm (x0,y0) (cực đại, cực tiểu) thì điều kiện cần là hoặc z không có
đạo hàm, hoặc có đạo hàm tại đó bằng 0, tức là: . Đặt .
a) Nếu A > 0 và ∆ > 0 thì hàm số đạt cực tiểu tại (x0,y0) .
Hình 6.1: Ba trường hợp thông dụng của bài toán tối ưu: điểm max, min và yên ngựa.
b) Nếu A < 0 và ∆ > 0 thì hàm số đạt cực đại tại (x0,y0).
c) Nếu ∆ < 0 thì hàm số không có cực trị.
d) Nếu ∆ = 0 thì không có kết luận gì, phải khảo sát thêm.
Ví dụ 6.6 Tìm cực trị hàm f(x,y) = x3 − x2 − y2 + 8.
Hướng dẫn. Tìm các điểm dừng
Suy ra (x0,y0) = (0,0) và (x0,y0) = (2/3,0).
Ta có f11′′ (x,y) = 6x − 2;f12′′ (x,y) = 0;f22′′ (x,y) = −2.
Tại các điểm dừng ta xét dấu của ∆ để suy ra điểm cực trị.
Ví dụ 6.7 Một hãng sản suất hai loại mặt hàng A và B. Chi phí sản xuất (cost product
function) hàng ngày x đơn vị mặt hàng A và y đơn vị B là
C(x,y) = 0.04x2 + 0.001xy + 0.001y2 + 4x + 2y + 500.
Giả sử giá (mỗi đơn vị) tương ứng là 15$ cho A và 9$ cho B. Tìm mức sản xuất x,y sao cho
hàm lợi nhuận π(x,y) = 15x + 9y − C(x,y) đạt cực đại. lOMoARcPSD| 36207943 46
CHƯƠNG 6. HÀM NHIỀU BIẾN (FUNCTION OF MULTI-VARIABLES) 6.4.2
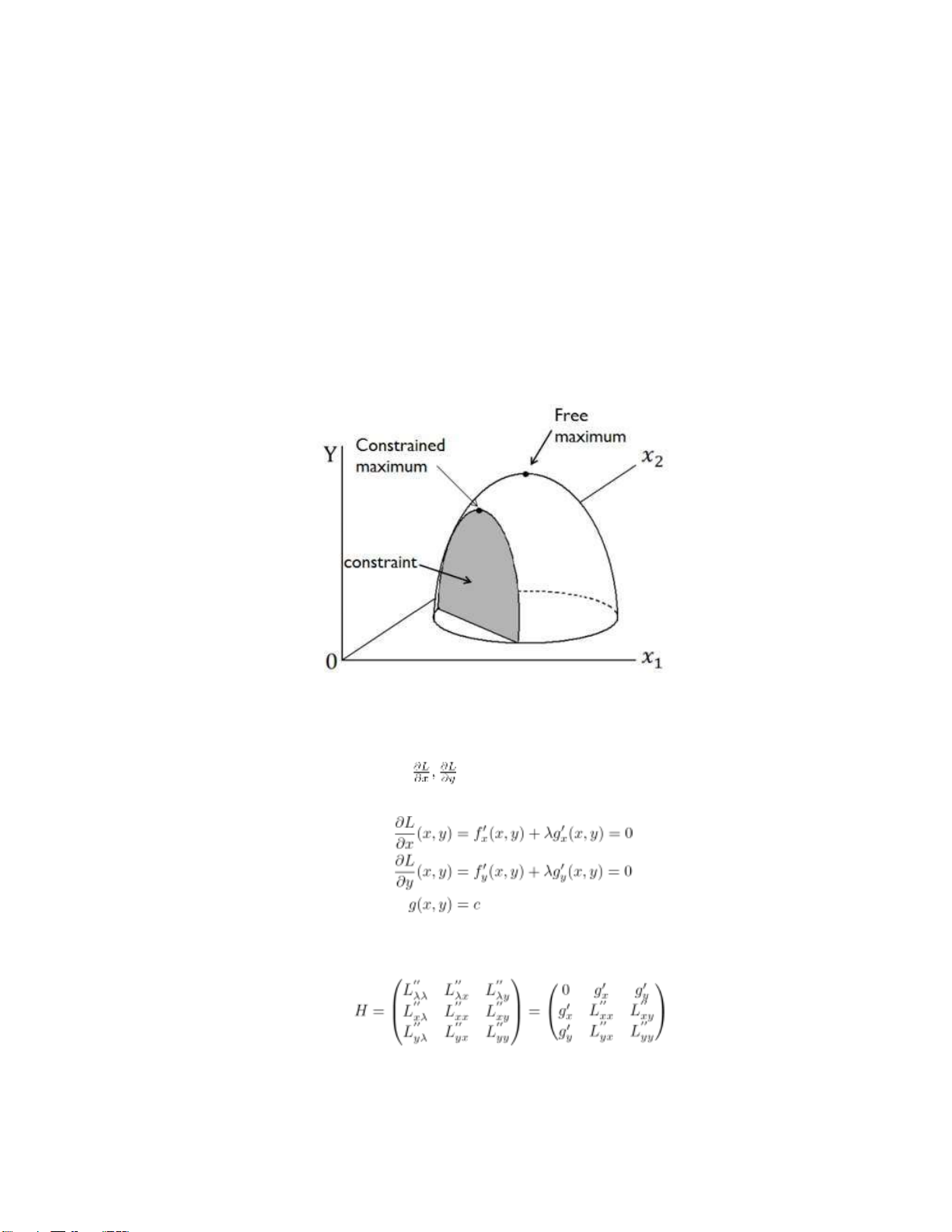
Cực trị có điều kiện (constrained optimization)
Tìm cực trị của hàm f(x,y) với x,y có ràng buộc điều kiện g(x,y) = c. Để giải bài toán này ta
có phương pháp Lagrange với các bước như sau. (I) Viết hàm Lagrange
L(x,y) = f(x,y) + λ(g(x,y) − c)
trong đó λ là một hằng số.
6.5. THỰC HÀNH TRÊN MÁY TÍNH
Hình 6.2: Cực trị có điều kiện.
(II) Tính các đạo hàm riêng
của hàm L theo các biến x,y
(III) Giải hệ phương trình sau để tìm điểm dừng x0,y0,λ0
Giá trị λ0 được gọi là nhân tử Lagrange. (IV) Lập ma trận Hessian
Tính định thức |H| tại các điểm dừng (x0,y0,λ0). lOMoARcPSD| 36207943 47
(i) Nếu định thức |H| < 0 thì hàm số đạt cực tiểu. (ii) Nếu
định thức |H| > 0 thì hàm số đạt cực đại.
6.5 Thực hành trên máy tính
Trong phần trước ta giải bài toán tối ưu bằng excel và ngôn ngữ lập trình R. Sau khi cài
đặt R và Rstudio, ta khởi động Rstudio và dùng một gói thư viện tối ưu để tìm lời giải.
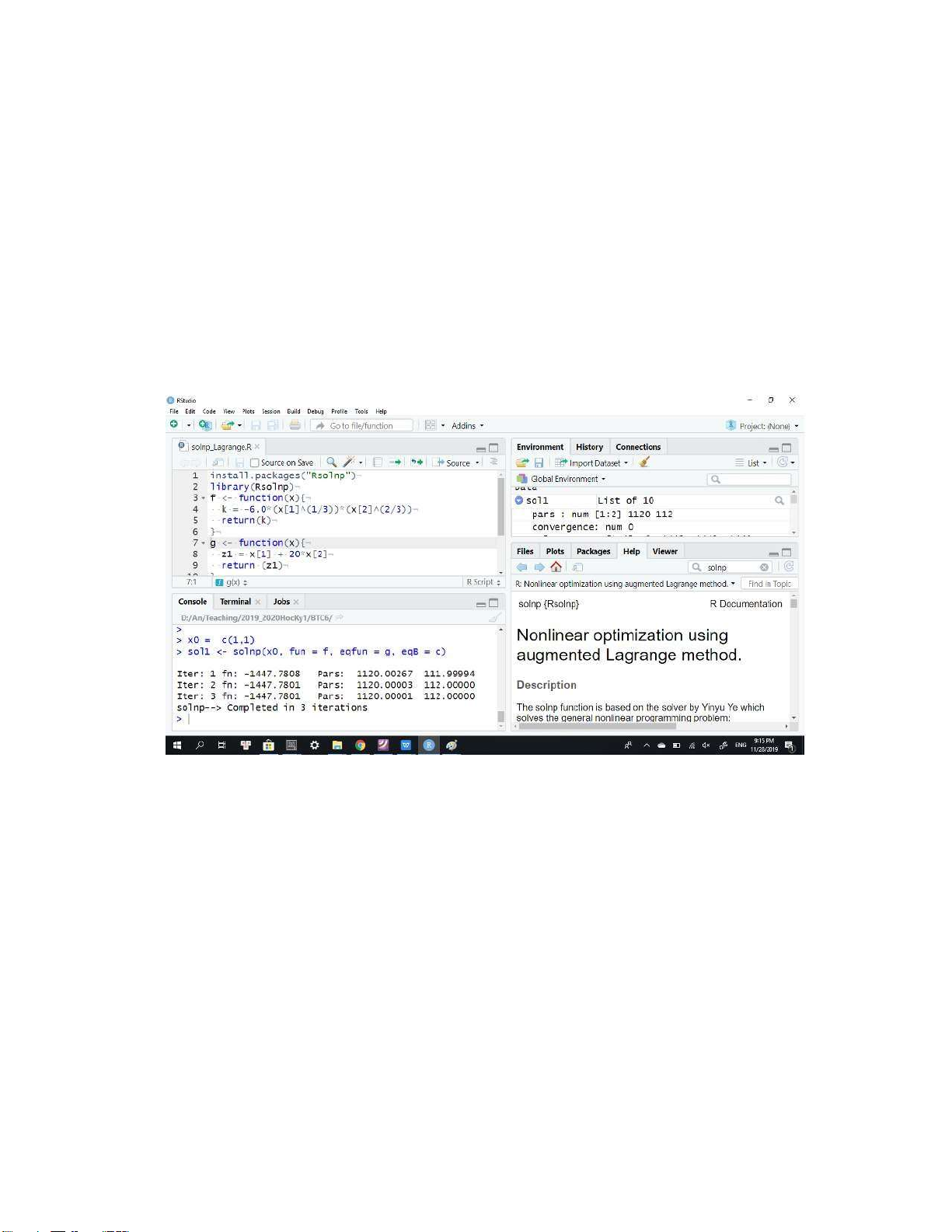
Có nhiều gói thư viện tối ưu và hàm tương ứng để tham khảo, bấm ở đây. Trong hình ??
ta dùng hàm solnp() để giải bài toán tối ưu có điều kiện:
Hình 6.3: Giải bài toán tối ưu có điều kiện bằng hàm solnp() trong R.
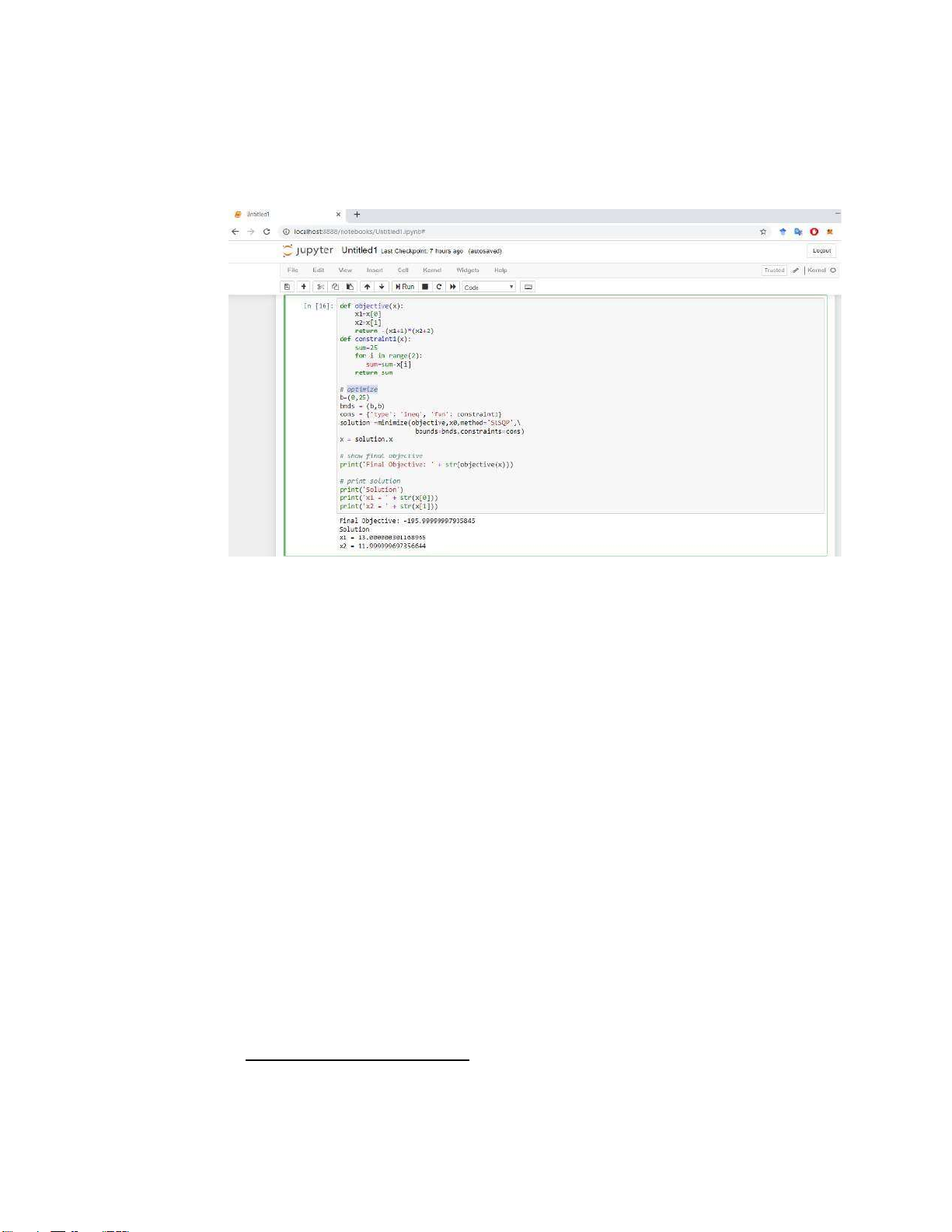
Phần tiếp theo ta sẽ thử nghiệm lập trình Python (một ngôn ngữ lập trình mở đang
rất thịnh hành hiện nay). Ta sẽ cài đặt Anaconda hoặc dùng Python online. lOMoARcPSD| 36207943 48
CHƯƠNG 6. HÀM NHIỀU BIẾN (FUNCTION OF MULTI-VARIABLES)
6.5. THỰC HÀNH TRÊN MÁY TÍNH
Hình 6.4: Cài đặt và khởi động Anacoda.
Hình 6.5: Cửa sổ Anacoda Nagigator. lOMoARcPSD| 36207943 49
Hình 6.6: Mở file Python nếu đã có sẵn hoặc mở một file mới.
Hình 6.7: Cửa sổ lập trình. lOMoARcPSD| 36207943 50
CHƯƠNG 6. HÀM NHIỀU BIẾN (FUNCTION OF MULTI-VARIABLES)
6.6. MỘT SỐ BÀI TẬP VÀ THỰC HÀNH CUỐI CHƯƠNG 6
Hình 6.8: Chạy chương trình và đọc kết quả bài toán tối ưu.
6.6 Một số bài tập và thực hành cuối chương 6
1. (Tiếng Anh học thuật và thực hành lập trình). Xem video hướng dẫn thực hành
và lập trình chạy ví dụ trong đó Video Python.
2. (Bài tập nhóm) Lập trình giải bài một số bài tập cuối chương Partial
Differentiation trong sách "Mathematics for economics and business", Ian
Jacques17. Mỗi nhóm làm một bài với nội dung ứng dụng khác nhau, giải thích
các hàm đã dùng và kết quả qua một bài trình bày.
3. (Hàm thuần nhất và bài toán quy mô sản xuất). Cho hàm sản xuất của một doanh
nghiệp là hàm Cobb Douglas Q = Q(K,L) = AKaLb, trong đó Q, K, L lần lượt là sản
lượng (quantity), lượng vốn (capital) và lượng lao động (labour); A, a, b là các
tham số dương. Đánh giá hiệu quả của quy mô sản xuất, biết rằng a = 0.3 và b =
0.5. Nếu doanh nghiệp muốn giảm 10% lượng nhân công L thì cần tăng lượng
vốn lên bao nhiêu phần trăm để duy trì mức sản lượng hiện tại?
4. (Ứng dụng của đạo hàm riêng: hàm biên, hệ số co giãn). Doanh nghiệp có hàm
sản xuất là Q = K(L+4), giá sản phẩm trên thị trường là P = 2(triuØng/snphm).
Giá thuê một đơn vị vốn là 1 triệu đồng và giá thuê môt đơn vị lao động là 0.4
17 http://93.174.95.29/_ads/96A8076441FD5FA8966D6B303EFE4497 lOMoAR cPSD| 36207943 51
triệu đồng. Chi phí cố định ban đầu là C0 = 100 triệu đồng. Xét tại vị trí K = 200,L = 30:
a. Xác định hàm chi phí, chi phí cận biên và hệ số co giãn.
b. Xác định hàm tổng doanh thu, doanh thu cận biên và hệ số co giãn.
c. Xác định hàm lợi nhuận, lợi nhuận cận biên và hệ số co giãn.
5. (Bài toán tối ưu tự do). Một doanh nghiệp độc quyền sản xuất hai loại hàng hóa.
Giả sử hàm cầu của chúng lần lượt là:
Q1 = 990 = P1 − P2,
q2 = 1390 − P1 − 2P2.
Hàm tổng chi phí là TC = Q21 + Q1Q2 + Q22.
a. Tìm hàm lợi nhuận của doanh nghiệp?
b. Tìm sản lượng mỗi loại hàng để lợi nhuận đạt tối ưu? Tính giá tại thời điểm đó?
6. (Bài toán tối ưu có điều kiện). Một người muốn tìm số giờ làm việc mỗi tuần để tối ưu
hóa hàm lợi ích U = 4E0.5F, trong đó E là tiền lương nhận được mỗi tuần($) và F là số
giờ họ không phải làm việc mỗi tuần (giờ). Biết rằng mỗi giờ làm việc họ được trả lương
20$ (sau khi đã trừ thuế).
a. Xác định hàm ràng buộc giữa E và F?
b. Người đó nên làm việc bao nhiêu giờ mỗi tuần để hàm lợi ích đạt tối ưu.
c. Nếu tiền lương mỗi giờ tăng lên thì người đó có nên tăng hay giảm số giờ làm
việc hàng tuần để đat lợi ích tối đa? lOMoARcPSD| 36207943
Chương7 Tích phân hàm một biến
Sau khi học xong chương này, người học có thể: -
Hiểu và có thể tìm được nguyên hàm, tích phân bất định, tích phân xác định của một số hàm kinh tế. -
Biết vận dụng tích phân để xử lý một số bài toán trong thực tiễn, cụ thể: xác định
được hàm kinh tế khi biết hàm biên tương ứng (ví dụ hàm lợi nhuận, doanh thu, chi phí);
tính được quỹ vốn khi biết hàm đầu tư; tìm được thặng dư tiêu dùng và thặng dư sản xuất. -
Có khái niệm sơ lược về tích phân suy rộng, ứng dụng của tích phân suy rộng trong thực tiễn. 7.1
Tích phân không xác định (nguyên hàm)
Định nghĩa 7.1 Cho hàm số f(x), hàm F(x) được gọi là một nguyên hàm của hàm . Ký hiệu
Z f(x)dx = F(x) + C.
Chú ý 7.1 Một số công thức tích phân bất định a.
Z [f(x) ± g(x)]dx = Z f(x)dx ± Z g(x)dx, b.
Z kf(x)dx = k Z f(x)dx, (k là hằng số,)
và một số tích phân đơn giản a. , 51 b. lOMoARcPSD| 36207943 53 c. 7.2
Tích phân xác định (tích phân Riemann)
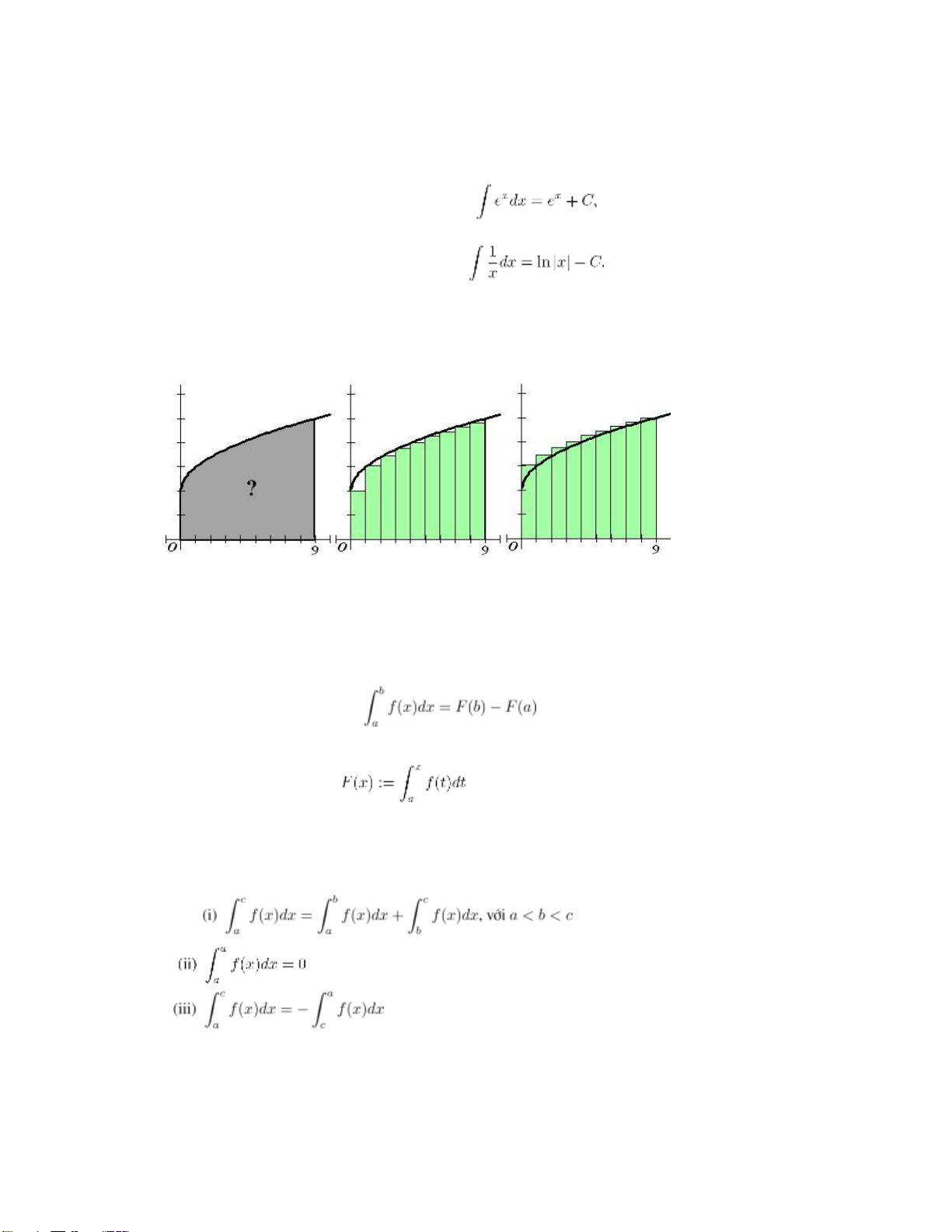
Ta đã biết một trong các bài toán xuất phát của tích phân xác định là để tính diện tích một
hình thang cong, hay một hình phẳng có hình dạng tùy ý.
Hình 7.1: Tích phân xác định, nguồn: http://www.hhofstede.nl/modules/ riemann.htm.
Định lý 7.1 Nếu f(x) là hàm liên tục trên [a,b] và F(x) là nguyên hàm của f thì ta có .
Định lý 7.2 Nếu f là hàm liên tục (hoặc ít nhất là khả tích, nghĩa là có thể lấy tích phân) trên
[a,b]. Với ∀x ∈ [a,b] hàm số có tính chất
F′(x) = f(x).
Một số tính chất đơn giản của tích phân xác định , , , lOMoARcPSD| 36207943 54
CHƯƠNG 7. TÍCH PHÂN HÀM MỘT BIẾN
7.3. CÁC PHƯƠNG PHÁP TÍNH TÍCH PHÂN
(iv) nếu hàm f(x) < 0 với mọi là giá trị diện
tích của miền giới hạn bởi hàm
7.3 Các phương pháp tính tích phân
• Phương pháp tích phân từng phần
• Phương pháp đổi biến
Nhận xét: Máy tính cầm tay có thể tính các tích phân xác định thông thường.
7.4 Ứng dụng của tích phân trong kinh tế
Trong phần này, ta sẽ nói tới việc ứng dụng tích phân để xác định các hàm chi phí, doanh
thu, lợi nhuận ... khi biết hàm biên tương ứng, xác định quỹ vốn khi biết hàm đầu tư, xác
định thặng dư tiêu dùng và thặng dư sản xuất khi biết hàm cầu và hàm cung của sản phẩm. 7.4.1
Xác định các hàm kinh tế khi biết hàm biên tương ứng
Ta đã biết hàm biên chi phí MC, hàm biên doanh thu MR, hàm biên lợi nhuận Mπ là xấp xỉ
đạo hàm của hàm C,R,π đang xét. Vậy hàm C,R,π là tích phân của các hàm biên.
MCVí dụ 7.1= 120+0Hàm doanh thu cận biên là.1Q2. Chi phí cố định là 50($)MR . Tính lợi
nhuận tối đa trong trường hợp= 360 − 0.5Q2, hàm chi phí biên là trên. Giải.
Hàm lợi nhuận là tích phân của hàm lợi nhuận biên, do đó:
π(Q) = Z (MR − MC)dQ = Z (240 − 0.6Q2)dQ = 240Q − 0.2Q3 + π0.
Khi sản xuất bằng 0 tức là Q = 0 ta có doanh thu R0 = 0, còn chi phí cố định
. Để tìm lợi nhuận tối đa, ta cần tìm Q ≥ 0 để lOMoARcPSD| 36207943 55 Q
Từ đó suy ra 240 − 0.6Q2 = 0 → Q = 20 (do Q > 0). Lợi nhuận tối đa đạt được khi Q = 20 là
maxπ = 240 × 20 − 0.2 × 203 − 50 = 3150($)..
7.4.2 Quỹ vốn và lượng đầu tư
Gọi K(t) là quỹ vốn, I(t) là lượng đầu tư tại thời điểm t. Khi đó I(t) là biên tế của quỹ vốn
K(t). Ta có biểu thức:
K0 là quỹ vốn ban đầu tại thời điểm ban đầu t = t0.
Ví dụ 7.2 Lượng đầu tư của vào một doanh nghiệp tại thời điểm t là I(t) = 30√t (triệu đồng).
Đơn vị của t tính theo năm.
a. Ban đầu quỹ vốn của doanh nghiệp là 100 triệu đồng. Xác định hàm quỹ vốn theothời gian của doanh nghiệp?
b. Tính tổng vốn tăng thêm từ cuối năm thứ nhất tới cuối năm thứ tư?
Giải. Quỹ vốn của doanh nghiệp là .
a. Theo đề bài quỹ vốn ban đầu là 100 triệu đồng, tức là tại t0 = 0 ta có K0 = 100 (triệu đồng). Suy ra (triệu đồng).
b. Tổng vốn tăng thêm từ cuối năm thứ nhất tới cuối năm thứ tư là:
K(4) − K(1) = (20 × 4 × √4 + 100) − (20 × 1 × √1 + 100) = 140 (triệu đồng).
7.4.3 Thặng dư tiêu dùng
Tại thời điểm người tiêu dùng đồng ý mua sản phẩm với mức giá P0, họ trả số tiền P0 cho
một đơn vị sản phẩm, tức là cho sản phẩm thứ Q0. Như vậy với những sản phẩm trước đó,
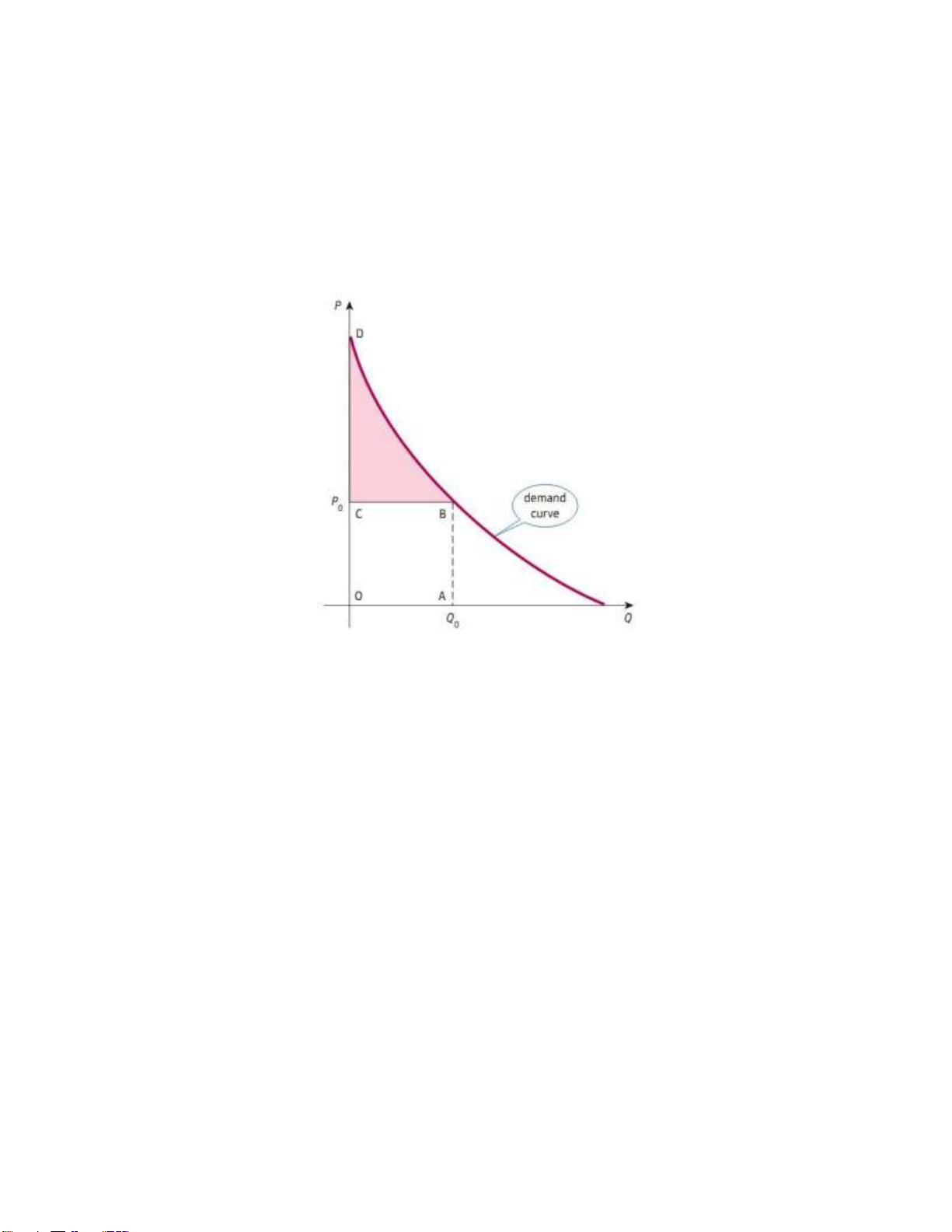
người tiêu dùng có thể đã đồng ý trả mức giá cao hơn để mua, xem đồ thị hàm cầu trong hình ??.
Thặng dư tiêu dùng tương ứng với sự "hài lòng" (satisfaction) khi người tiêu dùng mua hàng,
nó đo bằng diện tích phần tam giác cong BCD trong hình ??. Theo ý nghĩa của tích phân xác
định, khi ta xét tại điểm (Q0,P0) thì công thức tính thặng dư tiêu dùng là: Q0 Z
CS =D(Qd)dQd − P0Q0,
D(Qd) là hàm cầu. 0
Ví dụ 7.3 Cho hàm cầu P = 60 − 4Q. Tìm thặng dư tiêu dùng biết Q = 5. lOMoARcPSD| 36207943 56
CHƯƠNG 7. TÍCH PHÂN HÀM MỘT BIẾN
Giải. Do ta đang xét Q = 5 nên P = 40. Thặng dư tiêu dùng khi đó là: 5 Z CS +(60 −
4Q)dQ − 5 × 40 = 250 − 200 = 50. 0
7.4. ỨNG DỤNG CỦA TÍCH PHÂN TRONG KINH TẾ
Hình 7.2: Thặng dư tiêu dùng, nguồn: Ian Jacques, "Mathematics for economics and business".
Chú ý 7.2 Trong thực hành người ta hay xét thặng dư tiêu dùng ở điểm cân bằng thị trường.
Khi đó điểm (Q0,P0) trong công thức tính thặng dư tiêu dùng là điểm cân bằng thị trường.
7.4.4 Thặng dư sản xuất
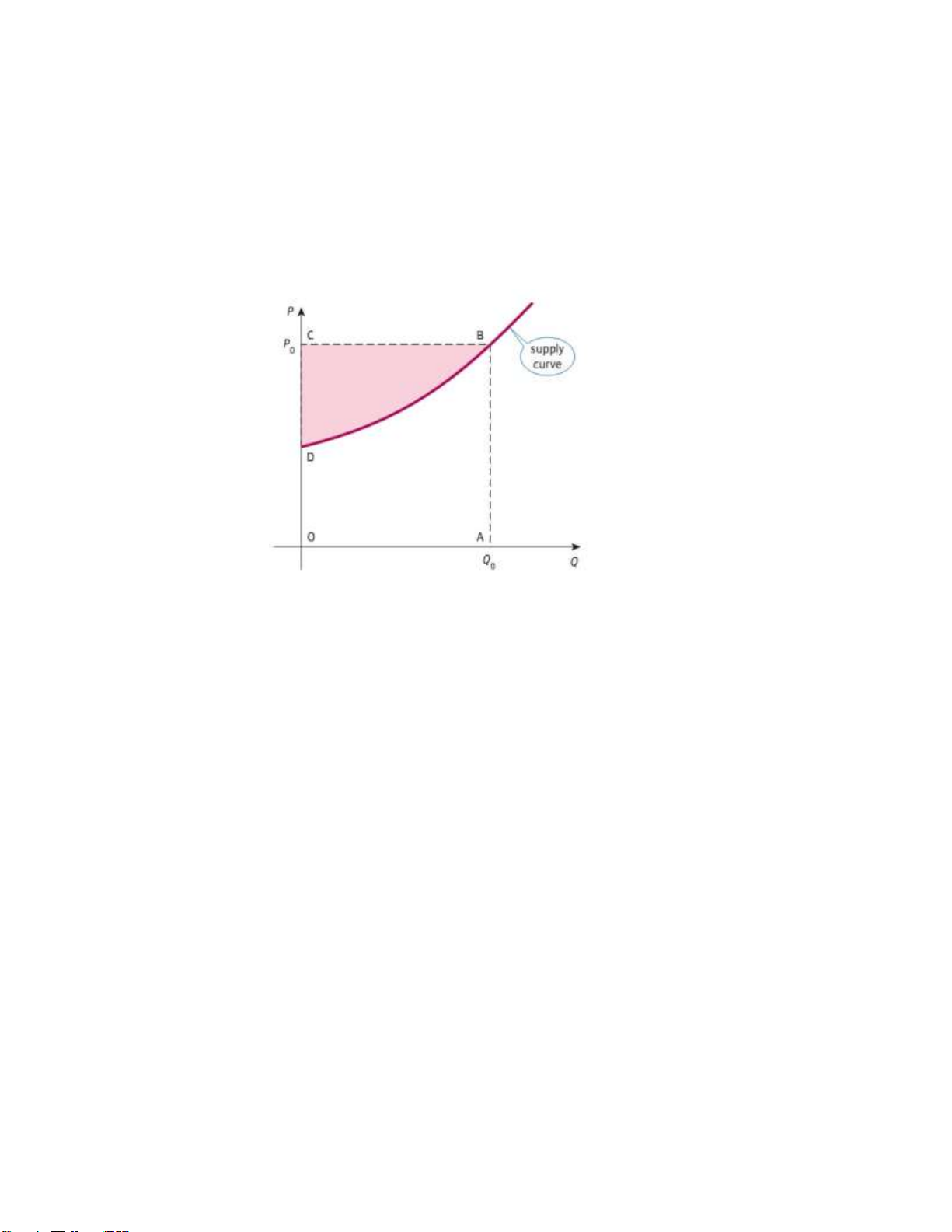
Thặng dư sản xuất (producer’s surplus) tại (Q0,P0) đo độ chênh lệch của doanh thu thực tế
với doanh số nhà sản xuất có thể đồng ý bán, xem hình ??. Công thức tính: Q0 Z PS =
P0Q0 −S(QS)dQS, S(QS) là hàm cung. 0
Chú ý 7.3 Trong thực tiễn, người ta hay xét thặng dư sản xuất tại thời điểm cân bằng thị
trường cung và cầu, do đó giá trị (Q0,P0) là giá trị tại thời điểm cân bằng.
Ví dụ 7.4 Giả sử hàm cầu P(QD) = 50−0.1QD và hàm cung P(QS) = 20+0.2QS. Thặng dư sản
xuất tại điểm cân bằng là bao nhiêu? lOMoARcPSD| 36207943 57
Hướng dẫn. Tại điểm cân bằng Q = 100,P(Q) = 40, giá trị của thặng dư sản xuất được tính qua công thức 1 Z 100 × 40 −00(20 +
0.2Q)dQ = 1000. 0
Hình 7.3: Thặng dư sản xuất, nguồn: Ian Jacques, "Mathematics for economics and business".
7.5 Tích phân suy rộng
Trong tài liệu này ta chỉ giới thiệu tích phân suy rộng loại có cận là +∞ hoặc −∞. Tích phân
suy rộng loại này có ứng dụng nhiều trong lý thuyết xác suất và thống kê. Phần này chúng ta
không đi sâu vào xét tính hội tụ của tích phân suy rộng.
Định nghĩa 7.2 Nếu tồn tại giới hạn bên phải hữu hạn thì ta đặt: Z +∞ c
f(x)dx := lim Z f(x)dx. a c→+∞ a c c Z
f(x)dx := lim Z f(x)dx. −∞ a→−∞ a +∞ b c Z
f(x)dx := lim Z f(x)dx + lim Z f(x)dx. −∞ a→−∞ a c→+∞ b lOMoARcPSD| 36207943 58
CHƯƠNG 7. TÍCH PHÂN HÀM MỘT BIẾN
Chú ý 7.4 Tính chất của tích phân suy rộng (với giả thiết các tích phân hội tụ) a. b. (k là hằng số).
Trường hợp cận dưới của tích phân là vô hạn ta có kết quả tương tự.
7.6. THỰC HÀNH TRÊN MÁY TÍNH
Ví dụ 7.5 Tính tích phân (theo nguyên hàm) a. ; b. Giải. a. . b. .
7.6 Thực hành trên máy tính
Việc tính toán tích phân xác định của các hàm thông dụng có thể thực hiện trên máy
tính cầm tay. Tuy nhiên với hàm phức tạp hoặc tích phân suy rộng, ta có thể cần tới
các công cụ mạnh hơn. Bên cạnh việc lập trình với mã nguồn mở trên R và Python, ta
cũng có một số các công cụ tích hợp sẵn trên web18 để tham khảo, xem hình ?? và ??.
7.7 Một số bài tập và thực hành cuối chương 7
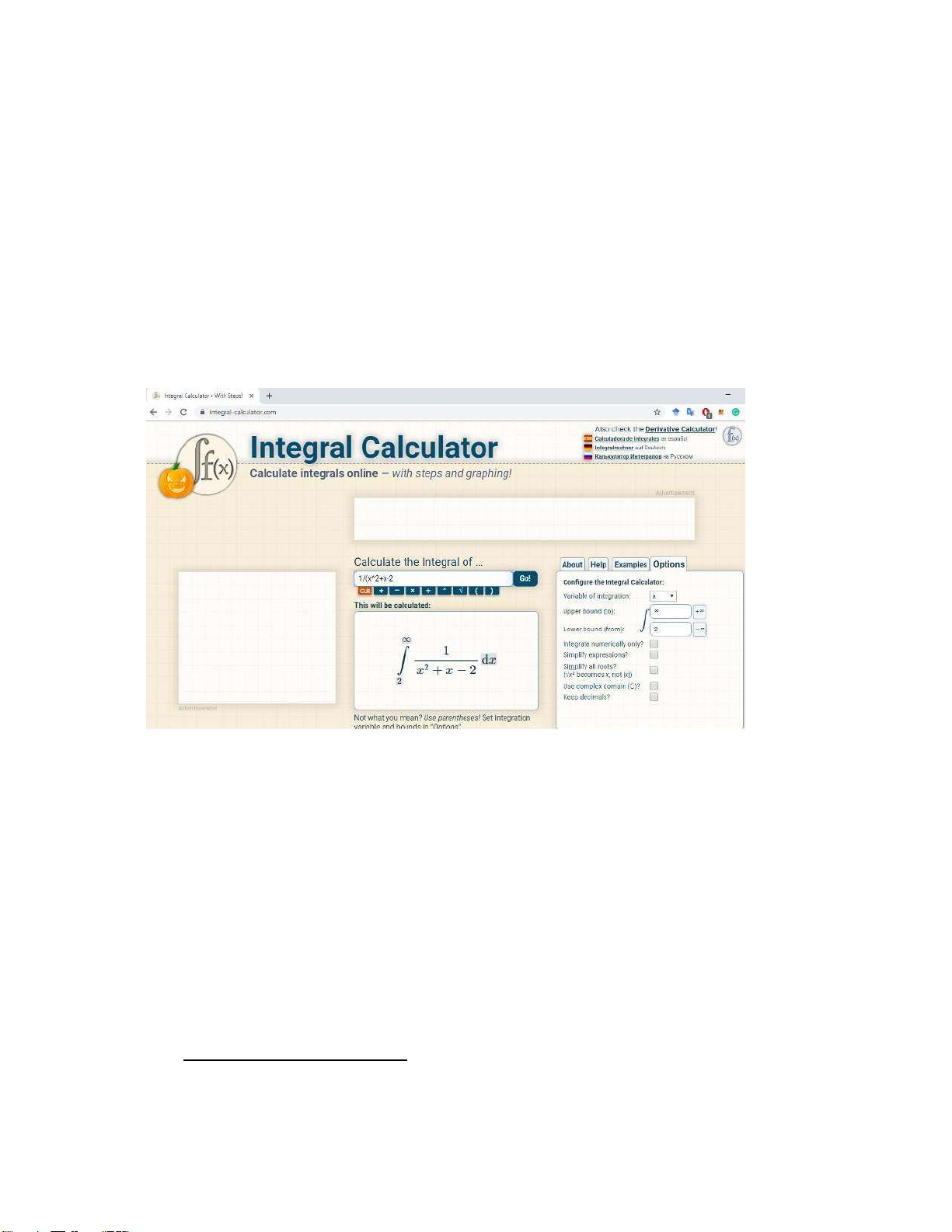
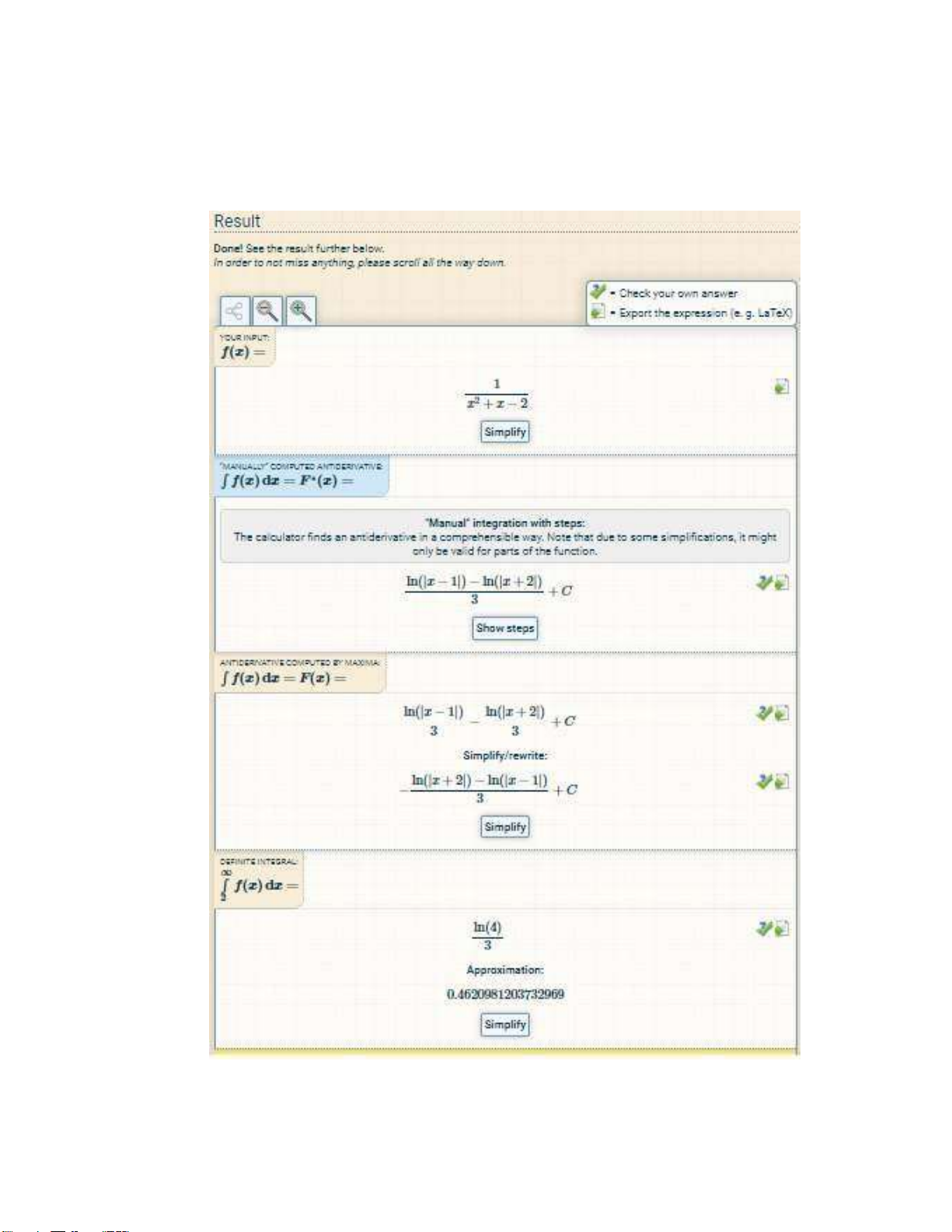
1. (Thực hành phần mềm). Sử dụng máy tính cầm tay và trang web integral-
calculator.com/ để tính một số tích phân bất định, tích phân xác định có cận ở vô
cùng, tích phân xác định phức tạp
2. (Bài tập rèn luyện tiếng Anh học thuật, bài tập nhóm). Sử dụng kiến thức tích phân
để giải một số bài tập ứng dụng cuối chương Integration và nghiên cứu vấn đề trữ 18 integral-calculator.com lOMoARcPSD| 36207943 59
lượng tài nguyên (ví dụ bài 7 trang 655) sách "Mathematics for economics and business"19.
3. Dòng đầu tư của một doanh nghiệp là hàm I(t) = 6000t0.5($), với t tính theo năm.
Tìm tổng lượng vốn gia tăng của doanh nghiệp từ cuối năm thứ nhất tới cuối năm thứ chín.
4. Tìm thặng dư tiêu dùng khi P = 36($), biết hàm cầu là P = 100 − Q2?
5. Tìm thặng dư tiêu dùng và thặng dư sản xuất tại thời điểm cân bằng thị trường,biết
P = 38 − Q2D, P = 6 + Q2S.
Hình 7.4: Tính toán với tích phân, nguồn integral-calculator.com
6. Hàm biên của tổng tiêu dùng quốc gia là MPC = 0.25 + Y −1/2. Khi không có thu nhập
(Y = 0), mức tiêu dùng tối thiểu là 10 (tỷ $). Tìm hàm tiêu dùng theo thu nhập Y và
tính mức tiêu dùng khi Y = 16 tỷ đô la.
19 http://93.174.95.29/_ads/96A8076441FD5FA8966D6B303EFE4497 lOMoARcPSD| 36207943 60
CHƯƠNG 7. TÍCH PHÂN HÀM MỘT BIẾN
7.7. MỘT SỐ BÀI TẬP VÀ THỰC HÀNH CUỐI CHƯƠNG 7 lOMoARcPSD| 36207943 61
Hình 7.5: Chi tiết tính toán với tích phân, nguồn integral-calculator.com
Tài liệu tham khảo lOMoARcPSD| 36207943
Một số dạng đề thi và giải mẫu 0.1 Đề mẫu 1 Câu 1. Giả sử Chọn đáp án đúng.
A. a = 0,b = 10,c = 9,d = 18 B. a =
C. a = 0,b = 10,c = 18,d = 10
0,b = 9,c = 10,d = 18 D. Một đáp án khác.
Câu 2. Tìm m để rank(B) = 2, trong đó A. m 6= 0
C. m = 0, hay m = 1 B. m 6= 1 D.
Câu 3. Xét một thị trường gồm ba loại hàng hoá. Hàm cung, hàm cầu và giá của chúng thoả mãn các điều kiện sau:
Qs1 = −10 + 6p1 − 5p2 + 3p3 Qs2 = −10 + 4p1 + 4p2 − 3p3 Qs3 = −20 − 3p1 + 2p2 + 3p3 Qd1 = 35 − 5p1 + 6p2 − 2p3
Qd2 = 30 + 5p1 − 6p2 + 2p3 Qd3 = 50 − 2p1 + 6p2 − 4p3
Xác định lượng cung và cầu cân bằng của từng loại hàng hoá.
A. Qs1 = Qd1 = 30;Qs2 = Qd2 = 35;Qs3 = Qd3 = 40
B. Qs1 = Qd1 = 40;Qs2 = Qd2 = 30;Qs3 = Qd3 = 35
C. Qs1 = Qd1 = 35;Qs2 = Qd2 = 30;Qs3 = Qd3 = 40 D. Một đáp án khác.
Câu 4. Giả sử một quốc gia có ba ngành sản xuất với ma trận hệ số đầu vào là
Biết nhu cầu cuối của các ngành lần lượt là 130,30,20. Tìm tổng đầu ra x1,x2,x3 của mỗi ngành.
A. x1 = 200,x2 = 300,x3 = 300 B. x1 =
C. x1 = 300,x2 = 200,x3 = 300
300,x2 = 200,x3 = 200 D. Một đáp án khác.
Câu 5. Xét các khẳng định dưới đây
1. Nếu hệ chứa vectơ 0 thì hệ phụ thuộc tuyến tính.
2. Hệ có chứa hai vectơ tỷ lệ thì phụ thuộc tuyến tính.
3. Nếu hệ chứa hệ con phụ thuộc tuyến tính thì hệ phụ thuộc tuyến tính.
4. Nếu hệ chứa hệ con độc lập tuyến tính thì hệ cũng độc lập tuyến tính.
Đếm số các khẳng định sai. 61 62 A. 0 B. 1 C. 2 D. 3
Câu 6. Tìm A−1, biết A. C. lOMoARcPSD| 36207943 B. D.
Câu 7. Trong R3, cho hệ vectơ . Xét các khẳng định dưới đây
1. Nếu m = 2 thì (B) là một cơ sở của R3.
2. Nếu (B) là cơ sở của R3 thì m 6= −1.
3. (B) là cơ sở của R3 khi và chỉ khi m 6= −1.
Đếm số các khẳng định sai. A. 0 B. 1 C. 2 D. 3 Câu 8. Cho ma trận
. Xét các khẳng định dưới đây
1. Tất cả các giá trị riêng của M là λ1 = 2 và λ2 = 8.
2. M chắc chắn chéo hoá được và dạng chéo của . 3. Các vectơ
là các vectơ riêng của M.
Đếm số các khẳng định sai. A. 0 B. 1 C. 2 D. 3
Câu 9. Tại một quốc gia, đầu tư cố định của chính phủ là 3500 (triệu USD), mức chi tiêu cố định
của chính phủ là 1500 (triệu USD), còn tổng thu nhập quốc dân Y , tổng mức tiêu dùng C và tổng thuế
T thoả mãn các điều kiện sau:
C = 2000 + 0.5(Y − T),
T = 4100 + 0.1Y.
Hãy xác định mức thu nhập quốc dân, tổng mức tiêu dùng và mức thuế ở trạng thái cân bằng kinh tế vĩ mô A. (4000,5000,9000) C. (5000,4000,9000) B. (9000,4000,5000) D. (4000,9000,2200)
Câu 10. Cho chi phí C = C(Q), doanh thu R = R(Q) và lợi nhuận π = π(Q) là các hàm khả vi theo biến
sản lượng Q không âm (trong giả thiết các yếu tố khác không đổi). Xét các khẳng định dưới đây.
1. Chi phí biên tại mức sản lượng Q = Qo là MC(Qo) ≡ C′(Qo).
2. Doanh thu biên MR(Qo) tại mức sản lượng Qo chính là xấp xỉ lượng thay đổi tương đối của
doanh thu khi sản lượng tăng tương đối lên 1% từ mức Qo lên mức Qo+1%Qo.
3. Hệ số co giãn ǫπQ(Qo) của lợi nhuận theo sản lượng tại mức Qo chính là xấp xỉ lượng thay đổi
tuyệt đối của lợi nhuận khi sản lượng tăng lên 1 đơn vị từ mức Qo lên mức Qo + 1.
Đếm số các khẳng định sai. 0.1. ĐỀ MẪU 1 63 A. 0 B. 1 C. 2 D. 3
Câu 11. Một công ty độc quyền sản xuất và tiêu thụ một loại sản phẩm trên thị trường. Giả sử
hàm cầu (theo giá P) của sản phẩm đó là Q = 101 − P và chi phí bình quân là
AC = Q2 + 3Q + 50 + 10Q−1. Tìm mức sản lượng tối ưu hoá lợi nhuận và tính mức giá tương ứng.
A. Q = 98,P = 3,πmax = 80
C. Q = 3,P = 98,πmax = 294
B. Q = 3,P = 98,πmax = 80 D. Một đáp án khác.
Câu 12. Giả sử doanh thu (đơn vị tính là triệu đồng) R = R(Q) theo sản lượng cầu Q của một doanh
nghiệp là một ẩn hàm xác định bởi phương trình theo tham số thời gian t như sau:
Q = Q(t) = 3t + 5,
R = R(t) = −3t3 + 225t + 20000. lOMoARcPSD| 36207943
Tìm mức sản lượng cầu Q(> 0) để tối ưu hoá doanh thu và tính doanh thu tối đa của doanh nghiệp đó.
A. Q = 5,Rmax = 20750 (triệu đồng) B. Q =
C. Q = 20,Rmax = 20750 (triệu đồng)
20,Rmax = 500 (triệu đồng) D. Một đáp án khác.
Câu 13. (Tự luận) Giả sử hàm cầu P = P(Q) biểu thị mối quan hê giữa giá bán một
đơn vị sản phẩm P (đơn vị USD) với sản lượng cầu Q (lượng sản phẩm bán được) là một hàm bậc
nhất. Biết rằng nếu giá mỗi đơn vị sản phẩm là P = 2000 USD thì sẽ bán được 200 đơn vị sản phẩm.
Nếu giảm giá mỗi đơn vị sản phẩm đi 250 USD thì lượng bán sẽ được tăng thêm 50 đơn vị sản phẩm.
Chi phí bình quân AC = 1500 USD. Tìm mức sản lượng cầu Q(> 0) để tối ưu hoá lợi nhuận và tính
mức giá P tương ứng với mức lợi nhuận π tối ưu đó.
Câu 14. (Tự luận) Một doanh nghiệp sản xuất độc quyền hai loại hàng hoá. Giả sử
ứng với các mức sản lượng Q1,Q2 (đơn vị sản phẩm) của từng loại hàng hoá, doanh nghiệp có hàm chi
phí (đơn vị tính là triệu đồng) như sau:
C = C(Q1,Q2) = (Q1 − 125)4/3 + (Q2 − 50)3 − 3(Q1 − 125)1/3(Q2 − 50)2 + 200
Tìm Q1,Q2 để chi phí đạt mức tối thiểu. Hướng dẫn giải.
Câu 1. Bằng cách nhân 2 ma trận bên tay trái của dấu ” = ”, ta sẽ được một ma trận cấp 2×2. Sau
đó so sánh ma trận này với ma trận bên phải của dấu ” = ”. Ta sẽ được một hệ 2 phương trình tuyến
tính theo hai ẩn a,b. Giải hệ phương trình này, ta sẽ được giá trị của a và b.
Câu 2. Ta có thể thực hiện các phép biến đổi sơ cấp trên dòng như sau:
d2 → d2 − md1,
d3 → d3 − md1.
Để rank(B) = 2 thì dòng 2 hoặc dòng 3 (của ma trận sau khi thực hiện các phép biến đổi sơ cấp bên
trên) phải khác 0 và dòng còn lại phải tỷ lệ với dòng đó. Trong trường hợp này ta có
Như vậy ta suy ra rank(B) = 2 khi và chỉ khi hoặc là , hoặc là 64
Giải các hệ phương trình, bất phương trình trên; ta sẽ được giá trị của m. Câu 3. Thị
trường đạt trạng thái cân bằng khi
Qs1 = Qd1,
Qs2 = Qd2,
Qs3 = Qd3.
Thế các hàm theo p1,p2,p3 vào hệ phương trên, ta sẽ được hệ phương trình tuyến tính 3 ẩn, 3 phương
trình. Giải hệ phương trình này, ta sẽ được giá cân bằng. Sau khi được giá cân bằng, thế vào lại các
hàm bên trên để đạt được sản lượng cung và cầu cân bằng của từng loại hàng hoá.
Câu 4. Đặt A là ma trận đầu vào. Theo mô hình Input-Output, đầu ra x1,x2,x3 là nghiệm của hệ .
Giải hệ phương trình trên, ta sẽ được tổng đầu ra của mỗi ngành. Câu 5.
1. Vì vectơ 0 luôn biểu diễn tuyến tính được qua mọi hệ vectơ nên hệ chứa vectơ 0 là một hệ phụ thuộc tuyến tính. lOMoARcPSD| 36207943
2. Nếu hệ 2 vectơ u,v tỷ lệ thì sẽ tồn tại 2 số thực α,β sao cho αu + βv = 0. Từ đó ta suy ra hệ phụ thuộc tuyến tính.
3. Giả sử hệ (B1) là một hệ phụ thuộc tuyến tính, nghĩa là vectơ 0 có một biểu diễn không tầm
thường theo các vectơ trong (B1) (gọi là biểu diễn số 1). Nếu hệ (B2) chứa (B1) thì vectơ 0 sẽ
có một biểu diễn không tầm thường trong (B2) đó là biểu diễn số 1 cộng với tích của hằng số
0 và các vectơ còn lại trong (B2). Nên hệ (B2) phụ thuộc tuyến tính.
4. Hệ (v1) với v1 6= 0 là một hệ độc lập tuyến tính. Nhưng hệ (v1,2v1) không phải là một hệ độc lập tuyến tính.
Câu 6. Ta có thể tính nghịch đảo của A bằng cách sử dụng các phép biến đổi sơ cấp trên dòng để đưa
[A|I] về dạng [I|B], trong đó I là ma trận đơn vị cấp 3. Lúc đó, ta có B là nghịch đảo của A.
Câu 7. Xét ma trận tạo thành từ các vectơ b1,b2,b3 như sau:
Thì ta có detA = −3m2 + 3. Do (B) là cơ sở của R3 khi và chỉ khi detA 6= 0. Nên (B) là cơ sở của R3 khi
và chỉ khi m 6= ±1.
Câu 8. Tìm đa thức đặc trưng của M : PM(λ) = det(M − λI2). Giải nghiệm của đa thức này để tìm các
giá trị riêng, từ đó tìm các vectơ riêng và suy ra tính chéo hoá của ma trận. Ngoài ra, để biết một
vectơ v có phải là vectơ riêng của M hay không thì ta chỉ cần kiểm tra xem Mv và v có tỷ lệ với nhau hay không.
Câu 9. Từ hệ phương trình ,
trong đó I = 1500 là mức chi tiêu của chính phủ, G = 3500 là mức đầu tư của chính phủ. Giải hệ
phương trình này ta sẽ được mức thu nhập quốc dân, mức tiêu dùng và mức thuế ở trạng thái cân
bằng kinh tế vĩ mô. Câu 10. Xem lại lý thuyết
Câu 11. Từ Q = 101 − P, ta suy ra P = 101 − Q. Và từ đó suy ra hàm lợi nhuận là π = PQ − C = PQ
− Q.AC = (101 − Q)Q − Q(Q2 + 3Q + 50 + 10Q−1).
Hàm này là một hàm bậc 3 theo biến Q. Bằng cách tính đạo hàm bậc nhất và bậc hai của π, ta sẽ suy
ra ra mức sản lượng tối ưu hoá lợi nhuận. 0.1. ĐỀ MẪU 1 65
Câu 12. Ta tính đạo hàm bậc nhất và bậc hai của R = R(Q) theo hàm ẩn cho bởi tham số: , và .
Giải phương trình RQ′ = 0 và tính RQ′′ tại các điểm đó, để suy ra các điểm cực trị. Từ đó suy ra sản
lượng cầu Q để tối ưu hoá doanh thu. Câu 13. Vì P là một hàm bậc nhất theo Q nên
P = a + bQ.
Tại mức giá P = 2000 USD thì bán được 200 đơn vị sản phẩm nên ta có
2000 = a + 200b.
Vì nếu giảm giá mỗi đơn vị sản phẩm đi 250 USD thì lượng bán ra sẽ được tăng thêm 50 đơn vị sản phẩm nên ta có
(2000 − 250) = a + (200 + 50)b.
Từ 2 phương trình tuyến tính trên, ta sẽ tìm ra được giá trị của a và b. Vì chi phí bình quân là AC =
1500. Nên ta có hàm lợi nhuận
π = PQ − Q.AC = Q(a + bQ) − 1500Q lOMoARcPSD| 36207943
là một hàm bậc 2 theo Q. Tính đạo hàm bậc nhất và bậc hai của hàm lợi nhuận này để suy ra sản
lượng cầu làm tối ưu hoá lợi nhuận.
Câu 14. Bằng cách tính các đạo hàm bậc nhất theo Q1 và Q2 của hàm C. Sau đó giải hệ phương trình
để tìm các điểm tới hạn. Cuối cùng ta tính các đạo hàm bậc 2, và thế các điểm tới hạn này vào để suy ra chi phi tối thiểu.