Giới thiệu Đại số tuyến tính môn Toán cao cấp | Trường Đại học Tôn Đức Thắng

LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT
• Check vector is a linear combination or not: 154 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 1:
• Step 1: create vectors v1, v2, v3 and w
• Step 2: create matrix A with columns v1, v2, v3
• Step 3: create matrix Aw with columns v1, v2, v3 and w
• If np.linalg.matrix_rank(A) = np.linalg.matrix_rank(Aw) then
w is linear combination of v1, v2, v3
• We have create function to Check_Linear_Combination 155 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT
• Check vectors are linearly independent or not: 156 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 2:
• Step 1: create vectors v1, v2, v3
• Step 2: create matrix A with columns v1, v2, v3
• Step 3: if np.linalg.matrix_rank(A) = A.shape[1] then v1, v2, v3 are linearly independent 157 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT
• Find a basis for the col (C) 158 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 3: • Step 1: create matrix C
• Step 2: res = sp.Matrix(C).rref()
• Step 3: basis_column_C = C[: , list(res[1])) #C[: , [0, 1]]
• Step 4: print("A basis for the column space of C=\n", basis_column_C)
• We can create the Third column of C by the basis:
• 2*basis_column_C[:, 0] + 8*basis_column_C[:, 1] 159 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT
• Find a basis for the row (C) 160 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 3:
• (b): Find a basis for the row. Step 1: create matrix CT = C.T
• Step 2: res_b = sp.Matrix(CT).rref()
• Step 3: basis_CT = CT[: , list(res_b[1]))
• Step 4: print("A basis for the row space of C=\n", np.transpose(basis_CT) • 161 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT
• Find a basis for the null-space of A2 and the stored answer as column vectors : 162 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT
• Find a basis for the null-space of A2 and the stored answer as column vectors (cont.): 163 MCS. Nguyen Van Khoa
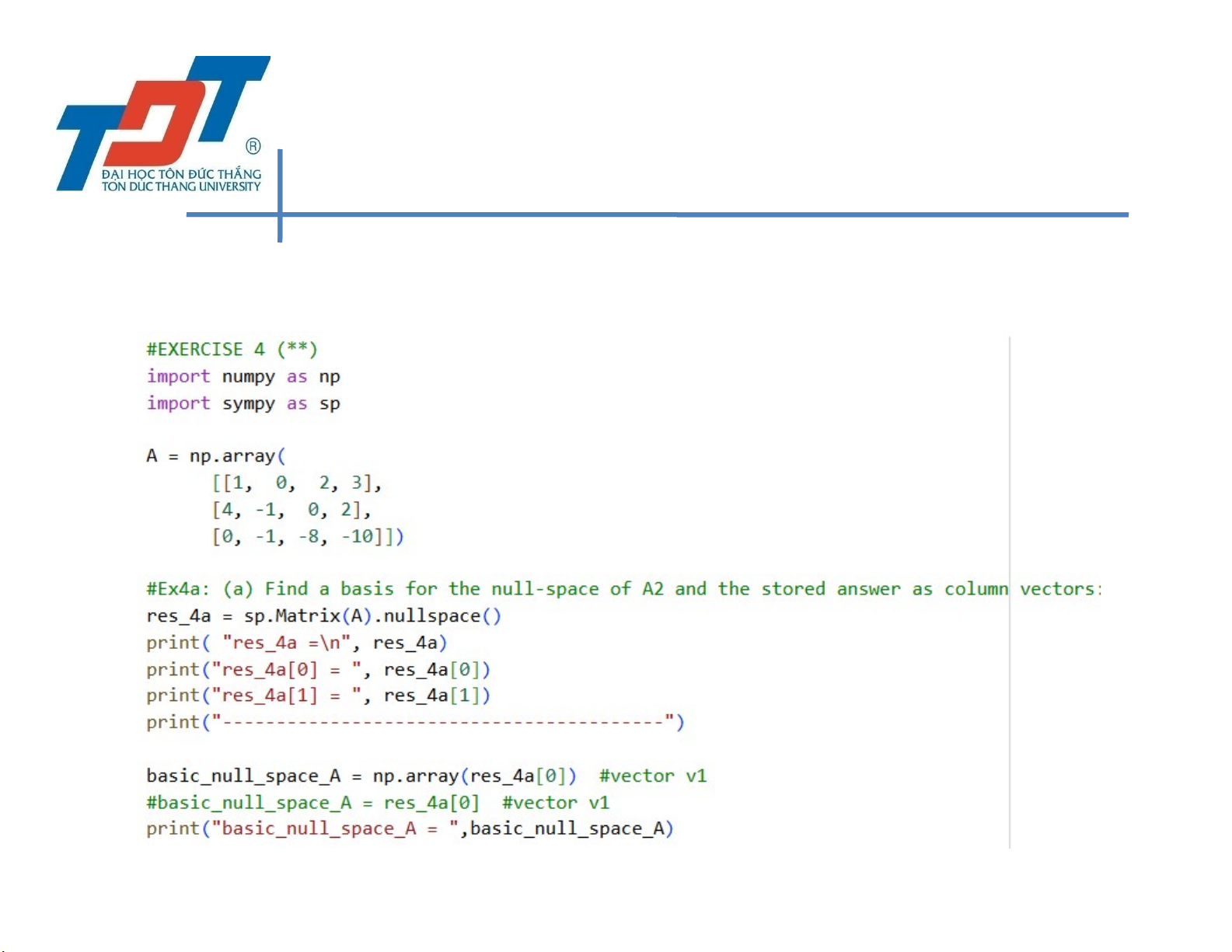
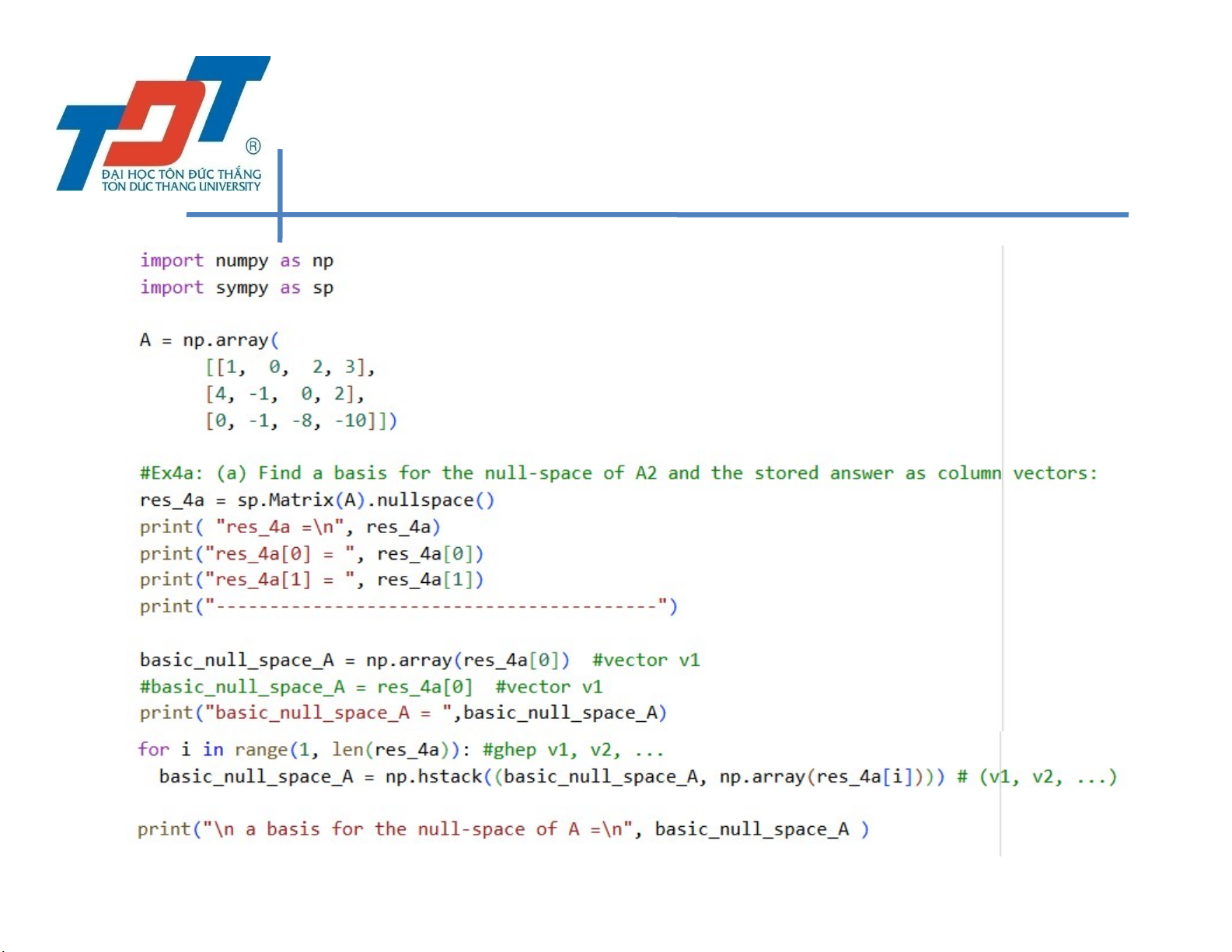
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 4:
• (a) Find a basis for the null-space of A2 and the stored answer as column vectors:
• res_4a = sp.Matrix(A).nullspace()
• basis_null_space_A = np.array(res_4a[0]) 164 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 4: 165 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 4:
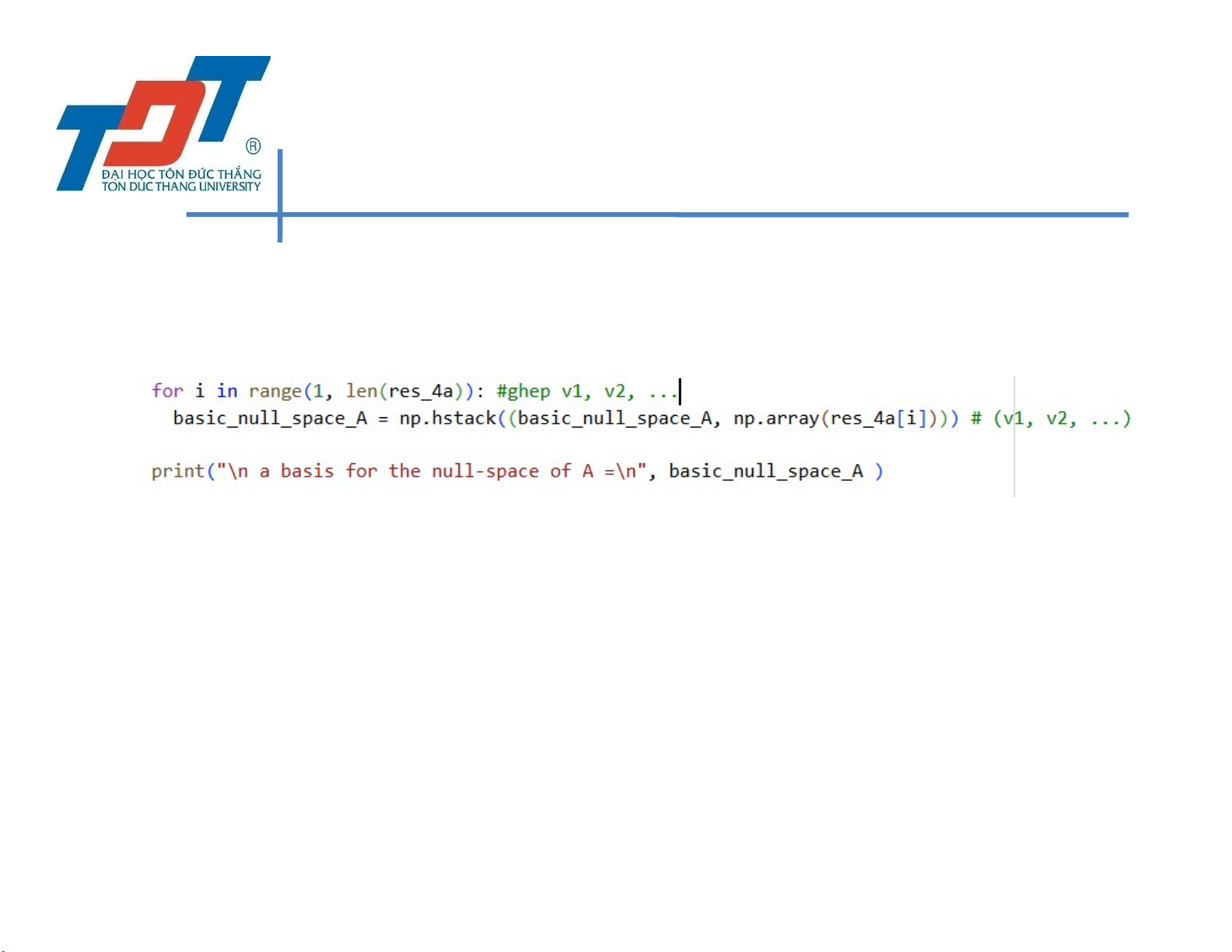
• (a) Find a basis for the null-space of A2 and the stored answer as column vectors (Cont.):
• for i in range(1, len(res_4a)): #ghép v1, v2, ... basis_null_space_A =
nh.hstack((np.array(basis_null_space_A , res_4a[i]))) #v1, v2, v3
• print(“Basis for the null-space of A = “, basis_null_space_A) 166 MCS. Nguyen Van Khoa
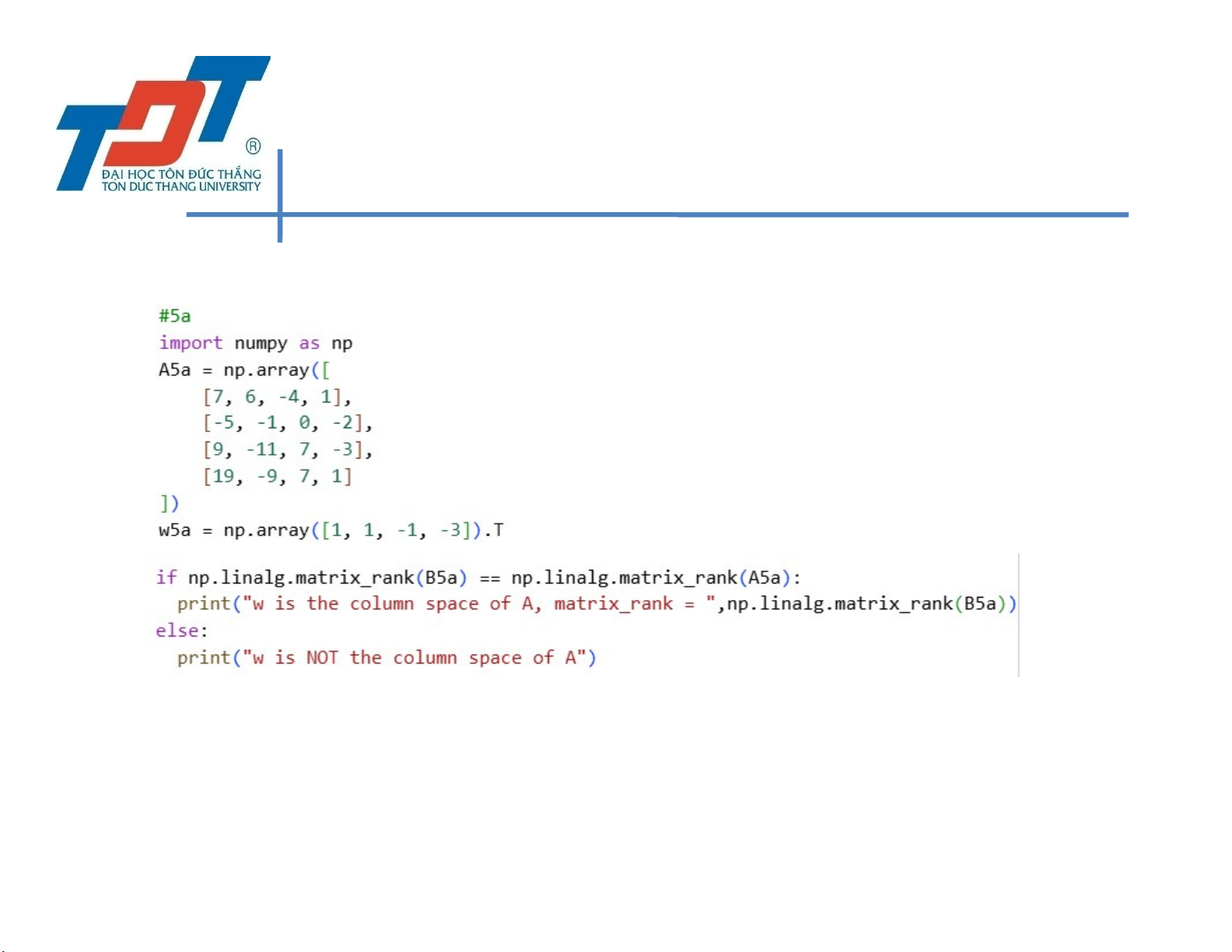
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 5:
• a) check w is the column space of A or not
• w is in the column space of matrix A if w is a linear
combination of the matrix's columns --> do similarly
• Step 1: Create matrix A; vector w = np.array([1, 1, -1, -3]).T 167 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 5 (cont.):
• Step 2: B = np.column_stack((A, w))
• Step 3: if np.matrix_rank(A) = np.matrix_rank(B) then • w is the column space of A
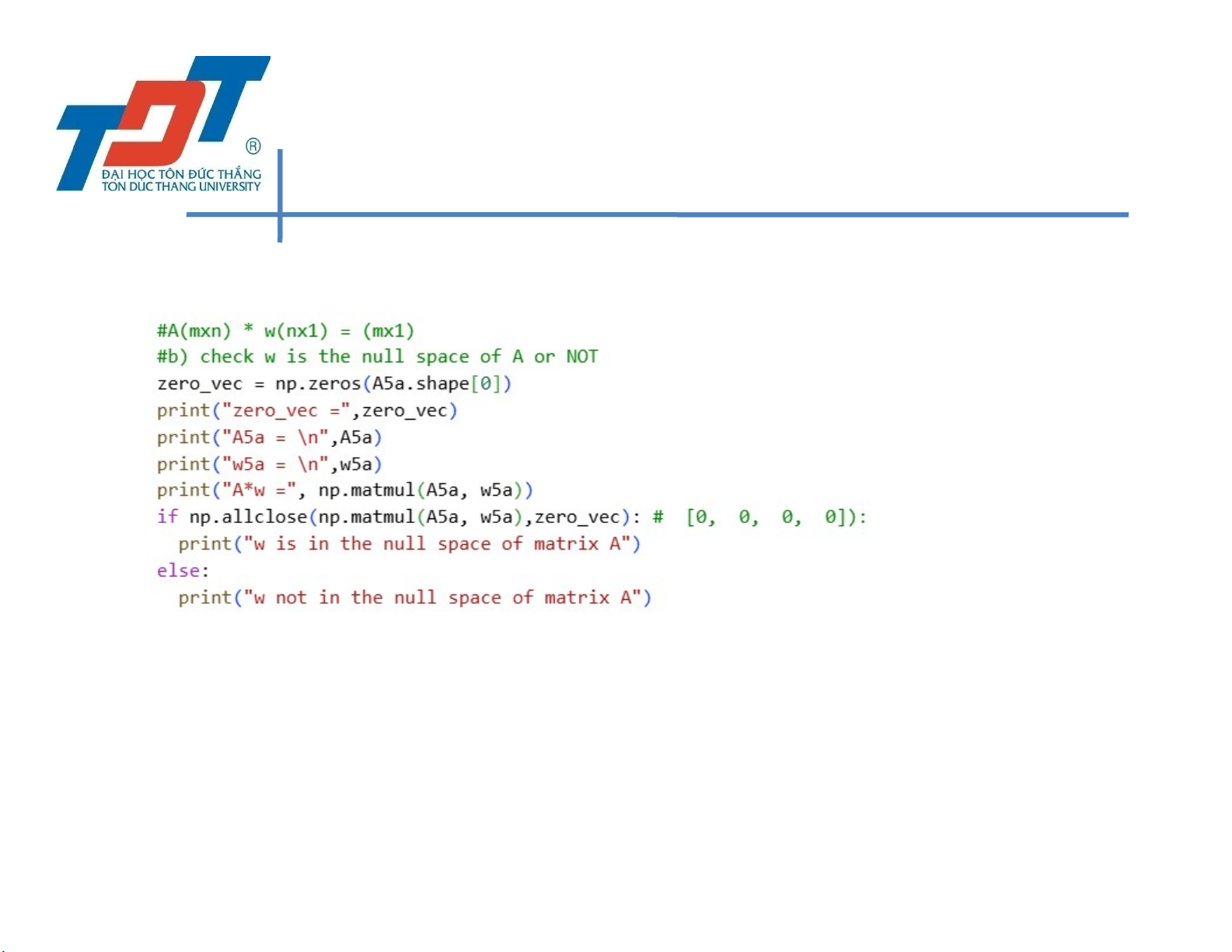
• check w is the null space of A or NOT
• Step 1: zero_vec = np.zeros(A.shape[0])
• Step 2: if np.allclose(np.matmul(A5a, w5a),zero_vec): # [0, 0, 0, 0]):
• Then w is in the null space of matrix A 168 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 5 (cont.): 169 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 5 (cont.): 170 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 6: • Do similarly Ex1 171 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT • Exercise 7:
• Find basis column, basis null-space for their span • Do similarly Ex3 172 MCS. Nguyen Van Khoa
LAB 8: LINEAR COMBINATION, LINEAR INDEPENDENT
• Exercise 8: HOMEWORK find Hilbert, Pascal, Magic Matrix 173 MCS. Nguyen Van Khoa