Giới thiệu và Phân tích Dữ liệu bài giảng môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 1: Giới thiêu chung về th ng kê ố
1. Thống kê là gì - là khoa h c v ọ ề thu thập, t ch ổ
ức, trình bày, phân tích, diễn giải dữ liệu ph c v ụ ụ
quá trình ra quyết định
2. Một số khái niệm thường dùng trong thống kê a. Tổng thể và mẫu: - Tổng thể bao g m toàn b ồ
ộ các đơn vị thuộc phạm vi đối tượng điều tra
+ Tham số: Các mức độ biểu hiện đặc điểm của t ng th ổ ể
+ Tổng điều tra: thu thập dữ liệu cho toàn bộ t ng th ổ ể
- Mẫu: là một phần c a t ủ ng ổ thể + Th ng kê: Các m ố
ức độ biểu hiện đặc điểm c a m ủ ẫu + Điều tra ch n m ọ
ẫu: thu thập dữ liệu c a m ủ ẫu b. Biến và dữ liệu
- Biến là đặc điểm của đơn vị t ng th ổ
ể hoặc mẫu được chọn ra để nghiên cứu.
- Dữ liệu là biểu hiện quan sát được c a m ủ t bi ộ ến - Biến bao g m ồ
+ Định tính – không đo đượ c bằng số
+ Định lượng: rời rạc + liên t c ụ
3. Thang đo trong thống kê: Định danh
Dữ liệu được biểu hiện không có quan hệ Biến định tính
bằng các đặc điểm, tính hơn kém chất Thứ bậc có quan hệ thứ bậc, hơn kém Khoảng
biểu hiện bằng con số và nằm trong m t ộ Biến định lượng
có đơn vị đo lường cụ khoảng Tỉ lệ thể bắt đầu từ 0
4. Thống kê mô tả và thống kê suy diễn: - Th ng kê mô t ố ả: t ch ổ
ức, tóm tắt, trình bày dữ liệu - Th ng ố
kê suy diễn: đưa ra kết luận về các tham số t ng ổ thể dựa trên các th ng ố kê mẫu
Bài 2: Trình bày dữ liệu b ng b ằ
ảng và đồ thị
1. Trình bày dữ liệu đơn biến a. Bảng: - Bảng tần s phân ph ố i: ố + Tần số: là s l
ố ần xuất hiện m t giá tr ộ ị lượng biến c th ụ ể nào đó + Bảng tần s phân ph ố i ố liệt kê s l
ố ần xuất hiện của các giá trị lượng biến dưới dạng bảng - B ng t ả n s ầ ố phân ph i g ố i ản đơn: + K thu ỹ
ật: coi mỗi giá trị lượng biến là m t t ộ ổ + Phạm vi áp d ng
ụ : Biến định tính + Biến rời rạc có ít giá trị - B ng t ả n s ầ ố phân ph i có kho ố ng cách t ả : ổ + K thu ỹ ật: ghép m t
ộ phạm vi lượng biến vào m t t ộ ổ + Phạm vi áp d ng
ụ : Biến rời rạc có nhiều giá trị + Biến liên t c ụ
+ Lý do tiến hành phân t v ổ ới khoảng cách tổ + Gồm: Bảng tần s ố có khoảng cách t
ổ bằng nhau + Bảng tần số có khoảng cách t không b ổ ằng nhau - M t s ộ thu ố ật ngữ:
+ Giới hạn dưới (ghd): giá trị thấp nhất c a m ủ t t ộ ổ. + Giới h n t
ạ rên (ght): giá trị cao nhất c a m ủ ột tổ
+ KCT: phạm vi lượng biến c a m ủ t t ộ ổ từ ghd đến ght + D y s  ố ph n ph  ối c n c  t ó n g i l ọ à dy s t
ố huộc tnh (phn t theo ổ biến
định tnh) và dy số lượng biến (phn tổ theo biến định lượng). b. Đồ thị: Biến
định Biểu đồ hình cột - 1 tr c bi ụ ểu diễn các thu c t ộ nh tính và biến giản đơn - Tr c ụ c n
 lại là tần số hoặc tuần suất xuất hiện rời rạc của từng loại thu c t ộ nh Series 2 5 0
Category 1Category 2Category 3Category 4 Series 2
Biểu đồ hình tròn - Sử d ng ụ biểu đồ tròn khi mu n ố mô tả, so sánh
tỉ lệ % xuất hiện c a các bi ủ ến.
- Biểu đồ tròn thường mô tả tần suất. Sales 1st Qtr 2nd Qtr 3rd Qtr 4th Qtr
Biến liên tục Biểu đồ tần s ố phân - Biểu đồ tần s ố phn phối m t ô ả th ng tin ô trong phối các bảng tần s ố phn phối c ó khoảng cách t ổ dưới dạng đồ thị + Đối xứng + Lệch phải + Lệch trái + Bimondal (2 đỉnh) Tiêu đề Biểu đồ 25 20 15 10 5 0 (5, 9] (13, 17] (21, 25] [1, 5] (9, 13] (17, 21] Biểu đồ hộp Đa giác tần số
- Đa giác tần số mô tả tần số và trị số giữa c a t ủ ổ cho các bảng tần s
ố phân phối có khoảng cách tổ.
2. Trình bày dữ liệu đa biến:
Biến định tính Bảng dữ liệu chéo - Cross-table được sử dụng để nghiên cứu mối và biến rời rạc
liên hệ giữa hai biến định tính hoặc biến rời rạc ít giá trị với ít giá trị.
- Lưu ý: khi xy dựng cross-table phải xác định được biến ph thu ụ c (dependent) và bi ộ ến độc lập (independent) để đưa
vào dng và cột cho phù hợp. Biểu đồ thanh Biến liên tục Đồ thị phân tán Bài 3: Các mứ th c độ ng kê mô t ố ả
1. Thống kê mô tả cho một biến:
a. Số tuyệt đối và số tương đối - S tuy ố ệt đối trong th ng kê bi ố
ểu hiện quy mô, số lượng của hiện tượng nghiên
cứu tại thời gian, địa điểm c ụ thể. + Đơn vị tính:
• Đơn vị hiện vật: cái, con, quả, chiếc, m, kg, giờ, ngày...
• Đơn vị giá trị: VND, USD,... - S
ố tương đối trong th ng kê bi ố
ểu hiện quan hệ so sánh giữa hai mức độ nào đó của hiện tượng + Đơn vị tính:
• lần, phần trăm (%), phần nghìn (‰)
• Đơn vị kép: người/km2, sản phẩm/người... - Các loại s ố tương đ i ố t = 𝑦1
Số tương đối động thái (tốc độ phát triển) 𝑦0(100) Số tương đối kế
Số tương đối nhiệm vụ Kn = 𝑦𝐾𝐻 hoạch KH 𝑦0 (100)
Số tương đối thực hiện Kt = 𝑦1 𝑦𝐾𝐻 (100) KH
Phản ánh tỷ trọng của từng bộ phận cấu
Số tương đối kết cấu thành trong m t t ộ ổng thể. Di= 𝑦1 ∑𝑦1 (100) so sánh
˗ hai hiện tượng cùng loại nhưng khác
Số tương đối không gian nhau về không gian
˗ hai mức độ giữa hai b ph ộ ận trong m t ộ tổng thể
Số tương đối cường độ
so sánh chỉ tiêu của hai hiện tượng khác
nhau nhưng có quan hệ với nhau.
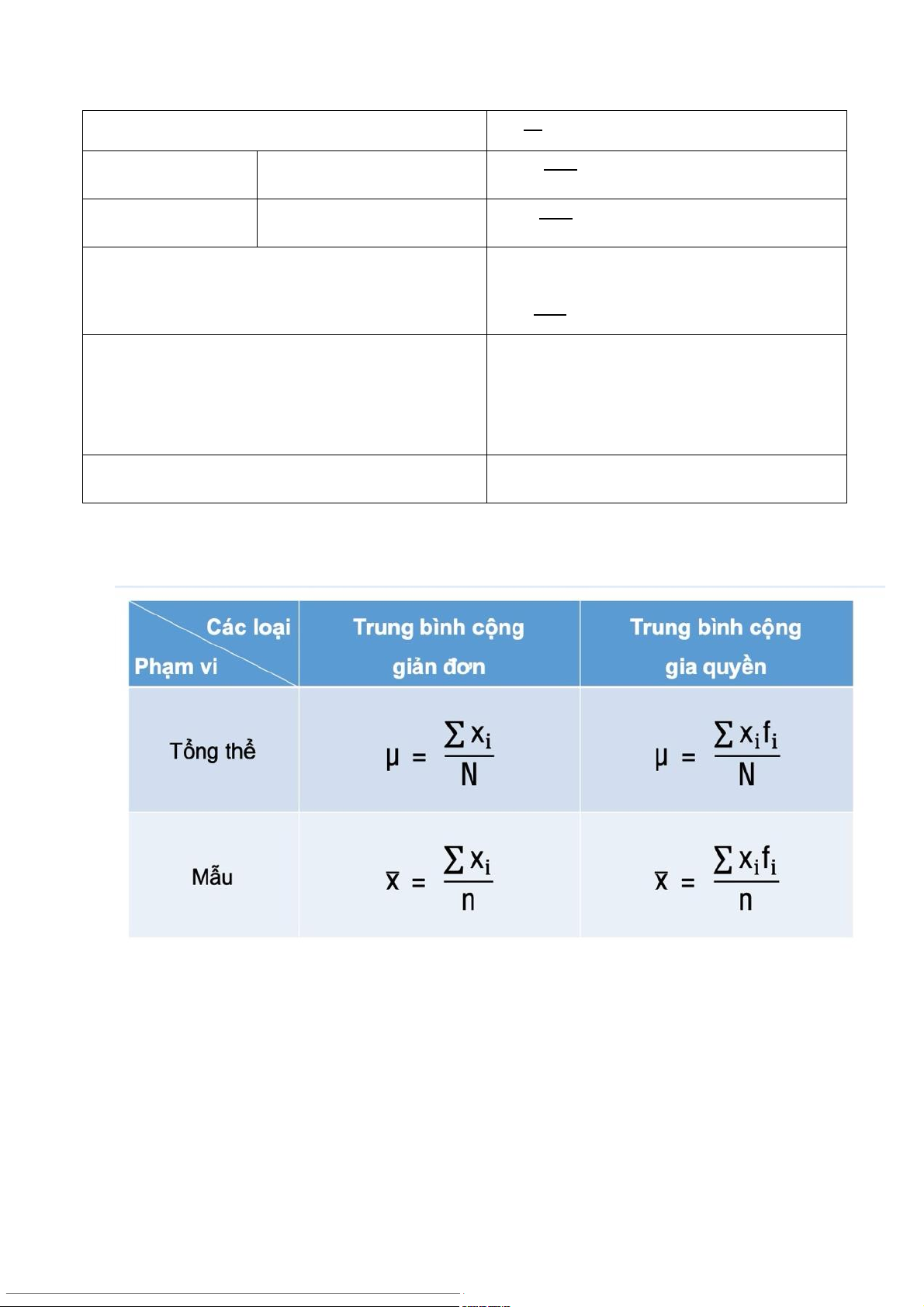
b. Các mức độ trung tâm (i) Số trung bình
- Đặc điểm trung bình c ng: ộ
• Dữ liệu sử ụng thang đo kho d ảng, t l ỷ ệ
• Tất cả các giá trị trong tổng thể đều tham gia vào công thức tính • Chỉ t
nh được một giá trị trung bình
• Tổng chênh lệch của các giá trị so với trung bình c ng b ộ ằng 0 • Chị ảnh hưở u
ng của giá trị đột xuất (ii) Số trung vị
- Giá trị lượng biến của đơn vị đứng ở vị trí chính giữa trong dãy s ố lượng biến + S ố đơn vị t ng th ổ
ể lẻ (∑𝑓𝑖= 2m+1): Me = xm+1 + S ố đơn vị t ng th ổ
ể chẵn (∑𝑓𝑖=2m): Me = 𝑥𝑚+ 𝑥𝑚+1 2 - Đặc điểm:
+ Không bị ảnh hưởng c a giá tr ủ ị t xu độ ất
+ Dữ liệu sử dụng thang đo thứ bậc, khoảng, t l ỷ ệ (iii) Mốt - M t là bi ố
ểu hiện xuất hiện ph bi
ổ ến nhất trong dãy số
- Xác định dựa vào tần số - Đặc điểm: + Dữ liệu sử d ng t ụ
ất cả các loại thang đo
+ Không bị ảnh hưởng c a giá tr ủ ị t xu độ ất (ngoại lai) + M t ộ s
ố trường hợp không có m t ho ố ặc có nhiều m t ố
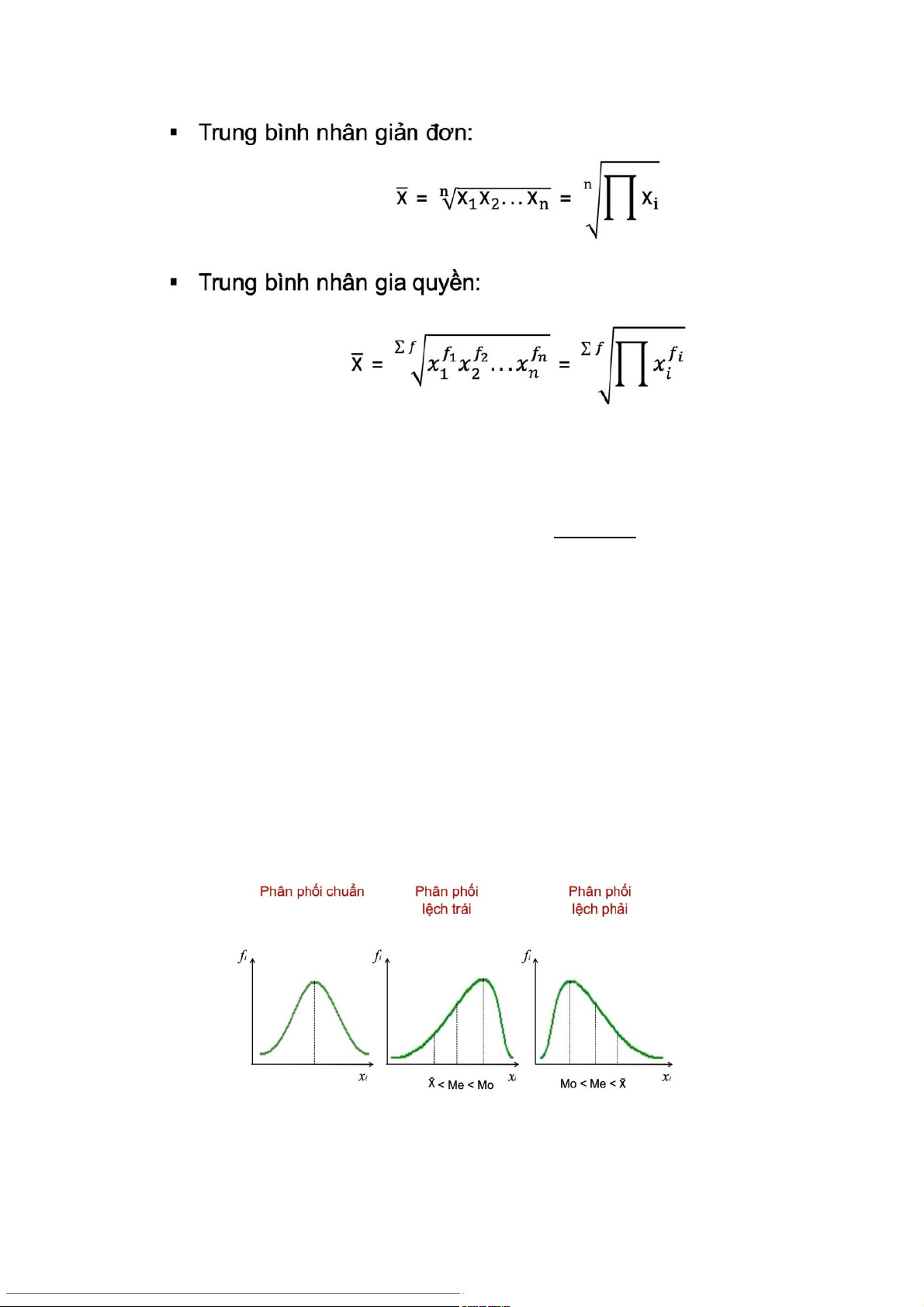
(iv) So sánh trung bình, trung vị, mốt
c. Các mức độ đo độ biến thiên
- Khoảng biến thiên: Là chênh lệch giữa giá trị lớn nhất và nhỏ nhất trong dãy s . ố R = xmax - xmin - Khoảng tứ phân vị:
+ Tứ phân vị: Các giá trị chia tập hợp dữ liệu (đ được sắp xếp từ nhỏ đến
lớn) thành 4 phần bằng nhau.
+ Thập phân vị: Các giá trị chia tập hợp dữ liệu (đ được sắp xếp từ nh ỏ
đến lớn) thành 10 phần bằng nhau.
+ Bách phân vị: Các giá trị chia tập hợp dữ liệu (đ được sắp xếp từ nh ỏ
đến lớn) thành 100 phần bằng nhau.
+ Cách xác định bách phân vị:
• Xác định vị trí c a phân ủ vị thứ p: Lp =(n+1) p • Tính giá trị c a phâ ủ
n vị thứ p dựa vào vị trí
+ Khoảng tứ phân vị là: Là chênh lệch giữa giá trị tứ phân vị thứ ba và tứ
phân vị thứ nhất. IQR = Q3 Q – 1
- Phương sai: Là trung bình c ng ộ c a
ủ tổng bình phương độ lệch so với s ố trung bình
- Độ lệch chuẩn: Là căn bậc hai của phương sai
+ Độ lệch chuẩn của tổng thể: σ = √σ 2
+ Độ lệch chuẩn của mẫu: S= √𝑆2 - Hệ số biến thiên: + Là s ố tương i
đố (%) tnh bằng cách so sánh giữa
độ lệch chuẩn với số trung bình c ng ộ V = S/𝑥 × 100 + Là thước đo
độ biến thin tương i, đố c
ó thể dng để so sánh giữa các
hiện tượng khác loại hoặc c ng lo  ại và c s
ó ố bình qun khác nhau
d. Hình dáng phân phối dãy số:
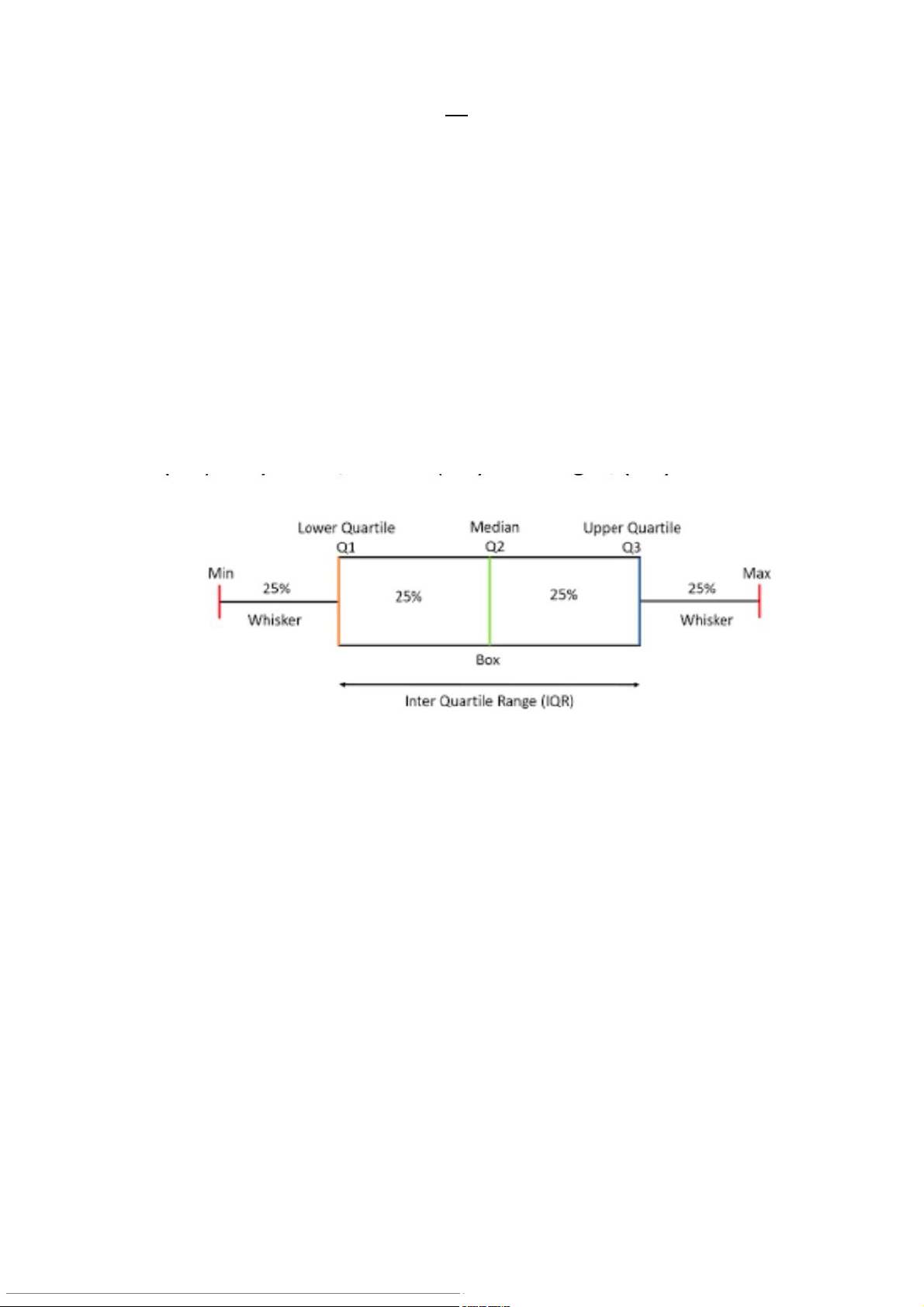
- Hệ số Skewness: là thước đo độ đối xứng của phân phối - Biểu đồ h p
ộ ria mèo (boxplot) biểu diễn 5 mức độ th ng ố
kê mô tả: giá trị lớn
nhất (max), giá trị nhỏ nhất (min), tứ phân vị thứ nhất (Q1), tứ phân vị thứ ba (Q3) và trung vị (Q2)
- Quy tắc 3 sigma: Đối với phân ph i chu ố ẩn:
+ Khoảng 68% các quan sát nằm trong phạm vi (+) và (-) 1 lần độ lệch chuẩn so với trung bình
+ Khoảng 95% các quan sát nằm trong phạm vi (+) và (-) 2 lần độ lệch chuẩn so với trung bình
+ Khoảng 99,7% các quan sát nằm trong khoảng (+) và (-) 3 lần độ lệch chuẩn so với trung bình
2. Thống kê mô tả phản ánh mối liên hệ:
a. Hiệp phương sai: Phản ánh chiều hướng của mối liên hệ
b. Hệ số tương quan: Phản ánh chiều hướng và cường độ của mối liên hệ
Bài 4: Tổng quan về xác suất và định lí giới hạn trung tâm
1. Tổng quan về xác suất:
a. Khái niệm về xác su t, bi ấ ến ng u nhiên: ẫ - Xác suất là:
+ khả năng mà một sự kiện có thể xảy ra.
+ X/S cung cấp mối liên hệ giữa t ng ổ thể và mẫu.
- X là biến ngẫu nhiên nếu giá trị c a X=x là ủ hoàn toàn ngẫu nhiên.
- Xác suất để X nhận giá trị x là p(x)=P(X=x). - Nếu m t bi ộ
ến ngẫu X nhận giá trị xi, khi đó 1. 0

2. ∑𝑝( 𝑥𝑖 𝑥𝑖) =1 b. Phân ph i xác su ố
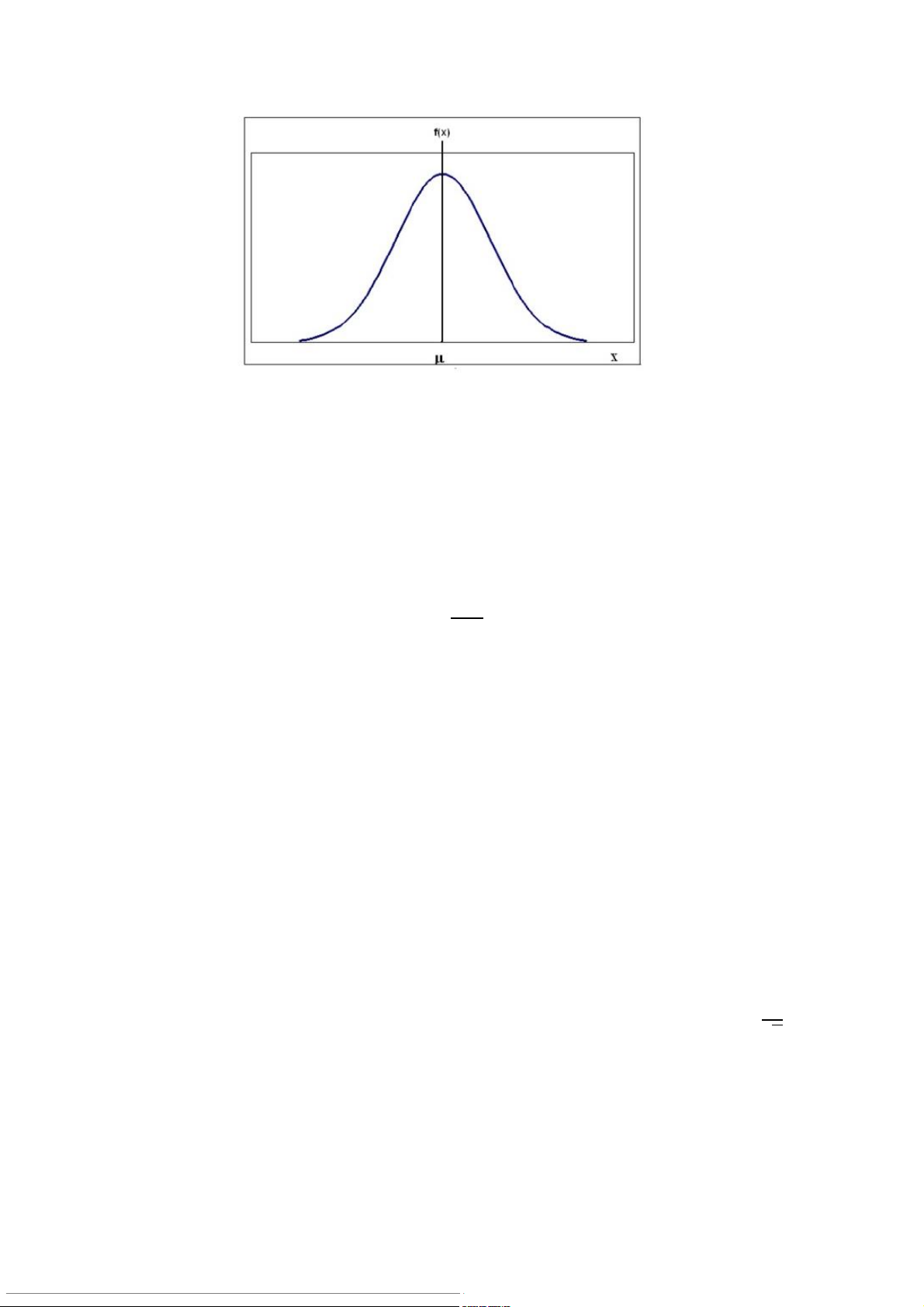
ất của biến ngẫu nhiên liên tục: - Phân ph i chu ố ẩn:
+ Dạng hình chuông, đối xứng qua giá trị trung tm μ, có đỉnh tại x=μ, đồ
thị tiệm cận 0 khi x→±∞. 1. E(X)=μ; V(X)=σ2
2. Diện tích dưới đường cong=1 3. Kí hiệu: X~N(μ,σ2).
4. Giá trị trung bình khácnhau–vị trí thay i d đổ ọc theo tr c x ụ
5. Phương sai khác nhau–đồ thị nh n ho ọ ặc thoải
+ Chuẩn hoá: Là quá trình chuyển một biến phân ph i chu ố ẩn về phân phối chuẩn hóa
+ Nếu X~N(μ,σ2), sử dụng công t ức dưới đy để h chuẩn hóa: Z = 𝑋−𝜇 𝜎 ~ N(0,1) -> Sử d ng b ụ ảng Z để tra X/S + Quy tắc đối xứng: • P(Z<-a) = P(Z>a) • P(Z>a) = 1 P(Z–
• P(a2. Định lí giới hạn trung tâm:
a. Phân phối của mẫu:
- Khi cỡ mẫu tăng ln (đặc biệt tăng đến vô hạn và tiệm cận về quy mô c a t ủ ng ổ
thể), phân phối của mẫu sẽ tiệm cận về phân ph i chu ố ẩn.
b. Phân phối của trung bình mẫu:
- Bất kể biến ngẫu nhin ban đầu có dạng phân phối như thế nào, khi cỡ mẫu tăng lên phân ph i
ố của các trung bình mẫu tiệm cận về phân ph i chu ố ẩn.
- Bất kể biến ngẫu nhin ban đầu có dạng phân phối như thế nào, với m t ộ cỡ mẫu
n, độ lệch chuẩn của các trung bình mẫu (sai s bình ố
quân chọn mẫu) bằng 𝜎 √𝑛, kí
hiệu là SE (Standard error of the mean).
-> Bất kể tổng thể có phân ph i th ố
ế nào (chuẩn hay không chuẩn), khi cỡ mẫu đủ
lớn phân phối của các trung bình mẫu sẽ tuân theo quy luật phân ph i ố chuẩn và
chúng ta có thể sử d ng th ụ
ống k Z để tính xác suất cho bất k gi ỳ á trị trung bình nào
c. Định lí giới hạn trung tâm: - Nếu X là m t
ộ biến ngẫu nhiên có giá trị trung bình là μ và phương sai là σ2, thì 𝑥 →N(𝜇,𝜎2𝑛) 𝑥−𝜇 𝜎
√𝑛 Z ~ N (0,1) as n → ∞
Bài 5: Ước lượng và kiểm định giả thuyết th ng kê ố
1. Ước lượng th ng kê: ố
a. Ước lượng (suy r ng) k ộ ết qu ả điều tra:
- Ước lượng điểm/ trung bình: thống kê tính từ mẫu được dng để ước lượng các tham s c ố a t ủ ổng thể
- Ước lượng bằng khoảng tin cậy: là khoảng giá trị được xác định từ th ng ố kê
mẫu mà với xác suất c th ụ ể, tham s c ố a t ủ ng
ổ thể sẽ thuộc khoảng đó - z,t làhệ s
ố tin cậy(giá trị tới hạn mức α c a
ủ phân phối chuẩn hoá và phân phối Student) - α m
– ức ý nghĩa (xác suất mắc sai lầm)
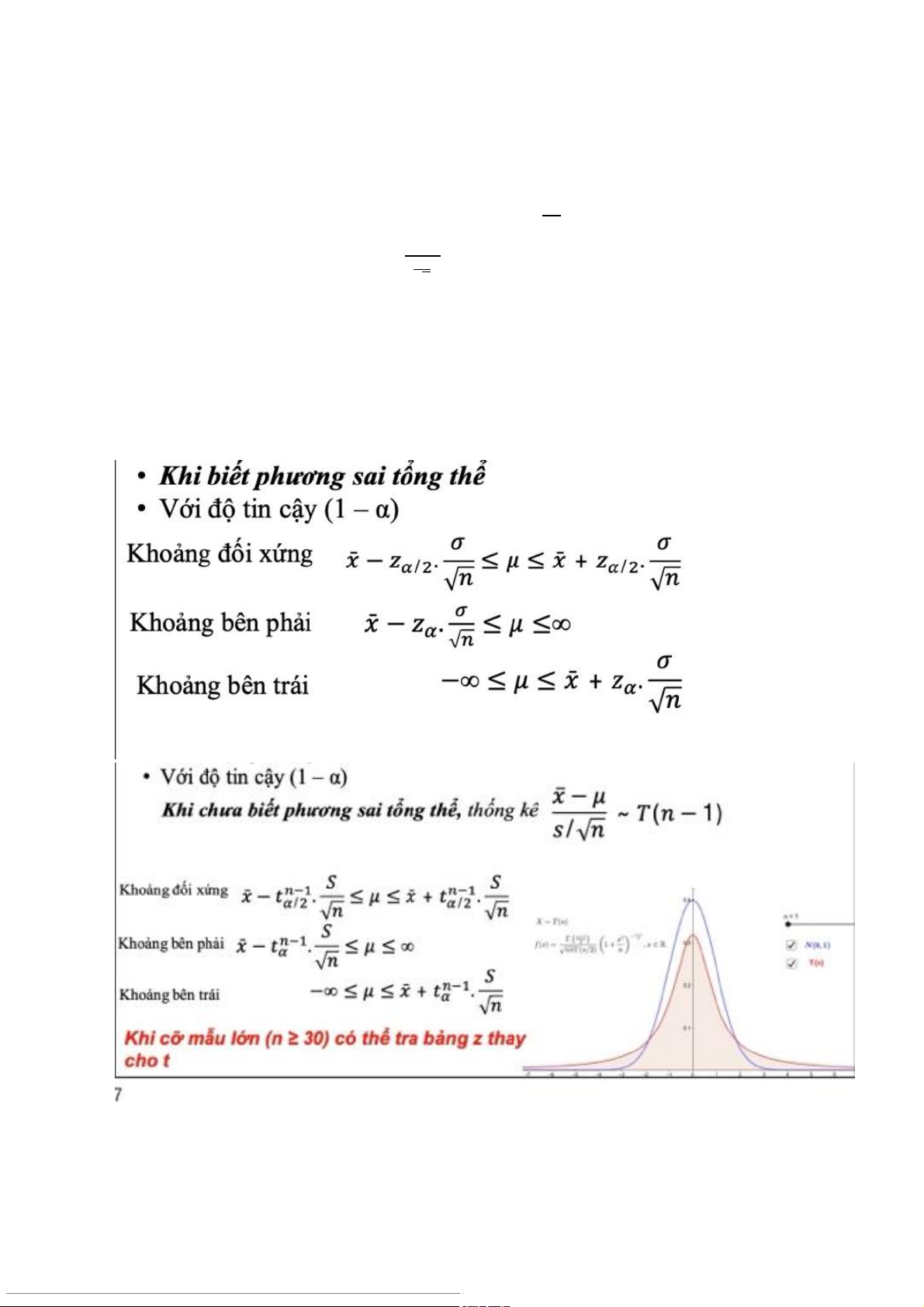
- (1-α) là xác suất hay trình độ tin cậy - Trong trường hợp t ng ổ
thể là hữu hạn, Chúng ta điều chỉnh phạm vi sai s trong ố
công thức xác định khoảng tin cậy. FPC=√𝑁−𝑛 𝑁−1
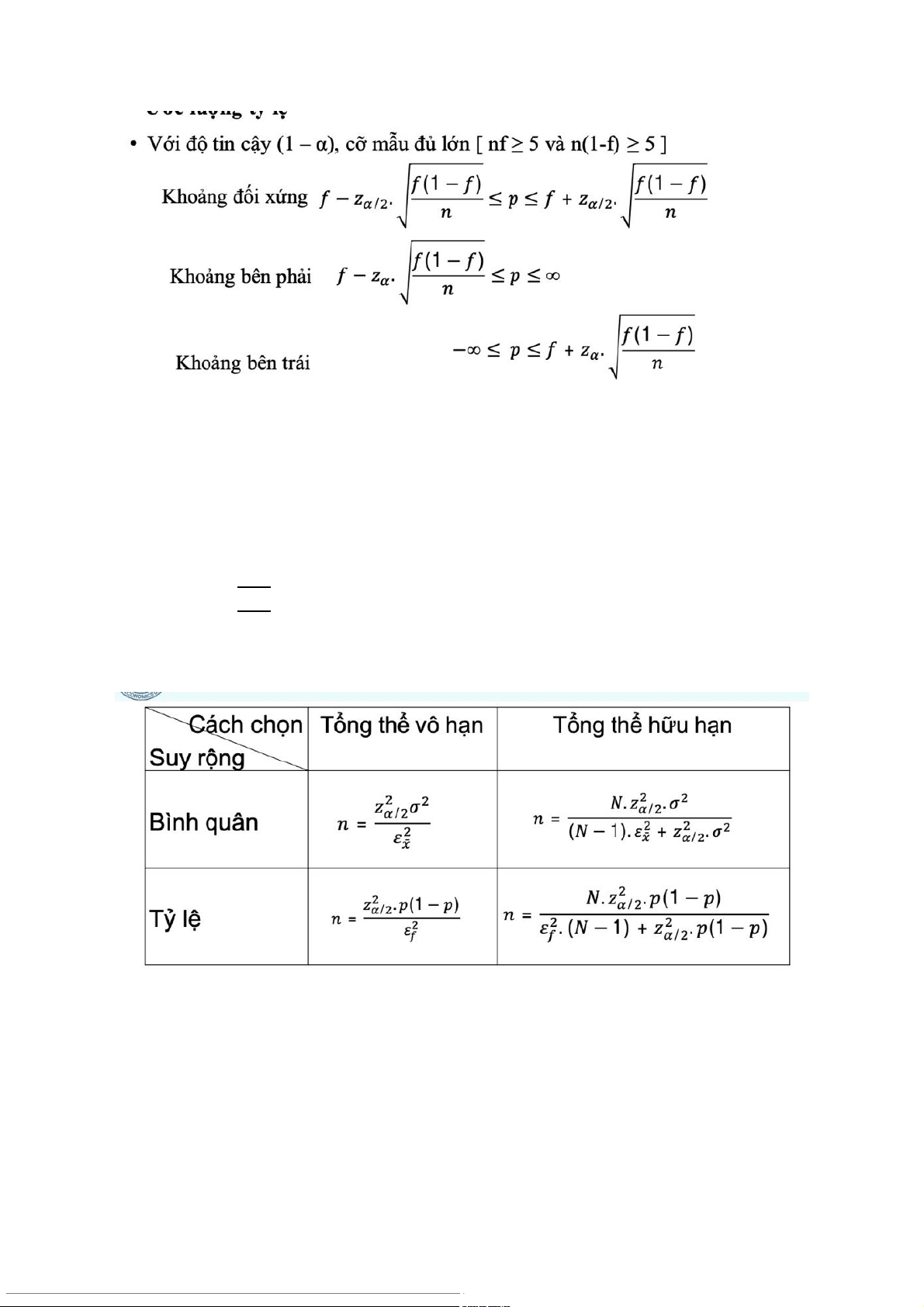
b. Xác định kích thước (quy mô) mẫu:
- Các yếu tố ảnh hưởng tới kch thước mẫu: + Hệ s tin c ố
ậy (z)/ Độ tin cậy của ước lượng
+ Phương sai (độ đồng đề u) của tổng thể + Phạm vi sai s ch ố n ọ mẫu/sai s ch ố n m ọ ẫu cho phép (𝜀) - M t s ộ
ố phương pháp xác định phương sai tổng thể:
+ Lấy phương sai lớn nhất hoặc t
ỷ lệ gần với 0,5 nhất trong các lần điều tra trước (nếu có)
+ Sử dụng kết quả c a nghiên c ủ
ứu có tính chất tương tự
+ Tiến hành nghiên cứu thử nghiệm + Lấy t
ỷ lệ bằng 0,5 hoặc ước lượng phương sai dựa vào khoảng biến thiên
𝜎 = 𝑅6= 𝑥𝑚𝑎𝑥− 𝑥𝑚𝑖𝑛 6
2. Kiểm định giả thuyết thống kê
a. Những vấn đề chung về kiểm định giá thuyết thống kê:
- Giả thuyết: là m t tuyên b ộ v ố ề tham s c ố a t ủ ng th ổ
ể cần được chứng minh
- Kiểm định giả thuyết là 1 quy trình dựa trên bằng chứng mẫu và lí thuyết xác suất để xác đ
ịnh xem giả thuyết đưa ra có phải là 1 tuyên bố hợp lí hay không
1) Bước 1: Nêu giả thuyết
- Giả thuyết không (H0): là tuyên b
ố về giá trị của tham s ố t ng ổ thể nhằm m c ụ
đch kiểm tra trn cơ ở bằng chứng c th ụ ể - Giả thuyết i
đố (H1): là tuyên bố được chấp nhận nếu dữ liệu mẫu cho hấy đủ
bằng chứng chứng minh giả thuyết là không sai 2) L ựa ch n m ọ ức ý nghĩa - Sai lầm loại I: bác b ỏ H0 khi H0 đúng
- Sai lầm loại II: chấp nhận H0 khi H0 sai 3) L ựa ch n ti ọ êu chu n ki ẩ ểm định
- Tiêu chuẩn kiểm định là giá trị được xác định từ dữ liệu mẫu, được sử dụng để
ra quyết định bác bỏ giả thuyết không
- Biết PS tổng thể (𝜎2): Zqs= 𝑥−𝜇0 𝜎 √𝑛
- Chưa biết PS tổng thể (𝑠2): Tqs= 𝑥−𝜇0  𝑠√𝑛
4) Xác định quy tắc ra quyết định:
- Quy tắc ra quyết định dựa vào miền bác bỏ
+ Nếu giá trị tiêu chuẩn kiểm định thu c ộ miền bác b ỏ (W ), có đủ cơ sở để bác bỏ H0 + Nếu giá trị c a t
ủ iêu chuẩn kiểm định không thu c mi ộ ền bác bỏ, chưa đủ cơ sở để bác bỏ H0
- Quy tắc ra quyết định dựa vào P-value:
+ P-value là xác suất c a giá ủ
trị tiêu chuẩn kiểm định từ ngưỡng tnh được
dựa trên thông tin mẫu với giả định giả thuyết không là đúng.
+ Các nguyên tắc ra quyết định để bác b gi
ỏ ả thuyết H0 với P-value là:
• Nếu p-value lớn hơn hoặc bằng α, chưa đủ cơ sở để bác bỏ giả thuyết H0.
• Nếu p-value nhỏ hơn α, bác bỏ giả thuyết H0.
- Quy tắc ra quyết định dựa vào Khoảng tin cậy: Bác bỏ giả thuyết H0 khi 𝜇0 không thu c kho ộ
ảng tin cậy (1 - 𝛼) của ước lượng giá trị trung bình. 5) Ra quyết định
- Xác định giá trị tiêu chuẩn kiểm định từ mẫu quan sát
- Dựa vào các quy tắc ra quyết định để ra quyết định. 6) Nêu kết luận - Có 2 trường hợp:
+ Nếu giá trị tiêu chuẩn kiểm định thu c ộ miền bác b /Giá tr ỏ ị xác suất nhỏ
hơn 𝛼=> Có đủ cơ sở
để bác bỏ giả thuyết H0
+ Nếu giá trị tiêu chuẩn kiểm định không thuộc miền bác bỏ/Giá trị xác
suất lớn hơn hoặc bằng 𝛼 => Chưa đủ cơ sở để bác b gi ỏ ả thuyết H0
b. Kiểm định giá trị trung bình của 1 tổng thể:
- Giả sử nghiên cứu biến ngẫu nhiên X phân phối chuẩn
- Chưa biết 𝜇 song có cơ sở để giả đị
nh nó bằng 𝜇0 (H0: 𝜇 = 𝜇 0)
- Để kiểm định giả thuyết trên, lấy ngẫu nhin n đơn vị từ đó tính các thống kê mẫu.
- Tiêu chuẩn kiểm định
- Biết PS tổng thể (𝜎2): Zqs= 𝑥−𝜇0 𝜎 √𝑛
Nếu H0 đúng -> th ng kê Z s ố
ẽ tuân theo quy luật pp chuẩn hoá
- Chưa biết PS tổng thể (𝑠2): Tqs= 𝑥−𝜇0  𝑠√𝑛
Nếu H0 đúng -> thống kê T sẽ tuân theo quy luật phân ph i ố Student với bậc tự do là n-1
c. Kiểm định tỉ lệ của 1 t ng th ổ ể:
- Giả sử nghiên cứu m t t ộ ng t ổ hể, t l ỷ ệ chung là p.
- Chưa biết p song có cơ sở để giả đị ằ nh nó b ng p0 (H0:p=p0)
- Để kiểm định giả thuyết trên, lấy mẫu n đơn vị từ đó tnh các thống kê của mẫu.
- Tiêu chuẩn kiểm định
Bài 6: Phân tích tương quan và hồi quy
1. Mối liên hệ giữa các hiện tượng
a. Liên hệ hàm số:
- Khái niệm: liên hệ hàm s là m ố i liên h ố ệ hoàn toàn chặt chẽ
- Đặc điểm: Liên hệ được biểu hiện trên từng đơn vị cá biệt
b. Liên hệ tương quan:
- Khái niệm: liên hệ tương quan là mối liên hệ không hoàn toàn chặt chẽ.
- Đặc điểm: Liên hệ không được biểu hiện trên từng đơn vị cá biệt mà phải quan sát s l ố ớn
2. Phân tích tương quan:
- Phn tch tương quan g m các k ồ thu ỹ
ật đo lường mối liên hệ giữa hai biến
- Hệ số tương quan đo lường mức độ chặt chẽ c a ủ m i li ố ên hệ tương quan tuyến tính giữa hai biến
r= (𝑥−𝑥)(𝑦−𝑦) (𝑛−1)𝑆𝑥𝑆𝑦 - Tác d ng: ụ
+ Xác định chiều hướng c a m ủ i l ố iên hệ
+ Đánh giá mức độ chặt chẽ c a liên h ủ
ệ tương quan tuyến tính
3. Phân tích hồi quy
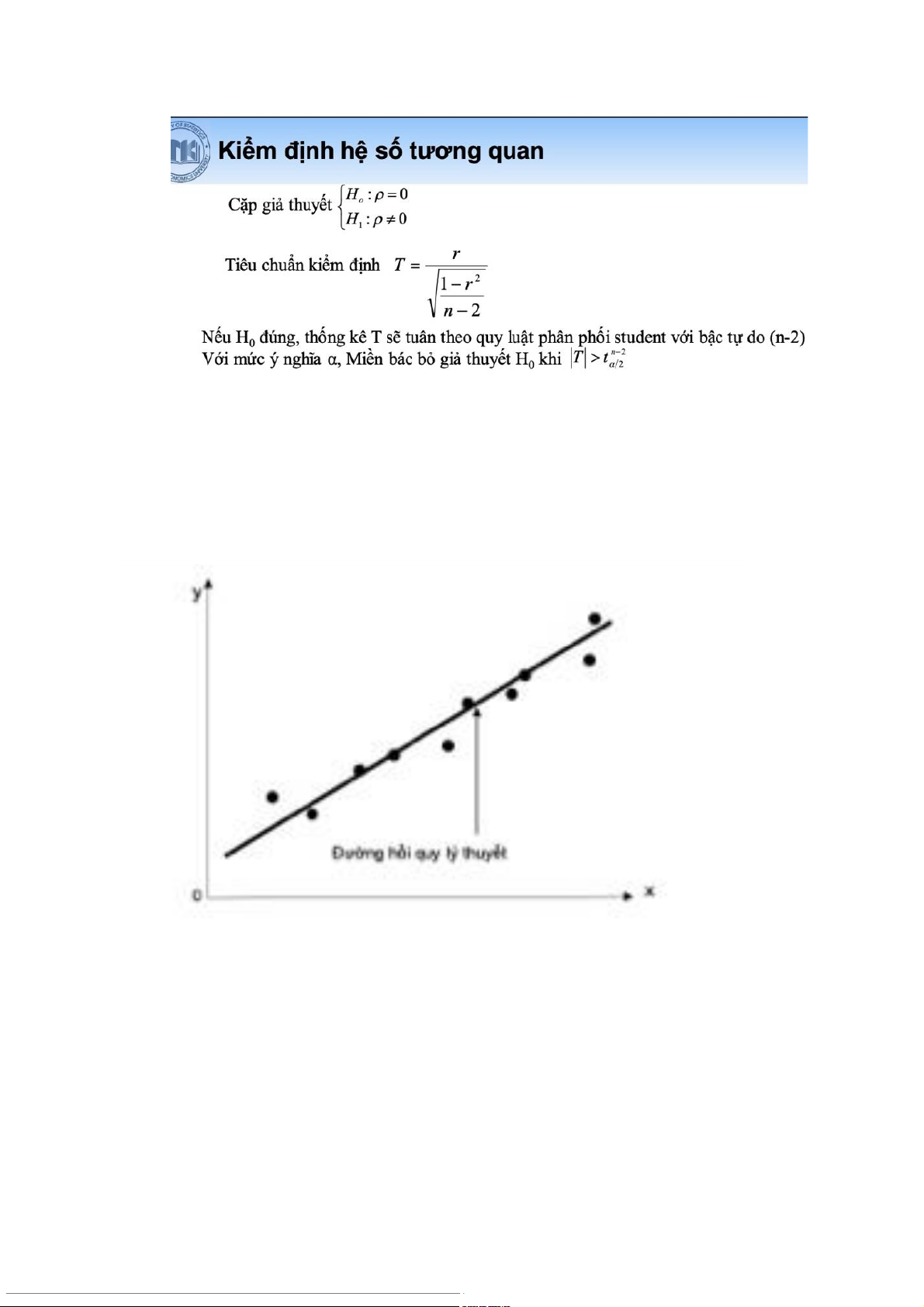
a. Phân tích hồi quy đơn: - Đường h i quy ồ
lý thuyết: là đường điều chỉnh bù trừ các chênh lệch ngẫu nhiên
nêu ra mối liên hệ cơ bản c a hi ủ ện tượng.
- Phương trình hồi quy: là phương trình xác định vị trí của đường h i ồ quy lý thuyết - Mô hình hồi quy t ng th ổ ể:
• 𝛼: phản ánh ảnh hưởng của các nguyên nhân khác (ngoài nguyên nhân x) tới kết quả y
• β: phản ánh ảnh hưởng trực tiếp c a nguyên nhân ủ x tới kết quả y. C th ụ ể,
khi x tăng thm 1 đơn vị thì y thay đổi trung bình β đơn vị
+ β > 0: x và y có mối liên hệ thuận (cùng chiều)
+ β < 0: x và y có mối liên hệ ịch (ngượ ngh c chiều)
- Phương trình hồi quy mẫu:
- Phương pháp OLS: Tìm các tham s sao c ố
ho tổng bình phương các chnh lệch
giữa giá trị thực tế và giá trị lý thuyết của tiêu thức kết quả là nh nh ỏ ất. + Giả thiết OLS:
• Giả thiết 1: Mô hình được ước lượng trn cơ sở mẫu ngẫu nhiên • Giả thiết 2: Kỳ ọ v ng toán của sai số ằ b ng không
• Giả thiết 3: Sai s tuân theo quy lu ố ật phân b chu ố ẩn
• Giả thiết 4: Phương sai của sai số bằng nhau (không đổi)
• Giả thiết 5: Không có tương quan giữa các phần dư (không có tự tương quan)
• Giả thiết 6: Giữa các biến c
độ lập không có tương quan tuyến tính hoàn hảo (đa c ng tuy ộ
ến) - Đối với hồi quy b i. ộ + N i dung: ộ b= ∑(𝑥𝑖 𝑛𝑖=1−𝑥 )( 𝑦𝑖−𝑦 ) ∑(𝑛𝑥𝑖 𝑖=1 −𝑥 )^2 a=𝑦-b𝑥
- Tính ∑𝑥, ∑𝑦, ∑𝑥 ∗ 𝑦, ∑𝑥^2 ∑ , 𝑦^2,
a= ∑𝑦 ∑𝑥2−∑𝑥∑𝑥y 𝑛∑𝑥2−(∑𝑥)2
b= 𝑛∑𝑥y− ∑𝑥∑𝑦 𝑛∑𝑥2−(∑𝑥)2
b. Phân tích hồi quy bội
- Bj: phản ánh ảnh hưởng thuần c a nguyên ủ
nhân xj tới kết quả y (khi các yếu tố
khác không đổi). Cụ thể, khi xj tăng thm 1 đơn vị thì y thay đổi trung bình βj đơn vị