Global Criterion Method: Understanding and Application | Môn Multi-Criteria Decision Making - Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 58504431
Global Criterion method
Question type: Use Global criterion method to solve the following problem
Multiple 𝑘 objectives: 𝑀𝑎𝑥/𝑀𝑖𝑛 𝑍𝑗
𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜: 𝑔𝑖(𝑥) How to do:
Step 1: Solve the problem with respect to each objective separately (Graphical method if 2 variables)
Step 2: Formulate Global Criterion objective and solve it to obtain the ideal value 𝑍𝑗∗(𝑥)
(Thế giá trị 𝒁𝒊 tìm ược ở từng corner points vào và tìm Min Z)
Note: Với “Minimize” objective, trên tử của công thức cần ổi lại thành 𝑍𝑗 𝑘𝑝 𝑍 𝑗
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 𝑍 = ∑ [ 𝑗∗(𝑥)
] , 𝑠. 𝑡 𝑡𝑜: 𝑔𝑖(𝑥) ≤ 𝑏𝑖; 𝑖 = 1,2, . . , 𝑚 𝑍 𝑗=1
𝑍𝑗∗(𝑥): 𝑡ℎ𝑒 𝑖𝑑𝑒𝑎𝑙 𝑣𝑎𝑙𝑢𝑒 𝑖𝑛 𝑠𝑡𝑒𝑝 1
Case 1: p=1: linear problem, giải bằng graphical method hoặc simplex
Case 2: p=2: nonlinear problem (không thi)
Example (Problem 2/ Homework 1) Consider the MODM problem:
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 𝑍1 = 𝑥1 + 3𝑥2
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 𝑍2 = 3𝑥1 − 𝑥2
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 𝑍3 = 3𝑥1 + 2𝑥2 Subject to 𝑥1 + 𝑥2 ≤ 12 −𝑥1 + 𝑥2 ≤ 2 4𝑥1 − 𝑥2 ≤ 18 2𝑥1 + 3𝑥2 ≥ 6 𝑥1 ≥ 0, 𝑥2 ≥ 0 lOMoAR cPSD| 58504431
(a) Determine the individual optimal solutions
(b) Identify the set of efficient solutions, build the payoff matrix
(c) Determine the “best” efficient solution by Global Criterion technique with 𝑝 = 1
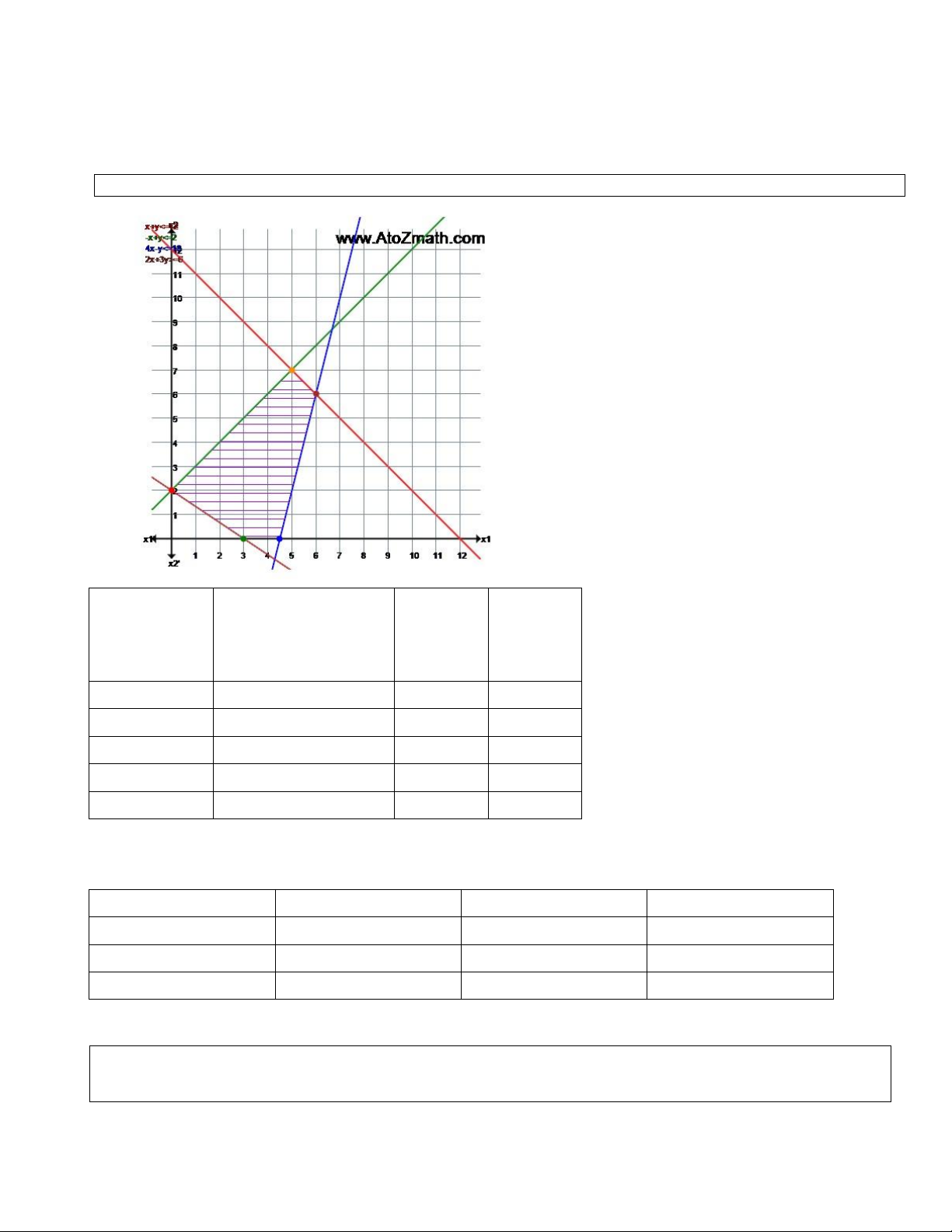
Step 1: Solve the problem with respect to each objective separately (Graphical method if 2 variables) Extreme Point Coordinates Z1 Z2 Z3 (x1,x2) A(0,2) 1(0)+3(2)=6 -2 4 B(3,0) 1(3)+3(0)=3 9 9 C(4.5,0) 1(4.5)+3(0)=4.5 13.5 13.5 D(6,6) 1(6)+3(6)=24 12 30 E(5,7) 1(5)+3(7)=26 8 29
Ideal/ Optimal objective values: 𝒁𝟏 = 𝟐𝟔, 𝒁𝟐 = 𝟏𝟑. 𝟓, 𝒁𝟑 = 𝟒 Set of
efficient solutions are points lying on the boundary ABCDE Payoff matrix: Z E(5,7) C(4.5, 0) A(0,2) Z1 26 4.5 6 Z2 8 13.5 -2 Z3 29 13.5 4
Step 2: Formulate Global Criterion objective and solve it to obtain the ideal value 𝑍𝑗∗(𝑥)
(Thế giá trị 𝒁𝒊 tìm ược ở từng corner points vào và tìm Min Z) lOMoAR cPSD| 58504431
Note: Với “Minimize” objective, trên tử của công thức cần ổi lại thành 𝑍𝑗 𝑘𝑝 𝑍 𝑗
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 𝑍 = ∑ [ 𝑗∗(𝑥)
] , 𝑠. 𝑡 𝑡𝑜: 𝑔𝑖(𝑥) ≤ 𝑏𝑖; 𝑖 = 1,2, . . , 𝑚 𝑍 𝑗=1
Global Criterion objective, 𝑝 = 1: 26 − 𝑍1 13.5 − 𝑍2 𝑍3 − 4
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 𝑍 = + + 26 Extreme Point Min Coordinates Max Z1 Max Z2 Min Z3 Z (x1,x2) A(0,2) 6 -2 4 1.92 B(3,0) 3 9 9 2.47 C(4.5,0) 4.5 13.5 13.5 3.2 D(6,6) 24 12 30 6.69 E(5,7) 26 8 29 6.65
A(0,2) is the best efficient solution Example practice
Question 1: (25 points)
Consider the following problem: Maximize Z1 = X1 + 3X2 Maximize Z2 = 3X1 − X2 Minimize Z3 = 3X1 + 2X2 Subject to: X1 + X2 ≤ 12 −X1 + X2 ≤ 2 4X1 − X2 ≤ 18 2X1 + 3X2 ≥ 6 X1 ≥ 0, X2 ≥ 0
Given payoff matrix as the following table: lOMoAR cPSD| 58504431 (5,7) (4.5, 0) (0,2) Z1 26 4.5 6 Z2 8 13.5 -2 Z3 17 9 4
Formulate MODM problem by using Global Criterion technique with p=1, p=2, p=∞ (5-10-10 pts) lOMoAR cPSD| 58504431 For p =1
Minimize Zd = 26−𝑋1−3𝑋2 +
13.5−3𝑋1+𝑋2 + 3𝑋1+2𝑋2−4 26 13.5 4 For p = 2 26−𝑋1−3𝑋22 13.5−3𝑋1+𝑋22 3𝑋1+2𝑋2−42 Minimize Zd = + + 26 13.5 4 For p = ∞ Let d∞ = max(
26−𝑋1−3𝑋2 , 13.5−3𝑋1+𝑋2 , 3𝑋1+2𝑋2−4) 26 13.5 4 Minimize d∞ S.t 26−𝑋1−3𝑋2 13.5−3𝑋1+𝑋2 ≤ d∞ 13.5 3𝑋1+2𝑋2−4 ≤ d∞ 4 X1 + X2 ≤ 12 −X1 + X2 ≤ 2 4X1 − X2 ≤ 18 2X1 + 3X2 ≥ 6
Compromise programming lOMoAR cPSD| 58504431
Question type: Use Compromise programming method to solve the following problem
Multiple 𝑘 objectives: 𝑀𝑎𝑥/𝑀𝑖𝑛 𝑍𝑗
𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜: 𝑔𝑖(𝑥)
𝐺𝑖𝑣𝑒𝑛 𝑝 = 1,2, . . , ∞, 𝐺𝑜𝑎𝑙 𝑤𝑒𝑖𝑔ℎ𝑡𝑠 𝑊1, 𝑊2, . . , 𝑊𝑖 How to do:
Step 1: Solve the problem with respect to each objective separately (Graphical method if 2 variables)
=> Ideal and anti-ideal solutions 𝑍𝑗∗ 𝑎𝑛𝑑 𝑍𝑗−
Step 2: Normalize distance 𝑑𝑗 for each corner point in graphical method:
|𝑍𝑗∗ − 𝑍𝑗(𝑥)| ; 𝑍𝑗: 𝑜𝑏𝑗𝑒𝑐𝑡𝑖𝑣𝑒 𝑗𝑡ℎ 𝑑𝑗 = 𝑗∗ − 𝑍𝑗−| |𝑍
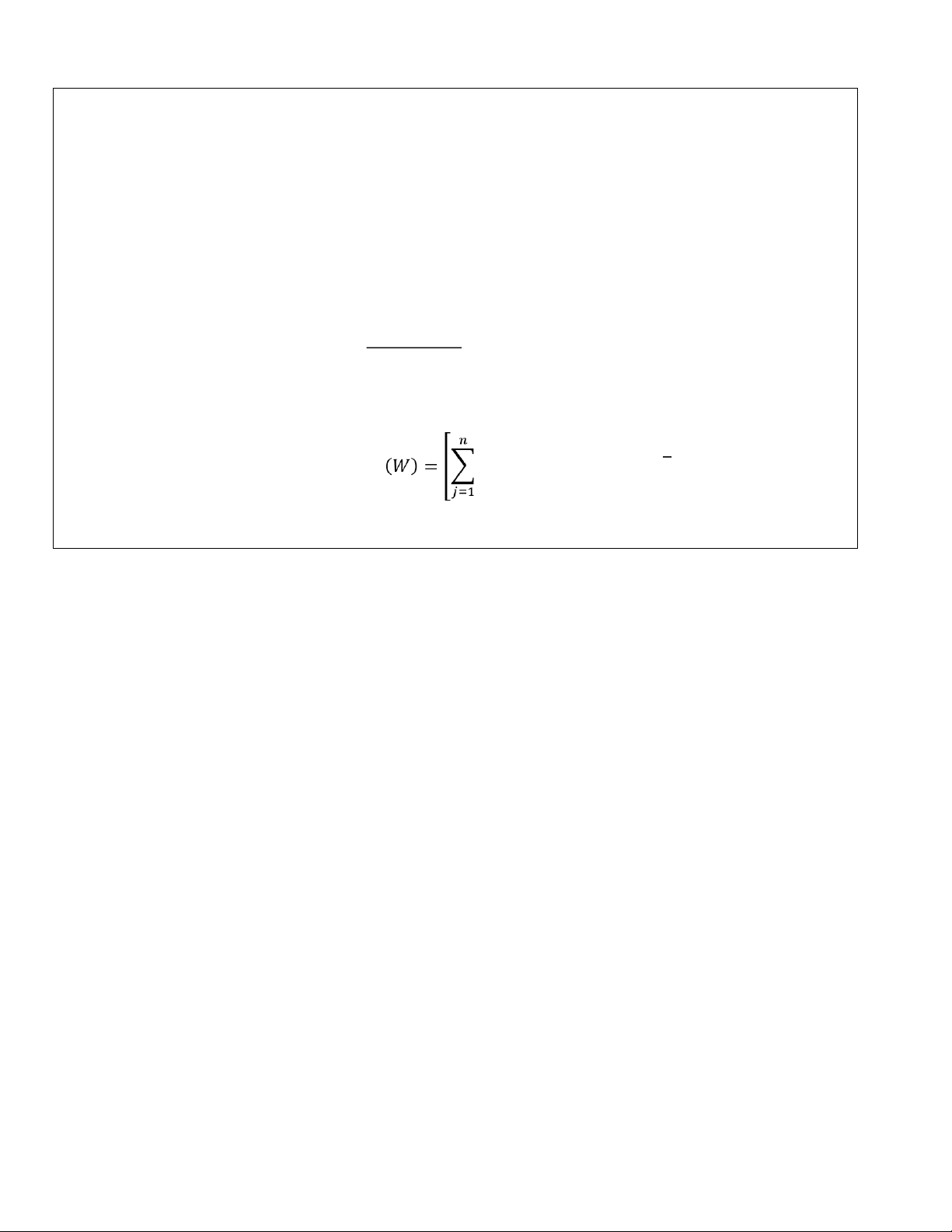
Step 3: Calculate 𝐿𝑝 for each corner point, 𝐺𝑖𝑣𝑒𝑛 𝑝 𝑎𝑛𝑑 𝑊𝑗 => Choose the point with the lowest 𝑳𝒑 1 𝑝 𝑝 𝐿𝑝(𝑊𝑗𝑑𝑗) ]
Example (Homework 7) Given the following problem:
𝑀𝑎𝑥 𝑍1 = 2𝑥1 + 3𝑥2
𝑀𝑎𝑥 𝑍2 = 3𝑥1 − 𝑥2 Subject to 2𝑥1 − 𝑥2 ≥ 0 3𝑥1 − 2𝑥2 + 1 ≥ 0 𝑥1 + 2𝑥2 − 13 ≤ 0 𝑥1 + 𝑥2 − 9 ≤ 0 3𝑥1 − 𝑥2 − 15 ≤ 0
(a) Solve the problem for goal 𝑍1 (b)
Solve the problem for goal 𝑍2
(c) Use the compromise method to solve two goals at the same time given 𝑊1 = 𝑊2 = 1 𝑎𝑛𝑑 𝑝 = 1 lOMoAR cPSD| 58504431
Step 1: Solve the problem with respect to each objective separately (Graphical method if 2
variables) => Ideal and anti-ideal solutions 𝑍𝑗∗ 𝑎𝑛𝑑 𝑍𝑗− Extreme Point Coordinates (x1,x2) Max Z1 Max Z2 O(0,0) 2(0)+3(0)=0 0 A(1,2) 2(1)+3(2)=8 1 B(3,5) 2(3)+3(5)=21 4 C(5,4) 2(5)+3(4)=22 11 D(6,3) 2(6)+3(3)=21 15 E(5,0) 2(5)+3(0)=10 15
Goal 1: Z1=22 at C(5,4); Goal 2: Z2=15 at D(6,3) and E(5,0)
➔ Goal 1: Ideal solution 𝑍 22, anti-ideal 𝑍1− = 0
➔ Goal 2: Ideal solution 𝑍 15, anti-ideal 𝑍2− = 0
Step 2: Normalize distance 𝑑𝑗 for each corner point in graphical method:
|𝑍𝑗∗ − 𝑍𝑗(𝑥)| ; 𝑍𝑗: 𝑜𝑏𝑗𝑒𝑐𝑡𝑖𝑣𝑒 𝑗𝑡ℎ 𝑑𝑗 = 𝑗∗ − 𝑍𝑗−| |𝑍 |22 − 𝑍1| |15 − 𝑍2| 𝑑1 = |22 − 0| ; 𝑑2 = |15 − 0| lOMoAR cPSD| 58504431
Step 3: Calculate 𝐿𝑝 for each corner point, 𝐺𝑖𝑣𝑒𝑛 𝑝 𝑎𝑛𝑑 𝑊𝑗 => Choose the point with the lowest 𝑳𝒑 1 𝑛 𝑝 𝑝
𝐿 ( 𝑊 ) =[ ∑ ( 𝑊 𝑑 ) ] 𝑝 𝑗 𝑗 𝑗=1
Given 𝑝 = 1, 𝑊1 = 𝑊2 = 𝑊3 = 1 |22 − 𝑍1| |15 − 𝑍2| 𝑀𝑖𝑛 𝐿1 = + 22 15 Extreme Point Max Coordinates Max Z1 𝐿1 (x1,x2) Z2 O(0,0) 2(0)+3(0)=0 0 2 A(1,2) 2(1)+3(2)=8 1 1.59 B(3,5) 2(3)+3(5)=21 4 0.78 C(5,4) 2(5)+3(4)=22 11 0.26 D(6,3) 2(6)+3(3)=21 15 0.045 E(5,0) 2(5)+3(0)=10 15 0.54
The compromise solution is D(6,3), Z1=21, Z2=15 DENOVO
The MOLP problem is formulated Max z1 = x1 + x2 Max z2 = x1 + 4x2 S.t 3x1 + 4x2 <= 60 x1 + 3x2 <= 30 x1 >=0, x2>=0 Input: p = (0.5,0.4), B =42 lOMoAR cPSD| 58504431 Answer 3 4
Unit cost v =p*A = [0.5,0.4] * [ ] = [1.9,3.2] 1 3 Max z1 = x1 + x2 Max z2 = x1 + 4x2 S.t 1.9x1 + 3.2x2 <= 42 x1,x2 >=0
=> z1* = 22.11, z2* = 52.50 Min B* = v*x = 1.9x1 + 3.2x2 S.t x1 + x2 >= 22.11 x1 + 4x2 >= 52.5
=> x1* = 11.98, x2* = 10.13
B* = vx* = 55.17 b* = Ax*, b1* = 76.48, b2* = 42.39 r = B/B* = 0.761
Optimal system design for B: x = rx*, b = rb*, z = rz*
X1 = 9.12, x2 = 7.71, b1 = 58.23, b2 = 32.25, z1 = 16.83, z2 = 39.96. Practice exercise lOMoAR cPSD| 58504431 GOAL PROGRAMMING PRE-EMPTIVE
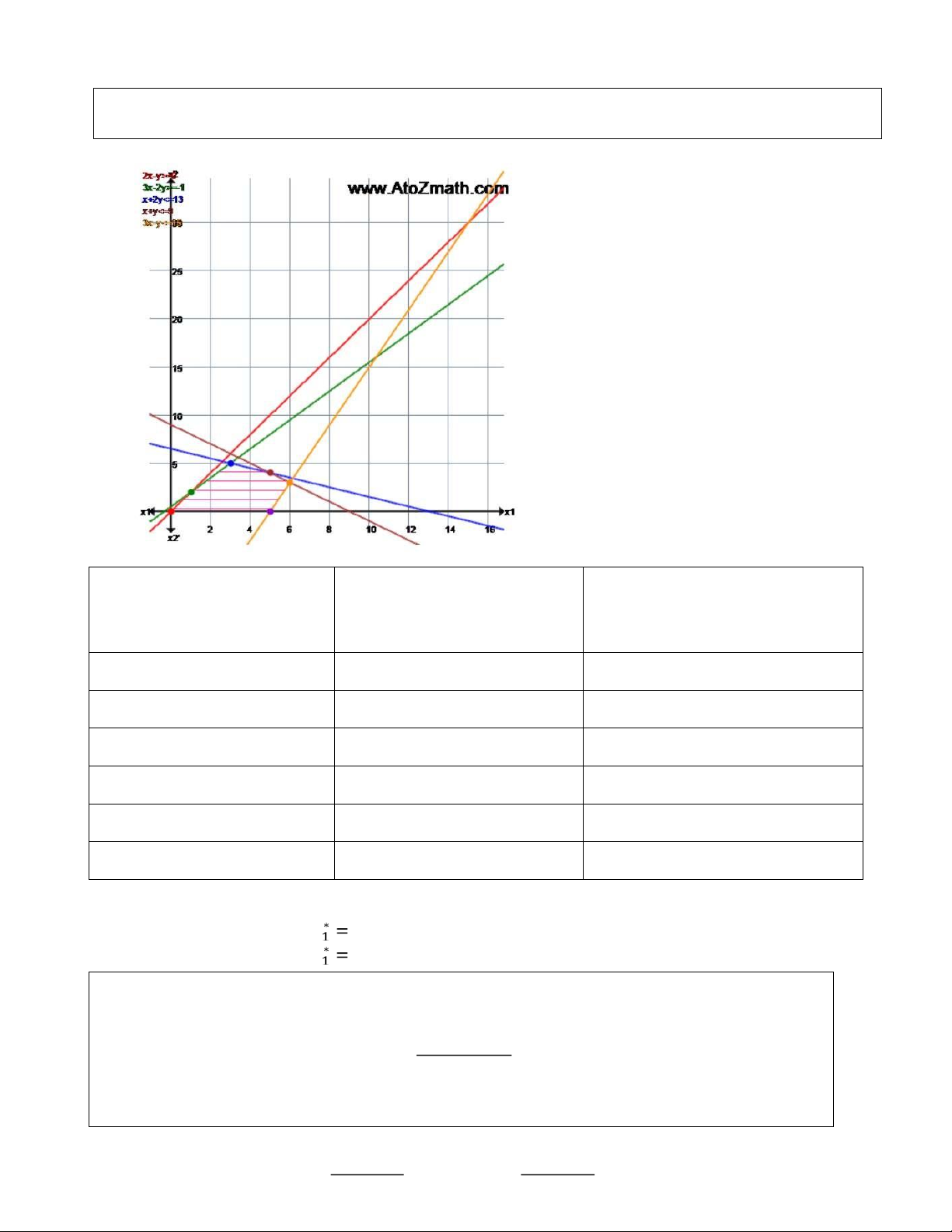
Suppose the weekly levels of two products to be manufactured are to be determined. Suppose
our first criterion relates to the amount of hours labour per week used to manufacture the two
products A and B. Assume our decision variables are x1: The number of products of type A manufactured per week
x2: The number of products of type B manufactured per week and each type A product takes 4
h to manufacture and each type B product takes 3h to manufacture. Suppose that the desired
level is to use no more than 120 h labour
The profit per item A is $100 and for product B is $150 per item. The company is
somewhat unsure about the level of profit to set as a target but give an initial estimate of $7000 per week.
The company has some strategic aims for their weekly production. They wish to maintain
production of at least 40 units of each of the products
The company has to purchase a minimum of 50l of this product weekly. Each item of
type A uses 2l of the product and each item of type B uses 1l of the product. Disposing of
unused product is prohibitively expensive. The second constraint relates to machine time,
which caps the maximum combined production of both products to 75 per week. lOMoAR cPSD| 58504431
Suppose that the company has a clear order in which they wish to see the
goals satisfied. An example of such an order could be Priority 1: Achieve the profit goal.
• Priority 2: Achieve the strategic production goals.
• Priority 3: Achieve the labour goal. SOLUTION
Note Objective: “<=” : min d + , “>=” : min d - lOMoAR cPSD| 58504431
Note: goal 2 không ược violate goal 1
The Growall Fertilizer Company produces three types of fertilizer—Supergro, Dynaplant, and
Soilsaver. The company has the capacity to produce a maximum of 2,000 tons of fertilizer in
a week. It costs $800 to produce a ton of Supergro, $1,500 for Dynaplant, and $500 for
Soilsaver. The production process requires 10 hours of labor for a ton of Supergro, 12 hours
for a ton of Dynaplant, and 18 hours for a ton of Soilsaver. The company has 800 hours of
normal production labor available each week. Each week the company can expect a demand
for 800 tons of Supergro, 900 tons of Dynaplant, and 1,100 tons of Soilsaver. The company
has established the following goals, in order of their priority: (1)
The company does not want to spend over $20,000 per week on production, if possible. (2)
The company would like to limit overtime to 100 hours per week. lOMoAR cPSD| 58504431 (3)
The company wants to meet demand for all three fertilizers;
however, it is twice as important to meet the demand for Supergro as it is to
meet the demand for Dynaplant, and it is twice as important to meet the demand for
Dynaplant as it is to meet the demand for Soilsaver. (4)
It is desirable to avoid producing undercapacity, if possible. (5)
Because of union agreements, the company wants to avoid underutilization of labor.
Formulate a goal programming model to determine the number of tons of each brand of
fertilizer to produce to satisfy the goals.
Conceptual Products is a computer company that produces the CP400 and the CP500
computers. The computers use different mother boards produced in abundant supply by the
company, but use the same cases and disk drives. The CP400 models use two floppy disk drives
and no zip disk drives whereas the CP500 models use one floppy disk drive and one zip disk
drive. The disk drives and cases are bought from vendors. There are 1000 floppy disk drives,
500 zip disk drives, and 600 cases available to Conceptual Products on a weekly basis. It takes
one hour to manufacture a CP400 and its profit is $200 and it takes one and one-half hours to
manufacture a CP500 and its profit is $500. Demand for CP 400 is 200 computers/week. lOMoAR cPSD| 58504431
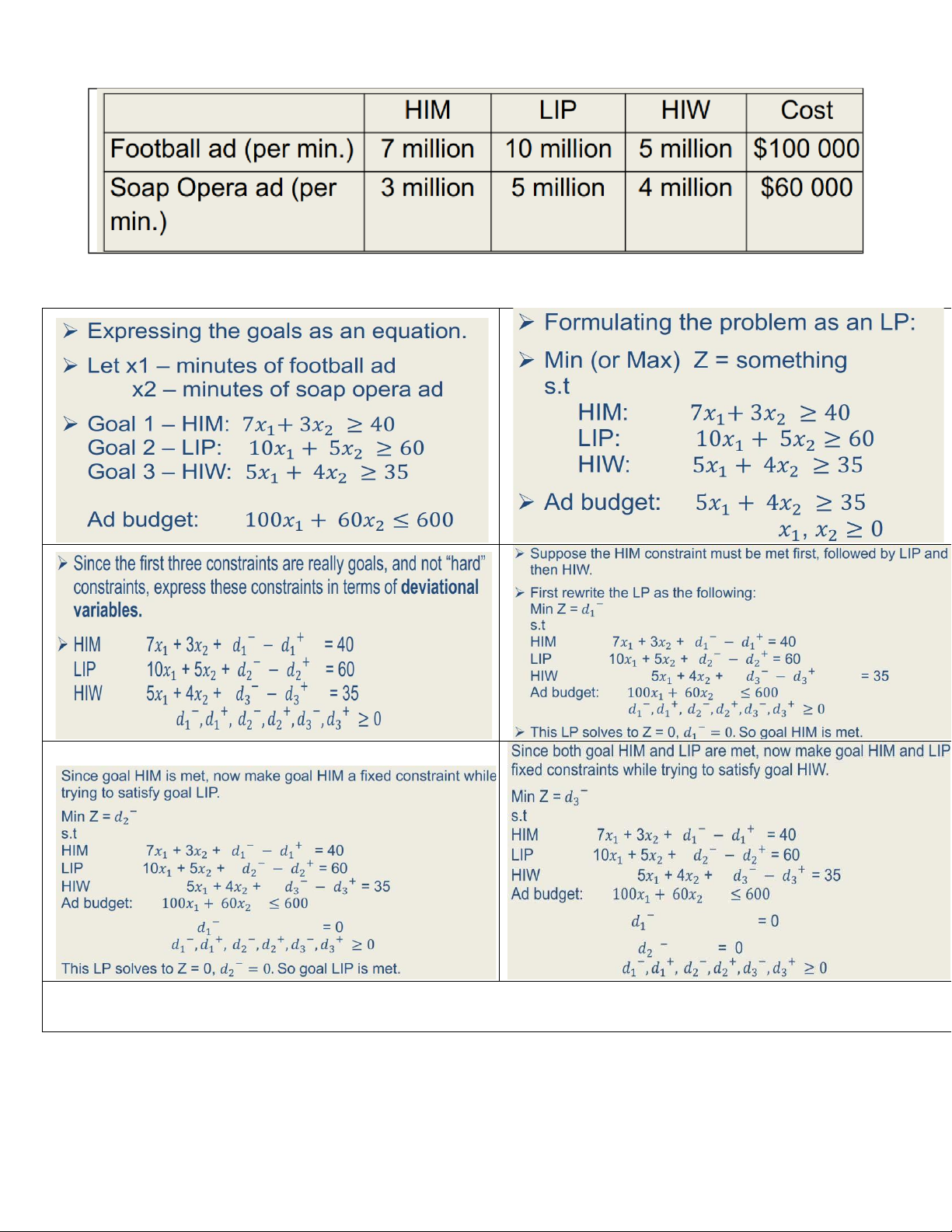
You work for an Advertising agency. A customer has identified three primary target audiences
they are trying to reach, and has an Advertising budget of $600000. They have expressed their
targets in the form of three goals:
• Goal 1 – Ads should be seen by at least 40 million high-income men (HIM)
• Goal 2 – Ads should be seen by at least 60 million low-income people (LIP)
• Goal 3 – Ads should be seen by at least 35 million high-income women (HIW)
You recognize that advertising during football games and soap operas will cover the
target audience. The table below indicates the number of viewers from the different
categories that will be viewing these types of programming. lOMoAR cPSD| 58504431
The goals can be ranked from most importance to least important. In this case, the most important goal preempts
all the other goals. Once the most important goal is met, the second goal is addressed, and so on. lOMoAR cPSD| 58504431 lOMoAR cPSD| 58504431
Let 𝑥1, 𝑥2 be the production length of part 1 and part 2
Let 𝑑𝑖−, 𝑑𝑖+ be amount the right-hand side of goal i is deficient and exceeded, respecti
We can now formulate the goals and objectives for each goal:
min: P1(d1+ + 𝑑2+), P2(d−3 + 𝑑4−), P3(d−5 ), P4(d+6 )
- Goal 1: 0.07x1 + 0.18x2 + d1− − d1+ = 600
0.2x1 + 0.23x2 + d−2 − d+2 = 500 - Goal
2: x1 + 𝑑3− − 𝑑3+ = 1650 x2 + 𝑑4− − 𝑑4+ = 1000
- Goal 3: 90𝑥1 + 100x2 + d−5 − d+5 = 300000 lOMoAR cPSD| 58504431
- Goal 4: 5.3𝑥1 + 3.7x2 + d−6 − d6+ = 1000 NON PRE-EMPTIVE
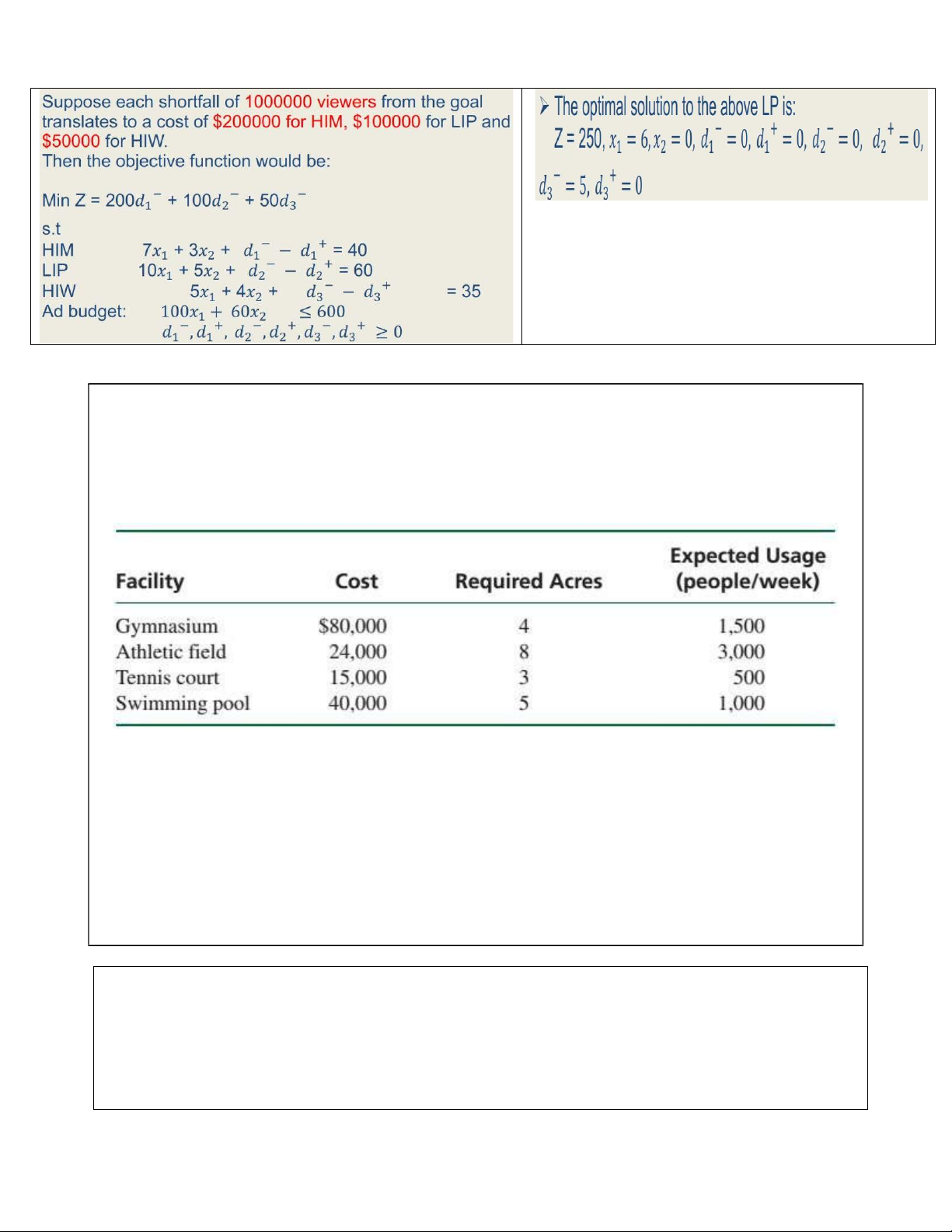
In the advertising example, the goals could readily be weighted by relative importance using the cost
penalties ($200000 for HIM, $100000 for LIP and $50000 for HIW). lOMoAR cPSD| 58504431
The Bay City Parks and Recreation Department has received a federal grant of $600,000 to
expand its public recreation facilities. City council representatives have demanded four
different types of facilities—gymnasiums, athletic fields, tennis courts, and swimming pools.
In fact, the demand by various communities in the city has been for 7 gyms, 10 athletic fields,
8 tenniscourts, and 12 swimming pools. Each facility costs a certain amount, requires a certain
numberof acres, and is expected to be used a certain amount, as follows:
‘The Parks and Recreation Department has located 50 acres of land for construction (although
more land could be located, if necessary). The department has established the following goals,
listed in order of their priority:
(1) The department wants to spend the total grant because any amount not spent must be returned to the government.
(2) The department wants the facilities to be used by a total of at least 20,000 people each week.
(3) The department wants to avoid having to secure more than the 50 acres of land already located.
(4) The department would like to meet the demands of the city council for new facilities.
However, this goal should be weighted according to the number of people expected to use each facility.
a. Formulate a goal programming model to determine how many of each type of facility
should be constructed to best achieve the city’s goals.
b. Solve this model by using the computer so that the solution values are integers. lOMoAR cPSD| 58504431
Computers Unlimited sells microcomputers and distributes them from three warehouses to four universities.
The available supply at the three warehouses, demand at the four universities, and shipping
costs are shown in the following table:
Instead of its original objective of cost minimization, Computers Unlimited has indicated the
following goals, arranged in order of their importance:
(1) A&M has been one of its better long-term customers, so Computers Unlimited wants to
meet all of A&M’s demands.
(2) Because of recent problems with a trucking union, it wants to ship at least 80 units from
the Washington warehouse to Central University.
(3) To maintain the best possible relations with all its customers, Computers Unlimited
would like to meet no less than 80% of each customer’s demand.
(4) It would like to keep total transportation costs to no more than 110% of the $22,470 total
cost achieved with the optimal allocation, using the transportation solution method.
(5) Because of dissatisfaction with the trucking firm it uses for the Atlanta-to-State
deliveries, it would like to minimize the number of units shipped over this route.