Hàm số lượng giác và phương trình lượng giác – Lê Minh Tâm

Tài liệu gồm 124 trang, được biên soạn bởi thầy giáo Lê Minh Tâm, phân loại và hướng dẫn giải các dạng bài tập chuyên đề hàm số lượng giác và phương trình lượng giác, giúp học sinh lớp 11 tham khảo khi học chương trình Đại số và Giải tích 11 chương 1

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

124 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU LƯU HÀNH NỘI BỘ
LÊ MINH TÂM
CHƯƠNG 01
HÀM SỐ LƯỢNG GIÁC
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 2
§1. HÀM SỐ LƯỢNG GIÁC .................................................................................................................... 4
I. ÔN TẬP ........................................................................................................................................................ 4
1.1. Các hệ thức cơ bản. ............................................................................................................................... 4
1.2. Cung liên kết. ......................................................................................................................................... 4
1.3. Công thức cộng. ..................................................................................................................................... 4
1.4. Công thức nhân và hạ bậc. .................................................................................................................. 4
1.5. Công thức biến đổi tổng thành tích. ................................................................................................... 5
1.6. Công thức biến đổi tích thành tổng. ................................................................................................... 5
1.7. Bảng giá trị lượng giác của một số góc đặc biệt. ............................................................................. 5
II. HÀM SỐ y = sinx VÀ HÀM SỐ y = cosx............................................................................................... 5
III. HÀM SỐ y = tanx Và HÀM SỐ y = cotx. ............................................................................................. 8
IV. BÀI TẬP. .................................................................................................................................................. 10
Dạng 01. TẬP XÁC ĐỊNH. ...................................................................................................................... 10
Dạng 02. TÍNH CHẴN LẺ. ...................................................................................................................... 13
Dạng 03. CHU KỲ HÀM SỐ. .................................................................................................................. 15
Dạng 04. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.................................................................. 17
§2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN ....................................................................................... 21
I. PHƯƠNG TRÌNH SinX = a VÀ PHƯƠNG TRÌNH CosX = a. ......................................................... 21
II. PHƯƠNG TRÌNH TanX = a VÀ PHƯƠNG TRÌNH CotX = a ....................................................... 23
III. BÀI TẬP. .................................................................................................................................................. 26
§3. PHƯƠNG TRÌNH BẬC HAI THEO HÀM LƯỢNG GIÁC ................................................................... 32
I. DẠNG CƠ BẢN. ....................................................................................................................................... 32
II. BÀI TẬP. ................................................................................................................................................... 33
§4. PHƯƠNG TRÌNH BẬC NHẤT VỚI HÀM SIN - COS ....................................................................... 43
I. DẠNG CƠ BẢN. ....................................................................................................................................... 43
II. BÀI TẬP. ................................................................................................................................................... 44
§4. PHƯƠNG TRÌNH ĐẲNG CẤP ........................................................................................................ 54
I. DẠNG CƠ BẢN. ....................................................................................................................................... 54
II. BÀI TẬP. ................................................................................................................................................... 55
HÀM SỐ LƯỢNG GIÁC
Trang 3
LÊ MINH TÂM
§5. PHƯƠNG TRÌNH ĐỐI XỨNG ........................................................................................................ 62
I. DẠNG CƠ BẢN. ....................................................................................................................................... 62
II. BÀI TẬP. ................................................................................................................................................... 62
§6. CÁC LOẠI PHƯƠNG TRÌNH KHÁC ................................................................................................ 68
I. BIẾN ĐỔI TÍCH THÀNH TỔNG. ........................................................................................................ 68
1.1. Ví dụ minh họa. ................................................................................................................................... 68
1.2. Bài tập rèn luyện. ................................................................................................................................ 68
II. BIẾN ĐỔI TỔNG THÀNH TÍCH. ....................................................................................................... 70
2.1. Ví dụ minh họa. ................................................................................................................................... 70
2.2. Bài tập rèn luyện. ................................................................................................................................ 70
III. TỔNG HỢP CÁC PHƯƠNG PHÁP. ................................................................................................. 73
3.1. Ví dụ minh họa. ................................................................................................................................... 73
3.2. Bài tập rèn luyện. ................................................................................................................................ 74
IV. PHƯƠNG TRÌNH CÓ ĐIỀU KIỆN. .................................................................................................. 75
4.1. Ví dụ minh họa. ................................................................................................................................... 76
4.2. Bài tập rèn luyện. ................................................................................................................................ 77
§7. TỔNG ÔN CHƯƠNG .......................................................................................................................91
Dạng 01. TẬP XÁC ĐỊNH. ...................................................................................................................... 91
Dạng 02. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.................................................................. 93
Dạng 03. PHƯƠNG TRÌNH LƯỢNG GIÁC. ...................................................................................... 96
Dạng 04. TỔNG HỢP PHƯƠNG TRÌNH LƯỢNG GIÁC. ............................................................ 113
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 4
§1. HÀM SỐ LƯỢNG GIÁC
I. ÔN TẬP
1.1. Các hệ thức cơ bản.
1tan .cot
22
1sin cos
2
2
1
1 tan
cos

2
2
1
1 cot
sin

1.2. Cung liên kết.
Cung đối nhau
Cung phụ nhau
Cung hơn kém
Cung hơn kém
2
cos cos
sin sin
tan tan
cot cot

sin sin
cos cos
tan tan
cot cot

2
2
2
2
sin cos
cos sin
tan cot
cot tan
















sin sin
cos cos
tan tan
cot cot


2
sin cos




2
cos sin



2
tan cot



2
cot tan



1.3. Công thức cộng.
sin sin cos sin cosa b a b b a
cos cos cos sin sina b a b a b
1
tan tan
tan
tan .tan
ab
ab
ab

1
tan tan
tan
tan .tan
ab
ab
ab

Hệ quả:
1
41
tan
tan
tan
x
x
x




và
1
41
tan
tan
tan
x
x
x




.
1.4. Công thức nhân và hạ bậc.
Nhân đôi
Hạ bậc
22sin sin cos
2
12
2
cos
sin
22
2cos cos sin
22
2 1 1 2cos sin
2
12
2
cos
cos
2
2
2
1
tan
tan
tan
2
12
12
cos
tan
cos
CHƯƠNG
HÀM SỐ LƯỢNG GIÁC
Trang 5
LÊ MINH TÂM
2
1
2
2
cot
cot
cot
2
12
12
cos
cot
cos
1.5. Công thức biến đổi tổng thành tích.
2
22
cos cos cos .cos
a b a b
ab


2
22
cos cos sin .sin
a b a b
ab

2
22
sin sin sin .cos
a b a b
ab


2
22
sin sin cos .sin
a b a b
ab


sin
tan tan
cos .cos
ab
ab
ab

sin
tan tan
cos .cos
ab
ab
ab

sin
cot cot
sin .sin
ab
ab
ab

sin
cot cot
sin .sin
ba
ab
ab

Đặc biệt
22
44
sin cos sin cosx x x x
22
44
sin cos sin cosx x x x
1.6. Công thức biến đổi tích thành tổng.
1
2
cos .cos cos cosa b a b a b


1
2
sin .sin cos cosa b a b a b


1
2
sin .cos sin sina b a b a b


1.7. Bảng giá trị lượng giác của một số góc đặc biệt.
Đơn vị
độ
o
0
o
30
45
o
o
60
o
90
o
120
135
o
o
150
o
180
o
360
Đơn vị
radian
0
6
4
3
2
2
3
3
4
5
6
2
sin
0
1
2
2
2
3
2
1
3
2
2
2
1
2
0
0
cos
1
3
2
2
2
1
2
0
1
2
2
2
3
2
1
1
tan
0
3
3
1
3
KXĐ
3
1
3
3
0
0
cot
KXĐ
3
1
3
3
0
3
3
1
3
KXĐ
KXĐ
II. Hàm Số y = sinx Và Hàm Số y = cosx.
Hàm số
sinyx
Hàm số
cosyx
1. Định
nghĩa:
Quy tắc đặt tương ứng mỗi số thực
x
với
sin
của góc lượng giác có số đo
x
rađian được gọi là hàm số
sin
, kí hiệu
sinyx
.
Quy tắc đặt tương ứng mỗi số thực
x
với
cos
của góc lượng giác có số đo
x
rađian được gọi là hàm số
cos
, kí hiệu
cosyx
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 6
2. Tập
xác định:
D
D
3. Tập
giá trị:
11;


11;


4. Tính
chất hàm
Là hàm số lẻ.
Là hàm số chẵn.
5. Chu kỳ
Chu kì
2
.
Chu kì
2
.
6. Đơn
điệu
Hàm số
+ Đồng biến trên mỗi khoảng
22
22
;kk



.
+ Nghịch biến trên mỗi khoảng
3
22
22
;kk




.
Hàm số
+ Đồng biến trên mỗi khoảng
22;kk

.
+ Nghịch biến trên mỗi khoảng
22;kk
.
7. Đồ thị
8. Giá trị
đặc biệt
12
2
sinx x k
.
0sinx x k
.
12
2
sinx x k
.
12cosx x k
.
0
2
cosx x k
.
12cosx x k
.
HÀM SỐ LƯỢNG GIÁC
Trang 7
LÊ MINH TÂM
Chú ý:
+) Hàm số
sin , cosy u x y u x

xác định
ux
có nghĩa.
+)
11sin ,cosxx
;
22
01sin ,cosxx
;
01sin , cosxx
.
Ví dụ 01.
Tìm tập xác định của các hàm số sau:
a.
4sinyx
. b.
2
31
1
sin
x
y
x
. c.
2cosyx
.
Lời giải
a.
4sinyx
.
Hàm số xác định với mọi số thực
x
nên hàm số có tập xác định
D
.
b.
2
31
1
sin
x
y
x
.
Hàm số xác định khi
2
1 0 1xx
.
Tập xác định
1\D
.
c.
2cosyx
.
Hàm số xác định khi
2 0 2xx
.
Tập xác định
2;D

.
Ví dụ 02.
Xét tính chẵn lẻ của các hàm số sau:
a.
2
3cos siny x x
. b.
2
12
13
sin
cos
x
y
x
.
Lời giải
a.
2
3cos siny x x
.
Hàm số có tập xác định
D
.
Lấy
x
ta có
x
và
22
33cos sin cos siny x x x x x y x
.
Do đó hàm số là hàm chẵn .
b.
2
12
13
sin
cos
x
y
x
Hàm số xác định khi
2
3 1 3 2
33
cos
k
x x k x k
.
Tập xác định
2
33
\
k
Dk



.
Ta thấy nếu
31cosx D x
mà
3 3 3 1cos cos cosx x x x D
Khi đó
2
2
12
12
13
13
sin
sin
cos
cos
x
x
y x y x
x
x


.
Do đó hàm số là hàm chẵn .
Ví dụ 03.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 8
a.
4 3 5sinyx
. b.
2 2 2 1sin cosy x x
. c.
44
sin , ;y x x



.
Lời giải
a.
4 3 5sinyx
.
Hàm số có tập xác định
D
.
Ta có
1 1 3 3 3 3 4 4 3 3 4 1 7sin sin sinx x x y
.
Do đó:
7 1 2
2
max siny x x k k
.
1 1 2
2
min siny x x k k
b.
21
2 2 2 1 3 2 2 1
33
sin cos sin cosy x x x x




Đặt
12
0
33
sin ;cos ;
ta có
3 2 2 1 3 2 1cos sin sin cos siny x x x
Ta có:
1 2 1 3 3 2 3 3 1 3 2 1 3 1sin sin sinx x x
Do đó:
13max y 
đạt được khi
21sin x

13min y 
đạt được khi
21sin x
.
c.
44
sin , ;y x x



Hàm số
sinyx
đồng biến trên khoảng
;
nên
Với
22
4 4 4 4 2 2
; sin sin sinx x y

.
Do đó
2
2
max y
đạt được khi
4
x
;
2
2
min y
đạt được khi
4
x 
.
III. Hàm Số y = tanx Và Hàm Số y = cotx.
Hàm số
tanyx
Hàm số
cotyx
1. Định
nghĩa:
Hàm số tang là hàm số được xác định bởi
công thức
0
sin
cos
cos
x
yx
x

, ký hiệu
tanyx
.
Hàm số côtang là hàm số được xác định
bởi công thức
0
cos
sin
sin
x
yx
x

, ký
hiệu
cotyx
.
2. Tập
xác
định:
2
\,D k k



\,D k k
3. Tập
giá trị:
11;


11;


HÀM SỐ LƯỢNG GIÁC
Trang 9
LÊ MINH TÂM
4. Tính
chất
hàm
Là hàm số lẻ.
Là hàm số lẻ.
5. Chu
kỳ
Chu kì .
Chu kì .
6. Đơn
điệu
Hàm số đồng biến trên mỗi khoảng
3
22
;kk




.
Hàm số nghịch biến trên mỗi khoảng
;kk
.
7. Đồ
thị
Chú ý:
- Hàm số
tany u x


xác định khi và chỉ khi
0cosux
.
- Hàm số
coty u x


xác định khi và chỉ khi
0sinux
.
Ví dụ 04.
Tìm tập xác định của các hàm số sau:
a.
4
tanyx




. b.
3
cotyx




.
Lời giải
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 10
a.
4
tanyx




.
Hàm số xác định khi
0
4 4 2 4
cos x x k x k k



Do đó hàm số có tập xác định
4
\D k k



.
b.
3
cotyx




Hàm số xác định khi
0
3 3 3
sin x x k x k k



Do đó hàm số có tập xác định
3
\D k k



.
IV. BÀI TẬP.
Dạng 01. TẬP XÁC ĐỊNH.
Phương pháp giải:
1.
fx
xac đinh
0fx
;
1
fx
xac đinh
0fx
.
2.
siny f x
xac đinh
fx
xac đinh.
3.
cosy f x
xac đinh
fx
xac đinh.
4.
tany f x
xac đinh
2
f x k k
.
5.
coty f x
xac đinh
f x k k
.
Bài 01.
Tìm tập xác định của các hàm số sau:
1.
1
23cos
y
x
2.
1 sinyx
3.
2
4
41
cos
sin
x
y
x
4.
2
1 cos
cos
x
y
x
Lời giải
1.
1
23cos
y
x
Điêu kiên:
3
2
26
cos ,x x k k
Tâp xác đinh của ham sô la
2
6
\,D k k



.
2.
1 sinyx
Điêu kiên:
1 0 1sin sinx x x
HÀM SỐ LƯỢNG GIÁC
Trang 11
LÊ MINH TÂM
Tâp xác đinh của ham sô la
D
.
3.
2
4
41
cos
sin
x
y
x
Điêu kiên:
2
2
6
5
2
1
6
4 1 0
2
2
6
7
2
6
sin sin ,
xk
xk
x x k
xk
xk



.
Tâp xác đinh của ham sô la
57
2 2 2 2
6 6 6 6
\ , , , ,kD k k k k



.
4.
2
1 cos
cos
x
y
x
Điêu kiên:
2
10
1
0
0
2
cos
cos
,
cos
cos
x
x
x k k
x
x

Tâp xác đinh của ham sô la
2
\ ,kDk



.
Bài 02.
Tìm tập xác định của các hàm số sau:
1.
1
3
cos
cot
x
y
x
2.
2
31
sin
tan
x
y
x
3.
2
3
cotyx




4.
2
4
tanyx




5.
tan coty x x
6.
2
1 tanyx
Lời giải
1.
1
3
cos
cot
x
y
x
Điêu kiên:
3
6
0
cot
,
sin
xk
x
k
x
xk




Tâp xác đinh của ham sô la
6
\ , ,D k k k



.
2.
2
31
sin
tan
x
y
x
Điêu kiên:
1
6
3
0
2
tan
,
cos
xk
x
k
xk
x






HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 12
Tâp xac định cua ham sô là
62
\ , ,kD k k



.
3.
2
3
cotyx




Điêu kiên:
2 0 2
3 3 6 2
sin ,
k
x x k x k



Tâp xác đinh của ham sô la
62
\,
k
Dk



.
4.
2
4
tanyx




Điêu kiên:
2 0 2
4 4 2 8 2
cos ,
k
x x k x k



Tâp xác đinh của ham sô la
82
\,
k
Dk



.
5.
tan coty x x
Điêu kiên:
0
2 0 2
0
2
cos
sin ,
sin
x
k
x x k x k
x
Tâp xác đinh của ham sô la
2
\,
k
Dk




.
6.
2
1 tanyx
Điêu kiên:
0
2
cos ,x x k k
.
Tâp xác đinh của ham sô la
2
\,D k k



.
HÀM SỐ LƯỢNG GIÁC
Trang 13
LÊ MINH TÂM
Dạng 02. TÍNH CHẴN LẺ.
Phương pháp giải:
1. Tập xác định
D
:
x D x D
..
2. Xét
fx
và
fx
.
– Nếu
,f x f x x D
thì hàm số chẵn trên
D
.
– Nếu
,f x f x x D
thì hàm số lẻ trên
D
.
Bài tập.
Xét tính chẵn, lẻ của hàm số:
1.
4
sinyx
; 2.
sin .cos
tan cot
xx
y
xx
; 3.
sin tan
sin cot
xx
y
xx
;
4.
4
3
1cos
sin
x
y
x
; 5.
4
cosyx




; 6.
tanyx
;
7.
2sin tany x x
; 8.
2
1
cos
sin
x
y
x
.
Lời giải
1.
4
sinyx
Tập xác định
,D x D x D
.
Đặt
4
siny f x x
.
Ta có:
4
44
sin sin sinf x x x x f x
.
Vậy hàm số đã cho là hàm số chẵn.
2.
sin .cos
tan cot
xx
y
xx
Tập xác định
2
\ , ,D k k x D x D



.
Đặt
sin .cos
tan cot
xx
y f x
xx

.
Ta có:
sin .cos
sin .cos sin .cos
tan cot tan cot
tan cot
xx
x x x x
f x f x
x x x x
xx

.
Vậy hàm số đã cho là hàm số chẵn.
3.
sin tan
sin cot
xx
y
xx
Tập xác định
15
2
22
\ , arccos , , ,D k m k m x D x D









.
Đặt
sin tan
sin cot
xx
y f x
xx

.
Ta có:
sin tan
sin tan sin tan
sin cot sin cot
sin cot
xx
x x x x
f x f x
x x x x
xx
.
Vậy hàm số đã cho là hàm số chẵn.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 14
4.
4
3
1cos
sin
x
y
x
Tập xác định
\ , ,D k k x D x D
.
Đặt
4
3
1cos
sin
x
y f x
x

.
Ta có:
4
4
33
1
1
cos
cos
sin sin
x
x
f x f x
xx


.
Vậy hàm số đã cho là hàm số lẻ.
5.
4
cosyx




Tập xác định
,D x D x D
.
Đặt
4
cosy f x x



.
Ta có:
44
cos cosf x x x
.
Ta thấy
,f x f x f x f x
.
Vậy hàm số đã cho là hàm số không chẵn, không lẻ.
6.
tanyx
Tập xác định
2
\,D k x D x D


.
Đặt
tany f x x
.
Ta có:
tan tanf x x x f x
.
Ta thấy
,f x f x f x f x
.
Vậy hàm số đã cho là hàm số chẵn.
7.
2sin tany x x
Tập xác định
2
\,D k x D x D


.
Đặt
2sin tany f x x x
.
Ta có:
2 2 2sin tan sin tan sin tanf x x x x x x x f x
.
Vậy hàm số đã cho là hàm số lẻ.
8.
2
1
cos
sin
x
y
x
Tập xác định
,D x D x D
.
Đặt
2
1
cos
sin
x
y f x
x

. Ta có:
22
11
cos
cos
sin sin
x
x
f x f x
xx
. Vậy hàm số đã cho là hàm số chẵn.
HÀM SỐ LƯỢNG GIÁC
Trang 15
LÊ MINH TÂM
Dạng 03. CHU KỲ HÀM SỐ.
Phương pháp giải:
Định nghĩa: Hàm số
y f x
xác định trên tập
D
được gọi là hàm số tuần hoàn nếu có số
0T
sao
cho với mọi
xD
ta có
x T D
và
f x T f x
.
Nếu có số
T
dương nhỏ nhất thỏa mãn các điều kiện trên thì hàm số đó được gọi là hàm số tuần hoàn
với chu kì
T
.
Lưu ý:
. Hàm số
sin cosf x a ux b vx c
( với
,uv
) là hàm số tuần hoàn với chu kì
2
,
T
uv
(
,uv
là ước chung lớn nhất).
Hàm số
.tan .cotf x a ux b vx c
(với
,uv
) là hàm tuần hoàn với chu kì
,
T
uv
.
1
y f x
có chu kỳ
1
T
;
2
y f x
có chu kỳ
2
T
Thì hàm số
12
y f x f x
có chu kỳ
T
là bội chung nhỏ nhất của
1
T
và
2
T
.
sinyx
: Tập xác định
DR
; tập giá trị
11;T



; hàm lẻ, chu kỳ
0
2T
.
siny ax b
có chu kỳ
0
2
T
a
siny f x
xác định
fx
xác định.
cosyx
: Tập xác định
DR
; Tập giá trị
11,T



; hàm chẵn, chu kỳ
0
2T
.
cosyx
có chu kỳ
0
2
T
a
cosy f x
xác định
fx
xác định.
tanyx
: Tập xác định
2
\,D k k Z


; tập giá trị
T
, hàm lẻ, chu kỳ
0
T
.
tany ax b
có chu kỳ
0
T
a
tany f x
xác định
2
f x k k
cotyx
: Tập xác định
\,D k k Z

; tập giá trị
T
, hàm lẻ, chu kỳ
0
T
.
coty ax b
có chu kỳ
0
T
a
coty f x
xác định
f x k k
.
Phương pháp chứng minh.
Tập xác định hàm số
,
x T D
D x D
x T D


.
1
Chứng minh:
,f x T f x x D
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 16
2
Giả sử có số
T
sao cho
0 TT

thỏa
,
x T D
f x T f x x D

vô lý.
Vậy hàm số
fx
là hàm tuần hoàn với chu kỳ
T
.
Bài 01.
Chứng minh rằng
2sinyx
tuần hoàn có chu kỳ .
Lời giải
Hàm số
2siny f x x
có tập xác định . Chọn số
0L 
Ta có:
xx
và
2 2 2 2sin sin sinf x L x x x f x


.
Vậy hàm số
fx
là hàm số tuần hoàn.
Ta sẽ chứng minh chu kỳ của nó là .
Thật vậy, giả sử hàm số
2sinf x x
có chu kỳ
A
mà
0 A
, khi đó ta có:
22sin sin ,x A x x


Cho
4
x
thì
2 2 1
4 2 2
sin sin sinAA



21cos :A
vô lý, vì
0 2 2A
Vậy chu kì tuần hoàn của hàm số
2sinyx
là .
Bài 02.
Chứng minh rằng
4
tanyx




tuần hoàn có chu kỳ .
Lời giải
Hàm số
4
tany f x x



có tập xác định
4
\,D k k



.
Chọn số
0L 
Ta có:
xx
và
44
tan tanf x L x x f x
.
Vậy hàm số
fx
là hàm số tuần hoàn.
Ta sẽ chứng minh chu kỳ của nó là .
Thật vậy, giả sử hàm số
4
tanyx




có chu kỳ
A
mà
0 A
, khi đó ta có:
44
tan tan ,x x x D
Cho
0x
thì
1
4
tan A




vô lý vì
0 A
.
Vậy chu kì tuần hoàn của hàm số
4
tanyx




là .
HÀM SỐ LƯỢNG GIÁC
Trang 17
LÊ MINH TÂM
Dạng 04. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.
Phương pháp giải:
Sử dụng tính chất
11sinx
và
11cosx
.
Bài tập.
Tìm GTNN và GTLN của các hàm số:
1.
2 3 4cosyx
; 2.
2
63cos siny x x
;
3.
2
2
45cos cos
y
xx

; 4.
42
25sin cosy x x
;
5.
2
25sin siny x x
; 6.
1
23sin
y
x
;
7.
42
21cos siny x x
; 8.
2
1
25sin cos
y
xx

;
9.
22cosyx
; 10.
44
sin cosy x x
.
Lời giải
1.
2 3 4cosyx
.
Điều kiện xác định:
3
2 3 0
2
cos cosx x x
.
Ta có:
11cosx
2 2 2 1 2 3 5 1 2 3 5 3 2 3 4 5 4cos cos cos cosx x x x
Vậy GTLN của hàm số là
54
khi
12cosx x k k
,
GTNN của hàm số là
3
khi
12cosx x k k
.
2.
2
63cos siny x x
.
Ta có:
2 2 2
6 3 1 6 3 6 4cos sin sin sin sin siny x x x x x x
.
Đặt
11sin , ;t x t


. Khi đó:
2
64y f t t t
xác định với
11;t



Bảng biến thiên
ft
:
Vậy GTLN của hàm số là
9
khi
12
2
sint x x k k
,
GTNN của hàm số là
3
khi
12
2
sint x x k k
.
3.
2
2
45cos cos
y
xx

.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 18
Đặt
11cos , ;t x t


. Khi đó:
22
4 5 4 5cos cosx x t t f t
xác định với
11;t



Bảng biến thiên
ft
:
Suy ra:
2
2
21
2 4 5 10 1
5
45
cos cos
cos cos
xx
xx

Vậy GTLN của hàm số là
1
khi
21f t t
12cosx x k k
,
GTNN của hàm số là
1
5
khi
10 1f t t
12cosx x k k
.
4.
42
25sin cosy x x
.
Ta có:
4 2 4 2 4 2
2 5 2 1 5 2 3sin cos sin sin sin siny x x x x x x
.
Đặt
2
01sin , ;t x t



. Khi đó:
2
23y f t t t
xác định với
01;t


.
Bảng biến thiên
ft
:
Vậy GTLN của hàm số là
6
khi
2
10
2
sin cosx x x k k
,
GTNN của hàm số là
3
khi
2
00sin sinx x x k k
.
5.
2
25sin siny x x
.
Đặt
11sin , ;t x t


. Khi đó:
2
25y f t t t
xác định với
11;t



.
Bảng biến thiên
ft
:
Vậy GTLN của hàm số là
8
khi
12
2
sinx x k k
,
HÀM SỐ LƯỢNG GIÁC
Trang 19
LÊ MINH TÂM
GTNN của hàm số là
4
khi
12
2
sinx x k k
.
6.
1
23sin
y
x
.
Điều kiện xác định:
3 0 3sin sinx x x
.
Ta có:
11sinx
1 1 1 1 1 1
2 3 4 2 3 2
24
2 3 2 2 2 3
sin sin
sin sin
xx
xx

Vậy GTLN của hàm số là
1
22
khi
12
2
sinx x k k
,
GTNN của hàm số là
1
4
khi
12
2
sinx x k k
.
7.
42
21cos siny x x
.
Ta có:
4 2 4 2 4 2
2 1 2 1 1 2 1cos sin cos cos cos cosy x x x x x x
.
Đặt
2
01cos , ;t x t



. Khi đó:
2
21y f t t t
xác định với
01;t


.
Bảng biến thiên
ft
:
Vậy GTLN của hàm số là
2
khi
2
10cos sinx x x k k
,
GTNN của hàm số là
1
khi
2
00
2
cos cosx x x k k
.
8.
2
1
25sin cos
y
xx

.
Ta có:
2 2 2
2 5 1 2 5 2 6sin cos cos cos cos cosy x x x x x x
.
Đặt
11cos , ;t x t


. Khi đó:
2
26y f t t t
xác định với
11;t



.
Bảng biến thiên
ft
:
Suy ra:
2
2
1 1 1
3 2 6 7
37
26
cos cos
cos cos
xx
xx
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 20
Vậy GTLN của hàm số là
1
3
khi
12cosx x k k
,
GTNN của hàm số là
1
7
khi
12cosx x k k
.
9.
22cosyx
.
Ta có:
1 2 1 1 2 2 3 1 2 2 3cos cos cosx x x
Vậy GTLN của hàm số là
3
khi
2 1 2 2cos x x k k x k k
,
GTNN của hàm số là
1
khi
2 1 2 2
2
cos x x k k x k k
.
10.
44
sin cosy x x
.
2
2 2 2 2 2
1
2 1 2
2
sin cos sin .cos siny x x x x y x
Ta có:
2 2 2
1 1 1 1
0 2 1 0 2 1 1 2
2 2 2 2
sin sin sinx x x
Vậy GTLN của hàm số là
1
khi
2
2 0 2 0 2
2
sin sin ,x x x k x k k
,
GTNN của hàm số là
1
2
khi
2
2 1 2 0 2
2 4 2
sin cos ,x x x k x k k
.
------------------HẾT------------------
HÀM SỐ LƯỢNG GIÁC
Trang 21
LÊ MINH TÂM
§2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
I. PHƯƠNG TRÌNH SinX = a VÀ PHƯƠNG TRÌNH CosX = a.
Phương trình SinX = m (1)
Phương trình CosX = a (2)
– Nếu
1:m
Phương trình vô nghiệm.
– Nếu
1
22
;m



thỏa mãn
sin .m
2
1
2
sin sin
xk
xk
xk

.
– Nếu
1:m
phương trình vô nghiệm.
– Nếu
10;m


thỏa mãn
cos .m
2
2
2
cos cos
xk
xk
xk

.
Chú ý: Nếu thỏa mãn
22
sin m
thì ta
viết
arcsin .m
Chú ý: Nếu
thỏa mãn
0
cos m

thì ta viết
arccos .m
Các trường hợp đặc biệt:
12
2
sin .x x k k
12
2
sin .x x k k
0sin .x x k k
Các trường hợp đặc biệt:
12cos .x x k k
12cos .x x k k
0
2
cos .x x k k
Ví dụ 01.
Giải các phương trình sau:
a.
3
2
sinx
. b.
1
3
sin x
.
c.
2
60
2
cos x
. d.
22sin x
.
e.
2
36
sin sinxx
. f.
22
4
sin cosxx




.
Lời giải
a.
3
2
sinx
2
3
2
3
2
3
sin sin
xk
xk
xk


.
b.
1
3
sin x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 22
1
2
3
1
2
3
arcsin
arcsin
xk
k
xk


.
c.
2
60
2
cos x
2
90 60
2
sin x
30 45 360 15 360
30 45
30 135 360 105 360
sin sin
x k x k
xk
x k x k



d.
22sin x
(1)
Vì
21
nên phương trình (1) vô nghiệm.
e.
2
36
sin sinxx
22
22
36
22
5 5 2
32
22
6 18 3
36
x x k
x k x k
k
x k x k
x x k






f.
22
4
sin cosxx




22
42
sin sinxx
2 2 2 0 2
4 2 4
16 2
2 2 2 4 2
4 2 4
,
x x k x k
x k k
x x k x k






Ví dụ 02.
Giải các phương trình sau:
a.
3
2
cosx 
. b.
1
5
cosx
.
c.
3
30
2
cos x
. d.
3
2
cos x
.
e.
2
2
35
cos cos
x
x




. f.
4
0
2 3 3
cos cos
x
x
.
Lời giải
a.
3
2
cosx 
5
6
cos cosx
5
2
6
,x k k
.
b.
1
5
cosx
HÀM SỐ LƯỢNG GIÁC
Trang 23
LÊ MINH TÂM
1
2
5
arccos ,x k k
.
c.
3
30
2
cos x
30 30 360 360
30 30
30 30 360 60 360
cos cos
x k x k
xk
x k x k



.
d.
3
2
cos x
(2)
Vì
3
1
2
nên phương trình (2) vô nghiệm.
e.
2
2
35
cos cos
x
x




2 11 2 10 10
2 2 2
3 5 5 3 33 11
2 9 2 10 10
2 2 2
5 3 5 3 27 9
x
x k x k x k
k
x
x k x k x k
.
f.
4
0
2 3 3
cos cos
x
x
44
2 3 3 2 3 3
20
22
cos cos
xx
xx
35
0
4 2 4 6
cos cos
xx
3
44
33
0
42
33
4 2 2 4
54
16
5
4
0
4 6 2 4 3
3
46
cos
cos
x
xx
xk
kk
k
xx
x
kk
xk















II. PHƯƠNG TRÌNH TANX = a VÀ PHƯƠNG TRÌNH COTX = a
Phương trình TanX = m (3)
Phương trình CotX = a (4)
– Với
22
, ; : tan .mm



3 tan tan .x x k
– Với
22
, ; : cot .mm



4 cot cot .x x k
Chú ý: Nếu thỏa mãn
22
tan m
thì ta
viết
arctan .m
Chú ý: Nếu thỏa mãn
22
cot m
thì ta
viết
arccot .m
Các trường hợp đặc biệt:
1
4
tan .x x k k
1
4
tan .x x k k
Các trường hợp đặc biệt:
1
4
cot .x x k k
1
4
cot .x x k k
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 24
0tan .x x k k
0
2
cot .x x k k
Chú ý:
2
2
,
sin sin
,
u v k k
uv
u v k k

2
2
,
cos cos
,
u v k k
uv
u v k k

22
hay
tan tan
u l v l l
uv
u v k k




hay
cot cot
u l v l l
uv
u v k k

CẦN NHỚ: Phương trình
tanxa
,
cot xa
luôn có nghiệm với
a
.
Ví dụ 03.
Giải các phương trình sau:
a.
1tanx
. b.
1
2
3
tan x 
. c.
0cotx
.
d.
32cot x 
. e.
3
20
4
tan tanxx



. f.
2
3
tan cotxx




.
g.
32
3
cot cotxx




.
Lời giải
a.
1tanx
.
Ta có:
1
44
tan tan tan ,x x x k k
.
b.
1
2
3
tan x 
Ta có:
1 1 1 1
22
3 3 2 3 2
tan arctan arctan ,x x k x k k
c.
0cot x
.
Ta có:
0
22
cot cot cot ,x x x k k
d.
32cot x 
.
Ta có
1
3 2 3 2 2
33
cot arccot arccot ,x x k x k k
e.
3
20
4
tan tanxx



.
Ta có:
2
33
2 4 2
2 0 2
33
44
2
44
tan tan tan tan , ,
x k x k
x x x x k n
x x n x n







Vậy phương trình đã cho vô nghiệm.
HÀM SỐ LƯỢNG GIÁC
Trang 25
LÊ MINH TÂM
Nhận xét: Việc giải dạng này theo chú ý ở trên cho kết quả nhanh, tuy nhiên nhiều bài học sinh sẽ khó
khăn trong việc nhìn nhận quan hệ bao hàm giữa các họ nghiệm. Nên sử dụng đường tròn lượng giác
để minh họa hoặc giải theo cách “dài” hơn như sau:
Điều kiện:
3
0
4
20
cos
cos
x
x




. Khi đó
3 3 3 3
2 0 2 2
4 4 4 4
tan tan tan tan ,x x x x x x k x k k
Thay vào điều kiện ta thấy không thỏa mãn. Vậy phương trình đã cho vô nghiệm.
f.
2
3
tan cotxx




.
22
22
2
3 3 2
12 2
32
tan cot tan tan , ,
xn
xn
x x x x k n
k
x
x x k




Vậy nghiệm của phương trình là
12 2
,
k
xk
.
g.
32
3
cot cotxx




.
Ta có:
2
2
32
3
32
3
3
cot cot , ,
xn
xn
x x k n
x x k
xk







Vậy nghiệm của phương trình là
3
,x k k
.
Tóm tắt như sau:
DẠNG CƠ BẢN:
2
2
,
sin sin
,
u v k k
uv
u v k k

2
2
,
cos cos
,
u v k k
uv
u v k k

22
hay
tan tan
u l v l l
uv
u v k k




hay
cot cot
u l v l l
uv
u v k k

TRƯỜNG HỢP ĐẶC BIỆT:
0sinx x k k
12
2
sinx x k k
12
2
sinx x k k
0
2
cosx x k k
12cosx x k k
12cosx x k k
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 26
III. BÀI TẬP.
Bài 01.
Giải các phương trình sau:
1.
1
2
32
sin x



2.
11
4
23
sin x




3.
35sin sinxx
4.
4 2 0
43
sin sinxx
5.
4 2 0
43
sin sinxx
. 6.
2 2 0cosx 
7.
0
3
3 15
2
cos x 
. 8.
2 1 2sin cosxx
9.
4
8
sin cosxx




. 10.
2 1 3 1 0sin cos .xx
11.
7 2 0
5
cos sin .xx



12.
1 2 3 0cos cos .xx
13.
2 3 4 0sin sin .xx
14.
6 4 5 8 0sin sin .xx
15.
2
20cos sin .xx
16.
22
2
4
sin cos .xx




17.
22
42sin cos .xx
Lời giải
1.
1
2
32
sin x



22
36
4
2
5
36
22
3 6 12
sin sin ( )
xk
xk
xk
x k x k
2.
11
4
23
sin x




11
42
23
11
42
23
arcsin
arcsin
xk
xk






1 1 1 1 1
42
2 3 8 4 3 2
1 1 1 1 1
42
2 3 4 8 4 3 2
arcsin arcsin
()
arcsin arcsin
k
x k x
k
k
x k x






3.
35sin sinxx
3 5 2 2 2
3 5 2 8 2
84
()
xk
x x k x k
k
k
x x k x k
x





HÀM SỐ LƯỢNG GIÁC
Trang 27
LÊ MINH TÂM
4.
4 2 0
43
sin sinxx
42
43
sin sinxx
4 2 2
22
43
24
12
19
19
4 2 2 6 2
72 3
4 3 12
()
x x k
xk
xk
kZ
k
x
x x k x k

5.
4 2 0
43
sin sinxx
42
43
sin sinxx
42
43
sin sinxx
7
7
4 2 2
62
43
72 3
12
11
11
4 2 2 2 2
4 3 12
24
()
k
x x k
x
xk
k
x x k x k
xk



6.
2 2 0cosx 
2
2
4
24
2
4
cos cos cos ( )
xk
x x k
xk

7.
0
3
3 15
2
cos x 
00
3 15 30cos cosx
0 0 0 0 0 0 0
0 0 0 0 0 0 0
3 15 30 360 3 15 360 5 120
3 15 30 360 3 45 360 15 120
. . .
()
. . .
x k x k x k
k
x k x k x k
8.
2 1 2sin( ) cos( )xx
2 1 2
2
sin( ) sinxx



32
2 1 2 2 3 2
2
22
12
2 1 2 2 3 1 2
6 3 3
22
()
xk
x x k x k
k
k
x
x x k x k






9.
4
8
sin cosxx




4
82
sin sinxx
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 28
52
4 2 5 2
8 2 8 8 5
5 5 2
4 2 3 2
8 2 8 24 3
()
k
x x k x k x
k
k
x x k x k x
10.
2 1 3 1 0sin cosxx
3 1 2 1cos sinxx
3 1 2 1cos sinxx
22
2
3 1 2 1 3 1 2 1 2
2
22
10 5
cos cos .
xk
x x x x k
xk
Vây nghiệm cua phương trình la:
22
2
xk
;
2
10 5
xk
.
11.
7 2 0
5
cos sinxx



72
5
cos sinxx



72
5
cos sinxx



32
3
50 5
7 2 7 2 2
2
2 5 10
30 9
cos cos .
xk
x x x x k
xk

Vây nghiệm cua phương trình la:
32
50 5
xk
;
2
30 9
xk
.
12.
1 2 3 0cos cosxx
1
2
2
2
3
3
cos
.
cos
x
xk
x VN

Vây nghiệm cua phương trình la:
2
2
3
.xk
13.
2 3 4 0sin sinxx
2 6 2 2 0sin sin .cosx x x
2 1 6 2 0sin cosxx
11
1
1
22
2
26
6
6
20
2
2
arccos
arccos
cos
.
sin
xk
xk
x
x
xk
xk







Vây nghiêm của phương trinh la:
11
26
arccosxk



;
2
xk
.
HÀM SỐ LƯỢNG GIÁC
Trang 29
LÊ MINH TÂM
14.
6 4 5 8 0sin sinxx
6 4 10 4 4 0sin sin .cosx x x
2 4 3 5 4 0sin cosxx
13
3
3
42
4
4 5 2
5
5
40
4
4
arccos
arccos
cos
.
sin
xk
xk
x
x
xk
xk







Vây nghiệm cua phương trình la:
13
4 5 2
arccosxk



;
4
xk
.
15.
2
20cos sinxx
2
2 0 2 0cos sin .cos cos cos sinx x x x x x
0
22
2 0 1 1
22
cos
cos sin
tan arctan
x k x k
x
xx
x x k







.
Vây nghiệm cua phương trình la:
2
xk
;
1
2
arctanxk
.
16.
22
2
4
sin cosxx




2
12
2
2
2
cos
sin
x
x





2
12
2
2
sin
sin
x
x

2
22
24
21
2 2 2 1 0 2 2
1
6 12
2
2
7
7
22
12
6
sin
sin sin
sin
x k x k
x
x x x k x k
x
xk
xk












Vây nghiệm cua phương trình la:
4
xk
;
12
xk
;
7
12
xk
.
17.
22
42sin cos .xx
Vi
22
0 1 0 4 1sin ; cos ;x x x
nên:
22
42sin cosxx
2
2
1 0 0
4 0 4 2 0
41
sin cos cos
sin sin .cos .cos
cos
x x x
x x x x
x



0
2
cos .x x k
Vây nghiêm cua phương trinh la:
2
xk
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 30
Bài 02.
Giải các phương trình sau:
1.
1
21
4
tan x 
2.
3
3
23
cot
x



3.
33
3
tan x



4.
1
4 20
3
cot x
5.
3 2 3 0tan x
6.
34tan tanxx
7.
5 8 1cot .cotxx
8.
2 3 0cot .sinxx
Lời giải
1.
1
21
4
tan x 
1 1 1 1
21
4 2 2 4
arctan arctanx k x k
k
.
2.
3
3
23
cot
x



33
2 3 6 2 6 9
xx
k k x k
k
.
3.
33
3
tan x



3
3 3 3
k
x k x
k
.
4.
1
4 20
3
cot x
4 20 60 180 4 80 180 20 45x k x k x k
k
.
5.
3 2 3 0tan x
2 3 2
3 6 2
tan
k
x x k x
k
.
6.
34tan tanxx
Điều kiện
3
30
63
2
40
4
2 8 4
cos
cos
k
x
xk
x
xk
x k x





k
.
Ta có
3 4 4 3tan tanx x x x k x k
k
.
Kết hợp điều kiện ta có nghiệm của phương trình là
xk
k
.
7.
5 8 1cot .cotxx
Điều kiện
5 0 5
5
8 0 8
8
sin
cos
k
x
x x k
x x k k
x





k
.
5 8 1 8 5 5 8 5
2 2 26 13
cot .cot cot tan cot
k
x x x x x x x k x



k
.
HÀM SỐ LƯỢNG GIÁC
Trang 31
LÊ MINH TÂM
Kết hợp điều kiện ta có nghiệm của phương trình là
26 13
k
x 
,
13 6km
k
.
8.
2 3 0cot .sinxx
Điều kiện
2 0 2
2
sin
k
x x k x
k
.
Ta có
20
2
42
2 3 0
2
30
3
3
cot
cot .sin
sin
k
x
x
xk
xx
k
x
xk
x


k
.
Kết hợp điều kiện ta có nghiệm của phương trình là
42
k
x 
;
3
3
m
x m n
;kn
.
------------------ HẾT------------------
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 32
§3. PHƯƠNG TRÌNH BẬC HAI THEO HÀM LƯỢNG GIÁC
I. DẠNG CƠ BẢN.
Dạng tổng quát:
2
0at bt c
,
trong đó
,,a b c
là hằng số
0a
và
t
là một trong các hàm lượng giác.
Phương pháp giải:
Quan sát và dùng các công thức biến đổi để đưa phương trình về cùng một hàm lượng
giác với cung góc giống nhau, chẳng hạn:
Dạng
Đặt ẩn phụ
Điều kiện
2
0sin sina X b X c
sintX
11t
2
0cos cosa X b X c
costX
11t
2
0tan tana X b X c
tantX
Không có điều kiện của
t
2
0cot cota X b X c
cottX
Không có điều kiện của
t
Nếu đặt
2
sintX
,
2
cos X
hoặc
sintX
,
costX
thì điều kiện là
01t
.
Ví dụ.
Giải các phương trình sau:
a.
2
2 1 0sin sinxx
b.
2
2 3 3 0tan tanxx
c.
24
3 2 2 0sin cosxx
d.
2
3 2 2 3 1cos cos sinx x x
.
Lời giải
a.
2
2 1 0sin sinxx
2
2
1
2 1 0 2
1
6
2
7
2
6
sin
sin sin
sin
xk
x
x x x k
x
xk



b.
2
2 3 3 0tan tanxx
2
2 3 3 0 3
3
tan tan tanx x x x k
c.
24
3 2 2 0sin cosxx
24
3 2 2 0sin cosxx
42
2 3 1 0cos cosxx
2
2
2
2
1
1
1
2
2
4
42
2
2
3
2
4
cos
cos
,
cos
cos
xk
xk
x
xk
x
kZ
k
xk
x
x
x
xk




HÀM SỐ LƯỢNG GIÁC
Trang 33
LÊ MINH TÂM
d.
2
3 2 2 3 1cos cos sinx x x
2
3 2 2 3 1cos cos sinx x x
22
3 1 2 1 2 3 1sin sin sinx x x
2
1
3 2 0 1 2
2
2
sin ( )
sin sin sin
sin ( )
xn
x x x x k
xl
II. BÀI TẬP.
Bài 01.
Giải các phương trình sau:
1.
2
2 3 1 0cos cosxx
2.
2
4 2 1 3 3 0cos cosxx
3.
2
2 2 2 3 1 2 3 0cos cosxx
4.
2
4
9 13 0
1
cos
tan
x
x
5.
2
44
36
cos cosxx
6.
2
2 5 3 0sin sinxx
7.
2
2 13 2 5 0sin sinxx
8.
2
4 4 3 0sin sinxx
9.
2 5 3 0cos sinxx
10.
5 2 7 0
2
cos sin
x
x
.
11.
2
2 3 1 0
33
cos cosxx
. 12.
4 12 5 0cos sin cos .x x x
13.
2
10sin cos .xx
14.
6 4 5 8 0sin sin .xx
15.
32
3 2 0sin sin sin .x x x
16.
2
3 1 3 0tan ( )tan .xx
17.
2
4 3 0cot cot .xx
18.
3
2
tan cot .xx
19.
2
3
23tan .
cos
x
x

20.
2
3
2 3 6 0cot .
sin
x
x
Lời giải
1.
2
2 3 1 0cos cosxx
2
1
1
2
3
2
cos
cos
xk
x
k
xk
x
.
2.
2
4 2 1 3 3 0cos cosxx
1
2
2
3
3
2
6
2
cos
cos
x
xk
k
xk
x
.
3.
2
2 2 2 3 1 2 3 0cos cosxx
33
21
3 3 1 3 3
2
22
2 2 2
33
2
2
cos ( )
arccos arccos
cos
x VN
x k x k
x


(
k
).
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 34
4.
2
4
9 13 0
1
cos
tan
x
x
.
Điều kiện
0cosx
.
2
1
9 13 4 0
9
1
4
cos
cos cos
cos
x
xx
x VN

2xk
(
k
).
5.
2
44
36
cos cosxx
2
1 4 4 0
33
sin sinxx
2
1
3
4 3 0 2
3 3 6
3
3
sin
sin sin
sin
x
x x x k
x VN








(
k
).
6.
2
2 5 3 0sin sinxx
1
2
3
2
2
sin
sin
x
xk
x VN

(
k
).
7.
2
2 13 2 5 0sin sinxx
13 149 1 13 149
2
2 2 2
13 149 1 13 149
2
2 2 2 2
sin arcsin
sin arcsin
x VN x k
x x k









(
k
).
8.
2
4 4 3 0sin sinxx
1
2
6
2
35
2
26
sin
sin
xk
x
x VN x k


(
k
).
9.
2 5 3 0cos sinxx
2
1 2 5 3 0sin sinxx
2
1
2
6
2 5 2 0
2
7
2
2
6
sin
sin sin
sin
xk
x
xx
x VN
xk



(
k
).
10.
5 2 7 0
2
cos sin
x
x
2
5 1 2 2 7 0
22
sin sin
xx



HÀM SỐ LƯỢNG GIÁC
Trang 35
LÊ MINH TÂM
2
1
2
10 2 12 0 2 4
6
2 2 2 2
25
sin
sin sin
sin
x
x x x
k x k
x
VN
(
k
).
11.
2
2 3 1 0
33
cos cosxx
2
3 1 0
33
2cos cosxx
(1)
Đặt
3
cos xt




11t
.
Pt (1)
2
3 1 02tt
1
2
1
t
t

2
2
2
33
3
12
2
2
2
3 2 3
33
2
2
2
1
3
3
3
4
2
2
3
3
cos cos
cos cos
xk
xk
x
xk
xk
kk
xk
xk
x
xk
xk









12.
4 12 5 0cos sin cos .x x x
2
2 2 6 2 5 01 sin sin .xx
2
2 2 6 2 4 0sin sin .xx
Đặt
2sin xt
11t
.
2
2 6 4 0.tt
2
1
3 2 0 2 1 2 2
2
2 2 4
(TM)
. sin sin .
(KTM)
t
t t x x k x k
t

13.
2
10sin cos .xx
22
1
1 1 0 2 0 2
2
cos
cos cos . cos cos . .
cos (KTM)
x
x x x x x k
x

14.
6 4 5 8 0sin sin .xx
6 4 10 4 4 0sin sin cos .x x x
2 4 3 5 4 0sin cos .xx
40
3
4
5
sin
cos
x
x

4
3
42
5
3
42
5
arccos ( )
arccos
xk
x k k
xk






4
13
4 5 2
13
4 5 2
arccos ( )
arccos
k
x
k
xk
k
x






.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 36
15.
32
3 2 0sin sin sin .x x x
(1)
Đặt
sinxt
11t
.
Pt (1)
32
3 2 0t t t
2
2
0
0
0
3 2 0 1
1
3 2 0
2
2
2
sin
( ).
sin
()
t
xk
t
x
t t t t k
x
tt
xk
t KTM


16.
2
3 1 3 0tan tan .xx
(1)
Đặt
tan .xt
Pt (1)
2
11
4
3 1 3 0
33
3
tan
. ( ).
tan
xk
tx
t t k
tx
xk






17.
2
4 3 0cot cot .xx
(1)
Đặt
cot .xt
Pt (1)
2
4 3 0.tt
1
3
t
t


1
3
cot
cot
x
x


1
1
3
tan
tan
x
x

4
1
3
( ).
arctan
xk
k
xk





18.
3
2
tan cot .xx
13
2
tan .
tan
x
x
(1)
Đặt
tanxt
0t
.
Pt (1)
2
13
0
2
t
t
2
2
22
2 3 2 0
1
11
2
22
arctan
tan
( ).
arctan
tan
xk
tx
t t k
xk
tx










19.
2
3
23tan .
cos
x
x

2
23
1 .
cos
cos
x
x
Đặt
1
cos
t
x
1
0 1 1,.t
t



2
1
1
1
2 3 1 0 1 2
1
1
2
2
. cos ( ).
t
t
t t x x k k
t
KTM
t
HÀM SỐ LƯỢNG GIÁC
Trang 37
LÊ MINH TÂM
20.
2
3
2 3 6 0cot .
sin
x
x
2
3 1 2 3 6 0cot cot .xx
2
3
6
3 2 3 3 0
3
3
3
cot
cot cot . ( ).
cot
x
xk
x x k
x
xk


Bài 02.
Giải các phương trình sau:
1.
2
2 3 2 2 2
6
sin cos cos .x x x



2.
14
2
cot tan .tan .sin .
x
x x x



3.
2
42
2
cot tan sin .
sin
x x x
x
4.
2 2 1 4 1 2 2
44
sin sin cos sinx x x x
5.
2
21
12
12
cos
cot sin sin .
tan
x
x x x
x
6.
2
5 2 3 1sin sin tan .x x x
7.
22
3 2 0cos cos cos ;x x x
8.
44
3
30
4 4 2
sin cos cos sin ;x x x x
9.
12
4
1
1
2
sin cos sin
cos ;
tan
x x x
x
x



10.
44
11
2
5 2 2 8 2
sin cos
cot ;
sin sin
xx
x
xx

11.
2
42
2
cot tan sin ;
sin
x x x
x
12.
62
3 4 8 2 3 0cos cos cos ;x x x
13.
24
2
cos
cot tan .
sin
x
xx
x

Lời giải
1.
2
2 3 2 2 2
6
sin cos cos .x x x



Ta co:
2
2 3 2 2 2
6
sin cos cosx x x



HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 38
2
13
4 2 2 2 2
2 2 6
sin cos cosx x x







2
2 2 2 2
6 6 6
sin .sin cos .cos cosx x x
2
2 2 2
66
cos cosxx
32
20
2
6
62
4
1
22
2
63
62
12
cos
.
cos
xk
x
xk
x k k
xk
x
xk










Vây nghiệm cua phương trình la:
32
xk
;
4
xk
;
12
x k k
.
2.
14
2
cot tan .tan .sin .
x
x x x



ĐKXĐ:
0
0 2 0 2
2
0
2
sin
cos sin .
cos
x
x x x k x k k
x
Ta co:
14
2
cot tan .tan .sin
x
x x x



2
14
2
sin .sin
cos
.sin
sin
cos .cos
x
x
x
x
x
x
x






2 2 2
44
22
cos .cos sin .sin cos
cos cos
.sin .sin
sin sin
cos .cos cos .cos
x x x
xx
xx
xx
xx
xx
xx
4
cos sin
sin cos
xx
xx
22
4cos sin sin .cosx x x x
22
1
6
12
2 2 1 2
55
2
22
6 12
sin sin .
xk
xk
x x k
x k x k


Đôi chiếu điêu kiên ta đươc nghiêm cua phương trinh la:
12
xk
;
5
12
x k k
.
HÀM SỐ LƯỢNG GIÁC
Trang 39
LÊ MINH TÂM
3.
2
42
2
cot tan sin .
sin
x x x
x
ĐKXĐ:
0
0 2 0 2
2
20
sin
cos sin .
sin
x
x x x k x k k
x
2
42
2
cot tan sin
sin
x x x
x
2
42
2
cos sin
sin
sin cos sin
xx
x
x x x
22
2
42
2
cos sin
sin
sin .cos sin
xx
x
x x x
2 2 2
42
22
cos
sin
sin sin
x
x
xx
2
2 1 2 2cos sinxx
2
2 1 2 1 2cos cosxx
2
21
2
2 2 2 1 0 2 2
1
33
2
2
cos
cos cos .
cos
xL
x x x k x k k
x

Đôi chiêu điêu kiện ta đươc nghiệm cua phương trinh la:
3
xk
k
.
4.
2 2 1 4 1 2 2
44
sin sin cos sinx x x x
2 2 1 4 1 2 2 2 2
4 4 4 4
sin sin cos .cos sin .sin sin .cos cos .sinx x x x x x



2 2 2 2
2 2 1 4 1 2 2 2 2
2 2 2 2
sin sin cos sin sin cosx x x x x x




2 2 1 4 1 2 2sin sin cosx x x
2
2 2 1 4 1 2 1 2sin sin sinx x x
2
1
2 2 2 2 2 4 0
2
2
sin
sin sin .
sin
x
x x x k
x VN

Vây nghiệm cua phương trinh đa cho là
2
xk
k
.
5.
2
21
12
12
cos
cot sin sin .
tan
x
x x x
x
ĐKXĐ:
0
2
0
1
4
sin
cos
tan
x
xk
xk
xk
x




.
2
21
12
12
cos
cot sin sin
tan
x
x x x
x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 40
22
2
1
1
cos cos sin
sin sin .cos
sin
sin
cos
x x x
x x x
x
x
x
2
cos cos sin cos sin
cos sin
sin sin .cos
sin cos sin
x x x x x
xx
x x x
x x x

01
1
2
cos sin
cos sin
cos cos sin sin cos sin
sin
cos sin
sin
xx
xx
x x x x x x
x
xx
x


Giai (1):
01
4
cos sin tan .x x x x k
Giai (2):
1
cos sin
sin
xx
x

2
1 sin .cos sinx x x
2 2 2
sin cos sin .cos sinx x x x x
2 2 2
2 0 2 1 0sin sin .cos cos tan tan .x x x x x x VN
Đôi chiêu điêu kiên ta đươc nghiêm của phương trinh la:
4
xk
k
.
6.
2
5 2 3 1sin sin tan .x x x
ĐKXĐ:
0
2
cosx x k k
.
2
5 2 3 1sin sin tanx x x
2
2
5 2 3 1
sin
sin sin .
cos
x
xx
x
2
2
5 2 3 1
1
sin
sin sin .
sin
x
xx
x
2
5 2 3
1
sin
sin .
sin
x
x
x
2
5 2 1 3sin sin sinx x x
2
1
2
6
2 3 2 0
2
5
2
2
6
sin
sin sin .
sin
xk
x
xx
x VN
xk



Đôi chiêu điêu kiện ta đươc nghiệm cua phương trinh la:
2
6
xk
;
5
2
6
xk
k
7.
22
3 2 0cos cos cosx x x
1 6 1 2
20
22
cos cos
cos
xx
x

2 6 2 1 2 0cos cos cos cosx x x x
6 2 1 0cos cosxx
HÀM SỐ LƯỢNG GIÁC
Trang 41
LÊ MINH TÂM
2
41
1
8 4 1 0 2 4 4 3 0
3
22
4
2
cos
cos cos cos cos , .
cos
x
k
x x x x x k
x vn

8.
44
3
30
4 4 2
sin cos cos sin ;x x x x
2
2 2 2 2
13
2 4 2
2 2 2
sin cos sin cos sin sinx x x x x x






2
1 1 3
1 2 4 2
2 2 2 2
sin sin sinx x x






2
2 2 4 2 3sin cos sinx x x
22
2 2 1 2 2 2 3sin sin sinx x x
2
21
2 2 2 0
22
4
sin
sin sin , .
sin
x
x x x k k
x vn

9.
12
4
1
1
2
sin cos sin
cos ;
tan
x x x
x
x



Điều kiện:
0
1
cos
.
tan
x
x

1
12
1
2
2
sin cos sin cos
cos
sin cos
cos
x x x x
x
xx
x

1 2 1sin cosxx
2
2
2
1
2
6
2 1 0 2
1
7
6
2
2
7
6
2
6
sin
sin sin ,
sin
x k l
x
xk
x x x k k
x
xk
xk




10.
44
11
2
5 2 2 8 2
sin cos
cot ;
sin sin
xx
x
xx

Điều kiện:
20sin x
2
1
12
4 2 1
2
5 2 8 2
sin
cos
sin sin
x
x
xx

2
8 4 1 2 20 2 5cos cosxx
2
9
2
2
4 2 20 2 9 0
1
6
2
2
cos
cos cos , .
cos
xl
x x x k k
x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 42
11.
2
42
2
cot tan sin ;
sin
x x x
x
Điều kiện:
20sin x
2
42
2
cot tan sin
sin
x x x
x
2
4 2 0
2
cos sin
sin
sin cos sin
xx
x
x x x
22
2
4 2 0
2
cos sin
sin
sin cos sin
x
x
x x x
2 2 2
4 2 0
22
cos
sin
sin sin
x
x
xx
2
2 2 4 2 2 0cos sinxx
22
21
2 2 1 2 1 0 2 2 2 1 0
1
3
2
2
cos ( )
cos cos cos cos , .
cos
xl
x x x x x k k
x

12.
62
3 4 8 2 3 0cos cos cos ;x x x
3
2
3 2 2 1 1 2 1 2 3 0cos cos cosx x x
2 2 3
6 2 3 1 3 2 3 2 2 1 2 3 0cos cos cos cos cosx x x x x
32
2 3 2 2 2 0cos cos cosx x x
2
20
2 2 3 2 2 0 2 1
42
22
cos
cos cos cos cos , .
cos
x
k
x
x x x x k
xk
x

13.
24
2
cos
cot tan .
sin
x
xx
x

Điều kiện:
20sin .x
Ta có:
24
2
cos
cot tan
sin
x
xx
x

24
0
2
cos sin cos
sin cos sin cos
x x x
x x x x
22
4
0
cos sin cos
sin cos sin cos
x x x
x x x x
24
0
cos cos
sin cos
xx
xx

2
21
2 4 0 2 2 2 1 0
1
3
2
2
cos ( )
cos cos cos cos , .
cos
xl
x x x x x k k
x

HÀM SỐ LƯỢNG GIÁC
Trang 43
LÊ MINH TÂM
§4. PHƯƠNG TRÌNH BẬC NHẤT VỚI HÀM SIN - COS
I. DẠNG CƠ BẢN.
Dạng tổng quát:
sin cos 1 ; ; a x b x c a b c
, và
22
0ab
.
Phương pháp giải:
Điều kiện có nghiệm của phương trình:
2 2 2
a b c
(kiểm tra trước khi giải)
* Chia 2 vế cho
22
ab
, thì
2 2 2 2 2 2
(*) sin cos
a b c
xx
a b a b a b
(**)
* Giả sử
22
cos
a
ab
,
22
sin
b
ab
,
02;


thì:
(**)
22
sin .cos cos .sin
c
xx
ab

22
sin
c
x
ab
: dạng cơ bản
Chú ý: hai công thức sử dụng nhiều nhất là:
sin .cos cos sin sin
cos .cos sin sin sin
a b a b a b
a b a b a b

Các dạng có cách giải tương tự:
22
22
22
2 2 2 2
0
cos
.sin .cos
sin
.sin .cos .sin .cos ,
pp
a b mx
a mx b mx a b
a b mx
a mx b mx c nx d nx a b c d

Chia cho
22
ab
.
Chú ý:
1
có nghiệm
2
có nghiệm
2 2 2
a b c
.
13
sin 3cos 2 sin cos 2sin
2 2 3
x x x x x







.
31
3sin cos 2 sin cos 2sin
2 2 6
x x x x x







.
11
sin cos 2 sin cos 2 sin
4
22
x x x x x






.
Ví dụ.
Giải các phương trình sau:
a.
31sin cosxx
b.
3 2 2 2cos sinxx
c.
3 3 3 2 2sin cos sinx x x
d.
2 3 2 3cos sin sin cosx x x x
Lời giải
a.
31sin cosxx
1 3 1
2 2 2
sin cosxx
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 44
2
2
1
36
6
5
32
2
2
36
2
sin
xk
xk
x
xk
xk




b.
3 2 2 2cos sinxx
3 1 2
22
2 2 2
cos sinxx
22
2
34
24
2
3 13
32
22
3 4 24
sin
xk
xk
x
x k x k




c.
3 3 3 2 2sin cos sinx x x
13
2
22
sin cos sinx x x
2 2 2
33
2
22
3
22
3 9 3
sin sin ,
x x k x k
x x k Z
k
x x k x









d.
2 3 2 3cos sin sin cosx x x x
1 3 3 1
22
2 2 2 2
cos sin sin cosx x x x
2
22
6 6 3
2
2
66
2 2 2
6 6 3
sin sin ,
k
x x k x
x x k Z
x x k x k






II. BÀI TẬP.
Bài 01.
Giải các phương trình sau:
1.
3 3 3 2 2sin cos sinx x x
2.
1sin cosxx
3.
6
2
sin cosxx
4.
5 2 12 2 13sin cosxx
5.
8 6 3 6 8sin cos sin cosx x x x
6.
7 2 3 2 7sin cos sin cosx x x x
7.
22sin cos .sin .cosx x x x
8.
2
2 3 2 3sin sinxx
9.
3
2 3 3 2 4sin cos .sin cos cos sinx x x x x x
Lời giải
1.
3 3 3 2 2sin cos sinx x x
13
3 3 2
22
sin cos sinx x x
HÀM SỐ LƯỢNG GIÁC
Trang 45
LÊ MINH TÂM
3 2 2 2
33
32
42
3
3 2 2
3 15 5
sin sin
x x k x k
xx
x x k x k









k
.
2.
1sin cosxx
2
2
1
44
21
2
44
2
2
2
44
sin sin
xk
xk
xx
xk
xk



k
.
3.
6
2
sin cosxx
2
2
63
43
12
2
5
4 2 4 2
22
4 3 12
sin sin
xk
xk
xx
x k x k

k
4.
5 2 12 2 13sin cosxx
5 12
2 2 1
13 13
sin cosxx
Đặt
5 12
13 13
cos ,sin
Ta có phương trình:
2 2 1sin .cos cos .sinxx
21sin x
22
2
xk
24
xk
,
k
5.
8 6 3 6 8sin cos sin cosx x x x
8 3 8 3 6 6sin cos sin cosx x x x
1 3 3 1
8 8 6 6
2 2 2 2
sin cos sin cosx x x x
86
36
sin sinxx
8 6 2
36
8 6 2
36
x x k
x x k
22
2
7
14 2
6
xk
xk


4
7
84 7
xk
k
x


k
6.
7 2 3 2 7sin cos sin cosx x x x
7 3 7 3 2 2sin cos sin cosx x x x
1 3 3 1
7 7 2 2
2 2 2 2
sin cos sin cosx x x x
72
63
cos cosxx
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 46
7 2 2
63
7 2 2
63
x x k
x x k
52
6
92
2
xk
xk

2
30 5
2
18 9
k
x
k
x

k
7.
22sin cos .sin .cosx x x x
2 2 2
4
sin sinxx



2
22
4
4
2
2
4
22
43
4
sin sin
xk
x x k
xx
k
x
x x k





k
Vì nghiệm
2
43
k
x 
chứa nghiệm
2
4
xk
nên pt có 1 họ nghiệm là
2
43
k
x 
,
k
8.
2
2 3 2 3sin sinxx
1 2 3 2 3cos sinxx
3 2 2 2sin cosxx
31
2 2 1
22
sin cosxx
21
6
sin x



22
62
xk
3
,x k k
9.
3
2 3 3 2 4sin cos .sin cos cos sinx x x x x x
2
1 2 2 3 3 2 4sin . sin cos .sin cos cosx x x x x x
2 2 3 3 2 4sin .cos cos .sin cos cosx x x x x x
3 3 3 2 4sin cos cosx x x
13
3 3 4
22
sin cos cosx x x
4 3 2 2
66
34
2
6
4 3 2
6 42 7
cos cos
x x k x k
x x k
k
x x k x









.
Bài 02.
Giải các phương trình sau:
1.
3 3 2
2
cos
cos
sin
x
x
x
. 2.
2
22
72
tan sin cos
x
x 
3.
44
3 cos sin sin cosx x x x
4.
3 2 2 2 2 2 2
6
cos sin sinx x x



5.
3 7 7 2 5
6
sin cos sinx x x



6.
2 3 2 2
2
sin x sin x



7.
3 2 2 0
3
cos sin cosx x x



. 8.
2 2 1 3cos cos sinx x x
.
HÀM SỐ LƯỢNG GIÁC
Trang 47
LÊ MINH TÂM
9.
3 1 3 1 1 3sin cosxx
. 10.
3
3 3 3 9 1 4 3sin cos sinx x x
.
11.
2 2 4 1 0
6
cos sin cosx x x



. 12.
4 2 3 2 0
44
sin cosxx
.
13.
8 2 6 2 5 7
44
sin .sin sin .cos cosx x x x x
.
14.
2
2 3 2 3 1
8 8 8
sin cos cosx x x
.
15.
2
1 2 3 2
33
3
21
cos cos cos
sin
cos cos
x x x
x
xx


.
16.
31
8sin
cos sin
x
xx

.
17.
3 3 2 2
2 2 2 2 2 0cos sin sin .cos cos .sinx x x x x x
.
18.
5 3 3 2 2 2 2cos sin sin cos sinx x x x x
.
Lời giải
1.
3 3 2
2
cos
cos
sin
x
x
x
.
Điều kiện xác định
xk
, (
k
).
3 3 2
2
cos
cos
sin
x
x
x
3 3 2 2 3 2 2 3cos sin cos sinx x x x
1 3 3
22
2 2 2
sin cosxx
3
22
3 3 2
cos sin sin cosxx
22
33
2
2
33
22
6
33
()
sin sin ( )
()
x k l
xk
x k Z
x k tm
xk




2.
2
22
72
tan sin cos
x
x 
12
7
tan sin cosxx
1
7
tan sin cosxx
7 7 7
sin sin cos cos cosxx
2
2
2
77
7
77
2
2
77
cos cos
xk
xk
xk
xk
xk





HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 48
3.
44
3 cos sin sin cosx x x x
2 2 2 2
3 cos sin cos sin sin cosx x x x x x
3 cos sin cos sin sin cosx x x x x x
4
20
0
4
1
2
4
31
6
61
4
31
2
4
6
sin
sin cos
arcsin
cos sin
sin
arcsin
xk
x
xx
x k k
xx
x
xk
















4.
3 2 2 2 2 2 2
6
cos sin sinx x x



31
2 2 2 2
2 2 6
cos sin sinx x x



2 2 2 2
6 6 6
cos cos sin sin sinx x x



2 2 2 2 2 2
6 6 4 6
cos sin sinx x x
5
2 1 2 2
12 12 2 24
sin x x k x k k



5.
3 7 7 2 5
6
sin cos sinx x x



31
7 7 5
2 2 6
sin cos sinx x x



7 7 5
6 6 6
cos sin sin cos sinx x x



7 5 2
66
75
7
66
7 5 2
96
66
sin sin
xk
x x k
x x k
xk
x x k

.
6.
2 3 2 2
2
sin sinxx



2 3 2 2cos sinxx
13
2 2 1 2 2 1
2 2 6 6
cos sin sin cos cos sinx x x x
2 1 2 2
6 6 2 6
sin x x k x k k



.
7.
3 2 2 0
3
cos sin cosx x x



HÀM SỐ LƯỢNG GIÁC
Trang 49
LÊ MINH TÂM
3 2 2
3
cos sin cosx x x



13
2
2 2 3
cos sin cosx x x



2
33
cos cosxx
2
22
32
33
33
2
22
2
3
33
3
k
x x k
xk
x
k
xk
x x k
xk






.
Vậy phương trình có hai họ nghiệm
2
2
3 3 3
,
k
x x k k
8.
2 2 1 3cos cos sinx x x
2 2 1 3cos cos sinx x x
22
13cos sin cos sinx x x x
13cos sin cos sin cos sinx x x x x x
1 3 0cos sin cos sinx x x x
0
1
4
1 3 0
13
cos sin
tan
cos sin
cos sin *
xx
x x k k
xx
xx


.
Phương trình (*) vô nghiệm do
2
22
1 1 1 3
Vậy phương trình có hai họ nghiệm
4
x k k
.
9.
3 1 3 1 1 3sin cosxx
3 1 3 1 1 3sin cosxx
31
1
13
sin cosxx
1
46
sin tan cosxx



5
1
12
sin tan .cosxx
5 5 5
12 12 12
sin .cos sin .cos cosxx
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 50
5
2
2
5
2
12 12
4
5
12 12
2
2
3
12 12
sin sin
xk
xk
xk
xk
xk





.
Vậy phương trình có hai họ nghiệm
4
22
23
,x k x k k
10.
3
3 3 3 9 1 4 3sin cos sinx x x
3
3 3 3 9 1 4 3sin cos sinx x x
3
3 3 4 3 3 9 1sin sin cosx x x
9 3 9 1sin cosxx
1 3 1
99
2 2 2
sin cosxx
2
92
3 6 18 9
9
72
36
92
3 6 54 9
sin sin
k
x k x
xk
k
x k x









.
Vậy phương trình có hai họ nghiệm
2 7 2
18 9 54 9
,
kk
x x k
11.
2 2 4 1 0
6
cos sin cosx x x



2 2 4 1 0
6
cos sin cosx x x



2 2 2 2 2 1 0
66
cos .cos sin .sin sinx x x



3 2 2 2 2 1 0cos sin sinx x x
3 2 2 1 0cos sinxx
3 1 1
22
2 2 2
cos sinxx
22
22
36
6
12
2
36
22
22
3 6 4
2
sin sin
xk
xk
xk
xk
x k x k
xk




.
Vậy phương trình có hai họ nghiệm
12 4
,x k x k k
12.
4 2 3 2 0
44
sin cosxx
4 2 3 2 0 4 2 3 2 0
4 4 2 4 4
sin cos cos cosx x x x
HÀM SỐ LƯỢNG GIÁC
Trang 51
LÊ MINH TÂM
4 2 3 2 0 4 2 3 2 0
4 4 4 4
cos cos cos cosx x x x
6 3 2
4
cos x



2
2
2
44
2
4 2 4
2
2
44
cos cos
xk
xk
xk
xk
xk





.
Vậy phương trình có hai họ nghiệm
22
2
,x k x k k
.
13.
8 2 6 2 5 7
44
sin .sin sin .cos cosx x x x x
8 2 6 2 5 7
44
sin .sin sin .cos cosx x x x x
8 2 3 3 5 7
2
sin .sin sin sin cosx x x x x






8 2 3 3 3 5 7sin .sin cos sin cosx x x x x
4 3 3 3 3 5 7cos cos cos sin cosx x x x x
4 3 4 3 3 3 5 7cos cos cos sin cosx x x x x
3 3 4 3 5sin cosxx
34
3 3 1
55
sin cosxx
3 3 1cos .sin sin .cosxx
(với
34
55
cos ,sin
)
31sin x
32
2
xk
2
3 6 3
()
k
xk
.
14.
2
2 3 2 3 1
8 8 8
sin cos cosx x x
2
2 3 2 3 1
8 8 8
sin .cos cosx x x
2
2 3 2 1 3
8 8 8
sin .cos cosx x x
3 2 2 3
44
sin x cos x
3 1 3
22
2 4 2 4 2
sin cosxx
5
22
2
3
12 3
24
2
3
2
12 2
2
22
8
12 3
sin ( )
xk
xk
xk
xk
xk





.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 52
15.
2
1 2 3 2
33
3
21
cos cos cos
sin
cos cos
x x x
x
xx


2
1 2 3 2
33
3
21
cos cos cos
sin
cos cos
x x x
x
xx


2
2
2 2 2 2
33
3
21
cos cos .cos
sin
cos cos
x x x
x
xx

2
2 2 2
33
3
21
cos (cos cos )
sin
cos cos
x x x
x
xx

2
2
2 2 1
2
33
3
21
cos cos cos
sin
cos cos
x x x
x
xx


3 3 3cos sinxx
33cos sinxx
3 1 3
222
cos sinxx
2
2
3
66
3
62
2
2
66
cos ( )
xk
xk
xk
xk
xk





.
16.
31
8sin
cos sin
x
xx

Điều kiện:
20
2
sin ;x x k k
.
Ta có:
31
8sin
cos sin
x
xx

3
8
sin cos
sin
cos .sin
xx
x
xx

4 2 3sin .sin sin cosx x x x
2 3 3cos cos sin cosx x x x
13
3
22
cos sin cosx x x
3
33
cos .cos sin .sin cosx x x
32
3
6
3
3
32
3
12 2
cos cos
x x k
xk
x x k
x x k
xk





.
17.
3 3 2 2
2 2 2 2 2 0cos sin sin .cos cos .sinx x x x x x
Ta có:
3 3 2 2
2 2 2 2 2 0cos sin sin .cos cos .sinx x x x x x
22
2 2 2 0cos cos sin sin cos sinx x x x x x
22
2 2 2cos sin cos sinx x x x
22cos sinxx
HÀM SỐ LƯỢNG GIÁC
Trang 53
LÊ MINH TÂM
7
2
2
1
43
12
42
22
4 3 12
cos
xk
xk
xk
x k x k





.
18.
5 3 3 2 2 2 2cos sin sin cos sinx x x x x
Ta có:
5 3 3 2 2 2 2cos sin sin cos sinx x x x x
33
5 3 4 4 3 2 2 2 2cos sin sin sin ( cos cos ) sinx x x x x x x
22
5 3 4 2 2 2 2cos sin cos sin cos sin sin sin .cos cos sinx x x x x x x x x x x
5 2 2 1 2 2 2 2cos sin sin cosx sin sinx x x x x
2 2 4 2 2 2 2sin cos sin sinx x x x
2 2 2 2 0sin sin cosx x x
2sin cosxx
22
4
sin x



1
4
sin x



2
4
()x k k
.
------------------ HẾT------------------
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 54
§4. PHƯƠNG TRÌNH ĐẲNG CẤP
I. DẠNG CƠ BẢN.
Dạng tổng quát:
22
1sin sin cos cosa x b x x c x d
,
, , ,a b c d
.
Phương pháp giải:
Bước 1: Kiểm tra
2
0
2
1
cos
sin
x
xk
x
có phải nghiệm hay không?
Bước 2: Khi
2
,x k k
2
0
1
cos
sin
x
x
. Chia hai vế (1) cho
2
cos x
:
22
2 2 2 2
1
1
sin sin cos cos
cos cos cos cos
x x x x
a b c d
x x x x
22
1tan tan tana x b x c d x
.
Bước 3: Đặt
tantx
để đưa về phương trình bậc hai theo ẩn
tx
.
Ví dụ.
Giải các phương trình sau:
a.
22
20sin sin cos cosx x x x
. b.
22
2 3 3 2sin sin cos cosx x x x
.
c.
22
3 2 1cos sin sinx x x
. d.
22
4 2 5 2 2 6 2 0sin sin cos cosx x x x
.
Lời giải
a.
22
20sin sin cos cosx x x x
22
20sin sin cos cosx x x x
(1)
* Với
2
0
2
1
cos
sin
x
xk
x
. Phương trình trở thành: 1 = 0 (vô lý)
Phương trình không nhận nghiệm
2
,x k k
* Với
2
,x k k
2
0
1
cos
sin
x
x
. Chia hai vế (1) cho
2
cos x
:
(1)
2
1
20
4
2
2
tan
tan tan
tan
arctan
xk
x
xx
x
xk


Vậy phương trình đã cho có hai họ nghiệm:
2
4
; arctanx k x k
,
k
.
b.
22
2 3 3 2sin sin cos cosx x x x
22
2 3 3 2sin sin cos cosx x x x
(2)
* Với
2
0
2
1
cos
sin
x
xk
x
. Phương trình trở thành: 2 = 2 (đúng)
HÀM SỐ LƯỢNG GIÁC
Trang 55
LÊ MINH TÂM
Phương trình nhận nghiệm
2
,x k k
* Với
2
,x k k
2
0
1
cos
sin
x
x
. Chia hai vế (2) cho
2
cos x
:
(2)
22
2 3 3 1 2 1tan tan tanx x x
3
3 3 3
36
tan tanx x x k
Vậy phương trình đã cho có hai họ nghiệm:
26
;x k x k
,
k
.
c.
22
3 2 1cos sin sinx x x
22
3 2 1cos sin sinx x x
22
3 2 1cos sin sinx x x
22
1
33
2 3 2 1 2
32
22
3
33
cos sin cos
xk
xk
x x x
xk
xk




d.
22
4 2 5 2 2 6 2 0sin sin cos cosx x x x
22
4 2 5 2 2 6 2 0sin sin cos cosx x x x
(3)
* Với
2
20
42
21
cos
sin
x
xk
x
. Phương trình trở thành: 4 = 0 (sai)
Phương trình không nhận nghiệm
42
,x k k
* Với
42
,x k k
2
20
21
cos
sin
x
x
. Chia hai vế (3) cho
2
2cos x
:
(2)
2
4 2 5 2 6 0tan tanxx
1
22
2
22
22
3
3
13
2
2
4
4
2 4 2
arctan
arctan
tan
arctan
tan
arctan
xk
xk
x
xk
x
xk










Vậy phương trình đã cho có hai họ nghiệm:
1 1 3
2
2 2 2 4 2
arctan ; arctanx k x k



,
k
.
II. BÀI TẬP.
Bài 01.
Giải các phương trình sau:
1.
22
2 3 3 4sin sin cos cosx x x x
2.
22
3 2 2 2 4 2 2sin sin cos cosx x x x
3.
22
2 3 3 3 1 1sin sin cos cosx x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 56
4.
22
3 4 8 3 9 0
22
sin sin cos
xx
x
5.
22
3 1 3 1 3 0sin sin .cos cosx x x x
6.
22
9 30 25 25sin sin .cos cosx x x x
7.
2
2 2 2 2sin sin cosx x x
8.
22
1
22
2
sin sin cosx x x
Lời giải
1.
22
2 3 3 4 1sin sin cos cosx x x x
Xét
2
01cos sinxx
, phương trình trở thành
24
(Vô lý)
2
x k k
không là nghiệm của phương trình.
Xét
0cosx
, chia cả hai vế của phương trình
1
cho
2
cos x
, ta được phương trình:
2
2 3 3 5 0tan tanxx
(phương trình vô nghiệm)
Vậy phương trình đã cho vô nghiệm.
2.
22
3 2 2 2 4 2 2 2sin sin cos cosx x x x
Xét
2
2 0 2 1cos sinxx
, phương trình trở thành
32
(Vô lý)
42
k
xk
không là nghiệm của phương trình.
Xét
20cos x
, chia cả hai vế của phương trình
2
cho
2
2cos x
, ta được:
2
1
2
22
2
2 2 6 0
2 3 1
3
2
arctan
tan
tan tan
tan
arctan
xk
x
x x k
x
xk


3.
22
2 3 3 3 1 1 3sin sin cos cosx x x
Xét
2
01cos sinxx
, phương trình trở thành
21
(Vô lý)
2
x k k
không là nghiệm của phương trình.
Xét
0cosx
, chia cả hai vế của phương trình
3
cho
2
cos x
, ta được:
2
1
4
3 3 3 3 0
3
3
6
tan
tan tan
tan
x
xk
x x k
x
xk


4.
22
3 4 8 3 9 0
22
sin sin cos
xx
x
Xét
2
01
22
cos sin
xx
, phương trình trở thành
30
(Vô lý)
2x k k
không là nghiệm của phương trình.
HÀM SỐ LƯỢNG GIÁC
Trang 57
LÊ MINH TÂM
Xét
0
2
cos
x
, chia cả hai vế của phương trình cho
2
2
cos
x
, ta được:
2
3 3 8
8 3 3
22
3
23
3 8 8 3 9 0
22
2
2
3
3
2
arctan
tan
tan tan
tan
x
xk
xx
k
x
xk



5.
22
3 1 3 1 3 0 5sin sin .cos cosx x x x
2 2 2 2
3 1 3 1 3 0sin sin .cos cos sin cosx x x x x x
22
1 3 3 0sin sin .cos cosx x x x
Xét
00cos sinxx
(loại vì
22
1sin cosxx
)
Xét
0cosx
chia cả 2 vế của phương trình
5
cho
2
cos x
ta được ;
2
1
4
1 3 3 0
3
3
tan
tan tan
tan
xk
x
xx
x
x


6.
22
9 30 25 25 6sin sin .cos cosx x x x
Xét
5
0
3
cos sinxx
(loại vì
22
1sin cosxx
)
Xét
0cosx
chia cả 2 vế của phương trình
6
cho
2
cos x
ta được :
22
9 30 25 25 1 0tan tan tanx x x
2
0
16 30 0
15
8
tan
tan tan
tan
x
xx
x
15
8
;
arctan
xk
k
xk


.
7.
2
2 2 2 2 7sin sin cosx x x
22
2 2 4 2sin .cos sin cosx x x x
22
2 2 4 2 0sin sin cos cosx x x x
(1).
Xét
01cos sinxx
. Suy ra
2
,x k k
là nghiệm của phương trình.
Xét
0cosx
chia cả 2 vế của phương trình
7
cho
2
cos x
ta được :
22
2 2 2 1 4 0tan tan tanx x x
1
4
tan ;x x k k
8.
22
1
2 2 8
2
sin sin cosx x x
2 2 2 2
1
22
2
sin sin .cos cos sin cosx x x x x x
22
15
20
22
sin sin .cos cosx x x x
Xét
0cosx
thay vào phương trình ta được
0sinx
(vô lý)
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 58
Xét
0cosx
chia cả 2 vế phương trình
8
cho
2
cos x
ta được;
2
1
15
20
4
5
22
5
tan
tan tan
tan
arctan
xk
x
xx
x
xk


Bài 02.
Giải các phương trình sau:
1.
3
2sin cosxx
2.
3 2 2
32sin sin cos sin cosx x x x x
3.
3
6 2 5 2sin cos sin cosx x x x
4.
3
40sin sin cosx x x
5.
4 2 2 4
3 4 0cos sin .cos sinx x x x
6.
2
2
2 3 1 1sin sin sin cos sin sinx x x x x x
7.
33
sin cos sin cosx x x x
8.
3
54
62
22
sin .cos
sin cos
cos
xx
xx
x

.
Lời giải
1.
3
2sin cosxx
Trường hợp 1: Xét
0cosx
0sinx
Thay
0cosx
vào
1
3
1 2 0sin x
0sinx
(mâu thuẫn)
Trường hợp 2: Xét
0cosx
3
32
32
1
1 2 2 1 1
4
sin
. .tan tan tan
cos cos
x
x x x x k k
xx
Vậy
4
|S k k


2.
3 2 2
32sin sin cos sin cosx x x x x
Trường hợp 1: Xét
0cosx
0sinx
Thay
0cosx
vào
2
3
2 3 0sin x
0sinx
(mâu thuẫn)
Trường hợp 2: Xét
0cosx
32
32
32
sin sin sin
.
cos
cos cos
x x x
x
xx
32
0
3 2 0 1
4
1
1
3
3
tan
tan tan tan tan
tan
arctan
xk
x
x x x x x k k
x
xk

(tmđk).
3.
3
6 2 5 2sin cos sin cosx x x x
Trường hợp 1: Xét
0cosx
0sinx
Thay
0cosx
vào
3 3 6 0 0sin sinxx
(mâu thuẫn)
Trường hợp 2: Xét
0cosx
HÀM SỐ LƯỢNG GIÁC
Trang 59
LÊ MINH TÂM
32
3 6 2 10sin cos sin cosx x x x
3
6
2 10
sin sin
.
cos
cos
xx
x
x
23
6 1 2 10 6 4 2 0 1
4
.tan tan tan tan tan tanx x x x x x x k k
Vậy
4
|S k k


4.
3
40sin sin cosx x x
Trường hợp 1: Xét
0cosx
0sinx
Thay
0cosx
vào
4
3
4 4 0sin sinxx
22
1 1 1
1 4 0 2
4 2 2 6
sin sin sin sin cosx x x x x x k k
Trường hợp 2: Xét
0cosx
3
3 3 2
1
4 4 0
sin sin
cos cos cos
xx
x x x
2 3 2
1 4 1 0tan tan tan tanx x x x
32
3 1 0 1
4
tan tan tan tanx x x x x k k
Vậy
46
,|S k k k


5.
4 2 2 4
3 4 0cos sin .cos sinx x x x
Trường hợp 1:
0
2
cos , x x k k
, khi đó
2
1sin x
.
Thay
2
01cos , sinxx
vào phương trình
1
ta được:
10
(Vô lý).
Vậy
2
, x k k
không là nghiệm của phương trình
1
.
Trường hợp 2:
0
2
cos , x x k k
*
.
4 2 2 4
4
34
10
cos sin .cos sin
cos
x x x x
x


24
24
3 4 0
sin sin
.
cos cos
xx
xx
42
4 3 0tan tanxx
2
22
4 3 0tan tanxx
2
2
4
1
1
1
4
3
3
3
3
3
tan
tan
tan
,
tan
tan
tan
xk
x
xk
x
x
k
x
x
xk
x
xk




(thoả
*
).
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 60
Vậy tập nghiệm của phương trình là
43
,,S k k k


.
6.
2
2
2 3 1 1sin sin sin cos sin sinx x x x x x
2
1 2 3 1 1 0sin sin sin cos sin sinx x x x x x
22
1 2 3 1 0sin sin sin .cos sinx x x x x


1 2 3 1 1 0sin sin . sin cos sin sinx x x x x x


22
1 2 3 0sin sin sin .cos cosx x x x x
22
10
2 3 0
sin
sin sin .cos cos
x
x x x x

22
22
1
2
2
2 3 0
2 3 0 2
sin
,
sin sin .cos cos
sin sin .cos cos
x
x k k
x x x x
x x x x

Giải phương trình
2
:
Trường hợp 1:
0
2
cos , x x k k
, khi đó
2
1sin x
.
Thay
2
01cos , sinxx
vào phương trình
2
ta được:
10
(Vô lý).
Vậy
2
, x k k
không là nghiệm của phương trình
2
.
Trường hợp 2:
0
2
cos , x x k k
*
.
22
2
23
10
sin sin .cos cos
cos
x x x x
x


2
2 3 0tan tanxx
1 1 3
1 1 3
tan arctan
arctan
tan
x x k
k
xk
x

(thoả
*
).
Vậy nghiệm của phương trình là
2
2
arctan ,
arctan
xk
x k k
xk


.
7.
33
sin cos sin cosx x x x
Trường hợp 1:
0
2
cos , x x k k
. Khi đó
1
1
sin
sin
x
x

.
Với
1sinx
: Thay
10sin , cosxx
vào phương trình
3
, ta được
11
(luôn đúng).
Với
1sinx 
: Thay
10sin , cosxx
vào phương trình
3
, ta được
11
(luôn đúng).
Vậy
2
, x k k
là nghiệm của phương trình
3
.
HÀM SỐ LƯỢNG GIÁC
Trang 61
LÊ MINH TÂM
Trường hợp 2:
0
2
cos , x x k k
.
33
33
3
sin cos sin cos
cos cos
x x x x
xx


3
22
11
1
sin
tan .
cos
cos cos
x
x
x
xx
3 2 2
1 1 1tan tan tan tanx x x x
3 3 2 2
1 1 2 0tan tan tan tan tan tanx x x x x x
: Phương trình vô nghiệm.
Vậy nghiệm của phương trình là
2
, x k k
.
8.
3
54
62
22
sin .cos
sin cos
cos
xx
xx
x

Điều kiện xác định:
2 0 2
2 4 2
cos * *x x k k x k k
.
3
5 2 2 2
4 6 2
22
. .sin .cos .cos
sin cos
cos
x x x
xx
x
3 3 2
6 2 5 2 6 2 10 5sin cos sin .cos sin cos sin .cos x x x x x x x x
Trường hợp 1:
0
2
cos , x x k k
. Khi đó
1
1
sin
sin
x
x

.
Với
1sinx
: Thay
10sin , cosxx
vào phương trình
5
, ta được
60
(vô lý).
Với
1sinx 
: Thay
10sin , cosxx
vào phương trình
5
, ta được
60
(vô lý).
Vậy
2
, x k k
không là nghiệm của phương trình
4
.
Trường hợp 2:
0
2
cos , x x k k
*
.
32
33
6 2 10
5
sin cos sin .cos
cos cos
x x x x
xx

2
1
6 2 10
sin sin
. . .
cos cos
cos
xx
xx
x
2
6 1 2 10tan tan tanx x x
3
6 6 10 2 0tan tan tanx x x
3
6 4 2 0 1
4
tan tan tan , x x x x k k
(thoả
*
).
So với điều kiện (
**
), ta thấy không thỏa mãn.
Vậy phương trình vô nghiệm.
------------------ HẾT------------------
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 62
§5. PHƯƠNG TRÌNH ĐỐI XỨNG
I. DẠNG CƠ BẢN.
Dạng tổng quát:
0sin cos sin cosa x x b x x c
, , ,a b c d
.
Phương pháp giải:
Đặt
2
4
sin cos sint x x x



, do đó
22
4
sintx



Với
sin cost x x
, khi đó
2
2
1
12
2
sin .cos sin .cos
t
t x x x x
.
Với
sin cost x x
, khi đó
2
2
1
12
2
sin .cos sin .cos
t
t x x x x
.
Lưu ý: khi đặt
sin cost x x
thì điều kiện là
2t
Ví dụ.
Giải phương trình sau:
2 6 2 1sin cos sin cosx x x x
Lời giải
Đặt
2
4
sin cos sint x x x



, do đó
22
4
sintx



.
sin cost x x
, khi đó
2
12sin cost x x
2
6 3 1sin cosx x t
.
22
1
1 2 3 1 2 3 2 5 0
5
3
t
t t t t
t
Kiểm tra điều kiện ta được
1t
. Khi đó :
2
2
1
44
21
44
2
2
2
2
44
sin sin
xk
xk
xx
xk
xk

.
II. BÀI TẬP.
Bài 01.
Giải các phương trình sau:
1.
2 2 3 3 5 0sin sin cosx x x
. 2.
2 6 2 0sin cos sin cosx x x x
.
3.
2 2 2 2 1sin cos sinx x x
. 4.
4 1 0sin cos sin cosx x x x
.
5.
2 1 0sin cos sin cosx x x x
. 6.
61sin .cos sin cosx x x x
.
7.
26sin cos sin .cosx x x x
. 8.
2 2 3 2sin cos sinx x x
.
9.
2 2 3 3 5 0sin sin cosx x x
. 10.
1 2 1 2sin cos sinxx
.
HÀM SỐ LƯỢNG GIÁC
Trang 63
LÊ MINH TÂM
Lời giải
1.
2 2 3 3 5 0sin sin cosx x x
.
Đặt
sin cost x x
2
4
sin x




2
22
1
2
;
sin cos
t
t
xx



.
Ta có
2
1
4 3 3 5 0
2
t
t



2
2 3 3 3 0tt
3
3
2
t
t
Do đó
6
42
6
44
sin
sin
x
x








6
2
42
36
2
42
6
2
44
36
2
44
arcsin
arcsin
()
arcsin
arcsin
xk
xk
k
xk
xk

















.
2.
2 6 2 0sin cos sin cosx x x x
.
Đặt
sin cost x x
2
4
sin x




2
22
1
2
;
sin cos
t
t
xx



.
Ta có
2
1
6 2 2 0
2
t
t



2
3 2 5 0tt
5
3
1
()
()
tl
tn

.
Do đó
21
4
sin x




1
4
2
sin x



2
44
3
2
44
xk
xk
2
2
2
xk
k
xk


3.
2 2 2 2 1sin cos sinx x x
.
Đặt
sin cost x x
2
4
sin x




2
22
1
2
;
sin cos
t
t
xx



.
Ta có
2
1
4 2 2 1 0
2
t
t



2
2 2 2 3 0tt
2
2
32
2
t
t

.
Do đó
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 64
2
2
42
sin x



1
42
sin x



2
46
7
2
46
xk
xk
2
12
17
2
12
xk
k
xk



4.
4 1 0sin cos sin cosx x x x
.
Đặt
sin cost x x
2
4
sin x




2
22
1
2
;
sin cos
t
t
xx



.
Ta có
2
1
4 1 0
2
t
t



2
2 1 0tt
1
2
1
t
t

.
Do đó
21
4
1
2
42
sin
sin
x
x







1
4
2
1
4
22
sin
sin
x
x







2
2
44
3
2
2
2
44
1
1
2
2
4
22
4
22
31
1
2
2
4
22
4
22
arcsin
arcsin
arcsin
arcsin
xk
xk
xk
xk
k
xk
xk
xk
xk













.
5.
2 1 0sin cos sin cosx x x x
.
Đặt
sin cost x x
2
4
sin x




2
22
1
2
;
sin cos
t
t
xx



.
Ta có
2
1
2 1 0
2
t
t
2
2 2 1 0tt
12
12
tn
tl
.
Do đó
HÀM SỐ LƯỢNG GIÁC
Trang 65
LÊ MINH TÂM
2 1 2
4
sin x



22
42
sin x



22
2
42
22
2
42
arcsin
arcsin
xk
xk
22
2
42
3 2 2
2
42
arcsin
arcsin
xk
k
xk

.
6.
6 1 1sin .cos sin cosx x x x
Đặt
2
22
2
1
4
2
;
sin cos sin
sin .cos
t
t x x x
t
xx






Thay vào
1
ta có được:
2
2
6 39
1
6 1 12 3 0
2
6 39 2 2;
t
t
t t t
t


78 6 2
6 39 2 6 39
4 4 2
* sin sint x x
78 6 2 78 6 2
22
4 2 4 2
78 6 2 5 78 6 2
22
4 2 4 2
arcsin arcsin
,.
arcsin arcsin
x k x k
k
x k x k









7.
2 6 1sin cos sin .cosx x x x
Đặt
2
22
2
1
4
2
;
sin cos sin
sin .cos
t
t x x x
t
xx






Thay vào
1
ta có được:
2
2
6
1
3
2 6 6 6
2
6
2
.
t
t
t t t
t

66
2
3 4 3
* sintx



33
22
4 3 4 3
3
43
3 5 3
22
4 3 4 3
arcsin arcsin
sin , .
arcsin arcsin
x k x k
xk
x k x k










6 6 3
2
2 4 2 4 2
* sin sint x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 66
2
2
43
12
4 19
22
4 3 12
,.
xk
xk
k
x k x k
8.
2 2 3 2 1sin cos sinx x x
1 2 2 3 2 2sin cos sin cosx x x x
Đặt
2
22
2
1
4
2
;
sin cos sin
sin .cos
t
t x x x
t
xx






Thay vào
2
ta có được:
2
2
1
2 2 3 2 2 2 2 0 2
2
.
t
t t t t
3
2 2 2 1 2 2
4 4 4 2 4
sin sin , .t x x x k x k k
9.
2 2 3 3 5 0 1sin sin cosx x x
1 4 3 3 5 0 2sin .cos sin cosx x x x
Đặt
2
22
2
1
4
2
;
sin cos sin
sin .cos
t
t x x x
t
xx






Thay vào
2
ta được:
2
2
3
1
2
4 3 3 5 0 2 3 3 3 0
2
3 2 2
..
;
t
t
t t t
t



3 3 6
2
2 4 2 4 4
* sin sint x x
66
22
4 4 4 4
6 3 6
22
4 4 4 4
arcsin arcsin
,.
arcsin arcsin
x k x k
k
x k x k







10.
1 2 1 2 1sin cos sinx x x
1 1 2 1 2 2sin cos sin .cosx x x x
Đặt
2
22
2
1
4
2
;
sin cos sin
sin .cos
t
t x x x
t
xx






Thay vào
2
ta được:
2
2
1
1
1 2 1 2 1 2 2 0
2
2
t
t
t t t
t

HÀM SỐ LƯỢNG GIÁC
Trang 67
LÊ MINH TÂM
1 2 1
4
* sintx



2
2
2
44
3
42
2
2
2
44
sin , .
xk
xk
xk
xk
xk







3
2 2 2 1 2 2
4 4 4 2 4
* sin sin , .t x x x k x k k
------------------ HẾT------------------
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 68
§6. CÁC LOẠI PHƯƠNG TRÌNH KHÁC
I. BIẾN ĐỔI TÍCH THÀNH TỔNG.
Phương pháp giải:
Dùng công thức biến đổi tích thành tổng, đặt nhân tử chung đưa về phương trình tích
1.1. Ví dụ minh họa.
Ví dụ.
Giải phương trình sau:
7 3 5sin .sin sin .sinx x x x
Lời giải
7 3 5sin .sin sin .sinx x x x
11
6 8 2 8
22
cos cos cos cosx x x x
6 2 2 4 2
2
62
6 2 2 8 2
4
cos cos , .
k
x
x x k x k
x x k
x x k x k k
x



Vậy phương trình có hai họ nghiệm
24
; ,
kk
x x k
.
1.2. Bài tập rèn luyện.
Bài tập.
Giải các phương trình sau:
1.
5 3 9 7sin .cos sin .cosx x x x
.
2.
3 2 6 4 6 0cos .cos sin .sin sin .sinx x x x x x
.
3.
4 5 4 3 2 0sin .sin sin .sin sin .sinx x x x x x
.
4.
2 2 3 7 7 2cos .cos .cos cosx x x x
.
Lời giải
1.
5 3 9 7sin .cos sin .cosx x x x
11
2 8 2 16
22
sin sin sin sinx x x x
16 8 2 8 2
4
16 8
16 8 2 24 2
24 12
sin sin , .
k
x
x x k x k
x x k
x x k x k k
x




Vậy phương trình có hai họ nghiệm
4 24 12
; ,
kk
x x k
.
2.
3 2 6 4 6 0cos .cos sin .sin sin .sinx x x x x x
1 1 1
4 2 4 8 2 10 0
2 2 2
cos cos cos cos cos cosx x x x x x
4 2 4 8 2 10 0cos cos cos cos cos cosx x x x x x
10 8 0cos cosxx
HÀM SỐ LƯỢNG GIÁC
Trang 69
LÊ MINH TÂM
9
90
18 9
2
2 9 0
0
2
2
cos
cos .cos , , .
cos
k
x
xk
x
x x k k
x
xk
xk




Vậy phương trình có hai họ nghiệm
18 9 2
; ,
k
x x k k
.
3.
4 5 4 3 2 0sin .sin sin .sin sin .sinx x x x x x
1 1 1
9 7 3 0
2 2 2
cos cos cos cos cos cosx x x x x x
9 7 3 0cos cos cos cos cos cosx x x x x x
9 7 3 0cos cos cos cosx x x x
3 9 7 0cos cos cos cosx x x x
2 2 2 8 0cos cos cos cosx x x x
2 8 0cos cos cosx x x
0
2 8 0
cos
cos cos
x
xx

2
22
0
8 2 2 6 2
82
3
8 2 2 10 2
5
cos
,.
cos cos
xk
x k x k
x
k
x x k x k x k
xx
x x k x k
k
x








Vậy phương trình có ba họ nghiệm
2 3 5
; ; ,
kk
x k x x k
.
4.
2 2 3 7 7 2cos .cos .cos cosx x x x
4 2 2 7 7 2cos cos .cos cosx x x x
2
2 2 1 2 2 7 7 2cos cos .cos cosx x x x
32
2 2 2 2 7 7 2cos cos cos cosx x x x
32
2 2 2 8 2 7 0cos cos cosx x x
2
2 1 2 2 2 7 0cos cos cosx x x
2
21
2 1 0
1 57
2
4
2 2 2 7 0
1 57
2
4
cos
cos
cos
cos cos
cos
x
x
x loai
xx
x loai


2 1 2 2
2
cos , .x x k x k k
Vậy phương trình có một họ nghiệm
2
x k k
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 70
II. BIẾN ĐỔI TỔNG THÀNH TÍCH.
Phương pháp giải:
Dùng công thức biến đổi tổng thành tích, đặt nhân tử chung đưa về phương trình tích
2.1. Ví dụ minh họa.
Ví dụ 01.
Giải phương trình sau:
5 3 4sin sin sinx x x
Lời giải
5 3 4sin sin sinx x x
5 3 4 0sin sin sinx x x
2 4 4 0sin cos sinx x x
4
40
4
4 2 1 0
1
2 1 0
2
2
3
,
sin
sin cos
cos
cos
k
x k k
x
x
xx
x
x
xk


k
Vậy
2
43
;|
k
S k k


.
Ví dụ 02.
Giải phương trình sau:
2 3 0sin sin sinx x x
Lời giải
2 3 0sin sin sinx x x
3 2 0sin sin sinx x x
2 2 2 0sin cos sinx x x
2 2 1 0sin cosxx
2
20
2
1
2
2 1 0
2
2
3
,
sin
cos
cos
k
x k k
x
x
x
x
xk



k
Vậy
2
2
23
;|
k
S k k


.
2.2. Bài tập rèn luyện.
Bài tập.
Giải các phương trình sau:
1.
3 2 5 0cos cos cosx x x
2.
22 3 18 3 14 10 0cos cos cos cosx x x x
3.
1 2 3 0cos cos cosx x x
4.
2 3 4 0cos cos cos cosx x x x
5.
1 3 2 2sin cos cos sin cosx x x x x
.
6.
2 3 4 2 3 4
sin sin sin sin cos cos cos cosx x x x x x x x
Lời giải
1.
3 2 5 0cos cos cosx x x
HÀM SỐ LƯỢNG GIÁC
Trang 71
LÊ MINH TÂM
5 3 5 0cos cos cos cosx x x x
2 3 2 2 4 0cos .cos cos .cosx x x x
3
4 3 2 4 0cos cos cos cos .cosx x x x x
2
4 3 2 4 0cos cos cos cosx x x x


2
2 2 1 2 2 2 1 0cos cos cos cosx x x x


2
4 2 2 1 0cos cos cosx x x


Trường Hợp 1:
0cosx
2
xk
Trường Hợp 2:
2
4 2 2 1 0cos cosxx
1 1 17
28
1 17
2
8
1 1 17
28
.arccos
cos
.arccos
xk
x
xk








k
Vậy
1 1 17
2 2 8
; .arccos |S k k k








.
2.
22 3 18 3 14 10 0cos cos cos cosx x x x
22 10 3 18 14 0cos cos cos cosx x x x
2 16 6 6 16 2 0cos .cos cos .cosx x x x
2 16 6 3 2 0cos cos cosx x x
3
16 4 2 0cos cosxx
16 0
20
cos
cos
x
x
32 16
42
k
x
k
x


k
Vậy
32 16 4 2
;|
kk
Sk


.
3.
1 2 3 0cos cos cosx x x
.
23
1 2 1 4 3 0cos cos cos cosx x x x
32
4 2 2 0cos cos cosx x x
2
2 2 1 0cos cos cosx x x
2
0
2
20
12
2 1 0
1
2
23
cos
cos
cos
cos cos
cos
xk
x
x
x x k k
xx
x x k

Vậy phương trình có các nghiệm là:
22
23
;;x k x k x k k
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 72
4.
2 3 4 0cos cos cos cosx x x x
4 2 3 0cos cos cos cosx x x x
5 3 5
2 2 0
2 2 2 2
cos cos cos cos
x x x x
53
20
2 2 2
cos cos cos
x x x



2
5
5
55
5
22
0
20
3
2
2
2
3
3
2 2 2
32
22
22
2
22
cos
cos
cos cos
cos cos
x
xk
k
x
x
xx
k x k k
xx
xx
x x x k
k







Vậy phương trình có các nghiệm là:
2
2
5 5 2
;;x k x k x k k
5.
1 3 2 2sin cos cos sin cosx x x x x
1 2 2 3 0cos sin sin cos cosx x x x x
2
2 2 2 2 0sin sin sin sin sinx x x x x
2 2 2 0sin sin sin sin sinx x x x x
2 2 1 0sin sin sinx x x
2
22
2
22
2
33
1
2
2
6
6
2
7
7
2
2
6
6
sin sin
sin
xk
x x k
x x k
xk
xx
k
xk
xk
x
xk
xk






Vậy phương trình có các nghiệm là:
27
2 2 2
3 3 6 6
; ; ;x k x k x k x k k
6.
2 3 4 2 3 4
sin sin sin sin cos cos cos cosx x x x x x x x
2 2 3 3 4 4
0sin cos sin cos sin cos sin cosx x x x x x x x
22
0
sin cos sin cos sin cos
sin cos sin sin cos cos sin cos sin cos
x x x x x x
x x x x x x x x x x
22
10sin cos sin cos sin sin cos cos sin cosx x x x x x x x x x
01
2 2 2 0 2
sin cos
sin sin cos cos
xx
x x x x

+ Giải
1
2
sin cos cos cosx x x x



HÀM SỐ LƯỢNG GIÁC
Trang 73
LÊ MINH TÂM
2
2
4
2
2
x x k
x k k
x x k

+ Giải
2 2 2 0sin cos sin cosx x x x
Đặt
2
1
2
2
sin cos sin cos .
t
x x t t x x
Khi đó phương trình trên trở thành:
2
1
4 3 0
3
t tm
tt
t loai


Với
1
1 1 2 1
44
2
sin cos sin sint x x x x
2
2
44
2
sin sin
xk
xk
xk

Vậy phương trình có các nghiệm là:
22
42
;;x k x k x k k
III. TỔNG HỢP CÁC PHƯƠNG PHÁP.
Phương pháp giải:
Sử dụng các công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc,
công thức biến đổi tích thành tổng, biến đổi tổng thành tích) để đưa về dạng phương trình
lượng giác cơ bản
3.1. Ví dụ minh họa.
Ví dụ 01.
Giải phương trình sau:
2 2 2
3
23
2
sin sin sinx x x
Lời giải
2 2 2
3
23
2
sin sin sinx x x
1 2 1 4 1 6 3cos cos cosx x x
.
2 4 6 0cos cos cosx x x
.
2 2 4 4 0cos cos cosx x x
.
4 2 2 1 0cos cosxx
.
4
40
8 4 8 4
2
2 2 1 0 1 2
2 2 2
2 3 3
cos
cos
cos
x k x k
xk
x
k
x
x x k x k








.
Ví dụ 02.
Giải phương trình sau:
2 2 2 2
3 4 5 6 1sin sin sin sinx x x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 74
Lời giải
2 2 2 2
3 4 5 6sin sin sin sinx x x x
1 6 1 8 1 10 1 12cos cos cos cosx x x x
.
6 8 10 12cos cos cos cosx x x x
.
7 11cos cos cos cosx x x x
.
7 11 0cos cos cosx x x
.
2
2
0
2
11 7 2
11 7
2
11 7 2
9
9
cos
cos cos
xk
xk
k
x
x
k
x x k x k
k
xx
x
x x k
k
x


.
3.2. Bài tập rèn luyện.
Bài tập.
Giải các phương trình sau:
1.
2 2 2
2 4 6sin sin sinx x x
. 2.
2 2 2 2
2 3 4 2cos cos cos cosx x x x
.
3.
2 2 2
3
345
2
cos cos cosx x x
. 4.
4
8 1 4cos cosxx
.
5.
44
4sin cos cosx x x
. 6.
2 2 2
3 2 3 0cos sin cosx x x
.
Lời giải
1
2 2 2
2 4 6 1sin sin sinx x x
.
Ta có:
1 1 4 1 8 1 12cos cos cosx x x
.
4 8 1 12cos cos cosx x x
.
2
2 6 2 2 6cos cos cosx x x
.
6 6 2 0cos cos cosx x x
.
6 2 4 2 0cos sin sinx x x
.
6 0 6 0
6
12 6
2
2 4 2 0 4 0
4
4
cos cos
,
sin sin sin
xk
xx
xk
k
x x x
xk
xk






.
2.
2 2 2 2
2 3 4 2cos cos cos cosx x x x
.
PT
2 4 6 8 0cos cos cos cosx x x x
2 3 2 7 0cos cos cos cosx x x x
.
2 3 7 0cos cos cosx x x
.
5 2 0cos cos cosx x x
.
22
0
5 0 5
2 10 5
20
2
2
42
cos
cos ,
cos
x k x k
x
x x k x k k
x
xk
xk











.
HÀM SỐ LƯỢNG GIÁC
Trang 75
LÊ MINH TÂM
3.
2 2 2
3
345
2
cos cos cosx x x
1 6 1 8 1 10 3
2 2 2 2
cos cos cosx x x
.
6 8 10 0cos cos cosx x x
2 8 2 8 0cos cos cosx x x
8 1 2 0cos cosxx
.
80
8
16 8
16 8
2
1 2 0
21
22
2
cos
cos
cos
k
k
x
x
x
xk
k k k
x
x
xk
xk







.
4.
4
8 1 4cos cosxx
2
2
12
8 2 2
2
cos
cos
x
x




2 2 1 0cos x
1
2
2
cos x
2
2
3
cos cosx
2
22
3
x k k
3
x k k
.
5.
44
4sin cos cosx x x
2
2 2 2 2 2
2 1 2 2sin cos sin cos sinx x x x x
22
1
1 2 1 2 2
2
sin sinxx
2
20sin x
20sin x
2x k k
2
k
xk
.
6.
2 2 2
3 2 3 0cos sin cosx x x
.
2
22
3 2 1 4 1 0sin sinxx
.
42
12 16 4 0sin sinxx
.
Đặt
2
01sin , ,t x t



. Phương trình trở thành
2
12 16 4 0tt
.
1
1
3
t
t
(thỏa mãn)
2
2
1
1
3
sin
sin
x
x
12
2 1 2 2
1
22
11
1 2 1 1 1
2 2 2
33
2 3 2 3
cos
cos
cos
cos arccos
arccos
x
x x k
xk
k
x
x x k
xk











.
IV. PHƯƠNG TRÌNH CÓ ĐIỀU KIỆN.
Phương pháp giải:
Sử dụng các công thức lượng giác đưa về phương trình lượng giác cơ bản và kết hợp điều
kiện để tìm nghiệm của phương trình.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 76
4.1. Ví dụ minh họa.
Ví dụ 01.
Tìm tổng các nghiệm trong khoảng
;
của phương trình:
32
34
sin cosxx
Lời giải
32
34
sin cosxx
32
3 2 2
3
3 4 12 5
32
32
34
3 2 2
3 4 12 5
sin sin (k )
x x k x k
xx
x x k x k






Trường hợp 1:
2
12 5
( ) ;x k k
1
65 55
25
2 1 0 1 2 5 2 1 0 1 2
24 24
12 5 12
{ ; ; ; ; } . ( )
k
kS
k
Trường hợp 2:
2
12 5
( ) ;x k k
2
55 65
5
2 1 0 1 2
24 24
12
{ ; ; ; ; }
k
kS
k
Vậy tổng các nghiệm trong khoảng
;
. của phương trình:
12
0S S S
Ví dụ 02.
Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình
22
2 5 1sin cosxx
Lời giải
22
2 5 1sin cosxx
22
3
2 5 1 4 10 4 10
7
sin sin cos 1 cos cos cos
xk
x x x x x x k
xk
.
Xét
00
3
x k k 
Xét
00
7
x k k 
Do
k
nên nghiệm dương nhỏ nhất
7
x
Tương tự tìm được nghiệm âm lớn nhất
7
x 
HÀM SỐ LƯỢNG GIÁC
Trang 77
LÊ MINH TÂM
4.2. Bài tập rèn luyện.
Bài 01.
Tìm tổng các nghiệm trong khoảng
;
của phương trình:
22
23
8
sin cosxx




Lời giải
22
23
8
sin osx c x




16
4
14
22
cos
cos
x
x





46
4
cos cosxx



4 6 2
85
4
46
3
4
4 6 2
48
cos cos ( )
xk
x x k
x x k
x x k x k




Trường hợp 1:
85
( ) ;x k k
1
45 35
5 4 3 2 1 0 1 2 3 4 10 5 4 3 3 4
88
55
{ ; ; ; ; ; ; ; ; ; } S . ( ... )
k
k
k
Trường hợp 2:
3
8
( ) ;x k k
2
5 11
01
88
4
{ ; }
k
kS
k
Vậy tổng các nghiệm trong khoảng
;
. của phương trình:
12
5
4
S S S
Bài 02.
Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình
2
2
23sin os osx c x c x
Lời giải
2
2
23sin cos cosx x x
2
2
2 2 3
4
sin cosxx






22
3
4
sin cosxx



HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 78
12
2
16
22
cos
cos
x
x





2 6 2
16 4
2
26
2
2 6 2
2 8 2
cos cos ( )
xk
x x k
x x k
x x k x k




Xét
1
0
16 4 4
x x k k 
Xét
1
0
8 2 4
x k k 
Do
k
nên nghiệm dương nhỏ nhất
16
x
Tương tự tìm được nghiệm âm lớn nhất
3
16
x 
Bài 03.
Tìm nghiệm dương nhỏ nhất của phương trình
1.
22
1
2
2
cos sinx x x






, 2.
2
2
1sin sinxx




.
Lời giải
1.
22
1
2
2
cos sinx x x






Ta có
22
1
2
2
cos sinx x x






22
1
2
22
cos cosx x x



22
22
1
22
22
1
22
22
,
x x x k
k
x x x k







22
22
11
22
22
11
22
22
,
x x x k
k
x x x k

2
13
1
24
2
( )
,
( )
xk
k
xk




+)
1
có nghiệm khi
33
0 0 1 2 3
44
, ; ; ; ...k k k k
HÀM SỐ LƯỢNG GIÁC
Trang 79
LÊ MINH TÂM
Khi đó
1
1 3 1 3
2 4 2 4
0 1 2 3
1 3 1 3
2 4 2 4
, ; ; ; ...
x k x k
k
x k x k






Suy ra nghiệm dương nhỏ nhất của
1
là
31
2
x
.
+)
2
có nghiệm dương nhỏ nhất là
1x
.
Vậy phương trình đã cho có nghiệm dương nhỏ nhất là
31
2
x
.
2.
2
2
1sin sinxx




Ta có
2
2
1sin sinxx




2
2
2
2
12
12
,
x x k
k
x x k

2
2
2
2
12
1 1 2
,
x x k
k
x x k

2
1
1
2
11
2
24
,
xk
k
xk




+)
1
có nghiệm dương nhỏ nhất là
1
2
x
.
+)
2
có nghiệm
11
0 0 1 2 3
44
, ; ; ; ....k k k k
Khi đó
2
1 1 1 1
2 4 2 4
0 1 2 3
1 1 1 1
2 4 2 4
, ; ; ; ....
x k x k
k
x k x k






2
có nghiệm dương nhỏ nhất là
51
2
x
.
Vậy phương trình đã cho có nghiệm dương nhỏ nhất là
1
2
x
.
Bài 04.
Tính tổng các nghiệm nằm trong khoảng
02;
của phương trình sau
3 1 3 1 2 2 2sin cos sinx x x
Lời giải
Ta có
3 1 3 1 2 2 2sin cos sinx x x
3 3 2 2 2sin cos cos sin sinx x x x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 80
3 1 3 1
22
2 2 2 2
sin cos cos sin sinx x x x x
22
66
sin cos sinx x x
5
2 2 2 2
6 4 12
sin sin sin sinx x x x
5
5
2
22
12
12
72
5
22
36 3
12
, ,
xk
x x k
kk
xk
x x k


+)
5
2
12
xk
,
02;x
5 5 19
0 2 2
12 24 24
kk
,
k
0k
5
12
x
.
+)
72
36 3
xk
,
02;x
7 2 7 65
02
36 3 12 24
kk
,
k
0 1 2;;k
7 31 55
36 36 36
;;x x x
.
Suy ra phương trình đã cho có tập nghiệm nằm trong khoảng
02;
là
5 7 31 55
12 36 36 36
; ; ;



Vậy tổng các nghiệm của phương trình đã cho nằm trong khoảng
02;
là
5 7 31 55
3
12 36 36 36
.
Bài 05.
Tìm nghiệm trên khoảng
,
của phương trình:
2
2 1 2 3 1 4sin sin sin sin .cosx x x x x
Lời giải
2
2 1 2 3 1 4sin sin sin sin .cosx x x x x
2
2 1 2 3 1 2 2 2sin sin sin sin .cos .cosx x x x x x
22
2 1 2 3 1 4 2sin sin sin cos .sin .cosx x x x x x
2
2 1 2 3 1 4 2 1 1sin sin sin cos .sin . sin sinx x x x x x x
2
10
2 3 1 2 2 1
sin
sin sin cos .sin . sin
x
x x x x x

Trường hợp 1:
1 0 1 2
2
sin sin , .x x x k k
Mà
2
,.xx
Trường hợp 2:
2
2 3 1 2 2 1sin sin cos .sin sinx x x x x
HÀM SỐ LƯỢNG GIÁC
Trang 81
LÊ MINH TÂM
2
2 3 1 3 1sin sin sin sin sinx x x x x
22
1 4 4 1 2 2 3 2 4
4 2 3 1 2 0
2 3 3 1 2 0
3 2 1 1 2 0
2 2 3 3
- cos - sin cos sin - cos - cos
cos - cos sin - sin
- sin sin sin - sin
sin
sin sin cos sin sin .si
i
n
- s n - sin
x x x
x
x
x x x x x x
x x x
x x x
x
x
x
xx
x




3
1
2
2
2
6
6
3 4 1 2 1 0
1
5
2
2
sin
sin sin sin
sin
x
x
x
k
x kx
x
k
xx

Mà
5
2 6 6
, , ,xx



Vậy
5
2 6 6
,,x



.
Bài 06.
Giải các phương trình sau
1.
3cot cotxx
2.
4 7 1cot .cotxx
Lời giải
1.
3cot cotxx
Điều kiện:
30
3
0
3
sin
,,
sin
k
x
x
k
k x k
x
xk

.
Ta có:
33
2
cot cot , ,
k
x x x x k k x k
Kết hợp điều kiện thì phương trình có nghiệm là
2
,x k k
.
2.
4 7 1cot .cotxx
Điều kiện:
40
4
70
7
sin
,
sin
k
x
x
k
k
x
x


.
Ta có:
4 7 1 4 7 4 7
2
cot .cot cot tan cot cotx x x x x x



47
2 22 11
,.
m
x x m x m
Giả sử
22 11 4
mk

2 4 11mk
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 82
42
42
2 4 11 4 2
11 5
kt
kt
tt
mt
mt



Giả sử
22 11 7
mk

7 14 22mk
7 22 14km
( phương trình vô nghiệm)
Vậy phương trình có nghiệm là
11 5
22 11
,
m
x m t t
.
Bài 07.
Giải phương trình lượng giác sau:
5
1
9
sin cot
cos
xx
x
Lời giải
+) Điều kiện
0
9
18 9
2
50
5
5
9c
,
n
os
,, ,
si
k
x
k
xk
x
x
x
l
xl
l k l




.
+) Với điều kiện trên, phương trình đã cho tương đương với
5 9 5sin cos cos sinx x x x
11
5 5 5 9 5 9
22
sin sin sin sinx x x x x x x x
6 4 14 4sin sin sin sinx x x x
14 6 2
14 6
14 6 2
sin sin
x x m
xx
x x m

82
4
20 2
20 10
,
m
m
m
x
xm
xm
x



.
+) Với
4
m
x
:
49
9 2 4 9 18 36 2 4
9 2 4
4 18 9
,
kt
mk
m k m t m t
m
t
k


.
5
5 4 4
5 20
45
,
lt
ml
m l m t
mt
t
.
Do đó phương trình có họ nghiệm
2 4 4
4
, , ,
m
x m t m t t
. Hay
42
,x m
m
+) Với
20 10
m
x 
:
18 1 20 18 20 1
20 10 18 9 10 180 9
m k m k
m k m k
(vô nghiệm).
1 2 4 1 4 2
20 10 5
ml
m l l m
(vô nghiệm).
Do đó phương trình có họ nghiệm
20 10
, m
m
x
thỏa mãn.
HÀM SỐ LƯỢNG GIÁC
Trang 83
LÊ MINH TÂM
Vậy phương trình đã cho có hai họ nghiệm
4 2 20 10
,,
mm
xx m
.
Bài 08.
Giải phương trình:
3 4 5cos tan sinx x x
Lời giải
+) Điều kiện
4 0 4
2 8 4
cos ,
k
x x k kx
.
+) Với điều kiện trên, phương trình đã cho
4 3 5 4sin cos sin cosx x x x
9 7 2
11
7 9 9 7
9 7 2
22
sin sin sin sin sin sin
x x m
x x x x x x
x x m

16 8 16 8
,
x m x m
mm
xx
m






.
+) Với
xm
:
8 1 2 8 2 1
84
k
m m k m k
(vô nghiệm).
Do đó họ nghiệm
,x mm
thỏa mãn.
+) Với
16 8
m
x 
:
1
2 1 4
16 8 8 4 8 16 4
m k m k
mk
(luôn đúng, vì một vế là số chẵn, một vế là
số lẻ). Do đó họ nghiệm
16 8
,
m
x m
thỏa mãn.
Vậy phương trình đã cho có hai họ nghiệm
16 8
,,
m
xm mx
.
Bài 09.
Giải phương trình:
2 3 7 2 3 7tan tan tan tan tan tanx x x x x x
Lời giải
+) Điều kiện
2
2 4 2
20
3 0 3
2 6 3
70
7
2
14 7
cos
cos ,
cos
k
x k x
x
k
x x k x
x
k
xk
x
k








.
+) Phương trình đã cho
2 3 7 1 3 7tan tan tan tan tanx x x x x
(1)
Nếu
2
1
3 7 1 0 3 7 0 3 0 3 1 0
3
tan tan tan tan tan tan
tan
x x x x x x
x
(vô
nghiệm). Do đó
3 7 1 0tan tanxx
. Khi đó
3 7 3 7
1 2 2 2 10
3 7 1 1 3 7
tan tan tan tan
( ) tan tan tan tan
tan tan tan tan
x x x x
x x x x
x x x x


HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 84
10 2 10 2
12
tan tan ,
l
x x x x l lx
.
+) Xét họ nghiệm
12
,
l
x l
. Ta có
3 6 3 1 2
12 4 2
lk
l k l k
2 4 2 1 2
12 6 3
lk
l k l k
37
37
7 6 12
7 6 12 3 7
7 6 12
12 14 7
kt
kt
lk
lk
lt
lk




37
6 12
6 12
, t
kt
lt
lt


.
Vậy phương trình có nghiệm,
3 1 2 2 1 2 6 12
12
,, , , ,
l
x l k l k l ltt
.
Bài 10.
Giải phương trình:
2
2
2 2 2 4
4cos
tan tan .tan
sin cos
xx
xx
xx



Lời giải
Điều kiện:
0
2
0
3
2
2
24
2
cos
,,
cos
x
xk
k x k k
x
xk









.
Ta có:
2
2
2 2 2 4
4cos
tan tan .tan
sin cos
xx
xx
xx



21
2 2 1
21
1
2 2 1
22
1
21
2
4cos sin
tan tan .
sin cos sin
4cos sin
tan .
sin .cos cos sin
4cos sin
.
cos sin
cos sin
cos sin
xx
xx
x x x
xx
x
x x x x
xx
xx
xx
xx







2
22
63
2
2
2
22
2
2
2
sin sin
k
x
x x k
x x k k
x x k
xk





Đối chiếu điều kiện thì phương trình có nghiệm là
5
22
66
;x k x k k
.
Bài 11.
Giải phương trình:
HÀM SỐ LƯỢNG GIÁC
Trang 85
LÊ MINH TÂM
2 2 2 1
3
cos cos
cot
sin
xx
x
x
Lời giải
Điều kiện:
30
30
0
3
sin
sin ,
sin
x
k
x x k
x
.
Ta có:
2
3
2 2 1 2 1
2 2 2 1
3
34
cos sin
cos ( cos ) cos
cot
sin sin
sin sin
xx
x x x
x
xx
xx



2
2
2 3 4
34
cos sin
cos
sin
sin sin
xx
x
x
xx

2cos cosxx
22
22
x x k
x x k

2
2
2
3
3
,
xk
k
xk
k
x
(Loại vì không thỏa mãn điều kiện)
Kết luận: Phương trình vô nghiệm.
Bài 12.
Giải các phương trình sau:
1.
23
3
23
sin sin sin
cos cos cos
x x x
x x x


2.
23
2
2
1
2
cos cos
cos tan
cos
xx
xx
x


.
3.
1 1 2
24cos sin sinx x x

. 4.
2
4
4
2 2 3
1
sin sin
tan
cos
xx
x
x

.
5.
3 5 7cos tan sinx x x
. 6.
2
1
21
sin cos
tan cot cot
xx
x x x

.
Lời giải
1.
23
3
23
sin sin sin
cos cos cos
x x x
x x x


32
3
32
sin sin sin
cos cos cos
x x x
x x x



2 2 2
3
2 2 2
sin os sin
cos cos cos
xc x x
x x x

2 2 1
3
2 2 1
sin os
cos cos
x c x
xx

, ĐK:
2 0 2 1 0cos ; cosxx
23tan x
2
3
xk
62
k
xk
(thoả mãn ĐK).
2.
23
2
2
1
2
cos cos
cos tan
cos
xx
xx
x


( ĐK:
0
2
cos , .x x k K
).
2
2
1
21cos tan cos
cos
PT x x x
x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 86
22
2 1 1cos tan cos tanx x x x
22
2 1 1cos tan cos tanx x x x
2
2 1 0cos cosxx
1
1
2
cos
cos
x
x

2
2
3
,
xk
K
xk


( Thoả mãn điều kiện).
3.
1 1 2
24cos sin sinx x x

Điều kiện:
0
20
40
cos
sin
sin
x
x
x
0
20
2 2 2 0
cos
sin cos
sin cos
x
xx
xx

40sin x
4xk
4
,
k
xk
.
1 1 2
2 2 2cos sin cos sin cos cos
PT
x x x x x x
11
1
2 2 2sin sin cosx x x
2 2 2 1sin cos cosx x x
2 2 1 2sin cos cosx x x
2
2 2 2sin cos sinx x x
2 2 0sin cos sinx x x
2
1 2 0sin sinxx
1
1
2
sin
sin
x
x

.
+) Xét
10sin cosxx
(Loại).
+)
1
2
sin x
2
6
5
2
6
,
xk
K
xk



.
Thử điều kiện
+)
4sin x
42
6
sin k




2
8
3
sin k




2
3
sin



3
2
0
( thoả mãn).
+)
4sin x
5
42
6
sin k




10
8
3
sin k




10
3
sin



3
30
3 3 2
sin sin
( thoả mãn).
Vậy phương trình có nghiệm:
2
6
5
2
6
,.
xk
K
xk


HÀM SỐ LƯỢNG GIÁC
Trang 87
LÊ MINH TÂM
4.
2
4
4
2 2 3
1
sin sin
tan
cos
xx
x
x

Điều kiện:
0
2
cosx x k k
.
Với điều kiện trên, ta có:
2
4
4
2 2 3
1
sin sin
tan
cos
xx
x
x

4 4 2
2 2 3sin cos sin sinx x x x
2
2 2 2 2 2 2
2 2 4 3sin cos sin cos sin cos sinx x x x x x x
2 2 2 2
1 2 2 3 4 3sin cos sin sin cos sinx x x x x x
2 2 2 2
4 3 2 2 3 1 0sin cos sin sin cos sinx x x x x x
22
2 2 3 1 2 3 1 0sin cos sin sinx x x x
22
2 3 1 2 1 0sin sin cosx x x
22
2 3 1 0 1
2 1 0 2
sin
sin cos
x
xx


Giải phương trình (1):
2
1
18 3
33
52
26
18 3
sin sin sin
k
x
x x k
k
x


Giải phương trình (2):
2 2 2
1 1 1 4 1 3 1 3
24
2 8 2 8 4 4 4 2
cos
sin cos sin cos arccos
xk
x x x x x k
Đối chiếu với điều kiện thì phương trình ban đầu có các họ nghiệm là:
2 5 2 1 3
18 3 18 3 4 4 2
; ; arccos
k k k
x x x k
.
5.
3 5 7cos tan sinx x x
Điều kiện:
50
10 5
cos
k
x x k
Với điều kiện trên, ta có:
3 5 7cos tan sinx x x
5
37
5
sin
cos sin
cos
x
xx
x

3 5 7 5cos sin sin cosx x x x
11
8 2 12 2
22
sin sin sin sinx x x x
12 8sin sinxx
12 8 2
12 8 2
x x k
k
x x k


HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 88
2
20 10
k
x
k
k
x


Đối chiếu với điều kiện thì phương trình ban đầu có các họ nghiệm là:
2 20 10
;
kk
x x k
.
6.
2
1
21
sin cos
tan cot cot
xx
x x x

Điều kiện:
2 1 2 0tan cot ; cot ; sinx x x x
Với điều kiện trên, ta có:
2
1
21
sin cos
tan cot cot
xx
x x x

2
1
2
2
sin cos
sin cos cos sin
cos sin cos sin
xx
x x x x
x x x x

2
2
1
22
2
sin sin cos
cos sin
sin cos
sin cos
x x x
xx
xx
xx

2
2
12
22
2
sin cos
sin
cos
. cos
xx
x
x
x
2 2 0sin cos sinx x x
0
3
2 2 1 0 2
2
4
2
sin ( )
sin cos
cos
x loai
x x x k k
x

Đối chiếu với điều kiện thì phương trình ban đầu có các họ nghiệm là:
3
2
4
x k k
Bài 13.
Giải các phương trình sau :
1.
11
2 2 2 2
2 2 2
tan cot sin
sin
x x x
x
.
1
2.
22
5
8 2 8
34
cos cos
sin cos
cos cos
xx
xx
xx



.
2
3.
2 3 5 2 3 5tan tan tan tan tan tanx x x x x x
.
3
Lời giải
1.
11
2 2 2 2
2 2 2
tan cot sin
sin
x x x
x
.
1
Đk:
0
20
20
22
cos
sin ( )
sin
x
x x k k
x
.
HÀM SỐ LƯỢNG GIÁC
Trang 89
LÊ MINH TÂM
Phương trình
1
2 2 1
22
22
sin cos
sin
cos sin sin
xx
x
x x x
22
4 2 2 2 1sin cos sinx x x
2 2 2 2
4 1 2 8 1sin sin sin .cosx x x x
22
2 1 4 0sin cosxx
2
2 1 2 1 2 0sin cosxx


2
2 1 2 2 0sin cosxx
02
1
23
2
sin
cos
x
x
.
Giải phương trình
2
:
0sinx
loại do
2 0 0sin sinxx
.
Giải phương trình
3
:
2
22
1
33
2
2
2
22
33
cos
x l x l
xl
x l x l






.
Kết hợp điều kiện
3
3
xl
l
xl


là nghiệm phương trình .
2.
22
5
8 2 8
34
cos cos
sin cos
cos cos
xx
xx
xx



.
2
Đk:
42
20
30
63
50
10 5
cos
cos ( )
cos
xk
x
x x k k
x
xk





.
Phương trình
2
2 3 5 2 3 5
2 3 5 2 3 5
sin sin sin sin sin sin
..
cos cos cos cos cos cos
x x x x x x
x x x x x x
2 3 5 3 2 5 5 3 2 2 3 5sin .cos .cos sin .cos .cos sin .cos .cos sin .sin .sinx x x x x x x x x x x x
5 2 3 3 2 5 3 2 2 3cos sin .cos sin .cos sin cos .cos sin .sinx x x x x x x x x x
5 5 5cos sin sin cosx x x x
5 5 0sin cos cosx x x
52
5
52
50
5
cos cos
sin
x x l
xx
x x l
x
xl

2
3
5
xl
x l l
xl
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 90
Kết hợp điều kiệnKết hợp điều kiện
2
3
5
xl
x l l
xl
là nghiệm phương trình .
3.
2 3 5 2 3 5tan tan tan tan tan tanx x x x x x
.
3
Đk:
0
2
30
63
cos
()
cos
xk
x
k
x
xk




.
Phương trình
3
2 2 2
5 3 8 2 3 8 3cos cos .cos cos .cos .cos cos .cos .cosx x x x x x x x x
2
5 3 4 4 4 2 3 0cos cos .cos cos cos .cos .cosx x x x x x x
1 1 1
2 2 8 8 3 3 0
2 2 2
cos cos cos sin .cos .cos .sinx x x x x x x
11
8 2 6 2 0
22
cos sin .sinx x x
11
8 4 8 0
22
cos cos cosx x x
1 8 2 4 0cos cosxx
2
2 4 2 4 0cos cosxx
40
84
41
2
cos
cos
l
x
x
l
x
l
x

Kết hợp điều kiện
84
l
x
l
xl

là nghiệm phương trình .
------------------ HẾT------------------
HÀM SỐ LƯỢNG GIÁC
Trang 91
LÊ MINH TÂM
§7. TỔNG ÔN CHƯƠNG
Dạng 01. TẬP XÁC ĐỊNH.
Phương pháp giải:
1.
fx
xac đinh
0fx
;
1
fx
xac đinh
0fx
.
2.
siny f x
xac đinh
fx
xac đinh.
3.
cosy f x
xac đinh
fx
xac đinh.
4.
tany f x
xac đinh
2
f x k k
.
5.
coty f x
xac đinh
f x k k
.
Bài tập
Tìm tập xác định của các hàm số sau:
a.
32cosyx
b.
1 cos
sin
x
y
x
c.
23
23
sin
cos
x
y
x
d.
11
sin cos
y
xx

e.
2
3
tanyx




f.
3cotyx
g.
4
3sin cos
y
xx
h.
23
21
sin tan
cos
xx
y
x
i.
6
1
cot
cos
x
y
x



k.
4
3
2
tan
sin
x
y
x



m.
32
2
43
54
sin cos
cos cos
xx
y
xx
Lời giải
a.
32cosyx
Hàm số
32cosyx
xác định khi
3 2 0cos x
(luôn đúng, vì
21cos ,xx
).
Vậy tập xác định của hàm số đã cho là .
b.
1 cos
sin
x
y
x
Hàm số
1 cos
sin
x
y
x
xác định khi
0sin ,x x k k
.
Vậy tập xác định của hàm số đã cho là
\,D k k
.
c.
23
23
sin
cos
x
y
x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 92
Hàm số
23
23
sin
cos
x
y
x
xác định khi
2 3 0cos x 
3
2
cosx
2
6
,x k k
.
Vậy tập xác định của hàm số đã cho là
2
6
\,D k k



.
d.
11
sin cos
y
xx

Hàm số
11
sin cos
y
xx

xác định khi
0
0
cos
sin
x
x
2
,
xk
k
xk


2
.,x k k
.
Vậy tập xác định của hàm số đã cho là
2
\ . ,D k k



.
e.
2
3
tanyx




Hàm số
2
3
tanyx




xác định khi
2 0 2
3 3 2 12 2
cos .x x k x k



Vậy tập xác định của hàm số đã cho là
12 2
\,D k k



.
f.
3cotyx
Hàm số
3cotyx
xác định khi
3 0 3 3sin .x x k x k
TXĐ:
3\,D k k
g.
4
3sin cos
y
xx
Hàm số
4
3sin cos
y
xx
xác định khi
3 0 0
3 3 3
sin cos sin .x x x x k x k



TXĐ:
3
\,D k k



.
h.
23
21
sin tan
cos
xx
y
x
Hàm số
23
21
sin tan
cos
xx
y
x
xác định khi
2
0
2
1
3
2
2
3
cos
cos
xk
x
xk
x
xk




.
TXĐ:
22
2 3 3
\ , , ,D k k k k



.
HÀM SỐ LƯỢNG GIÁC
Trang 93
LÊ MINH TÂM
i.
6
1
cot
cos
x
y
x



Hàm số
6
1
cot
cos
x
y
x



xác định khi
0
6
66
22
1
sin
cos
x
x k x k
x k x k
x








.
TXĐ:
2
6
\ , ,D k k k



k.
4
3
2
tan
sin
x
y
x



Hàm số
4
3
2
tan
sin
x
y
x



xác định khi
20
2
2
40
4
3
32
24 4
sin
cos
k
x
xk
x
x
k
xk
x





TXĐ:
2 24 4
\ , ,
kk
Dk



.
m.
32
2
43
54
sin cos
cos cos
xx
y
xx
Hàm số
22
2
43
54
sin cos
cos cos
xx
y
xx
xác định khi và chỉ khi
2
4 3 0
54
cos cosxx
7 3 13
20
2 40 2 40
cos cos
xx
73
7 3 17 2
0
2 40
2 40 2 140 7
13 7
13
2
0
2 40 2 20
2 40
cos
cos
x
x
k x k
x
x
k x k












.
TXĐ:
17 2 7
2
140 7 20
\ ; ,
k
D k k



.
Dạng 02. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.
Phương pháp giải:
Sử dụng tính chất
11sinx
và
11cosx
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 94
Bài tập.
Tìm GTNN và GTLN của các hàm số:
a.
25
4
cosyx



b.
2
41
4
sinyx



c.
2
5
3 2 1cos
y
x
d.
11sinyx
e.
sin cosy x x
.
f.
3 3 3sin cosy x x
.
g.
2
2 2 3sin cos cos sin .cosy x x x x x
.
h.
22
3 4 5 2sin sin .cos cosy x x x x
.
i.
2
2
sin cos
sin cos
xx
y
xx

.
Lời giải
a.
25
4
cosyx



Với
x
, ta có:
11
4
cos x



2 2 2
4
cos x



3 2 5 7
4
cos x



37y
Suy ra:
7max y
1
4
cos x



2
4
xk
2
4
xk
, với
k
3miny
1
4
cos x



2
4
xk
3
2
4
xk
, với
k
b.
2
41
4
sinyx



Với
x
, ta có:
01
4
sin x



2
01
4
sin x



2
1 4 1 3
4
sin x



13y
Suy ra:
3max y
1
4
sin x



2
42
xk
3
2
4
xk
, với
k
1min y 
0
4
sin x



4
xk
4
xk
, với
k
c.
2
5
3 2 1cos
y
x
Với
x
, ta có:
0 2 1cos x
2
0 2 1cos x
2
1 3 2 1 4cos x
HÀM SỐ LƯỢNG GIÁC
Trang 95
LÊ MINH TÂM
2
55
5
4
3 2 1cos x
Suy ra:
5max y
20cos x
2
2
xk
42
k
x
, với
k
.
5
4
min y
2
21cos x
2xk
2
k
x
, với
k
.
d.
11sinyx
Với
x
, ta có:
11sinx
11sinx
0 1 2sinx
0 1 2sinx
1 1 1 2 1sinx
1 2 1y
21maxy 
1sinx
2
2
xk
, với
k
1min y 
1sinx
2
2
xk
, với
k
e.
2
4
sin cos siny x x x



Với
x
, ta có:
11
4
sin x



2 2 2
4
sin x



22y
Suy ra:
2max y
1
4
sin x



2
42
xk
2
4
xk
, với
k
.
2min y 
1
4
sin x



2
42
xk
3
2
4
xk
, với
k
.
f.
13
3 3 3 2 3 3
22
sin cos sin . .cosy x x x x




Cách 1.
13
3 3 3 2 3 3
22
sin cos sin . .cosy x x x x




2 3 3 2 3
3 3 3
. cos sin sin cos sinx x x
Với
x
, ta có:
1 3 1
3
sin x



2 2 3 2
3
sin x



22y
Suy ra:
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 96
2maxy
31
3
sin x



32
32
xk
52
18 3
k
x
, với
k
2min y 
31
3
sin x



32
32
xk
2
18 3
k
x
, với
k
Cách 2. Phương trình
3 3 3sin cosy x x
có nghiệm khi và chỉ khi
2
2 2 2
1 3 4 2 2y y y
.
Vậy GTLN của
y
là
2
và GTNN của
y
là
2
.
g.
2
2 2 3sin cos cos sin .cosy x x x x x
1 2 2 2 3
1 2 2
1
1 2 2 2
2
sin .cos cos sin .cos
cos sin .cos
cos sin *
y x x x x x
y x x x
y x x
Phương trình ban đầu có nghiệm khi và chỉ khi (*) có nghiệm
2
22
2
1 17 17 17 17 17
2 1 1 1 1 1
2 4 2 2 2 2
y y y y



.
Vậy GTLN của
y
là
17
1
2
và GTNN của
y
là
17
1
2
.
h.
22
3 4 5 2sin sin .cos cosy x x x x
.
35
1 2 2 2 1 2 2
22
1 2 2 4 2
cos sin cos
sin cos *
y x x x
y x x
Phương trình ban đầu có nghiệm khi và chỉ khi (*) có nghiệm
2 2 2
2
2 4 1 1 20 2 5 1 2 5 1 2 5 1 2 5y y y y
.
Vậy GTLN của
y
là
1 2 5
và GTNN của
y
là
1 2 5
.
i.
2
2
sin cos
sin cos
xx
y
xx

22
2 1 2 0
sin cos sin cos
sin cos *
y x y x y x x
y x y x y
Phương trình ban đầu có nghiệm khi và chỉ khi (*) có nghiệm
2 2 2
2 1 2y y y
2 2 2
3 19 3 19
4 2 6 5 2 6 5 0
22
y y y y y y
Dạng 03. PHƯƠNG TRÌNH LƯỢNG GIÁC.
Phương pháp giải:
DẠNG CƠ BẢN:
2
2
,
sin sin
,
u v k k
uv
u v k k

2
2
,
cos cos
,
u v k k
uv
u v k k

HÀM SỐ LƯỢNG GIÁC
Trang 97
LÊ MINH TÂM
22
hay
tan tan
u l v l l
uv
u v k k




hay
cot cot
u l v l l
uv
u v k k

TRƯỜNG HỢP ĐẶC BIỆT:
0sinx x k k
12
2
sinx x k k
12
2
sinx x k k
0
2
cosx x k k
12cosx x k k
12cosx x k k
Bài 01.
Giải các phương trình sau:
a.
21cos x 
. b.
3
3
62
sin x




c.
21
5
cos x




d.
4 3 0cot x
e.
3 2 3 0tan x 
f.
0
3
cos x




g.
2 3 0
34
sin
x



h.
2
1
2
4
sin x
. i.
2
23
4
tan x




.
Lời giải
a.
21cos x 
22
2
,x k x k k
.
b.
3
3
62
sin x




2
32
6 3 6 3
3
2 5 2
63
32
6 3 18 3
sin sin ,
k
x k x
xk
k
x k x









c.
21
5
cos x




9
22
1
5 4 20
5 5 4
2
22
5 4 20
cos cos cos ,
x k x k
x x k
x k x k






d.
4 3 0cot x
44
6 6 24 4
cot cot ,
k
x x k x k
..
e.
3 2 3 0tan x 
3
2
3
tan x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 98
22
6 6 12 2
tan tan ,
k
x x k x k



.
f.
0
3
cos x




3 2 6
,x k x k k
.
g.
2 3 0
34
sin
x



3
3 4 2
sin
x



2
6
3 4 3
4
25
3 4 3
26
3 4 3 4
sin sin ,
x
k
xk
x
k
x
k x k




.
h.
2
1
2
4
sin x
1 4 1
24
cos x

1
4 4 4 2
2 3 3 12 2
cos cos cos ,
k
x x x k x k
.
i.
2
23
4
tan x




.
Điều kiện:
20
4
cos x




23
4
23
4
tan
tan
x
x







7
2
2
43
43
24 2
2
2
4 3 24 2
43
tan tan
,
tan tan
k
x
xk
x
k
k
x k x
x






đều thỏa mãn.
Vậy
7
24 2
24 2
,
k
x
k
k
x

là nghiệm của phương trình.
Bài 02.
Giải các phương trình sau:
a.
3 2 0sin cosxx
. b.
2
0
3
cos cosxx



.
HÀM SỐ LƯỢNG GIÁC
Trang 99
LÊ MINH TÂM
c.
2 30
2
cos cos
x
x
. d.
21tan .cotxx
.
e.
22
20sin cosxx
. f.
44
1
2 2 2
sin cos
xx

.
Lời giải
a.
3 2 0sin cosxx
.
32sin cosxx
.
2
2
3 2 2
1
10 5
2
2
4
3 2 2
2
2
2
sin , ,
k
x
x x k
x k k
x x k
xk


.
Vậy phương trình có nghiệm là
2
10 5
2
2
,
k
x
k
xk


.
b.
2
0
3
cos cosxx



.
3
20
3
cos cosx
.
0
3
cos x



.
23
xk
,k
.
6
xk
,k
.
Vậy phương trình có nghiệm là
6
xk
,k
.
c.
2 30
2
cos cos
x
x
.
2 30 180
2
cos cos
x
x
.
2 150 360
2
2 150 360
2
x
xk
x
xk
,k
.
100 240
60 240
xk
xk
,k
.
Vậy phương trình có nghiệm là
100 240
60 240
xk
k
xk
.
d.
21tan .cotxx
Điều kiện:
0
2
2
20
2
2
cos
,
sin
xm
x
xm
mn
xn
xn
x



.
Phương trình
1
2
tan
cot
x
x

2tan tanxx
2x x k
,k
xk
,k
.
Kết hợp với điều kiện ta có nghiệm của phương trình là
S 
.
e.
22
20sin cosxx
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 100
2
12
20
2
cos
cos
x
x
.
2
2 2 2 1 0cos cosxx
22
2
6
3
2
21
2
1
2
2
cos
cos
xk
xk
x
kk
x
xk
xk



.
Vậy phương trình có nghiệm là
6
2
xk
k
xk


.
f.
44
1
2 2 2
sin cos
xx

.
22
1
2 2 2 2 22
sin cos sin cos sin cos
x x x x x x
x
.
1
2 2 2 2
sin cos sin cos
x x x x
x
.
2
2
12
2
23
2
3
3
cos cos cos ,
xk
x x k
xk





.
Vậy phương trình có nghiệm là
3
2
2
2
3
2
,
xk
k
xk

.
Bài 03.
Tìm nghiệm của các phương trình sau trong các khoảng đã cho:
a.
1
2
2
sin x 
với
0;x
. b.
3
42
cos x




với
;x

.
c.
2 15 1tan x
với
180 90x
d.
1
3
3
cot x 
với
0
2
;x




. .
Lời giải
a.
1
2
2
sin x 
với
0;x
.
22
1
6
12
22
7
26
22
6 12
sin sin sin
xk
xk
x x k k
x k x k



.
HÀM SỐ LƯỢNG GIÁC
Trang 101
LÊ MINH TÂM
Vì
0;x
nên
1 1 13
0 0 1
1
12 12 12 12
7 7 7 5 0
0 0 1
12 12 12 12
k k k
k
k k k
k
k k k
.
Vậy
11
12 12
7
12
x
x
.
b.
3
42
cos x




với
;x

.
5
2
2
46
12
46
22
4 6 12
cos cos
xk
xk
x k k
x k x k


.
Vì
;x

nên
5
2
12
2
12
k
k
k
.
5 17 7 17 7
1 2 1 2
0
12 12 12 24 24
1 13 11 13 11 0
1 2 1 2
12 12 12 24 24
k k k
k
k k k
k
k k k

.
Vậy
5
12
12
x
x
.
c.
2 15 1tan x
với
180 90x
Ta có
2 15 1tan x
2 15 45 180 2 60 180 30 90. . .x k k x k k x k k
Vì
180 90x
180 30 90 90.kk
2
72
210 90 60
1
33
0
.
k
k k k k
k
k


Vậy phương trình có nghiệm
150
60
30
x
x
x

.
d.
1
3
3
cot x 
với
0
2
;x




.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 102
Ta có
1
33
3 9 3
3
cot
k
x x k k x k
.
Vì
0
2
;x




nên
0
2 9 3
k
k
.
1
1 1 7 1 21 1
0
0
2 9 3 18 3 9 18 3
k
kk
k k k k
k

.
Vậy
4
9
9
x
x


.
Bài 04.
Giải các phương trình sau:
a.
2
2 3 1 0cos cosxx
. b.
22
2 4 2 0sin cos sinx x x
.
c.
2
3 2 7 2 3 0sin cosxx
. d.
2
6 5 7 0cos sinxx
.
e.
2 3 4 0cos cosxx
. f.
2
6 3 12 7sin cosxx
.
g.
21
2
cos sin
x
x 
. h.
2
5 1 3sin sin cosx x x
.
i.
42
4 12 7sin cosxx
. k.
7 4 12tan cotxx
l.
2
2
1
3 5 0cot
cos
x
x
. m.
3
22sin cos sinx x x
n.
2
2
11
cos cos
cos
cos
xx
x
x
. o.
2
2tan cot tan cotx x x x
Lời giải
a.
2
2 3 1 0cos cosxx
.
2
1
1
2
3
2
cos
cos
xk
x
xk
x

.
Vậy nghiệm của phương trình ban đầu là:
2xk
;
2
3
xk
k
.
b.
22
2 4 2 0sin cos sinx x x
.
22
2 1 4 2 0sin sin sinx x x
.
2
2
2
1
1
3 4 1 0 2
1
3
3
1
2
3
sin
sin sin arccos
sin
arccos
xk
x
x x x k
x
xk

.
HÀM SỐ LƯỢNG GIÁC
Trang 103
LÊ MINH TÂM
Vậy nghiệm của phương trình ban đầu là:
2
2
xk
;
1
2
3
arccosxk
;
1
2
3
arccosxk
k
.
c.
2
3 2 7 2 3 0sin cosxx
.
2
3 1 2 7 2 3 0cos cosxx
.
2
3 2 7 2 0cos cosxx
.
20
2
7
2 4 2
2
3
cos
cos
x
k
x k x
x VN
.
Vậy nghiệm của phương trình ban đầu là:
42
k
xk
.
d.
2
6 5 7 0cos sinxx
.
22
1
2
6 1 5 7 0 6 5 1 0
1
3
sin
sin sin sin sin
sin
x
x x x x
x
.
+) Với
2
1
6
5
2
2
6
sin
xk
x
xk



.
+) Với
1
2
1
3
1
3
2
3
arcsin
sin
arcsin
xk
x
xk


.
Vậy nghiệm của phương trình ban đầu là:
2
6
xk
;
5
2
6
xk
;
1
2
3
arcsinxk
;
1
2
3
arcsinxk
k
.
e.
2 3 4 0cos cosxx
.
2
1
2 3 5 0 2
5
2
cos
cos cos
cos
x
x x x k
x VN
.
Vậy nghiệm của phương trình ban đầu là:
2xk
k
.
f.
2
6 3 12 7sin cosxx
.
2
16
6 2 6 1 7 0
2
cos
. cos
x
x
.
2
2 6 3 6 5 0cos cosxx
.
5
6
62
2
63
61
cos
cos
x VN
k
x k x
x

.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 104
Vậy nghiệm của phương trình ban đầu là:
63
k
x 
k
.
g.
21
2
cos sin
x
x 
.
2
2
22
2 2 0 2
2 2 2
0
2
sin
sin sin
sin
x
VN
x x x
k x k
x
.
Vậy nghiệm của phương trình ban đầu là:
2xk
k
.
h.
2
5 1 3sin sin cosx x x
22
5 5 1 3sin sin sinx x x
.
2
6 5 4 0sin sinxx
.
4
1
3
2
1 2 2
2
sin
sin .
sin
x vn
x x k k
x

i.
42
4 12 7sin cosxx
.
2
1 2 6 1 2 7 0cos cosxx
.
2
2 4 2 0cos cosxx
.
20
24
1 2 1
cos
cos
cos
x
x
x

.
2 0 2
2 4 2
cos .
k
x x k x k
.
k.
7 4 12tan cotxx
.
2
2
2
7 12 4 0
2
2
7
7
2
arctan
tan
tan tan
arctan
tan
xk
x
xx
k
xk
x
x k k






.
l.
2
2
1
3 5 0cot
cos
x
x
.
22
1 3 5 0
2
cot cotxx
x k k

.
2
4 4 0
1
4
2
cot
cot
x
x x k k
x k k


.
m.
3
22sin cos sinx x x
.
2
2 1 2 0sin sin cosx x x
.
HÀM SỐ LƯỢNG GIÁC
Trang 105
LÊ MINH TÂM
2 1 0cos sinxx
.
2
20
2 4 2
1
22
22
cos
sin
k
x k x
x
k
x
x k x k






.
n.
2
2
11
cos cos
cos
cos
xx
x
x
.
43
1
0
cos cosx x cosx
cosx
.
43
10
0
cos cos cos
cos
x x x
x
.
2
2
1 1 0
0
cos cos cos
cos
x x x
x
.
1
2
cos
k
x x k
.
o.
2
2tan cot tan cotx x x x
2
20
2
tan cot tan cotx x x x
k
xk

2
2
1 1 0
1
2
4
2 1 0
tan cot tan tan
tan
tan cot
tan tan
x x x x
x x k k
xx
xx

Bài 05.
Giải các phương trình sau:
a.
2 2 1sin cosxx
b.
6
55
2
cos sinxx
c.
3 2 2 2cos sinxx
d.
3 4 3 4 3 0sin cosxx
e.
3 2 2cos sin cosx x x
f.
7 5 3 5 7cos sin cos sinx x x x
g.
2 11 3 2 2 0sin cos sinx x x
Lời giải
a.
2 2 1sin cosxx
1 1 1
22
2 2 2
sin cosxx
1
22
44
2
cos sin sin cosxx
2
44
sin sinx



HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 106
22
22
4 4 4
2
22
22
4 4 2
,
x k x k
xk
k
xk
x k x k








b.
6
55
2
cos sinxx
6
25
42
sin x



3
5
42
sin x



5
43
sin sinx



2
52
52
4 3 60 5
12
52
5 2 5 2
4 3 12 12 5
,
k
x k x
xk
k
k
x k x k x







.
c.
3 2 2 2cos sinxx
3 1 2
22
2 2 2
cos sinxx
2
22
3 3 2
sin cos cos sinxx
2
34
sin sinx



22
22
34
12 24
55
2 2 2 2
3 4 12 24
,
xk
x k x k
k
x k x k x k






.
d.
3 4 3 4 3 0sin cosxx
3 4 3 4 3sin cosxx
3 1 1
44
2 2 2
sin cosxx
1
44
6 6 2
cos sin sin cosxx
4
66
sin sinx
42
42
66
2
4
42
42
3
32
66
,
k
xk
xk
x
k
k
xk
x
xk


.
e.
3 2 2cos sin cosx x x
HÀM SỐ LƯỢNG GIÁC
Trang 107
LÊ MINH TÂM
13
2
22
cos sin cosx x x
2
33
cos cos sin sin cosx x x
2 2 2
33
2
2
3
22
3 9 3
cos cos ,
x x k x k
x x k
k
x x k x









f.
7 5 3 5 7cos sin cos sinx x x x
7 5 3 5 3 7cos sin cos sinx x x x
7 3 7 3 5 5cos sin cos sinx x x x
7 3 7 3 5 5cos sin cos sinx x x x
1 3 3 1
7 7 5 5
2 2 2 2
cos sin cos sinx x x x
7 7 5 5
4 4 4 4
sin cos cos sin sin cos cos sinx x x x
7 5 2
44
75
3
44
7 5 2
24 6
44
sin sin ,
xk
x x k
x x k
k
x
x x k

.
g.
2 11 3 2 2 0sin cos sinx x x
2 11 3 2 2sin cos sinx x x
31
11 2 2
22
sin cos sinx x x
11 2 2
33
sin sin cos cos sinx x x
2
11 2 2
3 27 9
11 2
2 2 2
3
11 2 2
3 39 13
sin sin ,
k
x x k x
x x k
k
x x k x









Bài 06.
Giải các phương trình sau:
a.
3 2 2 3 0sin cos sinx x x
. b.
33
2sin os sin sin cosx c x x x x
.
c. d.
2 3 4 0cos cos cos cosx x x x
e.
5 2 3 0cos cos cosx x x
f.
2 5 7cos .cos cosx x x
.
g.
4 2 3 4sin .sin .sin sinx x x x
.
h.
3 2 6 4 6 0cos .cos sin .sin sin .sinx x x x x x
.
i.
22 3 18 3 14 10 0cos cos cos cosx x x x
.
k.
4 3 5 2 2 0sin sin sin .cosx x x x
.
Lời giải
cos cos2 cos3 0x x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 108
a.
3 2 2 3 0sin cos sinx x x
.
Đặt
2sin cos ,x x t t
2
21sin xt
, khi đó ta có pt:
2
3 2 1 3 0tt
2
2 3 1 0tt
1
1
2
()
()
t tm
t tm

.
+
2
1
11
2
4
2
2
sin cos sin
xk
t x x x k
xk





+
1
2
t
1
4
22
sin x



2
4
3
2
4
xk
xk
k
1
22
,sin
.
b.
33
2sin os sin sin cosx c x x x x
.
Đặt
2sin cos ,x x t t
2
21sin xt
, khi đó ta có pt:
2
2
1
11
2
t
t t t



32
2 2 0t t t
1
1
2
()
()
()
t tm
t tm
tl

+
11sin cost x x
1
4
2
sin x



2
2
2
xk
xk


k
.
+
11sin cost x x
1
4
2
sin x



2
2
2
xk
xk

k
c.
2 2 2 0cos cos cosx x x
20
42
2 2 1 0
2 1 0
2
3
cos
cos cos
cos
k
x
x
x x k
x
xk


Vậy
42
2
3
k
x
k
xk

d.
2 3 4 0cos cos cos cosx x x x
5 3 5
2 2 0
2 2 2 2
cos cos cos cos
x x x x
cos cos2 cos3 0x x x
HÀM SỐ LƯỢNG GIÁC
Trang 109
LÊ MINH TÂM
2
5
55
0
53
2
20
3
2 2 2 2
2
22
cos
cos cos cos
cos cos
k
x
x
x x x
x k k
xx
xk









.
Vậy:
2
55
2
2
k
x
x k k
xk


là nghiệm của phương trình.
e.
5 2 3 0cos cos cosx x x
5 2 3 0cos cos cosx x x
2 3 2 2 3 0cos .cos cosx x x
30
63
2 3 2 1 0
21
2
cos
cos cos ,
cos
k
x
x
x x k
x
xk



.
Vậy nghiệm của phương trình là
63
2
k
x
xk


,k
.
f.
2 5 7cos .cos cosx x x
1
7 3 7
2
cos cos cosx x x


7 3 2 7cos cos cosx x x
7 3 2
2
73
7 3 2
5
cos cos
k
x
x x k
x x k
k
x x k
x

g.
4 2 3 4sin .sin .sin sinx x x x
4 2 3 2 2 2sin .sin .sin sin .cosx x x x x
2 2 2 3 2 0sin . sin sin cosx x x x
2 2 4 2 0sin . cos cos cosx x x x
2
20
2
2 4 0
40
4
2
84
sin
sin cos
cos
k
xk
x
x
x x k
k
x
xk
x


h.
3 2 6 4 6 0cos .cos sin .sin sin .sinx x x x x x
3 6 4 2 0cos .cos sin sin sinx x x x x
3 2 6 3 0cos .cos sin .sin cosx x x x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 110
3 2 6 3 0cos cos sin sinx x x x
0
2
3 3 9 0
90
18 9
cos
cos cos cos cos
cos
xk
x
x x x x k
k
x
x


i.
22 3 18 3 14 10 0cos cos cos cosx x x x
.
22 10 3 18 14 0cos cos cos cosx x x x
2 16 6 6 16 2 0cos cos cos cosx x x x
2 16 6 3 2 0cos cos cosx x x
3
16 0
4 2 3 2 3 2 0
cos
cos cos cos
x
x x x
16
16 0
32 16
2
20
2
2
42
cos
cos
k
x
xk
x
k
x
k
xk
x




k.
4 3 5 2 2 0sin sin sin .cosx x x x
4 3 5 3 0sin sin sin sinxx x x
30
3
3 3 2 3 2 0
3
2
2
sin
sin sin cos .
cos
k
xx
x x x k
x VN

.
Bài 07.
Giải các phương trình sau:
a.
2 2 2
23sin sin sinx x x
. b.
2 2 2
3
23
2
sin sin sinx x x
.
c.
2 2 2
3 2 3 0cos sin cosx x x
d.
2 2 2 2
3 4 5 6sin cos sin cosx x x x
e.
4
8 1 4cos cosxx
. f.
44
4sin cos cosx x x
.
g.
44
sin cos cosx x x
. h.
66
1
2
sin cosxx
.
Lời giải
a.
2 2 2
23sin sin sinx x x
1 1 4 1
2 2 2
cos2 cos cos6x x x
10cos 2 +cos 4 +cos 6x x x
1 2 0cos 6 cos 3 .cosx x x
2
2 3 2 0cos cos3 .cosx x x
20cos 3 cos 3 cosx x x
HÀM SỐ LƯỢNG GIÁC
Trang 111
LÊ MINH TÂM
63
0
63
2
2
cos 3
,,
cos 3 cos
xk
xk
x
k l m
xl
xx
xm
xm


b.
2 2 2
3
23
2
sin sin sinx x x
1 1 4 1 3
2 2 2 2
cos2 cos cos6x x x
0cos 2 +cos 4 +cos 6xxx
2 6 4 0cos +cos +cosx x x
4 2 4 0cos .cos cosx x x
40
84
84
21
22
2
cos
,
cos -
xk
x
xk
kl
x
xl
xl




.
c.
2 2 2
3 2 3 0cos sin cosx x x
2
1 2 1 2
3 2 3 0
22
cos cos
cos
xx
x




2
6 2 4 2 0cos cos2xx
11
1
2
23
3
21
2
arccos
cos
,
cos
xk
x
kl
x
xl


d.
2 2 2 2
3 4 5 6sin cos sin cosx x x x
1 6 1 8 1 10 1 12
2 2 2 2
cos cos cos cosx x x x
6 8 10 12cos cos cos cosx x x x
10 6 12 8cos cos cos cosx x x x
2 8 2 2 10 2sin .sin sin .sinx x x x
2 2 10 8 0sin sin sinx x x
20
10 8
sin
sin sin
x
xx

2
2
2
10 8 2
9
10 8
9
22
, , ,
xk
xk
xk
k l m k l
x x l
xl
xl
x x km
xm

e.
4
8 1 4cos cosxx
.
Ta có
4
8 1 4cos cosxx
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 112
2
2
12
8 1 2 2 1
2
cos
cos
x
x



20
44
cos x x k k
.
f.
44
4sin cos cosx x x
.
Ta có
44
4sin cos cosx x x
2 2 2
1 2 2 2 1sin cos cosx x x
22
1
2 2 2 0
2
cos sinxx
2
3 2 1 0cos x
vô nghiệm.
g.
44
sin cos cosx x x
.
Ta có
44
sin cos cosx x x
22
sin cos cosx x x
2
12cos cosxx
2
2
1
2 1 0
1
2
3
2
cos
cos cos
cos
xk
x
xx
xk
x
k


h.
66
1
2
sin cosxx
.
Ta có
66
1
2
sin cosxx
3
2 2 2 2 2 2
1
3
2
sin cos sin cos sin cosx x x x x x
2
31
12
42
sin x
2
3
2
2
sin x
1 4 2
23
cos x

1 1 1 1
4 4 2 2
3 3 4 3
cos arccos arccosx x k x k k
HÀM SỐ LƯỢNG GIÁC
Trang 113
LÊ MINH TÂM
Dạng 04. TỔNG HỢP PHƯƠNG TRÌNH LƯỢNG GIÁC.
Bài tập.
Giải các phương trình sau:
1.
2 1 2cos cos cos sinx x x x
. 2.
2
3
1 sin cosxx
.
3.
2 3 4 0sin sin sin sinx x x x
. 4.
10 8 6 1 0cos cos cosx x x
.
5.
2
4 2 1sin cosxx
. 6.
1 2 2 0sin cos sin cosx x x x
.
7.
1 1 2 1tan sin tanx x x
. 8.
2
1 2 1sin cos sin cosx x x x
.
9.
2 1 2 2sin cos sin sin cosx x x x x
. 10.
44
2
44
cos sin sin
xx
x
.
11.
2 2 1 2 2 4sin cos sin sinx x x x
. 12.
2
2 2 7 1sin sin sinx x x
13.
2 2 2 4sin cos sin cos sin cosx x x x x x
. 14.
1
3sin cos
cos
xx
x

15.
2
2 1 2 2 3 4sin cos sin sin cosx x x x x
16.
2
2 2 3 1 3 3cos sin cos cos sinx x x x x
.
17.
22
4 3 4 3 2 3 4 0cos tan cos tanx x x x
.
18.
33
sin cos sin cosx x x x
.
19.
4
8 4 1cos cosxx
. 20.
22
3
24
2
sin sinxx
.
21.
33
43cos sin cos sinx x x x
. 22.
32
4 4 3 2 6 0sin sin sin cosx x x x
.
23.
2 2 2
2 1 2 3 2 1 0sin tan cosx x x
. 24.
2
1
21
cos cos
sin
sin cos
xx
x
xx

.
25.
2 2 1tan sinxx
. 26.
23tan tan sin .cosx x x x
.
27.
4 3 2 8sin cos cos sinx x x x
. 28.
57
2 3 1
22
sin cos sinx x x
.
29.
3 4 3tan cot sin cosx x x x
. 30.
44
1
22
sin cos
tan cot
sin
xx
xx
x

.
Lời giải
1.
2 1 2cos cos cos sinx x x x
22
12cos sin cos cos sinx x x x x
1 2 0cos sin cos cos sinx x x x x
10sin cos cos sinx x x x
2
2
2
1
42
2
0
0
4
4
sin
sin cos
cos sin
sin
xk
x
xx
xk
xx
x
xk












HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 114
Vậy phương trình có tập nghiệm
22
24
;;S k k k



.
2.
2
3
1 sin cosxx
2
2
11sin cos sinx x x
1 1 1 0sin sin cos sinx x x x


2
1
2
10
1 0 1
sin
sin cos sin cos
sin cos sin cos
xk
x
x x x x
x x x x


Đặt
22
4
sin cos sin ,t x x x t



2
2
1
12
2
sin cos sin cos
t
t x x x x
.
Khi đó
2
2
1
1
1 1 0 2 3 0
2
3
t TM
t
t t t
tl

.
Với
2
1
1 2 1
3
44
2
2
2
sin sin
xk
t x x
xk

.
Vậy phương trình có tập nghiệm
3
2 2 2
22
;;S k k k



.
3.
2 3 4 0sin sin sin sinx x x x
2 2 2 3 0sin cos sin cosx x x x
2 2 3 0cos sin sinx x x
2
2
0
2
2 3 2
23
5
2 3 2
2
cos
sin sin
xk
xk
x
k
x x k x
xx
x x k
xk



Vậy phương trình có tập nghiệm
2
2
25
;;
k
S k k



.
4.
10 8 6 1 0cos cos cosx x x
10 6 1 8 0cos cos cosx x x
2
2 8 2 2 4 0sin sin sinx x x
2
4 4 4 2 2 4 0sin cos sin sinx x x x
2 4 4 2 4 2 0sin sin cos sinx x x x
4 4 2 2 4 0sin sin cos cosx x x x
HÀM SỐ LƯỢNG GIÁC
Trang 115
LÊ MINH TÂM
4
4
40
2
20
2
4 2 2
42
4 2 2
3
sin
sin
cos cos
k
x
xk
x
k
xk
x
x
x x k
xk
xx
x x k
k
x

Vậy phương trình có tập nghiệm
43
;
kk
S



.
5.
2
4 2 1sin cosxx
2 2 2 2sin cos cosx x x
2 2 2 1 0cos sinxx
2
2 4 2
20
22
1
6 12
2
2
5
5
22
12
6
cos
sin
k
x k x
x
x k x k
x
xk
xk











Vậy phương trình có tập nghiệm
5
4 2 12 12
;;
k
S k k



.
6.
1 2 2 0sin cos sin cosx x x x
22
1 2 0sin cos sin cos cos sinx x x x x x
2
0sin cos sin cos cos sin cos sinx x x x x x x x
10sin cos sin cos cos sinx x x x x x
1 2 0sin cos cosx x x
0
1 2 0
sin cos
cos
xx
x


20
4
44
22
1
22
33
2
sin
cos
x
x k x k
k
x k x k
x











Vậy phương trình có các nghiệm
2
2
43
;x k x k k
7.
1 1 2 1tan sin tanx x x
.
Tập xác định
2
\,D k k



.
Ta có
1 1 2 1tan sin tanx x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 116
22
2
cos sin cos sin
sin cos sin cos
cos cos
x x x x
x x x x
xx




2
cos sin sin cos cos sinx x x x x x
22
cos sin cos sin cos sinx x x x x x
2 1 0cos sin cosx x x
0
2 1 0
sin cos
cos
xx
x


20
4
44
22
21
sin
cos
x
x k x k
k
x k x k
x










Vậy phương trình có các nghiệm
4
;x k x k k
8.
2
1 2 1sin cos sin cosx x x x
2
1 4 4 1sin sin cos sin cosx x x x x
2
4 4 1cos sin cos sin cos sin cosx x x x x x x
4 1 1sin cos sin sinx x x x
1 2 2 1 0sin sinxx
10
2 2 1 0
sin
sin
x
x


22
22
1
22
1
6 12
2
2
5
5
22
12
6
sin
sin
x k x k
x
x k x k k
x
xk
xk












Vậy phương trình có các nghiệm
5
2
2 12 12
;;x k x k x k k
9.
2 1 2 2sin cos sin sin cosx x x x x
2 1 2 2sin cos sin sin cos cosx x x x x x
2 1 2 2 1sin cos sin cos sinx x x x x
2 1 0sin cos sinx x x
2
1
6
2 1 0
5
2
2
0
6
0
4
4
sin
sin
cos sin
sin
xk
x
x
x k k
xx
x
xk







HÀM SỐ LƯỢNG GIÁC
Trang 117
LÊ MINH TÂM
Vậy phương trình có các nghiệm
5
22
6 6 4
;;x k x k x k k
10.
44
2
44
cos sin sin
xx
xx
2 2 2 2
2
4 4 4 4
cos sin cos sin sin
x x x x
x
2
22
cos cos
x
x



4
5
2 2 2
55
2 2 2 2
34
2 2 2
2 2 2 2 3 3
k
xx
x
x k k
k
x x k
x k k x







Vậy phương trình có các nghiệm
44
5 5 3 3
;
kk
x x k
11.
2 2 1 2 2 4sin cos sin sinx x x x
2
2 2 2 2 1 2 2sin cos sin cosx x x x
2 2 2 1 2 2cos sin cos cos sin cosx x x x x x
0
2 1 2 2
cos
sin cos sin cos
x
x x x x
0
2 2 2 2
cos
sin cos sin sin cos
x
x x x x x
0
2 2 3
cos
sin cos sin sin sin
x
x x x x x
2
32
48
5
32
4
16 2
2
0
2 2 3
4
cos
sin sin
x x k x k
k
x x k
x k x k
k
xx
x
x











12.
2
2 2 7 1sin sin sinx x x
2
7 1 2 2sin sin sinx x x
74sin sin cosx x x
2 4 3 4cos sin cosx x x
84
40
2
4 2 3 1 0
1
18 3
3
2
52
18 3
cos
cos sin
sin
k
x
x
k
x x x k
x
k
x


13.
2 2 2 4sin cos sin cos sin cosx x x x x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 118
2 2 4 2sin cos cos sin sinx x x x x
2 2 2 3sin cos cos cos sinx x x x x
0
23
sin
cos cos cos
x
x x x
0
0
11
42
2 4 2
3
2
3
2
sin
sin
cos cos
cos cos cos
k
xk
k
x
xk
x
x
xx
x x x



14.
1
3
2
sin cos ( : )
cos
x x ÐK x
x
k 
2
1
31tan
cos
x
x
22
0
3
3
3 1 1 0
3
tan
tan tan tan tan
tan
xk
x
x x x x k
kx
x

(tmđk).
15.
2
2 1 2 2 3 4sin cos sin sin cosx x x x x
2 2
2 1 2 2 3 4 2sin cos sin sin cos cosx x x x x x
22
2 1 2 2 3 4 2 1sin cos sin sin cos sinx x x x x x
2
1
2 2 3 2 2 1
sin
cos sin sin cos sin
x
x x x x x

22
1
2 2 3 2 1 2 1
sin
cos sin sin sin sin
x
x x x x x

2
2 2 2
1
2 1 2 3 2 2 1 2
sin
sin sin sin sin sin
x
x x x x x

4 3 2
1
8 4 6 5 1 0
sin
sin sin sin sin
x
x x x x

3
2
2
1
1
2
1
1 2 1 0
2
6
5
6
2
sin
sin
sin
sin sin
xk
x
x
kk
x
xx
k
x
x


 

16.
2
2 2 3 1 3 3cos sin cos cos sinx x x x x
.
Cách 1: Đặt
3cos sint x x
2 2 2 2
3 2 3 2 1 2 3cos sin sin cos cos sin cost x x x x x x x
Phương trình trở thành:
2
0
3
3
t
tt
t

.
HÀM SỐ LƯỢNG GIÁC
Trang 119
LÊ MINH TÂM
Với
0 3 0 3
3
cos sin tan ,t x x x x k k
.
Với
333 cos sinxxt 
2
3
6 2 6
2
3
cos cos ,
xk
xk
xk



.
Vậy nghiệm của phương trình là:
22
33
,,,x x k x k kk  
.
Cách 2:
2
2 2 3 1 3 3cos sin cos ( cos sin )x x x x x
2 3 2 2 3 3cos sin cos sinx x x x
2 1 3
36
cos cosxx
Đặt
6
tx
, ta được
2
0
2 1 3 2 3
3
2
cos
cos cos cos cos
cos
t
t t t t
t
Ta được nghiệm như cách 1.
17.
22
4 3 4 3 2 3 4 0cos tan cos tanx x x x
.
Điều kiện:
2
,x k k
.
Ta có
22
4 3 4 3 2 3 4 0cos tan cos tanx x x x
22
2 3 3 1 0cos .tanxx
2
2 3 0
6
2
6
31
6
cos
,
tan
xk
x
x k k
x
xk





Kết hợp điều kiện ta được nghiệm của phương trình là
2
6
,x k k
.
18.
33
sin cos sin cosx x x x
.
33
0sin sin cos cosx x x x
23
10sin sin cos cosx x x x
3 2 2
0 1 0cos cos sin cos cos cos sin cosx x x x x x x x
2
01
1 0 2
cos
cos sin cos
x
x x x
Ta có
1
2
,x k k
.
2 2 2 3sin cosxx
(Vô nghiệm vì
2
22
1 1 3
)
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 120
(Hoặc ta có
2
11
1 1 2 2
22
cos , sin cos sinx x x x
Vô nghiệm).
Vậy nghiệm của phương trình đã cho là
2
,x k k
.
19.
4
8 4 1cos cosxx
.
2
2
12
8 2 2 0
4
cos
cos
x
x
12
2 2 2
2 3 3
cos ,x x k x k k
.
Vậy nghiệm của phương trình là
3
,x k k
.
20.
22
3
24
2
sin sinxx
.
2
1 4 2 4 3 0cos sinxx
2
2 1 4 4 2 0cos cosxx
2
40
84
2 4 4 0
1
4
2
62
cos
cos cos
cos
k
x
x
x x k
k
x
x


.
Vậy nghiệm của phương trình là:
8 4 6 2
,,
kk
x x k
.
21.
33
43cos sin cos sinx x x x
.
33
4 3 4 0sin sin cos cosx x x x
Nếu
01
2
cos sinx x k x
không là nghiệm của phương trình.
Nếu
0cosx
, chia 2 vế của phương trình cho
3
cos x
ta được:
33
3 3 3 3
4 3 4 0
sin sin cos cos
cos cos cos cos
x x x x
x x x x
3
22
1
4 3 4 0
tan
tan
cos cos
x
x
xx
32
3 3 0tan tan tanx x x
2
1 3 0tan tanxx
4
1
3
3
3
tan
tan
xk
x
x k k
x
xk


.
22.
32
4 4 3 2 6 0sin sin sin cosx x x x
.
32
4 4 6 6 0sin sin sin cos cosx x x x x
2
4 1 6 1 0sin sin cos sinx x x x
HÀM SỐ LƯỢNG GIÁC
Trang 121
LÊ MINH TÂM
2
1 4 6 0sin sin cosx x x
2
1 4 6 4 0sin cos cosx x x
1
2
1
2
2
2
2
2
3
sin
cos
cos
x
xk
xk
xk
x loaïi

.
23.
2 2 2
2 1 2 3 2 1 0sin tan cosx x x
.
Điều kiện:
2
2 4 2
k
x k x k
.
Ta có
2 2 2
2 1 2 3 2 1 0sin tan cosx x x
2
2
22
3 2 0
2
cos .sin
cos
cos
xx
x
x
2 2 2
2 2 3 2
3 2 0 0
22
sin sin cos
cos
cos cos
x x x
x
xx
2 2 2 2 2
2 3 2 2 3 2 2 3sin cos sin cos tanx x x x x
23
3
tan x x k k
thoả mãn điều kiện.
Vậy nghiệm của phương tình là:
3
,x k k
.
24.
2
1
21
cos cos
sin
sin cos
xx
x
xx

.
Điều kiện:
01
4
sin cos tanx x x x k k
.
Ta có
2
1
21
cos cos
sin
sin cos
xx
x
xx

1 1 1 2 1sin sin cos sin sin cosx x x x x x
1 2 2 1 1 1 0sin sin cos sin sin cosx x x x x x
1 1 0sin sin .cos sin cosx x x x x
11
1 0 2
sin ( )
sin .cos sin cos ( )
x
x x x x

Giải
1()
:
12
2
sin ,x x k k
.
Giải
2()
:
10sin .cos sin cosx x x x
.
Đặt
2
4
sin cos sint x x x



,
22;t



2
1
2
sin .cos
t
xx

.
Ta được phương trình:
2
2
1
1 0 2 1 0 1
2
t
t t t t
.
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 122
Với
2
1 2 1
4 4 2
sin sint x x
2
2
44
2
5
2
2
44
,
xk
xk
k
xk
xk

Kết hợp điều kiện ta được nghiệm của phương trình là:
2xk
;
2
2
xk
,
k
.
25.
2 2 1tan sinxx
.
Điều kiện:
2
x k k
.
Ta có
2 2 1tan sinxx
2 2 1 2 2 0
sin
sin sin sin .cos cos
cos
x
x x x x x
x
2 2 0sin cos sin .cosx x x x
.
Đặt
2
4
sin cos sint x x x



,
22;t



2
1
2
sin .cos
t
xx

.
Ta được phương trình:
2
2
2
22
1
2
2 2 0 2 2 0
2
2 2 2
;
;
t
t
t t t
t




.
Với
2 2 1
2
2 4 2 4 2 6
sin sin sint x x
5
2
2
46
12
5 13
22
4 6 12
,
xk
xk
k
x k x k


.
Với
2 2 2 1
44
sin sint x x
22
4 2 4
,x k x k k
.
Kết hợp điều kiện ta được nghiệm của phương trình là:
5
2
12
xk
;
13
2
12
xk
,
2
4
,x k k
.
26.
23tan tan sin .cosx x x x
.
Điều kiện:
2
42
,
xk
k
k
x


Ta có:
23tan tan sin .cosx x x x
HÀM SỐ LƯỢNG GIÁC
Trang 123
LÊ MINH TÂM
2
3
2
sin sin
sin .cos
cos cos
xx
xx
xx
3 3 2sin sin .cos .cos .cosx x x x x
3 1 2 0sin cos .cos .cosx x x x
30
12
21
2
sin
cos
.cos
x
x
x
2
3
3
3
21
3
2 2 2 0
22
,
cos
cos cos
cos
k
x
k
xk
x
k
xk
x
xx
xk
x loaïi

Kiểm tra điều kiện suy ra nghiệm phương trình là
3
,
k
xk
.
27.
4 3 2 8sin cos cos sinx x x x
.
Ta có
4 3 2 8sin cos cos sinx x x x
2 3 2 2 8sin .cos sinx x x
3 4 8sin sinxx
4
4
40
4 3 2 4 0
42
3
24 2
6
4
2
42
24 2
6
sin
sin cos ,
cos
k
k
x
x
x
k
x x x k
xk
x
k
x
xk

28.
57
2 3 1
22
sin cos sinx x x
.
Ta có:
57
2 3 1
22
sin cos sinx x x
2 3 1cos sin sinx x x
2
0
1 2 2 1 0
1
2
2
sin
sin sin ,
sin
xk
x
x x k
x
xk

29.
3 4 3tan cot sin cosx x x x
Điều kiện:
2
,
k
xk
.
Ta có
3 4 3tan cot sin cosx x x x
3 4 3
sin cos
sin cos
cos sin
xx
xx
xx
22
3 4 3sin cos sin cos sin cosx x x x x x
3 3 2 2 0sin cos sin cos sinx x x x x
HÀM SỐ LƯỢNG GIÁC
LÊ MINH TÂM
Trang 124
3
3
30
2
3
2
3 2 2
3
42
93
tan
sin cos
,
sin sin
sin cos sin
xk
x
xx
x k k
xx
x x x
k
x








.
30.
44
1
22
sin cos
tan cot
sin
xx
xx
x

Điều kiện:
2
,
k
xk
.
Ta có
44
1
22
sin cos
tan cot
sin
xx
xx
x

4422
sin cos sin cosxxxx
2
2 2 2 2
21sin cos sin .cosx x x x
22
20sin .cosxx
20sin x
(loại)
Vậy phương trình đã cho vô nghiệm.
------------------ HẾT------------------
| 1/124
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LÊ MINH TÂM CHƯƠNG 01
HÀM SỐ LƯỢNG GIÁC
TÀI LIỆU LƯU HÀNH NỘI BỘ HÀM SỐ LƯỢNG GIÁC
§1. HÀM SỐ LƯỢNG GIÁC .................................................................................................................... 4
I. ÔN TẬP ........................................................................................................................................................ 4
1.1. Các hệ thức cơ bản. ............................................................................................................................... 4
1.2. Cung liên kết. ......................................................................................................................................... 4
1.3. Công thức cộng. ..................................................................................................................................... 4
1.4. Công thức nhân và hạ bậc. .................................................................................................................. 4
1.5. Công thức biến đổi tổng thành tích. ................................................................................................... 5
1.6. Công thức biến đổi tích thành tổng. ................................................................................................... 5
1.7. Bảng giá trị lượng giác của một số góc đặc biệt. ............................................................................. 5
II. HÀM SỐ y = sinx VÀ HÀM SỐ y = cosx............................................................................................... 5
III. HÀM SỐ y = tanx Và HÀM SỐ y = cotx. ............................................................................................. 8
IV. BÀI TẬP. .................................................................................................................................................. 10
Dạng 01. TẬP XÁC ĐỊNH. ...................................................................................................................... 10
Dạng 02. TÍNH CHẴN LẺ. ...................................................................................................................... 13
Dạng 03. CHU KỲ HÀM SỐ. .................................................................................................................. 15
Dạng 04. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.................................................................. 17
§2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN ....................................................................................... 21
I. PHƯƠNG TRÌNH SinX = a VÀ PHƯƠNG TRÌNH CosX = a. ......................................................... 21
II. PHƯƠNG TRÌNH TanX = a VÀ PHƯƠNG TRÌNH CotX = a ....................................................... 23
III. BÀI TẬP. .................................................................................................................................................. 26
§3. PHƯƠNG TRÌNH BẬC HAI THEO HÀM LƯỢNG GIÁC ................................................................... 32
I. DẠNG CƠ BẢN. ....................................................................................................................................... 32
II. BÀI TẬP. ................................................................................................................................................... 33
§4. PHƯƠNG TRÌNH BẬC NHẤT VỚI HÀM SIN - COS ....................................................................... 43
I. DẠNG CƠ BẢN. ....................................................................................................................................... 43
II. BÀI TẬP. ................................................................................................................................................... 44
§4. PHƯƠNG TRÌNH ĐẲNG CẤP ........................................................................................................ 54
I. DẠNG CƠ BẢN. ....................................................................................................................................... 54
II. BÀI TẬP. ................................................................................................................................................... 55 LÊ MINH TÂM Trang 2 HÀM SỐ LƯỢNG GIÁC
§5. PHƯƠNG TRÌNH ĐỐI XỨNG ........................................................................................................ 62
I. DẠNG CƠ BẢN. ....................................................................................................................................... 62
II. BÀI TẬP. ................................................................................................................................................... 62
§6. CÁC LOẠI PHƯƠNG TRÌNH KHÁC ................................................................................................ 68
I. BIẾN ĐỔI TÍCH THÀNH TỔNG. ........................................................................................................ 68
1.1. Ví dụ minh họa. ................................................................................................................................... 68
1.2. Bài tập rèn luyện. ................................................................................................................................ 68
II. BIẾN ĐỔI TỔNG THÀNH TÍCH. ....................................................................................................... 70
2.1. Ví dụ minh họa. ................................................................................................................................... 70
2.2. Bài tập rèn luyện. ................................................................................................................................ 70
III. TỔNG HỢP CÁC PHƯƠNG PHÁP. ................................................................................................. 73
3.1. Ví dụ minh họa. ................................................................................................................................... 73
3.2. Bài tập rèn luyện. ................................................................................................................................ 74
IV. PHƯƠNG TRÌNH CÓ ĐIỀU KIỆN. .................................................................................................. 75
4.1. Ví dụ minh họa. ................................................................................................................................... 76
4.2. Bài tập rèn luyện. ................................................................................................................................ 77
§7. TỔNG ÔN CHƯƠNG .......................................................................................................................91
Dạng 01. TẬP XÁC ĐỊNH. ...................................................................................................................... 91
Dạng 02. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.................................................................. 93
Dạng 03. PHƯƠNG TRÌNH LƯỢNG GIÁC. ...................................................................................... 96
Dạng 04. TỔNG HỢP PHƯƠNG TRÌNH LƯỢNG GIÁC. ............................................................ 113 Trang 3 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC CHƯƠNG
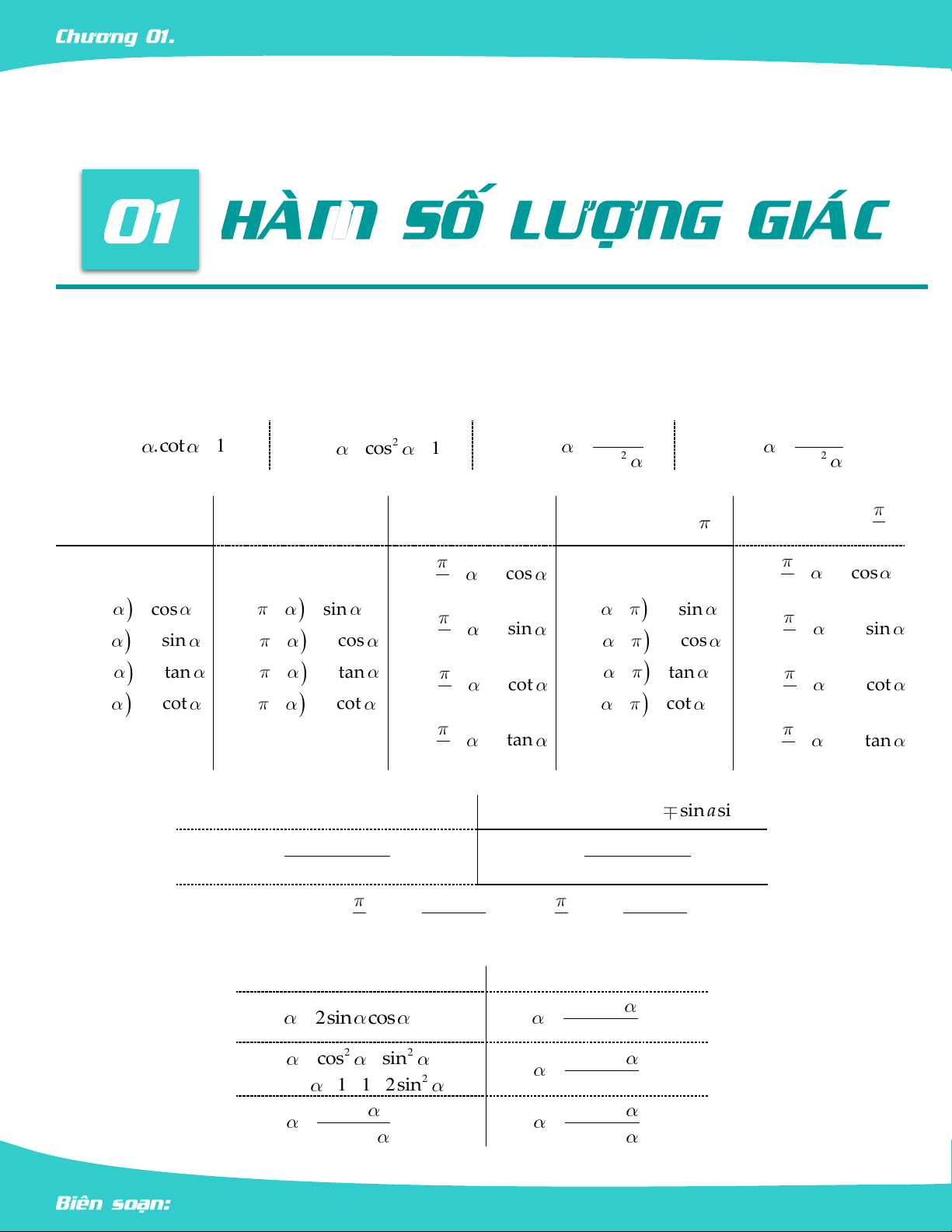
§1. HÀM SỐ LƯỢNG GIÁC I. ÔN TẬP
1.1. Các hệ thức cơ bản. 1 1 tan .cot 1 2 2 sin  cos  2 1 1 tan  2 1 cot  2 cos 2 sin
1.2. Cung liên kết.
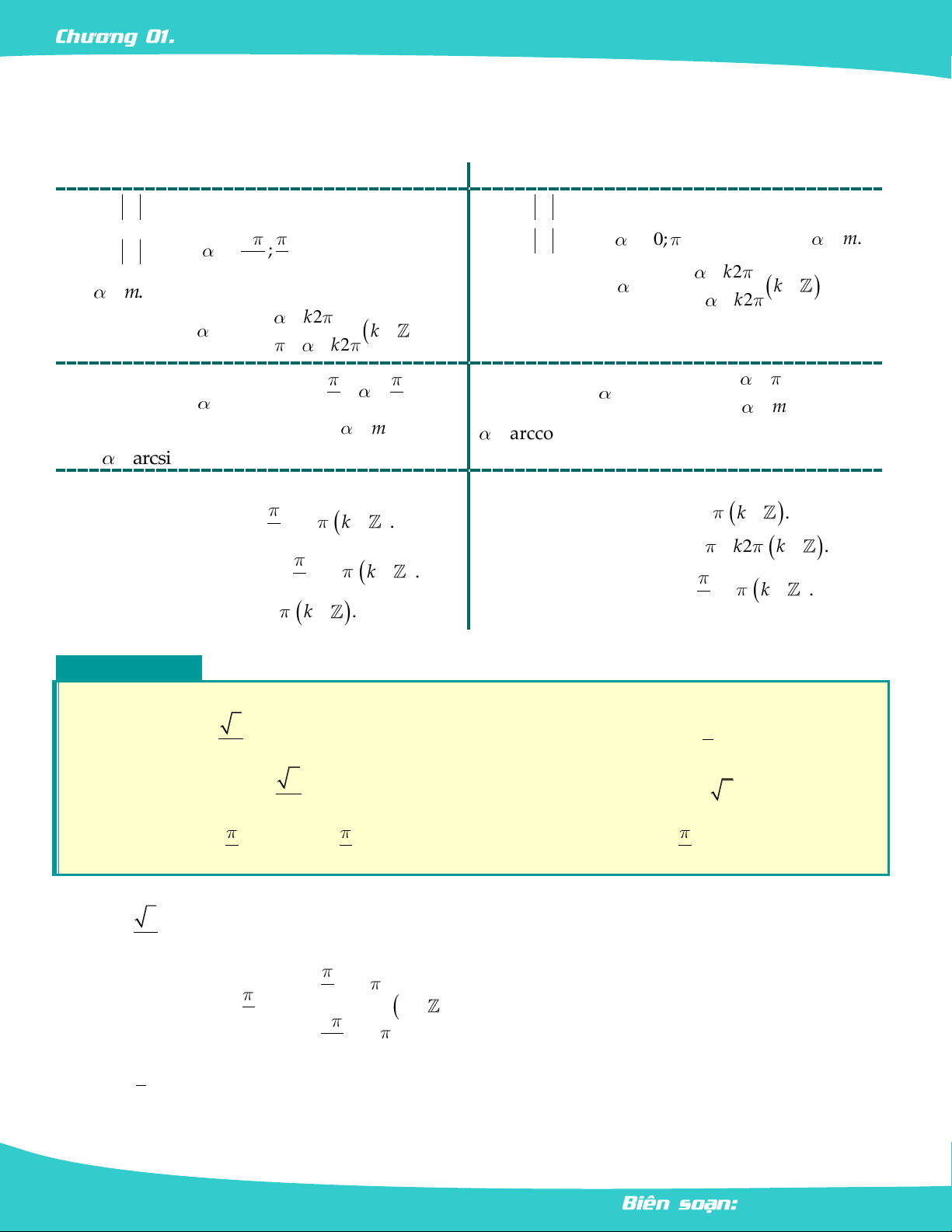
Cung đối nhau Cung bù nhau Cung phụ nhau Cung hơn kém Cung hơn kém 2     sin     cos sin     cos  2   2  cos    cos sin     sin   sin      sin   cos     sin cos      sin sin     sin cos      cos  2  cos      cos  2  tan     tan tan      tan   tan     tan   tan     cot tan      cot cot     cot cot      cot  2  cot     cot  2      cot     tan cot      tan  2   2 
1.3. Công thức cộng.
sina b  sin acosb  sinbcos a
cosa b  cos acosb sin asin b   tan a  tan b a b tan a tan b tan 
tan a b  1 tan . a tan b 1 tan . a tan b   1 tan x   1 tan x Hệ quả: tan  x    và tan  x    .  4  1 tan x  4  1 tan x
1.4. Công thức nhân và hạ bậc. Nhân đôi Hạ bậc 1 cos 2 sin2  2sin cos 2 sin  2 2 2 cos 2  cos sin 1 cos 2 2 cos  2 2  2cos 11 2sin 2 2 tan 1 cos 2 tan 2  2 tan  2 1 tan 1 cos 2 LÊ MINH TÂM Trang 4 HÀM SỐ LƯỢNG GIÁC 2 cot 1 1 cos 2 cot 2  2 cot  2 cot 1 cos 2
1.5. Công thức biến đổi tổng thành tích. a b a b a b a b
cos a  cos b  2cos .cos
cos a  cos b  2  sin .sin 2 2 2 2 a b a b a b a b
sin a  sin b  2sin .cos
sin a  sin b  2cos .sin 2 2 2 2
sin a b
sin a b
tan a  tan b
tan a  tan b  cos . a cos b cos . a cos b
sin a b
sin b a
cot a  cot b
cot a  cot b  sin . a sin b sin . a sin b Đặc biệt        
sin x  cos x  2 sin x   2 cos x     
sin x  cos x  2 sin x    2 cos x       4   4   4   4 
1.6. Công thức biến đổi tích thành tổng. 1 cos . a cos b  cos 
abcosab 2 1 sin . a sin b  cos 
abcosab 2 1 sin . a cos b  sin 
absinab 2
1.7. Bảng giá trị lượng giác của một số góc đặc biệt. Đơn vị o 0 o 30 45o o 60 o 90 o 120 135o o 150 o 180 o 360 độ Đơn vị 2 3 5 0 2 radian 6 4 3 2 3 4 6 1 1 sin 2 3 3 2 0 1 0 0 2 2 2 2 2 2 1 1 cos 3 2 1 0  2  3  1 1 2 2 2 2 2 2 tan 3 0 1 3 KXĐ  3  3 1  0 0 3 3 cot 3 3 KXĐ 3 1 0  1  3 KXĐ KXĐ 3 3
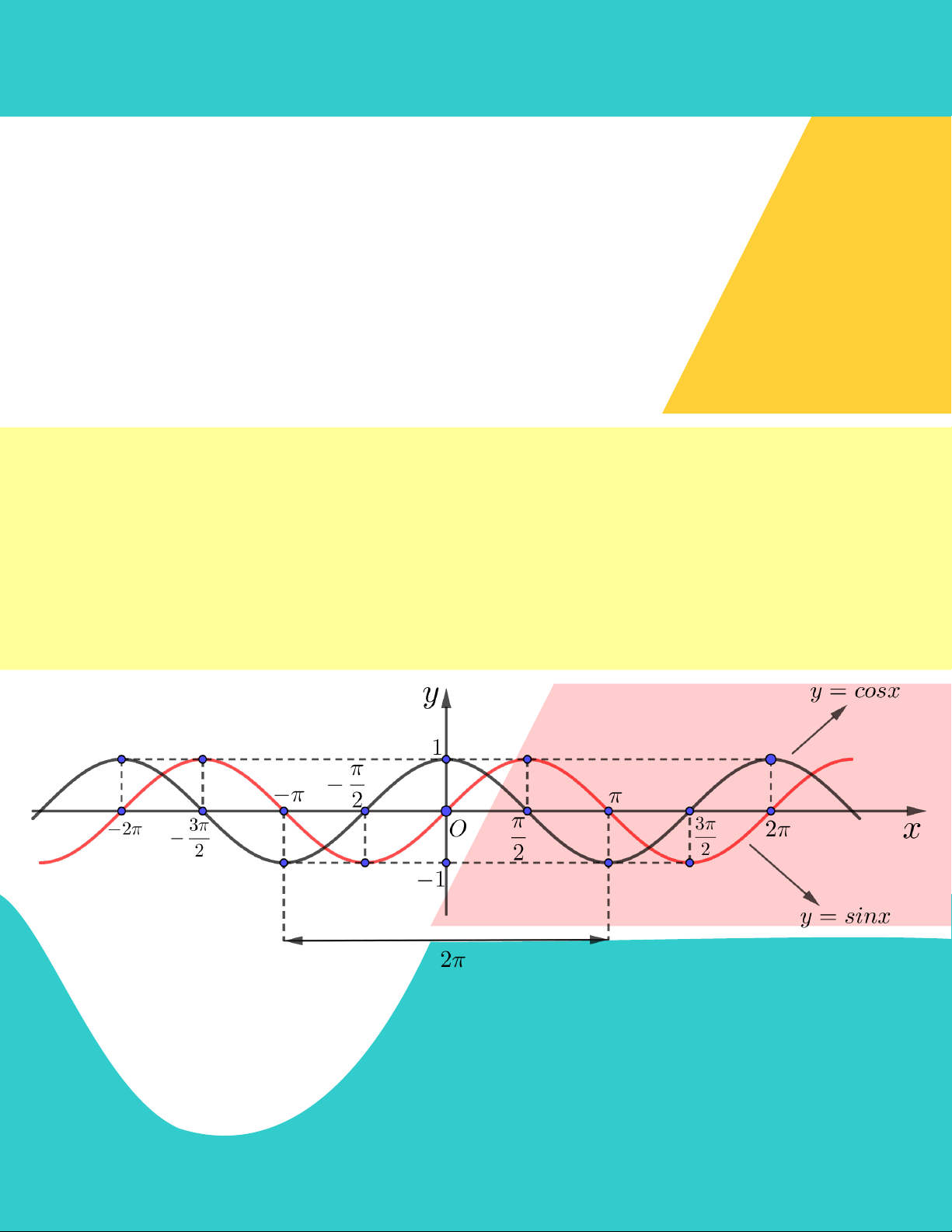
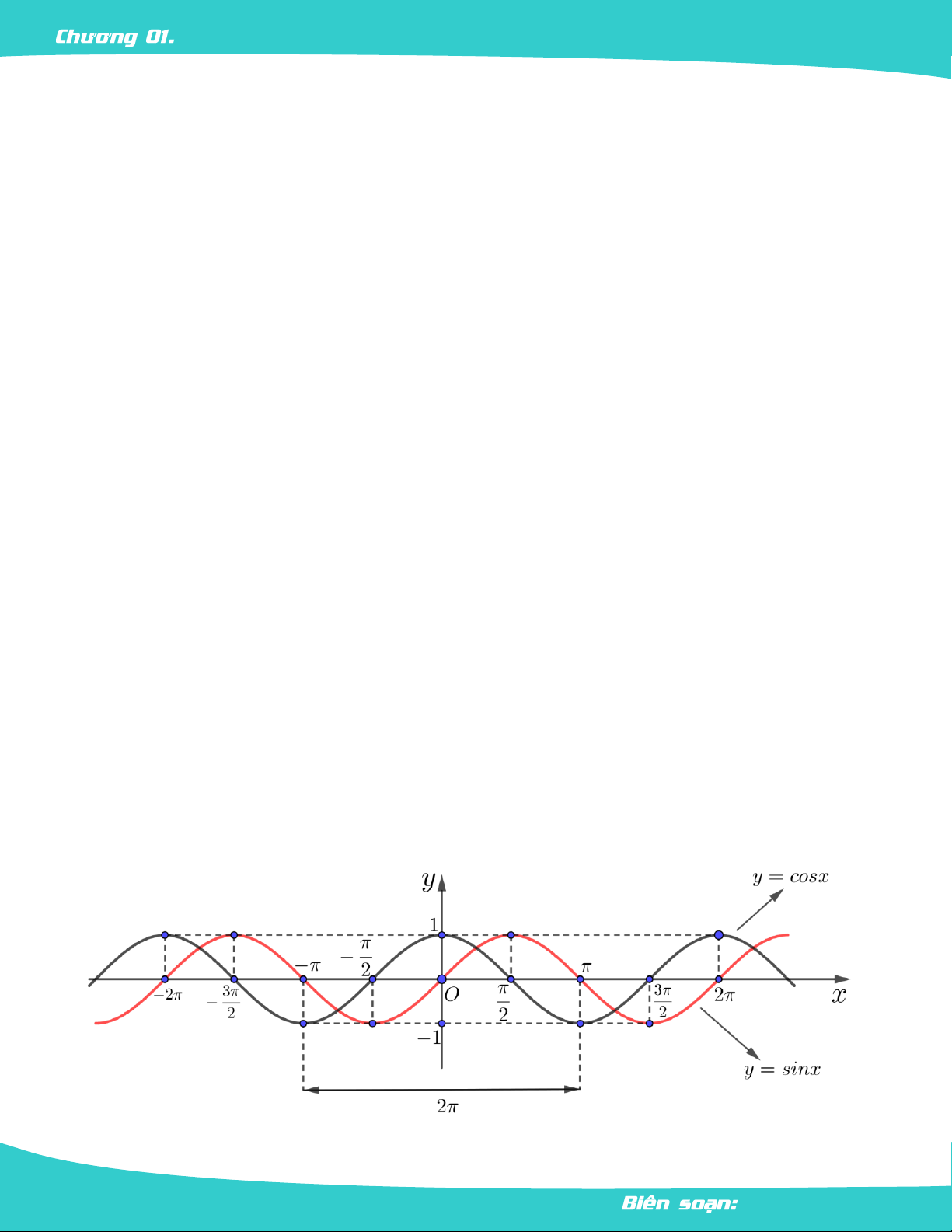
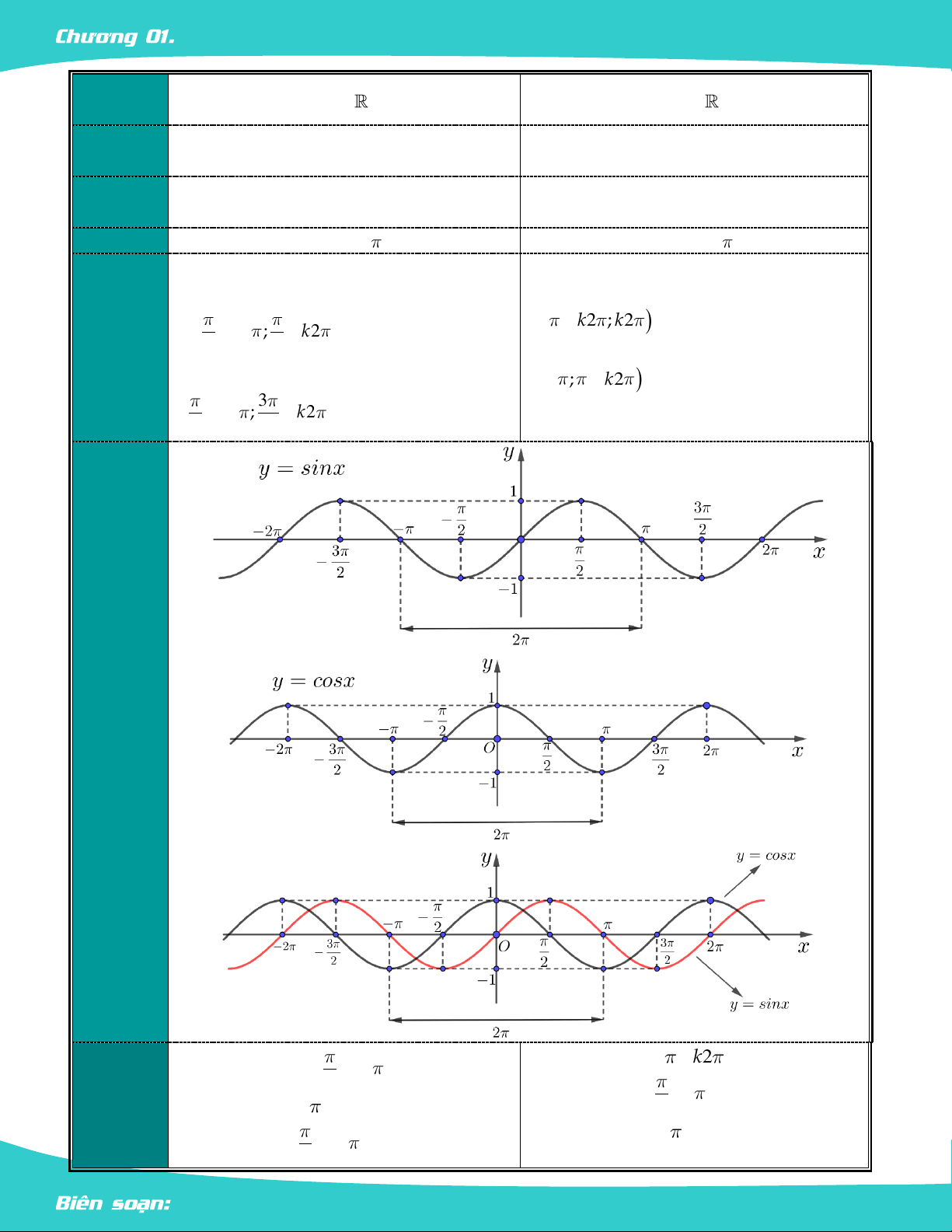
II. Hàm Số y = sinx Và Hàm Số y = cosx.
Hàm số y  sin x
Hàm số y  cos x
Quy tắc đặt tương ứng mỗi số thực x
Quy tắc đặt tương ứng mỗi số thực x 1. Định
với sin của góc lượng giác có số đo x
với cos của góc lượng giác có số đo x nghĩa:
rađian được gọi là hàm số sin , kí hiệu
rađian được gọi là hàm số cos , kí hiệu y  sin x . y  cos x . Trang 5 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 2. Tập D D xác định: 3. Tập  1  ;1    1  ;1   giá trị: 4. Tính Là hàm số lẻ. Là hàm số chẵn. chất hàm 5. Chu kỳ Chu kì 2 . Chu kì 2 . Hàm số Hàm số
+ Đồng biến trên mỗi khoảng
+ Đồng biến trên mỗi khoảng  
 k2 ;k2 . 6. Đơn   k2 ;   k2  .  2 2 
+ Nghịch biến trên mỗi khoảng điệu
+ Nghịch biến trên mỗi khoảng
k2 ;  k2 .  3   k2 ;   k2  .  2 2  7. Đồ thị cos x  1
  x   k2 . sin x  1
  x    k2 . 2 8. Giá trị
cos x  0  x   k .
sin x  0  x k . 2 đặc biệt
cos x 1 x k2 .
sin x  1  x   k2 . 2 LÊ MINH TÂM Trang 6 HÀM SỐ LƯỢNG GIÁC Chú ý:
+) Hàm số y  sin u
 x , y  cos u
 x xác định  ux có nghĩa. +) 1
  sin x,cos x 1 ; 2 2
0  sin x,cos x  1; 0  sin x , cos x  1. Ví dụ 01.
Tìm tập xác định của các hàm số sau: 3x 1
a. y  sin 4x . b. y  sin .
c. y  cos x  2 . 2 x 1 Lời giải
a. y  sin 4x .
Hàm số xác định với mọi số thực x nên hàm số có tập xác định D  . 3x 1 b. y  sin . 2 x 1 Hàm số xác định khi 2
x 1  0  x  1  .
Tập xác định D   \   1 .
c. y  cos x  2 .
Hàm số xác định khi x  2  0  x  2  .
Tập xác định D   2  ;   . Ví dụ 02.
Xét tính chẵn lẻ của các hàm số sau: 2 1 sin 2x a. 2
y  3cos x  sin x . b. y  1 . cos 3x Lời giải a. 2
y  3cos x  sin x .
Hàm số có tập xác định D  .
Lấy x ta có x
  và yx  cosx 2  sin x 2 3
 3cos x  sin x yx.
Do đó hàm số là hàm chẵn . 2 1 sin 2x
b. y  1cos3x k2
Hàm số xác định khi cos3x  1
  3x   k2  x   k . 3 3  k2 
Tập xác định D  \  k .  3 3 
Ta thấy nếu xD  cos3x  1  mà cos 3
x  cos3x  cos 3  x  1
  xD 2 2 1 sin 2  x 1 sin 2x
Khi đó y x      y x . 1 cos  3  x   1 cos 3x
Do đó hàm số là hàm chẵn . Ví dụ 03.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: Trang 7 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  
a. y  4  3sin5x .
b. y  2 sin 2x  cos 2x 1.
c. y  sin x, x   ;   .  4 4  Lời giải
a. y  4  3sin5x .
Hàm số có tập xác định D  . Ta có 1   sin x 1 3   3  sin x  3  3
  4  43sin x  3 4 1 y  7 .
Do đó: max y  7  sin x  1
  x    k2 k  . 2
min y  1  sin x  1  x
k2 k  2  2 1 
b. y  2 sin 2x  cos 2x 1  3  sin 2x  cos 2x  1   3 3   1 2 Đặt sin  ; cos   0;  ta có 3 3
y  3 cos sin 2x  sin cos 2x 1  3 sin2x   1 Ta có: 1
  sin2x   1  3  3 sin2x    3   3 1 3 sin2x  1 3 1
Do đó: max y  1 3 đạt được khi sin2x   1
min y  1 3 đạt được khi sin2x    1  .  
c. y  sin x, x   ;    4 4 
Hàm số y  sin x đồng biến trên khoảng  ;  nên       2 2 Với x   ;  sin   sin x  sin    y        .  4 4   4   4  2 2 2 2 Do đó max y
đạt được khi x  ; min y
đạt được khi x   . 2 4 2 4
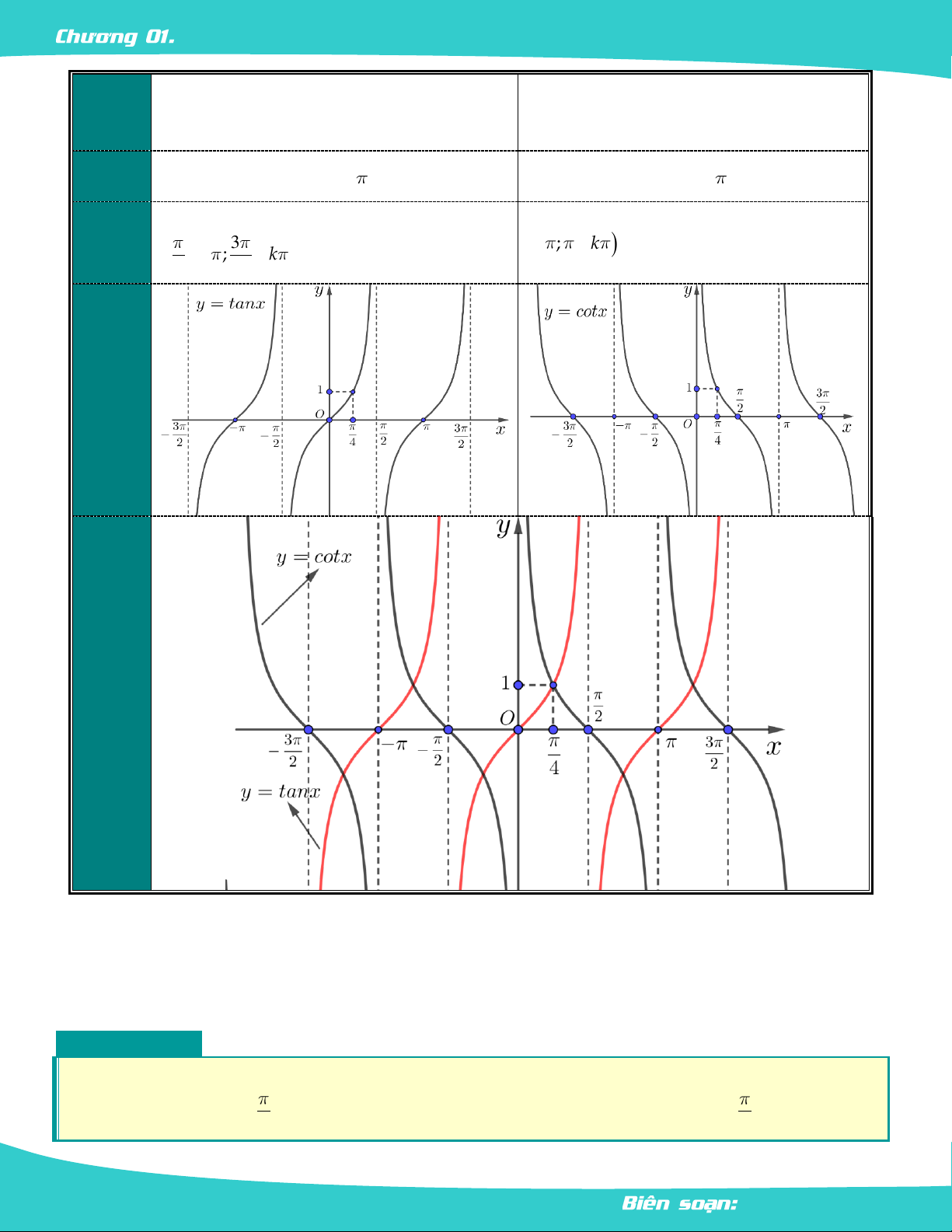
III. Hàm Số y = tanx Và Hàm Số y = cotx.
Hàm số y  tan x
Hàm số y  cot x
Hàm số tang là hàm số được xác định bởi
Hàm số côtang là hàm số được xác định 1. Định sin x cos x công thức y
cosx  0 , ký hiệu
bởi công thức y  sinx  0 , ký nghĩa: cos x sin x y  tan x .
hiệu y  cot x . 2. Tập   xác D
\  k , k   D   \ k , k    2  định: 3. Tập  1  ;1    1  ;1   giá trị: LÊ MINH TÂM Trang 8 HÀM SỐ LƯỢNG GIÁC 4. Tính chất Là hàm số lẻ. Là hàm số lẻ. hàm 5. Chu Chu kì . Chu kì . kỳ
Hàm số đồng biến trên mỗi khoảng Hàm số nghịch biến trên mỗi khoảng 6. Đơn  3 
k ; k  . điệuk ;   k  .  2 2  7. Đồ thị Chú ý:
- Hàm số y  tan u
 x xác định khi và chỉ khi cosux  0 .
- Hàm số y  cot u
 x xác định khi và chỉ khi sinux  0 . Ví dụ 04.
Tìm tập xác định của các hàm số sau:    
a. y  tan x    .
b. y  cot x    .  4   3  Lời giải Trang 9 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  
a. y  tan x    .  4   
Hàm số xác định khi cos x
 0  x    k x   k k      4  4 2 4  
Do đó hàm số có tập xác định D
\  k k   .  4   
b. y  cot x     3   
Hàm số xác định khi sin x
 0  x   k x   k k      3  3 3  
Do đó hàm số có tập xác định D
\  k k   .  3  IV. BÀI TẬP.
Dạng 01. TẬP XÁC ĐỊNH.
Phương pháp giải: 1 1.
f x xác định  f x  0 ;
xác định  f x  0 . f x
2. y  sin  f x xác định  f x xác định.
3. y  cos  f x xác định  f x xác định.
4. y  tan  f x xác định  f x   k k   . 2
5. y  cot  f x xác định  f x  k k   . Bài 01.
Tìm tập xác định của các hàm số sau: 1 1. y
2. y  1 sin x 2 cos x  3 4  cos x 1 cos x 3. y 4. y  2 4 sin x 1 2 cos x Lời giải 1
1. y  2cosx 3 3
Điều kiện: cos x
x    k2 ,k  2 6  
Tập xác định của hàm số là D
\  k2 , k   .  6 
2. y  1 sin x
Điều kiện: 1 sin x  0  sin x    1 x    LÊ MINH TÂM Trang 10 HÀM SỐ LƯỢNG GIÁC
Tập xác định của hàm số là D  . 4  cos x 3. y  2 4 sin x 1 x   k2  6   5 x   k2 1  Điều kiện: 2 6
4 sin x 1  0  sin x     , k  . 2
x    k2  6  7 x   k2  6  5 7 
Tập xác định của hàm số là D  \  k2 ,
k2 ,  k2 ,  k2 ,k   .  6 6 6 6  1 cos x 4. y  2 cos x 1 cos x 1   cos x  0 Điều kiện:  0  
x   k ,k  2 cos x cos x  0 2  
Tập xác định của hàm số là D
\  k ,k   .  2  Bài 02.
Tìm tập xác định của các hàm số sau: 1 cos x 2 sin x 1. y 2. y  cot x  3 3 tan x 1     3. y  cot  2  x
4. y  tan 2x     3   4 
5. y  tan x  cot x 6. 2 y  1 tan x Lời giải 1 cos x
1. y  cotx 3  co  t x   3
x    k Điều kiện:    6 , k  sin x  0 x   k  
Tập xác định của hàm số là D
\  k , k , k   .  6  2 sin x
2. y  3tanx1   1   tan x k x   Điều kiện: 6  3   , k   cos x   0 x   k  2 Trang 11 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  
Tập xác định của hàm số là D
\  k ,  k ,k   .  6 2    3. y  cot  2  x   3    k Điều kiện: sin
 2x  0   2x k x   , k     3  3 6 2  k
Tập xác định của hàm số là D  \  , k   .  6 2   
4. y  tan 2x     4    k
Điều kiện: cos 2x
 0  2x    k x   , k     4  4 2 8 2  k
Tập xác định của hàm số là D  \  , k   .  8 2 
5. y  tan x  cot x cos x  0 k Điều kiện: 
 sin 2x  0 2x k x  , k  sin x  0 2  k
Tập xác định của hàm số là D  \ , k   .  2  6. 2 y  1 tan x
Điều kiện: cos x  0  x   k ,k  . 2  
Tập xác định của hàm số là D
\  k , k   .  2  LÊ MINH TÂM Trang 12 HÀM SỐ LƯỢNG GIÁC
Dạng 02. TÍNH CHẴN LẺ.
Phương pháp giải:
1. Tập xác định D : x  Dx  D ..
2. Xét f x và f x.
– Nếu f x  f x , x
 D thì hàm số chẵn trên D .
– Nếu f x   f x , x
 D thì hàm số lẻ trên D . Bài tập.
Xét tính chẵn, lẻ của hàm số: sin . x cos x sin x  tan x 1. 4
y  sin x ; 2. y ; 3. y ; tan x  cot x sin x  cot x 4 cos x 1   4. y ;
5. y  cos x    ;
6. y  tan x ; 3 sin x  4  cos x
7. y  sin x  2tan x; 8. y . 2 1 sin x Lời giải 1. 4 y  sin x
Tập xác định D  , x
 D  xD.
Đặt y f x 4  sin x . 4
Ta có: f x 4 
x   x 4 sin sin
 sin x f x.
Vậy hàm số đã cho là hàm số chẵn. sin . x cos x
2. y  tanxcotx  
Tập xác định D
\k , k   , x
  D  xD .  2  x x
Đặt y f x sin .cos  . tan x  cot x
sin x .cos x sin . x cos x sin . x cos x
Ta có: f x         f x .
tan x  cot x  
 tan x  cot x tan x  cot x
Vậy hàm số đã cho là hàm số chẵn. sin x  tan x
3. y  sinxcotx       1 5 
Tập xác định D  \k ,  arccos 
  m2 , k,m , x
  D  xD . 2  2      x x
Đặt y f x sin tan  . sin x  cot x
sin x  tan x
sin x  tan x sin x  tan x
Ta có: f x         f x .
sin x  cot x  
sin x  cot x sin x  cot x
Vậy hàm số đã cho là hàm số chẵn. Trang 13 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 4 cos x 1 4. y  3 sin x
Tập xác định D  
\ k , k  , x
 D  xD . cos x 1
Đặt y f x 4  . 3 sin x 4 4 cos x 1 cos x 1
Ta có: f x       f x . 3 sin x 3   sin x
Vậy hàm số đã cho là hàm số lẻ.  
5. y  cos x     4 
Tập xác định D  , x
 D  xD.  
Đặt y f x  cos x    .  4     
Ta có: f x  cos x   cos x      .  4   4 
Ta thấy f x  f x , f x   f x .
Vậy hàm số đã cho là hàm số không chẵn, không lẻ.
6. y  tan x  
Tập xác định D
\  k  , x
  D  xD .  2 
Đặt y f x  tan x .
Ta có: f x  tan x  tan x f x .
Ta thấy f x  f x , f x   f x .
Vậy hàm số đã cho là hàm số chẵn.
7. y  sin x  2tan x  
Tập xác định D
\  k  , x
  D  xD .  2 
Đặt y f x  sin x  2tan x .
Ta có: f x  sinx  2tanx  sin x  2tan x  sin x  2tan x   f x .
Vậy hàm số đã cho là hàm số lẻ. cos x 8. y  2 1 sin x
Tập xác định D  , x
 D  xD. cos x
Đặt y f x  . Ta có: 2 1 sin x
  cosx cos x f x  
f x . Vậy hàm số đã cho là hàm số chẵn. 2 1 sin x 2   1 sin x LÊ MINH TÂM Trang 14 HÀM SỐ LƯỢNG GIÁC
Dạng 03. CHU KỲ HÀM SỐ.
Phương pháp giải:
Định nghĩa: Hàm số y f x xác định trên tập D được gọi là hàm số tuần hoàn nếu có số T  0 sao
cho với mọi xD ta có x T D và f x T  f x .
Nếu có số T dương nhỏ nhất thỏa mãn các điều kiện trên thì hàm số đó được gọi là hàm số tuần hoàn với chu kì T .  Lưu ý: . 2
Hàm số f x  asinux bcos vx c ( với u,v ) là hàm số tuần hoàn với chu kì T   ( u,vu , v
là ước chung lớn nhất).
 Hàm số f x  .atanux .bcotvx c (với u,v ) là hàm tuần hoàn với chu kì T   . u , v
y f x có chu kỳ T ; y f x có chu kỳ T 2   1   1 2
Thì hàm số y f x f x có chu kỳ T là bội chung nhỏ nhất của T và T . 1   2   1 2
y  sinx: Tập xác định D R ; tập giá trị T   1  ;1 
 ; hàm lẻ, chu kỳ T  2 . 0 2
y  sin ax b có chu kỳ T  0 a
y  sin  f x xác định  f x xác định.
y  cosx : Tập xác định D R ; Tập giá trị T   1  , 1 
 ; hàm chẵn, chu kỳ T  2 . 0 2
y  cos x có chu kỳ T  0 a
y  cos  f x xác định  f x xác định.   
y  tan x : Tập xác định D
\  k , k Z ; tập giá trị T
, hàm lẻ, chu kỳ T  .  2  0
y  tanax b có chu kỳ T  0 a
y  tan  f x xác định  f x 
k k  2
y  cot x : Tập xác định D   \ k , k  
Z ; tập giá trị T
, hàm lẻ, chu kỳ T  . 0
y  cot ax b có chu kỳ T  0 a
y  cot  f x xác định  f x  k k   .
Phương pháp chứng minh.
x T D
Tập xác định hàm số D, x   D   . x T   D
 1 Chứng minh: f xT  f x, x  D. Trang 15 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  x T   D
2 Giả sử có số T sao cho 0  T  T thỏa   vô lý. f
 x T  f x , x    D
Vậy hàm số f x là hàm tuần hoàn với chu kỳ T . Bài 01.
Chứng minh rằng y  sin 2x tuần hoàn có chu kỳ . Lời giải
Hàm số y f x  sin 2x có tập xác định . Chọn số L   0
Ta có: x  x   và f x L  sin 2
 x    sin 
2x 2   sin2x f x.
Vậy hàm số f x là hàm số tuần hoàn.
Ta sẽ chứng minh chu kỳ của nó là .
Thật vậy, giả sử hàm số f x  sin 2x có chu kỳ A mà 0  A  , khi đó ta có:
sin 2 x A  sin 2x, x          Cho x  thì sin 2  
A   sin  sin  2  A  1  4   4  2   2 
cos2A 1: vô lý, vì 0  2A  2
Vậy chu kì tuần hoàn của hàm số y  sin 2x là . Bài 02.  
Chứng minh rằng y  tan x  
 tuần hoàn có chu kỳ .  4  Lời giải    
Hàm số y f x  tan x  
 có tập xác định D  \  k , k   .  4   4 
Chọn số L   0    
Ta có: x  x   và f x L  tan x    tan x       f x .  4   4 
Vậy hàm số f x là hàm số tuần hoàn.
Ta sẽ chứng minh chu kỳ của nó là .  
Thật vậy, giả sử hàm số y  tan x  
 có chu kỳ A mà 0  A  , khi đó ta có:  4      tan x    tan x  , x       D  4   4   
Cho x  0 thì tan  A   1 
vô lý vì 0  A  .  4   
Vậy chu kì tuần hoàn của hàm số y  tan x    là .  4  LÊ MINH TÂM Trang 16 HÀM SỐ LƯỢNG GIÁC
Dạng 04. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.
Phương pháp giải:
Sử dụng tính chất 1   sinx 1 và 1   cosx 1. Bài tập.
Tìm GTNN và GTLN của các hàm số:
1. y  2 cos x  3  4 ; 2. 2
y  cos x  6sin x  3 ; 2 3. y ; 4. 4 2
y  sin x  2cos x  5; 2
cos x  4cos x  5 1 5. 2
y  sin x  2sin x  5; 6. y ; 2 sin x  3 1 7. 4 2
y  cos x  2sin x 1; 8. y ; 2
sin x  2cos x  5
9. y  2  cos 2x ; 10. 4 4
y  sin x  cos x . Lời giải
1. y  2 cos x  3  4 . 3 
Điều kiện xác định: 2cos x  3  0  cos x   x . 2 Ta có: 1   cosx 1  2
  2cosx  2 1 2cosx3  5 1 2cosx3  5  3
  2cosx3  4  5  4
Vậy GTLN của hàm số là 5  4 khi cos x 1  x k2 k   , GTNN của hàm số là 3  khi cos x  1
  x   k2 k . 2. 2
y  cos x  6sin x  3 . Ta có: 2
y  cos x  sin x    2  sin x 2 6 3 1
 6sin x  3  sin x  6sin x  4 .
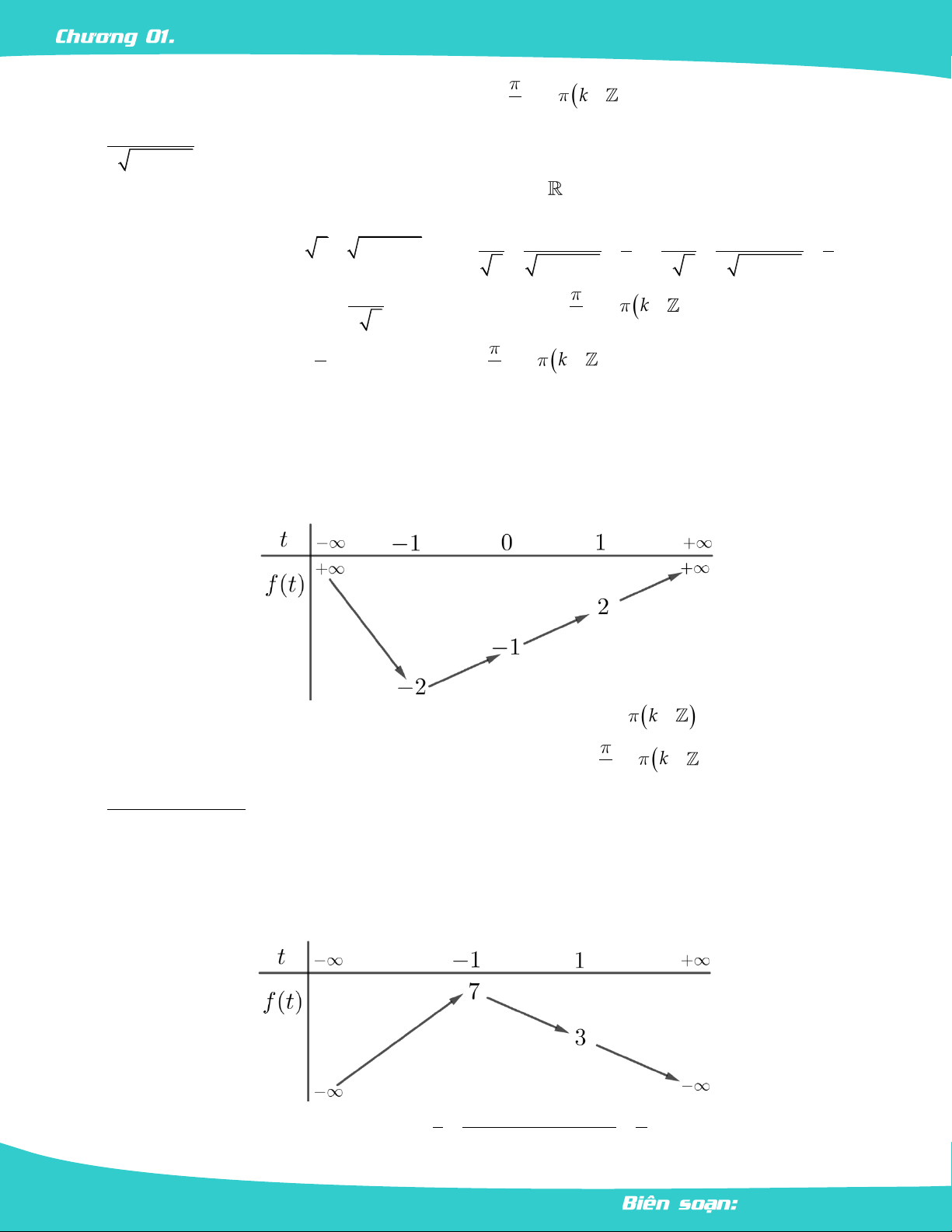
Đặt t  sin x,t   1  ;1 
 . Khi đó: y f t 2  t
  6t  4 xác định với t  1  ;1  
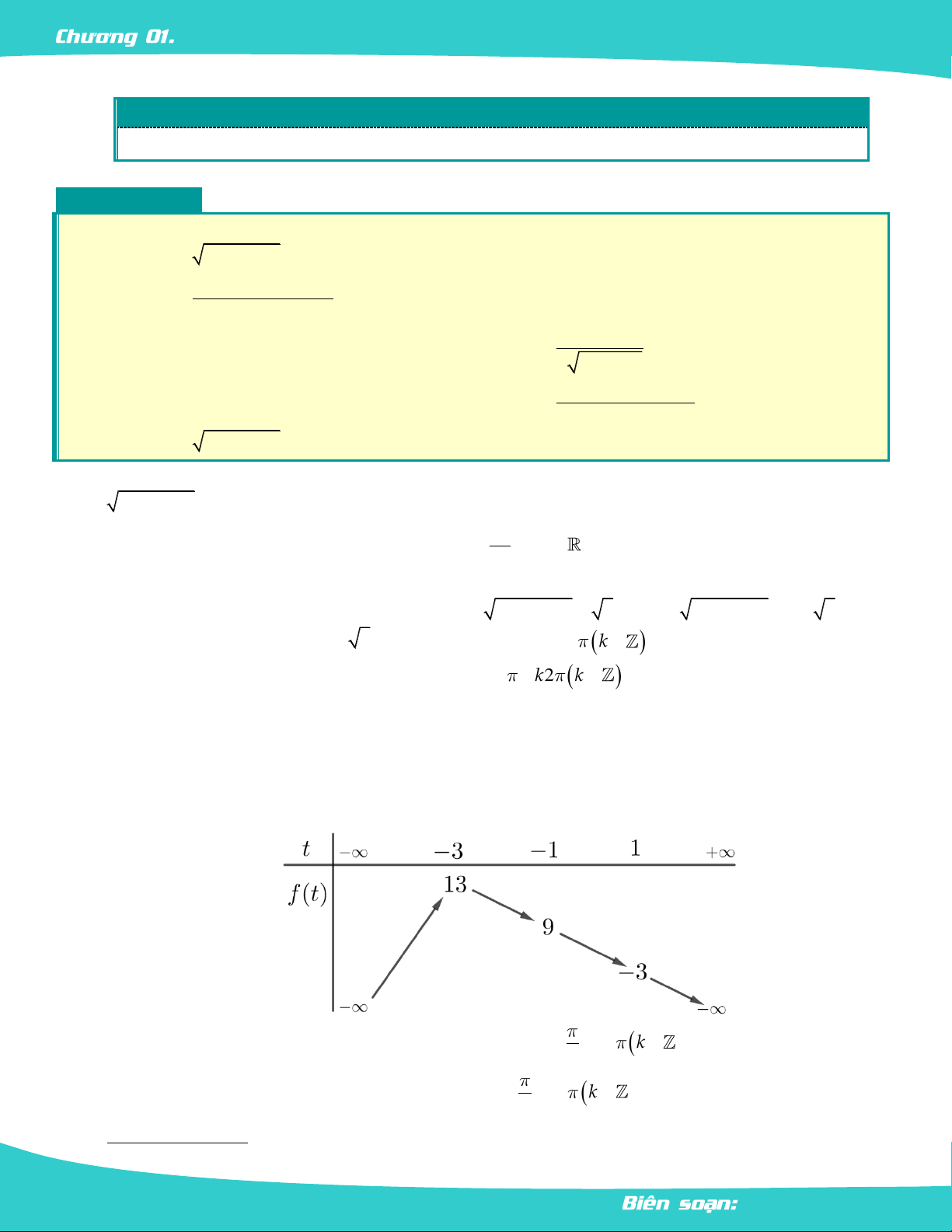
Bảng biến thiên f t :
Vậy GTLN của hàm số là 9 khi t  sin x  1
  x    k2 k , 2 GTNN của hàm số là 3
 khi t  sin x 1 x   k2 k . 2 2 3. y  . 2
cos x  4cos x  5 Trang 17 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
Đặt t  cos x,t   1  ;1   . Khi đó: 2 2
cos x  4cos x  5  t  4t  5  f t xác định với t   1  ;1  
Bảng biến thiên f t : 2 1 Suy ra: 2
2  cos x  4cos x  5  10  1   2
cos x  4cos x  5 5
Vậy GTLN của hàm số là 1 khi f t  2  t  1   cos x  1
  x   k2 k , 1 GTNN của hàm số là
khi f t 10  t 1  cos x 1  x k2 k   . 5 4. 4 2
y  sin x  2cos x  5. Ta có: 4 2 4
y  sin x  cos x   sin x   2  sin x 4 2 2 5 2 1
 5  sin x  2sin x  3 . Đặt 2
t  sin x,t  0;1 
 . Khi đó: y f t 2
t  2t  3 xác định với t  0;1   .
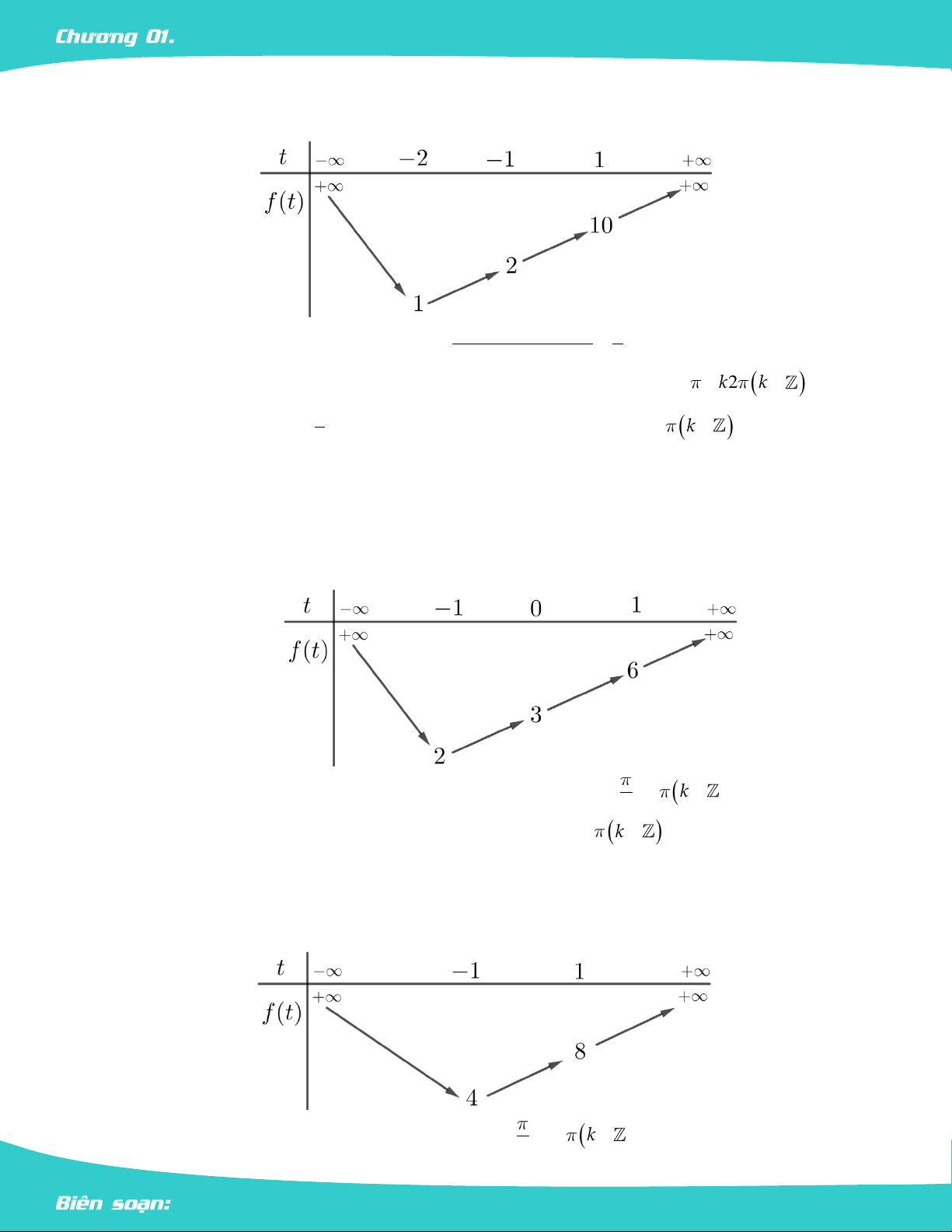
Bảng biến thiên f t :
Vậy GTLN của hàm số là 6 khi 2
sin x  1  cos x  0  x
k k  , 2
GTNN của hàm số là 3 khi 2
sin x  0  sin x  0  x k k   . 5. 2
y  sin x  2sin x  5.
Đặt t  sin x,t   1  ;1 
 . Khi đó: y f t 2
t  2t  5 xác định với t  1  ;1   .
Bảng biến thiên f t :
Vậy GTLN của hàm số là 8 khi sin x  1  x
k2 k  , 2 LÊ MINH TÂM Trang 18 HÀM SỐ LƯỢNG GIÁC
GTNN của hàm số là 4 khi sin x  1
  x    k2 k . 2 1 6. y . 2 sin x  3
Điều kiện xác định: sin x 3  0  sin x  3   x . Ta có: 1   sinx 1 1 1 1 1 1 1
 2  sin x  3  4  2  sin x  3  2       2 sin x  3 2 2 2 2 sin x  3 4 1
Vậy GTLN của hàm số là khi sin x  1
  x    k2 k , 2 2 2 1 GTNN của hàm số là
khi sin x  1  x
k2 k  . 4 2 7. 4 2
y  cos x  2sin x 1. Ta có: 4 2 4
y  cos x  sin x   cos x   2  cos x 4 2 2 1 2 1
1  cos x  2cos x 1. Đặt 2
t  cos x,t  0;1 
 . Khi đó: y f t 2
t  2t 1 xác định với t  0;1   .
Bảng biến thiên f t :
Vậy GTLN của hàm số là 2 khi 2
cos x 1  sin x  0  x k k   ,
GTNN của hàm số là 1 khi 2
cos x  0  cos x  0  x
k k  . 2 1 8. y . 2
sin x  2cos x  5 Ta có: 2
y  sin x  cos x    2  cos x 2 2 5 1
 2cos x  5  cos x  2cos x  6 .
Đặt t  cos x,t   1  ;1 
 . Khi đó: y f t 2  t
  2t  6 xác định với t  1  ;1   .
Bảng biến thiên f t : 1 1 1 Suy ra: 2
3   cos x  2cos x  6  7    2 3
cos x  2cos x  6 7 Trang 19 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 1
Vậy GTLN của hàm số là khi cos x  1
  x   k2 k , 3 1 GTNN của hàm số là
khi cos x 1  x k2 k   . 7
9. y  2  cos 2x . Ta có: 1
  cos2x 11 2 cos2x  3 1 2 cos2x  3
Vậy GTLN của hàm số là 3 khi cos 2x 1  2x k2 k    x k k   ,
GTNN của hàm số là 1 khi cos 2x  1
  2x   k2 k   x   k k  . 2 10. 4 4
y  sin x  cos x .
y  sin xcos x2 1 2 2 2 2 2  2sin .
x cos x y  1 sin 2x 2 1 1 1 1 Ta có: 2 2 2
0  sin 2x  1  0   sin 2x   11 sin 2x  2 2 2 2
Vậy GTLN của hàm số là 1 khi 2
sin 2x  0  sin 2x  0  2x k x k ,k   , 2 1 GTNN của hàm số là khi 2
sin 2x  1  cos 2x  0  2x
k x   k ,k  . 2 2 4 2
------------------HẾT------------------ LÊ MINH TÂM Trang 20 HÀM SỐ LƯỢNG GIÁC
§2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
I. PHƯƠNG TRÌNH SinX = a VÀ PHƯƠNG TRÌNH CosX = a.
Phương trình SinX = m (1)
Phương trình CosX = a (2)
– Nếu m  1: Phương trình vô nghiệm.
– Nếu m  1: phương trình vô nghiệm.   
– Nếu m  1   0;  
– Nếu m  1    ;   thỏa mãn   thỏa mãn cos . m  2 2    x   k2 2  cos x  cos   k  sin  . m . x     k2   x   k2 1  sin x  sin   k . x     k2        0 
Chú ý: Nếu  thì ta viết Chú ý: Nếu thỏa mãn  2 2 thì ta thỏa mãn cos   m sin   m  arccos . m viết  arcsin . m
Các trường hợp đặc biệt:
Các trường hợp đặc biệt:
 cos x 1 x k2 k  sin x  . 1  x
k2 k . 2  cos x  1
  x   k2 k .  sin x  1
  x    k2 k . 2
 cos x  0  x   k k .
 sin x  0  x k k . 2 Ví dụ 01.
Giải các phương trình sau: 3 1 a. sin x  . b. sin x  . 2 3
c. cos x   2 60  .
d. sin 2x  2 . 2       e. sin x   sin 2x      . f. sin  2x    cos 2x .  3   6   4  Lời giải 3 a. sin x  2 x   k2  3
 sin x  sin   k  . 3  2 x   k2  3 1 b. sin x  3 Trang 21 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  1
x  arcsin  k2  3   k .  1
x   arcsin  k2  3
c. cos x   2 60  2
 sin  x   2 90 60  2
   x    k
x     k   sin  x 30 45 360 15 360 30  sin 45     k 
30  x  135  k360 x  1  05  k360  
d. sin 2x  2 (1)
Vì 2  1 nên phương trình (1) vô nghiệm.     e. sin x   sin 2x       3   6     x
 2x   k2
x    k2 x   k2    3 6 2 2       k  5 5 2    x
  2x   k2 3x   k2 x   k  3 6  6  18 3   f. sin  2x    cos 2x  4       sin  2  x   sin  2  x   4   2   
 2x   2x k2 0x   k2   4 2 4      x    k ,k  16 2  
 2x    2x k2 4  x   k2  4 2  4 Ví dụ 02.
Giải các phương trình sau: 3 1 a. cos x   . b. cos x  . 2 5 3
c. cosx   3 30  . d. cos x  . 2 2  2 x   x 4   
e. cos 2x  cos    . f. cos     cos x   0  .  3 5   2 3   3  Lời giải 3
a. cos x   2 5  cos x  5 cos  x    k2 ,k  . 6 6 1 b. cos x  5 LÊ MINH TÂM Trang 22 HÀM SỐ LƯỢNG GIÁC 1
x  arccos  k2 ,k  . 5
c. cosx   3 30  2
x      k  x k   cosx   30 30 360 360 30  cos30     k . x  30  3  0  k360 x  6  0  k360   3 d. cos x  (2) 2 3 Vì
 1 nên phương trình (2) vô nghiệm. 2  2 x
e. cos 2x  cos     3 5   2 x 11 2  10 10 2x    k2 x   k2 x   k    3 5 5 3 33 11       k  .  x 2 9 2  10 10 2x    k2 x    k2 x    k  5 3 5 3  27 9  x 4    f. cos     cos x   0   2 3   3  x 4 x 4   x    x  2 3 3 2 3 3  2cos cos  0 2 2  3x   x 5   cos     cos    0    4 2   4 6    3x  3x 3x  4 4 cos   0      k   k x   k   4 2     4 2 2 4 3 3        k    x 5   x 5  x 4  16  cos    0     k    k x   k4        4 6 4 6 2 4 3  3 
II. PHƯƠNG TRÌNH TANX = a VÀ PHƯƠNG TRÌNH COTX = a
Phương trình TanX = m (3)
Phương trình CotX = a (4)     – Với m  ,    ; : tan    . m – Với m  ,   ; : cot    . m  2 2   2 2 
 3  tanx  tan  x  k .
4  cotx  cot  x  k .        
Chú ý: Nếu thỏa mãn  2
2 thì ta  Chú ý: Nếu thỏa mãn  2 2 thì ta tan   m cot   m viết  arctan . m viết  arccot . m
Các trường hợp đặc biệt:
Các trường hợp đặc biệt:
tan x 1  x   k k  .
cot x 1  x   k k  . 4 4  tan x  1
  x    k k .  cot x  1
  x    k k . 4 4 Trang 23 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
 tan x  0  x k k .
cot x  0  x   k k  . 2 Chú ý:
u v k2 , k
u v k2 , k
sinu  sin v  
cosu  cos v  
u   v k2 , k  
u  v k2 , k      u
   l  hay v   l l  u
  l hay v l l 
tanu  tan v   2  2 
 cot u  cot v  uvk k   u
  v k k  
CẦN NHỚ: Phương trình tan x a , cot x a luôn có nghiệm với a   . Ví dụ 03.
Giải các phương trình sau: 1
a. tan x 1.
b. tan 2x   .
c. cot x  0 . 3  3   2  d. cot3x  2  . e. tan   x
 tan 2x  0 . f. tan  x    cot x .  4   3    g. cot 3x     cot 2x .  3  Lời giải
a. tan x 1.
Ta có: tan x  1  tan x  tan
x   k ,k  . 4 4 1
b. tan 2x   3 1  1  1  1 
Ta có: tan 2x    2x  arctan 
k x  arctan   k ,k      3  3  2  3  2
c. cot x  0 .
Ta có: cot x  0  cot x  cot
x   k ,k  2 2 d. cot3x  2  . 1 Ta có cot 3x  2
  3x  arccot 2
  k x  arccot 2
  k ,k 3 3  3  e. tan   x   tan 2x  0.  4  Ta có:   2x   k x   k 3 3        2  4 2 tan   x
 tan 2x  0  tan 2x  tan x       , k ,n  4   4  3 3 2x x n     x    n  4  4
Vậy phương trình đã cho vô nghiệm. LÊ MINH TÂM Trang 24 HÀM SỐ LƯỢNG GIÁC
Nhận xét: Việc giải dạng này theo chú ý ở trên cho kết quả nhanh, tuy nhiên nhiều bài học sinh sẽ khó
khăn trong việc nhìn nhận quan hệ bao hàm giữa các họ nghiệm. Nên sử dụng đường tròn lượng giác
để minh họa hoặc giải theo cách “dài” hơn như sau:   3  cos   x  0  Điều kiện:   4  . Khi đó  cos 2x  0  3   3  3 3 tan
x  tan 2x  0  tan 2x  tan x   2x x
k x    k ,k       4   4  4 4
Thay vào điều kiện ta thấy không thỏa mãn. Vậy phương trình đã cho vô nghiệm.  2  f. tan  x    cot x .  3 
 x  nx  n 2 2         2 2  tan   x   cot x  tan   x   tan   x      , k ,n k   3   3   2  2  x   
x   x k  12 2  3 2 k
Vậy nghiệm của phương trình là x    , k  . 12 2   g. cot 3x     cot 2x .  3  Ta có:  2x n x n      2 cot 3  x    cot 2x     ,k ,n   3  3
x   2x k  3 x    k  3
Vậy nghiệm của phương trình là x   k ,k  . 3  Tóm tắt như sau: DẠNG CƠ BẢN:
u v k2 , k
u v k2 , k
sinu  sin v  
cosu  cos v  
u   v k2 , k  
u  v k2 , k      u
   l  hay v   l l  u
  l hay v l l 
tanu  tan v   2  2 
 cot u  cot v  uvk k   u
  v k k  
TRƯỜNG HỢP ĐẶC BIỆT:
 sin x  0  x k k 
 cos x  0  x   k k  2
 sin x 1 x   k2 k 
 cos x 1 x k2 k  2   cos x  1
  x   k2 k  sin x  1
  x    k2 k  2 Trang 25 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC III. BÀI TẬP. Bài 01.
Giải các phương trình sau:   1  1  1 1. sin 2x      2. sin 4x      3  2  2  3    
3. sin3x  sin5x 4. sin 4  x    sin 2  x   0   4   3      5. sin 4  x    sin 2  x   0  .
6. 2 cos x  2  0  4   3  3 7. cos 0 3x 15   .
8. sin2x   1  cos2  x 2   9. sin 4x     cos x .
10. sin2x   1  cos3x   1  0.  8   
11. cos 7x  sin 2  x   0  .
12. 1 2cos x3 cos x  0.  5 
13. sin2x 3sin4x  0.
14. 6sin4x 5sin8x  0.   15. 2
cos x  sin 2x  0. 16. 2 2 sin 2x  cos x   .  4  17. 2 2
sin x  cos 4x  2. Lời giải   1 1. sin 2x       3  2   2x     k2 x     k      3 6 4  sin 2  x    sin        (k  )  3   6   5  2x     k2 x   k  3 6  12  1  1 2. sin 4x      2  3  1  1  4x   arcsin    k2 2   3    1  1 
4x    arcsin    k2 2   3   1  1   1 1  1  k
4x    arcsin    k2 x    arcsin    2   3  8 4   3  2   (k  )  1  1   1 1  1  k
4x    arcsin    k2 x    arcsin    2   3  4 8 4   3  2
3. sin3x  sin5xx  k
3x  5x k2  2  x k2       (k  ) k 3
x   5x k2 8  x   k2 x    8 4 LÊ MINH TÂM Trang 26 HÀM SỐ LƯỢNG GIÁC     4. sin 4  x    sin 2  x   0   4   3       sin 4x   sin 2x       4   3     4x
 2x   k2 2x     k2 x    k   4 3 12 24       (k Z)  19 19   k 4x
  2x   k2 6x   k2 x    4 3  12  72 3     5. sin 4  x    sin 2  x   0   4   3       sin 4x    sin 2x       4   3       sin 4x   sin 2x       4   3    7  7 k 4x   2  x   k2 6x    k2 x     4 3 12 72 3       (k  )  11   11 4x
  2x   k2 2x   k2 x   k  4 3  12  24
6. 2 cos x  2  0 x   k2 2  4  cos x
 cos x  cos   (k  ) 2 4
x    k2  4 3 7. cos 0 3x 15   2  cos 0 x   0 3 15  cos30 0 0 0 0 0 0 0
3x 15  30  k 3 . 60
3x 15  k 3 . 60
x  5  k 1 . 20       (k  ) 0 0 0 0 0 0 0 3  x 15  3  0  k 3 . 60 3  x  4  5  k 3 . 60 x  1  5  k 1 . 20
8. sin(2x 1)  cos(2  x)  
 sin(2x 1)  sin  2   x   2     2x 1 
 2  x k2 x   3 k2 x   3  k2    2 2 2       (k  ) 1    k2 2x 1 
  2  x k2 3x  1 k2 x     2  2  6 3 3   9. sin 4x     cos x  8       sin 4x   sin     x   8   2  Trang 27 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC   5  k2 4x    x k2 5x   k2 x      8 2 8 8 5       (k  )   5  5 k2 4x
   x k2 3x   k2 x    8 2  8  24 3
10. sin2x   1  cos3x   1  0  cos3x  
1   sin 2x   1  cos3x   1  sin  2  x   1
x  2 k2       cos x   2 3 1  cos  2  x 1  3  x 1    2  x 1   k2   .  2   2  2
x    k  10 5 2
Vậy nghiệm của phương trình là: x
 2  k2 ; x    k . 2 10 5  
11. cos 7x  sin 2  x   0   5   
 cos7x  sin 2x     5     cos7x  sin 2  x     5   3 2 x   k 3      50 5  cos7x  cos  2  x   7  x    2  x   k2   .  2 5   10   2 x    k  30 9 3 2 2
Vậy nghiệm của phương trình là: x   k ; x    k . 50 5 30 9
12. 1 2cos x3 cos x  0  1 cos x    2  2  x    k2 .  cos x   VN 3 3 2
Vậy nghiệm của phương trình là: x    k2 . 3
13. sin2x  3sin4x  0  sin2x6sin2 . x cos2x  0
 sin2x1 6cos2x  0  1  1   1   1  x   arccos     k cos 2x    2x  arccos     k2 2          6  6 6 .  sin 2x  0 2  x kx k  2 1  1 
Vậy nghiệm của phương trình là: x   arccos   
k ; x k . 2  6  2 LÊ MINH TÂM Trang 28 HÀM SỐ LƯỢNG GIÁC
14. 6sin4x 5sin8x  0  6sin4x10sin4 . x cos4x  0
 2sin 4x35cos4x  0  1  3   3   3  x   arccos     k cos 4x    4x  arccos     k2 4          5  2 5 5 .  sin 4x  0 4  x kx k  4 1  3 
Vậy nghiệm của phương trình là: x   arccos   
k ; x k . 4  5  2 4 15. 2
cos x  sin 2x  0 2  cos x  2sin .
x cos x  0  cos xcos x  2sin x  0       cos x k x k x  0   2 2       .
cos x  2sin x  0 1 1   tan x
x  arctan  k  2  2 1
Vậy nghiệm của phương trình là: x
k ; x  arctan  k . 2 2   16. 2 2 sin 2x  cos x     4    1 cos 2x     2  2  sin 2x  2 1 sin 2x 2  sin 2x  2   2x   k2 x   k   2 4 sin 2x 1   2   
 2sin 2x  sin 2x 1  0 
 2x    k2 1  x    k sin 2x    6  12  2   7 7 2x   k2 x   k  6  12 7
Vậy nghiệm của phương trình là: x
k ; x    k ; x   k . 4 12 12 17. 2 2
sin x  cos 4x  2. Vì 2 2
0  sin x  1; 0  cos 4x  1; x  nên: 2 2
sin x  cos 4x  2 2 sin x 1 co  s x  0 co  s x  0       2 cos 4x 1 sin 4x  0 4  sin . x cos . x cos 2x  0
 cos x  0  x   k . 2
Vậy nghiệm của phương trình là: x   k . 2 Trang 29 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC Bài 02.
Giải các phương trình sau:  3x
1. tan  x   1 2 1  2. cot    3   4  2 3    3. tan 3  x    3  4. cot  x   1 4 20   3  3
5. 3 tan 2x  3  0
6. tan3x  tan4x 7. cot5 . x cot8x 1 8. cot 2 . x sin3x  0 Lời giải
1. tan  x   1 2 1  4 1 1 1 1
 2x 1 arctan  k x   arctan  k k . 4 2 2 4  3x2. cot    3    2 3  3x 3x      k
  k x   k k . 2 3 6 2 6 9   3. tan 3  x    3   3  k
 3x     k x  k . 3 3 3 4. cot  x   1 4 20  3
 4x20  60 1
k 80  4x  80  1
k 80  x  20  k45 k   .
5. 3 tan 2x  3  0 k
 tan 2x  3  2x   k x   k . 3 6 2
6. tan3x  tan4x   k 3     cos x k x 3x  0     Điều kiện 2 6 3      k . cos 4x  0 k 4x k    x    2  8 4
Ta có tan3x  tan4x  4x  3x k x k k   .
Kết hợp điều kiện ta có nghiệm của phương trình là x k k   . 7. cot5 . x cot8x 1  k  sin x 5x  0 5  x k  Điều kiện 5      k . cos8x  0 8x    k kx   8   k cot 5 .
x cot 8x  1  cot 8x  tan 5x  cot
 5x  8x   5x k x     k .  2  2 26 13 LÊ MINH TÂM Trang 30 HÀM SỐ LƯỢNG GIÁC k
Kết hợp điều kiện ta có nghiệm của phương trình là x  
, k 13m 6 k   . 26 13 8. cot 2 . x sin3x  0 k
Điều kiện sin 2x  0  2x k x  k . 2  k    cot x 2x  0 2x   k  Ta có  4 2 cot 2 .
x sin 3x  0    2   k . sin3x  0   k 3  x k x   3 k m
Kết hợp điều kiện ta có nghiệm của phương trình là x   ; x
m  3n k;n . 4 2 3
------------------ HẾT------------------ Trang 31 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
§3. PHƯƠNG TRÌNH BẬC HAI THEO HÀM LƯỢNG GIÁC I. DẠNG CƠ BẢN.
Dạng tổng quát: 2
at bt c  0 ,
trong đó a,b,c là hằng số a  0 và t là một trong các hàm lượng giác.
Phương pháp giải:
Quan sát và dùng các công thức biến đổi để đưa phương trình về cùng một hàm lượng
giác với cung góc giống nhau, chẳng hạn: Dạng
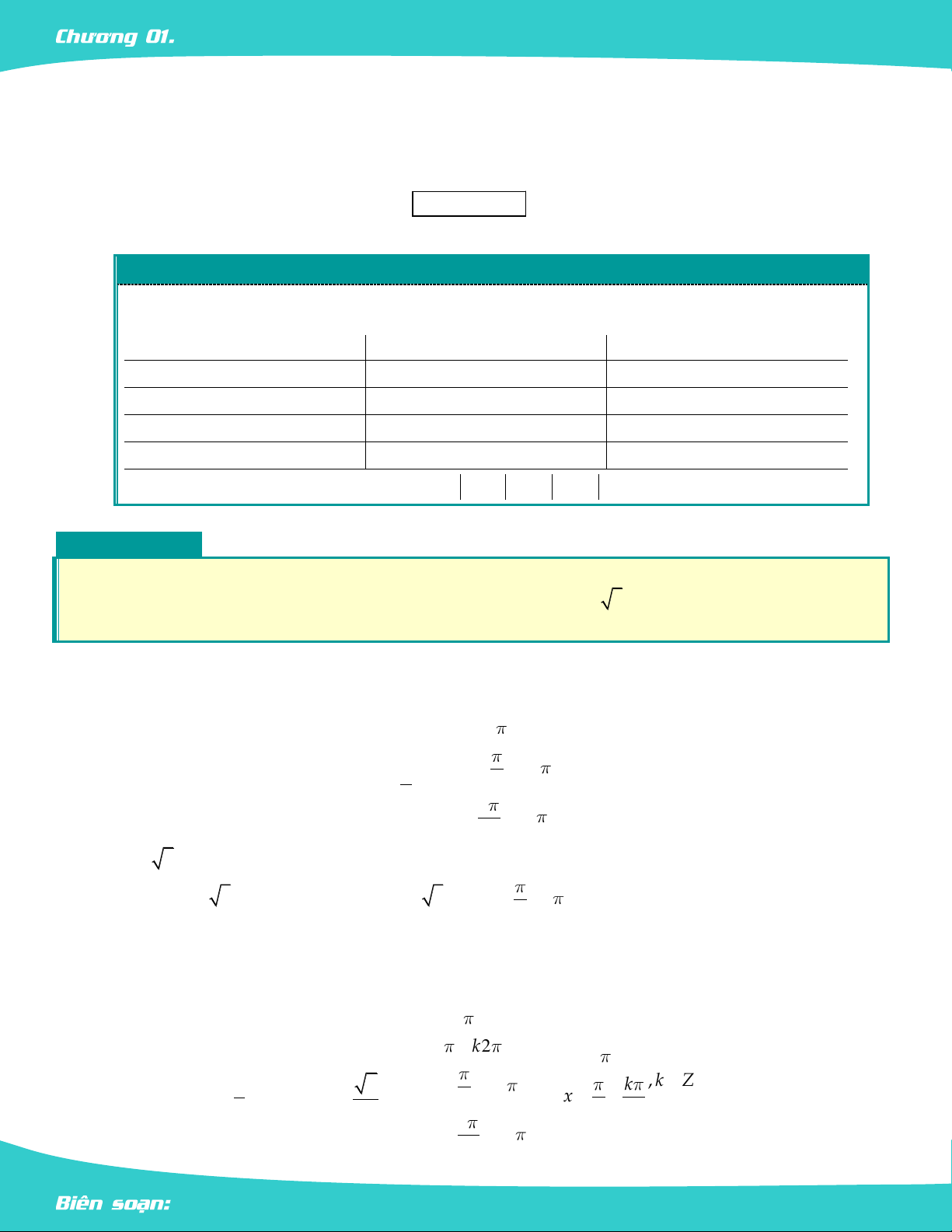
Đặt ẩn phụ Điều kiện 2
asin X bsin X c  0 t  sinX 1   t 1 2
acos X bcos X c  0 t  cosX 1   t 1 2
a tan X btan X c  0 t  tanX
Không có điều kiện của t 2
acot X bcot X c  0 t  cot X
Không có điều kiện của t Nếu đặt 2 t  sin X , 2
cos X hoặc t  sin X , t  cos X thì điều kiện là 0  t 1. Ví dụ.
Giải các phương trình sau: a. 2
2sin x  sin x 1  0 b. 2
tan x  2 3 tan x  3  0 c. 2 4
3sin x  2cos x  2  0 d. 2
3cos x  2cos 2x  3sin x 1. Lời giải a. 2
2sin x  sin x 1  0  x k2 sin x 1  2 
2 sin x  sin x 1  0 
 x    k2 1 sin x    6  2  7 x   k2  6 b. 2
tan x  2 3 tan x  3  0 2
tan x  2 3 tan x  3  0  tan x   3  x    k 3 c. 2 4
3sin x  2cos x  2  0 2 4
3sin x  2cos x  2  0 4 2
 2cos x 3cos x 1 0 x k2    2 x k2 cos x 1 cos x  1  x k      1    , k        Z x k k 2 2 2 cos x  cos x    4 x    2    2  4 2  3 x    k2  4 LÊ MINH TÂM Trang 32 HÀM SỐ LƯỢNG GIÁC d. 2
3cos x  2cos 2x  3sin x 1 2
3cos x  2cos 2x  3sin x 1   2  sin x   2 3 1
2 1 2 sin x  3sin x 1 sin x 1( ) n 2
 sin x  3sin x  2  0  
 sin x 1  x   k2
sin x  2(l) 2 II. BÀI TẬP. Bài 01.
Giải các phương trình sau: 1. 2
2cos x  3cos x 1  0 2. 2
4 cos x  21 3cos x  3  0 4 3. 2
2 cos 2x  2 3   1 cos 2x  3  0
4. 9 13cos x   0 2 1 tan x     5. 2 cos   x  4  cos   x  4  6. 2
2sin x  5sin x  3  0  3   6  7. 2
sin 2x 13sin 2x  5  0 8. 2
4sin x  4sin x  3  0 x
9. cos2x 5sin x 3  0
10. 5cos x  2sin  7  0 . 2  2    11. cos 2  x   3  cos  x  1  0  .
12. cos 4x 12sin xcos x  5  0.  3   3  13. 2
sin x  cos x 1  0.
14. 6sin4x 5sin8x  0. 15. 3 2
sin x  3sin x  2sin x  0. 16. 2
tan x  ( 3 1) tan x  3  0. 3 17. 2
cot x  4cot x  3  0.
18. tan x  cot x  . 2 3 3 19. 2 2 tan x  3  . 20.
 2 3 cot x  6  0. cos x 2 sin x Lời giải 1. 2
2cos x  3cos x 1  0 cos x 1 x k2    1  k   . cos x
x    k2  2  3 2. 2
4 cos x  21 3cos x  3  0  1  cos x   x    k2  2 3     k .  3  cos x x    k2    2  6 3. 2
2 cos 2x  2 3   1 cos 2x  3  0  3  3 cos 2x  1 (VN) 3  3 1 3  3 2    2x  arccos
k2  x   arccos  k ( k ).   2 2 2 3 3 cos 2x   2 Trang 33 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 4
4. 9 13cos x   0 . 2 1 tan x
Điều kiện cos x  0 . cos x 1 2 
 9 13cos x  4cos x  0  9    x k2 ( k  ). cos x  1 VN  4     5. 2 cos   x  4  cos   x  4   3   6      2  1 sin   x  4  sin   x  4  0   3   3     sin   x  1        3  2   sin  x  4sin  x  3  0   x       k2 ( k  ).  3   3     sin   x   VN 6 3   3  6. 2
2sin x  5sin x  3  0 sin x  1    
x    k  ( k  ). sin x  VN 2 3 2  2 7. 2
sin 2x 13sin 2x  5  0  13  149   sin x  VN 1 13 149 2 x  arcsin  k 2 2 2     ( k  ).  13  149  1 13  149 sin 2x  x   arcsin  k  2  2 2 2 8. 2
4sin x  4sin x  3  0  1  sin x x   k2   2 6     ( k  ). 3    sin x  VN 5 x   k2  2  6
9. cos2x 5sin x 3  0   2
1 2 sin x  5sin x  3  0   1 x    k2 sin x    2  6  2
 sin x  5sin x  2  0  2    ( k  ). sin x    VN  7 2 x   k2  6 x
10. 5cos x  2sin  7  0 2  x x 2  5 1 2  sin  2  sin  7  0  2  2 LÊ MINH TÂM Trang 34 HÀM SỐ LƯỢNG GIÁC  x sin 1 x xx 2 2  10  sin  2sin 12  0  
   k2  x   k4 ( k ). 2 2 x 6  sin  VN 2 2  2 5  2    11. cos 2  x   3  cos  x  1  0   3   3      2  2cos  x   3  cos  x  1  0  (1)  3   3    Đặt cos x     t  1   t   1 .  3   1  t  Pt (1) 2  2t   3t 1  0  2  t  1   2 x    k2   x   k2 3 3   3    1  2      2  cos  x  cos x     k2
x    k2   3  2 3  3 3   k    2 k      x   k2 cos x   1    cos
x    k2  3   3  3   4   x    k2
x    k2  3  3
12. cos 4x 12sin xcos x 5  0. 2
 1 2sin 2x  6sin2x 5  0. 2
 2sin 2x 6sin2x  4  0.
Đặt sin 2x t  1   t   1 . 2
 2t 6t  4  0. t 1 (TM) 2
t  3t  2  0.  
 sin 2x 1  sin  2x   k2  x   k . t  2   (KTM) 2 2 4 13. 2
sin x  cos x 1  0. cos x 1 2 2
 1 cos x  cos x 1  0.  cos x  cos x  2  0.    x k2 . cos x  2   (KTM)
14. 6sin4x 5sin8x  0.
 6sin4x10sin4xcos4x  0.
 2sin4x35cos4x  0.    kx  4x k    4 sin 4x  0         3 1 3 k 3              4x arccos   k2 (k ) x arccos   (k ) . cos 4x      5  4   5  2  5   3      1 3 k 4x   arccos     k2 x   arccos       5   4   5  2 Trang 35 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 15. 3 2
sin x  3sin x  2sin x  0. (1)
Đặt sin x t  1   t   1 . Pt (1) 3 2
t 3t  2t  0 t  0        t x k t 0 sin x 0 2 t  
 3t  2  0    t  1      (k  ). 2
t  3t  2  0 sin x  1 
x    k2 t  2  (KTM)    2 16. 2 tan x   3  
1 tan x  3  0. (1)
Đặt tan x t.     1 tan 1 x k t x  Pt (1) 2  t     4
3 1 t  3  0.       (k  ). t   3 tan x   3
x    k  3 17. 2
cot x  4cot x  3  0. (1)
Đặt cot x t. Pt (1) 2
t  4t 3  0.      tan x  1  x k t   1      cot x 1 4        1  (k  ). t  3   cot x  3   tan x    1      3 x arctan    k   3  3
18. tan x  cot x  . 2 1 3  tan x   . (1) tan x 2
Đặt tan x t t  0 . 1 3 Pt (1) 2  t    0 t 2 t  tan x  x  arctan 2 2 2  k    2
 2t  3t  2  0  1  1   1  (k  ).      t tan x   x  arctan     k  2  2   2  3 19. 2 2 tan x  3  . cos x 2 3  1 . 2 cos x cos x 1   Đặt  1
t t  0,1   1. cos xt  1 t 1  1  2   2  3 1  0. t t t   
 cos x 1  x   k2 1 (k  ). t  1   2 2 KTM t LÊ MINH TÂM Trang 36 HÀM SỐ LƯỢNG GIÁC 3 20.
 2 3 cot x  6  0. 2 sin x   2 3 cot x  
1  2 3 cot x  6  0.  cot x  3 x   k   2 6
 3cot x  2 3 cot x  3  0.       3 (k ). cot x       3 x k  3 Bài 02.
Giải các phương trình sau:   1. sin x  cos x2 2 3 2  2cos 2x   .  6   x
2. cot x  1  tan .
x tan .sin x  4.  2  2
3. cot x  tan x   4sin 2 . x sin 2x     4. 2 2 sin x  
1  4 sin x   1  cos 2x   sin 2x       4   4  cos 2x 1 5. 2 cot x 1   sin x  sin 2 . x 1 tan x 2
6. sin x     sin x 2 5 2 3 1 tan . x 7. 2 2
cos 3x cos 2x  cos x  0;     3 8. 4 4
sin x  cos x  cos  x    sin 3  x    0  ;  4   4  2   
1 sin x  cos 2xsin x     4  1 9.  cos x; 1 tan x 2 4 4 sin x  cos x 1 1 10.  cot 2x  ; 5sin 2x 2 8sin 2x 2
11. cot x  tan x  4sin 2x  ; sin 2x 12. 6 2
3cos 4x  8cos x  2cos x  3  0; 2 cos 4x
13. cot x  tan x  . sin 2x Lời giải   1. sin x  cos x2 2 3 2  2cos 2x   .  6  Ta có:    sin x  cos x2 2 3 2  2cos 2x     6  Trang 37 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 2  1 3     4 sin 2x  cos 2x   2 cos 2  x    2 2     6  2      2 sin 2 . x sin  cos 2 . x cos  cos 2x       6 6   6      2  2cos 2x   cos 2x       6   6  x   k      3 2 cos 2  x   0  2x    k  6     6 2      x   kk .     1  4 cos 2  x   2x     k2      6  2  6 3
x    k  12
Vậy nghiệm của phương trình là: x
k ; x   k ; x  
k k . 3 2 4 12  x
2. cot x  1  tan .
x tan .sin x  4.  2   sin x  0 
ĐKXĐ: cos x  0  sin 2x  0  2x k x k k  . 2  x cos  0  2 Ta có:  x  cot x  1  tan .
x tan .sin x  4  2   x   sin . x sin cos x  2   1 .sin x  4 sin x x  cos . x cos     2   x x   x  cos . x cos   sin . x sin   cos cos x  2 2 cos x 2    .sin x  4    .sin x  4 sin x x   sin x x cos . x cos  cos .xcos       2   2  cos x sin x    4 sin x cos x 2 2
 cos x  sin x  4sin . x cos x   2x   k2 x    k 1  6 12
 2sin 2x 1  sin 2x      k . 2  5 5  2x   k2 x   k  6  12 5
Đối chiếu điều kiện ta được nghiệm của phương trình là: x   k ; x
k k  . 12 12 LÊ MINH TÂM Trang 38 HÀM SỐ LƯỢNG GIÁC 2
3. cot x  tan x   4sin 2 . x sin 2x sin x  0 
ĐKXĐ: cos x  0  sin 2x  0  2x k x k k  . 2 sin2x  0  2
cot x  tan x   4sin 2x sin 2x cos x sin x 2     4sin 2x sin x cos x sin 2x 2 2 cos x  sin x 2    4s in2x sin . x cos x sin 2x 2 cos 2x 2    4sin 2x sin 2x sin 2x 2
 cos2x 1 2sin 2x
 cos x    2 2 1 2 1 cos 2x
cos 2x 1L  2 2
 2cos 2x  cos 2x 1  0   2x    k2       1 x k k . cos 2   3 3 x  2
Đối chiếu điều kiện ta được nghiệm của phương trình là: x  
k k . 3     4. 2 2 sin x  
1  4 sin x   1  cos 2x   sin 2x       4   4     2 2sin x  
1  4 sin x   1  cos 2 . x cos  sin 2 . x sin  sin 2 . x cos   cos 2 . x sin   4 4 4 4     
sin x    sin x   2 2 2 2 2 2 1 4 1   cos 2x  sin 2x  sin 2x  cos 2x   2 2 2 2     2 2sin x   1  4sin x   1  2 cos 2x
 sinx   sinx   2 2 2 1 4 1 2 1 2 sin x sin x 1 2
 2 2 sin x  22 2sinx4  0  
x   k . sin x   2  VN 2
Vậy nghiệm của phương trình đã cho là x
k k . 2 cos 2x 1 5. 2 cot x 1   sin x  sin 2 . x 1 tan x 2  sin x  0 x k    ĐKXĐ: 2 cos x  0   k .   tan x  1  x    k   4 cos 2x 1 2 cot x 1 
 sin x  sin 2x 1 tan x 2 Trang 39 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 2 2 cos x cos x  sin x 2  1   sin x  sin . x cos x sin x sin x 1 cosx cos x  sin x
cos xcos x  sin xcos x  sin x 2    sin x  sin . x cos x sin x cos x  sin x
cos x  sin x  0   1 cos x  sin x  
 cos xcos x  sin x  sin xcos x  sin x   1 sin x
 cos x  sin x 2 sin x
Giải (1): cos x  sin x  0  tan x  1  x   k . 4 1 Giải (2):
 cos x  sin x sin x 2 1 sin .
x cos x  sin x 2 2 2
 sin x  cos x  sin .
x cos x  sin x 2 2 2  2sin x sin .
x cos x  cos x  0  2 tan x  tan x 1  0VN.
Đối chiếu điều kiện ta được nghiệm của phương trình là: x
k k . 4
6. sin x     sin x 2 5 2 3 1 tan . x
ĐKXĐ: cos x  0  x
k k . 2
sin x     sin x 2 5 2 3 1 tan x sin x
 5sin x  2  31 sin x 2 . 2 cos x sin x
 5sin x  2  31 sin x 2 . 2 1 sin x 2 sin x
 5sin x  2  3.1sinx
  sinx    sinx 2 5 2 1  3sin x   1 x   k2 sin x   2  6
 2sin x  3sin x  2  0  2   .  sin x    VN  5 2 x   k2  6 5
Đối chiếu điều kiện ta được nghiệm của phương trình là: x   k2 ; x
k2 k  6 6 7. 2 2
cos 3xcos 2x  cos x  0 1 cos 6x 1 cos 2x  cos 2x   0 2 2
 cos2xcos6xcos2x1cos2x  0
 cos6xcos2x1 0 LÊ MINH TÂM Trang 40 HÀM SỐ LƯỢNG GIÁC cos4x 1 1    k
cos8x  cos 4x 2
1  0  2cos 4x  cos4x 3  0  3  x  , k  . 2 cos4x   vn 2  2     3 8. 4 4
sin x  cos x  cos  x    sin 3  x    0  ;  4   4  2      
sin x  cos x2 1 3 2 2 2 2
 2sin xcos x  sin 4  x    sin 2x  2   2  2  1 1     3 2
 1 sin 2x  sin 4  x    sin 2x  2 2   2  2  2
 2 sin 2x cos4x  sin2x  3 2   sin x   2 2 2
1 2 sin 2x  sin 2x  3 sin 2x 1 2
 sin 2x  sin 2x  2  0  
x   k ,k  . sin 2x  2   vn 4   
1 sin x  cos 2xsin x     4  1 9.  cos x; 1 tan x 2 cos x  0 Điều kiện:  . tan x  1
 sinxcos x 1 1 2 
sinxcosx 2 1   cos x sin x  cos x 2 cos x
1sinxcos2x 1 x   k2  l 2  sin x 1  x    k2  2   6  2
 sin x  sin x 1  0 
x    k2 1   , k  sin x    6  7   x   k2 2 7  6 x   k2  6 4 4 sin x  cos x 1 1 10.  cot 2x  ; 5sin 2x 2 8sin 2x
Điều kiện: sin 2x  0 1 2 1 sin 2x 4 cos 2x 1 2   5 sin 2x 8 sin 2x    2
8 4 1 cos 2x  20cos 2x  5  9 cos 2x   l 2 2
 4cos 2x  20cos 2x  9  0  
x    k ,k  . 1 6 cos2x   2 Trang 41 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 2
11. cot x  tan x  4sin 2x  ; sin 2x
Điều kiện: sin 2x  0 2
cot x  tan x  4sin 2x  sin2x cos x sin x 2    4sin 2x   0 sin x cos x sin 2x 2 2 cos x  sin 2   4sin 2x   0 sin x  cos x sin 2x 2 cos 2x 2   4sin 2x   0 sin 2x sin 2x 2
 2cos2x  4sin 2x  2  0
cos 2x 1(l) 2 cos  
2x  21 cos 2x 2
1  0  2cos 2x  cos 2x 1  0  1  x    k ,k  . cos2x   3  2 12. 6 2
3cos 4x  8cos x  2cos x  3  0;
  cos x    cos x3 2 3 2 2 1 1 2
 1 cos2x  3  0 2 2 3
 6cos 2x 313cos2x      
3cos 2x cos 2x 1 cos2x 3 0 3 2
 cos 2x 3cos 2x  2cos2x  0 cos 2x  0  kx   cos   2x  2
cos 2x  3cos 2x  2  0  cos 2x 1  4 2 , k  .   cos2x  2   x k 2 cos 4x
13. cot x  tan x  . sin 2x
Điều kiện: sin 2x  0. Ta có: 2 cos 4x
cot x  tan x  sin2x cos x sin x 2 cos 4x     0 sin x cos x 2 sin x cos x 2 2 cos x  sin x cos 4x    0 sin x cos x sin x cos x
cos 2x  cos 4x   0 sin x cos x
cos 2x 1(l) 2 cos  
2x  cos 4x  0  2
 cos 2x  cos 2x 1  0  1  x    k ,k  . cos2x   3  2 LÊ MINH TÂM Trang 42 HÀM SỐ LƯỢNG GIÁC
§4. PHƯƠNG TRÌNH BẬC NHẤT VỚI HÀM SIN - COS I. DẠNG CƠ BẢN.
Dạng tổng quát:
a sin x b cos x c   1 a ;b;  c  , và 2 2 a b  0 .
Phương pháp giải:
Điều kiện có nghiệm của phương trình: 2 2 2
a b c (kiểm tra trước khi giải) a b c * Chia 2 vế cho 2 2
a b , thì (*)  sin x  cos x  (**) 2 2 2 2 2 2 a b a b a b a b * Giả sử cos  , sin  ,   0; 2    thì: 2 2 a b 2 2 a b c (**)  sin . x cos  cos . x sin  2 2 a b c  sinx    : dạng cơ bản 2 2 a b
sin .acosb  cos asin b  sina   b
Chú ý: hai công thức sử dụng nhiều nhất là: cos .acosbsinasinb   sin  a b
Các dạng có cách giải tương tự: 2 2
a b cos mx . a sin mx  . b cos mx   2 2 a b  0 2 2 pp
a b sin mx Chia cho 2 2 a b . . a sin mx  . b cos mx  . c sin nx  . d cos nx,  2 2 2 2
a b c d   Chú ý:   
1 có nghiệm  2 có nghiệm 2 2 2
a b c .  1 3    
sin x  3 cos x  2 sin x
cos x   2sin x      . 2 2    3   3 1    
 3 sin x  cos x  2 sin x
cos x   2sin x      . 2 2    6        1 1
sin x  cos x  2 sin x  cos x  2 sin x      .  2 2   4  Ví dụ.
Giải các phương trình sau:
a. sin x  3 cos x 1 b.
3 cos 2x  sin 2x  2
c. sin3x  3 cos3x  2sin 2x
d. cos 2x  3 sin 2x  3 sin x  cos x Lời giải
a. sin x  3 cos x 1 1 3 1  sin x  cos x  2 2 2 Trang 43 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC   x    k2 x    k2 1     3 6 6  sin x         3  2  5  x    k2 x   k2  3 6  2 b.
3 cos 2x  sin 2x  2 3 1 2 
cos 2x  sin 2x  2 2 2  
 2x   k2 x    k 2    3 4 24  sin  2  x        3  2  3 13   2x   k2 x   k  3 4  24
c. sin3x  3 cos3x  2sin 2x 1 3  sin x  cos x  sin 2x 2 2   x   2x k2 x   k2     3 3  sin x    sin 2x     , k Z  3    2 k2 x
  2x k2 x    3  9 3
d. cos 2x  3 sin 2x  3 sin x  cos x 1 3 3 1  cos2x  sin 2x  sin x  cos x 2 2 2 2   k2
 2x   x k2 x        6 6 3  sin  2  x   sin   x      , k Z  6   6    2
 2x    x k2 x    k2  6 6  3 II. BÀI TẬP. Bài 01.
Giải các phương trình sau:
1. sin3x  3 cos3x  2sin 2x
2. sin x  cos x 1 6
3. sin x  cos x
4. 5sin2x 12cos2x 13 2
5. sin8x  cos 6x  3 sin 6x  cos8x
6. sin 7x  cos 2x  3 sin 2x  cos7x
7. sin x  cos x  2 2.sin . x cos x 8. 2
2sin x  3 sin 2x  3
9. sin x  cos . x sin x  cos x   3 2 3 3
2 cos 4x  sin xLời giải
1. sin3x  3 cos3x  2sin 2x 1 3  sin3x  cos3x  sin 2x 2 2 LÊ MINH TÂM Trang 44 HÀM SỐ LƯỢNG GIÁC   3x   2x k2 x   k2     3 3  sin 3  x    sin 2x     k .  3    4 2 3x
  2x k2 x   k  3  15 5
2. sin x  cos x 1
x   k2      1  x   k2 4 4   2 sin x   1   sin  x       2 k . 4 4      2
x     k2
x   k2  4 4 6
3. sin x  cos x  2   x    k2 x    k2 6 3      4 3 12  2 sin x     sin  x        k   4  2  4  2  5  x     k2 x   k2  4 3  12
4. 5sin2x 12cos2x 13 5 12  sin 2x  cos 2x  1 13 13 5 12 Đặt cos  ,sin  Ta có phương trình: 13 13  sin2 . x cos  cos2 .
x sin 1  sin2x   1  2x    k2  x
  k ,k  2 2 4
5. sin8x  cos 6x  3 sin 6x  cos8x
 sin8x  3cos8x  3sin6x  cos6x 1 3 3 1  sin8x  cos8x
sin 6x  cos 6x 2 2 2 2      sin 8x   sin 6x       3   6     8x
 6x   k2  2x   k2  x   k  3 6   2   4   k   7  7  k 8x
  6x   k2  14x   k2 x    3 6  6  84 7
6. sin 7x  cos 2x  3 sin 2x  cos7x
 sin7x  3cos7x  3sin2x  cos2x 1 3 3 1  sin7x  cos 7x
sin 2x  cos 2x 2 2 2 2      cos 7x   cos 2x       6   3  Trang 45 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC    k2 7x
 2x   k2  5x    k2  x     6 3   6   30 5   k     k2 7x   2  x   k2  9x   k2 x    6 3  2  18 9
7. sin x  cos x  2 2.sin . x cos x    2 sin x   2  sin 2x  4    2x x   k2 x   k2     4 4  sin x    sin 2x     k   4    k2 2x   x   k2 x    4  4 3 k2 k2 Vì nghiệm x   chứa nghiệm x
k2 nên pt có 1 họ nghiệm là x   , 4 3 4 4 3 k 8. 2
2sin x  3 sin 2x  3
1cos2x  3sin2x  3
 3 sin2x cos2x  2 3 1   
sin 2x  cos 2x  1  sin 2  x  1 
 2x    k2  x   k ,k  2 2  6  6 2 3
9. sin x  cos . x sin x  cos x   3 2 3 3
2 cos 4x  sin x  sin . x  2
1 2 sin x  cos .
x sin 2x  3 cos 3x  2 cos 4x  sin .
x cos 2x  cos .
x sin 2x  3 cos3x  2cos 4x
 sin3x  3cos3x  2cos4x 1 3  sin3x  cos3x  cos 4x 2 2   4x  3x   k2 x    k2     6 6  cos 3  x    cos 4x     k  .  6    k2 4x  3  x   k2 x    6  42 7 Bài 02.
Giải các phương trình sau: 3  3 cos 2x x 1.  cos x . 2. 2 tan sin x  2cos  2 2 sin x 7 2   3.  4 4
3 cos x  sin x  sin x  cos x 4.
3 cos 2x  sin 2x  2 sin 2  x   2 2   6      5.
3 sin 7x  cos7x  2 sin 5x    6. sin  2  x  3  sin   2x  2  6   2   
7. cos x  3 sin x  2 cos 2  x   0  .
8. 2 cos 2x  1 3cos x  sin x.  3  LÊ MINH TÂM Trang 46 HÀM SỐ LƯỢNG GIÁC 9.  3  
1 sin x   3  
1 cos x  1 3 . 10. 3
3sin3x  3 cos9x 1 4sin 3x .       11. 2 cos 2  x   4 
sin x cos x 1  0 .
12. 4 sin  x   2  cos  x   3 2  0  .  6   4   4      13. 8sin .
x sin 2x  6 sin  x  .cos  2  x  5  7  cos x .  4   4        14. 2
2 3 sin  x  cos x   2  cos  x   3 1  .  8   8   8 
1 cos x  cos 2x  cos3x 2 15.  3  3 sin x . 2  
2 cos x  cos x 1 3 3 1 16. 8sin x   . cos x sin x 17. 3 3 2 2
2 cos x  2sin x  2sin . x cos x  2cos .
x sin x  2  0 .
18. 5cos x  sin x  sin3x  cos3x  2 2 2  sin 2x. Lời giải 3  3 cos 2x 1.  cos x . 2 sin x
Điều kiện xác định x k , ( k  ).
3  3 cos 2x  cosx 2 sin x
 3  3 cos2x  sin2x  3cos2x sin2x  3 1 3 3  sin 2x  cos 2x  2 2 2 3
 cos sin 2x  sin cos 2x  3 3 2
2x   k2
x k (l)    3 3   sin 2  x    sin    (k Z)  3  3  2
x   k (tm) 2x    k2  6  3 3 x 2. 2 tan sin x  2cos  2 7 2
 tan sin x  cos x 1 2 7
 tan sin x  cos x 1 7
 sin sin x  cos cos x  cos 7 7 7
x   k2  2    x   k2 7 7   cosx    cos    7 k  7 7   
x     k2 x k2  7 7 Trang 47 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 3.  4 4
3 cos x  sin x  sin x  cos x   2 2 x x 2 2 3 cos sin
cos x  sin x  sin x  cos x
 3 cos x  sin xcosx  sin x  sin x  cosx
x    k     4  2 sin x   0
sin x  cos x   0    4   1    
 x   arcsin   k k   3 
cosxsinx 2    1     4  6   6 sin   x  1     4  3   1  x   arcsin   k2  4   6   
4. 3 cos 2x  sin 2x  2 sin 2  x   2 2   6  3 1     
cos 2x  sin 2x  sin 2  x   2   cos cos 2x  sin sin 2x  sin 2  x   2  2 2  6  6 6  6         cos 2  x    sin 2  x   2  2  sin 2  x    2   6   6   4 6    5  sin 2x   1  2x
  k2  x   k k     12  12 2 24   5.
3 sin 7x  cos 7x  2 sin 5x     6  3 1   
sin 7x  cos7x  sin 5x    2 2  6   
 cos sin 7x  sin cos7x  sin 5x    6 6  6 
7x  5x  k2 x k      6 6   sin 7  x    sin 5  x      k .  6   6   7 x   k 7x    5x k2  9 6  6 6   6. sin  2  x  3  sin   2x  2  2 
 cos2x  3sin2x  2 1 3  cos2x
sin 2x  1  sin cos 2x  cos sin 2x  1 2 2 6 6    sin 2x
 1  2x    k2  x   k k   .  6  6 2 6  
7. cos x  3 sin x  2 cos 2  x   0   3  LÊ MINH TÂM Trang 48 HÀM SỐ LƯỢNG GIÁC  
 cos x  3 sin x  2  cos 2x     3  1 3    cos x
sin x   cos 2x    2 2  3       cos x   cos  2x       3   3    2k x
  2x   2k  3x   2k x   3 3      k   3 3    .   
x    2k x      2   x   2  k  x   2 3 k 3   3    3 2k
Vậy phương trình có hai họ nghiệm x   , x
 2k k  3 3 3
8. 2 cos 2x  1 3cos x  sin x
 2cos 2x  1 3cosx sinx   2 2
cos x  sin x  1 3cos x  sin x
 cos x  sin xcos x  sin x  1 3cosx sin x
 cos x  sin xcosx sin x 1 3  0 
cos x  sin x  0
tan x  1  x   k k       4  .
cos x  sin x 1 3  0
cos x  sin x 1 3  *
Phương trình (*) vô nghiệm do     2 2 2 1 1 1 3
Vậy phương trình có hai họ nghiệm x
k k  . 4 9.  3  
1 sin x   3   1 cos x  1 3
  3  1sinx  3  1cosx 1 3 3 1  sin x  cos x  1 1 3    sin x  tan   cos x  1  4 6  5  sin x  tan .cos x  1 12 5 5 5  sin . x cos  sin .cos x  cos 12 12 12 Trang 49 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  5  x    2k x   2k  5    12 12 2  sin x    sin     k .  12  12 5 4   x     2k x   2k  12 12  3 4
Vậy phương trình có hai họ nghiệm x   2k ,x
 2k k  2 3 10. 3
3sin3x  3 cos9x 1 4sin 3x 3
 3sin3x  3cos9x 1 4sin 3x 3
 3sin3x  4sin 3x  3cos9x 1
 sin 9x  3 cos9x  1 1 3 1  sin9x  cos9x  2 2 2   2k 9x    2k x       3 6 18 9  sin 9  x    sin     k .  3  6   7 2k 9x     2k x    3 6  54 9 2k 7 2k
Vậy phương trình có hai họ nghiệm x   , x   k  18 9 54 9   11. 2 cos 2  x   4 
sin x cos x 1  0  6     2cos 2  x   4 
sin x cos x 1  0  6   
 2cos2 .xcos sin 2 .xsin  2  sin 2x 1  0  6 6 
 3 cos2x sin2x  2sin2x 1 0
 3 cos2x  sin2x 1 0 3 1 1 
cos 2x  sin 2x  2 2 2   
 2x   2k 2x    2k x     k     3 6 6 12  sin  2  x   sin       k .  3  6   
 2x    2k 2x   2k x   k  3 6  2  4
Vậy phương trình có hai họ nghiệm x  
k ,x   k k  12 4    
12. 4 sin  x   2  cos  x   3 2  0   4   4           4sin x   2  cos  x   3 2  0  4  cos   x   2  cos  x   3 2  0   4   4   2 4   4  LÊ MINH TÂM Trang 50 HÀM SỐ LƯỢNG GIÁC          4cos   x  2  cos  x   3 2  0  4  cos  x   2  cos  x   3 2  0   4   4   4   4     6cos x   3 2   4 
x  2k    2  x   2 4 4 k cos  x  cos         2 k . 4 2 4   
x     2k x  2k  4 4
Vậy phương trình có hai họ nghiệm x
 2k ,x  2k k . 2     13. 8sin .
x sin 2x  6 sin  x  .cos  2  x  5  7  cos x  4   4      8 sin .
x sin 2x  6 sin  x  .cos  2  x  5  7  cos x  4   4       8sin .
x sin 2x  3 sin   x  
 sin3x  5  7cos x   2   8sin .
x sin2x 3cos x 3sin3x  5 7cos x  4
 cos3x cosx3cosx 3sin3x  57cosx  4
 cos3x 4cosx3cosx3sin3x  57cosx
3sin3x4cos3x  5 3 4
 sin3x  cos3x 1 5 5  3 4
cos .sin3x sin .cos3x 1 (với cos  ,sin  ) 5 5  k
sin3x   1  3x    2 k2  x    (k  ) . 2 3 6 3       14. 2
2 3 sin  x  cos x   2  cos  x   3 1   8   8   8        2
2 3 sin  x  .cos x   2  cos  x   3 1   8   8   8        2
 2 3 sin x  .cos x   2  cos  x  1  3   8   8   8       3 sin 2  x   cos 2  x   3   4   4  3   1   3  sin 2x   cos 2x       2  4  2  4  2   5 2x    k2 x   k2 3     12 3 24  sin 2  x        (k  ) .  12  2  2 3  2x    k2 x   k2  12 3  8 Trang 51 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
1 cos x  cos 2x  cos3x 2 15.  3  3 sin x 2  
2 cos x  cos x 1 3
1 cos x  cos 2x  cos3x 2  3  3 sin x 2  
2 cos x  cos x 1 3 2 2 cos x  2 cos 2 . x cos x 2   3  3 sin x 2  
2 cos x  cos x 1 3 2 cos (
x cos x  cos 2 ) x 2   3  3 sin x 2  
2 cos x  cos x 1 3 2 cos x  2
2 cos x  cos x   1 2   3  3 sin x 2  
2 cos x  cos x 1 3
 3cos x  3  3 sin x
 3 cosx sinx  3 3 1 3 
cos x  sin x  2 2 2
x   k2    3  x   k2 6 6   cos x       3 (k  ) . 6 2   
x     k2 x k2  6 6 3 1 16. 8sin x   cos x sin x
Điều kiện: sin 2x  0  x k ;k  . 2 3 1 sin x  cos x Ta có: 8sin x   3  8sin x   4sin .
x sin 2x  3 sin x  cos x cos x sin x cos . x sin x
 2cos x  cos3x  3 sin x  1 3
cos x  cos x  sin x  cos3x 2 2
 cos .cos x  sin .sin x  cos3x 3 3   3x x   k2 x   k     3 6  cos x    cos3x     k .  3     3x  x   k2 x   k  3  12 2 17. 3 3 2 2
2 cos x  2sin x  2sin . x cos x  2cos .
x sin x  2  0 Ta có: 3 3 2 2
2 cos x  2sin x  2sin . x cos x  2cos .
x sin x  2  0 2
 cos xcos x  sin x 2 2
 2sin xcos x  sin x  2  0
 cos x  sin x 2 2
2 cos x  2 sin x  2
 2cos x  sin x  2 LÊ MINH TÂM Trang 52 HÀM SỐ LƯỢNG GIÁC   7 x    k2 x    k2 1    4 3 12  cos x        k .  4  2    x     k2 x   k2  4 3  12
18. 5cos x  sin x  sin3x  cos3x  2 2 2  sin 2x
Ta có: 5cos x  sin x  sin3x  cos3x  2 2 2  sin 2x
 cos x  sin x 3 3 5
 3sin x  4sin x (4cos x 3cos x)  2 2 2  sin2x
 cos x  sin x  cos x  sin x  cos x  sin x 2 2 5 3 4 sin x  sin .
x cos x  cos x  2 2 2  sin 2x
 5cos x  sin x sin x  cosx  2sin2x  
1  2 2 2  sin 2x
 sin x  cos x2sin2x  4  2 2 2  sin2x
 22  sin 2xsin x  cosx  2  0
 sin x  cos x  2    
 2 sin x   2   sin x  1 
x   k2 (k  ) .  4   4  4
------------------ HẾT------------------ Trang 53 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
§4. PHƯƠNG TRÌNH ĐẲNG CẤP I. DẠNG CƠ BẢN.
Dạng tổng quát: 2 2
a sin x b sin x cos x c cos x d   1 , a
 ,b,c ,d .
Phương pháp giải: cos x  0
Bước 1: Kiểm tra x   k  
có phải nghiệm hay không? 2 2 sin x 1 cos x  0
Bước 2: Khi x   k ,k    . Chia hai vế (1) cho 2 cos x : 2 2 sin x 1   2 2 sin x sin x cos x cos x 1 1  abcd 2 2 2 2 cos x cos x cos x cos x 2
a tan x b tan x c d  2 1 tan x .
Bước 3: Đặt t  tan x để đưa về phương trình bậc hai theo ẩn t x . Ví dụ.
Giải các phương trình sau: a. 2 2
sin x  sin xcos x  2cos x  0 . b. 2 2
2sin x  3 3 sin xcos x  cos x  2 . c. 2 2
cos x  3 sin 2x 1 sin x . d. 2 2
4sin 2x  5sin 2x cos 2x  6cos 2x  0 . Lời giải a. 2 2
sin x  sin xcos x  2cos x  0 2 2
sin x  sin xcos x  2cos x  0 (1) cos x  0 * Với x   k  
. Phương trình trở thành: 1 = 0 (vô lý) 2 2 sin x 1
 Phương trình không nhận nghiệm x   k ,k  2 cos x  0 * Với x   k ,k    . Chia hai vế (1) cho 2 cos x : 2 2 sin x 1  tan x 1 x   k  (1) 2
 tan x  tan x  2  0    4 tan x 2     x  arctan  2 k
Vậy phương trình đã cho có hai họ nghiệm: x
k ; x  arctan 2
  k , k  . 4 b. 2 2
2sin x  3 3 sin xcos x  cos x  2 2 2
2sin x  3 3 sin xcos x  cos x  2 (2) cos x  0 * Với x   k  
. Phương trình trở thành: 2 = 2 (đúng) 2 2 sin x 1 LÊ MINH TÂM Trang 54 HÀM SỐ LƯỢNG GIÁC
 Phương trình nhận nghiệm x   k ,k  2 cos x  0 * Với x   k ,k    . Chia hai vế (2) cho 2 cos x : 2 2 sin x 1 (2)  2 tan x  tan x    2 2 3 3 1 2 1 tan x 3
 3 3 tan x  3  tan x   x   k 3 6
Vậy phương trình đã cho có hai họ nghiệm: x
k ; x   k , k  . 2 6 c. 2 2
cos x  3 sin 2x 1 sin x 2 2
cos x  3 sin 2x 1 sin x 2 2
 cos x sin x  3sin2x 1
2x  2kx k 1    3 3 
 cos 2x  3 sin 2x 1  cos 2  x         3  2   x   k 2x    2k  3  3 3 d. 2 2
4sin 2x  5sin 2x cos 2x  6cos 2x  0 2 2
4sin 2x  5sin 2x cos 2x  6cos 2x  0 (3) cos2x  0 * Với x   k  
. Phương trình trở thành: 4 = 0 (sai) 2 4 2 sin 2x 1
 Phương trình không nhận nghiệm x   k ,k  4 2 cos2x  0 * Với x   k ,k    . Chia hai vế (3) cho 2 cos 2x : 4 2 2 sin 2x 1 (2)  2
4 tan 2x  5tan 2x  6  0  1   2 tan x x  arctan 2 2 2  k
x  arctan 2  k    2 2         3 3   tan 2x  2x  arctan    k  1  3       4   4 x arctan     k 2   4  2
Vậy phương trình đã cho có hai họ nghiệm: 1 1  3  
x  arctan 2  k ; x  arctan    k , k   . 2 2 2  4  2 II. BÀI TẬP. Bài 01.
Giải các phương trình sau: 1. 2 2
2sin x  3 3 sin xcos x  cos x  4 2. 2 2
3sin 2x  sin 2x cos 2x  4cos 2x  2 3. 2 sin   
sinxcosx   2 2 3 3 3 1 cos x  1  Trang 55 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC x x 4. 2 sin  sin x     2 3 4 8 3 9 cos  0 2 2 5. 2 sin x     2 3 1 3 sin .
x cos x  cos x 1 3  0 6. 2 2 9sin x  30sin .
x cos x  25cos x  25 7. 2
sin 2x  2sin x  2cos 2x 1 8. 2 2
sin x  sin 2x  2cos x  2 Lời giải 1. 2 2
2 sin x  3 3 sin x cos x  cos x  4  1 Xét 2
cos x  0  sin x 1, phương trình trở thành 2  4 (Vô lý)
x   k k  không là nghiệm của phương trình. 2
Xét cos x  0 , chia cả hai vế của phương trình   1 cho 2
cos x , ta được phương trình: 2 2
 tan x 3 3 tan x 5  0 (phương trình vô nghiệm)
Vậy phương trình đã cho vô nghiệm. 2. 2 2
3sin 2x  sin 2x cos 2x  4cos 2x  2 2 Xét 2
cos 2x  0  sin 2x 1, phương trình trở thành 3  2 (Vô lý)  k x  
k  không là nghiệm của phương trình. 4 2
Xét cos2x  0 , chia cả hai vế của phương trình 2 cho 2 cos 2x , ta được:  1 x  arctan      2    tan k 2x 2 2 2
tan 2x  tan 2x  6  0     k  tan 2x  3 1
x  arctan3 k  2 3. 2 sin   
sinxcosx   2 2 3 3 3 1 cos x  1  3 Xét 2
cos x  0  sin x 1, phương trình trở thành 2  1  (Vô lý)
x   k k  không là nghiệm của phương trình. 2
Xét cos x  0 , chia cả hai vế của phương trình 3 cho 2 cos x , ta được:  tan x  1  x    k   2 tan x     4 3 3 3 tan x  3  0      3 k  tan x         3 x k  6 x x 4. 2 sin  sin x     2 3 4 8 3 9 cos  0 2 2 x x Xét 2 cos  0  sin
1, phương trình trở thành 3  0 (Vô lý) 2 2
x   k2 k  không là nghiệm của phương trình. LÊ MINH TÂM Trang 56 HÀM SỐ LƯỢNG GIÁC x x Xét cos
 0 , chia cả hai vế của phương trình cho 2 cos , ta được: 2 2  x 8   3 3  3 3  8 tan  x  2arctan  k2 x x 2 3 tan  8tan  8 3 9 2 3 3  0     k  2 2  x  2 tan   3 x    k2    2  3 5. 2 sin x     2 3 1 3 sin .
x cos x  cos x 1 3  0 5 2  sin x     2 sin .
x cos x  cos x     2 2 3 1 3 1 3
sin x  cos x  0 2
 sin x     2 1 3 sin .
x cos x  3 cos x  0
Xét cos x  0  sin x  0 (loại vì 2 2
sin x  cos x 1)
Xét cos x  0 chia cả 2 vế của phương trình 5 cho 2 cos x ta được ;     tan  1 x k x   2 tan x    tan x 4 1 3  3  0     tan x  3 x    3 6. 2 2 9sin x  30sin .
x cos x  25cos x  25 6 5
Xét cos x  0  sin x   (loại vì 2 2
sin x  cos x 1) 3
Xét cos x  0 chia cả 2 vế của phương trình 6 cho 2 cos x ta được : tan x 0 2 tan x  tan x    2  9 30
25 25 1 tan x  0 2
 16tan x 30tan x 0 15 tan x  8 x k   15 ; k  . x arctan  k  8 7. 2
sin 2x  2sin x  2cos 2x 7 2 2  2sin .
x cos x  2sin x  4cos x  2 2 2  2sin x2sin c
x osx  4cos x  2  0 (1).
Xét cos x  0  sin x 1 . Suy ra x   k , k là nghiệm của phương trình. 2
Xét cos x  0 chia cả 2 vế của phương trình 7 cho 2 cos x ta được : 2
tan x  tan x   2 2 2
2 1 tan x  4  0  tan x 1 x   k ; k 4 1 8. 2 2
sin x  sin 2x  2cos x  8 2 1 2 2  sin x  2sin .
x cos x  2cos x   2 2
sin x  cos x 2 1 5 2 2  sin x  2sin .
x cos x  cos x  0 2 2
Xét cos x  0 thay vào phương trình ta được sin x  0 (vô lý) Trang 57 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
Xét cos x  0 chia cả 2 vế phương trình 8 cho 2 cos x ta được;  1 5 tan x 1 x   k 2 
tan x  2 tan x   0    4 2 2 tan x 5     x  arctan   5    k Bài 02.
Giải các phương trình sau: 1. 3 2sin x  cos x 2. 3 2 2
3sin x  2sin x cos x  sin x cos x 3. 3
6sin x  2cos x  5sin 2xcos x 4. 3
sin x  4sin x  cos x  0 5. 4 2 2 4 3cos x  4sin .
x cos x  sin x  0
6. sin x  sin xsin x  cos x 
 sinx sinx2 2 2 3 1 1 7. 3 3
sin x  cos x  sin x  cos x 5sin 4 . x cos x 8. 3
6 sin x  2cos x . 2 cos 2x Lời giải 1. 3 2sin x  cos x
Trường hợp 1: Xét cos x  0  sin x  0
Thay cos x  0 vào   1    3
1  2sin x  0  sin x  0 (mâu thuẫn)
Trường hợp 2: Xét cos x  0    3 sin x 1 3 2 1  2. 
 2.tan x 1 tan x  tan x 1  x   k k  3 2   cos x cos x 4  
Vậy S    k |k    4  2. 3 2 2
3sin x  2sin x cos x  sin xcos x
Trường hợp 1: Xét cos x  0  sin x  0
Thay cos x  0 vào 2    3
2  3sin x  0  sin x  0 (mâu thuẫn)
Trường hợp 2: Xét cos x  0 3 2 sin x sin x sin x  3.  2  3 2 cos x cos x cos x   x k tan x  0   3 2
 3tan x  2tan x  tan x  0  tan x  1
  x   kk    (tmđk). 4  1    1 tan x     3 x arctan k  3 3. 3
6sin x  2cos x  5sin 2xcos x
Trường hợp 1: Xét cos x  0  sin x  0
Thay cos x  0 vào 3  3  6sin x  0  sin x  0 (mâu thuẫn)
Trường hợp 2: Xét cos x  0 LÊ MINH TÂM Trang 58 HÀM SỐ LƯỢNG GIÁC    3 2
3  6sin x  2cos x  10sin x cos x 6 sin x sin x   2 10. 3 cos x cos x  .tan x 2  tan x 3 6 1
 2 10tan x  6tan x  4tan x  2  0  tan x 1 x   k k  4  
Vậy S    k |k    4  4. 3
sin x  4sin x  cos x  0
Trường hợp 1: Xét cos x  0  sin x  0
Thay cos x  0 vào 4    3
4  sin x  4sin x  0  sin x 1 1 1 2 1 4 sin x 2
 0  sin x   sin x    cos 2x   x    k k  4 2 2 6
Trường hợp 2: Xét cos x  0    3 sin x sin x 1 4   4   0 3 3 2 cos x cos x cos x  tan x 2  tan x 3  tan x   2 1 4 1 tan x  0 3 2  3
 tan x  tan x  tan x 1 0  tan x 1 x   k k  4  
Vậy S    k ,  k |k    4 6  5. 4 2 2 4 3cos x  4sin .
x cos x  sin x  0
Trường hợp 1: cos x  0  x
k , k , khi đó 2 sin x 1. 2 Thay 2
cos x  0, sin x  1 vào phương trình  
1 ta được: 1  0 (Vô lý). Vậy x
k , k  không là nghiệm của phương trình   1 . 2
Trường hợp 2: cos x  0  x
k , k  * . 2   4 2 2 4 3cos x  4 sin .
x cos x  sin x 1   0 4 cos x 2 4 sin x sin x  3 4.   0 2 4 cos x cos x 4 2
 tan x  4tan x 3  0 x   k  4 tan x 1       2   tan  1  x k x     tan x 1 tan x2 2 2  4
4 tan x  3  0     ,  
k  (thoả * ). 2 tan x  3 tan x  3  x   k   3 tan x   3 
x    k  3 Trang 59 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  
Vậy tập nghiệm của phương trình là S    k ,  k , k   .  4 3 
6. sin x  sin xsin x  cos x 
 sinx sinx2 2 2 3 1 1
 sin x sin xsin x  cos x 
 sinx sinx2 1 2 3 1 1  0    sin x 2
sin x  sin .xcos x   2 1 2
3 1 sin x  0  
 1 sin xsin .
x sin x  2cos x  3 1 sin x1 sin x  0  
   sin x 2 2 1 sin x  2 sin .
x cos x  3 cos x  0 1   sin x  0   2 2 sin x  2sin .
x cos x  3 cos x  0  sin x 1 x
k2 , k       2 2 2  sin x  2sin .
x cos x  3 cos x  0 2 2 sin x  2sin .
x cos x  3 cos x  0  2
Giải phương trình 2 :
Trường hợp 1: cos x  0  x
k , k , khi đó 2 sin x 1. 2 Thay 2
cos x  0, sin x  1 vào phương trình 2 ta được: 1 0 (Vô lý). Vậy x
k , k  không là nghiệm của phương trình 2 . 2
Trường hợp 2: cos x  0  x
k , k  * . 2   2 2 sin x  2sin .
x cos x  3 cos x 1   0 2 cos x tanx  1   1 3 
x  arctan  k 2
 tan x  2tanx  3  0     k     (thoả * ).  1   1 3  x arctan tan k xx   k2  2 
Vậy nghiệm của phương trình là x  arctan  k , k   .
x  arctan  k   7. 3 3
sin x  cos x  sin x  cos x sin x 1
Trường hợp 1: cos x  0  x
k , k . Khi đó  . 2 sin x  1  
Với sin x 1: Thay sin x 1, cos x  0 vào phương trình 3 , ta được 1 1 (luôn đúng). Với sin x  1  : Thay sin x  1
 , cos x  0 vào phương trình 3 , ta được 1   1  (luôn đúng). Vậy x
k , k  là nghiệm của phương trình 3 . 2 LÊ MINH TÂM Trang 60 HÀM SỐ LƯỢNG GIÁC
Trường hợp 2: cos x  0  x
k , k  . 2  sin x  cos x sin x  cos x 3 3 3   3 3 cos x cos x sin x 1 1 3  tan x 1 .  2 2
cos x cos x cos x 3
 tan x   tan x 2  tan x 2 1 1 1 tan x 3 3 2 2
 tan x 1 tanx  tan x 1 tan x  tan x  tan x  2  0 : Phương trình vô nghiệm.
Vậy nghiệm của phương trình là x
k , k . 2 5sin 4 . x cos x 8. 3
6 sin x  2cos x  2 cos 2x
Điều kiện xác định: cos 2x  0  2x
k k   x   kk  **. 2 4 2  . .sin . x cos . x cos x 4 5 2 2 2 3
 6sin x  2cos x  2 cos 2x 3 3 2
 6sin x  2cos x  5sin2 .
x cos x  6sin x  2cos x  10sin . x cos x 5 sin x 1
Trường hợp 1: cos x  0  x
k , k . Khi đó  . 2 sin x  1  
Với sin x 1: Thay sin x 1, cos x  0 vào phương trình 5 , ta được 6  0 (vô lý). Với sin x  1  : Thay sin x  1
 , cos x  0 vào phương trình 5, ta được 6   0 (vô lý). Vậy x
k , k  không là nghiệm của phương trình 4 . 2
Trường hợp 2: cos x  0  x
k , k  * . 2   3 2
6 sin x  2 cos x 10 sin . x cos x 5   3 3 cos x cos x sin x 1 sin x  6. .  2 10. 2 cos x cos x cos x  tan x 2 6
1 tan x  2  10 tan x 3
 6tan x  6tan x 10tan x  2  0 3
 6tan x  4tan x  2  0  tan x 1 x   k , k  (thoả * ). 4
So với điều kiện ( * * ), ta thấy không thỏa mãn.
Vậy phương trình vô nghiệm.
------------------ HẾT------------------ Trang 61 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
§5. PHƯƠNG TRÌNH ĐỐI XỨNG I. DẠNG CƠ BẢN.
Dạng tổng quát:
a sin x  cos x  b sin x cos x c  0 a
 ,b,c ,d .
Phương pháp giải:    
Đặt t  sin x  cos x  2 sin x  
 , do đó t  2 sin  x   2   4   4  2   t 1
Với t  sin x  cos x , khi đó 2 t  1 2 sin .
x cos x  sin . x cos x  . 2 2   1 t
Với t  sin x  cos x , khi đó 2 t  1 2 sin .
x cos x  sin . x cos x  . 2
Lưu ý: khi đặt t  sin x  cos x thì điều kiện là t  2 Ví dụ.
Giải phương trình sau:
2sin x  cos x  6sin xcos x  2   1 Lời giải    
Đặt t  sin x  cos x  2 sin x  
 , do đó t  2 sin  x   2  .  4   4 
t  sin x  cos x, khi đó 2
t 1 2sin xcos x  sin x cos x   2 6 3 t   1 . t 1    1  2t  3 2 t   2
1  2  3t  2t  5  0  5  t   3
Kiểm tra điều kiện ta được t  1. Khi đó :
x   k2 x k2 1      4 4  2 sin  x   1   sin  x       .  4   4   2  x   k2 x     k2  2  4 4 II. BÀI TẬP. Bài 01.
Giải các phương trình sau:
1. 2sin 2x  3 3 sin x  cos x  5  0 .
2. 2sin x  cos x  6sin xcos x  2  0 .
3. 2 2 sin x  cos x  2sin 2x 1.
4. sin x  cos x  4sin xcos x 1 0 .
5. sin x cos x  2 sin x  cos x 1  0 . 6. sin .
x cos x  6sin x  cos x 1.
7. sin x  cos x  2 6 sin .
x cos x .
8. 2 2 sin x  cos x  3 sin 2x .
9. 2sin 2x  3 3 sin x  cos x  5  0 .
10. 1 21 sin x  cos x  sin 2 . LÊ MINH TÂM Trang 62 HÀM SỐ LƯỢNG GIÁC Lời giải
1. 2sin 2x  3 3 sin x  cos x  5  0 .      t 2; 2   
Đặt t  sin x  cos x  2 sin x      .  4  2 t 1
sin xcos x   2 t  3 2  t 1  Ta có 4
  3 3t  5  0 2
 2t 3 3t 3  0   2   3 t   2   6 
x    arcsin   k2 4  2           6  3 6 sin x    x   arcsin   k2      4  2 4 2    Do đó   (k  ) .    6    6 sin x             x arcsin k2   4  4 4  4       3  6  x   arcsin   k2  4  4    
2. 2sin x  cos x  6sin xcos x  2  0 .      t 2; 2   
Đặt t  sin x  cos x  2 sin x      .  4  2 t 1
sin xcos x   2  5 2  t 1 t   (l) Ta có  6    2t  2  0 2
 3t  2t 5  0  3 . 2    t 1( ) n        x    k2 x k2 1  Do đó  2 sin  x   1   sin x     4 4    k   4   4  2 3  x   k2 x    k2     2 4 4
3. 2 2 sin x  cos x  2sin 2x 1.      t 2; 2   
Đặt t  sin x  cos x  2 sin x      .  4  2 1 t
sin xcos x   2  2    2  t 1 t  Ta có 4     2 2t 1  0 2
 2t  2 2t  3  0 2   . 2    3  2 t   2 Do đó Trang 63 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC     x     k2 x   k2 2   1   2 sin x       sin x      4 6   12   k   4  2  4  2  7 17  x    k2  x   k2  4 6  12
4. sin x  cos x  4sin xcos x 1 0 .      t 2; 2   
Đặt t  sin x  cos x  2 sin x      .  4  2 t 1
sin xcos x   2  1 2  t 1 t   Ta có  4     t 1  0 2  2
t t 1 0  2 . 2    t 1     2 sin  x   1    4  Do đó    1  2 sin  x       4  2    1 sin  x      4  2     1 sin  x       4  2 2
x   k2 x k2  4 4   3   x   k2 x    k2  2  4 4      1  k     1 . x    arcsin      k2 x   arcsin   k2  4   2 2  4  2 2    3  1    1  x   arcsin   k2 x    arcsin   k2  4    2 2  4   2 2 
5. sin x cos x  2 sin x  cos x 1  0 .      t 2; 2   
Đặt t  sin x  cos x  2 sin x      .  4  2 t 1
sin xcos x   2 2  t 1 t  1   2 n Ta có  2t 1  0 2
t  2 2t 1 0   . 2 t  1   2  l Do đó LÊ MINH TÂM Trang 64 HÀM SỐ LƯỢNG GIÁC  2  2     x   arcsin  k2 2  2 2 sin  x   1   2   sin x     4 2    4   4  2  2  2 x    arcsin  k2  4 2  2  2 x    arcsin  k2 4 2   k .  3 2  2 x   arcsin  k2  4 2 6. sin .
x cos x  6sin x  cos x 1   1 t   2; 2     
Đặt t  sin x  cos x  2 sin  x     2 1  4  t  sin . x cos x   2  2 t  6   39 1 t Thay vào   1 ta có được: 2
 6t 1  t 12t  3  0   2 t  6   39   2; 2        78  6 2 * t  6
  39  2 sin x   6
  39  sin x        4   4  2      78 6 2  78  6 2  x   arcsin   k2 x   arcsin    k2 4  2  4  2            ,k  .   78  6 2   5  78  6 2  x    arcsin   k2 x   arcsin   k2     4 2 4  2       
7. sin x  cos x  2 6 sin . x cos x   1 t   2; 2     
Đặt t  sin x  cos x  2 sin  x     2 1  4  t  sin . x cos x   2  6   2 t 1 t Thay vào   3 1 ta có được: 2 t  2 6.
 6t t  6   2  6 t    2 6   6 * t   2 sin x     3  4  3     3  3  x   arcsin   k2 x   arcsin   k2    4  3     4  3  3    sin x        ,k  .  4  3   3   5  3  x    arcsin   k2 x   arcsin   k2     4 3 4  3        6   6   3 * t    2 sin x     sin x        2  4  2  4  2 Trang 65 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC   x     k2 x     k2  4 3 12     ,k  .  4 19  x    k2 x   k2  4 3  12
8. 2 2 sin x  cos x  3  sin 2x   1
 1  2 2sinxcosx  32sinxcosx 2 t   2; 2     
Đặt t  sin x  cos x  2 sin  x     2 1  4  t  sin . x cos x   2 2 1 t
Thay vào 2 ta có được: 2 2 2.t  3  2
t  2 2t  2  0  t  2 2     3
t  2  2 sin x   2  sin x
 1  x    k2  x   k2 ,k      .  4   4  4 2 4
9. 2 sin 2x  3 3 sin x  cos x  5  0   1
 1  4sin .xcosx3 3sinxcosx5  0 2 t   2; 2     
Đặt t  sin x  cos x  2 sin  x     2 t 1  4  sin . x cos x   2  3 2 1 t t  
Thay vào 2 ta được: 2 4.
 3 3.t  5  0  2t  3 3t  3  0  2  2
t   3 2; 2    3   3   6 * t    2 sin x     sin x        2  4  2  4  4     6  6 
x   arcsin    k2
x    arcsin    k2 4  4  4  4            ,k  .  6  3  6    x    arcsin    k2 x   arcsin    k2     4 4 4  4       
10. 1 21 sin x  cos x  sin 2x   1
 1  1 21sinxcosx  2sin .xcosx 2 t   2; 2     
Đặt t  sin x  cos x  2 sin  x     2 1  4  t  sin . x cos x   2 2  t  1 1 t
Thay vào 2 ta được: 1 21 t 2  2
t  1 2t  2  0   2 t  2 LÊ MINH TÂM Trang 66 HÀM SỐ LƯỢNG GIÁC   * t  1   2 sin x   1   4 
x    k2  x k2   2 4 4  sin x        3 ,k    .  4  2    x   k2 x         k2  2 4   4      3
* t  2  2 sin x   2  sin x
 1  x    k2  x   k2 ,k      .  4   4  4 2 4
------------------ HẾT------------------ Trang 67 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
§6. CÁC LOẠI PHƯƠNG TRÌNH KHÁC
I. BIẾN ĐỔI TÍCH THÀNH TỔNG.
Phương pháp giải:
Dùng công thức biến đổi tích thành tổng, đặt nhân tử chung đưa về phương trình tích
1.1. Ví dụ minh họa. Ví dụ.
Giải phương trình sau: sin .
x sin7x  sin3 . x sin5x Lời giải sin .
x sin7x  sin3 . x sin5x 1
 cos x cos x 1 6 8
 cos2x cos8x 2 2  k x
6x  2x k2 4x k2  2
 cos6x  cos 2x       ,k  . 6  x  2  x k2 8  x k2  k x   4 k k
Vậy phương trình có hai họ nghiệm x  ; x  ,k   . 2 4
1.2. Bài tập rèn luyện. Bài tập.
Giải các phương trình sau: 1. sin5 .
x cos3x  sin9 .
x cos7x . 2. cos .
x cos3x sin2 .
x sin6x sin4 .
x sin6x  0 . 3. sin4 .
x sin5x  sin4 .
x sin3x sin2 .
x sin x  0. 4. 2cos . x cos2 .
x cos3x 7  7cos2x. Lời giải 1. sin5 .
x cos3x  sin9 . x cos7x 1
 sin x  sin x 1 2 8
 sin2x  sin16x 2 2  k x  16
x  8x k2 8  x k2  4
 sin16x  sin8x       ,k  . 16
x  8x k2 24  x   k2  k x    24 12 k k
Vậy phương trình có hai họ nghiệm x  ; x   ,k   . 4 24 12 2. cos .
x cos3x sin2 .
x sin6x sin4 . x sin6x  0 1
 cos x  cos x 1
 cos x cos x 1 4 2 4 8
 cos2x  cos10x  0 2 2 2
 cos4xcos2xcos4xcos8xcos2xco 1 s 0x  0  co 1
s 0x  cos8x  0 LÊ MINH TÂM Trang 68 HÀM SỐ LƯỢNG GIÁC   k 9     cos x k x 9x  0   2  2cos9 .
x cos x  0     ,k   18 9   ,k  . cos x  0   x   k x   k  2  2 k
Vậy phương trình có hai họ nghiệm x   ; x
k , k . 18 9 2 3. sin4 .
x sin5x  sin4 .
x sin3x sin2 . x sin x  0 1
 cosx cos x 1
 cosx cos x 1 9 7
 cosx cos3x  0 2 2 2
 cosxcos9xcosxcos7xcosxcos3x  0
 cosxcos9xcos7xcos3x  0
 cos3x  cosxcos9x  cos7x  0
 2cos2xcosx2cos8xcosx  0
 cos xcos2x cos8x  0 cos x  0
 cos2xcos8x 0    x   k x k x k        2 2 2  cos x  0    k    8
x  2x k2  6  x k2  x  ,k  . cos8x   cos 2x  3 8  x 2x k2 1     0x k2    kx     5 k k
Vậy phương trình có ba họ nghiệm x   k ; x  ; x  ,k   . 2 3 5 4. 2cos . x cos2 .
x cos3x 7  7cos2x
 cos4x  cos2x.cos2x 7  7cos2x   2
2 cos 2x 1 cos 2x.cos 2x  7  7cos 2x 3 2
 2cos 2x  cos 2x cos2x 7  7cos2x 3 2
 2cos 2x  cos 2x 8cos2x 7  0  cos x   2 2
1 2 cos 2x  cos 2x  7  0  cos 2x  1   cos 2x 1  0  1 57    cos 2x loai 2   2
 cos 2x cos 2x 7 0     4  1 57 cos2x  loai  4  cos2x  1
  2x   k2  x   k ,k . 2
Vậy phương trình có một họ nghiệm x
k k  . 2 Trang 69 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
II. BIẾN ĐỔI TỔNG THÀNH TÍCH.
Phương pháp giải:
Dùng công thức biến đổi tổng thành tích, đặt nhân tử chung đưa về phương trình tích
2.1. Ví dụ minh họa. Ví dụ 01.
Giải phương trình sau:
sin5x  sin3x  sin4x Lời giải
sin5x  sin3x  sin4x
 sin5xsin3xsin4x  0
 2sin4xcosxsin4x  0  k
4x k ,k  x   x   
 sin x cos x   sin 4 0 4 4 2 1  0      k  1  2  cos x 1  0 cos x    x    k2  2  3  k  Vậy S   ;
k2 |k   .  4 3  Ví dụ 02.
Giải phương trình sau:
sin x  sin2x  sin3x  0 Lời giải
sin x  sin2x  sin3x  0
 sinx  sin3xsin2x  0
 2sin2xcosxsin2x  0
 sin 2x2cosx   1  0  k
2x k ,k   sin x 2x  0   2      k  1  2  cos x 1  0   2 cos x   x    k2  2  3  k 2  Vậy S   ; 
k2 |k   .  2 3 
2.2. Bài tập rèn luyện. Bài tập.
Giải các phương trình sau:
1. cos x  cos3x  2cos5x  0
2. cos22x 3co 1 s 8x 3co 1 s 4x  co 1 s 0x  0
3. 1 cos x  cos 2x  cos3x  0
4. cos x  cos2x  cos3x  cos4x  0
5. 1 sin x  cos3x  cos x  sin2x  cos2x . 6. 2 3 4 2 3 4
sin x  sin x  sin x  sin x  cos x  cos x  cos x  cos x Lời giải
1. cos x  cos3x  2cos5x  0 LÊ MINH TÂM Trang 70 HÀM SỐ LƯỢNG GIÁC
 cos5x  cosxcos3x cos5x  0  2cos3 .
x cos2x  2cos4 . x cos x  0   3
4 cos x  3cos xcos 2x  cos 4 . x cos x  0  cos x  2
4 cos x  3cos 2x  cos 4x  0 
 cos x  cos x   2 2 2
1 cos 2x  2 cos 2x 1  0  2
 cos x 4cos 2x  cos 2x 1  0  
Trường Hợp 1: cos x  0  x   k 2
Trường Hợp 2: 2
4cos 2x  cos 2x 1  0  1 1 17  x   .arccos   k   2  8  1 17    cos 2x    k  8  1 1 17  x   .arccos    k  2  8           1 1 17 
Vậy S    k ;  .arccos 
  k |k   . 2 2  8     
2. cos22x 3co 1 s 8x 3co 1 s 4x  co 1 s 0x  0
 cos22x  cos10x3cos18x  cos14x  0  2co 1 s 6 .
x cos6x  6co 1 s 6 . x cos2x  0
 2cos16xcos6x 3cos2x  0  cos x 3 16 4 cos 2x  0  k    cos x 16x  0    32 16   k  cos 2x  0  k x    4 2  k k  Vậy S    ;  |k   . 32 16 4 2 
3. 1 cos x  cos 2x  cos3x  0 . 2 3
1 cosx  2cos x 1 4cos x 3cosx  0 3 2
 4cos x  2cos x  2cosx  0  cos x 2 2
2 cos x  cos x   1  0     cos x k x  0  2 2cos x  0      cos x  1
  x   k2 k  2   2
 cos x  cos x 1  0  1  cos x
x    k2  2  3
Vậy phương trình có các nghiệm là: x
k ; x   k2 ; x    k2 k  2 3 Trang 71 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
4. cos x  cos2x  cos3x  cos4x  0
 cosx  cos4xcos2x  cos3x  0 5x  3x  5xx   2cos cos   2   cos cos   0   2  2  2  2  5x  3x x   2cos cos  cos  0  2  2 2  5x  2   k x   k    5  5 x x 2 2 5 5 2 cos  0 cos  0     2 3 2  x x          k2  x   kk  3  x x  3xx   2 2  2 cos  cos cos  cos         2 2 2   2 3  x x x    k2      k2   2 2  2
Vậy phương trình có các nghiệm là: x   k ; x
k ; x    k2 k  5 5 2
5. 1 sin x  cos3x  cos x  sin2x  cos2x
 1cos2xsinx sin2xcos3x cosx  0 2
 2sin x  sinx sin2x 2sinxsin2x  0
 2sin xsin x sin2xsin x sin2x  0
 sin x sin2x2sin x   1  0 x  k2
x  2x k2   2
x   2x k2 x   k
sin x  sin 2x   3 3       1   2 k x k      sin x  
x    k2 6  2   6  7 x   k2  7  x   k2 6  6 2 7
Vậy phương trình có các nghiệm là: x  k2 ; x   k ; x    k2 ; x
k2 k  3 3 6 6 6. 2 3 4 2 3 4
sin x  sin x  sin x  sin x  cos x  cos x  cos x  cos x
 sin x  cos x   2 2
sin x  cos x   3 3
sin x  cos x   4 4
sin x  cos x  0
 sin x  cos x  sin x  cos xsin x  cos x
 sin x  cos x 2 2
sin x  sin x cos x  cos x  sin x  cos xsin x  cos x  0
 sin x  cos x 2 2
1 sin x  cos x  sin x  sin x cos x  cos x  sin x  cos x  0
sin x  cos x  0   1
 2sinxsinxcosx2cosx2 0  2   + Giải  
1  sin x  cos x  cos  x    cos x  2  LÊ MINH TÂM Trang 72 HÀM SỐ LƯỢNG GIÁC
  x xk2  2  
x   k k   4
  x  x k2  2
+ Giải 2  2sin x  cos x  sin xcos x  2  0 t
Đặt sin x  cos x t t   2 1
2  sin x cos x
. Khi đó phương trình trên trở thành: 2 t  1  tm 2  
t  4t  3  0  t  3   loai     1 Với t  1
  sin x  cos x  1   2 sin x   1   sin x         4   4  2      x    k2 sin x sin       2 k      4 4     
x   k2
Vậy phương trình có các nghiệm là: x
k ; x    k2 ; x   k2 k  4 2
III. TỔNG HỢP CÁC PHƯƠNG PHÁP.
Phương pháp giải:
Sử dụng các công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc,
công thức biến đổi tích thành tổng, biến đổi tổng thành tích) để đưa về dạng phương trình lượng giác cơ bản
3.1. Ví dụ minh họa. Ví dụ 01.
Giải phương trình sau: 3 2 2 2
sin x  sin 2x  sin 3x  2 Lời giải 3 2 2 2
sin x  sin 2x  sin 3x  2
1cos2x1cos4x1cos6x  3.
 cos2xcos4xcos6x  0 .
 2cos2xcos4xcos4x  0.
 cos4x2cos2x   1  0 .    4       cos x k x k x k 4x  0    2 8 4 8 4         k  . 2  cos 2x 1  0 1   2  cos 2x   2x    k2 x    k  2  3  3 Ví dụ 02.
Giải phương trình sau: 2 2 2 2
sin 3x  sin 4x  sin 5x  sin 6x   1 Trang 73 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC Lời giải 2 2 2 2
sin 3x  sin 4x  sin 5x  sin 6x
1cos6x1cos8x 1co 1 s 0x 1 co 1 s 2x .
 cos6xcos8x  co 1 s 0x  co 1 s 2x .
 cos7xcosx  co 1 s 1xcos x .
 cos xcos7x cos11x  0.   x   k x k     2  k 2   cos x x  0   k  2    11
x  7x k2  x    k .
cos11x  cos7x  2   k 11x  7  x k2  x   k  9 x    9
3.2. Bài tập rèn luyện. Bài tập.
Giải các phương trình sau: 1. 2 2 2
sin 2x  sin 4x  sin 6x . 2. 2 2 2 2
cos x  cos 2x  cos 3x  cos 4x  2 . 3 3. 2 2 2
cos 3x  cos 4x  cos 5x . 4. 4
8cos x 1 cos 4x . 2 5. 4 4
sin x  cos x  cos 4x . 6. 2 2 2
3cos 2x  3sin x  cos x  0 . Lời giải 1 2 2 2
sin 2x  sin 4x  sin 6x   1 . Ta có:  
1  1 cos 4x 1 cos8x  1 cos12x .
 cos4xcos8x 1co 1 s 2x . 2
 2cos6xcos2x  2cos 6x .
 cos6xcos6x cos2x  0 .  cos6x 2
 sin 4xsin 2x  0.     cos x k 6x  0 cos6x  0 6x   k   12 6      2   ,k   . 2 
 sin 4x sin 2x  0 sin 4x  0   4  x k x k  4 2. 2 2 2 2
cos x  cos 2x  cos 3x  cos 4x  2 .
PT  cos 2x  cos 4x  cos6x  cos8x  0
 2cos3xcosx2cos7xcosx  0.
 2cos xcos3x  cos7x  0.
 cosxcos5xcos2x  0.   x   k x   k   2 2 cos x  0     
 cos5x  0  5x   k x   k ,k     . 2  10 5 cos2x  0    2x   kx   k  2  4 2 LÊ MINH TÂM Trang 74 HÀM SỐ LƯỢNG GIÁC 3 3. 2 2 2
cos 3x  cos 4x  cos 5x  2
1 cos 6x 1 cos8x 1 cos10x 3     . 2 2 2 2
 cos6xcos8xco 1 s 0x  0
 2cos8xcos2xcos8x  0
 cos8x1 cos2x  0 .  k   k   cos x 8x  0 8x   k x         2 k   k  16 8 16 8   k  1  cos 2x  0   . cos  2x  1  2  x   k2 x   k  2 4. 4
8cos x 1 cos 4x 2 1 cos 2x  2  8  2   cos 2x  2   2cos2x1 0 1  2 cos 2x   2  cos2x  cos  2x  
k2 k   x    k k  . 2 3 3 3 5. 4 4
sin x  cos x  cos 4x
 sin xcos x2 2 2 2 2 2
 2sin xcos x 1 2sin 2x 1 k 2 2
1 sin 2x 1 2sin 2x 2
 sin 2x  0  sin2x  0  2x k k   x  k . 2 2 6. 2 2 2
3cos 2x  3sin x  cos x  0 .   sin x 2 2 2 3 2
1  4sin x 1  0 . 4 2
12sin x 16sin x  4  0 . Đặt 2
t  sin x, t  0 1 ,  
 . Phương trình trở thành 2
12t 16t  4  0 . t 1   1  (thỏa mãn) t   3 2 sin x 1   1  2 sin x   3 1 cos 2x  1 cos 2x  1  2x   k2 x   k   2   2    1  1   k . 1  cos 2x 1 cos2x
2x  arccos  k2 1 1    3  3
x   arccos  k  2 3  2 3
IV. PHƯƠNG TRÌNH CÓ ĐIỀU KIỆN.
Phương pháp giải:
Sử dụng các công thức lượng giác đưa về phương trình lượng giác cơ bản và kết hợp điều
kiện để tìm nghiệm của phương trình. Trang 75 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
4.1. Ví dụ minh họa. Ví dụ 01.
Tìm tổng các nghiệm trong khoảng  ;  của phương trình:     sin 3x   cos 2x       3   4  Lời giải     sin 3x   cos 2x       3   4   3  2 3x    2x k2 x   k 3       3 4 12 5  sin 3  x    sin  2  x      (k  )  3   4   3  2 3x     2x k2 x    k  3 4  12 5 2
Trường hợp 1: x   k (k  ) ;  12 5  65 55   k  2 5   24 24  k {  2; 1
 ;0;1; 2}  S  5.  ( 2  1 0 1 2)  1 12 5 12 k  2
Trường hợp 2: x    k (k  ) ;  12 5  55 65   k  5   24 24  k {  2; 1
 ;0;1; 2}  S   2 12 k 
Vậy tổng các nghiệm trong khoảng  ;  . của phương trình: S S S  0 1 2 Ví dụ 02.
Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình 2 2
sin 2x  cos 5x 1 Lời giải 2 2
sin 2x  cos 5x 1 x k  2 2 3
 sin 2x  sin 5x  1 cos4x  1 c 10
os x  cos4x  c 10 os x   k . x k  7 Xét x k  0  k  0 3 Xét x k  0  k  0 7
Do k  nên nghiệm dương nhỏ nhất x  7
Tương tự tìm được nghiệm âm lớn nhất x   7 LÊ MINH TÂM Trang 76 HÀM SỐ LƯỢNG GIÁC
4.2. Bài tập rèn luyện. Bài 01.
Tìm tổng các nghiệm trong khoảng  ;  của phương trình:   2 2 sin 2x  cos 3x     8  Lời giải   2 2 sin 2x  os c 3x     8    1 cos 6x    1 cos4x  4    2 2  
 cos4x  cos 6x     4   
 4x  6x   k2 x   k      cos  4x 4 8 5  cos 6  x       (k  )  4    3  4x  6  x   k2 x    k  4  8
Trường hợp 1: x
k (k  ) ;  8 5  45 35   k    8 8  k {  5; 4  ; 3  ; 2  ; 1
 ;0;1; 2;3; 4}  S 10.  ( 5
  4  3... 3 4)  1 5 5 k  3
Trường hợp 2: x  
k (k  ) ;  8  5 11   k    8
8  k {0;1}  S  2 4 k  5
Vậy tổng các nghiệm trong khoảng  ;  . của phương trình: S S S  1 2 4 Bài 02.
Tìm nghiệm dương nhỏ nhất và nghiệm âm lớn nhất của phương trình sinx o c sx2 2  2 o c s 3x Lời giải
sinxcosx2 2  2cos 3x 2    2
  2 sinx    2cos 3x   4    2 2  sin x     cos 3x  4  Trang 77 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC   1 cos 2x     2  1 cos 6x   2 2  
 2x  6x k2 x   k     2 16 4  cos  2  x   cos6x     (k  )  2     2x  6  x k2 x   k  2  8 2 1 Xét x x
k  0  k   16 4 4 1 Xét x
k  0  k   8 2 4
Do k  nên nghiệm dương nhỏ nhất x  16 3
Tương tự tìm được nghiệm âm lớn nhất x   16 Bài 03.
Tìm nghiệm dương nhỏ nhất của phương trình   1  1. 2 cos   x   
2x    sin  2 x  ,
2. sin  x   sin x 2 2 1   2    . Lời giải   1  1. 2
cos   x  2x    sin 2 x    2  Ta có   1  2
cos   x  2x    sin 2 x    2    1    2 2
 cos  x  2x    cos   x    2   2    1  2 2
  x  2x     x k2   2  2  , k    1  2 2
  x  2x      x k2   2  2  1 1 2 2 x  2x    x  2k  2 2   , k  1 1  2 2 x  2x
   x  2k  2 2 2  1  3  x      k 1 ( )  2 4 , k    x   k (2) 3 3 +)   1 có nghiệm khi
k  0  k   ,k   k 0;1;2;3.. . 4 4 LÊ MINH TÂM Trang 78 HÀM SỐ LƯỢNG GIÁC  1 3  1 3 x    kx     k Khi đó   2 4 2 4 1    
, k 0;1; 2;3..  .  1 3  1 3 x     kx     k  2 4  2 4 3 1
Suy ra nghiệm dương nhỏ nhất của   1 là x  . 2
+) 2 có nghiệm dương nhỏ nhất là x 1. 3 1
Vậy phương trình đã cho có nghiệm dương nhỏ nhất là x  . 2
2. sin  x  sin  x 2 2   1   Ta có  x 2 2 1  x k2
sin  x  sin  x 2 2   1         x   , k 2 2 1   x k2  1  x    k   1 x  2 2 1  x  2k    2     2 , k   x   , k 2 2 1 1 x  2k 1 1 x      k 2  2  4 1 +)  
1 có nghiệm dương nhỏ nhất là x  . 2 1 1
+) 2 có nghiệm   k  0  k   ,k   k 0;1; 2;3...  . 4 4  1 1  1 1 x    kx     k 2 4 2 4 Khi đó 2    
, k 0;1; 2;3...  .  1 1  1 1 x     kx     k  2 4  2 4    5 1
2 có nghiệm dương nhỏ nhất là x  . 2 1
Vậy phương trình đã cho có nghiệm dương nhỏ nhất là x  . 2 Bài 04.
Tính tổng các nghiệm nằm trong khoảng 0; 2  của phương trình sau
 3 1sinx 3 1cosx2 2sin2x Lời giải Ta có
 3 1sinx 3 1cosx2 2sin2x
  3sinx cosx 3cosxsinx  2 2 sin2x Trang 79 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  3 1   3 1   
sin x  cos x   
cos x  sin x   2 sin 2x  2 2   2 2           sin x    cos x   2  sin 2x  6   6     5   2 sin x  
 2 sin 2x  sin 2x  sin x       6 4   12   5  5 2x x   k2 x   k2   12 12   , k    , k  5 7 2   2x   x   k2 x   k  12  36 3 5 5 5 19 +) x
k2 , x0;2   0   k2  2    k
, k   k  5 0  x  . 12 12 24 24 12 7 2 7 2 7 65 +) x   k
, x 0; 2   0   k  2    k
, k   k 0;1;  2 36 3 36 3 12 24 7 31 55  x  ; x  ; x  . 36 36 36
Suy ra phương trình đã cho có tập nghiệm nằm trong khoảng 0; 2  là 5 7 31 55   ; ; ;  12 36 36 36 
Vậy tổng các nghiệm của phương trình đã cho nằm trong khoảng 0; 2  là 5 7 31 55     3 . 12 36 36 36 Bài 05.
Tìm nghiệm trên khoảng  ,  của phương trình: sinx  2 2
1 sin 2x  3sin x   1  sin 4 . x cos x Lời giải sinx  2 2
1 sin 2x  3sin x   1  sin 4 . x cos x
 sin x   2 2
1 sin 2x  3sin x   1  2 sin 2 . x cos 2 . x cos x
 sin x   2 sin
x  sin x   2 2 1 2 3 1  4 cos 2 . x sin . x cos x
 sin x   2 2
1 sin 2x  3sin x   1  4 cos 2 . x sin .
x 1 sin x1 sin x sin x 1  0   2
sin 2x  3sin x 1  2cos 2 . x sin . x  1  sin x 
Trường hợp 1: sin x 1  0  sin x  1   x   k2 ,k  . 2 
Mà x  ,   x  . 2
Trường hợp 2: 2
sin 2x  3sin x 1  2cos 2 .
x sin x1 sin x LÊ MINH TÂM Trang 80 HÀM SỐ LƯỢNG GIÁC 2
 sin 2x 3sin x 1 sin3x sinx1sinx 2 2
 sin 2x  2sin x  cos x  sin3x  sin3 . x sin x
 1- cos 4x - 4sin x 1 cos 2x  2sin3x - cos 2x - cos 4x
 cos 4x - cos 2x  sin3x -1 2sin x  0  2
- sin 3x sin x  sin 3x -1 2 sin x  0  sin3x 2 - i s n x   1 -1 2 sin x  0   x   k2  2       sin x 1 3  
3sin x  4 sin x   1  2  sin x   1  0   x   k2 1 sin x   6  2  5 x   k2  6   Mà x   ,  5  x  , ,   2 6 6   5  Vậy x   , ,  .  2 6 6  Bài 06.
Giải các phương trình sau
1. cot3x  cot x 2. cot 4 . x cot 7x 1 Lời giải
1. cot3x  cot xk sin3x  0 x k Điều kiện:   
3 ,k    x  ,k   . s  in x  0 3 x   k Ta có: k
cot 3x  cot x  3x x k ,k    x  ,k   2
Kết hợp điều kiện thì phương trình có nghiệm là x
k ,k . 2 2. cot 4 . x cot 7x 1  k  sin x 4x  0  Điều kiện: 4    ,k  . sin 7x  0 kx   7 Ta có:   cot 4 .
x cot 7x  1  cot 4x  tan 7x  cot 4x  cot  7  x   2  m
 4x   7x m x   ,m . 2 22 11 m k Giả sử  
 2 4m 11k 22 11 4 Trang 81 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
k  4t  2
k  4t  2   t    t  2  4  m  11  4t 2   
m 11t  5 m k Giả sử  
 714m  22k  7  22k 14m ( phương trình vô nghiệm) 22 11 7 m
Vậy phương trình có nghiệm là x  
, m  11t  5t   . 22 11 Bài 07.
Giải phương trình lượng giác sau:
sin x cot 5x 1 cos9x Lời giải k    cos x 9x  0 9  x   k  +) Điều kiện 18 9    2 , k,l    , k,l  . sin5x  0 l 5  x lx   5
+) Với điều kiện trên, phương trình đã cho tương đương với
 sinxcos5x  cos9xsin5x 1  sin 
xxsinxx 1 5 5   sin  
5x9xsin5x9x 2 2     x x m
sin6x sin4x  si 1 n 4x  14 6 2
sin4x  sin14x  sin 6x  14x  6x  m2  m x  8  x m2  4     , m  . 20x    m2 mx    20 10 m +) Với x  : 4 m k
k  4  9t  
 9m  2  4k  
 9m 18 36t m  2  4t, t  . 4 18 9 9
m  2  4k m ll  5t
 5m  4l  
m  4t, t  . 4 5 5  m  20t m m
Do đó phương trình có họ nghiệm x
,m  2  4t, m  4t, t  . Hay x   , m 4 4 2 m +) Với x   : 20 10 m k m k      
18m 1 20k 18m 20k 1 (vô nghiệm). 20 10 18 9 10 180 9 m l  
1 2m  4l 1 4l  2m (vô nghiệm). 20 10 5 m
Do đó phương trình có họ nghiệm x   , m thỏa mãn. 20 10 LÊ MINH TÂM Trang 82 HÀM SỐ LƯỢNG GIÁC m m
Vậy phương trình đã cho có hai họ nghiệm x   , x   , m . 4 2 20 10 Bài 08.
Giải phương trình:
cos3xtan4x  sin5x Lời giải k
+) Điều kiện cos 4x  0  4x
k x   , k  . 2 8 4
+) Với điều kiện trên, phương trình đã cho  sin4xcos3x  sin5xcos4x 1 
x x m
sin x  sin x 1 7
 sin x  sin9x 9 7 2
 sin9x  sin 7x   2 2 9x   7x   m2 x mx m       , m m m . x   x      16 8  16 8
+) Với x m : k m  
 8m 1 2k  8m  2k 1 (vô nghiệm). 8 4
Do đó họ nghiệm x m , m thỏa mãn. m +) Với x   : 16 8 m k m 1 k      
 2m 1 4k (luôn đúng, vì một vế là số chẵn, một vế là 16 8 8 4 8 16 4 m
số lẻ). Do đó họ nghiệm x   , m thỏa mãn. 16 8 m
Vậy phương trình đã cho có hai họ nghiệm x m , x   , m . 16 8 Bài 09.
Giải phương trình:
tan2xtan3xtan7x  tan2x  tan3x  tan7x Lời giải   k 2x   k x     2 4 2 cos 2x  0      k
+) Điều kiện cos3x  0  3
x   k  x   , k  . 2 6 3    cos 7x  0    k 7x   k x      2  14 7
+) Phương trình đã cho  tan 2xtan3xtan7x  
1  tan3x  tan 7x (1) 1 Nếu 2
tan 3x tan 7x 1  0  tan 3x  tan 7x  0  tan 3x
 0  tan 3x 1 0 (vô tan 3x
nghiệm). Do đó tan3xtan7x 1 0. Khi đó
tan 3x  tan 7x tan3x  tan 7x 1 ( )  tan 2x   tan 2x  
 tan 2x  tan10x
tan 3x tan 7x 1
1 tan 3x tan 7x Trang 83 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC l  tan10x  tan 2
x 10x  2
x l x  , l  . 12 l
+) Xét họ nghiệm x  , l  . Ta có 12 l k  
l  3 6k l  31 2k 12 4 2 l k  
l  2  4k l  21 2k 12 6 3 l kk  3 7t
k  3 7t  
 7l  6 12k     12 14 7 7
l  6 12k 7  l  6 12  37t k  3 7t  
l  6 12t, t  .
l  6 12t l
Vậy phương trình có nghiệm, x
, l  31 2k , l  21 2k , l  6 12t, l, t  . 12 Bài 10.
Giải phương trình: 4cos2xx  2  tan x  tan . x tan   
sin 2x  2 cos x  2 4  Lời giải  cos x  0 x   k    Điều kiện: 2   x   
,k   x   k ,k . cos   0 3 2       2 4 x   k2   2 4cos2xx  Ta có: 2  tan x  tan . x tan   
sin 2x  2 cos x  2 4  4cos2x 1 sin x   tan x  tan . x
sin 2x  2 cos x 1 sin x 4cos2x  1 sin x    tan . x 1   2 sin .
x cos x  2 cos x  1 sin x  4cos2x sin x 2   .
2 cos x sin x   1 cos x 1 sin x
 cos 2x  sin x   k2 x   2x k2 x       2  sin x  sin  2  x    k  6 3   k   2     x   2x k2 x   k2  2  2 5
Đối chiếu điều kiện thì phương trình có nghiệm là x   k2 ; x
k2 k  . 6 6 Bài 11.
Giải phương trình: LÊ MINH TÂM Trang 84 HÀM SỐ LƯỢNG GIÁC
cos2x2cos 2x   1  cotx sin 3x Lời giải sin3x  0 k Điều kiện: 
 sin3x  0  x  , k  . sin x  0 3 cos2x 2    2 1 2 sin   cos ( cos ) x x x  1 2 2 2 1  cos x Ta có:  cot x   3 sin 3x
3sin x  4 sin x sin x cos2x  2
3  4 sin x cos x   co 2 s x  cosx sin x  2 3  4 sin x sin x
2x x k2
 2x  x  k2 x k2  k2  2  x  , k k  x  3  3
(Loại vì không thỏa mãn điều kiện)
Kết luận: Phương trình vô nghiệm. Bài 12.
Giải các phương trình sau:
sin x  sin 2x  sin 3x 2 3
cos x  cos x 1 1.  3 2. 2
cos 2x  tan x .
cos x  cos 2x  cos3x 2 cos x  2
2  sin 2x sin 3x 4  1 1 2 3.   .
4. tan x 1  . cos x sin 2x sin 4x 4 cos x 1
2 sin x  cos x
5. cos3xtan5x  sin7x . 6. . tan x  cot 2x cot x 1 Lời giải
sin x  sin 2x  sin 3x 1.  3
cos x  cos 2x  cos3x
sin 3x  sin x  sin 2x   3
cos3x  cos x  cos 2x 2 sin 2x o
c sx  sin 2x   3
2 cos 2x cos x  cos 2x sin 2x2 o c sx   1  
, ĐK: cos 2x  0; 2cos x 1  0
cos x cos x   3 2 2 1  k
tan 2x  3  2x
k x  
k  (thoả mãn ĐK). 3 6 2 2 3
cos x  cos x 1 2. 2
cos 2x  tan x
( ĐK: cos x  0  x
k ,K  .). 2 cos x 2 1 2
PT  cos 2x  tan x  1 cos x  2 cos x Trang 85 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 2
 cos x  tan x   cos x   2 2 1 1 tan x 2 2
 cos2x  tan x 1cosx 1 tan x 2
 2cos x  cos x 1 0 cos x  1    1 cosx   2 x   k2   , K  
( Thoả mãn điều kiện). x    k2  3 1 1 2 3.   cos x sin 2x sin 4x cos x  0 cos x  0   k
Điều kiện: sin 2x  0  2sin x cos x  0
 sin4x  0  4x k x  , k    4 . sin 4x  0 
2 sin 2x cos 2x  0  1 1 2 PT    cos x 2 sin x cos x
2 sin x cos x cos 2x 1 1 1  2 sin x 2 sin x cos 2x
 2sinxcos2xcos2x 1
 2sinxcos2x 1cos2x 2
 2sinxcos2x  2sin x
 2sin xcos2x sinx  0 2
1 2sin x sin x  0 sin x  1    1  . sin x   2 +) Xét sin x  1
 cosx  0 (Loại). x   k2 1  +) sin x  6   , K  . 2  5 x   k2  6 Thử điều kiện    2   2  3 +) sin 4x  sin 4   k2   sin   k8   sin     0 ( thoả mãn).  6   3   3  2  5  10  10      3 +) sin 4x  sin 4   k2   sin   k8   sin    sin  3     sin    0    6   3   3   3   3  2 ( thoả mãn). x   k2 
Vậy phương trình có nghiệm: 6  , K  .  5 x   k2  6 LÊ MINH TÂM Trang 86 HÀM SỐ LƯỢNG GIÁC  2
2  sin 2x sin 3x 4 
4. tan x 1  4 cos x
Điều kiện: cos x  0  x
k k . 2
Với điều kiện trên, ta có:  2
2  sin 2x sin 3x 4  tan x 1  4 cos x 4 4
 sin x  cos x   2
2  sin 2xsin 3x
 sin xcos x2 2 2 2 2
 sin xcos x   2 2 2
2  4sin x cos xsin3x 2 2 2 2
1 2sin xcos x  2sin3x  4sin xcos xsin3x 2 2 2 2
 4sin xcos xsin3x  2sin xcos x 2sin3x   1  0 2 2
 2sin xcos x2sin3x   1  2sin3x   1  0
  sin x   2 2 2 3
1 2 sin x cos x   1  0 2sin3x 1  0  1   2 2
2sin x cos x 1  0  2  k2 x   1  Giải phương trình (1): 18 3 sin 3x
 sin3x  sin   k  2 6  5 k2 x    18 3 Giải phương trình (2): 1 1 1 cos 4x 1 3 1 3 k 2 2 2 sin x cos x   sin 2x  
  cos4x   x   arccos  k  2 8 2 8 4 4 4 2
Đối chiếu với điều kiện thì phương trình ban đầu có các họ nghiệm là: k2 5 k2 1 3 k x   ; x   ; x   arccos  k . 18 3 18 3 4 4 2
5. cos3xtan5x  sin7x k
Điều kiện: cos5x  0  x   k  10 5
Với điều kiện trên, ta có:
cos3xtan5x  sin7x sin 5x  cos3x  sin7x cos5x
 cos3xsin5x  sin7xcos5x 1
 sin x  sin x 1 8 2
 sin12x  sin2x 2 2  si 1 n 2x  sin8x 12
x  8x k2   k  12x  8x   k2 Trang 87 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  k x   2   k   k x    20 10
Đối chiếu với điều kiện thì phương trình ban đầu có các họ nghiệm là: k k x  ; x   k . 2 20 10 1
2 sin x  cos x6.  tan x  cot 2x cot x 1
Điều kiện: tan x  cot 2x ; cot x  1 ; sin 2x  0
Với điều kiện trên, ta có: 1
2 sin x  cos x  tan x  cot 2x cot x 1 1
2 sin x  cos x   sin x cos 2x cos x  sin x  cos x 2 sin x cos x sin x 1
2 sin x sin x  cos x   2
2 sin x  cos 2x cos x  sin x 2 sin x cos x 2 sin x cos x    2 sin x 1 cos 2x 2.  cos 2x 2
 2sin xcos x  2 sin x  0  x loai   sin x  cos x   sin 0 ( ) 3 2 2 1  0   x    k2   2 k    4 cos x  2 3
Đối chiếu với điều kiện thì phương trình ban đầu có các họ nghiệm là: x  
k2 k  4 Bài 13.
Giải các phương trình sau : 1 1
1. 2 tan x  cot 2x  2sin 2x  .   1 2 2 sin 2x cos x cos 5x   2. 2 2   8sin 2 x   8  cos x . 2 cos 3x cos x  4 
3. tan2x  tan3x  tan5x  tan2xtan3xtan5x . 3 Lời giải 1 1
1. 2 tan x  cot 2x  2sin 2x  .   1 2 2 sin 2x cos x  0 Đk: 
 sin 2x  0  x   k (k  ) . sin 2x  0 2 2 LÊ MINH TÂM Trang 88 HÀM SỐ LƯỢNG GIÁC 2 sin x cos 2x 1 Phương trình   1    2sin 2x  cos x sin 2x sin 2x 2 2
 4sin x  cos2x  2sin 2x 1 2  sin x   2  sin x 2 2 4 1 2  8sin . x cos x 1 2  sin x 2 2 1 4 cos x  0 2  2sin x 1   2 
1cos2x  0  sin x  0 2  2  2sin x 1
  2cos2x  0   1 . cos 2x  3  2
Giải phương trình 2 : sin x  0 loại do sin2x  0  sinx  0.  2  2x   l2 x   l 1   Giải phương trình  3 3
3 : cos 2x       l . 2  2  2x    l2 x    l  3  3 x  l
Kết hợp điều kiện  3  
l  là nghiệm phương trình .
x   l  3 cos x cos 5x   2. 2 2   8sin 2 x   8  cos x . 2 cos 3x cos x  4  x   k  4 2 cos 2x  0   
Đk: cos3x  0  x   k (k  ).  6 3   cos 5x  0  x   k  10 5 sin 2x sin 3x sin 5x
sin 2x sin 3x sin 5x Phương trình 2     . . cos 2x cos3x cos5x
cos 2x cos3x cos5x  sin2 . x cos3 .
x cos5x  sin3 . x cos 2 .
x cos5x  sin5 . x cos3 .
x cos 2x sin 2 . x sin3 . x sin5x  cos5xsin2 .
x cos3x  sin3 .
x cos 2x  sin5xcos3 .
x cos 2x  sin 2 . x sin 3x
 cos5xsin5x  sin5xcosx  sin5xcos5x cosx  0 x l
5x x l2 2   cos 5x  cos x     
5x  x l2   x ll . sin5x  0   3 5x l   x l  5 Trang 89 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC x l  2  
Kết hợp điều kiệnKết hợp điều kiện   x ll  
là nghiệm phương trình . 3  x l  5
3. tan2x  tan3x  tan5x  tan2xtan3xtan5x . 3    cos x k x  0  Đk: 2    (k  ) .  cos3x  0 x   k  6 3 Phương trình 3 2 2 2  cos x cos5 .
x cos3x  8cos 2 . x cos3 .
x cos x  8cos . x cos3 . x cos x 2  cos x cos5 .
x cos3x  4cos 4x  4cos 2x.cos3 . x cos x  0 1 1 1
  cos2x  cos2x  cos8x8sin3 . x cos3 . x cos . x sin x  0 2 2 2 1 1
  cos8x  2sin6 . x sin 2x  0 2 2 1 1
  cos8x  cos4x  cos8x  0 2 2
1cos8x2cos4x  0  l   cos x 4x  0  2
 2cos 4x  2cos4x  0 8 4     l  cos 4x 1  l x   2  l x  
Kết hợp điều kiện    8 4 l   
là nghiệm phương trình . x l
------------------ HẾT------------------ LÊ MINH TÂM Trang 90 HÀM SỐ LƯỢNG GIÁC
§7. TỔNG ÔN CHƯƠNG
Dạng 01. TẬP XÁC ĐỊNH.
Phương pháp giải: 1 1.
f x xác định  f x  0 ;
xác định  f x  0 . f x
2. y  sin  f x xác định  f x xác định.
3. y  cos  f x xác định  f x xác định.
4. y  tan  f x xác định  f x   k k   . 2
5. y  cot  f x xác định  f x  k k   . Bài tập
Tìm tập xác định của các hàm số sau: 1 cos x
a. y  3  cos 2x
b. y  sinx 2  3sin x 1 1 c. y d. y   2 cos x  3 sin x cos x  
e. y  tan 2x   
f. y  cot x   3  3  4
2 sin x  3tan x g. y h. y
3 sin x  cos x 2 cos x 1     cot x    tan  4  x   6   3  i. y k. y  1 cos x sin 2x
3sin 2x  cos x m. y   2    cos 4x   cos 3x       5   4  Lời giải
a. y  3  cos 2x
Hàm số y  3  cos 2x xác định khi 3 cos2x  0 (luôn đúng, vì cos 2x 1, x   ).
Vậy tập xác định của hàm số đã cho là . 1 cos x
b. y  sinx 1 cos x Hàm số y
xác định khi sin x  0  x k , k  . sin x
Vậy tập xác định của hàm số đã cho là D  
\ k , k   . 2  3sin x
c. y  2cosx 3 Trang 91 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 2  3sin x 3 Hàm số y
xác định khi 2 cos x  3  0  cos x
x    k2 ,k  . 2 cos x  3 2 6  
Vậy tập xác định của hàm số đã cho là D
\  k2 , k   .  6  1 1 d. y   sin x cos x  1 1 cos x  0 x   k Hàm số y   xác định khi    2 , k   x  . k , k  . sin x cos x sin x  0  2 x   k  
Vậy tập xác định của hàm số đã cho là D
\k. , k   .  2   
e. y  tan 2x     3     
Hàm số y  tan 2x  
 xác định khi cos 2x
 0  2x    k x     k .  3   3  3 2 12 2  
Vậy tập xác định của hàm số đã cho là D  \
k ,k  . 12 2 
f. y  cot x   3
Hàm số y  cot x  
3 xác định khi sin x  
3  0  x  3  k x  3  k . TXĐ: D  
\ 3 k , k   4
g. y  3sinxcosx 4 Hàm số y  xác định khi
3 sin x  cos x  
3 sin x  cos x  0  sin x
 0  x   k x     k .  3  3 3   TXĐ: D
\  k , k   .  3 
2 sin x  3tan x h. y  2 cos x 1 x   k  2 cos x  0 
2 sin x  3tan x   Hàm số y  xác định khi 
 x   k2 1 . 2 cos x 1 cos x  3   2
x    k2  3   TXĐ: D
\  k ,  k2 ,  k2 , k   .  2 3 3  LÊ MINH TÂM Trang 92 HÀM SỐ LƯỢNG GIÁC   cot x     6  i. y  1 cos x   cot x          6  sin x   0  x   kx   k Hàm số y  xác định khi   6    6   6 . 1 cos x      cos x 1 x k2 x k2   TXĐ: D
\  k , k2 , k    6    tan  4  x   3  k. y  sin 2x   tan  4  x   3  Hàm số y  xác định khi sin 2x  sin 2  0 k x 2x k x      2        cos  4   x  0   4  x   k k    3   3 2 x     24 4  k k  TXĐ: D  \ ,   , k   .  2 24 4 
3sin 2x  cos x m. y   2    cos 4x   cos 3x       5   4 
2 sin 2x  cos x Hàm số y
xác định khi và chỉ khi  2    cos 4x   cos 3x       5   4   2    cos 4  x    cos 3  x   0   5   4   7x 3   x 13   2cos   cos   0    2 40   2 40    7x 3  7x 3  17 2 cos   0      k x   k  2 40      2 40 2  140 7       .   x 13  x 13 7   cos   0    k x   k2     2 40 2 40 2  20  17 2k 7  TXĐ: D  \  ;
k2 ,k  . 140 7 20 
Dạng 02. GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT.
Phương pháp giải:
Sử dụng tính chất 1   sinx 1 và 1   cosx 1. Trang 93 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC Bài tập.
Tìm GTNN và GTLN của các hàm số:    
a. y  2 cos  x   5  b. 2
y  4 sin  x  1   4   4  5 c. y
d. y  1 sin x 1 2 3cos 2x 1
e. y  sin x  cos x .  
f. y sin 3x 3 cos 3x .
g. y  sin x  cos x2  2cos 2x  3sin . x cos x . h. 2 2
y  3sin x  4sin .
x cos x  5cos x  2 .
2 sin x  cos x i. y  .
sin x  cos x  2 Lời giải  
a. y  2 cos  x   5   4  Với x   , ta có:       1   cos x   1 
 2  2cos x   2   3  2cos x   5  7   4   4   4   3  y  7 Suy ra:  
max y  7  cos  x   1 
x   k2  x    k2 , với k  4  4 4  
min y  3  cos  x   1   x    3 k2  x
k2 , với k  4  4 4   b. 2
y  4 sin  x  1   4  Với x   , ta có:       0  sin  x  1  2  0  sin x   1  2  1   4sin  x  1  3   4   4   4   1   y  3 Suy ra:  
max y  3  sin  x   1   x    3 k2  x
k2 , với k  4  4 2 4   min y  1   sin  x   0 
x   k x   k , với k  4  4 4 5 c. y  2 3cos 2x 1 Với x   , ta có: 0  cos 2x  1 2  0  cos 2x 1 2
1 3cos 2x 1 4 LÊ MINH TÂM Trang 94 HÀM SỐ LƯỢNG GIÁC 5 5    5 2 4 3cos 2x 1 Suy ra: k
max y  5  cos2x  0  2x   k x   , với k  . 2 4 2 5 k min y  2
 cos 2x 1  2x k x  , với k  . 4 2
d. y  1 sin x 1 Với x   , ta có: 1   sinx 1  1
  sinx 1 0 1sinx  2
 0  1sinx  2  1
  1sin x 1 2 1
 1  y  2 1
max y  2 1  sin x  1
  x    k2 , với k 2 min y  1
  sinx 1  x   k2 , với k 2  
e. y  sin x  cos x  2 sin x     4  Với x   , ta có:   1   sin x   1   4   
  2  2 sin x   2   4    2  y  2 Suy ra:  
max y  2  sin  x   1 
x    k2  x   k2 , với k .  4  4 2 4  
min y   2  sin  x   1   x     3 k2  x  
k2 , với k .  4  4 2 4  1 3 
f. y  sin 3x  3 cos3x  2 sin 3 . x  .cos3x  2 2     1 3 
Cách 1. y  sin 3x  3 cos3x  2 sin 3 . x  .cos3x  2 2       
 2. cos sin3x  sin cos3x  2sin 3x       3 3   3  Với x   , ta có:     1   sin 3  x   1   2  2sin 3  x   2   2   y  2  3   3  Suy ra: Trang 95 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC   k max y  2  sin 3  x   1   3x    5 2 k2  x   , với k   3  3 2 18 3   k min y  2   sin 3x   1     3x     2 k2  x    , với k   3  3 2 18 3
Cách 2. Phương trình y  sin 3x  3 cos 3x có nghiệm khi và chỉ khi   2 2 2 2 1 3
y y  4  2  y  2 .
Vậy GTLN của y là 2 và GTNN của y là 2  .
g. y  sin x  cos x2  2cos 2x  3sin . x cos xy 1 2sin .
x cos x  2 cos 2x  3sin . x cos x
y 1  2cos 2x  sin . x cos x 1
y 1  2cos 2x  sin 2x * 2
Phương trình ban đầu có nghiệm khi và chỉ khi (*) có nghiệm 2  1   2   y  2 1  y  2 17 17 17 17 17 2 1     y 1  1  y  1   .  2  4 2 2 2 2 17 17
Vậy GTLN của y là 1
và GTNN của y là 1 . 2 2 h. 2 2
y  3sin x  4sin .
x cos x  5cos x  2 . 3
y    cos x 5 1 2
 2sin 2x  1 cos2x  2 2 2
y 1  2sin 2x  4cos 2x *
Phương trình ban đầu có nghiệm khi và chỉ khi (*) có nghiệm 
  2  y  2  y  2 2 2 4 1 1  20  2
 5  y 1 2 5 1 2 5  y 1 2 5 .
Vậy GTLN của y là 1 2 5 và GTNN của y là 1 2 5 .
2 sin x  cos x
i. y  sinxcosx2
y sin x y cos x  2y  2sin x  cos x
 y  2sin x  y  
1 cos x  2y  0 *
Phương trình ban đầu có nghiệm khi và chỉ khi (*) có nghiệm
 y  2  y  2   y2 2 1 2 3   19 3   19 2 2 2
 4y  2y  6y  5  2y  6y 5  0   y  2 2
Dạng 03. PHƯƠNG TRÌNH LƯỢNG GIÁC.
Phương pháp giải: DẠNG CƠ BẢN:
u v k2 , k
u v k2 , k
sinu  sin v  
cosu  cos v  
u   v k2 , k  
u  v k2 , k   LÊ MINH TÂM Trang 96 HÀM SỐ LƯỢNG GIÁC    u
   l  hay v   l l  u
  l hay v l l 
tanu  tan v   2  2 
 cot u  cot v  uvk k   u
  v k k  
TRƯỜNG HỢP ĐẶC BIỆT:
 sin x  0  x k k 
 cos x  0  x   k k  2
 sin x 1 x   k2 k 
 cos x 1 x k2 k  2   cos x  1
  x   k2 k  sin x  1
  x    k2 k  2 Bài 01.
Giải các phương trình sau:   3   a. cos2x  1  . b. sin 3x    
c. 2 cos  x   1   6  2  5   
d. cot 4x  3  0
e. 3tan 2x  3  0 f. cos   x  0   3   x  1   g. 2 sin   3  0   h. 2 sin 2x . i. 2 tan 2  x   3  .  3 4  4  4  Lời giải a. cos2x  1 
 2x   k2  x   k ,k . 2   3 b. sin 3x      6  2   k2 3x    k2 x       6 3 6 3  sin 3  x    sin     ,k    6  3  2  5 k2 3x    k2 x    6 3  18 3  
c. 2 cos  x   1   5    9 x    k2 x   k2 1       5 4 20  cos x     cos  x    cos     ,k    5  2  5  4   x     k2 x    k2  5 4  20
d. cot 4x  3  0 k
 cot 4x  cot  4x   k x   , k .. 6 6 24 4
e. 3tan 2x  3  0 3  tan 2x   3 Trang 97 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC   k  tan 2x  tan 
 2x    k x    , k    .  6  6 12 2   f. cos   x  0   3 
  x   k x    k ,k . 3 2 6  xg. 2 sin   3  0    3 4   x  3  sin      3 4  2  x     k2 x    k6 x    3 4 3 4  sin     sin     ,k   .  3 4  3  x 2 5     k2 x   k6 3 4 3  4 1 h. 2 sin 2x  4 1 cos 4x 1   2 4 1 k
 cos4x   cos4x  cos  4x    k2  x    , k  . 2 3 3 12 2   i. 2 tan 2  x   3  .  4    Điều kiện: cos 2  x   0   4     tan 2  x   3    4      tan 2  x    3    4       7 tan 2     tan k x 2x    kx   4 3     4 3 24 2      ,k    đều thỏa mãn.       k tan 2  x    tan  2x     k x         4   3  4 3  24 2   7 k x    Vậy 24 2 
,k   là nghiệm của phương trình.  k x     24 2 Bài 02.
Giải các phương trình sau:  2 
a. sin3x  cos2x  0. b. cos  x  
 cos x  0 .  3  LÊ MINH TÂM Trang 98 HÀM SỐ LƯỢNG GIÁC x c. cos
 cos2x 30 . d. tan .
x cot 2x 1. 2 x x 1 e. 2 2
sin x  cos 2x  0 . f. 4 4 sin  cos  . 2 2 2 Lời giải
a. sin3x  cos2x  0.
 sin3x  cos2x.   k2 3x   2x k2 x   1   2 2 10 5  sin 2x    , k    , k  . 4   3x
  2x k2 x   k2  2  2  k2 x   
Vậy phương trình có nghiệm là 10 5  , k  . x   k2  2  2  b. cos  x    cos x  0 .  3     
 2cos x  cos  0   .  3   3     cos x   0  .  x
  k ,k  .  x   k ,k  .  3  3 2 6
Vậy phương trình có nghiệm là x   k ,k  . 6 x c. cos
 cos2x 30 . 2 x
 cos  cos2x 30 180  . 2  x 2x 150   k360   2      x 100 k240 , k  .   , k  .  x x  6  0   k240 2x 150    k360  2 x  1  00  k240
Vậy phương trình có nghiệm là   k . x  6  0   k240 d. tan . x cot 2x 1        cos x m x  0 x   m  Điều kiện: 2    2   m,n . sin 2x  0 n  2x nx       2 1
Phương trình  tan x
 tanx  tan2x x  2xk ,k  x  k ,k . cot 2x
Kết hợp với điều kiện ta có nghiệm của phương trình là S   . e. 2 2
sin x  cos 2x  0 . Trang 99 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 1 cos 2x 2   cos 2x  0 . 2 2
 2cos 2x  cos2x 1 0   1  x    k cos 2x  2x    k2     2  k  6 3   k    . cos  2x  1  2  x   k2 x   k  2
x    k
Vậy phương trình có nghiệm là 6   k . x   k  2 x x 1 f. 4 4 sin  cos  . 2 2 2   x   x   x   x   x   x  1 2 2  sin    cos sin    cos sin    cos    .   2   2   x   2   2   2  2    x   x   x   x  1  sin    cos sin    cos   .   2   2   x   2  2   2 x   k2 1 2    3
 cos x    cos x  cos     , k  . 2  3   2 x    k2  3  2 x   k2 
Vậy phương trình có nghiệm là 3  , k  .  2 x    k2  3 Bài 03.
Tìm nghiệm của các phương trình sau trong các khoảng đã cho: 1   3
a. sin 2x   với x 0;  . b. cos x    
với x  ;  . 2  4  2 1  
c. tan2x 15 1với 1
 80  x  90 d. cot3x   với x    ; 0  . . 3  2  Lời giải 1
a. sin 2x   với x 0;  . 2   2x    k2 x     k 1    6 sin x    sin x  sin      k  12 2 2   k . 2  6   7  2x    k2 x   k  6  12 LÊ MINH TÂM Trang 100 HÀM SỐ LƯỢNG GIÁC Vì x 0;  nên   1  1 13 0    k  0    k 1  k         k     k    k  k 1 12 12 12 12   . 7 7 7 5    k  0 0   k  0   k 1   k   12  12  12 12  11 x      Vậy 12 12  . 7  x   12   3 b. cos x    
với x  ;  .  4  2   5 x    k2 x    k2      4 6  cos x    cos     k  12   k .  4   6    x     k2 x   k2  4 6  12  5    k2  
Vì x  ;  nên 12  k .     k2   12  5  17  7  17  7 1    2k 1  2k   k          k     k    k  k 0 12 12 12 24 24   . 1 13  11 13  11    k  0 1    2k 1  2k   k   12  12 12  24 24  5 x   Vậy 12  .  x   12
c. tan2x 15 1với 1
 80  x  90
Ta có tan2x 15 1
 2x 15  45 k 1
. 80k    2x  60  k 1
. 80k    x  30  k 9 . 0k   Vì 1
 80  x  90  1  80  30  9 .
k 0  90k   k  2    
  k.   k  7 2 210 90 60
   k  k   k  1   3 3 k  0 x  150 
Vậy phương trình có nghiệm x  60  .  x  30  1  
d. cot 3x   với x    ; 0 . 3  2  Trang 101 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 1 k Ta có cot 3x  
 3x    k k   x    k  . 3 3 9 3   Vì x    ; 0 nên  2  k      0k  . 2 9 3 1 1 k           k   7 k 1     k  21 1 k 0  
k  k  1   . 2 9 3 18 3 9 18 3  k  0  4 x    Vậy 9  .  x    9 Bài 04.
Giải các phương trình sau: a. 2
2cos x  3cos x 1  0 . b. 2 2
2sin x  cos x  4sin x  2  0 . c. 2
3sin 2x  7cos 2x  3  0 . d. 2
6cos x  5sin x  7  0 .
e. cos2x  3cos x  4  0 . f. 2
6sin 3x  cos12x  7 . x
g. cos x  2 sin 1 .
h. sin xsin x   2 5
1  cos x  3 . 2 i. 4 2
4sin x 12cos x  7 .
k. 7tan x  4cot x 12 1 l. 2
 3cot x 5  0 . m. 3
2sin x  cos 2x  sin x 2 cos x 1 1 2 n. 2 cos x   cos x .
o. tan x  cot x  tan x  cot x  2 2 cos x cos x Lời giải a. 2
2cos x  3cos x 1  0 . cos x 1 x k2    1   . cos x
x    k2  2  3
Vậy nghiệm của phương trình ban đầu là: x k2 ; x    k2 k . 3 b. 2 2
2sin x  cos x  4sin x  2  0 . 2  sin x   2 2
1 sin x  4sin x  2  0 . x   k2  2 sin x 1  1 2  
 3sin x  4sin x 1  0 
x  arccos  k2 1  . sin x   3  3  1
x  arccos  k2  3 LÊ MINH TÂM Trang 102 HÀM SỐ LƯỢNG GIÁC 1
Vậy nghiệm của phương trình ban đầu là: x
k2 ; x  arccos  k2 ; 2 3 1
x   arccos  k2 k . 3 c. 2
3sin 2x  7cos 2x  3  0 .   2
3 1 cos 2x  7 cos 2x  3  0 . 2
 3cos 2x 7cos2x  0 . cos 2x  0  k
x   k x    .
cos 2x  VN 2 7 2 4 2  3 k
Vậy nghiệm của phương trình ban đầu là: x   k . 4 2 d. 2
6cos x  5sin x  7  0 .  1    sin x  2  sin x 2 2 6 1
 5sin x  7  0  6
 sin x  5sin x 1  0   . 1 sin x   3 x   k2 1  +) Với 6 sin x    . 2  5 x   k2  6  1
x  arcsin  k2 1  +) Với 3 sin x    . 3  1
x   arcsin  k2  3 5 1
Vậy nghiệm của phương trình ban đầu là: x   k2 ; x
k2 ; x  arcsin  k2 ; 6 6 3 1
x   arcsin  k2 k . 3
e. cos2x  3cos x  4  0 . cos x 1 2 
 2cos x  3cos x 5  0    x k  . cos x  VN 2 5  2
Vậy nghiệm của phương trình ban đầu là: x k2 k   . f. 2
6sin 3x  cos12x  7 . 1 cos 6x 2  6.
 2cos 6x 1 7  0 . 2 2
 2cos 6x 3cos6x 5  0 .  5 cos 6x   VNk  2
 6x   k2  x    . 6 3 cos6x  1  Trang 103 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC k
Vậy nghiệm của phương trình ban đầu là: x   k . 6 3 x
g. cos x  2 sin 1 . 2  x  2 sin  VNx x x 2 2 2  2sin  2 sin  0  
  k x k2 . 2 2  x 2 sin  0  2
Vậy nghiệm của phương trình ban đầu là: x k2 k   .
h. sin xsin x   2 5
1  cos x  3 2 2
 5sin x 5sin x  sin x 1 3. 2
 6sin x 5sinx  4  0 .  4 sin x   vn 1 3  
 sin x    x    k2 k  .  1 2 2 sin x    2 i. 4 2
4sin x 12cos x  7 .    cos x2 1 2
 61 cos2x 7  0. 2
 cos 2x  4cos2x  0 . cos2x  0   cos2x  4  .  1    cos 2x  1 k
 cos2x  0  2x   k x   k .. 2 4 2
k. 7tan x  4cot x 12 . 2
7 tan x 12tan x  4  0 tan x  2
x  arctan 2  k             .
x k k   2 2 k  tan x   x  arctan     k  2  7   7  1 l. 2
 3cot x 5  0 . 2 cos x 2 2 1
  cot x  3cot x  5  0    .
x k k    2 2 4cot x  4  0            .
x k k   cot x 1 x k k  4  2 m. 3
2sin x  cos 2x  sin x .  sin x 2 2 sin x  
1  cos 2x  0 . LÊ MINH TÂM Trang 104 HÀM SỐ LƯỢNG GIÁC
 cos2x1sin x  0 .   k 2     cos x k x 2x  0   2 4 2       k . sin x 1   x   k2 x   k2  2  2 1 1 n. 2 cos x   cos x . 2 cos x cos x 4 3
cos x 1 cos x cosx   . cosx  0 4 3
cos x  cos x  cos x 1 0   . cos x  0
cosx 2  2 1
cos x  cos x   1  0   . cosx  0 k
 cos x 1 x  k  . 2 2
o. tan x  cot x  tan x  cot x  2
tanxcotx2 tanxcotx2  0    kx  k   2 2
tan x  cot x  1 
tan x  tan x 1 0    
 tan x 1 x   k k  2
tan x  cot x  2
tan x  2tan x 1 0 4 Bài 05.
Giải các phương trình sau: 6
a. sin 2x  cos 2x 1
b. cos5x  sin 5x  2
c. 3 cos 2x  sin 2x  2
d. 3sin 4x  3 cos 4x  3  0
e. cos x  3 sin x  2 cos 2x
f. cos 7x  sin 5x  3 cos5x  sin 7x
g. 2 sin11x  3 cos 2x  sin 2x  0 Lời giải
a. sin 2x  cos 2x 1 1 1 1  sin 2x  cos 2x  2 2 2 1
 cos sin 2x  sin cos 2x  4 4 2    sin 2x     sin  4  4 Trang 105 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC   2x    k2  x   k  2x   k2  4 4  4    2   , k     2x     k2 2  x   k2 x   k  4 4  2 6
b. cos5x  sin 5x  2   6  2 sin 5x      4  2   3  sin 5x      4  2    sin 5x     sin  4  3    k2 5x    k2 5x    k2 x     4 3 12 60 5       , k  .  5   k2 5x     k2 5x   k2 x    4 3  12  12 5
c. 3 cos 2x  sin 2x  2 3 1 2 
cos 2x  sin 2x  2 2 2 2
 sin cos 2x  cos sin 2x  3 3 2    sin  2x    sin  3  4   
 2x   k2 2x    k2 x     k   3 4 12 24       , k  .  5 5  
 2x    k2 2x   k2 x   k  3 4  12  24
d. 3sin 4x  3 cos 4x  3  0
 3sin 4x  3 cos 4x   3 3 1 1 
sin 4x  cos 4x   2 2 2 1
 cos sin 4x  sin cos4x   6 6 2      sin 4x   sin       6   6    k 4x     k2 4x k2 x    6 6  2    4   , k   .  4x   k2  k 4x     k2  3 x    6 6  3 2
e. cos x  3 sin x  2 cos 2x LÊ MINH TÂM Trang 106 HÀM SỐ LƯỢNG GIÁC 1 3  cos x  sin x  cos 2x 2 2
 cos cos x  sin sin x  cos 2x 3 3   x   2x k2 x    k2     3 3  cos x    cos 2x     , k   3    k2 x   2  x k2 x    3  9 3
f. cos 7x  sin 5x  3 cos5x  sin 7x
 cos7x  sin5x  3 cos5x  3 sin 7x
 cos7x  3 sin 7x  3 cos5x  sin5x
 cos7x  3 sin 7x  3 cos5x  sin5x 1 3 3 1  cos7x  sin 7x  cos5x  sin 5x 2 2 2 2
 sin cos7x  cos sin7x  sin cos5x  cos sin5x 4 4 4 4
 7x  5xk2 x k      4 4   sin  7  x   sin  5  x     , k k  .  4   4  3   x    7x   5x k2  24 6  4 4
g. 2 sin11x  3 cos 2x  sin 2x  0
 2sin11x  3 cos 2x  sin 2x 3 1  sin11x
cos 2x  sin 2x 2 2
 sin11x  sin cos2x  cos sin 2x 3 3   k2 11x   2x k2 x       3 27 9  sin11x  sin  2  x      , k   3   2  2 k2 11x   2x k2 x    3  39 13 Bài 06.
Giải các phương trình sau:
a. 3sinx  cos x  2sin 2x  3  0 . b. 3 3 sin x  o
c s x  sin 2x  sinx  cos x .
c. cos x  cos 2x  cos3x  0
d. cosx cos2x cos3x cos4x  0
e. cos x  cos5x  2cos3x  0 f. cos2 .
x cos5x  cos7x. g. 4sin . x sin2 .
x sin3x  sin4x . h. cos .
x cos3x sin2 .
x sin6x sin4 . x sin6x  0 .
i. cos22x 3co 1 s 8x 3co 1 s 4x  co 1 s 0x  0.
k. 4sin3x  sin5x  2sin . x cos2x  0 . Lời giải Trang 107 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
a. 3sinx  cos x  2sin 2x  3  0 .
Đặt s inx  cos x t, t  2 2
 sin2x t 1, khi đó ta có pt: t  1  (t ) m t   2  3 2 t   1  3  0 2
 2t 3t 1 0  1   . t  (t ) m  2     1  x   k2 + t   1
  sinx  cos x  1   sin x    2 k    4    2
x   k2   x    k2 1      1  + t  1  sin x     4   k  ,sin  . 2  4  2 2 3
x    k 2 2 2  4 b. 3 3 sin x  o
c s x  sin 2x  sinx  cos x .
Đặt s inx  cos x t, t  2 2
 sin2x t 1, khi đó ta có pt: t 1(t ) m 2  t 1  2 t 1
  t 1 t 3 2  t
  2t t  2  0  t  1  (t ) m  2   t  2  (l)       x   k2 + t  1
 sinxcosx  1  1  sin x       2 k .  4  2 
x   k2     x k2
+ t 1 sinx  cos x  1 1  sin x       k   4  2 x   k2  2
c. cos x  cos 2x  cos3x  0
 2cos2xcosxcos2x  0  k x    x  
 cos x cos x   cos 2 0 4 2 2 2 1  0     k  2  cos x 1  0
x    k2  3  k x    Vậy 4 2  k 
x    k2  3
d. cos x  cos2x  cos3x  cos4x  0 5x 3x 5x x  2cos cos  2cos cos  0 2 2 2 2 LÊ MINH TÂM Trang 108 HÀM SỐ LƯỢNG GIÁC  2k x   5x   5 5 cos  0   5x  3x x  2   2cos cos  cos  0    x   kk    . 2  2 2   3xx   2 cos  cos      2 2 x      k2    2k x    5 5   Vậy: x   kk  
là nghiệm của phương trình. 2 x   k2  
e. cos x  cos5x  2cos3x  0
 cosx  cos5x 2cos3x  0  2cos3 .
x cos2x  2cos3x  0  k x    x  
 cos xcos x   cos 3 0 6 3 2 3 2 1  0     , k . cos 2x  1  x   k  2  k x   
Vậy nghiệm của phương trình là 6 3   , k  . x   k  2 f. cos2 .
x cos5x  cos7x 1
 cos7x  cos3x  cos7x   2
 cos7xcos3x  2cos7xk x
7x  3x k2  2
 cos7x  cos3x     k  7  x  3  x k2  k x   5 g. 4sin . x sin2 .
x sin3x  sin4x  4sin . x sin2 .
x sin3x  2sin2 . x cos2x  2sin 2 .
x 2sin xsin3x  cos 2x  0  sin2 .
x cos 2x  cos 4x  cos 2x  0  k 2x k  sin x 2x  0   2
 sin 2xcos 4x  0      k  cos 4x  0 4x   kk  2 x    8 4 h. cos .
x cos3x sin2 .
x sin6x sin4 . x sin6x  0  cos .
x cos3x  sin 6xsin 4x  sin 2x  0  cos .
x cos3x  2sin6 .
x sin3xcos x  0 Trang 109 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
 cos xcos3x  2sin6xsin3x  0 x   kx  
 cos xcos x  cos x  cos x cos 0 2 3 3 9  0     k  cos9x  0  k x    18 9
i. cos22x 3co 1 s 8x 3co 1 s 4x  co 1 s 0x  0.
 cos22x  cos10x  3cos18x  cos14x  0  2co 1
s 6xcos6x  6co 1 s 6xcos2x  0
 2cos16xcos6x 3cos2x  0 cos16x  0   3 4
 cos 2x  3cos 2x  3cos 2x  0   k 16     cos x k x 16x  0   2 32 16       k  cos 2x  0   k 2x   k x    2  4 2
k. 4sin3x  sin5x  2sin . x cos2x  0
 4sin3xsin5xsin3xsinx  0  k
sin 3x  0  x   3
 3sin3x  2sin3xcos 2x  0   k ..  3
cos 2x   VN  2 Bài 07.
Giải các phương trình sau: 3 a. 2 2 2
sin x  sin 2x  sin 3x . b. 2 2 2
sin x  sin 2x  sin 3x  . 2 c. 2 2 2
3cos 2x  3sin x  cos x  0 d. 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x e. 4
8cos x 1 cos 4x . f. 4 4
sin x  cos x  cos 4x . 1 g. 4 4
sin x  cos x  cos x . h. 6 6
sin x  cos x . 2 Lời giải a. 2 2 2
sin x  sin 2x  sin 3x
1 cos2x 1 cos4x 1 cos6x    2 2 2
1cos 2x+cos 4x+cos 6x  0
1cos 6x2cos 3 . x cos x  0 2  2cos 3x  2cos3 . x cos x  0
 2cos 3xcos 3x cosx  0 LÊ MINH TÂM Trang 110 HÀM SỐ LƯỢNG GIÁC x   k   6 3   cos 3 x k x  0   6 3     x l  
k,l,m 
cos 3x  cos x  x mx m  2  2 3 b. 2 2 2
sin x  sin 2x  sin 3x  2
1 cos2x 1 cos4x 1 cos6x 3     2 2 2 2
 cos 2x+cos 4x+cos 6x  0  co 2 s + x co 6 s + x co 4 s x  0  co 4 s . x co 2 s x  co 4 s x  0      cos x k 4x  0 x   k   8 4    8 4   k,l . cos2x  1 -   2  x   l2 x   l  2 c. 2 2 2
3cos 2x  3sin x  cos x  0
1 cos2x  1 cos2x 2  3cos 2x  3   0    2  2 2
 6cos 2x  4cos2x  2  0  1 1  1
x   arccos  k cos 2x    2 3  3   k,l   cos  2x  1  x   l  2 d. 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x 1 co 6 s x 1 co 8 s x 1 co 1 s 0x 1 co 1 s 2x     2 2 2 2  c  o 6 s x co 8 s x  c  o 1 s 0x co 1 s 2x  co 1 s 0x  co 6 s x  co 1 s 2x  co 8 s x  2  sin8 .
x sin2x  2si 1 n 0 . x sin2x
 2sin2xsin10x  sin8x  0 sin 2x  0  sin10x sin   8   x  x k  2   2x kx k  
x   x l    x l
k,l,m  2 10 8 2   k,l   9  10
 x  8x kmx l  9 x   m  2 2 e. 4
8cos x 1 cos 4x . Ta có 4
8cos x 1 cos 4x Trang 111 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 2 1 cos 2x  2  8  1 2   cos 2x 1  2 
 cos2x  0  x   k k  . 4 4 f. 4 4
sin x  cos x  cos 4x . Ta có 4 4
sin x  cos x  cos 4x 2 2 2
1 2sin xcos x  2cos 2x 1 1 2 2
 2cos 2x  sin 2x  0 2 2
 3cos 2x 1 0 vô nghiệm. g. 4 4
sin x  cos x  cos x . Ta có 4 4
sin x  cos x  cos x 2 2
 sin x cos x  cosx 2
1 2cos x  cos x cos x  1  x   k2 2  
 2cos x  cos x 1  0  1  k  cosx
x    k2  2  3 1 h. 6 6
sin x  cos x . 2 1 Ta có 6 6
sin x  cos x  2
 sin x cos x3 1 2 2 2 2
3sin xcos x 2 2
sin x  cos x  2 3 1 2 1 sin 2x  4 2 2 2  sin 2x  3 1 cos 4x 2   2 3 1  1  1  1 
 cos 4x    4x  arccos 
k2  x   arccos   k2 k      3  3  4  3  LÊ MINH TÂM Trang 112 HÀM SỐ LƯỢNG GIÁC
Dạng 04. TỔNG HỢP PHƯƠNG TRÌNH LƯỢNG GIÁC. Bài tập.
Giải các phương trình sau:
1. cos 2x  1 2cos xcos x  sin x . 2.   x2 3 1 sin  cos x .
3. sin x  sin2x  sin3x  sin4x  0. 4. co 1
s 0x  cos8x  cos6x 1 0. 5. 2
sin 4x  2cos x 1.
6. 1 sin x  cos x  sin2x  cos2x  0 .
7. 1 tan x1 sin 2x 1 tan x .
8.   sin x2 1 2
cos x  1 sin x  cos x . x x
9. 2sin x  
1 2cos x  sin x  sin 2x  cos x . 10. 4 4 cos  sin  sin 2x . 4 4
11. sin 2x  cos 2x  1 2 sin 2x  sin 4x . 12. 2
2sin 2x  sin 7x 1  sin x 1
13. 2sin xcos2x  sin2xcos x  sin4xcos x . 14. 3 sin x  cos x  cosx
15. sin x   2 2
1 2  cos 2x  3sin x  sin 4x cos x 16. 2
2 cos x  2 3 sin x cos x 1  3  3 cos x  sin x . 17. 2 2
4cos x  3tan x  4 3 cos x  2 3 tan x  4  0 . 18. 3 3
sin x  cos x  sin x  cos x . 3 19. 4
8cos x  cos 4x 1. 20. 2 2
sin 2x  sin 4x  . 2 21.  3 3
4 cos x  sin x  cos x  3sin x . 22. 3 2
4sin x  4sin x  3sin 2x  6cos x  0. 2
cos xcos x   1 23.  2 sin x   2 tan x   2 2 1 2 3 2 cos x   1  0 . 24.  21 sin x sin x  . cos x
25. tan x  2 2 sin x  1 .
26. tan x  tan2x  sin3 .
x cos x .  5   7 
27. 4 3 sin xcos xcos 2x  sin8x . 28. sin 2x   3cos x   1     sin x .  2   2  4 4 sin x  cos x 1
29. tan x  3cot x  4sin x  3 cos x . 30.
 tan x  cot x . sin 2x 2 Lời giải
1. cos 2x  1 2cos xcos x  sin x 2 2
 cos x  sin x  1 2cosxcosx sinx
 cosx  sinx 1 2cosxcosx sin x  0
 sinx cosx  
1 cos x  sin x  0     2 x   k2 sin x     2
sin x  cos x 1 4 2       
 x   k2
cos x  sin x  0     sin   x  0    4 x   k   4 Trang 113 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC  
Vậy phương trình có tập nghiệm S    k2 ;  k2 ;  k  .  2 4  2.   x2 3 1 sin  cos x
   sin x2  cos x 2 1 1 sin x  1 sin x 1
  sin x  cos x  1sinx  0   sin x  1  x    k2     2
1 sin x cos x sin x cos x 0       1
  sin x  cos x  sin x cos x  0   1  
Đặt t  sin x  cos x  2 sin  x   , t  2  4  2 1 t 2
t 1 2sin xcos x  sin xcos x  . 2 2   t  1 1  TM t Khi đó   2   1  1 t
 0  t  2t  3  0   . 2 t  3  l x k2     1 Với t   1   2 sin x   1   sin x         3 .  4   4   2 x   k2  2  3 
Vậy phương trình có tập nghiệm S    k2 ; k2 ;  k2  .  2 2 
3. sin x  sin2x  sin3x  sin4x  0
 2sin2xcosx2sin3xcosx  0
 2cos xsin2x  sin3x  0   x   k x k     2 2  cos x  0   k2    2  x  3  x k2  x  sin 2x    sin 3x  5
2x  3x k2   x    k2     k2 
Vậy phương trình có tập nghiệm S    k ; ;   k2  .  2 5  4. co 1
s 0x  cos8x  cos6x 1 0
 cos10x cos6x1cos8x  0 2  2
 sin8xsin2x  2sin 4x  0 2  4
 sin4xcos4xsin2x  2sin 4x  0
 2sin4xsin4x 2cos4xsin2x  0
 4sin4xsin2xcos2x cos4x  0 LÊ MINH TÂM Trang 114 HÀM SỐ LƯỢNG GIÁC  k x   4 4x k  sin 4x  0   k  2x k x   sin  2x  0    2 
4x  2x k2 
cos4x  cos2xx k   4  x  2  x k2  k x   3  k k
Vậy phương trình có tập nghiệm S   ;  .  4 3  5. 2
sin 4x  2cos x 1
 2sin2xcos2x  cos2x
 cos2x2sin2x   1  0   k 2x   k x     2 4 2 cos 2x  0      
 2x   k2 1  x   k sin2x   6  12  2   5 5 2x   k2 x   k  6  12  k 5 
Vậy phương trình có tập nghiệm S    ;  k ;  k  .  4 2 12 12 
6. 1 sin x  cos x  sin2x  cos2x  0
 sin x  cos x    sin xcos x   2 2 1 2
cos x  sin x  0
 sin x  cosx sinx  cosx2 cosx  sinxcosx  sinx  0
 sinx  cosx1 sinx  cosx  cosx sinx  0
 sinx  cosx1 2cosx  0
sin x  cos x  0  12  cos x  0       2 sin x   0  x   k x    k      4  4 4     k   2 2 1    x   x    k2 x    k2 cos    3  3 2 2
Vậy phương trình có các nghiệm x  
k ; x  
k2 k  4 3
7. 1 tan x1 sin 2x 1 tan x .  
Tập xác định D
\  k , k   .  2  Ta có
1tanx1sin2x 1tanx Trang 115 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
 cos x  sin x    cos x  sin x 2 2
sin x  cos x  2 sin x cos x     cos x  cos x   x x x x2 cos sin sin cos
 cos x  sin x   x x 2 2 cos sin
cos x  sin x  cos x  sin x
 cosx  sin xcos2x   1  0
sin x  cos x  0  cos2x10       2 sin x   0  x   k x    k      4   4  4 k      2  xx k2 cos 2 1 x k
Vậy phương trình có các nghiệm x  
k ; x k k  4
8.   sin x2 1 2
cos x  1 sin x  cos x   2
1 4 sin x  4 sin xcos x  1 sin x  cos x 2
 cosx  4sin xcos x  4sin xcos x 1sin x cos x
 4sin xcos xsinx   1  sin x 1  sin x   1 2sin 2x   1  0 sin x 1  0
 2sin2x10   x    k2 x    k2   2 2 sin x  1       
 2x   k2 1  x   kk  sin2x   6  12  2   5 5 2x   k2 x   k  6  12 5
Vậy phương trình có các nghiệm x    k2 ; x   k ; x
k k  2 12 12
9. 2sin x  
1 2cos x  sin x  sin 2x  cos x  2sin x  
1 2cos x  sin x  2sin xcos x  cos x  2sinx  
1 2cos x  sin x  cos x2sin x   1  2sin x  
1 cos x  sin x  0  x   k2 1   6 sin x    2sin x 1  0 2  5      x
k2 k 
cos x  sin x  0     6 sin   x   0     4 
x    k  4 LÊ MINH TÂM Trang 116 HÀM SỐ LƯỢNG GIÁC 5
Vậy phương trình có các nghiệm x   k2 ; x
k2 ; x    k k  6 6 4 x x 10. 4 4 cos  sin x  sin 2x 4 4  x x  x x  2 2 2 2  cos  sin cos  sin     sin 2x  4 4  4 4  x    cos  cos  2  x  2  2   x 5xk4
  2x k2   k2 x      2 2 2 2 5 5       k   x 3   xk4
   2x k2   k2 x    2 2  2 2  3 3 k4 k4
Vậy phương trình có các nghiệm x   ; x    k  5 5 3 3
11. sin 2x  cos 2x  1 2 sin 2x  sin 4x 2
 sin 2x  2cos x  2 sin 2x1 2cos2x
 2cos xsin x cos x  2 2 cos xsin x1 2cos2x cos x  0
 sinxcosx 2sinx  12cos2x cos x  0
 sinxcosx 2sinx2 2sinxcos2x cos x  0
 sinxcosx 2sinx 2 
sin3xsinx   x   k x   k   2 2 cos x  0        
 3x x   k2
x    k  k  2 sin  x   2  sin 3x  4  8   4    5 k
3x   x   k2 x    4  16 2 12. 2
2sin 2x  sin 7x 1  sin x 2
 sin7x sin x 1 2sin 2x
 sin7xsinx  cos4x
 2cos4xsin3x  cos4xk x    8 4 cos 4x  0    k
 cos x sin x   2 4 2 3 1  0  1  x   k  sin3x   18 3  2  5 k2 x    18 3
13. 2sin xcos2x  sin2xcos x  sin4xcos x Trang 117 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
 2sin xcos2x  cos xsin4x sin2x
 2sinxcos2x  2cosxcos3xsinx sin x  0  cos2x   cos 3x cos x sin x  0 x k sin x  0   k  1 1     x  k k  
cos2x  cos4x  cos2x
cos 4x  cos 2xx  3  2 2  3 1
14. 3 sin x  cos x  (ÐK : x   k ) cos x 2 1  3 tan x 1 2 cos x   tan  0 x k x 2 2 
 3 tan x 1  tan x 1 tan x  3 tan x  0   
k  (tmđk). tan x 3   x   k  3
15. sin x   2 2
1 2  cos 2x  3sin x  sin 4x cos x  sin x   2
 cos x  sin x 2 2 1 2 2 3
 4sin xcos xcos 2x  sin x   2
 cos x  sin x  sin xcos x 2 2 1 2 2 3 4 2 1 sin x sin x  1    2
2  cos 2x  3sin x  2 sin x cos 2x  1  sin x sin x  1   2
2  cos 2x  3sin x  2sin x   2
1 2 sin x1 sin x sin x  1   2  12sin x2 2  3sin x   2
2 sin x  2 sin x 2 1 2 sin x sin x  1    4 3 2 8
 sin x  4sin x  6sin x  5sin x 1  0
x    k2  2 sin x  1   sin x  1            x   k k sin x   1 2sin x   2 3 1   1  0 sin x  6  2  5 x   k2  6 16. 2
2 cos x  2 3 sin x cos x 1  3  3 cos x  sin x .
Cách 1: Đặt t  3 cos x  sin x 2 2 2 2
t  3cos x  sin x  2 3sinxcosx  2cos x 1 2 3sinxcosxt  0
Phương trình trở thành: 2 t  3t   . t  3 LÊ MINH TÂM Trang 118 HÀM SỐ LƯỢNG GIÁC
Với t  0  3 cos x  sin x  0  tan x  3  x   k ,k  . 3
Với t  3  3 cos x  sin x  3 x k2   3   cos x    cos  ,k    .  6  2 6
x    k2  3
Vậy nghiệm của phương trình là: x
k ,x k2 ,x    k2 ,k  . 3 3 Cách 2: 2
2cos x  2 3 sin x cos x 1  3( 3 cos x  sin ) x
 cos 2x  3 sin 2x  2  3  3cosx sinx      cos 2x  1  3 cos x       3   6 
Đặt t x  , ta được 6 cost  0 2 
cos 2t 1  3 cos t  2 cos t  3 cos t   3 cos t   2
Ta được nghiệm như cách 1. 17. 2 2
4cos x  3tan x  4 3 cos x  2 3 tan x  4  0 . Điều kiện: x   k ,k  . 2 Ta có 2 2
4cos x  3tan x  4 3 cos x  2 3 tan x  4  0
  cosx  2  .tan x  2 2 3 3 1  0 x     k2 2cos x  3  0  6    
x    k2 ,k      6 3  tan x 1
x    k  6
Kết hợp điều kiện ta được nghiệm của phương trình là x    k2 ,k  . 6 18. 3 3
sin x  cos x  sin x  cos x . 3 3
 sin x sin x  cos x  cosx  0  sin x 2 sin x   3
1  cos x  cos x  0 3 2
 cos x  cos xsin x  cos x   cos x 2 0
cos x  sin x cos x   1  0 cos x  0   1   2
cos x  sin x cos x 1  0  2 Ta có   1  x   k ,k  . 2
2  sin2xcos2x  3 (Vô nghiệm vì  2 2 2 1 1  3 ) Trang 119 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC 1 1 (Hoặc ta có 2
cos x 1  1, sin x cos x   sin 2x    2 Vô nghiệm). 2 2
Vậy nghiệm của phương trình đã cho là x   k ,k  . 2 19. 4
8cos x  cos 4x 1. 1cos2x2 2  8  2cos 2x  0 4 1 2
 cos2x    2x  
k2  x    k ,k . 2 3 3
Vậy nghiệm của phương trình là x    k ,k  . 3 3 20. 2 2
sin 2x  sin 4x  . 2 2
1cos4x  2sin 4x 3  0   2
2 1 cos 4x  cos 4x  2  0  k cos 4x  0 x    2  8 4
 2cos 4x  cos 4x  0  1   k   . cos 4x    k  2 x     6 2 k k
Vậy nghiệm của phương trình là: x   , x    , k  . 8 4 6 2 21.  3 3
4 cos x  sin x  cos x  3sin x . 3 3
 4sin x 3sin x cos x  4cos x  0
Nếu cos x  0  x
k  sin x  1
 không là nghiệm của phương trình. 2
Nếu cos x  0 , chia 2 vế của phương trình cho 3 cos x ta được: 3 3 sin x sin x cos x cos x 4  3   4  0 3 3 3 3 cos x cos x cos x cos x tan x 1 3  4tan x 3   4  0 2 2 cos x cos x 3 2
 tan x  tan x 3tan x 3  0  tan x   2 1 tan x  3  0 x   k  4  tan x 1     x   kk . tan x    3 3 
x    k  3 22. 3 2
4sin x  4sin x  3sin 2x  6cos x  0. 3 2
 4sin x  4sin x  6sinxcosx  6cosx  0 2
 4sin xsinx  
1  6cos xsin x   1  0 LÊ MINH TÂM Trang 120 HÀM SỐ LƯỢNG GIÁC  sin x   2
1 4 sin x  6 cos x  0  sin x   2
1 4 cos x  6 cos x  4  0 sin x  1    x    k2 1    2 cos x     k   . 2 2 x     k cos x   loaïi 2 2  3 23.  2 sin x   2 tan x   2 2 1 2 3 2 cos x   1  0 . k Điều kiện: 2x
k x   k . 2 4 2 Ta có  2 sin x   2 tan x   2 2 1 2 3 2 cos x   1  0 2 cos 2 . x sin 2x   3cos 2x  0 2 cos 2x 2 2 2 sin 2x
sin 2x  3cos 2x   3cos 2x  0   0 cos 2x cos 2x 2 2 2 2 2
 sin 2x 3cos 2x  sin 2x  3cos 2x  tan 2x  3
 tan 2x   3  x    k k  thoả mãn điều kiện. 3
Vậy nghiệm của phương tình là: x  
k ,k  . 3 2
cos xcos x   1 24.  21 sin x sin x  . cos x
Điều kiện: sin x  cos x  0  tan x  1
  x    k k  . 4 2
cos xcos x   1 Ta có  21 sin x sin x  cos x
 1sin x1 sin xcosx  
1  21 sin xsin x  cos x
 1 sinx2sinx  2cosx1sinx1 sinxcosx   1  0
 1 sinx1 sin .
x cos x  sin x  cos x  0 sin x  1  1 ( )  1  sin .
x cos x  sin x  cos x  0 (2) Giải 1 ( ) : sin x  1
  x    k2 ,k  . 2 Giải (2) : 1 sin .
x cos x  sin x  cos x  0 .  
Đặt t  sin x  cos x  2 sin x  
 , t   2; 2   4    2 t 1  sin . x cos x  . 2 2 t 1 Ta được phương trình: 2 1
t  0  t  2t 1  0  t  1  . 2 Trang 121 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC     2 Với t  1   2 sin x   1   sin x         4   4  2
x    k2   x    k2 4 4     2 , k   5 
x    k2
x   k2  4 4
Kết hợp điều kiện ta được nghiệm của phương trình là: x   k2 ; x    k2 , k  . 2
25. tan x  2 2 sin x  1 . Điều kiện: x
k k . 2
Ta có tan x  2 2 sin x  1 sin x
 2 2 sin x 1 sin x  2 2 sin .
x cos x  cos x  0 cos x
 sin x  cos x  2 2 sin . x cos x  0 .  
Đặt t  sin x  cos x  2 sin x  
 , t   2; 2   4    2 1 t  sin . x cos x  . 2  2       2 t 2; 2 1 t Ta được phương trình: 2 t    2 2
 0  2t t  2  0  2  . 2
t   2  2; 2    2   2   1 Với t   2 sin x    sin x        sin 2  4  2  4  2 6   5 x    k2 x    k2  4 6 12     ,k   .  5 13  x    k2 x   k2  4 6  12    
Với t   2  2 sin  x    2   sin  x   1   4   4 
x     k2  x    k2 ,k  . 4 2 4
Kết hợp điều kiện ta được nghiệm của phương trình là: 5 13 x   k2 ; x
k2 , x    k2 ,k . 12 12 4
26. tan x  tan2x  sin3 . x cos x . x   k  2  , k  Điều kiện: kx    4 2
Ta có: tan x  tan2x  sin3 . x cos x LÊ MINH TÂM Trang 122 HÀM SỐ LƯỢNG GIÁC sin x sin 2x    sin3 . x cos x cos x cos 2x  sin3x  sin3 . x cos . x cos . x cos2x  sin3x1cos . x cos .
x cos 2x  0 sin3x  0   1 cos2x  .cos 2x  1  2  k x    k 3x k 3 x    k     3  x  , k  2    cos 2x  1
cos 2x cos 2x 2 0  3  x k cos 2x  2    loaïik
Kiểm tra điều kiện suy ra nghiệm phương trình là x  , k  . 3
27. 4 3 sin xcos xcos 2x  sin8x .
Ta có 4 3 sin xcos xcos 2x  sin8x  2 3 sin2 .
x cos 2x  sin8x
 3 sin4x  sin8xkk x x    4 4  x       k
 sin x  cos x sin 4 0 4 3 2 4  0 
 4x   k2      3 x , k   cos 4x  6 24 2   2  k
4x    k2 x      6  24 2  5   7  28. sin 2x   3cos x   1     sin x .  2   2   5   7  Ta có: sin 2x   3cos x   1     sin x  2   2 
 cos2x3sinx 1sinxx k sin x  0 2 
 1 2sin x  2sin x 1  0    , k  sin x 1 x   k2  2
29. tan x  3cot x  4sin x  3 cos xk Điều kiện: x  , k  . 2
Ta có tan x  3cot x  4sin x  3 cos x sin x cos x   3
 4sinx 3cosx cos x sin x 2 2
 sin x  3cos x  4sin xcos xsin x  3cosx
 sinx  3cosxsin x  3cosx 2sin2x  0 Trang 123 LÊ MINH TÂM HÀM SỐ LƯỢNG GIÁC
x    k  3 tan x   3 
sin x  3 cosx  0        
x    k2 ,k   .
sin x  3 cosx  2sin2x sin   x    sin 2x 3 3     4 k2 x    9 3 4 4 sin x  cos x 1 30.
 tan x  cot x sin 2x 2 k Điều kiện: x  , k  . 2 4 4 sin x  cos x 1 Ta có
 tan x  cot x sin 2x 2 4 4 2 2
 sin x  cos x  sin x  cos x
 sin xcos x2 2 2 2 2  2sin . x cos x  1 2 2  2sin .
x cos x  0  sin2x  0 (loại)
Vậy phương trình đã cho vô nghiệm.
------------------ HẾT------------------ LÊ MINH TÂM Trang 124