

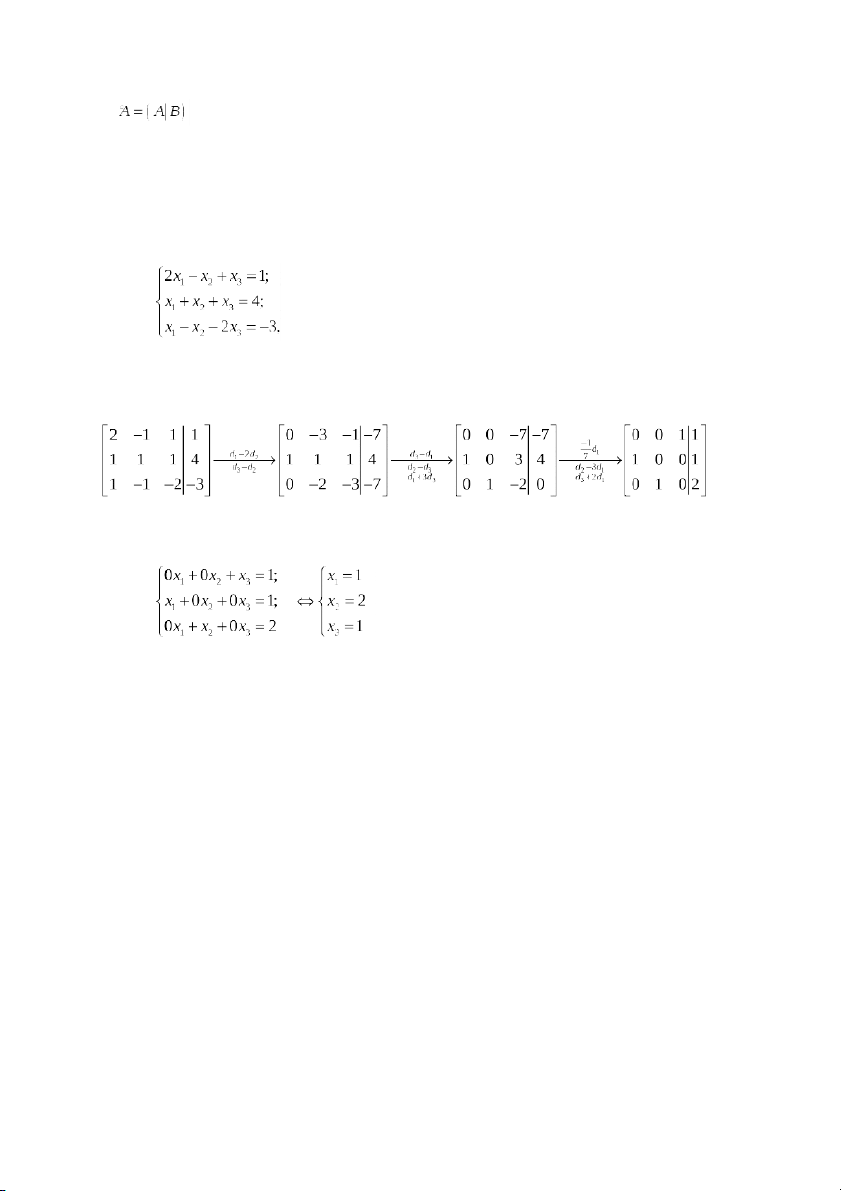

Preview text:
Phần mở đầu
Có thể nói đối với sinh viên khoa Toán nói riêng và sinh viên học toán nói
chung Đại số tuyến tính là một môn học rất quan trọng. Trong đó không thể nhắc
đến lý thuyết về hệ phương trình tuyến tính và một số ứng dụng của nó. Hệ phương
trình tuyến tính được hoàn thiện nhờ không gian vectơ, ma trận và định thức. Nó
có rất nhiều ứng dụng không những trong nhiều ngành toán học khác nhau như:
Đại số, Hình học, Giải tích, Lý thuyết phương trình vi phân, Phương trình đạo hàm
riêng, Qui hoạch tuyến tính mà còn trong cả nhiều lĩnh vực khoa học khác. Bản
thân em muốn tìm hiểu kĩ hơn về phương pháp giải dạng toán này và cũng có
mong muốn tìm hiểu sâu sắc hơn về các ứng dụng của hệ phương trình tuyến tính
trong một số lĩnh vực. Chính vì lý do đó, em đã chọn đề tài: “ Tìm hiểu một số ứng
dụng của hệ phương trình tuyến tính trong các bài toán thực tế ” để làm đề tài cho bài của mình. 1. Định nghĩa Hệ phương trình dạng: (1)
trong đó , ,... là các ẩn, là các hằng số , gọi là hệ phương trình tuyến tính ( m phương trình, n ẩn ). Kí hiệu A = (, x = ,
Khi đó, hệ phương trình nói trên có thể viết dưới dạng phương trình vectơ Ax =
Một nghiệm của hệ này là một vectơ sao cho Một hệ phương trình có ít nhất một nghiệm
được gọi là một hệ phương trình tương thích.
Hệ phương trình Ax = 0 được gọi là hệ phương trình tuyến tính thuần nhất liên kết với hệ Ax =
2. Một vài hệ phương trình đặc biệt 2.1 Hệ Cramer:
Hệ phương trình tuyến tính (1) được gọi là hệ Cramer nếu m = n (tức là số phương trình bằng
số ẩn) và ma trận các hệ số A không suy biến (hay det A 0) Ví dụ:
Hệ phương trình là hệ Cramer
a. Hệ phương trình tuyến tính thuần nhất:
- Nếu cột tự do của hệ bằng 0 (tức là ) thì hệ phương trình tuyến tính (1) được gọi là hệ
phương trình tuyến tính thuần nhất.
- Hệ này được gọi là hệ liên kết với hệ phương trình (1). 2.3 Nhận xét:
Hệ phương trình tuyến tính thuần nhất luôn có ít nhất một nghiệm là (
(0, 0,…0) và nghiệm này được gọi là nghiệm tầm thường của hệ
3. Một số định lí, hệ quả của hệ phương trình tuyến tính
Định lí 1: Đối với một hệ phương trình tuyến tính thì chỉ có một trong ba trường hợp nghiệm xảy ra là: Có một nghiệm duy nhất Vô nghiệm Có vô số nghiệm.
Hệ quả: Hệ phương trình tuyến tính thuần nhất hoặc chỉ có nghiệm tầm thường hoặc có vô số nghiệm.
Định nghĩa 1: Hai hệ phương trình có cùng số ẩn được gọi là tương đương nhau nếu chúng có cùng tập hợp nghiệm.
Định lí 2: Nếu hai hệ phương trình có hai ma trận hệ số mở rộng tương ứng tương đương dòng
với nhau thì chúng tương đương nhau. Hoặc có thể phát biểu lại như sau:
Cho hai hệ gồm m phương trình tuyến tính n ẩn trên K có dạng ma trận hóa lần lượt là
A= và C = . Khi đó nếu A : C thì hai hệ phương trình tương đương nhau.
Nhận xét: Ta có thể sử dụng các phép biến đổi sơ cấp trên dòng một cách tùy ý đối với ma trận
hóa của một hệ phương trình tuyến tính để đưa nó về dạng một hệ phương trình tuyến tính đơn giản hơn.
Ví dụ 1: Để giải hệ phương trình
ta tiến hành ma trận hóa và sử dụng các phép biến đổi sơ cấp trên dòng để đưa ma trận hóa về dạng đơn giản.
Vậy hệ đã cho tương đương với
Định lí 3: Giả sử là một nghiệm cho trước của hệ phương trình (1). Khi đó u là một nghiệm của
hệ (1) khi và chỉ khi u = , với v là nghiệm của hệ phương trình tuyến tính thuần nhất liên kết với hệ (1).
Nói cách khác nếu là các nghiệm của hệ phương trình tuyến tính thuần nhất liên kết thì ta có thể
viết nghiệm của hệ phương trình tuyến tính (1) là trong đó
Định nghĩa 2: Một nghiệm cố định của hệ phương trình tuyến tính (1) được gọi là nghiệm
riêng, còn nghiệm được gọi là nghiệm tổng quát của hệ.
Ví dụ 2: Xét hệ phương trình (2) sau:
Nhận xét hệ (2) có 1 nghiệm là
Xét hệ phương trình thuần nhất liên kết với hệ (2)
Hệ thuần nhất này có các nghiệm là ;
Khi đó nghiệm tổng quát của hệ phương trình ban đầu là



