Không gian Euclide - Đại số tuyến tính | Trường Đại học Thủ đô Hà Nội
Không gian Euclide - Đại số tuyến tính | Trường Đại học Thủ đô Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Đại số tuyến tính (SPT-2021B) 5 tài liệu
Trường: Đại học Thủ đô Hà Nội 603 tài liệu
Tác giả:
Preview text:
MôC LôC
4 Kh«ng gian Euclide vµ d¹ng toµn ph-¬ng 3 4.1
Kh«ng gian Euclide . . . . . . . . . . . . . . . . . . . . . . . . . . 3 4.1.1
TÝch v« h-íng vµ kh«ng gian Euclide . . . . . . . . . . . . 3 4.1.2
Qu¸ tr×nh trùc chuÈn hãa Gram-Smidt . . . . . . . . . . . 9
4.2 PhÐp biÕn ®æi trùc giao, phÐp biÕn ®æi ®èi xøng . . . . . . . . . . 13
4.3 D¹ng song tuyÕn tÝnh vµ d¹ng toµn ph-¬ng . . . . . . . . . . . . 27 4.3.1
D¹ng song tuyÕn tÝnh trªn kh«ng gian vÐc t¬ . . . . . . . 27 4.3.2
D¹ng toµn ph-¬ng . . . . . . . . . . . . . . . . . . . . . . 33 4.3.3
Ph©n lo¹i d¹ng toµn ph-¬ng . . . . . . . . . . . . . . . . . 48 1 ®¹i sè
S¸ch dïng cho sinh viªn tr-êng §¹i häc x©y dùng
vµ sinh viªn c¸c tr-êng §¹i häc, Cao ®¼ng kÜ thuËt 2 Ch-¬ng4 Kh«nggianEuclidevµd¹ngtoµn ph-¬ng 4.1 Kh«ng gianEuclide
4.1.1 TÝchv« h-íngvµ kh«nggian Euclide
§Þnh nghÜa 4.1.1 ChoE lµkh«nggianvÐc t¬ thùc. ¸nhx¹E2 → R ®-îcgäilµ
tÝchv« h-íng,kÝhiÖu x, y , nÕunãtháa m·nc¸ctÝnh chÊt •
x, x ≥ 0 víimäix ∈ E vµ x, x = 0 khivµ chØkhi x = 0. •
x, y = y, x víimäix, y ∈ E. •
αx, y = α x, y víimäiα ∈ R vµmäix, y ∈ E. •
x + y, z = x, z + y, z víimäix, y, z ∈ E. Kh kh ««nnggggiiaannv¬Ðc clit( t¬ E E
uclihd÷eu). h¹n chiÒucïng víi tÝch v« h-íng x,y ®-îc gäilµ
DÔ dµng chøng minh ®-îc c¸c tÝnh chÊt sau cña tÝch v« h-íng i) x, 0 = 0, x = 0 ∀x ∈ E ii)
z, x + y = z, x + z, y ∀x, y, z ∈ E
iii) α x, y = x, αy ∀x, y ∈ E,∀α ∈ R. 3 4
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng
VÝ dô 4.1.1 (C¸cvÝ dô vÒkh«nggianEuclide)
1. Trong kh«ng gian c¸c vÐc t¬ h×nh häc, nh- ®· biÕt tÝch v« h-íng − → − → − → − → a · b = |−
→a | · | b | cos(−→a , b )
tháa m·n c¸c yªu cÇu trªn, do vËy kh«ng gian c¸c vÐc t¬ h×nh häc lµ kh«ng − → − → b .
gian Euclide víi tÝch v« h-íng − → a , b = −→a ·
2. Trong kh«ng gian vÐc t¬ E cho hÖ c¬ së {e1, e2,...,en} vµ hai vÐc t¬ tïy ý x, y ∈ E n n x = x yiei. X iei, y = X i=1 i=1 BiÓu thøc n x X iyi x, y = x i=1 1y1 + x2y2 + · · · + xnyn =
tháa m·n c¸c yªu cÇu trong ®Þnh nghÜa tÝch v« h-íng. VËy kh«ng gian E
víi tÝch v« h-íng trªn lµ kh«ng gian Euclide.
§Æc biÖt kh«ng gian Rn lµ kh«ng gian Euclide víi tÝch v« h-íng
u, v = u1v1 + u2v2 + · · · + unvn
trong ®ã u = (u1, u 2,...,un), v = (v1, v 2,...,vn) ∈ Rn. TÝch v« h-íng nµy
trªn Rn còng ®-îc gäi lµ tÝchv«h-íngEuclide.
3. DÔ dµng chøng minh ®-îc trong R3 2, u3), v = (v1, v 2, v3)
u, v = u1v1 + 3u2v2 + 2u3v3, víi u = (u1, u
lµ tÝch v« h-íng. Víi tÝch v« h-íng ®ã, R3 lµ kh«ng gian Euclide.
4. KÝ hiÖu Pn[x] lµ kh«ng gian c¸c ®a thøc cã bËc kh«ng v-ît qu¸ n. DÔ dµng kiÓm tra
Z 1f(x)g(x)dx, ∀f, g∈ Pn[x] 0 f, g =
tháa m·n c¸c yªu cÇu cña tÝch v« h-íng. VËy Pn[x] lµ kh«ng gian Euclide n + 1 chiÒu. 4.1Kh«nggianEuclide 5 q §
g Þänilh µ n ®géhÜa dµi 4 c .ñ1a.2 v T Ðctro ¬ nxg,k k h Ý«hnigg ÖuianEuclideE, biÓuthøc x, x ∀x ∈ E ®-îc q |x| = x, x . VÝ dô 4.1.2
1. Trong kh«ng gian c¸c vÐc t¬ h×nh häc, víi tÝch v« h-íng − → − → − → a , a | · | b | cos(− →a , b ) − → b = |−→
®é dµi vÐc t¬ theo ®Þnh nghÜa trªn trïng víi ®é dµi h×nh häc ®o¹n th¼ng nèi gèc vµ ngän vÐc t¬.
2. Trong kh«ng gian R3 víi tÝch v« h-íng Euclide, ®é dµi cña x = (x1, x 2, x 3) b»ng q 1 + x22 + x23. |x| = x2
§é dµi vÐc t¬ hiÓn nhiªn cã c¸c tÝnh chÊt sau
i) |x| ≥ 0 ∀x ∈ E vµ |x| = 0 khi vµ chØ khi x = 0
ii) |α · x| = |α| · |x| ∀α ∈ R, ∀x ∈ E
iii) §é dµi vÐc t¬ tháa m·n bÊt ®¼ng thøc tam gi¸c
|x + y| ≤ |x| + |y| ∀x, y ∈ E.
BÊt ®¼ng thøc nµy sÏ ®-îc ph¸t biÓu l¹i vµ chøng minh trong ®Þnh lÝ 4.1.1 d-íi
®©y sö dông bÊt ®¼ng thøc Schwarz.
§Þnh lÝ 4.1.1 Trong kh«nggianEuclide E ta lu«n cãc¸cbÊt®¼ngthøcsau
(i) BÊt®¼ngthøc Schwarz: | u, v | ≤ |u| · |v| ∀u, v ∈ E
(ii) BÊt®¼ngthøc tam gi¸c: |u + v| ≤ |u| + |v| ∀u, v ∈ E 6
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng Chøngminh.
(i) BÊt ®¼ngthøcSchwarz: bÊt ®¼ng thøc hiÓn nhiªn ®óng khi u = 0.
XÐt tr-êng hîp |u| > 0, víi sè thùc t ∈ R bÊt k×
0 ≤ tu − v, tu − v = |u|2t2 − 2 u, v t + |v|2 (∗)
VÕ ph¶i cña bÊt ®¼ng thøc (∗) lµ tam thøc bËc hai kh«ng ©m víi mäi t ∈ R, suy ra biÖt thøc
∆′ = u, v 2−|u|2 · |v|2 ≤ 0 hay | u, v | ≤ |u| · |v|.
(ii) BÊt®¼ngthøc tamgi¸c: Thay t = −1 vµo (∗) vµ ¸p dông bÊt ®¼ng thøc
Schwarz: | u, v |2 ≤ |u| · |v| ta ®-îc |u + v|2 = |u| + 2
u, v +|v|2 ≤ |u|2 + 2|u| · |v| + |v|2 = (|u| + |v|)2
Suy ra bÊt ®¼ng thøc tam gi¸c: |u + v| ≤ |u| + |v|. VÝ dô 4.1.3
1. BÊt ®¼ng thøc Schwarz trong kh«ng gian Euclide Rn víi tÝch v« h-íng
u, v = u1v1 + u2v2 + · · · + unvn chÝnh lµ bÊt ®¼ng thøc Bunhiacèpki q 1 + u2 1 + v2 2 + · · · + u2 q 2 + · · · + v2n
|u1v1 + u2v2 + · · · + unvn| ≤ u2 n v2 2. V
S ícih twÝcahrz vc«ã hd-¹ínngg u,v = u1v1 + 3u2v2 + 2u3v3 trong R3, bÊt ®¼ng thøc q
1 + 3u22 + 2u2 q 1 + 3v22 + 2v23 |u1v1 + 3u2v2 + 2u3v3| ≤ u2 3 v2
3. BÊt ®¼ng thøc Schwarz vµ bÊt ®¼ng thøc tam gi¸c trong kh«ng gian Euclide 1 Z f(x)g(x)dx P 0 n[x] víi tÝch v« h-íng f, g = Z s s g2(x)dx 1 Z Z 0 1 0 1 0 f(x)g(x)dx ≤ f2(x)dx sZ sZ sZ (f(x) + g(x))2dx 10 1 0 1 0 f2(x)dx+ g2(x)dx≥ 4.1Kh«nggianEuclide 7
NhËnxÐt r»ng tÝchv« h-íng trongkh«ng gian Euclidelµ më réngkh¸i niÖm
tÝchv« h-íng cña2 vÐct¬h×nh häc. Trong kh«nggianEuclide ng-êitacòng ®Þnh
nghÜagãcgi÷ahaivÐct¬ u, v lµgãc ϕ, 0 ≤ ϕ ≤ π saocho . |u| u·,|v| cos ϕ = u, v
Theo bÊt ®¼ng thøc Schwarz | u, v | ≤ |u| · |v| hay ≤ 1, ®Þnh nghÜa
trªn hoµn toµn hîp lÝ. §Æc biÖt nÕu |u| · |v| u, v = 0,
u, v lµ hai vÐc t¬ kh¸c 0, khi ®ã gãc gi÷a hai vÐc t¬ u, v b»ng 900, ta nãi u
vu«nggãchoÆctrùc giaovíi v, kÝ hiÖu u⊥v.
§Þnh lÝ 4.1.2 (§Þnh lÝ Pitago trong kh«ng gian Euclide)
NÕuu vµv lµ 2 vÐct¬trùc giaotrongkh«ng gianEuclideth× |u + v|2 = |u|2 + |v|2. Chøngminh. Do u, v = 0 ta cã
|u + v|2 = u + v, u + v = u, u +2 u, v + v, v = |u|2 + |v|2.
C¸c kÕt qu¶ sau lµ hiÓn nhiªn, b¹n ®äc tù chøng minh
1. NÕu v trùc giao víi c¸c vÐc t¬ v1, v2,...,vk khi ®ã v trùc giao víi mäi vÐc
t¬ trong kh«ng gian con L(v1, v2,...,vk) sinh bëi v1, v2,...,vk.
2. TËp hîp c¸c vÐc t¬ trùc giao víi u1, u2,...,uk lµ kh«ng gian con cña E.
§Þnh lÝ 4.1.3 NÕuhÖc¸cvÐc t¬ B = {u1, u2,...,uk} kh¸c0 trongE ®«iméttrùc
giaovíinhauth× hÖB ®éclËp tuyÕn tÝnh.
Chøngminh. Gi¶ sö α1u1 + α2u2 + · · · + αkuk = 0. Nh©n v« h-íng c¶ hai vÕ víi ui, i = 1, n ta ®-îc
α1 u1, ui +α2 u2, ui + · · · + αi uk, ui + · · · + αk uk, ui = 0. 8
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng
Do um, ui = 0 víi mäi m 6= i, suy ra
αi ui, ui = 0 ⇒ αi = 0. ∀i = 1, n
VËy B = {u1, u2,...,uk} ®éc lËp tuyÕn tÝnh.
Tõ ®Þnh lÝ trªn suy ra nÕu trongkh«nggian Eucliden chiÒuE tånt¹i méthÖ
n vÐct¬kh¸c0,®«iméttrùc giaonhau,khi ®ãhÖ n vÐc t¬®ãlËpthµnhc¬sëcña
E. Ng-êi tagäic¬sënh-vËylµc¬sëtrùcgiaotrongE.
§Þnh nghÜa 4.1.3 B = {e1, e2, . . . , en} lµhÖc¬sëtrùcgiaotrongkh«nggian
EuclideE, ®ång thêi®é dµicñatõngvÐc t¬ trong B b»ng1
|e1| = |e2| = · · · = |en| = 1.
Khi®ãB = {e1, e2, . . . , en} ®-îcgäi lµ hÖ c¬së trùcchuÈncñaE.
Nh- vËy, hÖ {e1, e2, . . . , en} lµ mét c¬ së trùc chuÈn cña mét kh«ng gian Euclid n chiÒu khi vµ chØ khi (01 nÕnuÕ iu 6i== jj ei, ej =
Trong kh«ng gian Euclide c¸c vÐc t¬ cã ®é dµi b»ng 1 ®-îc gäi lµ vÐc t¬ ®¬nvÞ.
Do vËy ta th-êng nãi c¬ së trùc chuÈn lµ hÖ c¬ së trùc giao gåm c¸c vÐc t¬ ®¬n vÞ. NhËnxÐt r»ng nÕu
x = x1u1 + x2u2 + · · · + xnun, y = y1u1 + y2u2 + · · · + ynun haynãi c¸chkh¸c(x1, x 2,...,xn) vµ(y1, y
2,...,yn) lµ c¸ctäa®é cñax, y tronghÖ
c¬sëtrùcchuÈnB = {u1, u2,...,un} th×
< x, y >= x1y1 + x2y2 + · · · + xnyn. §Æc biÖt q 1 + x2 1 + y2 2 + · · · + x2 q 2 + · · · + y2n. |x| = x2 n, |y| = y2 VÝ dô 4.1.4 − → − → − →
1. Trong kh«ng gian vÐc t¬ h×nh häc, hÖ c¸c vÐc t¬ { i , j , k } (c¸c vÐc t¬
®¬n vÞ cña c¸c trôc täa ®é §Ò c¸c Oxyz) lËp thµnh mét c¬ së trùc chuÈn. 4.1Kh«nggianEuclide 9
2. Trong kh«ng gian Euclide R3 víi tÝch v« h-íng u, v = u1v1 + 3u2v2 + 2u3v3,
c¬ së chÝnh t¾c B = {e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1)} lµ hÖ
c¬ së trùc giao. Tuy nhiªn B kh«ng lµ hÖ c¬ së trùc chuÈn v× ®é dµi √ |e e2, 1√ e 2| = 3 6= 1. HÖ {e1, 1√3
2 3} lµ hÖ c¬ së trùc chuÈn cña R3.
3. Trong kh«ng gian Euclide Rn víi tÝch v« h-íng Euclide c¬ së chÝnh t¾c lµ hÖ u c , ¬ vsë =tru ù1v c 1c + h u u 2v Èn.2 + · · · + unvn,
4. Trong kh«ng gian Euclide E víi dim E = 2, cho hai vÐc t¬ ®¬n vÞ u vµ v
hîp víi nhau mét gãc 1200. Khi ®ã tån t¹i duy nhÊt vÐc t¬ ®¬n vÞ hîp víi
c¶ hai vÐc t¬ u vµ v c¸c gãc 1200.
ThËt vËy, tr-íc hÕt ta thÊy a = u + v lµ vÐc t¬ ®¬n vÞ do ®¼ng thøc sau Gä|ia|2 g = ãc giu÷ + a v,Ð u c + t¬va = = |u u |2 + + v |v v |2 íi + h 2 ai vÐc t u ¬ , v u v = µ 1 v + l 1 Çn −l- 2 ît co b s »n1g200 ϕ1, = ϕ 1. 2. 0 ⇒ ϕ . a, u 1 = a, u = u, u + v, u = 2 1 = 60 cos ϕ1 = |a| · |u| T-¬ng tù 0. a, v 1 ⇒ ϕ = a, v = u, v + v, v = 2 2 = 60 cos ϕ2 = |a| · |v|
VÐc t¬ a hîp víi u vµ v c¸c gãc 600, suy ra vÐc t¬ −a = −u − v hîp víi u vµ v c¸c gãc 1200.
PhÇn cßn l¹i, chøng minh ®ã lµ vÐc t¬ ®¬n vÞ duy nhÊt dµnh cho b¹n ®äc.
4.1.2 Qu¸ tr×nhtrùc chuÈnhãa Gram-Smidt
B©y giê chóng ta sÏ giíi thiÖu mét quy tr×nh x©y dùng hÖ c¬ së trùc chuÈn cña
kh«ng gian Euclide E tõ mét c¬ së bÊt k× cña E. Quy tr×nh nµy mang tªn qu¸
tr×nhtrùc chuÈnhãa Gram-Smidt.
Gi¶ sö u1, u2,...,un lµ mét hÖ c¬ së bÊt k× cña E. Ta sÏ kiÕn thiÕt hÖ c¬ së
trùc chuÈn e1, e2,...,en cña kh«ng gian E nh- sau. Tr-íc hÕt x©y dùng hÖ c¬ së
trùc giao v1, v2,...,vn cña E 10
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng 1. §Æt v1 = u1 6= 0 2. T×m v2 d-íi d¹ng v2 = u2 − αv1
sao cho v2⊥ v1. Sè thùc α t×m ®-îc tõ hÖ thøc u|v |2 0 = v 2,1 v1 2, v1 = u2, v1 −α v1, v1 ⇒ α =
Tõ c¸ch x©y dùng v1 vµ v2, dÔ dµng suy ra L(v1, v2) = L(u1, u2), ®ång
thêi v2 6= 0 do {ui} lµ hÖ c¬ së.
3. Víi k < n gi¶ sö ta ®· x©y dùng ®-îc hÖ trùc giao {v1, v2,...,vk}, vi 6= 0
∀i = 1, 2,...,k. Ta sÏ t×m vk+1 d-íi d¹ng
vk+1 = uk+1 − α1v1 − α2v2 − · · · − αkvk,
trong ®ã c¸c sè αi ∈ R, i = 1, 2,...,k cÇn ®-îc x¸c ®Þnh sao cho
vk+1⊥ vi hay vk+1, vi = 0 víi ∀i = 1, 2, ...,k vµ vk+1 6= 0. V c Ðc Çn tt¬×m α v i
k+1 6= 0 lµ hiÓn nhiªn. HÖ thøc
vk+1, vi = 0 kÐo theo c¸c gi¸ trÞ u ∀i = 1, k. |v 2 i| u k+1, vi k+1, vi −αi vi, vi = 0 ⇒ αi =
B»ng quy n¹p nh- trªn ta x©y dùng ®-îc hÖ c¬ së trùc giao v1, v2,...,vn
cña E vµ dÔ dµng nhËn thÊy
L(v1, v2,...,vm) = L(u1, u2,...,um) ∀m = 1, 2, ...,n.
4. Cuèi cïng hÖ c¬ së trùc chuÈn e1, e2,...,en cña kh«ng gian E nhËn ®-îc
tõ hÖ trùc giao v1, v2,...,vn b»ng c¸ch chuÈn hãa c¸c vÐc t¬ vi theo c«ng thøc v e i i = , i = 1, 2,...,n. |vi| 4.1Kh«nggianEuclide 11
NhËn xÐt r»ng nÕu u1, u2,...,un lµ mét hÖ vÐc t¬ bÊt k× (cã thÓ phô thuéc tuyÕn
tÝnh), ph-¬ng ph¸p Gram-Smidt nªu trªn vÉn cã thÓ ¸p dông ®Ó x©y dùng hÖ
trùc giao v1, v2,...,vk (k ≤ n) kh«ng chøa vÐc t¬ 0 tháa m·n tÝnh chÊt
L(v1, v2,...,vk) = L(u1, u2,...,uk).
(C¸c vÐc t¬ vi cã thÓ lµ vÐc t¬ 0 trong qu¸ tr×nh kiÕn thiÕt, ta cÇn lo¹i c¸c vÐc t¬ b»ng 0 ®ã.)
Qu¸ tr×nh trùc chuÈn hãa Gram-Smidt nªu trªn ®-îc gäi lµ ph-¬ngph¸p
Gram-Smidt, nã ®-îc thu gän trong ®Þnh lÝ sau
§Þnh lÝ 4.1.4 Gi¶sö{u1, u2,...,un} lµ mét hÖ c¬së bÊtk× cñakh«nggianEuclide
E. TrongE tånt¹i métc¬së trùcchuÈn {e1, e2,...,en} ®-îcx©ydùng bëiqu¸
tr×nhtrùc chuÈnhãa Gram-Smidt,hÖ c¬së ®ãcãtÝnh chÊt
L(e1, e2,...,em) = L(u1, u2,...,um) ∀m = 1, 2,...,n. VÝ dô 4.1.5 1. K g hia«n n gE g
ucilainde. DÔ dµng chØ ra hÖ c¸c vÐc t¬ R3 víi tÝch v« h-íng
x, y = x1y1 + 4x2y2 + x3y3 lµ kh«ng
B = {a1 = (1, 0, −1), a2 = (1, 1, 1), a3 = (1, 1, 3)}
lµ c¬ së cña R3. B»ng ph-¬ng ph¸p Gram-Smidt, h·y trùc chuÈn ho¸ hÖ vÐc t¬ B.
Ta cã nhËn xÐt r»ng 2 vÐc t¬ a1 = (1, 0, −1), a2 = (1, 1, 1) trùc giao nhau theo tÝch v« h-íng ®· cho
a1, a2 = 1 · 1 + 4 · 0 · 1 + (−1) · 1 = 0.
Theo ph-¬ng ph¸p Gram-Smidt, ta t×m vÐc t¬ thø ba v = a3 − α1a1 − α2a2
sao cho v⊥ a1, v⊥ a2. C¸c hÖ sè α1, α 2 ®-îc x¸c ®Þnh bëi c«ng thøc −2 4 = = −1, α = . a|a 2 |a 2 2| 3 1| 2 a α 3, a1 3, a2 1 = 2 = 12
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng Suy ra 4 2 v = a −1 3 + a1 − , , 23 3 a 3 2 = 3
KÝ hiÖu vÐc t¬ ®ång ph-¬ng víi v lµ u = (2, −1, 2). Nh- vËy hÖ 3 vÐc t¬
{a1 = (1, 0, −1), a2 = (1, 1, 1), u = (2, −1, 2)}
lµ hÖ trùc giao theo tÝch v« h-íng ®· cho trong R3. Trùc chuÈn hãa hÖ vÐc
t¬ trªn ta ®-îc hÖ c¬ së trùc chuÈn 1 1 1 e1 = √ (1, 0, −1), e2 = √ (1, 1, 1), e3 = √ (2, 2 6 −1, 2). 12
Ta dÔ dµng kiÓm tra tÝnh chÊt ph¸t biÓu trong ®Þnh lÝ 4.1.4
L(e1) = L(a1), L(e1, e2) = L(a1, a2), L(e1, e2, e3) = L(a1, a2, a3).
2. Trong kh«ng gian c¸c ®a thøc hÖ sè thùc cã bËc kh«ng v-ît qu¸ hai E = P2[x] víi tÝch v« h-íng 1 Z p(x)q(x)dx. p,q =−1
H·y trùc chuÈn hãa hÖ c¬ së B = {1, x, x 2} cña E.
Theo ph-¬ng ph¸p Gram-Smidt, tr-íc hÕt ta trùc giao hãa hÖ vÐc t¬ B.
⋆) §Æt f1 = 1 lµ vÐc t¬ ®Çu tiªn cña hÖ B.
⋆) §Æt f2 = x − α · 1 = x − α. Ta x¸c ®Þnh α ®Ó f1, f2 = 0 hay 1 1 · x dx R −1 = 0. 1, x 1 =
1, x −α f1, f1 = 0 ⇒ α = f1, f1 1 · 1 dx R −1 Do ®ã f2 = x − α = x.
4.2PhÐpbiÕn®æitrùcgiao,phÐp biÕn®æi®èixøng 13
⋆) §Æt f3 = x2 − α1f1 − α2f2. Khi ®ã 1 1 · x2dx R 1 −1 = 1 3 f1, f3 = 0 ⇒ f1, x 2 −α1 f1, f1 +0 = 0 ⇒ α1 = 1 · 1 dx R −1 1 R x · x2dx −1 = 0. 1 f2, f3 = 0 ⇒
f2, x2 −α2 f2, f2 = 0 ⇒ α2 = x · x dx R −1 Do ®ã f .
3 = x2 − α1f1 − α2f2 = x2 − 1 3 Nh- vËy f
lµ mét c¬ së trùc giao cña E. ChuÈn 1 = 1, f2 = x,f3 = x2 − 1 3
ho¸ chóng, ta ®-îc hÖ c¬ së trùc chuÈn cña E. 3. Tr m oÆn t gp k h h« ¼n n g g g x ia − n 2 E y u + cl z id = e0R3 lµ ví k i h t « Ýnch g v gi«a h n -í c n o g n cñ x a , y R3. = x1y1+2x2y2+2x3y3,
VÐc t¬ vu«ng gãc, theo tÝch v« h-íng ®· cho, víi mäi vÐc t¬ trong mÆt
ph¼ng x − 2y + z = 0 còng ®-îc gäi lµ vÐc t¬ ph¸p cña mÆt ph¼ng. ViÖc
t×m vÐc t¬ ph¸p cña mÆt ph¼ng cã thÓ ®-a vÒ viÖc trùc giao ho¸ hÖ c¬ së
gåm 3 vÐc t¬ {a, b, c} trong R3, víi {a, b} thuéc mÆt ph¼ng ®· cho.
Ch¼ng h¹n a = (1, 0, −1), b = (2, 1, 0) lµ 2 vÐc t¬ ®éc lËp tuyÕn tÝnh thuéc
mÆt ph¼ng x − 2y + z = 0. B»ng ph-¬ng ph¸p trùc giao ho¸ Gram-Smidt
tr×nh bµy trªn, ta dÔ dµng t×m ®-îc vÐc t¬ vu«ng gãc víi mÆt ph¼ng ®ã,
⊥L(a, b), cã d¹ng C(2, −2, 1), C ∈ R.
4.2 PhÐp biÕn ®æi trùcgiao, phÐp biÕn ®æi®èi xøng
§Þnh nghÜa 4.2.1 PhÐp biÕn®æituyÕn tÝnh f trong kh«nggianEuclideE ®-îc
gäi lµ phÐp biÕn®æitrùc giao nÕunã b¶otoµn tÝch v« h-íng: f(x), f(y) = x, y víimäi x, y ∈ E. 14
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng VÝ dô 4.2.1
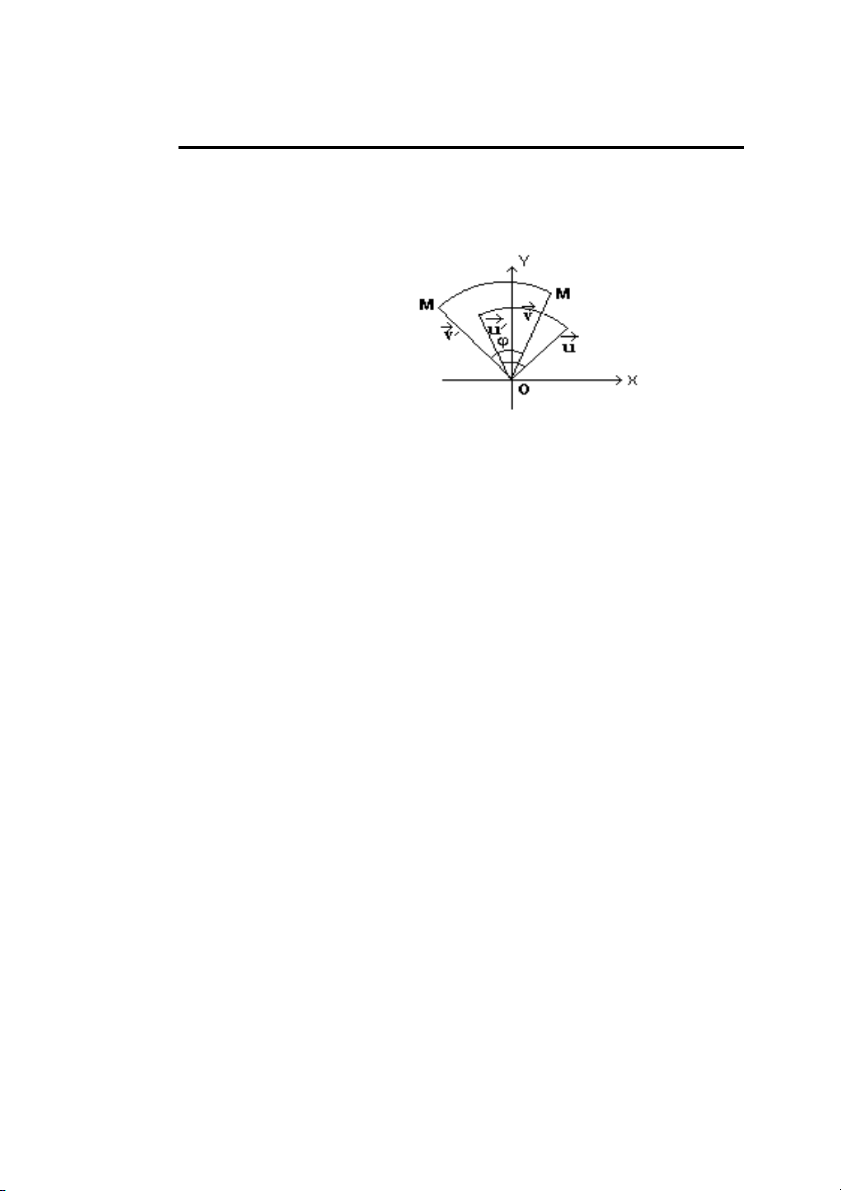
1. PhÐp quay t©m O trong mÆt ph¼ng xOyvíi gãc quay ϕ lµ phÐp biÕn ®æi trùc íng − → u , − → v = H×nh 4.1: PhÐp quay
ThËt vËy, kÝ hiÖu phÐp quay ®ã lµ T , nã quay mét gãc ϕ quanh t©m O − → − → biÕn − → u thµnh u′ vµ − → v thµnh v′ − → − → T − → u = u′, T − →v =v′ − → − → Khi ®ã |− →u | = | u′|, |−
→v | = | v′| vµ gãc gi÷a hai vÐc t¬ (−→u , −→v ) còng b»ng gãc − → − →
gi÷a hai vÐc t¬ ¶nh (u′, v′). Do vËy − → − → − → − → − → −
→u′| · | v′| cos(u′, v′) T − → u , T − → v = u′, v′ = | = |− →u | · |− →v | cos(− →u , − → u , − → v ) = − → v .
2. Trong kh«ng gian Euclide R2 (cã g¾n hÖ trôc täa ®é §Ò c¸c xOyvµ xÐt
tÝch v« h-íng Euclide), phÐp lÊy ®èi xøng qua ®-êng th¼ng, ch¼ng h¹n ®èi
xøng qua ®-êng ph©n gi¸c gãc phÇn t- thø nhÊt y = x lµ phÐp biÕn ®æi
trùc giao. KÝ hiÖu h lµ phÐp biÕn ®æi tuyÕn tÝnh ®ã
h(x,y) = (y,x) ∀(x,y) ∈ R2.
T-¬ng tù nh- trªn, tõ ý nghÜa h×nh häc ta thÊy phÐp lÊy ®èi xøng b¶o
toµn tÝch v« h-íng. Do vËy nã lµ phÐp biÕn ®æi trùc giao. C¬ së chÝnh t¾c
cña R2 còng lµ c¬ së trùc chuÈn − → − → E = { i = (1, 0), j = (0, 1)}
4.2PhÐpbiÕn®æitrùcgiao,phÐp biÕn®æi®èixøng 15
Ma trËn cña h trong c¬ së chÝnh t¾c ®ã b»ng 01 10 [h]E = .
§Þnh lÝ 4.2.1 §iÒukiÖncÇn vµ®ñ ®ÓphÐpbiÕn®æi tuyÕntÝnhf : E → E trong
trongkh«nggianEuclide lµphÐpbiÕn®æitrùcgiao,lµf b¶otoµn ®édµi. Nãic¸ch kh¸c |f(u)| = |u| víimäi u ∈ E.
Chøngminh. §iÒu kiÖn cÇn lµ hiÓn nhiªn
|f(u)|2 = f(u), f(u) = u, u = |u|2.
§Ó chøng minh ®iÒu kiÖn ®ñ, xÐt
|f(u + v)|2 = f(u + v), f(u + v) = f(u) + f(v), f(u) + f(v) = = |f f((uu)|)2, f+(u
2 ) +2 f(u), f(v) + f(v), f(v) = f(u), f(v) +|f(v)|2.
Theo gi¶ thiÕt cña ®iÒu kiÖn ®ñ |f(u)| = |u|, suy ra |f(u + v)|2 = |u|2 + 2 f(u), f(v) +|u|2
MÆt kh¸c còng tõ gi¶ thiÕt cña ®iÒu kiÖn ®ñ
|f(u + v)|2 = |u + v|2 = |u|2 + 2 u, v +|u|2.
So s¸nh 2 ®¼ng thøc trªn ta ®-îc f(u), f(v) = u, v víi mäi u, v ∈ E.
Nãi c¸ch kh¸c f lµ phÐp biÕn ®æi trùc giao. 16
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng NhËnxÐt
1. Do |f(u)| = |u| víi mäi u ∈ E suy ra Ker(f) = {0}, nãi c¸ch kh¸c f
lµ phÐp biÕn ®æi kh«ng suy biÕn, tån t¹i f−1. ¸nh x¹ ng-îc f−1 b¶o toµn
®é dµi, do vËy nã còng lµ phÐp biÕn ®æi trùc giao.
2. Theo ®Þnh lÝ trªn phÐp biÕn ®æi trùc giao b¶o toµn tÝch v« h-íng vµ ®é
dµi, do vËy nã ®-a hÖ c¬ së trùc chuÈn thµnh hÖ c¬ së trùc chuÈn. Cô thÓ
h¬n nÕu {u1, u2,...,un} lµ hÖ c¬ së trùc chuÈn cña E, khi ®ã {f(u1), f(u2), ...,f(un)}
còng lµ hÖ c¬ së trùc chuÈn.
3. §iÒu ng-îc l¹i còng ®óng, nÕu f chuyÓn hÖ c¬ së trùc chuÈn thµnh hÖ c¬
së trùc chuÈn th× f lµ phÐp biÕn ®æi trùc giao. n
ThËt vËy khi ®ã, gi¶ sö u = α2 X i . MÆt kh¸c P i=1 i=1 α n iui, suy ra |u|2 = n n |f(u)|2 = | α2 X αif(ui)|2 = X i . i=1 i=1
Do ®ã |f(u)| = |u| víi mäi u ∈ E, theo ®Þnh lÝ võa chøng minh, f lµ phÐp biÕn ®æi trùc giao.
VÒ ma trËn cña phÐp biÕn ®æi trùc giao, ta cã ®Þnh lÝ sau
§Þnh lÝ 4.2.2 Gi¶sö f lµ phÐp biÕn®æitrùc giaotrong E vµ ma trËncñaf trong
c¬sëtrùcchuÈnB = {e1, e2,...,en} cãd¹ng a11 a12 · · · a1n a21 a22 · · · a2n · · · · · · · · · · · · [f]B = A = an1 an2 · · · ann
Khi®ãma trËn cña ¸nh x¹ ng-îcf−1 trong c¬së B chÝnhlµ matrËnchuyÓnvÞ AT cñaA a11 a21 · · · an1 a12 a22 · · · an2 · · · · · · · · · · · · [f−1]B = A−1 = AT = a1n a2n · · · ann
4.2PhÐpbiÕn®æitrùcgiao,phÐp biÕn®æi®èixøng 17
Chøngminh. ViÖc chøng minh A−1 = AT t-¬ng ®-¬ng víi viÖc chøng minh
AT A = In (In lµ ma trËn ®¬n vÞ cÊp n).
ThËt vËy c¸c cét cña A lÇn l-ît lµ c¸c cét täa ®é cña c¸c vÐc t¬ f(e1), f(e2),...,f(en) n n f(ei) = aikek, f(ej) = X X ajkek ∀i,j = 1, n. k=1 k=1 Stu r y ªn ra {f(e f1()e
, f(e2),...,f (en)} còng lµ hÖ c¬ së trùc chuÈn cña E i), f (ej )
= a1ia1j + a2ia2j + · · · + anianj. MÆt kh¸c theo nhËn xÐt ë (1 0nÕunÕ iu =i j6= j f(ei), f(ej) = Do vËy ( hay AT A = In. 1 nÕu 0 i = nÕ ju i 6= j
a1ia1j + a2ia2j + · · · + anianj =
Ma trËn vu«ng A cã tÝnh chÊt AT A = In ®-îc gäi lµ matrËn trùc giao. Chi tiÕt
h¬n ng-êi ta th-êng nãi ma trËn trùc giao lµ ma trËn cã tÝnh chÊt (1 nÕu0 i =nÕ ju i 6= j
a1ia1j + a2ia2j + · · · + anianj = hoÆc (1 nÕu0 i =nÕ ju i 6= j
ai1aj1 + ai2aj2 + · · · + ainajn = víi mäi i,j = 1, 2,...,n.
Ta l-u ý tíi nhËn xÐt sau: nÕu f lµ phÐp biÕn ®æi tuyÕn tÝnh trong kh«ng
gian Euclide E vµ f cã c¸c vÐc t¬ riªng e1, e2,...,en lËp thµnh hÖ c¬ së trùc chuÈn
cña E, th× ma trËn A cña f trong c¬ së trùc chuÈn B bÊt k×, theo c«ng thøc (??)
trong ch-¬ng tr-íc, cã d¹ng A = T ΛT T hay Λ = T T AT. 18
Ch-¬ngIV. Kh«nggian Euclidevµ d¹ngtoµn ph-¬ng λ1 0 · · · 0 0 λ2 · · ·
0 lµ ma trËn chÐo, c¸c phÇn tö trªn ®-êng chÐo lµ c¸c trÞ ·· ·· · · · ·· Λ = 0 0 · · · λn
riªng cña f, T lµ ma trËn trùc giao (chuyÓn c¬ së trùc chuÈn B thµnh c¬ së trùc chuÈn {e1, e2,...,en}). VÝ dô 4.2.2
1. Trong vÝ dô 3.4.5 còng nh- vÝ dô 4.2.1 vÒ phÐp quay, ma trËn cña phÐp
quay t©m O, gãc quay ϕ trong c¬ së chÝnh t¾c cña mÆt ph¼ng xOy cos ϕ − sin ϕ cos ϕ sin ϕ A = sin ϕ cos ϕ ⇒ AT = − sin ϕ cos ϕ
Ma trËn cña phÐp quay lµ ma trËn trùc giao, ta dÔ dµng kiÓm tra hÖ thøc cos ϕ − sin ϕ 1 0 01 A−1 = AT hay cos ϕ sin ϕ = − sin ϕ cos ϕ sin ϕ cos ϕ
2. Còng trong vÝ dô 4.2.1, ma trËn cña phÐp lÊy ®èi xøng qua ®-êng ph©n
gi¸c gãc phÇn t- thø nhÊt y = x lµ ma trËn trùc giao 01 10 B = , hiÓn nhiªn B = BT = B−1.
3. Trong kh«ng gian Euclide R3 víi tÝch v« h-íng Euclide x, y = x1y1 + x2y2 + x3y3,
hÖ c¸c vÐc t¬ {a1 = (2, 0, 1), a2 = (1, 1, −2), a3 = (−1, 5, 2)} lµ hÖ c¬ së
trùc giao. ChuÈn ho¸ c¸c vÐc t¬ ®ã, ta ®-îc hÖ c¬ së trùc chuÈn cña R3 1 1 5 2 √ , 0, √ , −2 √ , √ , √ , 2 5 16 −1 30 30 B = √ , 6 √ , √ . KÝ hiÖu b1, b 5 6 30
2, b3 lÇn l-ît lµ c¸c vÐc t¬ trong c¬ së trùc chuÈn B, gäi
E = {e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1)} lµ hÖ c¬ së chÝnh t¾c cña
R3, khi ®ã phÐp biÕn ®æi tuyÕn tÝnh f : R3 → R3
f(e1) = b1, f(e2) = b2, f(e3) = b3
4.2PhÐpbiÕn®æitrùcgiao,phÐp biÕn®æi®èixøng 19
chuyÓn c¬ së trùc chuÈn E vµo c¬ së trùc chuÈn B. Do vËy f lµ phÐp biÕn
®æi trùc giao. Ma trËn cña f trong c¬ së chÝnh t¾c 2 1 √ √ −1 √ 5 6 30 0 1 5 √ √ 6 30 1 2 A = √ −2 √ √ 5 6 30
DÔ dµng kiÓm tra tÝnh chÊt AAT = I −1 T 3 hay A = A cña ma trËn trùc giao A.
§Þnh nghÜa 4.2.2 PhÐp biÕn®æituyÕn tÝnh f trong kh«nggianEuclideE ®-îc
gäilµphÐp biÕn ®æi®èi xøng nÕu f(x), y = x, f(y) víimäi x, y ∈ E
§Þnh lÝ 4.2.3 GäiA = (aij) lµma trËncñaphÐpbiÕn ®æi®èi xøng f trongmét
c¬sëtrùcchuÈn nµo®ã. Khi®ã
AT = A, (nãic¸chkh¸c A lµmatrËn ®èi xøng).
Chøngminh. Gi¶ sö A = (aij) lµ ma trËn cña phÐp biÕn ®æi ®èi xøng f trong c¬
së trùc chuÈn {e1, e2,...,en}. Khi ®ã aij = f(ej), ei vµ aji = ej, f(ei) Do mi fn lhµa pijh=Ðp aji bivÕíni ®
mæäii ®i,èji. xøng: f(ej),ei = ej,f(ei) , suy ra ®iÒu ph¶i chøng
PhÐp biÕn ®æi ®èi xøng cã c¸c tÝnh chÊt ®Æc biÖt ®-îc tr×nh bµy trong c¸c ®Þnh lÝ sau
§Þnh lÝ 4.2.4 NÕuλ vµµ lµhai gi¸trÞriªng kh¸cnhau cña phÐp biÕn®æi®èi
xøngf th×hai vÐct¬ riªngt-¬ng øngvíi λ vµµ trùcgiaonhau.
Chøngminh. Gäi e1 vµ e2 lµ hai vÐc t¬ riªng t-¬ng øng víi λ vµ µ. XÐt
λ e1, e2 = λe1, e2 = f(e1), e2 =
= e1, f(e2) = e1, µe2 = µ e1, e2
Do λ 6= µ suy ra e1, e2 = 0 hay e1⊥ e2. 20
Ch-¬ngIV. Kh«nggianEuclidevµ d¹ngtoµn ph-¬ng
§Þnh lÝ 4.2.5 PhÐp biÕn®æi ®èixøng trong kh«nggian Euclide cã ÝtnhÊt mét vÐc t¬riªng.
Chøngminh. Gäi A lµ ma trËn cña phÐp biÕn ®æi ®èi xøng f trong c¬ së
trùc chuÈn bÊt k× {e1, e2,...,en}. Tr-íc tiªn ta chøng minh ®a thøc ®Æc tr-ng
P (λ) = det(A − λI) cña f chØ cã nghiÖm thùc.
Gäi λ lµ nghiÖm bÊt k× (trong tr-êng sè phøc) cña ®a thøc ®Æc tr-ng. XÐt hÖ
ph-¬ng tr×nh tuyÕn tÝnh thuÇn nhÊt (A − λI)x = 0.
Do λ lµ nghiÖm cña ®a thøc ®Æc tr-ng nªn hÖ cã nghiÖm kh«ng tÇm th-êng x1 x2 . (C¸c nghiÖm x ..
1, x 2,...,xn cã thÓ lµ c¸c sè phøc kh«ng thùc). KÝ hiÖu x = xn x1
x2 . Do c¸c phÇn tö cña A lµ c¸c sè thùc ..
λ lµ sè phøc liªn hîp cña λ vµ x = xn
Ax = λx ⇒ Ax = λx ⇒ Ax = λx. MÆt kh¸c
λxT x = xT (Ax) = (xT (Ax))T = (Ax)Tx =
= xT AT x = xT Ax = λxT x = λxT x.
Suy ra λ = λ do x 6= 0. Nh- vËy mäi trÞ riªng λ cña phÐp biÕn ®æi ®èi xøng lu«n
lµ c¸c sè thùc. øng víi gi¸ trÞ riªng λ ®ã lµ vÐc t¬ riªng ®-îc tÝnh tõ hÖ ph-¬ng tr×nh (A − λI)x = 0.
§Þnh lÝ 4.2.6 PhÐp biÕn®æi ®èixøng trong kh«nggianEuclide n chiÒuE cãn vÐc
t¬riªngvµc¸c vÐct¬riªng ®ãlËpthµnh méthÖc¬sëtrùc chuÈncñaE.
Tõ ®Þnh lÝ nµy ta cã ngay nhËn xÐt
1. NÕu hÖ c¬ së B gåm n vÐc t¬ riªng cña phÐp biÕn ®æi ®èi xøng f, khi ®ã
ma trËn cña f trong c¬ së B cã d¹ng chÐo.