Hệ thống bài tập trắc nghiệm hàm số lượng giác và phương trình lượng giác

Tài liệu gồm 99 trang, được biên soạn bởi thầy giáo Lương Tuấn Đức (Giang Sơn), tuyển chọn hệ thống bài tập trắc nghiệm hàm số lượng giác và phương trình lượng giác trong chương trình Đại số và Giải tích 11 chương 1

45 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

99 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
C
C
H
H
U
U
Y
Y
Ê
Ê
N
N
Đ
Đ
Ề
Ề
HÀ
HÀ
M
M
S
S
Ố
Ố
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
VÀ
VÀ
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LỚP 11 THPT
o
o
T
T
Ậ
Ậ
P
P
XÁ
XÁ
C
C
Đ
Đ
Ị
Ị
N
N
H
H
(
(
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
)
)
o
o
C
C
H
H
U
U
KỲ
KỲ
(
(
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
)
)
o
o
M
M
I
I
N
N
M
M
A
A
X
X
(
(
C
C
Ơ
Ơ
BẢ
BẢ
N
N
)
)
o
o
TÍ
TÍ
N
N
H
H
C
C
H
H
Ẵ
Ẵ
N
N
LẺ
LẺ
VÀ ĐỒ THỊ
VÀ ĐỒ THỊ
(
(
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
)
)
o
o
TÍ
TÍ
N
N
H
H
Đ
Đ
Ơ
Ơ
N
N
Đ
Đ
I
I
Ệ
Ệ
U
U
(
(
C
C
Ơ
Ơ
BẢ
BẢ
N
N
)
)
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
C
C
Ơ
Ơ
BẢ
BẢ
N
N
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
B
B
Ậ
Ậ
C
C
N
N
H
H
Ấ
Ấ
T
T
S
S
I
I
N
N
,
,
C
C
O
O
S
S
(
(
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
)
)
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
C
C
H
H
Ứ
Ứ
A
A
Ẩ
Ẩ
N
N
M
M
Ẫ
Ẫ
U
U
T
T
H
H
Ứ
Ứ
C
C
(
(
C
C
Ơ
Ơ
BẢ
BẢ
N
N
)
)
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
DẠ
DẠ
N
N
G
G
TÍ
TÍ
C
C
H
H
(
(
C
C
Ơ
Ơ
BẢ
BẢ
N
N
)
)
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
ĐỐ
ĐỐ
I
I
X
X
Ứ
Ứ
N
N
G
G
(
(
C
C
Ơ
Ơ
BẢ
BẢ
N
N
)
)
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
ĐỒ
ĐỒ
N
N
G
G
B
B
Ậ
Ậ
C
C
(
(
C
C
Ơ
Ơ
BẢ
BẢ
N
N
)
)
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
Đ
Đ
A
A
T
T
H
H
Ứ
Ứ
C
C
+
+
Ẩ
Ẩ
N
N
PHỤ
PHỤ
(
(
C
C
Ơ
Ơ
B
B
Ả
Ả
N
N
)
)
o
o
HÀ
HÀ
M
M
S
S
Ố
Ố
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
(
(
V
V
Ậ
Ậ
N
N
D
D
Ụ
Ụ
N
N
G
G
C
C
A
A
O
O
)
)
o
o
P
P
H
H
Ư
Ư
Ơ
Ơ
N
N
G
G
TRÌ
TRÌ
N
N
H
H
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
(
(
V
V
Ậ
Ậ
N
N
DỤ
DỤ
N
N
G
G
C
C
A
A
O
O
)
)
o
o
Ô
Ô
N
N
T
T
Ậ
Ậ
P
P
T
T
Ổ
Ổ
N
N
G
G
H
H
Ợ
Ợ
P
P
L
L
ƯỢ
ƯỢ
N
N
G
G
GIÁ
GIÁ
C
C
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
;
;
T
T
E
E
L
L
0
0
3
3
3
3
3
3
2
2
7
7
5
5
3
3
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
1
1
0
0
/
/
2
2
0
0
2
2
0
0
2
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TẬP XÁC ĐỊNH PHẦN 1)
___________________________________________
Câu 1. Tìm tập xác định của hàm số
cos 2
y x
.
A.
B. [0;2] C. (0;2) D.
2;

Câu 2. Tìm điều kiện xác định của hàm số
1
tan
cos 2
y x
.
A.
2
x k
B.
2
2
x k
C.
2
4
x k
D.
Câu 3. Tập xác định của hàm số
tan 2
sin 1
x
y
x
là vòng tròn lượng giác bỏ đi bao nhiêu điểm ?
A. 4 B. 5 C. 2 D. 3
Câu 4. Tồn tại bao nhiêu số nguyên m lớn hơn – 6 để hàm số
3
4cos 3cos
y x x m
xác định với mọi x ?
A. 10 B. 6 C. 4 D. 5
Câu 5. Tìm tập xác định của hàm số
sin cos 3
y x x
.
A.
B. [0;2] C. (0;2) D.
2;

Câu 6. Tìm điều kiện xác định của hàm số
cos 4
sin 1
x
y
x
.
A.
2
x k
B.
2
2
x k
C.
2
4
x k
D.
Câu 7. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số
2
2cos2
y x m
có tập xác định
.
A. 0 B. 1 C. 5 D. 7
Câu 8. Tìm tập xác định của hàm số
2
cos 3
x
y
x
.
A.
B.
3;

C. (0;2) D.
2;

Câu 9. Tìm điều kiện tham số m để hàm số
1
( )
cos
f x
x m
có tập xác định
.
A. m > 0 B.
1
1
m
m
C. – 1 < m < 1 D. 0 < m < 1
Câu 10. Tìm điều kiện tham số m để hàm số
1
sin
y
x m
có tập xác định
.
A.
1
m
B.
1
1
m
m
C. 0 < m < 1 D.
1
m
Câu 11. Hàm số nào sau đây có tập xác định
?
A.
cos 1
sin 4
x
y
x
B.
1
tan
cos 4
y x
C.
sin 1
y x
D.
2cos 1
y x
Câu 12. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm
1
2
sin cos
y
x x
không xác định ?
A. 3 B. 2 C. 4 D. 1
Câu 13. Điều kiện xác định của hàm số
tan(2 )
4
y x
là
A.
4 2
k
x
B.
3
8 2
k
x
C.
2
x k
D.
2
2
x k
3
Câu 14. Hàm số nào sau đây có điều kiện xác định
2
x k
?
A.
2
1 1
cos 4 sin
y
x x
B.
cos 1
sin 4
x
y
x
C.
tan 3cot
y x x
D.
1
cos 1
y
x
Câu 15. Tồn tại bao nhiêu số nguyên x < 10 để hàm số
1
sin( )
x
y
x
xác định ?
A. 7 B. 4 C. 0 D. 8
Câu 16. Cho các hàm số
2
sin 1
; sin 4; ; cos 1
3 cos tan 1
x
y y x y y x
x x
. Có bao nhiêu hàm số
có tập xác định
?
A. 4 B. 1 C. 3 D. 2
Câu 17. Tồn tại bao nhiêu số nguyên
10;10
m
để hàm số
1
2cos2
y
x m
xác định với mọi giá trị x ?
A. 4 B. 14 C. 12 D. 10
Câu 18. Có bao nhiêu số nguyên
10;10
m
để hàm số
sin cos 1
y x x m
xác định với mọi giá trị x ?
A. 4 B. 14 C. 12 D. 10
Câu 19. Tồn tại bao nhiêu góc
0;2
x
để hàm số
tan(2 )
4
1 sin
8
x
y
x
không xác định ?
A. 4 B. 5 C. 6 D. 3
Câu 20. Tồn tại bao nhiêu góc
0;2
x
để hàm số
2 2
1 1
cos sin
4 cos2
y
x x
x
không xác định ?
A. 3 B. 2 C. 1 D. 4
Câu 21. Tồn tại bao nhiêu số nguyên
10;10
m
để hàm số
sin cos
y x x m
có tập xác định
?
A. 7 B. 11 C. 13 D. 12
Câu 22. Tồn tại bao nhiêu góc
0;2
x
để hàm số
2
1
9 4cos2
tan 1
y x
x
không xác định ?
A. 3 B. 4 C. 5 D. 6
Câu 23. Có bao nhiêu số nguyên
10;10
m
để hàm số 2sin3 3cos3
y x x m
có tập xác định
A. 7 B. 6 C. 3 D. 13
Câu 24. Tồn tại bao nhiêu góc
0;2
x
để hàm số
3
2 1
cos cos3 sin 9
y
x x x
không xác định ?
A. 7 B. 4 C. 5 D. 8
Câu 25. Tồn tại bao nhiêu số nguyên
10;10
m
để hàm số
1
3sin 4cos
y
x x m
có tập xác định
?
A. 7 B. 4 C. 3 D. 11
Câu 26. Tồn tại bao nhiêu góc
0;2
x
để hàm số
1
8 sin
1 cos2
y x
x
không xác định ?
A. 3 B. 4 C. 5 D. 6
Câu 27. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số
4sin3
y x m
có tập xác định
.
A. 6 B. 8 C. 5 D. 7
_________________________________
4
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TẬP XÁC ĐỊNH PHẦN 2)
___________________________________________
Câu 1. Tìm tập xác định của hàm số
1
cos 3
cos2 5
y x
x
.
A.
B. [0;2] C. (0;2) D.
2;

Câu 2. Cho các hàm số
2
2
1 1
sin cos 1; ; cos 1;
1 sin cos
3 3 cos2
y x x x x y y x y
x x
x x
.
Có bao nhiêu hàm số có tập xác định
A. 3 B. 2 C. 1 D. 4
Câu 3. Tồn tại bao nhiêu số nguyên dương m để hàm số
cos6 cos3 3
y x x m
xác định với mọi x.
A. 3 B. 1 C. 2 D. 4
Câu 4. Tồn tại bao nhiêu số nguyên m để hàm số cos2
y x m
không có tập xác định
.
A. 3 B. 2 C. 1 D. 4
Câu 5. Tìm điều kiện xác định của hàm số
2
1
2tan
cos sin 3
y x
x x
.
A.
2
x k
B.
2
2
x k
C.
2
4
x k
D.
Câu 6. Tìm tập xác định của hàm số
2sin cos 5
y x x
.
A.
B. [0;2] C. (0;2) D.
2;

Câu 7. Tìm điều kiện xác định của hàm số
4 sin 2
sin 1
x
y
x
.
A.
2
x k
B.
2
2
x k
C.
2
4
x k
D.
Câu 8. Cho các hàm số
2
3
1 1
sin 1; ; cos ; ; cot( 2)
5 cos2
1 sin
y x x y y x y y x
x x
x
.
Có bao nhiêu hàm số có tập xác định
A. 3 B. 2 C. 1 D. 4
Câu 9. Cho các hàm số
2
2
1 1
cos 3; ; cos 2;
1 cos
3 sin
y x x x y y x y
x
x x
.
Có bao nhiêu hàm số có tập xác định
A. 3 B. 2 C. 1 D. 4
Câu 10. Tìm tập xác định của hàm số
4 9
sin 3 3
x
y
x
.
A.
B.
3;

C. (0;2) D.
2;

Câu 11. Tìm điều kiện xác định của hàm số
2
1
cos 5
2tan tan 3
y x
x x
.
A.
2
x k
B.
2
2
x k
C.
2
4
x k
D.
Câu 12. Tìm điều kiện tham số m để hàm số
3
1
( )
4cos 3cos
f x
x x m
có tập xác định
.
5
A. m > 0 B.
1
1
m
m
C. – 1 < m < 1 D. 0 < m < 1
Câu 13. Tìm điều kiện tham số m để hàm số
1
2sin cos
y
x x m
có tập xác định
.
A.
1
m
B.
1
1
m
m
C. 0 < m < 1 D.
1
m
Câu 14. Hàm số nào sau đây có tập xác định
?
A.
4cos 1
4sin 2 9
x
y
B.
1
tan
cos 4
y x
C.
sin 1
y x
D.
2cos 1
y x
Câu 15. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm số
2 2
1
sin cos
y
x x
không xác định ?
A. 3 B. 2 C. 4 D. 1
Câu 16. Điều kiện xác định của hàm số
2
3tan(2 ) 4 1
4
y x x
là
A.
4 2
k
x
B.
3
8 2
k
x
C.
2
x k
D.
2
2
x k
Câu 17. Tìm tập xác định của hàm số
tan 2
2cos 7
x
y
x
.
A.
2
x k
B.
2
2
x k
C.
4 2
x k
D.
Câu 18. Tìm điều kiện xác định của hàm số
2
2
2
5 sin 2
cot 1
y x x x
x
.
A.
2
x k
B.
2
2
x k
C.
2
4
x k
D.
x k
Câu 19. Tồn tại bao nhiêu số nguyên x để hàm số
2 2
4
cos
x
y x
xác định ?
A. 13 B. 12 C. 14 D. 10
Câu 20. Tồn tại bao nhiêu số nguyên x để hàm số
2
1
cos 9
10 cos( 2)
y x
x
?
A. 6 B. 7 C. 2 D. 5
Câu 21. Tìm điều kiện xác định của hàm số
1
sin 2 1
y
x
.
A.
2
x k
B.
2
2
x k
C.
4
x k
D.
Câu 22. Tồn tại bao nhiêu số nguyên
20;20
m
để hàm số sau không có tập xác định
2 2
1 1
cos cos 2 cos cos
y
x x x x m
.
A. 34 B. 14 C. 27 D. 36
Câu 23. Tồn tại bao nhiêu số nguyên
20;20
m
để hàm số sau không có tập xác định
3
1
6sin 8sin
y
x x m
.
A. 34 B. 19 C. 24 D. 37
_________________________________
6
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – CHU KỲ PHẦN 1)
___________________________________________
Câu 1. Tìm chu kỳ của hàm số
sin
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 2. Tìm chu kỳ tuần hoàn của hàm số
cos2
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 3. Tìm chu kỳ của hàm số
2sin 2 cos2
y x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 4. Tìm chu kỳ tuần hoàn của hàm số
tan( )
3
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 5. Tìm chu kỳ của hàm số
4
sin 2 1993
9
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 6. Tìm chu kỳ tuần hoàn của hàm số
cot(2 ) 5
3
y x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 7. Tìm chu kỳ của hàm số
3
3sin 4sin 5
y x x
.
A.
2
T
B.
T
C.
4
T
D.
2
3
T
Câu 8. Tìm chu kỳ tuần hoàn của hàm số
3
8cos 6cos 4
y x x
.
A.
2
T
B.
T
C.
2
3
T
D.
8
T
Câu 9. Tìm chu kỳ của hàm số
3
4cos 2 3cos2 4tan 5
y x x x
.
A.
2
T
B.
T
C.
4
T
D.
3
T
Câu 10. Tìm chu kỳ tuần hoàn của hàm số
2
4sin 2 cos2 2cos 2
y x x x
.
A.
2
T
B.
T
C.
2
T
D.
8
T
Câu 11. Cho các hàm số
2
sin ; cos2 ; sin ; 2cos 3
3
y x y x y x y x
. Có bao nhiêu hàm số có chu
kỳ là
2
T
A. 3 B. 1 C. 2 D. 4
Câu 12. Tính tổng các giá trị m để hàm số sin
3
y mx
nhận chu kỳ
2
T
.
A. 3 B. 0 C. 1 D. 2
Câu 13. Tìm chu kỳ tuần hoàn của hàm số
4sin 9cos 1993
2 2
x x
y .
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 14. Tìm chu kỳ của hàm số
2 2
4sin 9cos
2 2
x x
y .
7
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 15. Tìm chu kỳ tuần hoàn của hàm số
2 2
cos 2 sin 2 6sin(4 5)
y x x x
A.
2
T
B.
T
C.
2
T
D.
8
T
Câu 16. Tìm chu kỳ của hàm số
cos9 cos4 sin 9 sin 4 1993
y x x x x
.
A.
2
T
B.
2
13
T
C.
13
T
D.
2
T
Câu 17. Tìm chu kỳ của hàm số
3
2
3tan tan
1 3tan
x x
y
x
.
A.
2
T
B.
T
C.
3
T
D.
8
T
Câu 18. Tìm chu kỳ của hàm số
4cot 9cot 1993cot
2 3
x x
y x .
A.
2
T
B.
6
T
C.
4
T
D.
3
T
Câu 19. Tồn tại bao nhiêu số nguyên dương n < 4 để hàm số
2 2
2sin 3cos ( )
y x nx
có chu kỳ
T
?
A. 4 B. 2 C. 3 D. 1
Câu 20. Tồn tại bao nhiêu số nguyên dương n < 10 để hàm số
4sin 2 9cos
2
nx
y x
có
T
?
A. 4 B. 2 C. 3 D. 1
Câu 21. Tìm m để hàm số
2
cos(2 1) sin 3
x
y x
m
có chu kỳ
3
T
.
A. m = 2 B. m = 1 C. m = 3 D. m = 4
Câu 22. Tồn tại bao nhiêu cặp số nguyên dương (m;n) để hàm số
26tan 4cot 2019
x x
y
m n
có
12
T
?
A. 16 B. 15 C. 10 D. 12
Câu 23. Cho các hàm số
2
4
cot ; tan ; sin ; sin cos
2 2 9
x x
y x y y y x x
. Tồn tại bao nhiêu hàm số
thỏa mãn điều kiện
( 2 ) ( )
f x k f x
?
A. 4 B. 2 C. 3 D. 1
Câu 24. Tìm chu kỳ của hàm số
tan 2 cot
2
x
y x
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 25. Tìm chu kỳ của hàm số
sin cos 4sin cos 9
y x x x x
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 26. Tìm chu kỳ của hàm số
2
3tan3 4cot 5sin
2
x
y x x
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 27. Tìm chu kỳ của hàm số
cot tan
y x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
_________________________________
8
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – CHU KỲ PHẦN 2)
___________________________________________
Câu 1. Tìm chu kỳ tuần hoàn của hàm số
2 2
6
2 2
sin tan
.cot tan
cos cot
x x
y x x
x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 2. Tìm chu kỳ của hàm số sin cos
3 6
y x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 3. Tìm chu kỳ tuần hoàn của hàm số
cos3 cos5 cos
y x x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 4. Tìm chu kỳ của hàm số
cot tan
1 tan .tan 2
x x
y
x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 5. Tìm chu kỳ tuần hoàn của hàm số
cot tan 2tan 2 4tan 4
y x x x x
.
A.
8
T
B.
T
C.
4
T
D.
2
T
Câu 6. Tìm chu kỳ của hàm số
1 cos2 sin 2
1 cos 2 sin 2
x x
y
x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 7. Tìm chu kỳ của hàm số
2 2 2 2
cos cos 60 cos 60 4sin
2
x
y x x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 8. Tìm chu kỳ của hàm số
sin sin3 sin 5
cos cos3 cos5
a a a
y
a a a
.
A.
2
5
T
B.
T
C.
3
T
D.
2
T
Câu 9. Tìm chu kỳ của hàm số
4sin sin sin sin
3 3
y x x x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 10. Tìm chu kỳ của hàm số
3
3sin3 4sin 3 cos 4
y x x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 11. Tìm chu kỳ của hàm số
2
sin 4
2cos cos3 cos5
x
y
x x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 12. Tìm chu kỳ của hàm số
4 4
sin cos 4
y x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 13. Tìm chu kỳ của hàm số
6 6
sin cos
y x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 14. Hàm số nào sau đây có chu kỳ khác
?
9
A. cos 2
4
y x
B.
tan 4
2
x
y
C.
sin cos cos2
y x x x
D.
2
sin
y x
Câu 15. Tìm chu kỳ của hàm số
sin
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 16. Hàm số nào sau đây có chu kỳ khác
2
A.
4cos
4
y x
B.
tan 4
2
x
y
C.
2
sin cos cos
2 2 2
x x x
y D.
2
sin
y x
Câu 17. Hàm số nào sau đây có chu kỳ tuần hoàn khác nhau
A.
cos ; cot
2
x
y x y B.
sin ; tan 2
y x y x
C.
cot 2 ; tan 2
y x y x
D.
2
sin cos cos ; tan
2 2 2 2
x x x x
y y
Câu 18. Tìm chu kỳ tuần hoàn của hàm số
3
sin 2cos
2 2
x x
y .
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 19. Hàm số nào sau đây thỏa mãn
( 2 ) ( )
f x k f x
?
A.
tan 4
2
x
y
B.
2 2
2sin 3cos
y x x
C.
cos cos3 sin
2
x
y x x D.
cos3 2
y x
Câu 20. Tìm chu kỳ của hàm số
2
2tan
6cot 2 3
1 tan
x
y x
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 21. Tìm chu kỳ tuần hoàn của hàm số
sin cos cos2 cos4
y x x x x
.
A.
2
T
B.
2
T
C.
4
T
D.
4
T
Câu 22. Tìm chu kỳ tuần hoàn của hàm số
(cos5 cos sin5 sin )cos4
y x x x x x
.
A.
2
T
B.
2
T
C.
4
T
D.
4
T
Câu 23. Tìm chu kỳ tuần hoàn của hàm số
3
1
(3sin 4sin )cos3 sin 4
y
x x x x
.
A.
T
B.
2
T
C.
4
T
D.
4
T
Câu 24. Tìm chu kỳ tuần hoàn của hàm số
sin cos cos 2 cos4 5
y x x x x
.
A.
2
T
B.
2
T
C.
4
T
D.
4
T
Câu 25. Tìm chu kỳ tuần hoàn của hàm số cos tan
3 6
y x x
.
A.
2
T
B.
2
T
C.
4
T
D.
4
T
Câu 26. Tồn tại bao nhiêu số nguyên dương n < 10 để hàm số
2cos 3tan 8
3 6
y x nx
có chu
kỳ tuần hoàn
2
T
?
A. 7 B. 9 C. 8 D. 5
_________________________________
10
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – MIN, MAX PHẦN 1)
___________________________________________
Câu 1. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos 3
y x
.
A. 4 B. 2 C. 6 D. 7
Câu 2. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos(3 ) 2
4
y x
.
A. 3 B. 4 C. 2 D. 5
Câu 3. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin 4 9 1993
y x
.
A. 3986 B. 2020 C. 1993 D. 3020
Câu 4. Tính tổng giá trị tham số m để tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau bằng 4
2
cos(2 ) 3 2
13
y x m m
.
A. 1 B. 2 C. 3 D. 4
Câu 5. Tìm giá trị nhỏ nhất của hàm số
2
tan 2 tan 5
y x x
.
A. 4 B. 7 C. 5 D. 3
Câu 6. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos sin
y x x
.
A. 4 B. 2 C. 0 D. 1
Câu 7. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos2 3sin 2
y x x
.
A. – 12 B. 10 C. – 10 D. 8
Câu 8. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
cos cos 4
y x x
.
A. 10 B. 9,75 C. 8,875 D. 7,75
Câu 9. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos2 cos 4
y x x
.
A. 9,25 B. 7,125 C. 8,5 D. 8,125
Câu 10. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 cos 4
y x
.
A. 15 B. 11 C. 10 D. 12
Câu 11. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
cos 4; 0;
3
y x x
.
A. 8,5 B. 9 C. 6 D. 7,5
Câu 12. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
4cos 3 3cos3 2
y x x
.
A. 4 B. 5 C. 4,5 D. 3
Câu 13. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1 cos4 2
y x
.
A. 4 B. 6 C.
4 2 2
D.
3 2
Câu 14. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
4cos 3cos 2sin 3 1
y x x x
.
A. – 4 B. – 2 C. – 3 D. 4
Câu 15. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin 2
3
y x
với
0;
3
x
.
A. – 0,5 B. – 1 C. 1 D. 0,25
Câu 16. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2cos 4sin 2 5
y x x
.
A. 6 B. 19 C. 20 D. – 7
Câu 17. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2 2
cos 3cos 5sin 5
y x x x
.
11
A.
65
8
B.
47
28
C.
215
28
D.
11
28
Câu 18. Tìm giá trị nhỏ nhất của hàm số
2
tan (cot 2) tan
y x x x
.
A. 4 B. – 1 C. 0 D. 2
Câu 19. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( ) cos5 cos sin5 sin 4sin3
f x x x x x x
.
A. – 15 B. – 8 C. 10 D. – 6
Câu 20. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2 2
4 5sin cos
y x x
.
A. 5 B. 11 C. 3 D. 8
Câu 21. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 8 sin cos
y x x
.
A. 4 B. 1 C. 3 D. – 2
Câu 22. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
sin sin
3
y x x
.
A. 2 B. – 1 C. 1 D. – 3
Câu 23. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số sin cos
3 3
y x x
.
A.
3 1
B.
3 1
C. – 2 D. 1
Câu 24. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
8cos 6cos 3
y x x
.
A. 3 B.
5
C.
2 3
D.
6
Câu 25. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2sin cos 3cos2 4
y x x x
.
A. 10 B. 8 C. 12 D. – 6
Câu 26. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4 4
3(cos sin ) sin 2 1
y x x x
.
A. – 3 B. – 2 C. 1 D. 4
Câu 27. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
3 2cos3 (3sin 4sin )
y x x x
.
A. 6 B. 8 C. 2 D. – 4
Câu 28. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4
2 sin
y
x
.
A. 4 B. 3 C.
16
3
D.
20
3
Câu 29. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
8
3 cos
y
x
.
A.
16
3
B. 6 C.
32
3
D. 8
Câu 30. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
3 1 cos
y
x
.
A. 2 B.
9 3 2
7
C.
3 2
D.
6 2
Câu 31. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
1
2 sin 3
y
x
.
A. 2 B.
2
2
C.
2
D.
3
2
_________________________________
12
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – MIN, MAX PHẦN 2)
___________________________________________
Câu 1. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
cos 2sin 2
y x x
.
A. 3 B. 1 C. 2 D. 1,5
Câu 2. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos2 3cos 1
y x x
trên miền
2
0;
3
.
A. – 9 B. 3 C. – 1 D. 6
Câu 3. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2(sin cos ) sin 2 3
y x x x
.
A. 4 B.
5 2 2
C. 3 D.
3 4 2
Câu 4. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin cos sin 2 1
y x x x
.
A. 2 B.
9 2
4
C. – 1 D.
5 2
4
Câu 5. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3(sin cos ) sin 2 3
y x x x
.
A. – 6 B. – 2 C. – 14 D . 3
Câu 6. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
(3 sin 2 ) 3 2sin cos
y x x x
trên
0;
2
.
A. 7 B. 8 C. 6 D. 10
Câu 7. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
cos 2 cos
3 3
y x x
trên
0;
.
A. – 1,25 B. – 1,125 C. – 2,25 D. – 2
Câu 8. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
6 6
sin cos
y x x
trên
;
2 2
.
A. 3 B. 1 C. 2 D. 4
Câu 9. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4 2
sin 2cos 1
y x x
.
A. 2 B. 1 C. 2 D. 0
Câu 10. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4 4
sin cos 4
y x x
.
A. 9,5 B. 6 C. 10 D. 8
Câu 11. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
6 6
sin cos
y x x
.
A. 1,25 B. 2 C. 1,5 D. 2,25
Câu 12. Gọi M, m tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2cos 1
cos 2
x
y
. Khi đó
A. 9M = m B. 9M + m = 0 C. M + m = 0 D. 2M + m = 0
Câu 13. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
12
7 4sin
y
x
trên miền
5
;
6 6
.
A. 4 B. 3 C.
16
3
D.
20
3
Câu 14. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2 2
3sin 4cos2 5cos
y x x x
.
A. 3 B. 8 C. 2 D. 10
Câu 15. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
(2sin cos )(3sin cos )
y x x x x
.
A. 4 B. 11,5 C. 12,5 D. 8,5
Câu 16. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
1 (sin 2 cos2 )
y x x
.
A. – 7 B. – 5 C. 5 D. – 2
13
Câu 17. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
5sin 12cos 10
y x x
.
A. 6 B. 23 C. 14 D. 11
Câu 18. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2sin 2 sin 1
4
y x x
.
A. 3 B. – 2 C. 1 D. 2
Câu 19. Hàm số
cos 2sin 3
2cos sin 4
x x
y
x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào đúng ?
A. 2M + N + 6 = 0 B. 4M = N C. M + 7N > 0 D. 2M – N < 2
Câu 20. Biểu thức
sin cos
2sin cos 3
x x
S
x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 2 B. 1 C. 3 D. 0
Câu 21. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2 cos2 cos 2 3
3
y x x
.
A. 7 B. 8 C. 6 D. 4
Câu 22. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2sin 2 (sin 2 4cos2 )
y x x x
.
A. – 16 B. – 7 C. 10 D. – 12
Câu 23. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4 4
sin cos
y x x
trên
0;
6
.
A.
13
8
B. 2 C.
11
8
D.
15
8
Câu 24. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2sin cos2
y x x
trên
0;
3
.
A. 3 B. 1 C. 2 D. 1,5
Câu 25. Tính giá trị lớn nhất của hàm số cot
4
y x
trên
3
;
4 4
.
A. 0 B. 2 C. 1 D. – 2
Câu 26. Ký hiệu M và N tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 cos
sin cos 2
x
y
x x
. Tính
giá trị của biểu thức M.N.
A. – 1 B.
2
C. 1,5 D. 2
Câu 27. Tính M + N với M, N tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin 1
cos sin 2
x
y
x x
.
A. 0 B. 1 C. 2 D. – 1
Câu 28. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
5
3sin 2 2cos 3; ;
6 4
y x x x
.
A. 6 B. 8 C. 4 D. 1
Câu 29. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( ) sin 2 cos2 3; ;
4 4
f x x x x
.
A. 5 B.
5 2
C.
4 2 2
D.
3 2 1
Câu 30. Hàm số
2cos 3sin 5
2sin 3cos 5
x x
y
x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính Q = M.N.
A. Q = 1 B. Q = 2 C. Q = 5 D. Q = 10
_________________________________
14
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH CHẴN, LẺ VÀ ĐỒ THỊ PHẦN 1)
___________________________________________
Câu 1. Hàm số nào sau đây là hàm số lẻ
A.
cos 1
sin 4
x
y
x
B.
1
tan
cos 4
y x
C.
sin
y x
D.
2cos 1
y x
Câu 2. Hàm số nào sau đây là hàm số chẵn
A.
cos(2 3)
y x
B.
2
sin
y x
C.
cos 2 1
y x
D.
sin 6
y x
Câu 3. Cho các hàm số
2
cos( 5); cos6 ; sin 2 ; cos3 cos
y x y x y x y x x
. Số lượng hàm số chẵn là
A. 3 B. 2 C. 4 D. 1
Câu 4. Hàm số
tan 4
y x
có đặc điểm
A. Đồ thị hàm số nằm phía trên trục hoành B. Hàm số lẻ
C. Hàm số chẵn D. Hàm số không chẵn, không lẻ
Câu 5. Có bao nhiêu số nguyên
20;20
m
để hàm số
cos cos3
y x x m
là hàm số chẵn ?
A. 37 B. 27 C. 39 D. 10
Câu 6. Đồ thị hàm số nào sau đây có tâm đối xứng là gốc tọa độ ?
A.
cos(2 3)
y x
B.
sin 6
y x
C.
sin 6 sin
y x x
D.
sin3
y x
Câu 7. Có bao nhiêu số nguyên
20;20
m
để hàm số
cot 5
y x m
là hàm số lẻ ?
A. 37 B. 1 C. 39 D. 10
Câu 8. Đồ thị hàm số nào sau đây có trục đối xứng là trục tung ?
A.
cos(3 1)
y x
B.
sin5
y x
C.
2
sin 5
y x
D.
2
cos 5 2
y x x
Câu 9. Đồ thị hàm số
sin 3
y x
có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành D. Luôn nằm bên trái trục tung
Câu 10. Tồn tại bao nhiêu hàm số mà đồ thị có tâm đối xứng là gốc tọa độ trong các hàm số sau
7
9
tan 2 .sin5 ; tan cot ; sin 2
2
y x x y x x y x
.
A. 0 B. 1 C. 2 D. 3
Câu 11. Cho các hàm số
2 2 2 2
sin 9 ; sin 5 cos9 ; sin cos(4 9) 1993; cos
y x y x x y x x y x
.
Có bao nhiêu hàm số mà đồ thị nhận trục tung là trục đối xứng ?
A. 3 B. 2 C. 1 D. 0
Câu 12. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx B. y = sinx
C. y = 1 + sinx D. y = cosx + 2
Câu 13. Tịnh tiến đồ thị
sin
y x
sang phải
2
đơn vị ta thu được đồ thị hàm số
( )
f x
. Khi đó
(491993)
f gần
nhất giá trị nào sau đây
A. – 0,56 B. – 0,73 C. 0,76 D. – 0,14
Câu 14. Tịnh tiến đồ thị hàm số
cos cos 2
y x x
lên phía trên tối thiểu bao nhiêu đơn vị để đồ thị thu được
15
không nằm phía dưới trục hoành ?
A. 1 B. 1,25 C. 1,75 D. 0,5
Câu 15. Cho các hàm số
3 2 2
cos3 cos ; cos cos ; sin ; sin 4 sin
y x x y x x y x y x x
. Tồn tại bao
nhiêu hàm số chẵn trong các hàm số đã cho ?
A. 3 B. 4 C. 2 D. 1
Câu 16. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx B. y = sinx
C. y = 1 + 2sinx D. y = 2cosx + 1
Câu 17. Đồ thị hàm số
cos2 5
y x
có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành D. Luôn nằm bên trái trục tung
Câu 18. Tịnh tiến đồ thị hàm số
3
( ) 3sin 4sin
g x x x
sang trái
2
đơn vị ta thu được đồ thị hàm số
( )
y f x
.
Hai đồ thị hàm số
( ), ( )
f x g x
cắt nhau tại bao nhiêu điểm có hoành độ thuộc khoảng
0;2
?
A. 5 B. 6 C. 3 D. 1
Câu 19. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx B. y = sinx
C. y = 1 + sinx D. y = cosx
Câu 20. Đồ thị hàm số
3
4cos 3cos 7
y x x
có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành D. Luôn nằm bên trái trục tung
Câu 21. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx
B. y = sinx + 2
C. y = 1 + sinx
D. y = cosx + 1
Câu 22. Tồn tại bao nhiêu số nguyên
20;20
m
để hàm số
cos2 1
sin( )
cos2 1
x
y mx
là hàm số chẵn ?
A. 10 B. 39 C. 20 D. 24
Câu 23. Tịnh tiến đồ thị hàm số
3
8cos 6cos 3
y x x
xuống dưới tối thiểu bao nhiêu đơn vị để đồ thị thu
được không nằm phía trên trục hoành ?
A. 1 B. 5 C. 4,75 D. 2,5
Câu 24. Hàm số
sin(3 1) 2
y x
có đặc điểm
A. Đồ thị hàm số nằm phía dưới trục hoành B. Hàm số chẵn
C. Hàm số lẻ D. Hàm số không chẵn, không lẻ
_________________________________
16
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH CHẴN, LẺ VÀ ĐỒ THỊ PHẦN 2)
___________________________________________
Câu 1. Hàm số
3
tan
y x x x
có đặc điểm
A. Hàm số chẵn B. Hàm số lẻ
C. Hàm số không chẵn, không lẻ D. Đồ thị hàm số nằm phía trên trục hoành
Câu 2. Có bao nhiêu điểm M (x;y) nằm trên đồ thị hàm số
sin
y x
thỏa mãn
4 9; cos
x y x
?
A. 4 B. 1 C. 3 D. 2
Câu 3. Cho các hàm số
1
sin sin 4 ; tan 4 ; sin ; cos 1; cos4
y x x y x x y y x y x
x
.
Biết rằng có a hàm số chẵn và b hàm số lẻ, tính 3a + 2b.
A. 5 B. 8 C. 11 D. 12
Câu 4. Tịnh tiến đồ thị
sin 2
y x
lên trên 2 đơn vị, sau đó sang phải
2
thu được đồ thị hàm số
( )
y f x
. Tính
tổng các giá trị m để đường thẳng y = m tiếp xúc với đồ thị
( )
y f x
.
A. 4 B. 2 C. 6 D. 7
Câu 5. Đồ thị hàm số nào sau đây luôn nằm phía dưới trục hoành
A.
cos3
y x
B.
sin 2 2
y x
C.
sin 2
3
y x
D.
cos3 cos6
y x x
Câu 6. Đồ thị hàm số nào sau đây tiếp xúc trục hoành ?
A.
cos3
y x
B.
sin 2 2
y x
C.
sin 6 1
y x
D.
tan 3
y x
Câu 7. Tồn tại bao nhiêu số nguyên dương m < 10 để hàm số
sin sin3 cos cos5 ( 1)
y x x m x x m x
là
hàm số chẵn ?
A. 4 B. 1 C. 2 D. 3
Câu 8. Hình vẽ bên là đồ thị hàm số nào ?
A.
2
cos 1
y x
B. y = 2 - sinx
C. y = 1 + cosx D. y = 2cosx
Câu 9. Có bao nhiêu hàm số có đồ thị nhận gốc tọa độ O làm tâm đối xứng:
2
1
cot ; sin 3 cos 2 ; sin ; 1993sin 4 9
1
y x x y x x y y x
.
A. 3 B. 1 C. 2 D. 4
Câu 10. Có bao nhiêu điểm M (x;y) có hoành độ trong khoảng
0;2
và cùng nằm trên hai đồ thị
2
2
cos
sin
y x
y x
A. 5 B. 4 C. 3 D. 2
Câu 11. Tịnh tiến đồ thị hàm số
2 sin
y x
sang phải
4
đơn vị ta thu được đồ thị (C). Khi đó (C) cắt đồ thị
hàm số
3cos
y x
tại bao nhiêu điểm có hoành độ thuộc
0;2
?
A. 3 B. 1 C. 2 D. 4
Câu 12. Tìm giá trị tham số m để đồ thị hàm số
cos2 cos3
y x x
tiếp xúc với đường thẳng y = m.
A. m = 5 B. m = 2 C. m = 1,5 D. m = 1
Câu 13. Hàm số nào sau đây là hàm số chẵn
17
A.
2
tan
tan 1
x
y
x
B.
3
cos .sin
y x x
C.
sin cos2
y x x
D.
2019cos 2020
y x
Câu 14. Tồn tại bao nhiêu đường cong có tâm đối xứng là gốc tọa độ
3
cot 4
cos .sin 4 ; ; cos 2020sin sin 2
cot 1 9
x
y x x y y x x x
.
A. 0 B. 1 C. 2 D. 3
Câu 15. Tồn tại bao nhiêu số nguyên m
10;10
để hàm số sau có đồ thị nhận trục Oy là trục đối xứng
3 2
cos cos4 ( 4)sin .sin 9
y x x m x x m
A. 0 B. 2 C. 3 D. 1
Câu 16. Đồ thị hàm số nào sau đây tiếp xúc trục hoành ?
A.
cos3
y x
B.
2
sin
y x
C.
3sin 6 1
y x
D.
tan 3
y x
Câu 17. Biết rằng đồ thị hàm số
2
sin 2
y x
tiếp xúc với trục hoành tại vô số điểm, trong đó có bao nhiêu điểm
có hoành độ thuộc
2;2
?
A. 4 B. 2 C. 3 D. 1
Câu 18. Tính tổng các giá trị m để đường thẳng y = m tiếp xúc đường cong
3sin 4cos
y x x
.
A. 5 B. 1 C. 0 D. 2
Câu 19. Hàm số
cos 4
6 sin
x
y
x
có đặc điểm
A. Hàm chẵn B. Hàm lẻ
C. Hàm không chẵn, không lẻ D. Đồ thị hàm số tiếp xúc trục hoành.
Câu 20. Tịnh tiến đồ thị
2 sin
y x
sang trái
4
đơn vị ta được đồ thị hàm số
A.
sin cos
y x x
B. 2 sin
4
y x
C.
sin
y x
D.
cos
y x
Câu 21. Đồ thị hàm số
tan 2
y x
cắt đường thẳng
2
y
tại bao nhiêu điểm có hoành độ thuộc
0;2
?
A. 5 B. 4 C. 6 D. 3
Câu 22. Tính tổng các giá trị m để đồ thị hàm số
cos2 sin
y x x
tiếp xúc với đường thẳng
y m
.
A. 1 B. 1,5 C.
7
8
D.
11
3
Câu 23. Cho
3
( ) 3 2
f x x x
. Tìm số nghiệm của phương trình
(tan 2 ) 0
f x
trong khoảng
0;2
.
A. 3 B. 6 C. 5 D. 8
Câu 24. Đồ thị hàm số nào sau đây nằm hoàn toàn phía trên đường thẳng y = 2 ?
A.
sin
2 cos
x
y
x
B.
3
4cos 3cos 3,5
y x x
C.
2cos2 cos
y x x
D.
sin3 sin 6 2
y x x
Câu 25. Tìm m để đồ thị hàm số
sin 4cos
y m x x
tiếp xúc đường thẳng y = 5.
A. m = 2 B. m = 3 C. m = 4 D. m = 1
Câu 26. Tồn tại bao nhiêu số thực m để đồ thị hàm số
3
( 3 2)sin 4cos
y m m x x
tiếp xúc với đường
thẳng đi qua hai điểm A (1;5), B (2;5) ?
A. 5 B. 4 C. 2 D. 1
_________________________________
18
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH ĐƠN ĐIỆU PHẦN 1)
___________________________________________
Câu 1. Hàm số
sin
y x
đồng biến trên khoảng nào sau đây
A.
;
2 2
B.
2
;
2 3
C.
4
;
2 3
D.
;
3
Câu 2. Hàm số
cos
y x
đồng biến trên khoảng nào sau đây
A.
;
2 2
B.
;0
C.
4
;
2 3
D.
;
3
Câu 3. Hàm số
cos2
y x
tăng trên khoảng
A.
;0
2
B.
;0
C.
4
;
2 3
D.
;
3
Câu 4. Trên miền
0;
2
, hàm số
sin cos
y x x
có đặc điểm
A. Đồng biến B. Nghịch biến
C. Không đổi D. Vừa đồng biến, vừa nghịch biến
Câu 5. Trên khoảng
0;2
, hàm số
sin 2
y x
có khoảng nghịch biến đầy đủ
;
a b
. Tính a + b
A.
B. 0,5
C. 0,75
D. 1,25
Câu 6. Trên khoảng
0;
, hàm số
cos2
y x
có khoảng nghịch biến đầy đủ
;
a b
. Tính a + b
A.
B. 0,5
C. 0,75
D. 1,25
Câu 7. Hàm số
2 2
sin 2cos
y x x
có khoảng đồng biến đầy đủ
2 ; 2
a k b k
. Tính a + b.
A.
B. 0,5
C. 0,75
D. 1,25
Câu 8. Hàm số
tan
y x
đồng biến trên khoảng nào sau đây
A.
;
2 2
B.
2
;
2 3
C.
4
;
2 3
D.
;
3
Câu 9. Khẳng định nào sau đây đúng đối với hàm số
4sin cos sin 2
6 6
y x x x
A. Hàm số đồng biến trên
0;
4
và
3
;
4
. B. Hàm số đồng biến trên
C. Hàm số nghịch biến trên
3
0;
4
D. Hàm số đồng biến trên
;
4
Câu 10. Khoảng đồng biến của hàm số
tan 2
y x
là ;
2 2
k k
a b
. Tính a + b.
A. 0 B. 0,5
C. 0,75
D. 1,25
Câu 11. Hàm số
tan
y x
đồng biến trên khoảng
A.
;
2 2
B.
2
;
2 3
C.
4
;
2 3
D.
;
3
Câu 12. Khoảng đồng biến đầy đủ của hàm số
sin cos
y x x
là
2 ; 2
a k b k
với
0, 0
a b
. Tính
giá trị biểu thức a + b.
A.
B. 0,5
C. 0,75
D. 1,25
Câu 13. Hàm số
cos
2
x
y có khoảng đồng biến là
4 ; 4
a k b k
với
0, 0
a b
. Tính a + b
19
A.
B. – 2
C. –
D. 1,5
Câu 14. Hàm số sin
2 3
x
y
có khoảng đồng biến là
4 ; 4
a k b k
với
0, 0
a b
. Tính a + b
A.
B.
4
3
C. –
D. 1,5
Câu 15. Hàm số
3
4cos 3cos 4
y x x
có khoảng nghịch biến
2 2
;
3 3
k k
a b
. Tính a + b
A.
3
B.
C. 2
D. 1,5
Câu 16. Tìm tất cả các khoảng nghịch biến của hàm số
cot
y x
A.
;
k k
B.
;2
k k
C. ;
2 2
k k
D. 2 ; 2
2 2
k k
Câu 17. Tìm số tự nhiên m để hàm số
sin
2
x
y
m
có khoảng đồng biến
5
4 ; 4
3 3
k k
A. m = 3 B. m = 2 C. m = 6 D. m = 4
Câu 18. Hàm số
2 2
3 3
cos sin
2 2
x x
y có khoảng nghịch biến
2 2
;
3 3
k k
a b
với
0, 0
a b
. Tính a + b
A.
3
B.
C. 2
D. 1,5
Câu 19. Hàm số
cos sin
y x x
có khoảng nghịch biến
2 ; 2
a k b k
. Tính a + b
A.
B. – 2
C. –
D. 1,5
Câu 20. Hàm số
2 2
cos 2 sin 2
y x x
có khoảng đồng biến ;
2 2
k k
a b
. Tính a + b
A. 0,5
B.
C. 0,25
D. 1,5
Câu 21. Hàm số
2
2cos 2 7
y x
có khoảng đồng biến ;
2 2
k k
a b
. Tính a + b
A. 0,5
B.
C. 0,25
D. 1,5
Câu 22. Hàm số sin cos
4 6 4 6
x x
y
có khoảng đồng biến là
4 ; 4
a k b k
với
0, 0
a b
.
Tính a + b
A.
B.
4
3
C. –
D. 1,5
Câu 23. Hàm số cot
x
y
a b
với
0, 0
a b
có khoảng nghịch biến
3 9
3 ; 3
4 4
k k
. Tính ab.
A. 12 B. 8 C. 6 D. 9
Câu 24. Hàm số
tan
x
y
a b
có khoảng đồng biến
7 3
2 ; 2
5 5
k k
. Tính ab.
A. 15 B. 10 C. 12 D. 20
Câu 25. Hàm số
4cos 9
4
y x
có khoảng nghịch biến
2 ; 2
a k b k
. Tính a + b
A.
B. – 2
C. –
D. 1,5
_________________________________
20
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH ĐƠN ĐIỆU PHẦN 2)
___________________________________________
Câu 1. Hàm số
3
3sin 3sin 4sin
3 2
x x
y x đồng biến trên khoảng nào sau đây
A.
;
2 2
B.
2
;
2 3
C.
4
;
2 3
D.
;
3
Câu 2. Hàm số
2 2
4cos 3sin
2 2
x x
y
đồng biến trên khoảng nào sau đây
A.
;
2 2
B.
;0
C.
4
;
2 3
D.
;
3
Câu 3. Hàm số
2
6 2sin
y x
tăng trên khoảng
A.
;0
2
B.
;0
C.
4
;
2 3
D.
;
3
Câu 4. Trên miền
0;
2
, hàm số
2 sin
4
y x
có đặc điểm
A. Đồng biến B. Nghịch biến
C. Không đổi D. Vừa đồng biến, vừa nghịch biến
Câu 5. Trên khoảng
0;2
, hàm số
sin cos cos
4 4 2
x x x
y có khoảng nghịch biến đầy đủ
;
a b
. Tính a + b
A.
B. 0,5
C. 0,75
D. 1,25
Câu 6. Hàm số
cos 3
y x n
có khoảng đồng biến ;
3 3
k k
a b
. Tồn tại bao nhiêu số nguyên âm n
sao cho
100
3
a b
?
A. 30 B. 45 C. 40 D. 36
Câu 7. Trên khoảng
0;
, hàm số
2 2
cos sin
y x x
có khoảng nghịch biến đầy đủ
;
a b
. Tính a + b
A.
B. 0,5
C. 0,75
D. 1,25
Câu 8. Tìm n để hàm số
3
4cos ( ) 3cos( )
y nx nx
có khoảng đồng biến ;
6 12 6
k k
.
A. n = 2 B. n = 3 C. n = 6 D. n = 4
Câu 9. Hàm số
2 2
2sin 6cos
y x x
có khoảng đồng biến đầy đủ
2 ; 2
a k b k
. Tính a + b.
A.
B. 0,5
C. 0,75
D. 1,25
Câu 10. Khoảng đồng biến của hàm số
2
sin cos
1 2sin
x x
y
x
là ;
2 2
k k
a b
. Tính a + b.
A. 0 B. 0,5
C. 0,75
D. 1,25
Câu 11. Hàm số
tan3
y x
có khoảng đồng biến ;
3 3
k k
a b
. Tính a + 2b.
A.
6
B. 0,5
C. 0,75
D. 1,25
Câu 12. Hàm số
cot( )
3
y mx
có khoảng nghịch biến ;
3 3
k k
a b
. Tìm m để
9
a b
.
A. m = 2 B. m = 3 C. m = 4 D. m = 6
21
Câu 13. Hàm số
3
8cos 6cos 5
y x x
có khoảng nghịch biến
2 2
;
3 3
k k
a b
với
0, 0
a b
. Tính
giá trị biểu thức a + b
A.
3
B.
C. 2
D. 1,5
Câu 14. Hàm số
4 2
8cos 8cos 1
y x x
có khoảng đồng biến
;
2 2
k k
a b
. Tính a + b
A. 0,5
B.
C. 0,25
D. 1,5
Câu 15. Hàm số
cos
3 4
x
y
có khoảng đồng biến
6 ; 6
a k b k
. Tính a + b.
A.
3
B.
C. 2
D. 1,5
Câu 16. Hàm số
1
sin 1
y
x
trên khoảng
;
2 2
có đặc điểm
A. Đồng biến B. Nghịch biến
C. Không đổi D. Vừa đồng biến vừa nghịch biến
Câu 17. Trên miền
0;2
, hàm số
3 cos sin
y x x
chia thành bao nhiêu khoảng đơn điệu rời nhau
A. 3 B. 2 C. 1 D. 4
Câu 18. Trên khoảng
31 33
;
4 4
x
khẳng định nào sau đây đúng
A. Hàm số
sin
y x
đồng biến B. Hàm số
cos
y x
nghịch biến
C. Hàm số
cot
y x
nghịch biến D. Hàm số
tan
y x
nghịch biến
Câu 19. Hàm số nào sau đây đồng biến trên khoảng
;
3 6
A.
tan 2
6
y x
B.
cot 2
6
y x
C.
sin 2
6
y x
D.
cos 2
6
y x
Câu 20. Hàm số cos 2
3
y x
có khoảng đồng biến đầy đủ là
;
a k b k
. Tính b – a.
A. 0,5
B.
C. 2
D. 1,5
Câu 21. Hàm số
sin cos
y x x
có khoảng nghịch biến
2 ; 2
a k b k
. Tính a + b
A.
B. – 2
C. –
D. 1,5
Câu 22. Hàm số
2
5cos 2 4
y x
có khoảng đồng biến ;
2 2
k k
a b
. Tính a + b
A. 0,5
B.
C. 0,25
D. 1,5
Câu 23. Hàm số
2
4 (sin 2 cos2 )
y x x
có khoảng nghịch biến ;
4 4
k k
a b
. Tính 3b – a.
A. 0,5
B.
C. 0,25
D. 1,5
Câu 24. Hàm số
3
4 2
4 8cos 8cos 1 3cos4
y x x x
khoảng đồng biến ;
6 6
k k
a b
. Tính a + b
A.
3
B.
C. 2
D.
12
_________________________________
22
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CƠ BẢN PHẦN 1)
___________________________________________
Câu 1. Tìm họ nghiệm của phương trình
sin 1
x
.
A.
2
2
x k
B.
2
x k
C.
2
x k
D.
2
x k
Câu 2. Tìm số nghiệm của phương trình
sin 0,3
x
trong khoảng
0;3
.
A. 4 B. 2 C. 3 D. 1
Câu 3. Tìm số nghiệm của phương trình
tan 0,4
trong khoảng
0;3
A. 3 B. 2 C. 4 D. 1
Câu 4. Tìm số điểm biểu diễn nghiệm phương trình
1
sin
3
x
trên vòng tròn lượng giác.
A. 3 B. 2 C. 1 D. 4
Câu 5. Tìm số điểm biểu diễn nghiệm phương trình
(sin 1)(sin 2)(2sin 1)
x x x
trên vòng tròn lượng giác.
A. 3 B. 4 C. 1 D. 2
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình
2sin
x m
có nghiệm ?
A. 4 B. 2 C. 5 D. 3
Câu 7. Tồn tại bao nhiêu số nguyên m thuộc [– 5;5] để phương trình
tan 2
x m
có nghiệm ?
A. 4 B. 2 C. 11 D. 20
Câu 8. Tồn tại bao nhiêu số nguyên m để phương trình
2sin
x m
có nghiệm thuộc
2
0;
3
?
A. 4 B. 2 C. 3 D. 5
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình
3sin
x m
có hai nghiệm thuộc
2
0;
3
?
A. 4 B. 3 C. 2 D. 0
Câu 10. Tìm số nghiệm của phương trình
2 2
(tan 1)(tan 4) 0
x x
trong khoảng
0;3
A. 12 B. 15 C. 14 D. 10
Câu 11. Tồn tại bao nhiêu số nguyên m nhỏ hơn 6 để phương trình
( 1)sin 2 0
m x m
có nghiệm ?
A. 5 B. 2 C. 4 D. 3
Câu 12. Tìm số điểm biểu diễn nghiệm phương trình
3
4cos 3cos 2cos3 1
x x x
trên vòng tròn lượng giác.
A. 4 B. 3 C. 1 D. 2
Câu 13. Tồn tại bao nhiêu số nguyên m nhỏ hơn 6 để phương trình
( 4).tan 0
m x m
có nghiệm ?
A. 5 B. 2 C. 4 D. 3
Câu 14. Tìm số nghiệm của phương trình
cos sin3
5
x x
trong đoạn
2
0;
3
.
A. 4 B. 3 C. 2 D. 5
Câu 15. Tìm số nghiệm của phương trình
sin3 cos cos3 (1 sin )
x x x x
trong đoạn
2
0;
3
.
A. 2 B. 3 C. 4 D. 5
Câu 16. Tìm số nghiệm của phương trình
cos sin 4 0
x x
trong đoạn
2
0;
3
.
A. 4 B. 3 C. 2 D. 5
23
Câu 17. Tồn tại bao nhiêu số nguyên m để phương trình
4sin
x m
có nghiệm thuộc
3
0;
2
?
A. 4 B. 7 C. 6 D. 5
Câu 18. Tồn tại bao nhiêu số nguyên m thuộc
3;3
để phương trình
2
2cos 1 cos(3 )
x x m
có nghiệm ?
A. 4 B. 2 C. 5 D. 3
Câu 19. Tồn tại bao nhiêu số nguyên m thuộc
10;10
để phương trình
cos4 cos sin 4 sin 2
x x x x m
có
nghiệm ?
A. 4 B. 5 C. 2 D. 3
Câu 20. Phương trình
2
2
2cos 3 1 4cos6
x x
có một phương trình hệ quả là
A.
cos3 2
B.
cos6 0,5
C.
1
cos6
3
x
D.
cos6 0
Câu 21. Tồn tại bao nhiêu số nguyên m thuộc
3;3
để phương trình
3
4cos 3cos 1
x x m
có nghiệm ?
A. 4 B. 5 C. 2 D. 3
Câu 22. Tồn tại bao nhiêu số nguyên m thuộc
10;10
để phương trình
sin 4 cos 4 2
x x m
có nghiệm ?
A. 4 B. 5 C. 3 D. 6
Câu 23. Phương trình
1
tan( 15 )
3
x
có bao nhiêu nghiệm thuộc
0 ;120
?
A. 3 B. 1 C. 2 D. 3
Câu 24. Tìm số nghiệm của phương trình
2
sin3 1 2cos
x x
trong khoảng
0;3
A. 3 B. 6 C. 7 D. 10
Câu 25. Tìm số nghiệm của phương trình
2sin 5cos 0
x x
trong khoảng
0;3
A. 3 B. 6 C. 7 D. 10
Câu 26. Tìm số nghiệm của phương trình
2
2cos 5sin 2 1
x x
trong khoảng
0;3
A. 3 B. 4 C. 7 D. 8
Câu 27. Tìm số nghiệm của phương trình
2sin 2 cos2 sin cos4 sin 4 cos 0
x x x x x x
trong khoảng
0;3
A. 13 B. 14 C. 10 D. 8
Câu 28. Tìm số nghiệm của phương trình
2 2
sin 2 cos 3 1
x x
trong khoảng
0;4
A. 16 B. 14 C. 20 D. 18
Câu 29. Tồn tại bao nhiêu số nguyên m thuộc
10;10
để phương trình
3 2
6sin 8sin 1
x x m
có nghiệm ?
A. 4 B. 5 C. 3 D. 6
Câu 30. Tìm số nghiệm của phương trình
3 cos2 cos 2 1 0
2
x x
trong khoảng
0;4
A. 5 B. 10 C. 7 D. 8
Câu 31. Một phương trình hệ quả của phương trình
sin 4 cos2 sin cos5
x x x x
là
A.
sin 4 sin 2 0
x x
B.
sin 4 sin 2
x x
C.
sin 4 sin 5
x x
D.
sin 4 sin
x x
Câu 32. Biết rằng tồn tại biến đổi
cos5 cos sin 6 sin 2 cos6 0 cos( ) cos( )
x x x x x ax bx
với a, b là các
số thực dương. Tính a + b.
A. 12 B. 10 C. 14 D. 16
_________________________________
24
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CƠ BẢN PHẦN 2)
___________________________________________
Câu 1. Tìm số nghiệm
0;2
của phương trình
cos tan3 1 sin
x x x
.
A. 4 B. 12 C. 16 D. 10
Câu 2. Tồn tại bao nhiêu số nguyên dương m để phương trình
( 3)cos2
m x m
có nghiệm
A. 4 B. 2 C. 3 D. 1
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
sin cos3 0
x x
A. 3 B. 2 C. 4 D. 5
Câu 4. Tồn tại bao nhiêu số nguyên m để phương trình
sin 5
x m
có nghiệm
;
6
A. 4 B. 2 C. 3 D. 1
Câu 5. Tính
cos2
x
biết rằng
3 3
1
cos cos3 sin sin 3
8
x x x x
.
A. – 0,5 B. 0,25 C. 0,5 D. 1
Câu 6. Tồn tại bao nhiêu số nguyên dương m để phương trình
tan 5
x m
có nghiệm
3
;
2
A. 4 B. 3 C. 1 D. 2
Câu 7. Tìm số nghiệm
0;20
của phương trình
1
sin
2
x
A. 2 B. 1 C. 3 D. 4
Câu 8. Phương trình
2sin3 cos sin 2 3 cos4
x x x x
có số nghiệm
0;2
là
A. 7 B. 8 C. 6 D. 10
Câu 9. Phương trình
3
2sin3 cos sin 4 sin 2 2
x x x x
có một hệ quả là
A.
sin 4 1
x
B.
sin 4 0,5
x
C.
sin3 0,5
x
D.
3
sin3
2
x
Câu 10. Có bao nhiêu số nguyên dương m để phương trình
2sin 5
x m
có hai nghiệm phân biệt
2
;
6 3
A. 3 B. 2 C. 1 D. 0
Câu 11. Phương trình
cos9 cos sin13 sin 3
x x x x
có một hệ quả là
A.
cos4 sin8
x x
B.
cos3 cos5
x x
C.
cos4 cos5
x x
D.
cos4 cos3
x x
Câu 12. Phương trình
2sin 4 3 4cos2
3
x x
có bao nhiêu nghiệm
0;2
A. 6 B. 5 C. 4 D. 3
Câu 13. Phương trình
2
sin cos2 2sin 2 1
x x x
có bao nhiêu nghiệm
0;100
A. 20 B. 200 C. 198 D. 196
Câu 14. Xác định số nghiệm
0;4
của phương trình
1
tan3
4
x
A. 14 B. 24 C. 18 D. 30
Câu 15. Phương trình
cos7 cos3 2cos5 0
x x x
có bao nhiêu nghiệm
0;2
A. 3 B. 2 C. 1 D. 4
Câu 16. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của phương trình
2cos3 cos 0,5 cos2
x x x
A. 4 B. 8 C. 12 D. 10
25
Câu 17. Phương trình
2
2sin3 sin cos4 cos 2 2
x x x x
có bao nhiêu nghiệm
0;100
A. 60 B. 99 C. 17 D. 80
Câu 18. Nghiệm dương nhỏ nhất của phương trình
cos5 cos sin10 sin 4
x x x x
gần nhất với
A. 0,52 B. 0,17 C. 0,76 D. 0,81
Câu 19. Phương trình
4 2
8cos 8cos 1 sin 4
x x x
có bao nhiêu nghiệm
0;30
A. 40 B. 240 C. 250 D. 300
Câu 20. Xác định số nghiệm
0;4
của phương trình
1
cos2
3
x
A. 4 B. 8 C. 6 D. 10
Câu 21. Phương trình
4 4
4cos 8sin cos 4 3
x x x
có bao nhiêu nghiệm
0;30
A. 40 B. 30 C. 25 D. 18
Câu 22. Tồn tại bao nhiêu số nguyên m để phương trình
3sin 2
x m
có hai nghiệm phân biệt
3
0;
2
A. 4 B. 2 C. 5 D. 6
Câu 23. Phương trình
4 2
4sin 2cos cos2 cos4 4
x x x x
có bao nhiêu nghiệm
0;30
A. 50 B. 70 C. 60 D. 34
Câu 24. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của phương trình
sin 6 sin 2 0,5tan 2
x x x
A. 4 B. 6 C. 12 D. 8
Câu 25. Phương trình
2 2 4
1 2sin sin 2 4sin cos2
x x x x
có bao nhiêu nghiệm
0;100
A. 60 B. 99 C. 17 D. 80
Câu 26. Xác định số nghiệm
0;30
của phương trình
(sin 3cos )(cos 2sin ) 0
x x x x
A. 10 B. 60 C. 40 D. 30
Câu 27. Tìm số nghiệm
0;30
của phương trình
cos cos2 cos3 cos 4
3
sin sin 2 sin 3 sin 4
x x x x
x x x x
A. 80 B. 90 C. 60 D. 75
Câu 28. Xác định số nghiệm
0;4
của phương trình
2
2cos 3 1 2sin 6
x x
A. 4 B. 6 C. 8 D. 10
Câu 29. Tìm số
0;4
của phương trình
sin cos cos2 cos4 cos8 0
x x x x x
A. 24 B. 32 C. 18 D. 40
Câu 30. Tìm một hệ quả của phương trình
cos7 sin8 cos3 sin 2
x x x x
.
A.
cos3 sin 2
x x
B.
cos2 sin3
x x
C.
2cos2 sin3
x x
D.
2cos2 3sin3
x x
Câu 31. Xác định số nghiệm
0;4
của phương trình
cos9 cos7 cos3 cos 0
x x x x
A. 34 B. 33 C. 32 D. 30
Câu 32. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của
sin sin3 sin 5 sin7 0
x x x x
A. 4 B. 6 C. 12 D. 8
Câu 33. Xác định số nghiệm
0;4
của phương trình
cos11 cos3 cos17 cos9
x x x x
A. 100 B. 95 C. 93 D. 104
Câu 34. Tồn tại bao nhiêu số nguyên dương m để phương trình
tan 5
x m
có đúng 2 nghiệm
3
;
2
A. 4 B. 2 C. 3 D. 1
26
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH BẬC NHẤT SIN, COS PHẦN 1)
___________________________________________
Câu 1. Phương trình
sin cos 1
x x
tương đương với phương trình nào sau đây
A.
1
sin
4
2
x
B.
1
sin
4
2
x
C.
sin 1
4
x
D.
sin 2
4
x
Câu 2. Tồn tại bao nhiêu số nguyên m để phương trình
3sin 4cos
x x m
có nghiệm ?
A. 10 B. 11 C. 12 D. 9
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 3sin cos
x x m
có nghiệm ?
A. 10 B. 11 C. 12 D. 9
Câu 4. Tồn tại bao nhiêu số nguyên m để phương trình
sin ( 1)cos 2 3 0
m x m x m
có nghiệm ?
A. 4 B. 5 C. 12 D. 9
Câu 5. Biết rằng
sin 3 cos 2 sin sin
x
x x x
n m
. Tính m + n biết m, n nguyên dương.
A. 7 B. 8 C. 6 D. 4
Câu 6. Có bao nhiêu nghiệm của phương trình
cos7 3sin 7 2
x x
thỏa mãn
2 6
5 7
x
?
A. 3 B. 7 C. 4 D. 2
Câu 7. Biết rằng 3 sin 2 cos2 2cos5 sin 2 sin
x x x x cx
a b
. Tính a + b + c với a, b, c là các
số nguyên dương.
A. 5 B. 17 C. 10 D. 13
Câu 8. Tìm phương trình tương đương với phương trình
1
3sin cos
cos
x x
x
.
A.
sin 1
6
x
B.
sin 1
6
x
C.
sin 3
6
x
D.
1
sin
6 2
x
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình
2 sin ( 2)cos 2
m x m x m
.
A. 2 B. 1 C. 3 D. 4
Câu 10. Tìm số nghiệm
0;2
của phương trình
sin sin 2 3(cos cos2 )
x x x x
.
A. 3 B. 4 C. 2 D. 1
Câu 11. Phương trình
cos 3sin 2cos3
x x x
có một họ nghiệm nào đó là
k
x
a b
với a, b nguyên
dương. Tính tổng số các ước dương của a và b.
A. 6 B. 4 C. 10 D. 12
Câu 12. Tìm số nghiệm
0;2
của phương trình
3
sin cos 3cos3 2(cos4 sin )
x x x x x
.
A. 7 B. 10 C. 8 D. 11
Câu 13. Tìm số nghiệm
0;2
của phương trình
3(sin 2 sin ) cos2 cos 2
x x x x
.
A. 7 B. 6 C. 3 D. 8
Câu 14. Tồn tại bao nhiêu số nguyên dương m để phương trình
2
( 1)sin 2cos 1
m x x m
.
A. 2 B. 1 C. 3 D. 4
Câu 15. Tìm số nghiệm
0;2
của phương trình
2
5sin 2 6cos 13
x x
.
A. 3 B. Vô nghiệm C. 6 D. 5
27
Câu 16. Tìm số nghiệm
0;2
của phương trình
2
sin 2 sin 0,5
x x .
A. 5 B. 4 C. 3 D. 6
Câu 17. Tìm số nghiệm
0;2
của phương trình
sin 2 sin5 cos
x x x
.
A. 10 B. 14 C. 9 D. 8
Câu 18. Tính a + b + c biết a, b, c là các số nguyên dương thỏa mãn
3
4cos 3sin3 3cos 2cos5 sin cos( )
x x x x ax cx
b
.
A. 15 B. 14 C. 12 D. 10
Câu 19. Tìm số nghiệm
0;
của phương trình
3sin sin 2
4 4
x x
.
A. 1 B. 3 C. 2 D. 4
Câu 20. Tìm số nghiệm
0;
của phương trình
sin 2 3 sin(2 ) 1
2
x x
.
A. 3 B. 7 C. 4 D. 2
Câu 21. Tồn tại bao nhiêu số nguyên m để phương trình
2
sin 2 2sin 3
m x x m
có nghiệm ?
A. 2 B. 1 C. 3 D. 4
Câu 22. Đoạn [a;b] gồm tất cả các giá trị m để phương trình
sin 2cos
sin cos 3
x x
m
x x
có nghiệm. Tính 7a – 5b.
A. 10 B. 1 C. – 10 D. 0
Câu 23. Đoạn [a;b] gồm tất cả các giá trị m để phương trình
sin 2cos 1
sin cos 2
x x
m
x x
có nghiệm. Tính a+ b.
A. 1 B. – 2 C. – 1 D. 2
Câu 24. Tìm số nghiệm
0;2
của phương trình
3(cos2 sin3 ) sin 2 cos3
x x x x
.
A. 5 B. 6 C. 3 D. 7
Câu 25. Phương trình
3 cos 2 sin 2 2sin 2 2 2
6
x x x
có một họ nghiệm nào đó là
5
x k
a
với
a nguyên dương. Số ước dương của a là
A. 6 B. 8 C. 7 D. 12
Câu 26. Tìm số nghiệm
0;
của phương trình
sin cos 2 2 sin cos
x x x x
A. 2 B. 3 C. 1 D. 4
Câu 27. Tìm số nghiệm
0;
của phương trình
2cos3 3sin cos 0
x x x
.
A. 2 B. 3 C. 1 D. 4
Câu 28. Tìm số nghiệm
0;2
của phương trình
(1 2sin )cos
3
(1 2sin )(1 sin )
x x
x x
.
A. 3 B. 7 C. 4 D. 2
Câu 29. Tìm số nghiệm
0;2
của phương trình
sin8 cos6 3(sin6 cos8 )
x x x x
.
A. 15 B. 14 C. 16 D. 12
Câu 30. Phương trình
sin3 3 cos3 2sin
x x x
có một họ nghiệm nào đó là
2
15
a
x k
b
với a, b nguyên
dương. Tính giá trị tổng a + b.
A. 7 B. 9 C. 10 D. 8
_________________________________
28
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH BẬC NHẤT SIN, COS PHẦN 2)
___________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m lớn hơn – 5 để phương trình
sin cos 2
m x x m
có nghiệm ?
A. 4 B. 5 C. 6 D. 2
Câu 2. Nghiệm dương nhỏ nhất của phương trình
4 4
4(sin cos ) 3sin 4 2
x x x
gần nhất với
A. 0,41 B. 0,24 C. 0,16 D. 0,72
Câu 3. Cho phương trình
2 cos2 3sin 2 sin 3 cos
x x x x
. Khi đó cos
6
x
có thể bằng
A. 0,2 B. – 0,5 C. – 1,2 D. – 2,5
Câu 4. Tồn tại bao nhiêu số nguyên dương k để phương trình
2
sin 2
2cos 1
3
x
x m
có nghiệm ?
A. 2 B. 1 C. 3 D. 4
Câu 5. Phương trình
2sin11 3sin 5 cos5 0
x x x
có 1 họ nghiệm
5
( 0, 0)
x a b
a b
. Tính a + b.
A. 45 B. 39 C. 20 D. 35
Câu 6. Biết rằng
2
4sin 9cos sin sin 97
x x m x m
. Khi đó
2 2
4tan 9cot
gần nhất
A. 10 B. 18 C. 19 D. 26
Câu 7. Có bao nhiêu số nguyên m < 18 để phương trình
2 sin cos 2 1cos2 2
m x x m x m
có nghiệm ?
A. 6 B. 10 C. 15 D. 12
Câu 8. Phương trình
2sin (cos 1) 3 cos2
x x x
có một họ nghiệm
4 2
( 0, 0)
x a b
a b
. Tính a + b.
A. 10 B. 12 C. 9 D. 13
Câu 9. Tồn tại bao nhiêu số nguyên m < 10 để phương trình
(cos 2)(sin cos 2 ) 0
x x m x m
có nghiệm
A. 2 B. 1 C. 3 D. 4
Câu 10. Biết
2(sin 3 cos ) 3cos2 sin 2
x x x x
có một họ nghiệm
2 ( 0, 0)
a
x k a b
b
, và
phân số
a
b
tối giản, tính a + b.
A. 10 B. 17 C. 19 D. 14
Câu 11. Tìm số nghiệm trong khoảng (– 1993;1993) của phương trình
2 2(sin cos )cos 3 cos2
x x x x
.
A. 1993 B. 2019 C. 0 D. 60
Câu 12. Tồn tại bao nhiêu số nguyên dương m < 10 để phương trình
2
3sin 2 2 cos 1
x m x m
có nghiệm ?
A. 10 B. 11 C. 6 D. 8
Câu 13. Biết rằng
3sin 4cos 5 sin 1
x x x
. Tính
4tan 9cot
.
A. 2 B. 4 C.
25
12
D.
11
13
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
cos3 3 sin 3 2cos
x x x
.
A. 8 B. 6 C. 10 D. 4
Câu 15. Phương trình
cos6 sin
3
cos sin 6
x x
x x
có một họ nghiệm
2
7
k
x
a
. Giá trị của a thuộc khoảng
A. (0;3) B. (3;7) C. (7;10) D. (10;15)
29
Câu 16. Phương trình
3
3sin3 4cos 3cos 2cos(1993 )
x x x x
có một họ nghiệm
( 0)
6
k
x a
a a
.
Tính giá trị biểu thức 2a – 3.
A. 1968 B. 1993 C. 2020 D. 1975
Câu 17. Phương trình
2sin cos 1
x x
có một phương trình hệ quả tan
2
x
k
, khi đó k thuộc khoảng
A. (0;1) B. (1;3) C. (3;4) D. (4;5)
Câu 18. Tồn tại bao nhiêu số nguyên dương a để phương trình
2sin cos 1
sin 2cos 3
x x
a
x x
có nghiệm ?
A. 3 B. 1 C. 2 D. 4
Câu 19. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của
2
(2 3)cos 2sin
2 4
1
2cos 1
x
x
.
A. 6 B. 2 C. 4 D. 8
Câu 20. Phương trình
sin 3cos 1
x x
có một phương trình hệ quả tan
2
x
k
, khi đó k thuộc khoảng
A. (0;1) B. (1;2) C. (– 1;0) B. (2;3)
Câu 21. Tìm số nghiệm
1993;1993
của phương trình
2
cos 2sin cos
3
2cos sin 1
x x x
x x
.
A. 1903 B. 1953 C. 1973 D. 1993
Câu 22. Tập hợp
;
S a b
bao gồm tất cả các giá trị m để phương trình
2 2
2sin sin cos cos
x x x x m
có
nghiệm. Tính giá trị
2 2
a b
.
A. 6 B. 5,5 C. 4 D. 6,5
Câu 23. Tồn tại bao nhiêu giá trị m để mọi nghiệm của phương trình
sin cos 1
x m x
cũng là nghiệm của
phương trình
2
sin cos
m x x m
.
A. 6 B. 2 C. 5 D. 4
Câu 24. Phương trình
3sin 2cos 2
x x
có một phương trình hệ quả là
A.
2
tan
2 3
x
B.
2
tan
2 5
x
C.
1
tan
2 2
x
D.
1
tan
2 3
x
Câu 25. Biết rằng
cos 3sin 3 (tan )(tan ) 0
2 2
x x
x x a b
. Tính a + b.
A. – 2 B. – 1,5 C. – 0,5 D. 2
Câu 26. Phương trình
2sin sin 2cos 3
6
x x x
có một phương trình hệ quả
1
tan
2
x a
b
, tính ab.
A. 18 B. 9 C. 4 D. 6
Câu 27. Tồn tại bao nhiêu số nguyên m để phương trình
sin 2cos 1
sin cos 2
x x
m
x x
có nghiệm ?
A. 4 B. 5 C. 9 D. 2
Câu 28. Phương trình
2cos cos 4sin 2 1
3
x x x
có một hệ quả là
tan 0
x a b
. Tính ab
A. 16 B. 24 C. 18 D. 10
Câu 29. Tồn tại bao nhiêu số nguyên m để phương trình
3
12cos 2 sin3 cos3 9cos2
x x x m x
có nghiệm
A. 10 B. 8 C. 7 D. 5
_________________________________
30
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CHỨA ẨN MẪU THỨC PHẦN 1)
___________________________________________
Câu 1. Tính a + b biết
sin cos 1 ( 0, 0)
a x b x a b
là một phương trình hệ quả của phương trình
1
3sin 2cos 3(1 tan )
cos
x x x
x
.
A. 4 B. 5 C. 3 D. 2
Câu 2. Tính tổng các nghiệm x thuộc
0;99
của phương trình
2 3
2
2
cos cos 1
cos2 tan
cos
x x
x x
.
A.
2209
3
B.
4
9
C.
1993
4
D.
2019
4
Câu 3. Tính a + b biết sin cos
x x a b
với a, b dương là một phương trình hệ quả của
3 2
2
3(1 sin )
3tan tan 8cos 0
cos 4 2
x x
x x
x
.
A. 3 B. 4 C. 5 D. 1
Câu 4. Tồn tại bao nhiêu nghiệm
2 ;2
của phương trình
2
1 cos2
1 cot 2
sin 2
x
x
x
.
A. 4 B. 6 C. 10 D. 12
Câu 5. Phương trình
2 2
cot tan
16(1 cos4 )
cos2
x x
x
x
có họ nghiệm
( , 0)
k
x a b
a b
. Tính a + b.
A. 24 B. 16 C. 20 D. 12
Câu 6. Phương trình
sin cot5
1
cos9
x x
x
có họ nghiệm
( , 0)
k
x a b
a b
. Tính a + b.
A. 24 B. 12 C. 30 D. 14
Câu 7. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1 1
2 sin
4 sin cos
x
x x
.
A. 4 B. 2 C. 3 D. 5
Câu 8. Tìm số nghiệm
2 ;2
của phương trình
2
2tan cot 3
sin 2
x x
.
A. 4 B. 3 C. 2 D. 5
Câu 9. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1
2tan cot 2sin 2
sin 2
x x x
x
.
A. 4 B. 6 C. 5 D. 8
Câu 10. Số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1 2(cos sin )
tan cot 2 cot 1
x x
x x x
là
A. 4 B. 6 C. 5 D. 2
Câu 11. Tìm số nghiệm
4 ;9
của phương trình
2
2
2 2
sin 2
tan
2
sin 4cos
2
x x
x
x
.
A. 8 B. 10 C. 9 D. 5
Câu 12. Tìm số nghiệm
4 ;9
của phương trình
4 4
4
sin 2 cos 2
cos 4
tan tan
4 4
x x
x
x x
.
A. 10 B. 25 C. 16 D. 26
31
Câu 13. Tìm số nghiệm
4 ;9
của phương trình
2 4
sin 2 cos 2 1
0
sin cos
x x
x x
.
A. 13 B. 14 C. 15 D. 16
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
4sin 2 6sin 9 3cos2
0
cos
x x x
.
A. 6 B. 2 C. 4 D. 5
Câu 15. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1 cos2 sin 2
2sin 1 cos2
x x
x x
.
A. 0 B. 2 C. 3 D. 4
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
1 sin 2
1 tan 2
cos 2
x
x
x
.
A. 4 B. 2 C. 3 D. 5
Câu 17. Tìm số nghiệm
4 ;9
của phương trình
2
sin (sin cos ) 1
0
cos sin 1
x x x
x x
.
A. 25 B. 22 C. 15 D. 7
Câu 18. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
sin5
1
5sin
x
x
.
A. 0 B. 2 C. 3 D. 4
Câu 19. Tìm số nghiệm
49 ;1993
của phương trình
1 tan
1 sin 2
1 tan
x
x
.
A. 4082 B. 4080 C. 2020 D. 1993
Câu 20. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
sin sin 2 sin 3
3
cos cos2 cos3
x x x
x x x
.
A. 3 B. 2 C. 5 D. 4
Câu 21. Tính tổng các nghiệm thuộc
0;2
của phương trình
1 1 2
cos sin 2 sin 4
x x x
.
A.
2
B.
C.
3
D.
1,5
Câu 22. Một phương trình hệ quả của phương trình
2 2
1
cos tan 2 cos 3
cos
x x x
x
là
A. cosx = 0,5 B. cosx = 1 C. cosx = 0,25 D.
1
cos
3
x
Câu 23. Phương trình
6 6
sin cos 1
4
tan .tan
4 4
x x
x x
có họ nghiệm
( 0, 0)
k
x a b
a b
. Tính a + 2b.
A. 12 B. 14 C. 10 D. 8
Câu 24. Tìm số nghiệm thuộc
0;2
của phương trình
2
cot 1
cos4 .cot 2 cos
2cot
x
x x x
.
A. 10 B. 8 C. 7 D. 6
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
tan 3
tan3
1 3 tan
x
x
x
.
A. 2 B. 3 C. 5 D. 4
_________________________________
32
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CHỨA ẨN MẪU THỨC PHẦN 2)
___________________________________________
Câu 1. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
cos2 3cot 2 sin 4
2
cot 2 cos 2
x x x
x x
A. 3 B. 2 C. 1 D. 4
Câu 2. Tìm số nghiệm thuộc
100 ;100
của phương trình
1 tan
1 sin 2
1 tan
x
x
x
.
A. 100 B. 199 C. 198 D. 56
Câu 3. Tìm số nghiệm thuộc khoảng (4;9) của phương trình
cos(2 )
0
1 tan(2 )
x
x
.
A. 4 B. 5 C. 3 D. 2
Câu 4. Tìm a + b biết
cos2 sin 2 1
a x b x
là hệ quả của
2
5
4sin sin
6 6
2tan 0
cos
x x
x
.
A. 4 B. 3 C. 2 D. 1
Câu 5. Phương trình
tan cot
6cos2 4sin 2
cot tan
x x
x x
x x
tương đương
(tan 2 )(tan 2 ) 0
x a x b
. Tính ab.
A. 4 B. – 5 C. – 2 D. 4
Câu 6. Phương trình
3 3
6cos 2 2sin 2
cos4
3cos2 sin 2
x x
x
x x
có một hệ quả là
A.
tan 2 3
x
B.
tan 2 2
C.
tan 2 1
D.
tan 2 4
Câu 7. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 3
2(cos 2sin )
sin 2
2sin 3cos
x x
x
x x
A. 3 B. 6 C. 4 D. 5
Câu 8. Tìm số nghiệm thuộc
100 ;100
của phương trình
4
3
4
1 cos
tan
1 sin
x
x
x
.
A. 100 B. 199 C. 198 D. 56
Câu 9. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 3
cos sin
cos2
2cos sin
x x
x
x x
A. 3 B. 4 C. 2 D. 5
Câu 10. Phương trình
2
cos (1 cot ) 3
3cos
sin cos
x x
x
x x
tương đương
2
(tan )(tan ) 0
x a x b
. Tính
1
ab
.
A. 5 B. – 3 C. – 2 D. – 4
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
2
cos 2
1
2
1
1 cos 2 cos 2
x
x x
A. 4 B. 2 C. 3 D. 6
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của
5sin 5tan
4(1 cot ) 0
sin tan
x x
x
x x
A. 2 B. 3 C. 4 D. 1
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
sin
2 cot
1 cos
x
x
A. 2 B. 3 C. 4 D. 1
33
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
3
2 2
sin tan
2tan 1 0
cos cot
x x
x
x x
A. 2 B. 3 C. 4 D. 1
Câu 15. Tính tổng các nghiệm thuộc
0;2
của phương trình
3(sin cos )
2cos 2
tan sin
x x
x
x x
.
A.
B. 2
C. 3
D. 0,5
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của
1
cos cot sin( )
sin
x x x
A. 2 B. 1 C. 3 D. 4
Câu 17. Tính
cos
x
khi phương trình
sin tan 9
1 cos 4
x x
x
có đúng một họ nghiệm dạng
cos
x m
.
A. 2 B. 3 C. 1 D. 4
Câu 18. Tính tổng các nghiệm thuộc
0;2
của phương trình
2
1 cos
tan
cos
x
x
x
.
A.
B. 2
C. 3
D. 0,5
Câu 19. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1 sin 2 1 tan
2. 3 0
1 sin 2 1 tan
x x
x x
A. 3 B. 2 C. 1 D. 4
Câu 20. Tính số nghiệm thuộc
0;2
của phương trình
2
1
1 cos 4
1 tan 2
x
.
A. 6 B. 7 C. 5 D. 4
Câu 21. Tính
cos6
x
khi góc x thỏa mãn
6 6
2
4 4
1 sin cos
2cos 3
1 sin cos
x x
x
x x
A. 1 B. 0,5 C. 0,25 D.
1
3
Câu 22. Tìm số nghiệm thuộc
100 ;100
của phương trình
1 cos
2
sin
2
x
x
.
A. 100 B. 50 C. 93 D. 42
Câu 23. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
sin 2 sin 1
. 1
1 cos 2 1 cos sin
x x
x x x
A. 2 B. 3 C. 1 D. 4
Câu 24. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
4
2 2
4sin 2
1 0
(1 cos2 ) cos
x
x x
A. 3 B. 5 C. 1 D. 4
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
cos2 1
cot 1 sin sin 2
1 tan 2
x
x x x
x
.
A. 3 B. 5 C. 1 D. 4
Câu 26. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của
2
3tan 6 2tan 2 cot 4
sin8
x x x
.
A. 4 B. 8 C. 10 D. 6
Câu 27. Tính số nghiệm thuộc
0;2
của phương trình
2
1 1
(4cos 2 3) 2
sin sin 3
x
x x
.
A. 8 B. 9 C. 11 D. 12
34
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐA THỨC + ẨN PHỤ P1)
___________________________________________
Câu 1. Phương trình
2
2sin sin 1 0
x x
có bao nhiêu nghiệm thuộc
0;3
?
A. 3 B. 4 C. 5 D. 6
Câu 2. Tính a + b biết rằng
2
2cos2 12sin 5 sin sin 5
x x a x b x
.
A. 15 B. 14 C. 16 D. 20
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình
2
2cos 5cos 2 0
x x
.
A. 3 B. 2 C. 4 D. 5
Câu 4. Phương trình
2
2 3
2tan 3
cot
x
có bao nhiêu nghiệm thuộc
0;3
?
A. 3 B. 6 C. 5 D. 8
Câu 5. Tìm số nghiệm thuộc
0;3
của phương trình
2
6cos 5sin 2
x x
.
A. 3 B. 4 C. 2 D. 5
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình
2cos2 sin
x x m
có nghiệm ?
A. 3 B. 6 C. 5 D. 10
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình
2
2cos2 3cos 2sin
x x x m
có nghiệm ?
A. 13 B. 7 C. 8 D. 10
Câu 8. Phương trình
4 2
4sin 12cos 7
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 2 C. 5 D. 4
Câu 9. Phương trình
cos4 9sin 2 8 0
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
Câu 10. Tìm số nghiệm thuộc
0;3
của phương trình
5cos 7 2sin
2
x
x .
A. 3 B. 4 C. 1 D. 2
Câu 11. Tồn tại bao nhiêu số nguyên m để phương trình
2
cos2 sin cos4
m x x x
có nghiệm
2
0;
3
A. 4 B. 8 C. 5 D. 6
Câu 12. Tìm số nghiệm thuộc
0;5
của phương trình
2
sin cos2 cos 2 0
x x x
.
A. 5 B. 4 C. 3 D. 2
Câu 13. Phương trình
2
cos4 12sin 1
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
Câu 14. Phương trình
2
8cos cos4 1
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 4
Câu 15. Tìm số nghiệm thuộc
0;3
của phương trình
4 4
5(1 cos ) 2 sin cos
x x x
.
A. 3 B. 4 C. 5 D. 2
Câu 16. Tìm số nghiệm thuộc
0;3
của phương trình
2
cos2 3cos 4cos
2
x
x x .
A. 3 B. 4 C. 5 D. 2
Câu 17. Phương trình
5tan 2cot 3 0
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 1 C. 5 D. 4
Câu 18. Phương trình
2
3cos4 2cos 3 1
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
35
A. 3 B. 2 C. 5 D. 4
Câu 19. Phương trình
4 4
cos2 sin cos
x x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
Câu 20. Tìm số nghiệm thuộc
0;2
của phương trình
4
2
4
3cot 5 0
sin
x
x
.
A. 3 B. 4 C. 5 D. 2
Câu 21. Tồn tại bao nhiêu số nguyên m nhỏ hơn 2 để phương trình
2
1
3tan
cos
x m
x
có nghiệm.
A. 4 B. 2 C. 3 D. 1
Câu 22. Phương trình
2
5
tan 7 0
cos
x
x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
Câu 23. Tồn tại tất cả bao nhiêu số nguyên m nhỏ hơn để phương trình
2
cos2 sin 2cos
x x x m
có nghiệm
2
0;
3
A. 4 B. 6 C. 2 D. 5
Câu 24. Tìm số nghiệm thuộc
0;2
của phương trình
2
1
cot 3
sin
x
.
A. 2 B. 3 C. 4 D. 5
Câu 25. Phương trình
4 4
sin cos sin 2 0,5
x x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng
giác ?
A. 3 B. 4 C. 5 D. 2
Câu 26. Phương trình
4 4
(2cos 2 5)cos (2cos2 5)sin 3
x x x x
có bao nhiêu điểm biểu diễn nghiệm trên
vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
Câu 27. Tìm số nghiệm thuộc
0;3
của phương trình
3 2
3sin 3cos 7sin cos2 1 0
x x x x
.
A. 3 B. 3 C. 5 D. 4
Câu 28. Phương trình
2
cos2 cos cos sin 1
4 4 2
x x x x
có bao nhiêu điểm biểu diễn nghiệm
trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
Câu 29. Tìm số nghiệm thuộc
0;2
của phương trình
4(sin3 cos2 ) 5(sin 1)
x x x
.
A. 2 B. 2 C. 3 D. 5
Câu 30. Tìm số nghiệm thuộc
0;2
của phương trình
2
2
2
2tan 5tan 5cot 4 0
sin
x x x
.
A. 3 B. 2 C. 1 D. 4
Câu 31. Tìm số nghiệm thuộc
0;2
của phương trình
2
2
1 1
sin sin
sin sin
x x
x x
.
A. 1 B. 2 C. 3 D. 4
Câu 32. Tìm số nghiệm thuộc
0;2
của phương trình
cos3 3cos2 2(1 cos )
x x x
.
A. 2 B. 2 C. 3 D. 5
Câu 33. Tìm số nghiệm thuộc
0;5
của phương trình
23sin sin3 24
x x
.
A. 5 B. 4 C. 3 D. 2
36
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐA THỨC + ẨN PHỤ P2)
___________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m để phương trình
1 cos 2
( 2)cos 2 0
2
x
m x m
có nghiệm ?
A. 3 B. 4 C. 5 D. 2
Câu 2. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
3 2
sin sin 2 cos
x x x
.
A. 3 B. 2 C. 1 D. 4
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình
3 2
cos4 cos6 4cos 2 2sin
x x x x m
có nghiệm ?
A. 4 B. 5 C. 3 D. 2
Câu 4. Phương trình
3
cot 2 cot 3 tan
x x x
có một họ nghiệm
( 0, 0)
k
x a b
a b
. Tính tích ab.
A. 10 B. 16 C. 20 D. 15
Câu 5. Tồn tại bao nhiêu số nguyên m < 100 để phương trình
2
4
tan 2
cot
x m
có nghiệm ?
A. 102 B. 93 C. 106 D. 97
Câu 6. Tồn tại bao nhiêu số nguyên m < 50 để phương trình
2
1
cot 2 2(cot tan )
tan 2
x x x m
x
có nghiệm
A. 52 B. 56 C. 49 D. 35
Câu 7. Phương trình
2
cot 4cot 2 tan 3 0
x x x
có hệ quả
5
cot
2
a
x
. Số ước dương của a là
A. 9 B. 8 C. 2 D. 4
Câu 8. Với
1994;1994
m , phương trình
cos3 1993cos
x x m
có tối đa bao nhiêu điểm biểu diễn
nghiệm trên vòng tròn lượng giác ?
A. 4 B. 2 C. 3 D. 1
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình
cos2 2cos 1
x x m
có nghiệm ?
A. 4 B. 2 C. 3 D. 5
Câu 10. Phương trình
2
cot 2 4(tan cot ) 8
x x x
có bao nhiêu nghiệm trên
0;2
?
A. 6 B. 4 C. 5 D. 10
Câu 11. Tồn tại bao nhiêu số nguyên m để phương trình sau có hai nghiệm phân biệt
3
;
2 2
.
2
cos (2 1)cos 2 0
x m x m
A. 3 B. 2 C. 1 D. 2
Câu 12. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
2
2
2cos
sin sin
1 sin
x
x x
x
.
A. 3 B. 2 C. 1 D. 4
Câu 13. Phương trình
4
sin 1 cos
x x
có một hệ quả là
2
cos cos 1 0 ( 0, 0)
a x b x a b
. Tính ab.
A. 2 B. 1 C. 3 D. 4
Câu 14. Phương trình
8 8
sin cos cos8
x x x
có một hệ quả
2
sin 2
a
x
b
(phân số tối giản). Tính b – a.
A. 6 B. 7 C. 2 D. 5
Câu 15. Tìm số nghiệm
4 ;9
của phương trình
6 6
sin cos sin 2 1
x x x
.
A. 25 B. 20 C. 23 D. 21
37
Câu 16. Phương trình
10 10 2
sin cos sin 2 1
x x x
có một quả
2
sin 2
a
x
b
(phân số tối giản). Tính b – a.
A. 2 B. 3 C. 1 D. 4
Câu 17. Phương trình
4 2 2
4sin 2sin cos4 sin 2 1
x x x x
đưa về
(cos2 ) 0
P x
với
2
( ) 1
P t at bt
.
Tính giá trị biểu thức ab.
A. – 7 B. – 6 C. 3 D. 2
Câu 18. Phương trình
4 4 2
8sin 4cos sin 2 4
x x x
có hệ quả là
(cos 2 )(cos2 ) 0
x a a b
. Tính ab.
A. 0 B. 2 C. 1 D. 3
Câu 19. Phương trình
2
tan 3tan 2cot 6 0
x x x
có hệ quả
tan 2
x a
. Số ước dương của a là
A. 4 B. 6 C. 8 D. 10
Câu 20. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
1
3tan cot 6
sin
x x
.
A. 6 B. 4 C. 8 D. 10
Câu 21. Phương trình
2 2
tan cot 2cot tan 2
2 2
x x
x x
có hệ quả
3 2
cot cot cot 1 0
a x b x c x
. Tính
tích abc.
A. 15 B. 12 C. – 56 D. – 28
Câu 22. Tồn tại bao nhiêu số nguyên m để phương trình
2
2sin ( 4)sin 2 0
x m x m
có hai nghiệm phân
biệt thuộc
;
6
.
A. 1 B. 2 C. 3 D. 5
Câu 23. Phương trình
3 3 2 2
tan cot tan cot 1
x x x x
có bao nhiêu nghiệm
4 ;9
A. 4 B. 2 C. 0 D. 3
Câu 24. Phương trình
2 2 2
cot 2 cot tan 2
x x x
đưa về
3 2
2 0
at bt ct
với
cot tan
t x x
. Tính ab.
A. 5 B. 4 C. 2 D. 3
Câu 25. Tìm số nghiệm trong khoảng
1993 ;1993
của phương trình
3 3
1
tan cot 3
sin 2
x x
x
.
A. 1994 B. 1993 C. 1992 D. 1996
Câu 26. Tìm số nghiệm trong khoảng
1993 ;1993
của phương trình
3 tan 3 cot 4
x x
.
A. 1994 B. 1993 C. 1992 D. 1996
Câu 27. Phương trình
2 2 2
1
cot 2 tan cot 3
sin 2
x x x
có hệ quả là
tan cot
x x a
. Số ước của a là
A. 4 B. 2 C. 6 D. 8
Câu 28. Phương trình
2 2
tan cot tan 5
2 2
x x
x
có bao nhiêu nghiệm trên
0;2
?
A. 4 B. 6 C. 5 D. 10
Câu 29. Phương trình
4 4
4cos 12sin 3 cos2
x x x
tương đương
(cos2 )(cos2 ) 0
x a x b
. Tính ab.
A. 0,5 B. 0,25 C. 1 D. 0,75
Câu 30. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
1
tan cot
sin
x x
x
A. 3 B. 4 C. 2 D. 5
_________________________________
38
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH TÍCH PHẦN 1)
___________________________________________
Câu 1. Tìm một phương trình hệ quả của phương trình
cos2 cos 4 sin sin 5
x x x x
.
A.
cos3 0
x
B.
cos3 1
x
C.
sin3 1
x
D.
2sin3 1
x
Câu 2. Tìm một phương trình hệ quả của phương trình
3 3
cos .sin3 sin cos3 sin 2
x x x x x
.
A.
3cos2 2
B.
3cos2 1
x
C.
sin 2 1
x
D.
3sin 2 1
x
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình
2
cos ( 2)cos 2 0
x m x m
có nghiệm ?
A. 3 B. 2 C. 1 D. 4
Câu 4. Tồn tại bao nhiêu số nguyên m để phương trình
2 2
sin (2 3)sin 3 0
x m x m m
có nghiệm ?
A. 3 B. 6 C. 5 D. 4
Câu 5. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
2 2
sin 3sin cos 2cos 0
x x x x
.
A. 4 B. 1 C. 2 D. 3
Câu 6. Tìm phương trình hệ quả của phương trình
2 2 2 2
cos cos 2 cos 3 cos 4 2
x x x x
.
A.
cos cos2 cos5 0
x x x
B.
cos sin 2 cos5 0
x x x
C.
sin cos cos3 0
x x x
D.
cos sin 2 cos5 0
x x x
Câu 7. Tính a + b biết
2
cos 2 cos2 1 0
a x b x
là một phương trình hệ quả của phương trình
cos cos4 cos 2 cos3 0
x x x x
A. 6 B. 5 C. 3 D. 2
Câu 8. Tính a + b biết
2
2 cos 2 cos2 1 0
a x b x
là một phương trình hệ quả của phương trình
cos cos4 cos 2 cos3 0
x x x x
A. 1 B. 0 C. 3 D. 2
Câu 9. Tính a + b biết
(sin cos ) sin cos 1 0
a x x b x x
là một phương trình hệ quả của phương trình
3
2cos cos2 sin 0
x x x
.
A. 5 B. 4 C. 3 D. 2
Câu 10. Tính a + b biết
2
cos 2 cos2 4 0
a x b x
là một phương trình hệ quả của
sin3 sin5
3 5
x x
.
A. 4 B. 2 C. 3 D. 5
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2 2
cos (1 cos ) sin (1 sin ) 2cos
x x x x x
.
A. 4 B. 3 C. 2 D. 1
Câu 12. Có bao nhiêu số nguyên m để phương trình
cos4 2( 3)cos2 6 1 0
x m x m
có nghiệm
0;
4
A. 2 B. 5 C. 3 D. 4
Câu 13. Tính a + b biết
sin 2 cos 7 0
a x b x
là một phương trình hệ quả của phương trình
9sin 6cos 3sin 2 cos2 8
x x x x
.
A. 5 B. 7 C. 6 D. 9
Câu 14. Tính a + b biết
(sin cos ) sin cos 1 0
a x x b x x
là một phương trình hệ quả của phương trình
2
2sin 3sin 1 cos3
x x x
.
A. 5 B. 3 C. 4 D. 2
Câu 15. Tập hợp
;
S a b
bao gồm tất cả các giá trị m để phương trình
sin5 sin
x m x
có nghiệm
x k
.
39
Tính giá trị của 4a + 2b.
A. 5 B. 2 C. 3 D. 4
Câu 16. Phương trình
2 2
sin 4 cos 6 sin 10,5 10
x x x
có bao nhiêu nghiệm thuộc
0;
2
?
A. 4 B. 5 C. 3 D. 2
Câu 17. Tính a + b biết
2
(cos sin ) (sin cos ) 0
x x a x x b
là một hệ quả của phương trình
2 2
cos 2 2(sin cos ) 3sin 2 3 0
x x x x
.
A. 5 B. 6 C. 4 D. 2
Câu 18. Tìm số nghiệm thuộc
0;3
của phương trình
4(sin3 cos2 ) 5(sin 1)
x x x
.
A. 6 B. 2 C. 3 D. 4
Câu 19. Tính tổng nghiệm nhỏ nhất và nghiệm lớn nhất trong khoảng
3 ;3
của phương trình
3
2sin cos2 cos 0
x x x
.
A.
2
B.
0,5
C.
0,25
D.
Câu 20. Tìm số nghiệm thuộc
100 ;100
của phương trình
6 6 8 8
sin cos 2(sin cos )
x x x x
.
A. 93 B. 56 C. 400 D. 201
Câu 21. Tìm số nghiệm thuộc
100 ;100
của phương trình
3 2
cos cos 2sin 2 0
x x x
.
A. 93 B. 56 C. 200 D. 201
Câu 22. Tồn tại bao nhiêu số nguyên m để phương trình
4 6
sin cos2 cos 0
x x m x
có nghiệm
0;
4
.
A. 2 B. 1 C. 0 D. 3
Câu 23. Tính a + b biết
;
S a b
gồm tất cả các giá trị m để phương trình sau có đúng hai nghiệm
2
0;
3
:
2
(cos 1)(cos2 cos ) sin
x x m x m x
.
A. – 1,5 B. 2 C. – 1 D. 3
Câu 24. Tìm số nghiệm thuộc
100 ;100
của phương trình sin 4 cos4 1 4 2 sin
4
x x x
.
A. 200 B. 198 C. 102 D. 93
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
(2sin 1)(2cos2 2sin 1) 3 4cos
x x x x
.
A. 5 B. 4 C. 6 D. 3
Câu 26. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
tan sin 1 tan .sin
x x x x
.
A. 5 B. 2 C. 3 D. 4
Câu 27. Tính tổng nghiệm lớn nhất và nghiệm nhỏ nhất thuộc
100 ;100
của phương trình
3 3
sin cos 1 0,5sin 2
x x x
.
A.
2
B.
0,5
C.
0,25
D. – 1,5
Câu 28. Tìm a + b biết
2
cos 2 cos2 0
a x b x
là một hệ quả của phương trình
tan tan3 2sin 2
x x x
.
A. 3 B. 4 C. 1 D. 2
Câu 29. Tìm số nghiệm thuộc
100 ;100
của phương trình
2(1 sin 2 ) 5(sin cos ) 3 0
x x x
.
A. 98 B. 190 C. 200 D. 152
_________________________________
40
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH TÍCH PHẦN 2)
___________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m để phương trình
2
cos (sin 2)cos (sin 2) 0
x x m x m x
có
nghiệm ?
A. 4 B. 2 C. 3 D. 5
Câu 2. Tìm số nghiệm
0;2
của phương trình
2 2
5 9
cos3 sin 7 2sin 2cos
4 2 2
x x
x x
.
A. 10 B. 7 C. 11 D. 5
Câu 3. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
4cos 2sin 3 cos2
x x x
.
A. 4 B. 2 C. 3 D. 5
Câu 4. Tính 4a + 9b biết
cos sin 6
a x b x
là một hệ quả của phương trình
4sin 2 3cos2 3(4sin 1)
x x x
.
A. 7 B. 3 C. 8 D. 6
Câu 5. Tính tổng các nghiệm thuộc
0;
của phương trình
2 2 2
sin cos 2 cos 3
x x x
.
A.
B.
4
3
C.
5
3
D.
2
Câu 6. Tính
cos4
khi
4 2
k
là một nghiệm của phương trình
2
sin 2 sin 6 3cos 2
x x x
.
A. 0,25 B. 0,125 C. – 0,125 D. – 0,5
Câu 7. Tính tổng các nghiệm của phương trình
2
(2cos 1)(2sin 2 1) 3 4sin
x x x
.
A. 1,5
B.
C. 2
D.
11
6
Câu 8. Tìm số nghiệm
0;2
của phương trình
tan 3cot 4(sin 3cos )
x x x x
.
A. 6 B. 5 C. 4 D. 3
Câu 9. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
2 2
sin cos4 2sin 2 4sin 3,5
4 2
x
x x x
.
A. 3 B. 4 C. 5 D. 2
Câu 10. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của
3sin cos 2 cos2 sin 2
x x x x
.
A. 5 B. 2 C. 4 D. 6
Câu 11. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
sin tan 2 3(sin 3 tan 2 ) 3 3
x x x x .
A. 3 B. 4 C. 5 D. 2
Câu 12. Phương trình
2
sin 2 (2sin cos ) 0
x m x x m
có nghiệm duy nhất khi
a
m
b
(a, b nguyên tố).
Tính a + b.
A. 7 B. 5 C. 10 D. 9
Câu 13. Phương trình
2sin cot 2sin 2 1
x x x
có phương trình hệ quả
(sin cos ) sin cos 0
a x x b x x
với a, b dương. Tính giá trị biểu thức a + b.
A. 4 B. 3 C. 2 D. 5
Câu 14. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
3 3
sin cos sin cos
x x x x
.
41
A. 6 B. 2 C. 1 D. 5
Câu 15. Phương trình
1 sin cos sin 2 2cos2 0
x x x x
có một hệ quả
cos sin 1 0
a x b x
với a, b
dương. Tìm 2a + b.
A. 7 B. 2 C. 6 D. 10
Câu 16. Tính abc biết phương trình
2 2
sin cos cos2 sin cos sin cos 0
x x x x x x x
tương đương
(sin cos )(sin )(cos ) 0
x a x x b x c
(a, b, c dương).
A. 2 B. 1 C. 3 D. 4
Câu 17. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của
3 3
sin 3sin 8cos 6cos
x x x x
.
A. 4 B. 1 C. 2 D. 3
Câu 18. Tồn tại bao nhiêu giá trị m để phương trình
2
sin (3 1)sin (2 1) 0
x m x m m
có nghiệm duy nhất.
A. 4 B. 1 C. 2 D. 3
Câu 19. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
2 2 2
sin 2sin 2sin sin cot 0
2 2
x x
x x x
.
A. 4 B. 2 C. 3 D. 5
Câu 20. Phương trình
1
sin 2 tan 1,5 cos2
2
x x x
tương đương
(sin 2 )(tan ) 0
x a x b
. Tính ab.
A. 1 B. 0,5 C. 0,25 D. 2
Câu 21. Tồn tại bao nhiêu số nguyên m để phương trình
sin 2 sin 2 4cos
x m x m x
có nghiệm ?
A. 4 B. 2 C. 5 D. 3
Câu 22. Phương trình
cos2 2cos 6sin 8
x x x
có một hệ quả
cos sin
x x a
, số ước của a là
A. 2 B. 4 C. 6 D. 8
Câu 23. Tìm số nghiệm
49;1993
của phương trình
cos2 3cos sin 2 0
x x x
.
A. 650 B. 542 C. 938 D. 1993
Câu 24. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của
sin 2 cos2 3sin cos 1
x x x x
A. 4 B. 2 C. 3 D. 5
Câu 25. Phương trình
sin 2 2cos2 1 sin 4cos
x x x x
có bao nhiêu nghiệm
49;1993
A. 193 B. 968 C. 702 D. 325
Câu 26. Phương trình
2sin 2 cos2 7sin 2cos 4
x x x x
tương đương phương trình
sin
x a
, khi đó
A.
1 1
;
5 4
a
B.
1 1
;
7 5
a
C.
1 1
;
4 3
a
D.
1
;1
3
a
Câu 27. Phương trình
sin3 cos3
2 sin
sin cos 4
x x
x
x x
có hệ quả
sin cos
x b x c
(b, c dương). Tính bc.
A. 0,25 B. 0,5 C. 1 D.
2
3
Câu 28. Tồn tại bao nhiêu số nguyên k để phương trình
4sin 2 cos cos3
x m x x
có nghiệm
0;
6
.
A. 5 B. 6 C. 3 D. 7
Câu 29. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của
3
4sin sin3 4cos cos
x x x x
.
A. 3 B. 2 C. 1 D. 4
Câu 30. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
sin3 cos3
1 sin 2
sin cos
x x
x
x x
.
A. 4 B. 2 C. 5 D. 1
42
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỐI XỨNG PHẦN 1)
___________________________________________
Câu 1. Phương trình
(2 2)(sin cos ) 2sin cos 2 2 1
x x x x
có bao nhiêu nghiệm
0;4
?
A. 2 B. 3 C. 4 D. 5
Câu 2. Phương trình
3(sin cos ) 2sin 2 3 0
x x x
có bao nhiêu nghiệm
0;4
?
A. 2 B. 4 C. 3 D. 5
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình
sin 2 3(sin cos ) 1
x x x m
có nghiệm ?
A. 4 B. 2 C. 9 D. 11
Câu 4. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
sin cos 4sin cos 1 0
x x x x
A. 3 B. 2 C. 1 D. 4
Câu 5. Phương trình
sin 2 12(sin cos ) 12 0
x x x
có phương trình hệ quả là
A.
sin cos 2
x x
B.
sin cos 1
x x
C.
sin cos 0
x x
D.
1
sin cos
2
x x
Câu 6. Phương trình
3 3
sin cos 1
x x
có bao nhiêu nghiệm
0;4
?
A. 2 B. 4 C. 3 D. 5
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình
3sin 2 4(sin cos )
x x x m
có nghiệm ?
A. 13 B. 12 C. 10 D. 11
Câu 8. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình
sin cos 4sin 2 1
x x x
.
A. 3 B. 4 C. 1 D. 2
Câu 9. Tìm một phương trình hệ quả của phương trình
cot tan sin cos
x x x x
.
A.
sin cos 1
x x
B.
1
sin cos
2
x x
C.
tan 1
x
D.
tan 1
x
Câu 10. Góc x thỏa mãn
1 1 10
cos sin
cos sin 3
x x
x x
thì cos
4
x
gần nhất với
A. – 0,55 B. – 0,25 C. 0,12 D. – 0,45
Câu 11. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
3 3
3
1 sin cos sin 2
2
x x x
.
A. 3 B. 4 C. 1 D. 2
Câu 12. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình
5 cos2 2(2 cos )(sin cos )
x x x x
.
A. 3 B. 2 C. 1 D. 4
Câu 13. Miền [a;b] gồm tất cả các giá trị m để phương trình sin 2 4(cos sin )
x x x m
có nghiệm. Tính a + b.
A. 1 B. 2 C. – 1 D. – 2
Câu 14. Tìm số nghiệm
0;4
của phương trình
sin cos sin cos 1
x x x x
.
A. 4 B. 3 C. 2 D. 1
Câu 15. Tìm số nghiệm
0;4
của phương trình
5sin 2 12 12(sin cos )
x x x
A. 5 B. 3 C. 4 D. 2
Câu 16. Tồn tại bao nhiêu số nguyên m để phương trình
sin cos 2(sin cos )
x x x x m
có nghiệm
0;
4
.
A. 2 B. 1 C. 3 D. 5
Câu 17. Tìm số nghiệm
0;4
của phương trình
cos sin sin cos 1
x x x x
.
43
A. 3 B. 4 C. 2 D. 5
Câu 18. Tìm số nghiệm
0;4
của phương trình
2 2
tan cot (tan cot ) 2 0
x x x x
.
A. 18 B. 14 C. 16 D. 15
Câu 19. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình
2 2
3(tan cot ) 4(tan cot ) 2 0
x x x x
.
A. 4 B. 3 C. 2 D. 1
Câu 20. Biết góc x thỏa mãn
sin 1 cos 1 1
x x
. Tính cos
4
x
.
A. 1 B.
1
2
C.
1
2
D. – 1
Câu 21. Tồn tại bao nhiêu số nguyên m để phương trình
sin cos 2 sin cos
x x x x m
có nghiệm
0;
4
.
A. 2 B. 1 C. 3 D. 5
Câu 22. Đặt
sin cos
x x t
thì phương trình
3 3
sin cos sin 2 1 ( ) 0
x x x P t
. Tính tổng các hệ số của
đa thức
( )
P t
A. 0 B. 2 C. 1 D. – 1
Câu 23. Đặt
sin cos
x x t
thì
3 2
2 sin3 cos3 sin cos 2 0
x x x x at bt ct
. Tính a – c.
A. 10 B. 6 C. 4 D. 2
Câu 24. Phương trình
1 1
2 (2 sin 2 ) tan cot 0
sin cos
x x x
x x
có một phương trình hệ quả là
A.
sin cos 1
x x
B.
1
sin cos
2
x x
C.
tan 1
x
D.
tan 1
x
Câu 25. Phương trình
3 3
tan cot tan cot 1
x x x x
có bao nhiêu nghiệm thuộc
0;4
?
A. Vô nghiệm B. 1 C. 4 D. 6
Câu 26. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
2 3 3
cot 2 cot tan 2
x x x
.
A. 3 B. 2 C. 4 D. 1
Câu 27. Tồn tại bao nhiêu số nguyên m để phương trình
2 2
tan cot tan cot
x x x x m
vô nghiệm ?
A. 3 B. 1 C. 2 D. 4
Câu 28. Tìm số nghiệm
0;4
của phương trình
3 3
1
tan cot 3
sin 2
x x
.
A. 3 B. 6 C. 4 D. 2
Câu 29. Tìm số nghiệm
0;6
của phương trình
3 tan 3 cot 4
x x
.
A. 3 B. 6 C. 4 D. 2
Câu 30. Tìm số nghiệm
0;6
của phương trình
3(tan cot ) 2(2 sin )
x x x
.
A. 6 B. 2 C. 3 D. 5
Câu 31. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình
3 3
sin cos 2(sin cos ) 1
x x x x
.
A. 1 B. 3 C. 2 D. 4
Câu 32. Tìm số nghiệm
0;6
của phương trình
2
2
2
2cot 5(tan cot ) 4 0
cos
x x x
A. 10 B. 12 C. 18 D. 14
44
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỐI XỨNG PHẦN 2)
___________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m để phương trình 4(sin cos ) 9sin cos
1993
m
x x x x có nghiệm
A. 31975 B. 21945 C. 20093 D. 31083
Câu 2. Tìm số nghiệm
0;6
của phương trình
sin cos sin cos 1
x x x x
.
A. 4 B. 6 C. 8 D. 12
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3(tan cot ) 2(2 sin 2 )
x x x
.
A. 3 B. 4 C. 2 D. 5
Câu 4. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của
6(sin cos ) sin cos 6 0
x x x x
A. 3 B. 2 C. 4 D. 1
Câu 5. Phương trình
sin3 cos3 2(sin cos ) 1
x x x x
có một hệ quả sin cos
x x a
. Số ước của a là
A. 2 B. 4 C. 1 D. 6
Câu 6. Tồn tại bao nhiêu số nguyên k để phương trình
2(sin cos ) 3sin cos 4
x x x x k
có nghiệm
A. 2 B. 1 C. 3 D. 4
Câu 7. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1 tan 2 2 sin
x x
.
A. 3 B. 2 C. 4 D. 5
Câu 8. Phương trình
3 3
sin cos sin cos 2
x x x x
đưa về đa thức
( ) 0
P t
với
sin cos
t x x
. Biết hệ số
cao nhất của
( )
P t
bằng 2, tính
(3)
P
.
A. 32 B. 18 C. 16 D. 20
Câu 9. Phương trình
cos sin 2sin cos 1
x x x x
có một hệ quả là
A.
cos sin 2
x x B.
cos sin 2
x x
C.
cos sin 1
x x
D.
1
cos sin
2
x x
Câu 10. Phương trình
2
3sin cos 3sin 2 8sin 1
x x x x
có một hệ quả là
6sin cos ( 2)
x b x a a
.
Tính giá trị biểu thức b – 2a.
A. 7 B. 6 C. 4 D. 5
Câu 11. Tồn tại bao nhiêu số nguyên dương m < 100 để phương trình
(sin cos ) sin 2 1 0
m x x x m
có
nghiệm
A. 3 B. 99 C. 80 D. 93
Câu 12. Biết rằng
3 3 3 2
sin cos sin 2 1 4 0
x x x at bt ct
với
sin cos
t x x
. Tính ab + c
A. – 1 B. 1 C. – 2 D. – 3
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
2
2
2tan 5tan 5cot 4 0
sin
x x x
x
.
A. 4 B. 3 C. 1 D. 2
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 3
sin cos 1
x x
A. 4 B. 2 C. 3 D. 1
Câu 15. Tồn tại bao nhiêu số nguyên m để phương trình
4(sin cos ) 9sin cos 1993
x x x x m
có nghiệm ?
A. 10 B. 16 C. 17 D. 7
Câu 16. Tồn tại bao nhiêu số nguyên m để phương trình
sin cos sin cos
x x x x m
có nghiệm
0;
4
45
A. 2 B. 1 C. 3 D. 4
Câu 17. Tính tổng các nghiệm của phương trình
sin cos sin cos 1
x x x x
trong khoảng
0;2
.
A.
B. 2
C. 3
D. 4
Câu 18. Tìm số nghiệm trong khoảng
0;2
của phương trình
3sin cos sin cos 3
x x x x
.
A. 3 B. 1 C. 0 D. 2
Câu 19. Tính
3 sin 2
khi
là nghiệm phương trình
sin cos 2(sin cos ) 2
x x x x
.
A. 3 B. 2 C. 3,5 D. 2,5
Câu 20. Tìm số nghiệm trong khoảng
0;2
của phương trình
sin cos 1 2sin cos2
x x x x
A. 2 B. 1 C. 3 D. 4
Câu 21. Điều kiện để phương trình
4(cos sin ) sin 2
x x x m
có nghiệm là
m a b c
. Tính abc.
A. 8 B. 10 C. 16 D. 4
Câu 22. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1 1 10
sin cos
sin cos 3
x x
x x
A. 4 B. 2 C. 3 D. 1
Câu 23. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 3 4 2 3 4
sin sin sin sin cos cos cos cos
x x x x x x x x
.
A. 4 B. 2 C. 1 D. 3
Câu 24. Tồn tại bao nhiêu số nguyên m để phương trình
2cos2 (sin cos )(sin cos ) 0
x x x m x x
có
nghiệm
0;
2
.
A. 4 B. 3 C. 5 D. 2
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
(tan 7)cot (cot 7) tan 14 0
x x x x
.
A. 4 B. 2 C. 3 D. 5
Câu 26. Tồn tại bao nhiêu số nguyên
93;93
m
để phương trình sau có nghiệm
2 2
tan cot (tan cot ) 2 0
x x m x x m
.
A. 180 B. 100 C. 69 D. 93
Câu 27. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 2 3 2
tan tan tan cot cot cot 6
x x x x x x
.
A. 4 B. 5 C. 3 D. 2
Câu 28. Tồn tại bao nhiêu số nguyên m
10;10
để phương trình sau có nghiệm
3 3
tan tan ( cot ) cot
x x m x m x
.
A. 3 B. 12 C. 16 D. 18
Câu 29. Tồn tại bao nhiêu số nguyên m để phương trình sau có nghiệm
sin cos 7sin cos
x x x x m
.
A. 6 B. 5 C. 4 D. 8
Câu 30. Có bao nhiêu số nguyên m để phương trình
(1 cos )(1 sin )
x x m
có đúng một nghiệm
0;
2
A. 2 B. 1 C. 3 D. 4
Câu 31. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 3
3
1 sin 2 cos 2 sin 4
2
x x x
.
A. 5 B. 4 C. 3 D. 2
46
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỒNG BẬC PHẦN 1)
___________________________________________
Câu 1. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
2cos 5sin cos 3sin 0
x x x x
.
A. 4 B. 5 C. 3 D. 6
Câu 2. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
2cos 4sin cos 4sin 1
x x x x
.
A. 4 B. 5 C. 3 D. 6
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
2cos 3 3 sin cos 4sin 4
x x x x
.
A. 4 B. 5 C. 3 D. 6
Câu 4. Tìm số nghiệm thuộc
0;3
của phương trình
2
sin 3sin cos 1
x x x
.
A. 5 B. 6 C. 2 D. 4
Câu 5. Nghiệm dương nhỏ nhất của phương trình
3
2 sin 2sin
4
x x
thuộc khoảng
A.
1
0;
2
B. (1;2) C. (2;3) D.
1
;1
2
Câu 6. Tìm số nghiệm thuộc
0;3
của phương trình
3
cos 2sin
x x
.
A. 5 B. 3 C. 2 D. 4
Câu 7. Nghiệm dương nhỏ nhất của phương trình
sin 2 2tan 3
x x
thuộc khoảng
A.
1
0;
2
B. (1;2) C. (2;3) D.
1
;1
2
Câu 8. Tìm số nghiệm thuộc
0;3
của phương trình
3
sin 2cos
x x
.
A. 5 B. 3 C. 2 D. 4
Câu 9. Tính b + c biết rằng phương trình
2
1 3sin 2 2tan (tan 1)(2 tan tan ) 0
x x x x b x c
.
A. 5 B. 4 C. 2 D. 3
Câu 10. Tìm số nghiệm thuộc
0;3
của phương trình
4 2 2 4
3cos 4sin cos sin 0
x x x x
A. 12 B. 16 C. 10 D. 8
Câu 11. Phương trình
2 2
8sin cos 2sin 4 3 3cos 4
x x x x
tương đương
(tan 2 )(tan 2 ) 0
x a x b
. Tính
giá trị biểu thức a + b + 2.
A. 2 B. 6 C. 3 D. 1
Câu 12. Tìm số nghiệm thuộc
0;3
của phương trình
2 2
tan sin 2sin 3(cos2 sin cos )
x x x x x x
.
A. 12 B. 16 C. 10 D. 8
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
7cos 4cos 4sin 2
x x x
.
A. 4 B. 5 C. 3 D. 6
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 2 3
cos 2sin cos 3sin 0
x x x x
.
A. 2 B. 5 C. 3 D. 4
Câu 15. Tồn tại bao nhiêu giá trị nguyên m để phương trình
2 2
3sin sin 2 4cos 0
x m x x
có nghiệm.
A. Vô số B. 12 C. 20 D. 15
47
Câu 16. Tồn tại bao nhiêu giá trị nguyên m để phương trình
2 2
sin ( 1)sin 2 ( 1)cos
x m x m x m
có
nghiệm
A. 5 B. 4 C. 3 D. 2
Câu 17. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
4sin 3 2 sin 2 8sin
x x x
.
A. 3 B. 5 C. 2 D. 4
Câu 18. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
sin (1 tan ) 3 3sin (cos sin )
x x x x x
.
A. 4 B. 3 C. 6 D. 5
Câu 19. Nghiệm dương nhỏ nhất của phương trình
3 3 2 2
sin 3 cos sin cos 3 sin cos
x x x x x x
thuộc
khoảng nào sau đây
A. (2;3) B. (1;2) C. (3;4) D. (0;1)
Câu 20. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
4 3 sin cos 4cos 2sin 2,5
x x x x
.
A. 4 B. 3 C. 6 D. 5
Câu 21. Phương trình
(1 tan )(1 sin 2 ) 1 tan
x x x
tương đương
(tan )(tan ) 0
x a x b
. Tính a + b.
A. – 1 B. 1 C. 0 D. 2
Câu 22. Tập hợp [a;b] gồm tất cả các giá trị a để phương trình
2 2
1
sin sin 2 2cos
2
x x x a
có nghiệm. Tính
giá trị biểu thức b – a.
A. 6 B.
10
C.
7
D.
2 5
Câu 23. Tính a + b + c biết rằng phương trình
3 3 2
4sin 3cos 3sin sin cos 0
x x x x x
tương đương
(tan )(tan )(tan ) 0
x a x b x c
.
A. 3 B. 1 C. 0 D. 2
Câu 24. Tính a + b biết rằng
3
sin sin 2 sin3 6cos
x x x x
tương đương
2
(tan )(tan ) 0
x a x b
A. 5 B. 4 C. 3 D. 2
Câu 25. Biết rằng
3
2cos 4sin ( ) 0
cos
x x P t
x
(đa thức hệ số nguyên) trong đó
tan
t x
. Tổng các hệ
số nguyên của đa thức
( ) 0
P t
là
A. 4 B. 0 C. 1 D. 2
Câu 26. Phương trình
sin cos2 6cos (1 2cos2 )
x x x x
tương đương
( ) 0
P t
với
tan
t x
. Tổng các nghiệm
của đa thức của đa thức
( ) 0
P t
là
A. 7 B. 6 C. 5 D. 8
Câu 27. Tìm số nghiệm thuộc
0;3
của phương trình
3
sin sin 2 sin3 6cos
x x x x
.
A. 5 B. 9 C. 12 D. 10
Câu 28. Tồn tại bao nhiêu số nguyên
7;7
m
để phương trình sau có nghiệm thuộc khoảng
0;
4
.
2 2
3sin (2 1)sin 2 ( 1)cos
x m x m x m
A. 10 B. 11 C. 13 D. 8
Câu 29. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của
sin3 cos3 2cos 0
x x x
.
A. 5 B. 4 C. 3 D. 6
_________________________________
48
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỒNG BẬC PHẦN 2)
___________________________________________
Câu 1. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 3 2
4sin 3cos 3sin sin cos 0
x x x x x
.
A. 3 B. 2 C. 4 D. 1
Câu 2. Nghiệm dương nhỏ nhất của phương trình
2
cos2 1
cot 1 sin sin 2
1 tan 2
x
x x x
thuộc khoảng
A.
1
0;
2
B. (1;2) C. (2;3) D.
1
;1
2
Câu 3. Phương trình
3 3 2
cos 4sin 3sin cos sin 0
x x x x x
tương đương với phương trình nào ?
A.
3 2
3 3 1 0; tan
t t t t x
B.
3 2
3 3 2 2 0; tan
t t t t x
C.
3 2
5 5 1 0; tan
t t t t x
D.
3 2
3 3 1 0; tan
t t t t x
.
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình
2 2
2sin (2 1)sin cos cos 0
x m x x m x
có 4 điểm
biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. Vô số C. 5 D. 10
Câu 4. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
2 2 cos ( ) 3cos sin 0
4
x x x
.
A. 3 B. 2 C. 4 D. 1
Câu 5. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 3
4(sin cos ) cos 3sin
x x x x
.
A. 3 B. 2 C. 6 D. 4
Câu 6. Phương trình
3
sin 2 sin
4
x x
có nghiệm
. Tính
3
2
(tan 1)
tan 1
.
A. 4 B. 2 C. 3 D. 5
Câu 7. Tồn tại bao nhiêu số nguyên m < 10 để phương trình
2 2
sin 2sin cos ( 1)cos
x x x m x
có nghiệm
A. 8 B. 12 C. 10 D. 8
Câu 8. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 2
sin 3cos 3sin cos 2sin
x x x x x
.
A. 3 B. 5 C. 2 D. 4
Câu 9. Tìm số nghiệm
(0;1993 )
của phương trình
sin cos cos3
x x x
.
A. 6230 B. 5977 C. 1288 D. 1394
Câu 10. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
sin3 cos sin cos
x x x x
.
A. 3 B. 2 C. 6 D. 4
Câu 11. Tìm số nghiệm
(0;1993 )
của phương trình
cos2 cos cos sin
x x x x
.
A. 3986 B. 3987 C. 3985 D. 2000
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
cos2 sin cos cos sin
x x x x x
A. 3 B. 4 C. 2 D. 5
Câu 13. Phương trình
2sin 3 cos
6
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
49
A. 4 B. 6 C. 2 D. 1
Câu 14. Tìm số nghiệm
0;5
của phương trình
2cos sin 2 sin cos
6
x x x x
A. 10 B. 15 C. 16 D. 20
Câu 15. Tồn tại bao nhiêu số nguyên m < 15 để phương trình
2 2
sin 4sin cos (4 )cos 0
x x x m x
có hai
nghiệm phân biệt thuộc
3
;
2
?
A. 6 B. 4 C. 3 D. 7
Câu 16. Tồn tại bao nhiêu số nguyên m để phương trình
2 2
sin ( 2)sin cos 2 cos 0
x m x x m x
có 4 điểm
biểu diễn nghiệm trên vòng tròn lượng giác ?
A. Vô số B. 2 C. 4 D. 6
Câu 17. Phương trình
4cos sin 2 cos
3 6
x x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn
lượng giác ?
A. 4 B. 6 C. 2 D. 1
Câu 18. Phương trình
2cos 3 cos 2sin
3
x x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn
lượng giác ?
A. 4 B. 6 C. 2 D. 1
Câu 19. Tồn tại bao nhiêu số nguyên m lớn hơn – 30 để phương trình sau có nghiệm thuộc
;
2
?
2 2
sin ( 4)sin cos 4 cos 0
x m x x m x
A. 29 B. 21 C. 40 D. 6
Câu 20. Phương trình
3
8sin cos
6
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 4 B. 6 C. 2 D. 1
Câu 21. Bao nhiêu số nguyên m < 15 để
2 2
sin 3sin cos (2 )cos 0
x x x m x
có nghiệm thuộc
;
2
?
A. 6 B. 13 C. 18 D. 7
Câu 22. Tồn tại bao nhiêu số nguyên m nhỏ hơn 10 để phương trình sau có nghiệm thuộc
3
;
2
?
2 2
sin ( 5)sin cos 5 cos 0
x m x x m x
A. 9 B. 25 C. 6 D. 4
Câu 23. Tồn tại bao nhiêu số nguyên m < 17 để phương trình
2 2
2sin 3sin cos (4 3 )cos 0
x x x m x
có hai
nghiệm phân biệt thuộc
;0
2
?
A. 4 B. 1 C. 3 D. 2
Câu 24. Tồn tại bao nhiêu số nguyên m lớn hơn – 7 để phương trình sau có nghiệm thuộc
;0
2
?
3 3
sin sin cos ( cos )
x x m x m x
A. 4 B. 6 C. 3 D. 10
_________________________________
50
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 1)
_______________________________________________________
Câu 1. Giả sử
sin
;cos ;tan
6
theo thứ tự lập thành một cấp số nhân. Tính
cos2
.
A.
3
2
B.
3
2
C.
1
2
D.
1
2
Câu 2. Tìm điều kiện tham số m để hàm số
2cos2 3cos
y x x m
xác định với mọi x.
A.
41
16
m
B.
41
8
m
C.
1
2
m
D.
11
23
m
Câu 3. Tồn tại bao nhiêu số nguyên m nhỏ hơn 2018 để
2 2
cos 4 sin 4 3sin8
x x x m
với mọi x.
A. 2016 B. 2015 C. 2014 D. 2018
Câu 4. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để
1
2sin3 2cos3
y
x x m
xác định với mọi x.
A. 7 B. 2 C. 6 D. 10
Câu 5. Hàm số
2cos 3sin 5
2sin 3cos 5
x x
y
x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính Q = M.N.
A. Q = 1 B. Q = 2 C. Q = 5 D. Q = 10
Câu 6. Ký hiệu S là tập giá trị của hàm số
sin cos
2sin cos 3
x x
y
x x
. Độ dài của S trên trục số bằng
A. 4 B. 2 C. 1 D. 1,5
Câu 7. Tồn tại bao nhiêu số nguyên m thuộc khoảng (– 27;27) sao cho
3 3
4cos 3cos 2 3sin 4sin
x x x x m
với mọi x.
A. 29 B. 35 C. 48 D. 24
Câu 8. Hàm số
cos 2
cos sin 2
x
y
x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào sau đây đúng ?
A. M + N = 3 B. M – N = 4 C. 2M + N = 6 D. M hữu tỷ.
Câu 9. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin 2cos 1
sin cos 2
x x
y
x x
trên
.
A.
1 2
B. 0 C. 1 D. – 1
Câu 10. Biểu thức
sin cos
2sin cos 3
x x
y
x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 3 B. 2 C. 6 D. 4
Câu 11. Tồn tại bao nhiêu số nguyên m nhỏ hơn 30 để hàm số
sin 6
sin 2 6
x
f x
x m
xác định trên
?
A. 10 B. ``9 C. 8 D. 29
Câu 12. Hàm số
2sin 2 cos2
sin 2 cos 2 3
x x
y
x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 4 B. 2 C. 3 D. 1
Câu 13. Tồn tại bao nhiêu số nguyên m lớn hơn – 2001 để hàm số
sin cos sin cos 2
2sin
x x x x
f x
x m
xác
định trên
;

?
A. 2017 B. 1999 C. 1998 D. 2002
51
Câu 16. Cho hàm số
4 4
2018
cos sin 3sin 2
f x
x x x m
. Tồn tại tất cả bao nhiêu số nguyên m trong khoảng
(– 40;40) để hàm số xác định với mọi giá trị x.
A. 20 B. 40 C. 72 D. 58
Câu 17. Tồn tại bao nhiêu số nguyên k lớn hơn – 13 thỏa mãn
4 4
2 2
sin cos 2
0,
cos sin 4sin 2
x x
x
x x x k
.
A. 30 B. 10 C. 14 D. 8
Câu 19. Tồn tại bao nhiêu số nguyên p sao cho
3
1,
sin cos
x
x x p
?
A. 3 B. 4 C. 0 D. 1
Câu 20. Tồn tại bao nhiêu số nguyên p sao cho
17
1,
sin cos
x
x x p
?
A. 13 B. 14 C. 10 D. 13
Câu 21. Cho hàm số
3
2
3sin 4sin 5cos3
x m
y
x x x m
. Tồn tại tất cả bao nhiêu số nguyên m nằm trong
khoảng (– 20;20) để hàm số xác định với mọi giá trị x.
A. 4 B. 12 C. 7 D. 28
Câu 22. Tính tổng tất cả các giá trị nguyên của hàm số
3sin cos 4
2sin cos 3
x x
y
x x
.
A. 8 B. 5 C. 6 D. 9
Câu 23. Tìm a để hàm số
3
2cos2 sin 1
2
f x x x a
đạt giá trị nhỏ nhất bằng 4.
A. a = 3 B. a = 2 C. a = 1 D. a =
47
16
Câu 24. Gọi n là số nguyên thỏa mãn
1 tan1 1 tan 2 1 tan3 ... 1 tan 45 2
n
. Khi đó
A.
n
[1;7] B.
n
[8;19] C.
n
[20;26] D.
n
[27;33]
Câu 25. Có bao nhiêu giá trị
0;2
để hai tập hợp sau trùng nhau
sin ,sin 2 ,sin3 ; cos ,cos2 ,cos3
S T
.
A. 1 B. 2 C. 3 D. 4
Câu 26. Tìm giá trị lớn nhất của hàm số
2 2
cos2 sin 3sin 4
2
x
y x x
trên
3
;
2 2
.
A. 5,5 B. 5 C.
89
16
D. 4
Câu 27. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 100 sao cho
2
3
4sin 3sin 6sin3 cos3 ,x x x x m x
.
A. 75 B. 60 C. 81 D. 97
Câu 28. Gọi M là tập giá trị của hàm số
2
2sin 3cos 4 2sin 3cos 5
S x x x x
. Tập hợp M chứa bao
nhiêu giá trị nguyên ?
A. 2 B. 3 C. 4 D. 1
Câu 29. Đồ thị của hàm số nào sau đây đối xứng qua trục tung ?
A.
2
1
sin
y
x
B.
sin 45
y x
C.
2 cos 45
y x
D.
sin 2
y x
__________________________________
52
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 2)
_______________________________________________________
Câu 1. Hàm số
2sin
6 4
y x
tuần hoàn với chu kỳ bao nhiêu ?
A. 24 B. 30 C. 4 D. 6
Câu 2. Tính tổng các giá trị a xảy ra để hàm số
cos sin 1
cos 2
x a x
y
x
có giá trị lớn nhất bằng 1 ?
A. 3 B. 0 C. 1 D. 2
Câu 3. Tìm giá trị lớn nhất của hàm số
13
sin 10cos
y x x
.
A. 11 B. 10 C. 9 D. 8,5
Câu 4. Hàm số
2sin 2 cos 2
sin 2 cos2 3
x x
y
x x
có thể nhận tất cả bao nhiêu giá trị nguyên ?
A. 1 B. 2 C. 3 D. 4
Câu 5. Hàm số
2
2018cos 5
5
x
y
tuần hoàn với chu kỳ bao nhiêu ?
A. 7 B. 10 C. 20 D. 5
Câu 6. Có bao nhiêu số nguyên m để hàm số
1 sin
2 cos
m x
g x
x
có giá trị nhỏ nhất M mà M < – 2 ?
A. 6 B. 7 C. 4 D. 5
Câu 7. Có bao nhiêu số thực m
4
sin cos 2
y x x m
có giá trị nhỏ nhất bằng 2 ?
A. 3 B. 2 C. 1 D. 4
Câu 8. Giá trị nhỏ nhất của hàm số
4 4
sin cos sin cos
y x x x x
là
A. 1,125 B. 1,25 C. 1 D. 2,25
Câu 9. Cho , , 0;
2
x y z x y z
. Tìm giá trị lớn nhất của biểu thức
1 tan tan 1 tan tan 1 tan tan
y x y z y x z
.
A.
1 2 2
B.
3 3
C. 2 D.
2 3
Câu 10. Giá trị lớn nhất của hàm số
2cos sin
4
y x x
là
A.
5 2 2
B.
5 2 2
C.
5 2 2
D.
5 2 2
Câu 11. Tìm giá trị nhỏ nhất của hàm số
2
2
1 tan 3
4cot 2
tan
x
y x
x
.
A. 0 B.
3 2 3
C.
2 2 2
D. – 1
Câu 12. Giá trị lớn nhất của hàm số
2 2
2 2
sin cos 1
1 1
x x
f x
x x
gần nhất với số nào
A. – 1 B. 2 C. – 0,25 D. – 0,125
Câu 13. Số giờ có ánh sáng của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số
lượng giác là
4 sin 60 10
178
y t
, với t là số nguyên và
0;365
t . Vào ngày nào trong năm thì thành
phố A có nhiều giờ ánh sáng mặt trời nhất ?
A. 28 tháng 5 B. 29 tháng 5 C. 30 tháng 5 D. 31 tháng 5
Câu 14. Cho
, 0;
2
x y
và
cos2 cos2 2sin( ) 2
x y x y
. Tìm giá trị nhỏ nhất của
4 4
sin cos
x y
P
x y
.
53
A.
3
B.
2
C.
2
3
D.
5
Câu 15. Tìm độ dài tập giá trị W của hàm số
sin cos cos sin
S x x x x
.
A. 2 B.
4
2
C.
2
D.
2 2
Câu 16. Tìm a để hàm số
2
2cos
5 3
ax
y
tuần hoàn với chu kỳ
5
.
A. a = 3 B. a = 4 C. a = 2 D. a = 6
Câu 17. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 2
5sin 1 5cos 1
y x x
.
A. 6 B. 1 +
2 2
C.
1 6 14
D.
2 3 15
Câu 18. Tìm giá trị lớn nhất của hàm số
2 2
1 1
cos 5 2sin
2 2
y x x
.
A.
5
1
2
B.
22
2
C.
11
2
D.
1 5
Câu 19. Cho hai số thực dương x, y thỏa mãn
cos( 1) 3 cos(3 ) 9 3 3
x y xy xy x y
. Giá trị nhỏ nhất
của biểu thức
( 2)
x y
gần nhất với
A. 2,39 B. 5,16 C. 4,23 D. 1,87
Câu 20. Cho hai số dương a, b thỏa mãn
sin(2 2 ) sin( ) 2 2
ab a b ab a b
. Giá trị nhỏ nhất của biểu
thức S = a + 2b là
A.
2 10 3
2
B.
10 3
2
C.
3 10 7
2
D.
2 10 3
5
Câu 21. Hàm số f (x) xác định trên R, thỏa mãn
1
tan sin 2 cos 2
2
f x x x
với
;
2 2
x
. Với a, b là hai số
thực thỏa mãn a + b = 1, tìm giá trị nhỏ nhất của S = f (a). f (b).
A.
1
25
B.
5 3 5
2
C.
5 3 5
2
D.
5 3 5
2
Câu 22. Cho x, y là hai số thực thỏa mãn cos2x + cos2y = 1. Tìm giá trị nhỏ nhất của biểu thức
2 2
tan tan
x y
.
A.
1
3
B.
2
3
C.
8
3
D. 3
Câu 23. Số giờ có ánh sáng của một thành phố X ở vĩ độ 40 độ Bắc trong ngày thứ t của một năm không nhuận
được cho bởi hàm số
3sin 80 12
182
d t t
, t nguyên và
0 365
t
. Vào ngày nào trong năm thì thành
phố X có nhiều giờ ánh sáng nhất ?
A. 262 B. 353 C. 80 D. 171
Câu 24. Hàm số
sin tan
4 6
x x
f x
có chu kỳ tuần hoàn nhỏ nhất là
A. 10
B. 24
C. 8
D. 14
Câu 25. Tìm giá trị lớn nhất của biểu thức
sin 1 3 sin
y x x
.
A. 4 B.
2 2
C.
3 2
D.
2 5
Câu 26. Tìm giá trị tham số m để hàm số ( ) cos 4 cos
f x x x m
có giá trị lớn nhất bằng
3 2
.
A. m = 3 B. m = 2 C.
2
m D.
2 2
m
Câu 27. Tìm giá trị nhỏ nhất của biểu thức
1 1
( ) ; 0;
2 cos 1 cos 2
f x x
x x
.
A. 1 B. 0,5 C.
4
3
D.
2
3
54
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 3)
_______________________________________________________
Câu 1. Tìm giá trị nhỏ nhất của
2
sin 1
cos (sin cos ) 4
x
y
x x x
với
;
4 2
x
.
A. 4 B. 4,25 C. 5 D. 5,25
Câu 2. Tìm giá trị lớn nhất của hàm số
5
sin 3 cos
y x x
A. 1 B. 2 C.
3
D.
2 3
Câu 3. Tính tổng giá trị lớn nhất, giá trị nhỏ nhât của hàm số
2
( ) sin 3sin 2
f x x x
.
A. 5 B. 6 C. 4 D. 2
Câu 4. Tồn tại bao nhiêu số nguyên x thuộc (0;100) để hàm số
3
4
sin 4 9
9
y x x x
đồng biến
A. 45 B. 30 C. 48 D. 36
Câu 5. Tìm điều kiện tham số m để bất phương trình
2
3sin 2 cos2
1
sin 2 4cos 1
x x
m
x x
đúng với mọi x.
A.
3 5
4
m B.
3 5 9
4
m
C.
65 9
4
m
D.
65 9
2
m
Câu 6. Tìm số tự tự nhiên n để tập giá trị của hàm số
1993sin cos cos2 cos4 ...cos( )
y x x x x nx
chứa 125 số
nguyên
A. n = 5 B. n = 6 C. n = 7 D. n = 4
Câu 7. Cho hai góc
, 0;
x y
thỏa mãn
3
x y
. Giá trị lớn nhất của
sin sin
x y
là
A. 1 B. 0,5 C. 0,75 D. 1,5
Câu 8. Cho tam giác ABC. Tìm giá trị lớn nhất của
cos2 cos 2 cos2
A B C
A. 1 B. 1,5 C. 2 D. 1,75
Câu 9. Cho hàm số
2
( ) 2
f x x x
. Tồn tại bao nhiêu số tự nhiên m để
sin cos 1
sin cos 3 49
x x m
f
x x
với mọi
x.
A. 130 B. 142 C. 143 D. 126
Câu 10. Tìm m để giá trị lớn nhất của hàm số
2
cos cos
y x x m
đạt giá trị nhỏ nhất.
A.
7
8
m
B. m = 2 C. m = 0 D.
3
8
m
Câu 11. Cho tam giác ABC. Tìm giá trị nhỏ nhất của biểu thức
2 2
sin sin sin
2 2 2
A B C
F
.
A. 1 B.
1
3
C.
1
27
D.
1
12
Câu 12. Có bao nhiêu số nguyên
10;10
m
để giá trị nhỏ nhất của hàm số
2
cos cos
y x x m
không
vượt quá 2.
A. 16 B. 5 C. 6 D. 7
Câu 13. Tổng giá trị lớn nhất và giá trị nhỏ nhất hàm số
2 2
2 4
cos cos 1
1 1
x x
y
x x
gần nhất với
A. 5 B. 4 C. 6 D. 7
Câu 14. Tìm giá trị nhỏ nhất của biểu thức
2 2
cos 2cos 5 cos 4cos 5
P x x x x
.
55
A. 4 B. 5 C. 2 D. 3
Câu 15. Tìm chu kỳ của hàm số
2
cos sin
2
x
y x
A. 3
B. 0,5
C.
D. 2
Câu 16. Cho tam giác ABC. Tập giá trị của hàm số
( , , ) sin sin sin sin sin sin
f A B C A B C A B C
.
A. (0;2) B. (1;2) C. (0;1) D. (2;3)
Câu 17. Cho tam giác ABC. Giá trị lớn nhất của
cos cos cos
2 2 2
A B C
H
gần nhất với số nào sau đây
A. 0,93 B. 0,77 C. 0,64 D. 0,52
Câu 18. Cho hàm số
( ) : (cot ) sin 2 cos2
f x f x x x
. Tìm giá trị lớn nhất của hàm số
2 2
(sin ). (cos )
f x f x
.
A.
6
125
B.
1
20
C.
19
500
D.
1
25
Câu 19. Tồn tại bao nhiêu số nguyên
2
m
sao cho giá trị lớn nhất hàm số sau nhỏ hơn 1993
4 4
sin cos sin cos
y x x m x x
.
A. 2020 B. 7964 C. 6930 D. 1945
Câu 20. Ký hiệu M là giá trị nhỏ nhất của
4 4 2
1 sin cos 2cos 2
y x x x
. Số ước dương của số tự
nhiên
6
M
khi đó là
A. 10 B. 12 C. 6 D. 16
Câu 21. Tìm giá trị nhỏ nhất của biểu thức
2
cos
2
x
P x
.
A. 2 B. 1 C. 1,5 D. 0,5
Câu 22. Tìm giá trị lớn nhất của biểu thức
(tan cot )(tan 2 cot 2 2)
Q x x x x
.
A. 1,5 B. 1 C. 0 D. – 1
Câu 23. Tìm điều kiện tham số a để
4 2 2
3cos 5cos3 36sin 15cos 36 24 12 0
x x x x a a
với mọi x.
A. 0 < a < 2 B. 1 < a < 2 C. 2 < a < 3 D. 0 < a < 1
Câu 24. Tìm chu kỳ của hàm số
3
8 20
3sin 4cos
9 10 27 20
x x
y
.
A. 14,5
B. 27
C.
3
3
D.
3
3
2
Câu 25. Giá trị nhỏ nhất của hàm số
1 2cos 1 2sin
y x x
gần nhất với
A. 1,65 B. 1,93 C. 2,13 D. 1,26
Câu 26. Tồn tại bao nhiêu số nguyên m lớn hơn – 7 để
2
3sin 0,5sin 2
x x m
đúng với mọi x
A. 5 B. 9 C. 6 D. 5
Câu 27. Tìm giá trị nhỏ nhất của biểu thức
4 4 4 2 2 4
9
sin (sin cos cos .sin 2 ) cos
8
P x y y x y x
.
A. 1 B. 0,5 C. 0,75 D. 0,25
Câu 28. Tồn tại bao nhiêu số nguyên
30;30
m
để giá trị lớn nhất của hàm số sau không lớn hơn 2
4 4
2(sin cos ) sin cos cos2
y x x m x x x
.
A. 4 B. 2 C. 5 D. 1
_________________________________
56
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 4)
_______________________________________________________
Câu 1. Tìm giá trị nhỏ nhất của biểu thức
cos sin
P x x
.
A. 1 B. 2 C. 0,5 D.
1
2
Câu 2. Tìm chu kỳ của hàm số
3 2
sin 3 2sin 2
y x x
.
A.
B. 2
C. 4
D. 0,5
Câu 3. Tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
cos sin
cos 1
x x
y
x
gần nhất với
A. 1,22 B. 1,42 C. 1,56 D. 1,78
Câu 4. Cho hàm số
2 2
( ) cos( ) cos( ( 2 1))
f x x x x
. Tìm x dương nhỏ nhất sao cho
( ) 0
f x
A.
3 1
2
x
B.
3 1
2
x
C.
3 2
2
x
D.
2 3
2
x
Câu 5. Tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1 2cos3 1 2sin3
y x x
gần nhất với
A. 1,56 B. 3,53 C. 2,72 D. 2,34
Câu 6. M là giao điểm của đường thẳng
3
x
y
và đồ thị hàm số
sin
y x
. Khoảng cách OM lớn nhất bằng
A. 3 B.
5
C.
10
D.
3 3
Câu 7. Đồ thị hàm số
5 3 4 2
(16sin 20sin 5sin )(16sin 5 20sin 5 5)
y x x x x x
tiếp xúc với đường thẳng
nào
A. y = 0,5 B. y = 1 C. y = 0,25 D.
2
y
Câu 8. Tìm tất cả các khoảng nghịch biến của hàm số
sin
y x
trên miền
0;2
.
A.
;2
B.
;
2
và
3
;2
2
C.
3
;
2 2
D.
0;
Câu 9. Hai hàm số
sin ; sin3
y x y x
cùng đồng biến trên khoảng nào dưới đây
A.
;
6 3
B.
;
3 2
C.
11
;2
6
D.
2
;
2 3
Câu 10. Tìm số thực k nhỏ nhất sao cho
2 2
cos cos cos( )
x y xy k
với mọi x.
A. k = 2 B. k = 3 C. k = 4 D. k = 1
Câu 11. Xác định số nghiệm thực phương trình
1978sin 197
x x
.
A. 1265 B. 1288 C. 1979 D. 1285
Câu 12. Tìm giá trị nhỏ nhất của biểu thức
2 sin
sin cos
3 cos
x
P x x
x
A. 0,5 B. 0 C. 0,25 D. 0,75
Câu 13. Ký hiệu M là giá trị lớn nhất của biểu thức
sin cos
2sin cos 3
x x
m
x x
. Giá trị nhỏ nhất của M là
A. 0,75 B. 0,5 C. 0,25 D. 1,25
Câu 14. Cho
2
2
x x
. Tìm số thực k lớn nhất sao cho
2
2
2cos sin 2
sin cos2
x x
k
x x
với mọi x.
A. k = 16 B. k = 10 C. k = 13 D. k = 12
Câu 15. Tồn tại bao nhiêu số nguyên k sao cho
2
sin cos 3 2 ,x x k k x
.
57
A. 2 B. 3 C. 1 D. 4
Câu 16. Đồ thị hàm số
( 2)
y f x
có đồ thị như hình
vẽ bên. Giá trị
(491993)
f
gần nhất giá trị nào
A. 0,045 B. 0,042
C. 0,048 D. 0,068
Câu 17. Đồ thị hàm số
2 2
2sin 2cos cos2
6
y x x x
luôn nằm phía trên đường thẳng nào sau đây
A. y = 0,26 B. y = 0,28 C. y = 1 D. 0,32
Câu 18. Tìm giá trị nhỏ nhất của biểu thức
2
( ) sin sin
3
f x x x
.
A. – 1 B. 0 C. – 2 D.
3
2
Câu 19. Cho hai số thực x, y thỏa mãn 0
4
x
và
3
4
x y
. Tính
(1 tan )(1 tan )
x y
.
A. 2 B. 1 C.
1
2
D.
3
2
Câu 20. Giả sử giá vé máy bay của hãng hàng không X trong tháng t là
( ) 110 2 15sin
6
t
s t t
với t là số
nguyên
1;12
, đơn vị nghìn USD. Tháng có giá vé cao nhất là
A. 12 B. 4 C. 3 D. 11
Câu 21. Hai điểm A, B thuộc đồ thị hàm số
sin
y x
như
hình vẽ. Các điểm C, D lần lượt là hình chiếu vuông góc
của A, B trên trục hoành sao cho
2
3
CD
. Tính BC.
A.
2
2
B. 0,5 C. 1 D.
3
2
Câu 22. Đồ thị hàm số ( ) cos 3sin
6 3
f x x x
tiếp xúc với đường thẳng nào sau đây
A. y = 2 B.
7
y
C.
7
2
y D.
3 2
y
Câu 23. Tồn tại bao nhiêu số nguyên n để hàm số
5
cos( )sin
x
y nx
n
tuần hoàn với chu kỳ
3
A. 6 B. 8 C. 12 D. 10
Câu 24. Cho đa giác lồi đều n cạnh có độ dài mỗi cạnh là t, diện tích của đa giác lồi đó được tính bằng
A.
2
2
sin
2
nt
n
S
B.
2
cot
2
nt
n
S
C.
2
2
cot
2sin
nt
n
S
n
D.
2
4tan
nt
S
n
Câu 25. Cho
sin sin ; cos cos
a x y b x y
. Tính theo a, b biểu thức
cos( )
a b
A.
2 2
2
ab
a b
B.
2 2
2 2
a b
a b
C.
2
ab
a b
D.
a b
a b
_________________________________
58
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 5)
_______________________________________________________
Câu 1. Cho x, y, z thỏa mãn
cos cos cos sin sin sin
cos( ) sin( )
x y z x y z
p
x y z x y z
.
Tính
cos( ) cos( ) cos( )
x y y z x z
.
A. p B. 2p C. 0,5p D.
2
p
Câu 2. Tập giá trị của hàm số
3
8cos 3 6cos3 5sin 3 2
y x x x
chứa bao nhiêu số nguyên
A. 3 B. 2 C. 11 D. 12
Câu 3. Khi giá trị lớn nhất của hàm số
4 2
8cos cos
y x a x b
đạt giá trị nhỏ nhất, hãy tính a + b.
A. – 8 B. – 9 C. 0 D. – 7
Câu 4. Giá trị lớn nhất của hàm số
4 2
8sin sin
y x a x b
bằng 1. Khi đó
A. a < 0, b < 0 B. a > 0, b > 0 C. a < 0, b > 0 D. a > 0, b < 0
Câu 5. Tồn tại bao nhiêu giá trị m để giá trị lớn nhất của hàm số
2
sin 2sin
y x x m
bằng 1
A. 0 B. 1 C. 4 D. 3
Câu 6. Giá trị lớn nhất của hàm số
2
sin 3 (cot cot3 )(4cos 3)
y x x x x
bằng
A. 2 B. 1 C. 0,5 D. 1,5
Câu 7. Tính tổng các giá trị sao cho giá trị lớn nhất của hàm số
4 2
( ) cos 8cos
f x x x m
bằng 5.
A. – 7 B. 7 C. 5 D. – 5
Câu 8. Giá trị lớn nhất của hàm số
4 2 2
(8cos 8cos 1) sin8
y x x x
gần nhất với
A. 1,27 B. 1,14 C. 1,22 D. 1,36
Câu 9. Tính tổng các giá trị m để giá trị nhỏ nhất của hàm số
2
4cos 2cos
y x x m
bằng 2
A. – 7,75 B. – 8 C. – 5,75 D. 2,2,5
Câu 10. Hàm số nào dưới đây có tính chất
( ) ( )
f x k f x
với mọi số nguyên k
A.
3
sin cos cos2
2
y x x x
B.
tan 2
cos2
sin 1
x
y x
x
C.
3
sin cos2 cos 2
2
y x x x
D.
2
sin .cos
y x x
Câu 11. Tìm giá trị nhỏ nhất của hàm số ( ) sin cos 3 cos
6 3
f x x x x
A. – 4 B. – 2 C.
2 3
D.
3
Câu 12. Giá trị nhỏ nhất của hàm số
4 4
1
sin cos
2
y x x
gần nhất với
A. 0,25 B. 0,33 C. 0,45 D. 0,5
Câu 13. Tính
sin
x
khi
4sin 12sin3 36sin9 27
1
1 2cos2 1 2cos6 1 2cos18 sin 27
x x x
x x x x
.
A. 0,5 B. 1 C. 0,25 D.
2
2
Câu 14. Đồ thị hàm số
2 8
8cot 2 tan
x x
tiếp xúc với đường thẳng nào sau đây
A. y = 6 B. y = 10 C. y = 12 D. y = 4
59
Câu 15. Tìm giá trị nhỏ nhất của biểu thức
10 10 8
1
sin cos cos 2
16
y x x x
.
A. 0,25 B. 0 C. 0,5 D. 0,15
Câu 16. Tìm giá trị lớn nhất của hàm số
2
1 1 1
cot 4 cot
sin sin 2 sin 2 sin 3 sin 3 sin 4
x x
x x x x x x
.
A. 0,5 B. 0,25 C. 1 D. 0,75
Câu 17. Tìm giá trị lớn nhất của hàm số
2 2
(cos 3 sin 2 sin 5 sin )(cos5 sin5 )
y x x x x x x
A. 2 B. 1 C.
2
D.
3
2
Câu 18. Tính
tan 27 tan
x x
khi
sin sin 3 sin9
0
cos3 cos9 cos27
x x x
x x x
A. 0,5 B. 0,25 C. 0 D. 1
Câu 19. Một vật nặng treo bởi một chiếc lò xo, chuyển động lên xuống qua vị trí
cân bằng như hình vẽ. Khoảng cách h từ vật đến vị trí cân bằng ở thời điểm t giây
được tính theo công thức h = |d| với
5sin 6 4cos6
d t t
với d được tính bằng
cm. Quy ước d > 0 khi vật ở trên cân bằng và d < 0 khi vật dưới vị trí cân bằng. Hỏi
trong giây đầu tiên có bao nhiêu thời điểm vật ở xa vị trí cân bằng nhất
A. 1 B. 4 C. 0 D. 2
Câu 20. Tập giá trị của hàm số
2
4sin
2 sin 2
6
x
y
x
chứa bao nhiêu số nguyên
A. 3 B. 2 C. 1 D. 4
Câu 21. Tìm giá trị lớn nhất của biểu thức
2 2 2 2
tan 4 tan 2 16tan 4 64cot 8 41
P x x x x
.
A. 2 B. 1 C. 1,5 D. – 1
Câu 22. Tính
sin
sin 27
x
x
khi góc x thỏa mãn
cos2 cos6 cos18
0
sin 3 sin 9 sin 27
x x x
x x x
A. 2 B. 1 C. 0,5 D. 0,25
Câu 23. Cho hàm số
sin
y x
. Tịnh tiến đồ thị hàm số đã cho sang trái
4
đơn vị, sau đó tịnh tiến lên trên 2
đơn vị, sau đó tịnh tiến sang phải
4
đơn vị ta thu được đồ thị (C). Hỏi (C) tiếp xúc với đường nào
A. y = 2 B.
2
y
C. y = 1 D. y = 1,5
Câu 24. Giá trị nhỏ nhất của
2
(tan tan 2 tan 2 tan3 tan 3 tan 4 3)tan tan 4 tan
y x x x x x x x x x
bằng
A. 0,25 B. – 0,25 C. 0,75 D. 0,5
Câu 25. Hàm số
2
tan tan 2 tan 4
tan8 2tan
cos2 cos4 cos8
x x x
y x x
x x x
có giá trị nhỏ nhất bằng
A. – 0,125 B. 0,25 C. – 0,25 D. 0,5
Câu 26. Giả sử tại Hà Nội, ngày có thời gian mặt trời chiếu sáng ngắn nhất trong năm 2014 là ngày 21/06/2014
(tức ngày thứ 172 của năm) khi mặt trời mọc lúc 06: 37 (6.62 giờ kể từ lúc nửa đêm). Ngày có thời gian mặt trời
chiếu sáng dài nhất trong năm 2014 là ngày 23/12/2014 khi mặt trời mọc lúc 04:50 (4.83 giờ kể từ lúc nửa đêm).
Biết rằng số giờ kể từ lúc nửa đêm đến khi mặt trời mọc của ngày thứ x trong năm được biểu diễn bởi hàm số
sin( )
y a b cx d
. Vậy ngày sớm nhất năm 2014 mặt trời mọc lúc 06:00 là
A. 13/02/2014 B/ 08/04/2014 C. 03/09/2014 D. 26/05/2014
_________________________________
60
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 1)
_______________________________________________________
Câu 1. Xác định số nghiệm thuộc
0;2
của phương trình
6 6
7
sin cos
8
x x
.
A. 6 B. 8 C. 10 D. 12
Câu 2. Phương trình
1 sin 2 cos 1 cos2 sin sin 2
x x x x x
có tổng các nghiệm trong khoảng
là
A. 0 B.
3
2
C.
2
3
D.
Câu 3. Tính hiệu nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình sau
2 2
4 3
sin tan cos cot 2sin cos
3
x x x x x x .
A.
3
2
B.
5
6
C.
5
6
D.
Câu 4. Tồn tại bao nhiêu số nguyên p nhỏ hơn 70 để phương trình sau có nghiệm
2 2
3sin 4cos 4 3sin 4cos 5
x x x x p
.
A. Vô số B. 69 C. 50 D. 32
Câu 5. Có bao nhiêu số
m
để phương trình
2
2sin 3cos 3 2sin 3cos 2
x x x x m
có nghiệm ?
A. 17 B. 26 C. 8 D. 36
Câu 6. Gọi S là tập hợp tất cả các nghiệm thuộc khoảng (0;2018) của phương trình
3 1 cos2 sin 2 4cos 8 4 3 1 sin
x x x x
.
Tính tổng tất cả các phần tử của S.
A.
103255
B.
310408
3
C.
312341
3
D.
102827
Câu 7. Cho
0
x
là nghiệm của phương trình
sin cos 2 sin cos 2
x x x x
. Tính
0
sin
4
x
.
A.
2
2
B. 1 C.
1
2
D.
2
2
Câu 8. Cho phương trình
2
sin
0
cos 3cos 2
x
x x
. Tính tổng tất cả các nghiệm trong đoạn
0;2018
của
phương trình trên.
A.
1018018
B.
1018080
C.
1018081
D.
1020100
Câu 9. Tập hợp các giá trị m để phương trình
cos2 2 1 cos 1 0
x m x m
có nghiệm
3
;
2 2
x
là
A. [0;1) B. (– 1;0) C. (0;1] D. [– 1;0)
Câu 10. Gọi m là nghiệm dương lớn nhất trên khoảng
0;100
của phương trình
2 2
2 1 3sin cos sin cos
0
2 2sin
x x x x
x
.
Giả sử m có dạng
; ,a a b
b
. Tính tổng a + b.
A. 100 B. 101 C. 102 D. 103
Câu 11. Trên vòng tròn lượng giác, các điểm biểu diễn nghiệm phương trình
tan tan 1
4
x x
tạo thành
61
đa giác H. Tính diện tích đa giác H.
A. 2 B.
3 10
5
C.
3 2
7
D.
2
Câu 12. Phương trình
2018
1 1 1 1
... 0
sin sin 2 sin 4 sin 2
x x x x
có nghiệm
2
2
a
k
x
b
, với a, b là các số
nguyên dương, b < 2018, k là số nguyên. Tính S = a + b.
A. S = 2017 B. S = 2018 C. S = 2019 D. S = 2020
Câu 13. Tính giá trị biểu thức sin
4
m
khi m là nghiệm lớn nhất thuộc khoảng
0;2
của phương trình
3cos cos2 cos3 1 2sin sin 2
x x x x x
.
A.
2
2
B.
2
2
C. 0 D. 1
Câu 14. Nghiệm của phương trình
2018 2018 2020 2020
sin cos 2 sin cos
x x x x
khi biểu diễn trên vòng tròn
lượng giác ứng với bao nhiêu vị trí ?
A. 3 B. 4 C. 6 D. 2020
Câu 15. Nghiệm âm lớn nhất của phương trình
2018 2018 2017
tan cot 2sin
4
x x x
là
a
x
b
, trong đó a và
b là các số nguyên, a < 0, a và b nguyên tố cùng nhau. Tính S = a + b.
A. S = 3 B. S = – 3 C. S = 4 D. S = – 1
Câu 16. Phương trình
sin
18
x
có tất cả bao nhiêu nghiệm thực ?
A. 1 B. 2 C. 3 D. Vô số
Câu 17. Phương trình
2
sin 3 9 16 80 0
4
x x x
có bao nhiêu nghiệm nguyên dương ?
A. 1 B. 3 C. 2 D. 4
Câu 18. Biểu diễn tập nghiệm của phương trình
cos cos2 cos3 0
x x x
trên đường tròn lượng giác ta được
số điểm cuối là
A. 2 B. 3 C. 5 D. 6
Câu 19. Đặt
cos
6
t x
thì phương trình
2 5
cos 2 4cos
3 6 2
x x
trở thành phương trình bậc
hai ẩn t có tổng các nghiệm là S và tích các nghiệm là P. Tính S + P.
A. 3,25 B. 2,75 C. 4,25 D. 6,25
Câu 20. Tổng các nghiệm của phương trình cos(sinx) = 1 trên
0;2
là
A. 0 B.
C. 2
D. 3
Câu 21. Tính tổng các phần tử của S với S là tập hợp tất cả các giá trị
0;4
để phương trình sau có
nghiệm kép:
2 2
9
2cos 3 7cos 3cos 0
4
x x
.
A. 16
B. 20
C. 15
D. 12
Câu 22. Có bao nhiêu số nguyên m để phương trình
6 6
sin cos 3sin cos 2 0,25
x x x x m
có nghiệm ?
A. 10 B. 13 C. 12 D. 18
______________________________________
62
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 2)
_______________________________________________________
Câu 1. Tìm điều kiện tham số m để phương trình
6 6
2 2
sin cos
2 tan 2
cos sin
x x
m x
x x
có nghiệm.
A. |m| > 0,25 B. |m| < 5 C. |m|
0,25
D. |m| > 1
Câu 2. Tồn tại bao nhiêu giá trị nguyên a để phương trình
3 2 2
cos 2 cos 2 sin
x x a x
có nghiệm
0;
6
x
?
A. 0 B. 2 C. 1 D. 3
Câu 3. Phương trình
6 6
sin cos 3sin cos 2 0
x x x x m
có nghiệm khi m thuộc đoạn [a;b]. Tính ab.
A. 2,25 B. 4,5 C.
75
16
D. 3,75
Câu 4. Tồn tại bao nhiêu giá trị nguyên m để phương trình
3
sin 2 sin 2
x m x
có nghiệm ?
A. 2 B. 3 C. 1 D. 0
Câu 5. Số các giá trị nguyên dương m nhỏ hơn 10 để phương trình sin ( 1)cos
cos
m
m x m x
x
có nghiệm là
A. 9 B. 10 C. 7 D. 8
Câu 6. Phương trình sin4x = tanx có nghiệm dạng
; cos
x k x marc n k
(k nguyên) thì m + n bằng
A.
3
2
B.
3
2
C.
3 1
2
D.
3 1
2
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình
2
sin 2 cos 2 | sin cos | 2cos
x x x x x m m
có
nghiệm thực ?
A. 2 B. 3 C. 5 D. 9
Câu 8. Tìm điều kiện tham số m để phương trình
2
cos 4 4tan
2 1 tan
x x
m
x
có nghiệm.
A. m – 2,5 hoặc m > 1,5 B.
1 1,5
m
C. – 2,5 < m < 0 D. m > 7
Câu 9. Có bao nhiêu số nguyên m để phương trình
sin 2 2 sin
4
x x m
có nghiệm ?
A. 3 B. 4 C. 5 D. 6
Câu 10. Tính tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
3 3
cos sin cos 2
x x x
.
A.
2
B.
5
4
C.
7
2
D.
4
Câu 11. Tồn tại bao nhiêu số nguyên a để phương trình
2
4sin cos 3 sin 2 cos 2
3 6
x x a x x
có
nghiệm ?
A. 5 B. 7 C. 10 D. 4
Câu 12. Có bao nhiêu số nguyên tham số m để phương trình 1 2cos 1 2sin
3
m
x x
có nghiệm.
A. 4 B. 5 C. 3 D. 2
Câu 13. Để phương trình
2 2 2
2
sin 2
1 tan cos 2
a x a
x x
có nghiệm thì tham số a thỏa mãn điều kiện gì ?
A. |a| > 1 B. |a|
2 C. |a|
3 D.
| | 1; 3
a a
Câu 14. Tìm điều kiện m để phương trình
2
sin 3sin cos 1 0
m x x x m
có đúng ba nghiệm
3
0;
2
x
.
A. m > – 1 B.
1
m
C. m < – 1 D.
1
m
63
Câu 15. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình sau có nghiệm thực
3
3
sin 3sin 4sin
x x x m m
.
A. 5 B. 7 C. 3 D. 2
Câu 16. Nửa khoảng (a;b] là tập hợp tất cả các giá trị m để phương trình
4 4 2
sin cos cos 4
x x x m
có bốn
nghiệm phân biệt thuộc đoạn
;
4 4
. Tính 64a + b.
A. 50 B. 48,5 C. 52,6 D. 69
Câu 17. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực.
2
sin sin
x m x m
.
A. 2 B. 1 C. 4 D. 3
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình
2 2
sin 4 sin 8 2
x m x m m
có nghiệm ?
A. 8 B. 6 C. 4 D. 2
Câu 19. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thực ?
2 2sin sin
m m x x
.
A. 0 B. 1 C. 3 D. 2
Câu 20. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
2
cos cos
x m x m
.
A. 3 B. 2 C. 5 D. 4
Câu 21. Tìm phương trình tương đương với phương trình
2
tan tan tan 3 3
3 3
x x x
.
A. cotx = 2 B.
cot3 3
x C.
tan 3
x D.
tan 3 3
x
Câu 22. Phương trình
2
4
cos cos
3
x
x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 4 B. 2 C. 5 D. 7
Câu 23. Có bao nhiêu số nguyên m để phương trình
2
cos 2 2 1 cos 2 3 2 0
x m x m m
có nghiệm.
A. 5 B. 2 C. 3 D. 4
Câu 24. Phương trình
4sin sin sin 2 cos3 1
3 3
x x x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng
tròn lượng giác ?
A. 7 B. 6 C. 5 D. 4
Câu 25. Có bao nhiêu giá trị nguyên của m để phương trình
3
3
3 3sin sin
m m x x
có nghiệm thực ?
A. 5 B. 7 C. 3 D. 2
Câu 26. Phương trình
10 10 6 6
2 2
sin cos sin cos
4 4cos 2 sin 2
x x x x
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn
lượng giác ?
A. 10 B. 6 C. 4 D. 8
Câu 27. Có bao nhiêu giá trị nguyên của m để phương trình
3
3
cos cos
m m x x
có nghiệm thực ?
A. 1 B. 7 C. 3 D. 2
Câu 28. Có bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
2
3
sin sin 1 1 cos2
x x x m m
.
A. 1 B. 2 C. 3 D. 5
_________________________________
64
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 3)
_______________________________________________________
Câu 1. Tìm tập hợp tất cả các giá trị tham số m để phương trình
cos2 2 1 cos 1 0
x m x m
có đúng hai
nghiệm
;
2 2
x
.
A. (– 1;0] B. [0;1) C. [0;1] D. (- 1;1)
Câu 2. Tồn tại bao nhiêu giá trị nguyên m để phương trình 2sinx + mcosx = 1 – m có nghiệm
;
2 2
x
.
A. 6 B. 7 C. 5 D. 4
Câu 3. Giả sử m là nghiệm dương nhỏ nhất của
cos 2 3 sin 2 3 sin cos 2
x x x x
. Mệnh đề nào sau đây
đúng ?
A. 0
12
m
B.
12 6
m
C.
6 3
m
D.
3 2
m
Câu 4. Tồn tại bao nhiêu số nguyên m thỏa mãn |m| < 20 để phương trình sau có nghiệm
4 4 6 6 2
4 sin cos 8 sin cos 4sin 4
x x x x x m
.
A. 34 B. 56 C. 20 D. 14
Câu 5. Tính tổng các nghiệm của phương trình
2cos3 (2cos2 1) 1
x x
trên đoạn
4 ;6
là
A. 61
B. 72
C. 50
D. 56
Câu 6. Tìm tập hợp tất cả các giá trị tham số m để phương trình
2
cos 1 cos 2 cos sin
x x m x m x
có đúng
hai nghiệm
2
0;
3
x
.
A. (– 1;1] B. (0;
1
2
] C.
1
1;
2
D.
1
1
2
m
Câu 7. Tồn tại bao nhiêu số nguyên của m để phương trình
2
2cos cos2 1
x m x m
có nghiệm thực
A. 3 B. 2 C. 5 D. 4
Câu 8. Tồn tại bao nhiêu giá trị nguyên của tham số
m
để phương trình sau có nghiệm thực
1 2 sin 2 2 cos4
m x m x
.
A. 3 B. 2 C. 5 D. 4
Câu 9. Phương trình
2 2 2
2cos 2cos 2 2cos 3 3 cos 4 2sin 2 1
x x x x x
có bao nhiêu nghiệm thực thuộc
khoảng (0;2018) ?
A. 2565 B. 2566 C. 2567 D. 2568
Câu 10. Số nghiệm thuộc đoạn [0;2017] của phương trình
1 cos 1 cos
4cos
sin
x x
x
là
A. 1285 B. 1284 C. 1988 D. 1260
Câu 11. Tìm giá trị nhỏ nhất của a để phương trình
6 6
sin cos | sin 2 |
x x a x
có nghiệm.
A. 0,5 B. 0,25 C. 2 D. 1,5
Câu 12. Tồn tại bao nhiêu giá trị nguyên của tham số
m
để phương trình có nghiệm thực.
3
3
3 6sin 2 4sin cos
m m x x x
.
A. 5 B. 7 C. 3 D. 1
Câu 13. Phương trình
1 2cos 1 cos
1
1 2cos sin
x x
x x
có bao nhiêu nghiệm thuộc khoảng
(0;2018 )
?
65
A. 3025 B. 3026 C. 3027 D. 3028
Câu 14. Có bao nhiêu giá trị nguyên của m để phương trình
3
3
5 5cos cos
m m x x
có nghiệm thực ?
A. 9 B. 8 C. 10 D. 11
Câu 15. Cho phương trình
3 tan 1(sin 2cos ) (sin 3cos )
x x x m x x
. Có bao nhiêu số nguyên m thuộc
đoạn [– 2018;2018] để phương trình đã cho có nghiệm thuộc đoạn
0;
2
?
A. 2015 B. 2018 C. 2016 D. 4036
Câu 16. Tập hợp S = (a;b) bao gồm tất cả các giá trị m để phương trình
sin 2 2 sin( ) 2 0
4
x x
có đúng
hai nghiệm thuộc khoảng
3
0;
4
. Tính
2 2
a b
.
A.
4 2 2
B. 10 C.
5 3 2
D.
7 2 5
Câu 17. Tính tổng các giá trị nguyên m trong đoạn [– 5;5] để phương trình
2
sin 3sin cos 1
m x x x m
có
đúng ba nghiệm thuộc khoảng
3
0;
2
.
A. – 14 B. 0 C. 15 D. – 10
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình
2
cos 1 4cos2 cos sin
x x m x m x
có đúng hai
nghiệm thuộc đoạn
2
0;
3
?
A. 1 B. 2 C. 3 D. 4
Câu 19. S = [a;b) là tập hợp tất cả các giá trị m để phương trình
2
1 cos cos4 cos sin
x x m x m x
có
đúng ba nghiệm phân biệt thuộc
2
0;
3
. Tính b + 2a.
A. 0 B. 1 C. 2 D. 3
Câu 20. Tìm số nghiệm của phương trình
2015 2016 2017 2018
sin cos 2 sin cos
x x x x
trên [– 10;30].
A. 46 B. 42 C. 44 D. 20
Câu 21. Có bao nhiêu số nguyên m để phương trình
3
sin( sin3 ) sin(3sin ) 4sin
m m x x x
có nghiệm ?
A. 4 B. 9 C. 8 D. 5
Câu 22. Tìm tập hợp tất cả các giá trị m để phương trình sau có nghiệm
0;
4
x
2 2 3 4
sin sin cos cos 2 3sin cos cos
x x x m x x x m x
A. (– 2;0) B. [– 3;1) C. (– 4;0) D. [– 1;3]
Câu 23. Tính tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
2
2sin 3 1 8sin 2 cos 2
4
x x x
.
A.
2
B. 1 C.
3
D.
4
Câu 24. Đoạn [a;b] là tập hợp tất cả các giá trị m để phương trình
1
1 sin sin
2
x x m
có nghiệm. Tính
giá trị biểu thức
2 2
a b
.
A. 5 B. 4,5 C. 6 D. 2,5
_________________________________
66
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 4)
_______________________________________________________
Câu 1. Phương trình
3(cot cos ) 5(tan sin ) 2
x x x x
có một phương trình hệ quả
1
sin
4
a
x
b
.
Tính giá trị biểu thức 4a + 9b + 1993.
A. 2000 B. 2019 C. 2020 D. 2017
Câu 2. Các nghiệm của phương trình
2
cos 3sin cos 1
x x x
khi biểu diễn trên vòng tròn lượng giác tạo thành
đa giác (H). Tính diện tích S của đa giác (H).
A. S = 6 B. S =
3 10
5
C. S =
8 10
5
D. S =
7 10
10
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình
7 4
cos sin 1
x x
.
A. 3 B. 2 C. 4 D. 1
Câu 4. Tìm số nghiệm trên
0;3
của phương trình
2
2 2
sin 3
sin sin sin 3
4
x
x x x
.
A. 7 B. 8 C. 5 D. 10
Câu 5. Phương trình
6
32cos cos6 1
x x
tương đương
2
cos 2 cos 2 1 0
a x b x
. Tính a + b.
A. 10 B. 11 C. 8 D. 9
Câu 6. Tìm số nghiệm thuộc khoảng
50;50
của phương trình
sin 2sin 2 sin 3 2 2
x x x .
A. 3 B. 2 C. 4 D. 0
Câu 7. Phương trình
2
6tan 5cot3 tan 2 cos 2 cos2 1 0
x x x a x b x
. Tính a + b.
A. 10 B. 11 C. 8 D. 9
Câu 8. Tìm số nghiệm thuộc
10 ;10
của phương trình
1
cot tan
sin
x x
x
.
A. 16 B. 12 C. 10 D. 7
Câu 9. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2cot 2 3cot3 tan 2
x x x
.
A. 3 B. 2 C. 4 D. 0
Câu 10. Tìm số nghiệm trên
0;3
của phương trình
20 20
sin cos 1
x x
.
A. 9 B. 7 C. 5 D. 10
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
(cos2 cos4 ) 6 2sin3
x x x
.
A. 3 B. 2 C. 4 D. 1
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình
2 2
cos3 2 cos 3 2(1 sin 2 )
x x x
.
A. 3 B. 2 C. 4 D. 1
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình
2 2
4cos 3tan 4 3cos 2 3 tan 4 0
x x x x
.
A. 3 B. 2 C. 4 D. 1
Câu 14. Tồn tại bao nhiêu số nguyên
50;50
a
để hai phương trình sau tương đương
1
sin cos2 sin 2 cos3 sin5
2
cos2 cos4 cos6 1
x x x x x
a x a x x
A. 50 B. 51 C. 52 D. 53
67
Câu 15. Tồn tại bao nhiêu số nguyên a để phương trình sau có nghiệm
2 2 2
(cos2 cos4 ) ( 4 3)( 4 6) 7 sin 3
x x a a a a x
.
A. 1 B. 2 C. 0 D. 3
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình
3 3
(1 tan )cos (1 cot )sin 2sin 2
x x x x x
.
A. 3 B. 2 C. 4 D. 1
Câu 17. Tìm số nghiệm thuộc
0;
của phương trình
2 2 2
4sin 2 sin 6 4sin 2 sin 6
x x x x
.
A. 6 B. 4 C. 3 D. 2
Câu 18. Tìm số nghiệm thuộc khoảng
50;50
của phương trình
sin cos sin cos 2
x x x x
.
A. 43 B. 27 C. 61 D. 35
Câu 19. Tính tổng các nghiệm thuộc
;
của phương trình
2
2sin 3 1 8sin 2 cos 2
4
x x x
.
A.
B.
2
C.
12
D.
3
Câu 20. Tìm số nghiệm trên
0;3
của phương trình
3
cos2 cos6 4(3sin 4sin 1) 0
x x x x
.
A. 5 B. 6 C. 4 D. 3
Câu 21. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình
1
( 1 cos cos )cos2 sin 4
2
x x x x
A. 3 B. 2 C. 4 D. 1
Câu 22. Tập hợp [a;b) gồm tất cả các giá trị tham số m để phương trình
cos2 (2 1)cos 1 0
x m x m
có
nghiệm
3
;
2 2
. Tính 2a + b.
A. 4 B. 3 C. 2 D. – 2
Câu 23. Tồn tại giá trị nguyên
50;50
a
để phương trình
1 1
cos sin
a
x x
có nghiệm ?
A. 99 B. 3 C. 100 D. 75
Câu 24. Tìm số nghiệm thuộc khoảng
50;50
của phương trình
2 2
sin 2 sin sin 2 sin 3
x x x x
.
A. 17 B. 16 C. 10 D. 46
Câu 25. Tìm số nghiệm thuộc khoảng
50;50
của phương trình
2 2 3 3
tan cot tan cot tan cot 6
x x x x x x
.
A. 31 B. 35 C. 32 D. 50
Câu 26. Tập hợp
;
S a b
gồm tất cả các giá trị m để phương trình
sin 4 tan
x m x
có nghiệm
x k
. Tính
a + b.
A. 3,5 B. 4,5 C. 3 D. 2
Câu 27. Giá trị a nhỏ nhất để phương trình
6 6
sin cos sin 2
x x a x
có nghiệm nằm trong khoảng nào
A. (2;3) B. (1;2) C.
1
;1
2
D.
1
0;
2
Câu 28. Tìm số nghiệm thuộc khoảng
0;50
của phương trình
cos2 1 sin 2 2 sin 2 cos
x x x x
.
A. 22 B. 26 C. 60 D. 37
_________________________________
68
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 5)
_______________________________________________________
Câu 1. Tìm số nghiệm
4 ;9
của phương trình
cos2 1 sin 2 2 sin cos
x x x x
.
A. 16 B. 20 C. 19 D. 12
Câu 2. Phương trình
3 3
4sin 4cos cos
6 6
x x x
có hệ quả
cos ; ;
x a b c
. Tính abc
A. – 1 B. 1 C. 0 D. – 0,5
Câu 3. Tập hợp
;
S a b
gồm tất cả các giá trị m để phương trình
6 6
2 2
sin cos
tan 2
cos sin
x x
m x
x x
có nghiệm. Tính
giá trị biểu thức b – a
A. 2 B. 0,5 C. 0,25 D. 1
Câu 4. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2tan tan 2 2tan tan3 tan 2 tan3 0
x x x x x x
A. 2 B. 3 C. 4 D. 1
Câu 5. Tìm số nghiệm
4 ;9
của phương trình
1 sin 2 cos sin
x x x
.
A. 25 B. 21 C. 10 D. 18
Câu 6. Nghiệm dương nhỏ nhất của phương trình
cot tan 2tan 2 4 tan 4 8 0
x x x x
gần nhất với
A. 0,2 B. 0,3 C. 0,5 D. 0,4
Câu 7. Tồn tại bao nhiêu số nguyên m < 10 để phương trình
8 8 2
sin cos cos 2
x x m x
có nghiệm
A. 8 B. 3 C. 9 D. 4
Câu 8. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 5
1945sin 2005cos 2005
x x
A. 1 B. 2 C. 3 D. 4
Câu 9. Tìm số nghiệm
4 ;9
của phương trình
1 4sin 2 cos sin
x x x
.
A. 25 B. 21 C. 10 D. 18
Câu 10. Cho phương trình
6 6 4 2 2 4
sin cos 8sin cos 8sin cos sin 2
x x x x x x a x
. Giá trị nguyên nhỏ nhất
của a để phương trình đã cho có nghiệm thuộc khoảng nào sau đây
A. (5;10) B. (0;5) C. (– 5;0) D. (– 10;– 5)
Câu 11. Tìm số nghiệm
4 ;9
của phương trình
2
2
4
cos cos
3
0
1 tan
x
x
x
.
A. 4 B. 12 C. 10 D. 6
Câu 12. Phương trình
2 2
sin cos 4 sin sin5 sin 3
x x x x x
có bao nhiêu nghiệm
4 ;9
A. 4 B. 3 C. 3 D. 7
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 4
1 cos 1 4cos 7cos
x x x
A. 2 B. 1 C. 3 D. 4
Câu 14. Tập hợp
;
S a b
gồm tất cả các giá trị m để phương trình
2
cos 4sin cos 2 0
m x x x m
có
nghiệm
0;
4
. Tính a + b.
A. 5 B.
11
3
C.
5
3
D. – 2
69
Câu 15. Tính tổng các nghiệm thuộc khoảng
0;2
của phương trình
sin3 sin
cos2 sin 2
1 cos2
x x
x x
x
.
A.
3,75
B.
4,75
C.
5
D.
2,25
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
31 50
sin 3 cos 3 1
x x
A. 12 B. 10 C. 11 D. 8
Câu 17. Phương trình
(sin cos )(sin 2 cos ) 2
x a x x a x
có một nghiệm
4
x k
. Tất cả các nghiệm
còn lại
0
x
của phương trình thỏa mãn
A.
0
16
sin 2
65
x
B.
0
16
sin 2
65
x C.
0
16
sin 2
63
x D.
0
13
sin 2
63
x
Câu 18. Tìm số nghiệm
(0;2 )
của phương trình
2
3tan 6 2tan 2 cot 4
sin8
x x x
.
A. 8 B. 7 C. 10 D. 6
Câu 19. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 3 2 5
(cos cos3 sin sin3 ) cos 2
x x x x x
A. 6 B. 5 C. 3 D. 4
Câu 20. Tìm số nghiệm
(0;2 )
của phương trình
3 3 3 3
sin sin 2 sin 3 (sin sin 2 sin 3 )
x x x x x x
.
A. 9 B. 7 C. 10 D. 6
Câu 21. Tìm số nghiệm
(0;2 )
của phương trình
5 5 3
4(sin cos cos sin ) sin 2 1
x x x x x
.
A. 4 B. 7 C. 10 D. 6
Câu 22. Tìm số nghiệm
(0;2 )
của phương trình
1 1
tan3
tan5 tan 2 cot 5 cot 2
x
x x x x
.
A. 19 B. 17 C. 10 D. 16
Câu 23. Tìm số nghiệm
(0;2 )
của phương trình
2
1 1
cot 7
tan3 tan 4 cot3 cot 4
x
x x x x
.
A. 28 B. 27 C. 20 D. 29
Câu 24. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2tan tan 4 tan5
x x x
A. 4 B. 2 C. 3 D. 5
Câu 25. Tìm số nghiệm
(0;2 )
của phương trình
2 2
sin 3 sin cos4 cos2 tan 6
x x x x x
A. 4 B. 10 C. 24 D. 18
Câu 26. Tìm số nghiệm
(0;2 )
của phương trình
2 2 3
sin 5 sin cos6 cos4 sin 1993
x x x x x
A. 1993 B. 3986 C. 2000 D. 1985
Câu 27. Tìm số nghiệm
(0;2 )
của phương trình
cot3 tan 2 tan 2 tan tan cot3 tan5
x x x x x x x
A. 8 B. 20 C. 30 D. 15
Câu 28. Phương trình
tan3 tan 1 tan 3 tan
x x x x
có bao nhiêu nghiệm
4 ;9
A. 70 B. 56 C. 40 D. 62
Câu 29. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
2 tan tan3 tan
x x x
A. 4 B. 2 C. 3 D. 5
Câu 30. Tìm số nghiệm
4 ;9
của phương trình
3 2
8sin sin3 2sin 3 3cos4 3
x x x x
A. 6 B. 9 C. 12 D. 10
Câu 31. Phương trình
5
16cos 1 5cos3 10cos
x x x
có bao nhiêu nghiệm
0;1993
A. 1000 B. 1993 C. 4982 D. 4980
70
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 6)
_______________________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên dương chẵn m để phương trình
sin 4cos 2 0
m x x m
?
A. 3 B. 1 C. 6 D. Vô sô
Câu 2. Phương trình
4cos cos2 cos4 1 cos3 cos5 cos7
x x x x x x
có bao nhiêu nghiệm
0;1993
A. 996 B. 968 C. 938 D. 1010
Câu 3. Tìm số biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
8cos cos3
3
x x
A. 10 B. 6 C. 8 D. 4
Câu 4. Phương trình
5
16sin 1 10sin 5sin3
x x x
có bao nhiêu nghiệm
0;1993
A. 4993 B. 4982 C. 1010 D. 1285
Câu 5. Có bao nhiêu số nguyên m để
2cos cos2 cos3 7cos2
x x x m x
có nghiệm duy nhất
0;
2
A. 1 B. 3 C. 11 D. 13
Câu 6. Biết phương trình
5 5 2
4cos sin 4sin cos sin 4
x x x x x m
có nghiệm
8
x
. Nghiệm dương nhỏ
nhất của phương trình thuộc khoảng nào dưới đây
A.
3 2
;
10 5
B.
2
;
5 2
C.
3
;
5 10
D.
0;
10
Câu 7. Tìm a + b với (a;b) là tập hợp tất cả các giá trị m để phương trình sau có 7 nghiệm
;3
2
sin3 sin cos sin
2 2
x m x x x
.
A. – 1 B. 2 C. 1 D. – 2
Câu 8. Tìm số nghiệm
0;20
của phương trình
2 2
(cos sin )sin5 1 0
x x x
.
A. 10 B. 9 C. 18 D. 17
Câu 9. Tìm số biểu diễn trên vòng tròn lượng giác nghiệm phương trình
sin (cos2 cos4 cos6 ) 1
x x x x
A. 1 B. 4 C. 2 D. 3
Câu 10. Tìm số nghiệm
0;20
của phương trình
sin 4 cos4 1 4(sin cos )
x x x x
.
A. 10 B. 19 C. 18 D. 17
Câu 11. Tồn tại bao nhiêu cặp số (x;y) với
, 0;20
x y
thỏa mãn điều kiện
2 2 2 2 2
2 2
1 1
(sin ) (cos ) 3,5 2sin sin
sin cos
x x y y
x x
A. 400 B. 350 C. 600 D. 210
Câu 12. Tìm số nghiệm
0;1993
của phương trình
2
sin 2 sin 2 0
5
x
x
A. 1993 B. 120 C. 542 D. 399
Câu 13. Tìm số nghiệm
0;20
của phương trình
4 4 4 2
1
sin sin cos sin 2
2 8 2
x
x x x
.
A. 10 B. 10 C. 18 D. 17
Câu 14. Tìm số nghiệm
0;1993
của phương trình
5 3
sin cos 1
x x
71
A. 1993 B. 2019 C. 1992 D. 1994
Câu 15. Xác định số nghiệm
2
2 0
x x m
khi hai phương trình sau tương đương
2 cos 2 3 sin 3
( 1)cos 3sin 0,75 2
m x x m
m x x m
A. 2 B. 1 C. 0 D. Không giải được
Câu 16. Tìm số nghiệm
0;1993
của phương trình
2
8cos4 cos 2 1 cos3 1 0
x x x
.
A. 1993 B. 2019 C. 1992 D. 1994
Câu 17. Khi
3
m
, khoảng (a;b) bao gồm tất cả các giá trị m để hai phương trình sau tương đương
cos ( 1)sin 2
( 3)cos (3 1)sin 5
m x m x m
m x m x m
Tính ab.
A. – 3 B. – 2 C. 1 D. 4
Câu 18. Tìm số nghiệm
0;1993
của phương trình
2
sin 2 sin 2 1 cos4
x x x
.
A. 1993 B. 998 C. 1995 D. 996
Câu 19. Xác định số nghiệm
0;4
của phương trình
2
tan ( 2) 1
3 4
x
x
A. 3 B. 2 C. 1 D. 4
Câu 20. Tính tổng các nghiệm của phương trình
2 2 2
2 4 cos( 3) 2cos
x x x x
.
A. 3 B. 2 C. 1 D. 4
Câu 21. Xác định số nghiệm
0;4
của phương trình
4
5cos
2
3 sin tan
cos
x
x x
x
A. 3 B. 2 C. 1 D. 4
Câu 22. Tìm số nghiệm
0;1993
của phương trình
2cos 2 sin10 3 2 2cos28 sin
x x x x
.
A. 1993 B. 998 C. 1995 D. 996
Câu 23. Xác định số nghiệm
0;
của phương trình
2 2 2 2
cos 4 cos 8 sin 12 sin 16 2
x x x x
A. 5 B. 12 C. 3 D. 2
Câu 24. Tìm số nghiệm
0;1993
của phương trình
3 3 4
sin cos 2 sin
x x x
A. 1990 B. 997 C. 996 D. 1995
Câu 25. Tìm số nghiệm
0;1993
của phương trình
2 2
1993 cos 3 sin sin 4 sin 2
x x x x x
A. 2 B. 1 C. 3 D. 4
Câu 26. Tìm số nghiệm
0;1993
của phương trình
2 2 2
2
sin sin sin cos 2
3 3 3
x x x x
A. 1991 B. 1993 C. 996 D. 997
Câu 27. Tìm số nghiệm
0;1993
của phương trình
2 2
2sin 3 sin cos 4 cos2 2
x x x x
A. 5979 B. 1288 C. 1975 D. 3986
Câu 28. Phương trình
2sin 4 2sin 3 2sin 1
6
x x x
có hai họ nghiệm
2
; 2
3
k
x x k
với
,
là các số dương nhỏ nhất có thể. Tích

gần nhất giá trị nào
A. 0,05 B. 0,09 C. 0,75 D. 0,93
_________________________________
72
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 7)
_______________________________________________________
Câu 1. M là số nghiệm
0;1993
của phương trình
tan 2 2 tan 1
4
x x
. Số ước của M là
A. 1993 B. 20 C. 30 D. 40
Câu 2. Tồn tại bao nhiêu số nguyên m để phương trình
cos3 2sin 2 cos 0
x x m x
có nghiệm
0;
2
A. 4 B. 2 C. 3 D. 1
Câu 3. Xác định số nghiệm
0;1993
của phương trình
sin 4
1
cos6
x
x
.
A. 9420 B. 7972 C. 1994 D. 9964
Câu 4. M là số nghiệm
0;1993
của phương trình
tan 4 tan3 tan 3
3
x x x
. Hai chữ số tận cùng
của M là
A. 52 B. 64 C. 24 D. 60
Câu 5. Tồn tại bao nhiêu số nguyên
10;10
m
để phương trình
2
sin3 sin (4 2 )sin
x m x m x
có đúng
năm nghiệm
0;2
A. 10 B. 12 C. 8 D. 16
Câu 6. Tìm số nghiệm thuộc (0;8) của phương trình
tan 2 .tan 7 1
x x
A. 60 B. 70 C. 68 D. 56
Câu 7. Biết rằng ; ;
2 2
k k
x x x k
(với
, ,
là các số âm lớn nhất) là ba họ nghiệm của
phương trình
sin 3 sin sin cos5
6 3
x x x x
. Tích ba số
, ,
gần nhất với
A. – 0,2 B. – 0,16 C. 0,15 D. – 0,56
Câu 8. Tính tổng các nghiệm thỏa mãn điều kiện
3
2
x
của phương trình
sin cos 1 sin
2 2
x x
x
A. 5
B. 6
C. 7
D. 4
Câu 9. Phương trình
tan 5 tan 3 tan 2 3
3
x x x
có bao nhiêu họ nghiệm rút gọn
A. 3 B. 4 C. 2 D. 1
Câu 10. Cho phương trình
2 2 2 2
tan .tan 3 .tan 4 tan tan 3 tan 4
x x x x x x
. Nghiệm dương lớn nhất trong
khoảng (0;100) của phương trình gần nhất số nào sau đây
A. 99,74 B. 97,38 C. 98,62 D. 99,18
Câu 11. Phương trình
2sin 5 2sin3 2sin 2 3
3
x x x
có bao nhiêu họ nghiệm rút gọn
A. 3 B. 4 C. 2 D. 1
Câu 12. Biết rằng hai phương trình sau đây tương đương
2
sin 2 2 2cos 2 sin
2sin cos2 sin 2 2 sin cos 1
a x x a x
x x x b b x x
Giá trị tích ab gần nhất với
A. 1,26 B. 1,41 C. 1,89 D. 1,35
73
Câu 13. Xác định số nghiệm
0;1993
của phương trình
tan tan 2 tan3 tan6
x x x x
A. 11993 B. 22353 C. 101010 D. 25295
Câu 14. Xác định số nghiệm
0;1993
của phương trình
3
sin sin 4cos sin
2 3 2 3 2
x x
x x
.
A. 1993 B. 1992 C. 540 D. 1285
Câu 15. Tìm số nghiệm
0;1993
của phương trình
2
cos sin 3 cos 2 1 4sin
3 3
x x x x
.
A. 1993 B. 1992 C. 540 D. 1285
Câu 16. Tìm số nghiệm của phương trình
2
2 2cos
x x
.
A. 3 B. 1 C. 2 D. 0
Câu 17. Phương trình
2 2
sin 4 cos 4 0,25 .sin 4 (2 1)sin cos 0
x x m x m x x
có hai nghiệm phân biệt thuộc
khoảng
;
4 2
khi
2 0,5
a b m
. Tính ab.
A. 6 B. 10 C. 12 D. 8
Câu 18. Xác định số nghiệm thuộc (0;5) của phương trình
1
cot 2 cot3 0
sin sin 2 sin 3
x x
x x x
.
A. 1 B. 2 C. 0 D. 3
Câu 19. Xác định số nghiệm
0;1993
của phương trình
sin (1 sin ) cos2 (1 cos2 ) 1
x x x x
.
A. 1993 B. 997 C. 994 D. 1285
Câu 20. Tồn tại bao nhiêu số nguyên
10;10
m
để hai phương trình sau tương đương
2
2sin cos2 1 cos2 cos3
4cos cos3 cos (4 )(1 cos2 )
x x x x
x x a x a x
A. 10 B. 16 C. 12 D. 18
Câu 21. Xác định số nghiệm thuộc (0;20) của phương trình
sin 3 cos sin cos sin 2
x x x x x
A. 10 B. 26 C. 6 D. 5
Câu 22. Tồn tại bao nhiêu số nguyên
10;10
m
để phương trình sau có nghiệm
2
(2 1)(sin cos ) (sin cos ) 2 2 2 0
m x x x x m m
A. 3 B. 4 C. 1 D. 2
Câu 23. Xác định số nghiệm thuộc (0;20) của phương trình
cos2 0,5sin 4 sin cos
x x x x
A. 15 B. 26 C. 10 D. 16
Câu 24. Cho phương trình
2 2
2tan 4cot tan 2 cot
2 2
x x
x x . Tổng nghiệm âm lớn nhất và nghiệm dương
nhỏ nhất của phương trình trên gần nhất với
A. 0,56 B. 0,26 C. 0,15 D. 0,43
Câu 25. Tìm số nghiệm
0;1993
của phương trình
2 2 2 2
3(tan tan 2 tan 3 ) (tan .tan 2 .tan3 )
x x x x x x
A. 1993 B. 1992 C. 994 D. 1997
Câu 26. Điều kiện để phương trình
sin cos 1 sin cos
x x m x x
có nghiệm là
m a
. Khi đó
3
3
a a
có giá
trị gần nhất với
A. 5 B. 4 C. 3 D. 6
_________________________________
74
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 8)
_______________________________________________________
C
C
â
â
u
u
1
1
.
.
Phương trình
2
cos cos 3 cos3 1 4sin
3 3
x x x x
có số họ nghiệm khác nhau là
A. 3 B. 4 C. 2 D. 0
C
C
â
â
u
u
2
2
.
.
Tồn tại bao nhiêu số nguyên m để phương trình
3
3
12 12sin sin
m m x x
có nghiệm
A. 23 B. 20 C. 6 D. 16
C
C
â
â
u
u
3
3
.
.
Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1
cot cot cot cot
6 6
3
x x x x
.
A. 5 B. 2 C. 4 D. 3
Câu 4. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
1 cos4 2 cos2 2
x m x m
.
A. 3 B. 2 C. 5 D. 4
C
C
â
â
u
u
5
5
.
.
T
T
ồ
ồ
n
n
tạ
tạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
l
l
ớ
ớ
n
n
h
h
ơ
ơ
n
n
–
–
8
8
để
để
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
trì
trì
n
n
h
h
2
sin 3sin cos 1 0
m x x x m
có đúng
ba nghiệm
3
0;
2
.
A. 4 B. 5 C. 3 D. 6
Câu 6. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
2
sin sin 3 5 cos2 4 cos2
x x m x m x m
.
A. 3 B. 4 C. 5 D. 6
C
C
â
â
u
u
7
7
.
.
Tập hợp
;
S a b
gồm tất cả các giá trị m để phương trình
3sin cos 0
x x m
có đúng ba nghiệm
thực thuộc
;2
6
. Tính a + b.
A. 1 B. 0 C. – 1 D. 3
Câu 8. Có tất cả bao nhiêu giá trị nguyên nhỏ hơn 30 của tham số m để phương trình sau có nghiệm thực ?
2
2 2 2
tan 6 1
1 sin sin 2 5 1 0
cos sin cos
x
m x m m x
x x m x
.
A. 8 B. 12 C. 40 D. 29
Câu 9. Tìm điều kiện tham số m để phương trình
sin
3 cos
x
x m
có nghiệm.
A.
2
2
m
m
B.
2
2
m
m
C.
3
3
m
m
D.
2 2
m
C
C
â
â
u
u
1
1
0
0
.
.
Tìm số nghiệm
0;1993
của phương trình
3 tan tan .tan 3 tan tan 2
6 6
x x x x x
A. 1993 B. 3986 C. 3984 D. 2020
Câu 11. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
5 2
sin sin 2cos2 4 cos 3 2cos
x x x m x m x m
.
A. 8 B. 5 C. 4 D. 6
C
C
â
â
u
u
1
1
2
2
.
.
Tìm số nghiệm
0;1993
của phương trình
2 2
3 tan tan tan tan
3 3
x x x x
75
A. 4993 B. 1993 C. 3985 D. 3986
C
C
â
â
u
u
1
1
3
3
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
5 5 5
sin 3cos 2cos sin 2 2sin cos
x x m x x m x x m
.
.
A
A
.
.
4
4
B
B
.
.
6
6
C
C
.
.
5
5
D
D
.
.
7
7
Câu 14. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực.
2
sin sin
x m x m
.
A. 2 B. 1 C. 4 D. 3
Câu 15. Có bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
2
3
sin sin 1 1 cos2
x x x m m
.
A. 1 B. 2 C. 3 D. 5
C
C
â
â
u
u
1
1
6
6
.
.
Tìm số nghiệm
0;2
của phương trình
sin 3 sin 2 sin
4 4
x x x
A. 3 B. 4 C. 5 D. 6
Câu 17. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
3
3
3
sin 2 2sin 8sin sin 2 27 3
x m x x x m
.
A. 10 B. 9 C. 11 D. 12
C
C
â
â
u
u
1
1
8
8
.
.
Phương trình
cot cot 2 cot3 3 cot tan3
x x x x x
có bao nhiêu nghiệm
0;2
A. 10 B. 16 C. 12 D. 14
C
C
â
â
u
u
1
1
9
9
.
.
Tìm điều kiện của m để phương trình
2
(sin 1)(cos cos ) 0
x x x m
có đúng năm nghiệm
0;2
A.
1
0
4
m
B.
1
0
4
m
C.
1
0
4
m
D.
1
0
4
m
C
C
â
â
u
u
2
2
0
0
.
.
Phương trình
2
6cos3 1 8sin cos3
x x x
tương đương
sin( ) sin( )
ax bx
. Tính a + b.
A. 10 B. 12 C. 7 D. 5
C
C
â
â
u
u
2
2
1
1
.
.
Tồn tại bao nhiêu số nguyên m để phương trình
sin 4cos 4
m x x
có nghiệm trên
0;
3
?
A. 4 B. 2 C. 3 D. 5
C
C
â
â
u
u
2
2
2
2
.
.
Xác định số nghiệm
0;2
của phương trình
2
4sin (2 2)sin 0
x x x x
.
A. 3 B. 4 C. 2 D. 5
C
C
â
â
u
u
2
2
3
3
.
.
Tồn tại bao nhiêu số nguyên dương m để phương trình
2 2
sin 2 2sin cos cos sin
x x x x m x
có
nhiều hơn một nghiệm
0;2
A. 3 B. 2 C. 4 D. 5
C
C
â
â
u
u
2
2
4
4
.
.
Xác định số họ nghiệm phân biệt của phương trình
3 1 3
sin sin
10 2 2 10 2
x x
A. 1 B. 3 C. 2 D. 4
C
C
â
â
u
u
2
2
5
5
.
.
C
C
h
h
o
o
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
.5 sin 5 5
x x
a x
;
;
a
a
l
l
à
à
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
h
h
ự
ự
c
c
.
.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
đ
đ
ã
ã
c
c
h
h
o
o
t
t
ồ
ồ
n
n
t
t
ạ
ạ
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
0
x
.
.
T
T
í
í
n
n
h
h
0 0 0
sin cos sin
2
x x x
.
.
A
A
.
.
1
1
B
B
.
.
2
2
C
C
.
.
4
4
D
D
.
.
3
3
C
C
â
â
u
u
2
2
6
6
.
.
Tìm số nghiệm
0;2
của phương trình
2 2
(3 4sin )(3 4sin 3 ) 1
x x
A. 16 B. 19 C. 20 D. 15
_________________________________
76
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 9)
_______________________________________________________
Câu 1. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
33
3
6sin 5 sin 3 sin 6sin 5 27
x m x x x m
.
A. 8 B. 19 C. 6 D. 7
Câu 2. Tập hợp
;
S a b
bao gồm tất cả các giá trị tham số m để phương trình sau có nghiệm thực
5 2
2sin sin 4 sin cos2 2 2 sin
x x m x x m x m
.
Tính giá trị biểu thức
8 5
b a
.
A. 8 B. 7 C. 4 D. 5
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
sin 2 cos 2 cos3 cos
x x x x
A. 4 B. 3 C. 5 D. 2
Câu 4. Tìm số nghiệm thuộc khoảng
của phương trình
3 2
cos 3 cos2 3cos 2 cos2 2
x x x x
A. 3 B. 2 C. 5 D. 4
Câu 5. Tập hợp
;
S a b
bao gồm tất cả các giá trị tham số m để phương trình sau có nghiệm thực
cos3 4cos 4 3 cos 6cos
x x m x m x
.
Tính giá trị biểu thức
8 5
b a
.
A. 8 B. 7 C. 4 D. 5
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình
cos3 cos2 cos 1
x x m x
có đúng bảy nghiệm khác
nhau thuộc khoảng
;2
2
A. 3 B. 5 C. 7 D. 1
Câu 7. Có bao nhiêu số nguyên m để phương trình
6 6
sin cos 3sin cos 0,25 2 0
x x x x m
có nghiệm
A. 13 B. 15 C. 7 D. 9
Câu 8.
C
C
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
cos cos
x m x m
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
A
A
.
.
3
3
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
4
4
Câu 9. Có bao nhiêu số nguyên dương m để phương trình
cos2 sin 0
x m x m
có nghiệm
A. 0 B. 1 C. 2 D. Vô số
Câu 10.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
1 2 sin 2 2 cos4
m x m x
.
.
A
A
.
.
3
3
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
4
4
Câu 11. Tìm điều kiện tham số m để phương trình
2 2
cos4 cos 3 sin
x x m x
có nghiệm 0;
12
x
A.
1
0;
12
m
B.
1
;2
2
m
C.
(0;1)
m
D.
1
1;
4
m
Câu 12. Tìm số nghiệm thuộc khoảng (0;20) của phương trình
2
4
2cos (sin cos ) 0
3
x
x x
A. 3 B. 2 C. 4 D. 5
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
tan 4cot 7 4tan cot
x x x x
A. 4 B. 3 C. 5 D. 2
77
Câu 14. Điều kiện để phương trình
sin 2 cos2 1 2
m x x m
có nghiệm
;
4 3
là
4
b
a m
c
. Tính
giá trị biểu thức a + b + c.
A. 10 B. 3 C. 7 D. 8
Câu 15. Tập hợp (a;b) gồm tất cả các giá trị m để phương trình
sin3 cos2 ( 1)sin 0
x m x m x m
có đúng
tám nghiệm phân biệt thuộc
0;3
. Tính 3a + b.
A. 0 B. 2 C. 3 D. 4
Câu 16. Tính tổng các nghiệm
(0;2 )
của phương trình
2
tan 2tan sin10 2 0
x x x
.
A. 2
B. 1,5
C.
D. 2,5
Câu 17. Tính tổng các nghiệm thuộc
của phương trình
2
cos4 6sin 2sin 0
x x x
A. 2
B. 1,5
C.
D. 2,5
Câu 18. Tìm số nghiệm thuộc
0;
của phương trình
cos cos3 cos2 cos 4 1
x x x x
A. 2 B. 3 C. 1 D. 4
Câu 19. Nghiệm dương nhỏ nhất của phương trình
4 4 2 2
sin cos sin 5 sin 2
x x x x
thuộc khoảng
A.
5
;
3 6
B.
0;
6
C.
;
6 3
D.
5 2
;
6 3
Câu 20. Có bao nhiêu số nguyên m để phương trình
3
3
5 5cos cos
m m x x
có nghiệm thực ?
A. 9 B. 8 C. 10 D. 11
Câu 21. Cho hàm số
4 2
( ) 4 3
f x x x
. Tìm số nghiệm thuộc
9
0;
2
của phương trình
(sin 2 2) 2
f x
.
A. 14 B. 13 C. 15 D. 16
Câu 22.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
sin 2cos 3 sin 2cos 3
2sin cos 4 2sin cos 4
x x x x
m
x x x x
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
k
k
h
h
i
i
v
v
à
à
c
c
h
h
ỉ
ỉ
k
k
h
h
i
i
;
m a b
.
.
T
T
í
í
n
n
h
h
g
g
i
i
á
á
t
t
r
r
ị
ị
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
b
b
–
–
a
a
.
.
A
A
.
.
–
–
1
1
3
3
8
8
,
,
7
7
5
5
B
B
.
.
–
–
1
1
2
2
0
0
,
,
2
2
5
5
C
C
.
.
–
–
6
6
,
,
2
2
5
5
D
D
.
.
–
–
1
1
2
2
9
9
,
,
5
5
Câu 23.
Tì
Tì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
r
r
ê
ê
n
n
khoả
khoả
n
n
g
g
0;6
của phương trình
2
4 4
sin sin 4 cos sin 3 cos
2 6 6 3
x x x
x x
A. 1 B. 2 C. 3 D. 4
Câu 24.
P
P
h
h
ư
ư
ơ
ơ
n
n
g
g
trì
trì
n
n
h
h
2
1 sin3 sin3 4cos 4cos
x x x x
có đặc điểm
A
A
.
.
Có
Có
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
u
u
y
y
n
n
h
h
ấ
ấ
t
t
0;
2
B. Có nghiệm
: cos(5 ) 0,5
C. Có hai nghiệm
(0; )
D. Có 10 nghiệm trong khoảng (0;10)
Câu 25. Nghiệm dương nhỏ nhất của phương trình
3 3
3sin cos tan cot
4 4
x x
x x
gần nhất số nào sau đây
A. 1,046 B. 1,047 C. 1,042 D. 0,269
Câu 26. Biết rằng phương trình
2 2
tan 4cot 3 cos(2 )
x x x m
có nghiệm. Tính
cos
m
.
A. – 0,5 B. – 0,6 C.
1
3
D.
1
4
Câu 27. Phương trình
2
9sin 3sin 2 4cos 4
x x x
có một hệ quả
sin cos 2
a x b x
. Tìm a + 2b.
A. 3 B. 4 C. 7 D. 8
_________________________________
78
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 10)
_______________________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m nhỏ hơn 50 để phương trình sau có nghiệm
2 2 4 3 2
sin 2( 1)sin 2 4 4 4 0
x m m x m m m m
.
A. 2 B. 1 C. 4 D. 10
Câu 2. Tìm số nghiệm thuộc khoảng (0;10) của phương trình
2
89
sin cos 4 9
16
x x x x
A. 2 B. 1 C. 0 D. 3
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình
2
2cos 3 (3 2 )cos3 2 0
x m x m
có đúng ba
nghiệm thực thuộc khoảng
;
6 3
A. 1 B. 2 C. 3 D. 4
Câu 4. Tồn tại bao nhiêu cặp số (x;y) với
0 10,0 10
x y
thỏa mãn đẳng thức
4 4
4 4
1 1
cos sin 8 0,5sin
cos sin
x x x
x x
.
A. 10 B. 12 C. 14 D. 16
Câu 5. Biết rằng khi
0
m m
thì phương trình
2 2
2sin (5 1)sin 2 2 0
x m x m m
có đúng năm nghiệm phân
biệt thuộc khoảng
;3
2
. Mệnh đề nào sau đây đúng
A.
0
3
m
B.
0
0,5
m
C.
0
3 7
;
5 10
m
D.
0
3 2
;
5 5
m
Câu 6. Có bao nhiêu số nguyên dương m để phương trình
2
sin sin
x m x m
có nghiệm thực.
A. 2 B. 1 C. 4 D. 3
Câu 7. Xác định số nghiệm thuộc khoảng (49;1993) của phương trình
tan tan 2 tan3
x x x
A. 93 B. 1858 C. 1945 D. 1802
Câu 8. Có bao nhiêu giá trị m để phương trình ẩn x:
3
3sin 4cos ( 4 3) 5
x x m m x m
vô nghiệm thực
A. 3 B. Vô số C. 1 D. 2
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình
3 3 2
sin 3sin 3 6 4
x x m m m
có nghiệm
A. 10 B. 3 C. 4 D. 2
Câu 10. Xác định số nghiệm thuộc khoảng (49;1993) của phương trình
4 4
sin cos sin cos
x x x x
A. 619 B. 542 C. 722 D. 968
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
5
sin 5cos sin
2 2
x x
x
A. 4 B. 2 C. 5 D. 6
Câu 12. Tồn tại bao nhiêu cặp số (x;y) với
0 10,0 10
x y
thỏa mãn
2 2
sin cos
8 8 10 cos2
x x
y
A. 18 B. 10 C. 20 D. 24
Câu 13. Biết rằng
, ( ; )
m m m
là điều kiện của m để hai phương trình sau tương đương
2
2
sin 2(2 1)sin 8 0
cos (3 2)cos 6 0
x m x m
x m x m
Tính
5 4 3
.
A. 3 B. 12 C. 2 D. 5
79
Câu 14. Tập hợp
;
S a b
gồm các giá trị m để phương trình
2sin 1
sin 3
x
m
có hai nghiệm
0;
. Tính
1
ab
A.10 B. – 12 C. – 14 D. – 15
Câu 15. Tìm số nghiệm thuộc
0;4
của phương trình
2 2
tan 8cos 3sin 2
x x x
.
A. 8 B. 4 C. 12 D. 10
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
5 7 3 5
1
cos sin (cos sin ).sin 2 cos sin
2
x x x x x x x
.
A. 5 B. 4 C. 6 D. 8
Câu 17. Tìm số nghiệm
0;2
của phương trình
6
4(sin cos ) cos6 3cos2
x x x x
A. 5 B. 4 C. 3 D. 7
Câu 18. Tìm số nghiệm
0;2
của phương trình
cos9 3cos3 sin 3 3sin
x x x x
A. 6 B. 2 C. 4 D. 5
Câu 19. Tìm số nghiệm
0;
của phương trình
tan 4 1
tan .tan3
tan 4 1
x
x x
A. 4 B. 2 C. 1 D. 3
Câu 20. Tìm số nghiệm
0;
của phương trình
2sin cos3 sin 2 1 sin 4
x x x x
A. 4 B. 2 C. 1 D. 3
Câu 21. Tập hợp
;
a b
gồm các giá trị m để phương trình
2cos2 (sin cos )(sin cos ) 0
x x x m x x
có
nghiệm thuộc
0;
2
. Tính
2 2
a b
.
A. 16 B. 8 C. 18 D. 4
Câu 22. Tìm số nghiệm thuộc
0;4
của phương trình
1
sin cos 2 tan
cos
x x x
x
.
A. 3 B. 4 C. 5 D. 6
Câu 23. Tìm số nghiệm thuộc (0;100) của phương trình
tan sin 2 2 cos2
x x x
.
A. 3 B. 4 C. 5 D. 6
Câu 24. Tìm số nghiệm
0;2
của phương trình
2 2
2cos9 (3 4sin )(3 4sin 3 ) 1
x x x
.
A. 45 B. 37 C. 32 D. 18
Câu 25. Tìm số nghiệm thuộc (0;1993) của phương trình
2 2 2
(1 tan )(1 tan 2 )(1 tan 4 ) 8
x x x
.
A. 4440 B. 5550 C. 3982 D. 1975
Câu 26. Tồn tại bao nhiêu số nguyên m để phương trình
2sin cos 1
x m x m
có nghiệm
;
2 2
A. 5 B. 4 C. 3 D. 6
Câu 27. Tìm số nghiệm thuộc (0;100) của phương trình
2 2 2
cot .(1 tan )(1 tan 2 )(1 tan 4 ) 8
x x x x
A. 230 B. 160 C. 254 D. 96
Câu 28. Phương trình
3 2 2 3
sin (3 4)sin cos (3 7)sin cos ( 3)cos 0
m x m x x m x x m x
có đúng ba
nghiệm thuộc khoảng
;0
2
khi và chỉ khi
;
m a b
. Tính 3a – 2b.
A. 1 B. 4 C. – 4 D. – 3
Câu 29. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
(cot cot3 )(4cos 3) 3
x x x
.
A. 4 B. 2 C. 6 D. 8
80
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P1)
_________________________________
Câu 1. Hàm số
tan 4
y x
có đặc điểm
A. Đồ thị hàm số nằm phía trên trục hoành B. Hàm số lẻ
C. Hàm số chẵn D. Hàm số không chẵn, không lẻ
Câu 2. Phương trình
3
sin 2
2
x có bao nhiêu nghiệm trong khoảng (0;10) ?
A. 10 B. 8 C. 7 D. 5
Câu 3. Tìm chu kỳ tuần hoàn của hàm số
cos2
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 4. Phương trình
sin cos 1
x x
có bao nhiêu nghiệm thuộc khoảng
0;30
?
A. 40 B. 29 C. 50 D. 31
Câu 5. Hàm số nào sau đây là hàm số lẻ
A.
cos 1
sin 4
x
y
x
B.
1
tan
cos 4
y x
C.
sin
y x
D.
2cos 1
y x
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình
sin 1 cos 2 0
m x m x m
vô nghiệm ?
A. 4 B. 3 C. 2 D. 5
Câu 7. Phương trình
2 2
2sin 5sin cos cos 2
x x x x
tương đương phương trình nào sau đây ?
A.
2
4 5 1 0; tan
t t t x
B.
2
4 7 3 0; tan
t t t x
C.
2
2 5 3 0; tan
t t t x
D.
2
3 5 2 0; tan
t t t x
Câu 8. Gọi M, m tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3sin 4cos
y x x
. Tính M – m.
A. 10 B. 20 C. 12 D. 10
Câu 9. Tìm chu kỳ của hàm số
2sin 2 cos2
y x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 10. Tìm điều kiện tham số m để hàm số
cos3
f x x m
xác định với mọi x.
A.
1
m
B.
1
m
C. m > 0 D. 0 < m < 1
Câu 11. Phương trình
sin cos sin cos 2
x x x x
có bao nhiêu nghiệm thực thuộc khoảng (0;2017) ?
A. 100 B. 0 C. 1009 D. 4
Câu 12. Hàm số
cos
y x
đồng biến trên khoảng nào sau đây
A.
;
2 2
B.
;0
C.
4
;
2 3
D.
;
3
Câu 13. Tìm tất cả các giá trị của tham số
m
để phương trình
sin cos 5
2 2
x x
m có nghiệm.
A.
2
2
m
m
B.
2
2
m
m
C.
2 2
m
D.
2 2
m
Câu 14. Gọi S là tập giá trị của hàm số
3
4cos 3cos 3
y x x
. Độ dài của S trên trục số là
A. 2 B.
3 2
C.
2 2
D.
2
Câu 15. Hàm số nào sau đây là hàm số chẵn
A.
cos(2 3)
y x
B.
2
sin
y x
C.
cos 2 1
y x
D.
sin 6
y x
81
Câu 16. Nếu đặt
sin cos
x x t
, phương trình
3 3
3
1 sin cos sin 2
2
x x x
tương đương phương trình nào ?
A.
3 2
3 3 5 0
t t t
B.
3 2
3 3 7 0
t t t
C.
3 2
3 4 0
t t
D.
3 2
2 4 0
t t t
Câu 17. Biểu thức
2 2
cos sin 4
P x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 4 B. 3 C. 1 D. 2
Câu 18. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình
2
sin 3cos 2 0
x x m
có nghiệm.
A. 8 B. 6 C. 18 D. 7
Câu 19. Hàm số
cos2
y x
tăng trên khoảng
A.
;0
2
B.
;0
C.
4
;
2 3
D.
;
3
Câu 20. Hàm số
2
sin 5cos 2
f x x x
có tập giá trị M. Độ dài của M trên trục số là
A. 9 B. 5 C. 10 D. 14
Câu 21. Cho các hàm số
2
cos( 5); cos6 ; sin 2 ; cos3 cos
y x y x y x y x x
. Số lượng hàm số chẵn là
A. 3 B. 2 C. 4 D. 1
Câu 22. Nếu đặt
sin cos
x x t
, phương trình
1 tan 2 2 sin
x x
tương đương phương trình nào sau đây ?
A.
2
2 2 0
t t
B.
2
2 2 0
t t
C.
2
2 2 1 0
t t
D.
2
2 2 1 0
t t
Câu 23. Trên miền
0;
2
, hàm số
sin cos
y x x
có đặc điểm
A. Đồng biến B. Nghịch biến
C. Không đổi D. Vừa đồng biến, vừa nghịch biến
Câu 24. Trên khoảng
0;2
, hàm số
sin 2
y x
có khoảng nghịch biến đầy đủ
;
a b
. Tính a + b
A.
B. 0,5
C. 0,75
D. 1,25
Câu 25. Tìm giá trị lớn nhất M và giá trị nhỏ nhất N của hàm số
2
2sin 3sin 1
y x x
.
A. M = 6; N =
1
8
B. M = 6; N = 0 C. M = 5; N = 1 D. M = 4; N = 2
Câu 26. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 2018 để
4
sin cos
f x x x m
xác định với mọi x.
A. 2015 B. 2016 C. 2017 D. 2018
Câu 27. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 10;10) để phương trình sau vô nghiệm
2 2
4sin 3 3sin 2 2cos
x x x m
.
A. 5 B. 4 C. 7 D. 6
Câu 28. Phương trình
3sin cos 1
x x
tương đương phương trình nào sau đây ?
A.
1
sin
6 2
x
B.
1
sin
6 2
x
C.
sin 1
6
x
D.
sin 1
3
x
Câu 29. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos(3 ) 2
4
y x
.
A. 3 B. 4 C. 2 D. 5
Câu 30. Phương trình
2sin 2 3 sin cos 3 0
x x x
có thể giải được bằng phép đặt ẩn phụ
sin cos
x x t
đưa về phương trình ẩn t. Tổng các nghiệm t của phương trình ẩn t là
A. – 2 B. 2 C. – 1,5 D. 1
_________________________________
82
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P2)
_________________________________
Câu 1. Phương trình
2 2
sin cos 3 1
x x
có một phương trình hệ quả là
A. sin3x = 0 B. sin4x = 0 C. sin5x = 0 D. sin5x = 1
Câu 2. Tìm chu kỳ tuần hoàn của hàm số
tan( )
3
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 3. Phương trình
4 4
1
sin cos
2 2 2
x x
tương đương phương trình nào sau đây ?
A.
cos 0
B.
sin 1
x
C.
1
cos
2
x
D.
1
cos
2
x
Câu 4. Hàm số
2
5sin cos2 sin 6
y x x x
có giá trị lớn nhất A và giá trị nhỏ nhất B. Tính 28B + A.
A. 152 B. 145 C. 120 D. 170
Câu 5. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx B. y = sinx
C. y = 1 + sinx D. y = cosx + 2
Câu 6. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin 4 9 1993
y x
.
A. 3986 B. 2020 C. 1993 D. 3020
Câu 7. Tính tổng giá trị tham số m để tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau bằng 4
2
cos(2 ) 3 2
13
y x m m
.
A. 1 B. 2 C. 3 D. 4
Câu 8. Phương trình
3
5sin 4 cos
6sin 2cos
2cos2
x x
x x
x
tương đương phương trình
3
tan tan 1 0
a x b x
. Tính
giá trị biểu thức a + b.
A. 3 B. 1 C. 2 D. 4
Câu 9. Tìm chu kỳ của hàm số
4
sin 2 1993
9
y x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 10. Có bao nhiêu giá trị nguyên m lớn hơn – 6 để hàm số
sin 2 3cos2
f x x x m
xác định với mọi
x.
A. 3 B. 2 C. 1 D. 4
Câu 11. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx B. y = sinx
C. y = 1 + 2sinx D. y = 2cosx + 1
Câu 12. Phương trình
sin 2 12 sin cos 12 0
x x x
tương đương phương trình nào sau đây ?
83
A.
2
12 13; sin cos
t t t x x
B.
2
12 13; sin cos
t t t x x
C.
2
12 11 0; sin cos
t t t x x
D.
2
12 8 0; sin cos
t t t x x
Câu 13. Biết
3
sin
2
và
2
. Giá trị của cos 2
3
bằng
A. 0 B. – 1 C. 0,5 D.
3
2
Câu 14. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để hàm số
2
tan 3tan
y x x m
xác định với mọi
2
x k
.
A. 10 B. 17 C. 5 D. 7
Câu 15. Phương trình
2
cos cos 2 0
x x
có bao nhiêu nghiệm trong đoạn
0;2
.
A. 1 B. 2 C. 4 D. 3
Câu 16. Biểu thức 3cos 2cos
4 3
M x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 4 B. 6 C. 5 D. 7
Câu 17. Phương trình
2
1 cos 4 sin 2 3cos 2
x x x
có tổng các nghiệm trong đoạn
0;
bằng bao nhiêu ?
A.
3
B.
2
3
C.
3
2
D.
Câu 18. Phương trình
2
2sin 1 2cos2 2sin 1 3 4cos
x x x x
tương đương phương trình nào ?
A.
2sin 1 cos2 0
x x
B.
2sin 1 cos3 0
x x
C.
2sin 1 cos 0
x x
D.
2sin 1 cos 2 1 0
x x
.
Câu 19. Cho phương trình
2
2 sin cos 4cos 5
m x x x m
, tồn tại bao nhiêu số nguyên m trong đoạn [– 3;2]
để phương trình đã cho có nghiệm ?
A. 3 B. 2 C. 6 D. 4
Câu 20. Số nghiệm thuộc đoạn
3
;
2
của phương trình
3
3sin cos 2
2
x x
là
A. 1 B. 2 C. 4 D. 3
Câu 21. Phương trình
2
4 4
sin 2 1
sin cos
2
x
x x
có bao nhiêu nghiệm trong đoạn
;
2 2
?
A. 1 B. 2 C. 3 D. 4
Câu 22. Biểu thức
2
1
sin cos
2
y x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 2 B. 1 C. 4 D. 3
Câu 23. Tồn tại bao nhiêu giá trị nguyên m để phương trình
2 3 sin cos cos2
x x x m
có nghiệm ?
A. 3 B. 5 C. 1 D. 2
Câu 24. Tìm tập xác định của hàm số
3 sin
1 sin 2
x
y
x
.
A. \
4
D k
B. \
2
D k
C. \ 2
2
D k
D.
D
Câu 25. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 3 để hàm số cos2 cos
y x x m
xác định với mọi x.
A. 4 B. 1 C. 2 D. 3
_________________________________
84
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P3)
_________________________________
Câu 1. Biểu diễn nghiệm của phương trình
4 4
4 sin cos sin 4 3 1 tan 2 tan 0
x x x x x
trên vòng tròn
lượng giác. Số điểm biểu diễn là
A. 10 B. 8 C. 12 D. 6
Câu 2. Đồ thị hàm số nào sau đây có tâm đối xứng là gốc tọa độ ?
A.
cos(2 3)
y x
B.
sin 6
y x
C.
sin 6 sin
y x x
D.
sin3
y x
Câu 3. Hàm số
sin
y x
đồng biến trên khoảng nào sau đây
A.
;
2 2
B.
2
;
2 3
C.
4
;
2 3
D.
;
3
Câu 4. Có bao nhiêu số nguyên
20;20
m
để hàm số
cot 5
y x m
là hàm số lẻ ?
A. 37 B. 1 C. 39 D. 10
Câu 5. Đồ thị hàm số nào sau đây có trục đối xứng là trục tung ?
A.
cos(3 1)
y x
B.
sin5
y x
C.
2
sin 5
y x
D.
2
cos 5 2
y x x
Câu 6. Có bao nhiêu giá trị nguyên m để phương trình
2
8sin 1 sin 2 2 6 0
x m x m
có nghiệm ?
A. 3 B. 5 C. 6 D. 2
Câu 7. Tìm chu kỳ tuần hoàn của hàm số
3
8cos 6cos 4
y x x
.
A.
2
T
B.
T
C.
2
3
T
D.
8
T
Câu 8. Tìm số nguyên a lớn nhất để phương trình
2 2
sin 2sin 2 3 cos 2
a x x a x
có nghiệm.
A. a = 3 B. a = 2 C. a = 1 D. a = - 1
Câu 9. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx B. y = sinx
C. y = 1 + sinx D. y = cosx
Câu 10. Phương trình
1 2cos 1 cos
1
1 2cos sin
x x
x x
có bao nhiêu nghiệm thuộc khoảng
0;2018
?
A. 3027 B. 2018 C. 2017 D. 3025
Câu 11. Tìm chu kỳ của hàm số
3
4cos 2 3cos2 4tan 5
y x x x
.
A.
2
T
B.
T
C.
4
T
D.
3
T
Câu 12. Phương trình
3 3
3
cos sin 3 sin cos3
8
x x x x
tương đương phương trình nào sau đây ?
A. 2sin4x = 1 B. 3sin4x = 1 C. cos4x = 0 D. 2cos4x = 1
Câu 13. Hình vẽ bên là đồ thị hàm số nào ?
A. y = tanx
B. y = sinx + 2
C. y = 1 + sinx
D. y = cosx + 1
85
Câu 14. Phương trình
sin cos sin 2cos 3 0
x x x x
có bao nhiêu nghiệm thực thuộc
3
;
4
?
A. 3 B. 0 C. 1 D. 2
Câu 15. Phương trình
3
sin sin 2 sin 3 6cos
x x x x
tương đương phương trình
0, tan
f t t x
. Tổng các
nghiệm t của phương trình ẩn t là
A. 1 B. 2 C. 3 D. 4
Câu 16. Số giá trị nguyên dương của tham số m để phương trình
4 3 cos sin 2 1 0
x x m
có nghiệm là
A. 6 B. 5 C. 4 D. 3
Câu 17. Tính tổng các nghiệm lớn nhất và nghiệm nhỏ nhất trong đoạn
0;2018
của phương trình
sin 3 cos 2sin3
x x x
.
A.
12109
6
m n
B.
12111
6
m n
C.
12107
6
m n
D.
12103
6
m n
Câu 18. Khoảng đồng biến của hàm số
tan 2
y x
là ;
2 2
k k
a b
. Tính a + b.
A. 0 B. 0,5
C. 0,75
D. 1,25
Câu 19. Hàm số
3sin 2018 4cos 2018
y x x m
đạt giá trị nhỏ nhất bằng 0. Tìm giá trị của m.
A. m = – 7 B. m = 5 C. m = – 5 D. m = 7
Câu 20. Tìm tất cả các giá trị m để phương trình
sin cos
1
2 sin cos
m x x
x x
có nghiệm.
A.
3
1
m
m
B.
3
1
m
m
C. [– 1;3] D.
1
1
m
m
Câu 21. Gọi S là tập hợp nghiệm thuộc khoảng
0;100
của phương trình
2
sin cos 3 cos 3
2 2
x x
x
,
tổng các phần tử của S là
A.
7400
3
B.
7525
3
C.
7375
3
D.
7550
3
Câu 22. Hàm số
tan
y x
đồng biến trên khoảng
A.
;
2 2
B.
2
;
2 3
C.
4
;
2 3
D.
;
3
Câu 23. Phương trình
sin3 2cos2 2sin 1 0
x x x
có bao nhiêu nghiệm thuộc khoảng
7
;0
8
?
A. 3 B. 1 C. 2 D. 0
Câu 24. Cho hàm số
2
sin cos
y x x
. Tính giá trị
2
2
7 1 min 16
S y max y
.
A.
25
16
S B. S = 25 C.
25 4 7
S D.
24 4 7
S
Câu 25. Hình vẽ bên là đồ thị hàm số
y f x
. Khi đó
giá trị f (2018) gần nhất với giá trị nào ?
A. 1,05 B. 0,69
C. 0,42 D. 0,75
_________________________________
86
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TÔNG HỢP – P4)
_________________________________
Câu 1. Tìm điều kiện tham số m để phương trình msinx + 8cosx = 10 có nghiệm ?
A.
6
m
B. |m| < 4 C.
6
m
D.
2
m
Câu 2. Phương trình
sin 3 sin sin 2 0
x x x
có bao nhiêu điểm biểu diễn nghiệm trên đường tròn lượng giác ?
A. 2 B. 3 C. 4 D. 1
Câu 3. Đồ thị hàm số nào sau đây nhận gốc tọa độ O làm tâm đối xứng ?
A. y = |sinx| B.
2
sin 4cos 2
y x x
C. y = sinx + 5 D. y = sin3x
Câu 4. Tìm tập hợp giá trị m để phương trình
3 2 3 2
sin sin 5sin 5
x x x m m m
có nghiệm.
A. (0;1) B. [– 1;1] C. (– 2;1] D. [0;1]
Câu 5. Có bao nhiêu số nguyên m < 26 để hàm số
2019
1
sin cos
m
f x
x x m
xác định với mọi x.
A. 20 B. 27 C. 26 D. 24
Câu 6. Tìm chu kỳ tuần hoàn của hàm số
2
4sin 2 cos 2 2cos 2
y x x x
.
A.
2
T
B.
T
C.
2
T
D.
8
T
Câu 7. Tìm điều kiện của m để phương trình
2 2
sin cos sin cos 0
m x x x x
có nghiệm.
A.
1
4
m
B. m > 0 C.
1
4
m
D. 1 < m < 2
Câu 8. Phương trình
4 4
1
sin cos
4 4
x x
có bao nhiêu nghiệm trên
2 ;3
?
A. 2 B. 3 C. 1 D. 4
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình
3
4cos 3cos cos6 2
x x x m
có nghiệm ?
A. 3 B. 4 C. 2 D. 1
Câu 10. Cho các hàm số
2
sin ; cos2 ; sin ; 2cos 3
3
y x y x y x y x
. Có bao nhiêu hàm số có chu
kỳ là
2
T
A. 3 B. 1 C. 2 D. 4
Câu 11. Có bao nhiêu giá trị nguyên m lớn hơn – 30 để hàm số sau xác định với mọi x.
7cos3 cos 4 sin sin 4 cos
y x x x x x m
.
A. 13 B. 7 C. 22 D. 25
Câu 12. Tồn tại bao nhiêu số nguyên m để phương trình
2
sin 2 sin 2 0
x m x m
có nghiệm ?
A. 3 B. 2 C. 4 D. 1
Câu 13. Phương trình
cos cos5 cos 2 cos 4
x x x x
có mấy điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 4 B. 2 C. 5 D. 6
Câu 14. Tìm giá trị nhỏ nhất của m để phương trình
2
sin 4sin 5
x x m
có nghiệm.
A. m = 1 B. m = 3 C. m =
10
D. m =
2
Câu 15. Có bao nhiêu giá trị nguyên m để phương trình sin cos sin cos
x x x x m
có nghiệm ?
A. 2 B. 4 C. 3 D. 7
Câu 16. Có bao nhiêu số nguyên m để phương trình
cos2 2 1 cos 1 0
x m x m
có nghiệm
3
;
2 2
.
A. 2 B. 1 C. 0 D. 3
87
Câu 17. Phương trình
3
4sin sin cos
x x x
có hai nghiệm âm liên tiếp lớn nhất là m và n. Tính m + n.
A.
B.
2
C.
4,5
D.
2,5
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình
cos2 6 sin 3 1
x m x m
có nghiệm
0;
.
A. 2 B. 1 C. 3 D. 0
Câu 19. Có bao nhiêu số nguyên m lớn hơn – 17 để hàm số
sin 2cos 6
2sin cos
x x
y
m x x
xác định với mọi x ?
A. 13 B. 9 C. 14 D. 5
Câu 20. Nghiệm âm lớn nhất của phương trình
sin 9 3 cos7 sin 7 3 cos9
x x x x
nằm trong miền nào ?
A.
;
6 12
B.
;0
12
C.
;
3 6
D.
;
2 3
Câu 21. Biểu thức
sin cos
2sin cos 3
x x
S
x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 2 B. 1 C. 3 D. 0
Câu 22. Khoảng đồng biến đầy đủ của hàm số
sin cos
y x x
là
2 ; 2
a k b k
với
0, 0
a b
. Tính
giá trị biểu thức a + b.
A.
B. 0,5
C. 0,75
D. 1,25
Câu 23. Có bao nhiêu giá trị nguyên m
(– 18;18) để hàm số
2
tan 6tan
f x x x m
xác định với mọi x.
A. 20 B. 17 C. 6 D. 9
Câu 24. Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng ?
A. y = cos2019x + 2 B.
sin
4
y x
C. y = tanx D. y =
sin 7
y x
Câu 25. Giá trị lớn nhất của hàm số
3 3
sin cos 8
y x x
là
A. 2 B. 9 C. 10 D. 8
Câu 26. Tồn tại bao nhiêu giá trị nguyên dương m để phương trình
4 4
sin cos sin cos
x x x x m
có nghiệm ?
A. 3 B. 4 C. 1 D. 2
Câu 27. Hàm số
cos
2
x
y có khoảng đồng biến là
4 ; 4
a k b k
với
0, 0
a b
. Tính a + b
A.
B. – 2
C. –
D. 1,5
Câu 28. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
cos cos 4
y x x
.
A. 10 B. 9,75 C. 8,875 D. 7,75
Câu 29. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos2 cos 4
y x x
.
A. 9,25 B. 7,125 C. 8,5 D. 8,125
Câu 30. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 cos 4
y x
.
A. 15 B. 11 C. 10 D. 12
Câu 31. Hàm số sin
2 3
x
y
có khoảng đồng biến là
4 ; 4
a k b k
với
0, 0
a b
. Tính a + b
A.
B.
4
3
C. –
D. 1,5
Câu 32. Có bao nhiêu số nguyên m để phương trình
2
2cos 3 3 2 cos3 2 0
x m x m
có đúng ba nghiệm
thuộc khoảng
;
6 3
?
A. 4 B. 1 C. 2 D. 3
_________________________________
88
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P5)
_________________________________
Câu 1. Gọi M, m tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3sin 2cos
y x x
. Tính M.m.
A. 10 B. – 13 C. 12 D. 10
Câu 2. Số nghiệm của phương trình
2
2sin 2 cos2 1 0
x x
trong đoạn
0;2018
là
A. 1008 B. 2018 C. 2017 D. 1009
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình
3
3
cos cos
4 5
m
x x
có nghiệm ?
A. 4 B. 3 C. 2 D. 1
Câu 4. Phương trình
3 2 2 3
sin 5sin cos 3sin cos 3cos 0
x x x x x x
tương đương với phương trình nào ?
A.
3 2
5 3 3 0; tan
t t t t x
B.
3 2
5 9 3 0; tan
t t t t x
C.
3 2
5 7 3 0; tan
t t t t x
D.
3 2
4 6 3 0; tan
t t t t x
Câu 5. Tìm chu kỳ tuần hoàn của hàm số
4sin 9cos 1993
2 2
x x
y .
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 6. Tìm chu kỳ của hàm số
2 2
4sin 9cos
2 2
x x
y .
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình
sin 5cos 2 5
m x x m
có nghiệm.
A. 5 B. 6 C. 7 D. 8
Câu 8. Phương trình
3
sin cos 4sin 0
x x x
tương đương phương trình nào sau đây ?
A.
3 2
3 1 0; tan
t t t t x
B.
3 2
3 2 4 0; tan
t t t t x
C.
3 2
3 2 6 0; tan
t t t t x
D.
3 2
3 3 2 8 0; tan
t t t t x
.
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình
2 sin cos 4cos2 3 4
m x x x m
có nghiệm.
A. 1 B. 2 C. 3 D. 4
Câu 10. Phương trình
(2 2)(sin cos ) 2sin cos 2 2 1
x x x x
có bao nhiêu nghiệm
0;4
?
A. 2 B. 3 C. 4 D. 5
Câu 11. Phương trình
3(sin cos ) 2sin 2 3 0
x x x
có bao nhiêu nghiệm
0;4
?
A. 2 B. 4 C. 3 D. 5
Câu 12. Hàm số
2
3cos2 4cos 5cos 3
y x x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính giá trị biểu
thức 4M + 5N.
A. 13 B. 16 C. 19 D. 12
Câu 13. Phương trình
3 1
8sin
cos sin
x
x x
tương đương phương trình
3 2
3 tan tan tan 0
x a x b x c
.
Giá trị biểu thức a + b + c gần nhất giá trị nào ?
A. – 2 B. – 3 C. – 4 D. 3
Câu 14. Hàm số
cos 2sin 3
2cos sin 4
x x
y
x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào đúng ?
A. 2M + N + 6 = 0 B. 4M = N C. M + 7N > 0 D. 2M – N < 2
Câu 15. Tồn tại bao nhiêu số nguyên m lớn hơn – 9 sao cho
2
2sin 3cos 4
x x m
với mọi x.
89
A. 7 B. 9 C. 10 D. 13
Câu 16. Phương trình
3 3 1
cos cos cos sin sin sin
2 2 2 2 2
x x x x
x x
có một phương trình hệ quả là
A.
cos sin 1
x x
B.
cos sin 0
x x
C.
cos2 sin 1
x x
D.
cos2 2sin 1
x x
Câu 17. Phương trình
2
cos4 cos2 5 sin 3
x x x
có một phương trình hệ quả là
A. sinx = 1 B. sin2x = 1 C. 2sin3x = 1 D. 4sinx = 1
Câu 18. Phương trình
tan 2sin 2 3
x x
tương đương phương trình
0; tan
f t t x
. Tổng các nghiệm của
phương trình
0
f t
là
A. 3 B. 2 C. 1 D. 5
Câu 19. Đồ thị hàm số
sin 3
y x
có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành D. Luôn nằm bên trái trục tung
Câu 20. Tồn tại bao nhiêu hàm số mà đồ thị có tâm đối xứng là gốc tọa độ trong các hàm số sau
7
9
tan 2 .sin5 ; tan cot ; sin 2
2
y x x y x x y x
.
A. 0 B. 1 C. 2 D. 3
Câu 21. Cho các hàm số
2 2 2 2
sin 9 ; sin 5 cos9 ; sin cos(4 9) 1993; cos
y x y x x y x x y x
.
Có bao nhiêu hàm số mà đồ thị nhận trục tung là trục đối xứng ?
A. 3 B. 2 C. 1 D. 0
Câu 22. Tìm điều kiện tham số m để phương trình
sin 1 3 cos 2
m x m x m
có nghiệm.
A.
3
m
B. Không tồn tại m C.
1
3
3
m
D.
1
3
m
Câu 23. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
215sin 2014cos
3 4
y x x
.
A. 2018 B. 0 C. 421 D. – 11
Câu 24. Phương trình
1 1
2sin3 2cos3
sin cos
x x
x x
có một phương trình hệ quả là
A. sin2x = – 1 B. sin2x = 1 C. cos2x = 1 D. tanx = 1
Câu 25. Giá trị pnhỏ nhất của hàm số
2
1
cos2
2cos 1
y x
x
là
A. 3 B. 2 C. 4 D. – 1
Câu 26. Phương trình
3 3 2
3cos 4sin sin cos 3sin 0
x x x x x
tương đương phương trình nào ?
A.
3 2
3 3 1 0; tan
t t t t x
B.
3 2
3 3 0; tan
t t t t x
C.
3 2
4 4 3 3 0; tan
t t t t x
D.
3 2
4 3 3 0; tan
t t t t x
Câu 27. Tìm tổng tất cả các nghiệm x thuộc đoạn
0;10
của phương trình
2
sin 2 3sin 2 2 0
x x
.
A.
105
2
B.
105
4
C.
297
4
D.
299
4
Câu 28. Phương trình
tan3 cot
x x
có bao nhiêu nghiệm thuộc
0;2
?
A. 7 nghiệm B. 4 nghiệm C. 8 nghiệm D. 5 nghiệm
_________________________________
90
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P6)
_________________________________
Câu 1. Phương trình
sin cos 1
x x
tương đương với phương trình nào sau đây
A.
1
sin
4
2
x
B.
1
sin
4
2
x
C.
sin 1
4
x
D.
sin 2
4
x
Câu 2. Tồn tại bao nhiêu số nguyên
10;10
m
để hàm số
sin cos
y x x m
có tập xác định
?
A. 7 B. 11 C. 13 D. 12
Câu 3. Tồn tại bao nhiêu góc
0;2
x
để hàm số
2
1
9 4cos 2
tan 1
y x
x
không xác định ?
A. 3 B. 4 C. 5 D. 6
Câu 4. Có bao nhiêu số nguyên m < 10 để phương trình
sin 1 cos
cos
m
m x m x
x
có nghiệm ?
A. 9 B. 6 C. 7 D. 8
Câu 5. Tồn tại bao nhiêu số nguyên dương n < 4 để hàm số
2 2
2sin 3cos ( )
y x nx
có chu kỳ
T
?
A. 4 B. 2 C. 3 D. 1
Câu 6. Tồn tại bao nhiêu số nguyên dương n < 10 để hàm số
4sin 2 9cos
2
nx
y x
có
T
?
A. 4 B. 2 C. 3 D. 1
Câu 7. Có bao nhiêu số nguyên m thỏa mãn đẳng thức
sin 2 2 sin
4
x x m
?
A. 4 B. 2 C. 3 D. 1
Câu 8. Tính tổng tất cả các giá trị nguyên m để
2 2
sin 2 1 sin cos 1 cos
x m x x m x m
là một phương
trình có nghiệm.
A. 1 B. 6 C. 3 D. 10
Câu 9. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
sin sin
3
y x x
.
A. 2 B. – 1 C. 1 D. – 3
Câu 10. Tính a + b biết
sin cos 1 ( 0, 0)
a x b x a b
là một phương trình hệ quả của phương trình
1
3sin 2cos 3(1 tan )
cos
x x x
x
.
A. 4 B. 5 C. 3 D. 2
Câu 11. Tính tổng các nghiệm x thuộc
0;99
của phương trình
2 3
2
2
cos cos 1
cos2 tan
cos
x x
x x
.
A.
2209
3
B.
4
9
C.
1993
4
D.
2019
4
Câu 12. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số sin cos
3 3
y x x
.
A.
3 1
B.
3 1
C. – 2 D. 1
Câu 13. Tìm tập hợp tất cả các giá trị m để phương trình
2
cos 1 cos 2 cos sin
x x m x m x
có đúng hai
nghiệm thuộc đoạn
2
0;
3
.
A. [0;1) B.
1
1;
2
C.
1
0;
2
D. (– 1;1]
91
Câu 14. Tìm m để đồ thị hàm số
sin 2 sin3 cos sin cos3 8
y x x x x x m
nhận gốc tọa độ làm tâm đối xứng.
A. m = 8 B. m = 3 C. m = 6 D. m = 2
Câu 15. Tồn tại bao nhiêu số nguyên
20;20
m
để hàm số
cos2 1
sin( )
cos2 1
x
y mx
là hàm số chẵn ?
A. 10 B. 39 C. 20 D. 24
Câu 16. Tịnh tiến đồ thị hàm số
3
8cos 6cos 3
y x x
xuống dưới tối thiểu bao nhiêu đơn vị để đồ thị thu
được không nằm phía trên trục hoành ?
A. 1 B. 5 C. 4,75 D. 2,5
Câu 17. Hỏi tồn tại bao nhiêu giá trị nguyên m để phương trình
cos2 2 1 cos 1
x m x m
có đúng hai nghiệm
;
2 2
?
A. 2 B. 3 C. 1 D. 4
Câu 18. Giả sử
2
3sin 2 cos 2 5
,
sin 2 4cos 1
x x a
x
x x b
. Tính a + 2b.
A. 77 B. 54 C. 19 D. 83
Câu 19. Phương trình
2
2sin sin 1 0
x x
có bao nhiêu nghiệm thuộc
0;3
?
A. 3 B. 4 C. 5 D. 6
Câu 20. Tính a + b biết rằng
2
2cos2 12sin 5 sin sin 5
x x a x b x
.
A. 15 B. 14 C. 16 D. 20
Câu 21. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình
2
2cos 5cos 2 0
x x
.
A. 3 B. 2 C. 4 D. 5
Câu 22. Tính tổng các giá trị tự nhiên m để hàm số
2
tan cos
2 4
x x
y
m
là hàm số tuần hoàn với
6
T
.
A. 3 B. 6 C. 9 D. Kết quả khác
Câu 23. Hàm số sin cos
4 6 4 6
x x
y
có khoảng đồng biến là
4 ; 4
a k b k
với
0, 0
a b
.
Tính a + b
A.
B.
4
3
C. –
D. 1,5
Câu 24. Tồn tại bao nhiêu số nguyên m để phương trình
3sin 4cos
x x m
có nghiệm ?
A. 10 B. 11 C. 12 D. 9
Câu 25. Tồn tại bao nhiêu số nguyên m để phương trình 3sin cos
x x m
có nghiệm ?
A. 10 B. 11 C. 12 D. 9
Câu 26. Hàm số cot
x
y
a b
với
0, 0
a b
có khoảng nghịch biến
3 9
3 ; 3
4 4
k k
. Tính ab.
A. 12 B. 8 C. 6 D. 9
Câu 27. Phương trình
2
2sin 2 5sin 2 2 0
x x
có hai họ nghiệm dạng
;
x k x k
. Khi đó tích
của

là
A.
2
5
144
B.
2
5
36
C.
2
5
36
D.
2
5
144
Câu 28. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số
4sin3
y x m
có tập xác định
.
A. 6 B. 8 C. 5 D. 7
_________________________________
92
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P7)
_________________________________
Câu 1. Tìm họ nghiệm của phương trình
sin 1
x
.
A.
2
2
x k
B.
2
x k
C.
2
x k
D.
2
x k
Câu 2. Cho các hàm số
2
sin ; cos2 ; sin ; 2cos 3
3
y x y x y x y x
. Có bao nhiêu hàm số có chu
kỳ là
2
T
A. 3 B. 1 C. 2 D. 4
Câu 3. Tìm số nghiệm của phương trình
sin 0,3
x
trong khoảng
0;3
.
A. 4 B. 2 C. 3 D. 1
Câu 4. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( ) cos5 cos sin5 sin 4sin3
f x x x x x x
.
A. – 15 B. – 8 C. 10 D. – 6
Câu 5. Tìm số nghiệm của phương trình
tan 0,4
trong khoảng
0;3
A. 3 B. 2 C. 4 D. 1
Câu 6. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
1 1
2 sin
4 sin cos
x
x x
.
A. 4 B. 2 C. 3 D. 5
Câu 7. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2 2
4 5sin cos
y x x
.
A. 5 B. 11 C. 3 D. 8
Câu 8. Tìm số nghiệm
2 ;2
của phương trình
2
2tan cot 3
sin 2
x x
.
A. 4 B. 3 C. 2 D. 5
Câu 9. Tính tổng các giá trị m để hàm số sin
3
y mx
nhận chu kỳ
2
T
.
A. 3 B. 0 C. 1 D. 2
Câu 10. Tồn tại bao nhiêu số nguyên m để phương trình
2cos2 sin
x x m
có nghiệm ?
A. 3 B. 6 C. 5 D. 10
Câu 11. Tìm điều kiện tham số m để hàm số
1
sin
y
x m
có tập xác định
.
A.
1
m
B.
1
1
m
m
C. 0 < m < 1 D.
1
m
Câu 12. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm
1
2
sin cos
y
x x
không xác định ?
A. 3 B. 2 C. 4 D. 1
Câu 13. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 8 sin cos
y x x
.
A. 4 B. 1 C. 3 D. – 2
Câu 14. Tồn tại bao nhiêu số nguyên m để phương trình
2
2cos2 3cos 2sin
x x x m
có nghiệm ?
A. 13 B. 7 C. 8 D. 10
Câu 15. Đồ thị hàm số
cos2 5
y x
có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
93
C. Luôn nằm phía dưới trục hoành D. Luôn nằm bên trái trục tung
Câu 16. Phương trình
4 2
4sin 12cos 7
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 2 C. 5 D. 4
Câu 17. Hàm số nào sau đây có tập xác định
?
A.
cos 1
sin 4
x
y
x
B.
1
tan
cos 4
y x
C.
sin 1
y x
D.
2cos 1
y x
Câu 18. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
(2sin 1)(2cos2 2sin 1) 3 4cos
x x x x
.
A. 5 B. 4 C. 6 D. 3
Câu 19. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
tan sin 1 tan .sin
x x x x
.
A. 5 B. 2 C. 3 D. 4
Câu 20. Tịnh tiến đồ thị hàm số
3
( ) 3sin 4sin
g x x x
sang trái
2
đơn vị ta thu được đồ thị hàm số
( )
y f x
.
Hai đồ thị hàm số
( ), ( )
f x g x
cắt nhau tại bao nhiêu điểm có hoành độ thuộc khoảng
0;2
?
A. 5 B. 6 C. 3 D. 1
Câu 21. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2 2
cos (1 cos ) sin (1 sin ) 2cos
x x x x x
.
A. 4 B. 3 C. 2 D. 1
Câu 22. Có bao nhiêu số nguyên m để phương trình
cos4 2( 3)cos2 6 1 0
x m x m
có nghiệm
0;
4
A. 2 B. 5 C. 3 D. 4
Câu 23. Tính tổng nghiệm lớn nhất và nghiệm nhỏ nhất thuộc
100 ;100
của phương trình
3 3
sin cos 1 0,5sin 2
x x x
.
A.
2
B.
0,5
C.
0,25
D. – 1,5
Câu 24. Phương trình
3 3
sin cos 1
x x
có bao nhiêu nghiệm
0;4
?
A. 2 B. 4 C. 3 D. 5
Câu 25. Tồn tại bao nhiêu số nguyên m để phương trình 3sin 2 4(sin cos )
x x x m
có nghiệm ?
A. 13 B. 12 C. 10 D. 11
Câu 26. Hàm số
sin
2 3
x
y
có khoảng đồng biến là
4 ; 4
a k b k
với
0, 0
a b
. Tính a + b
A.
B.
4
3
C. –
D. 1,5
Câu 27. Nghiệm dương nhỏ nhất của phương trình
3
2 sin 2sin
4
x x
thuộc khoảng
A.
1
0;
2
B. (1;2) C. (2;3) D.
1
;1
2
Câu 28. Tìm số nghiệm thuộc
0;3
của phương trình
3
cos 2sin
x x
.
A. 5 B. 3 C. 2 D. 4
Câu 29. Nghiệm dương nhỏ nhất của phương trình
sin 2 2tan 3
x x
thuộc khoảng
A.
1
0;
2
B. (1;2) C. (2;3) D.
1
;1
2
_________________________________
94
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P8)
_________________________________
Câu 1. Tính tổng các giá trị tham số m để hàm số
1 2
cot sin
3 2 3
x x
y
m
(m là số tự nhiên) tuần hoàn với
chu kỳ
6
.
A. 2 B. 6 C. 8 D. 12
Câu 2. Tính a + b biết
sin 2 cos 7 0
a x b x
là một phương trình hệ quả của phương trình
9sin 6cos 3sin 2 cos2 8
x x x x
.
A. 5 B. 7 C. 6 D. 9
Câu 3. Tồn tại bao nhiêu cặp số nguyên dương (m;n) để hàm số
26tan 4cot 2019
x x
y
m n
có
12
T
?
A. 16 B. 15 C. 10 D. 12
Câu 4. Tồn tại bao nhiêu số nguyên m thuộc [– 5;5] để phương trình
tan 2
x m
có nghiệm ?
A. 4 B. 2 C. 11 D. 20
Câu 5. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2sin cos 3cos2 4
y x x x
.
A. 10 B. 8 C. 12 D. – 6
Câu 6. Cho các hàm số
2
4
cot ; tan ; sin ; sin cos
2 2 9
x x
y x y y y x x
. Tồn tại bao nhiêu hàm số
thỏa mãn điều kiện
( 2 ) ( )
f x k f x
?
A. 4 B. 2 C. 3 D. 1
Câu 7. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
4 4
3(cos sin ) sin 2 1
y x x x
.
A. – 3 B. – 2 C. 1 D. 4
Câu 8. Tồn tại bao nhiêu số nguyên m để phương trình
2sin
x m
có nghiệm thuộc
2
0;
3
?
A. 4 B. 2 C. 3 D. 5
Câu 9. Tìm số nghiệm
4 ;9
của phương trình
2 4
sin 2 cos 2 1
0
sin cos
x x
x x
.
A. 13 B. 14 C. 15 D. 16
Câu 10. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
3 2cos3 (3sin 4sin )
y x x x
.
A. 6 B. 8 C. 2 D. – 4
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 2
4sin 2 6sin 9 3cos2
0
cos
x x x
.
A. 6 B. 2 C. 4 D. 5
Câu 12. Tồn tại bao nhiêu số nguyên m để phương trình
3sin
x m
có hai nghiệm thuộc
2
0;
3
?
A. 4 B. 3 C. 2 D. 0
Câu 13. Tính a + b biết
(sin cos ) sin cos 1 0
a x x b x x
là một phương trình hệ quả của phương trình
2
2sin 3sin 1 cos3
x x x
.
A. 5 B. 3 C. 4 D. 2
Câu 14. Phương trình
cos4 9sin 2 8 0
x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
95
Câu 15. Tìm số nghiệm thuộc
0;3
của phương trình
5cos 7 2sin
2
x
x .
A. 3 B. 4 C. 1 D. 2
Câu 16. Góc x thỏa mãn
1 1 10
cos sin
cos sin 3
x x
x x
thì cos
4
x
gần nhất với
A. – 0,55 B. – 0,25 C. 0,12 D. – 0,45
Câu 17. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
3 3
3
1 sin cos sin 2
2
x x x
.
A. 3 B. 4 C. 1 D. 2
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình
2
cos2 sin cos4
m x x x
có nghiệm
2
0;
3
A. 4 B. 8 C. 5 D. 6
Câu 19. Tìm số nghiệm thuộc
0;3
của phương trình
4 2 2 4
3cos 4sin cos sin 0
x x x x
A. 12 B. 16 C. 10 D. 8
Câu 20. Phương trình
2 2
8sin cos 2sin 4 3 3cos 4
x x x x
tương đương
(tan 2 )(tan 2 ) 0
x a x b
. Tính
giá trị biểu thức a + b + 2.
A. 2 B. 6 C. 3 D. 1
Câu 21. Tồn tại bao nhiêu hàm số mà đồ thị có tâm đối xứng là gốc tọa độ trong các hàm số sau
7
9
tan 2 .sin 5 ; tan cot ; sin 2
2
y x x y x x y x
.
A. 0 B. 1 C. 2 D. 3
Câu 22. Cho các hàm số
2 2 2 2
sin 9 ; sin 5 cos9 ; sin cos(4 9) 1993; cos
y x y x x y x x y x
.
Có bao nhiêu hàm số mà đồ thị nhận trục tung là trục đối xứng ?
A. 3 B. 2 C. 1 D. 0
Câu 23. Tìm chu kỳ của hàm số
sin cos 4sin cos 9
y x x x x
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 24. Hàm số nào sau đây có điều kiện xác định
2
x k
?
A.
2
1 1
cos 4 sin
y
x x
B.
cos 1
sin 4
x
y
x
C.
tan 3cot
y x x
D.
1
cos 1
y
x
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2
(2sin 1)(2cos2 2sin 1) 3 4cos
x x x x
.
A. 5 B. 4 C. 6 D. 3
Câu 26. Tồn tại bao nhiêu số nguyên x < 10 để hàm số
1
sin( )
x
y
x
xác định ?
A. 7 B. 4 C. 0 D. 8
Câu 27. Cho các hàm số
2
sin 1
; sin 4; ; cos 1
3 cos tan 1
x
y y x y y x
x x
. Có bao nhiêu hàm số
có tập xác định
?
A. 4 B. 1 C. 3 D. 2
_________________________________
96
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P9)
_________________________________
Câu 1. Tìm chu kỳ của hàm số
1 cos2 sin 2
1 cos 2 sin 2
x x
y
x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 2. Phương trình
cos 3sin 2cos3
x x x
có một họ nghiệm nào đó là
k
x
a b
với a, b nguyên
dương. Tính tổng số các ước dương của a và b.
A. 6 B. 4 C. 10 D. 12
Câu 3. Tìm số nghiệm
0;2
của phương trình
(1 2sin )cos
3
(1 2sin )(1 sin )
x x
x x
.
A. 3 B. 7 C. 4 D. 2
Câu 4. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm số
2 2
1
sin cos
y
x x
không xác định ?
A. 3 B. 2 C. 4 D. 1
Câu 5. Tịnh tiến đồ thị
sin 2
y x
lên trên 2 đơn vị, sau đó sang phải
2
thu được đồ thị hàm số
( )
y f x
. Tính
tổng các giá trị m để đường thẳng y = m tiếp xúc với đồ thị
( )
y f x
.
A. 4 B. 2 C. 6 D. 7
Câu 6. Đồ thị hàm số nào sau đây luôn nằm phía dưới trục hoành
A.
cos3
y x
B.
sin 2 2
y x
C.
sin 2
3
y x
D.
cos3 cos6
y x x
Câu 7. Biểu thức
sin cos
2sin cos 3
x x
S
x x
có thể nhận bao nhiêu giá trị nguyên ?
A. 2 B. 1 C. 3 D. 0
Câu 8. Tìm số nghiệm thuộc
0;3
của phương trình
4 4
5(1 cos ) 2 sin cos
x x x
.
A. 3 B. 4 C. 5 D. 2
Câu 9. Tồn tại bao nhiêu số nguyên k để phương trình
4sin 2 cos cos3
x m x x
có nghiệm
0;
6
.
A. 5 B. 6 C. 3 D. 7
Câu 10. Cho
3
( ) 3 2
f x x x
. Tìm số nghiệm của phương trình
(tan2 ) 0
f x
trong khoảng
0;2
.
A. 3 B. 6 C. 5 D. 8
Câu 11. Đồ thị hàm số nào sau đây nằm hoàn toàn phía trên đường thẳng y = 2 ?
A.
sin
2 cos
x
y
x
B.
3
4cos 3cos 3,5
y x x
C.
2cos2 cos
y x x
D.
sin3 sin6 2
y x x
Câu 12. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của
3
4sin sin3 4cos cos
x x x x
.
A. 3 B. 2 C. 1 D. 4
Câu 13. Tìm số nghiệm thuộc
0;3
của phương trình
2
cos2 3cos 4cos
2
x
x x
.
A. 3 B. 4 C. 5 D. 2
Câu 14. Hàm số
2
4 (sin 2 cos2 )
y x x
có khoảng nghịch biến ;
4 4
k k
a b
. Tính 3b – a.
97
A. 0,5
B.
C. 0,25
D. 1,5
Câu 15. Hàm số
3
4 2
4 8cos 8cos 1 3cos4
y x x x
khoảng đồng biến ;
6 6
k k
a b
. Tính a + b
A.
3
B.
C. 2
D.
12
Câu 16. Tìm chu kỳ tuần hoàn của hàm số
3
1
(3sin 4sin )cos3 sin 4
y
x x x x
.
A.
T
B.
2
T
C.
4
T
D.
4
T
Câu 17. Tìm chu kỳ của hàm số
sin sin3 sin 5
cos cos3 cos5
a a a
y
a a a
.
A.
2
5
T
B.
T
C.
3
T
D.
2
T
Câu 18. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
4cos 2sin 3 cos2
x x x
.
A. 4 B. 2 C. 3 D. 5
Câu 19. Tính 4a + 9b biết
cos sin 6
a x b x
là một hệ quả của phương trình
4sin 2 3cos2 3(4sin 1)
x x x
.
A. 7 B. 3 C. 8 D. 6
Câu 20. Tồn tại bao nhiêu số nguyên m để phương trình
4(sin cos ) 9sin cos 1993
x x x x m
có nghiệm ?
A. 10 B. 16 C. 17 D. 7
Câu 21. Tồn tại bao nhiêu số nguyên m thuộc
3;3
để phương trình
3
4cos 3cos 1
x x m
có nghiệm ?
A. 4 B. 5 C. 2 D. 3
Câu 22. Phương trình
sin 2 2cos2 1 sin 4cos
x x x x
có bao nhiêu nghiệm
49;1993
A. 193 B. 968 C. 702 D. 325
Câu 23. Phương trình
2sin 2 cos2 7sin 2cos 4
x x x x
tương đương phương trình
sin
x a
, khi đó
A.
1 1
;
5 4
a
B.
1 1
;
7 5
a
C.
1 1
;
4 3
a
D.
1
;1
3
a
Câu 24. Tồn tại bao nhiêu số nguyên m thuộc
10;10
để phương trình
sin 4 cos 4 2
x x m
có nghiệm ?
A. 4 B. 5 C. 3 D. 6
Câu 25. Tồn tại bao nhiêu số nguyên m để phương trình
sin cos sin cos
x x x x m
có nghiệm
0;
4
A. 2 B. 1 C. 3 D. 4
Câu 26. Tìm chu kỳ của hàm số
4sin sin sin sin
3 3
y x x x x
.
A.
2
T
B.
T
C.
4
T
D.
8
T
Câu 27. Tồn tại bao nhiêu số nguyên m để phương trình
2 2
2sin (2 1)sin cos cos 0
x m x x m x
có 4 điểm
biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. Vô số C. 5 D. 10
Câu 28. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3
2 2 cos ( ) 3cos sin 0
4
x x x
.
A. 3 B. 2 C. 4 D. 1
_________________________________
98
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P10)
_________________________________
Câu 1. Tìm chu kỳ tuần hoàn của hàm số
(cos5 cos sin5 sin )cos4
y x x x x x
.
A.
2
T
B.
2
T
C.
4
T
D.
4
T
Câu 2. Tìm số nghiệm
0;
của phương trình
2cos3 3sin cos 0
x x x
.
A. 2 B. 3 C. 1 D. 4
Câu 3. Hàm số
cos 2sin 3
2cos sin 4
x x
y
x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào đúng ?
A. 2M + N + 6 = 0 B. 4M = N C. M + 7N > 0 D. 2M – N < 2
Câu 4. Điều kiện xác định của hàm số
2
3tan(2 ) 4 1
4
y x x
là
A.
4 2
k
x
B.
3
8 2
k
x
C.
2
x k
D.
2
2
x k
Câu 5. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2 cos2 cos 2 3
3
y x x
.
A. 7 B. 8 C. 6 D. 4
Câu 6. Tìm số nghiệm
4 ;9
của phương trình
2
sin (sin cos ) 1
0
cos sin 1
x x x
x x
.
A. 25 B. 22 C. 15 D. 7
Câu 7. Hàm số
3
tan
y x x x
có đặc điểm
A. Hàm số chẵn B. Hàm số lẻ
C. Hàm số không chẵn, không lẻ D. Đồ thị hàm số nằm phía trên trục hoành
Câu 8. Có bao nhiêu điểm M (x;y) nằm trên đồ thị hàm số
sin
y x
thỏa mãn
4 9; cos
x y x
?
A. 4 B. 1 C. 3 D. 2
Câu 9. Phương trình
4 4
cos2 sin cos
x x x
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?
A. 3 B. 4 C. 5 D. 2
Câu 10. Tìm số nghiệm thuộc
0;2
của phương trình
4
2
4
3cot 5 0
sin
x
x
.
A. 3 B. 4 C. 5 D. 2
Câu 11. Tồn tại bao nhiêu số nguyên m < 10 để phương trình
2 2
sin 2sin cos ( 1)cos
x x x m x
có nghiệm
A. 8 B. 12 C. 10 D. 8
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
3 2
sin 3cos 3sin cos 2sin
x x x x x
.
A. 3 B. 5 C. 2 D. 4
Câu 13. Cho các hàm số
1
sin sin 4 ; tan 4 ; sin ; cos 1; cos4
y x x y x x y y x y x
x
.
Biết rằng có a hàm số chẵn và b hàm số lẻ, tính 3a + 2b.
A. 5 B. 8 C. 11 D. 12
Câu 14. Hàm số
2 2
3 3
cos sin
2 2
x x
y có khoảng nghịch biến
2 2
;
3 3
k k
a b
với
0, 0
a b
. Tính a + b
A.
3
B.
C. 2
D. 1,5
99
Câu 15. Tính tổng các nghiệm thuộc
0;2
của phương trình
1 1 2
cos sin 2 sin 4
x x x
.
A.
2
B.
C.
3
D.
1,5
Câu 16. Hàm số
cos sin
y x x
có khoảng nghịch biến
2 ; 2
a k b k
. Tính a + b
A.
B. – 2
C. –
D. 1,5
Câu 17. Tồn tại bao nhiêu số nguyên m để phương trình
sin 2 sin 2 4cos
x m x m x
có nghiệm ?
A. 4 B. 2 C. 5 D. 3
Câu 18. Tồn tại bao nhiêu số nguyên m thuộc
3;3
để phương trình
2
2cos 1 cos(3 )
x x m
có nghiệm ?
A. 4 B. 2 C. 5 D. 3
Câu 19. Tồn tại bao nhiêu số nguyên m thuộc
10;10
để phương trình
cos4 cos sin 4 sin 2
x x x x m
có
nghiệm ?
A. 4 B. 5 C. 2 D. 3
Câu 20. Phương trình
cos2 2cos 6sin 8
x x x
có một hệ quả
cos sin
x x a
, số ước của a là
A. 2 B. 4 C. 6 D. 8
Câu 21. Đồ thị hàm số nào sau đây tiếp xúc trục hoành ?
A.
cos3
y x
B.
sin 2 2
y x
C.
sin 6 1
y x
D.
tan 3
y x
Câu 22. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( ) sin 2 cos2 3; ;
4 4
f x x x x
.
A. 5 B.
5 2
C.
4 2 2
D.
3 2 1
Câu 23. Hàm số
2cos 3sin 5
2sin 3cos 5
x x
y
x x
có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính Q = M.N.
A. Q = 1 B. Q = 2 C. Q = 5 D. Q = 10
Câu 24. Tìm số nghiệm trong khoảng
0;2
của phương trình
3sin cos sin cos 3
x x x x
.
A. 3 B. 1 C. 0 D. 2
Câu 25. Tính
3 sin 2
khi
là nghiệm phương trình
sin cos 2(sin cos ) 2
x x x x
.
A. 3 B. 2 C. 3,5 D. 2,5
Câu 26. Tìm chu kỳ tuần hoàn của hàm số
2 2
6
2 2
sin tan
.cot tan
cos cot
x x
y x x
x x
.
A.
2
T
B.
T
C.
4
T
D.
2
T
Câu 27. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
sin5
1
5sin
x
x
.
A. 0 B. 2 C. 3 D. 4
Câu 28. Tìm tập xác định của hàm số
tan 2
2cos 7
x
y
x
.
A.
2
x k
B.
2
2
x k
C.
4 2
x k
D.
Câu 29. Tìm số nghiệm
0;2
của phương trình
3(sin 2 sin ) cos2 cos 2
x x x x
.
A. 7 B. 6 C. 3 D. 8
Câu 30. Tịnh tiến đồ thị
2 sin
y x
sang trái
4
đơn vị ta được đồ thị hàm số
A.
sin cos
y x x
B. 2 sin
4
y x
C.
sin
y x
D.
cos
y x
| 1/99
| | Tải xuống

Có thể bạn quan tâm:

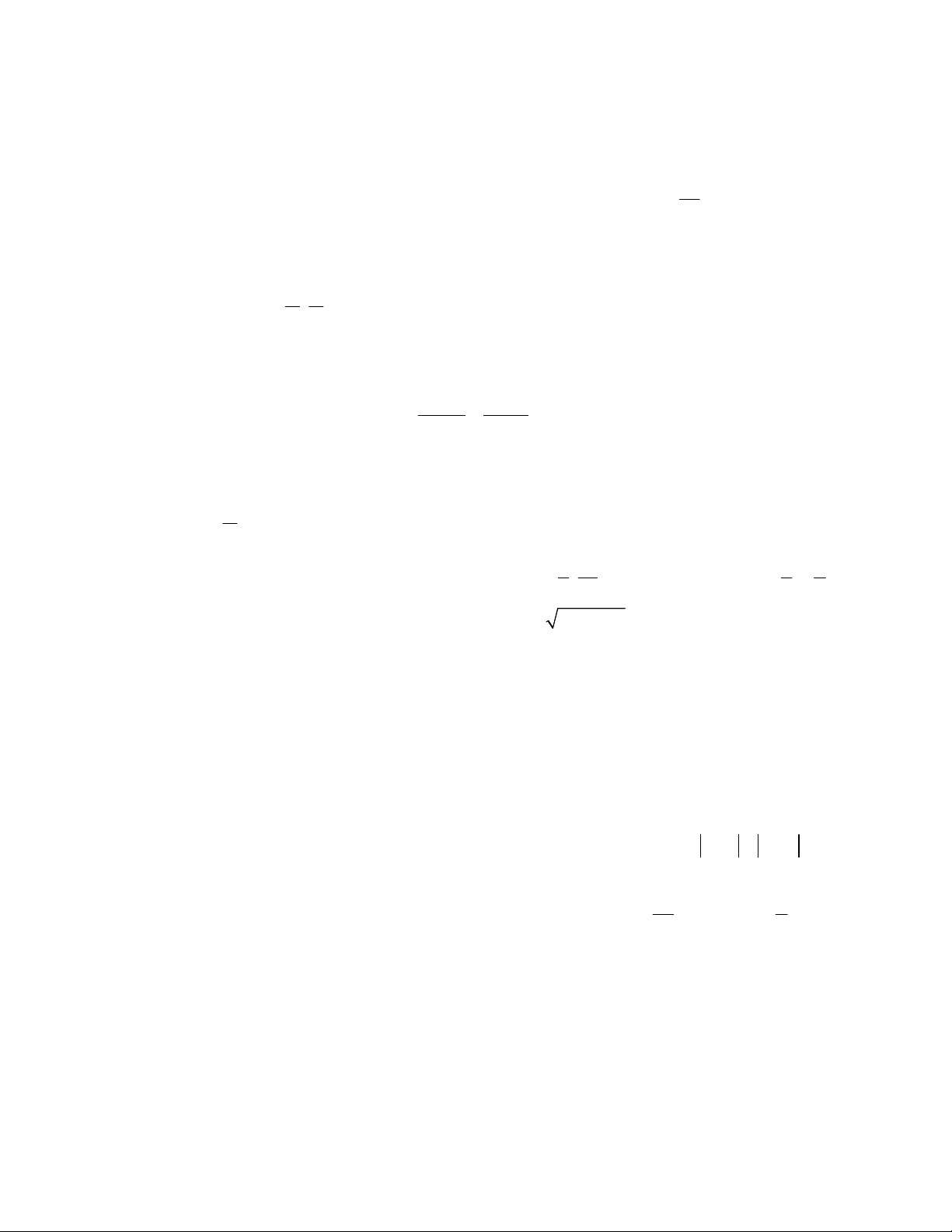
Preview text:

TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
-------------------------------------------------------------------------------------------- CHUYÊN ĐỀ
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
o TẬP XÁC ĐỊNH (CƠ BẢN) o CHU KỲ (CƠ BẢN) o MIN MAX (CƠ BẢN)
o TÍNH CHẴN LẺ VÀ ĐỒ THỊ (CƠ BẢN)
o TÍNH ĐƠN ĐIỆU (CƠ BẢN)
o PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
o PHƯƠNG TRÌNH LƯỢNG GIÁC BẬC NHẤT SIN, COS (CƠ BẢN)
o PHƯƠNG TRÌNH LƯỢNG GIÁC CHỨA ẨN MẪU THỨC (CƠ BẢN)
o PHƯƠNG TRÌNH LƯỢNG GIÁC DẠNG TÍCH (CƠ BẢN)
o PHƯƠNG TRÌNH LƯỢNG GIÁC ĐỐI XỨNG (CƠ BẢN)
o PHƯƠNG TRÌNH LƯỢNG GIÁC ĐỒNG BẬC (CƠ BẢN)
o PHƯƠNG TRÌNH LƯỢNG GIÁC ĐA THỨC + ẨN PHỤ (CƠ BẢN)
o HÀM SỐ LƯỢNG GIÁC (VẬN DỤNG CAO)
o PHƯƠNG TRÌNH LƯỢNG GIÁC (VẬN DỤNG CAO)
o ÔN TẬP TỔNG HỢP LƯỢNG GIÁC
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK); TEL 0333275320
THÀNH PHỐ THÁI BÌNH – THÁNG 10/2020 1
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TẬP XÁC ĐỊNH PHẦN 1)
___________________________________________
Câu 1. Tìm tập xác định của hàm số y  cos x  2 . A.  B. [0;2] C. (0;2) D.  2  ; 1
Câu 2. Tìm điều kiện xác định của hàm số y  tan x  . cos x  2    A. x   k B. x   k2 C. x   k2 D.  2 2 4 tan 2x
Câu 3. Tập xác định của hàm số y 
là vòng tròn lượng giác bỏ đi bao nhiêu điểm ? sin x 1 A. 4 B. 5 C. 2 D. 3
Câu 4. Tồn tại bao nhiêu số nguyên m lớn hơn – 6 để hàm số 3
y  4cos x  3cos x  m xác định với mọi x ? A. 10 B. 6 C. 4 D. 5
Câu 5. Tìm tập xác định của hàm số y  sin x  cos x  3 . A.  B. [0;2] C. (0;2) D.  2  ; cos x  4
Câu 6. Tìm điều kiện xác định của hàm số y  . sin x 1    A. x   k B. x    k2 C. x   k2 D.  2 2 4
Câu 7. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số 2
y  2cos 2x  m có tập xác định  . A. 0 B. 1 C. 5 D. 7 x  2
Câu 8. Tìm tập xác định của hàm số y  . cos x  3 A.  B.  3; C. (0;2) D.  2  ; 1
Câu 9. Tìm điều kiện tham số m để hàm số f (x)  có tập xác định  . cos x  m m  1 A. m > 0 B.  C. – 1 < m < 1 D. 0 < m < 1 m  1 1
Câu 10. Tìm điều kiện tham số m để hàm số y  có tập xác định  . sin x  m m  1 A. m  1 B.  C. 0 < m < 1 D. m  1 m  1
Câu 11. Hàm số nào sau đây có tập xác định  ? cos x 1 1 A. y  B. y  tan x  C. y  sin x 1 D. y  2cos x 1 sin x  4 cos x  4 1
Câu 12. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm y   2 không xác định ? sin x  cos x A. 3 B. 2 C. 4 D. 1 
Câu 13. Điều kiện xác định của hàm số y  tan(2x  ) là 4  k 3 k   A. x   B. x   C. x   k D. x    k2 4 2 8 2 2 2 2 
Câu 14. Hàm số nào sau đây có điều kiện xác định x   k ? 2 1 1 cos x 1 1 A. y   B. y  C. y  tan x  3cot x D. y  2 cos x 4  sin x sin x  4 cos x 1 x 1
Câu 15. Tồn tại bao nhiêu số nguyên x < 10 để hàm số y  xác định ? sin( x) A. 7 B. 4 C. 0 D. 8 sin x 1
Câu 16. Cho các hàm số y  ; y  sin x  4; y 
; y  cos x 1 . Có bao nhiêu hàm số 2 3  cos x tan x 1 có tập xác định  ? A. 4 B. 1 C. 3 D. 2 1
Câu 17. Tồn tại bao nhiêu số nguyên m  1
 0;10 để hàm số y 
xác định với mọi giá trị x ? 2cos 2x  m A. 4 B. 14 C. 12 D. 10
Câu 18. Có bao nhiêu số nguyên m  1
 0;10 để hàm số y  sin xcos x  m 1 xác định với mọi giá trị x ? A. 4 B. 14 C. 12 D. 10  tan(2x  )
Câu 19. Tồn tại bao nhiêu góc x 0;2  để hàm số 4 y  không xác định ?    1 sin x     8  A. 4 B. 5 C. 6 D. 3 1 1
Câu 20. Tồn tại bao nhiêu góc x 0;2  để hàm số y   không xác định ? 2 2 cos x  sin x 4  cos 2x A. 3 B. 2 C. 1 D. 4
Câu 21. Tồn tại bao nhiêu số nguyên m  1
 0;10 để hàm số y  sin x  cos x  m có tập xác định  ? A. 7 B. 11 C. 13 D. 12 1
Câu 22. Tồn tại bao nhiêu góc x 0;2  để hàm số y  9  4cos 2x  không xác định ? 2 tan x 1 A. 3 B. 4 C. 5 D. 6
Câu 23. Có bao nhiêu số nguyên m  1
 0;10 để hàm số y  2sin3x  3cos3x  m có tập xác định  A. 7 B. 6 C. 3 D. 13 2 1
Câu 24. Tồn tại bao nhiêu góc x 0;2  để hàm số y   không xác định ? 3 cos x  cos3x sin x  9 A. 7 B. 4 C. 5 D. 8 1
Câu 25. Tồn tại bao nhiêu số nguyên m  1
 0;10 để hàm số y  có tập xác định  ? 3sin x  4cos x  m A. 7 B. 4 C. 3 D. 11 1
Câu 26. Tồn tại bao nhiêu góc x 0;2  để hàm số y 
 8  sin x không xác định ? 1 cos 2x A. 3 B. 4 C. 5 D. 6
Câu 27. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số y  4sin 3x  m có tập xác định  . A. 6 B. 8 C. 5 D. 7
_________________________________ 3
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TẬP XÁC ĐỊNH PHẦN 2)
___________________________________________ 1
Câu 1. Tìm tập xác định của hàm số y  cos x  3  . cos 2x  5 A.  B. [0;2] C. (0;2) D.  2  ; Câu 2. Cho các hàm số 2 1 1
y  x  x  sin x cos x 1; y  ; y  cos x 1; y  . 2 3x  3  cos 2x 1 sin x cos x
Có bao nhiêu hàm số có tập xác định  A. 3 B. 2 C. 1 D. 4
Câu 3. Tồn tại bao nhiêu số nguyên dương m để hàm số y  cos6x  cos3x  3  m xác định với mọi x. A. 3 B. 1 C. 2 D. 4
Câu 4. Tồn tại bao nhiêu số nguyên m để hàm số y  cos 2x  m không có tập xác định  . A. 3 B. 2 C. 1 D. 4
Câu 5. Tìm điều kiện xác định của hàm số 2 1 y  2 tan x  . cos x  sin x  3    A. x   k B. x   k2 C. x   k2 D.  2 2 4
Câu 6. Tìm tập xác định của hàm số y  2sin x  cos x  5 . A.  B. [0;2] C. (0;2) D.  2  ; 4  sin 2x
Câu 7. Tìm điều kiện xác định của hàm số y  . sin x 1    A. x   k B. x    k2 C. x   k2 D.  2 2 4 Câu 8. Cho các hàm số 2 1 1 y  x  sin x 1; y  ; y  cos x ; y  ; y  cot(x  2) . 3 x  5  cos 2x 1 sin x
Có bao nhiêu hàm số có tập xác định  A. 3 B. 2 C. 1 D. 4 1 1 Câu 9. Cho các hàm số 2
y  x  x  cos x  3; y  ; y  cos x  2; y  . 2 x  3  sin x 1 cos x
Có bao nhiêu hàm số có tập xác định  A. 3 B. 2 C. 1 D. 4 4x  9
Câu 10. Tìm tập xác định của hàm số y  . sin 3x  3 A.  B.  3; C. (0;2) D.  2  ; 1
Câu 11. Tìm điều kiện xác định của hàm số y   cos x  5 . 2 2 tan x  tan x  3    A. x   k B. x   k2 C. x   k2 D.  2 2 4 1
Câu 12. Tìm điều kiện tham số m để hàm số f (x)  có tập xác định  . 3 4cos x  3cos x  m 4 m  1 A. m > 0 B.  C. – 1 < m < 1 D. 0 < m < 1 m  1 1
Câu 13. Tìm điều kiện tham số m để hàm số y  có tập xác định  . 2sin x cos x  m m  1 A. m  1 B.  C. 0 < m < 1 D. m  1 m  1
Câu 14. Hàm số nào sau đây có tập xác định  ? 4cos x 1 1 A. y  B. y  tan x  C. y  sin x 1 D. y  2cos x 1 4sin 2x  9 cos x  4 1
Câu 15. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm số y  không xác định ? 2 2 sin x  cos x A. 3 B. 2 C. 4 D. 1 
Câu 16. Điều kiện xác định của hàm số 2
y  3tan(2x  )  4 x 1 là 4  k 3 k   A. x   B. x   C. x   k D. x    k2 4 2 8 2 2 2 tan 2x
Câu 17. Tìm tập xác định của hàm số y  . 2cos x  7     A. x   k B. x   k2 C. x   k D.  2 2 4 2 2
Câu 18. Tìm điều kiện xác định của hàm số 2 y 
 5 x  x  sin x  2 . 2 cot x 1    A. x   k B. x   k2 C. x   k2 D. x  k 2 2 4 2 2 4  x
Câu 19. Tồn tại bao nhiêu số nguyên x để hàm số y   x xác định ? cos x A. 13 B. 12 C. 14 D. 10
Câu 20. Tồn tại bao nhiêu số nguyên x để hàm số 2 1 y  cos 9  x  ? 10  cos(x  2) A. 6 B. 7 C. 2 D. 5 1
Câu 21. Tìm điều kiện xác định của hàm số y  . sin 2x 1    A. x   k B. x    k2 C. x    k D.  2 2 4
Câu 22. Tồn tại bao nhiêu số nguyên m  2
 0;20để hàm số sau không có tập xác định  1 1 y   . 2 2
cos x  cos x  2 cos x  cos x  m A. 34 B. 14 C. 27 D. 36
Câu 23. Tồn tại bao nhiêu số nguyên m  2
 0;20để hàm số sau không có tập xác định  1 y  . 3 6sin x  8sin x  m A. 34 B. 19 C. 24 D. 37
_________________________________ 5
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – CHU KỲ PHẦN 1)
___________________________________________
Câu 1. Tìm chu kỳ của hàm số y  sin x . A. T  2 B. T   C. T  4 D. T  8
Câu 2. Tìm chu kỳ tuần hoàn của hàm số y  cos 2x . A. T  2 B. T   C. T  4 D. T  8
Câu 3. Tìm chu kỳ của hàm số y  2sin 2x cos 2x .  A. T  2 B. T   C. T  4 D. T  2 
Câu 4. Tìm chu kỳ tuần hoàn của hàm số y  tan(x  ) . 3 A. T  2 B. T   C. T  4 D. T  8  4 
Câu 5. Tìm chu kỳ của hàm số y  sin 2x  1993   .  9  A. T  2 B. T   C. T  4 D. T  8 
Câu 6. Tìm chu kỳ tuần hoàn của hàm số y  cot(2x  )  5 . 3  A. T  2 B. T   C. T  4 D. T  2
Câu 7. Tìm chu kỳ của hàm số 3
y  3sin x  4sin x  5 . 2 A. T  2 B. T   C. T  4 D. T  3
Câu 8. Tìm chu kỳ tuần hoàn của hàm số 3
y  8cos x  6cos x  4 . 2 A. T  2 B. T   C. T  D. T  8 3
Câu 9. Tìm chu kỳ của hàm số 3
y  4cos 2x  3cos 2x  4 tan x  5 .  A. T  2 B. T   C. T  4 D. T  3
Câu 10. Tìm chu kỳ tuần hoàn của hàm số 2
y  4sin 2x cos 2x  2cos 2x .  A. T  2 B. T   C. T  D. T  8 2    Câu 11. Cho các hàm số 2
y  sin x; y  cos 2x; y  sin x  ; y  2cos x  3  
. Có bao nhiêu hàm số có chu  3  kỳ là T  2 A. 3 B. 1 C. 2 D. 4   
Câu 12. Tính tổng các giá trị m để hàm số y  sin mx  
 nhận chu kỳ T  2 .  3  A. 3 B. 0 C. 1 D. 2 x x
Câu 13. Tìm chu kỳ tuần hoàn của hàm số y  4sin  9cos 1993. 2 2  A. T  2 B. T   C. T  4 D. T  2 x x
Câu 14. Tìm chu kỳ của hàm số 2 2 y  4sin  9cos . 2 2 6  A. T  2 B. T   C. T  4 D. T  2
Câu 15. Tìm chu kỳ tuần hoàn của hàm số 2 2
y  cos 2x  sin 2x  6sin(4x  5)  A. T  2 B. T   C. T  D. T  8 2
Câu 16. Tìm chu kỳ của hàm số y  cos9x cos4x  sin 9xsin 4x 1993. 2   A. T  2 B. T  C. T  D. T  13 13 2 3 3tan x  tan x
Câu 17. Tìm chu kỳ của hàm số y  . 2 1 3tan x  A. T  2 B. T   C. T  D. T  8 3 x x
Câu 18. Tìm chu kỳ của hàm số y  4cot x  9cot 1993cot . 2 3 A. T  2 B. T  6 C. T  4 D. T  3
Câu 19. Tồn tại bao nhiêu số nguyên dương n < 4 để hàm số 2 2
y  2sin x  3cos (nx) có chu kỳ T   ? A. 4 B. 2 C. 3 D. 1 nx
Câu 20. Tồn tại bao nhiêu số nguyên dương n < 10 để hàm số y  4sin 2x  9cos có T   ? 2 A. 4 B. 2 C. 3 D. 1  2x 
Câu 21. Tìm m để hàm số y  cos(2x 1)  sin  3   có chu kỳ T  3 .  m  A. m = 2 B. m = 1 C. m = 3 D. m = 4 x x
Câu 22. Tồn tại bao nhiêu cặp số nguyên dương (m;n) để hàm số y  26 tan
 4cot  2019 có T  12 ? m n A. 16 B. 15 C. 10 D. 12 x x    Câu 23. Cho các hàm số 2 4 y  cot ; x y  tan ; y  sin ; y  sin x  cos x  
. Tồn tại bao nhiêu hàm số 2 2  9 
thỏa mãn điều kiện f (x  2k )  f (x) ? A. 4 B. 2 C. 3 D. 1 x
Câu 24. Tìm chu kỳ của hàm số y  tan 2x  cot 2  A. T  2 B. T   C. T  4 D. T  2
Câu 25. Tìm chu kỳ của hàm số y  sin x  cos x  4sin x cos x  9  A. T  2 B. T   C. T  4 D. T  2 x
Câu 26. Tìm chu kỳ của hàm số 2
y  3tan 3x  4cot x  5sin 2  A. T  2 B. T   C. T  4 D. T  2
Câu 27. Tìm chu kỳ của hàm số y  cot x  tan x .  A. T  2 B. T   C. T  4 D. T  2
_________________________________ 7
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – CHU KỲ PHẦN 2)
___________________________________________ 2 2 sin x  tan x
Câu 1. Tìm chu kỳ tuần hoàn của hàm số 6 y  .cot x  tan x . 2 2 cos x  cot x  A. T  2 B. T   C. T  4 D. T  2      
Câu 2. Tìm chu kỳ của hàm số y  sin x   cos x     .  3   6  A. T  2 B. T   C. T  4 D. T  8
Câu 3. Tìm chu kỳ tuần hoàn của hàm số y  cos3x cos5x  cos x . A. T  2 B. T   C. T  4 D. T  8 cot x  tan x
Câu 4. Tìm chu kỳ của hàm số y  . 1 tan . x tan 2x  A. T  2 B. T   C. T  4 D. T  2
Câu 5. Tìm chu kỳ tuần hoàn của hàm số y  cot x  tan x  2 tan 2x  4 tan 4x .   A. T  B. T   C. T  4 D. T  8 2 1 cos 2x  sin 2x
Câu 6. Tìm chu kỳ của hàm số y  . 1 cos 2x  sin 2x A. T  2 B. T   C. T  4 D. T  8 x
Câu 7. Tìm chu kỳ của hàm số 2 2 y  x     x 2     x 2 cos cos 60 cos 60  4sin . 2  A. T  2 B. T   C. T  4 D. T  2 sin a  sin 3a  sin 5a
Câu 8. Tìm chu kỳ của hàm số y  . cos a  cos3a  cos5a 2   A. T  B. T   C. T  D. T  5 3 2      
Câu 9. Tìm chu kỳ của hàm số y  4sin x sin  x sin  x  sin x     .  3   3  A. T  2 B. T   C. T  4 D. T  8
Câu 10. Tìm chu kỳ của hàm số 3
y  3sin 3x  4sin 3x  cos 4x . A. T  2 B. T   C. T  4 D. T  8 2 sin 4x
Câu 11. Tìm chu kỳ của hàm số y  . 2cos x  cos3x  cos5x A. T  2 B. T   C. T  4 D. T  8
Câu 12. Tìm chu kỳ của hàm số 4 4 y  sin x  cos x  4 .  A. T  2 B. T   C. T  4 D. T  2
Câu 13. Tìm chu kỳ của hàm số 6 6 y  sin x  cos x .  A. T  2 B. T   C. T  4 D. T  2
Câu 14. Hàm số nào sau đây có chu kỳ khác  ? 8    x A. y  cos 2x    B. y  tan  4
C. y  sin x cos x  cos 2x D. 2 y  sin x  4  2
Câu 15. Tìm chu kỳ của hàm số y  sin x . A. T  2 B. T   C. T  4 D. T  8
Câu 16. Hàm số nào sau đây có chu kỳ khác 2    x x x x A. y  4cos x    B. y  tan  4 C. 2 y  sin cos  cos D. 2 y  sin x  4  2 2 2 2
Câu 17. Hàm số nào sau đây có chu kỳ tuần hoàn khác nhau x A. y  cos x; y  cot B. y  sin ; x y  tan 2x 2 x x x x C. y  cot 2 ; x y  tan 2x D. 2 y  sin cos  cos ; y  tan 2 2 2 2 x 3x
Câu 18. Tìm chu kỳ tuần hoàn của hàm số y  sin  2cos . 2 2  A. T  2 B. T   C. T  4 D. T  2
Câu 19. Hàm số nào sau đây thỏa mãn f (x  2k )  f (x) ? x x A. y  tan  4 B. 2 2 y  2sin x  3cos x
C. y  cos x cos3x  sin D. y  cos3x  2 2 2 2 tan x
Câu 20. Tìm chu kỳ của hàm số y   6cot 2x  3 2 1 tan x  A. T  2 B. T   C. T  4 D. T  2
Câu 21. Tìm chu kỳ tuần hoàn của hàm số y  sin xcos xcos 2x cos 4x .   A. T  2 B. T  C. T  4 D. T  2 4
Câu 22. Tìm chu kỳ tuần hoàn của hàm số y  (cos5x cos x  sin 5xsin x)cos 4x .   A. T  2 B. T  C. T  4 D. T  2 4 1
Câu 23. Tìm chu kỳ tuần hoàn của hàm số y  . 3
(3sin x  4sin x) cos3x  sin 4x   A. T   B. T  C. T  4 D. T  2 4
Câu 24. Tìm chu kỳ tuần hoàn của hàm số y  sin x cos x cos 2xcos 4x  5 .   A. T  2 B. T  C. T  4 D. T  2 4      
Câu 25. Tìm chu kỳ tuần hoàn của hàm số y  cos x   tan x      .  3   6    A. T  2 B. T  C. T  4 D. T  2 4      
Câu 26. Tồn tại bao nhiêu số nguyên dương n < 10 để hàm số y  2cos x   3tan nx   8     có chu  3   6 
kỳ tuần hoàn T  2 ? A. 7 B. 9 C. 8 D. 5
_________________________________ 9
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – MIN, MAX PHẦN 1)
___________________________________________
Câu 1. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos x  3. A. 4 B. 2 C. 6 D. 7 
Câu 2. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos(3x  )  2 . 4 A. 3 B. 4 C. 2 D. 5
Câu 3. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin 4x  9 1993 . A. 3986 B. 2020 C. 1993 D. 3020
Câu 4. Tính tổng giá trị tham số m để tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau bằng 4  2 y  cos(2x  )  m  3m  2. 13 A. 1 B. 2 C. 3 D. 4
Câu 5. Tìm giá trị nhỏ nhất của hàm số 2
y  tan x  2 tan x  5 . A. 4 B. 7 C. 5 D. 3
Câu 6. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos x  sin x . A. 4 B. 2 C. 0 D. 1
Câu 7. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos 2x  3sin 2x . A. – 12 B. 10 C. – 10 D. 8
Câu 8. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 y  cos x  cos x  4 . A. 10 B. 9,75 C. 8,875 D. 7,75
Câu 9. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos 2x  cos x  4 . A. 9,25 B. 7,125 C. 8,5 D. 8,125
Câu 10. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3 cos x  4 . A. 15 B. 11 C. 10 D. 12  2 
Câu 11. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos x  4; x  0;  . 3    A. 8,5 B. 9 C. 6 D. 7,5
Câu 12. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y  4cos 3x  3cos3x  2 . A. 4 B. 5 C. 4,5 D. 3
Câu 13. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  1 cos 4x  2. A. 4 B. 6 C. 4  2 2 D. 3 2
Câu 14. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y  4cos x  3cos x  2sin 3x 1. A. – 4 B. – 2 C. – 3 D. 4      
Câu 15. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin 2x    với x  0; .  3   3    A. – 0,5 B. – 1 C. 1 D. 0,25
Câu 16. Tìm tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y  2cos x  4sin 2x  5 . A. 6 B. 19 C. 20 D. – 7
Câu 17. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 2
y  cos x  3cos x  5sin x  5. 10 65 47 215 11 A. B. C. D. 8 28 28 28
Câu 18. Tìm giá trị nhỏ nhất của hàm số 2
y  tan x(cot x  2)  tan x . A. 4 B. – 1 C. 0 D. 2
Câu 19. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x)  cos5x cos x  sin 5xsin x  4sin 3x . A. – 15 B. – 8 C. 10 D. – 6
Câu 20. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 2 y  4  5sin x cos x . A. 5 B. 11 C. 3 D. 8
Câu 21. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3  8 sin x cos x . A. 4 B. 1 C. 3 D. – 2  2 
Câu 22. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin x  sin x    .  3  A. 2 B. – 1 C. 1 D. – 3      
Câu 23. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin x   cos x      .  3   3  A. 3 1 B.  3 1 C. – 2 D. 1
Câu 24. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y  8cos x  6cos x  3 . A. 3 B. 5 C. 2 3 D. 6
Câu 25. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2sin x cos x  3 cos 2x  4 . A. 10 B. 8 C. 12 D. – 6
Câu 26. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 4
y  3(cos x  sin x)  sin 2x 1. A. – 3 B. – 2 C. 1 D. 4
Câu 27. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y  3  2cos3x(3sin x  4sin x) . A. 6 B. 8 C. 2 D. – 4 4
Câu 28. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  . 2  sin x 16 20 A. 4 B. 3 C. D. 3 3 8
Câu 29. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  . 2 3  cos x 16 32 A. B. 6 C. D. 8 3 3 3
Câu 30. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  . 3  1 cos x 9  3 2 A. 2 B. C. 3  2 D. 6  2 7 1
Câu 31. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  . 2 2  sin 3x 2 3 A. 2 B. C. 2 D. 2 2
_________________________________ 11
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – MIN, MAX PHẦN 2)
___________________________________________
Câu 1. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y  cos x  2sin x  2 . A. 3 B. 1 C. 2 D. 1,5  2 
Câu 2. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos 2x  3cos x 1 trên miền 0;  . 3    A. – 9 B. 3 C. – 1 D. 6
Câu 3. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2(sin x  cos x)  sin 2x  3 . A. 4 B. 5  2 2 C. 3 D. 3  4 2
Câu 4. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin x  cos x  sin 2x 1. 9 2 5 2 A. 2 B.  C. – 1 D.  4 4
Câu 5. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3(sin x  cos x)  sin 2x  3 . A. – 6 B. – 2 C. – 14 D . 3   
Câu 6. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y  (3  sin 2x)  3  2sin x cos x trên 0;  . 2    A. 7 B. 8 C. 6 D. 10  2    
Câu 7. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos 2x   cos x      trên 0; .  3   3  A. – 1,25 B. – 1,125 C. – 2,25 D. – 2    
Câu 8. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 6 6
y  sin x  cos x trên  ;  . 2 2    A. 3 B. 1 C. 2 D. 4
Câu 9. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 2 y  sin x  2cos x 1. A. 2 B. 1 C. 2 D. 0
Câu 10. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 4 y  sin x  cos x  4 . A. 9,5 B. 6 C. 10 D. 8
Câu 11. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 6 6 y  sin x  cos x . A. 1,25 B. 2 C. 1,5 D. 2,25 2cos x 1
Câu 12. Gọi M, m tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  . Khi đó cos x  2 A. 9M = m B. 9M + m = 0 C. M + m = 0 D. 2M + m = 0 12   5 
Câu 13. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  trên miền  ; . 7  4sin x  6 6    16 20 A. 4 B. 3 C. D. 3 3
Câu 14. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 2
y  3sin x  4cos 2x  5cos x . A. 3 B. 8 C. 2 D. 10
Câu 15. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  (2sin x  cos x)(3sin x  cos x) . A. 4 B. 11,5 C. 12,5 D. 8,5
Câu 16. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y  1 (sin 2x  cos 2x) . A. – 7 B. – 5 C. 5 D. – 2 12
Câu 17. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  5sin x 12cos x 10 . A. 6 B. 23 C. 14 D. 11   
Câu 18. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2sin x  2 sin  x 1   .  4  A. 3 B. – 2 C. 1 D. 2 cos x  2sin x  3 Câu 19. Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào đúng ? 2cos x  sin x  4 A. 2M + N + 6 = 0 B. 4M = N C. M + 7N > 0 D. 2M – N < 2  Câu 20. Biểu thức sin x cos x S 
có thể nhận bao nhiêu giá trị nguyên ? 2sin x  cos x  3 A. 2 B. 1 C. 3 D. 0   2 
Câu 21. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2 cos 2x  cos 2x   3    .  3    A. 7 B. 8 C. 6 D. 4
Câu 22. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2sin 2x(sin 2x  4cos 2x) . A. – 16 B. – 7 C. 10 D. – 12   
Câu 23. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 4 y  sin x  cos x trên 0;  . 6    13 11 15 A. B. 2 C. D. 8 8 8   
Câu 24. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2
y  2sin x  cos 2x trên 0;  . 3    A. 3 B. 1 C. 2 D. 1,5     3  
Câu 25. Tính giá trị lớn nhất của hàm số y  cot x    trên  ; .  4   4 4    A. 0 B. 2 C. 1 D. – 2 2  cos x
Câu 26. Ký hiệu M và N tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  . Tính sin x  cos x  2
giá trị của biểu thức M.N. A. – 1 B. 2 C. 1,5 D. 2 sin x 1
Câu 27. Tính M + N với M, N tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  . cos x  sin x  2 A. 0 B. 1 C. 2 D. – 1    
Câu 28. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 5
y  3 sin 2x  2cos x  3; x   ;  . 6 4    A. 6 B. 8 C. 4 D. 1    
Câu 29. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x)  sin 2x  cos 2x  3; x   ;  . 4 4    A. 5 B. 5  2 C. 4  2 2 D. 3 2 1 2cos x  3sin x  5 Câu 30. Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính Q = M.N. 2sin x  3cos x  5 A. Q = 1 B. Q = 2 C. Q = 5 D. Q = 10
_________________________________ 13
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH CHẴN, LẺ VÀ ĐỒ THỊ PHẦN 1)
___________________________________________
Câu 1. Hàm số nào sau đây là hàm số lẻ cos x 1 1 A. y  B. y  tan x  C. y  sin x D. y  2cos x 1 sin x  4 cos x  4
Câu 2. Hàm số nào sau đây là hàm số chẵn A. y  cos(2x  3) B. 2 y  sin x C. y  cos 2x 1 D. y  sin x  6 Câu 3. Cho các hàm số 2
y  cos(x  5); y  cos6 ; x y  sin 2 ;
x y  cos3x cos x . Số lượng hàm số chẵn là A. 3 B. 2 C. 4 D. 1
Câu 4. Hàm số y  tan x  4 có đặc điểm
A. Đồ thị hàm số nằm phía trên trục hoành B. Hàm số lẻ C. Hàm số chẵn
D. Hàm số không chẵn, không lẻ
Câu 5. Có bao nhiêu số nguyên m  2
 0;20để hàm số y  cos xcos3x  m là hàm số chẵn ? A. 37 B. 27 C. 39 D. 10
Câu 6. Đồ thị hàm số nào sau đây có tâm đối xứng là gốc tọa độ ? A. y  cos(2x  3) B. y  sin x  6 C. y  sin 6xsin x D. y  sin 3x
Câu 7. Có bao nhiêu số nguyên m  2
 0;20để hàm số y  cot x  m  5 là hàm số lẻ ? A. 37 B. 1 C. 39 D. 10
Câu 8. Đồ thị hàm số nào sau đây có trục đối xứng là trục tung ? A. y  cos(3x 1) B. y  sin 5x C. 2 y  sin 5x D. 2 y  cos 5x  2x
Câu 9. Đồ thị hàm số y  sin x  3 có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành
D. Luôn nằm bên trái trục tung
Câu 10. Tồn tại bao nhiêu hàm số mà đồ thị có tâm đối xứng là gốc tọa độ trong các hàm số sau   7 9  y  tan 2 . x sin 5 ; x y  tan x  cot ; x y  sin 2x    .  2  A. 0 B. 1 C. 2 D. 3 Câu 11. Cho các hàm số 2 2 2 2
y  sin 9  x ; y  sin 5x  cos9 ; x
y  sin x  cos(4x  9) 1993; y  cos x .
Có bao nhiêu hàm số mà đồ thị nhận trục tung là trục đối xứng ? A. 3 B. 2 C. 1 D. 0
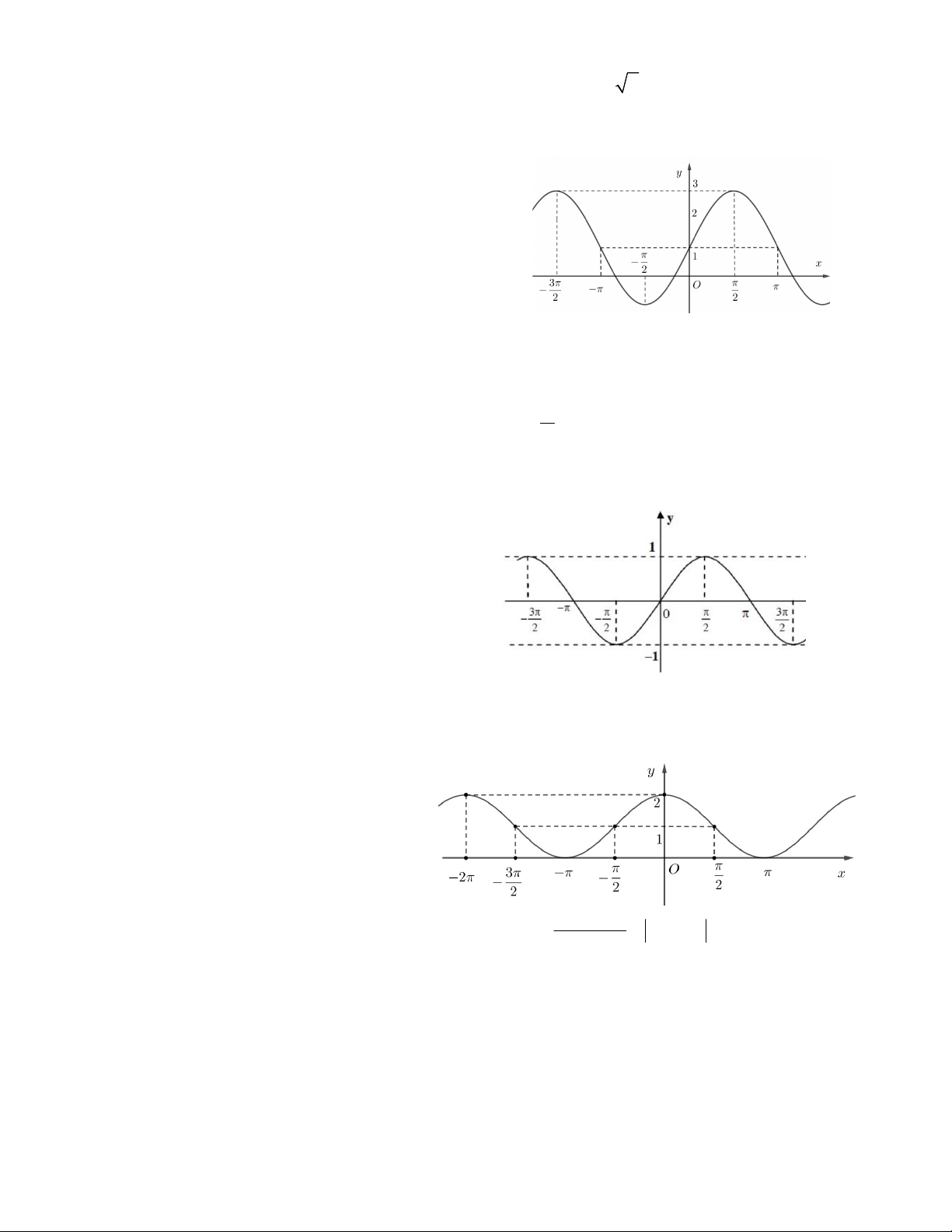
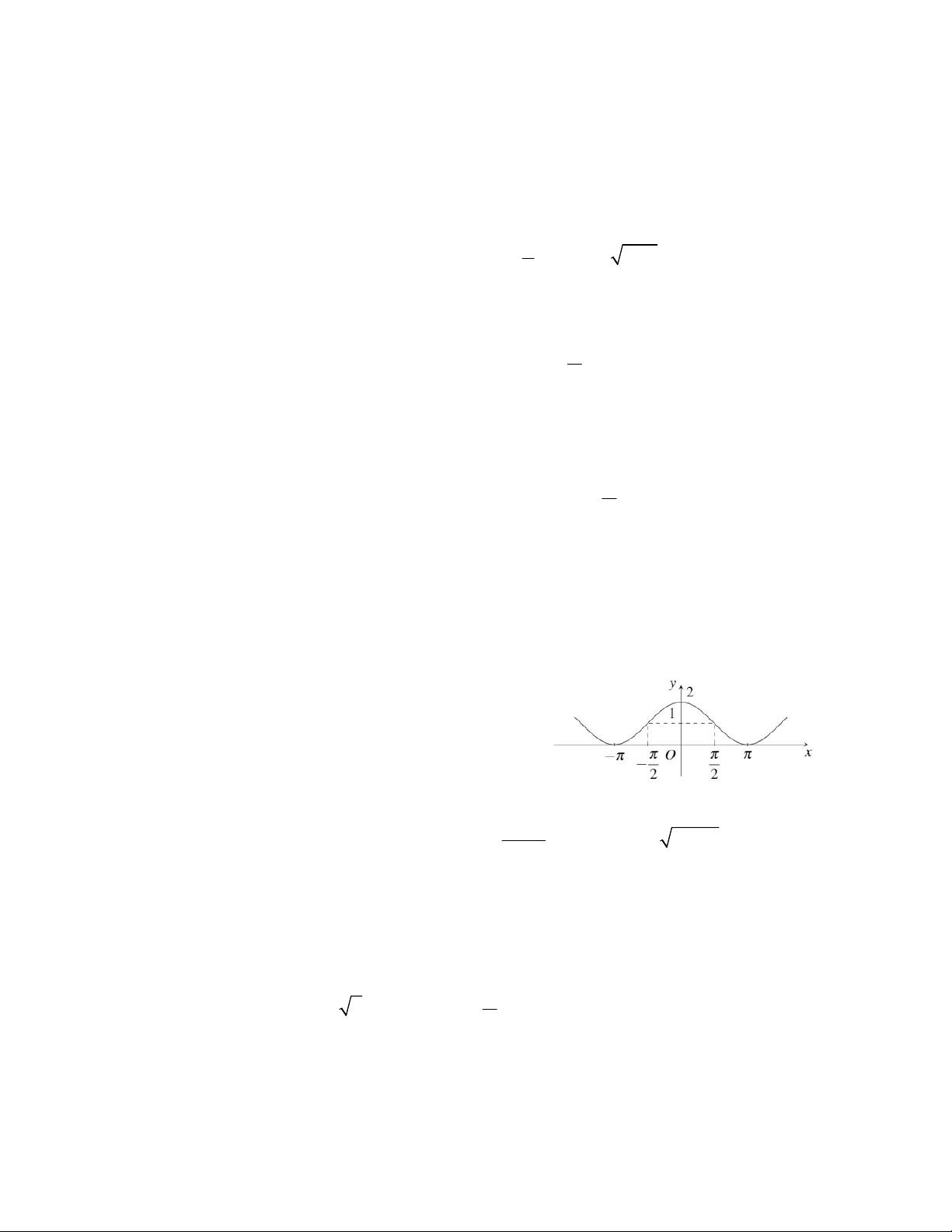
Câu 12. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx
C. y = 1 + sinx D. y = cosx + 2 
Câu 13. Tịnh tiến đồ thị y  sin x sang phải đơn vị ta thu được đồ thị hàm số f (x) . Khi đó f (491993) gần 2
nhất giá trị nào sau đây A. – 0,56 B. – 0,73 C. 0,76 D. – 0,14
Câu 14. Tịnh tiến đồ thị hàm số y  cos x  cos 2x lên phía trên tối thiểu bao nhiêu đơn vị để đồ thị thu được 14
không nằm phía dưới trục hoành ? A. 1 B. 1,25 C. 1,75 D. 0,5 Câu 15. Cho các hàm số 3 2 2 y  cos3x cos ; x y  cos x  cos ; x y  sin
x; y  sin 4xsin x . Tồn tại bao
nhiêu hàm số chẵn trong các hàm số đã cho ? A. 3 B. 4 C. 2 D. 1
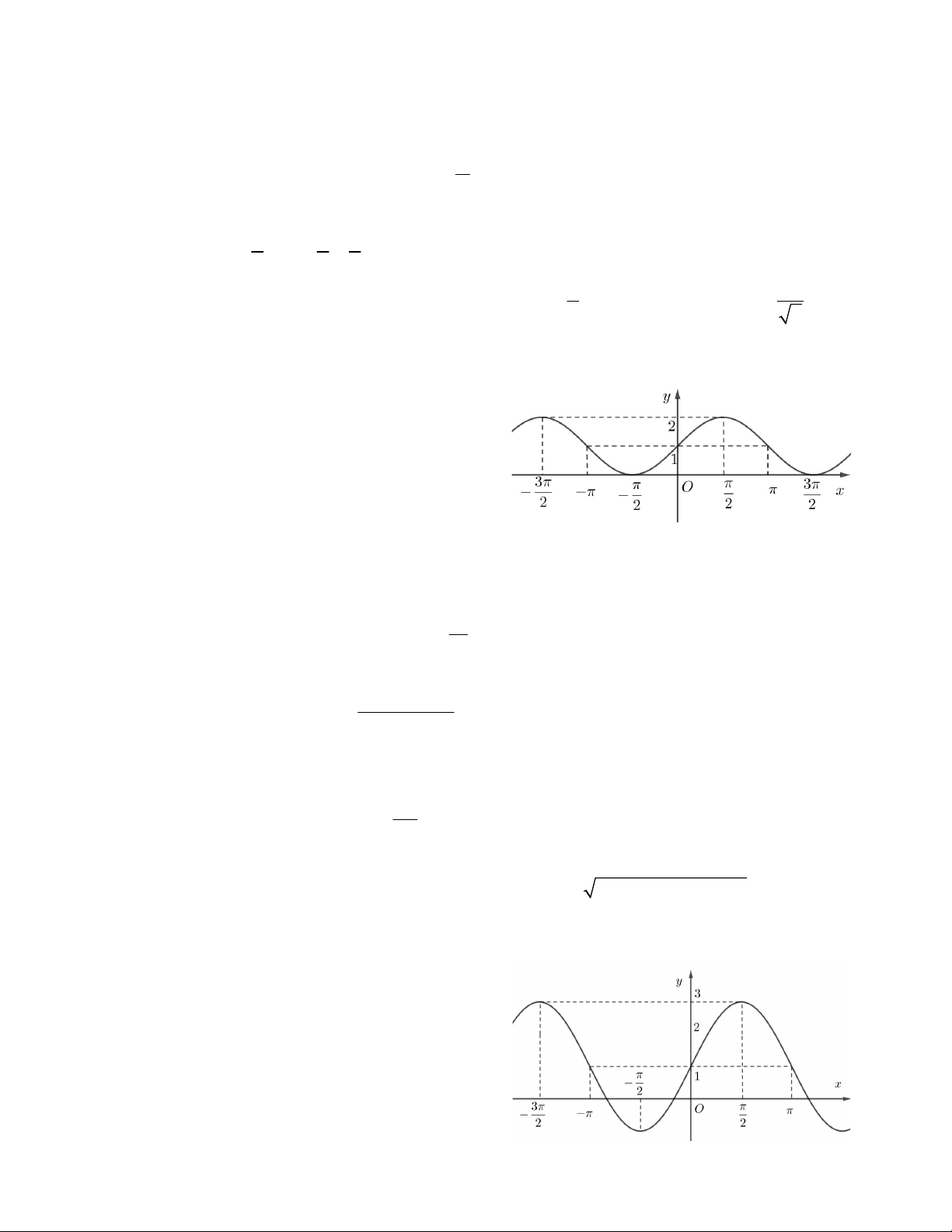
Câu 16. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx
C. y = 1 + 2sinx D. y = 2cosx + 1
Câu 17. Đồ thị hàm số y  cos 2x  5 có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành
D. Luôn nằm bên trái trục tung 
Câu 18. Tịnh tiến đồ thị hàm số 3
g(x)  3sin x  4sin x sang trái đơn vị ta thu được đồ thị hàm số y  f (x) . 2
Hai đồ thị hàm số f (x), g(x) cắt nhau tại bao nhiêu điểm có hoành độ thuộc khoảng 0;2  ? A. 5 B. 6 C. 3 D. 1
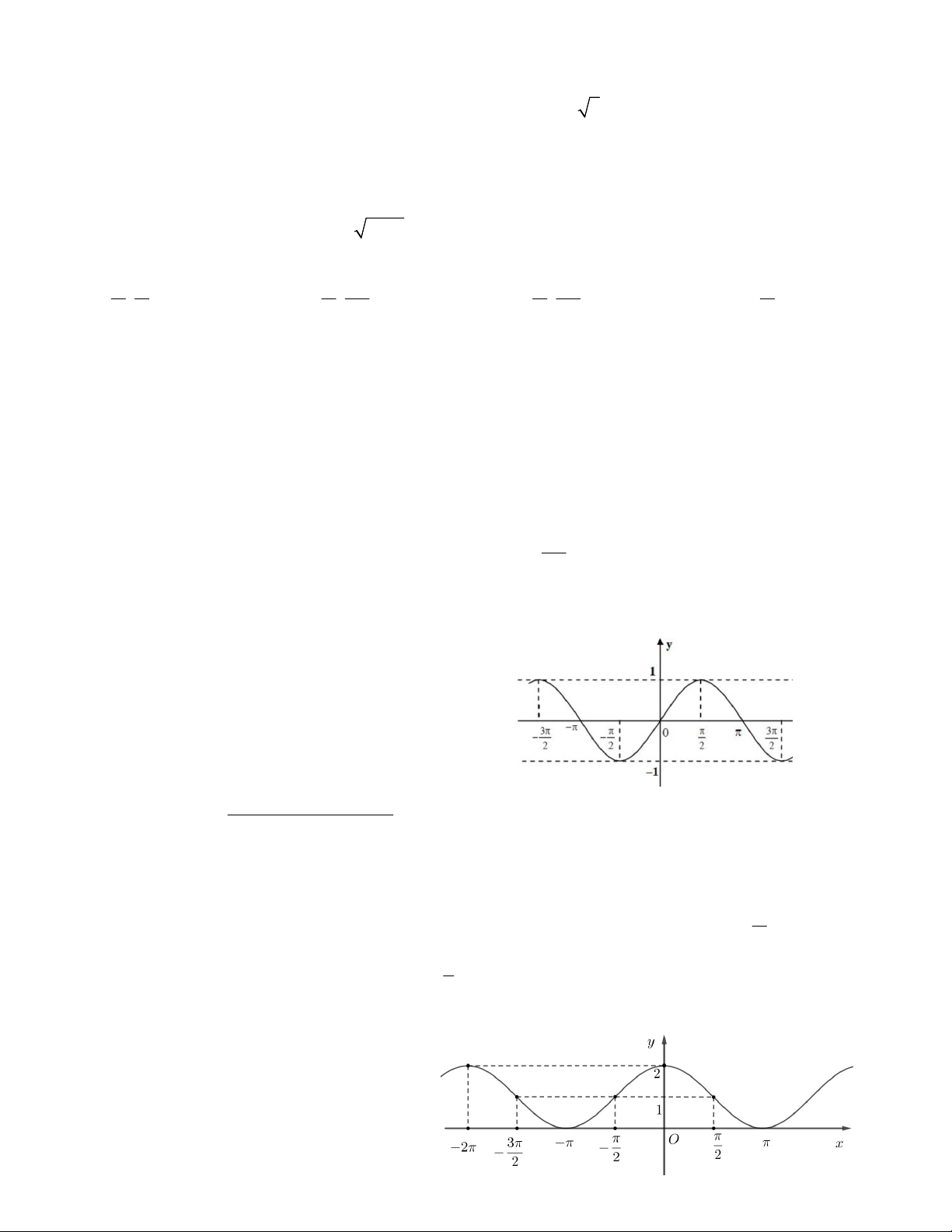
Câu 19. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx C. y = 1 + sinx D. y = cosx
Câu 20. Đồ thị hàm số 3
y  4cos x  3cos x  7 có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành
D. Luôn nằm bên trái trục tung
Câu 21. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx + 2 C. y = 1 + sinx D. y = cosx + 1 cos 2x 1
Câu 22. Tồn tại bao nhiêu số nguyên m  2
 0;20để hàm số y 
 sin(mx) là hàm số chẵn ? cos 2x 1 A. 10 B. 39 C. 20 D. 24
Câu 23. Tịnh tiến đồ thị hàm số 3
y  8cos x  6cos x  3 xuống dưới tối thiểu bao nhiêu đơn vị để đồ thị thu
được không nằm phía trên trục hoành ? A. 1 B. 5 C. 4,75 D. 2,5
Câu 24. Hàm số y  sin(3x 1)  2 có đặc điểm
A. Đồ thị hàm số nằm phía dưới trục hoành B. Hàm số chẵn C. Hàm số lẻ
D. Hàm số không chẵn, không lẻ
_________________________________ 15
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH CHẴN, LẺ VÀ ĐỒ THỊ PHẦN 2)
___________________________________________ Câu 1. Hàm số 3
y  x tan x  x có đặc điểm A. Hàm số chẵn B. Hàm số lẻ
C. Hàm số không chẵn, không lẻ
D. Đồ thị hàm số nằm phía trên trục hoành
Câu 2. Có bao nhiêu điểm M (x;y) nằm trên đồ thị hàm số y  sin x thỏa mãn 4  x  9; y  cos x ? A. 4 B. 1 C. 3 D. 2 1
Câu 3. Cho các hàm số y  sin xsin 4 ; x y  x tan 4 ;
x y  sin ; y  cos x 1; y  cos 4x . x
Biết rằng có a hàm số chẵn và b hàm số lẻ, tính 3a + 2b. A. 5 B. 8 C. 11 D. 12 
Câu 4. Tịnh tiến đồ thị y  sin 2x lên trên 2 đơn vị, sau đó sang phải thu được đồ thị hàm số y  f (x) . Tính 2
tổng các giá trị m để đường thẳng y = m tiếp xúc với đồ thị y  f (x) . A. 4 B. 2 C. 6 D. 7
Câu 5. Đồ thị hàm số nào sau đây luôn nằm phía dưới trục hoành    A. y  cos3x B. y  sin 2x  2 C. y  sin x   2   D. y  cos3x cos6x  3 
Câu 6. Đồ thị hàm số nào sau đây tiếp xúc trục hoành ? A. y  cos3x B. y  sin 2x  2 C. y  sin 6x 1 D. y  tan x  3
Câu 7. Tồn tại bao nhiêu số nguyên dương m < 10 để hàm số y  sin xsin 3x  mcos x cos5x  (m 1)x là hàm số chẵn ? A. 4 B. 1 C. 2 D. 3
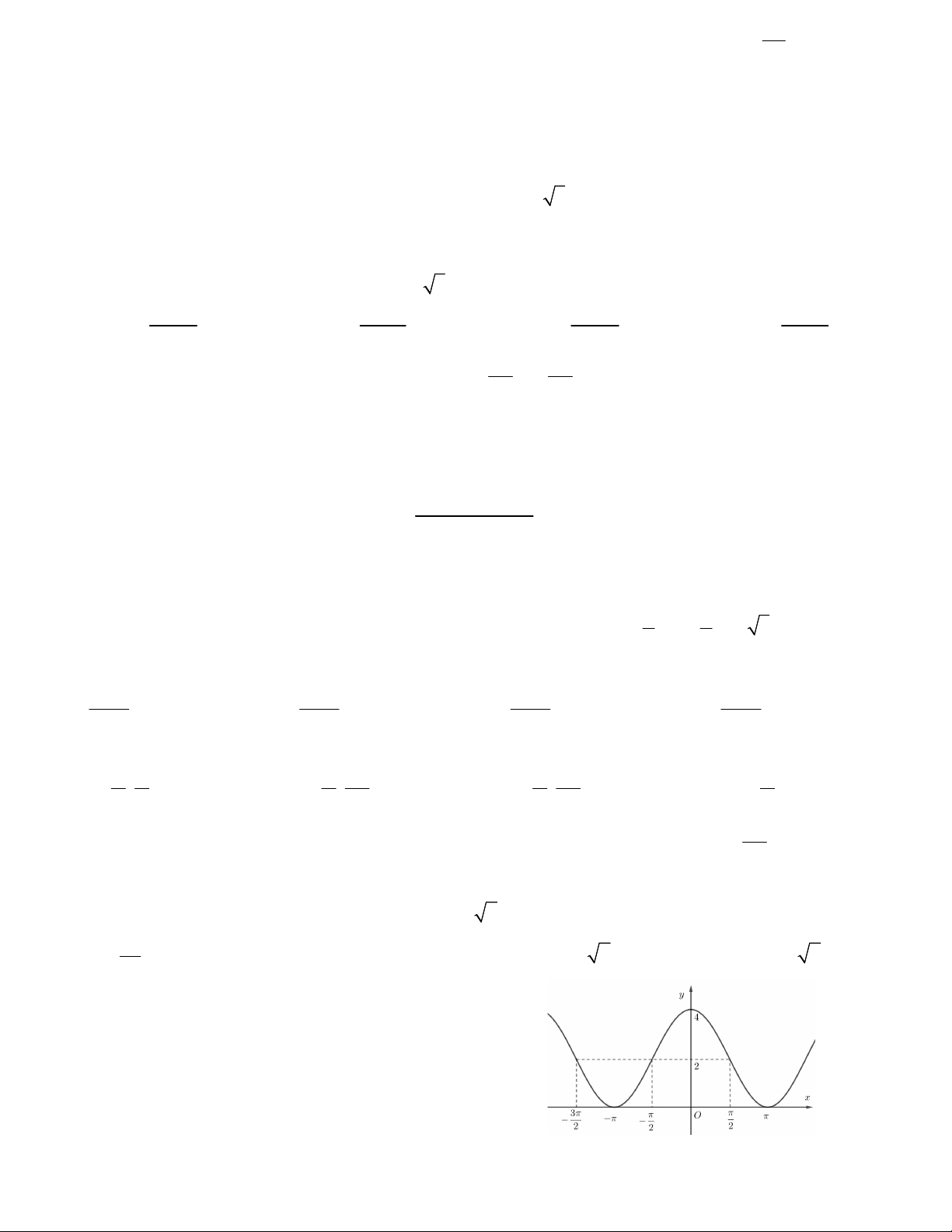
Câu 8. Hình vẽ bên là đồ thị hàm số nào ? A. 2
y  cos x 1 B. y = 2 - sinx C. y = 1 + cosx D. y = 2cosx
Câu 9. Có bao nhiêu hàm số có đồ thị nhận gốc tọa độ O làm tâm đối xứng: 1 y  x cot ; x y  sin 3x cos 2 ; x y  sin ; y  1993sin 4x  9 . 2 x 1 A. 3 B. 1 C. 2 D. 4 2 y  cos x
Câu 10. Có bao nhiêu điểm M (x;y) có hoành độ trong khoảng 0;2 và cùng nằm trên hai đồ thị  2 y  sin x A. 5 B. 4 C. 3 D. 2 
Câu 11. Tịnh tiến đồ thị hàm số y  2 sin x sang phải
đơn vị ta thu được đồ thị (C). Khi đó (C) cắt đồ thị 4
hàm số y  3cos x tại bao nhiêu điểm có hoành độ thuộc 0;2  ? A. 3 B. 1 C. 2 D. 4
Câu 12. Tìm giá trị tham số m để đồ thị hàm số y  cos 2x  cos3x tiếp xúc với đường thẳng y = m. A. m = 5 B. m = 2 C. m = 1,5 D. m = 1
Câu 13. Hàm số nào sau đây là hàm số chẵn 16 tan x A. y  B. 3 y  cos . x sin x 2 tan x 1 C. y  sin x cos 2x D. y  2019cos x  2020
Câu 14. Tồn tại bao nhiêu đường cong có tâm đối xứng là gốc tọa độ cot x 4 y  cos . x sin 4 ; x y 
; y  cos x  2020sin xsin 2x . 3 cot x 1 9 A. 0 B. 1 C. 2 D. 3
Câu 15. Tồn tại bao nhiêu số nguyên m  1
 0;10để hàm số sau có đồ thị nhận trục Oy là trục đối xứng 3 2
y  cos x cos 4x  (m  4)sin . x sin x  m  9 A. 0 B. 2 C. 3 D. 1
Câu 16. Đồ thị hàm số nào sau đây tiếp xúc trục hoành ? A. y  cos3x B. 2 y  sin x C. y  3sin 6x 1 D. y  tan x  3
Câu 17. Biết rằng đồ thị hàm số 2
y  sin 2x tiếp xúc với trục hoành tại vô số điểm, trong đó có bao nhiêu điểm
có hoành độ thuộc 2;2 ? A. 4 B. 2 C. 3 D. 1
Câu 18. Tính tổng các giá trị m để đường thẳng y = m tiếp xúc đường cong y  3sin x  4cos x . A. 5 B. 1 C. 0 D. 2 cos x  4 Câu 19. Hàm số y  có đặc điểm 6  sin x A. Hàm chẵn B. Hàm lẻ
C. Hàm không chẵn, không lẻ
D. Đồ thị hàm số tiếp xúc trục hoành. 
Câu 20. Tịnh tiến đồ thị y  2 sin x sang trái đơn vị ta được đồ thị hàm số 4 A. y  sin x  cos x B. y  2 sin x  C. y  sin x D. y  cos x 4
Câu 21. Đồ thị hàm số y  tan 2x cắt đường thẳng y  2 tại bao nhiêu điểm có hoành độ thuộc 0;2  ? A. 5 B. 4 C. 6 D. 3
Câu 22. Tính tổng các giá trị m để đồ thị hàm số y  cos 2x  sin x tiếp xúc với đường thẳng y  m . 7 11 A. 1 B. 1,5 C.  D. 8 3 Câu 23. Cho 3
f (x)  x  3x  2 . Tìm số nghiệm của phương trình f (tan 2x)  0 trong khoảng 0;2 . A. 3 B. 6 C. 5 D. 8
Câu 24. Đồ thị hàm số nào sau đây nằm hoàn toàn phía trên đường thẳng y = 2 ? sin x A. y  B. 3
y  4cos x  3cos x  3,5 2  cos x C. y  2cos 2x  cos x D. y  sin 3xsin 6x  2
Câu 25. Tìm m để đồ thị hàm số y  msin x  4cos x tiếp xúc đường thẳng y = 5. A. m = 2 B. m = 3 C. m = 4 D. m = 1
Câu 26. Tồn tại bao nhiêu số thực m để đồ thị hàm số 3
y  (m  3m  2)sin x  4cos x tiếp xúc với đường
thẳng đi qua hai điểm A (1;5), B (2;5) ? A. 5 B. 4 C. 2 D. 1
_________________________________ 17
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH ĐƠN ĐIỆU PHẦN 1)
___________________________________________
Câu 1. Hàm số y  sin x đồng biến trên khoảng nào sau đây       2    4     A.  ;   B.  ;   C.  ;   D.   ;    2 2   2 3   2 3   3 
Câu 2. Hàm số y  cos x đồng biến trên khoảng nào sau đây       4     A.  ;   B.    ;0 C.  ;   D.   ;    2 2   2 3   3 
Câu 3. Hàm số y  cos 2x tăng trên khoảng      4     A.  ;0   B.    ;0 C.  ;   D.   ;    2   2 3   3     Câu 4. Trên miền 0; 
 , hàm số y  sin x  cos x có đặc điểm  2  A. Đồng biến B. Nghịch biến C. Không đổi
D. Vừa đồng biến, vừa nghịch biến
Câu 5. Trên khoảng 0;2 , hàm số y  sin 2x có khoảng nghịch biến đầy đủ a;b . Tính a + b A.  B. 0,5 C. 0,75 D. 1,25
Câu 6. Trên khoảng 0;  , hàm số y  cos 2x có khoảng nghịch biến đầy đủ a;b. Tính a + b A.  B. 0,5 C. 0,75 D. 1,25 Câu 7. Hàm số 2 2
y  sin x  2cos x có khoảng đồng biến đầy đủ a  k2 ;b  k2  . Tính a + b. A.  B. 0,5 C. 0,75 D. 1,25
Câu 8. Hàm số y  tan x đồng biến trên khoảng nào sau đây       2    4     A.  ;   B.  ;   C.  ;   D.   ;    2 2   2 3   2 3   3       
Câu 9. Khẳng định nào sau đây đúng đối với hàm số y  4sin x  cos x   sin 2x      6   6      3 
A. Hàm số đồng biến trên 0;   và ; 
 . B. Hàm số đồng biến trên 0;   4   4   3    
C. Hàm số nghịch biến trên 0;  
D. Hàm số đồng biến trên ;    4   4   k k 
Câu 10. Khoảng đồng biến của hàm số y  tan 2x là a  ;b    . Tính a + b.  2 2  A. 0 B. 0,5 C. 0,75 D. 1,25
Câu 11. Hàm số y  tan x đồng biến trên khoảng       2    4     A.  ;   B.  ;   C.  ;   D.   ;    2 2   2 3   2 3   3 
Câu 12. Khoảng đồng biến đầy đủ của hàm số y  sin x  cos x là a  k2;b  k2  với a  0,b  0 . Tính
giá trị biểu thức a + b. A.  B. 0,5 C. 0,75 D. 1,25 x
Câu 13. Hàm số y  cos có khoảng đồng biến là a  k4;b  k4  với a  0,b  0. Tính a + b 2 18 A.  B. – 2 C. –  D. 1,5  x   Câu 14. Hàm số y  sin  
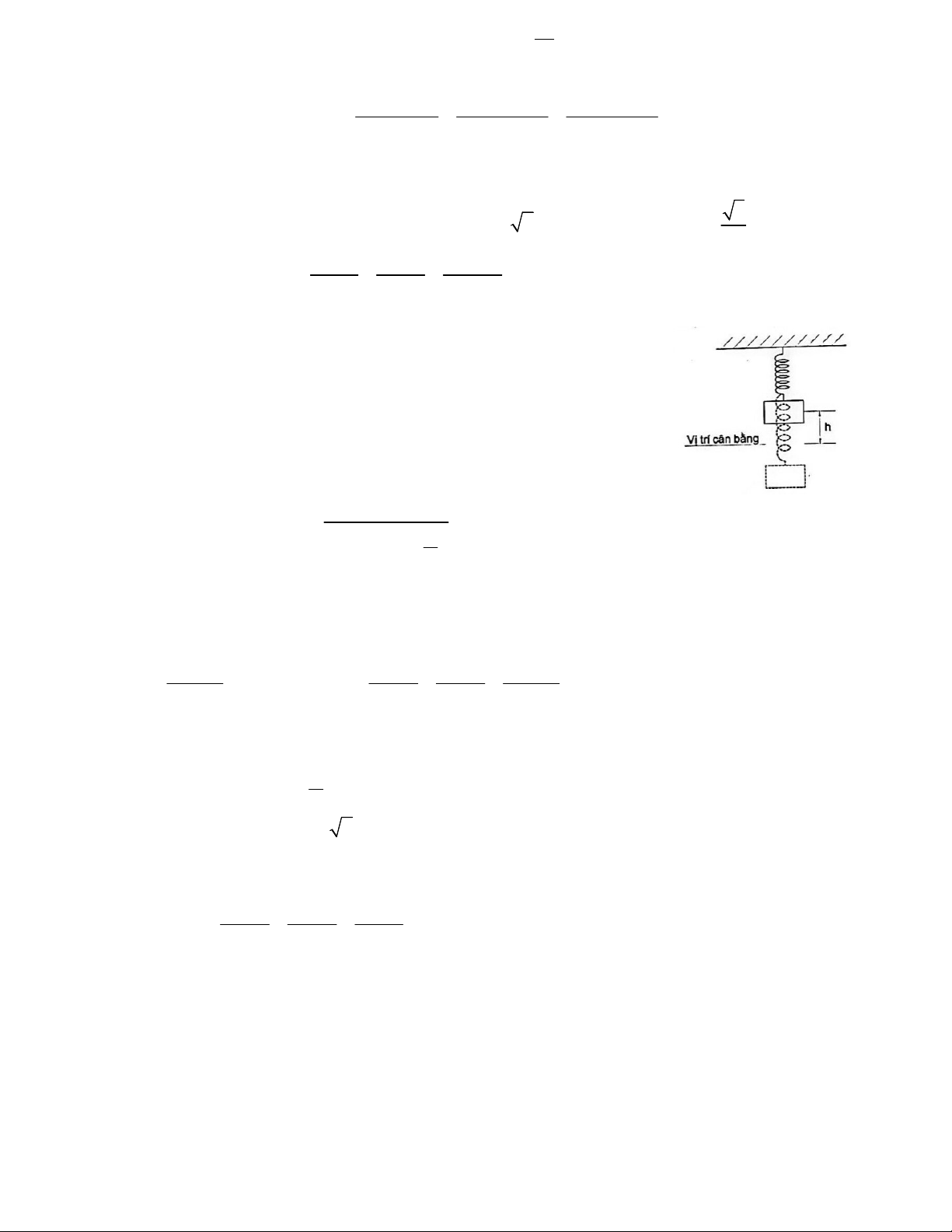
 có khoảng đồng biến là a  k4 ;b  k4  với a  0,b  0. Tính a + b  2 3  4 A.  B.   C. –  D. 1,5 3  k2 k2  Câu 15. Hàm số 3
y  4cos x  3cos x  4 có khoảng nghịch biến a  ;b    . Tính a + b  3 3   A. B.  C. 2 D. 1,5 3
Câu 16. Tìm tất cả các khoảng nghịch biến của hàm số y  cot x A. k;  k  B. k;2  k          C.   k ;  k   D.   2k ;  2k    2 2   2 2   x    5  
Câu 17. Tìm số tự nhiên m để hàm số y  sin  
 có khoảng đồng biến   k4 ;  k4    2 m   3 3  A. m = 3 B. m = 2 C. m = 6 D. m = 4 3x 3x  k2 k2  Câu 18. Hàm số 2 2 y  cos  sin
có khoảng nghịch biến a  ;b  
 với a  0,b  0 . Tính a + b 2 2  3 3   A. B.  C. 2 D. 1,5 3
Câu 19. Hàm số y  cos x  sin x có khoảng nghịch biến a  k2 ;b  k2  . Tính a + b A.  B. – 2 C. –  D. 1,5  k k  Câu 20. Hàm số 2 2
y  cos 2x  sin 2x có khoảng đồng biến a  ;b    . Tính a + b  2 2  A. 0,5 B.  C. 0,25 D. 1,5  k k  Câu 21. Hàm số 2
y  2cos 2x  7 có khoảng đồng biến a  ;b    . Tính a + b  2 2  A. 0,5 B.  C. 0,25 D. 1,5  x    x   Câu 22. Hàm số y  sin  cos    
 có khoảng đồng biến là a  k4 ;b  k4  với a  0,b  0 .  4 6   4 6  Tính a + b 4 A.  B.   C. –  D. 1,5 3  x    3 9  Câu 23. Hàm số y  cot  
 với a  0,b  0có khoảng nghịch biến   3k ;  3k   . Tính ab.  a b   4 4  A. 12 B. 8 C. 6 D. 9  x    7 3  Câu 24. Hàm số y  tan  
có khoảng đồng biến   2k ;  2k   . Tính ab.  a b   5 5  A. 15 B. 10 C. 12 D. 20   
Câu 25. Hàm số y  4cos x   9  
có khoảng nghịch biến a  k2 ;b  k2  . Tính a + b  4  A.  B. – 2 C. –  D. 1,5
_________________________________ 19
ÔN TẬP HÀM SỐ LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – TÍNH ĐƠN ĐIỆU PHẦN 2)
___________________________________________ x x Câu 1. Hàm số 3 y  3sin x  3sin  4sin
đồng biến trên khoảng nào sau đây 3 2       2    4     A.  ;   B.  ;   C.  ;   D.   ;    2 2   2 3   2 3   3  x x Câu 2. Hàm số 2 2 y  4cos  3sin
đồng biến trên khoảng nào sau đây 2 2       4     A.  ;   B.    ;0 C.  ;   D.   ;    2 2   2 3   3  Câu 3. Hàm số 2
y  6  2sin x tăng trên khoảng      4     A.  ;0   B.    ;0 C.  ;   D.   ;    2   2 3   3        Câu 4. Trên miền 0; 
 , hàm số y  2 sin x    có đặc điểm  2   4  A. Đồng biến B. Nghịch biến C. Không đổi
D. Vừa đồng biến, vừa nghịch biến x x x
Câu 5. Trên khoảng 0;2 , hàm số y  sin cos cos có khoảng nghịch biến đầy đủ a;b. Tính a + b 4 4 2 A.  B. 0,5 C. 0,75 D. 1,25  k k 
Câu 6. Hàm số y  cos3x  n có khoảng đồng biến a  ;b  
 . Tồn tại bao nhiêu số nguyên âm n  3 3  100 sao cho a  b  ? 3 A. 30 B. 45 C. 40 D. 36
Câu 7. Trên khoảng 0;  , hàm số 2 2
y  cos x  sin x có khoảng nghịch biến đầy đủ a;b. Tính a + b A.  B. 0,5 C. 0,75 D. 1,25  k  k 
Câu 8. Tìm n để hàm số 3
y  4cos (nx)  3cos(nx) có khoảng đồng biến ;    .  6 12 6  A. n = 2 B. n = 3 C. n = 6 D. n = 4 Câu 9. Hàm số 2 2
y  2sin x  6cos x có khoảng đồng biến đầy đủ a  k2 ;b  k2  . Tính a + b. A.  B. 0,5 C. 0,75 D. 1,25 sin x cos x  k k 
Câu 10. Khoảng đồng biến của hàm số y  là a  ;b  . Tính a + b. 2   1 2sin x  2 2  A. 0 B. 0,5 C. 0,75 D. 1,25  k k 
Câu 11. Hàm số y  tan 3x có khoảng đồng biến a  ;b    . Tính a + 2b.  3 3   A. B. 0,5 C. 0,75 D. 1,25 6   k k  
Câu 12. Hàm số y  cot(mx  ) có khoảng nghịch biến a  ;b  
 . Tìm m để a  b  . 3  3 3  9 A. m = 2 B. m = 3 C. m = 4 D. m = 6 20  k2 k2  Câu 13. Hàm số 3
y  8cos x  6cos x  5có khoảng nghịch biến a  ;b  
 với a  0,b  0 . Tính  3 3 
giá trị biểu thức a + b  A. B.  C. 2 D. 1,5 3  k k  Câu 14. Hàm số 4 2
y  8cos x  8cos x 1 có khoảng đồng biến a  ;b    . Tính a + b  2 2  A. 0,5 B.  C. 0,25 D. 1,5  x   Câu 15. Hàm số y  cos  
 có khoảng đồng biến a  k6;b  k6  . Tính a + b.  3 4   A. B.  C. 2 D. 1,5 3 1     Câu 16. Hàm số y  trên khoảng  ;   có đặc điểm sin x 1  2 2  A. Đồng biến B. Nghịch biến C. Không đổi
D. Vừa đồng biến vừa nghịch biến
Câu 17. Trên miền 0;2 , hàm số y  3 cos x  sin x chia thành bao nhiêu khoảng đơn điệu rời nhau A. 3 B. 2 C. 1 D. 4  31 33  Câu 18. Trên khoảng x  ; 
 khẳng định nào sau đây đúng  4 4 
A. Hàm số y  sin x đồng biến
B. Hàm số y  cos x nghịch biến
C. Hàm số y  cot x nghịch biến
D. Hàm số y  tan x nghịch biến    
Câu 19. Hàm số nào sau đây đồng biến trên khoảng  ;    3 6              A. y   tan 2x    B. y   cot 2x    C. y  sin 2x    D. y  cos 2x     6   6   6   6    
Câu 20. Hàm số y  cos 2x  
 có khoảng đồng biến đầy đủ là a  k;b  k  . Tính b – a.  3  A. 0,5 B.  C. 2 D. 1,5
Câu 21. Hàm số y  sin x  cos x có khoảng nghịch biến a  k2 ;b  k2  . Tính a + b A.  B. – 2 C. –  D. 1,5  k k  Câu 22. Hàm số 2
y  5cos 2x  4 có khoảng đồng biến a  ;b    . Tính a + b  2 2  A. 0,5 B.  C. 0,25 D. 1,5  k k  Câu 23. Hàm số 2
y  4  (sin 2x  cos 2x) có khoảng nghịch biến a  ;b    . Tính 3b – a.  4 4  A. 0,5 B.  C. 0,25 D. 1,5  k k  Câu 24. Hàm số y   x  x  3 4 2 4 8cos 8cos
1  3cos 4x khoảng đồng biến a  ;b    . Tính a + b  6 6    A. B.  C. 2 D. 3 12
_________________________________ 21
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CƠ BẢN PHẦN 1)
___________________________________________
Câu 1. Tìm họ nghiệm của phương trình sin x  1.   A. x   k2 B. x   k C. x    k2 D. x  k2 2 2
Câu 2. Tìm số nghiệm của phương trình sin x  0,3 trong khoảng 0;3  . A. 4 B. 2 C. 3 D. 1
Câu 3. Tìm số nghiệm của phương trình tan x  0, 4 trong khoảng 0;3  A. 3 B. 2 C. 4 D. 1 1
Câu 4. Tìm số điểm biểu diễn nghiệm phương trình sin x  trên vòng tròn lượng giác. 3 A. 3 B. 2 C. 1 D. 4
Câu 5. Tìm số điểm biểu diễn nghiệm phương trình (sin x 1)(sin x  2)(2sin x 1) trên vòng tròn lượng giác. A. 3 B. 4 C. 1 D. 2
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình 2sin x  m có nghiệm ? A. 4 B. 2 C. 5 D. 3
Câu 7. Tồn tại bao nhiêu số nguyên m thuộc [– 5;5] để phương trình tan x  2m có nghiệm ? A. 4 B. 2 C. 11 D. 20  2 
Câu 8. Tồn tại bao nhiêu số nguyên m để phương trình 2sin x  m có nghiệm thuộc 0;  ? 3    A. 4 B. 2 C. 3 D. 5  2 
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 3sin x  m có hai nghiệm thuộc 0;  ? 3    A. 4 B. 3 C. 2 D. 0
Câu 10. Tìm số nghiệm của phương trình 2 2
(tan x 1)(tan x  4)  0 trong khoảng 0;3  A. 12 B. 15 C. 14 D. 10
Câu 11. Tồn tại bao nhiêu số nguyên m nhỏ hơn 6 để phương trình (m 1)sin x  2  m  0 có nghiệm ? A. 5 B. 2 C. 4 D. 3
Câu 12. Tìm số điểm biểu diễn nghiệm phương trình 3
4cos x  3cos x  2cos3x 1trên vòng tròn lượng giác. A. 4 B. 3 C. 1 D. 2
Câu 13. Tồn tại bao nhiêu số nguyên m nhỏ hơn 6 để phương trình (m  4).tan x  m  0 có nghiệm ? A. 5 B. 2 C. 4 D. 3     2 
Câu 14. Tìm số nghiệm của phương trình cos x   sin 3x   trong đoạn 0; .  5   3    A. 4 B. 3 C. 2 D. 5  2 
Câu 15. Tìm số nghiệm của phương trình sin 3x cos x  cos3x(1 sin x) trong đoạn 0;  . 3    A. 2 B. 3 C. 4 D. 5  2 
Câu 16. Tìm số nghiệm của phương trình cos x  sin 4x  0 trong đoạn 0;  . 3    A. 4 B. 3 C. 2 D. 5 22  3 
Câu 17. Tồn tại bao nhiêu số nguyên m để phương trình 4sin x  m có nghiệm thuộc 0;  ? 2    A. 4 B. 7 C. 6 D. 5
Câu 18. Tồn tại bao nhiêu số nguyên m thuộc 3;3 để phương trình 2
2cos x 1  cos(3x  m) có nghiệm ? A. 4 B. 2 C. 5 D. 3
Câu 19. Tồn tại bao nhiêu số nguyên m thuộc 10;10 để phương trình cos 4xcos x  sin 4xsin x  2m có nghiệm ? A. 4 B. 5 C. 2 D. 3 Câu 20. Phương trình  x  2 2 2cos 3
1  4cos 6x có một phương trình hệ quả là 1 A. cos3x  2 B. cos6x  0,5 C. cos6x  D. cos6x  0 3
Câu 21. Tồn tại bao nhiêu số nguyên m thuộc 3;3 để phương trình 3
4cos x  3cos x  m 1 có nghiệm ? A. 4 B. 5 C. 2 D. 3
Câu 22. Tồn tại bao nhiêu số nguyên m thuộc 10;10 để phương trình sin 4x  cos 4x  2m có nghiệm ? A. 4 B. 5 C. 3 D. 6 1
Câu 23. Phương trình tan(x 15) 
có bao nhiêu nghiệm thuộc 0;120  ? 3 A. 3 B. 1 C. 2 D. 3
Câu 24. Tìm số nghiệm của phương trình 2
sin 3x 1  2cos x trong khoảng 0;3  A. 3 B. 6 C. 7 D. 10
Câu 25. Tìm số nghiệm của phương trình 2sin x  5cos x  0 trong khoảng 0;3  A. 3 B. 6 C. 7 D. 10
Câu 26. Tìm số nghiệm của phương trình 2
2cos x  5sin 2x 1trong khoảng 0;3  A. 3 B. 4 C. 7 D. 8
Câu 27. Tìm số nghiệm của phương trình 2sin 2x cos 2x  sin x cos 4x  sin 4xcos x  0 trong khoảng 0;3  A. 13 B. 14 C. 10 D. 8
Câu 28. Tìm số nghiệm của phương trình 2 2
sin 2x  cos 3x  1trong khoảng 0;4  A. 16 B. 14 C. 20 D. 18
Câu 29. Tồn tại bao nhiêu số nguyên m thuộc 10;10 để phương trình 3 2
6sin x  8sin x  m 1có nghiệm ? A. 4 B. 5 C. 3 D. 6   
Câu 30. Tìm số nghiệm của phương trình 3 cos 2x  cos 2x  1  0   trong khoảng 0;4   2  A. 5 B. 10 C. 7 D. 8
Câu 31. Một phương trình hệ quả của phương trình sin 4x cos 2x  sin x cos5x là A. sin 4x  sin 2x  0 B. sin 4x  sin 2x C. sin 4x  sin 5x D. sin 4x  sin x
Câu 32. Biết rằng tồn tại biến đổi cos5x cos x  sin 6xsin 2x  cos6x  0  cos(ax)  cos(bx) với a, b là các
số thực dương. Tính a + b. A. 12 B. 10 C. 14 D. 16
_________________________________ 23
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CƠ BẢN PHẦN 2)
___________________________________________
Câu 1. Tìm số nghiệm 0;2  của phương trình cos x tan 3x  1 sin x . A. 4 B. 12 C. 16 D. 10
Câu 2. Tồn tại bao nhiêu số nguyên dương m để phương trình (m  3) cos 2x  m có nghiệm A. 4 B. 2 C. 3 D. 1
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình sin x  cos3x  0 A. 3 B. 2 C. 4 D. 5  
Câu 4. Tồn tại bao nhiêu số nguyên m để phương trình sin x  m  5 có nghiệm  ;  6    A. 4 B. 2 C. 3 D. 1
Câu 5. Tính cos 2x biết rằng 3 3 1
cos x cos 3x  sin xsin 3x  . 8 A. – 0,5 B. 0,25 C. 0,5 D. 1  3 
Câu 6. Tồn tại bao nhiêu số nguyên dương m để phương trình tan x  m  5 có nghiệm   ;    2  A. 4 B. 3 C. 1 D. 2 1
Câu 7. Tìm số nghiệm  0;20  của phương trình sin x  2 A. 2 B. 1 C. 3 D. 4
Câu 8. Phương trình 2sin 3x cos x  sin 2x  3 cos 4x có số nghiệm 0;2  là A. 7 B. 8 C. 6 D. 10 Câu 9. Phương trình 3
2sin 3xcos x  sin 4x  sin 2x  2 có một hệ quả là 3 A. sin 4x  1 B. sin 4x  0,5 C. sin 3x  0,5 D. sin 3x  2  2 
Câu 10. Có bao nhiêu số nguyên dương m để phương trình 2sin x  m  5 có hai nghiệm phân biệt  ;  6 3    A. 3 B. 2 C. 1 D. 0
Câu 11. Phương trình cos9x  cos x  sin13x  sin 3x có một hệ quả là A. cos 4x  sin8x B. cos3x  cos5x C. cos 4x  cos5x D. cos 4x  cos3x   
Câu 12. Phương trình 2sin 4x   3  4cos2x  
có bao nhiêu nghiệm 0;2   3  A. 6 B. 5 C. 4 D. 3 Câu 13. Phương trình 2
sin x  cos 2x  2sin 2x  1có bao nhiêu nghiệm 0;100  A. 20 B. 200 C. 198 D. 196 1
Câu 14. Xác định số nghiệm 0;4 của phương trình tan 3x  4 A. 14 B. 24 C. 18 D. 30
Câu 15. Phương trình cos7x  cos3x  2cos5x  0 có bao nhiêu nghiệm 0;2  A. 3 B. 2 C. 1 D. 4
Câu 16. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của phương trình 2cos3x cos x  0,5  cos 2x A. 4 B. 8 C. 12 D. 10 24 Câu 17. Phương trình 2
2sin 3xsin x  cos 4x  cos 2x  2 có bao nhiêu nghiệm 0;100  A. 60 B. 99 C. 17 D. 80
Câu 18. Nghiệm dương nhỏ nhất của phương trình cos5x cos x  sin10xsin 4x gần nhất với A. 0,52 B. 0,17 C. 0,76 D. 0,81 Câu 19. Phương trình 4 2
8cos x  8cos x 1  sin 4x có bao nhiêu nghiệm 0;30  A. 40 B. 240 C. 250 D. 300 1
Câu 20. Xác định số nghiệm 0;4 của phương trình cos2x  3 A. 4 B. 8 C. 6 D. 10 Câu 21. Phương trình 4 4
4cos x  8sin x  cos 4x  3 có bao nhiêu nghiệm 0;30  A. 40 B. 30 C. 25 D. 18  3 
Câu 22. Tồn tại bao nhiêu số nguyên m để phương trình 3sin x  m  2 có hai nghiệm phân biệt  0;  2    A. 4 B. 2 C. 5 D. 6 Câu 23. Phương trình 4 2
4sin x  2cos x  cos 2x  cos 4x  4 có bao nhiêu nghiệm 0;30  A. 50 B. 70 C. 60 D. 34
Câu 24. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của phương trình sin 6x  sin 2x  0,5tan 2x A. 4 B. 6 C. 12 D. 8 Câu 25. Phương trình 2 2 4
1 2sin x  sin 2x  4sin x  cos 2x có bao nhiêu nghiệm 0;100  A. 60 B. 99 C. 17 D. 80
Câu 26. Xác định số nghiệm 0;30 của phương trình (sin x  3cos x)(cos x  2sin x)  0 A. 10 B. 60 C. 40 D. 30
cos x  cos 2x  cos3x  cos 4x
Câu 27. Tìm số nghiệm 0;30 của phương trình  3
sin x  sin 2x  sin 3x  sin 4x A. 80 B. 90 C. 60 D. 75
Câu 28. Xác định số nghiệm 0;4 của phương trình 2 2cos 3x  1 2sin 6x A. 4 B. 6 C. 8 D. 10
Câu 29. Tìm số 0;4 của phương trình sin xcos xcos2xcos 4x cos8x  0 A. 24 B. 32 C. 18 D. 40
Câu 30. Tìm một hệ quả của phương trình cos7x  sin8x  cos3x  sin 2x . A. cos3x  sin 2x B. cos 2x  sin 3x C. 2cos 2x  sin 3x D. 2cos 2x  3sin 3x
Câu 31. Xác định số nghiệm 0;4 của phương trình cos9x  cos7x  cos3x  cos x  0 A. 34 B. 33 C. 32 D. 30
Câu 32. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của sin x  sin 3x  sin 5x  sin 7x  0 A. 4 B. 6 C. 12 D. 8
Câu 33. Xác định số nghiệm 0;4 của phương trình cos11xcos3x  cos17xcos9x A. 100 B. 95 C. 93 D. 104 3
Câu 34. Tồn tại bao nhiêu số nguyên dương m để phương trình tan x  m  5 có đúng 2 nghiệm     ;  2    A. 4 B. 2 C. 3 D. 1 25
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH BẬC NHẤT SIN, COS PHẦN 1)
___________________________________________
Câu 1. Phương trình sin x  cos x  1tương đương với phương trình nào sau đây    1    1       A. sin x     B. sin x     C. sin x   1   D. sin x   2    4  2  4  2  4   4 
Câu 2. Tồn tại bao nhiêu số nguyên m để phương trình 3sin x  4cos x  m có nghiệm ? A. 10 B. 11 C. 12 D. 9
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 3sin x  cos x  m có nghiệm ? A. 10 B. 11 C. 12 D. 9
Câu 4. Tồn tại bao nhiêu số nguyên m để phương trình msin x  (m 1)cos x  2m  3  0 có nghiệm ? A. 4 B. 5 C. 12 D. 9  x  
Câu 5. Biết rằng sin x  3 cos x  2  sin x   sin  
. Tính m + n biết m, n nguyên dương.  n  m A. 7 B. 8 C. 6 D. 4 2 6
Câu 6. Có bao nhiêu nghiệm của phương trình cos7x  3 sin 7x   2 thỏa mãn  x  ? 5 7 A. 3 B. 7 C. 4 D. 2      
Câu 7. Biết rằng 3 sin 2x  cos 2x  2cos5x  sin 2x   sin  cx   
 . Tính a + b + c với a, b, c là các  a   b  số nguyên dương. A. 5 B. 17 C. 10 D. 13 1
Câu 8. Tìm phương trình tương đương với phương trình 3 sin x  cos x  . cos x             1 A. sin x   1   B. sin x   1   C. sin x   3   D. sin x      6   6   6   6  2
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình m  2 sin x  (m  2)cos x  m  2 . A. 2 B. 1 C. 3 D. 4
Câu 10. Tìm số nghiệm 0;2 của phương trình sin x  sin 2x  3(cos x  cos 2x). A. 3 B. 4 C. 2 D. 1  k
Câu 11. Phương trình cos x  3 sin x  2cos3x có một họ nghiệm nào đó là x   với a, b nguyên a b
dương. Tính tổng số các ước dương của a và b. A. 6 B. 4 C. 10 D. 12
Câu 12. Tìm số nghiệm 0;2 của phương trình 3
sin x  cos x  3 cos3x  2(cos 4x  sin x) . A. 7 B. 10 C. 8 D. 11
Câu 13. Tìm số nghiệm 0;2 của phương trình 3(sin 2x  sin x)  cos 2x  cos x  2 . A. 7 B. 6 C. 3 D. 8
Câu 14. Tồn tại bao nhiêu số nguyên dương m để phương trình 2
(m 1)sin x  2cos x  m 1. A. 2 B. 1 C. 3 D. 4
Câu 15. Tìm số nghiệm 0;2 của phương trình 2 5sin 2x  6cos x  13 . A. 3 B. Vô nghiệm C. 6 D. 5 26
Câu 16. Tìm số nghiệm0;2 của phương trình 2 sin 2x  sin x  0,5 . A. 5 B. 4 C. 3 D. 6
Câu 17. Tìm số nghiệm0;2 của phương trình sin x  2 sin 5x  cos x . A. 10 B. 14 C. 9 D. 8
Câu 18. Tính a + b + c biết a, b, c là các số nguyên dương thỏa mãn   3 
4cos x  3 sin 3x  3cos x  2cos 5x  sin ax   cos(cx)   .  b  A. 15 B. 14 C. 12 D. 10      
Câu 19. Tìm số nghiệm 0;  của phương trình 3 sin x   sin  x  2     .  4   4  A. 1 B. 3 C. 2 D. 4   
Câu 20. Tìm số nghiệm 0;  của phương trình sin
 2x  3 sin(2x  )  1   .  2  A. 3 B. 7 C. 4 D. 2
Câu 21. Tồn tại bao nhiêu số nguyên m để phương trình 2
msin 2x  2sin x  3m có nghiệm ? A. 2 B. 1 C. 3 D. 4 sin x  2cos x
Câu 22. Đoạn [a;b] gồm tất cả các giá trị m để phương trình
 m có nghiệm. Tính 7a – 5b. sin x  cos x  3 A. 10 B. 1 C. – 10 D. 0 sin x  2cos x 1
Câu 23. Đoạn [a;b] gồm tất cả các giá trị m để phương trình
 m có nghiệm. Tính a+ b. sin x  cos x  2 A. 1 B. – 2 C. – 1 D. 2
Câu 24. Tìm số nghiệm 0;2  của phương trình 3(cos2x  sin 3x)  sin 2x  cos3x . A. 5 B. 6 C. 3 D. 7    5
Câu 25. Phương trình 3 cos 2x  sin 2x  2sin 2x   2 2  
có một họ nghiệm nào đó là x   k với  6  a
a nguyên dương. Số ước dương của a là A. 6 B. 8 C. 7 D. 12
Câu 26. Tìm số nghiệm 0;  của phương trình sin x  cos x  2 2 sin x cos x A. 2 B. 3 C. 1 D. 4
Câu 27. Tìm số nghiệm 0;  của phương trình 2cos3x  3 sin x  cos x  0 . A. 2 B. 3 C. 1 D. 4 (1 2sin x)cos x
Câu 28. Tìm số nghiệm 0;2 của phương trình  3 . (1 2sin x)(1 sin x) A. 3 B. 7 C. 4 D. 2
Câu 29. Tìm số nghiệm 0;2 của phương trình sin8x  cos6x  3(sin 6x  cos8x) . A. 15 B. 14 C. 16 D. 12 a 2
Câu 30. Phương trình sin 3x  3 cos3x  2sin x có một họ nghiệm nào đó là x   k với a, b nguyên 15 b
dương. Tính giá trị tổng a + b. A. 7 B. 9 C. 10 D. 8
_________________________________ 27
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH BẬC NHẤT SIN, COS PHẦN 2)
___________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m lớn hơn – 5 để phương trình msin x  cos x  m  2 có nghiệm ? A. 4 B. 5 C. 6 D. 2
Câu 2. Nghiệm dương nhỏ nhất của phương trình 4 4
4(sin x  cos x)  3 sin 4x  2 gần nhất với A. 0,41 B. 0,24 C. 0,16 D. 0,72   
Câu 3. Cho phương trình 2  cos 2x  3 sin 2x  sin x  3 cos x . Khi đó cos x    có thể bằng  6  A. 0,2 B. – 0,5 C. – 1,2 D. – 2,5 x
Câu 4. Tồn tại bao nhiêu số nguyên dương k để phương trình 2 sin 2 2cos x   1 m có nghiệm ? 3 A. 2 B. 1 C. 3 D. 4 5 
Câu 5. Phương trình 2sin11x  3 sin 5x  cos5x  0có 1 họ nghiệm x   
(a  0,b  0). Tính a + b. a b A. 45 B. 39 C. 20 D. 35 Câu 6. Biết rằng x  x  m  x      2 4sin 9cos sin sin m  97 . Khi đó 2 2
4 tan   9cot  gần nhất A. 10 B. 18 C. 19 D. 26
Câu 7. Có bao nhiêu số nguyên m < 18 để phương trình 2msin x cos x  2m 1cos 2x  m  2 có nghiệm ? A. 6 B. 10 C. 15 D. 12 4 2
Câu 8. Phương trình 2sin x(cos x 1)  3 cos 2x có một họ nghiệm x  
(a  0,b  0) . Tính a + b. a b A. 10 B. 12 C. 9 D. 13
Câu 9. Tồn tại bao nhiêu số nguyên m < 10 để phương trình (cos x  2)(sin x  mcos x  2m)  0 có nghiệm A. 2 B. 1 C. 3 D. 4 a
Câu 10. Biết 2(sin x  3 cos x)  3 cos 2x  sin 2x có một họ nghiệm x  
 k2 (a  0,b  0), và b a
phân số tối giản, tính a + b. b A. 10 B. 17 C. 19 D. 14
Câu 11. Tìm số nghiệm trong khoảng (– 1993;1993) của phương trình 2 2(sin x  cos x)cos x  3  cos 2x . A. 1993 B. 2019 C. 0 D. 60
Câu 12. Tồn tại bao nhiêu số nguyên dương m < 10 để phương trình 2
3 sin 2x  2mcos x  1 m có nghiệm ? A. 10 B. 11 C. 6 D. 8
Câu 13. Biết rằng 3sin x  4cos x  5  sin  x    1. Tính 4 tan  9cot . 25 11 A. 2 B. 4 C. D. 12 13
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình cos3x  3 sin 3x  2cos x . A. 8 B. 6 C. 10 D. 4 cos 6x  sin x  2k Câu 15. Phương trình
 3 có một họ nghiệm x  
. Giá trị của a thuộc khoảng cos x  sin 6x a 7 A. (0;3) B. (3;7) C. (7;10) D. (10;15) 28  k Câu 16. Phương trình 3
3 sin 3x  4cos x  3cos x  2cos(1993x) có một họ nghiệm x   (a  0) . 6a a
Tính giá trị biểu thức 2a – 3. A. 1968 B. 1993 C. 2020 D. 1975 x
Câu 17. Phương trình 2sin x  cos x  1 có một phương trình hệ quả tan  k , khi đó k thuộc khoảng 2 A. (0;1) B. (1;3) C. (3;4) D. (4;5) 2sin x  cos x 1
Câu 18. Tồn tại bao nhiêu số nguyên dương a để phương trình  a có nghiệm ? sin x  2cos x  3 A. 3 B. 1 C. 2 D. 4   2 x  (2  3) cos x  2sin   
Câu 19. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của  2 4  1. 2cos x 1 A. 6 B. 2 C. 4 D. 8 x
Câu 20. Phương trình sin x  3cos x  1 có một phương trình hệ quả tan  k , khi đó k thuộc khoảng 2 A. (0;1) B. (1;2) C. (– 1;0) B. (2;3) cos x  2sin x cos x
Câu 21. Tìm số nghiệm  1
 993;1993 của phương trình  3 . 2 2cos x  sin x 1 A. 1903 B. 1953 C. 1973 D. 1993
Câu 22. Tập hợp S  a;b bao gồm tất cả các giá trị m để phương trình 2 2
2sin x  sin x cos x  cos x  m có nghiệm. Tính giá trị 2 2 a  b . A. 6 B. 5,5 C. 4 D. 6,5
Câu 23. Tồn tại bao nhiêu giá trị m để mọi nghiệm của phương trình sin x  m cos x  1cũng là nghiệm của phương trình 2 msin x  cos x  m . A. 6 B. 2 C. 5 D. 4
Câu 24. Phương trình 3sin x  2cos x  2 có một phương trình hệ quả là x 2 x 2 x 1 x 1 A. tan  B. tan  C. tan  D. tan  2 3 2 5 2 2 2 3 x x
Câu 25. Biết rằng cos x  3sin x  3  (tan  a)(tan  b)  0 . Tính a + b. 2 2 A. – 2 B. – 1,5 C. – 0,5 D. 2    x 1 a
Câu 26. Phương trình 2sin x   sin x  2cos x  3  
có một phương trình hệ quả tan  , tính ab.  6  2 b A. 18 B. 9 C. 4 D. 6 sin x  2cos x 1
Câu 27. Tồn tại bao nhiêu số nguyên m để phương trình  m có nghiệm ? sin x  cos x  2 A. 4 B. 5 C. 9 D. 2   
Câu 28. Phương trình 2cos x cos x   4sin 2x  1  
có một hệ quả là tan x  a  b  0 . Tính ab  3  A. 16 B. 24 C. 18 D. 10
Câu 29. Tồn tại bao nhiêu số nguyên m để phương trình 3
12cos 2x  sin 3x cos3x  m  9cos 2x có nghiệm A. 10 B. 8 C. 7 D. 5
_________________________________ 29
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CHỨA ẨN MẪU THỨC PHẦN 1)
___________________________________________
Câu 1. Tính a + b biết asin x  bcos x  1 (a  0,b  0) là một phương trình hệ quả của phương trình 1
3sin x  2cos x  3(1 tan x)  . cos x A. 4 B. 5 C. 3 D. 2 2 3 cos x  cos x 1
Câu 2. Tính tổng các nghiệm x thuộc 0;99của phương trình 2 cos 2x  tan x  . 2 cos x 2209 4 1993 2019 A.  B.  C.  D.  3 9 4 4
Câu 3. Tính a + b biết sin x  cos x  a  b với a, b dương là một phương trình hệ quả của    3 3(1 sin x) 2 x  3tan x  tan x   8cos   0 . 2   cos x  4 2  A. 3 B. 4 C. 5 D. 1 1 cos 2x
Câu 4. Tồn tại bao nhiêu nghiệm  2
  ;2  của phương trình 1 cot 2x  . 2 sin 2x A. 4 B. 6 C. 10 D. 12 2 2 cot x  tan x  k Câu 5. Phương trình
 16(1 cos4x)có họ nghiệm x   (a,b  0) . Tính a + b. cos 2x a b A. 24 B. 16 C. 20 D. 12 sin x cot 5x  k Câu 6. Phương trình
 1có họ nghiệm x   (a,b  0) . Tính a + b. cos9x a b A. 24 B. 12 C. 30 D. 14    1 1
Câu 7. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 sin x      .  4  sin x cos x A. 4 B. 2 C. 3 D. 5 2
Câu 8. Tìm số nghiệm  2
  ;2  của phương trình 2tan x  cot x   3 . sin 2x A. 4 B. 3 C. 2 D. 5 1
Câu 9. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 tan x  cot x  2sin 2x  . sin 2x A. 4 B. 6 C. 5 D. 8 1 2(cos x  sin x)
Câu 10. Số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  là tan x  cot 2x cot x 1 A. 4 B. 6 C. 5 D. 2 2 sin x  2 x
Câu 11. Tìm số nghiệm  4
  ;9  của phương trình 2  tan . 2 2 x 2 sin x  4cos 2 A. 8 B. 10 C. 9 D. 5 4 4 sin 2x  cos 2x
Câu 12. Tìm số nghiệm  4
  ;9  của phương trình 4  cos 4x .       tan  x tan  x      4   4  A. 10 B. 25 C. 16 D. 26 30 2 4 sin 2x  cos 2x 1
Câu 13. Tìm số nghiệm 4 ;9  của phương trình  0 . sin x cos x A. 13 B. 14 C. 15 D. 16
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
4sin 2x  6sin x  9  3cos 2x  0. cos x A. 6 B. 2 C. 4 D. 5 1 cos 2x sin 2x
Câu 15. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  . 2sin x 1 cos 2x A. 0 B. 2 C. 3 D. 4 1 sin 2x
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 1 tan 2x  . 2 cos 2x A. 4 B. 2 C. 3 D. 5 sin x(sin x  cos x) 1
Câu 17. Tìm số nghiệm  4
  ;9  của phương trình  0. 2 cos x  sin x 1 A. 25 B. 22 C. 15 D. 7 sin 5x
Câu 18. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  1. 5sin x A. 0 B. 2 C. 3 D. 4 1 tan x
Câu 19. Tìm số nghiệm  4
 9 ;1993 của phương trình  1 sin 2x . 1 tan x A. 4082 B. 4080 C. 2020 D. 1993 sin x  sin 2x  sin 3x
Câu 20. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  3 . cos x  cos 2x  cos3x A. 3 B. 2 C. 5 D. 4 1 1 2
Câu 21. Tính tổng các nghiệm thuộc 0;2 của phương trình   . cos x sin 2x sin 4x A. 2 B.  C. 3 D. 1,5  
Câu 22. Một phương trình hệ quả của phương trình 2 2 1
cos x  tan x  2 cos x   3   là  cos x  1 A. cosx = 0,5 B. cosx = 1 C. cosx = 0,25 D. cos x  3 6 6 sin x  cos x 1  k Câu 23. Phương trình
  có họ nghiệm x  
(a  0,b  0) . Tính a + 2b.       4 tan x  .tan x  a b      4   4  A. 12 B. 14 C. 10 D. 8 2 cot x 1
Câu 24. Tìm số nghiệm thuộc 0;2  của phương trình  cos 4 . x cot 2x  cos x . 2cot x A. 10 B. 8 C. 7 D. 6 tan x  3
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình tan 3x  . 1 3 tan x A. 2 B. 3 C. 5 D. 4
_________________________________ 31
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH CHỨA ẨN MẪU THỨC PHẦN 2)
___________________________________________ cos 2x  3cot 2x  sin 4x
Câu 1. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  2 cot 2x  cos 2x A. 3 B. 2 C. 1 D. 4 1 tan x
Câu 2. Tìm số nghiệm thuộc 100 ;100  của phương trình  1 sin 2x . 1 tan x A. 100 B. 199 C. 198 D. 56 cos(2 x)
Câu 3. Tìm số nghiệm thuộc khoảng (4;9) của phương trình  0 . 1 tan(2 x) A. 4 B. 5 C. 3 D. 2     5  4sin x  sin x      Câu 4. Tìm a + b biết  6   6
a cos 2x  bsin 2x  1là hệ quả của   2tan x  0 . 2 cos x A. 4 B. 3 C. 2 D. 1 tan x  cot x Câu 5. Phương trình
 6cos 2x  4sin 2x tương đương (tan 2x  a)(tan 2x  b)  0. Tính ab. cot x  tan x A. 4 B. – 5 C. – 2 D. 4 3 3 6cos 2x  2sin 2x Câu 6. Phương trình
 cos 4x có một hệ quả là 3cos 2x  sin 2x A. tan 2x  3 B. tan 2x  2 C. tan 2x  1 D. tan 2x  4 3 3 2(cos x  2sin x)
Câu 7. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  sin 2x 2sin x  3cos x A. 3 B. 6 C. 4 D. 5 4 1 cos x
Câu 8. Tìm số nghiệm thuộc 100 ;100  của phương trình 3 tan x  . 4 1 sin x A. 100 B. 199 C. 198 D. 56 3 3 cos x  sin x
Câu 9. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  cos 2x 2cos x  sin x A. 3 B. 4 C. 2 D. 5 2 cos x(1 cot x)  3 1 Câu 10. Phương trình  3cos x tương đương 2
(tan x  a)(tan x  b)  0. Tính . sin x  cos x ab A. 5 B. – 3 C. – 2 D. – 4   2  cos  2x    2  1
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  1 2 1 cos 2x cos 2x A. 4 B. 2 C. 3 D. 6 5sin x  5tan x
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của  4(1 cot x)  0 sin x  tan x A. 2 B. 3 C. 4 D. 1 sin x
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  2  cot x 1 cos x A. 2 B. 3 C. 4 D. 1 32 2 2 sin x  tan x
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3  2 tan x 1  0 2 2 cos x  cot x A. 2 B. 3 C. 4 D. 1 3(sin x  cos x)
Câu 15. Tính tổng các nghiệm thuộc 0;2 của phương trình  2cos x  2 . tan x  sin x A.  B. 2  C. 3  D. 0,5 1
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của cos x  cot x   sin(x   ) sin x A. 2 B. 1 C. 3 D. 4 sin x  tan x 9
Câu 17. Tính cos x khi phương trình
 có đúng một họ nghiệm dạng cos x  m . 1 cos x 4 A. 2 B. 3 C. 1 D. 4  x
Câu 18. Tính tổng các nghiệm thuộc 0;2 của phương trình 2 1 cos tan x  . cos x A.  B. 2  C. 3  D. 0,5 1 sin 2x 1 tan x
Câu 19. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  2.  3  0 1 sin 2x 1 tan x A. 3 B. 2 C. 1 D. 4 1
Câu 20. Tính số nghiệm thuộc 0;2 của phương trình  1 cos4x . 2 1 tan 2x A. 6 B. 7 C. 5 D. 4 6 6 1 sin x  cos x
Câu 21. Tính cos6x khi góc x thỏa mãn 2  2cos 3x 4 4 1 sin x  cos x 1 A. 1 B. 0,5 C. 0,25 D. 3 1 cos x
Câu 22. Tìm số nghiệm thuộc 100 ;100  của phương trình  2 . x sin 2 A. 100 B. 50 C. 93 D. 42 sin 2x sin x 1
Câu 23. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình .  1 1 cos 2x 1 cos x sin x A. 2 B. 3 C. 1 D. 4 4 4sin x 2
Câu 24. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  1  0 2 2 (1 cos 2x) cos x A. 3 B. 5 C. 1 D. 4
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình cos 2x 2 1 cot x 1   sin x  sin 2x . 1 tan x 2 A. 3 B. 5 C. 1 D. 4 2
Câu 26. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của 3tan 6x   2 tan 2x  cot 4x . sin8x A. 4 B. 8 C. 10 D. 6  1 1 
Câu 27. Tính số nghiệm thuộc 0;2 của phương trình 2  (4cos 2x  3)  2   .  sin x sin 3x  A. 8 B. 9 C. 11 D. 12 33
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐA THỨC + ẨN PHỤ P1)
___________________________________________ Câu 1. Phương trình 2
2sin x  sin x 1  0 có bao nhiêu nghiệm thuộc 0;3  ? A. 3 B. 4 C. 5 D. 6
Câu 2. Tính a + b biết rằng 2
2cos 2x 12sin x  5  asin x  bsin x  5 . A. 15 B. 14 C. 16 D. 20
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình 2
2cos x  5cos x  2  0 . A. 3 B. 2 C. 4 D. 5 Câu 4. Phương trình 2 2 3 2 tan x 
 3có bao nhiêu nghiệm thuộc 0;3  ? cot x A. 3 B. 6 C. 5 D. 8
Câu 5. Tìm số nghiệm thuộc 0;3  của phương trình 2 6cos x  5sin x  2 . A. 3 B. 4 C. 2 D. 5
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình 2cos 2x  sin x  m có nghiệm ? A. 3 B. 6 C. 5 D. 10
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình 2
2cos 2x  3cos x  2sin x  m có nghiệm ? A. 13 B. 7 C. 8 D. 10 Câu 8. Phương trình 4 2
4sin x 12cos x  7 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 2 C. 5 D. 4
Câu 9. Phương trình cos 4x  9sin 2x  8  0 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2 x
Câu 10. Tìm số nghiệm thuộc 0;3  của phương trình 5cos x  7  2sin . 2 A. 3 B. 4 C. 1 D. 2  2 
Câu 11. Tồn tại bao nhiêu số nguyên m để phương trình 2
m  cos 2x  sin x  cos 4x có nghiệm  0;  3    A. 4 B. 8 C. 5 D. 6
Câu 12. Tìm số nghiệm thuộc 0;5  của phương trình 2
sin x  cos 2x  cos x  2  0 . A. 5 B. 4 C. 3 D. 2 Câu 13. Phương trình 2
cos 4x 12sin x  1 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2 Câu 14. Phương trình 2
8cos x  cos 4x  1 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 4
Câu 15. Tìm số nghiệm thuộc 0;3  của phương trình 4 4
5(1 cos x)  2  sin x  cos x . A. 3 B. 4 C. 5 D. 2 x
Câu 16. Tìm số nghiệm thuộc 0;3  của phương trình 2 cos 2x  3cos x  4cos . 2 A. 3 B. 4 C. 5 D. 2
Câu 17. Phương trình 5tan x  2cot x  3  0 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 1 C. 5 D. 4 Câu 18. Phương trình 2
3cos 4x  2cos 3x  1 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? 34 A. 3 B. 2 C. 5 D. 4 Câu 19. Phương trình 4 4
cos 2x  sin x  cos x có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2 4
Câu 20. Tìm số nghiệm thuộc 0;2  của phương trình 4 3cot x   5  0 . 2 sin x A. 3 B. 4 C. 5 D. 2 1
Câu 21. Tồn tại bao nhiêu số nguyên m nhỏ hơn 2 để phương trình
 3tan x  m có nghiệm. 2 cos x A. 4 B. 2 C. 3 D. 1 Câu 22. Phương trình 2 5 tan x 
 7  0 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? cos x A. 3 B. 4 C. 5 D. 2
Câu 23. Tồn tại tất cả bao nhiêu số nguyên m nhỏ hơn để phương trình 2
cos 2x  sin x  2cos x  m có nghiệm  2   0;  3    A. 4 B. 6 C. 2 D. 5 1
Câu 24. Tìm số nghiệm thuộc 0;2  của phương trình  cot x  3 . 2 sin x A. 2 B. 3 C. 4 D. 5 Câu 25. Phương trình 4 4
sin x  cos x  sin 2x  0,5 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2 Câu 26. Phương trình 4 4
(2cos 2x  5)cos x  (2cos 2x  5)sin x  3 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2
Câu 27. Tìm số nghiệm thuộc 0;3  của phương trình 3 2
3sin x  3cos x  7sin x  cos 2x 1  0 . A. 3 B. 3 C. 5 D. 4       2
Câu 28. Phương trình cos 2x  cos x  cos x   sin x   1    
có bao nhiêu điểm biểu diễn nghiệm  4   4  2
trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2
Câu 29. Tìm số nghiệm thuộc 0;2  của phương trình 4(sin3x  cos2x)  5(sin x 1) . A. 2 B. 2 C. 3 D. 5 2
Câu 30. Tìm số nghiệm thuộc 0;2  của phương trình 2
 2 tan x  5tan x  5cot x  4  0. 2 sin x A. 3 B. 2 C. 1 D. 4 1 1
Câu 31. Tìm số nghiệm thuộc 0;2  của phương trình 2 sin x   sin x  . 2 sin x sin x A. 1 B. 2 C. 3 D. 4
Câu 32. Tìm số nghiệm thuộc 0;2  của phương trình cos3x  3cos 2x  2(1 cos x) . A. 2 B. 2 C. 3 D. 5
Câu 33. Tìm số nghiệm thuộc 0;5  của phương trình 23sin x  sin 3x  24 . A. 5 B. 4 C. 3 D. 2 35
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐA THỨC + ẨN PHỤ P2)
___________________________________________ 1 cos 2x
Câu 1. Tồn tại bao nhiêu số nguyên m để phương trình
 (m  2)cos x  2m  0 có nghiệm ? 2 A. 3 B. 4 C. 5 D. 2
Câu 2. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 3 2
sin x  sin x  2  cos x . A. 3 B. 2 C. 1 D. 4
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 3 2
cos 4x  cos6x  4cos 2x  2sin x  m có nghiệm ? A. 4 B. 5 C. 3 D. 2  k Câu 4. Phương trình 3
cot 2x  cot x  3  tan x có một họ nghiệm x  
(a  0,b  0) . Tính tích ab. a b A. 10 B. 16 C. 20 D. 15
Câu 5. Tồn tại bao nhiêu số nguyên m < 100 để phương trình 2 4 tan x   2  m có nghiệm ? cot x A. 102 B. 93 C. 106 D. 97
Câu 6. Tồn tại bao nhiêu số nguyên m < 50 để phương trình 2 1
cot 2x  2(cot x  tan x)   m có nghiệm tan 2x A. 52 B. 56 C. 49 D. 35 5   a Câu 7. Phương trình 2
cot x  4cot x  2 tan x  3  0 có hệ quả cot x 
. Số ước dương của a là 2 A. 9 B. 8 C. 2 D. 4 Câu 8. Với m  1
 994;1994, phương trình cos3x 1993cos x  m có tối đa bao nhiêu điểm biểu diễn
nghiệm trên vòng tròn lượng giác ? A. 4 B. 2 C. 3 D. 1
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình cos 2x  2cos x 1  m có nghiệm ? A. 4 B. 2 C. 3 D. 5 Câu 10. Phương trình 2
cot 2x  4(tan x  cot x)  8 có bao nhiêu nghiệm trên 0;2  ? A. 6 B. 4 C. 5 D. 10  3 
Câu 11. Tồn tại bao nhiêu số nguyên m để phương trình sau có hai nghiệm phân biệt  ;  . 2 2    2
cos x  (2m 1)cos x  2m  0 A. 3 B. 2 C. 1 D. 2 2 2cos x
Câu 12. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 2 sin x  sin x  . 1 sin x A. 3 B. 2 C. 1 D. 4 Câu 13. Phương trình 4
sin x  1 cos x có một hệ quả là 2
a cos x  bcos x 1  0 (a  0,b  0) . Tính ab. A. 2 B. 1 C. 3 D. 4 a Câu 14. Phương trình 8 8
sin x  cos x  cos8x có một hệ quả 2
sin 2x  (phân số tối giản). Tính b – a. b A. 6 B. 7 C. 2 D. 5
Câu 15. Tìm số nghiệm  4
  ;9  của phương trình 6 6
sin x  cos x  sin 2x  1. A. 25 B. 20 C. 23 D. 21 36 a Câu 16. Phương trình 10 10 2
sin x  cos x  sin 2x  1có một quả 2 sin 2x 
(phân số tối giản). Tính b – a. b A. 2 B. 3 C. 1 D. 4 Câu 17. Phương trình 4 2 2
4sin x  2sin x  cos 4x  sin 2x  1 đưa về P(cos 2x)  0 với 2 P(t)  at  bt 1.
Tính giá trị biểu thức ab. A. – 7 B. – 6 C. 3 D. 2 Câu 18. Phương trình 4 4 2
8sin x  4cos x  sin 2x  4 có hệ quả là (cos 2x  a)(cos 2a  b)  0 . Tính ab. A. 0 B. 2 C. 1 D. 3 Câu 19. Phương trình 2
tan x  3tan x  2cot x  6  0 có hệ quả tan x  a  2 . Số ước dương của a là A. 4 B. 6 C. 8 D. 10 1
Câu 20. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  3tan x  cot x  6 . 2 sin x A. 6 B. 4 C. 8 D. 10 x x Câu 21. Phương trình 2 2 tan  cot
 2cot x  tan x  2 có hệ quả 3 2
a cot x  bcot x  c cot x 1  0 . Tính 2 2 tích abc. A. 15 B. 12 C. – 56 D. – 28
Câu 22. Tồn tại bao nhiêu số nguyên m để phương trình 2
2sin x  (m  4)sin x  2m  0có hai nghiệm phân   biệt thuộc ;  . 6    A. 1 B. 2 C. 3 D. 5 Câu 23. Phương trình 3 3 2 2
tan x  cot x  tan x  cot x  1 có bao nhiêu nghiệm  4   ;9  A. 4 B. 2 C. 0 D. 3 Câu 24. Phương trình 2 2 2
cot 2x  cot x  tan x  2 đưa về 3 2
at  bt  ct  2  0 với t  cot x  tan x . Tính ab. A. 5 B. 4 C. 2 D. 3
Câu 25. Tìm số nghiệm trong khoảng 1993;1993  của phương trình 3 3 1 tan x  cot x   3 . sin 2x A. 1994 B. 1993 C. 1992 D. 1996
Câu 26. Tìm số nghiệm trong khoảng 1993;1993  của phương trình 3  tan x  3  cot x  4. A. 1994 B. 1993 C. 1992 D. 1996 1 Câu 27. Phương trình 2 2 2 cot 2x 
 tan x  cot x  3có hệ quả là tan x  cot x  a   . Số ước của a là sin 2x A. 4 B. 2 C. 6 D. 8 x x Câu 28. Phương trình 2 2 tan  cot
 tan x  5 có bao nhiêu nghiệm trên 0;2  ? 2 2 A. 4 B. 6 C. 5 D. 10 Câu 29. Phương trình 4 4
4cos x 12sin x  3  cos2x tương đương (cos 2x  a)(cos 2x  b)  0. Tính ab. A. 0,5 B. 0,25 C. 1 D. 0,75 1
Câu 30. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình tan x  cot x  2 sin x A. 3 B. 4 C. 2 D. 5
_________________________________ 37
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH TÍCH PHẦN 1)
___________________________________________
Câu 1. Tìm một phương trình hệ quả của phương trình cos 2x  cos 4x  sin x  sin 5x . A. cos3x  0 B. cos3x  1 C. sin 3x  1 D. 2sin 3x  1
Câu 2. Tìm một phương trình hệ quả của phương trình 3 3 cos .
x sin 3x  sin x cos3x  sin 2x . A. 3cos 2x  2 B. 3cos 2x  1 C. sin 2x  1 D. 3sin 2x  1
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 2
cos x  (m  2) cos x  2m  0 có nghiệm ? A. 3 B. 2 C. 1 D. 4
Câu 4. Tồn tại bao nhiêu số nguyên m để phương trình 2 2
sin x  (2m  3)sin x  m  3m  0 có nghiệm ? A. 3 B. 6 C. 5 D. 4
Câu 5. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 2 2
sin x  3sin x cos x  2cos x  0 . A. 4 B. 1 C. 2 D. 3
Câu 6. Tìm phương trình hệ quả của phương trình 2 2 2 2
cos x  cos 2x  cos 3x  cos 4x  2 . A. cos x cos 2x cos5x  0 B. cos x sin 2x cos5x  0 C. sin x cos xcos3x  0 D. cos xsin 2x cos5x  0 Câu 7. Tính a + b biết 2
a cos 2x  bcos 2x 1  0 là một phương trình hệ quả của phương trình
cos x cos 4x  cos 2x cos3x  0 A. 6 B. 5 C. 3 D. 2 Câu 8. Tính a + b biết 2
2a cos 2x  b cos 2x 1  0 là một phương trình hệ quả của phương trình
cos x cos 4x  cos 2x cos3x  0 A. 1 B. 0 C. 3 D. 2
Câu 9. Tính a + b biết a(sin x  cos x)  bsin x cos x 1  0 là một phương trình hệ quả của phương trình 3
2cos x  cos 2x  sin x  0 . A. 5 B. 4 C. 3 D. 2 sin 3x sin 5x Câu 10. Tính a + b biết 2
a cos 2x  bcos 2x  4  0 là một phương trình hệ quả của  . 3 5 A. 4 B. 2 C. 3 D. 5
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2 2
cos x(1 cos x)  sin x(1 sin x)  2cos x . A. 4 B. 3 C. 2 D. 1   
Câu 12. Có bao nhiêu số nguyên m để phương trình cos 4x  2(m  3) cos 2x  6m 1  0 có nghiệm 0;  4    A. 2 B. 5 C. 3 D. 4
Câu 13. Tính a + b biết a sin x  2bcos x  7  0 là một phương trình hệ quả của phương trình
9sin x  6cos x  3sin 2x  cos 2x  8 . A. 5 B. 7 C. 6 D. 9
Câu 14. Tính a + b biết a(sin x  cos x)  bsin x cos x 1  0 là một phương trình hệ quả của phương trình 2
2sin x  3sin x 1  cos3x . A. 5 B. 3 C. 4 D. 2
Câu 15. Tập hợp S   ;
a b bao gồm tất cả các giá trị m để phương trình sin5x  msin x có nghiệm x  k . 38
Tính giá trị của 4a + 2b. A. 5 B. 2 C. 3 D. 4    Câu 16. Phương trình 2 2
sin 4x  cos 6x  sin 10,5 10xcó bao nhiêu nghiệm thuộc 0;   ?  2  A. 4 B. 5 C. 3 D. 2 Câu 17. Tính a + b biết 2
(cos x  sin x)  a(sin x  cos x)  b  0 là một hệ quả của phương trình 2 2
cos 2x  2(sin x  cos x)  3sin 2x  3  0 . A. 5 B. 6 C. 4 D. 2
Câu 18. Tìm số nghiệm thuộc 0;3 của phương trình 4(sin 3x  cos2x)  5(sin x 1) . A. 6 B. 2 C. 3 D. 4
Câu 19. Tính tổng nghiệm nhỏ nhất và nghiệm lớn nhất trong khoảng  3
  ;3 của phương trình 3
2sin x  cos 2x  cos x  0 . A. 2 B. 0,5 C. 0, 25 D. 
Câu 20. Tìm số nghiệm thuộc  1
 00 ;100  của phương trình 6 6 8 8
sin x  cos x  2(sin x  cos x) . A. 93 B. 56 C. 400 D. 201
Câu 21. Tìm số nghiệm thuộc  1
 00 ;100  của phương trình 3 2
cos x  cos x  2sin x  2  0 . A. 93 B. 56 C. 200 D. 201   
Câu 22. Tồn tại bao nhiêu số nguyên m để phương trình 4 6
sin x  cos 2x  mcos x  0 có nghiệm  0;   .  4  A. 2 B. 1 C. 0 D. 3  2 
Câu 23. Tính a + b biết S  a;b gồm tất cả các giá trị m để phương trình sau có đúng hai nghiệm  0;  : 3    2
(cos x 1)(cos 2x  m cos x)  msin x . A. – 1,5 B. 2 C. – 1 D. 3   
Câu 24. Tìm số nghiệm thuộc  1
 00 ;100  của phương trình sin 4x  cos4x 1 4 2 sin x    .  4  A. 200 B. 198 C. 102 D. 93
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2
(2sin x 1)(2cos 2x  2sin x 1)  3  4cos x . A. 5 B. 4 C. 6 D. 3
Câu 26. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình tan x  sin x  1 tan . x sin x . A. 5 B. 2 C. 3 D. 4
Câu 27. Tính tổng nghiệm lớn nhất và nghiệm nhỏ nhất thuộc  1
 00 ;100  của phương trình 3 3
sin x  cos x  1 0,5sin 2x . A. 2 B. 0,5 C. 0, 25 D. – 1,5 Câu 28. Tìm a + b biết 2
a cos 2x  bcos 2x  0 là một hệ quả của phương trình tan x  tan 3x  2sin 2x . A. 3 B. 4 C. 1 D. 2
Câu 29. Tìm số nghiệm thuộc  1
 00 ;100  của phương trình 2(1 sin 2x)  5(sin x  cos x)  3  0 . A. 98 B. 190 C. 200 D. 152
_________________________________ 39
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH TÍCH PHẦN 2)
___________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m để phương trình 2
cos x  (sin x  m  2)cos x  m(sin x  2)  0 có nghiệm ? A. 4 B. 2 C. 3 D. 5   5x  9x
Câu 2. Tìm số nghiệm 0;2 của phương trình 2 2 cos3x  sin 7x  2sin   2cos   .  4 2  2 A. 10 B. 7 C. 11 D. 5
Câu 3. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 4cos x  2sin x  3  cos 2x . A. 4 B. 2 C. 3 D. 5
Câu 4. Tính 4a + 9b biết a cos x  bsin x  6 là một hệ quả của phương trình
4sin 2x  3cos 2x  3(4sin x 1) . A. 7 B. 3 C. 8 D. 6
Câu 5. Tính tổng các nghiệm thuộc 0; của phương trình 2 2 2 sin x  cos 2x  cos 3x . 4 5 A.  B. C. D. 2 3 3  k
Câu 6. Tính cos 4 khi   
là một nghiệm của phương trình 2
sin 2x  sin 6x  3cos 2x . 4 2 A. 0,25 B. 0,125 C. – 0,125 D. – 0,5
Câu 7. Tính tổng các nghiệm của phương trình 2
(2cos x 1)(2sin 2x 1)  3  4sin x . 11 A. 1,5 B.  C. 2 D. 6
Câu 8. Tìm số nghiệm 0;2 của phương trình tan x  3cot x  4(sin x  3 cos x) . A. 6 B. 5 C. 4 D. 3
Câu 9. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình   2 2 x 
sin x cos 4x  2sin 2x  4sin   3,5   .  4 2  A. 3 B. 4 C. 5 D. 2
Câu 10. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của 3sin x  cos x  2  cos 2x  sin 2x . A. 5 B. 2 C. 4 D. 6
Câu 11. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình
sin x tan 2x  3(sin x  3 tan 2x)  3 3 . A. 3 B. 4 C. 5 D. 2 a Câu 12. Phương trình 2
sin 2x  m(2sin x  cos x)  m  0 có nghiệm duy nhất khi m  (a, b nguyên tố). b Tính a + b. A. 7 B. 5 C. 10 D. 9
Câu 13. Phương trình 2sin x  cot x  2sin 2x 1có phương trình hệ quả a(sin x  cos x)  bsin xcos x  0
với a, b dương. Tính giá trị biểu thức a + b. A. 4 B. 3 C. 2 D. 5
Câu 14. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 3 3
sin x  cos x  sin x  cos x . 40 A. 6 B. 2 C. 1 D. 5
Câu 15. Phương trình 1 sin x  cos x  sin 2x  2cos 2x  0 có một hệ quả a cos x  bsin x 1  0 với a, b dương. Tìm 2a + b. A. 7 B. 2 C. 6 D. 10
Câu 16. Tính abc biết phương trình 2 2
sin x cos x  cos 2x  sin x  cos xsin x  cos x  0 tương đương
(sin x  a cos x)(sin x  b)(cos x  c)  0 (a, b, c dương). A. 2 B. 1 C. 3 D. 4
Câu 17. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của 3 3
sin x  3sin x  8cos x  6cos x . A. 4 B. 1 C. 2 D. 3
Câu 18. Tồn tại bao nhiêu giá trị m để phương trình 2
sin x  (3m 1)sin x  m(2m 1)  0 có nghiệm duy nhất. A. 4 B. 1 C. 2 D. 3
Câu 19. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 2 2 x 2 x sin x  2sin  2sin xsin  cot x  0 . 2 2 A. 4 B. 2 C. 3 D. 5 1
Câu 20. Phương trình sin 2x  tan x  1,5  cos 2x tương đương (sin 2x  a)(tan x  b)  0 . Tính ab. 2 A. 1 B. 0,5 C. 0,25 D. 2
Câu 21. Tồn tại bao nhiêu số nguyên m để phương trình sin 2x  msin x  2m  4cos x có nghiệm ? A. 4 B. 2 C. 5 D. 3
Câu 22. Phương trình cos 2x  2cos x  6sin x  8 có một hệ quả cos x  sin x  a , số ước của a là A. 2 B. 4 C. 6 D. 8
Câu 23. Tìm số nghiệm  4
 9;1993của phương trình cos2x  3cos x  sin x  2  0. A. 650 B. 542 C. 938 D. 1993
Câu 24. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của sin 2x  cos2x  3sin x  cos x  1 A. 4 B. 2 C. 3 D. 5
Câu 25. Phương trình sin 2x  2cos 2x  1 sin x  4cos x có bao nhiêu nghiệm  4  9;1993 A. 193 B. 968 C. 702 D. 325
Câu 26. Phương trình 2sin 2x  cos 2x  7sin x  2cos x  4 tương đương phương trình sin x  a , khi đó  1 1   1 1   1 1   1  A. a  ;   B. a  ;   C. a  ;   D. a  ;1    5 4   7 5   4 3   3  sin 3x cos3x    Câu 27. Phương trình   2 sin x  
 có hệ quả sin x  b cos x  c (b, c dương). Tính bc. sin x cos x  4  2 A. 0,25 B. 0,5 C. 1 D. 3   
Câu 28. Tồn tại bao nhiêu số nguyên k để phương trình 4sin 2x  mcos x  cos3x có nghiệm  0;  . 6    A. 5 B. 6 C. 3 D. 7
Câu 29. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của 3
4sin x  sin 3x  4cos x  cos x . A. 3 B. 2 C. 1 D. 4 sin 3x cos3x
Câu 30. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình   1 sin 2x . sin x cos x A. 4 B. 2 C. 5 D. 1 41
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỐI XỨNG PHẦN 1)
___________________________________________
Câu 1. Phương trình (2  2)(sin x  cos x)  2sin x cos x  2 2 1có bao nhiêu nghiệm 0;4  ? A. 2 B. 3 C. 4 D. 5
Câu 2. Phương trình 3(sin x  cos x)  2sin 2x  3  0 có bao nhiêu nghiệm 0;4  ? A. 2 B. 4 C. 3 D. 5
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình sin 2x  3(sin x  cos x)  m 1có nghiệm ? A. 4 B. 2 C. 9 D. 11
Câu 4. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình sin x  cos x  4sin x cos x 1  0 A. 3 B. 2 C. 1 D. 4
Câu 5. Phương trình sin 2x 12(sin x  cos x) 12  0 có phương trình hệ quả là 1
A. sin x  cos x  2 B. sin x  cos x  1 C. sin x  cos x  0 D. sin x  cos x  2 Câu 6. Phương trình 3 3
sin x  cos x  1có bao nhiêu nghiệm 0;4  ? A. 2 B. 4 C. 3 D. 5
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình 3sin 2x  4(sin x  cos x)  m có nghiệm ? A. 13 B. 12 C. 10 D. 11
Câu 8. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình sin x  cos x  4sin 2x  1. A. 3 B. 4 C. 1 D. 2
Câu 9. Tìm một phương trình hệ quả của phương trình cot x  tan x  sin x  cos x . 1 A. sin x  cos x  1 B. sin x  cos x  C. tan x  1  D. tan x  1 2 1 1 10   
Câu 10. Góc x thỏa mãn cos x   sin x   thì cos x    gần nhất với cos x sin x 3  4  A. – 0,55 B. – 0,25 C. 0,12 D. – 0,45
Câu 11. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 3 3 3
1 sin x  cos x  sin 2x . 2 A. 3 B. 4 C. 1 D. 2
Câu 12. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình
5  cos 2x  2(2  cos x)(sin x  cos x) . A. 3 B. 2 C. 1 D. 4
Câu 13. Miền [a;b] gồm tất cả các giá trị m để phương trình sin 2x  4(cos x  sin x)  m có nghiệm. Tính a + b. A. 1 B. 2 C. – 1 D. – 2
Câu 14. Tìm số nghiệm0;4  của phương trình sin x  cos x  sin xcos x  1. A. 4 B. 3 C. 2 D. 1
Câu 15. Tìm số nghiệm0;4  của phương trình 5sin 2x 12  12(sin x  cos x) A. 5 B. 3 C. 4 D. 2   
Câu 16. Tồn tại bao nhiêu số nguyên m để phương trình sin x cos x  2(sin x  cos x)  m có nghiệm  0;  . 4    A. 2 B. 1 C. 3 D. 5
Câu 17. Tìm số nghiệm0;4  của phương trình cos xsin x  sin x  cos x 1. 42 A. 3 B. 4 C. 2 D. 5
Câu 18. Tìm số nghiệm0;4  của phương trình 2 2
tan x  cot x  (tan x  cot x)  2  0 . A. 18 B. 14 C. 16 D. 15
Câu 19. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình 2 2
3(tan x  cot x)  4(tan x  cot x)  2  0 . A. 4 B. 3 C. 2 D. 1   
Câu 20. Biết góc x thỏa mãn sin x 1  cos x 1  1. Tính cos x    .  4  1 1 A. 1 B.  C. D. – 1 2 2   
Câu 21. Tồn tại bao nhiêu số nguyên m để phương trình sin x cos x  2 sin x  cos x  m có nghiệm  0;  . 4    A. 2 B. 1 C. 3 D. 5
Câu 22. Đặt sin x  cos x  t thì phương trình 3 3
sin x  cos x  sin 2x  1  P(t)  0 . Tính tổng các hệ số của đa thức P(t) A. 0 B. 2 C. 1 D. – 1
Câu 23. Đặt sin x  cos x  t thì 3 2
2  sin 3x  cos3x  sin x  cos x  at  bt  ct  2  0 . Tính a – c. A. 10 B. 6 C. 4 D. 2  1 1 
Câu 24. Phương trình 2  (2  sin 2x)   tan x  cot x  0  
có một phương trình hệ quả là  sin x cos x  1 A. sin x  cos x  1 B. sin x  cos x  C. tan x  1  D. tan x  1 2 Câu 25. Phương trình 3 3
tan x  cot x  tan x  cot x  1có bao nhiêu nghiệm thuộc 0;4  ? A. Vô nghiệm B. 1 C. 4 D. 6
Câu 26. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 2 3 3
cot 2x  cot x  tan x  2 . A. 3 B. 2 C. 4 D. 1
Câu 27. Tồn tại bao nhiêu số nguyên m để phương trình 2 2
tan x  cot x  tan x  cot x  m vô nghiệm ? A. 3 B. 1 C. 2 D. 4
Câu 28. Tìm số nghiệm 0;4  của phương trình 3 3 1 tan x  cot x   3 . sin 2x A. 3 B. 6 C. 4 D. 2
Câu 29. Tìm số nghiệm 0;6  của phương trình 3  tan x  3  cot x  4. A. 3 B. 6 C. 4 D. 2
Câu 30. Tìm số nghiệm 0;6  của phương trình 3(tan x  cot x)  2(2  sin x) . A. 6 B. 2 C. 3 D. 5
Câu 31. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của phương trình 3 3
sin x  cos x  2(sin x  cos x) 1. A. 1 B. 3 C. 2 D. 4 2
Câu 32. Tìm số nghiệm 0;6  của phương trình 2
 2cot x  5(tan x  cot x)  4  0 2 cos x A. 10 B. 12 C. 18 D. 14 43
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỐI XỨNG PHẦN 2)
___________________________________________ m
Câu 1. Tồn tại bao nhiêu số nguyên m để phương trình 4(sin x  cos x)  9sin x cos x  có nghiệm 1993 A. 31975 B. 21945 C. 20093 D. 31083
Câu 2. Tìm số nghiệm 0;6  của phương trình sin x  cos x  sin xcos x  1. A. 4 B. 6 C. 8 D. 12
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3(tan x  cot x)  2(2  sin 2x) . A. 3 B. 4 C. 2 D. 5
Câu 4. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm của 6(sin x  cos x)  sin xcos x  6  0 A. 3 B. 2 C. 4 D. 1
Câu 5. Phương trình sin 3x  cos3x  2(sin x  cos x)  1 có một hệ quả sin x  cos x  a . Số ước của a là A. 2 B. 4 C. 1 D. 6
Câu 6. Tồn tại bao nhiêu số nguyên k để phương trình 2(sin x  cos x)  3sin x cos x  4k có nghiệm A. 2 B. 1 C. 3 D. 4
Câu 7. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 1 tan x  2 2 sin x . A. 3 B. 2 C. 4 D. 5 Câu 8. Phương trình 3 3
sin x  cos x  sin x  cos x  2 đưa về đa thức P(t)  0 với t  sin x  cos x . Biết hệ số
cao nhất của P(t) bằng 2, tính P(3) . A. 32 B. 18 C. 16 D. 20
Câu 9. Phương trình cos x  sin x  2sin x cos x  1có một hệ quả là 1 A. cos x  sin x  2 B. cos x  sin x   2 C. cos x  sin x  1 D. cos x  sin x  2 Câu 10. Phương trình 2
3sin x  cos x  3sin 2x  8sin x  1 có một hệ quả là 6sin x  b cos x  a (a  2) .
Tính giá trị biểu thức b – 2a. A. 7 B. 6 C. 4 D. 5
Câu 11. Tồn tại bao nhiêu số nguyên dương m < 100 để phương trình m(sin x  cos x)  sin 2x  m 1  0 có nghiệm A. 3 B. 99 C. 80 D. 93 Câu 12. Biết rằng 3 3 3 2
sin x  cos x  sin 2x  1  at  bt  ct  4  0 với t  sin x  cos x . Tính ab + c A. – 1 B. 1 C. – 2 D. – 3
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
 2 tan x  5tan x  5cot x  4  0. 2 sin x A. 4 B. 3 C. 1 D. 2
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 3 sin x  cos x  1 A. 4 B. 2 C. 3 D. 1
Câu 15. Tồn tại bao nhiêu số nguyên m để phương trình 4(sin x  cos x)  9sin x cos x  m 1993 có nghiệm ? A. 10 B. 16 C. 17 D. 7   
Câu 16. Tồn tại bao nhiêu số nguyên m để phương trình sin x  cos x  sin x cos x  m có nghiệm  0;  4    44 A. 2 B. 1 C. 3 D. 4
Câu 17. Tính tổng các nghiệm của phương trình sin x cos x  sin x  cos x  1 trong khoảng 0;2 . A.  B. 2 C. 3 D. 4
Câu 18. Tìm số nghiệm trong khoảng 0;2  của phương trình 3sin xcos x  sin x  cos x  3. A. 3 B. 1 C. 0 D. 2
Câu 19. Tính 3  sin 2 khi  là nghiệm phương trình sin x cos x  2(sin x  cos x)  2 . A. 3 B. 2 C. 3,5 D. 2,5
Câu 20. Tìm số nghiệm trong khoảng 0;2  của phương trình sin x  cos x 1  2sin xcos2x A. 2 B. 1 C. 3 D. 4
Câu 21. Điều kiện để phương trình 4(cos x  sin x)  sin 2x  m có nghiệm là m  a b  c . Tính abc. A. 8 B. 10 C. 16 D. 4
Câu 22. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 1 1 10 sin x  cos x    sin x cos x 3 A. 4 B. 2 C. 3 D. 1
Câu 23. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 3 4 2 3 4
sin x  sin x  sin x  sin x  cos x  cos x  cos x  cos x . A. 4 B. 2 C. 1 D. 3
Câu 24. Tồn tại bao nhiêu số nguyên m để phương trình 2cos 2x  (sin x cos x  m)(sin x  cos x)  0 có    nghiệm  0;  . 2    A. 4 B. 3 C. 5 D. 2
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
(tan x  7)cot x  (cot x  7) tan x 14  0 . A. 4 B. 2 C. 3 D. 5
Câu 26. Tồn tại bao nhiêu số nguyên m  9  3;9 
3 để phương trình sau có nghiệm 2 2
tan x  cot x  m(tan x  cot x)  2m  0 . A. 180 B. 100 C. 69 D. 93
Câu 27. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 2 3 2
tan x  tan x  tan x  cot x  cot x  cot x  6 . A. 4 B. 5 C. 3 D. 2
Câu 28. Tồn tại bao nhiêu số nguyên m 1
 0;10 để phương trình sau có nghiệm 3 3
tan x  tan x  (m  cot x)  m  cot x . A. 3 B. 12 C. 16 D. 18
Câu 29. Tồn tại bao nhiêu số nguyên m để phương trình sau có nghiệm sin x  cos x  7sin x cos x  m . A. 6 B. 5 C. 4 D. 8   
Câu 30. Có bao nhiêu số nguyên m để phương trình (1 cos x)(1 sin x)  m có đúng một nghiệm  0;  2    A. 2 B. 1 C. 3 D. 4
Câu 31. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 3 3
1 sin 2x  cos 2x  sin 4x . 2 A. 5 B. 4 C. 3 D. 2 45
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỒNG BẬC PHẦN 1)
___________________________________________
Câu 1. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
2cos x  5sin x cos x  3sin x  0 . A. 4 B. 5 C. 3 D. 6
Câu 2. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
2cos x  4sin x cos x  4sin x  1. A. 4 B. 5 C. 3 D. 6
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
2cos x  3 3 sin x cos x  4sin x  4  . A. 4 B. 5 C. 3 D. 6
Câu 4. Tìm số nghiệm thuộc 0;3  của phương trình 2 sin x  3sin xcos x  1  . A. 5 B. 6 C. 2 D. 4   
Câu 5. Nghiệm dương nhỏ nhất của phương trình 3 2 sin x   2sin x   thuộc khoảng  4   1   1  A. 0;   B. (1;2) C. (2;3) D. ;1    2   2 
Câu 6. Tìm số nghiệm thuộc 0;3  của phương trình 3 cos x  2sin x . A. 5 B. 3 C. 2 D. 4
Câu 7. Nghiệm dương nhỏ nhất của phương trình sin 2x  2 tan x  3thuộc khoảng  1   1  A. 0;   B. (1;2) C. (2;3) D. ;1    2   2 
Câu 8. Tìm số nghiệm thuộc 0;3  của phương trình 3 sin x  2cos x . A. 5 B. 3 C. 2 D. 4
Câu 9. Tính b + c biết rằng phương trình 2
1 3sin 2x  2 tan x  (tan x 1)(2 tan x  b tan x  c)  0 . A. 5 B. 4 C. 2 D. 3
Câu 10. Tìm số nghiệm thuộc 0;3  của phương trình 4 2 2 4
3cos x  4sin xcos x  sin x  0 A. 12 B. 16 C. 10 D. 8 Câu 11. Phương trình 2 2
8sin xcos x  2sin 4x  3  3cos 4x tương đương (tan 2x  a)(tan 2x  b)  0 . Tính
giá trị biểu thức a + b + 2. A. 2 B. 6 C. 3 D. 1
Câu 12. Tìm số nghiệm thuộc 0;3  của phương trình 2 2
tan xsin x  2sin x  3(cos 2x  sin x cos x) . A. 12 B. 16 C. 10 D. 8
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3
7cos x  4cos x  4sin 2x . A. 4 B. 5 C. 3 D. 6
Câu 14. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 2 3
cos x  2sin x cos x  3sin x  0 . A. 2 B. 5 C. 3 D. 4
Câu 15. Tồn tại bao nhiêu giá trị nguyên m để phương trình 2 2
3sin x  msin 2x  4cos x  0 có nghiệm. A. Vô số B. 12 C. 20 D. 15 46
Câu 16. Tồn tại bao nhiêu giá trị nguyên m để phương trình 2 2
sin x  (m 1)sin 2x  (m 1)cos x  m có nghiệm A. 5 B. 4 C. 3 D. 2
Câu 17. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3
4sin x  3 2 sin 2x  8sin x . A. 3 B. 5 C. 2 D. 4
Câu 18. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2
sin x(1 tan x)  3  3sin x(cos x  sin x) . A. 4 B. 3 C. 6 D. 5
Câu 19. Nghiệm dương nhỏ nhất của phương trình 3 3 2 2
sin x  3 cos x  sin x cos x  3 sin x cos x thuộc khoảng nào sau đây A. (2;3) B. (1;2) C. (3;4) D. (0;1)
Câu 20. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
4 3 sin x cos x  4cos x  2sin x  2,5. A. 4 B. 3 C. 6 D. 5
Câu 21. Phương trình (1 tan x)(1 sin 2x)  1 tan x tương đương (tan x  a)(tan x  b)  0 . Tính a + b. A. – 1 B. 1 C. 0 D. 2 1
Câu 22. Tập hợp [a;b] gồm tất cả các giá trị a để phương trình 2 2
sin x  sin 2x  2cos x  a có nghiệm. Tính 2
giá trị biểu thức b – a. A. 6 B. 10 C. 7 D. 2 5
Câu 23. Tính a + b + c biết rằng phương trình 3 3 2
4sin x  3cos x  3sin x  sin xcos x  0 tương đương
(tan x  a)(tan x  b)(tan x  c)  0 . A. 3 B. 1 C. 0 D. 2
Câu 24. Tính a + b biết rằng 3
sin xsin 2x  sin 3x  6cos x tương đương 2
(tan x  a)(tan x  b)  0 A. 5 B. 4 C. 3 D. 2 3
Câu 25. Biết rằng 2cos x  4sin x 
 P(t)  0 (đa thức hệ số nguyên) trong đó t  tan x . Tổng các hệ cos x
số nguyên của đa thức P(t)  0 là A. 4 B. 0 C. 1 D. 2
Câu 26. Phương trình sin x cos 2x  6cos x(1 2cos 2x) tương đương P(t)  0 với t  tan x . Tổng các nghiệm
của đa thức của đa thức P(t)  0 là A. 7 B. 6 C. 5 D. 8
Câu 27. Tìm số nghiệm thuộc 0;3  của phương trình 3
sin xsin 2x  sin 3x  6cos x . A. 5 B. 9 C. 12 D. 10   
Câu 28. Tồn tại bao nhiêu số nguyên m  7
 ;7 để phương trình sau có nghiệm thuộc khoảng 0;   .  4  2 2
3sin x  (2m 1)sin 2x  (m 1)cos x  m A. 10 B. 11 C. 13 D. 8
Câu 29. Tìm số điểm biểu diễn nghiệm trên vòng tròn lượng giác của sin 3x  cos3x  2cos x  0 . A. 5 B. 4 C. 3 D. 6
_________________________________ 47
ÔN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN CƠ BẢN – PHƯƠNG TRÌNH ĐỒNG BẬC PHẦN 2)
___________________________________________
Câu 1. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 3 2
4sin x  3cos x  3sin x  sin x cos x  0 . A. 3 B. 2 C. 4 D. 1 cos 2x 1
Câu 2. Nghiệm dương nhỏ nhất của phương trình 2 cot x 1 
 sin x  sin 2x thuộc khoảng 1 tan x 2  1   1  A. 0;   B. (1;2) C. (2;3) D. ;1    2   2  Câu 3. Phương trình 3 3 2
cos x  4sin x  3sin xcos x  sin x  0 tương đương với phương trình nào ? A. 3 2
3t  3t  t 1  0;t  tan x B. 3 2
3t  3t  2t  2  0;t  tan x C. 3 2
5t  5t  t 1  0;t  tan x D. 3 2
3t  3t  t 1  0;t  tan x .
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 2 2
2sin x  (2m 1)sin x cos x  mcos x  0 có 4 điểm
biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. Vô số C. 5 D. 10
Câu 4. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  3
2 2 cos (x  )  3cos x  sin x  0 . 4 A. 3 B. 2 C. 4 D. 1
Câu 5. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 3
4(sin x  cos x)  cos x  3sin x . A. 3 B. 2 C. 6 D. 4    3 (tan 1) Câu 6. Phương trình 3 sin x   2 sin x  
có nghiệm x   . Tính .  4  2 tan  1 A. 4 B. 2 C. 3 D. 5
Câu 7. Tồn tại bao nhiêu số nguyên m < 10 để phương trình 2 2
sin x  2sin x cos x  (m 1)cos x có nghiệm A. 8 B. 12 C. 10 D. 8
Câu 8. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 2
sin x  3cos x  3sin xcos x  2sin x . A. 3 B. 5 C. 2 D. 4
Câu 9. Tìm số nghiệm  (0;1993 ) của phương trình sin x  cos x  cos3x . A. 6230 B. 5977 C. 1288 D. 1394
Câu 10. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3
sin 3x  cos x  sin x  cos x . A. 3 B. 2 C. 6 D. 4
Câu 11. Tìm số nghiệm  (0;1993 ) của phương trình cos 2x cos x  cos x  sin x . A. 3986 B. 3987 C. 3985 D. 2000
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3
cos 2xsin x  cos x  cos x  sin x A. 3 B. 4 C. 2 D. 5   
Câu 13. Phương trình 2sin 3x   cos x  
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?  6  48 A. 4 B. 6 C. 2 D. 1   
Câu 14. Tìm số nghiệm 0;5 của phương trình 2cos xsin 2x   sin x  cos x    6  A. 10 B. 15 C. 16 D. 20
Câu 15. Tồn tại bao nhiêu số nguyên m < 15 để phương trình 2 2
sin x  4sin x cos x  (4  ) m cos x  0 có hai  3 
nghiệm phân biệt thuộc  ;   ?  2  A. 6 B. 4 C. 3 D. 7
Câu 16. Tồn tại bao nhiêu số nguyên m để phương trình 2 2
sin x  (m  2)sin x cos x  2mcos x  0 có 4 điểm
biểu diễn nghiệm trên vòng tròn lượng giác ? A. Vô số B. 2 C. 4 D. 6      
Câu 17. Phương trình 4cos x  sin 2x   cos x    
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn  3   6  lượng giác ? A. 4 B. 6 C. 2 D. 1   
Câu 18. Phương trình 2cos 3x   cos x  2sin x  
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn  3  lượng giác ? A. 4 B. 6 C. 2 D. 1   
Câu 19. Tồn tại bao nhiêu số nguyên m lớn hơn – 30 để phương trình sau có nghiệm thuộc ;   ?  2  2 2
sin x  (m  4)sin x cos x  4mcos x  0 A. 29 B. 21 C. 40 D. 6    Câu 20. Phương trình 3 8sin x   cos x  
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ?  6  A. 4 B. 6 C. 2 D. 1   
Câu 21. Bao nhiêu số nguyên m < 15 để 2 2
sin x  3sin x cos x  (2  m) cos x  0 có nghiệm thuộc ;   ?  2  A. 6 B. 13 C. 18 D. 7  3 
Câu 22. Tồn tại bao nhiêu số nguyên m nhỏ hơn 10 để phương trình sau có nghiệm thuộc  ;   ?  2  2 2
sin x  (m  5)sin x cos x  5mcos x  0 A. 9 B. 25 C. 6 D. 4
Câu 23. Tồn tại bao nhiêu số nguyên m < 17 để phương trình 2 2
2sin x  3sin x cos x  (4  3m)cos x  0 có hai   
nghiệm phân biệt thuộc  ;0   ?  2  A. 4 B. 1 C. 3 D. 2   
Câu 24. Tồn tại bao nhiêu số nguyên m lớn hơn – 7 để phương trình sau có nghiệm thuộc  ;0   ?  2  3 3
sin x  sin x  mcos x  (mcos x) A. 4 B. 6 C. 3 D. 10
_________________________________ 49
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 1)
_______________________________________________________ sin Câu 1. Giả sử
;cos; tan theo thứ tự lập thành một cấp số nhân. Tính cos 2 . 6 3 3 1 1 A. B.  C. D.  2 2 2 2
Câu 2. Tìm điều kiện tham số m để hàm số y  2cos 2x  3cos x  m xác định với mọi x. 41 41 1 11 A. m   B. m   C. m  D. m   16 8 2 23
Câu 3. Tồn tại bao nhiêu số nguyên m nhỏ hơn 2018 để 2 2
cos 4x  sin 4x  3sin8x  m với mọi x. A. 2016 B. 2015 C. 2014 D. 2018 1
Câu 4. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để y  xác định với mọi x. 2sin 3x  2cos3x  m A. 7 B. 2 C. 6 D. 10 2cos x  3sin x  5 Câu 5. Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính Q = M.N. 2sin x  3cos x  5 A. Q = 1 B. Q = 2 C. Q = 5 D. Q = 10 sin x  cos x
Câu 6. Ký hiệu S là tập giá trị của hàm số y 
. Độ dài của S trên trục số bằng 2sin x  cos x  3 A. 4 B. 2 C. 1 D. 1,5
Câu 7. Tồn tại bao nhiêu số nguyên m thuộc khoảng (– 27;27) sao cho 3 x  x   3 4cos 3cos
2 3sin x  4sin x  mvới mọi x. A. 29 B. 35 C. 48 D. 24 cos x  2 Câu 8. Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào sau đây đúng ? cos x  sin x  2 A. M + N = 3 B. M – N = 4 C. 2M + N = 6 D. M hữu tỷ. sin x  2cos x 1
Câu 9. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên  . sin x  cos x  2 A. 1 2 B. 0 C. 1 D. – 1 sin x  cos x Câu 10. Biểu thức y 
có thể nhận bao nhiêu giá trị nguyên ? 2sin x  cos x  3 A. 3 B. 2 C. 6 D. 4 x 
Câu 11. Tồn tại bao nhiêu số nguyên m nhỏ hơn 30 để hàm số f  x sin 6  xác định trên  ? sin 2x  6m A. 10 B. ``9 C. 8 D. 29 2sin 2x  cos 2x Câu 12. Hàm số y 
có thể nhận bao nhiêu giá trị nguyên ? sin 2x  cos 2x  3 A. 4 B. 2 C. 3 D. 1 x  x  x x 
Câu 13. Tồn tại bao nhiêu số nguyên m lớn hơn – 2001 để hàm số f  x sin cos sin cos 2  xác 2sin x  m định trên  ;   ? A. 2017 B. 1999 C. 1998 D. 2002 50 2018
Câu 16. Cho hàm số f  x 
. Tồn tại tất cả bao nhiêu số nguyên m trong khoảng 4 4
cos x  sin x  3sin 2x  m
(– 40;40) để hàm số xác định với mọi giá trị x. A. 20 B. 40 C. 72 D. 58 4 4 sin x  cos x  2
Câu 17. Tồn tại bao nhiêu số nguyên k lớn hơn – 13 thỏa mãn  0, x    . 2 2
cos x  sin x  4sin 2x  k A. 30 B. 10 C. 14 D. 8 3
Câu 19. Tồn tại bao nhiêu số nguyên p sao cho  1, x    ? sin x  cos x  p A. 3 B. 4 C. 0 D. 1 17
Câu 20. Tồn tại bao nhiêu số nguyên p sao cho  1, x    ? sin x  cos x  p A. 13 B. 14 C. 10 D. 13 2x  m Câu 21. Cho hàm số y 
. Tồn tại tất cả bao nhiêu số nguyên m nằm trong 3
3sin x  4sin x  5cos3x  m
khoảng (– 20;20) để hàm số xác định với mọi giá trị x. A. 4 B. 12 C. 7 D. 28 3sin x  cos x  4
Câu 22. Tính tổng tất cả các giá trị nguyên của hàm số y  . 2sin x  cos x  3 A. 8 B. 5 C. 6 D. 9   
Câu 23. Tìm a để hàm số f  x 3  2cos 2x  sin x   a 1  
đạt giá trị nhỏ nhất bằng 4.  2  47 A. a = 3 B. a = 2 C. a = 1 D. a = 16
Câu 24. Gọi n là số nguyên thỏa mãn 1 tan1 1 tan 2 1 tan3 ...1 tan 45  2n      . Khi đó A. n [1;7] B. n [8;19] C. n [20;26] D. n [27;33]
Câu 25. Có bao nhiêu giá trị  0;2 để hai tập hợp sau trùng nhau
S  sin,sin 2,sin 3;T  cos,cos2,cos3 . A. 1 B. 2 C. 3 D. 4 x  3 
Câu 26. Tìm giá trị lớn nhất của hàm số 2 2 y  cos 2x  sin  3sin x  4 trên ; . 2  2 2    89 A. 5,5 B. 5 C. D. 4 16
Câu 27. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 100 sao cho  x  x2 3 4sin 3sin  6sin 3xcos3x  m, x    . A. 75 B. 60 C. 81 D. 97
Câu 28. Gọi M là tập giá trị của hàm số S   x  x2 2sin 3cos
 42sin x  3cos x  5. Tập hợp M chứa bao nhiêu giá trị nguyên ? A. 2 B. 3 C. 4 D. 1
Câu 29. Đồ thị của hàm số nào sau đây đối xứng qua trục tung ? 1 A. y 
B. y  sin x  45 
C. y  2 cosx  45  D. y  sin 2x 2 sin x
__________________________________ 51
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 2)
_______________________________________________________    Câu 1. Hàm số  y  2sin x  
 tuần hoàn với chu kỳ bao nhiêu ?  6 4  A. 24 B. 30 C. 4 D. 6  
Câu 2. Tính tổng các giá trị a xảy ra để hàm số cos x a sin x 1 y 
có giá trị lớn nhất bằng 1 ? cos x  2 A. 3 B. 0 C. 1 D. 2
Câu 3. Tìm giá trị lớn nhất của hàm số 13 y  sin x 10cos x . A. 11 B. 10 C. 9 D. 8,5  Câu 4. Hàm số 2sin 2x cos 2x y 
có thể nhận tất cả bao nhiêu giá trị nguyên ? sin 2x  cos 2x  3 A. 1 B. 2 C. 3 D. 4   Câu 5. Hàm số x 2  y  2018cos  5 
 tuần hoàn với chu kỳ bao nhiêu ?  5  A. 7 B. 10 C. 20 D. 5 
Câu 6. Có bao nhiêu số nguyên m để hàm số   1 msin x g x 
có giá trị nhỏ nhất M mà M < – 2 ? 2  cos x A. 6 B. 7 C. 4 D. 5
Câu 7. Có bao nhiêu số thực m 4
y  sin x  cos 2x  m có giá trị nhỏ nhất bằng 2 ? A. 3 B. 2 C. 1 D. 4
Câu 8. Giá trị nhỏ nhất của hàm số 4 4
y  sin x  cos x  sin x cos x là A. 1,125 B. 1,25 C. 1 D. 2,25 
Câu 9. Cho x, y, z  0; x  y  z  . Tìm giá trị lớn nhất của biểu thức 2
y  1 tan x tan y  1 tan z tan y  1 tan x tan z . A. 1 2 2 B. 3 3 C. 2 D. 2 3  
Câu 10. Giá trị lớn nhất của hàm số  y  2cos x  sin x    là  4  A. 5  2 2 B. 5  2 2 C. 5  2 2 D. 5  2 2  2 1 tan x 3 2 
Câu 11. Tìm giá trị nhỏ nhất của hàm số y  4cot 2x  . tan x A. 0 B. 3  2 3 C. 2  2 2 D. – 1
Câu 12. Giá trị lớn nhất của hàm số    2x   2x  f x  sin  cos 1  gần nhất với số nào 2   2   x 1  x 1 A. – 1 B. 2 C. – 0,25 D. – 0,125
Câu 13. Số giờ có ánh sáng của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số  lượng giác là y  4 sin
t  60 10, với t là số nguyên và t 0;36 
5 . Vào ngày nào trong năm thì thành 178
phố A có nhiều giờ ánh sáng mặt trời nhất ? A. 28 tháng 5 B. 29 tháng 5 C. 30 tháng 5 D. 31 tháng 5   4 4 sin x cos y Câu 14. Cho  x, y  0; 
 và cos 2x  cos 2 y  2sin(x  y)  2 . Tìm giá trị nhỏ nhất của P   .  2  x y 52 A. 3 B. 2 C. 2 D. 5   3 
Câu 15. Tìm độ dài tập giá trị W của hàm số S  sin x cos x  cos x sin x . A. 2 B. 4 2 C. 2 D. 2 2  
Câu 16. Tìm a để hàm số ax 2  y  2cos  
 tuần hoàn với chu kỳ 5 .  5 3  A. a = 3 B. a = 4 C. a = 2 D. a = 6
Câu 17. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2
y  5sin x 1  5cos x 1 . A. 6 B. 1 + 2 2 C. 1 6  14 D. 2  3  15 1 1
Câu 18. Tìm giá trị lớn nhất của hàm số 2 2 y   cos x  5  2sin x . 2 2 A. 5 1 B. 22 C. 11 D. 1 5 2 2 2
Câu 19. Cho hai số thực dương x, y thỏa mãn cos(x  y 1)  3  cos(3xy)  9xy  3x  3y . Giá trị nhỏ nhất
của biểu thức x(y  2) gần nhất với A. 2,39 B. 5,16 C. 4,23 D. 1,87
Câu 20. Cho hai số dương a, b thỏa mãn sin(2  2ab)  sin(a  b)  2ab  a  b  2 . Giá trị nhỏ nhất của biểu thức S = a + 2b là     A. 2 10 3 B. 10 3 C. 3 10 7 D. 2 10 3 2 2 2 5   
Câu 21. Hàm số f (x) xác định trên R, thỏa mãn  f  x 1 tan
 sin 2x  cos 2x với x   ;   . Với a, b là hai số 2  2 2 
thực thỏa mãn a + b = 1, tìm giá trị nhỏ nhất của S = f (a). f (b).    A. 1 B. 5 3 5 C. 5 3 5 D. 5 3 5 25 2 2 2
Câu 22. Cho x, y là hai số thực thỏa mãn cos2x + cos2y = 1. Tìm giá trị nhỏ nhất của biểu thức 2 2 tan x  tan y . A. 1 B. 2 C. 8 D. 3 3 3 3
Câu 23. Số giờ có ánh sáng của một thành phố X ở vĩ độ 40 độ Bắc trong ngày thứ t của một năm không nhuận   được cho bởi hàm số  d t   3sin t 80 12 
, t nguyên và 0  t  365 . Vào ngày nào trong năm thì thành 182   
phố X có nhiều giờ ánh sáng nhất ? A. 262 B. 353 C. 80 D. 171 x x
Câu 24. Hàm số f  x  sin  tan có chu kỳ tuần hoàn nhỏ nhất là 4 6 A. 10 B. 24 C. 8 D. 14
Câu 25. Tìm giá trị lớn nhất của biểu thức y  sin x 1  3  sin x . A. 4 B. 2 2 C. 3 2 D. 2 5
Câu 26. Tìm giá trị tham số m để hàm số f (x)  cos x  4  cos x  m có giá trị lớn nhất bằng 3 2 . A. m = 3 B. m = 2 C. m  2 D. m  2 2 1 1   
Câu 27. Tìm giá trị nhỏ nhất của biểu thức f (x)   ; x  0;   . 2  cos x 1 cos x  2  4 2 A. 1 B. 0,5 C. D. 3 3 53
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 3)
_______________________________________________________ 2 sin x 1    
Câu 1. Tìm giá trị nhỏ nhất của y   với x  ;   . cos x(sin x  cos x) 4  4 2  A. 4 B. 4,25 C. 5 D. 5,25
Câu 2. Tìm giá trị lớn nhất của hàm số 5 y  sin x  3 cos x A. 1 B. 2 C. 3 D. 2 3
Câu 3. Tính tổng giá trị lớn nhất, giá trị nhỏ nhât của hàm số 2
f (x)  sin x  3sin x  2 . A. 5 B. 6 C. 4 D. 2  4 
Câu 4. Tồn tại bao nhiêu số nguyên x thuộc (0;100) để hàm số 3 y  sin x   4x  9x   đồng biến  9  A. 45 B. 30 C. 48 D. 36 3sin 2x  cos 2x
Câu 5. Tìm điều kiện tham số m để bất phương trình
 m 1đúng với mọi x. 2 sin 2x  4cos x 1 3 5 3 5  9 65  9 65  9 A. m  B. m  C. m  D. m  4 4 4 2
Câu 6. Tìm số tự tự nhiên n để tập giá trị của hàm số y  1993sin x cos x cos 2x cos 4 . x ..cos(nx) chứa 125 số nguyên A. n = 5 B. n = 6 C. n = 7 D. n = 4 
Câu 7. Cho hai góc x, y 0; thỏa mãn x  y  . Giá trị lớn nhất của sin x  sin y là 3 A. 1 B. 0,5 C. 0,75 D. 1,5
Câu 8. Cho tam giác ABC. Tìm giá trị lớn nhất của cos 2A  cos 2B  cos 2C A. 1 B. 1,5 C. 2 D. 1,75  sin x  cos x 1  m Câu 9. Cho hàm số 2
f (x)  x  x  2 . Tồn tại bao nhiêu số tự nhiên m để f    với mọi
 sin x  cos x  3  49 x. A. 130 B. 142 C. 143 D. 126
Câu 10. Tìm m để giá trị lớn nhất của hàm số 2
y  cos x  cos x  m đạt giá trị nhỏ nhất. 7 3 A. m   B. m = 2 C. m = 0 D. m   8 8 A B C
Câu 11. Cho tam giác ABC. Tìm giá trị nhỏ nhất của biểu thức 2 2 F  sin sin sin . 2 2 2 1 1 1 A. 1 B. C. D. 3 27 12
Câu 12. Có bao nhiêu số nguyên m  1
 0;10để giá trị nhỏ nhất của hàm số 2
y  cos x  cos x  m không vượt quá 2. A. 16 B. 5 C. 6 D. 7 2x 4x
Câu 13. Tổng giá trị lớn nhất và giá trị nhỏ nhất hàm số y  cos  cos 1 gần nhất với 2 2 1 x 1 x A. 5 B. 4 C. 6 D. 7
Câu 14. Tìm giá trị nhỏ nhất của biểu thức 2 2
P  cos x  2cos x  5  cos x  4cos x  5 . 54 A. 4 B. 5 C. 2 D. 3 x
Câu 15. Tìm chu kỳ của hàm số 2 y  cos xsin 2 A. 3 B. 0,5 C.  D. 2
Câu 16. Cho tam giác ABC. Tập giá trị của hàm số f ( ,
A B,C)  sin A  sin B  sin C  sin Asin B sin C . A. (0;2) B. (1;2) C. (0;1) D. (2;3) A B C
Câu 17. Cho tam giác ABC. Giá trị lớn nhất của H  cos cos cos
gần nhất với số nào sau đây 2 2 2 A. 0,93 B. 0,77 C. 0,64 D. 0,52
Câu 18. Cho hàm số f (x) : f (cot x)  sin 2x  cos 2x . Tìm giá trị lớn nhất của hàm số 2 2 f (sin x). f (cos x) . 6 1 19 1 A. B. C. D. 125 20 500 25
Câu 19. Tồn tại bao nhiêu số nguyên m  2 sao cho giá trị lớn nhất hàm số sau nhỏ hơn 1993 4 4
y  sin x  cos x  msin x cos x . A. 2020 B. 7964 C. 6930 D. 1945
Câu 20. Ký hiệu M là giá trị nhỏ nhất của 4 4 2
y  1 sin x  cos x  2cos x  2 . Số ước dương của số tự nhiên 6 M khi đó là A. 10 B. 12 C. 6 D. 16 2 x
Câu 21. Tìm giá trị nhỏ nhất của biểu thức P  cos x  . 2 A. 2 B. 1 C. 1,5 D. 0,5
Câu 22. Tìm giá trị lớn nhất của biểu thức Q  (tan x  cot x)(tan 2x  cot 2x  2) . A. 1,5 B. 1 C. 0 D. – 1
Câu 23. Tìm điều kiện tham số a để 4 2 2
3cos x  5cos3x  36sin x 15cos x  36  24a 12a  0 với mọi x. A. 0 < a < 2 B. 1 < a < 2 C. 2 < a < 3 D. 0 < a < 1  8x    20x  
Câu 24. Tìm chu kỳ của hàm số y  3 3sin   4cos      .  9 10   27 20   A. 14,5 B. 27 C. 3 3  D. 3 3 2
Câu 25. Giá trị nhỏ nhất của hàm số y  1 2cos x  1 2sin x gần nhất với A. 1,65 B. 1,93 C. 2,13 D. 1,26
Câu 26. Tồn tại bao nhiêu số nguyên m lớn hơn – 7 để 2
3 sin x  0,5sin 2x  m đúng với mọi x A. 5 B. 9 C. 6 D. 5 9
Câu 27. Tìm giá trị nhỏ nhất của biểu thức 4 4 4 2 2 4
P  sin x(sin y  cos y  cos . x sin 2 y)  cos x . 8 A. 1 B. 0,5 C. 0,75 D. 0,25
Câu 28. Tồn tại bao nhiêu số nguyên m  3
 0;30để giá trị lớn nhất của hàm số sau không lớn hơn 2 4 4
y  2(sin x  cos x)  msin x cos xcos 2x . A. 4 B. 2 C. 5 D. 1
_________________________________ 55
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 4)
_______________________________________________________
Câu 1. Tìm giá trị nhỏ nhất của biểu thức P  cos x  sin x . 1 A. 1 B. 2 C. 0,5 D. 2
Câu 2. Tìm chu kỳ của hàm số 3 2 y  sin 3x  2sin 2x . A.  B. 2 C. 4 D. 0,5 cos x  sin x
Câu 3. Tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  gần nhất với 2 cos x 1 A. 1,22 B. 1,42 C. 1,56 D. 1,78 Câu 4. Cho hàm số 2 2
f (x)  cos( x )  cos( (x  2x 1)) . Tìm x dương nhỏ nhất sao cho f (x)  0 3 1 3 1 3  2 2  3 A. x  B. x  C. x  D. x  2 2 2 2
Câu 5. Tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  1 2cos3x  1 2sin3x gần nhất với A. 1,56 B. 3,53 C. 2,72 D. 2,34 x
Câu 6. M là giao điểm của đường thẳng y  và đồ thị hàm số y  sin x . Khoảng cách OM lớn nhất bằng 3 A. 3 B. 5 C. 10 D. 3 3 Câu 7. Đồ thị hàm số 5 3 4 2
y  (16sin x  20sin x  5sin x)(16sin 5x  20sin 5x  5) tiếp xúc với đường thẳng nào A. y = 0,5 B. y = 1 C. y = 0,25 D. y  2
Câu 8. Tìm tất cả các khoảng nghịch biến của hàm số y  sin x trên miền 0;2 .     3    3  A. ;2  B. ;   và ;2   C. ;   D. 0;   2   2   2 2 
Câu 9. Hai hàm số y  sin ;
x y  sin 3x cùng đồng biến trên khoảng nào dưới đây         11    2  A. ;   B. ;   C. ;2   D. ;    6 3   3 2   6   2 3 
Câu 10. Tìm số thực k nhỏ nhất sao cho 2 2
cos x  cos y  cos(xy)  k với mọi x. A. k = 2 B. k = 3 C. k = 4 D. k = 1
Câu 11. Xác định số nghiệm thực phương trình x  1978sin x 197 . A. 1265 B. 1288 C. 1979 D. 1285 2  sin x
Câu 12. Tìm giá trị nhỏ nhất của biểu thức P  sin x  cos x  3  cos x A. 0,5 B. 0 C. 0,25 D. 0,75 sin x  cos x
Câu 13. Ký hiệu M là giá trị lớn nhất của biểu thức
 m . Giá trị nhỏ nhất của M là 2sin x  cos x  3 A. 0,75 B. 0,5 C. 0,25 D. 1,25 2 2cos x  sin 2x Câu 14. Cho 2
x  2x . Tìm số thực k lớn nhất sao cho  k với mọi x. 2 sin x cos 2x A. k = 16 B. k = 10 C. k = 13 D. k = 12
Câu 15. Tồn tại bao nhiêu số nguyên k sao cho 2
sin x  cos x  3k  2k, x    . 56 A. 2 B. 3 C. 1 D. 4
Câu 16. Đồ thị hàm số y  f (x  2) có đồ thị như hình
vẽ bên. Giá trị f (491993) gần nhất giá trị nào A. 0,045 B. 0,042 C. 0,048 D. 0,068   
Câu 17. Đồ thị hàm số 2 2 y  2sin x   2cos x  cos 2x  
luôn nằm phía trên đường thẳng nào sau đây  6  A. y = 0,26 B. y = 0,28 C. y = 1 D. 0,32  2 
Câu 18. Tìm giá trị nhỏ nhất của biểu thức f (x)  sin x  sin x    .  3  3 A. – 1 B. 0 C. – 2 D. 2  3
Câu 19. Cho hai số thực x, y thỏa mãn 0  x  và x  y 
. Tính (1 tan x)(1 tan y) . 4 4 1 3 A. 2 B. 1 C. D.  2 2 t
Câu 20. Giả sử giá vé máy bay của hãng hàng không X trong tháng t là s(t)  110  2t 15sin với t là số 6
nguyên 1;12, đơn vị nghìn USD. Tháng có giá vé cao nhất là A. 12 B. 4 C. 3 D. 11
Câu 21. Hai điểm A, B thuộc đồ thị hàm số y  sin x như
hình vẽ. Các điểm C, D lần lượt là hình chiếu vuông góc 2
của A, B trên trục hoành sao cho CD  . Tính BC. 3 2 3 A. B. 0,5 C. 1 D. 2 2      
Câu 22. Đồ thị hàm số f (x)  cos x   3sin x    
 tiếp xúc với đường thẳng nào sau đây  6   3  7 A. y = 2 B. y  7 C. y  D. y  3 2 2 5x
Câu 23. Tồn tại bao nhiêu số nguyên n để hàm số y  cos(nx)sin
tuần hoàn với chu kỳ 3 n A. 6 B. 8 C. 12 D. 10
Câu 24. Cho đa giác lồi đều n cạnh có độ dài mỗi cạnh là t, diện tích của đa giác lồi đó được tính bằng    2 2 nt sin 2 nt cot 2 nt cot 2 nt A. n S  B. n S  C. n S  D. S  2 2   2 2sin 4 tan n n
Câu 25. Cho a  sin x  sin y; b  cos x  cos y . Tính theo a, b biểu thức cos(a  b) 2ab 2 2 a  b 2ab a  b A. B. C. D. 2 2 a  b 2 2 a  b a  b a  b
_________________________________ 57
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN HÀM SỐ LƯỢNG GIÁC – PHẦN 5)
_______________________________________________________ cos x  cos y  cos z sin x  sin y  sin z
Câu 1. Cho x, y, z thỏa mãn   p . cos(x  y  z) sin(x  y  z)
Tính cos(x  y)  cos( y  z)  cos(x  z) . p A. p B. 2p C. 0,5p D. 2
Câu 2. Tập giá trị của hàm số 3
y  8cos 3x  6cos3x  5sin 3x  2 chứa bao nhiêu số nguyên A. 3 B. 2 C. 11 D. 12
Câu 3. Khi giá trị lớn nhất của hàm số 4 2
y  8cos x  a cos x  b đạt giá trị nhỏ nhất, hãy tính a + b. A. – 8 B. – 9 C. 0 D. – 7
Câu 4. Giá trị lớn nhất của hàm số 4 2
y  8sin x  a sin x  b bằng 1. Khi đó A. a < 0, b < 0 B. a > 0, b > 0 C. a < 0, b > 0 D. a > 0, b < 0
Câu 5. Tồn tại bao nhiêu giá trị m để giá trị lớn nhất của hàm số 2
y  sin x  2sin x  m bằng 1 A. 0 B. 1 C. 4 D. 3
Câu 6. Giá trị lớn nhất của hàm số 2
y  sin 3x(cot x  cot 3x)(4cos x  3) bằng A. 2 B. 1 C. 0,5 D. 1,5
Câu 7. Tính tổng các giá trị sao cho giá trị lớn nhất của hàm số 4 2
f (x)  cos x  8cos x  m bằng 5. A. – 7 B. 7 C. 5 D. – 5
Câu 8. Giá trị lớn nhất của hàm số 4 2 2
y  (8cos x  8cos x 1)  sin 8x gần nhất với A. 1,27 B. 1,14 C. 1,22 D. 1,36
Câu 9. Tính tổng các giá trị m để giá trị nhỏ nhất của hàm số 2
y  4cos x  2cos x  m bằng 2 A. – 7,75 B. – 8 C. – 5,75 D. 2,2,5
Câu 10. Hàm số nào dưới đây có tính chất f (x  k )  f (x) với mọi số nguyên k 3 tan 2x A. y  sin x cos x  cos 2x B. y   cos 2x 2 sin x 1 3 C. y  sin x cos 2x  cos 2x D. 2 y  sin . x cos x 2      
Câu 11. Tìm giá trị nhỏ nhất của hàm số f (x)  sin x  cos x   3 cos x       6   3  A. – 4 B. – 2 C. 2 3 D.  3 1
Câu 12. Giá trị nhỏ nhất của hàm số 4 4
y  sin x  cos x gần nhất với 2 A. 0,25 B. 0,33 C. 0,45 D. 0,5 4sin x 12sin 3x 36sin 9x 27 Câu 13. Tính sin x khi    1.
1 2cos 2x 1 2cos 6x 1 2cos18x sin 27x 2 A. 0,5 B. 1 C. 0,25 D. 2
Câu 14. Đồ thị hàm số 2 8
8cot x  2 tan x tiếp xúc với đường thẳng nào sau đây A. y = 6 B. y = 10 C. y = 12 D. y = 4 58 1
Câu 15. Tìm giá trị nhỏ nhất của biểu thức 10 10 8 y  sin x  cos x  cos 2x . 16 A. 0,25 B. 0 C. 0,5 D. 0,15 1 1 1
Câu 16. Tìm giá trị lớn nhất của hàm số 2    cot 4x  cot x .
sin xsin 2x sin 2xsin 3x sin 3x sin 4x A. 0,5 B. 0,25 C. 1 D. 0,75
Câu 17. Tìm giá trị lớn nhất của hàm số 2 2
y  (cos 3x  sin 2x  sin 5xsin x)(cos5x  sin 5x) 3 A. 2 B. 1 C. 2 D. 2 sin x sin 3x sin 9x
Câu 18. Tính tan 27x  tan x khi    0 cos3x cos9x cos 27x A. 0,5 B. 0,25 C. 0 D. 1
Câu 19. Một vật nặng treo bởi một chiếc lò xo, chuyển động lên xuống qua vị trí
cân bằng như hình vẽ. Khoảng cách h từ vật đến vị trí cân bằng ở thời điểm t giây
được tính theo công thức h = |d| với d  5sin 6t  4cos6t với d được tính bằng
cm. Quy ước d > 0 khi vật ở trên cân bằng và d < 0 khi vật dưới vị trí cân bằng. Hỏi
trong giây đầu tiên có bao nhiêu thời điểm vật ở xa vị trí cân bằng nhất A. 1 B. 4 C. 0 D. 2 2 4sin x
Câu 20. Tập giá trị của hàm số y 
chứa bao nhiêu số nguyên    2  sin 2x     6  A. 3 B. 2 C. 1 D. 4
Câu 21. Tìm giá trị lớn nhất của biểu thức 2 2 2 2
P  tan x  4 tan 2x 16 tan 4x  64cot 8x  41. A. 2 B. 1 C. 1,5 D. – 1 sin x cos 2x cos 6x cos18x Câu 22. Tính khi góc x thỏa mãn    0 sin 27x sin 3x sin 9x sin 27x A. 2 B. 1 C. 0,5 D. 0,25
Câu 23. Cho hàm số y  sin x . Tịnh tiến đồ thị hàm số đã cho sang trái 4 đơn vị, sau đó tịnh tiến lên trên 2 
đơn vị, sau đó tịnh tiến sang phải đơn vị ta thu được đồ thị (C). Hỏi (C) tiếp xúc với đường nào 4 A. y = 2 B. y  2 C. y = 1 D. y = 1,5
Câu 24. Giá trị nhỏ nhất của 2
y  (tan x tan 2x  tan 2x tan 3x  tan 3x tan 4x  3) tan x  tan 4x  tan x bằng A. 0,25 B. – 0,25 C. 0,75 D. 0,5 tan x tan 2x tan 4x Câu 25. Hàm số 2 y   
 tan8x  2 tan x có giá trị nhỏ nhất bằng cos 2x cos 4x cos8x A. – 0,125 B. 0,25 C. – 0,25 D. 0,5
Câu 26. Giả sử tại Hà Nội, ngày có thời gian mặt trời chiếu sáng ngắn nhất trong năm 2014 là ngày 21/06/2014
(tức ngày thứ 172 của năm) khi mặt trời mọc lúc 06: 37 (6.62 giờ kể từ lúc nửa đêm). Ngày có thời gian mặt trời
chiếu sáng dài nhất trong năm 2014 là ngày 23/12/2014 khi mặt trời mọc lúc 04:50 (4.83 giờ kể từ lúc nửa đêm).
Biết rằng số giờ kể từ lúc nửa đêm đến khi mặt trời mọc của ngày thứ x trong năm được biểu diễn bởi hàm số
y  a  bsin(cx  d) . Vậy ngày sớm nhất năm 2014 mặt trời mọc lúc 06:00 là A. 13/02/2014 B/ 08/04/2014 C. 03/09/2014 D. 26/05/2014
_________________________________ 59
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 1)
_______________________________________________________
Câu 1. Xác định số nghiệm thuộc 0;2 của phương trình 6 6 7 sin x  cos x  . 8 A. 6 B. 8 C. 10 D. 12
Câu 2. Phương trình 1 sin 2xcos x  1 cos 2xsin x  sin 2x có tổng các nghiệm trong khoảng 0;  là 3 2 A. 0 B. C. D.  2 3
Câu 3. Tính hiệu nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình sau 2 2 4 3
sin x tan x  cos x cot x  2sin x cos x  . 3 3 5 5 A.  B. C.  D.  2 6 6
Câu 4. Tồn tại bao nhiêu số nguyên p nhỏ hơn 70 để phương trình sau có nghiệm  x  x2   x  x2 3sin 4cos 4 3sin 4cos  5  p . A. Vô số B. 69 C. 50 D. 32
Câu 5. Có bao nhiêu số m   để phương trình  x  x2 2sin 3cos
 32sin x  3cos x  2  m có nghiệm ? A. 17 B. 26 C. 8 D. 36
Câu 6. Gọi S là tập hợp tất cả các nghiệm thuộc khoảng (0;2018) của phương trình
3 1 cos 2x  sin 2x  4cos x  8  4 3   1 sin x .
Tính tổng tất cả các phần tử của S. 310408 312341 A. 103255 B.  C.  D. 102827 3 3   
Câu 7. Cho x là nghiệm của phương trình sin x cos x  2sin x  cos x  2. Tính sin x  . 0  0   4  2 1 2 A. B. 1 C. D.  2 2 2 sin x Câu 8. Cho phương trình
 0 . Tính tổng tất cả các nghiệm trong đoạn 0;2018 của 2 cos x  3cos x  2 phương trình trên. A. 1018018 B. 1018080 C. 1018081 D. 1020100   3 
Câu 9. Tập hợp các giá trị m để phương trình cos 2x  2m  
1 cos x  m 1  0 có nghiệm x   ;   là  2 2  A. [0;1) B. (– 1;0) C. (0;1] D. [– 1;0)
Câu 10. Gọi m là nghiệm dương lớn nhất trên khoảng 0;100  của phương trình  2 2
2 1 3sin x cos x  sin xcos x  0. 2  2sin x 
Giả sử m có dạng a  ;a,b   . Tính tổng a + b. b A. 100 B. 101 C. 102 D. 103   
Câu 11. Trên vòng tròn lượng giác, các điểm biểu diễn nghiệm phương trình tan x  tan x   1   tạo thành  4  60
đa giác H. Tính diện tích đa giác H. 3 10 3 2 A. 2 B. C. D. 2 5 7 1 1 1 1 k2 Câu 12. Phương trình    ...   0 có nghiệm x  , với a, b là các số 2018 sin x sin 2x sin 4x sin 2 x 2a  b
nguyên dương, b < 2018, k là số nguyên. Tính S = a + b. A. S = 2017 B. S = 2018 C. S = 2019 D. S = 2020   
Câu 13. Tính giá trị biểu thức sin m  
 khi m là nghiệm lớn nhất thuộc khoảng 0;2 của phương trình  4 
3cos x  cos 2x  cos3x 1  2sin xsin 2x . 2 2 A.  B. C. 0 D. 1 2 2
Câu 14. Nghiệm của phương trình 2018 2018 x  x   2020 2020 sin cos 2 sin x  cos
xkhi biểu diễn trên vòng tròn
lượng giác ứng với bao nhiêu vị trí ? A. 3 B. 4 C. 6 D. 2020     a
Câu 15. Nghiệm âm lớn nhất của phương trình 2018 2018 2017 tan x  cot x  2sin x   là x  , trong đó a và  4  b
b là các số nguyên, a < 0, a và b nguyên tố cùng nhau. Tính S = a + b. A. S = 3 B. S = – 3 C. S = 4 D. S = – 1 sin x  Câu 16. Phương trình 
có tất cả bao nhiêu nghiệm thực ? x 18 A. 1 B. 2 C. 3 D. Vô số   Câu 17. Phương trình   2 sin
3x  9x 16x  80   0có bao nhiêu nghiệm nguyên dương ? 4    A. 1 B. 3 C. 2 D. 4
Câu 18. Biểu diễn tập nghiệm của phương trình cos x  cos 2x  cos3x  0 trên đường tròn lượng giác ta được số điểm cuối là A. 2 B. 3 C. 5 D. 6     2     5 Câu 19. Đặt t  cos  x 
 thì phương trình cos 2x   4cos  x     
trở thành phương trình bậc  6   3   6  2
hai ẩn t có tổng các nghiệm là S và tích các nghiệm là P. Tính S + P. A. 3,25 B. 2,75 C. 4,25 D. 6,25
Câu 20. Tổng các nghiệm của phương trình cos(sinx) = 1 trên 0;2 là A. 0 B.  C. 2 D. 3
Câu 21. Tính tổng các phần tử của S với S là tập hợp tất cả các giá trị  0;4 để phương trình sau có nghiệm kép: 2 x      2 9 2cos
3 x  7cos   3cos   0 . 4 A. 16 B. 20 C. 15 D. 12
Câu 22. Có bao nhiêu số nguyên m để phương trình 6 6
sin x  cos x  3sin x cos x  2  0,25m có nghiệm ? A. 10 B. 13 C. 12 D. 18
______________________________________ 61
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 2)
_______________________________________________________ 6 6 
Câu 1. Tìm điều kiện tham số m để phương trình sin x cos x  2m tan 2x có nghiệm. 2 2 cos x  sin x A. |m| > 0,25 B. |m| < 5 C. |m|  0,25 D. |m| > 1  
Câu 2. Tồn tại bao nhiêu giá trị nguyên a để phương trình 3 2 2 
cos 2x  cos 2x  a sin x có nghiệm x  0;   ?  6  A. 0 B. 2 C. 1 D. 3 Câu 3. Phương trình 6 6
sin x  cos x  3sin x cos x  m  2  0 có nghiệm khi m thuộc đoạn [a;b]. Tính ab. 75 A. 2,25 B. 4,5 C. D. 3,75 16
Câu 4. Tồn tại bao nhiêu giá trị nguyên m để phương trình 3
sin x  2  m  sin x  2 có nghiệm ? A. 2 B. 3 C. 1 D. 0
Câu 5. Số các giá trị nguyên dương m nhỏ hơn 10 để phương trình m m sin x  (m 1) cos x  có nghiệm là cos x A. 9 B. 10 C. 7 D. 8
Câu 6. Phương trình sin4x = tanx có nghiệm dạng x  k ; x  marc cos n  k (k nguyên) thì m + n bằng    A. 3 B. 3  C. 3 1 D. 3 1 2 2 2 2
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình 2
sin 2x  cos 2x | sin x  cos x |  2cos x  m  m có nghiệm thực ? A. 2 B. 3 C. 5 D. 9 cos 4x 4 tan x
Câu 8. Tìm điều kiện tham số m để phương trình   m có nghiệm. 2 2 1 tan x
A. m – 2,5 hoặc m > 1,5 B. 1  m 1,5 C. – 2,5 < m < 0 D. m > 7  
Câu 9. Có bao nhiêu số nguyên m để phương trình  sin 2x  2 sin x   m   có nghiệm ?  4  A. 3 B. 4 C. 5 D. 6
Câu 10. Tính tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3 3 cos x  sin x  cos 2x .     A. B. 5 C. 7 D.  2 4 2 4     
Câu 11. Tồn tại bao nhiêu số nguyên a để phương trình  2 4sin x  cos x   a  3 sin 2x  cos 2x     có  3   6  nghiệm ? A. 5 B. 7 C. 10 D. 4 m
Câu 12. Có bao nhiêu số nguyên tham số m để phương trình 1 2cos x  1 2sin x  có nghiệm. 3 A. 4 B. 5 C. 3 D. 2 2 2 2 a sin x  a  2
Câu 13. Để phương trình 
có nghiệm thì tham số a thỏa mãn điều kiện gì ? 2 1 tan x cos 2x A. |a| > 1 B. |a|  2 C. |a|  3 D. | a | 1;a   3  
Câu 14. Tìm điều kiện m để phương trình 2 
m sin x  3sin x cos x  m 1  0 có đúng ba nghiệm 3 x  0;   .  2  A. m > – 1 B. m  1 C. m < – 1 D. m  1 62
Câu 15. Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để phương trình sau có nghiệm thực 3 3
sin x  3sin x  4sin x  m  m . A. 5 B. 7 C. 3 D. 2
Câu 16. Nửa khoảng (a;b] là tập hợp tất cả các giá trị m để phương trình 4 4 2
sin x  cos x  cos 4x  m có bốn   
nghiệm phân biệt thuộc đoạn   ;  . Tính 64a + b. 4 4    A. 50 B. 48,5 C. 52,6 D. 69
Câu 17. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực. 2 sin x  m  sin x  m . A. 2 B. 1 C. 4 D. 3
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình 2 x  m   2 sin
4 sin x  8m  2m có nghiệm ? A. 8 B. 6 C. 4 D. 2
Câu 19. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thực ?
m  2 m  2sin x  sin x . A. 0 B. 1 C. 3 D. 2
Câu 20. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực 2 cos x  m  cos x  m . A. 3 B. 2 C. 5 D. 4     
Câu 21. Tìm phương trình tương đương với phương trình 2  tan x  tan x   tan x   3 3     .  3   3  A. cotx = 2 B. cot 3x  3 C. tan x  3 D. tan 3x  3 4x Câu 22. Phương trình 2 cos
 cos x có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? 3 A. 4 B. 2 C. 5 D. 7
Câu 23. Có bao nhiêu số nguyên m để phương trình 2 cos 2x  2m  
1 cos 2x  3mm  2  0 có nghiệm. A. 5 B. 2 C. 3 D. 4      Câu 24. Phương trình  4sin x sin x  sin 2x   cos3x 1    
có bao nhiêu điểm biểu diễn nghiệm trên vòng  3   3  tròn lượng giác ? A. 7 B. 6 C. 5 D. 4
Câu 25. Có bao nhiêu giá trị nguyên của m để phương trình 3 3
m  3 m  3sin x  sin x có nghiệm thực ? A. 5 B. 7 C. 3 D. 2 10 10 6 6  
Câu 26. Phương trình sin x cos x sin x cos x 
có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn 2 2 4 4cos 2x  sin 2x lượng giác ? A. 10 B. 6 C. 4 D. 8
Câu 27. Có bao nhiêu giá trị nguyên của m để phương trình 3 3
m  m  cos x  cos x có nghiệm thực ? A. 1 B. 7 C. 3 D. 2
Câu 28. Có bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực x x  2 3 sin sin
1 1  cos 2x  m  m. A. 1 B. 2 C. 3 D. 5
_________________________________ 63
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 3)
_______________________________________________________
Câu 1. Tìm tập hợp tất cả các giá trị tham số m để phương trình cos 2x  2m  
1 cos x  m 1  0 có đúng hai    nghiệm  x   ;  . 2 2    A. (– 1;0] B. [0;1) C. [0;1] D. (- 1;1)   
Câu 2. Tồn tại bao nhiêu giá trị nguyên m để phương trình 2sinx + mcosx = 1 – m có nghiệm  x   ;  . 2 2    A. 6 B. 7 C. 5 D. 4
Câu 3. Giả sử m là nghiệm dương nhỏ nhất của cos 2x  3 sin 2x  3 sin x  cos x  2 . Mệnh đề nào sau đây đúng ?        A. 0  m  B.  m  C.  m  D.  m  12 12 6 6 3 3 2
Câu 4. Tồn tại bao nhiêu số nguyên m thỏa mãn |m| < 20 để phương trình sau có nghiệm  4 4 x  x   6 6 x  x 2 4 sin cos 8 sin cos  4sin 4x  m . A. 34 B. 56 C. 20 D. 14
Câu 5. Tính tổng các nghiệm của phương trình 2cos3x(2cos 2x 1)  1 trên đoạn  4  ;6 là A. 61 B. 72 C. 50 D. 56
Câu 6. Tìm tập hợp tất cả các giá trị tham số m để phương trình  x   x  m x 2 cos 1 cos 2 cos  msin x có đúng   hai nghiệm 2  x  0;  . 3    A. (– 1;1] B. (0; 1 ] C.  1  1;  D. 1   m  1 2 2    2
Câu 7. Tồn tại bao nhiêu số nguyên của m để phương trình 2
2cos x  m  cos 2x  m 1có nghiệm thực A. 3 B. 2 C. 5 D. 4
Câu 8. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
1 2 m  sin 2x  2m  cos 4x . A. 3 B. 2 C. 5 D. 4 Câu 9. Phương trình 2 2 2
2 cos x  2cos 2x  2cos 3x  3  cos 4x 2sin 2x  
1 có bao nhiêu nghiệm thực thuộc khoảng (0;2018) ? A. 2565 B. 2566 C. 2567 D. 2568 1 cos x  1 cos x
Câu 10. Số nghiệm thuộc đoạn [0;2017] của phương trình  4cos x là sin x A. 1285 B. 1284 C. 1988 D. 1260
Câu 11. Tìm giá trị nhỏ nhất của a để phương trình 6 6
sin x  cos x  a | sin 2x | có nghiệm. A. 0,5 B. 0,25 C. 2 D. 1,5
Câu 12. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm thực. 3 3
m  3 m  6sin 2x  4sin x cos x . A. 5 B. 7 C. 3 D. 1
1 2cos x1 cos x Câu 13. Phương trình 
 có bao nhiêu nghiệm thuộc khoảng (0;2018 ) ?  x 1 1 2cos sin x 64 A. 3025 B. 3026 C. 3027 D. 3028
Câu 14. Có bao nhiêu giá trị nguyên của m để phương trình 3 3
m  5 m  5cos x  cos x có nghiệm thực ? A. 9 B. 8 C. 10 D. 11
Câu 15. Cho phương trình 3 tan x 1(sin x  2cos x)  m(sin x  3cos x) . Có bao nhiêu số nguyên m thuộc   
đoạn [– 2018;2018] để phương trình đã cho có nghiệm thuộc đoạn 0;   ?  2  A. 2015 B. 2018 C. 2016 D. 4036 
Câu 16. Tập hợp S = (a;b) bao gồm tất cả các giá trị m để phương trình sin 2x  2 sin(x  )  2  0 có đúng 4  3 
hai nghiệm thuộc khoảng 0;   . Tính 2 2 a  b .  4  A. 4  2 2 B. 10 C. 5  3 2 D. 7  2 5
Câu 17. Tính tổng các giá trị nguyên m trong đoạn [– 5;5] để phương trình 2
msin x  3sin xcos x  m 1có  3 
đúng ba nghiệm thuộc khoảng 0;   .  2  A. – 14 B. 0 C. 15 D. – 10
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình  x   x  m x 2 cos 1 4cos 2 cos  msin x có đúng hai  2  nghiệm thuộc đoạn 0;  ? 3    A. 1 B. 2 C. 3 D. 4
Câu 19. S = [a;b) là tập hợp tất cả các giá trị m để phương trình   x x  m x 2 1 cos cos 4 cos  msin x có  2 
đúng ba nghiệm phân biệt thuộc 0;  . Tính b + 2a. 3    A. 0 B. 1 C. 2 D. 3
Câu 20. Tìm số nghiệm của phương trình 2015 2016 x  x   2017 2018 sin cos 2 sin x  cos x trên [– 10;30]. A. 46 B. 42 C. 44 D. 20
Câu 21. Có bao nhiêu số nguyên m để phương trình 3
m  sin(m  sin 3x)  sin(3sin x)  4sin x có nghiệm ? A. 4 B. 9 C. 8 D. 5   
Câu 22. Tìm tập hợp tất cả các giá trị m để phương trình sau có nghiệm x  0;    4  2 2 3 4
sin x  sin xcos x  mcos x  2 3sin xcos x  mcos x A. (– 2;0) B. [– 3;1) C. (– 4;0) D. [– 1;3]
Câu 23. Tính tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình    2 2sin 3x   1 8sin 2x cos 2x   .  4     A.  B. 1 C. D. 2 3 4 1
Câu 24. Đoạn [a;b] là tập hợp tất cả các giá trị m để phương trình 1 sin x  sin x   m có nghiệm. Tính 2 giá trị biểu thức 2 2 a  b . A. 5 B. 4,5 C. 6 D. 2,5
_________________________________ 65
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 4)
_______________________________________________________    1 a
Câu 1. Phương trình 3(cot x  cos x)  5(tan x  sin x)  2 có một phương trình hệ quả sin x     .  4  b
Tính giá trị biểu thức 4a + 9b + 1993. A. 2000 B. 2019 C. 2020 D. 2017
Câu 2. Các nghiệm của phương trình 2
cos x  3sin x cos x  1khi biểu diễn trên vòng tròn lượng giác tạo thành
đa giác (H). Tính diện tích S của đa giác (H). 3 10 8 10 7 10 A. S = 6 B. S = C. S = D. S = 5 5 10
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình 7 4 cos x  sin x  1. A. 3 B. 2 C. 4 D. 1 2 sin 3x
Câu 4. Tìm số nghiệm trên 0;3 của phương trình 2 2 sin x   sin xsin 3x . 4 A. 7 B. 8 C. 5 D. 10 Câu 5. Phương trình 6
32cos x  cos 6x  1 tương đương 2
a cos 2x  bcos 2x 1  0 . Tính a + b. A. 10 B. 11 C. 8 D. 9
Câu 6. Tìm số nghiệm thuộc khoảng 50;50 của phương trình sin x  2sin 2x  sin 3x  2 2 . A. 3 B. 2 C. 4 D. 0 Câu 7. Phương trình 2
6 tan x  5cot 3x  tan 2x  a cos 2x  bcos 2x 1  0 . Tính a + b. A. 10 B. 11 C. 8 D. 9 1
Câu 8. Tìm số nghiệm thuộc 10;10  của phương trình cot x  tan x  . sin x A. 16 B. 12 C. 10 D. 7
Câu 9. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2cot 2x  3cot 3x  tan 2x . A. 3 B. 2 C. 4 D. 0
Câu 10. Tìm số nghiệm trên 0;3 của phương trình 20 20 sin x  cos x  1. A. 9 B. 7 C. 5 D. 10
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2
(cos 2x  cos 4x)  6  2sin 3x . A. 3 B. 2 C. 4 D. 1
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình 2 2
cos3x  2  cos 3x  2(1 sin 2x) . A. 3 B. 2 C. 4 D. 1
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình 2 2
4cos x  3tan x  4 3 cos x  2 3 tan x  4  0 . A. 3 B. 2 C. 4 D. 1
Câu 14. Tồn tại bao nhiêu số nguyên a  5
 0;50để hai phương trình sau tương đương 1
sin x cos 2x  sin 2x cos3x  sin 5x 2
a cos 2x  a cos 4x  cos 6x  1 A. 50 B. 51 C. 52 D. 53 66
Câu 15. Tồn tại bao nhiêu số nguyên a để phương trình sau có nghiệm 2 2 2
(cos 2x  cos 4x)  (a  4a  3)(a  4a  6)  7  sin 3x . A. 1 B. 2 C. 0 D. 3
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình 3 3
(1 tan x) cos x  (1 cot x)sin x  2sin 2x . A. 3 B. 2 C. 4 D. 1
Câu 17. Tìm số nghiệm thuộc 0; của phương trình 2 2 2
4sin 2x  sin 6x  4sin 2xsin 6x . A. 6 B. 4 C. 3 D. 2
Câu 18. Tìm số nghiệm thuộc khoảng 50;50 của phương trình sin x  cos x  sin x  cos x  2 . A. 43 B. 27 C. 61 D. 35   
Câu 19. Tính tổng các nghiệm thuộc  
 ; của phương trình 2 2sin 3x   1 8sin 2x cos 2x   .  4     A.  B.  C. D. 2 12 3
Câu 20. Tìm số nghiệm trên 0;3 của phương trình 3
cos 2x  cos 6x  4(3sin x  4sin x 1)  0 . A. 5 B. 6 C. 4 D. 3
Câu 21. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình 1
( 1 cos x  cos x)cos 2x  sin 4x 2 A. 3 B. 2 C. 4 D. 1
Câu 22. Tập hợp [a;b) gồm tất cả các giá trị tham số m để phương trình cos 2x  (2m 1)cos x  m 1  0 có   3  nghiệm  ;  . Tính 2a + b.  2 2  A. 4 B. 3 C. 2 D. – 2 1 1
Câu 23. Tồn tại giá trị nguyên a  5
 0;50để phương trình   a có nghiệm ? cos x sin x A. 99 B. 3 C. 100 D. 75
Câu 24. Tìm số nghiệm thuộc khoảng 50;50 của phương trình 2 2
sin x  2  sin x  sin x 2  sin x  3 . A. 17 B. 16 C. 10 D. 46
Câu 25. Tìm số nghiệm thuộc khoảng 50;50 của phương trình 2 2 3 3
tan x  cot x  tan x  cot x  tan x  cot x  6 . A. 31 B. 35 C. 32 D. 50
Câu 26. Tập hợp S   ;
a b gồm tất cả các giá trị m để phương trình sin 4x  mtan x có nghiệm x  k . Tính a + b. A. 3,5 B. 4,5 C. 3 D. 2
Câu 27. Giá trị a nhỏ nhất để phương trình 6 6
sin x  cos x  a sin 2x có nghiệm nằm trong khoảng nào  1   1  A. (2;3) B. (1;2) C. ;1   D. 0;    2   2 
Câu 28. Tìm số nghiệm thuộc khoảng 0;50 của phương trình cos 2x  1 sin 2x  2 sin 2x  cos x . A. 22 B. 26 C. 60 D. 37
_________________________________ 67
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 5)
_______________________________________________________
Câu 1. Tìm số nghiệm  4
  ;9  của phương trình cos2x  1 sin 2x  2 sin x  cos x . A. 16 B. 20 C. 19 D. 12       Câu 2. Phương trình 3 3 4sin x   4cos x   cos x     có hệ quả cos x  ; a ; b  c . Tính abc  6   6  A. – 1 B. 1 C. 0 D. – 0,5 6 6 sin x  cos x
Câu 3. Tập hợp S  a;bgồm tất cả các giá trị m để phương trình
 m tan 2x có nghiệm. Tính 2 2 cos x  sin x
giá trị biểu thức b – a A. 2 B. 0,5 C. 0,25 D. 1
Câu 4. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình
2 tan x  tan 2x  2 tan x tan 3x  tan 2x tan 3x  0 A. 2 B. 3 C. 4 D. 1
Câu 5. Tìm số nghiệm  4
  ;9  của phương trình 1 sin 2x  cos x  sin x . A. 25 B. 21 C. 10 D. 18
Câu 6. Nghiệm dương nhỏ nhất của phương trình cot x  tan x  2 tan 2x  4 tan 4x  8  0 gần nhất với A. 0,2 B. 0,3 C. 0,5 D. 0,4
Câu 7. Tồn tại bao nhiêu số nguyên m < 10 để phương trình 8 8 2
sin x  cos x  mcos 2x có nghiệm A. 8 B. 3 C. 9 D. 4
Câu 8. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 5
1945sin x  2005cos x  2005 A. 1 B. 2 C. 3 D. 4
Câu 9. Tìm số nghiệm  4
  ;9  của phương trình 1 4sin 2x  cos x  sin x . A. 25 B. 21 C. 10 D. 18 Câu 10. Cho phương trình 6 6 4 2 2 4
sin x  cos x  8sin x cos x  8sin x cos x  a sin 2x . Giá trị nguyên nhỏ nhất
của a để phương trình đã cho có nghiệm thuộc khoảng nào sau đây A. (5;10) B. (0;5) C. (– 5;0) D. (– 10;– 5) 4x 2 cos  cos x
Câu 11. Tìm số nghiệm  4
  ;9  của phương trình 3  0 . 2 1 tan x A. 4 B. 12 C. 10 D. 6 Câu 12. Phương trình 2 2
sin x  cos 4x  sin x  sin 5xsin 3x có bao nhiêu nghiệm  4   ;9  A. 4 B. 3 C. 3 D. 7
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 4
1 cos x  1 4cos x  7 cos x A. 2 B. 1 C. 3 D. 4
Câu 14. Tập hợp S  a;bgồm tất cả các giá trị m để phương trình 2
mcos x  4sin x cos x  m  2  0 có    nghiệm  0;   . Tính a + b.  4  11 5 A. 5 B. C. D. – 2 3 3 68 sin 3x  sin x
Câu 15. Tính tổng các nghiệm thuộc khoảng 0;2 của phương trình  cos 2x  sin 2x . 1 cos 2x A. 3,75 B. 4,75 C. 5 D. 2,25
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 31 50 sin 3x  cos 3x  1 A. 12 B. 10 C. 11 D. 8 
Câu 17. Phương trình (sin x  a cos x)(sin x  2a cos x)  2 có một nghiệm x    k . Tất cả các nghiệm 4
còn lại x của phương trình thỏa mãn 0 16 16 16 13 A. sin 2x   B. sin 2x  C. sin 2x  D. sin 2x   0 65 0 65 0 63 0 63 2
Câu 18. Tìm số nghiệm  (0;2 ) của phương trình 3tan 6x   2 tan 2x  cot 4x . sin8x A. 8 B. 7 C. 10 D. 6
Câu 19. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 3 2 5
(cos x cos3x  sin xsin 3x)  cos 2x A. 6 B. 5 C. 3 D. 4
Câu 20. Tìm số nghiệm  (0;2 ) của phương trình 3 3 3 3
sin x  sin 2x  sin 3x  (sin x  sin 2x  sin 3x) . A. 9 B. 7 C. 10 D. 6
Câu 21. Tìm số nghiệm  (0;2 ) của phương trình 5 5 3
4(sin x cos x  cos xsin x)  sin 2x  1. A. 4 B. 7 C. 10 D. 6 1 1
Câu 22. Tìm số nghiệm  (0;2 ) của phương trình   tan 3x .
tan 5x  tan 2x cot 5x  cot 2x A. 19 B. 17 C. 10 D. 16 1 1
Câu 23. Tìm số nghiệm  (0;2 ) của phương trình 2  cot 7x  . tan 3x  tan 4x cot 3x  cot 4x A. 28 B. 27 C. 20 D. 29
Câu 24. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 tan x  tan 4x  tan 5x A. 4 B. 2 C. 3 D. 5
Câu 25. Tìm số nghiệm  (0;2 ) của phương trình 2 2
sin 3x  sin x  cos 4x cos 2x  tan 6x A. 4 B. 10 C. 24 D. 18
Câu 26. Tìm số nghiệm  (0;2 ) của phương trình 2 2 3
sin 5x  sin x  cos 6x cos 4x  sin 1993x A. 1993 B. 3986 C. 2000 D. 1985
Câu 27. Tìm số nghiệm  (0;2 ) của phương trình cot 3x tan 2x  tan 2x tan x  tan x cot 3x  tan 5x A. 8 B. 20 C. 30 D. 15
Câu 28. Phương trình tan 3x  tan x  1 tan 3x tan x có bao nhiêu nghiệm  4   ;9  A. 70 B. 56 C. 40 D. 62
Câu 29. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2  tan x tan 3x  tan x A. 4 B. 2 C. 3 D. 5
Câu 30. Tìm số nghiệm  4
  ;9  của phương trình 3 2
8sin xsin 3x  2sin 3x  3cos 4x  3 A. 6 B. 9 C. 12 D. 10 Câu 31. Phương trình 5
16cos x  1 5cos3x 10cos x có bao nhiêu nghiệm 0;1993  A. 1000 B. 1993 C. 4982 D. 4980 69
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 6)
_______________________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên dương chẵn m để phương trình m sin x  4cos x  m  2  0 ? A. 3 B. 1 C. 6 D. Vô sô
Câu 2. Phương trình 4cos x cos 2x cos 4x  1 cos3x  cos5x  cos 7x có bao nhiêu nghiệm 0;1993  A. 996 B. 968 C. 938 D. 1010   
Câu 3. Tìm số biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 8cos x   cos3x    3  A. 10 B. 6 C. 8 D. 4 Câu 4. Phương trình 5
16sin x  110sin x  5sin 3x có bao nhiêu nghiệm 0;1993  A. 4993 B. 4982 C. 1010 D. 1285   
Câu 5. Có bao nhiêu số nguyên m để 2cos x cos 2x cos3x  m  7cos 2x có nghiệm duy nhất  0;    2  A. 1 B. 3 C. 11 D. 13 
Câu 6. Biết phương trình 5 5 2
4cos xsin x  4sin x cos x  sin 4x  m có nghiệm x   . Nghiệm dương nhỏ 8
nhất của phương trình thuộc khoảng nào dưới đây  3 2   2     3     A. ;   B. ;   C. ;   D. 0;    10 5   5 2   5 10   10    
Câu 7. Tìm a + b với (a;b) là tập hợp tất cả các giá trị m để phương trình sau có 7 nghiệm  ;3    2       
sin 3x  msin x  cos x  sin x      .  2   2  A. – 1 B. 2 C. 1 D. – 2
Câu 8. Tìm số nghiệm  0;20  của phương trình 2 2
(cos x  sin x)sin5x 1  0 . A. 10 B. 9 C. 18 D. 17
Câu 9. Tìm số biểu diễn trên vòng tròn lượng giác nghiệm phương trình sin x(cos 2x  cos 4x  cos6x)  1 A. 1 B. 4 C. 2 D. 3
Câu 10. Tìm số nghiệm  0;20  của phương trình sin 4x  cos 4x 1 4(sin x  cos x) . A. 10 B. 19 C. 18 D. 17
Câu 11. Tồn tại bao nhiêu cặp số (x;y) với x, y  0;20  thỏa mãn điều kiện 2 1 2 2 1 2 2 (sin x  )  (cos x 
)  3,5  2sin y  sin y 2 2 sin x cos x A. 400 B. 350 C. 600 D. 210 2x
Câu 12. Tìm số nghiệm 0;1993  của phương trình sin 2x  sin  2  0 5 A. 1993 B. 120 C. 542 D. 399  x   1
Câu 13. Tìm số nghiệm  0;20  của phương trình 4 4 4 2 sin x  sin   cos x  sin 2x   .  2 8  2 A. 10 B. 10 C. 18 D. 17
Câu 14. Tìm số nghiệm 0;1993  của phương trình 5 3 sin x  cos x  1 70 A. 1993 B. 2019 C. 1992 D. 1994
Câu 15. Xác định số nghiệm 2
x  2x  m  0 khi hai phương trình sau tương đương
2mcos x  2 3 sin x  m  3
(m 1)cos x  3 sin x  0,75  2m A. 2 B. 1 C. 0 D. Không giải được
Câu 16. Tìm số nghiệm 0;1993  của phương trình 2
8cos 4x cos 2x  1 cos3x 1  0 . A. 1993 B. 2019 C. 1992 D. 1994
Câu 17. Khi m  3 , khoảng (a;b) bao gồm tất cả các giá trị m để hai phương trình sau tương đương
m cos x  (m 1)sin x  m  2
(m  3)cos x  (3m 1)sin x  5  m Tính ab. A. – 3 B. – 2 C. 1 D. 4
Câu 18. Tìm số nghiệm 0;1993  của phương trình 2
sin x  2  sin x  2  1 cos 4x . A. 1993 B. 998 C. 1995 D. 996 2x  
Câu 19. Xác định số nghiệm 0;4 của phương trình  tan (x  2)  1 3  4    A. 3 B. 2 C. 1 D. 4
Câu 20. Tính tổng các nghiệm của phương trình 2 2 2
x  2x  4  cos(x  3)  2cos x . A. 3 B. 2 C. 1 D. 4 4 x 5cos
Câu 21. Xác định số nghiệm 0;4 của phương trình 2 3  sin x  tan x  cos x A. 3 B. 2 C. 1 D. 4
Câu 22. Tìm số nghiệm 0;1993  của phương trình 2cos x  2 sin10x  3 2  2cos 28xsin x . A. 1993 B. 998 C. 1995 D. 996
Câu 23. Xác định số nghiệm 0; của phương trình 2 2 2 2
cos 4x  cos 8x  sin 12x  sin 16x  2 A. 5 B. 12 C. 3 D. 2
Câu 24. Tìm số nghiệm 0;1993  của phương trình 3 3 4
sin x  cos x  2  sin x A. 1990 B. 997 C. 996 D. 1995
Câu 25. Tìm số nghiệm 0;1993  của phương trình 2 2
1993x  cos 3x  sin x  sin 4xsin 2x A. 2 B. 1 C. 3 D. 4     2    
Câu 26. Tìm số nghiệm 0;1993  của phương trình 2 2 2 sin x   sin  x  sin x  cos 2x         3   3   3  A. 1991 B. 1993 C. 996 D. 997
Câu 27. Tìm số nghiệm 0;1993  của phương trình 2 2
2sin 3x  sin x  cos 4x cos 2x  2 A. 5979 B. 1288 C. 1975 D. 3986    k2 Câu 28. Phương trình 2sin
 4x  2sin 3x  2sin x  1  
có hai họ nghiệm x    ; x    k2 với  6  3
, là các số dương nhỏ nhất có thể. Tích  gần nhất giá trị nào A. 0,05 B. 0,09 C. 0,75 D. 0,93
_________________________________ 71
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 7)
_______________________________________________________   
Câu 1. M là số nghiệm 0;1993  của phương trình tan  2x  2 tan x  1   . Số ước của M là  4  A. 1993 B. 20 C. 30 D. 40   
Câu 2. Tồn tại bao nhiêu số nguyên m để phương trình cos3x  2sin 2x  mcos x  0 có nghiệm  0;    2  A. 4 B. 2 C. 3 D. 1 sin 4x
Câu 3. Xác định số nghiệm 0;1993  của phương trình  1. cos 6x A. 9420 B. 7972 C. 1994 D. 9964   
Câu 4. M là số nghiệm 0;1993  của phương trình tan
 4x  tan3x  tan x  3   . Hai chữ số tận cùng  3  của M là A. 52 B. 64 C. 24 D. 60
Câu 5. Tồn tại bao nhiêu số nguyên m  1
 0;10 để phương trình 2
sin 3x  msin x  (4  2m)sin x có đúng
năm nghiệm 0;2  A. 10 B. 12 C. 8 D. 16
Câu 6. Tìm số nghiệm thuộc (0;8) của phương trình tan 2 . x tan 7x  1 A. 60 B. 70 C. 68 D. 56 k k
Câu 7. Biết rằng x    ; x   
; x    k (với ,  , là các số âm lớn nhất) là ba họ nghiệm của 2 2       phương trình sin  3x  sin  x  sin x  cos5x    
. Tích ba số ,  , gần nhất với  6   3  A. – 0,2 B. – 0,16 C. 0,15 D. – 0,56 3 x x
Câu 8. Tính tổng các nghiệm thỏa mãn điều kiện x   
của phương trình sin  cos  1 sin x 2 2 2 A. 5 B. 6 C. 7 D. 4    Câu 9. Phương trình tan
 5x  tan 3x  tan 2x  3  
có bao nhiêu họ nghiệm rút gọn  3  A. 3 B. 4 C. 2 D. 1 Câu 10. Cho phương trình 2 2 2 2 tan . x tan 3 .
x tan 4x  tan x  tan 3x  tan 4x . Nghiệm dương lớn nhất trong
khoảng (0;100) của phương trình gần nhất số nào sau đây A. 99,74 B. 97,38 C. 98,62 D. 99,18    Câu 11. Phương trình 2sin
 5x  2sin 3x  2sin 2x  3  
có bao nhiêu họ nghiệm rút gọn  3  A. 3 B. 4 C. 2 D. 1
Câu 12. Biết rằng hai phương trình sau đây tương đương
asin 2x  2  2cos x  a 2 sin x 2
2sin x  cos 2x  sin 2x  b  2bsin x  cos x 1
Giá trị tích ab gần nhất với A. 1,26 B. 1,41 C. 1,89 D. 1,35 72
Câu 13. Xác định số nghiệm 0;1993  của phương trình tan x  tan 2x  tan 3x  tan 6x A. 11993 B. 22353 C. 101010 D. 25295 3    x   x 
Câu 14. Xác định số nghiệm 0;1993  của phương trình  sin  x  sin x  4cos sin      . 2  3  2  3 2  A. 1993 B. 1992 C. 540 D. 1285     2 
Câu 15. Tìm số nghiệm 0;1993  của phương trình cos  x  sin
 3x  cos 2x 1 4sin x     .  3   3  A. 1993 B. 1992 C. 540 D. 1285
Câu 16. Tìm số nghiệm của phương trình 2 2  x  2cos x . A. 3 B. 1 C. 2 D. 0 Câu 17. Phương trình 2 2 sin 4x  cos 4x  0,25 .
m sin 4x  (2m 1)sin x cos x  0 có hai nghiệm phân biệt thuộc     khoảng ; 
 khi 2 a  b  m  0,5. Tính ab.  4 2  A. 6 B. 10 C. 12 D. 8 1
Câu 18. Xác định số nghiệm thuộc (0;5) của phương trình cot 2x  cot 3x   0 . sin xsin 2x sin 3x A. 1 B. 2 C. 0 D. 3
Câu 19. Xác định số nghiệm 0;1993  của phương trình sin x(1 sin x)  cos 2x(1 cos2x)  1. A. 1993 B. 997 C. 994 D. 1285
Câu 20. Tồn tại bao nhiêu số nguyên m  1
 0;10 để hai phương trình sau tương đương
2sin x cos 2x  1 cos 2x  cos3x 2
4cos x  cos 3x  a cos x  (4  a)(1 cos 2x) A. 10 B. 16 C. 12 D. 18
Câu 21. Xác định số nghiệm thuộc (0;20) của phương trình sin 3x  cos x  sin x  cos x  sin 2x A. 10 B. 26 C. 6 D. 5
Câu 22. Tồn tại bao nhiêu số nguyên m  1
 0;10 để phương trình sau có nghiệm 2
(2m 1)(sin x  cos x)  (sin x  cos x)  2m  2m  2  0 A. 3 B. 4 C. 1 D. 2
Câu 23. Xác định số nghiệm thuộc (0;20) của phương trình cos 2x  0,5sin 4x  sin x  cos x A. 15 B. 26 C. 10 D. 16 x x Câu 24. Cho phương trình 2 2 2 tan x  4cot x  tan  2  cot
. Tổng nghiệm âm lớn nhất và nghiệm dương 2 2
nhỏ nhất của phương trình trên gần nhất với A. 0,56 B. 0,26 C. 0,15 D. 0,43
Câu 25. Tìm số nghiệm 0;1993  của phương trình 2 2 2 2
3(tan x  tan 2x  tan 3x)  (tan . x tan 2 . x tan 3x) A. 1993 B. 1992 C. 994 D. 1997
Câu 26. Điều kiện để phương trình sin x  cos x  m 1 sin x cos x có nghiệm là m  a . Khi đó 3 a  3a có giá trị gần nhất với A. 5 B. 4 C. 3 D. 6
_________________________________ 73
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 8)
_______________________________________________________     2 
Câu 1. Phương trình cos x   cos
 3x  cos3x  1 4sin x    
có số họ nghiệm khác nhau là  3   3  A. 3 B. 4 C. 2 D. 0
Câu 2. Tồn tại bao nhiêu số nguyên m để phương trình 3 3
m 12 m 12sin x  sin x có nghiệm A. 23 B. 20 C. 6 D. 16
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 1        cot x  cot  x  cot xcot  x     . 3  6   6  A. 5 B. 2 C. 4 D. 3
Câu 4. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
1 cos 4x  2 m  cos 2x  2m . A. 3 B. 2 C. 5 D. 4
Câu 5. Tồn tại bao nhiêu số nguyên m lớn hơn – 8 để phương trình 2
msin x  3sin x cos x  m 1  0 có đúng  3  ba nghiệm  0;   .  2  A. 4 B. 5 C. 3 D. 6
Câu 6. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực x x  2 sin sin
3  m  5  cos 2x  m  4 cos 2x  m . A. 3 B. 4 C. 5 D. 6
Câu 7. Tập hợp S  a;b gồm tất cả các giá trị m để phương trình 3 sin x  cos x  m  0 có đúng ba nghiệm    thực thuộc  ;2  . Tính a + b. 6    A. 1 B. 0 C. – 1 D. 3
Câu 8. Có tất cả bao nhiêu giá trị nguyên nhỏ hơn 30 của tham số m để phương trình sau có nghiệm thực ? 2 tan x  6 1   2 1 m  2 2      . x x  m x sin x m msin 2x 5 1 0 cos sin cos A. 8 B. 12 C. 40 D. 29
Câu 9. Tìm điều kiện tham số m để phương trình sin 3
x  cos x  m có nghiệm. m  2  m  2  m  3 A.  B.  C.  D. 2  m  2 m  2 m  2 m  3      
Câu 10. Tìm số nghiệm 0;1993  của phương trình 3 tan  x  tan . x tan  x  3 tan x  tan 2x      6   6  A. 1993 B. 3986 C. 3984 D. 2020
Câu 11. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực 5 x  x   2 sin sin
2cos 2x  4mcos x  m  3 2cos x  m . A. 8 B. 5 C. 4 D. 6  2   2 
Câu 12. Tìm số nghiệm 0;1993  của phương trình 3  tan x  tan  x  tan x tan  x      3   3  74 A. 4993 B. 1993 C. 3985 D. 3986
Câu 13. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực  x  x  m5   x  x  m5   x  x  m5 sin 3cos 2cos sin 2 2sin cos . A. 4 B. 6 C. 5 D. 7
Câu 14. Tồn tại bao nhiêu giá trị nguyên dương của tham số m để phương trình sau có nghiệm thực. 2 sin x  m  sin x  m . A. 2 B. 1 C. 4 D. 3
Câu 15. Có bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực x x  2 3 sin sin
1 1  cos 2x  m  m . A. 1 B. 2 C. 3 D. 5      
Câu 16. Tìm số nghiệm 0;2  của phương trình sin 3x   sin 2xsin x       4   4  A. 3 B. 4 C. 5 D. 6
Câu 17. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực 3 3 3
sin x  2m  2sin x  8sin x  sin x  2m  27  3 . A. 10 B. 9 C. 11 D. 12
Câu 18. Phương trình cot x  cot 2x  cot 3x  3 cot x tan 3x có bao nhiêu nghiệm 0;2  A. 10 B. 16 C. 12 D. 14
Câu 19. Tìm điều kiện của m để phương trình 2
(sin x 1)(cos x  cos x  m)  0có đúng năm nghiệm 0;2  1 1 1 1 A. 0  m  B.   m  0 C.   m  0 D. 0  m  4 4 4 4 Câu 20. Phương trình 2
6cos3x  1 8sin xcos3x tương đương sin(ax)  sin(bx) . Tính a + b. A. 10 B. 12 C. 7 D. 5   
Câu 21. Tồn tại bao nhiêu số nguyên m để phương trình msin x  4cos x  4 có nghiệm trên 0;   ?  3  A. 4 B. 2 C. 3 D. 5
Câu 22. Xác định số nghiệm 0;2  của phương trình 2
4sin x  (2x  2)sin x  x  0 . A. 3 B. 4 C. 2 D. 5
Câu 23. Tồn tại bao nhiêu số nguyên dương m để phương trình 2 2
sin 2x  2sin x  cos x  cos x  msin x có
nhiều hơn một nghiệm 0;2  A. 3 B. 2 C. 4 D. 5  3 x  1   3x 
Câu 24. Xác định số họ nghiệm phân biệt của phương trình sin   sin       10 2  2 10 2  A. 1 B. 3 C. 2 D. 4 Câu 25. Cho phương trình .5x sin 5 5x a x   
; a là tham số thực. Phương trình đã cho tồn tại nghiệm duy   
nhất x . Tính sin x  cos x  sin x  . 0 0 0  0   2  A. 1 B. 2 C. 4 D. 3
Câu 26. Tìm số nghiệm 0;2  của phương trình 2 2
(3  4sin x)(3  4sin 3x)  1 A. 16 B. 19 C. 20 D. 15
_________________________________ 75
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 9)
_______________________________________________________
Câu 1. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực 3 3 3
6sin x  5m  sin x  3  sin x  6sin x  5m  27 . A. 8 B. 19 C. 6 D. 7
Câu 2. Tập hợp S  a;b bao gồm tất cả các giá trị tham số m để phương trình sau có nghiệm thực 5 x  x   2 2sin sin
4msin x  cos 2x  2m  2 sin x  m .
Tính giá trị biểu thức b  8a  5. A. 8 B. 7 C. 4 D. 5
Câu 3. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2
sin 2x  cos 2x  cos 3x  cos x A. 4 B. 3 C. 5 D. 2
Câu 4. Tìm số nghiệm thuộc khoảng 0;  của phương trình 3 2
cos 3x  cos 2x  3cos 2x  cos 2x  2 A. 3 B. 2 C. 5 D. 4
Câu 5. Tập hợp S  a;b bao gồm tất cả các giá trị tham số m để phương trình sau có nghiệm thực
cos3x  4cos x  4m  3 cos x  m  6cos x .
Tính giá trị biểu thức b  8a  5. A. 8 B. 7 C. 4 D. 5
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình cos3x  cos 2x  m cos x  1có đúng bảy nghiệm khác   
nhau thuộc khoảng  ;2    2  A. 3 B. 5 C. 7 D. 1
Câu 7. Có bao nhiêu số nguyên m để phương trình 6 6
sin x  cos x  3sin x cos x  0,25m  2  0 có nghiệm A. 13 B. 15 C. 7 D. 9
Câu 8. Có bao nhiêu số nguyên m để phương trình 2
cos x  m  cos x  m có nghiệm thực A. 3 B. 2 C. 5 D. 4
Câu 9. Có bao nhiêu số nguyên dương m để phương trình cos 2x  m sin x  m  0 có nghiệm A. 0 B. 1 C. 2 D. Vô số
Câu 10. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực
1 2 m  sin 2x  2m  cos 4x . A. 3 B. 2 C. 5 D. 4   
Câu 11. Tìm điều kiện tham số m để phương trình 2 2
cos 4x  cos 3x  msin x có nghiệm x  0;    12   1   1   1  A. m  0;   B. m  ;2   C. m  (0;1) D. m  1  ;    12   2   4  4x
Câu 12. Tìm số nghiệm thuộc khoảng (0;20) của phương trình 2 2cos  (sin x  cos x)  0 3 A. 3 B. 2 C. 4 D. 5
Câu 13. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
tan x  4cot x  7  4 tan x  cot x A. 4 B. 3 C. 5 D. 2 76     b
Câu 14. Điều kiện để phương trình msin 2x  cos 2x 1  2m có nghiệm  ;   là a  m  . Tính  4 3  4  c
giá trị biểu thức a + b + c. A. 10 B. 3 C. 7 D. 8
Câu 15. Tập hợp (a;b) gồm tất cả các giá trị m để phương trình sin 3x  mcos 2x  (m 1)sin x  m  0 có đúng
tám nghiệm phân biệt thuộc 0;3  . Tính 3a + b. A. 0 B. 2 C. 3 D. 4
Câu 16. Tính tổng các nghiệm  (0;2 ) của phương trình 2
tan x  2 tan x  sin10x  2  0 . A. 2  B. 1,5  C.  D. 2,5 
Câu 17. Tính tổng các nghiệm thuộc 0;  của phương trình 2
cos 4x  6sin x  2sin x  0 A. 2  B. 1,5  C.  D. 2,5 
Câu 18. Tìm số nghiệm thuộc 0;  của phương trình cos x cos3x  cos 2xcos 4x  1 A. 2 B. 3 C. 1 D. 4
Câu 19. Nghiệm dương nhỏ nhất của phương trình 4 4 2 2
sin x  cos x  sin 5x  sin 2x thuộc khoảng   5          5 2  A. ;   B. 0;   C. ;   D. ;    3 6   6   6 3   6 3 
Câu 20. Có bao nhiêu số nguyên m để phương trình 3 3
m  5 m  5cos x  cos x có nghiệm thực ? A. 9 B. 8 C. 10 D. 11  9  Câu 21. Cho hàm số 4 2
f (x)  x  4x  3. Tìm số nghiệm thuộc 0; 
của phương trình f (sin 2x  2)  2 . 2    A. 14 B. 13 C. 15 D. 16 sin x  2cos x  3 sin x  2cos x  3 Câu 22. Phương trình  m 
có nghiệm khi và chỉ khi m a;b . Tính 2sin x  cos x  4 2sin x  cos x  4
giá trị biểu thức b – a. A. – 138,75 B. – 120,25 C. – 6,25 D. – 129,5
Câu 23. Tìm số nghiệm trên khoảng 0;6 của phương trình 2   4  4  x x  x sin x 
 sin x  4  cos  sin  3 cos      2   6 6  3 A. 1 B. 2 C. 3 D. 4 Câu 24. Phương trình 2
1 sin 3x  sin 3x  4cos x  4cos x có đặc điểm   
A. Có nghiệm duy nhất  0;  
B. Có nghiệm  : cos(5 )  0  ,5  2 
C. Có hai nghiệm  (0; )
D. Có 10 nghiệm trong khoảng (0;10) 3x 3x
Câu 25. Nghiệm dương nhỏ nhất của phương trình 3 sin x  cos x  tan  cot
gần nhất số nào sau đây 4 4 A. 1,046 B. 1,047 C. 1,042 D. 0,269
Câu 26. Biết rằng phương trình 2 2
tan x  4cot x  3  cos(2x  m) có nghiệm. Tính cos m . 1 1 A. – 0,5 B. – 0,6 C.  D. 3 4 Câu 27. Phương trình 2
9sin x  3sin 2x  4cos x  4 có một hệ quả a sin x  bcos x  2 . Tìm a + 2b. A. 3 B. 4 C. 7 D. 8
_________________________________ 77
VẬN DỤNG CAO – PHÂN LOẠI LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN PHƯƠNG TRÌNH LƯỢNG GIÁC – PHẦN 10)
_______________________________________________________
Câu 1. Tồn tại bao nhiêu số nguyên m nhỏ hơn 50 để phương trình sau có nghiệm 2 2 4 3 2
sin x  2(m  m 1)sin x  m  2m  4m  4m  4  0 . A. 2 B. 1 C. 4 D. 10
Câu 2. Tìm số nghiệm thuộc khoảng (0;10) của phương trình 2 89 sin x cos x  4x  9x  16 A. 2 B. 1 C. 0 D. 3
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 2
2cos 3x  (3  2m)cos3x  m  2  0 có đúng ba    
nghiệm thực thuộc khoảng  ;    6 3  A. 1 B. 2 C. 3 D. 4
Câu 4. Tồn tại bao nhiêu cặp số (x;y) với 0  x  10,0  y  10 thỏa mãn đẳng thức 4 4 1 1 cos x  sin x    8  0,5sin x . 4 4 cos x sin x A. 10 B. 12 C. 14 D. 16
Câu 5. Biết rằng khi m  m thì phương trình 2 2
2sin x  (5m 1)sin x  2m  2m  0 có đúng năm nghiệm phân 0   
biệt thuộc khoảng  ;3 
 . Mệnh đề nào sau đây đúng  2  3 7   3 2  A. m  3 B. m  0,5 C. m  ; D. m   ; 0 0 0 5 10   0  5 5  
Câu 6. Có bao nhiêu số nguyên dương m để phương trình 2
sin x  m  sin x  m có nghiệm thực. A. 2 B. 1 C. 4 D. 3
Câu 7. Xác định số nghiệm thuộc khoảng (49;1993) của phương trình tan x  tan 2x  tan 3x A. 93 B. 1858 C. 1945 D. 1802
Câu 8. Có bao nhiêu giá trị m để phương trình ẩn x: 3
3sin x  4cos x  (m  4m  3)x  m  5 vô nghiệm thực A. 3 B. Vô số C. 1 D. 2
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 3 3 2
sin x  3sin x  m  3m  6m  4 có nghiệm A. 10 B. 3 C. 4 D. 2
Câu 10. Xác định số nghiệm thuộc khoảng (49;1993) của phương trình 4 4
sin x  cos x  sin x  cos x A. 619 B. 542 C. 722 D. 968 5x x
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 sin  5cos xsin 2 2 A. 4 B. 2 C. 5 D. 6
Câu 12. Tồn tại bao nhiêu cặp số (x;y) với 0  x  10,0  y  10 thỏa mãn 2 2 sin x cos 8  8 x  10  cos 2y A. 18 B. 10 C. 20 D. 24
Câu 13. Biết rằng m    m    m   ,  (; ) là điều kiện của m để hai phương trình sau tương đương 2
sin x  2(2m 1)sin x  8m  0 2
cos x  (3m  2)cos x  6m  0
Tính 5  4  3 . A. 3 B. 12 C. 2 D. 5 78 2sin x 1 1
Câu 14. Tập hợp S   ;
a b gồm các giá trị m để phương trình
 m có hai nghiệm 0; . Tính sin x  3 ab A.10 B. – 12 C. – 14 D. – 15
Câu 15. Tìm số nghiệm thuộc 0;4 của phương trình 2 2
tan x  8cos x  3sin 2x . A. 8 B. 4 C. 12 D. 10
Câu 16. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 1 5 7 3 5
cos x  sin x  (cos x  sin x).sin 2x  cos x  sin x . 2 A. 5 B. 4 C. 6 D. 8
Câu 17. Tìm số nghiệm 0;2 của phương trình 6
4(sin x  cos x)  cos 6x  3cos 2x A. 5 B. 4 C. 3 D. 7
Câu 18. Tìm số nghiệm 0;2  của phương trình cos9x  3cos3x  sin 3x  3sin x A. 6 B. 2 C. 4 D. 5 tan 4x 1
Câu 19. Tìm số nghiệm 0;  của phương trình  tan . x tan 3x tan 4x 1 A. 4 B. 2 C. 1 D. 3
Câu 20. Tìm số nghiệm 0;  của phương trình 2sin x  cos3x  sin 2x  1 sin 4x A. 4 B. 2 C. 1 D. 3 Câu 21. Tập hợp  ;
a b gồm các giá trị m để phương trình 2cos2x  (sin xcos x  m)(sin x  cos x)  0có    nghiệm thuộc 0;  . Tính 2 2 a  b . 2    A. 16 B. 8 C. 18 D. 4 1
Câu 22. Tìm số nghiệm thuộc 0;4 của phương trình
 sin x  cos x  2  tan x . cos x A. 3 B. 4 C. 5 D. 6
Câu 23. Tìm số nghiệm thuộc (0;100) của phương trình tan x  sin 2x  2  cos 2x . A. 3 B. 4 C. 5 D. 6
Câu 24. Tìm số nghiệm 0;2  của phương trình 2 2
2cos9x(3  4sin x)(3  4sin 3x)  1. A. 45 B. 37 C. 32 D. 18
Câu 25. Tìm số nghiệm thuộc (0;1993) của phương trình 2 2 2
(1 tan x)(1 tan 2x)(1 tan 4x)  8 . A. 4440 B. 5550 C. 3982 D. 1975    
Câu 26. Tồn tại bao nhiêu số nguyên m để phương trình 2sin x  mcos x  1 m có nghiệm   ;  2 2    A. 5 B. 4 C. 3 D. 6
Câu 27. Tìm số nghiệm thuộc (0;100) của phương trình 2 2 2 cot .
x (1 tan x)(1 tan 2x)(1 tan 4x)  8 A. 230 B. 160 C. 254 D. 96 Câu 28. Phương trình 3 2 2 3
msin x  (3m  4)sin x cos x  (3m  7)sin xcos x  (m  3)cos x  0 có đúng ba   
nghiệm thuộc khoảng  ;0 
 khi và chỉ khi m a;b . Tính 3a – 2b.  2  A. 1 B. 4 C. – 4 D. – 3
Câu 29. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2
(cot x  cot 3x)(4cos x  3)  3 . A. 4 B. 2 C. 6 D. 8 79
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P1)
_________________________________
Câu 1. Hàm số y  tan x  4 có đặc điểm
A. Đồ thị hàm số nằm phía trên trục hoành B. Hàm số lẻ C. Hàm số chẵn
D. Hàm số không chẵn, không lẻ 3
Câu 2. Phương trình sin 2x 
có bao nhiêu nghiệm trong khoảng (0;10) ? 2 A. 10 B. 8 C. 7 D. 5
Câu 3. Tìm chu kỳ tuần hoàn của hàm số y  cos 2x . A. T  2 B. T   C. T  4 D. T  8
Câu 4. Phương trình sin x  cos x  1có bao nhiêu nghiệm thuộc khoảng 0;30  ? A. 40 B. 29 C. 50 D. 31
Câu 5. Hàm số nào sau đây là hàm số lẻ cos x 1 1 A. y  B. y  tan x  C. y  sin x D. y  2cos x 1 sin x  4 cos x  4
Câu 6. Tồn tại bao nhiêu số nguyên m để phương trình msin x  m  
1 cos x  m  2  0 vô nghiệm ? A. 4 B. 3 C. 2 D. 5 Câu 7. Phương trình 2 2
2sin x  5sin x cos x  cos x  2
 tương đương phương trình nào sau đây ? A. 2
4t  5t 1  0;t  tan x B. 2
4t  7t  3  0;t  tan x C. 2
2t  5t  3  0;t  tan x D. 2
3t  5t  2  0;t  tan x
Câu 8. Gọi M, m tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3sin x  4cos x . Tính M – m. A. 10 B. 20 C. 12 D. 10
Câu 9. Tìm chu kỳ của hàm số y  2sin 2x cos 2x .  A. T  2 B. T   C. T  4 D. T  2
Câu 10. Tìm điều kiện tham số m để hàm số f  x  cos3x  m xác định với mọi x. A. m  1 B. m  1 C. m > 0 D. 0 < m < 1
Câu 11. Phương trình sin x cos x  sin x  cos x  2 có bao nhiêu nghiệm thực thuộc khoảng (0;2017) ? A. 100 B. 0 C. 1009 D. 4
Câu 12. Hàm số y  cos x đồng biến trên khoảng nào sau đây       4     A.  ;   B.    ;0 C.  ;   D.   ;    2 2   2 3   3  x x
Câu 13. Tìm tất cả các giá trị của tham số m để phương trình msin  cos  5 có nghiệm. 2 2 m  2 m  2 A.  B.  C. 2  m  2 D. 2  m  2 m  2  m  2 
Câu 14. Gọi S là tập giá trị của hàm số 3
y  4cos x  3cos x  3 . Độ dài của S trên trục số là A. 2 B. 3  2 C. 2  2 D. 2
Câu 15. Hàm số nào sau đây là hàm số chẵn A. y  cos(2x  3) B. 2 y  sin x C. y  cos 2x 1 D. y  sin x  6 80
Câu 16. Nếu đặt sin x  cos x  t , phương trình 3 3 3
1 sin x  cos x  sin 2x tương đương phương trình nào ? 2 A. 3 2 t  3t  3t  5  0 B. 3 2 t  3t  3t  7  0 C. 3 2 t  3t  4  0 D. 3 2 t  t  2t  4  0 Câu 17. Biểu thức 2 2
P  cos x  sin x  4 có thể nhận bao nhiêu giá trị nguyên ? A. 4 B. 3 C. 1 D. 2
Câu 18. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình 2
sin x  3cos x  2  m  0 có nghiệm. A. 8 B. 6 C. 18 D. 7
Câu 19. Hàm số y  cos 2x tăng trên khoảng      4     A.  ;0   B.    ;0 C.  ;   D.   ;    2   2 3   3  Câu 20. Hàm số f  x 2
 sin x  5cos x  2 có tập giá trị M. Độ dài của M trên trục số là A. 9 B. 5 C. 10 D. 14 Câu 21. Cho các hàm số 2
y  cos(x  5); y  cos6 ; x y  sin 2 ;
x y  cos3x cos x . Số lượng hàm số chẵn là A. 3 B. 2 C. 4 D. 1
Câu 22. Nếu đặt sin x  cos x  t , phương trình 1 tan x  2 2 sin x tương đương phương trình nào sau đây ? A. 2 2t  t  2  0 B. 2 2t  t  2  0 C. 2 2t  t  2 1  0 D. 2 2t  t  2 1  0    Câu 23. Trên miền 0; 
 , hàm số y  sin x  cos x có đặc điểm  2  A. Đồng biến B. Nghịch biến C. Không đổi
D. Vừa đồng biến, vừa nghịch biến
Câu 24. Trên khoảng 0;2 , hàm số y  sin 2x có khoảng nghịch biến đầy đủ a;b. Tính a + b A.  B. 0,5 C. 0,75 D. 1,25
Câu 25. Tìm giá trị lớn nhất M và giá trị nhỏ nhất N của hàm số 2 y  2sin x  3sin x 1. 1 A. M = 6; N =  B. M = 6; N = 0 C. M = 5; N = 1 D. M = 4; N = 2 8
Câu 26. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 2018 để f x 4
 sin x  cos x  m xác định với mọi x. A. 2015 B. 2016 C. 2017 D. 2018
Câu 27. Tồn tại bao nhiêu giá trị nguyên m trong khoảng (– 10;10) để phương trình sau vô nghiệm 2 2
4sin x  3 3 sin 2x  2cos x  m . A. 5 B. 4 C. 7 D. 6
Câu 28. Phương trình 3 sin x  cos x  1tương đương phương trình nào sau đây ?    1    1       A. sin x     B. sin x     C. sin x   1   D. sin x   1    6  2  6  2  6   3  
Câu 29. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos(3x  )  2 . 4 A. 3 B. 4 C. 2 D. 5
Câu 30. Phương trình 2sin 2x  3sin x  cos x  3  0 có thể giải được bằng phép đặt ẩn phụ
sin x  cos x  t đưa về phương trình ẩn t. Tổng các nghiệm t của phương trình ẩn t là A. – 2 B. 2 C. – 1,5 D. 1
_________________________________ 81
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P2)
_________________________________ Câu 1. Phương trình 2 2
sin x  cos 3x  1có một phương trình hệ quả là A. sin3x = 0 B. sin4x = 0 C. sin5x = 0 D. sin5x = 1 
Câu 2. Tìm chu kỳ tuần hoàn của hàm số y  tan(x  ) . 3 A. T  2 B. T   C. T  4 D. T  8 x x Câu 3. Phương trình 4 4 1 sin  cos
 tương đương phương trình nào sau đây ? 2 2 2 1 1 A. cos x  0 B. sin x  1 C. cos x  D. cos x  2 2 Câu 4. Hàm số 2
y  5sin x  cos 2x  sin x  6 có giá trị lớn nhất A và giá trị nhỏ nhất B. Tính 28B + A. A. 152 B. 145 C. 120 D. 170
Câu 5. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx
C. y = 1 + sinx D. y = cosx + 2
Câu 6. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin 4x  9 1993 . A. 3986 B. 2020 C. 1993 D. 3020
Câu 7. Tính tổng giá trị tham số m để tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau bằng 4  2 y  cos(2x  )  m  3m  2. 13 A. 1 B. 2 C. 3 D. 4 x x Câu 8. Phương trình 3 5sin 4 cos 6sin x  2cos x 
tương đương phương trình 3
a tan x  b tan x 1  0. Tính 2cos 2x
giá trị biểu thức a + b. A. 3 B. 1 C. 2 D. 4  4 
Câu 9. Tìm chu kỳ của hàm số y  sin 2x  1993   .  9  A. T  2 B. T   C. T  4 D. T  8
Câu 10. Có bao nhiêu giá trị nguyên m lớn hơn – 6 để hàm số f x  sin 2x  3cos 2x  m xác định với mọi x. A. 3 B. 2 C. 1 D. 4
Câu 11. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx
C. y = 1 + 2sinx D. y = 2cosx + 1
Câu 12. Phương trình sin 2x 12sin x  cos x 12  0 tương đương phương trình nào sau đây ? 82 A. 2
t 12t  13;t  sin x  cos x B. 2
t 12t  13;t  sin x  cos x C. 2
t 12t 11  0;t  sin x  cos x D. 2
t 12t  8  0;t  sin x  cos x 3     Câu 13. Biết sin  và
    . Giá trị của cos 2    bằng 2 2  3  3 A. 0 B. – 1 C. 0,5 D.  2
Câu 14. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 10 để hàm số 2
y  tan x  3tan x  m xác định với mọi  x   k . 2 A. 10 B. 17 C. 5 D. 7 Câu 15. Phương trình 2
cos x  cos x  2  0có bao nhiêu nghiệm trong đoạn 0;2  . A. 1 B. 2 C. 4 D. 3      
Câu 16. Biểu thức M  3cos x   2cos x    
 có thể nhận bao nhiêu giá trị nguyên ?  4   3  A. 4 B. 6 C. 5 D. 7
Câu 17. Phương trình   x 2
1 cos 4 sin 2x  3cos 2x có tổng các nghiệm trong đoạn 0;  bằng bao nhiêu ?  2 3 A. B. C. D.  3 3 2 Câu 18. Phương trình  x   x  x   2 2sin 1 2cos 2 2sin
1  3  4cos x tương đương phương trình nào ? A. 2sin x   1 cos 2x  0 B. 2sin x   1 cos3x  0 C. 2sin x   1 cos x  0 D. 2sin x   1 cos2x   1  0 . Câu 19. Cho phương trình 2
2msin x cos x  4cos x  m  5 , tồn tại bao nhiêu số nguyên m trong đoạn [– 3;2]
để phương trình đã cho có nghiệm ? A. 3 B. 2 C. 6 D. 4  3   3 
Câu 20. Số nghiệm thuộc đoạn  ;   
của phương trình 3 sin x  cos  2x   là 2     2  A. 1 B. 2 C. 4 D. 3 2 sin 2x 1     Câu 21. Phương trình 4 4 sin x  cos x 
có bao nhiêu nghiệm trong đoạn  ; ? 2  2 2    A. 1 B. 2 C. 3 D. 4 Câu 22. Biểu thức 2 1
y  sin x  cos x  có thể nhận bao nhiêu giá trị nguyên ? 2 A. 2 B. 1 C. 4 D. 3
Câu 23. Tồn tại bao nhiêu giá trị nguyên m để phương trình 2 3 sin x cos x  cos 2x  m có nghiệm ? A. 3 B. 5 C. 1 D. 2 3  sin x
Câu 24. Tìm tập xác định của hàm số y  . 1 sin 2x      
A. D   \   k 
B. D   \   k 
C. D   \   2k  D. D    4   2   2 
Câu 25. Tồn tại bao nhiêu giá trị nguyên m lớn hơn – 3 để hàm số y  cos 2x  cos x  m xác định với mọi x. A. 4 B. 1 C. 2 D. 3
_________________________________ 83
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P3)
_________________________________
Câu 1. Biểu diễn nghiệm của phương trình  4 4
4 sin x  cos x  sin 4x 3 1 tan 2x tan x  0 trên vòng tròn
lượng giác. Số điểm biểu diễn là A. 10 B. 8 C. 12 D. 6
Câu 2. Đồ thị hàm số nào sau đây có tâm đối xứng là gốc tọa độ ? A. y  cos(2x  3) B. y  sin x  6 C. y  sin 6xsin x D. y  sin 3x
Câu 3. Hàm số y  sin x đồng biến trên khoảng nào sau đây       2    4     A.  ;   B.  ;   C.  ;   D.   ;    2 2   2 3   2 3   3 
Câu 4. Có bao nhiêu số nguyên m 20;20để hàm số y  cot x  m  5 là hàm số lẻ ? A. 37 B. 1 C. 39 D. 10
Câu 5. Đồ thị hàm số nào sau đây có trục đối xứng là trục tung ? A. y  cos(3x 1) B. y  sin 5x C. 2 y  sin 5x D. 2 y  cos 5x  2x
Câu 6. Có bao nhiêu giá trị nguyên m để phương trình 2 8sin x  m  
1 sin 2x  2m  6  0 có nghiệm ? A. 3 B. 5 C. 6 D. 2
Câu 7. Tìm chu kỳ tuần hoàn của hàm số 3
y  8cos x  6cos x  4 . 2 A. T  2 B. T   C. T  D. T  8 3
Câu 8. Tìm số nguyên a lớn nhất để phương trình 2 2
a sin x  2sin 2x  3a cos x  2 có nghiệm. A. a = 3 B. a = 2 C. a = 1 D. a = - 1
Câu 9. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx C. y = 1 + sinx D. y = cosx
1 2cos x1 cos x Câu 10. Phương trình 
 có bao nhiêu nghiệm thuộc khoảng 0;2018  ?  x 1 1 2cos sin x A. 3027 B. 2018 C. 2017 D. 3025
Câu 11. Tìm chu kỳ của hàm số 3
y  4cos 2x  3cos 2x  4 tan x  5 .  A. T  2 B. T   C. T  4 D. T  3 Câu 12. Phương trình 3 3 3
cos xsin 3x  sin x cos3x  tương đương phương trình nào sau đây ? 8 A. 2sin4x = 1 B. 3sin4x = 1 C. cos4x = 0 D. 2cos4x = 1
Câu 13. Hình vẽ bên là đồ thị hàm số nào ? A. y = tanx B. y = sinx + 2 C. y = 1 + sinx D. y = cosx + 1 84  3 
Câu 14. Phương trình sin x  cos xsin x  2cos x  3  0có bao nhiêu nghiệm thực thuộc  ;   ?  4  A. 3 B. 0 C. 1 D. 2 Câu 15. Phương trình 3
sin xsin 2x  sin 3x  6cos x tương đương phương trình f t  0,t  tan x . Tổng các
nghiệm t của phương trình ẩn t là A. 1 B. 2 C. 3 D. 4
Câu 16. Số giá trị nguyên dương của tham số m để phương trình 4 3 cos x  sin x  2m 1  0 có nghiệm là A. 6 B. 5 C. 4 D. 3
Câu 17. Tính tổng các nghiệm lớn nhất và nghiệm nhỏ nhất trong đoạn 0;2018 của phương trình
sin x  3 cos x  2sin 3x . 12109 12111 12107 12103 A. m  n   B. m  n   C. m  n   D. m  n   6 6 6 6  k k 
Câu 18. Khoảng đồng biến của hàm số y  tan 2x là a  ;b    . Tính a + b.  2 2  A. 0 B. 0,5 C. 0,75 D. 1,25
Câu 19. Hàm số y  3sin  x  2018  4cos x  2018  m đạt giá trị nhỏ nhất bằng 0. Tìm giá trị của m. A. m = – 7 B. m = 5 C. m = – 5 D. m = 7 msin x  cos x
Câu 20. Tìm tất cả các giá trị m để phương trình  1có nghiệm. 2  sin x  cos x m  3 m  3 m  1 A.  B.  C. [– 1;3] D.  m  1 m  1 m  1 2  x x 
Câu 21. Gọi S là tập hợp nghiệm thuộc khoảng 0;100  của phương trình sin  cos  3 cos x  3   ,  2 2 
tổng các phần tử của S là 7400 7525 7375 7550 A.  B.  C.  D.  3 3 3 3
Câu 22. Hàm số y  tan x đồng biến trên khoảng       2    4     A.  ;   B.  ;   C.  ;   D.   ;    2 2   2 3   2 3   3   7 
Câu 23. Phương trình sin 3x  2cos 2x  2sin x 1  0có bao nhiêu nghiệm thuộc khoảng  ;0   ?  8  A. 3 B. 1 C. 2 D. 0 Câu 24. Cho hàm số 2
y  sin x  cos x . Tính giá trị S    y2 2 7 1 min 16max y . 25 A. S  B. S = 25 C. S  25  4 7 D. S  24  4 7 16
Câu 25. Hình vẽ bên là đồ thị hàm số y  f  x . Khi đó
giá trị f (2018) gần nhất với giá trị nào ? A. 1,05 B. 0,69 C. 0,42 D. 0,75
_________________________________ 85
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P4)
_________________________________
Câu 1. Tìm điều kiện tham số m để phương trình msinx + 8cosx = 10 có nghiệm ? A. m  6 B. |m| < 4 C. m  6 D. m  2
Câu 2. Phương trình sin 3x  sin x  sin 2x  0 có bao nhiêu điểm biểu diễn nghiệm trên đường tròn lượng giác ? A. 2 B. 3 C. 4 D. 1
Câu 3. Đồ thị hàm số nào sau đây nhận gốc tọa độ O làm tâm đối xứng ? A. y = |sinx| B. 2 y  sin x  4cos 2x C. y = sinx + 5 D. y = sin3x
Câu 4. Tìm tập hợp giá trị m để phương trình 3 2 3 2
sin x  sin x  5sin x  m  m  5m có nghiệm. A. (0;1) B. [– 1;1] C. (– 2;1] D. [0;1] m 
Câu 5. Có bao nhiêu số nguyên m < 26 để hàm số f x 2019  1 xác định với mọi x. sin x  cos x  m A. 20 B. 27 C. 26 D. 24
Câu 6. Tìm chu kỳ tuần hoàn của hàm số 2
y  4sin 2x cos 2x  2cos 2x .  A. T  2 B. T   C. T  D. T  8 2
Câu 7. Tìm điều kiện của m để phương trình 2 2
m sin x  cos x  sin x cos x  0 có nghiệm. A. 1 m   B. m > 0 C. 1 m  D. 1 < m < 2 4 4   Câu 8. Phương trình  1 4 4 sin x  cos x    
có bao nhiêu nghiệm trên 2;3 ?  4  4 A. 2 B. 3 C. 1 D. 4
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 3
4cos x  3cos x  cos 6x  2  m có nghiệm ? A. 3 B. 4 C. 2 D. 1    Câu 10. Cho các hàm số 2
y  sin x; y  cos 2x; y  sin x  ; y  2cos x  3  
. Có bao nhiêu hàm số có chu  3  kỳ là T  2 A. 3 B. 1 C. 2 D. 4
Câu 11. Có bao nhiêu giá trị nguyên m lớn hơn – 30 để hàm số sau xác định với mọi x.
y  7 cos 3x  cos 4x sin x  sin 4x cos x  m . A. 13 B. 7 C. 22 D. 25
Câu 12. Tồn tại bao nhiêu số nguyên m để phương trình 2
sin x  m  2sin x  2m  0 có nghiệm ? A. 3 B. 2 C. 4 D. 1
Câu 13. Phương trình cos x cos5x  cos 2x cos 4x có mấy điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 4 B. 2 C. 5 D. 6
Câu 14. Tìm giá trị nhỏ nhất của m để phương trình 2
sin x  4sin x  5  m có nghiệm. A. m = 1 B. m = 3 C. m = 10 D. m = 2
Câu 15. Có bao nhiêu giá trị nguyên m để phương trình sin x  cos x  sin x cos x  m có nghiệm ? A. 2 B. 4 C. 3 D. 7   
Câu 16. Có bao nhiêu số nguyên m để phương trình  cos 2x  2m  
1 cos x  m 1  0 có nghiệm 3  ;   .  2 2  A. 2 B. 1 C. 0 D. 3 86 Câu 17. Phương trình 3
4sin x  sin x  cos x có hai nghiệm âm liên tiếp lớn nhất là m và n. Tính m + n. A.   B. 2 C. 4,5 D. 2,5
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình cos 2x  m  6sin x  3m 1có nghiệm 0;  . A. 2 B. 1 C. 3 D. 0 sin x  2 cos x  6
Câu 19. Có bao nhiêu số nguyên m lớn hơn – 17 để hàm số y  xác định với mọi x ? m  2sin x  cos x A. 13 B. 9 C. 14 D. 5
Câu 20. Nghiệm âm lớn nhất của phương trình sin 9x  3 cos7x  sin 7x  3 cos9x nằm trong miền nào ?            A.      ;  B.  ;0   C.  ;   D.  ;   6 12     12   3 6   2 3   Câu 21. Biểu thức sin x cos x S 
có thể nhận bao nhiêu giá trị nguyên ? 2sin x  cos x  3 A. 2 B. 1 C. 3 D. 0
Câu 22. Khoảng đồng biến đầy đủ của hàm số y  sin x  cos x là a  k2;b  k2  với a  0,b  0 . Tính
giá trị biểu thức a + b. A.  B. 0,5 C. 0,75 D. 1,25
Câu 23. Có bao nhiêu giá trị nguyên m (– 18;18) để hàm số f x 2
 tan x  6 tan x  m xác định với mọi x. A. 20 B. 17 C. 6 D. 9
Câu 24. Đồ thị hàm số nào sau đây nhận trục tung làm trục đối xứng ?   A. y = cos2019x + 2 B.  y  sin x    C. y = tanx D. y = y  sin 7x  4 
Câu 25. Giá trị lớn nhất của hàm số 3 3
y  sin x  cos x  8 là A. 2 B. 9 C. 10 D. 8
Câu 26. Tồn tại bao nhiêu giá trị nguyên dương m để phương trình 4 4
sin x  cos x  sin x cos x  m có nghiệm ? A. 3 B. 4 C. 1 D. 2 x
Câu 27. Hàm số y  cos có khoảng đồng biến là a  k4;b  k4  với a  0,b  0. Tính a + b 2 A.  B. – 2 C. –  D. 1,5
Câu 28. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 y  cos x  cos x  4 . A. 10 B. 9,75 C. 8,875 D. 7,75
Câu 29. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  cos 2x  cos x  4 . A. 9,25 B. 7,125 C. 8,5 D. 8,125
Câu 30. Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3 cos x  4 . A. 15 B. 11 C. 10 D. 12  x   Câu 31. Hàm số y  sin  
 có khoảng đồng biến là a  k4 ;b  k4  với a  0,b  0. Tính a + b  2 3  4 A.  B.   C. –  D. 1,5 3
Câu 32. Có bao nhiêu số nguyên m để phương trình 2
2 cos 3x  3  2mcos3x  m  2  0có đúng ba nghiệm    thuộc khoảng   ;   ?  6 3  A. 4 B. 1 C. 2 D. 3
_________________________________ 87
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P5)
_________________________________
Câu 1. Gọi M, m tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3sin x  2cos x . Tính M.m. A. 10 B. – 13 C. 12 D. 10
Câu 2. Số nghiệm của phương trình 2
2sin 2x  cos 2x 1  0 trong đoạn 0;2018 là A. 1008 B. 2018 C. 2017 D. 1009 m
Câu 3. Tồn tại bao nhiêu số nguyên m để phương trình 3 3 cos x  cos x  có nghiệm ? 4 5 A. 4 B. 3 C. 2 D. 1 Câu 4. Phương trình 3 2 2 3
sin x  5sin x cos x  3sin x cos x  3cos x  0 tương đương với phương trình nào ? A. 3 2
t  5t  3t  3  0;t  tan x B. 3 2
t  5t  9t  3  0;t  tan x C. 3 2
t  5t  7t  3  0;t  tan x D. 3 2
t  4t  6t  3  0;t  tan x x x
Câu 5. Tìm chu kỳ tuần hoàn của hàm số y  4sin  9cos 1993. 2 2  A. T  2 B. T   C. T  4 D. T  2 x x
Câu 6. Tìm chu kỳ của hàm số 2 2 y  4sin  9cos . 2 2  A. T  2 B. T   C. T  4 D. T  2
Câu 7. Tồn tại bao nhiêu số nguyên m để phương trình msin x  5cos x  2m  5 có nghiệm. A. 5 B. 6 C. 7 D. 8 Câu 8. Phương trình 3
sin x  cos x  4sin x  0 tương đương phương trình nào sau đây ? A. 3 2
3t  t  t 1  0;t  tan x B. 3 2
3t  t  2t  4  0;t  tan x C. 3 2
3t  t  2t  6  0;t  tan x D. 3 2
3t  3t  2t  8  0;t  tan x .
Câu 9. Tồn tại bao nhiêu số nguyên m để phương trình 2msin x cos x  4cos 2x  3m  4 có nghiệm. A. 1 B. 2 C. 3 D. 4
Câu 10. Phương trình (2  2)(sin x  cos x)  2sin x cos x  2 2 1có bao nhiêu nghiệm 0;4  ? A. 2 B. 3 C. 4 D. 5
Câu 11. Phương trình 3(sin x  cos x)  2sin 2x  3  0 có bao nhiêu nghiệm 0;4  ? A. 2 B. 4 C. 3 D. 5 Câu 12. Hàm số 2
y  3cos 2x  4cos x  5cos x  3 có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính giá trị biểu thức 4M + 5N. A. 13 B. 16 C. 19 D. 12 3 1
Câu 13. Phương trình 8sin x  
tương đương phương trình 3 2
3 tan x  a tan x  b tan x  c  0 . cos x sin x
Giá trị biểu thức a + b + c gần nhất giá trị nào ? A. – 2 B. – 3 C. – 4 D. 3 cos x  2sin x  3 Câu 14. Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào đúng ? 2cos x  sin x  4 A. 2M + N + 6 = 0 B. 4M = N C. M + 7N > 0 D. 2M – N < 2
Câu 15. Tồn tại bao nhiêu số nguyên m lớn hơn – 9 sao cho 2
2sin x  3cos x  4  m với mọi x. 88 A. 7 B. 9 C. 10 D. 13 x 3x x 3x 1
Câu 16. Phương trình cos x cos cos  sin xsin sin
 có một phương trình hệ quả là 2 2 2 2 2 A. cos x  sin x  1 B. cos x  sin x  0 C. cos 2x  sin x  1 D. cos 2x  2sin x  1 Câu 17. Phương trình  x  x2 cos 4 cos 2
 5  sin 3x có một phương trình hệ quả là A. sinx = 1 B. sin2x = 1 C. 2sin3x = 1 D. 4sinx = 1
Câu 18. Phương trình tan x  2sin 2x  3tương đương phương trình f t  0;t  tan x . Tổng các nghiệm của
phương trình f t  0 là A. 3 B. 2 C. 1 D. 5
Câu 19. Đồ thị hàm số y  sin x  3 có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành
C. Luôn nằm phía dưới trục hoành
D. Luôn nằm bên trái trục tung
Câu 20. Tồn tại bao nhiêu hàm số mà đồ thị có tâm đối xứng là gốc tọa độ trong các hàm số sau   7 9  y  tan 2 . x sin 5 ; x y  tan x  cot ; x y  sin 2x    .  2  A. 0 B. 1 C. 2 D. 3 Câu 21. Cho các hàm số 2 2 2 2
y  sin 9  x ; y  sin 5x  cos9 ; x
y  sin x  cos(4x  9) 1993; y  cos x .
Có bao nhiêu hàm số mà đồ thị nhận trục tung là trục đối xứng ? A. 3 B. 2 C. 1 D. 0
Câu 22. Tìm điều kiện tham số m để phương trình msin x  1 3m cos x  m  2 có nghiệm. 1 1 A. m  3 B. Không tồn tại m C.  m  3 D. m  3 3
Câu 23. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số       y  215sin x   2014cos x      .  3   4  A. 2018 B. 0 C. 421 D. – 11 1 1
Câu 24. Phương trình 2sin 3x   2cos3x 
có một phương trình hệ quả là sin x cos x A. sin2x = – 1 B. sin2x = 1 C. cos2x = 1 D. tanx = 1 1
Câu 25. Giá trị pnhỏ nhất của hàm số y  cos 2x  là 2 2cos x 1 A. 3 B. 2 C. 4 D. – 1 Câu 26. Phương trình 3 3 2
3cos x  4sin x  sin x cos x  3sin x  0 tương đương phương trình nào ? A. 3 2
3t  3t  t 1  0;t  tan x B. 3 2
t  t  3t  3  0;t  tan x C. 3 2
4t  4t  3t  3  0;t  tan x D. 3 2
4t  t  3t  3  0;t  tan x
Câu 27. Tìm tổng tất cả các nghiệm x thuộc đoạn 0;10 của phương trình 2
sin 2x  3sin 2x  2  0 . 105 105 297 299 A.  B.  C.  D.  2 4 4 4
Câu 28. Phương trình tan 3x  cot x có bao nhiêu nghiệm thuộc 0;2  ? A. 7 nghiệm B. 4 nghiệm C. 8 nghiệm D. 5 nghiệm
_________________________________ 89
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P6)
_________________________________
Câu 1. Phương trình sin x  cos x  1tương đương với phương trình nào sau đây    1    1       A. sin x     B. sin x     C. sin x   1   D. sin x   2    4  2  4  2  4   4 
Câu 2. Tồn tại bao nhiêu số nguyên m  1
 0;10 để hàm số y  sin x  cos x  m có tập xác định  ? A. 7 B. 11 C. 13 D. 12 1
Câu 3. Tồn tại bao nhiêu góc x 0;2  để hàm số y  9  4cos 2x  không xác định ? 2 tan x 1 A. 3 B. 4 C. 5 D. 6
Câu 4. Có bao nhiêu số nguyên m < 10 để phương trình m m sin x  m   1 cos x  có nghiệm ? cos x A. 9 B. 6 C. 7 D. 8
Câu 5. Tồn tại bao nhiêu số nguyên dương n < 4 để hàm số 2 2
y  2sin x  3cos (nx) có chu kỳ T   ? A. 4 B. 2 C. 3 D. 1 nx
Câu 6. Tồn tại bao nhiêu số nguyên dương n < 10 để hàm số y  4sin 2x  9cos có T   ? 2 A. 4 B. 2 C. 3 D. 1  
Câu 7. Có bao nhiêu số nguyên m thỏa mãn đẳng thức  sin 2x  2 sin x   m   ?  4  A. 4 B. 2 C. 3 D. 1
Câu 8. Tính tổng tất cả các giá trị nguyên m để 2 x  m   x x  m   2 sin 2 1 sin cos
1 cos x  m là một phương trình có nghiệm. A. 1 B. 6 C. 3 D. 10  2 
Câu 9. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin x  sin x    .  3  A. 2 B. – 1 C. 1 D. – 3
Câu 10. Tính a + b biết asin x  bcos x  1 (a  0,b  0) là một phương trình hệ quả của phương trình 1
3sin x  2cos x  3(1 tan x)  . cos x A. 4 B. 5 C. 3 D. 2 2 3 cos x  cos x 1
Câu 11. Tính tổng các nghiệm x thuộc 0;99của phương trình 2 cos 2x  tan x  . 2 cos x 2209 4 1993 2019 A.  B.  C.  D.  3 9 4 4      
Câu 12. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  sin x   cos x      .  3   3  A. 3 1 B.  3 1 C. – 2 D. 1
Câu 13. Tìm tập hợp tất cả các giá trị m để phương trình  x   x  m x 2 cos 1 cos 2 cos  msin x có đúng hai   nghiệm thuộc đoạn 2  0;  . 3    A. [0;1) B.  1    1  ;  C. 1 0;  D. (– 1;1] 2    2    90
Câu 14. Tìm m để đồ thị hàm số y  sin 2x  sin 3x cos x  sin x cos3x  m 8 nhận gốc tọa độ làm tâm đối xứng. A. m = 8 B. m = 3 C. m = 6 D. m = 2 cos 2x 1
Câu 15. Tồn tại bao nhiêu số nguyên m  2
 0;20để hàm số y 
 sin(mx) là hàm số chẵn ? cos 2x 1 A. 10 B. 39 C. 20 D. 24
Câu 16. Tịnh tiến đồ thị hàm số 3
y  8cos x  6cos x  3 xuống dưới tối thiểu bao nhiêu đơn vị để đồ thị thu
được không nằm phía trên trục hoành ? A. 1 B. 5 C. 4,75 D. 2,5
Câu 17. Hỏi tồn tại bao nhiêu giá trị nguyên m để phương trình cos 2x  2m  
1 cos x 1  m có đúng hai nghiệm       ;  ? 2 2    A. 2 B. 3 C. 1 D. 4  
Câu 18. Giả sử 3sin 2x cos 2x a 5  , x    . Tính a + 2b. 2 sin 2x  4cos x 1 b A. 77 B. 54 C. 19 D. 83 Câu 19. Phương trình 2
2sin x  sin x 1  0 có bao nhiêu nghiệm thuộc 0;3  ? A. 3 B. 4 C. 5 D. 6
Câu 20. Tính a + b biết rằng 2
2cos 2x 12sin x  5  asin x  bsin x  5 . A. 15 B. 14 C. 16 D. 20
Câu 21. Tìm số điểm biểu diễn trên vòng tròn lượng giác đối với nghiệm phương trình 2
2cos x  5cos x  2  0 . A. 3 B. 2 C. 4 D. 5 x  2x  
Câu 22. Tính tổng các giá trị tự nhiên m để hàm số y  tan  cos  
 là hàm số tuần hoàn với T  6 . 2  m 4  A. 3 B. 6 C. 9 D. Kết quả khác  x    x   Câu 23. Hàm số y  sin  cos    
 có khoảng đồng biến là a  k4 ;b  k4  với a  0,b  0 .  4 6   4 6  Tính a + b 4 A.  B.   C. –  D. 1,5 3
Câu 24. Tồn tại bao nhiêu số nguyên m để phương trình 3sin x  4cos x  m có nghiệm ? A. 10 B. 11 C. 12 D. 9
Câu 25. Tồn tại bao nhiêu số nguyên m để phương trình 3sin x  cos x  m có nghiệm ? A. 10 B. 11 C. 12 D. 9  x    3 9  Câu 26. Hàm số y  cot  
 với a  0,b  0có khoảng nghịch biến   3k ;  3k   . Tính ab.  a b   4 4  A. 12 B. 8 C. 6 D. 9 Câu 27. Phương trình 2
2sin 2x  5sin 2x  2  0 có hai họ nghiệm dạng x    k ; x    k . Khi đó tích của  là 2 5 2 5 2 5 2 5 A.  B. C.  D. 144 36 36 144
Câu 28. Tồn tại bao nhiêu số nguyên m lớn hơn – 10 để hàm số y  4sin 3x  m có tập xác định  . A. 6 B. 8 C. 5 D. 7
_________________________________ 91
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P7)
_________________________________
Câu 1. Tìm họ nghiệm của phương trình sin x  1.   A. x   k2 B. x   k C. x    k2 D. x  k2 2 2    Câu 2. Cho các hàm số 2 y  sin ; x y  cos 2 ; x y  sin x  ; y  2cos x  3  
. Có bao nhiêu hàm số có chu  3  kỳ là T  2 A. 3 B. 1 C. 2 D. 4
Câu 3. Tìm số nghiệm của phương trình sin x  0,3 trong khoảng 0;3  . A. 4 B. 2 C. 3 D. 1
Câu 4. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x)  cos5x cos x  sin 5xsin x  4sin 3x . A. – 15 B. – 8 C. 10 D. – 6
Câu 5. Tìm số nghiệm của phương trình tan x  0, 4 trong khoảng 0;3  A. 3 B. 2 C. 4 D. 1    1 1
Câu 6. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 sin x      .  4  sin x cos x A. 4 B. 2 C. 3 D. 5
Câu 7. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 2 2 y  4  5sin x cos x . A. 5 B. 11 C. 3 D. 8 2
Câu 8. Tìm số nghiệm  2
  ;2  của phương trình 2tan x  cot x   3 . sin 2x A. 4 B. 3 C. 2 D. 5   
Câu 9. Tính tổng các giá trị m để hàm số y  sin mx  
 nhận chu kỳ T  2 .  3  A. 3 B. 0 C. 1 D. 2
Câu 10. Tồn tại bao nhiêu số nguyên m để phương trình 2cos 2x  sin x  m có nghiệm ? A. 3 B. 6 C. 5 D. 10 1
Câu 11. Tìm điều kiện tham số m để hàm số y  có tập xác định  . sin x  m m  1 A. m  1 B.  C. 0 < m < 1 D. m  1 m  1 1
Câu 12. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm y   2 không xác định ? sin x  cos x A. 3 B. 2 C. 4 D. 1
Câu 13. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  3  8 sin x cos x . A. 4 B. 1 C. 3 D. – 2
Câu 14. Tồn tại bao nhiêu số nguyên m để phương trình 2
2cos 2x  3cos x  2sin x  m có nghiệm ? A. 13 B. 7 C. 8 D. 10
Câu 15. Đồ thị hàm số y  cos 2x  5 có đặc điểm
A. Luôn nằm phía trên trục hoành B. Tiếp xúc trục hoành 92
C. Luôn nằm phía dưới trục hoành
D. Luôn nằm bên trái trục tung Câu 16. Phương trình 4 2
4sin x 12cos x  7 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 2 C. 5 D. 4
Câu 17. Hàm số nào sau đây có tập xác định  ? cos x 1 1 A. y  B. y  tan x  C. y  sin x 1 D. y  2cos x 1 sin x  4 cos x  4
Câu 18. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2
(2sin x 1)(2cos 2x  2sin x 1)  3  4cos x . A. 5 B. 4 C. 6 D. 3
Câu 19. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình tan x  sin x  1 tan . x sin x . A. 5 B. 2 C. 3 D. 4 
Câu 20. Tịnh tiến đồ thị hàm số 3
g(x)  3sin x  4sin x sang trái đơn vị ta thu được đồ thị hàm số y  f (x) . 2
Hai đồ thị hàm số f (x), g(x) cắt nhau tại bao nhiêu điểm có hoành độ thuộc khoảng 0;2  ? A. 5 B. 6 C. 3 D. 1
Câu 21. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2 2
cos x(1 cos x)  sin x(1 sin x)  2cos x . A. 4 B. 3 C. 2 D. 1   
Câu 22. Có bao nhiêu số nguyên m để phương trình cos 4x  2(m  3) cos 2x  6m 1  0 có nghiệm 0;  4    A. 2 B. 5 C. 3 D. 4
Câu 23. Tính tổng nghiệm lớn nhất và nghiệm nhỏ nhất thuộc  1
 00 ;100  của phương trình 3 3
sin x  cos x  1 0,5sin 2x . A. 2 B. 0,5 C. 0, 25 D. – 1,5 Câu 24. Phương trình 3 3
sin x  cos x  1có bao nhiêu nghiệm 0;4  ? A. 2 B. 4 C. 3 D. 5
Câu 25. Tồn tại bao nhiêu số nguyên m để phương trình 3sin 2x  4(sin x  cos x)  m có nghiệm ? A. 13 B. 12 C. 10 D. 11  x   Câu 26. Hàm số y  sin  
 có khoảng đồng biến là a  k4 ;b  k4  với a  0,b  0 . Tính a + b  2 3  4 A.  B.   C. –  D. 1,5 3   
Câu 27. Nghiệm dương nhỏ nhất của phương trình 3 2 sin x   2sin x   thuộc khoảng  4   1   1  A. 0;   B. (1;2) C. (2;3) D. ;1    2   2 
Câu 28. Tìm số nghiệm thuộc 0;3  của phương trình 3 cos x  2sin x . A. 5 B. 3 C. 2 D. 4
Câu 29. Nghiệm dương nhỏ nhất của phương trình sin 2x  2 tan x  3thuộc khoảng  1   1  A. 0;   B. (1;2) C. (2;3) D. ;1    2   2 
_________________________________ 93
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P8)
_________________________________ x 1  2x  
Câu 1. Tính tổng các giá trị tham số m để hàm số y  cot  sin  
 (m là số tự nhiên) tuần hoàn với 3 2  m 3  chu kỳ 6 . A. 2 B. 6 C. 8 D. 12
Câu 2. Tính a + b biết asin x  2bcos x  7  0 là một phương trình hệ quả của phương trình
9sin x  6cos x  3sin 2x  cos 2x  8 . A. 5 B. 7 C. 6 D. 9 x x
Câu 3. Tồn tại bao nhiêu cặp số nguyên dương (m;n) để hàm số y  26 tan
 4cot  2019 có T  12 ? m n A. 16 B. 15 C. 10 D. 12
Câu 4. Tồn tại bao nhiêu số nguyên m thuộc [– 5;5] để phương trình tan x  2m có nghiệm ? A. 4 B. 2 C. 11 D. 20
Câu 5. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2sin x cos x  3 cos 2x  4 . A. 10 B. 8 C. 12 D. – 6 x x    Câu 6. Cho các hàm số 2 4
y  cot x; y  tan ; y  sin ; y  sin x  cos x  
 . Tồn tại bao nhiêu hàm số 2 2  9 
thỏa mãn điều kiện f (x  2k )  f (x) ? A. 4 B. 2 C. 3 D. 1
Câu 7. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 4 4
y  3(cos x  sin x)  sin 2x 1. A. – 3 B. – 2 C. 1 D. 4  2 
Câu 8. Tồn tại bao nhiêu số nguyên m để phương trình 2sin x  m có nghiệm thuộc 0;  ? 3    A. 4 B. 2 C. 3 D. 5 2 4 sin 2x  cos 2x 1
Câu 9. Tìm số nghiệm  4
  ;9  của phương trình  0 . sin x cos x A. 13 B. 14 C. 15 D. 16
Câu 10. Tính tích giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y  3  2cos3x(3sin x  4sin x) . A. 6 B. 8 C. 2 D. – 4
Câu 11. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2 2
4sin 2x  6sin x  9  3cos 2x  0. cos x A. 6 B. 2 C. 4 D. 5  2 
Câu 12. Tồn tại bao nhiêu số nguyên m để phương trình 3sin x  m có hai nghiệm thuộc 0;  ? 3    A. 4 B. 3 C. 2 D. 0
Câu 13. Tính a + b biết a(sin x  cos x)  bsin x cos x 1  0 là một phương trình hệ quả của phương trình 2
2sin x  3sin x 1  cos3x . A. 5 B. 3 C. 4 D. 2
Câu 14. Phương trình cos 4x  9sin 2x  8  0 có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2 94 x
Câu 15. Tìm số nghiệm thuộc 0;3  của phương trình 5cos x  7  2sin . 2 A. 3 B. 4 C. 1 D. 2 1 1 10   
Câu 16. Góc x thỏa mãn cos x   sin x   thì cos x    gần nhất với cos x sin x 3  4  A. – 0,55 B. – 0,25 C. 0,12 D. – 0,45
Câu 17. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 3 3 3
1 sin x  cos x  sin 2x . 2 A. 3 B. 4 C. 1 D. 2  2 
Câu 18. Tồn tại bao nhiêu số nguyên m để phương trình 2
m  cos 2x  sin x  cos 4x có nghiệm  0;  3    A. 4 B. 8 C. 5 D. 6
Câu 19. Tìm số nghiệm thuộc 0;3  của phương trình 4 2 2 4
3cos x  4sin x cos x  sin x  0 A. 12 B. 16 C. 10 D. 8 Câu 20. Phương trình 2 2
8sin xcos x  2sin 4x  3  3cos 4x tương đương (tan 2x  a)(tan 2x  b)  0 . Tính
giá trị biểu thức a + b + 2. A. 2 B. 6 C. 3 D. 1
Câu 21. Tồn tại bao nhiêu hàm số mà đồ thị có tâm đối xứng là gốc tọa độ trong các hàm số sau   7 9  y  tan 2 . x sin 5 ; x y  tan x  cot ; x y  sin 2x    .  2  A. 0 B. 1 C. 2 D. 3 Câu 22. Cho các hàm số 2 2 2 2
y  sin 9  x ; y  sin 5x  cos9 ; x
y  sin x  cos(4x  9) 1993; y  cos x .
Có bao nhiêu hàm số mà đồ thị nhận trục tung là trục đối xứng ? A. 3 B. 2 C. 1 D. 0
Câu 23. Tìm chu kỳ của hàm số y  sin x  cos x  4sin x cos x  9  A. T  2 B. T   C. T  4 D. T  2 
Câu 24. Hàm số nào sau đây có điều kiện xác định x   k ? 2 1 1 cos x 1 1 A. y   B. y  C. y  tan x  3cot x D. y  2 cos x 4  sin x sin x  4 cos x 1
Câu 25. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 2
(2sin x 1)(2cos 2x  2sin x 1)  3  4cos x . A. 5 B. 4 C. 6 D. 3 x 1
Câu 26. Tồn tại bao nhiêu số nguyên x < 10 để hàm số y  xác định ? sin( x) A. 7 B. 4 C. 0 D. 8 sin x 1
Câu 27. Cho các hàm số y  ; y  sin x  4; y 
; y  cos x 1 . Có bao nhiêu hàm số 2 3  cos x tan x 1 có tập xác định  ? A. 4 B. 1 C. 3 D. 2
_________________________________ 95
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P9)
_________________________________ 1 cos 2x  sin 2x
Câu 1. Tìm chu kỳ của hàm số y  . 1 cos 2x  sin 2x A. T  2 B. T   C. T  4 D. T  8  k
Câu 2. Phương trình cos x  3 sin x  2cos3x có một họ nghiệm nào đó là x   với a, b nguyên a b
dương. Tính tổng số các ước dương của a và b. A. 6 B. 4 C. 10 D. 12 (1 2sin x)cos x
Câu 3. Tìm số nghiệm 0;2 của phương trình  3 . (1 2sin x)(1 sin x) A. 3 B. 7 C. 4 D. 2 1
Câu 4. Có bao nhiêu điểm biểu diễn trên vòng tròn lượng giác để hàm số y  không xác định ? 2 2 sin x  cos x A. 3 B. 2 C. 4 D. 1 
Câu 5. Tịnh tiến đồ thị y  sin 2x lên trên 2 đơn vị, sau đó sang phải thu được đồ thị hàm số y  f (x) . Tính 2
tổng các giá trị m để đường thẳng y = m tiếp xúc với đồ thị y  f (x) . A. 4 B. 2 C. 6 D. 7
Câu 6. Đồ thị hàm số nào sau đây luôn nằm phía dưới trục hoành    A. y  cos3x B. y  sin 2x  2 C. y  sin x   2   D. y  cos3x cos6x  3   Câu 7. Biểu thức sin x cos x S 
có thể nhận bao nhiêu giá trị nguyên ? 2sin x  cos x  3 A. 2 B. 1 C. 3 D. 0
Câu 8. Tìm số nghiệm thuộc 0;3  của phương trình 4 4
5(1 cos x)  2  sin x  cos x . A. 3 B. 4 C. 5 D. 2   
Câu 9. Tồn tại bao nhiêu số nguyên k để phương trình 4sin 2x  mcos x  cos3x có nghiệm  0;  . 6    A. 5 B. 6 C. 3 D. 7 Câu 10. Cho 3
f (x)  x  3x  2 . Tìm số nghiệm của phương trình f (tan 2x)  0 trong khoảng 0;2 . A. 3 B. 6 C. 5 D. 8
Câu 11. Đồ thị hàm số nào sau đây nằm hoàn toàn phía trên đường thẳng y = 2 ? sin x A. y  B. 3
y  4cos x  3cos x  3,5 2  cos x C. y  2cos 2x  cos x D. y  sin 3xsin 6x  2
Câu 12. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm của 3
4sin x  sin 3x  4cos x  cos x . A. 3 B. 2 C. 1 D. 4 x
Câu 13. Tìm số nghiệm thuộc 0;3  của phương trình 2 cos 2x  3cos x  4cos . 2 A. 3 B. 4 C. 5 D. 2  k k  Câu 14. Hàm số 2
y  4  (sin 2x  cos 2x) có khoảng nghịch biến a  ;b    . Tính 3b – a.  4 4  96 A. 0,5 B.  C. 0,25 D. 1,5  k k  Câu 15. Hàm số y   x  x  3 4 2 4 8cos 8cos
1  3cos 4x khoảng đồng biến a  ;b    . Tính a + b  6 6    A. B.  C. 2 D. 3 12 1
Câu 16. Tìm chu kỳ tuần hoàn của hàm số y  . 3
(3sin x  4sin x) cos3x  sin 4x   A. T   B. T  C. T  4 D. T  2 4 sin a  sin 3a  sin 5a
Câu 17. Tìm chu kỳ của hàm số y  . cos a  cos3a  cos5a 2   A. T  B. T   C. T  D. T  5 3 2
Câu 18. Tìm số điểm trên vòng tròn lượng giác biểu diễn nghiệm phương trình 4cos x  2sin x  3  cos 2x . A. 4 B. 2 C. 3 D. 5
Câu 19. Tính 4a + 9b biết a cos x  bsin x  6 là một hệ quả của phương trình
4sin 2x  3cos 2x  3(4sin x 1) . A. 7 B. 3 C. 8 D. 6
Câu 20. Tồn tại bao nhiêu số nguyên m để phương trình 4(sin x  cos x)  9sin x cos x  m 1993 có nghiệm ? A. 10 B. 16 C. 17 D. 7
Câu 21. Tồn tại bao nhiêu số nguyên m thuộc 3;3 để phương trình 3
4cos x  3cos x  m 1 có nghiệm ? A. 4 B. 5 C. 2 D. 3
Câu 22. Phương trình sin 2x  2cos 2x  1 sin x  4cos x có bao nhiêu nghiệm  4  9;1993 A. 193 B. 968 C. 702 D. 325
Câu 23. Phương trình 2sin 2x  cos 2x  7sin x  2cos x  4 tương đương phương trình sin x  a , khi đó  1 1   1 1   1 1   1  A. a  ;   B. a  ;   C. a  ;   D. a  ;1    5 4   7 5   4 3   3 
Câu 24. Tồn tại bao nhiêu số nguyên m thuộc 10;10 để phương trình sin 4x  cos 4x  2m có nghiệm ? A. 4 B. 5 C. 3 D. 6   
Câu 25. Tồn tại bao nhiêu số nguyên m để phương trình sin x  cos x  sin x cos x  m có nghiệm  0;  4    A. 2 B. 1 C. 3 D. 4      
Câu 26. Tìm chu kỳ của hàm số y  4sin xsin  x sin  x  sin x     .  3   3  A. T  2 B. T   C. T  4 D. T  8
Câu 27. Tồn tại bao nhiêu số nguyên m để phương trình 2 2
2sin x  (2m 1)sin x cos x  mcos x  0 có 4 điểm
biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. Vô số C. 5 D. 10
Câu 28. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  3
2 2 cos (x  )  3cos x  sin x  0 . 4 A. 3 B. 2 C. 4 D. 1
_________________________________ 97
ÔN TẬP LƯỢNG GIÁC LỚP 11 THPT
(LỚP BÀI TOÁN TỔNG HỢP – P10)
_________________________________
Câu 1. Tìm chu kỳ tuần hoàn của hàm số y  (cos5x cos x  sin 5xsin x) cos 4x .   A. T  2 B. T  C. T  4 D. T  2 4
Câu 2. Tìm số nghiệm 0;  của phương trình 2cos3x  3 sin x  cos x  0 . A. 2 B. 3 C. 1 D. 4 cos x  2sin x  3 Câu 3. Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất N. Mệnh đề nào đúng ? 2cos x  sin x  4 A. 2M + N + 6 = 0 B. 4M = N C. M + 7N > 0 D. 2M – N < 2 
Câu 4. Điều kiện xác định của hàm số 2
y  3tan(2x  )  4 x 1 là 4  k 3 k   A. x   B. x   C. x   k D. x    k2 4 2 8 2 2 2   2 
Câu 5. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  2 cos 2x  cos 2x   3    .  3    A. 7 B. 8 C. 6 D. 4 sin x(sin x  cos x) 1
Câu 6. Tìm số nghiệm  4
  ;9  của phương trình  0. 2 cos x  sin x 1 A. 25 B. 22 C. 15 D. 7 Câu 7. Hàm số 3
y  x tan x  x có đặc điểm A. Hàm số chẵn B. Hàm số lẻ
C. Hàm số không chẵn, không lẻ
D. Đồ thị hàm số nằm phía trên trục hoành
Câu 8. Có bao nhiêu điểm M (x;y) nằm trên đồ thị hàm số y  sin x thỏa mãn 4  x  9; y  cos x ? A. 4 B. 1 C. 3 D. 2 Câu 9. Phương trình 4 4
cos 2x  sin x  cos x có bao nhiêu điểm biểu diễn nghiệm trên vòng tròn lượng giác ? A. 3 B. 4 C. 5 D. 2 4
Câu 10. Tìm số nghiệm thuộc 0;2  của phương trình 4 3cot x   5  0 . 2 sin x A. 3 B. 4 C. 5 D. 2
Câu 11. Tồn tại bao nhiêu số nguyên m < 10 để phương trình 2 2
sin x  2sin x cos x  (m 1)cos x có nghiệm A. 8 B. 12 C. 10 D. 8
Câu 12. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình 3 2
sin x  3cos x  3sin x cos x  2sin x . A. 3 B. 5 C. 2 D. 4 1
Câu 13. Cho các hàm số y  sin xsin 4 ; x y  x tan 4 ;
x y  sin ; y  cos x 1; y  cos 4x . x
Biết rằng có a hàm số chẵn và b hàm số lẻ, tính 3a + 2b. A. 5 B. 8 C. 11 D. 12 3x 3x  k2 k2  Câu 14. Hàm số 2 2 y  cos  sin
có khoảng nghịch biến a  ;b  
 với a  0,b  0. Tính a + b 2 2  3 3   A. B.  C. 2 D. 1,5 3 98 1 1 2
Câu 15. Tính tổng các nghiệm thuộc 0;2 của phương trình   . cos x sin 2x sin 4x A. 2 B.  C. 3 D. 1,5
Câu 16. Hàm số y  cos x  sin x có khoảng nghịch biến a  k2 ;b  k2  . Tính a + b A.  B. – 2 C. –  D. 1,5
Câu 17. Tồn tại bao nhiêu số nguyên m để phương trình sin 2x  msin x  2m  4cos x có nghiệm ? A. 4 B. 2 C. 5 D. 3
Câu 18. Tồn tại bao nhiêu số nguyên m thuộc 3;3 để phương trình 2
2cos x 1  cos(3x  m) có nghiệm ? A. 4 B. 2 C. 5 D. 3
Câu 19. Tồn tại bao nhiêu số nguyên m thuộc 10;10 để phương trình cos 4xcos x  sin 4xsin x  2m có nghiệm ? A. 4 B. 5 C. 2 D. 3
Câu 20. Phương trình cos 2x  2cos x  6sin x  8 có một hệ quả cos x  sin x  a , số ước của a là A. 2 B. 4 C. 6 D. 8
Câu 21. Đồ thị hàm số nào sau đây tiếp xúc trục hoành ? A. y  cos3x B. y  sin 2x  2 C. y  sin 6x 1 D. y  tan x  3    
Câu 22. Tính tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x)  sin 2x  cos 2x  3; x   ;  . 4 4    A. 5 B. 5  2 C. 4  2 2 D. 3 2 1 2cos x  3sin x  5 Câu 23. Hàm số y 
có giá trị lớn nhất M và giá trị nhỏ nhất N. Tính Q = M.N. 2sin x  3cos x  5 A. Q = 1 B. Q = 2 C. Q = 5 D. Q = 10
Câu 24. Tìm số nghiệm trong khoảng 0;2  của phương trình 3sin xcos x  sin x  cos x  3. A. 3 B. 1 C. 0 D. 2
Câu 25. Tính 3  sin 2 khi  là nghiệm phương trình sin x cos x  2(sin x  cos x)  2 . A. 3 B. 2 C. 3,5 D. 2,5 2 2 sin x  tan x
Câu 26. Tìm chu kỳ tuần hoàn của hàm số 6 y  .cot x  tan x . 2 2 cos x  cot x  A. T  2 B. T   C. T  4 D. T  2 sin 5x
Câu 27. Tìm số điểm biểu diễn trên vòng tròn lượng giác nghiệm phương trình  1. 5sin x A. 0 B. 2 C. 3 D. 4 tan 2x
Câu 28. Tìm tập xác định của hàm số y  . 2cos x  7     A. x   k B. x   k2 C. x   k D.  2 2 4 2
Câu 29. Tìm số nghiệm 0;2 của phương trình 3(sin 2x  sin x)  cos 2x  cos x  2 . A. 7 B. 6 C. 3 D. 8 
Câu 30. Tịnh tiến đồ thị y  2 sin x sang trái đơn vị ta được đồ thị hàm số 4 A. y  sin x  cos x B. y  2 sin x  C. y  sin x D. y  cos x 4 99