Hệ thống kiến thức và phương pháp giải Toán 11 GDPT 2018 – Võ Công Trường

Tài liệu Hệ thống kiến thức và phương pháp giải Toán 11 GDPT 2018 – Võ Công Trường gồm 44 trang, được biên soạn bởi thầy giáo Võ Công Trường, tổng hợp hệ thống kiến thức và phương pháp giải Toán 11 chương trình GDPT 2018.Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

3 2 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

44 trang 4 giờ trước

Tác giả:

Profile Lê Phương
2024-2025
sin
cosin
cotang
tang
0 (rad)
2
3
2
7
4
5
4
7
6
11
6
5
3
4
3
5
6
3
4
2
3
3
4
6
-1
2
-1
2
-
2
2
-
2
2
2
2
1
2
2
2
1
2
3
2
3
2
-
3
2
-
3
2
-
3
3
-
3
3
1
1
1
3
3
3
3
-1
-1
-1
-1
-
3
-
3
3
3
A'
B'
A
B
O
x
t
y
s
MỤC LỤC
PHẦN ĐẠI SỐ VÀ MỘT SỐ YẾU TỐ GIẢI TÍCH .................................................................................... 1
VẤN ĐỀ 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC ......................................... 1
I. GÓC LƯỢNG GIÁC, ................................................................................................................................. 1
II. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC .................................................................... 2
III. CÔNG THC LƯỢNG GÁC ................................................................................................................. 3
IV. HÀM SỐ LƯƠNG GIÁC ......................................................................................................................... 4
CÁC DẠNG TOÁN THƯỜNG GẶP ............................................................................................................ 4
Dạng 1: Tìm tập xác định ............................................................................................................................ 4
Dạng 2: Xét tính chẵn lẻ .............................................................................................................................. 5
Dạng 3: Xét tính tuần hoàn ......................................................................................................................... 5
Dạng 4: Sự biến thiên .................................................................................................................................. 5
Dạng 5: Tìm giá trị lớn nhất– nhỏ nhất của hàm số lượng giác .................................................................. 6
V. PHƯƠNG TRNH LƯỢNG GIÁC CƠ BN ........................................................................................... 6
PHƯƠNG PHÁP KIỂM TRA ĐIỀU KIỆN XÁC ĐỊNH CỦA PHƯƠNG TRNH .................................. 7
VẤN ĐỀ 2. DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN ......................................................................... 8
I. DÃY SỐ ...................................................................................................................................................... 8
II. CẤP SỐ CỘNG – CẤP SỐ NHÂN ........................................................................................................... 8
VẤN ĐỀ 3. GIỚI HẠN, HÀM SỐ LIÊN TỤC .............................................................................................. 9
I. GIỚI HẠN CỦA DÃY SỐ.......................................................................................................................... 9
II. GIỚI HẠN CỦA HÀM SỐ........................................................................................................................ 9
PHƯƠNG PHÁP TÌM GIỚI HẠN .............................................................................................................. 9
III. HÀM SỐ LIÊN TỤC .............................................................................................................................. 11
CÁC DẠNG TOÁN THƯỜNG GẶP .......................................................................................................... 11
VẤN ĐỀ 4: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT ................................................................................. 12
I. PHÉP TNH LŨY THỪA ......................................................................................................................... 12
II. PHÉP TÍNH LÔGARIT ........................................................................................................................... 12
III. HÀM SỐ MŨ VÀ HÀM SỐ LÔGART................................................................................................ 12
IV. PHƯƠNG TRNH, BẤT PHƯƠNG TRNH MŨ, LÔGARIT .............................................................. 13
VẤN ĐỀ 5. ĐẠO HÀM .................................................................................................................................. 14
I. CÔNG THC ĐẠO HÀM ....................................................................................................................... 14
II. TIẾP TUYẾN........................................................................................................................................... 14
PHẦN HÌNH HỌC VÀ ĐO LƯỜNG ........................................................................................................... 16
VẤN ĐỀ 6. ĐƯƠNG THẲNG VÀ MẶT PHẲNG. QUAN HỆ SONG SONG KHÔNG GIAN ............. 16
I. CHNG MINH QUAN HỆ SONG SONG .............................................................................................. 16
II. TM GIAO TUYẾN CỦA 2 MẶT PHẲNG............................................................................................ 17
III. TM GIAO ĐIỂM CỦA ĐƯƠNG THẲNG VÀ MẶT PHẲNG. .......................................................... 17
IV. TM THIẾT DIỆN CỦA HNH CHÓP, LĂNG TRỤ ĐƯỢC CẮT BỞI MỘT MẶT PHẲNG ........... 18
VẤN ĐỀ 7. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN ............................................................. 19
I. CHNG MINH QUAN HỆ VUÔNG GÓC. ............................................................................................ 19
II. TÌM HNH CHIẾU CỦA ĐIỂM LÊN MẶT PHẲNG ............................................................................ 20
III. GÓC ........................................................................................................................................................ 20
IV. KHONG CÁCH.................................................................................................................................. 21
V. THỂ TCH KHỐI ĐA DIỆN ................................................................................................................... 22
ỨNG DỤNG THỂ TÍCH ........................................................................................................................... 23
CÁC DẠNG HÌNH CHÓP THƯỜNG GẶP .............................................................................................. 23
HÌNH CHÓP CỤT .................................................................................................................................... 25
CÁC DẠNG HÌNH LĂNG TRỤ THƯỜNG GẶP ...................................................................................... 26
PHẦN THỐNG KÊ, XÁC SUẤT ................................................................................................................. 27
VẤN ĐỀ 8. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CHO MẪU SỐ LIỆU GHÉP NHÓM
.......................................................................................................................................................................... 27
I. SỐ TRUNG BNH VÀ MỐT CỦA MẪU SỐ LIỆU GHÉP NHÓM ....................................................... 27
II. TRUNG VỊ VÀ T PHÂN VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM ................................................... 28
I. BIẾN CỐ GIAO VÀ QUY TẮC NHÂN XÁC SUẤT ............................................................................. 29
II. BIẾN CỐ HỢP VÀ QUY TẮC CỘNG XÁC SUẤT .............................................................................. 29
PHỤ LỤC ........................................................................................................................................................ 30
TỔ HỢP, XÁC SUẤT .................................................................................................................................... 30
I. QUY TẮC ĐẾM ....................................................................................................................................... 30
II. HOÁN VỊ – CHỈNH HỢP – TỔ HỢP ..................................................................................................... 30
III. NHỊ THC NIU-TƠN ........................................................................................................................... 30
IV.XÁC SUẤT ............................................................................................................................................. 31
THỐNG KÊ .................................................................................................................................................... 34
I. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU ......................................... 34
II. CÁC SỐ ĐẶC TRƯNG ĐO MC ĐỘ PHÂN TÁN CỦA MẪU SỐ LIỆU .......................................... 35
HÌNH HỌC PHẲNG ..................................................................................................................................... 37
I. HỆ THC LƯỢNG TRONG TAM GIÁC ............................................................................................... 37
II. HỆ THC LƯỢNG TRONG T GIÁC ................................................................................................. 37
III. HỆ THC LƯỢNG TRONG ĐƯỜNG TRÒN ..................................................................................... 38
IV. TÂM CỦA TAM GIÁC ......................................................................................................................... 38
HÌNH HỌC TỌA ĐỘ TRONG MẶT PHẲNG ........................................................................................... 39
I. TỌA ĐỘ .................................................................................................................................................... 39
II. PHƯƠNG TRNH ĐƯỜNG THẲNG ..................................................................................................... 39
III. PHƯƠNG TRNH ĐƯỜNG TRÒN....................................................................................................... 39
CHUÊN ĐỀ 1. PHÉP BIẾN HÌNH TRONG MẶT PHẲNG ..................................................................... 40
I. PHÉP TỊNH TIẾN .................................................................................................................................... 40
II. PHÉP ĐỐI XNG TÂM ......................................................................................................................... 40
III. PHÉP ĐỐI XNG TRỤC ...................................................................................................................... 40
IV. PHÉP QUAY .......................................................................................................................................... 40
V. PHÉP DỜI HNH .................................................................................................................................... 41
VI. PHÉP VỊ TỰ .......................................................................................................................................... 41
VII. PHÉP ĐỒNG DẠNG ............................................................................................................................ 41
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 1 0983.900.570
PHẦN ĐẠI SỐ VÀ MỘT SỐ YẾU TỐ GIẢI TÍCH
VẤN ĐỀ 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
I. GÓC LƯỢNG GIÁC,
1.Góc lượng giác
Định nghĩa:
Nếu một tia
Om
quay quanh gốc
O
của nó theo một chiều cố định bắt đầu từ vị trí tia
Oa
và dừng ở vị trí
tia
Ob
thì ta nói tia
Om
quét một góc lưọng giác có tia đầu
Oa
, tia cuối
Ob
, kí hiệu
( )
,Oa Ob
.
sin
cosin
cotang
tang
0 (rad)
π
2
3
π
2
π
7
π
4
5
π
4
7
π
6
11
π
6
5
π
3
4
π
3
5
π
6
3
π
4
2
π
3
π
3
π
4
π
6
-1
2
-1
2
-
2
2
-
2
2
2
2
1
2
2
2
1
2
3
2
3
2
-
3
2
-
3
2
-
3
3
-
3
3
1
1
1
3
3
3
3
-1
-1
-1
-1
-
3
-
3
3
3
A'
B'
A
B
O
x
t
y
s
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 2 0983.900.570
Công thức tổng quát số đo góc lượng giác:
( ) ( )
, .360Oa Ob a k k= +
2.Đơn vị radian
( )
180rad
=
Công thức đổi đơn vị góc:
180
a
=
Quy tắc đổi đơn vi góc:
a)Đổi từ radian sang độ: Lấy số đo radian nhân
180
và rút gọn. Nếu số đo radian có chứa
thì chỉ cần
thay
bằng
180
và rút gọn.
b)Đổi từ độ sang radian: Lấy số đo độ nhân
180
và rút gọn.
3.Đường tròn lượng giác
Trong mặt phẳng tọa độ
Oxy
, cho đường tròn tâm
O
bán
kính bằng 1. Trên đường tròn này, chọn điểm
( )
1;0A
làm gốc,
chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là
chiều cùng chiều kim đồng hồ. Đường tròn cùng vởi gốc và
chiều như trên được gọi là đường tròn lượng giác.
Cho số đo góc
bất kì. Trên đường tròn lượng giác, ta
xác định được duy nhất một điểm
M
sao cho số đo góc lượng
giác
(,OA OM
) bằng
. Khi đó điểm
M
được gọi là điểm biểu
diễn của góc có số đo
trên đường tròn lượng giác.
Chú ý:
Công thức
( )
*
0
2
,k k n
n

= +
xác định n điểm
biểu diễn cách đều nhau một khoảng góc
2
n
trên đường tròn lượng giác, trong đó có một điểm biểu diễn góc
0
II. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
1.Giá trị lượng giác
Trên đường tròn lượng giác, gọi
M
là điểm biểu diễn góc lượng giác
có số đo
. Khi đó:
Tung độ
M
y
của
M
gọi là
sin
của
, kí hiệu
sin
.
Hoành độ
M
x
của
M
gọi là côsin của
, kí hiệu
cos
.
Nếu
0
M
x
thì ti số
sin
cos
M
M
y
x
=
gọi là tang của
, kí hiệu
tan
Nếu
0
M
y
thì tỉ sô
cos
sin
M
M
x
y
=
gọi là côtang của
, kí hiệu
cot
.
2.Hệ thức cơ bản và giá trị lượng giác của các góc có liên quan đặc biệt
a)Hệ thức cơ bản
22
22
22
sin cos 1; tan .cot 1
11
1 tan ; 1 cot
cos sin
a a a a
aa
aa
+ = =
+ = + =
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 3 0983.900.570
b)Giá trị lượng giác của các góc có liên quan đặc biệt
Cos đối
( )
( )
( )
( )
sin sin
cos cos
tan tan
cot cot




− = −
−=
− = −
− = −
Sin bù
( )
( )
( )
( )
sin sin
cos cos
tan tan
cot cot
−=
− = −
− = −
− = −
Chéo phụ
sin cos , cos sin
22
tan cot , cot tan
22


− = − =
− = − =
Tang, Cotang hơn kém
( )
( )
( )
( )
sin sin
cos cos
tan tan
cot cot
+ = −
+ = −
+=
+=
III. CÔNG THC LƯỢNG GÁC
1)Công thức cộng
( )
( )
( )
sin sin .cos cos .sin
cos cos .cos sin .sin
tan tan
tan
1 tan .tan
a b a b a b
a b a b a b
ab
ab
ab
=
=
=
2)Công thức nhân đôi
22
2
2
2
sin 2 2sin .cos
cos2 cos sin
2cos 1
1 2sin
2tan
tan2
1 tan
a a a
a a a
a
a
a
a
a
=
=−
=−
=−
=
−
3)Công thức biến đổi tch thành tổng
( ) ( )
( ) ( )
( ) ( )
1
cos .cos cos cos
2
1
sin .sin cos cos
2
1
sin .cos sin sin
2
a b a b a b
a b a b a b
a b a b a b
= + + −


= − − +


= + + −


4)Công thức biến đổi tổng thành tch
cos cos 2cos .cos
22
cos cos 2sin .sin
22
sin sin 2sin .cos
22
sin sin 2cos .sin
22
a b a b
ab
a b a b
ab
a b a b
ab
a b a b
ab
+−
+=
+−
− = −
+−
+=
+−
−=
5)Công thức h bc
2
1 cos2
cos
2
a
a
+
=
2
1 cos2
sin
2
a
a
−
=
2
1 cos2
tan
1 cos2
a
a
a
−
=
+
Quy tắc biển đổi lượng giác: Tùy theo các dấu hiệu mà áp dụng công thức thích hợp.
a)Không làm thay đổi góc → Hệ thức cơ bản
b)Góc là tổng hoặc hiệu → Công thức cộng
c)Góc có hệ số chẵn→ Công thức nhân đôi
d)Giá trị lượng giác có mũ chẵn→ Công thức hạ bậc
e)Có tích sin, cosin→ Công thức biến đổi tích thành tổng
f)Có tổng, hiệu sin, cosin→ Công thức biến đổi tổng thành tích
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 4 0983.900.570
IV. HÀM SỐ LƯƠNG GIÁC
1.
sinyx=
2.
cosyx=
TXĐ:
D =
. TGT:
1;1T =−
Tính chẵn lẻ: Là hàm lẻ Đồ thị đối xứng qua gốc
tọa độ
Tính tuần hoàn: Tuần hoàn với chu kì
2
Sự biến thiên: Đồng biến trên
;
22


−


; Nghịch
biến trên
3
;
22




Đồ thị:
TXĐ:
D =
. TGT:
1;1T =−
Tính chẵn chẵn: Là hàm lẻ Đồ thị đối xứng qua
trục tung.
Tính tuần hoàn: Tuần hoàn với chu kì
2
Sự biến thiên: Nghịch biến trên
( )
0;
; Đồng biến
trên
( )
;

Đồ thị:
3.
tanyx=
4.
cotyx=
TXĐ:
\/
2
D k k

= +


. TGT:
T =
Tính chẵn lẻ: Là hàm lẻ Đồ thị đối xứng qua gốc
tọa độ
Tính tuần hoàn: Tuần hoàn với chu kì
Sự biến thiên: Luôn đồng biến trên từng khoảng xác
định
;
22


−


;
3
;
22




Đồ thị:
TXĐ:
\/D k k
=
. TGT:
T =
Tính chẵn lẻ: Là hàm lẻ Đồ thị đối xứng qua gốc
tọa độ
Tính tuần hoàn: Tuần hoàn với chu kì
Sự biến thiên: Luôn nghịch biến trên từng khoảng
xác định
( )
0;
;
( )
;

Đồ thị:
CÁC DẠNG TOÁN THƯỜNG GẶP
Dng 1: Tìm tp xác định
1.Phương pháp:
B1: Lập điều kiện xác định (ĐKXĐ):
u
v
xác định khi
0v
u
xác định khi
0u
tanu
xác định khi
( )
,
2
u k k
+
cot u
xác định khi
( )
,u k k

B2: Giải ĐKXĐ → Tìm điều kiện của biến
B3: Tùy theo ĐK của biến, Ta kết luận TXĐ như sau:
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 5 0983.900.570
......
xa
xb
→
\ ; ;...D a b=
a x b
→
(
;D a b=
......
xa
xb
=
=
→
; ;...D a b=
Dng 2: Xét tnh chẵn lẻ
1.Định nghĩa:
( )
fx
là hàm chẵn
( ) ( )
,f x f x x D− =
( )
fx
là hàm lẻ
( ) ( )
,f x f x x D− = −
2.Tính chất:
2n
x
→ Chẵn;
21n
x
+
→ Lẻ
Hằng số → Chẵn
( )
fx
Chẵn
( )
f ax
Chẵn
( )
fx
Lẻ
( )
f ax
Lẻ
Chẵn Chẵn → Chẵn
Lẻ Lẻ → Lẻ
Chẵn Lẻ → Không Chẵn, Không Lẻ
Chẵn x() Chẵn → Chẵn
Lẻ x() Lẻ → Chẵn
Chẵn x() Lẻ → Lẻ
(Chẵn)
n
→ Chẵn
(Lẻ)
2n+1
→Lẻ
(Lẻ)
2n
→Chẵn
k.Chẵn → Chẵn
k.Lẻ → Lẻ
|Chẵn| → Chẵn; |Lẻ| → Chẵn
f Lẻ, g Chẵn
( )
fg
Chẵn
f Lẻ, g Lẻ
( )
fg
Lẻ
f Chẵn, g Chẵn (hay Lẻ)
( )
fg
Chẵn
Dng 3: Xét tnh tuần hoàn
1.Định nghĩa:
( )
fx
tuần hoàn với chu kì T Tồn tại số T dương nhỏ nhất sao cho:
( ) ( )
f x T f x=
2.Tính chất:
1
sin , cosy x y x==
tuần hoàn chu kì
2T
=
tan , coty x y x==
tuần hoàn chu kì
T
=
2
Nếu
( )
fx
tuần hoàn với chu kì T thì
( )
f ax b+
tuần hoàn với chu kì
'
T
T
a
=
( ) ( )
sin , cosy ax b y ax b= + = +
tuần hoàn chu kì
2
T
a
=
( ) ( )
tan , coty ax b y ax b= + = +
tuần hoàn chu kì
T
a
=
3
Nếu
sin , cosy u y u==
tuần hoàn chu kì
T
thì
22
sin , cosy u y u==
tuần hoàn chu kì
2
T
và
33
sin , cosy u y u==
tuần hoàn chu kì
T
Nếu
tan , coty u y u==
tuần hoàn chu kì
T
thì
22
tan , coty u y u==
và
33
tan , coty u y u==
tuần hoàn chu kì
T
4
Nếu
( )
fx
,
( )
gx
lần lượt tuần hoàn với chu kì
1
T
,
2
T
và
1
2
T
m
Tn
=
(tối giản)
thì
( ) ( )
f x g x
,
( ) ( )
( )
( )
.,
fx
f x g x
gx
tuần hoàn với chu kì
( )
*
12
..
,,
nT mT
T m n k
kk
= =
Nếu
1
T
,
2
T
là các số nguyên dương thì
( ) ( )
1 2 1 2
11
,,T BCNN T T LCM T T
kk
==
(Máy tính cầm tay)
Tổng, hiệu của 2 hàm sin, cos có chu kì tuần hoàn
T (như trên) với
1k =
Tích, thương của 2 hàm sin, cos có chu kì tuần
hoàn T (như trên) với với
2k =
Dng 4: Sự biến thiên
1.Hàm số lượng giác sơ cấp:
Hàm số
Chiều biến thiên
Khoảng (Trên ĐƯỜNG THẲNGLG)
sinyx=
Nghịch biến
Bên trái Oy
Đồng biến
Bên phải Oy
cosyx=
Nghịch biến
Phía trên Ox
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 6 0983.900.570
Đồng biến
Phía dưới Ox
tanyx=
Luôn Đồng biến
Không chứa
( )
,
2
x k k
= +
cotyx=
Luôn Nghịch biến
Không chứa
( )
,x k k
=
2.Tính chất cơ bản: Trên K
Hệ số a
( )
y f x=
( )
.y a f x b=+
0a
Đồng biến (Nghịch biến)
Đồng biến (Nghịch biến)
0a
Đồng biến (Nghịch biến)
Nghịch biến (Đồng biến)
Dng 5: Tìm giá trị lớn nhất– nhỏ nhất của hàm số lượng giác
1.Định nghĩa:
( )
( )
( )
00
,
max
:
K
f x M x K
f x M
x K f x M
=
=
( )
( )
( )
00
,
min
:
K
f x m x K
f x m
x K f x m
=
=
2.Phương pháp: Chặn hàm số
B1: Biến đổi hàm số đã cho đến khi chỉ còn chứa 1 HSLG (nếu được)
B2: Dùng Bất đẳng thức LG và Tính chất Bất đẳng thức → Biến đổi về dạng:
( )
m f x M
B3: Dùng định nghĩa → Xác định GTLN–GTNN:
( )
( )
min
min
K
K
f x m
f x M
=
=
3.Bất đẳng thức LG:
1 sin 1u−
1 cos 1u−
2
0 sin 1u
2
0 cos 1u
0 sin 1u
0 cos 1u
2
tan 0u
2
cot 0u
4.Tính chất Bất đẳng thức:
A B A C B C + +
AB
A C B D
CD
+ +
22
0
AB
AB
AB
( )
( )
. . 0
. . 0
AC B C C
AB
AC BC C



0
..
0
AB
AC B D
CD



33
33
AB
AB
AB

1
0 1 1A
A
1 1 1
00A B C
A B C
V. PHƯƠNG TRNH LƯỢNG GIÁC CƠ BN
Dng
( )
f u m=
Dng
( ) ( )
f u f v=
( )
( )
1
sin , ( 1 1)
sin sin , sin
2
,
2
u m m
um
uk
k
uk


−
= −
= =
=+

= − +
2
sin sin
2
u v k
uv
u v k

=+
=
= − +
( )
( )
1
cos , ( 1 1)
cos cos , cos
2
,
2
u m m
um
uk
k
uk



−
= −
= =
=+

= − +
cos cos 2u v u v k
= = +
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 7 0983.900.570
( )
( )
1
tan
tan tan , tan
,
um
um
u k k


−
=
= =
= +
tan tanu v u v k
= = +
1
cot
1
cot cot , tan
,
um
u
m
u k k


−
=


= =




= +
cot cotu v u v k
= = +
Trường hợp đặc biệt: Đối với phương trình
sin , cosu m u m==
Nếu
1m =
thì chỉ cần lấy 1 trong 2 công thức nghiệm.
Nếu
0m =
thì chỉ cần lấy 1 trong 2 công thức nghiệm và thay
2k
thành
k
Cụ thể:
sin 1 2
2
u u k
= = +
sin 1 2
2
u u k
= − = − +
sin 0u u k
= =
cos 1 2u u k
= =
cos 1 2u u k

= − = +
cos 0
2
u u k
= = +
PHƯƠNG PHÁP KIỂM TRA ĐIỀU KIỆN XÁC ĐỊNH CỦA PHƯƠNG TRÌNH
Bước 1. Xác định điểm biểu diễn công thức điều kiện xác định của phương trình và công thức nghiệm lên
Đường tròn lượng giác
Bước 2. Loại bỏ điểm biểu diễn trùng của công thức nghiệm so với điểm biểu diễn của điều kiện xác định.
Bước 3. Kết luận: Nghiệm của phương trình là công thức tổng quát xác định những điểm biểu diễn còn
lại.
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 8 0983.900.570
VẤN ĐỀ 2. DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN
I. DÃY SỐ
1.Định nghĩa
Dãy số là hàm số với đối số là số tự nhiên
2.Dãy số tăng, dãy số giảm
( )
n
u
là dãy số tăng
*
1
,
nn
u u n
+
;
( )
n
u
là dãy số giảm
*
1
,
nn
u u n
+
3.Dãy số bị chặn
( )
n
u
là dãy số bị chặn trên
*
:,
n
M u M n
.
( )
n
u
là dãy số bị chặn dưới
*
:,
n
m u m n
.
( )
n
u
là dãy số bị chặn
*
, : ,
n
m M m u M n
.
II. CẤP SỐ CỘNG – CẤP SỐ NHÂN
Cấp số cộng
Cấp số nhân
Định nghĩa
Dãy số
( )
n
u
là cấp số cộng
( )
*
1
,
nn
u u d n
+
= +
Dãy số
( )
n
u
là cấp số nhân
( )
*
1
,
nn
u u q n
+
=
Số hạng tổng quát
( )
*
1
( 1) ,
n
u u n d n= + −
( )
1*
1
.,
n
n
u u q n
−
=
Tính chất
( )
*
11
, 2 ,
2
kk
k
uu
u k k
−+
+
=
( )
2*
11
. , 2 ,
k k k
u u u k k
−+
=
Tổng n số hạng đầu
tiên
12
...
nn
S u u u= + + +
1
()
2
n
n
n u u
S
+
=
1
2 ( 1)
2
n
n
S u n d= + −
1
Khi 1:
n
q S nu==
1
1
1: .
1
n
n
q
q S u
q
−
=
−
Khi
Công sai, công bội
1nn
d u u
+
=−
;
km
uu
d
km
−
=
−
1n
n
u
q
u
+
=
;
km
k
m
u
q
u
−
=
CÁCH TÌM SỐ HẠNG DÃY SỐ TRUY HỒI BẰNG MÁY TÍNH CẦM TAY
DẠNG 1:
( )
( )
1
1
:
,
n
nn
u
u
u f u n
+
=
→ Công thức MTBT:
( )
1: , 1x x A f A x= + = −
→ CALC:
1
1;x A u==
Vi dụ:
( )
1
1
2
:
32
n
nn
u
u
u u n
+
=
=−
→
→ Tính được
2
4u =
,….. →
Tiếp tục tính được số
hạng tùy ý
DẠNG 2:
( )
( )
12
21
,
:
,,
n
n n n
uu
u
u f u u n
++
=
→ Công thức MTBT:
( )
1: , , 2 : :x x C f A B x A B B C= + = − = =
→ CALC:
12
1, ,x A u B u= = =
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 9 0983.900.570
VẤN ĐỀ 3. GIỚI HẠN, HÀM SỐ LIÊN TỤC
I. GIỚI HẠN CỦA DÃY SỐ
Giới hn hữu hn
Giới hn vô cực
1. Giới hạn đặc biệt:
•
1
lim 0
n
n
→+
=
;•
1
lim 0 ( )
k
n
k
n
+
→+
=
•
lim 0 ( 1)
n
n
qq
→+
=
; •
lim
n
CC
→+
=
2. Định lí: Cho
lim , lim
nn
u a v b==
. Ta có:
•
( )
lim
nn
u v a b =
•
( )
lim . .
nn
u v ab=
•
lim
n
n
u
a
vb
=
(nếu
0b
) •
lim
n
ua=
•
lim
n
ua=
(
,0
n
ua
)
3. Tổng của cấp số nhân lùi vô hạn
2
1
1
11
1
u
q
S u u q u q= + + + =
−
( )
1q
1. Giới hạn đặc biệt:
•
lim ( )
k
nk
+
= +
•
lim n = +
•
lim ( 1)
n
qq= +
2. Định lí:(Quy tắc về giới hạn vô cực)
0
a
n
n
u
v
→
;
0
0
a
n
n
u
v
→
;
0
[ . ]
a
nn
uv


→
(Dấu của giới hạn vô cực được xác định theo quy
tắc nhân dấu)
II. GIỚI HẠN CỦA HÀM SỐ
Giới hn hữu hn
Giới hn vô cực, giới hn ti vô cực
1. Giới hạn đặc biệt:
• ;•
0
lim
xx
CC
→
=
(C là hằng số)
2. Định lí: Cho , . Ta có:
• ; •
• ; • (nếu
0M
)
•
( )
( )
0fx
•
3. Giới hạn một bên:
1. Giới hạn đặc biệt:
• ; •
•
lim
x
CC
→
=
; •
2. Định lí: (Quy tắc về giới hạn vô cực)
()
0
()
L
fx
gx
→
;
0
0
()
()
L
fx
gx
→
;
0
[ ( ). ( )]
L
f x g x


→
(
0
hayx x x→ →
)
(Dấu của giới hạn vô cực được xác định theo quy
tắc nhân dấu)
PHƯƠNG PHÁP TM GIỚI HẠN
Dng vô định : ( Là giới hạn của thương mà tử và mẫu đều có giới hạn bằng 0:
0
0
()
()
fx
gx
)
a)Cách khử: Biến tử và mẫu thành tích rồi đơn giản (hết) nhân tử chung
b)Sơ đồ Hoocner: Dùng để tính giá trị đa thức hay phân tích đa thức thành nhân nhân tử.
1
a
Cộng
Bằng
0
x
Nhân
0
b
1 0 0 1
.b x b a=+
Cho
( )
1
0 1 1
. . ... .
nn
nn
f x a x a x a x a
−
−
= + + + +
có nghiệm
0
xx=
Hệ số
Nghiệm
0
a
1
a
2
a
…
1n
a
−
n
a
0
x
00
ba=
1 0 0 1
.b x b a=+
2 0 1 2
.b x b a=+
…
1 0 2 1
.
n n n
b x b a
− − −
=+
01
.0
n n n
b x b a
−
= + =
1n
x
−
2n
x
−
3n
x
−
0
1x =
0
0
lim
xx
xx
→
=
0
lim ( )
xx
f x L
→
=
0
lim ( )
xx
g x M
→
=
0
lim ( ) ( )
xx
f x g x L M
→
+ = +
0
lim ( ) ( )
xx
f x g x L M
→
− = −
0
lim ( ). ( ) .
xx
f x g x L M
→
=
0
()
lim
()
xx
f x L
g x M
→
=
0
lim ( )
xx
f x L
→
=
0
lim ( )
xx
f x L
→
=
0
lim ( )
xx
f x L
→
=
00
lim ( ) lim ( )
x x x x
f x f x L
−+
→→
==
lim
k
x
x
→+
= +
lim
k
x
neáu k chaün
x
neáu k leû
→−
+
=
−
lim 0
k
x
c
x
→
=
0
0
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 10 0983.900.570
Khi đó:
( ) ( )
( )
1 1 2
0 1 1 0 0 1 2 1
. . ... . . . ... .
n n n n
n n n n
f x a x a x a x a x x b x b x b x b
− − −
− − −
= + + + + = − + + + +
CÁC DẠNG THƯỜNG GẶP
Dạng 1.1: Giới hạn của phân thức hữu tỷ tại một điểm:
( )
( )
0
lim
xx
fx
gx
→
, với
( ) ( )
,f x g x
là các đa thức và
( ) ( )
00
0x g xf ==
PP: Phân tích cả tử và mẫu thành nhân tử và rút gọn nhân tử chung:
( )
( )
( ) ( )
( ) ( )
( )
( )
0 0 0
0
0
.
lim lim lim ...
.
x x x x x x
f x x x u x u x
g x x x v x v x
→ → →
−
= = =
−
VD:
Dạng 1.2:
( )
( )
0
lim
xx
fx
gx
→
, với
( ) ( )
,f x g x
là các biểu thức chứa căn cùng bậc và
( ) ( )
00
0x g xf ==
PP: Nhân biểu thức liên hợp (tương ứng) ở tử và mẫu để khử căn → Biến thành tích rồi đơn giản nhân tử
chung.
( )( )
( ) ( )
0 0 0
2
lim lim lim ...
..
x x x x x x
A B A B
A B A B
C
C A B C A B
→ → →
−+
−−
= = =
++
VD:
Dng vô định : (Là giới hạn của thương mà tử và mẫu đều có giới hạn vô cực:
()
()
fx
gx
)
CÁC DẠNG THƯỜNG GẶP
Dạng 2.1:
( ) ( )
,f x g x
là các đa thức →PP: Chia cả tử và mẫu cho luỹ thừa cao nhất của x.
VD:
Dạng 2.2:
( ) ( )
,f x g x
có chứa lũy thừa
k
x
và căn thức →PP: Rút lũy thừa cao nhất ra khỏi các căn rồi
chia cả tử và mẫu cho luỹ thừa cao nhất của x.
VD:
2
22
3
2
2 3 2 3
lim lim lim 1
33
3
. 1 . 1 1
x x x
xx
x
xx
xx
xx
→− →− →−
−
−−
= = = −
+−
− + − − + −
Giới hn của tổng, hiệu: (Chứa lũy thừa
k
x
)
CÁC DẠNG THƯỜNG GẶP
Dạng 3.1: Giới hạn tại vô cực của tổng, hiệu mà tổng hệ số các lũy thừa bậc cao nhất khác 0
PP: Rút lũy thừa bậc cao nhất làm nhân tử chung đưa về tích → Áp dụng quy tắc giới hạn của tích:
0
[ ( ). ( )]
L
f x g x


→
VD:
(
)
2
1
lim 2 lim 1 2
xx
x x x x
x
→− →−


+ − = − + − = −






Dạng 3.2: Giới hạn tại vô cực của tổng, hiệu mà tổng hệ số các lũy thừa bậc cao nhất bằng 0 (Dạng này
thường có căn)
3 2 2
2
2 2 2
8 ( 2)( 2 4) 2 4 12
lim lim lim 3
( 2)( 2) 2 4
4
x x x
x x x x x x
x x x
x
→ → →
− − + + + +
= = = =
− + +
−
( )( )
( )
0 0 0
2 4 2 4 2 4 1 1
lim lim lim
4
24
24
x x x
x x x
x
x
xx
→ → →
− − − − + −
= = =
+−
+−
2
2
2
2
53
2
2 5 3
lim lim 2
63
63
1
xx
xx
x
x
xx
x
x
→+ →+
+−
+−
==
++
++
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 11 0983.900.570
PP: Nhân chia biểu thức liên hợp để khử căn → Ta được giới hạn dạng vô định
VD:
III. HÀM SỐ LIÊN TỤC
1.Hàm số liên tục ti một điểm
( )
y f x=
liên tục tại
0
x
( ) ( )
0
0
lim
xx
f x f x
→
=
( )
y f x=
liên tục tại
0
x
( ) ( ) ( )
00
0
lim lim
x x x x
f x f x f x
−+
→→
==
2.Hàm số liên tục trên một khoảng
Hàm số liên tục trên một khoảng khi hàm số liên tục tại mọi điểm thuộc khoảng đó.
3.Hàm số liên tục trên một đon
Hàm số
( )
y f x=
liên tục trên một đoạn
;ab
nếu
( )
y f x=
liên tục trên
( )
;ab
và
( ) ( )
lim
xa
f x f a
+
→
=
( ) ( )
lim
xb
f x f b
−
→
=
4.Tnh chất
• Hàm số đa thức liên tục trên .
• Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
• Tổng hiệu, hiệu, tích, thương của các hàm số liên tục tại một điểm là hàm số liên tục tại điểm đó.
CÁC DẠNG TOÁN THƯỜNG GẶP
Dng 1: Xét tính liên tục của hàm số 𝒚 = 𝒇
(
𝒙
)
ti điểm 𝒙
𝟎
:
B1: Tính
( )
0
fx
.
B2: Tính
( )
0
lim
xx
fx
→
(Hay tính
( ) ( )
00
lim , lim
x x x x
f x f x
+−
→→
)
B3: So sánh ,
( )
0
fx
→ Kết luận.
Dng 2: Tìm tham số để hàm số 𝒚 = 𝒇
(
𝒙
)
liên tục ti điểm 𝒙
𝟎
:
B1: Tính
( )
0
fx
.
B2: Tính
( )
0
lim
xx
fx
→
(Hay tính
( ) ( )
00
lim , lim
x x x x
f x f x
+−
→→
)
B3: Cho =
( )
0
fx
(Hay cho
( ) ( ) ( )
00
0
lim lim
x x x x
f x f x f x
+−
→→
==
)→ Giải PT, HPT tìm tham số.
( )
( )( )
1 1 1
lim 1 lim lim 0
11
x x x
x x x x
xx
x x x x
→+ →+ →+
+ − + +
+ − = = =
+ + + +
0
lim ( )
xx
fx
→
0
lim ( )
xx
fx
→
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 12 0983.900.570
VẤN ĐỀ 4: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
I. PHÉP TNH LŨY THỪA
. .....
n
a a a a•=
(tích của n thừa số a)
( )
( )
0
1 , 0
1
, 0
n
n
aa
aa
a
−
• =
• =
.
m n m n
a a a
+
•=
m
mn
n
a
a
a
−
•=
( . ) .
n n n
ab a b•=
n
n
n
aa
bb

•=


.
( ) ( )
m n n m m n
a a a• = =
1
m
n
m
n
n
n
aa
aa
•=
•=
1a
:
( ) ( )
( ) ( )
f x g x
a a f x g x
01a
:
( ) ( )
( ) ( )
f x g x
a a f x g x
II. PHÉP TÍNH LÔGARIT
log
( , 0; 1)
a
b a b
a b a
• = =

log 1 0
a
•=
log 1
a
a•=
( )
log
a
a
•=
a
log
b
ab•=
1 2 1 2
1
12
2
log ( . ) log log
log log log
a a a
a a a
b b b b
b
bb
b
• = +

• = −


( )
log .log
aa
bb
•=
1
log log
a
a
bb
•=
log
log
log
1
log
log
c
a
c
a
b
b
b
a
b
a
•=
•=
log .log log
c a c
a b b•=
( )
log log
a
a
bb
•=
1a
:
log ( ) log ( )
( ) ( ) 0
aa
f x g x
f x g x
01a
:
log ( ) log ( )
0 ( ) ( )
aa
f x g x
f x g x
III. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARÍT
1. Hàm số mũ
x
ya=
( )
01a
1a
TXĐ:
D =
. TGT:
( )
0;T = +
.
Hàm số luôn đồng biến
Tiệm cận ngang là trục Ox
Đồ thị nằm phía trên trục hoành
01a
TXĐ:
D =
. TGT:
( )
0;T = +
.
Hàm số luôn nghịch biến
Tiệm cận ngang là trục Ox
Đồ thị nằm phía trên trục hoành
2. Hàm số logarit
log
a
yx=
,
( )
01a
1a
TXĐ:
( )
0;D = +
. TGT:
T =
.
Hàm số luôn đồng biến
Tiệm cận đứng là trục Oy
Đồ thị nằm phía bên phải trục tung
01a
TXĐ:
( )
0;D = +
. TGT:
T =
Hàm số luôn nghịch biến
Tiệm cận đứng là trục Oy
Đồ thị nằm phía bên phải trục tung
Chú ý : Đồ thị hàm số
x
ya=
và
log
a
yx=
(hai hàm ngược nhau) đối xứng nhau qua đường thẳng
yx=
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 13 0983.900.570
ĐIỀU KIỆN XÁC ĐỊNH CỦA HÀM SỐ MŨ, HÀM SỐ LOGARIT
Hàm số
Điều kiện xác định
Hàm mũ:
u
ya=
01a
u

Hàm logarit:
log
a
yu=
01
0
a
u

IV. PHƯƠNG TRNH, BẤT PHƯƠNG TRNH MŨ, LÔGARIT
Mũ
Logarit
Dng
,( 0 1 ),
u
a b a a=
0b
: Phương trình vô nghiệm
0 b
:
log
u
a
a b u b= =
Chú ý:
uv
a a u v= =
Dng
( )
log , 0, 1
a
u b a a=
Điều kiện:
0u
log
b
a
u b u a= =
Chú ý:
log log
aa
u v u v= =
(Điều kiện:
0; 0uv
)
Dng
,( 0 1 ),
u
a b a a
0b
: Bất phương trình có nghiệm với mọi
u
thỏa
điều kiện xác định.
0 b
:
log
u
a
a b u b
, khi
1a
log
u
a
a b u b
, khi
01a
Chú ý: Tương tự cho các bất phương trình:
0
u
a
;
0
u
a
;
0
u
a
Tổng quát
, khi 1
uv
a a u v a
, khi 0 1
uv
a a u v a
Dng
( )
log , 0, 1
a
u b a a
Điều kiện:
0u
log
b
a
u b u a
, khi
1a
log
b
a
u b u a
, khi
01a
Chú ý: Tương tự cho các bất phương trình:
log
a
ub
;
log
a
ub
;
log
a
ub
Tổng quát
log log , khi 1
aa
u v u v a
log log , khi 0 1
aa
u v u v a
(Điều kiện:
0; 0uv
)
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 14 0983.900.570
VẤN ĐỀ 5. ĐẠO HÀM
I. CÔNG THC ĐẠO HÀM
Hàm sơ cấp
Hàm hợp
Phép toán
( )
( )
( )
( )
1
2
0
1
.
1
2.
11
nn
C
x
x n x
x
x
xx
−
=
=
=
=
−

=


( ) ( )
.f u f u u

=


( )
( )
1
2
..
2.
1
nn
u nu u
u
u
u
u
uu
−
=
=
−

=


( )
( )
2
. . .
..
u v u v
u v u v u v
u u v v u
vv

=

=+

−

=


( )
2
..
.
k v k v
k k v
vv
=
−

=


(
k
là hằng số)
( )
( )
( )
( )
2
2
sin cos
cos sin
1
tan
cos
1
cot
sin
xx
xx
x
x
x
x
=
=−
=
−
=
( )
( )
( )
( )
2
2
sin .cos
cos .sin
tan
cos
cot
sin
u u u
u u u
u
u
u
u
u
u
=
=−
=
−
=
Đặc biệt
1
1
nn
n
xx
+
−

=


2
()
ax b ad bc
cx d cx d
+−

=

++

( )
( )
2
2
2
2adx aex bc cd
ax bx c
dx e
dx e
+ + −

++
=

+
+

( )
.ln
xx
a a a
=
( )
xx
ee
=
( )
.ln .
uu
a a a u
=
( )
.
uu
e e u
=
( )
1
log
.ln
a
x
xa
=
( )
1
ln x
x
=
( )
log
.ln
a
u
u
ua
=
( )
ln
u
u
u
=
QUY TẮC TM ĐẠO HÀM
Khi tìm đạo hàm của hàm số ta thực hiện theo thứ tự ưu tiên như sau:
PHÉP TOÁN
→
HÀM HỢP
→
SƠ CẤP.
II. TIẾP TUYẾN
1. Định lý
Phương trình tiếp tuyến của đường cong
( ) ( )
:C y f x=
tại tiếp điểm
( )
0 0
; M x y
có dạng:
( )
00
.y y k x x− = −
(*)
Trong đó:
0
x
: Hoành độ tiếp điểm;
( )
00
y y x=
: Tung độ tiếp điểm;
( )
0
k f x
=
: Hệ số góc của tiếp tuyến.
2. Quy tắc lp phương trình tiếp tuyến của đường cong
( )
y f x=
B1. Tìm đạo hàm
( )
''y f x=
B2. Dựa vào giả thiết, tính
( )
0 0 0
, , x y f x
.
B3. Thay vào phương trình (*), thu gọn, ta được phương trình tiếp tuyến cần tìm (Chú ý: So điều kiện, loại
phương trình nếu có)
3. Chú ý
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 15 0983.900.570
Đường thẳng
( )
:d y ax b=+
→ Hệ số góc
d
ka=
;
Đường thẳng
( )
:0d ax by c+ + =
.→ Hệ số góc
d
a
k
b
−
=
.
'
'
dd
d d k k=
;•
'
' . 1
dd
d d k k⊥ = −
4. Các dng phương trình tiếp tuyến
Giả thiết
Theo GT, Ta có:
Các đại lượng cần tính
Biết hoành độ tiếp điểm
0
x
Tính:
( )
00
y y x=
,
( )
0
k f x
=
Biết tung độ tiếp điểm
0
y
Từ:
( )
00
y y x=
→ Tính được
0
x
và
( )
0
k f x
=
Biết hệ số góc của tiếp
tuyến
k
Từ:
( )
0
k f x
=
→ Tính được
0
x
và
( )
00
y y x=
Biết tiếp tuyến song song
đường thẳng
( )
d
d
kk=
Từ:
( )
0
k f x
=
→ Tính được
0
x
và
( )
00
y y x=
(Chú ý loại phương trình tiếp tuyến trùng phương
trình đường thẳng d)
Biết tiếp tuyến vuông góc
đường thẳng
( )
d
1
.1
d
d
k k k
k
−
= − =
Từ:
( )
0
k f x
=
→ Tính được
0
x
và
( )
00
y y x=
Biết tiếp tuyến qua
( )
;
AA
A x y
( ) ( ) ( )
0 0 0
.
AA
y y x y x x x
− = −
Giải tìm
0
x
→ Tính
( )
00
y y x=
,
( )
0
k f x
=
Tiếp tuyến tại giao điểm
của
( ) ( )
:C y f x=
và
( )
:d y ax b=+
( )
00
f x ax b=+
Giải tìm
0
x
→ Tính
( )
00
y y x=
,
( )
0
k f x
=
Tiếp tuyến tại giao điểm
của
( )
C
và
Ox
0
0y =
Từ:
( )
00
y y x=
→ Tính được
0
x
và
( )
0
k f x
=
Tiếp tuyến tại giao điểm
của
( )
C
và
Oy
0
0x =
Tính:
( )
00
y y x=
,
( )
0
k f x
=
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 16 0983.900.570
PHẦN HÌNH HỌC VÀ ĐO LƯỜNG
VẤN ĐỀ 6. ĐƯƠNG THẲNG VÀ MẶT PHẲNG. QUAN HỆ SONG SONG KHÔNG GIAN
I. CHNG MINH QUAN HỆ SONG SONG
1. Chứng minh hai đường thẳng song song
Sử dụng kết quả hình học phẳng để chứng minh
a)Hình thang: Hai cạnh đáy song song
b)Các dạng hình bình hành (hình bình hành thường, hình thoi, hình chữ nhật, hình vuông): Hai cặp cạnh
đối song song và bằng nhau.
c)Đường trung bình:
Đường trung bình của tam giác: Đoạn thẳng nối trung điểm hai cạnh, song song và bằng nửa cạnh còn
lại.
Đường trung bình hình bình hành: Đoạn thẳng nối trung điểm hai cạnh đối, song song và bằng hai cạnh
còn lại.
Đường trung bình hình thang: Đoạn thẳng nối hai cạnh bên, song song và bằng trung bình cộng hai cạnh
đáy.
d)Định lý Thalès trong tam giác
Một đường thẳng chắn hai cạnh của tam giác theo các đoạn thẳng tương
ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại và ngược lại
AM AN
MN BC
AB AC
=
2. Chứng minh đường thẳng song song mặt phẳng
Cách
1
ĐL: Nếu đường thẳng d không
chứa trong mặt phẳng
( )
và
song song với đường thẳng d'
chứa trong mặt phẳng
( )
thì
đường thẳng d song song với
mặt phẳng
( )
.
()
'
' ( )
()
d
dd
d
d
Cách
2
ĐL: Nếu 2 mặt phẳng song
song thì mọi đường thẳng nằm
trong mặt phẳng này đều song
song với mặt phẳng kia.
()
( ) ( )
()
d
d
3. Chứng minh 2 mặt phẳng song song
Cách
1
ĐL: Nếu mặt phẳng này có
chứa 2 đường thẳng cắt nhau
cùng song song với mặt phẳng
kia thì hai mặt phẳng song song
nhau.
( )
( ) ,
,
( ) ( )
ab
a b I
ab
=
N
M
A
B
C
N
M
B
C
D
A
N
M
A
D
C
B
d'
d
α
d
β
α
b
a
α
β
I
C
B
A
N
M
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
2024-2025 17 0983.900.570
Cách
2
HQ: Nếu mặt phẳng này có
chứa 2 đường thẳng cắt nhau
lần lượt song song 2 đường
thẳng chứa trong mặt phẳng kia
thì hai mặt phẳng song song
nhau.
, ( )
', '
', ' ( )
( ) ( )
ab
a b I
a a b b
ab
=
II. TM GIAO TUYẾN CỦA 2 MẶT PHẲNG.
Cách
1
Tìm 2 điểm chung phân biệt
của 2 mặt phẳng
→
Giao tuyến
là đường thẳng đi qua 2 điểm
chung đó
( ) ( )
( ) ( )
( ) ( )
A
B
AB
AB





=
Cách
2
Tìm 1 điểm chung của 2 mặt
phẳng và chứng tỏ trong 2 mặt
phẳng lần lượt có chưa 2
đường thẳng song song nhau
→
Giao tuyến là đường thẳng
đi qua điểm chung và song
song 2 đường thẳng đó.
( ) ( )
( ) ( )
( ) ( ) ( )
,
I
ab
ab
Ix Ix a b





=
Cách
3
Tìm 1 điểm chung của 2 mặt
phẳng và chứng tỏ trong mặt
phẳng này có chưa 1 đường
thẳng song song với mặt phẳng
kia
→
Giao tuyến là đường
thẳng đi qua điểm chung và
song song đường thẳng đó.
( ) ( )
( )
( )
( ) ( ) ( )
I
a
a
Ix Ix a



=
III. TM GIAO ĐIỂM CỦA ĐƯƠNG THẲNG VÀ MẶT PHẲNG.
TH1
Nếu trong
( )
có chứa sẵn
đường thẳng a cắt b tại I thì I
là giao điểm của b và
( )
.
( )
( )
a
a b I
bI
=
=
a
b
a'
b'
β
α
I
d
β
α
B
A
d
a
b
α
β
I
d
a
α
β
I
Tìm giao
tuyến hai
mặt phẳng
Tìm một
điểm chung
Có một điểm chung
khác
Giao tuyến là đường
thẳng qua hai điểm
chung
Có hai đường thẳng
song song lần lượt chắ
trong hai mặt phảng
Gaio tuyến là đường
thẳng qua điểm
chung và song song
voiws hai đường
thẳng đó
Có một đường thẳng
nằm trong mặt phẳng
này và song song với
mặt phẳng kia
Giao tuyến là đường
thẳng qua điểm
chung và song song
và đường thẳng đó
b
a
α
I
| 1/44
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

sin y tang t 3 - 3 π 3 - 3 -1 3 2 3 1 3 B s 2π π 1 3 cotang 3 3 3π 2 2 π 4 2 4 1 3 5π π 2 3 6 6 - 2 2 π -1 1 0 (rad) x 2 2 A' - 3 -1 1 O 3 A cosin 2 2 2 2 -1 - 3 7π 2 3 11π - 2 6 6 5π 2 - 3 7π 4 2 4 4π -1 5π -1 3π 3 B' 3 2 - 3 2024-2025 MỤC LỤC
PHẦN ĐẠI SỐ VÀ MỘT SỐ YẾU TỐ GIẢI TÍCH .................................................................................... 1
VẤN ĐỀ 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC ......................................... 1
I. GÓC LƯỢNG GIÁC, ................................................................................................................................. 1
II. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC .................................................................... 2
III. CÔNG THỨC LƯỢNG GÍÁC ................................................................................................................. 3
IV. HÀM SỐ LƯƠNG GIÁC ......................................................................................................................... 4
CÁC DẠNG TOÁN THƯỜNG GẶP ............................................................................................................ 4
Dạng 1: Tìm tập xác định ............................................................................................................................ 4
Dạng 2: Xét tính chẵn lẻ .............................................................................................................................. 5
Dạng 3: Xét tính tuần hoàn ......................................................................................................................... 5
Dạng 4: Sự biến thiên .................................................................................................................................. 5
Dạng 5: Tìm giá trị lớn nhất– nhỏ nhất của hàm số lượng giác .................................................................. 6
V. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN ........................................................................................... 6
PHƯƠNG PHÁP KIỂM TRA ĐIỀU KIỆN XÁC ĐỊNH CỦA PHƯƠNG TRÌNH .................................. 7
VẤN ĐỀ 2. DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN ......................................................................... 8
I. DÃY SỐ ...................................................................................................................................................... 8
II. CẤP SỐ CỘNG – CẤP SỐ NHÂN ........................................................................................................... 8
VẤN ĐỀ 3. GIỚI HẠN, HÀM SỐ LIÊN TỤC .............................................................................................. 9
I. GIỚI HẠN CỦA DÃY SỐ.......................................................................................................................... 9
II. GIỚI HẠN CỦA HÀM SỐ........................................................................................................................ 9
PHƯƠNG PHÁP TÌM GIỚI HẠN .............................................................................................................. 9
III. HÀM SỐ LIÊN TỤC .............................................................................................................................. 11
CÁC DẠNG TOÁN THƯỜNG GẶP .......................................................................................................... 11
VẤN ĐỀ 4: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT ................................................................................. 12
I. PHÉP TÍNH LŨY THỪA ......................................................................................................................... 12
II. PHÉP TÍNH LÔGARIT ........................................................................................................................... 12
III. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARÍT................................................................................................ 12
IV. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ, LÔGARIT .............................................................. 13
VẤN ĐỀ 5. ĐẠO HÀM .................................................................................................................................. 14
I. CÔNG THỨC ĐẠO HÀM ....................................................................................................................... 14
II. TIẾP TUYẾN........................................................................................................................................... 14
PHẦN HÌNH HỌC VÀ ĐO LƯỜNG ........................................................................................................... 16
VẤN ĐỀ 6. ĐƯƠNG THẲNG VÀ MẶT PHẲNG. QUAN HỆ SONG SONG KHÔNG GIAN ............. 16
I. CHỨNG MINH QUAN HỆ SONG SONG .............................................................................................. 16
II. TÌM GIAO TUYẾN CỦA 2 MẶT PHẲNG............................................................................................ 17
III. TÌM GIAO ĐIỂM CỦA ĐƯƠNG THẲNG VÀ MẶT PHẲNG. .......................................................... 17
IV. TÌM THIẾT DIỆN CỦA HÌNH CHÓP, LĂNG TRỤ ĐƯỢC CẮT BỞI MỘT MẶT PHẲNG ........... 18
VẤN ĐỀ 7. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN ............................................................. 19
I. CHỨNG MINH QUAN HỆ VUÔNG GÓC. ............................................................................................ 19
II. TÌM HÌNH CHIẾU CỦA ĐIỂM LÊN MẶT PHẲNG ............................................................................ 20
III. GÓC ........................................................................................................................................................ 20
IV. KHOẢNG CÁCH.................................................................................................................................. 21
V. THỂ TÍCH KHỐI ĐA DIỆN ................................................................................................................... 22
ỨNG DỤNG THỂ TÍCH ........................................................................................................................... 23
CÁC DẠNG HÌNH CHÓP THƯỜNG GẶP .............................................................................................. 23
HÌNH CHÓP CỤT .................................................................................................................................... 25
CÁC DẠNG HÌNH LĂNG TRỤ THƯỜNG GẶP ...................................................................................... 26
PHẦN THỐNG KÊ, XÁC SUẤT ................................................................................................................. 27
VẤN ĐỀ 8. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CHO MẪU SỐ LIỆU GHÉP NHÓM
.......................................................................................................................................................................... 27
I. SỐ TRUNG BÌNH VÀ MỐT CỦA MẪU SỐ LIỆU GHÉP NHÓM ....................................................... 27
II. TRUNG VỊ VÀ TỨ PHÂN VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM ................................................... 28
I. BIẾN CỐ GIAO VÀ QUY TẮC NHÂN XÁC SUẤT ............................................................................. 29
II. BIẾN CỐ HỢP VÀ QUY TẮC CỘNG XÁC SUẤT .............................................................................. 29
PHỤ LỤC ........................................................................................................................................................ 30
TỔ HỢP, XÁC SUẤT .................................................................................................................................... 30
I. QUY TẮC ĐẾM ....................................................................................................................................... 30
II. HOÁN VỊ – CHỈNH HỢP – TỔ HỢP ..................................................................................................... 30
III. NHỊ THỨC NIU-TƠN ........................................................................................................................... 30
IV.XÁC SUẤT ............................................................................................................................................. 31
THỐNG KÊ .................................................................................................................................................... 34
I. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU ......................................... 34
II. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CỦA MẪU SỐ LIỆU .......................................... 35
HÌNH HỌC PHẲNG ..................................................................................................................................... 37
I. HỆ THỨC LƯỢNG TRONG TAM GIÁC ............................................................................................... 37
II. HỆ THỨC LƯỢNG TRONG TỨ GIÁC ................................................................................................. 37
III. HỆ THỨC LƯỢNG TRONG ĐƯỜNG TRÒN ..................................................................................... 38
IV. TÂM CỦA TAM GIÁC ......................................................................................................................... 38
HÌNH HỌC TỌA ĐỘ TRONG MẶT PHẲNG ........................................................................................... 39
I. TỌA ĐỘ .................................................................................................................................................... 39
II. PHƯƠNG TRÌNH ĐƯỜNG THẲNG ..................................................................................................... 39
III. PHƯƠNG TRÌNH ĐƯỜNG TRÒN....................................................................................................... 39
CHUÊN ĐỀ 1. PHÉP BIẾN HÌNH TRONG MẶT PHẲNG ..................................................................... 40
I. PHÉP TỊNH TIẾN .................................................................................................................................... 40
II. PHÉP ĐỐI XỨNG TÂM ......................................................................................................................... 40
III. PHÉP ĐỐI XỨNG TRỤC ...................................................................................................................... 40
IV. PHÉP QUAY .......................................................................................................................................... 40
V. PHÉP DỜI HÌNH .................................................................................................................................... 41
VI. PHÉP VỊ TỰ .......................................................................................................................................... 41
VII. PHÉP ĐỒNG DẠNG ............................................................................................................................ 41
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
PHẦN ĐẠI SỐ VÀ MỘT SỐ YẾU TỐ GIẢI TÍCH
VẤN ĐỀ 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC sin y tang t 3 - 3 π 3 - 3 -1 3 2 3 1 3 B s 2π π 1 3 cotang 3 3 3π 2 2 π 4 2 4 1 3 5π π 2 3 6 6 - 2 2 π -1 1 0 (rad) x 2 2 A' - 3 -1 1 O 3 A cosin 2 2 2 2 -1 - 3 7π 2 3 11π - 2 6 6 5π 2 - 3 7π 4 2 4 4π -1 5π -1 3π 3 B' 3 2 - 3 I. GÓC LƯỢNG GIÁC,
1.Góc lượng giác Định nghĩa:
Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí
tia Ob thì ta nói tia Om quét một góc lưọng giác có tia đầu Oa , tia cuối Ob , kí hiệu (Oa,Ob) . 2024-2025 1 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
Công thức tổng quát số đo góc lượng giác: (Oa,Ob) = a + k.360 (k  ) 2.Đơn vị radian
 (rad ) =180  
Công thức đổi đơn vị góc: 180 =  a
Quy tắc đổi đơn vi góc:
a)Đổi từ radian sang độ: Lấy số đo radian nhân 180
 và rút gọn. Nếu số đo radian có chứa  thì chỉ cần
thay  bằng 180 và rút gọn.
b)Đổi từ độ sang radian: Lấy số đo độ nhân và rút gọn. 180
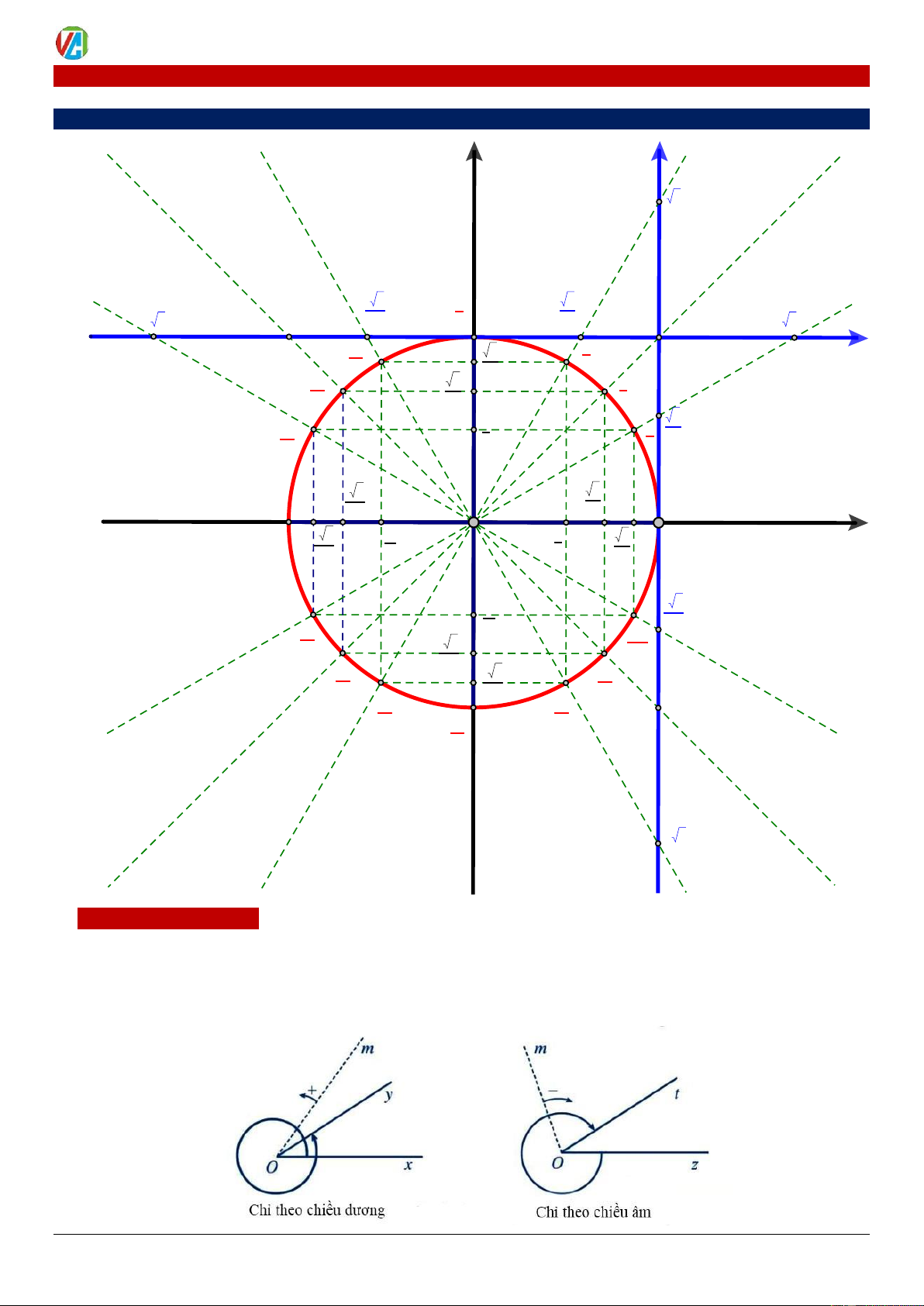
3.Đường tròn lượng giác
Trong mặt phẳng tọa độ Oxy , cho đường tròn tâm O bán
kính bằng 1. Trên đường tròn này, chọn điểm A(1;0) làm gốc,
chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là
chiều cùng chiều kim đồng hồ. Đường tròn cùng vởi gốc và
chiều như trên được gọi là đường tròn lượng giác.
Cho số đo góc  bất kì. Trên đường tròn lượng giác, ta
xác định được duy nhất một điểm M sao cho số đo góc lượng giác (O ,
A OM ) bằng  . Khi đó điểm M được gọi là điểm biểu
diễn của góc có số đo  trên đường tròn lượng giác. Chú ý: 2
Công thức  =  + k ( * k  , n
xác định n điểm 0 ) n 2
biểu diễn cách đều nhau một khoảng góc
trên đường tròn lượng giác, trong đó có một điểm biểu diễn góc n  0
II. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
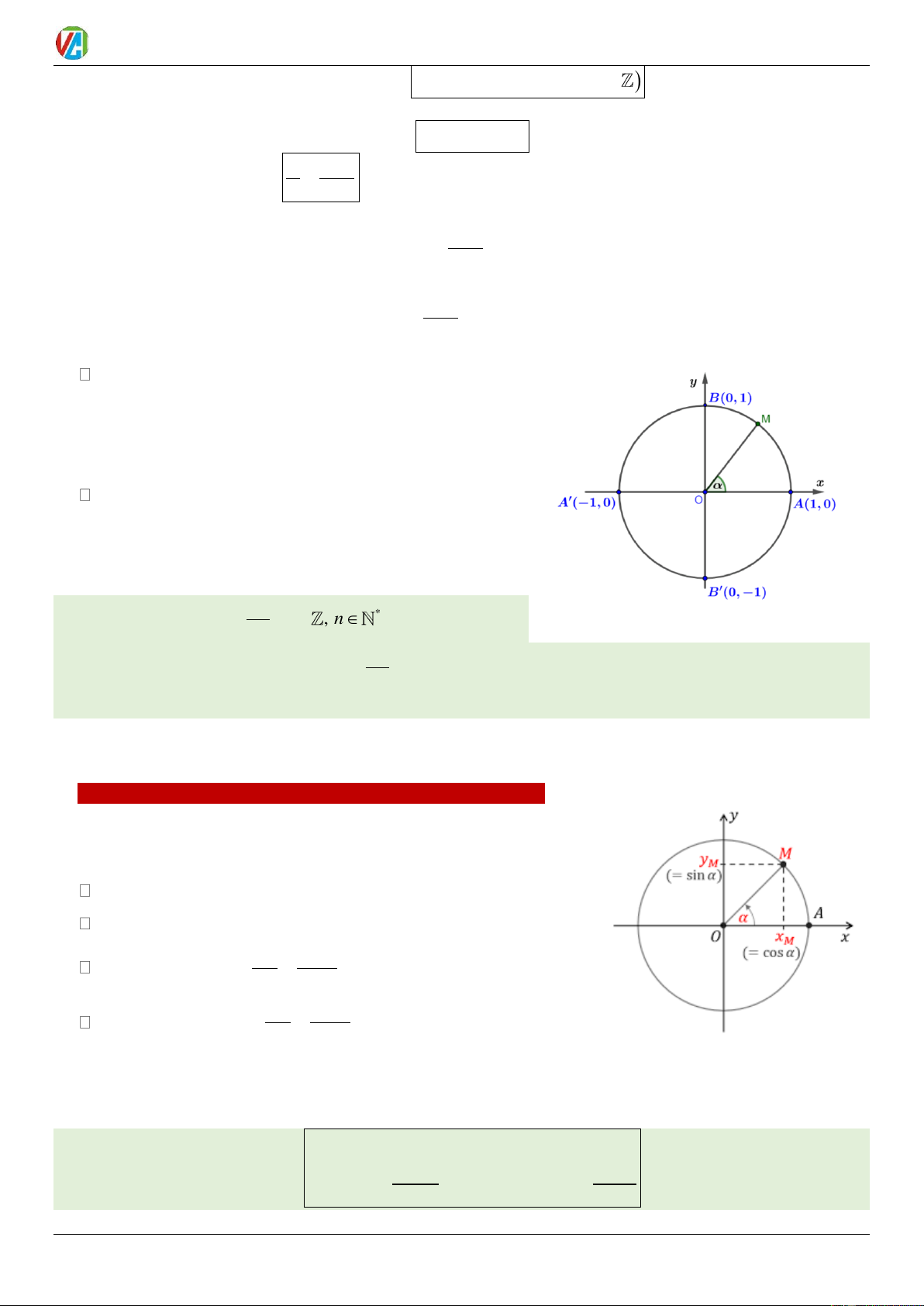
1.Giá trị lượng giác
Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo  . Khi đó:
Tung độ y của M gọi là sin của  , kí hiệu sin . M
Hoành độ x của M gọi là côsin của  , kí hiệu cos . M  Nếu y x  0 thì ti số sin M =
gọi là tang của  , kí hiệu tan M x cos M x
Nếu y  0 thì tỉ sô cos M =
gọi là côtang của  , kí hiệu M y sin M cot .
2.Hệ thức cơ bản và giá trị lượng giác của các góc có liên quan đặc biệt a)Hệ thức cơ bản 2 2
sin a + cos a = 1; tan . a cot a = 1 1 1 2 2 1+ tan a = ; 1+ cot a = 2 2 cos a sin a 2024-2025 2 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
b)Giá trị lượng giác của các góc có liên quan đặc biệt Cos đối Sin bù sin (  − ) = −sin sin ( − ) = sin cos (  − ) = cos cos ( − ) = − cos tan (  − ) = − tan tan ( − ) = − tan cot (  − ) = −cot cot ( − ) = − cot Chéo phụ
Tang, Cotang hơn kém       sin ( +  ) = −sin sin − = cos, cos − = sin      2   2  cos ( +  ) = −  cos       tan − = cot, cot − = tan     tan ( +  ) = tan  2   2  cot ( +  ) = cot
III. CÔNG THỨC LƯỢNG GÍÁC
1)Công thức cộng
2)Công thức nhân đôi
sin (a b) = sin .
a cos b  cos . a sin b sin 2a = 2sin . a cos a 2 2
cos (a b) = cos . a cos b sin . a sin b
cos 2a = cos a − sin a 2 (  = 2 cos a −1 a b) tan a tan b tan = 1 tan .atanb 2 = 1− 2sin a 2 tan a tan 2a = 2 1− tan a
3)Công thức biến đổi tích thành tổng
4)Công thức biến đổi tổng thành tích 1 a + b a − b cos . a cos b =
cos(a + b) + cos(a − b)  
cos a + cos b = 2 cos .cos 2 2 2 1 a + b a − b sin . a sin b =
cos(a − b) − cos(a + b)  
cos a − cos b = 2 − sin .sin 2 2 2 1 a + b a − b sin . a cos b =
sin (a + b) + sin (a −b)  
sin a + sin b = 2 sin .cos 2 2 2 a + b a − b
sin a − sin b = 2 cos .sin 2 2
5)Công thức hạ bậc 1+ cos 2a 2 cos a = 2 1− cos 2a 2 sin a = 2 1− cos 2a 2 tan a = 1+ cos 2a
Quy tắc biển đổi lượng giác: Tùy theo các dấu hiệu mà áp dụng công thức thích hợp.
a)Không làm thay đổi góc → Hệ thức cơ bản
b)Góc là tổng hoặc hiệu → Công thức cộng
c)Góc có hệ số chẵn→ Công thức nhân đôi
d)Giá trị lượng giác có mũ chẵn→ Công thức hạ bậc
e)Có tích sin, cosin→ Công thức biến đổi tích thành tổng
f)Có tổng, hiệu sin, cosin→ Công thức biến đổi tổng thành tích 2024-2025 3 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
IV. HÀM SỐ LƯƠNG GIÁC
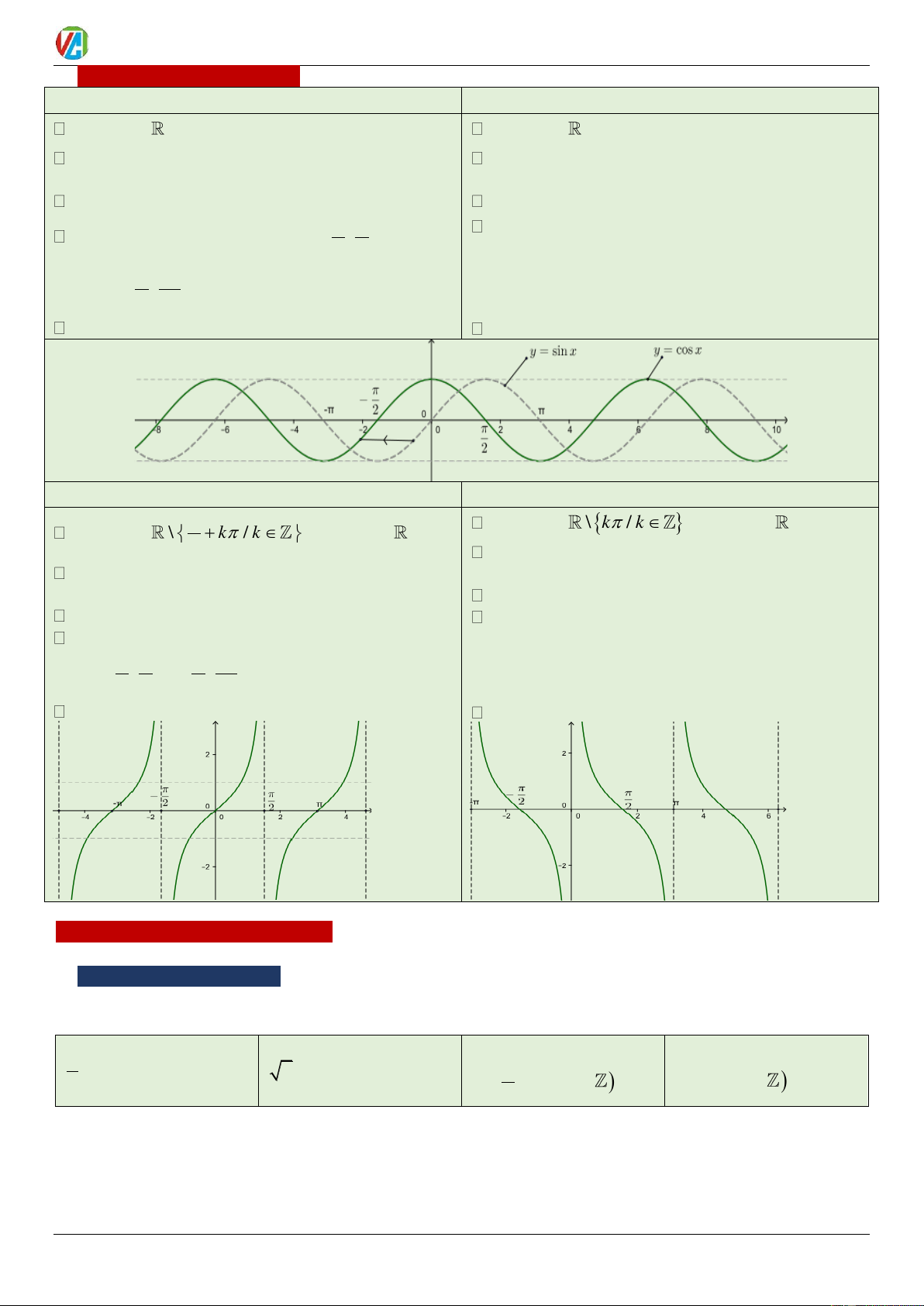
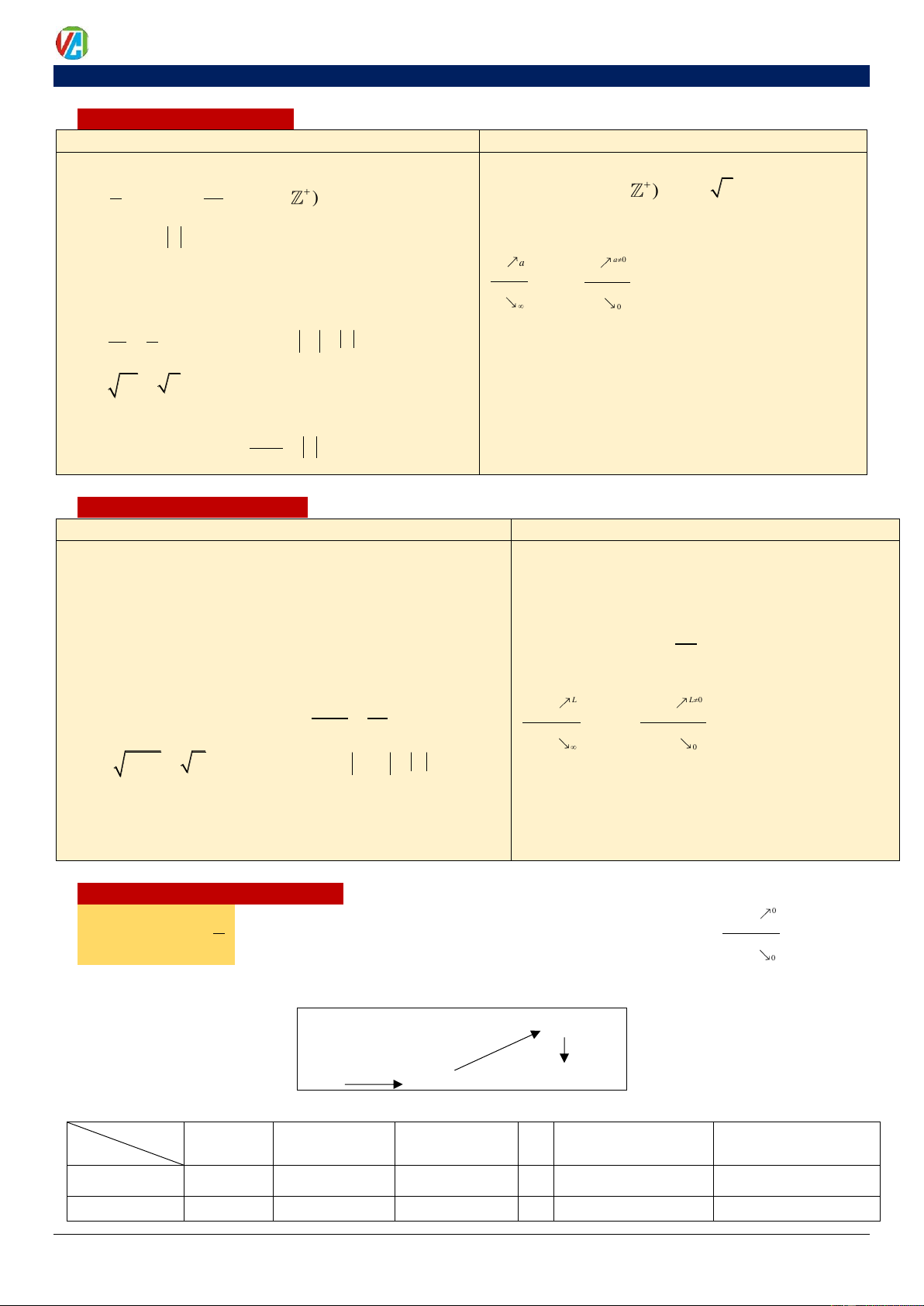
1. y = sin x
2. y = cos x TXĐ: D =
. TGT: T =  1 −  ;1 TXĐ: D =
. TGT: T =  1 −  ;1
Tính chẵn lẻ: Là hàm lẻ  Đồ thị đối xứng qua gốc
Tính chẵn chẵn: Là hàm lẻ  Đồ thị đối xứng qua tọa độ trục tung.
Tính tuần hoàn: Tuần hoàn với chu kì 2
Tính tuần hoàn: Tuần hoàn với chu kì 2     Sự biến
Sự biến thiên: Nghịch biến trên (0; ) ; Đồng biến
thiên: Đồng biến trên − ;   ; Nghịch  2 2  trên ( ;   )     biến trên 3 ;    2 2  Đồ thị: Đồ thị:
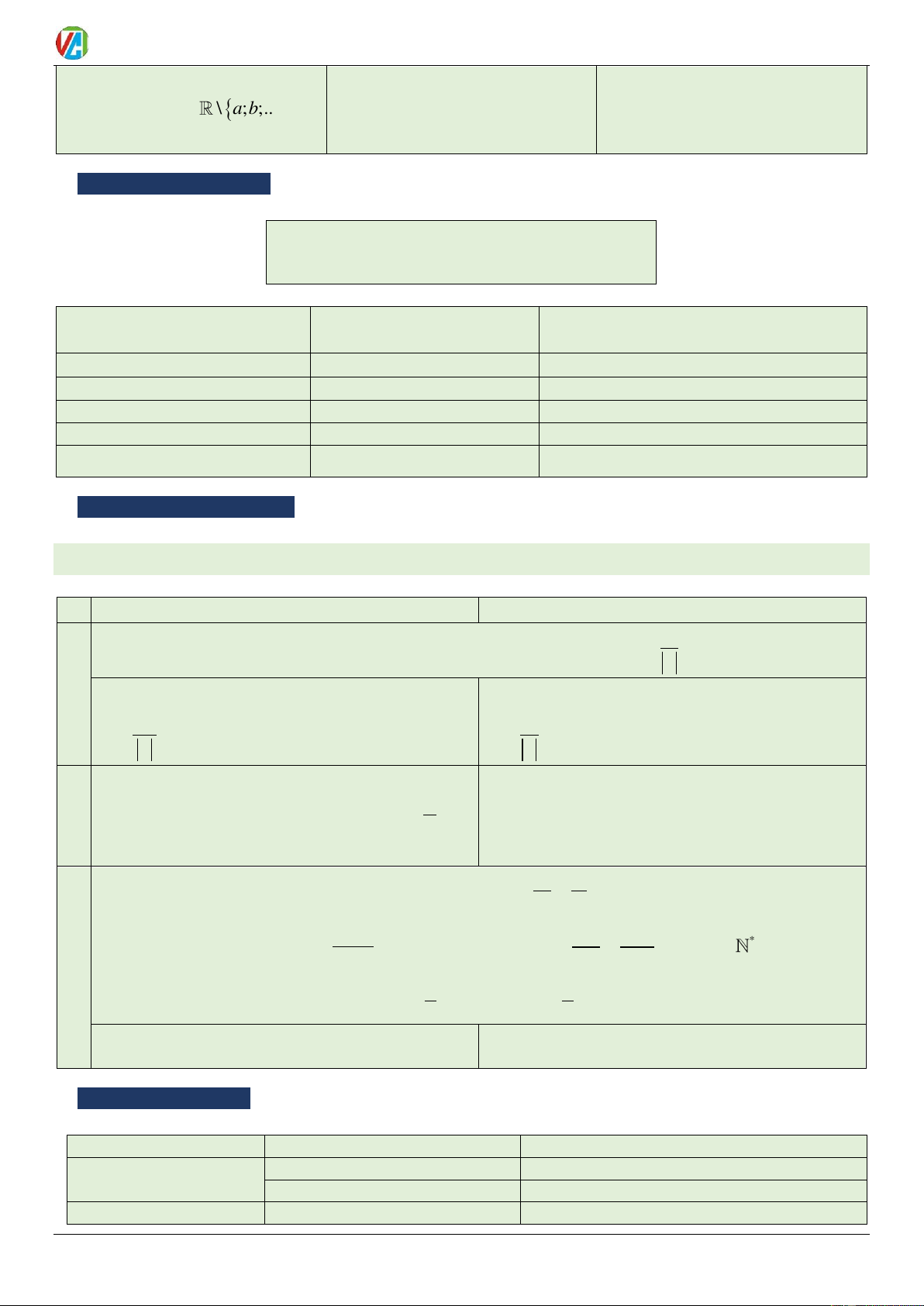
3. y = tan x
4. y = cot x   =   TXĐ: TXĐ: D \ k / k
. TGT: T = D =
\  + k / k   . TGT: T =  2 
Tính chẵn lẻ: Là hàm lẻ  Đồ thị đối xứng qua gốc
Tính chẵn lẻ: Là hàm lẻ  Đồ thị đối xứng qua gốc tọa độ tọa độ
Tính tuần hoàn: Tuần hoàn với chu kì 
Tính tuần hoàn: Tuần hoàn với chu kì 
Sự biến thiên: Luôn nghịch biến trên từng khoảng
Sự biến thiên: Luôn đồng biến trên từng khoảng xác xác định (0; ) ; (;   )
        định − 3 ;   ; ;    2 2   2 2  Đồ thị: Đồ thị:
CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1: Tìm tập xác định 1.Phương pháp:
B1: Lập điều kiện xác định (ĐKXĐ):
tan u xác định khi u
cot u xác định khi
xác định khi v  0
u xác định khi u  0  v u  + k,(k  )
u k ,(k  ) 2
B2: Giải ĐKXĐ → Tìm điều kiện của biến
B3: Tùy theo ĐK của biến, Ta kết luận TXĐ như sau: 2024-2025 4 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường x a
a x b → D = ( ; a b x = a   
x b → D = \ ; a ; b ..  . x = b  → D =  ; a ; b ..  . ......  ...... 
Dạng 2: Xét tính chẵn lẻ 1.Định nghĩa:
f ( x) là hàm chẵn  f (−x) = f ( x), x   D
f ( x) là hàm lẻ  f (−x) = − f ( x), x   D 2.Tính chất: 2 n
x → Chẵn; 2n 1 x + → Lẻ
f ( x) Chẵn  f (ax) Chẵn
f ( x) Lẻ  f (ax) Lẻ Hằng số → Chẵn
Chẵn  Chẵn → Chẵn Lẻ  Lẻ → Lẻ
Chẵn  Lẻ → Không Chẵn, Không Lẻ
Chẵn x() Chẵn → Chẵn Lẻ x() Lẻ → Chẵn Chẵn x() Lẻ → Lẻ (Chẵn)n → Chẵn (Lẻ)2n+1 →Lẻ (Lẻ)2n →Chẵn k.Chẵn → Chẵn k.Lẻ → Lẻ
|Chẵn| → Chẵn; |Lẻ| → Chẵn
f Lẻ, g Chẵn  f ( g ) Chẵn
f Lẻ, g Lẻ f ( g ) Lẻ
f Chẵn, g Chẵn (hay Lẻ) f ( g ) Chẵn
Dạng 3: Xét tính tuần hoàn 1.Định nghĩa:
f ( x) tuần hoàn với chu kì T  Tồn tại số T dương nhỏ nhất sao cho: f ( x T ) = f ( x) 2.Tính chất: 1 y = sin ,
x y = cos x tuần hoàn chu kì T = 2 y = tan ,
x y = cot x tuần hoàn chu kì T =  Nếu T
f ( x) tuần hoàn với chu kì T thì f (ax + b) tuần hoàn với chu kì T ' = a 2
y = sin (ax + b), y = cos(ax + b) tuần hoàn chu kì y = tan (ax + b), y = cot (ax + b) tuần hoàn chu kì 2  T = T = a a
Nếu y = sin u, y = cosu tuần hoàn chu kì T Nếu y = tan ,
u y = cot u tuần hoàn chu kì T T 3 thì 2 2 y = sin ,
u y = cos u tuần hoàn chu kì thì 2 2 y = tan , u y = cot u và 2 3 3 y = tan ,
u y = cot u tuần hoàn chu kì T và 3 3 y = sin ,
u y = cos u tuần hoàn chu kì T Nếu T m
f ( x) , g ( x) lần lượt tuần hoàn với chu kì T , T và 1 = (tối giản) 1 2 T n 2 f x . n T . m T
thì f ( x)  g ( x) , f ( x).g ( x) ( ) , tuần hoàn với chu kì 1 2 T = = ( * , m , n k  ) g ( x) 4 k k Nếu 1 1
T , T là các số nguyên dương thì T =
BCNN (T ,T = LCM T ,T (Máy tính cầm tay) 1 2 ) ( 1 2) 1 2 k k
Tổng, hiệu của 2 hàm sin, cos có chu kì tuần hoàn Tích, thương của 2 hàm sin, cos có chu kì tuần
T (như trên) với k = 1
hoàn T (như trên) với với k = 2
Dạng 4: Sự biến thiên
1.Hàm số lượng giác sơ cấp: Hàm số
Chiều biến thiên
Khoảng (Trên ĐƯỜNG THẲNGLG) Nghịch biến Bên trái Oy y = sin x Đồng biến Bên phải Oy y = cos x Nghịch biến Phía trên Ox 2024-2025 5 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường Đồng biến Phía dưới Ox y = tan x = +   Luôn Đồng biến Không chứa x k ,(k ) 2 y = cot x =   Luôn Nghịch biến
Không chứa x k ,(k )
2.Tính chất cơ bản: Trên K Hệ số a
y = f ( x) y = .
a f ( x) + b a  0
Đồng biến (Nghịch biến)
Đồng biến (Nghịch biến) a  0
Đồng biến (Nghịch biến)
Nghịch biến (Đồng biến)
Dạng 5: Tìm giá trị lớn nhất– nhỏ nhất của hàm số lượng giác 1.Định nghĩa:f
 (x)  M , x   Kf  (x)  , m x   K
 max f (x) = M
 min f (x) = m x   K : K f x = M   x   K : K f x = m  0 ( 0) 0 ( 0)
2.Phương pháp: Chặn hàm số
B1: Biến đổi hàm số đã cho đến khi chỉ còn chứa 1 HSLG (nếu được)
B2: Dùng Bất đẳng thức LG và Tính chất Bất đẳng thức → Biến đổi về dạng: m f ( x)  M
min f (x) = m
B3: Dùng định nghĩa → Xác định GTLN–GTNN: K  min f  (x) = MK
3.Bất đẳng thức LG:   1
−  sin u  1 2
0  sin u  1 0 sin u 1 2
tan u  0
−1  cos u  1 2
0  cos u  1
0  cos u  1 2
cot u  0
4.Tính chất Bất đẳng thức: A B 2 2 A B
A B A + C B + C
A + C B + D
A B  0   C   D  A B  . A C  . B C  (C  0) A B  0 3 3 A B A B     . A C  . B D A B    . A C  . B C  (C  0) C   D  0 3 3  A B 1 1 1 1 0  A  1  1
A B C  0  0    A A B C
V. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
Dạng f (u) = m
Dạng f (u) = f (v) sin u = , m ( 1 −  m 1)  sin u = sin, ( 1  = sin− (m))
u = v + k2
sin u = sin v  
u =  + k2
u =  − v + k2  , k  
u =  − + k2 cos u = , m ( 1 −  m 1)  cosu = cos, ( 1  = cos− (m))
cos u = cos vu = v + k 2
u =  + k2  , k   u =  − + k2 2024-2025 6 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường tan u = m  tan u = tan, ( 1  = tan− (m))
tan u = tan v u = v + k
u =  + k , k  cot u = m  −  1   1
 cot u = cot,  = tan   
cot u = cot v u = v + k   m 
u =  + k , k
Trường hợp đặc biệt: Đối với phương trình sin u = ,
m cos u = m
Nếu m = 1 thì chỉ cần lấy 1 trong 2 công thức nghiệm.
Nếu m = 0 thì chỉ cần lấy 1 trong 2 công thức nghiệm và thay k 2 thành kCụ thể:  
sin u = 1  u = + k2 sin u = 1
−  u = − + k2
sin u = 0  u = k 2 2 
cos u = 1  u = k 2
cos u = −1  u =  + k 2
cos u = 0  u = + k 2
PHƯƠNG PHÁP KIỂM TRA ĐIỀU KIỆN XÁC ĐỊNH CỦA PHƯƠNG TRÌNH
Bước 1. Xác định điểm biểu diễn công thức điều kiện xác định của phương trình và công thức nghiệm lên
Đường tròn lượng giác
Bước 2. Loại bỏ điểm biểu diễn trùng của công thức nghiệm so với điểm biểu diễn của điều kiện xác định.
Bước 3. Kết luận: Nghiệm của phương trình là công thức tổng quát xác định những điểm biểu diễn còn lại. 2024-2025 7 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
VẤN ĐỀ 2. DÃY SỐ – CẤP SỐ CỘNG – CẤP SỐ NHÂN I. DÃY SỐ 1.Định nghĩa
Dãy số là hàm số với đối số là số tự nhiên
2.Dãy số tăng, dãy số giảm (u là dãy số tăng *
u u , n  
; (u là dãy số giảm *
u u , n   n ) n ) n 1 + n n 1 + n
3.Dãy số bị chặn
(u là dãy số bị chặn trên *
 M  : u M , n   . n ) n
(u là dãy số bị chặn dưới *
 m : u m , n   . n ) n
(u là dãy số bị chặn *   ,
m M  : m u M , n   . n ) n
II. CẤP SỐ CỘNG – CẤP SỐ NHÂN Cấp số cộng Cấp số nhân
Dãy số (u là cấp số cộng
Dãy số (u là cấp số nhân n ) n ) Định nghĩa
u = u + d , n
u = u q , n   n+ n ( * 1 ) n+ n ( * 1 )
Số hạng tổng quát * n 1 − *
u = u + (n −1)d , n u = u .q , n n 1 ( ) n 1 ( ) u + u Tính chất k 1 − k 1 u + = , k k 2 u = u .u , k k  − k + ( * 2 , k k 1 1 ) k ( * 2 , ) 2 ( n u + u )
Tổng n số hạng đầu 1 n S =
Khi q =1: S = nu n n 1 tiên 2 1 n − q n Khi  =
S = u + u +...+ u q 1: S u . S =
u + n − d n 1 − n 2 ( 1) 1  n 1 2 n 1 q 2 u − u u − u
Công sai, công bội n+ d = u − u ; k m d = 1 q = ; k m k q = n 1 + n k − m u u n m
CÁCH TÌM SỐ HẠNG DÃY SỐ TRUY HỒI BẰNG MÁY TÍNH CẦM TAY u 
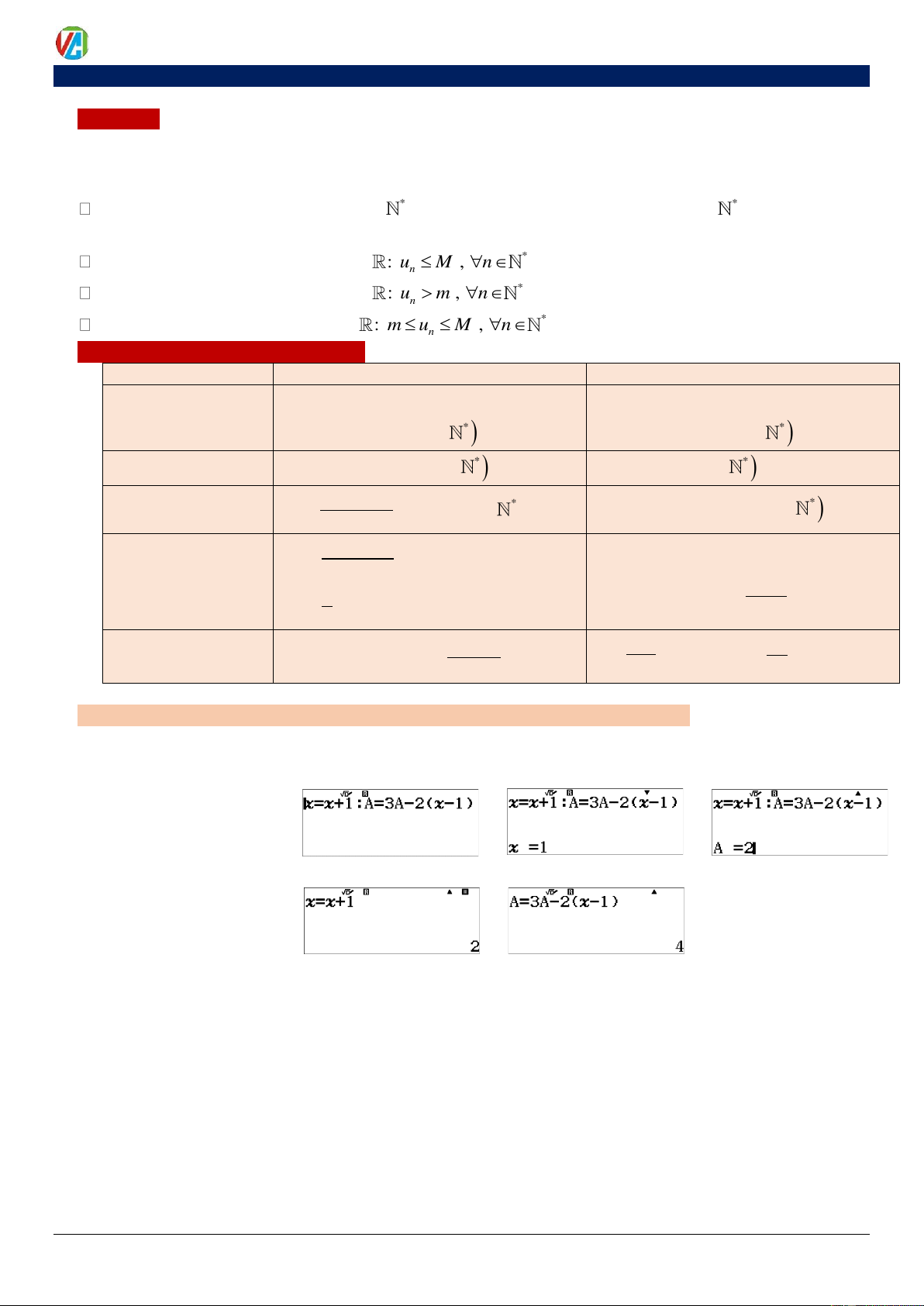
DẠNG 1: (u
→ Công thức MTBT: x = x +1: A = f ( , A x − )
1 → CALC: x = 1; A = u n ) 1 : u  = f u , n 1  n 1+ ( n ) Vi dụ: ( u  = u  → n ) 2 1
: u = 3u −2nn 1+ n
→ Tính được u = 4 ,….. →
Tiếp tục tính được số 2 hạng tùy ý DẠNG 2: ( uuu
→ Công thức MTBT: x = x +1: C = f ( , A ,
B x − 2) : A = B : B = C n ) , 1 2 : u
= f u ,u ,nn+2 ( n n 1+ )
→ CALC: x =1, A = u , B = u 1 2 2024-2025 8 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
VẤN ĐỀ 3. GIỚI HẠN, HÀM SỐ LIÊN TỤC
I. GIỚI HẠN CỦA DÃY SỐ
Giới hạn hữu hạn Giới hạn vô cực
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt: • 1 • k lim = 0;• 1 lim = 0 (k +  ) limn (k + = +
 ) • lim n = + n→+ n k n→+ n • lim n
q = + (q 1) • lim n
q = 0 ( q 1) ; • lim C = C
2. Định lí:(Quy tắc về giới hạn vô cực) n→+ n→+ a0
2. Định lí: Cho a limu = ,
a limv = b . Ta có: u u n n n → 0 ; n
→  ; [u .v ] →  • n n
lim(u v = a b • lim(u .v = a b v v n   n n ) . n n )  n 0  a0
(Dấu của giới hạn vô cực được xác định theo quy • u a lim n =
(nếu b  0 ) • lim u = a n tắc nhân dấu) v b n
• lim u = a (u , a  0 ) n n
3. Tổng của cấp số nhân lùi vô hạn u 2 1
S = u + u q + u q +  = ( q  ) 1 1 1 1 1− q
II. GIỚI HẠN CỦA HÀM SỐ
Giới hạn hữu hạn
Giới hạn vô cực, giới hạn tại vô cực
1. Giới hạn đặc biệt:
1. Giới hạn đặc biệt:
• lim x = x ;• lim C = C (C là hằng số) 0 lim k x = +
lim k + neáu k chaün x x→ x→x • ; • =  0 x 0 x→+ x→− − neáu k leû
2. Định lí: Cho lim f (x) = L , lim (
g x) = M . Ta có: x→x x→x c 0 0
• lim C = C ; • lim = 0
• lim  f (x) + (
g x) = L + M k
; • lim  f (x) − (
g x) = L − M x→ x→ x x→x x→x 0 0
2. Định lí: (Quy tắc về giới hạn vô cực) L L0 f (x) L • f (x) f (x) lim  f (x). (
g x) = L.M ; • lim =
(nếu M  0 ) → 0 ;
→  ; [f (x). g(x)] →  x→x x→x ( g x) M 0 0 g(x) g(x)    0  L0
• lim f (x) = L ( f (x)  0) • lim f (x) = L
( x → x hay x →  ) 0 x→x x→x 0 0
(Dấu của giới hạn vô cực được xác định theo quy
3. Giới hạn một bên: tắc nhân dấu)
lim f (x) = L  lim f (x) = lim f (x) = L x→x x x − x x + → → 0 0 0
PHƯƠNG PHÁP TÌM GIỚI HẠN 0 0  f (x) Dạng vô định
: ( Là giới hạn của thương mà tử và mẫu đều có giới hạn bằng 0: ) 0 g(x) 0
a)Cách khử: Biến tử và mẫu thành tích rồi đơn giản (hết) nhân tử chung
b)Sơ đồ Hoocner: Dùng để tính giá trị đa thức hay phân tích đa thức thành nhân nhân tử. a 1 Cộng Bằng x Nhân b
b = x .b + a 0 0 1 0 0 1 − Cho f ( x) n n 1
= a .x + a .x +...+ a .x + a có nghiệm x = x 0 1 n 1 − n 0
Hệ số a a a … a a Nghiệm 0 1 2 n 1 − n x b = a
b = x .b + a
b = x .b + a … b
= x .b + a b = x .b + a = 0 0 0 0 1 0 0 1 2 0 1 2 n 1 − 0 n−2 n 1 − n 0 n 1 − n n 1 x − n 2 x − n 3 x − 0 x = 1 2024-2025 9 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
Khi đó: f (x) n n 1
= a .x + a .x − +...+ a .x + a = x − x b x − +b x − + +b x +b n− n ( )( n 1 n 2 . . ... . 0 1 1 0 0 1 n−2 n 1 − )
CÁC DẠNG THƯỜNG GẶP f ( x)
Dạng 1.1: Giới hạn của phân thức hữu tỷ tại một điểm: lim
, với f ( x), g ( x) là các đa thức và
x→ x0 g ( x)
f ( x = g x = 0 0 ) ( 0)
PP: Phân tích cả tử và mẫu thành nhân tử và rút gọn nhân tử chung: f ( x)
(x − x .u x u x 0 ) ( ) ( ) lim = lim = lim = ... x→x x→x x→x − 0 g ( x) 0 ( x x .v x v x 0 ) ( ) 0 ( ) 3 2 2 x − 8
(x − 2)(x + 2x + 4) x + 2x + 4 12 VD: lim = lim = lim = = 3 2 x 2 → x 2 x − 4 → (x − 2)(x + 2) x 2 → x + 2 4 f ( x) Dạng 1.2: lim
, với f ( x), g ( x) là các biểu thức chứa căn cùng bậc và f ( x = g x = 0 0 ) ( 0)
x→ x0 g ( x)
PP: Nhân biểu thức liên hợp (tương ứng) ở tử và mẫu để khử căn → Biến thành tích rồi đơn giản nhân tử chung. −
(A− B)(A+ B A B ) 2 A − B lim = lim = lim = ... x→ → → 0 x x C 0 x
C.( A + B ) x 0
x C.( A + B ) 2 − 4 − x
(2− 4− x)(2+ 4− x) 1 1 VD: lim = lim = lim = x→0 x x→0 x (2 + 4 − x )
x→0 2 + 4 − x 4    f (x) Dạng vô định
: (Là giới hạn của thương mà tử và mẫu đều có giới hạn vô cực: ) g (x) 
CÁC DẠNG THƯỜNG GẶP
Dạng 2.1: f (x), g (x) là các đa thức →PP: Chia cả tử và mẫu cho luỹ thừa cao nhất của x. 5 3 2 2 + − 2 2x + 5x − 3 x x VD: lim = lim = 2 2
x→+ x + 6x + 3 x→+ 6 3 1+ + 2 x x
Dạng 2.2: f (x), g (x) có chứa lũy thừa k
x và căn thức →PP: Rút lũy thừa cao nhất ra khỏi các căn rồi
chia cả tử và mẫu cho luỹ thừa cao nhất của x. 3 2 − 2x − 3 2x − 3 VD: lim = lim = lim x = 1 − x→− 2 x + 3 x − x →− 3 x→− 3 − . x 1+ − x . − 1+ −1 2 2 x x
Giới hạn của tổng, hiệu: (Chứa lũy thừa k x )
CÁC DẠNG THƯỜNG GẶP
Dạng 3.1: Giới hạn tại vô cực của tổng, hiệu mà tổng hệ số các lũy thừa bậc cao nhất khác 0
PP: Rút lũy thừa bậc cao nhất làm nhân tử chung đưa về tích → Áp dụng quy tắc giới hạn của tích:
[f (x). g(x)] →     L0   1  VD: lim + − =
 − + −  = − →− ( 2 x x 2x) lim x 1 2   x x→−  x   
Dạng 3.2: Giới hạn tại vô cực của tổng, hiệu mà tổng hệ số các lũy thừa bậc cao nhất bằng 0 (Dạng này thường có căn) 2024-2025 10 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
PP: Nhân chia biểu thức liên hợp để khử căn → Ta được giới hạn dạng vô định  + x − x + x + x
lim ( 1+ x − x ) ( 1 )( 1 ) 1 VD: = lim = lim = 0 x→+ x→+ 1 x + x + x →+ 1+ x + x
III. HÀM SỐ LIÊN TỤC
1.Hàm số liên tục tại một điểm
y = f ( x) liên tục tại x  lim f ( x) = f ( x 0 ) 0 x→ 0 x
y = f ( x) liên tục tại x  lim f ( x) = lim f ( x) = f ( x − + 0 ) 0 x→ → 0 x x 0 x
2.Hàm số liên tục trên một khoảng
Hàm số liên tục trên một khoảng khi hàm số liên tục tại mọi điểm thuộc khoảng đó.
3.Hàm số liên tục trên một đoạn
Hàm số y = f (x) liên tục trên một đoạn  ;
a b nếu y = f ( x) liên tục trên ( ;
a b) và lim f ( x) = f (a) + x→a
lim f ( x) = f (b) − x b → 4.Tính chất
• Hàm số đa thức liên tục trên .
• Hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
• Tổng hiệu, hiệu, tích, thương của các hàm số liên tục tại một điểm là hàm số liên tục tại điểm đó.
CÁC DẠNG TOÁN THƯỜNG GẶP
Dạng 1: Xét tính liên tục của hàm số 𝒚 = 𝒇(𝒙) tại điểm 𝒙𝟎:
B1: Tính f ( x . 0 )
B2: Tính lim f ( x) (Hay tính lim f ( x), lim f ( x) ) x→ + − → → 0 x x 0 x x 0 x
B3: So sánh lim f (x) , f ( x → Kết luận. 0 ) x→x0
Dạng 2: Tìm tham số để hàm số 𝒚 = 𝒇(𝒙) liên tục tại điểm 𝒙𝟎:
B1: Tính f ( x . 0 )
B2: Tính lim f ( x) (Hay tính lim f ( x), lim f ( x) ) x→ + − → → 0 x x 0 x x 0 x
B3: Cho lim f (x) = f ( x (Hay cho lim f ( x) = lim f ( x) = f ( x )→ Giải PT, HPT tìm tham số. + − 0 ) 0 ) x→x x→ → 0 x x 0 x 0 2024-2025 11 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
VẤN ĐỀ 4: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
I. PHÉP TÍNH LŨY THỪA • n a = . a . a ....a m m a  1 : − a m+n m n m n n m n (tích của n thừa số a) • a
= a .a • a = • a = a n f ( x) g (x) a aaf ( ) x g( ) x 0 • 1
a = 1 , (a  0) n n    a a • n n a = a 0 a 1: n n n • ( . a ) b
= a .b • =   f ( x) g (x) aaf ( ) x g( ) x − n n 1 • a = , a   b b n ( 0) a m n n m . • ( ) = ( ) m n a a = a
II. PHÉP TÍNH LÔGARIT
• log b =   a = b • log (b .b ) = log b + log b log b a  1 : a a 1 2 a 1 a 2 • log c b = a
(a, b  0; a  1)  log f (x) log g(x) b  log a c a a 1 •   = − • log log b log b log 1 = 0 a a 1 a 2 1
f (x)  g(x)  0 a b  2  • log b = a   • log a =1  log a 0 a 1: • log (b ) a =.log b b a a   • = log f (x) log g(x) • log a = log . a log b log b a a c a c a ( ) 1 • log =
 0  f (x)  g(x)  b log b log a   a • b a = b a  • log =  (b ) log b a a
III. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARÍT 1. Hàm số mũ x
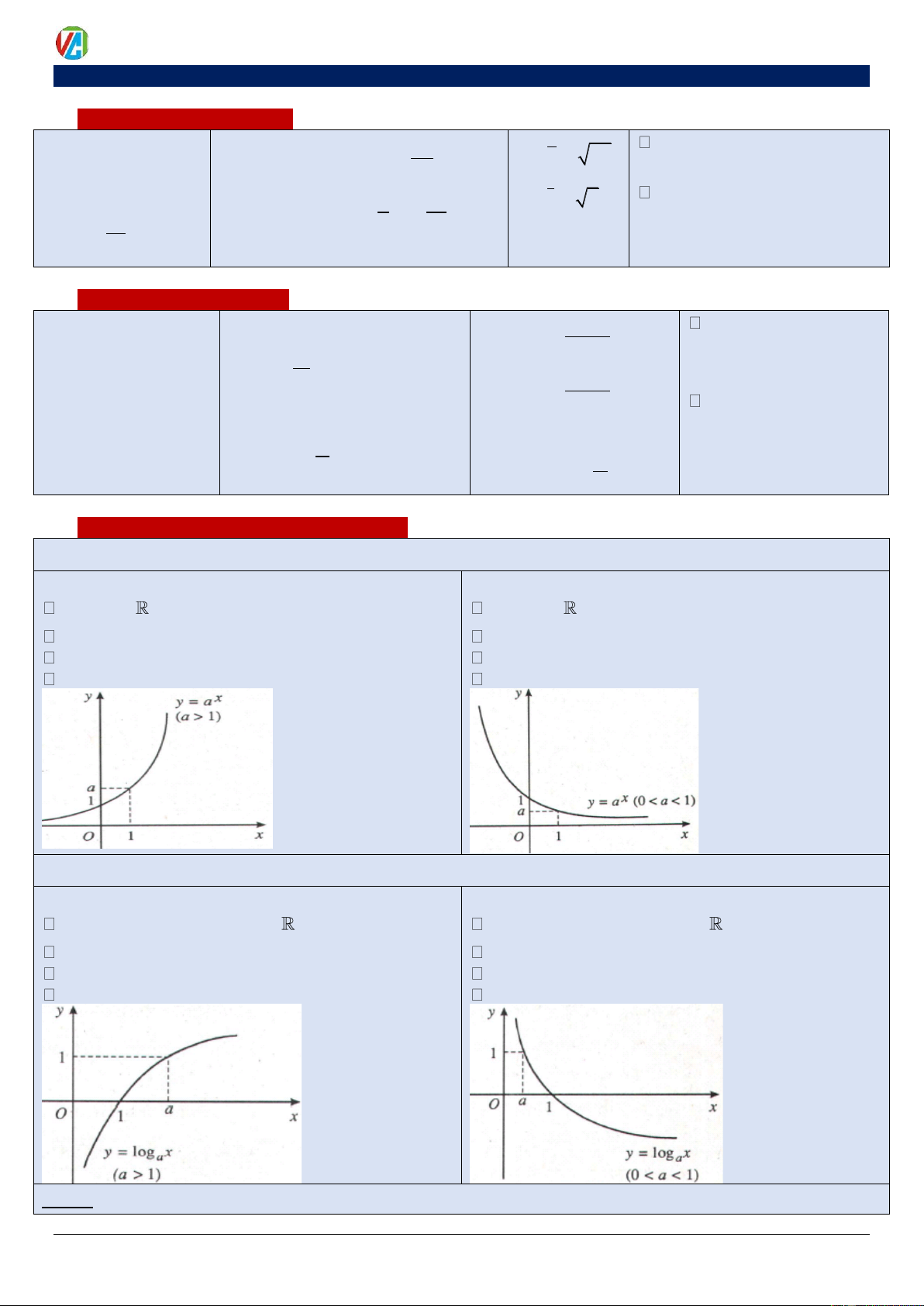
y = a (0  a  ) 1 a  1
0  a  1 TXĐ: D = . TGT: T = (0; +) . TXĐ: D = . TGT: T = (0; +) .
Hàm số luôn đồng biến
Hàm số luôn nghịch biến
Tiệm cận ngang là trục Ox
Tiệm cận ngang là trục Ox
Đồ thị nằm phía trên trục hoành
Đồ thị nằm phía trên trục hoành
2. Hàm số logarit y = log x , (0  a  ) 1 a a  1
0  a  1
TXĐ: D = (0;+) . TGT: T = .
TXĐ: D = (0;+) . TGT: T =
Hàm số luôn đồng biến
Hàm số luôn nghịch biến
Tiệm cận đứng là trục Oy
Tiệm cận đứng là trục Oy
Đồ thị nằm phía bên phải trục tung
Đồ thị nằm phía bên phải trục tung
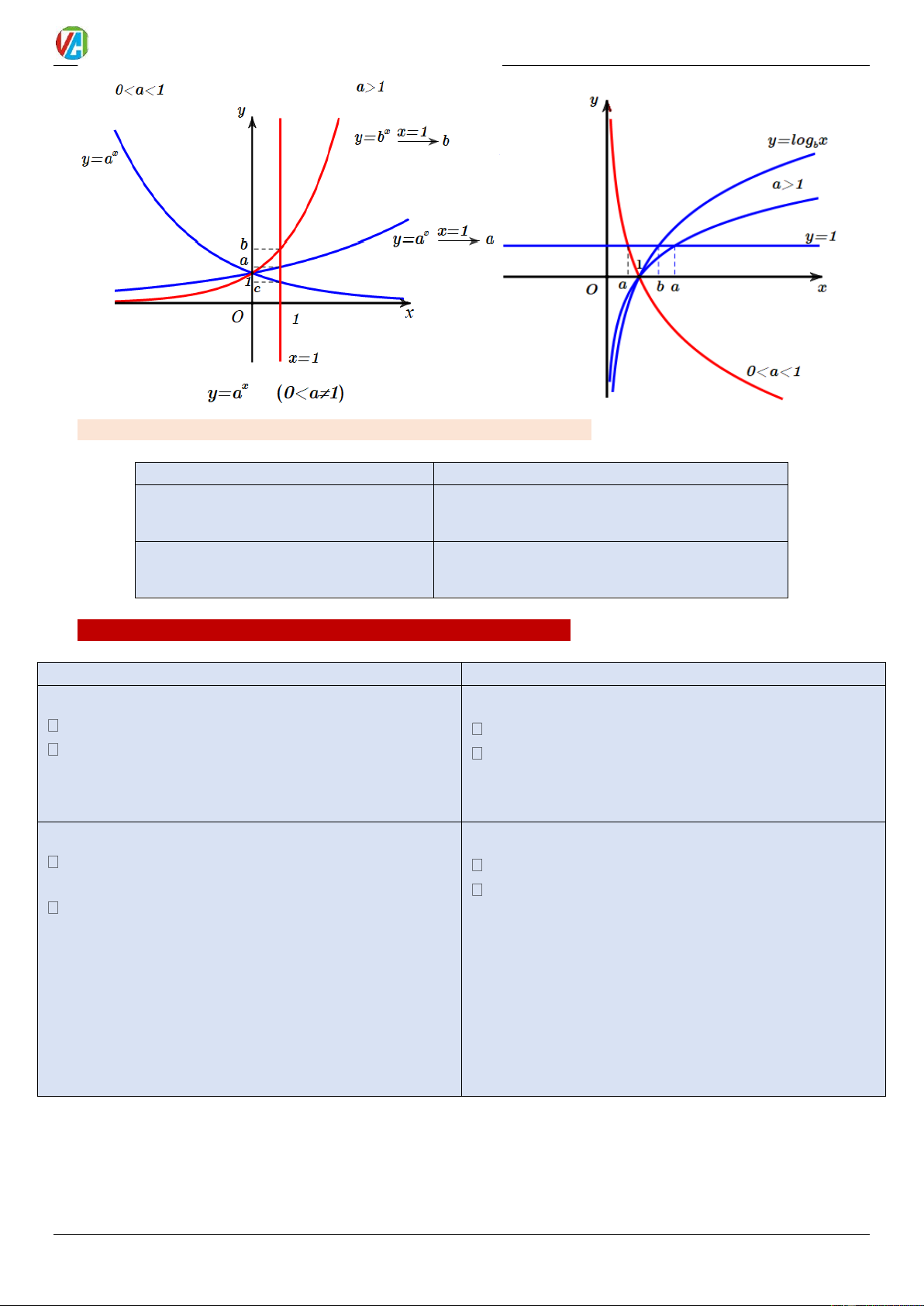
Chú ý : Đồ thị hàm số x
y = a và y = log x (hai hàm ngược nhau) đối xứng nhau qua đường thẳng y = x a 2024-2025 12 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
ĐIỀU KIỆN XÁC ĐỊNH CỦA HÀM SỐ MŨ, HÀM SỐ LOGARIT Hàm số
Điều kiện xác định 0  a  1 Hàm mũ: u y = a u   0  a  1
Hàm logarit: y = log u a u   0
IV. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ, LÔGARIT Mũ Logarit Dạng u
a = b ,(a  0, a  1 ) Dạng log u = ,
b (a  0, a  ) 1 a
b  0 : Phương trình vô nghiệm
Điều kiện: u  0 b  0 : u
a = b u = log b =  = a log b u b u a a Chú ý: u v
a = a u = v
Chú ý: log u = log v u = v a a
(Điều kiện: u  0; v  0 ) Dạng u
a b ,(a  0, a 1 )
Dạng log u  ,
b (a  0, a  ) 1 a
b  0 : Bất phương trình có nghiệm với mọi u thỏa
Điều kiện: u  0 điều kiện xác định. log b
u b u a , khi a  1 a b  0 : u
a b u  log b , khi a  1 a log b
u b u a , khi 0  a  1 a u
a b u  log b , khi 0  a  1 a
Chú ý: Tương tự cho các bất phương trình:
Chú ý: Tương tự cho các bất phương trình:
log u b ; log u b ; log u b a a a u a  0 ; u a  0 ; u a  0 Tổng quát Tổng quát
log u  log v u  , v khi a 1 u v a a
a a u  , v khi a 1
log u  log v u  ,
v khi 0  a 1 u v a a
a a u  ,
v khi 0  a 1
(Điều kiện: u  0; v  0 ) 2024-2025 13 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
VẤN ĐỀ 5. ĐẠO HÀM
I. CÔNG THỨC ĐẠO HÀM Hàm sơ cấp Hàm hợp Phép toán (    C ) = 0  f
 (u) = f  
(u).u
(u v) = u v (   x) = 1 (  n
(u.v) =  +  u ) n 1 = . n u − .uu .v u.v   ( n x ) n 1 = . n x −  u  u
u .v − v .u ( u) = =   2 (  2. uv v x ) 1 =   2. x  1  u −  (k.v) =  = k.v    2   u u
( k là hằng số) 1  1 −   −  = k k.v   =   2  x x 2  v v (   Đặc biệt sin x) = cos x
(sinu) = u .cosu    − (   1 n =
cos x) = − sin x (cosu) = u − .sin u   n n 1  x x + (  u  x) 1 tan = (tanu) =  ax + b ad − bc 2 cos x 2 cos u =   2  cx + d  (cx + d ) ( −  u −   x) 1 cot = (cotu) =  2 2 2 sin x 2 sin u
ax + bx + c
adx + 2aex + (bc − cd )   =   x x = u u =   dx + e  (dx + e)2
(a ) a .lna
(a ) a .ln .au (   x ) x e = e ( u) u e
= e .u (  u  x = (log u = a ) a ) 1 log . x ln a . u ln a ( ) 1  u  ln x = (lnu) = x u
QUY TẮC TÌM ĐẠO HÀM
Khi tìm đạo hàm của hàm số ta thực hiện theo thứ tự ưu tiên như sau:
PHÉP TOÁN → HÀM HỢP → SƠ CẤP. II. TIẾP TUYẾN 1. Định lý
Phương trình tiếp tuyến của đường cong (C) : y = f (x) tại tiếp điểm M (x ; y có dạng: 0 0 )
y − y = k. x − x (*) 0 ( 0 ) Trong đó:
x : Hoành độ tiếp điểm; 0
y = y x : Tung độ tiếp điểm; 0 ( 0)
k = f ( x : Hệ số góc của tiếp tuyến. 0 )
2. Quy tắc lập phương trình tiếp tuyến của đường cong y = f ( x)
B1. Tìm đạo hàm y ' = f '( x)
B2. Dựa vào giả thiết, tính x , y , f x . 0 0 ( 0)
B3. Thay vào phương trình (*), thu gọn, ta được phương trình tiếp tuyến cần tìm (Chú ý: So điều kiện, loại
phương trình nếu có) 3. Chú ý 2024-2025 14 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
Đường thẳng (d ) : y = ax + b → Hệ số góc k = a ; d − Đường thẳng ( a
d ) : ax + by + c = 0 .→ Hệ số góc k = . d b
d d '  k = k ;• d ⊥ d '  k .k = 1 − d d ' d d '
4. Các dạng phương trình tiếp tuyến Giả thiết
Theo GT, Ta có:
Các đại lượng cần tính
Biết hoành độ tiếp điểm x Tính: y = y x
, k = f ( x 0 ) 0 ( 0) 0
Biết tung độ tiếp điểm y
Từ: y = y x → Tính được x và k = f ( x 0 ) 0 ( 0) 0 0
Biết hệ số góc của tiếp
k = f x → Tính được x và y = y x 0 ( 0) tuyến k Từ: ( 0) 0 Biết
Từ: k = f ( x → Tính được x và y = y x 0 ( 0) 0 )
tiếp tuyến song song 0 =
đường thẳng ( k k d ) d
(Chú ý loại phương trình tiếp tuyến trùng phương
trình đường thẳng d)
Biết tiếp tuyến vuông góc 1 −
k.k = −1  k =
Từ: k = f ( x → Tính được x và y = y x 0 ( 0) 0 )
đường thẳng (d ) d k 0 d
Biết tiếp tuyến qua y − y(x = yx . x −x Giải tìm x → Tính y = y x , k = f (x 0 ) 0 ( 0) A 0 ) ( 0) ( A 0)
A( x ; y 0 A A )
Tiếp tuyến tại giao điểm
của (C) : y = f (x) và f (x = ax +b
Giải tìm x → Tính y = y x , k = f ( x 0 ) 0 ( 0) 0 ) 0 0
(d): y = ax +b
Tiếp tuyến tại giao điểm = =  của y = 0 Từ: y
y x → Tính được x và k f ( x 0 ) 0 ( 0)
(C ) và Ox 0 0
Tiếp tuyến tại giao điểm = =  của x = 0 Tính: y y x , k f ( x 0 ) 0 ( 0)
(C ) và Oy 0 2024-2025 15 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
PHẦN HÌNH HỌC VÀ ĐO LƯỜNG
VẤN ĐỀ 6. ĐƯƠNG THẲNG VÀ MẶT PHẲNG. QUAN HỆ SONG SONG KHÔNG GIAN
I. CHỨNG MINH QUAN HỆ SONG SONG
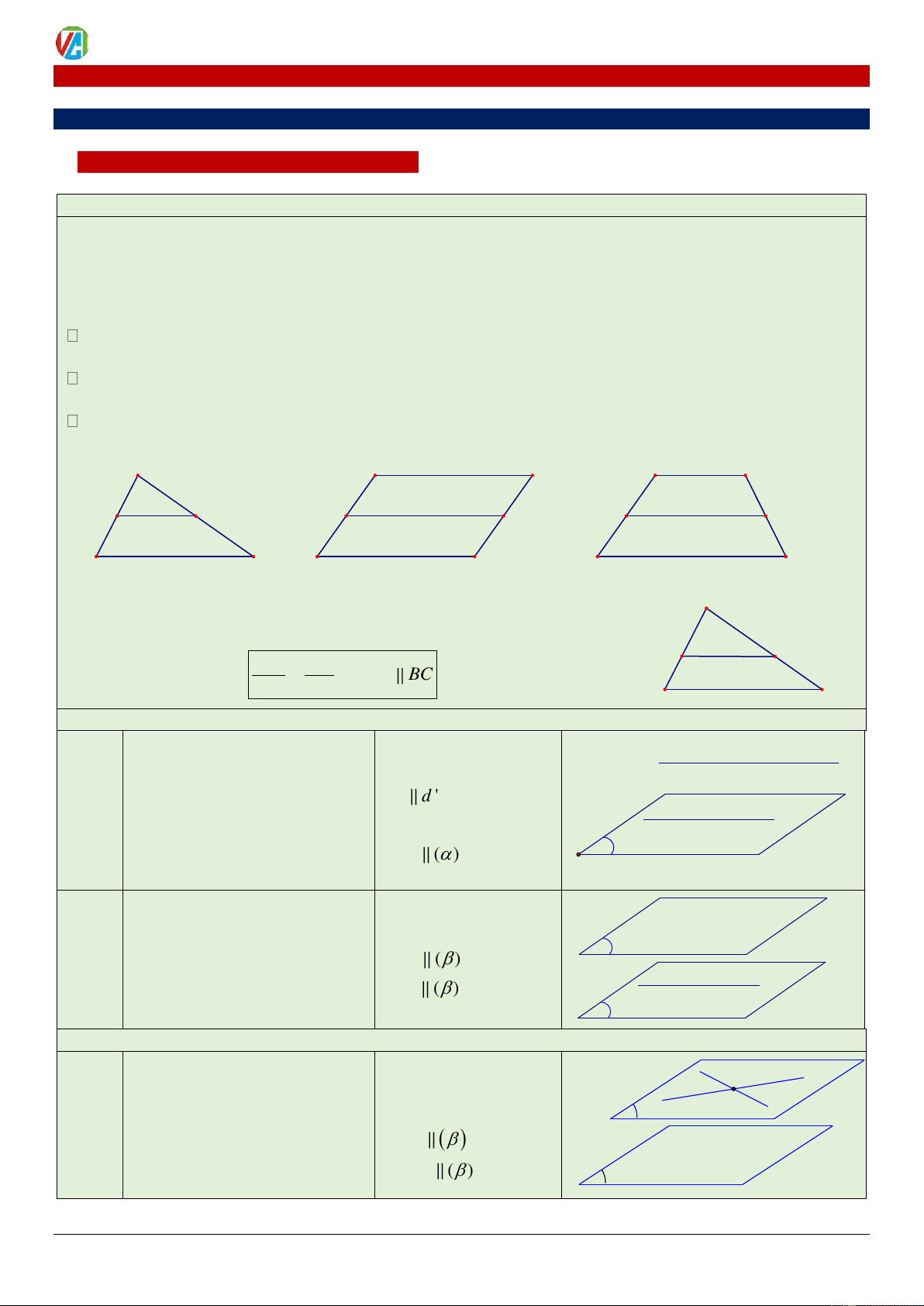
1. Chứng minh hai đường thẳng song song
Sử dụng kết quả hình học phẳng để chứng minh
a)Hình thang: Hai cạnh đáy song song
b)Các dạng hình bình hành (hình bình hành thường, hình thoi, hình chữ nhật, hình vuông): Hai cặp cạnh
đối song song và bằng nhau.
c)Đường trung bình:
Đường trung bình của tam giác: Đoạn thẳng nối trung điểm hai cạnh, song song và bằng nửa cạnh còn lại.
Đường trung bình hình bình hành: Đoạn thẳng nối trung điểm hai cạnh đối, song song và bằng hai cạnh còn lại.
Đường trung bình hình thang: Đoạn thẳng nối hai cạnh bên, song song và bằng trung bình cộng hai cạnh đáy. A A D A D N M M M N N B C B C B C
d)Định lý Thalès trong tam giác A
Một đường thẳng chắn hai cạnh của tam giác theo các đoạn thẳng tương
ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại và ngược lại N M AM AN =  MN BC AB AC B C
2. Chứng minh đường thẳng song song mặt phẳng
ĐL: Nếu đường thẳng d không
chứa trong mặt phẳng ( ) và d  ()  d' Cách
song song với đường thẳng d' d d ' 1
chứa trong mặt phẳng ( ) thì d '  ()  d
đường thẳng d song song với d () α
mặt phẳng ( ) .
ĐL: Nếu 2 mặt phẳng song d  () Cách
song thì mọi đường thẳng nằm  β () ( ) 2
trong mặt phẳng này đều song
song với mặt phẳng kia. d ( ) d α
3. Chứng minh 2 mặt phẳng song song
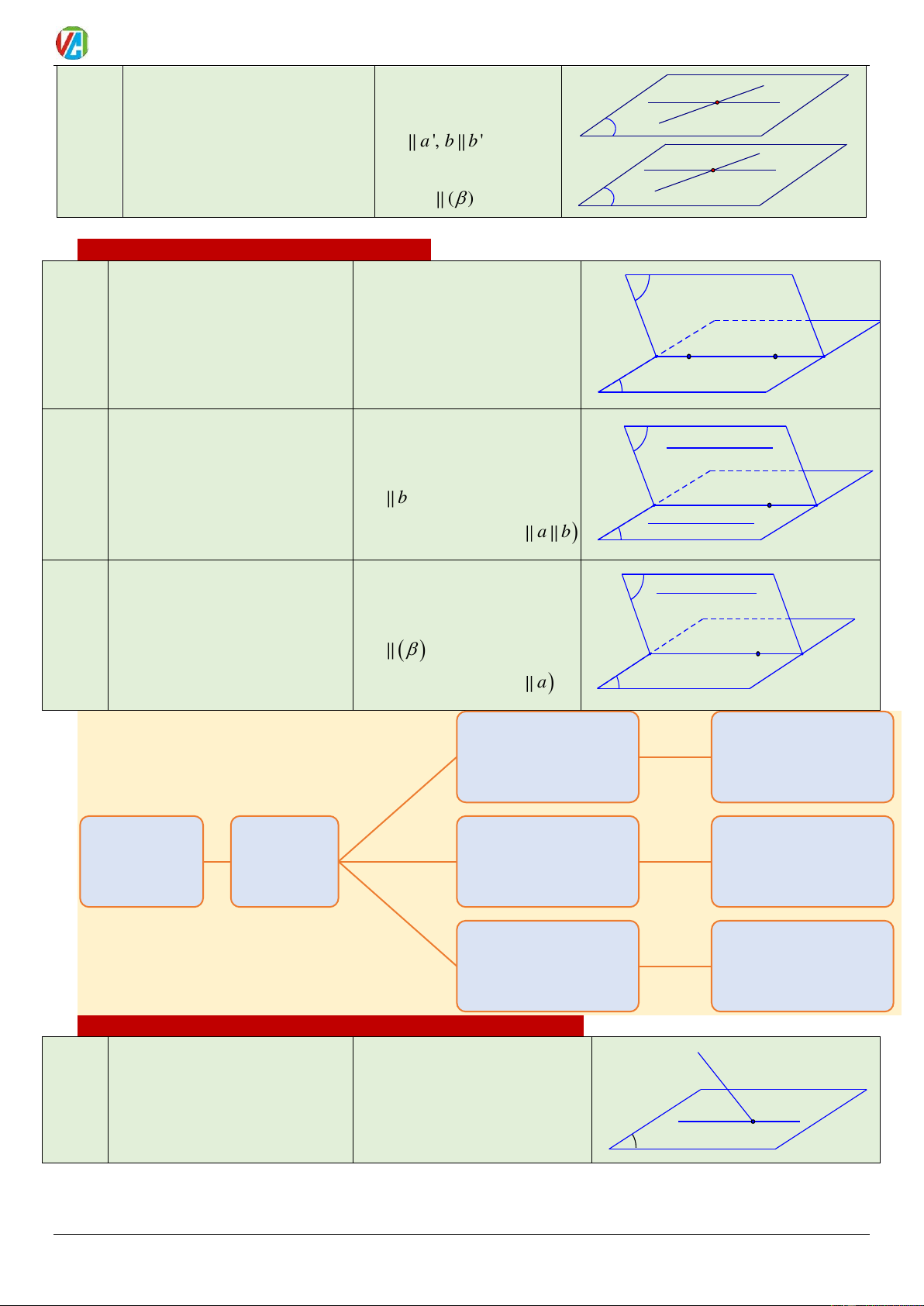
ĐL: Nếu mặt phẳng này có ( )  a,b a
chứa 2 đường thẳng cắt nhau b I Cách
a b = I α
cùng song song với mặt phẳng 1 a, b  ( )
kia thì hai mặt phẳng song song nhau.  () ( ) β 2024-2025 16 0983.900.570
Hê thống kiến thức và phương pháp giải Toán 11 Võ Công Trường
HQ: Nếu mặt phẳng này có a, b  ( )
chứa 2 đường thẳng cắt nhau a b = I a' Cách
lần lượt song song 2 đường b' β
a a ', b b ' 2
thẳng chứa trong mặt phẳng kia   
thì hai mặt phẳng song song a ', b ' ( ) a I nhau.  () ( ) b α
II. TÌM GIAO TUYẾN CỦA 2 MẶT PHẲNG. A( ) ( ) β
Tìm 2 điểm chung phân biệt
B ( ) ( ) Cách
của 2 mặt phẳng → Giao tuyến 1
là đường thẳng đi qua 2 điểm A Bd chung đó A B AB = ( )  ( ) α
Tìm 1 điểm chung của 2 mặt
phẳng và chứng tỏ trong 2 mặt I ( )  ( ) β  b
phẳng lần lượt có chưa 2 a  ( ), b  ( ) Cách
đường thẳng song song nhau 2 → a b d
Giao tuyến là đường thẳng
đi qua điểm chung và song  ( )( ) = I Ix ( Ix a b) α a
song 2 đường thẳng đó.
Tìm 1 điểm chung của 2 mặt
phẳng và chứng tỏ trong mặt I ( )  ( ) α  a
phẳng này có chưa 1 đường a  ( ) Cách
thẳng song song với mặt phẳng 3 a  ( ) d
kia→ Giao tuyến là đường
thẳng đi qua điểm chung và  ( )( ) = I Ix ( Ix a) β
song song đường thẳng đó. Có một điểm chung
Giao tuyến là đường
thẳng qua hai điểm khác chung
Gaio tuyến là đường Tìm giao Có hai đường thẳng thẳng qua điểm tuyến hai Tìm một điểm chung song song lần lượt chắ chung và song song mặt phẳng trong hai mặt phảng voiws hai đường thẳng đó Có một đường thẳng
Giao tuyến là đường nằm trong mặt phẳng thẳng qua điểm này và song song với chung và song song mặt phẳng kia
và đường thẳng đó
III. TÌM GIAO ĐIỂM CỦA ĐƯƠNG THẲNG VÀ MẶT PHẲNG. b
Nếu trong ( ) có chứa sẵn (   )  aTH1
đường thẳng a cắt b tại I thì I a b = I
là giao điểm của b và ( ) .
b ( ) = I a I α 2024-2025 17 0983.900.570