Hồi quy đơn và bội: Phân tích và đánh giá mô hình môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

X, Hồi quy đơn – Hồi quy bội Câu 50(tr428): BÀI LÀM
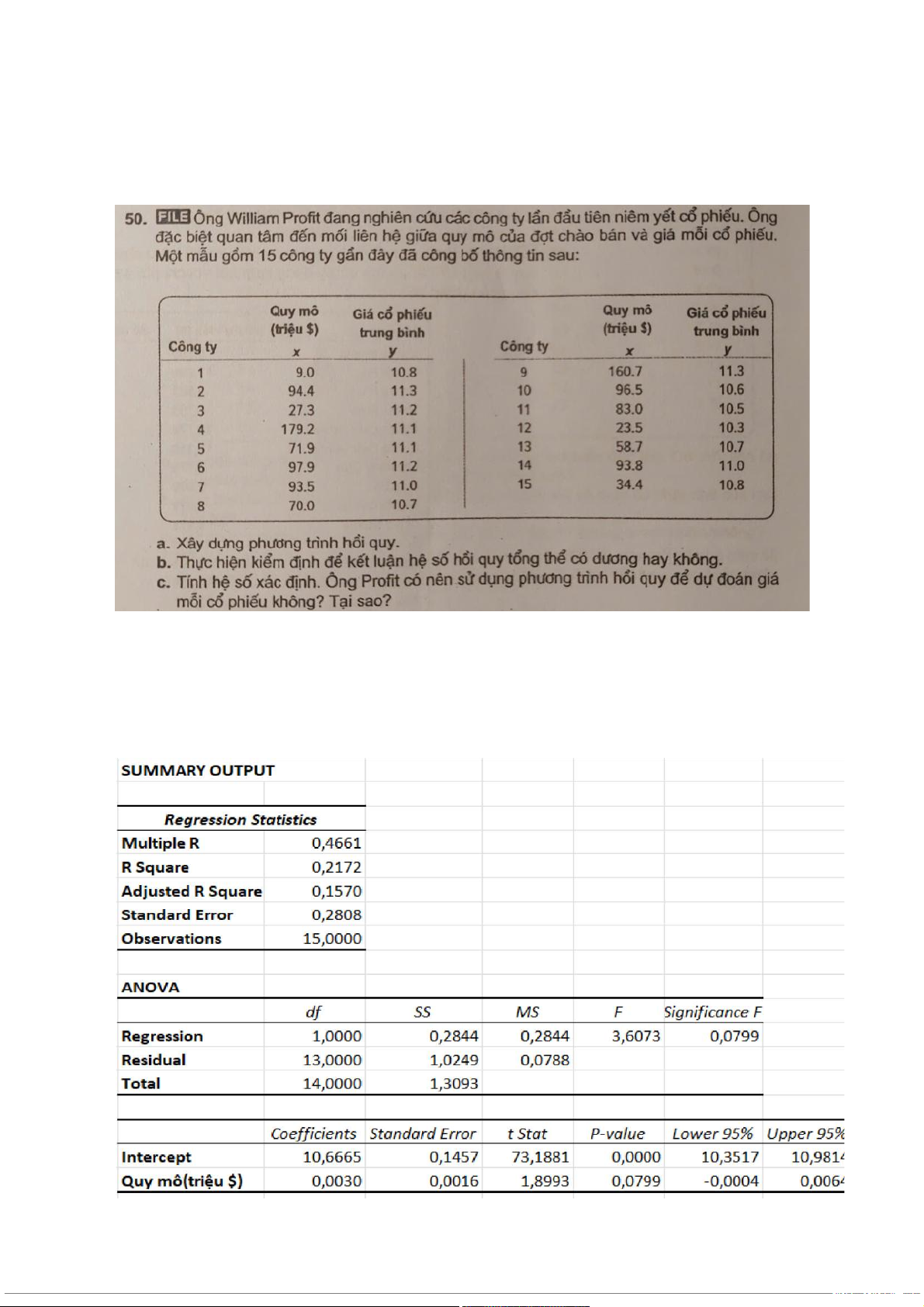
a, Sử dụng Microsoft Excel để tính toán các số liệu thống kê cần thiết cho phân tích:
Từ bảng trên, ta có phương trình hồi quy: Ŷi = 0,0030xi + 10,6665
b, Bước 1: Xét cặp giả thuyết H0: β1 ≤ 0 H1: β1 > 0
Bước 2: Tính tiêu chuẩn kiểm định t = 𝑆 𝑏 𝑒 1 (𝑏1) =0,003 0,0016 = 1,875
Bước 3: Xác định điều kiện bác bỏ H0
Ta có: df = n – 2 = 15 – 2 = 13 t =
13 1,771( Sử dụng mức ý nghĩa 5%, df=13) Ta có: 1,875 >
1,771 vì vậy bác bỏ giả thuyết H0
➔ Vậy hệ số hồi quy tổng thể có dương.
c, Từ bảng trên, ta có hệ số xác định r 2 = 0,2172
Không nên sử dụng phương trình hồi quy tuyến tính này để dự đoán giá mỗi cổ phiếu. Vì:
- Hệ số xác định (R Square) quá thấp: Giá trị R Square là 0,2172, nghĩa là
chỉ có khoảng 21,72% sự biến động của giá cổ phiếu được giải thích bởi
sự thay đổi của quy mô. Điều này cho thấy mô hình hồi quy tuyến tính
này không phù hợp để giải thích phần lớn sự biến động của giá cổ phiếu.
• Giá trị P-value của biến Quy mô (biến x) lớn hơn mức ý nghĩa 5%: Giá trị
P-value cho biến "Quy mô (triệu $)" là 0,0799. Nếu sử dụng mức ý nghĩa
là 0,05, thì giá trị P-value này lớn hơn 0,05. Điều này có nghĩa là hệ số
hồi quy của biến quy mô không có ý nghĩa ở mức ý nghĩa 5%. Vì vậy,
không có đủ bằng chứng để
➔ Quy mô có tác động đáng kể đến giá cổ phiếu trong mô hình này
Câu 30(tr484): Giám đốc các sự kiện đặc biệt của Sun City tin rằng số tiền chi
cho các màn bắn pháo hoa vào ngay 4 tháng 7 có thể dự đoán cho việc tham dự
Lễ hội mùa thu được tổ chức vào tháng 10. Cô thu thập dữ liệu sau đây để kiểm
tra sự nghi ngờ của mình: BÀI LÀM
a, Sử dụng Microsoft Excel để tính toán các số liệu thống kê cần thiết cho phân tích:
Từ bảng trên, ta có phương trình hồi quy: Ŷi = 0,7618xi + 1,7208 Hệ số xác định R
2 = 0,7604 Hệ số hồi quy b
1 = 0,7618. Có nghĩa là khi chi cho
bắn pháo hoa tăng 1(nghìn $) thì giá trị trung bình của số người dự lễ hội tăng 0,7618(nghìn người).
b, Đánh giá các giả thiết hồi quy:
- Giả thiết 1: Mối liên hệ là tuyến tính
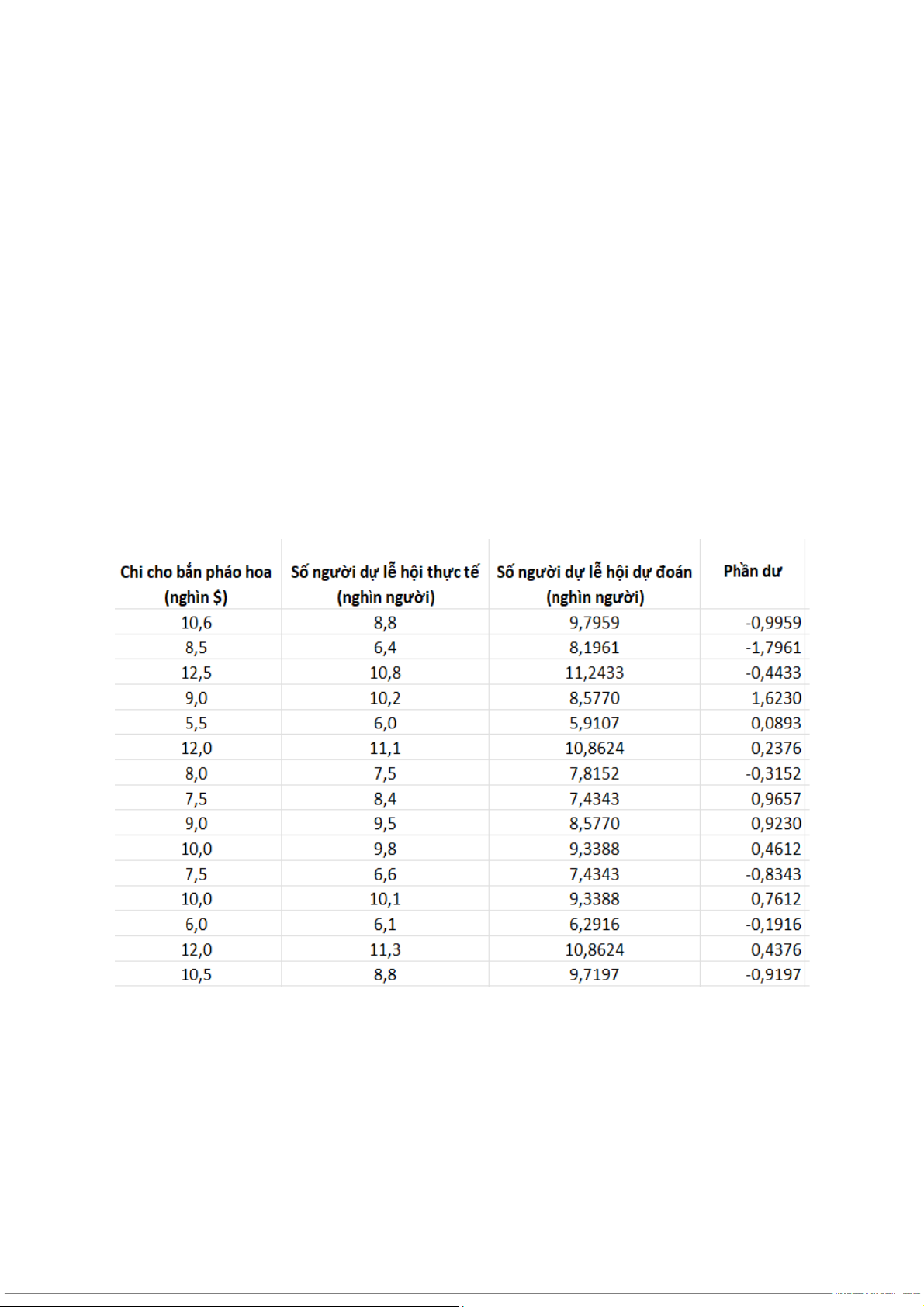
Phần dư được tính theo công thức:
Phần dư = Số người dự lễ hội thực tế - Số người dự lễ hội dự đoán
Số người dự lễ hội thực tế được lấy từ bảng, Số người dự lễ hội dự đoán được
tính bằng cách thay giá trị các biến x1, x2, x3 từ bảng số liệu vào phương trình
hồi quy. Từ đó, ta có Bảng: Phần dư của phương trình hồi quy
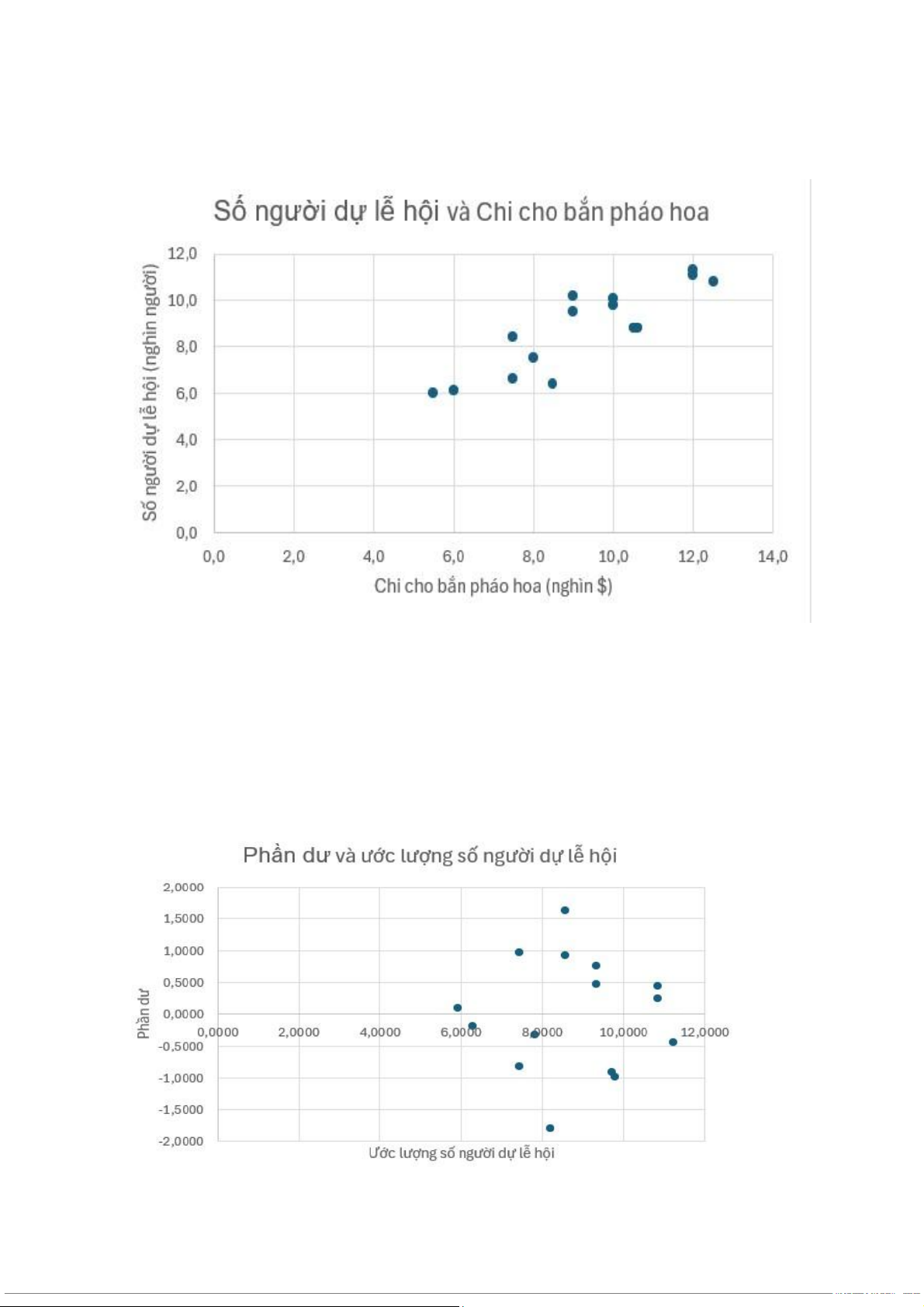
Từ bảng trên, ta có biểu đồ phân tán của chi cho bắn pháo hoa và số người dự lễ hội:
Biểu đồ phân tán của cặp biến số người dự lễ hội và chi cho bắn pháo hoa cho
thấy xu hướng tăng. Khi chi cho bắn pháo hoa tăng lên, số người dự lễ hội cũng
tăng. Các quan sát có xu hướng thể hiện đường tuyến tính.
- Giả thiết 2: Phương sai của phần dư bằng nhau tại mọi giá trị ước lượng
(phương sai sai số không đổi)
Từ bảng phần dư đã xây dựng ở trên, ta xây dựng biểu đồ phần dư:
Giả sử có mối liên hệ tuyến tính, sự phân bố của phần dư phải cho thấy tỷ lệ
bằng nhau của phần dư có giá trị âm và phần dư có giá trị dương xung quanh
giá trị 0. Các điểm quan sát không phân bố theo quy luật, phân bố trên và dưới
của đường thẳng đi qua điểm 0, vì vậy kết luận rằng giả thiết tuyến tính là hợp lý.
- Giả thiết 3: Phần dư tuân theo quy luật phân phối chuẩn
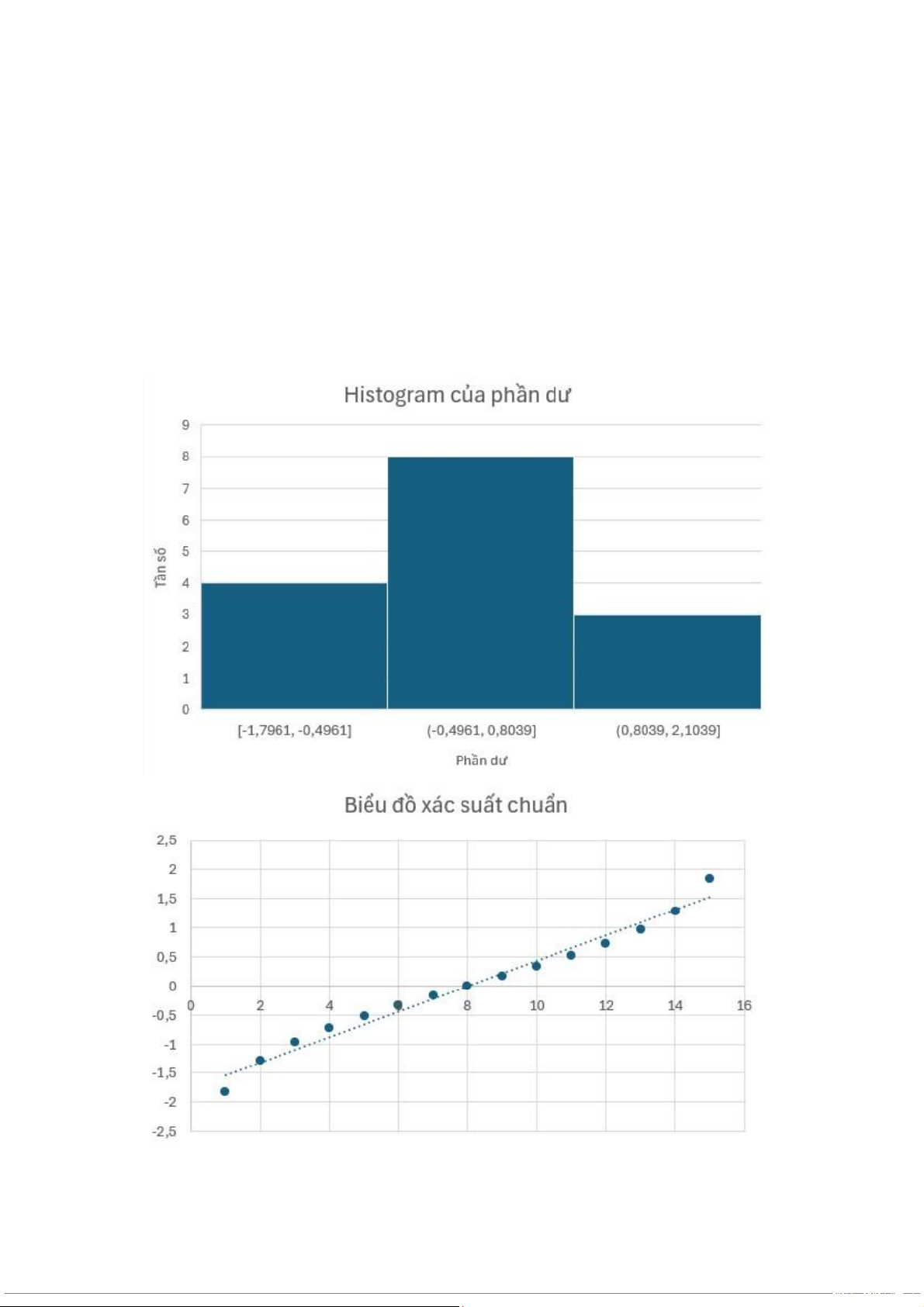
Từ số liệu từ bảng Phần dư đã xây dựng ở trên, sử dụng Microsoft Excel ta
xây dựng được biểu đồ Histogram của phần dư và biểu đồ xác suất chuẩn:
Ở biểu đồ Histogram của phần dư cho thấy các đặc điểm chính của một phân
phối chuẩn, phần lớn các quan sát ở giữa và tập trung quanh giá trị trung bình
bằng 0, với các tần số thấp hơn ở các phần đuôi của phân phối. Biểu đồ xác suất
chuẩn cho thấy các điểm được vẽ tiệm cận với một đường thẳng được vẽ từ góc
trái phía dưới đến góc phải phía trên của biểu đồ thì giả thiết về phần dư tuân
theo quy luật phân phối chuẩn được thỏa mãn.
- Giả thiết 4: Đa cộng tuyến
Với một biến độc lập duy nhất trong mô hình hồi quy, thì không thể xảy ra hiện tượng đa cộng tuyến.
 Phương trình này giải thích 76,04% sự thay đổi của số người dự lễ hội.
Các giả thiết của mô hình hồi quy bội là mối liên hệ tuyến tính, phần dư
tuân theo quy luật phân phối chuẩn và không có hiện tượng đa cộng tuyến đều được thỏa mãn.