





Preview text:
lOMoAR cPSD| 58605085
School of Industrial Engineering & Management (IEM) Inventory Management
International University, VNU-HCM
Instructor: Dr. Nguyen Van Hop Tr n Th Thanh Ngânầ ị – IELSIU18223 Homework 3
Problem 1: problem 6.2 page 224 Silver et.al. (1998) book
The demand pattern for another type of filter is: Jan Feb Mar Apr May June 18 31 23 95 29 37 July Aug Sept Oct Now Dec 50 39 30 88 22 36
These filters cost the company $4.75 each; ordering and carrying costs are as in Problem 6.1.
The variability coefficient equals 0.33. Use the Silver-Meal heuristic to determine the sizes and
timing of replenishments of stock. Solution: We have: c = $4.75 A = $35
r = 0.24 $/$/year = 0.02 $/$/month Ch =
0.02 × 4.75 = $0.095 /unit/month
Z1,1 = A + c × D1 = 35 + 4.75 × 18 = 120.5
Z1,2 = (A + c(D1 + D2) + Ch × D2)/2 = (35 + 4.75(18 + 31) + 0.095 × 31)/2 = 135.3475 > 120.5
So the heuristic sets Q1 = 18. Next:
Z2,2 = A + c × D2 = 35 + 4.75 × 31 = 182.25
Z2,3 = (A + c(D2 + D3) + Ch × D3)/2 = (35 + 4.75(31 + 23) + 0.095 × 23)/2 = 146.8425 < 182.25
Z2,4 = (A + c(D2 + D3 + D4) + 2Ch × D3 + Ch × D4)/3 = (35 + 4.75(31 + 23) + 0.095
× 23)/2 = 254.3283 > 146.8425
So the heuristic sets Q2 = 54. Same as above, we also have: Z4,4 = 486.25 Z4,5 = 313.3775 < 486.250 Z4,6 = 269.8450 < 313.3775 Z4,7 = 265.3213 < 269.8450 Z4,8 = 252.2710 < 265.3213 Z4,9 = 236.3508 < 252.2710
Z4,10 = 269.4664 > 236.3508
So the heuristic sets Q4 = 280. Next: Z10,10 = 453.00 Z10,11 = 279.7950 < 453.00 lOMoAR cPSD| 58605085
Z10,12 = 245.8100 < 279.7950
So the heuristic sets Q10 = 146.
Conclusion: - Ordering 18 patterns on January -
Ordering 54 patterns on February -
Ordering 280 patterns on April -
Ordering 146 patterns on October
Problem 2: problem 6.10 page 226 Silver et.al. (1998) book
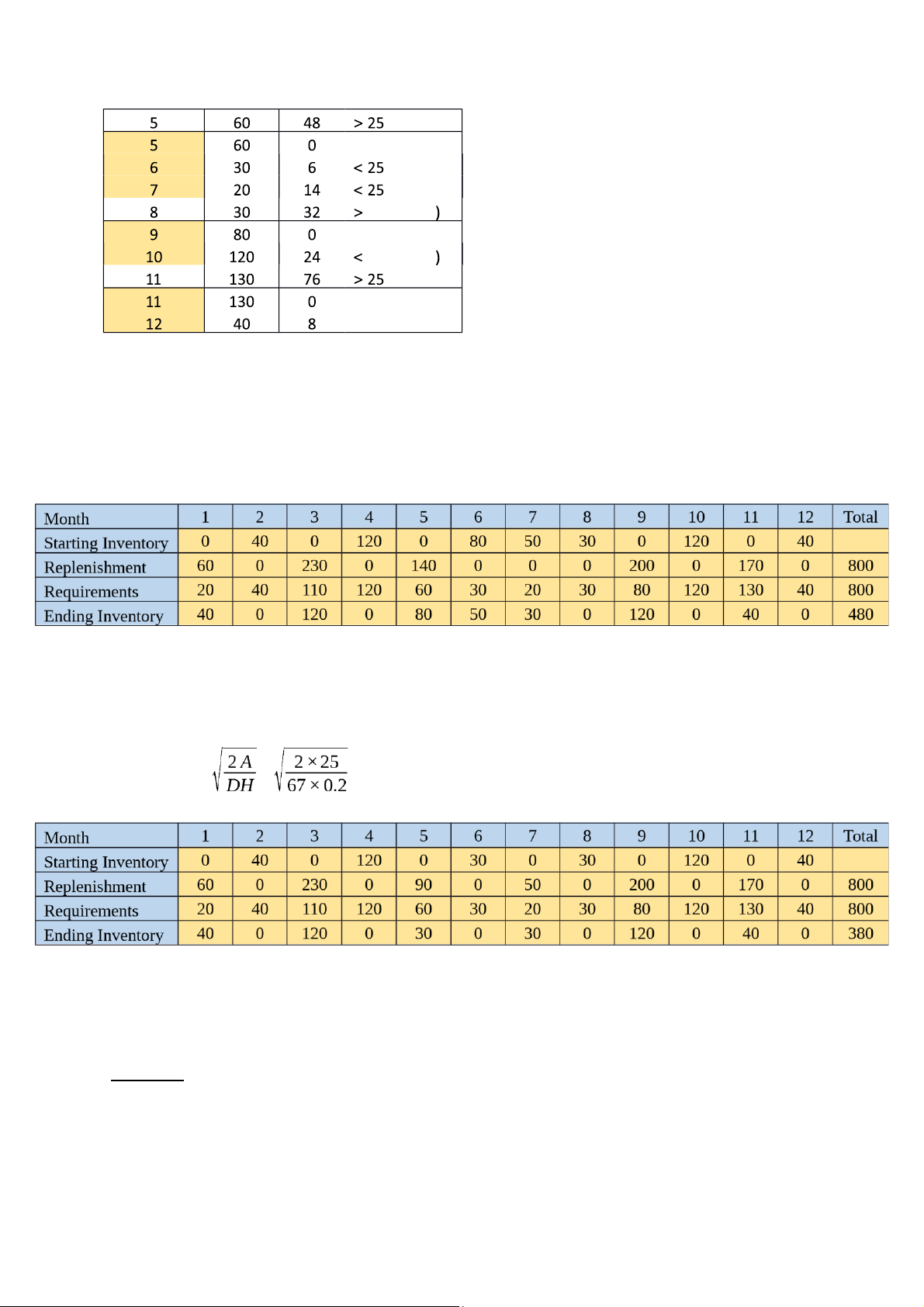
Consider a company facing a demand pattern and costs as follows: Month Sequential Number Requirements (Units) January 1 20 February 2 40 March 3 110 April 4 120 May 5 60 June 6 30 July 7 20 August 8 30 September 9 80 October 10 120 November 11 130 December 12 40 Total 800 A = $25.00 r (per month) =
$0.05 (carrying costs are very high in this industry) v = $4.00
Using a “three-month” decision rule, the replenishment schedule and associated costs are as follows: Month 1 2 3 4 5 6 7 8 9 10 11 12 Total Starting Inventory 0 150 110 0 90 30 0 110 80 0 170 40 Replenishment 170 0 0 210 0 0 130 0 0 290 0 0 800 Requirements 20 40 110 120 60 30 20 30 80 120 130 40 800 Ending Inventory 150 110 0 90 30 0 110 80 0 170 40 0 780 Total replenishment costs $100.00 lOMoAR cPSD| 58605085 Total carrying costs $156.00
Total replenishment + carrying $256.00
a. Construct a replenishment schedule and calculate the associated costs using the Fixed
Economic Order Quantity method.
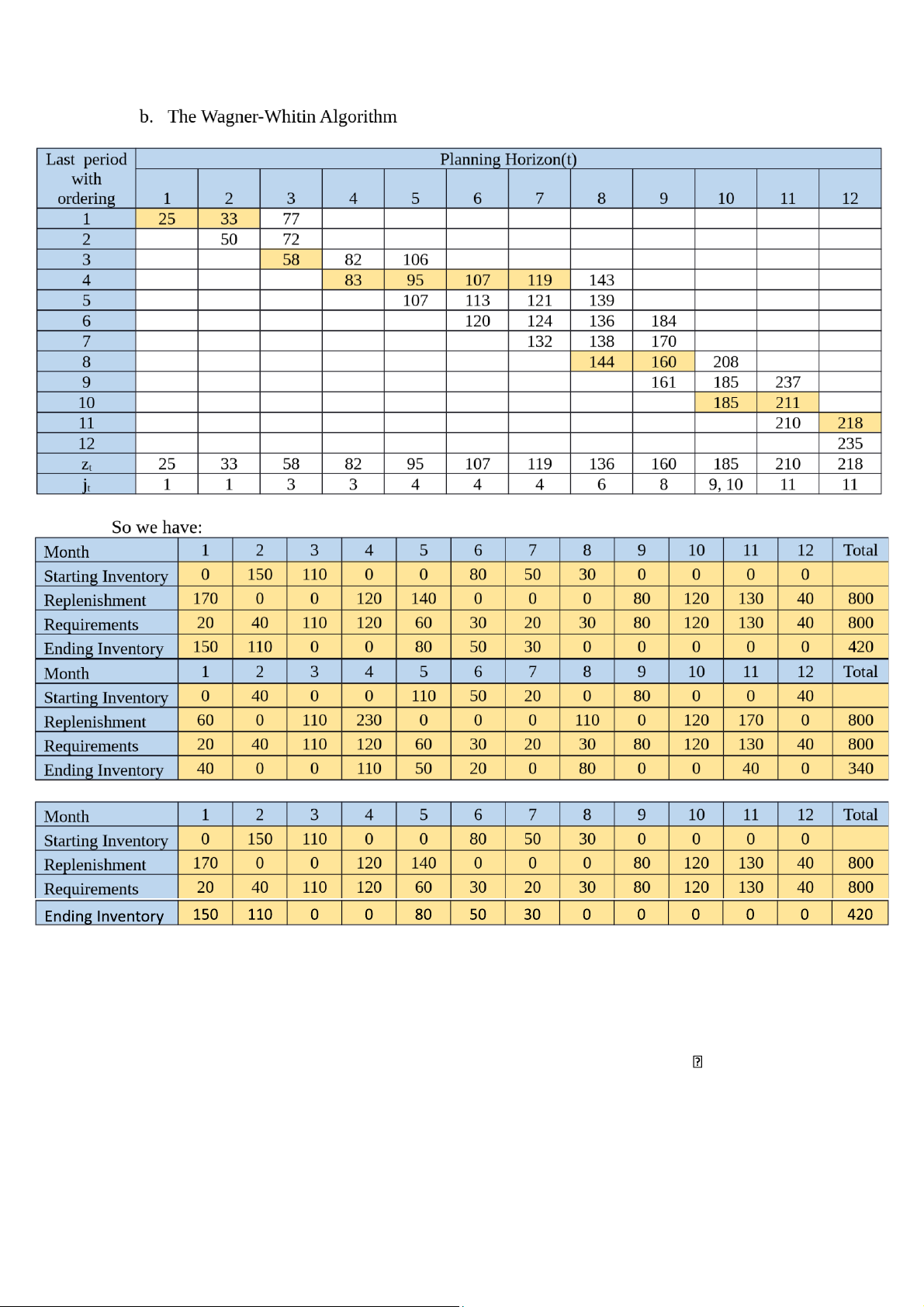
b. Repeat using the Wagner-Whitin Algorithm.
c. Repeat using the Silver-Meal Heuristic.
d. Repeat using the Least Unit Cost method.
e. Repeat using the Part-Period Balancing method.
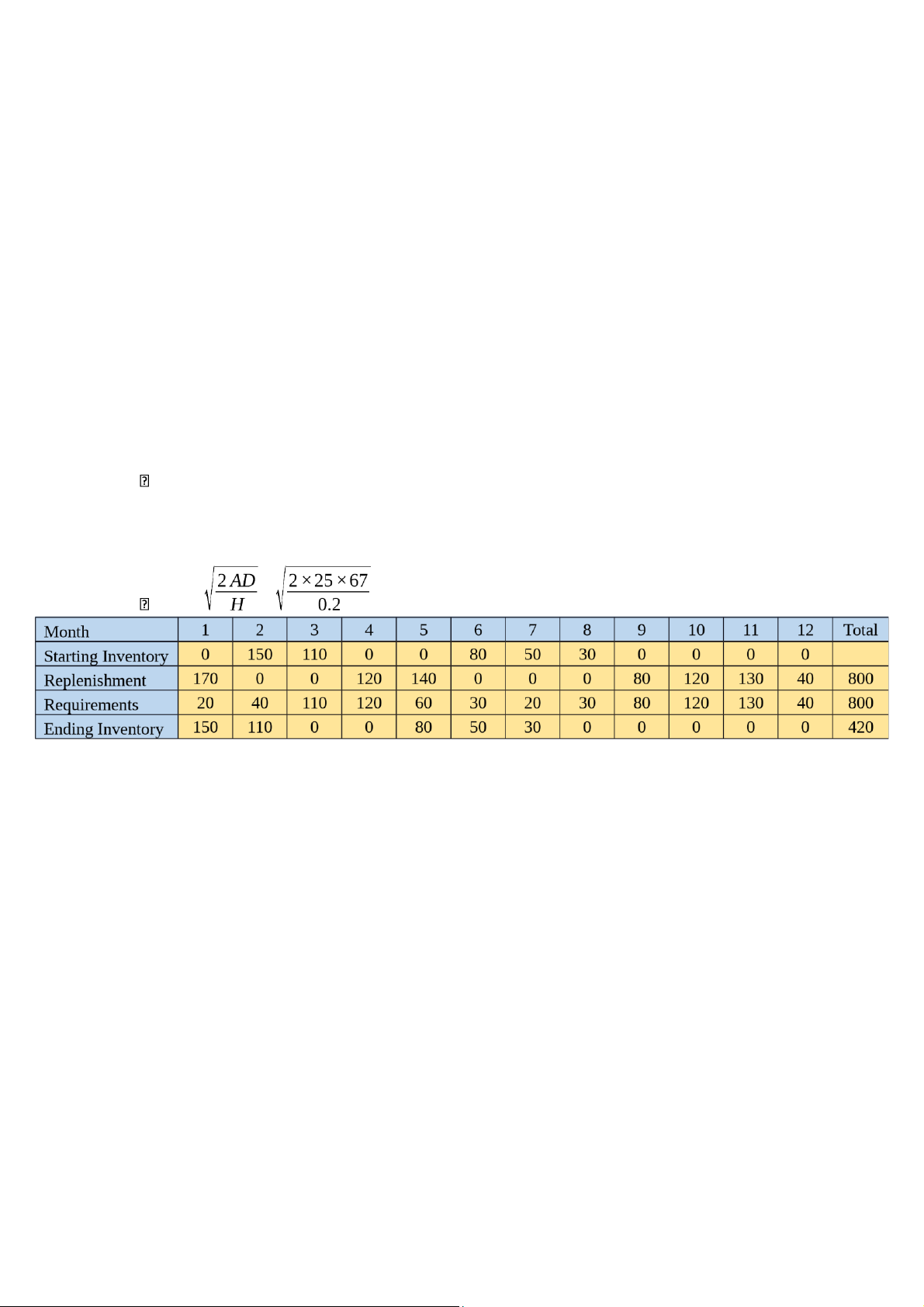
f. Repeat using the Periodic Order Quantity method. Solution: We have: At = $25 r = $0.05 v = $4 H = 0.05 × 4 = $0.2
a. The Fixed Economic Order Quantity method We get:
The average of the demand is: D = 67 unit per month EOQ = = = 129.42 = 130 unit
Total replenishment cost: 25 × 7 = $175
Total carrying costs: 420 × 0.2 = 84 Total: 175 + 84 = $259 lOMoAR cPSD| 58605085
Total replenishment cost: 25 × 6 = $150
Total carrying costs: 340 × 0.2 = 68 Total: 150 + 68 = $218 c. The Silver-Meal Heuristic
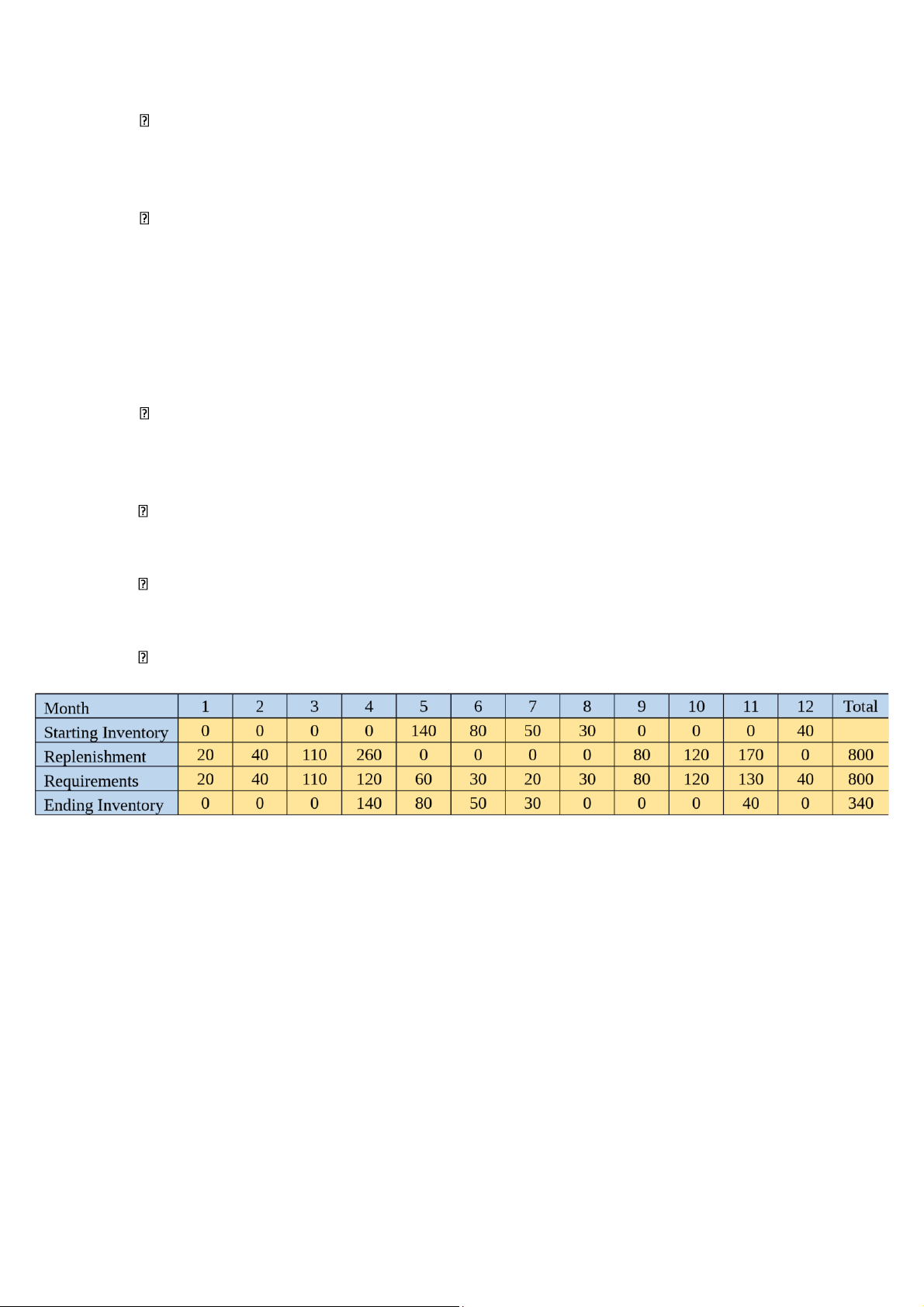
Z1,1 = A + c × D1 = 25 + 4 × 20 = 105
Z1,2 = (A + c(D1 + D2) + Ch × D2)/2 = (25 + 4(20 + 40) + 0.2 × 40)/2 = 136.5 > 105 So the heuristic sets Q1 = 20. Next:
Z2,2 = A + c × D2 = 25 + 4 × 40 = 185
Z2,3 = (A + c(D2 + D3) + Ch × D3)/2 = (25 + 4(40 + 110) + 0.2 × 110)/2 = 323.5 > 185 lOMoAR cPSD| 58605085
So the heuristic sets Q2 = 40. Same as above, we also have: Z3,3 = 465 Z3,4 = 484.5 > 465
So the heuristic sets Q3 = 110. Next: Z4,4 = 505 Z4,5 = 378.50 < 505 Z4,6 = 296.33 < 378.50 Z4,7 = 245.25 < 296.33 Z4,8 = 225.00 < 245.25 Z4,9 = 254.17 > 225.00
So the heuristic sets Q4 = 260. Next: Z9,9 = 345 Z9,10 = 424.50 > 345.00
So the heuristic sets Q9 = 80 Next: Z10,10 = 505 Z10,11 = 525.50 > 505.00
So the heuristic sets Q10 = 120 Next: Z11,11 = 545 Z11,12 = 356.50 < 545.00
So the heuristic sets Q11 = 170 So we have:
Total replenishment cost: 25 × 7 = $175
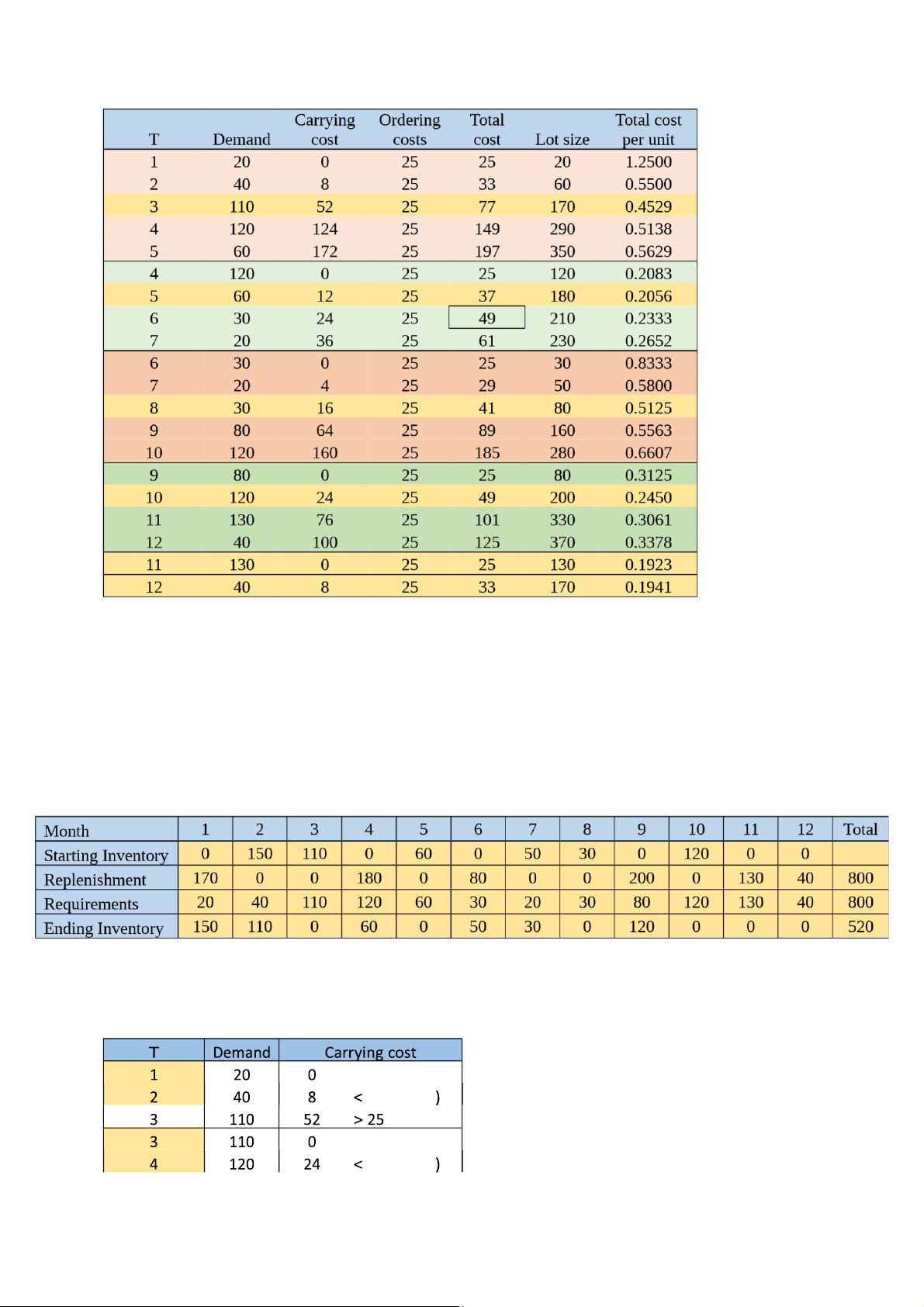
Total carrying costs: 340 × 0.2 = 68 Total: 175 + 68 = $243 d. The Least Unit Cost method lOMoAR cPSD| 58605085 So we will order with: - Q1 = 170 - Q4 = 180 - Q6 = 80 - Q9 = 200 - Q11 = 130 - Q12 = 40 Then, we have the result:
Total replenishment cost: 25 × 6 = $150
Total carrying costs: 520 × 0.2 = $104 Total: 150 + 104 = $254
e. The Part-Period Balancing method 25 (closer 25 (closer lOMoAR cPSD| 58605085 25 (closer 25 (closer So we will order with: - Q1 = 60 -
Q3 = 230 - Q5 = 110 - Q8 = 200 - Q10 = 120 - Q11 = 170 Then, we get the results:
Total replenishment cost: 25 × 5 = $125
Total carrying costs: 480 × 0.2 = $96 Total: 125 + 96 = $221
f. The Periodic Order Quantity method We have: T = = = 1.932 = 2 So we get:
Total replenishment cost: 25 × 6 = $150
Total carrying costs: 380 × 0.2 = $76 Total: 150 + 76 = $226
Problem3: solve problem 6.17 page 189 Silver et.al. (1998) book by dynamic programming approach Solution:
Holding cost: h = r × v = 1.05 × 65 = $68.25 lOMoAR cPSD| 58605085 Let z1* = 0 Node 2:
c1,2 = A + C × D1 = 50 + 65 ×350 = $22,800
z¿2 = $22,800 → p¿2=1 Node 3: c1,3 = $49,450
c2,3=$13,050 z¿3=min(z¿1+c1,3;z¿2+c2,3)=min
(49,450;35,850)=$35,850→p¿3=2 Node 4:
c1,4=A+C∗(D1+D2+D3)+h∗(D2+2 D3)=$ 49,450
c2,4=A+C∗(D2+D3)+h∗D3=$13,050 c3,4=A+C∗D3=$50 z →p Node 5:
c1,5=A+C∗(D1+D2+D3+D4)+h∗(D2+2 D3+3 D4)=$89912.5
c2,5=A+C∗(D2+D3+D4)+h∗(D3+2D4)=$ 43,275
c3,5=A+C∗(D3+D4)+h∗D4=$20,037.5 c4,5=A+C∗D4=$ 9,800 z
¿min (87662.5;66,975;55,887.5;45,650 )=$ 45,650 →p¿5=4
Node 6: c1,6=$258,912.5 c2,6=$178,150 c3,6=$120,787.5 c4,6=$76,425 c5,6=$32,550
z¿1+c1,6=$ 258,912.5
z¿2+c2,6=$ 200,950 z ¿
6 =minz¿3+c3,6=$
{15 6,637.5=$ 78,200→ p¿6=5
z¿4+c4,6=$112,275 z¿5+c5,6=$ 78,200
Node 7: c1,7=$502,662.5 c2,7=$380,950 c3,7=$282,637.5
c4,7=$197,325 c5,7=$112,500 c6,7=$39,050 z ¿ 1 +c1,7=$ 502,662.5 ¿
z2+c2,7=$ 403,750 lOMoAR cPSD| 58605085
z7¿=minz3¿+¿ c3,7=$ 318,487.5=$ 117,250→p7¿=6 z ¿ 4+c4,7=$233,175
z5 +c5,7=$ 158,150 z ¿
6 +c6,7=$117,250 Node 8: c1,8=$716,187.5
c2,8=$563,762.5 c3,8=$ 434,737.5 c4,8=$318,712.5 c5,8=$203,175 c6,8=$99,012.5 c7,8=$29,300 z ¿ ¿ ¿
1 +c1,8=$716,187.5
z2 +c2,8=$586,562.5 z3 +c3,8=$ 470,587.5 z ¿ ¿
8 =minz¿4+c4,8=$354,562.5=$146,550→p¿8=7 z5 +c5,8=$248,825 z ¿ ¿
6 +c6,8=$177,212.5
z7 +c7,8=$146,550
Node 9: c1,9=$906,150 c2,9=$729,837.5 c3,9=$576,925 c4,9=$ 437,012.5 c5,9=$297,587.5 c6,9=$169,537.5 c7,9=$75,937.5 c8,9=$22,800 z ¿
1 +c1,9=$906,150 z ¿
2 +c2,9=$752,637.5 z ¿
3 +c3,9=$612,775
z9¿=minz¿4¿+c4,9=$ 472,862.5=$ 169,350→ p9¿=8
z5+c5,9=$343,237.5
{z¿ 6+c6,9=$247,737.5 z ¿
7 +c7,9=$193,187.5 z ¿
8 +c8,9=$169,350
Node 10: c1,10=$1,028,350
c2,10=$838,387.5
c3,10=$671,825 c4,10=$518,262.5
c5,10=¿ $365,187.5 c6,10=$223,487.5
c7,10=$116,237.5
c8,10=$49,450 c9,10=$13,050 lOMoAR cPSD| 58605085 z ¿
1 +c1,10=$1,028,350 z ¿ ¿
2 +c2,10=$861,187.5 z3 +c3,10=$707,675 z ¿
4 +c4,10=$554,112.5 z ¿ 10 =minz ¿ ¿
5 +c5,10=$410,837.5=$182,400→p10 =9 z ¿ ¿ ¿
6 +c6,10=$301,687.5 z7 +c7,10=$233,487.5 z8 +c8,10=$196,000. z ¿
9 +c9,10=$182,400 Node 11: c1,11=$1,028,350 c2,11=$ 838,387.5
c3,11=$671,825 c4,11=$ 518,262.5 c5,11=¿ $365,187.5
c6,11=$223,487.5
c7,11=$116,237.5 c8,11=$
49,450 c9,11=$13,050 c10,11=$50 z ¿
1 +c1,11=$1,028,350 z ¿
2 +c2,11=$861,187.5 z ¿
3 +c3,11=$707,675 z ¿
4 +c4,11=$554,112.5 z11¿
=minz5¿¿+c5,11=$410,837.5=$182,400→p11¿
=9 z6+c6,11=$301,687.5 z ¿ ¿
7 +c7,11=$233,487.5 z8 +c8,11=$196,000 z ¿
9 +c9,11=$182,400
z10¿ +c10,11=$182,450
Node 12 c1,12=$1,140,475 c2,12=$940,275 c3,12=$763,475 c4,12=$599,675
c5,12=$436,362.5 c6,12=$284,425 lOMoAR cPSD| 58605085
c7,12=$166,937.5 c8,12=$59,200
c9,12=$43,275 c10,12=$
20,037.5 c11,12=$13,050 z ¿
1 +c1,12=$1,140,475 z ¿
2 +c2,12=$963,075 z ¿
3 +c3,12=$799,325 z ¿
4 +c4,12=$635,525 z ¿
5 +c5,12=$482,012.5 z ¿ ¿ ¿ 12
=minz6 +c6,12=$362,625 =$195,450→p12 =11 z ¿
7 +c7,12=$284,187.5 z ¿ ¿
8 +c8,12=$205,750 z9 +c9,12=$212,625
z10¿ +c10,12=$ 202,438
z11¿ +c11,12=$195,450
Node 13 c1,13=$1,303,625
c2,13=$1,089,775 c3,13=$899,325 c4,13=$721,875
c5,13=$544,912.5 c6,13=$379,325
c7,13=$248,187.5
c8,13=$157,512.5
c9,13=$97,225 c10,13=$ 60,337.5
c11,13=$36,450 c12,13=$ 13,050 z ¿
1 +c1,13=$ 1,303,625 z ¿ ¿
2 +c2,13=$1,112,575 z3 +c3,13=$
935,175 z¿4+c4,13=$757,725 z ¿
5 +c5,13=$590,562.5 z13¿
=minz¿6¿+c6,13=$ 457,525 =$ 205,250→p13¿
=12 z7+c7,13=$365,437.5 z ¿ ¿
8 +c8,13=$304,062.5 z9 +c9,13=$266,575 z10¿ +c10,13=$ 242,737.5 z11¿ lOMoAR cPSD| 58605085
+c11,13=$218,850 z12¿
+c12,13=$205,250 So, we have:




