23 trang 3 lượt tải

Hướng dẫn giải bài tập định hướng tuần 1-2-3 Dạng toán: bài toán điện tích điểm môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

5

Đặc điểm rất dễ nhận dạng của loại bài toán này là sự xuất hiện củacác điện tích điểm  trong đề bài do đó chúng ta cần nắm vững một số công thức và kiến thức liên quan tới điện tích điểm: o . Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem! 

Môn: Vật lý đại cương 2 298 tài liệu

Trường: Học viện Công Nghệ Bưu Chính Viễn Thông 1.7 K tài liệu

Tác giả:

Profile

VietJack

2 tuần trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/23
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
1
HƯỚNG D N GI I BÀI T P NH H NG TU N 1-2-3 Ẫ Ả Ậ ĐỊ ƯỚ Ầ
DẠNG TOÁN: BÀI TOÁN N TÍCH M ĐIỆ ĐIỂ
1. Nh n xét:ậ
- i i i Đặc đ ểm r t d nh n d ng c a lo i bài toán này là s xu t hi n c a các ấ ễ ậ ạ ủ ạ ự ấ ệ ủ đ ện tích đ ểm
trong bài do ó chúng ta c n n m v ng m t s công th c và ki n th c liên quan t i đề đ ầ ắ ữ ộ ố ứ ế ứ ớ
điệ ển tích đi m:
o L iực t ng tác gi a hai ươ ữ đ ện tích m: điể =

=
o Cườ độ ệ ường đi n tr ng: =

=
o Đ ệ ế ở đ ệ đ ểi n th gây b i i n tích i m: =

=
o Sơ đồ đổ ơ chuyển i công thức : tF E V ừ s đồ ướ ỉ ầ ớ d i ta thấy ch c n nh công
duy nh t công th c tính là có th suy ra công th c ấ ứ F ể ứ E, V
o Công d ch chuy n n tích m t v trí n v trí : = ị ể điệ điể q ừ ị A đế ị B A q(V
A
– V
B
)
o Hướng c a ủ điện tr ng gây b i n tích m: +: h ng ra, -: h ng v ườ ở điệ điể ướ ướ ề
- M ột s d ng bài t p n hình: ố ạ ậ điể
o Xác nh các i l ng c b n: đị đạ ượ ơ ả F, E, V, q, A
o Bài toán kế ợ độ ựt h p ng l c học: dây treo, trong môi tr ng xu t hi n l c y ườ ấ ệ ự đẩ
Acsimet (l c y Acsimet ự đẩ F
A
= – là tr ng l ng riêng c a ch t l ng) dV d ọ ượ ủ ấ ỏ
o Tìm v trí ng v i m t giá tr cho tr c nh v trí tri t tiêu,…. ị ứ ớ ộ ị ướ ư ị để E, F ệ
o Đ ắ ẽ đểuổi hình b t chữ nhìn hình v đư ậa ra nh n xét
2. H ng gi i: ướ ả
Bước 1: C n xác nh i l ng c n tìm ( ây chính là b c tóm t t) ầ đị đạ ượ ầ đ ướ ắ
Bước 2: Li t kê các công th c liên quan ánh d u nh ng i l ng ã bi t ệ ứ đ ấ ữ đạ ượ đ ế
Bước 3: Tìm liên h gi a i l ng ã bi t và i l ng c n tìm k t qu ệ ữ đạ ượ đ ế đạ ượ ầ ế ả
3. Bài t p minh hậ ọa:
Bài 1-5:
Hai qu cả ầu mang n có bán kính và điệ
khối l ng b ng nhau c treo hai u s i dây ượ ằ đượ ở đầ ợ
có chi u dài b ng nhau. Ng i ta nhúng chúng vào ề ằ ườ
m iột ch t ấ đ ện môi (d u) có kh i l ng riêng ầ ố ượ
ρ
1
và
hằng s n môi ố điệ
ε
. H i kh i l ng riêng c a qu ỏ ố ượ ủ ả
cầu
ρ
ph i b ng bao nhiêu góc gi a các s i dây ả ằ để ữ ợ
trong không khí và ch t n môi là nh nhau? ấ điệ ư
Tóm tắt:
Qu iả c u mang ầ đ ện: bán kính, kh i l ng nh nhau, ố ượ ư
ρ
Đ ệ ầi n môi: d u -
ρ
1
,
ε
Góc l ch trong không khí = góc l ch trong ch t n môi ệ ệ ấ điệ
F E V
- q - r
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
2
Xác nh đị
ρ
?
Giải:
- Nh n xét: ậ
- i i i Hai qu c u mang ả ầ đ ện bài toán đ ện tích đ ểm
- i Nhúng chúng vào m t ch t ộ ấ đ ện môi có s liên h t i l c y Acsimet liên quan t i ự ệ ớ ự đẩ ớ
độ ẽ ả ệng lực học s ph i li t kê lực tác d ng lên qu cụ ả ầu
- Góc gi a các s i dây trong không khí và ch t n môi là nh nhau kho ng cách gi a ữ ợ ấ điệ ư ả ữ
các qu c u là không ả ầ đổi.
- Xét tr ng h p 1:ườ ợ Đặt trong không khí
- M ỗi qu c u s ch u tác d ng c a 3 l c: ả ầ ẽ ị ụ ủ ự
o Trọng l c: ự P
o Lực y Coulomb: đẩ F
o Sức c ng dây: ă T
- T ừ hình v ta th y khi u ki n cân b ng thì: ẽ ấ ở điề ệ ằ
==
4
- Xét tr ng h p 2:ườ ợ Đặt trong d u ầ
- M ỗi qu c u s ch u tác d ng c a bả ầ ẽ ị ụ ủ ốn l c: ự
o Trọng l c: ự P
o Lực y Coulomb: đẩ F’
o Sức c ng dây: ă T’
o Lực y Acsimet: đẩ F
A
- T ừ hình v ta th y khi u ki n cân b ng thì: ẽ ấ ở điề ệ ằ
= ′ =
4 (−)
- K t h p hai tr ng h p trên trong ó thay: ế ợ ườ ợ đ m =
ρ
V; d =
ρ
1
g ta có:
!= !"
−1
Chú ý:
- Cần n m v ng công th c tính l c y Acsimetắ ữ ứ ự đẩ
- M ột s d ng bài m r ng liên quan t i bài toán:ố ạ ở ộ ớ
o Xác nh h ng s n môi c a ch t n môiđị ằ ố điệ ủ ấ điệ
o Xác nh kh i l ng riêng c a ch t n môiđị ố ượ ủ ấ điệ
o Xác nh góc l ch c a dây treođị ệ ủ
o Xác nh n tích c a qu cđị điệ ủ ả ầu
o …
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
3
Bài 1-9: Xác nh l c tác d ng lên m t n tích m q = 5/3.10-9 đị ự ụ ộ điệ điể
C t tâm n a vòng xuy n bán kính đặ ở ử ế r0 = 5 cm tích n u v i điệ đề ớ
điện tích = 3.10Q
-7
C (đặt trong chân không).
Tóm tắt:
Đ ệ đ ểi n tích i m = 5/3.10q
-9
C
Vòng xuy n: tâm O, ế r
0
= 5 cm, tích điện u, = 3.10đề Q
-7
C
Hệ trong chân không.
Xác nh l c đị ự F?
Giải:
- Nh n xét: ậ
- i Do có vòng xuy n tích ế đ ện u bài toán liên quan t i tính tích phân áp d ng đề ớ ụ
ph n)ương pháp tính tích phân (4 b c c bướ ơ ả
o Bướ ầc 1 – : vòng xuyVi phân v t thậ ể ến xét ph n tử cung tròn dl
o Bước 2 – : Xác nh dQđị $=%&= '

&
o Bước 3 – Xác nh dFđị : = '

='


(
&
o Bước 4 – Tính tích phân:
Phân tích hình v ta th y vector s g m hai thành ph n ẽ ấ dF ẽ ồ ầ dF
x
và dF
y
do tính i x ng c a vòng xuyđố ứ ủ ến nên F
y
= )*=0 nh v y ta cóư ậ
,= -,= -,) ) .=)'/012


(
& (trong ó đ α
là góc t o gi a vecto dF ạ ữ
và chi u d ng Ox – c ng có sách thì l i l y ề ươ ũ ạ ấ
α
là góc t o b i vecto dF v i ạ ở ớ
trục Oy và khi ó ta ph i i hàm cosđ ả đổ
α
thành hàm sin
α
d n n c n ẫ đế ậ
tích phân c ng thay i cho phù h p là t 0 n ũ đổ ợ ừ đế
π
)
Đế ạ đổn đây ta thấy có tích phân thì tính theo , trong khi l đó góc lα i thay i
tùy theo v trí trên vòng xuyị ế ả ố ệ ữn g ợi ý cho ta ph i tìm m i quan h gi a
α
và ta có m i quan h : dl ố ệ dl = r0d
α
thay vào bi u th c tính F và l y ể ứ ấ
tích phân từ −
n đế
= 3$456
4
7
=$
2≈1,14.107<=
- Chú ý:
- V ề c b n thì bài toán này s a v bài toán xác nh c ng n tr ng E sau ó suy ơ ả ẽ đư ề đị ườ độ điệ ườ đ
ra l c tác d ng ta ch c n nh công th c v c ng n tr ng gây b i m t n a ự ụ ỉ ầ ớ ứ ề ườ độ điệ ườ ở ộ ử
vòng xuy n t i tâm c a nó là: ế ạ ủ = $
2
- M ột bài toán m r ng suy ra t bài này chính là xác nh hi u n th gây b i n a vòng ở ộ ừ đị ệ điệ ế ở ử
xuyến t i tâm c a nó ta ch thay i t b c 2 ạ ủ ỉ đổ ừ ướ = '

và chú ý là i v i n th đố ớ điệ ế
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
4
là i l ng vô h ng nên ta ch c n áp d ng tr c ti p tích phân mà không c n ph i th c đạ ượ ướ ỉ ầ ụ ự ế ầ ả ự
hi u:ện phép chiế =3 $
4=$
4
- Ngoài ra có th có m t s bài toán liên quan nh : ể ộ ố ư
o Xác nh n tích đị điệ q, Q
o Xác nh bán kính, ng kính vòng xuyđị đườ ến
o Xác nh m t n dài trên vòng xuy n đị ậ độ điệ ế
o ….
Bài 1-11: Cho hai n tích và 2 t cách nhau 10 cm. H i t i m nào trên ng n i hai điệ q q đặ ỏ ạ điể đườ ố
điện tích ấy điện tr ng tri t tiêu. ườ ệ
Tóm tắt:
Hai n tích: và 2 điệ q q
r = 10 cm
M
∈
AB
E
M
= 0
Xác nh v trí đị ị M
Giải:
- Nh n xét:ậ Đây là bài toán xác nh v trí tri t tiêu ta c n chú ý các m sau: l n, d u c a đị ị ệ ầ điể độ ớ ấ ủ
đ ủ ố điệ đ ể ề độ ớn tích i m chi u và l n c a lực đ ệ ườ đội n, c ng điệ ườn tr ng, b trí các iệ ển tích đi m
(chú ý các b trí có tính i x ng cao). ố đố ứ
- Gi s n tích > 0: ả ử điệ q
- G ọi E
A là n tr ng t i gây b i n tích điệ ườ ạ M ở điệ q
- G ọi E
B
là n tr ng t i gây b i n tích 2 d nh n th y là hai vector c ng điệ ườ ạ M ở điệ q ễ ậ ấ ườ độ
điệ ườn tr ng E
A
và E
B
ng c chi u nhau t n t i m t v trí thích h p ượ ề ồ ạ ộ ị ợ để điện tr ng t ng ườ ổ
hợp t i M b tri t tiêu. ạ ị ệ
- Gi i i ả s ử đ ểm M cách đ ện tích m t kho ng xét u ki n tri t tiêu ta có: q ộ ả r điề ệ ệ
>
?????@
=A
????@
+A
????@
=0
?@
= 
("7)
⇒2 10− ⇒=4,14D4=( )
- Chú ý:
- i Đôi khi bài toán s h i v trí ẽ ỏ ị đ ểm M để E (ho c ặ F) t ng h p t i ó b ng 1 giá tr nào ó ổ ợ ạ đ ằ ị đ
khác 0
Bài 1-12: Xác nh c ng n tr ng t tâm c a m t l c giác u c nh a, bi t r ng 6 nh đị ườ độ điệ ườ đặ ở ủ ộ ụ đề ạ ế ằ đỉ
của nó có t: đặ
1. i 6 đ ện tích b ng nhau và cùng d u ằ ấ
2. i 3 đ ện tích âm, 3 điện tích d ng v tr s u b ng nhau ươ ề ị ố đề ằ
Tóm t t: ắ
O: tâm l c giác u cụ đề ạnh a
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
5
Xác nh đị E
0
:
- TH1: q
1 = q2 = q3 = q4 = q5 = q6 = q
- TH2: |q
1
| = |q
2
| = |q
3
| = |q
4
| = |q
5
| = |q
6
| (trong ó có 3 n tích d ng) đ điệ ươ
Giải:
- V i h b trí nh bài toán, ta d th y là có 4 cách b trí, và c n chú ý tính ch t i Nhận xét: ớ ệ ố ư ễ ấ ố ầ ấ đố
xứng đố ứ đềi x ng qua tâm của hình lục giác u.
- Xét xét tr ng h p 1 ch có m t cách b trí nh hình v ườ ợ ỉ ộ ố ư ẽ
- D ựa vào tính ch t i x ng ta th y các c p n tích m i ấ đố ứ ấ ặ điệ điể đố
xứng gây ra hai vector c ng n tr ng ng c chi u ườ độ điệ ườ ượ ề
nh iưng cùng l n độ ớ đ ện tr ng t ng h p gây b i hai n ườ ổ ợ ở điệ
tích m i x ng cùng d u là b ng 0. điể đố ứ ấ ằ
- i i Đối v i h b trí này, 6 ớ ệ ố đ ện tích đ ểm t ng ng v i 3 c p ươ đươ ớ ặ
điệ ện đi n tích m cùng d u i x ng qua tâm nên n điể ấ đố ứ điệ
trường t ng h p t i tâm l c giác u b ng 0. ổ ợ ạ ụ đề ằ
- Xét tr ng h p 2 có 3 cách b trí ườ ợ ố
Do tính ch t i x ng ta nh n ấ đố ứ ậ
thấy các c p ặ điện trường E
1
-
E
4
, E
2
-E
5
, E
3
-E
6
cùng chi u và ề
cùng l n. độ ớ
Các vector n tr ng t ng điệ ườ ổ
hợp E
14
, E
25
, E
36
cùng l n độ ớ
và t o v i nhau m t góc 120ạ ớ ộ
0
như hình v th y t ng n ẽ. Dễ ấ ổ điệ
trường t ng h p c a 3 vector ổ ợ ủ
này b ng 0 ằ E
O
= 0
Do tính ch t i x ng ta nh n ấ đố ứ ậ
th iấy các c p ặ đ ện tr ng ườ E
1
-
E
4
, E
2
-E
5
, E
3
-E
6
cùng chi u và ề
cùng l n. độ ớ
Các vector điện tr ng t ng ườ ổ
hợp E
14
, E
25
, E
36
cùng l n độ ớ
và có ph ng và chi u nh ươ ề ư
hình v . Áp d ng quy t c t ng ẽ ụ ắ ổ
hợp vector ta có:
=2
<E
= 4
E
=4

F
Do tính ch t i x ng ta nh n ấ đố ứ ậ
thấy các c p n tr ng ặ điệ ườ E
1
-
E
4
, E
3
-E
6
ng c chi u và cùng ượ ề
độ ớ ệ ườ ổ l n đi n tr ng t ng
hợp c a t ng c p này bủ ừ ặ ằng 0.
Cặp E
2
-E
5
cùng chi u và cùng ề
độ ớ l n
Vector n tr ng điệ ườ E
O
b ng ằ
vector E
25
có ph ng, chi u ươ ề
như hình v và có l n. ẽ độ ớ
=
G
=2
G
= 2

F
- Chú ý:
- Đây là bài toán n hình v vi c phân tích tích ch t i x ng tính n tr ng ho c l c điể ề ệ ấ đố ứ để điệ ườ ặ ự
t iổng h p t i m t v trí nào ó. bài ôi khi có th cho ta hợ ạ ộ ị đ Đề đ ể ệ đ ện tích c b trí theo đượ ố
một quy t c nào ó nh hình tam giác vuông, tam giác u, hình vuông, hình ch nh t,… ắ đ ư đề ữ ậ
- Cần n m v ng quy t c t ng h p vector và cách tính dài vector t ng h p nh (Pitago, ắ ữ ắ ổ ợ độ ổ ợ ư
Đị ườnh lý hàm số cos trong tam giác th ng)
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
6
Bài 1-13: Trên hình v AA’ là m t m t ph ng vô h n tích n u v i ẽ ộ ặ ẳ ạ điệ đề ớ
m iật độ đ ện m t ặ
σ
= 4.10
-9
C/cm
2
và B là m t qu c u tích n cùng d u ộ ả ầ điệ ấ
với điện tích trên m t ph ng. Khặ ẳ ối l ng qu c u = 1 , n tích c a ượ ả ầ m g điệ ủ
quả c u ầ q = 10
-9
C. H i s i dây treo qu c u l ch i m t góc b ng bao ỏ ợ ả ầ ệ đ ộ ằ
nhiêu so v i ph ng th ng ng. ớ ươ ẳ đứ
Tóm t t: ắ
σ
= 4.10
-9
C/cm
2
m = 1 g
q = 10
-9
C
Xác nh góc l ch đị ệ
α
Giải:
- Nh n xét: ây là bài toán cân b ng l c, d a vào d ki n bài ta th y mu n xác nh c góc ậ Đ ằ ự ự ữ ệ đề ấ ố đị đượ
α thì ta ph i i xác nh c l n c a ( ã bi t) và (ch a bi t) ph ng h ng là ph i i ả đ đị đượ độ ớ ủ P đ ế F ư ế ươ ướ ả đ
xác nh giá tr i l ng B n ch t c a l c là l c t nh n tác d ng lên n tích m đị ị đạ ượ F ả ấ ủ ự F ự ĩ điệ ụ điệ điể q
khi n tích này c t trong n tr ng c a m t ph ng vô h n tích n u điệ đượ đặ điệ ườ ủ ặ ẳ ạ điệ đề
- tr ng thái cân b ng qu c u ch u tác d ng b i ba l c: Ở ạ ằ ả ầ ị ụ ở ự
- Tr ọng l c: ự
?@
- L ực Coulomb: @
- L ực c ng dây: ă H
?@
- L c Coulomb tác d ng lên qu c u là: ự ụ ả ầ == I
JKK
L
(bi iểu th c màu chính là ứ đỏ đ ện tr ng ườ
gây b i m t ph ng vô h n tích n u) ở ặ ẳ ạ điệ đề
- T hình v ta có: ừ ẽ FM==N
2=0,223⇒≈13
- Chú ý:
- Công th c c n nh là n tr ng gây bứ ầ ớ điệ ườ ởi m t ph ng vô h n mang n u: ặ ẳ ạ điệ đề = P

- M ột s bài toán m r ng: ố ở ộ
o Xác nh l c c ng dây đị ự ă T
o Xác nh n tích đị điệ q
o Xác nh m t n m t đị ậ độ điệ ặ
σ
Bài 1-18: H t b i mang m t n tích = - 1,7.10ạ ụ ộ điệ q
-16
C ở gầ ộn m t
dây d n th ng kho ng 0,4 , g n ng trung tr c c a dây d n. ẫ ẳ ả m ở ầ đườ ự ủ ẫ
Đ ạ ẫ ệo n dây d n dài 150 cm, mang đi n tích q
1
= 2.10
-7
C. Xác định
lực tác d ng lên h t b i. Gi thi t r ng ụ ạ ụ ả ế ằ q
1
được phân b u trên s i ố đề ợ
dây và s có m t c a ự ặ ủ q
2
không nh h ng gì t i s phân b . ả ưở ớ ự ố
Tóm tắt:
Đ ệ đ ểi n tích i m: = - 1,7.10q
-16
C
a = 0,4 cm
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
7
Dây d n: = 150 ẫ l cm, q
1
= 2.10
-7
C
Xác nh l c đị ự F
Giải:
- Nh n xét:ậ Đây là m t bài toán tác d ng c a n tr ng gây b i m t s i dây dài vô h n (ho c ộ ụ ủ điệ ườ ở ộ ợ ạ ặ
hữu h n) tích ạ điện u lên mđề ột điện tích điểm q. bài này ta có th s d ng quy t c phân tách Ở ể ử ụ ắ r
2
a.b t công th c n tr ng gây b i n tích m (chú ý là ch c áp d ng khi m kh o ừ ứ điệ ườ ở điệ điể ỉ đượ ụ điể ả
sát n m r t g n ho c trên ng trung tr c trong ó a là kho ng cách tằ ấ ầ ặ đườ ụ đ ả ừ điểm ó t i trung m đ ớ điể
c i iủa s i dây và là kho ng cách tợ b ả ừ đ ểm ó n u mút c a dây) xác nh c ng đ đế đầ ủ để đị ườ độ đ ện
trường sau ó xác nh l c đ đị ự F: =⇒=
FQ
- Áp d ng quy t c phân tách ụ ắ r
2
ta có n tr ng gây b i s i dây d n th ng dài t i m n m trên điệ ườ ở ợ ẫ ẳ ạ điể ằ
đường trung trực của dây: ="
FQ ="
FRF+S&2T
- L c tác d ng lên n tích m ự ụ điệ điể q
1
là:
= = "
FRF+S&2T≈107"=
- Chú ý:
- Ở bài toán này ta hoàn toàn có th coi nh bài toán dây dài vô h n vì >> do ó áp d ng ể ư ạ l a đ ụ
đị ễ đượ đ ệnh lý O-G ta d dàng thu c công thức i n tr ng gây b i dây vô h n tích n u ườ ở ạ điệ đề q
tại m M cách dây m t kho ng là điể ộ ả a
= %2F=
2F&
- Rất d nh n th y n u tính theo công th c này thì bi u th c tính l c ễ ậ ấ ế ứ ể ứ ự F c ng s thay i ũ ẽ đổ
kết quả sai??? th c s thì k t qu v n s g n nh nhau do g n úng vô h n khi >> ự ự ế ả ẫ ẽ ầ ư ầ đ ạ l a.
- Các công th c c n nh : ứ ầ ớ
o =U

V=

VW
o =X
VY
- M ột s d ng bài m r ng liên quan t i các công th c ố ạ ở ộ ớ ứ
o Xác nh m t n dài đị ậ độ điệ
λ
o Xác nh kho ng cách t n tích đị ả ừ điệ q
o Xác nh dài c a dây d n đị độ ủ ẫ l
o Xác nh kho ng cách t n tích t i dây đị ả ừ điệ ớ a
o ….
Bài 1-24: Tính công c n thi t d ch chuy n m t n tích ầ ế để ị ể ộ điệ q = "
<107Z[ t m t m M cách qu ừ ộ điể ả
c i iầu tích đ ện bán kính = 1 r cm m t kho ng = 10 cm ra xa vô c c. Bi t qu c u có m t ộ ả R ự ế ả ầ ậ độ đ ện
mặt
σ
= 10
-11
C/cm
2
.
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
8
Tóm t t: ắ
q = "
<107Z[
Quả c u: = 1 ầ r cm,
σ
= 10
-11
C/cm
2
R = 10 cm
Xác nh đị A
R∞
Gi i:ả
- Nh n xét: ậ Đây là bài toán liên quan t i công d ch chuy n n tích m chúng ta quan tâm ớ ị ể điệ điể
tới công th c tính công d ch chuy n t v trí ứ ị ể ừ ị M
N A nào ó: đ MN = q(VM – VN) t công th c ừ ứ
này ta th y ph ng h ng c a bài toán là ph i i xác nh n th t i v trí và . Mà mu n ấ ươ ướ ủ ả đ đị điệ ế ạ ị M N ố
xác nh n th t i m t m nào ó tr c tiên ta ph i xác nh c hình d ng c a ngu n n đị điệ ế ạ ộ điể đ ướ ả đị đượ ạ ủ ồ điệ
tích gây ra t i m ó trong bài này là m t c u tích n u ta c n chú ý tính ch t n th ạ điể đ ặ ầ điệ đề ầ ấ điệ ế
gây b i m t c u tích n mở ặ ầ điệ ặt:
- i i Đ ện th t i m i ế ạ ọ đ ểm bên trong m t c u u b ng n th t i b m t c u bán kính ặ ầ đề ằ điệ ế ạ ề ặ ầ R
\]=1^_V/` =$
4a
- i i Đ ện th t i m t ế ạ ộ đ ểm cách tâm c u m t kho ng là: ầ ộ ả r > R
0^b =$
4
- i Đ ện th t i vô cùng luôn luôn b ng không ế ạ ằ
để ể ọ ườ ể ả ế đề hi u rõ công thức trên m i ng i có th tham kh o bài vi t chuyên ứng dụng tích phân
vào bài toán t nh n. ĩ điệ
- i v i bài toán ta ang kh o sát, m c n kh o sát n m ngoài m t c u nên ta áp d ng công Đố ớ đ ả điể ầ ả ằ ặ ầ ụ
thức:
c=( >−d)=>=$4(+a)=4N4(+a)=N
(+a)≈3,42.107Ze
- Chú ý:
- M ột s công th c c n quan tâm: ố ứ ầ
o Công d ch chuy n n tích t v trí M n v trí N: ị ể điệ ừ ị đế ị A
MN
= q(V
M
– V
N
)
o Đ ệ ế ở ả ầ ệ ặi n th gây b i qu c u tích đi n m t
\]=1^_V/` =$
4a
0^b =$
4
- M ột s bài toán m r ng: ố ở ộ
o Xác nh n tích m đị điệ điể q
o Xác nh bán kính c u đị ầ r
o Xác nh m t n m t đị ậ độ điệ ặ
σ
o …..
Bài 1-26: M t n tích m ộ điệ điể =<107f[ n m cách m t s i dây dài tích n u m t kho ng ằ ộ ợ điệ đề ộ ả r
1
= 4 . D i tác d ng c a n tr ng do s i dây gây ra, m t n tích d ch chuy n theo h ng cm ướ ụ ủ điệ ườ ợ ộ điệ ị ể ướ
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
9
đườ ứ ệ ườ ảng s c đi n tr ng kho ng r
2
= 2 . Khi ó l c n tr ng th c hi n m t công = 50.10cm đ ự điệ ườ ự ệ ộ A
-7
J. Tính m t dài c a dây. ậ độ ủ
Tóm tắt:
=2
3107f[
r
1
= 4 cm
r
2
= 2 cm
A = 50.10
-7
J
Xác nh m t dài c a dây đị ậ độ ủ
λ
.
Giải:
- Nh n xét: Ph ng h ng c a bài toán là ph i i tìm m i quan h gi a ậ ươ ướ ủ ả đ ố ệ ữ
λ
v i các i l ng ã ớ đạ ượ đ
biết. D th y d ki n ễ ấ ữ ệ sợi dây dài tích n u + điệ đề
λ
g i ý cho ta công th c xác nh n ợ ứ đị điệ
trường gây b i s i dây th ng dài ở ợ ẳ
λ
có liên quan t i . Ti p theo ta th y công thì th ng liên ớ E ế ấ A ườ
hệ v i mà gi a và có tớ V ữ V E ồn t i mạ ối quan h ta ệ đã liên h c i l ng ệ đượ đạ ượ
λ
với i l ng đạ ượ
đã biết là công . A
- Các m i liên h s d ng trong bài này là: ố ệ ử ụ
c=−
=−
= %
2
- Công mà l c n trự điệ ườ ệ để ị ể đ ệ ị đế ịng thực hi n d ch chuy n i n tích từ v trí 1 n v trí 2 là:
c=3 %
2

=%
2
&M
"
⇒%=2
c
&M
"
≈−6.10
7Z
[/
- Chú ý:
- Cần nh các công th c sau: ớ ứ
o =U

o
%=

i
W]
j
j
o c=
U

&M
- Bài toán m r ng: ở ộ
o Xác nh công d ch chuy n n tích đị ị ể điệ
o Xác nh n tích m đị điệ điể q
o ….
c=
%
2

TÍCH PHÂN T V Ừ Ị
TRÍ r1 r2
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
10
Bài 1-32: T i hai nh c a m t hình ch nh t (có các ạ đỉ C, D ủ ộ ữ ậ ABCD
c i iạnh AB = 4 m, BC = 3 m) ng i ta t hai ườ đặ đ ện tích đ ểm q1 = -
3.10
-8
C (t i ) và ạ C q
2
= 3.10
-8
C (t i ). Tính hi u n th gi a ạ D ệ điệ ế ữ A
và B.
Tóm t t: ắ
AB m = 4
BC m = 3
q
1
= - 3.10
-8
C
q2 = 3.10
-8
C
Xác nh hi u n thđị ệ điệ ế U
AB
Giải:
- Nh n xét:ậ ây là bài toán n th gây b i h n tích m khác v i n tr ng (ho c l c Đ điệ ế ở ệ điệ điể ớ điệ ườ ặ ự
đ đ ủiện), iệ ế đạ ượ ướ ỉ ầ đ ệ ến th là i l ng vô h ng nên ta ch c n tính i n th c a t ng n tích m gây ra ừ điệ điể
tại m c n xét sau ó c ng i s v i nhau. Hi u n th gi a hai m A và B c xác điể ầ đ ộ đạ ố ớ ệ điệ ế ữ điể đượ định
bằng công th c ứ U
AB
= V
A
- V
B
.
- n th t i là: Điệ ế ạ A i="i +i ="4c[+
4ck ≈36
- n th t i là: Điệ ế ạ B A="A +A ="4l[ +
4lk ≈−36
- Hi u n th gi a hai m là: ệ điệ ế ữ điể A, B U
AB
= V
A
- V
B
= 72 V
- Chú ý:
- Bài toán có th m r ng b ng cách b trí s l ng và v trí các n tích m theo các ể ở ộ ằ ố ố ượ ị điệ điể
hình khác nhau tính n th c a t ng m điệ ế ủ ừ điể c ng i s ộ đạ ố
- Công th c c n nh : ứ ầ ớ
Hi iệu đ ện th gi a hai m AB: ế ữ điể U
AB
= V
A
- V
B
Đ ệ ế ở đ ệ đ ểi n th gây b i i n tích i m: =

Bài 1-33: Tính công c a l c n tr ng khi d ch chuy n n ủ ự điệ ườ ị ể điệ
tích = 10q
-9
t m C n m n u = 6 , C ừ điể đế điể D ế a cm Q
1
=
"
<107f[, Q
2
= - 2.10
-9
. C
Tóm t t: ắ
q = 10
-9
C
a = 6 cm
Q1
= "
<107f[
Q
2
= - 2.10
-9
C
Tính công A
CD
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
11
Giải:
- Nh n xét:ậ ây là bài toán công d ch chuy n n tích ph i i xác nh n th t i C và D Đ ị ể điệ ả đ đị điệ ế ạ
áp d ng công th c: ụ ứ A
CD
= q(V
C
- V
D
).
- n th t i m là: Điệ ế ạ điể C m=$"
4F+$
4F
- n th t i m là: Điệ ế ạ điể D n=$"4√2F+$
4√2F
- Hi u n th gi a hai m là: ệ điệ ế ữ điể CD
pmn =m−n=14F($"+$)q1− 1
√2r≈58
- Công d ch chuy n n tích t n là: ị ể điệ q ừ C đế D
ACD = q.UCD = 0,58.10
-7
J
Bài 1-34: Gi a hai m t ph ng song song vô h n mang n u m t b ng nhau nh ng trái d u, ữ ặ ẳ ạ điệ đề ậ độ ằ ư ấ
cách nhau m t kho ng = 1 t n m ngang, có m t h t n mang kh i l ng = 5.10ộ ả d cm đặ ằ ộ ạ điệ ố ượ m
-14
kg.
Khi không có n tr ng, do s c c n c a không khí, h t r i v i t c không i điệ ườ ứ ả ủ ạ ơ ớ ố độ đổ v
1
. Khi gi a ữ
hai m t ph ng này có hi u n th = 600 thì h t r i ch m i v i v n t c ặ ẳ ệ điệ ế U V ạ ơ ậ đ ớ ậ ố u=v
. Tìm n điệ
tích c a h t. ủ ạ
Tóm t t: ắ
d = 1 cm
m = 5.10
-14
kg
U V = 600
u
=
u
"
2
Giải:
- Nh n xét: ậ Phân tích d ki n c a bài toán ta th y khi không có n tr ng d i tác d ng c a ữ ệ ủ ấ điệ ườ ướ ụ ủ
trọng l c h t b i s r i xu ng kèm theo là l c c n c a không khí, nh ng khi có n tr ng ự ạ ụ ẽ ơ ố ự ả ủ ư điệ ườ thì
hạt r i ch m ơ ậ đi có ngh a là n tr ng ã sinh ra m t l c tác d ng ng c h ng v i chi u ĩ điệ ườ đ ộ ự ụ ượ ướ ớ ề
của tr ng l c. H t r i v i t c không i gia t c r i c a v t b ng 0 t ng các vector ngo i ọ ự ạ ơ ớ ố độ đổ ố ơ ủ ậ ằ ổ ạ
lực tác d ng lên v t b tri t tiêu. ụ ậ ị ệ
- Khi không có n tr ng: điệ ườ
- H ạt ch u tác d ng c a hai l c: ị ụ ủ ự
o Trọng l c: ự
?@
o Lực c n: ả m
????@
- Do h t r i v i t c không i nên ta có: ạ ơ ớ ố độ đổ
o
?@
+m
????@
=0
?@
⇒=m⇒=6wu"=u" (1)
- Khi có n tr ng: điệ ườ
- H ạt ch u tác d ng c a hai l c: ị ụ ủ ự
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
12
o Trọng l c: ự
?@
o Lực c n: ả m
????@
′
o Lực Coulomb: đ
???@
- Do h t r i v i t c không i nên ta có: ạ ơ ớ ố độ đổ
o
?@
+m′
?????@
+đ
???@
=0
?@
⇒=my+đ⇒=6wu + =u+ (2)
- T (1) và (2) ta có: ừ
−=uu"⇒=q1−uu"r=pq1−u
u"r
Vì u=v
nên ta có: ="
z{
|≈4,17.107"~[
Bài 1-35: Có m t n tích m t t i tâm c a hai ng ộ điệ điể q đặ ạ O ủ đườ
tròn ng tâm bán kính và . Qua tâm ta v m t ng th ng đồ r R O ẽ ộ đườ ẳ
c iắt hai ng th ng c t hai ng tròn t i các đườ ẳ ắ đườ ạ đ ểm . A, B, C, D
1. i Tính công c a l c ủ ự đ ện tr ng khi d ch chuy n n tích ườ ị ể điệ q
0
từ B
C A và t ừ
D.
2. So sánh công c a l c t nh n khi d ch chuyủ ự ĩ điệ ị ển từ A
C
và t ừ B
D.
Tóm t t: ắ
Đ ệ đ ểi n tích i m t t i q đặ ạ O
Hai ng tròn ng tâm đườ đồ O: r, R
Xác nh đị A
BC
, A
AD
. So sánh A
AC
và A
BD
Giải:
- Nh n xét:ậ Đây là bài toán liên quan t i công d ch chuy n n tích ớ ị ể điệ điểm q
0
gây b i l c tở ự ĩnh
điệ ơ ản s ử dụng công thức c b n A12 = q0(V1 – V2). Ngoài ra, do tích ch t i x ng nên các m ấ đố ứ điể
nằm ng tròn có tâm là đườ điện tích điểm q s có cùng n th ẽ điệ ế đường ng th . đẳ ế
- Công d ch chuy n n tích ị ể điệ q0 t n là: ừ B đế C
A
BC
= q
0
(V
B
– V
C
)
- Công d ch chuy n n tích ị ể điệ q
0
t n là: ừ A đế D
A
AD
= q
0
(V
A
– V
D
)
do tính ch t ng th ng th ta có: ấ đườ ẳ ế V
B
= V
C
, V
A
= V
D
nên ta suy ra: A
BC
= A
AD
= 0
- Công d ch chuy n n tích ị ể điệ q
0
t n là: ừ A đế C
A
AC
= q
0
(V
A
– V
C
)
- Công d ch chuy n n tích ị ể điệ q
0
t n là: ừ B đế D
A
BD
= q
0
(V
B
– V
D
)
DẠNG TOÁN: ỨNG DỤNG TÍCH PHÂN
1. Nh n xét:ậ
- i Đặc đ ểm c a bài toán này là ph i s d ng ph ng pháp tính tích phân xác nh c ng ủ ả ử ụ ươ để đị ườ
độ đ ệ ườ ệ ệ ế ặ đạ ượ ữ đạ ượ i n tr ng, lực đi n, đi n th ho c các i l ng suy ra từ nh ng i l ng trên.
- Để gi i quy t các bài toán d ng này chúng ta c n trang b nh ng ki n th c c b n sau: ả ế ạ ầ ị ữ ế ứ ơ ả
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
13
o Kỹ ă ơ ả n ng tính tích phân các hàm c b n
o Mối liên h gi a các i l ng ệ ữ đạ ượ
o Tổng h p vector ợ
o Công th c tính l c t ng tác gi a hai n tích m. ứ ự ươ ữ điệ điể
o Công th c tính n tr ng gây b i n tích m. ứ điệ ườ ở điệ điể
o Công th c xác nh n th . ứ đị điệ ế
o Công th c xác nh di n tích vành tròn gi i h n b i hai ng tròn bán kính ứ đị ệ ớ ạ ở đườ R
1
và
R
2
: •=(a
−a")
o Công th c tính di n tích i c u: = 2 ứ ệ đớ ầ S πRh
o Nắm v ng m t s công th c g n úng ữ ộ ố ứ ầ đ
- Nhìn chung bài toán lo i này là r t a d ng, tuy nhiên n u chúng ta bi t c quan h ạ ấ đ ạ ế ế đượ ệ
giữa các i l ng v i nhau thì h u nh các bài toán này u có th a v d ng duy nh t đạ ượ ớ ầ ư đề ể đư ề ạ ấ
là xác nh c ng n tr ng gây b i m t v t th nào ó ph ng pháp quy v bài đị ườ độ điệ ườ ở ộ ậ ể đ ươ ề
toán n tr ng. Ví dđiệ ườ ụ
o Xác nh xác nh sđị F đị E ử d ng m i liên h = ụ ố ệ F qE
o Xác nh đị V
M
xác s d ng m i liên h định E ử ụ ố ệ
>
=− 6)
>
d
o
Xác nh đị U
MN xác nh đị E s d ng m i liên hử ụ ố ệ p
>€
=)6
€
>
o Xác nh đị A
MN
xác nh xác nh xác nh đị E đị V đị A
Nh v y ta th y các bài toán u i qua bài toán trung gian n tr ng bài toán xác ư ậ ấ đề đ điệ ườ
điệ ện đi n trường gây b i v t th óng vở ậ ể đ
ai trò r t quan tr ng. ấ ọ
2. H ng gi i: ướ ả
Bước 1 (vi phân v t thậ ể): áp d ng tích phân ta ph i ti n hành vi phân v t th : Để ụ ả ế ậ ể
- o Thanh, cung tròn, dây tròn chia thanh thành t ng ừ đ ạn dx vi phân chi u dài. ề
- M ặt ph ng vô h n, a tròn chia thành t ng vành tròn có bán kính trong ẳ ạ đĩ ừ x bán kính
ngoài + vi phân di n tích = 2 ( c xác nh b i công th c tính di n tích x dx ệ dS πxdx đượ đị ở ứ ệ
vành tròn, trong ó lo i b các giá tr đ ạ ỏ ị dx
2
do r t bé) ấ
- M ặt c u bán kính chia thành các i c u có ng cao ầ R đớ ầ đườ dx vi phân di n tích ệ dS =
2πRdx ( c xác nh b i công th c tính di n tích i c u). đượ đị ở ứ ệ đớ ầ
Bước 2 (Xác nh dq):đị Các bài toán l c n, n tr ng, n th th ng liên quan n giá tr ự điệ điệ ườ điệ ế ườ đế ị
đ điện tích do q ó phươ ướ đầ ầ ả đị ịng h ng u tiên c n ph i xác nh chính là giá tr dq. Thông thường
ta ph i tìm m i liên h gi a v i vi phân chi u dài/vi phân di n tích ả ố ệ ữ dq ớ ề ệ
- .d i dq = λ x ( : m t λ ậ độ đ ện dài = n tích c a v t thđiệ ủ ậ ể/độ ậ ể đơ ị dài v t th - n v : C/m)
- .d dq = σ S ( : m t σ ậ độ điệ ặ đn m t = iệ ủ ậ ể ệ ề ặ đơ ịn tích c a v t th /di n tích b m t – n v : C/m
2
)
- . dq = ρ dV ( : m t n kh i = n tích cρ ậ độ điệ ố điệ ủa v t th n tích b m t – n v : ậ ể/diệ ề ặ đơ ị
C/m
3
)dạng này thường dùng định lý O – G gi i cho n gi n) để ả đơ ả
Bước 3 (Xác nh các i l ng dF, dE, dV theo dq):đị đạ ượ Chú ý là hai i l ng , là hai i đạ ượ dF dE đạ
lượng có h ng áp d ng nguyên lý ch ng ch t tr c khi tính tích phân, i l ng ) ( n ướ ụ ồ ấ ướ đạ ượ dV điệ
th iế: cộng i s - c ng tr c tiđạ ố ộ ự ếp, l c và ự đ ện tr ng: ườ cộng vector u – chiế cộng).
Bước 4 (Tính tích phân): Xác c c n c a tích phân (d a vào giđịnh đượ ậ ủ ự ới h n c a v t th ), chú ý ạ ủ ậ ể
tính ch t i x ng c a v t th . ấ đố ứ ủ ậ ể
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
14
3. Bài t p minh h a: ậ ọ
Bài 1-16:
M t thanh kim lo i mang n tích = 2.10ộ ạ điệ q
-7
C.
Xác nh c ng n tr ng t i m t đị ườ độ điệ ườ ạ ộ điểm n m cách ằ
hai u thanh = 300 , cách trung m c a thanh đầ R cm điể ủ R
0
=
10 . cm
Tóm t t: ắ
q = 2.10
-7
C
R cm = 300
R
0
= 10 cm
Xác nh đị E
O
Giải:
- Nh n xét: ây là bài toán ng d ng tích phân i v i m t thanh kim lo i mang n tích ng ậ đ ứ ụ đố ớ ộ ạ điệ ứ
dụng các b c c b n gi i bài toán này. ướ ơ ả để ả
- B c 1 – Vi phân v t thướ ậ ể: Thanh kim lo i vi phân theo chi u dài ạ ề dx
- B c 2 – Vi phân n tích dq:ướ điệ G i ọ
λ là m t n dài trên thanh ta có ậ độ điệ =%•=W•
- B c 3 – Xác nh i l ng dE theo dqướ đị đạ ượ :
o Áp d ng công th c n tr ng gây b i n tích m ụ ứ điệ ườ ở điệ điể dq ta có:
=4=•
4&
o Do tính ch t i x ng n tr ng t ng c ng t i s n m trên ph ng và có chi u dài ấ đố ứ điệ ườ ổ ộ ạ O ẽ ằ ươ Ox ề
như hình v . Hình chi u c a ẽ ế ủ dE lên Ox có giá tr là: ị
‚=456=456•4&=a•4&=a•
4&(•+a)</
- B c 4 – Tính tích phân:ướ
o Đ ệ ưở ổ ợ ại n tr ng t ng h p t i là: O
= 3 a•
4&(•+a)</
W/
7W/ =23 a•
4&(•+a)</
W/
=a 2&3•
(•+a)</
W/
⇒= a2&1
a
•
ĥ+a
„
W/ =
4aa≈6000D/
- Chú ý:
- Cách tính tích phân d ng: ạ )‚
(‚
…V
)
(/
Xét tích phân †=)‚
(‚
…V
)
/
s d ng ph ng ử ụ ươ
pháp tích phân t ng ph n. ừ ầ
o Đặt ‡ˆ= "
√‚
…V
⇒ˆ=− ‚‚
(‚
…V
)
(/
u=•⇒u=• ta có:
†= •√•+F+3 ••(•+F)</ =•√•+F+3•+F−F•
(•+F)</
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
15
⇒†= •√•+F+3 •(•+F)"/−F3•
(•+F)</
Mà †=)‚
(‚
…V
)
/
nên ta có:
3•(•+F)</=1F•
å+F
- Nh ững bài toán m r ng: ở ộ
o Xác nh l c đị ự điện F
o Xác nh các i l ng liên quan t i công th c: đị đạ ượ ớ ứ R
0
, l, R, q,
λ
- Các công th c c n nh : ứ ầ ớ
o Đ ệ ườ ở ạ ả đ ệ ại n tr ng gây b i thanh kim lo i m nh mang i n tích tq i một điểm nằm cách
hai u thanh và cách trung m c a thanh đầ R điể ủ R
0
= 10 cm
=
4aa
o M iật độ đ ện dài: %=
W
o Tích phân c b n: ơ ả )‚
(‚
…V
)
(/
="
V
‚
√‚
…V
Bài 1-17: M t m t ph ng tích n u v i m t ộ ặ ẳ điệ đề ớ ậ độ
σ
. T i kho ng gi a c a m t có khoét m t l h ng ạ ả ữ ủ ặ ộ ỗ ổ
bán kính nh so v i kích th c c a m t. Tính a ỏ ớ ướ ủ ặ
c iường n tr ng t i m t độ điệ ườ ạ ộ đ ểm n m trên ng ằ đườ
thẳng vuông góc v i m t ph ng và i qua tâm c a ớ ặ ẳ đ ủ
lỗ h ng, cách tâm ó m t n là ổ đ ộ đoạ b
Tóm t t: ắ
Mặt ph ng: tích ẳ điện u, đề
∞
,
σ
Lỗ h ng: ổ a
O thu c tr c c a l và cách tâm m t kho ng ộ ụ ủ ỗ ộ ả b
Xác nh đị E
0
Giải:
- Nh n xét:ậ đây là bài toán ng d ng tích phân i v i m t m t ph ng mang n tích ng ứ ụ đố ớ ộ ặ ẳ điệ ứ
dụng các b c c b n gi i bài toán này. ướ ơ ả để ả
- B c 1 – Vi phân v t thướ ậ ể: M t ph ng vô h n vi phân theo hình vành kh n v i tâm là tâm ặ ẳ ạ ă ớ
của l tròn bán kính a. Khi ó vi phân di n tích hình vành kh n n m gi a hai ng tròn bán kính ỗ đ ệ ă ằ ữ đườ
x dS xdx x dx và là: x + dx = 2π (công th c này suy ra b ng cách l y di n tích hình tròn bán kính ứ ằ ấ ệ +
trừ i di n tích hình tròn bán kính đ ệ x và chú ý là b qua i l ng ỏ đạ ượ d
2
x vì nó quá nh ) ỏ
- B c 2 – Vi phân n tích dq:ướ điệ G i ọ σ là m t n m t ta có ậ độ điệ ặ =N•=N2 ••π
- B c 3 – Xác nh i l ng dE theo dqướ đị đạ ượ :
o Do tính i x ng nên n tr ng gây b i các ph n t n tích trên di n tích dS t i m đố ứ điệ ườ ở ầ ử điệ ệ ạ điể
O s có ph ng l p v i Ox m t góc và có cùng l n. Ta t ẽ ươ ậ ớ ộ α độ ớ đặ

?@
="
????@
+
????@
+⋯+Š
???@
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
16
⇒‚=("++⋯\)456= 456
4
Trong ó = đ dq dq
1
+ dq
2
+ …+ dq
i
, thay 456=Y,=N2 ••π ta có:
‚=QN••2<=QN••
2(•+Q)</
- B c 4 – Tính tích phân:ướ
o Đ ệ ườ ở ặ ẳi n tr ng gây b i toàn bộ m t ph ng là:
‹=3 QN••
2(•+Q)</
d
V=QN 43(•+Q)
(•+Q)</
d
V=− QN 21
√•+QŒV
d
⇒‹=QN2√F+Q=N
2R1+F
Q
- Chú ý:
- T i ừ bài toán này ta có th rút ra cách xác ể định đ ện tr ng gây b i m t s v t có hình d ng ườ ở ộ ố ậ ạ
tương t nh : ự ư
o Đĩ đ ệ đề Đ ệ ườa tròn mang i n u bán kính R i n tr ng E
0 l y tích phân t 0 ấ ừ R
đ đ ộ điệ ườ ở đĩn tr ng gây b i a tròn mang iệ đề ạn u t i m t iểm trên trục và n m cách ằ
tâm a m t kho ng là : đĩ ộ ả b
=− QN21
√•+QŒ
•=N
2
Ž
•
1− 1
R1+a
Q
•
‘
o Mặt ph ng vô h n không khoét l = 0 ẳ ạ ỗ a điện tr ng ườ =P

o Vành tròn bán kính trong là R
1
bán kính ngoài là R
2
l y tích phân tấ ừ a b
đ đ ụiệ ườ ở ệ đề ạn tr ng gây b i vành tròn mang đi n u t i một iểm trên tr c và nằm cách
tâm m t kho ng là : ộ ả b
=− QN21
å+QΥ
•
=N
2
Ž
•
1
R1+a"
Q−1
R1+a
Q
•
‘
- M ột s bài toán m r ng: ố ở ộ
o Xác nh các i l ng liên quan t i công th c: đị đạ ượ ớ ứ
σ
, a, b
- Các công th c c n nh : ứ ầ ớ
o Đ ệ ườ ở đĩ ệ đềi n tr ng gây b i a tròn bán kính tích R, đi n u
o Đ ệ ườ ở ặ ẳ ỗ ệ đềi n tr ng gây b i m t ph ng khoét l bán kính , tích a đi n u
o Đ ệ ườ ở ặ ẳ ạ ệ đềi n tr ng gây b i m t ph ng vô h n tích đi n u
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
17
Bài 1-29: Tính n th t i m t m n m trên điệ ế ạ ộ điể ằ
tr iục c a m t a tròn có tích ủ ộ đĩ đ ện u và cách đề
tâm a m t kho ng . a có bán kính và đĩ ộ ả h Đĩ R
m iật độ đ ện m t ặ
σ
.
Tóm t t: ắ
Đĩ ệ đềa tròn: tích đi n u, , R
σ
Đ ể ằ ủ đĩ ội m : nM m trên trục c a a, cách tâm m t
đoạn h
Xác nh đị V
M
Giải:
- Nh n xét:ậ ây là bài toán n th gây b i a tròn u ta có th s d ng ph ng pháp quy v đ điệ ế ở đĩ đề ể ử ụ ươ ề
bài toán n tr ng r i s d ng m i quan h gi a n th và n tr ng tìm ra điệ ườ ồ ử ụ ố ệ ữ điệ ế điệ ườ để điệ ế ạn th t i
điểm M.
- n tr ng gây b i a tròn t i m t m n m trên tr c và cách tâm a m t kho ng là là Điệ ườ ở đĩ ạ ộ điể ằ ụ đĩ ộ ả h
=N
2
Ž
•
1− 1
R1+a
ℎ
•
‘
- Áp d ng công th c liên h gi a n th và n tr ng là: ụ ứ ệ ữ điệ ế điệ ườ
>
=3 ℎ
d
=3
N
20
Ž
“
“
•
1− 1
”
1+a2
ℎ2
•
•
•
‘
ℎ
d
=N
2
(ℎ− aƒ
+ℎ
)–
d
Khi h ∞ thì nh v y ta có: h >> R √a+ℎ=ℎ ư ậ
>
=N
2
Sƒa
+ℎ
−ℎT
- Chú ý:
- Bài toán này hoàn toàn có th áp d ng ph ng pháp tích phân tính tr c ti p theo n th ể ụ ươ ự ế điệ ế
V
- M ột s bài toán m r ng: ố ở ộ
o Tính hi u n th gi a hai m trên tr c ệ điệ ế ữ điể ụ
o Tính công d ch chuy n n tích gi a hai m trên tr c ị ể điệ ữ điể ụ
o Xác nh các i l ng liên quan t i công th c đị đạ ượ ớ ứ
- Công th c c n nh là: ứ ầ ớ
o Đ ệ ế ở đĩ đ ệ đề ạ ội n th gây b i a tròn bán kính R tích i n u t i m t điểm trên tr c c a a ụ ủ đĩ
và cách tâm a m t kho ng : đĩ ộ ả h
>
=N
2
Sƒa
+ℎ
−ℎT
DẠ ĐỊNG TOÁN: ÁP DỤNG NH LÝ O - G
1. Nh n xét: ậ
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
18
- Có r t nhi u bài toán trong ó v t th có phân b n tích i x ng cao:ấ ề đ ậ ể ố điệ đố ứ
o Đố ẳi xứng ph ng
o Đố ầi xứng c u
o Đối xứng trụ
về ơ ả ể ử ươ c b n chúng ta hoàn toàn có th s dụng ph ng pháp tích phân tính các i l ng để đạ ượ
nh i i iư đ ện tr ng, l c ườ ự đ ện u ư đ ểm c a ph ng pháp tích phân là tính c h u h t các ủ ươ đượ ầ ế
lo iại v t th nh ng nh c ậ ể ư ượ đ ểm l n là i v i h có i x ng cao thì vi c tính toán l i khá ớ đố ớ ệ đố ứ ệ ạ
dài dòng gi i quy t bài toán i x ng cao ta s s d ng nh lý O – G. để ả ế đố ứ ẽ ử ụ đị
- Nh i ờ có nh lu t Gauss ta d dàng xác nh c c ng đị ậ ễ đị đượ ườ độ đ ện tr ng c a các v t th có ườ ủ ậ ể
sự phân b n tích i x ng cao. Thông qua vi c ta có th ố điệ đố ứ ệ lựa ch n m t Gauss h p lýọ ặ ợ ể
đư ứ đơ ả đị ậa ra công th c n giản mô t nh lu t Gauss:
].•= $
Trong ó đ E
n
là hình chi u c a vector lên vector pháp tuy n c a b m t Gauss ế ủ E ế ủ ề ặ
Như v y nhi m v c a bài toán lúc này ch là: ậ ệ ụ ủ ỉ
- Xác nh n tích S đị điệ
- Xác định n tích Q điệ
2. H ng gi i: ướ ả
Bước 1: Ch n m t kín bao quanh i t ng (m t Gauss): sao cho t i các ph n c a i tọ ặ đố ượ ặ ạ ầ ủ đố ượng
?@
//M?@ ho c ặ
?@
⊥M?@
v i ớ E
n
= h ng s . ằ ố
• Đố ẳ ặi xứng ph ng: chọn m t trụ. (1)
• Đố ầ ọ ặ ầ đồi xứng c u: ch n m t c u ng tâm. (2)
• Đố ụ ặ đồi xứng tr : chọn m t trụ ng trục. (3)
(1) (2) (3)
Bước 2: Áp d ng nh lu t Gauss: ụ đị ậ
˜ =™]`b ]c=
š$\]1\`
0
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
19
3. Bài t p minh h a: ậ ọ
Bài t p ví dậ ụ: Xác nh c ng n tr ng gây b i dây dài vô h n hình tr tích n u v i đị ườ độ điệ ườ ở ạ ụ điệ đề ớ
m i iật độ đ ện dài t i m t λ ạ ộ đ ểm cách tr c c a dây m t kho ng ụ ủ ộ ả R
Tóm t t: ắ
Dây vô h n: tích n u , hình tr ạ điệ đề λ ụ
M: cách tr c m t kho ng ụ ộ ả R
Xác nh đị E
M
Giải:
- Nh n xét: ậ
• Do tính ch t i x ng nên: ấ đố ứ
o
?@
vuông góc v i b m t tr c a dây – h ng ra m i h ng ớ ề ặ ụ ủ ướ ọ ướ
o Giá c a các ủ
?@
đều c t tr c c a dây i x ng tr ắ ụ ủ đố ứ ụ
• Lựa ch n m t Gauss: th a mãn tính ch t ta ch n m t tr bán kính ọ ặ đề ỏ ấ ọ ặ ụ R vecto c ng ườ độ
đ ủiệ ườ ớn tr ng vuông góc v i hai vector pháp tuyến c a mặ ẳt ph ng đáy và song song v i ớ
vector pháp tuy n c a m t cong ế ủ ặ thành ph n vuông góc b tri t tiêu ( ng v i hai m t ầ ị ệ ứ ớ ặ
bên).
- Ta có: ˜]`b =∮]c=š])c š=].Jœ•.ž Jœ•.ž trong đó: là di n tích m t bên hình ệ ặ
trụ
- n tích b bao b c b i m t Gauss chính là n tích c a Điệ ị ọ ở ặ điệ ủ
phần dây n m trong hình tr nên ta có: ằ ụ
$\]1\` =%Ÿ ˜ ]`b ='
¡¢ £¤
¥
=U¦
¥
- T công th c O - G (trong ó thay ừ ứ đ E
n
= E
M
) ta có:
§
¨
=
©
JœK
ª
K•
- Chú ý: c n nh công th c tính n tr ng gây ầ ớ ứ điệ ườ
bởi dây hình tr ụ
Bài 1-22: Gi a hai dây d n hình tr song song cách nhau ữ ẫ ụ
m iột kho ng ả l = 15 cm ng i ta t m t hi u ườ đặ ộ ệ đ ện thế U =
1500 V. Bán kính m i dây là = 0.1 . Hãy xác nh c ng ỗ r cm đị ườ
độ đ ệ ườ ạ ể ả ữ ợ i n tr ng t i trung đi m của kho ng cách gi a hai s i
dây bi t r ng s i dây t trong không khí. ế ằ ợ đặ
Tóm t t: ắ
Dây d n hình tr : 2 dây, t song song, bán kính = 0.1 ẫ ụ đặ r cm
l = 15 cm
U = 1500 V
ε
= 1
O trung m c a kho ng cách gi a hai s i dây điể ủ ả ữ ợ
Xác nh đị E
0
.
Gi i:ả
- Nh n xét:ậ Bài toán liên quan n dây d n hình tr i x ng tr áp d ng nh lý O-G đế ẫ ụ đố ứ ụ ụ đị để
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
DNK-2014
20
xác nh n tr ng gây b i t ng dây d n tr . Bài toán cho bi t ch c ch n c ng n đị điệ ườ ở ừ ẫ ụ ế U ắ ắ ườ độ điệ
trường s c tính thông qua giá tr ẽ đượ ị U.
- Xét tr ng h p t ng quát: gi s m M cách dây d n th nh t m t n là áp d ng ườ ợ ổ ả ử điể ẫ ứ ấ ộ đoạ x ụ định
lý O-G và nguyên lý ch ng ch t n tr ng ta có c ng ồ ấ điệ ườ ườ độ điện tr ng t i M là: ườ ạ
>=%2•+%2(&−•)=%2q1•+1
&−•r
- Nh ta ã bi t m i quan h gi a U và E là: nên ta có: ư đ ế ố ệ ữ -« = −§-.
−p=3p
¬
¬
=−3 %
2
W7
q1 •+1&−•r• = %2&M&−•
•Œ
W7 =%&M
&−
⇒%=− p
&M
&−=p
&M&−
- T i trung m thì = /2 ta có: ạ điể O x l
‹=2%&=2p
&.&M&−
≈4000D/
Bài 1-38: Cho qu c u tích n u v i m t n kh i ả ầ điệ đề ớ ậ độ điệ ố
ρ
, bán kính a. Tính hi u n th gi a ệ điệ ế ữ
hai m cách tâm l n l t là /2 và điể ầ ượ a a
Tóm tắt:
Qu iả c u: tích ầ đ ện u đề
ρ
, bán kính a
R
1
= /2 a
R
2
= a
Xác nh đị U
12
Giải:
- Bài toán xác nh hi u n th quy v bài toán xác nh n tr ng t i m n m Nhận xét: đị ệ điệ ế ề đị điệ ườ ạ điể ằ
trong m t c u áp d nh lý O-G do tính i x ng c u nên l a ch n m t kín là m t c u ặ ầ ụng đị đố ứ ầ ự ọ ặ ặ ầ
- Theo nh lý O-G ta có: đị
•=
⇔4=4
3<!
⇒= !
3
- Hi u n th gi a hai m 1 và 2 là: ệ điệ ế ữ điể
p" ="−= 3 
•
•
=3 !
3
V
V
=!
6„V
V=!F
8
- Chú ý:
- Các công th c c n nh : ứ ầ ớ
o Đ ệ ườ ạ ằi n tr ng t i một điểm n m trong m t c u tích n kh i: ặ ầ điệ ố = ®
<
o Mối liên h gi a n th và c ng n tr ng: ệ ữ điệ ế ườ độ điệ ườ "−=)
•
•

Tài liệu khác của Học viện Công Nghệ Bưu Chính Viễn Thông

Preview text:

Trần Thiên Đức – ductt111@gmail.com – ductt111.com
HƯỚNG DẪN GIẢI BÀI TẬP ĐỊNH HƯỚNG TUẦN 1-2-3
DẠNG TOÁN: BÀI TOÁN ĐIỆN TÍCH ĐIỂM
1. Nhận xét:
- Đặc điểm rất dễ nhận dạng của loại bài toán này là sự xuất hiện của các điện tích điểm
o Lực tương tác giữa hai điện tích điểm:  =  =  
trong đề bài  do đó chúng ta cần nắm vững một số công thức và kiến thức liên quan tới điện t o í ch C ưđờiể n m g :đ   ộ điện trường:  = 
=   =      
o Điện thế gây bởi điện tích điểm:  =         
o Sơ đồ chuyển đổi công thức F  E  V: từ sơ đồ dưới ta thấy chỉ cần nhớ công
duy nhất công thức tính F là có thể suy ra công thức E, V
o Công dịch chuyển điện Ft ích điểm q từ vị tríE A đến vị trí B: A = Vq - q - r (V – V )
o Hướng của điện trường gây bởi điện tích điểm: +: hướng ra, -: hướ A ng về B
- Một số dạng bài tập điển hình:
o Xác định các đại lượng cơ bản: F, E, V, q, A
o Bài toán kết hợp động lực học: dây treo, trong môi trường xuất hiện lực đẩy
Acsimet (lực đẩy Acsimet F = dV – d là trọng lượng riêng của chất lỏng)
o Tìm vị trí ứng với một giá trị Acho trước như vị trí để E, F triệt tiêu,….
o Đuổi hình bắt chữ  nhìn hình vẽ để đưa ra nhận xét
2. Hướng giải:
Bước 1: Cần xác định đại lượng cần tìm (đây chính là bước tóm tắt)
Bước 2: Liệt kê các công thức liên quan  đánh dấu những đại lượng đã biết
Bước 3: Tìm liên hệ giữa đại lượng đã biết và đại lượng cần tìm  kết quả
3. Bài tập minh họa:
Bài 1-5: Hai quả cầu mang điện có bán kính và
khối lượng bằng nhau được treo ở hai đầu sợi dây
có chiều dài bằng nhau. Người ta nhúng chúng vào m ρ
ột chất điện môi (dầu) có khối lượng riêng và ε 1
hằng số điện môi . Hỏi khối lượng riêng của quả ρ
cầu phải bằng bao nhiêu để góc giữa các sợi dây tro
T nógm kthắtô: n g khí và chất điện môi là như nhau? Qu ρ
ả cầu mang điện: bán kính, khối lượng như nhau, Điện môi: dầu - ρ , ε ệ 1
Góc l ch trong không khí = góc lệch trong chất điện môi 1 DNK-2014
Trần Thiên Đức – ductt111@gmail.com – ductt111.com Xác định ρ? Giải: - Nhận xét:
- Hai quả cầu mang điện  bài toán điện tích điểm
- Nhúng chúng vào một chất điện môi  có sự liên hệ tới lực đẩy Acsimet  liên quan tới
động lực học  sẽ phải liệt kê lực tác dụng lên quả cầu
- Góc giữa các sợi dây trong không khí và chất điện môi là như nhau  khoảng cách giữa
các quả cầu là không đổi.
- Xét trường hợp 1: Đặt trong không khí
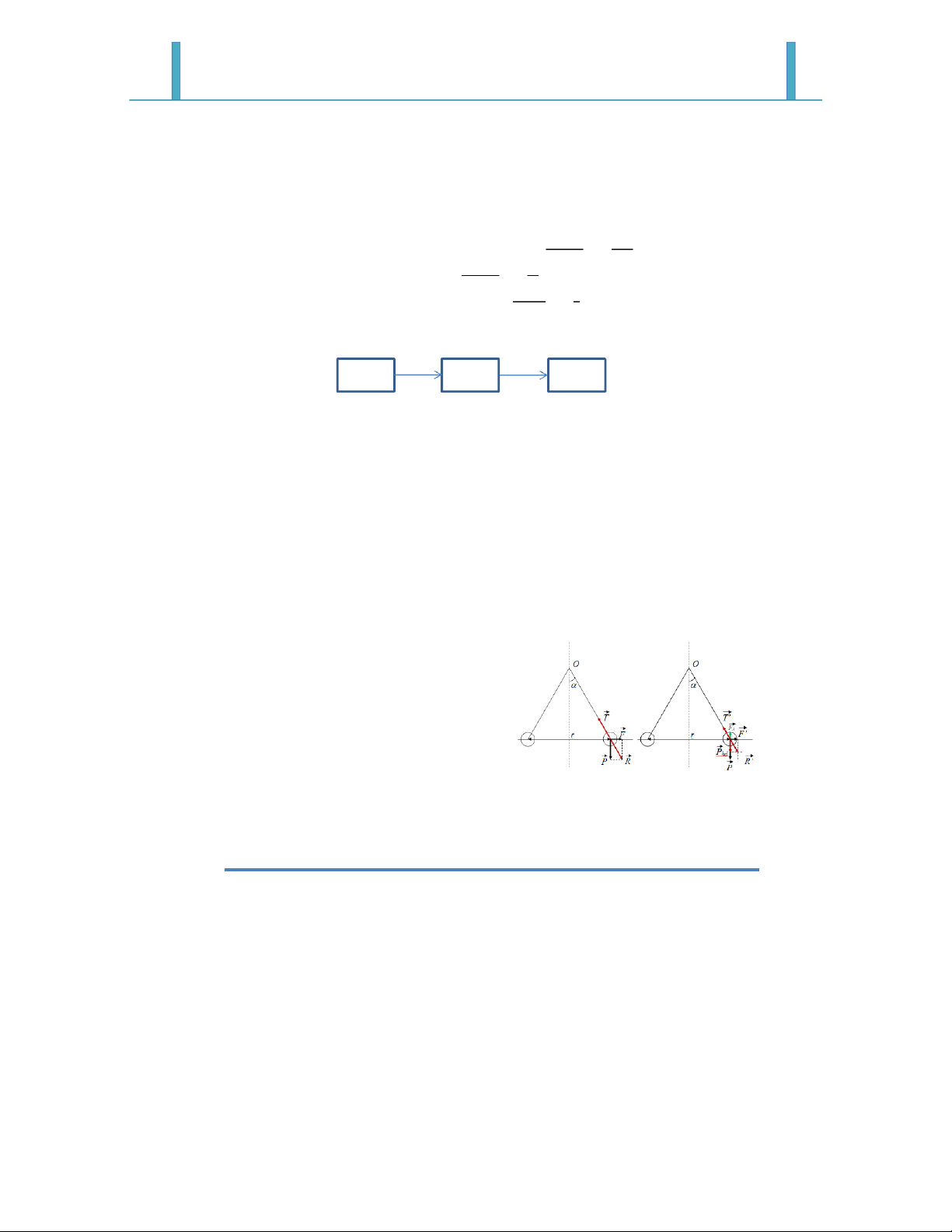
- Mỗi quả cầu sẽ chịu tác dụng của 3 lực: o Trọng lực: P o Lực đẩy Coulomb: F o Sức căng dây: T
- Từ hình vẽ ta thấy khi ở điều kiện cân bằng thì:
 = =4
- Xét trường hợp 2: Đặt trong dầu
- Mỗi quả cầu sẽ chịu tác dụng của bốn lực: o Trọng lực: P o Lực đẩy Coulomb: F’ o Sức căng dây: T’ o Lực đẩy Acsimet: F A
- Từ hình vẽ ta thấy khi ở điều kiện cân bằng thì:
 = ′ =
4( − )
- Kết hợp hai trường hợp trên trong đó thay: m = ρV; d = ρ1g ta có: ! = !"  − 1 Chú ý:
- Cần nắm vững công thức tính lực đẩy Acsimet
- Một số dạng bài mở rộng liên quan tới bài toán:
o Xác định hằng số điện môi của chất điện môi
o Xác định khối lượng riêng của chất điện môi
o Xác định góc lệch của dây treo
o Xác định điện tích của quả cầu o … DNK-2014 2
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
Bài 1-9: Xác định lực tác dụng lên một điện tích điểm q = 5/3.10-9
C đặt ở tâm nửa vòng xuyến bán kính r0 = 5 cm tích điện đều với
điện tích Q = 3.10-7 C (đặt trong chân không). Tóm tắt:
Điện tích điểm q = 5/3.10-9 C Vòng xuyến: tâm O, r -7
0 = 5 cm, tích điện đều, Q = 3.10 C Hệ trong chân không. Xác định lực F? Giải: - Nhận xét:
- Do có vòng xuyến tích điện đều  bài toán liên quan tới tính tích phân  áp dụng
phương pháp tính tích phân (4 bước cơ bản)
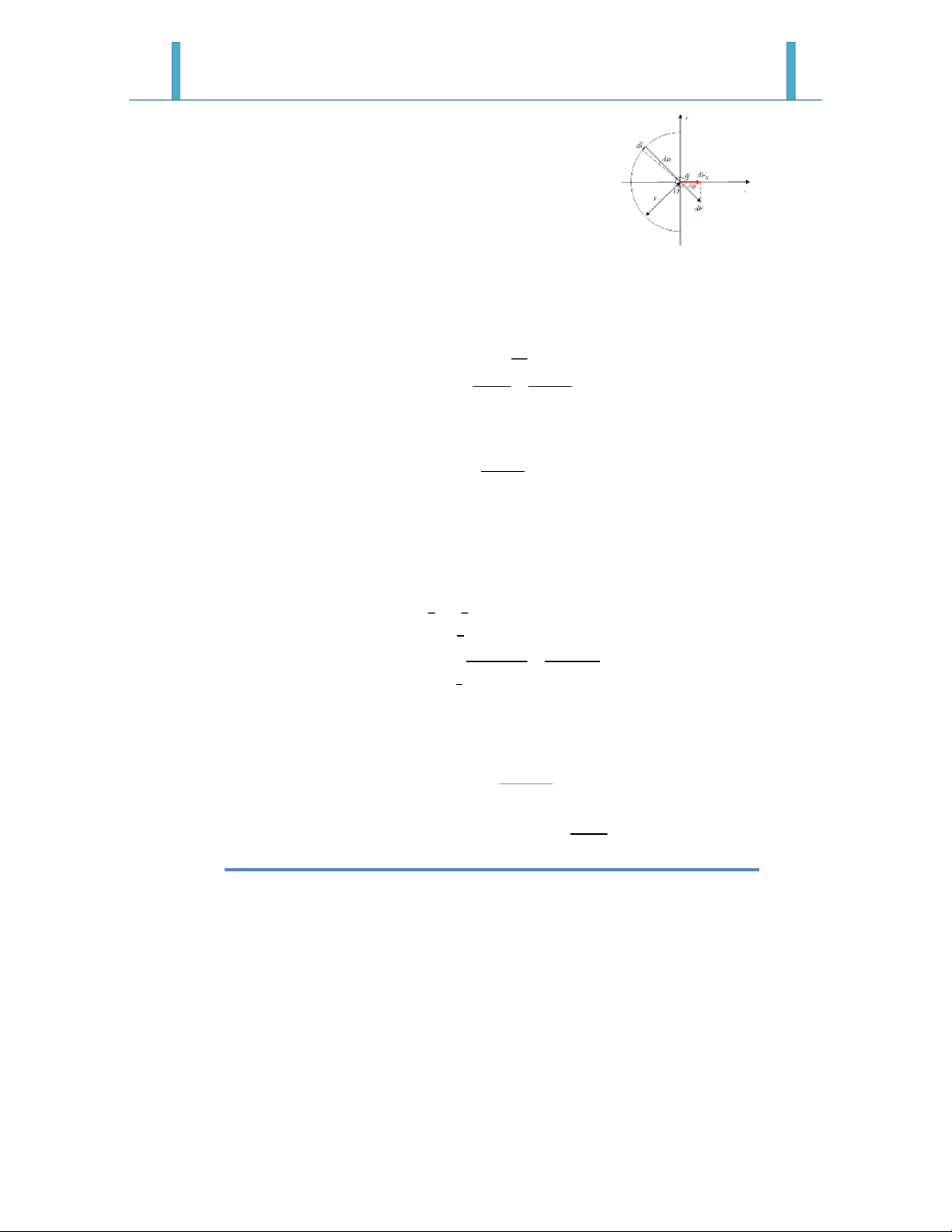
o Bước 1 – Vi phân vật thể: vòng xuyến  xét phần tử cung tròn dl
o Bước 2 – Xác định dQ: $ = %& = ' & 
o Bước 3 – Xác định dF:  = '  ='
( &
o Bước 4 – Tính tích phân:
 Phân tích hình vẽ ta thấy vector dF sẽ gồm hai thành phần dF x và dFy 
do tính đối xứng của vòng xuyến nên Fy = )*= 0 như vậy ta có , = )-, = )-,.=)'/012
đ α là góc tạo giữa vecto dF
( & (trong ó
và chiều dương Ox – cũng có sách thì lại lấy α là góc tạo bởi vecto dF với
trục Oy và khi đó ta phải đổi hàm cosα thành hàm sinα  dẫn đến cận
tích phân cũng thay đổi cho phù hợp là từ 0 đến π)
 Đến đây ta thấy có tích phân thì tính theo l, trong khi đó góc α lại thay đổi
tùy theo vị trí trên vòng xuyến  gợi ý cho ta phải tìm mối quan hệ giữa α
và dl  ta có mối quan hệ: dl = r0dα  thay vào biểu thức tính F và lấy tích phân từ − đế  n    = 3$ =45 $ 6 4
2≈ 1,14.107<=  7 - Chú ý:
- Về cơ bản thì bài toán này sẽ đưa về bài toán xác định cường độ điện trường E sau đó suy
ra lực tác dụng  ta chỉ cần nhớ công thức về cường độ điện trường gây bởi một nửa
vòng xuyến tại tâm của nó là:  = $ 2
- Một bài toán mở rộng suy ra từ bài này chính là xác định hiệu điện thế gây bởi nửa vòng
xuyến tại tâm của nó  ta chỉ thay đổi từ bước 2  = '
và chú ý là đối với điện thế  DNK-2014 3
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
là đại lượng vô hướng nên ta chỉ cần áp dụng trực tiếp tích phân mà không cần phải thực
hiện phép chiếu:  = 3 $ 4=$ 4
- Ngoài ra có thể có một số bài toán liên quan như:
o Xác định điện tích q, Q
o Xác định bán kính, đường kính vòng xuyến
o Xác định mật độ điện dài trên vòng xuyến o ….
Bài 1-11: Cho hai điện tích q và 2q đặt cách nhau 10 cm. Hỏi tại điểm nào trên đường nối hai
điện tích ấy điện trường triệt tiêu. Tóm tắt:
Hai điện tích: q và 2q r = 10 cm M ∈ AB EM = 0 Xác định vị trí M Giải:
- Nhận xét: Đây là bài toán xác định vị trí triệt tiêu  ta cần chú ý các điểm sau: độ lớn, dấu của
điện tích điểm  chiều và độ lớn của lực điện, cường độ điện trường, bố trí các điện tích điểm
(chú ý các bố trí có tính đối xứng cao).
- Giả sử điện tích q > 0:
- Gọi E A là điện trường tại M gây bởi điện tích q
- Gọi E B là điện trường tại M gây bởi điện tích 2q  dễ nhận thấy là hai vector cường độ
điện trường EA và EB ngược chiều nhau  tồn tại một vị trí thích hợp để điện trường tổng
hợp tại M bị triệt tiêu.
- Giả sử điểm M cách điện tích q một khoảng r  xét điều kiện triệt tiêu ta có: ?> ??@ = ?A?@ + ?A?@ = 0?@  
⇒ 2=(10 − )⇒  = 4,14D4  =   ("7) - Chú ý:
- Đôi khi bài toán sẽ hỏi vị trí điểm M để E (hoặc F) tổng hợp tại đó bằng 1 giá trị nào đó khác 0
Bài 1-12: Xác định cường độ điện trường đặt ở tâm của một lục giác đều cạnh a, biết rằng 6 đỉnh của nó có đặt:
1. 6 điện tích bằng nhau và cùng dấu
2. 3 điện tích âm, 3 điện tích dương về trị số đều bằng nhau Tóm tắt:
O: tâm lục giác đều cạnh a DNK-2014 4
Trần Thiên Đức – ductt111@gmail.com – ductt111.com Xác định E0:
- TH1: q 1 = q2 = q3 = q4 = q5 = q6 = q
- TH2: |q 1| = |q2| = |q3| = |q4| = |q5| = |q6| (trong đó có 3 điện tích dương) Giải:
- Nhận xét: Với hệ bố trí như bài toán, ta dễ thấy là có 4 cách bố trí, và cần chú ý tính chất đối
xứng đối xứng qua tâm của hình lục giác đều.
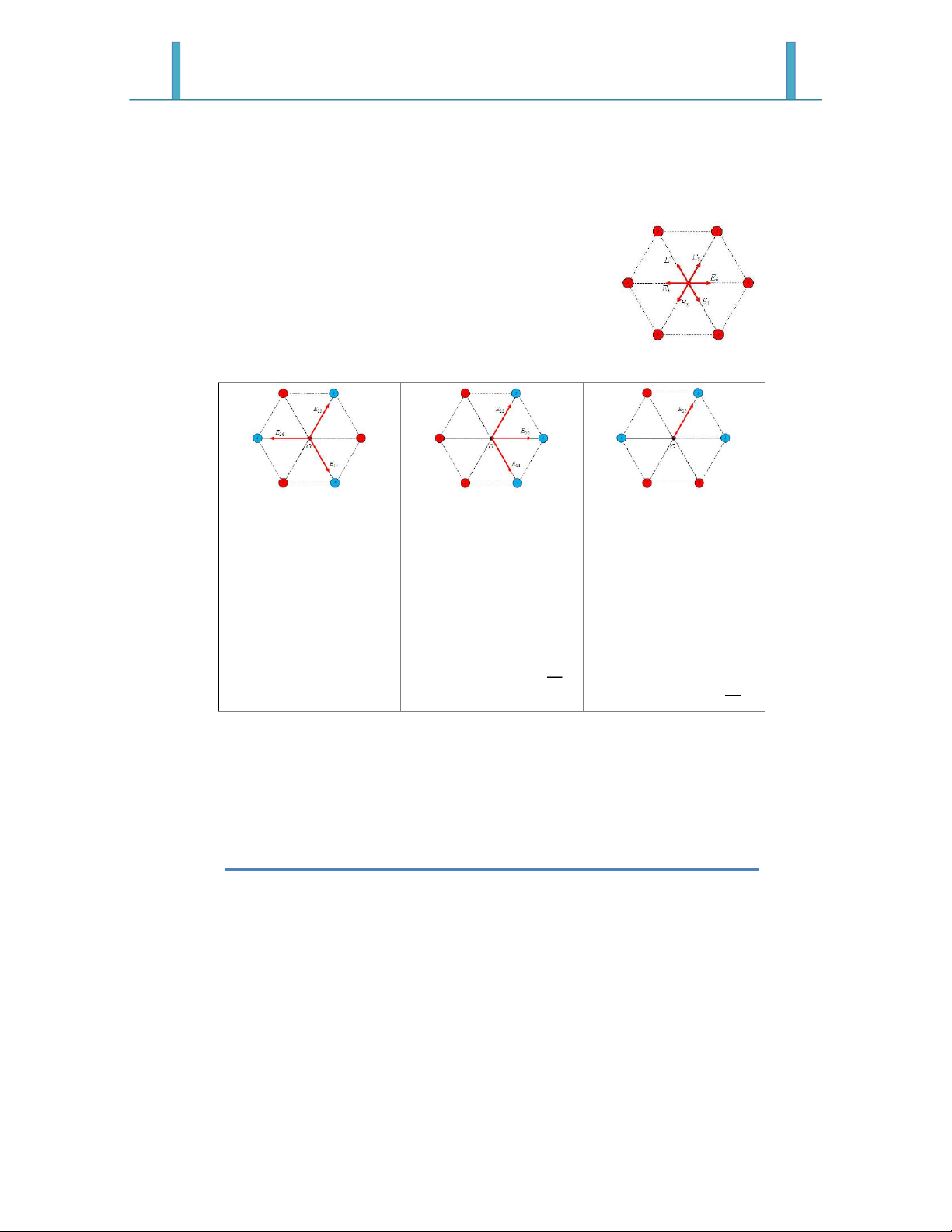
- Xét xét trường hợp 1  chỉ có một cách bố trí như hình vẽ
- Dựa vào tính chất đối xứng ta thấy các cặp điện tích điểm đối
xứng gây ra hai vector cường độ điện trường ngược chiều
nhưng cùng độ lớn  điện trường tổng hợp gây bởi hai điện
tích điểm đối xứng cùng dấu là bằng 0.
- Đối với hệ bố trí này, 6 điện tích điểm tương đương với 3 cặp đtirệưnờ nđgi ệtn ổ n tí g ch h ợ đ p itểạm i t â cù m nlg ụ c dgấiu á c đốềi u xbứ ằ n n g g 0q. ua tâm nên điện
- Xét trường hợp 2  có 3 cách bố trí
Do tính chất đối xứng ta nhận Do tính chất đối xứng ta nhận Do tính chất đối xứng ta nhận
thấy các cặp điện trường E1- thấy các cặp điện trường E1- thấy các cặp điện trường E1-
E4, E2-E5, E3-E6 cùng chiều và E4, E2-E5, E3-E6 cùng chiều và E4, E3-E6 ngược chiều và cùng cùng độ lớn. cùng độ lớn.
độ lớn  điện trường tổng
Các vector điện trường tổng Các vector điện trường tổng hợp của từng cặp này bằng 0.
hợp E14, E25, E36 cùng độ lớn hợp E14, E25, E36 cùng độ lớn Cặp E2-E5 cùng chiều và cùng
và tạo với nhau một góc 1200 và có phương và chiều như độ lớn
như hình vẽ. Dễ thấy tổng điện hình vẽ. Áp dụng quy tắc tổng Vector điện trường EO bằng
trường tổng hợp của 3 vector hợp vector ta có:
vector E25 có phương, chiều này bằng 0  EO = 0  
như hình vẽ và có độ lớn.  = 2
 = G = 2G = 2F - Chú ý:
- Đây là bài toán điển hình về việc phân tích tích chất đối xứng để tính điện trường hoặc lực
tổng hợp tại một vị trí nào đó. Đề bài đôi khi có thể cho ta hệ điện tích được bố trí theo
một quy tắc nào đó như hình tam giác vuông, tam giác đều, hình vuông, hình chữ nhật,…
- Cần nắm vững quy tắc tổng hợp vector và cách tính độ dài vector tổng hợp như (Pitago,
Định lý hàm số cos trong tam giác thường) DNK-2014 5
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
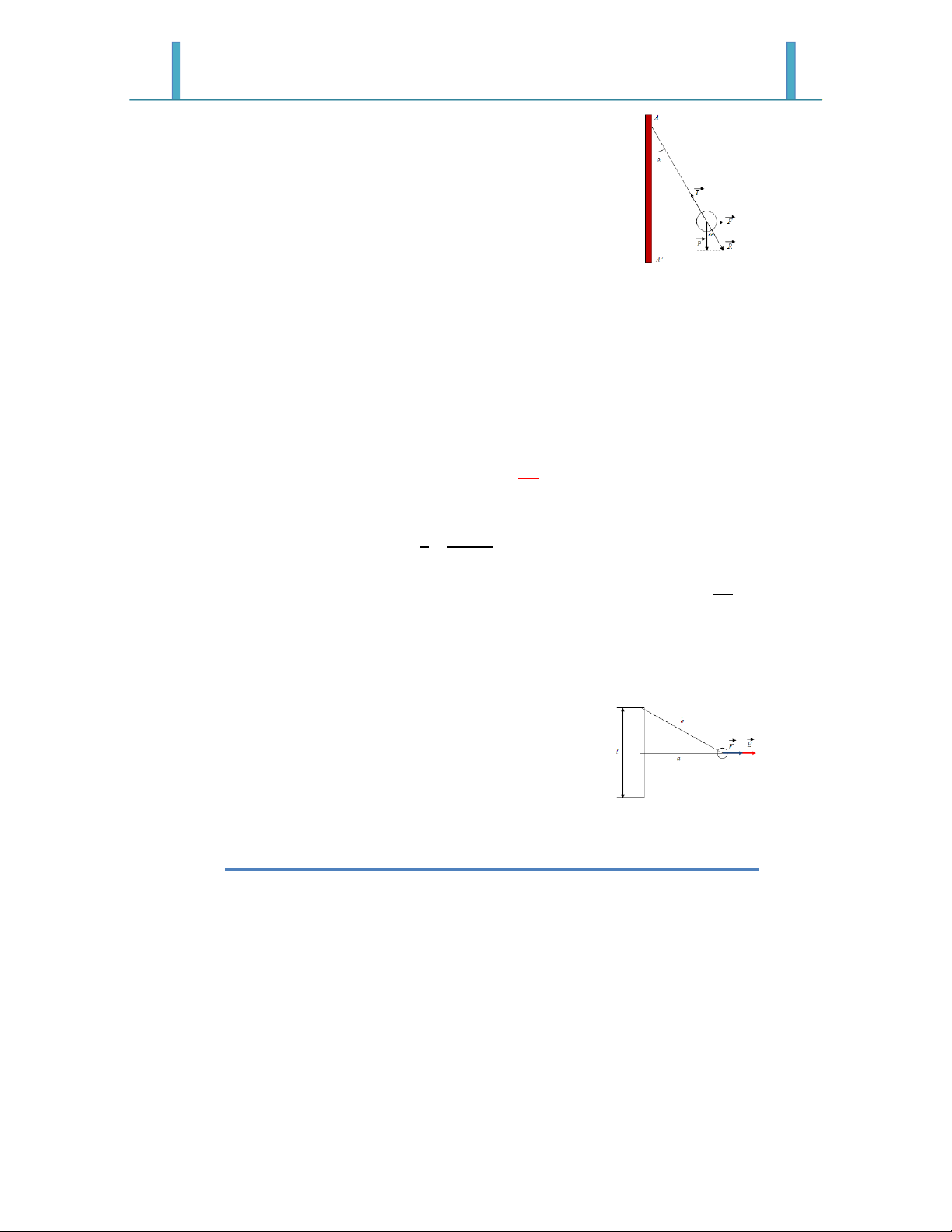
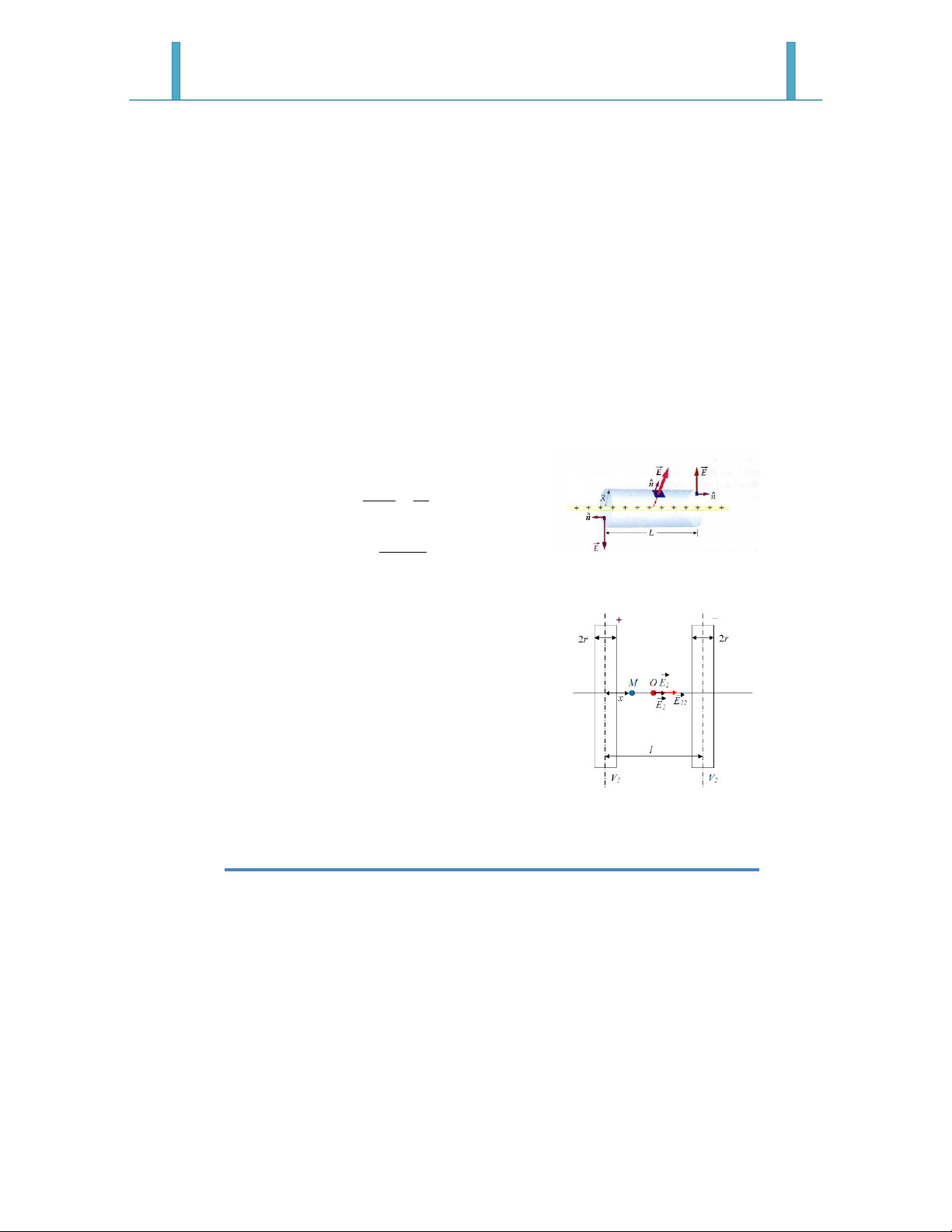
Bài 1-13: Trên hình vẽ AA’ là một mặt phẳng vô hạn tích điện đều với
mật độ điện mặt σ = 4.10-9 C/cm2 và B là một quả cầu tích điện cùng dấu
với điện tích trên mặt phẳng. Khối lượng quả cầu m = 1 g, điện tích của
quả cầu q = 10-9 C. Hỏi sợi dây treo quả cầu lệch đi một góc bằng bao
nhiêu so với phương thẳng đứng.
Tóm tắt: σ = 4.10-9 C/cm2 m = 1 g q = 10-9 C Xác định góc lệch α Giải:
- Nhận xét: Đây là bài toán cân bằng lực, dựa vào dữ kiện đề bài ta thấy muốn xác định được góc
α thì ta phải đi xác định được độ lớn của P (đã biết) và F (chưa biết)  phương hướng là phải đi
xác định giá trị đại lượng F  Bản chất của lực F là lực tĩnh điện tác dụng lên điện tích điểm q
khi điện tích này được đặt trong điện trường của mặt phẳng vô hạn tích điện đều
- Ở trạng thái cân bằng quả cầu chịu tác dụng bởi ba lực: - Trọng lực:  ?@ - Lực Coulomb: @ - Lực căng dây: H ?@
- Lực Coulomb tác dụng lên quả cầu là:  =  =  I (biểu thức màu đỏ chính là điện trường JKKL
gây bởi mặt phẳng vô hạn tích điện đều) - Từ hình vẽ ta có:
FM = =N2 = 0,223 ⇒  ≈ 13 - Chú ý:
- Công thức cần nhớ là điện trường gây bởi mặt phẳng vô hạn mang điện đều:  = P 
- Một số bài toán mở rộng:
o Xác định lực căng dây T
o Xác định điện tích q
o Xác định mật độ điện mặt σ
Bài 1-18: Hạt bụi mang một điện tích q = - 1,7.10-16 C ở gần một
dây dẫn thẳng khoảng 0,4 m, ở gần đường trung trực của dây dẫn.
Đoạn dây dẫn dài 150 cm, mang điện tích q1 = 2.10-7 C. Xác định
lực tác dụng lên hạt bụi. Giả thiết rằng q1 được phân bố đều trên sợi
dây và sự có mặt của q2 không ảnh hưởng gì tới sự phân bố.
Tóm tắt:
Điện tích điểm: q = - 1,7.10-16 C a = 0,4 cm DNK-2014 6
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
Dây dẫn: l = 150 cm, q1 = 2.10-7 C Xác định lực F Giải:
- Nhận xét: Đây là một bài toán tác dụng của điện trường gây bởi một sợi dây dài vô hạn (hoặc
hữu hạn) tích điện đều lên một điện tích điểm q. Ở bài này ta có thể sử dụng quy tắc phân tách r2
 a.b từ công thức điện trường gây bởi điện tích điểm (chú ý là chỉ được áp dụng khi điểm khảo
sát nằm rất gần hoặc trên đường trung trục trong đó a là khoảng cách từ điểm đó tới trung điểm
của sợi dây và b là khoảng cách từ điểm đó đến đầu mút của dây) để xác định cường độ điện
trường sau đó xác định lực F:  =  ⇒  =  FQ
- Áp dụng quy tắc phân tách r2 ta có điện trường gây bởi sợi dây dẫn thẳng dài tại điểm nằm trên
đường trung trực của dây:  =  F "Q =" FRF+ S&2T
- Lực tác dụng lên điện tích điểm q1 là:  =  = "
FRF+ S&2T≈ 107"= - Chú ý:
- Ở bài toán này ta hoàn toàn có thể coi như bài toán dây dài vô hạn vì l >> a do đó áp dụng
định lý O-G ta dễ dàng thu được công thức điện trường gây bởi dây vô hạn tích điện đều q
tại điểm M cách dây một khoảng là a  = %2F= 2F&
- Rất dễ nhận thấy nếu tính theo công thức này thì biểu thức tính lực F cũng sẽ thay đổi 
kết quả sai???  thực sự thì kết quả vẫn sẽ gần như nhau do gần đúng vô hạn khi l >> a.
- Các công thức cần nhớ: o  = U V=  VW o  = XVY
- Một số dạng bài mở rộng liên quan tới các công thức
o Xác định mật độ điện dài λ
o Xác định khoảng cách từ điện tích q
o Xác định độ dài của dây dẫn l
o Xác định khoảng cách từ điện tích tới dây a o ….
Bài 1-24: Tính công cần thiết để dịch chuyển một điện tích q = "<107Z[ từ một điểm M cách quả
cầu tích điện bán kính r = 1 cm một khoảng R = 10 cm ra xa vô cực. Biết quả cầu có mật độ điện mặt σ = 10-11 C/cm2. DNK-2014 7
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
Tóm tắt: q = "<107Z[
Quả cầu: r = 1 cm, σ = 10-11 C/cm2 R = 10 cm Xác định AR∞ Giải:
- Nhận xét: Đây là bài toán liên quan tới công dịch chuyển điện tích điểm  chúng ta quan tâm
tới công thức tính công dịch chuyển từ vị trí M  N nào đó: A MN = q(VM – VN)  từ công thức
này ta thấy phương hướng của bài toán là phải đi xác định điện thế tại vị trí M và N. Mà muốn
xác định điện thế tại một điểm nào đó trước tiên ta phải xác định được hình dạng của nguồn điện
tích gây ra tại điểm đó  trong bài này là mặt cầu tích điện đều  ta cần chú ý tính chất điện thế
gây bởi mặt cầu tích điện mặt:
- Điện thế tại mọi điểm bên trong mặt cầu đều bằng điện thế tại bề mặt cầu bán kính R \] = 1^_V/` =$ 4a
- Điện thế tại một điểm cách tâm cầu một khoảng r > R là: 0^b =$ 4
- Điện thế tại vô cùng luôn luôn bằng không
 để hiểu rõ công thức trên mọi người có thể tham khảo bài viết chuyên đề ứng dụng tích phân
vào bài toán tĩnh điện.
- Đối với bài toán ta đang khảo sát, điểm cần khảo sát nằm ngoài mặt cầu nên ta áp dụng công
thức: c =(>−d)=>=$4(+a) =44N(+a) =N
( + a) ≈ 3,42.107Ze - Chú ý:
- Một số công thức cần quan tâm:
o Công dịch chuyển điện tích từ vị trí M đến vị trí N: A MN = q(VM – VN)
o Điện thế gây bởi quả cầu tích điện mặt \] = 1^_V/` =$ 4a 0^b =$ 4
- Một số bài toán mở rộng:
o Xác định điện tích điểm q
o Xác định bán kính cầu r
o Xác định mật độ điện mặt σ o ….
Bài 1-26: Một điện tích điểm  = <107f[ nằm cách một sợi dây dài tích điện đều một khoảng r 1
= 4 cm. Dưới tác dụng của điện trường do sợi dây gây ra, một điện tích dịch chuyển theo hướng DNK-2014 8
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
đường sức điện trường khoảng r -7
2 = 2 cm. Khi đó lực điện trường thực hiện một công A = 50.10
J. Tính mật độ dài của dây.
Tóm tắt:  = 2 3107f[ r1 = 4 cm r2 = 2 cm A = 50.10-7 J
Xác định mật độ dài của dây λ. Giải:
- Nhận xét: Phương hướng của bài toán là phải đi tìm mối quan hệ giữa λ với các đại lượng đã
biết. Dễ thấy dữ kiện sợi dây dài tích điện đều + λ  gợi ý cho ta công thức xác định điện
trường gây bởi sợi dây thẳng dài  λ có liên quan tới E. Tiếp theo ta thấy công A thì thường liên
hệ với V mà giữa V và E có tồn tại mối quan hệ  ta đã liên hệ được đại lượng λ với đại lượng đã biết là công A.
- Các mối liên hệ sử dụng trong bài này là: c = −  = − % TÍCH PHÂN TỪ VỊ c =  = % 2  TRÍ r1  r2 2
- Công mà lực điện trường thực hiện để dịch chuyển điện tích từ vị trí 1 đến vị trí 2 là:  c = 3 % =%
&M  ⇒ % = 2c 2 
&M  ≈ −6.107Z[/  2     "  " - Chú ý:
- Cần nhớ các công thức sau: o  = U o % = i W]j j o c = U &M    - Bài toán mở rộng:
o Xác định công dịch chuyển điện tích
o Xác định điện tích điểm q o …. DNK-2014 9
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
Bài 1-32: Tại hai đỉnh C, D của một hình chữ nhật ABCD (có các
cạnh AB = 4 m, BC = 3 m) người ta đặt hai điện tích điểm q1 = -
3.10-8 C (tại C) và q2 = 3.10-8 C (tại D). Tính hiệu điện thế giữa A và B.
Tóm tắt: AB = 4 m BC = 3 m q1 = - 3.10-8 C q2 = 3.10-8 C
Xác định hiệu điện thế UAB Giải:
- Nhận xét: Đây là bài toán điện thế gây bởi hệ điện tích điểm  khác với điện trường (hoặc lực
điện), điện thế là đại lượng vô hướng nên ta chỉ cần tính điện thế của từng điện tích điểm gây ra
tại điểm cần xét sau đó cộng đại số với nhau. Hiệu điện thế giữa hai điểm A và B được xác định
bằng công thức UAB = VA - VB. - Điện thế tại A là:
i= "i + i ="4c[ +4ck ≈ 36 - Điện thế tại B là:
A= "A + A ="4l[ +4lk ≈ −36
- Hiệu điện thế giữa hai điểm A, B là: U AB = VA - VB = 72 V
- Chú ý: - Bài toán có thể mở rộng bằng cách bố trí số lượng và vị trí các điện tích điểm theo các
hình khác nhau  tính điện thế của từng điểm  cộng đại số - Công thức cần nhớ:
 Hiệu điện thế giữa hai điểm AB: U AB = VA - VB
 Điện thế gây bởi điện tích điểm:  =  
Bài 1-33: Tính công của lực điện trường khi dịch chuyển điện
tích q = 10-9 C từ điểm C đến điểm D nếu a = 6 cm, Q1 = " <107f[, Q 2 = - 2.10-9 C.
Tóm tắt: q = 10-9 C a = 6 cm Q = " 1 <107f[ Q2 = - 2.10-9 C Tính công ACD DNK-2014 10
Trần Thiên Đức – ductt111@gmail.com – ductt111.com Giải:
- Nhận xét: Đây là bài toán công dịch chuyển điện tích  phải đi xác định điện thế tại C và D 
áp dụng công thức: ACD = q(VC - VD).
- Điện thế tại điểm C là:
m=$"4F+$4F
- Điện thế tại điểm D là: n=$"4√2F+$ 4√2F
- Hiệu điện thế giữa hai điểm CD là:
pmn = m− n=1 4F($"+ $)q1 − 1√2r ≈ 58
- Công dịch chuyển điện tích q từ C đến D là: ACD = q.UCD = 0,58.10-7 J
Bài 1-34: Giữa hai mặt phẳng song song vô hạn mang điện đều mật độ bằng nhau nhưng trái dấu,
cách nhau một khoảng d = 1 cm đặt nằm ngang, có một hạt điện mang khối lượng m = 5.10-14 kg.
Khi không có điện trường, do sức cản của không khí, hạt rơi với tốc độ không đổi v1. Khi giữa
hai mặt phẳng này có hiệu điện thế U = 600 V thì hạt rơi chậm đi với vận tốc u=v . Tìm điện tích của hạt.
Tóm tắt: d = 1 cm m = 5.10-14 kg U = 600 V u u "  = 2 Giải:
- Nhận xét: Phân tích dữ kiện của bài toán ta thấy khi không có điện trường dưới tác dụng của
trọng lực hạt bụi sẽ rơi xuống kèm theo là lực cản của không khí, nhưng khi có điện trường thì
hạt rơi chậm đi  có nghĩa là điện trường đã sinh ra một lực tác dụng ngược hướng với chiều
của trọng lực. Hạt rơi với tốc độ không đổi  gia tốc rơi của vật bằng 0  tổng các vector ngoại
lực tác dụng lên vật bị triệt tiêu.
- Khi không có điện trường:
- Hạt chịu tác dụng của hai lực: o Trọng lực:  ?@ o Lực cản: m??@
- Do hạt rơi với tốc độ không đổi nên ta có:
o  ?@ + ?m?@ = 0?@ ⇒  = m⇒  = 6wu"= u" (1) - Khi có điện trường:
- Hạt chịu tác dụng của hai lực: DNK-2014 11
Trần Thiên Đức – ductt111@gmail.com – ductt111.com o Trọng lực:  ?@ o Lực cản: m??@ ′ o Lực Coulomb: đ??@
- Do hạt rơi với tốc độ không đổi nên ta có:
o  ?@ + ?m?′?@ + ?đ?@ = 0?@ ⇒  = my+ đ⇒  = 6wu+  = u+  (2) - Từ (1) và (2) ta có:
 −  = u" ⇒  =  q1 − uu"r =  pq1 − uu"r
Vì u=v  nên ta có:  = "z{ |≈ 4,17.107"~[
Bài 1-35: Có một điện tích điểm q đặt tại tâm O của hai đường
tròn đồng tâm bán kính r và R. Qua tâm O ta vẽ một đường thẳng
cắt hai đường thẳng cắt hai đường tròn tại các điểm A, B, C, D.
1. Tính công của lực điện trường khi dịch chuyển điện tích q 0
từ B  C và từ A  D.
2. So sánh công của lực tĩnh điện khi dịch chuyển từ A  C và t D. ừ B  Tóm tắt:
Điện tích điểm q đặt tại O
Hai đường tròn đồng tâm O: r, R
Xác định ABC, AAD. So sánh AAC và ABD Giải:
- Nhận xét: Đây là bài toán liên quan tới công dịch chuyển điện tích điểm q0 gây bởi lực tĩnh
điện  sử dụng công thức cơ bản A12 = q0(V1 – V2). Ngoài ra, do tích chất đối xứng nên các điểm
nằm đường tròn có tâm là điện tích điểm q sẽ có cùng điện thế  đường đẳng thế.
- Công dịch chuyển điện tích q0 từ B đến C là: ABC = q0(VB – VC)
- Công dịch chuyển điện tích q0 từ A đến D là: AAD = q0(VA – VD)
 do tính chất đường thẳng thế ta có: VB = VC, VA = V D nên ta suy ra: ABC = AAD = 0
- Công dịch chuyển điện tích q0 từ A đến C là: AAC = q0(VA – VC)
- Công dịch chuyển điện tích q0 từ B đến D là: ABD = q0(VB – VD)
DẠNG TOÁN: ỨNG DỤNG TÍCH PHÂN
1. Nhận xét:
- Đặc điểm của bài toán này là phải sử dụng phương pháp tính tích phân để xác định cường
độ điện trường, lực điện, điện thế hoặc các đại lượng suy ra từ những đại lượng trên.
- Để giải quyết các bài toán dạng này chúng ta cần trang bị những kiến thức cơ bản sau: DNK-2014 12
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
o Kỹ năng tính tích phân các hàm cơ bản
o Mối liên hệ giữa các đại lượng o Tổng hợp vector
o Công thức tính lực tương tác giữa hai điện tích điểm.
o Công thức tính điện trường gây bởi điện tích điểm.
o Công thức xác định điện thế.
o Công thức xác định diện tích vành tròn giới hạn bởi hai đường tròn bán kính R 1 và R2: • = (a− a")
o Công thức tính diện tích đới cầu: S = 2πRh
o Nắm vững một số công thức gần đúng
- Nhìn chung bài toán loại này là rất đa dạng, tuy nhiên nếu chúng ta biết được quan hệ
giữa các đại lượng với nhau thì hầu như các bài toán này đều có thể đưa về dạng duy nhất
là xác định cường độ điện trường gây bởi một vật thể nào đó  phương pháp quy về bài
toán điện trường. Ví dụ
o Xác định F  xác định E  sử dụng mối liên hệ F = qE o Xác định V >
M  xác định E  sử dụng mối liên hệ > = − )6 d o Xác định U €
MN  xác định E  sử dụng mối liên hệ p>€ =)6 >
o Xác định AMN  xác định E  xác định V  xác định A
 Như vậy ta thấy các bài toán đều đi qua bài toán trung gian điện trường  bài toán xác
điện điện trường gây bởi vật thể đóng vai trò rất quan trọng.
2. Hướng giải:
Bước 1 (vi phân vật thể): Để áp dụng tích phân ta phải tiến hành vi phân vật thể:
- Thanh, cung tròn, dây tròn  chia thanh thành từng đoạn dx  vi phân chiều dài.
- Mặt phẳng vô hạn, đĩa tròn  chia thành từng vành tròn có bán kính trong x bán kính
ngoài x + dx  vi phân diện tích dS = 2πxdx (được xác định bởi công thức tính diện tích
vành tròn, trong đó loại bỏ các giá trị dx2 do rất bé)
- Mặt cầu bán kính R  chia thành các đới cầu có đường cao dx  vi phân diện tích dS =
2πRdx (được xác định bởi công thức tính diện tích đới cầu).
Bước 2 (Xác định dq): Các bài toán lực điện, điện trường, điện thế thường liên quan đến giá trị
điện tích q  do đó phương hướng đầu tiên cần phải xác định chính là giá trị dq. Thông thường
ta phải tìm mối liên hệ giữa dq với vi phân chiều dài/vi phân diện tích
- dq = λ.dx (λ: mật độ điện dài = điện tích của vật thể/độ dài vật thể - đơn vị: C/m)
- dq = σ.dS (σ: mật độ điện mặt = điện tích của vật thể/diện tích bề mặt – đơn vị: C/m 2)
- dq = ρ.dV (ρ: mật độ điện khối = điện tích của vật thể/diện tích bề mặt – đơn vị:
C/m3)dạng này thường dùng định lý O – G để giải cho đơn giản)
Bước 3 (Xác định các đại lượng dF, dE, dV theo dq): Chú ý là hai đại lượng dF, dE là hai đại
lượng có hướng  áp dụng nguyên lý chồng chất trước khi tính tích phân, đại lượng dV ) (điện
thế: cộng đại số - cộng trực tiếp, lực và điện trường: cộng vector – chiếu cộng).
Bước 4 (Tính tích phân): Xác định được cận của tích phân (dựa vào giới hạn của vật thể), chú ý
tính chất đối xứng của vật thể. DNK-2014 13
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
3. Bài tập minh họa:
Bài 1-16: Một thanh kim loại mang điện tích q = 2.10-7 C.
Xác định cường độ điện trường tại một điểm nằm cách
hai đầu thanh R = 300 cm, cách trung điểm của thanh R0 = 10 cm. Tóm tắt: q = 2.10-7 C R = 300 cm R0 = 10 cm Xác định EO Giải:
- Nhận xét: đây là bài toán ứng dụng tích phân đối với một thanh kim loại mang điện tích  ứng
dụng các bước cơ bản để giải bài toán này.
- Bước 1 – Vi phân vật thể: Thanh kim loại  vi phân theo chiều dài dx
- Bước 2 – Vi phân điện tích dq: Gọi λ là mật độ điện dài trên thanh ta có  = %• = W•
- Bước 3 – Xác định đại lượng dE theo dq:
o Áp dụng công thức điện trường gây bởi điện tích điểm dq ta có:  =  4=• 4&
o Do tính chất đối xứng điện trường tổng cộng tại O sẽ nằm trên phương Ox và có chiều dài
như hình vẽ. Hình chiếu của dE lên Ox có giá trị là: ‚= 456 = 45 4 6     &•
=a4•&=a•
4&(•+ a)
- Bước 4 – Tính tích phân:
o Điện trưởng tổng hợp tại O là: W/ W/ W/  = 3 7W/ = 2 a 3  a• • =a 2&3•
4&(•+ a)
4&(•+ a)  (•+ a) ⇒  = a2 &1 • W/ = a „
4aa≈ 6000D/  ƒ•+ a - Chú ý:
- Cách tính tích phân dạng: )‚
 Xét tích phân † = )‚ ử ụ ươ (‚…V )(/
(‚…V)/ s d ng ph ng
pháp tích phân từng phần. o Đặt ‡ˆ = " ⇒ ˆ = − ‚‚ √‚ …V (‚ …V)(/
u = • ⇒ u = • ta có:
† = •√•+ F+ 3 •( • •
+ F) =• √•+ F+ 3 •+ F− F• (•+ F) DNK-2014 14
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
⇒ † = •√•+ F+ 3 •(•+ F)"/ − F3•(•+F)
Mà † = )‚(‚…V)/ nên ta có: 3• ( + F) =1F• √•+ F
- Những bài toán mở rộng:
o Xác định lực điện F
o Xác định các đại lượng liên quan tới công thức: R 0, l, R, q, λ
- Các công thức cần nhớ:
o Điện trường gây bởi thanh kim loại mảnh mang điện tích q tại một điểm nằm cách
hai đầu thanh R và cách trung điểm của thanh R0 = 10 cm  =  4aa
o Mật độ điện dài: % =  W o Tích phân cơ bản: ) ‚ ‚ = (‚ " …V )(/ V √‚ …V
Bài 1-17: Một mặt phẳng tích điện đều với mật độ
σ. Tại khoảng giữa của mặt có khoét một lỗ hổng
bán kính a nhỏ so với kích thước của mặt. Tính
cường độ điện trường tại một điểm nằm trên đường
thẳng vuông góc với mặt phẳng và đi qua tâm của
lỗ hổng, cách tâm đó một đoạn là b
Tóm tắt:
Mặt phẳng: tích điện đều, ∞, σ Lỗ hổng: a
O thuộc trục của lỗ và cách tâm một khoảng b Xác định E0 Giải:
- Nhận xét: đây là bài toán ứng dụng tích phân đối với một mặt phẳng mang điện tích  ứng
dụng các bước cơ bản để giải bài toán này.
- Bước 1 – Vi phân vật thể: Mặt phẳng vô hạn  vi phân theo hình vành khăn với tâm là tâm
của lỗ tròn bán kính a. Khi đó vi phân diện tích hình vành khăn nằm giữa hai đường tròn bán kính
x và x + dx là: dS = 2πxdx (công thức này suy ra bằng cách lấy diện tích hình tròn bán kính x + dx
trừ đi diện tích hình tròn bán kính x và chú ý là bỏ qua đại lượng d2x vì nó quá nhỏ)
- Bước 2 – Vi phân điện tích dq: Gọi σ là mật độ điện mặt ta có  = N• = N2π••
- Bước 3 – Xác định đại lượng dE theo dq:
o Do tính đối xứng nên điện trường gây bởi các phần tử điện tích trên diện tích dS tại điểm
O sẽ có phương lập với Ox một góc α và có cùng độ lớn. Ta đặt
?@ = ?"?@+ ??@+ ⋯ + ?Š?@ DNK-2014 15
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
⇒ ‚=("+ + ⋯ \)456 = 456 4
Trong đó dq = dq1 + dq2 + …+ dqi, thay 456 = Y,  = N2π•• ta có: ‚=QN•
2•<=QN•• 2(•+ Q)
- Bước 4 – Tính tích phân:
o Điện trường gây bởi toàn bộ mặt phẳng là:  d d ‹= 3V Q = N Q •N• 43V=(• − + Q Q N ) 21 d 2 √•+ QŒV (•+ Q) (•+ Q)
⇒ ‹=QN2√F+ Q=N 2R1 + F Q - Chú ý:
- Từ bài toán này ta có thể rút ra cách xác định điện trường gây bởi một số vật có hình dạng tương tự như:
o Đĩa tròn mang điện đều bán kính R  Điện trường E 0 lấy tích phân từ 0  R 
điện trường gây bởi đĩa tròn mang điện đều tại một điểm trên trục và nằm cách
tâm đĩa một khoảng là b: = − QN 21√• •=N + QŒ •1 − 1 ‘ 2  R1 + a Ž Q •
o Mặt phẳng vô hạn không khoét lỗ  a = 0  điện trường =P 
o Vành tròn bán kính trong là R 1 bán kính ngoài là R2  lấy tích phân từ a  b 
điện trường gây bởi vành tròn mang điện đều tại một điểm trên trục và nằm cách tâm một khoảng là b: = − QN 21 •  =N Q √• −1 + QŒ• • 1 ‘ 2   R1 + a" R1 + a Ž Q•
- Một số bài toán mở rộng:
o Xác định các đại lượng liên quan tới công thức: σ, a, b
- Các công thức cần nhớ:
o Điện trường gây bởi đĩa tròn bán kính R, tích điện đều
o Điện trường gây bởi mặt phẳng khoét lỗ bán kính a, tích điện đều
o Điện trường gây bởi mặt phẳng vô hạn tích điện đều DNK-2014 16
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
Bài 1-29: Tính điện thế tại một điểm nằm trên
trục của một đĩa tròn có tích điện đều và cách
tâm đĩa một khoảng h. Đĩa có bán kính R và mật độ điện mặt σ. Tóm tắt:
Đĩa tròn: tích điện đều, R, σ
Điểm M: nằm trên trục của đĩa, cách tâm một đoạn h Xác định VM Giải:
- Nhận xét: đây là bài toán điện thế gây bởi đĩa tròn đều  ta có thể sử dụng phương pháp quy về
bài toán điện trường rồi sử dụng mối quan hệ giữa điện thế và điện trường để tìm ra điện thế tại điểm M.
- Điện trường gây bởi đĩa tròn tại một điểm nằm trên trục và cách tâm đĩa một khoảng là h là =N • 1 − 1 ‘ 2  R1 + a Ž ℎ•
- Áp dụng công thức liên hệ giữa điện thế và điện trường là: d d N • 1− 1 ‘ =N d > = 3 ℎ = 3 “ • ℎ (ℎ − ƒa + ℎ)–  20“ • 2    ”1 + a2 Ž ℎ2•
Khi h  ∞ thì h >> R  √a+ ℎ= ℎ như vậy ta có: =N > Sƒa 2 + ℎ − ℎT  - Chú ý:
- Bài toán này hoàn toàn có thể áp dụng phương pháp tích phân tính trực tiếp theo điện thế V
- Một số bài toán mở rộng:
o Tính hiệu điện thế giữa hai điểm trên trục
o Tính công dịch chuyển điện tích giữa hai điểm trên trục
o Xác định các đại lượng liên quan tới công thức
- Công thức cần nhớ là:
o Điện thế gây bởi đĩa tròn bán kính R tích điện đều tại một điểm trên trục của đĩa
và cách tâm đĩa một khoảng h: =N > Sƒa 2 + ℎ − ℎT 
DẠNG TOÁN: ÁP DỤNG ĐỊNH LÝ O - G
1. Nhận xét: DNK-2014 17
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
- Có rất nhiều bài toán trong đó vật thể có phân bố điện tích đối xứng cao: o Đối xứng phẳng o Đối xứng cầu o Đối xứng trụ
 về cơ bản chúng ta hoàn toàn có thể sử dụng phương pháp tích phân để tính các đại lượng
như điện trường, lực điện  ưu điểm của phương pháp tích phân là tính được hầu hết các
loại vật thể nhưng nhược điểm lớn là đối với hệ có đối xứng cao thì việc tính toán lại khá
dài dòng  để giải quyết bài toán đối xứng cao ta sẽ sử dụng định lý O – G.
- Nhờ có định luật Gauss ta dễ dàng xác định được cường độ điện trường của các vật thể có
sự phân bố điện tích đối xứng cao. Thông qua việc lựa chọn mặt Gauss hợp lý ta có thể
đưa ra công thức đơn giản mô tả định luật Gauss: ].• = $ 
Trong đó En là hình chiếu của vector E lên vector pháp tuyến của bề mặt Gauss
Như vậy nhiệm vụ của bài toán lúc này chỉ là:
- Xác định điện tích S
- Xác định điện tích Q
2. Hướng giải:
Bước 1: Chọn mặt kín bao quanh đối tượng (mặt Gauss): sao cho tại các phần của đối tượng
?@//M?@ hoặc ?@ ⊥ M?@ với En = hằng số.
• Đối xứng phẳng: chọn mặt trụ. (1)
• Đối xứng cầu: chọn mặt cầu đồng tâm. (2)
• Đối xứng trụ: chọn mặt trụ đồng trục. (3) (1) (2) (3)
Bước 2: Áp dụng định luật Gauss: ˜ š$\]1\` ]`b = ™ ]c = 0 DNK-2014 18
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
3. Bài tập minh họa:
Bài tập ví dụ: Xác định cường độ điện trường gây bởi dây dài vô hạn hình trụ tích điện đều với
mật độ điện dài λ tại một điểm cách trục của dây một khoảng R Tóm tắt:
Dây vô hạn: tích điện đều λ, hình trụ
M: cách trục một khoảng R Xác định EM Giải: - Nhận xét:
• Do tính chất đối xứng nên:
o  ?@ vuông góc với bề mặt trụ của dây – hướng ra mọi hướng
o Giá của các ?@ đều cắt trục của dây  đối xứng trụ
• Lựa chọn mặt Gauss: đề thỏa mãn tính chất ta chọn mặt trụ bán kính R  vecto cường độ
điện trường vuông góc với hai vector pháp tuyến của mặt phẳng đáy và song song với
vector pháp tuyến của mặt cong  thành phần vuông góc bị triệt tiêu (ứng với hai mặt bên). - Ta có: ˜]`b =∮] š   c ]) = c
š= ]. Jœ•. ž trong đó:Jœ•. ž là diện tích mặt bên hình trụ
- Điện tích bị bao bọc bởi mặt Gauss chính là điện tích của
phần dây nằm trong hình trụ nên ta có:
$\]1\` = %Ÿ  ˜]`b =' ¡¢ £¤  =U¦ ¥ ¥
- Từ công thức O - G (trong đó thay En = EM) ta có: © § ¨ = JœKªK•
- Chú ý: cần nhớ công thức tính điện trường gây bởi dây hình trụ
Bài 1-22: Giữa hai dây dẫn hình trụ song song cách nhau
một khoảng l = 15 cm người ta đặt một hiệu điện thế U =
1500 V. Bán kính mỗi dây là r = 0.1 cm. Hãy xác định cường
độ điện trường tại trung điểm của khoảng cách giữa hai sợi
dây biết rằng sợi dây đặt trong không khí.
Tóm tắt:
Dây dẫn hình trụ: 2 dây, đặt song song, bán kính r = 0.1 cm l = 15 cm U = 1500 V ε = 1 O trung
điểm của khoảng cách giữa hai sợi dây Xác định E0. Giải:
- Nhận xét: Bài toán liên quan đến dây dẫn hình trụ  đối xứng trụ  áp dụng định lý O-G để DNK-2014 19
Trần Thiên Đức – ductt111@gmail.com – ductt111.com
xác định điện trường gây bởi từng dây dẫn trụ. Bài toán cho biết U  chắc chắn cường độ điện
trường sẽ được tính thông qua giá trị U.
- Xét trường hợp tổng quát: giả sử điểm M cách dây dẫn thứ nhất một đoạn là x  áp dụng định
lý O-G và nguyên lý chồng chất điện trường ta có cường độ điện trường tại M là:
>=%2•+%2(& − •) =%2q1•+1& −•r
- Như ta đã biết mối quan hệ giữa U và E là: -« = −§-. nên ta có: ¬ W7 −p = 3 p = − 3 q % 1
•+1& − •r• = %2&M & − • W7 =%&M  2 •Œ  & −  ¬ ⇒ % = − p & −  =p &M  &M & −  
- Tại trung điểm O thì x = l/2 ta có: ‹=2%&=2p &. &M & −   ≈ 4000D/
Bài 1-38: Cho quả cầu tích điện đều với mật độ điện khối ρ, bán kính a. Tính hiệu điện thế giữa
hai điểm cách tâm lần lượt là a/2 và a
Tóm tắt:
Quả cầu: tích điện đều ρ, bán kính a R1 = a/2 R2 = a Xác định U12 Giải:
- Nhận xét: Bài toán xác định hiệu điện thế  quy về bài toán xác định điện trường tại điểm nằm
trong mặt cầu  áp dụng định lý O-G  do tính đối xứng cầu nên lựa chọn mặt kín là mặt cầu
- Theo định lý O-G ta có: 
• =  ⇔ 4=4 3<! ⇒  = ! 3
- Hiệu điện thế giữa hai điểm 1 và 2 là: • V p = 3 =! V=!F
" = "− = 3 
3 6„V 8 • V 
- Chú ý: - Các công thức cần nhớ:
o Điện trường tại một điểm nằm trong mặt cầu tích điện khối:  = ® <
o Mối liên hệ giữa điện thế và cường độ điện trường: "− =)• •  DNK-2014 20

Tài liệu liên quan: