Hướng Dẫn Giải Bài Tập Lý Thuyết Đàn Hồi | Môn Cơ học kết cấu - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58933639 TRẦN CÔNG NGHỊ
HƯỚNG DẪN GIẢI BÀI TẬP
LÝ THUYẾT ĐÀN HỒI VÀ CƠ HỌC KẾT CẤU
(TÀI LIỆU HỌC TẬP DÀNH CHO SINH VIÊN KHOA ĐÓNG TÀU VÀ CÔNG TRÌNH NỔI) lOMoAR cPSD| 58933639 Chương 1
LÝ THUYẾT ĐÀN HỒI Tóm tắt Phương trình cân bằng: ∂σ (1.1) x ∂τxy ∂τxz ⎫ + + + X = 0⎪ ∂x ∂y ∂z ⎪
∂σ τ τy ∂ yx ∂ yz ⎪ + + + =Y 0⎬ ∂y ∂x ∂z ⎪
∂σz ∂τzx ∂τyz ⎪ + + + Z = 0⎪ ∂z ∂x ∂y ⎭
trong đó X, Y, Z – lực khối. ∂u ⎫ εx =⎪ ∂x ∂v ⎪ ε (1.2) y = ∂y ⎪ ∂w ⎪ εz = ⎪ ∂z ⎪
Phương trình biến dạng:
⎛∂u ∂v⎞⎬
γxy =⎜⎜∂y +∂x⎟⎟⎠⎪⎪ ⎝
⎛∂v ∂w⎞⎪
γyz =⎜⎜∂z +∂y ⎟⎟⎠⎪⎪
⎝ ⎛∂u ∂w⎞⎪ γzx =⎜ + ⎟⎪
⎝∂z ∂x ⎠⎭
Điều kiện tương hợp (liên tục): ⎪ lOMoAR cPSD| 58933639
∂∂2yεx ∂∂2xεy∂∂ ∂2x yγxy ⎫⎪
2 ∂ ε = ∂ ⎜⎛⎜− ∂γ∂xyz + ∂∂γyxz + ∂γ∂zxy ⎞⎟⎟⎠⎫⎪⎪ + = ⎪ 2 2 y z x ⎝ ∂
ε2∂ 2ε2z = ∂ 2γyz ∂z ∂y ∂ ∂y z ⎪ ⎪⎪⎬ và
∂ ∂x z ∂y ⎝ ∂x ∂y ∂z ⎠ ⎪ 2
∂ εy = ∂ ⎛⎜⎜∂γyz −∂γxz + ∂ ∂γ 2εz
∂ 2εx ∂ 2γxz ⎪ ∂ 2ε ∂ ⎛∂γ ∂γ ⎪ xy ⎞⎟⎟ ⎬⎪⎪ (1.3) 2 + 2 = ⎪ ∂x ∂z ∂ ∂x z ⎪⎭
2 ∂ ∂x yz = ∂z ⎜⎜⎝ ∂xyz + ∂∂γyxz −
∂zxy ⎞⎟⎟⎠ ⎪⎪⎭
Công thức chuyển của tensor ứng suất. Nếu ký hiệu ma trận các cosin góc giữa hai hệ trục là
[c], tensor ứng suất điểm trong hệ tọa độ Oxyz là [σ], tensor ứng suất trong hệ tọa độ mới [σ∗] tính theo công thức: [
σ* ]=[ ][ ][ ]c σ c T (1.4)
⎡cxx* cxy* cxz* ⎤ ⎡σ τ τx xy ⎢ cyy* ⎥ xz ⎤ czy*
với [ ]c = ⎢c cyz* ⎥; yx* [ ] c σ = ⎢⎢τ σ τxy y ⎢ zz* ⎥⎦ czx* ⎣ yz ⎥⎥ ⎢τ τ σxz yz z ⎥⎦ ⎣
Ứng suất chính xác định từ phương trình:
(σ σ τ τx − )k + yxl + zxm = 0⎫ ⎪ τ ⎪
xyk + (σ σ τy − )l + zym = 0⎬ (1.5) τ τ σ σxzk + yzl + ( z − )m = 0 ⎭
hoặc dưới dạng ma trận:
⎡σ σ τx − xy
τxz ⎤⎧k ⎫ ⎢ ⎥⎪ ⎪ ⎢ τ ⎥⎨
yx σ σ τy − yz l ⎬={0} (1.6) ⎢ τzx
τzy σ σz − ⎥⎦⎪⎩m⎪⎭ ⎣
trong đó tổng bình phương các cosin bằng đơn vị k2 + l 2 + m2 = 1. Lời giải hệ phương lOMoAR cPSD| 58933639 trình:
σ3 - σ2J1 + σJ2 – J3 = 0. (1.7)
trong đó J1 = σx + σy + σz J 2 2 2
2 = σyσz + σzσx + σxσy - τyx - τzx - τxy (1.8) J 2 2 2
3 = σxσyσz + 2τxyτyzτxz - τxy σz - τyz σx - τzx σy (1.9)
Các đại lượng J1, J2, J3 được gọi bất biến thứ nhất, bất biến thứ hai, và bất biến thứ ba của tenso ứng suất.
Trường hợp ứng suất phẳng, trong hệ tọa độ xOy ứng suất chính tính theo công thức: σx +σy 2 2 1 σ 4 1,2 =
± (σ σ τx − y ) + xy (1.10) 2
Hướng trục ứng suất chính tính từ công thức: 2τxy tg2θn = (1.11) σ σx − y
Ứng suất cắt lớn nhất: τmax,min =± (1.12) σx −σy tg2θs = 2 (1.13) τxy
Vòng tròn Mohr xây dựng từ phương trình: 2 2
⎛ σ σx + y ⎞ 2
⎛σ σx − y ⎞ ⎜⎝σ− ⎟⎟ +τ =⎜⎜ 2⎠⎟⎟ (1.14) ⎜ 2 ⎠ ⎝
Định luật Hooke áp dụng cho vật liệu đẳng hướng với mô đun đàn hồi E, hệ số Poisson ν. 1 [ ( )]⎫ 1 ⎫ εx = E σ νσ σx −
y + z ⎪ γxy = Gτxy ⎪ 1 ⎪⎪ 1 ⎪⎪ ε =σ νσ σ− ( + ) lOMoAR cPSD| 58933639 [ ] y y x
z ⎬ và γyz = τyz ⎬ (1.15) E ⎪ G ⎪ ε = 1 [σ νσ σ− ( )]⎪ γ = 1τ ⎪ + z z x y ⎪⎭ zx G zx ⎪⎭ E E trong đó G = (1.16) 2(1+ν)
Nếu ký hiệu: e =εx +εy +εz có thể viết: νE E ⎫
σx = (1+ν ν)(1− 2 )e + 1+νεx ⎪⎪ νE E ⎪ σy = e + εy ⎬ (1.17)
(1+ν ν)(1− 2 ) 1+ν ⎪ νE E ⎪
σz = (1+ν ν)(1− 2 )e + 1+νεz ⎪⎭
σ λx = e + 2Gεx ⎫ ⎪ σ λ ⎪
y = e + 2Gεy ⎬ (1.18) σ λz = e + 2Gεz ⎭ νE trong đó λ=
mang tên gọi hằng số Lamé. (1+ν ν)(1− 2 )
Hàm ứng suất Airy Φ(x,y) : ∇4Φ(x,y) = 0. ∂ Φ2 σx = ; σy = ; τxy =− ; ∂ ∂x y
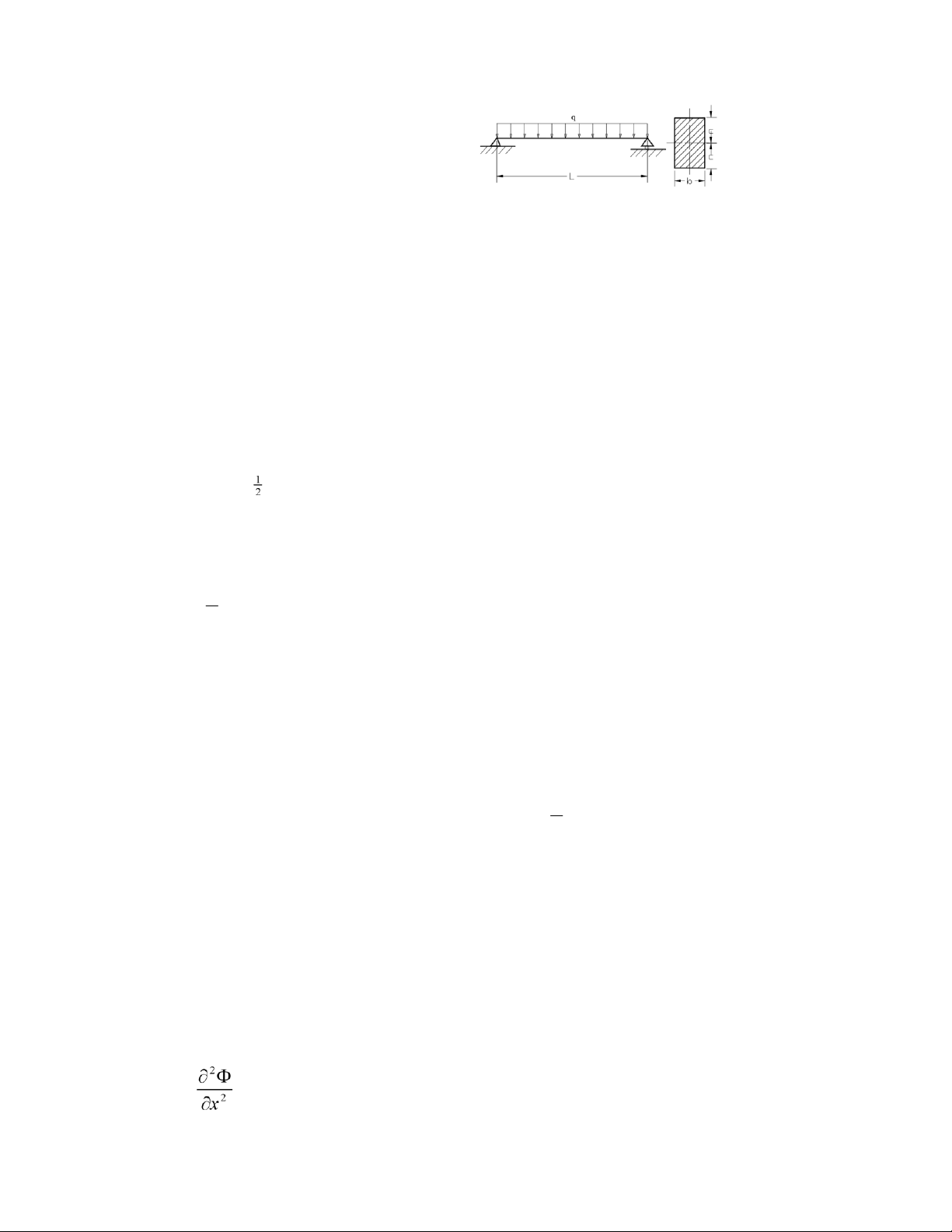
Ví dụ 1: Thành lập hàm ứng suất cho dầm dài L, hình 1.1, mặt cắt ngang hình chữ nhật cạnh đứng 2c,
chiều rộng b, chịu tác động tải phân bố đều q = const.
Điều kiện biên như sau: lOMoAR cPSD| 58933639 a) Tại x = 0: σx = 0; τxy = 0. b) Tại x = L: Hình 1.1 c ⎫ ∫τ ⎪ xybdy = qL − ⎪ c c ⎪ ∫σ ⎬ xbdy = 0 − ⎪ c c 2 ⎪
∫σx ybdy = qL ⎪ −c ⎭ c) Tại y = c: q σy =− ; τxy = 0 b d) Tại y = -c: σy = 0; τxy = 0.
Những nhận xét ban đầu:
- Điều kiện đầu tiên của a) trong trường hợp cụ thể không thể thỏa mãn. q
- Từ tính chất đối xứng của mặt cắt ngang và σy =− tại y = c và σy = 0 tại y = -c, có b
thể rút ra σy sẽ là hàm lẻ của y.
- Hàm σx cũng là hàm lẻ của y.
Hàm Airy nên viết dưới dạng:
Φ = Axy +Bx2 + Cx2y + Dy3 +Exy3 +Fx2y3 +Gy5 Có
thể thấy rằng: ∇4Φ(x,y) = 24Fy + 120Gy = 0.
Từ phương trình cuối suy ra F = -5G.
Ứng suất tính theo công thức sau: σx =
= 6Dy + 6Exy −30Gx y2 + 20Gy 3 lOMoAR cPSD| 58933639 σy = 2 B Cy Gy 3 ∂y ( 2 3 30Gxy 2 )
Từ công thức tính τxy có thể viết:
Thỏa mãn điều kiện τxy = 0 tại x = 0: A + 3Ey2 = 0, từ đó A = E = 0.
Thoả mãn τxy = 0 tại y = ±c có thể thấy:
0 = -(2Cx - 30Gc2x), hay là C = 15Gc2.
Giải phương trình xác định σy, thỏa mãn điều kiện biên cho phép xác định B, G: q 3 3 3
− = 2B + 30Gc −10Gc = 2B + 20Gc b
0 = 2B −30Gc3 +10Gc3 = 2B − 20Gc3
Từ đó có thể nhận được: q q B =− ; G =− 3 4b 40bc
Biết rằng momen quán tính mặt cắt ngang tính bằng I = bc3 , biểu thức của B và G sẽ có dạng: qc3 q B =− ; G =− 6I 60I
Hằng C tính theo G sẽ là: C = 15Gc2 = - (qc2)/(4I) Từ
phương trình xác định σx có thể viết: 2 3 q 2 q 3 σx
= 6Dy + 6Exy −30Gx y + 20Gy = 6Dy + x y − y 2I 3I
Thay biểu thức cuối vào điều kiện biên tại x = L có thể thấy: +c ⎞ 1 ⎛ q 2 q 3 2 ∫ − c⎜⎝6Dy +
2I x y − 3I y ⎟⎠ybdy = 2 qL qc 2
Từ đó có thể viết: D = lOMoAR cPSD| 58933639 30I
Trường ứng suất có dạng sau: ⎫
q ( 2 2 ) q 3 σx =
10I 5x + 2c y − 3I y ⎪ q ( ) 3 2 3 ⎪⎪ σy =−
2c + 3c y − y ⎬ 6I ⎪ q
τxy = 2I x c( 2 − y 2 ) ⎪⎪⎭
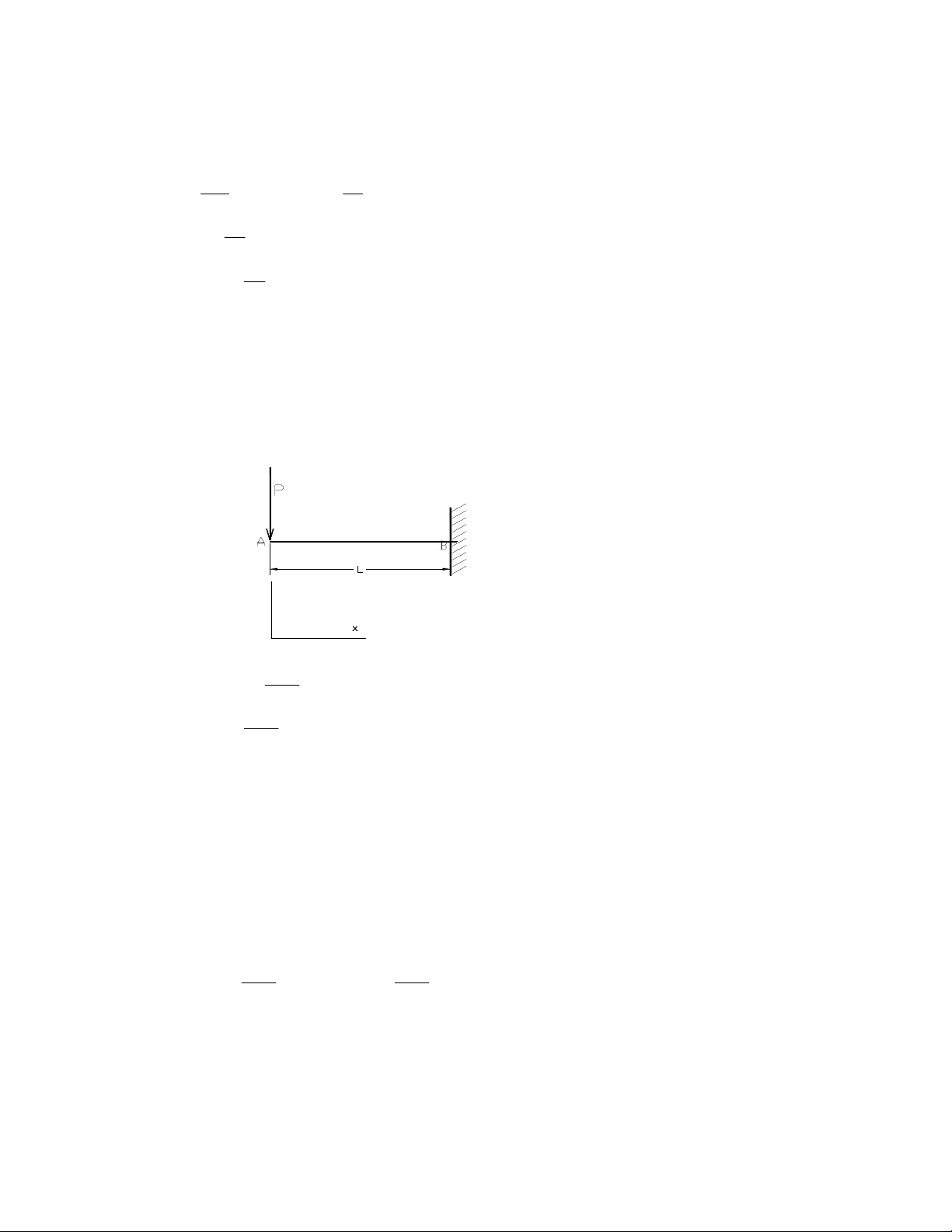
Ví dụ 2: Phương trình chuyển vị dầm trình bày tại hình 1.2 có dạng: Y Py ( 2 2 ) ⎫
u x y( , ) = 6EJ 6Lx −3x −υy ⎪⎬
v(x y, ) =− P [3Lx (
2 − x 2 −3υy 2 L − x)]⎪ 6EJ ⎭ Hình 1.2
Xác định chuyển vị điểm tại trục y = 0 và xác định trường ứng suất.
Chuyển vị theo phương thẳng đứng tại y = 0: P 2 3 Px 2 v(x,0) =− (3Lx − x
)=− (3L − x) 6EJ 6EJ
Góc xoay dầm tính theo công thức θxy 1 ⎛∂v ∂u ⎞ lOMoAR cPSD| 58933639
= 2⎜⎜⎝ ∂x − ∂y ⎟⎟⎠ , mang dạng sau: θ ) )
xy = ⎢− EJ(6Lx x−3 2 −3υy2 −6EJ(6Lx x−3 2 −3υy2 ⎥⎦=−6EJ(6Lx x−3 2 −3υy ) 2 2 6⎣
Tại y = 0 góc xoay sẽ là: P 2 θxy (x,0) =− (6Lx −3x ) 6EJ
Biến dạng trong dầm tính theo: ε υP (
x = ∂u = P (L − x y) ; εy = ∂v =− L − x y) ∂x EJ ∂y EJ lOMoAR cPSD| 58933639 ∂v ∂u γxy = + = ∂x ∂y − P (6Lx x−3 2
−3υy2)+ P (6Lx x−3 2 −3υy2)=0 6EJ 6EJ
Trường ứng suất tính theo cách sau: E ⎡ P
υ2 P1−υ ⎣EJ EJ ⎦ J ⎪ ⎤ E ⎡ υP υP ⎤ ⎪ P ⎬
⎫ σ σy = 1−υ2 ⎢⎣− EJ (L − x y) +
EJ (L − x y) ⎥⎦ x ⎪ = 0 = ⎪ 2 ⎢ τ ⎪ (L − xy = 0 ⎭ x y) − (L − x y) ⎥ = (L − x y) ⎪ 1⎡ P P ⎤ P lOMoAR cPSD| 58933639
Ví dụ 3: Sử dụng phương trình cân bằng trong “lý thuyết đàn hồi” thành lập hàm ứng suất σy , τxy dầm,
tiết diện dầm hình chữ nhật 2c x b, trong đó b – chiều rộng dầm, 2c – chiều cao dầm, chịu tải trọng
phân bố đều cường độ q(x) = const.
Ứng suất σx tính tại mặt cắt bất kỳ
của dầm, tại vị trí x, tính theo công thức: M x( ) σx = y (a) J
trong đó M = − qx2 (b) Hình 1.3 Hình 1.3
Nếu bỏ qua trọng lượng bản thân, lực khối dầm sẽ không được nhắc tới. Từ phương trình cân lOMoAR cPSD| 58933639 bằng đầy đủ: ∂σx ∂τxy ⎫ + + fBx = 0⎪ ∂x ∂y ⎪ (c)
∂τ σxy ∂ y ⎬⎪ có thể viết: + + fBy = 0 ∂x ∂y ⎪⎭ ∂τ q xy =− xy (d) ∂y J
Tiến hành tích phân phương trình đạo hàm riêng này sẽ nhận được: q 2' τxy =− xy = f x( ) (e) 2J
Để ý rằng, trường hợp không có ứng suất cắt tại mép trên và mép dưới của dầm, τxy = 0 tại
y = c và y = -c, hàm f(x) sẽ phải là: 2 qc f x( ) = x (f) 2J q 2 2'
Từ đây có thể viết: τxy =− x c( − y ) (g) 2J
Từ phương trình thứ hai của (c ) vớ FBy = 0 có thể viết: ∂σy q 2 2 =− (c − y ) ∂y 2J
Sau tích phân có thể nhận được: q 2 2 σy =−
y(3c − y ) + F x( ) (h) 6J
Điều kiện biên tại y = c: σ q y =−
b . Momen quán tính qua trục trung hòa mang giá trị J = b(2 c) 12 3 . lOMoAR cPSD| 58933639 qc 3
Từ đây xác định F(x) = − 3J
Hàm σy giờ có thể viết: q ( 3 2 3 ) σy =−
2c + 3c y − y 6J
Ví dụ 4: Dùng phương trình từ điều kiện tương hợp (liên tục) xác định chuyển vị trong mặt phẳng
xOy dầm công xôn nêu tại ví dụ 2. Mặt cắt dầm trong trường hợp này là hình chữ nhật, dày, độ
cứng EJ, hệ số Poisson ν. Y Hình 1.4
Momen uốn dầm tính theo công thức:
M = -P(L – x) 0 < x < L (a)
Các hàm ứng suất tính theo công thức quen thuộc sau: M P
σx =− y = y L( − x) (b) J J σy = 0; τxy = 0.
Từ định luật Hooke có thể viết các phương trình biến dạng: 1 P ε ) x =
(σ νσx − y = y L( − x) E EJ 1 ε ) ν P y =
(σ νσy −x =− y L( − x) lOMoAR cPSD| 58933639 E EJ 2(1+ν) γ = τ = 0 (c) xy xy E
Quan hệ biến dạng - chuyển vị cho phép viết: ∂u P =εx = y L( − x) ∂x EJ ∂v νP =ε (d) y =− y L( − x) ∂y EJ
Tiến hành tích phân hai phương trình đạo hàm riêng dạng (d) có thể nhận được: P u =
xy(2L − x) + f y( ) 2EJ νP 2 v=−
y (L − x) + F x( ) 2EJ
Hàm f(y) là hàm chỉ của y, hàm F(x) chỉ của x. ∂v ∂u
Sau tích phân, tiến hành thay vào hàm biến dạng góc γxy = + chúng ta có thể viết: ∂x ∂y ∂v ∂u νP 2 ∂F x( ) P ∂f y( ) γxy = + = y + +
x(2L − x) +
∂x ∂y 2EJ ∂x 2EJ ∂y
Thay biểu thức cuối vào (c ) sẽ nhận được phương trình: ∂F x( ) P ∂f y( ) νP 2 +
x(2L − x) = − y (e) ∂x 2EJ ∂y 2EJ
Phương trình (e) chỉ thỏa mãn khi cả hai vế là const, vídụ cả hai bằng C1. ∂F x( ) P ⎫ lOMoAR cPSD| 58933639
∂x + 2EJ x(2L − x) = C1 ⎪⎪⎬ ∂f y( ) νP 2 − y =−C1 ⎪ ∂y 2EJ ⎪⎭
Giải hệ phương trình này có thể viết: ⎫ P 2 F x( ) =− x
(3L − x) + C x1 + C2 ⎪⎪ 6EJ (f) νPy 3
⎬ f y( ) =− −C y1 + C3 ⎪⎪⎭ 6EJ
Hàm u và v giờ đây có dạng: P νP u
= 2EJ2 xy(2L − x) − 6EJ y 3 −C y1 + C3 ⎪⎬⎪⎫ (g) νPy P 2 ⎪ v=− 6EJ (L − x) −
6EJ x (3L − x) + C x1 + C2 ⎪⎭
Thỏa mãn điều kiện biên sau đây: tại x = y = 0: u = v = θxy = 0, các hằng số phải là C1
= C2 = C3 = 0. Từ đó có thể viết: P νP 3 ⎫ u =
xy(2L − x) − y ⎪
2EJ eEJ νP P ⎬ v -=
y 2 (L − x) − x 2 (3L − x)⎪ 2EJ 6EJ ⎭
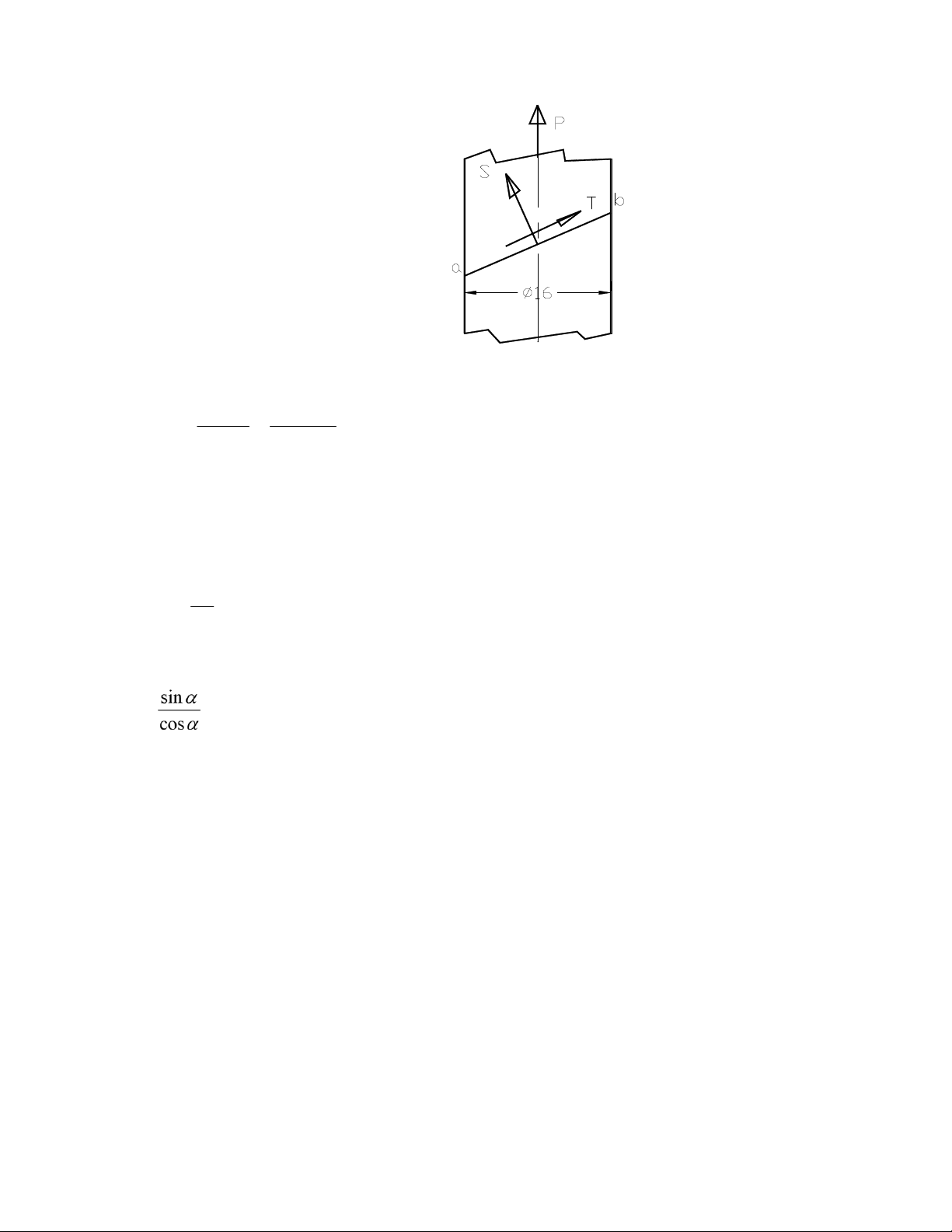
Ví dụ 5: Cho trước thép tròn đường kính φ16mm, chịu lực kéo dọc trục P = 40kN. Lực P gây ứng
suất cắt τ tại mặt cắt ab, giá trị của τ bằng 60% ứng suất pháp σ tại mặt ab đó. Xác định góc nghiêng mặt ab. lOMoAR cPSD| 58933639 Lời giải: Hình 1.5
Ứng suất pháp tính tại tiết diện trục thép tròn: P 40000 σ0 = 2 = 2
= 200MPa πd / 4 π.16 / 4
Ứng suất tính tại mặt cắt xiên ab: σ σ= 0 cos 2 α⎫⎪ τ=σ 20 sin 2α⎬⎪⎭
Từ điều kiện đề ra τ = 0,6σ hay là σ0sinαcosα = 0,6 σ0 cos2α có thể viết: = tgα= 0,6
Từ đó có thể xác định α = 31°.
Ví dụ 6: Trạng thái ứng suất tại điểm P biểu diễn bằng tensor ứng suất: ⎡14 7 − 7⎤ ⎢ 10 ⎥ σ 0 MPa . ij = ⎢ 7 0 ⎥ ⎢⎣− 7 35⎥⎦
Xác định ứng suất pháp và ứng suất tiếp tại mặt qua điểm, song song với mặt miêu tả bằng
phương trình 2x - y +3z = 9. Lời giải:
Cosin pháp tuyến mặt 2x - y +3z - 9 = 0 tính như sau: lOMoAR cPSD| 58933639 ⎫ 2 2 k = = ⎪ 22 + −( 1) 2 + 32 14 ⎪ ⎪ ( 1)− −1 ⎪ l = = ⎬ (a) 22 + −( 1) 2 + 32 14 ⎪ 3 3 ⎪ m = = ⎪ ⎪ 22 + −( 1) 2 + 32 14 ⎭
Ứng suất pháp tính theo công thức:
σ σ σ σ= xk 2 + yl 2 + zm 2 + 2τxykl + 2τyzlm + 2τzxmk (b)
trong đó, từ tensor ứng suất đọc được σx = 14, σy = 10, σz = 35; τxy = 7, τzx = -7, τyz = 0. Kết
quả ứng suất pháp, tính theo (b) sẽ là σ = 19,21 MPa.
Ứng suất tiếp tính theo công thức:
τ σ τ τ2 = ( xk + xyl + zxm)2 +(τ σ τxyk + yl + zxm)2 +(τ τ σzxk + yzl + zm)2 −σ2 (c)
Sau khi thay các giá trị ứng suất và k, l, m vào vế phải phương trình (c), ứng suất tiếp được tính như sau: τ = 14,95MPa.
Ví dụ 7: Trạng thái ứng suất tại điểm P, ghi trong hệ tọa độ Oxyz như sau: ⎡− 8 6 − 2⎤ ⎢ 4 ⎥ σ 2 MPa ij = ⎢ 6 2 ⎥ ⎢⎣− 2 − 5⎥⎦
Tính trạng thái ứng suất này trong hệ tọa độ Ox’y’z’, qua hai bước:lần đầu trục Oz xoay góc θ
= 45°, sau đó hệ trục vừa hình thành xoay quay trục Ox góc φ = 30°. Lời giải:
Sau lần xoay quanh trục Oz, hệ tọa độ mới có mối liên hệ với hệ tọa độ Oxyz theo quan hệ:
⎧x"⎫ ⎡ cosθ sinθ 0⎤⎧x⎫ ⎪ ⎪ ⎢ ⎥⎪ ⎪
⎨y"⎬= −⎢ sinθ θcos
0 ⎨y⎬ , với θ = 45° ⎥
⎪⎩z"⎪⎭ ⎢⎣ 0 0 lOMoAR cPSD| 58933639 1⎥⎦⎪⎩z⎪⎭
Lần xoay hệ trục sau thể hiện bằng quan hệ: ⎧x'⎫ ⎡1 0 0 ⎤⎧x"⎫ ⎪ ⎪ ⎢ ⎥⎪ ⎪ φ ⎨y'⎬= ⎢0
cosφ sin ⎥⎨y"⎬, với φ = 30°
⎪⎩z'⎪⎭ ⎢⎣0 − sinφ φcos ⎥⎦⎪⎩z"⎪⎭ Từ đó: ⎧x'⎫ ⎡ cosφ
sinθ cosφ 0 ⎤⎧x⎫ ⎪ ⎪
⎩z' ⎭ ⎢⎣ sinφ φsin − cosφ φ ⎪ ⎪ ⎢ φcos ⎥⎪ ⎪ ⎪ ⎪ φsin cos ⎥
⎨y'⎬= −⎢ sinφ φcos ⎦ ⎩z ⎭
sinφ ⎨y⎬=[C ]{ } x
X , Công thức tính chuyển ứng suất từ ⎥
hệ tọa độ Oxyz sang hệ tọa độ O’x’y’z’ có dạng: σ ]
ij ' =[Cx σij[Cx ]T
Sau khi thay θ = 45°, φ = 30° các thành phần ma trận [Cx] tính như sau: 2 2 2 2 0 ⎡⎤ 1 [ 4 6 4 6 2 C ] 2 2 3 x = −⎢⎢⎥⎥ ⎢⎣ 4 − 4 2 ⎥⎦
Các thành phần ứng suất điểm đang xét trong hệ tọa độ O’x’y’z’ sẽ là: 22
2 ⎛⎞ ⎛ 2 ⎞ ⎛ 2 ⎞⎛ 2 ⎞ ⎛⎞ ⎜⎟ ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎜⎟ 2
σx' =−8.⎜⎝ 2 ⎟⎠ + 4.⎜⎝ 2 ⎟⎠ +−5× + ×0 2 6⎝⎜ 2 ⎟⎠⎜⎝ 2 ⎟⎠+ 2×2⎜⎝ ⎡⎛ 2 ⎞ 1 ⎛ 6 ⎞⎤ ⎡⎛ 2 ⎞ 1 ⎛⎞⎤ ⎛ 2 ⎞ + 2× − × ×( 2) 0 ⎜ ⎟= 4MPa ⎜⎝ 2 ⎟⎠
⎛ 2 ⎞⎛ 6 ⎞ ⎛ 2 ⎞⎛ 6 ⎞ 1 ⎡⎛ 2 ⎞⎛ τx y' ' =−8⎜⎜⎝ 2 ⎟⎟⎠⎜⎜⎝− 4 ⎟⎠⎟+
4⎜⎝⎜ 2 ⎟⎟⎠⎜⎜⎝ 4 ⎠⎟⎟+ −( 5) 0x x 2 + 6⎣⎢⎢⎝⎜⎜ 2 ⎟⎟⎠⎜⎝⎜ 6 lOMoAR cPSD| 58933639 + 6 ⎞ ⎛ 2 ⎞⎛ 6 ⎞⎤
2⎢⎜⎜ 2 ⎟⎟⎠ 2 + 0x⎜⎜⎝ 4 ⎟⎟⎠⎥⎦⎥− 2⎢⎢⎣⎜⎜⎝ 2 ⎟⎠⎟ 2 + 0x⎜⎜⎝ 4 ⎟⎟⎠⎥⎥⎦ = 5,20MPa ⎢⎣⎝ 3 ⎡ ⎛ 2 ⎞⎛ 2 ⎞ ⎛ 2 ⎞⎛ 2 ⎞⎤ +6 ⎢ ⎜ ⎟⎜ − ⎟ +⎜ ⎟⎜ ⎟⎥ 2
⎜ 2 ⎟⎜ 4 ⎟ ⎜ 2 ⎟⎜ 4 ⎢ ⎟ ⎣ ⎝ ⎠⎝ ⎠ ⎝ ⎠⎝ ⎠⎥ ⎦ ⎛ 2 ⎞⎛ 2 ⎞ ⎛ 2 ⎞⎛ 2 ⎞ 2 ⎞⎤ ⎟⎥ =− M 3 Pa
τz x' ' =−8⎜⎜ 2 ⎟⎟⎠⎜⎜⎝ 4 ⎟⎟⎠+ 4⎜⎜⎝ 2 ⎟⎟⎠⎜⎝⎜− 4 ⎟⎠⎟+ −( 4 ⎟⎠⎥ 5) 0x x ⎦ ⎝ 6 6 + 4 ⎡⎛ 2 ⎞ 3 ⎛ 2 ⎞⎤ ⎡⎛ 2 ⎞ 3 ⎛
⎟⎟+⎜⎜ 2 ⎟⎟⎠⎜⎜⎝− 4
+ 2⎢⎣⎢⎜⎜⎝ 2 ⎟⎟⎠ 2 + 0x⎜⎜⎝− 4 ⎟⎟⎠⎦⎥⎥− 2⎢⎢⎣⎜⎝⎜ 2 ⎟⎟⎠ 2 + 0x⎜⎜⎝ ⎟⎟⎠⎥⎥⎦ 2 2 4 ⎠ ⎝
⎛ 46 ⎞⎠⎟⎟ + 4.⎛⎝⎜ 6 ⎞⎟ +−5×⎛⎜ 1⎟⎞
2 + 2×6⎛⎜⎜− 4 ⎟⎠⎟⎞ σy' =−8.⎜⎜ ⎜ 4 ⎟⎠ ⎝ 2⎠ ⎝ ⎝ ⎛ 6 ⎞ 1 ⎛ 6 ⎞ 1 × +0 2 ⎟⎠
+ 2× − ×( 2) ⎜ ⎟ + 2× − ×( 2) ⎜− ⎟ =−4,8MPa ⎜⎝ 4 ⎟⎠ 2 ⎜⎝ 4 ⎟⎠ 2
⎛ 2 ⎞⎛ 6 ⎞ ⎛ 2 ⎞⎛ 6 ⎞ 1 3 ⎡⎛ 2 ⎞⎛ 6 ⎞ ⎛ 2 ⎞⎛ 6 ⎞⎤ τy z' ' =−8⎜⎜ 4 ⎟⎠⎟⎜⎝⎜− 4 ⎠⎟⎟+ 4⎜⎝⎜− 2 ⎟⎠⎟⎜⎜⎝ 4 ⎟⎟⎠+ − ⎢⎜ ⎟ ⎟ ⎟
( 5)x 2 × 2 + 6⎣⎢ ⎝⎜− 4 ⎟⎠⎝⎜⎜− 4 ⎟⎠+⎜⎜⎝ 4 ⎟⎠⎝⎜⎜ 4 ⎟⎟⎠⎥⎦⎥ ⎝ ⎡⎛ 6 ⎞ 3 1 ⎛ 2 ⎞⎤ ⎡⎛ 3 ⎞⎛ 6 ⎞ 1 ⎛ 2 ⎞⎤
+ 2⎢⎣⎢⎜⎜⎝ 4 ⎟⎟⎠ 2 + 2⎜⎜⎝− 4 ⎟⎟⎠⎦⎥⎥− 2⎢⎢⎣⎝⎜⎜ 2 ⎟⎟⎠⎜⎝⎜− 4 ⎟⎟⎠+ 2 ⎜⎜⎝ 4 ⎟⎠⎟⎥⎥⎦ = 2,71MPa 2 2 ⎛ 2 ⎞ ⎛ 2 ⎞ ⎛ 3 ⎞⎛ 3 ⎞ ⎛ 2 ⎞⎛ 2 ⎞
σz' =−8.⎜⎝⎜ 4 ⎟⎟⎠ + 4.⎜⎜⎝− 4 ⎟⎟⎠ −5×⎜⎜⎝ ⎟⎜ ⎟+ 2×6⎜ ⎟⎜− ⎟+ 2 ⎟⎠⎜⎝ 2 ⎟⎠
⎜⎝ 4 ⎟⎠⎜⎝ 4 ⎟⎠ lOMoAR cPSD| 58933639 ⎛ 2 ⎞⎛ 3 ⎞ ⎛ 2 ⎞⎛ 3 ⎞ + 2× ×2 ⎜−
⎟⎜ ⎟+ 2× − ×( 2) ⎜ ⎟⎜ ⎟=−8,2MPa
⎜⎝ 4 ⎟⎠⎜⎝ 4 ⎟⎠
⎜⎝ 4 ⎟⎠⎜⎝ 4 ⎟⎠ Kết quả tính như sau: ⎡ 4 5,2 − 3 ⎤ ⎢ ⎥ σij '= ⎢5,2 − 4,8 2,7 ⎥MPa ⎢⎣− 3 2,7 − 8,2⎥⎦
Ví dụ 8: Xác định trục chính và ứng suất chính phần tử chiïu tác động ứng suất sau: σx = 500
kG/cm2, σy = 300 kG/cm2, τxy = 100 kG/cm2. Lời giải:
Công thức tính ứng suất chính: 2 σ σx + y
⎛σ σx + y ⎞ 2 σ1,2 = 2 ± ⎜⎜⎝ 2 ⎟⎟⎠ +τxy
Thay các giá trị đã cho vào biểu thức trên sẽ nhận được: 2 500 +300 ⎛ 500 +300 ⎞ 2 σ + 1 = ⎜
⎟ +100 = 400 +141,4 = 541,4 kG/cm2; 2 2 ⎝ ⎠ 2 500 +300 ⎛ 500 +300 ⎞ 2 − ⎜ ⎟ σ 1 =
+100 = 400 −141,4 = 258,6 kG/cm2; 2 2 ⎝ ⎠
Góc nghiêng trục chính so với trục Ox, Oy tính theo công thức: 2τxy tg2θ=− σ σx − y
Trường hợp này tg2θ = -1 và do vậy 2θ = -45°; θ = -22 ½ °
Ví dụ 9: Biết trước giá trị biến dạng điểm trong mặt phẳng 2D sau đây:
εx = 0,002; εy = -0,001; γxy = 0,003.
Xác định hướng chính và biến dạng chính. Lời giải:
Góc xoay hướng chính tính theo công thức: