Hướng dẫn ôn tập học kì 2 Toán 10 năm 2021 – 2022 trường Vinschool – Hà Nội

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 tài liệu đề cương hướng dẫn ôn tập học kì 2 môn Toán 10 năm học 2021 – 2022 trường Trung học Phổ thông Vinschool, thành phố Hà Nội.

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

13 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Trang 1/13
TRƯỜNG TRUNG HỌC VINSCHOOL
**********
HƯỚNG DẪN ÔN TẬP HỌC KÌ II NĂM HỌC 2021 - 2022
Môn Toán - Lớp 10 - Hệ Chuẩn Vinschool
I/ Lý thuyết
Chủ đề Nội dung
1. Dấu của nhị thức
bậc nhất
- Xét dấu của nhị thức bậc nhất.
- Giải bất phương trình tích, thương.
- Giải hệ bất phương trình một ẩn.
- Giải bất phương trình căn; bất phương trình chứa dấu giá trị
tuyệt đối.
- Biện luận phương trình, bất phương trình bậc hai một ẩn.
- Tìm tập xác định của hàm số.
2. Dấu tam thức bậc
hai
3. Giá trị lượng giác
của một cung
- Chuyển đổi đơn vị giữa độ và radian.
- Tính chiều dài cung.
- Biểu diễn cung.
- Tính giá trị lượng giác của một cung lượng giác.
4. Công thức lượng
giác
- Rút gọn biểu thức lượng giác.
- Chứng minh đẳng thức, bất đẳng thức lượng giác.
5. Hệ thức lượng
trong tam giác
- Giải tam giác.
- Tính diện tích tam giác.
- Ứng dụng vào thực tế.
6. Phương trình
đường thẳng
- Viết phương trình đường thẳng (tổng quát, tham số, chính tắc,
theo đoạn chắn).
- Xác định vị trí tương đối giữa hai đường thẳng.
- Tính khoảng cách từ một điểm đến một đường thẳng.
- Tính góc giữa hai đường thẳng.
7. Phương trình
đường tròn
- Viết phương trình đường tròn.
- Viết phương trình tiếp tuyến của đường tròn.
II/ Bài tập
Phần 1. Trắc nghiệm
Câu 1: Cho biểu thức
2 4.
f x x
Tìm tất cả các giá trị của
x
để
0
f x
.
A.
2; .
x

B.
1
; .
2
x

C.
;2 .
x
D.
2; .
x

Câu 2: Tập nghiệm của hệ bất phương trình
6 3
2 1
2
x
x
là
Trang 2/13
A.
5
;
2

. B.
5
;
2

. C.
5
;
2

. D.
5
;
2

.
Câu 3: Điều kiện xác định của bất phương trình
2 2 3 2 1
x x x
là
A.
x
. B.
;2
x 
. C.
1
;
2
x

. D.
1
;2
2
x
.
Câu 4: Có bao nhiêu số nguyên nhỏ hơn 10 thuộc tập nghiệm của bất phương trình
1 1
2 3 5
x x
?
A. Vô số. B. 4. C. 5. D. 6.
Câu 5: Tập nghiệm của bất phương trình
2022
0
3 6
x
là
A.
;2

. B.
;2

. C.
2;

. D.
2;

.
Câu 6: Tổng các nghiệm nguyên của bất phương trình
(3 )( 1) 0
x x
bằng
A. 1. B.
4
. C.
5
. D. 4.
Câu 7: Tập nghiệm của bất phương trình
1 1
x
là
A.
2;2
. B.
0;1
. C.
;2

. D.
0;2
.
Câu 8: Biết tập nghiệm của bất phương trình
2 1 2
x x
là đoạn
;
a b
. Khi đó, giá trị
b a
bằng
A.
4
3
. B.
8
3
. C. 4. D.
10
3
.
Câu 9: Tập nghiệm S của bất phương trình
2
2 1 0
x x
là
A.
1
; 1;
2
S

. B.
1
; 1;
2
S
 
.
C.
1
;1
2
S
. D.
1
;1
2
S
.
Câu 10: Tập nghiệm S của bất phương trình
2
4 4 0
x x
là
A.
\ 2
S
. B.
S
. C.
\ 2
S
. D.
2;S

.
Câu 11: Tam thức
2
–2 2 – 4
f x x m x m
âm với mọi
x
khi:
A.
14
m
hoặc
2
m
. B.
14 2
m
.
C.
2 14
m
. D.
14 2
m
.
Câu 12: Bất phương trình
2
0
x mx m
có nghiệm đúng với mọi
x
khi và chỉ khi:
Trang 3/13
A.
4
m
hoặc
0
m
. B.
4 0
m
.
C.
4
m
hoặc
0
m
. D.
4 0
m
.
Câu 13: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình
2
3 2 2 1 4 0
x m x m
vô nghiệm?
A. Vô số. B. 2. C. 3. D. 4.
Câu 14: Cho bất phương trình
2
2 1 1 0
f x mx m x m
(m là tham số). Gọi S là tập tất cả
các giá trị của m để bất phương trình có nghiệm. Khi đó, tập S là
A.
\ 0
S
. B.
1
;
8
S

. C.
1
;0 ;
8
S

. D.
0
S
.
Câu 15: Tìm tất cả các giá trị thực của tham số m để phương trình
2
( 1) 2 0
x m x m
có hai
nghiệm phân biệt
1 2
,
x x
khác 0 thỏa mãn
1 2
1 1
3
x x
.
A.
7
; 2; 1 7;
2
m
 
. B.
11
; 2 2;
10
m

.
C.
; 2 2; 1
m

. D.
7;m

.
Câu 16: Cung có số đo
70
bằng bao nhiêu rađian (làm tròn đến hàng phần nghìn)?
A. 2,443 rad. B. 1,222 rad. C. 2,943 rad. D. 1,412 rad.
Câu 17: Cung có số đo
5
rad
6
bằng bao nhiêu độ, phút, giây?
A.
47 44'47''
. B.
37 33'37 ''
. C.
150
. D.
30
.
Câu 18: Trên đường tròn lượng giác, cho điểm
3 1
;
2 2
M
. Khi đó, số đo cung
AM
(A là gốc
của đường tròn lược giác) bằng
A.
2
3
k
( ).
k
B.
2
3
k
( ).
k
C.
2
6
k
( ).
k
D.
2
6
k
( ).
k
Câu 19: Trên đường tròn lượng giác gốc
A
, cung lượng giác nào có các điểm biểu diễn tạo thành
tam giác đều?
A.
2
3
k
. B.
k
. C.
2
k
. D.
3
k
.
Câu 20: Trên đường tròn lượng giác gốc
A
, cung lượng giác nào có các điểm biểu diễn tạo thành
hình vuông
A.
2
k
. B.
k
. C.
2
3
k
. D.
3
k
.
Trang 4/13
Câu 21: Trên đường tròn lượng giác gốc
0;1
A
, có bao nhiêu điểm cuối
M
biểu diễn cung
AM
thỏa mãn sđ
2
3
AM k
,
k
?
A.
2
. B.
4
. C.
6
. D.
1
.
Câu 22: Có bao nhiêu điểm biễu diễn cung lượng giác có số đo ,
3 2
k
k
trên đường tròn
lượng giác gốc
1;0
A
.
A.
2
. B.
1
. C.
4
. D.
6
.
Câu 23: Hai góc lượng giác nào sau đây được biểu diễn bởi cùng một điểm trên đường tròn lượng
giác?
A.
6
và
5
6
. B.
3
và
3
. C.
2
và
5
2
. D.
0
và
3
.
Câu 24: Trên đường tròn lượng giác có điểm gốc là
A
, cho tam giác
OMB
và tam giác
ONB
là
các tam giác đều. Cung
có mút đầu là
A
và mút cuối trùng với
,
B M
hoặc
N
(
1;0 , 0;1
A B
)
. Số đo của cung
là
A.
6 3
k
. B.
2
2 3
k
. C.
2 3
k
. D.
2
6 3
k
.
Câu 25: Cho góc lượng giác
2
2
k
. Tìm
k
để
10 11 .
A.
4.
k
B.
5.
k
C.
6.
k
D.
7.
k
Câu 26: Một chiếc đồng hồ, có kim chỉ giờ
OG
chỉ số
9
và kim phút
OP
chỉ số
12
. Số đo của góc
lượng giác
,
OG OP
là
A. 2 ,
2
k k
. B.
0 0
270 360 , .
k k
C.
0 0
270 360 ,k k
. D.
9
2 ,
10
k k
.
Câu 27: Cho 0
2
. Khẳng định nào sau đây đúng?
A.
tan 0; cot 0
. B.
tan 0; cot 0
.
C.
tan 0; cot 0
. D.
tan 0; cot 0
.
Câu 28: Cho
3
2
. Khẳng định nào sau đây đúng?
A.
3
tan 0.
2
B.
3
tan 0.
2
C.
3
tan 0.
2
D.
3
tan 0.
2
Trang 5/13
Câu 29: Với mọi số thực
, ta có
9
sin
2
bằng
A.
sin
. B.
cos
. C.
sin
. D.
cos
.
Câu 30: Cho góc
thỏa mãn
12
sin
13
và
2
. Khi đó, giá trị
cos
bằng
A.
1
.
13
B.
5
.
13
C.
5
.
13
D.
1
.
13
Câu 31: Cho góc
thỏa mãn
4
tan
3
và
3
2
2
. Khi đó, giá trị
sin
bằng
A.
3
.
5
B.
3
.
5
C.
4
.
5
D.
4
.
5
Câu 32: Cho
3
sin
5
và
0 0
90 180
. Giá trị của biểu thức
cot 2tan
tan 3cot
E
là:
A.
2
57
. B.
2
57
. C.
4
57
. D.
4
57
.
Câu 33: Khẳng định nào sai trong các khẳng định sau?
A.
2
1 cos2
sin .
2
x
x
B.
2
1 cos 2
cos .
2
x
x
C.
sin 2sin cos .
2 2
x x
x D.
3 3
cos3 cos sin .
x x x
Câu 34: Khẳng định nào đúng trong các khẳng định sau?
A.
1
sin .sin cos cos .
2
a b a b a b
B.
sin sin 2sin .cos .
2 2
a b a b
a b
C.
2 tan
tan 2 .
1 tan
a
a
a
D.
2 2
cos2 sin cos .
a a a
Câu 35: Đơn giản biểu thức A cos sin cos sin
2 2 2 2
, ta có:
A.
2sin
A a
. B.
2cos
A a
. C.
sin – cos
A a a
. D.
0
A
.
Câu 36: Cho tam giác ABC. Hãy tìm mệnh đề sai
A.
sin cos
2 2
A C B
. B.
cos sin
2 2
A C B
. C.
sin
sin
A B C
. D.
cos cos
A B C
.
Câu 37: Cho biết
1
cot
2
x
. Giá trị biểu thức
2 2
2
sin sin .cos cos
A
x x x x
bằng
A. 6. B. 8. C. 10. D. 12.
Câu 38: Với mọi
, biểu thức:
9
cos + cos ... cos
5 5
A
nhận giá trị bằng:
Trang 6/13
A.
–10
. B.
10
. C.
0
. D.
5
.
Câu 39: Rút gọn
4
cos
4
cos
.
M x x
A.
n .
2
si
M
x
B.
sin .
2M
x
C.
s .
2
co
M
x
D.
cos .
2M
x
Câu 40: Rút gọn biểu thức
2 2
cos cos .
4 4
M
A.
sin 2 .
M
B.
cos 2 .
M
C.
cos 2 .
M
D.
sin 2 .
M
Câu 41: Rút gọn biểu thức
5 5
sin .cos sin .cos
A
.
A.
1
sin 2 .
2
B.
1
sin 4 .
2
C.
3
sin 4 .
4
D.
1
sin 4 .
4
Câu 42: Cho góc
thỏa mãn
3
cos
4
và
3
2
2
. Tính
cos .
3
P
A.
3 21
.
8
P
B.
3 21
.
8
P
C.
3 3 7
.
8
P
D.
3 3 7
.
8
P
Câu 43: Cho góc
thỏa mãn
4
cos
5
và
3
2
. Tính
tan
4
P
.
A.
1
.
7
P
B.
1
.
7
P
C.
7.
P
D.
7.
P
Câu 44: Giá trị lớn nhất
M
và nhỏ nhất
m
của biểu thức
3sin 2
P x
lần lượt là
A.
1, 5.
M m
B.
3, 1.
M m
C.
2, 2.
M m
D.
0, 2.
M m
Câu 45: Giá trị lớn nhất
M
và nhỏ nhất
m
của biểu thức
2 2
sin 2cos
P x x
lần lượt là
A.
3, 0.
M m
B.
2, 0.
M m
C.
2, 1.
M m
D.
3, 1.
M m
Câu 46: Cho tam giác ABC có
AB c
,
BC a
,
AC b
và R là bán kính đường tròn ngoại tiếp
tam giác ABC. Đẳng thức nào sau đây là đúng?
A.
sin sin sin
a b c
R
A B C
. B.
2
sin sin sin
a b c
R
A B C
.
C.
1
sin sin sin 2
a b c
A B C R
. D.
1
sin sin sin
a b c
A B C R
.
Câu 47: Cho tam giác ABC có
AB c
,
AC b
và
BC a
. Trung tuyến AM có độ dài là
A.
2 2 2
AM b c a
. B.
2 2 2
1
2 2
2
AM b c a
.
C.
2 2 2
3 2 2
AM a b c
. D.
2 2 2
2 2
AM b c a
.
Câu 48: Cho tam giác ABC có AB = 5, AC = 8 và
0
60 .
BAC
Khi đó, bán kính đường tròn nội tiếp
tam giác ABC bằng
A.
1.
B.
2.
C.
3.
D.
2 3.
Trang 7/13
Câu 49: Cho tam giác ABC có cạnh 6,b
8c
và góc
0
60A . Khi đó, độ dài cạnh a bằng
A. 2 13. B.
3 12.
C. 2 37. D. 20.
Câu 50: Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một
góc
0
60 . Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h. Sau 2
giờ, hai tàu cách nhau bao nhiêu km?
A. 13 km. B. 15 13 km. C. 20 13 km. D. 15 km.
Câu 51: Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội –
Huế), người ta cắm hai cọc AM và BN cao 1.5 mét so với mặt đất. Hai cọc này song song
và cách nhau 10 mét và thẳng hàng so với tim cột cờ (hình vẽ minh họa). Đặt giác kế tại
đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là
0
51 40
và
0
45 39
so với đường song song với mặt đất. Khi đó, chiều cao của cột cờ (làm tròn 0.01 mét)
bằng
A. 54.33 m. B. 56.88 m. C. 55.01 m. D. 32MN
54.63 m.
Câu 52: Để đo khoảng cách từ một vị trí N trên bờ sông đến một gốc cây tại A trên cù lao giữa
sông, người ta chọn một điểm M cùng ở trên bờ với N. Biết ta đo được m,
30AMN
,
42ANM
. Khoảng cách từ N đến gốc cây A bằng
A. 14,82AN
m. B. 15,82AN
m. C. 16,82AN
m. D. 17,82AN
m.
Câu 53: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) có phương trình
1 3
( ).
2 5
x t
t
y t
Vectơ nào sau đây là vectơ chỉ phương của đường thẳng (d)?
A.
1
(3; 5)u
. B.
2
(1; 2)u
. C.
3
(3; 2)u
. D.
4
(1; 5)u
.
Câu 54: Đường thẳng đi qua 2 điểm A(3; −1) và B(1; 5) có phương trình tổng quát là
Trang 8/13
A.
3 10 0.
x y
B.
3 6 0.
x y
C.
3 8 0.
x y
D.
3 6 0.
x y
Câu 55: Phương trình của đường thẳng đi qua 2 điểm A(0; −5) và B(3; 0) là
A.
1.
5 3
x y
B.
1.
5 3
x y
C.
1.
3 5
x y
D.
1.
5 3
x y
Câu 56: Trong mặt phẳng tọa độ Oxy, cho điểm
(7;4)
A và đường thẳng
:3 4 8 0
x y
. Khi đó,
khoảng cách từ điểm A đến đường thẳng
bằng
A.
13
.
5
B.
7
.
5
C.
3
.
5
D.
3
.
2
Câu 57: Tọa độ giao điểm của đường thẳng
15 2 10 0
x y
và trục tung là
A.
2
;5
3
. B. (0; −5). C. (0; 5). D. (−5; 0).
Câu 58: Tọa độ giao điểm của đường thẳng
0
: 4 3 26x y
và đường thẳng
3 4 7 0
: x yd
là
A. (2;
−6).
B. (5; 2). C. (
−2; 5).
D. (5;
−2).
Câu 59: Tọa độ giao điểm của đường thẳng
1
3 4
: ( )
2 5
x t
t
y t
và
2
1 4 '
: ( )
7 5 '
x t
t
y t
là
A. (−3; 2). B. (1; 7). C. (1; −3). D. (5; 1).
Câu 60: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng
1
: 2 1 0
x y
và
1
: 3 6 10 =0
x y
. Khẳng định nào sau đây đúng?
A.
1
song song với
2
. B.
1
cắt
2
nhưng
không vuông góc.
C.
1
và
2
trùng nhau. D.
1
vuông góc với
2
.
Câu 61: Trong mặt phẳng tọa độ Oxy, cho đường thẳng
12 5
: ( )
3 6
x t
t
y t
. Điểm nào sau đây
thuộc đường thẳng
A. M(7; 5). B. N(20; 9). C. P(12; 0) D. Q(13; 33).
Câu 62: Trong mặt phẳng tọa độ Oxy, cho đường thẳng
:
3 5
( )
1 4
x t
t
y t
. Khi đó, phương trình
tổng quát của đường thẳng
là
A.
4 5 17 0
x y
. B.
4 5 17 0
x y
. C.
4 5 17 0
x y
. D.
4 5 17 0
x y
.
Trang 9/13
Câu 63: Cho điểm
(0;1)
A và đường thẳng
1 2
:
x t
d
y t
. Tìm một điểm
M
trên
d
và cách
A
một
khoảng bằng
10
.
A.
2;3 .
B.
3;2 .
C.
3;2 .
D.
3; 2 .
Câu 64: Tính góc tạo bởi giữa hai đường thẳng
1
: 2 10 0
d x y
và
2
: 3 9 0.
d x y
A.
o
30 .
B.
o
45 .
C.
o
60 .
D.
o
135 .
Câu 65: Cho đường thẳng
1
0
:10 5 1d x y
và
2
2
:
1
x t
d
y t
. Tính cosin của góc tạo bởi giữa hai
đường thẳng đã cho.
A.
3 10
10
. B.
3
5
. C.
10
10
. D.
3
10
.
Câu 66: Cho hai đường thẳng
1
4 12 0
:3x yd
và
2
2
:
1 2
y
d
x at
t
. Tìm các giá trị của tham số
a
để
1
d
và
2
d
hợp với nhau một góc bằng
0
45 .
A.
2
7
a
hoặc
14.
a
B.
7
2
a
.
C.
5
a
hoặc
14.
a
D.
2
7
a
hoặc
5.
a
Câu 67: Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
1;1
A
,
4; 3
B
và đường thẳng
: 2 1 0
d x y
. Tìm điểm
M
thuộc
d
có tọa độ nguyên và thỏa mãn khoảng cách từ
M
đến đường thẳng
AB
bằng
6
.
A.
3;7 .
M
B.
7;3 .
M
C.
43; 27 .
M
D.
.
27
11
3;M
Câu 68: Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
3;0
A
và
0; 4
B
. Tìm điểm
M
thuộc trục tung sao cho diện tích tam giác
MAB
bằng
6.
A.
0;0
.
0; 8
M
M
B.
0; 8 .
M
C.
6;0 .
M
D.
0;0
.
0;6
M
M
Câu 69: Cho ba điểm di động
1 2 ;4 , 2 ;1 , 3 1;0 .
A m m B m m C m
Gọi
G
là trọng tâm
ABC
thì
G
nằm trên đường thẳng nào sau đây:
A.
1
.
3
y x
B.
1.
y x
C.
1
.
3
y x
D.
1.
y x
Trang 10/13
Câu 70: Cho đường thẳng
– 2 –1 2 –1 0.
: m x m y m
Với giá trị nào của
m
thì khoảng cách
từ điểm
2;3
đến
lớn nhất?
A.
11
.
5
m B.
11
.
5
m C.
11.
m
D.
11.
m
Câu 71: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):
2 2
( 1) ( 3) 3
x y
. Đường tròn (C)
có tâm I và bán kính R lần lượt là
A.
( 1;3), 3.
I R
B.
(1; 3), 3.
I R
C.
( 1;3), 3.
I R
D.
(1; 3), 3.
I R
Câu 72: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):
2 2
4 6 3 0
x y x y
. Đường tròn
(C) có bán kính bằng
A.
10
. B. 4. C. 55. D. 16.
Câu 73: Trong mặt phẳng tọa độ Oxy, đường tròn tâm
1;2
I
, bán kính
3
R
có phương trình là
A.
2 2
2 4 4 0.
x y x y
B.
2 2
2 4 4 0.
x y x y
C.
2 2
2 4 4 0.
x y x y
D.
2 2
2 4 4 0.
x y x y
Câu 74: Trong mặt phẳng tọa độ Oxy, cho hai điểm
3; 1 , 1; 5
A B
. Khi đó, đường tròn đường
kính AB có phương trình là
A.
2 2
2 3 5.
x y
B.
2 2
1 2 17.
x y
C.
2 2
2 3 5.
x y D.
2 2
2 3 5.
x y
Câu 75: Trong mặt phẳng tọa độ Oxy, cho phương trình
2 2
2 4 2 6 0 1
x y mx m y m
. Điều kiện của tham số
m
để
1
là phương
trình đường tròn là
A.
.
m
B.

;1 2; .
m
C.

;1 2; .
m
D.
 
1
; 2; .
3
m
Câu 76: Trong mặt phẳng tọa độ Oxy, cho phương trình
2 2
2 4( 2) 6
x y mx m y m
(1). Có
bao nhiêu giá trị nguyên của tham số m để (1) không phải là phương trình đường tròn?
A. 0. B. 1. C. 2. D. Vô số.
Câu 77: Đường tròn
2 2
: 12 14 4 0
C x y x y
có dạng tổng quát là:
A.
2 2
: 6 7 9.
C x y B.
2 2
: 6 7 81.
C x y
C.
2 2
: 6 7 89.
C x y D.
2 2
: 6 7 89.
C x y
Câu 78: Cho phương trình
2 2
2 2 0 1
x y ax by c
. Điều kiện để
1
là phương trình
đường tròn là:
Trang 11/13
A.
2 2
a b c
. B.
2 2
a b c
. C.
2 2
a b c
. D.
2 2
a b c
.
Câu 79: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
A.
2 2
4 10 6 2 0.
x y x y
B.
2 2
2 8 20 0.
x y x y
C.
2 2
2 4 8 1 0.
x y x y
D.
2 2
4 6 12 0.
x y x y
Câu 80: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
A.
2 2
2 4 9 0.
x y x y
B.
2 2
6 4 13 0.
x y x y
C.
2 2
2 2 8 4 6 0.
x y x y
D.
2 2
5 4 4 1 0.
x y x y
Câu 81: Cho đường tròn
2 2
: 1 2 8
C x y
. Viết phương trình tiếp tuyến
d
của
C
tại
điểm
3; 4
A
.
A.
: 1 0.
d x y B.
: 2 11 0.
d x y C.
: 7 0.
d x y D.
: 7 0.
d x y
Câu 82: Phương trình tiếp tuyến
d
của đường tròn
2 2
: 3 0
C x y x y
tại điểm
1; 1
N
là:
A.
: 3 2 0.
d x y B.
: 3 4 0.
d x y C.
: 3 4 0.
d x y D.
: 3 2 0.
d x y
Câu 83: Viết phương trình tiếp tuyến của đường tròn
2 2
2 4 25
: x yC , biết tiếp tuyến
vuông góc với đường thẳng
3 4 5 0
:
x yd .
A.
4 – 3 5 0
x y hoặc
4 – 3 – 45 0.
x y B.
4 3 5 0
x y hoặc
4 3 3 0.
x y
C.
4 3 29 0.
x y D.
4 3 29 0
x y hoặc
4 3 – 21 0.
x y
Câu 84: Cho đường tròn
2 2
( ) :( 1) ( 3) 4
C x y
và đường thẳng
:3 4 5 0
d x y
. Phương trình
của đường thẳng
d
song song với đường thẳng
d
và chắn trên
( )
C
một dây cung có độ
dài lớn nhất là
A.
4 3 13 0
x y
. B.
3 4 25 0
x y
. C.
3 4 15 0
x y
. D.
4 3 20 0
x y
.
Phần 2. Tự luận
Câu 1: Giải các bất phương trình sau:
a)
2
2 – 5 2 0
x x
; b)
2
3 – 4 4 0
x x
;
c)
2
16 40 25 0
x x
. d)
2 2
– 3 – 2 – 5 6 0
x x x x
;
e)
2
3
0
1 2
x x
x
; f)
2
2 5 1
6 7 3
x
x x x
.
Câu 2: Giải các bất phương trình sau:
a)
2 2
3 2 3 2
x x x x
; b)
2
4 12 5
x x x
;
Trang 12/13
c)
2
2 1 1
x x
; d)
2 1 2 3
x x
;
e)
2
3 10 2
x x x
; f)
3 3 2 3
x x
;
Câu 3: Tìm m để các phương trình sau thỏa điều kiện đã cho:
a)
2
( 1) 2( 1) 3 3 0
m x m x m
vô nghiệm;
b)
2
2( 1) 9 5 0
x m x m
có hai nghiệm âm phân biệt;
c)
2
( 2) 2 3 0
m x mx m
có hai nghiệm dương phân biệt;
d)
2
( 1) 2( 3) 3 0
m x m x m
có đúng một nghiệm âm.
Câu 4: Tính giá trị lượng giác còn lại của
biết:
a)
5
cos
13
và
3
2
2
; b)
sin 0,8
và
2
;
c)
15
tan
8
và
3
2
; d)
5
cot
3
và
3
2
2
.
Câu 5: Cho góc
thỏa mãn
4
sin
5
và
0;
2
. Tính
cos
,
tan
,
cot
,
sin 2
,
cos 2
,
sin
4
.
Câu 6: Cho
1
cot
2
x
. Tính giá trị của biểu thức
2
1
1 cos
A
x
.
Câu 7: Cho
3
sin
5
x
và
3
2
x
. Tính giá trị của biểu thức
1 tan
1 tan
x
A
x
.
Câu 8: Cho
cot 2
a
. Tính giá trị của biểu thức
2
2 2
1 sin
sin 3cos
a
A
a a
;
Câu 9: Chứng minh các đẳng thức sau:
a)
2
2
2
1 sin
1 2tan
1 sin
x
x
x
; b)
2
2 2
1 cos 1
tan .cot
1 sin cos
x
x x
x x
;
c)
sin 1 cos 2
1 cos sin sin
x x
x x x
; d)
cos 1
tan
1 sin cos
x
x
x x
;
e)
2
2
sin sin cos
sin cos
sin cos 1 tan
x x x
x x
x x x
; f)
2
1 cos
tan sin 2cos
sin
x
x x x
x
.
Câu 10: Rút gọn các biểu thức sau:
a)
sin 2
1 cos2
a
A
a
; b)
2
2cos 1
sin cos
a
B
a a
;
c)
cos2 cos4
sin 4 sin 2
a a
C
a a
; d)
sin sin3 sin5
cos cos3 cos5
a a a
D
a a a
;
e)
3 4cos 2 cos 4
3 4cos 2 cos 4
a a
E
a a
; f)
sin .cos tan .tan(5 )
2 2
F x x x x
Câu 11: Viết phương trình đường thẳng
trong mỗi trường hợp sau:
Trang 13/13
a)
đi qua điểm M(2; 4) và có hệ số góc k = 2;
b)
đi qua hai điểm A(–3; 0) và B(0; 5).
Câu 12: Lập phương trình đường thẳng
đi qua M(2; 3) và:
a)
song song với d:
13
3 5
x t
y t
. b)
vuông góc với trục tung Oy.
Câu 13: Cho đường thẳng
1
:3 4 1 0
d x y
và
2
15 12
:
1 5
x t
d
y t
.
Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho.
Câu 14: Tính khoảng cách giữa hai đường thẳng song song
1
: 6 – 8 3 0
x y
và
2
: 3 – 4 – 6 0
x y
Câu 15: Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai đường thẳng
1
:3 2 6 0
x y
và
2
: 3 2 3 0
x y
. Tìm điểm
M
thuộc trục hoành sao cho
M
cách đều hai đường thẳng
đã cho.
Câu 16: Xác định tâm và bán kính của các đường tròn có phương trình:
a)
2 2
( 5) ( 3) 1
x y
; b)
2
2
3
81
4
x y
;
c)
2 2
4 4 0
x y x y
; d)
2 2
6 0
x y y
;
Câu 17: Lập phương trình đường tròn trong các trường hợp sau:
a) Tâm P(1; - 3) và đi qua điểm Q(- 2; 4);
b) Đường kính AB với A(2; 3), B(- 1; -5);
c) Tâm I(4; 1) và tiếp xúc với đường thẳng
: 2 3 0
d x y
;
d) Đi qua ba điểm I(1; 2), J(- 5; 0) và K(- 2; 3).
Câu 18: Cho đường tròn (C):
2 2
6 2 6 0
x y x y
. Lập phương trình tiếp tuyến (d) của (C)
biết:
a) (d) tiếp xúc với (C) tại M(3; 1); b) (d) // (d’): 5x + 12y – 2021 = 0;
c) (d) vuông góc (d’): x + 2y = 0; d) (d) đi qua điểm N(1; 3).
---Hết---
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TRƯỜNG TRUNG HỌC VINSCHOOL **********
HƯỚNG DẪN ÔN TẬP HỌC KÌ II NĂM HỌC 2021 - 2022
Môn Toán - Lớp 10 - Hệ Chuẩn Vinschool I/ Lý thuyết Chủ đề Nội dung
1. Dấu của nhị thức - Xét dấu của nhị thức bậc nhất. bậc nhất
- Giải bất phương trình tích, thương.
2. Dấu tam thức bậc - Giải hệ bất phương trình một ẩn. hai
- Giải bất phương trình căn; bất phương trình chứa dấu giá trị tuyệt đối.
- Biện luận phương trình, bất phương trình bậc hai một ẩn.
- Tìm tập xác định của hàm số.
3. Giá trị lượng giác - Chuyển đổi đơn vị giữa độ và radian. của một cung - Tính chiều dài cung. - Biểu diễn cung.
- Tính giá trị lượng giác của một cung lượng giác.
4. Công thức lượng - Rút gọn biểu thức lượng giác. giác
- Chứng minh đẳng thức, bất đẳng thức lượng giác.
5. Hệ thức lượng - Giải tam giác. trong tam giác
- Tính diện tích tam giác.
- Ứng dụng vào thực tế. 6. Phương
trình - Viết phương trình đường thẳng (tổng quát, tham số, chính tắc, đường thẳng theo đoạn chắn).
- Xác định vị trí tương đối giữa hai đường thẳng.
- Tính khoảng cách từ một điểm đến một đường thẳng.
- Tính góc giữa hai đường thẳng. 7. Phương
trình - Viết phương trình đường tròn. đường tròn
- Viết phương trình tiếp tuyến của đường tròn. II/ Bài tập Phần 1. Trắc nghiệm
Câu 1: Cho biểu thức f x  2x  4. Tìm tất cả các giá trị của x để f x  0 . 1 A.  x 2; . B. x  ; .   C. x ;2. D. x 2;. 2  6x  3
Câu 2: Tập nghiệm của hệ bất phương trình  2x 1 là 2 Trang 1/13 5  5  5  5 A.     ;    . B.  ;   . C.  ;    . D. ;   . 2  2     2   2 
Câu 3: Điều kiện xác định của bất phương trình 2  x  2x  3  2x 1 là  1 1 A.   x   . B. x ;2. C. x   ;   . D. x  ; 2 . 2     2   
Câu 4: Có bao nhiêu số nguyên nhỏ hơn 10 thuộc tập nghiệm của bất phương trình 1 1  ? 2x  3 5  x A. Vô số. B. 4. C. 5. D. 6. 2022
Câu 5: Tập nghiệm của bất phương trình  0 là 3x  6 A.  ;  2. B.  ;  2 . C. 2; . D. 2; .
Câu 6: Tổng các nghiệm nguyên của bất phương trình (3  x)(x 1)  0 bằng A. 1. B. 4 . C. 5  . D. 4.
Câu 7: Tập nghiệm của bất phương trình x 1  1 là 2;2 0;  A. . B. 1 . C.  ;  2 . D. 0;2 .
Câu 8: Biết tập nghiệm của bất phương trình 2x 1  x  2 là đoạn a;b. Khi đó, giá trị b  a bằng 4 8 10 A. . B. . C. 4. D. . 3 3 3
Câu 9: Tập nghiệm S của bất phương trình 2 2x  x 1  0 là  1  1 A.   S   ;    1;   . B. S   ;   1;  .  2  2     1  1 C.   S   ;1   . D. S   ;1 .  2   2   
Câu 10: Tập nghiệm S của bất phương trình 2 x  4x  4  0 là A. S   \  2 . B. S   . C. S   \  2 . D. S  2; . Câu 11: Tam thức f  x 2
 –2x  m  2 x  m – 4 âm với mọi x khi:
A. m  14 hoặc m  2 . B. 14  m  2 . C. 2   m  14 . D. 14  m  2 .
Câu 12: Bất phương trình 2
x  mx  m  0 có nghiệm đúng với mọi x khi và chỉ khi: Trang 2/13
A. m  4 hoặc m  0 . B. 4  m  0 .
C. m  4 hoặc m  0 . D. 4  m  0 .
Câu 13: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình 2 3x  22m   1 x  m  4  0 vô nghiệm? A. Vô số. B. 2. C. 3. D. 4.
Câu 14: Cho bất phương trình f  x 2  mx  2m  
1 x  m 1  0 (m là tham số). Gọi S là tập tất cả
các giá trị của m để bất phương trình có nghiệm. Khi đó, tập S là  1 A.    S   \  0 . B. S   ;    . C. S    1 ;0  ;    . D. S    0 .  8   8 
Câu 15: Tìm tất cả các giá trị thực của tham số m để phương trình 2
x  (m 1)x  m  2  0 có hai 1 1
nghiệm phân biệt x , x khác 0 thỏa mãn   3. 1 2 x x 1 2  7 A.    m   ;    2  ;  1 7;    . B. m   11 ; 2  2  ;   .  2   10  C. m  ;  2  2  ;  1 . D. m 7; .
Câu 16: Cung có số đo 70 bằng bao nhiêu rađian (làm tròn đến hàng phần nghìn)? A. 2,443 rad. B. 1,222 rad. C. 2,943 rad. D. 1,412 rad. 5
Câu 17: Cung có số đo rad bằng bao nhiêu độ, phút, giây? 6 A. 4744'47 ' . B. 37 3  3'37 ' . C. 150 . D. 30 .  3 1  
Câu 18: Trên đường tròn lượng giác, cho điểm M  ;   
. Khi đó, số đo cung AM (A là gốc 2 2   
của đường tròn lược giác) bằng    
A.  k2 (k  ). B.   k2 (k ). C.  k2 (k ). D.   k2 (k ). 3 3 6 6
Câu 19: Trên đường tròn lượng giác gốc A , cung lượng giác nào có các điểm biểu diễn tạo thành tam giác đều? k2 k k A. . B. k . C. . D. . 3 2 3
Câu 20: Trên đường tròn lượng giác gốc A , cung lượng giác nào có các điểm biểu diễn tạo thành hình vuông k k2 k A. . B. k . C. . D. . 2 3 3 Trang 3/13 
Câu 21: Trên đường tròn lượng giác gốc A0; 
1 , có bao nhiêu điểm cuối M biểu diễn cung AM  
thỏa mãn sđ AM   k2 , k   ? 3 A. 2 . B. 4 . C. 6 . D. 1.  k
Câu 22: Có bao nhiêu điểm biễu diễn cung lượng giác có số đo 
, k  trên đường tròn 3 2
lượng giác gốc A1;0. A. 2 . B. 1. C. 4 . D. 6 .
Câu 23: Hai góc lượng giác nào sau đây được biểu diễn bởi cùng một điểm trên đường tròn lượng giác?  5    5 A. và . B. và  . C. và . D. 0 và 3 . 6 6 3 3 2 2
Câu 24: Trên đường tròn lượng giác có điểm gốc là A , cho tam giác OMB và tam giác ONB là
các tam giác đều. Cung  có mút đầu là A và mút cuối trùng với B, M hoặc N ( A1;0, B 0; 
1 ) . Số đo của cung  là    2    2 A.     k . B.    k . C.    k . D.    k . 6 3 2 3 2 3 6 3 
Câu 25: Cho góc lượng giác    k2 . Tìm k để 10    11. 2 A. k  4. B. k  5. C. k  6. D. k  7.
Câu 26: Một chiếc đồng hồ, có kim chỉ giờ OG chỉ số 9 và kim phút OP chỉ số12. Số đo của góc
lượng giác OG,OP là  A.  k2 , k  . B. 0 0  270  k360 , k  .  2 9 C. 0 0 270  k360 , k   . D.  k2 , k  . 10  Câu 27: Cho 0   
. Khẳng định nào sau đây đúng? 2
A. tan  0; cot  0 .
B. tan  0; cot  0 .
C. tan  0; cot  0 .
D. tan  0; cot  0 . 3 Câu 28: Cho    
. Khẳng định nào sau đây đúng? 2  3  3  3  3 A.     tan   0.   B. tan   0.   C. tan   0.   D. tan   0.    2   2   2   2  Trang 4/13  9
Câu 29: Với mọi số thực  , ta có  sin    bằng  2  A. sin . B. cos . C. sin . D.  cos . 12 
Câu 30: Cho góc  thỏa mãn sin 
và     . Khi đó, giá trị cos bằng 13 2 1 5 5 1 A. . B. . C.  . D.  . 13 13 13 13 4 3
Câu 31: Cho góc  thỏa mãn tan   và
   2 . Khi đó, giá trị sin bằng 3 2 3 3 4 4 A.  . B. . C.  . D. . 5 5 5 5 3 cot  2 tan Câu 32: Cho sin  và 0 0
90    180 . Giá trị của biểu thức E  là: 5 tan  3cot 2 2 4 4 A. . B.  . C. . D.  . 57 57 57 57
Câu 33: Khẳng định nào sai trong các khẳng định sau? 1 cos 2x 1 cos 2x A. 2 sin x  . B. 2 cos x  . 2 2 x x C. sin x  2sin cos . D. 3 3 cos3x  cos x  sin . x 2 2
Câu 34: Khẳng định nào đúng trong các khẳng định sau? 1 a  b a  b A. sin . a sin b   cos 
a bcosa b. a  b  2  B. sin sin 2sin .cos . 2 2 2 tan a C. tan 2a  . D. 2 2 cos 2a  sin a  cos . a 1 tan a           
Câu 35: Đơn giản biểu thức  A  cos   sin   cos   sin          , ta có:  2   2   2   2  A. A  2sin a . B. A  2cos a .
C. A  sin a – cos a . D. A  0 .
Câu 36: Cho tam giác ABC. Hãy tìm mệnh đề sai A  C B A  C B A. sin  cos . B. cos
 sin . C. sin  A  B  sin C . D. cos A  B  cosC . 2 2 2 2 1 2
Câu 37: Cho biết cot x  . Giá trị biểu thức A  bằng 2 2 2 sin x  sin . x cos x  cos x A. 6. B. 8. C. 10. D. 12.     9
Câu 38: Với mọi  , biểu thức:  A  cos + cos    ... cos       nhận giá trị bằng:  5   5  Trang 5/13 A. –10 . B. 10. C. 0 . D. 5 .      Câu 39: Rút gọn  M  cos x   cos x  .      4   4  A. M  2 sin . x B. M   2 sin . x C. M  2 cos . x D. M   2 cos . x     
Câu 40: Rút gọn biểu thức 2 2  M  cos   cos  .      4   4  A. M  sin 2. B. M  cos 2. C. M   cos 2. D. M   sin 2.
Câu 41: Rút gọn biểu thức 5 5
A  sin.cos   sin .cos . 1 1 3 1 A. sin 2. B.  sin 4. C. sin 4. D. sin 4. 2 2 4 4 3 3  
Câu 42: Cho góc  thỏa mãn  cos  và
   2 . Tính P  cos  .   4 2  3  3  21 3  21 3 3  7 3 3  7 A. P  . B. P  . C. P  . D. P  . 8 8 8 8 4 3  
Câu 43: Cho góc  thỏa mãn 
cos   và     . Tính P  tan     . 5 2  4  1 1 A. P   . B. P  . C. P  7. D. P  7. 7 7
Câu 44: Giá trị lớn nhất M và nhỏ nhất m của biểu thức P  3sin x  2 lần lượt là A. M 1, m  5  . B. M  3, m 1. C. M  2, m  2  . D. M  0, m  2  .
Câu 45: Giá trị lớn nhất M và nhỏ nhất m của biểu thức 2 2
P  sin x  2cos x lần lượt là A. M  3, m  0. B. M  2, m  0. C. M  2, m 1. D. M  3, m 1.
Câu 46: Cho tam giác ABC có AB  c , BC  a , AC  b và R là bán kính đường tròn ngoại tiếp
tam giác ABC. Đẳng thức nào sau đây là đúng? a b c a b c A.    R . B.    2R . sin A sin B sin C sin A sin B sin C a b c 1 a b c 1 C.    . D.    . sin A sin B sin C 2R sin A sin B sin C R
Câu 47: Cho tam giác ABC có AB  c , AC  b và BC  a . Trung tuyến AM có độ dài là 1 A. 2 2 2 AM  b  c a . B. 2 2 2 AM  2b  2c a . 2 C. 2 2 2 AM  3a  2b 2c . D. 2 2 2 AM  2b  2c a .
Câu 48: Cho tam giác ABC có AB = 5, AC = 8 và  0
BAC  60 . Khi đó, bán kính đường tròn nội tiếp tam giác ABC bằng A. 1. B. 2. C. 3. D. 2 3. Trang 6/13
Câu 49: Cho tam giác ABC có cạnh b  6, c  8 và góc  0
A  60 . Khi đó, độ dài cạnh a bằng A. 2 13. B. 3 12. C. 2 37. D. 20.
Câu 50: Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 0
60 . Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h. Sau 2
giờ, hai tàu cách nhau bao nhiêu km? A. 13 km. B. 15 13 km. C. 20 13 km. D. 15 km.
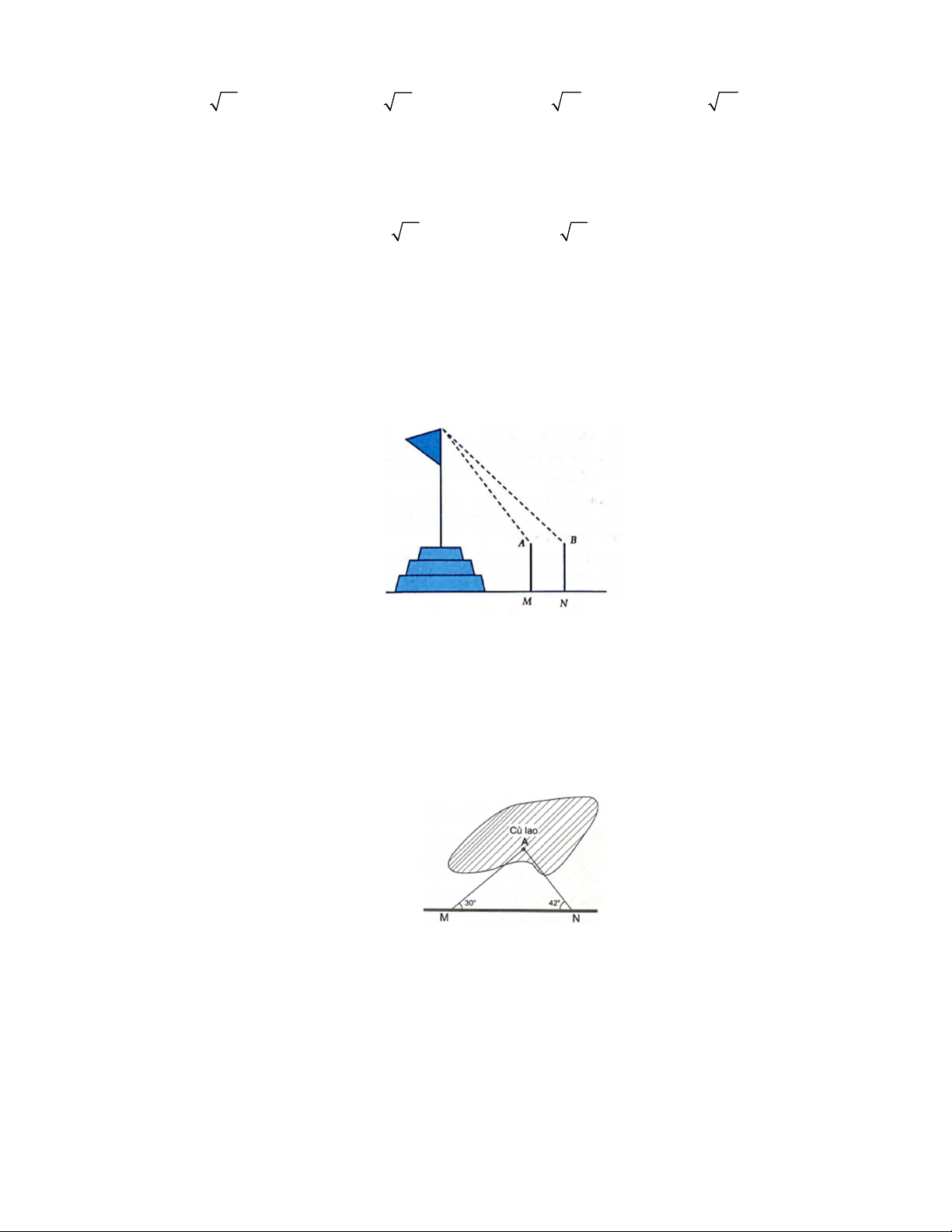
Câu 51: Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội –
Huế), người ta cắm hai cọc AM và BN cao 1.5 mét so với mặt đất. Hai cọc này song song
và cách nhau 10 mét và thẳng hàng so với tim cột cờ (hình vẽ minh họa). Đặt giác kế tại
đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 0 51 40 và 0 45 39
so với đường song song với mặt đất. Khi đó, chiều cao của cột cờ (làm tròn 0.01 mét) bằng A. 54.33 m. B. 56.88 m. C. 55.01 m. D. MN  32 54.63 m.
Câu 52: Để đo khoảng cách từ một vị trí N trên bờ sông đến một gốc cây tại A trên cù lao giữa
sông, người ta chọn một điểm M cùng ở trên bờ với N. Biết ta đo được m,  AMN  30, 
ANM  42 . Khoảng cách từ N đến gốc cây A bằng A. AN 14,82 m. B. AN 15,82 m. C. AN 16,82 m. D. AN 17,82 m. x  1 3t
Câu 53: Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) có phương trình  (t  ).  y  2   5t
Vectơ nào sau đây là vectơ chỉ phương của đường thẳng (d)?     A. u  (3; 5) . B. u  (1;2) . C. u  (3;2) . D. u  (1; 5  ) . 1 2 3 4
Câu 54: Đường thẳng đi qua 2 điểm A(3; −1) và B(1; 5) có phương trình tổng quát là Trang 7/13 A. 3x  y  10  0. B. 3x  y  6  0. C. 3x  y 8  0. D. x  3y  6  0.
Câu 55: Phương trình của đường thẳng đi qua 2 điểm A(0; −5) và B(3; 0) là x y x y x y x y A.  1. B.   1. C.  1. D.  1. 5 3 5 3 3 5 5 3
Câu 56: Trong mặt phẳng tọa độ Oxy, cho điểm (
A 7; 4) và đường thẳng  : 3x  4 y  8  0. Khi đó,
khoảng cách từ điểm A đến đường thẳng  bằng 13 7 3 3 A. . B. . C. . D. . 5 5 5 2
Câu 57: Tọa độ giao điểm của đường thẳng 15x  2y 10  0 và trục tung là  2 A.  ;5   . B. (0; −5). C. (0; 5). D. (−5; 0).  3 
Câu 58: Tọa độ giao điểm của đường thẳng  : 4x  3y  26  0 và đường thẳng d : 3x  4y  7  0 là A. (2; −6). B. (5; 2). C. (−2; 5). D. (5; −2). x  3   4t x  1 4t '
Câu 59: Tọa độ giao điểm của đường thẳng  :  (t  ) và  :  (t  ) là 1 y  2  5t 2  y  7  5t ' A. (−3; 2). B. (1; 7). C. (1; −3). D. (5; 1).
Câu 60: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng  : x  2 y 1  0 và  : 3  x  6y 10 =0 1 1
. Khẳng định nào sau đây đúng? A.  song song với  . B.  cắt  nhưng 1 2 1 2 không vuông góc. C.  và  trùng nhau. D.  vuông góc với 1 2 1  . 2 x  12  5t
Câu 61: Trong mặt phẳng tọa độ Oxy, cho đường thẳng  : 
(t  ) . Điểm nào sau đây  y  3  6t thuộc đường thẳng  A. M(7; 5). B. N(20; 9). C. P(12; 0) D. Q(13; 33). x  3  5t
Câu 62: Trong mặt phẳng tọa độ Oxy, cho đường thẳng  : 
(t  ) . Khi đó, phương trình  y  1 4t
tổng quát của đường thẳng  là A. 4x  5y 17  0 .
B. 4x  5y 17  0 . C. 4x  5y 17  0 . D. 4x  5y 17  0. Trang 8/13 x  1 2t Câu 63: Cho điểm (
A 0;1) và đường thẳng d : 
. Tìm một điểm M trên d và cách A một  y  t khoảng bằng 10 . A.  2;3. B. 3;2. C. 3;2. D. 3;2.
Câu 64: Tính góc tạo bởi giữa hai đường thẳng d : 2x  y 10  0 và d : x  3y  9  0. 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 135 . x  2  t
Câu 65: Cho đường thẳng d :10x  5y 1  0 và d :
. Tính cosin của góc tạo bởi giữa hai 1 2   y  1 t đường thẳng đã cho. 3 10 3 10 3 A. . B. . C. . D. . 10 5 10 10 x  2  at
Câu 66: Cho hai đường thẳng d : 3x  4y 12  0 và d :
. Tìm các giá trị của tham số a 1 2   y  1 2t
để d và d hợp với nhau một góc bằng 0 45 . 1 2 2 7
A. a  hoặc a  14. B. a  . 7 2 2
C. a  5 hoặc a  14. D. a  hoặc a  5. 7
Câu 67: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A1;  1 , B 4; 3   và đường thẳng
d : x  2 y 1  0 . Tìm điểm M thuộc d có tọa độ nguyên và thỏa mãn khoảng cách từ M
đến đường thẳng AB bằng 6 .  27 A.  M 3;7. B. M 7;3. C. M 43;27. D. M 3;  .    11 
Câu 68: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A3;0 và B0; 4   . Tìm điểm M
thuộc trục tung sao cho diện tích tam giác MAB bằng 6. M 0;0 M 0;0 A.  B. M 0; 8  . C. M 6;0. D.  . M    . 0; 8 M  0;6
Câu 69: Cho ba điểm di động A1 2 ; m 4m, B 2 ;
m 1 m,C 3m 1;0. Gọi G là trọng tâm ABC
thì G nằm trên đường thẳng nào sau đây: 1 1 A. y  x  . B. y  x 1. C. y  x  . D. y  x 1. 3 3 Trang 9/13
Câu 70: Cho đường thẳng  : m – 2 x  m – 
1 y  2m –1  0. Với giá trị nào của m thì khoảng cách
từ điểm 2;3 đến  lớn nhất? 11 11 A. m  . B. m   . C. m  11. D. m  11. 5 5
Câu 71: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): 2 2
(x 1)  ( y  3)  3 . Đường tròn (C)
có tâm I và bán kính R lần lượt là A. I ( 1  ;3), R  3. B. I (1; 3  ), R  3. C. I (1;3), R  3. D. I (1;3), R  3.
Câu 72: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): 2 2
x  y  4x  6y  3  0 . Đường tròn (C) có bán kính bằng A. 10 . B. 4. C. 55. D. 16.
Câu 73: Trong mặt phẳng tọa độ Oxy, đường tròn tâm I 1;2, bán kính R  3 có phương trình là A. 2 x  2 y 2x  4 y 4  0. B. 2 x  2 y 2x 4 y 4  0. C. 2 x  2 y 2x  4 y 4  0. D. 2 x  2 y 2x 4 y 4  0.
Câu 74: Trong mặt phẳng tọa độ Oxy, cho hai điểm A3;  1 , B 1; 
5 . Khi đó, đường tròn đường
kính AB có phương trình là
A. x  2 y 2 2 3  5.
B. x  2 y  2 1 2 17.
C. x  2 y  2 2 3  5.
D. x  2 y  2 2 3  5. Câu 75: Trong mặt phẳng tọa độ Oxy, cho phương trình 2 x  2
y 2mx  4m 2 y  6m  0  
1 . Điều kiện của tham số m để   1 là phương trình đường tròn là A. m  . B. m ;  1 2;.  1 C. m ;  1 2;. D. m 
 ; 2;  .  3
Câu 76: Trong mặt phẳng tọa độ Oxy, cho phương trình 2 2
x  y  2mx  4(m  2) y  m  6 (1). Có
bao nhiêu giá trị nguyên của tham số m để (1) không phải là phương trình đường tròn? A. 0. B. 1. C. 2. D. Vô số.
Câu 77: Đường tròn C 2 x  2 :
y 12x 14 y  4  0 có dạng tổng quát là:
A. C x  2 y  2 : 6 7  9.
B. C x  2 y  2 : 6 7  81.
C. C x  2 y 2 : 6 7  89.
D. C x  2 y 2 : 6 7  89. Câu 78: Cho phương trình 2 x  2
y 2ax 2by  c  0  
1 . Điều kiện để   1 là phương trình đường tròn là: Trang 10/13 A. 2  2 a b c . B. 2  2 a b c . C. 2  2 a b c . D. 2  2 a b c .
Câu 79: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 x  2 4 y 10x 6y 2  0. B. 2 x  2 y 2x 8y 20  0. C. 2 x  2 2 y 4x 8y 1 0. D. 2 x  2 y 4x 6y 12  0.
Câu 80: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 x  2 y 2x 4y  9  0. B. 2 x  2 y 6x  4 y 13  0. C. 2 x  2 2 2y 8x 4y 6  0. D. 2 x  2 5 4 y  x 4y 1 0.
Câu 81: Cho đường tròn C x  2 y  2 : 1
2  8 . Viết phương trình tiếp tuyến d của C tại điểm A3;4. A. d : x  y 1 0.
B. d : x 2y 11 0. C. d : x  y 7  0. D. d : x  y 7  0.
Câu 82: Phương trình tiếp tuyến d của đường tròn C 2 x  2 :
y 3x  y  0 tại điểm N 1;  1 là:
A. d : x 3y2  0. B. d : x 3y 4  0. C. d : x 3y 4  0. D. d : x 3y 2  0.
Câu 83: Viết phương trình tiếp tuyến của đường tròn C:x  2 y  2 2
4  25 , biết tiếp tuyến
vuông góc với đường thẳng d : 3x 4y 5  0 .
A. 4x – 3y 5  0 hoặc 4x – 3y – 45  0.
B. 4x 3y 5  0 hoặc 4x 3y 3  0. C. 4x 3y 29  0.
D. 4x 3y 29  0 hoặc 4x 3y – 21 0. Câu 84: Cho đường tròn 2 2
(C) : (x 1)  ( y  3)  4 và đường thẳng d : 3x  4 y  5  0 . Phương trình
của đường thẳng d song song với đường thẳng d và chắn trên (C) một dây cung có độ dài lớn nhất là A. 4x  3y 13  0 .
B. 3x  4y  25  0 . C. 3x  4y 15  0 . D. 4x  3y  20  0 . Phần 2. Tự luận
Câu 1: Giải các bất phương trình sau: a) 2 2x – 5x  2  0 ; b) 2 3x – 4x  4  0 ; c) 2 16x  40x  25  0 . d)  2 x  x  2 –
3 – 2 x – 5x  6  0 ; 2 x  x  3 2x  5 1 e)  0 ; f)  . 1 2x 2 x  6x  7 x  3
Câu 2: Giải các bất phương trình sau: a) 2 2
x  3x  2  x  3x  2 ; b) 2 x  4x 12  x  5; Trang 11/13 c) 2 2x 1  x 1; d) 2x 1  2x  3; e) 2 x  3x 10  x  2 ; f) 3x  3  2x  3 ;
Câu 3: Tìm m để các phương trình sau thỏa điều kiện đã cho: a) 2
(m 1)x  2(m 1)x  3m  3  0 vô nghiệm; b) 2
x  2(m 1)x  9m  5  0 có hai nghiệm âm phân biệt; c) 2
(m  2)x  2mx  m  3  0 có hai nghiệm dương phân biệt; d) 2
(m 1)x  2(m  3)x  m  3  0 có đúng một nghiệm âm.
Câu 4: Tính giá trị lượng giác còn lại của  biết: 5 3  a) cos  và
   2 ; b) sin  0,8 và     ; 13 2 2 15 3 5 3 c) tan  và     ; d) cot   và    2 . 8 2 3 2 4 
Câu 5: Cho góc  thỏa mãn sin  và     0; 
 . Tính cos , tan , cot , sin 2 , cos 2 , 5  2     sin     .  4  1 1
Câu 6: Cho cot x   . Tính giá trị của biểu thức A  . 2 2 1 cos x 3 3 1 tan x
Câu 7: Cho sin x   và   x 
. Tính giá trị của biểu thức A  . 5 2 1 tan x 2 1 sin a
Câu 8: Cho cot a  2 . Tính giá trị của biểu thức A  ; 2 2 sin a  3cos a
Câu 9: Chứng minh các đẳng thức sau: 2  2  a) 1 sin x 1 cos x 1 2  1 2 tan x ; b)  tan . x cot x  ; 2 1 sin x 2 2 1 sin x cos x sin x 1 cos x 2 cos x 1 c)   ; d)  tan x  ; 1 cos x sin x sin x 1 sin x cos x 2 sin x sin x  cos x 2 1 cos x  e)   sin x  cos x ; f) tan x  sin x  2cos x . 2   sin x  cos x 1 tan x sin x  
Câu 10: Rút gọn các biểu thức sau: sin 2a 2  a) 2cos a 1 A  ; b) B  ; 1 cos 2a sin a  cos a cos 2a  cos 4a sin a  sin 3a  sin 5a c) C  ; d) D  ; sin 4a  sin 2a cos a  cos 3a  cos5a 3  4cos 2a  cos 4a      e)  E  ; f) F  sin  x .cos x  tan  x .tan(5  x)     3  4cos 2a  cos 4a  2   2 
Câu 11: Viết phương trình đường thẳng  trong mỗi trường hợp sau: Trang 12/13
a)  đi qua điểm M(2; 4) và có hệ số góc k = 2;
b)  đi qua hai điểm A(–3; 0) và B(0; 5).
Câu 12: Lập phương trình đường thẳng  đi qua M(2; 3) và: x  13t a)  song song với d:  .
b)  vuông góc với trục tung Oy.  y  3 5t x  15 12t
Câu 13: Cho đường thẳng d : 3x  4y 1  0 và d : . 1 2   y  1 5t
Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho.
Câu 14: Tính khoảng cách giữa hai đường thẳng song song  : 6x – 8y  3  0 và  : 3x – 4y – 6  0 1 2
Câu 15: Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng  : 3x  2y  6  0 và 1
 : 3x  2y  3  0. Tìm điểm M thuộc trục hoành sao cho M cách đều hai đường thẳng 2 đã cho.
Câu 16: Xác định tâm và bán kính của các đường tròn có phương trình: 2  3 a) 2 2 
(x  5)  ( y  3)  1; b) 2 x  y   81   ;  4  c) 2 2
x  y  4x  y  4  0 ; d) 2 2 x  y  y  6  0 ;
Câu 17: Lập phương trình đường tròn trong các trường hợp sau:
a) Tâm P(1; - 3) và đi qua điểm Q(- 2; 4);
b) Đường kính AB với A(2; 3), B(- 1; -5);
c) Tâm I(4; 1) và tiếp xúc với đường thẳng d : 2x  y  3  0 ;
d) Đi qua ba điểm I(1; 2), J(- 5; 0) và K(- 2; 3).
Câu 18: Cho đường tròn (C): 2 2
x  y  6x  2y  6  0 . Lập phương trình tiếp tuyến (d) của (C) biết:
a) (d) tiếp xúc với (C) tại M(3; 1);
b) (d) // (d’): 5x + 12y – 2021 = 0;
c) (d) vuông góc (d’): x + 2y = 0;
d) (d) đi qua điểm N(1; 3). ---Hết--- Trang 13/13