Khảo sát kiến thức thi THPT Quốc gia lần 1 năm 2017 – 2018 Toán 10 trường Triệu Sơn 3 – Thanh Hóa

Đề khảo sát kiến thức thi THPT Quốc gia lần 1 năm học 2017 – 2018 Toán 10 trường THPT Triệu Sơn 3 – Thanh Hóa gồm 4 mã đề, mỗi đề gồm 50 câu hỏi trắc nghiệm, thời gian làm bài 90 phút, mời các bạn đón xem

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

27 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1/6 - Mã đề thi 134
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THANH HÓA
TRƯỜNG THPT TRIỆU SƠN 3
ĐỀ CHÍNH THỨC
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA
(Lần thứ 1)
NĂM HỌC 2017-2018
MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Mã đề thi
134
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
Câu 1: Tìm mệnh đề phủ định của mệnh đề:
2
, 50x Rx x∀∈ ++>
.
A.
2
, 5 0.x Rx x∃∈ + + <
B.
2
, 5 0.x Rx x∀∈ + + <
C.
2
, 5 0.x Rx x
∀∈ + + ≤
D.
Câu 2: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
22ym xm=−+
đồng biến trên
.
A.
2.m ≤
B.
2.m >
C.
2.
m
≥
D.
m 2.<
Câu 3: Trong hệ tọa độ
,Oxy
cho
2u ij
= −

và
v i xj= +

. Tìm
x
sao cho
u
và
v
cùng phương.
A.
1
2
x = −
. B.
1
4
x =
. C.
2x
=
. D.
1x = −
.
Câu 4: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A.
( )
[
)
−∞ − ∪ +∞; 2 5; .
B.
( ) ( )
−∞ − ∪ +∞; 2 5; .
C.
(
]
( )
−∞ − ∪ +∞; 2 5; .
D.
(
] [
)
−∞ − ∪ +∞; 2 5; .
Câu 5: Trong hệ tọa độ
,Oxy
cho
( )
(
)
2;5 , 3; 7ab
= = −

. Tính góc giữa hai véctơ
a
và
b
.
A.
60 .
o
B.
45 .
o
C.
135 .
o
D.
120 .
o
Câu 6: Tìm parabol
( )
2
: 3 2,
P y ax x= +−
biết rằng parabol có trục đối xứng
3.x = −
A.
2
3 2.yx x=+−
B.
2
1
2.
2
y xx= +−
C.
2
1
3 2.
2
yxx
= −−
D.
2
1
3 2.
2
yxx= +−
Câu 7: Trong hệ tọa độ
,Oxy
cho tam giác
ABC
có
( ) ( ) ( )
3;5 , 1;2 , 5;2 .ABC
Tìm tọa độ trọng tâm
G
của tam giác
.ABC
A.
( )
2;3 .G
B.
( )
3;3 .G
C.
( )
4;0 .G
D.
( )
3; 4 .G −
Câu 8: Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 9: Tìm nghiệm của hệ phương trình
2 30
.
42
xy
xy
−+=
−+ =
Trang 2/6 - Mã đề thi 134
A.
( ) ( )
, 2;1 .
xy =
B.
( )
10 1
, ;.
77
xy

=


C.
( )
10 1
, ;.
77
xy

= −


D.
( ) ( )
, 2; 1 .xy =−−
Câu 10: Điều kiện xác định của phương trình
123xx x−+ − = −
là:
A.
3.x >
B.
2.x
≥
C.
1.x ≥
D.
3.x ≥
Câu 11: Trong các hệ thức sau, hệ thức nào đúng?
A.
( )
2
.aa=

B.
.
aa
= ±

C.
( )
2
.aa=

D.
. ..
ab a b=

Câu 12: Tìm điều kiện của tham số
m
để hệ phương trình
1
mx y m
x my
−=
−+ =−
có nghiệm duy nhất.
A.
1.m = ±
B.
1.m
≠−
C.
1.m ≠
D.
1.m ≠±
Câu 13: Cho hàm số
( )
2
0y ax bx c a= ++ >
. Khẳng định nào sau đây là sai?
A. Đồ thị của hàm số có trục đối xứng là đường thẳng
.
2
b
x
a
= −
B. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.
C. Hàm số đồng biến trên khoảng
;.
2
b
a

− +∞


D. Hàm số nghịch biến trên khoảng
;.
2
b
a

−∞ −


Câu 14: Trong hệ tọa độ
,Oxy
cho
(
) ( )
3; 4 , 1; 2 .ab=−=−

Tìm tọa độ của
.ab+

A.
( )
4; 6 .
ab+= −

B.
( )
2; 2 .ab
+= −

C.
( )
4;6 .
ab
+=−

D.
( )
3; 8 .ab
+=−−

Câu 15: Hàm số
21yx= −
có đồ thị là hình nào trong các hình sau?
`
x
y
O
1
-1
Hình 1
x
y
O
1
-1
Hình 2
x
y
O
1
-1
Hình 3
x
y
O
1
-1
Hình 4
A. Hình 2 B. Hình 4. C. Hình 3. D. Hình 1.
Câu 16: Cho tam giác
.
ABC
Khẳng định nào sau đây đúng?
A.
.AB AC BC+=
  
B.
.AB CA CB+=
  
C.
.CA BA CB+=
  
D.
.AA BB AB+=
  
Câu 17: Đồ thị hình bên dưới là đồ thị của hàm số nào?
Trang 3/6 - Mã đề thi 134
`
x
y
O
1
1
A.
2
3 1.
yx x=−+
B.
2
2 3 1.yx x
= −+
C.
2
3 1.
yx x=−+ −
D.
2
2 3 1.
y xx=− +−
Câu 18: Phương trình
( )
2
0 0ax bx c a+ += ≠
có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
A.
0
.
0P
∆>
>
B.
0
.
0
S
∆>
<
C.
0
.
0P
∆≥
>
D.
0
.
0S
∆>
>
Câu 19: Cho tam giác đều
ABC
có cạnh bằng
a
. Tính
..AB AC
 
A.
2
3
..
2
AB AC a=
 
B.
2
1
..
2
AB AC a=
 
C.
2
1
..
2
AB AC a= −
 
D.
2
..AB AC a=
 
Câu 20: Cho
(
]
( )
;5 , 0;AB= −∞ = +∞
. Tìm
AB∩
.
A.
[
)
0;5 .
AB∩=
B.
( )
0;5 .AB∩=
C.
(
]
0;5 .AB∩=
D.
( )
;.AB∩ = −∞ +∞
Câu 21: Tìm tập xác định
D
của hàm số
(
)
1
1.fx x
x
= ++
A.
{ }
\0.D =
B.
{ }
\ 1; 0 .D = −
C.
[
) { }
1; \ 0 .D = − +∞
D.
[
)
1; .D = − +∞
Câu 22: Trong hệ tọa độ
,Oxy
cho
3ui j= +

và
( )
2; 1v = −
.Tính
.uv

.
A.
.1uv= −

. B.
.1uv=

. C.
( )
. 2; 3uv= −

. D.
. 52uv=

.
Câu 23: Đường thẳng nào sau đây song song với đường thẳng
2yx
=
?
A.
2
5.
2
yx
= −
B.
1 2.yx= −
C.
1
3.
2
yx= −
D.
2 2.yx=−+
Câu 24: Trong hệ tọa độ
,Oxy
cho véc tơ
( )
3; 4 .a = −
Đẳng thức nào sau đây đúng?
A.
5.a =
B.
3.a =
C.
4.a
=
D.
7.a
=
Câu 25: Cho phương trình
( )
(
)( )
2
1 –1 1 0x xx+ +=
. Phương trình nào sau đây tương đương với
phương trình đã cho?
A.
2
1 0.x +=
B.
1 0.x −=
C.
( )(
)
–1 1 0.xx
+=
D.
1 0.
x +=
Câu 26: Trong hệ tọa độ
,Oxy
cho
(
) ( )
2; 3 , 4;7 .AB−
Tìm tọa độ trung điểm
I
của đoạn thẳng
.AB
A.
( )
2;10 .I
B.
( )
6;4 .I
C.
( )
8; 21 .I −
D.
( )
3; 2 .I
Câu 27: Cho hàm số
( )
2
.fx x x= −
Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số
( )
fx
đối xứng qua trục hoành.
Trang 4/6 - Mã đề thi 134
B.
( )
fx
là hàm số chẵn.
C. Đồ thị của hàm số
( )
fx
đối xứng qua gốc tọa độ.
D.
( )
fx
là hàm số lẻ.
Câu 28: Tính tổng tất cả các nghiệm của phương trình
2 2 2.xx+= −
A.
1
.
2
B.
2
.
3
C.
6.
D.
20
.
3
Câu 29: Hãy liệt kê các phần tử của tập hợp
{ }
2
|2 5 3 0 .Xx x x= ∈ − +=
A.
{ }
1.X =
B.
3
.
2
X

=


C.
{ }
0.X =
D.
3
1; .
2
X

=


Câu 30: Cho
1
sin ,
3
α
=
với
00
90 180 .
α
<<
Tính
cos .
α
A.
2
cos .
3
α
=
B.
2
cos .
3
α
= −
C.
22
cos .
3
α
=
D.
22
cos .
3
α
= −
Câu 31: Tìm tất cả các giá trị của tham số
m
để hai đồ thị hàm số
2
23yx x=−− +
và
2
yx m= −
có
điểm chung.
A.
7
.
2
m = −
B.
7
.
2
m >−
C.
7
.
2
m ≥−
D.
7
.
2
m <−
Câu 32: Có tất cả bao nhiêu giá trị nguyên không dương của tham số
m
để phương trình
21
xm x+=−
có nghiệm duy nhất?
A.
4.
B.
3.
C.
1.
D.
2.
Câu 33: Cho hai tập
[ ]
(
]
0;5 ; 2 ;3 1
A B aa= = +
, với
1
a >−
. Tìm tất cả các giá trị của a để
A.
B∩ ≠∅
A.
5
2
.
1
3
a
a
<
≥−
B.
5
2
.
1
3
a
a
≥
<−
C.
15
.
32
a−≤<
D.
15
.
32
a−≤≤
Câu 34: Cho hai véc tơ
a
và
b
thỏa mãn các điều kiện
1
1,
2
ab= =

2 15.ab−=

Đặt
uab= +

và
2,.v ka b k=−∈

Tìm tất cả các giá trị của
k
sao cho
( )
0
, 60 .uv =

A.
35
4.
2
k = +
B.
35
4.
2
k = ±
C.
17
5.
2
k = +
D.
17
5.
2
k = ±
Câu 35: Đường thẳng
: 1,
xy
d
ab
+=
với
0; 0,ab≠≠
đi qua điểm
( )
1; 6M −
và tạo với các tia
,Ox Oy
một tam giác có diện tích bằng
4
. Tính
2
Sa b= +
.
A.
10.S =
B.
6.S =
C.
5 77
.
3
S
−+
=
D.
74
.
3
S = −
Câu 36: Cho biết
0m ≠
và
0n ≠
là các nghiệm của phương trình
2
0.
x mx n+ +=
Tính tổng
.mn+
A.
1
.
2
mn+=
B.
1
.
2
mn+=−
C.
1.mn+=−
D.
1.mn+=
Trang 5/6 - Mã đề thi 134
Câu 37: Cho tam giác
ABC
có
( ) ( ) ( )
2; 7 , 3; 5 , 1; 4A BC−−
. Biết rằng trực tâm của tam giác
ABC
là
điểm
;
ab
H
mn



, với
,, ,abmn
là các số nguyên dương và
a
m
,
b
n
là các phân số tối giản. Tính
.
ab
T
mn
= +
A.
95
.
9
T =
B.
43
.
4
T =
C.
72
.
7
T =
D.
54
.
5
T =
Câu 38: Biết rằng hàm số
(
)
2
0
y ax bx c a
= ++ ≠
đạt cực tiểu bằng
4
tại
2x =
và có đồ thị hàm số
đi qua điểm
( )
0;6A
. Tính tích
.P abc=
A.
6.P = −
B.
3.
P
= −
C.
6.P =
D.
3
.
2
P =
Câu 39: Cho mệnh đề:
2
, 2 0,x Rx a
∀∈ − + >
với
a
là số thực cho trước. Tìm
a
để mệnh đề đúng.
A.
2a ≤
. B.
2a >
. C.
2a ≥
. D.
2a =
.
Câu 40: Có tất cả bao nhiêu giá trị nguyên của tham số
[
]
10;10
m∈−
để phương trình
( )
( )
2
93 3m x mm
−= −
có nghiệm duy nhất ?
A.
2.
B.
21.
C.
19.
D.
18.
Câu 41: Giả sử phương trình
2
2 4 10x mx− −=
(với
m
là tham số) có hai nghiệm
12
, .xx
Tìm giá trị
nhỏ nhất của biểu thức
12
.Txx= −
A.
2
min .
3
T
=
B.
min 2.T =
C.
min 2.T =
D.
2
min .
2
T =
Câu 42: Cho 5 điểm phân biệt
, ,,,.M N PQR
Mệnh đề nào sau đây đúng?
A.
.MN PQ RN NP QR MP++++=
     
B.
.MN PQ RN NP QR PR++++=
     
C.
.MN PQ RN NP QR MR
++++=
     
D.
.MN PQ RN NP QR MN++++=
     
Câu 43: Cho hàm số
( )
2
f x ax bx c= ++
đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số
m
thì phương trình
( )
1fx m−=
có đúng
3
nghiệm phân biệt.
`
x
y
O
2
-1
3
A.
2 2.m−< <
B.
3.m =
C.
3.m >
D.
2.m =
Câu 44: Cho hình bình hành
.ABCD
Gọi
G
là trọng tâm của tam giác
ABC
. Mệnh đề nào sau đây
đúng?
A.
.GA GC GD CD++=
   
B.
.GA GC GD BD++=
   
C.
.GA GC GD O++=
  
D.
.GA GC GD DB++=
   
Câu 45: Cho tam giác
ABC
vuông cân tại
A
có
AB a=
. Tính
.AB AC+
 
Trang 6/6 - Mã đề thi 134
A.
2.
AB AC a+=
 
B.
2
.
2
a
AB AC+=
 
C.
2.AB AC a+=
 
D.
.AB AC a+=
 
Câu 46: Cho tứ giác
,ABCD
trên cạnh
,AB CD
lấy lần lượt các điểm
,MN
sao cho
32
AM AB
=
 
và
3 2.DN DC=
 
Tính vectơ
MN

theo hai vectơ
,.AD BC
 
A.
11
.
33
MN AD BC= +
  
B.
12
.
33
MN AD BC
= −
  
C.
12
.
33
MN AD BC
= +
  
D.
21
.
33
MN AD BC
= +
  
Câu 47: Gọi
S
là tập hợp các giá trị của tham số
m
sao cho parabol
( )
2
:4P y x xm=−+
cắt
Ox
tại
hai điểm phân biệt
, AB
thỏa mãn
3.OA OB
=
Tính tổng
T
các phần tử của
.S
A.
3.T
=
B.
15.T = −
C.
3
.
2
T =
D.
9.T = −
Câu 48: Trong hệ tọa độ
Oxy
, cho hai điểm
( ) ( )
2; 3, 3; 4.AB−−
Tìm tọa độ điểm
M
trên trục hoành
sao cho chu vi tam giác
AMB
nhỏ nhất.
A.
18
;0 .
7
M



B.
( )
4;0 .M
C.
(
)
3;0 .M
D.
17
;0 .
7
M



Câu 49: Cho hàm số
2
y ax bx c
= ++
có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng?
`
x
y
O
A.
0, 0, 0.abc
><<
B.
0, 0, 0.abc
><>
C.
0, 0, 0.abc
>>>
D.
0, 0, 0.abc
<<<
Câu 50: Cho biết tập hợp tất cả các giá trị của tham số
m
để phương trình
2
2
11
2 3 2 10x xm
xx

+ − + − +=


có nghiệm là
;
a
S
b

= − +∞

, với
,ab
là các số nguyên dương và
a
b
là phân số tối giản. Tính
.T ab= +
A.
13.
T =
B.
17.T =
C.
49.T =
D.
3.T =
----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Trang 1/6 - Mã đề thi 210
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THANH HÓA
TRƯỜNG THPT TRIỆU SƠN 3
ĐỀ CHÍNH THỨC
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA
(Lần thứ 1)
NĂM HỌC 2017-2018
MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Mã đề thi
210
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
Câu 1: Tìm tập xác định
D
của hàm số
( )
1
1.fx x
x
= ++
A.
{ }
\0.D
=
B.
[
)
1; .
D = − +∞
C.
{ }
\ 1; 0 .D = −
D.
[
) {
}
1; \ 0 .
D
= − +∞
Câu 2: Trong hệ tọa độ
,Oxy
cho
( ) ( )
2;5 , 3; 7ab= = −

. Tính góc giữa hai véctơ
a
và
b
.
A.
60 .
o
B.
45 .
o
C.
135 .
o
D.
120 .
o
Câu 3: Đường thẳng nào sau đây song song với đường thẳng
2
yx
=
?
A.
1
3.
2
yx= −
B.
2
5.
2
yx= −
C.
2 2.
yx=−+
D.
1 2.yx= −
Câu 4: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A.
( )
[
)
−∞ − ∪ +∞; 2 5; .
B.
(
] [
)
−∞ − ∪ +∞; 2 5; .
C.
(
]
( )
−∞ − ∪ +∞
; 2 5; .
D.
( ) ( )
−∞ − ∪ +∞; 2 5; .
Câu 5: Tìm parabol
( )
2
: 3 2,P y ax x
= +−
biết rằng parabol có trục đối xứng
3.
x = −
A.
2
3 2.yx x=+−
B.
2
1
3 2.
2
yxx= +−
C.
2
1
3 2.
2
yxx= −−
D.
2
1
2.
2
y xx= +−
Câu 6: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
22ym xm=−+
đồng biến trên
.
A.
2.m ≥
B.
2.m >
C.
2.
m ≤
D.
m 2.<
Câu 7: Cho
(
]
( )
;5 , 0;AB= −∞ = +∞
. Tìm
AB
∩
.
A.
(
]
0;5 .AB∩=
B.
( )
0;5 .AB∩=
C.
( )
;.AB∩ = −∞ +∞
D.
[
)
0;5 .AB∩=
Câu 8: Tìm nghiệm của hệ phương trình
2 30
.
42
xy
xy
−+=
−+ =
A.
( )
10 1
, ;.
77
xy

=


B.
( ) ( )
, 2; 1 .xy =−−
C.
( )
10 1
, ;.
77
xy

= −


D.
( ) ( )
, 2;1 .xy =
Câu 9: Điều kiện xác định của phương trình
123
xx x−+ − = −
là:
A.
3.x ≥
B.
2.x ≥
C.
1.x ≥
D.
3.x >
Câu 10: Hãy liệt kê các phần tử của tập hợp
{ }
2
|2 5 3 0 .Xx x x
= ∈ − +=
Trang 2/6 - Mã đề thi 210
A.
{ }
1.X =
B.
3
.
2
X

=


C.
{ }
0.X =
D.
3
1; .
2
X

=


Câu 11: Cho phương trình
( )
( )( )
2
1 –1 1 0x xx+ +=
. Phương trình nào sau đây tương đương với
phương trình đã cho?
A.
2
1 0.x
+=
B.
1 0.x −=
C.
( )( )
–1 1 0.xx+=
D.
1 0.x +=
Câu 12: Trong hệ tọa độ
,Oxy
cho tam giác
ABC
có
( ) ( ) ( )
3;5 , 1;2 , 5;2 .ABC
Tìm tọa độ trọng tâm
G
của tam giác
.
ABC
A.
(
)
2;3 .G
B.
(
)
4;0 .
G
C.
( )
3; 4 .G −
D.
( )
3;3 .G
Câu 13: Cho tam giác
.
ABC
Khẳng định nào sau đây đúng?
A.
.AB AC BC+=
  
B.
.AB CA CB+=
  
C.
.
CA BA CB
+=
  
D.
.AA BB AB+=
  
Câu 14: Trong hệ tọa độ
,Oxy
cho véc tơ
( )
3; 4 .a = −
Đẳng thức nào sau đây đúng?
A.
5.a =
B.
3.a =
C.
4.a =
D.
7.a =
Câu 15: Mệnh đề nào sau đây đúng?
A. Có vô số vectơ cùng phương với mọi vectơ.
B. Có duy nhất một vectơ cùng phương với mọi vectơ.
C. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 16: Trong hệ tọa độ
,Oxy
cho
( ) ( )
2; 3 , 4;7 .AB−
Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
A.
(
)
2;10 .
I
B.
( )
6;4 .
I
C.
( )
8; 21 .
I −
D.
( )
3; 2 .I
Câu 17: Phương trình
( )
2
0 0ax bx c a+ += ≠
có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
A.
0
.
0P
∆>
>
B.
0
.
0S
∆>
<
C.
0
.
0
P
∆≥
>
D.
0
.
0S
∆>
>
Câu 18: Tìm điều kiện của tham số
m
để hệ phương trình
1
mx y m
x my
−=
−+ =−
có nghiệm duy nhất.
A.
1.m ≠±
B.
1.m ≠−
C.
1.m ≠
D.
1.m = ±
Câu 19: Trong hệ tọa độ
,Oxy
cho
3ui j= +

và
( )
2; 1v
= −
.Tính
.uv

.
A.
.1uv=

. B.
. 52uv=

. C.
( )
. 2; 3uv
= −

. D.
.1
uv= −

.
Câu 20: Hàm số
21yx= −
có đồ thị là hình nào trong các hình sau?
`
x
y
O
1
-1
Hình 1
x
y
O
1
-1
Hình 2
x
y
O
1
-1
Hình 3
x
y
O
1
-1
Hình 4
Trang 3/6 - Mã đề thi 210
A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 3.
Câu 21: Trong hệ tọa độ
,Oxy
cho
( )
(
)
3; 4 , 1; 2 .
ab=−=−

Tìm tọa độ của
.ab+

A.
( )
2; 2 .
ab+= −

B.
( )
4; 6 .
ab
+= −

C.
( )
4;6 .
ab+=−

D.
( )
3; 8 .ab+=−−

Câu 22: Tìm mệnh đề phủ định của mệnh đề:
2
, 50
x Rx x
∀∈ ++>
.
A.
2
, 5 0.x Rx x∃∈ + + <
B.
C.
2
, 5 0.x Rx x
∀∈ + + ≤
D.
2
, 5 0.x Rx x∀∈ + + <
Câu 23: Cho tam giác đều
ABC
có cạnh bằng
a
. Tính
..AB AC
 
A.
2
3
..
2
AB AC a=
 
B.
2
1
..
2
AB AC a= −
 
C.
2
..AB AC a=
 
D.
2
1
..
2
AB AC a=
 
Câu 24: Trong các hệ thức sau, hệ thức nào đúng?
A.
.aa= ±

B.
( )
2
.aa=

C.
( )
2
.aa=

D.
. ..
ab a b=

Câu 25: Cho hàm số
( )
2
0y ax bx c a
= ++ >
. Khẳng định nào sau đây là sai?
A. Hàm số nghịch biến trên khoảng
;.
2
b
a

−∞ −


B. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.
C. Hàm số đồng biến trên khoảng
;.
2
b
a

− +∞


D. Đồ thị của hàm số có trục đối xứng là đường thẳng
.
2
b
x
a
= −
Câu 26: Cho hàm số
( )
2
.fx x x= −
Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số
( )
fx
đối xứng qua trục hoành.
B.
( )
fx
là hàm số chẵn.
C. Đồ thị của hàm số
( )
fx
đối xứng qua gốc tọa độ.
D.
( )
fx
là hàm số lẻ.
Câu 27: Tính tổng tất cả các nghiệm của phương trình
2 2 2.xx+= −
A.
1
.
2
B.
2
.
3
C.
6.
D.
20
.
3
Câu 28: Cho
1
sin ,
3
α
=
với
00
90 180 .
α
<<
Tính
cos .
α
A.
2
cos .
3
α
=
B.
2
cos .
3
α
= −
C.
22
cos .
3
α
=
D.
22
cos .
3
α
= −
Câu 29: Trong hệ tọa độ
,Oxy
cho
2u ij= −

và
v i xj
= +

. Tìm
x
sao cho
u
và
v
cùng phương.
A.
1
4
x =
. B.
1x = −
. C.
2x =
. D.
1
2
x = −
.
Trang 4/6 - Mã đề thi 210
Câu 30: Đồ thị hình bên dưới là đồ thị của hàm số nào?
`
x
y
O
1
1
A.
2
3 1.yx x=−+ −
B.
2
2 3 1.y xx
=− +−
C.
2
2 3 1.yx x= −+
D.
2
3 1.yx x
=−+
Câu 31: Cho hai tập
[ ]
(
]
0;5 ; 2 ;3 1A B aa= = +
, với
1a >−
. Tìm tất cả các giá trị của a để
A.B∩ ≠∅
A.
5
2
.
1
3
a
a
<
≥−
B.
5
2
.
1
3
a
a
≥
<−
C.
15
.
32
a
−≤<
D.
15
.
32
a
−≤≤
Câu 32: Biết rằng hàm số
( )
2
0y ax bx c a
= ++ ≠
đạt cực tiểu bằng
4
tại
2x =
và có đồ thị hàm số
đi qua điểm
( )
0;6A
. Tính tích
.P abc=
A.
6.P =
B.
6.P = −
C.
3.P = −
D.
3
.
2
P =
Câu 33: Trong hệ tọa độ
Oxy
, cho hai điểm
( ) ( )
2; 3, 3; 4.AB−−
Tìm tọa độ điểm
M
trên trục hoành
sao cho chu vi tam giác
AMB
nhỏ nhất.
A.
18
;0 .
7
M



B.
( )
4;0 .M
C.
( )
3;0 .M
D.
17
;0 .
7
M



Câu 34: Cho mệnh đề:
2
, 2 0,x Rx a∀∈ − + >
với
a
là số thực cho trước. Tìm
a
để mệnh đề đúng.
A.
2a =
. B.
2a ≥
. C.
2a >
. D.
2a ≤
.
Câu 35: Cho tứ giác
,ABCD
trên cạnh
,AB CD
lấy lần lượt các điểm
,MN
sao cho
32AM AB=
 
và
3 2.DN DC=
 
Tính vectơ
MN

theo hai vectơ
,.AD BC
 
A.
11
.
33
MN AD BC= +
  
B.
12
.
33
MN AD BC
= +
  
C.
12
.
33
MN AD BC
= −
  
D.
21
.
33
MN AD BC= +
  
Câu 36: Cho tam giác
ABC
có
( ) ( ) ( )
2; 7 , 3; 5 , 1; 4A BC−−
. Biết rằng trực tâm của tam giác
ABC
là
điểm
;
ab
H
mn



, với
,, ,abmn
là các số nguyên dương và
a
m
,
b
n
là các phân số tối giản. Tính
.
ab
T
mn
= +
A.
95
.
9
T =
B.
43
.
4
T =
C.
72
.
7
T =
D.
54
.
5
T =
Câu 37: Đường thẳng
: 1,
xy
d
ab
+=
với
0; 0,ab≠≠
đi qua điểm
( )
1; 6M −
và tạo với các tia
,Ox Oy
một tam giác có diện tích bằng
4
. Tính
2Sa b= +
.
Trang 5/6 - Mã đề thi 210
A.
10.S =
B.
74
.
3
S
= −
C.
6.S =
D.
5 77
.
3
S
−+
=
Câu 38: Giả sử phương trình
2
2 4 10
x mx− −=
(với
m
là tham số) có hai nghiệm
12
, .xx
Tìm giá trị
nhỏ nhất của biểu thức
12
.Txx
= −
A.
2
min .
3
T
=
B.
min 2.T =
C.
min 2.T =
D.
2
min .
2
T =
Câu 39: Có tất cả bao nhiêu giá trị nguyên của tham số
[ ]
10;10
m
∈−
để phương trình
( )
( )
2
93 3m x mm−= −
có nghiệm duy nhất ?
A.
2.
B.
21.
C.
19.
D.
18.
Câu 40: Cho hai véc tơ
a
và
b
thỏa mãn các điều kiện
1
1,
2
ab= =

2 15.
ab−=

Đặt
uab= +

và
2,.v ka b k=−∈

Tìm tất cả các giá trị của
k
sao cho
( )
0
, 60 .uv =

A.
35
4.
2
k = +
B.
17
5.
2
k = +
C.
17
5.
2
k = ±
D.
35
4.
2
k
= ±
Câu 41: Cho biết
0m ≠
và
0n ≠
là các nghiệm của phương trình
2
0.x mx n+ +=
Tính tổng
.mn+
A.
1
.
2
mn+=−
B.
1.mn+=
C.
1
.
2
mn
+=
D.
1.mn+=−
Câu 42: Cho hàm số
( )
2
f x ax bx c= ++
đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số
m
thì phương trình
(
)
1fx m
−=
có đúng
3
nghiệm phân biệt.
`
x
y
O
2
-1
3
A.
2 2.m−< <
B.
3.m =
C.
3.m >
D.
2.m =
Câu 43: Cho 5 điểm phân biệt
, ,,,.M NPQR
Mệnh đề nào sau đây đúng?
A.
.
MN PQ RN NP QR PR++++=
     
B.
.MN PQ RN NP QR MR++++=
     
C.
.MN PQ RN NP QR MP++++=
     
D.
.MN PQ RN NP QR MN++++=
     
Câu 44: Cho tam giác
ABC
vuông cân tại
A
có
AB a=
. Tính
.AB AC+
 
A.
2.AB AC a+=
 
B.
2
.
2
a
AB AC+=
 
C.
2.AB AC a+=
 
D.
.AB AC a+=
 
Câu 45: Cho hình bình hành
.ABCD
Gọi
G
là trọng tâm của tam giác
ABC
. Mệnh đề nào sau đây
đúng?
A.
.GA GC GD O++=
  
B.
.GA GC GD CD++=
   
C.
.GA GC GD BD++=
   
D.
.GA GC GD DB++=
   
Trang 6/6 - Mã đề thi 210
Câu 46: Gọi
S
là tập hợp các giá trị của tham số
m
sao cho parabol
( )
2
:4P y x xm=−+
cắt
Ox
tại
hai điểm phân biệt
,
AB
thỏa mãn
3.OA OB=
Tính tổng
T
các phần tử của
.S
A.
3.T =
B.
15.T = −
C.
9.T = −
D.
3
.
2
T =
Câu 47: Cho biết tập hợp tất cả các giá trị của tham số
m
để phương trình
2
2
11
2 3 2 10x xm
xx

+ − + − +=


có nghiệm là
;
a
S
b

= − +∞

, với
,ab
là các số nguyên dương và
a
b
là phân số tối giản. Tính
.T ab
= +
A.
17.T =
B.
49.T =
C.
3.T =
D.
13.T
=
Câu 48: Cho hàm số
2
y ax bx c
= ++
có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng?
`
x
y
O
A.
0, 0, 0.abc><<
B.
0, 0, 0.abc><>
C.
0, 0, 0.abc>>>
D.
0, 0, 0.abc<<<
Câu 49: Tìm tất cả các giá trị của tham số
m
để hai đồ thị hàm số
2
23yx x=−− +
và
2
yx m= −
có
điểm chung.
A.
7
.
2
m
≥−
B.
7
.
2
m <−
C.
7
.
2
m >−
D.
7
.
2
m = −
Câu 50: Có tất cả bao nhiêu giá trị nguyên không dương của tham số
m
để phương trình
21xm x+=−
có nghiệm duy nhất?
A.
1.
B.
2.
C.
4.
D.
3.
----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Trang 1/6 - Mã đề thi 356
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THANH HÓA
TRƯỜNG THPT TRIỆU SƠN 3
ĐỀ CHÍNH THỨC
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA
(Lần thứ 1)
NĂM HỌC 2017-2018
MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Mã đề thi
356
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
Câu 1: Tính tổng tất cả các nghiệm của phương trình
2 2 2.xx+= −
A.
2
.
3
B.
20
.
3
C.
1
.
2
D.
6.
Câu 2: Phương trình
( )
2
0 0ax bx c a+ += ≠
có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
A.
0
.
0P
∆>
>
B.
0
.
0S
∆>
<
C.
0
.
0P
∆≥
>
D.
0
.
0S
∆>
>
Câu 3: Tìm nghiệm của hệ phương trình
2 30
.
42
xy
xy
−+=
−+ =
A.
( )
10 1
, ;.
77
xy

=


B.
( ) (
)
, 2; 1 .xy =−−
C.
(
)
10 1
, ;.
77
xy

= −


D.
(
)
(
)
, 2;1 .
xy
=
Câu 4: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
22ym xm=−+
đồng biến trên
.
A.
2.
m ≥
B.
2.m
>
C.
m 2.<
D.
2.m ≤
Câu 5: Trong hệ tọa độ
,Oxy
cho
2u ij
= −

và
v i xj= +

. Tìm
x
sao cho
u
và
v
cùng phương.
A.
1
4
x =
. B.
1x = −
. C.
2x =
. D.
1
2
x = −
.
Câu 6: Cho tam giác
.ABC
Khẳng định nào sau đây đúng?
A.
.AB AC BC+=
  
B.
.AB CA CB+=
  
C.
.CA BA CB+=
  
D.
.AA BB AB+=
  
Câu 7: Cho
(
]
( )
;5 , 0;AB= −∞ = +∞
. Tìm
AB∩
.
A.
( )
;.AB∩ = −∞ +∞
B.
(
]
0;5 .AB
∩=
C.
[
)
0;5 .AB∩=
D.
( )
0;5 .AB∩=
Câu 8: Hãy liệt kê các phần tử của tập hợp
{ }
2
|2 5 3 0 .
Xx x x= ∈ − +=
A.
3
.
2
X

=


B.
{ }
1.X =
C.
{ }
0.X =
D.
3
1; .
2
X

=


Câu 9: Tìm mệnh đề phủ định của mệnh đề:
2
, 50x Rx x∀∈ ++>
.
A.
2
, 5 0.x Rx x∃∈ + + <
B.
C.
2
, 5 0.x Rx x∀∈ + + ≤
D.
2
, 5 0.x Rx x∀∈ + + <
Câu 10: Trong hệ tọa độ
,Oxy
cho
3ui j= +

và
( )
2; 1
v = −
.Tính
.uv

.
A.
.1uv=

. B.
. 52uv=

. C.
( )
. 2; 3uv= −

. D.
.1uv= −

.
Trang 2/6 - Mã đề thi 356
Câu 11: Cho phương trình
( )
( )( )
2
1 –1 1 0x xx+ +=
. Phương trình nào sau đây tương đương với
phương trình đã cho?
A.
1 0.x −=
B.
( )( )
–1 1 0.xx+=
C.
2
1 0.x +=
D.
1 0.x +=
Câu 12: Cho hàm số
( )
2
.fx x x= −
Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số
( )
fx
đối xứng qua gốc tọa độ.
B. Đồ thị của hàm số
( )
fx
đối xứng qua trục hoành.
C.
( )
fx
là hàm số lẻ.
D.
( )
fx
là hàm số chẵn.
Câu 13: Trong các hệ thức sau, hệ thức nào đúng?
A.
.aa= ±

B.
( )
2
.aa=

C.
(
)
2
.
aa
=

D.
. ..ab a b=

Câu 14: Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có vô số vectơ cùng phương với mọi vectơ.
C. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 15: Tìm điều kiện của tham số
m
để hệ phương trình
1
mx y m
x my
−=
−+ =−
có nghiệm duy nhất.
A.
1.m ≠±
B.
1.
m ≠−
C.
1.
m ≠
D.
1.m = ±
Câu 16: Cho
1
sin ,
3
α
=
với
00
90 180 .
α
<<
Tính
cos .
α
A.
2
cos .
3
α
=
B.
2
cos .
3
α
= −
C.
22
cos .
3
α
=
D.
22
cos .
3
α
= −
Câu 17: Trong hệ tọa độ
,Oxy
cho véc tơ
(
)
3; 4 .a = −
Đẳng thức nào sau đây đúng?
A.
3.a =
B.
5.
a =
C.
7.
a =
D.
4.
a =
Câu 18: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A.
( ) ( )
−∞ − ∪ +∞; 2 5; .
B.
(
]
( )
−∞ − ∪ +∞; 2 5; .
C.
( )
[
)
−∞ − ∪ +∞; 2 5; .
D.
(
] [
)
−∞ − ∪ +∞
; 2 5; .
Câu 19: Hàm số
21yx= −
có đồ thị là hình nào trong các hình sau?
Trang 3/6 - Mã đề thi 356
`
x
y
O
1
-1
Hình 1
x
y
O
1
-1
Hình 2
x
y
O
1
-1
Hình 3
x
y
O
1
-1
Hình 4
A. Hình 4. B. Hình 3. C. Hình 2. D. Hình 1.
Câu 20: Điều kiện xác định của phương trình
123
xx x−+ − = −
là:
A.
1.x ≥
B.
2.x
≥
C.
3.x >
D.
3.x ≥
Câu 21: Đường thẳng nào sau đây song song với đường thẳng
2yx=
?
A.
2
5.
2
yx= −
B.
1
3.
2
yx= −
C.
2 2.yx=−+
D.
1 2.yx= −
Câu 22: Cho tam giác đều
ABC
có cạnh bằng
a
. Tính
..AB AC
 
A.
2
3
..
2
AB AC a=
 
B.
2
1
..
2
AB AC a= −
 
C.
2
..AB AC a=
 
D.
2
1
..
2
AB AC a=
 
Câu 23: Trong hệ tọa độ
,Oxy
cho
( )
( )
2;5 , 3; 7ab
= = −

. Tính góc giữa hai véctơ
a
và
b
.
A.
135 .
o
B.
120 .
o
C.
60 .
o
D.
45 .
o
Câu 24: Trong hệ tọa độ
,Oxy
cho tam giác
ABC
có
( ) ( ) ( )
3;5 , 1;2 , 5;2 .ABC
Tìm tọa độ trọng tâm
G
của tam giác
.ABC
A.
( )
2;3 .G
B.
( )
4;0 .G
C.
( )
3;3 .G
D.
( )
3; 4 .G −
Câu 25: Tìm parabol
( )
2
: 3 2,P y ax x= +−
biết rằng parabol có trục đối xứng
3.
x = −
A.
2
1
2.
2
y xx= +−
B.
2
3 2.yx x=+−
C.
2
1
3 2.
2
yxx= +−
D.
2
1
3 2.
2
yxx= −−
Câu 26: Tìm tập xác định
D
của hàm số
( )
1
1.fx x
x
= ++
A.
{ }
\ 1; 0 .D = −
B.
[
)
1; .D = − +∞
C.
[
) { }
1; \ 0 .D = − +∞
D.
{ }
\0.D =
Câu 27: Trong hệ tọa độ
,
Oxy
cho
( ) ( )
2; 3 , 4;7 .AB−
Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
A.
( )
6;4 .I
B.
( )
3; 2 .
I
C.
( )
8; 21 .I −
D.
( )
2;10 .I
Câu 28: Đồ thị hình bên dưới là đồ thị của hàm số nào?
Trang 4/6 - Mã đề thi 356
`
x
y
O
1
1
A.
2
2 3 1.yx x
= −+
B.
2
2 3 1.y xx=− +−
C.
2
3 1.
yx x=−+ −
D.
2
3 1.
yx x
=−+
Câu 29: Cho hàm số
( )
2
0y ax bx c a= ++ >
. Khẳng định nào sau đây là sai?
A. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.
B. Hàm số nghịch biến trên khoảng
;.
2
b
a

−∞ −


C. Hàm số đồng biến trên khoảng
;.
2
b
a

− +∞


D. Đồ thị của hàm số có trục đối xứng là đường thẳng
.
2
b
x
a
= −
Câu 30: Trong hệ tọa độ
,Oxy
cho
( ) ( )
3; 4 , 1; 2 .
ab=−=−

Tìm tọa độ của
.ab
+

A.
( )
2; 2 .ab+= −

B.
(
)
4; 6 .ab+= −

C.
(
)
3; 8 .
ab+=−−

D.
( )
4;6 .ab+=−

Câu 31: Cho hai tập
[ ]
(
]
0;5 ; 2 ;3 1A B aa
= = +
, với
1a >−
. Tìm tất cả các giá trị của a để
A.B∩ ≠∅
A.
15
.
32
a−≤≤
B.
15
.
32
a
−≤<
C.
5
2
.
1
3
a
a
<
≥−
D.
5
2
.
1
3
a
a
≥
<−
Câu 32: Cho hàm số
( )
2
f x ax bx c= ++
đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số
m
thì phương trình
( )
1fx m−=
có đúng
3
nghiệm phân biệt.
`
x
y
O
2
-1
3
A.
3.m >
B.
2 2.m−< <
C.
2.m =
D.
3.m =
Câu 33: Tìm tất cả các giá trị của tham số
m
để hai đồ thị hàm số
2
23yx x=−− +
và
2
yx m= −
có
điểm chung.
A.
7
.
2
m ≥−
B.
7
.
2
m <−
C.
7
.
2
m >−
D.
7
.
2
m = −
Trang 5/6 - Mã đề thi 356
Câu 34: Cho tứ giác
,ABCD
trên cạnh
,AB CD
lấy lần lượt các điểm
,MN
sao cho
32AM AB
=
 
và
3 2.
DN DC
=
 
Tính vectơ
MN

theo hai vectơ
,.AD BC
 
A.
12
.
33
MN AD BC
= −
  
B.
12
.
33
MN AD BC
= +
  
C.
21
.
33
MN AD BC= +
  
D.
11
.
33
MN AD BC= +
  
Câu 35: Cho mệnh đề:
2
, 2 0,x Rx a
∀∈ − + >
với
a
là số thực cho trước. Tìm
a
để mệnh đề đúng.
A.
2a ≥
. B.
2a =
. C.
2a >
. D.
2a ≤
.
Câu 36: Đường thẳng
: 1,
xy
d
ab
+=
với
0; 0,ab
≠≠
đi qua điểm
( )
1; 6M −
và tạo với các tia
,Ox Oy
một tam giác có diện tích bằng
4
. Tính
2Sa b= +
.
A.
10.
S =
B.
74
.
3
S
= −
C.
6.S =
D.
5 77
.
3
S
−+
=
Câu 37: Cho hai véc tơ
a
và
b
thỏa mãn các điều kiện
1
1,
2
ab= =

2 15.ab−=

Đặt
uab
= +

và
2,.v ka b k=−∈

Tìm tất cả các giá trị của
k
sao cho
( )
0
, 60 .uv
=

A.
35
4.
2
k = +
B.
17
5.
2
k = +
C.
17
5.
2
k = ±
D.
35
4.
2
k = ±
Câu 38: Có tất cả bao nhiêu giá trị nguyên của tham số
[ ]
10;10
m∈−
để phương trình
( )
( )
2
93 3m x mm−= −
có nghiệm duy nhất ?
A.
2.
B.
21.
C.
19.
D.
18.
Câu 39: Cho tam giác
ABC
có
(
) ( ) ( )
2; 7 , 3; 5 , 1; 4
A BC−−
. Biết rằng trực tâm của tam giác
ABC
là
điểm
;
ab
H
mn



, với
,, ,abmn
là các số nguyên dương và
a
m
,
b
n
là các phân số tối giản. Tính
.
ab
T
mn
= +
A.
54
.
5
T =
B.
95
.
9
T
=
C.
72
.
7
T =
D.
43
.
4
T =
Câu 40: Cho 5 điểm phân biệt
, ,,,.M NPQR
Mệnh đề nào sau đây đúng?
A.
.MN PQ RN NP QR MN++++=
     
B.
.
MN PQ RN NP QR MP++++=
     
C.
.MN PQ RN NP QR PR++++=
     
D.
.MN PQ RN NP QR MR++++=
     
Câu 41: Cho hình bình hành
.ABCD
Gọi
G
là trọng tâm của tam giác
ABC
. Mệnh đề nào sau đây
đúng?
A.
.GA GC GD DB++=
   
B.
.GA GC GD CD++=
   
C.
.GA GC GD BD++=
   
D.
.GA GC GD O++=
  
Câu 42: Giả sử phương trình
2
2 4 10
x mx− −=
(với
m
là tham số) có hai nghiệm
12
, .xx
Tìm giá trị
nhỏ nhất của biểu thức
12
.Txx= −
A.
min 2.T
=
B.
2
min .
3
T =
C.
2
min .
2
T =
D.
min 2.T =
Trang 6/6 - Mã đề thi 356
Câu 43: Có tất cả bao nhiêu giá trị nguyên không dương của tham số
m
để phương trình
21xm x
+=−
có nghiệm duy nhất?
A.
1.
B.
2.
C.
4.
D.
3.
Câu 44: Trong hệ tọa độ
Oxy
, cho hai điểm
( ) ( )
2; 3, 3; 4.AB−−
Tìm tọa độ điểm
M
trên trục hoành
sao cho chu vi tam giác
AMB
nhỏ nhất.
A.
( )
3;0 .M
B.
17
;0 .
7
M



C.
18
;0 .
7
M



D.
( )
4;0 .M
Câu 45: Gọi
S
là tập hợp các giá trị của tham số
m
sao cho parabol
( )
2
:4P y x xm=−+
cắt
Ox
tại
hai điểm phân biệt
,
AB
thỏa mãn
3.OA OB=
Tính tổng
T
các phần tử của
.S
A.
3.T =
B.
15.T = −
C.
9.T = −
D.
3
.
2
T =
Câu 46: Biết rằng hàm số
( )
2
0y ax bx c a= ++ ≠
đạt cực tiểu bằng
4
tại
2x =
và có đồ thị hàm số
đi qua điểm
( )
0;6A
. Tính tích
.P abc
=
A.
3.P = −
B.
6.P = −
C.
3
.
2
P
=
D.
6.
P =
Câu 47: Cho tam giác
ABC
vuông cân tại
A
có
AB a=
. Tính
.AB AC+
 
A.
2.AB AC a+=
 
B.
.AB AC a+=
 
C.
2
.
2
a
AB AC
+=
 
D.
2.AB AC a+=
 
Câu 48: Cho hàm số
2
y ax bx c= ++
có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng?
`
x
y
O
A.
0, 0, 0.abc><>
B.
0, 0, 0.abc
><<
C.
0, 0, 0.abc
<<<
D.
0, 0, 0.abc>>>
Câu 49: Cho biết
0m ≠
và
0n ≠
là các nghiệm của phương trình
2
0.
x mx n+ +=
Tính tổng
.
mn+
A.
1.mn+=
B.
1
.
2
mn+=−
C.
1
.
2
mn+=
D.
1.mn+=−
Câu 50: Cho biết tập hợp tất cả các giá trị của tham số
m
để phương trình
2
2
11
2 3 2 10x xm
xx

+ − + − +=


có nghiệm là
;
a
S
b

= − +∞

, với
,ab
là các số nguyên dương và
a
b
là phân số tối giản. Tính
.T ab= +
A.
17.T =
B.
49.
T =
C.
3.T =
D.
13.T =
----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Trang 1/6 - Mã đề thi 483
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THANH HÓA
TRƯỜNG THPT TRIỆU SƠN 3
ĐỀ CHÍNH THỨC
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA
(Lần thứ 1)
NĂM HỌC 2017-2018
MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Mã đề thi
483
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
Câu 1: Tìm nghiệm của hệ phương trình
2 30
.
42
xy
xy
−+=
−+ =
A.
( )
(
)
, 2;1 .xy=
B.
( )
10 1
, ;.
77
xy

= −


C.
( ) ( )
, 2; 1 .xy =−−
D.
(
)
10 1
, ;.
77
xy

=


Câu 2: Đồ thị hình bên dưới là đồ thị của hàm số nào?
`
x
y
O
1
1
A.
2
2 3 1.yx x= −+
B.
2
2 3 1.y xx=− +−
C.
2
3 1.yx x=−+ −
D.
2
3 1.
yx x=−+
Câu 3: Tìm mệnh đề phủ định của mệnh đề:
2
, 50x Rx x∀∈ ++>
.
A.
2
, 5 0.x Rx x∃∈ + + <
B.
C.
2
, 5 0.x Rx x∀∈ + + ≤
D.
2
, 5 0.x Rx x∀∈ + + <
Câu 4: Hãy liệt kê các phần tử của tập hợp
{ }
2
|2 5 3 0 .Xx x x= ∈ − +=
A.
3
1; .
2
X

=


B.
{ }
0.X
=
C.
3
.
2
X

=


D.
{ }
1.X =
Câu 5: Hàm số
21
yx= −
có đồ thị là hình nào trong các hình sau?
`
x
y
O
1
-1
Hình 1
x
y
O
1
-1
Hình 2
x
y
O
1
-1
Hình 3
x
y
O
1
-1
Hình 4
A. Hình 4. B. Hình 3. C. Hình 2. D. Hình 1.
Câu 6: Cho tam giác đều
ABC
có cạnh bằng
a
. Tính
..AB AC
 
Trang 2/6 - Mã đề thi 483
A.
2
3
..
2
AB AC a
=
 
B.
2
1
..
2
AB AC a= −
 
C.
2
..AB AC a=
 
D.
2
1
..
2
AB AC a=
 
Câu 7: Đường thẳng nào sau đây song song với đường thẳng
2
yx
=
?
A.
2 2.yx=−+
B.
1 2.yx= −
C.
2
5.
2
yx= −
D.
1
3.
2
yx= −
Câu 8: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A.
(
]
( )
−∞ − ∪ +∞; 2 5; .
B.
(
] [
)
−∞ − ∪ +∞; 2 5; .
C.
( )
[
)
−∞ − ∪ +∞; 2 5; .
D.
( ) ( )
−∞ − ∪ +∞
; 2 5; .
Câu 9: Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có vô số vectơ cùng phương với mọi vectơ.
C. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 10: Tìm tất cả các giá trị của tham số
m
để hàm số
( )
22ym xm=−+
đồng biến trên
.
A.
2.
m ≥
B.
2.m
≤
C.
2.m >
D.
m 2.<
Câu 11: Cho hàm số
( )
2
.
fx x x= −
Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số
( )
fx
đối xứng qua gốc tọa độ.
B.
( )
fx
là hàm số chẵn.
C.
( )
fx
là hàm số lẻ.
D. Đồ thị của hàm số
( )
fx
đối xứng qua trục hoành.
Câu 12: Trong hệ tọa độ
,
Oxy
cho
3ui j= +

và
( )
2; 1v = −
.Tính
.uv

.
A.
.1uv=

. B.
. 52uv=

. C.
(
)
. 2; 3
uv= −

. D.
.1uv= −

.
Câu 13: Tìm parabol
( )
2
: 3 2,P y ax x= +−
biết rằng parabol có trục đối xứng
3.x = −
A.
2
1
2.
2
y xx= +−
B.
2
3 2.yx x=+−
C.
2
1
3 2.
2
yxx= +−
D.
2
1
3 2.
2
yxx= −−
Câu 14: Cho
(
]
( )
;5 , 0;AB= −∞ = +∞
. Tìm
AB∩
.
A.
( )
;.AB∩ = −∞ +∞
B.
( )
0;5 .AB∩=
C.
[
)
0;5 .AB∩=
D.
(
]
0;5 .AB∩=
Câu 15: Cho
1
sin ,
3
α
=
với
00
90 180 .
α
<<
Tính
cos .
α
A.
2
cos .
3
α
=
B.
2
cos .
3
α
= −
C.
22
cos .
3
α
=
D.
22
cos .
3
α
= −
Câu 16: Trong hệ tọa độ
,Oxy
cho véc tơ
( )
3; 4 .a = −
Đẳng thức nào sau đây đúng?
A.
3.a =
B.
4.a =
C.
7.a =
D.
5.a =
Trang 3/6 - Mã đề thi 483
Câu 17: Trong hệ tọa độ
,
Oxy
cho
2u ij
= −

và
v i xj= +

. Tìm
x
sao cho
u
và
v
cùng phương.
A.
1
2
x
= −
. B.
1
4
x
=
. C.
2x =
. D.
1x = −
.
Câu 18: Phương trình
( )
2
0 0ax bx c a+ += ≠
có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
A.
0
.
0
P
∆≥
>
B.
0
.
0
S
∆>
<
C.
0
.
0P
∆>
>
D.
0
.
0S
∆>
>
Câu 19: Điều kiện xác định của phương trình
123xx x
−+ − = −
là:
A.
1.x ≥
B.
2.
x
≥
C.
3.x >
D.
3.x
≥
Câu 20: Cho phương trình
( )
(
)( )
2
1 –1 1 0
x xx+ +=
. Phương trình nào sau đây tương đương với
phương trình đã cho?
A.
1 0.x −=
B.
1 0.x
+=
C.
2
1 0.x
+=
D.
( )( )
–1 1 0.xx+=
Câu 21: Cho tam giác
.
ABC
Khẳng định nào sau đây đúng?
A.
.
AB CA CB+=
  
B.
.CA BA CB+=
  
C.
.
AB AC BC+=
  
D.
.
AA BB AB
+=
  
Câu 22: Trong hệ tọa độ
,Oxy
cho
(
) (
)
2;5 , 3; 7ab
= = −

. Tính góc giữa hai véctơ
a
và
b
.
A.
135 .
o
B.
120 .
o
C.
60 .
o
D.
45 .
o
Câu 23: Trong hệ tọa độ
,
Oxy
cho tam giác
ABC
có
( ) (
) ( )
3;5 , 1;2 , 5;2 .ABC
Tìm tọa độ trọng tâm
G
của tam giác
.ABC
A.
( )
2;3 .G
B.
( )
4;0 .G
C.
( )
3;3 .G
D.
( )
3; 4 .G −
Câu 24: Tìm tập xác định
D
của hàm số
(
)
1
1.fx x
x
= ++
A.
[
) { }
1; \ 0 .D
= − +∞
B.
{ }
\ 1; 0 .D
= −
C.
{
}
\0.
D =
D.
[
)
1; .D = − +∞
Câu 25: Tính tổng tất cả các nghiệm của phương trình
2 2 2.xx+= −
A.
20
.
3
B.
2
.
3
C.
1
.
2
D.
6.
Câu 26: Trong hệ tọa độ
,
Oxy
cho
( ) ( )
2; 3 , 4;7 .AB−
Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
A.
( )
6;4 .
I
B.
( )
3; 2 .I
C.
( )
8; 21 .I −
D.
( )
2;10 .I
Câu 27: Trong hệ tọa độ
,Oxy
cho
( ) (
)
3; 4 , 1; 2 .ab=−=−

Tìm tọa độ của
.ab+

A.
( )
2; 2 .ab+= −

B.
( )
4; 6 .ab+= −

C.
( )
3; 8 .ab+=−−

D.
( )
4;6 .ab+=−

Câu 28: Cho hàm số
( )
2
0y ax bx c a= ++ >
. Khẳng định nào sau đây là sai?
A. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.
B. Hàm số nghịch biến trên khoảng
;.
2
b
a

−∞ −


C. Hàm số đồng biến trên khoảng
;.
2
b
a

− +∞


Trang 4/6 - Mã đề thi 483
D. Đồ thị của hàm số có trục đối xứng là đường thẳng
.
2
b
x
a
= −
Câu 29: Tìm điều kiện của tham số
m
để hệ phương trình
1
mx y m
x my
−=
−+ =−
có nghiệm duy nhất.
A.
1.m ≠−
B.
1.m ≠
C.
1.m = ±
D.
1.m ≠±
Câu 30: Trong các hệ thức sau, hệ thức nào đúng?
A.
( )
2
.
aa=

B.
( )
2
.aa=

C.
. ..ab a b=

D.
.aa= ±

Câu 31: Cho 5 điểm phân biệt
, ,,,.M N PQR
Mệnh đề nào sau đây đúng?
A.
.MN PQ RN NP QR MP++++=
     
B.
.MN PQ RN NP QR MR++++=
     
C.
.MN PQ RN NP QR PR++++=
     
D.
.
MN PQ RN NP QR MN++++=
     
Câu 32: Có tất cả bao nhiêu giá trị nguyên của tham số
[ ]
10;10m∈−
để phương trình
( )
(
)
2
93 3
m x mm−= −
có nghiệm duy nhất ?
A.
2.
B.
21.
C.
19.
D.
18.
Câu 33: Cho hàm số
2
y ax bx c= ++
có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng?
`
x
y
O
A.
0, 0, 0.abc><>
B.
0, 0, 0.
abc<<<
C.
0, 0, 0.abc>>>
D.
0, 0, 0.abc
><<
Câu 34: Cho tam giác
ABC
có
( ) ( )
( )
2; 7 , 3; 5 , 1; 4A BC−−
. Biết rằng trực tâm của tam giác
ABC
là
điểm
;
ab
H
mn



, với
,, ,abmn
là các số nguyên dương và
a
m
,
b
n
là các phân số tối giản. Tính
.
ab
T
mn
= +
A.
54
.
5
T =
B.
95
.
9
T =
C.
72
.
7
T =
D.
43
.
4
T =
Câu 35: Cho hai véc tơ
a
và
b
thỏa mãn các điều kiện
1
1,
2
ab= =

2 15.ab−=

Đặt
uab= +

và
2,.v ka b k=−∈

Tìm tất cả các giá trị của
k
sao cho
( )
0
, 60 .uv =

A.
35
4.
2
k = +
B.
17
5.
2
k = +
C.
17
5.
2
k = ±
D.
35
4.
2
k = ±
Câu 36: Cho mệnh đề:
2
, 2 0,x Rx a∀∈ − + >
với
a
là số thực cho trước. Tìm
a
để mệnh đề đúng.
A.
2a =
. B.
2a >
. C.
2a ≥
. D.
2a ≤
.
Câu 37: Giả sử phương trình
2
2 4 10x mx− −=
(với
m
là tham số) có hai nghiệm
12
, .xx
Tìm giá trị
nhỏ nhất của biểu thức
12
.Txx= −
Trang 5/6 - Mã đề thi 483
A.
min 2.T =
B.
min 2.T =
C.
2
min .
2
T =
D.
2
min .
3
T =
Câu 38: Cho hai tập
[ ]
(
]
0;5 ; 2 ;3 1A B aa= = +
, với
1a >−
. Tìm tất cả các giá trị của a để
A.
B∩ ≠∅
A.
15
.
32
a−≤<
B.
5
2
.
1
3
a
a
≥
<−
C.
15
.
32
a
−≤≤
D.
5
2
.
1
3
a
a
<
≥−
Câu 39: Biết rằng hàm số
( )
2
0
y ax bx c a
= ++ ≠
đạt cực tiểu bằng
4
tại
2x =
và có đồ thị hàm số
đi qua điểm
( )
0;6
A
. Tính tích
.P abc=
A.
3.P = −
B.
6.P
= −
C.
3
.
2
P =
D.
6.P =
Câu 40: Trong hệ tọa độ
Oxy
, cho hai điểm
( ) ( )
2; 3, 3; 4.AB−−
Tìm tọa độ điểm
M
trên trục hoành
sao cho chu vi tam giác
AMB
nhỏ nhất.
A.
( )
3;0 .M
B.
17
;0 .
7
M



C.
18
;0 .
7
M



D.
( )
4;0 .M
Câu 41: Cho biết tập hợp tất cả các giá trị của tham số
m
để phương trình
2
2
11
2 3 2 10x xm
xx

+ − + − +=


có nghiệm là
;
a
S
b

= − +∞

, với
,
ab
là các số nguyên dương và
a
b
là phân số tối giản. Tính
.T ab= +
A.
17.T =
B.
49.T =
C.
3.
T =
D.
13.T =
Câu 42: Có tất cả bao nhiêu giá trị nguyên không dương của tham số
m
để phương trình
21xm x+=−
có nghiệm duy nhất?
A.
4.
B.
1.
C.
2.
D.
3.
Câu 43: Cho hình bình hành
.ABCD
Gọi
G
là trọng tâm của tam giác
ABC
. Mệnh đề nào sau đây
đúng?
A.
.GA GC GD DB++=
   
B.
.GA GC GD BD++=
   
C.
.GA GC GD O
++=
  
D.
Câu 44: Cho hàm số
( )
2
f x ax bx c= ++
đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số
m
thì phương trình
( )
1fx m−=
có đúng
3
nghiệm phân biệt.
`
x
y
O
2
-1
3
A.
2 2.m−< <
B.
3.m >
C.
2.m =
D.
3.m =
Câu 45: Cho tam giác
ABC
vuông cân tại
A
có
AB a=
. Tính
.AB AC+
 
Trang 6/6 - Mã đề thi 483
A.
2.AB AC a
+=
 
B.
.AB AC a
+=
 
C.
2
.
2
a
AB AC+=
 
D.
2.AB AC a+=
 
Câu 46: Đường thẳng
: 1,
xy
d
ab
+=
với
0; 0,ab≠≠
đi qua điểm
( )
1; 6M −
và tạo với các tia
,Ox Oy
một tam giác có diện tích bằng
4
. Tính
2Sa b= +
.
A.
5 77
.
3
S
−+
=
B.
10.S =
C.
6.S
=
D.
74
.
3
S = −
Câu 47: Cho biết
0m
≠
và
0n ≠
là các nghiệm của phương trình
2
0.x mx n+ +=
Tính tổng
.mn+
A.
1.mn+=
B.
1
.
2
mn+=−
C.
1
.
2
mn+=
D.
1.mn+=−
Câu 48: Tìm tất cả các giá trị của tham số
m
để hai đồ thị hàm số
2
23yx x=−− +
và
2
yx m= −
có
điểm chung.
A.
7
.
2
m
<−
B.
7
.
2
m >−
C.
7
.
2
m ≥−
D.
7
.
2
m
= −
Câu 49: Gọi
S
là tập hợp các giá trị của tham số
m
sao cho parabol
( )
2
:4P y x xm=−+
cắt
Ox
tại
hai điểm phân biệt
, AB
thỏa mãn
3.OA OB=
Tính tổng
T
các phần tử của
.S
A.
3.T =
B.
15.T = −
C.
9.T = −
D.
3
.
2
T =
Câu 50: Cho tứ giác
,ABCD
trên cạnh
,AB CD
lấy lần lượt các điểm
,MN
sao cho
32AM AB
=
 
và
3 2.DN DC=
 
Tính vectơ
MN

theo hai vectơ
,.AD BC
 
A.
12
.
33
MN AD BC= −
  
B.
12
.
33
MN AD BC= +
  
C.
21
.
33
MN AD BC= +
  
D.
11
.
33
MN AD BC
= +
  
----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN ĐỀ KHẢO SÁT KIẾN THỨC (Lần 1) - MÔN TOÁN KHỐI 10
Câu
Mã 134
Mã 210
Mã 356
Mã 483
1.
D
D
B
B
2.
B
C
A
A
3.
A
B
C
B
4.
A
A
B
A
5.
C
B
D
D
6.
D
B
B
D
7.
B
A
B
C
8.
A
C
D
C
9.
C
A
B
A
10.
D
D
D
C
11.
C
C
B
B
12.
D
D
D
D
13.
B
B
B
C
14.
B
A
A
D
15.
D
B
A
D
16.
B
D
D
D
17.
B
A
B
A
18.
A
A
C
C
19.
B
D
D
D
20.
C
B
D
D
21.
C
A
A
A
22.
A
B
D
A
23.
A
D
A
C
24.
A
B
C
A
25.
C
B
C
A
26.
D
B
C
B
27.
B
D
B
A
28.
D
D
A
A
29.
D
D
A
D
30.
D
C
A
B
31.
C
C
B
D
32.
B
B
C
C
33.
C
D
A
D
34.
A
C
B
C
35.
A
B
C
A
36.
C
C
A
B
37.
C
A
A
B
38.
A
C
C
A
39.
B
C
C
B
40.
C
A
A
B
41.
B
D
C
C
42.
D
D
D
D
43.
D
D
D
B
44.
B
A
B
C
45.
A
C
C
D
46.
C
C
B
B
47.
D
C
D
D
48.
D
A
B
C
49.
A
A
D
C
50.
D
D
C
B
HƯỚNG DẪN MỘT SỐ CÂU VẬN DỤNG VÀ VẬN DỤNG CAO
ĐỀ KHẢO SÁT KIẾN THỨC (Lần 1) - MÔN TOÁN KHỐI 10
Câu 1: Đường thẳng
: 1,
xy
d
ab
+=
với
0; 0,ab≠≠
đi qua điểm
( )
1; 6M −
và tạo với các tia
,
Ox Oy
một
tam giác có diện tích bằng
4
. Tính
2Sa b= +
.
A.
74
.
3
S = −
B.
5 77
.
3
S
−+
=
C.
10.S =
D.
6.S =
Lời giải. Đường thẳng
:1
xy
d
ab
+=
đi qua điểm
( )
16
1; 6 1.M
ab
−
− → + =
( )
1
Ta có
( )
;0
d Ox A a∩=
;
( )
0;d Oy B b∩=
,
0, 0ab>>
(do
, AB
thuộc hai tia
Ox
,
Oy
).
Suy ra
OA a a
= =
và
OB b b= =
. Do đó, ta có
11
. 4 4.
22
ABC
S OAOB ab
∆
= = → =
( )
2
Từ
( )
1
và
( )
2
ta có hệ
16
1
60
8
1
4
2
a b ab
ab
ab
ab
−+=
−− =
⇒

=
=
Giải hệ ta được
2, 4.ab= =
Suy ra
2 10ab+=
.
Câu 2: Cho hai véc tơ
a
và
b
thỏa mãn các điều kiện
1
1,
2
ab= =

2 15.ab−=

Đặt
uab= +

và
2,.v ka b k=−∈

Tìm tất cả các giá trị của
k
sao cho
(
)
0
, 60 .
uv
=

A.
35
4.
2
k = +
B.
35
4.
2
k
= ±
C.
17
5.
2
k
= +
D.
17
5.
2
k
= ±
Lời giải.
Từ giả thiết
( )
2
1
2 15 2 15 .
2
ab ab ab− = ⇔− =⇒ =
 
.
( )(
)
9
. 23
2
uv a b ka b k=+ −=−

,
22
2
6, 4 2 4uu vv kk= = = = −+

( )
0
2
9
3
1 35
2
, 60 4 .
22
6. 4 2 4
k
uv k
kk
−
= ⇔ =⇔=+
−+

Câu 3: Gọi
S
là tập hợp các giá trị của tham số
m
sao cho parabol
( )
2
:4P y x xm=−+
cắt
Ox
tại hai
điểm phân biệt
, AB
thỏa mãn
3.OA OB=
Tính tổng
T
các phần tử của
.S
A.
3.T =
B.
9.T = −
C.
15.T = −
D.
3
.
2
T =
Lời giải. Phương trình hoành độ giao điểm:
2
4 0.x xm− +=
( )
*
Để
( )
P
cắt
Ox
tại hai điểm phân biệt
, AB
thì
( )
*
có hai nghiệm phân biệt
' 4 0 4.mm
⇔∆ = − > ⇔ <
Theo giả thiết
3
33 .
3
AB
AB
AB
xx
OA OB x x
xx
=
= → = ⇔
= −
TH1:
Viet
3
3 4 . 3.
.
AB
A B A B AB
AB
xx
x x x x m xx
xx m
=
= → + = → = =
=
TH2:
Viet
3
3 4 . 12
.
AB
A B A B AB
AB
xx
x x x x m xx
xx m
= −
= − → + = → = = −
=
.
Do đó
{ }
3; 12 9ST= − ⇒=−
Câu 4: Có tất cả bao nhiêu giá trị nguyên không dương của tham số
m
để phương trình
21xm x
+=−
có
nghiệm duy nhất?
A.
2.
B.
1.
C.
3.
D.
4.
Lời giải.
Phương trình
2
1
21
41
x
xm x
mx x
≥
+ = −⇔
=−+
Lập bảng biến thiên của hàm số
( )
2
41fx x x
=−+
trên
[
)
1; +∞
ta được
3m = −
hoặc
2m
>−
. Do đó có 3
giá trị nguyên không dương là:
3; 1; 0−−
.
Câu 5: Cho biết tập hợp tất cả các giá trị của tham số
m
để phương trình
2
2
11
2 3 2 10x xm
xx

+ − + − +=


có nghiệm là
;
a
S
b

= − +∞

, với
,ab
là các số nguyên dương và
a
b
là
phân số tối giản. Tính
.T ab= +
A.
13T =
B.
17.
T =
C.
49.T =
D.
3.T =
Lời giải.
Đặt
1
tx
x
= +
. Điều kiện
2t
≤−
hoặc
2.
t ≥
Phương trình trở thành
2
2 2 33
mt t= −−
.
Lập bảng biến thiên của hàm số
(
)
2
2 33
fx t t= −−
trên
(
] [
)
; 2 2;−∞ − ∪ +∞
ta được
1
2
m ≥−
.
Do đó
1, 2 3ab T= =⇒=
.
Câu 6: Cho tam giác
ABC
có
(
) (
)
(
)
2; 7 , 3; 5 , 1; 4
A BC−−
. Biết rằng trực tâm của tam giác
ABC
là điểm
;
ab
H
mn



, với
,, ,abmn
là các số nguyên dương và
a
m
,
b
n
là các phân số tối giản. Tính
.
ab
T
mn
= +
A.
43
.
4
T =
B.
54
.
5
T =
C.
72
.
7
T =
D.
95
.
9
T =
Lời giải. Gọi
( )
;H xy
. Giải hệ
.0
235 269 235 269 72
;
49 49 49 49 7
.0
AH BC
HT
BH AC
=

⇒ ⇒= + =


=
 
 
Câu 7: Trong hệ tọa độ
Oxy
, cho hai điểm
( ) ( )
2; 3, 3; 4.AB−−
Tìm tọa độ điểm
M
trên trục hoành sao cho
chu vi tam giác
AMB
nhỏ nhất.
A.
18
;0 .
7
M



B.
( )
4;0 .M
C.
( )
3;0 .M
D.
17
;0 .
7
M



Lời giải. Điểm
(
)
;0 .M Ox M m
∈⇒
Gọi
'B
là điểm đối xứng với
B
qua
Ox
thì
( )
' 3; 4B
.
Chu vi tam giác là:
''C AB AM BM AB AM B M AB AB
∆
=++=++ ≥+
không đổi
Do đó chu vi nhỏ nhất khi và chỉ khi
, ',AB M
thẳng hàng
',AB AM
⇔
 
cùng phương.
Ta có
( )
' 1; 7AB =

và
( )
2;3 .AM m= −

Để
,,ABM
thẳng hàng
2 3 17
.
17 7
m
m
−
⇔ =⇔=
-------------------------------
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

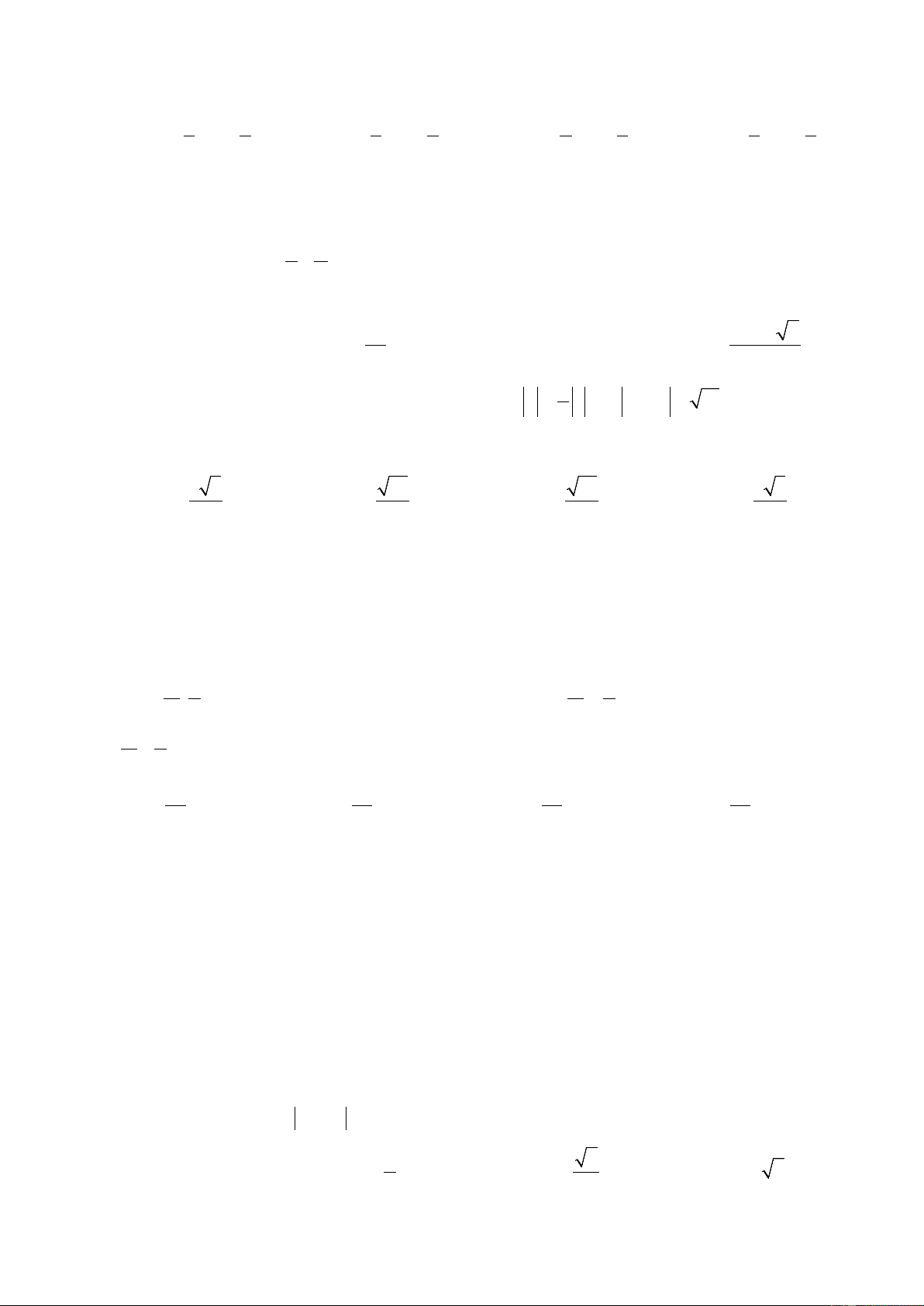
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA THANH HÓA (Lần thứ 1)
TRƯỜNG THPT TRIỆU SƠN 3 NĂM HỌC 2017-2018 ĐỀ CHÍNH THỨC MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề) Mã đề thi 134
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
Câu 1: Tìm mệnh đề phủ định của mệnh đề: 2 x
∀ ∈ R, x + x + 5 > 0. A. 2 x
∃ ∈ R, x + x + 5 < 0. B. 2 x
∀ ∈ R, x + x + 5 < 0. C. 2 x
∀ ∈ R, x + x + 5 ≤ 0. D. 2 x
∃ ∈ R, x + x + 5 ≤ 0.
Câu 2: Tìm tất cả các giá trị của tham số m để hàm số y = (m − 2) x + 2m đồng biến trên .  A. m ≤ 2. B. m > 2. C. m ≥ 2. D. m < 2.        
Câu 3: Trong hệ tọa độ Oxy, cho u = 2i − j và v = i + xj . Tìm x sao cho u và v cùng phương. 1 1 A. x = − . B. x = . C. x = 2 . D. x = 1 − . 2 4
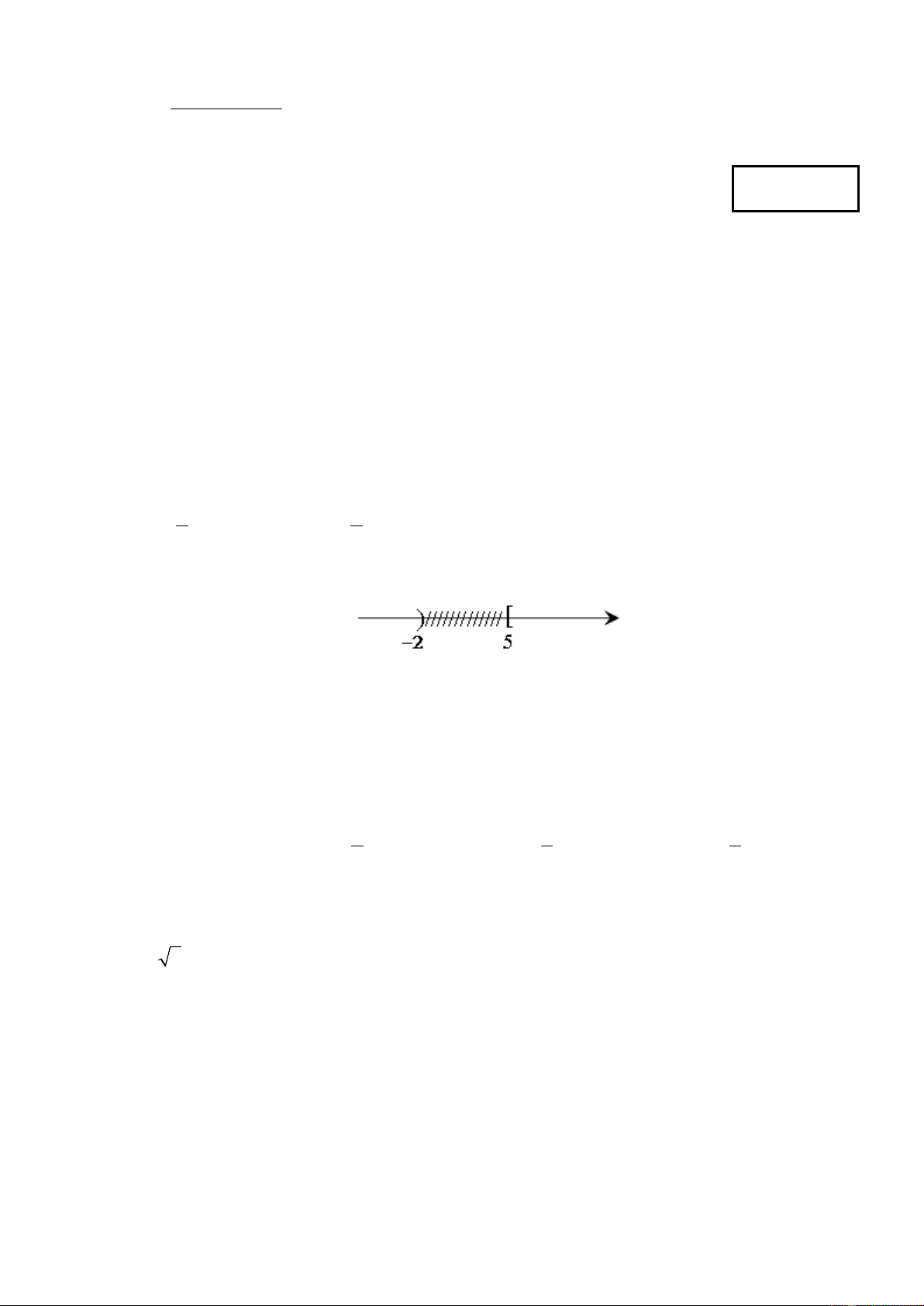
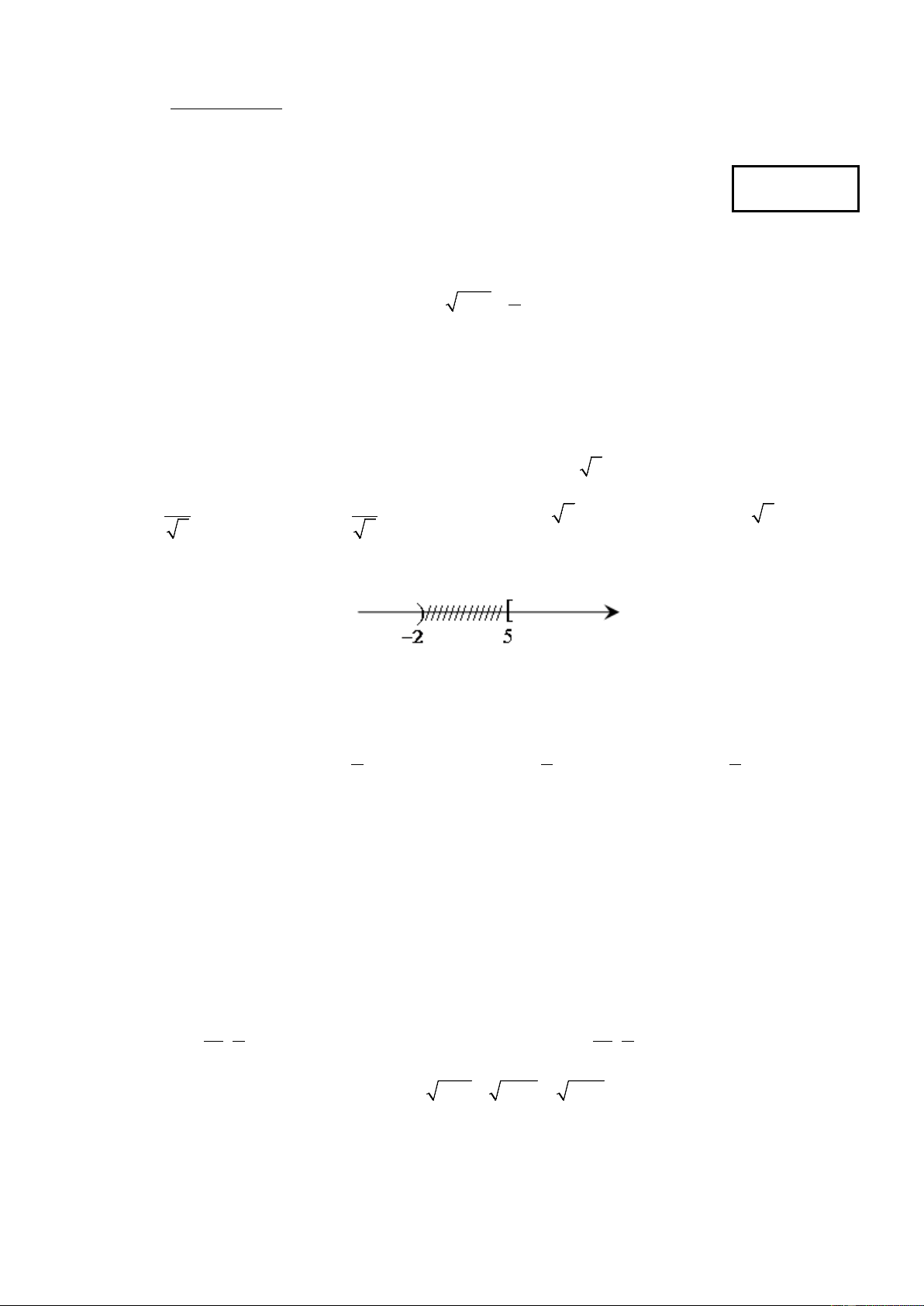
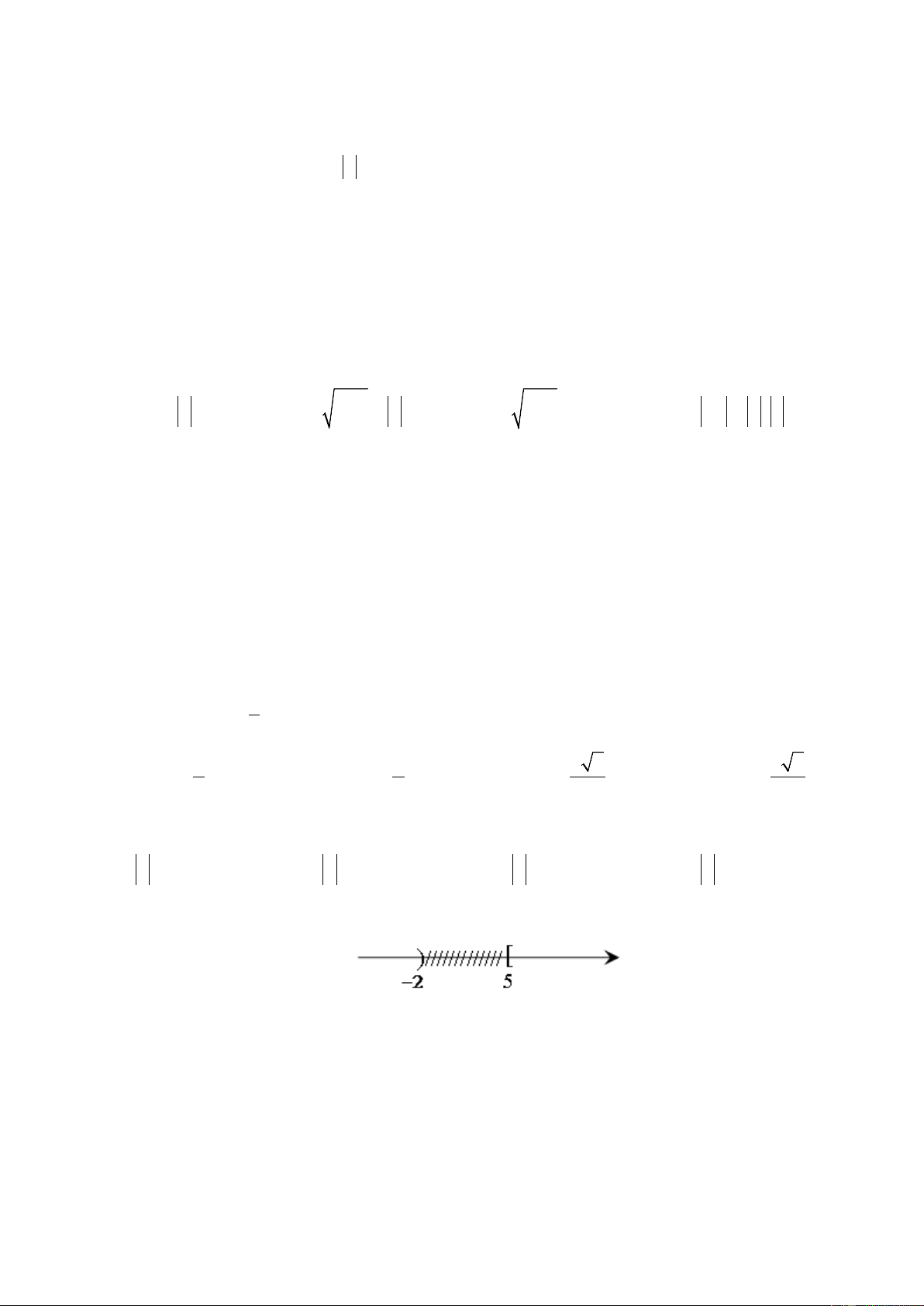
Câu 4: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A. (−∞;−2) ∪[5;+∞). B. (−∞;−2) ∪ (5;+∞). C. (−∞;−2] ∪ (5;+∞). D. (−∞;−2]∪[5;+∞).    
Câu 5: Trong hệ tọa độ Oxy, cho a = (2;5), b = (3; 7
− ) . Tính góc giữa hai véctơ a và b . A. 60 . o B. 45 . o C. 135 . o D. 120 . o
Câu 6: Tìm parabol ( P) 2
: y = ax + 3x − 2, biết rằng parabol có trục đối xứng x = 3. − 1 1 1 A. 2
y = x + 3x − 2. B. 2 y = x + x − 2. C. 2 y = x − 3x − 2. D. 2 y = x + 3x − 2. 2 2 2
Câu 7: Trong hệ tọa độ Oxy, cho tam giác ABC có A(3;5), B ( 1; 2), C (
5; 2). Tìm tọa độ trọng tâm
G của tam giác ABC. A. G ( 2;3). B. G (3;3). C. G (4;0). D. G ( 3 − ;4).
Câu 8: Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
2x − y + 3 = 0
Câu 9: Tìm nghiệm của hệ phương trình  . −x + 4y = 2
Trang 1/6 - Mã đề thi 134    
A. ( x, y) = (2; ) 1 . B. ( x y) 10 1 , = ; .   C. ( x y) 10 1 , = − ; . 
D. ( x, y) = ( 2; − − ) 1 .  7 7   7 7 
Câu 10: Điều kiện xác định của phương trình x −1 + x − 2 = x − 3 là: A. x > 3. B. x ≥ 2. C. x ≥ 1. D. x ≥ 3.
Câu 11: Trong các hệ thức sau, hệ thức nào đúng?           A. (a)2 = . a
B. a = ± a .
C. (a)2 = a . D. .
a b = a . b .
mx − y = m
Câu 12: Tìm điều kiện của tham số m để hệ phương trình  có nghiệm duy nhất. −x + my = 1 − A. m = 1. ± B. m ≠ 1. − C. m ≠ 1. D. m ≠ 1. ± Câu 13: Cho hàm số 2
y = ax + bx + c ( 0
a > ) . Khẳng định nào sau đây là sai? b
A. Đồ thị của hàm số có trục đối xứng là đường thẳng x = − . 2a
B. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.  b
C. Hàm số đồng biến trên khoảng − ; +∞ .    2a   b
D. Hàm số nghịch biến trên khoảng ; −∞ − .    2a     
Câu 14: Trong hệ tọa độ Oxy, cho a = (3; 4 − ), b = ( 1
− ;2). Tìm tọa độ của a + . b        
A. a + b = (4; 6 − ).
B. a + b = (2; 2 − ).
C. a + b = ( 4; − 6).
D. a + b = ( 3 − ; 8 − ).
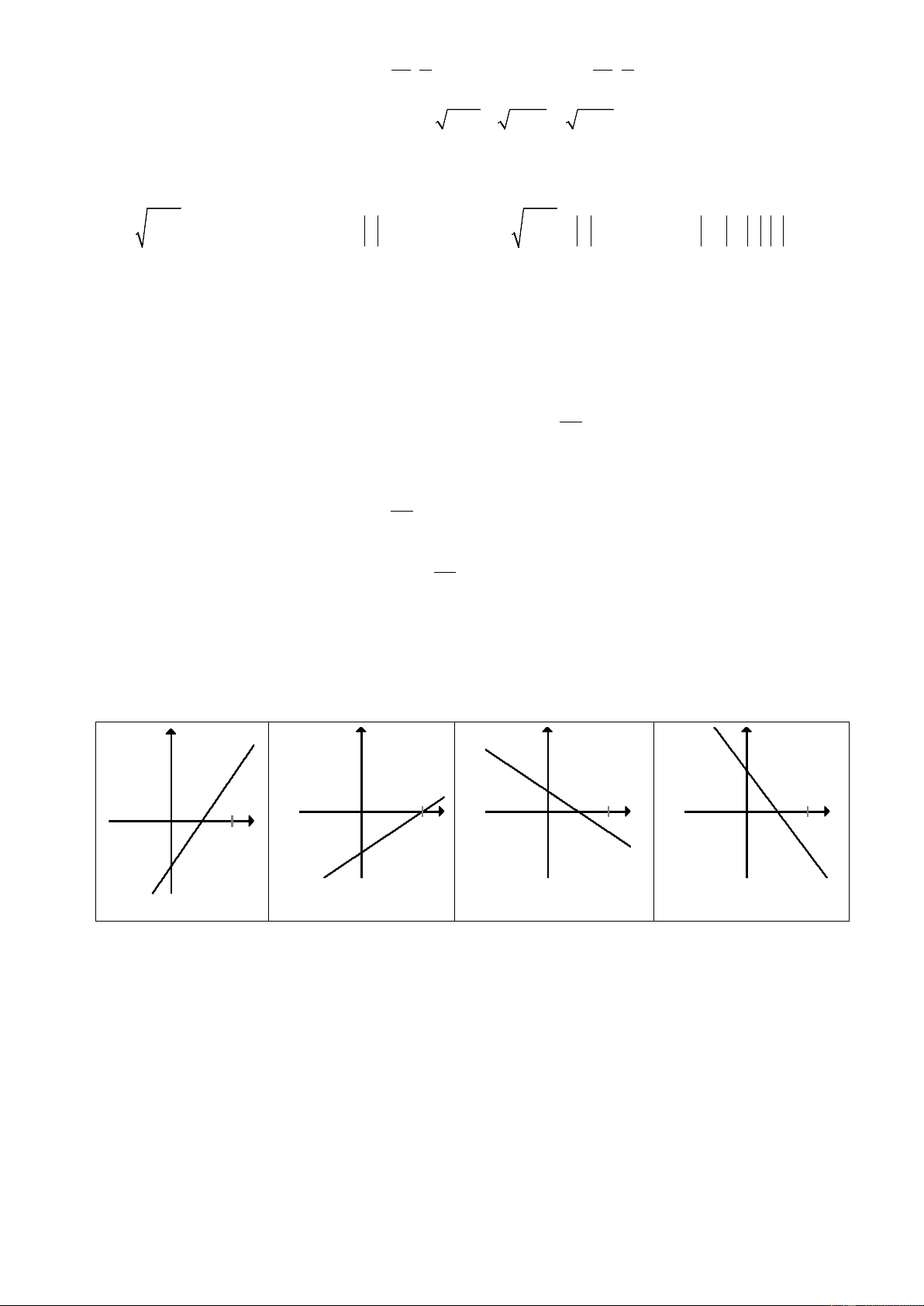
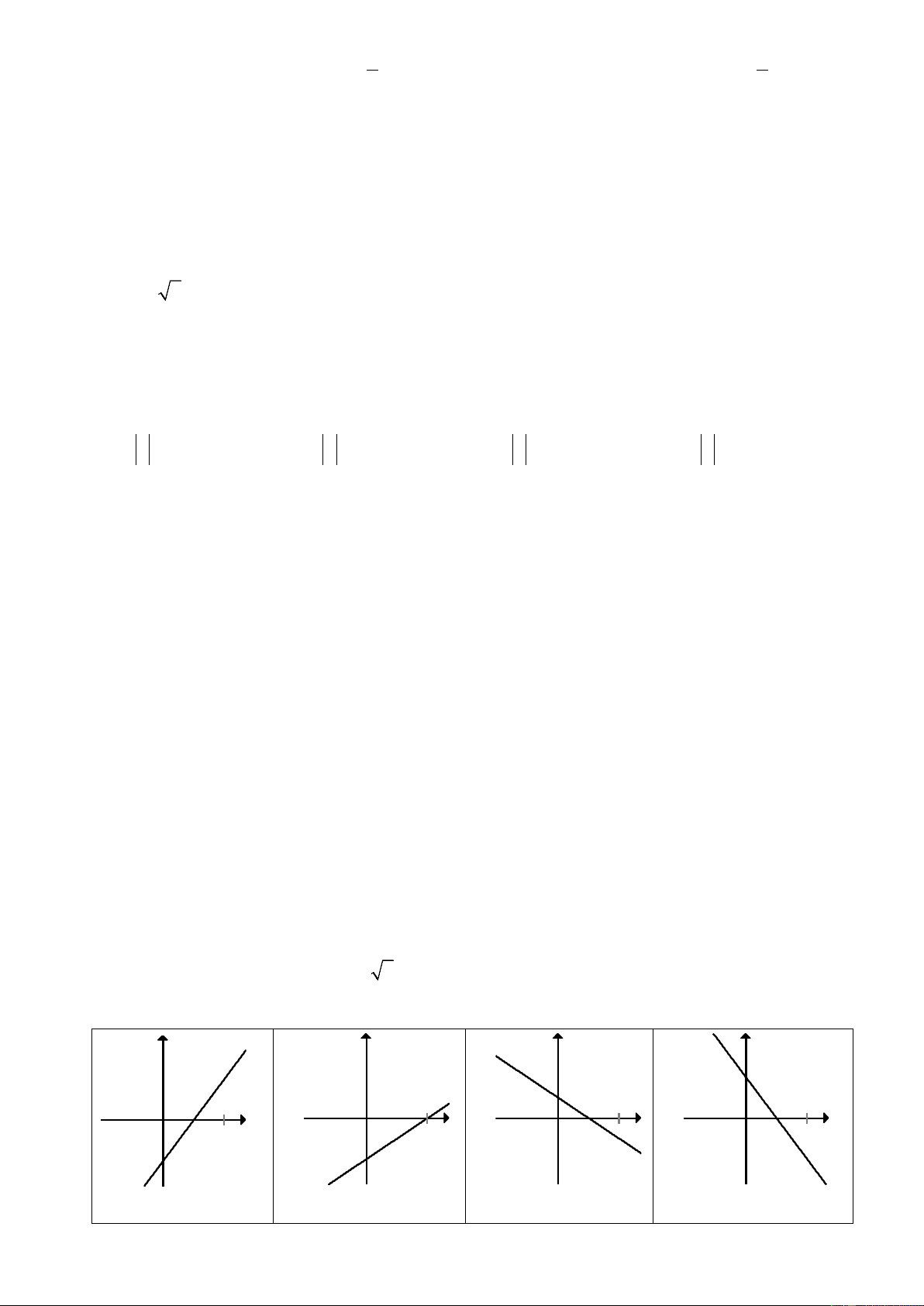
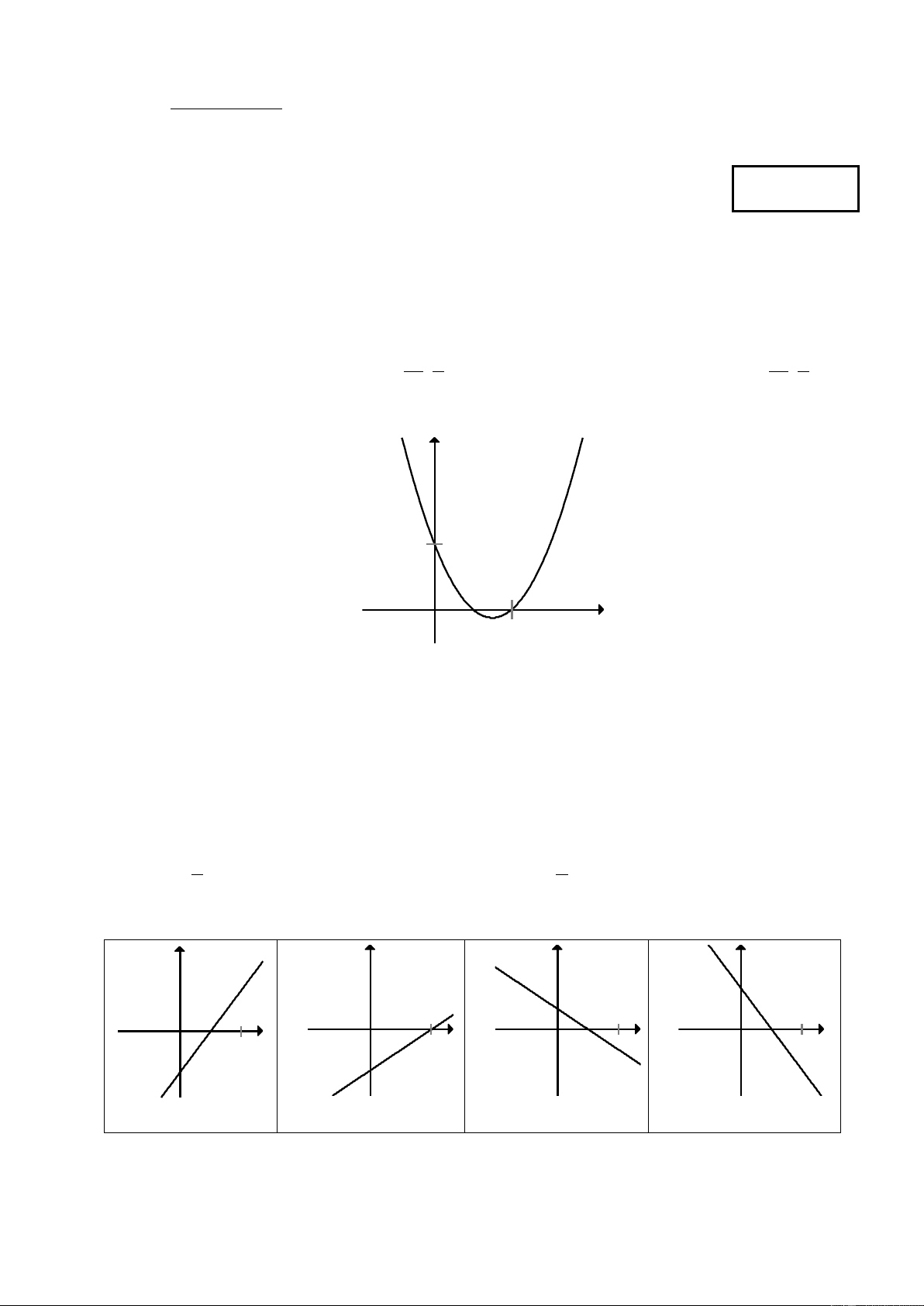
Câu 15: Hàm số y = 2x −1 có đồ thị là hình nào trong các hình sau? ` y y y y x x x x O O O O 1 1 1 1 -1 -1 -1 -1 Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2 B. Hình 4. C. Hình 3. D. Hình 1.
Câu 16: Cho tam giác ABC. Khẳng định nào sau đây đúng?
  
  
  
  
A. AB + AC = BC.
B. AB + CA = . CB
C. CA + BA = . CB
D. AA + BB = A . B
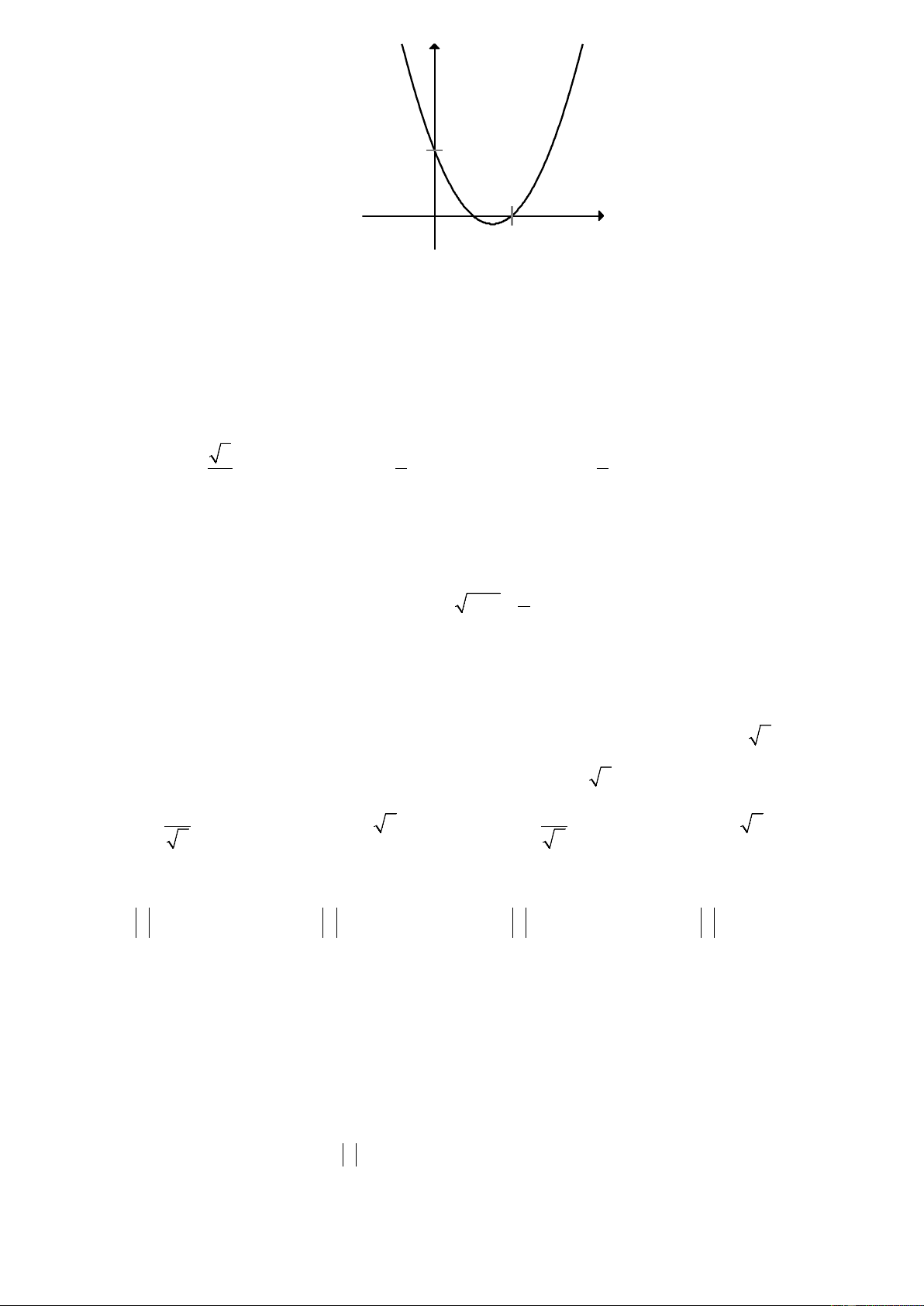
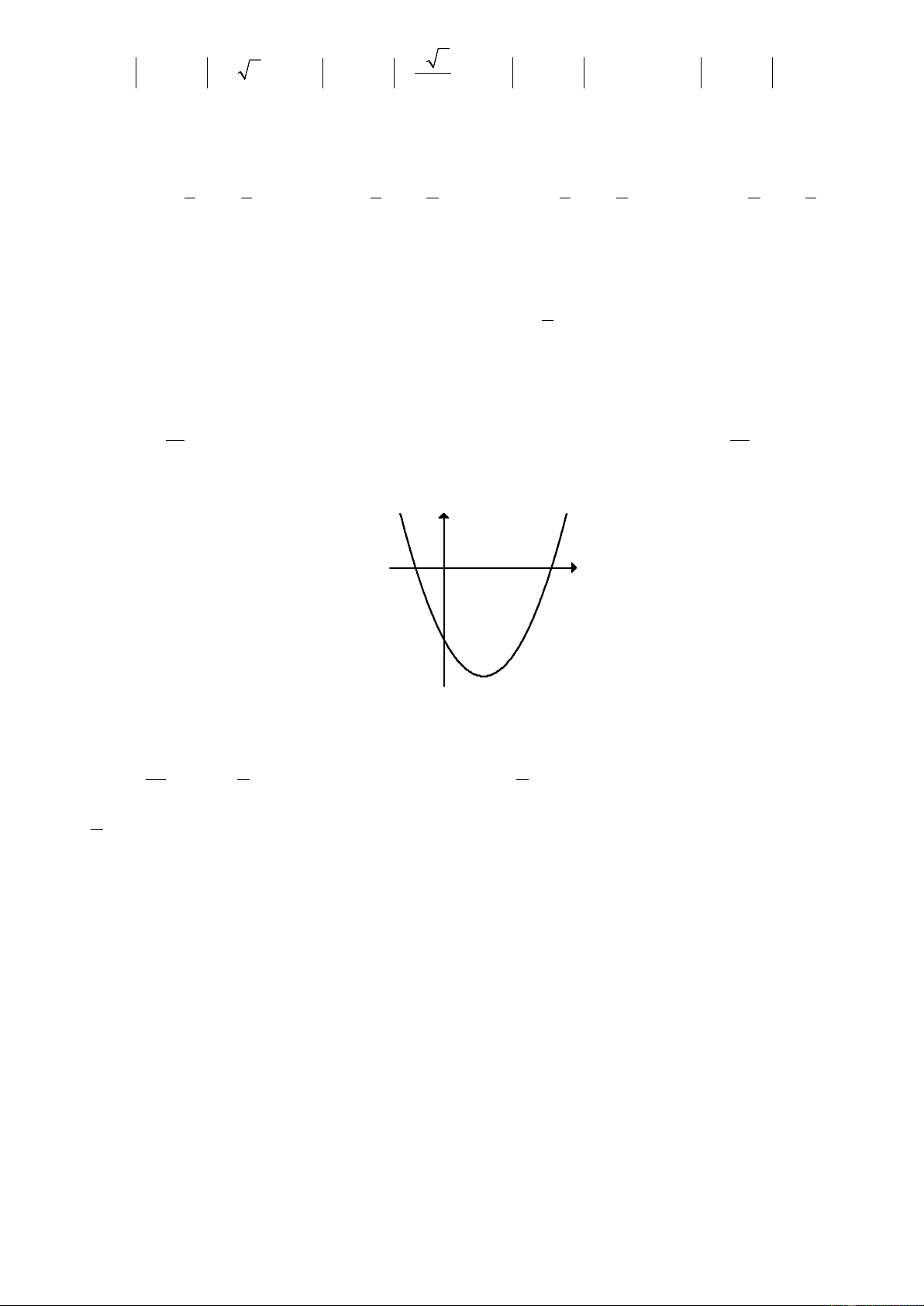
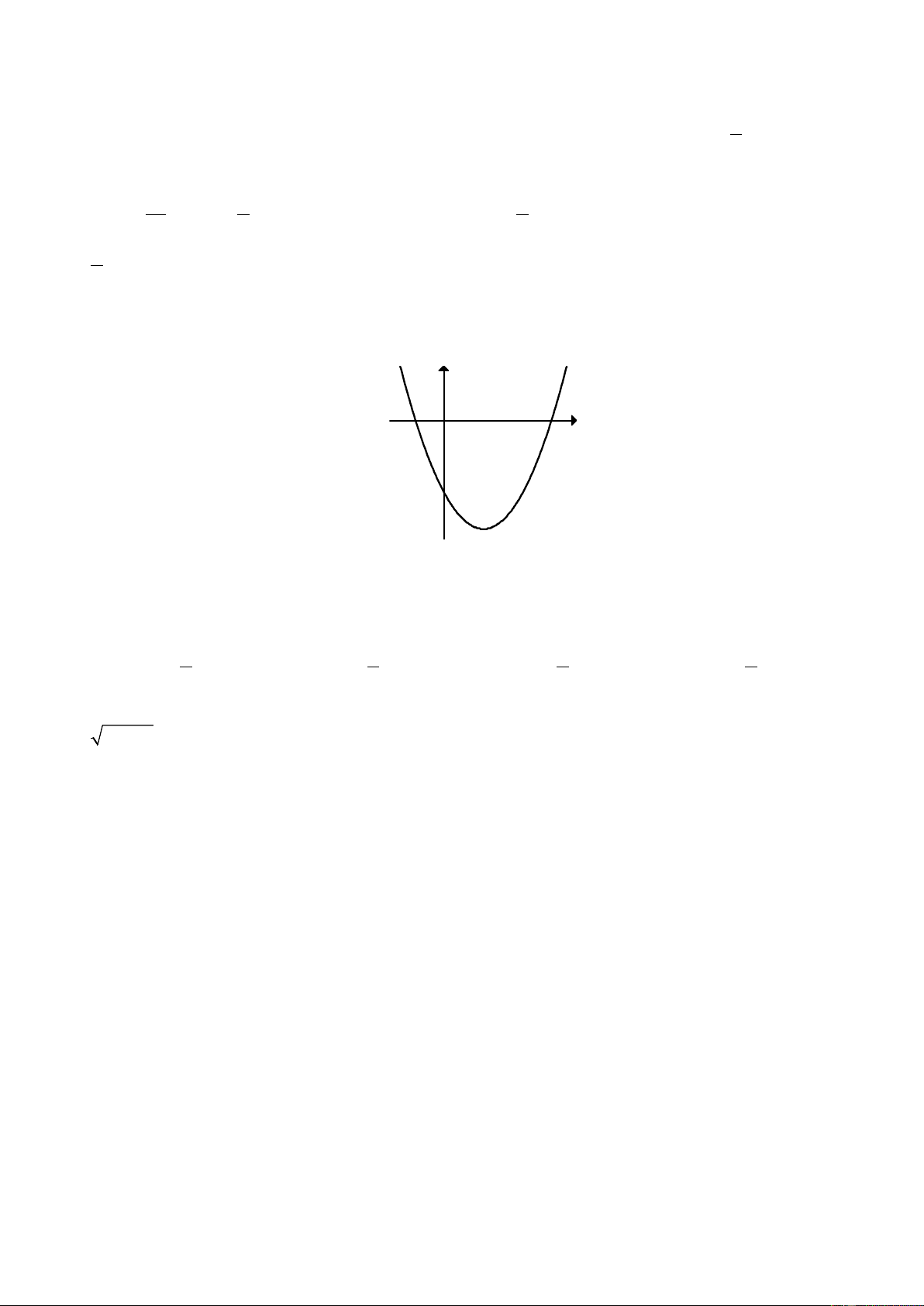
Câu 17: Đồ thị hình bên dưới là đồ thị của hàm số nào?
Trang 2/6 - Mã đề thi 134 y 1 1 x O ` A. 2
y = x − 3x +1. B. 2
y = 2x − 3x +1. C. 2
y = −x + 3x −1. D. 2 y = 2
− x + 3x −1.
Câu 18: Phương trình 2
ax + bx + c = ( 0 0
a ≠ ) có hai nghiệm phân biệt cùng dấu khi và chỉ khi: ∆ > 0 ∆ > 0 ∆ ≥ 0 ∆ > 0 A.  . B.  . C.  . D.  . P > 0 S < 0 P > 0 S > 0  
Câu 19: Cho tam giác đều ABC có cạnh bằng a . Tính A . B AC.   3   1   1   A. 2 A . B AC = a . B. 2 A . B AC = a . C. 2 A . B AC = − a . D. 2 A . B AC = a . 2 2 2
Câu 20: Cho A = ( ;
−∞ 5], B = (0;+∞) . Tìm A∩ B .
A. A ∩ B = [0;5).
B. A ∩ B = (0;5).
C. A ∩ B = (0;5].
D. A ∩ B = ( ; −∞ +∞).
Câu 21: Tìm tập xác định D của hàm số f ( x) 1 = x +1 + . x A. D =  \ { } 0 . B. D =  \ { 1 − ; } 0 . C. D = [ 1 − ;+∞) \{ } 0 . D. D = [ 1 − ;+∞).      
Câu 22: Trong hệ tọa độ Oxy, cho u = i + 3 j và v = (2; − ) 1 .Tính . u v .         A. . u v = 1 − . B. . u v = 1. C. . u v = (2; 3 − ) . D. . u v = 5 2 .
Câu 23: Đường thẳng nào sau đây song song với đường thẳng y = 2x ? 2 1 A. y = x − 5. B. y = 1− 2 . x C. y = x − 3.
D. y = − 2x + 2. 2 2 
Câu 24: Trong hệ tọa độ Oxy, cho véc tơ a = (3; 4
− ). Đẳng thức nào sau đây đúng?     A. a = 5. B. a = 3. C. a = 4. D. a = 7.
Câu 25: Cho phương trình ( 2 x + ) 1 ( x – ) 1 ( x + )
1 = 0 . Phương trình nào sau đây tương đương với phương trình đã cho? A. 2 x +1 = 0. B. x −1 = 0. C. ( x – ) 1 ( x + ) 1 = 0. D. x +1 = 0.
Câu 26: Trong hệ tọa độ Oxy, cho A(2; 3 − ), B(
4; 7). Tìm tọa độ trung điểm I của đoạn thẳng A . B A. I (2;10). B. I (6; 4). C. I (8; 2 − ) 1 . D. I (3; 2).
Câu 27: Cho hàm số f ( x) 2
= x − x . Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số f ( x) đối xứng qua trục hoành.
Trang 3/6 - Mã đề thi 134
B. f ( x) là hàm số chẵn.
C. Đồ thị của hàm số f ( x) đối xứng qua gốc tọa độ.
D. f ( x) là hàm số lẻ.
Câu 28: Tính tổng tất cả các nghiệm của phương trình x + 2 = 2 x − 2 . 1 2 20 A. . B. . C. 6. D. . 2 3 3
Câu 29: Hãy liệt kê các phần tử của tập hợp X = { 2
x ∈  | 2x − 5x + 3 = } 0 . 3  3 A. X = { } 1 . B. X =  . C. X = { } 0 . D. X = 1  ; . 2  2 1 Câu 30: Cho sin α = , với 0 0
90 < α < 180 . Tính cosα. 3 2 2 2 2 2 2 A. cosα = . B. cosα = − . C. cosα = . D. cosα = − . 3 3 3 3
Câu 31: Tìm tất cả các giá trị của tham số m để hai đồ thị hàm số 2
y = −x − 2x + 3 và 2
y = x − m có điểm chung. 7 7 7 7 A. m = − . B. m > − . C. m ≥ − . D. m < − . 2 2 2 2
Câu 32: Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình
2x + m = x −1 có nghiệm duy nhất? A. 4. B. 3. C. 1. D. 2.
Câu 33: Cho hai tập A = [0;5]; B = (2a;3a + ] 1 , với a > 1
− . Tìm tất cả các giá trị của a để A ∩ B ≠ . ∅  5  5 a <  a ≥  2 2 1 5 1 5 A.  . B.  . C. − ≤ a < . D. − ≤ a ≤ . 1  1  3 2 3 2 a ≥ −  a < −  3  3         
Câu 34: Cho hai véc tơ a và b thỏa mãn các điều kiện 1 a =
b = 1, a − 2b = 15. Đặt u = a + b và 2     
v = 2k a − b, k ∈ .
 Tìm tất cả các giá trị của k sao cho (u v) 0 , = 60 . 3 5 3 5 17 17 A. k = 4 + . B. k = 4 ± . C. k = 5 + . D. k = 5 ± . 2 2 2 2 x y
Câu 35: Đường thẳng d :
+ = 1, với a ≠ 0; b ≠ 0, đi qua điểm M ( 1
− ;6) và tạo với các tia Ox, Oy a b
một tam giác có diện tích bằng 4 . Tính S = a + 2b . 5 − + 7 7 74 A. S = 10. B. S = 6. C. S = . D. S = − . 3 3
Câu 36: Cho biết m ≠ 0 và n ≠ 0 là các nghiệm của phương trình 2
x + mx + n = 0. Tính tổng m + . n 1 1
A. m + n = .
B. m + n = − .
C. m + n = −1.
D. m + n = 1. 2 2
Trang 4/6 - Mã đề thi 134
Câu 37: Cho tam giác ABC có A( 2
− ;7), B(3;5),C (1; 4
− ) . Biết rằng trực tâm của tam giác ABC là điểm  a b b H ; 
 , với a,b, ,
m n là các số nguyên dương và a ,
là các phân số tối giản. Tính  m n m n a b T = + . m n 95 43 72 54 A. T = . B. T = . C. T = . D. T = . 9 4 7 5
Câu 38: Biết rằng hàm số 2
y = ax + bx + c ( 0
a ≠ ) đạt cực tiểu bằng 4 tại x = 2 và có đồ thị hàm số
đi qua điểm A(0;6). Tính tích P = . abc 3 A. P = 6. − B. P = 3. − C. P = 6. D. P = . 2
Câu 39: Cho mệnh đề: 2 x
∀ ∈ R, x − 2 + a > 0, với a là số thực cho trước. Tìm a để mệnh đề đúng. A. a ≤ 2 . B. a > 2 . C. a ≥ 2 . D. a = 2 .
Câu 40: Có tất cả bao nhiêu giá trị nguyên của tham số m ∈[ 10
− ;10] để phương trình ( 2
m − 9) x = 3m(m − 3) có nghiệm duy nhất ? A. 2. B. 21. C. 19. D. 18.
Câu 41: Giả sử phương trình 2
2x − 4mx −1 = 0 (với m là tham số) có hai nghiệm x , x . Tìm giá trị 1 2
nhỏ nhất của biểu thức T = x − x . 1 2 2 2 A. min T = . B. min T = 2. C. min T = 2. D. min T = . 3 2
Câu 42: Cho 5 điểm phân biệt M , N, P,Q, .
R Mệnh đề nào sau đây đúng?
     
     
A. MN + PQ + RN + NP + QR = . MP
B. MN + PQ + RN + NP + QR = P . R
     
     
C. MN + PQ + RN + NP + QR = . MR
D. MN + PQ + RN + NP + QR = MN. Câu 43: Cho hàm số ( ) 2
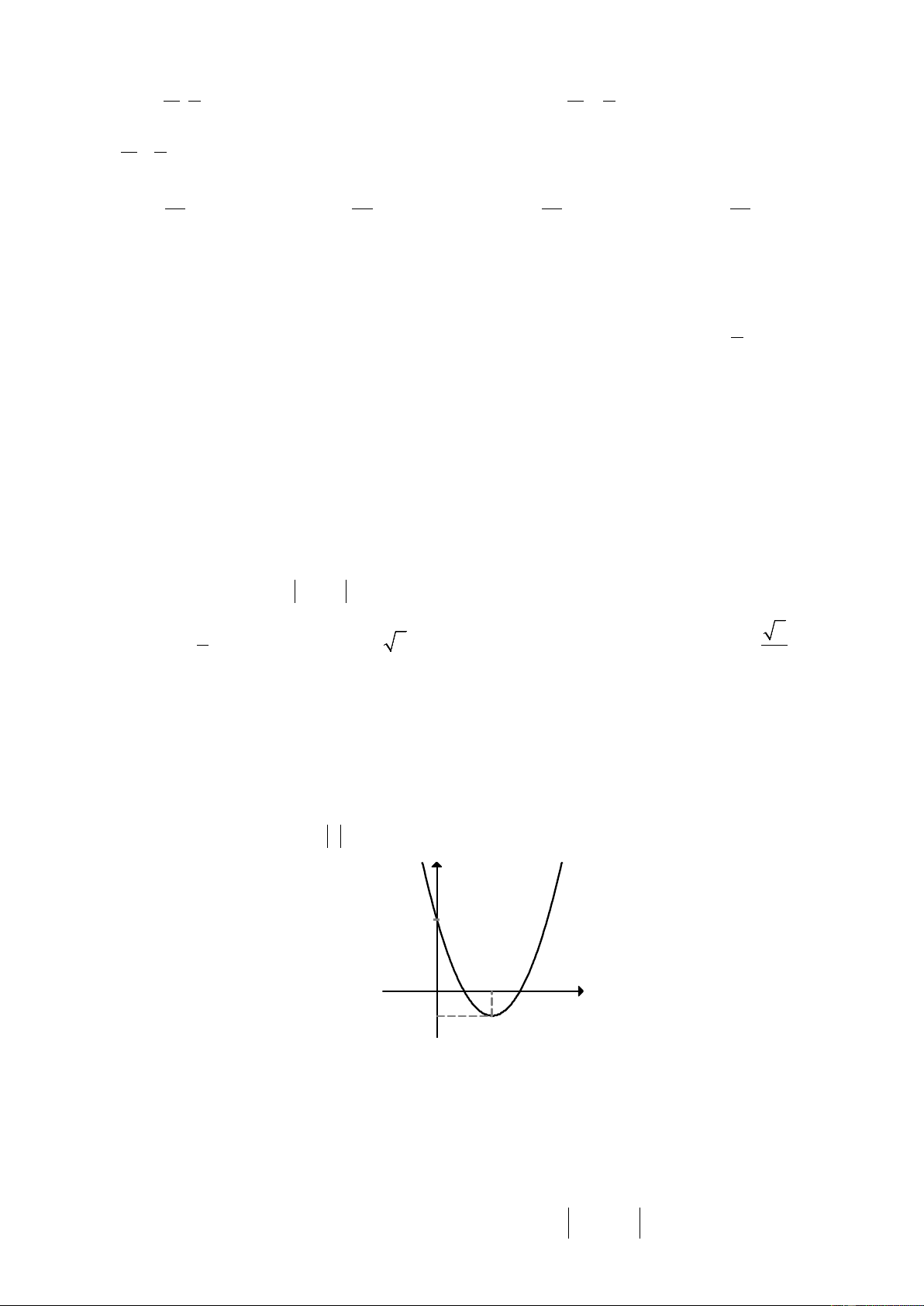
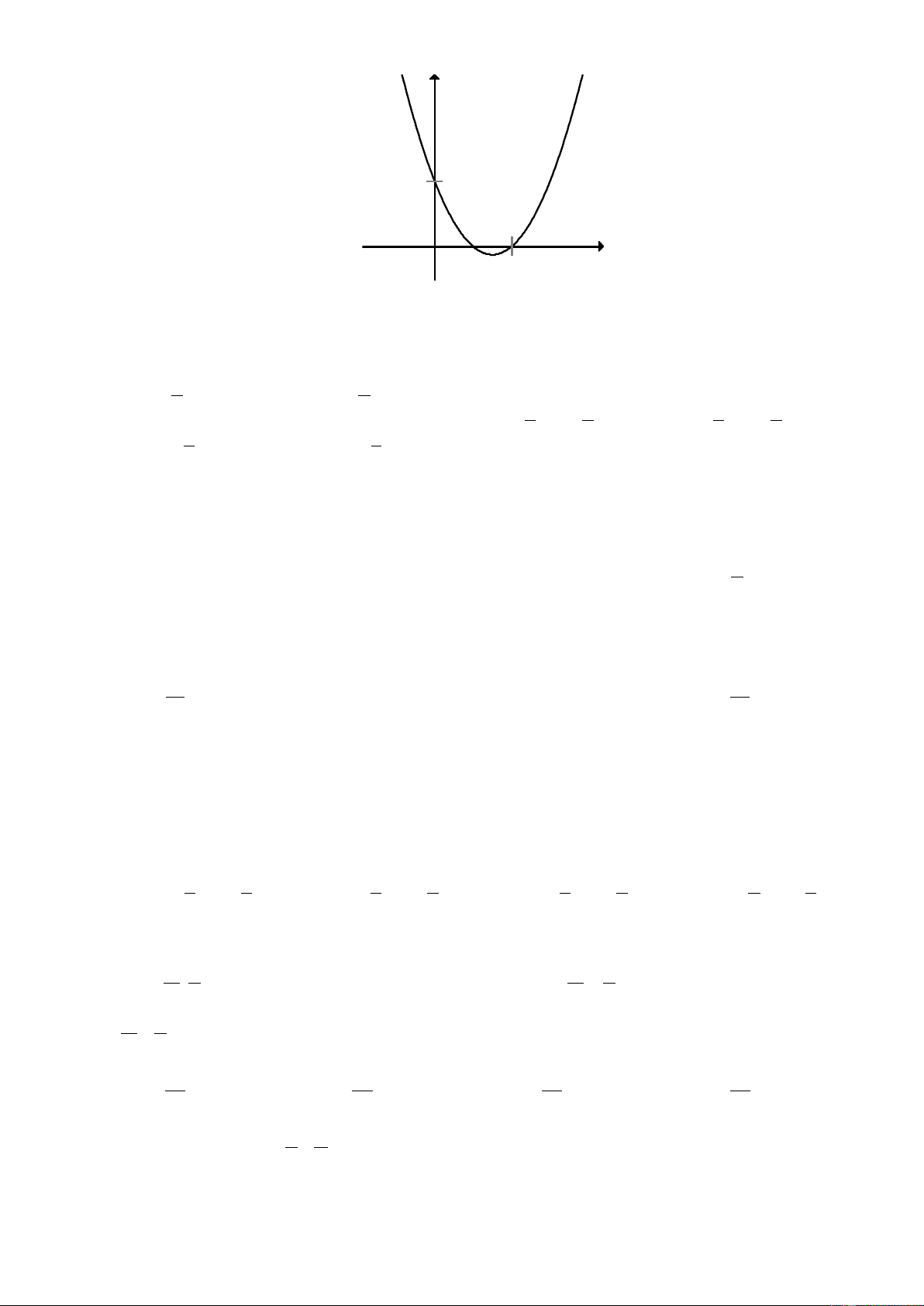
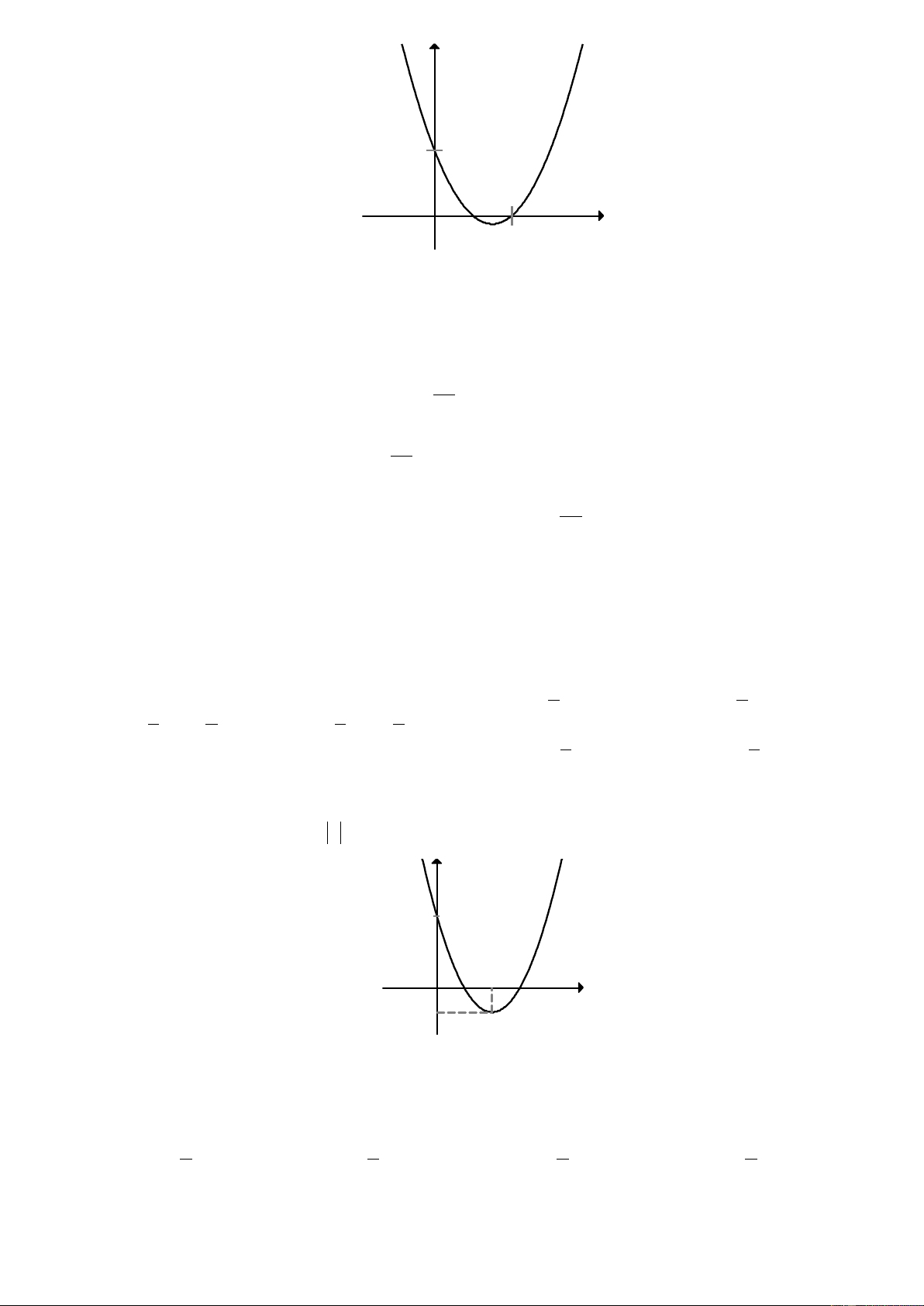
f x = ax + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số m thì phương trình f ( x ) −1= m có đúng 3 nghiệm phân biệt. y 3 x O 2 -1 ` A. 2 − < m < 2. B. m = 3. C. m > 3. D. m = 2.
Câu 44: Cho hình bình hành ABC .
D Gọi G là trọng tâm của tam giác ABC . Mệnh đề nào sau đây
đúng?    
   
A. GA + GC + GD = C . D
B. GA + GC + GD = B . D
   
   
C. GA + GC + GD = . O
D. GA + GC + GD = . DB  
Câu 45: Cho tam giác ABC vuông cân tại A có AB = a . Tính AB + AC .
Trang 5/6 - Mã đề thi 134  
  a 2    
A. AB + AC = a 2.
B. AB + AC = .
C. AB + AC = 2 . a
D. AB + AC = . a 2  
Câu 46: Cho tứ giác ABCD, trên cạnh AB, CD lấy lần lượt các điểm M , N sao cho 3 AM = 2 AB và     
3 DN = 2 DC. Tính vectơ MN theo hai vectơ AD, BC.
 1  1 
 1  2 
 1  2 
 2  1  A. MN = AD +
BC. B. MN = AD −
BC. C. MN = AD +
BC. D. MN = AD + BC. 3 3 3 3 3 3 3 3
Câu 47: Gọi S là tập hợp các giá trị của tham số m sao cho parabol ( P) 2
: y = x − 4x + m cắt Ox tại hai điểm phân biệt ,
A B thỏa mãn OA = 3 .
OB Tính tổng T các phần tử của S. 3 A. T = 3. B. T = 15. − C. T = . D. T = 9. − 2
Câu 48: Trong hệ tọa độ Oxy , cho hai điểm A(2; 3 − ), B(3; 4
− ). Tìm tọa độ điểm M trên trục hoành
sao cho chu vi tam giác AMB nhỏ nhất. 18  17  A. M ; 0 .   B. M (4;0). C. M (3;0). D. M ; 0 .    7   7  Câu 49: Cho hàm số 2
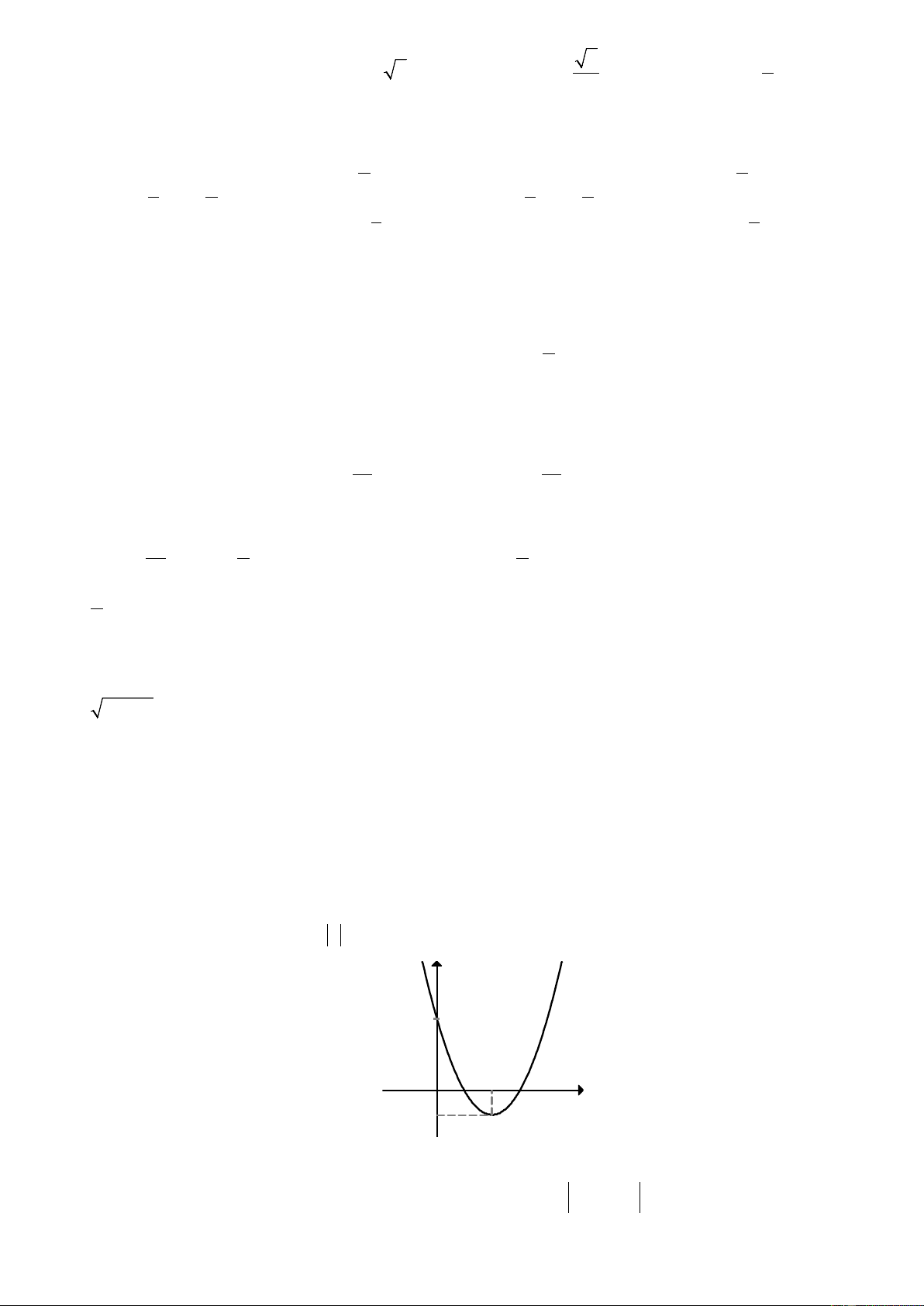
y = ax + bx + c có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng? y x O ` A. a > 0, b < 0, c < 0. B. a > 0, b < 0, 0 c > . C. a > 0, b > 0, 0 c > . D. a < 0, b < 0, c < 0.
Câu 50: Cho biết tập hợp tất cả các giá trị của tham số m để phương trình  1   1   a  2 2 x + − 3 x + − 2m +1 = 0    
có nghiệm là S = − ; +∞ 
 , với a,b là các số nguyên dương và 2  x   x   b
a là phân số tối giản. Tính T = a + .b b A. T = 13. B. T = 17. C. T = 49. D. T = 3. ----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Trang 6/6 - Mã đề thi 134
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA THANH HÓA (Lần thứ 1)
TRƯỜNG THPT TRIỆU SƠN 3 NĂM HỌC 2017-2018 ĐỀ CHÍNH THỨC MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề) Mã đề thi 210
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
Câu 1: Tìm tập xác định D của hàm số f ( x) 1 = x +1 + . x A. D =  \ { } 0 . B. D = [ 1 − ;+∞). C. D =  \ { 1 − ; } 0 . D. D = [ 1 − ;+∞) \{ } 0 .    
Câu 2: Trong hệ tọa độ Oxy, cho a = (2;5), b = (3; 7
− ) . Tính góc giữa hai véctơ a và b . A. 60 . o B. 45 . o C. 135 . o D. 120 . o
Câu 3: Đường thẳng nào sau đây song song với đường thẳng y = 2x ? 1 2 A. y = x − 3. B. y = x − 5.
C. y = − 2x + 2. D. y = 1− 2 . x 2 2
Câu 4: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A. (−∞;−2) ∪[5;+∞). B. (−∞;−2]∪[5;+∞). C. (−∞;−2] ∪ (5;+∞). D. (−∞;−2) ∪ (5;+∞).
Câu 5: Tìm parabol ( P) 2
: y = ax + 3x − 2, biết rằng parabol có trục đối xứng x = 3. − 1 1 1 A. 2
y = x + 3x − 2. B. 2 y = x + 3x − 2. C. 2 y = x − 3x − 2. D. 2 y = x + x − 2. 2 2 2
Câu 6: Tìm tất cả các giá trị của tham số m để hàm số y = (m − 2) x + 2m đồng biến trên .  A. m ≥ 2. B. m > 2. C. m ≤ 2. D. m < 2.
Câu 7: Cho A = ( ;
−∞ 5], B = (0;+∞) . Tìm A∩ B .
A. A ∩ B = (0;5].
B. A ∩ B = (0;5).
C. A ∩ B = ( ;
−∞ +∞). D. A∩ B = [0;5).
2x − y + 3 = 0
Câu 8: Tìm nghiệm của hệ phương trình  . −x + 4y = 2     A. ( x y) 10 1 , = ; .  
B. ( x, y) = ( 2; − − ) 1 . C. ( x y) 10 1 , = − ; . 
D. ( x, y) = (2; ) 1 .  7 7   7 7 
Câu 9: Điều kiện xác định của phương trình x −1 + x − 2 = x − 3 là: A. x ≥ 3. B. x ≥ 2. C. x ≥ 1. D. x > 3.
Câu 10: Hãy liệt kê các phần tử của tập hợp X = { 2
x ∈  | 2x − 5x + 3 = } 0 .
Trang 1/6 - Mã đề thi 210 3  3 A. X = { } 1 . B. X =  . C. X = { } 0 . D. X = 1  ; . 2  2
Câu 11: Cho phương trình ( 2 x + ) 1 ( x – ) 1 ( x + )
1 = 0 . Phương trình nào sau đây tương đương với phương trình đã cho? A. 2 x +1 = 0. B. x −1 = 0. C. ( x – ) 1 ( x + ) 1 = 0. D. x +1 = 0.
Câu 12: Trong hệ tọa độ Oxy, cho tam giác ABC có A(3;5), B ( 1; 2), C (
5; 2). Tìm tọa độ trọng tâm
G của tam giác ABC. A. G ( 2;3). B. G (4;0). C. G ( 3 − ;4). D. G (3;3).
Câu 13: Cho tam giác ABC. Khẳng định nào sau đây đúng?
  
  
  
  
A. AB + AC = BC.
B. AB + CA = . CB
C. CA + BA = . CB
D. AA + BB = A . B
Câu 14: Trong hệ tọa độ Oxy, cho véc tơ a = (3; 4
− ). Đẳng thức nào sau đây đúng?     A. a = 5. B. a = 3. C. a = 4. D. a = 7.
Câu 15: Mệnh đề nào sau đây đúng?
A. Có vô số vectơ cùng phương với mọi vectơ.
B. Có duy nhất một vectơ cùng phương với mọi vectơ.
C. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 16: Trong hệ tọa độ Oxy, cho A(2; 3 − ), B(
4; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB A. I (2;10). B. I (6; 4). C. I (8; 2 − ) 1 . D. I (3; 2).
Câu 17: Phương trình 2
ax + bx + c = ( 0 0
a ≠ ) có hai nghiệm phân biệt cùng dấu khi và chỉ khi: ∆ > 0 ∆ > 0 ∆ ≥ 0 ∆ > 0 A.  . B.  . C.  . D.  . P > 0 S < 0 P > 0 S > 0
mx − y = m
Câu 18: Tìm điều kiện của tham số m để hệ phương trình  có nghiệm duy nhất. −x + my = 1 − A. m ≠ 1. ± B. m ≠ 1. − C. m ≠ 1. D. m = 1. ±      
Câu 19: Trong hệ tọa độ Oxy, cho u = i + 3 j và v = (2; − ) 1 .Tính . u v .         A. . u v = 1. B. . u v = 5 2 . C. . u v = (2; 3 − ) . D. . u v = 1 − .
Câu 20: Hàm số y = 2x −1 có đồ thị là hình nào trong các hình sau? ` y y y y x x x x O 1 O 1 O 1 O 1 -1 -1 -1 -1 Hình 1 Hình 2 Hình 3 Hình 4
Trang 2/6 - Mã đề thi 210 A. Hình 4. B. Hình 1. C. Hình 2. D. Hình 3.    
Câu 21: Trong hệ tọa độ Oxy, cho a = (3; 4 − ), b = ( 1
− ;2). Tìm tọa độ của a + . b        
A. a + b = (2; 2 − ).
B. a + b = (4; 6 − ).
C. a + b = ( 4; − 6).
D. a + b = ( 3 − ; 8 − ).
Câu 22: Tìm mệnh đề phủ định của mệnh đề: 2 x
∀ ∈ R, x + x + 5 > 0. A. 2 x
∃ ∈ R, x + x + 5 < 0. B. 2 x
∃ ∈ R, x + x + 5 ≤ 0. C. 2 x
∀ ∈ R, x + x + 5 ≤ 0. D. 2 x
∀ ∈ R, x + x + 5 < 0.  
Câu 23: Cho tam giác đều ABC có cạnh bằng a . Tính A . B AC.   3   1     1 A. 2 A . B AC = a . B. 2 A . B AC = − a . C. 2 A . B AC = a . D. 2 A . B AC = a . 2 2 2
Câu 24: Trong các hệ thức sau, hệ thức nào đúng?          
A. a = ± a .
B. (a)2 = a . C. (a)2 = . a D. .
a b = a . b . Câu 25: Cho hàm số 2
y = ax + bx + c ( 0
a > ) . Khẳng định nào sau đây là sai?  b
A. Hàm số nghịch biến trên khoảng ; −∞ − .    2a
B. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.  b
C. Hàm số đồng biến trên khoảng − ; +∞ .    2ab
D. Đồ thị của hàm số có trục đối xứng là đường thẳng x = − . 2a
Câu 26: Cho hàm số f ( x) 2
= x − x . Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số f ( x) đối xứng qua trục hoành.
B. f ( x) là hàm số chẵn.
C. Đồ thị của hàm số f ( x) đối xứng qua gốc tọa độ.
D. f ( x) là hàm số lẻ.
Câu 27: Tính tổng tất cả các nghiệm của phương trình x + 2 = 2 x − 2 . 1 2 20 A. . B. . C. 6. D. . 2 3 3 1 Câu 28: Cho sin α = , với 0 0
90 < α < 180 . Tính cosα. 3 2 2 2 2 2 2 A. cosα = . B. cosα = − . C. cosα = . D. cosα = − . 3 3 3 3        
Câu 29: Trong hệ tọa độ Oxy, cho u = 2i − j và v = i + xj . Tìm x sao cho u và v cùng phương. 1 1 A. x = . B. x = 1 − . C. x = 2 . D. x = − . 4 2
Trang 3/6 - Mã đề thi 210
Câu 30: Đồ thị hình bên dưới là đồ thị của hàm số nào? y 1 1 x O ` A. 2
y = −x + 3x −1. B. 2 y = 2
− x + 3x −1. C. 2
y = 2x − 3x +1. D. 2
y = x − 3x +1.
Câu 31: Cho hai tập A = [0;5]; B = (2a;3a + ] 1 , với a > 1
− . Tìm tất cả các giá trị của a để A ∩ B ≠ . ∅  5  5 a <  a ≥  2 2 1 5 1 5 A.  . B.  . C. − ≤ a < . D. − ≤ a ≤ . 1  1  3 2 3 2 a ≥ −  a < −  3  3
Câu 32: Biết rằng hàm số 2
y = ax + bx + c ( 0
a ≠ ) đạt cực tiểu bằng 4 tại x = 2 và có đồ thị hàm số
đi qua điểm A(0;6). Tính tích P = . abc 3 A. P = 6. B. P = 6. − C. P = 3. − D. P = . 2
Câu 33: Trong hệ tọa độ Oxy , cho hai điểm A(2; 3 − ), B(3; 4
− ). Tìm tọa độ điểm M trên trục hoành
sao cho chu vi tam giác AMB nhỏ nhất. 18  17  A. M ; 0 .   B. M (4;0). C. M (3;0). D. M ; 0 .    7   7 
Câu 34: Cho mệnh đề: 2 x
∀ ∈ R, x − 2 + a > 0, với a là số thực cho trước. Tìm a để mệnh đề đúng. A. a = 2 . B. a ≥ 2 . C. a > 2 .
D. a ≤ 2 .  
Câu 35: Cho tứ giác ABCD, trên cạnh AB, CD lấy lần lượt các điểm M , N sao cho 3 AM = 2 AB và     
3 DN = 2 DC. Tính vectơ MN theo hai vectơ AD, BC.
 1  1 
 1  2 
 1  2 
 2  1  A. MN = AD +
BC. B. MN = AD +
BC. C. MN = AD −
BC. D. MN = AD + BC. 3 3 3 3 3 3 3 3
Câu 36: Cho tam giác ABC có A( 2
− ;7), B(3;5),C (1; 4
− ) . Biết rằng trực tâm của tam giác ABC là điểm  a b b H ; 
 , với a,b, ,
m n là các số nguyên dương và a ,
là các phân số tối giản. Tính  m n m n a b T = + . m n 95 43 72 54 A. T = . B. T = . C. T = . D. T = . 9 4 7 5 x y
Câu 37: Đường thẳng d :
+ = 1, với a ≠ 0; b ≠ 0, đi qua điểm M ( 1
− ;6) và tạo với các tia Ox, Oy a b
một tam giác có diện tích bằng 4 . Tính S = a + 2b .
Trang 4/6 - Mã đề thi 210 74 5 − + 7 7 A. S = 10. B. S = − . C. S = 6. D. S = . 3 3
Câu 38: Giả sử phương trình 2
2x − 4mx −1 = 0 (với m là tham số) có hai nghiệm x , x . Tìm giá trị 1 2
nhỏ nhất của biểu thức T = x − x . 1 2 2 2 A. min T = . B. min T = 2. C. min T = 2. D. min T = . 3 2
Câu 39: Có tất cả bao nhiêu giá trị nguyên của tham số m ∈[ 10
− ;10] để phương trình ( 2
m − 9) x = 3m(m − 3) có nghiệm duy nhất ? A. 2. B. 21. C. 19. D. 18.         
Câu 40: Cho hai véc tơ a và b thỏa mãn các điều kiện 1 a =
b = 1, a − 2b = 15. Đặt u = a + b và 2     
v = 2k a − b, k ∈ .
 Tìm tất cả các giá trị của k sao cho (u v) 0 , = 60 . 3 5 17 17 3 5 A. k = 4 + . B. k = 5 + . C. k = 5 ± . D. k = 4 ± . 2 2 2 2
Câu 41: Cho biết m ≠ 0 và n ≠ 0 là các nghiệm của phương trình 2
x + mx + n = 0. Tính tổng m + . n 1 1
A. m + n = − .
B. m + n = 1.
C. m + n = .
D. m + n = −1. 2 2 Câu 42: Cho hàm số ( ) 2
f x = ax + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số m thì phương trình f ( x ) −1= m có đúng 3 nghiệm phân biệt. y 3 x O 2 -1 ` A. 2 − < m < 2. B. m = 3. C. m > 3. D. m = 2.
Câu 43: Cho 5 điểm phân biệt M , N, P,Q, .
R Mệnh đề nào sau đây đúng?
     
     
A. MN + PQ + RN + NP + QR = P . R
B. MN + PQ + RN + NP + QR = . MR
     
     
C. MN + PQ + RN + NP + QR = . MP
D. MN + PQ + RN + NP + QR = MN.  
Câu 44: Cho tam giác ABC vuông cân tại A có AB = a . Tính AB + AC .  
  a 2    
A. AB + AC = a 2.
B. AB + AC = .
C. AB + AC = 2 . a
D. AB + AC = . a 2
Câu 45: Cho hình bình hành ABC .
D Gọi G là trọng tâm của tam giác ABC . Mệnh đề nào sau đây
đúng?    
   
A. GA + GC + GD = . O
B. GA + GC + GD = C . D
   
   
C. GA + GC + GD = B . D
D. GA + GC + GD = . DB
Trang 5/6 - Mã đề thi 210
Câu 46: Gọi S là tập hợp các giá trị của tham số m sao cho parabol ( P) 2
: y = x − 4x + m cắt Ox tại hai điểm phân biệt ,
A B thỏa mãn OA = 3 .
OB Tính tổng T các phần tử của S. 3 A. T = 3. B. T = 15. − C. T = 9. − D. T = . 2
Câu 47: Cho biết tập hợp tất cả các giá trị của tham số m để phương trình  1   1   a  2 2 x + − 3 x + − 2m +1 = 0    
có nghiệm là S = − ; +∞ 
 , với a,b là các số nguyên dương và 2  x   x   b
a là phân số tối giản. Tính T = a + .b b A. T = 17. B. T = 49. C. T = 3. D. T = 13. Câu 48: Cho hàm số 2
y = ax + bx + c có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng? y x O ` A. a > 0, b < 0, c < 0. B. a > 0, b < 0, 0 c > . C. a > 0, b > 0, 0 c > . D. a < 0, b < 0, c < 0.
Câu 49: Tìm tất cả các giá trị của tham số m để hai đồ thị hàm số 2
y = −x − 2x + 3 và 2
y = x − m có điểm chung. 7 7 7 7 A. m ≥ − . B. m < − . C. m > − . D. m = − . 2 2 2 2
Câu 50: Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình
2x + m = x −1 có nghiệm duy nhất? A. 1. B. 2. C. 4. D. 3. ----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Trang 6/6 - Mã đề thi 210
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA THANH HÓA (Lần thứ 1)
TRƯỜNG THPT TRIỆU SƠN 3 NĂM HỌC 2017-2018 ĐỀ CHÍNH THỨC MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề) Mã đề thi 356
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
Câu 1: Tính tổng tất cả các nghiệm của phương trình x + 2 = 2 x − 2 . 2 20 1 A. . B. . C. . D. 6. 3 3 2
Câu 2: Phương trình 2
ax + bx + c = ( 0 0
a ≠ ) có hai nghiệm phân biệt cùng dấu khi và chỉ khi: ∆ > 0 ∆ > 0 ∆ ≥ 0 ∆ > 0 A.  . B.  . C.  . D.  . P > 0 S < 0 P > 0 S > 0
2x − y + 3 = 0
Câu 3: Tìm nghiệm của hệ phương trình  . −x + 4y = 2     A. ( x y) 10 1 , = ; .  
B. ( x, y) = ( 2; − − ) 1 . C. ( x y) 10 1 , = − ; . 
D. ( x, y) = (2; ) 1 .  7 7   7 7 
Câu 4: Tìm tất cả các giá trị của tham số m để hàm số y = (m − 2) x + 2m đồng biến trên .  A. m ≥ 2. B. m > 2. C. m < 2. D. m ≤ 2.        
Câu 5: Trong hệ tọa độ Oxy, cho u = 2i − j và v = i + xj . Tìm x sao cho u và v cùng phương. 1 1 A. x = . B. x = 1 − . C. x = 2 . D. x = − . 4 2
Câu 6: Cho tam giác ABC. Khẳng định nào sau đây đúng?
  
  
  
  
A. AB + AC = BC.
B. AB + CA = . CB
C. CA + BA = . CB
D. AA + BB = A . B
Câu 7: Cho A = ( ;
−∞ 5], B = (0;+∞) . Tìm A∩ B .
A. A ∩ B = ( ;
−∞ +∞). B. A∩ B = (0;5].
C. A ∩ B = [0;5).
D. A ∩ B = (0;5).
Câu 8: Hãy liệt kê các phần tử của tập hợp X = { 2
x ∈  | 2x − 5x + 3 = } 0 . 3  3 A. X =  . B. X = { } 1 . C. X = { } 0 . D. X = 1  ; . 2  2
Câu 9: Tìm mệnh đề phủ định của mệnh đề: 2 x
∀ ∈ R, x + x + 5 > 0. A. 2 x
∃ ∈ R, x + x + 5 < 0. B. 2 x
∃ ∈ R, x + x + 5 ≤ 0. C. 2 x
∀ ∈ R, x + x + 5 ≤ 0. D. 2 x
∀ ∈ R, x + x + 5 < 0.      
Câu 10: Trong hệ tọa độ Oxy, cho u = i + 3 j và v = (2; − ) 1 .Tính . u v .         A. . u v = 1. B. . u v = 5 2 . C. . u v = (2; 3 − ) . D. . u v = 1 − .
Trang 1/6 - Mã đề thi 356
Câu 11: Cho phương trình ( 2 x + ) 1 ( x – ) 1 ( x + )
1 = 0 . Phương trình nào sau đây tương đương với phương trình đã cho? A. x −1 = 0. B. ( x – ) 1 ( x + ) 1 = 0. C. 2 x +1 = 0. D. x +1 = 0.
Câu 12: Cho hàm số f ( x) 2
= x − x . Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số f ( x) đối xứng qua gốc tọa độ.
B. Đồ thị của hàm số f ( x) đối xứng qua trục hoành.
C. f ( x) là hàm số lẻ.
D. f ( x) là hàm số chẵn.
Câu 13: Trong các hệ thức sau, hệ thức nào đúng?          
A. a = ± a .
B. (a)2 = a . C. (a)2 = . a D. .
a b = a . b .
Câu 14: Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có vô số vectơ cùng phương với mọi vectơ.
C. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
mx − y = m
Câu 15: Tìm điều kiện của tham số m để hệ phương trình  có nghiệm duy nhất. −x + my = 1 − A. m ≠ 1. ± B. m ≠ 1. − C. m ≠ 1. D. m = 1. ± 1 Câu 16: Cho sin α = , với 0 0
90 < α < 180 . Tính cosα. 3 2 2 2 2 2 2 A. cosα = . B. cosα = − . C. cosα = . D. cosα = − . 3 3 3 3 
Câu 17: Trong hệ tọa độ Oxy, cho véc tơ a = (3; 4
− ). Đẳng thức nào sau đây đúng?     A. a = 3. B. a = 5. C. a = 7. D. a = 4.
Câu 18: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A. (−∞;−2) ∪ (5;+∞). B. (−∞;−2] ∪ (5;+∞). C. (−∞;−2) ∪[5;+∞). D. (−∞;−2]∪[5;+∞).
Câu 19: Hàm số y = 2x −1 có đồ thị là hình nào trong các hình sau?
Trang 2/6 - Mã đề thi 356 ` y y y y x x x x O 1 O 1 O 1 O 1 -1 -1 -1 -1 Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 4. B. Hình 3. C. Hình 2. D. Hình 1.
Câu 20: Điều kiện xác định của phương trình x −1 + x − 2 = x − 3 là: A. x ≥ 1. B. x ≥ 2. C. x > 3. D. x ≥ 3.
Câu 21: Đường thẳng nào sau đây song song với đường thẳng y = 2x ? 2 1 A. y = x − 5. B. y = x − 3.
C. y = − 2x + 2. D. y = 1− 2 . x 2 2  
Câu 22: Cho tam giác đều ABC có cạnh bằng a . Tính A . B AC.   3   1     1 A. 2 A . B AC = a . B. 2 A . B AC = − a . C. 2 A . B AC = a . D. 2 A . B AC = a . 2 2 2    
Câu 23: Trong hệ tọa độ Oxy, cho a = (2;5), b = (3; 7
− ) . Tính góc giữa hai véctơ a và b . A. 135 . o B. 120 . o C. 60 . o D. 45 . o
Câu 24: Trong hệ tọa độ Oxy, cho tam giác ABC có A(3;5), B ( 1; 2), C (
5; 2). Tìm tọa độ trọng tâm
G của tam giác ABC. A. G ( 2;3). B. G (4;0). C. G (3;3). D. G ( 3 − ;4).
Câu 25: Tìm parabol ( P) 2
: y = ax + 3x − 2, biết rằng parabol có trục đối xứng x = 3. − 1 1 1 A. 2 y = x + x − 2. B. 2
y = x + 3x − 2. C. 2 y = x + 3x − 2. D. 2 y = x − 3x − 2. 2 2 2
Câu 26: Tìm tập xác định D của hàm số f ( x) 1 = x +1 + . x A. D =  \ { 1 − ; } 0 . B. D = [ 1 − ;+∞). C. D = [ 1 − ;+∞) \{ } 0 . D. D =  \ { } 0 .
Câu 27: Trong hệ tọa độ Oxy, cho A(2; 3 − ), B(
4; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB A. I (6; 4). B. I (3; 2). C. I (8; 2 − ) 1 . D. I (2;10).
Câu 28: Đồ thị hình bên dưới là đồ thị của hàm số nào?
Trang 3/6 - Mã đề thi 356 y 1 1 x O ` A. 2
y = 2x − 3x +1. B. 2 y = 2
− x + 3x −1. C. 2
y = −x + 3x −1. D. 2
y = x − 3x +1. Câu 29: Cho hàm số 2
y = ax + bx + c ( 0
a > ) . Khẳng định nào sau đây là sai?
A. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.  b
B. Hàm số nghịch biến trên khoảng ; −∞ − .    2a   b
C. Hàm số đồng biến trên khoảng − ; +∞ .    2ab
D. Đồ thị của hàm số có trục đối xứng là đường thẳng x = − . 2a    
Câu 30: Trong hệ tọa độ Oxy, cho a = (3; 4 − ), b = ( 1
− ;2). Tìm tọa độ của a + . b        
A. a + b = (2; 2 − ).
B. a + b = (4; 6 − ).
C. a + b = ( 3 − ; 8 − ).
D. a + b = ( 4; − 6).
Câu 31: Cho hai tập A = [0;5]; B = (2a;3a + ] 1 , với a > 1
− . Tìm tất cả các giá trị của a để A ∩ B ≠ . ∅  5  5 a < a ≥ 1 5 1 5   2 2 A. − ≤ a ≤ . B. − ≤ a < . C.  . D.  . 3 2 3 2 1  1  a ≥ −  a < −  3  3 Câu 32: Cho hàm số ( ) 2
f x = ax + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số m thì phương trình f ( x ) −1= m có đúng 3 nghiệm phân biệt. y 3 x O 2 -1 ` A. m > 3. B. 2 − < m < 2. C. m = 2. D. m = 3.
Câu 33: Tìm tất cả các giá trị của tham số m để hai đồ thị hàm số 2
y = −x − 2x + 3 và 2
y = x − m có điểm chung. 7 7 7 7 A. m ≥ − . B. m < − . C. m > − . D. m = − . 2 2 2 2
Trang 4/6 - Mã đề thi 356  
Câu 34: Cho tứ giác ABCD, trên cạnh AB, CD lấy lần lượt các điểm M , N sao cho 3 AM = 2 AB và     
3 DN = 2 DC. Tính vectơ MN theo hai vectơ AD, BC.
 1  2 
 1  2 
 2  1 
 1  1  A. MN = AD −
BC. B. MN = AD +
BC. C. MN = AD +
BC. D. MN = AD + BC. 3 3 3 3 3 3 3 3
Câu 35: Cho mệnh đề: 2 x
∀ ∈ R, x − 2 + a > 0, với a là số thực cho trước. Tìm a để mệnh đề đúng. A. a ≥ 2 . B. a = 2 . C. a > 2 . D. a ≤ 2 . x y
Câu 36: Đường thẳng d :
+ = 1, với a ≠ 0; b ≠ 0, đi qua điểm M ( 1
− ;6) và tạo với các tia Ox, Oy a b
một tam giác có diện tích bằng 4 . Tính S = a + 2b . 74 5 − + 7 7 A. S = 10. B. S = − . C. S = 6. D. S = . 3 3         
Câu 37: Cho hai véc tơ a và b thỏa mãn các điều kiện 1 a =
b = 1, a − 2b = 15. Đặt u = a + b và 2     
v = 2k a − b, k ∈ .
 Tìm tất cả các giá trị của k sao cho (u v) 0 , = 60 . 3 5 17 17 3 5 A. k = 4 + . B. k = 5 + . C. k = 5 ± . D. k = 4 ± . 2 2 2 2
Câu 38: Có tất cả bao nhiêu giá trị nguyên của tham số m ∈[ 10
− ;10] để phương trình ( 2
m − 9) x = 3m(m − 3) có nghiệm duy nhất ? A. 2. B. 21. C. 19. D. 18.
Câu 39: Cho tam giác ABC có A( 2
− ;7), B(3;5),C (1; 4
− ) . Biết rằng trực tâm của tam giác ABC là điểm  a b b H ; 
 , với a,b, ,
m n là các số nguyên dương và a ,
là các phân số tối giản. Tính  m n m n a b T = + . m n 54 95 72 43 A. T = . B. T = . C. T = . D. T = . 5 9 7 4
Câu 40: Cho 5 điểm phân biệt M , N, P,Q, .
R Mệnh đề nào sau đây đúng?
     
     
A. MN + PQ + RN + NP + QR = MN.
B. MN + PQ + RN + NP + QR = . MP
     
     
C. MN + PQ + RN + NP + QR = P . R
D. MN + PQ + RN + NP + QR = . MR
Câu 41: Cho hình bình hành ABC .
D Gọi G là trọng tâm của tam giác ABC . Mệnh đề nào sau đây
đúng?    
   
A. GA + GC + GD = . DB
B. GA + GC + GD = C . D
   
   
C. GA + GC + GD = B . D
D. GA + GC + GD = . O
Câu 42: Giả sử phương trình 2
2x − 4mx −1 = 0 (với m là tham số) có hai nghiệm x , x . Tìm giá trị 1 2
nhỏ nhất của biểu thức T = x − x . 1 2 2 2 A. min T = 2. B. min T = . C. min T = . D. min T = 2. 3 2
Trang 5/6 - Mã đề thi 356
Câu 43: Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình
2x + m = x −1 có nghiệm duy nhất? A. 1. B. 2. C. 4. D. 3.
Câu 44: Trong hệ tọa độ Oxy , cho hai điểm A(2; 3 − ), B(3; 4
− ). Tìm tọa độ điểm M trên trục hoành
sao cho chu vi tam giác AMB nhỏ nhất. 17  18  A. M (3;0). B. M ; 0 .   C. M ; 0 .   D. M (4;0).  7   7 
Câu 45: Gọi S là tập hợp các giá trị của tham số m sao cho parabol ( P) 2
: y = x − 4x + m cắt Ox tại hai điểm phân biệt ,
A B thỏa mãn OA = 3 .
OB Tính tổng T các phần tử của S. 3 A. T = 3. B. T = 15. − C. T = 9. − D. T = . 2
Câu 46: Biết rằng hàm số 2
y = ax + bx + c ( 0
a ≠ ) đạt cực tiểu bằng 4 tại x = 2 và có đồ thị hàm số
đi qua điểm A(0;6). Tính tích P = . abc 3 A. P = 3. − B. P = 6. − C. P = . D. P = 6. 2  
Câu 47: Cho tam giác ABC vuông cân tại A có AB = a . Tính AB + AC .    
  a 2  
A. AB + AC = 2 . a
B. AB + AC = . a
C. AB + AC = .
D. AB + AC = a 2. 2 Câu 48: Cho hàm số 2
y = ax + bx + c có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng? y x O ` A. a > 0, b < 0, 0 c > . B. a > 0, b < 0, c < 0. C. a < 0, b < 0, c < 0. D. a > 0, b > 0, 0 c > .
Câu 49: Cho biết m ≠ 0 và n ≠ 0 là các nghiệm của phương trình 2
x + mx + n = 0. Tính tổng m + . n 1 1
A. m + n = 1.
B. m + n = − .
C. m + n = .
D. m + n = −1. 2 2
Câu 50: Cho biết tập hợp tất cả các giá trị của tham số m để phương trình  1   1   a  2 2 x + − 3 x + − 2m +1 = 0    
có nghiệm là S = − ; +∞ 
 , với a,b là các số nguyên dương và 2  x   x   b
a là phân số tối giản. Tính T = a + .b b A. T = 17. B. T = 49. C. T = 3. D. T = 13. ----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Trang 6/6 - Mã đề thi 356
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT KIẾN THỨC THI THPT QUỐC GIA THANH HÓA (Lần thứ 1)
TRƯỜNG THPT TRIỆU SƠN 3 NĂM HỌC 2017-2018 ĐỀ CHÍNH THỨC MÔN: TOÁN KHỐI 10
Thời gian làm bài: 90 phút (Không kể thời gian giao đề) Mã đề thi 483
Họ, tên thí sinh:.........................................................Số báo danh: ......................Lớp:...........
2x − y + 3 = 0
Câu 1: Tìm nghiệm của hệ phương trình  . −x + 4y = 2    
A. ( x, y) = (2; ) 1 . B. ( x y) 10 1 , = − ; . 
C. ( x, y) = ( 2; − − ) 1 . D. ( x y) 10 1 , = ; .    7 7   7 7 
Câu 2: Đồ thị hình bên dưới là đồ thị của hàm số nào? y 1 1 x O ` A. 2
y = 2x − 3x +1. B. 2 y = 2
− x + 3x −1. C. 2
y = −x + 3x −1. D. 2
y = x − 3x +1.
Câu 3: Tìm mệnh đề phủ định của mệnh đề: 2 x
∀ ∈ R, x + x + 5 > 0. A. 2 x
∃ ∈ R, x + x + 5 < 0. B. 2 x
∃ ∈ R, x + x + 5 ≤ 0. C. 2 x
∀ ∈ R, x + x + 5 ≤ 0. D. 2 x
∀ ∈ R, x + x + 5 < 0.
Câu 4: Hãy liệt kê các phần tử của tập hợp X = { 2
x ∈  | 2x − 5x + 3 = } 0 .  3 3 A. X = 1  ; . B. X = { } 0 . C. X =  . D. X = { } 1 .  2 2
Câu 5: Hàm số y = 2x −1 có đồ thị là hình nào trong các hình sau? ` y y y y x x x x O 1 O 1 O 1 O 1 -1 -1 -1 -1 Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 4. B. Hình 3. C. Hình 2. D. Hình 1.  
Câu 6: Cho tam giác đều ABC có cạnh bằng a . Tính A . B AC.
Trang 1/6 - Mã đề thi 483   3   1     1 A. 2 A . B AC = a . B. 2 A . B AC = − a . C. 2 A . B AC = a . D. 2 A . B AC = a . 2 2 2
Câu 7: Đường thẳng nào sau đây song song với đường thẳng y = 2x ? 2 1
A. y = − 2x + 2. B. y = 1− 2 . x C. y = x − 5. D. y = x − 3. 2 2
Câu 8: Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A. (−∞;−2] ∪ (5;+∞). B. (−∞;−2]∪[5;+∞). C. (−∞;−2) ∪[5;+∞). D. (−∞;−2) ∪ (5;+∞).
Câu 9: Mệnh đề nào sau đây đúng?
A. Có duy nhất một vectơ cùng phương với mọi vectơ.
B. Có vô số vectơ cùng phương với mọi vectơ.
C. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
D. Không có vectơ nào cùng phương với mọi vectơ.
Câu 10: Tìm tất cả các giá trị của tham số m để hàm số y = (m − 2) x + 2m đồng biến trên .  A. m ≥ 2. B. m ≤ 2. C. m > 2. D. m < 2.
Câu 11: Cho hàm số f ( x) 2
= x − x . Khẳng định nào sau đây là đúng?
A. Đồ thị của hàm số f ( x) đối xứng qua gốc tọa độ.
B. f ( x) là hàm số chẵn.
C. f ( x) là hàm số lẻ.
D. Đồ thị của hàm số f ( x) đối xứng qua trục hoành.      
Câu 12: Trong hệ tọa độ Oxy, cho u = i + 3 j và v = (2; − ) 1 .Tính . u v .         A. . u v = 1. B. . u v = 5 2 . C. . u v = (2; 3 − ) . D. . u v = 1 − .
Câu 13: Tìm parabol ( P) 2
: y = ax + 3x − 2, biết rằng parabol có trục đối xứng x = 3. − 1 1 1 A. 2 y = x + x − 2. B. 2
y = x + 3x − 2. C. 2 y = x + 3x − 2. D. 2 y = x − 3x − 2. 2 2 2
Câu 14: Cho A = ( ;
−∞ 5], B = (0;+∞) . Tìm A∩ B .
A. A ∩ B = ( ;
−∞ +∞). B. A∩ B = (0;5).
C. A ∩ B = [0;5).
D. A ∩ B = (0;5]. 1 Câu 15: Cho sin α = , với 0 0
90 < α < 180 . Tính cosα. 3 2 2 2 2 2 2 A. cosα = . B. cosα = − . C. cosα = . D. cosα = − . 3 3 3 3 
Câu 16: Trong hệ tọa độ Oxy, cho véc tơ a = (3; 4
− ). Đẳng thức nào sau đây đúng?     A. a = 3. B. a = 4. C. a = 7. D. a = 5.
Trang 2/6 - Mã đề thi 483        
Câu 17: Trong hệ tọa độ Oxy, cho u = 2i − j và v = i + xj . Tìm x sao cho u và v cùng phương. 1 1 A. x = − . B. x = . C. x = 2 . D. x = 1 − . 2 4
Câu 18: Phương trình 2
ax + bx + c = ( 0 0
a ≠ ) có hai nghiệm phân biệt cùng dấu khi và chỉ khi: ∆ ≥ 0 ∆ > 0 ∆ > 0 ∆ > 0 A.  . B.  . C.  . D.  . P > 0 S < 0 P > 0 S > 0
Câu 19: Điều kiện xác định của phương trình x −1 + x − 2 = x − 3 là: A. x ≥ 1. B. x ≥ 2. C. x > 3. D. x ≥ 3.
Câu 20: Cho phương trình ( 2 x + ) 1 ( x – ) 1 ( x + )
1 = 0 . Phương trình nào sau đây tương đương với phương trình đã cho? A. x −1 = 0. B. x +1 = 0. C. 2 x +1 = 0. D. ( x – ) 1 ( x + ) 1 = 0.
Câu 21: Cho tam giác ABC. Khẳng định nào sau đây đúng?
  
  
  
  
A. AB + CA = . CB
B. CA + BA = . CB
C. AB + AC = BC.
D. AA + BB = A . B    
Câu 22: Trong hệ tọa độ Oxy, cho a = (2;5), b = (3; 7
− ) . Tính góc giữa hai véctơ a và b . A. 135 . o B. 120 . o C. 60 . o D. 45 . o
Câu 23: Trong hệ tọa độ Oxy, cho tam giác ABC có A(3;5), B ( 1; 2), C (
5; 2). Tìm tọa độ trọng tâm
G của tam giác ABC. A. G ( 2;3). B. G (4;0). C. G (3;3). D. G ( 3 − ;4).
Câu 24: Tìm tập xác định D của hàm số f ( x) 1 = x +1 + . x A. D = [ 1 − ;+∞) \{ } 0 . B. D =  \ { 1 − ; } 0 . C. D =  \ { } 0 . D. D = [ 1 − ;+∞).
Câu 25: Tính tổng tất cả các nghiệm của phương trình x + 2 = 2 x − 2 . 20 2 1 A. . B. . C. . D. 6. 3 3 2
Câu 26: Trong hệ tọa độ Oxy, cho A(2; 3 − ), B(
4; 7). Tìm tọa độ trung điểm I của đoạn thẳng AB A. I (6; 4). B. I (3; 2). C. I (8; 2 − ) 1 . D. I (2;10).    
Câu 27: Trong hệ tọa độ Oxy, cho a = (3; 4 − ), b = ( 1
− ;2). Tìm tọa độ của a + . b        
A. a + b = (2; 2 − ).
B. a + b = (4; 6 − ).
C. a + b = ( 3 − ; 8 − ).
D. a + b = ( 4; − 6). Câu 28: Cho hàm số 2
y = ax + bx + c ( 0
a > ) . Khẳng định nào sau đây là sai?
A. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.  b
B. Hàm số nghịch biến trên khoảng ; −∞ − .    2a   b
C. Hàm số đồng biến trên khoảng − ; +∞ .    2a
Trang 3/6 - Mã đề thi 483 b
D. Đồ thị của hàm số có trục đối xứng là đường thẳng x = − . 2a
mx − y = m
Câu 29: Tìm điều kiện của tham số m để hệ phương trình  có nghiệm duy nhất. −x + my = 1 − A. m ≠ 1. − B. m ≠ 1. C. m = 1. ± D. m ≠ 1. ±
Câu 30: Trong các hệ thức sau, hệ thức nào đúng?           A. (a)2 = . a
B. (a)2 = a . C. .
a b = a . b .
D. a = ± a .
Câu 31: Cho 5 điểm phân biệt M , N, P,Q, .
R Mệnh đề nào sau đây đúng?
     
     
A. MN + PQ + RN + NP + QR = . MP
B. MN + PQ + RN + NP + QR = . MR
     
     
C. MN + PQ + RN + NP + QR = P . R
D. MN + PQ + RN + NP + QR = MN.
Câu 32: Có tất cả bao nhiêu giá trị nguyên của tham số m ∈[ 10
− ;10] để phương trình ( 2
m − 9) x = 3m(m − 3) có nghiệm duy nhất ? A. 2. B. 21. C. 19. D. 18. Câu 33: Cho hàm số 2
y = ax + bx + c có đồ thị như hình bên dưới . Khẳng định nào sau đây đúng? y x O ` A. a > 0, b < 0, 0 c > . B. a < 0, b < 0, c < 0. C. a > 0, b > 0, 0 c > . D. a > 0, b < 0, c < 0.
Câu 34: Cho tam giác ABC có A( 2
− ;7), B(3;5),C (1; 4
− ) . Biết rằng trực tâm của tam giác ABC là điểm  a b b H ; 
 , với a,b, ,
m n là các số nguyên dương và a ,
là các phân số tối giản. Tính  m n m n a b T = + . m n 54 95 72 43 A. T = . B. T = . C. T = . D. T = . 5 9 7 4         
Câu 35: Cho hai véc tơ a và b thỏa mãn các điều kiện 1 a =
b = 1, a − 2b = 15. Đặt u = a + b và 2     
v = 2k a − b, k ∈ .
 Tìm tất cả các giá trị của k sao cho (u v) 0 , = 60 . 3 5 17 17 3 5 A. k = 4 + . B. k = 5 + . C. k = 5 ± . D. k = 4 ± . 2 2 2 2
Câu 36: Cho mệnh đề: 2 x
∀ ∈ R, x − 2 + a > 0, với a là số thực cho trước. Tìm a để mệnh đề đúng. A. a = 2 . B. a > 2 . C. a ≥ 2 . D. a ≤ 2 .
Câu 37: Giả sử phương trình 2
2x − 4mx −1 = 0 (với m là tham số) có hai nghiệm x , x . Tìm giá trị 1 2
nhỏ nhất của biểu thức T = x − x . 1 2
Trang 4/6 - Mã đề thi 483 2 2 A. min T = 2. B. min T = 2. C. min T = . D. min T = . 2 3
Câu 38: Cho hai tập A = [0;5]; B = (2a;3a + ] 1 , với a > 1
− . Tìm tất cả các giá trị của a để A ∩ B ≠ . ∅  5  5 a ≥ a < 1 5   2 1 5 2 A. − ≤ a < . B.  . C. − ≤ a ≤ . D.  . 3 2 1  3 2 1  a < −  a ≥ −  3  3
Câu 39: Biết rằng hàm số 2
y = ax + bx + c ( 0
a ≠ ) đạt cực tiểu bằng 4 tại x = 2 và có đồ thị hàm số
đi qua điểm A(0;6). Tính tích P = . abc 3 A. P = 3. − B. P = 6. − C. P = . D. P = 6. 2
Câu 40: Trong hệ tọa độ Oxy , cho hai điểm A(2; 3 − ), B(3; 4
− ). Tìm tọa độ điểm M trên trục hoành
sao cho chu vi tam giác AMB nhỏ nhất. 17  18  A. M (3;0). B. M ; 0 .   C. M ; 0 .   D. M (4;0).  7   7 
Câu 41: Cho biết tập hợp tất cả các giá trị của tham số m để phương trình  1   1   a  2 2 x + − 3 x + − 2m +1 = 0    
có nghiệm là S = − ; +∞ 
 , với a,b là các số nguyên dương và 2  x   x   b
a là phân số tối giản. Tính T = a + .b b A. T = 17. B. T = 49. C. T = 3. D. T = 13.
Câu 42: Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình
2x + m = x −1 có nghiệm duy nhất? A. 4. B. 1. C. 2. D. 3.
Câu 43: Cho hình bình hành ABC .
D Gọi G là trọng tâm của tam giác ABC . Mệnh đề nào sau đây
đúng?    
   
A. GA + GC + GD = . DB
B. GA + GC + GD = B . D
   
   
C. GA + GC + GD = . O
D. GA + GC + GD = C . D Câu 44: Cho hàm số ( ) 2
f x = ax + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số m thì phương trình f ( x ) −1= m có đúng 3 nghiệm phân biệt. y 3 x O 2 -1 ` A. 2 − < m < 2. B. m > 3. C. m = 2. D. m = 3.  
Câu 45: Cho tam giác ABC vuông cân tại A có AB = a . Tính AB + AC .
Trang 5/6 - Mã đề thi 483    
  a 2  
A. AB + AC = 2 . a
B. AB + AC = . a
C. AB + AC = .
D. AB + AC = a 2. 2 x y
Câu 46: Đường thẳng d :
+ = 1, với a ≠ 0; b ≠ 0, đi qua điểm M ( 1
− ;6) và tạo với các tia Ox, Oy a b
một tam giác có diện tích bằng 4 . Tính S = a + 2b . 5 − + 7 7 74 A. S = . B. S = 10. C. S = 6. D. S = − . 3 3
Câu 47: Cho biết m ≠ 0 và n ≠ 0 là các nghiệm của phương trình 2
x + mx + n = 0. Tính tổng m + . n 1 1
A. m + n = 1.
B. m + n = − .
C. m + n = .
D. m + n = −1. 2 2
Câu 48: Tìm tất cả các giá trị của tham số m để hai đồ thị hàm số 2
y = −x − 2x + 3 và 2
y = x − m có điểm chung. 7 7 7 7 A. m < − . B. m > − . C. m ≥ − . D. m = − . 2 2 2 2
Câu 49: Gọi S là tập hợp các giá trị của tham số m sao cho parabol ( P) 2
: y = x − 4x + m cắt Ox tại hai điểm phân biệt ,
A B thỏa mãn OA = 3 .
OB Tính tổng T các phần tử của S. 3 A. T = 3. B. T = 15. − C. T = 9. − D. T = . 2  
Câu 50: Cho tứ giác ABCD, trên cạnh AB, CD lấy lần lượt các điểm M , N sao cho 3 AM = 2 AB và     
3 DN = 2 DC. Tính vectơ MN theo hai vectơ AD, BC.
 1  2 
 1  2 
 2  1 
 1  1  A. MN = AD −
BC. B. MN = AD +
BC. C. MN = AD +
BC. D. MN = AD + BC. 3 3 3 3 3 3 3 3 ----------- HẾT ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Trang 6/6 - Mã đề thi 483
ĐÁP ÁN ĐỀ KHẢO SÁT KIẾN THỨC (Lần 1) - MÔN TOÁN KHỐI 10 Câu Mã 134 Mã 210 Mã 356 Mã 483 1. D D B B 2. B C A A 3. A B C B 4. A A B A 5. C B D D 6. D B B D 7. B A B C 8. A C D C 9. C A B A 10. D D D C 11. C C B B 12. D D D D 13. B B B C 14. B A A D 15. D B A D 16. B D D D 17. B A B A 18. A A C C 19. B D D D 20. C B D D 21. C A A A 22. A B D A 23. A D A C 24. A B C A 25. C B C A 26. D B C B 27. B D B A 28. D D A A 29. D D A D 30. D C A B 31. C C B D 32. B B C C 33. C D A D 34. A C B C 35. A B C A 36. C C A B 37. C A A B 38. A C C A 39. B C C B 40. C A A B 41. B D C C 42. D D D D 43. D D D B 44. B A B C 45. A C C D 46. C C B B 47. D C D D 48. D A B C 49. A A D C 50. D D C B
HƯỚNG DẪN MỘT SỐ CÂU VẬN DỤNG VÀ VẬN DỤNG CAO
ĐỀ KHẢO SÁT KIẾN THỨC (Lần 1) - MÔN TOÁN KHỐI 10 x y
Câu 1: Đường thẳng d :
+ = 1, với a ≠ 0; b ≠ 0, đi qua điểm M ( 1
− ;6) và tạo với các tia Ox, Oy một a b
tam giác có diện tích bằng 4 . Tính S = a + 2b . 74 5 − + 7 7 A. S = − . B. S = . C. S = 10. D. S = 6. 3 3
Lời giải. Đường thẳng x y − d :
+ =1 đi qua điểm M (− ) 1 6 1; 6  → + = 1. ( ) 1 a b a b
Ta có d ∩ Ox = A( ;
a 0) ; d ∩ Oy = B (0;b) , a > 0,b > 0 (do ,
A B thuộc hai tia Ox , Oy ).
Suy ra OA = a = a và OB = b = b . Do đó, ta có 1 1 S = . OA OB = 4  → ab = 4. (2) ABC ∆ 2 2  1 6 − + = 1   − − = Từ ( ) 6a b ab 0 a b 1 và (2) ta có hệ  ⇒  1  ab = 8 ab = 4 2
Giải hệ ta được a = 2,b = 4. Suy ra a + 2b =10.         
Câu 2: Cho hai véc tơ a và b thỏa mãn các điều kiện 1 a =
b = 1, a − 2b = 15. Đặt u = a + b và 2     
v = 2k a − b, k ∈ .
 Tìm tất cả các giá trị của k sao cho (u v) 0 , = 60 . 3 5 3 5 17 17 A. k = 4 + . B. k = 4 ± . C. k = 5 + . D. k = 5 ± . 2 2 2 2 Lời giải.      
Từ giả thiết a − b = ⇔ (a − b)2 1 2 15 2 =15 ⇒ . a b = . 2           2 2
u v = (a + b)( ka − b) 9 . 2 = 3k − , 2
u = u = 6, v = v = 4k − 2k + 4 2 9 ( −   u v) 3k 1 3 5 0 2 , = 60 ⇔ = ⇔ k = 4 + . 2 − + 2 2 6. 4k 2k 4
Câu 3: Gọi S là tập hợp các giá trị của tham số m sao cho parabol ( P) 2
: y = x − 4x + m cắt Ox tại hai điểm phân biệt ,
A B thỏa mãn OA = 3 .
OB Tính tổng T các phần tử của S. 3 A. T = 3. B. T = 9. − C. T = 15. − D. T = . 2
Lời giải. Phương trình hoành độ giao điểm: 2
x − 4x + m = 0. (*)
Để (P) cắt Ox tại hai điểm phân biệt ,
A B thì (*) có hai nghiệm phân biệt ⇔ ∆ ' = 4 − m > 0 ⇔ m < 4.  = Theo giả thiết x 3x OA = 3OB  → x = 3 A B x ⇔ . A Bx = 3 − xA Bx = 3x A B   TH1: Viet x = 3x 
→ x + x = 4 
→ m = x .x = 3. A B A B A B
x .x = mA Bx = 3 − x A B   TH2: Viet x = 3 − x 
→ x + x = 4 
→ m = x .x = 12 − . A B A B A B
x .x = mA B Do đó S = {3; 1 − } 2 ⇒ T = 9 −
Câu 4: Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình 2x + m = x −1 có nghiệm duy nhất? A. 2. B. 1. C. 3. D. 4. Lời giải.  ≥ Phương trình x 1
2x + m = x −1 ⇔  2
m = x − 4x +1
Lập bảng biến thiên của hàm số f (x) 2
= x − 4x +1 trên [1;+∞) ta được m = 3 − hoặc m > 2 − . Do đó có 3
giá trị nguyên không dương là: 3 − ; 1 − ;0 .
Câu 5: Cho biết tập hợp tất cả các giá trị của tham số
m để phương trình  1   1   a  2 2 x + − 3 x + − 2m +1 = 0    
có nghiệm là S = − ; +∞ 
 , với a,b là các số nguyên dương và a là 2  x   x   bb
phân số tối giản. Tính T = a + . b A. T = 13 B. T = 17. C. T = 49. D. T = 3. Lời giải. Đặt 1 t = x +
. Điều kiện t ≤ 2
− hoặc t ≥ 2. Phương trình trở thành 2
2m = 2t − 3t − 3 . x
Lập bảng biến thiên của hàm số f (x) 2
= 2t − 3t − 3 trên ( ; −∞ 2 − ]∪[2;+∞) ta được 1 m ≥ − . 2
Do đó a =1,b = 2 ⇒ T = 3 .
Câu 6: Cho tam giác ABC có A( 2
− ;7), B(3;5),C (1; 4
− ) . Biết rằng trực tâm của tam giác ABC là điểm  a b b a b H ; 
 , với a,b, ,
m n là các số nguyên dương và a ,
là các phân số tối giản. Tính T = + .  m n m n m n 43 54 72 95 A. T = . B. T = . C. T = . D. T = . 4 5 7 9    = Lời giải. Gọi AH .BC 0  235 269  235 269 72 H ( ;
x y ) . Giải hệ   ⇒ H ; ⇒ T = + =    =  49 49  49 49 7 BH .AC 0
Câu 7: Trong hệ tọa độ Oxy , cho hai điểm A(2; 3 − ), B(3; 4
− ). Tìm tọa độ điểm M trên trục hoành sao cho
chu vi tam giác AMB nhỏ nhất. 18  17  A. M ; 0 .   B. M (4;0). C. M (3;0). D. M ; 0 .    7   7 
Lời giải. Điểm M ∈Ox ⇒ M ( ;
m 0). Gọi B ' là điểm đối xứng với B qua Ox thì B '(3; 4) .
Chu vi tam giác là: C = AB + AM + BM = AB + AM + B ' M ≥ AB + AB ' ∆ không đổi
 
Do đó chu vi nhỏ nhất khi và chỉ khi ,
A B ', M thẳng hàng ⇔ AB ', AM cùng phương.  
Ta có AB ' = (1;7) và AM = (m − 2;3). Để m − ,
A B, M thẳng hàng 2 3 17 ⇔ = ⇔ m = . 1 7 7
-------------------------------
Document Outline

  • KSKT(LAN1)_TOÁN 10-2017_134.pdf
  • KSKT(LAN1)_TOÁN 10-2017_210.pdf
  • KSKT(LAN1)_TOÁN 10-2017_356.pdf
  • KSKT(LAN1)_TOÁN 10-2017_483.pdf
  • ĐÁP ÁN ĐỀ KHẢO SÁT KIẾN THỨC.pdf