
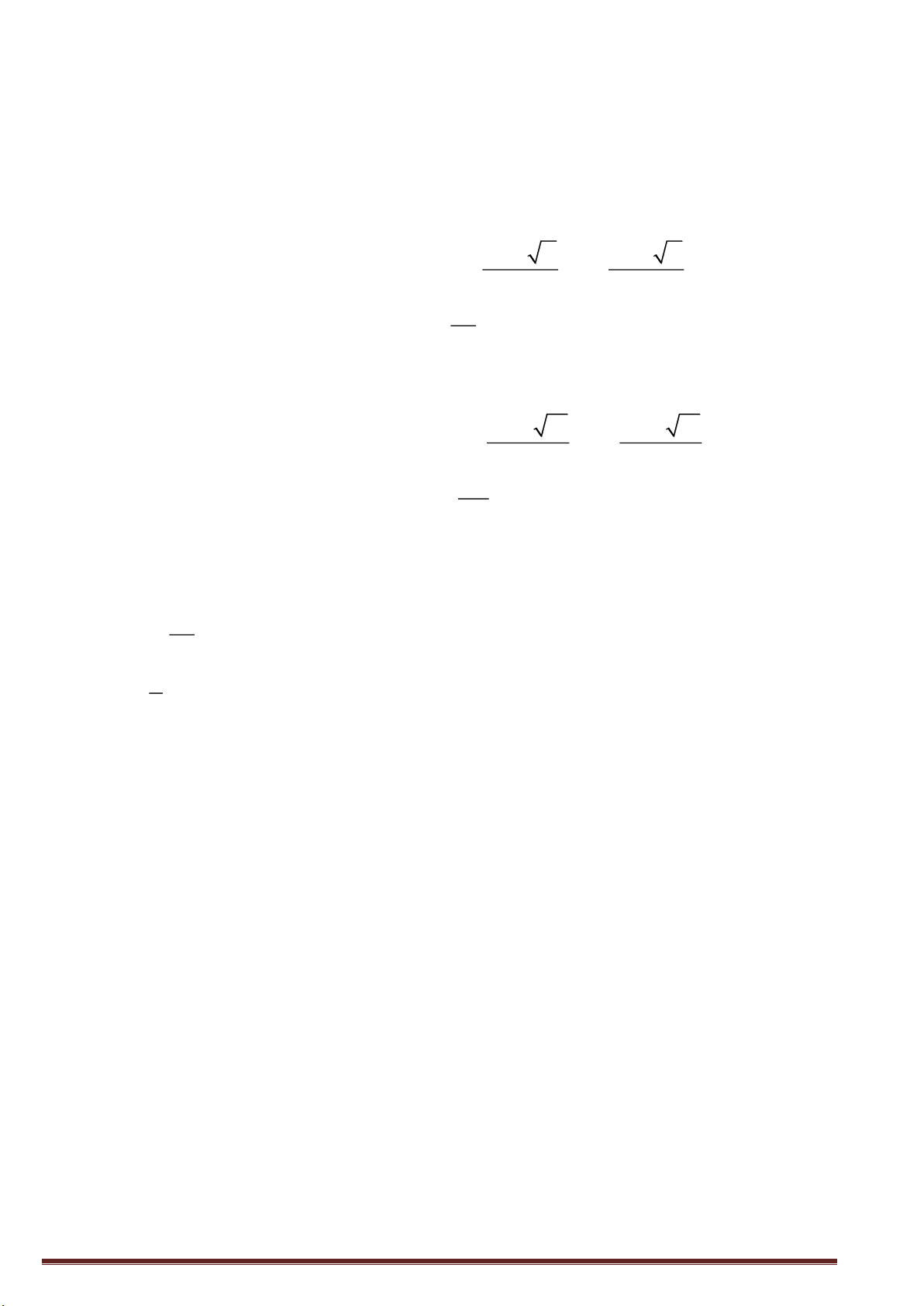


Preview text:
TỔNG HỢP KIẾN THỨC TOÁN 9
I. Tổng hợp kiến thức Toán đại số lớp 9
1. Chương 1: Căn bậc hai. Căn bậc ba
+ Điều kiện để căn thức có nghĩa:
A có nghĩa khi A 0
+ Các công thức biến đổi căn thức: 2 A A AB
A. B A 0; B 0 A A 2 A B A B B 0
A 0; B 0 B B 2 A B
A B A 0;B 0 2
A B A B A 0;B 0 A A B C A B C B 0 2
A 0; A B 2 B B A B A B C A B C
A 0;B 0; A B A B A B
+ 7 hằng đẳng thức đáng nhớ: a b2 2 2
a 2ab b 2 a b 2 2
a 2ab b a b3 3 2 2 3
a 3a b 3ab b a b3 3 2 2 3
a 3a b 3ab b 2 2
a b a ba b 3 3 2 2 a b a
b a ab b 3 3 2 2 a b a
b a ab b
2. Chương 2: Hàm số bậc nhất
* Hàm số y ax b a 0 có tính chất:
+ Hàm số đồng biến trên R khi a > 0
+ Hàm số nghịch biến trên R khi a < 0
* Hàm số y ax b a 0 có đồ thị là một đường thẳng đi qua điểm A(0; b) và B(-b/a; 0)
* Vị trí tương đối của hai đường thẳng: Xét đường thẳng y ax b d và y a ' x b 'd ' . Khi đó:
+ (d) và (d’) cắt nhau khi và chỉ khi a khác a’
+ (d) // (d’) khi và chỉ khi a = a’ và b khác b’
+ (d) trùng với (d’) khi và chỉ khi a = a’ và b = b’
3. Chương 3: Hệ hai phương trình bậc nhât hai ẩn
ax by c * Hệ phương trình:
a'x b' y c' a b
+ Hệ phương trình có nghiệm duy nhất a ' b ' a b c
+ Hệ phương trình vô nghiệm a ' b ' c ' a b c
+ Hệ phương trình có vô số nghiệm a ' b ' c '
* Giải bài toán bằng cách lập phương trình, hệ phương trình Trang 1
+ Bước 1: Lập phương trình hoặc hệ phương trình
+ Bước 2: Giải phương trình hoặc hệ phương trình
+ Bước 3: Kiểm tra các nghiệm của phương trình hoặc hệ phương trình nghiệm nào thích hợp với bài toán và kết luận
4. Chương 4: Phương trình bậc hai một ẩn * Phương trình 2
ax bx c 0a 0 + Công thức nghiệm: 2
b 4ac b b
- Nếu 0 , phương trình có hai nghiệm phân biệt x ; x 1 2 2a 2a b
- Nếu 0 , phương trình có nghiêm kép: x x 1 2 2a
- Nếu 0 , phương trình vô nghiệm
+ Công thức nghiệm thu gọn 2
' b' acb 2b' b' ' b' '
- Nếu ' 0 , phương trình có hai nghiệm phân biệt x ; x 1 2 a a b'
- Nếu ' 0 , phương trình có nghiệm kép x x 1 2 a
- Nếu ' 0 , phương trình vô nghiệm
* Hệ thức Vi ét và ứng dụng:
+ Hệ thức Vi ét: nếu x ; x là nghiệm của phương trình bậc hai 2
ax bx c 0a 0 thì 1 2 b
S x x 1 2 a c P x x 1 2 a * Hàm số 2
y ax a 0 có tính chất:
+ Nếu a > 0, hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
+ Nếu a < 0, hàm số đồng biến khi x < 0 và nghịch biến khi x > 0 * Hàm số 2
y ax a 0 là một đường cong parabol đi qua gốc tọa độ O (0;0)
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành
* Ví trí tương đối của đường thẳng và đường cong parabol: Xét đường thẳng y ax bd và 2
y ax P
+ (d) và (P) cắt nhau tại hai điểm, khi phương trình hoành độ giao điểm giữa đường thẳng và đường cong có hai nghiệm phân biệt
+ (d) tiếp xúc với (P) tại một điểm, khi phương trình hoành độ giao điểm giữa đường thẳng và đường cong có nghiêm kép
+ (d) không cắt (P), khi phương trình hoành độ giao điểm giữa đường thẳng và đường cong vô nghiệm
II. Tổng hợp kiến thức Toán hình lớp 9
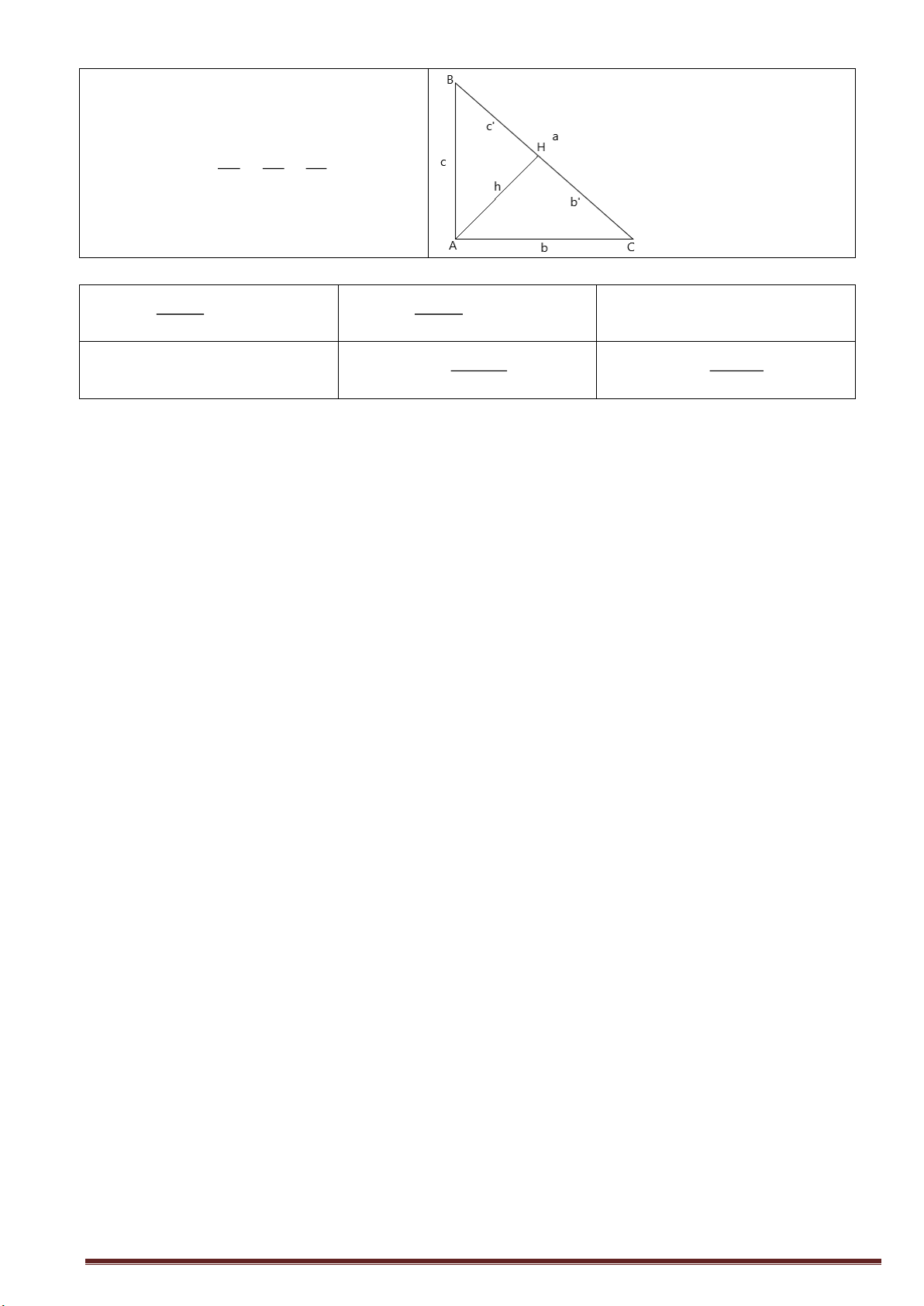
1. Chương 1: Hệ thức lượng trong tam giác vuông
* Hệ thức lượng trong tam giác vuông: Trang 2 2 2 b ab ' c ac ' 2
h b 'c ' ah bc 1 1 1 2 2 2
a b c 2 2 2 h b c
* Tỉ số lượng giác của góc nhọn: 0 sin 1;0 cos 1. Ta có: sin cos 2 2 sin cos 1 tan cot cos sin tan.cot 1 1 1 2 1 tan 2 1 cot 2 cos 2 sin
* Hệ thức về cạnh và góc trong tam giác vuông: b = a.sinB = a.cosC b = c.cotB = c.cotC c = a.sinC = a.cosB c = b.tanC = b.cotB
2. Chương 2, 3: Đường tròn và góc với đường tròn
* Quan hệ vuông góc giữa đường kính và dây: trong một đường tròn:
+ Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy
+ Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
* Liên hệ giữa dây và khoảng cách từ tâm đến dây: trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm
+ Hai dây cách đều tâm thì bằng nhau
+ Dây nào lớn hơn thì dây đó gần tâm hơn
+ Dây nào gần tâm hơn thì dây đó lớn hơn
* Liên hệ giữa cung và dây: trong một đường tròn hay trong hai đường tròn bằng nhau:
+ Hai cung bằng nhau căng hai dây bằng nhau
+ Hai dây bằng nhau căng ha cung bằng nhau
+ Cung lớn hơn căng dây lớn hơn
+ Dây lớn hơn căng cung lớn hơn
* Tiếp tuyến của đường tròn
+ Tính chất của tiếp tuyến: tiếp tuyến vuông góc với bán kính đi qua tiếp điểm
+ Dấu hiệu nhận biết tiếp tuyến
- Đường thẳng và đường tròn chỉ có một điểm chung
+ Khoảng cách từ tâm của đường tròn đến đường thẳng bằng bán kính
+ Đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó
+ Tính chất của 2 tiếp tuyến cắt nhau: nếu MA, MB là hai tiếp tuyến cắt nhau thì: - MA = MB
- MO là phân gác của góc AMB và OM là phân giác của góc AOB với O là tâm của đường tròn * Góc với đường tròn
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau
+ Các góc nội tiếp cùng chắn một cung thì bằng nhau
+ Các góc nội tiếp chắn các cung bằng nhau thì bằng nhau
+ Góc nội tiếp nhỏ hơn hoặc bằng 900 có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung
+ Góc nội tiếp chắn nửa đường tròn là góc vuông và ngược lại góc vuông nội tiếp thừ chắn nửa đường tròn
+ Góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau
* Với C là độ dài đường tròn, R là bán kính, l là độ dài cung thì:
+ Độ dài đường tròn: C 2 R Trang 3 0 Rn
+ Độ dài cung tròn: l 0 180 + Diện tích hình tròn: 2 S R 2 0 R n
+ Diện tích hình quạt tròn: S 0 360
3. Chương 4: Hình trụ, hình nón, hình cầu
* Với h là chiều cao và l là đường sinh thì:
+ Diện tích xung quanh của hình trụ: S 2 . R h xq 2
+ Diện tích toàn phần hình trụ: S 2 . R h 2 R tp
+ Thể tích của hình trụ: 2
V S.h R h
+ Diện tích xung quanh của hình nón: S Rl xq 2
+ Diện tích toàn phần hình nón: S Rl R tp 1 2
+ Thể tích hình nón: V R h 3
4. Các dạng bài tập thường gặp
* Chứng minh hai góc bằng nhau:
+ Chứng minh hai góc cùng bằng góc thứ ba
+ Chứng minh hai góc bằng với hai góc bằng nhau khác
+ Hai góc bằng tổng hoặc hiệu của hai góc theo thứ tự đôi một bằng nhau
+ Hai góc cùng phụ (hoặc cùng bù với góc thứ ba)
+ Hai góc cùng nhọn hoặc cùng tù có các cạnh đôi một song song hoặc vuông góc
+ Hai góc cùng ở vị trí so le trong, so le ngoài hoặc đồng vị
+ Hai góc ở vị trí đối đỉnh
+ Hai góc của cùng một tam giác câ hoặc đều
+ Hai góc tương ứng của hai tam giác bằng nhau hoặc đồng dạng
+ Hai góc nội tiếp cùng chắn một cung hoặc chắn hai cung bằng nhau
* Chứng minh hai đường thẳng song song
+ Chứng minh hai đường thẳng cùng song song với đường thẳng thứ ba
+ Chứng minh hai đường thẳng cùng vuông góc vớ đường thẳng thứ ba
+ Chứng minh chúng cùng tạo với một cát tuyến hai góc bằng nhau ở vị trí so le trong, vị trí so le ngoài
hoặc ở vị trí đồng vị
+ Là hai dây chắn giữa chúng hai cung bằng nhau trong một đường tròn
+ Chúng là hai cạnh đối của môt hình bình hành
* Chứng minh hai đường thẳng vuông góc
+ Chúng song song với hai đường thẳng vuông góc khác
+ Chứng minh chúng là chân đường cao trong một tam giác
+ Đường kính đi qua trung điểm của dây và dây
+ Chứng là phân giác của hai góc kề bù nhau
* Chứng minh ba đường thẳng đồng quy: chứng minh chúng là ba đường cao, ba đường trung tuyến, ba
đường trung trực hoặc ba đường phân giác trong
* Chứng minh hai tam giác bằng nhau: sử dụng các trường hợp bằng nhau của tam giác thường, tam giác vuông
* Chứng minh hai tam giác đồng dạng: sử dụng các trường hợp đồng dạng của tam giác thường, tam giác vuông
* Chứng minh đẳng thức hình học: sử dụng cặp cạnh tỉ lệ của hai tam giác đồng dạng
* Chứng minh tứ giác nội tiếp
+ Tứ giác có tổng hai góc bằng 1800
+ Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
+ Tứ giác có 4 đỉnh cách đều một điểm
+ Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc Trang 4
* Chứng minh tiếp tuyến của đường tròn
* Các bài toán tính độ dài cạnh, độ lớn góc Trang 5




