Lê Uyên Thi ĐỀ CƯƠNG ÔN TẬP PTĐL HK 22 - Tài liệu tham khảo | Đại học Hoa Sen

ĐỀ CƯƠNG ÔN TẬP MÔN PHÂN TÍCH ĐỊNH LƯỢNG
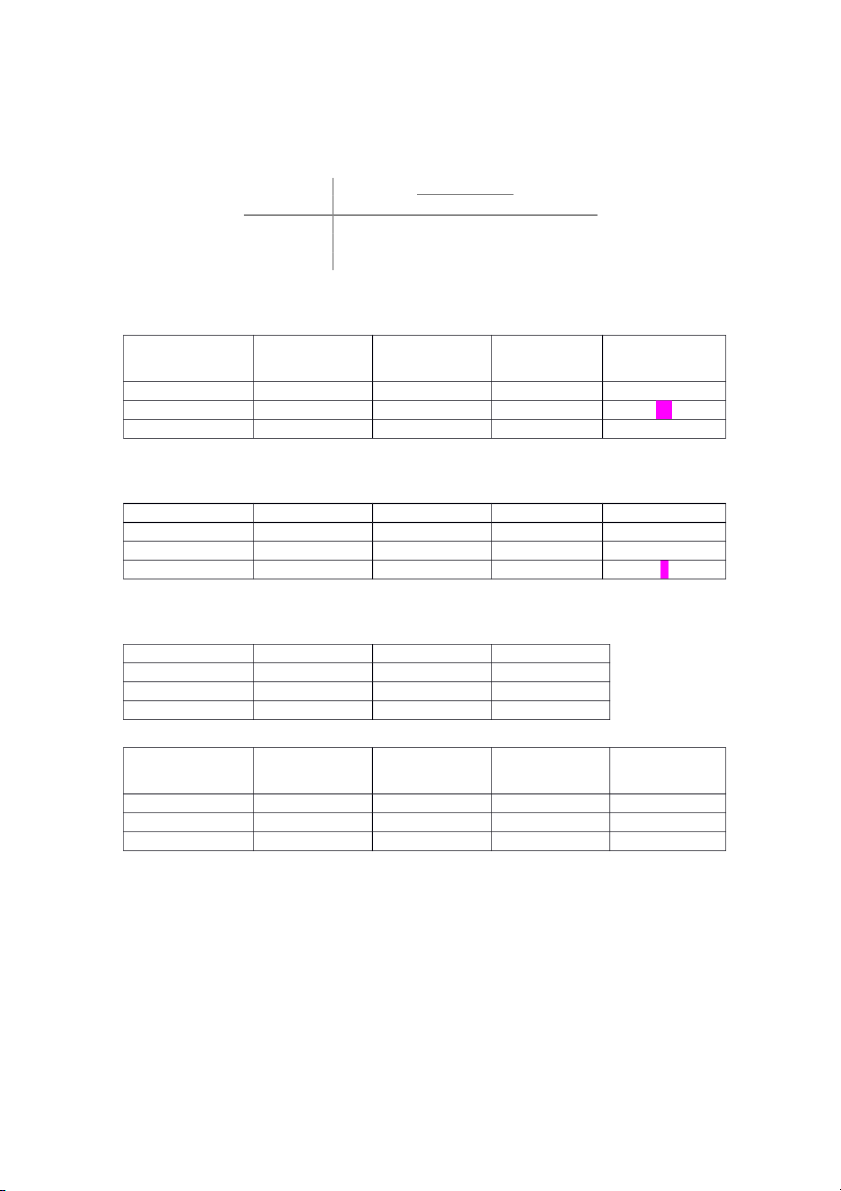
1. Một bảng payoff về profit được cho như sau: State of Nature Decision s1 s2 s3 d1 10 8 6 d2 14 15 2 d3 7 8 9
a. Người ra quyết định lạc quan (optimistic) nên đưa ra quyết định nào? Decision s1 s2 s3 Maximum payoff d1 10 8 6 10 d2 14 15 2 15 d3 7 8 9 9
Người lạc quan đưa ra quyết định d2
b. Người ra quyết định bảo thủ (conservative) nên đưa ra quyết định nào? Decision s1 s2 s3 Minimum payoff d1 10 8 6 6 d2 14 15 2 2 d3 7 8 9 7
Người bảo thủ đưa ra quyết định d3 c.
Quyết định nào nên được thực hiện với phương pháp minimax regret? Decision s1 s2 s3 d1 4 7 3 d2 0 0 7 d3 7 7 0 Decision s1 s2 s3 Maximum regret d1 4 7 3 7 d2 0 0 7 7 d3 7 7 0 7
Quyết định chọn cả 3 phương án d1, d2, d3
d. Nếu xác suất của và lần lượt là 0,5; 0,3 và 0,2 thì nên đưa ra quyết định nào với phương
pháp giá trị kỳ vọng (expected value)?
EV(d1) = 10*0.5 + 8*0.3 + 6*0.2 = 8.6
EV(d2) = 14*0.5 + 15*0.3 + 2*0.2 = 12.4
EV(d3) = 7*0.5 + 8*0.3 + 9*0.2 = 7.7
 Đưa ra quyết định với phương án d2
e. Giải lại bài toán trên với giả thiết đây là bảng payoff về Chi phí. Decision s1 s2 s3 Maximum payoff Minimum payoff d1 -10 -8 -6 -6 -10 d2 -14 -15 -2 -2 -15 d3 -7 -8 -9 -7 -9
Người lạc quan chọn phương án d2
Người bảo thủ chọn phương án d3 Decision s1 s2 s3 d1 3 0 4 d2 7 7 0 d3 0 0 7 Decision s1 s2 s3 Maximum regret d1 3 0 4 4 d2 7 7 0 7 d3 0 0 7 7
Quyết định chọn phương án d1
2. Một tiệm trà sữa cung cấp ra thị trường 2 loại trà sữa trân châu: Nguyên bản và Phong cách. Về
cơ bản, 2 loại sản phẩm này là sự pha trộn của các loại nguyên liệu gồm: trà, bột sữa, trân châu và
các loại topping hỗn hợp khác. Bảng bên dưới thể hiện lượng nguyên liệu cần thiết để làm ra 1 ly
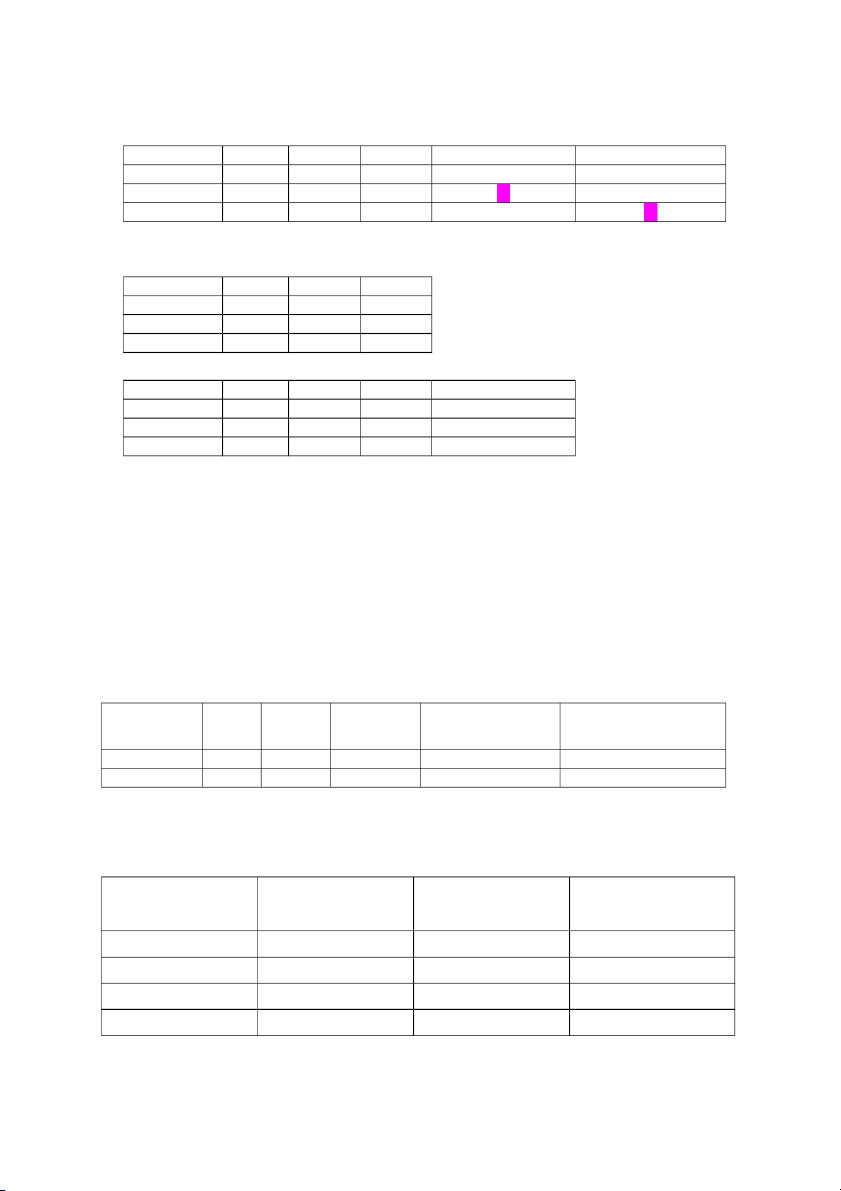
trà sữa mỗi loại và khoản tiền lời thu được trên 1 ly trà sữa. Loại trà sữa Trà Bột sữa Trân châu Topping hỗn hợp Tiền lời mỗi ly (nghìn (g) (g) (g) (g) VNĐ) Nguyên bản 10 20 20 - 10 Phong cách 5 25 - 30 12
Ở thời điểm hiện tại, lượng nguyên liệu có sẵn của Tiệm bao gồm: 1 kg trà, 3.2 kg bột sữa và 2 kg
trân châu và 2,4 kg topping hỗn hợp. Giả sử rằng Tiệm trà sữa quan tâm đến việc tối đa hóa lợi nhuận, hãy: Nguyên liệu Nguyên bản Phong cách Lượng nguyên liệu có sẵn Trà (kg) 0,01 0,005 1 Bột sữa (kg) 0,02 0,025 3,2 Trân châu (kg) 0,02 - 2 Topping hỗn hợp (kg) - 0,03 2,4 Tiền lời (nghìn VND) 10 12
a) Lập mô hình quy hoạch tuyến tính của bài toán trên; Gọi:
N: Số lượng nguyên liệu làm ra trà sữa nguyên bản
P: Số lượng nguyên liệu làm ra trà sữa phong cách
Hàm mục tiêu: Max {10N + 12P} Các ràng buộc:
RB1: Số lượng trà được sử dụng là 0,01N + 0,005P 1
RB 2: Số lượng bột sữa được sử dụng là 0,02N + 0,025P 3,2
RB 3: Số lượng trân châu được sử dụng là 0,02N 2
RB 4: Số lượng topping hỗn hợp được sử dụng là 0,03P 2,4
RB 4: Tính không âm của biến N, P 0 Mô hình
Hàm mục tiêu: Max {12P + 10N} Các ràng buộc:
b) Tìm nghiệm tối ưu của bài toán bằng phương pháp đồ thị. Từ đó xác định mức lợi nhuận tối ưu.
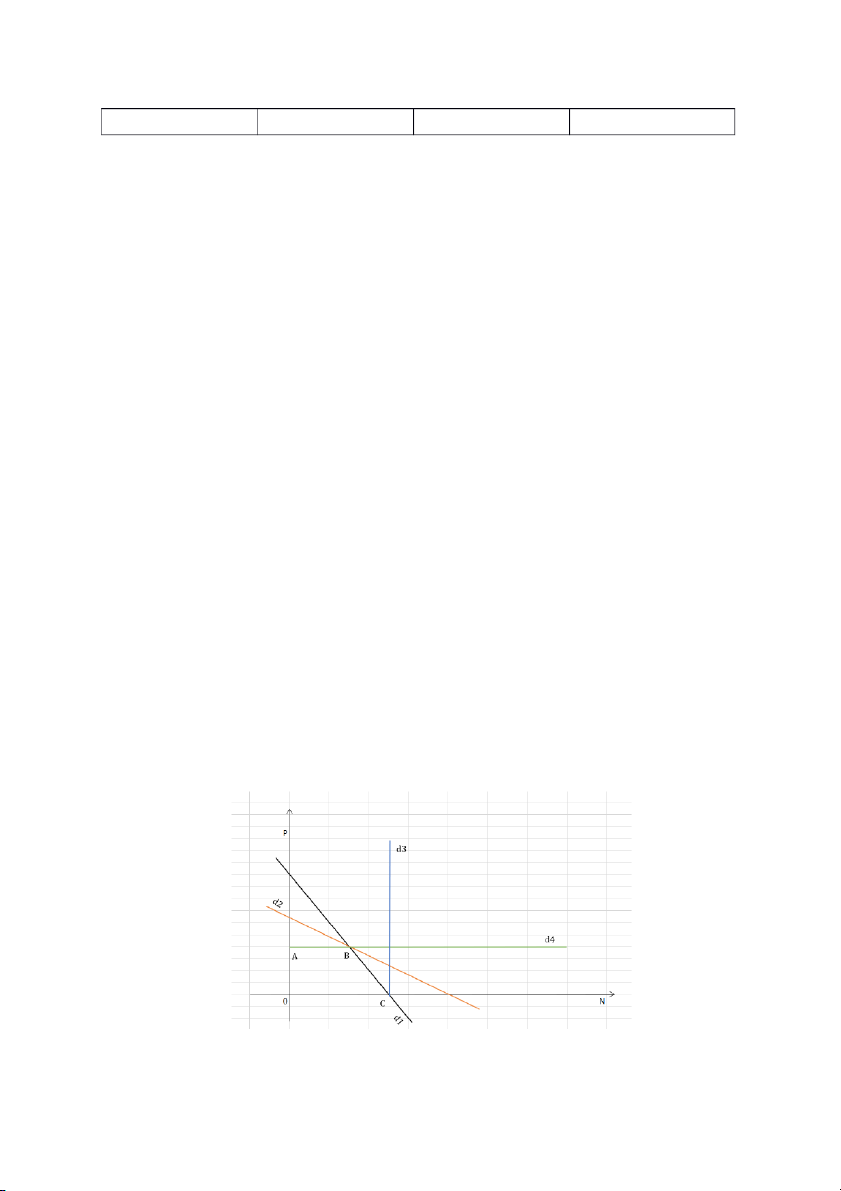
Miền xác định của bài toán là OABCD vì: RB 1:
Đường (d1): = 1 đi qua (100, 0) và (0, 200)
Lấy O (0, 0) thế vào ràng buộc 1: 0,01*0 + 0,005*0  Chọn miền chứa O RB 2:
Đường (d2): = 3,2 đi qua (160, 0) và (0,128)
Lấy O (0, 0) thế vào ràng buộc 1: 0,02*0 + 0,025*0  Chọn miền chứa O RB 3:
Đường (d3): = 2 đi qua (100,0) và song song trục OP
Lấy O (0, 0) thế vào ràng buộc 1: 0,02*0  Chọn miền chứa O RB 4:
Đường (d4): = 2,4 đi qua (0,80) và song song trục ON
Lấy O (0, 0) thế vào ràng buộc 1: 0,03*0  Chọn miền chứa O
O, A, B, C là các điểm cực biên của miền xác định O (0,0) => ; A (0,100) => ; B (60,80) => ; C (100,0) Với
A (0,100) => 10*0 + 12*100 = 1200
B (60,80) => 10*80 + 12*60 = 1560
C (100,0) => 10*100 + 12*0 = 1000
Lần lượt thế tọa độ các điểm cực biên vào hàm mục tiêu 10N + 12P, ta được hàm mục tiêu
đạt giá trị lớn nhất tại (N = 60; P = 80)
Mức lợi nhuận tối đa khi đó là: 10*80 + 12*60 = 1560
3. Công ty McCormick sản xuất hai sản phẩm có đóng góp lợi nhuận là $ 100 và $ 90 trên mỗi
tấn sản phẩm. Các yêu cầu về lao động để làm ra mỗi tấn sản phẩm và tổng số giờ lao động có
thể bố trí từ các bộ phận được thể hiện trong bảng sau:
Số giờ lao động cho mỗi tấn sản phẩm Bộ phận Sản phẩm 1 Sản phẩm 2 Số giờ sẵn có A 5 4 450 B 6 1 400 C 2,5 8 600
Với mục tiêu tối đa hóa lợi nhuận với 2 biến là số tấn sản phẩm mỗi loại. Kết quả thu được tử
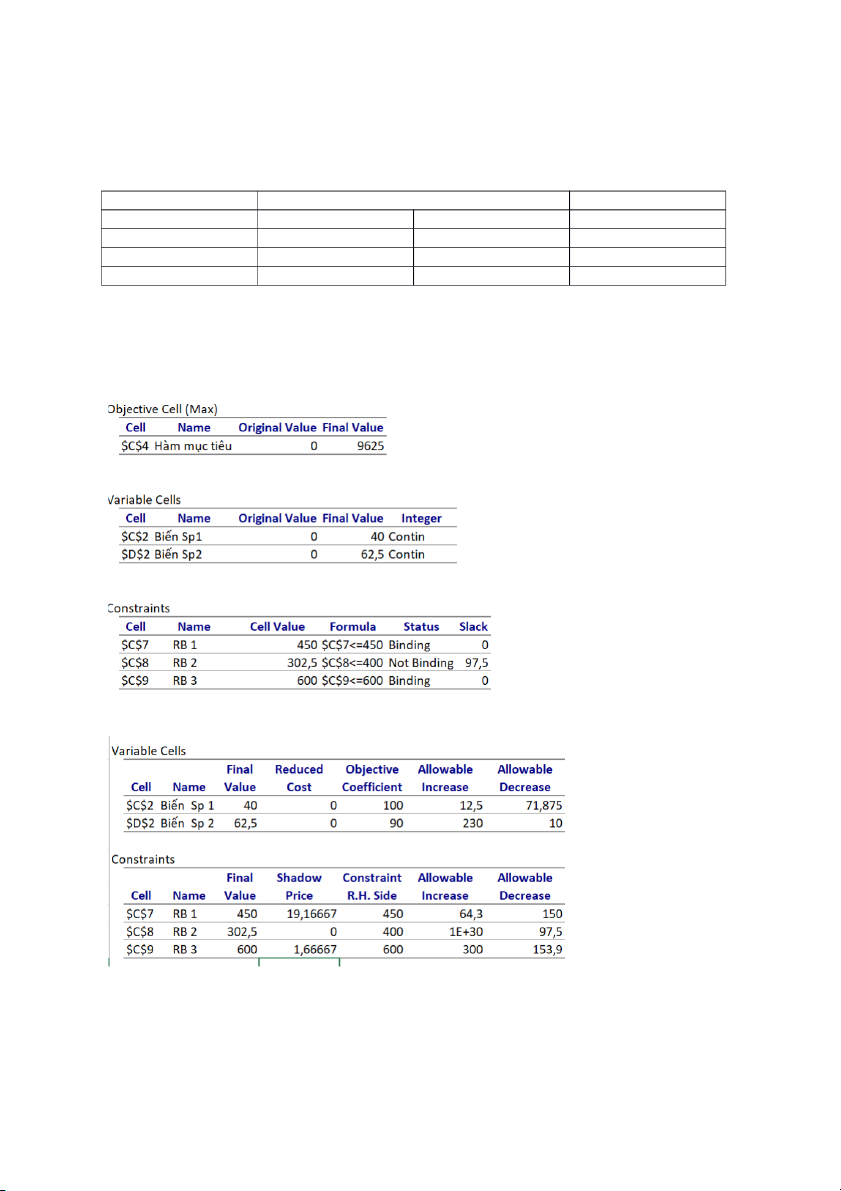
Excel Solver được thể hiện trong các bảng bên dưới. Answer Report: Sensitivity Report:
Dựa vào các bảng trên, hãy cho biết:
a) Công ty cần sản xuất bao nhiêu tấn sản phẩm mỗi loại? Mức lợi nhuận tối đa? Các Bộ
phận A, B, C đã sử dụng hết bao nhiêu giờ công lao động?
- Công ty cần sản xuất 40 tấn sản phẩm 1 và 62,5 tấn sản phẩm 2
- Mức lợi nhuận tối đa 9625$
- Bộ phận A sử dụng hết 450 giờ
- Bộ phận B sử dụng hết 302,5 giờ
- Bộ phận C sử dụng hết 600 giờ
b) Hãy giải thích các giá trị trong cột “Allowable Increase” và “Allowable Decrease” trong cả
2 bảng ở Sensitivity Report? Bảng 1
“Allowable Increase” và “Allowable Decrease” có nghĩa:
- Trong điều kiện các yếu tố khác không đổi, nếu đóng góp lợi nhuận của mỗi tấn sản phẩm
nằm trong khoảng từ 100 – 71,875 = $ 28,125 đến 100 + 12,5 = $ 112,5 thì nghiệm bài toán không đối.
- Trong điều kiện các yếu tố khác không đổi, nếu đóng góp lợi nhuận của mỗi tấn sản phẩm
trong khoảng từ 90 − 10 = $ 80 đến 90 + 230 = $ 320 thì nghiệm bài toán không đối. Bảng 2
“Allowable Increase” và “Allowable Decrease” có nghĩa: Trong điều kiện các yếu tố khác không đổi
- Nếu giá trị của hệ số tự do bên phải ràng buộc 1 dao động từ 450 − 150 = 300 đến 450 +
64,3 = 514,3 thì giá trị tối ưu của bài toán tăng 19,16667 trên mỗi đơn vị tăng thêm.
- Nếu giá trị của hệ số tự do bên phải ràng buộc 2 dao động từ 302,5 – 97,5 = 205 trở lên thì
giá trị tối ưu của bài toán không thay đổi.
- Nếu giá trị của hệ số tự do bên phải ràng buộc 1 dao động từ 600 – 153,9 = 446,1 đến 600 +
300 = 900 thì giá trị tối ưu của bài toán tăng 1,66667 trên mỗi đơn vị tăng thêm.
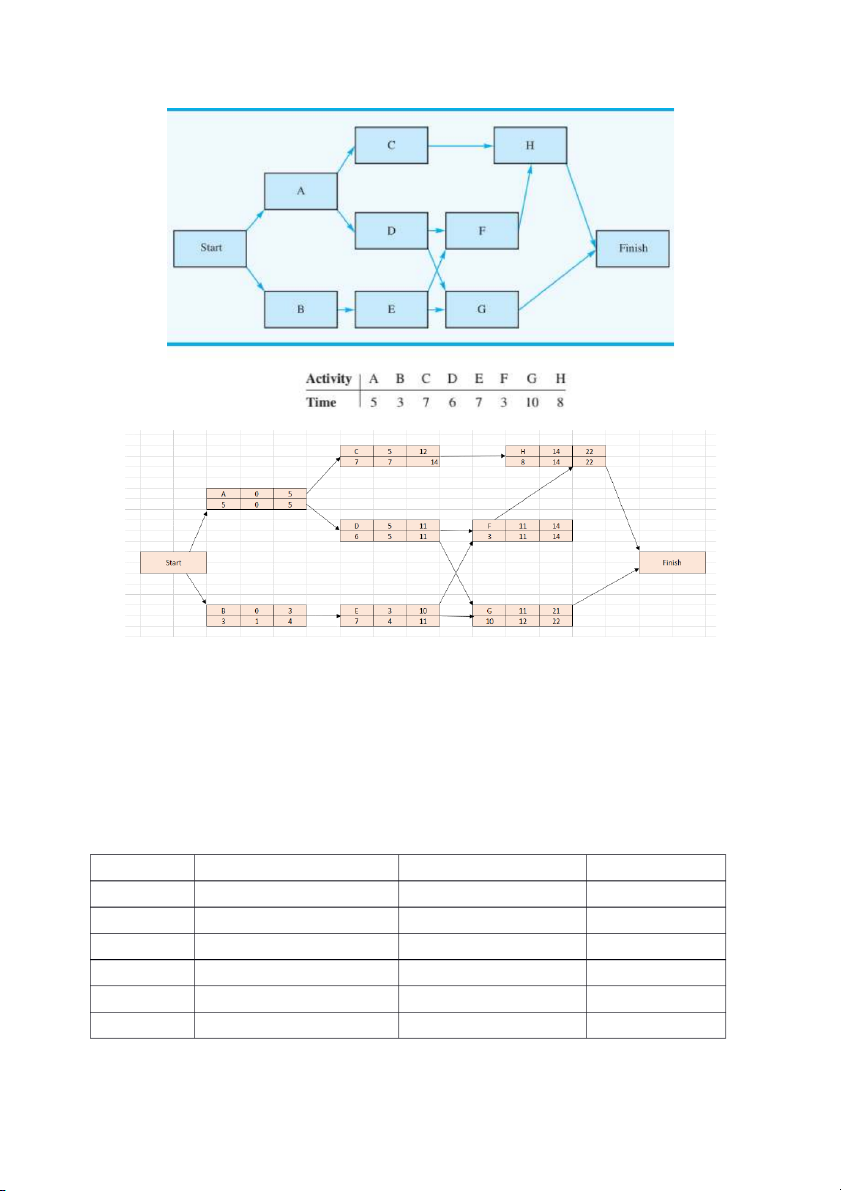
4. Giả sử một mạng dự án với thời gian hoạt động (tính theo tuần) được cho như sau:
a) Hãy xác định the critical path. Start-A-D-F-H-Finish.
b) Cần bao nhiêu thời gian để hoàn thành dự án này?
Thời gian hoàn thành dự kiến: 22 tuần
c) Những hoạt động nào có thể bị trì hoãn mà không làm chậm trễ toàn bộ dự án không? Nếu
được thì mỗi hoạt động có thể trì hoãn tối đa bao nhiêu tuần? Hoạt động
Thời gian bắt đầu sớm nhất
Thời gian bắt đầu trễ nhất Thời gian trì hoãn A 0 0 0 B 0 1 1 C 5 7 2 D 5 5 0 E 3 4 1 F 11 11 0 G 11 12 1 H 14 14 0
Các hoạt động B, C, E, G có thể bị trì hoãn. Thời gian trì hoãn được ghi chi tiết ở bảng trên.
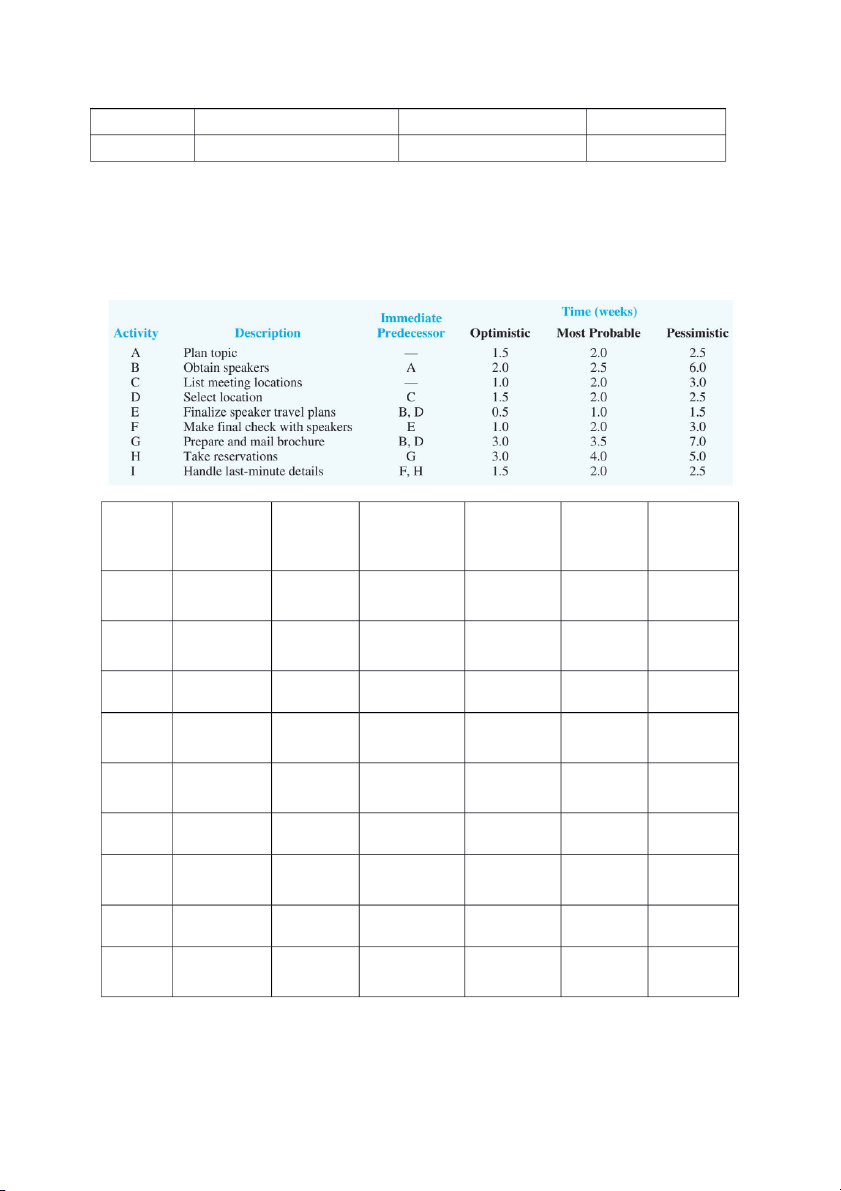
5. Doug Casey chịu trách nhiệm lập kế hoạch và điều phối chương trình đào tạo quản lý bán hàng
vào mùa xuân tới cho công ty của anh ấy. Doug liệt kê thông tin các hoạt động cho dự án như sau: Activity Immediate Optimistic Most Pessimistic Expected Variance Predecessor (a) Probable (m) (b) time A - 1.5 2.0 2.5 2 0.02777777 8 B A 2.0 2.5 6.0 3 0.44444444 4 C - 1.0 2.0 3.0 2 0.111111111 D C 1.5 2.0 2.5 2 0.02777777 8 E B, D 0.5 1.0 1.5 1 0.02777777 8 F E 1.0 2.0 3.0 2 0.111111111 G B, D 3.0 3.5 7.0 4 0.44444444 4 H G 3.0 4.0 5.0 4 0.111111111 I F, H 1.5 2.0 2.5 2 0.02777777 8
a) Hãy vẽ sơ đồ mạng dự án với thông tin thời gian hoàn thành trung bình của từng hoạt động;
b) Xác định Critical path. Từ đó tính thời gian trung bình hoàn thành dự án
Start-A-B-G-H-I. Thời gian trung bình hoàn thành dự án là 15 tuần
c) Tính xác suất hoàn thành dự án trong không quá 13 tuần? Từ 12 đến 14 tuần?
= t = tA + tB + tG + tH + tI = 15 2 2 = A + 2B + G + 2 H + 2 I = 1.555 => = 1.247 2 Không quá 13 tuần:
P (T13) = () + 0.5 (- 0.44520) + 0.5 = 0.0548 Từ 12 đến 14 tuần
P ( = () - () - – [- (0.8)] = (- 0.49180) – (- 0.28814) = - 0.2036
6. Giả sử rằng Công ty Đồ uống R&B có một sản phẩm nước giải khát với nhu cầu hàng năm
không đổi là 3600 lốc. Một lốc nước ngọt có giá R&B $ 3. Chi phí đặt hàng là $ 20 cho mỗi đơn
đặt hàng và chi phí giữ hàng là 25% giá trị của hàng tồn kho. R&B có 250 ngày làm việc mỗi
năm và thời gian giao hàng (the lead time) là 5 ngày. Dùng mô hình EOQ, hãy xác định: D = 3600 C = 3 Co = 20 I = 0.25 M = 250 m = 5 Ch = 0.25*3 = 0.75
a) Số lượng đặt hàng kinh tế Q = = = 438 (lốc)
b) Thời điểm tái đặt hàng d = = 14.4 r = d*m = 14.4*5 = 72 (lốc) c) Thời gian mỗi chu kỳ T = = 30.42 d) Tổng chi phí hàng năm TC = *Q* + = 20 = 328.63$
7. EL Computer sản xuất máy tính xách tay trên dây chuyền sản xuất có công suất hàng năm là
16.000 chiếc. EL Computer ước tính nhu cầu hàng năm đối với sản phẩm này ở mức 6000 chiếc.
Chi phí để thiết lập dây chuyền sản xuất là 2345 đô la và chi phí lưu trữ hàng năm là 20 đô la cho
mỗi đơn vị. Giả sử công ty làm việc 350 ngày mỗi năm. Dùng mô hình EOQ trong sản xuất, hãy xác định: D = 6000 p = 16000 M = 350 Ch = 20 Co = 2345
a) Kích thước/quy mô lô sản xuất tối ưu là bao nhiêu? Tính tổng chi phí tối ưu tương ứng. Q = = = 1500 (chiếc) TC = (1 - )*Q*C + *C h = (1 - )*1500*20 o + *2345 = 18755
b) Có bao nhiêu đợt sản xuất nên được thực hiện mỗi năm? Thời gian mỗi chu kỳ là bao nhiêu?
Số đợt sản xuất = = = 4
Thời gian 1 chu kỳ: T = = 87.5
c) Nếu thời gian thiết lập sản xuất là 5 ngày, thì điểm reorder point là gì?