Lecture 6: Decision Tree & Bayesian Classification | Môn Data Mining - Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 23136115 Introduction to Data Mining Lecture 6 – Activities
1. Exercises in Text [1] - 8.7
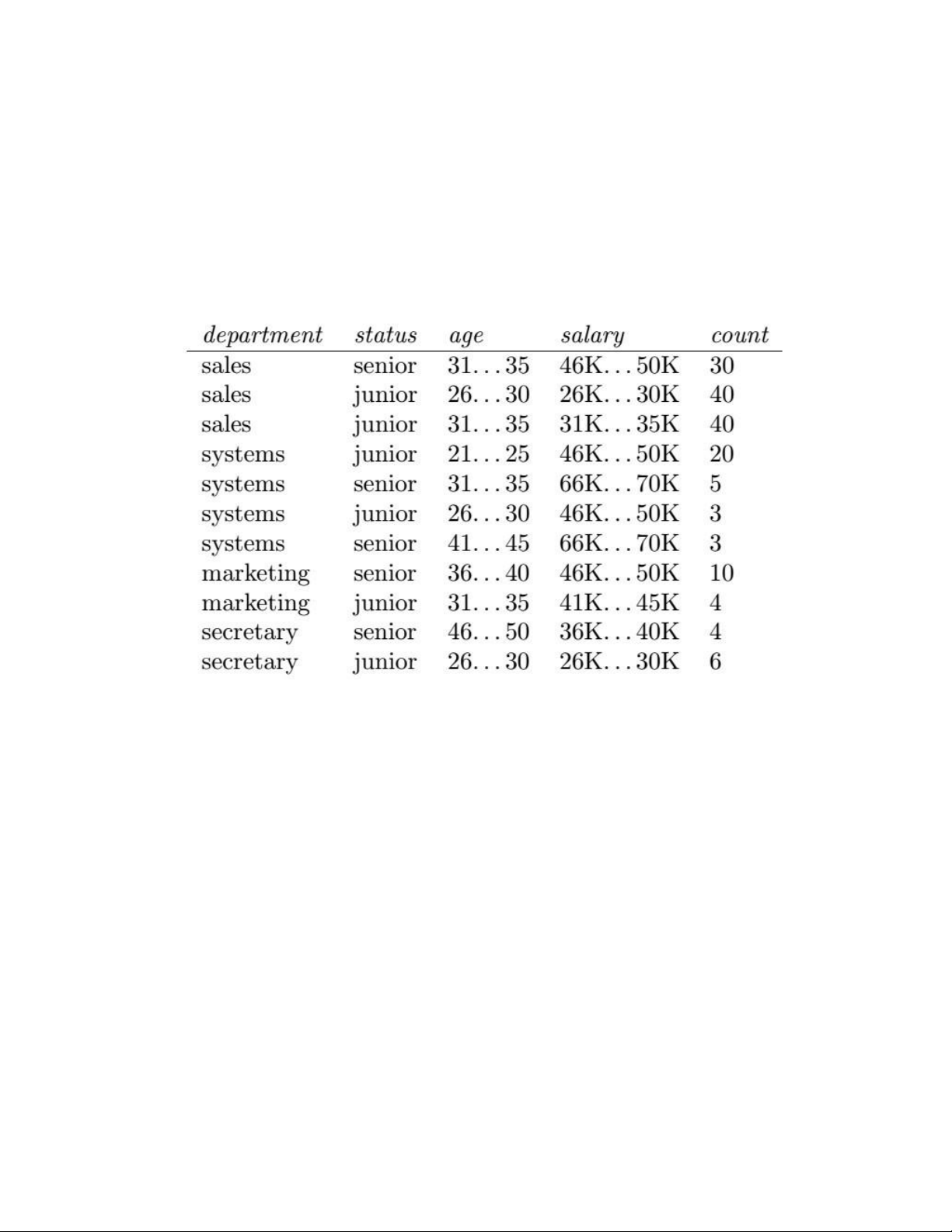
The following table consists of training data from an employee database. The data have been
generalized. For example, “31 . . . 35” for age represents the age range of 31 to 35. For a given row
entry, count represents the number of data tuples having the values for department, status, age, and salary given in that row.
Let status be the class label attribute.
(a) How would you modify the basic decision tree algorithm to take into consideration the count
of each generalized data tuple (i.e., of each row entry)?
(b) Use your algorithm to construct a decision tree from the given data.
(c) Given a data tuple having the values “systems”, “26. . . 30”, and “46–50K” for the attributes
department, age, and salary, respectively, what would a Na¨ıve Bayesian classification of the status for the tuple be? 1 Answers lOMoAR cPSD| 23136115 Introduction to Data Mining
(a) How would you modify the basic decision tree algorithm to take into consideration the count
of each generalized data tuple (i.e., of each row entry)?
The basic decision tree algorithm should be modified as follows to take into consideration the count
of each generalized data tuple.
• The count of each tuple must be integrated into the calculation of the attribute selection measure (such as information gain).
• Take the count into consideration to determine the most common class among the tuples.
(b) Use your algorithm to construct a decision tree from the given data. The resulting tree is: Info(D) = 0.899 Gain(Dept) = 0.0488 Gain(Age) = 0.4247 Gain(Salary) = 0.5375
Second level is Dept or Age b/c Gain = 1. We can choose one of them. Dept/Age is correct. But If
choosing Dept, the tree is simpler (less nodes). Therefore, Dept is preferred. More than that, dept
= secretary -> no instance, hence, the majority class which is junior is assigned as its leaf.
(c) Given a data tuple having the values “systems”, “26. . . 30”, and “46–50K” for the attributes
department, age, and salary, respectively, what would a Na¨ıve Bayesian classification of the status for the tuple be?
P (X|senior) = 18/52 × 0/52 × 40/52 = 0; << this case, the Laplacian correction was not used. 1
more tuple for each age group should be added. There are 6 groups of age => 18/52 × (0+1)/(52 +6) × 40/52 = 2 lOMoAR cPSD| 23136115 Introduction to Data Mining
P (X|junior) =23/113 × 49/113 × 23/113 = 0.018. Thus, a Na¨ıve Bayesian classification predicts
“junior”. => Laplacian correction: 23/113 × (49+1)/(113+6) × 23/113 = Other ways:
P (X|senior) = (18+1)/52+165 × (0+1)/(52 +165) × (40+1)/(52+165) =
P (X|junior) = (23+1)/(113+165) × (49+1)/(113+165) × (23+1)/(113+165) =
P (X|senior) = 18/52 × (0+6)/(52 +6) × 40/52 =
P (X|junior) = 23/113 × (49+6)/(113+6) × 23/113 = P(senior|X) = P(junior|X) =
Therefore, X belongs to class …