Lí thuyết và bài tập 33 câu về điện từ học môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Mục Lục
Câu 1: Phát biểu định luật Coulomb. Định nghĩa điện trường. Nêu đặc điểm của véctơ
cường độ điện trường. Phát biểu nguyên lý chồng chất điện trường. .................................... 3
Câu 2. Nêu cách xác định véctơ cường độ điện trường của điện tích điểm, hệ điện
tích điểm phân bố gián đoạn và hệ điện tích phân bố liên tục. Áp dụng cho lưỡng cực
điện, dây dẫn thẳng dài (vô hạn), vành tròn, đĩa tròn tích điện đều ................................ 4
Câu 3. Khảo sát trường hợp hạt tích điện đứng yên và chuyển động trong điện
trường đều. Nguyên tắc cấu tạo và hoạt động của ống tia âm cực. ............................... 7
Câu 4: Phát biểu và chứng minh định lý Ostrogradski-Gauss (Định luật Gauss). Áp dụng cho
trường hợp mặt cầu mang điện đều, mặt phẳng vô hạn mang điện đều, hai mặt phẳng mang
điện tích đối nhau, mặt trụ thẳng dài vô hạn mang điện đều. ................................................... 8
Câu 5: Tính công của lực tĩnh điện, từ đó chứng tỏ rằng điện trường là 1 trường thế 11
Câu 6: Dẫn ra công thức tính thế năng của điện tích trong điện trường. Nêu định
nghĩa, ý nghĩa của điện thế và hiệu điện thế. Nếu định nghĩa và các tính chất của mặt
đẳng thế. ............................................................................................................................ 12
Câu 7: Trình bày về mối liên hệ giữa cường độ điện trường và điện thế. Áp dụng cho
hai mặt phẳng song song vô hạn mang điện đều, trái dấu; mặt cầu mang điện đều;
mặt trụ thẳng dài vô hạn mang điện đều. ........................................................................ 13
Câu 8: Nêu điều kiện cân bằng tĩnh điện và tính chất của vật dẫn tích điện. Nêu định
nghĩa và công thức tính điện dung của vật dẫn cô lập. ................................................. 15
Câu 9: Định nghĩa hiện tượng điện hưởng. Thế nào là điện hưởng một phần, điện hưởng toàn
phần? Định nghĩa tụ điện. Tính điện dung của tụ phẳng, tụ trụ, và tụ cầu. ............................. 17
Câu 10. Chứng minh công thức tính năng lượng tương tác điện của hệ điện tích điểm, vật dẫn
cô lập tích điện, năng lượng tụ điện phẳng và năng lượng điện trường. .................................. 19
11. Dùng phương pháp ảnh điện để xác định lực tác dụng giữa một điện tích điểm và một mặt
phẳng kim loại vô hạn, tính điện dung của một dây dẫn hình trụ. .......................................... 21
Câu 12. Sự phân cực điện môi là gì? Giải thích hiện tượng phân cực điện môi. Định nghĩa và
công thức tính độ lớn của véctơ phân cực điện môi. Trình bày về mối liên hệ giữa véctơ phân
cực điện môi và mật độ điện mặt của các điện tích liên kết. Nêu công thức tính cường độ điện
trường và điện cảm trong điện môi. ...................................................................................... 23
13. Nêu công thức cường độ điện trường và điện cảm trong điện môi. Đặc điểm véctơ cường độ
điện trường và véctơ cảm ứng điện qua mặt phân cách của hai môi trường ............................ 27
Câu 14: Nội dung các định luật Kirchhoff ............................................................................. 28
Câu 15. Nêu định nghĩa, đặc điểm, ý nghĩa vật lý của véctơ mật độ dòng điện. Chứng minh công
thức định luật Ohm dạng vi phân. Tìm biểu thức suất điện động của nguồn điện trong trường
hợp tổng quát. ..................................................................................................................... 29
Câu 16. Tương tác từ là gì? Nêu nội dung của định luật Ampere. Định nghĩa từ trường. Nêu đặc
điểm của véctơ cảm ứng từ và véctơ cường độ từ trường. ...................................................... 30
Câu 17:Phát biểu nguyên lý chồng chất từ trường áp dụng cho dòng điện thẳng,dòng điện tròn :
........................................................................................................................................... 31
Câu 18: Định nghĩa từ thông. Nêu nội dung định lý Ostrogradski-Gauss (Định luật Gauss) đối
với từ trường. ...................................................................................................................... 34
Câu 19: Chứng minh định lý Ampere về dòng điện toàn phần. Áp dụng cho cuộn dây hình
xuyến, bên trong ống dây điện thẳng dài vô hạn. ................................................................... 36
Câu 20 : Nêu đặc điểm của lực từ (lực Ampere). Trình bày về tác dụng của từ trường đều lên
một mạch điện kín. Tính công của lực từ. .............................................................................. 38
Câu 21: Nêu đặc điểm của lực Lorentz. Nêu kết quả khảo sát chuyển động của hạt tích điện
trong từ trường đều (xét cả trường hợp hạt mang điện bay và từ trường theo phương không
vuông góc với đường sức từ trường đều). .............................................................................. 40
Câu 22: Trình bày về bộ lọc vận tốc và hiệu ứng hall ............................................................. 42
Câu 23: Định nghĩa hiện tượng cảm ứng điện từ. Nêu nội dung các định luật về hiện tượng cảm
ứng điện từ. Hiện tượng tự cảm là gì? Nêu định nghĩa, công thức tính độ tự cảm; công thức tính
suất điện động tự cảm. Giải thích định tính hiệu ứng bề mặt. ................................................. 43
Câu 24: Trình bày hiện tượng hỗ cảm. Nguyên tắc hoạt động, cấu tạo và phương trình của máy
biến thế................................................................................................................................ 44
Câu 25. Định nghĩa sóng điện từ. Nêu các tính chất tổng quát của sóng điện từ. Nêu đặc
điểm,phương trình của sóng điện từ phẳng, đơn sắc. Trình bày về năng lượng và năng thông
sóng điện từ. ........................................................................................................................ 46
Câu 26: Sự từ hóa là gì? Phân biệt các loại vật liệu từ. Nêu đặc điểm của mômen từ và
mômen động lượng của nguyên tử. Giải thích hiệu ứng nghịch từ. ............................. 49
b) Phân loại vật liệu từ: ................................................................................................ 49
Câu 27: Nêu đặc điểm của véctơ từ độ. Giải thích định tính hiện tượng nghịch từ và
thuận từ. Nêu các tính chất của vật liệu sắt từ (nhiệt độ Curie, hiện tượng từ trễ, Ferit
từ). Trình bày sơ lược về thuyết miền từ hóa tự nhiên. ................................................. 50
Câu 28: Trình bày về từ trường Trái Đất .......................................................................... 53
Câu 29: Nêu định nghĩa và đặc điểm của điện trường xoáy. Phát biểu luận điểm I của
Maxwell. Thành lập phương trình Maxwell - Faraday. Nêu định nghĩa và biểu thức của
dòng điện dịch. Phát biểu luận điểm II của Maxwell. Thành lập phương trình Maxwell-
Ampere. ............................................................................................................................. 54
Câu 30: Trường điện từ là gì? Viết hệ phương trình Maxwell. Trình bày về năng lượng
của trường điện từ, tính tương đối của trường điện từ và chuyển động của hạt mang
điện trong trường điện từ ................................................................................................ 57
Câu 31: Trình bày về dao động điện từ điều hòa, dao động điện từ tắt dần, và dao
động điện từ cưỡng bức. ................................................................................................. 59
Câu 32: Định nghĩa sóng điện từ. Nêu các tính chất tổng quát của sóng điện từ. Nêu
đặc điểm, phương trình của sóng điện từ phẳng, đơn sắc. Năng lượng và năng thông
sóng điện từ. ..................................................................................................................... 61
33. Trình bày về sự phát sóng điện từ của dao tử và áp suất sóng điện từ. ................ 63
CÂU HỎI LÝ THUYẾT:
Câu 1: Phát biểu định luật Coulomb. Định nghĩa điện trường. Nêu đặc điểm
của véctơ cường độ điện trường. Phát biểu nguyên lý chồng chất điện trường.
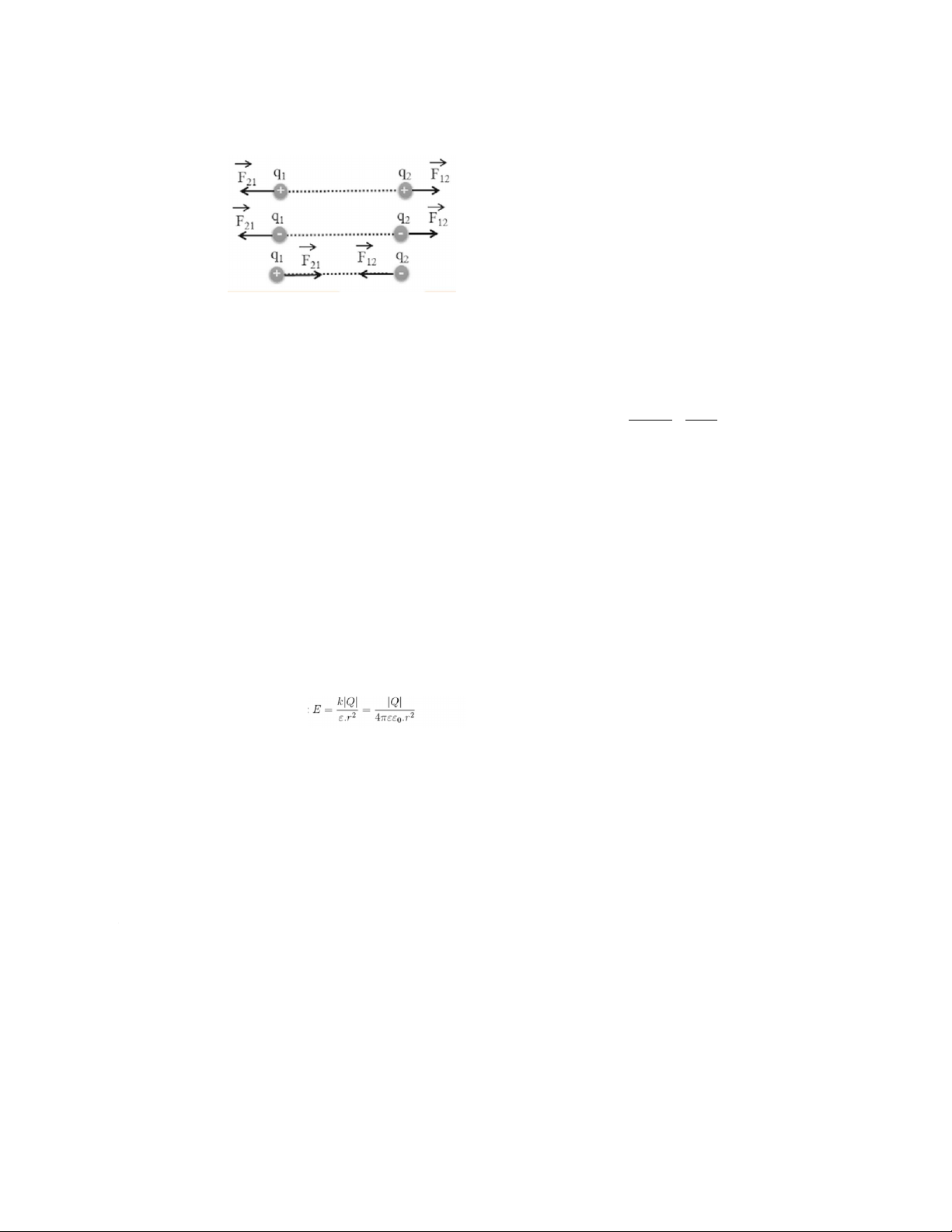
- Định luật Coulomb: lực tương tác tĩnh điện giữa 2 điện tích có phương
nằm trên đường nối 2 điện tích, có chiều như ảnh (hai điện tích cùng dấu
thì đẩy nhau, trái dấu thì hút nhau), có độ lớn tỉ lệ thuận với tích độ lớn
của 2 điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa 2 điện tích đó.
- Công thức tính độ lớn lực tương tác giữa 2 điện tích: F =  
 =  
+ q1, q2 là độ lớn 2 điện tích đang xét (đơn vị: C) + ε0 = 8, 86.10-12 C 2 N.m2
+ ε: hằng số điện môi của môi trường. Đối với môi trường chân không, ε = 1
- Điện trường: là khoảng không gian tồn tại xung quanh điện tích, có đặc
trưng là gây ra lực điện lên các điện tích đặt trong nó.
- Đặc điểm vectơ cường độ điện trường:
+ Phương: trên đường nối từ điện tích q đến điểm cần xét
+ Chiều: hướng ra xa điện tích q nếu q dương, hướng lại gần điện tích q nếu q âm + Độ lớn:
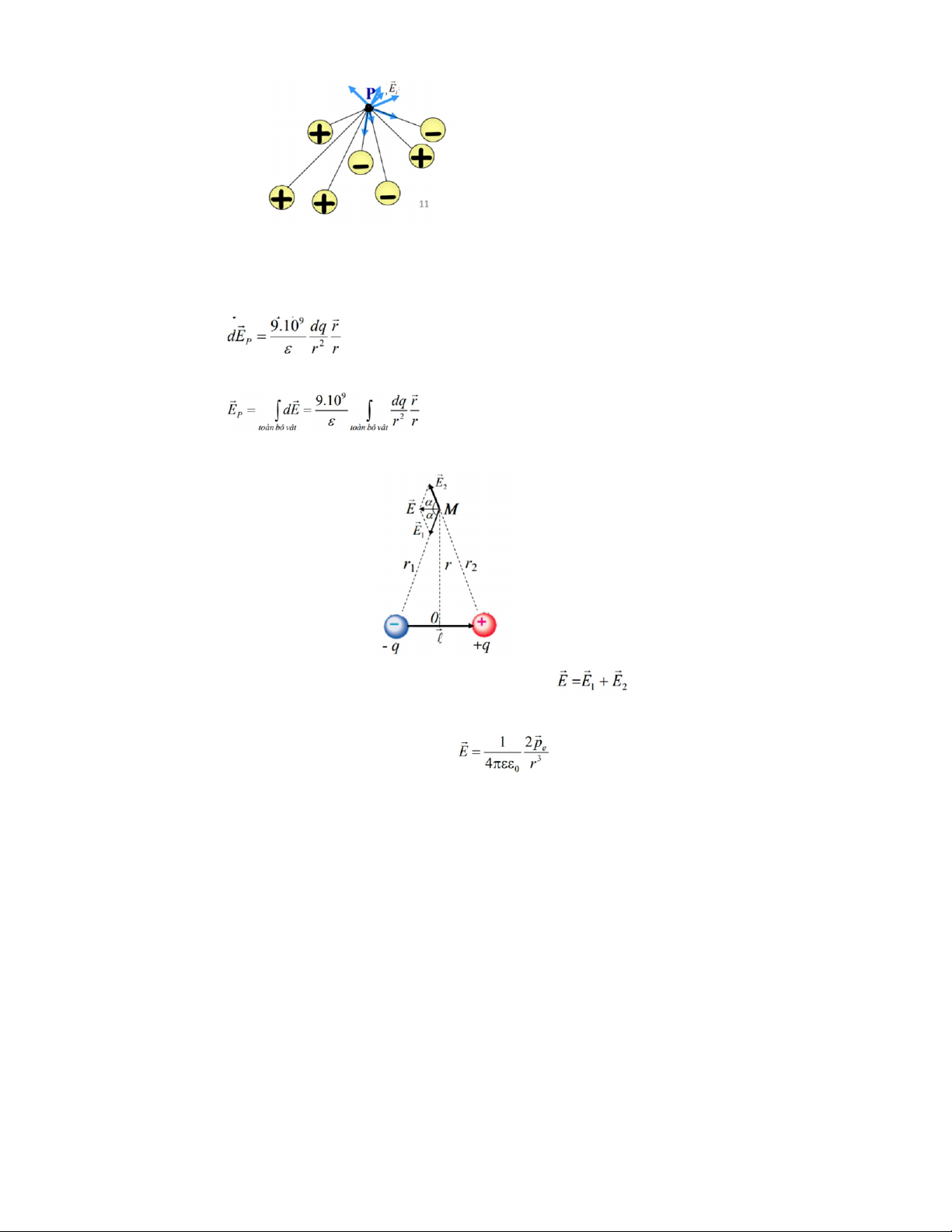
+ Nguyên lý chồng chất điện trường: Vecto cường độ điện trường của
một hệ điện tích điểm bằng tổng các vecto cường độ điện trường gây ra
bởi từng điện tích điểm của hệ
Câu 2. Nêu cách xác định véctơ cường độ điện trường của điện tích điểm, hệ
điện tích điểm phân bố gián đoạn và hệ điện tích phân bố liên tục. Áp dụng cho
lưỡng cực điện, dây dẫn thẳng dài (vô hạn), vành tròn, đĩa tròn tích điện đều
+) Khái niệm cường độ điện trường:Cường độ điện trường tại một điểm
là đại lượng vật lý có độ lớn bằng độ lớn của lực điện trường tác dụng lên
1 đơn vị điện tích đặt tại điểm đó
a. Điện tích điểm:
 Cường độ điện trường do một điện tích điểm Q tại một điểm trong
không gian được xác định bằng:
o 𝑘 =   : Hằng số điện trường
o Q: Điện tích gây ra điện trường,
o r: Khoảng cách từ điện tích đến điểm xét, o hằng số điện môi
b. Hệ điện tích điểm phân bố gián đoạn:
 Điện trường tại một điểm do hệ các điện tích điểm gây ra được tính
bằng cách tổng hợp véctơ cường độ điện trường của từng điện tích điểm tại điểm đó.
o Ei: Điện trường do điện tích qi gây ra tại điểm xét,
o : Khoảng cách từ qi đến điểm xét,
o : Véctơ đơn vị hướng từ đến điểm xét qi o
c. Hệ điện tích phân bố liên tục:
Chia vật thành vô số các phần tử vô cùng nhỏ điện tích dq
Điện trường gây bởi dq tại điểm P cách dq đoạn r:
Điện trường gây bởi vật mang điện tại P +) Áp dụng a. Lưỡng cực điện
 Xét tại điểm nằm trên đường trung trực (r>>l), ta có:
- Tại điểm nằm trên trục lưỡng cực
b. Dây dẫn thẳng dài vô hạn
 Chia dây thành các phần tử có độ dài dl, có điện tích dQ
 Xét điện trường tại dP gây bởi dQ
 Suy ra điện trường tại P gây bởi Q
c. Điện trường gây bởi vành tròn ( dây tròn )
 Chia dây thành các phần tử có độ dài dl, có điện tích
 điện trường tại P gây bởi dQ:
d. Đĩa tròn tích điện đều
 Chia đĩa thành các vành tròn bán kính x độ rộng dx:
 mỗi phần tử nhỏ có thể coi là một vòng dây tròn tâm O bán kính r.
Vòng daya này gây ra tại M vector điện trường dE nằm dọc theo trục Oz
Câu 3. Khảo sát trường hợp hạt tích điện đứng yên và chuyển động trong
điện trường đều. Nguyên tắc cấu tạo và hoạt động của ống tia âm cực.
1. Khảo sát trường hợp hạt tích điện đứng yên và chuyển động trong điện trường đều:
- Hạt tích điện đứng yên trong điện trường:
+ Lực điện tác dụng lên hạt sẽ làm nó trải qua một lực cản làm cho nó giữ nguyên trạng thái tĩnh.
+ Nếu hạt tích điện có độ lớn điện tích và khối lượng nhất định, sẽ có một điểm cân
bằng mà tại đó lực điện cân bằng với lực ma sát hoặc các lực khác.
- Hạt tích điện chuyển động trong điện trường đều:
+ Khi hạt mang điện tích q chuyển động trong một điện trường đều có cường
độ E, nó sẽ chịu một lực Lorentz: F=qE
+ Hạt sẽ chuyển động theo quỹ đạo thẳng hoặc cong tùy thuộc vào mối quan
hệ giữa tốc độ và cường độ điện trường.
+ Công thức cơ bản liên quan: F=ma =qE => a=qE/m
+ Tốc độ của hạt sẽ thay đổi theo thời gian, và hạt sẽ chuyển động với gia tốc phụ
thuộc vào khối lượng và điện tích của hạt.
2. Nguyên tắc cấu tạo và hoạt động của ống tia âm cực:
- Cấu tạo của ống tia âm cực:
+ Bao gồm các bộ phận chính: nguồn phát điện tử, ống phóng tia âm cực
(cathode ray tube), điện trường, từ trường, và màn hình.
+ Một ống tia âm cực gồm có:
` Nguồn phát điện tử (catot): phát ra các electron.
` Anot: nơi nhận electron, tạo ra một điện trường hướng về phía anode.
` Ống phóng (ray tube): môi trường chân không, nơi các electron di chuyển từ catot đến anot - Hoạt động:
+ Nguồn phát điện tử (cathode): phát ra các electron.
+ Điện trường: điện trường tác dụng lên các electron, đẩy chúng về phía anode.
+ Từ trường: nếu đặt từ trường quanh ống, nó sẽ làm lệch đường đi của electron theo quỹ đạo
cong, tùy thuộc vào từ trường và tốc độ của chúng.
+ Màn hình hiển thị: khi các electron va chạm với màn hình được phủ một lớp
phosphor, sẽ phát sáng tại điểm tiếp xúc.
Câu 4: Phát biểu và chứng minh định lý Ostrogradski-Gauss (Định luật
Gauss). Áp dụng cho trường hợp mặt cầu mang điện đều, mặt phẳng vô
hạn mang điện đều, hai mặt phẳng mang điện tích đối nhau, mặt trụ thẳng
dài vô hạn mang điện đều. Bài làm
● Phát biểu: Thông lượng điện cảm gửi qua một mặt kín bất kỳ bằng tổng đại
số các điện tích nằm trong mặt kín đó.
- Điện tích phân bố gián đoạn : 𝜙=𝐷 󰇍 =𝑑∑𝑆𝑞  
- Điện tích phân bố liên tục: 𝜙=∮𝐷  󰇍 ∮ 𝜌 𝑑𝑆= 𝑉 
Phương trình Poisson: 𝑑𝑖𝑣𝐷󰇍 = 𝜌, 𝑣ớ𝑖 𝑑𝑖𝑣𝐷󰇍 =  +  + ● Chứng minh:
Xét thông lượng điện cảm được gửi qua một diện tích dS có:
𝑑𝜙= 𝐷󰇍 𝑑𝑆 = D.ds.cos𝛼 (𝛼 𝑙à 𝑔ó𝑐 𝑡ạ𝑜 𝑏ở𝑖 𝐷󰇍 𝑣à 𝑝ℎá𝑝 𝑡𝑢𝑦ế𝑛 𝑛󰇍 )
= 𝐷𝑛.ds (𝐷𝑛 là hình chiếu của D trên 𝑛󰇍 )
Giả sử xét một mặt kín là một mặt cầu tâm O, bán kính R có: 𝜙 =  = ∫𝐷ds 4𝜋𝑟 = q
Kết luận: Từ thông gửi qua một mặt kín có giá trị bằng tổng điện tích chứa trong mặt ấy ● Áp dụng:
- Trường hợp 1: Mặt cầu mang điện đều
Cho mặt cầu tâm O, bán kính R.
● Điểm P bên ngoài, cách O một khoảng r (r > R).
+ Dựng mặt Gauss chứa điểm P, bán
kính r và bao quanh mặt cầu O.
- Thông lượng điện cảm qua mặt Gauss, bán kính r:
𝜙 = ∮ 𝐷 𝑑𝑆 = ∮ 𝐷 𝑑𝑆 = 𝐷∮ 𝑑𝑆 = 𝐷𝑆 = 𝐷4𝜋𝑟 (1)
Định lý Gauss: 𝜙= 𝑄 (2)
(1)(2) => 𝐷4𝜋𝑟 = Q => D = 
⇒ 𝐸 = = 
● Điểm P’ bên trong, cách O một khoảng r’ (r’ < R)
+ Dựng mặt Gauss là mặt cầu qua P’ bán kính r’ bao quanh mặt cầu O. + Tương tự : D =  
+ Do bên trong không có điện tích: Q = 0 => E =0
Trường hợp 2: Mặt phẳng vô hạn mang điện đều
- Qua M dựng mặt Gauss là mặt trụ có đáy
S, song song với mặt phẳng (trục vuông góc với mặt phẳng).
- Vector điện cảm có phương vuông góc với
mặt phẳng, chiều hướng ra xa mặt phẳng.
Khi đó, ta có thông lượng qua mặt trụ là:
𝜙 = ∮ 𝐷󰇍 𝑑𝑆 = +  ∫ 𝐷󰇍 𝑑𝑆  đá ∫ 𝐷󰇍 𝑑𝑆 ặ ê Lại có: ∫𝐷 󰇍 𝑑𝑆 ặ ê = 0
Áp dụng định lý O-G ta có: 𝜙 = ∫𝐷
 đá 󰇍 𝑑𝑆 = ∫𝐷. 𝑑𝑆  đá = D.2S (1)
Có: ∑𝑞 = 𝜎S
Thay vào (1) => D = ⇒ 𝐸 = =
- Trường hợp 3: Hai mặt phẳng mang điện tích đối nhau
- Áp dụng nguyên lý chồng chất điện trường:
𝐷󰇍 = 𝐷󰇍󰇍 + 𝐷󰇍 Thấy 𝐷
󰇍 󰇍,𝐷󰇍 cùng chiều với nhau
⇨ Độ lớn: D = 2D1 = 2 = 𝜎
⇨ E = = 
- Không gian bên ngoài 2 mặt phẳng: E = 0
- Trường hợp 4: Mặt trụ thẳng dài vô hạn mang điện đều
- Dựng mặt Gauss qua M là một mặt trụ đồng
trục có bán kính r > R, đô dài l. Vector điện cảm
phương vuông góc và hướng ra ngoài mặt trụ
⇨ Điện thông gửi qua mặt bên là Dn
Điện thông gửi qua 2 mặt đáy = 0.
- Thông lượng gửi qua mặt trụ là: 𝜙=∮𝐷 󰇍 =  𝑑 ∫ 𝑆 𝐷
 đá 󰇍 𝑑𝑆 + ∫𝐷 󰇍 𝑑𝑆 ặ ê Lại có: ∫ 𝐷󰇍 𝑑𝑆 = 0  đá ⇨ 𝜙 = ∫ 𝐷󰇍 𝑑𝑆 = = D = DSxq = D2𝜋𝑟𝑙 ặ ê ∫ 𝐷𝑑𝑆 ặ ê ∫ 𝑑𝑆 ặ ê
𝜙 = 𝜆𝑙 ( 𝜆: 𝑚ậ𝑡 độ đ𝑖ệ𝑛 𝑑à𝑖)
⇨ D =  ⇒ 𝐸 =  =     
Câu 5: Tính công của lực tĩnh điện, từ đó chứng tỏ rằng điện trường là 1 trường thế
 Xét điện tích thử q0 dịch chuyển từ M đến N trong điện trường gây
bởi q (đứng yên tại O). Lực tác dụng lên 𝑞 là 𝐹= 𝑞𝐸󰇍 ( 𝐸󰇍 : điện
trường do q gây ra tại vị trí 𝑞)
Công để dịch chuyển điện tích trên 1 đoạn 𝑑𝑠 vô cùng nhỏ: \
Như vậy, công để dịch chuyển điện tích từ M tới N có thể xác định bởi:
 Từ đây, có thể thấy rằng công của lực tĩnh điện trong chuyển rời 1
điện tích q0 không phụ thuộc vào hình dạng đường đi mà chỉ phụ
thuộc vào điểm đầu và điểm cuối. Như vậy, có thể kết luận điện
trường là trường thế.
 Để chứng minh điện trường là trường thế còn có thể xuất phát từ:
công dịch chuyển 1 điện tích q0 dọc theo 1 đường cong kín bằng 0
(điểm đầu trùng điểm cuối) :
Câu 6: Dẫn ra công thức tính thế năng của điện tích trong điện trường.
Nêu định nghĩa, ý nghĩa của điện thế và hiệu điện thế. Nếu định nghĩa và
các tính chất của mặt đẳng thế.
a) Dẫn ra công thức tính thế năng trong của điện tích trong điện trường:
+ Vì điện trường là một trường thế nên công của lực tĩnh điện trong dịch
chuyển 𝑞 bằng độ giảm thế năng của điện tích đó trong điện trường:
+ Thế năng của 𝑞 trong điện trường của một điện tích điểm q :
Xét 𝑞 dịch chuyển trong điện trường của q. Khi đó:
→ Biểu thức thế năng của 𝑞 đặt trong điện trường của điện tích điểm q
và cách điện tích này một khoảng bằng r là 𝑊 = 𝑞𝑞 4𝜋𝜀𝜀𝑟+ 𝐶
Quy ước chọn W của 𝑞 khi nó ở xa q vô cùng bằng không: 𝑊 = 0 → C = 0 → W =  
+ Thế năng của q0 trong điện trường của hệ điện tích điểm: W =∑𝑊= ∑   
+ Thế năng của q0 trong điện trường bất kỳ: 𝑊=𝑞𝐸 󰇍 𝑑𝑠 
b) Định nghĩa, ý nghĩa của điện thế và hiệu điện thế:
+ Định nghĩa: Tỷ số W/𝑞 không phụ thuộc vào điện tích 𝑞 mà chỉ phụ
thuộc vào các điện tích gây ra điện trường và vào vị trí điểm đang xét
trong điện trường. Vậy ta có thể dùng tỷ số đó để đặc trưng cho điện
trường tại điểm đang xét. V = W/𝑞 được gọi là điện thế của điện trường tại điểm đang xét. + Ý nghĩa:
+) Điện thế tại một điểm trong điện trường là một đại lượng về trị số bằng
công của lực tĩnh điện trong sự dịch
chuyển một đơn vị điện tích dương từ điểm đó ra xa vô cùng.
+) Hiệu điện thế giữa hai điểm M và N trong điện trường là một đại lượng
về trị số bằng công của lực tĩnh điện trong
sự dịch chuyển một đơn vị điện tích dương từ điểm M tới điểm N
c) Định nghĩa và các tính chất của mặt đẳng thế:
+ Định nghĩa: Mặt đẳng thế là quỹ tích của những điểm có cùng điện thế V = C = const
+ Ý nghĩa của mặt đẳng thế:
+) Các mặt đẳng thế không cắt nhau
+) Công của lực tĩnh điện trong sự dịch chuyển điện tích q0 trên mặt đẳng
thế bằng không : AMN = 𝑞(𝑣− 𝑣)= 0
+) Vectơ cường độ điện trường tại một điểm trên mặt đẳng thế vuông góc
với mặt đẳng thế tại điểm đó.
Câu 7: Trình bày về mối liên hệ giữa cường độ điện trường và điện thế. Áp
dụng cho hai mặt phẳng song song vô hạn mang điện đều, trái dấu; mặt
cầu mang điện đều; mặt trụ thẳng dài vô hạn mang điện đều. Trả lời:
a) Mối liên hệ giữa cường độ điện trường và điện thế:
+ Theo định nghĩa ta có: 𝑑𝐴 = 𝑞𝐸󰇍𝑑𝑠
+ Mà 𝑑𝐴 = 𝑞𝑉 − (𝑉 + 𝑑𝑉)= −𝑞𝑑𝑉
Do đó, ta có: 𝑑𝑉 = −𝐸󰇍𝑑𝑠= −𝐸. 𝑑𝑠. cos (𝛼) với α = (𝐸󰇍, 𝑑𝑠)
Kết luận 1: Vector cường độ điện trường luôn hướng theo chiều điện thế giảm.
Kết luận 2: Hình chiếu vector cường độ điện trường trên một phương nào
đó về trị số bằng độ giảm điện thế trên đơn vị dài của phương đó.
b) Áp dụng cho hai mặt phẳng song song vô hạn mạng điện đều; mặt
cầu mang điện đều; mặt trụ thẳng dài vô hạn mang điện đều
+ Xác định hiệu điện thế giữa hai mặt phẳng song song vô hạn mang điện đều, trái dấu:
 Ta có : 𝑑𝑉 = −𝐸 󰇍𝑑𝑠 (1)  Theo (1), ta có :       − =𝑑𝑉 𝑉− 𝑉=𝐸  󰇍 =𝑑  𝑠
𝐸𝑑𝑠 = 𝐸 𝑑𝑠 = 𝐸𝑑
Mà 𝐸 =  nên 𝑉− 𝑉=
+ Xác định hiệu điện thế giữa hai điểm trong điện trường của một mặt cầu mang điện đều:
Giả sử ta muốn xét hiệu điện thế giữa 2 điểm cách tâm quả cầu những đoạn R1 và R2
 Ta có : −𝑑𝑉 = 𝐸󰇍𝑑𝑟= 𝐸. 𝑑𝑟. cos(𝛼)= 𝐸𝑑𝑟 với 𝐸 là hình chiếu của
𝐸󰇍 lên phương pháp tuyến n của mặt cầu
 Mà mặt cầu là một mặt đẳng thế nên 𝐸󰇍 ↑↑ 𝐸
󰇍 󰇍 nên 𝐸= 𝐸 = 
Suy ra −𝑑𝑉 = .dr Từ đó ∫−    𝑑 =𝑉∫  
Hay 𝑉− 𝑉=  (−)
 Trong trường hợp R1 = R và R2 = ∞(V2 = 0), ta sẽ tìm được biểu
thức tính điện thế V của một mặt cầu mang điện đều V =  
+ Xác định hiệu điện thế giữa hai điểm trong điện trường của một mặt trụ
thẳng dài vô hạn mang điện đều
 Ta có 𝐸= 𝐸 =  == 
 Suy ra 𝑉− 𝑉=∫−𝑑𝑉 
=∫ 𝐸𝑑𝑟  =∫    = 𝑑𝑟 In( )
 Vậy 𝑉− 𝑉=  In 󰇡
󰇢=In 󰇡
󰇢=In()
Câu 8: Nêu điều kiện cân bằng tĩnh điện và tính chất của vật dẫn tích điện.
Nêu định nghĩa và công thức tính điện dung của vật dẫn cô lập.
• Điều kiện cân bằng tĩnh điện:
1. Vecto cường độ điện trường tại mọi điểm bên trong vật dẫn bằng
không:𝐸󰇍󰇍󰇍 = 0󰇍
2. Thành phần tiếp tuyến của vecto cường độ điện trường tại mọi điểm
trên mặt vật dẫn phải bằng không: 𝐸= 0󰇍, 𝐸󰇍 = 𝐸󰇍󰇍 Nếu 𝐸
󰇍 󰇍≠ 0󰇍,𝐸≠ 0󰇍 thì các electron tự do bên trong và trên bề mặt vật
dẫn sẽ chuyển dời có hướng → trái với điều kiện cân bằng đã đặt ra.
• Tính chất của vật dẫn mang điện:
Tính chất 1: Vật dẫn là vật đẳng thể
- Xét hai điểm M,N bất ký trên vật dẫn. Hiệu điện thể giữa 2 điểm đó là:
1. Bên trong vật dẫn: 𝐸󰇍 = 0󰇍 → 𝑉 tại mọi điểm bên trong vật dẫn đều bằng nhau.
2. Trên bề mặt vật dẫn: 𝐸= 0 → 𝑉 tại mọi điểm vật dẫn đều bằng nhau.
3. Do V có tính liên tục → điện thế tại mọi điểm của vật dẫn đều bằng nhau.
Tính chất 2: Khi vật dẫn ở trạng thái cân bằng tĩnh điện, điện tích
chỉ phân bố trên bề mặt vật dẫn. Bên trong vật dẫn điện tích bằng 0
- Giả sử truyền cho vật dẫn một điện tích q nào đó. Tưởng tượng lấy
một mặt kín (S) bất kỳ trong vật dẫn. Theo O-G, tổng đại số điện tích
nằm trong mặt kín (S) là:
- Bên trong vật dẫn: 𝐷󰇍 = 𝜀𝜀𝐸󰇍 = 0 ⇒ 𝛴𝑞= 0
- Vì mặt kín (S) được chọn bất kỳ ⇒ Ta kết luận: Tổng đại số điện tích
bên trong vật dẫn bằng không.
- Nếu ta truyền cho vật dẫn một điện tích q thì điện tích này sẽ chuyển
ra bề mặt vật dẫn và phân bố trên bề mặt vật dẫn đó.
- Đối với vật dẫn rỗng đã ở trạng thái cân bằng tinh điện, điện trường ở
phần rỗng và trong thành của vật dẫn rỗng cũng luôn bằng không.
- Nếu đem một quả cầu kim loại mang điện tích q cho tiếp xúc với mặt
trong của vật dẫn rỗng thì q sẽ truyền hết ra mặt ngoai vật dẫn rỗng →
Nguyên tắc máy phát tĩnh điện VandeGraf
- Vì điện trường bên trong vật dẫn rỗng bằng không → Vật dẫn rỗng có
tác dụng như 1 màn bảo vệ → Vật dẫn rỗng được gọi là màn điện
Tính chất 3: Sự phân bố điện tích trên mặt vật dẫn chỉ thuộc vào
hình dạng của mặt đó.
- Điện tích tập trung ở những chỗ có mũi nhọn. Ở những chỗ lõm điện
tích rất ít, hầu như bằng không
- Hiệu ứng mũi nhọn, gió điện: Giải phóng điện tích trên máy bay, phóng
điện bảo vệ máy điện, cột thu lôi.
• Định nghĩa điện dung của vật dẫn cô lập:
1. Vật dẫn cô lập: Một vât dẫn được gọi là cô lập về điện nếu gần nó
không có một vật nào khác có thể gây ra ảnh
hưởng đến sự phân bố điện tích trên vật dẫn đang xét.
2. Định nghĩa điện dung: Điện dung của một vật dẫn cô lập là một đại
lượng về trị số bằng điện tích cần truyền cho
vật dẫn để điện thế của vật tăng lên 1 đơn vị điện thế.
3. Công thức tính điện dung của vật dẫn cô lập:
Tính điện dung của quả cầu kim loại bán kinh R đặt trong môi trường có
h/s điện môi ε -Gọi Q là điện tích quả cầu.
- V là điện thế của quả cầu: 𝑉 =  ⇒ 𝐶 = = 4𝜋𝜀𝜀𝑅 (1)
- Nếu trong (1) chọn C = 1F, ε = 1
Câu 9: Định nghĩa hiện tượng điện hưởng. Thế nào là điện hưởng một
phần, điện hưởng toàn phần? Định nghĩa tụ điện. Tính điện dung của tụ
phẳng, tụ trụ, và tụ cầu. Bài làm
Định nghĩa hiện tượng điện hưởng: 1. Hiện tượng:
- Khi đặt một vật dẫn trung hòa trong điện trường ngoài E , hai phía của vật
dẫn xuất hiện các điện tích trái dấu gọi là các điện tích cảm ứng. Hiện tượng
này gọi là hiện tượng điện hưởng. 2. Giải thích:
- Dưới tác dụng của điện trường ngoài, các electron tự do trong vật dẫn chuyển
động ngược chiều với điện trường ngoài. Kết quả là mặt B tích điện “-”, mặt
C tích điện “+”, chúng có độ lớn bằng nhau, tạo nên điện trường E󰇍 bên trong vật dẫn
 Điện hưởng một phần và điện hưởng toàn phần:
1. Điện hưởng một phần:
- Chỉ một phần số đường cảm ứng điện của vật mang điện gặp vặt bị điện
hưởng, do đó độ lớn của điện tích cảm ứng nhỏ hơn độ lớn của điện tích trên vật mang điện: |q’| < |q|
2. Điện hưởng toàn phần:
- Khi vật dẫn (BC) bao bọc hoàn toàn vật mang điện A, toàn bộ đường
cảm ứng điện xuất phát từ A đến tận cùng trên vật dẫn (BC), ta có hiện
tượng điện hưởng toàn phần.
- Áp dụng định lý về các phần tử tương ứng → độ lớn của điện tích cảm
ứng bằng độ lớn của điện tích trên vật mang điện. |q’| = |q|
 Định nghĩa tụ điện: 1. Định nghĩa:
- Tụ điện là một hệ hai vật dẫn A và B sao cho vật dẫn B bao bọc hoàn
toàn vật dẫn A. Khi đó hai vật dẫn ở trạng thái điện hưởng toàn phần. 2. Tính chất:
a) Tính chất 1: q+ q= 0 (do điện hưởng toàn phần)
b) Tính chất 2: Gọi V1,V2 là điện thế của A và B
q= CV+ CV
q+ q′= CV+ CV
- Khi sử dụng tụ điện, 2 bản thường được nối với nguồn, nói chung q′ không xuất hiện.
q= CV+ CV
q= CV+ CV
 q+ q= (C + C)V+ (C + C) V = 0
- Do V, V tùy ý -> C + C = 0 và C + C = 0
- Do C = C -> C = C = C, C = C = − C q= C(V − V) q= −C(V − V) c) Tính chất 3: q= C(V − V) q= −C(V− V) (3)
- Vì C > 0, từ (3) suy ra q> 0 thì V> V
- Vậy trong tụ điện, điện thế của bản tích điện dương cao hơn điện thế của
bản tích điện âm q = q= − q được gọi là điện tích của tụ điện q = C(V − V)= CU
 Tính điện dung của một số tụ điện: 1. Tụ điện phẳng:
U = V − V= E. d =  d =  d C = 
  = 2. Tụ điện cầu:
U = V − V= E. d = (+) = (  )   C = 
  =    3. Tụ điện trụ:
U = V − V= ln = ln   C = 
  =  
Câu 10. Chứng minh công thức tính năng lượng tương tác điện của hệ
điện tích điểm, vật dẫn cô lập tích điện, năng lượng tụ điện phẳng và
năng lượng điện trường.
a) Năng lượng tương tác điện của hệ điện tích điểm
+) Hệ hai điện tích điểm :
Khi điện tích điểm q2 đặt trong điện trường của điện tích điểm q1 thế năng của q2 là: Wt =   
 với r12 là khoảng cách giữa 2 điện tích
Wt cũng là thế năng của q1 trong điện trường của q2. Ta nói Wt là thế năng
tương tác hay năng lượng tương tác điện của hệ 2 điện tích q1 và q2 ký hiệu là: W12 = W21 =    
W12 = W21 = q󰇡󰇢+ q󰇡󰇢 Mà ta có 
 = 𝑉 ,  = 𝑉
W12 = W21 = q𝑉+ q 𝑉
+) Hệ 3 điện tích điểm :
+)Hệ n điện tích điểm :
W = (q𝑉+ q𝑉+ ⋯ + q𝑉) =  ∑q𝑉 
b) Năng lượng điện của một vật dẫn cô lập tích điện
q : điện tích vật dẫn.
Chia vật dẫn thành những điện tích điểm dq
W = ∫𝑉𝑑𝑞 = 𝑉∫𝑑𝑞 =  𝑞𝑉
W = 𝑞𝑉 = 𝐶𝑉= 
c) Năng lượng tụ điện