








































































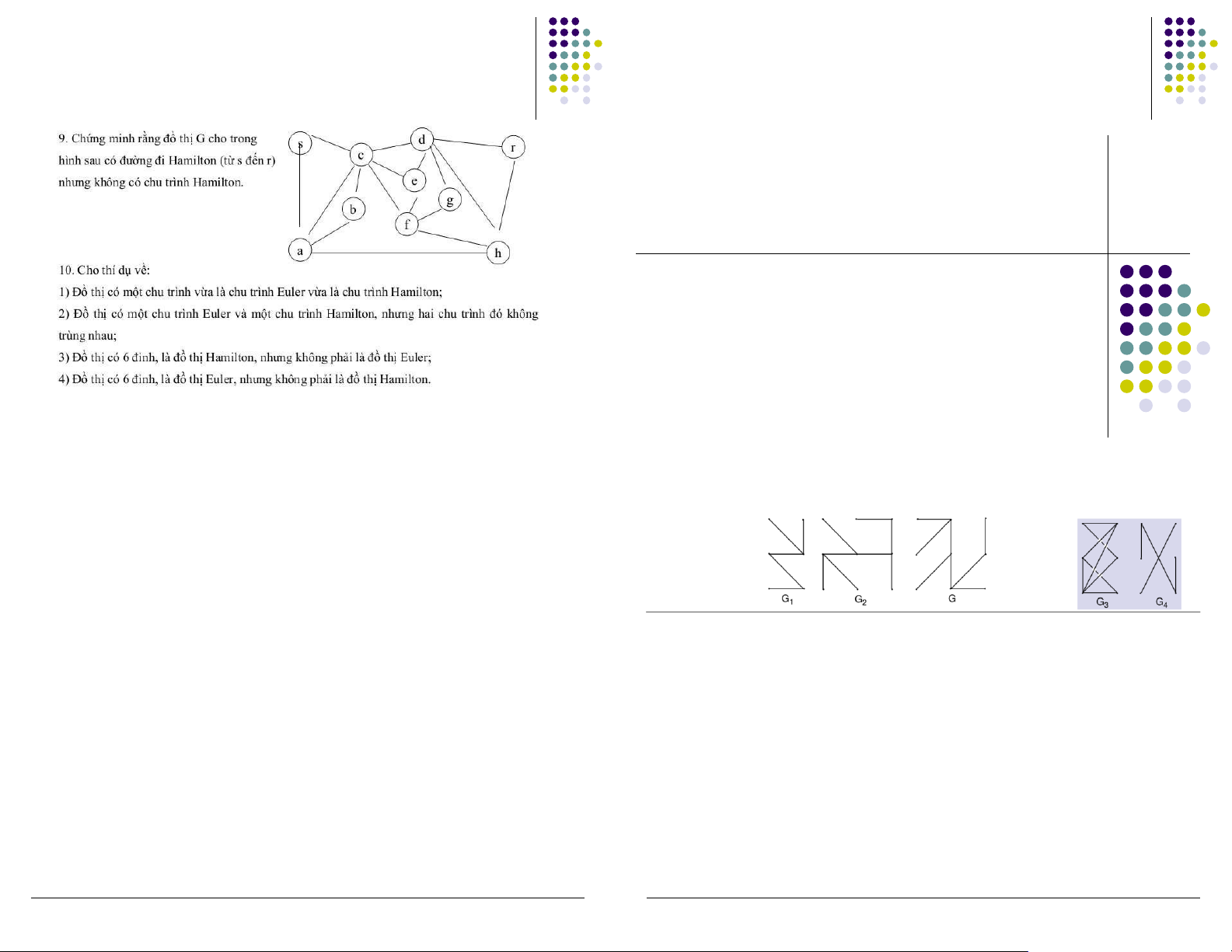



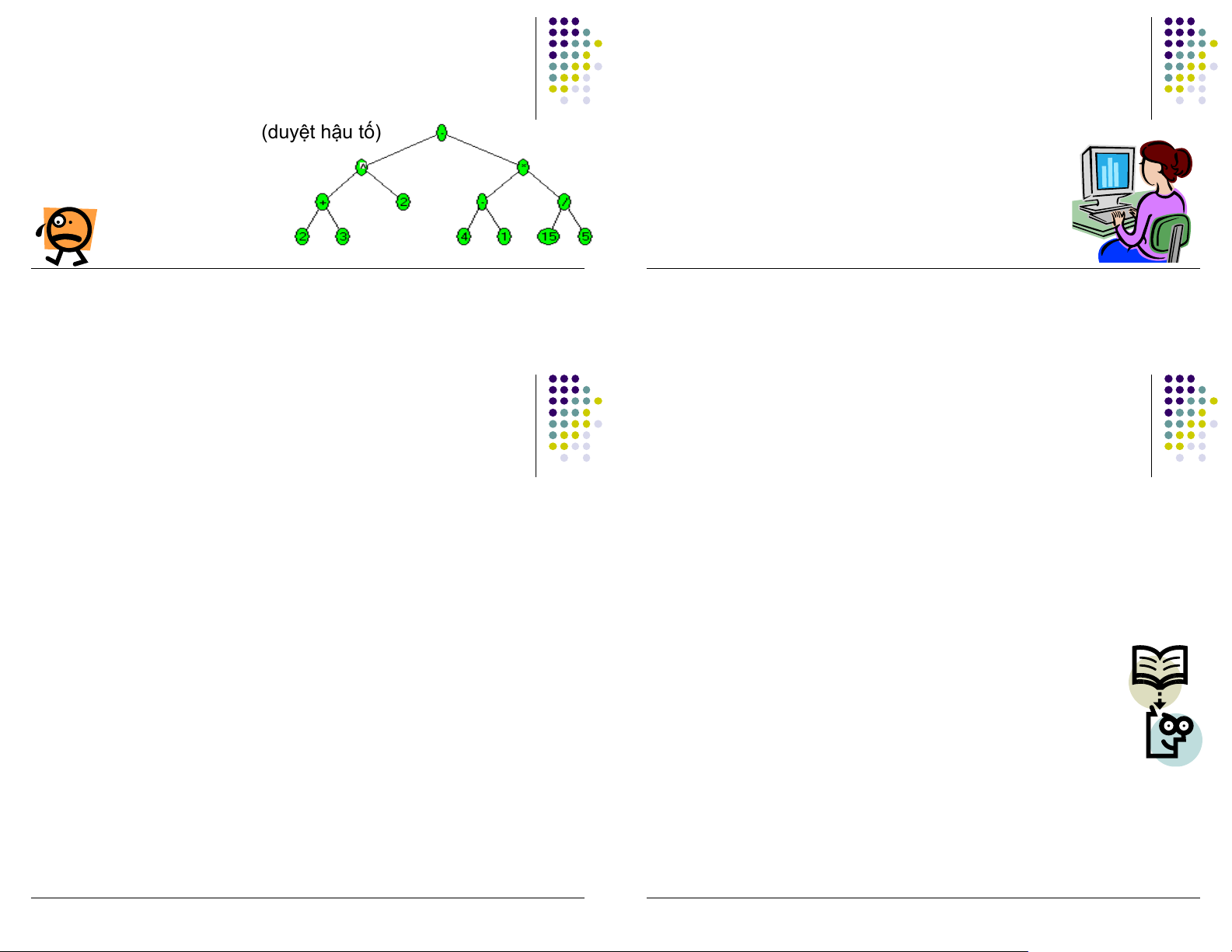







Preview text:
lOMoAR cPSD| 40425501
CHƯƠNG I: CƠ SỞ LÔGIC
CẤU TRÚC RỜI RẠC Mệnh ề
Biểu thức logic ( Dạng mệnh ề ) Qui tắc suy diễn Vị từ, lượng từ Quy nạp toán học 1 2 Mệnh đề
“ Toantính của chiếnlược gia44 tuổi ã suýt
Địnhnghĩa : Mệnh ề là một khẳng ịnh cógiá
thànhcông nếu ôngkhôngtính tới ột biến từ
trị chânlýxác ịnh, únghoặc sai.
những ngôisao ối phương”.
Câu hỏi, câu cảm thán, mệnh lệnh… không là mệnh ề. Nguồn : Ví dụ:
http://thethao.vnexpress.net/tin-tuc/champions-
- Đại học CNTT trựcthuộcĐHQG TP.HCM.
league/sneijder-ket-lieu-juventus-trong-con- -1+7=8. mua-tuyet-2922371.html - Hôm nay em ẹp quá! (k hông là mệnh ề)
- Hômnay ngày thứmấy ?(không là mệnh ề) 3 4
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Qui suy Qui suy tắc diễn tắc diễn 4. Qui tắc phản chứng : → pq → [( p q) 0] * Tổng quát: [( → → pp ... p ) q ] [( pp ... p q) 0] 1 2 n 1 2 n
Để chứng minh vế tráilà mộthằng úng ,ta
chứng minh nếu thêm phủ ịnhcủa qvào
cáctiên ề thì ượcmột mâu thuẫn . 29 30 Qui suy Qui suy tắc diễn tắc diễn 4. Qui tắc phản chứng : Chứng minh suy 5. luận :
Qui tắcchứng minhtheo trườnghợp : Ví dụ : p → r
[( p → r) ( q → r)] [( p q) → r] p → q * q Tổng quát: → s r → s [( → pq → ) ( → p q) ... ( p q)] Giải 1 2 n
: CM bằngphản chứng [( pp ... p ) → q] p → r 1 2 n p → q q → s r s 0 31 32
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Qui suy Suy luận lậpluận úng ( ) sau hay tắc diễn sai?
Ví dụ : Suy luận sau úng haysai p → q qr → s t → r p s → t
HD:Dùng phản ví dụ : Chọn
p=1, q=0, r=1, s=0, t=1 37 38 Qui tắc diễn suy 39 40
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 45 Vị từ - từ Vị từ - từ Lượng Lượng
Chop(x,y)là một vị từ theohai biến x,yxác ịnh
Ví dụ : Các mệnh ề sau úng haysai?
trênA B.Ta ịnhnghĩa các mệnh ề lượng từ hóa - 2 “ x R, ” x+6x+50 của p(x,y) như sau: - 2 “ x R, x+6x+50 ”
“ x A, y B,p(x, y)” “ x A,( y B,p(x, y))” - “ x R, y R,2x+y<1 ”
“ x A, y B,p(x, y)” “ x A,( y B,p(x, y))” - “ x R, y R,2x+y<1 ”
“ x A, y B,p(x, y)” “ x A,( y B,p(x, y))” - “ x R, y R,x+2y<1 ”
“ x A, y B,p(x, y)” “ x A,( y B,p(x, y))” - “ x R, y R,x+2y<1 ” 47 48
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 49 50 5 1 52
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Qui n Qui n ạp ạp
Cho n 0 N vàp(n) là một vị từ theo biến tự nhiênn n 0 .
*Nguyênlýquy nạpmạnh ( giảthiết úng ến k)
Để chứng minh tính úng ắncủamệnh ề : Môhìnhsuy diễn : n n 0 , p(n) tacó ( cơsở
thể dùngcác dạng nguyênlýquy nạp như sau: ) ( pn 0 ) + → + *Nguyênlýquy (GTQN ) knp 0 n ,( ) ( pn 1)... () pk ( pk 1)
nạpyếu ( giảthiết úng với k) 0 0 Môhìnhsuy diễn 0 nnpn ,() : ( cơ sở ) ( pn 0 ) G ( ) TQN kn p → + 0 k ,() ( pk 1) 0 nnpn ,() 57 58 Qui n ạp Ví dụ : Chứng 2 minh 1 ++++ −= 3 5 ... (2 n 1) n Ví dụ : Chứng minh 1 na 1 n a A = = , A 0 1 0 1 9 5 60
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
CÁC PHƯƠNG PHÁP ĐẾM TẬP HỢP
I. Tập hợp các tập hợp con. Biểu diễn tập hợp trên máy tính. 1.
Các phép toán tập hợp và các tính chất liên quan. Tập hợp
Khái niệm tích Descartes.
2. Quan hệ giữa các tập hợp
II. Nguyên lý cộng. Nguyên lý nhân.
Nguyên lý chuồng bồ câu.
3. Các cách xác ịnh tập hợp
III.Hoán vị, tổ hợp và chỉnh hợp. Công thức
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 nhị thức Newton.
4. Tập hợp các tập hợp con (Tập hợp lũy thừa)
IV.Hoán vị và tổ hợp lặp. 2 3
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
QUAN HỆ GIỮA CÁC TẬP HỢP
o Z = {…., 0, 1, 2, 3, …}. 8 QUAN HỆ GIỮA CÁC TẬP HỢP
Tập hợp bằng nhau: Hai tập hợp A và B ược gọi là
bằng nhau khi và chỉ khi chúng có cùng các phần
Ví dụ: Tập các số nguyên dương lẻ nhỏ hơn
tử, tức là mỗi phần tử thuộc A ều là phần tử thuộc B
10 là một tập con của tập các số nguyên
và ngược lại. Kí hiệu: A=B. Ví dụ: {1, 3, 5} và {3, 5,
dương nhỏ hơn 10 . 1}
Ghi chú: Khi muốn nhấn mạnh tập A là tập
con của tập B nhưng A≠B, ta viết A
Tập con: Tập A ược gọi là tập con của tập B khi và ⊂B và nói
rằng A là tập con thật sự của B.
chỉ khi mọi phần tử của A ều là phần tử của B. Nhận xét: Kí hiệu: A B.
o Nếu A⊆B và B⊆A thì A=B. o Tập
Nhận xét: (A B) x (x A → x B) là úng
rỗng là con của mọi tập hợp. o Mọi tập 6
hợp ều là tập con của chính nó. 7
CÁC CÁCH XÁC ĐỊNH TẬP HỢP
1. Liệt kê các phần tử
CÁC CÁCH XÁC ĐỊNH TẬP HỢP
Một tập hợp có thể ược xác ịnh bằng cách liệt
2. Chỉ ra các thuộc tính ặc trưng của phần tử
kê tất cả các phần tử của nó. Chúng ta sẽ dùng
Một tập hợp cũng có thể ược xác ịnh bằng
ký hiệu trong ó tất cả các phần tử của một tập
cách chỉ ra rõ các thuộc tính ặc trưng của các
hợp ược liệt kê ở giữa hai dấu móc. phần tử của nó. Ví dụ: o V = {a, e, i o, u} o
Cách viết: A={x U| p(x)} (A O = {1,3, 5, 7, 9} o
={x U:p(x)}) hay vắn tắt A={x| p(x)} (A N = {0, 1, 2, 3, …} ={x: p(x)}) Ví dụ:
▪V = {x | x là nguyên âm}
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 10
TẬP HỢP CÁC TẬP HỢP CON
▪O = {x | x là số nguyên dương nhỏ hơn 10}
▪A = {x | x = 2n, n N }
Cho tập X, tập tất cả các tập con của X
▪B = {n N | n là số nguyên tố} . 9
(còn gọi là tập lũy thừa của X) ược kí hiệu là
CÁC CÁCH XÁC ĐỊNH TẬP HỢP
P(X). Nói cách khác, P(X) là một tập hợp mà
mỗi phần tử của nó là một tập hợp con của
3. Cách xác ịnh tập hợp dưới dạng ảnh của một tập X. hợp khác Ví dụ: X={0, 1, 2}
P(X) = { , {0}, {1}, {2}, {0,1},
Cách viết: A={f(x)| x B} (A ={f(x): x B}) {0,2},{1,2},{0,1,23}}. Ví dụ: Chú ý: ▪A = {(2n+1)| n N} . ▪ X Y P(X) P(Y). ▪B = {2x| x R}
▪Nếu X có n phần tử (n N) thì P(X) có 2n phần tử. 11
BIỂU DIỄN TẬP HỢP TRÊN MÁY TÍNH
cách dùng sự sắp xếp tùy ý các phần tử của tập vũ trụ.
1. Phương pháp biểu diễn
▪ Có nhiều cách biểu diễn tập hợp trên máy tính. 12
BIỂU DIỄN CÁC TẬP HỢP TRÊN MÁY TÍNH
▪Ở ây chúng ta sẽ nói ến một phương pháp
lưu trữ các phần tử bằng
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
1. Phương pháp biểu diễn
Giả sử tập vũ trụ U là hữu hạn. Trước hết
sắp xếp tuỳ ý các phần tử của U, ví dụ a1, a2,
…,an, sau ó biểu diễn tập con A của U bằng
một xâu bit có chiều dài n, trong ó bit thứ i là
1 nếu ai thuộc A và là 0 nếu ai không thuộc A. 13
Cho U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} và sự sắp xếp các phần
tử trong U theo thứ tự tăng dần, tức là ai = i.
o Khi ó, chuỗi bit biểu diễn tập con A = {1, 2, 3, 4, 5} là 11111
00000; xâu bit biểu diễn tập con B = {1, 3, 5, 7, 9} là 10101 01010.
o Để nhận ược xâu bit cho các tập là hợp và giao của hai tập
hợp, ta sẽ thực hiện phép toán Boole trên các xâu bit biểu
diễn hai tập hợp ó.
o Xâu bit ối với hợp của hai tập là: 11111
00000 ∨ 10101 01010 = 11111 01010
A∪B = {1, 2, 3, 4, 5, 7, 9}.
o Xâu bit ối với giao của hai tập này là:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)
BIỂU DIỄN CÁC TẬP HỢP TRÊN MÁY TÍNH
CÁC PHÉP TO ÁN TẬP HỢ P lOMoAR cPSD| 40425501
2 . Ví dụ 11111
00000 ^ 10101 01010 = 10101 3. Phép hiệu 00000 A∩B = {1, 3, 5}. 14 1. Phép hợp
4. Các tính chất liên quan 2. Phép giao
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
CÁC PHÉP TOÁN TẬP HỢP 2 . Phép giao
CÁC PHÉP TOÁN TẬP HỢP
Định nghĩa: Giao của n tập hợp là một tập
hợp chứa các phần tử thuộc tất cả n tập hợp 2. Phép giao ó. Ta ký hiệu:
Định nghĩa: Cho A và B là hai tập hợp. Giao của hai tập hợp n
A và B, ược ký hiệu là A∩B, là tập hợp chứa các phần tử
thuộc cả hai tập A và B.
A A1 = 2 ... An Ai A∩B ={x| (x i=1
∈A)∧(x ∈B)}
ể chỉ giao của các tập hợp A1, A2, ..., An . Ví
dụ: Cho Ai= {i, i+1, i+2, …}. Khi ó:
Giản đồ Venn biểu diễn giao của A và B n Ví dụ: i i, 1,i 2,... = + +n Ai
o Cho A = {1, 2, 3} và B = {1, 3, 5} thì A∩B = {1, 3}.
= n n, + +1,n 2,...
o Cho M={1,2} và N={3,4} thì M∩N = ∅, khi ó ta nói M, N i=1 i=1 rời nhau. 18 19
CÁC PHÉP TOÁN TẬP HỢP 3. Phép hiệu
Giản đồ Venn biểu diễn hiệu A-B
Định nghĩa: Cho A và B là hai tập hợp, hiệu của A và B, ược
ký hiệu là A–B, là tập hợp chứa các phần tử thuộc A
Ví dụ: o Cho A={1, 2, 3} và B={1, 3, 5} thì A–B={2}; B–
nhưng không thuộc B. Hiệu của A và B cũng ược gọi là A={5}.
phần bù của B ối với A. 20
A–B={x| (x∈A) ∧ (x∉B)}
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 A A (B (B C) = (A C) = (A B) B) C C T nh kết hợp
CÁC PHÉP TOÁN TẬP HỢP A A (B (B C) = (A C) = (A B) B) (A (A C) C) T nh ph 3. Phép hiệu n phối
Nhận xét: A-B=B-A khi và chỉ khi A=B. Khi A = B AB ;A = B A B C ng thức De Morgan ó A-B=B-A=∅. 22
Định nghĩa: Cho U là tập vũ trụ. Phần bù TÍCH DESCARTES
của tập A, ược kí hiệu là Ā, là phần bù của
A ối với U: Ā={x| x∉A}.
Ví dụ: Cho A={a, e, i, o, u } thì Ā={b, c, d, f,
Định nghĩa 1: Cho hai tập A và B. Tích Descartes
g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, y, z} (ở
của A và B, ược ký hiệu là A B, là tập hợp gồm tất
cả các cặp (a, b) với a
ây tập vũ trụ là tập các chữ cái tiếng Anh). ∈A và b∈B.
A B={(a, b)| (a∈A) ∧ (b∈A)}. 21
Ví dụ: Cho A={1, 2}, B={a, b, c} thì:
CÁC TÍNH CHẤT LIÊN QUAN
A B={(1,a), (1, b), (1, c), (2, a), (2, b), (2, c)}
B A ={(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)} T nh chất TŒn gọi
A2=A A={(1, 1), (1, 2), (2, 1), (2, 2)}
A = A ; A U = A Phần tử trung h a
Nhận xét: A B ≠ B A.
A U = U ; A = T nh thống trị
A A = A ; A A = A T nh lũy đẳng 23 A =A U;A =A Φ Phần bø
A B = B A ; A B = B A T nh giao hoÆn
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
(có n tập A ở vế phải). TÍCH DESCARTES 25
LỰC LƯỢNG CỦA TẬP HỢP
Định nghĩa 2:Tích Descartes của n (n>1) tập hợp A1,
A2, …, An , ược ký hiệu bởi A1 A2 … An , là tập hợp
gồm tất cả các bộ n phần tử (a
*Số phần tử của một tập hợp hữu hạn A ược ký
1, a2, …, an) trong ó ai∈ A
hiệu là A và gọi là lực lượng của tập A. i với i=1, 2, …n.
*Nếu tập hợp A không hữu hạn, ta nói A là một tập
A1 A2 … An= {(a1, a2, …, an)| ai ∈Ai với i=1,2, …n}
vô hạn và viết: A = .
Ví dụ: Cho A={0, 1}, B = {1, 2}, C ={0, 1, 2} thì: A B * Quy ước: = 0.
C={(0,1,0), (0,1,1), (0,1,2), (0,2,0), (0,2,1), (0,2,2),
* Tính chất: Cho A, B là các tập hữu hạn. Khi ó:
(1,1,0), (1,1,1), (1,1,2)}. 1) A B = A + B - A B . 2) A B = A . B 3) P(A) = 2 A 24 TÍCH DESCARTES
VD: A= 1, 3, 5, 7 ; B= 3, 5,6 ; A B = {1,3,5,6,7};
A B={3,5} |A| = 4; |B|= 3; |A B|= 2; |A B |= 5; |AxB| = 12;|P(A)| =24=16 Ghi chú 26
Mệnh ề: Cho A và B là hai tập hữu hạn rời nhau,
▪ Lũy thừa bậc 2 Descartes (hay bình phương
Descartes) của tập A ược ịnh nghĩa là tích
nghĩa là A∩B = . Khi ó ta có: |A B| = |A|
Descartes của A với A: +|B| A2 = A×A
▪ Tương tự, lũy thừa Descartes bậc n của tập
A là tích Descartes của n tập A:
An = A×A×...×A
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) CÁC NGUYÊN LÝ lOMoAR cPSD| 40425501
1 .Nguyên lý cộng
* Tổng quát: Nếu A1, A2, …, An là các tập hữu hạn rời 27
nhau, nghĩa là Ai ∩ Aj = (i ≠ j; i, j=1, 2, …n) thì
| A1 A2 … An | = |A1| +|A2|+…+ |An| CÁC NGUYÊN LÝ
Vậy Ngọc sẽ có bao nhiêu cách chọn áo ể mặc. 1.Nguyên lý cộng Giải:
Ngọc có 5 cách chọn áo thun
Giả sử ể thực hiện một công việc nào ó, ta
Ngọc có 6 cách chọn áo sơ mi
có 2 phương pháp, trong ó: - Phương pháp 1
Vậy Ngọc sẽ có 5+6 =11 cách chọn áo ể mặc.
có n cách thực hiện
- Phương pháp 2 có m cách thực hiện Khi 29
ó, số cách thực hiện công việc trên là n + m Tổng quát? 28 CÁC NGUYÊN LÝ 1.Nguyên lý cộng
Ví dụ: Ngọc có 5 cái áo thun, 6 cái áo sơ mi.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 4042550 1 CÁC NGUYÊN LÝ CÁC NGUYÊN LÝ 2.Nguyên lý nhân
Mệnh ề: Cho A và B là hai tập hữu hạn. Khi ó ta có: 2.Nguyên lý nhân |A × B| = |A| .|B|
Giả sử ể thực hiên một công việc nào ó, ta
* Tổng quát: Nếu A1, A2, …, An là các tập hữu hạn
cần thực hiện 2 bước (giai oạn), trong ó - thì
Bước 1 có n cách thực hiện
| A1 × A2 × … × An | = |A1| .|A2|. … . |An|
- Bước 2 có m cách thực hiện Khi ó, số cách
thực hiện công việc trên là n.m Tổng quát? 30 31 CÁC NGUYÊN LÝ
Vậy Phúc muốn tới Trường Công Nghệ Thông Tin thì sẽ có 3.4=12 cách. 2.Nguyên lý nhân 32
Ví dụ: Bạn Phúc từ Quận 9 (A) muốn tới trường CÁC NGUYÊN LÝ
Công Nghệ Thông Tin (C), phải qua chặng Ngã tư
Thủ Đức (B). Biết từ A tới B có 3 tuyến xe buýt ể i, và
từ B tới C có 4 tuyến xe buýt ể i.
3.Nguyên lý chuồng bồ câu(Dirichlet) Giải:
Giai oạn 1 (A ến B): có 3 cách thực hiện
a. Giới thiệu
Giai oạn 2 (B ến C): có 4 cách thực hiện
Nguyên lý chuồng bồ câu ược phát triển từ mệnh
ề: “Giả sử có một àn chim bồ câu bay vào
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
chuồng. Nếu số chim nhiều hơn số ô trong
chuồng thì chắc chắn có ít nhất một ô chứa nhiều hơn một con chim.” 33 CÁC NGUYÊN LÝ
3.Nguyên lý chuồng bồ câu(Dirichlet)
b.Nguyên lý cơ bản
Nếu ta ặt n ối tượng nào ó vào k hộp, và số
hộp k nhỏ hơn số ối tượng n, thì có ít nhất một
hộp chứa từ 2 ối tượng trở lên.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)
CÁC NGUYÊN LÝ lOMoARcPSD|40425501
3.Nguyên lý chuồng bồ câu(Dirichlet)
b.Nguyên lý mở rộng
Nếu ta ặt n ối tượng vào k hộp thì sẽ tồn
tại một hộp chứa ít nhất là [n/k] ối tượng.
Chú ý: Ký hiệu [a] dùng ể chỉ số nguyên
nhỏ nhất lớn hơn hoặc bằng a. Ví dụ: [5]=5, [4/3]=2
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) HOÁN VỊ lOMoAR cPSD| 40425501 HOÁN VỊ 3 x = 3! x 2 1 Số cách chọn: b. Công thức:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Pn=n! = 1.2…(n-1).n 0! = 1
Ví dụ 2: Một oàn khách du lịch dự ịnh ến
tham quan 7 iểm A,B,C,D,E,F,G. Hỏi có bao
nhiêu cách chọn thứ tự tham quan? Giải:
Mỗi cách họ chọn thứ tự tham quan là một
hoán vị của tập A,B,C,D,E,F,G.
Do vậy oàn khách có tất cả: P7 = 7!=5040 cách
chọn thứ tự tham quan.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 TỔ HỢP
TỔ HỢP
Ví dụ: Cho tập A gồm 4 Giải:
số tự nhiên {1,2,3,4}. Tìm 1 2 3 4
Số oạn thẳng ược tạo thành từ 3 iểm
tất cả các tập con của A
A,B,C chính là số tổ hợp chập 2 của 3: C32
sao cho các tập con chỉ có 1 2 3 = 3
3 phần tử. Số tập con
Vậy có 3 oạn thẳng ược tạo thành từ 3 iểm 1 2 4
cóthểtìm ượclà𝑪𝟑 A,B,C. 𝟒=4
Ví dụ: Từ 3 iểm A,B và C, 1 3 4 43
bạn sẽ có bao nhiêu oạn thẳng ược tạo ra? 2 3 4 CHỈNH HỢP 42 44
CHỈNH HỢP a.Định nghĩa:
Cho tập hợp A gồm n phần tử (n>0). Mỗi bộ gồm
Nói cách khác, hai chỉnh hợp khác nhau khi và chỉ
k phần tử (1 k n) sắp thứ tự của tập A ược gọi là
khi hoặc có ít nhất một phần tử của chỉnh hợp này
một chỉnh hợp chập k của n phần tử. Số các chỉnh
không là phần tử của chỉnh hợp kia hoặc các phần
hợp chập k của n phần tử ược ký hiệu là . A k n
tử của 2 chỉnh hợp giống nhau nhưng ược sắp xếp
Nhận xét: Lập một chỉnh hợp chập k của n phần tử
theo thứ tự khác nhau. b.Công thức:
chính là lấy ra k phần tử từ n phần tử ó, có quan tâm ến thứ tự. = k n! , 1 k n. A
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 k=0 k=0 (
=C a C a bn0 n + n1 n−1 + +... C a bnk n k k− + +... C n n k− )! bnn n 45 CHỈNH HỢP
CÔNG THỨC NHỊ THỨC NEWTON
Ví dụ: Từ 3 iểm A,B và C sẽ lập ược bao nhiêu vector? Giải:
Số vector ược tạo thành từ 3 iểm A,B,C chính
là số chỉnhchập 2 của 3: A32 = 6
Vậy có 6 vector ược tạo thành từ 3 iểm A,B,C. Isaac Newton 47 (1643-1727)
CÔNG THỨC NHỊ THỨC NEWTON Ví dụ: 𝟐
𝒂 + 𝒃 𝟐 = 𝑪𝒌𝟐𝒂𝒏−𝒌𝒃𝑘 =
Định lý: Với a, b R và n là số nguyên dương 𝑘=0 ta có:
=𝑪𝟎𝟐𝒂𝟐𝒃𝟎+𝑪𝟏𝟐𝒂𝟏𝒃𝟏+𝑪𝟐𝟐𝒂𝟎𝒃𝟐 =𝒂2 +𝟐𝒂𝒃+𝒃2 n n 48 =
(a b+ =)n C a bnk n k k− C a bnk k n k− =
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
CÔNG THỨC NHỊ THỨC NEWTON
(1−x)n = ( 1)− kC xnk k =C x C xn0 0 − n1 1 + + −... ( 1)nC xnn n n n k=0 = (a b+ =) − − n C a bnk n k k C a bnk k n k = k=0 k=0
=C a C a bn0 n + n1 n−1 + +... C a bnk n k k− + +... C 50 b Ví dụ: nn n
(x y+ )6 =C x y C x y C x y C x y60 0 6 + 61 1 5 + 62 2 4 + 63 3 3 + Tính chất:
- Số các số hạng của công thức là n+1. + - C x y C x y C x y
Tổng các số mũ của a và b trong mỗi số hạng luôn luôn 64 4 2 + 65 5 1 + 66 6 0 =
bằng số mũ của nhị thức: k+n-k= n
= +y6 6xy5 +15x y2 4 +20x y3 3 +15x y4 2 +6x y x5 + 6
- Số hạng tổng quát của nhị thức là: T k n k k− k+1 =C a bn - Các
Ví dụ: Tìm hệ số của x4 trong khai triển (x2 -2)5
hệ số nhị thức cách ều hai số hạn ầu và cuối thì bằng nhau. 5 49
(x2 − =2)5 C x5k( ) ( 2)2 k − 5−k
Một số khai triển hay sử dụng: k=0 n
( )x2 k =4 k=2 2
Khi k = 2 thì hệ số của x4: C 2( 2)− 5 2− =−80 n = + =(1 1)n
Cnk = + + +Cn0 Cn1 5 ... Cnn k=0 51 n Downloaded by Mai Le
Thi Nguyet (hoathanvu729@gmail.com)
CÔNG THỨC NHỊ THỨC NEWTON
CÔNG THỨC NHỊ THỨC NE W TON lOMoAR cPSD| 40425501
HOÁN VỊ LẶP chuỗi là: n=7 Có 3 ký tự ‘A’
Do ó số chuỗi có ược là
a. Định nghĩa: Cho n ối tượng, trong ó có ni ối tượng
loại i giống hệt nhau (i =1,2,…,k) và n Có 2 ký tự ‘M’ 1+ n2,…+ nk= 7! =420
n. Mỗi cách sắp xếp có thứ tự n ối tượng ã cho gọi là Có 1 ký tự ‘Y’ 3!2!1!1!
một hoán vị lặp của n. b. Công thức: Có 1 ký tự ‘H’
Số hoán vị của n ối tượng, trong ó có nn 53 12 ối
tượng giống nhau thuộc loại 1, ối tượng giống nhau thuộc loại 2, n! …, n n n1 2! !... k!
nk ối tượng giống nhau thuộc loại k,
(n1+ n2,…+ nk= n) là 52
HOÁN VỊ LẶP
Ví dụ: Có bao nhiêu chuỗi ký tự khác nhau
nhận ược bằng cách sắp xếp lại các ký tự của chuỗi: “YAMAHAM”
Số ký tự có trong
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Khai triển mở rộng nhị thức Newton (a a 54
1 + 2 + +... ak)n =
Khai triển mở rộng nhị thức Newton Ví dụ:
Tìmhệsốcủa𝑢𝟏𝑣𝟐𝑤2𝑡𝟑 n n1+ + + =2 ... n nk n1,...,n nk
trongkhaitriển 𝑢+𝑣+𝑤+𝑡 8
a a1n1 2n2...aknk 𝟖 =
𝟖𝑢𝟏𝑣𝟐𝑤𝟐𝑡𝟑
với các số nguyên không âm n1,n2,…,nk thoả 𝒖+𝒗+𝒘+𝒕
n1+n2+…+nk = n, ký hiệu 𝟏, 𝟐, 𝟐, 𝟑 𝟏+𝟐+𝟐+𝟑
Vậy hệ số cần tìm:
n n1, n2,...,nk =
n n n1 2! n!...! k!
= 𝟏,𝟐,𝟐,𝟑𝟖 =𝟏!𝟐!𝟐!𝟑!𝟖! =𝟏𝟔𝟖𝟎 55
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
TỔ HỢP LẶP
K C32 = 3 2 12+ − = =C42 6
(Cụ thể AA, AB, AC, BB, BC, CC) 57 a. Định nghĩa:
TỔ HỢP LẶP
Mỗi cách chọn ra k vật từ n loại vật khác nhau
(trong ó mỗi loại vật có thể ược chọn lại nhiều
c. Hệ quả: Số nghiệm nguyên không âm (x1,x2,…,xn)
lần) ược gọi là tổ hợp lặp chập k của n. Số các tổ
(mỗi xi ều nguyên không âm) của phương trình x1+
hợp lặp chập k của n ược ký hiệu là x2+…+ xn= k là Knk
K Cnk = n kk+ −1 56
Số cách chia k vật ồng chất nhau vào n hộp phân
TỔ HỢP LẶP
biệt cũng chính bằng số tổ hợp lặp chập k của n. b. Công thức:
K Cnk = n kk+ −1
K Cnk = n kk+ −1 58
TỔ HỢP LẶP
Ví dụ: Có 3 loại nón A, B, C. An mua 2 cái nón.
Hỏi An có bao nhiêu cách chọn?
Bài 17: Phương trình X+Y+Z+T= 20 có bao
Ta có mỗi cách chọn là mỗi tổ hợp lặp chập 2
nhiêu nghiệm nguyên không âm ?
của 3. Số cách chọn: Lời giải :
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chọn 20 phần tử từ một tập có 4 loại, sao cho có 𝑲𝟐𝟎𝟒
X phần tử loại 1, Y phần tử loại 2 , có Z phần tử
=>Cách giải nhanh ối với bài toán tìm nghiệm
loại 3, có T phần tử loại 4. Vì vậy số nghiệm
nguyên không âm: x+y+z+t = n là 𝑲𝒏𝟒
bằng tổ hợp lặp chập 20 của 4 phần tử và bằng: 59
TỔ HỢP LẶP p = q – r 60
TỔ HỢP LẶP
Ví dụ: Tìm số nghiệm nguyên không âm của phương trình Ví dụ: x1+ x2 + x3 + x4 = 20 (1)
Trước hết ta tìm q.
Thỏa iều kiện x1 3; x2 2; x3 > 4 ( ). Đặt Giải:
x1’ = x1; x2’ = x2 – 2; x3’ = x3 - 5; x4’ = x4
Ta viết iều kiện ã cho thành x1 3; x2 2; x3 5.
Phương trình (1) trở thành
Xét các iều kiện sau:
x1’+ x2’ + x3’ + x4’ = 13 (2) Số nghiệm nguyên x2 2; x3 5 ( ) x1 4; x2 2; x3 5
không âm của phương trình (1) thỏa iều kiện (**) (
) Gọi p, q, r lần lượt là các số nghiệm nguyên
bằng số nghiệm nguyên không âm của phương trình
không âm của phương trình (1) thỏa các iều kiện (*),
(2) q K= 413 =C4 13 113+ − =C1613 (**), (***). Ta có: 61
tính chất. Biểu diễn quan hệ hai ngôi.
Nếu (a, b) R thì ta nói a có quan hệ R với b và ký hiệu
a R b; ngược lại nếu (a, b) R thì ta kí hiệu aRb.
Khi A = B, ta gọi R là một quan hệ hai ngôi trên A.
3.2. Quan hệ tương ương. Lớp tương ương. Ví dụ: Ā
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)
TỔ HỢP LẶP LOGO lOMoAR cPSD| 40425501 Ví dụ :
Tương tự , ta có: . 9 9 9 == rK = 4 C 491 +− C 12 13 9 =−= Hết pqrC − = 560 C − 220 = 340. 16 12 Vậy
số nghiệm nguyên không âm của phương
trình (1) thỏa iều kiện (*) là 340. 62 Chương 3. Quan hệ Quan hệ hai ngôi
1. Định nghĩa: Cho hai tập A, B. Ta gọi tập R là m ột quan 3. . Quan 1
hệ hai ngôi trên một tập hợp và các
hệ hai ngôi từ A ến B nếu R A x B . A
Sự phân hoạch thành các lớp tương ương. a1 b1 B a2 b2 a3 b3
3.3. Quan hệ thứ tự. Thứ tự toàn phần và bán phần. Biểu ồ
Hasse. Phần tử min và max.
Các phần tử tối tiểu và tối ại.
R = { (a1, b1), (a1, b3), (a3, b3) }
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 1 2
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Quan hệ hai ngôi Quan hệ hai ngôi 3
2. Các tính chất của quan hệ.
Định nghĩa: Giả sử R là một quan hệ hai ngôi trên tập A. 1. Định nghĩa.
Ví dụ: Cho A = {1, 2, 3, 4}, R là một quan hệ (hai ngôi) trên A
(a) Ta nói quan hệ R có tính phản xạ nếu và chỉ nếu
và R = {(a, b) A | a là ước của b}.
a R a , a A. Khi ó
R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4,4)}
Ví dụ: Trên tập A = {1, 2, 3, 4}, quan hệ
R1 = {(1,1), (1,2), (2,1), (2, 2), (3, 4), (4, 1), (4, 4)}
không phản xạ vì (3, 3) R1
R2 = {(1,1), (1,2), (1,4), (2, 2), (3, 3), (4, 1), (4, 4)}
phản xạ vì (1,1), (2, 2), (3, 3), (4, 4) R2 4 Quan hệ hai ngôi 5 Quan hệ hai ngôi
2. Các tính chất của quan hệ
2. Các tính chất của quan hệ. Ví dụ:
Định nghĩa: Giả sử R là một quan hệ hai ngôi trên tập A.
- Quan hệ ≤ trên Z phản xạ vì a ≤ a, a Z.
(b) Ta nói quan hệ R có tính ối xứng nếu và chỉ nếu a R b
- Quan hệ > trên Z không phản xạ vì 1 không lớn hơn 1. -
b R a , a, b A.
Quan hệ “ | ” (“ước số”) trên Z+ là phản xạ vì mọi số nguyên
dương a là ước của chính nó.
(c) Ta nói quan hệ R có tính phản xứng nếu và chỉ nếu
(a R b b R a) a = b , a, b A. Ví dụ: -
Quan hệ R1 = {(1,1), (1,2), (2,1)} trên tập A = {1, 2, 3, 4} là ối xứng.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Quan hệ hai ngôi lOMoAR cPSD| 40425501 -
Quan hệ ≤ trên Z không ối xứng, tuy nhiên nó phản
(a ≤ b) (b ≤ c) (a ≤ c)
xứng vì (a ≤ b) (b ≤ a) (a = b).
(a | b) (b | c) (a | c) -
Quan hệ“ | ” (“ước số”) trên Z+ không ối xứng, tuy
nhiên nó có tính phản xứng vì (a | b) (b | a) (a = b). 7
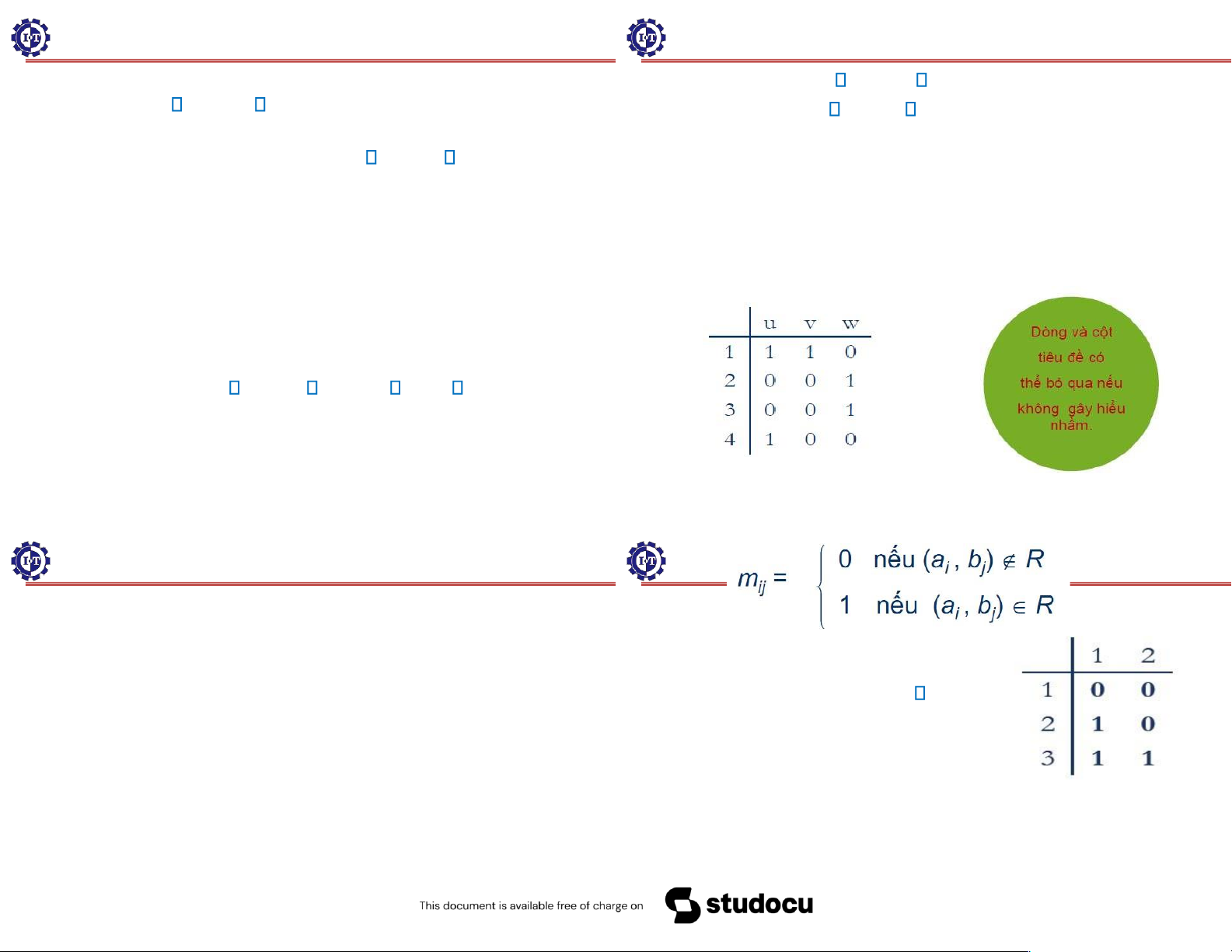
3. Biểu diễn quan hệ 6 Quan hệ hai ngôi Định nghĩa.
Cho R là quan hệ từ A = {1,2,3,4} ến B = {u,v,w},
2. Các tính chất của quan hệ
R = {(1,u),(1,v),(2,w),(3,w),(4,u)}.
Định nghĩa: Giả sử R là một quan hệ hai ngôi trên tập A.
Khi ó R có thể biễu diễn như sau
(d) Ta nói quan hệ R có tính bắc cầu (truyền) nếu và chỉ nếu
(a R b b R c) a R c , a,b,c A. Ví dụ:
- Quan hệ R = {(1,1), (1,2), (2,1), (2, 2), (1, 3), (2, 3)}
trên tập A = {1, 2, 3, 4} có tính bắc cầu.
Đây là ma trận cấp 4×3 biễu diễn cho
- Quan hệ ≤ và “|”trên Z có tính bắc cầu vì quan hệ R 8 Quan hệ hai ngôi
3. Biểu diễn Quan hệ
Định nghĩa. Cho R là quan hệ từ A = {a1, a2, …, am} ến
B = {b1, b2, …, bn}. Ma trận biểu diễn của R là ma trận
Ví dụ : Cho R là quan hệ từ A = {1,
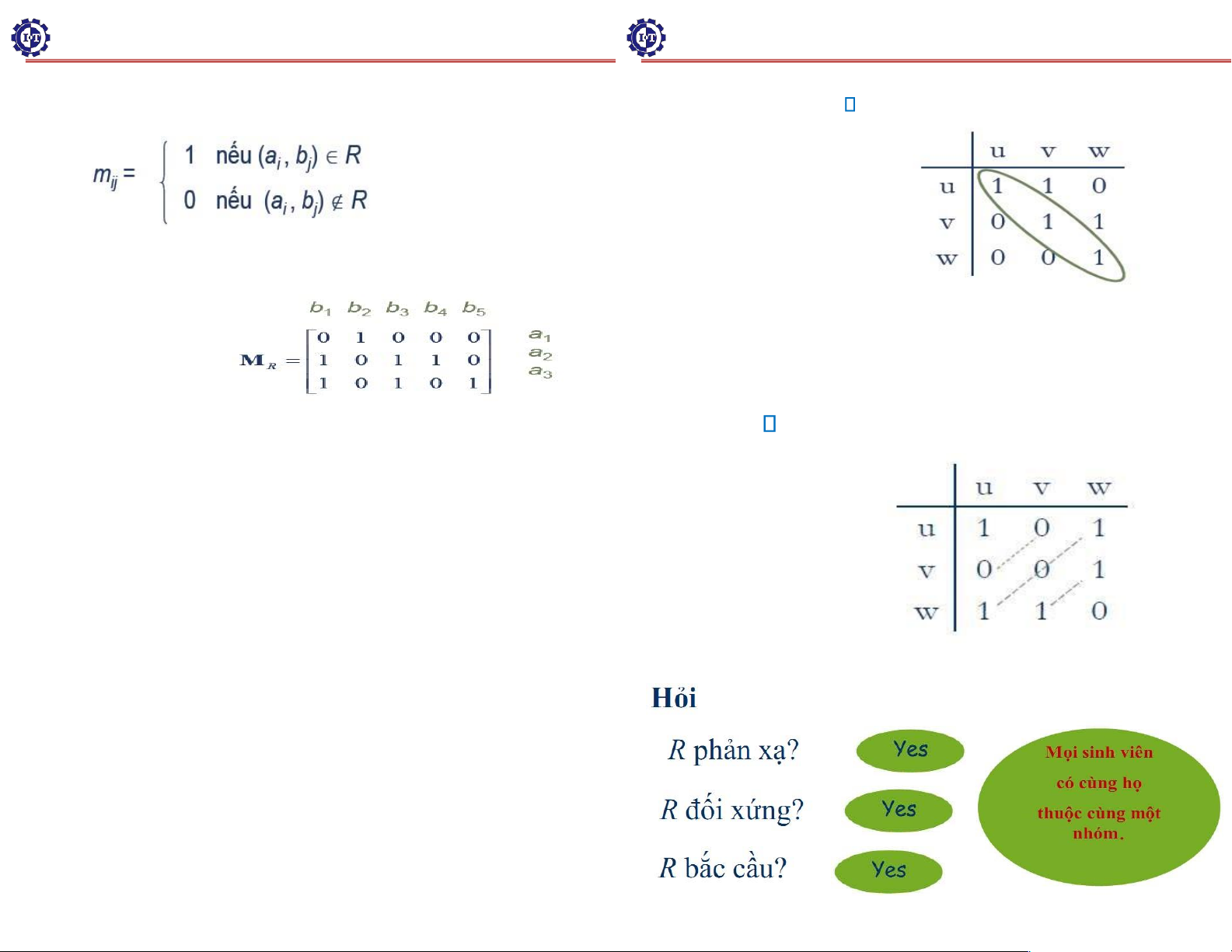
MR = [mij] mxn xác ịnh bởi:
2 , 3} ến B = {1, 2}: a R b a > b .
Khi ó ma trận biểu diễn của R là : 9
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Quan hệ hai ngôi lOMoAR cPSD| 40425501 Quan hệ hai ngôi
+) R là phản xạ nếu tất cả các phần tử trên ường chéo của M
3. Biểu diễn quan hệ
R ều bằng1: mii = 1, i.
Ví dụ: Cho R là quan hệ từ A = {a1, a2, a3} ến B = {b1, b2, b3,
b4, b5} ược biễu diễn bởi ma trận 11
3. Biểu diễn quan hệ
+) R là ối xứng nếu MR là ối xứng
Khi ó R gồm các cặp:{(a1, b2), (a2, b1), (a2, b3), (a2, b4), (a3,
mij = mji , i, j.
b1), (a3, b3), (a3, b5)}. 10 Quan hệ hai ngôi
3. Biểu diễn quan hệ
Cho R là quan hệ trên tập A, khi ó MR là ma trận vuông. 12 Quan hệ hai ngôi
3. Biểu diễn quan hệ
+) R là phản xứng nếu MR thỏa:
mij = 0 hoặc mji = 0 nếu i ≠ j
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Quan hệ hai ngôi lOMoAR cPSD| 40425501 13
Quan hệ tương ương 1. Định nghĩa.
Ví dụ: Cho S = {sinh viên của lớp}, gọi R là một
quan hệ trên S với R = {(a,b): a có cùng họ với b}. 14
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Quan hệ tương ương
Quan hệ tương ương 1. Định nghĩa.
1. Định nghĩa: Quan hệ R trên tập A ược gọi là tư
Ví dụ: Cho m là số nguyên dương và R là quan hệ trên Z :
ng ư ng nếu và chỉ nếu nó có tính chất phản xạ, ối
aRb (a – b) chia hết m xứng và bắc cầu.
Khi ó R là quan hệ tương ương. -
Rõ ràng quan hệ này có tính phản xạ và ối xứng. -
Cho a, b, c sao cho a – b và b – c chia hết cho m, khi ó a –
Ví dụ: Quan hệ R trên tập các chuỗi ký tự xác ịnh
c = a – b + b – c cũng chia hết cho m. Suy ra R có tính chất
bởi aRb nếu a và b có cùng ộ dài. Khi ó R là quan bắc cầu. hệ tương ương. -
Quan hệ này ược gọi là ồng dư modulo m và chúng
ta viết a b (mod m) thay vì aRb.
Ví dụ: Cho R là quan hệ trên tập R sao cho
Ví dụ: Cho | là quan hệ trên Z ược xác ịnh như sau:
aRb a – b Z a | b k Z: b = ka
Khi ó R là quan hệ tương ương.
Quan hệ | có là quan hệ tương ương? 15 16
Quan hệ tương ương
•Mỗi phần tử x [a]R ược gọi là một phần tử ại diện của lớp
tương ương [a]R .
2. Lớp tương ương
•Tập thương của A theo quan hệ R, ký hiệu là A/R, ược ịnh
Định nghĩa. Cho R là quan hệ tương ương trên A
nghĩa là tập tất cả các lớp tương ương của các phần và tử thuộc A, nghĩa là
a A . Lớp tư ng ư ng chứa a theo quan hệ R
ược ký hiệu bởi [a] A/R = { [a]
R hoặc [a] là tập hợp tất cả R | a A}
những phần tử có quan hệ R với a. 17
[a]R = {b A| b R a}
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Quan hệ tương ương (iii) [a]R [b]R ≠
Chú ý: Từ mệnh ề trên ta thấy rằng các lớp tương ương của
2. Lớp tương ương
các phần tử của tập A hoặc trùng nhau, hoặc rời nhau. Hơn
Ví dụ: Tìm các lớp tương ương modulo 8 chứa 0
nữa, hợp của tất cả các lớp tương ương này trùng với A, và 1?
cho nên tập A là hợp rời rạc của các lớp tương ương.Ta
cũng nói rằng tập A ược phân hoạch thành các lớp tương
Giải: Lớp tương ương modulo 8 chứa 0 gồm tất ương theo quan hệ R.
cả các số nguyên a chia hết cho 8. Do ó [0]8 ={ 19
…, – 16, – 8, 0, 8, 16, … }
Quan hệ tương ương Tương tự
3. Sự phân hoạch thành các lớp tương ương
[1]8 = {a | a chia 8 dư 1} = { …, – 15, – 7, 1, 9,
Chú ý: Cho {A1, A2, … } là phân hoạch A thành các tập con 17, … }
không rỗng, rời nhau. Khi ó có duy nhất quan hệ tương
ương trên A sao cho mỗi Ai là một lớp tương ương. 18
Thật vậy với mỗi a, b A, ta ặt a R b nếu có tập con Ai sao
Quan hệ tương ương
cho a, b Ai .
Dễ dàng chứng minh rằng R là quan hệ tương ương trên A
3. Sự phân hoạch thành các lớp tương ương Nhận và [a]R = A
xét: Trong ví dụ cuối, các lớp tương ương [0] i i 8 và [1]8 là nếu a A . rời nhau.
Mệnh ề. Cho R là quan hệ tương ương trên tập A. Với
mọi a,b A các iều kiện sau ây tương ương với nhau (i)a R b (ii)[a]R = [b]R 20
Quan hệ tương ương
Chúng lập thành phân hoạch của Z thành các tập con rời nhau. Chú ý rằng:
3. Sự phân hoạch thành các lớp tương ương
[0]m = [m]m = [2m]m = …
Ví dụ: Cho m là số nguyên dương, khi ó có m lớp ồng dư
[1]m = [m + 1]m = [2m +1]m
modulo m là [0]m , [1]m , …, [m – 1]m . = …
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Quan hệ thứ tự Quan hệ thứ tự lOMoAR cPSD| 40425501
…………………………………
[m – 1]m = [2m – 1]m = [3m – 1]m = …
Mỗi lớp tương ương này ược gọi là số nguyên modulo m. Tập
hợp các số nguyên modulo m ược ký hiệu bởi Zm , ó chính là
tập thương của Z theo quan hệ ồng dư modulo m.
Zm = Z/R = {[0]m , [1]m , …, [m – 1]m} 21 Quan hệ thứ tự 1. Định nghĩa
Ví dụ: Cho R là quan hệ trên tập số thực:
a R b nếu a ≤ b Hỏi: 22
1. Định nghĩa: Quan hệ R trên tập A ược gọi là
quan hệ thứ tự nếu và chỉ nếu nó có tính chất phản
xạ, phản xứng và bắc cầu.
Ta thường kí hiệu quan hệ thứ tự bởi .
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Cặp (A, ) ược gọi là tập sắp thứ tự (tập ược sắp) hay poset. 1. Định nghĩa.
Ví dụ: Quan hệ ước số “ | ”trên tập số nguyên dương
là quan hệ thứ tự, nghĩa là (Z+, | ) là poset 23 24 Quan hệ thứ tự Quan hệ thứ tự
Ví dụ: ( P(S), ) , ở ây P(S) là tập hợp các con của S, là một poset? 25 26
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Quan hệ thứ tự Quan hệ thứ tự
2. Thứ tự toàn phần và bán phần
2. Thứ tự toàn phần và bán phần
Định nghĩa. Các phần tử a và b của poset (S, ) gọi là so Ví dụ:
sánh ược nếu a b hoặc b a .
- Quan hệ “≤ ” trên tập số Z+ là thứ tự toàn phần. -
Trái lại thì ta nói a và b không so sánh ược.
Quan hệ ước số “ | ”trên tập hợp số Z+ không là thứ tự
toàn phần, vì các số 5 và 7 là không so sánh ược. - Với
Cho (S, ). Nếu hai phần tử tùy ý của S ều so sánh ược với
tập A cho trước, tập P(A) tất cả các tập con của A với quan
nhau thì ta gọi (S, ) là tập sắp thự tự toàn phần. Ta cũng
hệ là một tập ược sắp, nhưng không toàn phần khi A có
nói rằng là thứ tự toàn phần hay thứ tự tuyến tính trên S.
nhiều hơn một phần tử.
Trái lại thì ta nói là thứ tự bán phần. 27 28 Quan hệ thứ tự Quan hệ thứ tự
* Thứ tự từ iển
Ví dụ : Trên tập các chuỗi bit có ộ dài n ta có thể ịnh nghĩa thứ tự như sau: a …a 1 a 2
n ≤ b 1 b 2 …b n nếu a ,
i ≤ b i i .
Với thứ tự này thì các chuỗi 0110 và 1000 là không
so sánh ược với nhau. Chúng ta không thể nói chuỗi nào lớn hơn.
Trong tin học chúng ta thường sử dụng thứ tự toàn phần
trên các chuỗi bit. Đó là thứ tự từiển . Downloaded by Mai Le Thi
29 Nguyet (hoathanvu729@gmail.com) 30 lOMoAR cPSD| 40425501 Quan hệ thứ tự Quan hệ thứ tự
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Quan hệ thứ tự Quan hệ thứ tự 31 32 Quan hệ thứ tự Quan hệ thứ tự Downloaded by Mai Le Thi
33 Nguyet (hoathanvu729@gmail.com) 34 lOMoAR cPSD| 40425501 Quan hệ thứ tự Quan hệ thứ tự Quan hệ thứ tự Quan hệ thứ tự
3 . Biểu ồ Hasse
Ví dụ : Biểu ồ Hasse của P({a,b,c}) và biểu ồ Hasse của
các chuỗi bit ộ dài 3 với thứ tự từ iển . 3 7 38
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) 35 lOMoAR cPSD| 40425501 Quan hệ thứ tự Quan hệ thứ tự
4. Phần tử nhỏ nhất và phần tử lớn nhất. Định
4. Phần tử nhỏ nhất và phần tử lớn nhất.
nghĩa: Một phần tử a trong tập sắp thứ tự (S, ) ược
Định nghĩa: (Thứ tự tốt) gọi là:
Một tập hợp có thứ tự ược gọi là có thứ tự tốt (hay ược sắp
Phần tử nhỏ nhất nếu x S ta có a x.
tốt) nếu mọi tập con khác rỗng ều có phần tử nhỏ nhất.
Phần tử lớn nhất nếu x S ta có x a.
Nhận xét: Phần tử nhỏ nhất (lớn nhất) của một tập hợp (nếu
Ví dụ:
có) là duy nhất. Ta kí hiệu phần tử của tập hợp S là min(S), -
Tập hợp có thứ tự (N, ) là một tập hợp ược sắp tốt.
và kí hiệu phần tử lớn nhất của S là max(S).
- Tập hợp có thứ tự (Z, ) không phải là một tập hợp ược
Ví dụ: Trong tập có thứ tự (S, ), S={m Z|m^2 <100} có
sắp tốt vì Z không có phần tử nhỏ nhất. min(S) = -9, max(S) = 9.
Trong tập có thứ tự (A, ), A={x R|x^2 <100} không
có phần tử nhỏ nhất và cũng không có phần tử lớn nhất.
Cho tập B, ta biết (P(B), ) là tập có thứ tự. Với thứ tự 40
này thì min(P(B))= , max(P(B)) = B. 39 Quan hệ thứ tự Quan hệ thứ tự
5. Phần tử tối tiểu và phần tử tối ại. 5. Phần tử tối tiểu và phần tử tối ại. Định nghĩa: Một phần tử a trong tập sắp
thứ tự (S, ) ược Ví dụ: Xét poset có biểu ồ Hasse dưới ây: gọi là:
Phần tử tối tiểu nếu không tồn tại x S sao cho x a và x a.
Phần tử tối ại nếu không tồn tại x S sao cho x a và a x.
R = {(1,1), (2,2), (3,3), (1,2), (3,2)}. Dễ dàng kiểm chứng
rằng (S,R) là tập có thứ tự. Với thứ tự R này, S có hai
Nhận xét:
phần tử tối tiểu là 1 và 3. -
Phần tử tối tiểu (tối ại) của một tập có thứ tự không nhất
- Phần tử lớn nhất (nhỏ nhất) của một tập có thứ thiết là duy nhất.
tự, nếu có, là phần tử tối ại (tối tiểu) duy nhất của tập hợp
Ví dụ: Xét tập S = {1, 2, 3} với quan hệ R cho bởi ó. 41
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Quan hệ thứ tự Quan hệ thứ tự lOMoAR cPSD| 40425501
Mỗi ỉnh màu ỏ là tối ại.
Mỗi ỉnh màu xanh là tối tiểu.
Không có cung nào xuất phát từ iểm tối ại. Không có
cung nào kết thúc ở iểm tối tiểu. 42
5. Phần tử tối tiểu và phần tử tối ại.
Chú ý: Trong một poset S hữu hạn, phần tử tối tiểu và
phần tử tối ại luôn luôn tồn tại. A1,
Thật vậy, chúng ta xuất phát từ iểm bất kỳ a0 S. Nếu a0
không là phần tử tối tiểu thì a1 S: a1 a0 . Tiếp tục như vậy
cho ến khi tìm ược phần tử tối tiểu. Phần tử tối ại cũng tìm
ược bằng phương pháp tương tự. 43
5. Phần tử tối tiểu và phần tử tối đại.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Quan hệ thứ tự Quan hệ thứ tự lOMoAR cPSD| 40425501
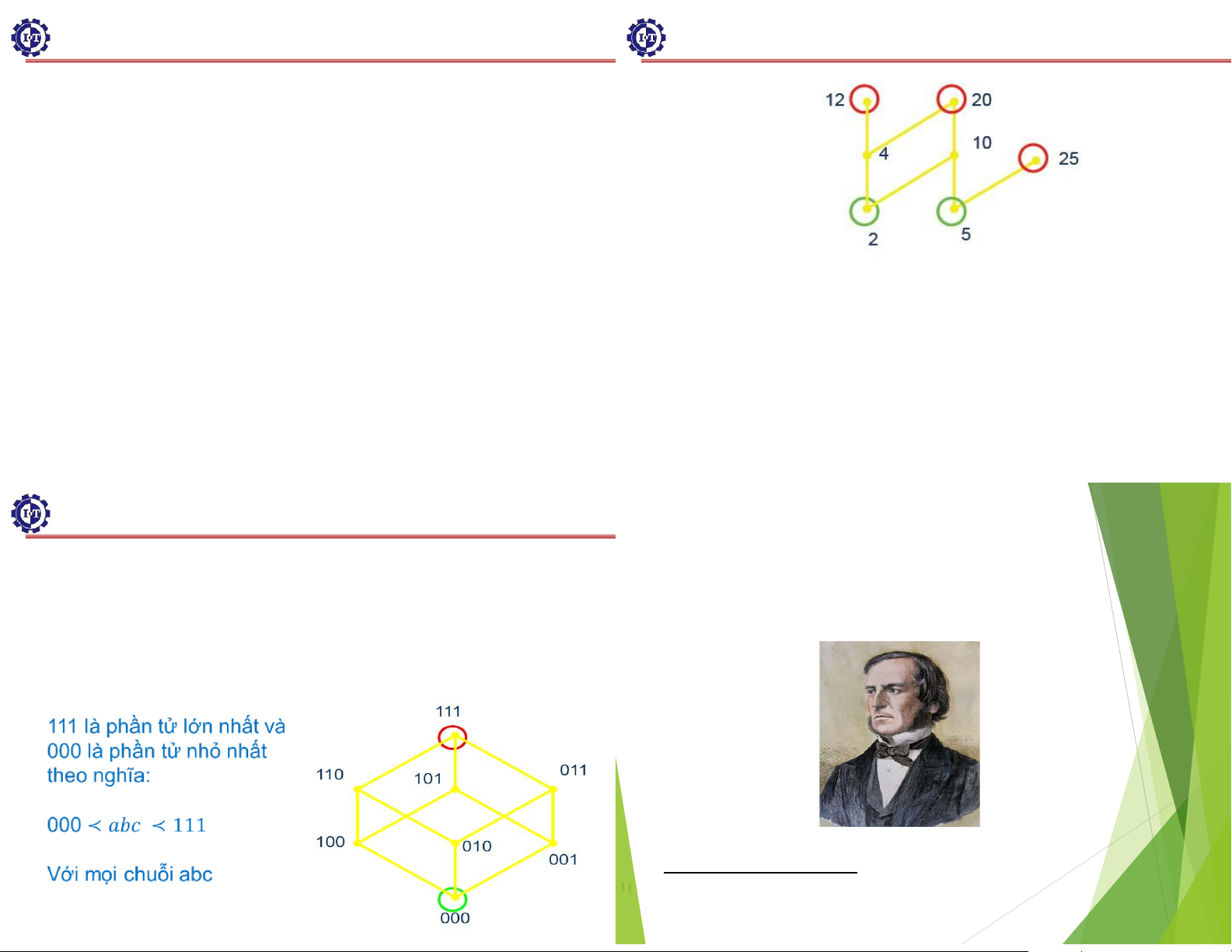
Ví dụ. Tìm phần tử tối ại, tối tiểu của poset ({2, 4, 5, 10, 12, 20, 25}, | ) ?
Giải: Từ biểu ồ Hasse, chúng ta thấy rằng 12, 20, 25 là các
phần tử tối ại, còn 2, 5 là các phần tử tối tiểu Như vậy phần
tử tối ại, tối tiểu của poset có thể không duy nhất. 44
5. Phần tử tối tiểu và phần tử tối ại.
Ví dụ: Tìm phần tử tối ại, tối tiểu của poset các chuỗi bit ộ dài 3?
Giải: Từ biểu ồ Hasse, chúng ta thấy rằng 111 là phần tử
tối ại duy nhất và 000 là phần tử tối tiểu duy nhất. Quan hệ thứ tự
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN BÀI THUYẾT TRÌNH
CHƯƠNG 4 :ĐẠI SỐ BOOLE
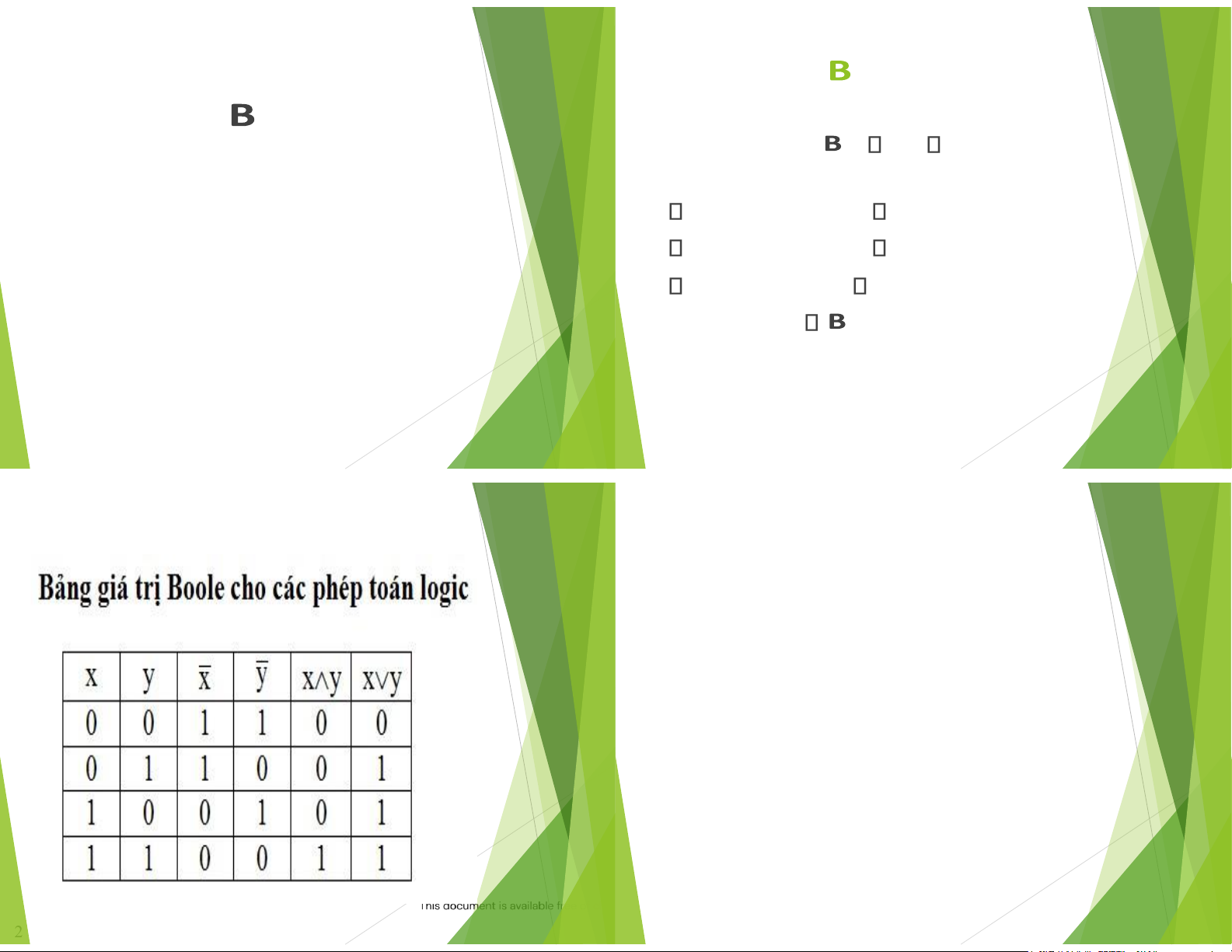
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) 4 5 lOMoAR cPSD| 40425501 N ỘI DUNG CH˝NH Đ ại s logic ố i s logic Đ ạ ố TrŒn t p logic , 0 ậ = 1 xØt cÆc phØp Đ ại s Boole ố toÆn logic Hm Boole (tch Boole) x y Cng th c đa th c t i thi u (t ng Boole) x y ứ ổ ứ ố ể (phØp bø) x
Bi ểu đ Karnaugh c a hm Boole ồ ủ trong đó x, y g ọi l cÆc bi n logic ế Ph ương phÆp Quine ho c bi n Boole. – McCluskey ặ ế
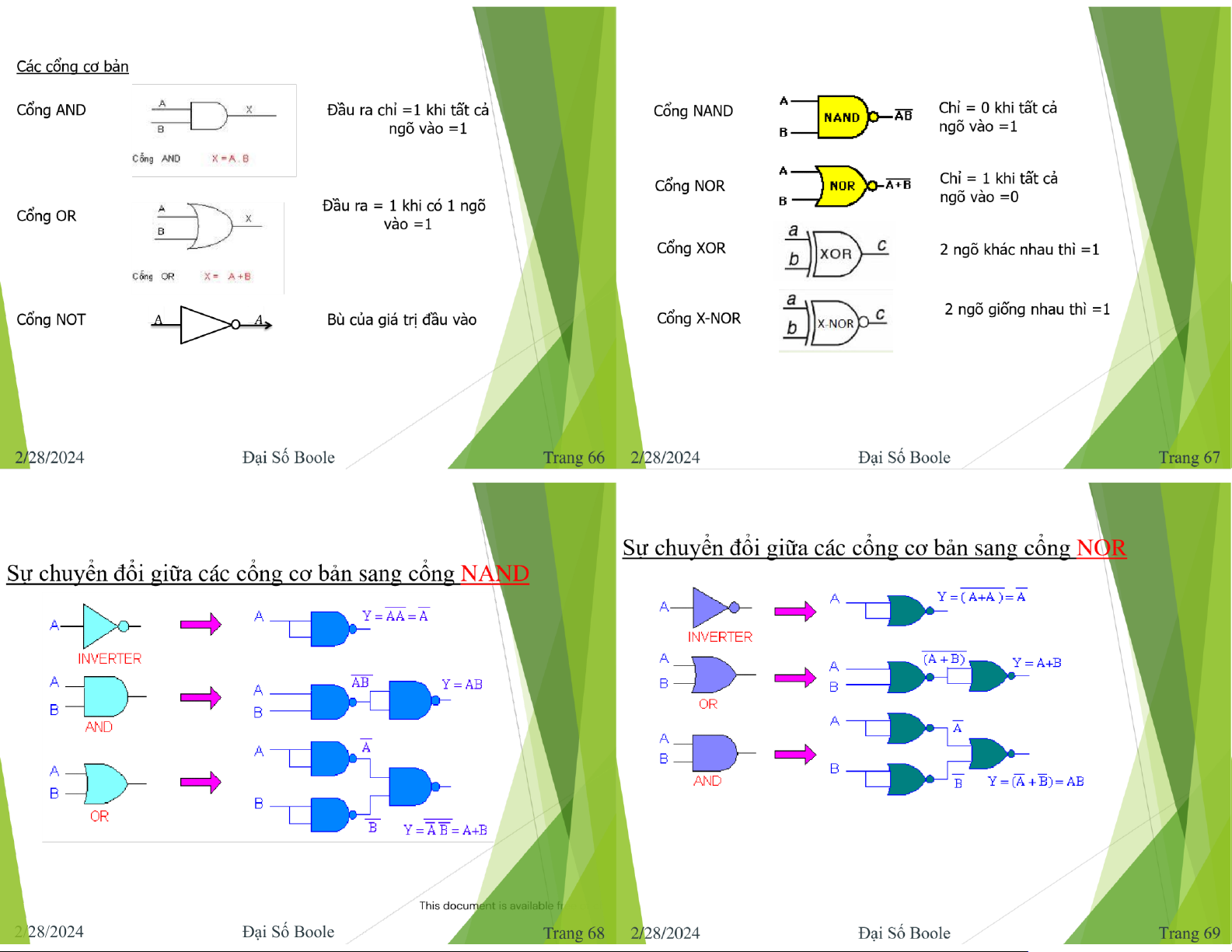
CÆc c ổng logic 2/28/2024 Đại Số Boole Trang 2 2/28/2024 Đại Số Boole Trang 3 CÆc h ằng đ ng th c logic ẳ ứ 1) Giao hoán
6 ) Luỹ ẳng 2) Kết hợp
7 ) Phần tử trung hoà 3) Phân phối
8 ) Phần tử bù
4) Luật bù kép 9 ) Luật thống trị 5) De Morgan
10 ) Luật hấp thu 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet Trang 4 2/28/2024 Trang 5 (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 Hm Boole
Cho f và g là hai hàm Boole n bi ến. Chúng ta có các đ nh nghĩa nh sau: Đ ị ư ịnh nghĩa : `nhx n ạ f:B → il thmBoolen Bg ọ m ộ bi 1) (f , …, x ) = f(x , …, x ) , …, x ) ến. g)(x 1 n 1 n g(x 1 n Hm 2) (f , …, x ) = f(x , …, x ) , …, x ) đ ồngnh tb ng1khi ul1,hm g)(x 1 n 1 n g(x 1 n ấ ằ ệ đ ồngnh tb ng0khi u l 0. T p t t c ấ ằ ệ ậ ấ ả
cÆc hm Boole n – bi ến k hi u l . ệ n 3) / / f ( x 1, …, x ) = (f(x , …, x )) n 1 n v ới m i x , …, x . ọ 1 n 2/28/2024 Đại Số Boole Trang 14 2/28/2024 Đại Số Boole Trang 15
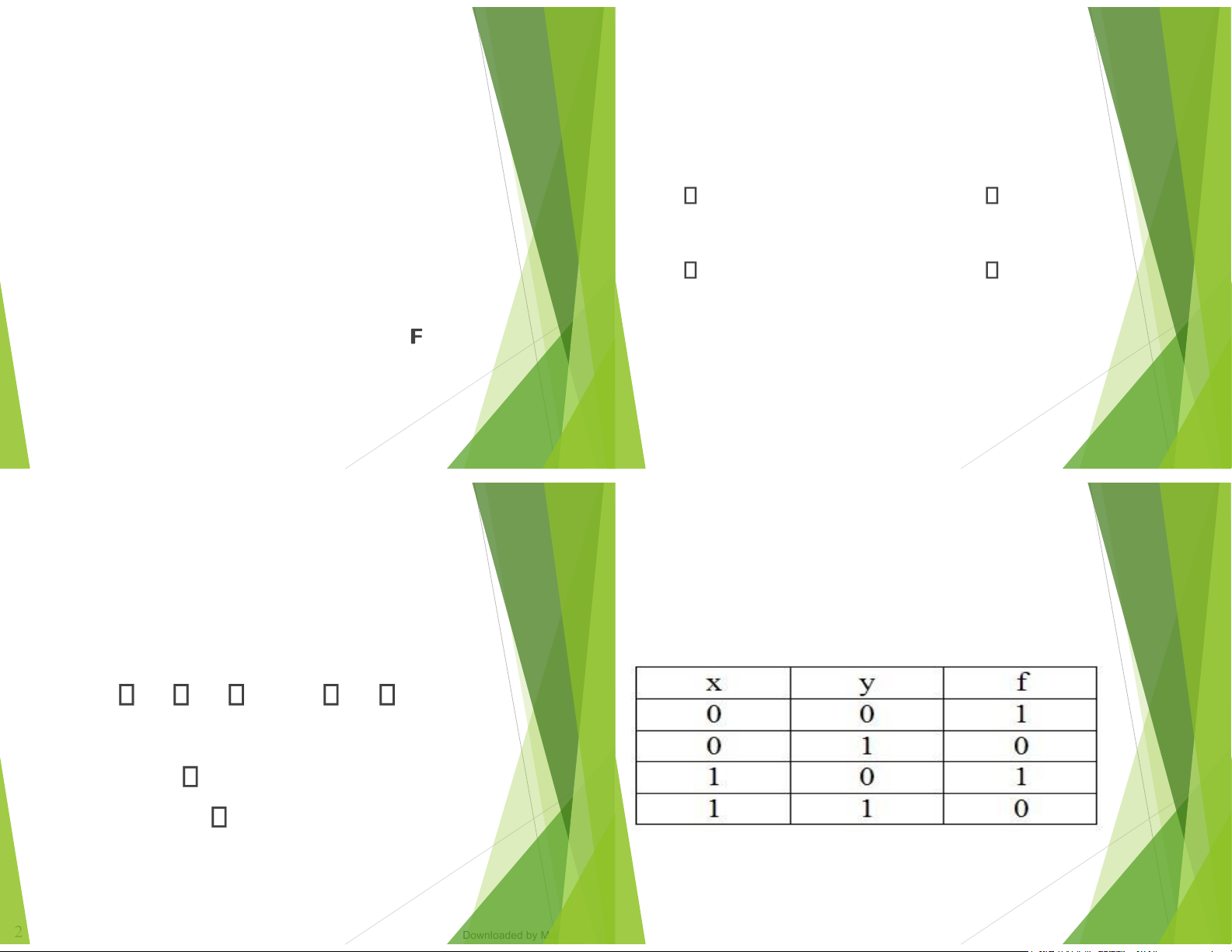
Cách thông thường nhất ể xác ịnh một hàm
Boole là dùng bảng giá trị. Ta có F
n cùng các phép toán này lập thành một ại số Boole. Ngoài ra còn có: Hàm Boole 2 biến f g f g = g f g = f trong ó nếu f g f(x … … 1, , x ) g(x , , x ). n 1 n 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole Trang 16 Trang 17 lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet
(hoathanvu729@gmail.com)2/28/2024 Đại Số Boole lOMoAR cPSD| 40425501 • C Ph 攃 Āp nhân Boole ∧
愃 Āc ph 攃 Āp to 愃 Ān trên h 愃 m : Với f,g Boole:
∈ F n , ta ịnh nghĩa tích Boole c甃ऀ a f và g: 𝒇∧𝒈= 𝒇𝒈
• Ph 攃 Āp c ⌀ng Boole ∨ : ∀ 𝑥= , Với f, g
𝑥 1 ,𝑥 2 ,…𝑥 𝑛 ∈𝐵 𝑛
∈ F n , ta ịnh nghĩa tổng Boole c甃ऀ a f và g: 𝒇∨𝒈=𝒇+𝒈− 𝒇𝒈 (f ∧ g)(x) = f(x)g(x) ∀ 𝑥= 𝑥 ,
1 ,𝑥 2 ,…𝑥 𝑛 ∈𝐵 𝑛 (f •
∨ g)(x) = f(x) + g(x) – f(x)g(x)
Ph 攃 Āp l Āy ph n b : ത 𝒇=𝟏−𝒇 2/28/2024 Đại Số Boole Trang 22 2/28/2024 Đại Số Boole Trang 23 Bi ऀ u thức Boole:
D愃⌀ng nối rời ch椃Ānh tắc c甃ऀ a hàm Boole:
Là một biểu thức ược tạo bởi các biến và các
Xét tập hợp các hàm Boole n biến F n
theo n biến x 1 , x 2 , …,x n . phép toán Boole. •
Mỗi hàm Boole x i hay 𝑥i ược gọi là một từ ơn . • ҧ
Đơn thức là tích khác không c甃ऀ a một số hữu hạn từ ơn. VD : E= (x ∧ y ∧ z ) ∨ (z
• Từ tối ti ऀ u (ơn thức tối ti ऀ ul) à tích khác không c甃ऀ a 甃Ā ∧𝑦ത)
Đểd ọc hơn, người ta có thể viết: n từ ơn. ng E = xyz + z
• Công thức a thức là công thức biểu di n hàm Boole 𝑦
thành tổng c甃ऀ a các ơn thức. ത
• D愃⌀ng nối rời ch椃Ānh t là ắc
công thức biểu di n hàm Boole thành tổng c甃ऀ a các t ừ tối tiểu. 2/28/2024 Đại Số Boole Downloaded by Ma T ir Le Th ang i Ng
24 uyet (hoathanvu729@gmail.com) Đại Số Boole Trang 25 lOMoAR cPSD| 40425501 ҧ 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet
(hoathanvu729@gmail.com)2/28/2024 Đại Số Boole lOMoAR cPSD| 40425501
Công thức a thức tối tiểu:
1. Đơn gi愃ऀ n hơn:
Cho hai công thức a thức c甃ऀ a một hàm Boole: 2.
Đơn gi愃ऀ n như nhau F = m 1 m m 2 3 ∨ ........ m k
Nếu F ơn giản hơn G và G ơn giản hơn F thì ta nói G = M F và G ơn giản như nhau. 1 M M 2 3 ∨ ........ M l
Ta nói rằng công thức F ơn giản hơn công thức G Ví dụ: nếu t n tại ơn ánh h: 1 ,2,…,𝑘
→{1,2,…,𝑙} sao cho với mọi 𝑖∈ ,
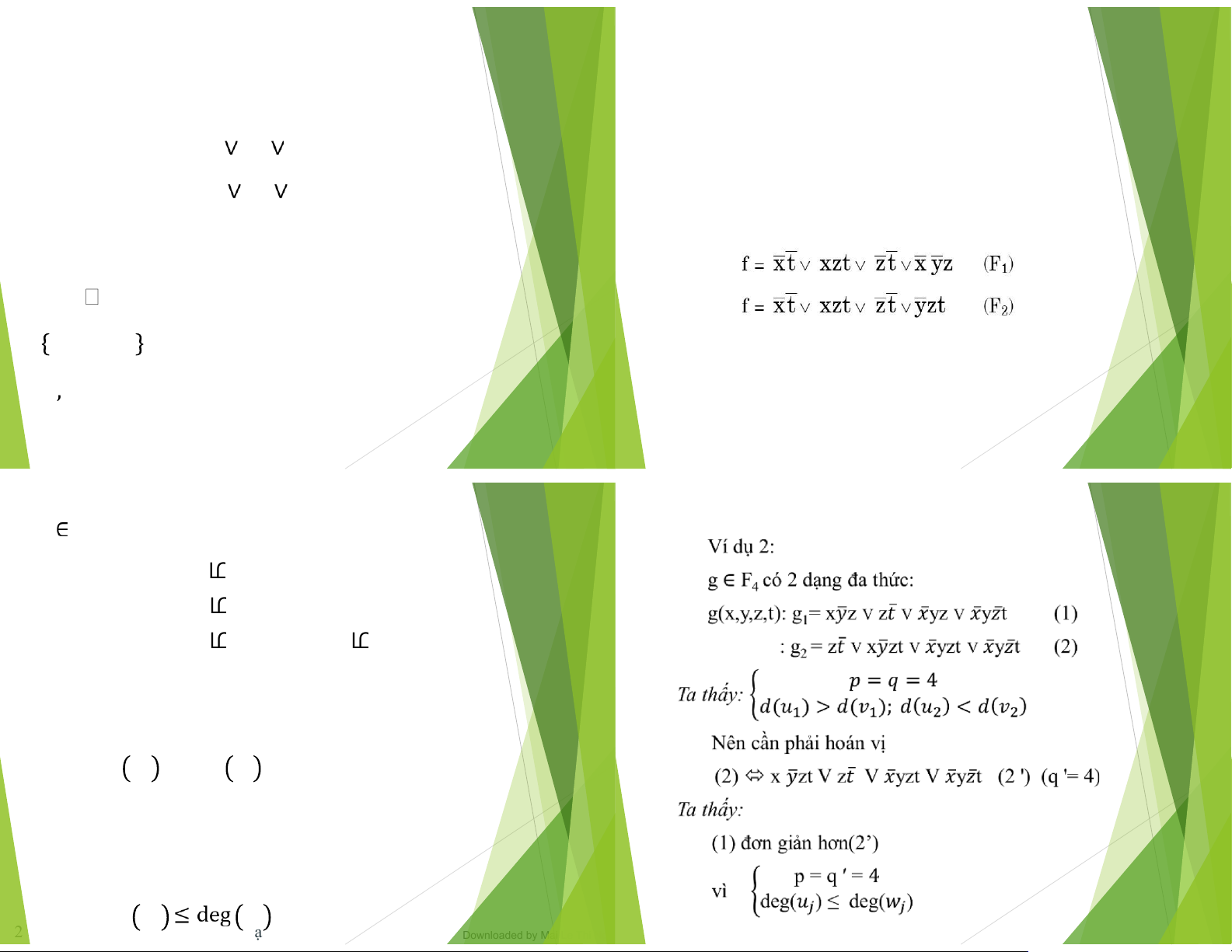
{1 2,…,𝑘 } thì số từ ơn c甃ऀ a 𝑚 không nhiều hơn số 𝑖 từ ơn c甃ऀ a 𝑀 ℎ( 𝑖 ) 2/28/2024 Đại Số Boole Trang 30 2/28/2024 Đại Số Boole Trang 31 f F 4 có 3 dạng a thức f(x,y,z,t): f 1 = ഥV yz V x x 𝑡 𝑥 𝑡 V xyz (1) : f = ഥ ҧ ഥ 𝑡 V yz V xഥ 2 y V yzt x (2) : f ഥ 𝑥 ഥ 𝑡 V 𝑥yzt V 𝑥 ഥ 3 yz V xy V yzt = x ഥ 𝑡 (3) ഥ ҧ ҧ ഥ
(1) và (2) ơn giản như nhau 𝑝=𝑞=4 Vì ൝
deg 𝑢 𝑗 = deg 𝑣 𝑗 =3
(2) ơn giản hơn (3) hay (3) phức tạp hơn (2) 𝑝=4 < 𝑞=5 Vì ൝ deg 2/28/2024 𝑢 𝑗 𝑣 Đại 𝑗 Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole Trang 32 Trang 33 lOMoAR cPSD| 40425501 B ản đ Karnaugh ồ
• Sử dụng bảng Karnaugh là phương pháp xác ịnh
công thức a thức tối tiểu. 3.
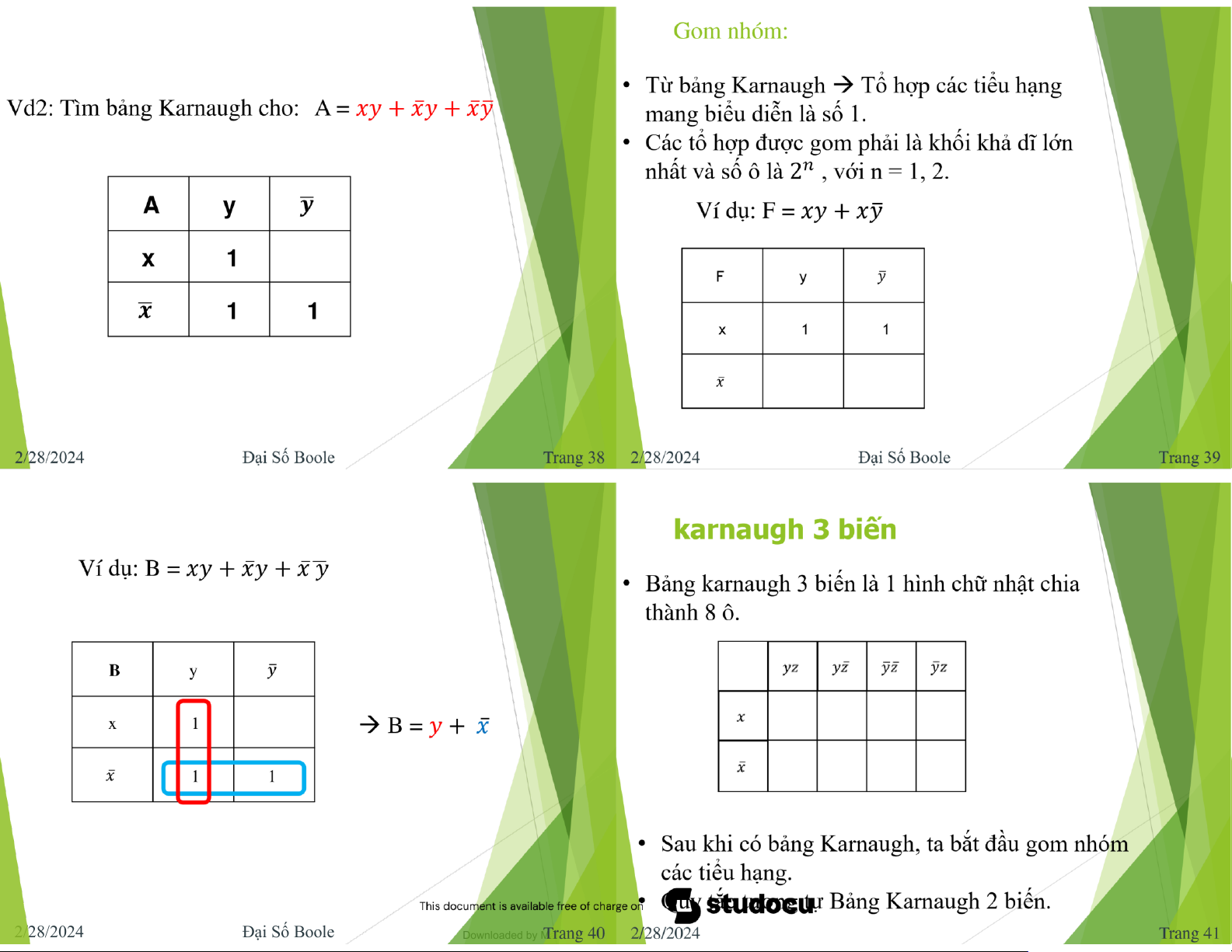
Công thức a thức tối ti ऀ u: • Quy tắc gom nhóm:
Công thức F c甃ऀ a hàm Boolef ược gọi là - Gom các tiểu hạng b mang iểu di n là số . 1 𝑛
- Khi gom Ô kế cận sẽ loại ược n biến. 2
Công thức a thức tối tiểu
Những biến bị loại là những biến khi ta i vòng qua các
nếu với bất kỳ công thức G c甃ऀ a f mà ơn giản hơn F
ô kế cận mà giá trị c甃ऀ a ch甃Āng t . h ay ổi
thì F và G ơn giản như nhau.
- Các vòng phải ược gom sao cho số ô có thể
vào trong vòng là lớn nhất và ể ạt ược iều ó,
thường ta phải gom cả những ô ã gom vào trong các vòng khác.
- Vòng gom phải là 1 hình chữ nhật. Đại Số Boole Trang 34 2/28/2024 Đại Số Boole Trang 35 Karnaugh 2 bi ến • Karnaugh 2 bi n
Đối với hàm Boole 2 biến x, y : ế
• Bảng karnaugh 2 biến có 4 ô vuông, trong ó:
Ô ược ánh số 1 ể biểu di n tiểu hạng có
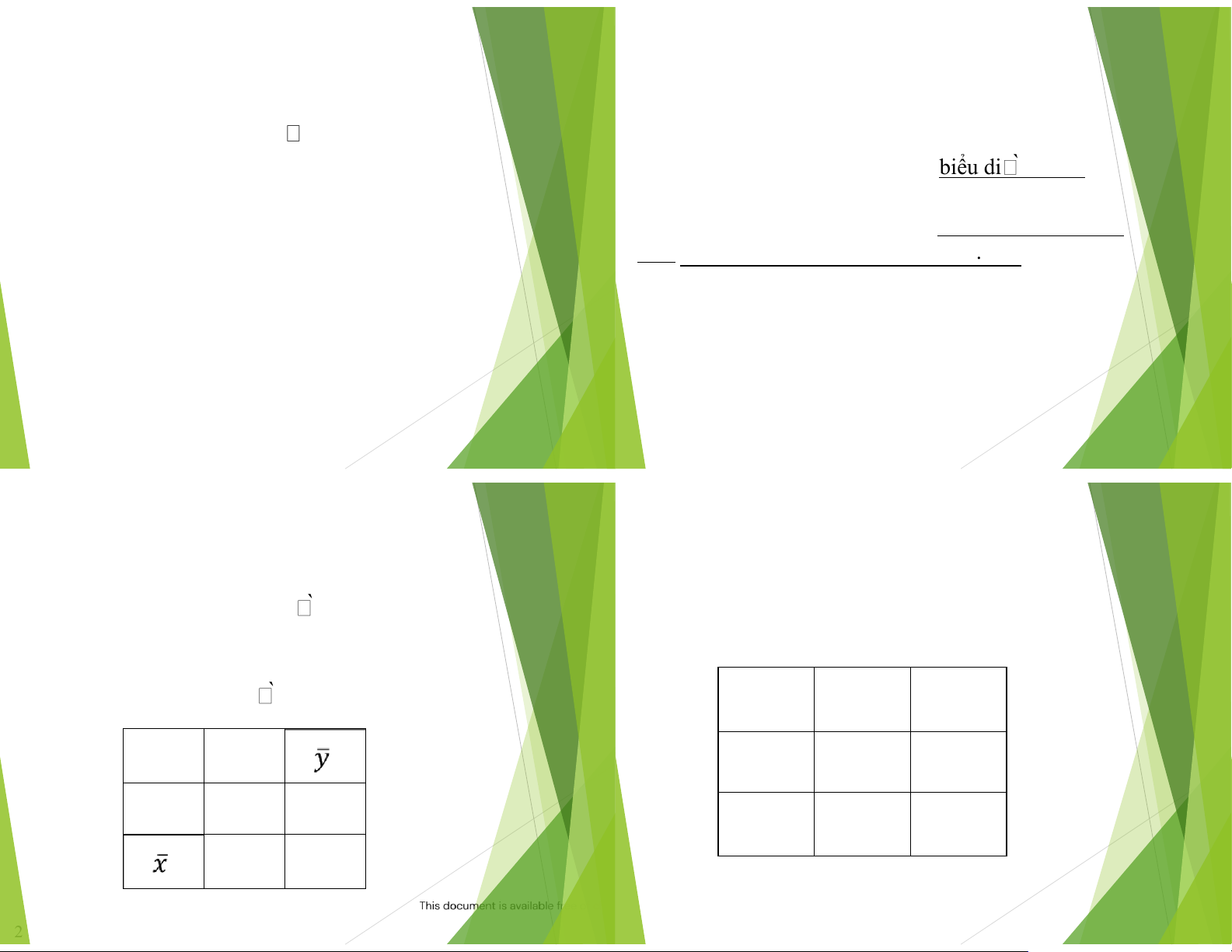
Vd1: Tìm bảng Karnaugh cho F = 𝑥𝑦 + 𝑥𝑦 mặt trong hàm. ത
Các ô ược cho là liền nhau nếu các tiểu hạng
mà ch甃Āng biểu di n chỉ khác nhau 1 biến. F y 𝑦 ത y x 1 1 x 𝑥 ҧ 2/28/2024 Đại Số Boole Trang 36
Downloaded by Mai Le Thi Nguyet 2/28/2024 Trang 37
(hoathanvu729@gmail.com)2/28/2024 Đại Số Boole lOMoAR cPSD| 40425501 2/28/2024 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 Ph甃ऀ c甃ऀ a tập X V dụ
Cho S = X1, …, Xn là họ các tập con c甃ऀ a
X. S gọi là ph甃ऀ c甃ऀ a X nếu X = X X = a, b, c, d i. A = a,b B = c,d
Ph甃ऀ tối tiểu c甃ऀ a X C = a,d D = b,c
Giả sử S là một ph甃ऀ c甃ऀ a X. S gọi là ph甃ऀ
A, B, C, D ph甃ऀ không tối tiểu.
tối tiểu c甃ऀ a X nếu với mọi i, S\Xi không
A, B , C, D là các ph甃ऀ tối tiểu. ph甃ऀ X.
A, C, D ph甃ऀ không tối tiểu. B, D không ph甃ऀ . 2/28/2024 Đại Số Boole Trang 47 2/28/2024 Đại Số Boole Trang 46
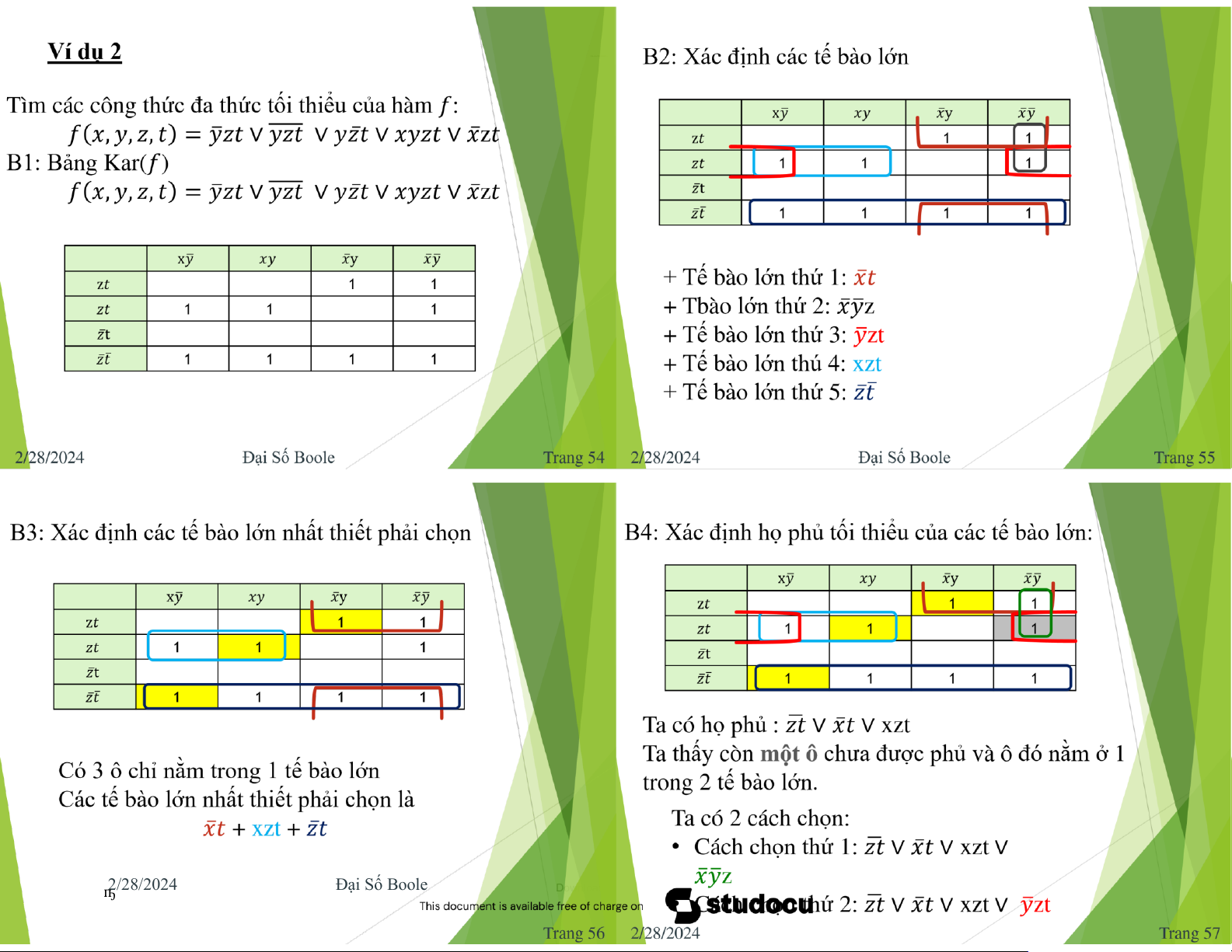
Thuật toán tìm công thức a thức tối tiểu
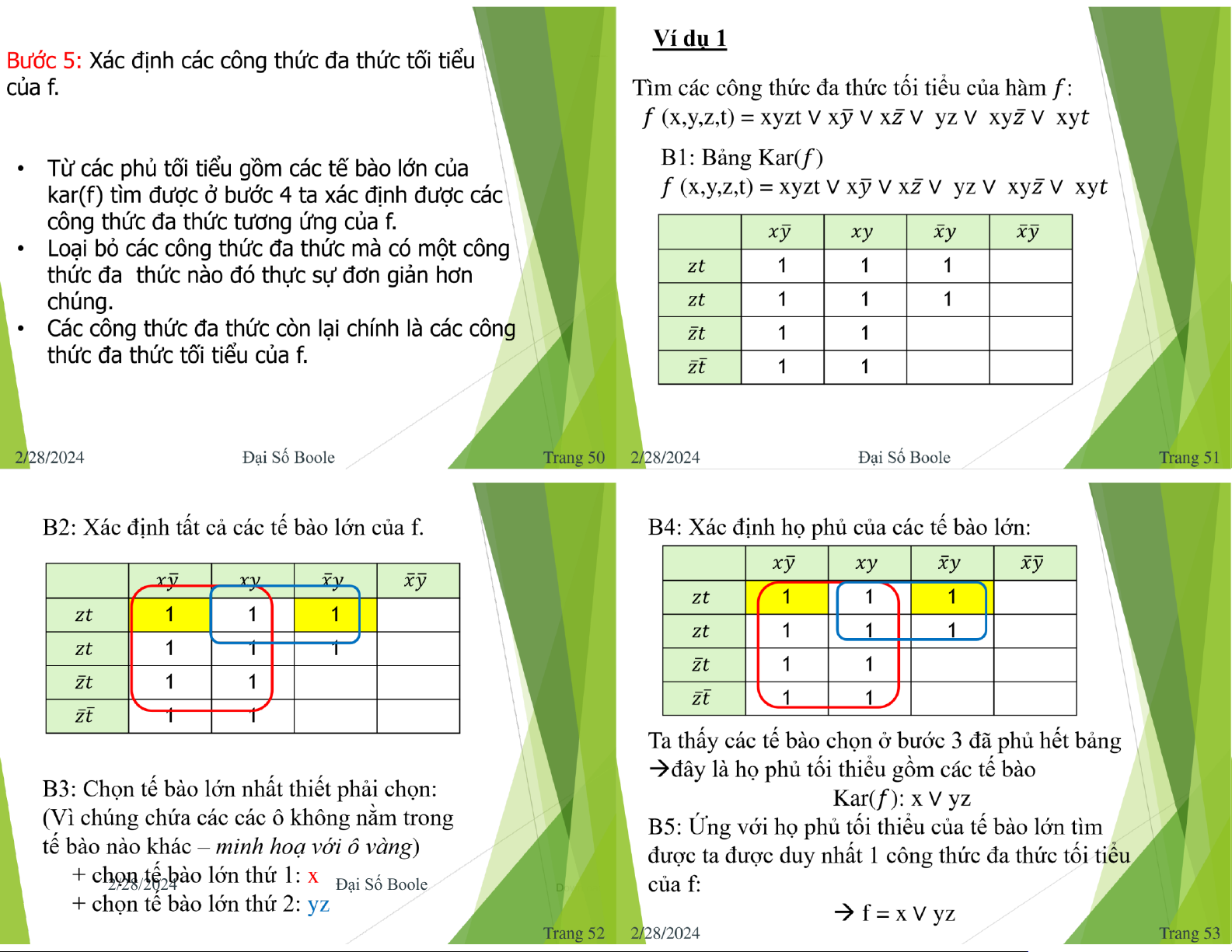
Bước 3: Xác ịnh các tế bào lớn nhất thiết phải Gồm 5 bước: chọn.
Ta nhất thiết phải chọn tế bào lớn T khi tồn tại
Bước 1: Vẽ biểu ồ karnaugh của f.
một ô của kar(f) mà ô này chỉ nằm trong tế
bào lớn T và không nằm trong bất kỳ tế bào
Bước 2: Xác ịnh tất cả các tế bào lớn của lớn nào khác. kar(f). Trang 48 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501
Bước 4: Xác ịnh các phủ tối tiểu gồm các tế bào lớn:
tế bào lớn này. Cứ tiếp tục như thế ta sẽ
tìm ược tất cả các phủ gồm các tế bào lớn
• Nếu các tế bào lớn chọn ược ở bước 3 ã phủ
ược kar(f) thì ta có duy nhất một phủ tối tiểu của kar(f).
gồm các tế bào lớn của kar(f).
o Loại bỏ các phủ không tối tiểu, ta tìm ược
tất cả các phủ tối tiểu gồm các tế bào lớn
• Nếu các tế bào lớn chọn ược ở bước 3 chưa phủ ược kar(f) thì: của kar(f). 2/28/2024 Trang 49
o Xét một ô chưa bị phủ, sẽ có ít nhất hai tế
b o lớn chứa ô này, ta chọn một trong các ҧ ҧ 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole Downloaded by Mai Le Thi Nguye ҧ t (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 ҧ ҧ ҧ ҧ ҧ ҧ ҧ 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole ҧ ҧ lOMoAR cPSD| 40425501 ҧ ҧ ҧ ҧ ҧ ҧ ҧ 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole
Phương pháp Quine-McCluskey lOMoAR cPSD| 40425501
B5: Xác ịnh công thức a thức cực tiểu :
Về cơ bản,phương phápQuine-McCluskey
Ta thấy 2 công thức ơn giản như nhau Phần cho nên cóhai phần .
ầu làtìmcác số hạng là ứng
công thức a thức tối thiểu c甃ऀ hàm 𝑓 là:
viên ể ưa vàokhai triểncựctiểuc甃ऀ a hàm a ഥ 𝑧𝑡
∨ 𝑥𝑡∨ xzt ∨ 𝑥𝑦 z
Boole như dướidạngchuẩntắctuyển . Phầnthứ ҧ ഥ hailàxác 𝑧𝑡
ịnh xemtrong số các ứng viên ó, ∨ 𝑥𝑡∨ xzt ∨ zt ҧ 𝑦ത
các số hạng nàolà thực sự dùng ược . 2/28/2024 Đại Số Boole Trang 58 2/28/2024 Đại Số Boole Trang 59
B ước 2: Lần lượt thực hiện tất cả các phép dán
Ph ương pháp Quine - McCluskey tìm dạng tổng
các biểu di n trong nhóm i với các biểu di n chuẩn tắc thu gọn:
trong nhóm i+1 (i=1, 2, …). Biểu di n nào tham
B ước 1: Viết vào cột thứ nhất các biểu di n c甃ऀ a
gia ít nhất một phép dán sẽ ược ghi nhận một
các nguyên nhân hạng n c甃ऀ a hàm Boole F . Các
dấu * bên cạnh. Kết quả dán ược ghi vào cột
biểu di n ược chia thành từng nhóm, các biểu tiếp theo.
di n trong mỗi nhóm có số các ký hiệu 1 bằng
nhau và các nhóm xếp theo thứ tự số các ký hiệu 1 tăng dần. B
ước 3: Lặp lại Bước 2 cho cột kế tiếp cho ến
khi không thu thêm ược cột nào mới. Khi ó
tất cả các biểu di n không có dấu * sẽ cho ta tất
cả các nguyên nhân nguyên tố c甃ऀ a F . 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole Trang 60 2/28/2024 Trang 61 lOMoAR cPSD| 40425501 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501 ҧ 2/28/2024 Đại Số Boole
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Đại Số Boole lOMoAR cPSD| 40425501
Các bước thiết kế logic tổng hợp:
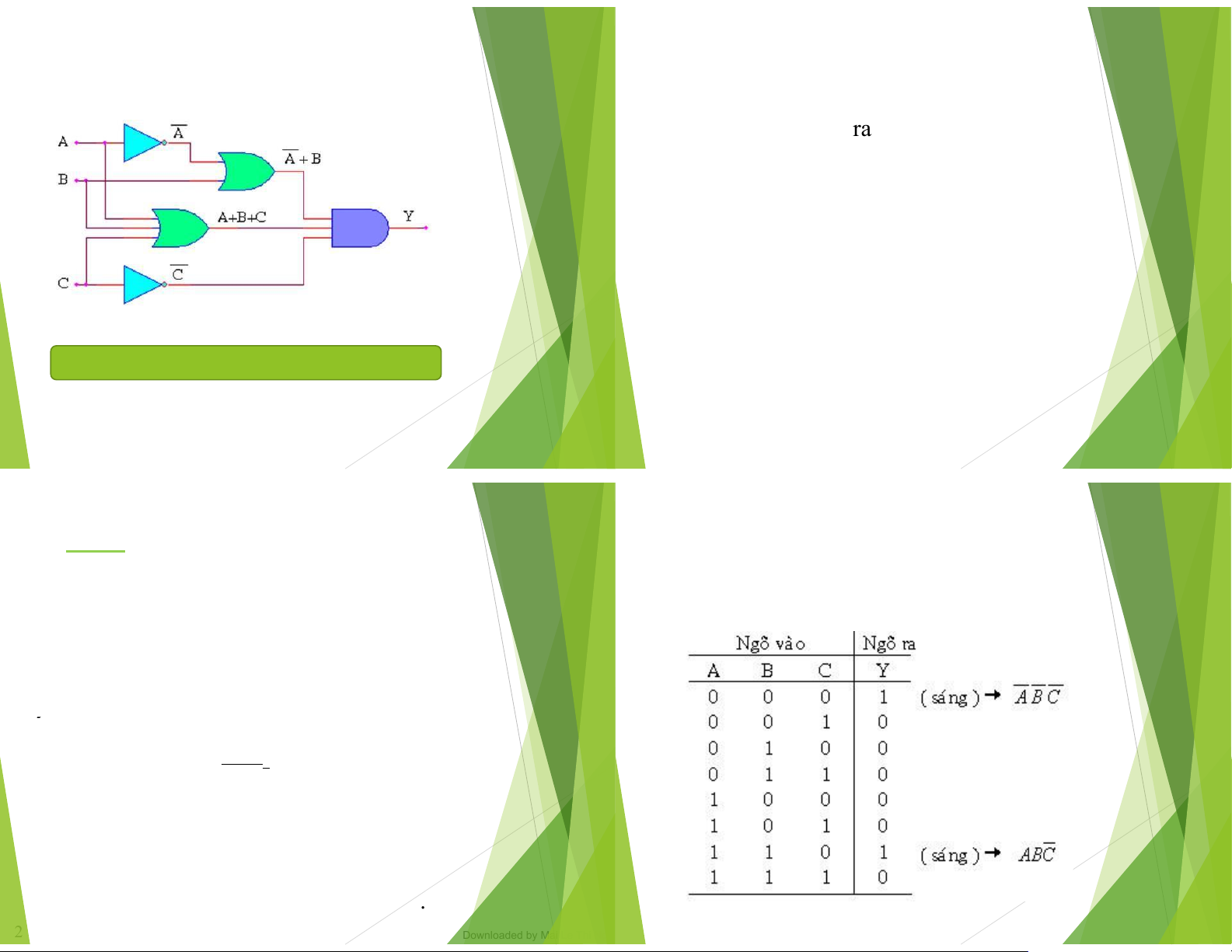
VD: Viết lại biểu thức logic sau từ mạch logic:
Bước 1: Đặt các biến cho ngõ vào và các hàm c甃ऀ a ngõ ra tương ứng.
Bước 2: Thiết lập bảng chân trị cho ngõ ra và ngõ vào
Bước 3: Viết biểu thức logic liên hệ giữa ngõ ra và các ngõ vào.
Bước 4: Tìm công thức a thức tối tiểu c甃ऀ a biểu
thức logic vừa tìm ược.
Bước 5: Từ biểu thức logic r甃Āt gọn chuyển sang Kết quả: mạch logic tương ứng
Y=( 𝐴+𝐵)(𝐴+𝐵+𝐶) 𝐶 2/28/2024 Đại Số Boole Trang 70 2/28/2024 Đại Số Boole Trang 71 V椃Ā Bước 2: dụ:
Một ngôi nhà có 3 công tắc, người ch甃ऀ nhà muốn Từ yêu
cầu bàitoánta có bảng chân trị :
bóng èn sáng khi cả 3 công tắc ều hở, hoặc khi
công tắc 1 và 2 óng còn công tắc thứ 3 hở. Hãy
thiết kế mạch logic thực hiện sao cho số cổng là 椃Āt nhất. Giải : Bước 1:
Gọi 3 công tắc lần lượt là A, B, C. Bóng èn là Y. ҧ ҧ
Trạng thái công tắc óng là logic 1, hở là 0.
Trạng thái èn sánglà logic1 và tắt là . 0 2/28/2024 Đại Số Boole Downloaded by Ma T ir Le Th ang i Ng 72 uyet (ho 2/ ath 28a/nvu 20 729 24 @gmail.com) Đại Số Boole Trang 73 lOMoAR cPSD| 40425501 Do ҧw nloa
ҧ ded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 2/28/2024
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Các khái niệm cơ bản Các khái niệm cơ bản
▪ Đồ thị (Graph) ▪ Đồ thị (Graph)
▪ G = (V, E) với V≠ ▪ Cạnh bội (song song)
▪ V: tập các ỉnh ▪ Hai cạnh phân biệt
▪ E: tập các cạnh cùng tương ứng với ▪ Cạnh e E x ▪ một cặp ỉnhB
ứng với 2 ỉnh v , w V ▪ A
v , w là 2 ỉnh kề (hay ▪ Đ n ồ thị C
liên kết) với nhau, e liên
thuộc với v và w
▪ Đồ thị không có vòng và yz cạnh song songD
▪ Ký hiệu: e = vw ( … ) ▪ Đa ồ thị
▪ v w : e ược gọi là
▪ Các ồ thị không phải là ơn ồ thị
vòng ( khuyên) tại v
Chương 1. Đại cương về ồ thị 2
Chương 1. Đại cương về ồ thị 3
▪ Kn: ơn ồ thị ầy ủ ▪ Đồ thị con
▪ Biểu diễn bằng ma trận
▪ Đồ thị G’ = (V’, E’)
Thường ược dùng ể biểu diễn trên máy tính
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ th ị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Các khái niệm cơ
bảnBiểu diễn ồ thị ▪ Đồ thị
(Graph)▪ Biểu diễn hình học ▪ Đồ thị ầy
ủ▪ Mỗi ỉnh một iểm
▪ Đồ thị mà mọi cặp ỉnh ều kề nhau▪ Mỗi
cạnh một ường (cong hoặc thẳng) nối 2 ỉnh liên thuộc với nó ▪
▪ V’ V, E’ E
▪ Đồ thị hữu hạn▪ 2
cách biểu diễn thường dùng
▪ E và V hữu hạn▪ Ma trận kề
▪ Đồ thị vô hạn▪ Ma trận liên thuộc 4 5
Biểu diễn ồ thị
▪ Một vòng ược tính là một cạnh (akk = 1)
Chương 1. Đại cương về ồ thị 6
▪ Biểu diễn bằng ma trận
Biểu diễn ồ thị ▪ Ma trận kề
▪ Ma trận vuông cấp n (số ỉnh của ồ thị)
▪ Biểu diễn bằng ma trận
▪ Các phần tử ược xác ịnh bởiaij ▪ = a ij
1: Nếu là một cạnh của vvi G j ▪ = a ij
0: Nếu không là một cạnh của vvi j G ▪ Tính chất
▪ Phụ thuộc vào thứ tự liệt kê của các ỉnh ▪ Ma trận là ối xứng
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chương 1. Đại cương về ồ thị 7 ▪ Ma trận kề ▪ Ví dụ 1 8
Biểu diễn ồ thị
Biểu diễn ồ thị
▪ Biểu diễn bằng ma trận
▪ Biểu diễn bằng ma trận ▪ Ma trận kề ▪ Ví dụ 2 ▪ Ma trận liên thuộc
▪ Ma trận M = ( )aij nxm B D A B C D E
▪ Các phần tử aij ược xác ịnh bởi A 0 1 1 0 ▪ = a ij
1: Nếu cạnh liên thuộc với ej v i của G 0A E =0 B ▪ a: : Nếu cạnh e C 1 0 1 1 1 ij
j không liên thuộc với vi C của G 1 1 0 1 2 D 0 1 1 1 2 ▪ Tính chất E 0 1 2 2 0
▪ Các cột tương ứng với các cạnh bội là giống nhau trong ma trân liên thuộc
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ th ị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
▪ Các vòng ứng với một cột có úng một phần tử bằng Biểu diễn ồ thị
1 ứng với ỉnh nối với vòng ó. 9
Biểu diễn ồ thị
▪ Biểu diễn bằng bảng (danh sách liền kề)
▪ Lưu trữ các ỉnh liền kề với một
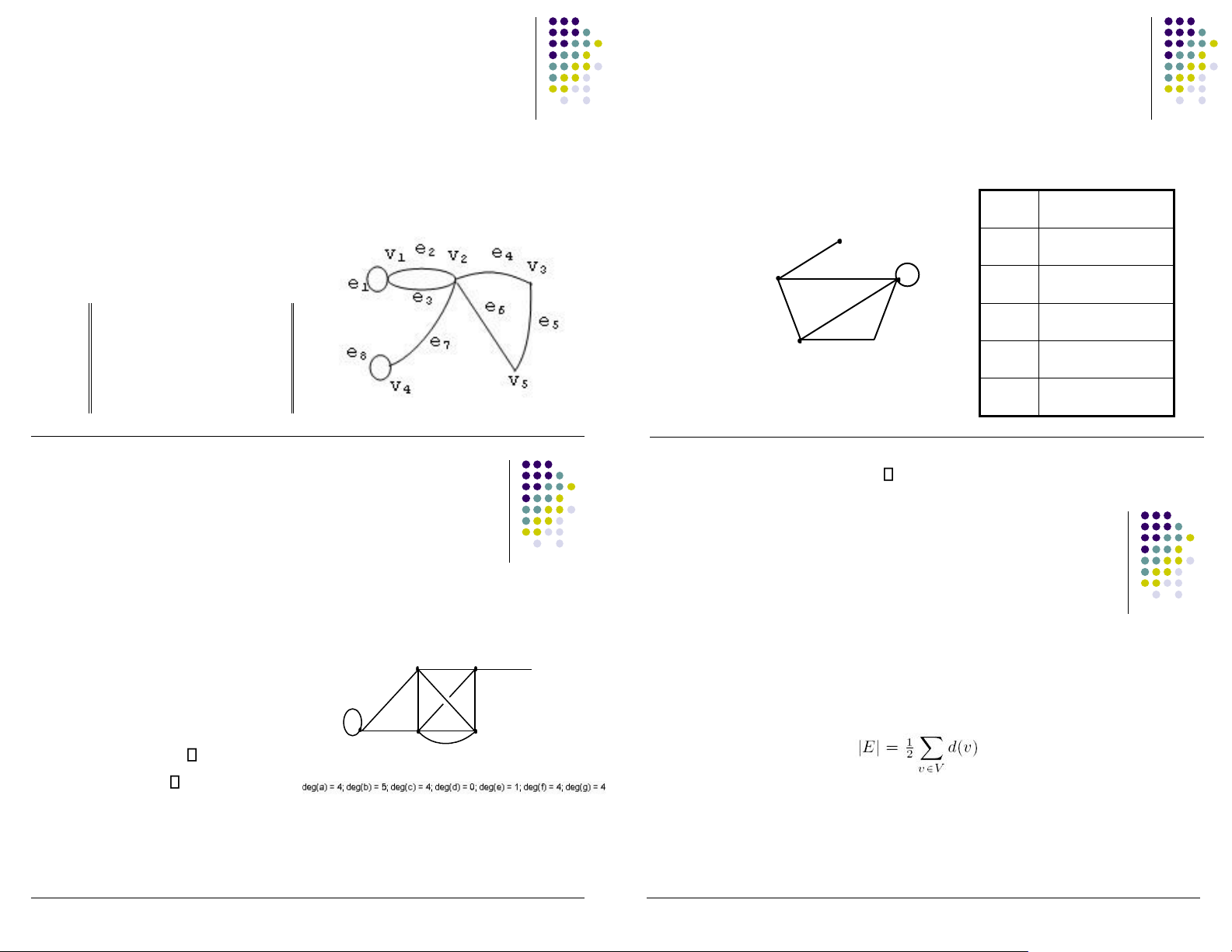
▪ Biểu diễn bằng ma trận ỉnh Đỉnh Đỉnh liền kề ▪ Ma liên thuộc b
▪ Ví dụ e e e e e e e e 1 2 3 4 5 6 7 8 a b, c, e c v a
11 1 1 0 0 0 0 0 v20 1 1 1 b a 0
1 1 0 v30 0 0 1 1 0 0 0 v40 c a, c, d, e 0
0 0 0 0 1 1 v50 0 0 0 1 1 0 e ▪ d Ví dụ 0 d c, e e a, c, d
Chương 1. Đại cương về ồ thị 10
Chương 1. Đại cương về ồ thị 11
▪ Đồ thị rỗng: deg(v)=0 v 12
Các khái niệm cơ bản ▪ Bậc của ỉnh
Các khái niệm cơ bản ▪
Đỉnh của ồ thị G có bậc là n nếu nó kề với n ỉnh ▪ Bậc của ỉnh khác. g f e
▪ Ký hiệu: deg(v) hay d(v) ▪ Định lý 1.1
▪ Mỗi vòng ược kể là 2
▪ Trong mọi ồ thị G = (V, E), tổng số bậc của các ỉnh của cạnh tới một ỉnh
G bằng 2 lần số cạnh của nó a c d ▪ b
Đỉnh cô lập deg(v)=0
▪ Đỉnh treo deg(v)=1 ▪ Hệ quả
▪ Cạnh treo có ầu mút là
▪ Trong mọi ồ thị G = (V, E) ta có ▪ Số ỉnh bậc một ỉnh treo
lẻ là một số chẵn
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ▪
Chương 1. Đại cương về ồ thị
Tổng bậc của ỉnh bậc lẻ là một số chẵn 14
Các khái niệm cơ bản 13
Các khái niệm cơ bản
▪ Chứng minh và giải toán bằng phương pháp ồ thị ▪ Bậc của ỉnh
1. Xây dựng ồ thị mô tả ầy ủ thông tin của bài toán ▪ Định lý 1.2 ▪
Mỗi ỉnh v V một ối tượng trong bài toán
▪ Trong mọi n ồ thị G = (V, E), nếu số ỉnh nhiều h n 1 ▪
Mỗi cạnh e E mối quan hệ giữa hai ối tượng
thì tồn tại ít nhất hai ỉnh cùng bậc. ▪
Vẽ ồ thị mô tả bài toán
2. Sử dụng các ịnh nghĩa, tính chất, ịnh lý, … suy ▪ Định lý 1.3
ra iều cần phải chứng minh
▪ Trong mọi n ồ thị G = (V, E), nếu số ỉnh nhiều h n 2
và có úng hai ỉnh cùng bậc thì hai ỉnh này không ồng
Chương 1. Đại cương về ồ thị 15
thời có bậc bằng 0 hoặc n-1. 16
Các khái niệm cơ bản
Các khái niệm cơ bản
▪ Một số bài toán ví dụ
▪ Một số bài toán ví dụ
Chứng minh rằng trong một cuộc họp tùy ý có ít
Chứng minh rằng số người mà mỗi người ã có một
nhất 2 ại biểu tham gia trở lên, luôn có ít nhất hai ại
số lẻ lần bắt tay nhau trên trái ất là một con số
biểu mà họ có số người quen bằng nhau trong các chẵn. ại biểu ến dự họp.
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ th ị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 17
Một số ồ thị ặc biệt
Một số ồ thị ặc biệt
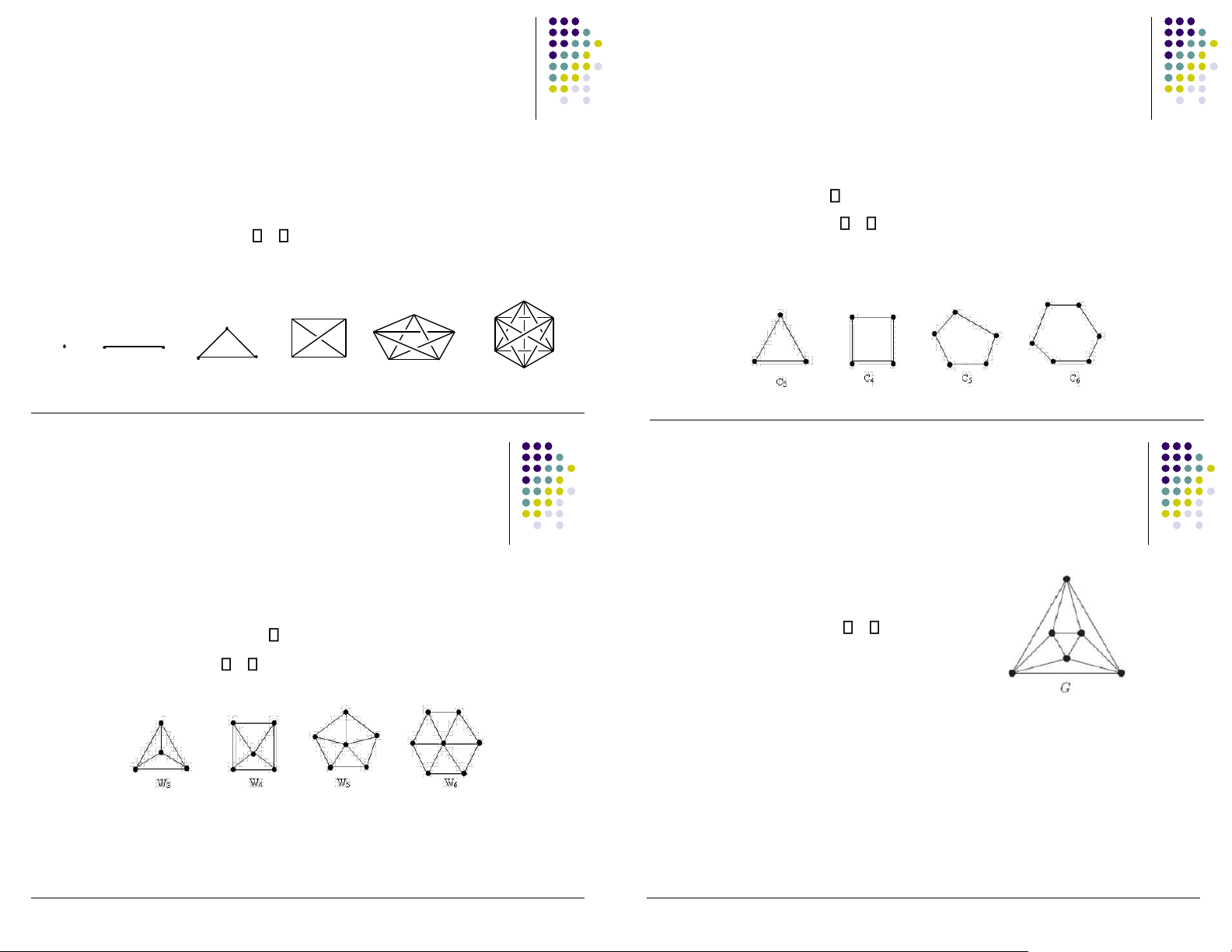
▪ Đồ thị vòng Cn
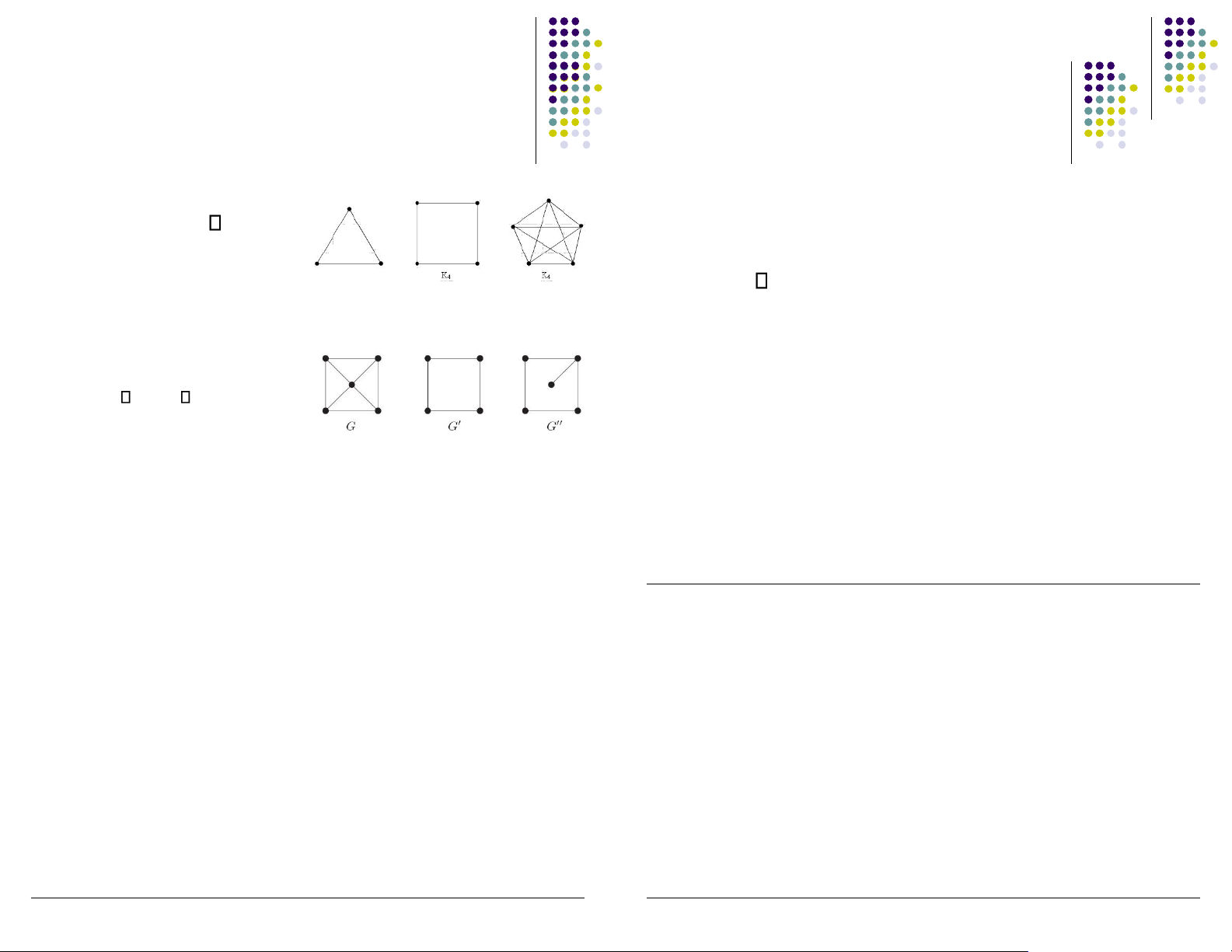
▪ Đồ thị ầy ủ Kn ▪ Đơn ồ thị ▪ Đơn ồ thị ▪
▪ Số ỉnh: |V| = n 3
Số ỉnh: |V| = n
▪ Bậc: deg(v) = 2, v V
▪ Bậc: deg(v) = n – 1, v V
▪ Số cạnh: | E | = n
▪ Số cạnh: |E| = n(n - 1) / 2 K 1 K 2 K K 3 4 K 5 K 6
Chương 1. Đại cương về ồ thị 18
Chương 1. Đại cương về ồ thị 19
Một số ồ thị ặc biệt
Một số ồ thị ặc biệt
▪ Đồ thị ều bậc k (Đồ thị k- ều)
▪ Đồ thị hình bánh xe Wn
▪ Mọi ỉnh ều có cùng bậc k
▪ Nối các ỉnh của Cn với một ỉnh mới u ta ược Wn
▪ Số ỉnh: |V| = n ▪
▪ Bậc: deg(v) = k, v V
Số ỉnh: |V| = n + 1, n 3 ▪ ▪
Số cạnh: |E| = n.k/2 Ví dụ:
Bậc: deg(v) = 3, v V \ {u}; deg(u) = n
▪ Số cạnh: |E| = 2n
▪ Cn là ồ thị ều bậc 2
▪ Kn là ồ thị ều bậc (n-1) 21 20
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Một số ồ thị ặc biệt
Một số ồ thị ặc biệt
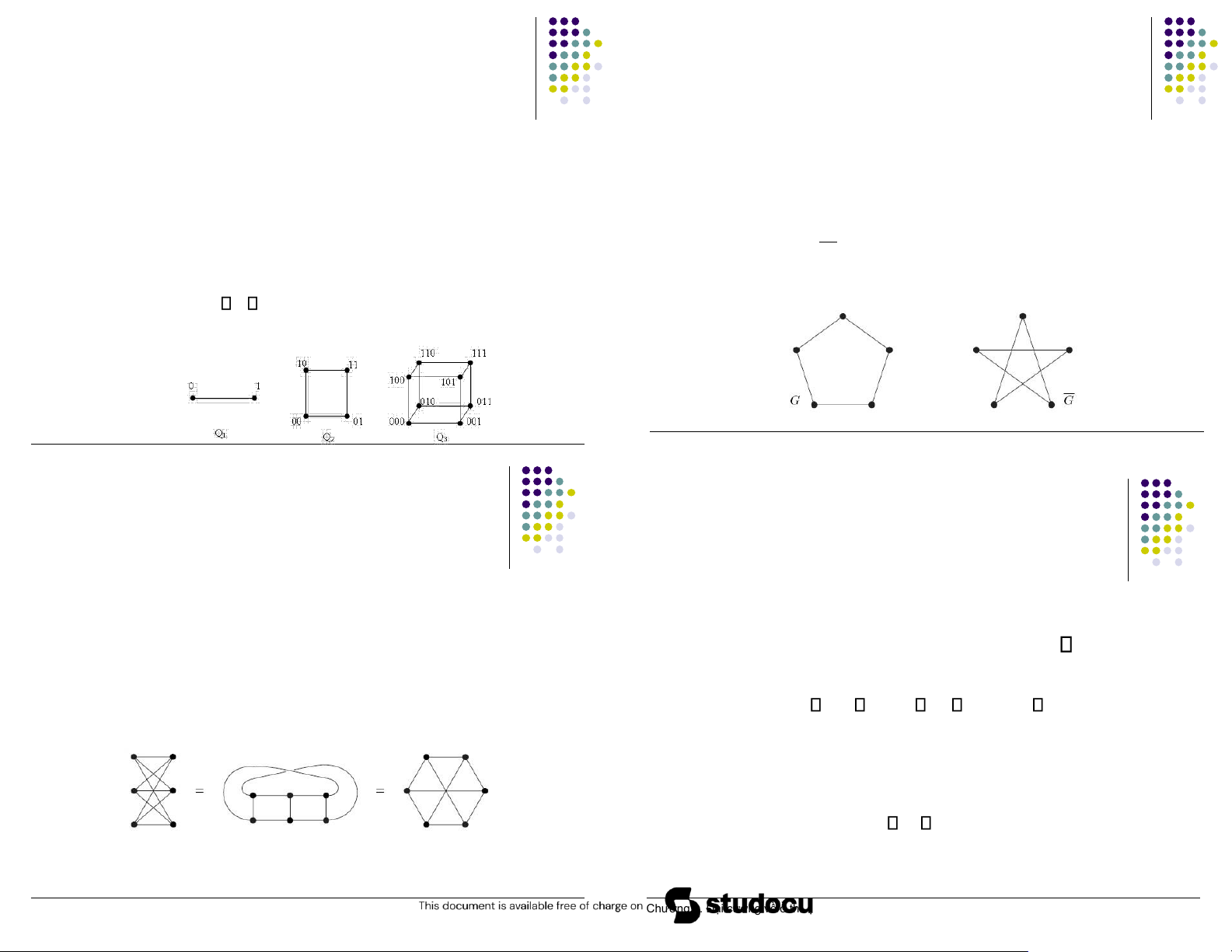
▪ Các khối n-lập phương Qn ▪ Đồ thị bù ▪ ▪
Có ỉnh, mỗi ỉnh ược biểu diễn bằng một dãy số nhị 2n
Hai ơn ồ thị G và G’ ược gọi là bù nhau phân với ộ dài n.
▪ chúng có chung các ỉnh ▪ ▪
Hai ỉnh là liền kề nếu và chỉ nếu các dãy nhị phân biểu diễn
Cạnh nào thuộc G thì không thuộc G’ và ngược lại
chúng chỉ khác nhau úng 1 bit. ▪ Ký hiệu: G’ = G ▪
Số ỉnh: |V| = 2n
▪ Bậc: deg(v) = n, v V
▪ Số cạnh: |E| = n. 2n−1
Chương 1. Đại cương về ồ thị 23
Chương 1. Đại cương về ồ thị 22 24
Một số ồ thị ặc biệt
Sự ẳng cấu giữa các ồ thị
▪ Đồ thị lưỡng phân ▪ Định nghĩa
▪ Một ồ thị G ược gọi là ồ thị lưỡng phân nếu tập các ỉnh của
G có thể phân thành 2 tập hợp không rỗng, rời nhau sao
▪ G(V, E) ẳng cầu với G’(V’, E’), (G G’) nếu
cho mỗi cạnh của G nối một ỉnh thuộc tập này ến một ỉnh
▪ Tồn tại song ánh f: V V’ ▪ Bảo toàn quan hệ liền kề: thuộc tập kia.
u,v V, uv E f(u)f(v) E’ ▪ Ký hiệu: Km,n
▪ G ẳng cấu với G’ thì ▪ |V| = |V’| ▪ |E| = |E’| ▪
deg(v) = deg(f(v)), v V K3,3
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ th ị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 25
Chương 1. Đại cương về ồ thị 26
Sự ẳng cấu giữa các ồ thị
Sự ẳng cấu giữa các ồ thị ▪ Định nghĩa ▪ Định nghĩa ▪
▪ Chứng minh 2 ồ thị ẳng cấu
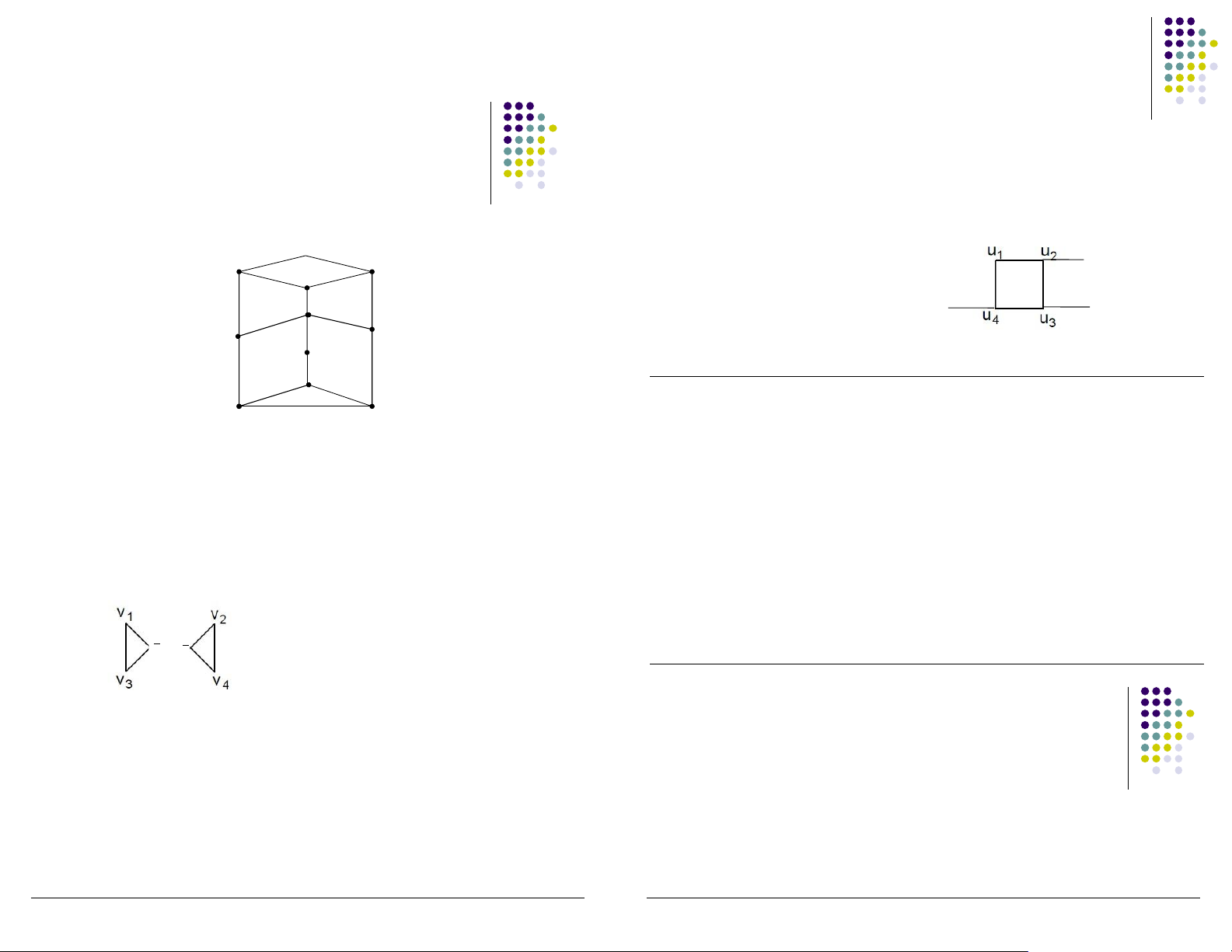
Chứng minh 2 ồ thị ẳng cấu ▪ ▪ Ví dụ 2 Điều kiện cần
▪ Xét số cạnh, số ỉnh, bậc của ỉnh ▪ Điều kiện ủ
▪ Xây dựng song ánh bảo toàn quan hệ liền kề ▪ Ví dụ 1: u1 u2 v1 v2 u4 u3 v3 v4 G = (V,E) H = (W,F)
Chương 1. Đại cương về ồ thị 27 28
Sự ẳng cấu giữa các ồ thị
Đồ thị có hướng ▪ Đồ thị tự bù ▪ Định nghĩa ▪ Định nghĩa ▪ G = (V, E)
▪ Đồ thị G tự bù nếu G ẳng cấu với phần bù của nó ▪ Tập ỉnh V
▪ Tập cạnh (cung) E = { (a, b) | a,b V } ▪ ▪ e = (a, b) E Ví dụ
▪ Ký hiệu: e = ab ▪ e có ▪ Định lý 1.4 hướng từ a ến b
▪ Hai ồ thị có ma trận liền kề (theo một thứ tự nào ó của
các ỉnh) bằng nhau thì ẳng cấu với nhau ▪ a: ỉnh ầu; b: ỉnh cuối ▪ e là khuyên (vòng) a b
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
▪ G ược gọi là ầy ủ nếu ồ thị vô hướng của nó là ầy ủ
Chương 1. Đại cương về ồ thị 30
Đồ thị có hướng 29
Đồ thị có hướng ▪ Bậc của ỉnh ▪ Bậc của ỉnh ▪ Định lý 1.5 ▪ Bậc vào
▪ Tổng bậc vào của các ỉnh bằng tổng bậc ra và bằng số
▪ deg - (v) = | { u | (u, v) E } | = số cạnh có ỉnh cuối là v cạnh của ồ thị ▪ Bậc ra
▪ deg + (v) = | { u | (v, u) E } | = số cạnh có ỉnh ầu là v |V| deg ( )+ v =
|V| deg ( )− v = | E | i=1 i=1
▪ Đồ thị cân bằng deg ( )+ v = deg ( ),− v v V ▪
Chú ý: Một khuyên (vòng) tại một ỉnh sẽ góp thêm một ơn
Chương 1. Đại cương về ồ thị 31
vị vào bậc vào và bậc ra của ỉnh này. 32
Đồ thị có hướng
Đường i và chu trình ▪ Bậc của ỉnh ▪ Đường i ▪ Ví dụ ▪ Định nghĩa ▪ ▪
Có một nhóm gồm 9 ội bóng bàn thi ấu vòng tròn một
Đường i có ộ dài n từ v0 ến vn với n là một số nguyên dương là lượt.
một dãy các cạnh liên tiếp v0v1, v1v2, …, vn-1vn
▪ v0: ỉnh ầu; vn: ỉnh cuối
▪ Hỏi sau khi có kết quả thi ấu của tất cả các ội có thể
có trường hợp bất kỳ ội nào trong 09 ội này cũng ều
▪ Ký hiệu: v0v1v2 … vn-1vn
thắng úng 05 ội khác trong nhóm ược không? (Lưu ường i v0 - vn
ý trong thi bóng bàn không có trận hòa)
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ th ị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chương 1. Đại cương về ồ thị 34
Đường i và chu trình ▪ Chu trình ▪ Định nghĩa ▪ Chu trình
▪ ường i khép kín (v0v1v2 … vn-1vnv0) ▪ ộ dài ít nhất là 3 33
Đường i và chu trình ▪ Chu trình ơn giản ▪ Đường i
▪ Chu trình không i qua cạnh nào quá 1 lần ▪ ▪ Chu trình sơ cấp Định nghĩa
▪ Chu trình không i qua ỉnh nào quá 1 lần (trừ ỉnh ầu, ỉnh
▪ Đường i ơn giản ( ường i ơn) cuối)
▪ Đường i không qua cạnh nào quá một lần ▪ Đường i sơ cấp
Chương 1. Đại cương về ồ thị 35
▪ Đường i không qua ỉnh nào quá một lần
▪ Đường i sơ cấp Đường i ơn giản ▪
Bậc của mọi ỉnh ều lớn hơn hoặc bằng 2 thì trong G luôn
tồn tại một chu trình sơ cấp ▪ Định lý 1.7
Đường i và chu trình
▪ G = (V, E) là một ồ thị vô hướng ▪
Số ỉnh lớn hơn hoặc bằng 4 ▪ Chu trình ▪
Bậc của mọi ỉnh ều lớn hơn hoặc bằng 3 thì trong G luôn ▪ Định lý 1.6
tồn tại một chu trình sơ cấp có ộ dài chẵn
▪ G = (V, E) là một ồ thị vô hướng 36 ▪
Số ỉnh lớn hơn hoặc bằng 3
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ thị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chú ý: Nếu v và u liên thông trong G thì thành phần liên
thông của G chứa v cũng là thành phần liên thông của G chứa u. Tính liên thông
▪ Tính liên thông trong ồ thị vô hướng ▪ Định nghĩa
▪ Hai ỉnh v, u trong ồ thị G ược
Chương 1. Đại cương về ồ thị 38
gọi là liên thông nếu tồn tại một
ường i nối chúng với nhau. Tính liên thông
▪ Đồ thị G gọi là liên thông nếu
▪ Tính liên thông trong ồ thị vô hướng
hai ỉnh phân biệt bất kỳ trong ồ
thị ều liên thông. Ngược lại thì ▪ Định lý 1.8
ta gọi là ồ thị không liên thông.
▪ Đồ thị G=(V, E) là liên thông khi và chỉ khi G có duy
nhất một thành phần liên thông.
(Sv tự chứng minh) 37 Tính liên thông
▪ Tính liên thông trong ồ thị vô hướng ▪ Định nghĩa ▪ Cho G = (V,E), v V .
▪ V’ là tập con của V gồm ỉnh v và tất cả các ỉnh liên thông với v trong G.
Chương 1. Đại cương về ồ thị ▪ 39
E’ là tập con của E gồm tất cả các cạnh nối các ỉnh thuộc V’.
Khi ó G’ = (V’, E’) gọi là thành phần liên thông của G chứa v.
▪ u là ỉnh cắt ( iểm khớp) số thành phần liên thông
tăng lên nếu bỏ u và các cạnh liên thuộc với nó. Tính liên thông
▪ e là cầu số thành phần liên thông tăng lên nếu bỏ cạnh e.
▪ Tính liên thông trong ồ thị vô hướng ▪ Đỉnh cắt và cầu
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ th ị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ▪ Liên thông mạnh
▪ Đồ thị có hướng G ược gọi là liên thông mạnh nếu giữa 2
ỉnh u,v bất kỳ trong G luôn có ường i từ v ến u và từ u ến v. ▪ Liên thông yếu
▪ Đồ thị có hướng G ược gọi là liên thông yếu nếu ồ thị vô hướng
tương ứng của nó là liên thông 40 Tính liên thông
Chương 1. Đại cương về ồ thị 42
▪ Tính liên thông trong ồ thị vô hướng Tính liên thông ▪ Định lý 1.9:
▪ Tính liên thông trong ồ thị có hướng
▪ Đơn ồ thị G = (V , E) có ▪ ▪ |V| = n 2 Định lý 1.10 ▪ ▪
Nếu ồ thị G có úng 2 ỉnh bậc lẻ thì 2 ỉnh này phải liên
deg(u) + deg(v) n, u,v V thì G là ồ thị liên thông thông với nhau ▪ Hệ quả:
▪ Đơn ồ thị G = (V , E), |V| = n có deg(v) n/2, v V thì ▪ Định lý 1.11
G là ồ thị liên thông
▪ Đồ thị G là một ồ thị lưỡng phân khi và chỉ khi mọi chu
trình của nó ều có ộ dài chẵn 41 Tính liên thông
▪ Tính liên thông trong ồ thị có hướng
Chương 1. Đại cương về ồ thị 43
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ thị
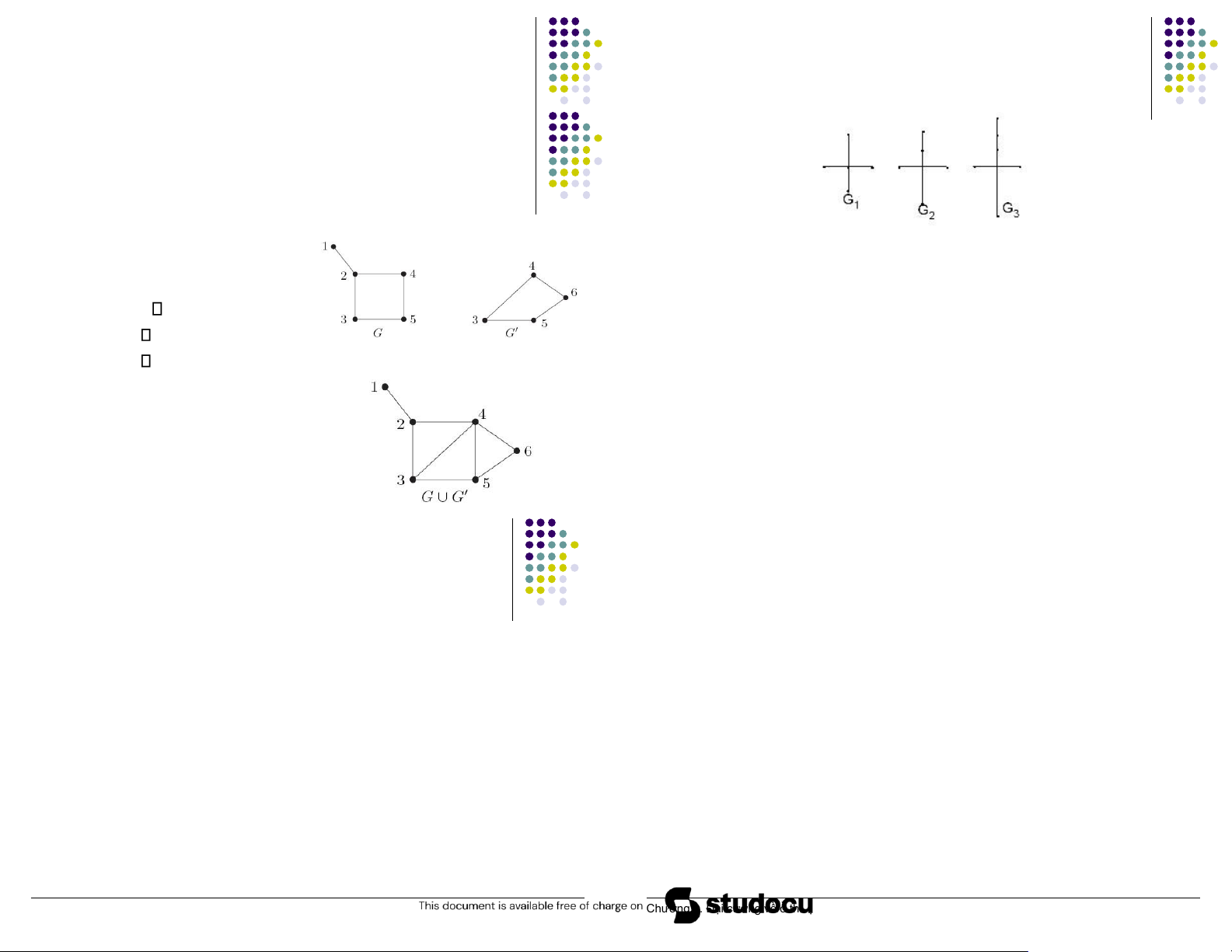
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Một số phép biến ổi ồ thị ▪ Hợp của 2 ồ thị 45 ▪ G = (V, E) ▪ G’ = (V’, E’)
▪ G’’ = G G’ = (V’’, E’’) ▪ V’’ = V V’ ▪ E’’ = E E’ 44
Một số phép biến ổi ồ thị
▪ Phép phân chia sơ cấp
▪ Phép thay thế cạnh e = uv của G bởi một ỉnh mới w cùng
với 2 cạnh uw và vw ▪ Đồng phôi
▪ G và G’ gọi là ồng phôi nếu chúng có thể nhận ược từ
cùng một ồ thị bằng một dãy các phép phân chia sơ cấp
▪ Hai ồ thị ồng phôi chưa chắc ẳng cấu với nhau
Chương 1. Đại cương về ồ thị
Chương 1. Đại cương về ồ th ị
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chu trình và ường i Euler
CHƯƠNG 5: CÁC KHÁI NIỆM CƠ
BẢN CỦA LÝ THUYẾT ĐỒ THỊ ▪ Bài toán
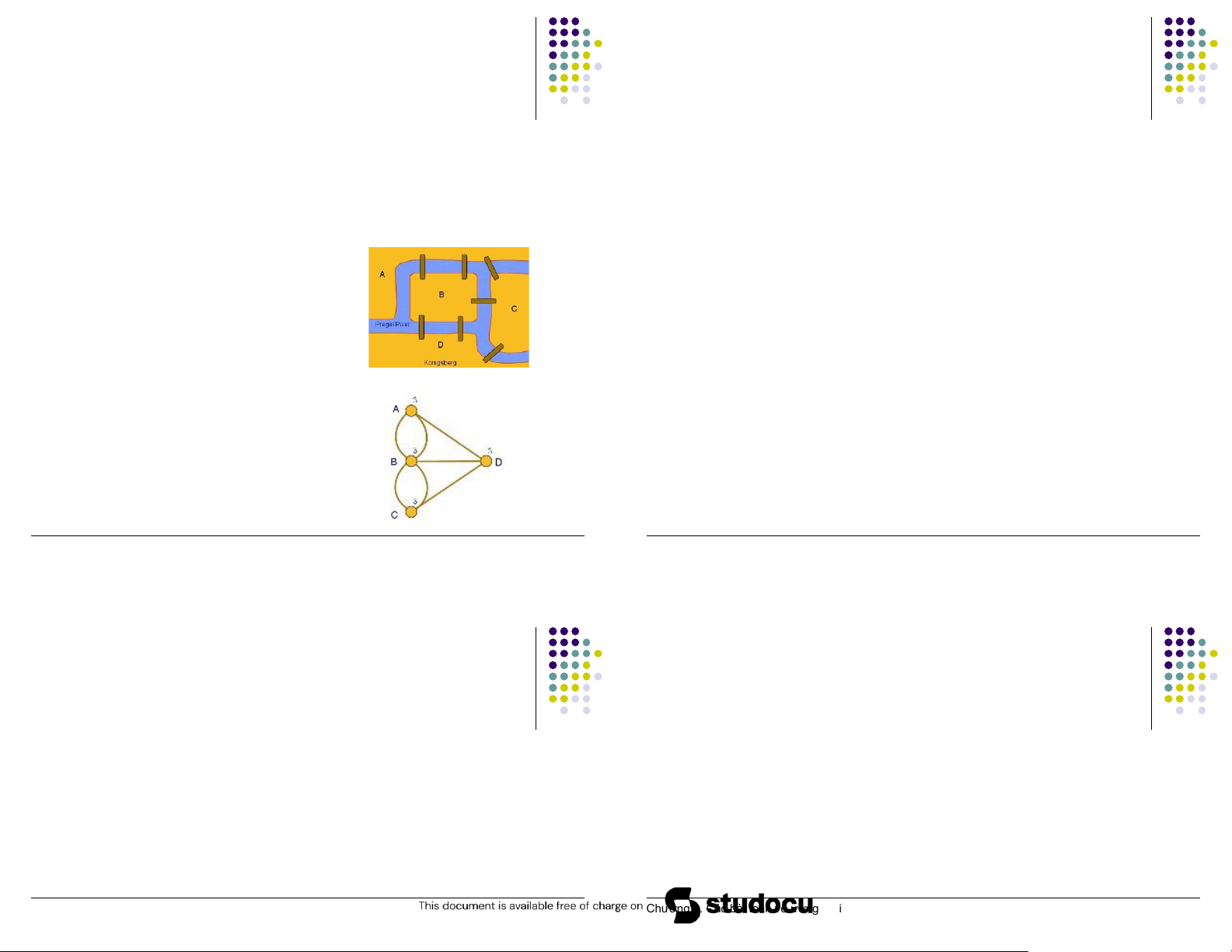
▪ Có thể xuất phát tại một
iểm nào ó trong thành phố,
i qua tất cả 7 cây cầu, mỗi PHẦN 2:
cây một lần, rồi trở về iểm xuất phát ược không?
- Chu trình và ường i Euler
▪ Leonhard Euler ã tìm ra lời
- Chu trình và ường i Hamilton
giải cho bài toán vào năm - Thuật toán Dijkstra 1736
Chương 2. Các bài toán về ường i 2 1
Leonhard Euler 1707 - 1783 Leonhard Euler 1707 - 1783 ▪ Leonhard Euler (15/04/1707 –
18/9/1783) là một nhà toán học và nhà vật lý ▪
Ông sinh và lớn lên tại Basel, và ược
xem là thần ồng toán học từ nhỏ. Ông làm giáo sư
học Thụy Sĩ. Ông (cùng với Archimedes và
toán học tại Sankt-Peterburg, sau ó tại Berlin, rồi trở
Newton) ược xem là một trong những nhà
lại SanktPeterburg. Ông là nhà toán học viết nhiều
toán học lừng lẫy nhất. Ông là người ầu tiên
nhất: tất cả các tài liệu ông viết chứa ầy 75 tập. Ông
sử dụng từ "hàm số" ( ược Gottfried Leibniz
là nhà toán học quan trọng nhất trong thế kỷ 18 và ã
ịnh nghĩa trong năm 1694) ể miêu tả một biểu
suy ra nhiều kết quả cho môn vi tích phân mới ược
thức có chứa các ối số, như y = F(x). Ông
thành lập. Ông bị mù hoàn toàn trong 17 năm cuối
cuộc ời, nhưng khoảng thời gian ó là lúc ông cho ra
cũng ược xem là người ầu tiên dùng vi tích
hơn nửa số bài ông viết. phân trong môn vật lý. 3
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 4
▪ Tên của ông ã ược ặt cho một miệng núi lửa
trên Mặt Trăng và cho tiểu hành tinh 2002.
Chu trình và ường i Euler
Chu trình và ường i Euler ▪ Bài toán ▪ Định nghĩa ▪ Môhìnhhóabàitoán
Cho ồ thị G=(V,E) liên thông ▪ Xây dựng ồ thị G ▪ ChutrìnhEuler
▪ Đỉnh : Cácvùng ất trong
▪ Chutrình ơn chứatấtcả các cạnhcủa ồ thị G. sơ ồ ▪ Đồ thị Euler ▪ Cạnh : cáccây cầunối giữa haivùng ất
▪ Đồ thị có chứamột chutrìnhEuler ▪ Yêu cầu ▪ Đường i Euler
▪ Tồntại haykhông một chutrình ơn trong a ▪ Đường iơn
chứatấtcả các cạnhcủa ồ thị G ồ thị G=(V,E)có chứa
tấtcả các cạnhcủa ồ thị?
Chương 2. Các bài toán về ường i 5
Chương 2. Các bài toán về ường i 6
Chu trình và ường i EulerChu
trình và ường i Euler ▪ Định nghĩa
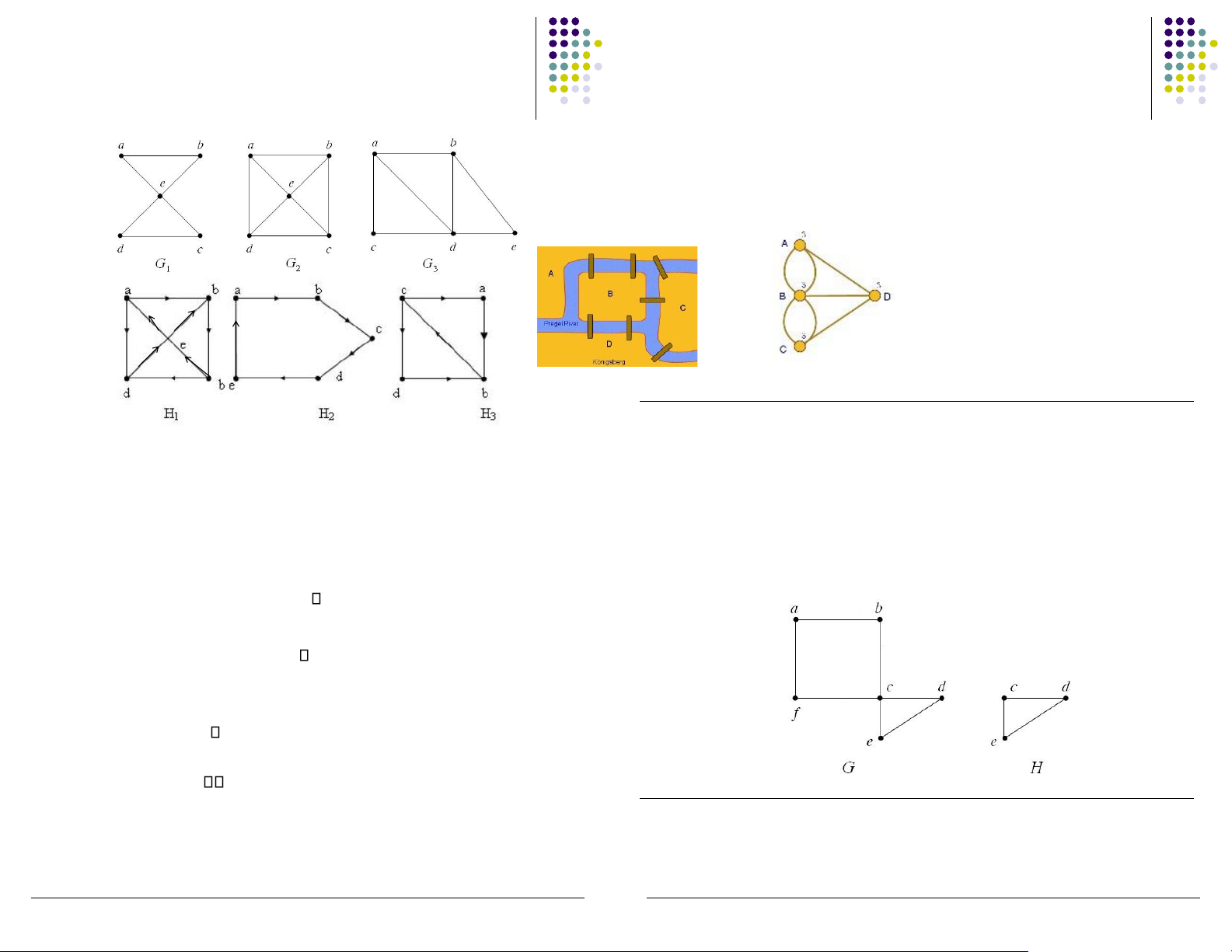
▪ Ví dụ: Chỉ ra ường i và chu trình Euler (nếu có) trong các ▪ Trong ồ thị vô hướng
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
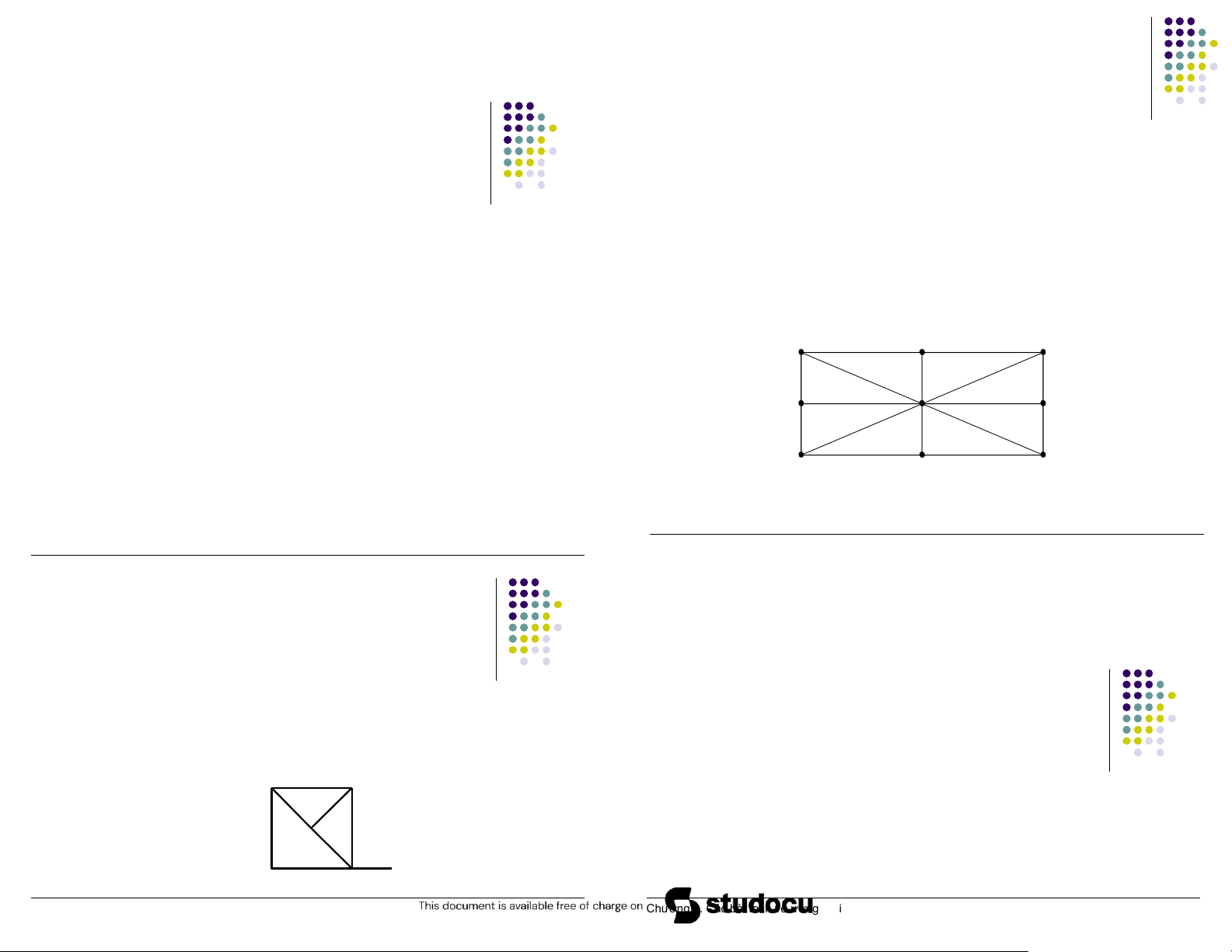
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ồ thị sau ây? ▪
Định lý về chu trình Euler ▪
Một ồ thị liên thông G=(V, E) có chu trình Euler khi và chỉ khi mỗi ỉnh
của nó ều có bậc chẵn. ▪
Áp dụng ịnh lý trên tìm lời giải cho bài toán mở ầu? 7 8
Chương 2. Các bài toán về ường i 9
Chu trình và ường i Euler
Chu trình và ường i Euler
▪ Trong ồ thị vô hướng
▪ Trong ồ thị vô hướng
▪ Các thuật toán tìm chu trình Euler:
▪ Các thuật toán tìm chu trình Euler: 1. Thuật toán Euler 1. Thuật toán Euler
Ký hiệu: C – chu trình Euler cần tìm của ồ thị G.
Ví dụ: Tìm chu trình Euler
Bước 1: Đặt H := G, k :=1, C := . Chọn ỉnh v bất kỳ của G.
Bước 2: Xuất phát từ v, xây dựng chu trình ơn bất kỳ Ck trong H. Nối Ck vào C, C := C Ck .
Bước 3: Loại khỏi H chu trình Ck . Nếu H chứa các ỉnh cô lập thì loại chúng ra khỏi H.
Bước 4: Nếu H = thì kết luận C là chu trình Euler cần tìm, kết thúc. Nếu H
thì chọn v là ỉnh chung của H và C. Đặt k:= k+1, quay lại bước 2.
Chương 2. Các bài toán về ường i 10
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chu trình và ường i Euler 2. Thuật toán Fleury:
Chu trình và ường i Euler Ví dụ: a b c d
Ví dụ: Tìm chu trình Euler i e h g f g abcfdcefghbga
Chương 2. Các bài toán về ường i 13 11
Chu trình và ường i Euler
▪ Trong ồ thị vô hướng
▪ Các thuật toán tìm chu trình Euler:
2. Thuật toán Fleury: Xuất phát từ một ỉnh bất kỳ của ồ thị và tuân theo hai quy tắc sau
Chu trình và ường i Euler
▪ Qui tắc 1: Mỗi khi i qua một cạnh nào thì
▪ Xóa cạnh vừa i qua ▪ Xóa ỉnh cô lập (nếu
▪ Trong ồ thị vô hướng có) ▪ Qui tắc 2:
▪ Định lý về ường i Euler
▪ Tại mỗi ỉnh, ta chỉ i theo một cạnh là cầu nếu
▪ Ví dụ: Đồ thị nào có ường i Euler?
không có sự lựa chọn nào khác.
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) 12
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i lOMoAR cPSD| 40425501
Chu trình và ường i Euler
▪ Trong ồ thị có hướng
▪ Định lý về chu trình Euler
▪ Đồ thị có hướng G=(V, E) có chu trình Euler khi và chỉ khi
▪ G liên thông mạnh
▪ deg+(v) = deg-(v), v V 15
Chu trình và ường i Euler
▪ Trong ồ thị vô hướng
▪ Định lý về ường i Euler 16
▪ Đồ thị liên thông G có ường i Euler, không có chu trình
Chu trình và ường i Euler
Euler khi và chỉ khi G có úng 2 ỉnh bậc lẻ
▪ Trong ồ thị có hướng
▪ Định lý về chu trình Euler
▪ Ví dụ: Đồ thị nào có chu trình Euler?
Chương 2. Các bài toán về ường i 14
Chương 2. Các bài toán về ường i 17
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chu trình và ường i Euler ▪ G liên thông yếu ▪
s V : deg+(s) = deg-(s) + 1 ▪
t V : deg+(t) = deg-(t) - 1
▪ Trong ồ thị có hướng
▪ deg+(v) = deg-(v), v V \ {s, t}
▪ Định lý về ường i Euler
▪ G = (V, E) là ồ thị có hướng
▪ G có ường i Euler nhưng không có chu trình Euler khi
Chương 2. Các bài toán về ường i 18 và chỉ khi
Chu trình & ường i Hamilton
Chu trình và ường i Euler ▪ Chu trình Hamilton
▪ Trong ồ thị có hướng ▪ Định nghĩa
▪ Định lý về ường i Euler ▪ Chu trình Hamilton ▪ ▪ Ví dụ
Chu trình bắt ầu từ một ỉnh v nào ó
qua tất cả các ỉnh còn lại mỗi ỉnh
úng một lần rồi quay trở về v ược gọi là chu trình Hamilton ▪ Đồ thị Hamilton ▪
Đồ thị có chứa chu trình Hamilton 20 19
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i lOMoAR cPSD| 40425501
Chu trình & ường i Hamilton
Chu trình & ường i Hamilton ▪ ▪ Chu trình Hamilton Chu trình Hamilton ▪ Điều kiện ủ ▪ Điều kiện ủ ▪ Định lý Ore (1960) ▪
Hệ quả (Định lý Dirac-1952)
▪ Cho G = (V, E) là một ơn ồ thị liên thông ▪
Cho G = (V, E) là một ơn ồ thị ▪ |V| = n 3 ▪ |V| = n 3
▪ deg(v) + deg(w) n, với mọi cặp ỉnh không liền kề v, w Khi ▪ deg(v) n/2, v V ó G có chu trình Hamilton
Khi ó G có chu trình Hamilton
Chương 2. Các bài toán về ường i 21
Chương 2. Các bài toán về ường i 22 23
Chu trình & ường i Hamilton
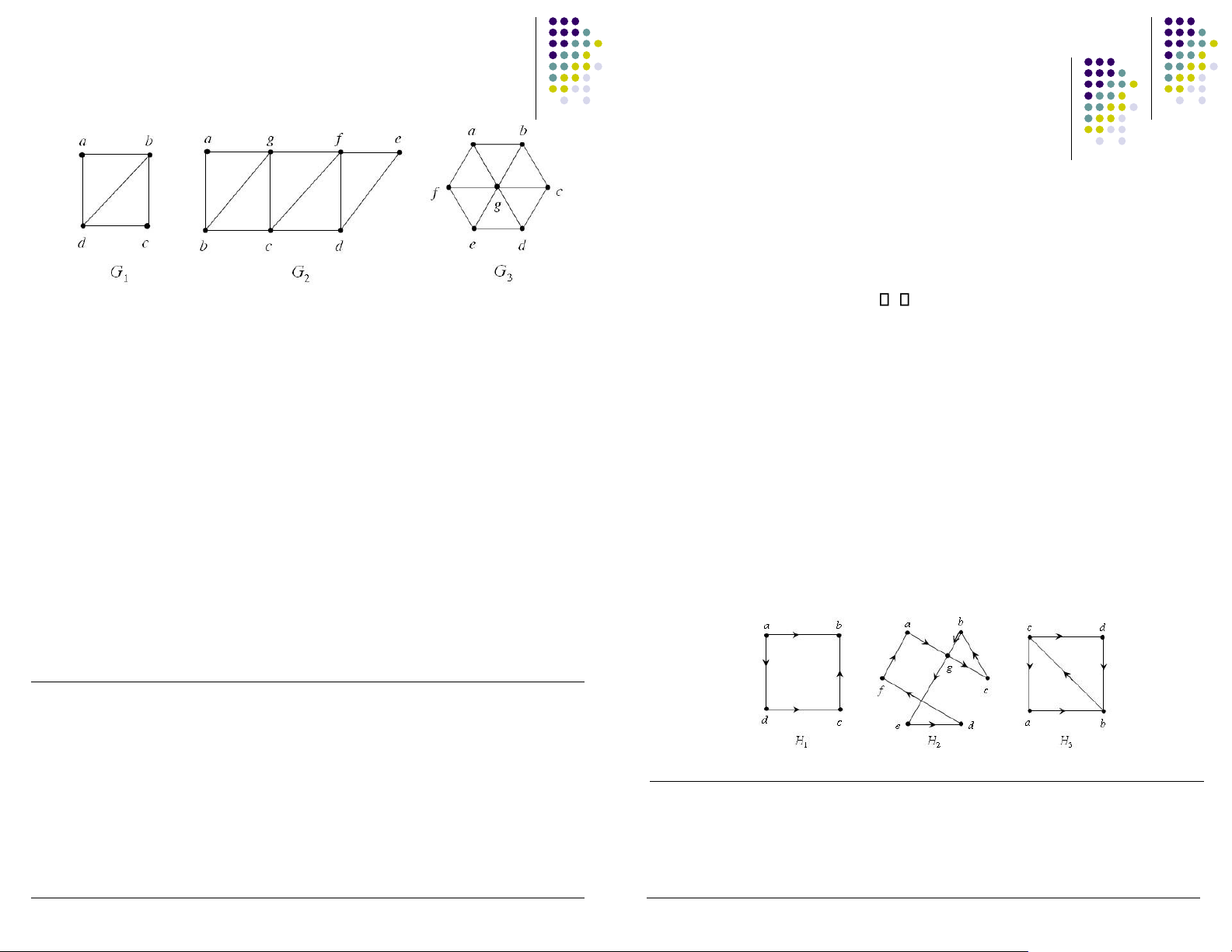
Chu trình & ường i Hamilton ▪ Chu trình Hamilton ▪ Chu trình Hamilton ▪ Điều kiện ủ ▪ Điều kiện ủ ▪ Định lý Pósa ▪ Ví dụ ▪
Cho G = (V, E) là một ơn ồ thị, |V| = n 3 ▪
|{v V: deg(v) k}| k-1 k [1, (n-1)/2) ▪
|{v V: deg(v) (n-1)/2}| (n-1)/2, nếu n lẻ
Khi ó G có chu trình Hamilton
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chu trình & ường i Hamilton
Chu trình & ường i Hamilton ▪ ▪ 24 Chu trình Hamilton Chu trình Hamilton ▪
Phương pháp tìm chu trình Hamilton ▪
Phương pháp tìm chu trình Hamilton ▪
Ví dụ 1: Tìm một chu trình Hamilton ▪
Qui tắc 1: Nếu tồn tại một ỉnh v của G có d(v)<=1 thì ồ thị
G không có chu trình Hamilton. a b c ▪
Qui tắc 2: Nếu ỉnh v có bậc là 2 thì cả 2 cạnh tới v ều phải thuộc chu trình Hamilton. e d f ▪
Qui tắc 3: Chu trình Hamilton không chứa bất kỳ chu trình con thực sự nào. ▪
Qui tắc 4: Trong quá trình xây dựng chu trình Hamilton, sau g
khi ã lấy 2 cạnh tới một ỉnh v ặt vào chu trình Hamilton rồi h i
thì không thể lấy thêm cạnh nào tới v nữa, do ó có thể xóa
mọi cạnh còn lại tới v.
Chương 2. Các bài toán về ường i 26
Chương 2. Các bài toán về ường i 25 d e f
Chu trình & ường i Hamilton 27 ▪ Chu trình Hamilton ▪
Phương pháp tìm chu trình Hamilton ▪ Ví dụ 2:
Chu trình & ường i Hamilton Đồ thị sau có chu trình Hamilton ▪ Chu trình Hamilton không? a b c ▪
Phương pháp tìm chu trình Hamilton ▪
Ví dụ 3: Đồ thị sau có chu trình Hamilton không?
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chu trình & ường i Hamilton
Chu trình & ường i Hamilton ▪ ▪ A u5u7 u B D C v v v v v v E 1 3 5 6 2 4 Không có ường i F H G Hamilton
Chương 2. Các bài toán về ường i 29 I J K Đường i Hamilton 28 ▪ Định lý König Đường i Hamilton ▪
Mọi ồ thị có hướng ầy ủ ( ồ thị vô hướng tương ứng là ▪
ầy ủ) ều có ường i Hamilton. Chứng minh (xem tài liệu) Định nghĩa ▪
Đường i sơ cấp i qua tất cả các ỉnh của ồ thị G ( i qua
mỗi ỉnh úng một lần). Ví dụ: 6 v 5 v 6
Chương 2. Các bài toán về ường i 30
Bài toán ường i ngắn nhất ▪ Mở ầu
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chu trình & ường i Hamilton
Chu trình & ường i Hamilton ▪ ▪
▪ Nhiều bài toán không chỉ quan tâm tồn tại hay =
không ường i giữa 2 ỉnh w p( ) w v v( i, i+1) ▪ i=1
Lựa chọn ường i với chi phí ít nhất Khoaíng caïch (dàûm) Boston Khoảng cách (dặm)
▪ Đường i ngắn nhất là ường i có trọng số nhỏ nhất 2534 860 Chicago 191 1855 908 957 722 New York San Francisco 32 834 760 349 2451 1090 Atlanta Los Angeles 595 Miam i 31
Bài toán ường i ngắn nhất ▪ Mở ầu
▪ Mô hình hóa bài toán về ồ thị có trọng số
▪ Đồ thị có hướng G = (V,E) với hàm trọng số W: E → R
(gán các giá trị thực cho các cạnh)
▪ Trọng số của ường i p = v1 → v2 → … → vk là k−1
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chương 2. Các bài toán về ường i 33
Bài toán ường i ngắn nhất ▪ Mở ầu
▪ Ví dụ: Đường i ngắn nhất giữa ỉnh 1 và 4:
Chương 2. Các bài toán về ường i 34
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Bài toán ường i ngắn nhất ▪ Thuật toán Dijkstra ▪ Ký hiệu:
▪ Nhãn của ỉnh v: L(v)
▪ Lưu trữ ộ dài ường i ngắn nhất từ a ến v ược biết cho ến thời iểm hiện tại
▪ Tập S: tập các ỉnh mà ường i ngắn nhất từ a ến chúng ã xác ịnh
Bài toán ường i ngắn nhất 36 ▪ Thuật toán Dijkstra
Bài toán ường i ngắn nhất ▪ Ý tưởng
▪ Ở mỗi lần lặp thì thuật toán sẽ tìm ra 1 ỉnh với ường i ▪ Thuật toán Dijkstra
ngắn nhất từ a tới ỉnh này là xác ịnh
▪ Thuật toán (Tìm ường i ngắn nhất từ a ến z) ▪ Bước 1: Khởi tạo
▪ L(a) = 0; L(v)=vo cung lon, S =
▪ Bước 2: Nếu z S thì kết thúc ▪ Bước 3: Chọn ỉnh ▪ Chọn u sao cho: L(u) = min { L(v) | v S}
▪ Đưa u vào tập S: S = S {u} ▪ Bước 4: Sửa nhãn
▪ Với mỗi ỉnh v (v S) kề với u 35
▪ L(v) = min { L(v); L(u) + w(uv) } (ký hiệu w(uv)=trọng số cạnh uv)
▪ Bước 5: Quay lại Bước 2
Chương 2. Các bài toán về ường i 37
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
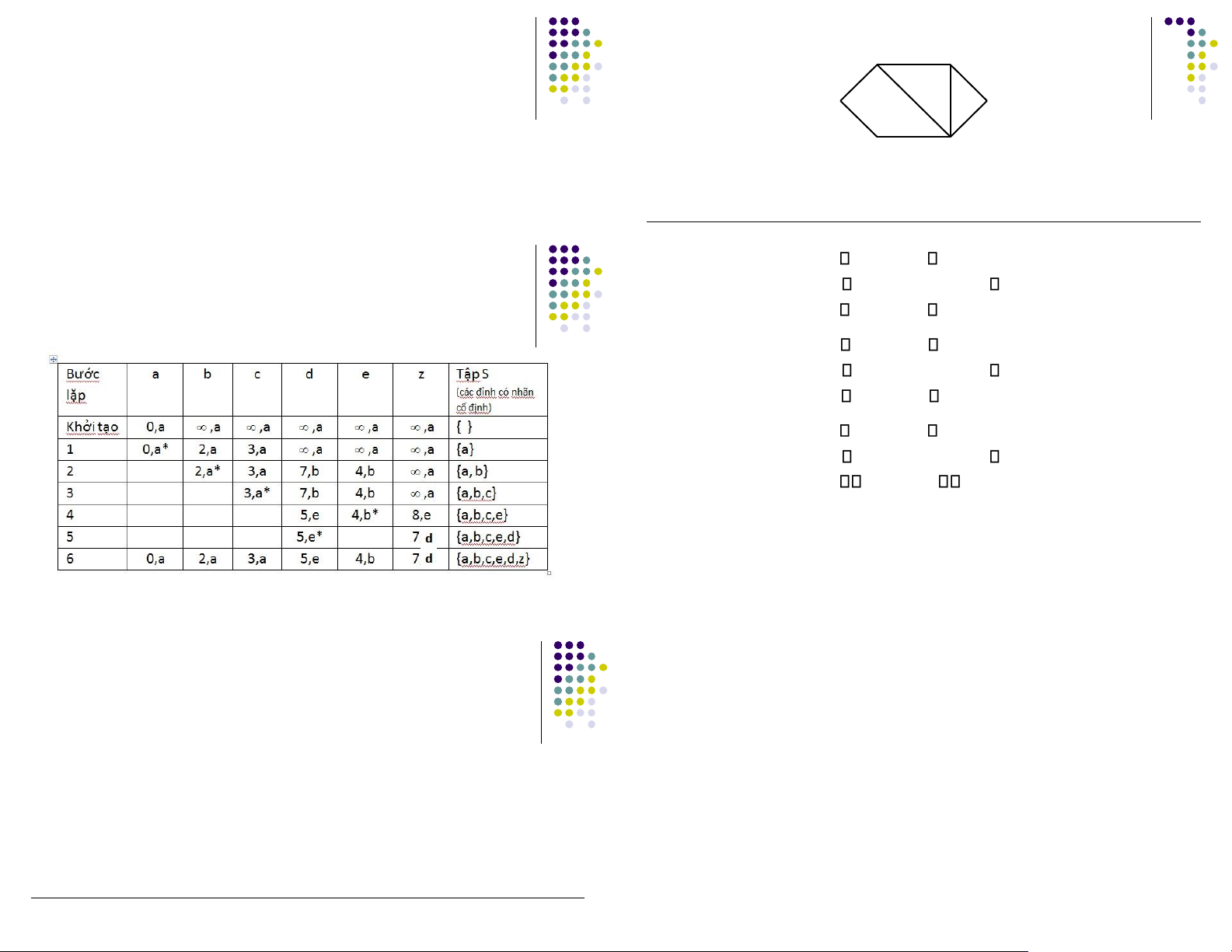
Bài toán ường i ngắn nhất 2 2 1 2 4 3 ▪ a z Thuật toán Dijkstra c 5 e ▪ Ví dụ
Đáp án: ường i ngắn nhất: abedz, ộ dài 7.
▪ Tìm ộ dài ường i ngắn nhất giữa ỉnh a và z? b 5 d
Chương 2. Các bài toán về ường i 38 A 0 7 2 0 0 0 B 7 0 3 2 1 0
Bài giải: Thuật toán Dijkstra cho bài toán ược trình bày trong bảng sau C 2 3 0 0 3 0 D 0 2 0 0 9 3 E 0 1 3 9 0 8 F 0 0 0 3 8 0 a) Vẽ ồ thị G
Dùng thuật toán Dijkstra:
b) Tìm ộ dài ường i ngắn nhất từ ỉnh a ến các
Đáp số: ường i ngắn nhất: abedz, ộ dài 7.
ỉnh còn lại của G? Chỉ ra các
Nếu hỏi ộ dài ngắn nhất i từ a ến d thì áp số là……?? Và ường ó là………. ường i ó. 39 40 Ví dụ
Cho ma trận kề của ơn ồ thị có trọng số G có dạng A B C D E F
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Chương 2. Các bài toán về ường i 41
Chương 2. Các bài toán về ường i 42
Bài toán ường i ngắn nhất
▪ Thuật toán tìm ường i ngắn nhất ▪ Thuật toán Dijkstra ▪ Định lý
Chương 2. Các bài toán về ường i
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
▪ Thuật toán Dijkstra tìm ược ường i ngắn nhất giữa 2
ỉnh trong ơn ồ thị liên thông, có trọng số. ▪ Nhận xét
▪ Chỉ úng cho ồ thị có trọng số không âm
▪ Nhãn sau cùng của mỗi ỉnh là ộ dài ường i ngắn nhất
từ ỉnh xuất phát ến nó. 43 44
Chương 2. Các bài toán về ường i
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 45 46
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 CHƯƠNG 6: CÂY
- Một số khái niệm cơ bản
- Cây m – phân và các tính chất
- Phép duyệt cây nhị phân
- Ký pháp nghịch ảo Ba Lan
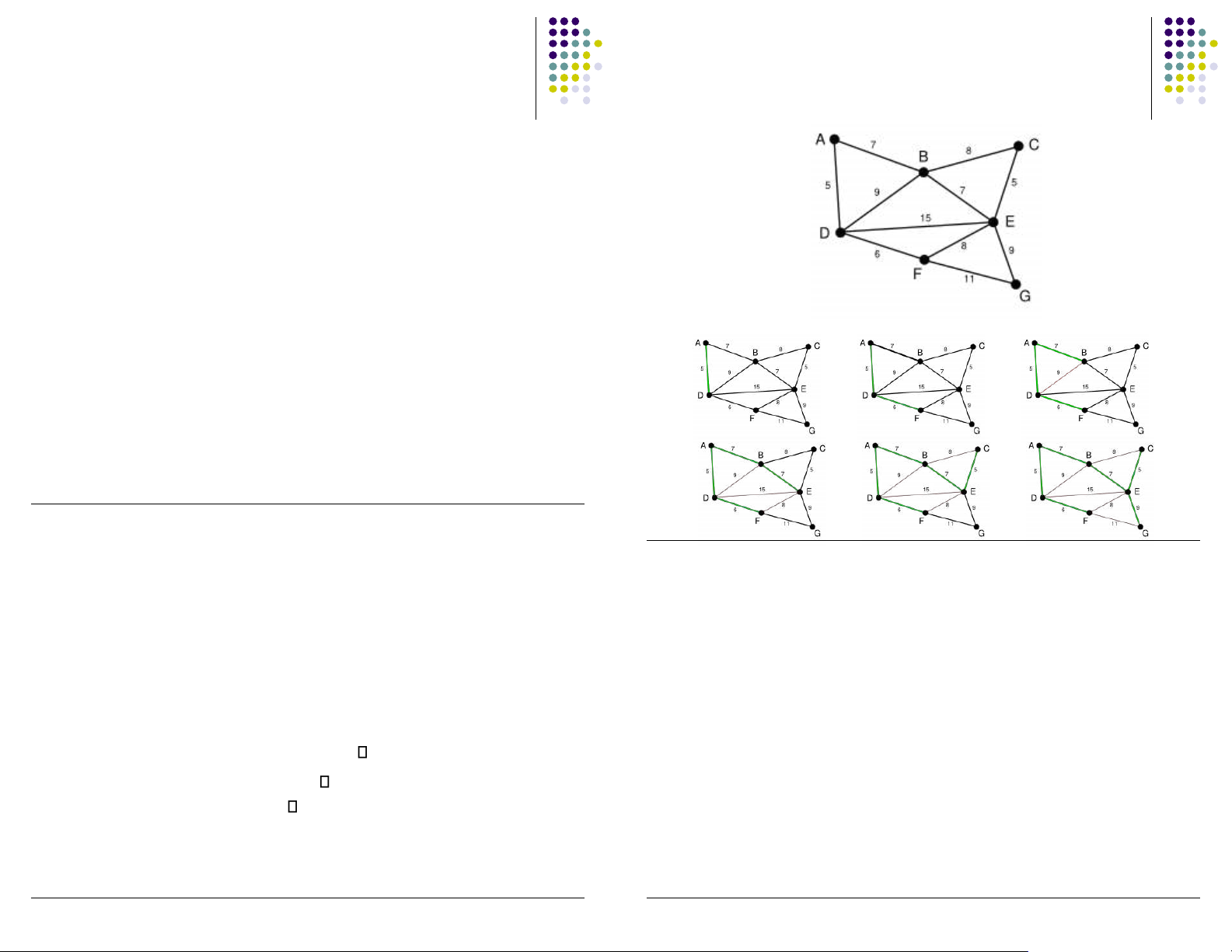
- Thuật toán Prim và Kruskal tìm cây khung
nhỏ nhất trong ồ thị liên thông có trọng số 47 1
Một số khái niệm cơ bản ▪ Cây ▪ Định nghĩa: Chương 2. Cây 2
▪ Cây là một ồ thị vô hướng, liên thông và không có chu
Một số khái niệm cơ bản trình s cấp
▪ Cây không có cạnh bội và khuyên ▪ Rừng
▪ Cây là một ơn ồ thị ▪ Định nghĩa: ▪ Ví dụ
▪ Rừng là một ồ thị vô hướng và không có chu trình
▪ Rừng có thể có nhiều thành phần liên thông
▪ Mỗi thành phần liên thông là một cây Chương 2. Cây Chương 2. Cây
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ▪ Ví dụ G Chương 2. Cây 3
Một số khái niệm cơ bản
Một số khái niệm cơ bản
▪ Định lý (Điều kiện ủ của cây) ▪ Cây có gốc
▪ Nếu mọi cặp ỉnh của một ồ thị vô hướng G luôn ▪ Định nghĩa
tồn tại một ường i sơ cấp duy nhất thì G là một
▪ Một cây với một ỉnh ược chọn làm gốc cây.
▪ Định hướng các cạnh trên cây từ gốc i ra
(Chứng minh SV tham khảo tài liệu) ▪ Ví dụ a f f h g h 4
▪ Cùng một cây, nếu chọn gốc khác nhau thì cây có gốc thu ược sẽ khác nhau 5
Một số khái niệm cơ bản ▪ Cây có gốc Chương 2. Cây Chương 2. Câ y
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Một số khái niệm cơ bản ▪ Một số khái niệm ▪ Định lý Daisy Chain ▪ Cha ▪ Lá
T là ồ thị có n ỉnh. Các mệnh ề tư ng ư ng: ▪ Anh em ▪ Đỉnh trong 1. T là một cây ▪ Tổ tiên ▪ Cây con
2. T không có chu trình và có n-1 cạnh ▪ Mức
3. T liên thông, mọi cạnh ều là cầu ▪ Chiều cao
4. Giữa hai ỉnh bất kỳ của T luôn tồn tại một ường i sơ cấp duy nhất
5. T không có chu trình và nếu thêm một cạnh mới nối
2 ỉnh bất kỳ của T thì sẽ tao ra một chu trình
6. T liên thông và có n-1 cạnh ▪ Con cháu Chương 2. Cây 6 Chương 2. Cây 7 8
Một số khái niệm cơ bản
Một số khái niệm cơ bản ▪ Cây m-phân
▪ Cây m-phân ▪ Ví dụ ▪ Định nghĩa ▪ Cây m-phân ▪ Cây có gốc ▪
Tất cả các ỉnh trong có không quá m con ▪ Cây m-phân ầy ủ T1 T2 T3 ▪ Cây có gốc
▪ T1: Cây nhị phân ầy ủ ▪
Tất cả các ỉnh trong có úng m con ▪ ▪ T m=2: Cây nhị phân 2: Cây tam phân ầy ủ
▪ T3: Cây tứ phân (không ầy ủ) Chương 2. Cây Chương 2. Cây
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 9
Một số tính chất của cây
Phép duyệt cây nhị phân ▪ Tính chất 1: ▪ Định nghĩa ▪
Cây n ỉnh (n 2) có ít nhất 2 ỉnh treo ▪ Duyệt cây ▪ ▪ Tính chất 2:
Liệt kê tất cả các ỉnh của cây theo một thứ tự xác ▪ ịnh, mỗi ỉnh một lần
Cây m-phân ầy ủ với i ỉnh trong có n = m.i + 1 ỉnh ▪ ▪ 3 phương pháp duyệt cây
Tính chất 3: Cho cây m-phân ầy ủ có n ỉnh, có i ỉnh
trong và l lá. Khi ó: ▪
Duyệt tiền tự (Pre-Oder) ▪ ▪ Duyệt trung tự (In-Oder)
i = (n -1)/m ▪ ▪
Duyệt hậu tự (Post-Oder)
l = [(m - 1)n + 1] / m
Cả 3 phương pháp duyệt trên ều ược ịnh nghĩa ệ quy ối ▪
l = (m - 1)i + 1
với cây nhị phân (mỗi nút có tối a 2 con lần lượt ược gọi ▪
n = l + i
là con trái và con phải của nút) Chương 2. Cây 10 Chương 2. Cây 11 12
Phép duyệt cây nhị phân
Phép duyệt cây nhị phân ▪ Định nghĩa ▪ Định nghĩa ▪ Duyệt tiền tự ▪ Duyệt trung tự 1. Duyệt nút gốc
1. Duyệt trung tự con trái
2. Duyệt tiền tự con trái 2. Duyệt nút gốc 1 2 2 3
3. Duyệt tiền tự con phải 1 3
3. Duyệt trung tự con phải Chương 2. Cây Chương 2. Câ y
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 13
Phép duyệt cây nhị phân
Phép duyệt cây nhị phân ▪ Định nghĩa ▪ Định nghĩa ▪ ▪ Duyệt hậu tự Ví dụ A ▪ Duyệt tiền tự
1. Duyệt hậu tự con trái ▪ A B D E C F B C
2. Duyệt hậu tự con phải ▪ Duyệt trung tự 3 ▪ D B E A C FF E D ▪ Duyệt hậu tự ▪ D E B F C A 1 2 3. Duyệt nút gốc Chương 2. Cây 15 Chương 2. Cây 14 16
Ký pháp nghịch ảo Ba Lan
Ký pháp nghịch ảo Ba Lan
▪ Cây biểu thức số học
▪ Cây biểu thức số học ▪ Là cây nhị phân ▪ Ví dụ: ▪
Mỗi nút trong biểu diễn cho một toán tử 2 ngôi
E = (2 + 3)^2 – (4 – 1)*(15/5) ▪
Mỗi nút lá biểu diễn cho một toán hạng của biểu thức
Nếu nút trong biểu diễn cho toán tử 2 ngôi và có 2 con: ▪
Con trái biểu diễn cho biểu thức E1 ▪
Con phải biểu diễn cho biểu thức E2 khi ó
nút trong này biểu diễn cho biểu thức E1 E2 Chương 2. Cây Chương 2. Cây
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 17
Ký pháp nghịch ảo Ba Lan
▪ Cây biểu thức số học ▪ Duyệt cây biểu thức ▪
Biểu thức tiền tố (duyệt tiền tự) - ^ + 2 3 2 * - 4 1 / 15 5 ▪
Biểu thức trung tố (duyệt trung tố) 2 + 3 ^ 2 - 4 - 1 * 15 / 5
Ký pháp nghịch ảo Ba Lan
▪ Cây biểu thức số học ▪
Ký pháp nghịch ảo Ba Lan
(Reverse Polish Notation – RPN) ▪
Biểu thức ở dạng hậu tố Chương 2. Cây Chương 2. Câ y
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ▪
Sử dụng ể tính giá trị biểu thức trên máy tính ▪
Biểu thức hậu tố (duyệt hậu tố)
▪ Tính từ trái qua phải
▪ Không sử dụng dấu ngoặc
▪ Sử dụng Stack (ngăn xếp) Chương 2. Cây 18 Chương 2. Cây 19 2 3 + 2 ^ 4 1 - 15 5 / * -
Ký pháp nghịch ảo Ba Lan
Ký pháp nghịch ảo Ba Lan ▪
Cây biểu thức số học ▪ Cây biểu thức số học ▪
Ký pháp nghịch ảo Ba Lan
▪ Ký pháp nghịch ảo Ba Lan
(Reverse Polish Notation – RPN)
(Reverse Polish Notation – RPN) ▪
Thuật toán tính giá trị biểu thức RPN Ví dụ: Tính giá trị biểu thức E = (2 + 3)^2 – (4 1)*(15/5) ▪
Đọc một ký hiệu (token)
- Biểu thức nhập dưới dạng ký pháp RPN ▪
Nếu ký hiệu là một số - E = 2 3 + 2 ^ 4 1 - 15 5 / * ▪ Đẩy vào Stack - Quá trình lưu trữ của cấu trúc Stack như sau: ▪
Ngược lại, ký hiệu là một toán tử ▪
Lấy ra 2 toán hạng từ Stack ▪
Tính giá trị theo toán tử ối với 2 toán hạng ▪ Đẩy kết quả vào Stack 20 21 Chương 2. Cây Chương 2. Cây
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Ký pháp nghịch ảo Ba Lan
Cây khung (Spanning Tree)
Ví dụ: E = 2 3 + 2 ^ 4 1 - 15 5 / * -
- Quá trình lưu trữ của cấu trúc Stack như sau: ▪ Định nghĩa
▪ Cây khung của ơn ồ thị G ▪ Đồ thị con của G
▪ Chứa tất cả các ỉnh của G
▪ Một ồ thị có thể có nhiều cây khung ▪ Ví dụ Chương 2. Cây 23 Chương 2. Cây 22 24
Cây khung (Spanning Tree)
Cây khung (Spanning Tree) ▪ Định lý
▪ Cây khung nhỏ nhất
▪ Một ơn ồ thị là liên thông khi và chỉ khi nó có cây khung ▪ Định nghĩa
(Chứng minh xem tài liệu) ▪
Cây khung nhỏ nhất trong một ồ thị liên thông,
có trọng số là một cây khung có tổng trọng số
trên các cạnh của nó là nhỏ nhất. Chương 2. Cây Chương 2. Câ y
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 25
Cây khung (Spanning Tree) ▪ Cây khung nhỏ nhất ▪ Thuật toán Prim
▪ Bắt ầu bằng việc chọn một ỉnh bất kỳ, ặt nó vào cây khung T.
▪ Trong khi cây khung T có ít hơn n ỉnh
▪ Ghép vào T cạnh có trọng số nhỏ nhất liên thuộc với một ỉnh của T
và không tạo ra chu trình trong T.
Chú ý: - Thuật toán dừng lại khi Tcó ủ n ỉnh hay (n-1) cạnh.
- Có nhiều hơn một cây khung nhỏ nhất ứng với một ồ thị liên thông có trọng số. Chương 2. Cây 26 Chương 2. Cây 27
Cây khung (Spanning Tree) ▪ Cây khung nhỏ nhất ▪ Thuật toán Prim ▪ Bước 1: Khởi tạo ▪
VT = {s}; ET = ; (VT – tập ỉnh; ET – tập cạnh) ▪
ds = 0; v VT dv = w(s, v), nếu s và v liền kề ▪
dv = , nếu s và v không liền kề ▪ Bước 2: Tìm cạnh Chương 2. Cây Chương 2. Cây
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ▪
Tìm u mà du = min {dv | v VT} ▪ VT = VT {u}; ▪
ET = ET {e} , e – cạnh nối u với một ỉnh của cây có trọng số du ▪ Nếu VT V thì dừng. ▪ Bước 3: Cập nhật nhãn ▪
dv = min {dv, w(u, v)} với v VT
Cây khung (Spanning Tree) ▪ Cây khung nhỏ nhất ▪ Thuật toán Kruskal
▪ Bắt ầu bằng việc chọn một cạnh có trọng số
nhỏ nhất, ặt nó vào cây khung T.
▪ Trong khi cây khung T có ít hơn (n-1) cạnh
▪ Ghép vào T cạnh có trọng số nhỏ nhất và không tạo 28 29 ra chu trình trong T. Chương 2. Cây 30 Chương 2. Cây Chương 2. Câ y
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 Chương 2. Cây 31 Chương 2. Cây Chương 2. Cây
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Cây khung (Spanning Tree) ▪ Cây khung nhỏ nhất
▪ Ví dụ: Tìm cây khung nhỏ nhất của ồ thị sau: ▪ 5 Dùng thuật toán Prim: a b 2 4 f c 3 6 e 1 d 4
Vậy cây khung nhỏ nhất với tập cạnh 5 a b 2 f c 3 1
có ộ dài (trọng số): 2+5+3+4+1=15 e d 4 33
Cây khung (Spanning Tree) ▪ Cây khung nhỏ nhất ▪ Thuật toán Kruskal ▪ Bước 1:
▪ Sắp xếp các cạnh của ồ thị G theo thứ tự có trọng số
không giảm: w(e1) w(e2) … w(em) ▪ ET = {e1} , i =1
▪ Bước 2: Tìm k = min { j | ET {ej} không có chu trình}
ET = ET {ek} ▪ Bước 3: i = i +1 Chương 2. Cây Chương 2. Câ y
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501 ▪ Nếu i = n-1 thì dừng
▪ Nếu i < n-1 thì quay lại bước 2 32
ây khung (Spanning Tree)
ây khung (Spanning Tree) ▪ Cây khung nhỏ nhất ▪ Cây khung nhỏ nhất
▪ Ví dụ: Tìm cây khung nhỏ nhất của ồ thị sau:
▪ Ví dụ: Tìm cây khung nhỏ nhất của ồ thị sau: 2a▪ 5 b 4 Sắp xếp các 2a▪ 5 b 4 Sắp xếp các
cạnh của ồ thị theo thứ Dùng thuật toán Kruskal:
cạnh của ồ thị theo thứ Dùng thuật toán Kruskal: f f
3 c tự có trọng số không giảm:
3 c tự có trọng số không giảm: 6 e 1 6 1 d e d 4 4
Vậy cây khung nhỏ nhất với tập cạnh
Vậy cây khung nhỏ nhất với tập cạnh
có ộ dài (trọng số): 1+2+3+4+5 =15
có ộ dài (trọng số): 1+2+3+4+5 =15 Chương 2. Cây 34 Chương 2. Cây 35
▪ Kruskal chọn cạnh có trọng số nhỏ nhất miễn là không tạo ra chu trình
▪ Thuật toán Prim hiệu quả hơn ối với các ồ thị dày
Cây khung (Spanning Tree) (số cạnh nhiều) ▪ Cây khung nhỏ nhất ▪ So sánh Prim và Kruskal ▪ 36
Prim chọn cạnh có trọng số nhỏ nhất liên thuộc với một
ỉnh ã thuộc cây và không tạo ra chu trình Chương 2. Cây Chương 2. Cây
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Cây khung (Spanning Tree)
▪ Một số bài toán ứng dụng ▪ Nối dây iện
▪ Trong một mặt phẳng toạ ộ cho N + 1 iểm, iểm ầu tiên
chính là gốc tọa ộ ược coi là nguồn iện duy nhất mà từ
ó ta nối dây cấp iện cho các nơi khác. Điểm thứ i trong
N iểm còn lại có toạ ộ là (Xi, Yi), là iểm ặt máy thứ i.
Mỗi iểm ặt máy có thể lấy trực tiếp từ nơi cấp iện ban
ầu hay gián tiếp qua một iểm ặt máy khác.
▪ Yêu cầu ưa ra phương án nối iện giữa các iểm ể mọi
nơi ặt máy ều có iện và tổng chiều dài dây cần thiết là ngắn nhất. 37 Chương 2. Cây Chương 2. Câ y
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Cây khung (Spanning Tree) Chương 2. Cây 39
▪ Một số bài toán ứng dụng
▪ Theo thiết kế, một mạng giao thông gồm N nút. Biết trước
chi phí ể xây dựng ường hai chiều trực tiếp từ nút i ến nút j.
Hai tuyến ường khác nhau không cắt nhau tại iểm không là
ầu mút. Hiện ã xây dựng ược K tuyến ường.
▪ Bài toán : Hệ thống ường ã xây dựng ã bảo ảm sự i lại
giữa hai nút bất kỳ chưa? Nếu chưa, hãy chọn một số
tuyến ường cần xây dựng thêm sao cho:
▪ Các tuyến ường sẽ xây dựng thêm cùng với các ường ã xây
dựng bảo ảm sự i lại giữa hai nút bất kỳ.
▪ Tổng kinh phí xây dựng các tuyến ường thêm vào là ít nhất. Chương 2. Cây 38
Cây khung (Spanning Tree)
▪ Cây khung lớn nhất ▪ Định nghĩa
▪ Cây khung lớn nhất trong một ồ thị liên thông,
có trọng số là một cây khung có tổng trọng số
trên các cạnh của nó là lớn nhất.
Tương tự trình bày thuật toán Prim và Kruskal ể tìm
cây khung lớn nhất trong ồ thị liên thông có trọng số !!!
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)







