Lý thuyết Chương 3: Hệ phương trình - Phương pháp Gauss-Seidel môn Phương pháp tính | Trường Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG CHƯƠNG 3 HỆ PHƯƠNG TRÌNH
PHƯƠNG PHÁP GAUSS-SEIDEL PHẦN 1. LÝ THUYẾT
Điều kiện: A là ma trận chéo trội nghiêm ngoặt Nội dung:
Phân tích 𝐴 = 𝐷 − 𝐿 − 𝑈 → 𝐴𝑋 = 𝐵 → 𝑋(𝑚) = 𝑇. 𝑋(𝑚−1) + 𝐶
Với 𝑇 = (𝐷 − 𝐿)−1𝑈, 𝐶 = (𝐷 − 𝐿)−1𝐵
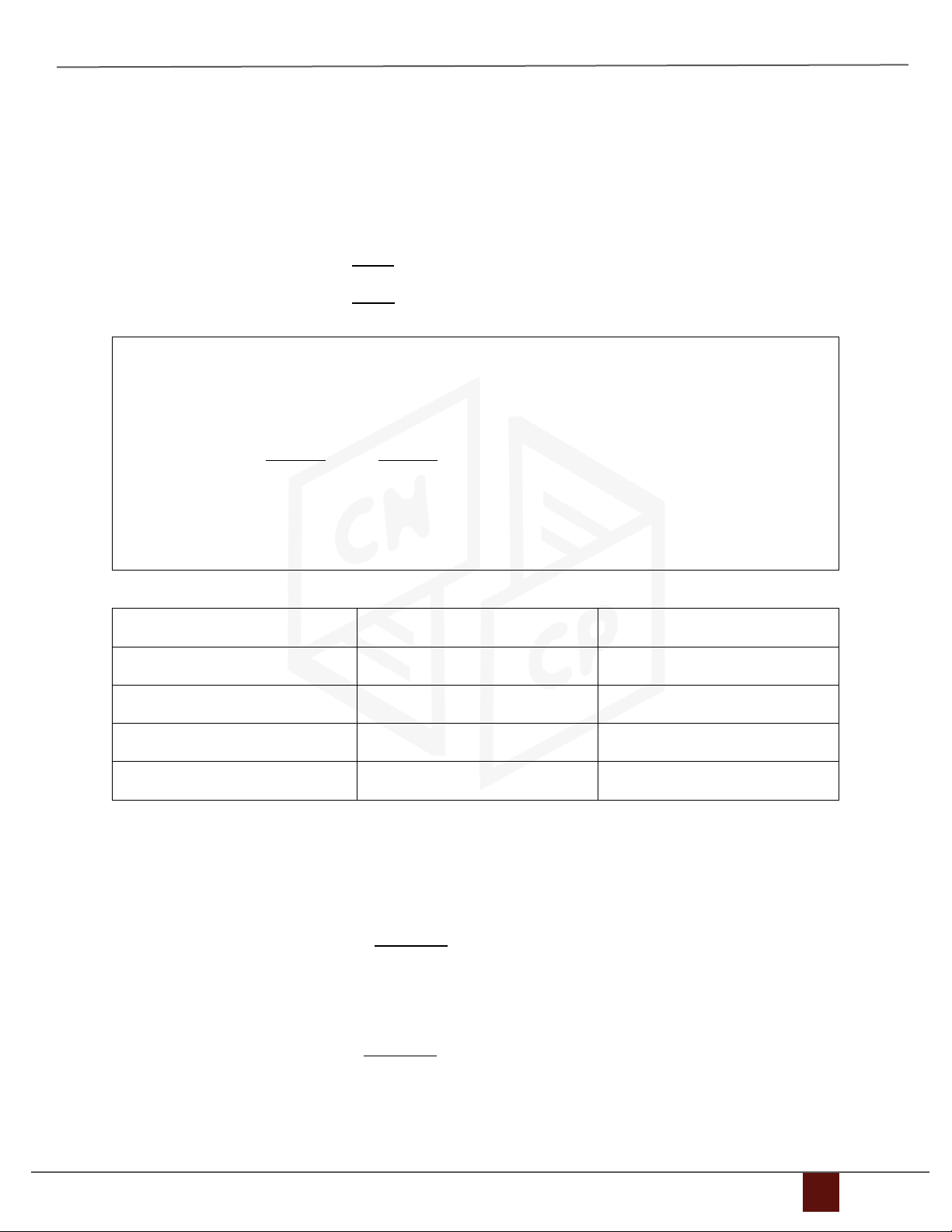
6.1 Dạng hệ phương trình 2 ẩn 16𝑥 Cho hệ phương trình {
1 − 5𝑥2 = 6 . Với 𝑥(0) = [0,7 0,8]𝑇. −5𝑥1 + 14𝑥2 = 6
Giải các bài toán sau bằng phương pháp gauss seidel
a/ Xác định ma trận D, L, U, T, C
b/ Tìm nghiệm gần đúng 𝑥(3)
c/ Tìm sai số nghiệm gần đúng 𝑥(3) tiên nghiệm và chuẩn 1
d/ Tìm sai số nghiệm gần đúng 𝑥(3) tiên nghiệm và chuẩn hàng
e/ Tìm sai số nghiệm gần đúng 𝑥(3) hậu nghiệm và chuẩn 1
f/ Tìm sai số nghiệm gần đúng 𝑥(3) hậu nghiệm và chuẩn hàng
g/ Theo công thức tiên nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3
h/ Theo công thức hậu nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3
k/ Theo công thức hậu nghiệm và chuẩn vô cùng, số bước lập cần thiết để sai số nhỏ hơn 10−3 Giải
(kết hợp với video bài giảng mới hiểu nha)
a/ Xác định ma trận D, L, U, T, C 16 −5 16 0 0 0 0 5 𝐴 = [ ] , 𝐷 = [ ] , 𝐿 = [ ] , 𝑈 = [ ] −5 14 0 14 5 0 0 0
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 1 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG 16 0 −1 0 5 0 5/16
𝑇 = (𝐷 − 𝐿)−1𝑈 = [ ] [ ] = [ ] −5 14 0 0 0 25/224 16 0 −1 6 3/8
𝐶 = (𝐷 − 𝐿)−1𝐵 = [ ] [ ] = [ ] −5 14 6 9/16
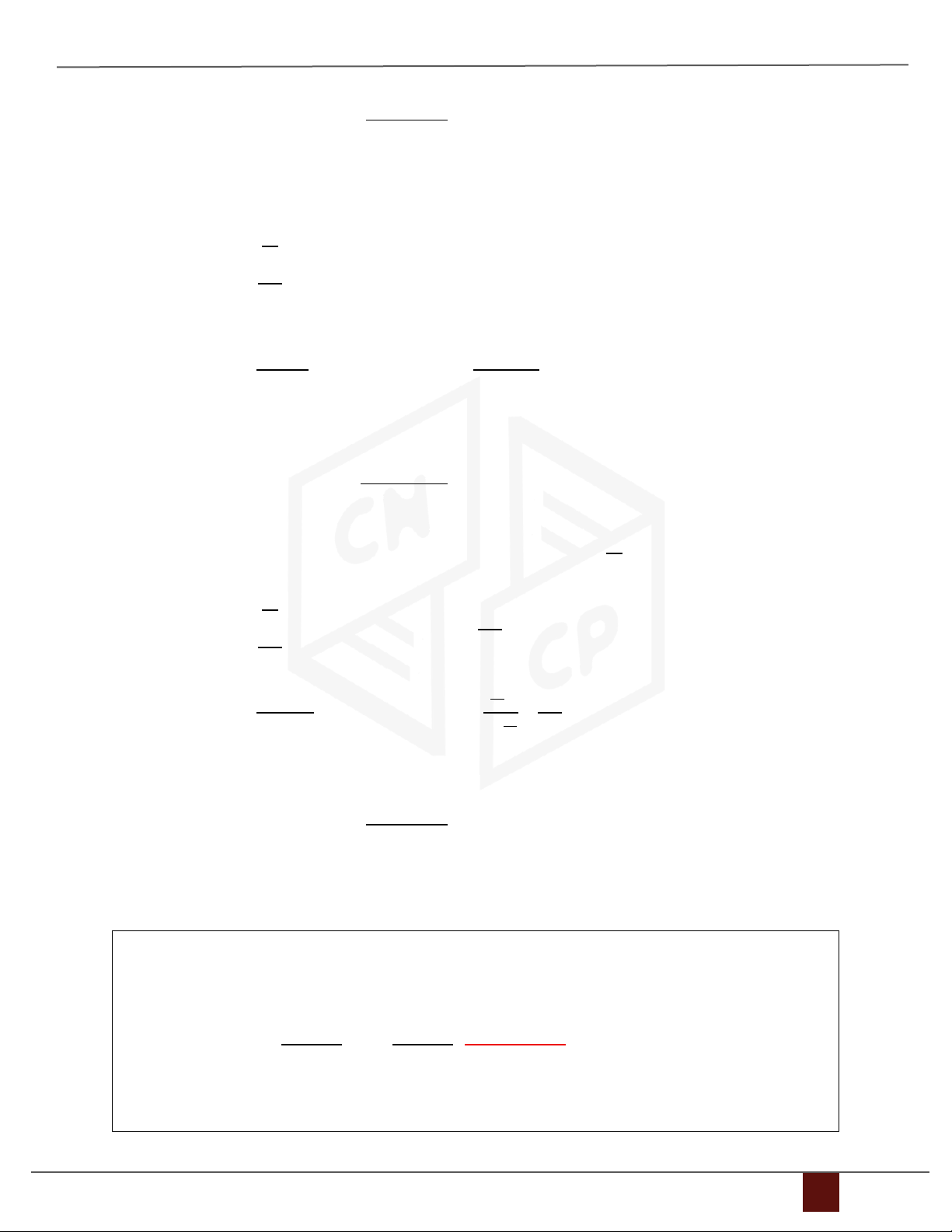
b/ Tìm nghiệm gần đúng 𝑥(3) 6+5𝑥2 16𝑥 𝑥1 = { 1 − 5𝑥2 = 6 → { 16 −5𝑥 6+5𝑥 1 + 14𝑥2 = 6 𝑥 1 2 = 14 𝑥 Đặt { 1 = 𝐴 𝑥2 = 𝐵 Bấm máy: 6 + 5𝐵 6 + 5𝐴 𝑀 = 𝑀 + 1: 𝐴 = : 𝐵 = 16 14 Nhấn CALC B=0,8 ;A=0,7 Kết quả n 𝑥 1 𝑥2 0 0,7 0,8 1 5/8 73/112 2 1037/1792 0,6352 3 0.5735 0,6334 Đánh giá sai số Công thức tiên nghiệm 𝑛 ||𝑇|| . ||𝑋(1) − 𝑋(0)|| 1 − ||𝑇|| Công thức hậu nghiệm ||𝑇||
. ||𝑋(𝑛) − 𝑋(𝑛−1)|| 1 − ||𝑇||
c/ Tìm sai số nghiệm gần đúng 𝑥(3) tiên nghiệm và chuẩn 1
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 2 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG 3
||𝑇||1 .||𝑋(1) − 𝑋(0)|| 1 − ||𝑇|| 1 1 0 5/16 Với 𝑇 = [
] → ||𝑇|| = 𝑀𝑎𝑥(0; 95/224) = 95/224 0 25/224 1 3 − 𝑋(1) − 𝑋(0) = [
40 ] → ||𝑋(1) − 𝑋(0)|| = 25/112 (nên dùng chức năng STO để lưu 83 − 1 560 giá trị) 3 ||𝑇|| Sai số cần tìm là: 1 (95/224)3 . ||𝑋(1) − 𝑋(0)|| = ∗ 25/112 (làm tròn lên) 1−||𝑇|| 1−95/224 1 1
d/Tìm sai số nghiệm gần đúng 𝑥(3) tiên nghiệm và chuẩn hàng 3
||𝑇||∞ .||𝑋(1) − 𝑋(0)|| 1 − ||𝑇|| ∞ ∞ 0 5/16 Với 5 𝑇 = [
] → ||𝑇|| = 𝑀𝑎𝑥(5/16; 25/224) = 0 25/224 ∞ 16 3 − 83 𝑋(1) − 𝑋(0) = [
40 ] → ||𝑋(1) − 𝑋(0)|| =
(nên dùng chức năng STO để lưu giá trị) 83 − ∞ 560 560 3 5 3 ||𝑇|| ( ) Sai số cần tìm là: ∞ 83
. ||𝑋(1) − 𝑋(0)|| = 16 ∗ (làm tròn lên) 1−||𝑇|| 5 1− 560 ∞ ∞ 16
e/Tìm sai số nghiệm gần đúng 𝑥(3) hậu và chuẩn 1
||𝑇||1 .||𝑋(3) − 𝑋(2)|| 1 − ||𝑇|| 1 1 0 5/16 Với 𝑇 = [
] → ||𝑇|| = 𝑀𝑎𝑥(0; 95/224) = 95/224 0 25/224 1 Bấm máy: 𝑥
{ 1 = 𝑋(𝑔𝑖á 𝑡𝑟ị ℎ𝑖ệ𝑛 𝑡ạ𝑖) = 𝐴(𝑔𝑖á 𝑡𝑟ị 𝑡𝑟ướ𝑐 đó)
𝑥2 = 𝑌(𝑔𝑖á 𝑡𝑟ị ℎ𝑖ệ𝑛 𝑡ạ𝑖) = 𝐵(𝑔𝑖á 𝑡𝑟ị 𝑡𝑟ướ𝑐 đó) 6 + 5𝐵 6 + 5𝑋 95/224 𝑀 = 𝑀 + 1: 𝑋 = : 𝑌 = :
(|X − A| + |Y − B|) : A = X: B 16 14 1 − ⏟ 95 / 224
sai số hậu nghiệm chuẩn cột = Y
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 3 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG Nhấn CALC B=0,8 ;A=0,7
Bấm tới lần lập thứ 3 ta được sai số
f/Tìm sai số nghiệm gần đúng x(3) hậu và chuẩn hàng ||T||∞ ||X(1) − X(0)|| 1 − ||T|| ∞ ∞ 0 5/16 Với 5 T = [
] → ||T|| = Max(5/16; 25/224) = 0 25/224 ∞ 16 Bấm máy: x
{ 1 = X(giá trị hiện tại) = A(giá trị trước đó)
x2 = Y(giá trị hiện tại) = B(giá trị trước đó) 6 + 5B 6 + 5X 5/16 5/16 M = M + 1: X = : Y = : . |X − A| : . |Y − B| : A 16 14 1 − ⏟ 5 / 16 1 − ⏟ 5 / 16 sai số 1 sai số 2 = X: B = Y Nhấn CALC B=0,8 ;A=0,7
Bấm máy đến lần lập thứ 3, sai số nào lớn hơn thì chọn sai số đó
g/ Theo công thức tiên nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3 0 5/16 Với 𝑇 = [
] → ||𝑇|| = 𝑀𝑎𝑥(0; 95/224) = 95/224 0 25/224 1 3 − 𝑋(1) − 𝑋(0) = [
40 ] → ||𝑋(1) − 𝑋(0)|| = 25/112 (nên dùng chức năng STO để lưu 83 − 1 560 giá trị) Theo đề yêu cầu: n n 95 ||𝑇|| ( ) 25 1
. ||𝑋(1) − 𝑋(0)|| < 10−3 <=> 224 .
< 10−3 → 𝑛 > 6,95 1 − ||𝑇|| 1 95 112 1 1 − 224
Vậy đến lần lập thứ 7 thì sai số nhở hơn 10−3
h/ Theo công thức hậu nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 4 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG 0 5/16 Với 𝑇 = [
] → ||𝑇|| = 𝑀𝑎𝑥(0; 95/224) = 95/224 0 25/224 1 Bấm máy: 𝑥
{ 1 = 𝑋(𝑔𝑖á 𝑡𝑟ị ℎ𝑖ệ𝑛 𝑡ạ𝑖) = 𝐴(𝑔𝑖á 𝑡𝑟ị 𝑡𝑟ướ𝑐 đó)
𝑥2 = 𝑌(𝑔𝑖á 𝑡𝑟ị ℎ𝑖ệ𝑛 𝑡ạ𝑖) = 𝐵(𝑔𝑖á 𝑡𝑟ị 𝑡𝑟ướ𝑐 đó) 6 + 5𝐵 6 + 5𝑋 95/224 𝑀 = 𝑀 + 1: 𝑋 = : 𝑌 = :
(|X − A| + |Y − B|) : A = X: B 16 14 1 − ⏟ 95 / 224
sai số hậu nghiệm chuẩn cột = Y Nhấn CALC B=0,8 ;A=0,7
Bấm đến khi nào sai số nhỏ hơn 10−3
k/ Theo công thức hậu nghiệm và chuẩn vô cùng, số bước lập cần thiết để sai số nhỏ hơn 10−3 0 5/16 Với 5 T = [
] → ||T|| = Max(5/16; 25/224) = 0 25/224 ∞ 16 Bấm máy: x
{ 1 = X(giá trị hiện tại) = A(giá trị trước đó)
x2 = Y(giá trị hiện tại) = B(giá trị trước đó) 6 + 5B 6 + 5X 5/16 5/16 M = M + 1: X = : Y = : . |X − A| : . |Y − B| : A 16 14 1 − ⏟ 5 / 16 1 − ⏟ 5 / 16 sai số 1 sai số 2 = X: B = Y Nhấn CALC B=0,8 ;A=0,7
Bấm đến khi nào sai số lớn hơn có giá trị nhỏ hơn 10−3 thì dừng lại
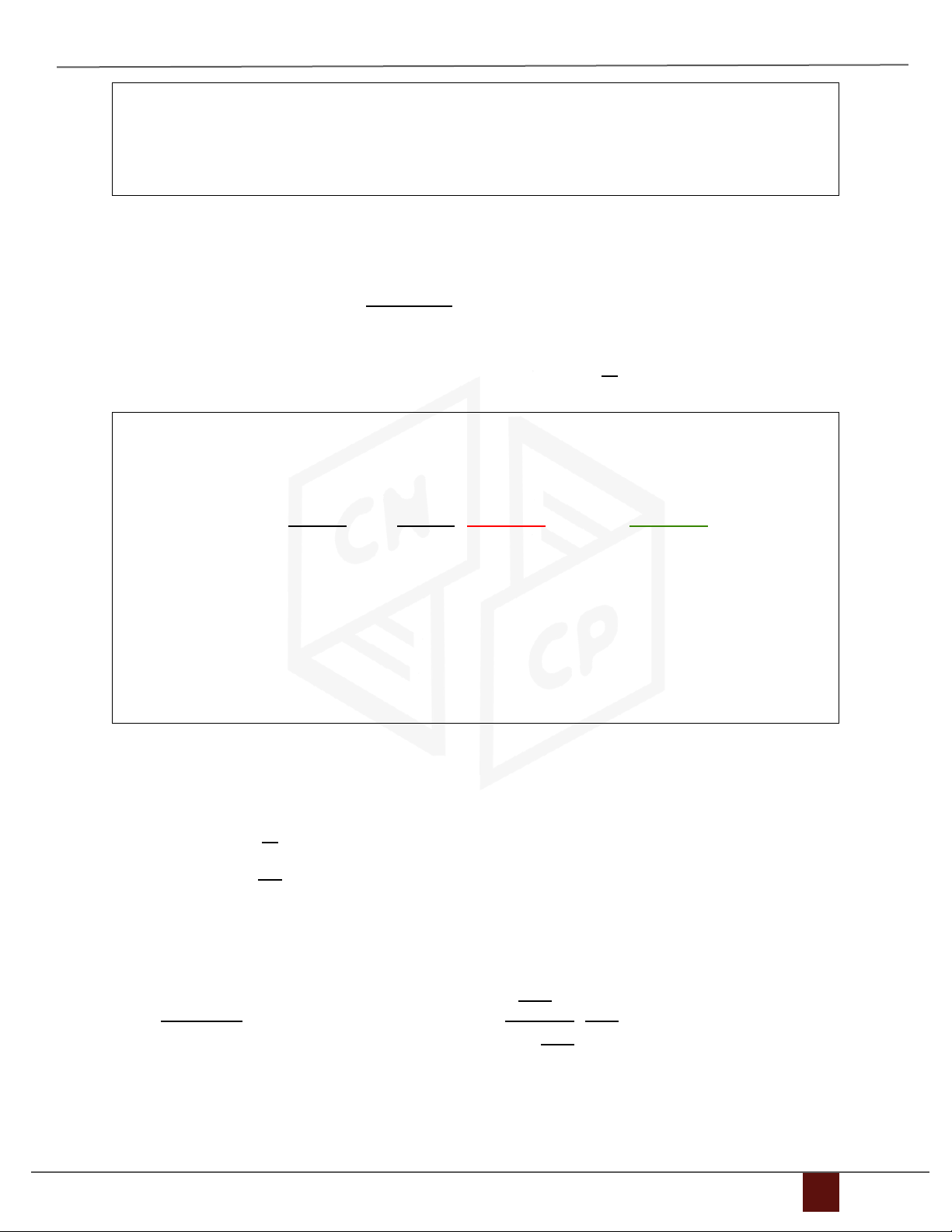
6.2 Dạng hệ phương trình 3 ẩn 2x1 − 0,2x2 − 0,3x3 = 2
Cho hệ phương trình {0,4x1 − 2x2 − 0,6x3 = −1. Với x(0) = [−2, −3, 1]T. 0,4x1 − 0,5x2 + 2x3 = 1
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 5 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG
a/ Xác định ma trận D, L, U, T, C
b/ Tìm nghiệm gần đúng x(3)
c/ Tìm sai số nghiệm gần đúng x(3) tiên nghiệm và chuẩn 1
d/ Tìm sai số nghiệm gần đúng x(3) tiên nghiệm và chuẩn hàng
e/ Tìm sai số nghiệm gần đúng x(3) hậu nghiệm và chuẩn 1
f/ Tìm sai số nghiệm gần đúng x(3) hậu nghiệm và chuẩn hàng
g/ Theo công thức tiên nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3
h/ Theo công thức hậu nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3
k/ Theo công thức hậu nghiệm và chuẩn vô cùng, số bước lập cần thiết để sai số nhỏ hơn 10−3 Giải
(kết hợp với video bài giảng mới hiểu nha)
a/ Xác định ma trận D, L, U, T, C 2 −0,2 −0,3 2 0 0 0 0 0 A = [0,4 −2
−0,6] , D = [0 −2 0] , L = [−0,4 0 0] , 0,4 −0,5 2 0 0 2 −0,4 0,5 0 0 0,2 0,3 U = [0 0 0,6] 0 0 0 2 0 0 −1 0 0,2 0,3 0 0,1 0,15 T = (D − L)−1U = [0,4 −2 0] [0 0 0,6] = [0 0,02 −0,27 ] 0,4 −0,5 2 0 0 0 0 −0,015 −0,097 2 0 0 −1 −2 C = (D − L)−1B = [0,4 −2 0] [−3] 0,4 −0,5 2 1
b/ Tìm nghiệm gần đúng x(3) 2 + 0,2x x 2 + 0,3x3 1 = 2x 2 1 − 0,2x2 − 0,3x3 = 2 −1 − 0,4x {0,4x 1 + 0,6x3 1 − 2x2 − 0,6x3 = −1 → x 2 = 0,4x −2 1 − 0,5x2 + 2x3 = 1 1 − 0,4x1 + 0,5x2 { x3 = 2
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 6 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG
x1 = X(giá trị hiện tại) = A(giá trị trước đó)
Đặt {x2 = Y(giá trị hiện tại) = B(giá trị trước đó)
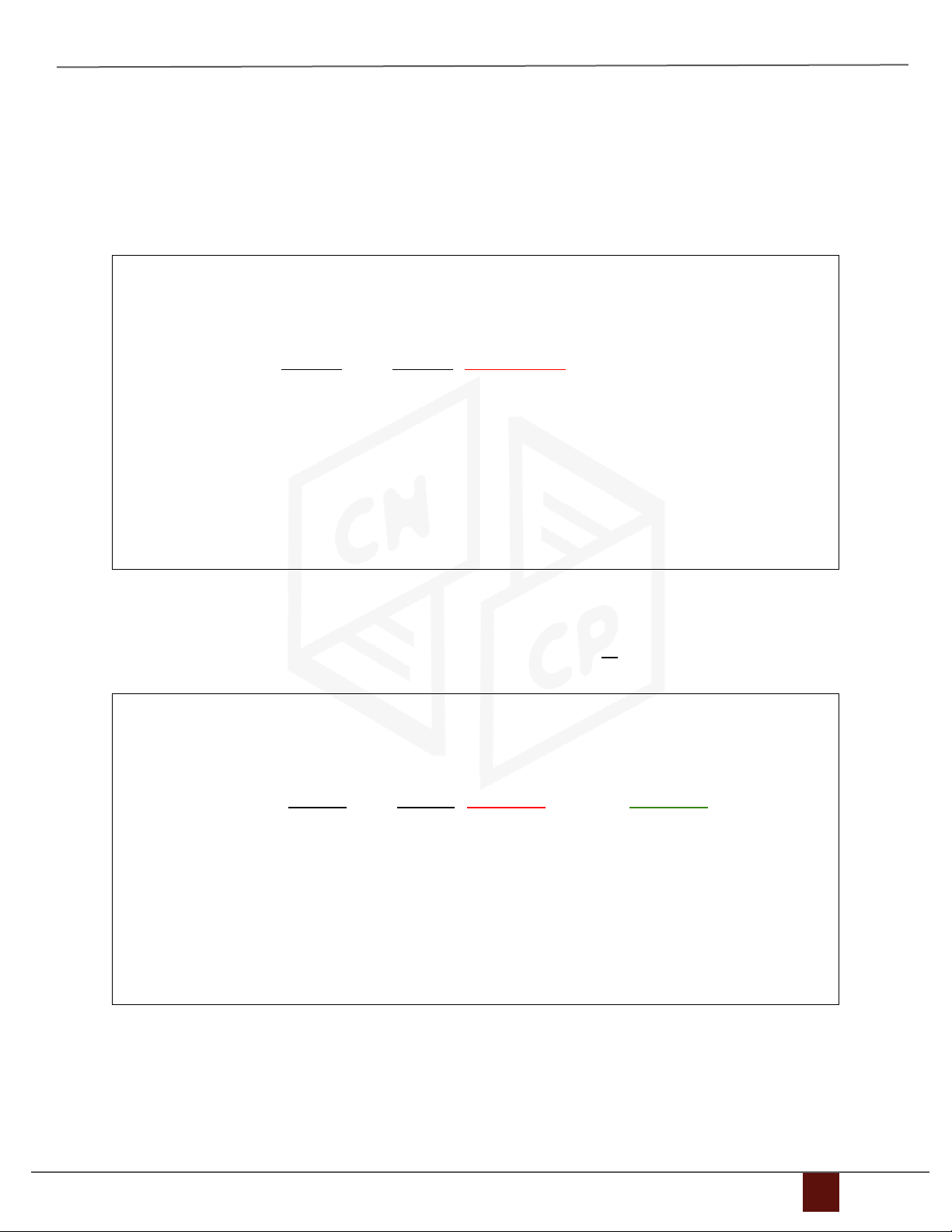
x3 = Z(giá trị hiện tại) = C(giá trị trước đó) Bấm máy: 2 + 0,2B + 0,3C −1 − 0,4A + 0,6C 1 − 0,4A + 0,5B M = M + 1: A = : B = : C = 2 −2 2 Nhấn CALC B=-3, C=1, A=-2 Kết quả n x 1 x2 x3 0 (khởi tạo giá trị) -2 -3 1 1 0,85 0,37 0,4225 2 8803/8000 0,593325 0,4283 3 1,1236 0.5962 0,4243 Đánh giá sai số Công thức tiên nghiệm n ||T|| . ||X(1) − X(0)|| 1 − ||T|| Công thức hậu nghiệm ||T|| . ||X(n) − X(n−1)|| 1 − ||T||
c/ Tìm sai số nghiệm gần đúng x(3) tiên nghiệm và chuẩn 1 3 ||T||1 .||X(1) − X(0)|| 1 − ||T|| 1 1 0 0,1 0,15 Với T = [0 0,02
−0,27 ] → ||T|| = Max(0; 0,135; 0,517) = 0,517 1 0 −0,015 −0,097 2,85
X(1) − X(0) = [ 3,37 ] → ||X(1) − X(0)|| = 6,7975 (nên dùng chức năng STO để lưu −0,5775 1 giá trị)
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 7 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG 3 ||T|| Sai số cần tìm là: 1 (0,517)3 . ||X(1) − X(0)|| = ∗ 6,7975 (làm tròn lên) 1−||T|| 1−0,517 1 1
d/Tìm sai số nghiệm gần đúng x(3) tiên nghiệm và chuẩn hàng 3 ||T||∞ .||X(1) − X(0)|| 1 − ||T|| ∞ ∞ 0 0,1 0,15 Với T = [0 0,02 −0,27 ] → ||T|| = 0,29 ∞ 0 −0,015 −0,097 2,85
X(1) − X(0) = [ 3,37 ] → ||X(1) − X(0)|| = 3,37 (nên dùng chức năng STO để lưu −0,5775 ∞ giá trị) 3 ||T|| Sai số cần tìm là: ∞ (0,29)3 . ||X(1) − X(0)|| = ∗ 3,37(làm tròn lên) 1−||T|| 1−0,29 ∞ ∞
e/Tìm sai số nghiệm gần đúng x(3) hậu và chuẩn 1 ||T||1 .||X(3) − X(2)|| 1 − ||T|| 1 1 0 0,1 0,15 Với T = [0 0,02
−0,27 ] → ||T|| = Max(0; 0,135; 0,517) = 0,517 1 0 −0,015 −0,097 Bấm máy: 2 + 0,2B + 0,3C −1 − 0,4X + 0,6C M = M + 1: X = : Y = : Z 2 −2 1 − 0,4X + 0,5Y 0,517 = :
(|X − A| + |Y − B| + |Z − C|) : A = X: B 2 1 − ⏟ 0 ,517
sai số hậu nghiệm chuẩn cột = Y: C = Z Nhấn CALC B=-3, C=1, A=-2
Bấm tới lần lập thứ 3 ta được sai số
f/Tìm sai số nghiệm gần đúng x(3) hậu nghiệm và chuẩn hàng ||T||∞ ||X(1) − X(0)|| 1 − ||T|| ∞ ∞
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 8 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG 0 0,1 0,15 Với T = [0 0,02 −0,27 ] → ||T|| = 0,29 ∞ 0 −0,015 −0,097 Bấm máy: 2 + 0,2B + 0,3C −1 − 0,4X + 0,6C M = M + 1: X = : Y = : Z 2 −2 1 − 0,4X + 0,5Y 0,29 029 0,29 = : . |X − A| : . |Y − B| : . |Z − C| : A = X: B 2 1 − ⏟ 0 ,29 1 − ⏟ 0 ,29 1 − ⏟ 0 ,29 sai số 1 sai số 2 sai số 3 = Y: C = Z Nhấn CALC B=-3, C=1, A=-2
Bấm máy đến lần lập thứ 3, sai số nào lớn nhất thì chọn sai số đó
g/ Theo công thức tiên nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3 0 0,1 0,15 Với T = [0 0,02
−0,27 ] → ||T|| = Max(0; 0,135; 0,517) = 0,517 1 0 −0,015 −0,097 2,85
X(1) − X(0) = [ 3,37 ] → ||X(1) − X(0)|| = 6,7975 (nên dùng chức năng STO để lưu −0,5775 1 giá trị) Theo đề yêu cầu: n ||𝑇|| (0,517)n 1
. ||𝑋(1) − 𝑋(0)|| < 10−3 <=>
. 6,7975 < 10−3 → 𝑛 > 14,48 1 − ||𝑇|| 1 1 − 0,517 1
Vậy đến lần lập thứ 15 thì sai số nhỏ hơn 10−3
h/ Theo công thức hậu nghiệm và chuẩn cột, số bước lập cần thiết để sai số nhỏ hơn 10−3 0 0,1 0,15 Với T = [0 0,02
−0,27 ] → ||T|| = Max(0; 0,135; 0,517) = 0,517 1 0 −0,015 −0,097 Bấm máy: 2 + 0,2B + 0,3C −1 − 0,4X + 0,6C M = M + 1: X = : Y = : Z 2 −2 1 − 0,4X + 0,5Y 0,517 = :
(|X − A| + |Y − B| + |Z − C|) : A = X: B 2 1 − ⏟ 0 ,517
sai số hậu nghiệm chuẩn cột = Y: C = Z
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 9 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG Nhấn CALC B=-3, C=1, A=-2
Bấm đến khi nào sai số nhỏ hơn 10−3
k/ Theo công thức hậu nghiệm và chuẩn vô cùng, số bước lập cần thiết để sai số nhỏ hơn 10−3 0 0,1 0,15 Với T = [0 0,02 −0,27 ] → ||T|| = 0,29 ∞ 0 −0,015 −0,097 Bấm máy: 2 + 0,2B + 0,3C −1 − 0,4X + 0,6C M = M + 1: X = : Y = : Z 2 −2 1 − 0,4X + 0,5Y 0,29 029 0,29 = : . |X − A| : . |Y − B| : . |Z − C| : A = X: B 2 1 − ⏟ 0 ,29 1 − ⏟ 0 ,29 1 − ⏟ 0 ,29 sai số 1 sai số 2 sai số 3 = Y: C = Z Nhấn CALC B=-3, C=1, A=-2
Bấm đến khi nào sai số lớn nhất có giá trị nhỏ hơn 10−3 thì dừng lại
Ma trận A được gọi là ma trận đường chéo trội nghiêm ngặt nếu thoả mãn điều kiện 𝑛 |𝑎 𝑖𝑖 | >
∑ |𝑎𝑖𝑗|, 𝑖 = 1,2 … , 𝑛 𝑗=1,𝑗≠𝑖 3 −0,2 2
Ví dụ: Ma trận 𝐴 = [ 0,9 2
0,5] Được gọi là ma trận đường chéo trội nghiêm 0,03 −0,4 0,8 |3| > |−0,2| + |2| ngặt vì { |2| > |0,9| + |0,5| |0,8| > |0,03| + | − 0,4|
PHẦN 2: PHẦN BÀI TẬP VỀ NHÀ
Lưu ý, thực hiện đổi đơn vị casio sang radian trước khi làm
Máy tính CASIO fx-580VNX
Đổi đơn vị sang RADIAN trước khi làm (SHIFT => MENU => 2 => 2)
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 10 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG 10 1 2 4
Câu 1: [CNCP] Cho hệ phương trình với ma trận bổ sung ( −1 10 −2 5 ).Xác 3 1 10 8
định nghiệm gần đúng 𝑋 thu được bằng phương pháp lặp Gauss-Seidel với xấp xỉ ban 1
đầu 𝑋0 = [0.204 0.645 0.673]𝑇.
A. [0.2009 0.66469 0.674261]𝑇
B. [0.2009 0.65469 0.674261]𝑇
C. [0.2119 0.65470 0.674261]𝑇
D. [0.2119 0.65469 0.674260]𝑇 11𝑥
E. Các câu khác đều saiCâu 2: [CNCP] Cho hệ phương trình { 1 − 2𝑥2 = 5. Với 5𝑥1 − 13𝑥2 = 7
𝑥(0) = [−1; 1.5]𝑇, sử dụng phương pháp
Gauss-Seidel, tìm chỉ số 𝑛 nhỏ
nhất để ‖𝑥(𝑛) − 𝑥(𝑛−1)‖ ≤ 0.0100 1 A. 5 B. 2 C. 4 D. 3
E. Các câu khác đều sai. 15𝑥
Câu 3: [CNCP] Cho hệ phương trình {
1 − 2𝑥2 = 3. Với 𝑥(0) = [1; −2]𝑇, sử dụng 5𝑥1 − 13𝑥2 = 2
phương pháp Gauss-Seidel, đánh giá sai số 𝛥𝑥(2) của vecto 𝑥(2) theo công thức hậu
nghiệm và chuẩn vô cùng là: A. 0.0401 B. 0.0779 C. 0.0708
D. 0.0400 E. Các câu khác đều sai.
[L.O.1] Sử dụng thông tin sau đây để trả lời câu hỏi từ 6 đến 7. Xét hệ phương trình −19 −9 −8 76
tuyến tính 𝐴𝑋 = 𝐵, với 𝐴 = ( 7 15 6 ) và 𝐵 = ( 2 ) 3 1 18 −172
Câu 4: [CNCP] Đặt 𝐴 = 𝐷 − 𝐿 − 𝑈 và 𝑇
𝑔 = (𝐷 − 𝐿)−1𝑈. Tìm chuẩn 1 của ma trận 𝑇𝑔
trong phương pháp lặp Gauss - Seidel. A. 0.5720 B. Các câu khác sai C. 0.9999 D. 0.7614 E. 0.8805
Câu 5: [CNCP] Sử dụng phương pháp lặp Gauss Seidel với nghiệm xấp xỉ ban đầu
𝑋(0) = [−4 2 − 9]𝑇 ta có thể tìm nghiệm xấp xỉ sau 3 lần lặp 𝑋(3) = [𝑎 𝑏 𝑐]𝑇. Tính 𝑐. A. Các câu khác sai B. -8.6116 C. -9.4473 D. -9.6765 E. -10.1155 15𝑥
Câu 6: [CNCP] Cho hệ phương trình {
1 − 2𝑥2 = 6. Với 𝑥(0) = [1.5 1]𝑇. Vecto 3𝑥1 + 11𝑥2 = 7
𝑥(3) tính theo phương pháp Gauss-Seidel là:
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 11 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG
A) [0.4655; 0.5190]𝑇
B) [0.4303; 0.4909]𝑇
C) [0.4655; 0.5094]𝑇 D)[0.4679; 0.5087]𝑇
E) Các câu khác đều sai 15𝑥
Câu 7: [CNCP] Cho hệ phương trình {
1 − 2𝑥2 = 6. Với 𝑥(0) = [1.5 1]𝑇, sử dụng 3𝑥1 + 11𝑥2 = 7
phương pháp Gauss-Seidel, tìm chỉ số 𝑛 nhỏ nhất để ‖𝑥(𝑛) − 𝑥(𝑛−1)‖ ≤ 0.0600 1 A) 2 B) 4 C) 3 D) 5
E) Các câu khác đều sai 15𝑥
Câu 8: [CNCP] Cho hệ phương trình {
1 − 2𝑥2 = 6. Với 𝑥(0) = [1.5 1]𝑇, sử dụng 3𝑥1 + 11𝑥2 = 7
phương pháp Gauss-Seidel, đánh giá sai số 𝛥𝑥(2) của vecto 𝑥(2) theo công thức tiên
nghiệm và chuẩn vô cùng là:
A) 0.0302 B) 0.0303 C) 0.0198 D) 0.0199
E) Các câu khác đều sai
Các câu hỏi từ câu 9 đến câu 10.
Cho hệ phương trình 4.6 1.6 1
𝐴𝑋 = 𝑏 với 𝐴 = (
), 𝑏 = ( ) và vecto ban đầu 𝑋(0) = 0.9 2.4 2 −1 ( ). −1
Câu 9: [CNCP] Sử dụng phương pháp lặp Gauss-Seidel, vecto nghiệm 𝑋(3) của hệ là
A. (2.9277, −1.1396)𝑇
B. Các câu khác đều sai
C. (−1.0723, 3.8604)𝑇
D. (−2.0723, 0.8604)𝑇
E. (−0.0723, 0.8604)𝑇
Câu 10: [CNCP] Đánh giá sai số tiên nghiệm của 𝑋(3) với chuẩn vô cùng
A. 0.8643 B. 0.105 C. 0.1005 D. 0.1206 E. Các câu khác đều sai 14 2 −1 −2
Cho phương trình 𝐴𝑋 = 𝐵 với 𝐴 = [ 1 14
2 ] và 𝐵 = [−1] . Hãy trả lời các câu 3 −1 13 −1
hỏi từ Câu 11 đến Câu 13.
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 12 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG
Câu 11: [CNCP] [L.O.1, L.O.2] Khi sử dụng phương pháp Gauss-Seidel, chuẩn vô cùng của ma trận TG là A. 0.2143 B. 0.2146
C. Các đáp án khác đều sai. D. 0.2148
Câu 12: [CNCP] [L.O.1, L.O.2] Khi sử dụng phương pháp Gauss-Seidel, với X(0) =
[0 3 0]𝑇 , tìm nghiệm gần đúng X(3) −0.1366 −0.1347 A. [−0.0544] B. [−0.0693] −0.0496 −0.0512 −0.1386 C. [−0.0544] −0.0491 −0.5714
D. Các đáp án khác đều sai. E. [−0.0306] 0.0526
Câu 13: [CNCP] [L.O.1, L.O.2] Đánh giá sai số nghiệm gần đúng X(3) theo công thức
tiên nghiệm và chuẩn vô cùng. A. 0.0734 B. 0.0061
C. Các đáp án khác đều sai. D. 0.0380 E. 0.0041 15𝑥 Câu 14: [CNCP] 1 Cho hệ { 1 − 𝑥2 = 1 với 𝑋(0) = ( ). −1.6𝑥1 + 20𝑥2 = 3.2 1.6
Sử dụng chuẩn vô cùng và sai số tiên nghiệm, so sánh tốc độ hội tụ của hai phương
pháp Gauss-Seidel bằng cách tính số lần lặp tối thiểu để nghiệm có sai số nhỏ hơn 10−5.
Câu 15: [CNCP] (L.O.1) Cho dạng tường minh của hệ phương trình 𝐴2×2𝑋2×1 =
𝐵2×1 trong phương pháp Gauss-Seidel là:
𝑥(𝑚) = 𝑎 + 1.6𝑏𝑥(𝑚−1) { 1 2
𝑥(𝑚) = 𝑐 + 𝑑𝑥(𝑚) 2 1
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 13 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG 𝑥(𝑚)
với 𝑋(𝑚) = ( 1 ). Dãy các vecto nghiệm gần đúng lần lượt như sau: 𝑋(0) = 𝑥(𝑚) 2 1 −0.1 0.09 ( ); 𝑋(1) = ( ); 𝑋(2) = (
). Hãy xác định a, b, c, d 0.7 0.33 0.27 Cho hệ phương trình 10 −2 1
𝐴𝑋 = 𝑏, với 𝐴 = (
), 𝑏 = ( ). Trả lời các câu hỏi từ 3 14 4 16 đến 18:
Câu 16: [CNCP] Tìm số điều kiện của ma trận A theo chuẩn vô cùng (lưu ý: số
điều kiện được làm tròn lên)
A) 1.7325. B) 1.1465. C) 1.3333. D) 1.8631. E) Các câu kia sai.
Câu 17: [CNCP] Sử dụng phương pháp Gauss-Seidel: 𝐴𝑋 = 𝑏 ⇔ 𝑋 = 𝑇𝑋 + 𝐶,
với 𝑇 = (𝐷 − 𝐿)−1𝑈, tìm chuẩn 1 của ma trận T (lưu ý: chuẩn được làm tròn lên).
A) 0.2429. B) 0.2001. C) 0.1572. D) 0.0879. E) Các câu kia sai.
Câu 18: [CNCP] Sử dụng phương pháp Gauss-Seidel, tính chỉ số n nhỏ nhất để 0.2
||𝑋𝑛 − 𝑋𝑛−1|| < 0.00007, với 𝑋0 = ( ) 0.1 A) 4. B) 5. C) 7. D) 6. E) Các câu kia sai. Cho hệ phương trình 11 −1 1
𝐴𝑋 = 𝑏, với 𝐴 = (
), 𝑏 = ( ). Trả lời các câu hỏi từ 2 17 3 19 đến 21:
Câu 19: [CNCP] Tìm số điều kiện của ma trận 𝐴 theo chuẩn 1 (lưu ý: số điều kiện làm tròn lên) A) 1.7214. B) 1.1573. C) 1.8427. D) Các câu kia sai. E) 1.8096.
Câu 20: [CNCP] Sử dụng phương pháp Gauss Seidel, 𝐴𝑋 = 𝑏 ⇔ 𝑋 = 𝑇𝑋 + 𝐶,
với 𝑇 = (𝐷 − 𝐿)−1𝑈. Tìm chuẩn vô cùng của ma trận 𝑇. A) 0.0910. B) 0.0908.
C) 0.0912. D) 0.0879. E) Các câu kia sai.
Câu 21: [CNCP] Sử dụng phương pháp Gauss Seidel, tìm nghiệm gần đúng 𝑋1 của hệ với 0.1 𝑋0 = ( ) 0.2
A) 𝑋1 = (0.1058,0.1640)𝑇.
B) 𝑋1 = (0.1045,0.1654)𝑇.
C) 𝑋1 = (0.1092,0.1648)𝑇. D) Các câu kia sai.
E) 𝑋1 = (0.1091,0.1636)𝑇.
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 14 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG Cho hệ phương trình 10 −2 1
𝐴𝑋 = 𝑏, với 𝐴 = (
), 𝑏 = ( ). Trả lời các câu hỏi từ 3 14 4 22 đến 24:
Câu 22: [CNCP] Tìm số điều kiện của ma trận A theo chuẩn vô cùng (lưu ý: số
điều kiện được làm tròn lên)
A) 1.7325. B) 1.1465. C) 1.3333. D) 1.8631. E) Các câu kia sai.
Câu 23: [CNCP] Sử dụng phương pháp Gauss-Seidel: 𝐴𝑋 = 𝑏 ⇔ 𝑋 = 𝑇𝑋 + 𝐶,
với 𝑇 = (𝐷 − 𝐿)−1𝑈, tìm chuẩn 1 của ma trận T (lưu ý: chuẩn được làm tròn lên).
A) 0.2429. B) 0.2001. C) 0.1572. D) 0.0879. E) Các câu kia sai.
Câu 24: [CNCP] Sử dụng phương pháp Gauss-Seidel, tính chỉ số n nhỏ nhất để 0.2
||𝑋𝑛 − 𝑋𝑛−1|| < 0.00007, với 𝑋0 = ( ) 0.1 B) 4. B) 5. C) 7. D) 6. E) Các câu kia sai.
[L.O.1] Sử dụng thông tin sau đây để trả lời câu hỏi từ 25 đến 26. Xét hệ phương −19 −9 −8 76
trình tuyến tính 𝐴𝑋 = 𝐵, với 𝐴 = ( 7 15 6 ) và 𝐵 = ( 2 ) 3 1 18 −172
Câu 25: [CNCP] Đặt 𝐴 = 𝐷 − 𝐿 − 𝑈 và 𝑇𝑔 = (𝐷 − 𝐿)−1𝑈. Tìm chuẩn 1 của ma
trận 𝑇𝑔 trong phương pháp lặp Gauss - Seidel. A. 0.5720 B. Các câu khác sai C. 0.9999 D. 0.7614 E. 0.8805
Câu 26: [CNCP] Sử dụng phương pháp lặp Gauss Seidel với nghiệm xấp xỉ ban
đầu 𝑋(0) = [−4 2 − 9]𝑇 ta có thể tìm nghiệm xấp xỉ sau 3 lần lặp 𝑋(3) = [𝑎 𝑏 𝑐]𝑇. Tính 𝑐.
A. Các câu khác sai B. -8.6116 C. -9.4473 D. -9.6765 E. -10.1155 6𝑥 − 3𝑦 = 3
Cho hệ phương trình tuyến tính 𝑥(0) {
Biết nghiệm ban đầu là ( 2𝑥 + 6𝑦 = 1 𝑦(0)) = 2 ( ). 1
Câu 27: [CNCP] Bằng phương pháp Gauss-Seidel, tính thành phần thứ hai của
vector nghiệm xấp xỉ sau ba bước lặp. A. 0.4802 B. 0.5182
C. 0.7676 D. -0.0046 E. 0.5342
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 15 HCMUT CNCP
LỚP PHƯƠNG PHÁP TÍNH PRO
NGUYỄN QUỐC VƯƠNG
Câu 28: [CNCP] Bằng phương pháp lặp Gauss-Seidel, sử dụng chuẩn 1, tính
sai số tiên nghiệm của vector nghiệm 𝑋(3). A. 2.0278 B. 2.4214 C. 1.926 D. 1.9288 E. 2.7448
TẠI BACHKHOACNCP.COM KHÓA HỌC PHƯƠNG PHÁP TÍNH 16