LÝ THUYẾT ĐIỀU KHIỂN TỰ ĐỘNG - Chương 1 đến Chương 5 Tổng Hợp. Môn Lý thuyết điều khiển tự động (UET) | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội.

lOMoAR cPSD| 59735516 Lý thuyết Chương 1:
Câu 1. Điều khiển là gì? Thế nào là quá trình điều khiển tự động? Ví dụ.
• Điều khiển là quá trình thu thập thông tin, xử lý thông tin và tác động lên hệ thống để
đáp ứng của hệ thống “gần” với mục đích định trước
• Điều khiển tự động là quá trình điều khiển không cần sự tác động của con người  Ví
dụ: Máy nướng bánh tự động
Câu 2. Nêu ý nghĩa của điều khiển tự động ?
• Đáp ứng của hệ thống thỏa mãn yêu cầu công nghệ • Tăng độ chính xác • Tăng năng suất
Câu 3. Nêu các nguyên tắc điều khiển cơ bản.
• Nguyên tắc ổn định hóa: Nguyên tắc này nhằm giữ tín hiệu ra ổn định và bằng giá trị hằng số định trước.
• Nguyên tắc điều khiển theo chương trình : Giữ cho tín hiệu ra thay đổi đúng theo một
hàm thời gian (chương trình) định trước.
• Nguyên tắc điều khiển thích nghi (tự chỉnh định) : Khi bộ điều khiển với thông số cố
định không thể đáp ứng được
Câu 4. Trình bày cấu trúc cơ bản của một hệ thống điều khiển. Mô tả các phần tử trong
hệ thống. Cho 03 ví dụ minh họa.
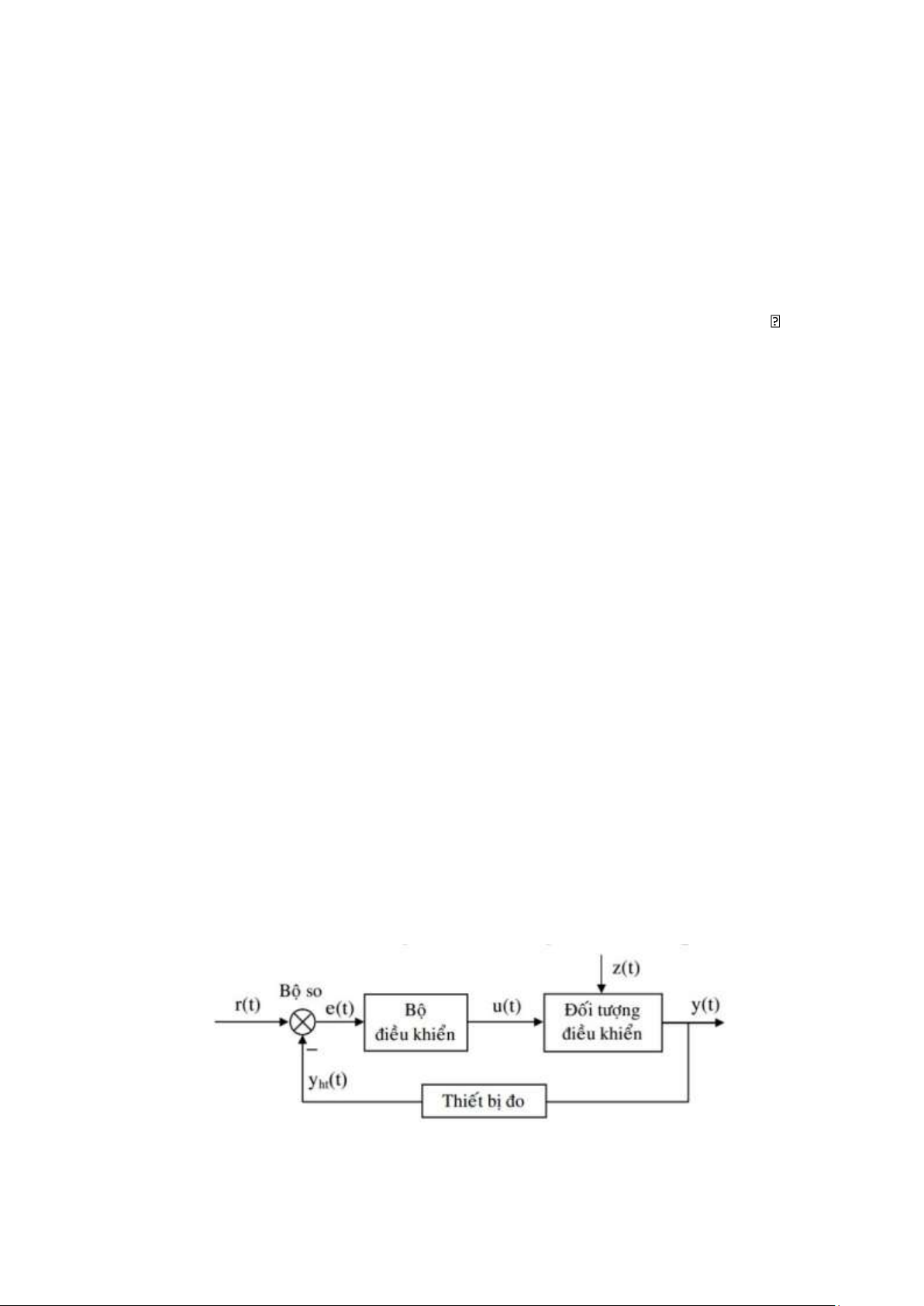
• Cấu trúc cơ bản của hệ thống điều khiển: gồm 3 thành phần cơ bản:
▫ r(t) : tín hiệu vào, tín hiệu chuẩn, tín hiệu đặt (giá trị đặt trước)
▫ u(t): tín hiệu điều khiển lOMoAR cPSD| 59735516
▫ y(t): tín hiệu ra, đại lượng cần được điều khiển, giá trị thực
▫ yht(t): tín hiệu hồi tiếp
▫ e(t): sai lệch giữa tín hiệu đặt và tín hiệu ra • 3 ví dụ: ▫ Động cơ điện ▫ Van ▫ Xi lanh lực
Câu 5. Phân loại các hệ thống điều khiển. • Phân loại tổng quát
Hệ thống điều khiển vòng kín (Closed-Loop Control System)
Hệ thống điều khiển vòng hở (Open-Loop Control System) Bộ điều khiển Đối tượng
• Phân loại theo đặc điểm mô tả toán học
Hệ thống tuyến tính:
▫ Mọi phần tử của hệ đều có quan hệ vào – ra là hàm tuyến tính.
▫ Hệ thống được mô tả bởi hệ phương trình vi phân/sai phân tuyến tính.
▫ Hệ tuyến tính chỉ là mô hình lý tưởng.
Hệ thống phi tuyến:
▫ Hệ có ít nhất một phần tử có quan hệ vào – ra là hàm phi tuyến.
▫ Hệ thống được mô tả bởi hệ phương trình vi phân/sai phân phi tuyến.
▫ Các hệ thống điều khiển thực tế đều có tính phi tuyến.
• Phân loại theo đặc điểm mô tả toán học Hệ thống liên tục:
▫ Các tín hiệu truyền trong hệ đều là hàm liên tục theo thời gian
▫ Hệ thống được mô tả bằng phương trình vi phân Hệ thống rời rạc:
▫ Tín hiệu ở một hay nhiều điểm của hệ là dạng chuỗi xung hoặc mã số
▫ Hệ thống được mô tả bằng phương trình sai phân
Hệ thống bất biến theo thời gian (hệ dừng): lOMoAR cPSD| 59735516
▫ Hệ số của phương trình vi phân/sai phân mô tả hệ thống là không đổi.
▫ Đáp ứng của hệ thống không phụ thuộc vào thời điểm mà tín hiệu vào được đặt vào hệ thống.
Hệ thống biến đổi theo thời gian (hệ không dừng):
▫ Hệ số của phương trình vi phân/sai phân mô tả hệ thống thay đổi theo thời gian. ▫
Đáp ứng của hệ thống phụ thuộc vào thời điểm mà tín hiệu vào được đặt vào hệ thống.
• Phân loại theo nguyên tắc điều khiển – mục tiêu điều khiển Điều khiển ổn định hóa:
▫ Nếu tín hiệu đặt r(t) = const, ta gọi là điều khiển ổn định hóa
Điều khiển theo chương trình:
▫ Nếu tín hiệu đặt r(t) là hàm thay đổi theo thời gian nhưng đã biết trước Điều khiển theo dõi:
▫ Tín hiệu vào r(t) là hàm không biết trước theo thời gian
• Phân loại theo dạng năng lượng sử dụng
Hệ thống điều khiển cơ khí
Hệ thống điều khiển điện
Hệ thống điều khiển khí nén
Hệ thống điều khiển thủy lực
Hệ thống điều khiển điện-khí nén, điện-thủy lực,…
• Phân loại theo số lượng ngõ và ngõ ra
Hệ thống một ngõ vào – một ngõ ra (hệ SISO)
Hệ thống nhiều ngõ vào – nhiều ngõ ra (hệ MIMO)
Câu 6. Trình bày ưu điểm và nhược điểm của bộ điều khiển vòng hở (open-loop) (không
phản hồi) và bộ điều khiển vòng kín (hệ thống điều khiển hồi tiếp) (closed-loop). Nêu 03 ví dụ. • Vòng hở Ưu:
o Đơn giản và dễ thiết kế o Chi phí thấp
o Không bị ảnh hưởng bởi dao động và nhiễu bên ngoài Nhược: lOMoAR cPSD| 59735516
o Không chính xác o Không tự điều chỉnh o Không ổn định • Vòng kín Ưu:
o Chính xác hơn o Tự điều chỉnh o Ổn định hơn Nhược:
o Phức tạp hơn o Chi phí cao hơn. o Có thể bị nhiễu
Câu 7. Trình bày các bước thiết kế một hệ thống điều khiển tự động + Câu 8. Nêu các bước
thiết kế hệ thống điều khiển.
• Xây dựng mô hình toán học của đối tượng.
• Chọn 1 nguyên tắc điều khiển cụ thể. Từ đó lựa chọn các thiết bị cụ thể để thực hiện
nguyên tắc điều khiển đã đề ra
• Kiểm tra về lý thuyết hiệu quả điều khiển trên các mặt, từ đó hiệu chỉnh phương án
chọn thiết bị, chọn nguyên tắc điều khiển khác hoặc hoàn thiện lại mô hình.
• Chế tạo, lắp ráp thiết bị từng phần. Kiểm tra, thí nghiệm thiết bị từng phần và hiệu chỉnh các sai sót.
• Chế tạo, lắp ráp thiết bị toàn bộ. Kiểm tra, thí nghiệm thiết bị toàn bộ. Hiệu chỉnh và
hoàn thành toàn bộ hệ thống điều khiển. Chương 2:
Câu 9. Khái niệm hàm truyền. Nêu các đặc tính cơ bản của hàm truyền.
• Hàm truyền của hệ thống là tỉ số giữa biến đổi Laplace của tín hiệu ra và biến đổi
Laplace của tín hiệu vào khi điều kiện đầu bằng 0
• Đặc tính cơ bản hàm truyền o Hàm truyền chỉ dùng cho phần tử và hệ thống tuyến tính bất biến.
o Biểu thức hàm truyền chỉ phụ thuộc vào các thông số là hệ số các đa thức tử
số và mẫu số và bậc của hệ thống mà không phụ thuộc vào thể loại và giá trị tín hiệu vào, ra.
o Việc giả thiết các điều kiện đầu bằng 0 là dựa trên quan điểm dùng hàm truyền
để nghiên cứu bản chất động học của hệ thống.
o Một hệ thống hay phần tử tuyến tính có tín hiệu vào r(t), tín hiệu ra y(t), sau
khi đã được mô hình hóa và có hàm truyền G(s) được biểu diễn đơn giản bằng một khối (block) lOMoAR cPSD| 59735516
o Sử dụng hàm truyền để mô tả và nghiên cứu hệ thống sẽ thuận lợi hơn nhiều
so với dùng phương trình vi phân. Với khái niệm này, quan hệ giữa tín hiệu
vào và ra có thể biểu diễn dưới dạng phương trình đại số.
o Đa thức mẫu số của hàm truyền được gọi là đa thức đặc tính. Nếu cho mẫu số
của hàm truyền bằng 0 ta có phương trình đặc tính
o Hàm truyền có thể biểu diễn dưới dạng điểm không – điểm cực.
Câu 10. Nêu ưu điểm và nhược điểm của phương pháp hàm truyền đạt. • Ưu
o Đơn giản hóa phân tích hệ thống o Dễ dàng phân tích trong miền tần số o
Thuận tiện cho việc sử dụng các công cụ toán học o Hỗ trợ thiết kế và tối ưu
hóa hệ thống o Khả năng phân tích các đặc tính động học • Nhược
o Chỉ áp dụng cho hệ thống tuyến tính và bất biến theo thời gian o Không cho
thông tin về trạng thái bên trong o Phức tạp khi hệ thống có nhiều đầu vào và
đầu ra o Khó khăn trong việc phân tích hệ thống phi tuyến o Giới hạn trong
việc phân tích các tín hiệu ngẫu nhiên
Câu 11. Trình bày các bước tìm hàm truyền của đối tượng.
• Bước 1: Thành lập phương trình vi phân mô tả quan hệ vào – ra của phần tử/hệ thống.
• Bước 2: Lấy biến đổi Laplace của phương trình vi phân, với giả thiết tất cả các điều kiện ban đầu bằng 0.
• Bước 3: Lập tỉ số tín hiệu ra Y(s) trên tín hiệu vào R(s). Tỉ số này chính là hàm truyền.
Câu 12. Thế nào là sơ đồ khối mô tả hệ thống. Mô tả các thành phần cơ bản trong sơ đồ khối.
• Sơ đồ khối của một hệ thống là hình vẽ mô tả chức năng của các phần tử và sự tác
động qua lại giữa các phần tử trong hệ thống.
• Sơ đồ khối có 4 thành phần chính: o Tín hiệu
o Khối chức năng : Tín hiệu ra của khối chức năng bằng tích tín hiệu vào và hàm truyền lOMoAR cPSD| 59735516
o Điểm rẽ nhánh : Tại điểm rẽ nhánh mọi tín hiệu đều bằng nhau o Bộ tổng :
Tín hiệu ra của bộ tổng bằng tổng đại số của các tín hiệu vào
Câu 13. Trình bày về các phép ghép nối sơ đồ khối cơ bản.
• Hệ thống nối tiếp:
▫ Hàm truyền tương đương: • Hệ thống song song:
▫ Hàm truyền tương đương: • Hồi tiếp âm:
▫ Hàm truyền tương đương:
▫ Hồi tiếp âm đơn vị H(s)=1 • Hồi tiếp dương:
▫ Hàm truyền tương đương:
Câu 14. Trình bày về các phép chuyển đổi nút trong đại số sơ đồ khối.
Chuyển điểm rẽ nhánh ra trước 1 khối: lOMoAR cPSD| 59735516
Chuyển điểm rẽ nhánh ra sau 1 khối:
Câu 15. Thế nào là graph tín hiệu. Mô tả các thành phần cơ bản trong graph tín hiệu. Phát biểu công thức Mason.
• Sơ đồ dòng tín hiệu (Graph tín hiệu) là một sơ đồ gồm các nhánh và nút
▫ Nút: một điểm biểu diễn một biến hay tín hiệu trong hệ thống
▫ Nhánh: đường nối trực tiếp 2 nút, trên mỗi nhánh có ghi mũi tên chỉ chiều truyền tín
hiệu và có ghi hàm truyền cho biết mối quan hệ giữa tín hiệu ở 2 nút.
▫ Nút nguồn: nút chỉ có các nhánh hướng ra.
▫ Nút đích: nút chỉ có các nhánh hướng vào.
▫ Nút hỗn hợp: nút có cả các nhánh ra và các nhánh vào • Công thức Mason
▫ Hàm truyền tương đương từ một nút nguồn đến một nút đích của hệ thống tự động
biểu diễn bằng sơ đồ dòng tín hiệu được cho bởi: lOMoAR cPSD| 59735516
Câu 16. Tóm tắt nội dung chương 2 trong 1 trang A4 theo Sơ đồ tư duy Mindmap Chương 3:
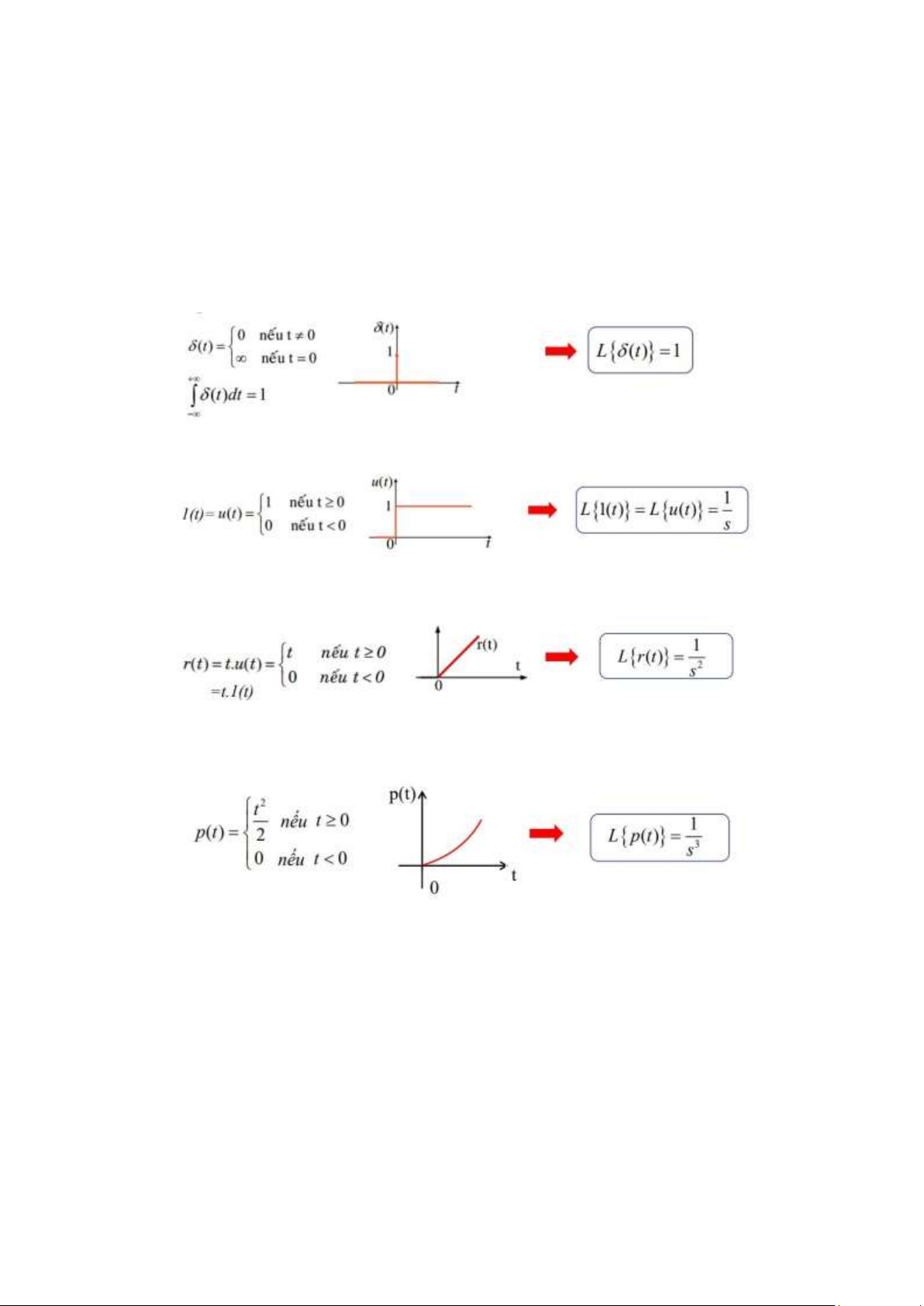
Câu 17. Nêu các tín hiệu tác động thử thường xuyên được sử dụng trong điều khiển tự
động. Biểu diễn chúng dưới miền thời gian và miền phức.
• Hàm xung đơn vị (impulse function): mô tả nhiễu tác động vào hệ thống
• Hàm bậc thang đơn vị (step function): khảo sát hệ thống điều khiển ổn định
• Hàm dốc đơn vị (ramp function): khảo sát hệ thống điều khiển theo dõi
• Hàm parabol đơn vị (parabolic function)
Câu 18. Trình bày các khái niệm trạng thái, vectơ trạng thái. Biểu diễn hệ phương trình trạng thái.
Câu 19. Thế nào là đặc tính động học của hệ thống? Các tín hiệu thử cơ bản? Trình bày về
đặc tính thời gian của hệ thống.+ Câu 20. Thế nào là đặc tính động học của hệ thống? Các tín hiệu thử cơ bản? lOMoAR cPSD| 59735516
• Trạng thái của một hệ thống là tập hợp nhỏ nhất các biến (gọi là biến trạng thái) mà
nếu biết giá trị của các biến này tại thời điểm t0 và biết các tín hiệu vào ở thời điểm
t>t0 , ta hoàn toàn có thể xác định được đáp ứng của hệ thống tại mọi thời điểm t  t0 .
• n biến trạng thái hợp thành vector cột gọi là vector trạng thái
• Hệ phương trình trạng thái
o x(t) là vectơ trạng thái o r(t) là tín
hiệu vào, y(t) là tín hiệu ra
▫ Với hệ tuyến tính bất biến MIMO thì A, B, C, D là các ma trận hệ số hằng
▫ Với hệ tuyến tính bất biến SISO thì A là ma trận, B là vectơ cột, C là vectơ hàng, D là hằng số
▫ Với hệ tuyến tính bất biến SISO có hàm truyền với bậc tử số nhỏ hơn bậc mẫu số
(hệ hợp thức chặt) thì D = 0
Câu 21. Nêu các khâu động học điển hình và khảo sát đặc tính thời gian của chúng
 Các khâu bậc 1, bậc 2:
▫ Khâu khuếch đại (tỷ lệ)
Hàm truyền: G(s) = K (K>0)
Đáp ứng xung g(t)=L-1  G(s) =L-1  K  =K.δ(t)
Đáp ứng bậc thang: h(t)=L-1 G(s) / s =L-1  K / s =K.1(t) Tổng quát: y(t)=K.r(t)
▫ Khâu quán tính bậc 1
Hàm truyền: 𝐆𝐬 = 𝐊 / (𝐓𝐬 + 1) Phương trình vi phân: Hàm xung: Hàm bậc thang: lOMoAR cPSD| 59735516 Hàm dốc: ▫ Khâu bậc 2
Hàm truyền 𝐆 𝐬 = 𝐊 / (𝐓𝟐𝐬𝟐 + 𝟐𝐓𝐬 + 1)
+ Đặc tính thời gian (1): Đáp ứng xung Đáp ứng bậcthang
+ Đặc tính thời gian (0<1) Đáp ứng xung Đáp ứng bậc thang ▫ Khâu trễ
Hàm truyền 𝐆𝐡 (𝐬)= 𝐆 (𝐬) 𝐞 −𝐓s
Đặc tính thời gian ▫ Đáp ứng xung: ▫ Đáp ứng nấc:  Khâu vi phân:
▫ Khâu vi phân lý tưởng
Hàm truyền 𝐆(𝐬) = 𝐊s
Phương trình vi phân y(t)=K * dr(t)/dt lOMoAR cPSD| 59735516
Đặc tính thời gian Y(s)=R(s).G(s)=K.s.R(s)
Đáp ứng xung: g(t)=L-1 G(s)  =L-1 Ks  =Kδ.(t)
Đáp ứng nấc: h(t)=L-1 H(s)  =L-1 K  =Kδ(t)
▫ Khâu vi phân là một thừa số động học thuần túy bậc 1
Hàm truyền 𝐆𝐬 = 𝐊(𝐓𝐬+1)
Đặc tính thời gian Y(s)=R(s).G(s)=K(Ts+1).R(s)
Đáp ứng xung g(t)=L-1 G(s)  =L-1 KTs + K =KTδ.(t)+ Kδ(t)
Đáp ứng nấc g(t)=L-1 H(s)  =L-1 KT +K/s  =KTδ(t) + K1(t) • Khâu tích phân
Hàm truyền: 𝐆𝐬 = 𝐊 / 𝐬 = 𝟏/ 𝐓s
Đặc tính thời gian Y(s)=R(s).G(s)=K/s R(s)
Đáp ứng xung: g(t)=L-1  G(s) =L-1  K/s =K.1(t)
Đáp ứng nấc: h(t)=L-1 H(s)  =L-1  K/s2 =K.t.1(t)
Câu 22. Khái niệm điểm không – điểm cực. Nêu ảnh hưởng của điểm không và điểm cực
lên đáp ứng của hệ thống.
• Điểm cực (pole) là nghiệm của mẫu số hàm truyền, tức là nghiệm của phương trình
đặc tính A(s) = 0. Do A(s) bậc n nên hệ thống có n điểm cực ký hiệu là pi , i=1, 2, …n 
Điểm không (zero) là nghiệm của tử số hàm truyền, tức là nghiệm của phương
trình B(s) = 0. Do B(s) bậc m nên hệ thống có m điểm không ký hiệu là zi , i = 1, 2, …m
• Ảnh Hưởng của Điểm Cực
Vị trí của Điểm Cực:
o Cực thực âm: Hệ thống ổn định và đáp ứng giảm dần về giá trị ổn định. o Cực
thực dương: Hệ thống không ổn định và đáp ứng tăng không giới hạn. o Cực
phức có phần thực âm: Hệ thống dao động tắt dần. o Cực phức có phần thực
dương: Hệ thống dao động không ổn định.
Đáp Ứng Thời Gian:
o Cực gần gốc tọa độ hơn dẫn đến đáp ứng chậm hơn. lOMoAR cPSD| 59735516
o Cực xa gốc tọa độ hơn dẫn đến đáp ứng nhanh hơn.  Ảnh Hưởng của Điểm Không
Vị trí của Điểm Không:
o Không thực âm: Tăng độ dốc của đáp ứng ban đầu và có thể tạo ra một đỉnh (overshoot) cao hơn.
o Không thực dương: Có thể làm cho đáp ứng ban đầu giảm tốc độ, thậm chí có
thể gây ra ngược dấu (inverted response) ban đầu trước khi trở về giá trị ổn định.
Đáp Ứng Thời Gian:
o Không gần gốc tọa độ hơn có thể làm cho đáp ứng trở nên nhanh hơn hoặc gây ra overshoot.
o Không xa gốc tọa độ hơn có thể làm giảm ảnh hưởng của điểm không đến đáp ứng của hệ thống.
Câu 23. Tóm tắt nội dung chương 3 trong 1 trang A4 theo Sơ đồ tư duy Mindmap Chương 4:
Câu 24. Thế nào là ổn định BIBO. Nêu ví dụ minh họa về hệ thống ổn định, biên giới ổn
định và không ổn định.
• Hệ thống được gọi là ổn định BIBO (Bounded Input – Bounded Output) nếu đáp ứng
của hệ bị chặn khi tín hiệu vào bị chặn. • Ví dụ
Hệ thống ổn định
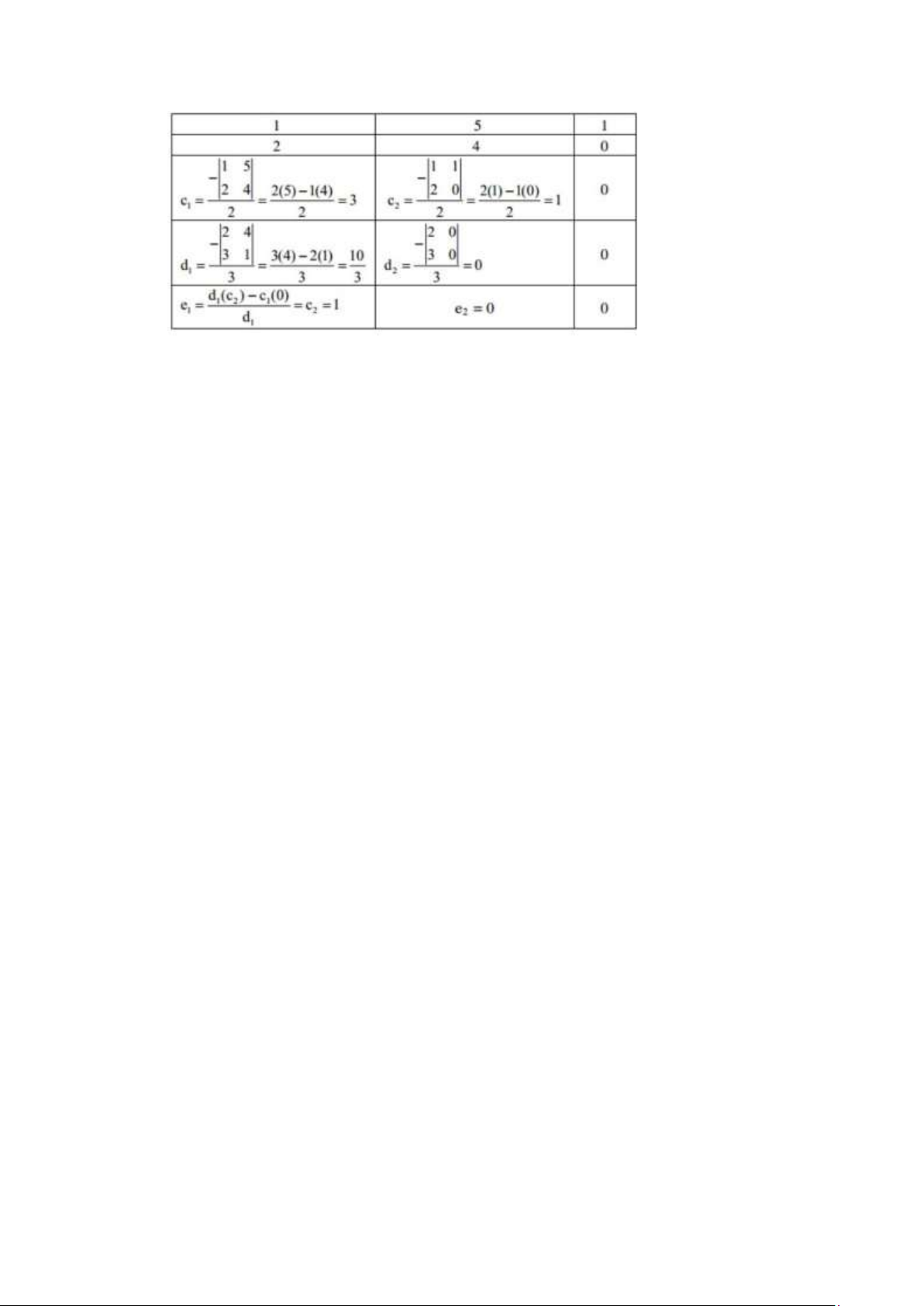
Hệ thống có phương trình đặc tính. s +2s +5s +4s+1=0
Sử dụng tiêu chuẩn Rout các phần tử ở cột 1 đều dương nên hệ thống ổn định. Tất cả
các nghiệm của phương trình đặc tính đều có phần thực âm (nằm bên trái trục ảo). lOMoAR cPSD| 59735516
Biên giới ổn định
Hàm truyền của một hệ thống dao động không tắt Điểm
cực: s=± j (phần thực bằng 0, phần ảo dương và âm) Đáp Ứng Bước: y(t)=sin(t) Đặc Điểm:
o Điểm cực nằm trên trục ảo của mặt phẳng phức. o Đáp ứng đầu ra là một hàm
dao động không tắt dần theo thời gian.
o Hệ thống biên giới ổn định vì đầu ra không tiến đến vô hạn nhưng cũng không ổn
định vì không tiến đến một giá trị cố định.
Biên giới không ổn định
Hàm truyền của một hệ thống có điểm cực tại gốc tọa độ: G(s)=1/
Điểm cực: s=0s = 0s=0 (trên trục ảo, tại gốc tọa độ) Đáp Ứng Bước:
y(t)=∫ t0u(τ)d τ = t nếu u(t) = 1 Đặc Điểm: lOMoAR cPSD| 59735516
o Điểm cực tại gốc tọa độ của mặt phẳng phức. o Đáp ứng đầu ra y(t)=ty(t) =
ty(t)=t tăng tuyến tính theo thời gian. o Hệ thống biên giới không ổn định vì đầu
ra không bị chặn và tiếp tục tăng trưởng.
Câu 25. Nêu định nghĩa phương trình đặc tính của hệ thống. Điều kiện cần và đủ để hệ
ổn định dựa vào các nghiệm của phương trình đặc tính như thế nào ?
• Phương trình đặc tính của hệ thống là phương trình vô hướng hay phương trình ma trận có dạng: det(A−λI)= 0
• Điều kiện cần để hệ thống ổn định là tất cả các hệ số của phương trình đặc tính phải khác 0 và cùng dấu.
Câu 26. Tiêu chuẩn ổn định đại số. Phát biểu tiêu chuẩn ổn định Routh + Câu 27.Phát biểu
tiêu chuẩn ổn định Hurwitz.
• Điều kiện cần và đủ để hệ thống ổn định là tất cả các phần tử nằm ở cột 1 của bảng Routh đều dương.
• Điều kiện cần và đủ để hệ thống ổn định là tất cả các định thức con chứa đường chéo
của ma trận Hurwitz đều dương.
Câu 28. Trình bày khái niệm quỹ đạo nghiệm số. Nêu các nguyên tắc xây dựng quỹ đạo nghiệm số.
• Quỹ đạo nghiệm số là tập hợp tất cả các nghiệm của phương trình đặc tính của hệ
thống khi một thông số nào đó trong hệ thay đổi từ 0 → ꝏ. Quỹ đạo nghiệm số được
dùng để khảo sát ảnh hưởng của thông số thay đổi đến chất lượng của hệ thống. • Quy tắc
o Quy tắc 1: Số nhánh của quỹ đạo nghiệm số = bậc của PTĐT = số cực của G0
(s) = n (n là số lượng cực). lOMoAR cPSD| 59735516
o Quy tắc 2: Các nhánh của quỹ đạo nghiệm xuất phát từ các cực của G0 (s) khi
K = 0. o Quy tắc 3: Khi K →  có m nhánh tiến tới m zero của G0 (s), còn lại
(n – m) nhánh tiến tới  theo các tiệm cận.
o Quy tắc 4: Góc của các tiệm cận với trục thực được xác định bởi:
o Quy tắc 5: Các tiệm cận cùng giao nhau tại
một điểm trên trục thực có hoành độ:
o Quy tắc 6: Quỹ đạo nghiệm đối xứng qua trục thực vì các nghiệm phức luôn có từng cặp liên hợp.
o Quy tắc 7: Điểm tách là điểm tại đó hai nhánh QĐN gặp nhau và sau đó tách
ra khi K tăng. Điểm tách nằm trên trục thực và là nghiệm của phương trình
dK/ds = 0 (suy ra từ 1+K.M(s)/N(s)=0).
o Quy tắc 8: Một điểm trên trục thực thuộc về QĐN nếu tổng số lượng điểm cực
và zero của G0 (s) bên phải nó là một số lẻ. o Quy tắc 9: Giao điểm của QĐN
với trục ảo có thể xác định bằng 2 cách:
▫ Cách 1: Dùng tiêu chuẩn Routh-Hurwitz để tìm K giới hạn rồi thay vào
PTĐT và giải tìm nghiệm ảo.
▫ Cách 2: Thay s = j vào PTĐT rồi cho phần thực và phần ảo bằng 0, sau
đó giải ra tìm  và K.
o Quy tắc 10: Góc xuất phát và góc đến của các nhánh được xác định từ điều
kiện pha. o Quy tắc 11: Giá trị K dọc theo QĐN có thể xác định từ điều kiện
biên độ. Câu 29. Trình bày các tiêu chuẩn chất lượng đánh giá hệ thống điều
khiển tự động. Phân tích sai số xác lập của hệ thống hồi tiếp âm.
• Các tiêu chuẩn chất lượng o Sai số xác lập o Đáp ứng quá độ ▫ Độ lọt vố
▫ Thời gian quá độ o Các tiêu chuẩn tối
ưu hóa quá độ o Quan hệ giữa đặc tính tần và sai số xác lập • Phân tích lOMoAR cPSD| 59735516
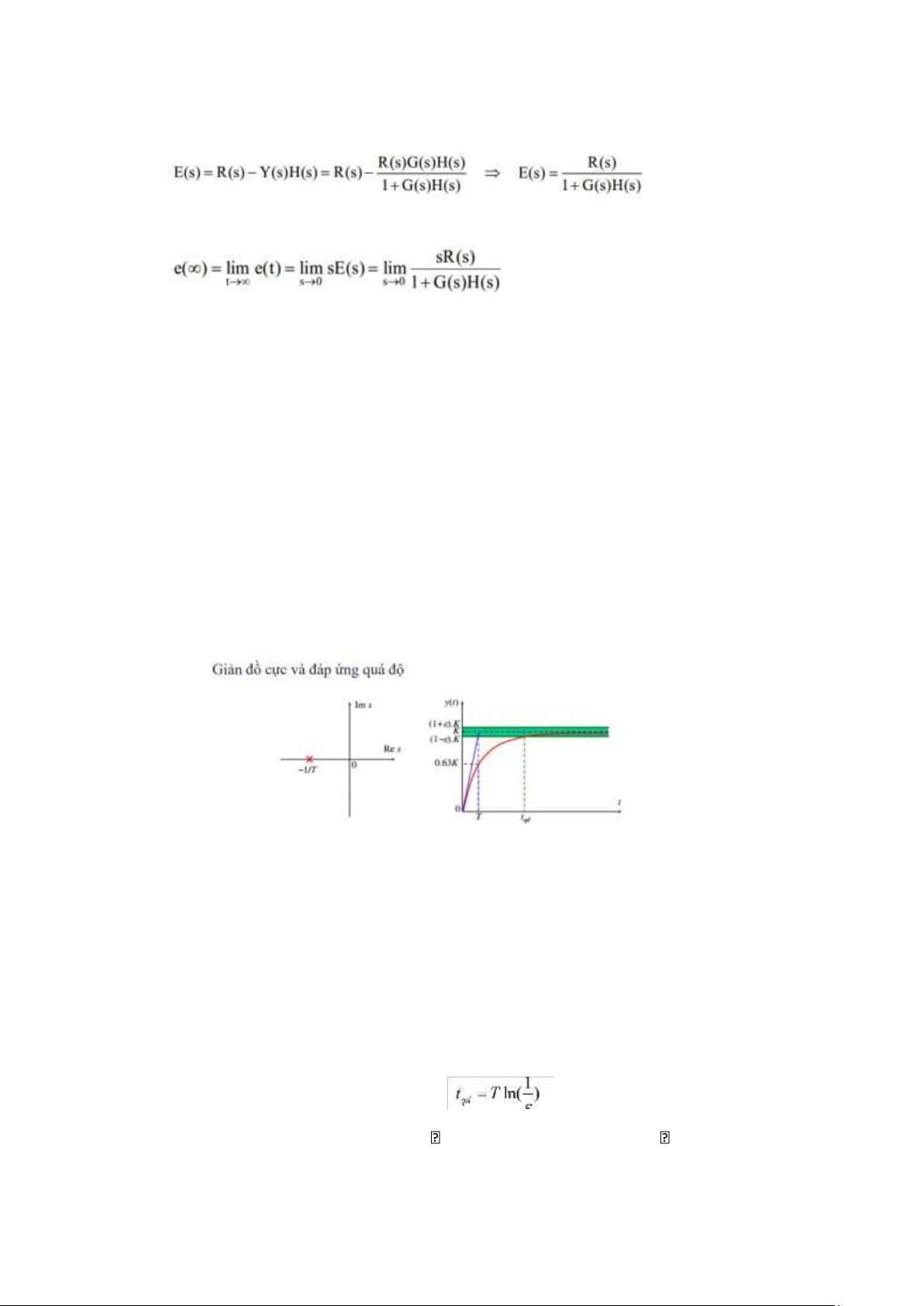
Sai số của hệ thống dưới dạng toán tử Laplace: Sai số xác lập:
Câu 30. Trình bày các thông số đặc trưng của quá trình quá độ.
• Các thông số chất lượng của đáp ứng quá độ:
- Thời gian quá độ (ts ) - Độ vọt lố (POT) - Sai số xác lập
Câu 31. Phân tích đáp ứng quá độ của hệ thống quán tính bậc nhất và hệ dao động tắt dần. • Hệ quán tính bậc 1:
o Hệ quán tính bậc 1 chỉ có 1 cực thực (-1/T), đáp ứng quá độ không có vọt lố.
o Hằng số thời gian T: là thời điểm đáp ứng của khâu quán tính bậc 1 đạt 63% giá trị xác lập.
o Cực thực càng nằm xa trục ảo thì hằng số thời gian T càng nhỏ, hệ thống đáp ứng càng nhanh.
o Thời gian quá độ của hệquán
tính bậc nhất là: o Với  = 0.02 (tiêu chuẩn 2%) hoặc  = 0.05 (tiêu chuẩn lOMoAR cPSD| 59735516
5%) o Cực nằm càng xa trục ảo đáp ứng của hệ càng nhanh, thời gian quá độ càng ngắn
Câu 32. Tóm tắt nội dung chương 4 trong 1 trang A4 theo Sơ đồ tư duy Mindmap Chương 5:
Câu 33. Các yêu cầu thiết kế hệ thống điều khiển tự động. Trình bày ảnh hưởng của các
khâu hiệu chỉnh cơ bản (P, PI, PID) lên chất lượng hệ thống. • Yêu cầu
o Hệ thống phải làm việc ổn định dưới tác động của tín hiệu vào (tín hiệu đặt) và tác động của nhiễu.
o Sai lệch tĩnh của hệ bằng 0 hoặc tín hiệu ra bám theo được tín hiệu vào trên 1 dải
tần số càng rộng càng tốt.
o Đáp ứng nhanh với sự thay đổi của trị số đặt chỉnh. Đạt các chỉ tiêu về thời gian
quá độ, độ vọt lố cho phép, độ dự trữ biên, dự trữ pha … o Hệ thống nhanh
chóng khử được ảnh hưởng của nhiễu. • Ảnh hưởng o Khâu P:
▫ Hệ số tỉ lệ càng lớn sai số xác lập càng nhỏ
▫ Tuy nhiên, hệ số tỉ lệ càng lớn độ vọt lố càng cao, hệ thống càng kém ổn định o Khâu PI:
▫ Giảm sai số xác lập, đối với tín hiệu vào là hàm nấc, hệ thống không có khâu
vi phân lý tưởng thì sai số sẽ bằng 0.
▫ Triệt tiêu nhiễu tần số cao.
▫ Chậm đáp ứng quá độ, tăng vọt lố. o Khâu PID:
▫ Cải thiện đáp ứng quá độ
▫ Giảm sai số xác lập
▫ Tăng bậc vô sai của hệ thống lOMoAR cPSD| 59735516
Câu 34. Trình bày 2 phương pháp của Ziegler – Nichols để xác định thông số bộ điều khiển PID.
Cách 1: Dựa vào đáp ứng quá độ của hệ hở
▫ Điều kiện để áp dụng phương pháp xấp xỉ mô hình bậc nhất có trễ của đối tượng là đối
tượng phải ổn định, không có dao động và ít nhất hàm quá độ của nó phải có dạng chữ S.
Cách 2: Dựa vào đáp ứng quá độ của hệ kín
▫ Tăng dần hệ số khuếch đại K của hệ kín đến giá trị giới hạn Kgh, khi đó đáp ứng ra của hệ
kín ở trạng thái xác lập là dao động ổn định với chu kì Tgh.
Câu 35. Tóm tắt nội dung chương 5 trong 1 trang A4 theo Sơ đồ tư duy Mindmap Thực hành
Câu 1 Ứng dụng Laplace giải phương trình vi phân:
1. Giải phương trình vi phân:
y ' '(t )+4 y(t )=9t
với điều kiện ban đầu y(0)=0; y’(0)=7 Giải Ta có :¿
 L{y (t)+4y(t)\}=L\{9t\
<=>s2Y (s)−7+4Y (s)= 92 s 2
<=>Y (s)= 74s +92 s +4 s •
Sử dụng phép laplace ngược ta có : y(t )=9s +19sin (¿2t)¿ 4
2. Giải hệ phương trình vi phân sau đây
x' (t)−2 x(t)+3 y(t)=0
{ y '(t)+2 x(t)− y(t)=0
với điều kiện ban đầu x(0)=8, và y(0)=3 Giải lOMoAR cPSD| 59735516
Ta có:{¿sX (s)−8−2X (s)+3Y (s)=0
¿sY (s)−3+2 X(s)−Y (s)=0 Hệ tương đương với :
¿sX (s)−8−2X (s)+3Y (s)=0
{ ¿sY (s)−3+2 X(s)−Y (s)=0
¿ X(s)= 28s−17 =s+51+ s−34 s −3s−4 { <=> s
¿Y (s)=s2 3s 4=s+1− s−4 − −
Sử dụng hàm Laplace ngược:
¿x(t)=5e−t+3e4t ¿
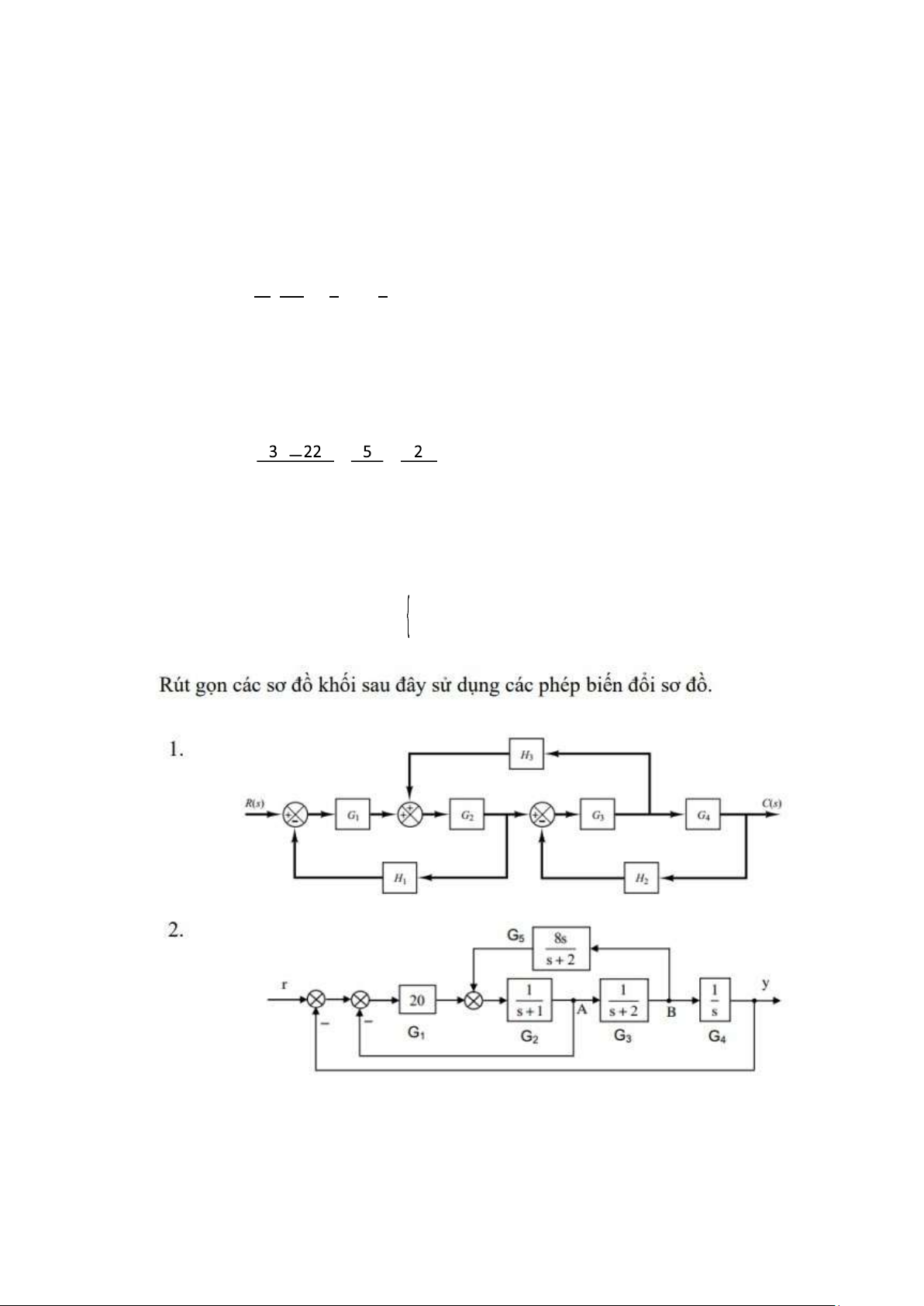
y(t)=5e−2t−2e4t Câu 2
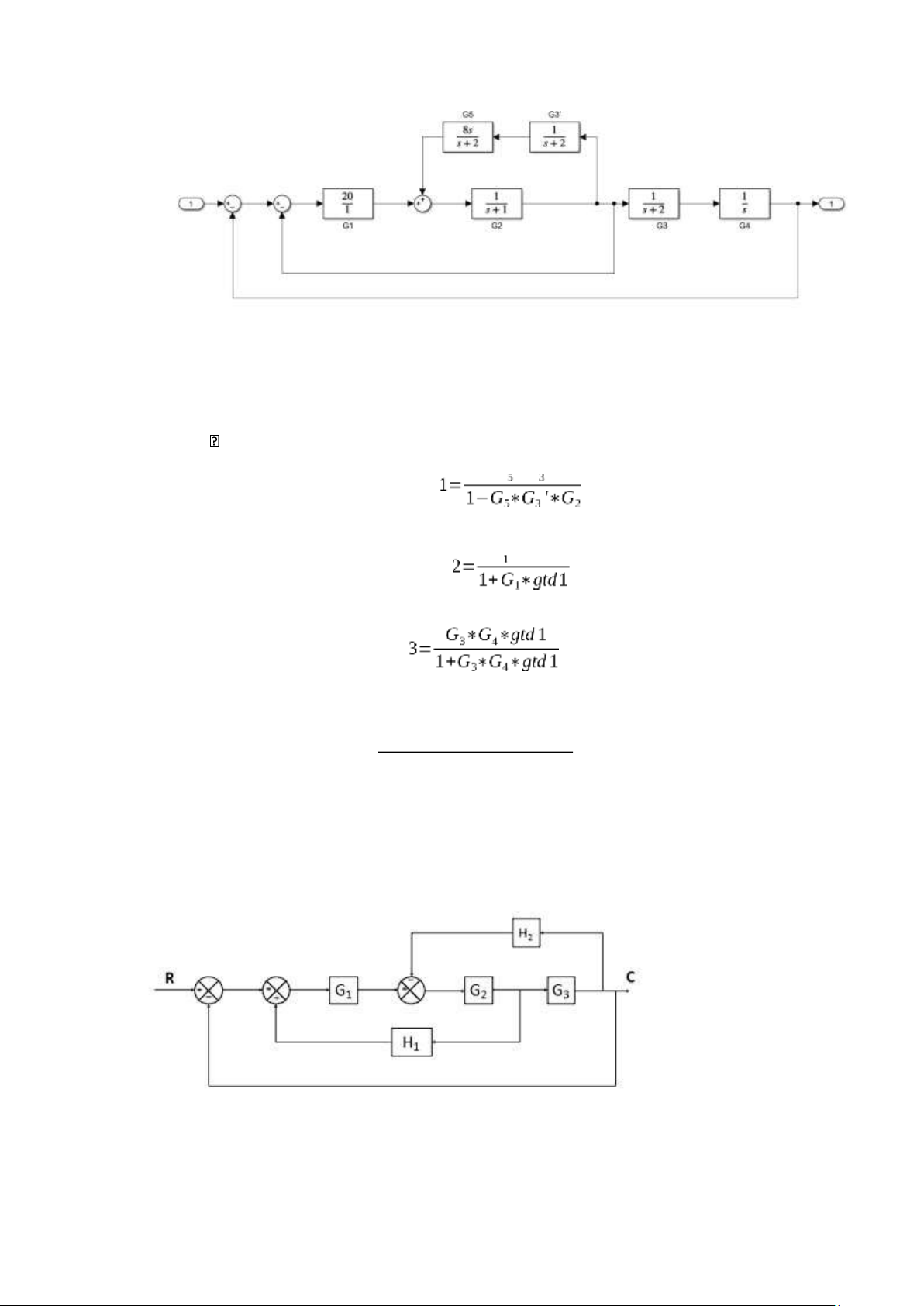
Chuyển nhánh B ra trước khối G3 ta có sơ đồ lOMoAR cPSD| 59735516 • Khi đó ta có : o
Khối gtd1 bao gồm ( G5 nối tiếp G3’) hồi tiếp dương với
G2 o Khối gtd2 bao gồm ( G1 nối tiếp với gtd1) hồi tiếp âm với 1
o Khối gtd3 bao gồm (gtd2 nối tiếp G3 nối tiếp G4) hồi tiếp âm với 1  Tính toán: G ∗G ' gtd G ∗gtd1 gtd gtd •
Kết quả thu được hàm truyền tương đương: Gtd= 4
3 20s+240 s +25s +80s +104 s+40
Câu 3: Cho hệ thống và sơ đồ vòng tín hiệu của nó như hình vẽ dưới đây. Tìm hàm
truyền của hệ thống theo 2 cách (sơ đồ khối và sơ đồ tín hiệu).
Biến đổi sơ đồ khối •
Chuyển điểm rẽ nhánh ra trước khối G3 ta có :