Lý thuyết và trắc nghiệm bài Phép đồng dạng Toán 11 (có lời giải)

Lý thuyết và trắc nghiệm bài Phép đồng dạng Toán 11 có lời giải và đáp án rất hay được soạn dưới dạng file word gồm 5 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

33 17 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Bài tập minh họa

Câu 1:   

   !"#$%

&'()*+', -./ *0, 

Lời giải

12  *+3, 4-./  ..

5*6 ) !"7 

890 : *+') 

: 

Trang 1

§➑. PHÉP ĐỒNG DẠNG

Chươn

g 1:

Tóm tắt lý thuyết

Ⓐ

➊Định nghĩa

 ;$ < !"-./=

>=?@A*6BC4D$9=C4

DCDE=CD

Nhận xét:

 ;FG;HF-./I

 ;*+'-./= !"-./J=J



D'();HF-./k*;HF-

./m#;HF-./pm

➋Tính chất: Phép đồng dạng tỉ số k:



Biến ba điểm thẳng hàng thành ba điểm thẳng

hàng và bảo toàn thứ tự giữa các điểm.



Biến đt  đt, tia  tia, đoạn thẳng  đoạn

thẳng.



Biến tam giác  tam giác đồng dạng với nó,

góc  góc bằng nó.



Biến đường tròn bán kính R  đường tròn bán

kính kR.

➌Hình đồng dạng

 Hai hình đgl đồng dạng với nhau nếu có một

PĐD biến hình này thành hình kia.



Phân dạng bài

tập

Ⓑ

K①Dạng 1:: Xác định ảnh của một hình qua một phép đồng dạng

L0 

MB * : 0

) * : L0 

Câu 2:   

   !"#$%&

'()*+', 4-./ *0, 

Lời giải

12  *+3, 4-./  .

.5*6 ) !"7 

890 : *+') : 

L0 N 0, 

 L0 

Câu 1:OP%&, *  *

& !"*6

Lời giải

;     !"  $   7



6 

Câu 2:OP%*Q$9= !"*6

Lời giải

M*Q * 

Trang 2

K②Dạng 2:Xác định ảnh của một hình qua một phép đồng dạng.

 6+RR*R G*Q $*Q



 R'(0, 40 

S5'(*+', -./ T*Q

#$%&'()$ !" L0

*Q !"*6

Dạng 1. Vận dụng lý thuyết

Câu 1:&=+.4=+sai?

A.T'()!#:!

B.T'():!*: !"#

: !"

C. ; !":#$(!

D.;!:#$( !"

Lời giải

Chọn C.

;!6:#$( !"

Câu 2: 1.3 !"*6-./ $B * P

 * 

A. B.

C. D.

Lời giải

Chọn C.

S3!U+V7;$  #2 !"-./

*6B $9=* PW

Q 

Dạng 2. Phương pháp tọa độ.

Câu 1: 2:  !" #$X*+'

, -./ */YPU $B B

2:

Trang 3

Bài tập rèn

luyện

Ⓒ

A. B.

C. D.

Lời giải

Chọn A.

Cách 1.

 ) 

7 

Cách 2.S3!U + 

-1

Chú ý: B.3!UQP.

 4*+', -./ ;*+')

$B B 7 

Câu 2: 2:  !" #$X*+'

, -./ */YPU $ 

 

A. B.

C. D.

Hướng dẫn giải

Chọn C.

Cách 1.

Trang 4

Z*+', -./ $B B 

[  Z/YPU$

  

Cách 2.

Z*+'7 0*7



Z/YPU7 0*

D)2 

Dạng 3. Nhận dạng phép đồng dạng, nhận dạng hình

Câu 1: O\L , 12 ]#B

 ; !"#$X*+',  -./   */

YP, $P& 

A. B.

C. D.

Hướng dẫn giải

Chọn C.

Trang 5

Bấm Tải xuống để xem toàn bộ.

| 1/5

| | Tải xuống

Preview text:

§➑. PHÉP ĐỒNG DẠNG

Chương 1:

Tóm tắt lý thuyết

Ⓐ

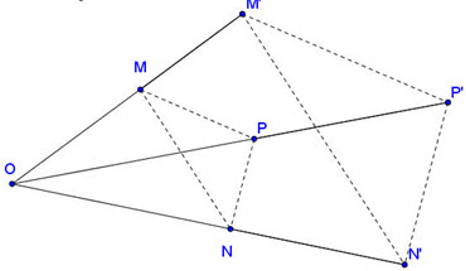
➊.Định nghĩa

Phép biến hình F đgl phép đồng dạng tỉ số k (k>0) nếu với hai điểm M, N bất kì có ảnh M′, N′ thì M′N′ = kMN.

⯎Nhận xét:

PDH là PĐD tỉ số 1.
Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|
Nếu thực hiện liên tiếp PĐD tỉ số k và PĐD tỉ số m ta được PĐD tỉ số pm

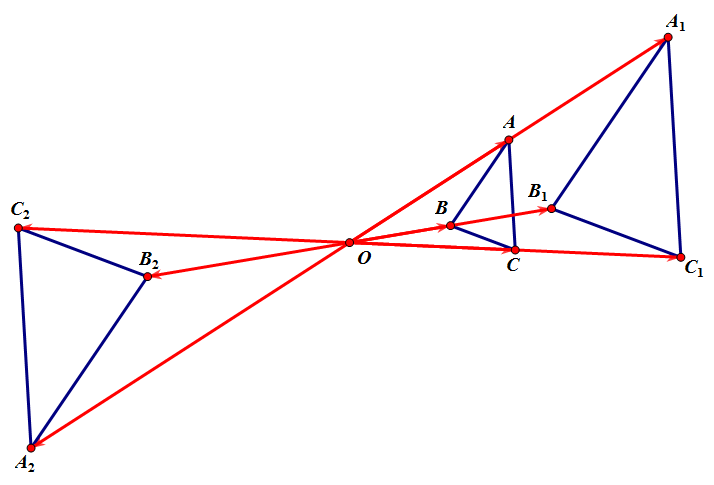
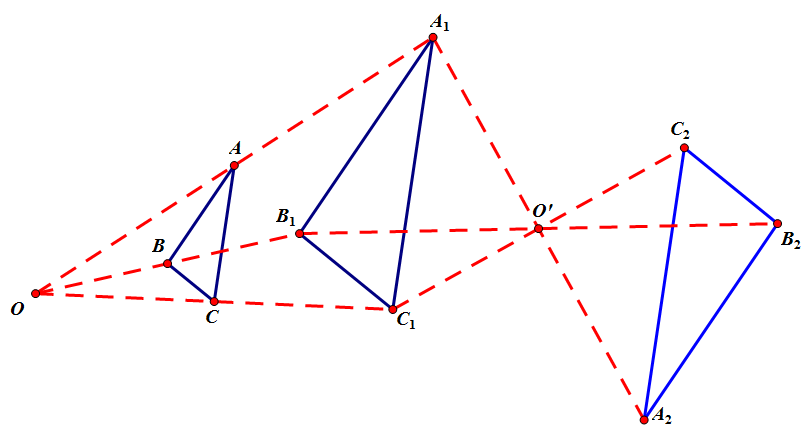
➋.Tính chất: Phép đồng dạng tỉ số k: Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm. Biến đt → đt, tia → tia, đoạn thẳng → đoạn thẳng. Biến tam giác → tam giác đồng dạng với nó, góc → góc bằng nó. Biến đường tròn bán kính R → đường tròn bán kính kR.

➌.Hình đồng dạng Hai hình đgl đồng dạng với nhau nếu có một PĐD biến hình này thành hình kia.

Phân dạng bài tập

Ⓑ

①. Dạng 1: : Xác định ảnh của một hình qua một phép đồng dạng

🞜Bài tập minh họa

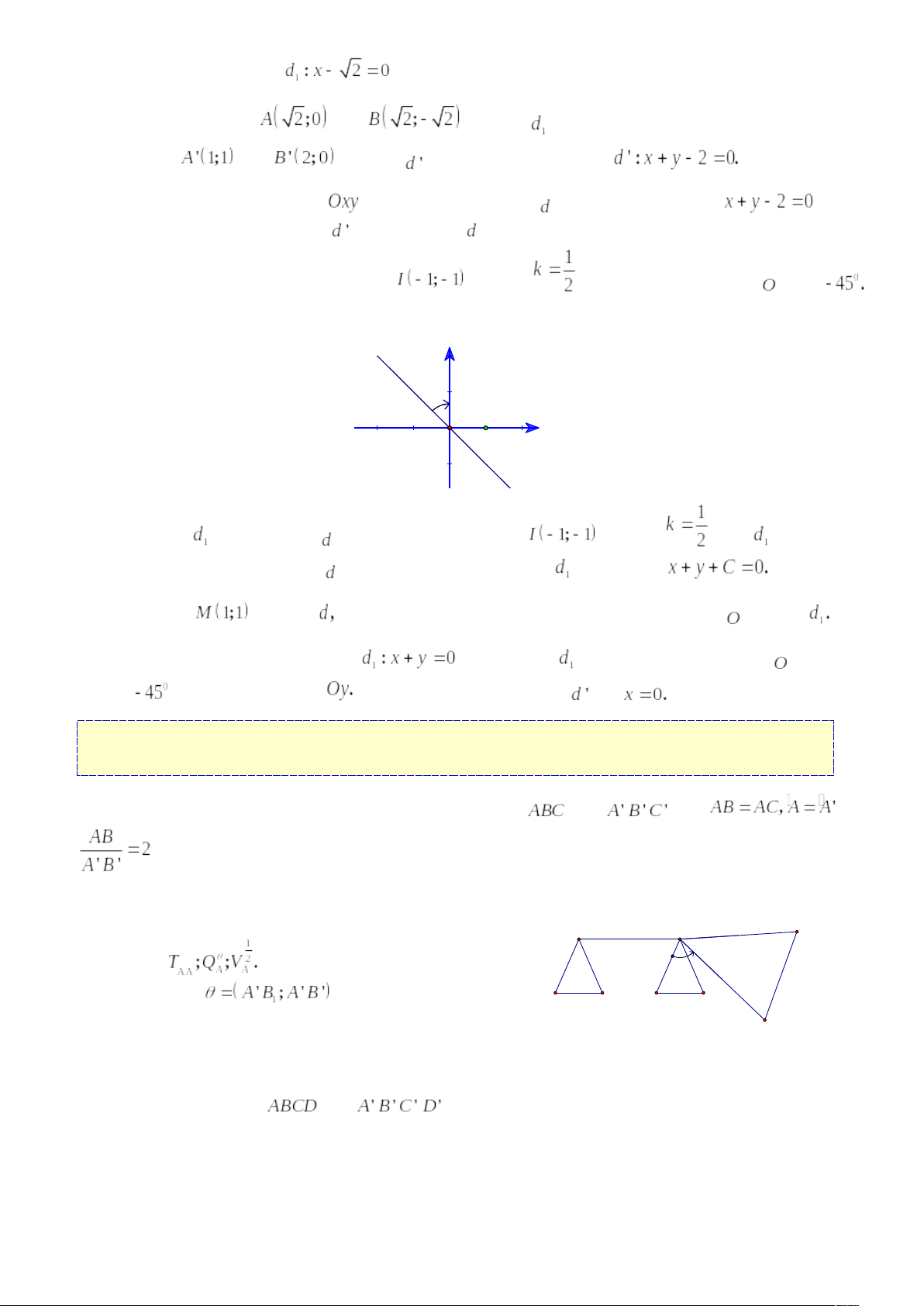
Câu 1: Trong mặt phẳng cho đường thẳng có phương trình . Viết phương trình đường thẳng là ảnh của qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm tỉ số và phép quay tâm góc

Lời giải

Gọi là ảnh của qua phép vị tử tâm , tỉ số . Vì song song hoặc trùng với nên phương trình của có dạng:

Lấy thuộc thì ảnh của nó qua phép vị tự nói trên là thuộc

Vậy phương trình của .

Xét hai điểm và thuộc thì ảnh của nó qua phép quay nói trên là và thuộc . Vậy phương trình

Câu 2: Trong mặt phẳng cho đường thẳng có phương trình . Viết phương trình đường thẳng là ảnh của qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm , tỉ số và phép quay tâm góc

Lời giải

Gọi là ảnh của qua phép vị tử tâm , tỉ số . Vì song song hoặc trùng với nên phương trình của có dạng:

Lấy thuộc thì ảnh của nó qua phép vị tự nói trên là thuộc

Vậy phương trình của . Ảnh của qua phép quay tâm góc là đường thẳng Vậy phương trình của là

②. Dạng 2: Xác định ảnh của một hình qua một phép đồng dạng.

Câu 1: Chứng minh rằng nếu hai tam giác cân và có và thì hai tam giác đó đồng dạng với nhau

Lời giải

Phép đồng dạng bao gồm:

Với

Câu 2: Chứng minh rằng hai hình vuông bất kì đồng dạng với nhau.

Lời giải

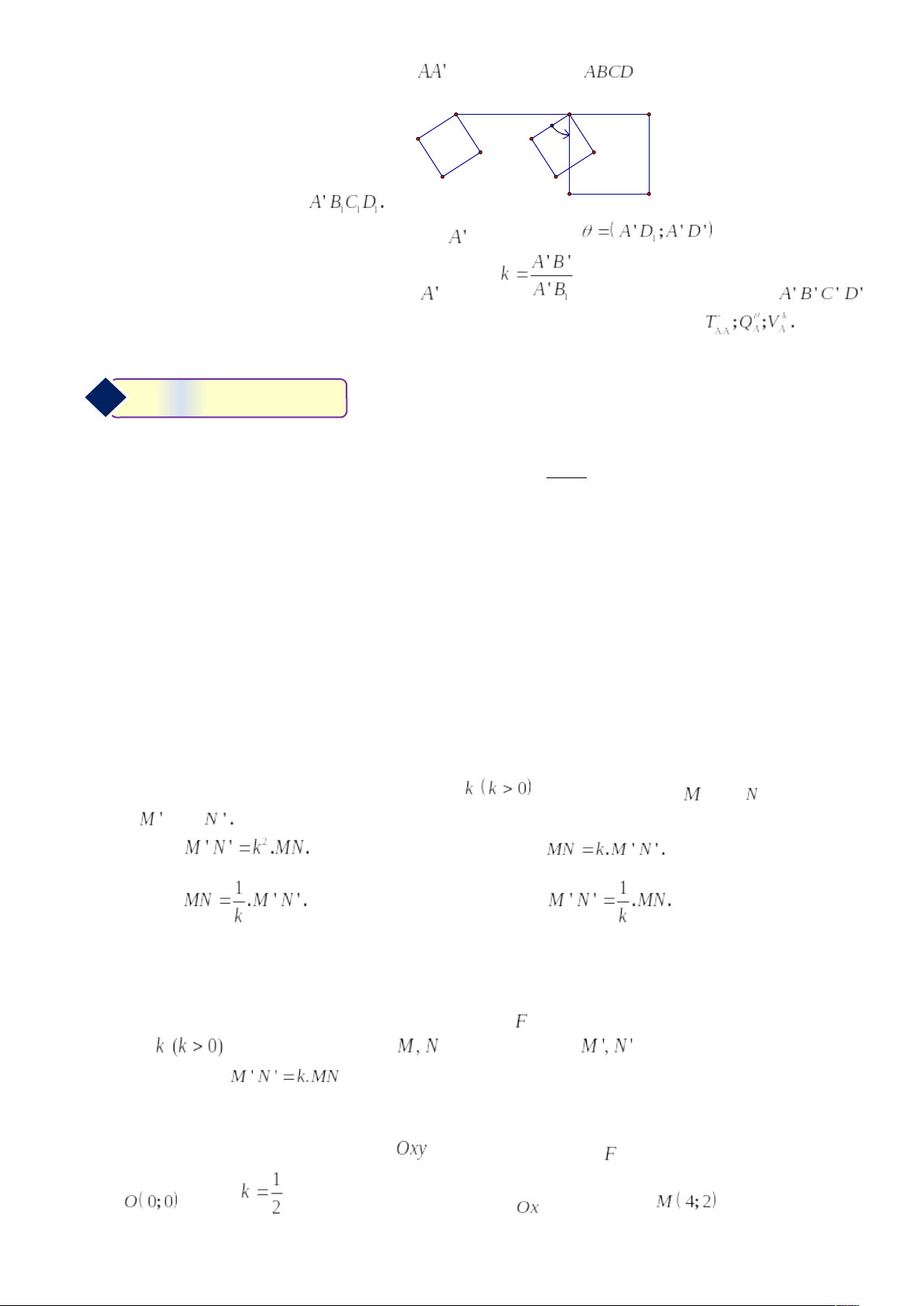
Xét hai hình vuông và .

Trước hết tịnh theo theo vectơ . Hình vuông biến thành hình vuông
Tiếp theo thực hiện phép quay tâm , góc quay .

Sau cùng thực hiện phép vị tự tâm tỉ số . Khi đó hình vuông có được bằng cách thự chiện liên tiếp ba phép đồng dạng Vậy hai hình vuông đồng dạng với nhau.

Bài tập rèn luyện

Ⓒ

⯎Dạng 1. Vận dụng lý thuyết

Câu 1:Trong các khẳng định sau, khẳng định nào sai?

A. Khi thực hiện liên tiếp hai phép dời hình ta được một phép dời hình.

B. Khi thực hiện liên tiếp một phép dời hình và một phép đồng dạng ta được một phép đồng dạng.

C. Phép đồng dạng là một trường hợp đặc biệt của phép dời hình.

D. Phép dời hình là một trường hợp đặc biệt của phép đồng dạng.

Lời giải

Chọn C.

Phép dời hình mới là một trường hợp đặc biệt của phép đồng dạng

Câu 2: Giả sử phép đồng dạng với tỉ số biến hai điểm và tương ứng thành và Ta có

A. B.

C. D.

Lời giải

Chọn C.

Sử dụng định nghĩa: Phép biến hình được gọi là phép đồng dạng tỉ số nếu với hai điểm bất kì và ảnh tương ứng của chúng ta luôn có .

⯎Dạng 2. Phương pháp tọa độ.

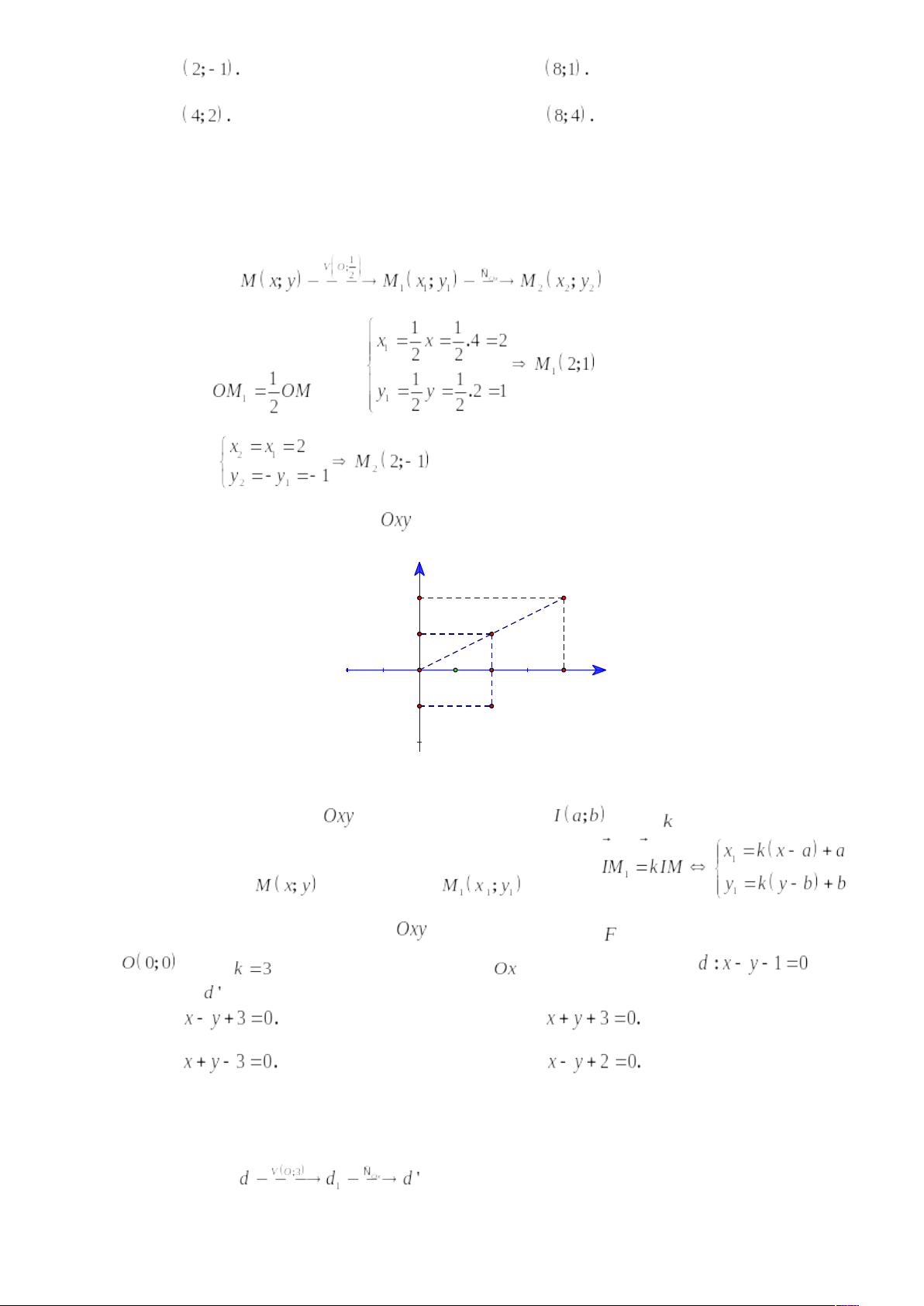
Câu 1: Trong mặt phẳng tọa độ phép đồng dạng hợp thành bởi phép vị tự tâm tỉ số và phép đối xứng trục biến điểm thành điểm có tọa độ

A. B.

C. D.

Lời giải

Chọn A.

Cách 1.

Ta có nên

Ta có:

Cách 2. Sử dụng đồ thị

Chú ý: Ta có thể sử dụng công thức sau

Trong mặt phẳng , cho phép vị tự tâm tỉ số . Phép vị tự trên biến điểm thành điểm . Ta có: .

Câu 2: Trong mặt phẳng tọa độ phép đồng dạng hợp thành bởi phép vị tự tâm tỉ số và phép đối xứng trục biến đường thẳng thành đường thẳng có phương trình