Thông tin
Quiz

Lý thuyết và trắc nghiệm bài Phương trình lượng giác cơ bản Toán 11 (có lời giải)

Lý thuyết và trắc nghiệm bài Phương trình lượng giác cơ bản Toán 11 có lời giải và đáp án rất hay được soạn dưới dạng file word gồm 29 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

Chủ đề:

Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT) 134 tài liệu

Môn:

Toán 11 3.3 K tài liệu

Thông tin:

32 trang 1 năm trước

Tác giả:

Thùy Dương (H)

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Lý thuyết và trắc nghiệm bài Phương trình lượng giác cơ bản Toán 11 (có lời giải)

50 25 lượt tải Tải xuống

Trang 1

§➋. PT LƯỢNG GIÁC CƠ BẢN

Chươn

g 1:

Tóm tắt lý thuyết

Ⓐ

➊Phương trình sinx = a



> 1: PT vô nghiệm



 1: PT có các nghiệm

. x = arcsina + k2, k  Z;

x =  – arcsina + k2, k  Z

Chú ý:



sinf(x) = sing(x) 



sinx = sin





Các trường hợp đặc biệt:

sinx = 1  x = + k2

sinx = –1  x = – + k2

sinx = 0  x = k

➋Phương trình cosx = a



> 1: PT vô nghiệm



 1: PT có các nghiệm

x = arccosa + k2, k  Z;

x = – arccosa + k2 , k  Z

Chú ý:



cosf(x) = cosg(x)  f(x) =  g(x) + k2, k  Z



cosx = cos

 x =  

+ k360

, k  Z

Các trường hợp đặc biệt:

cosx = 1  x = k2

cosx = –1  x =  + k2

cosx = 0  x = + k

. Bài tập minh họa:

Câu 1:  



B. 

C.  D. 

Lời giải

  

Trang 2

➌Phương trình tanx = a



ĐK: x  + k (k  Z).



PT có nghiệm x = arctana + k, k  Z;

Chú ý:



tanf(x) = tang(x) f(x) = g(x) + k, k  Z



tanx = tan





x =



+ k180

, k



Các trường hợp đặc biệt:

tanx = 1  x = + k

tanx = –1  x = – + k

tanx = 0  x = k

➍Phương trình cotx = a



ĐK: x  k (k  Z).



PT có nghiệm x = arccota + k, k  Z;

Chú ý:



cotf(x) = cotg(x)  f(x) = g(x) + k, k  Z



cotx = cot



 x =



+ k180

, k  Z

Các trường hợp đặc biệt:

cotx = 1  x = + k

cotx = –1  x = – + k

cotx = 0  x = + k

Phân dạng bài tập

Ⓑ

①Dạng 1:Phương trình sinx = a

Câu 2:  

A.  B. 

C.  D. 

Lời giải

Câu 3:  

A. 

B. 

C. 

D. 

Lời giải



Câu 4:  

A.  

B.  

C.  

D.  

Lời giải

  

Câu 5:  

A.  B. 

C.  D. 

Trang 3

Lời giải



. Bài tập minh họa:

Câu 1:  

A.  B. 

C.  D. 

Lời giải

 

Câu 2:  

A.  B. 

C.  D. 

Lời giải

 

Câu 3: !" 

A.  B.  C.  D. 

Lời giải

 

Câu 4:  

A.  B. 

C.  D. 

Lời giải

 

Trang 4

②Dạng 2:Phương trình cosx = a



Câu 5:  

A. 

B. 

C. 

D. 

Lời giải



. Bài tập minh họa:

Câu 1:  

A.  B. 

C.  D. 

Lời giải

 

Câu 2:  

A.  B.  C.  D. 

Lời giải



Câu 3:  

A.  B. 

C.  D. 

Lời giải

# $

Trang 5

③Dạng 3:Phương trình tanx = a

Câu 4: %&

'()





A.  B.  C.  D. 

Lời giải



*+ 

'() 

Câu 5: ," 

A.  B. 

C.  D. 

Lời giải

-.(

/0

1.(

. Bài tập minh họa:

Câu 1: 2/, 

A.  B.  C.  D. 

Lời giải

2/, 

Câu 2: ," 

A.   B.  

C.   D.  

Lời giải



 

Trang 6

④Dạng 4: Phương trình cotx = a



10)  

Câu 3: %& '() 

A.  B.  C.  D.

Lời giải

 

 ' 

Bài tập rèn luyện

Câu 1:  

A.  B. 

C.  D. 

Câu 2:  

A.  B. 

C.  D. 

Câu 3:  

A.  B. 

C.  D. 

Câu 4: !" 

A.  B.  C.  D. 

Câu 5: 134)15+6

A.  B. 

C. D. 

Câu 6:  

A.  B. 

Trang 7

C.  D. 

Câu 7: 78)15+6

A.  B.  C.  D. 

Câu 8:   7 

A.  B. 

C.  D. 

Câu 9: 





A.  B.  C.  D. 

Câu 10:  

A.  B. 

C.  D. 

Câu 11:  

A. 

B. 

C. 

D. 

Câu 12: 2/, 

A.  B.  C.  D. 

Câu 13:  

A.  B. 

C.  D. 

Trang 8

Câu 14:  

A.  B. 

C.  D. 

Câu 15:  

A.  B. 

C.  D. 

Câu 16: )")9:6

A.  B. 

C.  D. 

Câu 17:  

A.   B.  

C.   D.  

Câu 18:  

A.  B. 

C.  D. 

Câu 19: ;<1=)15+(<1=sai6

A.  B. 

C.  D. 

Câu 20:  

A.  B. 

C. D. 

Câu 21: )"4)'6

Trang 9

A.  B.  C.  D. 

Câu 22:  

A.  B. 

C.  D. 

Câu 23:  

A.  B. 

C.  D. 

Câu 24:  

A.  B. 

C.  D. 

Câu 25: ," 

A.   B.  

C.   D.  

Câu 26:  



B. 

C.  D. 

Câu 27: >8





A.  B.  C.  D. 

Câu 28: ;<1=)15+sai6

A. B.

C. D.

Câu 29:  (

A.  B.  C.  D. 

Câu 30:  

A. B.  C.  D. 

Câu 31:  

A.  B.  C.  D. 

Trang 10

Câu 32:  

A.  B.  C.  D. 

Câu 33: ?) )15+

A.  B.  C.  D. 

Câu 34: ?) )15+

A.  B.  C.  D. 

Câu 35: ?) 

A. B. C. D. .

Câu 36:  

A.  B.  C.  D. 

Câu 37: )"@4A1B@4A1B)sai6

A.  B. 

C.  D. 

Câu 38:  

A. B. 

C. D.

Câu 39:  7

A.  B.  C.  D. 

Câu 40:  

A.   B.  

C.   D.  

Câu 41:  

A.  B. 

Trang 11

C.  D. 

Câu 42: )15+9:6

A.  B. 

C.  D. 

Câu 43: 8 )()  A

4C2D 9E  &+'9 5&&

4F4)'6

A.  B.  C.  D. 

Câu 44:  

A.  B. 

C.  D. 

Câu 45: )()   4F

A.  B. 

C.  D. 

Câu 46: ," 

A.  B. 

C.  D. 

Câu 47: B," )()

4F *+ 4F4)'6

A.  B.  C.  D. 

Câu 48: %& '() 

A.  B.  C.  D.

Câu 49: ?)   9G2E15+

1!4C2D'1HI!"J1C)6

Trang 12

A. -C 1C  B. -C  1C



C. -C 1C  D. -C  1C



Câu 50:  

A.  B. 

C.  D. 

Câu 51:  4)''1)K 6

A. B. C. D.

Câu 52: %& '1)K 

A.  B.  C.  D. 

Câu 53: ""=& 1C 



A.  B.  C.  D. 

Câu 54:  4)''() 6

A. B. C. D.

Câu 55:  4)'7 6

A.  B.  C.  D. 

Câu 56:  "

A.  B. 

C.  D. 

Trang 13

Câu 57:  82K 9

 ;1L 6

A.  B.  C.  D. 

Câu 58: %& 7() 

A.  B.  C.  D. 

Câu 59: )2E15+M9E

 6

A.  B.  C.  D. 

Câu 60: %&

'()





A.  B.  C.  D. 

Câu 61: N@1HI!"9GOA   P

!"1C1&QR S& 



1!4C2D'1HI!"J1C)6

A. -C 1C B. -C   1C

C. -C 1C D. -C   1C

Câu 62: %& '1)K1)K 

A. T B. U C. V D. W

Câu 63:  

A.  B. 

C.  D. 

Câu 64: 





Trang 14

A.  B. 

C.  D. 

Câu 65:  

A.  B. 

C.  D. 

Câu 66: ?)    &   &    7       



A. W B. X C. U D. T

Câu 67:  

A.   B.  

C.   D.  

Câu 68:  

A.  B.  C.  D. 

Câu 69:  (

A.  B.  C.  D. 

Câu 70:  

A.  B.  C.  D. 

Câu 71: )")9:6

A.  B. 

C. D. 

Câu 72:  4)''() 6

A. B. C. D.

Câu 73: ?) ( ;1

4F

A. B. C. D.

Câu 74:   

Trang 15

A.  B. 

C.  D. 

Câu 75:  ,+)Y() 6

A.  B.  C.  D. 

Câu 76:  4)'71)K 6

A.  B.  C.  D. 

Câu 77: ," 

A.  B. 

C.  D. 

Câu 78: B5E,92/,

4F

A.  B.  C.  D. 

Câu 79: OA  "             2K  9

 9E "&+'2;1



4F

A. V B. T C. Z D. [

Câu 80:  9:( 

A.  B.  C.  D. 

Câu 81: %& '1)K 

A. V B. W C. T D. *:&

Câu 82: %& 71)K 

A.  B.  C.  D. 

Câu 83:  

A. . B. 

C.  D. 

Câu 84:  

Trang 16

A.  B. 

C.  D. 

Câu 85: ?  4)  '  "  =  +'      & m 1C    

6

A. B. C. D.

Câu 86: LB")1)K 

B. C. D.

Câu 87: LB," '1)K



A.  B.  C.  D. 

Câu 88:  9:(

A.  B.  C.  D.

Câu 89: )2E15+4C2D'1HI

!"W1C

A.  B.  C.  D. 

Câu 90: B" ' 

A.  B.  C.  D. 

Câu 91: ?)  &%&""=

+' 1C10)1\54'



A.  B.  C.  D.

Câu 92: ?)  LB"7

() '

Trang 17

A.  B.  C.  D. 

Câu 93: 2/,  

;1 4F

A. UW B. UT C. UV D. UU

BẢNG ĐÁP ÁN

1.D 2.C 3.A 4.B 5.C 6.B 7.A 8.C 9.D 10.C

11.A 12.B 13.A 14.D 15.A 16.B 17.C 18.D 19.A 20.A

21.D 22.C 23.C 24.D 25.D 26.B 27.C 28.C 29.A 30.D

31.C 32.C 33.C 34.B 35.C 36.C 37.D 38.C 39.C 40.D

41.A 42.C 43.C 44.A 45.D 46.A 47.D 48.D 49.D 50.A

51.D 52.A 53.D 54.B 55.D 56.D 57.A 58.C 59.C 60.D

61.A 62.D 63.B 64.C 65.A 66.D 67.C 68.A 69.B 70.B

71.D 72.B 73.A 74.B 75.C 76.C 77.D 78.C 79.D 80.C

81.C 82.C 83.D 84.D 85.B 86.C 87.B 88.D 89.C 90.D

91.D 92.B 93.C

Hướng dẫn giải

Câu 1: 

Câu 2:  

Câu 3:  

Câu 4:  

Câu 5: 

Câu 6:  

Câu 7: *E  

])1 78 

Câu 8:

Trang 18

Câu 9:  

Câu 10: 

 

Câu 11: 

Câu 12: 

2/, 

Câu 13: 



Câu 14:  

Câu 15: ^):R134 

Câu 16: *



'



9:

Câu 17:   

Câu 18:  

Câu 19: 

 

-"" 

Trang 19

Câu 20:  

Câu 21: ]) "= '"

 9:2)

Câu 22:  

Câu 23:   

Câu 24:         



*+ 

Câu 25: 

 

10)  

Câu 26:   

Câu 27:

Lời giải

Câu 28:

Lời giải

 %+?1""

Câu 29:

Lời giải

 ( 2) 

Câu 30:

Lời giải

*+8]

Câu 31:  

Câu 32: 

Câu 33: 

Trang 20

Câu 34: 

Câu 35:

Câu 36:



Câu 37: 

 '1""D

Câu 38: _ 

Câu 39:  *+ 7

10)

Câu 40:   

Câu 41: ^):R134 

Câu 42: `    9:



`   



`    



`          '       



Câu 43:  

*E %+ 9 

*+ 

Câu 44:  

Câu 45:  

Trang 21

%+)() 10)



Câu 46:  

Câu 47:  

*E 

*+ 

Câu 48:  

 ' 

Câu 49:  

?"!"  P!1!4C2D'

1HI!"4a"1C 9 

Câu 50:  # $

Câu 51: Cách 1:

 9E

`$ bK '

*+ WX'1)K

Cách 2:

Trang 22

]M1HI!"'1)K  W

c9E ?UX1)K9+'

d1)KW'+10)WUXeWX'

81"" D.

Câu 52:  

 

1! 

? "= R9E ' 

Câu 53:  

(9f( 

Câu 54:   

Trường hợp 1:  

* 

*+, "= R9EH!  

       

Trường hợp 2:  

* 

*+, "= R9EH!  

      

*+'() 10), 

Câu 55:   

Trang 23

 

%+  

*+  7 

Nhận xét: Hàm số tuần hoàn với chu kì , nên trên mỗi đoạn

có độ dài bằng một chu kì thì phương trình có đúng một nghiệm.

Mà đoạn được chia làm đoạn có độ dài bằng 1 chu kì

dạng , , …, nên phương trình

đã cho có nghiệm.

Câu 56: 

Câu 57:    

 

Câu 58: ?"U



`$N@ 

*+ W' 

?"W

>& &P)9E( 'd()

1724F( :1\



])1'  1\

Câu 59:  

Câu 60:  



*+ 

'() 

Trang 24

Câu 61: 

 

]c9)1HI!"1C4C2D

1C



1C 

Câu 62: T lun

gN@

?f7

gN@

?f7

*+W71)K 

Câu 63: 

Câu 64:



Trang 25

Câu 65: 



Câu 66: 

])1

H!U*E

]) '

%+ 1! 

H!W*E

]) '

%+ 1! 1! 

*+T7    



Câu 67:   

Câu 68: -.(  

 

;A!9E1.(1!  

Câu 69:  (9f(

Câu 70: 

Trang 26



Câu 71:  

 '9:

Câu 72:   

Trường hợp 1:  

* 

*+, "= R9EH!  

       

Trường hợp 2:  

* 

*+, "= R9EH!  

      

*+'() 10), 

Câu 73: 

(9f(

%+

Câu 74:    

;A*+ 

Câu 75:  

])

h3("2) 

Trang 27

*+

Câu 76:  



*+8+71)K  



*+8+771)K  

*+41P471)K 

Câu 77: -.(

/0

1.(

Câu 78:  

>U  E,

?8

>W  /,

?8

;1BP 

Câu 79: 



Trang 28

Câu 80: +) (

+) 9:(

?81""?

Câu 81: -;N- 

;1 

h ' ;A!9E1.(+



'1)K  

Câu 82:  

* U'1)K

Câu 83:  

  

  9:

*+8 

Câu 84:  

Câu 85: 10)19E

* '

*+'W"=8O

Câu 86:

Lời giải

-.(1Ci

Trang 29

;1 )"9E1(

*+B")1)K  

Câu 87: 



* ' 

`*E  %+ 

`*E c %+ 

*+B,"10)'  

Câu 88: ^)j+A 9:( 

Câu 89: ,+W1Ch9")1C1H<9:9E

kK1C 9E1HI!"⇒h9"1C4C

2D!"4 ⇒

-"" C.

Câu 90: 



h ' ]) '

Trang 30



Câu 91:

 10)19E

U

'

%+

Câu 92: 



`N@ 

]) * '(:"= 

`N@ 

]) * '"= 



*E 

Trang 31

*E 

])1'() 10) 9 

*+B"10))() 



Câu 93: Q"1= 

 



2/, 

Trang 32

Bấm Tải xuống để xem toàn bộ.

| 1/32

| | Tải xuống

Preview text:

§➋. PT LƯỢNG GIÁC CƠ BẢN

Chương 1:

Tóm tắt lý thuyết

Ⓐ

➊.Phương trình sinx = a

> 1: PT vô nghiệm
≤ 1: PT có các nghiệm

➀. x = arcsina + k2π, k ∈ Z;

➁. x = π – arcsina + k2π, k ∈ Z

🞜Chú ý:

sinf(x) = sing(x) ⇔
sinx = sinβ⁰ ⇔

🞜Các trường hợp đặc biệt:

➀.sinx = 1 ⇔ x = + k2π

➁.sinx = –1 ⇔ x = – + k2π

➂.sinx = 0 ⇔ x = kπ

➋. Phương trình cosx = a

> 1: PT vô nghiệm
≤ 1: PT có các nghiệm

➀.x = arccosa + k2π, k ∈ Z;

➁.x = – arccosa + k2π, k ∈ Z

🞜Chú ý:

cosf(x) = cosg(x) ⇔ f(x) = ± g(x) + k2π, k ∈ Z
cosx = cosβ⁰ ⇔ x = ± β⁰ + k360⁰, k ∈ Z

🞜Các trường hợp đặc biệt:

➀.cosx = 1 ⇔ x = k2π

➁.cosx = –1 ⇔ x = π + k2π

➂.cosx = 0 ⇔ x = + kπ

➌. Phương trình tanx = a

ĐK: x ≠ + kπ (k ∈ Z).
PT có nghiệm x = arctana + kπ, k ∈ Z;

🞜Chú ý:

tanf(x) = tang(x) ⇔f(x) = g(x) + kπ, k ∈ Z
tanx = tanβ⁰ ⇔ x = β⁰ + k180⁰, k ∈ Z

🞜Các trường hợp đặc biệt:

➀.tanx = 1 ⇔ x = + kπ

➁.tanx = –1 ⇔ x = – + kπ

➂.tanx = 0 ⇔ x = kπ

➍. Phương trình cotx = a

ĐK: x ≠ kπ (k ∈ Z).
PT có nghiệm x = arccota + kπ, k ∈ Z;

🞜Chú ý:

cotf(x) = cotg(x) ⇔ f(x) = g(x) + kπ, k ∈ Z
cotx = cotβ⁰ ⇔ x = β⁰ + k180⁰, k ∈ Z

🞜Các trường hợp đặc biệt:

➀.cotx = 1 ⇔ x = + kπ

➁.cotx = –1 ⇔ x = – + kπ

➂.cotx = 0 ⇔ x = + kπ

Phân dạng bài tập

Ⓑ

①. Dạng 1: Phương trình sinx = a

🗵. Bài tập minh họa:

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

Ta có: , .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

Tập nghiệm của phương trình là

A. .

B. .

C. .

D. .

Lời giải

Ta có

Nghiệm của phương trình là

A. ; .

B. ; .

C. ; .

D. ; .

Lời giải

Ta có: .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

②. Dạng 2: Phương trình cosx = a

🗵. Bài tập minh họa:

Giải phương trình sau .

A. . B. .

C. . D. .

Lời giải

Ta có: .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

Ta có .

Phương trình lượng giác có nghiệm là

A. . B. . C. . D. .

Lời giải

Ta có .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

Ta có .

Tập nghiệm của phương trình là

A. .

B. .

C. .

D. .

Lời giải

③. Dạng 3: Phương trình tanx = a

🗵. Bài tập minh họa:

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

Nghiệm của phương trình là:

A. . B. . C. . D. .

Lời giải

Nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

().

Số nghiệm của phương trình trên khoảng là

A. . B. . C. . D. .

Lời giải

Vậy phương trình có nghiệm trên khoảng .

Tất cả các nghiệm của phương trình là

A. . B. .

C. . D. .

Lời giải

Điều kiện

thỏa mãn điều kiện.

④. Dạng 4: Phương trình cotx = a

🗵. Bài tập minh họa:

Nghiệm dương nhỏ nhất của phương trình là

A. . B. . C. . D. .

Lời giải

Nghiệm dương nhỏ nhất của phương trình là .

Tất cả các nghiệm của phương trình là:

A. , . B. , .

C. , . D. , .

Lời giải

Ta có:

, .

Nghiệm của phương trình đã cho là: , .

Số nghiệm của phương trình trên khoảng là

A. . B. . C. . D.

Lời giải

Ta có: .

, mà nên .

🞜Bài tập rèn luyện

Nghiệm của phương trình là

A. . B. .

C. . D. .

Giải phương trình sau .

A. . B. .

C. . D. .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Phương trình lượng giác có nghiệm là

A. . B. . C. . D. .

Nghiệm đặc biệt nào sau đây là sai?

A. . B. .

C. D. .

Nghiệm của phương trình là

A. . B. .

C. . D. .

là một họ nghiệm của phương trình nào sau đây?

A. . B. . C. . D. .

Phương trình , thuộc có nghiệm là

A. . B. .

C. . D. .

Nghiệm của phương trình là

A. . B. . C. . D. .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Tập nghiệm của phương trình là

A. .

B. .

C. .

D. .

Nghiệm dương nhỏ nhất của phương trình là

A. . B. . C. . D. .

Phương trình có nghiệm là

A. . B. .

C. . D. .

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Phương trình có nghiệm là

A. . B. .

C. . D. .

Trong các phương trình sau, phương trình nào vô nghiệm?

A. . B. .

C. . D. .

Nghiệm của phương trình là

A. ; . B. ; .

C. ; . D. ; .

Phương trình có tập nghiệm là

A. . B. .

C. . D. .

Khẳng định nào sau đây là khẳng định sai?

A. . B. .

C. . D. .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Trong các phương trình sau có bao nhiêu phương trình có nghiệm?

A. . B. . C. . D. .

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Tất cả các nghiệm của phương trình là:

A. , . B. , .

C. , . D. , .

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Họ nghiệm của phương trình là:

A. . B. . C. . D. .

Khẳng định nào sau đây là sai?

A. B.

C. D.

Phương trình có nghiệm khi:

A. . B. . C. . D. .

Nghiệm của phương trình là

A. B. . C. . D. .

Nghiệm của phương trình là:

A. . B. . C. . D. .

Nghiệm của phương trình .

A. . B. . C. . D. .

Cho là nghiệm của phương trình nào sau đây

A. . B. . C. . D. .

Cho là nghiệm của phương trình nào sau đây

A. . B. . C. . D. .

Cho phương trình , nghiệm của phương trình là:

A. B. C. D. .

Phương trình có nghiệm là

A. . B. . C. . D. .

Trong các phép biến đổi sau, phép biến đổi nào sai?

A. . B. .

C. . D. .

Nghiệm của phương trình là

A. B. .

C. D.

Phương trình có một nghiệm là

A. . B. . C. . D. .

Giải phương trình .

A. , . B. , .

C. , . D. , .

Phương trình có nghiệm là:

A. . B. .

C. . D. .

Phương trình nào sau đây vô nghiệm?

A. . B. .

C. . D. .

Gọi là nghiệm trong khoảng của phương trình , nếu biểu diễn với , là hai số nguyên và là phân số tối giản thì bằng bao nhiêu?

A. . B. . C. . D. .

Nghiệm của phương trình: là.

A. . B. .

C. . D. .

Trong khoảng phương trình có tập nghiệm bằng

A. . B. .

C. . D. .

Tìm tất cả các nghiệm của phương trình .

A. . B. .

C. . D. .

Tổng tất cả các nghiệm của phương trình trong khoảng bằng . Vậy bằng bao nhiêu?

A. . B. . C. . D. .

Số nghiệm của phương trình trên khoảng là

A. . B. . C. . D.

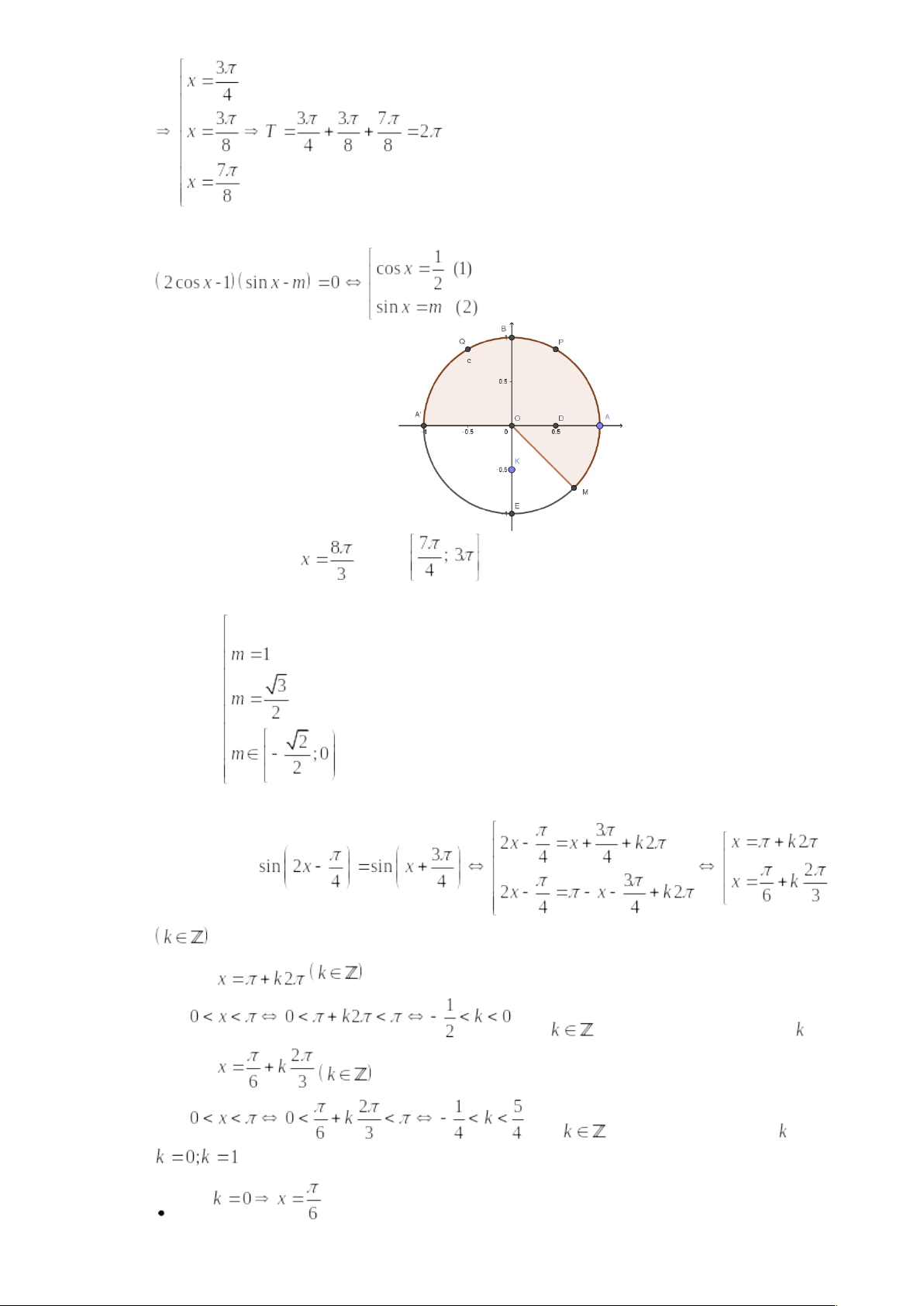
Cho như hình vẽ dưới đây. Nghiệm của phương trình được biểu diễn trên đường tròn lượng giác là những điểm nào?

A. Điểm , điểm . B. Điểm , điểm .

C. Điểm , điểm . D. Điểm , điểm .

Nghiệm của phương trình là

A. . B. .

C. . D. .

Phương trình có bao nhiêu nghiệm trên đoạn ?

A. B. C. D.

Số nghiệm của phương trình trên đoạn là

A. . B. . C. . D. .

Tập các giá trị của tham số để phương trình có nghiệm là

A. . B. . C. . D. .

Phương trình có bao nhiêu nghiệm trên khoảng ?

A. B. C. D.

Phương trình có bao nhiêu nghiệm thuộc ?

A. . B. . C. . D. .

Phương trình có các nghiệm là

A. . B. .

C. . D. .

Phương trình có hai họ nghiệm có dạng và , . Khi đó, tính ?

A. . B. . C. . D. .

Số nghiệm của phương trình: thuộc khoảng là

A. . B. . C. . D. .

Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình ?

A. . B. . C. . D. .

Số nghiệm của phương trình trên khoảng là

A. . B. . C. . D. .

Xét đường tròn lượng giác như hình vẽ. Biết lần lượt là các điểm đối xứng của qua gốc Nghiệm của phương trình được biểu diễn trên đường tròn lượng giác là những điểm nào?

A. Điểm , điểm B. Điểm điểm

C. Điểm điểm D. Điểm điểm

Số nghiệm của phương trình trên đoạn đoạn là

A. 3. B. 1. C. 4. D. 2.

Nghiệm của phương trình là

A. . B. .

C. . D. .

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Phương trình có tập nghiệm là

A. . B. .

C. . D. .

Cho hàm số, số nghiệm thuộc của phương trình là

A. 2. B. 0. C. 1. D. 3.

Nghiệm của phương trình là

A. ; . B. ; .

C. ; . D. ; .

Phương trình có nghiệm là

A. . B. . C. . D. .

Phương trình có nghiệm khi

A. . B. . C. . D. .

Tập nghiệm của phương trình là:

A. . B. . C. . D. .

Trong các phương trình sau phương trình nào vô nghiệm?

A. . B. .

C. D. .

Phương trình có bao nhiêu nghiệm trên khoảng ?

A. B. C. D.

Cho phương trình có nghiệm khi Khi đó bằng

A. B. C. D.

Tập nghiệm của phương trình là

A. . B. .

C. . D. .

Phương trình có mấy nghiệm trong nửa khoảng ?

A. . B. . C. . D. .

Phương trình có bao nhiêu nghiệm thuộc đoạn ?

A. . B. . C. . D. .

Tất cả các nghiệm của phương trình là

A. . B. .

C. . D. .

Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình bằng

A. . B. . C. . D. .

Biết các nghiệm của phương trình có dạng và ,; với là các số nguyên dương. Khi đó bằng

A. 4. B. 3. C. 5. D. 6.

Phương trình vô nghiệm khi là:

A. . B. . C. . D. .

Số nghiệm của phương trình trên đoạn là:

A. 4. B. 2. C. 3. D. Vô số.

Số nghiệm của phương trình thuộc đoạn là

A. . B. . C. . D. .

Giải phương trình .

A. . B. .

C. . D. .

Giải phương trình .

A. . B. .

C. . D. .

Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm?

A. B. C. D.

Tính tổng các nghiệm trong đoạn của phương trình:

A. B. C. D.

Tính tổng tất cả các nghiệm của phương trình trên đoạn .

A. . B. . C. . D. .

Phương trình: vô nghiệm khi m là:

A. . B. . C. . D.

Phương trình nào dưới đây có tập nghiệm biểu diễn trên đường tròn lượng giác là 2 điểm

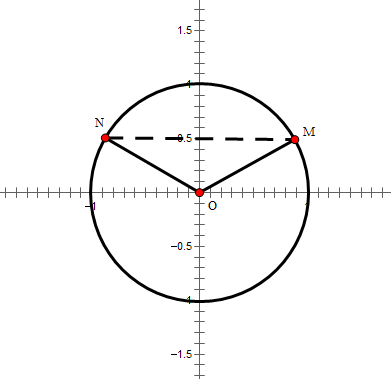
A. . B. . C. . D. .

Tìm tổng các nghiệm của phương trình trên .

A. . B. . C. . D. .

Cho phương trình là tham số. Số các giá trị nguyên của để phương trình đã cho có đúng hai nghiệm phân biệt trên là

A. . B. . C. . D.

Cho phương trình . Tính tổng các nghiệm thuộc khoảng của phương trình trên.

A. . B. . C. . D. .

Nghiệm dương nhỏ nhất của phương trình là . Khi đó bằng

A. 12. B. 13. C. 14. D. 11

BẢNG ĐÁP ÁN

1.D	2.C	3.A	4.B	5.C	6.B	7.A	8.C	9.D	10.C
11.A	12.B	13.A	14.D	15.A	16.B	17.C	18.D	19.A	20.A
21.D	22.C	23.C	24.D	25.D	26.B	27.C	28.C	29.A	30.D
31.C	32.C	33.C	34.B	35.C	36.C	37.D	38.C	39.C	40.D
41.A	42.C	43.C	44.A	45.D	46.A	47.D	48.D	49.D	50.A
51.D	52.A	53.D	54.B	55.D	56.D	57.A	58.C	59.C	60.D
61.A	62.D	63.B	64.C	65.A	66.D	67.C	68.A	69.B	70.B
71.D	72.B	73.A	74.B	75.C	76.C	77.D	78.C	79.D	80.C
81.C	82.C	83.D	84.D	85.B	86.C	87.B	88.D	89.C	90.D
91.D	92.B	93.C

Hướng dẫn giải

Câu 1:

Câu 2: Ta có: .

Câu 3: Ta có .

Câu 4: Ta có .

Câu 5:

Câu 6: .

Câu 7: Với ta có: .

Do đó là một họ nghiệm của phương trình .

Câu 8:

Câu 9: .

Câu 10:

Ta có .

Câu 11: Ta có

Câu 12:

Nghiệm dương nhỏ nhất của phương trình là .

Câu 13: Ta có

Câu 14: .

Câu 15: Theo công thức nghiệm đặc biệt thì .

Câu 16: Vì là nên phương trình vô nghiệm.

Câu 17: Ta có: .

Câu 18: .

Câu 19: Ta có:

⮚ .

Đáp án sai : .

Câu 20: .

Câu 21: Do có tập giá trị là nên các phương trình có nghiệm; phương trình vô nghiệm do

Câu 22: Ta có .

Câu 23: .

Câu 24: Ta có phương trình .

Vậy tập nghiệm của phương trình là .

Câu 25: Ta có:

, .

Nghiệm của phương trình đã cho là: , .

Câu 26: Ta có: , .

Câu 27:

Lời giải

Câu 28:

Lời giải

Ta có: Suy ra C là đáp án sai

Câu 29:

Lời giải

Phương trình có nghiệm khi do .

Câu 30:

Lời giải

. Vậy chọn D

Câu 31: .

Câu 32: Ta có:

Câu 33: Ta có:

Câu 34: Ta có:

Câu 35:

Câu 36:

Câu 37:

Ta có , nên đáp án D sai.

Câu 38: * Ta có: .

Câu 39: . Vậy là một nghiệm của pt đã cho.

Câu 40: Ta có , .

Câu 41: Theo công thức nghiệm đặc biệt thì .

Câu 42: + Phương trình phương trình vô nghiệm.

+ Phương trình phương trình có nghiệm.

+ Phương trình mà nên phương trình có nghiệm.

Câu 43: Phương trình .

Với . Suy ra và .

Vậy .

Câu 44: .

Câu 45: .

Suy ra trong khoảng phương trình đã cho có tập nghiệm là .

Câu 46: Ta có .

Câu 47: .

Với .

Vậy .

Câu 48: Ta có: .

, mà nên .

Câu 49: .

Các cung lượng giác , lần lượt được biểu diễn trên đường tròn lượng giác bởi các điểm và .

Câu 50: ().

Câu 51: Cách 1:

Ta có , với

+) Lại có nên

Vậy phương trình có 20 nghiệm trên đoạn

Cách 2:

Dùng đường tròn lượng giác, trên đoạn phương trình có 2 nghiệm, tương tự với Có 10 đoạn như vậy, trên mỗi đoạn có 2 nghiệm nên suy ra phương trình đã cho có 2.10=20 trên chọn đáp án D.

Câu 52: .

Ta có: .

Ta được .

Có giá trị , ứng với nghiệm của phương trình trên .

Câu 53: Ta có: có nghiệm

khi và chỉ khi .

Câu 54: Ta có: .

⮚ Trường hợp 1: .

Vì .

Vậy có tất cả có giá trị tương ứng với trường hợp có nghiệm là:

; ; ; ; ; ; ; .

⮚ Trường hợp 2: .

Vì .

Vậy có tất cả có giá trị tương ứng với trường hợp có nghiệm là:

; ; ; ; ; ; ;

Vậy trên khoảng phương trình đã cho có tất cả là nghiệm.

Câu 55: , mà .

, .

Suy ra , .

Vậy có nghiệm thuộc .

Nhận xét: Hàm số tuần hoàn với chu kì , nên trên mỗi đoạn có độ dài bằng một chu kì thì phương trình có đúng một nghiệm. Mà đoạn được chia làm đoạn có độ dài bằng 1 chu kì dạng , , …, nên phương trình đã cho có nghiệm.

Câu 56: Ta có:

Câu 57: .

Câu 58: Cách 1:

+) Xét .

Vậy phương trình có 2 nghiệm trên .

Cách 2:

Hàm số là hàm số tuần hoàn với chu kì . Trên mỗi khoảng có độ dài bằng chu kì thì phương trình luôn có đúng hai nghiệm.

Do đó trên thì phương trình có đúng hai nghiệm.

Câu 59: .

Câu 60: .

Vậy phương trình có nghiệm trên khoảng .

Câu 61: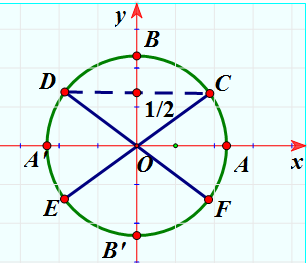

Ta có: .

Dựa vào đường tròn lượng giác ta có điểm biểu diễn nghiệm của phương trình là điểm điểm .

Câu 62: Tự luận

- Xét

Chỉ có một nghiệm

- Xét

Chỉ có một nghiệm

Vậy phương trình có 2 nghiệm thuộc đoạn .

Câu 63:

Câu 64: Ta có

Câu 65:

Câu 66: Ta có

Do đó

Trường hợp 1. Với

Do nên

Suy ra ta được .

Trường hợp 2. Với

Do nên

Suy ra ta được ta được .

Vậy có 3 nghiệm thuộc của phương trình là ; ; .

Câu 67: Ta có: .

Câu 68: Điều kiện: .

Ta có: .

Kết hợp với điều kiện ta được .

Câu 69: Phương trình có nghiệm khi và chỉ khi

Câu 70: Ta có:

Câu 71: .

Ta có nên phương trình vô nghiệm.

Câu 72: Ta có: .

⮚ Trường hợp 1: .

Vì .

Vậy có tất cả có giá trị tương ứng với trường hợp có nghiệm là:

; ; ; ; ; ; ; .

⮚ Trường hợp 2: .

Vì .

Vậy có tất cả có giá trị tương ứng với trường hợp có nghiệm là:

; ; ; ; ; ; ;

Vậy trên khoảng phương trình đã cho có tất cả là nghiệm.

Câu 73: Ta có:

Phương trình có nghiệm khi và chỉ khi

Suy ra:

Câu 74: Phương trình: .

Kết luận: Vậy phương trình tập nghiệm .

Câu 75: Ta có: .

Mặt khác do .

Vậy phương trình có nghiệm

Câu 76: Ta có .

Vậy họ nghiệm này có hai nghiệm thuộc đoạn là .

Vậy họ nghiệm này có một nghiệm thuộc đoạn là .

Vậy phương trình ban đầu có ba nghiệm thuộc đoạn .

Câu 77: Điều kiện

thỏa mãn điều kiện.

Câu 78: ;

TH1: ; lớn nhất

Chọn

TH2: ; nhỏ nhất

Chọn

Khi đó tổng cần tìm là: .

Câu 79:

Câu 80: +) , phương trình có nghiệm khi

+) , phương trình vô nghiệm khi

Chọn đáp án C

Câu 81: ĐKXĐ: .

Khi đó: .

Mà nên . Kết hợp với điều kiện, suy ra nghiệm của

phương trình trên đoạn là .

Câu 82: Ta có .

Vì Phương trình có 1 nghiệm trên đoạn

Câu 83: Ta có : .

Giải : .

Giải : , phương trình vô nghiệm.

Vậy phương trình có họ nghiệm là .

Câu 84: Ta có: .

Câu 85: Phương trình đã cho tương đương với phương trình

Vì nên

Vậy nên có 2 giá trị chọn B

Câu 86:

Lời giải

Điều kiện để phương trình có nghĩa

Khi đó, phương trình so sánh với đk

Vậy, tổng các nghiệm trong đoạn của phương trình là: .

Câu 87: Ta có .

Vì nên .

+ Với . Ta có . Suy ra .

+ Với . Tương tự . Suy ra .

Vậy tổng tất cả các nghiệm của phương trình đã cho trên là .

Câu 88: Theo lý thuyết phương trình vô nghiệm khi: .

Câu 89: Ta thấy 2 điểm M và N là các giao điểm của đường thẳng vuông góc với trục tung tại điểm với đường tròn lượng giác ⇒ M và N là các điểm biểu diễn tập nghiệm của phương trình lượng giác cơ bản: ⇒ Đáp án. C.