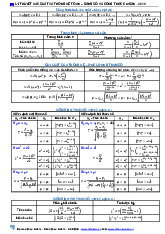
Preview text:
CHƯƠNG I: BIẾN CỐ - XÁC SUẤT CỦA BIẾN CỐ
1.3. Có 3 người, mỗi người bắn 1 viên đạn vào bia với xác suất bắn trúng bia của mỗi
người lần lượt là 0,7; 0,8; 0,9.
a. Tính xác suất để cả ba người bắn trúng bia.
b. Tính xác suất để có đúng 1 người bắn trúng bia.
c. Biết có đúng 1 người bắn trúng bia. Tính xác suất để đó là người thứ nhất. Giải
Gọi A là biến cố “người thứ I bắn trúng bia.” I=1,2,3. i
a) Gọi A là biến cố “cả ba người bắn trúng bia” A=A A A 1 2 3
P ( A )=P ( A A A )=P ( A ) P (A ) P ( A )=0,7.0,8 .0,9 1 2 3 1 2 3
b) Gọi B là biến cố có đúng một người bắn trúng bia B … P ( A B ) P( A A . A )
P( A ) P (A ) P( A ) c) P (A1)= 1 = 1 2 3 = 1 2 3
=0,7.0,2.0,1 /P(B). B P (B) P(B ) P ( B)
1.8. Một nhà máy sản xuất bóng đèn có 2 phân xưởng. Phân xưởng 1 sản xuất 60% tổng
số bóng đèn, phân xưởng 2 sản xuất 40% tổng số bóng đèn. Tỉ lệ bóng đèn không đạt tiêu
chuẩn của 2 phân xưởng lần lượt là 2% và 4%. Lấy ngẫu nhiên 1 bóng đèn của nhà máy đó để kiểm tra.
a. Tính xác suất để bóng đèn đó không đạt tiêu chuẩn.
b. Nếu bóng đèn được kiểm tra là bóng đèn không đạt tiêu chuẩn thì khả năng bóng đèn
đó do phân xưởng nào sản xuất nhiều hơn? Giải.
Gọi B là biến cố bóng đèn được chọn không đạt tiêu chuẩn.
Gọi A là biến cố “bóng đèn được chọn là bóng thuộc phân xưởng i” i=1,2 i
{A , A } là hệ đầy đủ các biến cố. 1 2
P ( B )=P (A ) P(B|A )+P ( A )P ( B|A ) 1 1 2 2 0,6.0,02+0,4.0,04=¿
b)P ( A |B)=… 1
P ( A |B)=¿… 2 1
CHƯƠNG II: ĐẠI LƯỢNG NGẪU NHIÊN
Dạng 1. Tính các tham số đặc trưng và phân phối xác suất.
2.1. Có 2 xạ thủ, mỗi người bắn 1 viên đạn vào bia với xác suất bắn trúng bia của mỗi
người lần lượt là 0,7; 0,8. Hỏi trung bình có bao nhiêu viên đạn trúng bia?
Gọi X là số viên đạn trúng bia.
X là số viên đạn trúng bia của người thứ i i
Ta có: X =X +X suy ra E ( X )=E( X )+E (X )=0,7+0,8. 1 2 1 2
Mà X A (0,7) ; X A (0,8) suy ra E ( X )=0,7 ; E( X )=0,8 1 2 1 2
Cách 2: X :0,1,2
Gọi A là biến cố người thứ I bắn trúng bia i
P (X=0 )=P ( A . A )=0,3.0,2 1 2
P ( X=1 )=P ( A . A )+P ( A . A ) 1 2 1 2
2.7. Một xạ thủ bắn 5 phát đạn vào một mục tiêu. Xác suất bắn trúng mục tiêu của xạ thủ đó là 0,8.
a. Tính xác suất để xạ thủ bắn trúng mục tiêu 2 lần.
b. Tính xác suất để có ít nhất một lần xạ thủ bắn trúng mục tiêu.
c. Tính xác suất để có ít nhất 3 lần xạ thủ bắn trúng mục tiêu.
d. Hỏi trung bình có bao nhiêu lần xạ thủ bắn trúng mục tiêu.
Gọi X là số viên đạn trúng bia trong 5 viên. X B(5;0,8) 2
P ( X=2 )=C . 0,82.0,23 5 E(X)=n.p
2.13. Chiều dài của một loại sản phẩm được chế tạo trên máy tự động là đại lượng ngẫu
nhiên có phân phối chuẩn với độ lệch tiêu chuẩn là 1,5 .
cm Sản phẩm được coi là đạt tiêu
chuẩn nếu chiều dài của nó sai lệch so với chiều dài trung bình không quá 2,94 . cm
a. Tính tỷ lệ sản phẩm đạt tiêu chuẩn.
b. Tính xác suất để trong 4 sản phẩm có ít nhất một sản phẩm đạt tiêu chuẩn.
c. Mỗi sản phẩm đạt tiêu chuẩn bán được lãi 20 nghìn đồng, mỗi sản phẩm không đạt
tiêu chuẩn bị lỗ 5 nghìn đồng. Hỏi nếu sản suất và tiêu thụ 1000 sản phẩm thì trung bình lãi được bao nhiêu tiền. 2
Gọi X là chiều dài của sản phẩm loại đó (cm). X N (a;1,52)
Tỷ lệ sản phẩm đạt tiêu chuẩn
P (|X − a|≤2,94 )=P( −2,94 ≤ X − a ≤2,94) =P (a −2,94 ≤ X ≤ a+2,94)
¿ Φ(a+2,94−a)−Φ(a−2,94−a) 1,5 1,5
¿ Φ(2,94)−Φ(−2,94)=2Φ(2,94 )=2Φ(1,96)=2.0,475=0,95 1,5 1,5 1,5
Gọi Y là số sản phẩm đạt tiêu chuẩn trong 4 sản phẩm được sản xuất. Y B(4 ; 0,95 )
Tính P (Y ≥ 4)
d) Gọi Z là số sản phẩm đạt tiêu chuẩn trong 1000 sản phẩm được sản xuất. Z B(1000 ; 0,95)
Gọi T là tiền lãi khi sản xuất và tiêu thụ 1000 sản phẩm này (nghìn đồng)
T =20. Z −5( 1000 − Z)=25 Z −5000
E ( T )=25 E (Z ) −5000=25.1000.0,95 −5000
CHƯƠNG III: ƯỚC LƯỢNG THAM SỐ
Dạng 1. Xác định khoảng tin cậy khi ước lượng vọng toán
Bài 3.3. Trong một hồ nuôi cá chép, người ta bắt lên 100 con thì thấy:
Khối lượng (g) 400 - 430 430 - 460 460 - 490 490 - 520 520 - 550 550 - 580 Số con cá 4 16 24 32 18 6
Hãy ước lượng khối lượng trung bình của toàn bộ cá chép trong hồ với độ tin cậy 99%.
Gọi X là khối lượng của một con cá chép trong hồ (g). đặt E ( X )=a; D ( X )=σ2
Đây là bài toán ước lượng giá trị trung bình.
Ta có n=100>30, σ chưa biết nên khoảng tin cậy của a là ( x−ε ; x+ε ;) trong đó s ε =u . α √n 2
Theo bài ta có dãy thống kê dạng điểm 41 50 X (g) 445 475 535 565 5 5 n 4 16 24 32 18 6 3
x= 1 (4.415+ 16.445+24.475+32.505+18.535+6.565 )=493,6 100
s2= 1 ( 4.4152+16.4452+24.4752+ 32.5052+ 18.5352+ 6.5652)− 493,62=1364,04 100 s= √1001364,04=37,119 99 =u =2,58
α =1 − γ=1− 0,99=0,01 suy ra uα 0,005 2 Vậy ε = 2,58.37,119=9,5767 √100
Vậy khối lượng trung bình của cá chép trong hồ nằm trong khoảng ()
Dạng 2. Xác định khoảng tin cậy khi ước lượng xác suất
Bài 3.11. Kiểm tra khối lượng 100 sản phẩm trong 1 kho hàng được kết quả:
Khối lượng (kg) 1,8 1,9 2,0 2,1 2,2 Số sản phẩm 10 15 30 20 25
Căn cứ vào mẫu trên, hãy ước lượng số sản phẩm trong kho hàng với độ tin cậy 0,95.
Biết rằng trong kho hàng có 2000 sản phẩm khối lượng không quá 2,0 kg.
Gọi p là tỷ lệ sản phẩm có khối lượng không quá 2kg
Đây là bài toán ước lương cho p. +
Theo bài ra ta có f = 10+15 30 =0,55. 0 100
Nên n.f (1− f )=100.0,55 .0,45=24,75>20 nên khoảng tin cậy của p là 0 0 ( √f (1−f ) √f (1−f ) 0 0 0 0 f −u ; f +u ) 0 α √n 0 α /2 √ n 2 Với = =
α =1 −0,95=0,05 suy ra u u 1,96 α 0,025 2 Nên √ 0,55.0,45 √0,55.0,45
p ∈(0,55−1,96. ; 0,55+1,96. ) √ 100 √100
Gọi N là số sản phẩm trong kho hàng suy ra 4 √ 0,55.0,45 √0,55.0,45
p= 2000 ∈(0,55−1,96. ; 0,55+1,96. ) N √100 √100
Dạng 1. Kiểm định vọng toán
4.1. Khối lượng trung bình 1 loại sản phẩm theo quy định là 500 gam. Người ta nghi ngờ
khối lượng các s/phẩm sản xuất ra nhiều hơn so với quy định nên lấy 81 sản phẩm để kiểm
tra thì thấy khối lượng trung bình là 505 gam, độ lệch tiêu chuẩn mẫu điều chỉnh là 30 gam.
Dựa vào kết quả thu được, hãy kiểm định nghi ngờ trên với mức ý nghĩa 0,025. 5