



Preview text:
lOMoAR cPSD| 58675420
MÔ HÌNH HÓA VÀ PHÂN TÍCH HỆ THỐNG CƠ KHÍ
Năm học: HKII 2023-2024 Bài 1:
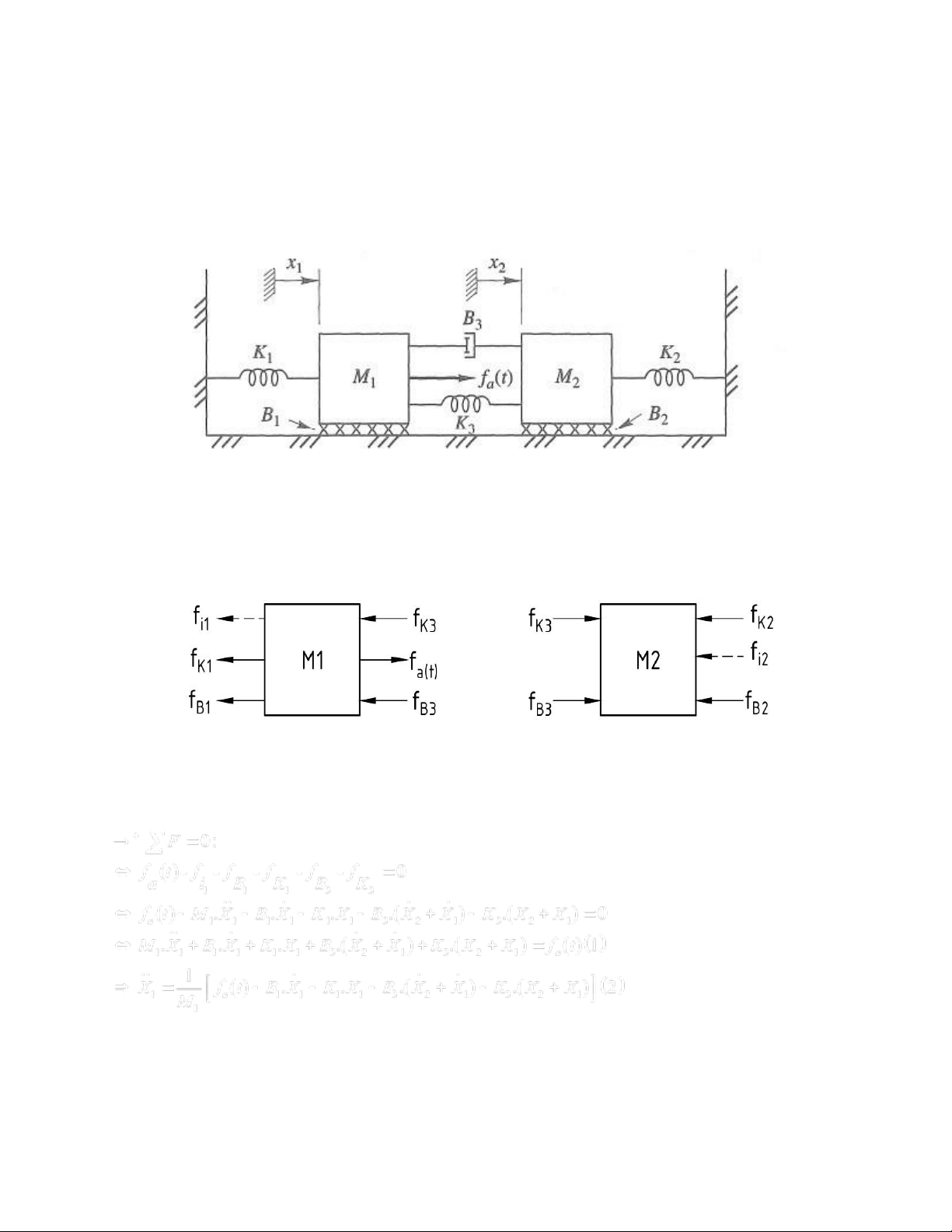
Cho hệ thống cơ khí như hình vẽ.
Cho: M1= 50 kg, M2=5 kg, B1= 10 N-s/m, B2= 10 N-s/m, B3= 20 N-s/m, K₁=10 N/m, K₂= 10 N/m, K3= 10 N/m. Tìm:
a) Vẽ sơ đồ vật thể tự do của hệ thống (Free Body Diagram )
b) Viết phương trình trạng thái chuyển động của hệ thống theo góc x1 và x2 dùng nguyên lý
Da’lembert Với vật M1: Với vật M2: lOMoAR cPSD| 58675420
c) Viết phương trình chuyển động của thanh dùng hàm truyền Laplace và lập công thức tính
hàm truyền Laplace của hệ thống Với vật M1:
- Biến đổi Laplace 2 vế với ĐKĐ = 0, ta được: Với vật M2:
- Biến đổi Laplace 2 vế với ĐKĐ = 0, ta được:
Thay phương trình (6) vào phương trình (5), ta được: lOMoAR cPSD| 58675420
Thay phương trình (7) vào (6), ta được:
Hàm truyền Laplace của hệ thống: từ phương trình (7) và (8)
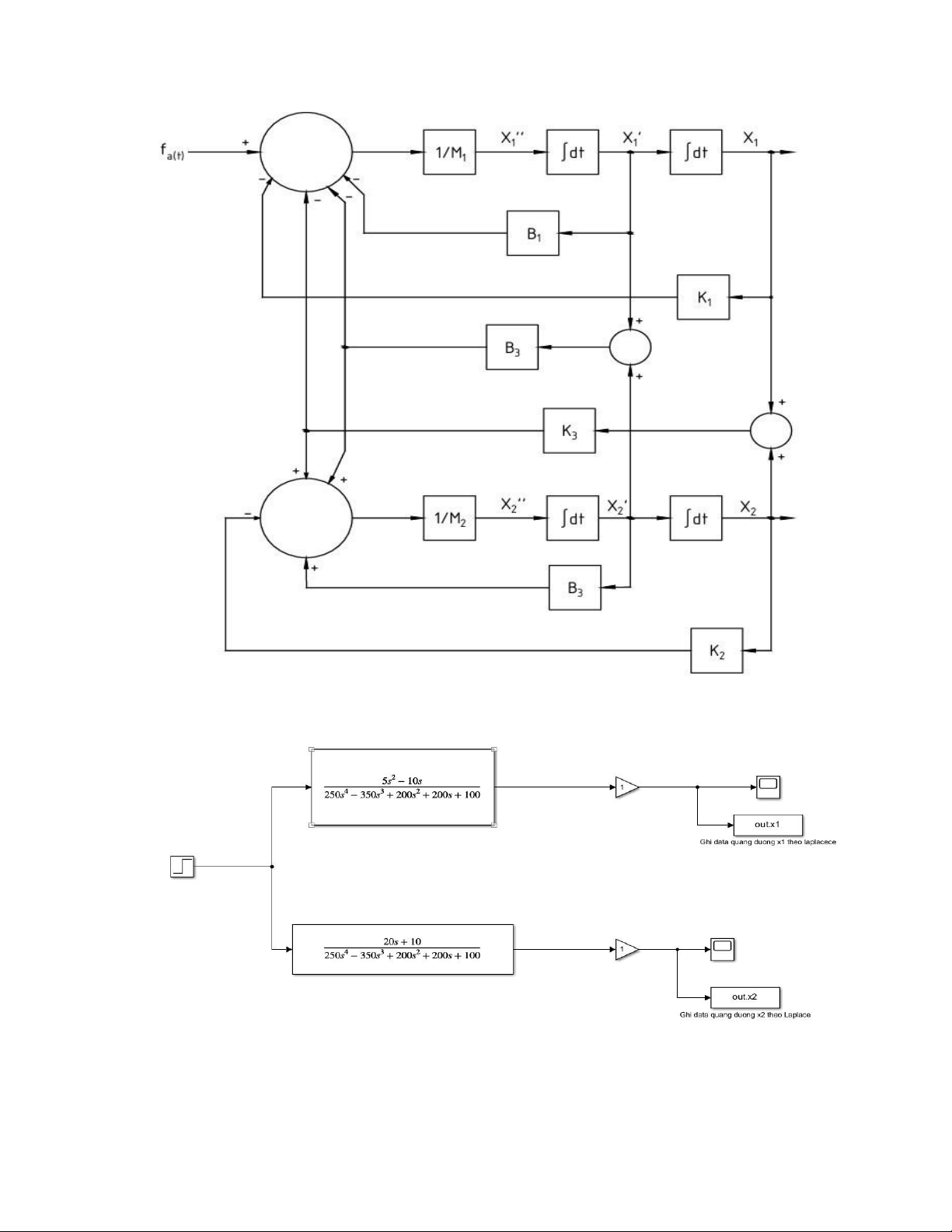
d) Vẽ sơ đồ khối dùng lý thuyết khối block diagram cho phương trình vi phân Da’lembert lOMoAR cPSD| 58675420
e) Vẽ sơ đồ khối dùng lý thuyết khối block diagram cho hàm truyền truyền Laplace
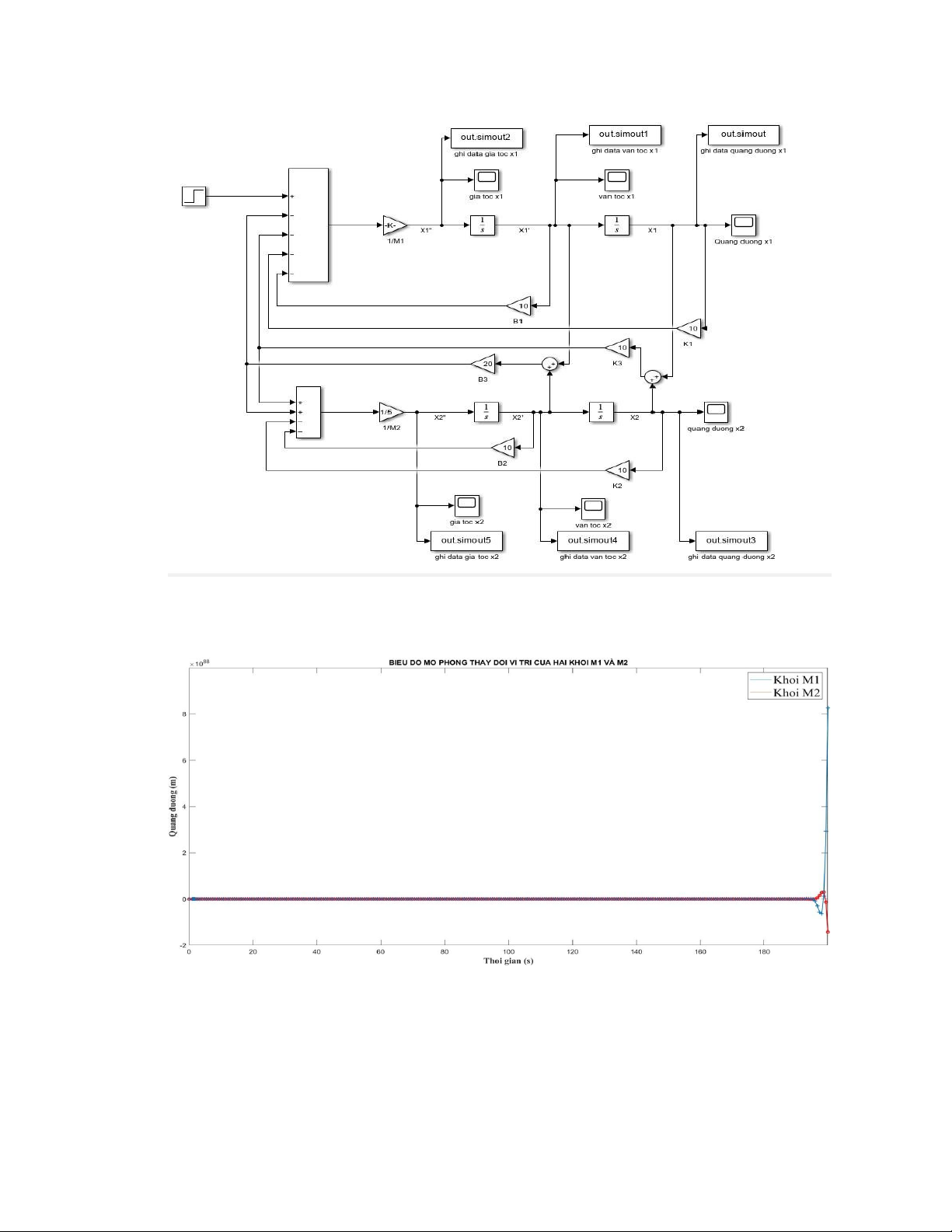
f) Vẽ sơ đồ khối dùng matlab Simulink lOMoAR cPSD| 58675420
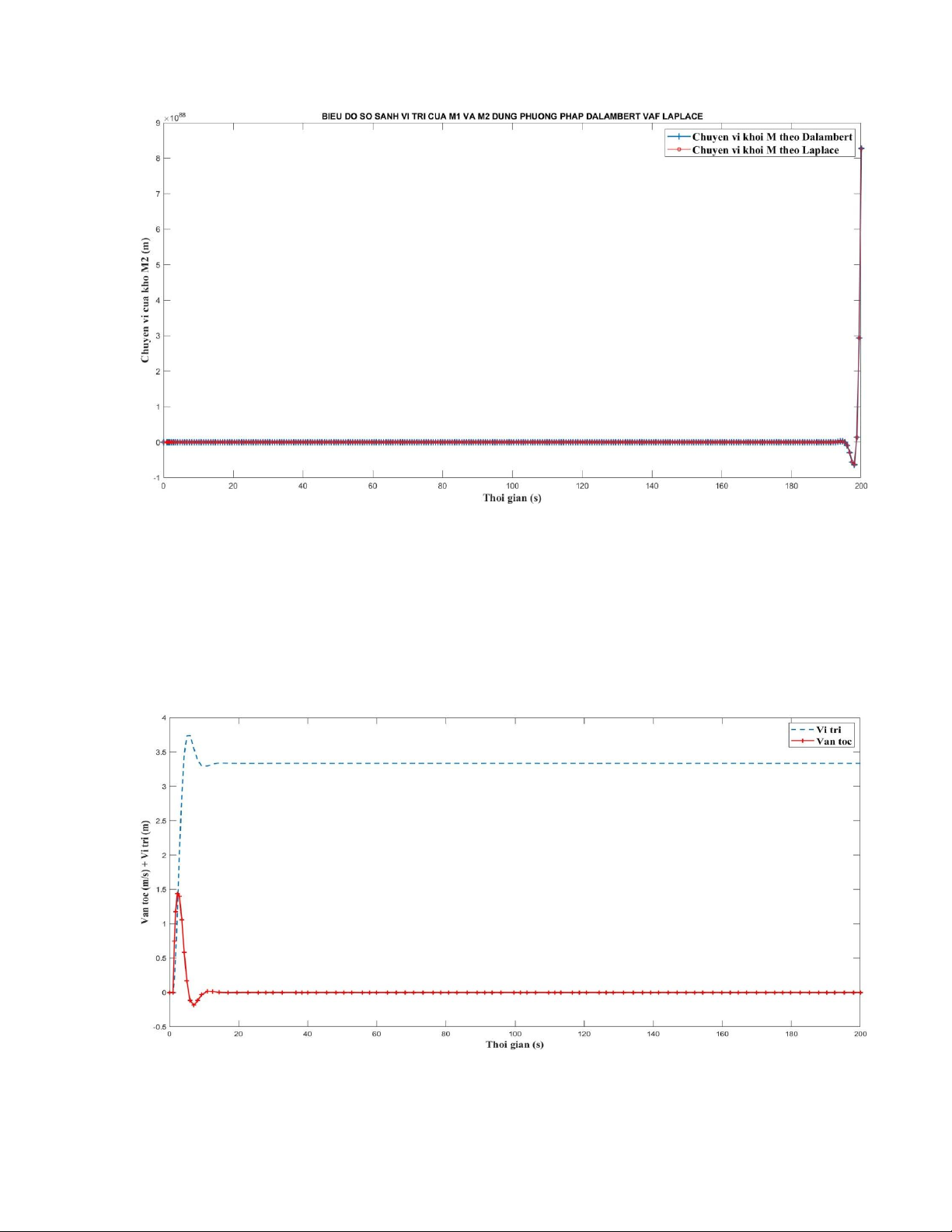
g) Cho lực dẫn fa(t) lên hệ thống tăng từ 0 N đến 100 N tại thời điểm t=1 s. Vẽ biểu đồ mô
phỏng sự thay đổi của vị trí của hai khối vật x1(t), x2(t) của hệ trong 200 giây đầu tiên.
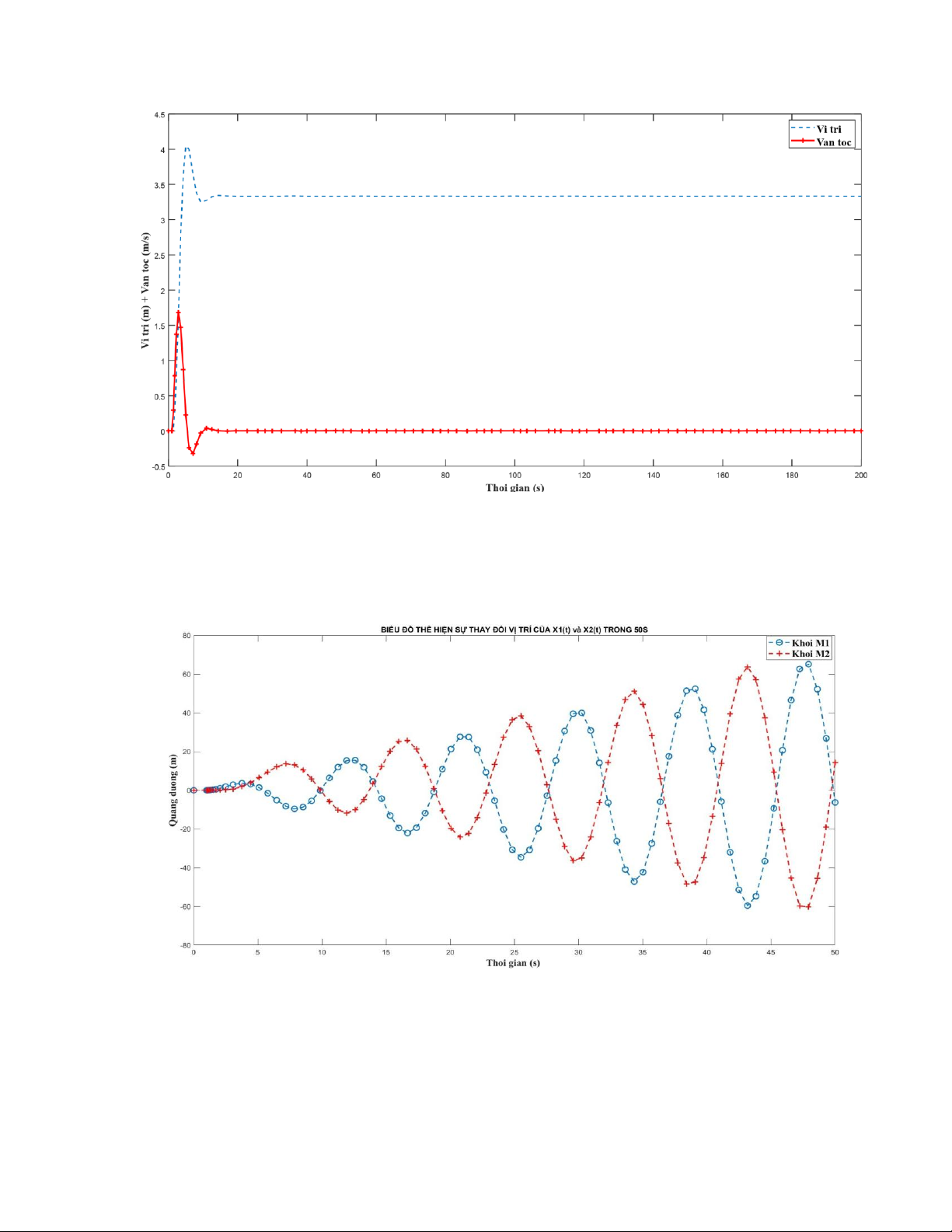
h) Cho lực dẫn fa(t) lên hệ thống tăng từ 0 N đến 100 N tại thời điểm t=1 s. Vẽ biểu đồ mô
phỏng sự thay đổi vận tốc của hai khối vật của cơ hệ trong 200 giây đầu tiên. lOMoAR cPSD| 58675420
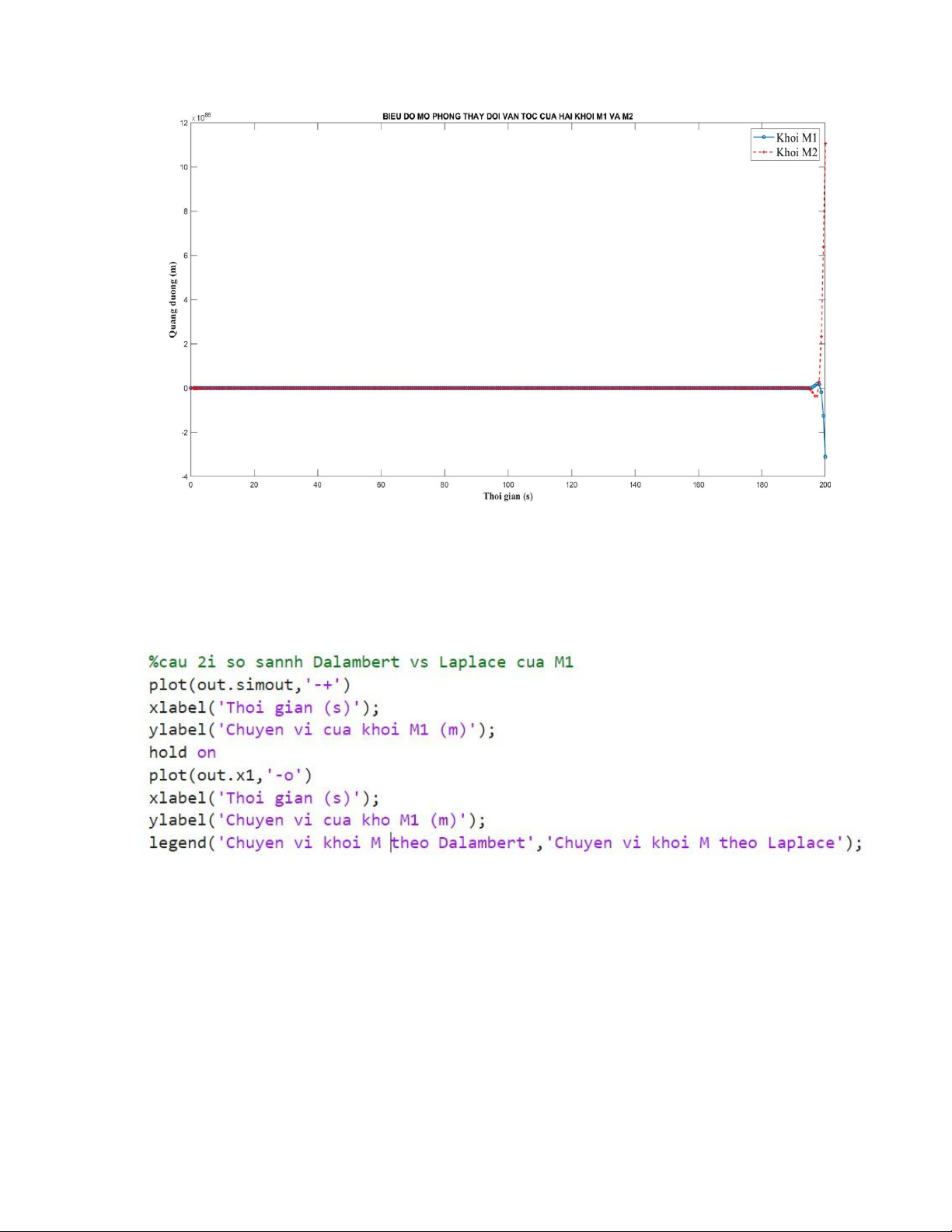
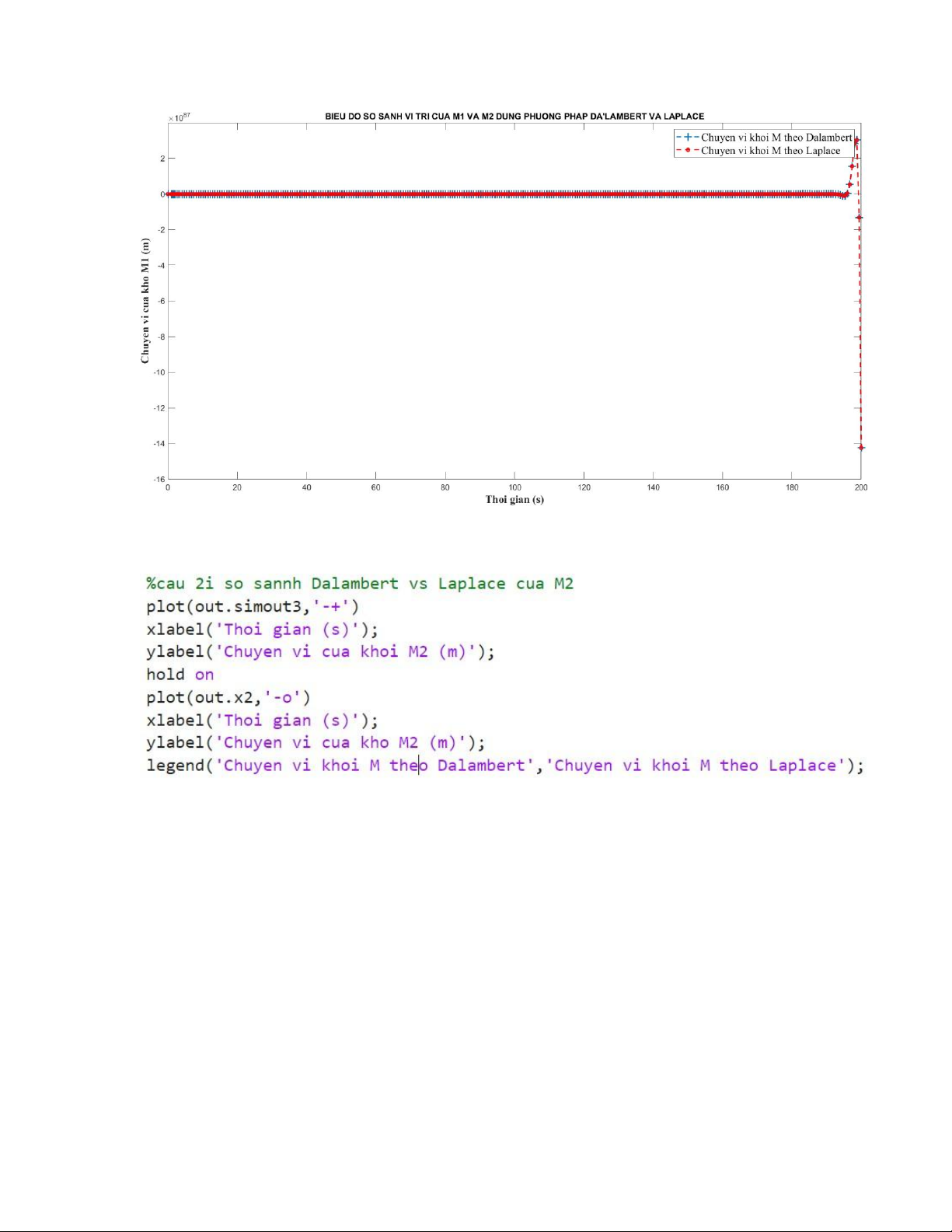
i) Viết đoạn code trong matlab, để vẽ biểu đồ so sánh vị trí x1(t), x2(t) của hệ thống dùng
phương pháp giải Da’lembert và phương pháp giải Laplace - Với M1 + Code Matlab:
+ Biểu đồ so sánh vị trí của M1 hệ thống dùng phương pháp giải Da’lembert và phương pháp giải Laplace: lOMoAR cPSD| 58675420 - Với M2: + Code Matlab
+ Biểu đồ so sánh vị trí M2 của hệ thống dùng phương pháp giải Da’lembert và phương pháp giải Laplace: lOMoAR cPSD| 58675420
j) Nếu biểu đồ vị trí, vận tốc chưa hội tụ, SV thay đổi giá trị khối lượng m, độ cứng k, giảm
chấn B để tìm ra biểu đồ hội tụ
Với việc thay đổi các giá trị m, B và K nhận thấy rằng với các giá trị:
M1= 50 kg, M2=5 kg, B1= 20 N-s/m, B2= 10 N-s/m, B3= 20 N-s/m, K₁=10 N/m, K₂= 20 N/m, K3= 10 N/m. lOMoAR cPSD| 58675420
Bài 2: Cho hình vẽ trên (bài 1). Cho M1= 20 kg, M2=20 kg, B1= 0 N-s/m, B2= 0 N-s/m, B3= 0 Ns/m,
K₁=10 N/m, K₂= 10 N/m, K3= 10 N/m.
a) Cho lực dẫn fa(t) lên hệ thống tăng từ 0 N đến 40 N tại thời điểm t=1 s. Vẽ biểu đồ mô
phỏng sự thay đổi của vị trí của hai khối vật x1(t), x2(t) của hệ trong 50 giây đầu tiên.
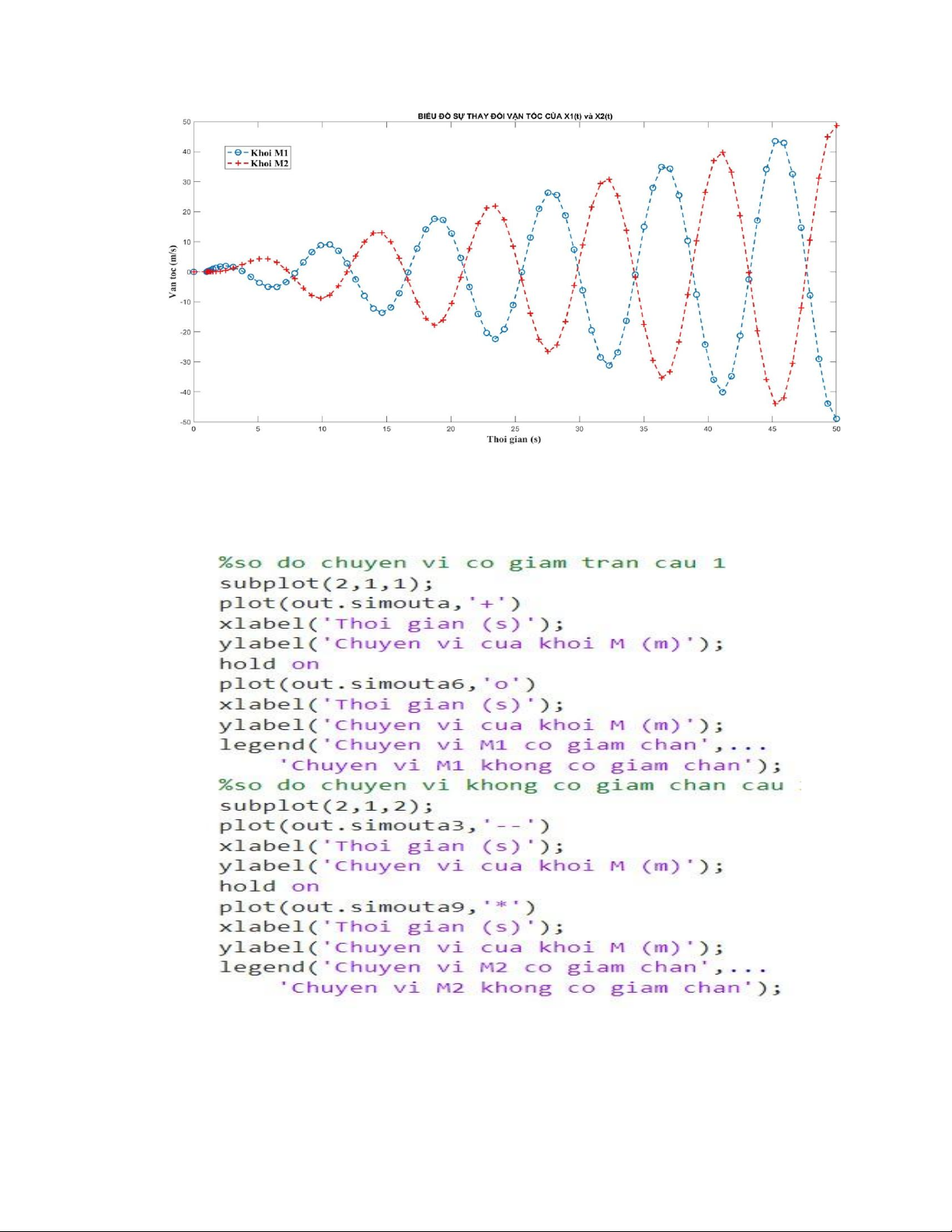
b) Cho lực dẫn fa(t) lên hệ thống tăng từ 0 N đến 40 N tại thời điểm t=1 s. Vẽ biểu đồ mô
phỏng sự thay đổi vận tốc của hai khối vật của cơ hệ trong 50 giây đầu tiên. lOMoAR cPSD| 58675420
c) Viết matlab code để vẽ biểu đồ so sánh 02 trường hợp:
- So sánh vị trí x1(t), x2(t) có giảm chấn (câu 1) và vị trí x1(t), x2(t) không có giảm
chấn (câu 2) + Code Matlab: + Biểu đồ so sánh lOMoAR cPSD| 58675420
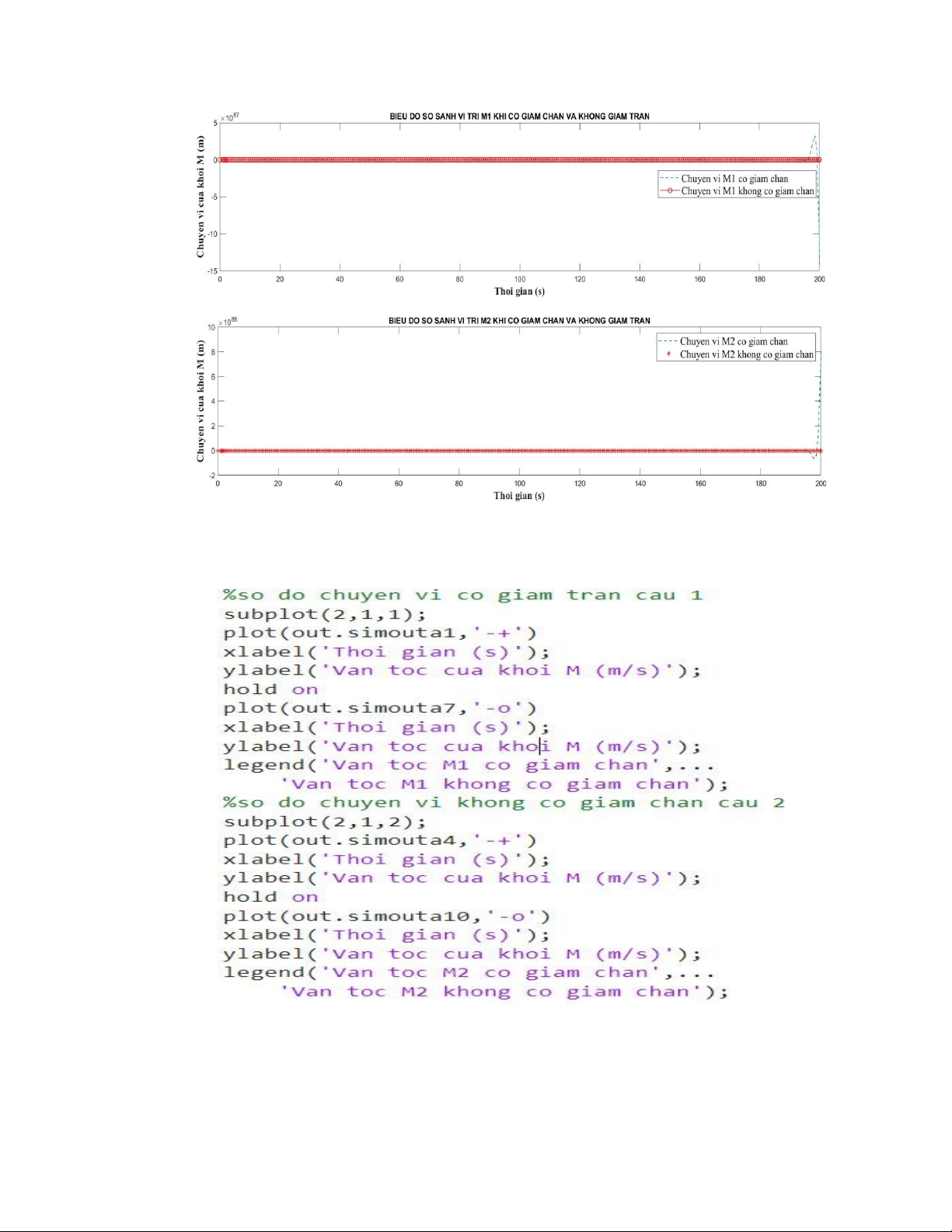
- So sánh vận tốc hai khối vật (x’1 và x’2) có giảm chấn (câu 1) và vận tốc hai
khối vật (x’1 và x’2) không có giảm chấn (câu 2) + Code Matlab: + Biểu đồ so sánh lOMoAR cPSD| 58675420
Bài 3: Cho B và K thay đổi trong một khoảng (SV tự cho B và K khoảng biến thiên), vẽ biểu đồ
gia tốc của hai khối vật và rút ra kết luận: làm thế nào để tăng tốc độ đáp ứng của hệ thống.
Trường hợp 1: thay đổi giá trị K trong khoảng [1-100] N và giữ nguyên giá trị B
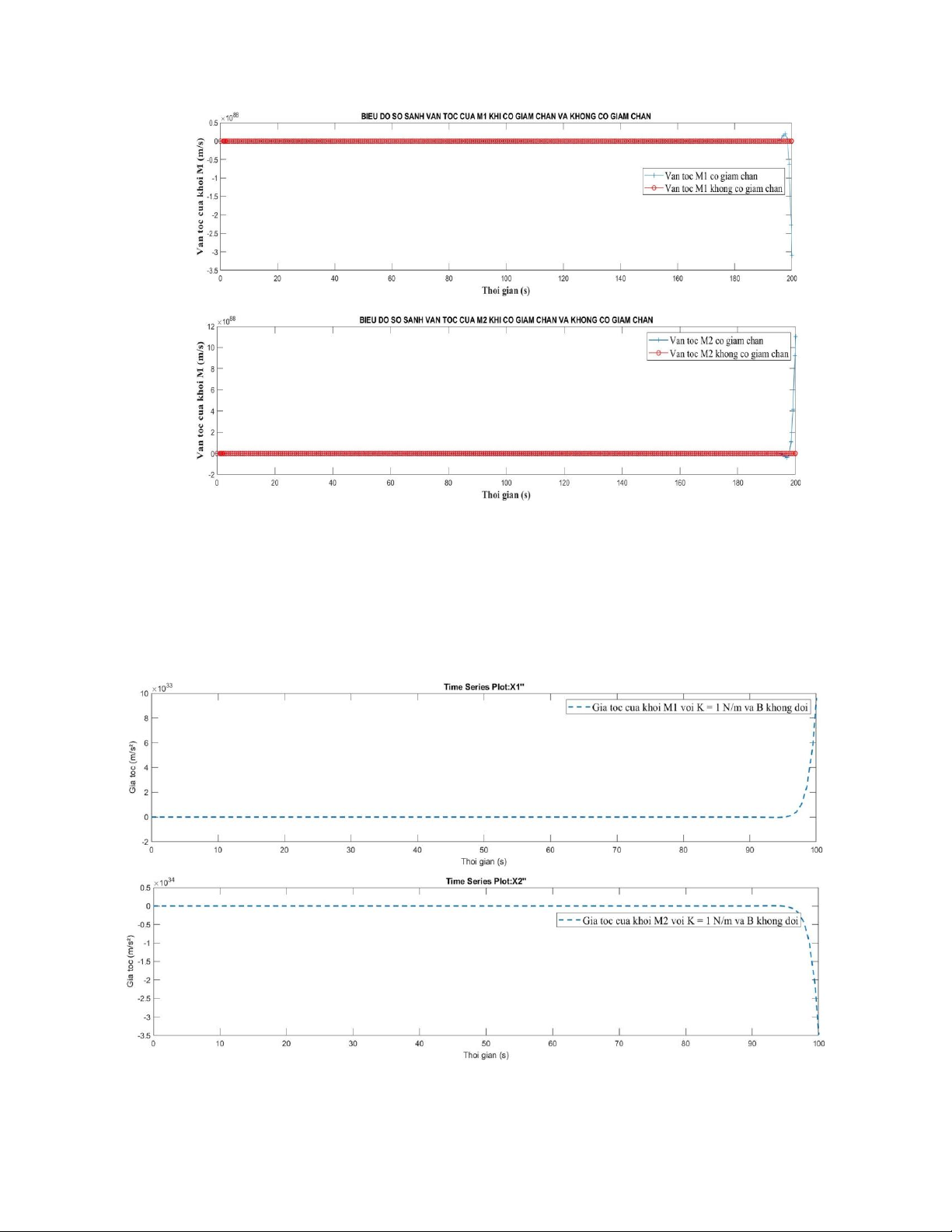
+ Giá trị K = 1 N/m , B không đổi
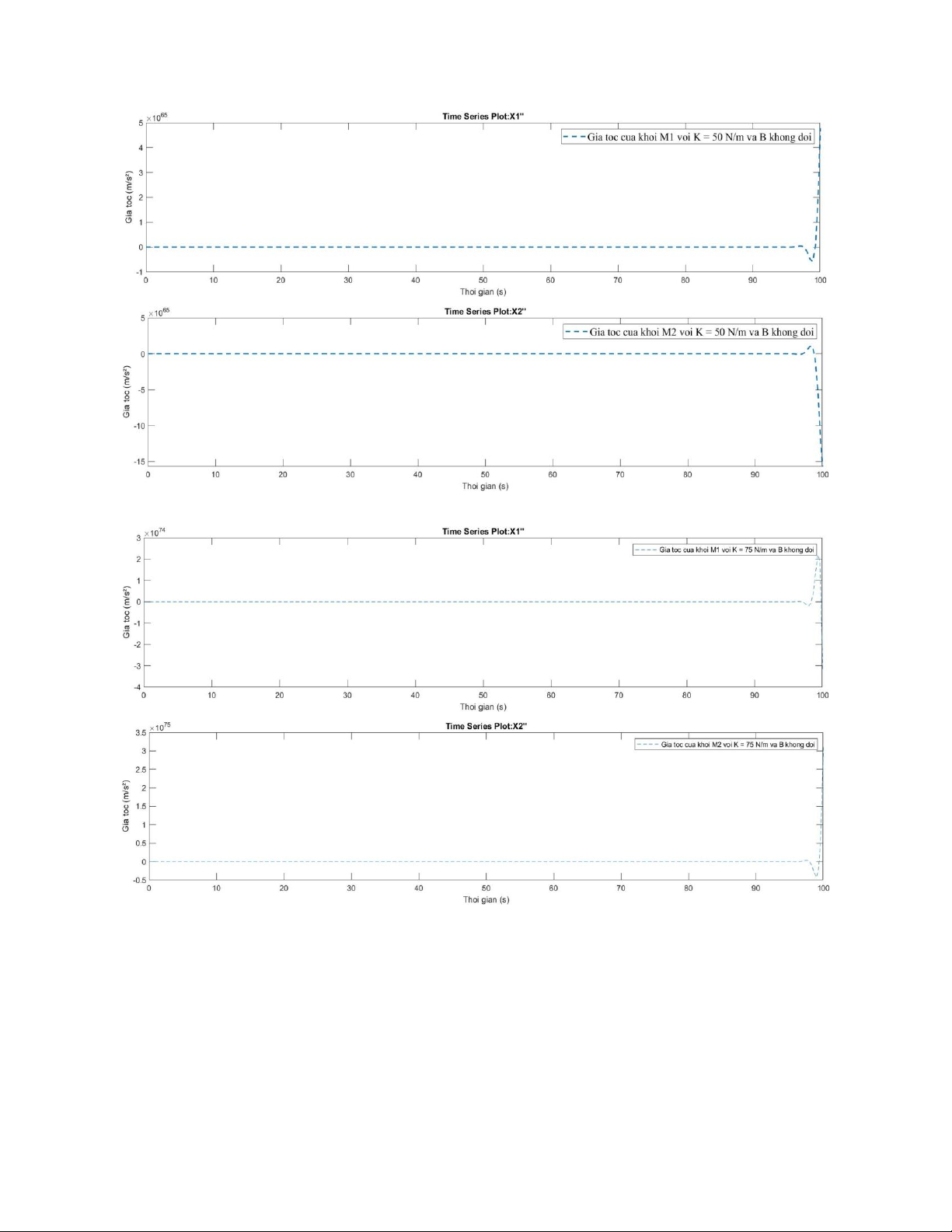
+ Giá trị K = 50 N/m , B không đổi lOMoAR cPSD| 58675420
+ Giá trị K = 75 N/m , B không đổi
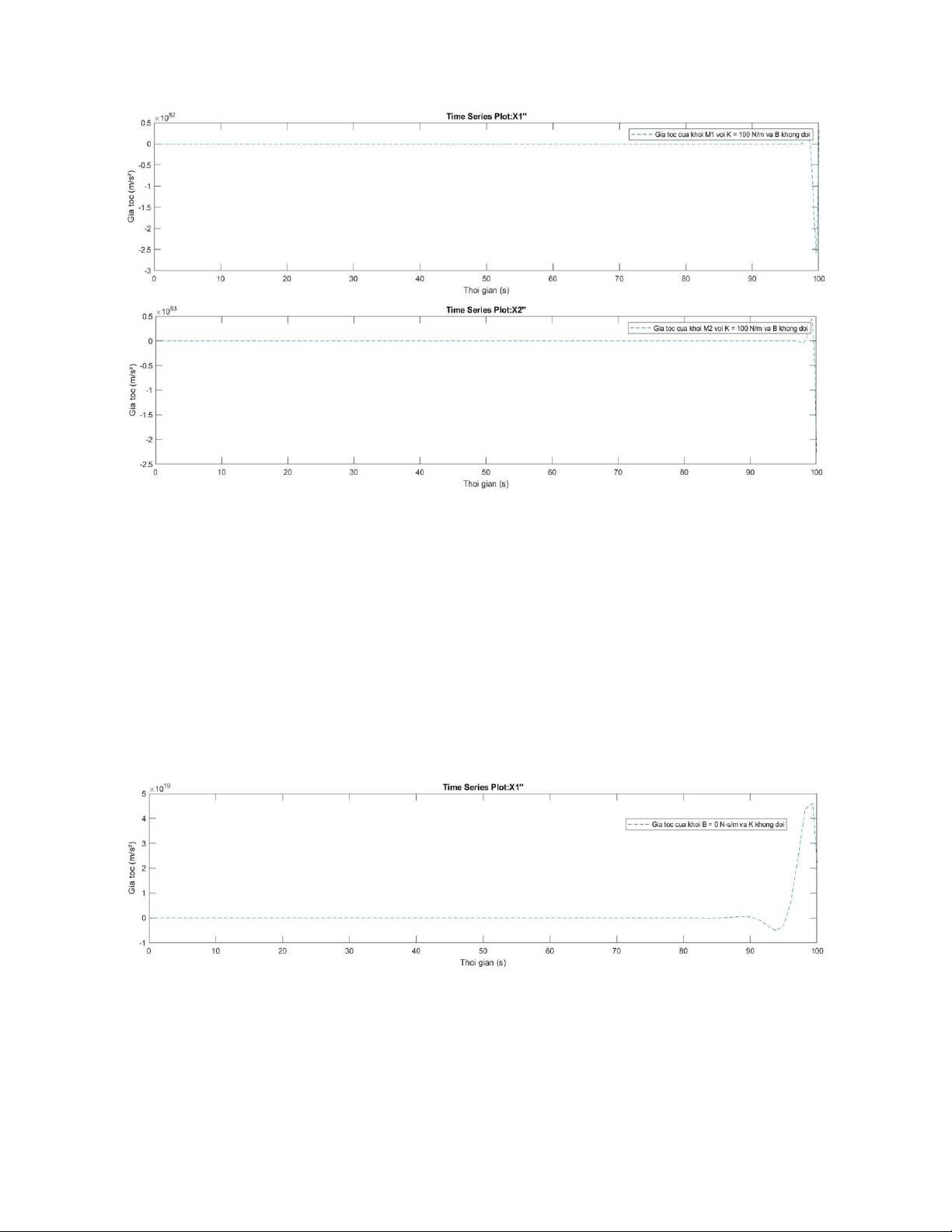
+ Giá trị K = 100 N/m , B không đổi lOMoAR cPSD| 58675420
Kết luận: khi tăng giá trị K trong khoảng [1-100] N/m và giữ nguyên B, ta nhận thấy +
Biều đồ gia tốc của hai khối không dao động trong phần lớn thời gian và dao động đột
ngột tại gần cuối thời gian, không ổn định lại về 0. + Hệ thống phản ứng chậm hơn, dao động nhiều hơn.
Nhận xét: Khi tăng K => hệ thống trở nên phản ứng chậm hơn với lực tác động => thời
gian đáp ứng tăng => hệ thống phản hồi chậm hơn
Trường hợp 2: thay đổi giá trị B trong khoảng [1-100] và giữ nguyên K
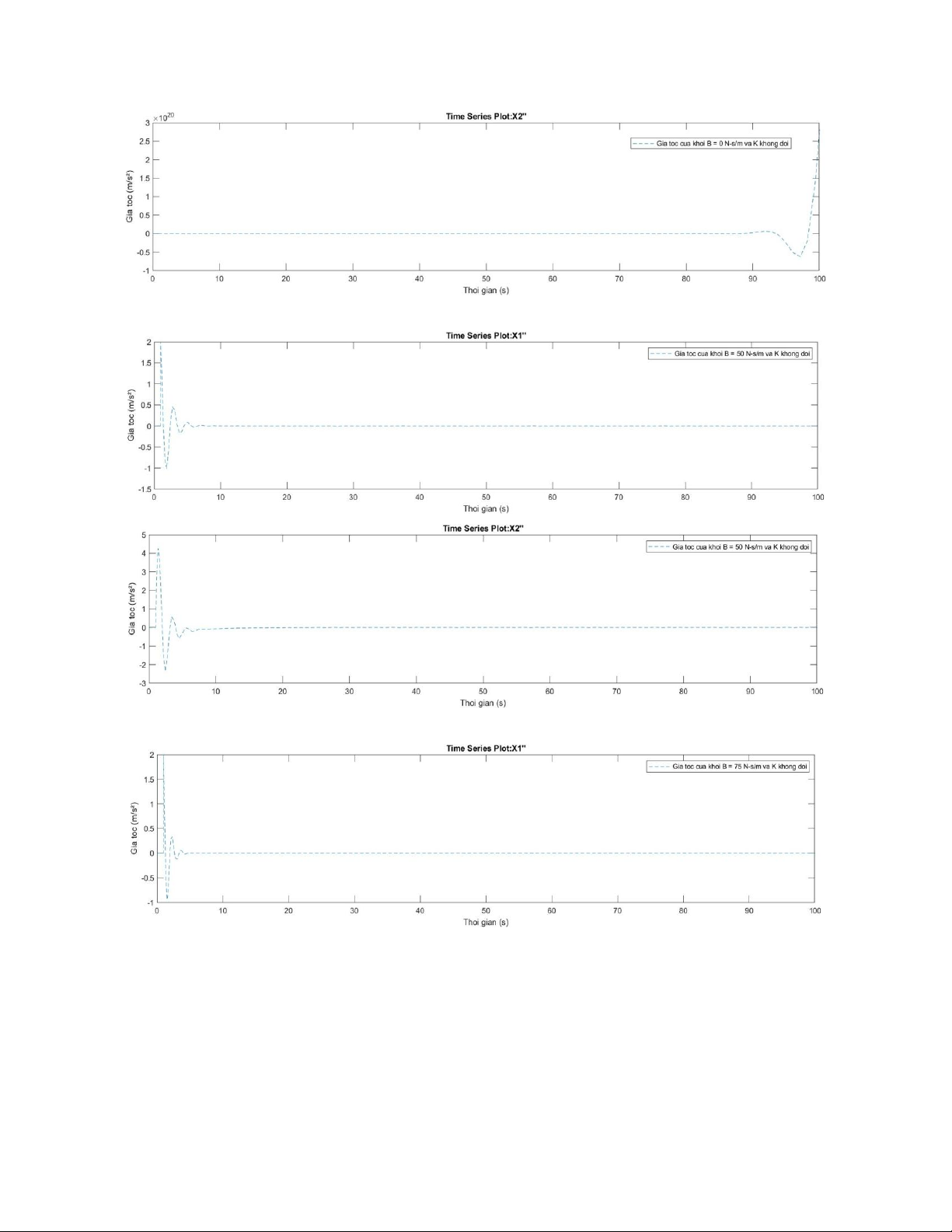
+ Giá trị B = 0 N-s/m , K không đổi lOMoAR cPSD| 58675420
+ Giá trị B = 50 N-s/m , K không đổi
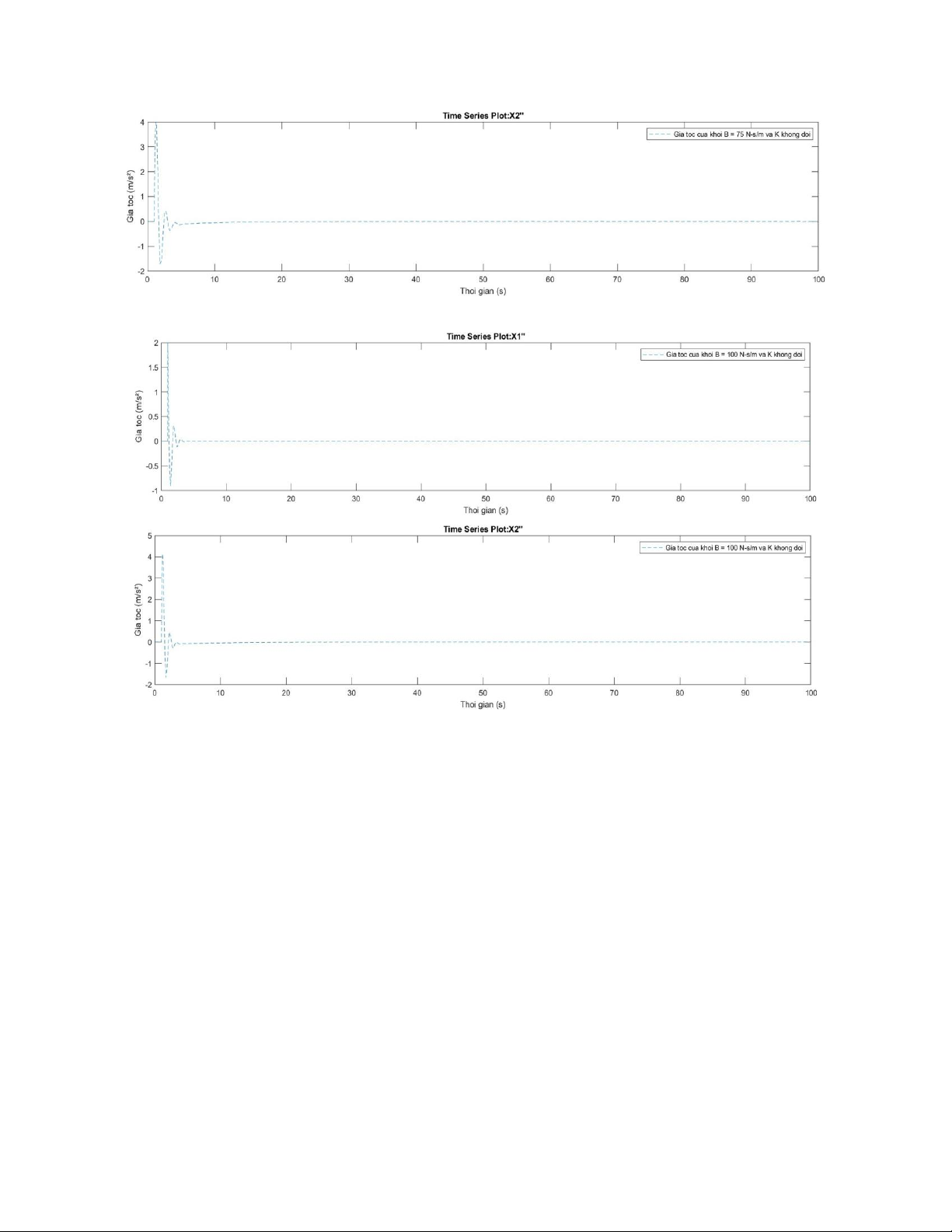
+ Giá trị B = 75 N-s/m , K không đổi lOMoAR cPSD| 58675420
+ Giá trị B = 100 N-s/m , K không đổi
Kết luận: khi tăng giá trị B trong khoảng [1-100] N-s/m và giữ nguyên K, ta nhận thấy +
Biều đồ gia tốc của hai khối giảm giao động và nhanh chóng ổn định về 0.
+ Hệ thống phản ứng nhanh hơn, ít dao động hơn.
Nhận xét: Khi tăng B => hệ thống trở nên nhạy hơn với lực tác động => thời gian đáp ứng
giảm => hệ thống phản hồi nhanh hơn
=> So sánh tốc độ đáp ứng
- Khi tăng giá trị độ cứng K của lò xo: hệ thống phản ứng chậm hơn và dao động lớn hơn
- Khi tăng giá trị giảm chấn B: hệ thống phản ứng nhạy hơn và tiến tới ổn định nhanh
hơnPHẦN 3: KẾT LUẬN VÀ KIẾN NGHỊ 1. Kết luận
Qua quá trình mô phỏng và phân tích hệ dao động cơ học bằng Simulink và ngôn ngữ
MATLAB, bài tiểu luận đã rút ra được một số kết luận quan trọng: lOMoAR cPSD| 58675420
Hệ cơ học có giảm chấn cho thấy khả năng hội tụ nhanh hơn, ổn định hơn và làm suy giảm
dao động theo thời gian, trong khi hệ không có giảm chấn dao động liên tục và không tự ổn định.
Khối lượng, độ cứng và hệ số giảm chấn ảnh hưởng rõ rệt đến trạng thái ổn định của hệ:
khi các tham số này được lựa chọn phù hợp, hệ có thể đạt được trạng thái hội tụ cả về vị trí và vận tốc.
Mô phỏng bằng Simulink giúp trực quan hóa rõ ràng động học hệ cơ, từ đó hỗ trợ rất tốt cho
việc phân tích, điều chỉnh và thiết kế hệ thống điều khiển dao động. 2. Kiến nghị
Về nội dung môn học: Nên tiếp tục lồng ghép nhiều bài tập mô phỏng thực tiễn bằng
Simulink để giúp sinh viên hiểu sâu và ứng dụng tốt kiến thức lý thuyết vào thực tế.
Về cách thức giảng dạy: Giảng viên nên kết hợp giữa lý thuyết truyền thống và hướng dẫn
trực tiếp trên phần mềm để sinh viên nắm vững kiến thức và kỹ năng xử lý mô hình kỹ thuật trên
công cụ hiện đại, đồng thời khuyến khích sinh viên tự sáng tạo trong mô hình hóa và điều chỉnh hệ thống. KẾT LUẬN BÁO CÁO
Qua quá trình mô hình hóa, phân tích và mô phỏng hệ thống cơ học gồm 2 khối M1, M2; 3
giảm chấn B và 3 lò xo K, báo cáo đã tiếp cận một cách toàn diện từ việc xây dựng phương trình
chuyển động theo nguyên lý D’Alembert, chuyển đổi sang miền Laplace, đến việc triển khai mô
hình khối và thực hiện mô phỏng trên MATLAB/Simulink.
Kết quả mô phỏng cho thấy ảnh hưởng rõ rệt của các tham số hệ thống như hệ số giảm chấn
(B) và độ cứng lò xo (K) đến hành vi động lực học của thanh. Khi tăng độ cứng K, hệ có xu hướng
phản ứng chậm hơn, tuy nhiên cũng dễ gây dao động mạnh nếu không được giảm chấn hợp lý.
Ngược lại, nếu tăng hệ số giảm chấn, hệ sẽ đáp ứng nhanh hơn và tính ổn định nhanh chóng. Do
đó, việc lựa chọn thông số phù hợp là cực kỳ quan trọng để đảm bảo tốc độ đáp ứng cao mà vẫn duy trì tính ổn định.
Thông qua phân tích trong bài, có thể thấy rằng: để tăng tốc độ đáp ứng của hệ thống, cần
phải tăng giảm chấn B một cách hợp lý đồng thời lựa chọn giá trị độ cứng K tối ưu – đủ để hạn
chế dao động nhưng không làm chậm phản ứng của hệ. Việc điều chỉnh linh hoạt các thông số này
sẽ giúp hệ thống đạt hiệu suất cao trong thực tế. lOMoAR cPSD| 58675420
Báo cáo cũng là minh chứng rõ ràng cho tầm quan trọng của mô hình hóa và mô phỏng trong
việc phân tích, tối ưu và thiết kế các hệ thống cơ khí hiện đại.



