Bài giảng Giải tích Nguyễn Hữu Nhân Chương 1. MỘT BIẾN
Giới hạn của dãy số thực
1.1.1 Các định nghĩa
Định nghĩa 1.1 Dãy số là một phép cho tương ứng (ánh xạ) mỗi số tự nhiên n khác 0 với một
số thực, kí hiệu
Ký hiệu dãy số thực là
được gọi là số hạng tổng quát
Ví dụ 1: Hai dãy số sau là các ví dụ về dãy số: = = +
Định nghĩa 1.2. Cho dãy số
. Xét một dãy các số tự nhiên tăng ngặt     +
và các phần tử tương ứng của dãy số Khi đó, được gọi là của dãy Kí hiệu:
Định nghĩa 1.3. Dãy số
được gọi là bị chặn
nếu tồn tại một số thực M sao cho:    Dãy số
được gọi là bị chặn dưới nếu tồn tại một số thực m sao cho:    Dãy số
được gọi là bị chặn nếu vừa bị chặn trên và vừa bị chặn dưới. Trong Ví dụ 1, dãy
chỉ bị chặn dưới (bởi 0) và không bị chặn trê bị
chặn dưới bởi 0 và bị chặn trên bởi Ví dụ 2: Dãy số = + (ứng với n là số lẻ)
(ứng với n là số chẵn) +
Trong Ví dụ 2, ta dẽ dàng thấy rằng giá trị của
càng bé “dần về 0” khi n càng lớn. Số
0 trong trường hợp này gọi là giới hạn của dãy số thực Định nghĩa 1. Dãy số
được gọi là có giới hạn là a, viết là
= nếu ta có thể làm →+
gần a một cách tùy ý khi lấy n lớn một cách thích hợp.
Bài giảng Giải tích Nguyễn Hữu Nhân Dãy số có giới hạn
hội tụ. Ngược lạ phân kỳ
Định nghĩa chính xác về mặt toán được phát biểu dưới dạng mệnh đề như sau: = nếu:      −   →+ Ví dụ 3: =
hội tụ và có giới hạn bằng 0, =
hội tụ và có giới hạn + bằng 1. − = phân kỳ, = phân kỳ. +
Định nghĩa 1.5. Dãy số
có giới hạn là vô cùng, kí hiệu:
=  nếu ta có thể làm cho →+
lớn số dương M tùy ý bằng việc lấy n lớn một cách thích hợp.
Định nghĩa chính xác về mặt toán được phát biểu dưới dạng mệnh đề như sau: iết là: =  nếu:   (lớn tùy ý    →+ Ví dụ 4: Dãy số = = + →+ ính chất Nếu dãy số
có giới hạn thì giới hạn đó là duy nhất.
hội tụ thì bị chặn. Nếu dãy
hội tụ và có giới hạn là a thì mọi dãy con
của nó cũng hội tụ và có giới hạn là a. Nếu = =     →+ →+ Nếu     = = = →+ →+ →+ Nếu = = →+ →+ Nếu =    =   →+ →+ Định lý 1.
luật giới hạn hữu hạn Giả sử = = . Khi đó: →+ →+ (  ) =  =  →+ →+ →+ ( ) = = →+ →+ →+ ( ) =  =    →+ →+ Nếu  →+ = = →+ →+
Bài giảng Giải tích Nguyễn Hữu Nhân
Ví dụ 5: Tính các giới hạn sau: + + − + − →+ − + →+ − + − + − + − →+ + − →+ − + − + + + − − →+ →+
1.2. Giới hạn hàm số Khái niệm hàm số Định nghĩa
X và Y là hai tập hợp khác rỗng Ánh xạ là phép cho tương ứng mỗi 
duy nhất phần tử  được gọi là một ánh xạ từ X vào Y. Kí hiệu: →
Ví dụ 1. Xét hai tập hợp = =
. Khi đó, ta có thể thiết lập một ánh xạ từ như sau: →
Định nghĩa 1.9. Hàm số thực là một ánh xạ từ tập con
của tập hợp số thực Nghĩa 
được gọi là tập xác định =
 được gọi là tập giá trị của hàm số. ụ 2. (a) Hàm số = có tập xác định là và tập giá trị là + (b) Hàm số = có tập xác định là + và tập giá trị là
trên các hàm số thực Giả sử
→ là hai hàm số xác định trên hàm số + → − → → xác định bởi
Bài giảng Giải tích Nguyễn Hữu Nhân + = + − = − = à nếu    thì hàm số → xác định bởi   =     Nếu
là một số thực thì kí hiệu chỉ hàm số → xác định bởi =
Định nghĩa 1.10. Cho 2 hàm số →
→ thỏa miền giá trị của hàm nằm
trong miền xác định của hàm g. Hợp của 2 hàm số , kí hiệu
, là một hàm số được xác định bởi: ( )   Ví dụ 3 hàm số = = . Khi đó, ta có: = = =
Định nghĩa 1.11. Hàm số f được gọi là hàm số một đối một, hay viết đơn giản là hàm số 1
(còn gọi hàm số đơn ánh) nếu nó không nhận cùng một giá trị hai lần. Nghĩ là, nếu  
Hàm số 1 1 chỉ cắt các đường thẳng có phương nằm ngang (song song với trục Ox) tại một điểm.
Ví dụ 4. (a) Hàm số = là hàm số 1 (b) Hàm số = không là hàm số 1
Định nghĩa 1.12. Cho f là một hàm số 1 1 có miền xác định D và miền giá trị T. Hàm số
ngược của hàm số f, kí hiệu − , là một hàm số có miền xác định là T, miền giá trị D và được xác định bởi: − =  = với mọi 
Bài giảng Giải tích Nguyễn Hữu Nhân Ví dụ 5. Hàm số
= có hàm số ngược là − = , vì nếu = , khi đó: − − = = =
(i) Miền xác định của chính là miền giá trị của − và ngược lại. −
là hàm số ngược của hàm số , không đồng nhất là hàm số:
Tiếp theo, ta giới thiệu về một số hàm số sơ cấp thường gặp bao gồm: hàm đa thức,
hàm phân thức hữu tỉ, hàm mũ, hàm logarit, hàm lũy thừa, hàm lượng giác, hàm lượng giác ngược.
Hàm đa thức Hàm đa thức bậc hệ số thực là hàm số dạng: − = = + + + + − trong đó   Tập xác định: =
Hàm phân thức hữu tỉ Hàm phân thức là thương của hai đa thức có dạng: − + + + + − = = = − + + + + − Tập xác định: = 
Hàm số mũ Hàm số mũ là hàm số dạng: = =   Tập xác định: = Tập giá trị: = + Sự biến thiên
Nếu  thì hàm số tăng trên
Nếu   thì hàm số giảm trên
Hàm số logarit Hàm số logarit là hàm số dạng: = =   Tập xác định: = + Tập giá trị: = Sự biến thiên
Nếu  thì hàm số tăng trên +
Nếu   thì hàm số giảm trên + Hàm lũy thừa
àm lũy thừa là hàm số dạng:  = =   Tập xác định: = + Hàm lượng giác = = = = Tập xác định: = Tập giá trị: = − Chu kỳ tuần hoàn  = = = =  
Tập xác định của hàm tan:  =   , của hàm cot:  
Bài giảng Giải tích Nguyễn Hữu Nhân =   Tập giá trị: = Chu kỳ tuần hoàn 
Hàm lượng giác ngược = = = = Tập xác định: = −    
Tập giá trị của arcsin là : = −   , của arccos là: =    = = = = Tập xác định: =    
Tập giá trị của arctan là : = −   , của arccot là: =   
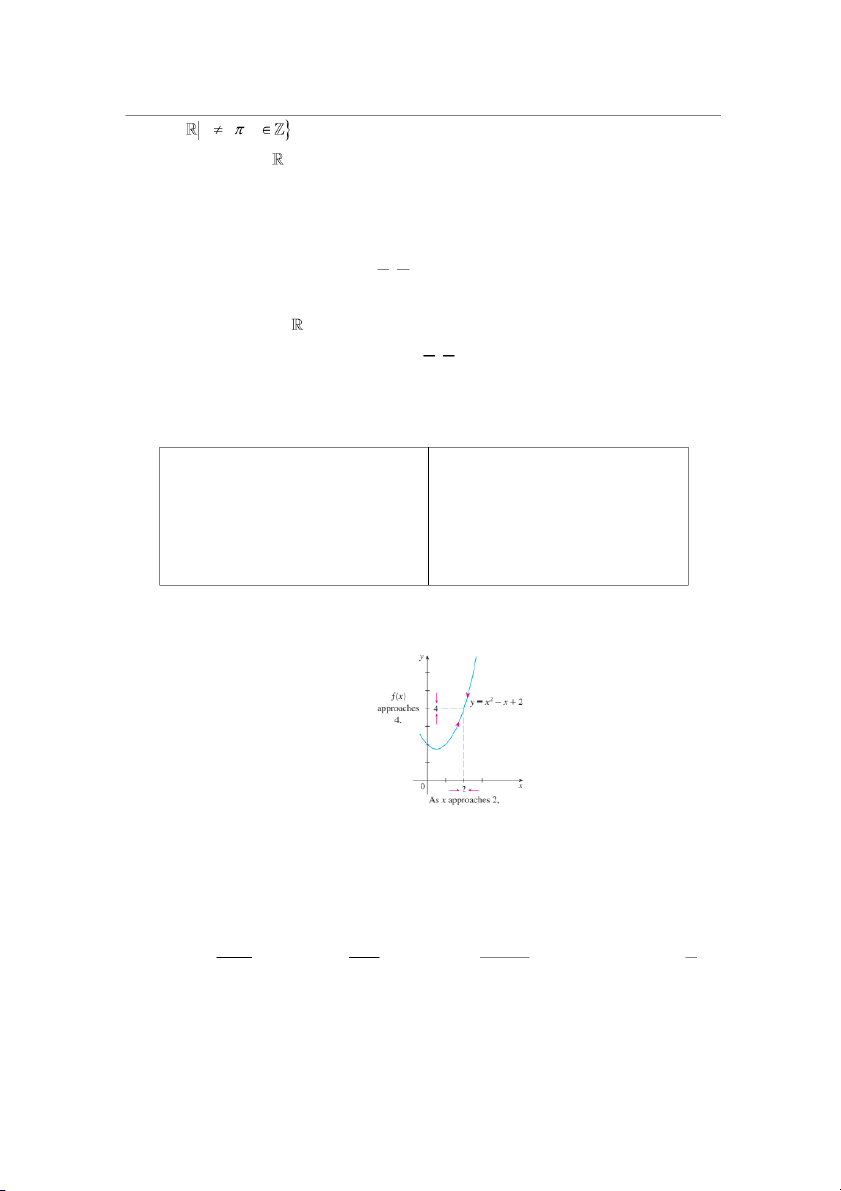
1.2.2. Giới hạn hàm số Xét hàm số =
− +, ta xét các giá trị của hàm gần 2 như sau
Ta thấy rằng (trực quan) khi giá trị của càng gần 2 (cả hai phía) thì giá trị của hàm số
càng gần 4. Ta nói 4 là giới hạn của hàm số tiến tới 2. Viết là: − + = → Định nghĩa 1.
Hàm số f được là có giới hạn là L khi x dần về a viế = , nếu →
ta có thể làm giá trị của f gần L tùy ý bởi việc cho x gần a (cả hai phía nhưng khác a) một cách thích hợp.
Ví dụ . Ước lượng giá trị của các giới hạn: −      → − → → − →  
Bài giảng Giải tích Nguyễn Hữu Nhân . (i) Hàm số
) có thể không xác định tại nhưng giới hạn của nó khi tiến về vẫn có thể tồn tại.
(ii) Để chứng minh không tồn tại
, ta có thể chứng minh theo như sau: → Hoặc chứng minh = + (hoặc ∞), → Hoặc chỉ ra hai dãy cùng tiến về nhưng các dãy ( ) (
) tiến về hai giá trị khác nhau dụ
Trong định nghĩa giới hạn, ta thấy rằng khi càng gần về cả hai phía thì hàm số
càng gần một giá trị duy nhất . Tuy nhiên, có nhiều hàm số mà khi càng gần từ phía bên
phải và khi càng gần từ phía bên trái thì hàm số
) lại không tiến về một giá trị
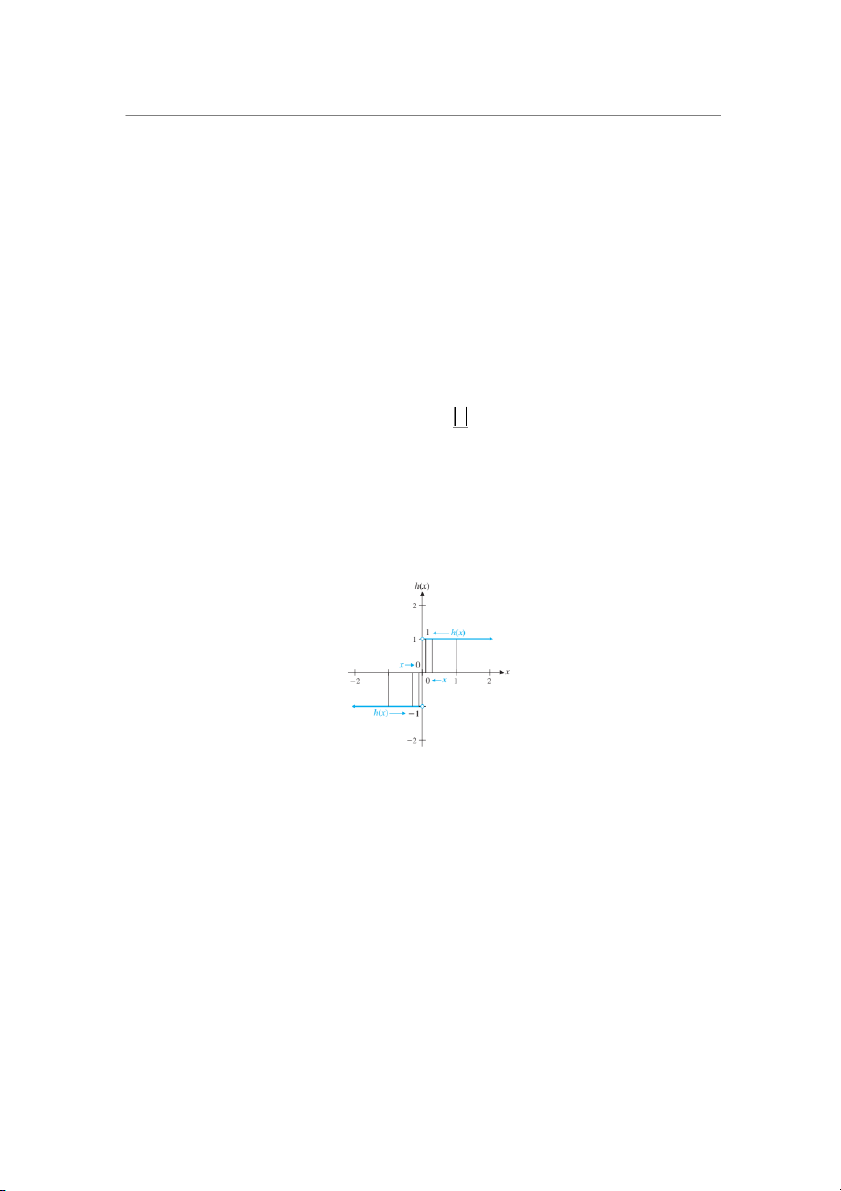
nhất. Chẳng hạn, ta xét giới hạn của hàm số = dần về 0.
Hàm số trên xác định tại mọi giá trị thực , trừ tại 0. Ta chú ý rằng nếu =. Nếu = − gần 0 (cả hai phía) thì ) không gần một giá
trị đặc biệt duy nhất. Do đó, không tồn tại
(cũng không tồn tại giá trị của hàm số → tại 0).
Trong ví dụ trên, ta thấy rằng các giá trị của
) càng gần hai giá trị khác nhau phụ
thuộc vào việc tiến về 0 theo hướng bên phải hay hướng bên trái. Một cách tự nhiên điều này
gợi dẫn cho ta đến khái niệm "giới hạn một phía" sau đây. Định nghĩa 1.
gọi L là giới hạn bên trái của f(x), viế =
nếu ta có thể làm − →
giá trị của f(x) gần L tùy ý bởi việc lấy các giá trị x nhỏ hơn a và gần a một cách thích hợp.
gọi L là giới hạn bên phải của f(x), viết =
nếu ta có thể làm giá trị của + →
ần L tùy ý bởi việc lấy các giá trị x lớn hơn a và gần a một cách thích hợp.
Định lí sau đây cho ta mối liên hệ giữa các giới hạn bên trái, giới hạn bên phải và giới hạn
của hàm số tại một điểm.
Bài giảng Giải tích Nguyễn Hữu Nhân Định lí 1.
Giới hạn hàm số f(x) khi x tiến về a tồn tại khi và chỉ khi cùng tồn tại giới hạn
bên trái và giới hạn bên phải của f(x), và chúng bằng nhau. Nghĩa là, = khi và chỉ khi = = → − + → → Ví dụ
Cho hàm số H(x) xác định bởi:  +  =  −  c giới hạn: → →−
. Các phép toán về giới hạn Định lí 1.1
Nếu tồn tại các giới hạn
và chúng hữu hạn thì → →    =  → → →  = → → → → = với  → → → = =
, với mọi k là số nguyên dương và khi k chẵn thì ta phải → →
có thêm giả thiết  Hệ quả 1.1 = → →     = →  →  Định lý 1.1
(giới hạn kẹp) Nếu 
 với mọi x thuộc vào một “lân cận”
đó của điểm a và = = = → → → Ví dụ Tính các giới hạn sau: − + + → →− → + → − – Vô cùng lớn –
Định nghĩa 1.19. Hàm số được gọi là một tiến về nếu = →
Bài giảng Giải tích Nguyễn Hữu Nhân Ví dụ 1. Hàm số = − là một VCB khi → − = → ố = + là một VCB khi → + = → 1.3.2. Vô cùng lớn
Định nghĩa 1.20. Hàm số
được gọi là một vô cùng lớn tiến về nếu =  → Ví dụ 2: Hàm số =
là một VCL khi x tiến về 0 = + →
1.3.3. Các dạng giới hạn vô định
quá trình tính toán về giới hạn, ta có thể gặp một số dạng giới hạn sau đây:    − 
được gọi là các giới hạn dạng vô định. Các giới hạn dạng vô định này cũng 
bắt gặp trong một số bài toán thực tiễn. Chẳng hạn, bài toán mở đầu sau đây là ứng dụng của
việc tính toán (khử) dạng vô định
Bài toán mở đầu. Giả sử một sự cố vỡ đường ống dẫn dầu ở một vùng biển tạo ra một
lớp dầu dày (mét) tại vị trí cách chổ ống bị vỡ (mét). Việc xác định độ dày của lớp dầu ngay tại vị trí vỡ (
0) là vấn đề khó khăn. Tuy nhiên giả sử rằng, khi 0 thì độ dày của lớp
dầu được xác định bởi + = + +
Khi đó, việc tính (ước lượng) độ dày của lớp dầu ngay tại vị trí ống dầu bị vỡ được xác
định nhờ vào việc tính giới hạn của hàm số trên k
tiến về 0. (xem Ví dụ 4
Để khử các dạng vô định này ta thường dùng một trong các cách sau:
1) Đối với dạng vô định
hoặc  −  và có chứa căn thức bậc hai hoặc căn thức bậc ba: Sử dụng lượng hợp tương ứng. 
Đối với dạng vô định
mà tử số và mẫu số là các đa thức: Thực hiện chia cả tử và  mẫu cho thừa số , với
là bậc cao nhất của đa thức ở tử số và mẫu số  
Đối với dạng vô định  Sử dụng giới hạn + = + =   + →+ →     hoặc − = − =   + →+ →  
Bài giảng Giải tích Nguyễn Hữu Nhân
Ngoài ra, khi gặp giới hạn dạng vô định (thông thường là dạng ) mà có chứa hàm số
lượng giác hoặc hàm số mũ hoặc hàm số logarit, ta sử dụng một số giới hạn đặc biệt sau đây để
khử các dạng vô định tương ứng. = = → → + = → − =  → + − = → Ví dụ Tính các giới hạn sau: − + + − →+ + → + → − + − − + − + →+ ( ) → − → −  −  + + −   →+  −  → →
Ví dụ 4. (Bài toán mở đầu) Xác định độ dày của lớp dầu loang trong Bài toán mở đầu bằng
cách tính giới hạn khi tiến về 0 của hàm số: + = + + Định nghĩa 1.2 tiến về = đ → ếu = được gọi l ậc ơn ếu =  được gọi l ậc ấp ơn ếu  =  được gọi l ậc. Đặc biệt, nếu = được gọi l tương đương ệu: ụ = − ậc ơn = − →