Một phương pháp tính độ tin cậy của công trình có biến mờ tham gia | Trường Đại học Kinh tế – Luật

lOMoAR cPSD| 46348410
Một phương pháp tính độ tin cậy của công trình có biến mờ tham gia 1. Mở đầu
Việc tính toán độ tin cậy (ĐTC) của các hệ điện, hệ cơ khí đã được phát triển sớm, cho đến
nay đã có nhiều tài liệu đề cập đến [1,2,...].
Ứng dụng lý thuyết ĐTC vào đánh goá an toàn của công trình xây dựng, được phát triển
chậm hơn, song cho đến nay cũng đã đạt nhiều thành tựu to lớn[3,4,5,6...]. Công cụ toán
học để giải quyết bài toán ĐTC của các lĩnh vực là lý thuyết xác suất thống kê và quá trình ngẫu nhiên.
Bước sang thế kỷ 21, nhân loại ngày càng nhận ra rằng khí hậu toàn cầu đã thay đổi về cơ
bản, các số liệu cũ là không đáng tin cậy, nạn khủng bố lan tràn, trong khi đó công trình
xây dựng là đối tượng bị động hứng chịu tai hoạ.
Một vấn đề có tính toàn cầu trong thế kỷ 21 là nhân loại đang phải hành động và giải quyết
trong điều kiện thiếu thông tin, không chắc chắn, mơ hồ, nghĩa là thông tin mờ. Do đó,
người ta đã tìm đến một công cụ toán học mới, thích hợp là “toán học mờ”, cụ thể là lý
thuyết tập mờ [7,8]. Cho đến nay, đã có nhiều tài liệu bàn về tập mờ và điều khiển mờ [9,10,..].
Việc ứng dụng lý thuyết mờ vào tính độ tin cậy cũng đã đề cập đến trong thời gian gần đây
[11,12,...], song chỉ xét cho cấu kiện hay yếu tố đơn giản, chưa xét cho công trình (hệ nhiều yếu tố).
Trong các công trình [13,14,15], chúng tôi bàn đến, một số vấn đề cơ bản của việc ứng
dụng lý thuyết tập mờ vào đánh giá tính an toàn của hệ thống.
Trong bài này chúng tôi đề nghị một phương pháp tính độ tin cậy của công trình có biến mờ.
Theo những thông tin mà chúng tôi nhận được thì cho đến nay chưa có công trình nghiên
cứu nào đề xuất phương pháp tính ĐTC của công trình chứa các tham số tiền định, ngẫu
nhiên và mờ cùng tham gia.
Phương pháp mà chúng tôi đề xuất gồm các bước cơ bản sau:
Chọn và phân loại tham số, xác suất các tiết diện nguy hiểm của công trình, bổ sung số
liệu, thực hiện phép hồi quy mờ, xác định ứng suất (nội lực) mờ tại các tiết diện nguy hiểm,
tính ĐTC của công trình có biến mờ tham gia.
Để minh hoạ cho phương pháp, chúng tôi đưa ra một thí dụ đơn giản (song vẫn thực hiện
đủ các bước) là tấm chữ nhật, tựa bản lề theo các cạnh chịu tải trọng ngang.
2. Phương pháp tính độ tin cậy của công trình có biến mờ tham gia
Phương pháp gồm các bước sau:
Bước 1: Chọn và phân loại biến số
Một công trình xây dựng, nói chung số tham số hình học, vật liệu và tải trọng (môi trường)
tham gia là rất lớn. Các biến số trên có các đặc trưng khác nhau và chứa các lượng thông
tin khác nhau. Do đó, căn cứ vào lượng thông tin về các tham số mà phân loại thành tiền
định, ngẫu nhiên và mờ. lOMoAR cPSD| 46348410 a.
Biến tiền định là biến có phương sai bé, đồng thời độ nhạy cảm của các đại lượng
đặctrưng cho độ bền, ổn định, dao động của công trình đối với các đại lượng đó là bé. Để
đáp ứng được các yêu cầu đó thì lượng thông tin cần phải khá đầy đủ. b.
Biến ngẫu nhiên là các đại lượng ngẫu nhiên, có đủ số liệu để xử lý tìm ra được
cácđặc trưng bằng số của chúng và khẳng định nó thuộc loại phân phối thống kê nào, do
đó phải thoả mãn các tiêu chuẩn phù hợp của lý thuyết thống kê. c.
Biến mờ là biến thiếu số liệu quan sát đo đạc, giá trị của nó mơ hồ, không chắc
chắn,không rõ quy luật biến đổi.
Trong bài này xét các biến mờ ước định được cận trên và cận dưới của miền biến thiên,
song không rõ quy luật lấy giá trị của chúng trong đó.
Các tác giả đã xét các biến “ngẫu nhiên mờ” trong đó kỳ vọng và phương sai là các số mờ
[12], để dễ ứng dụng chúng tôi tạm chia ra ba loại như trên.
Bước 2: Xác định các tiết diện nguy hiểm của công trình
Khi tính ĐTC của công trình ta không tính tại mọi tiết diện của công trình mà chỉ tính tại tiết diện nguy hiểm.
Đối với các biến tiền định và ngẫu nhiên thì theo quy phạm về dung sai trong xây dựng cho
phép biến thiên nhỏ quanh kỳ vọng, do đó các loại biến này không gây ra thay đổi vị trí
các tiết diện nguy hiểm.
Đối với các biến mờ thì ta không rõ quy luật biến thiên, nên phải căn cứ vào đặc diểm của
công trình để dự đoán về tiết diện nguy hiểm, thường người ta phải phân ra 2 miền giá trị
âm và dương để tính tiết diện nguy hiểm.
Từ các ý kiến, ta có thể chọn tiết diện nguy hiểm bằng cách tính kết cấu theo phương pháp
tiền định (chẳng hạn dùng SAP 2000), đầu vào là giá trị đại diện cho biến mờ trong các
vùng trái dấu hoặc giá trị trung bình khi không đổi dấu. Với cách làm trên ta xác định được
nội lực, từ đó suy ra các tiết diện nguy hiểm.
Các tiết diện nguy hiểm của bước này có thể phải điều chỉnh khi ta tính được giá trị trung
tâm của biến mờ ở bước sau.
Bước 3: Bổ sung số liệu do thiếu hoặc không rõ ràng
Khi thiếu số liệu hoặc số liệu không rõ ràng thì việc thực hiện thuật toán hồi quy để tìm
ứng suất (hay cường độ ứng suất) không thực hiện được hoặc kết quả không đáng tin cậy.
Do đó, ta phải bổ sung số liệu. Trước hết bổ sung số liệu đầu vào. Việc bổ sung số liệu đầu
vào được thực hiện theo các thuật toán mô phỏng Monte - Carlo [1,16].
Giả sử bằng “số ngẫu nhiên” của mô phỏng Monte - Carlo trong đoạn [0,1] là K thì số liệu
bổ sung của chúng ta trên đoạn là: A+(b-a)K (với b> a)
Từ các số liệu đã có và số liệu bổ sung với các tổ hợp khác nhau ta tìm được noọ lực tương
ứng của công trình qua các thuật toán phân tích kết cấu (chẳng hạn SAP 2000) tại tiết diện nguy hiểm.
Bước 4: Thực hiện phép hồi quy tuyến tính mờ từ các số liệu đầu vào (các Xi) và đầu ra lOMoAR cPSD| 46348410
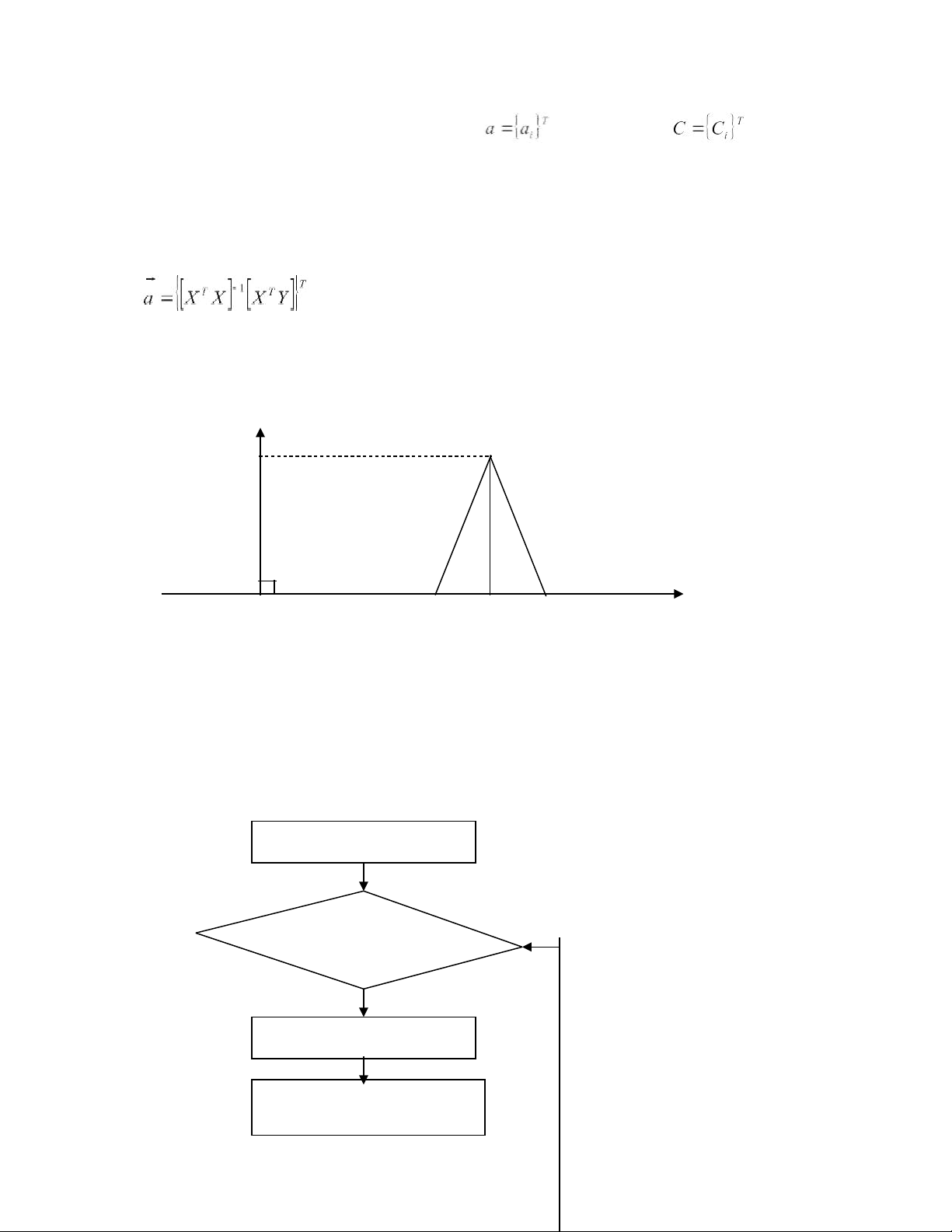
(ứng suất tương ứng), đê tìm giá trị trung tâm và các độ rộng [17,18] (hình 1)
Trong bước này có 3 việc phải làm:
a. Tìm giá trị trung tâm của các hệ số mờ (mờ tam giác cân). Để thực hiện bước này ta
dùng thuật toán hồi quy thông thường đối với các tổ hợp của giá trị đầu vào X và đầu ra
(ứng suất)Y. Ta tìm được vectơ a theo công thức:
b. Tìm các độ rộng Ci của các hệ số mờ tam giác Ai = (ai , ci)
Áp dụng nguyên lý mở rộng của Zadeh (1978) về xác định ảnh của một tập mờ qua một
hàm để tìm các độ rộng Ci của các hệ số Ai của hàm hồi quy. Để tìm Ci ta phải giải một bài toán cực trị[11,17]. μ X l Hình 1 0 a-c ai a+ci X
Bước 5: Xác định các ứng suất mờ tại các tiết diện nguy hiểm
Sau khi có các ai và ci (i= 1,....,n) ta tìm ứng suất mờ.
Bước 6: Tính độ tin cậy của công trình có biến mờ tham gia
Dùng mô hình giao thoa giữa hàm lệ thuộc của ứng suất mờ và hàm mật độ của đặc trưng
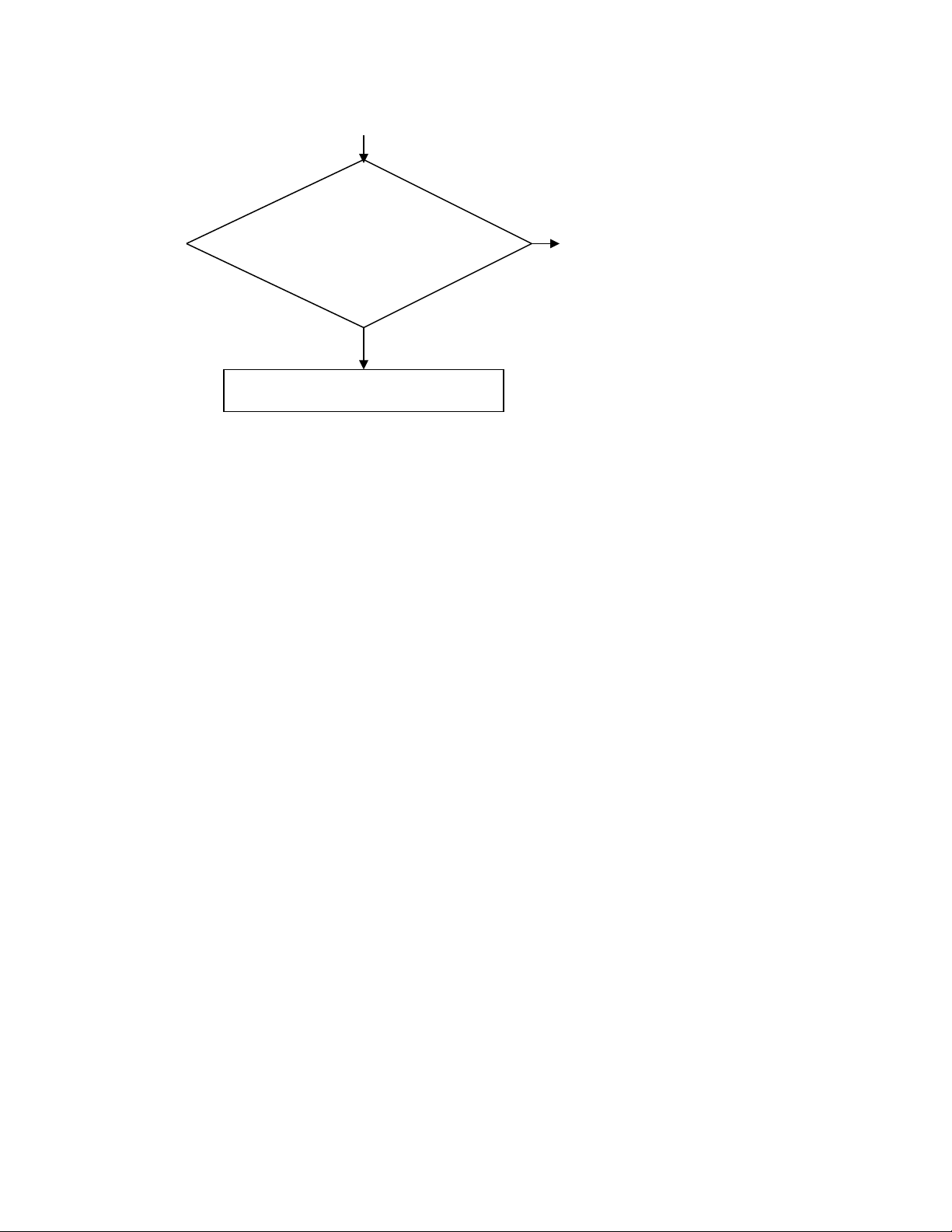
sức bền vật liệu ta tính được độ tin cậy. Sáu bước trên có thể tóm tắt trong sơ đồ khối sau:
Chọn và phân loại biến số Xác định tiết
diện nguy hiểm của công trình
Bổ sung số liệu đầu vào
Tìm ứng suất tương ứng
với các tổ hợp đầu vào lOMoAR cPSD| 46348410 Hồi quy tuyến tính mờ
để tìm giá trị trung tâm và độ
rộng của ứng suất mờ
Tính độ tin cậy của công trình 3. Thí dụ
Tính độ tin cậy của tấm chữ nhật bằng thép, liên kết khớp tại 4 biên, có các kích thước cạnh
ngắn l1= 1,2m; cạnh dài l2 = 2m; chiều dày δ =12mm; chịu tải trọng ngang phân bố đều q, 25kN/m2 ≤ q
≤ 35 kN/m2 không rõ quy luật phân bố.
Về vật liệu: Môđun đàn hồi 1,8.108kN/m2 ≤ E ≤ 2,4.108kN/m2.
Hệ số Poat - xông μ = 0,3 Lời giải:
1. Chọn và phân loại biến số: Các biến tham gia vào bài toán gồm: l1, l2, δ, q, E, μ. Việc
phân loại các biến tuỳ thuộc vào lượng thông tin thu được về chúng. Nhằm mục đích minh
hoạ cho phương pháp trên, chúng tôi giả định như sau:
- l1, l2 và μ là các biến tiền định, nghĩa là phương sai bằng ;
- δ là biến ngẫu nhiên, biết kỳ vọng và phương sai;- E và q là biến mờ,
chỉ biết cận trên và dưới.
2. Xác định tiết diện nguy hiểm
Giải bài toán bằng phương pháp phần tử hữu hạn với các giá trị l1 = 1,2m, l2 = 2,0m, μ = 0,3
Còn các biến mờ ta chọn giá trị trung bình:
Q = 30kN/m2 ; E = 2.1.108kN/m2
Tấm được chia thành các phần tử chữ nhật 0,25m x 0,15m.
Độ võng lớn nhất tại tâm của tấm Wmax = 1.622cm.
Úng suất lớn nhât tại tâm: - Mặt trên: lOMoAR cPSD| 46348410 (góc 900) - Mặt dưới: (góc 900)
Như vậy điểm nguy hiểm của mzựt trung bình là tâm của tấm.
3. Bổ sung số liệu
Các biến tiền định thì có giá trị xác định.
Các biến ngẫu nhiên, là các biến đã có quy luật phân phối ta bổ sung bằng cách mô phỏng Monte - Carlo.
Gọi K là tập số ngẫu nhiên trong đoạn tương ứng với biến số đang xét, thì số liệu mô phỏng
trong đoạn tương ứng với khoảng 3σ: μδ = 12mm; σδ = 1,2mm Ta có: σ = a+(b-a) K
Đối với các biến mờ, ta chưa rõ quyluật nhận các giá trị của chúng trong khoảng giữa cận
trên và cận dưới. Vì vậy phải giả định các phân bố khác nhau, tính toán theo từng dạng.
Dùng phương pháp “khoang vùng” đã nêu trong phần trên để đánh giá.
Gọi K’ là tập số mô phỏng biến mờ trong [0,1] của q, và K’’ là tập số mô phỏng biến mờ trong [0,1] của E, ta có:
Q = 25kN/m2 + (35 – 25)kN/m2 K’
E = 2,1.108kN/m2 + (2,4 – 1,8) kN/m2.K’’. 4.
Tìm tập giá trị ứng suất tại tâm của tấm tương ứng với các tổ hợp của
số liệu đầu vàoDùng SAP 2000 tính với các tổ khác nhau của số liệu đầu vào, ta tìm được:
σ(i)max , σ(i)min (mặt trên và mặt dưới)
Chẳng hạn, ta tim được bảng ghi giá trị của σ(i)max như sau:
-88476,73 , - 88473,12, - 88469,13, - 88477,16, - 88479,12... 5.
Thực hiện phép hồi quy tuyến tính mờ để tìm ứng suất mờChọn hàm hồi quy có dạng:
Y = A1l1 + A2l2 + A3μ + A4δ + A5q + A6E + A7l21 + A8l22 + A9μ2 + A10δ2 + A11q2 + A12E vì giả
thiết các biến l1, l2, μ là tiền định, δ là ngẫu nhiên. Còn 4 hệ số mờ tam giác chưa xác định: A5 = (a5, c5), A6 = (a6, c6)
A11 = (a11, c11) A12 = (a12 , c12) lOMoAR cPSD| 46348410
a. Thực hiện phép hồi quy ta tìm được giá trị Theo công thức:
Trong đó là vectơ đầu vào ,
là vectơ đầu ra. b. Tính các độ rộng Ci
Việc này được thực hiên theo nguyên lý mở rộng của Zadeh [8,11] Cụ
thể là giải bài toán cực trị đối với các biến Ci sau: Với các điều kiện
Trong đó H là mức mờ.
Với H=0,5, kết quả tính toán ghi trong bảng sau: H =
a 358,6 216,3 -880 11,0 -55,4 -48,1 258,1 -0,108 21,70 -14,7 25,30 10,11 0,5 C 0 0 0 0 0 0 0 0 0,657 0,029 1,280 0,492
6. Tính độ tin cậy theo các mức mờ với μσ0 = 3,6.105kN/m2; σσ0 = 0,2.105kN/m2 H 0,1 0,2 0,3 0,4 0,5 PS 0,99620 0,99570 0,99505 0,99416 0,99286 H 0,6 0,7 0,8 0,9 PS 0,99077 0,99680 0,97631 0,91122 4. Kết luận
Trong bài này các tác giả đề nghị một cách tìm độ tin cậy của công trình có biến mờ tham
gia cùng với các biến tiền định và ngẫu nhiên. Để thực hiện phương pháp trên chúng tôi đã
dùng phương pháp phần tử hữu hạn, kỹ thuật mô phỏng Monte - Carlo, phép hồi quy tuyến
tính mờ và phương pháp tính độ tin cậy theo mô hình giao thoa giữa ứng suất mờ và sức bền ngẫu nhiên.
Ứng dụng lý thuyết tập mờ vào tính toán độ tin cậy của công trình là lĩnh vực mới mẻ. Do
đó, phương pháp mà chúng tôi nêu ra có thể coi là bước đầu, cần được hoàn thiện thêm. Vì
chưa có phương pháp tính độ tin cậy cho công trình có biến mờ tham gia nên việc so sánh
chưa thực hiện được. Song nếu coi biến mờ là biến ngẫu nhiên biết đủ các đặc trưng bằng
số thì có thể tính được độ tin cậy. Đó là một trong các vấn đề cần nghiên cứu tiếp, do khuôn
khổ của một bài báo ở đây đã không trình bày. Công trình này hoàn thành với sự hỗ trợ của
chương trình nghiên cứu cơ bản trong khoa học tự nhiên - Ngành cơ học.
GS.TS. Nguyễn Văn Phó; ThS. Nguyễn đình Xắn.
(Nguồn tin: T/C KHCN Xây dựng, số 3/2005)